title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅C++|| Java || Python || Solution using Backtracking (faster 80.39%(98 ms), memory 100%(8.6 mb)) | maximum-number-of-achievable-transfer-requests | 1 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n\nThe `maximumRequests` function initializes a vector `v` of size `n` with all elements initialized to 0. This vector represents the current state of the buildings. Each element in the vector represents the net change in the number of requests for a particular building. Positive values indicate that there are more requests for that building, while negative values indicate that there are more requests to leave that building.\n\nThe function then calls a helper function `helper` with the initial index set to 0. The `helper` function is a recursive function that tries to fulfill each request and computes the maximum number of requests that can be fulfilled.\n\nIn the `helper` function, if the index reaches the end of the requests vector (`index == requests.size()`), it checks if all buildings have zero net requests. If they do, it returns 0, indicating that all requests have been fulfilled. Otherwise, it returns a large negative value `INT_MIN`, indicating that this state is not valid.\n\nIf the index is not at the end of the requests vector, the function proceeds to handle the current request. It decreases the net request count for the building at `requests[index][0]` and increases the count for the building at `requests[index][1]`. It then recursively calls the `helper` function with the index incremented by 1.\n\nAfter the recursive call, the function restores the net request counts for the current request by increasing the count for the building at `requests[index][0]` and decreasing the count for the building at `requests[index][1]`. This is done to backtrack and consider other possible combinations of requests.\n\nThe function then calculates two values: `take` and `notTake`. `take` represents the maximum number of requests that can be fulfilled if the current request is taken into account. It adds 1 to the result of the recursive call (`1 + helper(index + 1, n, requests, v)`).\n\n`notTake` represents the maximum number of requests that can be fulfilled if the current request is not taken into account. It calls the recursive function without changing the net request counts (`helper(index + 1, n, requests, v)`).\n\nFinally, the function returns the maximum value between `take` and `notTake`, representing the maximum number of requests that can be fulfilled considering the current state.\n\n\n\n# Code\n\n# C++\n```\nclass Solution {\n \n\n int helper(int index, int n,vector<vector<int>>& requests,vector<int> &v){\n\n if(index==requests.size()){\n for(int i=0;i<n;i++){\n if(v[i]!=0) return INT_MIN;\n }\n return 0;\n }\n\n v[requests[index][0]]-=1;\n v[requests[index][1]]+=1;\n int take=1+helper(index+1,n,requests,v);\n v[requests[index][0]]+=1;\n v[requests[index][1]]-=1;\n int notTake=helper(index+1,n,requests,v);\n\n\n return max(take,notTake);\n }\n\n\npublic:\n int maximumRequests(int n, vector<vector<int>>& requests) {\n vector<int> v(n,0);\n return helper(0,n, requests,v);\n }\n};\n```\n# Java\n```\nclass Solution {\n private int helper(int index, int n, List<List<Integer>> requests, List<Integer> v) {\n if (index == requests.size()) {\n for (int i = 0; i < n; i++) {\n if (v.get(i) != 0)\n return Integer.MIN_VALUE;\n }\n return 0;\n }\n \n v.set(requests.get(index).get(0), v.get(requests.get(index).get(0)) - 1);\n v.set(requests.get(index).get(1), v.get(requests.get(index).get(1)) + 1);\n int take = 1 + helper(index + 1, n, requests, v);\n v.set(requests.get(index).get(0), v.get(requests.get(index).get(0)) + 1);\n v.set(requests.get(index).get(1), v.get(requests.get(index).get(1)) - 1);\n int notTake = helper(index + 1, n, requests, v);\n \n return Math.max(take, notTake);\n }\n \n public int maximumRequests(int n, List<List<Integer>> requests) {\n List<Integer> v = new ArrayList<>(n);\n for (int i = 0; i < n; i++) {\n v.add(0);\n }\n return helper(0, n, requests, v);\n }\n}\n\n```\n\n# Python\n\n```\nclass Solution:\n def helper(self, index, n, requests, v):\n if index == len(requests):\n for i in range(n):\n if v[i] != 0:\n return float(\'-inf\')\n return 0\n\n v[requests[index][0]] -= 1\n v[requests[index][1]] += 1\n take = 1 + self.helper(index + 1, n, requests, v)\n v[requests[index][0]] += 1\n v[requests[index][1]] -= 1\n notTake = self.helper(index + 1, n, requests, v)\n\n return max(take, notTake)\n\n def maximumRequests(self, n, requests):\n v = [0] * n\n return self.helper(0, n, requests, v)\n\n``` | 1 | You are given an integer array `jobs`, where `jobs[i]` is the amount of time it takes to complete the `ith` job.
There are `k` workers that you can assign jobs to. Each job should be assigned to **exactly** one worker. The **working time** of a worker is the sum of the time it takes to complete all jobs assigned to them. Your goal is to devise an optimal assignment such that the **maximum working time** of any worker is **minimized**.
_Return the **minimum** possible **maximum working time** of any assignment._
**Example 1:**
**Input:** jobs = \[3,2,3\], k = 3
**Output:** 3
**Explanation:** By assigning each person one job, the maximum time is 3.
**Example 2:**
**Input:** jobs = \[1,2,4,7,8\], k = 2
**Output:** 11
**Explanation:** Assign the jobs the following way:
Worker 1: 1, 2, 8 (working time = 1 + 2 + 8 = 11)
Worker 2: 4, 7 (working time = 4 + 7 = 11)
The maximum working time is 11.
**Constraints:**
* `1 <= k <= jobs.length <= 12`
* `1 <= jobs[i] <= 107` | Think brute force When is a subset of requests okay? |
Backtracking Solution (Java, Python, C++) | maximum-number-of-achievable-transfer-requests | 1 | 1 | **Java**\n```\nclass Solution {\n int answer = 0;\n public int maximumRequests(int n, int[][] requests) {\n int[] inDegree = new int[n];\n helper(0,0,inDegree,requests);\n return answer;\n }\n private void helper(int index,int count, int[] indegree,int[][] requests) {\n if(index == requests.length) {\n \n for(int i: indegree) {\n if(i != 0) return; \n }\n answer = Math.max(answer, count);\n return;\n }\n \n \n indegree[requests[index][0]]--;\n indegree[requests[index][1]]++;\n helper(index + 1, count + 1, indegree,requests);\n indegree[requests[index][0]]++;\n indegree[requests[index][1]]--;\n helper(index + 1, count, indegree, requests);\n }\n}\n```\n\n**C++**\n\n```\nclass Solution {\npublic:\n int answer = 0;\n int maximumRequests(int n, vector<vector<int>>& requests) {\n answer = 0;\n vector<int> inDegree(n, 0);\n helper(0, 0, inDegree, requests);\n return answer;\n }\n void helper(int index, int count, vector<int>& inDegree, vector<vector<int>>& requests) {\n if (index == requests.size()) {\n for (int i : inDegree) {\n if (i != 0)\n return;\n }\n answer = max(answer, count);\n return;\n }\n inDegree[requests[index][0]]++;\n inDegree[requests[index][1]]--;\n helper(index + 1, count + 1, inDegree, requests);\n inDegree[requests[index][0]]--;\n inDegree[requests[index][1]]++;\n helper(index + 1, count, inDegree, requests);\n }\n};\n```\n\n**Python3**\n\n\n```\nclass Solution:\n def maximumRequests(self, n: int, requests: List[List[int]]) -> int:\n self.answer = 0\n in_degree = [0] * n\n self.helper(0, 0, in_degree, requests)\n return self.answer\n \n def helper(self, index, count, in_degree, requests):\n if index == len(requests):\n for i in in_degree:\n if i != 0:\n return\n self.answer = max(self.answer, count)\n return\n\n in_degree[requests[index][0]] += 1\n in_degree[requests[index][1]] -= 1\n self.helper(index + 1, count + 1, in_degree, requests)\n in_degree[requests[index][0]] -= 1\n in_degree[requests[index][1]] += 1\n self.helper(index + 1, count, in_degree, requests)\n```\n | 1 | We have `n` buildings numbered from `0` to `n - 1`. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.
You are given an array `requests` where `requests[i] = [fromi, toi]` represents an employee's request to transfer from building `fromi` to building `toi`.
**All buildings are full**, so a list of requests is achievable only if for each building, the **net change in employee transfers is zero**. This means the number of employees **leaving** is **equal** to the number of employees **moving in**. For example if `n = 3` and two employees are leaving building `0`, one is leaving building `1`, and one is leaving building `2`, there should be two employees moving to building `0`, one employee moving to building `1`, and one employee moving to building `2`.
Return _the maximum number of achievable requests_.
**Example 1:**
**Input:** n = 5, requests = \[\[0,1\],\[1,0\],\[0,1\],\[1,2\],\[2,0\],\[3,4\]\]
**Output:** 5
**Explantion:** Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.
**Example 2:**
**Input:** n = 3, requests = \[\[0,0\],\[1,2\],\[2,1\]\]
**Output:** 3
**Explantion:** Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests.
**Example 3:**
**Input:** n = 4, requests = \[\[0,3\],\[3,1\],\[1,2\],\[2,0\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 20`
* `1 <= requests.length <= 16`
* `requests[i].length == 2`
* `0 <= fromi, toi < n` | null |
Backtracking Solution (Java, Python, C++) | maximum-number-of-achievable-transfer-requests | 1 | 1 | **Java**\n```\nclass Solution {\n int answer = 0;\n public int maximumRequests(int n, int[][] requests) {\n int[] inDegree = new int[n];\n helper(0,0,inDegree,requests);\n return answer;\n }\n private void helper(int index,int count, int[] indegree,int[][] requests) {\n if(index == requests.length) {\n \n for(int i: indegree) {\n if(i != 0) return; \n }\n answer = Math.max(answer, count);\n return;\n }\n \n \n indegree[requests[index][0]]--;\n indegree[requests[index][1]]++;\n helper(index + 1, count + 1, indegree,requests);\n indegree[requests[index][0]]++;\n indegree[requests[index][1]]--;\n helper(index + 1, count, indegree, requests);\n }\n}\n```\n\n**C++**\n\n```\nclass Solution {\npublic:\n int answer = 0;\n int maximumRequests(int n, vector<vector<int>>& requests) {\n answer = 0;\n vector<int> inDegree(n, 0);\n helper(0, 0, inDegree, requests);\n return answer;\n }\n void helper(int index, int count, vector<int>& inDegree, vector<vector<int>>& requests) {\n if (index == requests.size()) {\n for (int i : inDegree) {\n if (i != 0)\n return;\n }\n answer = max(answer, count);\n return;\n }\n inDegree[requests[index][0]]++;\n inDegree[requests[index][1]]--;\n helper(index + 1, count + 1, inDegree, requests);\n inDegree[requests[index][0]]--;\n inDegree[requests[index][1]]++;\n helper(index + 1, count, inDegree, requests);\n }\n};\n```\n\n**Python3**\n\n\n```\nclass Solution:\n def maximumRequests(self, n: int, requests: List[List[int]]) -> int:\n self.answer = 0\n in_degree = [0] * n\n self.helper(0, 0, in_degree, requests)\n return self.answer\n \n def helper(self, index, count, in_degree, requests):\n if index == len(requests):\n for i in in_degree:\n if i != 0:\n return\n self.answer = max(self.answer, count)\n return\n\n in_degree[requests[index][0]] += 1\n in_degree[requests[index][1]] -= 1\n self.helper(index + 1, count + 1, in_degree, requests)\n in_degree[requests[index][0]] -= 1\n in_degree[requests[index][1]] += 1\n self.helper(index + 1, count, in_degree, requests)\n```\n | 1 | You are given an integer array `jobs`, where `jobs[i]` is the amount of time it takes to complete the `ith` job.
There are `k` workers that you can assign jobs to. Each job should be assigned to **exactly** one worker. The **working time** of a worker is the sum of the time it takes to complete all jobs assigned to them. Your goal is to devise an optimal assignment such that the **maximum working time** of any worker is **minimized**.
_Return the **minimum** possible **maximum working time** of any assignment._
**Example 1:**
**Input:** jobs = \[3,2,3\], k = 3
**Output:** 3
**Explanation:** By assigning each person one job, the maximum time is 3.
**Example 2:**
**Input:** jobs = \[1,2,4,7,8\], k = 2
**Output:** 11
**Explanation:** Assign the jobs the following way:
Worker 1: 1, 2, 8 (working time = 1 + 2 + 8 = 11)
Worker 2: 4, 7 (working time = 4 + 7 = 11)
The maximum working time is 11.
**Constraints:**
* `1 <= k <= jobs.length <= 12`
* `1 <= jobs[i] <= 107` | Think brute force When is a subset of requests okay? |
Python Solution || Backtracking | maximum-number-of-achievable-transfer-requests | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe will maintain a list **out_in_degree** of length n.\nWhile traversing requests[i] = [fromi, toi], we will subtract -1 from out_in_degree[fromi] and add +1 to out_in_degree[toi] and when we reach to the end of requests then we will check if out_in_degree[] is balenced or not(all elements =0). If it is balenced then we will take our ans otherwise will backtrack\n\n\n# Code\n```\nclass Solution:\n def maximumRequests(self, n: int, requests: List[List[int]]) -> int:\n global ans\n ans = 0\n out_in_degree = [0]*n\n def backtrack(index, requests,out_in_degree,count):\n global ans \n if index == len(requests):\n for item in out_in_degree:\n if item != 0: # not zero means unbalenced out_in_degree\n return\n ans = max(ans, count)\n return\n \n #consider current requests[index]\n out_in_degree[requests[index][0]]-=1\n out_in_degree[requests[index][1]]+=1\n backtrack(index+1, requests, out_in_degree,count+1)\n\n #do not consider current requests[index]\n out_in_degree[requests[index][0]]+=1\n out_in_degree[requests[index][1]]-=1\n backtrack(index+1, requests, out_in_degree,count)\n\n backtrack(0,requests,out_in_degree,0)\n return ans\n \n \n``` | 1 | We have `n` buildings numbered from `0` to `n - 1`. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.
You are given an array `requests` where `requests[i] = [fromi, toi]` represents an employee's request to transfer from building `fromi` to building `toi`.
**All buildings are full**, so a list of requests is achievable only if for each building, the **net change in employee transfers is zero**. This means the number of employees **leaving** is **equal** to the number of employees **moving in**. For example if `n = 3` and two employees are leaving building `0`, one is leaving building `1`, and one is leaving building `2`, there should be two employees moving to building `0`, one employee moving to building `1`, and one employee moving to building `2`.
Return _the maximum number of achievable requests_.
**Example 1:**
**Input:** n = 5, requests = \[\[0,1\],\[1,0\],\[0,1\],\[1,2\],\[2,0\],\[3,4\]\]
**Output:** 5
**Explantion:** Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.
**Example 2:**
**Input:** n = 3, requests = \[\[0,0\],\[1,2\],\[2,1\]\]
**Output:** 3
**Explantion:** Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests.
**Example 3:**
**Input:** n = 4, requests = \[\[0,3\],\[3,1\],\[1,2\],\[2,0\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 20`
* `1 <= requests.length <= 16`
* `requests[i].length == 2`
* `0 <= fromi, toi < n` | null |
Python Solution || Backtracking | maximum-number-of-achievable-transfer-requests | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe will maintain a list **out_in_degree** of length n.\nWhile traversing requests[i] = [fromi, toi], we will subtract -1 from out_in_degree[fromi] and add +1 to out_in_degree[toi] and when we reach to the end of requests then we will check if out_in_degree[] is balenced or not(all elements =0). If it is balenced then we will take our ans otherwise will backtrack\n\n\n# Code\n```\nclass Solution:\n def maximumRequests(self, n: int, requests: List[List[int]]) -> int:\n global ans\n ans = 0\n out_in_degree = [0]*n\n def backtrack(index, requests,out_in_degree,count):\n global ans \n if index == len(requests):\n for item in out_in_degree:\n if item != 0: # not zero means unbalenced out_in_degree\n return\n ans = max(ans, count)\n return\n \n #consider current requests[index]\n out_in_degree[requests[index][0]]-=1\n out_in_degree[requests[index][1]]+=1\n backtrack(index+1, requests, out_in_degree,count+1)\n\n #do not consider current requests[index]\n out_in_degree[requests[index][0]]+=1\n out_in_degree[requests[index][1]]-=1\n backtrack(index+1, requests, out_in_degree,count)\n\n backtrack(0,requests,out_in_degree,0)\n return ans\n \n \n``` | 1 | You are given an integer array `jobs`, where `jobs[i]` is the amount of time it takes to complete the `ith` job.
There are `k` workers that you can assign jobs to. Each job should be assigned to **exactly** one worker. The **working time** of a worker is the sum of the time it takes to complete all jobs assigned to them. Your goal is to devise an optimal assignment such that the **maximum working time** of any worker is **minimized**.
_Return the **minimum** possible **maximum working time** of any assignment._
**Example 1:**
**Input:** jobs = \[3,2,3\], k = 3
**Output:** 3
**Explanation:** By assigning each person one job, the maximum time is 3.
**Example 2:**
**Input:** jobs = \[1,2,4,7,8\], k = 2
**Output:** 11
**Explanation:** Assign the jobs the following way:
Worker 1: 1, 2, 8 (working time = 1 + 2 + 8 = 11)
Worker 2: 4, 7 (working time = 4 + 7 = 11)
The maximum working time is 11.
**Constraints:**
* `1 <= k <= jobs.length <= 12`
* `1 <= jobs[i] <= 107` | Think brute force When is a subset of requests okay? |
Easy python soln beats 71.7% in memory | design-parking-system | 0 | 1 | # Easy python solution\n\n# Code\n```\nclass ParkingSystem(object):\n def __init__(self, big, medium, small):\n self.ar=[big,medium,small]\n def addCar(self, carType):\n if self.ar[carType-1]>0:\n self.ar[carType-1]-=1\n return True\n return False\n``` | 1 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
Python short and clean. 2-liner. | design-parking-system | 0 | 1 | # Approach\n1. Store the available `slots` in an array.\n\n2. For each call to `addCar`, decrement the count if `count > -1`. Return `True` if `count > -1` else `False`.\n\n# Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\nfor both `init` and `addCar` methods.\n\n# Code\n```python\nclass ParkingSystem:\n\n def __init__(self, big: int, medium: int, small: int):\n self.slots = [0, big, medium, small]\n\n def addCar(self, car_type: int) -> bool:\n self.slots[car_type] = count = max(self.slots[car_type] - 1, -1)\n return count > -1\n\n\n``` | 2 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | design-parking-system | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution\n\n# Search \uD83D\uDC49 `Design Parking System By Tech Wired` \n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\nThe approach for the "Design Parking System" problem is to maintain a data structure that keeps track of the number of available parking spots for each car type. In this case, we can use a list or an array to store the available spots for big, medium, and small cars.\n\nInitialize the parking system: In the constructor or initialization method, store the number of available spots for each car type in the data structure (list or array).\n\nAdd a car: In the addCar method, check if there is an available spot for the specified car type. If the number of available spots for that car type is greater than 0, decrement the count of available spots for that car type and return true to indicate a successful addition. Otherwise, return false to indicate that no parking spot is available for that car type.\n\n# Intuition:\nThe parking system is designed to keep track of available parking spots for different car types. By maintaining the count of available spots for each car type, we can efficiently check and manage the parking availability for incoming cars.\n\nWhen initializing the parking system, we store the initial count of available spots for each car type. This allows us to keep track of the available spots throughout the parking process.\n\nWhen adding a car, we check if there is an available spot for the specified car type. If so, we decrement the count of available spots for that car type and indicate a successful addition. Otherwise, we indicate that no parking spot is available for that car type.\n\n\n\n```Python []\nclass ParkingSystem:\n def __init__(self, big: int, medium: int, small: int):\n self.spots = [big, medium, small]\n\n def addCar(self, carType: int) -> bool:\n if self.spots[carType - 1] > 0:\n self.spots[carType - 1] -= 1\n return True\n else:\n return False\n\n```\n```Java []\nclass ParkingSystem {\n private int[] spots;\n\n public ParkingSystem(int big, int medium, int small) {\n spots = new int[]{big, medium, small};\n }\n\n public boolean addCar(int carType) {\n if (spots[carType - 1] > 0) {\n spots[carType - 1]--;\n return true;\n } else {\n return false;\n }\n }\n}\n\n```\n```C++ []\nclass ParkingSystem {\nprivate:\n int spots[3];\n\npublic:\n ParkingSystem(int big, int medium, int small) {\n spots[0] = big;\n spots[1] = medium;\n spots[2] = small;\n }\n\n bool addCar(int carType) {\n if (spots[carType - 1] > 0) {\n spots[carType - 1]--;\n return true;\n } else {\n return false;\n }\n }\n};\n\n```\n | 10 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
python 3 - simple iteration | design-parking-system | 0 | 1 | # Complexity\n- Time complexity:\n__init__ : O(1)\naddCar: O(1)\n\n- Space complexity:\n__init__ : O(1)\naddCar: O(1)\n\n# Code\n```\nclass ParkingSystem:\n\n def __init__(self, big: int, medium: int, small: int):\n self.space = [0, big, medium, small]\n \n def addCar(self, carType: int) -> bool:\n if self.space[carType] > 0:\n self.space[carType] -= 1\n return True\n return False\n\n \n\n\n# Your ParkingSystem object will be instantiated and called as such:\n# obj = ParkingSystem(big, medium, small)\n# param_1 = obj.addCar(carType)\n``` | 5 | Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the `ParkingSystem` class:
* `ParkingSystem(int big, int medium, int small)` Initializes object of the `ParkingSystem` class. The number of slots for each parking space are given as part of the constructor.
* `bool addCar(int carType)` Checks whether there is a parking space of `carType` for the car that wants to get into the parking lot. `carType` can be of three kinds: big, medium, or small, which are represented by `1`, `2`, and `3` respectively. **A car can only park in a parking space of its** `carType`. If there is no space available, return `false`, else park the car in that size space and return `true`.
**Example 1:**
**Input**
\[ "ParkingSystem ", "addCar ", "addCar ", "addCar ", "addCar "\]
\[\[1, 1, 0\], \[1\], \[2\], \[3\], \[1\]\]
**Output**
\[null, true, true, false, false\]
**Explanation**
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
**Constraints:**
* `0 <= big, medium, small <= 1000`
* `carType` is `1`, `2`, or `3`
* At most `1000` calls will be made to `addCar` | Think about how we can calculate the i-th number in the running sum from the (i-1)-th number. |
[Python] Clean and Fast Solution | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | ```python\nclass Solution:\n # 668 ms, 99.52%. Time: O(NlogN). Space: O(N)\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n \n def is_within_1hr(t1, t2):\n h1, m1 = t1.split(":")\n h2, m2 = t2.split(":")\n if int(h1) + 1 < int(h2): return False\n if h1 == h2: return True\n return m1 >= m2\n \n records = collections.defaultdict(list)\n for name, time in zip(keyName, keyTime):\n records[name].append(time)\n \n rv = []\n for person, record in records.items():\n record.sort()\n\t\t\t# Loop through 2 values at a time and check if they are within 1 hour.\n if any(is_within_1hr(t1, t2) for t1, t2 in zip(record, record[2:])):\n rv.append(person)\n return sorted(rv)\n \n``` | 10 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Beat 100% 650ms easy understanding hashtable python3 | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | https://leetcode.com/problems/alert-using-same-key-card-three-or-more-times-in-a-one-hour-period/submissions/933863150/?submissionId=933863150\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHashtable \n\n# Complexity\n- Time complexity: O(N log N)\n N = number of emplyees\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom datetime import time\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n empl, ans = {}, []\n for index, name in enumerate(keyName):\n if name in empl: \n empl[name].append(int(keyTime[index][:2] + keyTime[index][3:]))\n else:\n empl[name] = [int(keyTime[index][:2] + keyTime[index][3:])]\n for n, t in empl.items():\n t.sort()\n for i in range(len(t)-2):\n if t[i+2] - t[i] <= 100:\n ans.append(n)\n break\n return sorted(ans)\n``` | 3 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Python3 | Dict + Sort | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | ```\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n key_time = {}\n for index, name in enumerate(keyName):\n key_time[name] = key_time.get(name, [])\n key_time[name].append(int(keyTime[index].replace(":", "")))\n ans = []\n for name, time_list in key_time.items():\n time_list.sort()\n n = len(time_list)\n for i in range(n-2):\n if time_list[i+2] - time_list[i] <= 100:\n ans.append(name)\n break\n return sorted(ans)\n ```\n \n \n \n \n \n \n\t\t | 4 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
python dict | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n data = {}\n for i in range(len(keyName)):\n if keyName[i] not in data:\n data[keyName[i]] = [int(keyTime[i][0]+keyTime[i][1])*60+int(keyTime[i][3]+keyTime[i][4])]\n else:\n data[keyName[i]].append(int(keyTime[i][0]+keyTime[i][1])*60+(int(keyTime[i][3]+keyTime[i][4])))\n final = []\n for k in data.keys():\n data[k].sort()\n for i in range(len((data[k]))-2):\n if data[k][i+2] - data[k][i] <=60 and data[k][i+1] - data[k][i]<60:\n final.append(k)\n break\n \n return sorted(set(final))\n\n\n\n\n\n\n\n\n \n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Very simple easy for beginners using hashmap and sorting !!!! | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n res=[]\n a=[]\n for i in keyTime:\n a.append((int(i[0]+i[1])*60+(int(i[3]+i[4]))))\n d={}\n for i in range(len(keyName)):\n if keyName[i] not in d:\n d[keyName[i]]=[a[i]]\n else:\n d[keyName[i]].append(a[i])\n for i in d:\n d[i].sort()\n for i in d:\n flag=1\n for j in range(2,len(d[i])):\n if d[i][j]-d[i][j-2]<=60:\n flag=0\n break\n if flag==0:\n res.append(i)\n res.sort()\n return res\n\n\n\n\n\n \n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
[Python] Sliding Window, HashMap | Clean and Fast Solution | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGrouping the times by each person will make the check much easier.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use a hashmap to group every person\'s time together and then check if any of them swiped more than three times.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n def to_min(time):\n h, m = time.split(":")\n return int(h) * 60 + int(m)\n \n records = collections.defaultdict(list)\n for name, time in zip(keyName, keyTime):\n records[name].append(to_min(time))\n\n rv = []\n for person, record in records.items():\n if len(record) < 3:\n continue\n record.sort()\n for r in range(2, len(record)):\n if record[r] - record[r - 2] <= 60:\n rv.append(person)\n break\n return sorted(rv)\n \n \n\n \n\n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Python - Sorting and Min Heap | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nProcessing entries in increasing order of keyTime ensures that the timestamps to follow will always be greater and that\'s why the size of heap can be limited to 3 and the first timestamp can be deleted from the heap as that would never be a part of a 1 hour window in the future.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nProcess the entries in increasing order of keyTime. Only process an employee if that hasn\'t been already identified in the result. Convert the given time into a timestamp value using (hours*60) + minutes and add these timestamps to a heap maintained for each employee in a employees dict. If the heap reaches a size of 3 then check if those 3 values are within 1 hour window, if yes add employee to result and delete from employees dict, else remove the first timestamp and keep the other 2 in the heap to compare with any following timestamps.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n# Code\n```\nimport heapq as hq\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n employees = {}\n res = set()\n\n def get_timestamp(emp_time):\n hours, minutes = list(map(int, emp_time.split(":")))\n return (hours*60) + minutes\n\n def is_within_hour(t1, t2, t3):\n if t2-t1 <= 60 and t3-t2 <= 60 and t3-t1 <= 60:\n return True\n return False\n\n combined_sorted = sorted(zip(keyName, keyTime), key=lambda x: x[1]) \n \n for emp_name, emp_time in combined_sorted:\n if emp_name not in res:\n if emp_name not in employees:\n employees[emp_name] = []\n emp_ts = get_timestamp(emp_time)\n hq.heappush(employees[emp_name], emp_ts)\n\n if len(employees[emp_name]) == 3:\n t1 = hq.heappop(employees[emp_name])\n t2 = hq.heappop(employees[emp_name])\n t3 = hq.heappop(employees[emp_name])\n if is_within_hour(t1, t2, t3):\n res.add(emp_name)\n del employees[emp_name]\n else:\n hq.heappush(employees[emp_name], t2)\n hq.heappush(employees[emp_name], t3)\n\n res = sorted(list(res))\n return res\n\n \n\n \n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Python 3 solution | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]:\n nameToMinutes = collections.defaultdict(list)\n\n for name, time in zip(keyName, keyTime):\n minutes = self._getMinutes(time)\n nameToMinutes[name].append(minutes)\n\n return sorted([name for name, minutes in nameToMinutes.items()\n if self._hasAlert(minutes)])\n\n def _hasAlert(self, minutes: List[int]) -> bool:\n if len(minutes) > 70:\n return True\n minutes.sort()\n for i in range(2, len(minutes)):\n if minutes[i - 2] + 60 >= minutes[i]:\n return True\n return False\n\n def _getMinutes(self, time: str) -> int:\n h, m = map(int, time.split(\':\'))\n return 60 * h + m\n\n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
Python Easy to Understand | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | \n# Code\n```\nclass Solution:\n def alertNames(self, keyname: List[str], keytime: List[str]) -> List[str]:\n keytime_mins=[]\n for i in keytime:\n h,m=i.split(\':\')\n keytime_mins.append(int(h)*60+int(m))\n d={}\n for i in range(len(keyname)):\n if keyname[i] not in d.keys():\n d[keyname[i]]=[keytime_mins[i]]\n else:\n \n d[keyname[i]].append(keytime_mins[i])\n res=[]\n for i in d.keys():\n l=d[i]\n l.sort()\n if len(l)<3:\n continue\n for j in range(2,len(l)):\n if l[j]-l[j-2]<=60:\n res.append(i)\n break\n res.sort()\n return res\n\n\n\n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
dict by name, sort and run sliding window of length 2 | alert-using-same-key-card-three-or-more-times-in-a-one-hour-period | 0 | 1 | \n# Code\n```\ndef alertNames(self, name: List[str], time: List[str]) -> List[str]:\n n = len(name)\n def time2int(time):\n h, m = time.split(":")\n return int(h)*60 + int(m)\n data = defaultdict(list)\n for i in range(n):\n data[name[i]].append(time2int(time[i]))\n ret = []\n for name in sorted(data.keys()):\n if len(data[name]) < 3:\n continue\n data[name].sort()\n for i in range(2, len(data[name])):\n if data[name][i] - data[name][i-2] <= 60:\n ret.append(name)\n break\n return ret\n``` | 0 | LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an **alert** if any worker uses the key-card **three or more times** in a one-hour period.
You are given a list of strings `keyName` and `keyTime` where `[keyName[i], keyTime[i]]` corresponds to a person's name and the time when their key-card was used **in a** **single day**.
Access times are given in the **24-hour time format "HH:MM "**, such as `"23:51 "` and `"09:49 "`.
Return a _list of unique worker names who received an alert for frequent keycard use_. Sort the names in **ascending order alphabetically**.
Notice that `"10:00 "` - `"11:00 "` is considered to be within a one-hour period, while `"22:51 "` - `"23:52 "` is not considered to be within a one-hour period.
**Example 1:**
**Input:** keyName = \[ "daniel ", "daniel ", "daniel ", "luis ", "luis ", "luis ", "luis "\], keyTime = \[ "10:00 ", "10:40 ", "11:00 ", "09:00 ", "11:00 ", "13:00 ", "15:00 "\]
**Output:** \[ "daniel "\]
**Explanation:** "daniel " used the keycard 3 times in a one-hour period ( "10:00 ", "10:40 ", "11:00 ").
**Example 2:**
**Input:** keyName = \[ "alice ", "alice ", "alice ", "bob ", "bob ", "bob ", "bob "\], keyTime = \[ "12:01 ", "12:00 ", "18:00 ", "21:00 ", "21:20 ", "21:30 ", "23:00 "\]
**Output:** \[ "bob "\]
**Explanation:** "bob " used the keycard 3 times in a one-hour period ( "21:00 ", "21:20 ", "21:30 ").
**Constraints:**
* `1 <= keyName.length, keyTime.length <= 105`
* `keyName.length == keyTime.length`
* `keyTime[i]` is in the format **"HH:MM "**.
* `[keyName[i], keyTime[i]]` is **unique**.
* `1 <= keyName[i].length <= 10`
* `keyName[i] contains only lowercase English letters.` | Use a map to count the frequencies of the numbers in the array. An optimal strategy is to remove the numbers with the smallest count first. |
[Python & C++] (Greedy) Easy python solution. { Explained using images} | find-valid-matrix-given-row-and-column-sums | 0 | 1 | \nIntuition : To fill matrix, based on the fact of making, the total sum on both of the row and column to zero.\nLets take this example: RowSum = [14, 9] and ColSum = [ 6 , 9 , 8 ]\nso create a empty matrix initially with zero filled.\n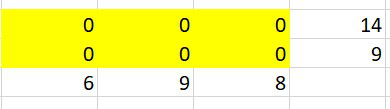\nNow start from the top left corner of matrx and go on filling it.\nFor cell (0,0) select the minimum of both rowSum and colSum and update the cell value with the minimum.\nAnd decrease the selected value in rowSum and colSum respectively as shown below.\n\n\nSo for the cell (0,0), colSum =6 and rowSum = 14, hence choose min(14,6), which is 6. Therefore fill (0,0) with 6 and substract 6 from both rowSum and colSum.\n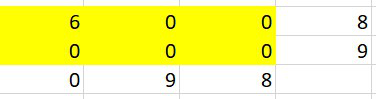\n\nNow fill the (0,1) cell similarly. Min(8,9) is 8, hence fill the cell with 8 and decrease 8 from both of them.\n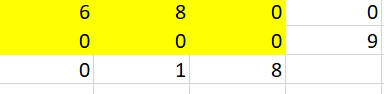\nAnd similarly you can fill the whole matrix, as shown below step by step.\n(As cell (0,2) and (1,0) will be filled with zero, They arent shown here)\n\nFor cell (1,1)\n4. 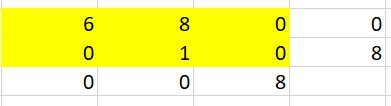\n\nFor cell (1,2)\n5. \n\n\n\n\nPYTHON:\n```\n\ndef restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n c, r = len(colSum), len(rowSum)\n mat = [[0 for i in range(c)] for i in range(r)]\n for i in range(r):\n for j in range(c):\n rsum, csum= rowSum[i], colSum[j]\n minn = min(rsum, csum)\n mat[i][j] = minn\n\t\t\t\trowSum[i]-=minn\n\t\t\t\tcolSum[j]-=minn\n return mat\n```\n\nC++\n```\n vector<vector<int>> restoreMatrix(vector<int>& rowSum, vector<int>& colSum) {\n int m = rowSum.size();\n\t\tint n = colSum.size();\n vector<vector<int>> mat(m, vector<int>(n, 0));\n for (int i = 0; i < m; i++) {\n for (int j = 0 ; j < n; j++) {\n mat[i][j] = min(rowSum[i], colSum[j]);\n rowSum[i] -= mat[i][j];\n colSum[j] -= mat[i][j];\n }\n }\n return mat;\n }\n``` | 61 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
[Python & C++] (Greedy) Easy python solution. { Explained using images} | find-valid-matrix-given-row-and-column-sums | 0 | 1 | \nIntuition : To fill matrix, based on the fact of making, the total sum on both of the row and column to zero.\nLets take this example: RowSum = [14, 9] and ColSum = [ 6 , 9 , 8 ]\nso create a empty matrix initially with zero filled.\n\nNow start from the top left corner of matrx and go on filling it.\nFor cell (0,0) select the minimum of both rowSum and colSum and update the cell value with the minimum.\nAnd decrease the selected value in rowSum and colSum respectively as shown below.\n\n\nSo for the cell (0,0), colSum =6 and rowSum = 14, hence choose min(14,6), which is 6. Therefore fill (0,0) with 6 and substract 6 from both rowSum and colSum.\n\n\nNow fill the (0,1) cell similarly. Min(8,9) is 8, hence fill the cell with 8 and decrease 8 from both of them.\n\nAnd similarly you can fill the whole matrix, as shown below step by step.\n(As cell (0,2) and (1,0) will be filled with zero, They arent shown here)\n\nFor cell (1,1)\n4. \n\nFor cell (1,2)\n5. \n\n\n\n\nPYTHON:\n```\n\ndef restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n c, r = len(colSum), len(rowSum)\n mat = [[0 for i in range(c)] for i in range(r)]\n for i in range(r):\n for j in range(c):\n rsum, csum= rowSum[i], colSum[j]\n minn = min(rsum, csum)\n mat[i][j] = minn\n\t\t\t\trowSum[i]-=minn\n\t\t\t\tcolSum[j]-=minn\n return mat\n```\n\nC++\n```\n vector<vector<int>> restoreMatrix(vector<int>& rowSum, vector<int>& colSum) {\n int m = rowSum.size();\n\t\tint n = colSum.size();\n vector<vector<int>> mat(m, vector<int>(n, 0));\n for (int i = 0; i < m; i++) {\n for (int j = 0 ; j < n; j++) {\n mat[i][j] = min(rowSum[i], colSum[j]);\n rowSum[i] -= mat[i][j];\n colSum[j] -= mat[i][j];\n }\n }\n return mat;\n }\n``` | 61 | A **good meal** is a meal that contains **exactly two different food items** with a sum of deliciousness equal to a power of two.
You can pick **any** two different foods to make a good meal.
Given an array of integers `deliciousness` where `deliciousness[i]` is the deliciousness of the `ith` item of food, return _the number of different **good meals** you can make from this list modulo_ `109 + 7`.
Note that items with different indices are considered different even if they have the same deliciousness value.
**Example 1:**
**Input:** deliciousness = \[1,3,5,7,9\]
**Output:** 4
**Explanation:** The good meals are (1,3), (1,7), (3,5) and, (7,9).
Their respective sums are 4, 8, 8, and 16, all of which are powers of 2.
**Example 2:**
**Input:** deliciousness = \[1,1,1,3,3,3,7\]
**Output:** 15
**Explanation:** The good meals are (1,1) with 3 ways, (1,3) with 9 ways, and (1,7) with 3 ways.
**Constraints:**
* `1 <= deliciousness.length <= 105`
* `0 <= deliciousness[i] <= 220` | Find the smallest rowSum or colSum, and let it be x. Place that number in the grid, and subtract x from rowSum and colSum. Continue until all the sums are satisfied. |
Python Beats 99.83% with Illustration | find-valid-matrix-given-row-and-column-sums | 0 | 1 | **The example are there to just confuse you so forget about the example.**\n\n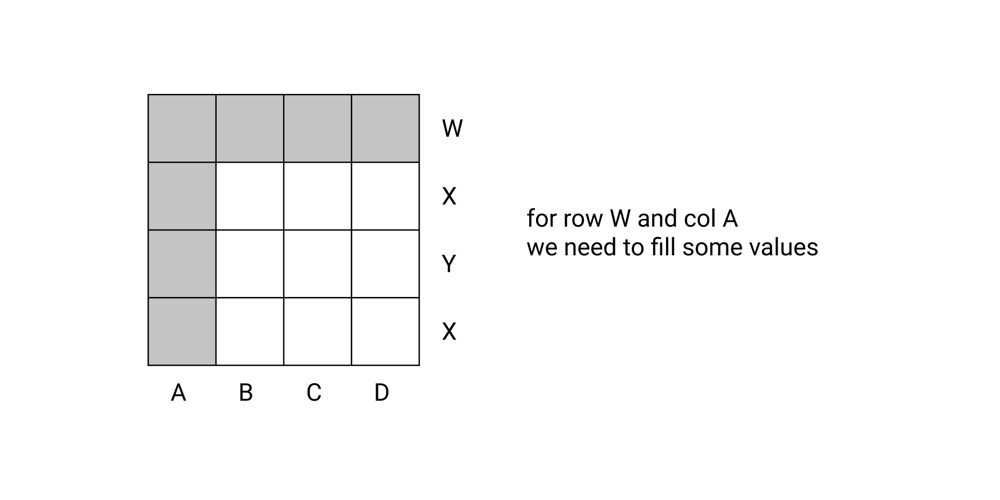\n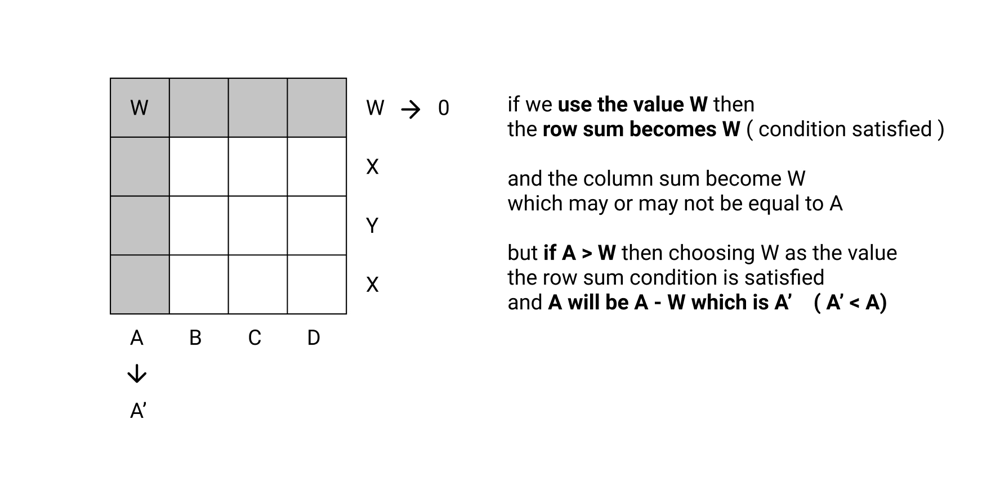\n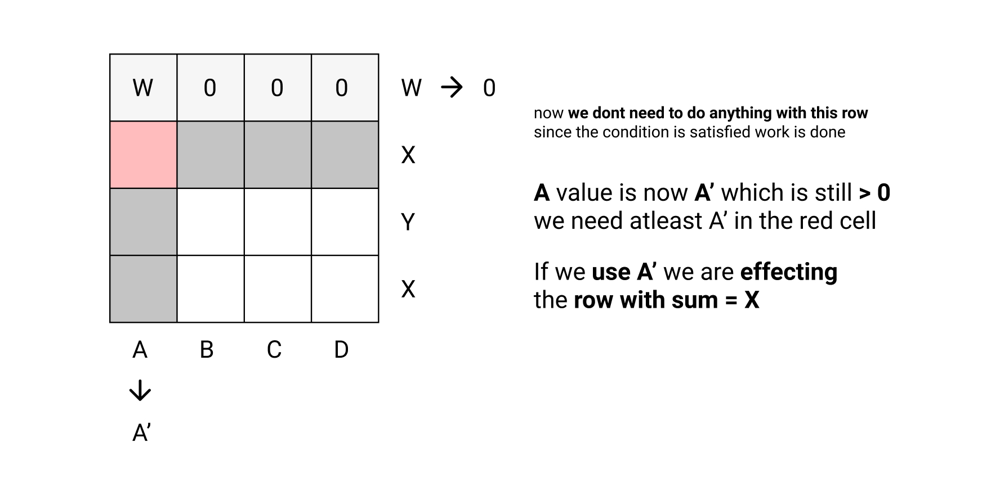\n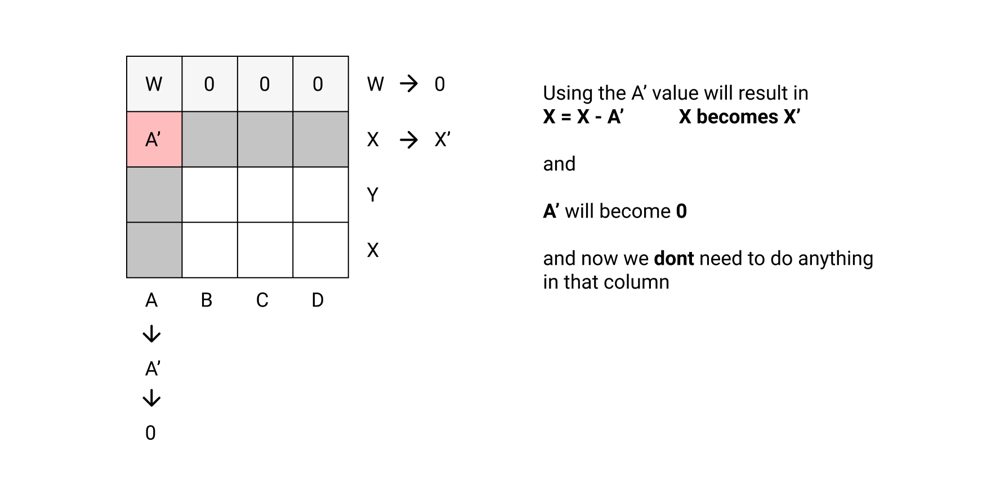\n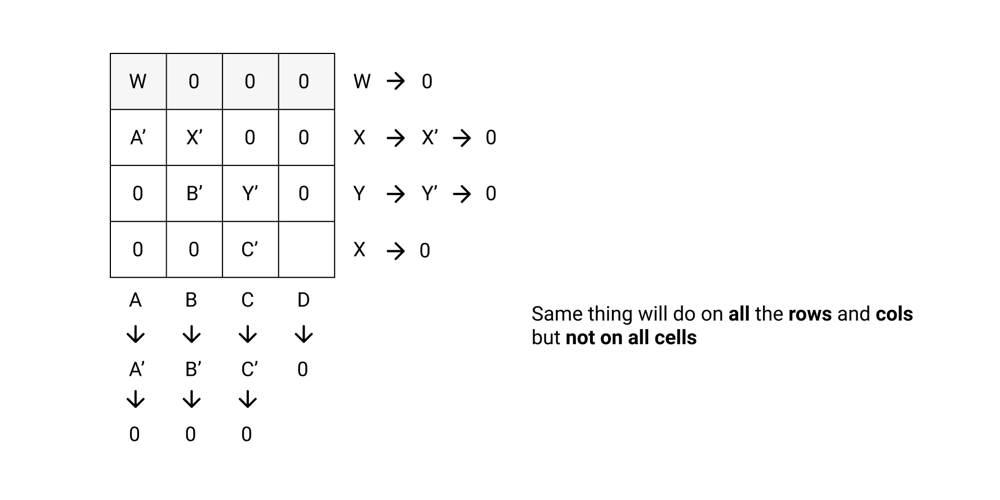\n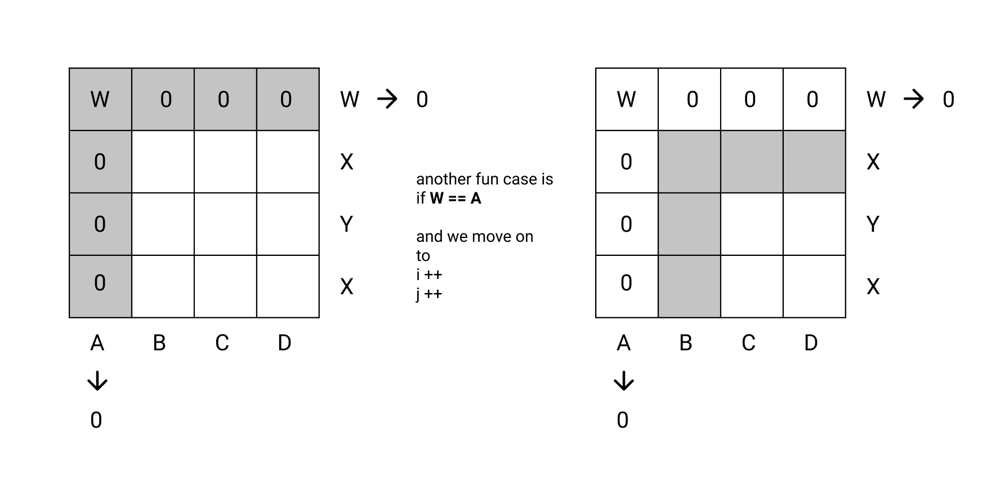\n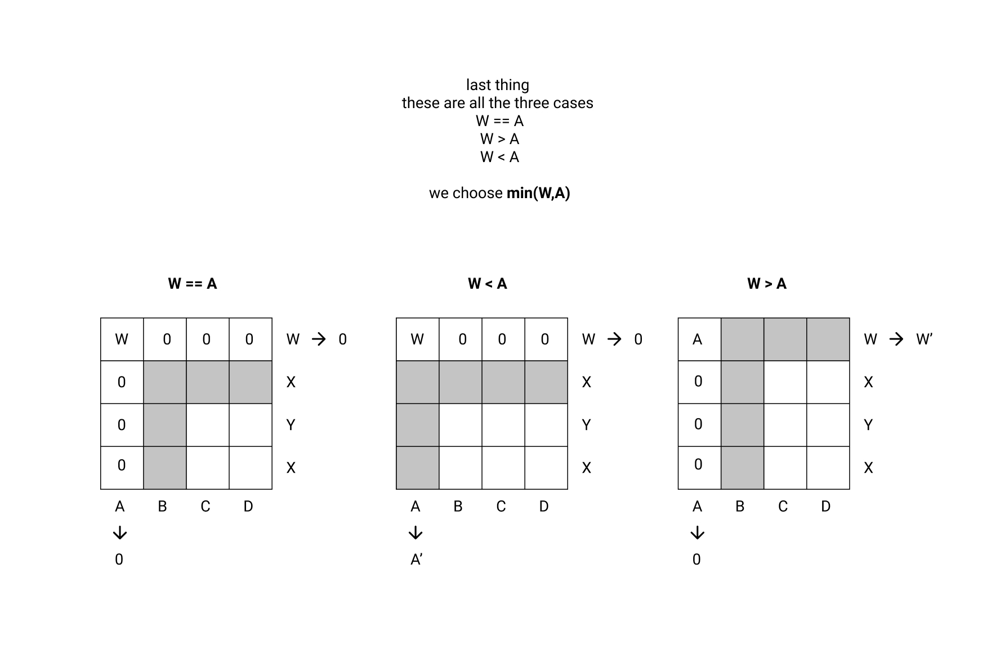\n\n\n\n\n```python\nclass Solution:\n def restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n col_sum = colSum\n row_sum = rowSum\n \n mat = [[0]*len(col_sum) for i in range(len(row_sum))]\n i = 0\n j = 0\n while i < len(row_sum) and j < len(col_sum):\n mat[i][j] = min(row_sum[i], col_sum[j])\n if row_sum[i] == col_sum[j]:\n i += 1\n j += 1\n elif row_sum[i] > col_sum[j]:\n row_sum[i] -= col_sum[j]\n j += 1\n else:\n col_sum[j] -= row_sum[i]\n i += 1\n\n return mat\n``` | 35 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
Python Beats 99.83% with Illustration | find-valid-matrix-given-row-and-column-sums | 0 | 1 | **The example are there to just confuse you so forget about the example.**\n\n\n\n\n\n\n\n\n\n\n\n\n```python\nclass Solution:\n def restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n col_sum = colSum\n row_sum = rowSum\n \n mat = [[0]*len(col_sum) for i in range(len(row_sum))]\n i = 0\n j = 0\n while i < len(row_sum) and j < len(col_sum):\n mat[i][j] = min(row_sum[i], col_sum[j])\n if row_sum[i] == col_sum[j]:\n i += 1\n j += 1\n elif row_sum[i] > col_sum[j]:\n row_sum[i] -= col_sum[j]\n j += 1\n else:\n col_sum[j] -= row_sum[i]\n i += 1\n\n return mat\n``` | 35 | A **good meal** is a meal that contains **exactly two different food items** with a sum of deliciousness equal to a power of two.
You can pick **any** two different foods to make a good meal.
Given an array of integers `deliciousness` where `deliciousness[i]` is the deliciousness of the `ith` item of food, return _the number of different **good meals** you can make from this list modulo_ `109 + 7`.
Note that items with different indices are considered different even if they have the same deliciousness value.
**Example 1:**
**Input:** deliciousness = \[1,3,5,7,9\]
**Output:** 4
**Explanation:** The good meals are (1,3), (1,7), (3,5) and, (7,9).
Their respective sums are 4, 8, 8, and 16, all of which are powers of 2.
**Example 2:**
**Input:** deliciousness = \[1,1,1,3,3,3,7\]
**Output:** 15
**Explanation:** The good meals are (1,1) with 3 ways, (1,3) with 9 ways, and (1,7) with 3 ways.
**Constraints:**
* `1 <= deliciousness.length <= 105`
* `0 <= deliciousness[i] <= 220` | Find the smallest rowSum or colSum, and let it be x. Place that number in the grid, and subtract x from rowSum and colSum. Continue until all the sums are satisfied. |
[C++/Python3] Greedy | Fill Minimum Element Left | O(n*m) | find-valid-matrix-given-row-and-column-sums | 0 | 1 | **Thought Process**\n\nIterate through each row and column one by one, for each `i` (row) and `j` (column) pick the minimum element between `rowSum[i]` and `colSum[j]` and assign `el = min(rowSum[i], colSum[j])` and reduce this `el` from both sum entries respectively.\n\nTada!\n\n**Time Complexity** : `O(n*m)`\n**Space Complexity**: `O(n*m) aux space : O(1)`\n\n[C++]\n```\nclass Solution {\npublic:\n vector<vector<int>> restoreMatrix(vector<int>& rs, vector<int>& cs) {\n int rows = rs.size();\n int cols = cs.size();\n int req;\n vector<vector<int>> ans(rows, vector<int>(cols, 0));\n for(int i=0; i<rows; i++) {\n for(int j=0; j<cols; j++) {\n req = min(rs[i], cs[j]);\n ans[i][j] = req;\n rs[i] -= req;\n cs[j] -= req;\n }\n }\n return ans;\n }\n};\n```\n\n[Python3]\n```\nclass Solution:\n def restoreMatrix(self, rs: List[int], cs: List[int]) -> List[List[int]]:\n row = len(rs)\n col = len(cs)\n ans = [[0 for i in range(col)] for j in range(row)]\n for i in range(row):\n for j in range(col):\n el = min(rs[i], cs[j])\n ans[i][j] = el\n rs[i] -= el\n cs[j] -= el\n return ans\n``` | 12 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
[C++/Python3] Greedy | Fill Minimum Element Left | O(n*m) | find-valid-matrix-given-row-and-column-sums | 0 | 1 | **Thought Process**\n\nIterate through each row and column one by one, for each `i` (row) and `j` (column) pick the minimum element between `rowSum[i]` and `colSum[j]` and assign `el = min(rowSum[i], colSum[j])` and reduce this `el` from both sum entries respectively.\n\nTada!\n\n**Time Complexity** : `O(n*m)`\n**Space Complexity**: `O(n*m) aux space : O(1)`\n\n[C++]\n```\nclass Solution {\npublic:\n vector<vector<int>> restoreMatrix(vector<int>& rs, vector<int>& cs) {\n int rows = rs.size();\n int cols = cs.size();\n int req;\n vector<vector<int>> ans(rows, vector<int>(cols, 0));\n for(int i=0; i<rows; i++) {\n for(int j=0; j<cols; j++) {\n req = min(rs[i], cs[j]);\n ans[i][j] = req;\n rs[i] -= req;\n cs[j] -= req;\n }\n }\n return ans;\n }\n};\n```\n\n[Python3]\n```\nclass Solution:\n def restoreMatrix(self, rs: List[int], cs: List[int]) -> List[List[int]]:\n row = len(rs)\n col = len(cs)\n ans = [[0 for i in range(col)] for j in range(row)]\n for i in range(row):\n for j in range(col):\n el = min(rs[i], cs[j])\n ans[i][j] = el\n rs[i] -= el\n cs[j] -= el\n return ans\n``` | 12 | A **good meal** is a meal that contains **exactly two different food items** with a sum of deliciousness equal to a power of two.
You can pick **any** two different foods to make a good meal.
Given an array of integers `deliciousness` where `deliciousness[i]` is the deliciousness of the `ith` item of food, return _the number of different **good meals** you can make from this list modulo_ `109 + 7`.
Note that items with different indices are considered different even if they have the same deliciousness value.
**Example 1:**
**Input:** deliciousness = \[1,3,5,7,9\]
**Output:** 4
**Explanation:** The good meals are (1,3), (1,7), (3,5) and, (7,9).
Their respective sums are 4, 8, 8, and 16, all of which are powers of 2.
**Example 2:**
**Input:** deliciousness = \[1,1,1,3,3,3,7\]
**Output:** 15
**Explanation:** The good meals are (1,1) with 3 ways, (1,3) with 9 ways, and (1,7) with 3 ways.
**Constraints:**
* `1 <= deliciousness.length <= 105`
* `0 <= deliciousness[i] <= 220` | Find the smallest rowSum or colSum, and let it be x. Place that number in the grid, and subtract x from rowSum and colSum. Continue until all the sums are satisfied. |
50% TC and 67% SC easy python solution | find-valid-matrix-given-row-and-column-sums | 0 | 1 | ```\ndef restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n\tr = len(rowSum)\n\tc = len(colSum)\n\tans = [[-1 for _ in range(c)] for _ in range(r)]\n\tfor i in range(r):\n\t\tfor j in range(c):\n\t\t\tif(rowSum[i] <= colSum[j]):\n\t\t\t\tans[i][j] = rowSum[i]\n\t\t\t\tcolSum[j] -= rowSum[i]\n\t\t\t\trowSum[i] = 0\n\t\t\telse:\n\t\t\t\tans[i][j] = colSum[j]\n\t\t\t\trowSum[i] -= colSum[j]\n\t\t\t\tcolSum[j] = 0\n\treturn ans\n``` | 1 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
50% TC and 67% SC easy python solution | find-valid-matrix-given-row-and-column-sums | 0 | 1 | ```\ndef restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n\tr = len(rowSum)\n\tc = len(colSum)\n\tans = [[-1 for _ in range(c)] for _ in range(r)]\n\tfor i in range(r):\n\t\tfor j in range(c):\n\t\t\tif(rowSum[i] <= colSum[j]):\n\t\t\t\tans[i][j] = rowSum[i]\n\t\t\t\tcolSum[j] -= rowSum[i]\n\t\t\t\trowSum[i] = 0\n\t\t\telse:\n\t\t\t\tans[i][j] = colSum[j]\n\t\t\t\trowSum[i] -= colSum[j]\n\t\t\t\tcolSum[j] = 0\n\treturn ans\n``` | 1 | A **good meal** is a meal that contains **exactly two different food items** with a sum of deliciousness equal to a power of two.
You can pick **any** two different foods to make a good meal.
Given an array of integers `deliciousness` where `deliciousness[i]` is the deliciousness of the `ith` item of food, return _the number of different **good meals** you can make from this list modulo_ `109 + 7`.
Note that items with different indices are considered different even if they have the same deliciousness value.
**Example 1:**
**Input:** deliciousness = \[1,3,5,7,9\]
**Output:** 4
**Explanation:** The good meals are (1,3), (1,7), (3,5) and, (7,9).
Their respective sums are 4, 8, 8, and 16, all of which are powers of 2.
**Example 2:**
**Input:** deliciousness = \[1,1,1,3,3,3,7\]
**Output:** 15
**Explanation:** The good meals are (1,1) with 3 ways, (1,3) with 9 ways, and (1,7) with 3 ways.
**Constraints:**
* `1 <= deliciousness.length <= 105`
* `0 <= deliciousness[i] <= 220` | Find the smallest rowSum or colSum, and let it be x. Place that number in the grid, and subtract x from rowSum and colSum. Continue until all the sums are satisfied. |
[Python3] Good enough | find-valid-matrix-given-row-and-column-sums | 0 | 1 | ``` Python3 []\nclass Solution:\n def restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n matrix = [[0]*len(colSum) for _ in range(len(rowSum))]\n \n rows = []\n for i,x in enumerate(rowSum):\n heapq.heappush(rows, (x,i))\n \n cols = []\n for i,x in enumerate(colSum):\n heapq.heappush(cols, (x,i))\n\n while rows and cols:\n row = heapq.heappop(rows)\n col = heapq.heappop(cols)\n minn = min(row[0],col[0])\n\n matrix[row[1]][col[1]] = minn\n\n if row[0]-minn:\n heapq.heappush(rows, (row[0]-minn, row[1]))\n if col[0]-minn:\n heapq.heappush(cols, (col[0]-minn, col[1]))\n \n return matrix\n``` | 0 | You are given two arrays `rowSum` and `colSum` of non-negative integers where `rowSum[i]` is the sum of the elements in the `ith` row and `colSum[j]` is the sum of the elements of the `jth` column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of **non-negative** integers of size `rowSum.length x colSum.length` that satisfies the `rowSum` and `colSum` requirements.
Return _a 2D array representing **any** matrix that fulfills the requirements_. It's guaranteed that **at least one** matrix that fulfills the requirements exists.
**Example 1:**
**Input:** rowSum = \[3,8\], colSum = \[4,7\]
**Output:** \[\[3,0\],
\[1,7\]\]
**Explanation:**
0th row: 3 + 0 = 3 == rowSum\[0\]
1st row: 1 + 7 = 8 == rowSum\[1\]
0th column: 3 + 1 = 4 == colSum\[0\]
1st column: 0 + 7 = 7 == colSum\[1\]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: \[\[1,2\],
\[3,5\]\]
**Example 2:**
**Input:** rowSum = \[5,7,10\], colSum = \[8,6,8\]
**Output:** \[\[0,5,0\],
\[6,1,0\],
\[2,0,8\]\]
**Constraints:**
* `1 <= rowSum.length, colSum.length <= 500`
* `0 <= rowSum[i], colSum[i] <= 108`
* `sum(rowSum) == sum(colSum)` | If we can make m or more bouquets at day x, then we can still make m or more bouquets at any day y > x. We can check easily if we can make enough bouquets at day x if we can get group adjacent flowers at day x. |
[Python3] Good enough | find-valid-matrix-given-row-and-column-sums | 0 | 1 | ``` Python3 []\nclass Solution:\n def restoreMatrix(self, rowSum: List[int], colSum: List[int]) -> List[List[int]]:\n matrix = [[0]*len(colSum) for _ in range(len(rowSum))]\n \n rows = []\n for i,x in enumerate(rowSum):\n heapq.heappush(rows, (x,i))\n \n cols = []\n for i,x in enumerate(colSum):\n heapq.heappush(cols, (x,i))\n\n while rows and cols:\n row = heapq.heappop(rows)\n col = heapq.heappop(cols)\n minn = min(row[0],col[0])\n\n matrix[row[1]][col[1]] = minn\n\n if row[0]-minn:\n heapq.heappush(rows, (row[0]-minn, row[1]))\n if col[0]-minn:\n heapq.heappush(cols, (col[0]-minn, col[1]))\n \n return matrix\n``` | 0 | A **good meal** is a meal that contains **exactly two different food items** with a sum of deliciousness equal to a power of two.
You can pick **any** two different foods to make a good meal.
Given an array of integers `deliciousness` where `deliciousness[i]` is the deliciousness of the `ith` item of food, return _the number of different **good meals** you can make from this list modulo_ `109 + 7`.
Note that items with different indices are considered different even if they have the same deliciousness value.
**Example 1:**
**Input:** deliciousness = \[1,3,5,7,9\]
**Output:** 4
**Explanation:** The good meals are (1,3), (1,7), (3,5) and, (7,9).
Their respective sums are 4, 8, 8, and 16, all of which are powers of 2.
**Example 2:**
**Input:** deliciousness = \[1,1,1,3,3,3,7\]
**Output:** 15
**Explanation:** The good meals are (1,1) with 3 ways, (1,3) with 9 ways, and (1,7) with 3 ways.
**Constraints:**
* `1 <= deliciousness.length <= 105`
* `0 <= deliciousness[i] <= 220` | Find the smallest rowSum or colSum, and let it be x. Place that number in the grid, and subtract x from rowSum and colSum. Continue until all the sums are satisfied. |
Python3 fast solution with mathematical derivation | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe need to sort server_id in range: [i, i+k)\nso we have:\ni <= server_id + m*k < i+k\n-> server_id + m*k = i + x where x in range[0, k)\n-> server_id % k + 0 = i % k + x\n-> x = server_id % k - i % k\nthat means we can use id = i + x = i + (server_id - i) % k as key of the heap\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n\n available_servers = list(range(k))\n busy_servers = []\n cnt = [0] * k\n\n for i in range(len(arrival)):\n start, duration = arrival[i], load[i]\n while busy_servers and busy_servers[0][0] <= start:\n _, server = heapq.heappop(busy_servers)\n heapq.heappush(available_servers, i + (server - i) % k)\n if available_servers:\n server = heapq.heappop(available_servers) % k\n cnt[server] += 1\n heapq.heappush(busy_servers, (start + duration, server))\n\n mx = max(cnt)\n return [i for i in range(len(cnt)) if cnt[i] == mx]\n \n \n\n\n\n\n``` | 2 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python3 fast solution with mathematical derivation | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe need to sort server_id in range: [i, i+k)\nso we have:\ni <= server_id + m*k < i+k\n-> server_id + m*k = i + x where x in range[0, k)\n-> server_id % k + 0 = i % k + x\n-> x = server_id % k - i % k\nthat means we can use id = i + x = i + (server_id - i) % k as key of the heap\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n\n available_servers = list(range(k))\n busy_servers = []\n cnt = [0] * k\n\n for i in range(len(arrival)):\n start, duration = arrival[i], load[i]\n while busy_servers and busy_servers[0][0] <= start:\n _, server = heapq.heappop(busy_servers)\n heapq.heappush(available_servers, i + (server - i) % k)\n if available_servers:\n server = heapq.heappop(available_servers) % k\n cnt[server] += 1\n heapq.heappush(busy_servers, (start + duration, server))\n\n mx = max(cnt)\n return [i for i in range(len(cnt)) if cnt[i] == mx]\n \n \n\n\n\n\n``` | 2 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python, using only heaps | find-servers-that-handled-most-number-of-requests | 0 | 1 | Solution using three heaps. First heap is used to quickly free up the nodes. Then we split the servers to those that come after the `server_id` which is current server and those that come before, for loopback.\n```\ndef busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n\tbusy_jobs = [] # heap (job_end_time, node) to free up the nodes quickly\n\tafter = [] # heap (nodes) free after current server\n\tbefore = list(range(k)) # heap (nodes) to use for loopback\n\trequests_handled = [0] * k\n\n\tfor i, (arrvl, ld) in enumerate(zip(arrival, load)):\n\t\tserver_id = i % k\n\t\tif server_id == 0: # loopback\n\t\t\tafter = before\n\t\t\tbefore = []\n\n\t\twhile busy_jobs and busy_jobs[0][0] <= arrvl:\n\t\t\tfreed_node = heapq.heappop(busy_jobs)[1]\n\t\t\tif freed_node < server_id: heapq.heappush(before, freed_node)\n\t\t\telse: heapq.heappush(after, freed_node)\n\n\t\tuse_queue = after if after else before\n\t\tif not use_queue: continue # request dropped\n\t\tusing_node = heapq.heappop(use_queue)\n\t\trequests_handled[using_node] += 1\n\t\theapq.heappush(busy_jobs, (arrvl + ld, using_node))\n\n\tmaxreqs = max(requests_handled)\n\treturn [i for i, handled in enumerate(requests_handled) if handled == maxreqs]\n``` | 90 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python, using only heaps | find-servers-that-handled-most-number-of-requests | 0 | 1 | Solution using three heaps. First heap is used to quickly free up the nodes. Then we split the servers to those that come after the `server_id` which is current server and those that come before, for loopback.\n```\ndef busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n\tbusy_jobs = [] # heap (job_end_time, node) to free up the nodes quickly\n\tafter = [] # heap (nodes) free after current server\n\tbefore = list(range(k)) # heap (nodes) to use for loopback\n\trequests_handled = [0] * k\n\n\tfor i, (arrvl, ld) in enumerate(zip(arrival, load)):\n\t\tserver_id = i % k\n\t\tif server_id == 0: # loopback\n\t\t\tafter = before\n\t\t\tbefore = []\n\n\t\twhile busy_jobs and busy_jobs[0][0] <= arrvl:\n\t\t\tfreed_node = heapq.heappop(busy_jobs)[1]\n\t\t\tif freed_node < server_id: heapq.heappush(before, freed_node)\n\t\t\telse: heapq.heappush(after, freed_node)\n\n\t\tuse_queue = after if after else before\n\t\tif not use_queue: continue # request dropped\n\t\tusing_node = heapq.heappop(use_queue)\n\t\trequests_handled[using_node] += 1\n\t\theapq.heappush(busy_jobs, (arrvl + ld, using_node))\n\n\tmaxreqs = max(requests_handled)\n\treturn [i for i, handled in enumerate(requests_handled) if handled == maxreqs]\n``` | 90 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python, Two PriorityQueue back and forth O(n log k) | find-servers-that-handled-most-number-of-requests | 0 | 1 | Idea is simple:\n\nUse a priority queue `available` to keep track of the available servers. When a server get a job, remove it from `available` and put it in another PriorityQueue `busy` whose priority is given by the done time. \n\nOn the arrival each job, check if any of the jobs in `busy` are done. If so, put them back in `available` with the **appropriate index**. So when the `i`-th job comes in, `min(available)` is at least `i`, at most `i+k-1`.\n\nNote that the length of `available` and `busy` are at most `k`. So the heaps are not too big and the complexity is O(n log k) -- every job goes in the priority queue `busy` once, goes out at most once, and when it goes out it go into `available` once.\n\nShort annotated version:\n```\nclass Solution:\n def busiestServers(self, k: int, A: List[int], B: List[int]) -> List[int]:\n available = list(range(k)) # already a min-heap\n busy = [] \n res = [0] * k\n for i, a in enumerate(A):\n while busy and busy[0][0] <= a: # these are done, put them back as available\n _, x = heapq.heappop(busy)\n heapq.heappush(available, i + (x-i)%k) # invariant: min(available) is at least i, at most i+k-1\n if available: \n j = heapq.heappop(available) % k\n heapq.heappush(busy, (a+B[i],j))\n res[j] += 1\n a = max(res)\n return [i for i in range(k) if res[i] == a]\n``` | 44 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python, Two PriorityQueue back and forth O(n log k) | find-servers-that-handled-most-number-of-requests | 0 | 1 | Idea is simple:\n\nUse a priority queue `available` to keep track of the available servers. When a server get a job, remove it from `available` and put it in another PriorityQueue `busy` whose priority is given by the done time. \n\nOn the arrival each job, check if any of the jobs in `busy` are done. If so, put them back in `available` with the **appropriate index**. So when the `i`-th job comes in, `min(available)` is at least `i`, at most `i+k-1`.\n\nNote that the length of `available` and `busy` are at most `k`. So the heaps are not too big and the complexity is O(n log k) -- every job goes in the priority queue `busy` once, goes out at most once, and when it goes out it go into `available` once.\n\nShort annotated version:\n```\nclass Solution:\n def busiestServers(self, k: int, A: List[int], B: List[int]) -> List[int]:\n available = list(range(k)) # already a min-heap\n busy = [] \n res = [0] * k\n for i, a in enumerate(A):\n while busy and busy[0][0] <= a: # these are done, put them back as available\n _, x = heapq.heappop(busy)\n heapq.heappush(available, i + (x-i)%k) # invariant: min(available) is at least i, at most i+k-1\n if available: \n j = heapq.heappop(available) % k\n heapq.heappush(busy, (a+B[i],j))\n res[j] += 1\n a = max(res)\n return [i for i in range(k) if res[i] == a]\n``` | 44 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python - super readable solution - SortedList + Heap | find-servers-that-handled-most-number-of-requests | 0 | 1 | #### The basic approach to this question is:\n* iterate arrival and load values\n\t* Identify all available servers\n\t* Find the next available server and increase its handle count\n\t* Mark it is busy\n\n* return all servers that reached the same request handled count\n\n#### The main problem here is find an efficient method to:\n* Know at any time which servers are available and which are busy\n\t* My implementation here is inspired by the question [Meetings Rooms II](https://leetcode.com/problems/meeting-rooms-ii/). We can use a min heap holding the end time of each meeting (busy time in our case) to know which servers are **busy** and when they are going to be **available again**.\n* Find the **correct** next available server\n\t* In order to comply with the defined routing algorithm in the question, I keep a sorted list of the avaiable servers indices.\tThis gives me the ability to do a binary search (O(logk)) in order to find the next available server\n\t\n\n\n\n\n```\nimport heapq\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n # map server to its handle count\n server_busy_count = [0] * k\n \n # init heap\n busy_servers_heap = []\n \n # init available servers sortedlist -> klogk\n available_servers = SortedList([idx for idx in range(k)])\n \n # iterate arrivals\n for req_idx, (curr_arrival, curr_load) in enumerate(zip(arrival, load)):\n # pop all available servers from heap\n while busy_servers_heap and curr_arrival >= busy_servers_heap[0][0]:\n _, server_idx = heapq.heappop(busy_servers_heap)\n \n # add servers to available sorted list\n available_servers.add(server_idx)\n \n # all servers are busy -> drop request\n if not available_servers: continue\n \n # binary search on available list to find the correct available server\n desired_server_idx = req_idx % k\n next_idx = available_servers.bisect_left(desired_server_idx)\n \n # no bigger idx found, use the first available server\n if next_idx == len(available_servers):\n next_idx = 0\n \n # select server by the next_idx calculated\n selected_server = available_servers[next_idx]\n \n # increase selected server handle count\n server_busy_count[selected_server] += 1\n \n # add selected server with end time to the heap\n heapq.heappush(busy_servers_heap, (curr_arrival + curr_load, selected_server))\n \n # pop selected servers from the available list\n available_servers.remove(selected_server)\n \n # return all servers the handled the max request count\n max_busy = max(server_busy_count)\n return [idx for idx in range(k) if server_busy_count[idx] == max_busy] \n```\n\n\n#### Please upvote if you find this solution helpful, so it could help others as well :) | 2 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python - super readable solution - SortedList + Heap | find-servers-that-handled-most-number-of-requests | 0 | 1 | #### The basic approach to this question is:\n* iterate arrival and load values\n\t* Identify all available servers\n\t* Find the next available server and increase its handle count\n\t* Mark it is busy\n\n* return all servers that reached the same request handled count\n\n#### The main problem here is find an efficient method to:\n* Know at any time which servers are available and which are busy\n\t* My implementation here is inspired by the question [Meetings Rooms II](https://leetcode.com/problems/meeting-rooms-ii/). We can use a min heap holding the end time of each meeting (busy time in our case) to know which servers are **busy** and when they are going to be **available again**.\n* Find the **correct** next available server\n\t* In order to comply with the defined routing algorithm in the question, I keep a sorted list of the avaiable servers indices.\tThis gives me the ability to do a binary search (O(logk)) in order to find the next available server\n\t\n\n\n\n\n```\nimport heapq\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n # map server to its handle count\n server_busy_count = [0] * k\n \n # init heap\n busy_servers_heap = []\n \n # init available servers sortedlist -> klogk\n available_servers = SortedList([idx for idx in range(k)])\n \n # iterate arrivals\n for req_idx, (curr_arrival, curr_load) in enumerate(zip(arrival, load)):\n # pop all available servers from heap\n while busy_servers_heap and curr_arrival >= busy_servers_heap[0][0]:\n _, server_idx = heapq.heappop(busy_servers_heap)\n \n # add servers to available sorted list\n available_servers.add(server_idx)\n \n # all servers are busy -> drop request\n if not available_servers: continue\n \n # binary search on available list to find the correct available server\n desired_server_idx = req_idx % k\n next_idx = available_servers.bisect_left(desired_server_idx)\n \n # no bigger idx found, use the first available server\n if next_idx == len(available_servers):\n next_idx = 0\n \n # select server by the next_idx calculated\n selected_server = available_servers[next_idx]\n \n # increase selected server handle count\n server_busy_count[selected_server] += 1\n \n # add selected server with end time to the heap\n heapq.heappush(busy_servers_heap, (curr_arrival + curr_load, selected_server))\n \n # pop selected servers from the available list\n available_servers.remove(selected_server)\n \n # return all servers the handled the max request count\n max_busy = max(server_busy_count)\n return [idx for idx in range(k) if server_busy_count[idx] == max_busy] \n```\n\n\n#### Please upvote if you find this solution helpful, so it could help others as well :) | 2 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
[Python3] summarizing 3 approaches | find-servers-that-handled-most-number-of-requests | 0 | 1 | **Approach 1** - heap only \nI was completely amazed to learn this solution from @warmr0bot in this [post](https://leetcode.com/problems/find-servers-that-handled-most-number-of-requests/discuss/876883/Python-using-only-heaps). Here, the trick is to relocate a freed server to a later place by circularly adjusting its index. In this way, when we are looking server `ii` at position `i` where `ii < i`, we will free `ii` to a place `ii + x*k` where `x` is enough so that `ii+x*k` bearly passes `i`. Mathematically, `i + (ii-i)%k` does the trick. \n\nImplementation \n```\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n busy = [] # min-heap\n free = list(range(k)) # min-heap \n freq = [0]*k\n \n for i, (ta, tl) in enumerate(zip(arrival, load)): \n while busy and busy[0][0] <= ta: \n _, ii = heappop(busy)\n heappush(free, i + (ii - i) % k) # circularly relocate it\n if free: \n ii = heappop(free) % k \n freq[ii] += 1\n heappush(busy, (ta+tl, ii))\n \n mx = max(freq)\n return [i for i, x in enumerate(freq) if x == mx]\n```\n\n**Approach 2** - Fenwick tree\nThis is my original approach, but it is really slow (8000+ms). Here, we use a Fenwick tree to label free servers and use binary search to locate the left-most free servers past a give index `i`. \n\n```\nclass Fenwick: \n\tdef __init__(self, n: int):\n\t\tself.nums = [0]*(n+1)\n\n\tdef sum(self, k: int) -> int: \n\t\t"""Return the sum of nums[:k]."""\n\t\tans = 0\n\t\twhile k:\n\t\t\tans += self.nums[k]\n\t\t\tk -= k & -k # unset last set bit \n\t\treturn ans\n\n\tdef add(self, k: int, x: int) -> None: \n\t\tk += 1\n\t\twhile k < len(self.nums): \n\t\t\tself.nums[k] += x\n\t\t\tk += k & -k \n \n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n freq = [0]*k # counter \n pq = [] # min-heap \n \n fw = Fenwick(k) # count of available servers \n for i in range(k): fw.add(i, 1) \n \n for i, (ta, tl) in enumerate(zip(arrival, load)): \n i %= k \n while pq and pq[0][0] <= ta: \n _, ii = heappop(pq) # release servers \n fw.add(ii, 1)\n \n if fw.sum(k):\n if fw.sum(k) - fw.sum(i): lo, hi, x = i, k, fw.sum(i)\n else: lo, hi, x = 0, i, 0\n \n while lo < hi: \n mid = lo + hi >> 1\n if fw.sum(mid) - x: hi = mid\n else: lo = mid + 1\n fw.add(lo-1, -1)\n freq[lo-1] += 1\n heappush(pq, (ta+tl, lo-1))\n \n mx = max(freq)\n return [i for i, x in enumerate(freq) if x == mx]\n```\n\n**Approach 3** - SortedList\n`SortedList` is an interesting data structure of `sortedcontainers` which is an external library and doesn\'t come with Python by default. I believe the underlying data structure is a balanced bst. \n\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n freq = [0]*k\n busy = [] # min-heap \n free = SortedList(range(k)) # balanced bst\n \n for i, (ta, tl) in enumerate(zip(arrival, load)): \n while busy and busy[0][0] <= ta: \n _, ii = heappop(busy)\n free.add(ii)\n \n if free: \n ii = free.bisect_left(i%k) % len(free)\n server = free.pop(ii)\n freq[server] += 1\n heappush(busy, (ta+tl, server))\n \n mx = max(freq)\n return [i for i, x in enumerate(freq) if x == mx]\n``` | 16 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
[Python3] summarizing 3 approaches | find-servers-that-handled-most-number-of-requests | 0 | 1 | **Approach 1** - heap only \nI was completely amazed to learn this solution from @warmr0bot in this [post](https://leetcode.com/problems/find-servers-that-handled-most-number-of-requests/discuss/876883/Python-using-only-heaps). Here, the trick is to relocate a freed server to a later place by circularly adjusting its index. In this way, when we are looking server `ii` at position `i` where `ii < i`, we will free `ii` to a place `ii + x*k` where `x` is enough so that `ii+x*k` bearly passes `i`. Mathematically, `i + (ii-i)%k` does the trick. \n\nImplementation \n```\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n busy = [] # min-heap\n free = list(range(k)) # min-heap \n freq = [0]*k\n \n for i, (ta, tl) in enumerate(zip(arrival, load)): \n while busy and busy[0][0] <= ta: \n _, ii = heappop(busy)\n heappush(free, i + (ii - i) % k) # circularly relocate it\n if free: \n ii = heappop(free) % k \n freq[ii] += 1\n heappush(busy, (ta+tl, ii))\n \n mx = max(freq)\n return [i for i, x in enumerate(freq) if x == mx]\n```\n\n**Approach 2** - Fenwick tree\nThis is my original approach, but it is really slow (8000+ms). Here, we use a Fenwick tree to label free servers and use binary search to locate the left-most free servers past a give index `i`. \n\n```\nclass Fenwick: \n\tdef __init__(self, n: int):\n\t\tself.nums = [0]*(n+1)\n\n\tdef sum(self, k: int) -> int: \n\t\t"""Return the sum of nums[:k]."""\n\t\tans = 0\n\t\twhile k:\n\t\t\tans += self.nums[k]\n\t\t\tk -= k & -k # unset last set bit \n\t\treturn ans\n\n\tdef add(self, k: int, x: int) -> None: \n\t\tk += 1\n\t\twhile k < len(self.nums): \n\t\t\tself.nums[k] += x\n\t\t\tk += k & -k \n \n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n freq = [0]*k # counter \n pq = [] # min-heap \n \n fw = Fenwick(k) # count of available servers \n for i in range(k): fw.add(i, 1) \n \n for i, (ta, tl) in enumerate(zip(arrival, load)): \n i %= k \n while pq and pq[0][0] <= ta: \n _, ii = heappop(pq) # release servers \n fw.add(ii, 1)\n \n if fw.sum(k):\n if fw.sum(k) - fw.sum(i): lo, hi, x = i, k, fw.sum(i)\n else: lo, hi, x = 0, i, 0\n \n while lo < hi: \n mid = lo + hi >> 1\n if fw.sum(mid) - x: hi = mid\n else: lo = mid + 1\n fw.add(lo-1, -1)\n freq[lo-1] += 1\n heappush(pq, (ta+tl, lo-1))\n \n mx = max(freq)\n return [i for i, x in enumerate(freq) if x == mx]\n```\n\n**Approach 3** - SortedList\n`SortedList` is an interesting data structure of `sortedcontainers` which is an external library and doesn\'t come with Python by default. I believe the underlying data structure is a balanced bst. \n\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n freq = [0]*k\n busy = [] # min-heap \n free = SortedList(range(k)) # balanced bst\n \n for i, (ta, tl) in enumerate(zip(arrival, load)): \n while busy and busy[0][0] <= ta: \n _, ii = heappop(busy)\n free.add(ii)\n \n if free: \n ii = free.bisect_left(i%k) % len(free)\n server = free.pop(ii)\n freq[server] += 1\n heappush(busy, (ta+tl, server))\n \n mx = max(freq)\n return [i for i, x in enumerate(freq) if x == mx]\n``` | 16 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python3 - simulate servers using sorted list and heap | find-servers-that-handled-most-number-of-requests | 0 | 1 | ```\nfrom sortedcontainers import SortedList\nfrom heapq import heappush, heappop\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n processed = [0]*k\n ready = SortedList(list(range(k)))\n processing = [] # (ready time, server number)\n for i, a, l in zip(range(len(arrival)), arrival, load):\n while processing and processing[0][0] <= a:\n _, s = heappop(processing)\n ready.add(s)\n \n if not ready:\n continue\n index = ready.bisect_left(i%k)\n if index == len(ready):\n index = 0\n s = ready[index]\n ready.pop(index)\n processed[s] += 1\n heappush(processing, (a+l, s))\n\n m = max(processed)\n return [i for i in range(k) if processed[i] == m]\n\n``` | 0 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python3 - simulate servers using sorted list and heap | find-servers-that-handled-most-number-of-requests | 0 | 1 | ```\nfrom sortedcontainers import SortedList\nfrom heapq import heappush, heappop\n\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n processed = [0]*k\n ready = SortedList(list(range(k)))\n processing = [] # (ready time, server number)\n for i, a, l in zip(range(len(arrival)), arrival, load):\n while processing and processing[0][0] <= a:\n _, s = heappop(processing)\n ready.add(s)\n \n if not ready:\n continue\n index = ready.bisect_left(i%k)\n if index == len(ready):\n index = 0\n s = ready[index]\n ready.pop(index)\n processed[s] += 1\n heappush(processing, (a+l, s))\n\n m = max(processed)\n return [i for i in range(k) if processed[i] == m]\n\n``` | 0 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Intuitive, straightforward solution with binary search tree in Python with explaination | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem can be solved by using heaps with some tricky properties. The heap solution is good and smart, but less intuitive and not that easy to understand. Fortunately, this problem can also be solved in a very intuitive approach in the same time complexity by using an ordered container. In Python, we can happily employ the powerful `SortedList` or `SortedSet` in this problem. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis straightforward solution maintains a priority queue (i.e., `heapq`) for the requests under processing and a table for the available servers by using `SortedSet`. At each time step, we clean done requests from the queue for freeing servers. Then, we look up the available server for the arrival request. When a server is found, we assign the request to the server, and update the priority queue and the `SortedSet` accordingly. \n\nLike a balanced binary search tree, the operations including adding a server, removing a server, and finding a server can be performed in $$O(\\log k)$$ with `SortedSet`, where $$k$$ is the number of servers. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity is $$O(n \\log k)$$ where $$n$$ is the number of requests and $$k$$ is the number of servers. Note that the complexity of this solution is the same as the heap solution. The heap solution is faster due to its less overhead, but this solution is more straightforward and easy to understand. \n\n# Code\n```\nfrom sortedcontainers import SortedSet\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n requests = []\n servers = SortedSet(range(k))\n counter = defaultdict(int)\n for i, (t, d) in enumerate(zip(arrival, load)):\n while len(requests) and requests[0][0] <= t:\n servers.add(requests[0][1])\n heapq.heappop(requests)\n if len(servers) == 0:\n continue\n p = servers.bisect_left(i % k)\n server = servers[p] if p < len(servers) else servers[0]\n servers.remove(server)\n heapq.heappush(requests, (t+d, server))\n counter[server] += 1\n max_loads = max(counter.values())\n return [s for s, c in counter.items() if c == max_loads]\n``` | 0 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Intuitive, straightforward solution with binary search tree in Python with explaination | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem can be solved by using heaps with some tricky properties. The heap solution is good and smart, but less intuitive and not that easy to understand. Fortunately, this problem can also be solved in a very intuitive approach in the same time complexity by using an ordered container. In Python, we can happily employ the powerful `SortedList` or `SortedSet` in this problem. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis straightforward solution maintains a priority queue (i.e., `heapq`) for the requests under processing and a table for the available servers by using `SortedSet`. At each time step, we clean done requests from the queue for freeing servers. Then, we look up the available server for the arrival request. When a server is found, we assign the request to the server, and update the priority queue and the `SortedSet` accordingly. \n\nLike a balanced binary search tree, the operations including adding a server, removing a server, and finding a server can be performed in $$O(\\log k)$$ with `SortedSet`, where $$k$$ is the number of servers. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity is $$O(n \\log k)$$ where $$n$$ is the number of requests and $$k$$ is the number of servers. Note that the complexity of this solution is the same as the heap solution. The heap solution is faster due to its less overhead, but this solution is more straightforward and easy to understand. \n\n# Code\n```\nfrom sortedcontainers import SortedSet\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n requests = []\n servers = SortedSet(range(k))\n counter = defaultdict(int)\n for i, (t, d) in enumerate(zip(arrival, load)):\n while len(requests) and requests[0][0] <= t:\n servers.add(requests[0][1])\n heapq.heappop(requests)\n if len(servers) == 0:\n continue\n p = servers.bisect_left(i % k)\n server = servers[p] if p < len(servers) else servers[0]\n servers.remove(server)\n heapq.heappush(requests, (t+d, server))\n counter[server] += 1\n max_loads = max(counter.values())\n return [s for s, c in counter.items() if c == max_loads]\n``` | 0 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python3 | binary search tree solution | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing Binary search Tree though it looks big logic is pretty simple for all operations\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BSTNode:\n def __init__(self,val,left=None,right=None):\n self.val = val\n self.leftCount,self.rightCount = 0,0\n self.there = True\n self.left = left\n #self.par = None\n self.right = right\n\nclass Tree:\n def __init__(self,k):\n self.root = self.makingTree(0,k-1)[0]\n\n \n def makingTree(self,i,j):\n if j<i:return None,0\n mid = (i+j)//2\n l,r = self.makingTree(i,mid-1),self.makingTree(mid+1,j)\n root = BSTNode(mid,l[0],r[0])\n root.leftCount = l[1]\n root.rightCount = r[1]\n return root,1+root.leftCount+root.rightCount\n\n def findBetterLeastThan(self,val):\n a = float(\'inf\')\n temp = self.root\n while temp.val!=val:\n if temp.val>val:\n a = min(a,self.findLeast(temp))\n temp = temp.left\n else:temp = temp.right\n a = min(a,self.findLeast(temp))\n return a\n \n def findLeast(self,node):\n ans = float(\'inf\')\n if node.there:return node.val\n temp = node.right\n while temp:\n if temp.there:\n ans = min(ans,temp.val)\n if temp.leftCount:\n temp = temp.left\n elif temp.rightCount:\n temp = temp.right\n else:break\n return ans\n\n def abbaLeast(self):\n ans = float(\'inf\')\n temp = self.root\n while temp:\n if temp.there:\n ans = min(ans,temp.val)\n if temp.leftCount:\n temp = temp.left\n elif temp.rightCount:\n temp = temp.right\n else:break\n return ans\n\n def allotNode(self,val):\n temp = self.root\n while temp.val!=val:\n if temp.val<val:\n temp.rightCount -= 1\n temp = temp.right\n else:\n temp.leftCount -= 1\n temp = temp.left\n temp.there = False\n\n def freeNode(self,val):\n temp = self.root\n while temp.val!=val:\n if temp.val<val:\n temp.rightCount += 1\n temp = temp.right\n else:\n temp.leftCount += 1\n temp = temp.left\n temp.there = True\n\n def getAlloted(self,val):\n a = self.findBetterLeastThan(val)\n if a==float(\'inf\'):\n a = self.abbaLeast()\n if a!=float(\'inf\'):\n self.allotNode(a)\n return a\n return -1\n \n def printTree(self):\n arr = []\n def getThis(root=self.root):\n if not root:return\n getThis(root.left)\n arr.append([root.val,root.there])\n getThis(root.right)\n getThis()\n print(arr)\n \n \nfrom collections import defaultdict\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n freeAt = defaultdict(list)\n count = [0]*k\n arr = set()\n allotments = defaultdict(lambda:-1)\n for i in range(len(arrival)):\n arr.add(arrival[i])\n allotments[arrival[i]] = i\n arr.add(arrival[i]+load[i])\n arr = sorted(list(arr))\n root = Tree(k)\n for i in arr:\n for node in freeAt[i]:\n root.freeNode(node)\n if allotments[i]+1:\n comp = root.getAlloted(allotments[i]%k)\n #print(allotments[i],allotments[i]%k,i,arrival[allotments[i]]+load[allotments[i]],comp)\n #if i==94:root.printTree()\n if comp+1:\n count[comp]+=1\n freeAt[arrival[allotments[i]]+load[allotments[i]]].append(comp)\n go = max(count)\n ans = []\n #print(arr)\n for i in range(len(count)):\n if count[i]==go:ans.append(i)\n #print(count)\n return ans\n\n\n \n``` | 0 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python3 | binary search tree solution | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing Binary search Tree though it looks big logic is pretty simple for all operations\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BSTNode:\n def __init__(self,val,left=None,right=None):\n self.val = val\n self.leftCount,self.rightCount = 0,0\n self.there = True\n self.left = left\n #self.par = None\n self.right = right\n\nclass Tree:\n def __init__(self,k):\n self.root = self.makingTree(0,k-1)[0]\n\n \n def makingTree(self,i,j):\n if j<i:return None,0\n mid = (i+j)//2\n l,r = self.makingTree(i,mid-1),self.makingTree(mid+1,j)\n root = BSTNode(mid,l[0],r[0])\n root.leftCount = l[1]\n root.rightCount = r[1]\n return root,1+root.leftCount+root.rightCount\n\n def findBetterLeastThan(self,val):\n a = float(\'inf\')\n temp = self.root\n while temp.val!=val:\n if temp.val>val:\n a = min(a,self.findLeast(temp))\n temp = temp.left\n else:temp = temp.right\n a = min(a,self.findLeast(temp))\n return a\n \n def findLeast(self,node):\n ans = float(\'inf\')\n if node.there:return node.val\n temp = node.right\n while temp:\n if temp.there:\n ans = min(ans,temp.val)\n if temp.leftCount:\n temp = temp.left\n elif temp.rightCount:\n temp = temp.right\n else:break\n return ans\n\n def abbaLeast(self):\n ans = float(\'inf\')\n temp = self.root\n while temp:\n if temp.there:\n ans = min(ans,temp.val)\n if temp.leftCount:\n temp = temp.left\n elif temp.rightCount:\n temp = temp.right\n else:break\n return ans\n\n def allotNode(self,val):\n temp = self.root\n while temp.val!=val:\n if temp.val<val:\n temp.rightCount -= 1\n temp = temp.right\n else:\n temp.leftCount -= 1\n temp = temp.left\n temp.there = False\n\n def freeNode(self,val):\n temp = self.root\n while temp.val!=val:\n if temp.val<val:\n temp.rightCount += 1\n temp = temp.right\n else:\n temp.leftCount += 1\n temp = temp.left\n temp.there = True\n\n def getAlloted(self,val):\n a = self.findBetterLeastThan(val)\n if a==float(\'inf\'):\n a = self.abbaLeast()\n if a!=float(\'inf\'):\n self.allotNode(a)\n return a\n return -1\n \n def printTree(self):\n arr = []\n def getThis(root=self.root):\n if not root:return\n getThis(root.left)\n arr.append([root.val,root.there])\n getThis(root.right)\n getThis()\n print(arr)\n \n \nfrom collections import defaultdict\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n freeAt = defaultdict(list)\n count = [0]*k\n arr = set()\n allotments = defaultdict(lambda:-1)\n for i in range(len(arrival)):\n arr.add(arrival[i])\n allotments[arrival[i]] = i\n arr.add(arrival[i]+load[i])\n arr = sorted(list(arr))\n root = Tree(k)\n for i in arr:\n for node in freeAt[i]:\n root.freeNode(node)\n if allotments[i]+1:\n comp = root.getAlloted(allotments[i]%k)\n #print(allotments[i],allotments[i]%k,i,arrival[allotments[i]]+load[allotments[i]],comp)\n #if i==94:root.printTree()\n if comp+1:\n count[comp]+=1\n freeAt[arrival[allotments[i]]+load[allotments[i]]].append(comp)\n go = max(count)\n ans = []\n #print(arr)\n for i in range(len(count)):\n if count[i]==go:ans.append(i)\n #print(count)\n return ans\n\n\n \n``` | 0 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python (Simple Heap) | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def busiestServers(self, k, arrival, load):\n available, busy, dict1 = [i for i in range(k)], [], collections.defaultdict(int)\n\n for i,start in enumerate(arrival):\n while busy and busy[0][0] <= start:\n heapq.heappush(available,i + (heapq.heappop(busy)[1] - i)%k)\n\n if available:\n j = heapq.heappop(available)%k\n dict1[j] += 1\n heapq.heappush(busy,(start+load[i],j))\n\n max_val = max(dict1.values())\n\n return [key for key,val in dict1.items() if val == max_val]\n\n\n\n \n\n\n\n\n\n\n\n``` | 0 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python (Simple Heap) | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def busiestServers(self, k, arrival, load):\n available, busy, dict1 = [i for i in range(k)], [], collections.defaultdict(int)\n\n for i,start in enumerate(arrival):\n while busy and busy[0][0] <= start:\n heapq.heappush(available,i + (heapq.heappop(busy)[1] - i)%k)\n\n if available:\n j = heapq.heappop(available)%k\n dict1[j] += 1\n heapq.heappush(busy,(start+load[i],j))\n\n max_val = max(dict1.values())\n\n return [key for key,val in dict1.items() if val == max_val]\n\n\n\n \n\n\n\n\n\n\n\n``` | 0 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Python3 | Two Heap Solution | Explained and Commented | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to prioritize our useage of the servers in a set range. This is similar to modular arithmetic, so we should look for a priority queue solution that can use a modular approach, like a circular priority queue. In this case, we arrive at the solution through comparison of the server ids, which are in order of the ith server to be processed at any given point in time. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up a list of servers currently available, called servers. \nSet up an empty list of servers processing. \nSet up a number of tasks by server of size k and value 0 to start. \nLoop over the indices of your arrival index \n- As you do, get the arrival time and the load size for the current arrival\n- While you have servers processing, and the servers that are processing have a finish time before the current arrival time \n - Get the prior_task and server_id by popping off from the servers_processing \n - Push into the servers heap this server by its identification key at this point in the circular priority queue of servers with key value of arrival_index + (server_id - arrival_index) % k. See comments for details. \n- Then, if you have servers avaialble \n - Pop out the most recent to complete one in ith order by using a heappop from servers and taking modulo of k for the value. This is needed to turn the arrival_index + (server_id - arrival_index) % k back into the correct server_id. For completeness, see example after time complexity. \n - Increment the number of tasks by server at this server by 1 \n - Push this ((arrival_time + load_size), server) back into servers processing \n\nAt end, get your highest productivity (number of tasks cleared by a server) \nUse list comprehension to build the list of server for server in your range of servers if number of tasks by server at server is equal to highest productivity (as requested by problem) \n\n# Complexity\n- Time complexity: We need to process N arrivals \n- During each arrival, we might process up to the ith arrival in a pop push fashion, necessitating an amount of work at most equal to N log N (where we go until the last prossible process before popping everything off of the servers processing before pushing them back into the arrivals) \n- During each arrival, we may also do a 2 log N amount of work for popping from the servers and pushing to the servers processing. \n- This gives an overall runtime of N log N. \n\n- Space complexity: At worst, we will store the entire space in the processing of this at least twice (Once for the heaps, and once for the return list if eveyrone processed only one item). So, we have O(N) space. \n\nExample for completeness \nConsider the test case below \nk = 3 \nArrivals = [1,2,3,4,8,9,10]\nLoads = [5,2,10,3,1,2,2]\n\nAt arrival index 0, we have arrival time 1 and load size five\nWe\'ll end up popping server 0 and incrementing tasks at 0 \nThis leaves us at end of arrival index 0 in state of \nServers -> [1, 2]\nNumber_of_tasks_per_server = [1, 0, 0]\nprocessing_servers -> [(6, 0)]\n\nAt arrival index 1, we have arrival time 2 and load size 2 \nWe\'ll end up popping server 1 and incrementing tasks at 1 \nThis leaves us at end of arrival index 1 in state of \nServers -> [2]\nNumber_of_tasks_per_server = [1, 1, 0]\nprocessing_servers = [(4, 1), (6, 0)]\n\nAt arrival index 2, we have arrival time of 3 and load size of 10 \nWe\'ll end up popping server 2 and incrementing tasks at 2 \nThis leaves uas at end of arrival index 2 in state of \nServers -> []\nNumber_of_tasks_per_server -> [1, 1, 1]\nprocessing_servers = [(4, 1), (6, 0), (13, 2)]\n\nAt arrival index 3, we have arrival time of 4 and load size of 3\nWe now have a servers_processing[0][0] that is <= arrival time\nSo, we pop from processing servers to get \n- prior_task, server_id = 4, 1\n- arrival_index = 3 \n- 3 + (1 - 3) mod 3 = 4 \n- servers -> [4]\nWe now will pop server 4, however! we will do mod k on it (as we did on the others) and get a result of 1 (the server we started with!)\nWe increment server 1 then and push in a node of (7, 1)\nWe end arrival index 3 with \nServers -> []\nNumber_of_tasks_per_server = [1, 2, 1]\nProcessing_servers = [(6, 0), (7, 1), (13, 2)]\n\nThe rest are left as an exercise but hopefully this has helped you get the process so you can check the rest. If not, please post in the comments about what can be made more clear and I\'ll do my best. \n\n# Code\n```\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n # heap of servers currently available \n servers = list(range(k))\n # heap of servers currently processing \n servers_processing = []\n # number of tasks at this server over time \n number_of_tasks_by_server = [0]*k\n\n # for each arrival in arrival\n for arrival_index in range(len(arrival)) : \n # get the arrival time and load size \n arrival_time = arrival[arrival_index]\n load_size = load[arrival_index]\n # while you have servers that were processing and have now finished \n while servers_processing and servers_processing[0][0] <= arrival_time : \n # finish those tasks you have completed \n prior_task, server_id = heapq.heappop(servers_processing)\n # print("Prior task at ", server_id, " now completed.")\n # push back into servers the current server_id at it\'s heap key \n # the heap key is determined as arrival_index + (server_id - arrival_index) % k \n # this is because we are in a limited space (go to ith server until k, then loop back)\n # so, server_id + m*k = i + x \n # where we have x going from 0 up to but not including k and i as some time quality \n # we then take modular of k of both sides \n # server_id % k + 0 (as m*k%k == 0) = i % k + x (as c % k == c iff c in [0, k)) \n # x = server_id % k - i % k \n # we then simplify by joining similar modulo\'s \n # x = (server_id - i) % k \n # With x equal to this, if we use i as arrival index and go back to line 23 \n # we get server_id + mk = arrival_index + (server_id - arrival_index) % k \n # This means we can use arrival_index + (server_id - arrival_index) % k as our heap key \n # and that in doing so, it will map to a specific server id \n heapq.heappush(servers, arrival_index + (server_id - arrival_index)%k)\n # if you have servers available \n if servers : \n # get the next server by using heapq.heappop and keeping within k \n server = heapq.heappop(servers)%k\n # at this server, up the tasks by one \n number_of_tasks_by_server[server] += 1 \n # push this server into our servers processing with finish time of arrival_time plus load_size\n heapq.heappush(servers_processing, ((arrival_time+load_size), server))\n # else : \n # print("No servers available, dropping task ", arrival_index, " of size ", load_size)\n\n highest_productivity = max(number_of_tasks_by_server)\n return [server for server in range(k) if number_of_tasks_by_server[server]==highest_productivity]\n``` | 0 | You have `k` servers numbered from `0` to `k-1` that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but **cannot handle more than one request at a time**. The requests are assigned to servers according to a specific algorithm:
* The `ith` (0-indexed) request arrives.
* If all servers are busy, the request is dropped (not handled at all).
* If the `(i % k)th` server is available, assign the request to that server.
* Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the `ith` server is busy, try to assign the request to the `(i+1)th` server, then the `(i+2)th` server, and so on.
You are given a **strictly increasing** array `arrival` of positive integers, where `arrival[i]` represents the arrival time of the `ith` request, and another array `load`, where `load[i]` represents the load of the `ith` request (the time it takes to complete). Your goal is to find the **busiest server(s)**. A server is considered **busiest** if it handled the most number of requests successfully among all the servers.
Return _a list containing the IDs (0-indexed) of the **busiest server(s)**_. You may return the IDs in any order.
**Example 1:**
**Input:** k = 3, arrival = \[1,2,3,4,5\], load = \[5,2,3,3,3\]
**Output:** \[1\]
**Explanation:**
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
**Example 2:**
**Input:** k = 3, arrival = \[1,2,3,4\], load = \[1,2,1,2\]
**Output:** \[0\]
**Explanation:**
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
**Example 3:**
**Input:** k = 3, arrival = \[1,2,3\], load = \[10,12,11\]
**Output:** \[0,1,2\]
**Explanation:** Each server handles a single request, so they are all considered the busiest.
**Constraints:**
* `1 <= k <= 105`
* `1 <= arrival.length, load.length <= 105`
* `arrival.length == load.length`
* `1 <= arrival[i], load[i] <= 109`
* `arrival` is **strictly increasing**. | null |
Python3 | Two Heap Solution | Explained and Commented | find-servers-that-handled-most-number-of-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to prioritize our useage of the servers in a set range. This is similar to modular arithmetic, so we should look for a priority queue solution that can use a modular approach, like a circular priority queue. In this case, we arrive at the solution through comparison of the server ids, which are in order of the ith server to be processed at any given point in time. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up a list of servers currently available, called servers. \nSet up an empty list of servers processing. \nSet up a number of tasks by server of size k and value 0 to start. \nLoop over the indices of your arrival index \n- As you do, get the arrival time and the load size for the current arrival\n- While you have servers processing, and the servers that are processing have a finish time before the current arrival time \n - Get the prior_task and server_id by popping off from the servers_processing \n - Push into the servers heap this server by its identification key at this point in the circular priority queue of servers with key value of arrival_index + (server_id - arrival_index) % k. See comments for details. \n- Then, if you have servers avaialble \n - Pop out the most recent to complete one in ith order by using a heappop from servers and taking modulo of k for the value. This is needed to turn the arrival_index + (server_id - arrival_index) % k back into the correct server_id. For completeness, see example after time complexity. \n - Increment the number of tasks by server at this server by 1 \n - Push this ((arrival_time + load_size), server) back into servers processing \n\nAt end, get your highest productivity (number of tasks cleared by a server) \nUse list comprehension to build the list of server for server in your range of servers if number of tasks by server at server is equal to highest productivity (as requested by problem) \n\n# Complexity\n- Time complexity: We need to process N arrivals \n- During each arrival, we might process up to the ith arrival in a pop push fashion, necessitating an amount of work at most equal to N log N (where we go until the last prossible process before popping everything off of the servers processing before pushing them back into the arrivals) \n- During each arrival, we may also do a 2 log N amount of work for popping from the servers and pushing to the servers processing. \n- This gives an overall runtime of N log N. \n\n- Space complexity: At worst, we will store the entire space in the processing of this at least twice (Once for the heaps, and once for the return list if eveyrone processed only one item). So, we have O(N) space. \n\nExample for completeness \nConsider the test case below \nk = 3 \nArrivals = [1,2,3,4,8,9,10]\nLoads = [5,2,10,3,1,2,2]\n\nAt arrival index 0, we have arrival time 1 and load size five\nWe\'ll end up popping server 0 and incrementing tasks at 0 \nThis leaves us at end of arrival index 0 in state of \nServers -> [1, 2]\nNumber_of_tasks_per_server = [1, 0, 0]\nprocessing_servers -> [(6, 0)]\n\nAt arrival index 1, we have arrival time 2 and load size 2 \nWe\'ll end up popping server 1 and incrementing tasks at 1 \nThis leaves us at end of arrival index 1 in state of \nServers -> [2]\nNumber_of_tasks_per_server = [1, 1, 0]\nprocessing_servers = [(4, 1), (6, 0)]\n\nAt arrival index 2, we have arrival time of 3 and load size of 10 \nWe\'ll end up popping server 2 and incrementing tasks at 2 \nThis leaves uas at end of arrival index 2 in state of \nServers -> []\nNumber_of_tasks_per_server -> [1, 1, 1]\nprocessing_servers = [(4, 1), (6, 0), (13, 2)]\n\nAt arrival index 3, we have arrival time of 4 and load size of 3\nWe now have a servers_processing[0][0] that is <= arrival time\nSo, we pop from processing servers to get \n- prior_task, server_id = 4, 1\n- arrival_index = 3 \n- 3 + (1 - 3) mod 3 = 4 \n- servers -> [4]\nWe now will pop server 4, however! we will do mod k on it (as we did on the others) and get a result of 1 (the server we started with!)\nWe increment server 1 then and push in a node of (7, 1)\nWe end arrival index 3 with \nServers -> []\nNumber_of_tasks_per_server = [1, 2, 1]\nProcessing_servers = [(6, 0), (7, 1), (13, 2)]\n\nThe rest are left as an exercise but hopefully this has helped you get the process so you can check the rest. If not, please post in the comments about what can be made more clear and I\'ll do my best. \n\n# Code\n```\nclass Solution:\n def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:\n # heap of servers currently available \n servers = list(range(k))\n # heap of servers currently processing \n servers_processing = []\n # number of tasks at this server over time \n number_of_tasks_by_server = [0]*k\n\n # for each arrival in arrival\n for arrival_index in range(len(arrival)) : \n # get the arrival time and load size \n arrival_time = arrival[arrival_index]\n load_size = load[arrival_index]\n # while you have servers that were processing and have now finished \n while servers_processing and servers_processing[0][0] <= arrival_time : \n # finish those tasks you have completed \n prior_task, server_id = heapq.heappop(servers_processing)\n # print("Prior task at ", server_id, " now completed.")\n # push back into servers the current server_id at it\'s heap key \n # the heap key is determined as arrival_index + (server_id - arrival_index) % k \n # this is because we are in a limited space (go to ith server until k, then loop back)\n # so, server_id + m*k = i + x \n # where we have x going from 0 up to but not including k and i as some time quality \n # we then take modular of k of both sides \n # server_id % k + 0 (as m*k%k == 0) = i % k + x (as c % k == c iff c in [0, k)) \n # x = server_id % k - i % k \n # we then simplify by joining similar modulo\'s \n # x = (server_id - i) % k \n # With x equal to this, if we use i as arrival index and go back to line 23 \n # we get server_id + mk = arrival_index + (server_id - arrival_index) % k \n # This means we can use arrival_index + (server_id - arrival_index) % k as our heap key \n # and that in doing so, it will map to a specific server id \n heapq.heappush(servers, arrival_index + (server_id - arrival_index)%k)\n # if you have servers available \n if servers : \n # get the next server by using heapq.heappop and keeping within k \n server = heapq.heappop(servers)%k\n # at this server, up the tasks by one \n number_of_tasks_by_server[server] += 1 \n # push this server into our servers processing with finish time of arrival_time plus load_size\n heapq.heappush(servers_processing, ((arrival_time+load_size), server))\n # else : \n # print("No servers available, dropping task ", arrival_index, " of size ", load_size)\n\n highest_productivity = max(number_of_tasks_by_server)\n return [server for server in range(k) if number_of_tasks_by_server[server]==highest_productivity]\n``` | 0 | You are assigned to put some amount of boxes onto **one truck**. You are given a 2D array `boxTypes`, where `boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi]`:
* `numberOfBoxesi` is the number of boxes of type `i`.
* `numberOfUnitsPerBoxi` is the number of units in each box of the type `i`.
You are also given an integer `truckSize`, which is the **maximum** number of **boxes** that can be put on the truck. You can choose any boxes to put on the truck as long as the number of boxes does not exceed `truckSize`.
Return _the **maximum** total number of **units** that can be put on the truck._
**Example 1:**
**Input:** boxTypes = \[\[1,3\],\[2,2\],\[3,1\]\], truckSize = 4
**Output:** 8
**Explanation:** There are:
- 1 box of the first type that contains 3 units.
- 2 boxes of the second type that contain 2 units each.
- 3 boxes of the third type that contain 1 unit each.
You can take all the boxes of the first and second types, and one box of the third type.
The total number of units will be = (1 \* 3) + (2 \* 2) + (1 \* 1) = 8.
**Example 2:**
**Input:** boxTypes = \[\[5,10\],\[2,5\],\[4,7\],\[3,9\]\], truckSize = 10
**Output:** 91
**Constraints:**
* `1 <= boxTypes.length <= 1000`
* `1 <= numberOfBoxesi, numberOfUnitsPerBoxi <= 1000`
* `1 <= truckSize <= 106` | To speed up the next available server search, keep track of the available servers in a sorted structure such as an ordered set. To determine if a server is available, keep track of the end times for each task in a heap and add the server to the available set once the soonest task ending time is less than or equal to the next task to add. |
Easiest solution in python. | special-array-with-x-elements-greater-than-or-equal-x | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def specialArray(self, nums: List[int]) -> int:\n nums.sort()\n for i in range(max(nums)+1):\n y=len(nums)-bisect.bisect_left(nums,i)\n if y==i:\n return i\n return -1\n\n \n \n``` | 2 | You are given an array `nums` of non-negative integers. `nums` is considered **special** if there exists a number `x` such that there are **exactly** `x` numbers in `nums` that are **greater than or equal to** `x`.
Notice that `x` **does not** have to be an element in `nums`.
Return `x` _if the array is **special**, otherwise, return_ `-1`. It can be proven that if `nums` is special, the value for `x` is **unique**.
**Example 1:**
**Input:** nums = \[3,5\]
**Output:** 2
**Explanation:** There are 2 values (3 and 5) that are greater than or equal to 2.
**Example 2:**
**Input:** nums = \[0,0\]
**Output:** -1
**Explanation:** No numbers fit the criteria for x.
If x = 0, there should be 0 numbers >= x, but there are 2.
If x = 1, there should be 1 number >= x, but there are 0.
If x = 2, there should be 2 numbers >= x, but there are 0.
x cannot be greater since there are only 2 numbers in nums.
**Example 3:**
**Input:** nums = \[0,4,3,0,4\]
**Output:** 3
**Explanation:** There are 3 values that are greater than or equal to 3.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | null |
Easiest solution in python. | special-array-with-x-elements-greater-than-or-equal-x | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def specialArray(self, nums: List[int]) -> int:\n nums.sort()\n for i in range(max(nums)+1):\n y=len(nums)-bisect.bisect_left(nums,i)\n if y==i:\n return i\n return -1\n\n \n \n``` | 2 | You are starving and you want to eat food as quickly as possible. You want to find the shortest path to arrive at any food cell.
You are given an `m x n` character matrix, `grid`, of these different types of cells:
* `'*'` is your location. There is **exactly one** `'*'` cell.
* `'#'` is a food cell. There may be **multiple** food cells.
* `'O'` is free space, and you can travel through these cells.
* `'X'` is an obstacle, and you cannot travel through these cells.
You can travel to any adjacent cell north, east, south, or west of your current location if there is not an obstacle.
Return _the **length** of the shortest path for you to reach **any** food cell_. If there is no path for you to reach food, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "O ", "O ", "O ", "X "\],\[ "X ", "O ", "O ", "# ", "O ", "X "\],\[ "X ", "X ", "X ", "X ", "X ", "X "\]\]
**Output:** 3
**Explanation:** It takes 3 steps to reach the food.
**Example 2:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "# ", "X "\],\[ "X ", "X ", "X ", "X ", "X "\]\]
**Output:** -1
**Explanation:** It is not possible to reach the food.
**Example 3:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "O ", "X ", "O ", "# ", "O ", "X "\],\[ "X ", "O ", "O ", "X ", "O ", "O ", "X ", "X "\],\[ "X ", "O ", "O ", "O ", "O ", "# ", "O ", "X "\],\[ "X ", "X ", "X ", "X ", "X ", "X ", "X ", "X "\]\]
**Output:** 6
**Explanation:** There can be multiple food cells. It only takes 6 steps to reach the bottom food.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[row][col]` is `'*'`, `'X'`, `'O'`, or `'#'`.
* The `grid` contains **exactly one** `'*'`. | Count the number of elements greater than or equal to x for each x in the range [0, nums.length]. If for any x, the condition satisfies, return that x. Otherwise, there is no answer. |
Python Brute Force 62.06% Faster | special-array-with-x-elements-greater-than-or-equal-x | 0 | 1 | ```\nclass Solution:\n def specialArray(self, nums: List[int]) -> int:\n c=0\n for i in range(1,1001):\n c=0\n for j in nums:\n if i<=j:\n c+=1\n if i==c:\n return i\n \n return -1\n``` | 1 | You are given an array `nums` of non-negative integers. `nums` is considered **special** if there exists a number `x` such that there are **exactly** `x` numbers in `nums` that are **greater than or equal to** `x`.
Notice that `x` **does not** have to be an element in `nums`.
Return `x` _if the array is **special**, otherwise, return_ `-1`. It can be proven that if `nums` is special, the value for `x` is **unique**.
**Example 1:**
**Input:** nums = \[3,5\]
**Output:** 2
**Explanation:** There are 2 values (3 and 5) that are greater than or equal to 2.
**Example 2:**
**Input:** nums = \[0,0\]
**Output:** -1
**Explanation:** No numbers fit the criteria for x.
If x = 0, there should be 0 numbers >= x, but there are 2.
If x = 1, there should be 1 number >= x, but there are 0.
If x = 2, there should be 2 numbers >= x, but there are 0.
x cannot be greater since there are only 2 numbers in nums.
**Example 3:**
**Input:** nums = \[0,4,3,0,4\]
**Output:** 3
**Explanation:** There are 3 values that are greater than or equal to 3.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | null |
Python Brute Force 62.06% Faster | special-array-with-x-elements-greater-than-or-equal-x | 0 | 1 | ```\nclass Solution:\n def specialArray(self, nums: List[int]) -> int:\n c=0\n for i in range(1,1001):\n c=0\n for j in nums:\n if i<=j:\n c+=1\n if i==c:\n return i\n \n return -1\n``` | 1 | You are starving and you want to eat food as quickly as possible. You want to find the shortest path to arrive at any food cell.
You are given an `m x n` character matrix, `grid`, of these different types of cells:
* `'*'` is your location. There is **exactly one** `'*'` cell.
* `'#'` is a food cell. There may be **multiple** food cells.
* `'O'` is free space, and you can travel through these cells.
* `'X'` is an obstacle, and you cannot travel through these cells.
You can travel to any adjacent cell north, east, south, or west of your current location if there is not an obstacle.
Return _the **length** of the shortest path for you to reach **any** food cell_. If there is no path for you to reach food, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "O ", "O ", "O ", "X "\],\[ "X ", "O ", "O ", "# ", "O ", "X "\],\[ "X ", "X ", "X ", "X ", "X ", "X "\]\]
**Output:** 3
**Explanation:** It takes 3 steps to reach the food.
**Example 2:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "# ", "X "\],\[ "X ", "X ", "X ", "X ", "X "\]\]
**Output:** -1
**Explanation:** It is not possible to reach the food.
**Example 3:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "O ", "X ", "O ", "# ", "O ", "X "\],\[ "X ", "O ", "O ", "X ", "O ", "O ", "X ", "X "\],\[ "X ", "O ", "O ", "O ", "O ", "# ", "O ", "X "\],\[ "X ", "X ", "X ", "X ", "X ", "X ", "X ", "X "\]\]
**Output:** 6
**Explanation:** There can be multiple food cells. It only takes 6 steps to reach the bottom food.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[row][col]` is `'*'`, `'X'`, `'O'`, or `'#'`.
* The `grid` contains **exactly one** `'*'`. | Count the number of elements greater than or equal to x for each x in the range [0, nums.length]. If for any x, the condition satisfies, return that x. Otherwise, there is no answer. |
Basic binary search with two pointers | special-array-with-x-elements-greater-than-or-equal-x | 0 | 1 | \n# Code\n```\nclass Solution:\n def specialArray(self, nums: List[int]) -> int:\n n = len(nums)\n l, r = 0, n\n while(l<=r):\n mid = (l+r)//2\n count = 0 \n for i in nums:\n if(i>=mid):\n count +=1\n\n if (count == mid): return mid\n elif count > mid:\n l = mid + 1\n else : \n r = mid - 1\n\n return -1 \n\n\n\n\n``` | 1 | You are given an array `nums` of non-negative integers. `nums` is considered **special** if there exists a number `x` such that there are **exactly** `x` numbers in `nums` that are **greater than or equal to** `x`.
Notice that `x` **does not** have to be an element in `nums`.
Return `x` _if the array is **special**, otherwise, return_ `-1`. It can be proven that if `nums` is special, the value for `x` is **unique**.
**Example 1:**
**Input:** nums = \[3,5\]
**Output:** 2
**Explanation:** There are 2 values (3 and 5) that are greater than or equal to 2.
**Example 2:**
**Input:** nums = \[0,0\]
**Output:** -1
**Explanation:** No numbers fit the criteria for x.
If x = 0, there should be 0 numbers >= x, but there are 2.
If x = 1, there should be 1 number >= x, but there are 0.
If x = 2, there should be 2 numbers >= x, but there are 0.
x cannot be greater since there are only 2 numbers in nums.
**Example 3:**
**Input:** nums = \[0,4,3,0,4\]
**Output:** 3
**Explanation:** There are 3 values that are greater than or equal to 3.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 1000` | null |
Basic binary search with two pointers | special-array-with-x-elements-greater-than-or-equal-x | 0 | 1 | \n# Code\n```\nclass Solution:\n def specialArray(self, nums: List[int]) -> int:\n n = len(nums)\n l, r = 0, n\n while(l<=r):\n mid = (l+r)//2\n count = 0 \n for i in nums:\n if(i>=mid):\n count +=1\n\n if (count == mid): return mid\n elif count > mid:\n l = mid + 1\n else : \n r = mid - 1\n\n return -1 \n\n\n\n\n``` | 1 | You are starving and you want to eat food as quickly as possible. You want to find the shortest path to arrive at any food cell.
You are given an `m x n` character matrix, `grid`, of these different types of cells:
* `'*'` is your location. There is **exactly one** `'*'` cell.
* `'#'` is a food cell. There may be **multiple** food cells.
* `'O'` is free space, and you can travel through these cells.
* `'X'` is an obstacle, and you cannot travel through these cells.
You can travel to any adjacent cell north, east, south, or west of your current location if there is not an obstacle.
Return _the **length** of the shortest path for you to reach **any** food cell_. If there is no path for you to reach food, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "O ", "O ", "O ", "X "\],\[ "X ", "O ", "O ", "# ", "O ", "X "\],\[ "X ", "X ", "X ", "X ", "X ", "X "\]\]
**Output:** 3
**Explanation:** It takes 3 steps to reach the food.
**Example 2:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "X ", "O ", "X "\],\[ "X ", "O ", "X ", "# ", "X "\],\[ "X ", "X ", "X ", "X ", "X "\]\]
**Output:** -1
**Explanation:** It is not possible to reach the food.
**Example 3:**
**Input:** grid = \[\[ "X ", "X ", "X ", "X ", "X ", "X ", "X ", "X "\],\[ "X ", "\* ", "O ", "X ", "O ", "# ", "O ", "X "\],\[ "X ", "O ", "O ", "X ", "O ", "O ", "X ", "X "\],\[ "X ", "O ", "O ", "O ", "O ", "# ", "O ", "X "\],\[ "X ", "X ", "X ", "X ", "X ", "X ", "X ", "X "\]\]
**Output:** 6
**Explanation:** There can be multiple food cells. It only takes 6 steps to reach the bottom food.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[row][col]` is `'*'`, `'X'`, `'O'`, or `'#'`.
* The `grid` contains **exactly one** `'*'`. | Count the number of elements greater than or equal to x for each x in the range [0, nums.length]. If for any x, the condition satisfies, return that x. Otherwise, there is no answer. |
🐍🏋️♂️ The GigaChad Pythonista's Solution 🏋️♂️ Bitwise Blast! 💥 Explanation 🚀 | even-odd-tree | 0 | 1 | # Intuition\n> "Always determine evenness using bitwise operations." - Jason Statham.\n\nBitwise operations are often overlooked, but they can offer neat solutions to certain problems. In our case, we\'re dealing with binary trees and odd/even numbers, which makes it a perfect fit for bit manipulation. Let\'s briefly dive into the two bitwise operations we use:\n\n1. `x & 1`: This operation checks the least significant bit of a number. If it\'s 1, the number is odd; if it\'s 0, the number is even. Essentially, it\'s a way to check if a number is odd or even.\n2. `x ^= 1`: This operation flips the least significant bit of a number. If it\'s 1, it becomes 0, and vice versa. Basically, it\'s a way to switch between 0 and 1.\n\nNow that we\'re armed with these handy bit operations, let\'s use them to solve the problem at hand. The idea is to interpret each level of the binary tree as a binary level, where 1 represents odd, and 0 represents even. This way, we can verify if the binary tree follows the rules by simply traversing it level by level.\n\n# Approach\nWe start with the root level as an odd level (`bit_level = 1`). We use a stack to store the nodes at each level in left to right order.\n\n1. We traverse each level node by node. We use `stack[i]` to access each node as we loop through the stack. First, we check if the node value\'s parity matches the level\'s parity using the bit operation `stack[i].val & 1 != bit_level`. The `!=` operator is used here because the parity of the level and the node values should be different; odd levels should have odd values and even levels should have even values.\n2. Then, we check whether the node values at the level follow the correct order (strictly increasing for odd levels and strictly decreasing for even levels). We use the following check:\n```python\nstack[i].val > stack[i+1].val == bool(bit_level) or stack[i].val == stack[i+1].val\n```\nThis checks if the order of values is correct, and if there are any equal values, which are not allowed.\n3. We toggle the `bit_level` using `bit_level ^= 1` for the next level. This operation flips the bit of `bit_level`, switching between 1 and 0 for subsequent levels.\n4. Finally, if all checks pass, we return `True`.\n\n# Complexity\n- Time complexity: O(n), where n is the number of nodes in the tree. Each node is visited exactly once.\n- Space complexity: O(n), where n is the number of nodes in the tree. In the worst case, all nodes could end up in the stack.\n\n____\n\nThis solution is more for fun and to practice bitwise manipulation. It may not be necessary for this problem, but bitwise manipulation can be a powerful tool in various situations. So, take this as an opportunity to revisit and refresh your bitwise operation skills! \uD83D\uDE04\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:\n bit_level = 1\n stack = [root] if root else []\n\n while stack:\n for i in range(len(stack)):\n if stack[i].val & 1 != bit_level: \n return False\n if i < len(stack) - 1 and ((stack[i].val > stack[i+1].val) == bool(bit_level) or stack[i].val == stack[i+1].val):\n return False\n bit_level ^= 1\n stack = [node for n in stack for node in (n.left, n.right) if node]\n\n return True\n \n``` | 8 | A binary tree is named **Even-Odd** if it meets the following conditions:
* The root of the binary tree is at level index `0`, its children are at level index `1`, their children are at level index `2`, etc.
* For every **even-indexed** level, all nodes at the level have **odd** integer values in **strictly increasing** order (from left to right).
* For every **odd-indexed** level, all nodes at the level have **even** integer values in **strictly decreasing** order (from left to right).
Given the `root` of a binary tree, _return_ `true` _if the binary tree is **Even-Odd**, otherwise return_ `false`_._
**Example 1:**
**Input:** root = \[1,10,4,3,null,7,9,12,8,6,null,null,2\]
**Output:** true
**Explanation:** The node values on each level are:
Level 0: \[1\]
Level 1: \[10,4\]
Level 2: \[3,7,9\]
Level 3: \[12,8,6,2\]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
**Example 2:**
**Input:** root = \[5,4,2,3,3,7\]
**Output:** false
**Explanation:** The node values on each level are:
Level 0: \[5\]
Level 1: \[4,2\]
Level 2: \[3,3,7\]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
**Example 3:**
**Input:** root = \[5,9,1,3,5,7\]
**Output:** false
**Explanation:** Node values in the level 1 should be even integers.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 106` | Do a simple tree traversal, try to check if the current node is lonely or not. Node is lonely if at least one of the left/right pointers is null. |
Python solution using breadth search first algorithm | even-odd-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn this approach we travel the tree using breadth first search algorithm. We store each node with it\'s index level in the queue. We go through the node and if this is the first node in the index, we make sure that it is either odd or even depending on the index, then if it is not the first one in the index, we make sure that is has the correct relationship with the node before it in the same index. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:\n queue = [(root, 0)]\n current_value = 0\n current_index = 0\n # breadth-first search algorithm\n while queue:\n root, index = queue.pop(0)\n # even index\n if index % 2 == 0:\n # value should be odd\n if root.val % 2 == 0:\n return False\n # any node in the same even index should be bigger than last\n if index == current_index and root.val <= current_value:\n return False\n # odd index\n else:\n # value should be even\n if root.val % 2 != 0:\n return False\n # any node in the same odd index should be less than last\n if index == current_index and root.val >= current_value:\n return False\n # update the value and index\n current_index = index\n current_value = root.val\n if root.left:\n queue.append((root.left, index + 1))\n if root.right:\n queue.append((root.right, index + 1))\n return True\n``` | 1 | A binary tree is named **Even-Odd** if it meets the following conditions:
* The root of the binary tree is at level index `0`, its children are at level index `1`, their children are at level index `2`, etc.
* For every **even-indexed** level, all nodes at the level have **odd** integer values in **strictly increasing** order (from left to right).
* For every **odd-indexed** level, all nodes at the level have **even** integer values in **strictly decreasing** order (from left to right).
Given the `root` of a binary tree, _return_ `true` _if the binary tree is **Even-Odd**, otherwise return_ `false`_._
**Example 1:**
**Input:** root = \[1,10,4,3,null,7,9,12,8,6,null,null,2\]
**Output:** true
**Explanation:** The node values on each level are:
Level 0: \[1\]
Level 1: \[10,4\]
Level 2: \[3,7,9\]
Level 3: \[12,8,6,2\]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
**Example 2:**
**Input:** root = \[5,4,2,3,3,7\]
**Output:** false
**Explanation:** The node values on each level are:
Level 0: \[5\]
Level 1: \[4,2\]
Level 2: \[3,3,7\]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
**Example 3:**
**Input:** root = \[5,9,1,3,5,7\]
**Output:** false
**Explanation:** Node values in the level 1 should be even integers.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 106` | Do a simple tree traversal, try to check if the current node is lonely or not. Node is lonely if at least one of the left/right pointers is null. |
Python3 Runtime:838ms 44.05% || Memory: 40.8mb 57.22% # O(n) || O(h) | even-odd-tree | 0 | 1 | I added prev = 0 because we can\'t campare with NoneType at `comparison` variable\n```\nfrom collections import deque\n# Runtime:838ms 44.05% || Memory: 40.8mb 57.22%\n# O(n) || O(h); where h is the height of the tree\n\nclass Solution:\n def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return False\n\n level = 0\n evenOddLevel = {0:1, 1:0}\n queue = deque([root])\n\n while queue:\n prev = 0\n for _ in range(len(queue)):\n currNode = queue.popleft()\n comparison = {0:prev < currNode.val, 1:prev > currNode.val}\n if currNode.val % 2 != evenOddLevel[level % 2]:\n return False\n else:\n if prev != 0 and comparison[level % 2]:\n prev = currNode.val\n elif prev == 0:\n prev = currNode.val\n else:\n return False\n\n if currNode.left:\n queue.append(currNode.left)\n\n if currNode.right:\n queue.append(currNode.right)\n\n level += 1\n\n return True\n```\nPS: All the questions I solved I push it here https://github.com/ArshErgon/Leetcode-Question-Solution be a part of it, share your answers in your own language if you want to contribute in it. | 1 | A binary tree is named **Even-Odd** if it meets the following conditions:
* The root of the binary tree is at level index `0`, its children are at level index `1`, their children are at level index `2`, etc.
* For every **even-indexed** level, all nodes at the level have **odd** integer values in **strictly increasing** order (from left to right).
* For every **odd-indexed** level, all nodes at the level have **even** integer values in **strictly decreasing** order (from left to right).
Given the `root` of a binary tree, _return_ `true` _if the binary tree is **Even-Odd**, otherwise return_ `false`_._
**Example 1:**
**Input:** root = \[1,10,4,3,null,7,9,12,8,6,null,null,2\]
**Output:** true
**Explanation:** The node values on each level are:
Level 0: \[1\]
Level 1: \[10,4\]
Level 2: \[3,7,9\]
Level 3: \[12,8,6,2\]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
**Example 2:**
**Input:** root = \[5,4,2,3,3,7\]
**Output:** false
**Explanation:** The node values on each level are:
Level 0: \[5\]
Level 1: \[4,2\]
Level 2: \[3,3,7\]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
**Example 3:**
**Input:** root = \[5,9,1,3,5,7\]
**Output:** false
**Explanation:** Node values in the level 1 should be even integers.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 106` | Do a simple tree traversal, try to check if the current node is lonely or not. Node is lonely if at least one of the left/right pointers is null. |
even-odd-tree | even-odd-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return True\n t = deque([root])\n count = 0\n while t:\n a = len(t)\n l = []\n for i in range((a)):\n node = t.popleft()\n if node.left:\n t.append(node.left)\n if node.right:\n t.append(node.right)\n if count%2==0 and node.val%2!=0:\n if len(l)==0:\n l.append(node.val)\n elif node.val>l[-1]:\n l.append(node.val)\n else:\n return False\n elif count%2==0 and node.val%2==0: \n return False\n elif count%2!=0 and node.val%2==0:\n if len(l)==0:\n l.append(node.val)\n elif node.val<l[-1]:\n l.append(node.val)\n else:\n return False\n else:\n return False\n count+=1\n return True\n\n \n \n \n\n\n \n \n \n \n\n \n``` | 0 | A binary tree is named **Even-Odd** if it meets the following conditions:
* The root of the binary tree is at level index `0`, its children are at level index `1`, their children are at level index `2`, etc.
* For every **even-indexed** level, all nodes at the level have **odd** integer values in **strictly increasing** order (from left to right).
* For every **odd-indexed** level, all nodes at the level have **even** integer values in **strictly decreasing** order (from left to right).
Given the `root` of a binary tree, _return_ `true` _if the binary tree is **Even-Odd**, otherwise return_ `false`_._
**Example 1:**
**Input:** root = \[1,10,4,3,null,7,9,12,8,6,null,null,2\]
**Output:** true
**Explanation:** The node values on each level are:
Level 0: \[1\]
Level 1: \[10,4\]
Level 2: \[3,7,9\]
Level 3: \[12,8,6,2\]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
**Example 2:**
**Input:** root = \[5,4,2,3,3,7\]
**Output:** false
**Explanation:** The node values on each level are:
Level 0: \[5\]
Level 1: \[4,2\]
Level 2: \[3,3,7\]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
**Example 3:**
**Input:** root = \[5,9,1,3,5,7\]
**Output:** false
**Explanation:** Node values in the level 1 should be even integers.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 106` | Do a simple tree traversal, try to check if the current node is lonely or not. Node is lonely if at least one of the left/right pointers is null. |
Solution using BFS | even-odd-tree | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:\n if not root:\n return False\n\n queue = deque([root])\n level = 0\n\n while queue:\n level_list = []\n for _ in range(len(queue)):\n node = queue.popleft()\n # check if both level and node value are even or odd\n if level % 2 == node.val % 2:\n return False\n \n level_list.append(node.val)\n\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n\n # evaluate if the logic of strictly decreasing/increasing order applies to the level list\n if level % 2 == 0:\n for i in range(len(level_list)-1):\n if (level_list[i+1] - level_list[i]) <= 0:\n return False\n \n else:\n for i in range(len(level_list)-1):\n if (level_list[i+1] - level_list[i]) >= 0:\n return False\n\n level += 1 \n\n return True\n\n\n\n \n``` | 0 | A binary tree is named **Even-Odd** if it meets the following conditions:
* The root of the binary tree is at level index `0`, its children are at level index `1`, their children are at level index `2`, etc.
* For every **even-indexed** level, all nodes at the level have **odd** integer values in **strictly increasing** order (from left to right).
* For every **odd-indexed** level, all nodes at the level have **even** integer values in **strictly decreasing** order (from left to right).
Given the `root` of a binary tree, _return_ `true` _if the binary tree is **Even-Odd**, otherwise return_ `false`_._
**Example 1:**
**Input:** root = \[1,10,4,3,null,7,9,12,8,6,null,null,2\]
**Output:** true
**Explanation:** The node values on each level are:
Level 0: \[1\]
Level 1: \[10,4\]
Level 2: \[3,7,9\]
Level 3: \[12,8,6,2\]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.
**Example 2:**
**Input:** root = \[5,4,2,3,3,7\]
**Output:** false
**Explanation:** The node values on each level are:
Level 0: \[5\]
Level 1: \[4,2\]
Level 2: \[3,3,7\]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.
**Example 3:**
**Input:** root = \[5,9,1,3,5,7\]
**Output:** false
**Explanation:** Node values in the level 1 should be even integers.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 106` | Do a simple tree traversal, try to check if the current node is lonely or not. Node is lonely if at least one of the left/right pointers is null. |
[Python / C++] 3 Simple Steps | maximum-number-of-visible-points | 0 | 1 | ```html5\n<b>Time Complexity: O(n·log(n))\nSpace Complexity: O(n)</b>\n```\n<iframe src="https://leetcode.com/playground/YyWmsvj7/shared" frameBorder="0" width="100%" height="750"></iframe>\n\n**Notes:**\n1. ```math.atan2(y,x)``` is used instead of ```math.atan``` because it accounts for the sign of x and y. \n```html5\n math.atan2(-1, -1) * (180 / π) = -135°\n\tmath.atan2(1, 1) * (180 / π) = 45°\n\tmath.atan(1/1) * (180 / π) = 45°\n\tmath.atan(-1/-1) * (180 / π) = 45°\n```\n\n2. Python: Step 2 is written for readability. It is more efficient to replace step 2 with the following code:\n```python\n\tangles = sorted((angle_from_me(p) for p in points))\n\tif not angles: return points_on_me\n\tmax_angle = angles[-1]\n\tfor a in angles:\n\t\tif a + 360 > max_angle + angle: break\n\t\tangles.append(a + 360)\n```\n\n3. C++: `double` is used for angles for higher precision. If you are using C++ and obtaining a result that contains one or two points more than the expected result for just a few of the test cases, try increasing the precision by using `double`. | 43 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
[Python / C++] 3 Simple Steps | maximum-number-of-visible-points | 0 | 1 | ```html5\n<b>Time Complexity: O(n·log(n))\nSpace Complexity: O(n)</b>\n```\n<iframe src="https://leetcode.com/playground/YyWmsvj7/shared" frameBorder="0" width="100%" height="750"></iframe>\n\n**Notes:**\n1. ```math.atan2(y,x)``` is used instead of ```math.atan``` because it accounts for the sign of x and y. \n```html5\n math.atan2(-1, -1) * (180 / π) = -135°\n\tmath.atan2(1, 1) * (180 / π) = 45°\n\tmath.atan(1/1) * (180 / π) = 45°\n\tmath.atan(-1/-1) * (180 / π) = 45°\n```\n\n2. Python: Step 2 is written for readability. It is more efficient to replace step 2 with the following code:\n```python\n\tangles = sorted((angle_from_me(p) for p in points))\n\tif not angles: return points_on_me\n\tmax_angle = angles[-1]\n\tfor a in angles:\n\t\tif a + 360 > max_angle + angle: break\n\t\tangles.append(a + 360)\n```\n\n3. C++: `double` is used for angles for higher precision. If you are using C++ and obtaining a result that contains one or two points more than the expected result for just a few of the test cases, try increasing the precision by using `double`. | 43 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
Angle sliding window (intuition behind polar coordinates) | maximum-number-of-visible-points | 0 | 1 | # Intuition\nThe maximum number of points within the given Field Of View (FOV) is the maximum of the number of points contained in the interval window $$[\\theta, \\theta+ FOV]$$ of size $$FOV$$, which starts at angle $$x$$ and considers the angle range up to $$x+FOV$$ inclusive.\nTo attain this, every point has to be represented by its angle with respect to the x-axis relative to the observer (horizontal axis).\nSince the problem assumes that we are able to observe:\n- all points in the interval FOV up to infinity\n- all points which are behind others in the same line of sight\n\nThen we do not care about the distance of any point from the observer location. Only the angle at which is located is relevant so solve the problem \n# Real world application\nThis problem provides a simplified setting in which points captured by a LiDAR sensor have to be filtered so as to consider only the ones falling within the field of view of a given RGB camera sensor.\nE.g. to obtian occupancy maps of the environment for an autonomous driving application.\n\n## Simplified algorithm\nNote: the below simplified algorithm gives only a simple intuition about a sliding window solution which is then refined in the actual approach. \nThis one would give "off by 1" or "off by 2 errors" due to the rounding of angles to integers. Nevertheless, it gives a proper intuition about the refinement steps.\n1. Represent all points with respect to the observer location (perform a translation) \n2. Transform all points to polar coordinates such that they are represented by distance(not needed for this problem) and an integer angle with respect to the observer.\n3. Create a count vector of size $360+FOV$, with index that represents the angle and value the frequency (e.g. number of points) represented by that angle (ignore points exactly at observer location). Note that the array considers also FOV bonus locations in order to evaluate all possible windows that are placed in an interval that crosses angle 360 and 0 (which represent the same angular location).\n4. Given the obtained counts, transform such array to a prefix sum array.\n5. Compute number of points within window of size $FOV$ starting at \n $x \\in [0,360]$ by means of the prefix sum computedbefore $cur\\_count = prefix\\_sum[x+FOV]-prefix\\_sum[x-1] $\n6. Return $max_{i}(cur\\_count_i) + K$, where K is the number of previously ignored points.\n\n# Approach\nNote: this will be an in depth explanation that covers deeply all concepts.\nJust glance through it if you want to just see the code.\nFurthermore, the general setting of this problem is that of an engineering problem more than a CS one.\nSo you might need a bit more math knowledge for this.\n\n#### Three concepts are fundamental to fully understand this problem:\n* **Calculus**: any point x,y in cartesian coordinates can be mapped to another set of coordinates u,v.\nSince the field of view (FOV for short) is here represented by an angle, it would be neat **to have points and FOV in the same unit of measurement e.g. angles**. **Polar coordinates** allow to map a point **x,y in cartesian coordinates (x,y) to polar(radius,angle)**.\nThis is achieved as follows:\n. $$radius = (x^2+y^2)^{\\frac{1}{2}}$$\n. $$angle=arctan(y/x)$$\n\nRead here for more details https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates ). Here radius is not relevant since the problem states that you can "see" behind points on the same line of sight, otherwise you would need it. \n\n\n* **Sliding window**: Now that the field of view and the points are represent both as angles, we can\nconceptualize the field of view as a window/interval/range which has size equal to the provided field of view angle ). Hence the problem is reduced to finding the sliding window that contains the maximum number of points. \nStill, where should we slide the window that represents the field of view?\nIt should be slid by placing it at any of the points x,y represented by their angle $\\theta$, and considering the FOV area after it: this is represented by the interval $[\\theta, \\theta + FOV]$, in which $FOV$ is basically the sliding window size.\n\n* **Coordinate translation**: \npoints have to be represented with respect to the observer location, since the field of view has to be considered based on that position. \nUp to now, the location of the observer (given in the problem as "location")\nhas not been taken into account when considering angles and sliding windows. Indeed the data is given to us with respect to the origin of the plane. \nHowever, as stated in the problem, we need to determine all quantities with respect to the observer\'s field of view.\nThis can be solved by simply translating all points such that they are represented with respect to the observer location, rather than the origin of the axis.\nAs an example, if the observer is located at location=$(x_{obs}=1,y_{obs}=1)$ (with respect to the origin $(0,0)$), a point $(x=1,y=0)$ (also with respect to the origin), \nthe observer would see it exactly below its location, thus at \n$(x_{new}=0,y_{new}=-1)$. Therefore to achieve this result, every point has to be represented relative to the observer location.\nThis is mathematically achieved by a simple translation:\n. $$x_{new}=x-x_{obs}$$\n. $$y_{new}=y-y_{obs}$$\n\n* **Edge cases**\n All points that after the translations are exactly below the observer are deemed at angle 0 (because $arctan(0)=0$) with respect to it. Still, any points located exactly at the observer location has to be considered as visible by any field of view sliding window. Thus, these are excluded and added back to the result after all computations are performed.\n\n# Complexity\nN = number of points\n- Time complexity:\n$$O(N \\log N)$$\n\n- Space complexity:\n$$O(N)$$\n# Code\n```\n\n\nclass Solution:\n def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:\n t = Solution.t\n to_angle = Solution.to_angle \n \n points_at_location = 0\n angles = []\n for point in points:\n x1,y1 = t(*point, *location)\n if x1 == 0 and y1 == 0:\n points_at_location += 1\n continue\n ang = to_angle(x1,y1) \n angles.append(ang)\n\n if ang >= 0 and ang < angle:\n angles.append(ang+360)\n angles = sorted(angles)\n max_s = 0\n j = 0\n for i in range(0, len(angles)):\n \n while angles[i]-angles[j] > angle:\n j += 1\n\n max_s = max(i-j+1, max_s)\n return max_s + points_at_location\n\n\n def t(x,y, x0,y0):\n x1 = x-x0\n y1 = y-y0\n return x1,y1\n \n def to_angle(x,y):\n angle = (math.atan2(y,x)/(math.pi))*180 \n if angle < 0:\n angle += 360\n return angle\n``` | 5 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
Angle sliding window (intuition behind polar coordinates) | maximum-number-of-visible-points | 0 | 1 | # Intuition\nThe maximum number of points within the given Field Of View (FOV) is the maximum of the number of points contained in the interval window $$[\\theta, \\theta+ FOV]$$ of size $$FOV$$, which starts at angle $$x$$ and considers the angle range up to $$x+FOV$$ inclusive.\nTo attain this, every point has to be represented by its angle with respect to the x-axis relative to the observer (horizontal axis).\nSince the problem assumes that we are able to observe:\n- all points in the interval FOV up to infinity\n- all points which are behind others in the same line of sight\n\nThen we do not care about the distance of any point from the observer location. Only the angle at which is located is relevant so solve the problem \n# Real world application\nThis problem provides a simplified setting in which points captured by a LiDAR sensor have to be filtered so as to consider only the ones falling within the field of view of a given RGB camera sensor.\nE.g. to obtian occupancy maps of the environment for an autonomous driving application.\n\n## Simplified algorithm\nNote: the below simplified algorithm gives only a simple intuition about a sliding window solution which is then refined in the actual approach. \nThis one would give "off by 1" or "off by 2 errors" due to the rounding of angles to integers. Nevertheless, it gives a proper intuition about the refinement steps.\n1. Represent all points with respect to the observer location (perform a translation) \n2. Transform all points to polar coordinates such that they are represented by distance(not needed for this problem) and an integer angle with respect to the observer.\n3. Create a count vector of size $360+FOV$, with index that represents the angle and value the frequency (e.g. number of points) represented by that angle (ignore points exactly at observer location). Note that the array considers also FOV bonus locations in order to evaluate all possible windows that are placed in an interval that crosses angle 360 and 0 (which represent the same angular location).\n4. Given the obtained counts, transform such array to a prefix sum array.\n5. Compute number of points within window of size $FOV$ starting at \n $x \\in [0,360]$ by means of the prefix sum computedbefore $cur\\_count = prefix\\_sum[x+FOV]-prefix\\_sum[x-1] $\n6. Return $max_{i}(cur\\_count_i) + K$, where K is the number of previously ignored points.\n\n# Approach\nNote: this will be an in depth explanation that covers deeply all concepts.\nJust glance through it if you want to just see the code.\nFurthermore, the general setting of this problem is that of an engineering problem more than a CS one.\nSo you might need a bit more math knowledge for this.\n\n#### Three concepts are fundamental to fully understand this problem:\n* **Calculus**: any point x,y in cartesian coordinates can be mapped to another set of coordinates u,v.\nSince the field of view (FOV for short) is here represented by an angle, it would be neat **to have points and FOV in the same unit of measurement e.g. angles**. **Polar coordinates** allow to map a point **x,y in cartesian coordinates (x,y) to polar(radius,angle)**.\nThis is achieved as follows:\n. $$radius = (x^2+y^2)^{\\frac{1}{2}}$$\n. $$angle=arctan(y/x)$$\n\nRead here for more details https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates ). Here radius is not relevant since the problem states that you can "see" behind points on the same line of sight, otherwise you would need it. \n\n\n* **Sliding window**: Now that the field of view and the points are represent both as angles, we can\nconceptualize the field of view as a window/interval/range which has size equal to the provided field of view angle ). Hence the problem is reduced to finding the sliding window that contains the maximum number of points. \nStill, where should we slide the window that represents the field of view?\nIt should be slid by placing it at any of the points x,y represented by their angle $\\theta$, and considering the FOV area after it: this is represented by the interval $[\\theta, \\theta + FOV]$, in which $FOV$ is basically the sliding window size.\n\n* **Coordinate translation**: \npoints have to be represented with respect to the observer location, since the field of view has to be considered based on that position. \nUp to now, the location of the observer (given in the problem as "location")\nhas not been taken into account when considering angles and sliding windows. Indeed the data is given to us with respect to the origin of the plane. \nHowever, as stated in the problem, we need to determine all quantities with respect to the observer\'s field of view.\nThis can be solved by simply translating all points such that they are represented with respect to the observer location, rather than the origin of the axis.\nAs an example, if the observer is located at location=$(x_{obs}=1,y_{obs}=1)$ (with respect to the origin $(0,0)$), a point $(x=1,y=0)$ (also with respect to the origin), \nthe observer would see it exactly below its location, thus at \n$(x_{new}=0,y_{new}=-1)$. Therefore to achieve this result, every point has to be represented relative to the observer location.\nThis is mathematically achieved by a simple translation:\n. $$x_{new}=x-x_{obs}$$\n. $$y_{new}=y-y_{obs}$$\n\n* **Edge cases**\n All points that after the translations are exactly below the observer are deemed at angle 0 (because $arctan(0)=0$) with respect to it. Still, any points located exactly at the observer location has to be considered as visible by any field of view sliding window. Thus, these are excluded and added back to the result after all computations are performed.\n\n# Complexity\nN = number of points\n- Time complexity:\n$$O(N \\log N)$$\n\n- Space complexity:\n$$O(N)$$\n# Code\n```\n\n\nclass Solution:\n def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:\n t = Solution.t\n to_angle = Solution.to_angle \n \n points_at_location = 0\n angles = []\n for point in points:\n x1,y1 = t(*point, *location)\n if x1 == 0 and y1 == 0:\n points_at_location += 1\n continue\n ang = to_angle(x1,y1) \n angles.append(ang)\n\n if ang >= 0 and ang < angle:\n angles.append(ang+360)\n angles = sorted(angles)\n max_s = 0\n j = 0\n for i in range(0, len(angles)):\n \n while angles[i]-angles[j] > angle:\n j += 1\n\n max_s = max(i-j+1, max_s)\n return max_s + points_at_location\n\n\n def t(x,y, x0,y0):\n x1 = x-x0\n y1 = y-y0\n return x1,y1\n \n def to_angle(x,y):\n angle = (math.atan2(y,x)/(math.pi))*180 \n if angle < 0:\n angle += 360\n return angle\n``` | 5 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
[Hashmap + Prefix sum + Sliding window] Runtime beats 99% of users with Python3 | maximum-number-of-visible-points | 0 | 1 | # Intuition\n1. Use hashmap to record the same angle and number of itmes.\n2. Sort unique angles in the hashmap.\n3. Calculate the num of points from first angle to the last angle: sum_list. Then the point number between i-th angle and j-th angle will be: \n * ```if j > i: num = sum_list[j] - sum_list[i]```\n * ```if j <= i: num = sum_list[j] + sum_list[-1] - sum_list[i]```\n4. Remember to consider the boundary condition, if the range of all angle is smaller than the filed of view angle, we can directly return all point number.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlog) for sort, O(n) for sliding window because right idx will be at most 2n.\n\n- Space complexity:\nO(n)\n\n# Code\n```\nimport math\nfrom collections import defaultdict\nclass Solution:\n def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:\n angle_map = defaultdict(int)\n origin_point_num = 0\n for point in points:\n if point == location:\n origin_point_num += 1\n continue\n q = math.degrees(math.atan2(point[1] - location[1], point[0] - location[0]))\n angle_map[q] += 1\n \n if origin_point_num == len(points):\n return origin_point_num\n \n angle_keys = sorted(list(angle_map.keys()))\n \n n = len(angle_keys)\n sum_list = [0] * (n+1)\n cur_sum = 0\n for i in range(1, n+1):\n cur_sum += angle_map[angle_keys[i-1]]\n sum_list[i] = cur_sum\n \n max_num = 0\n max_angle_diff = angle_keys[-1] - angle_keys[0]\n if max_angle_diff <= angle:\n return sum_list[-1] + origin_point_num\n \n right_idx = 1\n for i in range(n):\n # right_idx > i\n angle_diff = 0\n while right_idx < n:\n points_num = sum_list[(right_idx)] - sum_list[i]\n max_num = max(max_num, points_num)\n angle_diff = angle_keys[right_idx] - angle_keys[i]\n if angle_diff > angle:\n break\n right_idx += 1\n\n if angle_diff > angle:\n continue\n\n while right_idx <= n + i:\n right_rem_idx = right_idx % n\n points_num = sum_list[right_rem_idx] + sum_list[-1] - sum_list[i]\n max_num = max(max_num, points_num)\n angle_diff = 360 + angle_keys[right_rem_idx] - angle_keys[i]\n if angle_diff > angle:\n break\n right_idx += 1\n return max_num + origin_point_num\n``` | 0 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
[Hashmap + Prefix sum + Sliding window] Runtime beats 99% of users with Python3 | maximum-number-of-visible-points | 0 | 1 | # Intuition\n1. Use hashmap to record the same angle and number of itmes.\n2. Sort unique angles in the hashmap.\n3. Calculate the num of points from first angle to the last angle: sum_list. Then the point number between i-th angle and j-th angle will be: \n * ```if j > i: num = sum_list[j] - sum_list[i]```\n * ```if j <= i: num = sum_list[j] + sum_list[-1] - sum_list[i]```\n4. Remember to consider the boundary condition, if the range of all angle is smaller than the filed of view angle, we can directly return all point number.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlog) for sort, O(n) for sliding window because right idx will be at most 2n.\n\n- Space complexity:\nO(n)\n\n# Code\n```\nimport math\nfrom collections import defaultdict\nclass Solution:\n def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:\n angle_map = defaultdict(int)\n origin_point_num = 0\n for point in points:\n if point == location:\n origin_point_num += 1\n continue\n q = math.degrees(math.atan2(point[1] - location[1], point[0] - location[0]))\n angle_map[q] += 1\n \n if origin_point_num == len(points):\n return origin_point_num\n \n angle_keys = sorted(list(angle_map.keys()))\n \n n = len(angle_keys)\n sum_list = [0] * (n+1)\n cur_sum = 0\n for i in range(1, n+1):\n cur_sum += angle_map[angle_keys[i-1]]\n sum_list[i] = cur_sum\n \n max_num = 0\n max_angle_diff = angle_keys[-1] - angle_keys[0]\n if max_angle_diff <= angle:\n return sum_list[-1] + origin_point_num\n \n right_idx = 1\n for i in range(n):\n # right_idx > i\n angle_diff = 0\n while right_idx < n:\n points_num = sum_list[(right_idx)] - sum_list[i]\n max_num = max(max_num, points_num)\n angle_diff = angle_keys[right_idx] - angle_keys[i]\n if angle_diff > angle:\n break\n right_idx += 1\n\n if angle_diff > angle:\n continue\n\n while right_idx <= n + i:\n right_rem_idx = right_idx % n\n points_num = sum_list[right_rem_idx] + sum_list[-1] - sum_list[i]\n max_num = max(max_num, points_num)\n angle_diff = 360 + angle_keys[right_rem_idx] - angle_keys[i]\n if angle_diff > angle:\n break\n right_idx += 1\n return max_num + origin_point_num\n``` | 0 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
1610. Maximum Number of Visible Points | maximum-number-of-visible-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def visiblePoints(\n self, points: List[List[int]], angle: int, location: List[int]\n ) -> int:\n v = []\n x, y = location\n same = 0\n for xi, yi in points:\n if xi == x and yi == y:\n same += 1\n else:\n v.append(atan2(yi - y, xi - x))\n v.sort()\n n = len(v)\n v += [deg + 2 * pi for deg in v]\n t = angle * pi / 180\n mx = max((bisect_right(v, v[i] + t) - i for i in range(n)), default=0)\n return mx + same\n``` | 0 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
1610. Maximum Number of Visible Points | maximum-number-of-visible-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def visiblePoints(\n self, points: List[List[int]], angle: int, location: List[int]\n ) -> int:\n v = []\n x, y = location\n same = 0\n for xi, yi in points:\n if xi == x and yi == y:\n same += 1\n else:\n v.append(atan2(yi - y, xi - x))\n v.sort()\n n = len(v)\n v += [deg + 2 * pi for deg in v]\n t = angle * pi / 180\n mx = max((bisect_right(v, v[i] + t) - i for i in range(n)), default=0)\n return mx + same\n``` | 0 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
Sliding Window on a circle | maximum-number-of-visible-points | 0 | 1 | \n# Code\n```\nclass Solution:\n def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:\n vectors = [(p1-location[0],p2-location[1]) for p1,p2 in points]\n pi = 3.141592653589793238462643383279502884197\n def myatan(a1,a2):\n if a1 > 0:\n return atan(a2/a1) / pi*180\n elif a1<0:\n return atan(a2/a1) / pi*180 + 180\n else:\n return 90 if a2>0 else -90\n myvectors = [v for v in vectors if v!=(0,0)]\n angles = sorted([myatan(a1,a2) for a1,a2 in myvectors])\n \n i,j = 0,0\n n = len(angles)\n less = len(vectors) - n\n res = 0\n angles += [x+360 for x in angles] // this line is crucial for sliding windows to work on a circle\n n = len(angles)\n while j<n:\n while angles[j]-angles[i] > angle:\n i += 1\n j += 1\n res = max(res,j-i)\n return res+less\n \n \n``` | 0 | You are given an array `points`, an integer `angle`, and your `location`, where `location = [posx, posy]` and `points[i] = [xi, yi]` both denote **integral coordinates** on the X-Y plane.
Initially, you are facing directly east from your position. You **cannot move** from your position, but you can **rotate**. In other words, `posx` and `posy` cannot be changed. Your field of view in **degrees** is represented by `angle`, determining how wide you can see from any given view direction. Let `d` be the amount in degrees that you rotate counterclockwise. Then, your field of view is the **inclusive** range of angles `[d - angle/2, d + angle/2]`.
Your browser does not support the video tag or this video format.
You can **see** some set of points if, for each point, the **angle** formed by the point, your position, and the immediate east direction from your position is **in your field of view**.
There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.
Return _the maximum number of points you can see_.
**Example 1:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,3\]\], angle = 90, location = \[1,1\]
**Output:** 3
**Explanation:** The shaded region represents your field of view. All points can be made visible in your field of view, including \[3,3\] even though \[2,2\] is in front and in the same line of sight.
**Example 2:**
**Input:** points = \[\[2,1\],\[2,2\],\[3,4\],\[1,1\]\], angle = 90, location = \[1,1\]
**Output:** 4
**Explanation:** All points can be made visible in your field of view, including the one at your location.
**Example 3:**
**Input:** points = \[\[1,0\],\[2,1\]\], angle = 13, location = \[1,1\]
**Output:** 1
**Explanation:** You can only see one of the two points, as shown above.
**Constraints:**
* `1 <= points.length <= 105`
* `points[i].length == 2`
* `location.length == 2`
* `0 <= angle < 360`
* `0 <= posx, posy, xi, yi <= 100` | Simulate the process, create an array nums and return the Bitwise XOR of all elements of it. |
Sliding Window on a circle | maximum-number-of-visible-points | 0 | 1 | \n# Code\n```\nclass Solution:\n def visiblePoints(self, points: List[List[int]], angle: int, location: List[int]) -> int:\n vectors = [(p1-location[0],p2-location[1]) for p1,p2 in points]\n pi = 3.141592653589793238462643383279502884197\n def myatan(a1,a2):\n if a1 > 0:\n return atan(a2/a1) / pi*180\n elif a1<0:\n return atan(a2/a1) / pi*180 + 180\n else:\n return 90 if a2>0 else -90\n myvectors = [v for v in vectors if v!=(0,0)]\n angles = sorted([myatan(a1,a2) for a1,a2 in myvectors])\n \n i,j = 0,0\n n = len(angles)\n less = len(vectors) - n\n res = 0\n angles += [x+360 for x in angles] // this line is crucial for sliding windows to work on a circle\n n = len(angles)\n while j<n:\n while angles[j]-angles[i] > angle:\n i += 1\n j += 1\n res = max(res,j-i)\n return res+less\n \n \n``` | 0 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
🥇 C++ | PYTHON | JAVA || EXPLAINED || ; ] ✅ | minimum-one-bit-operations-to-make-integers-zero | 1 | 1 | **UPVOTE IF HELPFuuL**\n\n# Intuition\nAssume a number `1101001`\nStarting from left to right to save number of operations\n`1000000->0` takes 2^7-1 = 127 steps \n`0100000->0` takes 2^6-1 = 63 steps \n`0001000->0` takes 2^4-1 = 15 steps \n`0000001->0` takes 2^1-1 = 1 step \n\nHence Can be said\n`1 -> 0` needs `1` operation,\n`2 -> 0` needs `3` operations,\n`4 -> 0` needs `7` operations,\n`2^k` needs `2^(k+1)-1` operations.\n\n# Approach\n\n`1101001` : Required steps = 127-63+15-1 = 78\n\n- Let steps `x` to convert `000000` to `100000`.\n- But, since `1101001` already has 1 in the 5th bit from right, some steps will be saved. \n- Saved steps `y = Number of steps needed to convert 000000 to 100000`\n- Hence not all the `2^(6+1) - 1` steps to convert `1000000 -> 0` as `0100000` can be obtained in less number of steps.\n\nFor `0100000 -> 0`, we need to add its `2^6-1` steps\nFor `0001000 -> 0`, we need to add its `2^4-1` steps\nFor `0000001 -> 0`, we need to add its `2^1-1` steps\n\nResult = `2^(7)-1` - `2^6-1` + `2^4-1` - `2^1-1`\n\n# Complexity\n- Time complexity: O ( log N )\n- Space complexity: O ( 1 )\n\n``` Python []\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n res = 0\n while n:\n res = -res - (n ^ (n - 1))\n n &= n - 1\n return abs(res)\n```\n``` C++ []\nclass Solution {\npublic:\n int minimumOneBitOperations(int n) {\n int res;\n for (res = 0; n > 0; n &= n - 1)\n res = -(res + (n ^ (n - 1)));\n return abs(res);\n }\n};\n```\n\n``` JAVA []\nclass Solution {\n public int minimumOneBitOperations(int n) {\n int multiplier = 1;\n int res = 0;\n while (n > 0) {\n res += n ^ (n - 1) * multiplier;\n multiplier = -1 * multiplier;\n n &= n - 1;\n }\n return Math.abs(res);\n }\n}\n```\n\n**UPVOTE IF HELPFuuL**\n\n\n\n | 91 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
🥇 C++ | PYTHON | JAVA || EXPLAINED || ; ] ✅ | minimum-one-bit-operations-to-make-integers-zero | 1 | 1 | **UPVOTE IF HELPFuuL**\n\n# Intuition\nAssume a number `1101001`\nStarting from left to right to save number of operations\n`1000000->0` takes 2^7-1 = 127 steps \n`0100000->0` takes 2^6-1 = 63 steps \n`0001000->0` takes 2^4-1 = 15 steps \n`0000001->0` takes 2^1-1 = 1 step \n\nHence Can be said\n`1 -> 0` needs `1` operation,\n`2 -> 0` needs `3` operations,\n`4 -> 0` needs `7` operations,\n`2^k` needs `2^(k+1)-1` operations.\n\n# Approach\n\n`1101001` : Required steps = 127-63+15-1 = 78\n\n- Let steps `x` to convert `000000` to `100000`.\n- But, since `1101001` already has 1 in the 5th bit from right, some steps will be saved. \n- Saved steps `y = Number of steps needed to convert 000000 to 100000`\n- Hence not all the `2^(6+1) - 1` steps to convert `1000000 -> 0` as `0100000` can be obtained in less number of steps.\n\nFor `0100000 -> 0`, we need to add its `2^6-1` steps\nFor `0001000 -> 0`, we need to add its `2^4-1` steps\nFor `0000001 -> 0`, we need to add its `2^1-1` steps\n\nResult = `2^(7)-1` - `2^6-1` + `2^4-1` - `2^1-1`\n\n# Complexity\n- Time complexity: O ( log N )\n- Space complexity: O ( 1 )\n\n``` Python []\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n res = 0\n while n:\n res = -res - (n ^ (n - 1))\n n &= n - 1\n return abs(res)\n```\n``` C++ []\nclass Solution {\npublic:\n int minimumOneBitOperations(int n) {\n int res;\n for (res = 0; n > 0; n &= n - 1)\n res = -(res + (n ^ (n - 1)));\n return abs(res);\n }\n};\n```\n\n``` JAVA []\nclass Solution {\n public int minimumOneBitOperations(int n) {\n int multiplier = 1;\n int res = 0;\n while (n > 0) {\n res += n ^ (n - 1) * multiplier;\n multiplier = -1 * multiplier;\n n &= n - 1;\n }\n return Math.abs(res);\n }\n}\n```\n\n**UPVOTE IF HELPFuuL**\n\n\n\n | 91 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
Python3 Solution | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | \n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n ans=0\n while n:\n ans=-ans-(n^(n-1))\n n&=n-1\n return abs(ans) \n``` | 7 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
Python3 Solution | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | \n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n ans=0\n while n:\n ans=-ans-(n^(n-1))\n n&=n-1\n return abs(ans) \n``` | 7 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
Simple Pattern Recognition + Recursion | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem you have to observe pattern.\nThinking for this problem makes it HARD...\nbut as soon as you decode the logic, it is EASY to code.\n\nI have mentioned some testcases with the output in the code.\n\n**TIP :**\nFor every ***n*** which can be written in terms of power(***k***) of 2\noutput : 2**(k+1)-1\n\n\nfor example :\nn = 4\no/p = 7 \n\nNow try to recursively reduce the number to the nearest lower power of 2 and subtract the results as shown in following example :\n\nlet **n = 14**\nnearest lower power of 2 = **8**\nwe can calulate the ans for **8** (which will be 15) .......(i)\nnow residue = 14-8 = **6**\n\nwe will solve for **6**...\nagain repeating the same process..\nnearest lower power of 2 = **4**\nwe can calulate the ans for **4** (which will be 7) ......(ii)\nnow residue = 6-4 = **2**\n\nnow for **2** (base case)\nwe get result = **3** ...........(iii)\n\nNow final output will be calculated as\n\nans = 15-(7-3) [using eq.(i),(ii),(iii)]\nans = 15-(4)\n**ans = 11**\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet the number be X\n**Step1**: \nCalculate the lower nearest power of 2 (i.e. 2^k).\n\n**Step2:** \nCalculate the Residue (X-(2^k)).\n\n**Step3:** \nRepeat the process for the Residue untill the base case is reached.\n\n\n# Complexity\n- Time complexity: $$O(32+32)$$ ~ $$O(1)$$\n Here the total number of bits used is 32. \n So the maximum recursion calls may go upto 32\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n \'\'\'\n For refference testcases\n 1 : 1\n 2 : 3\n 3 : 2\n 4 : 7\n 5 : 6\n 6 : 4\n 7 : 5\n 8 : 15\n 9 : 14\n 10 : 12\n 11 : 13\n 12 : 8\n 13 : 9\n 14 : 11\n 15 : 10\n 16 : 31\n \'\'\'\n\n # helper fuction \n def helper(x) :\n mapper = {0:0,1:1,2:3,3:2}\n if x in mapper :\n return mapper[x]\n else:\n k = (int)(math.log(x,2))\n main = (2**(k+1))-1\n residue = x - (2**k)\n return main - helper(residue)\n\n\n ans = helper(n)\n return ans\n \n``` | 2 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
Simple Pattern Recognition + Recursion | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem you have to observe pattern.\nThinking for this problem makes it HARD...\nbut as soon as you decode the logic, it is EASY to code.\n\nI have mentioned some testcases with the output in the code.\n\n**TIP :**\nFor every ***n*** which can be written in terms of power(***k***) of 2\noutput : 2**(k+1)-1\n\n\nfor example :\nn = 4\no/p = 7 \n\nNow try to recursively reduce the number to the nearest lower power of 2 and subtract the results as shown in following example :\n\nlet **n = 14**\nnearest lower power of 2 = **8**\nwe can calulate the ans for **8** (which will be 15) .......(i)\nnow residue = 14-8 = **6**\n\nwe will solve for **6**...\nagain repeating the same process..\nnearest lower power of 2 = **4**\nwe can calulate the ans for **4** (which will be 7) ......(ii)\nnow residue = 6-4 = **2**\n\nnow for **2** (base case)\nwe get result = **3** ...........(iii)\n\nNow final output will be calculated as\n\nans = 15-(7-3) [using eq.(i),(ii),(iii)]\nans = 15-(4)\n**ans = 11**\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet the number be X\n**Step1**: \nCalculate the lower nearest power of 2 (i.e. 2^k).\n\n**Step2:** \nCalculate the Residue (X-(2^k)).\n\n**Step3:** \nRepeat the process for the Residue untill the base case is reached.\n\n\n# Complexity\n- Time complexity: $$O(32+32)$$ ~ $$O(1)$$\n Here the total number of bits used is 32. \n So the maximum recursion calls may go upto 32\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n \'\'\'\n For refference testcases\n 1 : 1\n 2 : 3\n 3 : 2\n 4 : 7\n 5 : 6\n 6 : 4\n 7 : 5\n 8 : 15\n 9 : 14\n 10 : 12\n 11 : 13\n 12 : 8\n 13 : 9\n 14 : 11\n 15 : 10\n 16 : 31\n \'\'\'\n\n # helper fuction \n def helper(x) :\n mapper = {0:0,1:1,2:3,3:2}\n if x in mapper :\n return mapper[x]\n else:\n k = (int)(math.log(x,2))\n main = (2**(k+1))-1\n residue = x - (2**k)\n return main - helper(residue)\n\n\n ans = helper(n)\n return ans\n \n``` | 2 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
[Python 3]Two DPs | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | For each bit, in order to convert it to zero, we should have the right bits set to `1000...` and call it R. thus it takes 1 + ones(n[1:]) + zero(R)\nwhere one is to transform the string to `1000...` and zero is to transform the string to all zeros.\n\n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n \n n = bin(n)[2:]\n \n @cache\n def zero(n):\n if \'1\' not in n:\n return 0\n elif n[0] == \'0\':\n return zero(n[1:])\n else:\n if n == \'1\': return 1\n new = \'1\' + \'0\' * (len(n) - 2)\n return 1 + zero(new) + ones(n[1:])\n \n @cache\n def ones(n):\n if n == \'1\' or n[0] == \'1\' and n.count(\'1\') == 1:\n return 0\n elif n[0] == \'1\':\n return zero(n[1:])\n else:\n if n == \'0\': return 1\n new = \'1\' + \'0\' * (len(n) - 2)\n return 1 + zero(new) + ones(n[1:])\n \n return zero(n) | 2 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
[Python 3]Two DPs | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | For each bit, in order to convert it to zero, we should have the right bits set to `1000...` and call it R. thus it takes 1 + ones(n[1:]) + zero(R)\nwhere one is to transform the string to `1000...` and zero is to transform the string to all zeros.\n\n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n \n n = bin(n)[2:]\n \n @cache\n def zero(n):\n if \'1\' not in n:\n return 0\n elif n[0] == \'0\':\n return zero(n[1:])\n else:\n if n == \'1\': return 1\n new = \'1\' + \'0\' * (len(n) - 2)\n return 1 + zero(new) + ones(n[1:])\n \n @cache\n def ones(n):\n if n == \'1\' or n[0] == \'1\' and n.count(\'1\') == 1:\n return 0\n elif n[0] == \'1\':\n return zero(n[1:])\n else:\n if n == \'0\': return 1\n new = \'1\' + \'0\' * (len(n) - 2)\n return 1 + zero(new) + ones(n[1:])\n \n return zero(n) | 2 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
Python3: Math and Dynamic Programming | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | # Intuition\n\nI found this problem to be brutal, it took me literally HOURS to come up with it. So I guess I won\'t work at Oracle where this is asked apparently.\n\nIMO this is one of the hardest problems because you have to spend a LOT of time getting the alternating moves insight, then figure out that the move sequences are kind of like the Tower of Hanoi puzzle, and THEN you have to do the DP stuff and avoid off-by-one errors.\n\nAnyway, I\'ll skip all the false routes I went through (you can see them in the comments for honesty) and explain the answer I came up with.\n\n## Toggling is Idempotent\n\nSomething is idempotent if doing it twice is the same as not doing it at all. In mathier terms, it means an operation is its own inverse.\n\nToggling bits is its own inverse: if you toggle a bit twice, the second toggle undoes the first toggle.\n\nBoth operations (A and B) toggle bits, so **A and B are idempotent**.\n\n## The Shortest Sequences Alternate A and B\n\nSince we know they\'re idempotent, let\'s look at a sample sequence of moves:\n```\nAAABABABBAAABBBAABABB\n```\nWe know they\'re idempotent so we can reduce them as follows:\n```\nAAABABABBAAABBBAABABB\n ABABA A B BA # pairs AA and BB cancel: idempotent\n ABAB A # more pairs of AA and BB cancel\n # so in the end, the operations alternate\n```\nSo the equivalent sequence is just `ABABA`. **The shortest sequence alternates: `..ABABn` or `..BABAn`**\n\nNote: BAn means\n* apply `A` to `n`\n* then apply `B` to the result, `An`\n\nTherefore **the easiest solution is to simulate ..ABABn and ..BABAn directly, and exit when one of those goes to zero**. This solution is pretty slow though, because the sequence of moves is like the Tower of Hanoi solution: 1 bit takes one operation, then 2 bits takes about twice as many operations, and 3 bits takes another twice as many operations, and so on.\n\n## Speeding Up: Look at What the Operations Do:\n\n### A: Toggles the Ones Bit\n\n`An` is `A^1`: the right-most bit is flipped.\n\n### B: Toggles the Bit Right of the LSB\n\n`Bn` takes the bit `b` at position `i-1`, followed by all zeros (therefore `b` is the LSB), and toggles `b<<1`.\n\n### Clearing a Specific Bit\n\nAs we iterate `..BAn` and `..ABn`, suppose we have some remainder\n```\nr = 1100110100\n```\nTo clear the third bit, we need\n* to set the second bit to one: `ops[2]`\n* then apply `B` to toggle the third bit off: 1 operation\n* then set the second bit back to zero: `ops[2]`\n\nSo we need to toggle the second bit. To do that, we\'d:\n* toggle the first bit to one: `ops[1] = 1` operation\n* use B to toggle the second bit: 1 operation\n* toggle the first bit to zero: `ops[1] = 1` again\n\nSo a pattern emerges\n* toggling the last bit costs one operation: A\n* toggling bit `i` requires `ops[i] = ops[i-1] + 1 + ops[i-1]` operations\n * `ops[i]` to turn the next bit on\n * 1 operation `B` to toggle `i`\n * `ops[i]` to turn the next bit off again\n * so a total of `ops[i] = 2*ops[i-1]+1`.\n\nDynamic programming!\n\n### What are the moves?\n\nToggling the last bit is clearly A.\n\nToggling any other bit is B.\n\nThe move sequences of `ops[i]` are as follows:\n* `ops[1]`: toggle first bit: `A`\n* `ops[2]`: toggle second bit: `ABA`\n* `ops[3]`: toggle third: turn second on, do B, turn second off:\n * i.e. `ABA + B + ABA == ABABABA`\n\n### Putting it All Together\n\nSo for each current bit we can do the following:\n* if the current bit is 1:\n * if there\'s a higher bit, we need to toggle the next bit up. This is because that next bit is the most significant bit, or we need to set that bit to 1 later anyway to toggle off an even higher bit\n * then we need to clear this bit\n* if the current bit is 0:\n * we won\'t spend moves to toggle the current bit, because it\'s not set\n * we can\'t use operation B here because the current bit isn\'t set\n* then we move on to the next bit\n\nThis is the sequence `..ABABn`.\n\n**Final insight:** remember that there are TWO unique candidates for the shortest sequence: `..ABABn` and `..BABAn`.\n\nSo we really need to do this algorithm twice:\n* once with `..ABABn`: the above steps\n* again with `..BABAn == ..ABAB(An) == ..ABAB(n^1)`\n\n# Approach\n\nHere are some details:\n* I used DP to get the moves needed to toggle the current bit: `cost` is `ops[i]` for the current `i`, updated in place\n* `n` in the loop is really `<prefix><currentBit>`, where we\'ve shifted away all the zeros\n* `baOps` is the algorithm above, which toggles the next bit (`n^2` in the loop), and THEN toggles the current bit. i.e. applies `..A` to it. Or in other words, `AB..ABABn`\n\nSo finally the answer is the lesser of\n* `baOps(n)` to clear `n` using `..ABn` directly\n* `baOps(n^1)+1` to first get `An` (1 op), then do `..AB(An) == ..BAn`\n\n# Complexity\n- Time complexity: logarithmic. Two passes over the set bits of `n`, one for `A` first and another for `B` first.\n\n- Space complexity: constant: just a bunch of counters and in-place DP\n\n# Code\n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n # FIRST: misunderstood problem, mixed up left and right\n # NEXT: wrote an algo before understanding the logic of n=6, and thus got wrong answers after a bunch of work\n\n\n # NOW: logically approach n=6 and go from there\n\n # INSIGHT: from having wrangled with this problem for a good long while:\n # operations are idempotent: A and B toggle\n # so sequences of A and B are idempotent e.g. if you do AB, then the inverse is BA because BAAB = BB = B\n # (so take a sequence, and apply in reverse order)\n \n # and because of the idempotence, the only move sequences are ...ABA or ...BAB\n\n # so we can apply A first, or B first (and can only do B if n is not a power of two, otherwise there\'s no prior bit to toggle)\n # although applying this to B would would just make a larger number, so we\'d find that\n # A first wins)\n\n # if n == 0: return 0\n # if n == 1: return 1\n\n # brute force: simulate the moves. We only have ...ABA or ...BAB to contend with\n # this looks like towers of Hanoi basically so setting and clearing a bit takes O(n**2) operations\n\n # ...ABA: clears LSB first. good if prior bit isn\'t 1. Otherwise we\'d clear LSB, then have to set LSB again to get 1, THEN apply B\n # ...BAB: clears second-to-last bit first, if there is one. Then the later ABABA before the ...BAB will clear the LSB\n\n # to clear bit i, starting at zero, where later bits are zero:\n # ops(0) is 1: apply A\n # ops(1) is 3: apply A to get 11, then B to get 01, then A to get 0\n # ops(2): set bit 1 in ops(1), then apply B to get 010, then apply ops(1) again to get 000.\n\n # so ops[i] = 2*ops[i-1]+1\n\n # now we put it all together:\n # if second to LSB is set, toggle it first with B to get some m < n.\n # then for each set bit we find, we need to clear it with ops[i] which is an ...ABA sequence\n\n # if n is a power of 2, it\'s 100..0. So our only option is to do A to get a suffix of 1, then B to get 11, then A for 10, etc. as we build up to clearing msb\n # if n isn\'t a power of 2, then it looks like 10..010..0\n # so applying B first gets us 10..110..0: it gets us one step closer to clearing MSB if it doesn\'t already.\n # then we apply the ..ABA sequence, Towers of Hanoi style\n\n # if n < 2:\n # return n # 0: already cleared. 1: apply A\n\n # l = n&-n\n # ans = 0\n # if n > l: # n not a power of two\n # ans += 1\n # n ^= l<<1 # toggle bit just right of lsb\n\n # cost = 0 # cost to clear prior bit; these are the ..ABA operations now\n # while n:\n # cost = 2*cost+1 # to clear next bit: set prior, clear current, unset prior\n # if n & 1: ans += cost\n # n >>= 1\n\n # return ans\n\n # 101001110\n # 101001000 in 1+ops(1): toggle prior, do b to clear prior, toggle 1 again\n # \n # \n # 1001: toggle 10: 1 op, then clear 1: 1 op. 2 ops\n # 1010: toggle 100 in 1 op, then clear 10 in 3 ops: 4 ops\n # 1100: toggle 1000 in 1 op, then clear 100 in 7 ps: 8 ops\n # total: 14 ops :)\n\n\n # pattern: if there\'s a larger bit, toggle it. We need to clear it if the next is msb, otherwise\n # we need to propagate up there\n # then we need to clear current bit by setting lower bit, using B, then clearing lower bit (i.e. pay cost)\n\n # for each bit: if there\'s a larger bit, and the current bit is set, toggle the next bit up using B\n # then use an ABAB.. sequence of `cost` moves to toggle off the current bit\n\n # cost = 0 # ops needed to clear current bit\n # ans = 0\n # while n:\n # cost = 2*cost + 1\n \n # if (n & 1) and (n > 1): # higher bit is set\n # n ^= 2\n # ans += 1\n\n # if n & 1:\n # ans += cost\n\n # n >>= 1\n\n # return ans\n\n # I think I see the problem now:\n # doing ... X 1 => ... !X 1 is B first\n # versus => ... !X 0 is A first\n # one is better than the other\n\n # so what we need to do is the above TWICE:\n # once on n: apply B, then A, then B, then A\n # once on n ^ 1: apply A, then apply B, then A, then B, ...\n # return the cheaper one\n\n def baOps(m: int) -> int:\n """Returns the number of operations we do if we start with B, then A, then B, etc."""\n ans = 0\n cost = 0 # cost to toggle current bit\n while m:\n cost = 2*cost + 1 # toggle lower bit to true, use B to toggle this, then toggle lower bit off again\n\n if (m&1) and (m>1):\n # current bit is set, and a higher bit is set: toggle next bit with B\n m ^= 2\n ans += 1\n\n if m&1:\n ans += cost\n\n m >>= 1\n\n return ans\n\n # choices: A and B are idempotent: A*A*n == n; B*B*n == n\n # so a sequence of moves like this: AABBAABABBBBABAAABBB \n # reduces to BA AB A B\n # B B A B\n # A B\n # In general: it\'s just ...*A*B*A*B, or ..*B*A*B*A\n # baOps counts ops for ...*A*B so we try\n # ...A*B*n: baOps\n # ...A*B*A*n == ...A*B(A*n) => 1 + baOps(n^1)\n return min(baOps(n), 1 + baOps(n^1))\n``` | 1 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
Python3: Math and Dynamic Programming | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | # Intuition\n\nI found this problem to be brutal, it took me literally HOURS to come up with it. So I guess I won\'t work at Oracle where this is asked apparently.\n\nIMO this is one of the hardest problems because you have to spend a LOT of time getting the alternating moves insight, then figure out that the move sequences are kind of like the Tower of Hanoi puzzle, and THEN you have to do the DP stuff and avoid off-by-one errors.\n\nAnyway, I\'ll skip all the false routes I went through (you can see them in the comments for honesty) and explain the answer I came up with.\n\n## Toggling is Idempotent\n\nSomething is idempotent if doing it twice is the same as not doing it at all. In mathier terms, it means an operation is its own inverse.\n\nToggling bits is its own inverse: if you toggle a bit twice, the second toggle undoes the first toggle.\n\nBoth operations (A and B) toggle bits, so **A and B are idempotent**.\n\n## The Shortest Sequences Alternate A and B\n\nSince we know they\'re idempotent, let\'s look at a sample sequence of moves:\n```\nAAABABABBAAABBBAABABB\n```\nWe know they\'re idempotent so we can reduce them as follows:\n```\nAAABABABBAAABBBAABABB\n ABABA A B BA # pairs AA and BB cancel: idempotent\n ABAB A # more pairs of AA and BB cancel\n # so in the end, the operations alternate\n```\nSo the equivalent sequence is just `ABABA`. **The shortest sequence alternates: `..ABABn` or `..BABAn`**\n\nNote: BAn means\n* apply `A` to `n`\n* then apply `B` to the result, `An`\n\nTherefore **the easiest solution is to simulate ..ABABn and ..BABAn directly, and exit when one of those goes to zero**. This solution is pretty slow though, because the sequence of moves is like the Tower of Hanoi solution: 1 bit takes one operation, then 2 bits takes about twice as many operations, and 3 bits takes another twice as many operations, and so on.\n\n## Speeding Up: Look at What the Operations Do:\n\n### A: Toggles the Ones Bit\n\n`An` is `A^1`: the right-most bit is flipped.\n\n### B: Toggles the Bit Right of the LSB\n\n`Bn` takes the bit `b` at position `i-1`, followed by all zeros (therefore `b` is the LSB), and toggles `b<<1`.\n\n### Clearing a Specific Bit\n\nAs we iterate `..BAn` and `..ABn`, suppose we have some remainder\n```\nr = 1100110100\n```\nTo clear the third bit, we need\n* to set the second bit to one: `ops[2]`\n* then apply `B` to toggle the third bit off: 1 operation\n* then set the second bit back to zero: `ops[2]`\n\nSo we need to toggle the second bit. To do that, we\'d:\n* toggle the first bit to one: `ops[1] = 1` operation\n* use B to toggle the second bit: 1 operation\n* toggle the first bit to zero: `ops[1] = 1` again\n\nSo a pattern emerges\n* toggling the last bit costs one operation: A\n* toggling bit `i` requires `ops[i] = ops[i-1] + 1 + ops[i-1]` operations\n * `ops[i]` to turn the next bit on\n * 1 operation `B` to toggle `i`\n * `ops[i]` to turn the next bit off again\n * so a total of `ops[i] = 2*ops[i-1]+1`.\n\nDynamic programming!\n\n### What are the moves?\n\nToggling the last bit is clearly A.\n\nToggling any other bit is B.\n\nThe move sequences of `ops[i]` are as follows:\n* `ops[1]`: toggle first bit: `A`\n* `ops[2]`: toggle second bit: `ABA`\n* `ops[3]`: toggle third: turn second on, do B, turn second off:\n * i.e. `ABA + B + ABA == ABABABA`\n\n### Putting it All Together\n\nSo for each current bit we can do the following:\n* if the current bit is 1:\n * if there\'s a higher bit, we need to toggle the next bit up. This is because that next bit is the most significant bit, or we need to set that bit to 1 later anyway to toggle off an even higher bit\n * then we need to clear this bit\n* if the current bit is 0:\n * we won\'t spend moves to toggle the current bit, because it\'s not set\n * we can\'t use operation B here because the current bit isn\'t set\n* then we move on to the next bit\n\nThis is the sequence `..ABABn`.\n\n**Final insight:** remember that there are TWO unique candidates for the shortest sequence: `..ABABn` and `..BABAn`.\n\nSo we really need to do this algorithm twice:\n* once with `..ABABn`: the above steps\n* again with `..BABAn == ..ABAB(An) == ..ABAB(n^1)`\n\n# Approach\n\nHere are some details:\n* I used DP to get the moves needed to toggle the current bit: `cost` is `ops[i]` for the current `i`, updated in place\n* `n` in the loop is really `<prefix><currentBit>`, where we\'ve shifted away all the zeros\n* `baOps` is the algorithm above, which toggles the next bit (`n^2` in the loop), and THEN toggles the current bit. i.e. applies `..A` to it. Or in other words, `AB..ABABn`\n\nSo finally the answer is the lesser of\n* `baOps(n)` to clear `n` using `..ABn` directly\n* `baOps(n^1)+1` to first get `An` (1 op), then do `..AB(An) == ..BAn`\n\n# Complexity\n- Time complexity: logarithmic. Two passes over the set bits of `n`, one for `A` first and another for `B` first.\n\n- Space complexity: constant: just a bunch of counters and in-place DP\n\n# Code\n```\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n # FIRST: misunderstood problem, mixed up left and right\n # NEXT: wrote an algo before understanding the logic of n=6, and thus got wrong answers after a bunch of work\n\n\n # NOW: logically approach n=6 and go from there\n\n # INSIGHT: from having wrangled with this problem for a good long while:\n # operations are idempotent: A and B toggle\n # so sequences of A and B are idempotent e.g. if you do AB, then the inverse is BA because BAAB = BB = B\n # (so take a sequence, and apply in reverse order)\n \n # and because of the idempotence, the only move sequences are ...ABA or ...BAB\n\n # so we can apply A first, or B first (and can only do B if n is not a power of two, otherwise there\'s no prior bit to toggle)\n # although applying this to B would would just make a larger number, so we\'d find that\n # A first wins)\n\n # if n == 0: return 0\n # if n == 1: return 1\n\n # brute force: simulate the moves. We only have ...ABA or ...BAB to contend with\n # this looks like towers of Hanoi basically so setting and clearing a bit takes O(n**2) operations\n\n # ...ABA: clears LSB first. good if prior bit isn\'t 1. Otherwise we\'d clear LSB, then have to set LSB again to get 1, THEN apply B\n # ...BAB: clears second-to-last bit first, if there is one. Then the later ABABA before the ...BAB will clear the LSB\n\n # to clear bit i, starting at zero, where later bits are zero:\n # ops(0) is 1: apply A\n # ops(1) is 3: apply A to get 11, then B to get 01, then A to get 0\n # ops(2): set bit 1 in ops(1), then apply B to get 010, then apply ops(1) again to get 000.\n\n # so ops[i] = 2*ops[i-1]+1\n\n # now we put it all together:\n # if second to LSB is set, toggle it first with B to get some m < n.\n # then for each set bit we find, we need to clear it with ops[i] which is an ...ABA sequence\n\n # if n is a power of 2, it\'s 100..0. So our only option is to do A to get a suffix of 1, then B to get 11, then A for 10, etc. as we build up to clearing msb\n # if n isn\'t a power of 2, then it looks like 10..010..0\n # so applying B first gets us 10..110..0: it gets us one step closer to clearing MSB if it doesn\'t already.\n # then we apply the ..ABA sequence, Towers of Hanoi style\n\n # if n < 2:\n # return n # 0: already cleared. 1: apply A\n\n # l = n&-n\n # ans = 0\n # if n > l: # n not a power of two\n # ans += 1\n # n ^= l<<1 # toggle bit just right of lsb\n\n # cost = 0 # cost to clear prior bit; these are the ..ABA operations now\n # while n:\n # cost = 2*cost+1 # to clear next bit: set prior, clear current, unset prior\n # if n & 1: ans += cost\n # n >>= 1\n\n # return ans\n\n # 101001110\n # 101001000 in 1+ops(1): toggle prior, do b to clear prior, toggle 1 again\n # \n # \n # 1001: toggle 10: 1 op, then clear 1: 1 op. 2 ops\n # 1010: toggle 100 in 1 op, then clear 10 in 3 ops: 4 ops\n # 1100: toggle 1000 in 1 op, then clear 100 in 7 ps: 8 ops\n # total: 14 ops :)\n\n\n # pattern: if there\'s a larger bit, toggle it. We need to clear it if the next is msb, otherwise\n # we need to propagate up there\n # then we need to clear current bit by setting lower bit, using B, then clearing lower bit (i.e. pay cost)\n\n # for each bit: if there\'s a larger bit, and the current bit is set, toggle the next bit up using B\n # then use an ABAB.. sequence of `cost` moves to toggle off the current bit\n\n # cost = 0 # ops needed to clear current bit\n # ans = 0\n # while n:\n # cost = 2*cost + 1\n \n # if (n & 1) and (n > 1): # higher bit is set\n # n ^= 2\n # ans += 1\n\n # if n & 1:\n # ans += cost\n\n # n >>= 1\n\n # return ans\n\n # I think I see the problem now:\n # doing ... X 1 => ... !X 1 is B first\n # versus => ... !X 0 is A first\n # one is better than the other\n\n # so what we need to do is the above TWICE:\n # once on n: apply B, then A, then B, then A\n # once on n ^ 1: apply A, then apply B, then A, then B, ...\n # return the cheaper one\n\n def baOps(m: int) -> int:\n """Returns the number of operations we do if we start with B, then A, then B, etc."""\n ans = 0\n cost = 0 # cost to toggle current bit\n while m:\n cost = 2*cost + 1 # toggle lower bit to true, use B to toggle this, then toggle lower bit off again\n\n if (m&1) and (m>1):\n # current bit is set, and a higher bit is set: toggle next bit with B\n m ^= 2\n ans += 1\n\n if m&1:\n ans += cost\n\n m >>= 1\n\n return ans\n\n # choices: A and B are idempotent: A*A*n == n; B*B*n == n\n # so a sequence of moves like this: AABBAABABBBBABAAABBB \n # reduces to BA AB A B\n # B B A B\n # A B\n # In general: it\'s just ...*A*B*A*B, or ..*B*A*B*A\n # baOps counts ops for ...*A*B so we try\n # ...A*B*n: baOps\n # ...A*B*A*n == ...A*B(A*n) => 1 + baOps(n^1)\n return min(baOps(n), 1 + baOps(n^1))\n``` | 1 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
A step-by-step understandable (but longer) solution | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | # Intuition\nThe intuition is to break the whole conversion process into four core operations (AnyToZero, AnyToPower, PowerToZero, and ZeroToPower) based on the two given basic operations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nFor example, if we want to convert any n-bit string ?????? into 0, there are two conditions:\n\n* The string is 1?????\nIn this case, we need to convert the remaining string ????? into 10...0, then we can remove the leading 1, and the remaining problem is to convert a 2-power (10...0) into 0.\n\n* The string is 0?????\nIn this case, the problem is reduced to a smaller problem - converting a (n-1)-bit string ????? into 0.\n\n\n\nThe above figure shows the relationship between the four core operations. The only problem is that the resulted code runs too slow due to the inefficient implementation of PowerToZero().\n\nLooking into the implementation of PowerToZero() and ZeroToPower(), we can find that they are exactly the same. Thus, we can re-implement PowerToZero() to recursively call it self. Then, it is not easy to get the mathematical formula.\n\n\n\n\n\n# Code\n```\nclass Solution:\n\n def AnyToZero(self, s): # n-bit string -> zero\n if len(s)==1: return int(s[0]==\'1\')\n\n if s[0]==\'1\':\n return self.AnyToPower(s[1:])+1+self.PowerToZero(len(s[1:]))\n else:\n return self.AnyToZero(s[1:])\n\n def AnyToPower(self, s): # n-bit string -> 1 + (n-1)-bit zeros\n if len(s)==1: return int(s[0]==\'0\')\n\n if s[0]==\'1\':\n return self.AnyToZero(s[1:])\n else:\n return self.AnyToPower(s[1:])+1+self.PowerToZero(len(s[1:]))\n\n def PowerToZero(self, n): # n-bit 10000...0 -> 0\n return 2**n-1\n\n def minimumOneBitOperations(self, num: int) -> int:\n return self.AnyToZero(bin(num)[2:])\n``` | 1 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
A step-by-step understandable (but longer) solution | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | # Intuition\nThe intuition is to break the whole conversion process into four core operations (AnyToZero, AnyToPower, PowerToZero, and ZeroToPower) based on the two given basic operations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nFor example, if we want to convert any n-bit string ?????? into 0, there are two conditions:\n\n* The string is 1?????\nIn this case, we need to convert the remaining string ????? into 10...0, then we can remove the leading 1, and the remaining problem is to convert a 2-power (10...0) into 0.\n\n* The string is 0?????\nIn this case, the problem is reduced to a smaller problem - converting a (n-1)-bit string ????? into 0.\n\n\n\nThe above figure shows the relationship between the four core operations. The only problem is that the resulted code runs too slow due to the inefficient implementation of PowerToZero().\n\nLooking into the implementation of PowerToZero() and ZeroToPower(), we can find that they are exactly the same. Thus, we can re-implement PowerToZero() to recursively call it self. Then, it is not easy to get the mathematical formula.\n\n\n\n\n\n# Code\n```\nclass Solution:\n\n def AnyToZero(self, s): # n-bit string -> zero\n if len(s)==1: return int(s[0]==\'1\')\n\n if s[0]==\'1\':\n return self.AnyToPower(s[1:])+1+self.PowerToZero(len(s[1:]))\n else:\n return self.AnyToZero(s[1:])\n\n def AnyToPower(self, s): # n-bit string -> 1 + (n-1)-bit zeros\n if len(s)==1: return int(s[0]==\'0\')\n\n if s[0]==\'1\':\n return self.AnyToZero(s[1:])\n else:\n return self.AnyToPower(s[1:])+1+self.PowerToZero(len(s[1:]))\n\n def PowerToZero(self, n): # n-bit 10000...0 -> 0\n return 2**n-1\n\n def minimumOneBitOperations(self, num: int) -> int:\n return self.AnyToZero(bin(num)[2:])\n``` | 1 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
[We💕Simple] One Liner! - Explanations. | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | ```Kotlin []\nclass Solution {\n fun minimumOneBitOperations(n: Int): Int =\n if (n != 0) n.takeHighestOneBit() * 2 - 1 - minimumOneBitOperations(n - n.takeHighestOneBit()) else 0\n}\n```\n```Python []\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n return 2**n.bit_length()-1 - self.minimumOneBitOperations(n-2**(n.bit_length()-1)) if n else 0\n\n```\n\nThe intuition behind solving this problem lies in carefully manipulating the binary representation of the integer `n` to transform it into 0, adhering to the specific operations allowed. Here\'s the breakdown of the thought process:\n\n1. **Binary Transformation Logic**: The operations outlined in the problem let us manipulate individual bits of `n`. The first operation is straightforward, allowing us to flip the rightmost bit. The second operation, however, is more complex, requiring the (i-1)th bit to be 1, with all bits from (i-2)th to the 0th being 0, to flip the ith bit.\n2. **Starting with the Highest Significant Bit**: The key strategy is to commence the transformation from the highest significant bit (HSB) of `n`. This bit, located at position `k` (using 0-based indexing from the right), is pivotal as it holds the highest value in the binary representation.\n3. **Operations to Flip the HSB**: To flip the HSB (let\'s say, the kth bit), we need all bits below it (from `k-1` to `0`) to be set to `1`. This precondition leads to a recursive pattern. Flipping the kth bit involves setting all bits below it to `1` (a sequence of operations), flipping the kth bit itself (one operation), and then resetting the lower bits back to `0` (another sequence of operations).\n4. **Recursive Operation Count**: The recursive nature of the problem is evident here. The total number of operations to flip the kth bit can be expressed as `count(k) = count(k-1) + 1 + count(k-1)`, where `count(k-1)` represents the number of operations needed to set all bits of a number (with its HSB at the `k-1`th position) to `1`. This simplifies to `2^k - 1`, making the expression `n.takeHighestOneBit() * 2 - 1` for the total operations needed.\n5. **Applying the Logic Recursively**: After handling the HSB, the same logic is applied to the remaining number. This approach effectively breaks down the problem into smaller sub-problems, each dealing with the next highest bit, following the same pattern until the number is reduced to 0.\n | 1 | Given an integer `n`, you must transform it into `0` using the following operations any number of times:
* Change the rightmost (`0th`) bit in the binary representation of `n`.
* Change the `ith` bit in the binary representation of `n` if the `(i-1)th` bit is set to `1` and the `(i-2)th` through `0th` bits are set to `0`.
Return _the minimum number of operations to transform_ `n` _into_ `0`_._
**Example 1:**
**Input:** n = 3
**Output:** 2
**Explanation:** The binary representation of 3 is "11 ".
"11 " -> "01 " with the 2nd operation since the 0th bit is 1.
"01 " -> "00 " with the 1st operation.
**Example 2:**
**Input:** n = 6
**Output:** 4
**Explanation:** The binary representation of 6 is "110 ".
"110 " -> "010 " with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010 " -> "011 " with the 1st operation.
"011 " -> "001 " with the 2nd operation since the 0th bit is 1.
"001 " -> "000 " with the 1st operation.
**Constraints:**
* `0 <= n <= 109` | Keep a map of each name and the smallest valid integer that can be appended as a suffix to it. If the name is not present in the map, you can use it without adding any suffixes. If the name is present in the map, append the smallest proper suffix, and add the new name to the map. |
[We💕Simple] One Liner! - Explanations. | minimum-one-bit-operations-to-make-integers-zero | 0 | 1 | ```Kotlin []\nclass Solution {\n fun minimumOneBitOperations(n: Int): Int =\n if (n != 0) n.takeHighestOneBit() * 2 - 1 - minimumOneBitOperations(n - n.takeHighestOneBit()) else 0\n}\n```\n```Python []\nclass Solution:\n def minimumOneBitOperations(self, n: int) -> int:\n return 2**n.bit_length()-1 - self.minimumOneBitOperations(n-2**(n.bit_length()-1)) if n else 0\n\n```\n\nThe intuition behind solving this problem lies in carefully manipulating the binary representation of the integer `n` to transform it into 0, adhering to the specific operations allowed. Here\'s the breakdown of the thought process:\n\n1. **Binary Transformation Logic**: The operations outlined in the problem let us manipulate individual bits of `n`. The first operation is straightforward, allowing us to flip the rightmost bit. The second operation, however, is more complex, requiring the (i-1)th bit to be 1, with all bits from (i-2)th to the 0th being 0, to flip the ith bit.\n2. **Starting with the Highest Significant Bit**: The key strategy is to commence the transformation from the highest significant bit (HSB) of `n`. This bit, located at position `k` (using 0-based indexing from the right), is pivotal as it holds the highest value in the binary representation.\n3. **Operations to Flip the HSB**: To flip the HSB (let\'s say, the kth bit), we need all bits below it (from `k-1` to `0`) to be set to `1`. This precondition leads to a recursive pattern. Flipping the kth bit involves setting all bits below it to `1` (a sequence of operations), flipping the kth bit itself (one operation), and then resetting the lower bits back to `0` (another sequence of operations).\n4. **Recursive Operation Count**: The recursive nature of the problem is evident here. The total number of operations to flip the kth bit can be expressed as `count(k) = count(k-1) + 1 + count(k-1)`, where `count(k-1)` represents the number of operations needed to set all bits of a number (with its HSB at the `k-1`th position) to `1`. This simplifies to `2^k - 1`, making the expression `n.takeHighestOneBit() * 2 - 1` for the total operations needed.\n5. **Applying the Logic Recursively**: After handling the HSB, the same logic is applied to the remaining number. This approach effectively breaks down the problem into smaller sub-problems, each dealing with the next highest bit, following the same pattern until the number is reduced to 0.\n | 1 | There is a biker going on a road trip. The road trip consists of `n + 1` points at different altitudes. The biker starts his trip on point `0` with altitude equal `0`.
You are given an integer array `gain` of length `n` where `gain[i]` is the **net gain in altitude** between points `i` and `i + 1` for all (`0 <= i < n)`. Return _the **highest altitude** of a point._
**Example 1:**
**Input:** gain = \[-5,1,5,0,-7\]
**Output:** 1
**Explanation:** The altitudes are \[0,-5,-4,1,1,-6\]. The highest is 1.
**Example 2:**
**Input:** gain = \[-4,-3,-2,-1,4,3,2\]
**Output:** 0
**Explanation:** The altitudes are \[0,-4,-7,-9,-10,-6,-3,-1\]. The highest is 0.
**Constraints:**
* `n == gain.length`
* `1 <= n <= 100`
* `-100 <= gain[i] <= 100` | The fastest way to convert n to zero is to remove all set bits starting from the leftmost one. Try some simple examples to learn the rule of how many steps are needed to remove one set bit. consider n=2^k case first, then solve for all n. |
A very simple solution. O(n) Time, O(1) Space | maximum-nesting-depth-of-the-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere isnt any need to use stack to solve this. You just need to observe that the deepest VPS has the highest consecutive opening brackets. So the max value that V(variable defined in my code) takes, is our answer.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxDepth(self, s: str) -> int:\n v=0\n res=0\n\n #Handle base case\n if not s:\n return 0\n \n #Iterate through the string\n for i in s:\n if i==\'(\':\n v+=1\n res=max(res,v)\n elif i==\')\':\n v-=1\n return res\n``` | 0 | A string is a **valid parentheses string** (denoted **VPS**) if it meets one of the following:
* It is an empty string `" "`, or a single character not equal to `"( "` or `") "`,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are **VPS**'s, or
* It can be written as `(A)`, where `A` is a **VPS**.
We can similarly define the **nesting depth** `depth(S)` of any VPS `S` as follows:
* `depth( " ") = 0`
* `depth(C) = 0`, where `C` is a string with a single character not equal to `"( "` or `") "`.
* `depth(A + B) = max(depth(A), depth(B))`, where `A` and `B` are **VPS**'s.
* `depth( "( " + A + ") ") = 1 + depth(A)`, where `A` is a **VPS**.
For example, `" "`, `"()() "`, and `"()(()()) "` are **VPS**'s (with nesting depths 0, 1, and 2), and `")( "` and `"(() "` are not **VPS**'s.
Given a **VPS** represented as string `s`, return _the **nesting depth** of_ `s`.
**Example 1:**
**Input:** s = "(1+(2\*3)+((8)/4))+1 "
**Output:** 3
**Explanation:** Digit 8 is inside of 3 nested parentheses in the string.
**Example 2:**
**Input:** s = "(1)+((2))+(((3))) "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of digits `0-9` and characters `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* It is guaranteed that parentheses expression `s` is a **VPS**. | null |
A very simple solution. O(n) Time, O(1) Space | maximum-nesting-depth-of-the-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere isnt any need to use stack to solve this. You just need to observe that the deepest VPS has the highest consecutive opening brackets. So the max value that V(variable defined in my code) takes, is our answer.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxDepth(self, s: str) -> int:\n v=0\n res=0\n\n #Handle base case\n if not s:\n return 0\n \n #Iterate through the string\n for i in s:\n if i==\'(\':\n v+=1\n res=max(res,v)\n elif i==\')\':\n v-=1\n return res\n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Simple stack solution | maximum-nesting-depth-of-the-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxDepth(self, s: str) -> int:\n stack = []\n maxi = 0\n for char in s:\n if char == \'(\':\n stack.append(char)\n if len(stack) > maxi:\n maxi = len(stack)\n elif char == \')\':\n stack.pop(-1)\n return maxi\n``` | 1 | A string is a **valid parentheses string** (denoted **VPS**) if it meets one of the following:
* It is an empty string `" "`, or a single character not equal to `"( "` or `") "`,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are **VPS**'s, or
* It can be written as `(A)`, where `A` is a **VPS**.
We can similarly define the **nesting depth** `depth(S)` of any VPS `S` as follows:
* `depth( " ") = 0`
* `depth(C) = 0`, where `C` is a string with a single character not equal to `"( "` or `") "`.
* `depth(A + B) = max(depth(A), depth(B))`, where `A` and `B` are **VPS**'s.
* `depth( "( " + A + ") ") = 1 + depth(A)`, where `A` is a **VPS**.
For example, `" "`, `"()() "`, and `"()(()()) "` are **VPS**'s (with nesting depths 0, 1, and 2), and `")( "` and `"(() "` are not **VPS**'s.
Given a **VPS** represented as string `s`, return _the **nesting depth** of_ `s`.
**Example 1:**
**Input:** s = "(1+(2\*3)+((8)/4))+1 "
**Output:** 3
**Explanation:** Digit 8 is inside of 3 nested parentheses in the string.
**Example 2:**
**Input:** s = "(1)+((2))+(((3))) "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of digits `0-9` and characters `'+'`, `'-'`, `'*'`, `'/'`, `'('`, and `')'`.
* It is guaranteed that parentheses expression `s` is a **VPS**. | null |
Simple stack solution | maximum-nesting-depth-of-the-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxDepth(self, s: str) -> int:\n stack = []\n maxi = 0\n for char in s:\n if char == \'(\':\n stack.append(char)\n if len(stack) > maxi:\n maxi = len(stack)\n elif char == \')\':\n stack.pop(-1)\n return maxi\n``` | 1 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
C++/Python adjacent Matrix and degree array->O(V+E) | maximal-network-rank | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWith the hint "The network rank of two vertices is almost the sum of their degrees", it is a little bit clearer. But\n"almost" means that is not exactly, so what is the exception?\n\n1.The edge that connecting these both vertices.\n2.It could be 0 if these is no path connecting these both vertices!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe implementation assumes that the graph for this infastruture is connected.\n1. Declare the containers for adjacent matrix and degrees\n2. Compute degree for each vertex and build the adjacent matrix.\n3. Compute the rank every pair (i, j) and find the maximal rank.\n\nThe step 3 costs $V(V-1)/2$ iterations which can be furthermore improved. Is it possible replace step 3 by other procedure with average runtime $O(V)$?\n# 1st solution needs run time O(V^2+E) but can be improved to O(V+E) in average\n\nThe 2nd approach is proceeded as follows:\n\n1. Construct array i_max storing the indexes i\'s with maximal degree.Since some graph has more vertices with the same max degree.\n2. Deal with the case of array i_max having more than 1 elements. If |i_max|=O(1), it\'s fine. But at worse, there are $O(V)$ such elements and there are $O(V^2)$ edges among them, it\'s rare; in that case TC remains still $O(V^2+E)$.\n3. Deal with the case of the array i_max having only 1 element. The process is "almost" to find the second biggest degree. In this case, running time can be reduced to $O(V+E)$.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(V^2+E)\\to O(V+E)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(V+E)$$\n# Code\n```\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n vector<unordered_set<int>> adj(n);\n vector<int> deg(n, 0);\n for (auto& edge: roads){\n int v=edge[0], w=edge[1];\n deg[v]++;\n deg[w]++;\n adj[v].insert(w);\n adj[w].insert(v);\n }\n\n int max_rank=0;\n for(int i=0; i<n; i++){//Supposed that this graph is connected\n for(int j=0; j<i; j++){\n int rank=deg[i]+deg[j]-adj[i].count(j);\n max_rank=max(max_rank, rank);\n }\n }\n return max_rank;\n }\n};\n```\n# Code with O(V+E) time complexity\n\n\n```C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n vector<bitset<101>> adj(n);\n vector<int> deg(n, 0);\n for (auto& edge: roads){\n int v=edge[0], w=edge[1];\n deg[v]++;\n deg[w]++;\n adj[v][w]=adj[w][v]=1;\n }\n \n //Supposed that this graph is connected\n int deg_max=*max_element(deg.begin(), deg.end());\n vector<int> i_max; //some graph has more vertices with max deg\n for(int i=0; i<n; i++)\n if(deg[i]==deg_max) i_max.push_back(i);\n int s_deg=i_max.size();\n\n // cout<<"i_max.size="<<s_deg<<endl;\n if (s_deg>1){\n for (int i=1; i<s_deg; i++){\n for (int j=0; j<i; j++)\n if (adj[i_max[i]][i_max[j]]==0) //no edge between\n return 2*deg_max;\n }\n return 2*deg_max-1;//all vertices with max deg have edges mutual\n }\n //The following deals with the case s_deg=1. i.e. only one max deg\n int i_max0=i_max[0];\n int max_rank=0;\n //Find the max_rank by considering \n //rank=deg_max+deg[j]-adj[i_max0][j]\n for(int j=0; j<n; j++){\n if (j==i_max0) continue;\n int rank=deg_max+deg[j]-adj[i_max0][j];\n // cout<<rank<<endl;\n max_rank=max(max_rank, rank);\n }\n return max_rank;\n }\n};\n```\n```python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n adj=[set() for _ in range(n)]\n deg=[0]*n\n for edge in roads:\n v, w=edge\n deg[v]+=1\n deg[w]+=1\n adj[v].add(w)\n adj[w].add(v)\n\n deg_max=max(deg)\n i_max=[]\n for i in range(n):\n if deg[i]==deg_max: i_max.append(i)\n s_deg=len(i_max)\n # More than 1 max deg\n if s_deg>1:\n for i in range(s_deg):\n for j in range(i):\n if i_max[j] not in adj[i_max[i]]:\n return 2*deg_max\n return 2*deg_max-1\n\n # Only one max deg\n i_max0=i_max[0]\n max_rank=0\n for j in range(n):\n if j==i_max0: continue\n rank=deg_max+deg[j]\n if j in adj[i_max0]: rank-=1\n max_rank=max(max_rank, rank)\n \n return max_rank\n``` | 6 | There is an infrastructure of `n` cities with some number of `roads` connecting these cities. Each `roads[i] = [ai, bi]` indicates that there is a bidirectional road between cities `ai` and `bi`.
The **network rank** of **two different cities** is defined as the total number of **directly** connected roads to **either** city. If a road is directly connected to both cities, it is only counted **once**.
The **maximal network rank** of the infrastructure is the **maximum network rank** of all pairs of different cities.
Given the integer `n` and the array `roads`, return _the **maximal network rank** of the entire infrastructure_.
**Example 1:**
**Input:** n = 4, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 4
**Explanation:** The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
**Example 2:**
**Input:** n = 5, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\],\[2,3\],\[2,4\]\]
**Output:** 5
**Explanation:** There are 5 roads that are connected to cities 1 or 2.
**Example 3:**
**Input:** n = 8, roads = \[\[0,1\],\[1,2\],\[2,3\],\[2,4\],\[5,6\],\[5,7\]\]
**Output:** 5
**Explanation:** The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
**Constraints:**
* `2 <= n <= 100`
* `0 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 2`
* `0 <= ai, bi <= n-1`
* `ai != bi`
* Each pair of cities has **at most one** road connecting them. | Compute all sums and save it in array. Then just go from LEFT to RIGHT index and calculate answer modulo 1e9 + 7. |
C++/Python adjacent Matrix and degree array->O(V+E) | maximal-network-rank | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWith the hint "The network rank of two vertices is almost the sum of their degrees", it is a little bit clearer. But\n"almost" means that is not exactly, so what is the exception?\n\n1.The edge that connecting these both vertices.\n2.It could be 0 if these is no path connecting these both vertices!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe implementation assumes that the graph for this infastruture is connected.\n1. Declare the containers for adjacent matrix and degrees\n2. Compute degree for each vertex and build the adjacent matrix.\n3. Compute the rank every pair (i, j) and find the maximal rank.\n\nThe step 3 costs $V(V-1)/2$ iterations which can be furthermore improved. Is it possible replace step 3 by other procedure with average runtime $O(V)$?\n# 1st solution needs run time O(V^2+E) but can be improved to O(V+E) in average\n\nThe 2nd approach is proceeded as follows:\n\n1. Construct array i_max storing the indexes i\'s with maximal degree.Since some graph has more vertices with the same max degree.\n2. Deal with the case of array i_max having more than 1 elements. If |i_max|=O(1), it\'s fine. But at worse, there are $O(V)$ such elements and there are $O(V^2)$ edges among them, it\'s rare; in that case TC remains still $O(V^2+E)$.\n3. Deal with the case of the array i_max having only 1 element. The process is "almost" to find the second biggest degree. In this case, running time can be reduced to $O(V+E)$.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(V^2+E)\\to O(V+E)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(V+E)$$\n# Code\n```\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n vector<unordered_set<int>> adj(n);\n vector<int> deg(n, 0);\n for (auto& edge: roads){\n int v=edge[0], w=edge[1];\n deg[v]++;\n deg[w]++;\n adj[v].insert(w);\n adj[w].insert(v);\n }\n\n int max_rank=0;\n for(int i=0; i<n; i++){//Supposed that this graph is connected\n for(int j=0; j<i; j++){\n int rank=deg[i]+deg[j]-adj[i].count(j);\n max_rank=max(max_rank, rank);\n }\n }\n return max_rank;\n }\n};\n```\n# Code with O(V+E) time complexity\n\n\n```C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n vector<bitset<101>> adj(n);\n vector<int> deg(n, 0);\n for (auto& edge: roads){\n int v=edge[0], w=edge[1];\n deg[v]++;\n deg[w]++;\n adj[v][w]=adj[w][v]=1;\n }\n \n //Supposed that this graph is connected\n int deg_max=*max_element(deg.begin(), deg.end());\n vector<int> i_max; //some graph has more vertices with max deg\n for(int i=0; i<n; i++)\n if(deg[i]==deg_max) i_max.push_back(i);\n int s_deg=i_max.size();\n\n // cout<<"i_max.size="<<s_deg<<endl;\n if (s_deg>1){\n for (int i=1; i<s_deg; i++){\n for (int j=0; j<i; j++)\n if (adj[i_max[i]][i_max[j]]==0) //no edge between\n return 2*deg_max;\n }\n return 2*deg_max-1;//all vertices with max deg have edges mutual\n }\n //The following deals with the case s_deg=1. i.e. only one max deg\n int i_max0=i_max[0];\n int max_rank=0;\n //Find the max_rank by considering \n //rank=deg_max+deg[j]-adj[i_max0][j]\n for(int j=0; j<n; j++){\n if (j==i_max0) continue;\n int rank=deg_max+deg[j]-adj[i_max0][j];\n // cout<<rank<<endl;\n max_rank=max(max_rank, rank);\n }\n return max_rank;\n }\n};\n```\n```python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n adj=[set() for _ in range(n)]\n deg=[0]*n\n for edge in roads:\n v, w=edge\n deg[v]+=1\n deg[w]+=1\n adj[v].add(w)\n adj[w].add(v)\n\n deg_max=max(deg)\n i_max=[]\n for i in range(n):\n if deg[i]==deg_max: i_max.append(i)\n s_deg=len(i_max)\n # More than 1 max deg\n if s_deg>1:\n for i in range(s_deg):\n for j in range(i):\n if i_max[j] not in adj[i_max[i]]:\n return 2*deg_max\n return 2*deg_max-1\n\n # Only one max deg\n i_max0=i_max[0]\n max_rank=0\n for j in range(n):\n if j==i_max0: continue\n rank=deg_max+deg[j]\n if j in adj[i_max0]: rank-=1\n max_rank=max(max_rank, rank)\n \n return max_rank\n``` | 6 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Python3 Solution | maximal-network-rank | 0 | 1 | \n```\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n g=[[False]*n for _ in range(n)]\n for x,y in roads:\n g[x][y]=g[y][x]=True\n\n ans=0\n for i in range(n):\n for j in range(n):\n if i==j:\n continue\n\n cur=0\n for k in range(n):\n if k!=i and k!=j:\n if g[i][k]:\n cur+=1\n\n if g[j][k]:\n cur+=1\n\n if g[i][j]:\n cur+=1\n\n ans=max(cur,ans)\n\n return ans \n``` | 3 | There is an infrastructure of `n` cities with some number of `roads` connecting these cities. Each `roads[i] = [ai, bi]` indicates that there is a bidirectional road between cities `ai` and `bi`.
The **network rank** of **two different cities** is defined as the total number of **directly** connected roads to **either** city. If a road is directly connected to both cities, it is only counted **once**.
The **maximal network rank** of the infrastructure is the **maximum network rank** of all pairs of different cities.
Given the integer `n` and the array `roads`, return _the **maximal network rank** of the entire infrastructure_.
**Example 1:**
**Input:** n = 4, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 4
**Explanation:** The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
**Example 2:**
**Input:** n = 5, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\],\[2,3\],\[2,4\]\]
**Output:** 5
**Explanation:** There are 5 roads that are connected to cities 1 or 2.
**Example 3:**
**Input:** n = 8, roads = \[\[0,1\],\[1,2\],\[2,3\],\[2,4\],\[5,6\],\[5,7\]\]
**Output:** 5
**Explanation:** The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
**Constraints:**
* `2 <= n <= 100`
* `0 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 2`
* `0 <= ai, bi <= n-1`
* `ai != bi`
* Each pair of cities has **at most one** road connecting them. | Compute all sums and save it in array. Then just go from LEFT to RIGHT index and calculate answer modulo 1e9 + 7. |
Python3 Solution | maximal-network-rank | 0 | 1 | \n```\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n g=[[False]*n for _ in range(n)]\n for x,y in roads:\n g[x][y]=g[y][x]=True\n\n ans=0\n for i in range(n):\n for j in range(n):\n if i==j:\n continue\n\n cur=0\n for k in range(n):\n if k!=i and k!=j:\n if g[i][k]:\n cur+=1\n\n if g[j][k]:\n cur+=1\n\n if g[i][j]:\n cur+=1\n\n ans=max(cur,ans)\n\n return ans \n``` | 3 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Python Elegant & Short | Vertex Degrees | maximal-network-rank | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n graph = defaultdict(set)\n\n for u, v in roads:\n graph[u].add(v)\n graph[v].add(u)\n\n return max(\n len(graph[i]) + len(graph[j]) - (i in graph[j])\n for i in range(n)\n for j in range(i + 1, n)\n )\n``` | 2 | There is an infrastructure of `n` cities with some number of `roads` connecting these cities. Each `roads[i] = [ai, bi]` indicates that there is a bidirectional road between cities `ai` and `bi`.
The **network rank** of **two different cities** is defined as the total number of **directly** connected roads to **either** city. If a road is directly connected to both cities, it is only counted **once**.
The **maximal network rank** of the infrastructure is the **maximum network rank** of all pairs of different cities.
Given the integer `n` and the array `roads`, return _the **maximal network rank** of the entire infrastructure_.
**Example 1:**
**Input:** n = 4, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 4
**Explanation:** The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
**Example 2:**
**Input:** n = 5, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\],\[2,3\],\[2,4\]\]
**Output:** 5
**Explanation:** There are 5 roads that are connected to cities 1 or 2.
**Example 3:**
**Input:** n = 8, roads = \[\[0,1\],\[1,2\],\[2,3\],\[2,4\],\[5,6\],\[5,7\]\]
**Output:** 5
**Explanation:** The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
**Constraints:**
* `2 <= n <= 100`
* `0 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 2`
* `0 <= ai, bi <= n-1`
* `ai != bi`
* Each pair of cities has **at most one** road connecting them. | Compute all sums and save it in array. Then just go from LEFT to RIGHT index and calculate answer modulo 1e9 + 7. |
Python Elegant & Short | Vertex Degrees | maximal-network-rank | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n graph = defaultdict(set)\n\n for u, v in roads:\n graph[u].add(v)\n graph[v].add(u)\n\n return max(\n len(graph[i]) + len(graph[j]) - (i in graph[j])\n for i in range(n)\n for j in range(i + 1, n)\n )\n``` | 2 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Optimized Solution | C++, Java, Python | With Explanation | maximal-network-rank | 1 | 1 | # Intuition\nCounting degree for all cities and checking for all possible pairs of cities also gives us a AC but do we really need to check for all pairs of cities?\n\n# Approach\nThere are just 2 cases to consider here.\n\n##### **Case 1: Multiple Cities with Max Degree:**\nIf all of maxDegree cities are directly connected answer will be `2 * maxDegree - 1` as the edge that connects any two maxDegree cities will be only counted once.\nOtherwise, answer will `2 * maxDegree` as we can consider any 2 disconnected cities for maximal network rank.\n\n##### **Case 2: Single Cities with Max Degree:**\nIf the single maxDegree city is directly connected to all secondMaxDegree cities the answer will be `maxDegree + secMaxDegree - 1` as the edge which directly connects them both will be counted once.\nOtherwise, answer will be `maxDegree + secMaxDegree` as we can consider any disconnected second max degree city for maximal network rank.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n // Make a adjacency matrix for the graph\n // and store degree count for each vertex\n vector<int> degrees(n, 0);\n vector<vector<bool>> isConnected(n, vector<bool>(n, 0));\n for(auto road : roads) {\n int a = road[0], b = road[1];\n degrees[a]++;\n degrees[b]++;\n isConnected[a][b] = 1;\n isConnected[b][a] = 1;\n }\n\n // Find out maximum & second maximum degrees in the graph\n int maxDegree = 0, secMaxDegree = 0;\n for(int degree : degrees) {\n if(degree > maxDegree) {\n secMaxDegree = maxDegree;\n maxDegree = degree;\n }\n else if(degree > secMaxDegree && degree != maxDegree) {\n secMaxDegree = degree;\n }\n }\n\n // store cities/vertices with max & second max degree count\n vector<int> maxCities, secMaxCities;\n for(int city = 0; city < n; city++) {\n if(degrees[city] == maxDegree) {\n maxCities.push_back(city);\n }\n else if(degrees[city] == secMaxDegree) {\n secMaxCities.push_back(city);\n }\n }\n\n // if we are having more than 1 cities with max degrees\n if(maxCities.size() > 1) {\n for(int i = 0; i < maxCities.size(); i++) {\n for(int j = i + 1; j < maxCities.size(); j++) {\n int u = maxCities[i], v = maxCities[j];\n // If any of 2 max degree cities are not directly connected\n // then answer is (2 * maxDegree)\n if(!isConnected[u][v]) {\n return (2 * maxDegree);\n }\n }\n }\n\n // If all of them are directly connected\n // then answer is (2 * maxDegree - 1)\n return (2 * maxDegree) - 1;\n }\n \n // If there is a single max Degree city\n int u = maxCities[0];\n for(int i = 0; i < secMaxCities.size(); i++) {\n int v = secMaxCities[i];\n\n // If any of max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree)\n if(!isConnected[u][v]) {\n return (maxDegree + secMaxDegree);\n }\n }\n\n // If all max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree - 1)\n return (maxDegree + secMaxDegree - 1);\n }\n};\n```\n``` Java []\nclass Solution {\n public int maximalNetworkRank(int n, int[][] roads) {\n // Make a adjacency matrix for the graph\n // and store degree count for each vertex\n int[] degrees = new int[n];\n boolean[][] isConnected = new boolean[n][n];\n for (int[] road : roads) {\n int a = road[0], b = road[1];\n degrees[a]++;\n degrees[b]++;\n isConnected[a][b] = true;\n isConnected[b][a] = true;\n }\n\n // Find out maximum & second maximum degrees in the graph\n int maxDegree = 0, secMaxDegree = 0;\n for (int degree : degrees) {\n if (degree > maxDegree) {\n secMaxDegree = maxDegree;\n maxDegree = degree;\n } else if (degree > secMaxDegree && degree != maxDegree) {\n secMaxDegree = degree;\n }\n }\n\n // store cities/vertices with max & second max degree count\n List<Integer> maxCities = new ArrayList<>();\n List<Integer> secMaxCities = new ArrayList<>();\n for (int city = 0; city < n; city++) {\n if (degrees[city] == maxDegree) {\n maxCities.add(city);\n } else if (degrees[city] == secMaxDegree) {\n secMaxCities.add(city);\n }\n }\n\n // if we are having more than 1 cities with max degrees\n if (maxCities.size() > 1) {\n for (int i = 0; i < maxCities.size(); i++) {\n for (int j = i + 1; j < maxCities.size(); j++) {\n int u = maxCities.get(i), v = maxCities.get(j);\n // If any of 2 max degree cities are not directly connected\n // then answer is (2 * maxDegree)\n if (!isConnected[u][v]) {\n return (2 * maxDegree);\n }\n }\n }\n\n // If all of them are directly connected\n // then answer is (2 * maxDegree - 1)\n return (2 * maxDegree) - 1;\n }\n\n // If there is a single max Degree city\n int u = maxCities.get(0);\n for (int i = 0; i < secMaxCities.size(); i++) {\n int v = secMaxCities.get(i);\n\n // If any of max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree)\n if (!isConnected[u][v]) {\n return (maxDegree + secMaxDegree);\n }\n }\n\n // If all max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree - 1)\n return (maxDegree + secMaxDegree - 1);\n }\n}\n```\n```Python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n # Make a adjacency matrix for the graph\n # and store degree count for each vertex\n degrees = [0] * n\n isConnected = [[False] * n for _ in range(n)]\n for road in roads:\n a, b = road[0], road[1]\n degrees[a] += 1\n degrees[b] += 1\n isConnected[a][b] = True\n isConnected[b][a] = True\n\n # Find out maximum & second maximum degrees in the graph\n maxDegree = 0\n secMaxDegree = 0\n for degree in degrees:\n if degree > maxDegree:\n secMaxDegree = maxDegree\n maxDegree = degree\n elif degree > secMaxDegree and degree != maxDegree:\n secMaxDegree = degree\n\n # store cities/vertices with max & second max degree count\n maxCities = []\n secMaxCities = []\n for i in range(n):\n if degrees[i] == maxDegree:\n maxCities.append(i)\n elif degrees[i] == secMaxDegree:\n secMaxCities.append(i)\n\n # if we are having more than 1 cities with max degrees\n if len(maxCities) > 1:\n for i in range(len(maxCities)):\n for j in range(i + 1, len(maxCities)):\n u, v = maxCities[i], maxCities[j]\n # If any of 2 max degree cities are not directly connected\n # then answer is (2 * maxDegree)\n if not isConnected[u][v]:\n return 2 * maxDegree\n\n # If all of them are directly connected\n # then answer is (2 * maxDegree - 1)\n return 2 * maxDegree - 1\n\n # If there is a single max Degree city\n u = maxCities[0]\n for i in range(len(secMaxCities)):\n v = secMaxCities[i]\n\n # If any of max degree - second max degree cities \n # are not directly connected\n # then answer is (maxDegree + secondMaxDegree)\n if not isConnected[u][v]:\n return maxDegree + secMaxDegree\n\n # If all max degree - second max degree cities \n # are not directly connected\n return maxDegree + secMaxDegree - 1\n\n```\n# Complexity\n- Time complexity:\n$$O(n)$$ for the average case,\nbut $$O(n^2)$$ at the worst case if all cities have same degree and they all are directly connected we will end up checking all pairs of cities.\n\n- Space complexity:\n$$O(n^2)$$, Majorly for the adjacency Matrix. | 6 | There is an infrastructure of `n` cities with some number of `roads` connecting these cities. Each `roads[i] = [ai, bi]` indicates that there is a bidirectional road between cities `ai` and `bi`.
The **network rank** of **two different cities** is defined as the total number of **directly** connected roads to **either** city. If a road is directly connected to both cities, it is only counted **once**.
The **maximal network rank** of the infrastructure is the **maximum network rank** of all pairs of different cities.
Given the integer `n` and the array `roads`, return _the **maximal network rank** of the entire infrastructure_.
**Example 1:**
**Input:** n = 4, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 4
**Explanation:** The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
**Example 2:**
**Input:** n = 5, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\],\[2,3\],\[2,4\]\]
**Output:** 5
**Explanation:** There are 5 roads that are connected to cities 1 or 2.
**Example 3:**
**Input:** n = 8, roads = \[\[0,1\],\[1,2\],\[2,3\],\[2,4\],\[5,6\],\[5,7\]\]
**Output:** 5
**Explanation:** The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
**Constraints:**
* `2 <= n <= 100`
* `0 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 2`
* `0 <= ai, bi <= n-1`
* `ai != bi`
* Each pair of cities has **at most one** road connecting them. | Compute all sums and save it in array. Then just go from LEFT to RIGHT index and calculate answer modulo 1e9 + 7. |
Optimized Solution | C++, Java, Python | With Explanation | maximal-network-rank | 1 | 1 | # Intuition\nCounting degree for all cities and checking for all possible pairs of cities also gives us a AC but do we really need to check for all pairs of cities?\n\n# Approach\nThere are just 2 cases to consider here.\n\n##### **Case 1: Multiple Cities with Max Degree:**\nIf all of maxDegree cities are directly connected answer will be `2 * maxDegree - 1` as the edge that connects any two maxDegree cities will be only counted once.\nOtherwise, answer will `2 * maxDegree` as we can consider any 2 disconnected cities for maximal network rank.\n\n##### **Case 2: Single Cities with Max Degree:**\nIf the single maxDegree city is directly connected to all secondMaxDegree cities the answer will be `maxDegree + secMaxDegree - 1` as the edge which directly connects them both will be counted once.\nOtherwise, answer will be `maxDegree + secMaxDegree` as we can consider any disconnected second max degree city for maximal network rank.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n // Make a adjacency matrix for the graph\n // and store degree count for each vertex\n vector<int> degrees(n, 0);\n vector<vector<bool>> isConnected(n, vector<bool>(n, 0));\n for(auto road : roads) {\n int a = road[0], b = road[1];\n degrees[a]++;\n degrees[b]++;\n isConnected[a][b] = 1;\n isConnected[b][a] = 1;\n }\n\n // Find out maximum & second maximum degrees in the graph\n int maxDegree = 0, secMaxDegree = 0;\n for(int degree : degrees) {\n if(degree > maxDegree) {\n secMaxDegree = maxDegree;\n maxDegree = degree;\n }\n else if(degree > secMaxDegree && degree != maxDegree) {\n secMaxDegree = degree;\n }\n }\n\n // store cities/vertices with max & second max degree count\n vector<int> maxCities, secMaxCities;\n for(int city = 0; city < n; city++) {\n if(degrees[city] == maxDegree) {\n maxCities.push_back(city);\n }\n else if(degrees[city] == secMaxDegree) {\n secMaxCities.push_back(city);\n }\n }\n\n // if we are having more than 1 cities with max degrees\n if(maxCities.size() > 1) {\n for(int i = 0; i < maxCities.size(); i++) {\n for(int j = i + 1; j < maxCities.size(); j++) {\n int u = maxCities[i], v = maxCities[j];\n // If any of 2 max degree cities are not directly connected\n // then answer is (2 * maxDegree)\n if(!isConnected[u][v]) {\n return (2 * maxDegree);\n }\n }\n }\n\n // If all of them are directly connected\n // then answer is (2 * maxDegree - 1)\n return (2 * maxDegree) - 1;\n }\n \n // If there is a single max Degree city\n int u = maxCities[0];\n for(int i = 0; i < secMaxCities.size(); i++) {\n int v = secMaxCities[i];\n\n // If any of max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree)\n if(!isConnected[u][v]) {\n return (maxDegree + secMaxDegree);\n }\n }\n\n // If all max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree - 1)\n return (maxDegree + secMaxDegree - 1);\n }\n};\n```\n``` Java []\nclass Solution {\n public int maximalNetworkRank(int n, int[][] roads) {\n // Make a adjacency matrix for the graph\n // and store degree count for each vertex\n int[] degrees = new int[n];\n boolean[][] isConnected = new boolean[n][n];\n for (int[] road : roads) {\n int a = road[0], b = road[1];\n degrees[a]++;\n degrees[b]++;\n isConnected[a][b] = true;\n isConnected[b][a] = true;\n }\n\n // Find out maximum & second maximum degrees in the graph\n int maxDegree = 0, secMaxDegree = 0;\n for (int degree : degrees) {\n if (degree > maxDegree) {\n secMaxDegree = maxDegree;\n maxDegree = degree;\n } else if (degree > secMaxDegree && degree != maxDegree) {\n secMaxDegree = degree;\n }\n }\n\n // store cities/vertices with max & second max degree count\n List<Integer> maxCities = new ArrayList<>();\n List<Integer> secMaxCities = new ArrayList<>();\n for (int city = 0; city < n; city++) {\n if (degrees[city] == maxDegree) {\n maxCities.add(city);\n } else if (degrees[city] == secMaxDegree) {\n secMaxCities.add(city);\n }\n }\n\n // if we are having more than 1 cities with max degrees\n if (maxCities.size() > 1) {\n for (int i = 0; i < maxCities.size(); i++) {\n for (int j = i + 1; j < maxCities.size(); j++) {\n int u = maxCities.get(i), v = maxCities.get(j);\n // If any of 2 max degree cities are not directly connected\n // then answer is (2 * maxDegree)\n if (!isConnected[u][v]) {\n return (2 * maxDegree);\n }\n }\n }\n\n // If all of them are directly connected\n // then answer is (2 * maxDegree - 1)\n return (2 * maxDegree) - 1;\n }\n\n // If there is a single max Degree city\n int u = maxCities.get(0);\n for (int i = 0; i < secMaxCities.size(); i++) {\n int v = secMaxCities.get(i);\n\n // If any of max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree)\n if (!isConnected[u][v]) {\n return (maxDegree + secMaxDegree);\n }\n }\n\n // If all max degree - second max degree cities \n // are not directly connected\n // then answer is (maxDegree + secondMaxDegree - 1)\n return (maxDegree + secMaxDegree - 1);\n }\n}\n```\n```Python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n # Make a adjacency matrix for the graph\n # and store degree count for each vertex\n degrees = [0] * n\n isConnected = [[False] * n for _ in range(n)]\n for road in roads:\n a, b = road[0], road[1]\n degrees[a] += 1\n degrees[b] += 1\n isConnected[a][b] = True\n isConnected[b][a] = True\n\n # Find out maximum & second maximum degrees in the graph\n maxDegree = 0\n secMaxDegree = 0\n for degree in degrees:\n if degree > maxDegree:\n secMaxDegree = maxDegree\n maxDegree = degree\n elif degree > secMaxDegree and degree != maxDegree:\n secMaxDegree = degree\n\n # store cities/vertices with max & second max degree count\n maxCities = []\n secMaxCities = []\n for i in range(n):\n if degrees[i] == maxDegree:\n maxCities.append(i)\n elif degrees[i] == secMaxDegree:\n secMaxCities.append(i)\n\n # if we are having more than 1 cities with max degrees\n if len(maxCities) > 1:\n for i in range(len(maxCities)):\n for j in range(i + 1, len(maxCities)):\n u, v = maxCities[i], maxCities[j]\n # If any of 2 max degree cities are not directly connected\n # then answer is (2 * maxDegree)\n if not isConnected[u][v]:\n return 2 * maxDegree\n\n # If all of them are directly connected\n # then answer is (2 * maxDegree - 1)\n return 2 * maxDegree - 1\n\n # If there is a single max Degree city\n u = maxCities[0]\n for i in range(len(secMaxCities)):\n v = secMaxCities[i]\n\n # If any of max degree - second max degree cities \n # are not directly connected\n # then answer is (maxDegree + secondMaxDegree)\n if not isConnected[u][v]:\n return maxDegree + secMaxDegree\n\n # If all max degree - second max degree cities \n # are not directly connected\n return maxDegree + secMaxDegree - 1\n\n```\n# Complexity\n- Time complexity:\n$$O(n)$$ for the average case,\nbut $$O(n^2)$$ at the worst case if all cities have same degree and they all are directly connected we will end up checking all pairs of cities.\n\n- Space complexity:\n$$O(n^2)$$, Majorly for the adjacency Matrix. | 6 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
✅ 100% 2-Approaches - O(n+r) & O(n^2) - Iterative Pairwise Comparison & Direct Connection Check | maximal-network-rank | 1 | 1 | # Problem Understanding\n\nIn the "Maximal Network Rank" problem, we are given an integer `n` representing the number of cities and a list of roads connecting these cities. Each road connects two distinct cities and is bidirectional. The task is to compute the maximal network rank of the infrastructure, which is defined as the maximum network rank of all pairs of different cities. The network rank of two different cities is the total number of directly connected roads to either city.\n\nFor instance, given `n = 4` and roads = `[[0,1],[0,3],[1,2],[1,3]]`, the output should be 4. This is because cities 0 and 1 have a combined network rank of 4.\n\n---\n\n# Live Coding in Python\n### Approach 1/2 - O(n^2):\nhttps://youtu.be/4jT0UeXl4U0\n\n### Approach 2/2 - O(n+r):\nhttps://youtu.be/E0CdCD_kDPY\n\n# Approach Comparison:\n\n\n\n\n## Approach 1/2: Iterative Pairwise Comparison\n\n- **Strategy**: This approach calculates the degree of each city and then iterates over every possible pair of cities to compute their combined network rank.\n \n- **Key Data Structures**:\n - Degree List: To store the number of roads connected to each city.\n - Road Set: For quick lookup of roads.\n \n- **Major Steps**:\n - Calculate the degree of each city.\n - Iterate over all possible pairs of cities.\n - For each pair, compute the network rank and update the max rank.\n \n- **Complexity**:\n - **Time**: $$O(n^2)$$ due to iterating over all pairs of cities.\n - **Space**: $$O(n + \\text{len(roads)})$$. The degree list occupies $$O(n)$$ and the road set occupies $$O(\\text{len(roads)})$$.\n\n**Approach 2/2: Degree Counting with Direct Connection Check**\n\n- **Strategy**: Instead of exhaustive pairwise comparison, this method identifies cities with the highest and second-highest degrees, and then restricts checks to a smaller subset of cities.\n\n- **Key Data Structures**:\n - Degree List: To store the number of roads connected to each city.\n - Road Set: For quick O(1) lookup of roads.\n \n- **Major Steps**:\n - Calculate the degree of each city.\n - Identify the highest and second-highest degree cities.\n - Check direct connections among these cities to compute the maximal rank.\n \n- **Complexity**:\n - **Time**: $$O(n + \\text{len(roads)})$$ derived from counting degrees and checking direct connections among a few cities.\n - **Space**: $$O(n + \\text{len(roads)})$$. The degree list occupies $$O(n)$$ and the road set occupies $$O(\\text{len(roads)})$$.\n\n---\n\n### Differences:\n\n- **Strategy**: The first approach involves a brute-force method of iterating through all pairs of cities. In contrast, the second approach is more optimized, focusing on cities with the highest and second-highest degrees.\n \n- **Efficiency**: The second approach is generally more efficient as it avoids unnecessary computations by restricting the checks to a subset of city pairs.\n \n- **Complexity**: The time complexity of the first approach is quadratic ($$O(n^2)$$), while the second approach has a linear time complexity ($$O(n + \\text{len(roads)})$$), making the latter more scalable for larger inputs.\n\nBy understanding the differences between these two approaches, one can appreciate the importance of optimizing algorithms and the benefits it brings in terms of efficiency and scalability.\n\n\n# Approach 1/2: Iterative Pairwise Comparison\n\nTo solve the "Maximal Network Rank" problem, we first compute the degree of each city (number of roads connected to it). Then, we iterate over every possible pair of cities to compute their combined network rank.\n\n## Key Data Structures:\n- **Degree List**: A list that stores the number of roads connected to each city.\n- **Road Set**: A set that stores the roads for quick look-up.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Initialize a list `degree` of size `n` with zeros.\n - Initialize an empty set `road_set`.\n \n2. **Processing Each Road**:\n - For each road connecting cities `a` and `b` :\n - Increment the degree of both `a` and `b`.\n - Add the road to `road_set`.\n \n3. **Iterate Over All City Pairs**:\n - For each pair of distinct cities `i` and `j`:\n - Compute their network rank as the sum of their degrees.\n - If they are directly connected, subtract 1 from the rank.\n - Update the `max_rank` with the current rank if it\'s higher.\n\n4. **Wrap-up**:\n - Return the computed `max_rank`.\n\n## Example:\n\nBased on the breakdown, here\'s how the algorithm processes the given example:\n\n1. **Input**: \n - Number of cities `n = 4`\n - Roads: `[ [0,1], [0,3], [1,2], [1,3] ]`\n\n2. **Degree Calculation**: \n After processing all the roads, the degree of connection for each city is as follows:\n - City 0 is connected to 2 other cities.\n - City 1 is connected to 3 other cities.\n - City 2 is connected to 1 other city.\n - City 3 is connected to 2 other cities.\n \n Hence, the degree list is: `[2, 3, 1, 2]`.\n\n3. **Network Rank Calculation for Each Pair**: \n For each unique pair of cities, we calculate their network rank:\n - Pair (0, 1): Network Rank = 4\n - Pair (0, 2): Network Rank = 3\n - Pair (0, 3): Network Rank = 3\n - Pair (1, 2): Network Rank = 3\n - Pair (1, 3): Network Rank = 4\n - Pair (2, 3): Network Rank = 3\n\n4. **Result**: \n The maximal network rank among all pairs of cities is 4.\n\n### Summary:\n\nGiven the input `n = 4` and roads `[ [0,1], [0,3], [1,2], [1,3] ]`:\n\nAfter processing all roads, the degree list is `[2, 3, 1, 2]`. Iterating over city pairs, the pairs (0, 1) and (1, 3) both give a network rank of 4, which is the maximum. Thus, the output is 4.\n\n---\n\n# Complexity 1/2:\n\n**Time Complexity:** \n- The solution has a time complexity of $$ O(n^2) $$. This is because we iterate over all pairs of cities, resulting in $$ O(n^2) $$ complexity.\n\n**Space Complexity:** \n- The space complexity is $$ O(n + \\text{len(roads)}) $$. The `degree` list takes $$ O(n) $$ space, and the `road_set` takes $$ O(\\text{len(roads)}) $$ space.\n\n---\n\n# Performance 1/2:\n\nGiven the constraints, this solution is optimal and will efficiently handle scenarios where `n` is up to 100.\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Rust | 39 | 25% | 3.3 | 25% |\n| Java | 40 | 16.8% | 44.8 | 8.4% |\n| Go | 80 | 6.6% | 7.5 | 45.45% |\n| JavaScript | 83 | 91.80% | 50.5 | 44.26% |\n| C++ | 94 | 56.78% | 39.0 | 37.23% |\n| C# | 144 | 82.86% | 85.4 | 5.71% |\n| Python3 | 297 | 93.4% | 18.6 | 15.22% |\n\n\n\n\n---\n\n# Code 1/2\n\n``` Python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n degree = [0] * n\n for a, b in roads:\n degree[a] += 1\n degree[b] += 1\n road_set = set(tuple(road) for road in roads)\n max_rank = 0\n for i in range(n):\n for j in range(i+1, n):\n rank = degree[i] + degree[j]\n if (i, j) in road_set or (j, i) in road_set:\n rank -= 1\n max_rank = max(max_rank, rank)\n return max_rank\n```\n``` C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n vector<int> degree(n, 0);\n set<pair<int, int>> road_set;\n \n for (auto& road : roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n road_set.insert({road[0], road[1]});\n road_set.insert({road[1], road[0]});\n }\n\n int max_rank = 0;\n for (int i = 0; i < n; ++i) {\n for (int j = i+1; j < n; ++j) {\n int rank = degree[i] + degree[j];\n if (road_set.find({i, j}) != road_set.end()) {\n rank--;\n }\n max_rank = max(max_rank, rank);\n }\n }\n\n return max_rank;\n }\n};\n```\n``` Java []\nclass Solution {\n public int maximalNetworkRank(int n, int[][] roads) {\n int[] degree = new int[n];\n Set<String> roadSet = new HashSet<>();\n \n for (int[] road : roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n roadSet.add(road[0] + "," + road[1]);\n roadSet.add(road[1] + "," + road[0]);\n }\n\n int maxRank = 0;\n for (int i = 0; i < n; i++) {\n for (int j = i+1; j < n; j++) {\n int rank = degree[i] + degree[j];\n if (roadSet.contains(i + "," + j)) {\n rank--;\n }\n maxRank = Math.max(maxRank, rank);\n }\n }\n\n return maxRank;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number[][]} roads\n * @return {number}\n */\nvar maximalNetworkRank = function(n, roads) {\n let degree = new Array(n).fill(0);\n let roadSet = new Set();\n\n for (let road of roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n roadSet.add(road[0] + \',\' + road[1]);\n roadSet.add(road[1] + \',\' + road[0]);\n }\n\n let maxRank = 0;\n for (let i = 0; i < n; i++) {\n for (let j = i+1; j < n; j++) {\n let rank = degree[i] + degree[j];\n if (roadSet.has(i + \',\' + j)) {\n rank--;\n }\n maxRank = Math.max(maxRank, rank);\n }\n }\n\n return maxRank;\n};\n```\n``` C# []\npublic class Solution {\n public int MaximalNetworkRank(int n, int[][] roads) {\n int[] degree = new int[n];\n HashSet<string> roadSet = new HashSet<string>();\n \n foreach (int[] road in roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n roadSet.Add(road[0] + "," + road[1]);\n roadSet.Add(road[1] + "," + road[0]);\n }\n\n int maxRank = 0;\n for (int i = 0; i < n; i++) {\n for (int j = i+1; j < n; j++) {\n int rank = degree[i] + degree[j];\n if (roadSet.Contains(i + "," + j)) {\n rank--;\n }\n maxRank = Math.Max(maxRank, rank);\n }\n }\n\n return maxRank;\n }\n}\n```\n``` Go []\nfunc maximalNetworkRank(n int, roads [][]int) int {\n degree := make([]int, n)\n roadSet := make(map[string]bool)\n\n for _, road := range roads {\n degree[road[0]]++\n degree[road[1]]++\n roadSet[fmt.Sprintf("%d,%d", road[0], road[1])] = true\n roadSet[fmt.Sprintf("%d,%d", road[1], road[0])] = true\n }\n\n maxRank := 0\n for i := 0; i < n; i++ {\n for j := i+1; j < n; j++ {\n rank := degree[i] + degree[j]\n if _, exists := roadSet[fmt.Sprintf("%d,%d", i, j)]; exists {\n rank--\n }\n if rank > maxRank {\n maxRank = rank\n }\n }\n }\n\n return maxRank\n}\n```\n``` Rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn maximal_network_rank(n: i32, roads: Vec<Vec<i32>>) -> i32 {\n let mut degree = vec![0; n as usize];\n let mut road_set = HashSet::new();\n\n for road in &roads {\n degree[road[0] as usize] += 1;\n degree[road[1] as usize] += 1;\n road_set.insert(format!("{},{}", road[0], road[1]));\n road_set.insert(format!("{},{}", road[1], road[0]));\n }\n\n let mut max_rank = 0;\n for i in 0..n {\n for j in i+1..n {\n let rank = degree[i as usize] + degree[j as usize];\n let rank = if road_set.contains(&format!("{},{}", i, j)) {\n rank - 1\n } else {\n rank\n };\n max_rank = max_rank.max(rank);\n }\n }\n\n max_rank\n }\n}\n```\n\n# Approach 2/2: Degree Counting with Direct Connection Check\n\nTo solve the "Maximal Network Rank" problem in a more optimized manner, we focus on reducing the redundant work by using the degree counting method. Instead of iterating through all pairs of cities, which is inefficient, we first identify cities with the highest and second-highest degrees. By doing so, we can restrict our checks to a smaller subset of cities, thus saving time.\n\n## Key Data Structures:\n- **Degree List**: A list that stores the number of roads connected to each city.\n- **Road Set**: A set to store the roads for quick O(1) lookup.\n\n## Enhanced Breakdown:\n1. **Degree Calculation**:\n - Initialize a list called `degrees` of size `n` with zeros.\n - For every road in the given list of roads, increment the degree of both connected cities.\n\n2. **Identifying Key Nodes**:\n - Sort the unique degrees in descending order.\n - Identify the highest and second-highest degrees.\n - Count the number of cities with the highest and second-highest degrees.\n\n3. **Maximal Rank Calculation**:\n - If there are multiple cities with the highest degree, check the direct connections among them. The rank is based on these connections.\n - If there\'s only one city with the highest degree, check its direct connections with cities having the second-highest degree. The rank is based on these connections.\n\n4. **Wrap-up**:\n - Return the computed maximal network rank.\n\n---\n\n## Complexity 2/2:\n\n**Time Complexity**:\n- The solution has a time complexity of $$O(n + \\text{len(roads)})$$. This is derived from counting degrees and checking direct connections among a few cities, rather than iterating over all pairs.\n\n**Space Complexity**:\n- The space complexity is $$O(n+\\text{len(roads)})$$. The degree list occupies $$O(n)$$ space and the road set occupies $$O(\\text{len(roads)})$$ space.\n\n---\n\n# Performance 2/2:\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Java | 4 | 88.27% | 44.1 | 55.78% |\n| Rust | 7 | 100% | 2.4 | 100% |\n| Go | 27 | 100% | 7.3 | 75.76% |\n| C++ | 49 | 99.25% | 27.9 | 97.68% |\n| JavaScript | 73 | 100% | 47.4 | 98.36% |\n| C# | 144 | 82.86% | 85.4 | 5.71% |\n| Python3 | 268 | 100% | 17.7 | 99.13% |\n\n\n\n\n# Code 2/2\n``` Python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n degrees = [0] * n\n for u, v in roads:\n degrees[u] += 1\n degrees[v] += 1\n\n sorted_degrees = sorted(set(degrees), reverse=True)\n max_deg = sorted_degrees[0]\n second_max_deg = sorted_degrees[1] if len(sorted_degrees) > 1 else 0\n\n max_count = degrees.count(max_deg)\n second_max_count = degrees.count(second_max_deg)\n\n if max_count > 1:\n directly_connected = sum(1 for u, v in roads if degrees[u] == max_deg and degrees[v] == max_deg)\n possible_connections = max_count * (max_count - 1) // 2\n return 2 * max_deg - 1 if possible_connections == directly_connected else 2 * max_deg\n\n direct_connections_to_second = sum(1 for u, v in roads if (degrees[u], degrees[v]) in [(max_deg, second_max_deg), (second_max_deg, max_deg)])\n return max_deg + second_max_deg - 1 if second_max_count == direct_connections_to_second else max_deg + second_max_deg\n```\n``` C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, std::vector<std::vector<int>>& roads) {\n std::vector<int> degrees(n, 0);\n for (auto& road : roads) {\n degrees[road[0]]++;\n degrees[road[1]]++;\n }\n \n std::unordered_set<int> unique_degrees(degrees.begin(), degrees.end());\n std::vector<int> sorted_degrees(unique_degrees.begin(), unique_degrees.end());\n std::sort(sorted_degrees.rbegin(), sorted_degrees.rend());\n \n int max_deg = sorted_degrees[0];\n int second_max_deg = sorted_degrees.size() > 1 ? sorted_degrees[1] : 0;\n \n int max_count = std::count(degrees.begin(), degrees.end(), max_deg);\n int second_max_count = std::count(degrees.begin(), degrees.end(), second_max_deg);\n \n if (max_count > 1) {\n int directly_connected = 0;\n for (auto& road : roads) {\n if (degrees[road[0]] == max_deg && degrees[road[1]] == max_deg)\n directly_connected++;\n }\n int possible_connections = max_count * (max_count - 1) / 2;\n return possible_connections == directly_connected ? 2 * max_deg - 1 : 2 * max_deg;\n }\n \n int direct_connections_to_second = 0;\n for (auto& road : roads) {\n if ((degrees[road[0]] == max_deg && degrees[road[1]] == second_max_deg) ||\n (degrees[road[0]] == second_max_deg && degrees[road[1]] == max_deg))\n direct_connections_to_second++;\n }\n \n return second_max_count == direct_connections_to_second ? max_deg + second_max_deg - 1 : max_deg + second_max_deg;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int maximalNetworkRank(int n, int[][] roads) {\n int[] degrees = new int[n];\n for (int[] road : roads) {\n degrees[road[0]]++;\n degrees[road[1]]++;\n }\n \n Set<Integer> uniqueDegrees = new HashSet<>();\n for (int degree : degrees) {\n uniqueDegrees.add(degree);\n }\n \n List<Integer> sortedDegrees = new ArrayList<>(uniqueDegrees);\n Collections.sort(sortedDegrees, Collections.reverseOrder());\n\n int maxDeg = sortedDegrees.get(0);\n int secondMaxDeg = sortedDegrees.size() > 1 ? sortedDegrees.get(1) : 0;\n\n int maxCount = 0;\n for (int degree : degrees) {\n if (degree == maxDeg) maxCount++;\n }\n\n int secondMaxCount = 0;\n for (int degree : degrees) {\n if (degree == secondMaxDeg) secondMaxCount++;\n }\n\n if (maxCount > 1) {\n int directlyConnected = 0;\n for (int[] road : roads) {\n if (degrees[road[0]] == maxDeg && degrees[road[1]] == maxDeg)\n directlyConnected++;\n }\n int possibleConnections = maxCount * (maxCount - 1) / 2;\n return possibleConnections == directlyConnected ? 2 * maxDeg - 1 : 2 * maxDeg;\n }\n\n int directConnectionsToSecond = 0;\n for (int[] road : roads) {\n if ((degrees[road[0]] == maxDeg && degrees[road[1]] == secondMaxDeg) ||\n (degrees[road[0]] == secondMaxDeg && degrees[road[1]] == maxDeg))\n directConnectionsToSecond++;\n }\n\n return secondMaxCount == directConnectionsToSecond ? maxDeg + secondMaxDeg - 1 : maxDeg + secondMaxDeg;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int MaximalNetworkRank(int n, int[][] roads) {\n int[] degrees = new int[n];\n foreach (var road in roads) {\n degrees[road[0]]++;\n degrees[road[1]]++;\n }\n\n HashSet<int> uniqueDegrees = new HashSet<int>(degrees);\n List<int> sortedDegrees = uniqueDegrees.ToList();\n sortedDegrees.Sort((a, b) => b.CompareTo(a));\n\n int maxDeg = sortedDegrees[0];\n int secondMaxDeg = sortedDegrees.Count > 1 ? sortedDegrees[1] : 0;\n\n int maxCount = degrees.Count(degree => degree == maxDeg);\n int secondMaxCount = degrees.Count(degree => degree == secondMaxDeg);\n\n if (maxCount > 1) {\n int directlyConnected = 0;\n foreach (var road in roads) {\n if (degrees[road[0]] == maxDeg && degrees[road[1]] == maxDeg)\n directlyConnected++;\n }\n int possibleConnections = maxCount * (maxCount - 1) / 2;\n return possibleConnections == directlyConnected ? 2 * maxDeg - 1 : 2 * maxDeg;\n }\n\n int directConnectionsToSecond = 0;\n foreach (var road in roads) {\n if ((degrees[road[0]] == maxDeg && degrees[road[1]] == secondMaxDeg) ||\n (degrees[road[0]] == secondMaxDeg && degrees[road[1]] == maxDeg))\n directConnectionsToSecond++;\n }\n\n return secondMaxCount == directConnectionsToSecond ? maxDeg + secondMaxDeg - 1 : maxDeg + secondMaxDeg;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number[][]} roads\n * @return {number}\n */\nvar maximalNetworkRank = function(n, roads) {\n let degrees = Array(n).fill(0);\n roads.forEach(([u, v]) => {\n degrees[u]++;\n degrees[v]++;\n });\n\n let uniqueDegrees = [...new Set(degrees)].sort((a, b) => b - a);\n let maxDeg = uniqueDegrees[0];\n let secondMaxDeg = uniqueDegrees.length > 1 ? uniqueDegrees[1] : 0;\n\n let maxCount = degrees.filter(degree => degree === maxDeg).length;\n let secondMaxCount = degrees.filter(degree => degree === secondMaxDeg).length;\n\n if (maxCount > 1) {\n let directlyConnected = roads.filter(([u, v]) => degrees[u] === maxDeg && degrees[v] === maxDeg).length;\n let possibleConnections = maxCount * (maxCount - 1) / 2;\n return possibleConnections === directlyConnected ? 2 * maxDeg - 1 : 2 * maxDeg;\n }\n\n let directConnectionsToSecond = roads.filter(([u, v]) => \n (degrees[u] === maxDeg && degrees[v] === secondMaxDeg) || \n (degrees[u] === secondMaxDeg && degrees[v] === maxDeg)\n ).length;\n\n return secondMaxCount === directConnectionsToSecond ? maxDeg + secondMaxDeg - 1 : maxDeg + secondMaxDeg;\n }\n\n```\n``` Go []\n{\n degrees := make([]int, n)\n for _, road := range roads {\n degrees[road[0]]++\n degrees[road[1]]++\n }\n\n uniqueDegrees := []int{}\n m := make(map[int]bool)\n for _, item := range degrees {\n if _, value := m[item]; !value {\n m[item] = true\n uniqueDegrees = append(uniqueDegrees, item)\n }\n }\n sort.Sort(sort.Reverse(sort.IntSlice(uniqueDegrees)))\n\n maxDeg := uniqueDegrees[0]\n secondMaxDeg := 0\n if len(uniqueDegrees) > 1 {\n secondMaxDeg = uniqueDegrees[1]\n }\n\n maxCount, secondMaxCount := 0, 0\n for _, degree := range degrees {\n if degree == maxDeg {\n maxCount++\n } else if degree == secondMaxDeg {\n secondMaxCount++\n }\n }\n\n if maxCount > 1 {\n directlyConnected := 0\n for _, road := range roads {\n if degrees[road[0]] == maxDeg && degrees[road[1]] == maxDeg {\n directlyConnected++\n }\n }\n possibleConnections := maxCount * (maxCount - 1) / 2\n if directlyConnected == possibleConnections {\n return 2*maxDeg - 1\n }\n return 2 * maxDeg\n }\n\n directConnectionsToSecond := 0\n for _, road := range roads {\n if (degrees[road[0]] == maxDeg && degrees[road[1]] == secondMaxDeg) || \n (degrees[road[0]] == secondMaxDeg && degrees[road[1]] == maxDeg) {\n directConnectionsToSecond++\n }\n }\n\n if directConnectionsToSecond == secondMaxCount {\n return maxDeg + secondMaxDeg - 1\n }\n return maxDeg + secondMaxDeg\n}\n```\n``` Rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn maximal_network_rank(n: i32, roads: Vec<Vec<i32>>) -> i32 {\n let mut degrees = vec![0; n as usize];\n for road in &roads {\n degrees[road[0] as usize] += 1;\n degrees[road[1] as usize] += 1;\n }\n\n let mut unique_degrees: HashSet<_> = degrees.iter().cloned().collect();\n let mut sorted_degrees: Vec<_> = unique_degrees.iter().cloned().collect();\n sorted_degrees.sort();\n sorted_degrees.reverse();\n\n let max_deg = sorted_degrees[0];\n let second_max_deg = if sorted_degrees.len() > 1 {\n sorted_degrees[1]\n } else {\n 0\n };\n\n let max_count = degrees.iter().filter(|&°| deg == max_deg).count();\n let second_max_count = degrees.iter().filter(|&°| deg == second_max_deg).count();\n\n if max_count > 1 {\n let directly_connected = roads.iter().filter(|road| degrees[road[0] as usize] == max_deg && degrees[road[1] as usize] == max_deg).count();\n let possible_connections = max_count * (max_count - 1) / 2;\n return if possible_connections == directly_connected {\n 2 * max_deg - 1\n } else {\n 2 * max_deg\n };\n } else {\n let direct_connections_to_second = roads.iter().filter(|road| {\n (degrees[road[0] as usize] == max_deg && degrees[road[1] as usize] == second_max_deg) ||\n (degrees[road[0] as usize] == second_max_deg && degrees[road[1] as usize] == max_deg)\n }).count();\n return if second_max_count == direct_connections_to_second {\n max_deg + second_max_deg - 1\n } else {\n max_deg + second_max_deg\n };\n }\n }\n}\n\n```\n\nThis problem beautifully showcases the importance of understanding the underlying structures of a network and the power of pairwise comparison. Keep coding and keep learning! \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB | 82 | There is an infrastructure of `n` cities with some number of `roads` connecting these cities. Each `roads[i] = [ai, bi]` indicates that there is a bidirectional road between cities `ai` and `bi`.
The **network rank** of **two different cities** is defined as the total number of **directly** connected roads to **either** city. If a road is directly connected to both cities, it is only counted **once**.
The **maximal network rank** of the infrastructure is the **maximum network rank** of all pairs of different cities.
Given the integer `n` and the array `roads`, return _the **maximal network rank** of the entire infrastructure_.
**Example 1:**
**Input:** n = 4, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 4
**Explanation:** The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
**Example 2:**
**Input:** n = 5, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\],\[2,3\],\[2,4\]\]
**Output:** 5
**Explanation:** There are 5 roads that are connected to cities 1 or 2.
**Example 3:**
**Input:** n = 8, roads = \[\[0,1\],\[1,2\],\[2,3\],\[2,4\],\[5,6\],\[5,7\]\]
**Output:** 5
**Explanation:** The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
**Constraints:**
* `2 <= n <= 100`
* `0 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 2`
* `0 <= ai, bi <= n-1`
* `ai != bi`
* Each pair of cities has **at most one** road connecting them. | Compute all sums and save it in array. Then just go from LEFT to RIGHT index and calculate answer modulo 1e9 + 7. |
✅ 100% 2-Approaches - O(n+r) & O(n^2) - Iterative Pairwise Comparison & Direct Connection Check | maximal-network-rank | 1 | 1 | # Problem Understanding\n\nIn the "Maximal Network Rank" problem, we are given an integer `n` representing the number of cities and a list of roads connecting these cities. Each road connects two distinct cities and is bidirectional. The task is to compute the maximal network rank of the infrastructure, which is defined as the maximum network rank of all pairs of different cities. The network rank of two different cities is the total number of directly connected roads to either city.\n\nFor instance, given `n = 4` and roads = `[[0,1],[0,3],[1,2],[1,3]]`, the output should be 4. This is because cities 0 and 1 have a combined network rank of 4.\n\n---\n\n# Live Coding in Python\n### Approach 1/2 - O(n^2):\nhttps://youtu.be/4jT0UeXl4U0\n\n### Approach 2/2 - O(n+r):\nhttps://youtu.be/E0CdCD_kDPY\n\n# Approach Comparison:\n\n\n\n\n## Approach 1/2: Iterative Pairwise Comparison\n\n- **Strategy**: This approach calculates the degree of each city and then iterates over every possible pair of cities to compute their combined network rank.\n \n- **Key Data Structures**:\n - Degree List: To store the number of roads connected to each city.\n - Road Set: For quick lookup of roads.\n \n- **Major Steps**:\n - Calculate the degree of each city.\n - Iterate over all possible pairs of cities.\n - For each pair, compute the network rank and update the max rank.\n \n- **Complexity**:\n - **Time**: $$O(n^2)$$ due to iterating over all pairs of cities.\n - **Space**: $$O(n + \\text{len(roads)})$$. The degree list occupies $$O(n)$$ and the road set occupies $$O(\\text{len(roads)})$$.\n\n**Approach 2/2: Degree Counting with Direct Connection Check**\n\n- **Strategy**: Instead of exhaustive pairwise comparison, this method identifies cities with the highest and second-highest degrees, and then restricts checks to a smaller subset of cities.\n\n- **Key Data Structures**:\n - Degree List: To store the number of roads connected to each city.\n - Road Set: For quick O(1) lookup of roads.\n \n- **Major Steps**:\n - Calculate the degree of each city.\n - Identify the highest and second-highest degree cities.\n - Check direct connections among these cities to compute the maximal rank.\n \n- **Complexity**:\n - **Time**: $$O(n + \\text{len(roads)})$$ derived from counting degrees and checking direct connections among a few cities.\n - **Space**: $$O(n + \\text{len(roads)})$$. The degree list occupies $$O(n)$$ and the road set occupies $$O(\\text{len(roads)})$$.\n\n---\n\n### Differences:\n\n- **Strategy**: The first approach involves a brute-force method of iterating through all pairs of cities. In contrast, the second approach is more optimized, focusing on cities with the highest and second-highest degrees.\n \n- **Efficiency**: The second approach is generally more efficient as it avoids unnecessary computations by restricting the checks to a subset of city pairs.\n \n- **Complexity**: The time complexity of the first approach is quadratic ($$O(n^2)$$), while the second approach has a linear time complexity ($$O(n + \\text{len(roads)})$$), making the latter more scalable for larger inputs.\n\nBy understanding the differences between these two approaches, one can appreciate the importance of optimizing algorithms and the benefits it brings in terms of efficiency and scalability.\n\n\n# Approach 1/2: Iterative Pairwise Comparison\n\nTo solve the "Maximal Network Rank" problem, we first compute the degree of each city (number of roads connected to it). Then, we iterate over every possible pair of cities to compute their combined network rank.\n\n## Key Data Structures:\n- **Degree List**: A list that stores the number of roads connected to each city.\n- **Road Set**: A set that stores the roads for quick look-up.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Initialize a list `degree` of size `n` with zeros.\n - Initialize an empty set `road_set`.\n \n2. **Processing Each Road**:\n - For each road connecting cities `a` and `b` :\n - Increment the degree of both `a` and `b`.\n - Add the road to `road_set`.\n \n3. **Iterate Over All City Pairs**:\n - For each pair of distinct cities `i` and `j`:\n - Compute their network rank as the sum of their degrees.\n - If they are directly connected, subtract 1 from the rank.\n - Update the `max_rank` with the current rank if it\'s higher.\n\n4. **Wrap-up**:\n - Return the computed `max_rank`.\n\n## Example:\n\nBased on the breakdown, here\'s how the algorithm processes the given example:\n\n1. **Input**: \n - Number of cities `n = 4`\n - Roads: `[ [0,1], [0,3], [1,2], [1,3] ]`\n\n2. **Degree Calculation**: \n After processing all the roads, the degree of connection for each city is as follows:\n - City 0 is connected to 2 other cities.\n - City 1 is connected to 3 other cities.\n - City 2 is connected to 1 other city.\n - City 3 is connected to 2 other cities.\n \n Hence, the degree list is: `[2, 3, 1, 2]`.\n\n3. **Network Rank Calculation for Each Pair**: \n For each unique pair of cities, we calculate their network rank:\n - Pair (0, 1): Network Rank = 4\n - Pair (0, 2): Network Rank = 3\n - Pair (0, 3): Network Rank = 3\n - Pair (1, 2): Network Rank = 3\n - Pair (1, 3): Network Rank = 4\n - Pair (2, 3): Network Rank = 3\n\n4. **Result**: \n The maximal network rank among all pairs of cities is 4.\n\n### Summary:\n\nGiven the input `n = 4` and roads `[ [0,1], [0,3], [1,2], [1,3] ]`:\n\nAfter processing all roads, the degree list is `[2, 3, 1, 2]`. Iterating over city pairs, the pairs (0, 1) and (1, 3) both give a network rank of 4, which is the maximum. Thus, the output is 4.\n\n---\n\n# Complexity 1/2:\n\n**Time Complexity:** \n- The solution has a time complexity of $$ O(n^2) $$. This is because we iterate over all pairs of cities, resulting in $$ O(n^2) $$ complexity.\n\n**Space Complexity:** \n- The space complexity is $$ O(n + \\text{len(roads)}) $$. The `degree` list takes $$ O(n) $$ space, and the `road_set` takes $$ O(\\text{len(roads)}) $$ space.\n\n---\n\n# Performance 1/2:\n\nGiven the constraints, this solution is optimal and will efficiently handle scenarios where `n` is up to 100.\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Rust | 39 | 25% | 3.3 | 25% |\n| Java | 40 | 16.8% | 44.8 | 8.4% |\n| Go | 80 | 6.6% | 7.5 | 45.45% |\n| JavaScript | 83 | 91.80% | 50.5 | 44.26% |\n| C++ | 94 | 56.78% | 39.0 | 37.23% |\n| C# | 144 | 82.86% | 85.4 | 5.71% |\n| Python3 | 297 | 93.4% | 18.6 | 15.22% |\n\n\n\n\n---\n\n# Code 1/2\n\n``` Python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n degree = [0] * n\n for a, b in roads:\n degree[a] += 1\n degree[b] += 1\n road_set = set(tuple(road) for road in roads)\n max_rank = 0\n for i in range(n):\n for j in range(i+1, n):\n rank = degree[i] + degree[j]\n if (i, j) in road_set or (j, i) in road_set:\n rank -= 1\n max_rank = max(max_rank, rank)\n return max_rank\n```\n``` C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, vector<vector<int>>& roads) {\n vector<int> degree(n, 0);\n set<pair<int, int>> road_set;\n \n for (auto& road : roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n road_set.insert({road[0], road[1]});\n road_set.insert({road[1], road[0]});\n }\n\n int max_rank = 0;\n for (int i = 0; i < n; ++i) {\n for (int j = i+1; j < n; ++j) {\n int rank = degree[i] + degree[j];\n if (road_set.find({i, j}) != road_set.end()) {\n rank--;\n }\n max_rank = max(max_rank, rank);\n }\n }\n\n return max_rank;\n }\n};\n```\n``` Java []\nclass Solution {\n public int maximalNetworkRank(int n, int[][] roads) {\n int[] degree = new int[n];\n Set<String> roadSet = new HashSet<>();\n \n for (int[] road : roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n roadSet.add(road[0] + "," + road[1]);\n roadSet.add(road[1] + "," + road[0]);\n }\n\n int maxRank = 0;\n for (int i = 0; i < n; i++) {\n for (int j = i+1; j < n; j++) {\n int rank = degree[i] + degree[j];\n if (roadSet.contains(i + "," + j)) {\n rank--;\n }\n maxRank = Math.max(maxRank, rank);\n }\n }\n\n return maxRank;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number[][]} roads\n * @return {number}\n */\nvar maximalNetworkRank = function(n, roads) {\n let degree = new Array(n).fill(0);\n let roadSet = new Set();\n\n for (let road of roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n roadSet.add(road[0] + \',\' + road[1]);\n roadSet.add(road[1] + \',\' + road[0]);\n }\n\n let maxRank = 0;\n for (let i = 0; i < n; i++) {\n for (let j = i+1; j < n; j++) {\n let rank = degree[i] + degree[j];\n if (roadSet.has(i + \',\' + j)) {\n rank--;\n }\n maxRank = Math.max(maxRank, rank);\n }\n }\n\n return maxRank;\n};\n```\n``` C# []\npublic class Solution {\n public int MaximalNetworkRank(int n, int[][] roads) {\n int[] degree = new int[n];\n HashSet<string> roadSet = new HashSet<string>();\n \n foreach (int[] road in roads) {\n degree[road[0]]++;\n degree[road[1]]++;\n roadSet.Add(road[0] + "," + road[1]);\n roadSet.Add(road[1] + "," + road[0]);\n }\n\n int maxRank = 0;\n for (int i = 0; i < n; i++) {\n for (int j = i+1; j < n; j++) {\n int rank = degree[i] + degree[j];\n if (roadSet.Contains(i + "," + j)) {\n rank--;\n }\n maxRank = Math.Max(maxRank, rank);\n }\n }\n\n return maxRank;\n }\n}\n```\n``` Go []\nfunc maximalNetworkRank(n int, roads [][]int) int {\n degree := make([]int, n)\n roadSet := make(map[string]bool)\n\n for _, road := range roads {\n degree[road[0]]++\n degree[road[1]]++\n roadSet[fmt.Sprintf("%d,%d", road[0], road[1])] = true\n roadSet[fmt.Sprintf("%d,%d", road[1], road[0])] = true\n }\n\n maxRank := 0\n for i := 0; i < n; i++ {\n for j := i+1; j < n; j++ {\n rank := degree[i] + degree[j]\n if _, exists := roadSet[fmt.Sprintf("%d,%d", i, j)]; exists {\n rank--\n }\n if rank > maxRank {\n maxRank = rank\n }\n }\n }\n\n return maxRank\n}\n```\n``` Rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn maximal_network_rank(n: i32, roads: Vec<Vec<i32>>) -> i32 {\n let mut degree = vec![0; n as usize];\n let mut road_set = HashSet::new();\n\n for road in &roads {\n degree[road[0] as usize] += 1;\n degree[road[1] as usize] += 1;\n road_set.insert(format!("{},{}", road[0], road[1]));\n road_set.insert(format!("{},{}", road[1], road[0]));\n }\n\n let mut max_rank = 0;\n for i in 0..n {\n for j in i+1..n {\n let rank = degree[i as usize] + degree[j as usize];\n let rank = if road_set.contains(&format!("{},{}", i, j)) {\n rank - 1\n } else {\n rank\n };\n max_rank = max_rank.max(rank);\n }\n }\n\n max_rank\n }\n}\n```\n\n# Approach 2/2: Degree Counting with Direct Connection Check\n\nTo solve the "Maximal Network Rank" problem in a more optimized manner, we focus on reducing the redundant work by using the degree counting method. Instead of iterating through all pairs of cities, which is inefficient, we first identify cities with the highest and second-highest degrees. By doing so, we can restrict our checks to a smaller subset of cities, thus saving time.\n\n## Key Data Structures:\n- **Degree List**: A list that stores the number of roads connected to each city.\n- **Road Set**: A set to store the roads for quick O(1) lookup.\n\n## Enhanced Breakdown:\n1. **Degree Calculation**:\n - Initialize a list called `degrees` of size `n` with zeros.\n - For every road in the given list of roads, increment the degree of both connected cities.\n\n2. **Identifying Key Nodes**:\n - Sort the unique degrees in descending order.\n - Identify the highest and second-highest degrees.\n - Count the number of cities with the highest and second-highest degrees.\n\n3. **Maximal Rank Calculation**:\n - If there are multiple cities with the highest degree, check the direct connections among them. The rank is based on these connections.\n - If there\'s only one city with the highest degree, check its direct connections with cities having the second-highest degree. The rank is based on these connections.\n\n4. **Wrap-up**:\n - Return the computed maximal network rank.\n\n---\n\n## Complexity 2/2:\n\n**Time Complexity**:\n- The solution has a time complexity of $$O(n + \\text{len(roads)})$$. This is derived from counting degrees and checking direct connections among a few cities, rather than iterating over all pairs.\n\n**Space Complexity**:\n- The space complexity is $$O(n+\\text{len(roads)})$$. The degree list occupies $$O(n)$$ space and the road set occupies $$O(\\text{len(roads)})$$ space.\n\n---\n\n# Performance 2/2:\n\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Java | 4 | 88.27% | 44.1 | 55.78% |\n| Rust | 7 | 100% | 2.4 | 100% |\n| Go | 27 | 100% | 7.3 | 75.76% |\n| C++ | 49 | 99.25% | 27.9 | 97.68% |\n| JavaScript | 73 | 100% | 47.4 | 98.36% |\n| C# | 144 | 82.86% | 85.4 | 5.71% |\n| Python3 | 268 | 100% | 17.7 | 99.13% |\n\n\n\n\n# Code 2/2\n``` Python []\nclass Solution:\n def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:\n degrees = [0] * n\n for u, v in roads:\n degrees[u] += 1\n degrees[v] += 1\n\n sorted_degrees = sorted(set(degrees), reverse=True)\n max_deg = sorted_degrees[0]\n second_max_deg = sorted_degrees[1] if len(sorted_degrees) > 1 else 0\n\n max_count = degrees.count(max_deg)\n second_max_count = degrees.count(second_max_deg)\n\n if max_count > 1:\n directly_connected = sum(1 for u, v in roads if degrees[u] == max_deg and degrees[v] == max_deg)\n possible_connections = max_count * (max_count - 1) // 2\n return 2 * max_deg - 1 if possible_connections == directly_connected else 2 * max_deg\n\n direct_connections_to_second = sum(1 for u, v in roads if (degrees[u], degrees[v]) in [(max_deg, second_max_deg), (second_max_deg, max_deg)])\n return max_deg + second_max_deg - 1 if second_max_count == direct_connections_to_second else max_deg + second_max_deg\n```\n``` C++ []\nclass Solution {\npublic:\n int maximalNetworkRank(int n, std::vector<std::vector<int>>& roads) {\n std::vector<int> degrees(n, 0);\n for (auto& road : roads) {\n degrees[road[0]]++;\n degrees[road[1]]++;\n }\n \n std::unordered_set<int> unique_degrees(degrees.begin(), degrees.end());\n std::vector<int> sorted_degrees(unique_degrees.begin(), unique_degrees.end());\n std::sort(sorted_degrees.rbegin(), sorted_degrees.rend());\n \n int max_deg = sorted_degrees[0];\n int second_max_deg = sorted_degrees.size() > 1 ? sorted_degrees[1] : 0;\n \n int max_count = std::count(degrees.begin(), degrees.end(), max_deg);\n int second_max_count = std::count(degrees.begin(), degrees.end(), second_max_deg);\n \n if (max_count > 1) {\n int directly_connected = 0;\n for (auto& road : roads) {\n if (degrees[road[0]] == max_deg && degrees[road[1]] == max_deg)\n directly_connected++;\n }\n int possible_connections = max_count * (max_count - 1) / 2;\n return possible_connections == directly_connected ? 2 * max_deg - 1 : 2 * max_deg;\n }\n \n int direct_connections_to_second = 0;\n for (auto& road : roads) {\n if ((degrees[road[0]] == max_deg && degrees[road[1]] == second_max_deg) ||\n (degrees[road[0]] == second_max_deg && degrees[road[1]] == max_deg))\n direct_connections_to_second++;\n }\n \n return second_max_count == direct_connections_to_second ? max_deg + second_max_deg - 1 : max_deg + second_max_deg;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int maximalNetworkRank(int n, int[][] roads) {\n int[] degrees = new int[n];\n for (int[] road : roads) {\n degrees[road[0]]++;\n degrees[road[1]]++;\n }\n \n Set<Integer> uniqueDegrees = new HashSet<>();\n for (int degree : degrees) {\n uniqueDegrees.add(degree);\n }\n \n List<Integer> sortedDegrees = new ArrayList<>(uniqueDegrees);\n Collections.sort(sortedDegrees, Collections.reverseOrder());\n\n int maxDeg = sortedDegrees.get(0);\n int secondMaxDeg = sortedDegrees.size() > 1 ? sortedDegrees.get(1) : 0;\n\n int maxCount = 0;\n for (int degree : degrees) {\n if (degree == maxDeg) maxCount++;\n }\n\n int secondMaxCount = 0;\n for (int degree : degrees) {\n if (degree == secondMaxDeg) secondMaxCount++;\n }\n\n if (maxCount > 1) {\n int directlyConnected = 0;\n for (int[] road : roads) {\n if (degrees[road[0]] == maxDeg && degrees[road[1]] == maxDeg)\n directlyConnected++;\n }\n int possibleConnections = maxCount * (maxCount - 1) / 2;\n return possibleConnections == directlyConnected ? 2 * maxDeg - 1 : 2 * maxDeg;\n }\n\n int directConnectionsToSecond = 0;\n for (int[] road : roads) {\n if ((degrees[road[0]] == maxDeg && degrees[road[1]] == secondMaxDeg) ||\n (degrees[road[0]] == secondMaxDeg && degrees[road[1]] == maxDeg))\n directConnectionsToSecond++;\n }\n\n return secondMaxCount == directConnectionsToSecond ? maxDeg + secondMaxDeg - 1 : maxDeg + secondMaxDeg;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int MaximalNetworkRank(int n, int[][] roads) {\n int[] degrees = new int[n];\n foreach (var road in roads) {\n degrees[road[0]]++;\n degrees[road[1]]++;\n }\n\n HashSet<int> uniqueDegrees = new HashSet<int>(degrees);\n List<int> sortedDegrees = uniqueDegrees.ToList();\n sortedDegrees.Sort((a, b) => b.CompareTo(a));\n\n int maxDeg = sortedDegrees[0];\n int secondMaxDeg = sortedDegrees.Count > 1 ? sortedDegrees[1] : 0;\n\n int maxCount = degrees.Count(degree => degree == maxDeg);\n int secondMaxCount = degrees.Count(degree => degree == secondMaxDeg);\n\n if (maxCount > 1) {\n int directlyConnected = 0;\n foreach (var road in roads) {\n if (degrees[road[0]] == maxDeg && degrees[road[1]] == maxDeg)\n directlyConnected++;\n }\n int possibleConnections = maxCount * (maxCount - 1) / 2;\n return possibleConnections == directlyConnected ? 2 * maxDeg - 1 : 2 * maxDeg;\n }\n\n int directConnectionsToSecond = 0;\n foreach (var road in roads) {\n if ((degrees[road[0]] == maxDeg && degrees[road[1]] == secondMaxDeg) ||\n (degrees[road[0]] == secondMaxDeg && degrees[road[1]] == maxDeg))\n directConnectionsToSecond++;\n }\n\n return secondMaxCount == directConnectionsToSecond ? maxDeg + secondMaxDeg - 1 : maxDeg + secondMaxDeg;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number[][]} roads\n * @return {number}\n */\nvar maximalNetworkRank = function(n, roads) {\n let degrees = Array(n).fill(0);\n roads.forEach(([u, v]) => {\n degrees[u]++;\n degrees[v]++;\n });\n\n let uniqueDegrees = [...new Set(degrees)].sort((a, b) => b - a);\n let maxDeg = uniqueDegrees[0];\n let secondMaxDeg = uniqueDegrees.length > 1 ? uniqueDegrees[1] : 0;\n\n let maxCount = degrees.filter(degree => degree === maxDeg).length;\n let secondMaxCount = degrees.filter(degree => degree === secondMaxDeg).length;\n\n if (maxCount > 1) {\n let directlyConnected = roads.filter(([u, v]) => degrees[u] === maxDeg && degrees[v] === maxDeg).length;\n let possibleConnections = maxCount * (maxCount - 1) / 2;\n return possibleConnections === directlyConnected ? 2 * maxDeg - 1 : 2 * maxDeg;\n }\n\n let directConnectionsToSecond = roads.filter(([u, v]) => \n (degrees[u] === maxDeg && degrees[v] === secondMaxDeg) || \n (degrees[u] === secondMaxDeg && degrees[v] === maxDeg)\n ).length;\n\n return secondMaxCount === directConnectionsToSecond ? maxDeg + secondMaxDeg - 1 : maxDeg + secondMaxDeg;\n }\n\n```\n``` Go []\n{\n degrees := make([]int, n)\n for _, road := range roads {\n degrees[road[0]]++\n degrees[road[1]]++\n }\n\n uniqueDegrees := []int{}\n m := make(map[int]bool)\n for _, item := range degrees {\n if _, value := m[item]; !value {\n m[item] = true\n uniqueDegrees = append(uniqueDegrees, item)\n }\n }\n sort.Sort(sort.Reverse(sort.IntSlice(uniqueDegrees)))\n\n maxDeg := uniqueDegrees[0]\n secondMaxDeg := 0\n if len(uniqueDegrees) > 1 {\n secondMaxDeg = uniqueDegrees[1]\n }\n\n maxCount, secondMaxCount := 0, 0\n for _, degree := range degrees {\n if degree == maxDeg {\n maxCount++\n } else if degree == secondMaxDeg {\n secondMaxCount++\n }\n }\n\n if maxCount > 1 {\n directlyConnected := 0\n for _, road := range roads {\n if degrees[road[0]] == maxDeg && degrees[road[1]] == maxDeg {\n directlyConnected++\n }\n }\n possibleConnections := maxCount * (maxCount - 1) / 2\n if directlyConnected == possibleConnections {\n return 2*maxDeg - 1\n }\n return 2 * maxDeg\n }\n\n directConnectionsToSecond := 0\n for _, road := range roads {\n if (degrees[road[0]] == maxDeg && degrees[road[1]] == secondMaxDeg) || \n (degrees[road[0]] == secondMaxDeg && degrees[road[1]] == maxDeg) {\n directConnectionsToSecond++\n }\n }\n\n if directConnectionsToSecond == secondMaxCount {\n return maxDeg + secondMaxDeg - 1\n }\n return maxDeg + secondMaxDeg\n}\n```\n``` Rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn maximal_network_rank(n: i32, roads: Vec<Vec<i32>>) -> i32 {\n let mut degrees = vec![0; n as usize];\n for road in &roads {\n degrees[road[0] as usize] += 1;\n degrees[road[1] as usize] += 1;\n }\n\n let mut unique_degrees: HashSet<_> = degrees.iter().cloned().collect();\n let mut sorted_degrees: Vec<_> = unique_degrees.iter().cloned().collect();\n sorted_degrees.sort();\n sorted_degrees.reverse();\n\n let max_deg = sorted_degrees[0];\n let second_max_deg = if sorted_degrees.len() > 1 {\n sorted_degrees[1]\n } else {\n 0\n };\n\n let max_count = degrees.iter().filter(|&°| deg == max_deg).count();\n let second_max_count = degrees.iter().filter(|&°| deg == second_max_deg).count();\n\n if max_count > 1 {\n let directly_connected = roads.iter().filter(|road| degrees[road[0] as usize] == max_deg && degrees[road[1] as usize] == max_deg).count();\n let possible_connections = max_count * (max_count - 1) / 2;\n return if possible_connections == directly_connected {\n 2 * max_deg - 1\n } else {\n 2 * max_deg\n };\n } else {\n let direct_connections_to_second = roads.iter().filter(|road| {\n (degrees[road[0] as usize] == max_deg && degrees[road[1] as usize] == second_max_deg) ||\n (degrees[road[0] as usize] == second_max_deg && degrees[road[1] as usize] == max_deg)\n }).count();\n return if second_max_count == direct_connections_to_second {\n max_deg + second_max_deg - 1\n } else {\n max_deg + second_max_deg\n };\n }\n }\n}\n\n```\n\nThis problem beautifully showcases the importance of understanding the underlying structures of a network and the power of pairwise comparison. Keep coding and keep learning! \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB | 82 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Python 85% | maximal-network-rank | 0 | 1 | # Code\n```\nclass Solution:\n def maximalNetworkRank(self, n: int, A: List[List[int]]) -> int:\n\n # Create connection dict and store edges in "edgesSet"\n conn = defaultdict(list)\n edgesSet = set()\n for a, b in A:\n conn[a] += [b]\n conn[b] += [a]\n edgesSet |= set([(a, b), (b, a)])\n \n # Create an inverseIndex: invMap[number_of_edges] -> Nodes\n # Also create a sorted list of numConn\n invMap = defaultdict(list)\n numConn = set()\n for k, v in conn.items():\n numConn.add(len(v))\n invMap[len(v)] += [k]\n numConn = list(numConn)\n numConn.sort(reverse = True)\n\n # From larger numConn, calculate the network rank\n res = 0\n for i in range(len(numConn)):\n if res > numConn[i]*2: # early break\n return res\n for j in range(i, len(numConn)):\n if i == j and len(invMap[numConn[i]]) == 1: # skip condition\n continue\n # minus one if every pair of nodes in edgeSet\n res = max(res, numConn[i] + numConn[j] - all([(a, b) in edgesSet for a, b in product(invMap[numConn[i]], invMap[numConn[j]]) if a != b]))\n return res\n``` | 1 | There is an infrastructure of `n` cities with some number of `roads` connecting these cities. Each `roads[i] = [ai, bi]` indicates that there is a bidirectional road between cities `ai` and `bi`.
The **network rank** of **two different cities** is defined as the total number of **directly** connected roads to **either** city. If a road is directly connected to both cities, it is only counted **once**.
The **maximal network rank** of the infrastructure is the **maximum network rank** of all pairs of different cities.
Given the integer `n` and the array `roads`, return _the **maximal network rank** of the entire infrastructure_.
**Example 1:**
**Input:** n = 4, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 4
**Explanation:** The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
**Example 2:**
**Input:** n = 5, roads = \[\[0,1\],\[0,3\],\[1,2\],\[1,3\],\[2,3\],\[2,4\]\]
**Output:** 5
**Explanation:** There are 5 roads that are connected to cities 1 or 2.
**Example 3:**
**Input:** n = 8, roads = \[\[0,1\],\[1,2\],\[2,3\],\[2,4\],\[5,6\],\[5,7\]\]
**Output:** 5
**Explanation:** The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
**Constraints:**
* `2 <= n <= 100`
* `0 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 2`
* `0 <= ai, bi <= n-1`
* `ai != bi`
* Each pair of cities has **at most one** road connecting them. | Compute all sums and save it in array. Then just go from LEFT to RIGHT index and calculate answer modulo 1e9 + 7. |
Python 85% | maximal-network-rank | 0 | 1 | # Code\n```\nclass Solution:\n def maximalNetworkRank(self, n: int, A: List[List[int]]) -> int:\n\n # Create connection dict and store edges in "edgesSet"\n conn = defaultdict(list)\n edgesSet = set()\n for a, b in A:\n conn[a] += [b]\n conn[b] += [a]\n edgesSet |= set([(a, b), (b, a)])\n \n # Create an inverseIndex: invMap[number_of_edges] -> Nodes\n # Also create a sorted list of numConn\n invMap = defaultdict(list)\n numConn = set()\n for k, v in conn.items():\n numConn.add(len(v))\n invMap[len(v)] += [k]\n numConn = list(numConn)\n numConn.sort(reverse = True)\n\n # From larger numConn, calculate the network rank\n res = 0\n for i in range(len(numConn)):\n if res > numConn[i]*2: # early break\n return res\n for j in range(i, len(numConn)):\n if i == j and len(invMap[numConn[i]]) == 1: # skip condition\n continue\n # minus one if every pair of nodes in edgeSet\n res = max(res, numConn[i] + numConn[j] - all([(a, b) in edgesSet for a, b in product(invMap[numConn[i]], invMap[numConn[j]]) if a != b]))\n return res\n``` | 1 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.