title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python, one pass, no additional memory | slowest-key | 0 | 1 | ```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n max_dur = releaseTimes[0]\n max_key = keysPressed[0]\n \n for i in range(1, len(releaseTimes)):\n if releaseTimes[i] - releaseTimes[i-1] > max_dur:\n max_dur = releaseTimes[i] - releaseTimes[i-1]\n max_key = keysPressed[i]\n elif releaseTimes[i] - releaseTimes[i-1] == max_dur and max_key < keysPressed[i]:\n max_key = keysPressed[i]\n \n return max_key \n```\t\t\n\t\t | 9 | A newly designed keypad was tested, where a tester pressed a sequence of `n` keys, one at a time.
You are given a string `keysPressed` of length `n`, where `keysPressed[i]` was the `ith` key pressed in the testing sequence, and a sorted list `releaseTimes`, where `releaseTimes[i]` was the time the `ith` key was released. Both arrays are **0-indexed**. The `0th` key was pressed at the time `0`, and every subsequent key was pressed at the **exact** time the previous key was released.
The tester wants to know the key of the keypress that had the **longest duration**. The `ith` keypress had a **duration** of `releaseTimes[i] - releaseTimes[i - 1]`, and the `0th` keypress had a duration of `releaseTimes[0]`.
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key **may not** have had the same **duration**.
_Return the key of the keypress that had the **longest duration**. If there are multiple such keypresses, return the lexicographically largest key of the keypresses._
**Example 1:**
**Input:** releaseTimes = \[9,29,49,50\], keysPressed = "cbcd "
**Output:** "c "
**Explanation:** The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
**Example 2:**
**Input:** releaseTimes = \[12,23,36,46,62\], keysPressed = "spuda "
**Output:** "a "
**Explanation:** The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
**Constraints:**
* `releaseTimes.length == n`
* `keysPressed.length == n`
* `2 <= n <= 1000`
* `1 <= releaseTimes[i] <= 109`
* `releaseTimes[i] < releaseTimes[i+1]`
* `keysPressed` contains only lowercase English letters. | We want to make the smaller digits the most significant digits in the number. For each index i, check the smallest digit in a window of size k and append it to the answer. Update the indices of all digits in this range accordingly. |
Python, one pass, no additional memory | slowest-key | 0 | 1 | ```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n max_dur = releaseTimes[0]\n max_key = keysPressed[0]\n \n for i in range(1, len(releaseTimes)):\n if releaseTimes[i] - releaseTimes[i-1] > max_dur:\n max_dur = releaseTimes[i] - releaseTimes[i-1]\n max_key = keysPressed[i]\n elif releaseTimes[i] - releaseTimes[i-1] == max_dur and max_key < keysPressed[i]:\n max_key = keysPressed[i]\n \n return max_key \n```\t\t\n\t\t | 9 | You are given an array of `events` where `events[i] = [startDayi, endDayi, valuei]`. The `ith` event starts at `startDayi` and ends at `endDayi`, and if you attend this event, you will receive a value of `valuei`. You are also given an integer `k` which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the **entire** event. Note that the end day is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return _the **maximum sum** of values that you can receive by attending events._
**Example 1:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,1\]\], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
**Example 2:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,10\]\], k = 2
**Output:** 10
**Explanation:** Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.
**Example 3:**
**Input:** events = \[\[1,1,1\],\[2,2,2\],\[3,3,3\],\[4,4,4\]\], k = 3
**Output:** 9
**Explanation:** Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
**Constraints:**
* `1 <= k <= events.length`
* `1 <= k * events.length <= 106`
* `1 <= startDayi <= endDayi <= 109`
* `1 <= valuei <= 106` | Get for each press its key and amount of time taken. Iterate on the presses, maintaining the answer so far. The current press will change the answer if and only if its amount of time taken is longer than that of the previous answer, or they are equal but the key is larger than that of the previous answer. |
use dictionary | slowest-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slowestKey(self, times,keys):\n i=1\n md={}\n md.update({keys[0]:times[0]})\n while i<len(keys):\n if keys[i] in md and times[i]-times[i-1]>md[keys[i]]:\n md.update({keys[i]:times[i]-times[i-1]})\n elif keys[i] not in md:\n md.update({keys[i]:times[i]-times[i-1]})\n i=i+1\n md=dict(sorted(md.items(),reverse=True))\n return max(md,key=md.get)\n``` | 0 | A newly designed keypad was tested, where a tester pressed a sequence of `n` keys, one at a time.
You are given a string `keysPressed` of length `n`, where `keysPressed[i]` was the `ith` key pressed in the testing sequence, and a sorted list `releaseTimes`, where `releaseTimes[i]` was the time the `ith` key was released. Both arrays are **0-indexed**. The `0th` key was pressed at the time `0`, and every subsequent key was pressed at the **exact** time the previous key was released.
The tester wants to know the key of the keypress that had the **longest duration**. The `ith` keypress had a **duration** of `releaseTimes[i] - releaseTimes[i - 1]`, and the `0th` keypress had a duration of `releaseTimes[0]`.
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key **may not** have had the same **duration**.
_Return the key of the keypress that had the **longest duration**. If there are multiple such keypresses, return the lexicographically largest key of the keypresses._
**Example 1:**
**Input:** releaseTimes = \[9,29,49,50\], keysPressed = "cbcd "
**Output:** "c "
**Explanation:** The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
**Example 2:**
**Input:** releaseTimes = \[12,23,36,46,62\], keysPressed = "spuda "
**Output:** "a "
**Explanation:** The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
**Constraints:**
* `releaseTimes.length == n`
* `keysPressed.length == n`
* `2 <= n <= 1000`
* `1 <= releaseTimes[i] <= 109`
* `releaseTimes[i] < releaseTimes[i+1]`
* `keysPressed` contains only lowercase English letters. | We want to make the smaller digits the most significant digits in the number. For each index i, check the smallest digit in a window of size k and append it to the answer. Update the indices of all digits in this range accordingly. |
use dictionary | slowest-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slowestKey(self, times,keys):\n i=1\n md={}\n md.update({keys[0]:times[0]})\n while i<len(keys):\n if keys[i] in md and times[i]-times[i-1]>md[keys[i]]:\n md.update({keys[i]:times[i]-times[i-1]})\n elif keys[i] not in md:\n md.update({keys[i]:times[i]-times[i-1]})\n i=i+1\n md=dict(sorted(md.items(),reverse=True))\n return max(md,key=md.get)\n``` | 0 | You are given an array of `events` where `events[i] = [startDayi, endDayi, valuei]`. The `ith` event starts at `startDayi` and ends at `endDayi`, and if you attend this event, you will receive a value of `valuei`. You are also given an integer `k` which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the **entire** event. Note that the end day is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return _the **maximum sum** of values that you can receive by attending events._
**Example 1:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,1\]\], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
**Example 2:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,10\]\], k = 2
**Output:** 10
**Explanation:** Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.
**Example 3:**
**Input:** events = \[\[1,1,1\],\[2,2,2\],\[3,3,3\],\[4,4,4\]\], k = 3
**Output:** 9
**Explanation:** Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
**Constraints:**
* `1 <= k <= events.length`
* `1 <= k * events.length <= 106`
* `1 <= startDayi <= endDayi <= 109`
* `1 <= valuei <= 106` | Get for each press its key and amount of time taken. Iterate on the presses, maintaining the answer so far. The current press will change the answer if and only if its amount of time taken is longer than that of the previous answer, or they are equal but the key is larger than that of the previous answer. |
My Solution :) BEATS 79.66 % RUNTIME | slowest-key | 0 | 1 | # Intuition\n1. Initialize a dictionary prev to keep track of the previous release time for each key. The first entry in the dictionary is initialized with the first key and its corresponding release time from keysPressed and releaseTimes.\n\n2. Initialize a variable maximumTime with the first release time from releaseTimes.\n\n3. Initialize a list elements with the first key from keysPressed.\n\n4. Iterate over the remaining elements of releaseTimes and keysPressed, starting from index 1.\n\n5. For each iteration, calculate the duration of the current key press by subtracting the previous release time from the current release time. Store this duration in the prev dictionary with the current key as the key and the duration as the value.\n\n6. If the duration of the current key press is greater than the current maximumTime, update elements with a list containing only the current key, and update maximumTime with the duration of the current key press.\n\n7. If the duration of the current key press is equal to the current maximumTime, append the current key to elements.\n\n8. After iterating through all the key presses, elements will contain all the keys that were pressed for the longest duration. Sort elements in ascending order and return the last element, which will be the key pressed for the longest duration.\n\n# Approach\nThe approach essentially keeps track of the duration of each key press and compares it with the previous maximum duration encountered. If a longer duration is found, the list of keys pressed for the longest duration is updated. Finally, the last key in the sorted list is returned as the answer.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n prev = {keysPressed[0]: releaseTimes[0]}\n maximumTime = releaseTimes[0]\n elements = [keysPressed[0]]\n for i in range(1, len(releaseTimes)):\n prev[keysPressed[i]] = releaseTimes[i]-releaseTimes[i-1]\n if prev[keysPressed[i]] > maximumTime:\n elements = [] + [keysPressed[i]]\n maximumTime = prev[keysPressed[i]]\n elif prev[keysPressed[i]] == maximumTime:\n elements.append(keysPressed[i])\n return sorted(elements)[-1]\n``` | 0 | A newly designed keypad was tested, where a tester pressed a sequence of `n` keys, one at a time.
You are given a string `keysPressed` of length `n`, where `keysPressed[i]` was the `ith` key pressed in the testing sequence, and a sorted list `releaseTimes`, where `releaseTimes[i]` was the time the `ith` key was released. Both arrays are **0-indexed**. The `0th` key was pressed at the time `0`, and every subsequent key was pressed at the **exact** time the previous key was released.
The tester wants to know the key of the keypress that had the **longest duration**. The `ith` keypress had a **duration** of `releaseTimes[i] - releaseTimes[i - 1]`, and the `0th` keypress had a duration of `releaseTimes[0]`.
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key **may not** have had the same **duration**.
_Return the key of the keypress that had the **longest duration**. If there are multiple such keypresses, return the lexicographically largest key of the keypresses._
**Example 1:**
**Input:** releaseTimes = \[9,29,49,50\], keysPressed = "cbcd "
**Output:** "c "
**Explanation:** The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
**Example 2:**
**Input:** releaseTimes = \[12,23,36,46,62\], keysPressed = "spuda "
**Output:** "a "
**Explanation:** The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
**Constraints:**
* `releaseTimes.length == n`
* `keysPressed.length == n`
* `2 <= n <= 1000`
* `1 <= releaseTimes[i] <= 109`
* `releaseTimes[i] < releaseTimes[i+1]`
* `keysPressed` contains only lowercase English letters. | We want to make the smaller digits the most significant digits in the number. For each index i, check the smallest digit in a window of size k and append it to the answer. Update the indices of all digits in this range accordingly. |
My Solution :) BEATS 79.66 % RUNTIME | slowest-key | 0 | 1 | # Intuition\n1. Initialize a dictionary prev to keep track of the previous release time for each key. The first entry in the dictionary is initialized with the first key and its corresponding release time from keysPressed and releaseTimes.\n\n2. Initialize a variable maximumTime with the first release time from releaseTimes.\n\n3. Initialize a list elements with the first key from keysPressed.\n\n4. Iterate over the remaining elements of releaseTimes and keysPressed, starting from index 1.\n\n5. For each iteration, calculate the duration of the current key press by subtracting the previous release time from the current release time. Store this duration in the prev dictionary with the current key as the key and the duration as the value.\n\n6. If the duration of the current key press is greater than the current maximumTime, update elements with a list containing only the current key, and update maximumTime with the duration of the current key press.\n\n7. If the duration of the current key press is equal to the current maximumTime, append the current key to elements.\n\n8. After iterating through all the key presses, elements will contain all the keys that were pressed for the longest duration. Sort elements in ascending order and return the last element, which will be the key pressed for the longest duration.\n\n# Approach\nThe approach essentially keeps track of the duration of each key press and compares it with the previous maximum duration encountered. If a longer duration is found, the list of keys pressed for the longest duration is updated. Finally, the last key in the sorted list is returned as the answer.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n prev = {keysPressed[0]: releaseTimes[0]}\n maximumTime = releaseTimes[0]\n elements = [keysPressed[0]]\n for i in range(1, len(releaseTimes)):\n prev[keysPressed[i]] = releaseTimes[i]-releaseTimes[i-1]\n if prev[keysPressed[i]] > maximumTime:\n elements = [] + [keysPressed[i]]\n maximumTime = prev[keysPressed[i]]\n elif prev[keysPressed[i]] == maximumTime:\n elements.append(keysPressed[i])\n return sorted(elements)[-1]\n``` | 0 | You are given an array of `events` where `events[i] = [startDayi, endDayi, valuei]`. The `ith` event starts at `startDayi` and ends at `endDayi`, and if you attend this event, you will receive a value of `valuei`. You are also given an integer `k` which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the **entire** event. Note that the end day is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return _the **maximum sum** of values that you can receive by attending events._
**Example 1:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,1\]\], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
**Example 2:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,10\]\], k = 2
**Output:** 10
**Explanation:** Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.
**Example 3:**
**Input:** events = \[\[1,1,1\],\[2,2,2\],\[3,3,3\],\[4,4,4\]\], k = 3
**Output:** 9
**Explanation:** Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
**Constraints:**
* `1 <= k <= events.length`
* `1 <= k * events.length <= 106`
* `1 <= startDayi <= endDayi <= 109`
* `1 <= valuei <= 106` | Get for each press its key and amount of time taken. Iterate on the presses, maintaining the answer so far. The current press will change the answer if and only if its amount of time taken is longer than that of the previous answer, or they are equal but the key is larger than that of the previous answer. |
Python Simple Soluiton - Hashmap! | slowest-key | 0 | 1 | \n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n\n hashmap: dict = { keysPressed[0]:releaseTimes[0] }\n for index in range(1, len(releaseTimes)):\n \n difference: int = releaseTimes[index] - releaseTimes[index - 1]\n hashmap[keysPressed[index]] = hashmap.get(keysPressed[index], 0)\n if difference > hashmap.get(keysPressed[index]):\n hashmap[keysPressed[index]] = difference\n \n maximum: int = max(hashmap.values()) \n longest: list = sorted(letter for letter, value in hashmap.items() if value == maximum)[-1]\n return longest\n``` | 0 | A newly designed keypad was tested, where a tester pressed a sequence of `n` keys, one at a time.
You are given a string `keysPressed` of length `n`, where `keysPressed[i]` was the `ith` key pressed in the testing sequence, and a sorted list `releaseTimes`, where `releaseTimes[i]` was the time the `ith` key was released. Both arrays are **0-indexed**. The `0th` key was pressed at the time `0`, and every subsequent key was pressed at the **exact** time the previous key was released.
The tester wants to know the key of the keypress that had the **longest duration**. The `ith` keypress had a **duration** of `releaseTimes[i] - releaseTimes[i - 1]`, and the `0th` keypress had a duration of `releaseTimes[0]`.
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key **may not** have had the same **duration**.
_Return the key of the keypress that had the **longest duration**. If there are multiple such keypresses, return the lexicographically largest key of the keypresses._
**Example 1:**
**Input:** releaseTimes = \[9,29,49,50\], keysPressed = "cbcd "
**Output:** "c "
**Explanation:** The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
**Example 2:**
**Input:** releaseTimes = \[12,23,36,46,62\], keysPressed = "spuda "
**Output:** "a "
**Explanation:** The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
**Constraints:**
* `releaseTimes.length == n`
* `keysPressed.length == n`
* `2 <= n <= 1000`
* `1 <= releaseTimes[i] <= 109`
* `releaseTimes[i] < releaseTimes[i+1]`
* `keysPressed` contains only lowercase English letters. | We want to make the smaller digits the most significant digits in the number. For each index i, check the smallest digit in a window of size k and append it to the answer. Update the indices of all digits in this range accordingly. |
Python Simple Soluiton - Hashmap! | slowest-key | 0 | 1 | \n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n\n hashmap: dict = { keysPressed[0]:releaseTimes[0] }\n for index in range(1, len(releaseTimes)):\n \n difference: int = releaseTimes[index] - releaseTimes[index - 1]\n hashmap[keysPressed[index]] = hashmap.get(keysPressed[index], 0)\n if difference > hashmap.get(keysPressed[index]):\n hashmap[keysPressed[index]] = difference\n \n maximum: int = max(hashmap.values()) \n longest: list = sorted(letter for letter, value in hashmap.items() if value == maximum)[-1]\n return longest\n``` | 0 | You are given an array of `events` where `events[i] = [startDayi, endDayi, valuei]`. The `ith` event starts at `startDayi` and ends at `endDayi`, and if you attend this event, you will receive a value of `valuei`. You are also given an integer `k` which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the **entire** event. Note that the end day is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return _the **maximum sum** of values that you can receive by attending events._
**Example 1:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,1\]\], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
**Example 2:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,10\]\], k = 2
**Output:** 10
**Explanation:** Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.
**Example 3:**
**Input:** events = \[\[1,1,1\],\[2,2,2\],\[3,3,3\],\[4,4,4\]\], k = 3
**Output:** 9
**Explanation:** Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
**Constraints:**
* `1 <= k <= events.length`
* `1 <= k * events.length <= 106`
* `1 <= startDayi <= endDayi <= 109`
* `1 <= valuei <= 106` | Get for each press its key and amount of time taken. Iterate on the presses, maintaining the answer so far. The current press will change the answer if and only if its amount of time taken is longer than that of the previous answer, or they are equal but the key is larger than that of the previous answer. |
python beats 93% | slowest-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n data ={keysPressed[0]:releaseTimes[0]}\n for i in range(1,len(releaseTimes)):\n if keysPressed[i] in data:\n if( releaseTimes[i] - releaseTimes[i-1])> data[keysPressed[i]]:\n data[keysPressed[i]] =releaseTimes[i] - releaseTimes[i-1]\n elif keysPressed[i] not in data:\n data[keysPressed[i]] =( releaseTimes[i] - releaseTimes[i-1])\n data1 = dict(sorted(data.items(), key=lambda item: (item[1], item[0]),))\n return list(data1.keys())[-1]\n\n\n \n\n\n \n``` | 0 | A newly designed keypad was tested, where a tester pressed a sequence of `n` keys, one at a time.
You are given a string `keysPressed` of length `n`, where `keysPressed[i]` was the `ith` key pressed in the testing sequence, and a sorted list `releaseTimes`, where `releaseTimes[i]` was the time the `ith` key was released. Both arrays are **0-indexed**. The `0th` key was pressed at the time `0`, and every subsequent key was pressed at the **exact** time the previous key was released.
The tester wants to know the key of the keypress that had the **longest duration**. The `ith` keypress had a **duration** of `releaseTimes[i] - releaseTimes[i - 1]`, and the `0th` keypress had a duration of `releaseTimes[0]`.
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key **may not** have had the same **duration**.
_Return the key of the keypress that had the **longest duration**. If there are multiple such keypresses, return the lexicographically largest key of the keypresses._
**Example 1:**
**Input:** releaseTimes = \[9,29,49,50\], keysPressed = "cbcd "
**Output:** "c "
**Explanation:** The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
**Example 2:**
**Input:** releaseTimes = \[12,23,36,46,62\], keysPressed = "spuda "
**Output:** "a "
**Explanation:** The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
**Constraints:**
* `releaseTimes.length == n`
* `keysPressed.length == n`
* `2 <= n <= 1000`
* `1 <= releaseTimes[i] <= 109`
* `releaseTimes[i] < releaseTimes[i+1]`
* `keysPressed` contains only lowercase English letters. | We want to make the smaller digits the most significant digits in the number. For each index i, check the smallest digit in a window of size k and append it to the answer. Update the indices of all digits in this range accordingly. |
python beats 93% | slowest-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n data ={keysPressed[0]:releaseTimes[0]}\n for i in range(1,len(releaseTimes)):\n if keysPressed[i] in data:\n if( releaseTimes[i] - releaseTimes[i-1])> data[keysPressed[i]]:\n data[keysPressed[i]] =releaseTimes[i] - releaseTimes[i-1]\n elif keysPressed[i] not in data:\n data[keysPressed[i]] =( releaseTimes[i] - releaseTimes[i-1])\n data1 = dict(sorted(data.items(), key=lambda item: (item[1], item[0]),))\n return list(data1.keys())[-1]\n\n\n \n\n\n \n``` | 0 | You are given an array of `events` where `events[i] = [startDayi, endDayi, valuei]`. The `ith` event starts at `startDayi` and ends at `endDayi`, and if you attend this event, you will receive a value of `valuei`. You are also given an integer `k` which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the **entire** event. Note that the end day is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return _the **maximum sum** of values that you can receive by attending events._
**Example 1:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,1\]\], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
**Example 2:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,10\]\], k = 2
**Output:** 10
**Explanation:** Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.
**Example 3:**
**Input:** events = \[\[1,1,1\],\[2,2,2\],\[3,3,3\],\[4,4,4\]\], k = 3
**Output:** 9
**Explanation:** Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
**Constraints:**
* `1 <= k <= events.length`
* `1 <= k * events.length <= 106`
* `1 <= startDayi <= endDayi <= 109`
* `1 <= valuei <= 106` | Get for each press its key and amount of time taken. Iterate on the presses, maintaining the answer so far. The current press will change the answer if and only if its amount of time taken is longer than that of the previous answer, or they are equal but the key is larger than that of the previous answer. |
Easy python Solution. Beats 90%. Dictionary. | slowest-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n## *Use a python dictionary to calculate the hold time for each key.*\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Store the largest the hold time for each key using a dictionary.\n2. Find the key that was pressesd for the longest time.\n a. In case there are two or more keys with the same holding time return the lexicographically largest key. \n b. In order to find the lexicographically largest key use build in ord() method that return the position of a character in the ASCII table.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n ans = 0\n mx = 0\n statistic = {keysPressed[0]: releaseTimes[0]}\n\n for i in range(1, len(releaseTimes)):)\n reliase_time = (releaseTimes[i] - releaseTimes[i-1])\n if keysPressed[i] not in statistic \\\n or reliase_time > statistic[keysPressed[i]]:\n statistic[keysPressed[i]] = (reliase_time)\n \n for key, value in statistic.items():\n if value > mx:\n mx = value\n ans = key\n elif value == mx:\n if ord(key) > ord(ans):\n mx = value\n ans = key\n\n return ans\n\n```\n# Please UPVOTE !!! | 0 | A newly designed keypad was tested, where a tester pressed a sequence of `n` keys, one at a time.
You are given a string `keysPressed` of length `n`, where `keysPressed[i]` was the `ith` key pressed in the testing sequence, and a sorted list `releaseTimes`, where `releaseTimes[i]` was the time the `ith` key was released. Both arrays are **0-indexed**. The `0th` key was pressed at the time `0`, and every subsequent key was pressed at the **exact** time the previous key was released.
The tester wants to know the key of the keypress that had the **longest duration**. The `ith` keypress had a **duration** of `releaseTimes[i] - releaseTimes[i - 1]`, and the `0th` keypress had a duration of `releaseTimes[0]`.
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key **may not** have had the same **duration**.
_Return the key of the keypress that had the **longest duration**. If there are multiple such keypresses, return the lexicographically largest key of the keypresses._
**Example 1:**
**Input:** releaseTimes = \[9,29,49,50\], keysPressed = "cbcd "
**Output:** "c "
**Explanation:** The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
**Example 2:**
**Input:** releaseTimes = \[12,23,36,46,62\], keysPressed = "spuda "
**Output:** "a "
**Explanation:** The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
**Constraints:**
* `releaseTimes.length == n`
* `keysPressed.length == n`
* `2 <= n <= 1000`
* `1 <= releaseTimes[i] <= 109`
* `releaseTimes[i] < releaseTimes[i+1]`
* `keysPressed` contains only lowercase English letters. | We want to make the smaller digits the most significant digits in the number. For each index i, check the smallest digit in a window of size k and append it to the answer. Update the indices of all digits in this range accordingly. |
Easy python Solution. Beats 90%. Dictionary. | slowest-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n## *Use a python dictionary to calculate the hold time for each key.*\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Store the largest the hold time for each key using a dictionary.\n2. Find the key that was pressesd for the longest time.\n a. In case there are two or more keys with the same holding time return the lexicographically largest key. \n b. In order to find the lexicographically largest key use build in ord() method that return the position of a character in the ASCII table.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slowestKey(self, releaseTimes: List[int], keysPressed: str) -> str:\n ans = 0\n mx = 0\n statistic = {keysPressed[0]: releaseTimes[0]}\n\n for i in range(1, len(releaseTimes)):)\n reliase_time = (releaseTimes[i] - releaseTimes[i-1])\n if keysPressed[i] not in statistic \\\n or reliase_time > statistic[keysPressed[i]]:\n statistic[keysPressed[i]] = (reliase_time)\n \n for key, value in statistic.items():\n if value > mx:\n mx = value\n ans = key\n elif value == mx:\n if ord(key) > ord(ans):\n mx = value\n ans = key\n\n return ans\n\n```\n# Please UPVOTE !!! | 0 | You are given an array of `events` where `events[i] = [startDayi, endDayi, valuei]`. The `ith` event starts at `startDayi` and ends at `endDayi`, and if you attend this event, you will receive a value of `valuei`. You are also given an integer `k` which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the **entire** event. Note that the end day is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return _the **maximum sum** of values that you can receive by attending events._
**Example 1:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,1\]\], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
**Example 2:**
**Input:** events = \[\[1,2,4\],\[3,4,3\],\[2,3,10\]\], k = 2
**Output:** 10
**Explanation:** Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do **not** have to attend k events.
**Example 3:**
**Input:** events = \[\[1,1,1\],\[2,2,2\],\[3,3,3\],\[4,4,4\]\], k = 3
**Output:** 9
**Explanation:** Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
**Constraints:**
* `1 <= k <= events.length`
* `1 <= k * events.length <= 106`
* `1 <= startDayi <= endDayi <= 109`
* `1 <= valuei <= 106` | Get for each press its key and amount of time taken. Iterate on the presses, maintaining the answer so far. The current press will change the answer if and only if its amount of time taken is longer than that of the previous answer, or they are equal but the key is larger than that of the previous answer. |
1️⃣-liner_brute_force.py😁 | arithmetic-subarrays | 0 | 1 | # Code\n```js\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n return[all(arr[i+1]-arr[i]==arr[1]-arr[0]for i in range(len(arr)-1))for arr in[sorted(nums[a:b+1])for a,b in zip(l,r)]] \n```\n\n | 5 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
1️⃣-liner_brute_force.py😁 | arithmetic-subarrays | 0 | 1 | # Code\n```js\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n return[all(arr[i+1]-arr[i]==arr[1]-arr[0]for i in range(len(arr)-1))for arr in[sorted(nums[a:b+1])for a,b in zip(l,r)]] \n```\n\n | 5 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | arithmetic-subarrays | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(With Sorting)***\n1. **check function:** Sorts the given array and checks if the elements form an arithmetic sequence by verifying if the difference between consecutive elements remains constant.\n1. **checkArithmeticSubarrays function:** Loops through the provided ranges `l` and `r` to extract subarrays from `nums`, then checks each subarray using the `check` function to determine if they form arithmetic sequences.\n1. **ans vector:** Stores the boolean results indicating whether each subarray is an arithmetic sequence or not.\n1. **Return:** Returns the vector containing results for each subarray\'s arithmetic sequence check.\n\n# Complexity\n- *Time complexity:*\n $$O(m\u22C5n\u22C5logn)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to check if the given array forms an arithmetic sequence\n bool check(vector<int>& arr) {\n sort(arr.begin(), arr.end()); // Sort the array\n int diff = arr[1] - arr[0]; // Calculate the difference between the first two elements\n \n // Check if the difference remains the same for consecutive elements\n for (int i = 2; i < arr.size(); i++) {\n if (arr[i] - arr[i - 1] != diff) {\n return false; // If the difference changes, it\'s not an arithmetic sequence\n }\n }\n \n return true; // If all differences are the same, it\'s an arithmetic sequence\n }\n \n // Function to check arithmetic subarrays in the given range\n vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {\n vector<bool> ans; // Vector to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < l.size(); i++) {\n // Extract the subarray from nums using the given range [l[i], r[i]]\n vector<int> arr(begin(nums) + l[i], begin(nums) + r[i] + 1);\n ans.push_back(check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n }\n};\n\n\n```\n```C []\nbool check(int arr[], int size) {\n // Sort the array\n // (Implementation of sorting is not provided here)\n\n int diff = arr[1] - arr[0]; // Calculate the difference between the first two elements\n \n // Check if the difference remains the same for consecutive elements\n for (int i = 2; i < size; i++) {\n if (arr[i] - arr[i - 1] != diff) {\n return false; // If the difference changes, it\'s not an arithmetic sequence\n }\n }\n\n return true; // If all differences are the same, it\'s an arithmetic sequence\n}\n\n// Function to check arithmetic subarrays in the given range\nvoid checkArithmeticSubarrays(int nums[], int numsSize, int l[], int r[], int queriesSize) {\n bool ans[queriesSize]; // Array to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < queriesSize; i++) {\n int subarraySize = r[i] - l[i] + 1;\n int arr[subarraySize]; // Create a subarray\n \n // Extract the subarray from nums using the given range [l[i], r[i]]\n int index = 0;\n for (int j = l[i]; j <= r[i]; j++) {\n arr[index++] = nums[j];\n }\n \n ans[i] = check(arr, subarraySize); // Check if the subarray forms an arithmetic sequence\n }\n \n // Printing the results\n for (int i = 0; i < queriesSize; i++) {\n if (ans[i]) {\n printf("true ");\n } else {\n printf("false ");\n }\n }\n printf("\\n");\n}\n\n\n```\n\n```Java []\nclass Solution {\n public Boolean check(int[] arr) {\n Arrays.sort(arr);\n int diff = arr[1] - arr[0];\n \n for (int i = 2; i < arr.length; i++) {\n if (arr[i] - arr[i - 1] != diff) {\n return false;\n }\n }\n \n return true;\n }\n \n public List<Boolean> checkArithmeticSubarrays(int[] nums, int[] l, int[] r) {\n List<Boolean> ans = new ArrayList();\n for (int i = 0; i < l.length; i++) {\n int[] arr = new int[r[i] - l[i] + 1];\n for (int j = 0; j < arr.length; j++) {\n arr[j] = nums[l[i] + j];\n }\n \n ans.add(check(arr));\n }\n\n return ans;\n }\n}\n\n```\n\n```python3 []\n\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def check(arr):\n arr.sort()\n diff = arr[1] - arr[0]\n \n for i in range(2, len(arr)):\n if arr[i] - arr[i - 1] != diff:\n return False\n \n return True\n \n ans = []\n for i in range(len(l)):\n arr = nums[l[i] : r[i] + 1]\n ans.append(check(arr))\n \n return ans\n\n```\n```javascript []\nfunction check(arr) {\n arr.sort((a, b) => a - b); // Sort the array\n let diff = arr[1] - arr[0]; // Calculate the difference between the first two elements\n\n // Check if the difference remains the same for consecutive elements\n for (let i = 2; i < arr.length; i++) {\n if (arr[i] - arr[i - 1] !== diff) {\n return false; // If the difference changes, it\'s not an arithmetic sequence\n }\n }\n\n return true; // If all differences are the same, it\'s an arithmetic sequence\n}\n\nfunction checkArithmeticSubarrays(nums, l, r) {\n const ans = [];\n\n // Iterate through the ranges and check each subarray\n for (let i = 0; i < l.length; i++) {\n const arr = nums.slice(l[i], r[i] + 1); // Extract the subarray from nums using the given range [l[i], r[i]]\n ans.push(check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n\n return ans; // Return the results for each subarray\n}\n\n```\n\n---\n\n#### ***Approach 2(Without Sorting)***\n1. **Libraries included:**\n\n - **<vector>:** To use the `vector` container for arrays.\n - **<unordered_set>:** To utilize an unordered set for efficient element lookup.\n - **<climits>:** For using `INT_MAX` and `INT_MIN` constants for integer limits.\n1. **Class Solution:**\n\n - Contains two methods:\n - **bool check(vector<int>& arr):** Checks if an array forms an arithmetic sequence.\n - **vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r):** Checks arithmetic subarrays in the given range.\n1. **bool check(vector<int>& arr) function:**\n\n - Calculates minimum and maximum elements in the array and stores them in `minElement` and `maxElement`.\n - Populates an `unordered_set` named `arrSet` with elements from the array `arr`.\n - Determines if the array elements can form an arithmetic sequence:\n - Computes the expected common difference diff if the elements are in an arithmetic sequence.\n - Validates the sequence by checking if the elements satisfy the arithmetic sequence condition:\n - Verifies the evenly spaced property using the modulus operation.\n - Validates if the expected elements are present by checking each one against the set.\n1. **vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) function:**\n\n - Iterates through the ranges defined by vectors `l` and `r`.\n - Extracts subarrays from `nums` based on the provided range.\n - Applies the `check` function to each subarray and stores the result in the `ans` vector.\n1. **Overall Process:**\n\n - The code first defines methods to verify if a given array is an arithmetic sequence and then applies this check to multiple subarrays within a range.\n\n# Complexity\n- *Time complexity:*\n $$O(m\u22C5n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to check if the given array forms an arithmetic sequence\n bool check(vector<int>& arr) {\n int minElement = INT_MAX; // Variable to store the minimum element in the array\n int maxElement = INT_MIN; // Variable to store the maximum element in the array\n unordered_set<int> arrSet; // Set to store elements of the array\n \n // Finding minimum and maximum elements and populating the set\n for (int num : arr) {\n minElement = min(minElement, num);\n maxElement = max(maxElement, num);\n arrSet.insert(num);\n }\n \n // Check if the elements can form an arithmetic sequence\n if ((maxElement - minElement) % (arr.size() - 1) != 0) {\n return false; // If not evenly spaced, it\'s not an arithmetic sequence\n }\n \n int diff = (maxElement - minElement) / (arr.size() - 1); // Calculate the common difference\n int curr = minElement + diff; // Initialize current element\n \n // Check for each expected element in the sequence\n while (curr < maxElement) {\n if (arrSet.find(curr) == arrSet.end()) {\n return false; // If any element is missing, it\'s not an arithmetic sequence\n }\n curr += diff; // Move to the next expected element\n }\n \n return true; // If all conditions satisfy, it\'s an arithmetic sequence\n }\n \n // Function to check arithmetic subarrays in the given range\n vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {\n vector<bool> ans; // Vector to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < l.size(); i++) {\n // Extract the subarray from nums using the given range [l[i], r[i]]\n vector<int> arr(begin(nums) + l[i], begin(nums) + r[i] + 1);\n ans.push_back(check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n }\n};\n\n\n\n```\n```C []\n\nint check(int arr[], int size) {\n int minElement = INT_MAX; // Variable to store the minimum element in the array\n int maxElement = INT_MIN; // Variable to store the maximum element in the array\n int arrSet[MAX_SIZE] = {0}; // Array to store elements of the array\n \n // Finding minimum and maximum elements and populating the set\n for (int i = 0; i < size; i++) {\n minElement = (arr[i] < minElement) ? arr[i] : minElement;\n maxElement = (arr[i] > maxElement) ? arr[i] : maxElement;\n arrSet[arr[i]] = 1;\n }\n \n // Check if the elements can form an arithmetic sequence\n if ((maxElement - minElement) % (size - 1) != 0) {\n return 0; // If not evenly spaced, it\'s not an arithmetic sequence\n }\n \n int diff = (maxElement - minElement) / (size - 1); // Calculate the common difference\n int curr = minElement + diff; // Initialize current element\n \n // Check for each expected element in the sequence\n while (curr < maxElement) {\n if (arrSet[curr] == 0) {\n return 0; // If any element is missing, it\'s not an arithmetic sequence\n }\n curr += diff; // Move to the next expected element\n }\n \n return 1; // If all conditions satisfy, it\'s an arithmetic sequence\n}\n\n// Function to check arithmetic subarrays in the given range\nint* checkArithmeticSubarrays(int* nums, int* l, int* r, int size) {\n int* ans = (int*)malloc(size * sizeof(int)); // Array to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < size; i++) {\n int subArraySize = r[i] - l[i] + 1;\n int subArray[subArraySize];\n \n // Extract the subarray from nums using the given range [l[i], r[i]]\n for (int j = l[i], k = 0; j <= r[i]; j++, k++) {\n subArray[k] = nums[j];\n }\n \n ans[i] = check(subArray, subArraySize); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n}\n\n\n```\n\n```Java []\nclass Solution {\n public Boolean check(int[] arr) {\n int minElement = Integer.MAX_VALUE;\n int maxElement = Integer.MIN_VALUE;\n Set<Integer> arrSet = new HashSet();\n \n for (int num : arr) {\n minElement = Math.min(minElement, num);\n maxElement = Math.max(maxElement, num);\n arrSet.add(num);\n }\n \n if ((maxElement - minElement) % (arr.length - 1) != 0) {\n return false;\n }\n \n int diff = (maxElement - minElement) / (arr.length - 1);\n int curr = minElement + diff;\n \n while (curr < maxElement) {\n if (!arrSet.contains(curr)) {\n return false;\n }\n \n curr += diff;\n }\n \n return true;\n }\n \n public List<Boolean> checkArithmeticSubarrays(int[] nums, int[] l, int[] r) {\n List<Boolean> ans = new ArrayList();\n for (int i = 0; i < l.length; i++) {\n int[] arr = new int[r[i] - l[i] + 1];\n for (int j = 0; j < arr.length; j++) {\n arr[j] = nums[l[i] + j];\n }\n \n ans.add(check(arr));\n }\n\n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def check(arr):\n min_element = min(arr)\n max_element = max(arr)\n\n if (max_element - min_element) % (len(arr) - 1) != 0:\n return False\n\n diff = (max_element - min_element) / (len(arr) - 1)\n \n arr_set = set(arr)\n curr = min_element + diff\n while curr < max_element:\n if curr not in arr_set:\n return False\n \n curr += diff\n \n return True\n\n ans = []\n for i in range(len(l)):\n arr = nums[l[i] : r[i] + 1]\n ans.append(check(arr))\n \n return ans\n\n\n```\n```javascript []\nclass Solution {\n check(arr) {\n let minElement = Number.MAX_SAFE_INTEGER; // Variable to store the minimum element in the array\n let maxElement = Number.MIN_SAFE_INTEGER; // Variable to store the maximum element in the array\n let arrSet = new Set(); // Set to store elements of the array\n \n // Finding minimum and maximum elements and populating the set\n arr.forEach(num => {\n minElement = Math.min(minElement, num);\n maxElement = Math.max(maxElement, num);\n arrSet.add(num);\n });\n \n // Check if the elements can form an arithmetic sequence\n if ((maxElement - minElement) % (arr.length - 1) !== 0) {\n return false; // If not evenly spaced, it\'s not an arithmetic sequence\n }\n \n let diff = (maxElement - minElement) / (arr.length - 1); // Calculate the common difference\n let curr = minElement + diff; // Initialize current element\n \n // Check for each expected element in the sequence\n while (curr < maxElement) {\n if (!arrSet.has(curr)) {\n return false; // If any element is missing, it\'s not an arithmetic sequence\n }\n curr += diff; // Move to the next expected element\n }\n \n return true; // If all conditions satisfy, it\'s an arithmetic sequence\n }\n \n checkArithmeticSubarrays(nums, l, r) {\n let ans = []; // Array to store results\n \n // Iterate through the ranges and check each subarray\n for (let i = 0; i < l.length; i++) {\n // Extract the subarray from nums using the given range [l[i], r[i]]\n let arr = nums.slice(l[i], r[i] + 1);\n ans.push(this.check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n }\n}\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 29 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | arithmetic-subarrays | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(With Sorting)***\n1. **check function:** Sorts the given array and checks if the elements form an arithmetic sequence by verifying if the difference between consecutive elements remains constant.\n1. **checkArithmeticSubarrays function:** Loops through the provided ranges `l` and `r` to extract subarrays from `nums`, then checks each subarray using the `check` function to determine if they form arithmetic sequences.\n1. **ans vector:** Stores the boolean results indicating whether each subarray is an arithmetic sequence or not.\n1. **Return:** Returns the vector containing results for each subarray\'s arithmetic sequence check.\n\n# Complexity\n- *Time complexity:*\n $$O(m\u22C5n\u22C5logn)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to check if the given array forms an arithmetic sequence\n bool check(vector<int>& arr) {\n sort(arr.begin(), arr.end()); // Sort the array\n int diff = arr[1] - arr[0]; // Calculate the difference between the first two elements\n \n // Check if the difference remains the same for consecutive elements\n for (int i = 2; i < arr.size(); i++) {\n if (arr[i] - arr[i - 1] != diff) {\n return false; // If the difference changes, it\'s not an arithmetic sequence\n }\n }\n \n return true; // If all differences are the same, it\'s an arithmetic sequence\n }\n \n // Function to check arithmetic subarrays in the given range\n vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {\n vector<bool> ans; // Vector to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < l.size(); i++) {\n // Extract the subarray from nums using the given range [l[i], r[i]]\n vector<int> arr(begin(nums) + l[i], begin(nums) + r[i] + 1);\n ans.push_back(check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n }\n};\n\n\n```\n```C []\nbool check(int arr[], int size) {\n // Sort the array\n // (Implementation of sorting is not provided here)\n\n int diff = arr[1] - arr[0]; // Calculate the difference between the first two elements\n \n // Check if the difference remains the same for consecutive elements\n for (int i = 2; i < size; i++) {\n if (arr[i] - arr[i - 1] != diff) {\n return false; // If the difference changes, it\'s not an arithmetic sequence\n }\n }\n\n return true; // If all differences are the same, it\'s an arithmetic sequence\n}\n\n// Function to check arithmetic subarrays in the given range\nvoid checkArithmeticSubarrays(int nums[], int numsSize, int l[], int r[], int queriesSize) {\n bool ans[queriesSize]; // Array to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < queriesSize; i++) {\n int subarraySize = r[i] - l[i] + 1;\n int arr[subarraySize]; // Create a subarray\n \n // Extract the subarray from nums using the given range [l[i], r[i]]\n int index = 0;\n for (int j = l[i]; j <= r[i]; j++) {\n arr[index++] = nums[j];\n }\n \n ans[i] = check(arr, subarraySize); // Check if the subarray forms an arithmetic sequence\n }\n \n // Printing the results\n for (int i = 0; i < queriesSize; i++) {\n if (ans[i]) {\n printf("true ");\n } else {\n printf("false ");\n }\n }\n printf("\\n");\n}\n\n\n```\n\n```Java []\nclass Solution {\n public Boolean check(int[] arr) {\n Arrays.sort(arr);\n int diff = arr[1] - arr[0];\n \n for (int i = 2; i < arr.length; i++) {\n if (arr[i] - arr[i - 1] != diff) {\n return false;\n }\n }\n \n return true;\n }\n \n public List<Boolean> checkArithmeticSubarrays(int[] nums, int[] l, int[] r) {\n List<Boolean> ans = new ArrayList();\n for (int i = 0; i < l.length; i++) {\n int[] arr = new int[r[i] - l[i] + 1];\n for (int j = 0; j < arr.length; j++) {\n arr[j] = nums[l[i] + j];\n }\n \n ans.add(check(arr));\n }\n\n return ans;\n }\n}\n\n```\n\n```python3 []\n\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def check(arr):\n arr.sort()\n diff = arr[1] - arr[0]\n \n for i in range(2, len(arr)):\n if arr[i] - arr[i - 1] != diff:\n return False\n \n return True\n \n ans = []\n for i in range(len(l)):\n arr = nums[l[i] : r[i] + 1]\n ans.append(check(arr))\n \n return ans\n\n```\n```javascript []\nfunction check(arr) {\n arr.sort((a, b) => a - b); // Sort the array\n let diff = arr[1] - arr[0]; // Calculate the difference between the first two elements\n\n // Check if the difference remains the same for consecutive elements\n for (let i = 2; i < arr.length; i++) {\n if (arr[i] - arr[i - 1] !== diff) {\n return false; // If the difference changes, it\'s not an arithmetic sequence\n }\n }\n\n return true; // If all differences are the same, it\'s an arithmetic sequence\n}\n\nfunction checkArithmeticSubarrays(nums, l, r) {\n const ans = [];\n\n // Iterate through the ranges and check each subarray\n for (let i = 0; i < l.length; i++) {\n const arr = nums.slice(l[i], r[i] + 1); // Extract the subarray from nums using the given range [l[i], r[i]]\n ans.push(check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n\n return ans; // Return the results for each subarray\n}\n\n```\n\n---\n\n#### ***Approach 2(Without Sorting)***\n1. **Libraries included:**\n\n - **<vector>:** To use the `vector` container for arrays.\n - **<unordered_set>:** To utilize an unordered set for efficient element lookup.\n - **<climits>:** For using `INT_MAX` and `INT_MIN` constants for integer limits.\n1. **Class Solution:**\n\n - Contains two methods:\n - **bool check(vector<int>& arr):** Checks if an array forms an arithmetic sequence.\n - **vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r):** Checks arithmetic subarrays in the given range.\n1. **bool check(vector<int>& arr) function:**\n\n - Calculates minimum and maximum elements in the array and stores them in `minElement` and `maxElement`.\n - Populates an `unordered_set` named `arrSet` with elements from the array `arr`.\n - Determines if the array elements can form an arithmetic sequence:\n - Computes the expected common difference diff if the elements are in an arithmetic sequence.\n - Validates the sequence by checking if the elements satisfy the arithmetic sequence condition:\n - Verifies the evenly spaced property using the modulus operation.\n - Validates if the expected elements are present by checking each one against the set.\n1. **vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) function:**\n\n - Iterates through the ranges defined by vectors `l` and `r`.\n - Extracts subarrays from `nums` based on the provided range.\n - Applies the `check` function to each subarray and stores the result in the `ans` vector.\n1. **Overall Process:**\n\n - The code first defines methods to verify if a given array is an arithmetic sequence and then applies this check to multiple subarrays within a range.\n\n# Complexity\n- *Time complexity:*\n $$O(m\u22C5n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n // Function to check if the given array forms an arithmetic sequence\n bool check(vector<int>& arr) {\n int minElement = INT_MAX; // Variable to store the minimum element in the array\n int maxElement = INT_MIN; // Variable to store the maximum element in the array\n unordered_set<int> arrSet; // Set to store elements of the array\n \n // Finding minimum and maximum elements and populating the set\n for (int num : arr) {\n minElement = min(minElement, num);\n maxElement = max(maxElement, num);\n arrSet.insert(num);\n }\n \n // Check if the elements can form an arithmetic sequence\n if ((maxElement - minElement) % (arr.size() - 1) != 0) {\n return false; // If not evenly spaced, it\'s not an arithmetic sequence\n }\n \n int diff = (maxElement - minElement) / (arr.size() - 1); // Calculate the common difference\n int curr = minElement + diff; // Initialize current element\n \n // Check for each expected element in the sequence\n while (curr < maxElement) {\n if (arrSet.find(curr) == arrSet.end()) {\n return false; // If any element is missing, it\'s not an arithmetic sequence\n }\n curr += diff; // Move to the next expected element\n }\n \n return true; // If all conditions satisfy, it\'s an arithmetic sequence\n }\n \n // Function to check arithmetic subarrays in the given range\n vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {\n vector<bool> ans; // Vector to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < l.size(); i++) {\n // Extract the subarray from nums using the given range [l[i], r[i]]\n vector<int> arr(begin(nums) + l[i], begin(nums) + r[i] + 1);\n ans.push_back(check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n }\n};\n\n\n\n```\n```C []\n\nint check(int arr[], int size) {\n int minElement = INT_MAX; // Variable to store the minimum element in the array\n int maxElement = INT_MIN; // Variable to store the maximum element in the array\n int arrSet[MAX_SIZE] = {0}; // Array to store elements of the array\n \n // Finding minimum and maximum elements and populating the set\n for (int i = 0; i < size; i++) {\n minElement = (arr[i] < minElement) ? arr[i] : minElement;\n maxElement = (arr[i] > maxElement) ? arr[i] : maxElement;\n arrSet[arr[i]] = 1;\n }\n \n // Check if the elements can form an arithmetic sequence\n if ((maxElement - minElement) % (size - 1) != 0) {\n return 0; // If not evenly spaced, it\'s not an arithmetic sequence\n }\n \n int diff = (maxElement - minElement) / (size - 1); // Calculate the common difference\n int curr = minElement + diff; // Initialize current element\n \n // Check for each expected element in the sequence\n while (curr < maxElement) {\n if (arrSet[curr] == 0) {\n return 0; // If any element is missing, it\'s not an arithmetic sequence\n }\n curr += diff; // Move to the next expected element\n }\n \n return 1; // If all conditions satisfy, it\'s an arithmetic sequence\n}\n\n// Function to check arithmetic subarrays in the given range\nint* checkArithmeticSubarrays(int* nums, int* l, int* r, int size) {\n int* ans = (int*)malloc(size * sizeof(int)); // Array to store results\n \n // Iterate through the ranges and check each subarray\n for (int i = 0; i < size; i++) {\n int subArraySize = r[i] - l[i] + 1;\n int subArray[subArraySize];\n \n // Extract the subarray from nums using the given range [l[i], r[i]]\n for (int j = l[i], k = 0; j <= r[i]; j++, k++) {\n subArray[k] = nums[j];\n }\n \n ans[i] = check(subArray, subArraySize); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n}\n\n\n```\n\n```Java []\nclass Solution {\n public Boolean check(int[] arr) {\n int minElement = Integer.MAX_VALUE;\n int maxElement = Integer.MIN_VALUE;\n Set<Integer> arrSet = new HashSet();\n \n for (int num : arr) {\n minElement = Math.min(minElement, num);\n maxElement = Math.max(maxElement, num);\n arrSet.add(num);\n }\n \n if ((maxElement - minElement) % (arr.length - 1) != 0) {\n return false;\n }\n \n int diff = (maxElement - minElement) / (arr.length - 1);\n int curr = minElement + diff;\n \n while (curr < maxElement) {\n if (!arrSet.contains(curr)) {\n return false;\n }\n \n curr += diff;\n }\n \n return true;\n }\n \n public List<Boolean> checkArithmeticSubarrays(int[] nums, int[] l, int[] r) {\n List<Boolean> ans = new ArrayList();\n for (int i = 0; i < l.length; i++) {\n int[] arr = new int[r[i] - l[i] + 1];\n for (int j = 0; j < arr.length; j++) {\n arr[j] = nums[l[i] + j];\n }\n \n ans.add(check(arr));\n }\n\n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def check(arr):\n min_element = min(arr)\n max_element = max(arr)\n\n if (max_element - min_element) % (len(arr) - 1) != 0:\n return False\n\n diff = (max_element - min_element) / (len(arr) - 1)\n \n arr_set = set(arr)\n curr = min_element + diff\n while curr < max_element:\n if curr not in arr_set:\n return False\n \n curr += diff\n \n return True\n\n ans = []\n for i in range(len(l)):\n arr = nums[l[i] : r[i] + 1]\n ans.append(check(arr))\n \n return ans\n\n\n```\n```javascript []\nclass Solution {\n check(arr) {\n let minElement = Number.MAX_SAFE_INTEGER; // Variable to store the minimum element in the array\n let maxElement = Number.MIN_SAFE_INTEGER; // Variable to store the maximum element in the array\n let arrSet = new Set(); // Set to store elements of the array\n \n // Finding minimum and maximum elements and populating the set\n arr.forEach(num => {\n minElement = Math.min(minElement, num);\n maxElement = Math.max(maxElement, num);\n arrSet.add(num);\n });\n \n // Check if the elements can form an arithmetic sequence\n if ((maxElement - minElement) % (arr.length - 1) !== 0) {\n return false; // If not evenly spaced, it\'s not an arithmetic sequence\n }\n \n let diff = (maxElement - minElement) / (arr.length - 1); // Calculate the common difference\n let curr = minElement + diff; // Initialize current element\n \n // Check for each expected element in the sequence\n while (curr < maxElement) {\n if (!arrSet.has(curr)) {\n return false; // If any element is missing, it\'s not an arithmetic sequence\n }\n curr += diff; // Move to the next expected element\n }\n \n return true; // If all conditions satisfy, it\'s an arithmetic sequence\n }\n \n checkArithmeticSubarrays(nums, l, r) {\n let ans = []; // Array to store results\n \n // Iterate through the ranges and check each subarray\n for (let i = 0; i < l.length; i++) {\n // Extract the subarray from nums using the given range [l[i], r[i]]\n let arr = nums.slice(l[i], r[i] + 1);\n ans.push(this.check(arr)); // Check if the subarray forms an arithmetic sequence\n }\n \n return ans; // Return the results for each subarray\n }\n}\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 29 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
📌📌C++/JAVA/Python3- Most intuitive, concise, and interview friendly code for beginners | arithmetic-subarrays | 1 | 1 | # **Intuition**\n\n* For each query, bring out the required vector to check.\n* sort the array for easy AP check\n* If the size is less than two, then it is surely following AP.\n* else we\'ll check for all the values. If at any place it does not follow the progression, then it is not an AP following the sequence.\n\n--------------------------------------\n```Time complexity :``` **O(n*log(n))*** for sorting, and we are running the loop for m times, so overall time complexity will be ***O(n.m.log(n))*** \n# C++\n```\nclass Solution {\npublic:\n vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {\n vector<bool> ans;\n for(int i = 0; i < l.size(); i++){\n vector<int> vec(nums.begin()+l[i], nums.begin()+r[i]+1);\n sort(vec.begin(), vec.end());\n \n if(vec.size() < 2) ans.push_back(true);\n else{\n bool flag = true;\n int diff = vec[1] - vec[0];\n for(int j = 1; j < vec.size(); j++){\n if(vec[j] - vec[j-1] != diff) flag = false;\n }\n ans.push_back(flag);\n }\n }\n return ans;\n }\n};\n```\n\n----------------------------------\n----------------------------------\n# Java\n```\nclass Solution {\n public List<Boolean> checkArithmeticSubarrays(int[] nums, int[] l, int[] r) {\n List<Boolean> ans = new ArrayList<>();\n for (int i = 0; i < l.length; i++) {\n int[] subArray = Arrays.copyOfRange(nums, l[i], r[i] + 1);\n Arrays.sort(subArray);\n \n if (subArray.length < 2) {\n ans.add(true);\n } else {\n boolean flag = true;\n int diff = subArray[1] - subArray[0];\n for (int j = 1; j < subArray.length; j++) {\n if (subArray[j] - subArray[j - 1] != diff) {\n flag = false;\n break;\n }\n }\n ans.add(flag);\n }\n }\n return ans;\n }\n}\n\n```\n----------------------------------------\n--------------------------------------------------------------------\n# Python3\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums, l, r):\n ans = []\n for i in range(len(l)):\n subArray = nums[l[i]:r[i] + 1]\n subArray.sort()\n \n if len(subArray) < 2:\n ans.append(True)\n else:\n flag = True\n diff = subArray[1] - subArray[0]\n for j in range(1, len(subArray)):\n if subArray[j] - subArray[j - 1] != diff:\n flag = False\n break\n ans.append(flag)\n return ans\n\n``` | 4 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
📌📌C++/JAVA/Python3- Most intuitive, concise, and interview friendly code for beginners | arithmetic-subarrays | 1 | 1 | # **Intuition**\n\n* For each query, bring out the required vector to check.\n* sort the array for easy AP check\n* If the size is less than two, then it is surely following AP.\n* else we\'ll check for all the values. If at any place it does not follow the progression, then it is not an AP following the sequence.\n\n--------------------------------------\n```Time complexity :``` **O(n*log(n))*** for sorting, and we are running the loop for m times, so overall time complexity will be ***O(n.m.log(n))*** \n# C++\n```\nclass Solution {\npublic:\n vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {\n vector<bool> ans;\n for(int i = 0; i < l.size(); i++){\n vector<int> vec(nums.begin()+l[i], nums.begin()+r[i]+1);\n sort(vec.begin(), vec.end());\n \n if(vec.size() < 2) ans.push_back(true);\n else{\n bool flag = true;\n int diff = vec[1] - vec[0];\n for(int j = 1; j < vec.size(); j++){\n if(vec[j] - vec[j-1] != diff) flag = false;\n }\n ans.push_back(flag);\n }\n }\n return ans;\n }\n};\n```\n\n----------------------------------\n----------------------------------\n# Java\n```\nclass Solution {\n public List<Boolean> checkArithmeticSubarrays(int[] nums, int[] l, int[] r) {\n List<Boolean> ans = new ArrayList<>();\n for (int i = 0; i < l.length; i++) {\n int[] subArray = Arrays.copyOfRange(nums, l[i], r[i] + 1);\n Arrays.sort(subArray);\n \n if (subArray.length < 2) {\n ans.add(true);\n } else {\n boolean flag = true;\n int diff = subArray[1] - subArray[0];\n for (int j = 1; j < subArray.length; j++) {\n if (subArray[j] - subArray[j - 1] != diff) {\n flag = false;\n break;\n }\n }\n ans.add(flag);\n }\n }\n return ans;\n }\n}\n\n```\n----------------------------------------\n--------------------------------------------------------------------\n# Python3\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums, l, r):\n ans = []\n for i in range(len(l)):\n subArray = nums[l[i]:r[i] + 1]\n subArray.sort()\n \n if len(subArray) < 2:\n ans.append(True)\n else:\n flag = True\n diff = subArray[1] - subArray[0]\n for j in range(1, len(subArray)):\n if subArray[j] - subArray[j - 1] != diff:\n flag = False\n break\n ans.append(flag)\n return ans\n\n``` | 4 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Simple solution for noobs brute-force | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n res=[]\n \n for i in range(len(l)):\n sub=nums[l[i]:r[i]+1]\n sub.sort()\n count=False\n d=sub[1]-sub[0]\n for j in range(1,len(sub)):\n if sub[j]-d==sub[j-1]:\n count=True\n else:\n count=False\n break\n res.append(count)\n return res\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Simple solution for noobs brute-force | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n res=[]\n \n for i in range(len(l)):\n sub=nums[l[i]:r[i]+1]\n sub.sort()\n count=False\n d=sub[1]-sub[0]\n for j in range(1,len(sub)):\n if sub[j]-d==sub[j-1]:\n count=True\n else:\n count=False\n break\n res.append(count)\n return res\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Easy python sorting array | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n m=[]\n for i in range(len(l)):\n k=nums[l[i]:r[i]+1]\n k.sort()\n l1=[k[i+1]-k[i] for i in range(len(k)-1)] \n if len(set(l1))==1:\n m.append(True)\n else:\n m.append(False)\n return m\n\n\n \n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Easy python sorting array | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n m=[]\n for i in range(len(l)):\n k=nums[l[i]:r[i]+1]\n k.sort()\n l1=[k[i+1]-k[i] for i in range(len(k)-1)] \n if len(set(l1))==1:\n m.append(True)\n else:\n m.append(False)\n return m\n\n\n \n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Disgusting one-liner (Python) | arithmetic-subarrays | 0 | 1 | Quite possibly the worst code I\'ve ever written.\nI wanted to see if it was possible.\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n return [all([k-(nums2[1]-nums2[0])==nums2[index] for index,k in enumerate(nums2[1:])]) for e,i in zip(l,r) if (nums2 := sorted(nums[e:i+1]))]\n\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Disgusting one-liner (Python) | arithmetic-subarrays | 0 | 1 | Quite possibly the worst code I\'ve ever written.\nI wanted to see if it was possible.\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n return [all([k-(nums2[1]-nums2[0])==nums2[index] for index,k in enumerate(nums2[1:])]) for e,i in zip(l,r) if (nums2 := sorted(nums[e:i+1]))]\n\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
SImple python solution using sorting | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n##### Check if each subarry can be rearranged into a arithmetic sequence.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. #### Extract the subarray \n2. #### Check Arithmetic sequence \n3. #### Store the result\n\n# Complexity\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def isarith(nums):\n nums.sort()\n return len(set(nums[i]-nums[i-1] for i in range(1,len(nums))))==1\n return [isarith(nums[i:j+1]) for i,j in zip(l,r)]\n \n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
SImple python solution using sorting | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n##### Check if each subarry can be rearranged into a arithmetic sequence.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. #### Extract the subarray \n2. #### Check Arithmetic sequence \n3. #### Store the result\n\n# Complexity\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def isarith(nums):\n nums.sort()\n return len(set(nums[i]-nums[i-1] for i in range(1,len(nums))))==1\n return [isarith(nums[i:j+1]) for i,j in zip(l,r)]\n \n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Set Approach Runtime 165ms | arithmetic-subarrays | 0 | 1 | # Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n n=len(l)\n ans=[True for i in range(n)]\n for i in range(n):\n lf,rg=l[i],r[i]\n t=nums[lf:rg+1]\n mini,maxi,s=min(t),max(t),set(t)\n d=(maxi-mini)//(rg-lf)\n if (maxi-mini)%(rg-lf)!=0:\n ans[i]=False\n continue\n if d==0:\n continue\n for j in range(mini,maxi+1,d):\n if j not in s:\n ans[i]=False\n break\n return ans\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Set Approach Runtime 165ms | arithmetic-subarrays | 0 | 1 | # Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n n=len(l)\n ans=[True for i in range(n)]\n for i in range(n):\n lf,rg=l[i],r[i]\n t=nums[lf:rg+1]\n mini,maxi,s=min(t),max(t),set(t)\n d=(maxi-mini)//(rg-lf)\n if (maxi-mini)%(rg-lf)!=0:\n ans[i]=False\n continue\n if d==0:\n continue\n for j in range(mini,maxi+1,d):\n if j not in s:\n ans[i]=False\n break\n return ans\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Optimized solution O(MlogN) — SegmentTree + Cumsum + Cumsum of squares | arithmetic-subarrays | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. In the original solution, the author offered to find minimal and maximal elements just passing through the array for $$O(N)$$. We can optimize the complexity to $$O(logN)$$ using two segment trees.\n2. To check if the subarray is the arithmetic progression we can calculate the sum of elements and sum of squares of elements and compare them to expected ones.\nTo find the sum of elements and sum of squares of elements for $$O(1)$$ we have to use precalculated cumulative sum.\n \n## Expected sum of elements \nSum of the arithmetic progression formula can be easily googled:\n\n$$S=\\frac{(2a_0+d(n-1)) \\cdot n}{2}$$\n\nAnd we can calculate the sum of the arithmetic progression suqares:\n$$S^2=\\sum_{i=0}^{n-1}(a_0+di)^2 = \\sum_{i=0}^{n-1}(a_0^2+2 a_0di+d^2i^2)=a_0^2 \\cdot n+2a_0d\\sum_{i=0}^{n-1}i+d^2\\sum_{i=0}^{n-1}i^2=a_0^2 \\cdot n+2a_0d \\cdot \\frac{n(n-1)}2+d^2 \\cdot \\frac{n(n-1)(2n-1)}6$$\n\nWhere $$a_0$$ is the first element of the progression and $$d$$ is the common difference of successive members.\n# Complexity\n- Time complexity: $$O(N+MlogN)$$.\n$$O(N)$$ is used for the precalculations of segment trees and cumulative sums.\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nimport math\nimport operator\n\nfrom itertools import accumulate\n\n\nclass SegmentTree:\n def __init__(self, length, neutral_element=0, operator=operator.add):\n self.operator = operator\n self.neutral_element = neutral_element\n self._length = length\n self._inner_size = 1 << math.ceil(math.log2(length))\n self._array = [neutral_element] * (self._inner_size * 2 - 1)\n\n def __len__(self):\n return self._length\n\n @staticmethod\n def from_array(array, neutral_element=0, operator=operator.add):\n result = SegmentTree(len(array), neutral_element, operator)\n result.build(array)\n return result\n\n def build(self, array):\n if len(array) != self._length:\n raise ValueError(\'There are different lengths of arrays\')\n self._build(array, 0, 0, self._inner_size)\n\n def _build(self, array, st_index, st_left, st_right):\n if st_right - st_left == 1:\n if st_left < len(array):\n self._array[st_index] = array[st_left]\n return\n\n st_mid = (st_left + st_right) // 2\n self._build(array, 2 * st_index + 1, st_left, st_mid)\n self._build(array, 2 * st_index + 2, st_mid, st_right)\n self._array[st_index] = self.operator(\n self._array[2 * st_index + 1],\n self._array[2 * st_index + 2]\n )\n\n def _update_index(self, index, right_bound=False):\n if not isinstance(index, int):\n raise TypeError(f\'Expected int, got: {type(index)}\')\n if not (-self._length - right_bound <= index < self._length + right_bound):\n raise IndexError(f\'index should be between 0 and {self._length + right_bound}\')\n if index < 0:\n index += self._length\n return index\n\n def __getitem__(self, index):\n if not isinstance(index, slice):\n index = self._update_index(index)\n return self._array[index - self._inner_size]\n if index.step is not None:\n raise ValueError(f\'Steps are not supported\')\n start_index = self._update_index(index.start)\n end_index = self._update_index(index.stop, True)\n return self._get(start_index, end_index, 0, 0, self._inner_size)\n\n def _get(self, left, right, st_index, st_left, st_right):\n if st_left >= right or left >= st_right:\n return self.neutral_element\n\n if left <= st_left and st_right <= right:\n return self._array[st_index]\n\n st_mid = (st_left + st_right) // 2\n\n lvalue = self._get(left, right, 2 * st_index + 1, st_left, st_mid)\n rvalue = self._get(left, right, 2 * st_index + 2, st_mid, st_right)\n\n return self.operator(lvalue, rvalue)\n\n def __setitem__(self, index, value):\n index = self._update_index(index)\n self._set(index, value, 0, 0, self._inner_size)\n\n def _set(self, index, value, st_index, st_left, st_right):\n if st_right - st_left == 1:\n self._array[st_index] = value\n return\n\n st_mid = (st_left + st_right) // 2\n if index < st_mid:\n self._set(index, value, 2 * st_index + 1, st_left, st_mid)\n else:\n self._set(index, value, 2 * st_index + 2, st_mid, st_right)\n\n self._array[st_index] = self.operator(\n self._array[2 * st_index + 1],\n self._array[2 * st_index + 2]\n )\n\n def __iter__(self):\n for i in range(self._length):\n yield self._array[i - self._inner_size]\n\n\nclass Solution:\n def checkArithmeticSubarrays(self, nums: list[int], l: list[int], r: list[int]) -> list[bool]:\n cumsum = list(accumulate(nums))\n squared_cumsum = list(accumulate(value ** 2 for value in nums))\n\n min_segment_tree = SegmentTree.from_array(nums, neutral_element=math.inf, operator=min)\n max_segment_tree = SegmentTree.from_array(nums, neutral_element=-math.inf, operator=max)\n \n m = len(l)\n result = [False] * m\n for i, left, right in zip(range(m), l, r):\n length = right - left + 1\n if length <= 2:\n result[i] = True\n continue\n\n min_value = min_segment_tree[left: right + 1]\n max_value = max_segment_tree[left: right + 1]\n\n diff, mod = divmod(max_value - min_value, length - 1)\n if mod != 0:\n continue\n\n expected_sum = (min_value + max_value) * length // 2\n real_sum = cumsum[right] - (cumsum[left - 1] if left else 0)\n\n if expected_sum != real_sum:\n continue\n\n expected_squared_sum = min_value ** 2 * length \\\n + diff * min_value * length * (length - 1) \\\n + diff ** 2 * (length - 1) * length * (2 * length - 1) // 6\n real_squared_sum = squared_cumsum[right] - (squared_cumsum[left - 1] if left else 0)\n\n if expected_squared_sum != real_squared_sum:\n continue\n\n result[i] = True\n\n return result\n\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Optimized solution O(MlogN) — SegmentTree + Cumsum + Cumsum of squares | arithmetic-subarrays | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. In the original solution, the author offered to find minimal and maximal elements just passing through the array for $$O(N)$$. We can optimize the complexity to $$O(logN)$$ using two segment trees.\n2. To check if the subarray is the arithmetic progression we can calculate the sum of elements and sum of squares of elements and compare them to expected ones.\nTo find the sum of elements and sum of squares of elements for $$O(1)$$ we have to use precalculated cumulative sum.\n \n## Expected sum of elements \nSum of the arithmetic progression formula can be easily googled:\n\n$$S=\\frac{(2a_0+d(n-1)) \\cdot n}{2}$$\n\nAnd we can calculate the sum of the arithmetic progression suqares:\n$$S^2=\\sum_{i=0}^{n-1}(a_0+di)^2 = \\sum_{i=0}^{n-1}(a_0^2+2 a_0di+d^2i^2)=a_0^2 \\cdot n+2a_0d\\sum_{i=0}^{n-1}i+d^2\\sum_{i=0}^{n-1}i^2=a_0^2 \\cdot n+2a_0d \\cdot \\frac{n(n-1)}2+d^2 \\cdot \\frac{n(n-1)(2n-1)}6$$\n\nWhere $$a_0$$ is the first element of the progression and $$d$$ is the common difference of successive members.\n# Complexity\n- Time complexity: $$O(N+MlogN)$$.\n$$O(N)$$ is used for the precalculations of segment trees and cumulative sums.\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nimport math\nimport operator\n\nfrom itertools import accumulate\n\n\nclass SegmentTree:\n def __init__(self, length, neutral_element=0, operator=operator.add):\n self.operator = operator\n self.neutral_element = neutral_element\n self._length = length\n self._inner_size = 1 << math.ceil(math.log2(length))\n self._array = [neutral_element] * (self._inner_size * 2 - 1)\n\n def __len__(self):\n return self._length\n\n @staticmethod\n def from_array(array, neutral_element=0, operator=operator.add):\n result = SegmentTree(len(array), neutral_element, operator)\n result.build(array)\n return result\n\n def build(self, array):\n if len(array) != self._length:\n raise ValueError(\'There are different lengths of arrays\')\n self._build(array, 0, 0, self._inner_size)\n\n def _build(self, array, st_index, st_left, st_right):\n if st_right - st_left == 1:\n if st_left < len(array):\n self._array[st_index] = array[st_left]\n return\n\n st_mid = (st_left + st_right) // 2\n self._build(array, 2 * st_index + 1, st_left, st_mid)\n self._build(array, 2 * st_index + 2, st_mid, st_right)\n self._array[st_index] = self.operator(\n self._array[2 * st_index + 1],\n self._array[2 * st_index + 2]\n )\n\n def _update_index(self, index, right_bound=False):\n if not isinstance(index, int):\n raise TypeError(f\'Expected int, got: {type(index)}\')\n if not (-self._length - right_bound <= index < self._length + right_bound):\n raise IndexError(f\'index should be between 0 and {self._length + right_bound}\')\n if index < 0:\n index += self._length\n return index\n\n def __getitem__(self, index):\n if not isinstance(index, slice):\n index = self._update_index(index)\n return self._array[index - self._inner_size]\n if index.step is not None:\n raise ValueError(f\'Steps are not supported\')\n start_index = self._update_index(index.start)\n end_index = self._update_index(index.stop, True)\n return self._get(start_index, end_index, 0, 0, self._inner_size)\n\n def _get(self, left, right, st_index, st_left, st_right):\n if st_left >= right or left >= st_right:\n return self.neutral_element\n\n if left <= st_left and st_right <= right:\n return self._array[st_index]\n\n st_mid = (st_left + st_right) // 2\n\n lvalue = self._get(left, right, 2 * st_index + 1, st_left, st_mid)\n rvalue = self._get(left, right, 2 * st_index + 2, st_mid, st_right)\n\n return self.operator(lvalue, rvalue)\n\n def __setitem__(self, index, value):\n index = self._update_index(index)\n self._set(index, value, 0, 0, self._inner_size)\n\n def _set(self, index, value, st_index, st_left, st_right):\n if st_right - st_left == 1:\n self._array[st_index] = value\n return\n\n st_mid = (st_left + st_right) // 2\n if index < st_mid:\n self._set(index, value, 2 * st_index + 1, st_left, st_mid)\n else:\n self._set(index, value, 2 * st_index + 2, st_mid, st_right)\n\n self._array[st_index] = self.operator(\n self._array[2 * st_index + 1],\n self._array[2 * st_index + 2]\n )\n\n def __iter__(self):\n for i in range(self._length):\n yield self._array[i - self._inner_size]\n\n\nclass Solution:\n def checkArithmeticSubarrays(self, nums: list[int], l: list[int], r: list[int]) -> list[bool]:\n cumsum = list(accumulate(nums))\n squared_cumsum = list(accumulate(value ** 2 for value in nums))\n\n min_segment_tree = SegmentTree.from_array(nums, neutral_element=math.inf, operator=min)\n max_segment_tree = SegmentTree.from_array(nums, neutral_element=-math.inf, operator=max)\n \n m = len(l)\n result = [False] * m\n for i, left, right in zip(range(m), l, r):\n length = right - left + 1\n if length <= 2:\n result[i] = True\n continue\n\n min_value = min_segment_tree[left: right + 1]\n max_value = max_segment_tree[left: right + 1]\n\n diff, mod = divmod(max_value - min_value, length - 1)\n if mod != 0:\n continue\n\n expected_sum = (min_value + max_value) * length // 2\n real_sum = cumsum[right] - (cumsum[left - 1] if left else 0)\n\n if expected_sum != real_sum:\n continue\n\n expected_squared_sum = min_value ** 2 * length \\\n + diff * min_value * length * (length - 1) \\\n + diff ** 2 * (length - 1) * length * (2 * length - 1) // 6\n real_squared_sum = squared_cumsum[right] - (squared_cumsum[left - 1] if left else 0)\n\n if expected_squared_sum != real_squared_sum:\n continue\n\n result[i] = True\n\n return result\n\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Simple python solution with explanation | arithmetic-subarrays | 0 | 1 | \n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n #variable to store the result\n n=[]\n for i in range(len(l)):\n #taking the subarray which is need to be checked and sorted\n a=nums[l[i]:r[i]+1]\n a.sort()\n check=[]\n #calculating the difference to check whether it is a arithematic subarray\n for j in range(len(a)-1):\n val=a[j+1]-a[j]\n check.append(val)\n check.sort()\n if check[0]==check[-1]:\n n.append(True)\n else:\n n.append(False)\n return n\n\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Simple python solution with explanation | arithmetic-subarrays | 0 | 1 | \n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n #variable to store the result\n n=[]\n for i in range(len(l)):\n #taking the subarray which is need to be checked and sorted\n a=nums[l[i]:r[i]+1]\n a.sort()\n check=[]\n #calculating the difference to check whether it is a arithematic subarray\n for j in range(len(a)-1):\n val=a[j+1]-a[j]\n check.append(val)\n check.sort()\n if check[0]==check[-1]:\n n.append(True)\n else:\n n.append(False)\n return n\n\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Easy Solutions in python code 👍🙏 | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n res = []\n\n for i in range(len(l)):\n n = sorted(nums[l[i]:r[i] + 1])\n j = 2\n while j < len(n):\n if n[j] - n[j - 1] != n[1] - n[0]:\n break\n j += 1\n res.append(j == len(n))\n\n return res\n \n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Easy Solutions in python code 👍🙏 | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n res = []\n\n for i in range(len(l)):\n n = sorted(nums[l[i]:r[i] + 1])\n j = 2\n while j < len(n):\n if n[j] - n[j - 1] != n[1] - n[0]:\n break\n j += 1\n res.append(j == len(n))\n\n return res\n \n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Python3 Solution | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirstly, we realize we have to check whether the subarray is arithmetic or not. For this condition to be true, the differences between consecutive elements must be the same. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo check whether the differences bewteen consecutive elements are the same, this is easily done by sorting our subarray. Since the values are now in order, if the differences are not the same in any consecutive pairs of elements, we know that this can\'t be an artihmetic sequence. \n# Complexity\n- Time complexity: $$O(n*logn)$$ From sorting the subarrays.\n<!-- Add your time complexity here, e.g. $$O(n^2)$$ -->\n- Space complexity: $$O(n)$$ From creating a new array to put in our subarray values.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n\n m = len(l)\n res = []\n\n for i in range(m):\n passes = True\n left = l[i]\n right = r[i]\n arr = [] \n for j in range(left,right+1):\n arr.append(nums[j])\n arr.sort()\n\n first,second=0,1\n diff = arr[second]-arr[first]\n while(second < len(arr)):\n if(arr[second] - arr[first] != diff):\n passes = False\n break\n first += 1\n second += 1\n if(passes):\n res.append(True)\n else:\n res.append(False)\n \n return res\n\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Python3 Solution | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirstly, we realize we have to check whether the subarray is arithmetic or not. For this condition to be true, the differences between consecutive elements must be the same. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo check whether the differences bewteen consecutive elements are the same, this is easily done by sorting our subarray. Since the values are now in order, if the differences are not the same in any consecutive pairs of elements, we know that this can\'t be an artihmetic sequence. \n# Complexity\n- Time complexity: $$O(n*logn)$$ From sorting the subarrays.\n<!-- Add your time complexity here, e.g. $$O(n^2)$$ -->\n- Space complexity: $$O(n)$$ From creating a new array to put in our subarray values.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n\n m = len(l)\n res = []\n\n for i in range(m):\n passes = True\n left = l[i]\n right = r[i]\n arr = [] \n for j in range(left,right+1):\n arr.append(nums[j])\n arr.sort()\n\n first,second=0,1\n diff = arr[second]-arr[first]\n while(second < len(arr)):\n if(arr[second] - arr[first] != diff):\n passes = False\n break\n first += 1\n second += 1\n if(passes):\n res.append(True)\n else:\n res.append(False)\n \n return res\n\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Simple Brute-Force + Sorting approach | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* Since \'n\' ranges from [2, 500], we can apply a brute-force approach. \n* Here we created a query list store all the queries.(to improve the readability) \n* check - The code checks for each query whether the list is valid or not.\n* we append corresponding boolean value to the res\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def check(u,v):\n lis = nums[u:v+1]\n lis.sort()\n if v - u == 0 : return False\n elif v - u == 1: return True\n else:\n diff = lis[1] - lis[0]\n if any(lis[i+1] - lis[i] != diff for i in range(len(lis)-1)) : return False\n return True\n queries , res = list(zip(l,r)) , []\n for u,v in queries:\n if check(u,v):\n res.append(True)\n else: \n res.append(False)\n return res\n``` | 1 | A sequence of numbers is called **arithmetic** if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence `s` is arithmetic if and only if `s[i+1] - s[i] == s[1] - s[0]` for all valid `i`.
For example, these are **arithmetic** sequences:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not **arithmetic**:
1, 1, 2, 5, 7
You are given an array of `n` integers, `nums`, and two arrays of `m` integers each, `l` and `r`, representing the `m` range queries, where the `ith` query is the range `[l[i], r[i]]`. All the arrays are **0-indexed**.
Return _a list of_ `boolean` _elements_ `answer`_, where_ `answer[i]` _is_ `true` _if the subarray_ `nums[l[i]], nums[l[i]+1], ... , nums[r[i]]` _can be **rearranged** to form an **arithmetic** sequence, and_ `false` _otherwise._
**Example 1:**
**Input:** nums = `[4,6,5,9,3,7]`, l = `[0,0,2]`, r = `[2,3,5]`
**Output:** `[true,false,true]`
**Explanation:**
In the 0th query, the subarray is \[4,6,5\]. This can be rearranged as \[6,5,4\], which is an arithmetic sequence.
In the 1st query, the subarray is \[4,6,5,9\]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is `[5,9,3,7]. This` can be rearranged as `[3,5,7,9]`, which is an arithmetic sequence.
**Example 2:**
**Input:** nums = \[-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10\], l = \[0,1,6,4,8,7\], r = \[4,4,9,7,9,10\]
**Output:** \[false,true,false,false,true,true\]
**Constraints:**
* `n == nums.length`
* `m == l.length`
* `m == r.length`
* `2 <= n <= 500`
* `1 <= m <= 500`
* `0 <= l[i] < r[i] < n`
* `-105 <= nums[i] <= 105` | If the range (high - low + 1) is even, the number of even and odd numbers in this range will be the same. If the range (high - low + 1) is odd, the solution will depend on the parity of high and low. |
Simple Brute-Force + Sorting approach | arithmetic-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* Since \'n\' ranges from [2, 500], we can apply a brute-force approach. \n* Here we created a query list store all the queries.(to improve the readability) \n* check - The code checks for each query whether the list is valid or not.\n* we append corresponding boolean value to the res\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkArithmeticSubarrays(self, nums: List[int], l: List[int], r: List[int]) -> List[bool]:\n def check(u,v):\n lis = nums[u:v+1]\n lis.sort()\n if v - u == 0 : return False\n elif v - u == 1: return True\n else:\n diff = lis[1] - lis[0]\n if any(lis[i+1] - lis[i] != diff for i in range(len(lis)-1)) : return False\n return True\n queries , res = list(zip(l,r)) , []\n for u,v in queries:\n if check(u,v):\n res.append(True)\n else: \n res.append(False)\n return res\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
【Video】Simple Solution with Min Heap and BFS - Python, JavaScript, Java and C++ | path-with-minimum-effort | 1 | 1 | # Intuition\r\nUsing min heap and BFS.\r\n\r\n---\r\n\r\n# Solution Video\r\n\r\nhttps://youtu.be/yQtfAG1wI48\r\n\r\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\r\n\r\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\r\n\r\n**\u25A0 Subscribe URL**\r\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\r\n\r\nSubscribers: 2,350\r\nThank you for your support!\r\n\r\n---\r\n\r\n# Approach\r\nThis is based on Python. Other might be different a bit.\r\n\r\n### Algorithm Overview:\r\n1. **Input Validation:**\r\n - Check if the input `heights` is empty. If it is, return 0 (no effort needed).\r\n\r\n2. **Initialization:**\r\n - Initialize variables: `rows`, `cols` to store the number of rows and columns in `heights`.\r\n - Create a min heap `min_heap` to store tuples (effort, row, col) starting with (0, 0, 0).\r\n - Initialize `max_effort` to 0, which stores the maximum effort encountered so far.\r\n - Create a set `visited` to keep track of visited cells.\r\n\r\n3. **Dijkstra\'s Algorithm using Heap:**\r\n - Begin a loop while the min heap is not empty:\r\n - Pop the tuple with the smallest effort from the min heap.\r\n - Update `max_effort` if the current effort is greater than `max_effort`.\r\n - If the current cell is the bottom-right cell, return `max_effort`.\r\n - Mark the current cell as visited.\r\n\r\n4. **Explore Neighbors:**\r\n - Iterate through the four directions (down, up, right, left):\r\n - Calculate the new row and column based on the current direction.\r\n - If the new cell is within the grid bounds and has not been visited:\r\n - Calculate the new effort for this step.\r\n - If the new effort is less than the effort for the current cell, update the heap and set `new_effort`.\r\n\r\n5. **Return Maximum Effort:**\r\n - If the bottom-right cell is not reached, return `max_effort`.\r\n\r\n### Detailed Explanation:\r\n1. **Input Validation:**\r\n - Check if `heights` is an empty list. If so, return 0 indicating no effort is needed.\r\n\r\n2. **Initialization:**\r\n - Get the number of rows `rows` and columns `cols` in the input grid.\r\n - Create a min heap `min_heap` and initialize `max_effort` to store the maximum effort encountered so far.\r\n - Create a set `visited` to keep track of visited cells.\r\n\r\n3. **Dijkstra\'s Algorithm using Heap:**\r\n - While the min heap is not empty:\r\n - Pop the tuple with the smallest effort from the min heap.\r\n - Update `max_effort` if the current effort is greater than `max_effort`.\r\n - If the current cell is the bottom-right cell, return `max_effort`.\r\n - Mark the current cell as visited.\r\n\r\n4. **Explore Neighbors:**\r\n - Iterate through the four directions (down, up, right, left):\r\n - Calculate the new row and column based on the current direction.\r\n - If the new cell is within the grid bounds and has not been visited:\r\n - Calculate the new effort for this step.\r\n - If the new effort is less than the effort for the current cell, update the heap and set `new_effort`.\r\n\r\n5. **Return Maximum Effort:**\r\n - If the bottom-right cell is not reached, return `max_effort`.\r\n\r\nThis algorithm uses Dijkstra\'s algorithm to find the path with the minimum effort. It explores cells in a priority-based manner, where the priority is the effort required to reach the cell. The min heap helps in efficiently selecting cells with the minimum effort.\r\n\r\n# Complexity\r\n\r\n### Time Complexity:\r\n- The main loop in Dijkstra\'s algorithm iterates until the min heap is empty or until reaching the bottom-right cell.\r\n- Extracting the minimum from the min heap (heapify) and pushing elements into the min heap takes O(log n) time, where n is the number of elements in the heap.\r\n- In the worst case, the min heap can contain all cells (rows * columns).\r\n\r\nTherefore, the overall time complexity is approximately `O((R * C) * log(R * C))`, where R is the number of rows and C is the number of columns in the grid. The log term arises from the heap operations.\r\n\r\n### Space Complexity:\r\n- The `min_heap` can have at most R * C elements, so the space complexity for the min heap is O(R * C) and `visited` also has (R * C) data.\r\n- Other variables (e.g., `max_effort`, `effort`, `cur_row`, `cur_col`, `new_row`, `new_col`, `new_effort`) and constants use O(1) additional space.\r\n\r\nTherefore, the overall space complexity is `O(R * C)` due to the min heap, where R is the number of rows and C is the number of columns in the grid.\r\n\r\n```python []\r\nclass Solution:\r\n def minimumEffortPath(self, heights):\r\n if not heights:\r\n return 0\r\n \r\n rows, cols = len(heights), len(heights[0])\r\n min_heap = [(0, 0, 0)] # (effort, row, col)\r\n max_effort = 0\r\n visited = set()\r\n\r\n while min_heap:\r\n effort, cur_row, cur_col = heapq.heappop(min_heap)\r\n\r\n max_effort = max(max_effort, effort)\r\n if (cur_row, cur_col) == (rows - 1, cols - 1):\r\n return max_effort\r\n visited.add((cur_row, cur_col))\r\n\r\n for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:\r\n new_row, new_col = cur_row + dr, cur_col + dc\r\n\r\n if 0 <= new_row < rows and 0 <= new_col < cols and(new_row, new_col) not in visited:\r\n new_effort = abs(heights[new_row][new_col] - heights[cur_row][cur_col])\r\n heapq.heappush(min_heap, (new_effort, new_row, new_col))\r\n \r\n return max_effort\r\n```\r\n```javascript []\r\n/**\r\n * @param {number[][]} heights\r\n * @return {number}\r\n */\r\nvar minimumEffortPath = function(heights) {\r\n const rows = heights.length, cols = heights[0].length;\r\n const curEffort = Array.from(Array(rows), () => Array(cols).fill(Infinity));\r\n const minHeap = [[0, 0, 0]]; // [effort, row, col]\r\n \r\n curEffort[0][0] = 0;\r\n const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];\r\n \r\n while (minHeap.length > 0) {\r\n const [effort, row, col] = minHeap.shift();\r\n \r\n if (effort > curEffort[row][col]) continue;\r\n \r\n if (row === rows - 1 && col === cols - 1) return effort;\r\n \r\n for (const [dr, dc] of directions) {\r\n const newRow = row + dr, newCol = col + dc;\r\n if (newRow >= 0 && newRow < rows && newCol >= 0 && newCol < cols) {\r\n const newEffort = Math.max(effort, Math.abs(heights[row][col] - heights[newRow][newCol]));\r\n if (newEffort < curEffort[newRow][newCol]) {\r\n curEffort[newRow][newCol] = newEffort;\r\n minHeap.push([newEffort, newRow, newCol]);\r\n minHeap.sort((a, b) => a[0] - b[0]);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n};\r\n```\r\n```java []\r\nclass Solution {\r\n public int minimumEffortPath(int[][] heights) {\r\n if (heights.length == 0) {\r\n return 0;\r\n }\r\n \r\n int rows = heights.length;\r\n int cols = heights[0].length;\r\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[0] - b[0]); // [effort, row, col]\r\n minHeap.offer(new int[]{0, 0, 0});\r\n int maxEffort = 0;\r\n Set<String> visited = new HashSet<>();\r\n\r\n while (!minHeap.isEmpty()) {\r\n int[] current = minHeap.poll();\r\n int effort = current[0];\r\n int curRow = current[1];\r\n int curCol = current[2];\r\n\r\n maxEffort = Math.max(maxEffort, effort);\r\n if (curRow == rows - 1 && curCol == cols - 1) {\r\n return maxEffort;\r\n }\r\n visited.add(curRow + "," + curCol);\r\n\r\n int[][] directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\r\n for (int[] direction : directions) {\r\n int newRow = curRow + direction[0];\r\n int newCol = curCol + direction[1];\r\n\r\n if (0 <= newRow && newRow < rows && 0 <= newCol && newCol < cols &&\r\n !visited.contains(newRow + "," + newCol)) {\r\n int newEffort = Math.abs(heights[newRow][newCol] - heights[curRow][curCol]);\r\n minHeap.offer(new int[]{newEffort, newRow, newCol});\r\n }\r\n }\r\n }\r\n \r\n return maxEffort; \r\n }\r\n}\r\n```\r\n```C++ []\r\nclass Solution {\r\npublic:\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n if (heights.empty()) {\r\n return 0;\r\n }\r\n \r\n int rows = heights.size();\r\n int cols = heights[0].size();\r\n std::priority_queue<std::vector<int>, std::vector<std::vector<int>>, std::greater<std::vector<int>>> minHeap; // {effort, row, col}\r\n minHeap.push({0, 0, 0});\r\n int maxEffort = 0;\r\n std::set<std::string> visited;\r\n\r\n while (!minHeap.empty()) {\r\n auto current = minHeap.top();\r\n minHeap.pop();\r\n int effort = current[0];\r\n int curRow = current[1];\r\n int curCol = current[2];\r\n\r\n maxEffort = std::max(maxEffort, effort);\r\n if (curRow == rows - 1 && curCol == cols - 1) {\r\n return maxEffort;\r\n }\r\n visited.insert(std::to_string(curRow) + "," + std::to_string(curCol));\r\n\r\n std::vector<std::vector<int>> directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\r\n for (const auto& direction : directions) {\r\n int newRow = curRow + direction[0];\r\n int newCol = curCol + direction[1];\r\n\r\n if (0 <= newRow && newRow < rows && 0 <= newCol && newCol < cols &&\r\n visited.find(std::to_string(newRow) + "," + std::to_string(newCol)) == visited.end()) {\r\n int newEffort = std::abs(heights[newRow][newCol] - heights[curRow][curCol]);\r\n minHeap.push({newEffort, newRow, newCol});\r\n }\r\n }\r\n }\r\n \r\n return maxEffort; \r\n }\r\n};\r\n```\r\n | 8 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
【Video】Simple Solution with Min Heap and BFS - Python, JavaScript, Java and C++ | path-with-minimum-effort | 1 | 1 | # Intuition\r\nUsing min heap and BFS.\r\n\r\n---\r\n\r\n# Solution Video\r\n\r\nhttps://youtu.be/yQtfAG1wI48\r\n\r\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\r\n\r\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\r\n\r\n**\u25A0 Subscribe URL**\r\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\r\n\r\nSubscribers: 2,350\r\nThank you for your support!\r\n\r\n---\r\n\r\n# Approach\r\nThis is based on Python. Other might be different a bit.\r\n\r\n### Algorithm Overview:\r\n1. **Input Validation:**\r\n - Check if the input `heights` is empty. If it is, return 0 (no effort needed).\r\n\r\n2. **Initialization:**\r\n - Initialize variables: `rows`, `cols` to store the number of rows and columns in `heights`.\r\n - Create a min heap `min_heap` to store tuples (effort, row, col) starting with (0, 0, 0).\r\n - Initialize `max_effort` to 0, which stores the maximum effort encountered so far.\r\n - Create a set `visited` to keep track of visited cells.\r\n\r\n3. **Dijkstra\'s Algorithm using Heap:**\r\n - Begin a loop while the min heap is not empty:\r\n - Pop the tuple with the smallest effort from the min heap.\r\n - Update `max_effort` if the current effort is greater than `max_effort`.\r\n - If the current cell is the bottom-right cell, return `max_effort`.\r\n - Mark the current cell as visited.\r\n\r\n4. **Explore Neighbors:**\r\n - Iterate through the four directions (down, up, right, left):\r\n - Calculate the new row and column based on the current direction.\r\n - If the new cell is within the grid bounds and has not been visited:\r\n - Calculate the new effort for this step.\r\n - If the new effort is less than the effort for the current cell, update the heap and set `new_effort`.\r\n\r\n5. **Return Maximum Effort:**\r\n - If the bottom-right cell is not reached, return `max_effort`.\r\n\r\n### Detailed Explanation:\r\n1. **Input Validation:**\r\n - Check if `heights` is an empty list. If so, return 0 indicating no effort is needed.\r\n\r\n2. **Initialization:**\r\n - Get the number of rows `rows` and columns `cols` in the input grid.\r\n - Create a min heap `min_heap` and initialize `max_effort` to store the maximum effort encountered so far.\r\n - Create a set `visited` to keep track of visited cells.\r\n\r\n3. **Dijkstra\'s Algorithm using Heap:**\r\n - While the min heap is not empty:\r\n - Pop the tuple with the smallest effort from the min heap.\r\n - Update `max_effort` if the current effort is greater than `max_effort`.\r\n - If the current cell is the bottom-right cell, return `max_effort`.\r\n - Mark the current cell as visited.\r\n\r\n4. **Explore Neighbors:**\r\n - Iterate through the four directions (down, up, right, left):\r\n - Calculate the new row and column based on the current direction.\r\n - If the new cell is within the grid bounds and has not been visited:\r\n - Calculate the new effort for this step.\r\n - If the new effort is less than the effort for the current cell, update the heap and set `new_effort`.\r\n\r\n5. **Return Maximum Effort:**\r\n - If the bottom-right cell is not reached, return `max_effort`.\r\n\r\nThis algorithm uses Dijkstra\'s algorithm to find the path with the minimum effort. It explores cells in a priority-based manner, where the priority is the effort required to reach the cell. The min heap helps in efficiently selecting cells with the minimum effort.\r\n\r\n# Complexity\r\n\r\n### Time Complexity:\r\n- The main loop in Dijkstra\'s algorithm iterates until the min heap is empty or until reaching the bottom-right cell.\r\n- Extracting the minimum from the min heap (heapify) and pushing elements into the min heap takes O(log n) time, where n is the number of elements in the heap.\r\n- In the worst case, the min heap can contain all cells (rows * columns).\r\n\r\nTherefore, the overall time complexity is approximately `O((R * C) * log(R * C))`, where R is the number of rows and C is the number of columns in the grid. The log term arises from the heap operations.\r\n\r\n### Space Complexity:\r\n- The `min_heap` can have at most R * C elements, so the space complexity for the min heap is O(R * C) and `visited` also has (R * C) data.\r\n- Other variables (e.g., `max_effort`, `effort`, `cur_row`, `cur_col`, `new_row`, `new_col`, `new_effort`) and constants use O(1) additional space.\r\n\r\nTherefore, the overall space complexity is `O(R * C)` due to the min heap, where R is the number of rows and C is the number of columns in the grid.\r\n\r\n```python []\r\nclass Solution:\r\n def minimumEffortPath(self, heights):\r\n if not heights:\r\n return 0\r\n \r\n rows, cols = len(heights), len(heights[0])\r\n min_heap = [(0, 0, 0)] # (effort, row, col)\r\n max_effort = 0\r\n visited = set()\r\n\r\n while min_heap:\r\n effort, cur_row, cur_col = heapq.heappop(min_heap)\r\n\r\n max_effort = max(max_effort, effort)\r\n if (cur_row, cur_col) == (rows - 1, cols - 1):\r\n return max_effort\r\n visited.add((cur_row, cur_col))\r\n\r\n for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:\r\n new_row, new_col = cur_row + dr, cur_col + dc\r\n\r\n if 0 <= new_row < rows and 0 <= new_col < cols and(new_row, new_col) not in visited:\r\n new_effort = abs(heights[new_row][new_col] - heights[cur_row][cur_col])\r\n heapq.heappush(min_heap, (new_effort, new_row, new_col))\r\n \r\n return max_effort\r\n```\r\n```javascript []\r\n/**\r\n * @param {number[][]} heights\r\n * @return {number}\r\n */\r\nvar minimumEffortPath = function(heights) {\r\n const rows = heights.length, cols = heights[0].length;\r\n const curEffort = Array.from(Array(rows), () => Array(cols).fill(Infinity));\r\n const minHeap = [[0, 0, 0]]; // [effort, row, col]\r\n \r\n curEffort[0][0] = 0;\r\n const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];\r\n \r\n while (minHeap.length > 0) {\r\n const [effort, row, col] = minHeap.shift();\r\n \r\n if (effort > curEffort[row][col]) continue;\r\n \r\n if (row === rows - 1 && col === cols - 1) return effort;\r\n \r\n for (const [dr, dc] of directions) {\r\n const newRow = row + dr, newCol = col + dc;\r\n if (newRow >= 0 && newRow < rows && newCol >= 0 && newCol < cols) {\r\n const newEffort = Math.max(effort, Math.abs(heights[row][col] - heights[newRow][newCol]));\r\n if (newEffort < curEffort[newRow][newCol]) {\r\n curEffort[newRow][newCol] = newEffort;\r\n minHeap.push([newEffort, newRow, newCol]);\r\n minHeap.sort((a, b) => a[0] - b[0]);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n};\r\n```\r\n```java []\r\nclass Solution {\r\n public int minimumEffortPath(int[][] heights) {\r\n if (heights.length == 0) {\r\n return 0;\r\n }\r\n \r\n int rows = heights.length;\r\n int cols = heights[0].length;\r\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[0] - b[0]); // [effort, row, col]\r\n minHeap.offer(new int[]{0, 0, 0});\r\n int maxEffort = 0;\r\n Set<String> visited = new HashSet<>();\r\n\r\n while (!minHeap.isEmpty()) {\r\n int[] current = minHeap.poll();\r\n int effort = current[0];\r\n int curRow = current[1];\r\n int curCol = current[2];\r\n\r\n maxEffort = Math.max(maxEffort, effort);\r\n if (curRow == rows - 1 && curCol == cols - 1) {\r\n return maxEffort;\r\n }\r\n visited.add(curRow + "," + curCol);\r\n\r\n int[][] directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\r\n for (int[] direction : directions) {\r\n int newRow = curRow + direction[0];\r\n int newCol = curCol + direction[1];\r\n\r\n if (0 <= newRow && newRow < rows && 0 <= newCol && newCol < cols &&\r\n !visited.contains(newRow + "," + newCol)) {\r\n int newEffort = Math.abs(heights[newRow][newCol] - heights[curRow][curCol]);\r\n minHeap.offer(new int[]{newEffort, newRow, newCol});\r\n }\r\n }\r\n }\r\n \r\n return maxEffort; \r\n }\r\n}\r\n```\r\n```C++ []\r\nclass Solution {\r\npublic:\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n if (heights.empty()) {\r\n return 0;\r\n }\r\n \r\n int rows = heights.size();\r\n int cols = heights[0].size();\r\n std::priority_queue<std::vector<int>, std::vector<std::vector<int>>, std::greater<std::vector<int>>> minHeap; // {effort, row, col}\r\n minHeap.push({0, 0, 0});\r\n int maxEffort = 0;\r\n std::set<std::string> visited;\r\n\r\n while (!minHeap.empty()) {\r\n auto current = minHeap.top();\r\n minHeap.pop();\r\n int effort = current[0];\r\n int curRow = current[1];\r\n int curCol = current[2];\r\n\r\n maxEffort = std::max(maxEffort, effort);\r\n if (curRow == rows - 1 && curCol == cols - 1) {\r\n return maxEffort;\r\n }\r\n visited.insert(std::to_string(curRow) + "," + std::to_string(curCol));\r\n\r\n std::vector<std::vector<int>> directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\r\n for (const auto& direction : directions) {\r\n int newRow = curRow + direction[0];\r\n int newCol = curCol + direction[1];\r\n\r\n if (0 <= newRow && newRow < rows && 0 <= newCol && newCol < cols &&\r\n visited.find(std::to_string(newRow) + "," + std::to_string(newCol)) == visited.end()) {\r\n int newEffort = std::abs(heights[newRow][newCol] - heights[curRow][curCol]);\r\n minHeap.push({newEffort, newRow, newCol});\r\n }\r\n }\r\n }\r\n \r\n return maxEffort; \r\n }\r\n};\r\n```\r\n | 8 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Rust/Python BFS with explanation | path-with-minimum-effort | 0 | 1 | # Intuition\nThere are at least two possible solutions here. One involves dijkstra where you maintain the min-heap of positions with smallest effor seen so far. But you can also adjust a standard BFS to solve the problem.\n\nTo do this, create a frontier which starts with `(0, 0)` and maintain your current knowledge of effort. This will be a matrix where all elements are some maximum value and the value at the start position `(0, 0)` is `0`.\n\nNow do standard BFS where you constantly build a new frontier from the previous one by taking a position and trying to go in 4 directions. When you do this you check than the next value is within the range and also check the effor to reach that cell. How to calculate the effort?\n\nIt is max between the effort of the cell you came from and the current effor to reach the new cell which is the absolute difference between the values. So basically `max(E[y][x], abs(M[y][x] - M[y_][x_]))`. And if this effort is smaller than the effort we have before we add it into the frontier and update the effort in our effort matrix.\n\n\n# Code\n```Rust []\nimpl Solution {\n pub fn minimum_effort_path(M: Vec<Vec<i32>>) -> i32 {\n let (Y, X) = (M.len(), M[0].len());\n let mut frontier = vec![(0, 0)];\n let mut E = vec![vec![i32::MAX; X]; Y];\n E[0][0] = 0;\n let dirs = [-1, 0, 1, 0, -1];\n \n while !frontier.is_empty() {\n let mut new_frontier = Vec::new();\n for (y, x) in frontier {\n for i in 0 .. 4 {\n let y_ = (y as i32 + dirs[i]) as usize;\n let x_ = (x as i32 + dirs[i + 1]) as usize;\n\n if y_ < Y && x_ < X {\n let e = (M[y][x] - M[y_][x_]).abs().max(E[y][x]);\n if e < E[y_][x_] {\n E[y_][x_] = e;\n new_frontier.push((y_, x_));\n }\n }\n }\n }\n\n frontier = new_frontier;\n }\n \n return E[Y - 1][X - 1];\n }\n}\n```\n```python []\nclass Solution:\n def minimumEffortPath(self, M: List[List[int]]) -> int:\n frontier = [(0, 0)] \n Y, X = len(M), len(M[0])\n E = [[float(\'inf\')] * X for _ in range(Y)]\n E[0][0] = 0\n\n while frontier:\n new_frontier = []\n for y, x in frontier:\n for y_, x_ in [(y + 1, x), (y - 1, x), (y, x + 1), (y, x - 1)]:\n if y_ < 0 or x_ < 0 or y_ >= Y or x_ >= X:\n continue\n\n effort = max(E[y][x], abs(M[y][x] - M[y_][x_]))\n if effort < E[y_][x_]:\n E[y_][x_] = effort\n new_frontier.append((y_, x_))\n \n frontier = new_frontier\n \n return E[-1][-1]\n``` | 1 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Rust/Python BFS with explanation | path-with-minimum-effort | 0 | 1 | # Intuition\nThere are at least two possible solutions here. One involves dijkstra where you maintain the min-heap of positions with smallest effor seen so far. But you can also adjust a standard BFS to solve the problem.\n\nTo do this, create a frontier which starts with `(0, 0)` and maintain your current knowledge of effort. This will be a matrix where all elements are some maximum value and the value at the start position `(0, 0)` is `0`.\n\nNow do standard BFS where you constantly build a new frontier from the previous one by taking a position and trying to go in 4 directions. When you do this you check than the next value is within the range and also check the effor to reach that cell. How to calculate the effort?\n\nIt is max between the effort of the cell you came from and the current effor to reach the new cell which is the absolute difference between the values. So basically `max(E[y][x], abs(M[y][x] - M[y_][x_]))`. And if this effort is smaller than the effort we have before we add it into the frontier and update the effort in our effort matrix.\n\n\n# Code\n```Rust []\nimpl Solution {\n pub fn minimum_effort_path(M: Vec<Vec<i32>>) -> i32 {\n let (Y, X) = (M.len(), M[0].len());\n let mut frontier = vec![(0, 0)];\n let mut E = vec![vec![i32::MAX; X]; Y];\n E[0][0] = 0;\n let dirs = [-1, 0, 1, 0, -1];\n \n while !frontier.is_empty() {\n let mut new_frontier = Vec::new();\n for (y, x) in frontier {\n for i in 0 .. 4 {\n let y_ = (y as i32 + dirs[i]) as usize;\n let x_ = (x as i32 + dirs[i + 1]) as usize;\n\n if y_ < Y && x_ < X {\n let e = (M[y][x] - M[y_][x_]).abs().max(E[y][x]);\n if e < E[y_][x_] {\n E[y_][x_] = e;\n new_frontier.push((y_, x_));\n }\n }\n }\n }\n\n frontier = new_frontier;\n }\n \n return E[Y - 1][X - 1];\n }\n}\n```\n```python []\nclass Solution:\n def minimumEffortPath(self, M: List[List[int]]) -> int:\n frontier = [(0, 0)] \n Y, X = len(M), len(M[0])\n E = [[float(\'inf\')] * X for _ in range(Y)]\n E[0][0] = 0\n\n while frontier:\n new_frontier = []\n for y, x in frontier:\n for y_, x_ in [(y + 1, x), (y - 1, x), (y, x + 1), (y, x - 1)]:\n if y_ < 0 or x_ < 0 or y_ >= Y or x_ >= X:\n continue\n\n effort = max(E[y][x], abs(M[y][x] - M[y_][x_]))\n if effort < E[y_][x_]:\n E[y_][x_] = effort\n new_frontier.append((y_, x_))\n \n frontier = new_frontier\n \n return E[-1][-1]\n``` | 1 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
✅ 97.67% Optimal Dijkstra with Heap | path-with-minimum-effort | 1 | 1 | # Comprehensive Guide to Solving "Path With Minimum Effort": Conquering the Terrain Efficiently\r\n\r\n## Introduction & Problem Statement\r\n\r\nGreetings, algorithmic adventurers! Today\'s quest leads us through a matrix of heights, representing terrains that a hiker needs to cross. The task is to find the path that requires the minimum effort. The effort is calculated as the maximum absolute difference in heights between two consecutive cells of the route. Intriguing, isn\'t it?\r\n\r\n## Key Concepts and Constraints\r\n\r\n### What Makes This Problem Unique?\r\n\r\n1. **Graph Representation**: \r\n This problem can be mapped to a graph where each cell in the 2D matrix is a node. The edges connecting these nodes represent the "effort" required to move from one cell to another.\r\n\r\n2. **Variants of Shortest Path Algorithms**: \r\n The objective is similar to finding the shortest path, but with a different metric. We need to minimize the maximum absolute difference between adjacent nodes.\r\n\r\n3. **Constraints**: \r\n - $$1 \\leq \\text{rows, columns} \\leq 100$$\r\n - $$1 \\leq \\text{heights}[i][j] \\leq 10^6$$\r\n\r\n### Strategies to Tackle the Problem\r\n\r\n1. **Dijkstra\'s Algorithm**: \r\n A classic algorithm for finding the shortest path in a weighted graph, adapted for this problem.\r\n\r\n---\r\n\r\n## Live Coding Dijkstra\'s + Explain\r\nhttps://youtu.be/4VsdOZnViYc?si=4zNaGwKudgqIpyTc\r\n\r\n## Dijkstra\'s Algorithm Explained\r\n\r\n### What is Dijkstra\'s Algorithm?\r\n\r\nDijkstra\'s Algorithm is a classic graph algorithm that finds the shortest path from a source node to all other nodes in a weighted graph. In this case, the graph is represented by a 2D grid of cells, where each cell is a node and the edges between them represent the effort to move from one cell to another.\r\n\r\n### Mechanics of Dijkstra\'s Algorithm in "Path With Minimum Effort"\r\n\r\n1. **Initialize Priority Queue**: \r\n - The algorithm starts at the top-left corner (the source). The priority queue is initialized to store the effort needed to reach each cell from the source. The effort for the source itself is zero.\r\n\r\n2. **Distance Matrix**: \r\n - A 2D array keeps track of the minimum effort required to reach each cell. Initially, this is set to infinity for all cells except the source.\r\n\r\n3. **Iterate and Update Distances**: \r\n - The algorithm pops the cell with the smallest effort from the priority queue and explores its neighbors. The effort required to reach a neighbor is updated if a smaller effort is found.\r\n\r\n4. **Early Exit**: \r\n - The algorithm stops when it reaches the bottom-right corner, returning the effort required to get there.\r\n\r\n### Time and Space Complexity\r\n\r\n- **Time Complexity**: $$O(M \\times N \\log(M \\times N))$$, where $$M$$ and $$N$$ are the dimensions of the grid. This is primarily due to the operations on the priority queue.\r\n- **Space Complexity**: $$O(M \\times N)$$, needed for the distance matrix and the priority queue.\r\n\r\n# Code Dijkstra\r\n``` Python []\r\nclass Solution:\r\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\r\n rows, cols = len(heights), len(heights[0])\r\n directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]\r\n dist = [[math.inf for _ in range(cols)] for _ in range(rows)]\r\n dist[0][0] = 0\r\n minHeap = [(0, 0, 0)] \r\n \r\n while minHeap:\r\n effort, x, y = heappop(minHeap)\r\n\r\n if x == rows - 1 and y == cols - 1:\r\n return effort\r\n \r\n for dx, dy in directions:\r\n nx, ny = x + dx, y + dy\r\n \r\n if 0 <= nx < rows and 0 <= ny < cols:\r\n new_effort = max(effort, abs(heights[x][y] - heights[nx][ny]))\r\n \r\n if new_effort < dist[nx][ny]:\r\n dist[nx][ny] = new_effort\r\n heappush(minHeap, (new_effort, nx, ny))\r\n```\r\n``` Rust []\r\nuse std::collections::BinaryHeap;\r\nuse std::cmp::Reverse;\r\n\r\nimpl Solution {\r\n pub fn minimum_effort_path(heights: Vec<Vec<i32>>) -> i32 {\r\n let rows = heights.len();\r\n let cols = heights[0].len();\r\n let mut dist = vec![vec![i32::MAX; cols]; rows];\r\n let mut min_heap: BinaryHeap<Reverse<(i32, usize, usize)>> = BinaryHeap::new();\r\n \r\n dist[0][0] = 0;\r\n min_heap.push(Reverse((0, 0, 0)));\r\n \r\n let directions = [(0, 1), (0, -1), (1, 0), (-1, 0)];\r\n \r\n while let Some(Reverse((effort, x, y))) = min_heap.pop() {\r\n if effort > dist[x][y] {\r\n continue;\r\n }\r\n if x == rows - 1 && y == cols - 1 {\r\n return effort;\r\n }\r\n for (dx, dy) in directions.iter() {\r\n let nx = (x as i32 + dx) as usize;\r\n let ny = (y as i32 + dy) as usize;\r\n if nx < rows && ny < cols {\r\n let new_effort = std::cmp::max(effort, (heights[x][y] - heights[nx][ny]).abs());\r\n if new_effort < dist[nx][ny] {\r\n dist[nx][ny] = new_effort;\r\n min_heap.push(Reverse((new_effort, nx, ny)));\r\n }\r\n }\r\n }\r\n }\r\n -1\r\n }\r\n}\r\n```\r\n``` Go []\r\ntype Item struct {\r\n\teffort, x, y int\r\n}\r\n\r\ntype PriorityQueue []Item\r\n\r\nfunc (pq PriorityQueue) Len() int { return len(pq) }\r\n\r\nfunc (pq PriorityQueue) Less(i, j int) bool {\r\n\treturn pq[i].effort < pq[j].effort\r\n}\r\n\r\nfunc (pq PriorityQueue) Swap(i, j int) {\r\n\tpq[i], pq[j] = pq[j], pq[i]\r\n}\r\n\r\nfunc (pq *PriorityQueue) Push(x interface{}) {\r\n\t*pq = append(*pq, x.(Item))\r\n}\r\n\r\nfunc (pq *PriorityQueue) Pop() interface{} {\r\n\told := *pq\r\n\tn := len(old)\r\n\titem := old[n-1]\r\n\t*pq = old[0 : n-1]\r\n\treturn item\r\n}\r\n\r\nfunc minimumEffortPath(heights [][]int) int {\r\n\trows, cols := len(heights), len(heights[0])\r\n\tdist := make([][]int, rows)\r\n\tfor i := range dist {\r\n\t\tdist[i] = make([]int, cols)\r\n\t\tfor j := range dist[i] {\r\n\t\t\tdist[i][j] = math.MaxInt32\r\n\t\t}\r\n\t}\r\n\tdist[0][0] = 0\r\n\tdirections := [][2]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}\r\n\r\n\tpq := &PriorityQueue{Item{0, 0, 0}}\r\n\theap.Init(pq)\r\n\r\n\tfor pq.Len() > 0 {\r\n\t\titem := heap.Pop(pq).(Item)\r\n\t\teffort, x, y := item.effort, item.x, item.y\r\n\t\tif effort > dist[x][y] {\r\n\t\t\tcontinue\r\n\t\t}\r\n\t\tif x == rows-1 && y == cols-1 {\r\n\t\t\treturn effort\r\n\t\t}\r\n\t\tfor _, dir := range directions {\r\n\t\t\tnx, ny := x+dir[0], y+dir[1]\r\n\t\t\tif nx >= 0 && nx < rows && ny >= 0 && ny < cols {\r\n\t\t\t\tnewEffort := int(math.Max(float64(effort), math.Abs(float64(heights[x][y]-heights[nx][ny]))))\r\n\t\t\t\tif newEffort < dist[nx][ny] {\r\n\t\t\t\t\tdist[nx][ny] = newEffort\r\n\t\t\t\t\theap.Push(pq, Item{newEffort, nx, ny})\r\n\t\t\t\t}\r\n\t\t\t}\r\n\t\t}\r\n\t}\r\n\treturn -1\r\n}\r\n```\r\n``` C++ []\r\nclass Solution {\r\npublic:\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n int rows = heights.size(), cols = heights[0].size();\r\n vector<vector<int>> dist(rows, vector<int>(cols, INT_MAX));\r\n priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> minHeap;\r\n minHeap.emplace(0, 0, 0);\r\n dist[0][0] = 0;\r\n \r\n int directions[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\r\n \r\n while (!minHeap.empty()) {\r\n auto [effort, x, y] = minHeap.top();\r\n minHeap.pop();\r\n \r\n if (effort > dist[x][y]) continue;\r\n \r\n if (x == rows - 1 && y == cols - 1) return effort;\r\n \r\n for (auto& dir : directions) {\r\n int nx = x + dir[0], ny = y + dir[1];\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n int new_effort = max(effort, abs(heights[x][y] - heights[nx][ny]));\r\n if (new_effort < dist[nx][ny]) {\r\n dist[nx][ny] = new_effort;\r\n minHeap.emplace(new_effort, nx, ny);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n};\r\n```\r\n``` Java []\r\npublic class Solution {\r\n public int minimumEffortPath(int[][] heights) {\r\n int rows = heights.length, cols = heights[0].length;\r\n int[][] dist = new int[rows][cols];\r\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\r\n minHeap.add(new int[]{0, 0, 0});\r\n \r\n for (int i = 0; i < rows; i++) {\r\n for (int j = 0; j < cols; j++) {\r\n dist[i][j] = Integer.MAX_VALUE;\r\n }\r\n }\r\n dist[0][0] = 0;\r\n \r\n int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\r\n \r\n while (!minHeap.isEmpty()) {\r\n int[] top = minHeap.poll();\r\n int effort = top[0], x = top[1], y = top[2];\r\n \r\n if (effort > dist[x][y]) continue;\r\n \r\n if (x == rows - 1 && y == cols - 1) return effort;\r\n \r\n for (int[] dir : directions) {\r\n int nx = x + dir[0], ny = y + dir[1];\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n int new_effort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));\r\n if (new_effort < dist[nx][ny]) {\r\n dist[nx][ny] = new_effort;\r\n minHeap.add(new int[]{new_effort, nx, ny});\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n}\r\n```\r\n``` C# []\r\npublic class Solution {\r\n public int MinimumEffortPath(int[][] heights) {\r\n int rows = heights.Length, cols = heights[0].Length;\r\n int[,] dist = new int[rows, cols];\r\n var minHeap = new SortedSet<(int effort, int x, int y)>();\r\n minHeap.Add((0, 0, 0));\r\n \r\n for (int i = 0; i < rows; i++) {\r\n for (int j = 0; j < cols; j++) {\r\n dist[i, j] = int.MaxValue;\r\n }\r\n }\r\n dist[0, 0] = 0;\r\n \r\n int[][] directions = new int[][] { new int[]{ 0, 1 }, new int[]{ 0, -1 }, new int[]{ 1, 0 }, new int[]{ -1, 0 }};\r\n \r\n while (minHeap.Count > 0) {\r\n var (effort, x, y) = minHeap.Min;\r\n minHeap.Remove(minHeap.Min);\r\n \r\n if (effort > dist[x, y]) continue;\r\n \r\n if (x == rows - 1 && y == cols - 1) return effort;\r\n \r\n foreach (var dir in directions) {\r\n int nx = x + dir[0], ny = y + dir[1];\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n int new_effort = Math.Max(effort, Math.Abs(heights[x][y] - heights[nx][ny]));\r\n if (new_effort < dist[nx, ny]) {\r\n dist[nx, ny] = new_effort;\r\n minHeap.Add((new_effort, nx, ny));\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n}\r\n```\r\n``` JavaScript []\r\n/**\r\n * @param {number[][]} heights\r\n * @return {number}\r\n */\r\nvar minimumEffortPath = function(heights) {\r\n const rows = heights.length, cols = heights[0].length;\r\n const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity));\r\n const minHeap = [[0, 0, 0]]; // [effort, x, y]\r\n \r\n dist[0][0] = 0;\r\n const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];\r\n \r\n while (minHeap.length > 0) {\r\n const [effort, x, y] = minHeap.shift();\r\n \r\n if (effort > dist[x][y]) continue;\r\n \r\n if (x === rows - 1 && y === cols - 1) return effort;\r\n \r\n for (const [dx, dy] of directions) {\r\n const nx = x + dx, ny = y + dy;\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));\r\n if (newEffort < dist[nx][ny]) {\r\n dist[nx][ny] = newEffort;\r\n minHeap.push([newEffort, nx, ny]);\r\n minHeap.sort((a, b) => a[0] - b[0]);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n};\r\n```\r\n``` PHP []\r\nclass Solution {\r\n\r\n function minimumEffortPath($heights) {\r\n $rows = count($heights);\r\n $cols = count($heights[0]);\r\n $dist = array_fill(0, $rows, array_fill(0, $cols, PHP_INT_MAX));\r\n \r\n $minHeap = new SplPriorityQueue();\r\n $minHeap->insert([0, 0, 0], 0);\r\n \r\n $dist[0][0] = 0;\r\n $directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];\r\n \r\n while (!$minHeap->isEmpty()) {\r\n list($effort, $x, $y) = $minHeap->extract();\r\n \r\n if ($effort > $dist[$x][$y]) continue;\r\n \r\n if ($x === $rows - 1 && $y === $cols - 1) return $effort;\r\n \r\n foreach ($directions as $dir) {\r\n list($dx, $dy) = $dir;\r\n $nx = $x + $dx;\r\n $ny = $y + $dy;\r\n \r\n if ($nx >= 0 && $nx < $rows && $ny >= 0 && $ny < $cols) {\r\n $newEffort = max($effort, abs($heights[$x][$y] - $heights[$nx][$ny]));\r\n if ($newEffort < $dist[$nx][$ny]) {\r\n $dist[$nx][$ny] = $newEffort;\r\n $minHeap->insert([$newEffort, $nx, $ny], -$newEffort);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n}\r\n```\r\n\r\n## Performance\r\n\r\n| Language | Algorithm | Time (ms) | Memory (MB) |\r\n|-------------|-----------|-----------|-------------|\r\n| Rust | Dijkstra | 22 | 2.4 |\r\n| Java | Dijkstra | 40 | 44.4 |\r\n| Go | Dijkstra | 73 | 7.7 |\r\n| C++ | Dijkstra | 111 | 20.5 |\r\n| JavaScript | Dijkstra | 152 | 51.9 |\r\n| PHP | Dijkstra | 191 | 22.6 |\r\n| C# | Dijkstra | 261 | 65 |\r\n| Python3 | Dijkstra | 515 | 17.8 |\r\n\r\n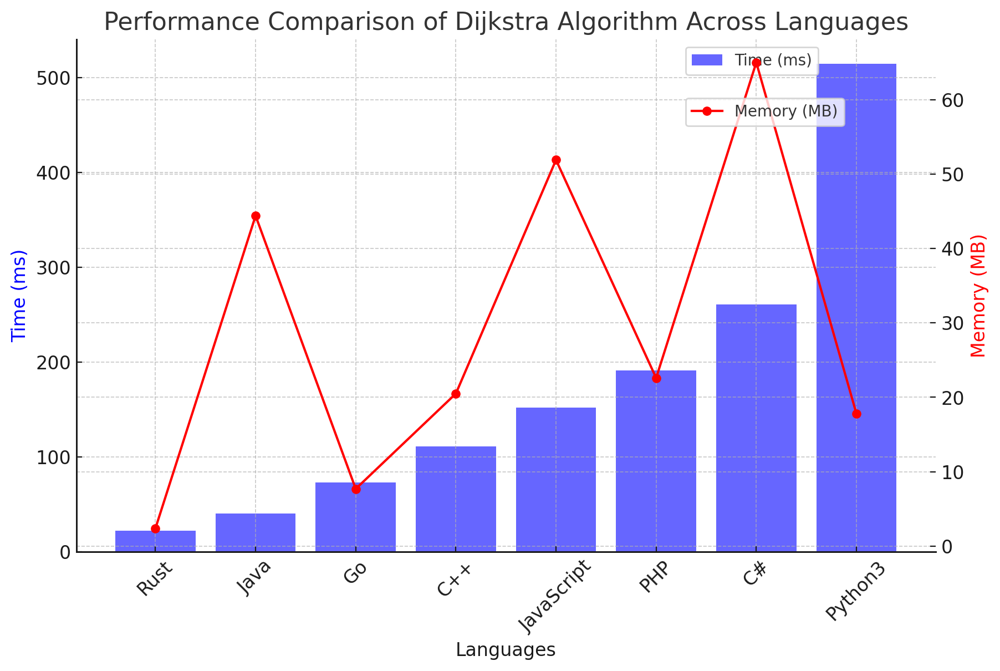\r\n\r\n\r\n## Code Highlights and Best Practices\r\n\r\n- Dijkstra\'s algorithm is straightforward to implement and can be optimized using a 2D array for storing distances.\r\n\r\nMastering these algorithms will not only help you solve this particular problem but will also give you tools that are highly applicable in various domains. So, are you ready to find the path with minimum effort? Let\'s do it! | 95 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
✅ 97.67% Optimal Dijkstra with Heap | path-with-minimum-effort | 1 | 1 | # Comprehensive Guide to Solving "Path With Minimum Effort": Conquering the Terrain Efficiently\r\n\r\n## Introduction & Problem Statement\r\n\r\nGreetings, algorithmic adventurers! Today\'s quest leads us through a matrix of heights, representing terrains that a hiker needs to cross. The task is to find the path that requires the minimum effort. The effort is calculated as the maximum absolute difference in heights between two consecutive cells of the route. Intriguing, isn\'t it?\r\n\r\n## Key Concepts and Constraints\r\n\r\n### What Makes This Problem Unique?\r\n\r\n1. **Graph Representation**: \r\n This problem can be mapped to a graph where each cell in the 2D matrix is a node. The edges connecting these nodes represent the "effort" required to move from one cell to another.\r\n\r\n2. **Variants of Shortest Path Algorithms**: \r\n The objective is similar to finding the shortest path, but with a different metric. We need to minimize the maximum absolute difference between adjacent nodes.\r\n\r\n3. **Constraints**: \r\n - $$1 \\leq \\text{rows, columns} \\leq 100$$\r\n - $$1 \\leq \\text{heights}[i][j] \\leq 10^6$$\r\n\r\n### Strategies to Tackle the Problem\r\n\r\n1. **Dijkstra\'s Algorithm**: \r\n A classic algorithm for finding the shortest path in a weighted graph, adapted for this problem.\r\n\r\n---\r\n\r\n## Live Coding Dijkstra\'s + Explain\r\nhttps://youtu.be/4VsdOZnViYc?si=4zNaGwKudgqIpyTc\r\n\r\n## Dijkstra\'s Algorithm Explained\r\n\r\n### What is Dijkstra\'s Algorithm?\r\n\r\nDijkstra\'s Algorithm is a classic graph algorithm that finds the shortest path from a source node to all other nodes in a weighted graph. In this case, the graph is represented by a 2D grid of cells, where each cell is a node and the edges between them represent the effort to move from one cell to another.\r\n\r\n### Mechanics of Dijkstra\'s Algorithm in "Path With Minimum Effort"\r\n\r\n1. **Initialize Priority Queue**: \r\n - The algorithm starts at the top-left corner (the source). The priority queue is initialized to store the effort needed to reach each cell from the source. The effort for the source itself is zero.\r\n\r\n2. **Distance Matrix**: \r\n - A 2D array keeps track of the minimum effort required to reach each cell. Initially, this is set to infinity for all cells except the source.\r\n\r\n3. **Iterate and Update Distances**: \r\n - The algorithm pops the cell with the smallest effort from the priority queue and explores its neighbors. The effort required to reach a neighbor is updated if a smaller effort is found.\r\n\r\n4. **Early Exit**: \r\n - The algorithm stops when it reaches the bottom-right corner, returning the effort required to get there.\r\n\r\n### Time and Space Complexity\r\n\r\n- **Time Complexity**: $$O(M \\times N \\log(M \\times N))$$, where $$M$$ and $$N$$ are the dimensions of the grid. This is primarily due to the operations on the priority queue.\r\n- **Space Complexity**: $$O(M \\times N)$$, needed for the distance matrix and the priority queue.\r\n\r\n# Code Dijkstra\r\n``` Python []\r\nclass Solution:\r\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\r\n rows, cols = len(heights), len(heights[0])\r\n directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]\r\n dist = [[math.inf for _ in range(cols)] for _ in range(rows)]\r\n dist[0][0] = 0\r\n minHeap = [(0, 0, 0)] \r\n \r\n while minHeap:\r\n effort, x, y = heappop(minHeap)\r\n\r\n if x == rows - 1 and y == cols - 1:\r\n return effort\r\n \r\n for dx, dy in directions:\r\n nx, ny = x + dx, y + dy\r\n \r\n if 0 <= nx < rows and 0 <= ny < cols:\r\n new_effort = max(effort, abs(heights[x][y] - heights[nx][ny]))\r\n \r\n if new_effort < dist[nx][ny]:\r\n dist[nx][ny] = new_effort\r\n heappush(minHeap, (new_effort, nx, ny))\r\n```\r\n``` Rust []\r\nuse std::collections::BinaryHeap;\r\nuse std::cmp::Reverse;\r\n\r\nimpl Solution {\r\n pub fn minimum_effort_path(heights: Vec<Vec<i32>>) -> i32 {\r\n let rows = heights.len();\r\n let cols = heights[0].len();\r\n let mut dist = vec![vec![i32::MAX; cols]; rows];\r\n let mut min_heap: BinaryHeap<Reverse<(i32, usize, usize)>> = BinaryHeap::new();\r\n \r\n dist[0][0] = 0;\r\n min_heap.push(Reverse((0, 0, 0)));\r\n \r\n let directions = [(0, 1), (0, -1), (1, 0), (-1, 0)];\r\n \r\n while let Some(Reverse((effort, x, y))) = min_heap.pop() {\r\n if effort > dist[x][y] {\r\n continue;\r\n }\r\n if x == rows - 1 && y == cols - 1 {\r\n return effort;\r\n }\r\n for (dx, dy) in directions.iter() {\r\n let nx = (x as i32 + dx) as usize;\r\n let ny = (y as i32 + dy) as usize;\r\n if nx < rows && ny < cols {\r\n let new_effort = std::cmp::max(effort, (heights[x][y] - heights[nx][ny]).abs());\r\n if new_effort < dist[nx][ny] {\r\n dist[nx][ny] = new_effort;\r\n min_heap.push(Reverse((new_effort, nx, ny)));\r\n }\r\n }\r\n }\r\n }\r\n -1\r\n }\r\n}\r\n```\r\n``` Go []\r\ntype Item struct {\r\n\teffort, x, y int\r\n}\r\n\r\ntype PriorityQueue []Item\r\n\r\nfunc (pq PriorityQueue) Len() int { return len(pq) }\r\n\r\nfunc (pq PriorityQueue) Less(i, j int) bool {\r\n\treturn pq[i].effort < pq[j].effort\r\n}\r\n\r\nfunc (pq PriorityQueue) Swap(i, j int) {\r\n\tpq[i], pq[j] = pq[j], pq[i]\r\n}\r\n\r\nfunc (pq *PriorityQueue) Push(x interface{}) {\r\n\t*pq = append(*pq, x.(Item))\r\n}\r\n\r\nfunc (pq *PriorityQueue) Pop() interface{} {\r\n\told := *pq\r\n\tn := len(old)\r\n\titem := old[n-1]\r\n\t*pq = old[0 : n-1]\r\n\treturn item\r\n}\r\n\r\nfunc minimumEffortPath(heights [][]int) int {\r\n\trows, cols := len(heights), len(heights[0])\r\n\tdist := make([][]int, rows)\r\n\tfor i := range dist {\r\n\t\tdist[i] = make([]int, cols)\r\n\t\tfor j := range dist[i] {\r\n\t\t\tdist[i][j] = math.MaxInt32\r\n\t\t}\r\n\t}\r\n\tdist[0][0] = 0\r\n\tdirections := [][2]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}\r\n\r\n\tpq := &PriorityQueue{Item{0, 0, 0}}\r\n\theap.Init(pq)\r\n\r\n\tfor pq.Len() > 0 {\r\n\t\titem := heap.Pop(pq).(Item)\r\n\t\teffort, x, y := item.effort, item.x, item.y\r\n\t\tif effort > dist[x][y] {\r\n\t\t\tcontinue\r\n\t\t}\r\n\t\tif x == rows-1 && y == cols-1 {\r\n\t\t\treturn effort\r\n\t\t}\r\n\t\tfor _, dir := range directions {\r\n\t\t\tnx, ny := x+dir[0], y+dir[1]\r\n\t\t\tif nx >= 0 && nx < rows && ny >= 0 && ny < cols {\r\n\t\t\t\tnewEffort := int(math.Max(float64(effort), math.Abs(float64(heights[x][y]-heights[nx][ny]))))\r\n\t\t\t\tif newEffort < dist[nx][ny] {\r\n\t\t\t\t\tdist[nx][ny] = newEffort\r\n\t\t\t\t\theap.Push(pq, Item{newEffort, nx, ny})\r\n\t\t\t\t}\r\n\t\t\t}\r\n\t\t}\r\n\t}\r\n\treturn -1\r\n}\r\n```\r\n``` C++ []\r\nclass Solution {\r\npublic:\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n int rows = heights.size(), cols = heights[0].size();\r\n vector<vector<int>> dist(rows, vector<int>(cols, INT_MAX));\r\n priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> minHeap;\r\n minHeap.emplace(0, 0, 0);\r\n dist[0][0] = 0;\r\n \r\n int directions[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\r\n \r\n while (!minHeap.empty()) {\r\n auto [effort, x, y] = minHeap.top();\r\n minHeap.pop();\r\n \r\n if (effort > dist[x][y]) continue;\r\n \r\n if (x == rows - 1 && y == cols - 1) return effort;\r\n \r\n for (auto& dir : directions) {\r\n int nx = x + dir[0], ny = y + dir[1];\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n int new_effort = max(effort, abs(heights[x][y] - heights[nx][ny]));\r\n if (new_effort < dist[nx][ny]) {\r\n dist[nx][ny] = new_effort;\r\n minHeap.emplace(new_effort, nx, ny);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n};\r\n```\r\n``` Java []\r\npublic class Solution {\r\n public int minimumEffortPath(int[][] heights) {\r\n int rows = heights.length, cols = heights[0].length;\r\n int[][] dist = new int[rows][cols];\r\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\r\n minHeap.add(new int[]{0, 0, 0});\r\n \r\n for (int i = 0; i < rows; i++) {\r\n for (int j = 0; j < cols; j++) {\r\n dist[i][j] = Integer.MAX_VALUE;\r\n }\r\n }\r\n dist[0][0] = 0;\r\n \r\n int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\r\n \r\n while (!minHeap.isEmpty()) {\r\n int[] top = minHeap.poll();\r\n int effort = top[0], x = top[1], y = top[2];\r\n \r\n if (effort > dist[x][y]) continue;\r\n \r\n if (x == rows - 1 && y == cols - 1) return effort;\r\n \r\n for (int[] dir : directions) {\r\n int nx = x + dir[0], ny = y + dir[1];\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n int new_effort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));\r\n if (new_effort < dist[nx][ny]) {\r\n dist[nx][ny] = new_effort;\r\n minHeap.add(new int[]{new_effort, nx, ny});\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n}\r\n```\r\n``` C# []\r\npublic class Solution {\r\n public int MinimumEffortPath(int[][] heights) {\r\n int rows = heights.Length, cols = heights[0].Length;\r\n int[,] dist = new int[rows, cols];\r\n var minHeap = new SortedSet<(int effort, int x, int y)>();\r\n minHeap.Add((0, 0, 0));\r\n \r\n for (int i = 0; i < rows; i++) {\r\n for (int j = 0; j < cols; j++) {\r\n dist[i, j] = int.MaxValue;\r\n }\r\n }\r\n dist[0, 0] = 0;\r\n \r\n int[][] directions = new int[][] { new int[]{ 0, 1 }, new int[]{ 0, -1 }, new int[]{ 1, 0 }, new int[]{ -1, 0 }};\r\n \r\n while (minHeap.Count > 0) {\r\n var (effort, x, y) = minHeap.Min;\r\n minHeap.Remove(minHeap.Min);\r\n \r\n if (effort > dist[x, y]) continue;\r\n \r\n if (x == rows - 1 && y == cols - 1) return effort;\r\n \r\n foreach (var dir in directions) {\r\n int nx = x + dir[0], ny = y + dir[1];\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n int new_effort = Math.Max(effort, Math.Abs(heights[x][y] - heights[nx][ny]));\r\n if (new_effort < dist[nx, ny]) {\r\n dist[nx, ny] = new_effort;\r\n minHeap.Add((new_effort, nx, ny));\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n}\r\n```\r\n``` JavaScript []\r\n/**\r\n * @param {number[][]} heights\r\n * @return {number}\r\n */\r\nvar minimumEffortPath = function(heights) {\r\n const rows = heights.length, cols = heights[0].length;\r\n const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity));\r\n const minHeap = [[0, 0, 0]]; // [effort, x, y]\r\n \r\n dist[0][0] = 0;\r\n const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];\r\n \r\n while (minHeap.length > 0) {\r\n const [effort, x, y] = minHeap.shift();\r\n \r\n if (effort > dist[x][y]) continue;\r\n \r\n if (x === rows - 1 && y === cols - 1) return effort;\r\n \r\n for (const [dx, dy] of directions) {\r\n const nx = x + dx, ny = y + dy;\r\n if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {\r\n const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));\r\n if (newEffort < dist[nx][ny]) {\r\n dist[nx][ny] = newEffort;\r\n minHeap.push([newEffort, nx, ny]);\r\n minHeap.sort((a, b) => a[0] - b[0]);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n};\r\n```\r\n``` PHP []\r\nclass Solution {\r\n\r\n function minimumEffortPath($heights) {\r\n $rows = count($heights);\r\n $cols = count($heights[0]);\r\n $dist = array_fill(0, $rows, array_fill(0, $cols, PHP_INT_MAX));\r\n \r\n $minHeap = new SplPriorityQueue();\r\n $minHeap->insert([0, 0, 0], 0);\r\n \r\n $dist[0][0] = 0;\r\n $directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];\r\n \r\n while (!$minHeap->isEmpty()) {\r\n list($effort, $x, $y) = $minHeap->extract();\r\n \r\n if ($effort > $dist[$x][$y]) continue;\r\n \r\n if ($x === $rows - 1 && $y === $cols - 1) return $effort;\r\n \r\n foreach ($directions as $dir) {\r\n list($dx, $dy) = $dir;\r\n $nx = $x + $dx;\r\n $ny = $y + $dy;\r\n \r\n if ($nx >= 0 && $nx < $rows && $ny >= 0 && $ny < $cols) {\r\n $newEffort = max($effort, abs($heights[$x][$y] - $heights[$nx][$ny]));\r\n if ($newEffort < $dist[$nx][$ny]) {\r\n $dist[$nx][$ny] = $newEffort;\r\n $minHeap->insert([$newEffort, $nx, $ny], -$newEffort);\r\n }\r\n }\r\n }\r\n }\r\n return -1;\r\n }\r\n}\r\n```\r\n\r\n## Performance\r\n\r\n| Language | Algorithm | Time (ms) | Memory (MB) |\r\n|-------------|-----------|-----------|-------------|\r\n| Rust | Dijkstra | 22 | 2.4 |\r\n| Java | Dijkstra | 40 | 44.4 |\r\n| Go | Dijkstra | 73 | 7.7 |\r\n| C++ | Dijkstra | 111 | 20.5 |\r\n| JavaScript | Dijkstra | 152 | 51.9 |\r\n| PHP | Dijkstra | 191 | 22.6 |\r\n| C# | Dijkstra | 261 | 65 |\r\n| Python3 | Dijkstra | 515 | 17.8 |\r\n\r\n\r\n\r\n\r\n## Code Highlights and Best Practices\r\n\r\n- Dijkstra\'s algorithm is straightforward to implement and can be optimized using a 2D array for storing distances.\r\n\r\nMastering these algorithms will not only help you solve this particular problem but will also give you tools that are highly applicable in various domains. So, are you ready to find the path with minimum effort? Let\'s do it! | 95 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Python3 Solution | path-with-minimum-effort | 0 | 1 | \r\n```\r\nclass Solution:\r\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\r\n m=len(heights)\r\n n=len(heights[0])\r\n queue={(0,0):0}\r\n seen={(0,0):0}\r\n ans=inf\r\n while queue:\r\n newqueue={}\r\n for (i,j),h in queue.items():\r\n if i==(m-1) and j==(n-1):\r\n ans=min(ans,h)\r\n for x,y in (i-1,j),(i,j-1),(i,j+1),(i+1,j):\r\n if 0<=x<m and 0<=y<n:\r\n hi=max(h,abs(heights[i][j]-heights[x][y]))\r\n\r\n if hi<seen.get((x,y),inf):\r\n seen[(x,y)]=hi\r\n newqueue[(x,y)]=hi\r\n queue=newqueue\r\n return ans \r\n``` | 1 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Python3 Solution | path-with-minimum-effort | 0 | 1 | \r\n```\r\nclass Solution:\r\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\r\n m=len(heights)\r\n n=len(heights[0])\r\n queue={(0,0):0}\r\n seen={(0,0):0}\r\n ans=inf\r\n while queue:\r\n newqueue={}\r\n for (i,j),h in queue.items():\r\n if i==(m-1) and j==(n-1):\r\n ans=min(ans,h)\r\n for x,y in (i-1,j),(i,j-1),(i,j+1),(i+1,j):\r\n if 0<=x<m and 0<=y<n:\r\n hi=max(h,abs(heights[i][j]-heights[x][y]))\r\n\r\n if hi<seen.get((x,y),inf):\r\n seen[(x,y)]=hi\r\n newqueue[(x,y)]=hi\r\n queue=newqueue\r\n return ans \r\n``` | 1 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
🚀 99.92% || Dijkstra's Algorithm || Binary Search || Commented Code 🚀 | path-with-minimum-effort | 1 | 1 | # Problem Description\r\nYou are a hiker preparing for an upcoming hike and need to plan your route efficiently. Given a 2D array of heights representing the elevation of each cell, your objective is to find the path from the **top-left** cell to the **bottom-right** cell with the **minimum** effort for the whole path.\r\nThe **effort** of a route is defined as the **maximum** absolute difference in heights between **two consecutive** cells along the path. Your goal is to determine the **minimum** effort needed to traverse from the **starting** point to the **destination** in this manner.\r\n\r\n- Constraints:\r\n - `rows == heights.length`\r\n - `columns == heights[i].length`\r\n - `1 <= rows, columns <= 100`\r\n - `1 <= heights[i][j] <= 10e6`\r\n \r\n\r\n---\r\n\r\n\r\n\r\n# Intuition\r\nHello There\uD83D\uDE00\r\nLet\'s take a look on our interesting problem\uD83D\uDE80\r\nOur problem says that we have matrix `M * N` of cells and each cell has some value of **height**.\r\nour goal is to find the path that has **minimum** effort for the `top-left` cell to the `bottom-right` cell.\r\n- Let\'s focus on **two important** things:\r\n - We want to find a **path** between two cells.\r\n - We want to **minimize** some obejective.\r\n\r\n## Dijkstra\'s Algorithm\r\nIt looks something that **Dijkstra\'s Algorithm** can solve !\r\n\r\nBut what is **DIJKSTRA** ?!!\r\nDijkstra\'s Algorithm is an algorithm to find the **shortest** path between two nodes in a **graph** or two cells in a **matrix** like our problem. \r\nIt\'s part of a **family** of algorithms designed to uncover the shortest path between nodes or cells **like** BFS, Bellman-Ford Algorithm, Floyd-Warsahll Algorithm. Each algorithm has its **unique** applications.\r\n- Let\'s focus on Dijkstra\'s Algorithm:\r\n - **Nature:** It\'s a single-source, multiple-destination algorithm. In simpler terms, it pinpoints the shortest path from a starting node to any other node in our graph.\r\n - **Constraints:** Dijkstra\'s Algorithm is suitable for graphs or problems featuring positive weights. If we encounter negative weights, we\'d choose alternative algorithms such as Bellman-Ford.\r\n \r\nAnd there you have it! Dijkstra\'s Algorithm is the **key** to our problem, well-known for tackling precisely these types of challenges.\r\n\r\n\r\n## Binary Search\r\nAnother **interesting** approach to solve this problem is to use **binary search**. But how? What if we shift our **perspective** a bit?\r\n\r\nI put it in this post because I found it a **unique** solution to a problem that we can solve using Dijkstra\'s Algorithm. \r\n\r\nInstead of focusing solely on finding the **shortest** path between the starting and ending cells, let\'s consider **traversing** the entire matrix. We can approach this much like a **DFS** (Depth-First Search) like any other simple problem.\r\n\r\n**Picture** this: As we navigate through the matrix using **DFS**, we\'re mindful of this **effort limit**. The goal? To reach the end cell while ensuring that our **maximum** effort remains below this specified **limit**.\r\n\r\nNow, here comes the interesting part\u2014let\'s integrate **binary search** into this. We\'ll perform a binary search around this **limit effort** in our DFS traversal. By doing so, we can effectively hone in on the optimal effort threshold that guarantees our success in reaching the end cell. If we achieve this within the defined effort threshold, it indicates a **possibility** to reach the goal cell with an even **lower** effort.\r\n\r\nIn essence, this creative approach combines the power of binary search with **DFS**, enriching our problem-solving repertoire.\r\n\r\n---\r\n\r\n\r\n# Proposed Approaches\r\n## Dijkstra\'s Algorithm\r\n### Steps\r\n- Create a 2D `effort` array and define **directional** **changes** using `dx` and `dy`.\r\n- Initialize cell `efforts` to **maximum** value.\r\n- Call **dijkstra** to find the **minimum** effort.\r\n- Initialize a `priority` queue to store (-effort, {x, y}) to make it return the **minimum** element.\r\n- Push the `top-left` cell into the queue with `initial` effort as `0`.\r\n- While the priority queue is **not empty**:\r\n - **Pop** the cell with the **least** effort.\r\n - If cost is **greater** than existing effort, **skip**.\r\n - If at **bottom-right** cell, **return minimum** effort.\r\n - **Explore** four directions, update efforts, and push to queue if lower effort found.\r\n- **Return** the minimum effort from top-left to bottom-right cell.\r\n\r\n### Complexity\r\n- **Time complexity:**$$O(M * N * log(M * N))$$\r\nThe time complexity for Dijkstra\'s Algorithm is `O(E * log(E))`, where `E` is the number of edges in the graph. In our case, we can consider the number of edges are `M * N`.\r\n- **Space complexity:**$$O(M * N)$$\r\nSince we are storing the minimum effort for the path from the starting point to each cell, then the space complexity is `O(M * N)`.\r\n\r\n---\r\n## Binary Search\r\n### Steps\r\n- **Create** a 2D array `visited` to track visited cells and define **directional changes** using `dx` and `dy`.\r\n- Set the **lower** and **upper** limits for `binary search`.\r\n- Perform `binary search` to find the minimum effort needed:\r\n - Use `DFS` to traverse the matrix within the effort **limits**.\r\n - **Update** the search **range** accordingly based on `DFS` results.\r\n- `Depth-First Search` (DFS) Function:\r\n - Mark the current cell as **visited**.\r\n - **Stop** if the bottom-right cell is reached.\r\n - **Explore** each direction (up, down, left, right):\r\n - Check if the new coordinates are within **bounds**.\r\n - Move to the next cell if the effort is within the specified **limit**.\r\n- Return **minimum** effort\r\n\r\n### Complexity\r\n- **Time complexity:**$$O(M * N * log(10^6))$$\r\nThe time complexity for **Binary Search** is `log(upper_bound - lower_bound)` and in our case the maximum range in `10^6`. and since we are doing **DFS** in each iteration knowing that the time complexity for the single **DFS** is O(N * M) then the total time complexity is `O(M * N * log(10^6))`.\r\n- **Space complexity:**$$O(M * N)$$\r\nSince we are storing the visited array for each cell and the **DFS** recursion stack complexity is also `O(M * N)`, then the space complexity is `O(M * N)`.\r\n\r\n\r\n---\r\n\r\n\r\n# Code\r\n## Dijkstra\'s Algorithm\r\n```C++ []\r\nclass Solution {\r\nprivate:\r\n int effort[105][105]; // Store effort for each cell\r\n int dx[4] = {0, 1, -1, 0}; // Changes in x coordinate for each direction\r\n int dy[4] = {1, 0, 0, -1}; // Changes in y coordinate for each direction\r\n\r\npublic:\r\n // Dijkstra\'s Algorithm to find minimum effort\r\n int dijkstra(vector<vector<int>>& heights) {\r\n int rows = heights.size();\r\n int cols = heights[0].size();\r\n\r\n // Priority queue to store {effort, {x, y}}\r\n std::priority_queue<std::pair<int, std::pair<int, int>>> pq;\r\n pq.push({0, {0, 0}}); // Start from the top-left cell\r\n effort[0][0] = 0; // Initial effort at the starting cell\r\n\r\n while (!pq.empty()) {\r\n auto current = pq.top().second;\r\n int cost = -pq.top().first; // Effort for the current cell\r\n pq.pop();\r\n\r\n int x = current.first;\r\n int y = current.second;\r\n\r\n // Skip if we\'ve already found a better effort for this cell\r\n if (cost > effort[x][y])\r\n continue;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == rows - 1 && y == cols - 1)\r\n return cost;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + dx[i];\r\n int new_y = y + dy[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= rows || new_y < 0 || new_y >= cols)\r\n continue;\r\n\r\n // Calculate new effort for the neighboring cell\r\n int new_effort = std::max(effort[x][y], std::abs(heights[x][y] - heights[new_x][new_y]));\r\n\r\n // Update effort if a lower effort is found for the neighboring cell\r\n if (new_effort < effort[new_x][new_y]) {\r\n effort[new_x][new_y] = new_effort;\r\n pq.push({-new_effort, {new_x, new_y}});\r\n }\r\n }\r\n }\r\n return effort[rows - 1][cols - 1]; // Minimum effort for the path to the bottom-right cell\r\n }\r\n\r\n // Function to find the minimum effort path\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n // Initialize effort for each cell to maximum value\r\n for (int i = 0; i < heights.size(); i++) {\r\n for (int j = 0; j < heights[i].size(); j++) {\r\n effort[i][j] = INT_MAX;\r\n }\r\n }\r\n return dijkstra(heights); // Find minimum effort using dijkstra\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n private int[][] effort = new int[105][105]; // Store effort for each cell\r\n private int[] dx = {0, 1, -1, 0}; // Changes in x coordinate for each direction\r\n private int[] dy = {1, 0, 0, -1}; // Changes in y coordinate for each direction\r\n\r\n // Dijkstra\'s Algorithm to find minimum effort\r\n private int dijkstra(int[][] heights) {\r\n int rows = heights.length;\r\n int cols = heights[0].length;\r\n\r\n // Priority queue to store {effort, {x, y}}\r\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(-a[0], -b[0]));\r\n pq.add(new int[]{0, 0, 0}); // Start from the top-left cell\r\n effort[0][0] = 0; // Initial effort at the starting cell\r\n\r\n while (!pq.isEmpty()) {\r\n int[] current = pq.poll();\r\n int cost = -current[0]; // Effort for the current cell\r\n\r\n int x = current[1];\r\n int y = current[2];\r\n\r\n // Skip if we\'ve already found a better effort for this cell\r\n if (cost > effort[x][y])\r\n continue;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == rows - 1 && y == cols - 1)\r\n return cost;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + dx[i];\r\n int new_y = y + dy[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= rows || new_y < 0 || new_y >= cols)\r\n continue;\r\n\r\n // Calculate new effort for the neighboring cell\r\n int new_effort = Math.max(effort[x][y], Math.abs(heights[x][y] - heights[new_x][new_y]));\r\n\r\n // Update effort if a lower effort is found for the neighboring cell\r\n if (new_effort < effort[new_x][new_y]) {\r\n effort[new_x][new_y] = new_effort;\r\n pq.add(new int[]{-new_effort, new_x, new_y});\r\n }\r\n }\r\n }\r\n return effort[rows - 1][cols - 1]; // Minimum effort for the path to the bottom-right cell\r\n }\r\n\r\n // Function to find the minimum effort path\r\n public int minimumEffortPath(int[][] heights) {\r\n int rows = heights.length;\r\n int cols = heights[0].length;\r\n\r\n // Initialize effort for each cell to maximum value\r\n for (int i = 0; i < rows; i++) {\r\n Arrays.fill(effort[i], Integer.MAX_VALUE);\r\n }\r\n\r\n return dijkstra(heights); // Find minimum effort using dijkstra\r\n }\r\n}\r\n```\r\n```Python []\r\nclass Solution:\r\n def __init__(self):\r\n self.effort = [[float(\'inf\')] * 105 for _ in range(105)]\r\n self.dx = [0, 1, -1, 0]\r\n self.dy = [1, 0, 0, -1]\r\n\r\n def dijkstra(self, heights) -> int:\r\n rows = len(heights)\r\n cols = len(heights[0])\r\n\r\n pq = [(0, 0, 0)] # Priority queue to store (-effort, x, y)\r\n self.effort[0][0] = 0 # Initial effort at the starting cell\r\n\r\n while pq:\r\n cost, x, y = heapq.heappop(pq)\r\n\r\n # Skip if we\'ve already found a better effort for this cell\r\n if cost > self.effort[x][y]:\r\n continue\r\n\r\n # Stop if we\'ve reached the bottom-right cell\r\n if x == rows - 1 and y == cols - 1:\r\n return cost\r\n\r\n # Explore each direction (up, down, left, right)\r\n for i in range(4):\r\n new_x = x + self.dx[i]\r\n new_y = y + self.dy[i]\r\n\r\n # Check if the new coordinates are within bounds\r\n if not (0 <= new_x < rows and 0 <= new_y < cols):\r\n continue\r\n\r\n # Calculate new effort for the neighboring cell\r\n new_effort = max(self.effort[x][y], abs(heights[x][y] - heights[new_x][new_y]))\r\n\r\n # Update effort if a lower effort is found for the neighboring cell\r\n if new_effort < self.effort[new_x][new_y]:\r\n self.effort[new_x][new_y] = new_effort\r\n heapq.heappush(pq, (new_effort, new_x, new_y))\r\n\r\n return self.effort[rows - 1][cols - 1] # Minimum effort for the path to the bottom-right cell\r\n\r\n def minimumEffortPath(self, heights) -> int:\r\n rows = len(heights)\r\n cols = len(heights[0])\r\n\r\n # Initialize effort for each cell to maximum value\r\n for i in range(rows):\r\n for j in range(cols):\r\n self.effort[i][j] = float(\'inf\')\r\n\r\n return self.dijkstra(heights) # Find minimum effort using dijkstra\r\n```\r\n\r\n## Binary Search\r\n```C++ []\r\nclass Solution {\r\nprivate:\r\n bool visited[105][105]; // Visited cells tracker\r\n int directions_x[4] = {0, 1, -1, 0}; // Changes in x coordinate for four directions\r\n int directions_y[4] = {1, 0, 0, -1}; // Changes in y coordinate for four directions\r\n int numRows, numCols; // Number of rows and columns in the matrix\r\n\r\npublic:\r\n\r\n // Depth-First Search to explore the path with a given limit effort\r\n void dfs(int x, int y, int limitEffort, vector<vector<int>>& heights){\r\n if (visited[x][y])\r\n return;\r\n visited[x][y] = true;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == numRows - 1 && y == numCols - 1)\r\n return ;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + directions_x[i];\r\n int new_y = y + directions_y[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= numRows || new_y < 0 || new_y >= numCols)\r\n continue;\r\n \r\n // Go to next cell if the effort is within limit\r\n int newEffort = abs(heights[x][y] - heights[new_x][new_y]);\r\n if (newEffort <= limitEffort)\r\n dfs(new_x, new_y, limitEffort, heights);\r\n }\r\n }\r\n\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n numRows = heights.size(); \r\n numCols = heights[0].size();\r\n\r\n // Bound for our binary search\r\n int lowerLimit = 0, upperLimit = 1e6;\r\n\r\n while (lowerLimit < upperLimit) {\r\n int mid = (upperLimit + lowerLimit) / 2;\r\n memset(visited, 0, sizeof visited);\r\n dfs(0, 0, mid, heights);\r\n\r\n if (visited[numRows - 1][numCols - 1])\r\n upperLimit = mid;\r\n else\r\n lowerLimit = mid + 1;\r\n }\r\n\r\n return lowerLimit;\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n private boolean[][] visited; // Visited cells tracker\r\n private int[] directions_x = {0, 1, -1, 0}; // Changes in x coordinate for four directions\r\n private int[] directions_y = {1, 0, 0, -1}; // Changes in y coordinate for four directions\r\n private int numRows, numCols; // Number of rows and columns in the matrix\r\n\r\n // Depth-First Search to explore the path with a given limit effort\r\n private void dfs(int x, int y, int limitEffort, int[][] heights) {\r\n if (visited[x][y])\r\n return;\r\n visited[x][y] = true;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == numRows - 1 && y == numCols - 1)\r\n return;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + directions_x[i];\r\n int new_y = y + directions_y[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= numRows || new_y < 0 || new_y >= numCols)\r\n continue;\r\n\r\n // Go to next cell if the effort is within limit\r\n int newEffort = Math.abs(heights[x][y] - heights[new_x][new_y]);\r\n if (newEffort <= limitEffort)\r\n dfs(new_x, new_y, limitEffort, heights);\r\n }\r\n }\r\n\r\n public int minimumEffortPath(int[][] heights) {\r\n numRows = heights.length;\r\n numCols = heights[0].length;\r\n\r\n // Initialize visited array\r\n visited = new boolean[numRows][numCols];\r\n\r\n // Bound for our binary search\r\n int lowerLimit = 0, upperLimit = 1_000_000;\r\n\r\n while (lowerLimit < upperLimit) {\r\n int mid = (upperLimit + lowerLimit) / 2;\r\n for (boolean[] row : visited) {\r\n Arrays.fill(row, false);\r\n }\r\n\r\n dfs(0, 0, mid, heights);\r\n\r\n if (visited[numRows - 1][numCols - 1])\r\n upperLimit = mid;\r\n else\r\n lowerLimit = mid + 1;\r\n }\r\n\r\n return lowerLimit;\r\n }\r\n}\r\n```\r\n```Python []\r\nclass Solution:\r\n def __init__(self):\r\n self.visited = [] # Visited cells tracker\r\n self.directions_x = [0, 1, -1, 0] # Changes in x coordinate for four directions\r\n self.directions_y = [1, 0, 0, -1] # Changes in y coordinate for four directions\r\n self.numRows = 0\r\n self.numCols = 0\r\n\r\n # Depth-First Search to explore the path with a given maximum effort\r\n def dfs(self, x, y, limit_effort, heights) -> None:\r\n if self.visited[x][y]:\r\n return\r\n self.visited[x][y] = True\r\n\r\n # Stop if we\'ve reached the bottom-right cell\r\n if x == self.numRows - 1 and y == self.numCols - 1:\r\n return\r\n\r\n # Explore each direction (up, down, left, right)\r\n for i in range(4):\r\n new_x = x + self.directions_x[i]\r\n new_y = y + self.directions_y[i]\r\n\r\n # Check if the new coordinates are within bounds\r\n if new_x < 0 or new_x >= self.numRows or new_y < 0 or new_y >= self.numCols:\r\n continue\r\n\r\n # Go to next cell if the effort is within maximum\r\n new_effort = abs(heights[x][y] - heights[new_x][new_y])\r\n if new_effort <= limit_effort:\r\n self.dfs(new_x, new_y, limit_effort, heights)\r\n\r\n def minimumEffortPath(self, heights) -> int:\r\n self.numRows = len(heights)\r\n self.numCols = len(heights[0])\r\n\r\n # Initialize visited array\r\n self.visited = [[False for _ in range(self.numCols)] for _ in range(self.numRows)]\r\n\r\n # Bound for our binary search\r\n lower_limit, upper_limit = 0, 1000000\r\n\r\n while lower_limit < upper_limit:\r\n mid = (upper_limit + lower_limit) // 2\r\n\r\n # Reset visited array\r\n self.visited = [[False for _ in range(self.numCols)] for _ in range(self.numRows)]\r\n\r\n self.dfs(0, 0, mid, heights)\r\n\r\n if self.visited[self.numRows - 1][self.numCols - 1]:\r\n upper_limit = mid\r\n else:\r\n lower_limit = mid + 1\r\n\r\n return lower_limit\r\n```\r\n\r\n\r\n\r\n\r\n | 59 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
🚀 99.92% || Dijkstra's Algorithm || Binary Search || Commented Code 🚀 | path-with-minimum-effort | 1 | 1 | # Problem Description\r\nYou are a hiker preparing for an upcoming hike and need to plan your route efficiently. Given a 2D array of heights representing the elevation of each cell, your objective is to find the path from the **top-left** cell to the **bottom-right** cell with the **minimum** effort for the whole path.\r\nThe **effort** of a route is defined as the **maximum** absolute difference in heights between **two consecutive** cells along the path. Your goal is to determine the **minimum** effort needed to traverse from the **starting** point to the **destination** in this manner.\r\n\r\n- Constraints:\r\n - `rows == heights.length`\r\n - `columns == heights[i].length`\r\n - `1 <= rows, columns <= 100`\r\n - `1 <= heights[i][j] <= 10e6`\r\n \r\n\r\n---\r\n\r\n\r\n\r\n# Intuition\r\nHello There\uD83D\uDE00\r\nLet\'s take a look on our interesting problem\uD83D\uDE80\r\nOur problem says that we have matrix `M * N` of cells and each cell has some value of **height**.\r\nour goal is to find the path that has **minimum** effort for the `top-left` cell to the `bottom-right` cell.\r\n- Let\'s focus on **two important** things:\r\n - We want to find a **path** between two cells.\r\n - We want to **minimize** some obejective.\r\n\r\n## Dijkstra\'s Algorithm\r\nIt looks something that **Dijkstra\'s Algorithm** can solve !\r\n\r\nBut what is **DIJKSTRA** ?!!\r\nDijkstra\'s Algorithm is an algorithm to find the **shortest** path between two nodes in a **graph** or two cells in a **matrix** like our problem. \r\nIt\'s part of a **family** of algorithms designed to uncover the shortest path between nodes or cells **like** BFS, Bellman-Ford Algorithm, Floyd-Warsahll Algorithm. Each algorithm has its **unique** applications.\r\n- Let\'s focus on Dijkstra\'s Algorithm:\r\n - **Nature:** It\'s a single-source, multiple-destination algorithm. In simpler terms, it pinpoints the shortest path from a starting node to any other node in our graph.\r\n - **Constraints:** Dijkstra\'s Algorithm is suitable for graphs or problems featuring positive weights. If we encounter negative weights, we\'d choose alternative algorithms such as Bellman-Ford.\r\n \r\nAnd there you have it! Dijkstra\'s Algorithm is the **key** to our problem, well-known for tackling precisely these types of challenges.\r\n\r\n\r\n## Binary Search\r\nAnother **interesting** approach to solve this problem is to use **binary search**. But how? What if we shift our **perspective** a bit?\r\n\r\nI put it in this post because I found it a **unique** solution to a problem that we can solve using Dijkstra\'s Algorithm. \r\n\r\nInstead of focusing solely on finding the **shortest** path between the starting and ending cells, let\'s consider **traversing** the entire matrix. We can approach this much like a **DFS** (Depth-First Search) like any other simple problem.\r\n\r\n**Picture** this: As we navigate through the matrix using **DFS**, we\'re mindful of this **effort limit**. The goal? To reach the end cell while ensuring that our **maximum** effort remains below this specified **limit**.\r\n\r\nNow, here comes the interesting part\u2014let\'s integrate **binary search** into this. We\'ll perform a binary search around this **limit effort** in our DFS traversal. By doing so, we can effectively hone in on the optimal effort threshold that guarantees our success in reaching the end cell. If we achieve this within the defined effort threshold, it indicates a **possibility** to reach the goal cell with an even **lower** effort.\r\n\r\nIn essence, this creative approach combines the power of binary search with **DFS**, enriching our problem-solving repertoire.\r\n\r\n---\r\n\r\n\r\n# Proposed Approaches\r\n## Dijkstra\'s Algorithm\r\n### Steps\r\n- Create a 2D `effort` array and define **directional** **changes** using `dx` and `dy`.\r\n- Initialize cell `efforts` to **maximum** value.\r\n- Call **dijkstra** to find the **minimum** effort.\r\n- Initialize a `priority` queue to store (-effort, {x, y}) to make it return the **minimum** element.\r\n- Push the `top-left` cell into the queue with `initial` effort as `0`.\r\n- While the priority queue is **not empty**:\r\n - **Pop** the cell with the **least** effort.\r\n - If cost is **greater** than existing effort, **skip**.\r\n - If at **bottom-right** cell, **return minimum** effort.\r\n - **Explore** four directions, update efforts, and push to queue if lower effort found.\r\n- **Return** the minimum effort from top-left to bottom-right cell.\r\n\r\n### Complexity\r\n- **Time complexity:**$$O(M * N * log(M * N))$$\r\nThe time complexity for Dijkstra\'s Algorithm is `O(E * log(E))`, where `E` is the number of edges in the graph. In our case, we can consider the number of edges are `M * N`.\r\n- **Space complexity:**$$O(M * N)$$\r\nSince we are storing the minimum effort for the path from the starting point to each cell, then the space complexity is `O(M * N)`.\r\n\r\n---\r\n## Binary Search\r\n### Steps\r\n- **Create** a 2D array `visited` to track visited cells and define **directional changes** using `dx` and `dy`.\r\n- Set the **lower** and **upper** limits for `binary search`.\r\n- Perform `binary search` to find the minimum effort needed:\r\n - Use `DFS` to traverse the matrix within the effort **limits**.\r\n - **Update** the search **range** accordingly based on `DFS` results.\r\n- `Depth-First Search` (DFS) Function:\r\n - Mark the current cell as **visited**.\r\n - **Stop** if the bottom-right cell is reached.\r\n - **Explore** each direction (up, down, left, right):\r\n - Check if the new coordinates are within **bounds**.\r\n - Move to the next cell if the effort is within the specified **limit**.\r\n- Return **minimum** effort\r\n\r\n### Complexity\r\n- **Time complexity:**$$O(M * N * log(10^6))$$\r\nThe time complexity for **Binary Search** is `log(upper_bound - lower_bound)` and in our case the maximum range in `10^6`. and since we are doing **DFS** in each iteration knowing that the time complexity for the single **DFS** is O(N * M) then the total time complexity is `O(M * N * log(10^6))`.\r\n- **Space complexity:**$$O(M * N)$$\r\nSince we are storing the visited array for each cell and the **DFS** recursion stack complexity is also `O(M * N)`, then the space complexity is `O(M * N)`.\r\n\r\n\r\n---\r\n\r\n\r\n# Code\r\n## Dijkstra\'s Algorithm\r\n```C++ []\r\nclass Solution {\r\nprivate:\r\n int effort[105][105]; // Store effort for each cell\r\n int dx[4] = {0, 1, -1, 0}; // Changes in x coordinate for each direction\r\n int dy[4] = {1, 0, 0, -1}; // Changes in y coordinate for each direction\r\n\r\npublic:\r\n // Dijkstra\'s Algorithm to find minimum effort\r\n int dijkstra(vector<vector<int>>& heights) {\r\n int rows = heights.size();\r\n int cols = heights[0].size();\r\n\r\n // Priority queue to store {effort, {x, y}}\r\n std::priority_queue<std::pair<int, std::pair<int, int>>> pq;\r\n pq.push({0, {0, 0}}); // Start from the top-left cell\r\n effort[0][0] = 0; // Initial effort at the starting cell\r\n\r\n while (!pq.empty()) {\r\n auto current = pq.top().second;\r\n int cost = -pq.top().first; // Effort for the current cell\r\n pq.pop();\r\n\r\n int x = current.first;\r\n int y = current.second;\r\n\r\n // Skip if we\'ve already found a better effort for this cell\r\n if (cost > effort[x][y])\r\n continue;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == rows - 1 && y == cols - 1)\r\n return cost;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + dx[i];\r\n int new_y = y + dy[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= rows || new_y < 0 || new_y >= cols)\r\n continue;\r\n\r\n // Calculate new effort for the neighboring cell\r\n int new_effort = std::max(effort[x][y], std::abs(heights[x][y] - heights[new_x][new_y]));\r\n\r\n // Update effort if a lower effort is found for the neighboring cell\r\n if (new_effort < effort[new_x][new_y]) {\r\n effort[new_x][new_y] = new_effort;\r\n pq.push({-new_effort, {new_x, new_y}});\r\n }\r\n }\r\n }\r\n return effort[rows - 1][cols - 1]; // Minimum effort for the path to the bottom-right cell\r\n }\r\n\r\n // Function to find the minimum effort path\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n // Initialize effort for each cell to maximum value\r\n for (int i = 0; i < heights.size(); i++) {\r\n for (int j = 0; j < heights[i].size(); j++) {\r\n effort[i][j] = INT_MAX;\r\n }\r\n }\r\n return dijkstra(heights); // Find minimum effort using dijkstra\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n private int[][] effort = new int[105][105]; // Store effort for each cell\r\n private int[] dx = {0, 1, -1, 0}; // Changes in x coordinate for each direction\r\n private int[] dy = {1, 0, 0, -1}; // Changes in y coordinate for each direction\r\n\r\n // Dijkstra\'s Algorithm to find minimum effort\r\n private int dijkstra(int[][] heights) {\r\n int rows = heights.length;\r\n int cols = heights[0].length;\r\n\r\n // Priority queue to store {effort, {x, y}}\r\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(-a[0], -b[0]));\r\n pq.add(new int[]{0, 0, 0}); // Start from the top-left cell\r\n effort[0][0] = 0; // Initial effort at the starting cell\r\n\r\n while (!pq.isEmpty()) {\r\n int[] current = pq.poll();\r\n int cost = -current[0]; // Effort for the current cell\r\n\r\n int x = current[1];\r\n int y = current[2];\r\n\r\n // Skip if we\'ve already found a better effort for this cell\r\n if (cost > effort[x][y])\r\n continue;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == rows - 1 && y == cols - 1)\r\n return cost;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + dx[i];\r\n int new_y = y + dy[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= rows || new_y < 0 || new_y >= cols)\r\n continue;\r\n\r\n // Calculate new effort for the neighboring cell\r\n int new_effort = Math.max(effort[x][y], Math.abs(heights[x][y] - heights[new_x][new_y]));\r\n\r\n // Update effort if a lower effort is found for the neighboring cell\r\n if (new_effort < effort[new_x][new_y]) {\r\n effort[new_x][new_y] = new_effort;\r\n pq.add(new int[]{-new_effort, new_x, new_y});\r\n }\r\n }\r\n }\r\n return effort[rows - 1][cols - 1]; // Minimum effort for the path to the bottom-right cell\r\n }\r\n\r\n // Function to find the minimum effort path\r\n public int minimumEffortPath(int[][] heights) {\r\n int rows = heights.length;\r\n int cols = heights[0].length;\r\n\r\n // Initialize effort for each cell to maximum value\r\n for (int i = 0; i < rows; i++) {\r\n Arrays.fill(effort[i], Integer.MAX_VALUE);\r\n }\r\n\r\n return dijkstra(heights); // Find minimum effort using dijkstra\r\n }\r\n}\r\n```\r\n```Python []\r\nclass Solution:\r\n def __init__(self):\r\n self.effort = [[float(\'inf\')] * 105 for _ in range(105)]\r\n self.dx = [0, 1, -1, 0]\r\n self.dy = [1, 0, 0, -1]\r\n\r\n def dijkstra(self, heights) -> int:\r\n rows = len(heights)\r\n cols = len(heights[0])\r\n\r\n pq = [(0, 0, 0)] # Priority queue to store (-effort, x, y)\r\n self.effort[0][0] = 0 # Initial effort at the starting cell\r\n\r\n while pq:\r\n cost, x, y = heapq.heappop(pq)\r\n\r\n # Skip if we\'ve already found a better effort for this cell\r\n if cost > self.effort[x][y]:\r\n continue\r\n\r\n # Stop if we\'ve reached the bottom-right cell\r\n if x == rows - 1 and y == cols - 1:\r\n return cost\r\n\r\n # Explore each direction (up, down, left, right)\r\n for i in range(4):\r\n new_x = x + self.dx[i]\r\n new_y = y + self.dy[i]\r\n\r\n # Check if the new coordinates are within bounds\r\n if not (0 <= new_x < rows and 0 <= new_y < cols):\r\n continue\r\n\r\n # Calculate new effort for the neighboring cell\r\n new_effort = max(self.effort[x][y], abs(heights[x][y] - heights[new_x][new_y]))\r\n\r\n # Update effort if a lower effort is found for the neighboring cell\r\n if new_effort < self.effort[new_x][new_y]:\r\n self.effort[new_x][new_y] = new_effort\r\n heapq.heappush(pq, (new_effort, new_x, new_y))\r\n\r\n return self.effort[rows - 1][cols - 1] # Minimum effort for the path to the bottom-right cell\r\n\r\n def minimumEffortPath(self, heights) -> int:\r\n rows = len(heights)\r\n cols = len(heights[0])\r\n\r\n # Initialize effort for each cell to maximum value\r\n for i in range(rows):\r\n for j in range(cols):\r\n self.effort[i][j] = float(\'inf\')\r\n\r\n return self.dijkstra(heights) # Find minimum effort using dijkstra\r\n```\r\n\r\n## Binary Search\r\n```C++ []\r\nclass Solution {\r\nprivate:\r\n bool visited[105][105]; // Visited cells tracker\r\n int directions_x[4] = {0, 1, -1, 0}; // Changes in x coordinate for four directions\r\n int directions_y[4] = {1, 0, 0, -1}; // Changes in y coordinate for four directions\r\n int numRows, numCols; // Number of rows and columns in the matrix\r\n\r\npublic:\r\n\r\n // Depth-First Search to explore the path with a given limit effort\r\n void dfs(int x, int y, int limitEffort, vector<vector<int>>& heights){\r\n if (visited[x][y])\r\n return;\r\n visited[x][y] = true;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == numRows - 1 && y == numCols - 1)\r\n return ;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + directions_x[i];\r\n int new_y = y + directions_y[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= numRows || new_y < 0 || new_y >= numCols)\r\n continue;\r\n \r\n // Go to next cell if the effort is within limit\r\n int newEffort = abs(heights[x][y] - heights[new_x][new_y]);\r\n if (newEffort <= limitEffort)\r\n dfs(new_x, new_y, limitEffort, heights);\r\n }\r\n }\r\n\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n numRows = heights.size(); \r\n numCols = heights[0].size();\r\n\r\n // Bound for our binary search\r\n int lowerLimit = 0, upperLimit = 1e6;\r\n\r\n while (lowerLimit < upperLimit) {\r\n int mid = (upperLimit + lowerLimit) / 2;\r\n memset(visited, 0, sizeof visited);\r\n dfs(0, 0, mid, heights);\r\n\r\n if (visited[numRows - 1][numCols - 1])\r\n upperLimit = mid;\r\n else\r\n lowerLimit = mid + 1;\r\n }\r\n\r\n return lowerLimit;\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n private boolean[][] visited; // Visited cells tracker\r\n private int[] directions_x = {0, 1, -1, 0}; // Changes in x coordinate for four directions\r\n private int[] directions_y = {1, 0, 0, -1}; // Changes in y coordinate for four directions\r\n private int numRows, numCols; // Number of rows and columns in the matrix\r\n\r\n // Depth-First Search to explore the path with a given limit effort\r\n private void dfs(int x, int y, int limitEffort, int[][] heights) {\r\n if (visited[x][y])\r\n return;\r\n visited[x][y] = true;\r\n\r\n // Stop if we\'ve reached the bottom-right cell\r\n if (x == numRows - 1 && y == numCols - 1)\r\n return;\r\n\r\n // Explore each direction (up, down, left, right)\r\n for (int i = 0; i < 4; i++) {\r\n int new_x = x + directions_x[i];\r\n int new_y = y + directions_y[i];\r\n\r\n // Check if the new coordinates are within bounds\r\n if (new_x < 0 || new_x >= numRows || new_y < 0 || new_y >= numCols)\r\n continue;\r\n\r\n // Go to next cell if the effort is within limit\r\n int newEffort = Math.abs(heights[x][y] - heights[new_x][new_y]);\r\n if (newEffort <= limitEffort)\r\n dfs(new_x, new_y, limitEffort, heights);\r\n }\r\n }\r\n\r\n public int minimumEffortPath(int[][] heights) {\r\n numRows = heights.length;\r\n numCols = heights[0].length;\r\n\r\n // Initialize visited array\r\n visited = new boolean[numRows][numCols];\r\n\r\n // Bound for our binary search\r\n int lowerLimit = 0, upperLimit = 1_000_000;\r\n\r\n while (lowerLimit < upperLimit) {\r\n int mid = (upperLimit + lowerLimit) / 2;\r\n for (boolean[] row : visited) {\r\n Arrays.fill(row, false);\r\n }\r\n\r\n dfs(0, 0, mid, heights);\r\n\r\n if (visited[numRows - 1][numCols - 1])\r\n upperLimit = mid;\r\n else\r\n lowerLimit = mid + 1;\r\n }\r\n\r\n return lowerLimit;\r\n }\r\n}\r\n```\r\n```Python []\r\nclass Solution:\r\n def __init__(self):\r\n self.visited = [] # Visited cells tracker\r\n self.directions_x = [0, 1, -1, 0] # Changes in x coordinate for four directions\r\n self.directions_y = [1, 0, 0, -1] # Changes in y coordinate for four directions\r\n self.numRows = 0\r\n self.numCols = 0\r\n\r\n # Depth-First Search to explore the path with a given maximum effort\r\n def dfs(self, x, y, limit_effort, heights) -> None:\r\n if self.visited[x][y]:\r\n return\r\n self.visited[x][y] = True\r\n\r\n # Stop if we\'ve reached the bottom-right cell\r\n if x == self.numRows - 1 and y == self.numCols - 1:\r\n return\r\n\r\n # Explore each direction (up, down, left, right)\r\n for i in range(4):\r\n new_x = x + self.directions_x[i]\r\n new_y = y + self.directions_y[i]\r\n\r\n # Check if the new coordinates are within bounds\r\n if new_x < 0 or new_x >= self.numRows or new_y < 0 or new_y >= self.numCols:\r\n continue\r\n\r\n # Go to next cell if the effort is within maximum\r\n new_effort = abs(heights[x][y] - heights[new_x][new_y])\r\n if new_effort <= limit_effort:\r\n self.dfs(new_x, new_y, limit_effort, heights)\r\n\r\n def minimumEffortPath(self, heights) -> int:\r\n self.numRows = len(heights)\r\n self.numCols = len(heights[0])\r\n\r\n # Initialize visited array\r\n self.visited = [[False for _ in range(self.numCols)] for _ in range(self.numRows)]\r\n\r\n # Bound for our binary search\r\n lower_limit, upper_limit = 0, 1000000\r\n\r\n while lower_limit < upper_limit:\r\n mid = (upper_limit + lower_limit) // 2\r\n\r\n # Reset visited array\r\n self.visited = [[False for _ in range(self.numCols)] for _ in range(self.numRows)]\r\n\r\n self.dfs(0, 0, mid, heights)\r\n\r\n if self.visited[self.numRows - 1][self.numCols - 1]:\r\n upper_limit = mid\r\n else:\r\n lower_limit = mid + 1\r\n\r\n return lower_limit\r\n```\r\n\r\n\r\n\r\n\r\n | 59 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Thought Process from Naive BFS to Dijkstra | path-with-minimum-effort | 0 | 1 | **TLDR**: Naive BFS doesn\'t work because you only visit the node once, and therefore you **only consider one of many paths.** Secondly, a naive BFS will give you the path with minimal nodes visited and doesn\'t care about the `effort`. In this problem, though, we can clearly see that `optimal path != path with minimal length` (look at **Example 3**), which naive BFS is unable to differentiate.\n\n# Thought Process\n\nWhen a question asks about something related to shortest path, always consider how BFS can help because that\'s what BFS does. However after a few minutes of thinking, I quickly realize that a simple naive BFS would not work.\n\nBefore going further, here is the pseudocode of naive BFS:\n```\nqueue = []\nvisited = set()\nwhile queue:\n\tme = queue.popleft()\n\tfor every neighbor of me:\n\t\tif neighbor not in visited:\n\t\t\tvisited.add(neighbor)\n\t\t\tqueue.append(neighbor)\n```\nConsider the **Example 1**. If you loop the neighbors in the following order: **right,left,bottom,up** then you would find the below path before other possible paths\n\n\nThat\'s great. Although it is not the optimal path, at least you found a path to the destination and you know the `effort` here is 3. Now, you can look for other better paths right? Unfortunately, in naive BFS, you only visit a node exactly once. This means that unless you reset the `visited` set, you can\'t find other way to the destination. Remember, by now, the destination itself is already marked as visited right? So you will not visit it again.\n\nInterestingly, if you loop your neighbors in the following order: **bottom,right,left,up**, then you will find optimal path.\n\n\nSo the order of iterating the neighbor clearly matters. But wait a minute! that\'s no longer the scope of BFS!\n\n> In BFS, the order of looping the neighbors should never affect the answer. BFS should find the shortest path regardless of how you iterate your neighbors. \n\nIt is true our BFS has found the path with minimal length (i.e. both of the above paths visit 4 nodes). However, our BFS cannot differentiate the `effort` of the two paths above. In fact, once you introduce any notion of weight to the graph, BFS will fail since BFS doesn\'t really care about weight. And so, naive BFS would not work for this problem. We need to modify our stupid BFS.\n\nFortunately, we\'re close. At this point, I know that the logic for visiting a node is messed up; I cannot just visit a node once and call it a day, I need to visit it more than once. Where in the code that is responsible of whether or not I should visit a node?\n\nThat\'s right. It\'s this dude:\n```\nif neighbor not in visited:\n\t# visit neighbor\n```\nSo we need to change the logic and how we store the BFS\'s visited state. How? Well, ask this question.\n\n> When would I ever bother to visit a node for the second time?\n\nThe answer is \n\n> when we found a better path (i.e. lower cost)\n\nAnd this answer should be sufficient to give me a hint that instead of a visited set, we need to store **a cost in dictionary**. Hence, the modified BFS should look like the following (pseudocode):\n```python\nqueue = []\ncost = {} # dictionary, instead of a set\nwhile queue:\n\tme = queue.popleft()\n\tfor every neighbor of me:\n\t\tnew_cost = compute_cost()\n\t\tif new_cost < cost[neighbor]: # better path!\n\t\t\tcost[neighbor] = new_cost\n\t\t\tqueue.append(neighbor)\n```\n\n**And this modified BFS is actually what Dijkstra does :)**.\n\n## Solution\nFor reference, this is just one way of implementing the Dijkstra\'s algorithm (no priority queue).\n\n```python\nfrom collections import deque\n\nclass Solution:\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\n H = len(heights)\n W = len(heights[0])\n\n queue = deque([])\n queue.append((0, 0))\n\n cost = { (row, col): float(\'inf\') for col in range(W) for row in range(H) }\n cost[(0, 0)] = 0\n\n directions = [[1,0], [0,1], [-1,0], [0,-1]]\n \n def inside(row, col):\n return 0 <= row < H and 0 <= col < W\n \n while queue:\n row, col = queue.popleft()\n current_height = heights[row][col]\n current_cost = cost[(row, col)]\n\n for d_row, d_col in directions:\n new_row = row + d_row\n new_col = col + d_col\n\n if inside(new_row, new_col):\n neighbor_height = heights[new_row][new_col]\n new_cost = max(current_cost, abs(neighbor_height - current_height))\n if new_cost < cost[(new_row, new_col)]:\n cost[(new_row, new_col)] = new_cost\n queue.append((new_row, new_col))\n \n return cost[(H - 1, W - 1)]\n```\n\n# Analysis\nRight now we have working answer. But it is `O(V^2)`. Where `V` is the number of nodes (H * W). We could optimize the Dijkstra\'s algorithm with minimizing heap (or priority queue, if you will) instead of a simple queue. That will bring the complexity down to `O(ElgV)`. I\'m sure every other posts would have already had this solution.\n | 285 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
Thought Process from Naive BFS to Dijkstra | path-with-minimum-effort | 0 | 1 | **TLDR**: Naive BFS doesn\'t work because you only visit the node once, and therefore you **only consider one of many paths.** Secondly, a naive BFS will give you the path with minimal nodes visited and doesn\'t care about the `effort`. In this problem, though, we can clearly see that `optimal path != path with minimal length` (look at **Example 3**), which naive BFS is unable to differentiate.\n\n# Thought Process\n\nWhen a question asks about something related to shortest path, always consider how BFS can help because that\'s what BFS does. However after a few minutes of thinking, I quickly realize that a simple naive BFS would not work.\n\nBefore going further, here is the pseudocode of naive BFS:\n```\nqueue = []\nvisited = set()\nwhile queue:\n\tme = queue.popleft()\n\tfor every neighbor of me:\n\t\tif neighbor not in visited:\n\t\t\tvisited.add(neighbor)\n\t\t\tqueue.append(neighbor)\n```\nConsider the **Example 1**. If you loop the neighbors in the following order: **right,left,bottom,up** then you would find the below path before other possible paths\n\n\nThat\'s great. Although it is not the optimal path, at least you found a path to the destination and you know the `effort` here is 3. Now, you can look for other better paths right? Unfortunately, in naive BFS, you only visit a node exactly once. This means that unless you reset the `visited` set, you can\'t find other way to the destination. Remember, by now, the destination itself is already marked as visited right? So you will not visit it again.\n\nInterestingly, if you loop your neighbors in the following order: **bottom,right,left,up**, then you will find optimal path.\n\n\nSo the order of iterating the neighbor clearly matters. But wait a minute! that\'s no longer the scope of BFS!\n\n> In BFS, the order of looping the neighbors should never affect the answer. BFS should find the shortest path regardless of how you iterate your neighbors. \n\nIt is true our BFS has found the path with minimal length (i.e. both of the above paths visit 4 nodes). However, our BFS cannot differentiate the `effort` of the two paths above. In fact, once you introduce any notion of weight to the graph, BFS will fail since BFS doesn\'t really care about weight. And so, naive BFS would not work for this problem. We need to modify our stupid BFS.\n\nFortunately, we\'re close. At this point, I know that the logic for visiting a node is messed up; I cannot just visit a node once and call it a day, I need to visit it more than once. Where in the code that is responsible of whether or not I should visit a node?\n\nThat\'s right. It\'s this dude:\n```\nif neighbor not in visited:\n\t# visit neighbor\n```\nSo we need to change the logic and how we store the BFS\'s visited state. How? Well, ask this question.\n\n> When would I ever bother to visit a node for the second time?\n\nThe answer is \n\n> when we found a better path (i.e. lower cost)\n\nAnd this answer should be sufficient to give me a hint that instead of a visited set, we need to store **a cost in dictionary**. Hence, the modified BFS should look like the following (pseudocode):\n```python\nqueue = []\ncost = {} # dictionary, instead of a set\nwhile queue:\n\tme = queue.popleft()\n\tfor every neighbor of me:\n\t\tnew_cost = compute_cost()\n\t\tif new_cost < cost[neighbor]: # better path!\n\t\t\tcost[neighbor] = new_cost\n\t\t\tqueue.append(neighbor)\n```\n\n**And this modified BFS is actually what Dijkstra does :)**.\n\n## Solution\nFor reference, this is just one way of implementing the Dijkstra\'s algorithm (no priority queue).\n\n```python\nfrom collections import deque\n\nclass Solution:\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\n H = len(heights)\n W = len(heights[0])\n\n queue = deque([])\n queue.append((0, 0))\n\n cost = { (row, col): float(\'inf\') for col in range(W) for row in range(H) }\n cost[(0, 0)] = 0\n\n directions = [[1,0], [0,1], [-1,0], [0,-1]]\n \n def inside(row, col):\n return 0 <= row < H and 0 <= col < W\n \n while queue:\n row, col = queue.popleft()\n current_height = heights[row][col]\n current_cost = cost[(row, col)]\n\n for d_row, d_col in directions:\n new_row = row + d_row\n new_col = col + d_col\n\n if inside(new_row, new_col):\n neighbor_height = heights[new_row][new_col]\n new_cost = max(current_cost, abs(neighbor_height - current_height))\n if new_cost < cost[(new_row, new_col)]:\n cost[(new_row, new_col)] = new_cost\n queue.append((new_row, new_col))\n \n return cost[(H - 1, W - 1)]\n```\n\n# Analysis\nRight now we have working answer. But it is `O(V^2)`. Where `V` is the number of nodes (H * W). We could optimize the Dijkstra\'s algorithm with minimizing heap (or priority queue, if you will) instead of a simple queue. That will bring the complexity down to `O(ElgV)`. I\'m sure every other posts would have already had this solution.\n | 285 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
12 Line Python | path-with-minimum-effort | 0 | 1 | ```python\nclass Solution:\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\n d = [[float(\'inf\')] * len(heights[0]) for _ in range(len(heights))]\n d[0][0] = 0\n q = [(0, 0, 0)]\n while q:\n e, x, y = heappop(q)\n if (x, y) == (len(heights) - 1, len(heights[0]) - 1): return e\n for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n if 0 <= x+dx < len(heights) and 0 <= y+dy < len(heights[0]) and max(e, abs(heights[x][y] - heights[x+dx][y+dy])) < d[x+dx][y+dy]:\n d[x+dx][y+dy] = max(e, abs(heights[x][y] - heights[x+dx][y+dy]))\n heappush(q, (d[x+dx][y+dy], x+dx, y+dy))\n``` | 0 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
12 Line Python | path-with-minimum-effort | 0 | 1 | ```python\nclass Solution:\n def minimumEffortPath(self, heights: List[List[int]]) -> int:\n d = [[float(\'inf\')] * len(heights[0]) for _ in range(len(heights))]\n d[0][0] = 0\n q = [(0, 0, 0)]\n while q:\n e, x, y = heappop(q)\n if (x, y) == (len(heights) - 1, len(heights[0]) - 1): return e\n for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n if 0 <= x+dx < len(heights) and 0 <= y+dy < len(heights[0]) and max(e, abs(heights[x][y] - heights[x+dx][y+dy])) < d[x+dx][y+dy]:\n d[x+dx][y+dy] = max(e, abs(heights[x][y] - heights[x+dx][y+dy]))\n heappush(q, (d[x+dx][y+dy], x+dx, y+dy))\n``` | 0 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
✔Graph || Binary Search 📈✨|| Medium-->Easy🏆 || Easy to understand 😎|| #Beginner | path-with-minimum-effort | 1 | 1 | # Intuition\r\n- The problem requires finding the minimum effort path from the top-left corner of a 2D grid to the bottom-right corner. \r\n- The effort of a path is defined as the maximum absolute difference in heights between adjacent cells along the path. We need to minimize this maximum effort.\r\n\r\n# Approach\r\n1. We can use a binary search approach to find the minimum effort required for the path. We initialize the lower bound `l` as 0 and the upper bound `r` as a very large value (1e9 + 2) since the effort cannot exceed this upper limit.\r\n\r\n1. In each iteration of the binary search, we calculate the middle value mid between `l` and `r`.\r\n\r\n1. We use depth-first search (DFS) to check if there exists a path from the top-left corner to the bottom-right corner with a maximum effort not exceeding `mid`. The DFS function ok explores the grid and marks cells as visited if they can be reached with an effort less than or equal to `mid`.\r\n\r\n1. **If the bottom-right corner is marked** as visited after the DFS, it means there is a path with an effort not exceeding mid, so we update the upper bound r to mid.\r\n\r\n1. If the bottom-right corner is not marked as visited after the DFS, it means there is no path with an effort less than` mid`, so we update the lower bound `l` to `mid + 1.`\r\n\r\n1. We repeat the binary search until` l` is less than `r`. Finally, `l` will represent the minimum effort required to reach the destination.\r\n\r\n# Complexity\r\n- Time complexity:\r\n- The binary search runs in O(log(1e9 + 2)) time, which is effectively O(1).\r\n- **The DFS function ok explores each cell at most once, so its time complexity is O(N * M)**, where N is the number of rows and M is the number of columns in the grid.\r\n- **The overall time complexity of the solution is O(log(1e9 + 2) * N * M)**, which simplifies to `O(N * M).`\r\n\r\n- Space complexity:\r\n- **The space complexity is dominated by the vis array, which is O(N * M) since it has the same dimensions as the grid.**\r\n- **The recursive DFS stack may require additional space, but in the worst case, it won\'t exceed O(N * M)** since each cell is visited at most once.\r\n`The overall space complexity of the solution is O(N * M).`\r\n\r\n# PLEASE UPVOTE\u2764\uD83D\uDE0D\r\n\r\n\r\n# Code\r\n```\r\nclass Solution {\r\npublic:\r\n \r\n int vis[105][105]; // Declare a 2D array to mark visited cells.\r\n vector<pair<int,int>>dir={{1,0},{-1,0},{0,-1},{0,1}}; // Define 4 possible directions to move: down, up, left, right.\r\n\r\n // Depth-first search function to explore cells with a maximum difference of \'mid\'.\r\n void ok(int x, int y, int mid, vector<vector<int>>& heights) {\r\n if (!vis[x][y]) { // If the cell has not been visited.\r\n vis[x][y] = 1; // Mark the cell as visited.\r\n int n = heights.size(); // Get the number of rows in the \'heights\' matrix.\r\n int m = heights[0].size(); // Get the number of columns in the \'heights\' matrix.\r\n \r\n // Loop through the four possible directions.\r\n for (int i = 0; i < 4; i++) {\r\n int X = x + dir[i].first; // Calculate the new row coordinate.\r\n int Y = y + dir[i].second; // Calculate the new column coordinate.\r\n \r\n // Check if the new coordinates are out of bounds.\r\n if (X < 0 || X >= n || Y < 0 || Y >= m)\r\n continue; // Skip this direction if out of bounds.\r\n \r\n // Check if the absolute difference between the heights is less than or equal to \'mid\'.\r\n if (abs(heights[x][y] - heights[X][Y]) <= mid)\r\n ok(X, Y, mid, heights); // Recursively explore this direction.\r\n }\r\n }\r\n }\r\n \r\n // Function to find the minimum effort path using binary search.\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n int l = 0; // Initialize the left bound of the binary search.\r\n int r = 1e9 + 2; // Initialize the right bound of the binary search.\r\n int n = heights.size(); // Get the number of rows in the \'heights\' matrix.\r\n int m = heights[0].size(); // Get the number of columns in the \'heights\' matrix.\r\n \r\n while (l < r) { // Perform binary search until the left bound is less than the right bound.\r\n int mid = (l + r) / 2; // Calculate the middle value.\r\n memset(vis, 0, sizeof(vis)); // Initialize the visited array to 0.\r\n ok(0, 0, mid, heights); // Start the depth-first search with \'mid\' as the maximum difference.\r\n \r\n if (vis[n - 1][m - 1] == 1)\r\n r = mid; // If the destination cell is reachable, update the right bound.\r\n else\r\n l = mid + 1; // If the destination cell is not reachable, update the left bound.\r\n }\r\n \r\n return l; // Return the minimum effort required to reach the destination.\r\n }\r\n};\r\n\r\n```\r\n# JAVA\r\n```\r\nclass Solution {\r\n int[][] vis = new int[105][105];\r\n int[][] dir = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};\r\n\r\n void ok(int x, int y, int mid, int[][] heights) {\r\n if (vis[x][y] == 0) {\r\n vis[x][y] = 1;\r\n int n = heights.length;\r\n int m = heights[0].length;\r\n\r\n for (int i = 0; i < 4; i++) {\r\n int X = x + dir[i][0];\r\n int Y = y + dir[i][1];\r\n\r\n if (X < 0 || X >= n || Y < 0 || Y >= m)\r\n continue;\r\n\r\n if (Math.abs(heights[x][y] - heights[X][Y]) <= mid)\r\n ok(X, Y, mid, heights);\r\n }\r\n }\r\n }\r\n\r\n public int minimumEffortPath(int[][] heights) {\r\n int l = 0;\r\n int r = 1000000002;\r\n int n = heights.length;\r\n int m = heights[0].length;\r\n\r\n while (l < r) {\r\n int mid = (l + r) / 2;\r\n vis = new int[105][105];\r\n ok(0, 0, mid, heights);\r\n\r\n if (vis[n - 1][m - 1] == 1)\r\n r = mid;\r\n else\r\n l = mid + 1;\r\n }\r\n\r\n return l;\r\n }\r\n}\r\n\r\n```\r\n# PYTHON\r\n```\r\nclass Solution:\r\n def __init__(self):\r\n self.vis = [[0] * 105 for _ in range(105)]\r\n self.dir = [(1, 0), (-1, 0), (0, -1), (0, 1)]\r\n\r\n def ok(self, x, y, mid, heights):\r\n if not self.vis[x][y]:\r\n self.vis[x][y] = 1\r\n n = len(heights)\r\n m = len(heights[0])\r\n\r\n for i in range(4):\r\n X = x + self.dir[i][0]\r\n Y = y + self.dir[i][1]\r\n\r\n if X < 0 or X >= n or Y < 0 or Y >= m:\r\n continue\r\n\r\n if abs(heights[x][y] - heights[X][Y]) <= mid:\r\n self.ok(X, Y, mid, heights)\r\n\r\n def minimumEffortPath(self, heights):\r\n l = 0\r\n r = 1000000002\r\n n = len(heights)\r\n m = len(heights[0])\r\n\r\n while l < r:\r\n mid = (l + r) // 2\r\n self.vis = [[0] * 105 for _ in range(105)]\r\n self.ok(0, 0, mid, heights)\r\n\r\n if self.vis[n - 1][m - 1] == 1:\r\n r = mid\r\n else:\r\n l = mid + 1\r\n\r\n return l\r\n\r\n```\r\n# JAVASCRIPT\r\n```\r\nclass Solution {\r\n constructor() {\r\n this.vis = new Array(105).fill(null).map(() => new Array(105).fill(0));\r\n this.dir = [[1, 0], [-1, 0], [0, -1], [0, 1]];\r\n }\r\n\r\n ok(x, y, mid, heights) {\r\n if (!this.vis[x][y]) {\r\n this.vis[x][y] = 1;\r\n const n = heights.length;\r\n const m = heights[0].length;\r\n\r\n for (let i = 0; i < 4; i++) {\r\n const X = x + this.dir[i][0];\r\n const Y = y + this.dir[i][1];\r\n\r\n if (X < 0 || X >= n || Y < 0 || Y >= m)\r\n continue;\r\n\r\n if (Math.abs(heights[x][y] - heights[X][Y]) <= mid)\r\n this.ok(X, Y, mid, heights);\r\n }\r\n }\r\n }\r\n\r\n minimumEffortPath(heights) {\r\n let l = 0;\r\n let r = 1000000002;\r\n const n = heights.length;\r\n const m = heights[0].length;\r\n\r\n while (l < r) {\r\n const mid = Math.floor((l + r) / 2);\r\n this.vis = new Array(105).fill(null).map(() => new Array(105).fill(0));\r\n this.ok(0, 0, mid, heights);\r\n\r\n if (this.vis[n - 1][m - 1] === 1)\r\n r = mid;\r\n else\r\n l = mid + 1;\r\n }\r\n\r\n return l;\r\n }\r\n}\r\n\r\n```\r\n# GO\r\n```\r\npackage main\r\n\r\nimport "math"\r\n\r\ntype Solution struct {\r\n\tvis [105][105]int\r\n\tdir [][2]int\r\n}\r\n\r\nfunc (s *Solution) ok(x, y, mid int, heights [][]int) {\r\n\tif s.vis[x][y] == 0 {\r\n\t\ts.vis[x][y] = 1\r\n\t\tn := len(heights)\r\n\t\tm := len(heights[0])\r\n\r\n\t\tdirections := [][2]int{{1, 0}, {-1, 0}, {0, -1}, {0, 1}}\r\n\r\n\t\tfor i := 0; i < 4; i++ {\r\n\t\t\tX := x + directions[i][0]\r\n\t\t\tY := y + directions[i][1]\r\n\r\n\t\t\tif X < 0 || X >= n || Y < 0 || Y >= m {\r\n\t\t\t\tcontinue\r\n\t\t\t}\r\n\r\n\t\t\tif int(math.Abs(float64(heights[x][y]-heights[X][Y]))) <= mid {\r\n\t\t\t\ts.ok(X, Y, mid, heights)\r\n\t\t\t}\r\n\t\t}\r\n\t}\r\n}\r\n\r\nfunc (s *Solution) minimumEffortPath(heights [][]int) int {\r\n\tl := 0\r\n\tr := int(1e9 + 2)\r\n\tn := len(heights)\r\n\tm := len(heights[0])\r\n\r\n\tfor l < r {\r\n\t\tmid := (l + r) / 2\r\n\t\ts.vis = [105][105]int{}\r\n\r\n\t\ts.ok(0, 0, int(mid), heights)\r\n\r\n\t\tif s.vis[n-1][m-1] == 1 {\r\n\t\t\tr = int(mid)\r\n\t\t} else {\r\n\t\t\tl = int(mid) + 1\r\n\t\t}\r\n\t}\r\n\r\n\treturn l\r\n}\r\n\r\nfunc main() {\r\n\t// Create an instance of Solution and call minimumEffortPath here with your input data.\r\n}\r\n\r\n```\r\n# PLEASE UPVOTE\u2764\uD83D\uDE0D | 16 | You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
**Example 1:**
**Input:** heights = \[\[1,2,2\],\[3,8,2\],\[5,3,5\]\]
**Output:** 2
**Explanation:** The route of \[1,3,5,3,5\] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of \[1,2,2,2,5\], where the maximum absolute difference is 3.
**Example 2:**
**Input:** heights = \[\[1,2,3\],\[3,8,4\],\[5,3,5\]\]
**Output:** 1
**Explanation:** The route of \[1,2,3,4,5\] has a maximum absolute difference of 1 in consecutive cells, which is better than route \[1,3,5,3,5\].
**Example 3:**
**Input:** heights = \[\[1,2,1,1,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,2,1,2,1\],\[1,1,1,2,1\]\]
**Output:** 0
**Explanation:** This route does not require any effort.
**Constraints:**
* `rows == heights.length`
* `columns == heights[i].length`
* `1 <= rows, columns <= 100`
* `1 <= heights[i][j] <= 106` | Can we use the accumulative sum to keep track of all the odd-sum sub-arrays ? if the current accu sum is odd, we care only about previous even accu sums and vice versa. |
✔Graph || Binary Search 📈✨|| Medium-->Easy🏆 || Easy to understand 😎|| #Beginner | path-with-minimum-effort | 1 | 1 | # Intuition\r\n- The problem requires finding the minimum effort path from the top-left corner of a 2D grid to the bottom-right corner. \r\n- The effort of a path is defined as the maximum absolute difference in heights between adjacent cells along the path. We need to minimize this maximum effort.\r\n\r\n# Approach\r\n1. We can use a binary search approach to find the minimum effort required for the path. We initialize the lower bound `l` as 0 and the upper bound `r` as a very large value (1e9 + 2) since the effort cannot exceed this upper limit.\r\n\r\n1. In each iteration of the binary search, we calculate the middle value mid between `l` and `r`.\r\n\r\n1. We use depth-first search (DFS) to check if there exists a path from the top-left corner to the bottom-right corner with a maximum effort not exceeding `mid`. The DFS function ok explores the grid and marks cells as visited if they can be reached with an effort less than or equal to `mid`.\r\n\r\n1. **If the bottom-right corner is marked** as visited after the DFS, it means there is a path with an effort not exceeding mid, so we update the upper bound r to mid.\r\n\r\n1. If the bottom-right corner is not marked as visited after the DFS, it means there is no path with an effort less than` mid`, so we update the lower bound `l` to `mid + 1.`\r\n\r\n1. We repeat the binary search until` l` is less than `r`. Finally, `l` will represent the minimum effort required to reach the destination.\r\n\r\n# Complexity\r\n- Time complexity:\r\n- The binary search runs in O(log(1e9 + 2)) time, which is effectively O(1).\r\n- **The DFS function ok explores each cell at most once, so its time complexity is O(N * M)**, where N is the number of rows and M is the number of columns in the grid.\r\n- **The overall time complexity of the solution is O(log(1e9 + 2) * N * M)**, which simplifies to `O(N * M).`\r\n\r\n- Space complexity:\r\n- **The space complexity is dominated by the vis array, which is O(N * M) since it has the same dimensions as the grid.**\r\n- **The recursive DFS stack may require additional space, but in the worst case, it won\'t exceed O(N * M)** since each cell is visited at most once.\r\n`The overall space complexity of the solution is O(N * M).`\r\n\r\n# PLEASE UPVOTE\u2764\uD83D\uDE0D\r\n\r\n\r\n# Code\r\n```\r\nclass Solution {\r\npublic:\r\n \r\n int vis[105][105]; // Declare a 2D array to mark visited cells.\r\n vector<pair<int,int>>dir={{1,0},{-1,0},{0,-1},{0,1}}; // Define 4 possible directions to move: down, up, left, right.\r\n\r\n // Depth-first search function to explore cells with a maximum difference of \'mid\'.\r\n void ok(int x, int y, int mid, vector<vector<int>>& heights) {\r\n if (!vis[x][y]) { // If the cell has not been visited.\r\n vis[x][y] = 1; // Mark the cell as visited.\r\n int n = heights.size(); // Get the number of rows in the \'heights\' matrix.\r\n int m = heights[0].size(); // Get the number of columns in the \'heights\' matrix.\r\n \r\n // Loop through the four possible directions.\r\n for (int i = 0; i < 4; i++) {\r\n int X = x + dir[i].first; // Calculate the new row coordinate.\r\n int Y = y + dir[i].second; // Calculate the new column coordinate.\r\n \r\n // Check if the new coordinates are out of bounds.\r\n if (X < 0 || X >= n || Y < 0 || Y >= m)\r\n continue; // Skip this direction if out of bounds.\r\n \r\n // Check if the absolute difference between the heights is less than or equal to \'mid\'.\r\n if (abs(heights[x][y] - heights[X][Y]) <= mid)\r\n ok(X, Y, mid, heights); // Recursively explore this direction.\r\n }\r\n }\r\n }\r\n \r\n // Function to find the minimum effort path using binary search.\r\n int minimumEffortPath(vector<vector<int>>& heights) {\r\n int l = 0; // Initialize the left bound of the binary search.\r\n int r = 1e9 + 2; // Initialize the right bound of the binary search.\r\n int n = heights.size(); // Get the number of rows in the \'heights\' matrix.\r\n int m = heights[0].size(); // Get the number of columns in the \'heights\' matrix.\r\n \r\n while (l < r) { // Perform binary search until the left bound is less than the right bound.\r\n int mid = (l + r) / 2; // Calculate the middle value.\r\n memset(vis, 0, sizeof(vis)); // Initialize the visited array to 0.\r\n ok(0, 0, mid, heights); // Start the depth-first search with \'mid\' as the maximum difference.\r\n \r\n if (vis[n - 1][m - 1] == 1)\r\n r = mid; // If the destination cell is reachable, update the right bound.\r\n else\r\n l = mid + 1; // If the destination cell is not reachable, update the left bound.\r\n }\r\n \r\n return l; // Return the minimum effort required to reach the destination.\r\n }\r\n};\r\n\r\n```\r\n# JAVA\r\n```\r\nclass Solution {\r\n int[][] vis = new int[105][105];\r\n int[][] dir = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};\r\n\r\n void ok(int x, int y, int mid, int[][] heights) {\r\n if (vis[x][y] == 0) {\r\n vis[x][y] = 1;\r\n int n = heights.length;\r\n int m = heights[0].length;\r\n\r\n for (int i = 0; i < 4; i++) {\r\n int X = x + dir[i][0];\r\n int Y = y + dir[i][1];\r\n\r\n if (X < 0 || X >= n || Y < 0 || Y >= m)\r\n continue;\r\n\r\n if (Math.abs(heights[x][y] - heights[X][Y]) <= mid)\r\n ok(X, Y, mid, heights);\r\n }\r\n }\r\n }\r\n\r\n public int minimumEffortPath(int[][] heights) {\r\n int l = 0;\r\n int r = 1000000002;\r\n int n = heights.length;\r\n int m = heights[0].length;\r\n\r\n while (l < r) {\r\n int mid = (l + r) / 2;\r\n vis = new int[105][105];\r\n ok(0, 0, mid, heights);\r\n\r\n if (vis[n - 1][m - 1] == 1)\r\n r = mid;\r\n else\r\n l = mid + 1;\r\n }\r\n\r\n return l;\r\n }\r\n}\r\n\r\n```\r\n# PYTHON\r\n```\r\nclass Solution:\r\n def __init__(self):\r\n self.vis = [[0] * 105 for _ in range(105)]\r\n self.dir = [(1, 0), (-1, 0), (0, -1), (0, 1)]\r\n\r\n def ok(self, x, y, mid, heights):\r\n if not self.vis[x][y]:\r\n self.vis[x][y] = 1\r\n n = len(heights)\r\n m = len(heights[0])\r\n\r\n for i in range(4):\r\n X = x + self.dir[i][0]\r\n Y = y + self.dir[i][1]\r\n\r\n if X < 0 or X >= n or Y < 0 or Y >= m:\r\n continue\r\n\r\n if abs(heights[x][y] - heights[X][Y]) <= mid:\r\n self.ok(X, Y, mid, heights)\r\n\r\n def minimumEffortPath(self, heights):\r\n l = 0\r\n r = 1000000002\r\n n = len(heights)\r\n m = len(heights[0])\r\n\r\n while l < r:\r\n mid = (l + r) // 2\r\n self.vis = [[0] * 105 for _ in range(105)]\r\n self.ok(0, 0, mid, heights)\r\n\r\n if self.vis[n - 1][m - 1] == 1:\r\n r = mid\r\n else:\r\n l = mid + 1\r\n\r\n return l\r\n\r\n```\r\n# JAVASCRIPT\r\n```\r\nclass Solution {\r\n constructor() {\r\n this.vis = new Array(105).fill(null).map(() => new Array(105).fill(0));\r\n this.dir = [[1, 0], [-1, 0], [0, -1], [0, 1]];\r\n }\r\n\r\n ok(x, y, mid, heights) {\r\n if (!this.vis[x][y]) {\r\n this.vis[x][y] = 1;\r\n const n = heights.length;\r\n const m = heights[0].length;\r\n\r\n for (let i = 0; i < 4; i++) {\r\n const X = x + this.dir[i][0];\r\n const Y = y + this.dir[i][1];\r\n\r\n if (X < 0 || X >= n || Y < 0 || Y >= m)\r\n continue;\r\n\r\n if (Math.abs(heights[x][y] - heights[X][Y]) <= mid)\r\n this.ok(X, Y, mid, heights);\r\n }\r\n }\r\n }\r\n\r\n minimumEffortPath(heights) {\r\n let l = 0;\r\n let r = 1000000002;\r\n const n = heights.length;\r\n const m = heights[0].length;\r\n\r\n while (l < r) {\r\n const mid = Math.floor((l + r) / 2);\r\n this.vis = new Array(105).fill(null).map(() => new Array(105).fill(0));\r\n this.ok(0, 0, mid, heights);\r\n\r\n if (this.vis[n - 1][m - 1] === 1)\r\n r = mid;\r\n else\r\n l = mid + 1;\r\n }\r\n\r\n return l;\r\n }\r\n}\r\n\r\n```\r\n# GO\r\n```\r\npackage main\r\n\r\nimport "math"\r\n\r\ntype Solution struct {\r\n\tvis [105][105]int\r\n\tdir [][2]int\r\n}\r\n\r\nfunc (s *Solution) ok(x, y, mid int, heights [][]int) {\r\n\tif s.vis[x][y] == 0 {\r\n\t\ts.vis[x][y] = 1\r\n\t\tn := len(heights)\r\n\t\tm := len(heights[0])\r\n\r\n\t\tdirections := [][2]int{{1, 0}, {-1, 0}, {0, -1}, {0, 1}}\r\n\r\n\t\tfor i := 0; i < 4; i++ {\r\n\t\t\tX := x + directions[i][0]\r\n\t\t\tY := y + directions[i][1]\r\n\r\n\t\t\tif X < 0 || X >= n || Y < 0 || Y >= m {\r\n\t\t\t\tcontinue\r\n\t\t\t}\r\n\r\n\t\t\tif int(math.Abs(float64(heights[x][y]-heights[X][Y]))) <= mid {\r\n\t\t\t\ts.ok(X, Y, mid, heights)\r\n\t\t\t}\r\n\t\t}\r\n\t}\r\n}\r\n\r\nfunc (s *Solution) minimumEffortPath(heights [][]int) int {\r\n\tl := 0\r\n\tr := int(1e9 + 2)\r\n\tn := len(heights)\r\n\tm := len(heights[0])\r\n\r\n\tfor l < r {\r\n\t\tmid := (l + r) / 2\r\n\t\ts.vis = [105][105]int{}\r\n\r\n\t\ts.ok(0, 0, int(mid), heights)\r\n\r\n\t\tif s.vis[n-1][m-1] == 1 {\r\n\t\t\tr = int(mid)\r\n\t\t} else {\r\n\t\t\tl = int(mid) + 1\r\n\t\t}\r\n\t}\r\n\r\n\treturn l\r\n}\r\n\r\nfunc main() {\r\n\t// Create an instance of Solution and call minimumEffortPath here with your input data.\r\n}\r\n\r\n```\r\n# PLEASE UPVOTE\u2764\uD83D\uDE0D | 16 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Sorting - GroupBy - DSU | rank-transform-of-a-matrix | 0 | 1 | # Complexity\n```haskell\nTime complexity: O(nlogn + n * A(n))\nSpace complexity: O(n)\n```\n# Code\n```\nclass Solution:\n def matrixRankTransform(self, M: List[List[int]]) -> List[List[int]]:\n mr = [0 for _ in M]\n mc = [0 for _ in range(len(M[0]))]\n ii = sorted([(i, j) for j in range(len(M[0])) for i in range(len(M))], key=lambda x: M[x[0]][x[1]])\n rr = [[0 for _ in r] for r in M]\n for _, gg in groupby(ii, lambda x: M[x[0]][x[1]]):\n gg = list(gg)\n pp = [jj for jj in range(len(gg))]\n ra = [1 for _ in range(len(gg))]\n def find(a: int) -> int:\n if a != pp[a]:\n pp[a] = find(pp[a])\n return pp[a]\n def join(a: int, b: int):\n pa = find(a)\n pb = find(b)\n if pa == pb: return\n if ra[pa] > ra[pb]:\n pp[pb] = pa\n ra[pa] += ra[pb]\n else:\n pp[pa] = pb\n ra[pb] += ra[pa]\n \n rd, cd = {}, {}\n for aa in range(len(gg)):\n join(aa, rd.get(gg[aa][0], aa))\n join(aa, cd.get(gg[aa][1], aa))\n rd[gg[aa][0]] = aa\n cd[gg[aa][1]] = aa\n \n mnn = defaultdict(int)\n for aa in range(len(gg)):\n p = find(aa)\n mnn[p] = max(mnn[p], max(mr[gg[aa][0]], mc[gg[aa][1]]) + 1)\n \n for aa in range(len(gg)):\n mn = mnn[find(aa)]\n rr[gg[aa][0]][gg[aa][1]] = mn\n mr[gg[aa][0]] = mn\n mc[gg[aa][1]] = mn\n \n return rr\n``` | 0 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Rank Transform of a Matrix | rank-transform-of-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea behind this algorithm is to iterate through the elements of the matrix in ascending order, maintaining a data structure (DSU - Disjoint Set Union) to keep track of the connected components based on the values. We also keep track of the rank for each element in the matrix.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a DSU (Disjoint Set Union) class to manage connected components. Initialize a dictionary p to store the parent of each element, initially set to itself.\n\nCreate a rank list to store the rank of each element. Initialize it with zeros.\n\nCreate a defaultdict d to group elements with the same value in the matrix.\n\nIterate through the matrix elements, and for each element a:\n\nAppend the coordinates of the element to d[a].\nIterate through the values in ascending order, using the sorted(d) loop:\n\nFor each value a, create a list of connected components by merging rows and columns based on the positions of elements with value a. This is done using the DSU class and the union method.\nFor each connected component, find the maximum rank among its elements and assign it to all elements in the component.\n\nUpdate the matrix with the computed ranks.\n\nReturn the modified matrix.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m * n * log(m * n)) \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(m * n)\n\n# Code\n```\nfrom collections import defaultdict\nfrom itertools import product\n\nclass DSU:\n def __init__(self, graph):\n self.p = {i: i for i in graph}\n\n def find(self, x):\n if self.p[x] != x:\n self.p[x] = self.find(self.p[x])\n return self.p[x]\n\n def union(self, x, y):\n self.p[self.find(x)] = self.find(y)\n\n def groups(self):\n ans = defaultdict(list)\n for el in self.p.keys():\n ans[self.find(el)].append(el)\n return ans\n\nclass Solution:\n def matrixRankTransform(self, matrix):\n n, m = len(matrix), len(matrix[0])\n rank = [0] * (m + n)\n d = defaultdict(list)\n\n for i, j in product(range(n), range(m)):\n d[matrix[i][j]].append([i, j])\n\n for a in sorted(d):\n graph = [i for i, j in d[a]] + [j + n for i, j in d[a]]\n dsu = DSU(graph)\n for i, j in d[a]:\n dsu.union(i, j + n)\n\n for group in dsu.groups().values():\n mx = max(rank[i] for i in group)\n for i in group:\n rank[i] = mx + 1\n\n for i, j in d[a]:\n matrix[i][j] = rank[i]\n\n return matrix\n\n``` | 0 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
Python3 || DSU Algorithm | rank-transform-of-a-matrix | 0 | 1 | \n# Code\n```\nclass Solution:\n def matrixRankTransform(self, matrix: List[List[int]]) -> List[List[int]]:\n\n m = len(matrix)\n n = len(matrix[0])\n\n # Iterate over all elements and create a map with that element along with its parent array to get connected components for all equal values\n\n union_graph = {}\n for i in range(m):\n for j in range(n):\n value = matrix[i][j]\n if(value not in union_graph):\n union_graph[value] = {}\n self.union(i, ~j, union_graph[value])\n \n value_graph = {}\n\n for i in range(m):\n for j in range(n):\n value = matrix[i][j]\n if(value not in value_graph):\n value_graph[value] = {}\n parent = self.find(i, union_graph[value])\n if(parent not in value_graph[value]):\n value_graph[value][parent] = []\n value_graph[value][parent].append([i, j])\n\n answer = [[0] * n for _ in range(m)]\n row_rank_max = [0] * m\n col_rank_max = [0] * n\n\n for value in sorted(value_graph.keys()):\n for points in value_graph[value].values():\n rank = 1\n for i, j in points:\n rank = max(rank, max(row_rank_max[i], col_rank_max[j]) + 1)\n for i, j in points:\n answer[i][j] = rank\n row_rank_max[i] = max(row_rank_max[i], rank)\n col_rank_max[j] = max(col_rank_max[j], rank)\n return answer\n\n\n\n def find(self, x, parent):\n if(x == parent[x]):\n return x\n parent[x] = self.find(parent[x], parent)\n return parent[x]\n \n def union(self, x, y, parent):\n parent.setdefault(x, x)\n parent.setdefault(y, y)\n\n root_x = self.find(x, parent)\n root_y = self.find(y, parent)\n parent[root_x] = root_y\n \n\n``` | 0 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
[C++ || Python || Java] Union find with path compression | rank-transform-of-a-matrix | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n\n> **Vote welcome if this solution helped.**\n---\n\n# Intuition\n- TBD\n\n# Approach\n- TBD\n\n# Complexity\n- Time complexity: $O(mn\\log(mn))$\n- Space complexity: $O(mn)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {\n int m = matrix.size(), n = matrix[0].size();\n vector<vector<int>> res(m, vector<int>(n, 0));\n map<int, vector<pair<int, int>>> mp;\n for (int i = 0; i < m; ++i) \n for (int j = 0; j < n; ++j) \n mp[matrix[i][j]].push_back(make_pair(i, j));\n vector<int> fa(m+n), maxx(m), row(m, 0), col(n, 0);\n function<int(int)> getFa = [&](int x) -> int {\n return x == fa[x] ? x : (fa[x] = getFa(fa[x]));\n };\n for (auto &[k, v]: mp) {\n for (auto &[i, j]: v) fa[i] = fa[m+j] = i, maxx[i] = 0;\n for (auto &[i, j]: v) fa[getFa(m+j)] = getFa(i);\n for (auto &[i, j]: v) maxx[getFa(i)] = max(maxx[getFa(i)], max(row[i], col[j]));\n for (auto &[i, j]: v) row[i] = col[j] = res[i][j] = maxx[getFa(i)] + 1;\n }\n return res;\n }\n};\n```\n``` Java []\nclass Solution {\n public int getFa(int []fa, int x) {\n if (x != fa[x]) fa[x] = getFa(fa, fa[x]);\n return fa[x];\n }\n public int[][] matrixRankTransform(int[][] matrix) {\n int m = matrix.length, n = matrix[0].length;\n int [][]res = new int[m][n];\n TreeMap<Integer, List<int[]>> mp = new TreeMap<>();\n for (int i = 0; i < m; ++i) \n for (int j = 0; j < n; ++j) \n mp.computeIfAbsent(matrix[i][j], k -> new ArrayList<>()).add(new int[]{i, j});\n int []fa = new int[m+n];\n int []maxx = new int[m];\n int []row = new int[m];\n int []col = new int[n];\n for (var v: mp.values()) {\n for (var p: v) {\n fa[p[0]] = fa[m+p[1]] = p[0]; \n maxx[p[0]] = 0;\n }\n for (var p: v) \n fa[getFa(fa, m+p[1])] = getFa(fa, p[0]);\n for (var p: v) \n maxx[getFa(fa, p[0])] = Math.max(maxx[getFa(fa, p[0])], Math.max(row[p[0]], col[p[1]]));\n for (var p: v) \n row[p[0]] = col[p[1]] = res[p[0]][p[1]] = maxx[getFa(fa, p[0])] + 1;\n }\n return res;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def matrixRankTransform(self, matrix: List[List[int]]) -> List[List[int]]:\n m, n = len(matrix), len(matrix[0])\n res = [[0 for j in range(n)] for i in range(m)]\n mp = defaultdict(list)\n for i in range(m):\n for j in range(n):\n mp[matrix[i][j]].append((i,j))\n fa, maxx, row, col = [0]*(m+n), [0]*m, [0]*m, [0]*n\n def getFa(x):\n if x != fa[x]: fa[x] = getFa(fa[x])\n return fa[x]\n for k, v in sorted(mp.items()):\n for (i, j) in v:\n fa[i] = fa[m+j] = i\n maxx[i] = 0\n for (i, j) in v:\n fa[getFa(m+j)] = getFa(i)\n for (i, j) in v:\n maxx[getFa(i)] = max(maxx[getFa(i)], row[i], col[j])\n for (i, j) in v:\n row[i] = col[j] = res[i][j] = maxx[getFa(i)] + 1\n return res\n```\n | 0 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
[Python3] UF | rank-transform-of-a-matrix | 0 | 1 | Learned this approach from @lee215 in this [post](https://leetcode.com/problems/rank-transform-of-a-matrix/discuss/909142/Python-Union-Find). \n```\nclass Solution:\n def matrixRankTransform(self, matrix: List[List[int]]) -> List[List[int]]:\n m, n = len(matrix), len(matrix[0]) # dimension \n # mapping from value to index \n mp = {} \n for i in range(m):\n for j in range(n): \n mp.setdefault(matrix[i][j], []).append((i, j))\n \n def find(p):\n """Find root of p."""\n if p != parent[p]:\n parent[p] = find(parent[p])\n return parent[p]\n \n rank = [0]*(m+n)\n ans = [[0]*n for _ in range(m)]\n \n for k in sorted(mp): # from minimum to maximum \n parent = list(range(m+n))\n for i, j in mp[k]: \n ii, jj = find(i), find(m+j) # find \n parent[ii] = jj # union \n rank[jj] = max(rank[ii], rank[jj]) # max rank \n \n seen = set()\n for i, j in mp[k]:\n ii = find(i)\n if ii not in seen: rank[ii] += 1\n seen.add(ii)\n rank[i] = rank[m+j] = ans[i][j] = rank[ii]\n return ans \n``` | 5 | Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`.
The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules:
* The rank is an integer starting from `1`.
* If two elements `p` and `q` are in the **same row or column**, then:
* If `p < q` then `rank(p) < rank(q)`
* If `p == q` then `rank(p) == rank(q)`
* If `p > q` then `rank(p) > rank(q)`
* The **rank** should be as **small** as possible.
The test cases are generated so that `answer` is unique under the given rules.
**Example 1:**
**Input:** matrix = \[\[1,2\],\[3,4\]\]
**Output:** \[\[1,2\],\[2,3\]\]
**Explanation:**
The rank of matrix\[0\]\[0\] is 1 because it is the smallest integer in its row and column.
The rank of matrix\[0\]\[1\] is 2 because matrix\[0\]\[1\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[0\] is 2 because matrix\[1\]\[0\] > matrix\[0\]\[0\] and matrix\[0\]\[0\] is rank 1.
The rank of matrix\[1\]\[1\] is 3 because matrix\[1\]\[1\] > matrix\[0\]\[1\], matrix\[1\]\[1\] > matrix\[1\]\[0\], and both matrix\[0\]\[1\] and matrix\[1\]\[0\] are rank 2.
**Example 2:**
**Input:** matrix = \[\[7,7\],\[7,7\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Example 3:**
**Input:** matrix = \[\[20,-21,14\],\[-19,4,19\],\[22,-47,24\],\[-19,4,19\]\]
**Output:** \[\[4,2,3\],\[1,3,4\],\[5,1,6\],\[1,3,4\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 500`
* `-109 <= matrix[row][col] <= 109` | Use two HashMap to store the counts of distinct letters in the left and right substring divided by the current index. |
heap | sort-array-by-increasing-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom heapq import heappush,heappop\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n d={}\n for i in range(len(nums)):\n if(nums[i] in d):\n d[nums[i]]+=1\n else:\n d[nums[i]]=1\n heap=[]\n arr=[]\n for i in d:\n heappush(heap,[d[i],-i])\n while(heap):\n m,n=heappop(heap)\n for i in range(m):\n arr.append(n*(-1))\n return(arr)\n \n \n``` | 3 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Python keep it simple | sort-array-by-increasing-frequency | 0 | 1 | # Complexity\n- Time complexity:$$O(nlogn)$$\n- Space complexity:$$O(n)$$\n\n# Code\n```\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n counts_dict = Counter(nums)\n return sorted(nums, key = lambda x: (counts_dict[x], -x))\n``` | 1 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Python 3 solution - with process of thinking and improvement | sort-array-by-increasing-frequency | 0 | 1 | # Part 1\n\nSunday morning, Spotify, coffee, console... Task from the list of tasks to solve later.\nLet\'s go!\n\n```python\n~ \u276F python3 at 10:38:03\nPython 3.9.1 (default, Feb 3 2021, 07:38:02)\n[Clang 12.0.0 (clang-1200.0.32.29)] on darwin\nType "help", "copyright", "credits" or "license" for more information.\n>>> nums = [1,1,2,2,2,6,6,4,4,5,5,3]\n```\n\nOk, so I need to count frequency of each of the unique values... First idea - use `Counter`. This returns `collection` type of object:\n\n```python\n>>> d = Counter(nums)\n>>> d\nCounter({2: 3, 1: 2, 6: 2, 4: 2, 5: 2, 3: 1})\n>>> type(d)\n<class \'collections.Counter\'>\n```\n\nNow I need to sort those values following the requirements in the description. \'Counter\' object has no attribute \'sort\', and \'sorted\' will only sort values, not frequencies. Googling options, found this [StackOverflow question](https://stackoverflow.com/q/20950650/4440387) with lots of useful answers. Reading... Let\'s try easier object:\n\n```python\n>>> r = Counter(nums).most_common()\n```\n\nThis returns a list of tuples, where first number is value and second - its\' frequency. Can I sort it in the same command? Jumping to the [official documentation](https://docs.python.org/3/library/collections.html#collections.Counter.most_common). Nope, not sortable in the command itself, moreover: "*Elements with equal counts are ordered in the order first encountered*". Ok, let\'s sort it directly, first by values in the decreasing order, then by frequencies in the increasing.\n\n```\n>>> r.sort(key = lambda x: x[0], reverse=True)\n>>> r.sort(key = lambda x: x[1])\n>>> r\n[(3, 1), (6, 2), (5, 2), (4, 2), (1, 2), (2, 3)]\n```\n\nLooks promising. Now I want to expand those tuples into a single list... Still browsing answers to the same [question](https://stackoverflow.com/q/20950650/4440387). Remembering that I can expand tuple and get every number from it by using this:\n\n```\n>>> a, b = (3, 2)\n>>> a\n3\n>>> b\n2\n```\n\nso then I can repeat every value by the number of its\' frequency like so:\n\n```\n>>> [3]*2\n[3, 3]\n```\n\nAha. Now I need an empty list to combine all those tuples into a single list:\n\n```\nt = []\nfor i in r:\n a, b = i\n t.extend([a] * b)\n\n>>> t\n[3, 6, 6, 5, 5, 4, 4, 1, 1, 2, 2, 2]\n```\n\nWoo-hoo! That\'s what I need. So the complete solution now looks like this:\n\n```\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n \n r = Counter(nums).most_common()\n r.sort(key = lambda x: x[0], reverse=True)\n r.sort(key = lambda x: x[1])\n \n t = []\n for i in r:\n a, b = i\n t.extend([a]*b)\n \n return t\n```\n\n**Result**:\nRuntime: 52 ms, faster than 63.30% of Python3 online submissions for Sort Array by Increasing Frequency.\nMemory Usage: 14.2 MB, less than 58.20% of Python3 online submissions for Sort Array by Increasing Frequency.\n\nNot the best, but the task is solved.\n\n# Part 2\n\nNow it\'s time for another *fun* - can I make it one-liner or optimize the solution in any other way?\n\nLooking at sorting lines... Can I sort it in one go? Yes! So, first we sort by values in the reverse order (`-x[0]`) and then by their frequencies (`x[1]`) in direct order. \n```\n>>> r.sort(key = lambda x: (x[1], -x[0]))\n```\n\nBasically, it\'s the same operation as the above but now coded in one line. Love Python :) Same logic applies to the tuple expansion part and it allows to save another line:\n\n```\nt = []\nfor i in r:\n\tt += ([i[0]] * i[1])\n```\n\nAnd then I thought - if I can sort by value and its\' frequency why do I need intermediate list? Can I sort the original list the same way?! Let\'s see...\n\n```python\n>>> nums\n[1, 1, 2, 2, 2, 6, 6, 4, 4, 5, 5, 3]\n>>> r = Counter(nums)\n>>> r\nCounter({2: 3, 1: 2, 6: 2, 4: 2, 5: 2, 3: 1})\n>>> nums.sort(key=lambda x: (r[x], -x))\n>>> nums\n[3, 6, 6, 5, 5, 4, 4, 1, 1, 2, 2, 2]\n```\n\nVoila! That feels sooo good. But `x.sort` makes it in-place and I need to return an object... So, I need to change it to `sorted` then:\n\n```\n>>> result = sorted(nums, key=lambda x: (r[x], -x))\n>>> result\n[3, 6, 6, 5, 5, 4, 4, 1, 1, 2, 2, 2]\n```\n\nPerfect. So the final variant would be:\n```python\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n r = Counter(nums)\n return sorted(nums, key=lambda x: (r[x], -x))\n```\n\nAnd it\'s even faster!\n\nRuntime: 44 ms, faster than 95.07% of Python3 online submissions for Sort Array by Increasing Frequency.\nMemory Usage: 14.3 MB, less than 58.20% of Python3 online submissions for Sort Array by Increasing Frequency.\n\n**NOTE**\n* If you want to downvote this post, please, be brave and comment why. This will help me and others to learn from it.\n* If you think that others can learn something from this post, then please, upvote it. Thanks. | 261 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Python || 94.84% Faster || Max Heap | sort-array-by-increasing-frequency | 0 | 1 | ```\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n c=Counter(nums)\n pq=[]\n for item,freq in c.items():\n heapq.heappush(pq,(-freq,item)) # \'-\' because we are using max heap\n result=[]\n while pq:\n freq, item = heapq.heappop(pq)\n freq*=-1\n while freq:\n result.append(item)\n freq-=1\n return result[::-1]\n```\n**An upvote will be encouraging** | 1 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Python Easy Solution || Sorting || Hashmap | sort-array-by-increasing-frequency | 0 | 1 | # Code\n```\nclass Solution:\n def sort(self,nums: list)-> list:\n i=0\n while(i<len(nums)):\n swapped=0\n j=0\n while(j<len(nums)-i-1):\n if nums[j]>nums[j+1]:\n \n nums[j+1],nums[j]=nums[j],nums[j+1]\n swapped=1\n j+=1\n if swapped==0:\n break\n i+=1\n return(nums)\n\n def frequencySort(self, nums: List[int]) -> List[int]:\n dic=dict()\n res=[]\n new=[]\n \n for i in nums:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n\n for i in dic:\n if dic[i] not in res:\n res.append(dic[i])\n res=Solution.sort(self,res)\n\n for i in res:\n temp=[]\n for j in dic:\n if dic[j]==i:\n temp+=[j]*i\n if len(temp)>1:\n temp=Solution.sort(self,temp)\n temp.reverse()\n new+=temp\n return new \n``` | 1 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
2 lines solution very easy | sort-array-by-increasing-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n freq_map = Counter(nums)\n \n nums.sort(key=lambda x: (freq_map[x], -x))\n \n return nums\n \n``` | 2 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Easiest one line solution in python | sort-array-by-increasing-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n return sorted(sorted(nums,reverse=1),key=nums.count)\n\n #please do upvote it will encourage me alot\n\t\t\n\t\t\n \n``` | 11 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Easiest & Shortest readable HashMap/HashTable Solution. | sort-array-by-increasing-frequency | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Consider example:\n - `nums = [3, 4, 2, 1, 2, 1]` \n- First dictionary will store the frequency of the numbers\n - `firstDic = {2: 2, 1: 2, 3: 1, 4: 1}`\n- Second dictionary will store all the values with same frequency, meaning if two numbers occured twice then they are stored in same list. In our example, 3 and 4 appeared once so they are stored in same list and 2 and 1 appeared twice so they are stored in the same list.\n - `secondDic = {1: [3, 4], 2: [2, 1]}`\n- Create a list which will store our final answer.\n- Iterate over sorted keys of secondDic, because we want to add the numbers with lesser frequencies first.\n- `sorted(x*secondDic[x], reverse = True)`: this statement gets the element of the list in descending order, because when two numbers have same frequencies then we have to add the number who is bigger than the other one, and `x` is multiplied because x is the key which shows the number appeared x times, so we have to add the elements x times.\n- Keep extending the answer list till no elements left.\n\n\n### I hope you understood my solution, it was quite unique! \n# Code\n```\nclass Solution:\n def frequencySort(self, nums: List[int]) -> List[int]:\n firstDic = Counter(nums)\n secondDic = {}\n for i, j in firstDic.items():\n if j not in secondDic:\n secondDic[j] = [i]\n else:\n secondDic[j] += [i]\n \n ans = []\n for x in sorted(secondDic):\n ans.extend(sorted(x*secondDic[x], reverse = True))\n \n return ans\n\n``` | 1 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Easy Python Solution with Explanation | sort-array-by-increasing-frequency | 0 | 1 | \tfrom collections import Counter\n\tclass Solution:\n\t\tdef frequencySort(self, nums: List[int]) -> List[int]:\n\t\t\td = Counter(nums)\n\t\t\tdef check(x):\n\t\t\t\treturn d[x]\n\n\t\t\tnums.sort(reverse=True)\n\t\t\tnums.sort(key=check)\n\t\t\treturn nums\n\t\t\t\nSo the basic idea is we use the Python\'s inbuilt sort function with a custom method which returns the frequency of that element in the array to sort. So, first we create a frequency array using the Python\'s Counter function *(This returns a dictionary, the same could have been manually using a blank dictionary but since we can utilise the capabilities of Python, that is what we do here.)* \n\nand we create a new function which returns the frequency of that element in our array *(The same could have been done easier with a lambda function as well, but this was my first instinct so I went with this)*\n\nNow, we reversed sorted the list first normally so that when sorting the second time using our custom sort, our answer comes out to be what we want, *(decreasing order for elements with the same frequency)* \n\nNext we use our custom sort function which generates a frequency wise + decreasing order for same frequency elements. Our inbuilt custom sort is stable, meaning it won\'t change the relative order among elements. \n\nExample:\n\tIn Stable Frequency Wise Sort:\n\t`[1,3,3,2,4] --> [1,2,4,3,3] (relative order of 1,2,4 is maintained)`\n\tIn Unstable Frequency Wise Sort:\n\t`[1,3,3,2,4] --> [4,1,2,3,3] (relative order of 1,2,4 is not maintained)`\n\t\n\n**Note:** We can achieve this in one sort also by instead of returning a single key in our *check* function, we return a tuple of keys. \n\nSo that would make our *check* function something like: \n\n```\ndef check(x):\n\treturn (d[x], -x)\n```\nThe purpose of *-x* is because in case of elements with the same frequency, we want them sorted in reverse sorted order.\n\nExample: `nums = [1,2,3,4]`\n\nSo, for this list, the element:\n* 1 --> (1, -1)\n* 2 --> (1, -2)\n* 3 --> (1, -3)\n* 4 --> (1, -4)\n* element --> (frequency of element, -element)\n\nSo, first our list is sorted based on the first element, so since all are 1. Nothing happens. Next, we sort all the 1s based on the second element. So, -4 is the smallest so, that comes first, then -3 then -2 and lastly -1.\n\nSo the order becomes: (1, -4) , (1, -3), (1, -2), (1, -1) which means [4,3,2,1]. Which is what we wanted. \n\nPlease feel free to ask anything here, I will be happy to help/respond. | 32 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
✅98.74%🔥Easy Solution🔥with explanation🔥 | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | 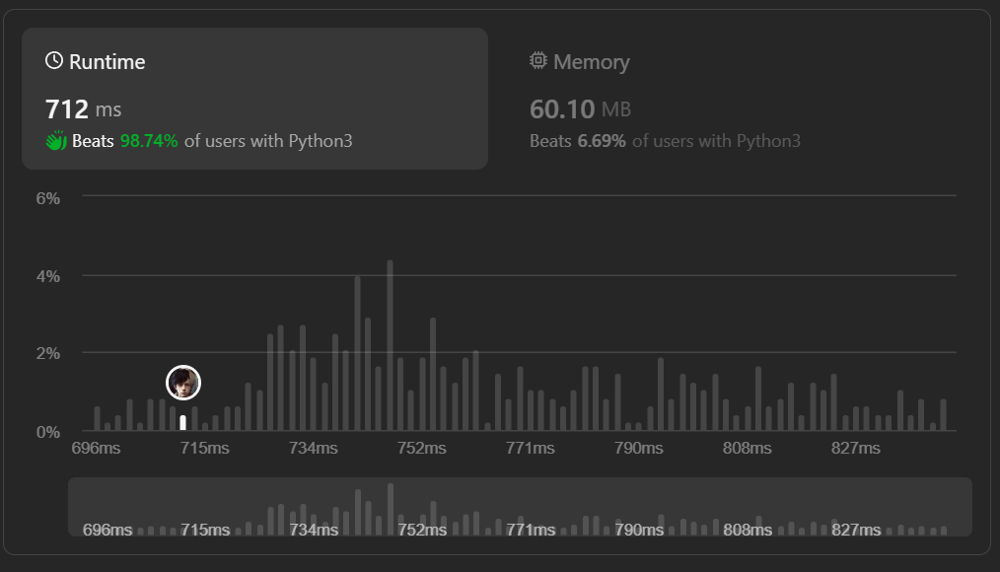\n\n---\n# Intuition\n##### The problem asks for the widest vertical area between two points on a 2D plane. To find this, we can sort the given points based on their x-coordinates. After sorting, we can iterate through the sorted points and calculate the horizontal distance between consecutive points. The maximum of these distances will be the widest vertical area.\n---\n\n# Approach\n 1. #### Sort the points based on their x-coordinates.\n 2. #### Initialize a variable `max_width` to store the maximum width.\n 3. #### Iterate through the sorted points starting from index 1.\n 4. #### For each pair of consecutive points, calculate the width by subtracting the x-coordinate of the previous point from the x-coordinate of the current point.\n 5. #### Update `max_width` with the maximum of its current value and the calculated width.\n 6. #### After the iteration, `max_width` will contain the result.\n---\n# Complexity\n- ### Time complexity:\n##### $$O(n * log(n))$$ due to the sorting operation, where n is the number of points.\n- ### Space complexity:\n##### $$O(1)$$ as we use a constant amount of space for variables.\n---\n# Code\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: x[0])\n\n max_width = 0\n\n for i in range(1, len(points)):\n width = points[i][0] - points[i-1][0]\n max_width = max(max_width, width)\n\n return max_width\n```\n```C++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(std::vector<std::vector<int>>& points) {\n std::sort(points.begin(), points.end(), [](const auto& a, const auto& b) {\n return a[0] < b[0];\n });\n\n int max_width = 0;\n\n for (int i = 1; i < points.size(); ++i) {\n int width = points[i][0] - points[i - 1][0];\n max_width = std::max(max_width, width);\n }\n\n return max_width;\n }\n};\n```\n```javascript []\nvar maxWidthOfVerticalArea = function(points) {\n points.sort((a, b) => a[0] - b[0]);\n\n let maxWidth = 0;\n\n for (let i = 1; i < points.length; i++) {\n let width = points[i][0] - points[i - 1][0];\n maxWidth = Math.max(maxWidth, width);\n }\n\n return maxWidth;\n};\n\n```\n```java []\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));\n\n int max_width = 0;\n\n for (int i = 1; i < points.length; i++) {\n int width = points[i][0] - points[i - 1][0];\n max_width = Math.max(max_width, width);\n }\n\n return max_width;\n }\n}\n```\n```C# []\npublic class Solution {\n public int MaxWidthOfVerticalArea(int[][] points) {\n Array.Sort(points, (a, b) => a[0].CompareTo(b[0]));\n\n int maxWidth = 0;\n\n for (int i = 1; i < points.Length; i++) {\n int width = points[i][0] - points[i - 1][0];\n maxWidth = Math.Max(maxWidth, width);\n }\n\n return maxWidth;\n }\n}\n```\n```PHP []\nclass Solution {\n function maxWidthOfVerticalArea($points) {\n usort($points, function ($a, $b) {\n return $a[0] - $b[0];\n });\n\n $maxWidth = 0;\n\n for ($i = 1; $i < count($points); $i++) {\n $width = $points[$i][0] - $points[$i - 1][0];\n $maxWidth = max($maxWidth, $width);\n }\n\n return $maxWidth;\n }\n}\n\n```\n```ruby []\ndef max_width_of_vertical_area(points)\n points.sort! { |a, b| a[0] - b[0] }\n\n max_width = 0\n\n (1...points.length).each do |i|\n width = points[i][0] - points[i - 1][0]\n max_width = [max_width, width].max\n end\n\n max_width\nend\n\n```\n---\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n | 62 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
✅98.74%🔥Easy Solution🔥with explanation🔥 | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | \n\n---\n# Intuition\n##### The problem asks for the widest vertical area between two points on a 2D plane. To find this, we can sort the given points based on their x-coordinates. After sorting, we can iterate through the sorted points and calculate the horizontal distance between consecutive points. The maximum of these distances will be the widest vertical area.\n---\n\n# Approach\n 1. #### Sort the points based on their x-coordinates.\n 2. #### Initialize a variable `max_width` to store the maximum width.\n 3. #### Iterate through the sorted points starting from index 1.\n 4. #### For each pair of consecutive points, calculate the width by subtracting the x-coordinate of the previous point from the x-coordinate of the current point.\n 5. #### Update `max_width` with the maximum of its current value and the calculated width.\n 6. #### After the iteration, `max_width` will contain the result.\n---\n# Complexity\n- ### Time complexity:\n##### $$O(n * log(n))$$ due to the sorting operation, where n is the number of points.\n- ### Space complexity:\n##### $$O(1)$$ as we use a constant amount of space for variables.\n---\n# Code\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: x[0])\n\n max_width = 0\n\n for i in range(1, len(points)):\n width = points[i][0] - points[i-1][0]\n max_width = max(max_width, width)\n\n return max_width\n```\n```C++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(std::vector<std::vector<int>>& points) {\n std::sort(points.begin(), points.end(), [](const auto& a, const auto& b) {\n return a[0] < b[0];\n });\n\n int max_width = 0;\n\n for (int i = 1; i < points.size(); ++i) {\n int width = points[i][0] - points[i - 1][0];\n max_width = std::max(max_width, width);\n }\n\n return max_width;\n }\n};\n```\n```javascript []\nvar maxWidthOfVerticalArea = function(points) {\n points.sort((a, b) => a[0] - b[0]);\n\n let maxWidth = 0;\n\n for (let i = 1; i < points.length; i++) {\n let width = points[i][0] - points[i - 1][0];\n maxWidth = Math.max(maxWidth, width);\n }\n\n return maxWidth;\n};\n\n```\n```java []\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));\n\n int max_width = 0;\n\n for (int i = 1; i < points.length; i++) {\n int width = points[i][0] - points[i - 1][0];\n max_width = Math.max(max_width, width);\n }\n\n return max_width;\n }\n}\n```\n```C# []\npublic class Solution {\n public int MaxWidthOfVerticalArea(int[][] points) {\n Array.Sort(points, (a, b) => a[0].CompareTo(b[0]));\n\n int maxWidth = 0;\n\n for (int i = 1; i < points.Length; i++) {\n int width = points[i][0] - points[i - 1][0];\n maxWidth = Math.Max(maxWidth, width);\n }\n\n return maxWidth;\n }\n}\n```\n```PHP []\nclass Solution {\n function maxWidthOfVerticalArea($points) {\n usort($points, function ($a, $b) {\n return $a[0] - $b[0];\n });\n\n $maxWidth = 0;\n\n for ($i = 1; $i < count($points); $i++) {\n $width = $points[$i][0] - $points[$i - 1][0];\n $maxWidth = max($maxWidth, $width);\n }\n\n return $maxWidth;\n }\n}\n\n```\n```ruby []\ndef max_width_of_vertical_area(points)\n points.sort! { |a, b| a[0] - b[0] }\n\n max_width = 0\n\n (1...points.length).each do |i|\n width = points[i][0] - points[i - 1][0]\n max_width = [max_width, width].max\n end\n\n max_width\nend\n\n```\n---\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n | 62 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
【Video】Give me 5 minutes - How we think about a solution + Bonus code in Python | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | # Intuition\nSort x-coordinates\n\n---\n\n# Solution Video\n\nhttps://youtu.be/q628cVxEFvU\n\n\u25A0 Timeline of the video\n\n`0:06` Explain key points\n`3:16` Coding\n`4:38` Time Complexity and Space Complexity\n`4:57` Step by step algorithm of my solution code\n`5:08` Bonus coding in Python\n`6:19` Time Complexity and Space Complexity for Bonus\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,571\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nWe need to find widest vertical area, so simply we sort x-coordinates in input array, then find the widest area.\n\n```\nInput: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]\n```\nWe don\'t need `y-coordinates`, so take `all x-coordinates` only and sort them.\n\n```\n[[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]\n\u2193\n[3,9,1,1,5,8]\n\u2193\nx_sorted = [1, 1, 3, 5, 8, 9]\n```\nSince it\'s sorted, the latter number should be larger. Width between two points should be\n\n```\nwidth = (number at current index + 1) - (number at current index)\n```\nLet\'s see one by one. Number of loop should be `length of x_sorted - 1` to prevent out of bounds\n\n```\nindex = 0\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 0), 1 - 1)\n\nfirst 1 from index 1\nsecond 1 from index 0\n\nmax_width = 0\n```\n```\nindex = 1\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 0), 3 - 1)\n\n3 from index 2\n1 from index 1\n\nmax_width = 2\n```\n```\nindex = 2\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 2), 5 - 3)\n\n5 from index 3\n3 from index 2\n\nmax_width = 2\n```\n```\nindex = 3\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 2), 8 - 5)\n\n8 from index 4\n5 from index 3\n\nmax_width = 3\n```\n```\nindex = 4\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 3), 9 - 8)\n\n9 from index 5\n8 from index 4\n\nmax_width = 3\n```\n```\nOutput: 3\n```\n\nEasy!\uD83D\uDE04\nLet\'s see solution codes.\n\n---\n\n# Complexity & Solution codes\n- Time complexity: $$O(n log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log n)$$ or $$O(n)$$\nDepends on language you use. Sorting need some extra space.\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x_sorted = sorted([x for x, _ in points])\n\n max_width = 0\n for i in range(len(x_sorted) - 1):\n max_width = max(max_width, x_sorted[i + 1] - x_sorted[i])\n\n return max_width \n```\n```javascript []\n/**\n * @param {number[][]} points\n * @return {number}\n */\nvar maxWidthOfVerticalArea = function(points) {\n const xSorted = points.map(([x, _]) => x).sort((a, b) => a - b);\n\n let maxWidth = 0;\n for (let i = 0; i < xSorted.length - 1; i++) {\n maxWidth = Math.max(maxWidth, xSorted[i + 1] - xSorted[i]);\n }\n\n return maxWidth; \n};\n```\n```java []\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n int[] xSorted = Arrays.stream(points).mapToInt(point -> point[0]).sorted().toArray();\n\n int maxWidth = 0;\n for (int i = 0; i < xSorted.length - 1; i++) {\n maxWidth = Math.max(maxWidth, xSorted[i + 1] - xSorted[i]);\n }\n\n return maxWidth; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n vector<int> xSorted;\n for (const auto& point : points) {\n xSorted.push_back(point[0]);\n }\n\n sort(xSorted.begin(), xSorted.end());\n\n int maxWidth = 0;\n for (int i = 0; i < xSorted.size() - 1; i++) {\n maxWidth = max(maxWidth, xSorted[i + 1] - xSorted[i]);\n }\n\n return maxWidth; \n }\n};\n```\n\n## Step by step algorithm\n\n1. **Sorting the x-coordinates:**\n ```python\n x_sorted = sorted([x for x, _ in points])\n ```\n This line creates a list `x_sorted` by extracting the x-coordinates from the input `points` and sorting them in ascending order.\n\n2. **Initializing the maximum width variable:**\n ```python\n max_width = 0\n ```\n Here, `max_width` is initialized to zero. This variable will be used to track the maximum width between consecutive x-coordinates.\n\n3. **Iterating through the sorted list:**\n ```python\n for i in range(len(x_sorted) - 1):\n ```\n The loop iterates through the sorted list of x-coordinates. The `- 1` ensures that the loop doesn\'t go out of bounds, as we are comparing each element with the next one.\n\n4. **Calculating and updating the maximum width:**\n ```python\n max_width = max(max_width, x_sorted[i + 1] - x_sorted[i])\n ```\n Within the loop, the width between the current x-coordinate (`x_sorted[i]`) and the next one (`x_sorted[i + 1]`) is calculated. If this width is greater than the current `max_width`, it updates `max_width` to store the maximum width encountered so far.\n\n5. **Returning the maximum width:**\n ```python\n return max_width\n ```\n Finally, the function returns the maximum width between consecutive x-coordinates.\n\nIn summary, the algorithm sorts the x-coordinates, iterates through the sorted list, calculates the width between consecutive x-coordinates, and keeps track of the maximum width encountered. The sorted order ensures that the latter number in each pair is larger, simplifying the width calculation. The final result is the maximum width between any two consecutive x-coordinates.\n\n\n---\n\n# Bonus\n\nIn python, if we can use `itertools.pairwise`\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x_sorted = sorted([x for x, _ in points])\n return max(x2 - x1 for x1, x2 in itertools.pairwise(x_sorted)) \n```\n`itertools.pairwise` takes adjacent two numbers like\n```\n[1,2,3,4,5]\n\u2193\nx1, x2\n1, 2: first loop\n2, 3: second loop\n3, 4: third loop\n4, 5: fourth loop\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/buy-two-chocolates/solutions/4427319/video-give-me-5-minutes-how-we-think-about-a-solution-bonus-codes-in-python/\n\nvideo\nhttps://youtu.be/nMRj-C4yzpI\n\n\u25A0 Timeline of the video\n\n`0:03` Explain key points\n`2:40` coding\n`4:49` Time Complexity and Space Complexity\n`5:02` Step by step algorithm of my solution code\n | 49 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
【Video】Give me 5 minutes - How we think about a solution + Bonus code in Python | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | # Intuition\nSort x-coordinates\n\n---\n\n# Solution Video\n\nhttps://youtu.be/q628cVxEFvU\n\n\u25A0 Timeline of the video\n\n`0:06` Explain key points\n`3:16` Coding\n`4:38` Time Complexity and Space Complexity\n`4:57` Step by step algorithm of my solution code\n`5:08` Bonus coding in Python\n`6:19` Time Complexity and Space Complexity for Bonus\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,571\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nWe need to find widest vertical area, so simply we sort x-coordinates in input array, then find the widest area.\n\n```\nInput: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]\n```\nWe don\'t need `y-coordinates`, so take `all x-coordinates` only and sort them.\n\n```\n[[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]\n\u2193\n[3,9,1,1,5,8]\n\u2193\nx_sorted = [1, 1, 3, 5, 8, 9]\n```\nSince it\'s sorted, the latter number should be larger. Width between two points should be\n\n```\nwidth = (number at current index + 1) - (number at current index)\n```\nLet\'s see one by one. Number of loop should be `length of x_sorted - 1` to prevent out of bounds\n\n```\nindex = 0\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 0), 1 - 1)\n\nfirst 1 from index 1\nsecond 1 from index 0\n\nmax_width = 0\n```\n```\nindex = 1\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 0), 3 - 1)\n\n3 from index 2\n1 from index 1\n\nmax_width = 2\n```\n```\nindex = 2\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 2), 5 - 3)\n\n5 from index 3\n3 from index 2\n\nmax_width = 2\n```\n```\nindex = 3\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 2), 8 - 5)\n\n8 from index 4\n5 from index 3\n\nmax_width = 3\n```\n```\nindex = 4\n\n[1, 1, 3, 5, 8, 9]\n\nmax_width = max(max_width(= 3), 9 - 8)\n\n9 from index 5\n8 from index 4\n\nmax_width = 3\n```\n```\nOutput: 3\n```\n\nEasy!\uD83D\uDE04\nLet\'s see solution codes.\n\n---\n\n# Complexity & Solution codes\n- Time complexity: $$O(n log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log n)$$ or $$O(n)$$\nDepends on language you use. Sorting need some extra space.\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x_sorted = sorted([x for x, _ in points])\n\n max_width = 0\n for i in range(len(x_sorted) - 1):\n max_width = max(max_width, x_sorted[i + 1] - x_sorted[i])\n\n return max_width \n```\n```javascript []\n/**\n * @param {number[][]} points\n * @return {number}\n */\nvar maxWidthOfVerticalArea = function(points) {\n const xSorted = points.map(([x, _]) => x).sort((a, b) => a - b);\n\n let maxWidth = 0;\n for (let i = 0; i < xSorted.length - 1; i++) {\n maxWidth = Math.max(maxWidth, xSorted[i + 1] - xSorted[i]);\n }\n\n return maxWidth; \n};\n```\n```java []\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n int[] xSorted = Arrays.stream(points).mapToInt(point -> point[0]).sorted().toArray();\n\n int maxWidth = 0;\n for (int i = 0; i < xSorted.length - 1; i++) {\n maxWidth = Math.max(maxWidth, xSorted[i + 1] - xSorted[i]);\n }\n\n return maxWidth; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n vector<int> xSorted;\n for (const auto& point : points) {\n xSorted.push_back(point[0]);\n }\n\n sort(xSorted.begin(), xSorted.end());\n\n int maxWidth = 0;\n for (int i = 0; i < xSorted.size() - 1; i++) {\n maxWidth = max(maxWidth, xSorted[i + 1] - xSorted[i]);\n }\n\n return maxWidth; \n }\n};\n```\n\n## Step by step algorithm\n\n1. **Sorting the x-coordinates:**\n ```python\n x_sorted = sorted([x for x, _ in points])\n ```\n This line creates a list `x_sorted` by extracting the x-coordinates from the input `points` and sorting them in ascending order.\n\n2. **Initializing the maximum width variable:**\n ```python\n max_width = 0\n ```\n Here, `max_width` is initialized to zero. This variable will be used to track the maximum width between consecutive x-coordinates.\n\n3. **Iterating through the sorted list:**\n ```python\n for i in range(len(x_sorted) - 1):\n ```\n The loop iterates through the sorted list of x-coordinates. The `- 1` ensures that the loop doesn\'t go out of bounds, as we are comparing each element with the next one.\n\n4. **Calculating and updating the maximum width:**\n ```python\n max_width = max(max_width, x_sorted[i + 1] - x_sorted[i])\n ```\n Within the loop, the width between the current x-coordinate (`x_sorted[i]`) and the next one (`x_sorted[i + 1]`) is calculated. If this width is greater than the current `max_width`, it updates `max_width` to store the maximum width encountered so far.\n\n5. **Returning the maximum width:**\n ```python\n return max_width\n ```\n Finally, the function returns the maximum width between consecutive x-coordinates.\n\nIn summary, the algorithm sorts the x-coordinates, iterates through the sorted list, calculates the width between consecutive x-coordinates, and keeps track of the maximum width encountered. The sorted order ensures that the latter number in each pair is larger, simplifying the width calculation. The final result is the maximum width between any two consecutive x-coordinates.\n\n\n---\n\n# Bonus\n\nIn python, if we can use `itertools.pairwise`\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x_sorted = sorted([x for x, _ in points])\n return max(x2 - x1 for x1, x2 in itertools.pairwise(x_sorted)) \n```\n`itertools.pairwise` takes adjacent two numbers like\n```\n[1,2,3,4,5]\n\u2193\nx1, x2\n1, 2: first loop\n2, 3: second loop\n3, 4: third loop\n4, 5: fourth loop\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/buy-two-chocolates/solutions/4427319/video-give-me-5-minutes-how-we-think-about-a-solution-bonus-codes-in-python/\n\nvideo\nhttps://youtu.be/nMRj-C4yzpI\n\n\u25A0 Timeline of the video\n\n`0:03` Explain key points\n`2:40` coding\n`4:49` Time Complexity and Space Complexity\n`5:02` Step by step algorithm of my solution code\n | 49 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
✅☑Beats 100% || [C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n#### ***Approach 1(Sorting)***\n1. **Sorting Points:**\n\n- The function begins by sorting the `points` vector based on the x-coordinate of each point. This is done using `sort(points.begin(), points.end())`.\n1. **Calculating Maximum Width:**\n\n- It then iterates through the sorted points.\n- For each pair of consecutive points, it calculates the difference in x-coordinates (`points[i][0] - points[i-1][0]`).\n- It updates the `diff` variable to hold the maximum difference encountered while traversing the sorted points.\n1. **Returning the Maximum Width:**\n\n- Finally, it returns the maximum `diff`, which represents the maximum width between two consecutive x-coordinates among the sorted points.\n\n\n# Complexity\n- Time complexity:\n $$O(nlogn)$$\n \n\n- Space complexity:\n $$O(logn)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n sort(points.begin(),points.end());\n int diff =0;\n for(int i =1;i<points.size();i++){\n diff = max(diff,points[i][0]-points[i-1][0]);\n }\n return diff;\n }\n};\n\n\n\n\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));\n int diff = 0;\n for (int i = 1; i < points.length; i++) {\n diff = Math.max(diff, points[i][0] - points[i - 1][0]);\n }\n return diff;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort()\n diff = 0\n for i in range(1, len(points)):\n diff = max(diff, points[i][0] - points[i - 1][0])\n return diff\n\n\n\n```\n```javascript []\nvar maxWidthOfVerticalArea = function(points) {\n points.sort((a, b) => a[0] - b[0]);\n let diff = 0;\n for (let i = 1; i < points.length; i++) {\n diff = Math.max(diff, points[i][0] - points[i - 1][0]);\n }\n return diff;\n};\n\n\n```\n\n---\n\n#### ***Approach 2(With Sets)***\n1. The function `maxWidthOfVerticalArea` takes a vector of vectors points representing coordinates.\n1. It utilizes a set `xCoordinates` to store unique x-coordinates from the input points.\n1. Iterates through each point, extracting its x-coordinate and inserts it into the set.\n1. Initializes variables `maxDiff` to keep track of the maximum difference between x-coordinates and `prevX` to hold the previous x-coordinate.\n1. Iterates through the set of x-coordinates:\n - Updates `maxDiff` by finding the maximum difference between the current x-coordinate and the previous x-coordinate.\n - Updates `prevX` with the current x-coordinate for the next iteration.\n1. Returns the `maxDiff`, which represents the maximum width of the vertical area.\n\n\n# Complexity\n- Time complexity:\n $$O(nlogn)$$\n \n\n- Space complexity:\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n set<int> xCoordinates; // Using a set to store unique x-coordinates\n \n for (const auto& point : points) {\n xCoordinates.insert(point[0]); // Inserting x-coordinates into the set\n }\n \n int maxDiff = 0;\n int prevX = INT_MIN;\n \n for (int x : xCoordinates) {\n if (prevX != INT_MIN) {\n maxDiff = max(maxDiff, x - prevX); // Calculate the maximum difference\n }\n prevX = x;\n }\n \n return maxDiff;\n }\n};\n\n\n\n```\n```Java []\n\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Set<Integer> xCoordinates = new TreeSet<>();\n \n for (int[] point : points) {\n xCoordinates.add(point[0]);\n }\n \n int maxDiff = 0;\n Integer prevX = null;\n \n for (int x : xCoordinates) {\n if (prevX != null) {\n maxDiff = Math.max(maxDiff, x - prevX);\n }\n prevX = x;\n }\n \n return maxDiff;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x_coordinates = sorted(set(point[0] for point in points))\n max_diff = 0\n prev_x = None\n \n for x in x_coordinates:\n if prev_x is not None:\n max_diff = max(max_diff, x - prev_x)\n prev_x = x\n \n return max_diff\n\n\n\n```\n```javascript []\n\nvar maxWidthOfVerticalArea = function(points) {\n let xCoordinates = new Set();\n \n for (let point of points) {\n xCoordinates.add(point[0]);\n }\n \n let maxDiff = 0;\n let prevX = null;\n \n for (let x of [...xCoordinates].sort((a, b) => a - b)) {\n if (prevX !== null) {\n maxDiff = Math.max(maxDiff, x - prevX);\n }\n prevX = x;\n }\n \n return maxDiff;\n};\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 39 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
✅☑Beats 100% || [C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n#### ***Approach 1(Sorting)***\n1. **Sorting Points:**\n\n- The function begins by sorting the `points` vector based on the x-coordinate of each point. This is done using `sort(points.begin(), points.end())`.\n1. **Calculating Maximum Width:**\n\n- It then iterates through the sorted points.\n- For each pair of consecutive points, it calculates the difference in x-coordinates (`points[i][0] - points[i-1][0]`).\n- It updates the `diff` variable to hold the maximum difference encountered while traversing the sorted points.\n1. **Returning the Maximum Width:**\n\n- Finally, it returns the maximum `diff`, which represents the maximum width between two consecutive x-coordinates among the sorted points.\n\n\n# Complexity\n- Time complexity:\n $$O(nlogn)$$\n \n\n- Space complexity:\n $$O(logn)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n sort(points.begin(),points.end());\n int diff =0;\n for(int i =1;i<points.size();i++){\n diff = max(diff,points[i][0]-points[i-1][0]);\n }\n return diff;\n }\n};\n\n\n\n\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));\n int diff = 0;\n for (int i = 1; i < points.length; i++) {\n diff = Math.max(diff, points[i][0] - points[i - 1][0]);\n }\n return diff;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort()\n diff = 0\n for i in range(1, len(points)):\n diff = max(diff, points[i][0] - points[i - 1][0])\n return diff\n\n\n\n```\n```javascript []\nvar maxWidthOfVerticalArea = function(points) {\n points.sort((a, b) => a[0] - b[0]);\n let diff = 0;\n for (let i = 1; i < points.length; i++) {\n diff = Math.max(diff, points[i][0] - points[i - 1][0]);\n }\n return diff;\n};\n\n\n```\n\n---\n\n#### ***Approach 2(With Sets)***\n1. The function `maxWidthOfVerticalArea` takes a vector of vectors points representing coordinates.\n1. It utilizes a set `xCoordinates` to store unique x-coordinates from the input points.\n1. Iterates through each point, extracting its x-coordinate and inserts it into the set.\n1. Initializes variables `maxDiff` to keep track of the maximum difference between x-coordinates and `prevX` to hold the previous x-coordinate.\n1. Iterates through the set of x-coordinates:\n - Updates `maxDiff` by finding the maximum difference between the current x-coordinate and the previous x-coordinate.\n - Updates `prevX` with the current x-coordinate for the next iteration.\n1. Returns the `maxDiff`, which represents the maximum width of the vertical area.\n\n\n# Complexity\n- Time complexity:\n $$O(nlogn)$$\n \n\n- Space complexity:\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n set<int> xCoordinates; // Using a set to store unique x-coordinates\n \n for (const auto& point : points) {\n xCoordinates.insert(point[0]); // Inserting x-coordinates into the set\n }\n \n int maxDiff = 0;\n int prevX = INT_MIN;\n \n for (int x : xCoordinates) {\n if (prevX != INT_MIN) {\n maxDiff = max(maxDiff, x - prevX); // Calculate the maximum difference\n }\n prevX = x;\n }\n \n return maxDiff;\n }\n};\n\n\n\n```\n```Java []\n\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Set<Integer> xCoordinates = new TreeSet<>();\n \n for (int[] point : points) {\n xCoordinates.add(point[0]);\n }\n \n int maxDiff = 0;\n Integer prevX = null;\n \n for (int x : xCoordinates) {\n if (prevX != null) {\n maxDiff = Math.max(maxDiff, x - prevX);\n }\n prevX = x;\n }\n \n return maxDiff;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x_coordinates = sorted(set(point[0] for point in points))\n max_diff = 0\n prev_x = None\n \n for x in x_coordinates:\n if prev_x is not None:\n max_diff = max(max_diff, x - prev_x)\n prev_x = x\n \n return max_diff\n\n\n\n```\n```javascript []\n\nvar maxWidthOfVerticalArea = function(points) {\n let xCoordinates = new Set();\n \n for (let point of points) {\n xCoordinates.add(point[0]);\n }\n \n let maxDiff = 0;\n let prevX = null;\n \n for (let x of [...xCoordinates].sort((a, b) => a - b)) {\n if (prevX !== null) {\n maxDiff = Math.max(maxDiff, x - prevX);\n }\n prevX = x;\n }\n \n return maxDiff;\n};\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 39 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
6 methods||Beats 100%||Python liners, C++ set/priority_queue/sort&adjacent_difference | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnly x-coordinate is important.\n\nUsing sorting is easy; a 2 line code for python\nThe 2nd Python code is also 2 line code which uses the matrix-transpose-like zip & beats 100% in speed.\n\nC++ has 3 solutions, not only uses sort, but also `set` & `priority_queue`.\n\nMy own Python 1-liner is made thanks to comments of @Sergei & @maria_q pointing out the solutions of @MikPosp\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince the constraints `0 <= xi, yi <= 10^9`, using counting sort is not possible. The normal sort is very useful.\n\nBesides the normal sorting, there are other methods:\n- ordered set (C++ set)\n- max Heap (C++ priority_queue )\n\nDue to implementation experience, the performance of priority_queue is superior to the one of set.\n\nThe C++ solutions drop out the info on y-coordinates.\nThe implementation using x-sort&adjacent_difference is the fast one.\n|Method|Elasped Time|speed record|Memory|\n|---|---|---|---|\n|C++ priority_queue|157 ms| 98.06%|67.26MB|\n|C++ set| 199 ms|79.19%|79.97MB|\n|C++ x-sort&adjacent_difference|121ms|99.68% |66.98MB| \n|Python sort|731 ms|84.94%|60.28MB|\n|Python sort+ sorted(list(zip(*points))[0])|677ms|100%|59.62MB\n|Python 1-liner|657ms|100%|60.03MB|\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n $$O(n\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Python 1-liner\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max([x1-x0 for x0, x1 in pairwise(sorted(list(zip(*points))[0]))])\n \n```\n# Python Code 2-liner using sorted\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x=[x0 for x0, _ in sorted(points)]\n return max([x[i+1]-x[i] for i in range(len(x)-1)])\n \n```\n# Python 2-line Code using sorted(list(zip(*points))[0]) 677ms Beats 100%\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x= sorted(list(zip(*points))[0])\n return max([x[i+1]-x[i] for i in range(len(x)-1)])\n \n```\n# C++ using Max Heap\uFF08priority_queue\uFF09157 ms Beats 98.06%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n priority_queue<int> pq;//Max heap\n for(auto& coord: points)\n pq.push(coord[0]);\n int mdiff=0, prev=pq.top();\n while(!pq.empty()){\n int curr=pq.top();\n pq.pop();\n mdiff=max(mdiff, prev-curr);\n prev=curr;\n }\n return mdiff; \n }\n};\n```\n# C++ using set\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n set<int> x;\n for(auto& coord: points)\n x.insert(coord[0]);\n int mdiff=0, prev=*x.begin();\n for (int x1: x){\n mdiff=max(mdiff, x1-prev);\n prev=x1;\n }\n return mdiff; \n }\n};\n\n```\n# C++ using x-sorting&adjacent_difference 121ms Beats 99.68%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n vector<int> x;\n for (auto& coord: points)\n x.push_back(coord[0]);\n sort(x.begin(), x.end());\n adjacent_difference(x.begin(), x.end(), x.begin());\n\n return *max_element(x.begin()+1, x.end()); \n }\n};\n```\n\n\n | 15 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
6 methods||Beats 100%||Python liners, C++ set/priority_queue/sort&adjacent_difference | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnly x-coordinate is important.\n\nUsing sorting is easy; a 2 line code for python\nThe 2nd Python code is also 2 line code which uses the matrix-transpose-like zip & beats 100% in speed.\n\nC++ has 3 solutions, not only uses sort, but also `set` & `priority_queue`.\n\nMy own Python 1-liner is made thanks to comments of @Sergei & @maria_q pointing out the solutions of @MikPosp\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince the constraints `0 <= xi, yi <= 10^9`, using counting sort is not possible. The normal sort is very useful.\n\nBesides the normal sorting, there are other methods:\n- ordered set (C++ set)\n- max Heap (C++ priority_queue )\n\nDue to implementation experience, the performance of priority_queue is superior to the one of set.\n\nThe C++ solutions drop out the info on y-coordinates.\nThe implementation using x-sort&adjacent_difference is the fast one.\n|Method|Elasped Time|speed record|Memory|\n|---|---|---|---|\n|C++ priority_queue|157 ms| 98.06%|67.26MB|\n|C++ set| 199 ms|79.19%|79.97MB|\n|C++ x-sort&adjacent_difference|121ms|99.68% |66.98MB| \n|Python sort|731 ms|84.94%|60.28MB|\n|Python sort+ sorted(list(zip(*points))[0])|677ms|100%|59.62MB\n|Python 1-liner|657ms|100%|60.03MB|\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n $$O(n\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Python 1-liner\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max([x1-x0 for x0, x1 in pairwise(sorted(list(zip(*points))[0]))])\n \n```\n# Python Code 2-liner using sorted\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x=[x0 for x0, _ in sorted(points)]\n return max([x[i+1]-x[i] for i in range(len(x)-1)])\n \n```\n# Python 2-line Code using sorted(list(zip(*points))[0]) 677ms Beats 100%\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x= sorted(list(zip(*points))[0])\n return max([x[i+1]-x[i] for i in range(len(x)-1)])\n \n```\n# C++ using Max Heap\uFF08priority_queue\uFF09157 ms Beats 98.06%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n priority_queue<int> pq;//Max heap\n for(auto& coord: points)\n pq.push(coord[0]);\n int mdiff=0, prev=pq.top();\n while(!pq.empty()){\n int curr=pq.top();\n pq.pop();\n mdiff=max(mdiff, prev-curr);\n prev=curr;\n }\n return mdiff; \n }\n};\n```\n# C++ using set\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n set<int> x;\n for(auto& coord: points)\n x.insert(coord[0]);\n int mdiff=0, prev=*x.begin();\n for (int x1: x){\n mdiff=max(mdiff, x1-prev);\n prev=x1;\n }\n return mdiff; \n }\n};\n\n```\n# C++ using x-sorting&adjacent_difference 121ms Beats 99.68%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n vector<int> x;\n for (auto& coord: points)\n x.push_back(coord[0]);\n sort(x.begin(), x.end());\n adjacent_difference(x.begin(), x.end(), x.begin());\n\n return *max_element(x.begin()+1, x.end()); \n }\n};\n```\n\n\n | 15 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Easy solution using sets || c++ || java || python | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nGiven the problem description, our focus is solely on the x coordinates, disregarding the y coordinates. In this context, we can efficiently address the issue by gathering and sorting all x coordinates, utilizing a set to eliminate duplicates. Subsequently, we can iterate through the sorted set, monitoring the maximum difference between adjacent points.\n\n# Complexity\n- Time complexity:\nThe dominant factor in the time complexity is the insertion of elements into the set (s.insert(i[0])), which takes O(log n) time for each element. If there are \'n\' elements, the overall time complexity becomes O(n log n).\n- Space complexity:\nThe set s stores the unique x-coordinates from the input points. In the worst case, all x-coordinates are distinct, and the set will have \'n\' elements, resulting in O(n) space complexity.\n```c++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n set<int> s;\n int res = 0;\n for (auto i : points)\n {\n s.insert(i[0]);\n }\n for (auto it = next(begin(s)); it != end(s); ++it)\n {\n res = max(res, *it - *prev(it));\n }\n return res;\n }\n};\n```\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points):\n s = set()\n res = 0\n for i in points:\n s.add(i[0])\n sorted_set = sorted(s)\n for i in range(1, len(sorted_set)):\n res = max(res, sorted_set[i] - sorted_set[i-1])\n return res\n\n```\n```java []\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Set<Integer> set = new HashSet<>();\n int res = 0;\n for (int[] point : points) {\n set.add(point[0]);\n }\n Integer[] sortedSet = set.toArray(new Integer[0]);\n Arrays.sort(sortedSet);\n for (int i = 1; i < sortedSet.length; i++) {\n res = Math.max(res, sortedSet[i] - sortedSet[i - 1]);\n }\n return res;\n }\n}\n```\n\n\n | 8 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Easy solution using sets || c++ || java || python | widest-vertical-area-between-two-points-containing-no-points | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nGiven the problem description, our focus is solely on the x coordinates, disregarding the y coordinates. In this context, we can efficiently address the issue by gathering and sorting all x coordinates, utilizing a set to eliminate duplicates. Subsequently, we can iterate through the sorted set, monitoring the maximum difference between adjacent points.\n\n# Complexity\n- Time complexity:\nThe dominant factor in the time complexity is the insertion of elements into the set (s.insert(i[0])), which takes O(log n) time for each element. If there are \'n\' elements, the overall time complexity becomes O(n log n).\n- Space complexity:\nThe set s stores the unique x-coordinates from the input points. In the worst case, all x-coordinates are distinct, and the set will have \'n\' elements, resulting in O(n) space complexity.\n```c++ []\nclass Solution {\npublic:\n int maxWidthOfVerticalArea(vector<vector<int>>& points) {\n set<int> s;\n int res = 0;\n for (auto i : points)\n {\n s.insert(i[0]);\n }\n for (auto it = next(begin(s)); it != end(s); ++it)\n {\n res = max(res, *it - *prev(it));\n }\n return res;\n }\n};\n```\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points):\n s = set()\n res = 0\n for i in points:\n s.add(i[0])\n sorted_set = sorted(s)\n for i in range(1, len(sorted_set)):\n res = max(res, sorted_set[i] - sorted_set[i-1])\n return res\n\n```\n```java []\nclass Solution {\n public int maxWidthOfVerticalArea(int[][] points) {\n Set<Integer> set = new HashSet<>();\n int res = 0;\n for (int[] point : points) {\n set.add(point[0]);\n }\n Integer[] sortedSet = set.toArray(new Integer[0]);\n Arrays.sort(sortedSet);\n for (int i = 1; i < sortedSet.length; i++) {\n res = Math.max(res, sortedSet[i] - sortedSet[i - 1]);\n }\n return res;\n }\n}\n```\n\n\n | 8 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
✅Python || Beats 100% Runtime | 99.58% Memory | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | \n# What is the Problem \n- Problem nature: The problem involves finding the maximum width of a vertical area formed by points on a 2D plane.\n- Key insight: The widths of vertical areas are determined solely by the differences in x-coordinates of points.\n- Focus on x-coordinates: We can focus on extracting and sorting the x-coordinates to efficiently calculate the widths.\n\n\n# What we do\n1. Extract and sort x-coordinates:\n - Obtain a list of x-coordinates from the input points.\n - Sort the x-coordinates in descending order to ensure consecutive points form vertical areas.\n2. Calculate widths:\n - Iterate through the sorted x-coordinates, calculating the difference between consecutive values to obtain the widths of vertical areas.\n4. Find maximum width:\n - Return the maximum width found among all calculated widths.\n\n# Complexity\n- Time complexity:\n - Both solutions have a time complexity of $$O(n\\ log\\ n)$$, primarily due to the sorting operation.\n- Space complexity:\n - The first solution has a space complexity of $O(n)$ due to the additional memo list.\n - The second solution optimizes space usage to $O(1)$ by modifying the input list directly.\n\n# Code\n\n\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n (memo := [i[0] for i in points]).sort(reverse= True)\n\n return max(memo[i-1] - memo[i]for i in range(1, len(memo)))\n```\n\n# Memory Optimized version ->\n\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n\n for ind, val in enumerate(points):\n points[ind] = val[0]\n points.sort(reverse=True)\n\n for i in range(1, len(points)):\n points[i-1] = points[i-1] - points[i]\n \n return max(points[:-1])\n```\n\n# Upvote pl\n\n\n\n | 3 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
✅Python || Beats 100% Runtime | 99.58% Memory | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | \n# What is the Problem \n- Problem nature: The problem involves finding the maximum width of a vertical area formed by points on a 2D plane.\n- Key insight: The widths of vertical areas are determined solely by the differences in x-coordinates of points.\n- Focus on x-coordinates: We can focus on extracting and sorting the x-coordinates to efficiently calculate the widths.\n\n\n# What we do\n1. Extract and sort x-coordinates:\n - Obtain a list of x-coordinates from the input points.\n - Sort the x-coordinates in descending order to ensure consecutive points form vertical areas.\n2. Calculate widths:\n - Iterate through the sorted x-coordinates, calculating the difference between consecutive values to obtain the widths of vertical areas.\n4. Find maximum width:\n - Return the maximum width found among all calculated widths.\n\n# Complexity\n- Time complexity:\n - Both solutions have a time complexity of $$O(n\\ log\\ n)$$, primarily due to the sorting operation.\n- Space complexity:\n - The first solution has a space complexity of $O(n)$ due to the additional memo list.\n - The second solution optimizes space usage to $O(1)$ by modifying the input list directly.\n\n# Code\n\n\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n (memo := [i[0] for i in points]).sort(reverse= True)\n\n return max(memo[i-1] - memo[i]for i in range(1, len(memo)))\n```\n\n# Memory Optimized version ->\n\n\n```python []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n\n for ind, val in enumerate(points):\n points[ind] = val[0]\n points.sort(reverse=True)\n\n for i in range(1, len(points)):\n points[i-1] = points[i-1] - points[i]\n \n return max(points[:-1])\n```\n\n# Upvote pl\n\n\n\n | 3 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
✅ One Line Solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Code #1 - The Most Concise\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max(b-a for (a,_),(b,_) in pairwise(sorted(points)))\n```\n\n# Code #2\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max(starmap(sub, pairwise(sorted(next(zip(*points)))[::-1])))\n```\n\n# Code #3\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return (p:=sorted(points)) and max(b-a for (a,_),(b,_) in zip(p, p[1:]))\n``` | 4 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
✅ One Line Solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Code #1 - The Most Concise\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max(b-a for (a,_),(b,_) in pairwise(sorted(points)))\n```\n\n# Code #2\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max(starmap(sub, pairwise(sorted(next(zip(*points)))[::-1])))\n```\n\n# Code #3\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return (p:=sorted(points)) and max(b-a for (a,_),(b,_) in zip(p, p[1:]))\n``` | 4 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Python3 Soltion | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | \n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort()\n n=len(points)\n ans=0\n for i in range(1,n):\n ans=max(ans,(points[i][0]-points[i-1][0]))\n return ans \n \n``` | 3 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Python3 Soltion | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | \n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort()\n n=len(points)\n ans=0\n for i in range(1,n):\n ans=max(ans,(points[i][0]-points[i-1][0]))\n return ans \n \n``` | 3 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
[We💕Simple] One Liner! (Beat 100%) | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | ``` Kotlin []\nclass Solution {\n fun maxWidthOfVerticalArea(points: Array<IntArray>): Int =\n points.map { it[0] }.sorted().zipWithNext { a, b -> b - a }.max()\n}\n```\n.\n``` Python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max([\n y-x\n for x,y in pairwise(sorted(p[0] for p in points))\n ])\n``` | 2 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
[We💕Simple] One Liner! (Beat 100%) | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | ``` Kotlin []\nclass Solution {\n fun maxWidthOfVerticalArea(points: Array<IntArray>): Int =\n points.map { it[0] }.sorted().zipWithNext { a, b -> b - a }.max()\n}\n```\n.\n``` Python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max([\n y-x\n for x,y in pairwise(sorted(p[0] for p in points))\n ])\n``` | 2 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Normal Approach to problem solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs per given question, whatever the value of y-coordinate we need the maxwidth/max difference between x-coordinates so that no other x-coordinate in between those points.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we create a new list to store all the x-coordinates.\nSort it and then assume max width is in between first two x-coordinates and Run a loop until size(x-coordinates array)-1 by checking any where i and i+1 x-coordinate diff is less or more than our maxwidth.\nYou can understand by seeing the code!\nThank You... \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n a=[]\n for i in points:\n a.append(i[0])\n a.sort()\n maxwidth=a[1]-a[0]\n for i in range(2,len(a)-1):\n if maxwidth<a[i+1]-a[i]:\n maxwidth=a[i+1]-a[i]\n return maxwidth\n\n\n \n\n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Normal Approach to problem solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs per given question, whatever the value of y-coordinate we need the maxwidth/max difference between x-coordinates so that no other x-coordinate in between those points.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we create a new list to store all the x-coordinates.\nSort it and then assume max width is in between first two x-coordinates and Run a loop until size(x-coordinates array)-1 by checking any where i and i+1 x-coordinate diff is less or more than our maxwidth.\nYou can understand by seeing the code!\nThank You... \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n a=[]\n for i in points:\n a.append(i[0])\n a.sort()\n maxwidth=a[1]-a[0]\n for i in range(2,len(a)-1):\n if maxwidth<a[i+1]-a[i]:\n maxwidth=a[i+1]-a[i]\n return maxwidth\n\n\n \n\n``` | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Easy approach // Beat 100% user | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n l=[]\n for i in range(len(points)):\n l.append(points[i][0])\n l.sort()\n if(len(l)==0 or len(l)==1):\n return 0\n c=0\n for i in range(len(l)-1,0,-1):\n d=l[i]-l[i-1]\n if(c<d):\n c=d\n return c\n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Easy approach // Beat 100% user | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n l=[]\n for i in range(len(points)):\n l.append(points[i][0])\n l.sort()\n if(len(l)==0 or len(l)==1):\n return 0\n c=0\n for i in range(len(l)-1,0,-1):\n d=l[i]-l[i-1]\n if(c<d):\n c=d\n return c\n``` | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Fastest Python Solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFaster than 100% of solutions. We can reword the question to find the maximum distance between two adjacent points\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince we have to find max distance between 2 points, the y co-ordinate doesnt matter. The question mentions to not worry about the ht of points or abt the y co-ordinate. \n\nSince we dont need the y co-ordinates, we will only take into account the x co-ordinates. \n\n1) Create an array with only x co-ordinates\n2) Sort them, because in a graph all values are sorted. \n3) Iterate over the x co-ordinate array and find the difference between successive elements. \n4) Take the highest difference and return it.\n\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe sorting takes O(n log n) and the loop takes O(n) time. Using that we get O(n log n + n), which if solved further will become O(n log (n+1)), since we only consider n, we get O(n log n) as time complexity\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n\n x_cor = [i for i,j in points]\n\n x_cor.sort()\n ans = 0\n\n for i in range(len(x_cor)-1):\n if ans < x_cor[i+1] - x_cor[i]:\n ans = x_cor[i+1] - x_cor[i] \n return ans\n \n```\n# Line by Line code explanation\n\n```\nx_cor = [i for i,j in points]\n\n```\n\nIn this we make use of list comprehension. In the above line we add i to the array. Since points is an 2D array having only 2 element in the inside array, we can make use tuple unpacking to get co-ordinates. \n\nUsing for i,j in points, we get the 2 co-ordinates present in the 1st sub array. Since the 1st co-ordinate will be x, i will represent x co-ordinate and j will represent y. \n\n\n```\nx_cor.sort()\n```\nSorting the x_cor we will get the co-ordinates in the same order as an typical graph. A graph has sorted values in the ascending order. \nSorting it will give an clear picture of who is the neighbour.\n\n```\nans = 0\n\nfor i in range(len(x_cor)-1):\n if ans < x_cor[i+1] - x_cor[i]:\n ans = x_cor[i+1] - x_cor[i]\n```\nIn this, we intialize a variable with value 0. Then we iterate over the array x_cor. Taking `len(x_cor)-1`, as we are making use of the present element and the successive element. \n\nWhen the loop will reacht the last element, it will try to compare the last element and the element after that, which doesnt exist. Hence we will get an array. \n\nUsing `len(x_cor)-1`, we will iterate till only the second last element. The second last and last element will operated on. | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Fastest Python Solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFaster than 100% of solutions. We can reword the question to find the maximum distance between two adjacent points\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince we have to find max distance between 2 points, the y co-ordinate doesnt matter. The question mentions to not worry about the ht of points or abt the y co-ordinate. \n\nSince we dont need the y co-ordinates, we will only take into account the x co-ordinates. \n\n1) Create an array with only x co-ordinates\n2) Sort them, because in a graph all values are sorted. \n3) Iterate over the x co-ordinate array and find the difference between successive elements. \n4) Take the highest difference and return it.\n\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe sorting takes O(n log n) and the loop takes O(n) time. Using that we get O(n log n + n), which if solved further will become O(n log (n+1)), since we only consider n, we get O(n log n) as time complexity\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n\n x_cor = [i for i,j in points]\n\n x_cor.sort()\n ans = 0\n\n for i in range(len(x_cor)-1):\n if ans < x_cor[i+1] - x_cor[i]:\n ans = x_cor[i+1] - x_cor[i] \n return ans\n \n```\n# Line by Line code explanation\n\n```\nx_cor = [i for i,j in points]\n\n```\n\nIn this we make use of list comprehension. In the above line we add i to the array. Since points is an 2D array having only 2 element in the inside array, we can make use tuple unpacking to get co-ordinates. \n\nUsing for i,j in points, we get the 2 co-ordinates present in the 1st sub array. Since the 1st co-ordinate will be x, i will represent x co-ordinate and j will represent y. \n\n\n```\nx_cor.sort()\n```\nSorting the x_cor we will get the co-ordinates in the same order as an typical graph. A graph has sorted values in the ascending order. \nSorting it will give an clear picture of who is the neighbour.\n\n```\nans = 0\n\nfor i in range(len(x_cor)-1):\n if ans < x_cor[i+1] - x_cor[i]:\n ans = x_cor[i+1] - x_cor[i]\n```\nIn this, we intialize a variable with value 0. Then we iterate over the array x_cor. Taking `len(x_cor)-1`, as we are making use of the present element and the successive element. \n\nWhen the loop will reacht the last element, it will try to compare the last element and the element after that, which doesnt exist. Hence we will get an array. \n\nUsing `len(x_cor)-1`, we will iterate till only the second last element. The second last and last element will operated on. | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Easy python solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\nto be consistent in leetcode\n\n# Approach\nused sorting,difference and iterative method\n\n# Complexity\n- beats 100% users in python by time\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n60.5 MB\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n l=len(points)\n print(l)\n s=[]\n for i in range(len(points)):\n s.append(points[i][0])\n s.sort()\n c=0\n for i in range(1,l):\n d=s[i]-s[i-1]\n if(c<d):\n c=d\n return c\n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Easy python solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\nto be consistent in leetcode\n\n# Approach\nused sorting,difference and iterative method\n\n# Complexity\n- beats 100% users in python by time\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n60.5 MB\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n l=len(points)\n print(l)\n s=[]\n for i in range(len(points)):\n s.append(points[i][0])\n s.sort()\n c=0\n for i in range(1,l):\n d=s[i]-s[i-1]\n if(c<d):\n c=d\n return c\n``` | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
✅ 100% SPEED SOLUTION IN 1 LINE! 😲😲 | FROM USERS 🐋 TO USERS 🐳 | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O (n*log(n))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max(cur - prev for prev, cur in pairwise(sorted([point[0] for point in points])))\n \n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
✅ 100% SPEED SOLUTION IN 1 LINE! 😲😲 | FROM USERS 🐋 TO USERS 🐳 | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O (n*log(n))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n return max(cur - prev for prev, cur in pairwise(sorted([point[0] for point in points])))\n \n``` | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
PYTHON3 SOLUTION | RUNTIME BEATS 100% 🐍 | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe just have to find the width of the widest area. Because of the infinite height, the y coordinates can be ignored.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can find the width simply by subtracting two x coordinates.\nWhile finding the maximum pair, we have to make sure that no other numbers are between them.\nHence, we sort the x coordinates.\nNow, we can say that there are no elements between any two adjacent coordinates\nThe maximum difference between any two adjacent elements is our answer.\n\n# Code\n```python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x = sorted([i for i, j in points]) # stores only x coordinates in sorted order\n ans = 0\n for i in range(1, len(x)):\n ans = max(ans, x[i] - x[i - 1]) # ans will be the max distance between any two coordinates\n return ans\n```\n\nHope this helped you :) | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
PYTHON3 SOLUTION | RUNTIME BEATS 100% 🐍 | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe just have to find the width of the widest area. Because of the infinite height, the y coordinates can be ignored.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can find the width simply by subtracting two x coordinates.\nWhile finding the maximum pair, we have to make sure that no other numbers are between them.\nHence, we sort the x coordinates.\nNow, we can say that there are no elements between any two adjacent coordinates\nThe maximum difference between any two adjacent elements is our answer.\n\n# Code\n```python3 []\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n x = sorted([i for i, j in points]) # stores only x coordinates in sorted order\n ans = 0\n for i in range(1, len(x)):\n ans = max(ans, x[i] - x[i - 1]) # ans will be the max distance between any two coordinates\n return ans\n```\n\nHope this helped you :) | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
My Solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | Given n points on a 2D plane where points[i] = [xi, yi], Return the widest vertical area between two points such that no points are inside the area.\n\nA vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.\n\nNote that points on the edge of a vertical area are not considered included in the area.\n\n \n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: x[0])\n maxi=float(\'-inf\')\n for i in range(len(points)-1):\n maxi=max(abs(points[i+1][0]-points[i][0]),maxi)\n\n return maxi\n\n \n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
My Solution | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | Given n points on a 2D plane where points[i] = [xi, yi], Return the widest vertical area between two points such that no points are inside the area.\n\nA vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.\n\nNote that points on the edge of a vertical area are not considered included in the area.\n\n \n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n points.sort(key=lambda x: x[0])\n maxi=float(\'-inf\')\n for i in range(len(points)-1):\n maxi=max(abs(points[i+1][0]-points[i][0]),maxi)\n\n return maxi\n\n \n``` | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.