title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Easy Solution || A Sorting Approach || Python || Beats 100% | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # BEATS\n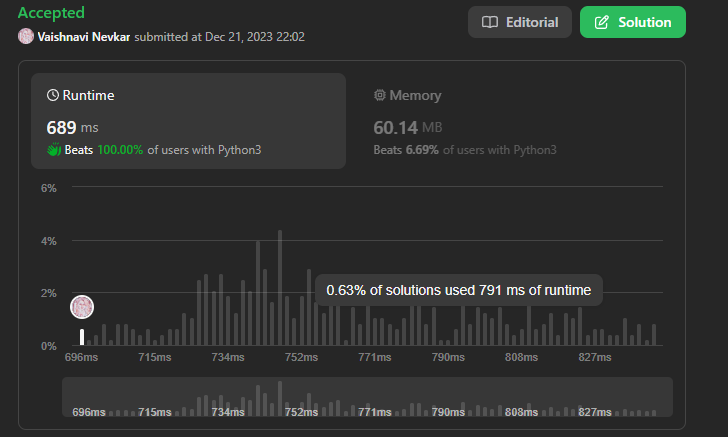\n\n\n# Intuition\nThe problem involves finding the widest vertical area between two points without including any points within the area. Since the goal is to maximize the width, it\'s essential to consider the x-coordinates of the given points. The intuition is to sort these x-coordinates and then find the maximum difference between consecutive elements.\n\n# Approach\n1. **Extract X-coordinates:** Start by extracting the x-coordinates of the given points and store them in an array.\n2. **Sort the Array:** Sort the array of x-coordinates to have them in ascending order.\n3. **Calculate Differences:** Iterate through the sorted array and calculate the differences between consecutive x-coordinates. Store these differences in another array.\n4. **Find Maximum Difference:** Sort the array of differences and return the maximum difference, as it represents the widest vertical area.\n\n# Complexity\n- **Time complexity:** The time complexity is dominated by the sorting step, which is O(n log n), where n is the number of points.\n- **Space complexity:** The space complexity is O(n), where n is the number of points, as we use additional arrays to store x-coordinates and differences.\n\nThis approach ensures an efficient way to find the widest vertical area by leveraging the sorted order of x-coordinates.\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n k=[]\n for i in points:\n k.append(i[0])\n k.sort()\n l=[]\n for i in range(len(k)-1):\n l.append(k[i+1]-k[i])\n l.sort()\n return l[-1]\n``` | 1 | Given `n` `points` on a 2D plane where `points[i] = [xi, yi]`, Return _the **widest vertical area** between two points such that no points are inside the area._
A **vertical area** is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The **widest vertical area** is the one with the maximum width.
Note that points **on the edge** of a vertical area **are not** considered included in the area.
**Example 1:**
**Input:** points = \[\[8,7\],\[9,9\],\[7,4\],\[9,7\]\]
**Output:** 1
**Explanation:** Both the red and the blue area are optimal.
**Example 2:**
**Input:** points = \[\[3,1\],\[9,0\],\[1,0\],\[1,4\],\[5,3\],\[8,8\]\]
**Output:** 3
**Constraints:**
* `n == points.length`
* `2 <= n <= 105`
* `points[i].length == 2`
* `0 <= xi, yi <= 109` | Use dynamic programming. The state of the DP can be the current index and the remaining characters to delete. Having a prefix sum for each character can help you determine for a certain character c in some specific range, how many characters you need to delete to merge all occurrences of c in that range. |
Easy Solution || A Sorting Approach || Python || Beats 100% | widest-vertical-area-between-two-points-containing-no-points | 0 | 1 | # BEATS\n\n\n\n# Intuition\nThe problem involves finding the widest vertical area between two points without including any points within the area. Since the goal is to maximize the width, it\'s essential to consider the x-coordinates of the given points. The intuition is to sort these x-coordinates and then find the maximum difference between consecutive elements.\n\n# Approach\n1. **Extract X-coordinates:** Start by extracting the x-coordinates of the given points and store them in an array.\n2. **Sort the Array:** Sort the array of x-coordinates to have them in ascending order.\n3. **Calculate Differences:** Iterate through the sorted array and calculate the differences between consecutive x-coordinates. Store these differences in another array.\n4. **Find Maximum Difference:** Sort the array of differences and return the maximum difference, as it represents the widest vertical area.\n\n# Complexity\n- **Time complexity:** The time complexity is dominated by the sorting step, which is O(n log n), where n is the number of points.\n- **Space complexity:** The space complexity is O(n), where n is the number of points, as we use additional arrays to store x-coordinates and differences.\n\nThis approach ensures an efficient way to find the widest vertical area by leveraging the sorted order of x-coordinates.\n\n# Code\n```\nclass Solution:\n def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:\n k=[]\n for i in points:\n k.append(i[0])\n k.sort()\n l=[]\n for i in range(len(k)-1):\n l.append(k[i+1]-k[i])\n l.sort()\n return l[-1]\n``` | 1 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
97% TC and 95% SC easy python solution with explanation | count-substrings-that-differ-by-one-character | 0 | 1 | Believe me, this ques is like must to have in the mind, as this gonna help you solve many such questions.\n1. We have to calculate all substrings which differ by just a character.\n2. So, maintain 2 states, first one will be for the count of substrings which is present in "t" string as well(all characters equal). The second one will keep the count with 1 different character.\n3. Traverse the 2 strings using 2 pointers using 2 loops. If the char which are being pointed are same, which means we will have our ans from already differed strings, which already have a character different. So just use that.\n4. If they are different, then go for all the strings which have all the characters same, because the current is gonna be a different one.\n5. Now just keep maintaining these 2 states for all the indices.\n6. Didn\'t get it, read it for 3-4 times atleast. And you\'re free to comment down :)\n```\ndef countSubstrings(self, s: str, t: str) -> int:\n\tls, lt = len(s), len(t)\n\tequal_prev, unequal_prev = [0] * (lt+1), [0] * (lt+1)\n\tans = 0\n\tfor i in range(ls):\n\t\tequal_curr, unequal_curr = [0] * (lt+1), [0] * (lt+1)\n\t\tfor j in range(lt):\n\t\t\tif(s[i] == t[j]):\n\t\t\t\tequal_curr[j+1] = 1+equal_prev[j]\n\t\t\tunequal_curr[j+1] = 1+equal_prev[j] if(s[i] != t[j]) else unequal_prev[j]\n\t\t\tans += unequal_curr[j+1]\n\t\tequal_prev, unequal_prev = equal_curr, unequal_curr\n\treturn ans\n``` | 6 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
97% TC and 95% SC easy python solution with explanation | count-substrings-that-differ-by-one-character | 0 | 1 | Believe me, this ques is like must to have in the mind, as this gonna help you solve many such questions.\n1. We have to calculate all substrings which differ by just a character.\n2. So, maintain 2 states, first one will be for the count of substrings which is present in "t" string as well(all characters equal). The second one will keep the count with 1 different character.\n3. Traverse the 2 strings using 2 pointers using 2 loops. If the char which are being pointed are same, which means we will have our ans from already differed strings, which already have a character different. So just use that.\n4. If they are different, then go for all the strings which have all the characters same, because the current is gonna be a different one.\n5. Now just keep maintaining these 2 states for all the indices.\n6. Didn\'t get it, read it for 3-4 times atleast. And you\'re free to comment down :)\n```\ndef countSubstrings(self, s: str, t: str) -> int:\n\tls, lt = len(s), len(t)\n\tequal_prev, unequal_prev = [0] * (lt+1), [0] * (lt+1)\n\tans = 0\n\tfor i in range(ls):\n\t\tequal_curr, unequal_curr = [0] * (lt+1), [0] * (lt+1)\n\t\tfor j in range(lt):\n\t\t\tif(s[i] == t[j]):\n\t\t\t\tequal_curr[j+1] = 1+equal_prev[j]\n\t\t\tunequal_curr[j+1] = 1+equal_prev[j] if(s[i] != t[j]) else unequal_prev[j]\n\t\t\tans += unequal_curr[j+1]\n\t\tequal_prev, unequal_prev = equal_curr, unequal_curr\n\treturn ans\n``` | 6 | There is an integer array `nums` that consists of `n` **unique** elements, but you have forgotten it. However, you do remember every pair of adjacent elements in `nums`.
You are given a 2D integer array `adjacentPairs` of size `n - 1` where each `adjacentPairs[i] = [ui, vi]` indicates that the elements `ui` and `vi` are adjacent in `nums`.
It is guaranteed that every adjacent pair of elements `nums[i]` and `nums[i+1]` will exist in `adjacentPairs`, either as `[nums[i], nums[i+1]]` or `[nums[i+1], nums[i]]`. The pairs can appear **in any order**.
Return _the original array_ `nums`_. If there are multiple solutions, return **any of them**_.
**Example 1:**
**Input:** adjacentPairs = \[\[2,1\],\[3,4\],\[3,2\]\]
**Output:** \[1,2,3,4\]
**Explanation:** This array has all its adjacent pairs in adjacentPairs.
Notice that adjacentPairs\[i\] may not be in left-to-right order.
**Example 2:**
**Input:** adjacentPairs = \[\[4,-2\],\[1,4\],\[-3,1\]\]
**Output:** \[-2,4,1,-3\]
**Explanation:** There can be negative numbers.
Another solution is \[-3,1,4,-2\], which would also be accepted.
**Example 3:**
**Input:** adjacentPairs = \[\[100000,-100000\]\]
**Output:** \[100000,-100000\]
**Constraints:**
* `nums.length == n`
* `adjacentPairs.length == n - 1`
* `adjacentPairs[i].length == 2`
* `2 <= n <= 105`
* `-105 <= nums[i], ui, vi <= 105`
* There exists some `nums` that has `adjacentPairs` as its pairs. | Take every substring of s, change a character, and see how many substrings of t match that substring. Use a Trie to store all substrings of t as a dictionary. |
Python (Simple DP) | count-substrings-that-differ-by-one-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s, t):\n n, m = len(s), len(t)\n\n match = [[0 for _ in range(m+1)] for _ in range(n+1)]\n matchone = [[0 for _ in range(m+1)] for _ in range(n+1)]\n\n for i in range(1,n+1):\n for j in range(1,m+1):\n if s[i-1] == t[j-1]:\n match[i][j] = 1 + match[i-1][j-1]\n matchone[i][j] = matchone[i-1][j-1]\n else:\n match[i][j] = 0\n matchone[i][j] = 1 + match[i-1][j-1]\n\n return sum([sum(i) for i in matchone])\n\n\n \n \n``` | 1 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python (Simple DP) | count-substrings-that-differ-by-one-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s, t):\n n, m = len(s), len(t)\n\n match = [[0 for _ in range(m+1)] for _ in range(n+1)]\n matchone = [[0 for _ in range(m+1)] for _ in range(n+1)]\n\n for i in range(1,n+1):\n for j in range(1,m+1):\n if s[i-1] == t[j-1]:\n match[i][j] = 1 + match[i-1][j-1]\n matchone[i][j] = matchone[i-1][j-1]\n else:\n match[i][j] = 0\n matchone[i][j] = 1 + match[i-1][j-1]\n\n return sum([sum(i) for i in matchone])\n\n\n \n \n``` | 1 | There is an integer array `nums` that consists of `n` **unique** elements, but you have forgotten it. However, you do remember every pair of adjacent elements in `nums`.
You are given a 2D integer array `adjacentPairs` of size `n - 1` where each `adjacentPairs[i] = [ui, vi]` indicates that the elements `ui` and `vi` are adjacent in `nums`.
It is guaranteed that every adjacent pair of elements `nums[i]` and `nums[i+1]` will exist in `adjacentPairs`, either as `[nums[i], nums[i+1]]` or `[nums[i+1], nums[i]]`. The pairs can appear **in any order**.
Return _the original array_ `nums`_. If there are multiple solutions, return **any of them**_.
**Example 1:**
**Input:** adjacentPairs = \[\[2,1\],\[3,4\],\[3,2\]\]
**Output:** \[1,2,3,4\]
**Explanation:** This array has all its adjacent pairs in adjacentPairs.
Notice that adjacentPairs\[i\] may not be in left-to-right order.
**Example 2:**
**Input:** adjacentPairs = \[\[4,-2\],\[1,4\],\[-3,1\]\]
**Output:** \[-2,4,1,-3\]
**Explanation:** There can be negative numbers.
Another solution is \[-3,1,4,-2\], which would also be accepted.
**Example 3:**
**Input:** adjacentPairs = \[\[100000,-100000\]\]
**Output:** \[100000,-100000\]
**Constraints:**
* `nums.length == n`
* `adjacentPairs.length == n - 1`
* `adjacentPairs[i].length == 2`
* `2 <= n <= 105`
* `-105 <= nums[i], ui, vi <= 105`
* There exists some `nums` that has `adjacentPairs` as its pairs. | Take every substring of s, change a character, and see how many substrings of t match that substring. Use a Trie to store all substrings of t as a dictionary. |
Python3 solution with explanations | count-substrings-that-differ-by-one-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nxayy, xxbyy differs with two prefixing chars, and two suffixing chars\ntotal number of substrings that differs with one char is 9:\nwe could pick 0,1,2 x from left, and 1,2,3 chars from ayy\nso the 3 times 3 equals 9\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str, t: str) -> int:\n # xxayy, xxbyy differs with two prefixing chars, and two suffixing chars\n # total number of substrings that differs with one char is 9:\n # we could pick 0,1,2 x from left, and 1,2,3 chars from ayy\n # so the 3 times 3 equals 9\n\n # Therefore, we could precompute two arrays dpl[][], dpr[][]\n # dpl is the number of same chars on the left, for s[i] and t[j]\n # dpr is the number of same cahrs on the right, for s[i] and t[j]\n # dpl[i][j] = dpl[i-1][j-1] + 1 if s[i] == t[j], else 0\n # dpr[i][j] = dpr[i+1][j+1] + 1 if s[i] == t[j], else 0\n # to get the answer, we need to sum all (dpl+1)(dpr+1)\n dpl = [[0 for y in range(len(t))] for x in range(len(s))]\n dpr = [[0 for y in range(len(t))] for x in range(len(s))]\n\n # Initialze dpl, dpr\n for i in range(len(s)):\n for j in range(len(t)):\n if i != 0 and j != 0:\n dpl[i][j] = dpl[i-1][j-1] + 1 if s[i-1] == t[j-1] else 0\n \n for i in range(len(s)-1, -1, -1):\n for j in range(len(t)-1, -1, -1):\n if i != len(s) - 1 and j != len(t) - 1:\n dpr[i][j] = dpr[i+1][j+1] + 1 if s[i+1] == t[j+1] else 0\n cnt = 0\n for i in range(len(s)):\n for j in range(len(t)):\n if s[i] != t[j]:\n lop = dpl[i][j] + 1\n rop = dpr[i][j] + 1\n cnt += lop * rop \n \n return cnt\n \n \n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python3 solution with explanations | count-substrings-that-differ-by-one-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nxayy, xxbyy differs with two prefixing chars, and two suffixing chars\ntotal number of substrings that differs with one char is 9:\nwe could pick 0,1,2 x from left, and 1,2,3 chars from ayy\nso the 3 times 3 equals 9\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def countSubstrings(self, s: str, t: str) -> int:\n # xxayy, xxbyy differs with two prefixing chars, and two suffixing chars\n # total number of substrings that differs with one char is 9:\n # we could pick 0,1,2 x from left, and 1,2,3 chars from ayy\n # so the 3 times 3 equals 9\n\n # Therefore, we could precompute two arrays dpl[][], dpr[][]\n # dpl is the number of same chars on the left, for s[i] and t[j]\n # dpr is the number of same cahrs on the right, for s[i] and t[j]\n # dpl[i][j] = dpl[i-1][j-1] + 1 if s[i] == t[j], else 0\n # dpr[i][j] = dpr[i+1][j+1] + 1 if s[i] == t[j], else 0\n # to get the answer, we need to sum all (dpl+1)(dpr+1)\n dpl = [[0 for y in range(len(t))] for x in range(len(s))]\n dpr = [[0 for y in range(len(t))] for x in range(len(s))]\n\n # Initialze dpl, dpr\n for i in range(len(s)):\n for j in range(len(t)):\n if i != 0 and j != 0:\n dpl[i][j] = dpl[i-1][j-1] + 1 if s[i-1] == t[j-1] else 0\n \n for i in range(len(s)-1, -1, -1):\n for j in range(len(t)-1, -1, -1):\n if i != len(s) - 1 and j != len(t) - 1:\n dpr[i][j] = dpr[i+1][j+1] + 1 if s[i+1] == t[j+1] else 0\n cnt = 0\n for i in range(len(s)):\n for j in range(len(t)):\n if s[i] != t[j]:\n lop = dpl[i][j] + 1\n rop = dpr[i][j] + 1\n cnt += lop * rop \n \n return cnt\n \n \n``` | 0 | There is an integer array `nums` that consists of `n` **unique** elements, but you have forgotten it. However, you do remember every pair of adjacent elements in `nums`.
You are given a 2D integer array `adjacentPairs` of size `n - 1` where each `adjacentPairs[i] = [ui, vi]` indicates that the elements `ui` and `vi` are adjacent in `nums`.
It is guaranteed that every adjacent pair of elements `nums[i]` and `nums[i+1]` will exist in `adjacentPairs`, either as `[nums[i], nums[i+1]]` or `[nums[i+1], nums[i]]`. The pairs can appear **in any order**.
Return _the original array_ `nums`_. If there are multiple solutions, return **any of them**_.
**Example 1:**
**Input:** adjacentPairs = \[\[2,1\],\[3,4\],\[3,2\]\]
**Output:** \[1,2,3,4\]
**Explanation:** This array has all its adjacent pairs in adjacentPairs.
Notice that adjacentPairs\[i\] may not be in left-to-right order.
**Example 2:**
**Input:** adjacentPairs = \[\[4,-2\],\[1,4\],\[-3,1\]\]
**Output:** \[-2,4,1,-3\]
**Explanation:** There can be negative numbers.
Another solution is \[-3,1,4,-2\], which would also be accepted.
**Example 3:**
**Input:** adjacentPairs = \[\[100000,-100000\]\]
**Output:** \[100000,-100000\]
**Constraints:**
* `nums.length == n`
* `adjacentPairs.length == n - 1`
* `adjacentPairs[i].length == 2`
* `2 <= n <= 105`
* `-105 <= nums[i], ui, vi <= 105`
* There exists some `nums` that has `adjacentPairs` as its pairs. | Take every substring of s, change a character, and see how many substrings of t match that substring. Use a Trie to store all substrings of t as a dictionary. |
Python3 Dynamic Programming O(n^2) Runtime + Space | count-substrings-that-differ-by-one-character | 0 | 1 | # Code\n```\nclass Solution:\n\n def countSubstrings(self, s: str, t: str) -> int:\n\n m, n = len(s), len(t)\n \n # O(n^2) space\n left = [[0] * (n+1) for _ in range(m+1)]\n right = [[0] * (n+1) for _ in range(m+1)]\n\n for i in range(m):\n for j in range(n):\n if s[i] == t[j]:\n left[i+1][j+1] = 1 + left[i][j]\n\n for i in range(m - 1, -1, -1):\n for j in range(n - 1, -1, -1):\n if s[i] == t[j]:\n right[i][j] = 1 + right[i+1][j+1]\n \n answer = 0\n for i in range(m):\n for j in range(n): \n if s[i] != t[j]:\n answer += (left[i][j] + 1) * (right[i+1][j+1] + 1)\n return answer\n \n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python3 Dynamic Programming O(n^2) Runtime + Space | count-substrings-that-differ-by-one-character | 0 | 1 | # Code\n```\nclass Solution:\n\n def countSubstrings(self, s: str, t: str) -> int:\n\n m, n = len(s), len(t)\n \n # O(n^2) space\n left = [[0] * (n+1) for _ in range(m+1)]\n right = [[0] * (n+1) for _ in range(m+1)]\n\n for i in range(m):\n for j in range(n):\n if s[i] == t[j]:\n left[i+1][j+1] = 1 + left[i][j]\n\n for i in range(m - 1, -1, -1):\n for j in range(n - 1, -1, -1):\n if s[i] == t[j]:\n right[i][j] = 1 + right[i+1][j+1]\n \n answer = 0\n for i in range(m):\n for j in range(n): \n if s[i] != t[j]:\n answer += (left[i][j] + 1) * (right[i+1][j+1] + 1)\n return answer\n \n``` | 0 | There is an integer array `nums` that consists of `n` **unique** elements, but you have forgotten it. However, you do remember every pair of adjacent elements in `nums`.
You are given a 2D integer array `adjacentPairs` of size `n - 1` where each `adjacentPairs[i] = [ui, vi]` indicates that the elements `ui` and `vi` are adjacent in `nums`.
It is guaranteed that every adjacent pair of elements `nums[i]` and `nums[i+1]` will exist in `adjacentPairs`, either as `[nums[i], nums[i+1]]` or `[nums[i+1], nums[i]]`. The pairs can appear **in any order**.
Return _the original array_ `nums`_. If there are multiple solutions, return **any of them**_.
**Example 1:**
**Input:** adjacentPairs = \[\[2,1\],\[3,4\],\[3,2\]\]
**Output:** \[1,2,3,4\]
**Explanation:** This array has all its adjacent pairs in adjacentPairs.
Notice that adjacentPairs\[i\] may not be in left-to-right order.
**Example 2:**
**Input:** adjacentPairs = \[\[4,-2\],\[1,4\],\[-3,1\]\]
**Output:** \[-2,4,1,-3\]
**Explanation:** There can be negative numbers.
Another solution is \[-3,1,4,-2\], which would also be accepted.
**Example 3:**
**Input:** adjacentPairs = \[\[100000,-100000\]\]
**Output:** \[100000,-100000\]
**Constraints:**
* `nums.length == n`
* `adjacentPairs.length == n - 1`
* `adjacentPairs[i].length == 2`
* `2 <= n <= 105`
* `-105 <= nums[i], ui, vi <= 105`
* There exists some `nums` that has `adjacentPairs` as its pairs. | Take every substring of s, change a character, and see how many substrings of t match that substring. Use a Trie to store all substrings of t as a dictionary. |
Python 3 || 7 lines using transpose of target || T/M: 84% / 79% | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | ```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n \n m, n = len(words[0]),len(target)\n ans = [1]+ [0]*n\n words = list(map(Counter,zip(*map(list,words))))\n\n for word in words:\n for i in reversed(range(n)):\n ans[i+1] += ans[i] * word[target[i]] %1000000007\n\n return ans[n] %1000000007\n\n```\n[https://leetcode.com/problems/number-of-ways-to-form-a-target-string-given-a-dictionary/submissions/934810558/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*). | 3 | You are given a list of strings of the **same length** `words` and a string `target`.
Your task is to form `target` using the given `words` under the following rules:
* `target` should be formed from left to right.
* To form the `ith` character (**0-indexed**) of `target`, you can choose the `kth` character of the `jth` string in `words` if `target[i] = words[j][k]`.
* Once you use the `kth` character of the `jth` string of `words`, you **can no longer** use the `xth` character of any string in `words` where `x <= k`. In other words, all characters to the left of or at index `k` become unusuable for every string.
* Repeat the process until you form the string `target`.
**Notice** that you can use **multiple characters** from the **same string** in `words` provided the conditions above are met.
Return _the number of ways to form `target` from `words`_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** words = \[ "acca ", "bbbb ", "caca "\], target = "aba "
**Output:** 6
**Explanation:** There are 6 ways to form target.
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "caca ")
**Example 2:**
**Input:** words = \[ "abba ", "baab "\], target = "bab "
**Output:** 4
**Explanation:** There are 4 ways to form target.
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 2 ( "abba ")
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 3 ( "baab ")
"bab " -> index 0 ( "baab "), index 2 ( "baab "), index 3 ( "baab ")
"bab " -> index 1 ( "abba "), index 2 ( "baab "), index 3 ( "baab ")
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* All strings in `words` have the same length.
* `1 <= target.length <= 1000`
* `words[i]` and `target` contain only lowercase English letters. | null |
Python 3 || 7 lines using transpose of target || T/M: 84% / 79% | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | ```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n \n m, n = len(words[0]),len(target)\n ans = [1]+ [0]*n\n words = list(map(Counter,zip(*map(list,words))))\n\n for word in words:\n for i in reversed(range(n)):\n ans[i+1] += ans[i] * word[target[i]] %1000000007\n\n return ans[n] %1000000007\n\n```\n[https://leetcode.com/problems/number-of-ways-to-form-a-target-string-given-a-dictionary/submissions/934810558/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*). | 3 | You are given a **(0-indexed)** array of positive integers `candiesCount` where `candiesCount[i]` represents the number of candies of the `ith` type you have. You are also given a 2D array `queries` where `queries[i] = [favoriteTypei, favoriteDayi, dailyCapi]`.
You play a game with the following rules:
* You start eating candies on day `**0**`.
* You **cannot** eat **any** candy of type `i` unless you have eaten **all** candies of type `i - 1`.
* You must eat **at least** **one** candy per day until you have eaten all the candies.
Construct a boolean array `answer` such that `answer.length == queries.length` and `answer[i]` is `true` if you can eat a candy of type `favoriteTypei` on day `favoriteDayi` without eating **more than** `dailyCapi` candies on **any** day, and `false` otherwise. Note that you can eat different types of candy on the same day, provided that you follow rule 2.
Return _the constructed array_ `answer`.
**Example 1:**
**Input:** candiesCount = \[7,4,5,3,8\], queries = \[\[0,2,2\],\[4,2,4\],\[2,13,1000000000\]\]
**Output:** \[true,false,true\]
**Explanation:**
1- If you eat 2 candies (type 0) on day 0 and 2 candies (type 0) on day 1, you will eat a candy of type 0 on day 2.
2- You can eat at most 4 candies each day.
If you eat 4 candies every day, you will eat 4 candies (type 0) on day 0 and 4 candies (type 0 and type 1) on day 1.
On day 2, you can only eat 4 candies (type 1 and type 2), so you cannot eat a candy of type 4 on day 2.
3- If you eat 1 candy each day, you will eat a candy of type 2 on day 13.
**Example 2:**
**Input:** candiesCount = \[5,2,6,4,1\], queries = \[\[3,1,2\],\[4,10,3\],\[3,10,100\],\[4,100,30\],\[1,3,1\]\]
**Output:** \[false,true,true,false,false\]
**Constraints:**
* `1 <= candiesCount.length <= 105`
* `1 <= candiesCount[i] <= 105`
* `1 <= queries.length <= 105`
* `queries[i].length == 3`
* `0 <= favoriteTypei < candiesCount.length`
* `0 <= favoriteDayi <= 109`
* `1 <= dailyCapi <= 109` | For each index i, store the frequency of each character in the ith row. Use dynamic programing to calculate the number of ways to get the target string using the frequency array, |
python 3 - top down dp | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | # Intuition\nThis question\'s constraints are quite harsh imo.\n\nThere are 2 state variables:\n1.index of target\n2.index of word in words list\n\nYou can\'t save indexes of all characters in each word in a defaultdict(list) and then do binary search, which will cost you log(n) time and get TLE. This was my first trial mistake.\n\nYou need to save frequency of characters in each index of words.\n\n# Approach\ntop down dp\n\n# Complexity\n- Time complexity:\nO(mn + nl) -> read all characters in words and do dp\n\n- Space complexity:\nO(mn + nl) -> mapp\'s size and dp\'s cache size\n\nm = len(words)\nn = len(words[0])\nl = len(target)\n\n# Code\n```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n import collections\n\n mapp = collections.defaultdict(collections.Counter) # char index in word: {char: freq}\n for word in words:\n for char_ind, char in enumerate(word):\n mapp[char_ind][char] += 1\n\n @lru_cache(None)\n def dp(it, iw): # return int, possibility\n nonlocal target\n if it == len(target): # reached terminal\n return 1\n if iw == len(words[0]): # need more char but can\'t get more\n return 0\n\n if target[it] in mapp[iw]:\n r1 = dp(it + 1, iw + 1) # take iw for it, you have mapp[iw][target[it]] extra combinations\n r2 = dp(it, iw + 1) # skip iw\n return r1 * mapp[iw][target[it]] + r2\n else:\n r1 = dp(it, iw + 1)\n return r1\n\n mod = 10 ** 9 + 7\n return dp(0, 0) % mod\n``` | 1 | You are given a list of strings of the **same length** `words` and a string `target`.
Your task is to form `target` using the given `words` under the following rules:
* `target` should be formed from left to right.
* To form the `ith` character (**0-indexed**) of `target`, you can choose the `kth` character of the `jth` string in `words` if `target[i] = words[j][k]`.
* Once you use the `kth` character of the `jth` string of `words`, you **can no longer** use the `xth` character of any string in `words` where `x <= k`. In other words, all characters to the left of or at index `k` become unusuable for every string.
* Repeat the process until you form the string `target`.
**Notice** that you can use **multiple characters** from the **same string** in `words` provided the conditions above are met.
Return _the number of ways to form `target` from `words`_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** words = \[ "acca ", "bbbb ", "caca "\], target = "aba "
**Output:** 6
**Explanation:** There are 6 ways to form target.
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "caca ")
**Example 2:**
**Input:** words = \[ "abba ", "baab "\], target = "bab "
**Output:** 4
**Explanation:** There are 4 ways to form target.
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 2 ( "abba ")
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 3 ( "baab ")
"bab " -> index 0 ( "baab "), index 2 ( "baab "), index 3 ( "baab ")
"bab " -> index 1 ( "abba "), index 2 ( "baab "), index 3 ( "baab ")
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* All strings in `words` have the same length.
* `1 <= target.length <= 1000`
* `words[i]` and `target` contain only lowercase English letters. | null |
python 3 - top down dp | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | # Intuition\nThis question\'s constraints are quite harsh imo.\n\nThere are 2 state variables:\n1.index of target\n2.index of word in words list\n\nYou can\'t save indexes of all characters in each word in a defaultdict(list) and then do binary search, which will cost you log(n) time and get TLE. This was my first trial mistake.\n\nYou need to save frequency of characters in each index of words.\n\n# Approach\ntop down dp\n\n# Complexity\n- Time complexity:\nO(mn + nl) -> read all characters in words and do dp\n\n- Space complexity:\nO(mn + nl) -> mapp\'s size and dp\'s cache size\n\nm = len(words)\nn = len(words[0])\nl = len(target)\n\n# Code\n```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n import collections\n\n mapp = collections.defaultdict(collections.Counter) # char index in word: {char: freq}\n for word in words:\n for char_ind, char in enumerate(word):\n mapp[char_ind][char] += 1\n\n @lru_cache(None)\n def dp(it, iw): # return int, possibility\n nonlocal target\n if it == len(target): # reached terminal\n return 1\n if iw == len(words[0]): # need more char but can\'t get more\n return 0\n\n if target[it] in mapp[iw]:\n r1 = dp(it + 1, iw + 1) # take iw for it, you have mapp[iw][target[it]] extra combinations\n r2 = dp(it, iw + 1) # skip iw\n return r1 * mapp[iw][target[it]] + r2\n else:\n r1 = dp(it, iw + 1)\n return r1\n\n mod = 10 ** 9 + 7\n return dp(0, 0) % mod\n``` | 1 | You are given a **(0-indexed)** array of positive integers `candiesCount` where `candiesCount[i]` represents the number of candies of the `ith` type you have. You are also given a 2D array `queries` where `queries[i] = [favoriteTypei, favoriteDayi, dailyCapi]`.
You play a game with the following rules:
* You start eating candies on day `**0**`.
* You **cannot** eat **any** candy of type `i` unless you have eaten **all** candies of type `i - 1`.
* You must eat **at least** **one** candy per day until you have eaten all the candies.
Construct a boolean array `answer` such that `answer.length == queries.length` and `answer[i]` is `true` if you can eat a candy of type `favoriteTypei` on day `favoriteDayi` without eating **more than** `dailyCapi` candies on **any** day, and `false` otherwise. Note that you can eat different types of candy on the same day, provided that you follow rule 2.
Return _the constructed array_ `answer`.
**Example 1:**
**Input:** candiesCount = \[7,4,5,3,8\], queries = \[\[0,2,2\],\[4,2,4\],\[2,13,1000000000\]\]
**Output:** \[true,false,true\]
**Explanation:**
1- If you eat 2 candies (type 0) on day 0 and 2 candies (type 0) on day 1, you will eat a candy of type 0 on day 2.
2- You can eat at most 4 candies each day.
If you eat 4 candies every day, you will eat 4 candies (type 0) on day 0 and 4 candies (type 0 and type 1) on day 1.
On day 2, you can only eat 4 candies (type 1 and type 2), so you cannot eat a candy of type 4 on day 2.
3- If you eat 1 candy each day, you will eat a candy of type 2 on day 13.
**Example 2:**
**Input:** candiesCount = \[5,2,6,4,1\], queries = \[\[3,1,2\],\[4,10,3\],\[3,10,100\],\[4,100,30\],\[1,3,1\]\]
**Output:** \[false,true,true,false,false\]
**Constraints:**
* `1 <= candiesCount.length <= 105`
* `1 <= candiesCount[i] <= 105`
* `1 <= queries.length <= 105`
* `queries[i].length == 3`
* `0 <= favoriteTypei < candiesCount.length`
* `0 <= favoriteDayi <= 109`
* `1 <= dailyCapi <= 109` | For each index i, store the frequency of each character in the ith row. Use dynamic programing to calculate the number of ways to get the target string using the frequency array, |
Python3 Solution | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | \n```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n n=len(words[0])\n m=len(target)\n mod=10**9+7\n dp=[0]*(m+1)\n dp[0]=1\n count=[[0]*26 for _ in range(n)]\n for i in range(n):\n for word in words:\n count[i][ord(word[i])-ord(\'a\')]+=1\n\n for i in range(n):\n for j in range(m-1,-1,-1):\n dp[j+1]+=dp[j]*count[i][ord(target[j])-ord(\'a\')]\n dp[j+1]%=mod\n\n return dp[m] \n``` | 1 | You are given a list of strings of the **same length** `words` and a string `target`.
Your task is to form `target` using the given `words` under the following rules:
* `target` should be formed from left to right.
* To form the `ith` character (**0-indexed**) of `target`, you can choose the `kth` character of the `jth` string in `words` if `target[i] = words[j][k]`.
* Once you use the `kth` character of the `jth` string of `words`, you **can no longer** use the `xth` character of any string in `words` where `x <= k`. In other words, all characters to the left of or at index `k` become unusuable for every string.
* Repeat the process until you form the string `target`.
**Notice** that you can use **multiple characters** from the **same string** in `words` provided the conditions above are met.
Return _the number of ways to form `target` from `words`_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** words = \[ "acca ", "bbbb ", "caca "\], target = "aba "
**Output:** 6
**Explanation:** There are 6 ways to form target.
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "caca ")
**Example 2:**
**Input:** words = \[ "abba ", "baab "\], target = "bab "
**Output:** 4
**Explanation:** There are 4 ways to form target.
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 2 ( "abba ")
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 3 ( "baab ")
"bab " -> index 0 ( "baab "), index 2 ( "baab "), index 3 ( "baab ")
"bab " -> index 1 ( "abba "), index 2 ( "baab "), index 3 ( "baab ")
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* All strings in `words` have the same length.
* `1 <= target.length <= 1000`
* `words[i]` and `target` contain only lowercase English letters. | null |
Python3 Solution | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | \n```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n n=len(words[0])\n m=len(target)\n mod=10**9+7\n dp=[0]*(m+1)\n dp[0]=1\n count=[[0]*26 for _ in range(n)]\n for i in range(n):\n for word in words:\n count[i][ord(word[i])-ord(\'a\')]+=1\n\n for i in range(n):\n for j in range(m-1,-1,-1):\n dp[j+1]+=dp[j]*count[i][ord(target[j])-ord(\'a\')]\n dp[j+1]%=mod\n\n return dp[m] \n``` | 1 | You are given a **(0-indexed)** array of positive integers `candiesCount` where `candiesCount[i]` represents the number of candies of the `ith` type you have. You are also given a 2D array `queries` where `queries[i] = [favoriteTypei, favoriteDayi, dailyCapi]`.
You play a game with the following rules:
* You start eating candies on day `**0**`.
* You **cannot** eat **any** candy of type `i` unless you have eaten **all** candies of type `i - 1`.
* You must eat **at least** **one** candy per day until you have eaten all the candies.
Construct a boolean array `answer` such that `answer.length == queries.length` and `answer[i]` is `true` if you can eat a candy of type `favoriteTypei` on day `favoriteDayi` without eating **more than** `dailyCapi` candies on **any** day, and `false` otherwise. Note that you can eat different types of candy on the same day, provided that you follow rule 2.
Return _the constructed array_ `answer`.
**Example 1:**
**Input:** candiesCount = \[7,4,5,3,8\], queries = \[\[0,2,2\],\[4,2,4\],\[2,13,1000000000\]\]
**Output:** \[true,false,true\]
**Explanation:**
1- If you eat 2 candies (type 0) on day 0 and 2 candies (type 0) on day 1, you will eat a candy of type 0 on day 2.
2- You can eat at most 4 candies each day.
If you eat 4 candies every day, you will eat 4 candies (type 0) on day 0 and 4 candies (type 0 and type 1) on day 1.
On day 2, you can only eat 4 candies (type 1 and type 2), so you cannot eat a candy of type 4 on day 2.
3- If you eat 1 candy each day, you will eat a candy of type 2 on day 13.
**Example 2:**
**Input:** candiesCount = \[5,2,6,4,1\], queries = \[\[3,1,2\],\[4,10,3\],\[3,10,100\],\[4,100,30\],\[1,3,1\]\]
**Output:** \[false,true,true,false,false\]
**Constraints:**
* `1 <= candiesCount.length <= 105`
* `1 <= candiesCount[i] <= 105`
* `1 <= queries.length <= 105`
* `queries[i].length == 3`
* `0 <= favoriteTypei < candiesCount.length`
* `0 <= favoriteDayi <= 109`
* `1 <= dailyCapi <= 109` | For each index i, store the frequency of each character in the ith row. Use dynamic programing to calculate the number of ways to get the target string using the frequency array, |
Python DP (Memoization) | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | ```\nclass word_index:\n def __init__(self):\n self.char_set = set()\n self.frequencies = defaultdict(int)\n def add_char(self, char):\n self.char_set.add(char)\n self.frequencies[char] += 1\n\nclass Solution(object):\n def numWays(self, words, target):\n # seperate each word into its characters and map them to an index\n # ["acca", "bbbb", "caca"] -> {1: set([a, b, c]), 2: set([c, b, a]), 3: set([c, b]), 4: set([a, b])}\n # add frequency array to each index to avoid word collisions\n\n # solve using dp\n # let dp[i][k] be the number of ways to form target[i:] at index k\n # if k == m: res = 1\n # if i == n: res = 0\n # dp[i][k] = include * freq + skip\n \n n = len(words[0])\n m = len(target)\n\n word_map = defaultdict(word_index)\n\n for word in words:\n for i in range(n):\n word_map[i].add_char(word[i])\n \n dp = [[None] * m for i in range(n)]\n\n def solve(i, k):\n if k == m:\n return 1\n elif i == n:\n return 0\n elif dp[i][k] is not None:\n return dp[i][k]\n\n if target[k] in word_map[i].char_set:\n dp[i][k] = solve(i + 1, k + 1) * word_map[i].frequencies[target[k]] + solve(i + 1, k) \n else:\n dp[i][k] = solve(i + 1, k)\n return dp[i][k]\n \n mod = 10**9 + 7\n return solve(0, 0) % mod\n``` | 1 | You are given a list of strings of the **same length** `words` and a string `target`.
Your task is to form `target` using the given `words` under the following rules:
* `target` should be formed from left to right.
* To form the `ith` character (**0-indexed**) of `target`, you can choose the `kth` character of the `jth` string in `words` if `target[i] = words[j][k]`.
* Once you use the `kth` character of the `jth` string of `words`, you **can no longer** use the `xth` character of any string in `words` where `x <= k`. In other words, all characters to the left of or at index `k` become unusuable for every string.
* Repeat the process until you form the string `target`.
**Notice** that you can use **multiple characters** from the **same string** in `words` provided the conditions above are met.
Return _the number of ways to form `target` from `words`_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** words = \[ "acca ", "bbbb ", "caca "\], target = "aba "
**Output:** 6
**Explanation:** There are 6 ways to form target.
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "caca ")
**Example 2:**
**Input:** words = \[ "abba ", "baab "\], target = "bab "
**Output:** 4
**Explanation:** There are 4 ways to form target.
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 2 ( "abba ")
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 3 ( "baab ")
"bab " -> index 0 ( "baab "), index 2 ( "baab "), index 3 ( "baab ")
"bab " -> index 1 ( "abba "), index 2 ( "baab "), index 3 ( "baab ")
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* All strings in `words` have the same length.
* `1 <= target.length <= 1000`
* `words[i]` and `target` contain only lowercase English letters. | null |
Python DP (Memoization) | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | ```\nclass word_index:\n def __init__(self):\n self.char_set = set()\n self.frequencies = defaultdict(int)\n def add_char(self, char):\n self.char_set.add(char)\n self.frequencies[char] += 1\n\nclass Solution(object):\n def numWays(self, words, target):\n # seperate each word into its characters and map them to an index\n # ["acca", "bbbb", "caca"] -> {1: set([a, b, c]), 2: set([c, b, a]), 3: set([c, b]), 4: set([a, b])}\n # add frequency array to each index to avoid word collisions\n\n # solve using dp\n # let dp[i][k] be the number of ways to form target[i:] at index k\n # if k == m: res = 1\n # if i == n: res = 0\n # dp[i][k] = include * freq + skip\n \n n = len(words[0])\n m = len(target)\n\n word_map = defaultdict(word_index)\n\n for word in words:\n for i in range(n):\n word_map[i].add_char(word[i])\n \n dp = [[None] * m for i in range(n)]\n\n def solve(i, k):\n if k == m:\n return 1\n elif i == n:\n return 0\n elif dp[i][k] is not None:\n return dp[i][k]\n\n if target[k] in word_map[i].char_set:\n dp[i][k] = solve(i + 1, k + 1) * word_map[i].frequencies[target[k]] + solve(i + 1, k) \n else:\n dp[i][k] = solve(i + 1, k)\n return dp[i][k]\n \n mod = 10**9 + 7\n return solve(0, 0) % mod\n``` | 1 | You are given a **(0-indexed)** array of positive integers `candiesCount` where `candiesCount[i]` represents the number of candies of the `ith` type you have. You are also given a 2D array `queries` where `queries[i] = [favoriteTypei, favoriteDayi, dailyCapi]`.
You play a game with the following rules:
* You start eating candies on day `**0**`.
* You **cannot** eat **any** candy of type `i` unless you have eaten **all** candies of type `i - 1`.
* You must eat **at least** **one** candy per day until you have eaten all the candies.
Construct a boolean array `answer` such that `answer.length == queries.length` and `answer[i]` is `true` if you can eat a candy of type `favoriteTypei` on day `favoriteDayi` without eating **more than** `dailyCapi` candies on **any** day, and `false` otherwise. Note that you can eat different types of candy on the same day, provided that you follow rule 2.
Return _the constructed array_ `answer`.
**Example 1:**
**Input:** candiesCount = \[7,4,5,3,8\], queries = \[\[0,2,2\],\[4,2,4\],\[2,13,1000000000\]\]
**Output:** \[true,false,true\]
**Explanation:**
1- If you eat 2 candies (type 0) on day 0 and 2 candies (type 0) on day 1, you will eat a candy of type 0 on day 2.
2- You can eat at most 4 candies each day.
If you eat 4 candies every day, you will eat 4 candies (type 0) on day 0 and 4 candies (type 0 and type 1) on day 1.
On day 2, you can only eat 4 candies (type 1 and type 2), so you cannot eat a candy of type 4 on day 2.
3- If you eat 1 candy each day, you will eat a candy of type 2 on day 13.
**Example 2:**
**Input:** candiesCount = \[5,2,6,4,1\], queries = \[\[3,1,2\],\[4,10,3\],\[3,10,100\],\[4,100,30\],\[1,3,1\]\]
**Output:** \[false,true,true,false,false\]
**Constraints:**
* `1 <= candiesCount.length <= 105`
* `1 <= candiesCount[i] <= 105`
* `1 <= queries.length <= 105`
* `queries[i].length == 3`
* `0 <= favoriteTypei < candiesCount.length`
* `0 <= favoriteDayi <= 109`
* `1 <= dailyCapi <= 109` | For each index i, store the frequency of each character in the ith row. Use dynamic programing to calculate the number of ways to get the target string using the frequency array, |
Python DP | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | ```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n n, m = len(words[0]), len(target)\n maps = [Counter() for _ in range(n)]\n for word in words:\n for i, c in enumerate(word):\n maps[i][c] += 1\n @cache\n def dp(i, j):\n if j >= m: return 1\n if i >= n: return 0\n v = maps[i][target[j]]\n return dp(i + 1, j) + dp(i + 1, j + 1) * v\n return dp(0, 0) % (10 ** 9 + 7)\n``` | 1 | You are given a list of strings of the **same length** `words` and a string `target`.
Your task is to form `target` using the given `words` under the following rules:
* `target` should be formed from left to right.
* To form the `ith` character (**0-indexed**) of `target`, you can choose the `kth` character of the `jth` string in `words` if `target[i] = words[j][k]`.
* Once you use the `kth` character of the `jth` string of `words`, you **can no longer** use the `xth` character of any string in `words` where `x <= k`. In other words, all characters to the left of or at index `k` become unusuable for every string.
* Repeat the process until you form the string `target`.
**Notice** that you can use **multiple characters** from the **same string** in `words` provided the conditions above are met.
Return _the number of ways to form `target` from `words`_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** words = \[ "acca ", "bbbb ", "caca "\], target = "aba "
**Output:** 6
**Explanation:** There are 6 ways to form target.
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "caca ")
**Example 2:**
**Input:** words = \[ "abba ", "baab "\], target = "bab "
**Output:** 4
**Explanation:** There are 4 ways to form target.
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 2 ( "abba ")
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 3 ( "baab ")
"bab " -> index 0 ( "baab "), index 2 ( "baab "), index 3 ( "baab ")
"bab " -> index 1 ( "abba "), index 2 ( "baab "), index 3 ( "baab ")
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* All strings in `words` have the same length.
* `1 <= target.length <= 1000`
* `words[i]` and `target` contain only lowercase English letters. | null |
Python DP | number-of-ways-to-form-a-target-string-given-a-dictionary | 0 | 1 | ```\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n n, m = len(words[0]), len(target)\n maps = [Counter() for _ in range(n)]\n for word in words:\n for i, c in enumerate(word):\n maps[i][c] += 1\n @cache\n def dp(i, j):\n if j >= m: return 1\n if i >= n: return 0\n v = maps[i][target[j]]\n return dp(i + 1, j) + dp(i + 1, j + 1) * v\n return dp(0, 0) % (10 ** 9 + 7)\n``` | 1 | You are given a **(0-indexed)** array of positive integers `candiesCount` where `candiesCount[i]` represents the number of candies of the `ith` type you have. You are also given a 2D array `queries` where `queries[i] = [favoriteTypei, favoriteDayi, dailyCapi]`.
You play a game with the following rules:
* You start eating candies on day `**0**`.
* You **cannot** eat **any** candy of type `i` unless you have eaten **all** candies of type `i - 1`.
* You must eat **at least** **one** candy per day until you have eaten all the candies.
Construct a boolean array `answer` such that `answer.length == queries.length` and `answer[i]` is `true` if you can eat a candy of type `favoriteTypei` on day `favoriteDayi` without eating **more than** `dailyCapi` candies on **any** day, and `false` otherwise. Note that you can eat different types of candy on the same day, provided that you follow rule 2.
Return _the constructed array_ `answer`.
**Example 1:**
**Input:** candiesCount = \[7,4,5,3,8\], queries = \[\[0,2,2\],\[4,2,4\],\[2,13,1000000000\]\]
**Output:** \[true,false,true\]
**Explanation:**
1- If you eat 2 candies (type 0) on day 0 and 2 candies (type 0) on day 1, you will eat a candy of type 0 on day 2.
2- You can eat at most 4 candies each day.
If you eat 4 candies every day, you will eat 4 candies (type 0) on day 0 and 4 candies (type 0 and type 1) on day 1.
On day 2, you can only eat 4 candies (type 1 and type 2), so you cannot eat a candy of type 4 on day 2.
3- If you eat 1 candy each day, you will eat a candy of type 2 on day 13.
**Example 2:**
**Input:** candiesCount = \[5,2,6,4,1\], queries = \[\[3,1,2\],\[4,10,3\],\[3,10,100\],\[4,100,30\],\[1,3,1\]\]
**Output:** \[false,true,true,false,false\]
**Constraints:**
* `1 <= candiesCount.length <= 105`
* `1 <= candiesCount[i] <= 105`
* `1 <= queries.length <= 105`
* `queries[i].length == 3`
* `0 <= favoriteTypei < candiesCount.length`
* `0 <= favoriteDayi <= 109`
* `1 <= dailyCapi <= 109` | For each index i, store the frequency of each character in the ith row. Use dynamic programing to calculate the number of ways to get the target string using the frequency array, |
Image Explanation🏆- [DP - Complete Intuition] - C++/Java/Python | number-of-ways-to-form-a-target-string-given-a-dictionary | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Number of Ways to Form a Target String Given a Dictionary` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n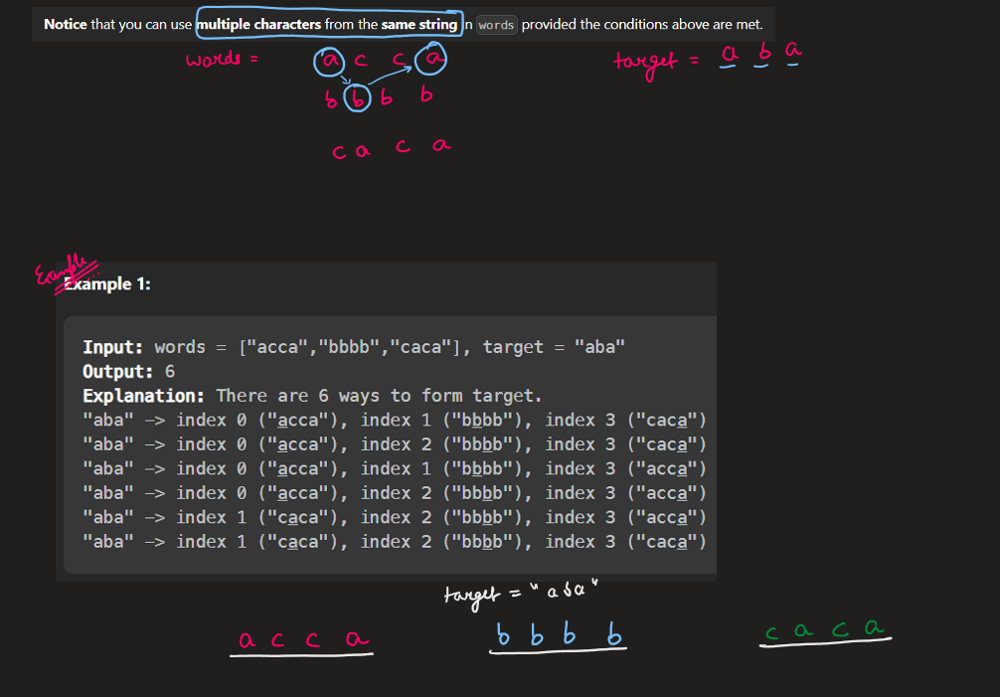\n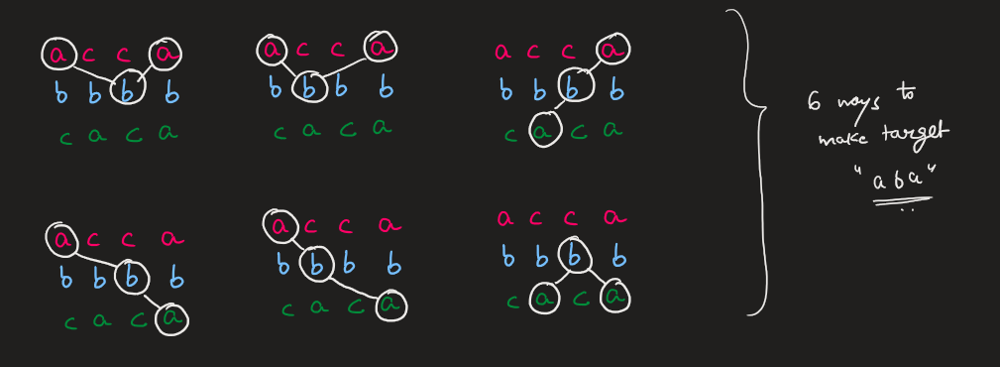\n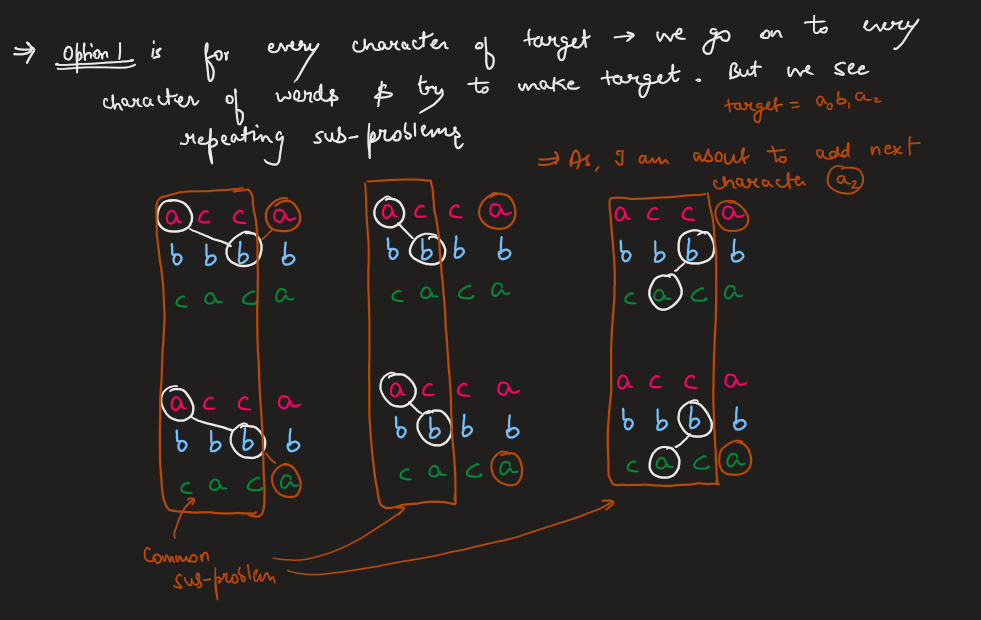\n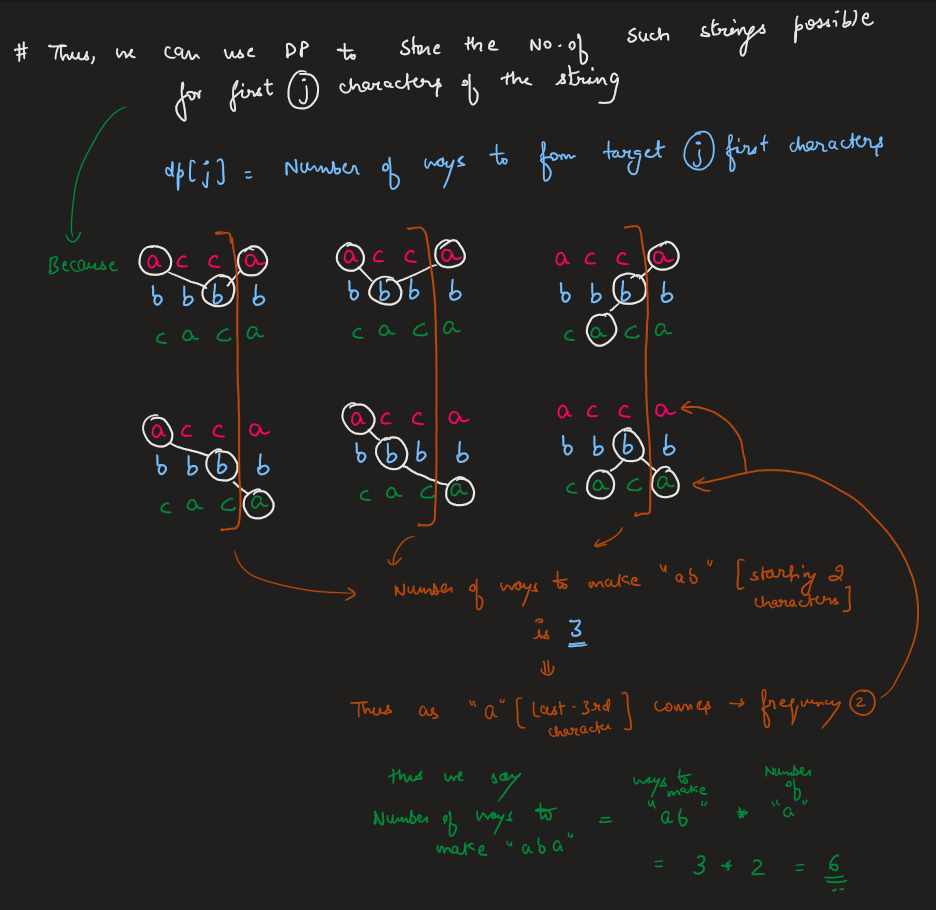\n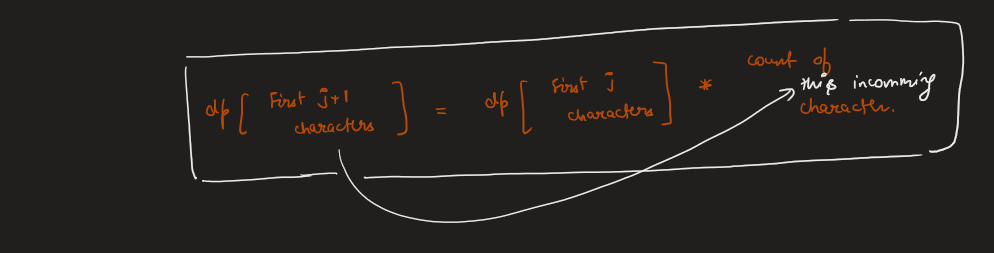\n\n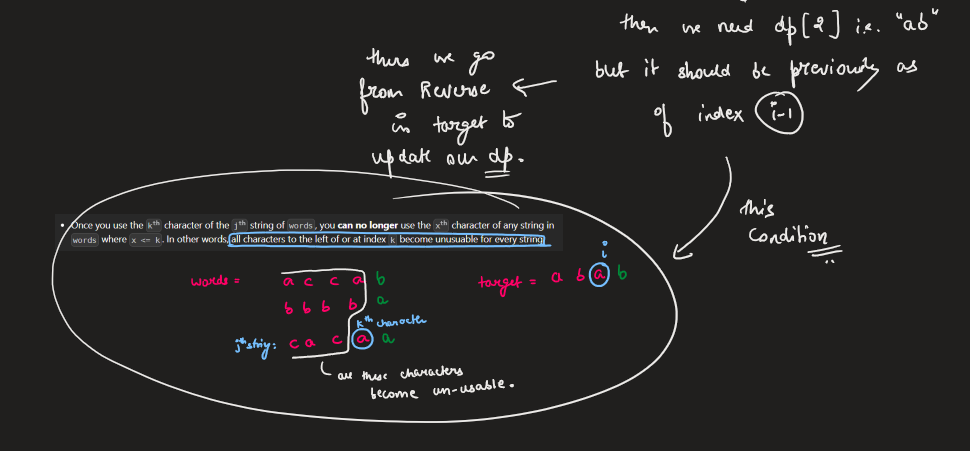\n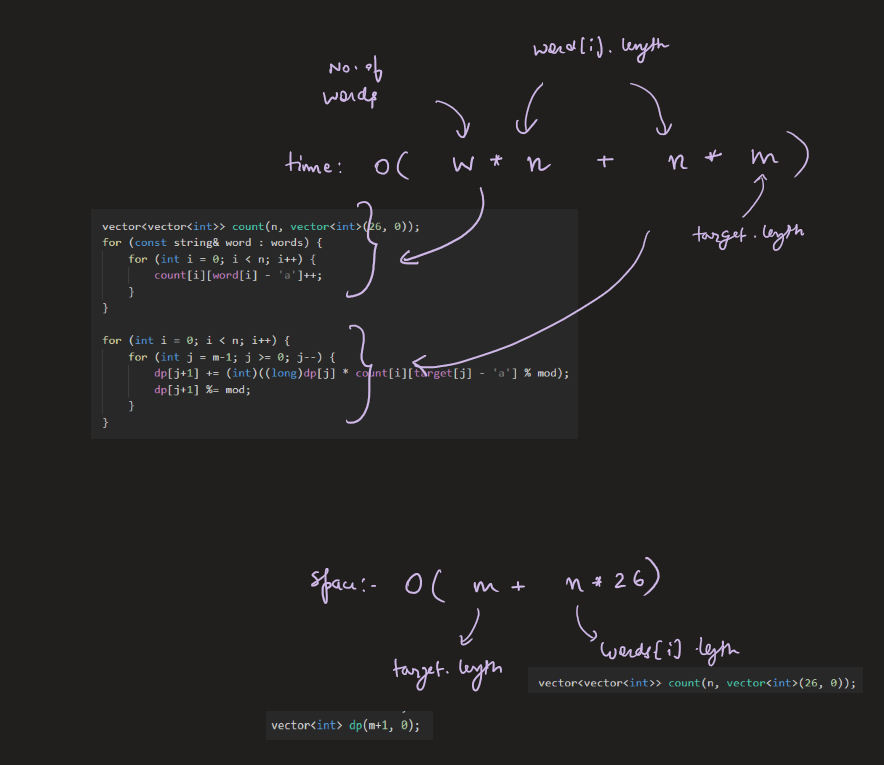\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numWays(vector<string>& words, string target) {\n int n = words[0].size();\n int m = target.size();\n int mod = 1000000007;\n vector<int> dp(m+1, 0);\n dp[0] = 1;\n \n vector<vector<int>> count(n, vector<int>(26, 0));\n for (const string& word : words) {\n for (int i = 0; i < n; i++) {\n count[i][word[i] - \'a\']++;\n }\n }\n \n for (int i = 0; i < n; i++) {\n for (int j = m-1; j >= 0; j--) {\n dp[j+1] += (int)((long)dp[j] * count[i][target[j] - \'a\'] % mod);\n dp[j+1] %= mod;\n }\n }\n \n return dp[m];\n }\n};\n```\n```Java []\nclass Solution {\n public int numWays(String[] words, String target) {\n int n = words[0].length();\n int m = target.length();\n int mod = 1000000007;\n int[] dp = new int[m+1];\n dp[0] = 1;\n \n int[][] count = new int[n][26];\n for (String word : words) {\n for (int i = 0; i < n; i++) {\n count[i][word.charAt(i) - \'a\']++;\n }\n }\n \n for (int i = 0; i < n; i++) {\n for (int j = m-1; j >= 0; j--) {\n dp[j+1] += (int)((long)dp[j] * count[i][target.charAt(j) - \'a\'] % mod);\n dp[j+1] %= mod;\n }\n }\n \n return dp[m];\n }\n}\n```\n```Python []\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n n = len(words[0])\n m = len(target)\n mod = 10**9 + 7\n dp = [0] * (m+1)\n dp[0] = 1\n \n count = [[0] * 26 for _ in range(n)]\n for i in range(n):\n for word in words:\n count[i][ord(word[i]) - ord(\'a\')] += 1\n \n for i in range(n):\n for j in range(m-1, -1, -1):\n dp[j+1] += dp[j] * count[i][ord(target[j]) - ord(\'a\')]\n dp[j+1] %= mod\n \n return dp[m]\n```\n | 57 | You are given a list of strings of the **same length** `words` and a string `target`.
Your task is to form `target` using the given `words` under the following rules:
* `target` should be formed from left to right.
* To form the `ith` character (**0-indexed**) of `target`, you can choose the `kth` character of the `jth` string in `words` if `target[i] = words[j][k]`.
* Once you use the `kth` character of the `jth` string of `words`, you **can no longer** use the `xth` character of any string in `words` where `x <= k`. In other words, all characters to the left of or at index `k` become unusuable for every string.
* Repeat the process until you form the string `target`.
**Notice** that you can use **multiple characters** from the **same string** in `words` provided the conditions above are met.
Return _the number of ways to form `target` from `words`_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** words = \[ "acca ", "bbbb ", "caca "\], target = "aba "
**Output:** 6
**Explanation:** There are 6 ways to form target.
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "caca ")
"aba " -> index 0 ( "acca "), index 1 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 0 ( "acca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "acca ")
"aba " -> index 1 ( "caca "), index 2 ( "bbbb "), index 3 ( "caca ")
**Example 2:**
**Input:** words = \[ "abba ", "baab "\], target = "bab "
**Output:** 4
**Explanation:** There are 4 ways to form target.
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 2 ( "abba ")
"bab " -> index 0 ( "baab "), index 1 ( "baab "), index 3 ( "baab ")
"bab " -> index 0 ( "baab "), index 2 ( "baab "), index 3 ( "baab ")
"bab " -> index 1 ( "abba "), index 2 ( "baab "), index 3 ( "baab ")
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 1000`
* All strings in `words` have the same length.
* `1 <= target.length <= 1000`
* `words[i]` and `target` contain only lowercase English letters. | null |
Image Explanation🏆- [DP - Complete Intuition] - C++/Java/Python | number-of-ways-to-form-a-target-string-given-a-dictionary | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Number of Ways to Form a Target String Given a Dictionary` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n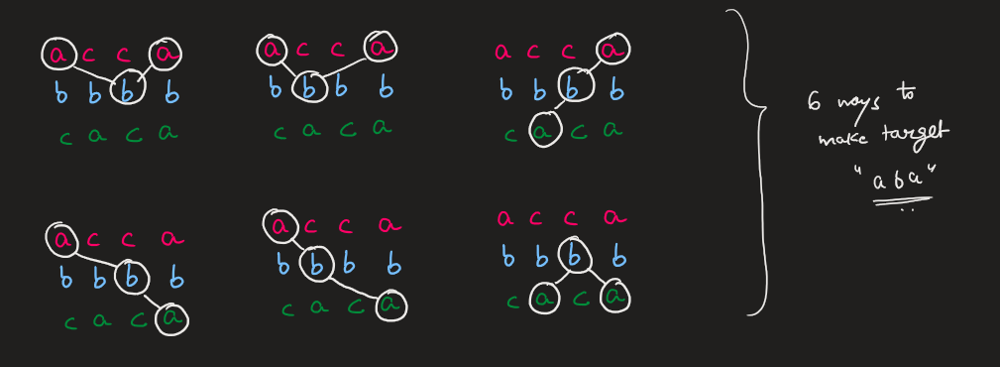\n\n\n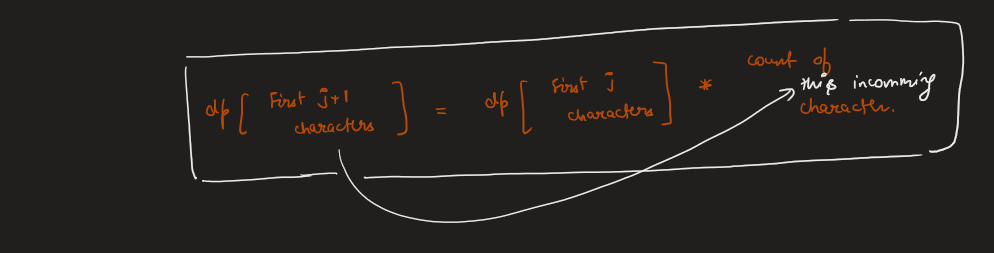\n\n\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numWays(vector<string>& words, string target) {\n int n = words[0].size();\n int m = target.size();\n int mod = 1000000007;\n vector<int> dp(m+1, 0);\n dp[0] = 1;\n \n vector<vector<int>> count(n, vector<int>(26, 0));\n for (const string& word : words) {\n for (int i = 0; i < n; i++) {\n count[i][word[i] - \'a\']++;\n }\n }\n \n for (int i = 0; i < n; i++) {\n for (int j = m-1; j >= 0; j--) {\n dp[j+1] += (int)((long)dp[j] * count[i][target[j] - \'a\'] % mod);\n dp[j+1] %= mod;\n }\n }\n \n return dp[m];\n }\n};\n```\n```Java []\nclass Solution {\n public int numWays(String[] words, String target) {\n int n = words[0].length();\n int m = target.length();\n int mod = 1000000007;\n int[] dp = new int[m+1];\n dp[0] = 1;\n \n int[][] count = new int[n][26];\n for (String word : words) {\n for (int i = 0; i < n; i++) {\n count[i][word.charAt(i) - \'a\']++;\n }\n }\n \n for (int i = 0; i < n; i++) {\n for (int j = m-1; j >= 0; j--) {\n dp[j+1] += (int)((long)dp[j] * count[i][target.charAt(j) - \'a\'] % mod);\n dp[j+1] %= mod;\n }\n }\n \n return dp[m];\n }\n}\n```\n```Python []\nclass Solution:\n def numWays(self, words: List[str], target: str) -> int:\n n = len(words[0])\n m = len(target)\n mod = 10**9 + 7\n dp = [0] * (m+1)\n dp[0] = 1\n \n count = [[0] * 26 for _ in range(n)]\n for i in range(n):\n for word in words:\n count[i][ord(word[i]) - ord(\'a\')] += 1\n \n for i in range(n):\n for j in range(m-1, -1, -1):\n dp[j+1] += dp[j] * count[i][ord(target[j]) - ord(\'a\')]\n dp[j+1] %= mod\n \n return dp[m]\n```\n | 57 | You are given a **(0-indexed)** array of positive integers `candiesCount` where `candiesCount[i]` represents the number of candies of the `ith` type you have. You are also given a 2D array `queries` where `queries[i] = [favoriteTypei, favoriteDayi, dailyCapi]`.
You play a game with the following rules:
* You start eating candies on day `**0**`.
* You **cannot** eat **any** candy of type `i` unless you have eaten **all** candies of type `i - 1`.
* You must eat **at least** **one** candy per day until you have eaten all the candies.
Construct a boolean array `answer` such that `answer.length == queries.length` and `answer[i]` is `true` if you can eat a candy of type `favoriteTypei` on day `favoriteDayi` without eating **more than** `dailyCapi` candies on **any** day, and `false` otherwise. Note that you can eat different types of candy on the same day, provided that you follow rule 2.
Return _the constructed array_ `answer`.
**Example 1:**
**Input:** candiesCount = \[7,4,5,3,8\], queries = \[\[0,2,2\],\[4,2,4\],\[2,13,1000000000\]\]
**Output:** \[true,false,true\]
**Explanation:**
1- If you eat 2 candies (type 0) on day 0 and 2 candies (type 0) on day 1, you will eat a candy of type 0 on day 2.
2- You can eat at most 4 candies each day.
If you eat 4 candies every day, you will eat 4 candies (type 0) on day 0 and 4 candies (type 0 and type 1) on day 1.
On day 2, you can only eat 4 candies (type 1 and type 2), so you cannot eat a candy of type 4 on day 2.
3- If you eat 1 candy each day, you will eat a candy of type 2 on day 13.
**Example 2:**
**Input:** candiesCount = \[5,2,6,4,1\], queries = \[\[3,1,2\],\[4,10,3\],\[3,10,100\],\[4,100,30\],\[1,3,1\]\]
**Output:** \[false,true,true,false,false\]
**Constraints:**
* `1 <= candiesCount.length <= 105`
* `1 <= candiesCount[i] <= 105`
* `1 <= queries.length <= 105`
* `queries[i].length == 3`
* `0 <= favoriteTypei < candiesCount.length`
* `0 <= favoriteDayi <= 109`
* `1 <= dailyCapi <= 109` | For each index i, store the frequency of each character in the ith row. Use dynamic programing to calculate the number of ways to get the target string using the frequency array, |
C++/Python Solution | check-array-formation-through-concatenation | 0 | 1 | ### C++\n**Runtime: 8 ms, faster than 58.49% of C++ online submissions for Check Array Formation Through Concatenation.\nMemory Usage: 10.2 MB, less than 76.10% of C++ online submissions for Check Array Formation Through Concatenation.**\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n vector<int> ps(101,-1);\n for(int i=0;i<pieces.size();i++)\n {\n ps[pieces[i][0]]=i;\n }\n for(int i=0;i<arr.size();)\n {\n int p=ps[arr[i]];\n if(p==-1)\n {\n return false;\n }\n for(int j=0;j<pieces[p].size();j++)\n {\n if(pieces[p][j]!=arr[i++])\n return false;\n }\n }\n return true;\n \n }\n};\n```\n\n### Python\n```\nclass Solution:\n def canFormArray(self, arr, pieces):\n d = {x[0]: x for x in pieces}\n return list(chain(*[d.get(num, []) for num in arr])) == arr\n``` | 1 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
C++/Python Solution | check-array-formation-through-concatenation | 0 | 1 | ### C++\n**Runtime: 8 ms, faster than 58.49% of C++ online submissions for Check Array Formation Through Concatenation.\nMemory Usage: 10.2 MB, less than 76.10% of C++ online submissions for Check Array Formation Through Concatenation.**\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n vector<int> ps(101,-1);\n for(int i=0;i<pieces.size();i++)\n {\n ps[pieces[i][0]]=i;\n }\n for(int i=0;i<arr.size();)\n {\n int p=ps[arr[i]];\n if(p==-1)\n {\n return false;\n }\n for(int j=0;j<pieces[p].size();j++)\n {\n if(pieces[p][j]!=arr[i++])\n return false;\n }\n }\n return true;\n \n }\n};\n```\n\n### Python\n```\nclass Solution:\n def canFormArray(self, arr, pieces):\n d = {x[0]: x for x in pieces}\n return list(chain(*[d.get(num, []) for num in arr])) == arr\n``` | 1 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
"Python" easy explanation blackboard | check-array-formation-through-concatenation | 0 | 1 | * **Simple and easy python3 solution**\n* **The approch is well explained in the below image**\n\n\n\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n keys, ans = {}, []\n for piece in pieces:\n keys[piece[0]] = piece\n for a in arr:\n if a in keys:\n ans.extend(keys[a])\n return \'\'.join(map(str, arr)) == \'\'.join(map(str, ans))\n``` | 29 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
"Python" easy explanation blackboard | check-array-formation-through-concatenation | 0 | 1 | * **Simple and easy python3 solution**\n* **The approch is well explained in the below image**\n\n\n\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n keys, ans = {}, []\n for piece in pieces:\n keys[piece[0]] = piece\n for a in arr:\n if a in keys:\n ans.extend(keys[a])\n return \'\'.join(map(str, arr)) == \'\'.join(map(str, ans))\n``` | 29 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
simple code made using dict and beat 90% | check-array-formation-through-concatenation | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## create a dictionary\n # key: head number of piece\n # value: all number of single piece\n mapping = { piece[0]: piece for piece in pieces }\n \n result = []\n \n # try to make array from pieces\n for number in arr:\n \n result += mapping.get( number, [] )\n \n # check they are the same or not\n return result == arr\n``` | 1 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
simple code made using dict and beat 90% | check-array-formation-through-concatenation | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## create a dictionary\n # key: head number of piece\n # value: all number of single piece\n mapping = { piece[0]: piece for piece in pieces }\n \n result = []\n \n # try to make array from pieces\n for number in arr:\n \n result += mapping.get( number, [] )\n \n # check they are the same or not\n return result == arr\n``` | 1 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
Python O(n) by dictionary [w/ Comment] | check-array-formation-through-concatenation | 0 | 1 | Python O(n) by dictionary\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## dictionary\n # key: head number of piece\n # value: all number of single piece\n mapping = { piece[0]: piece for piece in pieces }\n \n result = []\n \n # try to make array from pieces\n for number in arr:\n \n result += mapping.get( number, [] )\n \n # check they are the same or not\n return result == arr\n```\n\n---\n\nReference:\n\n[1] [Python official docs about dictionary.get( ..., default value)](https://docs.python.org/3/library/stdtypes.html#dict.get)\n | 15 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
Python O(n) by dictionary [w/ Comment] | check-array-formation-through-concatenation | 0 | 1 | Python O(n) by dictionary\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## dictionary\n # key: head number of piece\n # value: all number of single piece\n mapping = { piece[0]: piece for piece in pieces }\n \n result = []\n \n # try to make array from pieces\n for number in arr:\n \n result += mapping.get( number, [] )\n \n # check they are the same or not\n return result == arr\n```\n\n---\n\nReference:\n\n[1] [Python official docs about dictionary.get( ..., default value)](https://docs.python.org/3/library/stdtypes.html#dict.get)\n | 15 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
[Python3] 2-line O(N) | check-array-formation-through-concatenation | 0 | 1 | Algo\nWe can leverage on the fact that the integers in `pieces` are distinct and define a mapping `mp` to map from the first element of piece to piece. Then, we could linearly scan `arr` and check if what\'s in arr `arr[i:i+len(mp[x])]` is the same as the one in piece `mp[x]`. \n\nImplementation\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n i = 0\n while i < len(arr): \n if (x := arr[i]) not in mp or mp[x] != arr[i:i+len(mp[x])]: return False \n i += len(mp[x])\n return True \n```\n\nEdited on 11/01/2020 \nAdding a 2-line implementation \n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n return sum((mp.get(x, []) for x in arr), []) == arr\n```\n\nAnalysis\nTime complexity `O(N)`\nSpace complexity `O(N)` | 11 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
[Python3] 2-line O(N) | check-array-formation-through-concatenation | 0 | 1 | Algo\nWe can leverage on the fact that the integers in `pieces` are distinct and define a mapping `mp` to map from the first element of piece to piece. Then, we could linearly scan `arr` and check if what\'s in arr `arr[i:i+len(mp[x])]` is the same as the one in piece `mp[x]`. \n\nImplementation\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n i = 0\n while i < len(arr): \n if (x := arr[i]) not in mp or mp[x] != arr[i:i+len(mp[x])]: return False \n i += len(mp[x])\n return True \n```\n\nEdited on 11/01/2020 \nAdding a 2-line implementation \n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n return sum((mp.get(x, []) for x in arr), []) == arr\n```\n\nAnalysis\nTime complexity `O(N)`\nSpace complexity `O(N)` | 11 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
check-array-formation-through-concatenation | check-array-formation-through-concatenation | 0 | 1 | # Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {}\n l = []\n for i in pieces:\n if i[0] not in d:\n d[i[0]]= i\n for i in arr:\n if d.get(i) is not None:\n l+= d[i]\n return l==arr\n\n\n \n``` | 0 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
check-array-formation-through-concatenation | check-array-formation-through-concatenation | 0 | 1 | # Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {}\n l = []\n for i in pieces:\n if i[0] not in d:\n d[i[0]]= i\n for i in arr:\n if d.get(i) is not None:\n l+= d[i]\n return l==arr\n\n\n \n``` | 0 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
My Solution :) | check-array-formation-through-concatenation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n allOne = []\n onePiece = [x for x in pieces if len(x) == 1]\n morePiece = [x for x in pieces if len(x) > 1]\n for x in morePiece:\n allOne += x\n \n for x in onePiece:\n allOne += x\n for x in allOne:\n if x not in arr:\n return False\n\n for x in morePiece:\n if arr.index(x[-1])-arr.index(x[0]) != len(x)-1:\n return False\n for x in onePiece:\n if x[0] not in arr:\n return False\n return True\n``` | 0 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
My Solution :) | check-array-formation-through-concatenation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n allOne = []\n onePiece = [x for x in pieces if len(x) == 1]\n morePiece = [x for x in pieces if len(x) > 1]\n for x in morePiece:\n allOne += x\n \n for x in onePiece:\n allOne += x\n for x in allOne:\n if x not in arr:\n return False\n\n for x in morePiece:\n if arr.index(x[-1])-arr.index(x[0]) != len(x)-1:\n return False\n for x in onePiece:\n if x[0] not in arr:\n return False\n return True\n``` | 0 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
Python solution | check-array-formation-through-concatenation | 0 | 1 | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n is_concatenated, index, _len = True, 0, len(pieces)\n\n while pieces:\n if pieces[0][0] not in arr: return False\n start = arr.index(pieces[0][0])\n if arr[start:len(pieces[0]) + start] != pieces[0]: return False\n del pieces[0]\n \n return is_concatenated\n``` | 0 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
Python solution | check-array-formation-through-concatenation | 0 | 1 | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n is_concatenated, index, _len = True, 0, len(pieces)\n\n while pieces:\n if pieces[0][0] not in arr: return False\n start = arr.index(pieces[0][0])\n if arr[start:len(pieces[0]) + start] != pieces[0]: return False\n del pieces[0]\n \n return is_concatenated\n``` | 0 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
One line not readable solution beats 94.12 % of users with Python 3 | check-array-formation-through-concatenation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n\n \n\n return reduce(lambda x, y: x + y, [{piece[0] : piece for piece in pieces}.get(item, []) for item in arr]) == arr\n\n\n\n \n``` | 0 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
One line not readable solution beats 94.12 % of users with Python 3 | check-array-formation-through-concatenation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n\n \n\n return reduce(lambda x, y: x + y, [{piece[0] : piece for piece in pieces}.get(item, []) for item in arr]) == arr\n\n\n\n \n``` | 0 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
Python O(n) by dictionary | check-array-formation-through-concatenation | 0 | 1 | # Intuition\nPython O(n) by dictionary\n\n# Approach\nPython O(n) by dictionary\n# Complexity\n- Time complexity:\n$$O(n)$$ \n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {}\n l = []\n for i in pieces:\n d[i[0]] = i\n for i in arr:\n if i in d:\n l.append(d[i])\n if "".join(str(i) for i in arr) == "".join(str(j) for i in l for j in i):\n return True\n else:\n return False\n``` | 0 | You are given an array of **distinct** integers `arr` and an array of integer arrays `pieces`, where the integers in `pieces` are **distinct**. Your goal is to form `arr` by concatenating the arrays in `pieces` **in any order**. However, you are **not** allowed to reorder the integers in each array `pieces[i]`.
Return `true` _if it is possible_ _to form the array_ `arr` _from_ `pieces`. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[15,88\], pieces = \[\[88\],\[15\]\]
**Output:** true
**Explanation:** Concatenate \[15\] then \[88\]
**Example 2:**
**Input:** arr = \[49,18,16\], pieces = \[\[16,18,49\]\]
**Output:** false
**Explanation:** Even though the numbers match, we cannot reorder pieces\[0\].
**Example 3:**
**Input:** arr = \[91,4,64,78\], pieces = \[\[78\],\[4,64\],\[91\]\]
**Output:** true
**Explanation:** Concatenate \[91\] then \[4,64\] then \[78\]
**Constraints:**
* `1 <= pieces.length <= arr.length <= 100`
* `sum(pieces[i].length) == arr.length`
* `1 <= pieces[i].length <= arr.length`
* `1 <= arr[i], pieces[i][j] <= 100`
* The integers in `arr` are **distinct**.
* The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct). | Try to solve it by keeping for each file chunk, the users who have this chunk. Try to solve it by keeping all the users in the system with their owned chunks, and when you request a chunk, check all users for it. |
Python O(n) by dictionary | check-array-formation-through-concatenation | 0 | 1 | # Intuition\nPython O(n) by dictionary\n\n# Approach\nPython O(n) by dictionary\n# Complexity\n- Time complexity:\n$$O(n)$$ \n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {}\n l = []\n for i in pieces:\n d[i[0]] = i\n for i in arr:\n if i in d:\n l.append(d[i])\n if "".join(str(i) for i in arr) == "".join(str(j) for i in l for j in i):\n return True\n else:\n return False\n``` | 0 | You are given an integer array `nums` where the `ith` bag contains `nums[i]` balls. You are also given an integer `maxOperations`.
You can perform the following operation at most `maxOperations` times:
* Take any bag of balls and divide it into two new bags with a **positive** number of balls.
* For example, a bag of `5` balls can become two new bags of `1` and `4` balls, or two new bags of `2` and `3` balls.
Your penalty is the **maximum** number of balls in a bag. You want to **minimize** your penalty after the operations.
Return _the minimum possible penalty after performing the operations_.
**Example 1:**
**Input:** nums = \[9\], maxOperations = 2
**Output:** 3
**Explanation:**
- Divide the bag with 9 balls into two bags of sizes 6 and 3. \[**9**\] -> \[6,3\].
- Divide the bag with 6 balls into two bags of sizes 3 and 3. \[**6**,3\] -> \[3,3,3\].
The bag with the most number of balls has 3 balls, so your penalty is 3 and you should return 3.
**Example 2:**
**Input:** nums = \[2,4,8,2\], maxOperations = 4
**Output:** 2
**Explanation:**
- Divide the bag with 8 balls into two bags of sizes 4 and 4. \[2,4,**8**,2\] -> \[2,4,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,**4**,4,4,2\] -> \[2,2,2,4,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,**4**,4,2\] -> \[2,2,2,2,2,4,2\].
- Divide the bag with 4 balls into two bags of sizes 2 and 2. \[2,2,2,2,2,**4**,2\] -> \[2,2,2,2,2,2,2,2\].
The bag with the most number of balls has 2 balls, so your penalty is 2, and you should return 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= maxOperations, nums[i] <= 109` | Note that the distinct part means that every position in the array belongs to only one piece Note that you can get the piece every position belongs to naively |
Beginner-friendly || Simple solution with Dynamic Programming in Python3 / TypeScript | count-sorted-vowel-strings | 0 | 1 | # Intuition\nLet\'s briefly explain what the problem is:\n- there\'s an integer `n`\n- our goal is to find **how many** distinct and **lexicographically** correct strings exist, which are created from **vowels**\n\nThe approach is straightforward: if we represent the final string as a **tree with nodes**, this helps to find the correct strings as long as we visit all of the nodes in this tree.\n\n```\n# (\' \')\n# / / | \\ \\\n# (a) (e) (i) (o) (u)\n# .....\n# and so on\n\n# Two things we only care about are lexicographical correctness\n# and count of vowels in a particular string\n\nn = 3\n# Valid: [aei, eio, iou, ...]\n# Invalid: [a, ie, uoi, ...] \n```\n\n# Approach\n1. define `dp` with `s` and `k`, that\'re a particular string and it\'s length\n2. if `k == n`, we\'ve founded a valid combination, so return `1`\n3. otherwise collect a **sum** of valid combinations, that\'re along in `dp(x, k + 1)` way, if a particular string is **fits** the conditions above\n4. return `dp(\'a\', 0)` as a starting point\n\n# Complexity\n- Time complexity: **O(N)**, since we\'re working with `n`- subproblems\n\n- Space complexity: **O(N)**, the same for storing\n\n# Code in Python3\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n @cache\n def dp(s, k):\n if k == n: return 1\n\n return sum([dp(x, k + 1) for x in [\'a\',\'e\',\'i\',\'o\',\'u\'] if s <= x])\n\n return dp(\'a\', 0)\n```\n\n# Code in TypeScript\n```\nfunction countVowelStrings(n: number): number {\n const cache = {}\n\n const keify = (i: string, j: number) => `${i}-${j}`\n\n const dp = (s: string, k: number) => {\n const key = keify(s, k)\n\n if (key in cache) return cache[key]\n if (k === n) return 1\n\n let result = 0\n\n for (const char of [\'a\', \'e\', \'i\', \'o\', \'u\']) {\n if (s <= char) result += dp(char, k + 1)\n }\n\n return cache[key] = result\n }\n\n return dp(\'a\', 0)\n};\n``` | 1 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
Beginner-friendly || Simple solution with Dynamic Programming in Python3 / TypeScript | count-sorted-vowel-strings | 0 | 1 | # Intuition\nLet\'s briefly explain what the problem is:\n- there\'s an integer `n`\n- our goal is to find **how many** distinct and **lexicographically** correct strings exist, which are created from **vowels**\n\nThe approach is straightforward: if we represent the final string as a **tree with nodes**, this helps to find the correct strings as long as we visit all of the nodes in this tree.\n\n```\n# (\' \')\n# / / | \\ \\\n# (a) (e) (i) (o) (u)\n# .....\n# and so on\n\n# Two things we only care about are lexicographical correctness\n# and count of vowels in a particular string\n\nn = 3\n# Valid: [aei, eio, iou, ...]\n# Invalid: [a, ie, uoi, ...] \n```\n\n# Approach\n1. define `dp` with `s` and `k`, that\'re a particular string and it\'s length\n2. if `k == n`, we\'ve founded a valid combination, so return `1`\n3. otherwise collect a **sum** of valid combinations, that\'re along in `dp(x, k + 1)` way, if a particular string is **fits** the conditions above\n4. return `dp(\'a\', 0)` as a starting point\n\n# Complexity\n- Time complexity: **O(N)**, since we\'re working with `n`- subproblems\n\n- Space complexity: **O(N)**, the same for storing\n\n# Code in Python3\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n @cache\n def dp(s, k):\n if k == n: return 1\n\n return sum([dp(x, k + 1) for x in [\'a\',\'e\',\'i\',\'o\',\'u\'] if s <= x])\n\n return dp(\'a\', 0)\n```\n\n# Code in TypeScript\n```\nfunction countVowelStrings(n: number): number {\n const cache = {}\n\n const keify = (i: string, j: number) => `${i}-${j}`\n\n const dp = (s: string, k: number) => {\n const key = keify(s, k)\n\n if (key in cache) return cache[key]\n if (k === n) return 1\n\n let result = 0\n\n for (const char of [\'a\', \'e\', \'i\', \'o\', \'u\']) {\n if (s <= char) result += dp(char, k + 1)\n }\n\n return cache[key] = result\n }\n\n return dp(\'a\', 0)\n};\n``` | 1 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Python Best Solution | count-sorted-vowel-strings | 0 | 1 | \n# Code\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n mul=1\n j=1\n for i in range(5,5+n):\n mul=(mul*i)//j\n j+=1\n return mul\n \n``` | 11 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
Python Best Solution | count-sorted-vowel-strings | 0 | 1 | \n# Code\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n mul=1\n j=1\n for i in range(5,5+n):\n mul=(mul*i)//j\n j+=1\n return mul\n \n``` | 11 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
✅🔥DP & 5 Variables Approach - C++/Java/Python | count-sorted-vowel-strings | 1 | 1 | # Intuition\n\n- Here we can observe a pattern to this problem.\n\n```\n\t\t a e i o u\n n=1 1 1 1 1 1 /a, e, i, o, u\n n=2 5 4 3 2 1 /a-> aa,ae,ai,ao,au | e-> ee,ei,eo,eu | i-> ii,io,iu | o-> oo,ou | u-> uu\n n=3 15 10 6 3 1\n```\n\n- If we observe from last there will be only 1 element which will start with u. Every other element will have the count of previous count + next element count. As example\nin n=2, i will be previous i(1) + count of next element, o(2) \u2192 3\nin n=3, e will be previous e(4) + count of next element, i(6) \u2192 10\n\n# Approach 01\n1. Using ***5 variables.***\n1. Initialize variables a, e, i, o, and u to 1, representing the count of strings ending with each vowel.\n2. Iterate from n-1 to 0 using a loop, updating the count for each vowel as follows:\n - Increment the count of strings ending with \'o\' (o += u).\n - Increment the count of strings ending with \'i\' (i += o).\n - Increment the count of strings ending with \'e\' (e += i).\n - Increment the count of strings ending with \'a\' (a += e).\n3. After the loop, the sum of counts for all vowels (a+e+i+o+u) represents the total count of strings of length n that consist only of vowels and are lexicographically sorted.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(n), where algorithm iterates through the loop n times, and each iteration involves constant time operations.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we use a constant amount of space for variables regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n \n while(--n){\n o += u;\n i += o;\n e += i;\n a += e;\n }\n \n return a+e+i+o+u;\n }\n};\n```\n```Java []\nclass Solution {\n public int countVowelStrings(int n) {\n int a = 1, e = 1, i = 1, o = 1, u = 1;\n\n while (--n > 0) {\n o += u;\n i += o;\n e += i;\n a += e;\n }\n\n return a + e + i + o + u;\n }\n}\n```\n```python []\nclass Solution(object):\n def countVowelStrings(self, n):\n a, e, i, o, u = 1, 1, 1, 1, 1\n\n while n > 1:\n o += u\n i += o\n e += i\n a += e\n n -= 1\n\n return a + e + i + o + u\n```\n\n---\n\n\n\n# Approach 02\n\n1. Using ***Dynamic Programing(dp).***\n2. Initialize a vector dp of size 5 (representing the vowels) with all elements set to 1. This vector will store the count of strings ending with each vowel.\n3. Iterate n-1 times (since we already have the count for n=1).\n4. In each iteration, update the count in the dp vector by summing up the counts of strings ending with each vowel from right to left. This step corresponds to extending the strings by adding one more character.\n5. After the iterations, the sum of counts in the dp vector represents the total number of strings of length n that can be formed using vowels.\n6. Return the sum as the result.\n\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(3n) - The algorithm iterates n-1 times, and each iteration involves updating the vector in constant time.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we use a constant amount of space for variables regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> dp(5, 1);\n int ans = 0;\n \n while(--n){\n for(int i=3; i>=0; i--){\n dp[i] += dp[i+1];\n }\n }\n \n for(auto x:dp) ans += x;\n \n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int countVowelStrings(int n) {\n int[] dp = new int[]{1, 1, 1, 1, 1};\n int ans = 0;\n\n while (--n > 0) {\n for (int i = 3; i >= 0; i--) {\n dp[i] += dp[i + 1];\n }\n }\n\n for (int x : dp) {\n ans += x;\n }\n\n return ans;\n }\n}\n```\n```python []\nclass Solution(object):\n def countVowelStrings(self, n):\n dp = [[0] * 5 for _ in range(n + 1)]\n\n for j in range(5):\n dp[1][j] = 1\n\n for i in range(2, n + 1):\n for j in range(5):\n for k in range(j, 5):\n dp[i][j] += dp[i - 1][k]\n\n result = sum(dp[n])\n return result\n```\n\n---\n\n> **Please upvote this solution**\n> | 183 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
✅🔥DP & 5 Variables Approach - C++/Java/Python | count-sorted-vowel-strings | 1 | 1 | # Intuition\n\n- Here we can observe a pattern to this problem.\n\n```\n\t\t a e i o u\n n=1 1 1 1 1 1 /a, e, i, o, u\n n=2 5 4 3 2 1 /a-> aa,ae,ai,ao,au | e-> ee,ei,eo,eu | i-> ii,io,iu | o-> oo,ou | u-> uu\n n=3 15 10 6 3 1\n```\n\n- If we observe from last there will be only 1 element which will start with u. Every other element will have the count of previous count + next element count. As example\nin n=2, i will be previous i(1) + count of next element, o(2) \u2192 3\nin n=3, e will be previous e(4) + count of next element, i(6) \u2192 10\n\n# Approach 01\n1. Using ***5 variables.***\n1. Initialize variables a, e, i, o, and u to 1, representing the count of strings ending with each vowel.\n2. Iterate from n-1 to 0 using a loop, updating the count for each vowel as follows:\n - Increment the count of strings ending with \'o\' (o += u).\n - Increment the count of strings ending with \'i\' (i += o).\n - Increment the count of strings ending with \'e\' (e += i).\n - Increment the count of strings ending with \'a\' (a += e).\n3. After the loop, the sum of counts for all vowels (a+e+i+o+u) represents the total count of strings of length n that consist only of vowels and are lexicographically sorted.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(n), where algorithm iterates through the loop n times, and each iteration involves constant time operations.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we use a constant amount of space for variables regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n \n while(--n){\n o += u;\n i += o;\n e += i;\n a += e;\n }\n \n return a+e+i+o+u;\n }\n};\n```\n```Java []\nclass Solution {\n public int countVowelStrings(int n) {\n int a = 1, e = 1, i = 1, o = 1, u = 1;\n\n while (--n > 0) {\n o += u;\n i += o;\n e += i;\n a += e;\n }\n\n return a + e + i + o + u;\n }\n}\n```\n```python []\nclass Solution(object):\n def countVowelStrings(self, n):\n a, e, i, o, u = 1, 1, 1, 1, 1\n\n while n > 1:\n o += u\n i += o\n e += i\n a += e\n n -= 1\n\n return a + e + i + o + u\n```\n\n---\n\n\n\n# Approach 02\n\n1. Using ***Dynamic Programing(dp).***\n2. Initialize a vector dp of size 5 (representing the vowels) with all elements set to 1. This vector will store the count of strings ending with each vowel.\n3. Iterate n-1 times (since we already have the count for n=1).\n4. In each iteration, update the count in the dp vector by summing up the counts of strings ending with each vowel from right to left. This step corresponds to extending the strings by adding one more character.\n5. After the iterations, the sum of counts in the dp vector represents the total number of strings of length n that can be formed using vowels.\n6. Return the sum as the result.\n\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(3n) - The algorithm iterates n-1 times, and each iteration involves updating the vector in constant time.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we use a constant amount of space for variables regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> dp(5, 1);\n int ans = 0;\n \n while(--n){\n for(int i=3; i>=0; i--){\n dp[i] += dp[i+1];\n }\n }\n \n for(auto x:dp) ans += x;\n \n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int countVowelStrings(int n) {\n int[] dp = new int[]{1, 1, 1, 1, 1};\n int ans = 0;\n\n while (--n > 0) {\n for (int i = 3; i >= 0; i--) {\n dp[i] += dp[i + 1];\n }\n }\n\n for (int x : dp) {\n ans += x;\n }\n\n return ans;\n }\n}\n```\n```python []\nclass Solution(object):\n def countVowelStrings(self, n):\n dp = [[0] * 5 for _ in range(n + 1)]\n\n for j in range(5):\n dp[1][j] = 1\n\n for i in range(2, n + 1):\n for j in range(5):\n for k in range(j, 5):\n dp[i][j] += dp[i - 1][k]\n\n result = sum(dp[n])\n return result\n```\n\n---\n\n> **Please upvote this solution**\n> | 183 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
✅ Python 4 approaches (DP, Maths) | count-sorted-vowel-strings | 0 | 1 | 1. ##### DP Tabulation\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [[0] * 6 for _ in range(n+1)]\n for i in range(1, 6):\n dp[1][i] = i\n \n for i in range(2, n+1):\n dp[i][1]=1\n for j in range(2, 6):\n dp[i][j] = dp[i][j-1] + dp[i-1][j]\n \n return dp[n][5]\n```\n**Time = O(n)**\n**Space = O(n)**\n\n---\n2. ##### O(1) Space\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [1] * 5\n \n for i in range(2, n+1):\n for j in range(4, -1, -1):\n dp[j] += sum(dp[:j]) \n \n return sum(dp)\n```\n\nAlternative solution shared by [@koacosmos](https://leetcode.com/koacosmos/)\n\n```\nclass Solution:\n def countVowelStrings(self, k: int) -> int: \n dp = [1] * 5\n \n for _ in range(1, k):\n for i in range(1, 5): \n dp[i] = dp[i] + dp[i-1]\n \n return sum(dp)\n```\n**Time = O(n)**\n**Space = O(1)**\n\n---\n\n3. ##### Mathematical equation using [Combinations with repetition](https://en.wikipedia.org/wiki/Combination#Number_of_combinations_with_repetition)\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n return (n + 4) * (n + 3) * (n + 2) * (n + 1) // 24;\n```\n\n---\nSolution shared by [@nithinmanne1](https://leetcode.com/nithinmanne1/) using Python internal library.\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n return math.comb(n + 4, 4)\n```\n\n**Time = O(1)\nSpace = O(1)**\n\n----\n\nOther contributers of this post:\n1. [@nithinmanne1](https://leetcode.com/nithinmanne1/)\n2. [@koacosmos](https://leetcode.com/koacosmos/)\n\n---\n\n***Please upvote if you find it useful*** | 50 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
✅ Python 4 approaches (DP, Maths) | count-sorted-vowel-strings | 0 | 1 | 1. ##### DP Tabulation\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [[0] * 6 for _ in range(n+1)]\n for i in range(1, 6):\n dp[1][i] = i\n \n for i in range(2, n+1):\n dp[i][1]=1\n for j in range(2, 6):\n dp[i][j] = dp[i][j-1] + dp[i-1][j]\n \n return dp[n][5]\n```\n**Time = O(n)**\n**Space = O(n)**\n\n---\n2. ##### O(1) Space\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [1] * 5\n \n for i in range(2, n+1):\n for j in range(4, -1, -1):\n dp[j] += sum(dp[:j]) \n \n return sum(dp)\n```\n\nAlternative solution shared by [@koacosmos](https://leetcode.com/koacosmos/)\n\n```\nclass Solution:\n def countVowelStrings(self, k: int) -> int: \n dp = [1] * 5\n \n for _ in range(1, k):\n for i in range(1, 5): \n dp[i] = dp[i] + dp[i-1]\n \n return sum(dp)\n```\n**Time = O(n)**\n**Space = O(1)**\n\n---\n\n3. ##### Mathematical equation using [Combinations with repetition](https://en.wikipedia.org/wiki/Combination#Number_of_combinations_with_repetition)\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n return (n + 4) * (n + 3) * (n + 2) * (n + 1) // 24;\n```\n\n---\nSolution shared by [@nithinmanne1](https://leetcode.com/nithinmanne1/) using Python internal library.\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n return math.comb(n + 4, 4)\n```\n\n**Time = O(1)\nSpace = O(1)**\n\n----\n\nOther contributers of this post:\n1. [@nithinmanne1](https://leetcode.com/nithinmanne1/)\n2. [@koacosmos](https://leetcode.com/koacosmos/)\n\n---\n\n***Please upvote if you find it useful*** | 50 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Dynamic Programming - Python [100%] [Explanation + code] | count-sorted-vowel-strings | 0 | 1 | In this problem, the pattern I observed was prepending \'a\' to all the strings of length n-1 does not affect any order. Similarly, \'e\' can be prepended to strings starting with \'e\' and greater vowels and so on.\n\nSo we have our subproblem.\n\n**How do we fill the DP Table?**\nLets, take an example of n = 3\n\n\n\nFor n = 1, number of strings starting with u is 1, with o is 2 (including the ones starting with u) and so on.\nFor n = 2, number of strings starting with u is 1, but for o its (number of strings of length 2 starting with u + number of strings of length 1 starting with o) and so on.\ndp[i][j] represents total no. of string of length i , starting with characters of column j and after j. (Thanks @[rkm_coder](https://leetcode.com/rkm_coder/) for the correction)\n\nThe recursive expression is : dp[i][j] = dp[i - 1][j] + dp[i][j + 1]\n\nFinally, we will get our answer at dp[n][0]\n\nThe running time of my algorithm is **O(n)**\n\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n dp = [[i for i in range(5,0,-1)] for _ in range(n)] # intialize dp matrix\n \n for i in range(1,n):\n for j in range(3,-1,-1):\n dp[i][j] = dp[i - 1][j] + dp[i][j + 1] # dp expression\n \n return dp[n-1][0]\n```\n\nAlso check out Java implementation here: https://leetcode.com/problems/count-sorted-vowel-strings/discuss/918728/java-dp-beats-100 | 103 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
Dynamic Programming - Python [100%] [Explanation + code] | count-sorted-vowel-strings | 0 | 1 | In this problem, the pattern I observed was prepending \'a\' to all the strings of length n-1 does not affect any order. Similarly, \'e\' can be prepended to strings starting with \'e\' and greater vowels and so on.\n\nSo we have our subproblem.\n\n**How do we fill the DP Table?**\nLets, take an example of n = 3\n\n\n\nFor n = 1, number of strings starting with u is 1, with o is 2 (including the ones starting with u) and so on.\nFor n = 2, number of strings starting with u is 1, but for o its (number of strings of length 2 starting with u + number of strings of length 1 starting with o) and so on.\ndp[i][j] represents total no. of string of length i , starting with characters of column j and after j. (Thanks @[rkm_coder](https://leetcode.com/rkm_coder/) for the correction)\n\nThe recursive expression is : dp[i][j] = dp[i - 1][j] + dp[i][j + 1]\n\nFinally, we will get our answer at dp[n][0]\n\nThe running time of my algorithm is **O(n)**\n\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n dp = [[i for i in range(5,0,-1)] for _ in range(n)] # intialize dp matrix\n \n for i in range(1,n):\n for j in range(3,-1,-1):\n dp[i][j] = dp[i - 1][j] + dp[i][j + 1] # dp expression\n \n return dp[n-1][0]\n```\n\nAlso check out Java implementation here: https://leetcode.com/problems/count-sorted-vowel-strings/discuss/918728/java-dp-beats-100 | 103 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Easy method for beginners to understand | count-sorted-vowel-strings | 0 | 1 | # Intuition\nWe need to just calculate the permutation for given value n (Eg n=3\n then result = 5*(5+1)*(5+2)//(1*2*3)= 35)\n\n# Code\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n mul=1\n j=1\n for i in range(5,5+n):\n mul=(mul*i)//j\n j+=1\n return mul\n \n``` | 1 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
Easy method for beginners to understand | count-sorted-vowel-strings | 0 | 1 | # Intuition\nWe need to just calculate the permutation for given value n (Eg n=3\n then result = 5*(5+1)*(5+2)//(1*2*3)= 35)\n\n# Code\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n mul=1\n j=1\n for i in range(5,5+n):\n mul=(mul*i)//j\n j+=1\n return mul\n \n``` | 1 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
3 different solutions (backtracking, dynamic programming, math) | count-sorted-vowel-strings | 0 | 1 | \n\n**Backtracking solution:**\n**Time complexity:** `O(n^5)`\nWe try all the possibilities where adding the new vowel doesn\'t break the lexicographic order. For example, if the last character of our actual possibility is \'e\', we can\'t add an \'a\' after it.\n```\ndef count(n, last=\'\'):\n if n == 0:\n return 1\n else:\n nb = 0\n for vowel in [\'a\', \'e\', \'i\', \'o\', \'u\']:\n if last <= vowel:\n nb += count(n-1, vowel)\n return nb\n```\n\n\n**Dynamic programming solution:**\n**Time complexity:** `O(n)`\nWe use a dp matrix of n rows and 5 columns (one column for each vowel) where the number of strings of size k that start with a vowel v is the sum of strings of size k-1 with whom we can add the vowel v from the beginning without breaking the order\nWe can add \'a\' before any vowel string without breaking the order, so the number of strings of size k that start with \'a\' is the number of strings of size k-1 that start with \'a\', \'e\', \'i\', \'o\', or \'u\'\nWe can add \'e\' before strings that start with \'e\', \'i\', \'o\', or \'u\' without breaking the order, so the number of strings of size k that start with \'e\' is the number of strings of size k-1 that start with \'e\', \'i\', \'o\', or \'u\'\nSame logic with remaining vowels (\'i\' -> \'i\', \'o\', or \'u\' / \'o\' -> \'o\' or \'u\' / \'u\' -> \'u\')\nAfter filling the matrix, the last row will contain the numbers of strings of size n with each vowel, we do the sum\n```\ndef count(n):\n NB_VOWELS = 5\n dp = [[0]*NB_VOWELS for i in range(n)]\n dp[0] = [1]*NB_VOWELS\n for i in range(1, len(dp)):\n dp[i][0] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # a\n dp[i][1] = dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # e\n dp[i][2] = dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # i\n dp[i][3] = dp[i-1][3] + dp[i-1][4] # o\n dp[i][4] = dp[i-1][4] # u\n return sum(dp[-1])\n```\n\n\n**Math solution:**\n**Time complexity:** `O(1)`\nThe number of possible sorted strings that we can get by taking n vowels from 5 possible vowels is the number of possible combinations with repetition that we can get by taking n elements from 5 possible elements, and we have a mathematical law for that\n\n\n\n```\ndef count(n):\n return (n+4)*(n+3)*(n+2)*(n+1)//24\n```\n\n\n\n\n\n | 30 | Given an integer `n`, return _the number of strings of length_ `n` _that consist only of vowels (_`a`_,_ `e`_,_ `i`_,_ `o`_,_ `u`_) and are **lexicographically sorted**._
A string `s` is **lexicographically sorted** if for all valid `i`, `s[i]` is the same as or comes before `s[i+1]` in the alphabet.
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** The 5 sorted strings that consist of vowels only are `[ "a ", "e ", "i ", "o ", "u "].`
**Example 2:**
**Input:** n = 2
**Output:** 15
**Explanation:** The 15 sorted strings that consist of vowels only are
\[ "aa ", "ae ", "ai ", "ao ", "au ", "ee ", "ei ", "eo ", "eu ", "ii ", "io ", "iu ", "oo ", "ou ", "uu "\].
Note that "ea " is not a valid string since 'e' comes after 'a' in the alphabet.
**Example 3:**
**Input:** n = 33
**Output:** 66045
**Constraints:**
* `1 <= n <= 50` | null |
3 different solutions (backtracking, dynamic programming, math) | count-sorted-vowel-strings | 0 | 1 | \n\n**Backtracking solution:**\n**Time complexity:** `O(n^5)`\nWe try all the possibilities where adding the new vowel doesn\'t break the lexicographic order. For example, if the last character of our actual possibility is \'e\', we can\'t add an \'a\' after it.\n```\ndef count(n, last=\'\'):\n if n == 0:\n return 1\n else:\n nb = 0\n for vowel in [\'a\', \'e\', \'i\', \'o\', \'u\']:\n if last <= vowel:\n nb += count(n-1, vowel)\n return nb\n```\n\n\n**Dynamic programming solution:**\n**Time complexity:** `O(n)`\nWe use a dp matrix of n rows and 5 columns (one column for each vowel) where the number of strings of size k that start with a vowel v is the sum of strings of size k-1 with whom we can add the vowel v from the beginning without breaking the order\nWe can add \'a\' before any vowel string without breaking the order, so the number of strings of size k that start with \'a\' is the number of strings of size k-1 that start with \'a\', \'e\', \'i\', \'o\', or \'u\'\nWe can add \'e\' before strings that start with \'e\', \'i\', \'o\', or \'u\' without breaking the order, so the number of strings of size k that start with \'e\' is the number of strings of size k-1 that start with \'e\', \'i\', \'o\', or \'u\'\nSame logic with remaining vowels (\'i\' -> \'i\', \'o\', or \'u\' / \'o\' -> \'o\' or \'u\' / \'u\' -> \'u\')\nAfter filling the matrix, the last row will contain the numbers of strings of size n with each vowel, we do the sum\n```\ndef count(n):\n NB_VOWELS = 5\n dp = [[0]*NB_VOWELS for i in range(n)]\n dp[0] = [1]*NB_VOWELS\n for i in range(1, len(dp)):\n dp[i][0] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # a\n dp[i][1] = dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # e\n dp[i][2] = dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # i\n dp[i][3] = dp[i-1][3] + dp[i-1][4] # o\n dp[i][4] = dp[i-1][4] # u\n return sum(dp[-1])\n```\n\n\n**Math solution:**\n**Time complexity:** `O(1)`\nThe number of possible sorted strings that we can get by taking n vowels from 5 possible vowels is the number of possible combinations with repetition that we can get by taking n elements from 5 possible elements, and we have a mathematical law for that\n\n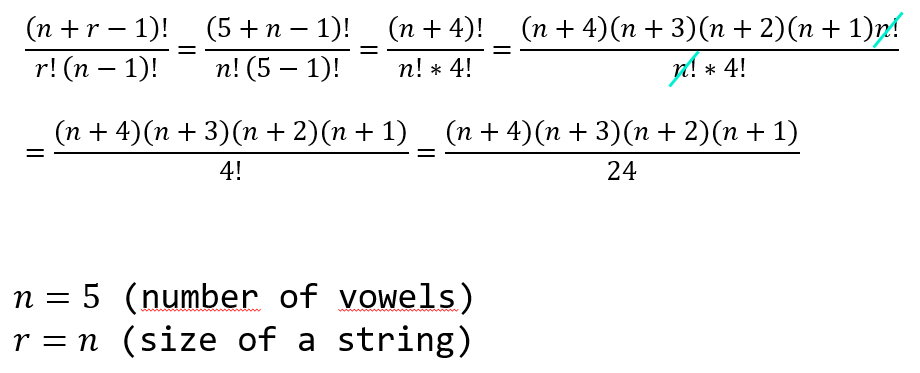\n\n```\ndef count(n):\n return (n+4)*(n+3)*(n+2)*(n+1)//24\n```\n\n\n\n\n\n | 30 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Python | Min Heap | With Explanation | Easy to Understand | furthest-building-you-can-reach | 0 | 1 | ```\nclass Solution:\n def furthestBuilding(self, heights: List[int], bricks: int, ladders: int) -> int:\n # prepare: use a min heap to store each difference(climb) between two contiguous buildings\n # strategy: use the ladders for the longest climbs and the bricks for the shortest climbs\n \n min_heap = []\n n = len(heights)\n \n for i in range(n-1):\n climb = heights[i+1] - heights[i]\n \n if climb <= 0:\n continue\n \n # we need to use a ladder or some bricks, always take the ladder at first\n if climb > 0:\n heapq.heappush(min_heap, climb)\n \n # ladders are all in used, find the current shortest climb to use bricks instead!\n if len(min_heap) > ladders:\n # find the current shortest climb to use bricks\n brick_need = heapq.heappop(min_heap)\n bricks -= brick_need\n \n if bricks < 0:\n return i\n \n return n-1\n```\n\n**Upvote if it is helpful for you, many thanks!**\n | 36 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
Python | Min Heap | With Explanation | Easy to Understand | furthest-building-you-can-reach | 0 | 1 | ```\nclass Solution:\n def furthestBuilding(self, heights: List[int], bricks: int, ladders: int) -> int:\n # prepare: use a min heap to store each difference(climb) between two contiguous buildings\n # strategy: use the ladders for the longest climbs and the bricks for the shortest climbs\n \n min_heap = []\n n = len(heights)\n \n for i in range(n-1):\n climb = heights[i+1] - heights[i]\n \n if climb <= 0:\n continue\n \n # we need to use a ladder or some bricks, always take the ladder at first\n if climb > 0:\n heapq.heappush(min_heap, climb)\n \n # ladders are all in used, find the current shortest climb to use bricks instead!\n if len(min_heap) > ladders:\n # find the current shortest climb to use bricks\n brick_need = heapq.heappop(min_heap)\n bricks -= brick_need\n \n if bricks < 0:\n return i\n \n return n-1\n```\n\n**Upvote if it is helpful for you, many thanks!**\n | 36 | There are `n` buildings in a line. You are given an integer array `heights` of size `n` that represents the heights of the buildings in the line.
The ocean is to the right of the buildings. A building has an ocean view if the building can see the ocean without obstructions. Formally, a building has an ocean view if all the buildings to its right have a **smaller** height.
Return a list of indices **(0-indexed)** of buildings that have an ocean view, sorted in increasing order.
**Example 1:**
**Input:** heights = \[4,2,3,1\]
**Output:** \[0,2,3\]
**Explanation:** Building 1 (0-indexed) does not have an ocean view because building 2 is taller.
**Example 2:**
**Input:** heights = \[4,3,2,1\]
**Output:** \[0,1,2,3\]
**Explanation:** All the buildings have an ocean view.
**Example 3:**
**Input:** heights = \[1,3,2,4\]
**Output:** \[3\]
**Explanation:** Only building 3 has an ocean view.
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 109` | Assume the problem is to check whether you can reach the last building or not. You'll have to do a set of jumps, and choose for each one whether to do it using a ladder or bricks. It's always optimal to use ladders in the largest jumps. Iterate on the buildings, maintaining the largest r jumps and the sum of the remaining ones so far, and stop whenever this sum exceeds b. |
Python 3 || 13 lines, iterative & recursive versions , w/example || T/M: 94% / 81% | kth-smallest-instructions | 0 | 1 | The iterative version:\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n\n (v, h), ans = destination, \'\' # Example: destination = [3, 4] k = 16 \n\n while h and v: # h v k c Ans \n # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\n c = comb(h+v-1,v) # 4 3 16 comb(6,3) = 20 "H"\n # 3 3 16 comb(5,3) = 10 "HV" \n if c < k: # 3 2 6 comb(4,2) = 6 "HVH"\n ans+= \'V\' # 2 2 6 comb(3,1) = 3 "HVHV"\n v-= 1 # 2 1 3 comb(2,1) = 2 "HVHV"\n k-= c # 2 0 1 "HVHVV"\n else: \n ans+= \'H\' # return "HVHVV" + "H"*2 = "HVHVVHH"\n h-= 1\n \n if not h: ans+= \'V\'*v\n if not v: ans+= \'H\'*h \n \n return ans\n```\n[https://leetcode.com/problems/kth-smallest-instructions/submissions/903074964/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1).\n\n_______\n\nThe recursive version:\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n\n v, h = destination\n\n def dp(h: int,v: int,k: int)-> str:\n\n if not h: return \'V\'*v\n if not v: return \'H\'*h\n\n c = comb(h+v-1,v)\n\n if c < k: return \'V\' + dp(h ,v-1,k - c)\n else : return \'H\' + dp(h-1,v ,k)\n \n return dp(h,v,k)\n``` | 3 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Python 3 || 13 lines, iterative & recursive versions , w/example || T/M: 94% / 81% | kth-smallest-instructions | 0 | 1 | The iterative version:\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n\n (v, h), ans = destination, \'\' # Example: destination = [3, 4] k = 16 \n\n while h and v: # h v k c Ans \n # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\n c = comb(h+v-1,v) # 4 3 16 comb(6,3) = 20 "H"\n # 3 3 16 comb(5,3) = 10 "HV" \n if c < k: # 3 2 6 comb(4,2) = 6 "HVH"\n ans+= \'V\' # 2 2 6 comb(3,1) = 3 "HVHV"\n v-= 1 # 2 1 3 comb(2,1) = 2 "HVHV"\n k-= c # 2 0 1 "HVHVV"\n else: \n ans+= \'H\' # return "HVHVV" + "H"*2 = "HVHVVHH"\n h-= 1\n \n if not h: ans+= \'V\'*v\n if not v: ans+= \'H\'*h \n \n return ans\n```\n[https://leetcode.com/problems/kth-smallest-instructions/submissions/903074964/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1).\n\n_______\n\nThe recursive version:\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n\n v, h = destination\n\n def dp(h: int,v: int,k: int)-> str:\n\n if not h: return \'V\'*v\n if not v: return \'H\'*h\n\n c = comb(h+v-1,v)\n\n if c < k: return \'V\' + dp(h ,v-1,k - c)\n else : return \'H\' + dp(h-1,v ,k)\n \n return dp(h,v,k)\n``` | 3 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Solution | kth-smallest-instructions | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int getCount(int h, int v)\n {\n if(h == 0 || v == 0) return 1;\n long long res = 1;\n if(h < v) swap(h, v);\n for(int i = h + 1; i <= (h+v); i++) res *= i;\n for(int i = 1; i <= v; i++) res /= i;\n return (int)res;\n }\n string kthSmallestPath(vector<int>& dest, int k) {\n int h = dest[1];\n int v = dest[0];\n int len = h + v;\n string res;\n for(int i = 0; i < len; i++)\n {\n if(h == 0) \n {\n v--;\n res.push_back(\'V\');\n continue;\n }\n if(v == 0) \n {\n h--;\n res.push_back(\'H\');\n continue;\n }\n int cnt = getCount(h - 1, v);\n if(cnt >= k)\n {\n res.push_back(\'H\');\n h--;\n }\n else\n {\n k -= cnt;\n v--;\n res.push_back(\'V\');\n }\n }\n return res;\n }\n};\n```\n```Python3 []\nclass Solution:\n def kthSmallestPath(self, D, K):\n K -= 1\n V, H = D\n ans = \'\'\n while K and H and V:\n C = comb(H + V - 1, H - 1)\n if C <= K:\n ans, V, K = ans + \'V\', V - 1, K - C\n else:\n ans, H = ans + \'H\', H - 1\n return ans + \'H\' * H + \'V\' * V\n```\n```Java []\nclass Solution {\n public String kthSmallestPath(int[] destination, int k) {\n int m = destination[0] + 1;\n int n = destination[1] + 1;\n int[][] dp = new int[m][n];\n for (int i = 0; i < m; i++) dp[i][n-1] = 1; \n for (int j = 0; j < n; j++) dp[m-1][j] = 1; \n for (int i = m-2; i >= 0; i--) {\n for (int j = n-2; j >= 0; j--) {\n dp[i][j] = dp[i+1][j] + dp[i][j+1];\n }\n }\n int i = 0;\n int j = 0;\n StringBuilder sb = new StringBuilder();\n while (i < m-1 && j < n-1) {\n if (k <= dp[i][j+1]) {\n j++;\n sb.append(\'H\');\n } \n else {\n k -= dp[i][j+1];\n i++;\n sb.append(\'V\');\n }\n }\n for (; i < m-1; i++) sb.append(\'V\');\n for (; j < n-1; j++) sb.append(\'H\');\n return sb.toString();\n }\n}\n```\n | 1 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Solution | kth-smallest-instructions | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int getCount(int h, int v)\n {\n if(h == 0 || v == 0) return 1;\n long long res = 1;\n if(h < v) swap(h, v);\n for(int i = h + 1; i <= (h+v); i++) res *= i;\n for(int i = 1; i <= v; i++) res /= i;\n return (int)res;\n }\n string kthSmallestPath(vector<int>& dest, int k) {\n int h = dest[1];\n int v = dest[0];\n int len = h + v;\n string res;\n for(int i = 0; i < len; i++)\n {\n if(h == 0) \n {\n v--;\n res.push_back(\'V\');\n continue;\n }\n if(v == 0) \n {\n h--;\n res.push_back(\'H\');\n continue;\n }\n int cnt = getCount(h - 1, v);\n if(cnt >= k)\n {\n res.push_back(\'H\');\n h--;\n }\n else\n {\n k -= cnt;\n v--;\n res.push_back(\'V\');\n }\n }\n return res;\n }\n};\n```\n```Python3 []\nclass Solution:\n def kthSmallestPath(self, D, K):\n K -= 1\n V, H = D\n ans = \'\'\n while K and H and V:\n C = comb(H + V - 1, H - 1)\n if C <= K:\n ans, V, K = ans + \'V\', V - 1, K - C\n else:\n ans, H = ans + \'H\', H - 1\n return ans + \'H\' * H + \'V\' * V\n```\n```Java []\nclass Solution {\n public String kthSmallestPath(int[] destination, int k) {\n int m = destination[0] + 1;\n int n = destination[1] + 1;\n int[][] dp = new int[m][n];\n for (int i = 0; i < m; i++) dp[i][n-1] = 1; \n for (int j = 0; j < n; j++) dp[m-1][j] = 1; \n for (int i = m-2; i >= 0; i--) {\n for (int j = n-2; j >= 0; j--) {\n dp[i][j] = dp[i+1][j] + dp[i][j+1];\n }\n }\n int i = 0;\n int j = 0;\n StringBuilder sb = new StringBuilder();\n while (i < m-1 && j < n-1) {\n if (k <= dp[i][j+1]) {\n j++;\n sb.append(\'H\');\n } \n else {\n k -= dp[i][j+1];\n i++;\n sb.append(\'V\');\n }\n }\n for (; i < m-1; i++) sb.append(\'V\');\n for (; j < n-1; j++) sb.append(\'H\');\n return sb.toString();\n }\n}\n```\n | 1 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
[Python] Simple & Fast Solution, explained | kth-smallest-instructions | 0 | 1 | **Observations**\n1. We know for certain number of **\'H\'** and **\'V\'**, the total number of instructions are **comb(h + v, v)**\n2. They should be sorted **lexicographically**, which means: the **order** of instructions with first character of **\'H\'** are always smaller than instructions with first character of **\'V\'**:\nFor example, **destination = [2,3], k = 1**:\n["**H**HHVV", "**H**HVHV", "**H**HVVH", "**H**VHHV", "**H**VHVH", "**H**VVHH", "**V**HHHV", "**V**HHVH", "**V**HVHH", "**V**VHHH"]\n3. If the first character is **\'H\'**, we know there will be **comb(h + v - 1, v)** number of instructions for the rest of characters because we used **one** **\'H\'**.\n\n**Algo**\n1. Use the above 3 facts, we know after sored, **comb(h + v - 1, v)** number of instructions starting with **\'H\'**, and the rest of the instructions are starting with **\'V\'**\n2. Based on value of **k**, we will know which **group** the kth instructions belongs to\n3. Then we can get the characters one by one\n4. Available characters will be **decreasing** until one of them hit **0**\n\n**Code:**\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n v, h = destination\n res = \'\'\n while h > 0 and v > 0:\n pre = comb(h + v - 1, v)\n \n if k <= pre:\n res += \'H\'\n h -= 1\n else:\n res += \'V\'\n v -= 1\n k -= pre\n\n if h == 0:\n res += \'V\' * v\n if v == 0:\n res += \'H\' * h\n \n return res\n```\n**Runtime: 32ms** | 17 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
[Python] Simple & Fast Solution, explained | kth-smallest-instructions | 0 | 1 | **Observations**\n1. We know for certain number of **\'H\'** and **\'V\'**, the total number of instructions are **comb(h + v, v)**\n2. They should be sorted **lexicographically**, which means: the **order** of instructions with first character of **\'H\'** are always smaller than instructions with first character of **\'V\'**:\nFor example, **destination = [2,3], k = 1**:\n["**H**HHVV", "**H**HVHV", "**H**HVVH", "**H**VHHV", "**H**VHVH", "**H**VVHH", "**V**HHHV", "**V**HHVH", "**V**HVHH", "**V**VHHH"]\n3. If the first character is **\'H\'**, we know there will be **comb(h + v - 1, v)** number of instructions for the rest of characters because we used **one** **\'H\'**.\n\n**Algo**\n1. Use the above 3 facts, we know after sored, **comb(h + v - 1, v)** number of instructions starting with **\'H\'**, and the rest of the instructions are starting with **\'V\'**\n2. Based on value of **k**, we will know which **group** the kth instructions belongs to\n3. Then we can get the characters one by one\n4. Available characters will be **decreasing** until one of them hit **0**\n\n**Code:**\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n v, h = destination\n res = \'\'\n while h > 0 and v > 0:\n pre = comb(h + v - 1, v)\n \n if k <= pre:\n res += \'H\'\n h -= 1\n else:\n res += \'V\'\n v -= 1\n k -= pre\n\n if h == 0:\n res += \'V\' * v\n if v == 0:\n res += \'H\' * h\n \n return res\n```\n**Runtime: 32ms** | 17 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
✔ Python3 Solution | Combination | kth-smallest-instructions | 0 | 1 | # Solution - 1\n```Python\nclass Solution:\n def kthSmallestPath(self, D, K):\n K -= 1\n V, H = D\n ans = \'\'\n while K and H and V:\n C = comb(H + V - 1, H - 1)\n if C <= K:\n ans, V, K = ans + \'V\', V - 1, K - C\n else:\n ans, H = ans + \'H\', H - 1\n return ans + \'H\' * H + \'V\' * V\n```\n\n# Solution - 2\n```Python\nclass Solution:\n def kthSmallestPath(self, D, K):\n K -= 1\n V, H = D\n C = comb(H + V - 1, H - 1)\n ans = \'\'\n while K and H and V:\n if C <= K:\n ans, V, K = ans + \'V\', V - 1, K - C\n C *= (V + 1)\n else:\n ans, H = ans + \'H\', H - 1\n C *= H\n C //= (V + H)\n return ans + \'H\' * H + \'V\' * V\n``` | 2 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
✔ Python3 Solution | Combination | kth-smallest-instructions | 0 | 1 | # Solution - 1\n```Python\nclass Solution:\n def kthSmallestPath(self, D, K):\n K -= 1\n V, H = D\n ans = \'\'\n while K and H and V:\n C = comb(H + V - 1, H - 1)\n if C <= K:\n ans, V, K = ans + \'V\', V - 1, K - C\n else:\n ans, H = ans + \'H\', H - 1\n return ans + \'H\' * H + \'V\' * V\n```\n\n# Solution - 2\n```Python\nclass Solution:\n def kthSmallestPath(self, D, K):\n K -= 1\n V, H = D\n C = comb(H + V - 1, H - 1)\n ans = \'\'\n while K and H and V:\n if C <= K:\n ans, V, K = ans + \'V\', V - 1, K - C\n C *= (V + 1)\n else:\n ans, H = ans + \'H\', H - 1\n C *= H\n C //= (V + H)\n return ans + \'H\' * H + \'V\' * V\n``` | 2 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
[Python3] greedy | kth-smallest-instructions | 0 | 1 | Algo \nGiven `m` H and `n` V to place, we check if it is possible to place H. If so, decrement `n`; otherwise decrement `m`. Since there are `comb(m+n-1, n-1)` instructions starting with H, the condition to check for placing H is `comb(m+n-1, n-1) >= k`. \n\nImplementation \n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n m, n = destination # m "V" & n "H" in total \n ans = ""\n while n: \n kk = comb(m+n-1, n-1) # (m+n-1 choose n-1) instructions starting with "H" \n if kk >= k: \n ans += "H"\n n -= 1\n else: \n ans += "V"\n m -= 1\n k -= kk \n return ans + m*"V"\n```\n\nAnalysis\nTime complexity `O(M*N + N^2)`\nSpace complexity `O(M+N)` | 5 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
[Python3] greedy | kth-smallest-instructions | 0 | 1 | Algo \nGiven `m` H and `n` V to place, we check if it is possible to place H. If so, decrement `n`; otherwise decrement `m`. Since there are `comb(m+n-1, n-1)` instructions starting with H, the condition to check for placing H is `comb(m+n-1, n-1) >= k`. \n\nImplementation \n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n m, n = destination # m "V" & n "H" in total \n ans = ""\n while n: \n kk = comb(m+n-1, n-1) # (m+n-1 choose n-1) instructions starting with "H" \n if kk >= k: \n ans += "H"\n n -= 1\n else: \n ans += "V"\n m -= 1\n k -= kk \n return ans + m*"V"\n```\n\nAnalysis\nTime complexity `O(M*N + N^2)`\nSpace complexity `O(M+N)` | 5 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Recursive Combinatorics 99% runtime | kth-smallest-instructions | 0 | 1 | # Intuition\nWe might be tempted to brute force enumerate all strings then sort and get the top K. But, a quick calculation shows that if we naively enumerate even the top K strings, it is too much (nCr)\n\nThis motivates us to find a more guided approach towards finding the best string. The key insight is found by playing with strings: if we place a certain letter (V/H), how many completed strings will start with said letter?\n\nFor example, if we have a string of length 1, H, then: (r+c-1)C(c-1) strings will start with this starting string. Not only that, we know that all (r+c-1)C(c-1) go before any string that starts with V. This means if k <= (r+c-1)C(c-1), it must be true that our answer starts with H! \n\nWe can repeat this process recursively, choosing to add "H" or "V" based on whether our target string k lies within the set of strings beginning with each letter. Eventually, we can narrow down and get our answer.\n\n# Code\n```\nfrom math import comb\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n def rec(r,c,kp): \n if kp <= 1 and (r == 0 or c == 0):\n a = ""\n if r > 0:\n a = "V"*r\n elif c > 0:\n a = "H"*c\n return a\n a = ""\n if c > 0:\n lower = comb(r+c-1,c-1) # say we take a column away\n if lower >= kp:\n a += "H" + rec(r,c-1,kp)\n else:\n a += "V" + rec(r-1,c,kp-lower)\n else: # everything is either a row or done\n a += rec(r-1,c,kp) + "V"\n\n return a\n return rec(destination[0], destination[1], k)\n``` | 0 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Recursive Combinatorics 99% runtime | kth-smallest-instructions | 0 | 1 | # Intuition\nWe might be tempted to brute force enumerate all strings then sort and get the top K. But, a quick calculation shows that if we naively enumerate even the top K strings, it is too much (nCr)\n\nThis motivates us to find a more guided approach towards finding the best string. The key insight is found by playing with strings: if we place a certain letter (V/H), how many completed strings will start with said letter?\n\nFor example, if we have a string of length 1, H, then: (r+c-1)C(c-1) strings will start with this starting string. Not only that, we know that all (r+c-1)C(c-1) go before any string that starts with V. This means if k <= (r+c-1)C(c-1), it must be true that our answer starts with H! \n\nWe can repeat this process recursively, choosing to add "H" or "V" based on whether our target string k lies within the set of strings beginning with each letter. Eventually, we can narrow down and get our answer.\n\n# Code\n```\nfrom math import comb\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n def rec(r,c,kp): \n if kp <= 1 and (r == 0 or c == 0):\n a = ""\n if r > 0:\n a = "V"*r\n elif c > 0:\n a = "H"*c\n return a\n a = ""\n if c > 0:\n lower = comb(r+c-1,c-1) # say we take a column away\n if lower >= kp:\n a += "H" + rec(r,c-1,kp)\n else:\n a += "V" + rec(r-1,c,kp-lower)\n else: # everything is either a row or done\n a += rec(r-1,c,kp) + "V"\n\n return a\n return rec(destination[0], destination[1], k)\n``` | 0 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Python Combinatorial solution. Beats 95%. 10 lines | kth-smallest-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPython combinatorial search. Beats 97%. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRecursive combinatorial search\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(destination[0] + destination[1])\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(destination[0] + destination[1]) \n\n# Code\n```\nimport math\nclass Solution:\n def kthSmallestPath(self, destination: list[int], k: int) -> str:\n def choose(n, k):\n return math.factorial(n) / (math.factorial(n-k)*math.factorial(k))\n def helper(n, k, rank) -> str:\n if k == 0:\n return \'H\' * n\n elif n == k:\n return \'V\' * n\n if rank <= choose(n-1, k):\n # we know path must start with a 0 (\'H\')\n return \'H\' + helper(n-1, k, rank)\n else:\n # we know path must start with a 1 (\'V\')\n return \'V\' + helper(n-1, k-1, rank - choose(n-1, k))\n return helper(destination[0]+destination[1], destination[0], k)\n``` | 0 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Python Combinatorial solution. Beats 95%. 10 lines | kth-smallest-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPython combinatorial search. Beats 97%. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRecursive combinatorial search\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(destination[0] + destination[1])\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(destination[0] + destination[1]) \n\n# Code\n```\nimport math\nclass Solution:\n def kthSmallestPath(self, destination: list[int], k: int) -> str:\n def choose(n, k):\n return math.factorial(n) / (math.factorial(n-k)*math.factorial(k))\n def helper(n, k, rank) -> str:\n if k == 0:\n return \'H\' * n\n elif n == k:\n return \'V\' * n\n if rank <= choose(n-1, k):\n # we know path must start with a 0 (\'H\')\n return \'H\' + helper(n-1, k, rank)\n else:\n # we know path must start with a 1 (\'V\')\n return \'V\' + helper(n-1, k-1, rank - choose(n-1, k))\n return helper(destination[0]+destination[1], destination[0], k)\n``` | 0 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Good combinatorics problem | Commented and Explained | kth-smallest-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOne of the best ways to solve a search space sometimes is to DFS. This is one of those times thanks to the fact that Bob is picky. Because Bob is picky, we can use that to prune the dfs space as we go along, thus providing a way to quickly and readily match up and eliminate possible dead ends quickly. \n\nThis is mainly due to the fact that Bob\'s pickiness allows us to use a combinatorial calculation to determine WHEN we add a \'V\' to our path string, rather than trying to find WHERE in the graph we should do so; this reduces our search space complexity greatly at the cost of combinatorial calculations. Luckily, nice people out there have done n choose k for a quite large range, so calculating that is of less concern. \n\nWith that in hand, we merely need to stay in our bounded space of k, moves horizontal and moves vertical and we can get to an answer that uses up Bob\'s exhaustive nature. Then we can simply concat the remaining in lexicographically smallest order and it\'s solved. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nReduce K by 1 for off by 1 indexing (annoying monopoly rule people) \n\nGet change in rows and change in columns as the value of destination unpacked \n\nSet an empty path string \n\n- While you have k, dr, and dc greater than 0 \n - get directional options - 1 choose horizontal options minus 1 \n - if this value is lte k\n - we can afford a V \n - So, add a V to the path string \n - reduce our number of vertical options \n - and reduce our value of k by the combinatorial value \n - otherwise, we can\'t afford a V \n - add an H to the path string and reduce our number of horizontal options \n\nWhen done, bob still may not have arrived. \nSo, to keep it lexicographically smallest \n- If you still have dc options gt 0 \n - add H dc times to the path string \n- If you still have dr options gt 0 \n - add V dr times to the path string \n\nNow we know Bob has made it, send him his path string that he\'ll be OK with \n\n\n# Complexity\n- Time complexity : O(N ^ 2)\n - O(N) for math combinations it turns out \n - Gotta do that at least N times as well to make up for search space at the worst (if Bob was not, in fact, actually that picky)\n - At worst O(N * N) or O(N^2), where N is size of grid space \n\n- Space complexity : O(P) \n - O(P) have to store the path string of size P \n\n# Code\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str :\n # off by 1 indexing \n k-=1\n # get destination row and column \n dr, dc = destination\n # set up path string \n path_string = "" \n # while you still have moves to make, and have not reached the goal \n while k and dr and dc : \n # evaluates n choose k, in this case n is directional space of dr + dc - 1 \n # and k is choosing space of only dc - 1 \n # remember dc, change in cols, is horizontal! \n current_combination_value = math.comb(dr+dc - 1, dc - 1) \n # if the value produced is lte k \n if current_combination_value <= k : \n # we can afford a \'V\' here, which is a large value lexicographically \n path_string += "V"\n # we\'ve used up a vertical directional movement, a change in rows \n dr -= 1 \n # so, we also need to lower k by this combination value\n # this is equivalent to cutting off any future V\'s of at most this value as well \n k -= current_combination_value\n else : \n # otherwise, we should just add an h and decrement our horizontal option space\n path_string += "H" \n dc -= 1 \n # when done with above, path string still may not be fully built. To ensure it \n # if we have any horizontal components left \n if (dc > 0) :\n path_string = path_string + "H" * dc\n # then if we have any vertical components left \n if (dr > 0) : \n path_string = path_string + "V" * dr\n # now we\'re all set \n return path_string\n``` | 0 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Good combinatorics problem | Commented and Explained | kth-smallest-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOne of the best ways to solve a search space sometimes is to DFS. This is one of those times thanks to the fact that Bob is picky. Because Bob is picky, we can use that to prune the dfs space as we go along, thus providing a way to quickly and readily match up and eliminate possible dead ends quickly. \n\nThis is mainly due to the fact that Bob\'s pickiness allows us to use a combinatorial calculation to determine WHEN we add a \'V\' to our path string, rather than trying to find WHERE in the graph we should do so; this reduces our search space complexity greatly at the cost of combinatorial calculations. Luckily, nice people out there have done n choose k for a quite large range, so calculating that is of less concern. \n\nWith that in hand, we merely need to stay in our bounded space of k, moves horizontal and moves vertical and we can get to an answer that uses up Bob\'s exhaustive nature. Then we can simply concat the remaining in lexicographically smallest order and it\'s solved. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nReduce K by 1 for off by 1 indexing (annoying monopoly rule people) \n\nGet change in rows and change in columns as the value of destination unpacked \n\nSet an empty path string \n\n- While you have k, dr, and dc greater than 0 \n - get directional options - 1 choose horizontal options minus 1 \n - if this value is lte k\n - we can afford a V \n - So, add a V to the path string \n - reduce our number of vertical options \n - and reduce our value of k by the combinatorial value \n - otherwise, we can\'t afford a V \n - add an H to the path string and reduce our number of horizontal options \n\nWhen done, bob still may not have arrived. \nSo, to keep it lexicographically smallest \n- If you still have dc options gt 0 \n - add H dc times to the path string \n- If you still have dr options gt 0 \n - add V dr times to the path string \n\nNow we know Bob has made it, send him his path string that he\'ll be OK with \n\n\n# Complexity\n- Time complexity : O(N ^ 2)\n - O(N) for math combinations it turns out \n - Gotta do that at least N times as well to make up for search space at the worst (if Bob was not, in fact, actually that picky)\n - At worst O(N * N) or O(N^2), where N is size of grid space \n\n- Space complexity : O(P) \n - O(P) have to store the path string of size P \n\n# Code\n```\nclass Solution:\n def kthSmallestPath(self, destination: List[int], k: int) -> str :\n # off by 1 indexing \n k-=1\n # get destination row and column \n dr, dc = destination\n # set up path string \n path_string = "" \n # while you still have moves to make, and have not reached the goal \n while k and dr and dc : \n # evaluates n choose k, in this case n is directional space of dr + dc - 1 \n # and k is choosing space of only dc - 1 \n # remember dc, change in cols, is horizontal! \n current_combination_value = math.comb(dr+dc - 1, dc - 1) \n # if the value produced is lte k \n if current_combination_value <= k : \n # we can afford a \'V\' here, which is a large value lexicographically \n path_string += "V"\n # we\'ve used up a vertical directional movement, a change in rows \n dr -= 1 \n # so, we also need to lower k by this combination value\n # this is equivalent to cutting off any future V\'s of at most this value as well \n k -= current_combination_value\n else : \n # otherwise, we should just add an h and decrement our horizontal option space\n path_string += "H" \n dc -= 1 \n # when done with above, path string still may not be fully built. To ensure it \n # if we have any horizontal components left \n if (dc > 0) :\n path_string = path_string + "H" * dc\n # then if we have any vertical components left \n if (dr > 0) : \n path_string = path_string + "V" * dr\n # now we\'re all set \n return path_string\n``` | 0 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Is k small enough to insert symbol H at the end of the string? | kth-smallest-instructions | 0 | 1 | # Intuition\nWe iteratively add symbols from the the beggining of the string to its end. What we can do is to think of when the first symbol is "H" and when it is \'V\'. In fact if k is "too large" then it\'s \'V\'. In fact too large means it\'s larger then (n choose h-1) where n is the length of the string and h is the number of "H" in it. So if it\'s smaller we return \'H\' + kthSmallestPath((v,h-1), k). otherwise we insert V and change k: k = k - (n choose h-1)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import factorial\nclass Solution:\n def perm(self, destination) -> int:\n return factorial(destination[1]+destination[0]) // factorial(destination[0]) // factorial(destination[1])\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n if k==0:\n return \'H\' * destination[1] + \'V\' * destination[0]\n if destination[1]==0:\n return \'V\' * destination[0]\n ans = \'\' \n while k-1>=self.perm((destination[0], destination[1]-1)) and destination[0]>0:\n k = k - self.perm((destination[0], destination[1]-1))\n destination = destination[0]-1, destination[1]\n ans = ans + \'V\'\n if destination[0]==0:\n return ans + \'H\' * destination[1]\n if k-1<self.perm((destination[0], destination[1]-1)):\n return ans + \'H\' + self.kthSmallestPath((destination[0], destination[1]-1), k)\n return ans\n\n \n``` | 0 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Is k small enough to insert symbol H at the end of the string? | kth-smallest-instructions | 0 | 1 | # Intuition\nWe iteratively add symbols from the the beggining of the string to its end. What we can do is to think of when the first symbol is "H" and when it is \'V\'. In fact if k is "too large" then it\'s \'V\'. In fact too large means it\'s larger then (n choose h-1) where n is the length of the string and h is the number of "H" in it. So if it\'s smaller we return \'H\' + kthSmallestPath((v,h-1), k). otherwise we insert V and change k: k = k - (n choose h-1)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import factorial\nclass Solution:\n def perm(self, destination) -> int:\n return factorial(destination[1]+destination[0]) // factorial(destination[0]) // factorial(destination[1])\n def kthSmallestPath(self, destination: List[int], k: int) -> str:\n if k==0:\n return \'H\' * destination[1] + \'V\' * destination[0]\n if destination[1]==0:\n return \'V\' * destination[0]\n ans = \'\' \n while k-1>=self.perm((destination[0], destination[1]-1)) and destination[0]>0:\n k = k - self.perm((destination[0], destination[1]-1))\n destination = destination[0]-1, destination[1]\n ans = ans + \'V\'\n if destination[0]==0:\n return ans + \'H\' * destination[1]\n if k-1<self.perm((destination[0], destination[1]-1)):\n return ans + \'H\' + self.kthSmallestPath((destination[0], destination[1]-1), k)\n return ans\n\n \n``` | 0 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Tracing Path from 2D array | kth-smallest-instructions | 0 | 1 | ### Thought Process 1:Greedy TLE\n`Why not store all possible paths and return the k-1 th path`\n```\nclass Solution:\n def kthSmallestPath(self, arr: List[int], k: int) -> str:\n row = arr[0]\n col = arr[1]\n self.path = []\n def f(i,j,s):\n if i == row and j == col:\n # reached destination so store the path\n self.path.append(s)\n if i>row or j>col:return\n f(i,j+1,s+"H") # lets move right\n f(i+1,j,s+"V") # lets move down\n f(0,0,"")\n return self.path[k-1]\n# Note to keep the path list sorted we need to move RIGHT first then DOWN\n# If we move DOWN first and then RIGHT we need to sort them\n```\n### Improving Thought Process 1: Improved Greedy TLE\n`\nDo we really need to store all paths?\n`\n`We are finding paths in sorted manner.So cant we use this to our advantage?`\n`So , basically we can return k-1th path and stop searching for next paths`\n```\n# We will store only the answer now. Not the complete list\n# We will return once we reach k-1th path\nclass Solution:\n def kthSmallestPath(self, arr: List[int], k: int) -> str:\n row = arr[0]\n col = arr[1]\n\n self.k = k\n self.ans = ""\n @cache\n def f(i,j,s):\n if i == row and j == col: # reached destination\n self.k -= 1\n if self.k == 0: # checking if its our k-1th path\n self.ans = s\n return True # If yes, return True and store the answer\n return False\n if self.k == 0: # This will stop seaching for next\n self.ans = s # store the answer and return True\n return True\n if i>row or j>col:return False\n return f(i,j+1,s+"H") or f(i+1,j,s+"V")\n f(0,0,"")\n return self.ans # return answer\n```\n\n### Issue With Recurion:\n`As k value is very high` $^nC_r(row+col,row)$ `for this memory wont suffice`\n`From above we are able to travel [0,0] to [r,c]`\n`Cant we store the possible paths for each cell?`\n```\n def f(i,j):\n if i == row and j == col: # reached destination\n return 1\n if i>row or j>col:\n return 0 # out of bound\n right = f(i,j+1) # move right\n down = f(i+1,j) # move down\n return right+down # total paths\n f(0,0)\n # Equvalent Code in 2d array\n dp = [[0]*(col+1) for _ in range(row+1)]\n for i in range(row,-1,-1):\n for j in range(col,-1,-1):\n if i == row and j == col:\n dp[i][j] = 1\n continue\n right,down = 0,0\n if j+1<=col:\n right = dp[i][j+1]\n if i+1<=row:\n down = dp[i+1][j]\n dp[i][j] = right+down\n```\n```\nfor [2,2]\nnCr = (2+2,2) = 6 i.e total possible paths for [2,2]\n\no/p:\n 6 3 1\n 3 2 1\n 1 1 1\n\neach cell denotes total paths current cell to [2,2]\ncell [0,1] = 3 i.e from [0,1] to [2,2] we have 3 paths [HVV,VHV,VVH]\ncell [1,0] = 3 i.e from [0,1] to [2,2] we have 3 paths [HHV,HVH,VHH]\ncell [0,0] = 6 i.e from [0,0] to [2,2] we have 6 possible paths\n```\n### Whats Next?\n`We have all possible paths in a 2D list`\n`Now we need to extract the k-1th path from it`\n\n`To do so we need to follow 2 rules:`\n```\nwe are currently at [0,0]\nSo,\n should we move [0,1] i.e (i,j+1) - "H"\n should we move [1,0] i.e (i+1,j) - "V"\n\nmove to (i,j+1) if dp[i][j+1] >=k -> (k remains same j+=1 add "H")\nmove to (i+1,j) if dp[i][j+1] < k -> (k = k - dp[i][j+1] i+=1 add "V")\n\nNow we would have reached one of the boundary (row or column)\nif we have not reached end of row: add "V"\nif we have not reached end of col: add "H"\n```\n```\nclass Solution:\n def kthSmallestPath(self, arr: List[int], k: int) -> str:\n row = arr[0]\n col = arr[1]\n // Creating dp for all possible paths\n dp = [[0]*(col+1) for _ in range(row+1)]\n for i in range(row,-1,-1):\n for j in range(col,-1,-1):\n if i == row and j == col:\n dp[i][j] = 1\n continue\n right,down = 0,0\n if j+1<=col:\n right = dp[i][j+1]\n if i+1<=row:\n down = dp[i+1][j]\n dp[i][j] = right+down\n \n\n i,j = 0,0 //stating point [0,0]\n s = "" // answer\n while i<row and j<col: // iterate until we have hit one of boundary\n if dp[i][j+1]>=k: // move horizontal\n j += 1\n s += "H"\n else: // move vertical\n k -= dp[i][j+1]\n i +=1\n s += "V"\n while i<row: // we can move down as i<row so add "V"\n s += "V"\n i += 1\n while j<col: // we can move right as j<col so add "H"\n s += "H"\n j += 1\n return s\n\n```\n\n### Extra\n`Exchange "H" and "V" and it will give lexicographically largest`\n\n | 0 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Tracing Path from 2D array | kth-smallest-instructions | 0 | 1 | ### Thought Process 1:Greedy TLE\n`Why not store all possible paths and return the k-1 th path`\n```\nclass Solution:\n def kthSmallestPath(self, arr: List[int], k: int) -> str:\n row = arr[0]\n col = arr[1]\n self.path = []\n def f(i,j,s):\n if i == row and j == col:\n # reached destination so store the path\n self.path.append(s)\n if i>row or j>col:return\n f(i,j+1,s+"H") # lets move right\n f(i+1,j,s+"V") # lets move down\n f(0,0,"")\n return self.path[k-1]\n# Note to keep the path list sorted we need to move RIGHT first then DOWN\n# If we move DOWN first and then RIGHT we need to sort them\n```\n### Improving Thought Process 1: Improved Greedy TLE\n`\nDo we really need to store all paths?\n`\n`We are finding paths in sorted manner.So cant we use this to our advantage?`\n`So , basically we can return k-1th path and stop searching for next paths`\n```\n# We will store only the answer now. Not the complete list\n# We will return once we reach k-1th path\nclass Solution:\n def kthSmallestPath(self, arr: List[int], k: int) -> str:\n row = arr[0]\n col = arr[1]\n\n self.k = k\n self.ans = ""\n @cache\n def f(i,j,s):\n if i == row and j == col: # reached destination\n self.k -= 1\n if self.k == 0: # checking if its our k-1th path\n self.ans = s\n return True # If yes, return True and store the answer\n return False\n if self.k == 0: # This will stop seaching for next\n self.ans = s # store the answer and return True\n return True\n if i>row or j>col:return False\n return f(i,j+1,s+"H") or f(i+1,j,s+"V")\n f(0,0,"")\n return self.ans # return answer\n```\n\n### Issue With Recurion:\n`As k value is very high` $^nC_r(row+col,row)$ `for this memory wont suffice`\n`From above we are able to travel [0,0] to [r,c]`\n`Cant we store the possible paths for each cell?`\n```\n def f(i,j):\n if i == row and j == col: # reached destination\n return 1\n if i>row or j>col:\n return 0 # out of bound\n right = f(i,j+1) # move right\n down = f(i+1,j) # move down\n return right+down # total paths\n f(0,0)\n # Equvalent Code in 2d array\n dp = [[0]*(col+1) for _ in range(row+1)]\n for i in range(row,-1,-1):\n for j in range(col,-1,-1):\n if i == row and j == col:\n dp[i][j] = 1\n continue\n right,down = 0,0\n if j+1<=col:\n right = dp[i][j+1]\n if i+1<=row:\n down = dp[i+1][j]\n dp[i][j] = right+down\n```\n```\nfor [2,2]\nnCr = (2+2,2) = 6 i.e total possible paths for [2,2]\n\no/p:\n 6 3 1\n 3 2 1\n 1 1 1\n\neach cell denotes total paths current cell to [2,2]\ncell [0,1] = 3 i.e from [0,1] to [2,2] we have 3 paths [HVV,VHV,VVH]\ncell [1,0] = 3 i.e from [0,1] to [2,2] we have 3 paths [HHV,HVH,VHH]\ncell [0,0] = 6 i.e from [0,0] to [2,2] we have 6 possible paths\n```\n### Whats Next?\n`We have all possible paths in a 2D list`\n`Now we need to extract the k-1th path from it`\n\n`To do so we need to follow 2 rules:`\n```\nwe are currently at [0,0]\nSo,\n should we move [0,1] i.e (i,j+1) - "H"\n should we move [1,0] i.e (i+1,j) - "V"\n\nmove to (i,j+1) if dp[i][j+1] >=k -> (k remains same j+=1 add "H")\nmove to (i+1,j) if dp[i][j+1] < k -> (k = k - dp[i][j+1] i+=1 add "V")\n\nNow we would have reached one of the boundary (row or column)\nif we have not reached end of row: add "V"\nif we have not reached end of col: add "H"\n```\n```\nclass Solution:\n def kthSmallestPath(self, arr: List[int], k: int) -> str:\n row = arr[0]\n col = arr[1]\n // Creating dp for all possible paths\n dp = [[0]*(col+1) for _ in range(row+1)]\n for i in range(row,-1,-1):\n for j in range(col,-1,-1):\n if i == row and j == col:\n dp[i][j] = 1\n continue\n right,down = 0,0\n if j+1<=col:\n right = dp[i][j+1]\n if i+1<=row:\n down = dp[i+1][j]\n dp[i][j] = right+down\n \n\n i,j = 0,0 //stating point [0,0]\n s = "" // answer\n while i<row and j<col: // iterate until we have hit one of boundary\n if dp[i][j+1]>=k: // move horizontal\n j += 1\n s += "H"\n else: // move vertical\n k -= dp[i][j+1]\n i +=1\n s += "V"\n while i<row: // we can move down as i<row so add "V"\n s += "V"\n i += 1\n while j<col: // we can move right as j<col so add "H"\n s += "H"\n j += 1\n return s\n\n```\n\n### Extra\n`Exchange "H" and "V" and it will give lexicographically largest`\n\n | 0 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
Python (Simple DP) | kth-smallest-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthSmallestPath(self, destination, k):\n i,j = destination\n\n @lru_cache(None)\n def dfs(i,j,k):\n if k == 1:\n return "H"*j + "V"*i\n else:\n val = math.comb(i+j-1,j-1)\n\n if k <= val:\n return "H" + dfs(i,j-1,k)\n else:\n return "V" + dfs(i-1,j,k-val)\n\n return dfs(i,j,k)\n\n\n\n\n\n\n``` | 0 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Python (Simple DP) | kth-smallest-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthSmallestPath(self, destination, k):\n i,j = destination\n\n @lru_cache(None)\n def dfs(i,j,k):\n if k == 1:\n return "H"*j + "V"*i\n else:\n val = math.comb(i+j-1,j-1)\n\n if k <= val:\n return "H" + dfs(i,j-1,k)\n else:\n return "V" + dfs(i-1,j,k-val)\n\n return dfs(i,j,k)\n\n\n\n\n\n\n``` | 0 | You are controlling a robot that is located somewhere in a room. The room is modeled as an `m x n` binary grid where `0` represents a wall and `1` represents an empty slot.
The robot starts at an unknown location in the room that is guaranteed to be empty, and you do not have access to the grid, but you can move the robot using the given API `Robot`.
You are tasked to use the robot to clean the entire room (i.e., clean every empty cell in the room). The robot with the four given APIs can move forward, turn left, or turn right. Each turn is `90` degrees.
When the robot tries to move into a wall cell, its bumper sensor detects the obstacle, and it stays on the current cell.
Design an algorithm to clean the entire room using the following APIs:
interface Robot {
// returns true if next cell is open and robot moves into the cell.
// returns false if next cell is obstacle and robot stays on the current cell.
boolean move();
// Robot will stay on the same cell after calling turnLeft/turnRight.
// Each turn will be 90 degrees.
void turnLeft();
void turnRight();
// Clean the current cell.
void clean();
}
**Note** that the initial direction of the robot will be facing up. You can assume all four edges of the grid are all surrounded by a wall.
**Custom testing:**
The input is only given to initialize the room and the robot's position internally. You must solve this problem "blindfolded ". In other words, you must control the robot using only the four mentioned APIs without knowing the room layout and the initial robot's position.
**Example 1:**
**Input:** room = \[\[1,1,1,1,1,0,1,1\],\[1,1,1,1,1,0,1,1\],\[1,0,1,1,1,1,1,1\],\[0,0,0,1,0,0,0,0\],\[1,1,1,1,1,1,1,1\]\], row = 1, col = 3
**Output:** Robot cleaned all rooms.
**Explanation:** All grids in the room are marked by either 0 or 1.
0 means the cell is blocked, while 1 means the cell is accessible.
The robot initially starts at the position of row=1, col=3.
From the top left corner, its position is one row below and three columns right.
**Example 2:**
**Input:** room = \[\[1\]\], row = 0, col = 0
**Output:** Robot cleaned all rooms.
**Constraints:**
* `m == room.length`
* `n == room[i].length`
* `1 <= m <= 100`
* `1 <= n <= 200`
* `room[i][j]` is either `0` or `1`.
* `0 <= row < m`
* `0 <= col < n`
* `room[row][col] == 1`
* All the empty cells can be visited from the starting position. | There are nCr(row + column, row) possible instructions to reach (row, column). Try building the instructions one step at a time. How many instructions start with "H", and how does this compare with k? |
get-maximum-in-generated-array | get-maximum-in-generated-array | 0 | 1 | # Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n nums = []\n nums.append(0)\n nums.append(1)\n for i in range(2,n+1):\n if i%2==0:\n nums.append(nums[i//2])\n else:\n nums.append(nums[i//2] + nums[(i//2) + 1])\n if n==0:\n return 0\n return max(nums)\n\n \n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
get-maximum-in-generated-array | get-maximum-in-generated-array | 0 | 1 | # Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n nums = []\n nums.append(0)\n nums.append(1)\n for i in range(2,n+1):\n if i%2==0:\n nums.append(nums[i//2])\n else:\n nums.append(nums[i//2] + nums[(i//2) + 1])\n if n==0:\n return 0\n return max(nums)\n\n \n``` | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
bottom up approach easiest 9 lines code python | get-maximum-in-generated-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n tb=[0,1]\n if n==0:\n return 0\n for i in range(2,n+1):\n if i%2==0:\n tb.append(tb[i//2])\n else:\n tb.append(tb[i//2]+tb[(i//2)+1])\n return max(tb)\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
bottom up approach easiest 9 lines code python | get-maximum-in-generated-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n tb=[0,1]\n if n==0:\n return 0\n for i in range(2,n+1):\n if i%2==0:\n tb.append(tb[i//2])\n else:\n tb.append(tb[i//2]+tb[(i//2)+1])\n return max(tb)\n``` | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Simplest code with runtime 45 ms | get-maximum-in-generated-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n dp=[0,1]\n for i in range(2,n+1):\n dp += [dp[i//2] if i%2==0 else dp[i//2]+ dp[i//2+1]]\n return max(dp[:n+1])\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Simplest code with runtime 45 ms | get-maximum-in-generated-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n dp=[0,1]\n for i in range(2,n+1):\n dp += [dp[i//2] if i%2==0 else dp[i//2]+ dp[i//2+1]]\n return max(dp[:n+1])\n``` | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
✅Python3 || 23ms/Beats 97.74% | get-maximum-in-generated-array | 0 | 1 | \n\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!!\n\n# Python3\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n dp=[0,1]\n for i in range(2,n + 1):\n dp + =[dp[i//2] if i % 2==0 else dp[i//2] + dp[i//2 + 1]]\n return max(dp[:n + 1])\n\n``` | 14 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
✅Python3 || 23ms/Beats 97.74% | get-maximum-in-generated-array | 0 | 1 | \n\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!!\n\n# Python3\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n dp=[0,1]\n for i in range(2,n + 1):\n dp + =[dp[i//2] if i % 2==0 else dp[i//2] + dp[i//2 + 1]]\n return max(dp[:n + 1])\n\n``` | 14 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Awesome Code--->Python3 | get-maximum-in-generated-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n if n<2:\n return n\n nums=[0]*(n+1)\n nums[0]=0\n nums[1]=1\n for i in range(2,n+1):\n if i%2==0:\n nums[i]=nums[i//2]\n else:\n nums[i]=nums[i//2]+nums[i//2+1]\n return max(nums)\n #please upvote me it would encourage me alot\n\n``` | 4 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Awesome Code--->Python3 | get-maximum-in-generated-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n if n<2:\n return n\n nums=[0]*(n+1)\n nums[0]=0\n nums[1]=1\n for i in range(2,n+1):\n if i%2==0:\n nums[i]=nums[i//2]\n else:\n nums[i]=nums[i//2]+nums[i//2+1]\n return max(nums)\n #please upvote me it would encourage me alot\n\n``` | 4 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Python simple solution | get-maximum-in-generated-array | 0 | 1 | **Python :**\n\n```\ndef getMaximumGenerated(self, n: int) -> int:\n\tif not n:\n\t\treturn n\n\n\tnums = [0] * (n + 1)\n\tnums[1] = 1\n\n\tfor i in range(2, n + 1): \n\t\tif i % 2:\n\t\t\tnums[i] = nums[i // 2] + nums[i // 2 + 1]\n\n\t\telse:\n\t\t\tnums[i] = nums[i // 2]\n\n\treturn max(nums)\n```\n\n**Like it ? please upvote !** | 8 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Python simple solution | get-maximum-in-generated-array | 0 | 1 | **Python :**\n\n```\ndef getMaximumGenerated(self, n: int) -> int:\n\tif not n:\n\t\treturn n\n\n\tnums = [0] * (n + 1)\n\tnums[1] = 1\n\n\tfor i in range(2, n + 1): \n\t\tif i % 2:\n\t\t\tnums[i] = nums[i // 2] + nums[i // 2 + 1]\n\n\t\telse:\n\t\t\tnums[i] = nums[i // 2]\n\n\treturn max(nums)\n```\n\n**Like it ? please upvote !** | 8 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Simple Python Solution | get-maximum-in-generated-array | 0 | 1 | **Upvote if the solution if helpful. Comment for any doubts or suggestions.**\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n if n < 2:\n return n\n arr = [0]*(n+1)\n arr[1] = 1\n max_num = 0\n for i in range(2, n+1):\n if i%2 == 0:\n arr[i] = arr[i//2]\n else:\n arr[i] = arr[i//2] + arr[i//2 + 1]\n max_num = max(max_num, arr[i])\n return max_num\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Simple Python Solution | get-maximum-in-generated-array | 0 | 1 | **Upvote if the solution if helpful. Comment for any doubts or suggestions.**\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n if n < 2:\n return n\n arr = [0]*(n+1)\n arr[1] = 1\n max_num = 0\n for i in range(2, n+1):\n if i%2 == 0:\n arr[i] = arr[i//2]\n else:\n arr[i] = arr[i//2] + arr[i//2 + 1]\n max_num = max(max_num, arr[i])\n return max_num\n``` | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
DP | Python3 | get-maximum-in-generated-array | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n dp = [0] * (n + 2)\n dp[1] = 1 \n ans = 0\n for i in range(1, n // 2 + 1):\n dp[i * 2] = dp[i]\n dp[i * 2 + 1] = dp[i] + dp[i + 1]\n ans = max(dp[:n + 1])\n return ans\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
DP | Python3 | get-maximum-in-generated-array | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n dp = [0] * (n + 2)\n dp[1] = 1 \n ans = 0\n for i in range(1, n // 2 + 1):\n dp[i * 2] = dp[i]\n dp[i * 2 + 1] = dp[i] + dp[i + 1]\n ans = max(dp[:n + 1])\n return ans\n``` | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Python generators are like space shuttles | get-maximum-in-generated-array | 0 | 1 | Constructive solutions were posted before, but did you know that generators allow you get rid of used array parts, like a space shuttle gets rid of spent fuel tanks?\n\n```\nfrom queue import deque\n\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n \n def arrgen(n):\n yield 0\n q = deque([1])\n while True:\n yield q[0]\n q.append(q[0])\n q.append(q[0]+q[1])\n q.popleft()\n \n g = arrgen(n)\n return max(next(g) for _ in range(n+1)) | 12 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Python generators are like space shuttles | get-maximum-in-generated-array | 0 | 1 | Constructive solutions were posted before, but did you know that generators allow you get rid of used array parts, like a space shuttle gets rid of spent fuel tanks?\n\n```\nfrom queue import deque\n\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n \n def arrgen(n):\n yield 0\n q = deque([1])\n while True:\n yield q[0]\n q.append(q[0])\n q.append(q[0]+q[1])\n q.popleft()\n \n g = arrgen(n)\n return max(next(g) for _ in range(n+1)) | 12 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Easy Python Solution O(n) with Explanation | get-maximum-in-generated-array | 0 | 1 | \tclass Solution:\n\t\tdef getMaximumGenerated(self, n: int) -> int:\n\t\t\tif n==0: return 0\n\t\t\tarr = [0, 1]\n\t\t\tfor i in range(2, n+1):\n\t\t\t\tif i%2==0:\n\t\t\t\t\tarr.append(arr[i//2])\n\t\t\t\telse:\n\t\t\t\t\tarr.append(arr[i//2] + arr[i//2 + 1])\n\t\t\treturn max(arr)\n\t\t\t\nThe Basic Idea is that given our constraints and the Question itself, we can simply just generate the array by simulating what is needed. So, we start with our base array of `[0, 1]` and for any `N > 1` we generate the array as following:\n* If our index is even: we divide the index by 2 and append that result to our base array.\n* If our index is odd: we divide the index by 2 ( and considering only the integer of it, so 7//2 = 3 and not 3.5 ) and use that index and the next of that index.\n\nWe hence generate the entire array from 0 to N, so N+1 elements, and our job now is to only find the maximum of this array. \n\n**Note:** This takes a O(N) time and O(N) space in generating the array. | 8 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Easy Python Solution O(n) with Explanation | get-maximum-in-generated-array | 0 | 1 | \tclass Solution:\n\t\tdef getMaximumGenerated(self, n: int) -> int:\n\t\t\tif n==0: return 0\n\t\t\tarr = [0, 1]\n\t\t\tfor i in range(2, n+1):\n\t\t\t\tif i%2==0:\n\t\t\t\t\tarr.append(arr[i//2])\n\t\t\t\telse:\n\t\t\t\t\tarr.append(arr[i//2] + arr[i//2 + 1])\n\t\t\treturn max(arr)\n\t\t\t\nThe Basic Idea is that given our constraints and the Question itself, we can simply just generate the array by simulating what is needed. So, we start with our base array of `[0, 1]` and for any `N > 1` we generate the array as following:\n* If our index is even: we divide the index by 2 and append that result to our base array.\n* If our index is odd: we divide the index by 2 ( and considering only the integer of it, so 7//2 = 3 and not 3.5 ) and use that index and the next of that index.\n\nWe hence generate the entire array from 0 to N, so N+1 elements, and our job now is to only find the maximum of this array. \n\n**Note:** This takes a O(N) time and O(N) space in generating the array. | 8 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.