title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python3 [runtime faster than 90.82%, memory less than 93.18%] + testing | design-an-ordered-stream | 0 | 1 | ```\n"""\nexercise: 1656. Design an Ordered Stream\nhttps://leetcode.com/problems/design-an-ordered-stream/\ncompany: Bloomberg\n"""\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(idKey,value)\n\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.pairs = dict()\n self.pointer = 0\n\n def insert(self, idKey: int, value: str) -> list[str]:\n self.pairs[idKey] = value\n\n temp = list()\n while self.pointer + 1 in self.pairs:\n self.pointer += 1\n\n temp.append(self.pairs[self.pointer])\n\n return temp\n\n\nif __name__ == \'__main__\':\n os = OrderedStream(5)\n\n assert os.insert(3, "ccccc").__eq__([])\n assert os.insert(1, "aaaaa").__eq__([\'aaaaa\'])\n assert os.insert(2, "bbbbb").__eq__(["bbbbb", "ccccc"])\n assert os.insert(5, "eeeee").__eq__([])\n assert os.insert(4, "ddddd").__eq__(["ddddd", "eeeee"])\n | 1 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Python3 [runtime faster than 90.82%, memory less than 93.18%] + testing | design-an-ordered-stream | 0 | 1 | ```\n"""\nexercise: 1656. Design an Ordered Stream\nhttps://leetcode.com/problems/design-an-ordered-stream/\ncompany: Bloomberg\n"""\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(idKey,value)\n\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.pairs = dict()\n self.pointer = 0\n\n def insert(self, idKey: int, value: str) -> list[str]:\n self.pairs[idKey] = value\n\n temp = list()\n while self.pointer + 1 in self.pairs:\n self.pointer += 1\n\n temp.append(self.pairs[self.pointer])\n\n return temp\n\n\nif __name__ == \'__main__\':\n os = OrderedStream(5)\n\n assert os.insert(3, "ccccc").__eq__([])\n assert os.insert(1, "aaaaa").__eq__([\'aaaaa\'])\n assert os.insert(2, "bbbbb").__eq__(["bbbbb", "ccccc"])\n assert os.insert(5, "eeeee").__eq__([])\n assert os.insert(4, "ddddd").__eq__(["ddddd", "eeeee"])\n | 1 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Python3 Solution + Better Description Because This One Is Really Bad | design-an-ordered-stream | 0 | 1 | The description as of June 13th, 2022 mentions nothing a ptr. There is a ptr that should be initialized at 1. If an item is inserted with an idKey above the ptr, return nothing. If an item is inserted that matches the ptr, return the largest chunk of contiguous values above the ptr. The ptr should update to the index immediately after the returned chunk. \n\n```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.ptr = 1\n self.hashmap = dict()\n \n\n def insert(self, idKey: int, value: str) -> List[str]:\n self.hashmap[idKey] = value\n output = []\n if idKey > self.ptr:\n return output\n \n while idKey in self.hashmap:\n output.append(self.hashmap[idKey])\n idKey += 1\n self.ptr = idKey\n \n return output\n``` | 11 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Python3 Solution + Better Description Because This One Is Really Bad | design-an-ordered-stream | 0 | 1 | The description as of June 13th, 2022 mentions nothing a ptr. There is a ptr that should be initialized at 1. If an item is inserted with an idKey above the ptr, return nothing. If an item is inserted that matches the ptr, return the largest chunk of contiguous values above the ptr. The ptr should update to the index immediately after the returned chunk. \n\n```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.ptr = 1\n self.hashmap = dict()\n \n\n def insert(self, idKey: int, value: str) -> List[str]:\n self.hashmap[idKey] = value\n output = []\n if idKey > self.ptr:\n return output\n \n while idKey in self.hashmap:\n output.append(self.hashmap[idKey])\n idKey += 1\n self.ptr = idKey\n \n return output\n``` | 11 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
python 3 || simple solution | design-an-ordered-stream | 0 | 1 | ```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.stream = [\'\'] * (n + 1)\n self.i = 0\n\n def insert(self, idKey: int, value: str) -> List[str]:\n self.stream[idKey - 1] = value\n res = []\n\n while self.stream[self.i]:\n res.append(self.stream[self.i])\n self.i += 1\n \n return res | 2 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
python 3 || simple solution | design-an-ordered-stream | 0 | 1 | ```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.stream = [\'\'] * (n + 1)\n self.i = 0\n\n def insert(self, idKey: int, value: str) -> List[str]:\n self.stream[idKey - 1] = value\n res = []\n\n while self.stream[self.i]:\n res.append(self.stream[self.i])\n self.i += 1\n \n return res | 2 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Python using dict, 212ms 14.6MB | design-an-ordered-stream | 0 | 1 | ```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.seen = {}\n self.ptr = 1\n\n def insert(self, id: int, value: str) -> List[str]:\n seen, ptr = self.seen, self.ptr\n \n seen[id] = value\n result = []\n while ptr in seen:\n result.append(seen[ptr])\n del seen[ptr]\n ptr += 1\n \n self.ptr = ptr\n return result\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(id,value)\n``` | 16 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Python using dict, 212ms 14.6MB | design-an-ordered-stream | 0 | 1 | ```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.seen = {}\n self.ptr = 1\n\n def insert(self, id: int, value: str) -> List[str]:\n seen, ptr = self.seen, self.ptr\n \n seen[id] = value\n result = []\n while ptr in seen:\n result.append(seen[ptr])\n del seen[ptr]\n ptr += 1\n \n self.ptr = ptr\n return result\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(id,value)\n``` | 16 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Python Commented beats 90% | Iteration, Codesplitting | design-an-ordered-stream | 0 | 1 | class OrderedStream:\n\n def __init__(self, n: int):\n self.arr = [None]*n # initialize the array for size n\n self.ptr = 0 # remeber where the stream pointer is at\n def get_chunk(self):\n chunk = []\n \n # Construct the next chunk by checking bounds, and ensuring value is not None\n while self.ptr < len(self.arr) and self.arr[self.ptr]:\n chunk.append(self.arr[self.ptr])\n self.ptr+=1 # Update the pointer\n return chunk\n def insert(self, idKey: int, value: str) -> List[str]:\n # set the arr\'s 0-indexed value to the incoming value\n self.arr[idKey-1] = value\n return self.get_chunk() # then return the chunk | 2 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Python Commented beats 90% | Iteration, Codesplitting | design-an-ordered-stream | 0 | 1 | class OrderedStream:\n\n def __init__(self, n: int):\n self.arr = [None]*n # initialize the array for size n\n self.ptr = 0 # remeber where the stream pointer is at\n def get_chunk(self):\n chunk = []\n \n # Construct the next chunk by checking bounds, and ensuring value is not None\n while self.ptr < len(self.arr) and self.arr[self.ptr]:\n chunk.append(self.arr[self.ptr])\n self.ptr+=1 # Update the pointer\n return chunk\n def insert(self, idKey: int, value: str) -> List[str]:\n # set the arr\'s 0-indexed value to the incoming value\n self.arr[idKey-1] = value\n return self.get_chunk() # then return the chunk | 2 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Beats 74.34%of users with Python3 | determine-if-two-strings-are-close | 0 | 1 | \n\n# Approach\n- The approach taken in the code is to use the Counter class from the collections module to count the frequency of characters in both input strings.\n- The code first checks if the lengths of the two strings are different, and if so, returns False because strings of different lengths cannot be close.\n- Then, it compares the sets of keys (characters) in both frequency dictionaries. If they are not the same, the strings cannot be close, so it returns False.\n- Next, the code sorts the dictionaries based on the frequency of characters.\n- Finally, it checks if the lists of frequencies in both dictionaries are the same. \n- If they are, the strings are close, and the function returns True; otherwise, it returns False.\n\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def closeStrings(self, word1: str, word2: str) -> bool:\n if len(word1) != len(word2):\n return False\n frequency1 = Counter(word1)\n frequency2 = Counter(word2)\n if set(frequency1.keys()) != set(frequency2.keys()):\n return False\n frequency1 = dict(sorted(frequency1.items(), key=lambda item: item[1]))\n frequency2 = dict(sorted(frequency2.items(), key=lambda item: item[1]))\n return [frequency for frequency in frequency1.values()] == [frequency for frequency in frequency2.values()]\n``` | 2 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
Three line, simple & fast solution | determine-if-two-strings-are-close | 0 | 1 | # Intuition\nTwo strings are close if they share the same characters and character frequencies, regardless of order.\n \n\n# Approach\n- **Character Set Comparison**: Ensure both strings contain identical characters.\n- **Frequency Comparison**: Check if the character frequencies match across both strings.\n\n# Complexity\n- Time complexity: $$O(n log(n\n))$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nfrom collections import Counter\nclass Solution:\n def closeStrings(self, word1: str, word2: str) -> bool:\n a = Counter(word1)\n b = Counter(word2)\n\n return sorted(a.keys()) == sorted(b.keys()) and sorted(a.values()) == sorted(b.values())\n``` | 3 | Two strings are considered **close** if you can attain one from the other using the following operations:
* Operation 1: Swap any two **existing** characters.
* For example, `abcde -> aecdb`
* Operation 2: Transform **every** occurrence of one **existing** character into another **existing** character, and do the same with the other character.
* For example, `aacabb -> bbcbaa` (all `a`'s turn into `b`'s, and all `b`'s turn into `a`'s)
You can use the operations on either string as many times as necessary.
Given two strings, `word1` and `word2`, return `true` _if_ `word1` _and_ `word2` _are **close**, and_ `false` _otherwise._
**Example 1:**
**Input:** word1 = "abc ", word2 = "bca "
**Output:** true
**Explanation:** You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc " -> "acb "
Apply Operation 1: "acb " -> "bca "
**Example 2:**
**Input:** word1 = "a ", word2 = "aa "
**Output:** false
**Explanation:** It is impossible to attain word2 from word1, or vice versa, in any number of operations.
**Example 3:**
**Input:** word1 = "cabbba ", word2 = "abbccc "
**Output:** true
**Explanation:** You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba " -> "caabbb "
`Apply Operation 2: "`caabbb " -> "baaccc "
Apply Operation 2: "baaccc " -> "abbccc "
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` contain only lowercase English letters. | If k ≥ arr.length return the max element of the array. If k < arr.length simulate the game until a number wins k consecutive games. |
✅ 96.51% Sliding Window | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Comprehensive Guide to Solving "Minimum Operations to Reduce X to Zero"\n\n## Introduction & Problem Statement\n\nGiven an integer array `nums` and an integer `x`, the task is to find the minimum number of operations to reduce `x` to exactly 0 by removing either the leftmost or rightmost element from the array `nums` in each operation. What makes this problem intriguing is that it\'s not a straightforward minimization problem; it involves searching for subarrays, working with prefix sums, and applying two-pointer techniques.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Array Constraints**: \n - $$1 \\leq \\text{nums.length} \\leq 10^5$$\n - $$1 \\leq \\text{nums}[i] \\leq 10^4$$\n \n2. **Target Number `x`**:\n - $$1 \\leq x \\leq 10^9$$\n\n3. **Operations**: \n You can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from $$ x $$.\n\n4. **Minimization Objective**: \n The goal is to minimize the number of operations to reduce $$ x $$ to zero.\n\n---\n\n## One Primary Strategy to Solve the Problem:\n\n## Live Coding & Explain\nhttps://youtu.be/3dhzAV81hBI?si=QgcosgkvdbMBBKtq\n\n# Approach: Sliding Window with Prefix Sum\n\nTo solve this problem, we apply the Sliding Window technique with a twist involving Prefix Sum. We use two pointers, `left` and `right`, to traverse the array `nums` and find the longest subarray whose sum equals the total sum of elements in `nums` minus `x`.\n\n## Key Data Structures:\n\n- **max_len**: An integer to store the length of the longest subarray that can be excluded to make the sum equal to `x`.\n- **cur_sum**: An integer to store the sum of elements in the current subarray.\n\n## Enhanced Breakdown:\n\n1. **Initialize and Calculate the Target**:\n - Compute `target = sum(nums) - x`, as we\'re interested in finding a subarray with this sum.\n - Initialize `max_len`, `cur_sum`, and `left` to 0.\n \n2. **Check for Edge Cases**:\n - If `target` is zero, it means we need to remove all elements to make the sum equal to `x`. In this case, return the total number of elements, `n`.\n\n3. **Traverse the Array with Two Pointers**:\n - Iterate through `nums` using a `right` pointer.\n - Update `cur_sum` by adding the current element `nums[right]`.\n \n4. **Sliding Window Adjustment**:\n - If `cur_sum` exceeds `target`, slide the `left` pointer to the right by one position and decrease `cur_sum` by `nums[left]`.\n\n5. **Update Max Length**:\n - If `cur_sum` matches `target`, update `max_len` with the length of the current subarray, which is `right - left + 1`.\n\n6. **Conclude and Return**:\n - After the loop, if `max_len` is non-zero, return `n - max_len`. Otherwise, return -1, indicating it\'s not possible to reduce `x` to zero.\n\n## Complexity Analysis:\n\n**Time Complexity**: \n- Since we traverse the array only once, the time complexity is $$ O(n) $$.\n\n**Space Complexity**: \n- The algorithm uses only a constant amount of extra space, thus having a space complexity of $$ O(1) $$.\n\n---\n\n# Code\n``` Python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target, n = sum(nums) - x, len(nums)\n \n if target == 0:\n return n\n \n max_len = cur_sum = left = 0\n \n for right, val in enumerate(nums):\n cur_sum += val\n while left <= right and cur_sum > target:\n cur_sum -= nums[left]\n left += 1\n if cur_sum == target:\n max_len = max(max_len, right - left + 1)\n \n return n - max_len if max_len else -1\n```\n``` Go []\nfunc minOperations(nums []int, x int) int {\n target, n := -x, len(nums)\n for _, num := range nums {\n target += num\n }\n \n if target == 0 {\n return n\n }\n \n maxLen, curSum, left := 0, 0, 0\n \n for right, val := range nums {\n curSum += val\n for left <= right && curSum > target {\n curSum -= nums[left]\n left++\n }\n if curSum == target {\n if right - left + 1 > maxLen {\n maxLen = right - left + 1\n }\n }\n }\n \n if maxLen != 0 {\n return n - maxLen\n }\n return -1\n}\n```\n``` Rust []\nimpl Solution {\n pub fn min_operations(nums: Vec<i32>, x: i32) -> i32 {\n let mut target: i32 = -x;\n let n = nums.len() as i32;\n \n for &num in &nums {\n target += num;\n }\n \n if target == 0 {\n return n;\n }\n \n let (mut max_len, mut cur_sum, mut left) = (0, 0, 0);\n \n for right in 0..n as usize {\n cur_sum += nums[right];\n while left <= right as i32 && cur_sum > target {\n cur_sum -= nums[left as usize];\n left += 1;\n }\n if cur_sum == target {\n max_len = std::cmp::max(max_len, right as i32 - left + 1);\n }\n }\n \n if max_len != 0 { n - max_len } else { -1 }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int target = 0, n = nums.size();\n for (int num : nums) target += num;\n target -= x;\n \n if (target == 0) return n;\n \n int max_len = 0, cur_sum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n cur_sum += nums[right];\n while (left <= right && cur_sum > target) {\n cur_sum -= nums[left];\n left++;\n }\n if (cur_sum == target) {\n max_len = max(max_len, right - left + 1);\n }\n }\n \n return max_len ? n - max_len : -1;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int minOperations(int[] nums, int x) {\n int target = -x, n = nums.length;\n for (int num : nums) target += num;\n \n if (target == 0) return n;\n \n int maxLen = 0, curSum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum == target) {\n maxLen = Math.max(maxLen, right - left + 1);\n }\n }\n \n return maxLen != 0 ? n - maxLen : -1;\n }\n}\n```\n``` PHP []\nclass Solution {\n function minOperations($nums, $x) {\n $target = 0;\n $n = count($nums);\n foreach ($nums as $num) $target += $num;\n $target -= $x;\n \n if ($target === 0) return $n;\n \n $maxLen = $curSum = $left = 0;\n \n for ($right = 0; $right < $n; ++$right) {\n $curSum += $nums[$right];\n while ($left <= $right && $curSum > $target) {\n $curSum -= $nums[$left];\n $left++;\n }\n if ($curSum === $target) {\n $maxLen = max($maxLen, $right - $left + 1);\n }\n }\n \n return $maxLen ? $n - $maxLen : -1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} x\n * @return {number}\n */\nvar minOperations = function(nums, x) {\n let target = -x, n = nums.length;\n for (let num of nums) target += num;\n \n if (target === 0) return n;\n \n let maxLen = 0, curSum = 0, left = 0;\n \n for (let right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum === target) {\n maxLen = Math.max(maxLen, right - left + 1);\n }\n }\n \n return maxLen ? n - maxLen : -1;\n};\n```\n``` C# []\npublic class Solution {\n public int MinOperations(int[] nums, int x) {\n int target = -x, n = nums.Length;\n foreach (int num in nums) target += num;\n \n if (target == 0) return n;\n \n int maxLen = 0, curSum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum == target) {\n maxLen = Math.Max(maxLen, right - left + 1);\n }\n }\n \n return maxLen != 0 ? n - maxLen : -1;\n }\n}\n```\n\n## Performance\n\n| Language | Fastest Runtime (ms) | Memory Usage (MB) |\n|-----------|----------------------|-------------------|\n| Java | 4 | 56 |\n| Rust | 15 | 3 |\n| JavaScript| 76 | 52.8 |\n| C++ | 110 | 99 |\n| Go | 137 | 8.6 |\n| C# | 236 | 54.6 |\n| PHP | 340 | 31.8 |\n| Python3 | 913 | 30.2 |\n\n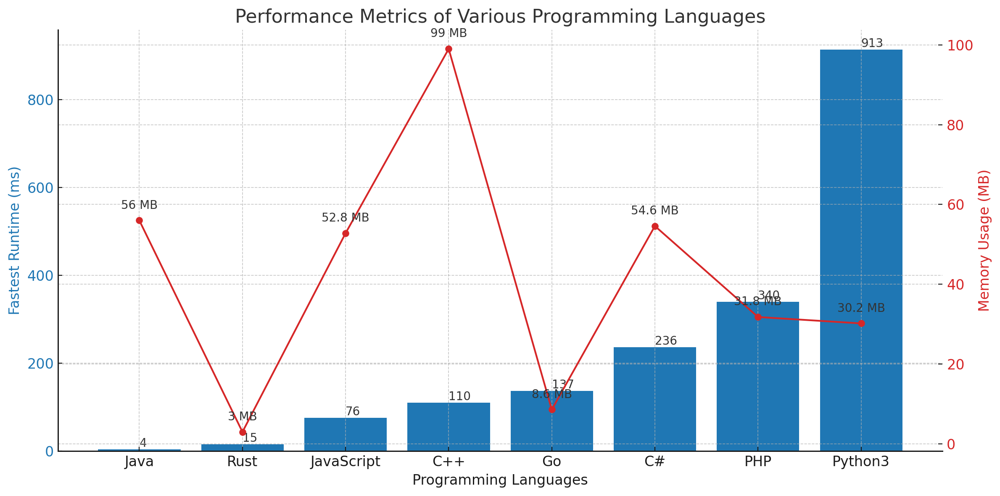\n\n\n## Live Coding in Rust\nhttps://youtu.be/CU93rMboS7w?si=r2ryBueD4fCiKZ7w\n\n## Conclusion\n\nThe problem "Minimum Operations to Reduce X to Zero" may look complicated initially due to its minimization objective. However, understanding the underlying logic of subarray sums and applying a sliding window approach can simplify it. This not only solves the problem efficiently but also enhances one\'s understanding of array manipulation techniques. Happy coding! | 140 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
✅ 96.51% Sliding Window | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Comprehensive Guide to Solving "Minimum Operations to Reduce X to Zero"\n\n## Introduction & Problem Statement\n\nGiven an integer array `nums` and an integer `x`, the task is to find the minimum number of operations to reduce `x` to exactly 0 by removing either the leftmost or rightmost element from the array `nums` in each operation. What makes this problem intriguing is that it\'s not a straightforward minimization problem; it involves searching for subarrays, working with prefix sums, and applying two-pointer techniques.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Array Constraints**: \n - $$1 \\leq \\text{nums.length} \\leq 10^5$$\n - $$1 \\leq \\text{nums}[i] \\leq 10^4$$\n \n2. **Target Number `x`**:\n - $$1 \\leq x \\leq 10^9$$\n\n3. **Operations**: \n You can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from $$ x $$.\n\n4. **Minimization Objective**: \n The goal is to minimize the number of operations to reduce $$ x $$ to zero.\n\n---\n\n## One Primary Strategy to Solve the Problem:\n\n## Live Coding & Explain\nhttps://youtu.be/3dhzAV81hBI?si=QgcosgkvdbMBBKtq\n\n# Approach: Sliding Window with Prefix Sum\n\nTo solve this problem, we apply the Sliding Window technique with a twist involving Prefix Sum. We use two pointers, `left` and `right`, to traverse the array `nums` and find the longest subarray whose sum equals the total sum of elements in `nums` minus `x`.\n\n## Key Data Structures:\n\n- **max_len**: An integer to store the length of the longest subarray that can be excluded to make the sum equal to `x`.\n- **cur_sum**: An integer to store the sum of elements in the current subarray.\n\n## Enhanced Breakdown:\n\n1. **Initialize and Calculate the Target**:\n - Compute `target = sum(nums) - x`, as we\'re interested in finding a subarray with this sum.\n - Initialize `max_len`, `cur_sum`, and `left` to 0.\n \n2. **Check for Edge Cases**:\n - If `target` is zero, it means we need to remove all elements to make the sum equal to `x`. In this case, return the total number of elements, `n`.\n\n3. **Traverse the Array with Two Pointers**:\n - Iterate through `nums` using a `right` pointer.\n - Update `cur_sum` by adding the current element `nums[right]`.\n \n4. **Sliding Window Adjustment**:\n - If `cur_sum` exceeds `target`, slide the `left` pointer to the right by one position and decrease `cur_sum` by `nums[left]`.\n\n5. **Update Max Length**:\n - If `cur_sum` matches `target`, update `max_len` with the length of the current subarray, which is `right - left + 1`.\n\n6. **Conclude and Return**:\n - After the loop, if `max_len` is non-zero, return `n - max_len`. Otherwise, return -1, indicating it\'s not possible to reduce `x` to zero.\n\n## Complexity Analysis:\n\n**Time Complexity**: \n- Since we traverse the array only once, the time complexity is $$ O(n) $$.\n\n**Space Complexity**: \n- The algorithm uses only a constant amount of extra space, thus having a space complexity of $$ O(1) $$.\n\n---\n\n# Code\n``` Python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target, n = sum(nums) - x, len(nums)\n \n if target == 0:\n return n\n \n max_len = cur_sum = left = 0\n \n for right, val in enumerate(nums):\n cur_sum += val\n while left <= right and cur_sum > target:\n cur_sum -= nums[left]\n left += 1\n if cur_sum == target:\n max_len = max(max_len, right - left + 1)\n \n return n - max_len if max_len else -1\n```\n``` Go []\nfunc minOperations(nums []int, x int) int {\n target, n := -x, len(nums)\n for _, num := range nums {\n target += num\n }\n \n if target == 0 {\n return n\n }\n \n maxLen, curSum, left := 0, 0, 0\n \n for right, val := range nums {\n curSum += val\n for left <= right && curSum > target {\n curSum -= nums[left]\n left++\n }\n if curSum == target {\n if right - left + 1 > maxLen {\n maxLen = right - left + 1\n }\n }\n }\n \n if maxLen != 0 {\n return n - maxLen\n }\n return -1\n}\n```\n``` Rust []\nimpl Solution {\n pub fn min_operations(nums: Vec<i32>, x: i32) -> i32 {\n let mut target: i32 = -x;\n let n = nums.len() as i32;\n \n for &num in &nums {\n target += num;\n }\n \n if target == 0 {\n return n;\n }\n \n let (mut max_len, mut cur_sum, mut left) = (0, 0, 0);\n \n for right in 0..n as usize {\n cur_sum += nums[right];\n while left <= right as i32 && cur_sum > target {\n cur_sum -= nums[left as usize];\n left += 1;\n }\n if cur_sum == target {\n max_len = std::cmp::max(max_len, right as i32 - left + 1);\n }\n }\n \n if max_len != 0 { n - max_len } else { -1 }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int target = 0, n = nums.size();\n for (int num : nums) target += num;\n target -= x;\n \n if (target == 0) return n;\n \n int max_len = 0, cur_sum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n cur_sum += nums[right];\n while (left <= right && cur_sum > target) {\n cur_sum -= nums[left];\n left++;\n }\n if (cur_sum == target) {\n max_len = max(max_len, right - left + 1);\n }\n }\n \n return max_len ? n - max_len : -1;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int minOperations(int[] nums, int x) {\n int target = -x, n = nums.length;\n for (int num : nums) target += num;\n \n if (target == 0) return n;\n \n int maxLen = 0, curSum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum == target) {\n maxLen = Math.max(maxLen, right - left + 1);\n }\n }\n \n return maxLen != 0 ? n - maxLen : -1;\n }\n}\n```\n``` PHP []\nclass Solution {\n function minOperations($nums, $x) {\n $target = 0;\n $n = count($nums);\n foreach ($nums as $num) $target += $num;\n $target -= $x;\n \n if ($target === 0) return $n;\n \n $maxLen = $curSum = $left = 0;\n \n for ($right = 0; $right < $n; ++$right) {\n $curSum += $nums[$right];\n while ($left <= $right && $curSum > $target) {\n $curSum -= $nums[$left];\n $left++;\n }\n if ($curSum === $target) {\n $maxLen = max($maxLen, $right - $left + 1);\n }\n }\n \n return $maxLen ? $n - $maxLen : -1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} x\n * @return {number}\n */\nvar minOperations = function(nums, x) {\n let target = -x, n = nums.length;\n for (let num of nums) target += num;\n \n if (target === 0) return n;\n \n let maxLen = 0, curSum = 0, left = 0;\n \n for (let right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum === target) {\n maxLen = Math.max(maxLen, right - left + 1);\n }\n }\n \n return maxLen ? n - maxLen : -1;\n};\n```\n``` C# []\npublic class Solution {\n public int MinOperations(int[] nums, int x) {\n int target = -x, n = nums.Length;\n foreach (int num in nums) target += num;\n \n if (target == 0) return n;\n \n int maxLen = 0, curSum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum == target) {\n maxLen = Math.Max(maxLen, right - left + 1);\n }\n }\n \n return maxLen != 0 ? n - maxLen : -1;\n }\n}\n```\n\n## Performance\n\n| Language | Fastest Runtime (ms) | Memory Usage (MB) |\n|-----------|----------------------|-------------------|\n| Java | 4 | 56 |\n| Rust | 15 | 3 |\n| JavaScript| 76 | 52.8 |\n| C++ | 110 | 99 |\n| Go | 137 | 8.6 |\n| C# | 236 | 54.6 |\n| PHP | 340 | 31.8 |\n| Python3 | 913 | 30.2 |\n\n\n\n\n## Live Coding in Rust\nhttps://youtu.be/CU93rMboS7w?si=r2ryBueD4fCiKZ7w\n\n## Conclusion\n\nThe problem "Minimum Operations to Reduce X to Zero" may look complicated initially due to its minimization objective. However, understanding the underlying logic of subarray sums and applying a sliding window approach can simplify it. This not only solves the problem efficiently but also enhances one\'s understanding of array manipulation techniques. Happy coding! | 140 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
🚀95.97% || Two Pointers - Sliding Window || Commented Code🚀 | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Porblem Description\nGiven an array of integers, `nums`, and an integer `x`. Each element in `nums` can be subtracted from x. The **goal** is to reduce `x` to exactly `0` using a **minimum** number of operations.\n\nIn each **operation**, you can choose to **remove** either the `leftmost` or the `rightmost` element from the array `nums` and subtract its value from `x`.\n\n- **Constraints:**\n- `1 <= nums.length <= 10e5`\n- `1 <= nums[i] <= 10e4`\n- `1 <= x <= 10e9`\n\n---\n\n\n\n# Intuition\nHello There\uD83D\uDE00\nLet\'s take a look on our today\'s interesting problem\uD83D\uDE80\n\nToday we have **two things**, **array** of intergers and **number** `x`.\nWe can do **one** operation **each** time select `rightmost` or `leftmost` item from the array and **subtract** it from `x`.\nThe goal is to make `x` equal to `zero`.\n\nLook interesting \uD83E\uDD2F\nLet\'s **simplify** our problem a little ?\nWe only need to know **sum** of numbers from `right` and `left` that equal to `x`.\nBut how we get this number ?\uD83E\uDD14\nLet\'s see this example:\n```\nnums = (3, 4, 7, 1, 3, 8, 2, 4), x = 9\n```\nwe can see here that the answer of minimum elements from `left` and `right` (operations) is `3` which are `(3, 2, 4)`\nThere is also something interesting.\uD83E\uDD29\nWe can see that there is a subarray that we **didn\'t touch** which is `(4, 7, 1, 3, 8)`\n\nLet\'s make a **relation** between them\uD83D\uDE80\n```\nsum(3, 4, 7, 1, 3, 8, 2, 4) = sum(4, 7, 1, 3, 8) + sum(3, 2, 4)\nsum(3, 4, 7, 1, 3, 8, 2, 4) = sum(4, 7, 1, 3, 8) + x\nsum(3, 4, 7, 1, 3, 8, 2, 4) - x = sum(4, 7, 1, 3, 8) \n23 = sum(4, 7, 1, 3, 8) \n```\nWe can see something here.\uD83D\uDE00\nThat the `sum subarray` that I talked about before is the `sum of the whole array - x`\n\nOk we made a **relation** between them but **why** I walked through all of this ?\n\nThe reason is that we can **utilize** an efficient technique that is called **Two Pointers**.\uD83D\uDE80\uD83D\uDE80\n\nThats it, instead of finding the **minimum** number of operations from `leftmost` and `rightmost` elements. We can find the **continous subarray** that **anyother** element in the array is the **answer** to our **minimum** operations.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n# Approach\n1. Calculate the total sum of elements.\n2. Compute the target value as the difference between the total sum and the provided target `x`.\n3. Check if the target value is `negative`; if so, return `-1` as the target sum is not achievable.\n4. Check if the target value is `zero`; if so, **return** the **size** of nums since we need to subtract **all** of the elements from x.\n5. Initialize pointers `leftIndex` and `rightIndex` to track a sliding window.\n6. Within the loop, check if `currentSum` exceeds the target value. If it does, increment `leftIndex` and update `currentSum`.\n7. Whenever `currentSum` equals the target value, calculate the **minimum** number of operations required and update `minOperations`.\n8. **Return** the **minimum** number of operations.\n\n---\n\n\n\n# Complexity\n- **Time complexity:**$$O(N)$$\nIn this method we have two pointers, each of them can iterate over the array at most once. So the complexity is `2 * N` which is `O(N)`.\n- **Space complexity:**$$O(1)$$\nWe are storing couple of variables and not storing arrays or other data structure so the complexity is `O(1)`.\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int targetSum) {\n int totalSum = accumulate(nums.begin(), nums.end(), 0);\n int target = totalSum - targetSum; // Calculate the target sum difference\n\n if (target < 0)\n return -1; // Return -1 if target sum is not achievable\n\n if (target == 0)\n return nums.size(); // Return the number of elements if target sum is 0\n\n int n = nums.size(); // Number of elements in the vector\n int minOperations = INT_MAX; // Minimum operations to achieve the target sum\n int currentSum = 0; // Current sum of elements\n int leftIndex = 0, rightIndex = 0; // Pointers for the sliding window\n\n while (rightIndex < n) {\n currentSum += nums[rightIndex];\n rightIndex++;\n\n while (currentSum > target && leftIndex < n) {\n currentSum -= nums[leftIndex];\n leftIndex++;\n }\n\n if (currentSum == target)\n minOperations = min(minOperations, n - (rightIndex - leftIndex));\n }\n\n return (minOperations == INT_MAX) ? -1 : minOperations; // Return the minimum operations or -1 if not possible\n }\n};\n```\n```Java []\nclass Solution {\n public int minOperations(int[] nums, int targetSum) {\n int totalSum = Arrays.stream(nums).sum();\n int target = totalSum - targetSum; // Calculate the target sum difference\n\n if (target < 0)\n return -1; // Return -1 if target sum is not achievable\n\n if (target == 0)\n return nums.length; // Return the number of elements if target sum is 0\n\n int n = nums.length; // Number of elements in the array\n int minOperations = Integer.MAX_VALUE; // Minimum operations to achieve the target sum\n int currentSum = 0; // Current sum of elements\n int leftIndex = 0, rightIndex = 0; // Pointers for the sliding window\n\n while (rightIndex < n) {\n currentSum += nums[rightIndex];\n rightIndex++;\n\n while (currentSum > target && leftIndex < n) {\n currentSum -= nums[leftIndex];\n leftIndex++;\n }\n\n if (currentSum == target)\n minOperations = Math.min(minOperations, n - (rightIndex - leftIndex));\n }\n\n return (minOperations == Integer.MAX_VALUE) ? -1 : minOperations; // Return the minimum operations or -1 if not possible\n }\n}\n```\n```Python []\nclass Solution:\n def minOperations(self, nums, targetSum) -> int:\n totalSum = sum(nums)\n target = totalSum - targetSum # Calculate the target sum difference\n\n if target < 0:\n return -1 # Return -1 if target sum is not achievable\n\n if target == 0:\n return len(nums) # Return the number of elements if target sum is 0\n\n n = len(nums) # Number of elements in the list\n minOperations = float(\'inf\') # Minimum operations to achieve the target sum\n currentSum = 0 # Current sum of elements\n leftIndex = 0\n rightIndex = 0 # Pointers for the sliding window\n\n while rightIndex < n:\n currentSum += nums[rightIndex]\n rightIndex += 1\n\n while currentSum > target and leftIndex < n:\n currentSum -= nums[leftIndex]\n leftIndex += 1\n\n if currentSum == target:\n minOperations = min(minOperations, n - (rightIndex - leftIndex))\n\n return -1 if minOperations == float(\'inf\') else minOperations # Return the minimum operations or -1 if not possible\n```\n\n\n\n | 60 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
🚀95.97% || Two Pointers - Sliding Window || Commented Code🚀 | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Porblem Description\nGiven an array of integers, `nums`, and an integer `x`. Each element in `nums` can be subtracted from x. The **goal** is to reduce `x` to exactly `0` using a **minimum** number of operations.\n\nIn each **operation**, you can choose to **remove** either the `leftmost` or the `rightmost` element from the array `nums` and subtract its value from `x`.\n\n- **Constraints:**\n- `1 <= nums.length <= 10e5`\n- `1 <= nums[i] <= 10e4`\n- `1 <= x <= 10e9`\n\n---\n\n\n\n# Intuition\nHello There\uD83D\uDE00\nLet\'s take a look on our today\'s interesting problem\uD83D\uDE80\n\nToday we have **two things**, **array** of intergers and **number** `x`.\nWe can do **one** operation **each** time select `rightmost` or `leftmost` item from the array and **subtract** it from `x`.\nThe goal is to make `x` equal to `zero`.\n\nLook interesting \uD83E\uDD2F\nLet\'s **simplify** our problem a little ?\nWe only need to know **sum** of numbers from `right` and `left` that equal to `x`.\nBut how we get this number ?\uD83E\uDD14\nLet\'s see this example:\n```\nnums = (3, 4, 7, 1, 3, 8, 2, 4), x = 9\n```\nwe can see here that the answer of minimum elements from `left` and `right` (operations) is `3` which are `(3, 2, 4)`\nThere is also something interesting.\uD83E\uDD29\nWe can see that there is a subarray that we **didn\'t touch** which is `(4, 7, 1, 3, 8)`\n\nLet\'s make a **relation** between them\uD83D\uDE80\n```\nsum(3, 4, 7, 1, 3, 8, 2, 4) = sum(4, 7, 1, 3, 8) + sum(3, 2, 4)\nsum(3, 4, 7, 1, 3, 8, 2, 4) = sum(4, 7, 1, 3, 8) + x\nsum(3, 4, 7, 1, 3, 8, 2, 4) - x = sum(4, 7, 1, 3, 8) \n23 = sum(4, 7, 1, 3, 8) \n```\nWe can see something here.\uD83D\uDE00\nThat the `sum subarray` that I talked about before is the `sum of the whole array - x`\n\nOk we made a **relation** between them but **why** I walked through all of this ?\n\nThe reason is that we can **utilize** an efficient technique that is called **Two Pointers**.\uD83D\uDE80\uD83D\uDE80\n\nThats it, instead of finding the **minimum** number of operations from `leftmost` and `rightmost` elements. We can find the **continous subarray** that **anyother** element in the array is the **answer** to our **minimum** operations.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n# Approach\n1. Calculate the total sum of elements.\n2. Compute the target value as the difference between the total sum and the provided target `x`.\n3. Check if the target value is `negative`; if so, return `-1` as the target sum is not achievable.\n4. Check if the target value is `zero`; if so, **return** the **size** of nums since we need to subtract **all** of the elements from x.\n5. Initialize pointers `leftIndex` and `rightIndex` to track a sliding window.\n6. Within the loop, check if `currentSum` exceeds the target value. If it does, increment `leftIndex` and update `currentSum`.\n7. Whenever `currentSum` equals the target value, calculate the **minimum** number of operations required and update `minOperations`.\n8. **Return** the **minimum** number of operations.\n\n---\n\n\n\n# Complexity\n- **Time complexity:**$$O(N)$$\nIn this method we have two pointers, each of them can iterate over the array at most once. So the complexity is `2 * N` which is `O(N)`.\n- **Space complexity:**$$O(1)$$\nWe are storing couple of variables and not storing arrays or other data structure so the complexity is `O(1)`.\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int targetSum) {\n int totalSum = accumulate(nums.begin(), nums.end(), 0);\n int target = totalSum - targetSum; // Calculate the target sum difference\n\n if (target < 0)\n return -1; // Return -1 if target sum is not achievable\n\n if (target == 0)\n return nums.size(); // Return the number of elements if target sum is 0\n\n int n = nums.size(); // Number of elements in the vector\n int minOperations = INT_MAX; // Minimum operations to achieve the target sum\n int currentSum = 0; // Current sum of elements\n int leftIndex = 0, rightIndex = 0; // Pointers for the sliding window\n\n while (rightIndex < n) {\n currentSum += nums[rightIndex];\n rightIndex++;\n\n while (currentSum > target && leftIndex < n) {\n currentSum -= nums[leftIndex];\n leftIndex++;\n }\n\n if (currentSum == target)\n minOperations = min(minOperations, n - (rightIndex - leftIndex));\n }\n\n return (minOperations == INT_MAX) ? -1 : minOperations; // Return the minimum operations or -1 if not possible\n }\n};\n```\n```Java []\nclass Solution {\n public int minOperations(int[] nums, int targetSum) {\n int totalSum = Arrays.stream(nums).sum();\n int target = totalSum - targetSum; // Calculate the target sum difference\n\n if (target < 0)\n return -1; // Return -1 if target sum is not achievable\n\n if (target == 0)\n return nums.length; // Return the number of elements if target sum is 0\n\n int n = nums.length; // Number of elements in the array\n int minOperations = Integer.MAX_VALUE; // Minimum operations to achieve the target sum\n int currentSum = 0; // Current sum of elements\n int leftIndex = 0, rightIndex = 0; // Pointers for the sliding window\n\n while (rightIndex < n) {\n currentSum += nums[rightIndex];\n rightIndex++;\n\n while (currentSum > target && leftIndex < n) {\n currentSum -= nums[leftIndex];\n leftIndex++;\n }\n\n if (currentSum == target)\n minOperations = Math.min(minOperations, n - (rightIndex - leftIndex));\n }\n\n return (minOperations == Integer.MAX_VALUE) ? -1 : minOperations; // Return the minimum operations or -1 if not possible\n }\n}\n```\n```Python []\nclass Solution:\n def minOperations(self, nums, targetSum) -> int:\n totalSum = sum(nums)\n target = totalSum - targetSum # Calculate the target sum difference\n\n if target < 0:\n return -1 # Return -1 if target sum is not achievable\n\n if target == 0:\n return len(nums) # Return the number of elements if target sum is 0\n\n n = len(nums) # Number of elements in the list\n minOperations = float(\'inf\') # Minimum operations to achieve the target sum\n currentSum = 0 # Current sum of elements\n leftIndex = 0\n rightIndex = 0 # Pointers for the sliding window\n\n while rightIndex < n:\n currentSum += nums[rightIndex]\n rightIndex += 1\n\n while currentSum > target and leftIndex < n:\n currentSum -= nums[leftIndex]\n leftIndex += 1\n\n if currentSum == target:\n minOperations = min(minOperations, n - (rightIndex - leftIndex))\n\n return -1 if minOperations == float(\'inf\') else minOperations # Return the minimum operations or -1 if not possible\n```\n\n\n\n | 60 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
Simple Python Solution | minimum-operations-to-reduce-x-to-zero | 0 | 1 | # Complexity\n- Time complexity: **O(N)**\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n n = len(nums)\n totalSum = sum(nums)\n if totalSum == x:\n return n\n target = totalSum - x\n hashmap = { 0: -1 }\n currLen, currSum = 0, 0\n for i in range(len(nums)):\n currSum += nums[i]\n j = hashmap.get(currSum - target, i)\n currLen = max(currLen, i - j)\n hashmap[currSum] = i\n return n - currLen if currLen > 0 else -1\n``` | 1 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
Simple Python Solution | minimum-operations-to-reduce-x-to-zero | 0 | 1 | # Complexity\n- Time complexity: **O(N)**\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n n = len(nums)\n totalSum = sum(nums)\n if totalSum == x:\n return n\n target = totalSum - x\n hashmap = { 0: -1 }\n currLen, currSum = 0, 0\n for i in range(len(nums)):\n currSum += nums[i]\n j = hashmap.get(currSum - target, i)\n currLen = max(currLen, i - j)\n hashmap[currSum] = i\n return n - currLen if currLen > 0 else -1\n``` | 1 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
Python 3 | Beats 92.74% Time | Beats 100% Memory | Sliding Window Solution | minimum-operations-to-reduce-x-to-zero | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n \n def minOperations(self, nums: List[int], x: int) -> int:\n \n # sliding window solution\n \n # target will represent the subarray that is not needed \n # when our subarray equals to target then everything outside, will be the number of operations to reduce x to zero\n target = sum(nums) - x\n\n # !!! if our target is 0 then the whole array is needed to reduce x to 0 !!!\n if target == 0:\n return len(nums)\n\n l, r = 0, 0\n # curr_sum will keep track of the sum of our current subarray\n curr_sum = 0\n\n # operations will be infinite for now since we want the MINIMUM NUMBER of operations\n operations = float(\'inf\')\n\n for r in range(len(nums)):\n curr_sum += nums[r]\n\n # if curr_sum is greater than our target then we want to shrink our window\n # also do some out of bounds checking\n while curr_sum >= target and l < len(nums):\n # if the current sum == target then we have the window that we don\'t need\n if curr_sum == target:\n # update the operations \n # the whole array - the sub array will equal to x\n # * it represents the outside operations that can reduce x to zero\n operations = min(operations, len(nums) - (r - l + 1))\n\n # shrink the window\n curr_sum -= nums[l]\n l += 1\n\n return operations if operations != float(\'inf\') else -1\n \n\n\n``` | 1 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
Python 3 | Beats 92.74% Time | Beats 100% Memory | Sliding Window Solution | minimum-operations-to-reduce-x-to-zero | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n \n def minOperations(self, nums: List[int], x: int) -> int:\n \n # sliding window solution\n \n # target will represent the subarray that is not needed \n # when our subarray equals to target then everything outside, will be the number of operations to reduce x to zero\n target = sum(nums) - x\n\n # !!! if our target is 0 then the whole array is needed to reduce x to 0 !!!\n if target == 0:\n return len(nums)\n\n l, r = 0, 0\n # curr_sum will keep track of the sum of our current subarray\n curr_sum = 0\n\n # operations will be infinite for now since we want the MINIMUM NUMBER of operations\n operations = float(\'inf\')\n\n for r in range(len(nums)):\n curr_sum += nums[r]\n\n # if curr_sum is greater than our target then we want to shrink our window\n # also do some out of bounds checking\n while curr_sum >= target and l < len(nums):\n # if the current sum == target then we have the window that we don\'t need\n if curr_sum == target:\n # update the operations \n # the whole array - the sub array will equal to x\n # * it represents the outside operations that can reduce x to zero\n operations = min(operations, len(nums) - (r - l + 1))\n\n # shrink the window\n curr_sum -= nums[l]\n l += 1\n\n return operations if operations != float(\'inf\') else -1\n \n\n\n``` | 1 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
Maximum length subarray sum equal K | minimum-operations-to-reduce-x-to-zero | 0 | 1 | # Approach\nIf we have to find ***X as sum from starting and ending of array***, \nSo we basically need to find - \n ***maximum length of subarray*** with `sum = total-x`\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target = sum(nums) - x\n mini = 1e9\n j = 0\n summ = 0\n if target < 0: return -1 \n for i in range(len(nums)):\n summ+=nums[i]\n while summ > target and j < len(nums):\n summ -= nums[j]\n j+=1\n if summ == target:\n mini = min(mini,(len(nums)- (i-j+1)))\n if mini == 1e9: mini = -1\n return mini\n\n \n``` | 1 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
Maximum length subarray sum equal K | minimum-operations-to-reduce-x-to-zero | 0 | 1 | # Approach\nIf we have to find ***X as sum from starting and ending of array***, \nSo we basically need to find - \n ***maximum length of subarray*** with `sum = total-x`\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target = sum(nums) - x\n mini = 1e9\n j = 0\n summ = 0\n if target < 0: return -1 \n for i in range(len(nums)):\n summ+=nums[i]\n while summ > target and j < len(nums):\n summ -= nums[j]\n j+=1\n if summ == target:\n mini = min(mini,(len(nums)- (i-j+1)))\n if mini == 1e9: mini = -1\n return mini\n\n \n``` | 1 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
How we think about a solution - O(n) time, O(1) space - Python, JavaScript, Java, C++ | minimum-operations-to-reduce-x-to-zero | 1 | 1 | Welcome to my article. Before starting the article, why do I have to get multiple downvotes for a miniute every day? That is obviously deliberate downvotes. I can tell who is doing it. Please show your respect to others! Thanks.\n\n# Intuition\nTry to find target number with sum(nums) - x which is `unnecessary numbers`\n\n---\n\n# Solution Video\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/RUF-4_3fzew\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Minimum Operations to Reduce X to Zero \n`1:13` How we think about a solution\n`3:47` Explain how to solve Minimum Operations to Reduce X to Zero\n`13:00` Coding\n`15:26` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,382\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nWe have two choices to take numbers from left or right side. But problem is we don\'t know what numbers are coming next, next next or next next next...so it\'s tough to manage left and right numbers at the same time.\n\nThat\'s why I changed my idea to this. We have to subtract some numbers from `x`. In other words, If we can calculate numbers which don\'t need for `x` and subtract the `unnecessary numbers` from `total number` of input array, we can get `x`. That formula is\n\n```\ntotal numbers in array - unnecessary numbers = x\n```\n\nAnd an important point is that as I told you, we have two choices to take numbers from left side or right side. That\'s why `position of unnecessary numbers` is around middle of input array for the most cases and `it is consecutive places`.\n\nLet\'s see concrete expamle.\n```\nInput: nums = [3,2,20,1,1,3], x = 10\n```\n\ncalculation of `unnecessary numbers` is\n```\ntotal numbers in array - unnecessary numbers = x\n\u2193\ntotal numbers in array - x = unnecessary numbers\n\n30 - 10 = 20\n\n30: total number of input array\n10: x\n20: unnecessary numbers \n```\n\n\nAt first, we have to find `20` from `input array`. Let\'s break the numbers into small pieces.\n\n```\n[3,2] = 5\n[20] = 20\n[1,1,3] = 5\n\n[3,2] is an case where we take 3 and 2 from left side.\n[1,1,3] is an case where we take 3, 1 and 1 from right side.\nThe total of [3,2] and [1,1,3] is 10 (3+2+1+1+3) which is x.\n```\nIn this case, if we can find `[20]`, all we have to do is to calculate this.\n```\n6 - 1 = 5\n\n6: total length of input array\n1: length of [20]\n5: length of [3,2] + [1,1,3]\n```\n```\nOutput : 5 (minimum number of operations to make x zero)\n```\n\n`position of unnecessary numbers` is around middle of input array and it is `consective places`, so looks like we can use `sliding window` technique to find `length of array for unnecessary numbers`.\n\n\n### Overview Algorithm\n1. Calculate the target sum as the sum of `nums` minus `x`.\n2. Check if the target sum is negative, return -1 if it is.\n3. Initialize variables `left`, `cur_sum`, and `max_sub_length`.\n4. Iterate through the `nums` array using a sliding window approach to find the longest subarray with the sum equal to the target.\n\n### Detailed Explanation\n1. Calculate the target sum:\n - Calculate the `target` as the sum of `nums` minus `x`. This is the sum we want to achieve by finding a subarray in the given array.\n\n2. Check if the target sum is negative:\n - If `target` is less than 0, it means it\'s not possible to achieve the target sum by removing elements from the array. Return -1.\n\n3. Initialize variables:\n - `left`: Initialize a pointer to the left end of the window.\n - `cur_sum`: Initialize a variable to keep track of the current sum in the window.\n - `max_sub_length`: Initialize a variable to keep track of the maximum subarray length with the sum equal to the target.\n\n4. Iterate through the array using a sliding window:\n - Start a loop over the array using the right pointer.\n - Update the current sum by adding the current element at the right pointer.\n - Check if the current sum is greater than the target:\n - If the current sum exceeds the target, move the left pointer to the right until the current sum is less than or equal to the target.\n - Check if the current sum is equal to the target:\n - If the current sum equals the target, update the maximum subarray length if needed.\n - At each iteration, keep track of the maximum subarray length found so far.\n\n5. Return the result:\n - After the loop, return -1 if no valid subarray was found (max_sub_length remains as initialized), or return the difference between the total length of the array and the maximum subarray length.\n\nThis algorithm efficiently finds the longest subarray with a sum equal to the target sum using a sliding window approach.\n\n# How it works\nLet\'s think about this input.\n```\nInput: nums = [3,2,20,1,1,3], x = 10\n\ntarget(unnecessary numbers) = 20 (fixed)\ncur_sum = 0\nleft = 0\nright = 0\nmax_sub_length = 0\nn = 6 (fixed)\n```\niteration thorugh input array one by one\n```\nwhen right = 0, add 3 to cur_sum\n\ncur_sum = 3\nleft = 0\nmax_sub_length = 0\n```\n\n```\nwhen right = 1, add 2 to cur_sum\n\ncur_sum = 5\nleft = 0\nmax_sub_length = 0\n```\n\n```\nwhen right = 2, add 20 to cur_sum\n\ncur_sum = 25 \u2192 20(while loop, 25 - 3 - 2)\nleft = 0 \u2192 2 (while loop, 0 + 1 + 1)\nmax_sub_length = 1 (if statement, max(-inf, 2 - 2 + 1))\n```\n\n```\nwhen right = 3, add 1 to cur_sum\n\ncur_sum = 21 \u2192 1(while loop, 21 - 20)\nleft = 2 \u2192 3 (while loop, 2 + 1)\nmax_sub_length = 1\n```\n\n```\nwhen right = 4, add 1 to cur_sum\n\ncur_sum = 2\nleft = 3\nmax_sub_length = 1\n```\n\n```\nwhen right = 5, add 3 to cur_sum\n\ncur_sum = 5\nleft = 3\nmax_sub_length = 1\n```\n\n```\nreturn 6(n) - 1(max_sub_length)\n```\n\n```\nOutput: 5 (operations)\n```\n\n\n\n\n# Complexity\n- Time complexity: O(n)\n`n` is the length of the input nums array. This is because there is a single loop that iterates through the elements of the array once.\n\n\n- Space complexity: O(1)\nbecause the code uses a constant amount of additional memory regardless of the size of the input nums array. The space used for variables like `target`, `left`, `cur_sum`, `max_sub_length`, and `n` does not depend on the size of the input array and remains constant.\n\n\n```python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target = sum(nums) - x\n \n if target < 0:\n return -1\n \n left = 0\n cur_sum = 0\n max_sub_length = float(\'-inf\')\n n = len(nums)\n \n for right in range(n):\n cur_sum += nums[right]\n \n while cur_sum > target:\n cur_sum -= nums[left]\n left += 1\n \n if cur_sum == target:\n max_sub_length = max(max_sub_length, right - left + 1)\n \n return -1 if max_sub_length == float(\'-inf\') else n - max_sub_length\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} x\n * @return {number}\n */\nvar minOperations = function(nums, x) {\n const target = nums.reduce((acc, num) => acc + num, 0) - x;\n \n if (target < 0) {\n return -1;\n }\n \n let left = 0;\n let curSum = 0;\n let maxSubLength = Number.NEGATIVE_INFINITY;\n const n = nums.length;\n \n for (let right = 0; right < n; right++) {\n curSum += nums[right];\n \n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n \n if (curSum === target) {\n maxSubLength = Math.max(maxSubLength, right - left + 1);\n }\n }\n \n return maxSubLength === Number.NEGATIVE_INFINITY ? -1 : n - maxSubLength; \n};\n```\n```java []\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int target = 0;\n for (int num : nums) {\n target += num;\n }\n target -= x;\n\n if (target < 0) {\n return -1;\n }\n\n int left = 0;\n int curSum = 0;\n int maxSubLength = Integer.MIN_VALUE;\n int n = nums.length;\n\n for (int right = 0; right < n; right++) {\n curSum += nums[right];\n\n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n\n if (curSum == target) {\n maxSubLength = Math.max(maxSubLength, right - left + 1);\n }\n }\n\n return maxSubLength == Integer.MIN_VALUE ? -1 : n - maxSubLength; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int target = 0;\n for (int i : nums) {\n target += i;\n }\n target -= x;\n\n if (target < 0) {\n return -1;\n }\n\n int left = 0;\n int curSum = 0;\n int maxSubLength = INT_MIN;\n int n = nums.size();\n\n for (int right = 0; right < n; right++) {\n curSum += nums[right];\n\n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n\n if (curSum == target) {\n maxSubLength = std::max(maxSubLength, right - left + 1);\n }\n }\n\n return maxSubLength == INT_MIN ? -1 : n - maxSubLength; \n }\n};\n```\n\n\n---\n\nThank you for reading such a long article. \n\n\u2B50\uFE0F Please upvote it if you understand how we think about a solution and don\'t forget to subscribe to my youtube channel!\n\n\nMy next post for daily coding challenge on Sep 21, 2023\nhttps://leetcode.com/problems/median-of-two-sorted-arrays/solutions/4070884/my-thought-process-ologminn-m-time-o1-space-python-javascript-java-c/\n\nHave a nice day!\n\n\n | 39 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
How we think about a solution - O(n) time, O(1) space - Python, JavaScript, Java, C++ | minimum-operations-to-reduce-x-to-zero | 1 | 1 | Welcome to my article. Before starting the article, why do I have to get multiple downvotes for a miniute every day? That is obviously deliberate downvotes. I can tell who is doing it. Please show your respect to others! Thanks.\n\n# Intuition\nTry to find target number with sum(nums) - x which is `unnecessary numbers`\n\n---\n\n# Solution Video\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/RUF-4_3fzew\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Minimum Operations to Reduce X to Zero \n`1:13` How we think about a solution\n`3:47` Explain how to solve Minimum Operations to Reduce X to Zero\n`13:00` Coding\n`15:26` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,382\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nWe have two choices to take numbers from left or right side. But problem is we don\'t know what numbers are coming next, next next or next next next...so it\'s tough to manage left and right numbers at the same time.\n\nThat\'s why I changed my idea to this. We have to subtract some numbers from `x`. In other words, If we can calculate numbers which don\'t need for `x` and subtract the `unnecessary numbers` from `total number` of input array, we can get `x`. That formula is\n\n```\ntotal numbers in array - unnecessary numbers = x\n```\n\nAnd an important point is that as I told you, we have two choices to take numbers from left side or right side. That\'s why `position of unnecessary numbers` is around middle of input array for the most cases and `it is consecutive places`.\n\nLet\'s see concrete expamle.\n```\nInput: nums = [3,2,20,1,1,3], x = 10\n```\n\ncalculation of `unnecessary numbers` is\n```\ntotal numbers in array - unnecessary numbers = x\n\u2193\ntotal numbers in array - x = unnecessary numbers\n\n30 - 10 = 20\n\n30: total number of input array\n10: x\n20: unnecessary numbers \n```\n\n\nAt first, we have to find `20` from `input array`. Let\'s break the numbers into small pieces.\n\n```\n[3,2] = 5\n[20] = 20\n[1,1,3] = 5\n\n[3,2] is an case where we take 3 and 2 from left side.\n[1,1,3] is an case where we take 3, 1 and 1 from right side.\nThe total of [3,2] and [1,1,3] is 10 (3+2+1+1+3) which is x.\n```\nIn this case, if we can find `[20]`, all we have to do is to calculate this.\n```\n6 - 1 = 5\n\n6: total length of input array\n1: length of [20]\n5: length of [3,2] + [1,1,3]\n```\n```\nOutput : 5 (minimum number of operations to make x zero)\n```\n\n`position of unnecessary numbers` is around middle of input array and it is `consective places`, so looks like we can use `sliding window` technique to find `length of array for unnecessary numbers`.\n\n\n### Overview Algorithm\n1. Calculate the target sum as the sum of `nums` minus `x`.\n2. Check if the target sum is negative, return -1 if it is.\n3. Initialize variables `left`, `cur_sum`, and `max_sub_length`.\n4. Iterate through the `nums` array using a sliding window approach to find the longest subarray with the sum equal to the target.\n\n### Detailed Explanation\n1. Calculate the target sum:\n - Calculate the `target` as the sum of `nums` minus `x`. This is the sum we want to achieve by finding a subarray in the given array.\n\n2. Check if the target sum is negative:\n - If `target` is less than 0, it means it\'s not possible to achieve the target sum by removing elements from the array. Return -1.\n\n3. Initialize variables:\n - `left`: Initialize a pointer to the left end of the window.\n - `cur_sum`: Initialize a variable to keep track of the current sum in the window.\n - `max_sub_length`: Initialize a variable to keep track of the maximum subarray length with the sum equal to the target.\n\n4. Iterate through the array using a sliding window:\n - Start a loop over the array using the right pointer.\n - Update the current sum by adding the current element at the right pointer.\n - Check if the current sum is greater than the target:\n - If the current sum exceeds the target, move the left pointer to the right until the current sum is less than or equal to the target.\n - Check if the current sum is equal to the target:\n - If the current sum equals the target, update the maximum subarray length if needed.\n - At each iteration, keep track of the maximum subarray length found so far.\n\n5. Return the result:\n - After the loop, return -1 if no valid subarray was found (max_sub_length remains as initialized), or return the difference between the total length of the array and the maximum subarray length.\n\nThis algorithm efficiently finds the longest subarray with a sum equal to the target sum using a sliding window approach.\n\n# How it works\nLet\'s think about this input.\n```\nInput: nums = [3,2,20,1,1,3], x = 10\n\ntarget(unnecessary numbers) = 20 (fixed)\ncur_sum = 0\nleft = 0\nright = 0\nmax_sub_length = 0\nn = 6 (fixed)\n```\niteration thorugh input array one by one\n```\nwhen right = 0, add 3 to cur_sum\n\ncur_sum = 3\nleft = 0\nmax_sub_length = 0\n```\n\n```\nwhen right = 1, add 2 to cur_sum\n\ncur_sum = 5\nleft = 0\nmax_sub_length = 0\n```\n\n```\nwhen right = 2, add 20 to cur_sum\n\ncur_sum = 25 \u2192 20(while loop, 25 - 3 - 2)\nleft = 0 \u2192 2 (while loop, 0 + 1 + 1)\nmax_sub_length = 1 (if statement, max(-inf, 2 - 2 + 1))\n```\n\n```\nwhen right = 3, add 1 to cur_sum\n\ncur_sum = 21 \u2192 1(while loop, 21 - 20)\nleft = 2 \u2192 3 (while loop, 2 + 1)\nmax_sub_length = 1\n```\n\n```\nwhen right = 4, add 1 to cur_sum\n\ncur_sum = 2\nleft = 3\nmax_sub_length = 1\n```\n\n```\nwhen right = 5, add 3 to cur_sum\n\ncur_sum = 5\nleft = 3\nmax_sub_length = 1\n```\n\n```\nreturn 6(n) - 1(max_sub_length)\n```\n\n```\nOutput: 5 (operations)\n```\n\n\n\n\n# Complexity\n- Time complexity: O(n)\n`n` is the length of the input nums array. This is because there is a single loop that iterates through the elements of the array once.\n\n\n- Space complexity: O(1)\nbecause the code uses a constant amount of additional memory regardless of the size of the input nums array. The space used for variables like `target`, `left`, `cur_sum`, `max_sub_length`, and `n` does not depend on the size of the input array and remains constant.\n\n\n```python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target = sum(nums) - x\n \n if target < 0:\n return -1\n \n left = 0\n cur_sum = 0\n max_sub_length = float(\'-inf\')\n n = len(nums)\n \n for right in range(n):\n cur_sum += nums[right]\n \n while cur_sum > target:\n cur_sum -= nums[left]\n left += 1\n \n if cur_sum == target:\n max_sub_length = max(max_sub_length, right - left + 1)\n \n return -1 if max_sub_length == float(\'-inf\') else n - max_sub_length\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} x\n * @return {number}\n */\nvar minOperations = function(nums, x) {\n const target = nums.reduce((acc, num) => acc + num, 0) - x;\n \n if (target < 0) {\n return -1;\n }\n \n let left = 0;\n let curSum = 0;\n let maxSubLength = Number.NEGATIVE_INFINITY;\n const n = nums.length;\n \n for (let right = 0; right < n; right++) {\n curSum += nums[right];\n \n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n \n if (curSum === target) {\n maxSubLength = Math.max(maxSubLength, right - left + 1);\n }\n }\n \n return maxSubLength === Number.NEGATIVE_INFINITY ? -1 : n - maxSubLength; \n};\n```\n```java []\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int target = 0;\n for (int num : nums) {\n target += num;\n }\n target -= x;\n\n if (target < 0) {\n return -1;\n }\n\n int left = 0;\n int curSum = 0;\n int maxSubLength = Integer.MIN_VALUE;\n int n = nums.length;\n\n for (int right = 0; right < n; right++) {\n curSum += nums[right];\n\n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n\n if (curSum == target) {\n maxSubLength = Math.max(maxSubLength, right - left + 1);\n }\n }\n\n return maxSubLength == Integer.MIN_VALUE ? -1 : n - maxSubLength; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int target = 0;\n for (int i : nums) {\n target += i;\n }\n target -= x;\n\n if (target < 0) {\n return -1;\n }\n\n int left = 0;\n int curSum = 0;\n int maxSubLength = INT_MIN;\n int n = nums.size();\n\n for (int right = 0; right < n; right++) {\n curSum += nums[right];\n\n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n\n if (curSum == target) {\n maxSubLength = std::max(maxSubLength, right - left + 1);\n }\n }\n\n return maxSubLength == INT_MIN ? -1 : n - maxSubLength; \n }\n};\n```\n\n\n---\n\nThank you for reading such a long article. \n\n\u2B50\uFE0F Please upvote it if you understand how we think about a solution and don\'t forget to subscribe to my youtube channel!\n\n\nMy next post for daily coding challenge on Sep 21, 2023\nhttps://leetcode.com/problems/median-of-two-sorted-arrays/solutions/4070884/my-thought-process-ologminn-m-time-o1-space-python-javascript-java-c/\n\nHave a nice day!\n\n\n | 39 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
✅97.65%🔥Sum of Subarray Reduction🔥 | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Problem\n\n### This problem involves finding the minimum number of operations to reduce the sum of elements in the array nums to exactly zero, given that you can perform operations to remove elements from either the left or right end of the array.\n---\n# Solution\n\n##### **1.** Calculate the total sum of all elements in the nums array and store it in the variable total.\n\n##### **2.** Calculate the target value that we want to reach, which is target = total - x. Essentially, we want to find a subarray whose sum is equal to target.\n\n##### **3.** Initialize two pointers, left and right, both starting at index 0, and a variable running_sum to keep track of the sum of elements within the sliding window.\n\n##### **4.** Initialize a variable max_length to -1. This variable will be used to keep track of the maximum length of a subarray with a sum equal to target.\n\n#### **5.** Iterate through the nums array using the right pointer. At each step, add the value at nums[right] to running_sum.\n\n#### **6.** Check if running_sum is greater than target. If it is, this means the current subarray sum is too large. In this case, we need to shrink the sliding window by incrementing the left pointer and subtracting the value at nums[left] from running_sum until running_sum is less than or equal to target.\n\n#### **7.** Once the sliding window is valid (i.e., running_sum is equal to target), calculate its length (right - left + 1) and update max_length if this length is greater than the current maximum length.\n\n#### **8.** Continue this process until you\'ve iterated through the entire nums array.\n\n#### **9.** After the loop, check if max_length has been updated. If it has, it means we found a subarray with the sum equal to target. The minimum number of operations required to reduce x to zero is equal to n - max_length, where n is the length of the original array nums. If max_length is still -1, return -1 to indicate that it\'s not possible to reduce x to zero.\n---\n# Summary\n\n#### In summary, the algorithm uses a sliding window approach to find the subarray with the sum equal to the target, and then calculates the minimum number of operations required based on the length of that subarray. If no such subarray exists, it returns -1.\n\n---\n# Code\n```Python3 []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n total = sum(nums)\n target = total - x\n left = 0\n n = len(nums)\n max_length = -1\n running_sum = 0\n\n for right in range(n):\n running_sum += nums[right]\n\n #shrink sliding window to make sure running_sum is not greater than target\n while running_sum > target and left <= right:\n running_sum -= nums[left]\n left += 1\n\n #now we have a avalid sliding window\n if running_sum == target:\n max_length = max(max_length, right - left + 1)\n \n return n - max_length if max_length != -1 else -1\n```\n```python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n total = sum(nums)\n target = total - x\n left = 0\n n = len(nums)\n max_length = -1\n running_sum = 0\n\n for right in range(n):\n running_sum += nums[right]\n\n #shrink sliding window to make sure running_sum is not greater than target\n while running_sum > target and left <= right:\n running_sum -= nums[left]\n left += 1\n\n #now we have a avalid sliding window\n if running_sum == target:\n max_length = max(max_length, right - left + 1)\n \n return n - max_length if max_length != -1 else -1\n```\n```C# []\npublic class Solution {\n public int MinOperations(int[] nums, int x) {\n int total = nums.Sum();\n int target = total - x;\n int left = 0;\n int n = nums.Length;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = Math.Max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(std::vector<int>& nums, int x) {\n int total = std::accumulate(nums.begin(), nums.end(), 0);\n int target = total - x;\n int left = 0;\n int n = nums.size();\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = std::max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n};\n\n```\n```C []\nint minOperations(int* nums, int numsSize, int x) {\n int total = 0;\n for (int i = 0; i < numsSize; i++) {\n total += nums[i];\n }\n\n int target = total - x;\n int left = 0;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < numsSize; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n int currentLength = right - left + 1;\n maxLength = (maxLength == -1) ? currentLength : (currentLength > maxLength ? currentLength : maxLength);\n }\n }\n\n return (maxLength != -1) ? numsSize - maxLength : -1;\n}\n\n```\n```Java []\npublic class Solution {\n public int minOperations(int[] nums, int x) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n\n int target = total - x;\n int left = 0;\n int n = nums.length;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = Math.max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n}\n\n```\n```Go []\nfunc minOperations(nums []int, x int) int {\n total := 0\n for _, num := range nums {\n total += num\n }\n\n target := total - x\n left := 0\n n := len(nums)\n maxLength := -1\n runningSum := 0\n\n for right := 0; right < n; right++ {\n runningSum += nums[right]\n\n for runningSum > target && left <= right {\n runningSum -= nums[left]\n left++\n }\n\n if runningSum == target {\n currentLength := right - left + 1\n if maxLength == -1 || currentLength > maxLength {\n maxLength = currentLength\n }\n }\n }\n\n if maxLength != -1 {\n return n - maxLength\n }\n\n return -1\n}\n\n```\n\n\n | 11 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
✅97.65%🔥Sum of Subarray Reduction🔥 | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Problem\n\n### This problem involves finding the minimum number of operations to reduce the sum of elements in the array nums to exactly zero, given that you can perform operations to remove elements from either the left or right end of the array.\n---\n# Solution\n\n##### **1.** Calculate the total sum of all elements in the nums array and store it in the variable total.\n\n##### **2.** Calculate the target value that we want to reach, which is target = total - x. Essentially, we want to find a subarray whose sum is equal to target.\n\n##### **3.** Initialize two pointers, left and right, both starting at index 0, and a variable running_sum to keep track of the sum of elements within the sliding window.\n\n##### **4.** Initialize a variable max_length to -1. This variable will be used to keep track of the maximum length of a subarray with a sum equal to target.\n\n#### **5.** Iterate through the nums array using the right pointer. At each step, add the value at nums[right] to running_sum.\n\n#### **6.** Check if running_sum is greater than target. If it is, this means the current subarray sum is too large. In this case, we need to shrink the sliding window by incrementing the left pointer and subtracting the value at nums[left] from running_sum until running_sum is less than or equal to target.\n\n#### **7.** Once the sliding window is valid (i.e., running_sum is equal to target), calculate its length (right - left + 1) and update max_length if this length is greater than the current maximum length.\n\n#### **8.** Continue this process until you\'ve iterated through the entire nums array.\n\n#### **9.** After the loop, check if max_length has been updated. If it has, it means we found a subarray with the sum equal to target. The minimum number of operations required to reduce x to zero is equal to n - max_length, where n is the length of the original array nums. If max_length is still -1, return -1 to indicate that it\'s not possible to reduce x to zero.\n---\n# Summary\n\n#### In summary, the algorithm uses a sliding window approach to find the subarray with the sum equal to the target, and then calculates the minimum number of operations required based on the length of that subarray. If no such subarray exists, it returns -1.\n\n---\n# Code\n```Python3 []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n total = sum(nums)\n target = total - x\n left = 0\n n = len(nums)\n max_length = -1\n running_sum = 0\n\n for right in range(n):\n running_sum += nums[right]\n\n #shrink sliding window to make sure running_sum is not greater than target\n while running_sum > target and left <= right:\n running_sum -= nums[left]\n left += 1\n\n #now we have a avalid sliding window\n if running_sum == target:\n max_length = max(max_length, right - left + 1)\n \n return n - max_length if max_length != -1 else -1\n```\n```python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n total = sum(nums)\n target = total - x\n left = 0\n n = len(nums)\n max_length = -1\n running_sum = 0\n\n for right in range(n):\n running_sum += nums[right]\n\n #shrink sliding window to make sure running_sum is not greater than target\n while running_sum > target and left <= right:\n running_sum -= nums[left]\n left += 1\n\n #now we have a avalid sliding window\n if running_sum == target:\n max_length = max(max_length, right - left + 1)\n \n return n - max_length if max_length != -1 else -1\n```\n```C# []\npublic class Solution {\n public int MinOperations(int[] nums, int x) {\n int total = nums.Sum();\n int target = total - x;\n int left = 0;\n int n = nums.Length;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = Math.Max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(std::vector<int>& nums, int x) {\n int total = std::accumulate(nums.begin(), nums.end(), 0);\n int target = total - x;\n int left = 0;\n int n = nums.size();\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = std::max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n};\n\n```\n```C []\nint minOperations(int* nums, int numsSize, int x) {\n int total = 0;\n for (int i = 0; i < numsSize; i++) {\n total += nums[i];\n }\n\n int target = total - x;\n int left = 0;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < numsSize; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n int currentLength = right - left + 1;\n maxLength = (maxLength == -1) ? currentLength : (currentLength > maxLength ? currentLength : maxLength);\n }\n }\n\n return (maxLength != -1) ? numsSize - maxLength : -1;\n}\n\n```\n```Java []\npublic class Solution {\n public int minOperations(int[] nums, int x) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n\n int target = total - x;\n int left = 0;\n int n = nums.length;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = Math.max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n}\n\n```\n```Go []\nfunc minOperations(nums []int, x int) int {\n total := 0\n for _, num := range nums {\n total += num\n }\n\n target := total - x\n left := 0\n n := len(nums)\n maxLength := -1\n runningSum := 0\n\n for right := 0; right < n; right++ {\n runningSum += nums[right]\n\n for runningSum > target && left <= right {\n runningSum -= nums[left]\n left++\n }\n\n if runningSum == target {\n currentLength := right - left + 1\n if maxLength == -1 || currentLength > maxLength {\n maxLength = currentLength\n }\n }\n }\n\n if maxLength != -1 {\n return n - maxLength\n }\n\n return -1\n}\n\n```\n\n\n | 11 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
🔥98.80% Acceptance📈 rate | Using Sliding Window🧭 | Explained in details✅ | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to find a subarray with the maximum possible sum (equal to targetSum) within the given nums array. The goal is to minimize the number of operations to reduce x to 0. By calculating the maximum subarray length, we can determine the minimum number of operations required.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Calculate the targetSum by iterating through the nums array and subtract x from the sum of all elements. If targetSum is negative, it means there is no solution, so return -1.\n\n2. Initialize two pointers, left and right, both initially at the beginning of the array. Also, initialize currentSum and maxLength to 0 and -1, respectively.\n\n3. Iterate through the nums array using the right pointer. At each step, add the current element to currentSum.\n\n4. Check if currentSum is greater than targetSum. If it is, it means the current subarray sum is too large. In this case, move the left pointer to the right to reduce the subarray size until currentSum is less than or equal to targetSum.\n\n5. If currentSum becomes equal to targetSum, update maxLength to be the maximum of its current value and the length of the current subarray (right - left + 1).\n\n6. Repeat steps 3-5 until the right pointer reaches the end of the array.\n\n7. Finally, return n - maxLength as the minimum number of operations needed. If maxLength remains -1, return -1, indicating that n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the nums array twice: once to calculate targetSum and once to find the maximum subarray length. Each iteration takes O(n) time.\nTherefore, the overall time complexity is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because the code uses a constant amount of extra space, regardless of the size of the input array nums.\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int targetSum = 0;\n for (int num : nums) {\n targetSum += num;\n }\n targetSum -= x;\n if (targetSum < 0) return -1; // If x is greater than the sum of all elements, no solution exists.\n\n int left = 0;\n int currentSum = 0;\n int maxLength = -1;\n\n for (int right = 0; right < n; right++) {\n currentSum += nums[right];\n\n while (currentSum > targetSum) {\n currentSum -= nums[left];\n left++;\n }\n\n if (currentSum == targetSum) {\n maxLength = max(maxLength, right - left + 1);\n }\n }\n\n return (maxLength == -1) ? -1 : n - maxLength;\n }\n};\n\n``` | 3 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
🔥98.80% Acceptance📈 rate | Using Sliding Window🧭 | Explained in details✅ | minimum-operations-to-reduce-x-to-zero | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to find a subarray with the maximum possible sum (equal to targetSum) within the given nums array. The goal is to minimize the number of operations to reduce x to 0. By calculating the maximum subarray length, we can determine the minimum number of operations required.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Calculate the targetSum by iterating through the nums array and subtract x from the sum of all elements. If targetSum is negative, it means there is no solution, so return -1.\n\n2. Initialize two pointers, left and right, both initially at the beginning of the array. Also, initialize currentSum and maxLength to 0 and -1, respectively.\n\n3. Iterate through the nums array using the right pointer. At each step, add the current element to currentSum.\n\n4. Check if currentSum is greater than targetSum. If it is, it means the current subarray sum is too large. In this case, move the left pointer to the right to reduce the subarray size until currentSum is less than or equal to targetSum.\n\n5. If currentSum becomes equal to targetSum, update maxLength to be the maximum of its current value and the length of the current subarray (right - left + 1).\n\n6. Repeat steps 3-5 until the right pointer reaches the end of the array.\n\n7. Finally, return n - maxLength as the minimum number of operations needed. If maxLength remains -1, return -1, indicating that n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the nums array twice: once to calculate targetSum and once to find the maximum subarray length. Each iteration takes O(n) time.\nTherefore, the overall time complexity is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because the code uses a constant amount of extra space, regardless of the size of the input array nums.\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int targetSum = 0;\n for (int num : nums) {\n targetSum += num;\n }\n targetSum -= x;\n if (targetSum < 0) return -1; // If x is greater than the sum of all elements, no solution exists.\n\n int left = 0;\n int currentSum = 0;\n int maxLength = -1;\n\n for (int right = 0; right < n; right++) {\n currentSum += nums[right];\n\n while (currentSum > targetSum) {\n currentSum -= nums[left];\n left++;\n }\n\n if (currentSum == targetSum) {\n maxLength = max(maxLength, right - left + 1);\n }\n }\n\n return (maxLength == -1) ? -1 : n - maxLength;\n }\n};\n\n``` | 3 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
✅ [C++/Python] Simple Solution w/ Explanation | Sliding Window | minimum-operations-to-reduce-x-to-zero | 0 | 1 | Sometimes, converting a problem into some other familiar one helps a lot. This question is one of them.\nLet me state a different problem, and your task is to relate how solving this problem will help in solving the actual one.\n> Given an array containing integers, your task is to find the length of the longest subarray with a given sum.\n\nIf you were able to relate, congratulations! \uD83C\uDF89\nAnd if not, don\'t worry; it happens with all of us (or maybe use hints \uD83D\uDE09).\nContinue reading below to find the solution.\n___\n___\n\u2705 **Solution I - Sliding Window [Accepted]**\n\nWe need to make `prefix_sum + suffix_sum = x`. But instead of this, finding a subarray whose sum is `sum(nums) - x` will do the job. Now we only need to maximize the length of this subarray to minimize the length of `prefix + suffix`, which can be done greedily. By doing this, we can get the minimum length, i.e., the minimum number of operations to reduce `x` to exactly `0` (if possible).\n\nIf you haven\'t heard the term "sliding window" before, visit [this link](https://stackoverflow.com/questions/8269916/what-is-sliding-window-algorithm-examples).\n\n1. Let us take a sliding window whose ends are defined by `start_idx` and `end_idx`.\n2. If the sum of this sliding window (subarray) exceeds the target, keep reducing the window size (by increasing `start_idx`) until its sum becomes `<= target`.\n3. If the sum becomes equal to the target, compare the length, and store if it exceeds the previous length.\n4. Return `-1` if the sum of the sliding window never becomes equal to `target`.\n\n<iframe src="https://leetcode.com/playground/PoeSGL3x/shared" frameBorder="0" width="1080" height="450"></iframe>\n\n- **Time Complexity:** `O(n)`\n- **Space Complexity:** `O(1)`\n\n___\n___\nIf you like the solution, please **upvote**! \uD83D\uDD3C\nFor any questions, or discussions, comment below. \uD83D\uDC47\uFE0F\n | 203 | You are given an integer array `nums` and an integer `x`. In one operation, you can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from `x`. Note that this **modifies** the array for future operations.
Return _the **minimum number** of operations to reduce_ `x` _to **exactly**_ `0` _if it is possible__, otherwise, return_ `-1`.
**Example 1:**
**Input:** nums = \[1,1,4,2,3\], x = 5
**Output:** 2
**Explanation:** The optimal solution is to remove the last two elements to reduce x to zero.
**Example 2:**
**Input:** nums = \[5,6,7,8,9\], x = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[3,2,20,1,1,3\], x = 10
**Output:** 5
**Explanation:** The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104`
* `1 <= x <= 109` | For each row of the grid calculate the most right 1 in the grid in the array maxRight. To check if there exist answer, sort maxRight and check if maxRight[i] ≤ i for all possible i's. If there exist an answer, simulate the swaps. |
✅ [C++/Python] Simple Solution w/ Explanation | Sliding Window | minimum-operations-to-reduce-x-to-zero | 0 | 1 | Sometimes, converting a problem into some other familiar one helps a lot. This question is one of them.\nLet me state a different problem, and your task is to relate how solving this problem will help in solving the actual one.\n> Given an array containing integers, your task is to find the length of the longest subarray with a given sum.\n\nIf you were able to relate, congratulations! \uD83C\uDF89\nAnd if not, don\'t worry; it happens with all of us (or maybe use hints \uD83D\uDE09).\nContinue reading below to find the solution.\n___\n___\n\u2705 **Solution I - Sliding Window [Accepted]**\n\nWe need to make `prefix_sum + suffix_sum = x`. But instead of this, finding a subarray whose sum is `sum(nums) - x` will do the job. Now we only need to maximize the length of this subarray to minimize the length of `prefix + suffix`, which can be done greedily. By doing this, we can get the minimum length, i.e., the minimum number of operations to reduce `x` to exactly `0` (if possible).\n\nIf you haven\'t heard the term "sliding window" before, visit [this link](https://stackoverflow.com/questions/8269916/what-is-sliding-window-algorithm-examples).\n\n1. Let us take a sliding window whose ends are defined by `start_idx` and `end_idx`.\n2. If the sum of this sliding window (subarray) exceeds the target, keep reducing the window size (by increasing `start_idx`) until its sum becomes `<= target`.\n3. If the sum becomes equal to the target, compare the length, and store if it exceeds the previous length.\n4. Return `-1` if the sum of the sliding window never becomes equal to `target`.\n\n<iframe src="https://leetcode.com/playground/PoeSGL3x/shared" frameBorder="0" width="1080" height="450"></iframe>\n\n- **Time Complexity:** `O(n)`\n- **Space Complexity:** `O(1)`\n\n___\n___\nIf you like the solution, please **upvote**! \uD83D\uDD3C\nFor any questions, or discussions, comment below. \uD83D\uDC47\uFE0F\n | 203 | There are `n` cars traveling at different speeds in the same direction along a one-lane road. You are given an array `cars` of length `n`, where `cars[i] = [positioni, speedi]` represents:
* `positioni` is the distance between the `ith` car and the beginning of the road in meters. It is guaranteed that `positioni < positioni+1`.
* `speedi` is the initial speed of the `ith` car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the **slowest** car in the fleet.
Return an array `answer`, where `answer[i]` is the time, in seconds, at which the `ith` car collides with the next car, or `-1` if the car does not collide with the next car. Answers within `10-5` of the actual answers are accepted.
**Example 1:**
**Input:** cars = \[\[1,2\],\[2,1\],\[4,3\],\[7,2\]\]
**Output:** \[1.00000,-1.00000,3.00000,-1.00000\]
**Explanation:** After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
**Example 2:**
**Input:** cars = \[\[3,4\],\[5,4\],\[6,3\],\[9,1\]\]
**Output:** \[2.00000,1.00000,1.50000,-1.00000\]
**Constraints:**
* `1 <= cars.length <= 105`
* `1 <= positioni, speedi <= 106`
* `positioni < positioni+1` | Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray. Finding the maximum subarray is standard and can be done greedily. |
[Python3] top-down dp | maximize-grid-happiness | 0 | 1 | \n```\nclass Solution:\n def getMaxGridHappiness(self, m: int, n: int, introvertsCount: int, extrovertsCount: int) -> int:\n \n @cache\n def fn(prev, i, j, intro, extro): \n """Return max grid happiness at (i, j)."""\n if i == m: return 0 # no more position\n if j == n: return fn(prev, i+1, 0, intro, extro)\n if intro == extro == 0: return 0 \n \n prev0 = prev[:j] + (0,) + prev[j+1:]\n ans = fn(prev0, i, j+1, intro, extro)\n if intro: \n val = 120 \n if i and prev[j]: # neighbor from above \n val -= 30 \n if prev[j] == 1: val -= 30 \n else: val += 20 \n if j and prev[j-1]: # neighbor from left \n val -= 30 \n if prev[j-1] == 1: val -= 30 \n else: val += 20 \n prev0 = prev[:j] + (1,) + prev[j+1:]\n ans = max(ans, val + fn(prev0, i, j+1, intro-1, extro))\n if extro: \n val = 40 \n if i and prev[j]: \n val += 20 \n if prev[j] == 1: val -= 30 \n else: val += 20 \n if j and prev[j-1]: \n val += 20 \n if prev[j-1] == 1: val -= 30 \n else: val += 20 \n prev0 = prev[:j] + (2,) + prev[j+1:]\n ans = max(ans, val + fn(prev0, i, j+1, intro, extro-1))\n return ans \n \n return fn((0,)*n, 0, 0, introvertsCount, extrovertsCount)\n``` | 3 | You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts.
You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid.
The **happiness** of each person is calculated as follows:
* Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert).
* Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert).
Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell.
The **grid happiness** is the **sum** of each person's happiness. Return _the **maximum possible grid happiness**._
**Example 1:**
**Input:** m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
**Output:** 240
**Explanation:** Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 \* 30) (0 neighbors) = 120
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
The grid happiness is 120 + 60 + 60 = 240.
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
**Example 2:**
**Input:** m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
**Output:** 260
**Explanation:** Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 \* 20) (2 neighbors) = 80
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
The grid happiness is 90 + 80 + 90 = 260.
**Example 3:**
**Input:** m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
**Output:** 240
**Constraints:**
* `1 <= m, n <= 5`
* `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)` | Partition the array by common integers, and choose the path with larger sum with a DP technique. |
[Python3] top-down dp | maximize-grid-happiness | 0 | 1 | \n```\nclass Solution:\n def getMaxGridHappiness(self, m: int, n: int, introvertsCount: int, extrovertsCount: int) -> int:\n \n @cache\n def fn(prev, i, j, intro, extro): \n """Return max grid happiness at (i, j)."""\n if i == m: return 0 # no more position\n if j == n: return fn(prev, i+1, 0, intro, extro)\n if intro == extro == 0: return 0 \n \n prev0 = prev[:j] + (0,) + prev[j+1:]\n ans = fn(prev0, i, j+1, intro, extro)\n if intro: \n val = 120 \n if i and prev[j]: # neighbor from above \n val -= 30 \n if prev[j] == 1: val -= 30 \n else: val += 20 \n if j and prev[j-1]: # neighbor from left \n val -= 30 \n if prev[j-1] == 1: val -= 30 \n else: val += 20 \n prev0 = prev[:j] + (1,) + prev[j+1:]\n ans = max(ans, val + fn(prev0, i, j+1, intro-1, extro))\n if extro: \n val = 40 \n if i and prev[j]: \n val += 20 \n if prev[j] == 1: val -= 30 \n else: val += 20 \n if j and prev[j-1]: \n val += 20 \n if prev[j-1] == 1: val -= 30 \n else: val += 20 \n prev0 = prev[:j] + (2,) + prev[j+1:]\n ans = max(ans, val + fn(prev0, i, j+1, intro, extro-1))\n return ans \n \n return fn((0,)*n, 0, 0, introvertsCount, extrovertsCount)\n``` | 3 | This is an **interactive problem**.
There is a robot in a hidden grid, and you are trying to get it from its starting cell to the target cell in this grid. The grid is of size `m x n`, and each cell in the grid is either empty or blocked. It is **guaranteed** that the starting cell and the target cell are different, and neither of them is blocked.
You want to find the minimum distance to the target cell. However, you **do not know** the grid's dimensions, the starting cell, nor the target cell. You are only allowed to ask queries to the `GridMaster` object.
Thr `GridMaster` class has the following functions:
* `boolean canMove(char direction)` Returns `true` if the robot can move in that direction. Otherwise, it returns `false`.
* `void move(char direction)` Moves the robot in that direction. If this move would move the robot to a blocked cell or off the grid, the move will be **ignored**, and the robot will remain in the same position.
* `boolean isTarget()` Returns `true` if the robot is currently on the target cell. Otherwise, it returns `false`.
Note that `direction` in the above functions should be a character from `{'U','D','L','R'}`, representing the directions up, down, left, and right, respectively.
Return _the **minimum distance** between the robot's initial starting cell and the target cell. If there is no valid path between the cells, return_ `-1`.
**Custom testing:**
The test input is read as a 2D matrix `grid` of size `m x n` where:
* `grid[i][j] == -1` indicates that the robot is in cell `(i, j)` (the starting cell).
* `grid[i][j] == 0` indicates that the cell `(i, j)` is blocked.
* `grid[i][j] == 1` indicates that the cell `(i, j)` is empty.
* `grid[i][j] == 2` indicates that the cell `(i, j)` is the target cell.
There is exactly one `-1` and `2` in `grid`. Remember that you will **not** have this information in your code.
**Example 1:**
**Input:** grid = \[\[1,2\],\[-1,0\]\]
**Output:** 2
**Explanation:** One possible interaction is described below:
The robot is initially standing on cell (1, 0), denoted by the -1.
- master.canMove('U') returns true.
- master.canMove('D') returns false.
- master.canMove('L') returns false.
- master.canMove('R') returns false.
- master.move('U') moves the robot to the cell (0, 0).
- master.isTarget() returns false.
- master.canMove('U') returns false.
- master.canMove('D') returns true.
- master.canMove('L') returns false.
- master.canMove('R') returns true.
- master.move('R') moves the robot to the cell (0, 1).
- master.isTarget() returns true.
We now know that the target is the cell (0, 1), and the shortest path to the target cell is 2.
**Example 2:**
**Input:** grid = \[\[0,0,-1\],\[1,1,1\],\[2,0,0\]\]
**Output:** 4
**Explanation:** The minimum distance between the robot and the target cell is 4.
**Example 3:**
**Input:** grid = \[\[-1,0\],\[0,2\]\]
**Output:** -1
**Explanation:** There is no path from the robot to the target cell.
**Constraints:**
* `1 <= n, m <= 500`
* `m == grid.length`
* `n == grid[i].length`
* `grid[i][j]` is either `-1`, `0`, `1`, or `2`.
* There is **exactly one** `-1` in `grid`.
* There is **exactly one** `2` in `grid`. | For each cell, it has 3 options, either it is empty, or contains an introvert, or an extrovert. You can do DP where you maintain the state of the previous row, the number of remaining introverts and extroverts, the current row and column, and try the 3 options for each cell. Assume that the previous columns in the current row already belong to the previous row. |
ez C/C++/Python string||0ms Beats 100% | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nString concatenation vs pointers\n# Approach\n<!-- Describe your approach to solving the problem. -->\nC code is also provided which is rare. No string copy is used for this solution.\n\nPython code is 1-line code.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {\n int n1=word1.size(), n2=word2.size();\n for(int i=1; i<n1; i++)\n word1[0]+=word1[i];\n for(int i=1; i<n2; i++)\n word2[0]+=word2[i];\n return word1[0]==word2[0]; \n }\n};\n```\n# C code\n```\n#pragma GCC optimize("O3", "unroll-loops")\n\nbool arrayStringsAreEqual(char** word1, int word1Size, char** word2, int word2Size) {\n int j1=strlen(word1[0]), j2=strlen(word2[0]);\n int len1= j1, len2=j2, count=0, k1=0, k2=0;\n \n for (register int i1=0, i2=0; i1<word1Size && i2<word2Size; count++) {\n if (word1[i1][k1]!=word2[i2][k2]) return 0;\n k1++, k2++;\n if (k1==j1){\n k1=0, i1++;\n j1=(i1<word1Size) ? strlen(word1[i1]) : 0;\n len1+=j1;\n }\n \n if( k2==j2){\n k2=0, i2++;\n j2=(i2<word2Size) ? strlen(word2[i2]) : 0;\n len2+=j2;\n }\n \n }\n// printf("count=%d len1=%d len2=%d \\n", count, len1, len2);\n return count == len1 && count == len2;\n}\n\n```\n#python 1 line\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return "".join(word1)=="".join(word2)\n \n``` | 7 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
ez C/C++/Python string||0ms Beats 100% | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nString concatenation vs pointers\n# Approach\n<!-- Describe your approach to solving the problem. -->\nC code is also provided which is rare. No string copy is used for this solution.\n\nPython code is 1-line code.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {\n int n1=word1.size(), n2=word2.size();\n for(int i=1; i<n1; i++)\n word1[0]+=word1[i];\n for(int i=1; i<n2; i++)\n word2[0]+=word2[i];\n return word1[0]==word2[0]; \n }\n};\n```\n# C code\n```\n#pragma GCC optimize("O3", "unroll-loops")\n\nbool arrayStringsAreEqual(char** word1, int word1Size, char** word2, int word2Size) {\n int j1=strlen(word1[0]), j2=strlen(word2[0]);\n int len1= j1, len2=j2, count=0, k1=0, k2=0;\n \n for (register int i1=0, i2=0; i1<word1Size && i2<word2Size; count++) {\n if (word1[i1][k1]!=word2[i2][k2]) return 0;\n k1++, k2++;\n if (k1==j1){\n k1=0, i1++;\n j1=(i1<word1Size) ? strlen(word1[i1]) : 0;\n len1+=j1;\n }\n \n if( k2==j2){\n k2=0, i2++;\n j2=(i2<word2Size) ? strlen(word2[i2]) : 0;\n len2+=j2;\n }\n \n }\n// printf("count=%d len1=%d len2=%d \\n", count, len1, len2);\n return count == len1 && count == len2;\n}\n\n```\n#python 1 line\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return "".join(word1)=="".join(word2)\n \n``` | 7 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
✅☑[C++/Java/Python/JavaScript] || One-Line Code || 3 Approaches || Beats 100% || EXPLAINED🔥 | check-if-two-string-arrays-are-equivalent | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Built in Function)***\n\n1. Use built-in function accumulate to add the two string vectors.\n2. Compare them, if equal then true else false.\n\n# Complexity\n- *Time complexity:*\n $$O(word1.size() + word2.size())$$\n \n\n- *Space complexity:*\n $$O(word1 + word2)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool arrayStringsAreEqual(std::vector<std::string>& word1, std::vector<std::string>& word2) {\n // Using std::accumulate to concatenate strings in word1 and word2\n return (accumulate(word1.begin(), word1.end(), string("")))==(accumulate(word2.begin(), word2.end(), string("")));\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n#include <string.h>\n\nint main() {\n char* word1[] = {"hello", "world"};\n char* word2[] = {"helloworld"};\n\n char s1[100] = ""; // Ensure this size is big enough to hold the concatenated strings\n char s2[100] = "";\n\n for (int i = 0; i < sizeof(word1) / sizeof(word1[0]); i++) {\n strcat(s1, word1[i]);\n }\n\n for (int i = 0; i < sizeof(word2) / sizeof(word2[0]); i++) {\n strcat(s2, word2[i]);\n }\n\n printf("%s\\n", strcmp(s1, s2) == 0 ? "true" : "false");\n\n return 0;\n}\n\n\n\n\n```\n```Java []\n\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n // Using String.join to concatenate strings in word1 and word2\n String s1 = String.join("", word1);\n String s2 = String.join("", word2);\n \n return s1.equals(s2);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n # Using join to concatenate strings in word1 and word2\n s1 = \'\'.join(word1)\n s2 = \'\'.join(word2)\n \n return s1 == s2\n\n\n\n```\n```javascript []\nfunction arrayStringsAreEqual(word1, word2) {\n let s1 = word1.join(\'\');\n let s2 = word2.join(\'\');\n\n return s1 === s2;\n}\n\nlet word1 = ["hello", "world"];\nlet word2 = ["helloworld"];\n\nconsole.log(arrayStringsAreEqual(word1, word2)); // Outputs: true\n\n\n```\n\n---\n\n#### ***Approach 2(Concatenate and Compare)***\n\n1. **Initialization:**\n\n - It creates two empty strings: `word1Combined` and `word2Combined` to store the combined strings from `word1` and `word2`, respectively.\n1. **Combining Strings:**\n\n - It then iterates through each string in `word1` (using a for-each loop) and concatenates (combines) these strings together into the `word1Combined` string.\n - Similarly, it does the same for `word2`, combining all the strings in word2 into the `word2Combined` string.\n1. **Comparison:**\n\n - After combining all strings, the function compares `word1Combined` and `word2Combined`.\n - If the two combined strings are exactly the same, the function returns `true`, indicating that the concatenated strings from `word1` are equal to the concatenated strings from `word2`. Otherwise, it returns `false`.\n\n# Complexity\n- *Time complexity:*\n $$O(n*k)$$\n \n\n- *Space complexity:*\n $$O(n*k)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {\n // Creates a new string by combining all the strings in word1.\n string word1Combined;\n for (string s : word1) {\n word1Combined += s;\n }\n // Creates a new string by combining all the strings in word2.\n string word2Combined;\n for (string s : word2) {\n word2Combined += s;\n }\n // Returns true if both string are the same.\n return word1Combined == word2Combined;\n }\n};\n\n\n```\n```C []\n\nint arrayStringsAreEqual(char** word1, int word1Size, char** word2, int word2Size) {\n // Combining strings in word1\n char word1Combined[1000] = ""; // Assuming maximum length of combined string as 1000, adjust accordingly\n for (int i = 0; i < word1Size; i++) {\n strcat(word1Combined, word1[i]);\n }\n\n // Combining strings in word2\n char word2Combined[1000] = ""; // Assuming maximum length of combined string as 1000, adjust accordingly\n for (int i = 0; i < word2Size; i++) {\n strcat(word2Combined, word2[i]);\n }\n\n // Comparing the combined strings\n return strcmp(word1Combined, word2Combined) == 0;\n}\n\n\n```\n```Java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n // Creates a new string by combining all the strings in word1.\n StringBuilder word1Combined = new StringBuilder();\n for (String s : word1) {\n word1Combined.append(s);\n }\n // Creates a new string by combining all the strings in word2.\n StringBuilder word2Combined = new StringBuilder();\n for (String s : word2) {\n word2Combined.append(s);\n }\n // Returns true if both string are the same.\n return word1Combined.compareTo(word2Combined) == 0;\n }\n}\n\n\n```\n```python3 []\ndef arrayStringsAreEqual(word1, word2):\n # Combining strings in word1\n word1_combined = \'\'.join(word1)\n\n # Combining strings in word2\n word2_combined = \'\'.join(word2)\n\n # Comparing the combined strings\n return word1_combined == word2_combined\n\nword1 = ["hello", "world"]\nword2 = ["helloworld"]\n\nresult = arrayStringsAreEqual(word1, word2)\nprint(result)\n\n\n\n```\n```javascript []\nfunction arrayStringsAreEqual(word1, word2) {\n // Combining strings in word1\n const word1Combined = word1.join(\'\');\n\n // Combining strings in word2\n const word2Combined = word2.join(\'\');\n\n // Comparing the combined strings\n return word1Combined === word2Combined;\n}\n\nconst word1 = ["hello", "world"];\nconst word2 = ["helloworld"];\n\nconst result = arrayStringsAreEqual(word1, word2);\nconsole.log(result);\n\n\n```\n\n---\n\n#### ***Approach 3(Two Pointers)***\n1. **Initialization of Pointers:**\n\n - `word1Pointer` and `word2Pointer` are initialized to keep track of the current position of the words in `word1` and `word2` vectors, respectively.\n - `string1Pointer` and `string2Pointer` are initialized to keep track of the current character within the words pointed by `word1Pointer` and `word2Pointer`.\n1. **Comparison Loop:**\n\n - The code uses a while loop to compare characters in the strings pointed by `word1Pointer` and `word2Pointer`.\n - It continues looping until either one of the vectors reaches the end (`word1Pointer < word1.size()` and `word2Pointer < word2.size()`).\n1. **Character Comparison:**\n\n - For each pair of strings in word1 and word2, it compares the characters at the positions indicated by `string1Pointer` and `string2Pointer`.\n - If the characters at the current positions are not equal, it returns `false`, indicating that the strings are not equal.\n1. **Advancing Pointers:**\n\n - After comparing characters, it increments `string1Pointer` and `string2Pointer` to move to the next characters in the current words.\n - If the `string1Pointer` reaches the end of a word in `word1`, it moves to the next word by incrementing `word1Pointer` and resets `string1Pointer` to `0`.\n - Similarly, if the `string2Pointer` reaches the end of a word in `word2`, it advances `word2Pointer` and resets `string2Pointer` to `0`.\n1. **Final Check:**\n\n - After the loop, it checks if both vectors (`word1` and `word2`) have been completely traversed. If yes, it returns `true`, indicating that all strings in both vectors are equal; otherwise, it returns `false`.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n*k)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {\n // Pointers to mark the current word in the given two lists.\n int word1Pointer = 0, word2Pointer = 0;\n // Pointers to mark the character in the string pointed by the above pointers.\n int string1Pointer = 0, string2Pointer = 0;\n \n // While we still have the string in any of the two given lists.\n while (word1Pointer < word1.size() && word2Pointer < word2.size()) {\n // If the characters at the two string are same, increment the string pointers\n // Otherwise return false.\n if (word1[word1Pointer][string1Pointer++] != word2[word2Pointer][string2Pointer++]) {\n return false;\n }\n // If the string pointer reaches the end of string in the list word1, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string1Pointer == word1[word1Pointer].size()) {\n word1Pointer++;\n string1Pointer = 0;\n }\n // If the string pointer reaches the end of string in the list word2, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string2Pointer == word2[word2Pointer].size()) {\n word2Pointer++;\n string2Pointer = 0;\n }\n }\n // Strings in both the lists should be traversed.\n return word1Pointer == word1.size() && word2Pointer == word2.size();\n }\n};\n\n\n```\n```C []\n\n\n\n\n```\n```Java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n // Pointers to mark the current word in the given two lists.\n int word1Pointer = 0, word2Pointer = 0;\n // Pointers to mark the character in the string pointed by the above pointers.\n int string1Pointer = 0, string2Pointer = 0;\n \n // While we still have the string in any of the two given lists.\n while (word1Pointer < word1.length && word2Pointer < word2.length) {\n // If the characters at the two string are same, increment the string pointers\n // Otherwise return false.\n if (word1[word1Pointer].charAt(string1Pointer++) != \n word2[word2Pointer].charAt(string2Pointer++)) {\n return false;\n }\n // If the string pointer reaches the end of string in the list word1, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string1Pointer == word1[word1Pointer].length()) {\n word1Pointer++;\n string1Pointer = 0;\n }\n // If the string pointer reaches the end of string in the list word2, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string2Pointer == word2[word2Pointer].length()) {\n word2Pointer++;\n string2Pointer = 0;\n }\n }\n // Strings in both the lists should be traversed.\n return word1Pointer == word1.length && word2Pointer == word2.length;\n }\n}\n\n\n```\n```python3 []\n\n\n\n```\n```javascript []\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
✅☑[C++/Java/Python/JavaScript] || One-Line Code || 3 Approaches || Beats 100% || EXPLAINED🔥 | check-if-two-string-arrays-are-equivalent | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Built in Function)***\n\n1. Use built-in function accumulate to add the two string vectors.\n2. Compare them, if equal then true else false.\n\n# Complexity\n- *Time complexity:*\n $$O(word1.size() + word2.size())$$\n \n\n- *Space complexity:*\n $$O(word1 + word2)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool arrayStringsAreEqual(std::vector<std::string>& word1, std::vector<std::string>& word2) {\n // Using std::accumulate to concatenate strings in word1 and word2\n return (accumulate(word1.begin(), word1.end(), string("")))==(accumulate(word2.begin(), word2.end(), string("")));\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n#include <string.h>\n\nint main() {\n char* word1[] = {"hello", "world"};\n char* word2[] = {"helloworld"};\n\n char s1[100] = ""; // Ensure this size is big enough to hold the concatenated strings\n char s2[100] = "";\n\n for (int i = 0; i < sizeof(word1) / sizeof(word1[0]); i++) {\n strcat(s1, word1[i]);\n }\n\n for (int i = 0; i < sizeof(word2) / sizeof(word2[0]); i++) {\n strcat(s2, word2[i]);\n }\n\n printf("%s\\n", strcmp(s1, s2) == 0 ? "true" : "false");\n\n return 0;\n}\n\n\n\n\n```\n```Java []\n\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n // Using String.join to concatenate strings in word1 and word2\n String s1 = String.join("", word1);\n String s2 = String.join("", word2);\n \n return s1.equals(s2);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n # Using join to concatenate strings in word1 and word2\n s1 = \'\'.join(word1)\n s2 = \'\'.join(word2)\n \n return s1 == s2\n\n\n\n```\n```javascript []\nfunction arrayStringsAreEqual(word1, word2) {\n let s1 = word1.join(\'\');\n let s2 = word2.join(\'\');\n\n return s1 === s2;\n}\n\nlet word1 = ["hello", "world"];\nlet word2 = ["helloworld"];\n\nconsole.log(arrayStringsAreEqual(word1, word2)); // Outputs: true\n\n\n```\n\n---\n\n#### ***Approach 2(Concatenate and Compare)***\n\n1. **Initialization:**\n\n - It creates two empty strings: `word1Combined` and `word2Combined` to store the combined strings from `word1` and `word2`, respectively.\n1. **Combining Strings:**\n\n - It then iterates through each string in `word1` (using a for-each loop) and concatenates (combines) these strings together into the `word1Combined` string.\n - Similarly, it does the same for `word2`, combining all the strings in word2 into the `word2Combined` string.\n1. **Comparison:**\n\n - After combining all strings, the function compares `word1Combined` and `word2Combined`.\n - If the two combined strings are exactly the same, the function returns `true`, indicating that the concatenated strings from `word1` are equal to the concatenated strings from `word2`. Otherwise, it returns `false`.\n\n# Complexity\n- *Time complexity:*\n $$O(n*k)$$\n \n\n- *Space complexity:*\n $$O(n*k)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {\n // Creates a new string by combining all the strings in word1.\n string word1Combined;\n for (string s : word1) {\n word1Combined += s;\n }\n // Creates a new string by combining all the strings in word2.\n string word2Combined;\n for (string s : word2) {\n word2Combined += s;\n }\n // Returns true if both string are the same.\n return word1Combined == word2Combined;\n }\n};\n\n\n```\n```C []\n\nint arrayStringsAreEqual(char** word1, int word1Size, char** word2, int word2Size) {\n // Combining strings in word1\n char word1Combined[1000] = ""; // Assuming maximum length of combined string as 1000, adjust accordingly\n for (int i = 0; i < word1Size; i++) {\n strcat(word1Combined, word1[i]);\n }\n\n // Combining strings in word2\n char word2Combined[1000] = ""; // Assuming maximum length of combined string as 1000, adjust accordingly\n for (int i = 0; i < word2Size; i++) {\n strcat(word2Combined, word2[i]);\n }\n\n // Comparing the combined strings\n return strcmp(word1Combined, word2Combined) == 0;\n}\n\n\n```\n```Java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n // Creates a new string by combining all the strings in word1.\n StringBuilder word1Combined = new StringBuilder();\n for (String s : word1) {\n word1Combined.append(s);\n }\n // Creates a new string by combining all the strings in word2.\n StringBuilder word2Combined = new StringBuilder();\n for (String s : word2) {\n word2Combined.append(s);\n }\n // Returns true if both string are the same.\n return word1Combined.compareTo(word2Combined) == 0;\n }\n}\n\n\n```\n```python3 []\ndef arrayStringsAreEqual(word1, word2):\n # Combining strings in word1\n word1_combined = \'\'.join(word1)\n\n # Combining strings in word2\n word2_combined = \'\'.join(word2)\n\n # Comparing the combined strings\n return word1_combined == word2_combined\n\nword1 = ["hello", "world"]\nword2 = ["helloworld"]\n\nresult = arrayStringsAreEqual(word1, word2)\nprint(result)\n\n\n\n```\n```javascript []\nfunction arrayStringsAreEqual(word1, word2) {\n // Combining strings in word1\n const word1Combined = word1.join(\'\');\n\n // Combining strings in word2\n const word2Combined = word2.join(\'\');\n\n // Comparing the combined strings\n return word1Combined === word2Combined;\n}\n\nconst word1 = ["hello", "world"];\nconst word2 = ["helloworld"];\n\nconst result = arrayStringsAreEqual(word1, word2);\nconsole.log(result);\n\n\n```\n\n---\n\n#### ***Approach 3(Two Pointers)***\n1. **Initialization of Pointers:**\n\n - `word1Pointer` and `word2Pointer` are initialized to keep track of the current position of the words in `word1` and `word2` vectors, respectively.\n - `string1Pointer` and `string2Pointer` are initialized to keep track of the current character within the words pointed by `word1Pointer` and `word2Pointer`.\n1. **Comparison Loop:**\n\n - The code uses a while loop to compare characters in the strings pointed by `word1Pointer` and `word2Pointer`.\n - It continues looping until either one of the vectors reaches the end (`word1Pointer < word1.size()` and `word2Pointer < word2.size()`).\n1. **Character Comparison:**\n\n - For each pair of strings in word1 and word2, it compares the characters at the positions indicated by `string1Pointer` and `string2Pointer`.\n - If the characters at the current positions are not equal, it returns `false`, indicating that the strings are not equal.\n1. **Advancing Pointers:**\n\n - After comparing characters, it increments `string1Pointer` and `string2Pointer` to move to the next characters in the current words.\n - If the `string1Pointer` reaches the end of a word in `word1`, it moves to the next word by incrementing `word1Pointer` and resets `string1Pointer` to `0`.\n - Similarly, if the `string2Pointer` reaches the end of a word in `word2`, it advances `word2Pointer` and resets `string2Pointer` to `0`.\n1. **Final Check:**\n\n - After the loop, it checks if both vectors (`word1` and `word2`) have been completely traversed. If yes, it returns `true`, indicating that all strings in both vectors are equal; otherwise, it returns `false`.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n*k)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {\n // Pointers to mark the current word in the given two lists.\n int word1Pointer = 0, word2Pointer = 0;\n // Pointers to mark the character in the string pointed by the above pointers.\n int string1Pointer = 0, string2Pointer = 0;\n \n // While we still have the string in any of the two given lists.\n while (word1Pointer < word1.size() && word2Pointer < word2.size()) {\n // If the characters at the two string are same, increment the string pointers\n // Otherwise return false.\n if (word1[word1Pointer][string1Pointer++] != word2[word2Pointer][string2Pointer++]) {\n return false;\n }\n // If the string pointer reaches the end of string in the list word1, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string1Pointer == word1[word1Pointer].size()) {\n word1Pointer++;\n string1Pointer = 0;\n }\n // If the string pointer reaches the end of string in the list word2, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string2Pointer == word2[word2Pointer].size()) {\n word2Pointer++;\n string2Pointer = 0;\n }\n }\n // Strings in both the lists should be traversed.\n return word1Pointer == word1.size() && word2Pointer == word2.size();\n }\n};\n\n\n```\n```C []\n\n\n\n\n```\n```Java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n // Pointers to mark the current word in the given two lists.\n int word1Pointer = 0, word2Pointer = 0;\n // Pointers to mark the character in the string pointed by the above pointers.\n int string1Pointer = 0, string2Pointer = 0;\n \n // While we still have the string in any of the two given lists.\n while (word1Pointer < word1.length && word2Pointer < word2.length) {\n // If the characters at the two string are same, increment the string pointers\n // Otherwise return false.\n if (word1[word1Pointer].charAt(string1Pointer++) != \n word2[word2Pointer].charAt(string2Pointer++)) {\n return false;\n }\n // If the string pointer reaches the end of string in the list word1, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string1Pointer == word1[word1Pointer].length()) {\n word1Pointer++;\n string1Pointer = 0;\n }\n // If the string pointer reaches the end of string in the list word2, \n // Move to the next string in the list and, reset the string pointer to 0.\n if (string2Pointer == word2[word2Pointer].length()) {\n word2Pointer++;\n string2Pointer = 0;\n }\n }\n // Strings in both the lists should be traversed.\n return word1Pointer == word1.length && word2Pointer == word2.length;\n }\n}\n\n\n```\n```python3 []\n\n\n\n```\n```javascript []\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
Simple Single Line Code. | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return \'\'.join(word1) == \'\'.join(word2)\n\n\n\n \n``` | 3 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Simple Single Line Code. | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return \'\'.join(word1) == \'\'.join(word2)\n\n\n\n \n``` | 3 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
[Java/C++/Python]Beats 100% || Well explained || | check-if-two-string-arrays-are-equivalent | 1 | 1 | # Approach\n1. **StringBuilder Initialization:**\n - **Why StringBuilder?** StringBuilder is used for efficient string concatenation. It allows you to build strings dynamically, especially when dealing with a sequence of concatenations.\n2. **Concatenation Using For Loops:**\n - **Why For Loops?** For loops are used to iterate over each string in the input arrays (word1 and word2). This is necessary to concatenate each string together. Without a loop, you would need to manually concatenate each string, making the code less readable and maintainable.\n3. **StringBuilder to String Conversion:**\n - **Why Convert to String?** The toString method is used to obtain the final string representations of the concatenated content in each StringBuilder. This is essential because the equals method, which we use for comparison, is defined for strings, not for StringBuilder objects.\n4. **Comparison Using equals:**\n - **Why equals?** The equals method is used to compare the content of the two strings (str1 and str2). This ensures that the content, not just the references, is being compared. Since StringBuilder does not override the equals method, we convert the StringBuilder objects to strings before performing the comparison.\n\n\n\n# Complexity\n- Time complexity: O(m+n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Java\n```\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n\n // Step 1: Initialize StringBuilder objects\n StringBuilder sb1 = new StringBuilder();\n StringBuilder sb2 = new StringBuilder();\n\n // Step 2: Concatenate strings from the first array (word1) using a loop\n for (String str : word1) {\n sb1.append(str);\n }\n\n // Step 3: Concatenate strings from the second array (word2) using a loop\n for (String str : word2) {\n sb2.append(str);\n }\n\n // Step 4: Convert StringBuilder objects to strings\n String str1 = sb1.toString();\n String str2 = sb2.toString();\n\n // Step 5: Compare the strings using the equals method\n return str1.equals(str2);\n }\n}\n\n```\n# C++\n```\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) \n {\n int wordIdx1 = 0, wordIdx2 = 0, chIdx1 = 0, chIdx2 = 0;\n while(true)\n {\n char ch1 = word1[wordIdx1][chIdx1];\n char ch2 = word2[wordIdx2][chIdx2];\n if (ch1 != ch2) return false;\n \n chIdx1++; //incrementing the character index of current word from "word1"\n chIdx2++; //incrementing the character index of current word from "word2";\n //=========================================================\n if (chIdx1 == word1[wordIdx1].size()) //if current word from "word1" is over\n { \n wordIdx1++; //move to next word in "word1"\n chIdx1 = 0; //reset character index to 0\n }\n if (chIdx2 == word2[wordIdx2].size()) //if current word from "word2" is over\n { \n wordIdx2++; //move to next word in "word2"\n chIdx2 = 0; //reset character index to 0\n }\n //=================================================================\n if (wordIdx1 == word1.size() && wordIdx2 == word2.size()) break; // words in both arrays are finished\n \n if (wordIdx1 == word1.size() || wordIdx2 == word2.size()) return false;\n //if words in any onr of the arrays are finished and other still has some words in it\n //then there is no way same string could be formed on concatenation\n }\n return true; \n }\n};\n```\n# Python\n```\nclass Solution(object):\n def arrayStringsAreEqual(self, word1, word2):\n i1 = l1 = 0 # element index and list index of word1\n i2 = l2 = 0 # element index and list index of word1\n while l1 < len(word1) or l2 < len(word2):\n if l1 == len(word1) or l2 == len(word2): # If word1 is end or word2 is end\n return False\n if word1[l1][i1] != word2[l2][i2]: # If diff char between word1 and word2\n return False\n i1 += 1\n i2 += 1\n if i1 == len(word1[l1]):\n i1 = 0\n l1 += 1\n if i2 == len(word2[l2]):\n i2 = 0\n l2 += 1\n return True\n``` | 2 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
[Java/C++/Python]Beats 100% || Well explained || | check-if-two-string-arrays-are-equivalent | 1 | 1 | # Approach\n1. **StringBuilder Initialization:**\n - **Why StringBuilder?** StringBuilder is used for efficient string concatenation. It allows you to build strings dynamically, especially when dealing with a sequence of concatenations.\n2. **Concatenation Using For Loops:**\n - **Why For Loops?** For loops are used to iterate over each string in the input arrays (word1 and word2). This is necessary to concatenate each string together. Without a loop, you would need to manually concatenate each string, making the code less readable and maintainable.\n3. **StringBuilder to String Conversion:**\n - **Why Convert to String?** The toString method is used to obtain the final string representations of the concatenated content in each StringBuilder. This is essential because the equals method, which we use for comparison, is defined for strings, not for StringBuilder objects.\n4. **Comparison Using equals:**\n - **Why equals?** The equals method is used to compare the content of the two strings (str1 and str2). This ensures that the content, not just the references, is being compared. Since StringBuilder does not override the equals method, we convert the StringBuilder objects to strings before performing the comparison.\n\n\n\n# Complexity\n- Time complexity: O(m+n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Java\n```\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n\n // Step 1: Initialize StringBuilder objects\n StringBuilder sb1 = new StringBuilder();\n StringBuilder sb2 = new StringBuilder();\n\n // Step 2: Concatenate strings from the first array (word1) using a loop\n for (String str : word1) {\n sb1.append(str);\n }\n\n // Step 3: Concatenate strings from the second array (word2) using a loop\n for (String str : word2) {\n sb2.append(str);\n }\n\n // Step 4: Convert StringBuilder objects to strings\n String str1 = sb1.toString();\n String str2 = sb2.toString();\n\n // Step 5: Compare the strings using the equals method\n return str1.equals(str2);\n }\n}\n\n```\n# C++\n```\nclass Solution {\npublic:\n bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) \n {\n int wordIdx1 = 0, wordIdx2 = 0, chIdx1 = 0, chIdx2 = 0;\n while(true)\n {\n char ch1 = word1[wordIdx1][chIdx1];\n char ch2 = word2[wordIdx2][chIdx2];\n if (ch1 != ch2) return false;\n \n chIdx1++; //incrementing the character index of current word from "word1"\n chIdx2++; //incrementing the character index of current word from "word2";\n //=========================================================\n if (chIdx1 == word1[wordIdx1].size()) //if current word from "word1" is over\n { \n wordIdx1++; //move to next word in "word1"\n chIdx1 = 0; //reset character index to 0\n }\n if (chIdx2 == word2[wordIdx2].size()) //if current word from "word2" is over\n { \n wordIdx2++; //move to next word in "word2"\n chIdx2 = 0; //reset character index to 0\n }\n //=================================================================\n if (wordIdx1 == word1.size() && wordIdx2 == word2.size()) break; // words in both arrays are finished\n \n if (wordIdx1 == word1.size() || wordIdx2 == word2.size()) return false;\n //if words in any onr of the arrays are finished and other still has some words in it\n //then there is no way same string could be formed on concatenation\n }\n return true; \n }\n};\n```\n# Python\n```\nclass Solution(object):\n def arrayStringsAreEqual(self, word1, word2):\n i1 = l1 = 0 # element index and list index of word1\n i2 = l2 = 0 # element index and list index of word1\n while l1 < len(word1) or l2 < len(word2):\n if l1 == len(word1) or l2 == len(word2): # If word1 is end or word2 is end\n return False\n if word1[l1][i1] != word2[l2][i2]: # If diff char between word1 and word2\n return False\n i1 += 1\n i2 += 1\n if i1 == len(word1[l1]):\n i1 = 0\n l1 += 1\n if i2 == len(word2[l2]):\n i2 = 0\n l2 += 1\n return True\n``` | 2 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
Rust/Python/Go oneliners and then a normal solution in py | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\nIn all high-level languages you can just use some sort of join to create strings and check if they are the same. This gives you an easy 1 line solution wich runs in $O(n + m)$\n\n```Rust []\nimpl Solution {\n pub fn array_strings_are_equal(word1: Vec<String>, word2: Vec<String>) -> bool {\n return word1.join("") == word2.join("");\n }\n}\n```\n```Go []\nimport "strings"\n\nfunc arrayStringsAreEqual(word1 []string, word2 []string) bool {\n return strings.Join(word1, "") == strings.Join(word2, "")\n}\n```\n```Python []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return "".join(word1) == "".join(word2)\n```\n\nBut this is definitely not what people are looking for in the interview. Finding a function in a documentation is not that hard. So they want you to do this with pointers where you move over words and over positions. So here is a normal solution which uses $O(1)$ space and also fails early\n\n# Code\n```\nclass Solution(object):\n def arrayStringsAreEqual(self, word1, word2):\n w1, p1, w2, p2 = 0, 0, 0, 0\n while w1 < len(word1) or w2 < len(word2):\n if w1 == len(word1) or w2 == len(word2) or word1[w1][p1] != word2[w2][p2]:\n return False\n\n p1, p2 = p1 + 1, p2 + 1\n if p1 == len(word1[w1]):\n w1, p1 = w1 + 1, 0\n if p2 == len(word2[w2]):\n w2, p2 = w2 + 1, 0\n\n return True\n``` | 2 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Rust/Python/Go oneliners and then a normal solution in py | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\nIn all high-level languages you can just use some sort of join to create strings and check if they are the same. This gives you an easy 1 line solution wich runs in $O(n + m)$\n\n```Rust []\nimpl Solution {\n pub fn array_strings_are_equal(word1: Vec<String>, word2: Vec<String>) -> bool {\n return word1.join("") == word2.join("");\n }\n}\n```\n```Go []\nimport "strings"\n\nfunc arrayStringsAreEqual(word1 []string, word2 []string) bool {\n return strings.Join(word1, "") == strings.Join(word2, "")\n}\n```\n```Python []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return "".join(word1) == "".join(word2)\n```\n\nBut this is definitely not what people are looking for in the interview. Finding a function in a documentation is not that hard. So they want you to do this with pointers where you move over words and over positions. So here is a normal solution which uses $O(1)$ space and also fails early\n\n# Code\n```\nclass Solution(object):\n def arrayStringsAreEqual(self, word1, word2):\n w1, p1, w2, p2 = 0, 0, 0, 0\n while w1 < len(word1) or w2 < len(word2):\n if w1 == len(word1) or w2 == len(word2) or word1[w1][p1] != word2[w2][p2]:\n return False\n\n p1, p2 = p1 + 1, p2 + 1\n if p1 == len(word1[w1]):\n w1, p1 = w1 + 1, 0\n if p2 == len(word2[w2]):\n w2, p2 = w2 + 1, 0\n\n return True\n``` | 2 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
✅✅|| ONE LINE || EASY PEASY || Java, Python, C#, Rust, Ruby || 🔥🔥🔥 | check-if-two-string-arrays-are-equivalent | 1 | 1 | # Description\n\n## Intuition\nThe problem seems to be about comparing two lists of strings and checking if the concatenation of strings in each list results in equal strings. The provided code uses the `join` method to concatenate the strings in both lists and then compares the resulting strings.\n\n## Approach\nThe approach taken in the code is straightforward. It joins the strings in both lists and checks if the resulting strings are equal. If they are equal, the function returns `True`; otherwise, it returns `False`.\n\n## Complexity\n- **Time complexity:** The time complexity is dominated by the `join` operation, which is linear in the total length of the strings in the input lists. Let\'s denote the total length of all strings in `word1` as \\(m\\) and in `word2` as \\(n\\). Therefore, the time complexity is \\(O(m + n)\\).\n- **Space complexity:** The space complexity is also \\(O(m + n)\\) as the `join` method creates new strings that are the concatenation of the input strings.\n\n## Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n| :--- | :---:| :---: | \nJava | 1 | 40.6 |\nPython3 | 43 | 16.3 |\nC# | 87 | 40.9 |\nRust | 1 | 2.1 |\nRuby | 55 | 210.9 |\n\n## Code\n```python []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return "".join(word1) == "".join(word2)\n```\n```Java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n return String.join("", word1).equals(String.join("", word2));\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool ArrayStringsAreEqual(string[] word1, string[] word2) {\n return string.Concat(word1) == string.Concat(word2);\n }\n}\n```\n``` Ruby []\ndef array_strings_are_equal(word1, word2)\n word1.join == word2.join\nend\n```\n``` Rust []\nimpl Solution {\n pub fn array_strings_are_equal(word1: Vec<String>, word2: Vec<String>) -> bool {\n word1.concat() == word2.concat()\n }\n}\n```\n\n\n- Please upvote me !!!\n | 33 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
✅✅|| ONE LINE || EASY PEASY || Java, Python, C#, Rust, Ruby || 🔥🔥🔥 | check-if-two-string-arrays-are-equivalent | 1 | 1 | # Description\n\n## Intuition\nThe problem seems to be about comparing two lists of strings and checking if the concatenation of strings in each list results in equal strings. The provided code uses the `join` method to concatenate the strings in both lists and then compares the resulting strings.\n\n## Approach\nThe approach taken in the code is straightforward. It joins the strings in both lists and checks if the resulting strings are equal. If they are equal, the function returns `True`; otherwise, it returns `False`.\n\n## Complexity\n- **Time complexity:** The time complexity is dominated by the `join` operation, which is linear in the total length of the strings in the input lists. Let\'s denote the total length of all strings in `word1` as \\(m\\) and in `word2` as \\(n\\). Therefore, the time complexity is \\(O(m + n)\\).\n- **Space complexity:** The space complexity is also \\(O(m + n)\\) as the `join` method creates new strings that are the concatenation of the input strings.\n\n## Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n| :--- | :---:| :---: | \nJava | 1 | 40.6 |\nPython3 | 43 | 16.3 |\nC# | 87 | 40.9 |\nRust | 1 | 2.1 |\nRuby | 55 | 210.9 |\n\n## Code\n```python []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return "".join(word1) == "".join(word2)\n```\n```Java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n return String.join("", word1).equals(String.join("", word2));\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool ArrayStringsAreEqual(string[] word1, string[] word2) {\n return string.Concat(word1) == string.Concat(word2);\n }\n}\n```\n``` Ruby []\ndef array_strings_are_equal(word1, word2)\n word1.join == word2.join\nend\n```\n``` Rust []\nimpl Solution {\n pub fn array_strings_are_equal(word1: Vec<String>, word2: Vec<String>) -> bool {\n word1.concat() == word2.concat()\n }\n}\n```\n\n\n- Please upvote me !!!\n | 33 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
Python | Zip Chains, O(1) Space | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n\nThe focus of this problem is on developing a solution with $$O(1)$$ space usage. In most languages, this requires maintaining pointers manually, but not in Python (#blessed). \n\n# Approach\n\nThe following solution is my favorite:\n```py\nclass Solution:\n def arrayStringsAreEqual(self, word1: list[str], word2: list[str]) -> bool:\n return all(starmap(eq, zip_longest(chain.from_iterable(word1), chain.from_iterable(word2))))\n```\n\nA couple of side notes:\n- `x == y for x, y in zip_longest(...)` also works and some may find it easier to read;\n- `zip` instead of `zip_longest` doesn\'t work if one wordlist is a (strict) prefix of another;\n- `zip(..., strict=True)` is a reasonable alternative that produces an exception instead of a sentinel value;\n- `chain(*words)` results in a correct answer but uses $$O(N)$$ space.\n\n# Complexity\n\nHere $$N$$ is the number of strings in the list and $$K$$ is the maximum length of a string in it.\n\n- Time complexity: $$O(N \\cdot K)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code\n\n```py\nclass Solution:\n def arrayStringsAreEqual(self, word1: list[str], word2: list[str]) -> bool:\n return all(starmap(eq, zip_longest(chain.from_iterable(word1), chain.from_iterable(word2))))\n``` | 6 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Python | Zip Chains, O(1) Space | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n\nThe focus of this problem is on developing a solution with $$O(1)$$ space usage. In most languages, this requires maintaining pointers manually, but not in Python (#blessed). \n\n# Approach\n\nThe following solution is my favorite:\n```py\nclass Solution:\n def arrayStringsAreEqual(self, word1: list[str], word2: list[str]) -> bool:\n return all(starmap(eq, zip_longest(chain.from_iterable(word1), chain.from_iterable(word2))))\n```\n\nA couple of side notes:\n- `x == y for x, y in zip_longest(...)` also works and some may find it easier to read;\n- `zip` instead of `zip_longest` doesn\'t work if one wordlist is a (strict) prefix of another;\n- `zip(..., strict=True)` is a reasonable alternative that produces an exception instead of a sentinel value;\n- `chain(*words)` results in a correct answer but uses $$O(N)$$ space.\n\n# Complexity\n\nHere $$N$$ is the number of strings in the list and $$K$$ is the maximum length of a string in it.\n\n- Time complexity: $$O(N \\cdot K)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code\n\n```py\nclass Solution:\n def arrayStringsAreEqual(self, word1: list[str], word2: list[str]) -> bool:\n return all(starmap(eq, zip_longest(chain.from_iterable(word1), chain.from_iterable(word2))))\n``` | 6 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
Easy Python Solution || One liner.......... || Beginner Friendly | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this function is to check if two lists of strings, word1 and word2, would be equal when their elements are concatenated into single strings.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The function uses the join method to concatenate all strings in both word1 and word2 into single strings.\n- It then compares the two resulting strings to check if they are equal.\n- The function returns True if the concatenated strings are equal and False otherwise.\n```\n return \'\'.join(word1) == \'\'.join(word2)\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is dependent on the length of the concatenated strings, which is proportional to the sum of the lengths of all strings in word1 and word2.\nLet n be the total number of characters in both lists, the time complexity is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is determined by the space required to store the concatenated strings.\nThe join operation creates a new string, so the space complexity is O(n), where n is the total number of characters in both lists.\n# Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return \'\'.join(word1) == \'\'.join(word2)\n```\n- If you don\'t know join() method, you can use the below code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n # Initialize two empty strings to store concatenated strings of word1 and word2\n s1, s2 = \'\', \'\'\n \n # Concatenate each string in word1 to form s1\n for i in word1:\n s1 += i\n \n # Concatenate each string in word2 to form s2\n for i in word2:\n s2 += i\n \n # Check if the two concatenated strings are equal\n return s1 == s2\n\n```\n\n---\n# Please upvote my solution if you like it...\n---\n\n | 1 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Easy Python Solution || One liner.......... || Beginner Friendly | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this function is to check if two lists of strings, word1 and word2, would be equal when their elements are concatenated into single strings.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The function uses the join method to concatenate all strings in both word1 and word2 into single strings.\n- It then compares the two resulting strings to check if they are equal.\n- The function returns True if the concatenated strings are equal and False otherwise.\n```\n return \'\'.join(word1) == \'\'.join(word2)\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is dependent on the length of the concatenated strings, which is proportional to the sum of the lengths of all strings in word1 and word2.\nLet n be the total number of characters in both lists, the time complexity is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is determined by the space required to store the concatenated strings.\nThe join operation creates a new string, so the space complexity is O(n), where n is the total number of characters in both lists.\n# Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return \'\'.join(word1) == \'\'.join(word2)\n```\n- If you don\'t know join() method, you can use the below code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n # Initialize two empty strings to store concatenated strings of word1 and word2\n s1, s2 = \'\', \'\'\n \n # Concatenate each string in word1 to form s1\n for i in word1:\n s1 += i\n \n # Concatenate each string in word2 to form s2\n for i in word2:\n s2 += i\n \n # Check if the two concatenated strings are equal\n return s1 == s2\n\n```\n\n---\n# Please upvote my solution if you like it...\n---\n\n | 1 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
🔥 Easy solution | JAVA | Python 3 🔥| | check-if-two-string-arrays-are-equivalent | 1 | 1 | # Intuition\nCheck If Two String Arrays are Equivalent\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**String.join:** \n 1. This method concatenates all the strings in the array into a single string without any delimiter. \n 2. It\'s used here to create two strings, joinedWord1 and joinedWord2, by joining all strings in word1 and word2, respectively.\n\n**Comparison:** \n 1. The method then uses the equals() method to compare the two resulting strings, joinedWord1 and joinedWord2. \n 2. If they are equal, it returns true; otherwise, it returns false.\n\n**boolean:** \n - Returns true if the concatenated strings from word1 and word2 are equal. Otherwise, it returns false.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m + k)$$\n - Where \'m\' is the total number of characters in word1 and \'k\' is the total number of characters in word2.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n String joinedWord1 = String.join("", word1);\n String joinedWord2 = String.join("", word2);\n\n return joinedWord1.equals(joinedWord2);\n \n }\n}\n```\n```python []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n joined_word1 = "".join(word1)\n joined_word2 = "".join(word2)\n if (joined_word1==joined_word2):\n return True\n else:\n return False \n```\n\n | 1 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
🔥 Easy solution | JAVA | Python 3 🔥| | check-if-two-string-arrays-are-equivalent | 1 | 1 | # Intuition\nCheck If Two String Arrays are Equivalent\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**String.join:** \n 1. This method concatenates all the strings in the array into a single string without any delimiter. \n 2. It\'s used here to create two strings, joinedWord1 and joinedWord2, by joining all strings in word1 and word2, respectively.\n\n**Comparison:** \n 1. The method then uses the equals() method to compare the two resulting strings, joinedWord1 and joinedWord2. \n 2. If they are equal, it returns true; otherwise, it returns false.\n\n**boolean:** \n - Returns true if the concatenated strings from word1 and word2 are equal. Otherwise, it returns false.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m + k)$$\n - Where \'m\' is the total number of characters in word1 and \'k\' is the total number of characters in word2.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public boolean arrayStringsAreEqual(String[] word1, String[] word2) {\n String joinedWord1 = String.join("", word1);\n String joinedWord2 = String.join("", word2);\n\n return joinedWord1.equals(joinedWord2);\n \n }\n}\n```\n```python []\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n joined_word1 = "".join(word1)\n joined_word2 = "".join(word2)\n if (joined_word1==joined_word2):\n return True\n else:\n return False \n```\n\n | 1 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
O(1) Space | no while loop | easy to understand | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Complexity\n- Time complexity: $$O(N*K)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n p2, i2 = 0, 0\n\n for part in word1:\n for letter in part:\n if i2 >= len(word2[p2]):\n i2 = 0\n p2 += 1\n if p2 >= len(word2):\n return False\n if letter != word2[p2][i2]:\n return False\n i2 += 1\n # check if the pointer on the last part of the second word and we\'ve already checked last letter in this part\n if p2 == len(word2) - 1 and i2 >= len(word2[p2]):\n return True\n\n return False\n \n``` | 1 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
O(1) Space | no while loop | easy to understand | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Complexity\n- Time complexity: $$O(N*K)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n p2, i2 = 0, 0\n\n for part in word1:\n for letter in part:\n if i2 >= len(word2[p2]):\n i2 = 0\n p2 += 1\n if p2 >= len(word2):\n return False\n if letter != word2[p2][i2]:\n return False\n i2 += 1\n # check if the pointer on the last part of the second word and we\'ve already checked last letter in this part\n if p2 == len(word2) - 1 and i2 >= len(word2[p2]):\n return True\n\n return False\n \n``` | 1 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
Simple one line python solution | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return True if \'\'.join(word1)==\'\'.join(word2) else False\n``` | 1 | Given two string arrays `word1` and `word2`, return `true` _if the two arrays **represent** the same string, and_ `false` _otherwise._
A string is **represented** by an array if the array elements concatenated **in order** forms the string.
**Example 1:**
**Input:** word1 = \[ "ab ", "c "\], word2 = \[ "a ", "bc "\]
**Output:** true
**Explanation:**
word1 represents string "ab " + "c " -> "abc "
word2 represents string "a " + "bc " -> "abc "
The strings are the same, so return true.
**Example 2:**
**Input:** word1 = \[ "a ", "cb "\], word2 = \[ "ab ", "c "\]
**Output:** false
**Example 3:**
**Input:** word1 = \[ "abc ", "d ", "defg "\], word2 = \[ "abcddefg "\]
**Output:** true
**Constraints:**
* `1 <= word1.length, word2.length <= 103`
* `1 <= word1[i].length, word2[i].length <= 103`
* `1 <= sum(word1[i].length), sum(word2[i].length) <= 103`
* `word1[i]` and `word2[i]` consist of lowercase letters. | Work backwards: try to go from nums to arr. You should try to divide by 2 as much as possible, but you can only divide by 2 if everything is even. |
Simple one line python solution | check-if-two-string-arrays-are-equivalent | 0 | 1 | # Code\n```\nclass Solution:\n def arrayStringsAreEqual(self, word1: List[str], word2: List[str]) -> bool:\n return True if \'\'.join(word1)==\'\'.join(word2) else False\n``` | 1 | The **beauty** of a string is the difference in frequencies between the most frequent and least frequent characters.
* For example, the beauty of `"abaacc "` is `3 - 1 = 2`.
Given a string `s`, return _the sum of **beauty** of all of its substrings._
**Example 1:**
**Input:** s = "aabcb "
**Output:** 5
**Explanation:** The substrings with non-zero beauty are \[ "aab ", "aabc ", "aabcb ", "abcb ", "bcb "\], each with beauty equal to 1.
**Example 2:**
**Input:** s = "aabcbaa "
**Output:** 17
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | Concatenate all strings in the first array into a single string in the given order, the same for the second array. Both arrays represent the same string if and only if the generated strings are the same. |
✔️ [Python3] GREEDY FILLING (🌸¬‿¬), Explained | smallest-string-with-a-given-numeric-value | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nSince we are forming the lexicographically smallest string, we just simply fill our result with `a`s ( o\u02D8\u25E1\u02D8o). But hold on, that result will not necessarily have the required score c(\uFF9F.\uFF9F*) Ummm\u2026 Ok, then we can add some `z`s to the back of the result until the score reaches the required value, so be it (\uFFE2_\uFFE2;). Ofc if we are missing less than 26 to the required score, we add something that is less than `z`.\n\nTime: **O(n)** - iterations\nSpace: **O(n)** - for list of chars\n\nRuntime: 393 ms, faster than **73.27%** of Python3 online submissions for Smallest String With A Given Numeric Value.\nMemory Usage: 15.4 MB, less than **68.20%** of Python3 online submissions for Smallest String With A Given Numeric Value.\n\n```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n res, k, i = [\'a\'] * n, k - n, n - 1\n while k:\n k += 1\n if k/26 >= 1:\n res[i], k, i = \'z\', k - 26, i - 1\n else:\n res[i], k = chr(k + 96), 0\n\n return \'\'.join(res)\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 64 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
✔️ [Python3] GREEDY FILLING (🌸¬‿¬), Explained | smallest-string-with-a-given-numeric-value | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nSince we are forming the lexicographically smallest string, we just simply fill our result with `a`s ( o\u02D8\u25E1\u02D8o). But hold on, that result will not necessarily have the required score c(\uFF9F.\uFF9F*) Ummm\u2026 Ok, then we can add some `z`s to the back of the result until the score reaches the required value, so be it (\uFFE2_\uFFE2;). Ofc if we are missing less than 26 to the required score, we add something that is less than `z`.\n\nTime: **O(n)** - iterations\nSpace: **O(n)** - for list of chars\n\nRuntime: 393 ms, faster than **73.27%** of Python3 online submissions for Smallest String With A Given Numeric Value.\nMemory Usage: 15.4 MB, less than **68.20%** of Python3 online submissions for Smallest String With A Given Numeric Value.\n\n```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n res, k, i = [\'a\'] * n, k - n, n - 1\n while k:\n k += 1\n if k/26 >= 1:\n res[i], k, i = \'z\', k - 26, i - 1\n else:\n res[i], k = chr(k + 96), 0\n\n return \'\'.join(res)\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 64 | You are given an undirected graph defined by an integer `n`, the number of nodes, and a 2D integer array `edges`, the edges in the graph, where `edges[i] = [ui, vi]` indicates that there is an **undirected** edge between `ui` and `vi`. You are also given an integer array `queries`.
Let `incident(a, b)` be defined as the **number of edges** that are connected to **either** node `a` or `b`.
The answer to the `jth` query is the **number of pairs** of nodes `(a, b)` that satisfy **both** of the following conditions:
* `a < b`
* `incident(a, b) > queries[j]`
Return _an array_ `answers` _such that_ `answers.length == queries.length` _and_ `answers[j]` _is the answer of the_ `jth` _query_.
Note that there can be **multiple edges** between the same two nodes.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,4\],\[1,3\],\[2,3\],\[2,1\]\], queries = \[2,3\]
**Output:** \[6,5\]
**Explanation:** The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers\[0\] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers\[1\] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.
**Example 2:**
**Input:** n = 5, edges = \[\[1,5\],\[1,5\],\[3,4\],\[2,5\],\[1,3\],\[5,1\],\[2,3\],\[2,5\]\], queries = \[1,2,3,4,5\]
**Output:** \[10,10,9,8,6\]
**Constraints:**
* `2 <= n <= 2 * 104`
* `1 <= edges.length <= 105`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= queries.length <= 20`
* `0 <= queries[j] < edges.length` | Think greedily. If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index. |
[Java/Python 3] Two O(n) codes w/ brief explanation and analysis. | smallest-string-with-a-given-numeric-value | 1 | 1 | **Mehtod 1: Greedily reversely place values**\n\n1. Make sure each value of the n characters is at least `1`: initialized all as `\'a\'`;\n2. Put as more value at the end of the String as possible.\n```java\n public String getSmallestString(int n, int k) {\n k -= n;\n char[] ans = new char[n];\n Arrays.fill(ans, \'a\');\n while (k > 0) {\n ans[--n] += Math.min(k, 25);\n k -= Math.min(k, 25);\n }\n return String.valueOf(ans);\n }\n```\n```python\n def getSmallestString(self, n: int, k: int) -> str:\n ans = [\'a\'] * n\n k -= n\n while k > 0:\n n -= 1 \n ans[n] = chr(ord(\'a\') + min(25, k))\n k -= min(25, k)\n return \'\'.join(ans)\n```\n\n**Analysis:**\nTime & space: O(n)\n\n----\n**Method 2: Math**\nCompute the total number of `z` at the end, and the number of not `a` characters right before those `z`: `r`; The remaining are `a`\'s .\n```java\n public String getSmallestString(int n, int k) {\n int z = (k - n) / 25, r = (k - n) % 25;\n return (z == n ? "" : "a".repeat(n - z - 1) + (char)(\'a\' + r)) + "z".repeat(z);\n }\n```\n```python\n def getSmallestString(self, n: int, k: int) -> str:\n z, r = divmod(k - n, 25)\n return (\'\' if z == n else \'a\' * (n - z - 1) + chr(ord(\'a\') + r)) + \'z\' * z\n```\nThe above codes can be further simplified as follows:\n\n```java\n public String getSmallestString(int n, int k) {\n int z = (k - n - 1) / 25, r = (k - n - 1) % 25;\n return "a".repeat(n - z - 1) + (char)(\'a\' + r + 1) + "z".repeat(z);\n }\n```\n```python\n def getSmallestString(self, n: int, k: int) -> str:\n z, r = divmod(k - n, 25)\n return \'a\' * (n - z - 1) + chr(ord(\'a\') + r) * (n > z) + \'z\' * z\n```\n**Analysis:**\nTime & space: O(n)\n | 63 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
[Java/Python 3] Two O(n) codes w/ brief explanation and analysis. | smallest-string-with-a-given-numeric-value | 1 | 1 | **Mehtod 1: Greedily reversely place values**\n\n1. Make sure each value of the n characters is at least `1`: initialized all as `\'a\'`;\n2. Put as more value at the end of the String as possible.\n```java\n public String getSmallestString(int n, int k) {\n k -= n;\n char[] ans = new char[n];\n Arrays.fill(ans, \'a\');\n while (k > 0) {\n ans[--n] += Math.min(k, 25);\n k -= Math.min(k, 25);\n }\n return String.valueOf(ans);\n }\n```\n```python\n def getSmallestString(self, n: int, k: int) -> str:\n ans = [\'a\'] * n\n k -= n\n while k > 0:\n n -= 1 \n ans[n] = chr(ord(\'a\') + min(25, k))\n k -= min(25, k)\n return \'\'.join(ans)\n```\n\n**Analysis:**\nTime & space: O(n)\n\n----\n**Method 2: Math**\nCompute the total number of `z` at the end, and the number of not `a` characters right before those `z`: `r`; The remaining are `a`\'s .\n```java\n public String getSmallestString(int n, int k) {\n int z = (k - n) / 25, r = (k - n) % 25;\n return (z == n ? "" : "a".repeat(n - z - 1) + (char)(\'a\' + r)) + "z".repeat(z);\n }\n```\n```python\n def getSmallestString(self, n: int, k: int) -> str:\n z, r = divmod(k - n, 25)\n return (\'\' if z == n else \'a\' * (n - z - 1) + chr(ord(\'a\') + r)) + \'z\' * z\n```\nThe above codes can be further simplified as follows:\n\n```java\n public String getSmallestString(int n, int k) {\n int z = (k - n - 1) / 25, r = (k - n - 1) % 25;\n return "a".repeat(n - z - 1) + (char)(\'a\' + r + 1) + "z".repeat(z);\n }\n```\n```python\n def getSmallestString(self, n: int, k: int) -> str:\n z, r = divmod(k - n, 25)\n return \'a\' * (n - z - 1) + chr(ord(\'a\') + r) * (n > z) + \'z\' * z\n```\n**Analysis:**\nTime & space: O(n)\n | 63 | You are given an undirected graph defined by an integer `n`, the number of nodes, and a 2D integer array `edges`, the edges in the graph, where `edges[i] = [ui, vi]` indicates that there is an **undirected** edge between `ui` and `vi`. You are also given an integer array `queries`.
Let `incident(a, b)` be defined as the **number of edges** that are connected to **either** node `a` or `b`.
The answer to the `jth` query is the **number of pairs** of nodes `(a, b)` that satisfy **both** of the following conditions:
* `a < b`
* `incident(a, b) > queries[j]`
Return _an array_ `answers` _such that_ `answers.length == queries.length` _and_ `answers[j]` _is the answer of the_ `jth` _query_.
Note that there can be **multiple edges** between the same two nodes.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,4\],\[1,3\],\[2,3\],\[2,1\]\], queries = \[2,3\]
**Output:** \[6,5\]
**Explanation:** The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers\[0\] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers\[1\] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.
**Example 2:**
**Input:** n = 5, edges = \[\[1,5\],\[1,5\],\[3,4\],\[2,5\],\[1,3\],\[5,1\],\[2,3\],\[2,5\]\], queries = \[1,2,3,4,5\]
**Output:** \[10,10,9,8,6\]
**Constraints:**
* `2 <= n <= 2 * 104`
* `1 <= edges.length <= 105`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= queries.length <= 20`
* `0 <= queries[j] < edges.length` | Think greedily. If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index. |
[Python] Simple solution - Greedy - O(N) [Explanation + Code + Comment] | smallest-string-with-a-given-numeric-value | 0 | 1 | The lexicographically smallest string of length n could be \'aaa\'.. of length n\nThe constraint is that the numeric value must be k.\nTo satisfy this constraint, we will greedily add either \'z\' or character form of (k - value) to the string.\n\nFor eg. \nn = 3, k = 32\nInitially, ans = \'aaa\', val = 3, i =2\nSince val!=k\nans = \'aaz\', val = 28, i = 1\nSince, val!=k\nk - val = 4\nans = \'adz\', val = 0 \nSince, val == k\nbreak\n\nFinal answer = \'adz\'\n\nRunning time: O(N)\nMemory: O(1)\n\n```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n ans = [\'a\']*n # Initialize the answer to be \'aaa\'.. length n\n val = n #Value would be length as all are \'a\'\n \n for i in range(n-1, -1, -1): \n if val == k: # if value has reached k, we have created our lexicographically smallest string\n break\n val -= 1 # reduce value by one as we are removing \'a\' and replacing by a suitable character\n ans[i] = chr(96 + min(k - val, 26)) # replace with a character which is k - value or \'z\'\n val += ord(ans[i]) - 96 # add the value of newly appended character to value\n \n return \'\'.join(ans) # return the ans string in the by concatenating the list\n``` | 17 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
[Python] Simple solution - Greedy - O(N) [Explanation + Code + Comment] | smallest-string-with-a-given-numeric-value | 0 | 1 | The lexicographically smallest string of length n could be \'aaa\'.. of length n\nThe constraint is that the numeric value must be k.\nTo satisfy this constraint, we will greedily add either \'z\' or character form of (k - value) to the string.\n\nFor eg. \nn = 3, k = 32\nInitially, ans = \'aaa\', val = 3, i =2\nSince val!=k\nans = \'aaz\', val = 28, i = 1\nSince, val!=k\nk - val = 4\nans = \'adz\', val = 0 \nSince, val == k\nbreak\n\nFinal answer = \'adz\'\n\nRunning time: O(N)\nMemory: O(1)\n\n```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n ans = [\'a\']*n # Initialize the answer to be \'aaa\'.. length n\n val = n #Value would be length as all are \'a\'\n \n for i in range(n-1, -1, -1): \n if val == k: # if value has reached k, we have created our lexicographically smallest string\n break\n val -= 1 # reduce value by one as we are removing \'a\' and replacing by a suitable character\n ans[i] = chr(96 + min(k - val, 26)) # replace with a character which is k - value or \'z\'\n val += ord(ans[i]) - 96 # add the value of newly appended character to value\n \n return \'\'.join(ans) # return the ans string in the by concatenating the list\n``` | 17 | You are given an undirected graph defined by an integer `n`, the number of nodes, and a 2D integer array `edges`, the edges in the graph, where `edges[i] = [ui, vi]` indicates that there is an **undirected** edge between `ui` and `vi`. You are also given an integer array `queries`.
Let `incident(a, b)` be defined as the **number of edges** that are connected to **either** node `a` or `b`.
The answer to the `jth` query is the **number of pairs** of nodes `(a, b)` that satisfy **both** of the following conditions:
* `a < b`
* `incident(a, b) > queries[j]`
Return _an array_ `answers` _such that_ `answers.length == queries.length` _and_ `answers[j]` _is the answer of the_ `jth` _query_.
Note that there can be **multiple edges** between the same two nodes.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,4\],\[1,3\],\[2,3\],\[2,1\]\], queries = \[2,3\]
**Output:** \[6,5\]
**Explanation:** The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers\[0\] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers\[1\] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.
**Example 2:**
**Input:** n = 5, edges = \[\[1,5\],\[1,5\],\[3,4\],\[2,5\],\[1,3\],\[5,1\],\[2,3\],\[2,5\]\], queries = \[1,2,3,4,5\]
**Output:** \[10,10,9,8,6\]
**Constraints:**
* `2 <= n <= 2 * 104`
* `1 <= edges.length <= 105`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= queries.length <= 20`
* `0 <= queries[j] < edges.length` | Think greedily. If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index. |
✅ Python Solution | smallest-string-with-a-given-numeric-value | 0 | 1 | ```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n ans = \'\'\n while (n - 1) * 26 >= k:\n ans += \'a\'\n n -= 1; k -= 1\n ans += chr(ord(\'a\') + (k % 26 or 26) - 1)\n ans += \'z\' * (n - 1)\n return ans\n``` | 3 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
✅ Python Solution | smallest-string-with-a-given-numeric-value | 0 | 1 | ```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n ans = \'\'\n while (n - 1) * 26 >= k:\n ans += \'a\'\n n -= 1; k -= 1\n ans += chr(ord(\'a\') + (k % 26 or 26) - 1)\n ans += \'z\' * (n - 1)\n return ans\n``` | 3 | You are given an undirected graph defined by an integer `n`, the number of nodes, and a 2D integer array `edges`, the edges in the graph, where `edges[i] = [ui, vi]` indicates that there is an **undirected** edge between `ui` and `vi`. You are also given an integer array `queries`.
Let `incident(a, b)` be defined as the **number of edges** that are connected to **either** node `a` or `b`.
The answer to the `jth` query is the **number of pairs** of nodes `(a, b)` that satisfy **both** of the following conditions:
* `a < b`
* `incident(a, b) > queries[j]`
Return _an array_ `answers` _such that_ `answers.length == queries.length` _and_ `answers[j]` _is the answer of the_ `jth` _query_.
Note that there can be **multiple edges** between the same two nodes.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,4\],\[1,3\],\[2,3\],\[2,1\]\], queries = \[2,3\]
**Output:** \[6,5\]
**Explanation:** The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers\[0\] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers\[1\] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.
**Example 2:**
**Input:** n = 5, edges = \[\[1,5\],\[1,5\],\[3,4\],\[2,5\],\[1,3\],\[5,1\],\[2,3\],\[2,5\]\], queries = \[1,2,3,4,5\]
**Output:** \[10,10,9,8,6\]
**Constraints:**
* `2 <= n <= 2 * 104`
* `1 <= edges.length <= 105`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= queries.length <= 20`
* `0 <= queries[j] < edges.length` | Think greedily. If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index. |
[Python3] O(n) time and O(1) space complexity solution | smallest-string-with-a-given-numeric-value | 0 | 1 | ``` python3\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n result =[0]*n\n for position in range(n-1,-1,-1):\n add = min(k -position,26)\n result[position] = chr(ord("a")+add -1)\n k-=add\n \n return "".join(result)\n```\n\nComplexity :\n\nTime : O(n), as we iterate over n positions to build the result.\n\nSpace : O(1), as we use constant extra space to store add and position variables. | 3 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
[Python3] O(n) time and O(1) space complexity solution | smallest-string-with-a-given-numeric-value | 0 | 1 | ``` python3\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n result =[0]*n\n for position in range(n-1,-1,-1):\n add = min(k -position,26)\n result[position] = chr(ord("a")+add -1)\n k-=add\n \n return "".join(result)\n```\n\nComplexity :\n\nTime : O(n), as we iterate over n positions to build the result.\n\nSpace : O(1), as we use constant extra space to store add and position variables. | 3 | You are given an undirected graph defined by an integer `n`, the number of nodes, and a 2D integer array `edges`, the edges in the graph, where `edges[i] = [ui, vi]` indicates that there is an **undirected** edge between `ui` and `vi`. You are also given an integer array `queries`.
Let `incident(a, b)` be defined as the **number of edges** that are connected to **either** node `a` or `b`.
The answer to the `jth` query is the **number of pairs** of nodes `(a, b)` that satisfy **both** of the following conditions:
* `a < b`
* `incident(a, b) > queries[j]`
Return _an array_ `answers` _such that_ `answers.length == queries.length` _and_ `answers[j]` _is the answer of the_ `jth` _query_.
Note that there can be **multiple edges** between the same two nodes.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,4\],\[1,3\],\[2,3\],\[2,1\]\], queries = \[2,3\]
**Output:** \[6,5\]
**Explanation:** The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers\[0\] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers\[1\] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.
**Example 2:**
**Input:** n = 5, edges = \[\[1,5\],\[1,5\],\[3,4\],\[2,5\],\[1,3\],\[5,1\],\[2,3\],\[2,5\]\], queries = \[1,2,3,4,5\]
**Output:** \[10,10,9,8,6\]
**Constraints:**
* `2 <= n <= 2 * 104`
* `1 <= edges.length <= 105`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= queries.length <= 20`
* `0 <= queries[j] < edges.length` | Think greedily. If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index. |
Easy to understand with comments | smallest-string-with-a-given-numeric-value | 0 | 1 | we start from the back , keep adding the highest letter possible to the result , highest possible letter is k-(remaining spaces)(remaining as we subtract the value of k by the value of each letter added, the remaining spaces are n - current length of result)\n```\ndef getSmallestString(self, n: int, k: int) -> str:\n l=[]\n count=0\n for i in range(n):\n # check if we can put \'z\' \n if k-26>((n-2)-i): \n l.append(chr(26+96))\n k=k-26\n # if we cant we put highest possible letter and put a\'s after it\n else:\n l.append(chr(k-(n-1-i)+96))\n break\n while len(l)!=n:\n l.append(chr(97))\n return ("".join(l))[::-1]\n\'\'\' | 2 | The **numeric value** of a **lowercase character** is defined as its position `(1-indexed)` in the alphabet, so the numeric value of `a` is `1`, the numeric value of `b` is `2`, the numeric value of `c` is `3`, and so on.
The **numeric value** of a **string** consisting of lowercase characters is defined as the sum of its characters' numeric values. For example, the numeric value of the string `"abe "` is equal to `1 + 2 + 5 = 8`.
You are given two integers `n` and `k`. Return _the **lexicographically smallest string** with **length** equal to `n` and **numeric value** equal to `k`._
Note that a string `x` is lexicographically smaller than string `y` if `x` comes before `y` in dictionary order, that is, either `x` is a prefix of `y`, or if `i` is the first position such that `x[i] != y[i]`, then `x[i]` comes before `y[i]` in alphabetic order.
**Example 1:**
**Input:** n = 3, k = 27
**Output:** "aay "
**Explanation:** The numeric value of the string is 1 + 1 + 25 = 27, and it is the smallest string with such a value and length equal to 3.
**Example 2:**
**Input:** n = 5, k = 73
**Output:** "aaszz "
**Constraints:**
* `1 <= n <= 105`
* `n <= k <= 26 * n` | Keep track of the parent (previous position) to avoid considering an invalid path. Use DFS or BFS and keep track of visited cells to see if there is a cycle. |
Easy to understand with comments | smallest-string-with-a-given-numeric-value | 0 | 1 | we start from the back , keep adding the highest letter possible to the result , highest possible letter is k-(remaining spaces)(remaining as we subtract the value of k by the value of each letter added, the remaining spaces are n - current length of result)\n```\ndef getSmallestString(self, n: int, k: int) -> str:\n l=[]\n count=0\n for i in range(n):\n # check if we can put \'z\' \n if k-26>((n-2)-i): \n l.append(chr(26+96))\n k=k-26\n # if we cant we put highest possible letter and put a\'s after it\n else:\n l.append(chr(k-(n-1-i)+96))\n break\n while len(l)!=n:\n l.append(chr(97))\n return ("".join(l))[::-1]\n\'\'\' | 2 | You are given an undirected graph defined by an integer `n`, the number of nodes, and a 2D integer array `edges`, the edges in the graph, where `edges[i] = [ui, vi]` indicates that there is an **undirected** edge between `ui` and `vi`. You are also given an integer array `queries`.
Let `incident(a, b)` be defined as the **number of edges** that are connected to **either** node `a` or `b`.
The answer to the `jth` query is the **number of pairs** of nodes `(a, b)` that satisfy **both** of the following conditions:
* `a < b`
* `incident(a, b) > queries[j]`
Return _an array_ `answers` _such that_ `answers.length == queries.length` _and_ `answers[j]` _is the answer of the_ `jth` _query_.
Note that there can be **multiple edges** between the same two nodes.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,4\],\[1,3\],\[2,3\],\[2,1\]\], queries = \[2,3\]
**Output:** \[6,5\]
**Explanation:** The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers\[0\] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers\[1\] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.
**Example 2:**
**Input:** n = 5, edges = \[\[1,5\],\[1,5\],\[3,4\],\[2,5\],\[1,3\],\[5,1\],\[2,3\],\[2,5\]\], queries = \[1,2,3,4,5\]
**Output:** \[10,10,9,8,6\]
**Constraints:**
* `2 <= n <= 2 * 104`
* `1 <= edges.length <= 105`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= queries.length <= 20`
* `0 <= queries[j] < edges.length` | Think greedily. If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index. |
Easy python solution of O(n) TC | ways-to-make-a-fair-array | 0 | 1 | ```\ndef waysToMakeFair(self, nums: List[int]) -> int:\n\teven, odd = [0], [0]\n\tfor i in range(len(nums)):\n\t\tif(i % 2):\n\t\t\todd.append(odd[-1] + nums[i])\n\t\t\teven.append(even[-1])\n\t\telse:\n\t\t\teven.append(even[-1] + nums[i])\n\t\t\todd.append(odd[-1])\n\tans = 0\n\tfor i in range(1, len(nums)+1):\n\t\te_l, o_l = even[i-1], odd[i-1]\n\t\te_r, o_r = even[-1]-even[i], odd[-1]-odd[i]\n\t\tif(e_l + o_r == e_r + o_l):\n\t\t\tans += 1\n\treturn ans\n``` | 2 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
WEEB EXPLAINS PYTHON/C++ DP/PREFIX SUM SOLN | ways-to-make-a-fair-array | 0 | 1 | My initial sketch for the question:\n\t\n\nHere is my explanation for my messy sketch:\n\t\n\tCorrection : \n\t- At odd idx, prefixOdd at current idx == prefixOdd at the **next** idx (not previous idx)\n\t- At even idx, prefixEven at current idx == prefixEven at the **next** idx (not previous idx)\n\t\n\n\n**Python**\n\n\tclass Solution:\n\t\tdef waysToMakeFair(self, nums: List[int]) -> int:\n\t\t\tif len(nums) == 1:\n\t\t\t\treturn 1\n\n\t\t\tif len(nums) == 2:\n\t\t\t\treturn 0\n\n\t\t\tprefixEven = sum(nums[2::2])\n\t\t\tprefixOdd = sum(nums[1::2])\n\t\t\tresult = 0\n\n\t\t\tif prefixEven == prefixOdd and len(set(nums)) == 1:\n\t\t\t\tresult += 1\n\n\t\t\tfor i in range(1,len(nums)):\n\t\t\t\tif i == 1:\n\t\t\t\t\tprefixOdd, prefixEven = prefixEven, prefixOdd \n\n\t\t\t\tif i > 1:\n\t\t\t\t\tif i % 2 == 0:\n\t\t\t\t\t\tprefixEven -= nums[i-1]\n\t\t\t\t\t\tprefixEven += nums[i-2]\n\n\t\t\t\t\telse:\n\t\t\t\t\t\tprefixOdd -= nums[i-1]\n\t\t\t\t\t\tprefixOdd += nums[i-2]\n\n\t\t\t\tif prefixOdd == prefixEven:\n\t\t\t\t\tresult += 1\n\n\t\t\treturn result\n\n**C++**\n\n\tclass Solution {\n\tpublic:\n\t\tint waysToMakeFair(vector<int>& nums) {\n\t\t\tif (nums.size() == 1) return 1;\n\n\t\t\tif (nums.size() == 2) return 0;\n\n\t\t\tlong int prefixEven = 0;\n\t\t\tlong int prefixOdd = 0;\n\t\t\tset<int> set;\n\t\t\tint result = 0;\n\n\t\t\tfor (int i=1; i < nums.size(); i++){\n\t\t\t\tif (i % 2 == 1) prefixOdd += nums[i];\n\n\t\t\t\telse{\n\t\t\t\t\tprefixEven += nums[i];\n\t\t\t\t}\n\n\t\t\t\tif (set.find(nums[i]) == set.end()) set.insert(nums[i]);\n\t\t\t}\n\n\t\t\tif (prefixOdd == prefixEven){\n\t\t\t\tif (set.size() == 1) result++;\n\t\t\t}\n\n\n\t\t\tfor (int i=1; i < nums.size(); i++){\n\t\t\t\tif (i == 1){\n\t\t\t\t\tlong int temp = prefixEven;\n\t\t\t\t\tprefixEven = prefixOdd;\n\t\t\t\t\tprefixOdd = temp;\n\n\t\t\t\t}\n\n\t\t\t\tif (i > 1){\n\t\t\t\t\tif (i % 2 == 0){\n\t\t\t\t\t\tprefixEven -= nums[i-1];\n\t\t\t\t\t\tprefixEven += nums[i-2];\n\t\t\t\t\t}\n\n\t\t\t\t\telse{\n\t\t\t\t\t\tprefixOdd -= nums[i-1];\n\t\t\t\t\t\tprefixOdd += nums[i-2];\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\tif (prefixEven == prefixOdd) result++;\n\t\t\t}\n\n\t\t\treturn result;\n\t\t}\n\t};\n\nEnough coding, dp takes a toll on your brain\nEspecially this one, its just one BIG pattern spotting question\nHave a break, watch some anime instead\nCheck out **\u30EF\u30FC\u30AD\u30F3\u30B0!! (Working!!)**\n\n# Episodes: 13 (1st Season) + 13 (2nd Season) + 14 (3rd Season)\n# Genres: Comedy, Romance, Slice of Life\n# Demographic: Seinen\n\nThere is an alternative setting for this anime, its called **WWW.Working!!** which is a side story of this anime.\nAnyways, watch this show to kill some time.\nAlso, please give this an upvote if u find this post useful, tq | 6 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
[Python3] O(N) - Simple code + Explanation | ways-to-make-a-fair-array | 0 | 1 | The key thing to notice is that when you remove an element at index i, the odd sum and even sum for elements less that i remains unchanged and the odd sum and even sum for elements greater than i switches.\n\nAfter removing element at index i, array is fair if odd_sum of elements greater than i + even_sum of elements less than = odd_sum of elements less than i + even_sum of elements greater than i\n\nRunning time: O(N)\nMemory : O(N)\n\n```\nclass Solution:\n def waysToMakeFair(self, nums: List[int]) -> int:\n odd_sum_r, even_sum_r = 0,0\n odd_sum_l, even_sum_l = 0,0\n sum_arr = []\n ans = 0\n \n for i in range(len(nums)-1, -1, -1):\n sum_arr.append([odd_sum_r, even_sum_r, odd_sum_l, even_sum_l])\n if i%2:\n odd_sum_r += nums[i]\n else:\n even_sum_r += nums[i]\n \n sum_arr = sum_arr[::-1]\n for i in range(len(nums)):\n sum_arr[i][2], sum_arr[i][3] = odd_sum_l, even_sum_l\n if i%2:\n odd_sum_l += nums[i]\n else:\n even_sum_l += nums[i]\n \n for i in range(len(nums) - 1, -1, -1):\n if sum_arr[i][2] + sum_arr[i][1] == sum_arr[i][3] + sum_arr[i][0]:\n ans += 1\n \n return ans\n``` | 7 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
✔ Python3 Solution | Clean & Concise | ways-to-make-a-fair-array | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```Python\nclass Solution:\n def waysToMakeFair(self, A):\n ans, cur = 0, sum(A[::2]) - sum(A[1::2])\n for i in A:\n if i == cur: ans += 1\n cur = (i << 1) - cur\n return ans\n``` | 2 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
intuitive prefix sum approach explained | ways-to-make-a-fair-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can see that when we remove an index, all elements AFTER that original index now swap parity (even or oddness). even becomes odd, odd becomes even.\nWe can use this to help us.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe just have to pre-process the array, we have a oddPrefix and an evenPrefix array. They will store prefix sum of all even / odd elements up till each index. Then we iterate through the array again, at each step calculating the even and odd sums on the left and right after removing the current element.\nif the even and odd sums of array after removal are equal, increment count\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def waysToMakeFair(self, nums: List[int]) -> int:\n # when removing an index, all elements after it swap parity\n # even become odd, odd become even\n # find prefix sum up to a certain point for even and oodd\n\n evenPrefix = [0] * len(nums)\n oddPrefix = [0] * len(nums)\n evenCurr = 0\n oddCurr = 0\n for i in range(len(nums)):\n if i % 2 == 0:\n evenCurr += nums[i]\n else:\n oddCurr += nums[i]\n evenPrefix[i] = evenCurr\n oddPrefix[i] = oddCurr\n count = 0\n for i in range(len(nums)):\n # if we remove index i\n if i % 2 == 0: #if even\n evenLeft = evenPrefix[i] - nums[i]\n oddLeft = oddPrefix[i]\n # on right side, new even is old odd\n if i < len(nums) - 1:\n evenRight = oddPrefix[-1] - oddPrefix[i]\n oddRight = evenPrefix[-1] - evenPrefix[i]\n else:\n evenRight = 0\n oddRight = 0\n if evenLeft + evenRight == oddLeft + oddRight:\n count += 1\n else:\n oddLeft = oddPrefix[i] - nums[i]\n evenLeft = evenPrefix[i]\n if i < len(nums) - 1:\n evenRight = oddPrefix[-1] - oddPrefix[i]\n oddRight = evenPrefix[-1] - evenPrefix[i]\n else:\n evenRight = 0\n oddRight = 0\n if evenLeft + evenRight == oddLeft + oddRight:\n count += 1\n return count\n \n\n ## remove index 1, evenleflt is 2, oddleft is 0, even right is 5 - 1 = 4\n ## oddright is 8 - 8 = 0\n``` | 0 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
Beats 99.63%, "Efficient Energy Management: The Task of Minimum Effort" | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n The idea is to sort the tasks based on the difference between the actual and minimum energy required.\n This way, we prioritize tasks with a larger energy difference, making it easier to manage energy.\n\n# Approach\n1. Sort the tasks based on the difference between actual and minimum energy.\n 2. Initialize variables ans and cur to track the minimum initial energy and current energy level.\n 3. Iterate through the sorted tasks:\n a. If the current energy is less than the minimum required for the task, update ans and cur accordingly.\n b. Subtract the actual energy spent on the task from the current energy.\n 4. Return the minimum initial energy needed (ans).\n\n# Complexity\n# - Time complexity: O(nlogn) due to sorting, where n is the number of tasks.\n# - Space complexity: O(1) as we are using a constant amount of space.\n\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n ans = cur = 0\n for a, m in sorted(tasks, key=lambda x: x[0] - x[1]):\n if cur < m:\n ans += m - cur\n cur = m\n cur -= a\n return ans\n | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Beats 99.63%, "Efficient Energy Management: The Task of Minimum Effort" | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n The idea is to sort the tasks based on the difference between the actual and minimum energy required.\n This way, we prioritize tasks with a larger energy difference, making it easier to manage energy.\n\n# Approach\n1. Sort the tasks based on the difference between actual and minimum energy.\n 2. Initialize variables ans and cur to track the minimum initial energy and current energy level.\n 3. Iterate through the sorted tasks:\n a. If the current energy is less than the minimum required for the task, update ans and cur accordingly.\n b. Subtract the actual energy spent on the task from the current energy.\n 4. Return the minimum initial energy needed (ans).\n\n# Complexity\n# - Time complexity: O(nlogn) due to sorting, where n is the number of tasks.\n# - Space complexity: O(1) as we are using a constant amount of space.\n\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n ans = cur = 0\n for a, m in sorted(tasks, key=lambda x: x[0] - x[1]):\n if cur < m:\n ans += m - cur\n cur = m\n cur -= a\n return ans\n | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Beats 95%, "Efficient Energy Management: The Task of Minimum Effort" | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n The idea is to sort the tasks based on the difference between the actual and minimum energy required.\n\n This way, we prioritize tasks with a larger energy difference, making it easier to manage energy.\n\n\n# Approach\n1. Sort the tasks based on the difference between actual and minimum energy.\n2. Initialize variables ans and cur to track the minimum initial energy and current energy level.\n3. Iterate through the sorted tasks:\n a. If the current energy is less than the minimum required for the task, update ans and cur accordingly.\n b. Subtract the actual energy spent on the task from the current energy.\n 4. Return the minimum initial energy needed (ans).\n\n# Complexity\n# - Time complexity: O(nlogn) due to sorting, where n is the number of tasks.\n# - Space complexity: O(1) as we are using a constant amount of space.\n\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n ans = cur = 0\n for a, m in sorted(tasks, key=lambda x: x[0] - x[1]):\n if cur < m:\n ans += m - cur\n cur = m\n cur -= a\n return ans\n | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Beats 95%, "Efficient Energy Management: The Task of Minimum Effort" | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n The idea is to sort the tasks based on the difference between the actual and minimum energy required.\n\n This way, we prioritize tasks with a larger energy difference, making it easier to manage energy.\n\n\n# Approach\n1. Sort the tasks based on the difference between actual and minimum energy.\n2. Initialize variables ans and cur to track the minimum initial energy and current energy level.\n3. Iterate through the sorted tasks:\n a. If the current energy is less than the minimum required for the task, update ans and cur accordingly.\n b. Subtract the actual energy spent on the task from the current energy.\n 4. Return the minimum initial energy needed (ans).\n\n# Complexity\n# - Time complexity: O(nlogn) due to sorting, where n is the number of tasks.\n# - Space complexity: O(1) as we are using a constant amount of space.\n\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n ans = cur = 0\n for a, m in sorted(tasks, key=lambda x: x[0] - x[1]):\n if cur < m:\n ans += m - cur\n cur = m\n cur -= a\n return ans\n | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
sorting + binary search | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n \n\n tasks.sort(key = lambda x: x[0]-x[1])\n\n\n l = 0 \n r = 0\n for a, m in tasks:\n r = max(a, m, r)\n r *= len(tasks)\n def is_valid(e):\n for a, m in tasks:\n if e < m:\n return False\n if e < a:\n return False\n e -=a\n \n return True\n\n while l <= r:\n mid = l + (r-l)//2\n\n if is_valid(mid):\n r = mid-1\n else:\n l = mid +1\n return l\n\n \n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
sorting + binary search | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n \n\n tasks.sort(key = lambda x: x[0]-x[1])\n\n\n l = 0 \n r = 0\n for a, m in tasks:\n r = max(a, m, r)\n r *= len(tasks)\n def is_valid(e):\n for a, m in tasks:\n if e < m:\n return False\n if e < a:\n return False\n e -=a\n \n return True\n\n while l <= r:\n mid = l + (r-l)//2\n\n if is_valid(mid):\n r = mid-1\n else:\n l = mid +1\n return l\n\n \n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Heap solution Python | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\nThink about dont want to waste any resource as much as possible => start with a task that has minimum gap => least time waste. In this part, you can either sort by (start-end) or just put that into heap. The rest of the algorithm is explained below\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHave a heap to store tuple (gap, start, end) which is sorted by gap.\nAt each step, take out (gap, start, end):\n\n - total_time = min(total_time + start, end time)\n\n=> be greedy by taking the min of these two (intuition, why do we have to waste time for nothing, just take the one that is just enough)\n=> return total_time\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n heap = []\n for i in range(len(tasks)):\n heapq.heappush(heap, (tasks[i][1] - tasks[i][0], tasks[i][0], tasks[i][1]))\n \n total_time = 0\n while heap:\n gap, start, end = heapq.heappop(heap)\n total_time = max(end, total_time + start)\n return total_time\n \n \n \n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Heap solution Python | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\nThink about dont want to waste any resource as much as possible => start with a task that has minimum gap => least time waste. In this part, you can either sort by (start-end) or just put that into heap. The rest of the algorithm is explained below\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHave a heap to store tuple (gap, start, end) which is sorted by gap.\nAt each step, take out (gap, start, end):\n\n - total_time = min(total_time + start, end time)\n\n=> be greedy by taking the min of these two (intuition, why do we have to waste time for nothing, just take the one that is just enough)\n=> return total_time\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n heap = []\n for i in range(len(tasks)):\n heapq.heappush(heap, (tasks[i][1] - tasks[i][0], tasks[i][0], tasks[i][1]))\n \n total_time = 0\n while heap:\n gap, start, end = heapq.heappop(heap)\n total_time = max(end, total_time + start)\n return total_time\n \n \n \n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
python | minimum-initial-energy-to-finish-tasks | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n\n m = max(y for x, y in tasks)\n n = m + sum(x for x, y in tasks)\n res = float(\'inf\')\n\n # binary search between m, n\n # print(n, m)\n\n tasks.sort(key =lambda x: x[1]-x[0], reverse=True)\n # print(tasks)\n while n>=m:\n \n mid = (n+m)//2\n # print(mid)\n curr = mid\n flag = False\n for i in range(len(tasks)):\n if curr>=tasks[i][1]:\n curr-=tasks[i][0]\n else:\n flag = True\n # print(tasks[i][1], curr)\n break\n if flag:\n n, m = n, mid+1\n else:\n if mid<res:\n res = mid\n n, m = mid-1, m\n \n return res\n\n\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
python | minimum-initial-energy-to-finish-tasks | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n\n m = max(y for x, y in tasks)\n n = m + sum(x for x, y in tasks)\n res = float(\'inf\')\n\n # binary search between m, n\n # print(n, m)\n\n tasks.sort(key =lambda x: x[1]-x[0], reverse=True)\n # print(tasks)\n while n>=m:\n \n mid = (n+m)//2\n # print(mid)\n curr = mid\n flag = False\n for i in range(len(tasks)):\n if curr>=tasks[i][1]:\n curr-=tasks[i][0]\n else:\n flag = True\n # print(tasks[i][1], curr)\n break\n if flag:\n n, m = n, mid+1\n else:\n if mid<res:\n res = mid\n n, m = mid-1, m\n \n return res\n\n\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
[Python3] Simple Greedy Solution + Sorting | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\nWe want to greedily choose the tasks - this should be clear since there exists an optimal ordering that will give us a minimal result, which is determined by some sorted property.\n\n# Approach\nAt first I tried sorting by required energy, but this doesn\'t work because the actual energy could be close to the required, so we won\'t have much energy leftover. The idea is that we want to carry over as much energy as possible for the next jobs, so instead sort by the difference between required and actual. This will provide us with the greatest energy carryover, which will in turn minimize the total energy we need to start with as the jobs where (required - actual) is minimal, will have energy available for consumption.\n\n# Complexity\n- Time complexity:\nO(nlogn) (due to sorting)\n\n- Space complexity:\nO(n) (if you sort in place, you can make it O(1))\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n\n order = sorted(tasks, key = lambda x: -(x[1] - x[0]))\n \n min_energy = 0\n curr_energy = 0\n for actual, required in order:\n if curr_energy < required:\n min_energy += (required - curr_energy)\n curr_energy = required - actual\n else:\n curr_energy -= actual\n \n return min_energy\n\n\n\n\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
[Python3] Simple Greedy Solution + Sorting | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\nWe want to greedily choose the tasks - this should be clear since there exists an optimal ordering that will give us a minimal result, which is determined by some sorted property.\n\n# Approach\nAt first I tried sorting by required energy, but this doesn\'t work because the actual energy could be close to the required, so we won\'t have much energy leftover. The idea is that we want to carry over as much energy as possible for the next jobs, so instead sort by the difference between required and actual. This will provide us with the greatest energy carryover, which will in turn minimize the total energy we need to start with as the jobs where (required - actual) is minimal, will have energy available for consumption.\n\n# Complexity\n- Time complexity:\nO(nlogn) (due to sorting)\n\n- Space complexity:\nO(n) (if you sort in place, you can make it O(1))\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n\n order = sorted(tasks, key = lambda x: -(x[1] - x[0]))\n \n min_energy = 0\n curr_energy = 0\n for actual, required in order:\n if curr_energy < required:\n min_energy += (required - curr_energy)\n curr_energy = required - actual\n else:\n curr_energy -= actual\n \n return min_energy\n\n\n\n\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Perfection | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n tasks.sort()\n dic=dict()\n for i in tasks:\n if i[1]-i[0] in dic:dic[i[1]-i[0]].append(i)\n else:dic[i[1]-i[0]]=[i]\n vals,arr,res=sorted(dic.keys()),[],0\n for i in vals:\n for j in dic[i]:\n arr.append(j)\n for i in range(len(arr)):\n if res+arr[i][0]>=arr[i][1]:res+=arr[i][0]\n else:res=arr[i][1]\n return res\n\n \n \n \n\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Perfection | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n tasks.sort()\n dic=dict()\n for i in tasks:\n if i[1]-i[0] in dic:dic[i[1]-i[0]].append(i)\n else:dic[i[1]-i[0]]=[i]\n vals,arr,res=sorted(dic.keys()),[],0\n for i in vals:\n for j in dic[i]:\n arr.append(j)\n for i in range(len(arr)):\n if res+arr[i][0]>=arr[i][1]:res+=arr[i][0]\n else:res=arr[i][1]\n return res\n\n \n \n \n\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Binary search solution | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n def check(ans):\n for i in tasks:\n if ans >= i[1] :\n ans -= i[0]\n else :\n return False\n break\n return True\n tasks.sort(key = lambda x : x[1]-x[0],reverse = True) \n l = 0\n h = 10**9\n while l <= h :\n mid = l+(h-l)//2 \n if check(mid):\n ans = mid \n h = mid-1\n else :\n l = mid +1\n return ans \n\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Binary search solution | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n def check(ans):\n for i in tasks:\n if ans >= i[1] :\n ans -= i[0]\n else :\n return False\n break\n return True\n tasks.sort(key = lambda x : x[1]-x[0],reverse = True) \n l = 0\n h = 10**9\n while l <= h :\n mid = l+(h-l)//2 \n if check(mid):\n ans = mid \n h = mid-1\n else :\n l = mid +1\n return ans \n\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Python (Simple Maths) | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks):\n tasks.sort(key = lambda x:(x[1]-x[0]),reverse=True)\n min_val, curr = 0, 0\n\n for i,j in tasks:\n if curr < j:\n min_val += j-curr\n curr = j\n curr -= i \n\n return min_val\n\n\n\n\n \n\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Python (Simple Maths) | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks):\n tasks.sort(key = lambda x:(x[1]-x[0]),reverse=True)\n min_val, curr = 0, 0\n\n for i,j in tasks:\n if curr < j:\n min_val += j-curr\n curr = j\n curr -= i \n\n return min_val\n\n\n\n\n \n\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Python3 solution using merge sort | minimum-initial-energy-to-finish-tasks | 0 | 1 | \n# Approach\n### 1. Sort the algorithm using merge sort so that the arrays inside the tasks array have descending differences between the actual energy and the minimum energy\n### 2. Add each of the differences between the minimum between the arrays to the first minimum\n\n# Complexity\n- Time complexity:\n$$O(nlog(n))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n energy = tasks[0][1]\n result = tasks[0][1]\n def mergeSort(arr):\n if len(arr) > 1:\n mid = len(arr) // 2\n sub_array1 = arr[:mid]\n sub_array2 = arr[mid:]\n\n mergeSort(sub_array1)\n mergeSort(sub_array2)\n i = j = k = 0\n while i < len(sub_array1) and j < len(sub_array2):\n if sub_array1[i][1] - sub_array1[i][0] > sub_array2[j][1] - sub_array2[j][0]:\n arr[k] = sub_array1[i]\n i += 1\n else:\n arr[k] = sub_array2[j]\n j += 1\n k += 1\n while i < len(sub_array1):\n arr[k] = sub_array1[i]\n i += 1\n k += 1\n \n while j < len(sub_array2):\n arr[k] = sub_array2[j]\n j += 1\n k += 1\n\n mergeSort(tasks)\n\n for element in tasks:\n if element[1] > energy:\n result = result + element[1] - energy\n energy = energy + element[1] - energy\n energy = energy - element[0]\n return result\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
Python3 solution using merge sort | minimum-initial-energy-to-finish-tasks | 0 | 1 | \n# Approach\n### 1. Sort the algorithm using merge sort so that the arrays inside the tasks array have descending differences between the actual energy and the minimum energy\n### 2. Add each of the differences between the minimum between the arrays to the first minimum\n\n# Complexity\n- Time complexity:\n$$O(nlog(n))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n energy = tasks[0][1]\n result = tasks[0][1]\n def mergeSort(arr):\n if len(arr) > 1:\n mid = len(arr) // 2\n sub_array1 = arr[:mid]\n sub_array2 = arr[mid:]\n\n mergeSort(sub_array1)\n mergeSort(sub_array2)\n i = j = k = 0\n while i < len(sub_array1) and j < len(sub_array2):\n if sub_array1[i][1] - sub_array1[i][0] > sub_array2[j][1] - sub_array2[j][0]:\n arr[k] = sub_array1[i]\n i += 1\n else:\n arr[k] = sub_array2[j]\n j += 1\n k += 1\n while i < len(sub_array1):\n arr[k] = sub_array1[i]\n i += 1\n k += 1\n \n while j < len(sub_array2):\n arr[k] = sub_array2[j]\n j += 1\n k += 1\n\n mergeSort(tasks)\n\n for element in tasks:\n if element[1] > energy:\n result = result + element[1] - energy\n energy = energy + element[1] - energy\n energy = energy - element[0]\n return result\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
O(n * log(n)) solution | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this problem is to minimize the effort required to complete a given list of tasks. Each task has a minimum and maximum effort required to complete it. The solution should aim to find the minimum effort required to complete all tasks while still meeting the minimum effort requirement for each task.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach taken in the provided code is to first sort the tasks by the difference between the maximum and minimum effort required. The tasks are then iterated through and the effort required for each task is set to the maximum of the current effort plus the minimum effort required for the task and the maximum effort required for the task. This ensures that the effort required for each task is at least the minimum required, but no more than the maximum required.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * log(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x: x[1] - x[0])\n effort = 0\n for task in tasks:\n effort = max(effort + task[0], task[1])\n return effort\n``` | 0 | You are given an array `tasks` where `tasks[i] = [actuali, minimumi]`:
* `actuali` is the actual amount of energy you **spend to finish** the `ith` task.
* `minimumi` is the minimum amount of energy you **require to begin** the `ith` task.
For example, if the task is `[10, 12]` and your current energy is `11`, you cannot start this task. However, if your current energy is `13`, you can complete this task, and your energy will be `3` after finishing it.
You can finish the tasks in **any order** you like.
Return _the **minimum** initial amount of energy you will need_ _to finish all the tasks_.
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[4,8\]\]
**Output:** 8
**Explanation:**
Starting with 8 energy, we finish the tasks in the following order:
- 3rd task. Now energy = 8 - 4 = 4.
- 2nd task. Now energy = 4 - 2 = 2.
- 1st task. Now energy = 2 - 1 = 1.
Notice that even though we have leftover energy, starting with 7 energy does not work because we cannot do the 3rd task.
**Example 2:**
**Input:** tasks = \[\[1,3\],\[2,4\],\[10,11\],\[10,12\],\[8,9\]\]
**Output:** 32
**Explanation:**
Starting with 32 energy, we finish the tasks in the following order:
- 1st task. Now energy = 32 - 1 = 31.
- 2nd task. Now energy = 31 - 2 = 29.
- 3rd task. Now energy = 29 - 10 = 19.
- 4th task. Now energy = 19 - 10 = 9.
- 5th task. Now energy = 9 - 8 = 1.
**Example 3:**
**Input:** tasks = \[\[1,7\],\[2,8\],\[3,9\],\[4,10\],\[5,11\],\[6,12\]\]
**Output:** 27
**Explanation:**
Starting with 27 energy, we finish the tasks in the following order:
- 5th task. Now energy = 27 - 5 = 22.
- 2nd task. Now energy = 22 - 2 = 20.
- 3rd task. Now energy = 20 - 3 = 17.
- 1st task. Now energy = 17 - 1 = 16.
- 4th task. Now energy = 16 - 4 = 12.
- 6th task. Now energy = 12 - 6 = 6.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= actuali <= minimumi <= 104` | For the node i, calculate the height of each of its children and keep the first and second maximum heights (max1_i , max2_i). Check all nodes and return max( 2 + max1_i + max2_i ). |
O(n * log(n)) solution | minimum-initial-energy-to-finish-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this problem is to minimize the effort required to complete a given list of tasks. Each task has a minimum and maximum effort required to complete it. The solution should aim to find the minimum effort required to complete all tasks while still meeting the minimum effort requirement for each task.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach taken in the provided code is to first sort the tasks by the difference between the maximum and minimum effort required. The tasks are then iterated through and the effort required for each task is set to the maximum of the current effort plus the minimum effort required for the task and the maximum effort required for the task. This ensures that the effort required for each task is at least the minimum required, but no more than the maximum required.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * log(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def minimumEffort(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x: x[1] - x[0])\n effort = 0\n for task in tasks:\n effort = max(effort + task[0], task[1])\n return effort\n``` | 0 | Given a binary string `s` **without leading zeros**, return `true` _if_ `s` _contains **at most one contiguous segment of ones**_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "1001 "
**Output:** false
**Explanation:** The ones do not form a contiguous segment.
**Example 2:**
**Input:** s = "110 "
**Output:** true
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`.
* `s[0]` is `'1'`. | We can easily figure that the f(x) : does x solve this array is monotonic so binary Search is doable Figure a sorting pattern |
Simplest code with runtime 40ms | maximum-repeating-substring | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n if len(sequence)<len(word):\n return 0\n k=1\n ans=0\n\n while k*word in sequence:\n ans+=1\n k+=1\n return ans \n``` | 1 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
Simplest code with runtime 40ms | maximum-repeating-substring | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n if len(sequence)<len(word):\n return 0\n k=1\n ans=0\n\n while k*word in sequence:\n ans+=1\n k+=1\n return ans \n``` | 1 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Python, binary search on the length of the subsequence | maximum-repeating-substring | 0 | 1 | ```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n if word not in sequence:\n return 0\n\n left = 1\n right = len(sequence) // len(word)\n while left <= right:\n mid = (left + right) // 2\n if word * mid in sequence:\n left = mid + 1\n else:\n right = mid - 1 \n \n return left - 1\n``` | 23 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
Python, binary search on the length of the subsequence | maximum-repeating-substring | 0 | 1 | ```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n if word not in sequence:\n return 0\n\n left = 1\n right = len(sequence) // len(word)\n while left <= right:\n mid = (left + right) // 2\n if word * mid in sequence:\n left = mid + 1\n else:\n right = mid - 1 \n \n return left - 1\n``` | 23 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
python3 easy way | maximum-repeating-substring | 0 | 1 | ```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n if len(sequence) < len(word):\n return 0\n ans = 0\n k = 1\n while word*k in sequence:\n ans += 1\n k += 1\n return ans\n``` | 10 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
python3 easy way | maximum-repeating-substring | 0 | 1 | ```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n if len(sequence) < len(word):\n return 0\n ans = 0\n k = 1\n while word*k in sequence:\n ans += 1\n k += 1\n return ans\n``` | 10 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Python3: O(N^2) solution intuitive | maximum-repeating-substring | 0 | 1 | O(n^2) still but found it to be more intuitive than the top solutions\n\n# Code\n```\nclass Solution:\n def maxRepeating(self, sequence: str, word: str) -> int:\n i = 0\n j = 0\n max_ct = 0\n\n if len(word) > len(sequence):\n return 0\n\n ct = 0\n while i < len(sequence):\n while sequence[j:j+len(word)] == word:\n ct += 1\n j += len(word)\n max_ct = max(max_ct, ct)\n ct = 0\n i += 1\n j = i\n return max_ct\n``` | 2 | For a string `sequence`, a string `word` is **`k`\-repeating** if `word` concatenated `k` times is a substring of `sequence`. The `word`'s **maximum `k`\-repeating value** is the highest value `k` where `word` is `k`\-repeating in `sequence`. If `word` is not a substring of `sequence`, `word`'s maximum `k`\-repeating value is `0`.
Given strings `sequence` and `word`, return _the **maximum `k`\-repeating value** of `word` in `sequence`_.
**Example 1:**
**Input:** sequence = "ababc ", word = "ab "
**Output:** 2
**Explanation: ** "abab " is a substring in "ababc ".
**Example 2:**
**Input:** sequence = "ababc ", word = "ba "
**Output:** 1
**Explanation: ** "ba " is a substring in "ababc ". "baba " is not a substring in "ababc ".
**Example 3:**
**Input:** sequence = "ababc ", word = "ac "
**Output:** 0
**Explanation: ** "ac " is not a substring in "ababc ".
**Constraints:**
* `1 <= sequence.length <= 100`
* `1 <= word.length <= 100`
* `sequence` and `word` contains only lowercase English letters. | Given the character counts, under what conditions can a palindrome be formed ? From left to right, use bitwise xor-operation to compute for any prefix the number of times modulo 2 of each digit. (mask ^= (1<<(s[i]-'0')). Expected complexity is O(n*A) where A is the alphabet (10). |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.