title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution ( 96.51% Faster) | get-maximum-in-generated-array | 0 | 1 | ```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n l1 = [0,1]\n if n == 2 or n == 1:\n return (1)\n elif n == 0:\n return (0)\n for i in range(1,n):\n l1.append(l1[i])\n if (i * 2) == n:\n break\n l1.append((l1[i]) + (l1[i+1]))\n if (((i * 2)+1) == n):\n break\n return (max(l1))\n\n``` | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Solution ( 96.51% Faster) | get-maximum-in-generated-array | 0 | 1 | ```\nclass Solution:\n def getMaximumGenerated(self, n: int) -> int:\n l1 = [0,1]\n if n == 2 or n == 1:\n return (1)\n elif n == 0:\n return (0)\n for i in range(1,n):\n l1.append(l1[i])\n if (i * 2) == n:\n break\n l1.append((l1[i]) + (l1[i+1]))\n if (((i * 2)+1) == n):\n break\n return (max(l1))\n\n``` | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Python 90% Faster Simple Code easy understanding | get-maximum-in-generated-array | 0 | 1 | class Solution:\n def getMaximumGenerated(self, n: int) -> int:\n if n == 0: return 0\n \n nums = [0, 1]\n for i in range(2, n+1):\n if i % 2 == 0:\n nums.append(nums[i//2])\n else:\n nums.append(nums[(i-1)//2]+ nums[(i+1)//2])\n \n return max(nums)\n\t\t\n\t\t\n\t\tPlease Upvote if you find the solution Helpful. Thank You. | 1 | You are given an integer `n`. A **0-indexed** integer array `nums` of length `n + 1` is generated in the following way:
* `nums[0] = 0`
* `nums[1] = 1`
* `nums[2 * i] = nums[i]` when `2 <= 2 * i <= n`
* `nums[2 * i + 1] = nums[i] + nums[i + 1]` when `2 <= 2 * i + 1 <= n`
Return _the **maximum** integer in the array_ `nums`.
**Example 1:**
**Input:** n = 7
**Output:** 3
**Explanation:** According to the given rules:
nums\[0\] = 0
nums\[1\] = 1
nums\[(1 \* 2) = 2\] = nums\[1\] = 1
nums\[(1 \* 2) + 1 = 3\] = nums\[1\] + nums\[2\] = 1 + 1 = 2
nums\[(2 \* 2) = 4\] = nums\[2\] = 1
nums\[(2 \* 2) + 1 = 5\] = nums\[2\] + nums\[3\] = 1 + 2 = 3
nums\[(3 \* 2) = 6\] = nums\[3\] = 2
nums\[(3 \* 2) + 1 = 7\] = nums\[3\] + nums\[4\] = 2 + 1 = 3
Hence, nums = \[0,1,1,2,1,3,2,3\], and the maximum is max(0,1,1,2,1,3,2,3) = 3.
**Example 2:**
**Input:** n = 2
**Output:** 1
**Explanation:** According to the given rules, nums = \[0,1,1\]. The maximum is max(0,1,1) = 1.
**Example 3:**
**Input:** n = 3
**Output:** 2
**Explanation:** According to the given rules, nums = \[0,1,1,2\]. The maximum is max(0,1,1,2) = 2.
**Constraints:**
* `0 <= n <= 100` | Keep track of how many positive numbers are missing as you scan the array. |
Python 90% Faster Simple Code easy understanding | get-maximum-in-generated-array | 0 | 1 | class Solution:\n def getMaximumGenerated(self, n: int) -> int:\n if n == 0: return 0\n \n nums = [0, 1]\n for i in range(2, n+1):\n if i % 2 == 0:\n nums.append(nums[i//2])\n else:\n nums.append(nums[(i-1)//2]+ nums[(i+1)//2])\n \n return max(nums)\n\t\t\n\t\t\n\t\tPlease Upvote if you find the solution Helpful. Thank You. | 1 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Python3 | 98.24% | Greedy Approach | Easy to Understand | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | # Python3 | 98.24% | Greedy Approach | Easy to Understand\n```\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n for char, freq in cnt.items():\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n used_frequencies.add(freq)\n \n return deletions\n``` | 22 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
Python3 | 98.24% | Greedy Approach | Easy to Understand | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | # Python3 | 98.24% | Greedy Approach | Easy to Understand\n```\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n for char, freq in cnt.items():\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n used_frequencies.add(freq)\n \n return deletions\n``` | 22 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
Simple Approach Using SortedDict | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code\n```\nfrom sortedcontainers import SortedDict\n\nclass Solution:\n def minDeletions(self, s: str) -> int:\n freqToCnt = SortedDict(Counter(Counter(s).values()))\n deletions = 0\n i = -1\n while i >= -len(freqToCnt):\n freq, cnt = freqToCnt.peekitem(i)\n if cnt > 1:\n deletions += cnt - 1\n if freq > 1:\n freqToCnt[freq-1] = freqToCnt.get(freq-1, 0) + cnt - 1\n\n i -= 1\n \n return deletions\n``` | 4 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
Simple Approach Using SortedDict | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code\n```\nfrom sortedcontainers import SortedDict\n\nclass Solution:\n def minDeletions(self, s: str) -> int:\n freqToCnt = SortedDict(Counter(Counter(s).values()))\n deletions = 0\n i = -1\n while i >= -len(freqToCnt):\n freq, cnt = freqToCnt.peekitem(i)\n if cnt > 1:\n deletions += cnt - 1\n if freq > 1:\n freqToCnt[freq-1] = freqToCnt.get(freq-1, 0) + cnt - 1\n\n i -= 1\n \n return deletions\n``` | 4 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
O(n) Time, O(1) Space Solution - Python, JavaScript, Java, C++ | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Intuition\nUsing HashMap to count each character and Set to keep unique frequency of chracters.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/2CXjNZa0ldo\n\nMinor update:\nIn the video, I use Set and variable name is "uniq_set". It\'s a little bit weird because values in Set are usually unique, so we should use variable name like "freq_set".\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\nThe next subscriber is exact 2300.\n\u2B50\uFE0F Today is my birthday. Please give me the gift of subscribing to my channel\uFF01\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2299\nThank you for your support!\n\n---\n\n# Approach\n\n```\nInput: s = "aaabbbcc"\n```\n\n## \u25A0 Step 1\nCreate HashMap`chars`. key is character and value is frequency of the character.\n```\nchars = {"a": 3, "b": 3, "c": 2}\n```\n\nInitialize `freq_set` with Set and `count` with 0. `freq_set` is used to keep unique frequency of chracters and `count` is return value.\n\n## \u25A0 Step 2\nStart iteration with `chars`.\n\n##### 2-1\nReagarding `"a": 3` in HashMap, `freq` is now `3`. `freq` doesn\'t meet the condition below\n```\nwhile freq > 0 and freq in freq_set:\n```\nSo, just add `3` to `freq_set`\n```\nNow freq_set = {3}, count = 0\n```\n\n##### 2-2\nReagarding `"b": 3` in HashMap, `freq` is now `3`. `freq` meets the `while condition` above, so we need to add `-1` to `freq`. Now `freq = 2` and add `1` to `count`. Then, check the `while condition` again. `freq` doesn\'t meet the condition, so add `freq = 2` to `freq_set` .\n\n```\nNow freq_set = {2, 3}, count = 1\n```\n\n##### 2-3\nReagarding `"c": 2` in HashMap, `freq` is now `2`. `freq` meets the `while condition` above, so we need to add `-1` to `freq`. Now `freq = 1` and add `1` to `count`. Then check the `while condition` again. `freq` doesn\'t meet the condition, so add `1` to `freq_set`.\n```\nNow freq_set = {1, 2, 3}, count = 2\n```\n\n```\nOutput: 2\n```\n\n# Complexity\n- Time complexity: O(n)\nWe count frequency of each character and store them to HashMap. For example, `Input: s = "aaabbbcc"`, we count them 8 times. `Input: s = "aaabbbccdd"`, we count them 10 times. It depends on length of input string.\n\n- Space complexity: O(1)\nWe will not store more than 26 different frequencies. Because we have constraint saying "s contains only lowercase English letters". It does not grow with length of input string or something. In the worst case O(26) \u2192 O(1)\n\n```python []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n chars = Counter(s)\n\n freq_set = set()\n count = 0\n\n for freq in chars.values():\n while freq > 0 and freq in freq_set:\n freq -= 1\n count += 1\n \n freq_set.add(freq)\n\n return count\n```\n```javascript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar minDeletions = function(s) {\n const chars = new Map();\n for (const char of s) {\n chars.set(char, (chars.get(char) || 0) + 1);\n }\n\n const freqSet = new Set();\n let count = 0;\n\n for (let freq of chars.values()) {\n while (freq > 0 && freqSet.has(freq)) {\n freq--;\n count++;\n }\n\n freqSet.add(freq);\n }\n\n return count; \n};\n```\n```Java []\nclass Solution {\n public int minDeletions(String s) {\n Map<Character, Integer> chars = new HashMap<>();\n for (char c : s.toCharArray()) {\n chars.put(c, chars.getOrDefault(c, 0) + 1);\n }\n\n Set<Integer> freqSet = new HashSet<>();\n int count = 0;\n\n for (int freq : chars.values()) {\n while (freq > 0 && freqSet.contains(freq)) {\n freq--;\n count++;\n }\n freqSet.add(freq);\n }\n\n return count; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n unordered_map<char, int> chars;\n for (char c : s) {\n chars[c]++;\n }\n\n unordered_set<int> freqSet;\n int count = 0;\n\n for (const auto& pair : chars) {\n int freq = pair.second;\n while (freq > 0 && freqSet.count(freq)) {\n freq--;\n count++;\n }\n freqSet.insert(freq);\n }\n\n return count; \n }\n};\n```\n | 33 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
O(n) Time, O(1) Space Solution - Python, JavaScript, Java, C++ | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Intuition\nUsing HashMap to count each character and Set to keep unique frequency of chracters.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/2CXjNZa0ldo\n\nMinor update:\nIn the video, I use Set and variable name is "uniq_set". It\'s a little bit weird because values in Set are usually unique, so we should use variable name like "freq_set".\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\nThe next subscriber is exact 2300.\n\u2B50\uFE0F Today is my birthday. Please give me the gift of subscribing to my channel\uFF01\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2299\nThank you for your support!\n\n---\n\n# Approach\n\n```\nInput: s = "aaabbbcc"\n```\n\n## \u25A0 Step 1\nCreate HashMap`chars`. key is character and value is frequency of the character.\n```\nchars = {"a": 3, "b": 3, "c": 2}\n```\n\nInitialize `freq_set` with Set and `count` with 0. `freq_set` is used to keep unique frequency of chracters and `count` is return value.\n\n## \u25A0 Step 2\nStart iteration with `chars`.\n\n##### 2-1\nReagarding `"a": 3` in HashMap, `freq` is now `3`. `freq` doesn\'t meet the condition below\n```\nwhile freq > 0 and freq in freq_set:\n```\nSo, just add `3` to `freq_set`\n```\nNow freq_set = {3}, count = 0\n```\n\n##### 2-2\nReagarding `"b": 3` in HashMap, `freq` is now `3`. `freq` meets the `while condition` above, so we need to add `-1` to `freq`. Now `freq = 2` and add `1` to `count`. Then, check the `while condition` again. `freq` doesn\'t meet the condition, so add `freq = 2` to `freq_set` .\n\n```\nNow freq_set = {2, 3}, count = 1\n```\n\n##### 2-3\nReagarding `"c": 2` in HashMap, `freq` is now `2`. `freq` meets the `while condition` above, so we need to add `-1` to `freq`. Now `freq = 1` and add `1` to `count`. Then check the `while condition` again. `freq` doesn\'t meet the condition, so add `1` to `freq_set`.\n```\nNow freq_set = {1, 2, 3}, count = 2\n```\n\n```\nOutput: 2\n```\n\n# Complexity\n- Time complexity: O(n)\nWe count frequency of each character and store them to HashMap. For example, `Input: s = "aaabbbcc"`, we count them 8 times. `Input: s = "aaabbbccdd"`, we count them 10 times. It depends on length of input string.\n\n- Space complexity: O(1)\nWe will not store more than 26 different frequencies. Because we have constraint saying "s contains only lowercase English letters". It does not grow with length of input string or something. In the worst case O(26) \u2192 O(1)\n\n```python []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n chars = Counter(s)\n\n freq_set = set()\n count = 0\n\n for freq in chars.values():\n while freq > 0 and freq in freq_set:\n freq -= 1\n count += 1\n \n freq_set.add(freq)\n\n return count\n```\n```javascript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar minDeletions = function(s) {\n const chars = new Map();\n for (const char of s) {\n chars.set(char, (chars.get(char) || 0) + 1);\n }\n\n const freqSet = new Set();\n let count = 0;\n\n for (let freq of chars.values()) {\n while (freq > 0 && freqSet.has(freq)) {\n freq--;\n count++;\n }\n\n freqSet.add(freq);\n }\n\n return count; \n};\n```\n```Java []\nclass Solution {\n public int minDeletions(String s) {\n Map<Character, Integer> chars = new HashMap<>();\n for (char c : s.toCharArray()) {\n chars.put(c, chars.getOrDefault(c, 0) + 1);\n }\n\n Set<Integer> freqSet = new HashSet<>();\n int count = 0;\n\n for (int freq : chars.values()) {\n while (freq > 0 && freqSet.contains(freq)) {\n freq--;\n count++;\n }\n freqSet.add(freq);\n }\n\n return count; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n unordered_map<char, int> chars;\n for (char c : s) {\n chars[c]++;\n }\n\n unordered_set<int> freqSet;\n int count = 0;\n\n for (const auto& pair : chars) {\n int freq = pair.second;\n while (freq > 0 && freqSet.count(freq)) {\n freq--;\n count++;\n }\n freqSet.insert(freq);\n }\n\n return count; \n }\n};\n```\n | 33 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
[ Python / Java / C++] 🔥100% | ✅ MAP | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | ```Python []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n counts=Counter(s)\n res=0\n set1=set()\n for i in counts:\n frec=counts[i]\n if frec in set1:\n while frec in set1 and frec>0: \n frec-=1\n res+=1\n \n set1.add(frec) \n return res\n```\n```Java []\nclass Solution {\n public int minDeletions(String s) {\n if(s.length() == 0) return 0 ;\n \n int[] arr = new int[26] ;\n for(int i = 0 ; i < s.length() ; i++){\n char ch = s.charAt(i) ;\n arr[ch - \'a\'] ++ ;\n }\n HashSet<Integer> mp = new HashSet<>() ;\n int count = 0 ;\n for(int i = 0 ; i < 26 ; i++){\n int f = arr[i] ;\n \n if(! mp.contains(f) )\n mp.add(f) ;\n else{\n while(f > 0 && mp.contains(f) ){\n f -- ;\n count ++ ;\n }\n mp.add(f) ;\n }\n }\n return count ;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n map<int , vector<char> , greater<int>> m;\n int curr = 1;\n unordered_map<char , int> mp;\n for(int i =0 ; i< s.size() ; i++){\n mp[s[i]]++;\n }\n for(auto e : mp){\n m[e.second].push_back(e.first);\n }\n int count = 0;\n for( auto e : m){\n if(e.second.size() > 1){\n for( int i = 1 ; i< e.second.size() ; i++ ){\n if( e.first > 0){\n m[e.first-1].push_back(e.second[i]);\n count++;\n }\n }\n }\n }\n return count;\n }\n};\n | 3 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
[ Python / Java / C++] 🔥100% | ✅ MAP | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | ```Python []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n counts=Counter(s)\n res=0\n set1=set()\n for i in counts:\n frec=counts[i]\n if frec in set1:\n while frec in set1 and frec>0: \n frec-=1\n res+=1\n \n set1.add(frec) \n return res\n```\n```Java []\nclass Solution {\n public int minDeletions(String s) {\n if(s.length() == 0) return 0 ;\n \n int[] arr = new int[26] ;\n for(int i = 0 ; i < s.length() ; i++){\n char ch = s.charAt(i) ;\n arr[ch - \'a\'] ++ ;\n }\n HashSet<Integer> mp = new HashSet<>() ;\n int count = 0 ;\n for(int i = 0 ; i < 26 ; i++){\n int f = arr[i] ;\n \n if(! mp.contains(f) )\n mp.add(f) ;\n else{\n while(f > 0 && mp.contains(f) ){\n f -- ;\n count ++ ;\n }\n mp.add(f) ;\n }\n }\n return count ;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n map<int , vector<char> , greater<int>> m;\n int curr = 1;\n unordered_map<char , int> mp;\n for(int i =0 ; i< s.size() ; i++){\n mp[s[i]]++;\n }\n for(auto e : mp){\n m[e.second].push_back(e.first);\n }\n int count = 0;\n for( auto e : m){\n if(e.second.size() > 1){\n for( int i = 1 ; i< e.second.size() ; i++ ){\n if( e.first > 0){\n m[e.first-1].push_back(e.second[i]);\n count++;\n }\n }\n }\n }\n return count;\n }\n};\n | 3 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
✅ 98.18% Greedy & Heap & Sorting | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Comprehensive Guide to Solving "Minimum Deletions to Make Character Frequencies Unique"\n\n## Introduction & Problem Statement\n\nWelcome, code enthusiasts! Today, we\'re tackling an intriguing problem: **Minimum Deletions to Make Character Frequencies Unique**. Given a string `s` , the goal is to delete the minimum number of characters so that no two characters have the same frequency.\n\nFor instance, if the input string is "aaabbbcc", you can delete two \'b\'s to make the string "aaabcc", ensuring that each character has a unique frequency.\n\n## Key Concepts and Constraints\n\n### What Makes this Problem Unique?\n\n1. **Character Frequency**: \n Each character in the string `s` has a frequency, and we need to make sure no two characters share the same frequency after deletions.\n\n2. **Minimum Deletions**:\n The goal is to achieve this with the fewest number of deletions.\n\n3. **Constraints**: \n - The length of the string `s` , `n` , is between `1` and `10^5` .\n - The string `s` contains only lowercase English letters.\n\n---\n\n# Strategies to Tackle the Problem:\n\n## Live Coding & Explain Greedy\nhttps://youtu.be/QkCo8HhiwYU?si=zPPAMxrpL0a0c4Ns\n\n## Greedy Algorithm 1/3: Minimizing Deletions Step by Step\n\n### What is a Greedy Algorithm?\nA Greedy Algorithm makes choices that seem the best at the moment. In the context of this problem, we\'ll try to make each character frequency unique by making the fewest number of changes to the existing frequencies.\n\n### Detailed Steps\n\n1. **Step 1: Count Frequencies** \n - **Why Count Frequencies?**: \n Before we can decide which characters to delete, we need to know how often each character appears. This is done using a frequency counter, stored in a dictionary `cnt`.\n \n2. **Step 2: Iterate and Minimize**\n - **Why Iterate Through Frequencies?**: \n We need to ensure that all character frequencies are unique. To do this, we iterate through the `cnt` dictionary. If a frequency is already used, we decrement it by 1 until it becomes unique, keeping track of these decrements in a variable `deletions`.\n\n3. **Step 3: Return Deletions**\n - **What is the Output?**: \n The function returns the total number of deletions (`deletions`) required to make all character frequencies unique.\n\n#### Time and Space Complexity\n- **Time Complexity**: $$O(n)$$, as you only iterate through the list once.\n- **Space Complexity**: $$O(n)$$, to store the frequencies in `cnt` and the used frequencies in `used_frequencies`.\n\n## Code Greedy\n``` Python []\n# Greedy Approach\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n for char, freq in cnt.items():\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n used_frequencies.add(freq)\n \n return deletions\n```\n``` Go []\nfunc minDeletions(s string) int {\n cnt := make(map[rune]int)\n deletions := 0\n used_frequencies := make(map[int]bool)\n \n for _, c := range s {\n cnt[c]++\n }\n \n for _, freq := range cnt {\n for freq > 0 && used_frequencies[freq] {\n freq--\n deletions++\n }\n used_frequencies[freq] = true\n }\n \n return deletions\n}\n```\n``` Rust []\nuse std::collections::HashMap;\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn min_deletions(s: String) -> i32 {\n let mut cnt = HashMap::new();\n let mut deletions = 0;\n let mut used_frequencies = HashSet::new();\n \n for c in s.chars() {\n *cnt.entry(c).or_insert(0) += 1;\n }\n \n for freq in cnt.values() {\n let mut f = *freq;\n while f > 0 && used_frequencies.contains(&f) {\n f -= 1;\n deletions += 1;\n }\n used_frequencies.insert(f);\n }\n \n deletions\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minDeletions(std::string s) {\n std::unordered_map<char, int> cnt;\n int deletions = 0;\n std::unordered_set<int> used_frequencies;\n \n for (char c : s) {\n cnt[c]++;\n }\n \n for (auto& kv : cnt) {\n int freq = kv.second;\n while (freq > 0 && used_frequencies.find(freq) != used_frequencies.end()) {\n freq--;\n deletions++;\n }\n used_frequencies.insert(freq);\n }\n \n return deletions;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int minDeletions(String s) {\n HashMap<Character, Integer> cnt = new HashMap<>();\n int deletions = 0;\n HashSet<Integer> used_frequencies = new HashSet<>();\n \n for (char c : s.toCharArray()) {\n cnt.put(c, cnt.getOrDefault(c, 0) + 1);\n }\n \n for (int freq : cnt.values()) {\n while (freq > 0 && used_frequencies.contains(freq)) {\n freq--;\n deletions++;\n }\n used_frequencies.add(freq);\n }\n \n return deletions;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar minDeletions = function(s) {\n const cnt = {};\n let deletions = 0;\n const used_frequencies = new Set();\n \n for (const c of s) {\n cnt[c] = (cnt[c] || 0) + 1;\n }\n \n for (const freq of Object.values(cnt)) {\n let f = freq;\n while (f > 0 && used_frequencies.has(f)) {\n f--;\n deletions++;\n }\n used_frequencies.add(f);\n }\n \n return deletions;\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param String $s\n * @return Integer\n */\n function minDeletions($s) {\n $cnt = [];\n $deletions = 0;\n $used_frequencies = [];\n \n foreach (str_split($s) as $c) {\n $cnt[$c] = ($cnt[$c] ?? 0) + 1;\n }\n \n foreach ($cnt as $freq) {\n while ($freq > 0 && in_array($freq, $used_frequencies)) {\n $freq--;\n $deletions++;\n }\n $used_frequencies[] = $freq;\n }\n \n return $deletions;\n}\n}\n```\n``` C# []\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution {\n public int MinDeletions(string s) {\n Dictionary<char, int> cnt = new Dictionary<char, int>();\n int deletions = 0;\n HashSet<int> used_frequencies = new HashSet<int>();\n \n foreach (char c in s) {\n if (cnt.ContainsKey(c)) cnt[c]++;\n else cnt[c] = 1;\n }\n \n foreach (int freqReadOnly in cnt.Values) {\n int freq = freqReadOnly;\n while (freq > 0 && used_frequencies.Contains(freq)) {\n freq--;\n deletions++;\n }\n used_frequencies.Add(freq);\n }\n \n return deletions;\n }\n}\n```\n\n---\n\n## Sorting Algorithm 2/3: Sort and Minimize\n\n### Detailed Steps\n\n#### Step 1: Count and Sort Frequencies\n\n- **Why Sort?**: \n Sorting brings an order to the chaos. When you sort the frequencies in descending order, you can start adjusting from the highest frequency downwards. This is beneficial because higher frequencies have a greater range of potential unique lower frequencies they can be adjusted to. For example, a frequency of 10 can be decreased to any of 9, 8, 7, ... until it becomes unique, giving us more "room" to make adjustments.\n\n#### Step 2: Iterate and Minimize\n\n- **Why Iterate Through Sorted Frequencies?**: \n After sorting, the frequencies are now in an ordered list, `sorted_freqs`. We iterate through this list, and for each frequency, we decrease it until it becomes unique. The advantage of working with sorted frequencies is that we can minimize the number of operations by taking advantage of the "room" lower frequencies offer for adjustment.\n\n#### Step 3: Early Exit Optimization\n\n- **Why Early Exit?**: \n An important optimization is to exit the loop early when you find a frequency that is already unique. In a sorted list, if you encounter a frequency that is unique, then all frequencies that come after it in the list will also be unique. This is because they will all be smaller and we have already confirmed that larger frequencies are unique.\n\n#### Step 4: Return Deletions\n\n- **What is the output?**: \n After iterating through `sorted_freqs` and making the necessary adjustments, we return the total number of deletions required to make the frequencies unique.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$ O(n \\log n) $$ due to sorting. Sorting the frequencies is the most time-consuming part here.\n- **Space Complexity**: $$ O(n) $$ for storing frequencies and used frequencies.\n\n## Code Sorting\n``` Python []\n# Sorting Approach\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n sorted_freqs = sorted(cnt.values(), reverse=True)\n \n for freq in sorted_freqs:\n if freq not in used_frequencies: # Early exit condition\n used_frequencies.add(freq)\n continue \n\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n\n used_frequencies.add(freq)\n \n return deletions\n```\n``` Go []\nfunc minDeletions(s string) int {\n\tcnt := make(map[rune]int)\n\tdeletions := 0\n\tused_frequencies := make(map[int]bool)\n\n\tfor _, c := range s {\n\t\tcnt[c]++\n\t}\n\n\tsortedFreqs := make([]int, 0, len(cnt))\n\tfor _, freq := range cnt {\n\t\tsortedFreqs = append(sortedFreqs, freq)\n\t}\n\tsort.Sort(sort.Reverse(sort.IntSlice(sortedFreqs)))\n\n\tfor _, freq := range sortedFreqs {\n\t\tfor freq > 0 && used_frequencies[freq] {\n\t\t\tfreq--\n\t\t\tdeletions++\n\t\t}\n\t\tused_frequencies[freq] = true\n\t}\n\n\treturn deletions\n}\n```\n\n---\n\n## Heap / Priority Queue 3/3: Prioritize Frequencies to Adjust\n\n### Detailed Steps\n\n#### Step 1: Count Frequencies and Build Heap\n\n- **Why Use a Heap?**: \n A min-heap is a specialized tree-based data structure that keeps the smallest element at the top. In the context of this problem, the smallest frequency will always be at the top of the heap. This allows us to focus on making the smallest frequencies unique first, which is generally easier and requires fewer adjustments.\n\n#### Step 2: Iterate and Minimize Using Heap\n\n- **Why Heap?**: \n The heap automatically "tells" us which frequency should be adjusted next (it will be the smallest one). We pop this smallest frequency and make it unique by decrementing it until it no longer matches any other frequency. The advantage here is that the heap dynamically updates, so after each adjustment, the next smallest frequency is ready for us to examine.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$ O(n \\log n) $$ due to heap operations. Each insertion and removal from the heap takes $$ \\log n $$ time, and we may need to do this $$ n $$ times.\n- **Space Complexity**: $$ O(n) $$ for storing the frequencies in `cnt` and the used frequencies in `used_frequencies`.\n\n\n## Code Heap\n``` Python []\n# Heap / Priority Queue Approach\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n heap = list(cnt.values())\n heapq.heapify(heap)\n \n while heap:\n freq = heapq.heappop(heap)\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n used_frequencies.add(freq)\n \n return deletions\n```\n``` Go []\nimport (\n\t"container/heap"\n\t"fmt"\n)\n\ntype IntHeap []int\n\nfunc (h IntHeap) Len() int { return len(h) }\nfunc (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }\nfunc (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *IntHeap) Push(x interface{}) {\n\t*h = append(*h, x.(int))\n}\n\nfunc (h *IntHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\tx := old[n-1]\n\t*h = old[0 : n-1]\n\treturn x\n}\n\nfunc minDeletions(s string) int {\n\tcnt := make(map[rune]int)\n\tdeletions := 0\n\tused_frequencies := make(map[int]bool)\n\n\tfor _, c := range s {\n\t\tcnt[c]++\n\t}\n\n\th := &IntHeap{}\n\theap.Init(h)\n\n\tfor _, freq := range cnt {\n\t\theap.Push(h, freq)\n\t}\n\n\tfor h.Len() > 0 {\n\t\tfreq := heap.Pop(h).(int)\n\t\tfor freq > 0 && used_frequencies[freq] {\n\t\t\tfreq--\n\t\t\tdeletions++\n\t\t}\n\t\tused_frequencies[freq] = true\n\t}\n\n\treturn deletions\n}\n```\n\n---\n\n## Performance\n\n| Language | Approach | Execution Time (ms) | Memory Usage (MB) |\n|------------|-----------|---------------------|-------------------|\n| Rust | Greedy | 31 | 2.5 |\n| Go | Heap | 51 | 6.8 |\n| Java | Greedy | 50 | 45 |\n| C++ | Greedy | 75 | 17.5 |\n| Go | Greedy | 62 | 6.6 |\n| PHP | Greedy | 95 | 26.2 |\n| Python3 | Heap | 99 | 17.1 |\n| Python3 | Greedy | 105 | 17.2 |\n| C# | Greedy | 105 | 42.8 |\n| Python3 | Sorting | 106 | 17.1 |\n| JavaScript | Greedy | 125 | 48.4 |\n\n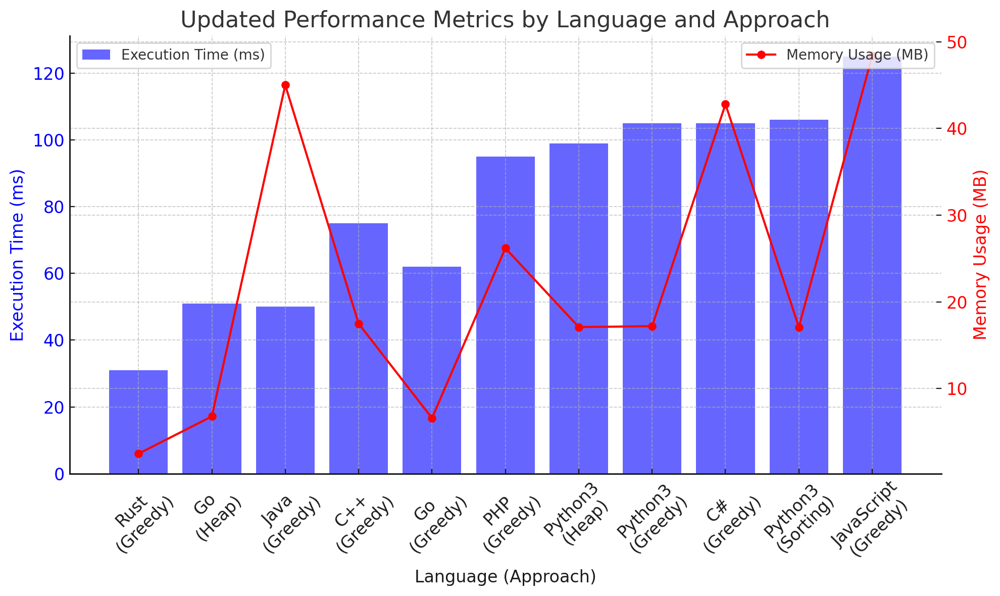\n\n\n## Live Coding & Explain Heap & Sort\nhttps://youtu.be/myQ6RGLyaDM?si=5nfp8jnnsp_srtCz\n\n## Code Highlights and Best Practices\n\n- The Greedy Algorithm is simple and efficient, making it a go-to approach for this problem.\n- The Sorting Algorithm provides another effective way to tackle this problem but with a slight overhead due to sorting.\n- The Heap / Priority Queue approach adds a layer of optimization by prioritizing which frequencies to adjust first.\n\nBy mastering these approaches, you\'ll be well-equipped to tackle other frequency-based or deletion-minimizing problems, which are common in coding interviews and competitive programming. So, are you ready to make some string frequencies unique? Let\'s get coding!\n\n\n | 106 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
✅ 98.18% Greedy & Heap & Sorting | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Comprehensive Guide to Solving "Minimum Deletions to Make Character Frequencies Unique"\n\n## Introduction & Problem Statement\n\nWelcome, code enthusiasts! Today, we\'re tackling an intriguing problem: **Minimum Deletions to Make Character Frequencies Unique**. Given a string `s` , the goal is to delete the minimum number of characters so that no two characters have the same frequency.\n\nFor instance, if the input string is "aaabbbcc", you can delete two \'b\'s to make the string "aaabcc", ensuring that each character has a unique frequency.\n\n## Key Concepts and Constraints\n\n### What Makes this Problem Unique?\n\n1. **Character Frequency**: \n Each character in the string `s` has a frequency, and we need to make sure no two characters share the same frequency after deletions.\n\n2. **Minimum Deletions**:\n The goal is to achieve this with the fewest number of deletions.\n\n3. **Constraints**: \n - The length of the string `s` , `n` , is between `1` and `10^5` .\n - The string `s` contains only lowercase English letters.\n\n---\n\n# Strategies to Tackle the Problem:\n\n## Live Coding & Explain Greedy\nhttps://youtu.be/QkCo8HhiwYU?si=zPPAMxrpL0a0c4Ns\n\n## Greedy Algorithm 1/3: Minimizing Deletions Step by Step\n\n### What is a Greedy Algorithm?\nA Greedy Algorithm makes choices that seem the best at the moment. In the context of this problem, we\'ll try to make each character frequency unique by making the fewest number of changes to the existing frequencies.\n\n### Detailed Steps\n\n1. **Step 1: Count Frequencies** \n - **Why Count Frequencies?**: \n Before we can decide which characters to delete, we need to know how often each character appears. This is done using a frequency counter, stored in a dictionary `cnt`.\n \n2. **Step 2: Iterate and Minimize**\n - **Why Iterate Through Frequencies?**: \n We need to ensure that all character frequencies are unique. To do this, we iterate through the `cnt` dictionary. If a frequency is already used, we decrement it by 1 until it becomes unique, keeping track of these decrements in a variable `deletions`.\n\n3. **Step 3: Return Deletions**\n - **What is the Output?**: \n The function returns the total number of deletions (`deletions`) required to make all character frequencies unique.\n\n#### Time and Space Complexity\n- **Time Complexity**: $$O(n)$$, as you only iterate through the list once.\n- **Space Complexity**: $$O(n)$$, to store the frequencies in `cnt` and the used frequencies in `used_frequencies`.\n\n## Code Greedy\n``` Python []\n# Greedy Approach\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n for char, freq in cnt.items():\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n used_frequencies.add(freq)\n \n return deletions\n```\n``` Go []\nfunc minDeletions(s string) int {\n cnt := make(map[rune]int)\n deletions := 0\n used_frequencies := make(map[int]bool)\n \n for _, c := range s {\n cnt[c]++\n }\n \n for _, freq := range cnt {\n for freq > 0 && used_frequencies[freq] {\n freq--\n deletions++\n }\n used_frequencies[freq] = true\n }\n \n return deletions\n}\n```\n``` Rust []\nuse std::collections::HashMap;\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn min_deletions(s: String) -> i32 {\n let mut cnt = HashMap::new();\n let mut deletions = 0;\n let mut used_frequencies = HashSet::new();\n \n for c in s.chars() {\n *cnt.entry(c).or_insert(0) += 1;\n }\n \n for freq in cnt.values() {\n let mut f = *freq;\n while f > 0 && used_frequencies.contains(&f) {\n f -= 1;\n deletions += 1;\n }\n used_frequencies.insert(f);\n }\n \n deletions\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minDeletions(std::string s) {\n std::unordered_map<char, int> cnt;\n int deletions = 0;\n std::unordered_set<int> used_frequencies;\n \n for (char c : s) {\n cnt[c]++;\n }\n \n for (auto& kv : cnt) {\n int freq = kv.second;\n while (freq > 0 && used_frequencies.find(freq) != used_frequencies.end()) {\n freq--;\n deletions++;\n }\n used_frequencies.insert(freq);\n }\n \n return deletions;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int minDeletions(String s) {\n HashMap<Character, Integer> cnt = new HashMap<>();\n int deletions = 0;\n HashSet<Integer> used_frequencies = new HashSet<>();\n \n for (char c : s.toCharArray()) {\n cnt.put(c, cnt.getOrDefault(c, 0) + 1);\n }\n \n for (int freq : cnt.values()) {\n while (freq > 0 && used_frequencies.contains(freq)) {\n freq--;\n deletions++;\n }\n used_frequencies.add(freq);\n }\n \n return deletions;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar minDeletions = function(s) {\n const cnt = {};\n let deletions = 0;\n const used_frequencies = new Set();\n \n for (const c of s) {\n cnt[c] = (cnt[c] || 0) + 1;\n }\n \n for (const freq of Object.values(cnt)) {\n let f = freq;\n while (f > 0 && used_frequencies.has(f)) {\n f--;\n deletions++;\n }\n used_frequencies.add(f);\n }\n \n return deletions;\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param String $s\n * @return Integer\n */\n function minDeletions($s) {\n $cnt = [];\n $deletions = 0;\n $used_frequencies = [];\n \n foreach (str_split($s) as $c) {\n $cnt[$c] = ($cnt[$c] ?? 0) + 1;\n }\n \n foreach ($cnt as $freq) {\n while ($freq > 0 && in_array($freq, $used_frequencies)) {\n $freq--;\n $deletions++;\n }\n $used_frequencies[] = $freq;\n }\n \n return $deletions;\n}\n}\n```\n``` C# []\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution {\n public int MinDeletions(string s) {\n Dictionary<char, int> cnt = new Dictionary<char, int>();\n int deletions = 0;\n HashSet<int> used_frequencies = new HashSet<int>();\n \n foreach (char c in s) {\n if (cnt.ContainsKey(c)) cnt[c]++;\n else cnt[c] = 1;\n }\n \n foreach (int freqReadOnly in cnt.Values) {\n int freq = freqReadOnly;\n while (freq > 0 && used_frequencies.Contains(freq)) {\n freq--;\n deletions++;\n }\n used_frequencies.Add(freq);\n }\n \n return deletions;\n }\n}\n```\n\n---\n\n## Sorting Algorithm 2/3: Sort and Minimize\n\n### Detailed Steps\n\n#### Step 1: Count and Sort Frequencies\n\n- **Why Sort?**: \n Sorting brings an order to the chaos. When you sort the frequencies in descending order, you can start adjusting from the highest frequency downwards. This is beneficial because higher frequencies have a greater range of potential unique lower frequencies they can be adjusted to. For example, a frequency of 10 can be decreased to any of 9, 8, 7, ... until it becomes unique, giving us more "room" to make adjustments.\n\n#### Step 2: Iterate and Minimize\n\n- **Why Iterate Through Sorted Frequencies?**: \n After sorting, the frequencies are now in an ordered list, `sorted_freqs`. We iterate through this list, and for each frequency, we decrease it until it becomes unique. The advantage of working with sorted frequencies is that we can minimize the number of operations by taking advantage of the "room" lower frequencies offer for adjustment.\n\n#### Step 3: Early Exit Optimization\n\n- **Why Early Exit?**: \n An important optimization is to exit the loop early when you find a frequency that is already unique. In a sorted list, if you encounter a frequency that is unique, then all frequencies that come after it in the list will also be unique. This is because they will all be smaller and we have already confirmed that larger frequencies are unique.\n\n#### Step 4: Return Deletions\n\n- **What is the output?**: \n After iterating through `sorted_freqs` and making the necessary adjustments, we return the total number of deletions required to make the frequencies unique.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$ O(n \\log n) $$ due to sorting. Sorting the frequencies is the most time-consuming part here.\n- **Space Complexity**: $$ O(n) $$ for storing frequencies and used frequencies.\n\n## Code Sorting\n``` Python []\n# Sorting Approach\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n sorted_freqs = sorted(cnt.values(), reverse=True)\n \n for freq in sorted_freqs:\n if freq not in used_frequencies: # Early exit condition\n used_frequencies.add(freq)\n continue \n\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n\n used_frequencies.add(freq)\n \n return deletions\n```\n``` Go []\nfunc minDeletions(s string) int {\n\tcnt := make(map[rune]int)\n\tdeletions := 0\n\tused_frequencies := make(map[int]bool)\n\n\tfor _, c := range s {\n\t\tcnt[c]++\n\t}\n\n\tsortedFreqs := make([]int, 0, len(cnt))\n\tfor _, freq := range cnt {\n\t\tsortedFreqs = append(sortedFreqs, freq)\n\t}\n\tsort.Sort(sort.Reverse(sort.IntSlice(sortedFreqs)))\n\n\tfor _, freq := range sortedFreqs {\n\t\tfor freq > 0 && used_frequencies[freq] {\n\t\t\tfreq--\n\t\t\tdeletions++\n\t\t}\n\t\tused_frequencies[freq] = true\n\t}\n\n\treturn deletions\n}\n```\n\n---\n\n## Heap / Priority Queue 3/3: Prioritize Frequencies to Adjust\n\n### Detailed Steps\n\n#### Step 1: Count Frequencies and Build Heap\n\n- **Why Use a Heap?**: \n A min-heap is a specialized tree-based data structure that keeps the smallest element at the top. In the context of this problem, the smallest frequency will always be at the top of the heap. This allows us to focus on making the smallest frequencies unique first, which is generally easier and requires fewer adjustments.\n\n#### Step 2: Iterate and Minimize Using Heap\n\n- **Why Heap?**: \n The heap automatically "tells" us which frequency should be adjusted next (it will be the smallest one). We pop this smallest frequency and make it unique by decrementing it until it no longer matches any other frequency. The advantage here is that the heap dynamically updates, so after each adjustment, the next smallest frequency is ready for us to examine.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$ O(n \\log n) $$ due to heap operations. Each insertion and removal from the heap takes $$ \\log n $$ time, and we may need to do this $$ n $$ times.\n- **Space Complexity**: $$ O(n) $$ for storing the frequencies in `cnt` and the used frequencies in `used_frequencies`.\n\n\n## Code Heap\n``` Python []\n# Heap / Priority Queue Approach\nclass Solution:\n def minDeletions(self, s: str) -> int:\n cnt = Counter(s)\n deletions = 0\n used_frequencies = set()\n \n heap = list(cnt.values())\n heapq.heapify(heap)\n \n while heap:\n freq = heapq.heappop(heap)\n while freq > 0 and freq in used_frequencies:\n freq -= 1\n deletions += 1\n used_frequencies.add(freq)\n \n return deletions\n```\n``` Go []\nimport (\n\t"container/heap"\n\t"fmt"\n)\n\ntype IntHeap []int\n\nfunc (h IntHeap) Len() int { return len(h) }\nfunc (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }\nfunc (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *IntHeap) Push(x interface{}) {\n\t*h = append(*h, x.(int))\n}\n\nfunc (h *IntHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\tx := old[n-1]\n\t*h = old[0 : n-1]\n\treturn x\n}\n\nfunc minDeletions(s string) int {\n\tcnt := make(map[rune]int)\n\tdeletions := 0\n\tused_frequencies := make(map[int]bool)\n\n\tfor _, c := range s {\n\t\tcnt[c]++\n\t}\n\n\th := &IntHeap{}\n\theap.Init(h)\n\n\tfor _, freq := range cnt {\n\t\theap.Push(h, freq)\n\t}\n\n\tfor h.Len() > 0 {\n\t\tfreq := heap.Pop(h).(int)\n\t\tfor freq > 0 && used_frequencies[freq] {\n\t\t\tfreq--\n\t\t\tdeletions++\n\t\t}\n\t\tused_frequencies[freq] = true\n\t}\n\n\treturn deletions\n}\n```\n\n---\n\n## Performance\n\n| Language | Approach | Execution Time (ms) | Memory Usage (MB) |\n|------------|-----------|---------------------|-------------------|\n| Rust | Greedy | 31 | 2.5 |\n| Go | Heap | 51 | 6.8 |\n| Java | Greedy | 50 | 45 |\n| C++ | Greedy | 75 | 17.5 |\n| Go | Greedy | 62 | 6.6 |\n| PHP | Greedy | 95 | 26.2 |\n| Python3 | Heap | 99 | 17.1 |\n| Python3 | Greedy | 105 | 17.2 |\n| C# | Greedy | 105 | 42.8 |\n| Python3 | Sorting | 106 | 17.1 |\n| JavaScript | Greedy | 125 | 48.4 |\n\n\n\n\n## Live Coding & Explain Heap & Sort\nhttps://youtu.be/myQ6RGLyaDM?si=5nfp8jnnsp_srtCz\n\n## Code Highlights and Best Practices\n\n- The Greedy Algorithm is simple and efficient, making it a go-to approach for this problem.\n- The Sorting Algorithm provides another effective way to tackle this problem but with a slight overhead due to sorting.\n- The Heap / Priority Queue approach adds a layer of optimization by prioritizing which frequencies to adjust first.\n\nBy mastering these approaches, you\'ll be well-equipped to tackle other frequency-based or deletion-minimizing problems, which are common in coding interviews and competitive programming. So, are you ready to make some string frequencies unique? Let\'s get coding!\n\n\n | 106 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
Simplest Python solution. Counter + check for values | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDeletions(self, s: str) -> int:\n d = Counter(s)\n ans = 0\n seen = set()\n for k, v in d.items():\n while v and v in seen:\n ans += 1\n v -= 1\n seen.add(v)\n return ans\n``` | 5 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
Simplest Python solution. Counter + check for values | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minDeletions(self, s: str) -> int:\n d = Counter(s)\n ans = 0\n seen = set()\n for k, v in d.items():\n while v and v in seen:\n ans += 1\n v -= 1\n seen.add(v)\n return ans\n``` | 5 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
✅99.32%☑️Greedy+Heap|🔥|Beginner Friendly✅☑️||Full Explanation🔥||C++||Java||Python✅☑️ | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Problem Understanding\nThe given problem **asks you to find the minimum number of characters you need to delete from a string s to make it "good."** A string is **considered "good" if there are no two different characters in it that have the same frequency.**\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this approach is that by **sorting the frequencies in non-decreasing order**, you can start from the highest frequency characters **and gradually decrease their frequencies by deleting characters until they become unique.** This ensures that you delete the minimum number of characters necessary to satisfy the condition of having no two different characters with the same frequency.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initialize a vector freq of size 26** (for the lowercase English letters) to store the frequency of each character in the input string s. Initialize all elements of freq to 0.\n\n2. **Iterate through the characters of the string s and update the frequency of each character in the freq vector**.\n\n3. **Sort the freq vector** in ascending order. This will arrange the frequencies in non-decreasing order.\n\n4. Initialize a **variable del to keep track of the minimum deletions** required and set it to 0.\n\n5. Iterate through the sorted freq vector in reverse order, starting **from index 24 (since there are 26 lowercase English letters).**\n\n6. Inside the loop, check **if the current frequency freq[i] is greater than or equal to the next frequency freq[i+1]**. If it is, then you need to delete some characters to make them unique.\n\n7. Calculate the number of characters to delete to make freq[i] less than freq[i+1]. **This is done by subtracting freq[i+1] - 1 from freq[i] and setting freq[i] to this new value**. Update the del variable by adding this difference.\n\n8. Continue this process until you have iterated through all frequencies, or until you encounter a frequency of 0, indicating that there are no more characters of that frequency.\n\n9. **Finally, return the value of del**, which represents the minimum number of deletions required to make the string "good."\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(k), where k=26\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n# Code(Greedy Approach)\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n // Create a vector to store the frequency of each lowercase English letter (fixed size of 26).\n vector<int> freq(26, 0);\n\n // Iterate through the characters of the input string s to count their frequencies.\n for (char c : s) {\n freq[c - \'a\']++; // Increment the corresponding frequency counter.\n }\n\n // Sort the frequency vector in non-decreasing order.\n sort(freq.begin(), freq.end());\n\n // Initialize a variable to keep track of the minimum number of deletions needed.\n int del = 0;\n\n // Iterate through the sorted frequency vector in reverse order.\n for (int i = 24; i >= 0; i--) {\n // If the current frequency is 0, break the loop (no more characters with this frequency).\n if (freq[i] == 0) {\n break;\n }\n \n // Check if the current frequency is greater than or equal to the next frequency.\n if (freq[i] >= freq[i + 1]) {\n int prev = freq[i];\n // Reduce the current frequency to make it one less than the next frequency.\n freq[i] = max(0, freq[i + 1] - 1);\n // Update the deletion count by the difference between previous and current frequency.\n del += prev - freq[i];\n }\n }\n\n // Return the minimum number of deletions required to make the string "good."\n return del;\n }\n};\n```\n```Java []\nimport java.util.Arrays;\n\npublic class Solution {\n public int minDeletions(String s) {\n int[] freq = new int[26]; // Create an array to store character frequencies\n \n for (char c : s.toCharArray()) {\n freq[c - \'a\']++; // Count the frequency of each character\n }\n \n Arrays.sort(freq); // Sort frequencies in ascending order\n \n int del = 0; // Initialize the deletion count\n \n for (int i = 24; i >= 0; i--) {\n if (freq[i] == 0) {\n break; // No more characters with this frequency\n }\n \n if (freq[i] >= freq[i + 1]) {\n int prev = freq[i];\n freq[i] = Math.max(0, freq[i + 1] - 1);\n del += prev - freq[i]; // Update the deletion count\n }\n }\n \n return del; // Return the minimum deletions required\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n freq = [0] * 26 # Create a list to store character frequencies\n \n for c in s:\n freq[ord(c) - ord(\'a\')] += 1 # Count the frequency of each character\n \n freq.sort() # Sort frequencies in ascending order\n \n del_count = 0 # Initialize the deletion count\n \n for i in range(24, -1, -1):\n if freq[i] == 0:\n break # No more characters with this frequency\n \n if freq[i] >= freq[i + 1]:\n prev = freq[i]\n freq[i] = max(0, freq[i + 1] - 1)\n del_count += prev - freq[i] # Update the deletion count\n \n return del_count # Return the minimum deletions required\n\n```\n```Javascript []\nvar minDeletions = function(s) {\n let freq = new Array(26).fill(0); // Create an array to store character frequencies\n \n for (let i = 0; i < s.length; i++) {\n freq[s.charCodeAt(i) - \'a\'.charCodeAt(0)]++; // Count the frequency of each character\n }\n \n freq.sort((a, b) => a - b); // Sort frequencies in ascending order\n \n let del = 0; // Initialize the deletion count\n \n for (let i = 24; i >= 0; i--) {\n if (freq[i] === 0) {\n break; // No more characters with this frequency\n }\n \n if (freq[i] >= freq[i + 1]) {\n let prev = freq[i];\n freq[i] = Math.max(0, freq[i + 1] - 1);\n del += prev - freq[i]; // Update the deletion count\n }\n }\n \n return del; // Return the minimum deletions required\n};\n\n```\n# Code using Heap Method\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n // Create an unordered map to count the frequency of each character.\n unordered_map<char, int> mp;\n\n // Iterate through the characters in the input string \'s\'.\n for (auto &it : s) {\n mp[it]++; // Increment the character\'s frequency in the map.\n }\n\n // Create a max-heap (priority queue) to store character frequencies in decreasing order.\n priority_queue<int> pq;\n\n // Populate the max-heap with character frequencies from the map.\n for (auto &it : mp) {\n pq.push(it.second);\n }\n\n // Initialize a variable to keep track of the minimum number of deletions needed.\n int count = 0;\n\n // Continue as long as there are at least two frequencies in the max-heap.\n while (pq.size() != 1) {\n int top = pq.top(); // Get the character frequency with the highest count.\n pq.pop(); // Remove it from the max-heap.\n\n // Check if the next character in the max-heap has the same frequency as \'top\' (and it\'s not zero).\n if (pq.top() == top && top != 0) {\n count++; // Increment the deletion count.\n pq.push(top - 1); // Decrease \'top\' frequency by 1 and push it back into the max-heap.\n }\n }\n\n // Return the minimum number of deletions required to make the string "good."\n return count;\n }\n};\n\n```\n```java []\nimport java.util.HashMap;\nimport java.util.PriorityQueue;\nimport java.util.Map;\n\npublic class Solution {\n public int minDeletions(String s) {\n // Create a HashMap to count the frequency of each character.\n Map<Character, Integer> frequencyMap = new HashMap<>();\n\n // Iterate through the characters in the input string \'s\'.\n for (char c : s.toCharArray()) {\n frequencyMap.put(c, frequencyMap.getOrDefault(c, 0) + 1);\n }\n\n // Create a max-heap (PriorityQueue) to store character frequencies in decreasing order.\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);\n\n // Populate the max-heap with character frequencies from the map.\n maxHeap.addAll(frequencyMap.values());\n\n // Initialize a variable to keep track of the minimum number of deletions needed.\n int count = 0;\n\n // Continue as long as there are at least two frequencies in the max-heap.\n while (maxHeap.size() > 1) {\n int top = maxHeap.poll(); // Get the character frequency with the highest count.\n\n // Check if the next character in the max-heap has the same frequency as \'top\' (and it\'s not zero).\n if (maxHeap.peek() != null && maxHeap.peek() == top && top != 0) {\n count++; // Increment the deletion count.\n maxHeap.add(top - 1); // Decrease \'top\' frequency by 1 and push it back into the max-heap.\n }\n }\n\n // Return the minimum number of deletions required to make the string "good."\n return count;\n }\n}\n\n```\n---\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n\n | 189 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
✅99.32%☑️Greedy+Heap|🔥|Beginner Friendly✅☑️||Full Explanation🔥||C++||Java||Python✅☑️ | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Problem Understanding\nThe given problem **asks you to find the minimum number of characters you need to delete from a string s to make it "good."** A string is **considered "good" if there are no two different characters in it that have the same frequency.**\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this approach is that by **sorting the frequencies in non-decreasing order**, you can start from the highest frequency characters **and gradually decrease their frequencies by deleting characters until they become unique.** This ensures that you delete the minimum number of characters necessary to satisfy the condition of having no two different characters with the same frequency.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initialize a vector freq of size 26** (for the lowercase English letters) to store the frequency of each character in the input string s. Initialize all elements of freq to 0.\n\n2. **Iterate through the characters of the string s and update the frequency of each character in the freq vector**.\n\n3. **Sort the freq vector** in ascending order. This will arrange the frequencies in non-decreasing order.\n\n4. Initialize a **variable del to keep track of the minimum deletions** required and set it to 0.\n\n5. Iterate through the sorted freq vector in reverse order, starting **from index 24 (since there are 26 lowercase English letters).**\n\n6. Inside the loop, check **if the current frequency freq[i] is greater than or equal to the next frequency freq[i+1]**. If it is, then you need to delete some characters to make them unique.\n\n7. Calculate the number of characters to delete to make freq[i] less than freq[i+1]. **This is done by subtracting freq[i+1] - 1 from freq[i] and setting freq[i] to this new value**. Update the del variable by adding this difference.\n\n8. Continue this process until you have iterated through all frequencies, or until you encounter a frequency of 0, indicating that there are no more characters of that frequency.\n\n9. **Finally, return the value of del**, which represents the minimum number of deletions required to make the string "good."\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(k), where k=26\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n# Code(Greedy Approach)\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n // Create a vector to store the frequency of each lowercase English letter (fixed size of 26).\n vector<int> freq(26, 0);\n\n // Iterate through the characters of the input string s to count their frequencies.\n for (char c : s) {\n freq[c - \'a\']++; // Increment the corresponding frequency counter.\n }\n\n // Sort the frequency vector in non-decreasing order.\n sort(freq.begin(), freq.end());\n\n // Initialize a variable to keep track of the minimum number of deletions needed.\n int del = 0;\n\n // Iterate through the sorted frequency vector in reverse order.\n for (int i = 24; i >= 0; i--) {\n // If the current frequency is 0, break the loop (no more characters with this frequency).\n if (freq[i] == 0) {\n break;\n }\n \n // Check if the current frequency is greater than or equal to the next frequency.\n if (freq[i] >= freq[i + 1]) {\n int prev = freq[i];\n // Reduce the current frequency to make it one less than the next frequency.\n freq[i] = max(0, freq[i + 1] - 1);\n // Update the deletion count by the difference between previous and current frequency.\n del += prev - freq[i];\n }\n }\n\n // Return the minimum number of deletions required to make the string "good."\n return del;\n }\n};\n```\n```Java []\nimport java.util.Arrays;\n\npublic class Solution {\n public int minDeletions(String s) {\n int[] freq = new int[26]; // Create an array to store character frequencies\n \n for (char c : s.toCharArray()) {\n freq[c - \'a\']++; // Count the frequency of each character\n }\n \n Arrays.sort(freq); // Sort frequencies in ascending order\n \n int del = 0; // Initialize the deletion count\n \n for (int i = 24; i >= 0; i--) {\n if (freq[i] == 0) {\n break; // No more characters with this frequency\n }\n \n if (freq[i] >= freq[i + 1]) {\n int prev = freq[i];\n freq[i] = Math.max(0, freq[i + 1] - 1);\n del += prev - freq[i]; // Update the deletion count\n }\n }\n \n return del; // Return the minimum deletions required\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n freq = [0] * 26 # Create a list to store character frequencies\n \n for c in s:\n freq[ord(c) - ord(\'a\')] += 1 # Count the frequency of each character\n \n freq.sort() # Sort frequencies in ascending order\n \n del_count = 0 # Initialize the deletion count\n \n for i in range(24, -1, -1):\n if freq[i] == 0:\n break # No more characters with this frequency\n \n if freq[i] >= freq[i + 1]:\n prev = freq[i]\n freq[i] = max(0, freq[i + 1] - 1)\n del_count += prev - freq[i] # Update the deletion count\n \n return del_count # Return the minimum deletions required\n\n```\n```Javascript []\nvar minDeletions = function(s) {\n let freq = new Array(26).fill(0); // Create an array to store character frequencies\n \n for (let i = 0; i < s.length; i++) {\n freq[s.charCodeAt(i) - \'a\'.charCodeAt(0)]++; // Count the frequency of each character\n }\n \n freq.sort((a, b) => a - b); // Sort frequencies in ascending order\n \n let del = 0; // Initialize the deletion count\n \n for (let i = 24; i >= 0; i--) {\n if (freq[i] === 0) {\n break; // No more characters with this frequency\n }\n \n if (freq[i] >= freq[i + 1]) {\n let prev = freq[i];\n freq[i] = Math.max(0, freq[i + 1] - 1);\n del += prev - freq[i]; // Update the deletion count\n }\n }\n \n return del; // Return the minimum deletions required\n};\n\n```\n# Code using Heap Method\n```C++ []\nclass Solution {\npublic:\n int minDeletions(string s) {\n // Create an unordered map to count the frequency of each character.\n unordered_map<char, int> mp;\n\n // Iterate through the characters in the input string \'s\'.\n for (auto &it : s) {\n mp[it]++; // Increment the character\'s frequency in the map.\n }\n\n // Create a max-heap (priority queue) to store character frequencies in decreasing order.\n priority_queue<int> pq;\n\n // Populate the max-heap with character frequencies from the map.\n for (auto &it : mp) {\n pq.push(it.second);\n }\n\n // Initialize a variable to keep track of the minimum number of deletions needed.\n int count = 0;\n\n // Continue as long as there are at least two frequencies in the max-heap.\n while (pq.size() != 1) {\n int top = pq.top(); // Get the character frequency with the highest count.\n pq.pop(); // Remove it from the max-heap.\n\n // Check if the next character in the max-heap has the same frequency as \'top\' (and it\'s not zero).\n if (pq.top() == top && top != 0) {\n count++; // Increment the deletion count.\n pq.push(top - 1); // Decrease \'top\' frequency by 1 and push it back into the max-heap.\n }\n }\n\n // Return the minimum number of deletions required to make the string "good."\n return count;\n }\n};\n\n```\n```java []\nimport java.util.HashMap;\nimport java.util.PriorityQueue;\nimport java.util.Map;\n\npublic class Solution {\n public int minDeletions(String s) {\n // Create a HashMap to count the frequency of each character.\n Map<Character, Integer> frequencyMap = new HashMap<>();\n\n // Iterate through the characters in the input string \'s\'.\n for (char c : s.toCharArray()) {\n frequencyMap.put(c, frequencyMap.getOrDefault(c, 0) + 1);\n }\n\n // Create a max-heap (PriorityQueue) to store character frequencies in decreasing order.\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);\n\n // Populate the max-heap with character frequencies from the map.\n maxHeap.addAll(frequencyMap.values());\n\n // Initialize a variable to keep track of the minimum number of deletions needed.\n int count = 0;\n\n // Continue as long as there are at least two frequencies in the max-heap.\n while (maxHeap.size() > 1) {\n int top = maxHeap.poll(); // Get the character frequency with the highest count.\n\n // Check if the next character in the max-heap has the same frequency as \'top\' (and it\'s not zero).\n if (maxHeap.peek() != null && maxHeap.peek() == top && top != 0) {\n count++; // Increment the deletion count.\n maxHeap.add(top - 1); // Decrease \'top\' frequency by 1 and push it back into the max-heap.\n }\n }\n\n // Return the minimum number of deletions required to make the string "good."\n return count;\n }\n}\n\n```\n---\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n\n | 189 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
No Priority Queue, No Heap, No Sorting! 10 Liner Solution using hashmap and counters! | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor each letter check if a previous letter has the same count. If Yes? Keep on decreasing until we get a unique count (we might even make it 0 i.e. delete that letter altogether!)\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a counter to track the counts. E.g. `{a: 2, b:2, c:1}`.\nWe have a variable `ans=0` to store the number of deletions.\nNow we keep a hash map that stores the letters and their counts in the final good string.\nThe computation goes on as :\nThe Hash Map now has:`{2:a}`. Next we try to add b for index 2 again. But we see that 2 already exists in the keys. This means we previously have some other letter (here a) that has the same count. In order to make it a *good string* we delete 1 from count of b and increase 1 for our ans (ans+=1).\nCounter Now : `{a:2, b:1, c:1}`. Since hash map does not have 1 as the key we can add b to the Hash Map. \nHash Map now: `{2:a, 1:b}`.\nNext, we cannot add c to the hash map as count[\'c\'] is 1 (Counter: `{a:2, b:1, c:1}`) and we already have b mapped to the index 1. Hence, we have no other choice but to delete c from the string. Hence count[\'c\']-=1 and ans+=1.\nHence, counter is now `{a:2, b:1, c:0}`.\nNote, that we do not add any letter for index = 0 in hash Map as the hash map only stores letters that appear in the final string.\nWe return ans = 2.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDeletions(self, s: str) -> int:\n count, hashMap, ans = collections.Counter(s), dict(), 0\n for i in count.keys():\n while count[i] > 0 and count[i] in hashMap.keys():\n ans += 1\n count[i] -= 1\n if count[i] != 0:\n hashMap[count[i]] = i\n return ans\n \n``` | 2 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
No Priority Queue, No Heap, No Sorting! 10 Liner Solution using hashmap and counters! | minimum-deletions-to-make-character-frequencies-unique | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor each letter check if a previous letter has the same count. If Yes? Keep on decreasing until we get a unique count (we might even make it 0 i.e. delete that letter altogether!)\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a counter to track the counts. E.g. `{a: 2, b:2, c:1}`.\nWe have a variable `ans=0` to store the number of deletions.\nNow we keep a hash map that stores the letters and their counts in the final good string.\nThe computation goes on as :\nThe Hash Map now has:`{2:a}`. Next we try to add b for index 2 again. But we see that 2 already exists in the keys. This means we previously have some other letter (here a) that has the same count. In order to make it a *good string* we delete 1 from count of b and increase 1 for our ans (ans+=1).\nCounter Now : `{a:2, b:1, c:1}`. Since hash map does not have 1 as the key we can add b to the Hash Map. \nHash Map now: `{2:a, 1:b}`.\nNext, we cannot add c to the hash map as count[\'c\'] is 1 (Counter: `{a:2, b:1, c:1}`) and we already have b mapped to the index 1. Hence, we have no other choice but to delete c from the string. Hence count[\'c\']-=1 and ans+=1.\nHence, counter is now `{a:2, b:1, c:0}`.\nNote, that we do not add any letter for index = 0 in hash Map as the hash map only stores letters that appear in the final string.\nWe return ans = 2.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDeletions(self, s: str) -> int:\n count, hashMap, ans = collections.Counter(s), dict(), 0\n for i in count.keys():\n while count[i] > 0 and count[i] in hashMap.keys():\n ans += 1\n count[i] -= 1\n if count[i] != 0:\n hashMap[count[i]] = i\n return ans\n \n``` | 2 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
Minimum Deletions to Make Character Frequencies Unique Java Python and CPP | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Intuition\nThe problem seems to be about finding the minimum number of deletions required to make all characters in the given string appear with unique frequencies. To do this, we can keep track of the frequency of each character and then iteratively check and possibly reduce the frequency of characters until all frequencies are unique.\n\n# Approach\n1. Initialize an array `freq` of size 26 to store the frequency of each lowercase alphabet. Initialize a HashSet `hs` to keep track of frequencies encountered so far.\n2. Iterate through the input string `s`, and for each character, update its frequency in the `freq` array.\n3. Iterate through the `freq` array, and for each frequency `i`, perform the following steps:\n - While `i` is greater than 0 and `hs` already contains `i`, increment a counter `count` and decrement `i`.\n - Add the updated `i` to the `hs` set to mark it as encountered.\n4. After processing all frequencies in the `freq` array, return the `count` as the minimum number of deletions required to make all frequencies unique.\n\n# Complexity\n- Time complexity: The code iterates through the input string once to calculate the frequency of characters, and then it iterates through the frequency array. Therefore, the time complexity is O(n), where n is the length of the input string `s`.\n\n- Space complexity: The code uses two data structures of constant size (freq array of size 26 and HashSet). Thus, the space complexity is O(1), as it does not depend on the size of the input string.\n\n```Java []\nclass Solution {\n public int minDeletions(String s) {\n char freq[] = new char[26];\n for(int i=0;i<s.length();i++){\n freq[s.charAt(i)-\'a\']++;\n }\n HashSet<Integer> hs = new HashSet<>();\n int count =0;\n for(int i :freq){\n while(i>0 && hs.contains(i)){\n count++;\n i--;\n }\n hs.add(i);\n }\n return count;\n }\n}\n```\n```CPP []\nclass Solution {\npublic:\n int minDeletions(string s) {\n vector<int> freq(26, 0);\n for (char c : s) {\n freq[c - \'a\']++;\n }\n \n unordered_set<int> hs;\n int count = 0;\n for (int i : freq) {\n while (i > 0 && hs.count(i)) {\n count++;\n i--;\n }\n hs.insert(i);\n }\n \n return count;\n }\n};\n\n```\n```python []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n freq = [0] * 26\n for char in s:\n freq[ord(char) - ord(\'a\')] += 1\n \n hs = set()\n count = 0\n for i in freq:\n while i > 0 and i in hs:\n count += 1\n i -= 1\n hs.add(i)\n \n return count\n\n```\n\n | 1 | A string `s` is called **good** if there are no two different characters in `s` that have the same **frequency**.
Given a string `s`, return _the **minimum** number of characters you need to delete to make_ `s` _**good**._
The **frequency** of a character in a string is the number of times it appears in the string. For example, in the string `"aab "`, the **frequency** of `'a'` is `2`, while the **frequency** of `'b'` is `1`.
**Example 1:**
**Input:** s = "aab "
**Output:** 0
**Explanation:** `s` is already good.
**Example 2:**
**Input:** s = "aaabbbcc "
**Output:** 2
**Explanation:** You can delete two 'b's resulting in the good string "aaabcc ".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc ".
**Example 3:**
**Input:** s = "ceabaacb "
**Output:** 2
**Explanation:** You can delete both 'c's resulting in the good string "eabaab ".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Observe that shifting a letter x times has the same effect of shifting the letter x + 26 times. You need to check whether k is large enough to cover all shifts with the same remainder after modulo 26. |
Minimum Deletions to Make Character Frequencies Unique Java Python and CPP | minimum-deletions-to-make-character-frequencies-unique | 1 | 1 | # Intuition\nThe problem seems to be about finding the minimum number of deletions required to make all characters in the given string appear with unique frequencies. To do this, we can keep track of the frequency of each character and then iteratively check and possibly reduce the frequency of characters until all frequencies are unique.\n\n# Approach\n1. Initialize an array `freq` of size 26 to store the frequency of each lowercase alphabet. Initialize a HashSet `hs` to keep track of frequencies encountered so far.\n2. Iterate through the input string `s`, and for each character, update its frequency in the `freq` array.\n3. Iterate through the `freq` array, and for each frequency `i`, perform the following steps:\n - While `i` is greater than 0 and `hs` already contains `i`, increment a counter `count` and decrement `i`.\n - Add the updated `i` to the `hs` set to mark it as encountered.\n4. After processing all frequencies in the `freq` array, return the `count` as the minimum number of deletions required to make all frequencies unique.\n\n# Complexity\n- Time complexity: The code iterates through the input string once to calculate the frequency of characters, and then it iterates through the frequency array. Therefore, the time complexity is O(n), where n is the length of the input string `s`.\n\n- Space complexity: The code uses two data structures of constant size (freq array of size 26 and HashSet). Thus, the space complexity is O(1), as it does not depend on the size of the input string.\n\n```Java []\nclass Solution {\n public int minDeletions(String s) {\n char freq[] = new char[26];\n for(int i=0;i<s.length();i++){\n freq[s.charAt(i)-\'a\']++;\n }\n HashSet<Integer> hs = new HashSet<>();\n int count =0;\n for(int i :freq){\n while(i>0 && hs.contains(i)){\n count++;\n i--;\n }\n hs.add(i);\n }\n return count;\n }\n}\n```\n```CPP []\nclass Solution {\npublic:\n int minDeletions(string s) {\n vector<int> freq(26, 0);\n for (char c : s) {\n freq[c - \'a\']++;\n }\n \n unordered_set<int> hs;\n int count = 0;\n for (int i : freq) {\n while (i > 0 && hs.count(i)) {\n count++;\n i--;\n }\n hs.insert(i);\n }\n \n return count;\n }\n};\n\n```\n```python []\nclass Solution:\n def minDeletions(self, s: str) -> int:\n freq = [0] * 26\n for char in s:\n freq[ord(char) - ord(\'a\')] += 1\n \n hs = set()\n count = 0\n for i in freq:\n while i > 0 and i in hs:\n count += 1\n i -= 1\n hs.add(i)\n \n return count\n\n```\n\n | 1 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
✔ Python3 Solution | Sorting | O(nlogn) | sell-diminishing-valued-colored-balls | 0 | 1 | # Complexity\n- Time complexity: $$O(nlogn)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxProfit(self, A, O):\n nsum = lambda n : (n * (n + 1)) // 2\n A.sort(reverse = True)\n A.append(0)\n ans, mod = 0, 10 ** 9 + 7\n for i in range(len(A) - 1):\n if (i + 1) * (A[i] - A[i + 1]) > O:\n k, l = O // (i + 1), O % (i + 1)\n return (ans + (i + 1) * (nsum(A[i]) - nsum(A[i] - k)) + l * (A[i] - k)) % mod\n ans = (ans + (i + 1) * (nsum(A[i]) - nsum(A[i + 1]))) % mod\n O -= (i + 1) * (A[i] - A[i + 1])\n return ans\n``` | 1 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
✔ Python3 Solution | Sorting | O(nlogn) | sell-diminishing-valued-colored-balls | 0 | 1 | # Complexity\n- Time complexity: $$O(nlogn)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxProfit(self, A, O):\n nsum = lambda n : (n * (n + 1)) // 2\n A.sort(reverse = True)\n A.append(0)\n ans, mod = 0, 10 ** 9 + 7\n for i in range(len(A) - 1):\n if (i + 1) * (A[i] - A[i + 1]) > O:\n k, l = O // (i + 1), O % (i + 1)\n return (ans + (i + 1) * (nsum(A[i]) - nsum(A[i] - k)) + l * (A[i] - k)) % mod\n ans = (ans + (i + 1) * (nsum(A[i]) - nsum(A[i + 1]))) % mod\n O -= (i + 1) * (A[i] - A[i + 1])\n return ans\n``` | 1 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
[Python3] Greedy | sell-diminishing-valued-colored-balls | 0 | 1 | Algo \nFirst, it should be clear that we want to sell from the most abundant balls as much as possible as it is valued more than less abundant balls. In the spirit of this, we propose the below algo \n1) sort inventory in reverse order and append 0 at the end (for termination); \n2) scan through the inventory, and add the difference between adjacent categories to answer. \n\nAssume `inventory = [2,8,4,10,6]`. Then, we traverse inventory following 10->8->6->4->2->0. The evolution of inventory becomes \n```\n10 | 8 | 6 | 4 | 2\n 8 | 8 | 6 | 4 | 2\n 6 | 6 | 6 | 4 | 2\n 4 | 4 | 4 | 4 | 2\n 2 | 2 | 2 | 2 | 2 \n 0 | 0 | 0 | 0 | 0 \n```\nOf course, if in any step, we have enough order, return the answer. \n\n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n inventory.sort(reverse=True) # inventory high to low \n inventory += [0]\n ans = 0\n k = 1\n for i in range(len(inventory)-1): \n if inventory[i] > inventory[i+1]: \n if k*(inventory[i] - inventory[i+1]) < orders: \n ans += k*(inventory[i] + inventory[i+1] + 1)*(inventory[i] - inventory[i+1])//2 # arithmic sum \n orders -= k*(inventory[i] - inventory[i+1])\n else: \n q, r = divmod(orders, k)\n ans += k*(2*inventory[i] - q + 1) * q//2 + r*(inventory[i] - q)\n return ans % 1_000_000_007\n k += 1\n```\n\nEdited on 10/08/2020\nAdding binary serach solution \n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n fn = lambda x: sum(max(0, xx - x) for xx in inventory) # balls sold \n \n # last true binary search \n lo, hi = 0, 10**9\n while lo < hi: \n mid = lo + hi + 1 >> 1\n if fn(mid) >= orders: lo = mid\n else: hi = mid - 1\n \n ans = sum((x + lo + 1)*(x - lo)//2 for x in inventory if x > lo)\n return (ans - (fn(lo) - orders) * (lo + 1)) % 1_000_000_007\n``` | 36 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
[Python3] Greedy | sell-diminishing-valued-colored-balls | 0 | 1 | Algo \nFirst, it should be clear that we want to sell from the most abundant balls as much as possible as it is valued more than less abundant balls. In the spirit of this, we propose the below algo \n1) sort inventory in reverse order and append 0 at the end (for termination); \n2) scan through the inventory, and add the difference between adjacent categories to answer. \n\nAssume `inventory = [2,8,4,10,6]`. Then, we traverse inventory following 10->8->6->4->2->0. The evolution of inventory becomes \n```\n10 | 8 | 6 | 4 | 2\n 8 | 8 | 6 | 4 | 2\n 6 | 6 | 6 | 4 | 2\n 4 | 4 | 4 | 4 | 2\n 2 | 2 | 2 | 2 | 2 \n 0 | 0 | 0 | 0 | 0 \n```\nOf course, if in any step, we have enough order, return the answer. \n\n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n inventory.sort(reverse=True) # inventory high to low \n inventory += [0]\n ans = 0\n k = 1\n for i in range(len(inventory)-1): \n if inventory[i] > inventory[i+1]: \n if k*(inventory[i] - inventory[i+1]) < orders: \n ans += k*(inventory[i] + inventory[i+1] + 1)*(inventory[i] - inventory[i+1])//2 # arithmic sum \n orders -= k*(inventory[i] - inventory[i+1])\n else: \n q, r = divmod(orders, k)\n ans += k*(2*inventory[i] - q + 1) * q//2 + r*(inventory[i] - q)\n return ans % 1_000_000_007\n k += 1\n```\n\nEdited on 10/08/2020\nAdding binary serach solution \n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n fn = lambda x: sum(max(0, xx - x) for xx in inventory) # balls sold \n \n # last true binary search \n lo, hi = 0, 10**9\n while lo < hi: \n mid = lo + hi + 1 >> 1\n if fn(mid) >= orders: lo = mid\n else: hi = mid - 1\n \n ans = sum((x + lo + 1)*(x - lo)//2 for x in inventory if x > lo)\n return (ans - (fn(lo) - orders) * (lo + 1)) % 1_000_000_007\n``` | 36 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
85% TC and 84% SC easy python solution | sell-diminishing-valued-colored-balls | 0 | 1 | ```\ndef maxProfit(self, inventory: List[int], orders: int) -> int:\n\tinventory.sort()\n\ti, j = 1, inventory[-1]\n\tans = -1\n\tdef isValid(v):\n\t\tt = orders\n\t\tm = bisect_left(inventory, v)\n\t\tfor i in range(m, len(inventory)):\n\t\t\tt -= inventory[i] - v\n\t\t\tif(t <= 0):\n\t\t\t\treturn 1\n\t\tif(t <= len(inventory)-m):\n\t\t\treturn 1\n\t\treturn 0\n\twhile(i <= j):\n\t\tmid = i + (j-i) // 2\n\t\tif(isValid(mid)):\n\t\t\tans = mid\n\t\t\ti = mid+1\n\t\telse:\n\t\t\tj = mid-1\n\tif(ans == -1):\n\t\treturn -1\n\tans, v = 0, ans\n\tfor i in range(len(inventory)):\n\t\tif(inventory[i] > v):\n\t\t\tans = (ans + ((inventory[i]+1)*inventory[i])//2 - ((v+1)*v)//2) % 1000000007\n\t\t\torders -= inventory[i] - v\n\tif(orders):\n\t\tans = (ans + v * orders) % 1000000007\n\treturn ans\n``` | 1 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
85% TC and 84% SC easy python solution | sell-diminishing-valued-colored-balls | 0 | 1 | ```\ndef maxProfit(self, inventory: List[int], orders: int) -> int:\n\tinventory.sort()\n\ti, j = 1, inventory[-1]\n\tans = -1\n\tdef isValid(v):\n\t\tt = orders\n\t\tm = bisect_left(inventory, v)\n\t\tfor i in range(m, len(inventory)):\n\t\t\tt -= inventory[i] - v\n\t\t\tif(t <= 0):\n\t\t\t\treturn 1\n\t\tif(t <= len(inventory)-m):\n\t\t\treturn 1\n\t\treturn 0\n\twhile(i <= j):\n\t\tmid = i + (j-i) // 2\n\t\tif(isValid(mid)):\n\t\t\tans = mid\n\t\t\ti = mid+1\n\t\telse:\n\t\t\tj = mid-1\n\tif(ans == -1):\n\t\treturn -1\n\tans, v = 0, ans\n\tfor i in range(len(inventory)):\n\t\tif(inventory[i] > v):\n\t\t\tans = (ans + ((inventory[i]+1)*inventory[i])//2 - ((v+1)*v)//2) % 1000000007\n\t\t\torders -= inventory[i] - v\n\tif(orders):\n\t\tans = (ans + v * orders) % 1000000007\n\treturn ans\n``` | 1 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
Binary search | sell-diminishing-valued-colored-balls | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, inventory, orders: int) -> int:\n left = 0\n right = max(inventory)\n while right - left > 1:\n middle = (left + right) // 2\n sold_balls = sum(i - middle for i in inventory if i > middle)\n if sold_balls > orders:\n left = middle\n else:\n right = middle\n sold_balls = 0\n total_value = 0\n for i in inventory:\n if i > right:\n sold_balls += i - right\n total_value += (i + right + 1) * (i - right) // 2\n if sold_balls < orders:\n total_value += (orders - sold_balls) * right\n return total_value % 1_000_000_007\n``` | 14 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
Binary search | sell-diminishing-valued-colored-balls | 0 | 1 | ```\nclass Solution:\n def maxProfit(self, inventory, orders: int) -> int:\n left = 0\n right = max(inventory)\n while right - left > 1:\n middle = (left + right) // 2\n sold_balls = sum(i - middle for i in inventory if i > middle)\n if sold_balls > orders:\n left = middle\n else:\n right = middle\n sold_balls = 0\n total_value = 0\n for i in inventory:\n if i > right:\n sold_balls += i - right\n total_value += (i + right + 1) * (i - right) // 2\n if sold_balls < orders:\n total_value += (orders - sold_balls) * right\n return total_value % 1_000_000_007\n``` | 14 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
find error | sell-diminishing-valued-colored-balls | 0 | 1 | can anybody help me to find my mistake?? why my answer is not right\n# Code\n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n res = 0\n sorted(inventory)\n while orders>0:\n for i in range(len(inventory)):\n while inventory[i]>1:\n res += inventory[i]\n inventory[i] -= 1\n orders -= 1\n if orders == 0:\n return res\n return res\n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
find error | sell-diminishing-valued-colored-balls | 0 | 1 | can anybody help me to find my mistake?? why my answer is not right\n# Code\n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n res = 0\n sorted(inventory)\n while orders>0:\n for i in range(len(inventory)):\n while inventory[i]>1:\n res += inventory[i]\n inventory[i] -= 1\n orders -= 1\n if orders == 0:\n return res\n return res\n``` | 0 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
[Python3] Heap 680 ms | sell-diminishing-valued-colored-balls | 0 | 1 | ```py3\nclass Solution:\n def maxProfit(self, h: List[int], orders: int) -> int:\n MOD = int(1e9 + 7)\n def series_sum_length(b, i):\n a = b - (i - 1)\n a_quotient, a_remainder = divmod(a * i, 2)\n b_quotient, b_remainder = divmod(b * i, 2)\n result = (a_quotient % MOD + b_quotient % MOD + b_remainder % MOD) % MOD\n return int(result)\n h = [-v for v in h]\n heapify(h)\n ans = 0\n multiplier = 1\n ret = False\n while orders > 0:\n last = heappop(h)\n if not h:\n return (ans + series_sum_length(-last, orders)) % MOD\n ball = heappop(h)\n while ball == last:\n multiplier += 1\n if not h:\n ret = True\n break\n ball = heappop(h)\n res, rem = divmod(orders, multiplier)\n if ret or res < ball - last:\n ans += (series_sum_length(-last, res) * multiplier) % MOD\n ans %= MOD\n ans += ((-last - res) * rem) % MOD\n return ans % MOD\n ans += (series_sum_length(-last, ball - last) * multiplier) % MOD\n ans %= MOD\n res -= ball - last\n orders = multiplier * res + rem\n heappush(h, ball)\n heappush(h, ball)\n return ans\n\n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
[Python3] Heap 680 ms | sell-diminishing-valued-colored-balls | 0 | 1 | ```py3\nclass Solution:\n def maxProfit(self, h: List[int], orders: int) -> int:\n MOD = int(1e9 + 7)\n def series_sum_length(b, i):\n a = b - (i - 1)\n a_quotient, a_remainder = divmod(a * i, 2)\n b_quotient, b_remainder = divmod(b * i, 2)\n result = (a_quotient % MOD + b_quotient % MOD + b_remainder % MOD) % MOD\n return int(result)\n h = [-v for v in h]\n heapify(h)\n ans = 0\n multiplier = 1\n ret = False\n while orders > 0:\n last = heappop(h)\n if not h:\n return (ans + series_sum_length(-last, orders)) % MOD\n ball = heappop(h)\n while ball == last:\n multiplier += 1\n if not h:\n ret = True\n break\n ball = heappop(h)\n res, rem = divmod(orders, multiplier)\n if ret or res < ball - last:\n ans += (series_sum_length(-last, res) * multiplier) % MOD\n ans %= MOD\n ans += ((-last - res) * rem) % MOD\n return ans % MOD\n ans += (series_sum_length(-last, ball - last) * multiplier) % MOD\n ans %= MOD\n res -= ball - last\n orders = multiplier * res + rem\n heappush(h, ball)\n heappush(h, ball)\n return ans\n\n``` | 0 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
[Python] Greedy & Math | sell-diminishing-valued-colored-balls | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n inv, curOrders, curSum, MOD = sorted(inventory, reverse=True) + [0], 0, 0, 1000000007\n for i in range(1, len(inv)):\n if inv[i - 1] == inv[i]: continue\n increments = i * (inv[i - 1] - inv[i])\n if increments + curOrders < orders:\n curOrders += increments\n curSum += ((inv[i - 1] + inv[i] + 1) * increments // 2) % MOD\n continue\n q, r = divmod(orders - curOrders, i)\n return (curSum + q * i * (2 * inv[i - 1] - q + 1) // 2 + (inv[i - 1] - q) * r) % MOD\n``` | 0 | You have an `inventory` of different colored balls, and there is a customer that wants `orders` balls of **any** color.
The customer weirdly values the colored balls. Each colored ball's value is the number of balls **of that color** you currently have in your `inventory`. For example, if you own `6` yellow balls, the customer would pay `6` for the first yellow ball. After the transaction, there are only `5` yellow balls left, so the next yellow ball is then valued at `5` (i.e., the value of the balls decreases as you sell more to the customer).
You are given an integer array, `inventory`, where `inventory[i]` represents the number of balls of the `ith` color that you initially own. You are also given an integer `orders`, which represents the total number of balls that the customer wants. You can sell the balls **in any order**.
Return _the **maximum** total value that you can attain after selling_ `orders` _colored balls_. As the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** inventory = \[2,5\], orders = 4
**Output:** 14
**Explanation:** Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.
**Example 2:**
**Input:** inventory = \[3,5\], orders = 6
**Output:** 19
**Explanation:** Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.
**Constraints:**
* `1 <= inventory.length <= 105`
* `1 <= inventory[i] <= 109`
* `1 <= orders <= min(sum(inventory[i]), 109)` | Use a stack to keep opening brackets. If you face single closing ')' add 1 to the answer and consider it as '))'. If you have '))' with empty stack, add 1 to the answer, If after finishing you have x opening remaining in the stack, add 2x to the answer. |
[Python] Greedy & Math | sell-diminishing-valued-colored-balls | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxProfit(self, inventory: List[int], orders: int) -> int:\n inv, curOrders, curSum, MOD = sorted(inventory, reverse=True) + [0], 0, 0, 1000000007\n for i in range(1, len(inv)):\n if inv[i - 1] == inv[i]: continue\n increments = i * (inv[i - 1] - inv[i])\n if increments + curOrders < orders:\n curOrders += increments\n curSum += ((inv[i - 1] + inv[i] + 1) * increments // 2) % MOD\n continue\n q, r = divmod(orders - curOrders, i)\n return (curSum + q * i * (2 * inv[i - 1] - q + 1) // 2 + (inv[i - 1] - q) * r) % MOD\n``` | 0 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
python3 SortedList Soultion in O(nlogn) | create-sorted-array-through-instructions | 0 | 1 | ```\nfrom sortedcontainers import SortedList\nclass Solution:\n def createSortedArray(self, ins: List[int]) -> int:\n mod = 10**9+7\n dicti = defaultdict(int)\n s1 = SortedList()\n sum_ = 0\n \n for i in range(len(ins)):\n dicti[ins[i]] += 1\n s1.add(ins[i])\n if i == 0:\n sum_ = (sum_+0)%mod\n else:\n leftIndex = s1.bisect_left(ins[i])\n small = leftIndex - 0\n big = len(s1) - leftIndex\n if dicti[ins[i]]>0:\n big -= dicti[ins[i]]\n sum_ = (sum_+min(small,big))%mod\n return sum_ | 6 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
python3 SortedList Soultion in O(nlogn) | create-sorted-array-through-instructions | 0 | 1 | ```\nfrom sortedcontainers import SortedList\nclass Solution:\n def createSortedArray(self, ins: List[int]) -> int:\n mod = 10**9+7\n dicti = defaultdict(int)\n s1 = SortedList()\n sum_ = 0\n \n for i in range(len(ins)):\n dicti[ins[i]] += 1\n s1.add(ins[i])\n if i == 0:\n sum_ = (sum_+0)%mod\n else:\n leftIndex = s1.bisect_left(ins[i])\n small = leftIndex - 0\n big = len(s1) - leftIndex\n if dicti[ins[i]]>0:\n big -= dicti[ins[i]]\n sum_ = (sum_+min(small,big))%mod\n return sum_ | 6 | You are given a string array `features` where `features[i]` is a single word that represents the name of a feature of the latest product you are working on. You have made a survey where users have reported which features they like. You are given a string array `responses`, where each `responses[i]` is a string containing space-separated words.
The **popularity** of a feature is the number of `responses[i]` that contain the feature. You want to sort the features in non-increasing order by their popularity. If two features have the same popularity, order them by their original index in `features`. Notice that one response could contain the same feature multiple times; this feature is only counted once in its popularity.
Return _the features in sorted order._
**Example 1:**
**Input:** features = \[ "cooler ", "lock ", "touch "\], responses = \[ "i like cooler cooler ", "lock touch cool ", "locker like touch "\]
**Output:** \[ "touch ", "cooler ", "lock "\]
**Explanation:** appearances( "cooler ") = 1, appearances( "lock ") = 1, appearances( "touch ") = 2. Since "cooler " and "lock " both had 1 appearance, "cooler " comes first because "cooler " came first in the features array.
**Example 2:**
**Input:** features = \[ "a ", "aa ", "b ", "c "\], responses = \[ "a ", "a aa ", "a a a a a ", "b a "\]
**Output:** \[ "a ", "aa ", "b ", "c "\]
**Constraints:**
* `1 <= features.length <= 104`
* `1 <= features[i].length <= 10`
* `features` contains no duplicates.
* `features[i]` consists of lowercase letters.
* `1 <= responses.length <= 102`
* `1 <= responses[i].length <= 103`
* `responses[i]` consists of lowercase letters and spaces.
* `responses[i]` contains no two consecutive spaces.
* `responses[i]` has no leading or trailing spaces. | This problem is closely related to finding the number of inversions in an array if i know the position in which i will insert the i-th element in I can find the minimum cost to insert it |
With python sortedlist all problems like this shall be categorized as easy... | create-sorted-array-through-instructions | 0 | 1 | ```\nfrom sortedcontainers import SortedList\nclass Solution:\n def createSortedArray(self, instructions: List[int]) -> int:\n res = 0\n sl = SortedList([])\n for n in instructions:\n i = sl.bisect_left(n)\n j = sl.bisect_right(n)\n a = len(sl)\n res += min(i,a-j)\n sl.add(n)\n return res % (10**9+7)\n\n \n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
With python sortedlist all problems like this shall be categorized as easy... | create-sorted-array-through-instructions | 0 | 1 | ```\nfrom sortedcontainers import SortedList\nclass Solution:\n def createSortedArray(self, instructions: List[int]) -> int:\n res = 0\n sl = SortedList([])\n for n in instructions:\n i = sl.bisect_left(n)\n j = sl.bisect_right(n)\n a = len(sl)\n res += min(i,a-j)\n sl.add(n)\n return res % (10**9+7)\n\n \n``` | 0 | You are given a string array `features` where `features[i]` is a single word that represents the name of a feature of the latest product you are working on. You have made a survey where users have reported which features they like. You are given a string array `responses`, where each `responses[i]` is a string containing space-separated words.
The **popularity** of a feature is the number of `responses[i]` that contain the feature. You want to sort the features in non-increasing order by their popularity. If two features have the same popularity, order them by their original index in `features`. Notice that one response could contain the same feature multiple times; this feature is only counted once in its popularity.
Return _the features in sorted order._
**Example 1:**
**Input:** features = \[ "cooler ", "lock ", "touch "\], responses = \[ "i like cooler cooler ", "lock touch cool ", "locker like touch "\]
**Output:** \[ "touch ", "cooler ", "lock "\]
**Explanation:** appearances( "cooler ") = 1, appearances( "lock ") = 1, appearances( "touch ") = 2. Since "cooler " and "lock " both had 1 appearance, "cooler " comes first because "cooler " came first in the features array.
**Example 2:**
**Input:** features = \[ "a ", "aa ", "b ", "c "\], responses = \[ "a ", "a aa ", "a a a a a ", "b a "\]
**Output:** \[ "a ", "aa ", "b ", "c "\]
**Constraints:**
* `1 <= features.length <= 104`
* `1 <= features[i].length <= 10`
* `features` contains no duplicates.
* `features[i]` consists of lowercase letters.
* `1 <= responses.length <= 102`
* `1 <= responses[i].length <= 103`
* `responses[i]` consists of lowercase letters and spaces.
* `responses[i]` contains no two consecutive spaces.
* `responses[i]` has no leading or trailing spaces. | This problem is closely related to finding the number of inversions in an array if i know the position in which i will insert the i-th element in I can find the minimum cost to insert it |
python3 segment tree | create-sorted-array-through-instructions | 0 | 1 | \n# Code\n```\nimport bisect\n\nclass SegmentTree:\n def __init__(self,arr):\n self.arr = arr\n self.n = len(arr)\n self.tree = [0] * (2 * self.n)\n self.build(self.arr)\n\n def build(self,arr):\n for i in range(self.n):\n self.tree[self.n + i] = arr[i]\n for i in range(self.n - 1, 0, -1):\n self.tree[i] = self.tree[2 * i] + self.tree[2 * i + 1]\n\n # 0 indexed\n def update(self,p, value):\n p += self.n\n self.tree[p] = value\n while p > 1:\n if p % 2 == 0:\n sibling = p + 1\n else:\n sibling = p - 1\n self.tree[p // 2] = self.tree[p] + self.tree[sibling]\n p //= 2\n\n #l inclusive r exclusive [l,r)\n def query(self,l, r):\n res = 0\n l += self.n\n r += self.n\n while l < r:\n if l % 2 == 1:\n res += self.tree[l]\n l += 1\n if r % 2 == 1:\n r -= 1\n res += self.tree[r]\n l //= 2\n r //= 2\n return res\n\n\nclass Solution:\n def createSortedArray(self, instructions) -> int:\n ans = 0\n t = SegmentTree([0 for x in range(int(1e5)+1)])\n for e in instructions:\n l = t.query(0,e)\n r = t.query(e+1,100001)\n ans+=min(l,r)\n t.update(e,t.tree[t.n+e]+1)\n \n return ans%1000000007\n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
python3 segment tree | create-sorted-array-through-instructions | 0 | 1 | \n# Code\n```\nimport bisect\n\nclass SegmentTree:\n def __init__(self,arr):\n self.arr = arr\n self.n = len(arr)\n self.tree = [0] * (2 * self.n)\n self.build(self.arr)\n\n def build(self,arr):\n for i in range(self.n):\n self.tree[self.n + i] = arr[i]\n for i in range(self.n - 1, 0, -1):\n self.tree[i] = self.tree[2 * i] + self.tree[2 * i + 1]\n\n # 0 indexed\n def update(self,p, value):\n p += self.n\n self.tree[p] = value\n while p > 1:\n if p % 2 == 0:\n sibling = p + 1\n else:\n sibling = p - 1\n self.tree[p // 2] = self.tree[p] + self.tree[sibling]\n p //= 2\n\n #l inclusive r exclusive [l,r)\n def query(self,l, r):\n res = 0\n l += self.n\n r += self.n\n while l < r:\n if l % 2 == 1:\n res += self.tree[l]\n l += 1\n if r % 2 == 1:\n r -= 1\n res += self.tree[r]\n l //= 2\n r //= 2\n return res\n\n\nclass Solution:\n def createSortedArray(self, instructions) -> int:\n ans = 0\n t = SegmentTree([0 for x in range(int(1e5)+1)])\n for e in instructions:\n l = t.query(0,e)\n r = t.query(e+1,100001)\n ans+=min(l,r)\n t.update(e,t.tree[t.n+e]+1)\n \n return ans%1000000007\n``` | 0 | You are given a string array `features` where `features[i]` is a single word that represents the name of a feature of the latest product you are working on. You have made a survey where users have reported which features they like. You are given a string array `responses`, where each `responses[i]` is a string containing space-separated words.
The **popularity** of a feature is the number of `responses[i]` that contain the feature. You want to sort the features in non-increasing order by their popularity. If two features have the same popularity, order them by their original index in `features`. Notice that one response could contain the same feature multiple times; this feature is only counted once in its popularity.
Return _the features in sorted order._
**Example 1:**
**Input:** features = \[ "cooler ", "lock ", "touch "\], responses = \[ "i like cooler cooler ", "lock touch cool ", "locker like touch "\]
**Output:** \[ "touch ", "cooler ", "lock "\]
**Explanation:** appearances( "cooler ") = 1, appearances( "lock ") = 1, appearances( "touch ") = 2. Since "cooler " and "lock " both had 1 appearance, "cooler " comes first because "cooler " came first in the features array.
**Example 2:**
**Input:** features = \[ "a ", "aa ", "b ", "c "\], responses = \[ "a ", "a aa ", "a a a a a ", "b a "\]
**Output:** \[ "a ", "aa ", "b ", "c "\]
**Constraints:**
* `1 <= features.length <= 104`
* `1 <= features[i].length <= 10`
* `features` contains no duplicates.
* `features[i]` consists of lowercase letters.
* `1 <= responses.length <= 102`
* `1 <= responses[i].length <= 103`
* `responses[i]` consists of lowercase letters and spaces.
* `responses[i]` contains no two consecutive spaces.
* `responses[i]` has no leading or trailing spaces. | This problem is closely related to finding the number of inversions in an array if i know the position in which i will insert the i-th element in I can find the minimum cost to insert it |
Python (Simple Segment Tree) | create-sorted-array-through-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SegmentTree:\n def __init__(self,n):\n self.tree = [0]*n\n\n def query(self,left,right,n):\n total = 0\n left += n\n right += n\n\n while left < right:\n if left&1:\n total += self.tree[left]\n left += 1\n left = left//2\n\n if right&1:\n right -= 1\n total += self.tree[right]\n right = right//2\n\n return total\n\n def update(self,index,value,n):\n index += n\n self.tree[index] += value\n\n while index > 1:\n index = index//2\n self.tree[index] = self.tree[2*index] + self.tree[2*index+1]\n\n\nclass Solution:\n def createSortedArray(self, instructions):\n m, cost = max(instructions)+1, 0\n result = SegmentTree(2*m)\n\n for x in instructions:\n left_cost = result.query(0,x,m)\n right_cost = result.query(x+1,m,m)\n cost += min(left_cost,right_cost)\n result.update(x,1,m)\n\n return cost%(10**9+7)\n\n\n\n\n\n\n\n\n\n \n \n \n``` | 0 | Given an integer array `instructions`, you are asked to create a sorted array from the elements in `instructions`. You start with an empty container `nums`. For each element from **left to right** in `instructions`, insert it into `nums`. The **cost** of each insertion is the **minimum** of the following:
* The number of elements currently in `nums` that are **strictly less than** `instructions[i]`.
* The number of elements currently in `nums` that are **strictly greater than** `instructions[i]`.
For example, if inserting element `3` into `nums = [1,2,3,5]`, the **cost** of insertion is `min(2, 1)` (elements `1` and `2` are less than `3`, element `5` is greater than `3`) and `nums` will become `[1,2,3,3,5]`.
Return _the **total cost** to insert all elements from_ `instructions` _into_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`
**Example 1:**
**Input:** instructions = \[1,5,6,2\]
**Output:** 1
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 5 with cost min(1, 0) = 0, now nums = \[1,5\].
Insert 6 with cost min(2, 0) = 0, now nums = \[1,5,6\].
Insert 2 with cost min(1, 2) = 1, now nums = \[1,2,5,6\].
The total cost is 0 + 0 + 0 + 1 = 1.
**Example 2:**
**Input:** instructions = \[1,2,3,6,5,4\]
**Output:** 3
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 2 with cost min(1, 0) = 0, now nums = \[1,2\].
Insert 3 with cost min(2, 0) = 0, now nums = \[1,2,3\].
Insert 6 with cost min(3, 0) = 0, now nums = \[1,2,3,6\].
Insert 5 with cost min(3, 1) = 1, now nums = \[1,2,3,5,6\].
Insert 4 with cost min(3, 2) = 2, now nums = \[1,2,3,4,5,6\].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.
**Example 3:**
**Input:** instructions = \[1,3,3,3,2,4,2,1,2\]
**Output:** 4
**Explanation:** Begin with nums = \[\].
Insert 1 with cost min(0, 0) = 0, now nums = \[1\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3\].
Insert 3 with cost min(1, 0) = 0, now nums = \[1,3,3,3\].
Insert 2 with cost min(1, 3) = 1, now nums = \[1,2,3,3,3\].
Insert 4 with cost min(5, 0) = 0, now nums = \[1,2,3,3,3,4\].
Insert 2 with cost min(1, 4) = 1, now nums = \[1,2,2,3,3,3,4\].
Insert 1 with cost min(0, 6) = 0, now nums = \[1,1,2,2,3,3,3,4\].
Insert 2 with cost min(2, 4) = 2, now nums = \[1,1,2,2,2,3,3,3,4\].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.
**Constraints:**
* `1 <= instructions.length <= 105`
* `1 <= instructions[i] <= 105` | Keep track of prefix sums to quickly look up what subarray that sums "target" can be formed at each step of scanning the input array. It can be proved that greedily forming valid subarrays as soon as one is found is optimal. |
Python (Simple Segment Tree) | create-sorted-array-through-instructions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SegmentTree:\n def __init__(self,n):\n self.tree = [0]*n\n\n def query(self,left,right,n):\n total = 0\n left += n\n right += n\n\n while left < right:\n if left&1:\n total += self.tree[left]\n left += 1\n left = left//2\n\n if right&1:\n right -= 1\n total += self.tree[right]\n right = right//2\n\n return total\n\n def update(self,index,value,n):\n index += n\n self.tree[index] += value\n\n while index > 1:\n index = index//2\n self.tree[index] = self.tree[2*index] + self.tree[2*index+1]\n\n\nclass Solution:\n def createSortedArray(self, instructions):\n m, cost = max(instructions)+1, 0\n result = SegmentTree(2*m)\n\n for x in instructions:\n left_cost = result.query(0,x,m)\n right_cost = result.query(x+1,m,m)\n cost += min(left_cost,right_cost)\n result.update(x,1,m)\n\n return cost%(10**9+7)\n\n\n\n\n\n\n\n\n\n \n \n \n``` | 0 | You are given a string array `features` where `features[i]` is a single word that represents the name of a feature of the latest product you are working on. You have made a survey where users have reported which features they like. You are given a string array `responses`, where each `responses[i]` is a string containing space-separated words.
The **popularity** of a feature is the number of `responses[i]` that contain the feature. You want to sort the features in non-increasing order by their popularity. If two features have the same popularity, order them by their original index in `features`. Notice that one response could contain the same feature multiple times; this feature is only counted once in its popularity.
Return _the features in sorted order._
**Example 1:**
**Input:** features = \[ "cooler ", "lock ", "touch "\], responses = \[ "i like cooler cooler ", "lock touch cool ", "locker like touch "\]
**Output:** \[ "touch ", "cooler ", "lock "\]
**Explanation:** appearances( "cooler ") = 1, appearances( "lock ") = 1, appearances( "touch ") = 2. Since "cooler " and "lock " both had 1 appearance, "cooler " comes first because "cooler " came first in the features array.
**Example 2:**
**Input:** features = \[ "a ", "aa ", "b ", "c "\], responses = \[ "a ", "a aa ", "a a a a a ", "b a "\]
**Output:** \[ "a ", "aa ", "b ", "c "\]
**Constraints:**
* `1 <= features.length <= 104`
* `1 <= features[i].length <= 10`
* `features` contains no duplicates.
* `features[i]` consists of lowercase letters.
* `1 <= responses.length <= 102`
* `1 <= responses[i].length <= 103`
* `responses[i]` consists of lowercase letters and spaces.
* `responses[i]` contains no two consecutive spaces.
* `responses[i]` has no leading or trailing spaces. | This problem is closely related to finding the number of inversions in an array if i know the position in which i will insert the i-th element in I can find the minimum cost to insert it |
Python Easy Solution | defuse-the-bomb | 0 | 1 | # Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n res=[]\n if k>0: \n first=sum(code[:k])\n for i in range(len(code)):\n first=first-code[i]+code[(k+i)%(len(code))]\n res.append(first)\n elif k<0:\n first=sum(code[k:])\n print(first)\n for i in range(len(code)):\n res.append(first)\n first=first+code[i]-code[(k+i)%(len(code))]\n else:\n res=[0]*len(code)\n return res\n```\n\n***Please Upvote*** | 1 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python Easy Solution | defuse-the-bomb | 0 | 1 | # Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n res=[]\n if k>0: \n first=sum(code[:k])\n for i in range(len(code)):\n first=first-code[i]+code[(k+i)%(len(code))]\n res.append(first)\n elif k<0:\n first=sum(code[k:])\n print(first)\n for i in range(len(code)):\n res.append(first)\n first=first+code[i]-code[(k+i)%(len(code))]\n else:\n res=[0]*len(code)\n return res\n```\n\n***Please Upvote*** | 1 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Easy Python Solution | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n ind = 0\n li = [0 for i in range(len(code))]\n if k>0:\n for j in range(len(code)):\n sum = 0\n ind = j\n for i in range(k):\n if ind+1 >= len(code):\n sum += code[(ind+1)%len(code)]\n else:\n sum += code[ind+1]\n ind += 1\n li[j] = sum\n elif k<0:\n r = -k\n for j in range(len(code)):\n sum = 0\n ind = j\n for i in range(r):\n if ind-1 <0:\n sum += code[ind-1]\n ind -= 1\n else:\n sum += code[ind-1]\n ind -= 1\n li[j] = sum\n return li\n\n\n\n``` | 1 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Easy Python Solution | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n ind = 0\n li = [0 for i in range(len(code))]\n if k>0:\n for j in range(len(code)):\n sum = 0\n ind = j\n for i in range(k):\n if ind+1 >= len(code):\n sum += code[(ind+1)%len(code)]\n else:\n sum += code[ind+1]\n ind += 1\n li[j] = sum\n elif k<0:\n r = -k\n for j in range(len(code)):\n sum = 0\n ind = j\n for i in range(r):\n if ind-1 <0:\n sum += code[ind-1]\n ind -= 1\n else:\n sum += code[ind-1]\n ind -= 1\n li[j] = sum\n return li\n\n\n\n``` | 1 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Python 3 - O(n) - sliding window with array rotation | defuse-the-bomb | 0 | 1 | # Intuition\nOn close inspection we find that K<0 case solution is just a rotated form of K>0 solution\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nReturn 0 array for k==0 case and for other case find the next k sum array by sliding window technique and in case the k value is negative then rotate the ans list by k-1.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n ans=[]\n s=0\n if k==0:\n ans = [0]*len(code)\n else:\n absK=abs(k)\n s=sum(code[0:absK])\n for i in range(len(code)):\n s=s-code[i]+code[(i+absK)%len(code)]\n ans.append(s)\n if k<0:\n ans=ans[k-1:]+ans[:k-1]\n return ans\n``` | 2 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python 3 - O(n) - sliding window with array rotation | defuse-the-bomb | 0 | 1 | # Intuition\nOn close inspection we find that K<0 case solution is just a rotated form of K>0 solution\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nReturn 0 array for k==0 case and for other case find the next k sum array by sliding window technique and in case the k value is negative then rotate the ans list by k-1.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n ans=[]\n s=0\n if k==0:\n ans = [0]*len(code)\n else:\n absK=abs(k)\n s=sum(code[0:absK])\n for i in range(len(code)):\n s=s-code[i]+code[(i+absK)%len(code)]\n ans.append(s)\n if k<0:\n ans=ans[k-1:]+ans[:k-1]\n return ans\n``` | 2 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Pyhton3, beats 100%, double the code array | defuse-the-bomb | 0 | 1 | Double the ```code``` array so that it\'s easy to iterate.\n```class Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k==0: return [0 for i in code]\n temp = code\n code = code*2\n for i in range(len(temp)):\n if k>0:\n temp[i] = sum(code[i+1:i+k+1])\n else:\n temp[i] = sum(code[i+len(temp)+k:i+len(temp)])\n return temp | 20 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Pyhton3, beats 100%, double the code array | defuse-the-bomb | 0 | 1 | Double the ```code``` array so that it\'s easy to iterate.\n```class Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k==0: return [0 for i in code]\n temp = code\n code = code*2\n for i in range(len(temp)):\n if k>0:\n temp[i] = sum(code[i+1:i+k+1])\n else:\n temp[i] = sum(code[i+len(temp)+k:i+len(temp)])\n return temp | 20 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
simple list slicing and loop process that beats 100% | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n# **O**(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# **O**(n)\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k>0:\n final=code+code[:k]\n for i in range(len(code)):\n code[i]=sum(final[i+1:k+1+i])\n return code\n if k==0:\n new=[0]*len(code)\n return new\n else:\n final=code[k:]+code\n for i in range(len(code)):\n code[i]=sum(final[i:i-k])\n return code\n``` | 2 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
simple list slicing and loop process that beats 100% | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n# **O**(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# **O**(n)\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k>0:\n final=code+code[:k]\n for i in range(len(code)):\n code[i]=sum(final[i+1:k+1+i])\n return code\n if k==0:\n new=[0]*len(code)\n return new\n else:\n final=code[k:]+code\n for i in range(len(code)):\n code[i]=sum(final[i:i-k])\n return code\n``` | 2 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
simple and easy | defuse-the-bomb | 0 | 1 | ```\noutput = []\nfor i in range(len(code)):\n\tif k > 0:\n\t\tsum = 0\n\t\tj = i+1\n\t\tm = k\n\t\twhile(m):\n\t\t\tsum+=code[j%len(code)]\n\t\t\tm-=1\n\t\t\tj+=1\n\t\toutput.append(sum)\n\n\telif k == 0:\n\t\toutput.append(0)\n\n\telse:\n\t\tsum = 0\n\t\tj = i-1\n\t\tm = k\n\t\twhile(m):\n\t\t\tsum+=code[j%len(code)]\n\t\t\tm+=1\n\t\t\tj-=1\n\t\toutput.append(sum)\n\nreturn output\n``` | 7 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
simple and easy | defuse-the-bomb | 0 | 1 | ```\noutput = []\nfor i in range(len(code)):\n\tif k > 0:\n\t\tsum = 0\n\t\tj = i+1\n\t\tm = k\n\t\twhile(m):\n\t\t\tsum+=code[j%len(code)]\n\t\t\tm-=1\n\t\t\tj+=1\n\t\toutput.append(sum)\n\n\telif k == 0:\n\t\toutput.append(0)\n\n\telse:\n\t\tsum = 0\n\t\tj = i-1\n\t\tm = k\n\t\twhile(m):\n\t\t\tsum+=code[j%len(code)]\n\t\t\tm+=1\n\t\t\tj-=1\n\t\toutput.append(sum)\n\nreturn output\n``` | 7 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Python Solution | defuse-the-bomb | 0 | 1 | ```python\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k == 0:\n return [0] * len(code)\n data = code + code\n result = [sum(data[i + 1: i + 1 + abs(k)]) for i in range(len(code))]\n\t\t# result = []\n # for i in range(len(code)):\n # result.append(sum(data[i + 1: i + 1 + abs(k)]))\n if 0 > k:\n return result[k - 1:] + result[:k - 1]\n return result\n```\n | 3 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python Solution | defuse-the-bomb | 0 | 1 | ```python\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k == 0:\n return [0] * len(code)\n data = code + code\n result = [sum(data[i + 1: i + 1 + abs(k)]) for i in range(len(code))]\n\t\t# result = []\n # for i in range(len(code)):\n # result.append(sum(data[i + 1: i + 1 + abs(k)]))\n if 0 > k:\n return result[k - 1:] + result[:k - 1]\n return result\n```\n | 3 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Python Solution | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n\n decrypted_code = []\n n = len(code)\n if k == 0:\n decrypted_code = [0] * len(code)\n elif k > 0:\n code = code * 2\n for i in range(n):\n code[i] = sum(code[i+1:i+1+k])\n decrypted_code.append(code[i])\n elif k < 0:\n code = code * 2\n for i in range(n):\n start = n+i-abs(k)\n decrypted_code.append(sum(code[start:n+i]))\n return decrypted_code\n \n\n\n \n``` | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python Solution | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n\n decrypted_code = []\n n = len(code)\n if k == 0:\n decrypted_code = [0] * len(code)\n elif k > 0:\n code = code * 2\n for i in range(n):\n code[i] = sum(code[i+1:i+1+k])\n decrypted_code.append(code[i])\n elif k < 0:\n code = code * 2\n for i in range(n):\n start = n+i-abs(k)\n decrypted_code.append(sum(code[start:n+i]))\n return decrypted_code\n \n\n\n \n``` | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
easy solution using array-manipulations | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsince the array is circular append same array at end of array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n> if key 0 store array of zeros in output\n\n> if key +ve prepare a temporary array of (array + array) & store sum of next k elements in output, iterate over the entire code & store output\n\n> if key -ve prepare a temporary array of (array + array) & store sum of previous k elements in output, iterate over the entire code & store output\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n\n # case 3 | k [zero]\n if k == 0:\n return [0] * len(code) # array of zero\'s as expected\n\n # case 1 | k [+ve] \n elif k > 0:\n op = [] # array to store output\n for i in range(0, len(code)): # iterate on all elements in code\n temp = code + code # to manipulate circularity of array\n\n op.append(sum(temp[i+1 : i+k+1])) # sum of next k elements\n return op # manipulated output\n\n # case 2 | k [-ve] \n elif k < 0:\n op = [] # array to store output\n for i in range(0, len(code)): # iterate on all elements in code\n temp = code + code # to manipulate circularity of array\n\n # since k -ve we manipulate the current_index = length_of_code + current_index\n op.append(sum(temp[k+(len(code)+i) : len(code)+i])) # sum of previous k elements\n return op # manipulated output\n``` | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
easy solution using array-manipulations | defuse-the-bomb | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsince the array is circular append same array at end of array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n> if key 0 store array of zeros in output\n\n> if key +ve prepare a temporary array of (array + array) & store sum of next k elements in output, iterate over the entire code & store output\n\n> if key -ve prepare a temporary array of (array + array) & store sum of previous k elements in output, iterate over the entire code & store output\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n\n # case 3 | k [zero]\n if k == 0:\n return [0] * len(code) # array of zero\'s as expected\n\n # case 1 | k [+ve] \n elif k > 0:\n op = [] # array to store output\n for i in range(0, len(code)): # iterate on all elements in code\n temp = code + code # to manipulate circularity of array\n\n op.append(sum(temp[i+1 : i+k+1])) # sum of next k elements\n return op # manipulated output\n\n # case 2 | k [-ve] \n elif k < 0:\n op = [] # array to store output\n for i in range(0, len(code)): # iterate on all elements in code\n temp = code + code # to manipulate circularity of array\n\n # since k -ve we manipulate the current_index = length_of_code + current_index\n op.append(sum(temp[k+(len(code)+i) : len(code)+i])) # sum of previous k elements\n return op # manipulated output\n``` | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Python Solution for beginners and basic | defuse-the-bomb | 0 | 1 | # Intuition\nThe problem involves decrypting a given circular array based on a given key \'k\'. \nWe need to replace each element in the array according to specific rules based on the value of \'k\'.\n\n# Approach\n1. If k is non-negative, calculate the sum of the next \'k\' elements for each element in the array.\n2. If k is negative, calculate the sum of the previous \'k\' elements for each element in the array.\n3. Use modular arithmetic to handle the circular nature of the array.\n\n# Complexity\n- Time complexity:\nO(n), where \'n\' is the length of the input array \'code\'.\n\n- Space complexity:\nO(n), as we use additional space to store the decrypted array.\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k>=0:\n ran = k\n new = []\n for i in range(1,len(code)+1):\n lst = []\n for j in range(i%len(code),k+i%len(code)):\n lst.append(code[j%len(code)])\n new.append(sum(lst))\n return new\n elif k<0:\n start = len(code)\n end = 2*len(code)\n new = []\n for i in range(start-1,end-1):\n lst = []\n for j in range(i%len(code),i%len(code)+k,-1):\n lst.append(code[j])\n new.append(sum(lst))\n return new\n``` | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
Python Solution for beginners and basic | defuse-the-bomb | 0 | 1 | # Intuition\nThe problem involves decrypting a given circular array based on a given key \'k\'. \nWe need to replace each element in the array according to specific rules based on the value of \'k\'.\n\n# Approach\n1. If k is non-negative, calculate the sum of the next \'k\' elements for each element in the array.\n2. If k is negative, calculate the sum of the previous \'k\' elements for each element in the array.\n3. Use modular arithmetic to handle the circular nature of the array.\n\n# Complexity\n- Time complexity:\nO(n), where \'n\' is the length of the input array \'code\'.\n\n- Space complexity:\nO(n), as we use additional space to store the decrypted array.\n\n# Code\n```\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n if k>=0:\n ran = k\n new = []\n for i in range(1,len(code)+1):\n lst = []\n for j in range(i%len(code),k+i%len(code)):\n lst.append(code[j%len(code)])\n new.append(sum(lst))\n return new\n elif k<0:\n start = len(code)\n end = 2*len(code)\n new = []\n for i in range(start-1,end-1):\n lst = []\n for j in range(i%len(code),i%len(code)+k,-1):\n lst.append(code[j])\n new.append(sum(lst))\n return new\n``` | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
THE BEST SOLUTiON EVER by PRODONiK (Java, C++, C#, Python, Ruby) | defuse-the-bomb | 1 | 1 | \n\n# Intuition\nI aimed to decrypt an encoded message by summing up specific elements based on the provided key value.\n\n# Approach\nI checked whether the key value was negative, and if so, I reversed the array before decryption. Then, I iterated through the array and calculated the sum of specific elements based on the key. Finally, if the array was reversed, I reversed it back.\n\n# Complexity\n- Time complexity: O(n), where n is the length of the input array.\n- Space complexity: O(n), as I used an additional array to store the decrypted values.\n\n# Code\n```java []\nclass Solution {\n public int[] decrypt(int[] code, int k) {\n int length = code.length;\n int[] results = new int[length];\n boolean reversed = false;\n\n if (k < 0) {\n reverse(length, code);\n k *= -1;\n reversed = true;\n }\n\n for (int i = 0; i < length; i++) {\n int element = 0;\n for (int j = 1; j < k + 1; j++) {\n element += code[(i + j) % length];\n }\n results[i] = element;\n }\n\n if (reversed) {\n reverse(length, results);\n }\n\n return results;\n }\n\n private void reverse(int length, int[] code) {\n for (int i = 0; i < length / 2; i++) {\n int temp = code[i];\n code[i] = code[length - i - 1];\n code[length - i - 1] = temp;\n }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> decrypt(std::vector<int>& code, int k) {\n int length = code.size();\n std::vector<int> results(length, 0);\n bool reversed = false;\n\n if (k < 0) {\n reverse(length, code);\n k *= -1;\n reversed = true;\n }\n\n for (int i = 0; i < length; i++) {\n int element = 0;\n for (int j = 1; j < k + 1; j++) {\n element += code[(i + j) % length];\n }\n results[i] = element;\n }\n\n if (reversed) {\n reverse(length, results);\n }\n\n return results;\n }\n\nprivate:\n void reverse(int length, std::vector<int>& code) {\n for (int i = 0; i < length / 2; i++) {\n int temp = code[i];\n code[i] = code[length - i - 1];\n code[length - i - 1] = temp;\n }\n }\n};\n```\n``` C# []\npublic class Solution {\n public int[] Decrypt(int[] code, int k) {\n int length = code.Length;\n int[] results = new int[length];\n bool reversed = false;\n\n if (k < 0) {\n Reverse(length, code);\n k *= -1;\n reversed = true;\n }\n\n for (int i = 0; i < length; i++) {\n int element = 0;\n for (int j = 1; j < k + 1; j++) {\n element += code[(i + j) % length];\n }\n results[i] = element;\n }\n\n if (reversed) {\n Reverse(length, results);\n }\n\n return results;\n }\n\n private void Reverse(int length, int[] code) {\n for (int i = 0; i < length / 2; i++) {\n int temp = code[i];\n code[i] = code[length - i - 1];\n code[length - i - 1] = temp;\n }\n }\n}\n```\n``` Python []\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n length = len(code)\n results = [0] * length\n reversed = k < 0\n if k < 0:\n code = reversed(code)\n k *= (k < 0) * -1\n\n for i in range(length):\n element = 0\n for j in range(1, k + 1):\n element += code[(i + j) % length]\n results[i] = element\n\n if reversed:\n results = reversed(results)\n\n return results\n```\n```Ruby []\ndef decrypt(code, k)\n length = code.length\n results = Array.new(length, 0)\n reversed = false\n\n if k < 0\n reverse(length, code)\n k *= -1\n reversed = true\n end\n\n (0...length).each do |i|\n element = 0\n (1..k).each do |j|\n element += code[(i + j) % length]\n end\n results[i] = element\n end\n\n reverse(length, results) if reversed\n\n results\nend\n\ndef reverse(length, array)\n (0...(length / 2)).each do |i|\n array[i], array[length - i - 1] = array[length - i - 1], array[i]\n end\nend\n```\n | 0 | You have a bomb to defuse, and your time is running out! Your informer will provide you with a **circular** array `code` of length of `n` and a key `k`.
To decrypt the code, you must replace every number. All the numbers are replaced **simultaneously**.
* If `k > 0`, replace the `ith` number with the sum of the **next** `k` numbers.
* If `k < 0`, replace the `ith` number with the sum of the **previous** `k` numbers.
* If `k == 0`, replace the `ith` number with `0`.
As `code` is circular, the next element of `code[n-1]` is `code[0]`, and the previous element of `code[0]` is `code[n-1]`.
Given the **circular** array `code` and an integer key `k`, return _the decrypted code to defuse the bomb_!
**Example 1:**
**Input:** code = \[5,7,1,4\], k = 3
**Output:** \[12,10,16,13\]
**Explanation:** Each number is replaced by the sum of the next 3 numbers. The decrypted code is \[7+1+4, 1+4+5, 4+5+7, 5+7+1\]. Notice that the numbers wrap around.
**Example 2:**
**Input:** code = \[1,2,3,4\], k = 0
**Output:** \[0,0,0,0\]
**Explanation:** When k is zero, the numbers are replaced by 0.
**Example 3:**
**Input:** code = \[2,4,9,3\], k = -2
**Output:** \[12,5,6,13\]
**Explanation:** The decrypted code is \[3+9, 2+3, 4+2, 9+4\]. Notice that the numbers wrap around again. If k is negative, the sum is of the **previous** numbers.
**Constraints:**
* `n == code.length`
* `1 <= n <= 100`
* `1 <= code[i] <= 100`
* `-(n - 1) <= k <= n - 1` | Consider a strategy where the choice of bulb with number i is increasing. In such a strategy, you no longer need to worry about bulbs that have been set to the left. |
THE BEST SOLUTiON EVER by PRODONiK (Java, C++, C#, Python, Ruby) | defuse-the-bomb | 1 | 1 | \n\n# Intuition\nI aimed to decrypt an encoded message by summing up specific elements based on the provided key value.\n\n# Approach\nI checked whether the key value was negative, and if so, I reversed the array before decryption. Then, I iterated through the array and calculated the sum of specific elements based on the key. Finally, if the array was reversed, I reversed it back.\n\n# Complexity\n- Time complexity: O(n), where n is the length of the input array.\n- Space complexity: O(n), as I used an additional array to store the decrypted values.\n\n# Code\n```java []\nclass Solution {\n public int[] decrypt(int[] code, int k) {\n int length = code.length;\n int[] results = new int[length];\n boolean reversed = false;\n\n if (k < 0) {\n reverse(length, code);\n k *= -1;\n reversed = true;\n }\n\n for (int i = 0; i < length; i++) {\n int element = 0;\n for (int j = 1; j < k + 1; j++) {\n element += code[(i + j) % length];\n }\n results[i] = element;\n }\n\n if (reversed) {\n reverse(length, results);\n }\n\n return results;\n }\n\n private void reverse(int length, int[] code) {\n for (int i = 0; i < length / 2; i++) {\n int temp = code[i];\n code[i] = code[length - i - 1];\n code[length - i - 1] = temp;\n }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> decrypt(std::vector<int>& code, int k) {\n int length = code.size();\n std::vector<int> results(length, 0);\n bool reversed = false;\n\n if (k < 0) {\n reverse(length, code);\n k *= -1;\n reversed = true;\n }\n\n for (int i = 0; i < length; i++) {\n int element = 0;\n for (int j = 1; j < k + 1; j++) {\n element += code[(i + j) % length];\n }\n results[i] = element;\n }\n\n if (reversed) {\n reverse(length, results);\n }\n\n return results;\n }\n\nprivate:\n void reverse(int length, std::vector<int>& code) {\n for (int i = 0; i < length / 2; i++) {\n int temp = code[i];\n code[i] = code[length - i - 1];\n code[length - i - 1] = temp;\n }\n }\n};\n```\n``` C# []\npublic class Solution {\n public int[] Decrypt(int[] code, int k) {\n int length = code.Length;\n int[] results = new int[length];\n bool reversed = false;\n\n if (k < 0) {\n Reverse(length, code);\n k *= -1;\n reversed = true;\n }\n\n for (int i = 0; i < length; i++) {\n int element = 0;\n for (int j = 1; j < k + 1; j++) {\n element += code[(i + j) % length];\n }\n results[i] = element;\n }\n\n if (reversed) {\n Reverse(length, results);\n }\n\n return results;\n }\n\n private void Reverse(int length, int[] code) {\n for (int i = 0; i < length / 2; i++) {\n int temp = code[i];\n code[i] = code[length - i - 1];\n code[length - i - 1] = temp;\n }\n }\n}\n```\n``` Python []\nclass Solution:\n def decrypt(self, code: List[int], k: int) -> List[int]:\n length = len(code)\n results = [0] * length\n reversed = k < 0\n if k < 0:\n code = reversed(code)\n k *= (k < 0) * -1\n\n for i in range(length):\n element = 0\n for j in range(1, k + 1):\n element += code[(i + j) % length]\n results[i] = element\n\n if reversed:\n results = reversed(results)\n\n return results\n```\n```Ruby []\ndef decrypt(code, k)\n length = code.length\n results = Array.new(length, 0)\n reversed = false\n\n if k < 0\n reverse(length, code)\n k *= -1\n reversed = true\n end\n\n (0...length).each do |i|\n element = 0\n (1..k).each do |j|\n element += code[(i + j) % length]\n end\n results[i] = element\n end\n\n reverse(length, results) if reversed\n\n results\nend\n\ndef reverse(length, array)\n (0...(length / 2)).each do |i|\n array[i], array[length - i - 1] = array[length - i - 1], array[i]\n end\nend\n```\n | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Time O(n)/ Space O(1) Solution | minimum-deletions-to-make-string-balanced | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n[ Flip String to Monotone Increasing](https://leetcode.com/problems/flip-string-to-monotone-increasing/solutions/2912351/flip-string-to-monotone-increasing//)\n\nExactly Same\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n rightDel = s.count(\'a\')\n leftDel = 0\n ans = rightDel\n for i in range(len(s)):\n if s[i] == \'b\':\n leftDel += 1\n else:\n rightDel -= 1\n ans = min(ans,leftDel+rightDel)\n return ans\n\n``` | 2 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
Time O(n)/ Space O(1) Solution | minimum-deletions-to-make-string-balanced | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n[ Flip String to Monotone Increasing](https://leetcode.com/problems/flip-string-to-monotone-increasing/solutions/2912351/flip-string-to-monotone-increasing//)\n\nExactly Same\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n rightDel = s.count(\'a\')\n leftDel = 0\n ans = rightDel\n for i in range(len(s)):\n if s[i] == \'b\':\n leftDel += 1\n else:\n rightDel -= 1\n ans = min(ans,leftDel+rightDel)\n return ans\n\n``` | 2 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
✔ Python3 Solution | Clean & Concise | O(1) Space | minimum-deletions-to-make-string-balanced | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```Python\nclass Solution:\n def minimumDeletions(self, s):\n ans, count = 0, 0\n for i in s:\n if i == \'b\':\n count += 1\n elif count:\n ans += 1\n count -= 1\n return ans\n``` | 2 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
✔ Python3 Solution | Clean & Concise | O(1) Space | minimum-deletions-to-make-string-balanced | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```Python\nclass Solution:\n def minimumDeletions(self, s):\n ans, count = 0, 0\n for i in s:\n if i == \'b\':\n count += 1\n elif count:\n ans += 1\n count -= 1\n return ans\n``` | 2 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
Python easy to read and understand | stack | minimum-deletions-to-make-string-balanced | 0 | 1 | **Count the total number of ba pairs**\n```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n stack, res = [], 0\n for i in range(len(s)):\n if stack and s[i] == "a" and stack[-1] == "b":\n stack.pop()\n res += 1\n else:\n stack.append(s[i])\n return res | 9 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
Python easy to read and understand | stack | minimum-deletions-to-make-string-balanced | 0 | 1 | **Count the total number of ba pairs**\n```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n stack, res = [], 0\n for i in range(len(s)):\n if stack and s[i] == "a" and stack[-1] == "b":\n stack.pop()\n res += 1\n else:\n stack.append(s[i])\n return res | 9 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
[Python] DP solution easy to understand | minimum-deletions-to-make-string-balanced | 0 | 1 | * O(n) for loop each character of the string s\n* Track the minimum number of deletions to make a balanced string till current character, either ending with \'a\' or \'b\'.\n* In the end, find the min of these two numbers\n```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n # track the minimum number of deletions to make the current string balanced ending with \'a\', \'b\'\n end_a, end_b = 0,0 \n for val in s:\n if val == \'a\':\n # to end with \'a\', nothing to do with previous ending with \'a\'\n # to end with \'b\', need to delete the current \'a\' from previous ending with \'b\'\n end_b += 1\n else:\n # to end with \'a\', need to delete the current \'b\' from previous ending with \'a\'\n # to end with \'b\', nothing to do, so just pick smaller of end_a, end_b\n end_a, end_b = end_a+1, min(end_a, end_b)\n return min(end_a, end_b)\n``` | 14 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
[Python] DP solution easy to understand | minimum-deletions-to-make-string-balanced | 0 | 1 | * O(n) for loop each character of the string s\n* Track the minimum number of deletions to make a balanced string till current character, either ending with \'a\' or \'b\'.\n* In the end, find the min of these two numbers\n```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n # track the minimum number of deletions to make the current string balanced ending with \'a\', \'b\'\n end_a, end_b = 0,0 \n for val in s:\n if val == \'a\':\n # to end with \'a\', nothing to do with previous ending with \'a\'\n # to end with \'b\', need to delete the current \'a\' from previous ending with \'b\'\n end_b += 1\n else:\n # to end with \'a\', need to delete the current \'b\' from previous ending with \'a\'\n # to end with \'b\', nothing to do, so just pick smaller of end_a, end_b\n end_a, end_b = end_a+1, min(end_a, end_b)\n return min(end_a, end_b)\n``` | 14 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
Simple python solution using dynamic programming | minimum-deletions-to-make-string-balanced | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n a_cnt = s.count(\'a\')\n result = a_cnt\n left_b = 0\n right_a = a_cnt\n\n for char in s:\n if char == \'a\':\n right_a -= 1\n else:\n left_b += 1\n result = min(result, right_a + left_b)\n\n return result\n\n``` | 2 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
Simple python solution using dynamic programming | minimum-deletions-to-make-string-balanced | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n a_cnt = s.count(\'a\')\n result = a_cnt\n left_b = 0\n right_a = a_cnt\n\n for char in s:\n if char == \'a\':\n right_a -= 1\n else:\n left_b += 1\n result = min(result, right_a + left_b)\n\n return result\n\n``` | 2 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
70% TC and 78% SC easy python solution | minimum-deletions-to-make-string-balanced | 0 | 1 | ```\ndef minimumDeletions(self, s: str) -> int:\n\tstart = [0]\n\tlast = [0]\n\tfor i in s:\n\t\tstart.append(start[-1] + int(i=="b"))\n\tfor i in s[::-1]:\n\t\tlast.append(last[-1] + int(i=="a"))\n\tans = 10000000000\n\tfor i in range(len(start)):\n\t\tans = min(ans, start[i] + last[-i-1])\n\treturn ans\n``` | 1 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
70% TC and 78% SC easy python solution | minimum-deletions-to-make-string-balanced | 0 | 1 | ```\ndef minimumDeletions(self, s: str) -> int:\n\tstart = [0]\n\tlast = [0]\n\tfor i in s:\n\t\tstart.append(start[-1] + int(i=="b"))\n\tfor i in s[::-1]:\n\t\tlast.append(last[-1] + int(i=="a"))\n\tans = 10000000000\n\tfor i in range(len(start)):\n\t\tans = min(ans, start[i] + last[-i-1])\n\treturn ans\n``` | 1 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
Python Stack | Beats 95% | minimum-deletions-to-make-string-balanced | 0 | 1 | ```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n count = 0\n stack = [] \n for c in s:\n if c == \'b\':\n stack.append(c)\n elif stack:\n stack.pop()\n count += 1\n return count\n \n``` | 4 | You are given a string `s` consisting only of characters `'a'` and `'b'`.
You can delete any number of characters in `s` to make `s` **balanced**. `s` is **balanced** if there is no pair of indices `(i,j)` such that `i < j` and `s[i] = 'b'` and `s[j]= 'a'`.
Return _the **minimum** number of deletions needed to make_ `s` _**balanced**_.
**Example 1:**
**Input:** s = "aababbab "
**Output:** 2
**Explanation:** You can either:
Delete the characters at 0-indexed positions 2 and 6 ( "aababbab " -> "aaabbb "), or
Delete the characters at 0-indexed positions 3 and 6 ( "aababbab " -> "aabbbb ").
**Example 2:**
**Input:** s = "bbaaaaabb "
**Output:** 2
**Explanation:** The only solution is to delete the first two characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is `'a'` or `'b'`. | Start DFS from each leaf node. stop the DFS when the number of steps done > distance. If you reach another leaf node within distance steps, add 1 to the answer. Note that all pairs will be counted twice so divide the answer by 2. |
Python Stack | Beats 95% | minimum-deletions-to-make-string-balanced | 0 | 1 | ```\nclass Solution:\n def minimumDeletions(self, s: str) -> int:\n count = 0\n stack = [] \n for c in s:\n if c == \'b\':\n stack.append(c)\n elif stack:\n stack.pop()\n count += 1\n return count\n \n``` | 4 | Design a queue-like data structure that moves the most recently used element to the end of the queue.
Implement the `MRUQueue` class:
* `MRUQueue(int n)` constructs the `MRUQueue` with `n` elements: `[1,2,3,...,n]`.
* `int fetch(int k)` moves the `kth` element **(1-indexed)** to the end of the queue and returns it.
**Example 1:**
**Input:**
\[ "MRUQueue ", "fetch ", "fetch ", "fetch ", "fetch "\]
\[\[8\], \[3\], \[5\], \[2\], \[8\]\]
**Output:**
\[null, 3, 6, 2, 2\]
**Explanation:**
MRUQueue mRUQueue = new MRUQueue(8); // Initializes the queue to \[1,2,3,4,5,6,7,8\].
mRUQueue.fetch(3); // Moves the 3rd element (3) to the end of the queue to become \[1,2,4,5,6,7,8,3\] and returns it.
mRUQueue.fetch(5); // Moves the 5th element (6) to the end of the queue to become \[1,2,4,5,7,8,3,6\] and returns it.
mRUQueue.fetch(2); // Moves the 2nd element (2) to the end of the queue to become \[1,4,5,7,8,3,6,2\] and returns it.
mRUQueue.fetch(8); // The 8th element (2) is already at the end of the queue so just return it.
**Constraints:**
* `1 <= n <= 2000`
* `1 <= k <= n`
* At most `2000` calls will be made to `fetch`.
**Follow up:** Finding an `O(n)` algorithm per `fetch` is a bit easy. Can you find an algorithm with a better complexity for each `fetch` call? | You need to find for every index the number of Bs before it and the number of A's after it You can speed up the finding of A's and B's in suffix and prefix using preprocessing |
Python, DFS (issue with 121 test case solved) | minimum-jumps-to-reach-home | 0 | 1 | **UPD:**\n\nI believe I have found the issue: I should be able to go back more if my back step is larger than my forward step. Thanks to @ShidaLei\n for pointing it out.\n\n----------------------------------------------------------------------------------------------------------------\nUpdated, working DFS solution, still not 100% about the "toofar" condition, one possibly could come up with test cases where this still breaks:\n```\ndef minimumJumps(self, forbidden: List[int], a: int, b: int, x: int) -> int:\n\tforbidden = set(forbidden)\n\ttoofar = max(forbidden) + b if a < b else x\n\tminsofar = -1\n\n\tposition_cost = {} # only record the cost when jumping forward\n\tdef minjumps(cur_pos = 0, jumped_back = False, jumpsmade = 0):\n\t\tnonlocal minsofar, toofar\n\t\tif cur_pos < 0 or \\\n\t\t cur_pos in forbidden or \\\n\t\t cur_pos - b > toofar or \\\n\t\t minsofar > -1 and jumpsmade > minsofar: return \n\n\t\tif cur_pos == x:\n\t\t\tminsofar = jumpsmade if minsofar == -1 else min(minsofar, jumpsmade)\n\t\t\treturn\n\n\t\tif jumped_back: # can only jump forward at this point\n\t\t\tminjumps(cur_pos + a, False, jumpsmade + 1)\n\t\t\treturn\n\t\telif cur_pos not in position_cost: position_cost[cur_pos] = jumpsmade\n\t\telif jumpsmade >= position_cost[cur_pos]: return\n\t\telse: position_cost[cur_pos] = jumpsmade\n\n\t\tminjumps(cur_pos + a, False, jumpsmade + 1)\n\t\tminjumps(cur_pos - b, True, jumpsmade + 1)\n\n\tminjumps()\n\treturn minsofar\n```\n\nTest case, for which I used to end up with `-1` instead of `121`:\n```\n[162,118,178,152,167,100,40,74,199,186,26,73,200,127,30,124,193,84,184,36,103,149,153,9,54,154,133,95,45,198,79,157,64,122,59,71,48,177,82,35,14,176,16,108,111,6,168,31,134,164,136,72,98]\n29\n98\n80\n``` | 22 | A certain bug's home is on the x-axis at position `x`. Help them get there from position `0`.
The bug jumps according to the following rules:
* It can jump exactly `a` positions **forward** (to the right).
* It can jump exactly `b` positions **backward** (to the left).
* It cannot jump backward twice in a row.
* It cannot jump to any `forbidden` positions.
The bug may jump forward **beyond** its home, but it **cannot jump** to positions numbered with **negative** integers.
Given an array of integers `forbidden`, where `forbidden[i]` means that the bug cannot jump to the position `forbidden[i]`, and integers `a`, `b`, and `x`, return _the minimum number of jumps needed for the bug to reach its home_. If there is no possible sequence of jumps that lands the bug on position `x`, return `-1.`
**Example 1:**
**Input:** forbidden = \[14,4,18,1,15\], a = 3, b = 15, x = 9
**Output:** 3
**Explanation:** 3 jumps forward (0 -> 3 -> 6 -> 9) will get the bug home.
**Example 2:**
**Input:** forbidden = \[8,3,16,6,12,20\], a = 15, b = 13, x = 11
**Output:** -1
**Example 3:**
**Input:** forbidden = \[1,6,2,14,5,17,4\], a = 16, b = 9, x = 7
**Output:** 2
**Explanation:** One jump forward (0 -> 16) then one jump backward (16 -> 7) will get the bug home.
**Constraints:**
* `1 <= forbidden.length <= 1000`
* `1 <= a, b, forbidden[i] <= 2000`
* `0 <= x <= 2000`
* All the elements in `forbidden` are distinct.
* Position `x` is not forbidden. | null |
Fast Python and C++ solution with explanation - BFS | minimum-jumps-to-reach-home | 0 | 1 | The objective is to find the minimum number of hops. BFS is the ideal candidate for this question since it will provide the shortest path.\n**Solution:**\n1. We start exploring from `0` position. \n2. At each position, we can either go forward by `a` and go backward by `b`. Thing to note here is we cannot go backward twice in a row so we will maintain a flag `isForward` to signal if the previous jump was a `forward` jump.\n3. If the previous jump was `isForward` then we have 2 positions we can go to from current position `pos` -> `pos+a` and `pos-b`\n4. If the previous jump was not `isForward` then we can go to 1 position only from current position `pos` -> `pos+a`\n5. To avoid going to the same `pos` multiple times we will maintain a `visited` data-structure which will keep track of already visited positions. We will also add forbidden positions to this data structure.\n6. The tricky bit is to figure out when the forward limit. Since the question mentions that the max x is 2000. The absolute limit is `2000 + a + b`. As anything beyond this limit will always be greater than x because there is only one backward move allowed. So any position above this limit will not be added to the search queue.\n7. Keep exploring the positions in the `queue` until you reach destination `x` in which case `return hops` or until the `queue` is empty in which case `return -1`\n\nPython\n```\nclass Solution:\n def minimumJumps(self, forbidden: List[int], a: int, b: int, x: int) -> int:\n limit = 2000 + a + b\n visited = set(forbidden)\n myque = collections.deque([(0, True)]) # (pos, isForward) \n hops = 0\n while(myque):\n l = len(myque)\n while(l > 0):\n l -= 1\n pos, isForward = myque.popleft()\n if pos == x:\n return hops\n if pos in visited: continue\n visited.add(pos)\n if isForward:\n nxt_jump = pos - b\n if nxt_jump >= 0:\n myque.append((nxt_jump, False))\n nxt_jump = pos + a\n if nxt_jump <= limit:\n myque.append((nxt_jump, True))\n hops += 1\n return -1\n```\n\nC++\n```\nclass Solution {\npublic:\n int minimumJumps(vector<int>& forbidden, int a, int b, int x) {\n int limit = 2000 + a + b;\n std::queue<std::pair<int, int>> cur;\n cur.push({0, 1});\n std::unordered_set<int> visited;\n for (auto& x : forbidden){\n visited.insert(x);\n }\n \n int hops = 0;\n while(!cur.empty()){\n int size = cur.size();\n while(size--){\n auto it = cur.front(); cur.pop();\n int num = it.first;\n int forward = it.second;\n if (num == x) return hops;\n if (visited.count(num) != 0)\n continue;\n visited.insert(num);\n if (forward){\n int nxt = num - b;\n if (nxt >= 0){\n cur.push({nxt, 0});\n }\n }\n int nxt = num + a;\n if (nxt <= limit){\n cur.push({nxt, 1});\n }\n }\n ++hops;\n }\n return -1;\n \n }\n}; | 23 | A certain bug's home is on the x-axis at position `x`. Help them get there from position `0`.
The bug jumps according to the following rules:
* It can jump exactly `a` positions **forward** (to the right).
* It can jump exactly `b` positions **backward** (to the left).
* It cannot jump backward twice in a row.
* It cannot jump to any `forbidden` positions.
The bug may jump forward **beyond** its home, but it **cannot jump** to positions numbered with **negative** integers.
Given an array of integers `forbidden`, where `forbidden[i]` means that the bug cannot jump to the position `forbidden[i]`, and integers `a`, `b`, and `x`, return _the minimum number of jumps needed for the bug to reach its home_. If there is no possible sequence of jumps that lands the bug on position `x`, return `-1.`
**Example 1:**
**Input:** forbidden = \[14,4,18,1,15\], a = 3, b = 15, x = 9
**Output:** 3
**Explanation:** 3 jumps forward (0 -> 3 -> 6 -> 9) will get the bug home.
**Example 2:**
**Input:** forbidden = \[8,3,16,6,12,20\], a = 15, b = 13, x = 11
**Output:** -1
**Example 3:**
**Input:** forbidden = \[1,6,2,14,5,17,4\], a = 16, b = 9, x = 7
**Output:** 2
**Explanation:** One jump forward (0 -> 16) then one jump backward (16 -> 7) will get the bug home.
**Constraints:**
* `1 <= forbidden.length <= 1000`
* `1 <= a, b, forbidden[i] <= 2000`
* `0 <= x <= 2000`
* All the elements in `forbidden` are distinct.
* Position `x` is not forbidden. | null |
Python3 - BFS - beats 100% - with Explanation 🔥🔥🔥 | minimum-jumps-to-reach-home | 0 | 1 | # Intuition\r\n- We use BFS to find the minimum number of jumps required to reach the target position from the starting position.\r\n\r\n- We consider two types of moves: a forward jump of size \'a\', and a backward jump of size \'b\'.\r\n\r\n- We avoid forbidden positions, jumping backwards twice in a row and jumping into negative positions. \r\n\r\n- We keep track of positions that we have already visited to avoid revisiting them. Those can be added into set of forbidden positions.\r\n\r\n- If we cannot reach the target position from the starting position, we return -1.\r\n\r\n# Approach\r\n- We use BFS to explore all possible positions that we can reach from the starting position within a maximum of two forward jumps.\r\n- We start by setting upper and lower limits for the search, based on the target position and the highest forbidden position, and the minimum allowed position (0).\r\n- We create a queue to keep track of the positions to explore, their corresponding number of steps, and a boolean flag to indicate if we can or cannot make a backward jump from the current position.\r\n- For each position in the queue, we explore all possible forward jumps and backward jumps, as long as they are within the upper and lower limits and not forbidden, and we also use the boolean flag to prevent going backwards twice in a row.\r\n- If we reach the target position, we return the corresponding number of steps.\r\n- If we exhaust all possible positions to explore without reaching the target position, we return -1 to indicate that the target is unreachable\r\n\r\n# Complexity\r\n- Time complexity: **O(U)**\r\n- Where U is the upper limit of the search space. In worse case scenario, the algorithm will have to explore all positions between in range(0, U)\r\n\r\n- Space complexity: **O(U)**\r\n- We need to keep track of all positions between 0 and U, and each position can be added to the queue at most once.\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def minimumJumps(self, forbidden: List[int], a: int, b: int, x: int) -> int:\r\n # Create a set of forbidden positions, set the lower limit to 0, and set the upper limit to the maximum of the goal position, \r\n # the maximum of the forbidden positions, and the sum of the jump lengths.\r\n forbidden, lower, upper = set(forbidden), 0, max(x, max(forbidden)) + a + b\r\n if 0 in forbidden:\r\n return -1\r\n \r\n # Initialize a queue to hold the positions to be explored, set the number of steps to -1, and add the starting position to the queue.\r\n queue, steps = deque(), -1\r\n queue.append((0, True))\r\n forbidden.add(0)\r\n \r\n # Loop through the positions in the queue until the queue is empty.\r\n while queue:\r\n # Increment the number of steps.\r\n steps += 1\r\n \r\n # Loop through the positions in the queue that were added in the previous iteration.\r\n for i in range(len(queue)):\r\n # Remove the first position from the queue.\r\n pos, canBackwards = queue.popleft()\r\n \r\n # Check if the current position is the goal position, if so, return the number of steps.\r\n if pos == x:\r\n return steps\r\n \r\n # Check if it is possible to jump backwards from the current position and if the new position is not forbidden.\r\n if (canBackwards and pos - b > 0 and pos-b not in forbidden):\r\n # Add the new position to the queue with canBackwards set to False, and add it to the forbidden set.\r\n queue.append((pos-b, False))\r\n forbidden.add(pos-b)\r\n \r\n # Check if it is possible to jump forwards from the current position and if the new position is not forbidden.\r\n if (pos+a <= upper and pos+a not in forbidden):\r\n # Add the new position to the queue with canBackwards set to True, and add it to the forbidden set.\r\n queue.append((pos+a, True))\r\n forbidden.add(pos+a)\r\n \r\n # If the goal position is not reached, return -1.\r\n return -1\r\n\r\n\r\n``` | 3 | A certain bug's home is on the x-axis at position `x`. Help them get there from position `0`.
The bug jumps according to the following rules:
* It can jump exactly `a` positions **forward** (to the right).
* It can jump exactly `b` positions **backward** (to the left).
* It cannot jump backward twice in a row.
* It cannot jump to any `forbidden` positions.
The bug may jump forward **beyond** its home, but it **cannot jump** to positions numbered with **negative** integers.
Given an array of integers `forbidden`, where `forbidden[i]` means that the bug cannot jump to the position `forbidden[i]`, and integers `a`, `b`, and `x`, return _the minimum number of jumps needed for the bug to reach its home_. If there is no possible sequence of jumps that lands the bug on position `x`, return `-1.`
**Example 1:**
**Input:** forbidden = \[14,4,18,1,15\], a = 3, b = 15, x = 9
**Output:** 3
**Explanation:** 3 jumps forward (0 -> 3 -> 6 -> 9) will get the bug home.
**Example 2:**
**Input:** forbidden = \[8,3,16,6,12,20\], a = 15, b = 13, x = 11
**Output:** -1
**Example 3:**
**Input:** forbidden = \[1,6,2,14,5,17,4\], a = 16, b = 9, x = 7
**Output:** 2
**Explanation:** One jump forward (0 -> 16) then one jump backward (16 -> 7) will get the bug home.
**Constraints:**
* `1 <= forbidden.length <= 1000`
* `1 <= a, b, forbidden[i] <= 2000`
* `0 <= x <= 2000`
* All the elements in `forbidden` are distinct.
* Position `x` is not forbidden. | null |
[Python3] BFS - easy understanding | minimum-jumps-to-reach-home | 0 | 1 | ```\ndef minimumJumps(self, forbidden: List[int], a: int, b: int, x: int) -> int:\n visited = set()\n q = deque([(0, 0)])\n forbidden = set(forbidden)\n furthest = max(x, max(forbidden)) + a + b\n \n res = 0\n while q:\n n = len(q)\n for _ in range(n):\n p, is_back = q.popleft()\n if p in forbidden or (p, is_back) in visited or p < 0 or p > furthest:\n continue\n if p == x:\n return res \n visited.add((p, is_back))\n q.append((p + a, 0))\n if not is_back:\n q.append((p - b, 1))\n \n res += 1\n return -1\n``` | 5 | A certain bug's home is on the x-axis at position `x`. Help them get there from position `0`.
The bug jumps according to the following rules:
* It can jump exactly `a` positions **forward** (to the right).
* It can jump exactly `b` positions **backward** (to the left).
* It cannot jump backward twice in a row.
* It cannot jump to any `forbidden` positions.
The bug may jump forward **beyond** its home, but it **cannot jump** to positions numbered with **negative** integers.
Given an array of integers `forbidden`, where `forbidden[i]` means that the bug cannot jump to the position `forbidden[i]`, and integers `a`, `b`, and `x`, return _the minimum number of jumps needed for the bug to reach its home_. If there is no possible sequence of jumps that lands the bug on position `x`, return `-1.`
**Example 1:**
**Input:** forbidden = \[14,4,18,1,15\], a = 3, b = 15, x = 9
**Output:** 3
**Explanation:** 3 jumps forward (0 -> 3 -> 6 -> 9) will get the bug home.
**Example 2:**
**Input:** forbidden = \[8,3,16,6,12,20\], a = 15, b = 13, x = 11
**Output:** -1
**Example 3:**
**Input:** forbidden = \[1,6,2,14,5,17,4\], a = 16, b = 9, x = 7
**Output:** 2
**Explanation:** One jump forward (0 -> 16) then one jump backward (16 -> 7) will get the bug home.
**Constraints:**
* `1 <= forbidden.length <= 1000`
* `1 <= a, b, forbidden[i] <= 2000`
* `0 <= x <= 2000`
* All the elements in `forbidden` are distinct.
* Position `x` is not forbidden. | null |
[Python3] Dead simple backtracking - faster than 98% | distribute-repeating-integers | 0 | 1 | 1. Sort the `quantity` array in reverse order, since allocating larger quantities first will more quickly reduce the search space.\n2. Get the frequency of each number in `nums`, ignoring the actual numbers.\n3. Then further get the count of each frequency, storing this in `freqCounts`. We do this so that in our backtracking step, we don\'t try allocating a quantity to two different but equal frequencies, as they would have an equivalent result.\n4. In the backtracking, we try allocating each quantity to each unique frequency, simply decrementing and incrementing the frequency counts in each step.\n```\nfrom collections import Counter, defaultdict\n\nclass Solution:\n def canDistribute(self, nums: List[int], quantity: List[int]) -> bool:\n quantity.sort(reverse=True)\n freqCounts = defaultdict(int, Counter(Counter(nums).values()))\n def backtrack(i: int = 0) -> bool:\n if i == len(quantity):\n return True\n \n for freq, count in list(freqCounts.items()):\n if freq >= quantity[i] and count > 0:\n freqCounts[freq] -= 1\n freqCounts[freq - quantity[i]] += 1\n if backtrack(i + 1):\n return True\n freqCounts[freq] += 1\n freqCounts[freq - quantity[i]] -= 1\n \n return False\n \n return backtrack()\n``` | 6 | You are given an array of `n` integers, `nums`, where there are at most `50` unique values in the array. You are also given an array of `m` customer order quantities, `quantity`, where `quantity[i]` is the amount of integers the `ith` customer ordered. Determine if it is possible to distribute `nums` such that:
* The `ith` customer gets **exactly** `quantity[i]` integers,
* The integers the `ith` customer gets are **all equal**, and
* Every customer is satisfied.
Return `true` _if it is possible to distribute_ `nums` _according to the above conditions_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], quantity = \[2\]
**Output:** false
**Explanation:** The 0th customer cannot be given two different integers.
**Example 2:**
**Input:** nums = \[1,2,3,3\], quantity = \[2\]
**Output:** true
**Explanation:** The 0th customer is given \[3,3\]. The integers \[1,2\] are not used.
**Example 3:**
**Input:** nums = \[1,1,2,2\], quantity = \[2,2\]
**Output:** true
**Explanation:** The 0th customer is given \[1,1\], and the 1st customer is given \[2,2\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 1000`
* `m == quantity.length`
* `1 <= m <= 10`
* `1 <= quantity[i] <= 105`
* There are at most `50` unique values in `nums`. | Disconnect node p from its parent and append it to the children list of node q. If q was in the sub-tree of node p (case 1), get the parent node of p and replace p in its children list with q. If p was the root of the tree, make q the root of the tree. |
[Python3] Dead simple backtracking - faster than 98% | distribute-repeating-integers | 0 | 1 | 1. Sort the `quantity` array in reverse order, since allocating larger quantities first will more quickly reduce the search space.\n2. Get the frequency of each number in `nums`, ignoring the actual numbers.\n3. Then further get the count of each frequency, storing this in `freqCounts`. We do this so that in our backtracking step, we don\'t try allocating a quantity to two different but equal frequencies, as they would have an equivalent result.\n4. In the backtracking, we try allocating each quantity to each unique frequency, simply decrementing and incrementing the frequency counts in each step.\n```\nfrom collections import Counter, defaultdict\n\nclass Solution:\n def canDistribute(self, nums: List[int], quantity: List[int]) -> bool:\n quantity.sort(reverse=True)\n freqCounts = defaultdict(int, Counter(Counter(nums).values()))\n def backtrack(i: int = 0) -> bool:\n if i == len(quantity):\n return True\n \n for freq, count in list(freqCounts.items()):\n if freq >= quantity[i] and count > 0:\n freqCounts[freq] -= 1\n freqCounts[freq - quantity[i]] += 1\n if backtrack(i + 1):\n return True\n freqCounts[freq] += 1\n freqCounts[freq - quantity[i]] -= 1\n \n return False\n \n return backtrack()\n``` | 6 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Simple and clear python3 solutions | Backtracking + Recursion | distribute-repeating-integers | 0 | 1 | # Complexity\n- Time complexity: $$O(n + m \\cdot log(m) + k^m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k + m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nwhere `n = nums.length`, `m = quantity.length`, `k = nums.unique`\n\n# Code\n``` python3 []\nclass Solution:\n def canDistribute(self, nums: List[int], quantity: List[int]) -> bool:\n data = list(Counter(nums).values())\n quantity.sort(reverse=True)\n\n k = len(data)\n m = len(quantity)\n\n def recursive(j):\n if j == m:\n return True\n elem = quantity[j]\n\n for i in range(k):\n if data[i] >= elem:\n data[i] -= elem\n if recursive(j + 1):\n return True\n data[i] += elem\n return False\n \n return recursive(0)\n``` | 0 | You are given an array of `n` integers, `nums`, where there are at most `50` unique values in the array. You are also given an array of `m` customer order quantities, `quantity`, where `quantity[i]` is the amount of integers the `ith` customer ordered. Determine if it is possible to distribute `nums` such that:
* The `ith` customer gets **exactly** `quantity[i]` integers,
* The integers the `ith` customer gets are **all equal**, and
* Every customer is satisfied.
Return `true` _if it is possible to distribute_ `nums` _according to the above conditions_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], quantity = \[2\]
**Output:** false
**Explanation:** The 0th customer cannot be given two different integers.
**Example 2:**
**Input:** nums = \[1,2,3,3\], quantity = \[2\]
**Output:** true
**Explanation:** The 0th customer is given \[3,3\]. The integers \[1,2\] are not used.
**Example 3:**
**Input:** nums = \[1,1,2,2\], quantity = \[2,2\]
**Output:** true
**Explanation:** The 0th customer is given \[1,1\], and the 1st customer is given \[2,2\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 1000`
* `m == quantity.length`
* `1 <= m <= 10`
* `1 <= quantity[i] <= 105`
* There are at most `50` unique values in `nums`. | Disconnect node p from its parent and append it to the children list of node q. If q was in the sub-tree of node p (case 1), get the parent node of p and replace p in its children list with q. If p was the root of the tree, make q the root of the tree. |
Simple and clear python3 solutions | Backtracking + Recursion | distribute-repeating-integers | 0 | 1 | # Complexity\n- Time complexity: $$O(n + m \\cdot log(m) + k^m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k + m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nwhere `n = nums.length`, `m = quantity.length`, `k = nums.unique`\n\n# Code\n``` python3 []\nclass Solution:\n def canDistribute(self, nums: List[int], quantity: List[int]) -> bool:\n data = list(Counter(nums).values())\n quantity.sort(reverse=True)\n\n k = len(data)\n m = len(quantity)\n\n def recursive(j):\n if j == m:\n return True\n elem = quantity[j]\n\n for i in range(k):\n if data[i] >= elem:\n data[i] -= elem\n if recursive(j + 1):\n return True\n data[i] += elem\n return False\n \n return recursive(0)\n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python - 8 lines | distribute-repeating-integers | 0 | 1 | # Complexity\n- Time complexity:\n$$O(C 2^n)$$\n\n\n# Code\n```\nclass Solution:\n def canDistribute(self, nums, quantity) -> bool:\n quantity, A = sorted(quantity, reverse=True), list(Counter(nums).values())\n def check(customer):\n for i in range(len(A)):\n if A[i] >= quantity[customer]:\n A[i] -= quantity[customer]\n if customer + 1 == len(quantity) or check(customer + 1): return True\n A[i] += quantity[customer]\n return check(0) \n``` | 0 | You are given an array of `n` integers, `nums`, where there are at most `50` unique values in the array. You are also given an array of `m` customer order quantities, `quantity`, where `quantity[i]` is the amount of integers the `ith` customer ordered. Determine if it is possible to distribute `nums` such that:
* The `ith` customer gets **exactly** `quantity[i]` integers,
* The integers the `ith` customer gets are **all equal**, and
* Every customer is satisfied.
Return `true` _if it is possible to distribute_ `nums` _according to the above conditions_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], quantity = \[2\]
**Output:** false
**Explanation:** The 0th customer cannot be given two different integers.
**Example 2:**
**Input:** nums = \[1,2,3,3\], quantity = \[2\]
**Output:** true
**Explanation:** The 0th customer is given \[3,3\]. The integers \[1,2\] are not used.
**Example 3:**
**Input:** nums = \[1,1,2,2\], quantity = \[2,2\]
**Output:** true
**Explanation:** The 0th customer is given \[1,1\], and the 1st customer is given \[2,2\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 1000`
* `m == quantity.length`
* `1 <= m <= 10`
* `1 <= quantity[i] <= 105`
* There are at most `50` unique values in `nums`. | Disconnect node p from its parent and append it to the children list of node q. If q was in the sub-tree of node p (case 1), get the parent node of p and replace p in its children list with q. If p was the root of the tree, make q the root of the tree. |
Python - 8 lines | distribute-repeating-integers | 0 | 1 | # Complexity\n- Time complexity:\n$$O(C 2^n)$$\n\n\n# Code\n```\nclass Solution:\n def canDistribute(self, nums, quantity) -> bool:\n quantity, A = sorted(quantity, reverse=True), list(Counter(nums).values())\n def check(customer):\n for i in range(len(A)):\n if A[i] >= quantity[customer]:\n A[i] -= quantity[customer]\n if customer + 1 == len(quantity) or check(customer + 1): return True\n A[i] += quantity[customer]\n return check(0) \n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Backtracking with Memoization | Commented and Explained | distribute-repeating-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe know we only have 10 customers at worst. We also know we have at most 50 unique items in our set up. We can backtrack on the customers and on the items, and can limit ourselves to only as many items as we have customers if we go in greatest reversed order of items present. This lets us limit ourselves appropriately to a space at worst of 10^10. We can allow ourselves to stop early by utilizing a backtracking string to target the current items and current customers as a key, thus letting us memoize results and reduce computational time altogether. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind your number of items, your number of customers, and then check to make sure you at least have enough items to match customers before any combinations. \n\nThen, get the frequency of your items. \nTurn nums into the sorted form of the frequencies (not the items, the frequencies) in reverse order for as many as you have customers. This lets you focus on a subset of size 10^10 at worst. \n\nSort your quantities in reverse. \n\nIf your sum of item frequencies is less than the sum of your quantity, you can also return False already. \n\nOtherwise, set up a memo \n\nDuring the backtracking phase, pass in the current items, customer index, and current customer statuses \n- Build a backtrack key using the items sorted | customer status sorted as a string \n- If your customer index is past the total number number of customers, set memo at backtrack key to true and return true \n- If you have the backtrack key in the memo, return what you found already and skip the preprocess. This is the reason for the sorting as it combines similar set ups with different location strings. \n- otherwise, get the current amount as quantity at customer index \n- set your current item index to 0 \n- while your current item index is in range of your current items length \n - if the item here is not big enough -> move forward by 1 until it is \n - otherwise \n - if the current item index is greater than 0 and we have matching items here \n - go until the last version of these if you can \n - if you end up out of range, break \n - otherwise if you end up at a bad spot, move forward one and continue \n - otherwise try to use the current item to satisfy the current customer, updating in both lists appropriately \n - make a temp key of doing so \n - if you have seen this temp key and it doesn\'t work \n - unset what you did and move forward one and continue \n - if you saw it and it did work \n - set memo for the backtrack key and return True \n - otherwise, go check it out\n - then update the memo\n - if it was true, update memo for backtrack key and return \n - otherwise, undo the look, move forward and continue \n- if you never got a success in the loop, update the memo here and return False \n\nTo solve, kick off backtrack with nums, 0, quantity \n\n# Complexity\n- Time complexity : O (Sum m! / (i!(m-i)!) for i in range 1, m-1, where m is number of customers)\n - O(10^10) at worst since we do 10^10 considerations in our backtracking is the naive amount \n - However, we can limit down since our sort for the backtrack keys worked (never caused an error) to O(3629822) operations, since we now know that we are dealing with combinatory states where no repeats are allowed and order doesn\'t matter (otherwise, the backtrack keys would have caused a problem). Due to this, we get the time complexity of combinations with no repeats instead of permutations with repeats for the backtrack process. \n - This puts our overall time complexity in the form of O(Sum m!/(i!(m-i)!) for i in range 1, m-1), where m is the number of customers according to the problem statement. For comparison sakes, this is about 2750 times faster than O(10^10)\n\n- Space complexity : Due to backtracking nature, we match our space complexity unfortunately, but due handidly beat the space in the other case due to our size reduction. If someone is interested, this can potentially be done in bottom up form and save us the massive amounts of space with the time savings. \n\n# Code\n```\nclass Solution:\n def canDistribute(self, nums: List[int], quantity: List[int]) -> bool :\n \'\'\'\n at most 50 unique values in the array \n customer quantities -> no more than 10 customers -> m \n -> each customer can order between 1 and 10^5, the number of items range as well \n nums -> amount of items \n want to distribute nums so that \n each customer gets exactly customer_i items (so if there are not exactly i items not gonna work)\n the integers that compose the ith customer order are all equal and sum to customer i items \n every customer can be satisfied \n \n \'\'\'\n # get number of items and number of customers \n number_of_items = len(nums)\n number_of_customers = len(quantity) \n # before doing frequency work, if you do not have enough items, you\'ll never satisfy everyone \n if number_of_items < number_of_customers : \n return False \n # find out your frequency of your items \n frequency_of_items = collections.Counter(nums)\n # and limit yourself to the best for your customers \n nums = sorted(frequency_of_items.values(), reverse=True)[:number_of_customers]\n quantity.sort(reverse = True)\n # if you still can\'t satisfy everyone, don\'t try and return False \n if sum(nums) < sum(quantity) : \n return False \n # set up a memo to track your progress \n self.memo = dict() \n\n def backtrack(current_items, customer_index, current_customers) :\n # set up a backtrack key where you use the sorted form of each to capture as many possible alternate substates as you can \n backtrack_key = "".join([str(c_it) for c_it in sorted(current_items)]) + "-" + "".join([str(c_c) for c_c in sorted(current_customers)]) \n # if you reached the end, mark it and return True. Otherwise, if you\'ve seen this, return what you already found! \n if customer_index == number_of_customers : \n self.memo[backtrack_key] = True\n return True \n elif backtrack_key in self.memo : \n return self.memo[backtrack_key]\n\n # figure out how much you have \n current_amount = quantity[customer_index]\n\n # consider all your items \n c_i = 0 \n while c_i < len(current_items) :\n # if we have an item that is gte here \n if current_items[c_i] >= current_amount :\n # if we are past 0 and have a matching situation \n if c_i > 0 and current_items[c_i] == current_items[c_i - 1] :\n # go until you run out of room, or until you run out of matches, or until you run into a problem \n while c_i < len(current_items) and current_items[c_i] == current_items[c_i - 1] and current_items[c_i] >= current_amount : \n c_i += 1 \n # if you ran out of room, nothing to do here, break \n if c_i >= len(current_items) : \n break \n elif current_items[c_i] < current_amount :\n # otherwise, if you ran out items, skip on to the next \n c_i += 1 \n continue \n # otherwise, if you have not run out room, and you do have an item worth looking at \n # look at it \n current_items[c_i] -= current_amount\n current_customers[customer_index] = 0 \n # get the key \n temp_key = "".join([str(c_it) for c_it in sorted(current_items)]) + "-" + "".join([str(c_c) for c_c in sorted(current_customers)])\n # check if you have it and it doesn\'t work \n if temp_key in self.memo and self.memo[temp_key] == False :\n # if it doesn\'t, unset the looking and then move forward one \n current_items[c_i] += current_amount\n current_customers[customer_index] = current_amount\n c_i += 1 \n continue \n elif temp_key in self.memo and self.memo[temp_key] == True : \n # if you have the key and it worked already, skip out of there after resetting your backtrack key as well \n self.memo[backtrack_key] = True\n return True \n elif temp_key not in self.memo : \n # otherwise if we have not seen this thing, set up a temp result and lock it in \n temp_result = backtrack(current_items, customer_index + 1, current_customers) \n self.memo[temp_key] = temp_result \n if temp_result == True : \n # on success, update and return \n self.memo[backtrack_key] = True \n return True \n else : \n # on failure, unset and continue \n current_items[c_i] += current_amount \n current_customers[customer_index] = current_amount\n c_i += 1 \n continue \n else : \n c_i += 1 \n continue \n\n # if you ran out of room or weren\'t able to make it work -> set False and return it \n self.memo[backtrack_key] = False\n return False \n \n # kick it off with our altered nums and quantities \n return backtrack(nums, 0, quantity)\n``` | 0 | You are given an array of `n` integers, `nums`, where there are at most `50` unique values in the array. You are also given an array of `m` customer order quantities, `quantity`, where `quantity[i]` is the amount of integers the `ith` customer ordered. Determine if it is possible to distribute `nums` such that:
* The `ith` customer gets **exactly** `quantity[i]` integers,
* The integers the `ith` customer gets are **all equal**, and
* Every customer is satisfied.
Return `true` _if it is possible to distribute_ `nums` _according to the above conditions_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], quantity = \[2\]
**Output:** false
**Explanation:** The 0th customer cannot be given two different integers.
**Example 2:**
**Input:** nums = \[1,2,3,3\], quantity = \[2\]
**Output:** true
**Explanation:** The 0th customer is given \[3,3\]. The integers \[1,2\] are not used.
**Example 3:**
**Input:** nums = \[1,1,2,2\], quantity = \[2,2\]
**Output:** true
**Explanation:** The 0th customer is given \[1,1\], and the 1st customer is given \[2,2\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 1000`
* `m == quantity.length`
* `1 <= m <= 10`
* `1 <= quantity[i] <= 105`
* There are at most `50` unique values in `nums`. | Disconnect node p from its parent and append it to the children list of node q. If q was in the sub-tree of node p (case 1), get the parent node of p and replace p in its children list with q. If p was the root of the tree, make q the root of the tree. |
Backtracking with Memoization | Commented and Explained | distribute-repeating-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe know we only have 10 customers at worst. We also know we have at most 50 unique items in our set up. We can backtrack on the customers and on the items, and can limit ourselves to only as many items as we have customers if we go in greatest reversed order of items present. This lets us limit ourselves appropriately to a space at worst of 10^10. We can allow ourselves to stop early by utilizing a backtracking string to target the current items and current customers as a key, thus letting us memoize results and reduce computational time altogether. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind your number of items, your number of customers, and then check to make sure you at least have enough items to match customers before any combinations. \n\nThen, get the frequency of your items. \nTurn nums into the sorted form of the frequencies (not the items, the frequencies) in reverse order for as many as you have customers. This lets you focus on a subset of size 10^10 at worst. \n\nSort your quantities in reverse. \n\nIf your sum of item frequencies is less than the sum of your quantity, you can also return False already. \n\nOtherwise, set up a memo \n\nDuring the backtracking phase, pass in the current items, customer index, and current customer statuses \n- Build a backtrack key using the items sorted | customer status sorted as a string \n- If your customer index is past the total number number of customers, set memo at backtrack key to true and return true \n- If you have the backtrack key in the memo, return what you found already and skip the preprocess. This is the reason for the sorting as it combines similar set ups with different location strings. \n- otherwise, get the current amount as quantity at customer index \n- set your current item index to 0 \n- while your current item index is in range of your current items length \n - if the item here is not big enough -> move forward by 1 until it is \n - otherwise \n - if the current item index is greater than 0 and we have matching items here \n - go until the last version of these if you can \n - if you end up out of range, break \n - otherwise if you end up at a bad spot, move forward one and continue \n - otherwise try to use the current item to satisfy the current customer, updating in both lists appropriately \n - make a temp key of doing so \n - if you have seen this temp key and it doesn\'t work \n - unset what you did and move forward one and continue \n - if you saw it and it did work \n - set memo for the backtrack key and return True \n - otherwise, go check it out\n - then update the memo\n - if it was true, update memo for backtrack key and return \n - otherwise, undo the look, move forward and continue \n- if you never got a success in the loop, update the memo here and return False \n\nTo solve, kick off backtrack with nums, 0, quantity \n\n# Complexity\n- Time complexity : O (Sum m! / (i!(m-i)!) for i in range 1, m-1, where m is number of customers)\n - O(10^10) at worst since we do 10^10 considerations in our backtracking is the naive amount \n - However, we can limit down since our sort for the backtrack keys worked (never caused an error) to O(3629822) operations, since we now know that we are dealing with combinatory states where no repeats are allowed and order doesn\'t matter (otherwise, the backtrack keys would have caused a problem). Due to this, we get the time complexity of combinations with no repeats instead of permutations with repeats for the backtrack process. \n - This puts our overall time complexity in the form of O(Sum m!/(i!(m-i)!) for i in range 1, m-1), where m is the number of customers according to the problem statement. For comparison sakes, this is about 2750 times faster than O(10^10)\n\n- Space complexity : Due to backtracking nature, we match our space complexity unfortunately, but due handidly beat the space in the other case due to our size reduction. If someone is interested, this can potentially be done in bottom up form and save us the massive amounts of space with the time savings. \n\n# Code\n```\nclass Solution:\n def canDistribute(self, nums: List[int], quantity: List[int]) -> bool :\n \'\'\'\n at most 50 unique values in the array \n customer quantities -> no more than 10 customers -> m \n -> each customer can order between 1 and 10^5, the number of items range as well \n nums -> amount of items \n want to distribute nums so that \n each customer gets exactly customer_i items (so if there are not exactly i items not gonna work)\n the integers that compose the ith customer order are all equal and sum to customer i items \n every customer can be satisfied \n \n \'\'\'\n # get number of items and number of customers \n number_of_items = len(nums)\n number_of_customers = len(quantity) \n # before doing frequency work, if you do not have enough items, you\'ll never satisfy everyone \n if number_of_items < number_of_customers : \n return False \n # find out your frequency of your items \n frequency_of_items = collections.Counter(nums)\n # and limit yourself to the best for your customers \n nums = sorted(frequency_of_items.values(), reverse=True)[:number_of_customers]\n quantity.sort(reverse = True)\n # if you still can\'t satisfy everyone, don\'t try and return False \n if sum(nums) < sum(quantity) : \n return False \n # set up a memo to track your progress \n self.memo = dict() \n\n def backtrack(current_items, customer_index, current_customers) :\n # set up a backtrack key where you use the sorted form of each to capture as many possible alternate substates as you can \n backtrack_key = "".join([str(c_it) for c_it in sorted(current_items)]) + "-" + "".join([str(c_c) for c_c in sorted(current_customers)]) \n # if you reached the end, mark it and return True. Otherwise, if you\'ve seen this, return what you already found! \n if customer_index == number_of_customers : \n self.memo[backtrack_key] = True\n return True \n elif backtrack_key in self.memo : \n return self.memo[backtrack_key]\n\n # figure out how much you have \n current_amount = quantity[customer_index]\n\n # consider all your items \n c_i = 0 \n while c_i < len(current_items) :\n # if we have an item that is gte here \n if current_items[c_i] >= current_amount :\n # if we are past 0 and have a matching situation \n if c_i > 0 and current_items[c_i] == current_items[c_i - 1] :\n # go until you run out of room, or until you run out of matches, or until you run into a problem \n while c_i < len(current_items) and current_items[c_i] == current_items[c_i - 1] and current_items[c_i] >= current_amount : \n c_i += 1 \n # if you ran out of room, nothing to do here, break \n if c_i >= len(current_items) : \n break \n elif current_items[c_i] < current_amount :\n # otherwise, if you ran out items, skip on to the next \n c_i += 1 \n continue \n # otherwise, if you have not run out room, and you do have an item worth looking at \n # look at it \n current_items[c_i] -= current_amount\n current_customers[customer_index] = 0 \n # get the key \n temp_key = "".join([str(c_it) for c_it in sorted(current_items)]) + "-" + "".join([str(c_c) for c_c in sorted(current_customers)])\n # check if you have it and it doesn\'t work \n if temp_key in self.memo and self.memo[temp_key] == False :\n # if it doesn\'t, unset the looking and then move forward one \n current_items[c_i] += current_amount\n current_customers[customer_index] = current_amount\n c_i += 1 \n continue \n elif temp_key in self.memo and self.memo[temp_key] == True : \n # if you have the key and it worked already, skip out of there after resetting your backtrack key as well \n self.memo[backtrack_key] = True\n return True \n elif temp_key not in self.memo : \n # otherwise if we have not seen this thing, set up a temp result and lock it in \n temp_result = backtrack(current_items, customer_index + 1, current_customers) \n self.memo[temp_key] = temp_result \n if temp_result == True : \n # on success, update and return \n self.memo[backtrack_key] = True \n return True \n else : \n # on failure, unset and continue \n current_items[c_i] += current_amount \n current_customers[customer_index] = current_amount\n c_i += 1 \n continue \n else : \n c_i += 1 \n continue \n\n # if you ran out of room or weren\'t able to make it work -> set False and return it \n self.memo[backtrack_key] = False\n return False \n \n # kick it off with our altered nums and quantities \n return backtrack(nums, 0, quantity)\n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python (Simple Backtracking) | distribute-repeating-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canDistribute(self, nums, quantity):\n n, m = len(nums), len(quantity)\n\n dict1 = collections.Counter(nums)\n\n quantity.sort(reverse = True)\n\n def dfs(i):\n if i == m:\n return True \n\n for key,val in dict1.items():\n if val >= quantity[i]:\n dict1[key] -= quantity[i]\n\n if dfs(i+1):\n return True\n\n dict1[key] += quantity[i]\n\n return False \n\n return dfs(0)\n\n\n\n \n\n\n\n \n\n\n\n \n \n \n``` | 0 | You are given an array of `n` integers, `nums`, where there are at most `50` unique values in the array. You are also given an array of `m` customer order quantities, `quantity`, where `quantity[i]` is the amount of integers the `ith` customer ordered. Determine if it is possible to distribute `nums` such that:
* The `ith` customer gets **exactly** `quantity[i]` integers,
* The integers the `ith` customer gets are **all equal**, and
* Every customer is satisfied.
Return `true` _if it is possible to distribute_ `nums` _according to the above conditions_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], quantity = \[2\]
**Output:** false
**Explanation:** The 0th customer cannot be given two different integers.
**Example 2:**
**Input:** nums = \[1,2,3,3\], quantity = \[2\]
**Output:** true
**Explanation:** The 0th customer is given \[3,3\]. The integers \[1,2\] are not used.
**Example 3:**
**Input:** nums = \[1,1,2,2\], quantity = \[2,2\]
**Output:** true
**Explanation:** The 0th customer is given \[1,1\], and the 1st customer is given \[2,2\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 1000`
* `m == quantity.length`
* `1 <= m <= 10`
* `1 <= quantity[i] <= 105`
* There are at most `50` unique values in `nums`. | Disconnect node p from its parent and append it to the children list of node q. If q was in the sub-tree of node p (case 1), get the parent node of p and replace p in its children list with q. If p was the root of the tree, make q the root of the tree. |
Python (Simple Backtracking) | distribute-repeating-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canDistribute(self, nums, quantity):\n n, m = len(nums), len(quantity)\n\n dict1 = collections.Counter(nums)\n\n quantity.sort(reverse = True)\n\n def dfs(i):\n if i == m:\n return True \n\n for key,val in dict1.items():\n if val >= quantity[i]:\n dict1[key] -= quantity[i]\n\n if dfs(i+1):\n return True\n\n dict1[key] += quantity[i]\n\n return False \n\n return dfs(0)\n\n\n\n \n\n\n\n \n\n\n\n \n \n \n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
[Python3] simple solution | design-an-ordered-stream | 0 | 1 | \n```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.data = [None]*n\n self.ptr = 0 # 0-indexed \n\n def insert(self, id: int, value: str) -> List[str]:\n id -= 1 # 0-indexed \n self.data[id] = value \n if id > self.ptr: return [] # not reaching ptr \n \n while self.ptr < len(self.data) and self.data[self.ptr]: self.ptr += 1 # update self.ptr \n return self.data[id:self.ptr]\n``` | 55 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
[Python3] simple solution | design-an-ordered-stream | 0 | 1 | \n```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.data = [None]*n\n self.ptr = 0 # 0-indexed \n\n def insert(self, id: int, value: str) -> List[str]:\n id -= 1 # 0-indexed \n self.data[id] = value \n if id > self.ptr: return [] # not reaching ptr \n \n while self.ptr < len(self.data) and self.data[self.ptr]: self.ptr += 1 # update self.ptr \n return self.data[id:self.ptr]\n``` | 55 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Python solution with a hint before the solution. | design-an-ordered-stream | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIf you don\'t want to go through my code, I suggest you to watch the example video and observe the "ptr" and how it is incrementing and returning things based on the ptr value.\n\n# Code\n```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.arr = [""] * n\n self.ptr = 0\n\n def insert(self, idKey: int, value: str) -> List[str]:\n self.arr[idKey-1] = value\n res = []\n if self.ptr == idKey - 1:\n while self.ptr < len(self.arr) and self.arr[self.ptr] != "":\n print(self.ptr)\n res.append(self.arr[self.ptr])\n self.ptr += 1\n\n return res\n\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(idKey,value)\n``` | 2 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Python solution with a hint before the solution. | design-an-ordered-stream | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIf you don\'t want to go through my code, I suggest you to watch the example video and observe the "ptr" and how it is incrementing and returning things based on the ptr value.\n\n# Code\n```\nclass OrderedStream:\n\n def __init__(self, n: int):\n self.arr = [""] * n\n self.ptr = 0\n\n def insert(self, idKey: int, value: str) -> List[str]:\n self.arr[idKey-1] = value\n res = []\n if self.ptr == idKey - 1:\n while self.ptr < len(self.arr) and self.arr[self.ptr] != "":\n print(self.ptr)\n res.append(self.arr[self.ptr])\n self.ptr += 1\n\n return res\n\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(idKey,value)\n``` | 2 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Latest Python solution explained for newly updated description: Faster than 90% | design-an-ordered-stream | 0 | 1 | The idea behind this problem is simple but the description is confusing.\nSo let me explain a bit.\n\nBasically , we need to store every incoming value at the given index. And \nwith every incoming index, we have to check\n\n* If the current index is less than the incoming index, the we have to return\n an empty list\n\n* Else , we have to return an sliced list from the incoming index to the first index\n where there is no insertion till yet.\n\nSolution:\n* Initialize a list of size n with None\n* Maintain the current index with self.ptr\n* For every insert call, with idKey, value \n * Assign the list[idKey-1] to the value # Since array is 0-index reduce 1\n * Check if the current index is less than incoming index(idKey-1) and return []\n * Else return sliced list from incoming index(idKey-1) till we do not encounter None.\n\n\n```\nclass OrderedStream:\n\n def __init__(self, n):\n self.stream = [None]*n\n self.ptr = 0\n\n def insert(self, idKey, value):\n idKey -= 1\n self.stream[idKey] = value\n if self.ptr < idKey:\n return []\n else:\n while self.ptr < len(self.stream) and self.stream[self.ptr] is not None:\n self.ptr += 1\n return self.stream[idKey:self.ptr]\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(idKey,value)\n``` | 29 | There is a stream of `n` `(idKey, value)` pairs arriving in an **arbitrary** order, where `idKey` is an integer between `1` and `n` and `value` is a string. No two pairs have the same `id`.
Design a stream that returns the values in **increasing order of their IDs** by returning a **chunk** (list) of values after each insertion. The concatenation of all the **chunks** should result in a list of the sorted values.
Implement the `OrderedStream` class:
* `OrderedStream(int n)` Constructs the stream to take `n` values.
* `String[] insert(int idKey, String value)` Inserts the pair `(idKey, value)` into the stream, then returns the **largest possible chunk** of currently inserted values that appear next in the order.
**Example:**
**Input**
\[ "OrderedStream ", "insert ", "insert ", "insert ", "insert ", "insert "\]
\[\[5\], \[3, "ccccc "\], \[1, "aaaaa "\], \[2, "bbbbb "\], \[5, "eeeee "\], \[4, "ddddd "\]\]
**Output**
\[null, \[\], \[ "aaaaa "\], \[ "bbbbb ", "ccccc "\], \[\], \[ "ddddd ", "eeeee "\]\]
**Explanation**
// Note that the values ordered by ID is \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc "); // Inserts (3, "ccccc "), returns \[\].
os.insert(1, "aaaaa "); // Inserts (1, "aaaaa "), returns \[ "aaaaa "\].
os.insert(2, "bbbbb "); // Inserts (2, "bbbbb "), returns \[ "bbbbb ", "ccccc "\].
os.insert(5, "eeeee "); // Inserts (5, "eeeee "), returns \[\].
os.insert(4, "ddddd "); // Inserts (4, "ddddd "), returns \[ "ddddd ", "eeeee "\].
// Concatentating all the chunks returned:
// \[\] + \[ "aaaaa "\] + \[ "bbbbb ", "ccccc "\] + \[\] + \[ "ddddd ", "eeeee "\] = \[ "aaaaa ", "bbbbb ", "ccccc ", "ddddd ", "eeeee "\]
// The resulting order is the same as the order above.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= id <= n`
* `value.length == 5`
* `value` consists only of lowercase letters.
* Each call to `insert` will have a unique `id.`
* Exactly `n` calls will be made to `insert`. | Notice that the constraints are small enough for a brute force solution to pass. Loop through all triplets, and count the ones that are good. |
Latest Python solution explained for newly updated description: Faster than 90% | design-an-ordered-stream | 0 | 1 | The idea behind this problem is simple but the description is confusing.\nSo let me explain a bit.\n\nBasically , we need to store every incoming value at the given index. And \nwith every incoming index, we have to check\n\n* If the current index is less than the incoming index, the we have to return\n an empty list\n\n* Else , we have to return an sliced list from the incoming index to the first index\n where there is no insertion till yet.\n\nSolution:\n* Initialize a list of size n with None\n* Maintain the current index with self.ptr\n* For every insert call, with idKey, value \n * Assign the list[idKey-1] to the value # Since array is 0-index reduce 1\n * Check if the current index is less than incoming index(idKey-1) and return []\n * Else return sliced list from incoming index(idKey-1) till we do not encounter None.\n\n\n```\nclass OrderedStream:\n\n def __init__(self, n):\n self.stream = [None]*n\n self.ptr = 0\n\n def insert(self, idKey, value):\n idKey -= 1\n self.stream[idKey] = value\n if self.ptr < idKey:\n return []\n else:\n while self.ptr < len(self.stream) and self.stream[self.ptr] is not None:\n self.ptr += 1\n return self.stream[idKey:self.ptr]\n\n\n# Your OrderedStream object will be instantiated and called as such:\n# obj = OrderedStream(n)\n# param_1 = obj.insert(idKey,value)\n``` | 29 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.