title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python] 4 ways to attack | goal-parser-interpretation | 0 | 1 | Just while loop with carefully incrementing counter is good enough:\n```\n# runtime beats 32% ; memory beats 99.76%\ndef interpret(command):\n \n return_string = ""\n i = 0\n while i < len(command):\n if command[i] == "G":\n return_string += \'G\'\n i += 1\n elif command[i:i + 2] == \'()\':\n return_string += \'o\'\n i += 2\n else:\n \'\'\'when command[i:i+3] == "Cal)"\n or command[i] == \'(\'\n but command[i+1] != \')\'\n \'\'\'\n return_string += \'al\'\n i += 4\n \n return return_string\n```\nUse for loop if you want:\n```\n# runtime beats 64%; memory beats 66%\ndef interpret(command):\n \n return_string = ""\n tmp = ""\n for each in command:\n if each == "G":\n return_string += "G"\n tmp = ""\n else:\n tmp += each\n if tmp == \'()\':\n return_string += \'o\'\n tmp = ""\n if tmp == \'(al)\':\n return_string += \'al\'\n tmp = ""\n \n return return_string\n```\nWant to get fancier than that? Enter dictionary:\n```\n# runtime beats 19% ; memory beats 38%\ndef interpret(command):\n list1 = []\n str1 = ""\n parser_table = {\'G\':\'G\',\n \'()\':\'o\',\n \'(al)\':\'al\'\n }\n for each in command:\n str1 += each\n if str1 in parser_table:\n list1.append(parser_table[str1])\n str1 = ""\n \n return \'\'.join(list1)\n```\nOne must always know the builtins of one\'s language:\n```\n# runtime beats 68% ; memory beats 38%\ndef interpret(command): \n command = command.replace("()","o")\n command = command.replace(\'(al)\',\'al\')\n return command\n\t\t# try one liner with this\n``` | 38 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Python Two pointer well explain solution quick and still mantain O(1) space complexity | max-number-of-k-sum-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to use a `two-pointer` approach on a sorted array. Sorting the array allows us to efficiently find pairs of numbers that sum up to the target value `k`. The two pointers (`left` and `right`) are initialized at the beginning and end of the sorted array, and we move them towards each other based on the sum of the numbers at those positions.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Sort the array:** We begin by sorting the input array nums. Sorting is essential for the two-pointer approach. using the `nums.sort()`\n\n**Iterate with two pointers:** Use a while loop to iterate until `left` pointer is less than `right` pointer.\n - If the sum of `nums[left]` and `nums[right]` is equal to the target k, we have found a pair, so we increment the operation count and move both pointers towards the center\n - If the sum is less than **k**, we need a larger sum, so we move the left pointer to the right.\n - If the sum is greater than **k**, we need a smaller sum, so we move the right pointer to the left.\n\n**Return the count:** After the while loop completes, return the operation count, which represents the maximum number of pairs that can be formed to achieve the target sum.\n\n\n \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is dominated by the sorting step, which is typically O(n log n) for the average case. The two-pointer traversal of the sorted array is O(n), so the overall time complexity is **O(n log n)**\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is **O(1)** because the algorithm uses a constant amount of extra space for the pointers and variables, regardless of the input size.\n# Code\n```\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n nums.sort()\n\n left = 0 \n right = len(nums) - 1\n operation = 0 \n\n while left < right:\n if ((nums[left] + nums[right]) == k):\n operation += 1\n left +=1 \n right -=1\n elif((nums[left] + nums[right]) < k):\n left += 1\n else:\n right -= 1\n return operation\n\n```\n\n## Please upvote this solution if you enjoyed it\n | 10 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
Python Two pointer well explain solution quick and still mantain O(1) space complexity | max-number-of-k-sum-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to use a `two-pointer` approach on a sorted array. Sorting the array allows us to efficiently find pairs of numbers that sum up to the target value `k`. The two pointers (`left` and `right`) are initialized at the beginning and end of the sorted array, and we move them towards each other based on the sum of the numbers at those positions.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Sort the array:** We begin by sorting the input array nums. Sorting is essential for the two-pointer approach. using the `nums.sort()`\n\n**Iterate with two pointers:** Use a while loop to iterate until `left` pointer is less than `right` pointer.\n - If the sum of `nums[left]` and `nums[right]` is equal to the target k, we have found a pair, so we increment the operation count and move both pointers towards the center\n - If the sum is less than **k**, we need a larger sum, so we move the left pointer to the right.\n - If the sum is greater than **k**, we need a smaller sum, so we move the right pointer to the left.\n\n**Return the count:** After the while loop completes, return the operation count, which represents the maximum number of pairs that can be formed to achieve the target sum.\n\n\n \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is dominated by the sorting step, which is typically O(n log n) for the average case. The two-pointer traversal of the sorted array is O(n), so the overall time complexity is **O(n log n)**\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is **O(1)** because the algorithm uses a constant amount of extra space for the pointers and variables, regardless of the input size.\n# Code\n```\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n nums.sort()\n\n left = 0 \n right = len(nums) - 1\n operation = 0 \n\n while left < right:\n if ((nums[left] + nums[right]) == k):\n operation += 1\n left +=1 \n right -=1\n elif((nums[left] + nums[right]) < k):\n left += 1\n else:\n right -= 1\n return operation\n\n```\n\n## Please upvote this solution if you enjoyed it\n | 10 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
[Python 3] Two solution with Counter and two points || beats 99% | max-number-of-k-sum-pairs | 0 | 1 | ```python3 []\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n res, d = 0, Counter(nums)\n for val1, cnt in d.items():\n val2 = k - val1\n # it\'s trick to get rid of duplicates pairs, consider only pairs where val1 >= val2\n if val2 < val1 or val2 not in d: continue \n res += min(cnt, d[val2]) if val1 != val2 else cnt//2\n \n return res\n```\n```python3 []\nclass Solution:\n def maxOperations2(self, nums: List[int], k: int) -> int:\n nums.sort()\n res, l, r = 0, 0 ,len(nums) - 1\n\n while l < r:\n S = nums[l] + nums[r]\n if S > k:\n r -= 1\n elif S < k:\n l += 1\n else:\n res += 1\n l += 1\n r -= 1\n return res\n\n```\n\n\n | 16 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
[Python 3] Two solution with Counter and two points || beats 99% | max-number-of-k-sum-pairs | 0 | 1 | ```python3 []\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n res, d = 0, Counter(nums)\n for val1, cnt in d.items():\n val2 = k - val1\n # it\'s trick to get rid of duplicates pairs, consider only pairs where val1 >= val2\n if val2 < val1 or val2 not in d: continue \n res += min(cnt, d[val2]) if val1 != val2 else cnt//2\n \n return res\n```\n```python3 []\nclass Solution:\n def maxOperations2(self, nums: List[int], k: int) -> int:\n nums.sort()\n res, l, r = 0, 0 ,len(nums) - 1\n\n while l < r:\n S = nums[l] + nums[r]\n if S > k:\n r -= 1\n elif S < k:\n l += 1\n else:\n res += 1\n l += 1\n r -= 1\n return res\n\n```\n\n\n | 16 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
99% CPU, 92% RAM:π±βπ Suboptimal but Purr-fectly Playful: Sort + Binary Search π | max-number-of-k-sum-pairs | 0 | 1 | # \uD83D\uDC31 Cat-tastic Intuition \uD83D\uDC31\nWhy chase the optimal mouse when we can have some fun with a playful, yet speedy, kitty solution? Let\'s use some purr-fect library functions to give us a little boost!\n\n# \uD83D\uDC3E Feline Approach \uD83D\uDC3E\nSure, sorting is like the classic cat nap \u2013 everyone does it. But why not add a twist with a game of binary search? It\'s like the laser pointer game for our sorted array, helping us pounce over numbers that just won\'t play nice.\n\n# \uD83D\uDC08 Complexity Whiskers \uD83D\uDC08\n- **Time complexity:** $$O(n)log(n)$$ \u2013 Technically, it\'s a tad slower than the optimal $$O(n)$$ (which is like a cat sprinting after a toy). But hey, our library functions are like catnip, making everything more fun and fast!\n \n- **Space complexity:** $$O(1)$$ \u2013 Meow-tastic! Python lets us sort in place, just like how cats always find the purr-fect spot to curl up.\n\n# \uD83D\uDC31\u200D\uD83D\uDCBB Code Time! \uD83D\uDC31\u200D\uD83D\uDCBB\n```\nfrom bisect import bisect_left, bisect_right\n\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n nums.sort() # Time to line up our yarn balls!\n operations = 0 # Here\'s where we\'ll count our playful pounces.\n\n # Two paws are better than one! Let\'s use two pointers.\n left, right = 0, len(nums) - 1\n \n while left < right:\n total = nums[left] + nums[right]\n \n if total == k: # Did we catch the yarn ball?\n operations += 1\n left += 1\n right -= 1\n elif total < k:\n # Pounce to the leftmost yarn ball that\'s k - nums[right] or bigger.\n left = bisect.bisect_left(nums, k - nums[right], lo=left + 1, hi=right)\n else: # total > k\n # Hop to the rightmost yarn ball that\'s k - nums[left] or smaller.\n right = bisect.bisect_right(nums, k - nums[left], lo=left, hi=right) - 1\n # Remember, bisect_right is a sneaky kitty:\n # If there\'s a yarn ball with the same value, \n # it\'ll try to jump just past it.\n \n return operations\n```\n\n# \uD83D\uDC3E Paws & Reflect \uD83D\uDC3E\nIf my kitty solution made you purr, please give it an upvote! And remember, it\'s not always about catching the mouse \u2013 sometimes, it\'s about the chase! \uD83D\uDC31\uD83E\uDDF6\uD83D\uDC3E | 7 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
99% CPU, 92% RAM:π±βπ Suboptimal but Purr-fectly Playful: Sort + Binary Search π | max-number-of-k-sum-pairs | 0 | 1 | # \uD83D\uDC31 Cat-tastic Intuition \uD83D\uDC31\nWhy chase the optimal mouse when we can have some fun with a playful, yet speedy, kitty solution? Let\'s use some purr-fect library functions to give us a little boost!\n\n# \uD83D\uDC3E Feline Approach \uD83D\uDC3E\nSure, sorting is like the classic cat nap \u2013 everyone does it. But why not add a twist with a game of binary search? It\'s like the laser pointer game for our sorted array, helping us pounce over numbers that just won\'t play nice.\n\n# \uD83D\uDC08 Complexity Whiskers \uD83D\uDC08\n- **Time complexity:** $$O(n)log(n)$$ \u2013 Technically, it\'s a tad slower than the optimal $$O(n)$$ (which is like a cat sprinting after a toy). But hey, our library functions are like catnip, making everything more fun and fast!\n \n- **Space complexity:** $$O(1)$$ \u2013 Meow-tastic! Python lets us sort in place, just like how cats always find the purr-fect spot to curl up.\n\n# \uD83D\uDC31\u200D\uD83D\uDCBB Code Time! \uD83D\uDC31\u200D\uD83D\uDCBB\n```\nfrom bisect import bisect_left, bisect_right\n\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n nums.sort() # Time to line up our yarn balls!\n operations = 0 # Here\'s where we\'ll count our playful pounces.\n\n # Two paws are better than one! Let\'s use two pointers.\n left, right = 0, len(nums) - 1\n \n while left < right:\n total = nums[left] + nums[right]\n \n if total == k: # Did we catch the yarn ball?\n operations += 1\n left += 1\n right -= 1\n elif total < k:\n # Pounce to the leftmost yarn ball that\'s k - nums[right] or bigger.\n left = bisect.bisect_left(nums, k - nums[right], lo=left + 1, hi=right)\n else: # total > k\n # Hop to the rightmost yarn ball that\'s k - nums[left] or smaller.\n right = bisect.bisect_right(nums, k - nums[left], lo=left, hi=right) - 1\n # Remember, bisect_right is a sneaky kitty:\n # If there\'s a yarn ball with the same value, \n # it\'ll try to jump just past it.\n \n return operations\n```\n\n# \uD83D\uDC3E Paws & Reflect \uD83D\uDC3E\nIf my kitty solution made you purr, please give it an upvote! And remember, it\'s not always about catching the mouse \u2013 sometimes, it\'s about the chase! \uD83D\uDC31\uD83E\uDDF6\uD83D\uDC3E | 7 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Easy HashMap Solution : Java π | max-number-of-k-sum-pairs | 1 | 1 | # Easy HashMap Solution : \n# Java Code : \n```\nclass Solution {\n public int maxOperations(int[] nums, int target) {\n HashMap<Integer,Integer> hmap = new HashMap<>();\n int count = 0;\n for(int i = 0;i<nums.length;i++)\n {\n if(hmap.containsKey(target-nums[i]) == true)\n {\n count++;\n if(hmap.get(target-nums[i]) == 1)\n hmap.remove(target-nums[i]);\n else\n hmap.put(target-nums[i],hmap.get(target-nums[i])-1);\n }\n else\n {\n hmap.put(nums[i],hmap.getOrDefault(nums[i],0)+1);\n }\n }\n return count;\n }\n}\n\n```\n---\n#### *Please don\'t forget to upvote if you\'ve liked mu solution.* \uD83D\uDD25\n--- | 10 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
Easy HashMap Solution : Java π | max-number-of-k-sum-pairs | 1 | 1 | # Easy HashMap Solution : \n# Java Code : \n```\nclass Solution {\n public int maxOperations(int[] nums, int target) {\n HashMap<Integer,Integer> hmap = new HashMap<>();\n int count = 0;\n for(int i = 0;i<nums.length;i++)\n {\n if(hmap.containsKey(target-nums[i]) == true)\n {\n count++;\n if(hmap.get(target-nums[i]) == 1)\n hmap.remove(target-nums[i]);\n else\n hmap.put(target-nums[i],hmap.get(target-nums[i])-1);\n }\n else\n {\n hmap.put(nums[i],hmap.getOrDefault(nums[i],0)+1);\n }\n }\n return count;\n }\n}\n\n```\n---\n#### *Please don\'t forget to upvote if you\'ve liked mu solution.* \uD83D\uDD25\n--- | 10 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Using Python Dictionary | max-number-of-k-sum-pairs | 0 | 1 | # Code\n```\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n\n d = {}\n count = 0\n\n for x in nums:\n if d.get(k - x, 0) > 0:\n count+=1\n d[k-x]-=1\n else:\n d[x] = d.get(x, 0) + 1\n\n return count\n``` | 7 | You are given an integer array `nums` and an integer `k`.
In one operation, you can pick two numbers from the array whose sum equals `k` and remove them from the array.
Return _the maximum number of operations you can perform on the array_.
**Example 1:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 2
**Explanation:** Starting with nums = \[1,2,3,4\]:
- Remove numbers 1 and 4, then nums = \[2,3\]
- Remove numbers 2 and 3, then nums = \[\]
There are no more pairs that sum up to 5, hence a total of 2 operations.
**Example 2:**
**Input:** nums = \[3,1,3,4,3\], k = 6
**Output:** 1
**Explanation:** Starting with nums = \[3,1,3,4,3\]:
- Remove the first two 3's, then nums = \[1,4,3\]
There are no more pairs that sum up to 6, hence a total of 1 operation.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 109` | The key is to find the longest non-decreasing subarray starting with the first element or ending with the last element, respectively. After removing some subarray, the result is the concatenation of a sorted prefix and a sorted suffix, where the last element of the prefix is smaller than the first element of the suffix. |
Using Python Dictionary | max-number-of-k-sum-pairs | 0 | 1 | # Code\n```\nclass Solution:\n def maxOperations(self, nums: List[int], k: int) -> int:\n\n d = {}\n count = 0\n\n for x in nums:\n if d.get(k - x, 0) > 0:\n count+=1\n d[k-x]-=1\n else:\n d[x] = d.get(x, 0) + 1\n\n return count\n``` | 7 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Simplest Python solution | concatenation-of-consecutive-binary-numbers | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n res = ""\n for x in range(1, n+1):\n res += bin(x)[2:]\n return int(res, 2) % (10**9+7)\n``` | 1 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
Simplest Python solution | concatenation-of-consecutive-binary-numbers | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n res = ""\n for x in range(1, n+1):\n res += bin(x)[2:]\n return int(res, 2) % (10**9+7)\n``` | 1 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
π₯ [LeetCode The Hard Way] π₯ Explained Line By Line | concatenation-of-consecutive-binary-numbers | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n**Approach 1: Bit Manipulation**\n\n**C++**\n\n```cpp\n// Time Complexity: O(N)\n// Space Complexity: O(1)\nclass Solution {\npublic:\n // the idea is to use bit manipulation to set the current number based on the previous number\n // for example, \n // n = 1, ans = 0b1\n // n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n // i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n // n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n // i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n // n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n // i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n // so now we can see a pattern here\n // we need to shift `l` bits of the previous ans to the left and add the current `i` \n // how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n int concatenatedBinary(int n) {\n // `l` is the bit length to be shifted\n int M = 1e9 + 7, l = 0;\n // use long here as it potentially could overflow for int\n long ans = 0;\n for (int i = 1; i <= n; i++) {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if ((i & (i - 1)) == 0) l += 1;\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M;\n }\n return ans;\n }\n};\n```\n\n**Java**\n\n```java\n// Time Complexity: O(N)\n// Space Complexity: O(1)\nclass Solution {\n // the idea is to use bit manipulation to set the current number based on the previous number\n // for example, \n // n = 1, ans = 0b1\n // n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n // i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n // n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n // i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n // n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n // i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n // so now we can see a pattern here\n // we need to shift `l` bits of the previous ans to the left and add the current `i` \n // how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n public int concatenatedBinary(int n) {\n // `l` is the bit length to be shifted\n int M = 1000000007, l = 0;\n // use long here as it potentially could overflow for int\n long ans = 0;\n for (int i = 1; i <= n; i++) {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if ((i & (i - 1)) == 0) l += 1;\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M;\n }\n return (int) ans;\n }\n}\n```\n\n**Python**\n\n```py\n# Time Complexity: O(N)\n# Space Complexity: O(1)\nclass Solution:\n # the idea is to use bit manipulation to set the current number based on the previous number\n # for example, \n # n = 1, ans = 0b1\n # n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n # i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n # n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n # i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n # n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n # i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n # so now we can see a pattern here\n # we need to shift `l` bits of the previous ans to the left and add the current `i` \n # how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n def concatenatedBinary(self, n: int) -> int:\n M = 10 ** 9 + 7\n # `l` is the bit length to be shifted\n l, ans = 0, 0\n for i in range(1, n + 1):\n # i & (i - 1) means removing the rightmost set bit\n # e.g. 100100 -> 100000\n # 000001 -> 000000\n # 000000 -> 000000\n # after removal, if it is 0, then it means it is power of 2\n # as all power of 2 only contains 1 set bit\n # if it is power of 2, we increase the bit length `l`\n if i & (i - 1) == 0:\n l += 1\n # (ans << l) means shifting the orginal answer `l` bits to th left\n # (x | i) means using OR operation to set the bit\n # e.g. 0001 << 3 = 0001000\n # e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M\n return ans\n```\n\n**Go**\n\n```go\n// Time Complexity: O(N)\n// Space Complexity: O(1)\n\n// the idea is to use bit manipulation to set the current number based on the previous number\n// for example, \n// n = 1, ans = 0b1\n// n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n// i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n// n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n// i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n// n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n// i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n// so now we can see a pattern here\n// we need to shift `l` bits of the previous ans to the left and add the current `i` \n// how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\nfunc concatenatedBinary(n int) int {\n // `l` is the bit length to be shifted\n ans, l, M := 0, 0, 1_000_000_007\n for i := 1; i <= n; i++ {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if (i & (i - 1) == 0) {\n l += 1\n }\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M\n } \n return ans\n}\n``` | 71 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
π₯ [LeetCode The Hard Way] π₯ Explained Line By Line | concatenation-of-consecutive-binary-numbers | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n**Approach 1: Bit Manipulation**\n\n**C++**\n\n```cpp\n// Time Complexity: O(N)\n// Space Complexity: O(1)\nclass Solution {\npublic:\n // the idea is to use bit manipulation to set the current number based on the previous number\n // for example, \n // n = 1, ans = 0b1\n // n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n // i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n // n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n // i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n // n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n // i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n // so now we can see a pattern here\n // we need to shift `l` bits of the previous ans to the left and add the current `i` \n // how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n int concatenatedBinary(int n) {\n // `l` is the bit length to be shifted\n int M = 1e9 + 7, l = 0;\n // use long here as it potentially could overflow for int\n long ans = 0;\n for (int i = 1; i <= n; i++) {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if ((i & (i - 1)) == 0) l += 1;\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M;\n }\n return ans;\n }\n};\n```\n\n**Java**\n\n```java\n// Time Complexity: O(N)\n// Space Complexity: O(1)\nclass Solution {\n // the idea is to use bit manipulation to set the current number based on the previous number\n // for example, \n // n = 1, ans = 0b1\n // n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n // i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n // n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n // i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n // n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n // i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n // so now we can see a pattern here\n // we need to shift `l` bits of the previous ans to the left and add the current `i` \n // how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n public int concatenatedBinary(int n) {\n // `l` is the bit length to be shifted\n int M = 1000000007, l = 0;\n // use long here as it potentially could overflow for int\n long ans = 0;\n for (int i = 1; i <= n; i++) {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if ((i & (i - 1)) == 0) l += 1;\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M;\n }\n return (int) ans;\n }\n}\n```\n\n**Python**\n\n```py\n# Time Complexity: O(N)\n# Space Complexity: O(1)\nclass Solution:\n # the idea is to use bit manipulation to set the current number based on the previous number\n # for example, \n # n = 1, ans = 0b1\n # n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n # i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n # n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n # i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n # n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n # i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n # so now we can see a pattern here\n # we need to shift `l` bits of the previous ans to the left and add the current `i` \n # how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n def concatenatedBinary(self, n: int) -> int:\n M = 10 ** 9 + 7\n # `l` is the bit length to be shifted\n l, ans = 0, 0\n for i in range(1, n + 1):\n # i & (i - 1) means removing the rightmost set bit\n # e.g. 100100 -> 100000\n # 000001 -> 000000\n # 000000 -> 000000\n # after removal, if it is 0, then it means it is power of 2\n # as all power of 2 only contains 1 set bit\n # if it is power of 2, we increase the bit length `l`\n if i & (i - 1) == 0:\n l += 1\n # (ans << l) means shifting the orginal answer `l` bits to th left\n # (x | i) means using OR operation to set the bit\n # e.g. 0001 << 3 = 0001000\n # e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M\n return ans\n```\n\n**Go**\n\n```go\n// Time Complexity: O(N)\n// Space Complexity: O(1)\n\n// the idea is to use bit manipulation to set the current number based on the previous number\n// for example, \n// n = 1, ans = 0b1\n// n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n// i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n// n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n// i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n// n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n// i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n// so now we can see a pattern here\n// we need to shift `l` bits of the previous ans to the left and add the current `i` \n// how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\nfunc concatenatedBinary(n int) int {\n // `l` is the bit length to be shifted\n ans, l, M := 0, 0, 1_000_000_007\n for i := 1; i <= n; i++ {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if (i & (i - 1) == 0) {\n l += 1\n }\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M\n } \n return ans\n}\n``` | 71 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
[ Python ] β
β
Simple Python Solution Using Bin Function π₯³βπ | concatenation-of-consecutive-binary-numbers | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 3110 ms, faster than 38.58% of Python3 online submissions for Concatenation of Consecutive Binary Numbers.\n# Memory Usage: 15.9 MB, less than 22.05% of Python3 online submissions for Concatenation of Consecutive Binary Numbers.\n\n\tclass Solution:\n\t\tdef concatenatedBinary(self, n: int) -> int:\n\n\t\t\tbinary = \'\'\n\n\t\t\tfor num in range(1, n+1):\n\n\t\t\t\tbinary = binary + bin(num)[2:]\n\n\t\t\tresult = int(binary, 2)\n\n\t\t\treturn result % (10**9 + 7)\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 3 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
[ Python ] β
β
Simple Python Solution Using Bin Function π₯³βπ | concatenation-of-consecutive-binary-numbers | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 3110 ms, faster than 38.58% of Python3 online submissions for Concatenation of Consecutive Binary Numbers.\n# Memory Usage: 15.9 MB, less than 22.05% of Python3 online submissions for Concatenation of Consecutive Binary Numbers.\n\n\tclass Solution:\n\t\tdef concatenatedBinary(self, n: int) -> int:\n\n\t\t\tbinary = \'\'\n\n\t\t\tfor num in range(1, n+1):\n\n\t\t\t\tbinary = binary + bin(num)[2:]\n\n\t\t\tresult = int(binary, 2)\n\n\t\t\treturn result % (10**9 + 7)\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 3 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
β
β SIMPLE PYTHON3 SOLUTION β
β O)n log n ) time | concatenation-of-consecutive-binary-numbers | 0 | 1 | ***UPVOTE*** if it is helpfull\n```\n\nclass Solution:\n def countBits(self,x):\n ab = 0\n while x:\n x >>= 1\n ab += 1\n return ab\n def concatenatedBinary(self, n: int) -> int:\n res = 0\n mod = 10**9 + 7\n for i in range(1, n+1):\n res = ((res << self.countBits(i)) + i) % mod\n return res\n``` | 2 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
β
β SIMPLE PYTHON3 SOLUTION β
β O)n log n ) time | concatenation-of-consecutive-binary-numbers | 0 | 1 | ***UPVOTE*** if it is helpfull\n```\n\nclass Solution:\n def countBits(self,x):\n ab = 0\n while x:\n x >>= 1\n ab += 1\n return ab\n def concatenatedBinary(self, n: int) -> int:\n res = 0\n mod = 10**9 + 7\n for i in range(1, n+1):\n res = ((res << self.countBits(i)) + i) % mod\n return res\n``` | 2 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Python Elegant & Short | One line | Reducing | concatenation-of-consecutive-binary-numbers | 0 | 1 | ```\nclass Solution:\n """\n Time: O(n*log(n))\n Memory: O(1)\n """\n\n MOD = 10 ** 9 + 7\n\n def concatenatedBinary(self, n: int) -> int:\n return reduce(lambda x, y: ((x << y.bit_length()) | y) % self.MOD, range(1, n + 1))\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 2 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
Python Elegant & Short | One line | Reducing | concatenation-of-consecutive-binary-numbers | 0 | 1 | ```\nclass Solution:\n """\n Time: O(n*log(n))\n Memory: O(1)\n """\n\n MOD = 10 ** 9 + 7\n\n def concatenatedBinary(self, n: int) -> int:\n return reduce(lambda x, y: ((x << y.bit_length()) | y) % self.MOD, range(1, n + 1))\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 2 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
πOne-Liner explanation and code || Python3 Solution and Explanation | concatenation-of-consecutive-binary-numbers | 0 | 1 | ##### Just in one-line, the answer is completed\uD83D\uDE01\n#### **Explanation:**\nAll we have to do is converting every number in the range of 1 to n using bin() function and make them as a list\n```[bin(i) for i in range(1,n+1)]```\n\nIn that, we have to remove the first 2 charfacters because every bin conversion will have \'0b\' in the front\n```[bin(i)[2:] for i in range(1,n+1)]```\n\nAnd then we have to join all the bin\'s in the list using "".join() method\n```"".join([bin(i)[2:] for i in range(1,n+1)])```\n\nNow, converting bin into decimal in python is int(bin_string,2)\n ```int("".join([bin(i)[2:] for i in range(1,n+1)]),2)```\n \nAt last this number has to be mod with 1000000007\n```int("".join([bin(i)[2:] for i in range(1,n+1)]),2)%1000000007```\n\nAt last, return the final answer!\n\n#### **Code:**\n\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return int("".join([bin(i)[2:] for i in range(1,n+1)]),2)%1000000007\n```\n\nThat\'s it! As simple as that!\nThank you for viewing my solution.. and feel free to comment if you don\'t understand or if you have a better solution or if you have any changes for this code\uD83D\uDE0A\n | 1 | Given an integer `n`, return _the **decimal value** of the binary string formed by concatenating the binary representations of_ `1` _to_ `n` _in order, **modulo**_ `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 1
**Explanation: ** "1 " in binary corresponds to the decimal value 1.
**Example 2:**
**Input:** n = 3
**Output:** 27
**Explanation:** In binary, 1, 2, and 3 corresponds to "1 ", "10 ", and "11 ".
After concatenating them, we have "11011 ", which corresponds to the decimal value 27.
**Example 3:**
**Input:** n = 12
**Output:** 505379714
**Explanation**: The concatenation results in "1101110010111011110001001101010111100 ".
The decimal value of that is 118505380540.
After modulo 109 + 7, the result is 505379714.
**Constraints:**
* `1 <= n <= 105` | Use dynamic programming to solve this problem with each state defined by the city index and fuel left. Since the array contains distinct integers fuel will always be spent in each move and so there can be no cycles. |
πOne-Liner explanation and code || Python3 Solution and Explanation | concatenation-of-consecutive-binary-numbers | 0 | 1 | ##### Just in one-line, the answer is completed\uD83D\uDE01\n#### **Explanation:**\nAll we have to do is converting every number in the range of 1 to n using bin() function and make them as a list\n```[bin(i) for i in range(1,n+1)]```\n\nIn that, we have to remove the first 2 charfacters because every bin conversion will have \'0b\' in the front\n```[bin(i)[2:] for i in range(1,n+1)]```\n\nAnd then we have to join all the bin\'s in the list using "".join() method\n```"".join([bin(i)[2:] for i in range(1,n+1)])```\n\nNow, converting bin into decimal in python is int(bin_string,2)\n ```int("".join([bin(i)[2:] for i in range(1,n+1)]),2)```\n \nAt last this number has to be mod with 1000000007\n```int("".join([bin(i)[2:] for i in range(1,n+1)]),2)%1000000007```\n\nAt last, return the final answer!\n\n#### **Code:**\n\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return int("".join([bin(i)[2:] for i in range(1,n+1)]),2)%1000000007\n```\n\nThat\'s it! As simple as that!\nThank you for viewing my solution.. and feel free to comment if you don\'t understand or if you have a better solution or if you have any changes for this code\uD83D\uDE0A\n | 1 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Python (Simple DP) | minimum-incompatibility | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumIncompatibility(self, nums, k):\n length = len(nums)//k\n \n @lru_cache(None)\n def dfs(nums):\n if not nums: return 0\n \n min_val = float("inf")\n \n for i in itertools.combinations(nums,length):\n if len(set(i)) < length: continue\n \n new_nums = list(nums)\n \n for j in i:\n new_nums.remove(j)\n \n min_val = min(min_val,max(i)-min(i)+dfs(tuple(new_nums)))\n \n return min_val\n \n result = dfs(tuple(nums))\n \n return result if result != float("inf") else -1\n\n \n \n \n\n\n``` | 1 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
[Python] simple backtracking beats 100% | minimum-incompatibility | 0 | 1 | 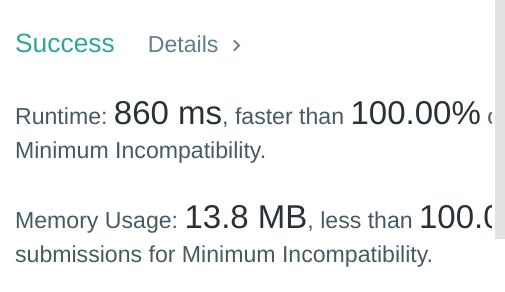\n```python\nclass Solution(object):\n def minimumIncompatibility(self, nums, k):\n nums.sort(reverse = True)\n upperbound = len(nums) // k\n arr = [[] for _ in range(k)]\n self.res = float(\'inf\')\n def assign(i):\n if i == len(nums):\n self.res = min(self.res, sum(arr[i][0]-arr[i][-1] for i in range(k)))\n return True\n flag = 0\n for j in range(k):\n if not arr[j] or (len(arr[j]) < upperbound and arr[j][-1] != nums[i]):\n arr[j].append(nums[i])\n if assign(i+1):\n flag += 1\n arr[j].pop()\n if flag >= 2: break\n return flag != 0\n if max(collections.Counter(nums).values()) > k: return -1\n assign(0)\n return self.res\n```\n\nBacktracking is a very time consuming algorithm. If we don\'t have early break, its time complexity will be O(n!) (for example Hamiltonian and NQueens problems). So we usually need to have an early break condition, which is a tricky part.\n\nIn this case, I implemented backtracking with two attemps (nums[i] can be assigned to arr[j] and arr[j+1]). A simple and fast solution. | 8 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
python3 dfs backtrack with pruning | minimum-incompatibility | 0 | 1 | Easy to think of backtrack, but pruning is crucial to avoid TLE. Two pruning steps are adopted: first cut all branches with incompatibility larger than already known minimum; second we consider only empty buckets two remove the symmetry between buckets.\n\n# Code\n```\nclass Solution:\n def minimumIncompatibility(self, nums: List[int], k: int) -> int:\n self.buckets = [[] for i in range(k)]\n self.res = float(\'inf\')\n self.n = len(nums)\n self.target = self.n // k\n nums.sort()\n counter = Counter(nums)\n m = max(counter.values())\n self.cur_res = 0\n if m > k:return -1\n def dfs(i):\n if self.cur_res > self.res:#pruning, remove all redundant branches with too large sums\n return \n if i == self.n:\n self.res = min(self.res,self.cur_res)\n return\n for j in range(k):\n if len(self.buckets[j])<self.target and nums[i] not in self.buckets[j]:\n self.buckets[j].append(nums[i])\n if len(self.buckets[j])>1:self.cur_res += self.buckets[j][-1] - self.buckets[j][-2] \n dfs(i+1)\n if len(self.buckets[j])>1:self.cur_res -= self.buckets[j][-1] - self.buckets[j][-2]\n self.buckets[j].pop()\n if self.buckets[j] == []:// pruning 2: all empty buckets are the same, so this would remove all branches with the same combination\n break\n dfs(0)\n return self.res if self.res<float(\'inf\') else -1\n\n\n\n``` | 0 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
Bitmask DP - [33%, 6%] | minimum-incompatibility | 0 | 1 | # Complexity\nTime complexity: $O(2^n + 2^{n/k})$\nSpace complexity: $O(2^n + 2^{n/k})$\n\n# Code\n```python\nclass Solution:\n def minimumIncompatibility(self, A: List[int], K: int) -> int:\n S = len(A) // K\n # pre-calc the bitmasks\n M = reduce(lambda M, i: {\n n | (1 << i) for i in range(len(A)) \n for n in M if (n >> i) & 1 == 0 \n and all((n >> j) & 1 == 0 or A[j] != A[i] for j in range(len(A)))\n },\n range(S),\n {0}\n )\n\n # find \'incompatability\' for each mask \n D = {\n m: max(A[i] for i in range(len(A)) if (m >> i) & 1)\\\n - min(A[i] for i in range(len(A)) if (m >> i) & 1)\\\n for m in M\n }\n \n @cache\n def f(m: int) -> int:\n if m == (1 << len(A)) - 1: return 0\n return min(\n (f(m | nm) + D[nm] for nm in M if not (nm & m)), default=maxsize\n )\n\n return f(0) if f(0) < maxsize else -1\n \n``` | 0 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
[Python3] backtracking | minimum-incompatibility | 0 | 1 | **Algo**\nThis is an organized brute force approach. We simply put the elements following the rule into stacks and compute incompatibility. Here, the two tricks are \n1) `if cand + len(nums) - i > ans: return` meaning that if there is no chance for the current run to get smaller incompability we simply return;\n2) `len(stack[ii]) < len(nums)//k and (not stack[ii] or stack[ii][-1] != nums[i]) and (not ii or stack[ii-1] != stack[ii])` meaning current stack has enough space for an extra element, `nums[i]` hasn\'t been added to this stack yet, and it is different from the previous stack (otherwise what\'s the point of adding it to an identical stack). \n\nWithout these two tricks, one would have TLE. \n\n**Implementation**\n```\nclass Solution:\n def minimumIncompatibility(self, nums: List[int], k: int) -> int:\n nums.sort()\n \n def fn(i, cand): \n """Populate stack and compute minimum incompatibility."""\n nonlocal ans \n if cand + len(nums) - i - sum(not x for x in stack) > ans: return \n if i == len(nums): ans = cand\n else: \n for ii in range(k): \n if len(stack[ii]) < len(nums)//k and (not stack[ii] or stack[ii][-1] != nums[i]) and (not ii or stack[ii-1] != stack[ii]): \n stack[ii].append(nums[i])\n if len(stack[ii]) == 1: fn(i+1, cand)\n else: fn(i+1, cand + stack[ii][-1] - stack[ii][-2])\n stack[ii].pop()\n \n ans = inf\n stack = [[] for _ in range(k)]\n fn(0, 0)\n return ans if ans < inf else -1\n```\n\nFor those who are uncomfortable with `nonlocal` variables, an alternative implementation is given below \n```\nclass Solution:\n def minimumIncompatibility(self, nums: List[int], k: int) -> int:\n nums.sort()\n \n def fn(i, cand=0, ans=inf):\n """Return minimum incompatibility via backtracking."""\n if cand + len(nums) - i - sum(not x for x in stack) >= ans: return ans # early return \n if i == len(nums): return cand\n for ii in range(k): \n if len(stack[ii]) < len(nums)//k and (not stack[ii] or stack[ii][-1] != nums[i]) and (not ii or stack[ii-1] != stack[ii]): \n stack[ii].append(nums[i])\n if len(stack[ii]) == 1: ans = fn(i+1, cand, ans)\n else: ans = fn(i+1, cand + stack[ii][-1] - stack[ii][-2], ans)\n stack[ii].pop()\n return ans \n \n stack = [[] for _ in range(k)]\n ans = fn(0)\n return ans if ans < inf else -1\n``` | 4 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
[Python] Easy-Understanding DFS with Memo | minimum-incompatibility | 0 | 1 | **Idea:**\nLet\'s assume the problem is for dictionary `d,` we need to divide them into `k` groups with each group size as `count`, we can pick a group of numbers first and transform the problem to a sub-problem of `(new_d, k - 1, count)`\n**Implementation**\nUse `frozenset` to hash\n```\nimport collections\nclass Solution:\n def minimumIncompatibility(self, nums: List[int], k: int) -> int:\n @lru_cache(None)\n def dfs(d, k, count):\n d = dict(d)\n # Special cases\n if k == 1:\n if len(d) >= count:\n return max(d.keys()) - min(d.keys())\n else:\n return -1\n if count == 1:\n return 0\n if len(d) < count:\n return -1\n for key in d:\n if d[key] > k:\n return -1\n \n # Pick a group first\n from itertools import combinations \n res = float(\'inf\')\n perm = combinations(d.keys(), count) \n for i in list(perm):\n gap = max(i) - min(i)\n for cur in i:\n d[cur] -= 1\n if d[cur] == 0:\n del d[cur]\n \n # Update result\n nex = dfs(frozenset(d.items()), k - 1, count)\n if nex != -1:\n res = min(res, gap + nex)\n for cur in i:\n if cur not in d:\n d[cur] = 0\n d[cur] += 1\n\n return res if res != float(\'inf\') else -1\n \n d = {}\n for num in nums:\n if num not in d:\n d[num] = 0\n d[num] += 1\n \n return dfs(frozenset(d.items()), k, len(nums) // k)\n``` | 2 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
Backtracking + smart optimizations = crazy performance (31ms for Python) | minimum-incompatibility | 0 | 1 | # Intuition\n\nThe base idea is backtracking. All possible combinations of subsets are checked using a recursion.\n\nIdeas used to implement major backtracking optimizations:\n\n1. Backtrack greedily: try combinations with close (to each other) numbers first.\n2. Exit the current backtracking branch as soon as it\'s clear that the minimum score won\'t be beaten. The greedier the combinataion, the higher the chance for it to be the best, therefore the best combination is found quickly, and the rest combinations are skipped early.\n3. Avoid walking same combinations:\n - Don\'t walk same subsets in different order.\n - Don\'t walk elements of a subset in different order.\n\n# Approach\n\nThe description implies that you are familiar with the concept of backtracking. The combinations are build subset by subset, each subset is built number by number on is a separate recursion step.\n\nA dictionary is used to store the count of each number in `nums`. It\'s implemented with an array because the variety of numbers is very small and it\'s much faster than a hash-map.\n\nThe backtracking uses it to detect which numbers are not "put" into the subsets yet. The actual subsets aren\'t built, it is not necessary. The dictionary is changed temporarily during the backtracking.\n\nThe current minimum sum of incompatibilities (`minScore`) is also stored globally so that any backtracking branch knows the minimum sum and can exit.\n\nThe state of backtracking is defined by 3 more values:\n\n- `involvedNumsCount` \u2014 the count of numbers from `nums` that has already been "put" into the subsets. When it\'s equal `len(nums)`, the process is complete (all the numbers have been "put" into the subsets).\n- `score` \u2014 the current sum of incompatibilities. It\'s calculated even if the current subset is incomplete. It\'s possible due to this property:\n ```\n score\n = subset[m-1] - subset[0]\n = (subset[m-1] - subset[m-2])\n + ...\n + (subset[2] - subset[1])\n + (subset[1] - subset[0])\n ```\n where `m` is the size of a complete subset.\n- `lastNum` \u2014 if the current subset is incomplete, stores the last number of the subset, otherwise stores `None`. Required to calculate the score for the next step using the formula above, and to know the largest number in the subset.\n\nThe code of the recursion step continues the current combination of subsets. It checks each not yet involved number greedily: from the smallest to the largest. Since the variety of numbers is very limited, a simple loop from `1` to `n` is used.\n\n- If this is a start of a new subset (`lastNum` is `None`), only the first available number is cheched. It\'s excessive to check the other numbers because the first available number is a part of some subset anyway. Checking other numbers would lead to building the same combination of subsets in different order (the order of subsets doesn\'t affect the score).\n- If this is a continuation of an incomplete subset, check only available numbers that are greater than any number inside the current subset. It ensures that permutations of a subset aren\'t checked (the order inside the subsets doesn\'t affect the score).\n\nBefore going into the next recursion step, the algorithm checks whether it\'s impossible to beat the best score in the current situation. If yes, the backtracking branch exits. It\'s checked by comparing the most optimistic final score with the current minimum final score (`minScore`). The optimistic score is calculated assuming that the rest subsets will contain only adjecent numbers.\n\n# Complexity\n- Time complexity:\n\nI don\'t know, sorry.\n\nIf there was no fast exit, the number of steps would be the number of ways to split `nums` into `k` equal subsets: `O(n! / ((n/k)!)^k / k!)` (in the worst case).\n\n- Space complexity:\n\nThe `nums` counter and the depth of the recursion. Both are `O(n)` in the worst case.\n\n# Code\n```python\nclass Solution:\n def minimumIncompatibility(self, nums: List[int], k: int) -> int:\n n = len(nums)\n subsetSize = int(n / k)\n numCounts = [0] * (n + 1)\n for num in nums:\n numCounts[num] += 1\n minScore = math.inf\n\n def backtrack(involvedNumsCount, currentScore, lastNum):\n nonlocal minScore\n\n if involvedNumsCount == n:\n minScore = currentScore\n return\n\n involvedNumsCount += 1\n subsetEnd = involvedNumsCount % subsetSize == 0\n\n if lastNum is None:\n for num in range(1, n + 2 - subsetSize):\n if numCounts[num] == 0:\n continue\n\n numCounts[num] -= 1\n backtrack(involvedNumsCount, currentScore, None if subsetEnd else num)\n numCounts[num] += 1\n\n # Avoids checking same subsets in different order\n break\n else:\n numsLeft = n - involvedNumsCount\n # Assuming that the other numbers are adjacent\n optimisticRestScore = numsLeft - floor(numsLeft / subsetSize)\n \n # `lastNum + 1` as the start avoids checking permutations of subsets\n for num in range(lastNum + 1, n + 1):\n if numCounts[num] == 0:\n continue\n\n nextScore = currentScore + num - lastNum\n if nextScore + optimisticRestScore >= minScore:\n # The next nums will give even bigger score\n return\n\n numCounts[num] -= 1\n backtrack(involvedNumsCount, nextScore, None if subsetEnd else num)\n numCounts[num] += 1\n \n backtrack(0, 0, None)\n return minScore if minScore is not math.inf else -1\n``` | 0 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions β
| invalid-tweets | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef invalid_tweets(tweets: pd.DataFrame) -> pd.DataFrame:\n return tweets[\n tweets[\'content\'].str.len() > 15\n ][[\'tweet_id\']]\n```\n```SQL []\nSELECT tweet_id\n FROM Tweets\n WHERE length(content) >= 16;\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to upvote for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n | 16 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
π₯Simple using Set, Subsetπ₯ | count-the-number-of-consistent-strings | 0 | 1 | # Approach\n\n1. Given a list of words and a string allowed containing characters that are considered allowed.\n2. Utilize a list comprehension to iterate through each word x in the words list.\n3. For each word, create a set of its characters (`set(x)`) and check if this set is a ***subset*** of the set of allowed characters (`set(allowed)`).\n4. Sum the number of words for which the condition in step 3 is true.\n# Code\n```\nclass Solution:\n def countConsistentStrings(self, allowed: str, words: List[str]) -> int:\n return sum(1 for x in words if set(x).issubset(set(allowed)))\n```\nplease upvote :D | 2 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current β1β groups. At each step (going backwards) you need to split one group and update the map. |
π₯Simple using Set, Subsetπ₯ | count-the-number-of-consistent-strings | 0 | 1 | # Approach\n\n1. Given a list of words and a string allowed containing characters that are considered allowed.\n2. Utilize a list comprehension to iterate through each word x in the words list.\n3. For each word, create a set of its characters (`set(x)`) and check if this set is a ***subset*** of the set of allowed characters (`set(allowed)`).\n4. Sum the number of words for which the condition in step 3 is true.\n# Code\n```\nclass Solution:\n def countConsistentStrings(self, allowed: str, words: List[str]) -> int:\n return sum(1 for x in words if set(x).issubset(set(allowed)))\n```\nplease upvote :D | 2 | There is an undirected weighted connected graph. You are given a positive integer `n` which denotes that the graph has `n` nodes labeled from `1` to `n`, and an array `edges` where each `edges[i] = [ui, vi, weighti]` denotes that there is an edge between nodes `ui` and `vi` with weight equal to `weighti`.
A path from node `start` to node `end` is a sequence of nodes `[z0, z1, z2, ..., zk]` such that `z0 = start` and `zk = end` and there is an edge between `zi` and `zi+1` where `0 <= i <= k-1`.
The distance of a path is the sum of the weights on the edges of the path. Let `distanceToLastNode(x)` denote the shortest distance of a path between node `n` and node `x`. A **restricted path** is a path that also satisfies that `distanceToLastNode(zi) > distanceToLastNode(zi+1)` where `0 <= i <= k-1`.
Return _the number of restricted paths from node_ `1` _to node_ `n`. Since that number may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2,3\],\[1,3,3\],\[2,3,1\],\[1,4,2\],\[5,2,2\],\[3,5,1\],\[5,4,10\]\]
**Output:** 3
**Explanation:** Each circle contains the node number in black and its `distanceToLastNode value in blue.` The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5
**Example 2:**
**Input:** n = 7, edges = \[\[1,3,1\],\[4,1,2\],\[7,3,4\],\[2,5,3\],\[5,6,1\],\[6,7,2\],\[7,5,3\],\[2,6,4\]\]
**Output:** 1
**Explanation:** Each circle contains the node number in black and its `distanceToLastNode value in blue.` The only restricted path is 1 --> 3 --> 7.
**Constraints:**
* `1 <= n <= 2 * 104`
* `n - 1 <= edges.length <= 4 * 104`
* `edges[i].length == 3`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= weighti <= 105`
* There is at most one edge between any two nodes.
* There is at least one path between any two nodes. | A string is incorrect if it contains a character that is not allowed Constraints are small enough for brute force |
Python 3 solution 100 faster than any other codes | count-the-number-of-consistent-strings | 0 | 1 | - We know that sets in python are actually implemented by hash tables, which means you can search a member in set by `O(1)`. Therfore, first we create a set from `allowed` string and check that every letter of each word to be in the allowed string. If its not, we increase the `count`. By the end of the program we know the number of wrong words, so we just need to return the difference of `allowed` length and `count`\n- Complexity: `O(nd)`\nIf we assume we have `n` words, we should iterate on all of them and also iterate on each letter which we assumed the average length of words is `d`. So the time complexity is `O(nd)`.\n- Code:\n```\nclass Solution:\n def countConsistentStrings(self, allowed: str, words: List[str]) -> int:\n allowed = set(allowed)\n count = 0\n \n for word in words:\n for letter in word:\n if letter not in allowed:\n count += 1\n break\n \n return len(words) - count\n``` | 82 | You are given a string `allowed` consisting of **distinct** characters and an array of strings `words`. A string is **consistent** if all characters in the string appear in the string `allowed`.
Return _the number of **consistent** strings in the array_ `words`.
**Example 1:**
**Input:** allowed = "ab ", words = \[ "ad ", "bd ", "aaab ", "baa ", "badab "\]
**Output:** 2
**Explanation:** Strings "aaab " and "baa " are consistent since they only contain characters 'a' and 'b'.
**Example 2:**
**Input:** allowed = "abc ", words = \[ "a ", "b ", "c ", "ab ", "ac ", "bc ", "abc "\]
**Output:** 7
**Explanation:** All strings are consistent.
**Example 3:**
**Input:** allowed = "cad ", words = \[ "cc ", "acd ", "b ", "ba ", "bac ", "bad ", "ac ", "d "\]
**Output:** 4
**Explanation:** Strings "cc ", "acd ", "ac ", and "d " are consistent.
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= allowed.length <= 26`
* `1 <= words[i].length <= 10`
* The characters in `allowed` are **distinct**.
* `words[i]` and `allowed` contain only lowercase English letters. | Since the problem asks for the latest step, can you start the searching from the end of arr? Use a map to store the current β1β groups. At each step (going backwards) you need to split one group and update the map. |
Python 3 solution 100 faster than any other codes | count-the-number-of-consistent-strings | 0 | 1 | - We know that sets in python are actually implemented by hash tables, which means you can search a member in set by `O(1)`. Therfore, first we create a set from `allowed` string and check that every letter of each word to be in the allowed string. If its not, we increase the `count`. By the end of the program we know the number of wrong words, so we just need to return the difference of `allowed` length and `count`\n- Complexity: `O(nd)`\nIf we assume we have `n` words, we should iterate on all of them and also iterate on each letter which we assumed the average length of words is `d`. So the time complexity is `O(nd)`.\n- Code:\n```\nclass Solution:\n def countConsistentStrings(self, allowed: str, words: List[str]) -> int:\n allowed = set(allowed)\n count = 0\n \n for word in words:\n for letter in word:\n if letter not in allowed:\n count += 1\n break\n \n return len(words) - count\n``` | 82 | There is an undirected weighted connected graph. You are given a positive integer `n` which denotes that the graph has `n` nodes labeled from `1` to `n`, and an array `edges` where each `edges[i] = [ui, vi, weighti]` denotes that there is an edge between nodes `ui` and `vi` with weight equal to `weighti`.
A path from node `start` to node `end` is a sequence of nodes `[z0, z1, z2, ..., zk]` such that `z0 = start` and `zk = end` and there is an edge between `zi` and `zi+1` where `0 <= i <= k-1`.
The distance of a path is the sum of the weights on the edges of the path. Let `distanceToLastNode(x)` denote the shortest distance of a path between node `n` and node `x`. A **restricted path** is a path that also satisfies that `distanceToLastNode(zi) > distanceToLastNode(zi+1)` where `0 <= i <= k-1`.
Return _the number of restricted paths from node_ `1` _to node_ `n`. Since that number may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2,3\],\[1,3,3\],\[2,3,1\],\[1,4,2\],\[5,2,2\],\[3,5,1\],\[5,4,10\]\]
**Output:** 3
**Explanation:** Each circle contains the node number in black and its `distanceToLastNode value in blue.` The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5
**Example 2:**
**Input:** n = 7, edges = \[\[1,3,1\],\[4,1,2\],\[7,3,4\],\[2,5,3\],\[5,6,1\],\[6,7,2\],\[7,5,3\],\[2,6,4\]\]
**Output:** 1
**Explanation:** Each circle contains the node number in black and its `distanceToLastNode value in blue.` The only restricted path is 1 --> 3 --> 7.
**Constraints:**
* `1 <= n <= 2 * 104`
* `n - 1 <= edges.length <= 4 * 104`
* `edges[i].length == 3`
* `1 <= ui, vi <= n`
* `ui != vi`
* `1 <= weighti <= 105`
* There is at most one edge between any two nodes.
* There is at least one path between any two nodes. | A string is incorrect if it contains a character that is not allowed Constraints are small enough for brute force |
π€―Optimized-Without-Extra-Space.pyπ | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | \n# Complexity\n- Time complexity:\n $$O(n)$$ \n- Space complexity:\n $$O(n)$$ --> $$O(1)$$\n`Just use one variable for Prefix sum instead of an arr`\n`Suffix sum = Sum - PrefixSum`\n# Code\n```js\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n pr=[None]*len(nums)\n pr[0]=nums[0]\n for i in range(1,len(nums)):pr[i]=pr[i-1]+nums[i]\n su=[None]*len(nums)\n su[len(nums)-1]=nums[len(nums)-1]\n for i in range(len(nums)-2,-1,-1):su[i]=su[i+1]+nums[i]\n return [(nums[i]*(i+1)-pr[i])+su[i]-nums[i]*(len(nums)-i) for i in range(len(nums))]\n```\n```py\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n sm,pr=sum(nums),0\n for i in range(len(nums)):\n pr+=nums[i]\n nums[i]=(((i+1)*nums[i]-pr)+(sm-pr)-(len(nums)-i-1)*nums[i])\n return nums\n```\n\n | 8 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
π€―Optimized-Without-Extra-Space.pyπ | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | \n# Complexity\n- Time complexity:\n $$O(n)$$ \n- Space complexity:\n $$O(n)$$ --> $$O(1)$$\n`Just use one variable for Prefix sum instead of an arr`\n`Suffix sum = Sum - PrefixSum`\n# Code\n```js\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n pr=[None]*len(nums)\n pr[0]=nums[0]\n for i in range(1,len(nums)):pr[i]=pr[i-1]+nums[i]\n su=[None]*len(nums)\n su[len(nums)-1]=nums[len(nums)-1]\n for i in range(len(nums)-2,-1,-1):su[i]=su[i+1]+nums[i]\n return [(nums[i]*(i+1)-pr[i])+su[i]-nums[i]*(len(nums)-i) for i in range(len(nums))]\n```\n```py\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n sm,pr=sum(nums),0\n for i in range(len(nums)):\n pr+=nums[i]\n nums[i]=(((i+1)*nums[i]-pr)+(sm-pr)-(len(nums)-i-1)*nums[i])\n return nums\n```\n\n | 8 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
π PrefixSum & SuffixSum || Explained Intuition π | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # Problem Description\n\nGiven a **sorted** integer array `nums`, create and return an array result of the same length, where each element `result[i]` represents the sum of absolute differences between `nums[i]` and all other elements in the array, **excluding** itself.\n\n- Constraints:\n - `result[i] = |nums[0]-nums[i]| + |nums[1]-nums[i]| +......+ |nums[n]-nums[i]|` \n - $2 <= nums.length <= 10^5$\n - $1 <= nums[i] <= nums[i + 1] <= 10^4$\n\n\n---\n\n\n\n# Intuition\n\n\nHi there,\uD83D\uDE04\n\nLet\'s take a look\uD83D\uDC40 at our today\'s problem.\nWe have a **sorted** integer array and we are required to return an array such that for each element `i` in the **result** array, it equals the **absolute** **difference** of element `i` in original array and all other elements.\nIn other words, `result[i] = |nums[0]-nums[i]| + |nums[1]-nums[i]| +......+ |nums[n]-nums[i]|`\n\nSeem interesting problem.\uD83E\uDD29\n**First** thing that we can think of is our **big guy**\uD83D\uDCAA Brute Force, by looping with **nested loop** and for each element we compute the absolute difference between them and add it to our `result[i]`.\nFor us, this solution is inefficient since it takes $O(N^2)$ and will give us headace\uD83D\uDE02.\n\nHow can we improve this?\uD83E\uDD14\nSince for each element we want to compute the absolute difference between them and other elements in the array.\nWe can first thing **sum** all the elements of the array and for each element `i` we compute `|sum - nums[i] * size of arrray|` which means that we actually compute differece between each element and the current element.\nIt\'s code will be:\n```cpp\nvector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size(), sum = 0;\n vector<int> ans(n);\n for(int i = 0 ; i < n ; i ++){\n sum += nums[i] ;\n }\n for(int i = 0 ; i < n ; i ++){\n int cur = abs(sum - nums[i] * n) ;\n ans[i] = cur ;\n }\n return ans;\n }\n```\nThis may look right from first look but unfortunately it is not valid answer.\uD83D\uDE14\n\nLet\'s see some examples to see why it is not valid:\n```\nnums = [2,3,5]\nsum = 10\nfor 2: |10 - 2 * 3| = |2 - 2 + 3 - 2 + 5 - 2| = |8 - 4| = 4\nfor 3: |10 - 3 * 3| = |2 - 3 + 3 - 3 + 5 - 3| = |7 - 6| = 1\nfor 5: |10 - 5 * 3| = |2 - 5 + 3 - 5 + 5 - 5| = |5 - 10| = 5\n```\n```\nnums = [1,4,6,8,10]\nsum = 29\nfor 1: |29 - 1 * 5| = |1 - 1 + 4 - 1 + 6 - 1 + 8 - 1 + 10 - 1| = |28 - 4| = 24\nfor 4: |29 - 4 * 5| = |1 - 4 + 4 - 4 + 6 - 4 + 8 - 4 + 10 - 4| = |25 - 16| = 9\n.\n.\n.\n```\n\nI think we got why it is wrong...\uD83D\uDE22\nWhat we are doing is\n`|nums[i] - nums[0] + nums[i] - nums[1] +..... nums[n] - nums[i]|` \nand this is far from our objective which is \n`|nums[0]-nums[i]| + |nums[1]-nums[i]| +......+ |nums[n]-nums[i]|`.\n\nNow we reached here, How can we get the right formula.\uD83E\uDD14\nWe can think about one thing.\nWhen is `|nums[i] - nums[0] + nums[i] - nums[1] +..... ` is equal to `|nums[0]-nums[i]| + |nums[1]-nums[i]| +......` ?\uD83E\uDD28\nI know that I said earlier that they are two different things but they can be equal in one case.... Actually two cases.\uD83E\uDD2F\n\nWhen `nums[i]` is greater than all other elements in the array so \n```\nnums[i]-nums[0] = |nums[0]-nums[i]|\nnums[i]-nums[1] = |nums[1]-nums[i]|\nnums[i]-nums[2] = |nums[2]-nums[i]|\n.\n.\nand so on so forth\n```\n\nand when `nums[i]` is smaller than all other elements in the array so \n```\nnums[0]-nums[i] = |nums[0]-nums[i]|\nnums[1]-nums[i] = |nums[1]-nums[i]|\nnums[2]-nums[i] = |nums[2]-nums[i]|\n.\n.\nand so on so forth\n```\n\nSince our array is already **sorted**, we can use these two cases to compute our objective so for each element we can use the **sum** trick two times -which was invalid first but now are valid-.\uD83E\uDD29\n\n**First time**, with all the elements **before** the current element since it is **greater** than them all and for this we can use **prefix** array to get immediately the sum of all elements **before** current element.\n\n**Second time**, with all the elements **after** the current element since it is **smaller** than them all and for this we can use **suffix** array to get immediately the sum of all elements **after** current element.\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n# Approach\n\n1. **Initialization:** Obtain the size of the input array `nums` and create a result array of the same size.\n ```cpp\n int n = nums.size();\n vector<int> result(n);\n ```\n2. **Prefix and Suffix Sums:** Create two additional arrays, `prefixSum` and `suffixSum`, to store the cumulative sums from the beginning and end of the `nums` array, respectively. Initialize the first element of both arrays -Don\'t forget that the input array is sorted- .\n ```cpp\n vector<int> prefixSum(n), suffixSum(n);\n prefixSum[0] = nums[0];\n suffixSum[n - 1] = nums[n - 1];\n ```\n3. **Calculate Sums in One Loop:** Use a single loop to calculate both the prefix and suffix sums simultaneously.\n ```cpp\n for (int i = 1; i < n; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[n - i - 1] = suffixSum[n - i] + nums[n - i - 1];\n }\n ```\n4. **Calculate Absolute Differences:** Iterate through the array and compute the absolute differences using the prefix and suffix sums.\n ```cpp\n for (int i = 0; i < n; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (n - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n ```\n5. **Return** the calculated result array.\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we are **looping** over the input array **two** time, one time to calculate `prefix` and `suffix` arrays and another time to calculate the result which costs us `2 * N` so time complexity is `O(N)`.\nWhere `N` is the size of the input array.\n- **Space complexity:** $O(N)$\nSince are storing two arrays of the same length of the input array which are the prefix and suffix arrays which costs us `2 * N` so space complexity is `O(N)`.\n\n\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size();\n vector<int> result(n);\n vector<int> prefixSum(n), suffixSum(n);\n \n // Calculate and initialize the prefix sums & suffixSum array\n prefixSum[0] = nums[0];\n suffixSum[n - 1] = nums[n - 1];\n \n // Calculate the prefix sums & suffixSum array in one loop\n for (int i = 1; i < n; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[n - i - 1] = suffixSum[n - i] + nums[n - i - 1];\n }\n \n // Calculate absolute differences and update the result array\n for (int i = 0; i < n; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (n - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n \n return result;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n int[] prefixSum = new int[n];\n int[] suffixSum = new int[n];\n\n // Calculate and initialize the prefix sums & suffixSum array\n prefixSum[0] = nums[0];\n suffixSum[n - 1] = nums[n - 1];\n\n // Calculate the prefix sums & suffixSum array in one loop\n for (int i = 1; i < n; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[n - i - 1] = suffixSum[n - i] + nums[n - i - 1];\n }\n\n // Calculate absolute differences and update the result array\n for (int i = 0; i < n; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (n - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n result = [0] * n\n prefix_sum = [0] * n\n suffix_sum = [0] * n\n\n # Calculate and initialize the prefix sums & suffix_sum array\n prefix_sum[0] = nums[0]\n suffix_sum[n - 1] = nums[n - 1]\n\n # Calculate the prefix sums & suffix_sum array in one loop\n for i in range(1, n):\n prefix_sum[i] = prefix_sum[i - 1] + nums[i]\n suffix_sum[n - i - 1] = suffix_sum[n - i] + nums[n - i - 1]\n\n # Calculate absolute differences and update the result array\n for i in range(n):\n current_absolute_diff = ((nums[i] * i) - prefix_sum[i]) + (suffix_sum[i] - (nums[i] * (n - i - 1)))\n result[i] = current_absolute_diff\n\n return result\n```\n```C []\nint* getSumAbsoluteDifferences(int* nums, int numsSize, int* returnSize) {\n int* result = (int*)malloc(numsSize * sizeof(int));\n *returnSize = numsSize;\n\n int* prefixSum = (int*)malloc(numsSize * sizeof(int));\n int* suffixSum = (int*)malloc(numsSize * sizeof(int));\n\n // Calculate and initialize the prefix sums & suffixSum array\n prefixSum[0] = nums[0];\n suffixSum[numsSize - 1] = nums[numsSize - 1];\n\n // Calculate the prefix sums & suffixSum array in one loop\n for (int i = 1; i < numsSize; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[numsSize - i - 1] = suffixSum[numsSize - i] + nums[numsSize - i - 1];\n }\n\n // Calculate absolute differences and update the result array\n for (int i = 0; i < numsSize; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (numsSize - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n\n // Free dynamically allocated memory\n free(prefixSum);\n free(suffixSum);\n\n return result;\n}\n```\n\n\n\n | 93 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
π PrefixSum & SuffixSum || Explained Intuition π | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # Problem Description\n\nGiven a **sorted** integer array `nums`, create and return an array result of the same length, where each element `result[i]` represents the sum of absolute differences between `nums[i]` and all other elements in the array, **excluding** itself.\n\n- Constraints:\n - `result[i] = |nums[0]-nums[i]| + |nums[1]-nums[i]| +......+ |nums[n]-nums[i]|` \n - $2 <= nums.length <= 10^5$\n - $1 <= nums[i] <= nums[i + 1] <= 10^4$\n\n\n---\n\n\n\n# Intuition\n\n\nHi there,\uD83D\uDE04\n\nLet\'s take a look\uD83D\uDC40 at our today\'s problem.\nWe have a **sorted** integer array and we are required to return an array such that for each element `i` in the **result** array, it equals the **absolute** **difference** of element `i` in original array and all other elements.\nIn other words, `result[i] = |nums[0]-nums[i]| + |nums[1]-nums[i]| +......+ |nums[n]-nums[i]|`\n\nSeem interesting problem.\uD83E\uDD29\n**First** thing that we can think of is our **big guy**\uD83D\uDCAA Brute Force, by looping with **nested loop** and for each element we compute the absolute difference between them and add it to our `result[i]`.\nFor us, this solution is inefficient since it takes $O(N^2)$ and will give us headace\uD83D\uDE02.\n\nHow can we improve this?\uD83E\uDD14\nSince for each element we want to compute the absolute difference between them and other elements in the array.\nWe can first thing **sum** all the elements of the array and for each element `i` we compute `|sum - nums[i] * size of arrray|` which means that we actually compute differece between each element and the current element.\nIt\'s code will be:\n```cpp\nvector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size(), sum = 0;\n vector<int> ans(n);\n for(int i = 0 ; i < n ; i ++){\n sum += nums[i] ;\n }\n for(int i = 0 ; i < n ; i ++){\n int cur = abs(sum - nums[i] * n) ;\n ans[i] = cur ;\n }\n return ans;\n }\n```\nThis may look right from first look but unfortunately it is not valid answer.\uD83D\uDE14\n\nLet\'s see some examples to see why it is not valid:\n```\nnums = [2,3,5]\nsum = 10\nfor 2: |10 - 2 * 3| = |2 - 2 + 3 - 2 + 5 - 2| = |8 - 4| = 4\nfor 3: |10 - 3 * 3| = |2 - 3 + 3 - 3 + 5 - 3| = |7 - 6| = 1\nfor 5: |10 - 5 * 3| = |2 - 5 + 3 - 5 + 5 - 5| = |5 - 10| = 5\n```\n```\nnums = [1,4,6,8,10]\nsum = 29\nfor 1: |29 - 1 * 5| = |1 - 1 + 4 - 1 + 6 - 1 + 8 - 1 + 10 - 1| = |28 - 4| = 24\nfor 4: |29 - 4 * 5| = |1 - 4 + 4 - 4 + 6 - 4 + 8 - 4 + 10 - 4| = |25 - 16| = 9\n.\n.\n.\n```\n\nI think we got why it is wrong...\uD83D\uDE22\nWhat we are doing is\n`|nums[i] - nums[0] + nums[i] - nums[1] +..... nums[n] - nums[i]|` \nand this is far from our objective which is \n`|nums[0]-nums[i]| + |nums[1]-nums[i]| +......+ |nums[n]-nums[i]|`.\n\nNow we reached here, How can we get the right formula.\uD83E\uDD14\nWe can think about one thing.\nWhen is `|nums[i] - nums[0] + nums[i] - nums[1] +..... ` is equal to `|nums[0]-nums[i]| + |nums[1]-nums[i]| +......` ?\uD83E\uDD28\nI know that I said earlier that they are two different things but they can be equal in one case.... Actually two cases.\uD83E\uDD2F\n\nWhen `nums[i]` is greater than all other elements in the array so \n```\nnums[i]-nums[0] = |nums[0]-nums[i]|\nnums[i]-nums[1] = |nums[1]-nums[i]|\nnums[i]-nums[2] = |nums[2]-nums[i]|\n.\n.\nand so on so forth\n```\n\nand when `nums[i]` is smaller than all other elements in the array so \n```\nnums[0]-nums[i] = |nums[0]-nums[i]|\nnums[1]-nums[i] = |nums[1]-nums[i]|\nnums[2]-nums[i] = |nums[2]-nums[i]|\n.\n.\nand so on so forth\n```\n\nSince our array is already **sorted**, we can use these two cases to compute our objective so for each element we can use the **sum** trick two times -which was invalid first but now are valid-.\uD83E\uDD29\n\n**First time**, with all the elements **before** the current element since it is **greater** than them all and for this we can use **prefix** array to get immediately the sum of all elements **before** current element.\n\n**Second time**, with all the elements **after** the current element since it is **smaller** than them all and for this we can use **suffix** array to get immediately the sum of all elements **after** current element.\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n# Approach\n\n1. **Initialization:** Obtain the size of the input array `nums` and create a result array of the same size.\n ```cpp\n int n = nums.size();\n vector<int> result(n);\n ```\n2. **Prefix and Suffix Sums:** Create two additional arrays, `prefixSum` and `suffixSum`, to store the cumulative sums from the beginning and end of the `nums` array, respectively. Initialize the first element of both arrays -Don\'t forget that the input array is sorted- .\n ```cpp\n vector<int> prefixSum(n), suffixSum(n);\n prefixSum[0] = nums[0];\n suffixSum[n - 1] = nums[n - 1];\n ```\n3. **Calculate Sums in One Loop:** Use a single loop to calculate both the prefix and suffix sums simultaneously.\n ```cpp\n for (int i = 1; i < n; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[n - i - 1] = suffixSum[n - i] + nums[n - i - 1];\n }\n ```\n4. **Calculate Absolute Differences:** Iterate through the array and compute the absolute differences using the prefix and suffix sums.\n ```cpp\n for (int i = 0; i < n; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (n - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n ```\n5. **Return** the calculated result array.\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we are **looping** over the input array **two** time, one time to calculate `prefix` and `suffix` arrays and another time to calculate the result which costs us `2 * N` so time complexity is `O(N)`.\nWhere `N` is the size of the input array.\n- **Space complexity:** $O(N)$\nSince are storing two arrays of the same length of the input array which are the prefix and suffix arrays which costs us `2 * N` so space complexity is `O(N)`.\n\n\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size();\n vector<int> result(n);\n vector<int> prefixSum(n), suffixSum(n);\n \n // Calculate and initialize the prefix sums & suffixSum array\n prefixSum[0] = nums[0];\n suffixSum[n - 1] = nums[n - 1];\n \n // Calculate the prefix sums & suffixSum array in one loop\n for (int i = 1; i < n; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[n - i - 1] = suffixSum[n - i] + nums[n - i - 1];\n }\n \n // Calculate absolute differences and update the result array\n for (int i = 0; i < n; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (n - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n \n return result;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n int[] prefixSum = new int[n];\n int[] suffixSum = new int[n];\n\n // Calculate and initialize the prefix sums & suffixSum array\n prefixSum[0] = nums[0];\n suffixSum[n - 1] = nums[n - 1];\n\n // Calculate the prefix sums & suffixSum array in one loop\n for (int i = 1; i < n; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[n - i - 1] = suffixSum[n - i] + nums[n - i - 1];\n }\n\n // Calculate absolute differences and update the result array\n for (int i = 0; i < n; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (n - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n\n return result;\n }\n}\n```\n```Python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n result = [0] * n\n prefix_sum = [0] * n\n suffix_sum = [0] * n\n\n # Calculate and initialize the prefix sums & suffix_sum array\n prefix_sum[0] = nums[0]\n suffix_sum[n - 1] = nums[n - 1]\n\n # Calculate the prefix sums & suffix_sum array in one loop\n for i in range(1, n):\n prefix_sum[i] = prefix_sum[i - 1] + nums[i]\n suffix_sum[n - i - 1] = suffix_sum[n - i] + nums[n - i - 1]\n\n # Calculate absolute differences and update the result array\n for i in range(n):\n current_absolute_diff = ((nums[i] * i) - prefix_sum[i]) + (suffix_sum[i] - (nums[i] * (n - i - 1)))\n result[i] = current_absolute_diff\n\n return result\n```\n```C []\nint* getSumAbsoluteDifferences(int* nums, int numsSize, int* returnSize) {\n int* result = (int*)malloc(numsSize * sizeof(int));\n *returnSize = numsSize;\n\n int* prefixSum = (int*)malloc(numsSize * sizeof(int));\n int* suffixSum = (int*)malloc(numsSize * sizeof(int));\n\n // Calculate and initialize the prefix sums & suffixSum array\n prefixSum[0] = nums[0];\n suffixSum[numsSize - 1] = nums[numsSize - 1];\n\n // Calculate the prefix sums & suffixSum array in one loop\n for (int i = 1; i < numsSize; ++i) {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n suffixSum[numsSize - i - 1] = suffixSum[numsSize - i] + nums[numsSize - i - 1];\n }\n\n // Calculate absolute differences and update the result array\n for (int i = 0; i < numsSize; ++i) {\n int currentAbsoluteDiff = ((nums[i] * i) - prefixSum[i]) + (suffixSum[i] - (nums[i] * (numsSize - i - 1)));\n result[i] = currentAbsoluteDiff;\n }\n\n // Free dynamically allocated memory\n free(prefixSum);\n free(suffixSum);\n\n return result;\n}\n```\n\n\n\n | 93 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
γVideoγGive me 10 minutes - How we think about a solution. | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # Intuition\nCalcuate left side and right side.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bwQh44GWME8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve this question\n`1:56` Calculate left total\n`6:32` Calculate right total\n`11:12` Create answers\n`11:51` Coding\n`14:14` Time Complexity and Space Complexity\n`14:39` Summary of the algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,217\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nThis is brute force solution.\n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n res = []\n\n for i in range(n):\n current_sum = 0\n\n for j in range(n):\n current_sum += abs(nums[i] - nums[j])\n\n res.append(current_sum)\n\n return res\n```\nBut I got `Time Limit Exceeded`. lol\n\nLook at Example 1.\n```\nInput: nums = [2,3,5]\n```\n```\nOutput: [4,3,5]\n\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\nLet\'s focus on this.\n```\n0 + 1 + 3 = 4\n1 + 0 + 2 = 3\n3 + 2 + 0 = 5\n```\nEach calculation has `0`. It means `current number` - `current number`. Look at positions for other numbers.\n```\n0 + 1 + 3 = 4\nWe have `1` and `3` on the right of `0`.\n\n1 + 0 + 2 = 3\nWe have `1` on the left of `0` and `2` on the right of `0`.\n\n3 + 2 + 0 = 5\nWe have `3` and `2` on the left of `0`.\n```\n\n---\n\n\u2B50\uFE0F Points\n\nWe should calculate left total and right total from 0 position, so that we will get the right answer.\n\n---\n\n- How we calculate both totals?\n\nLet\'s say we call left total `prefix` and right total `suffix`\n\n```\nInput: nums = [2,3,5]\n```\n\n```\nprefix_sum = 0\nsuffix_sum = 10 (= sum(nums))\n```\n### How to use prefix_sum\n`prefix_sum` is total of numbers we already met in the iteration.\n\nTo understand my idea easily, let me explain it when `index = 1`. In solution code, we start iteration from `index 0`. \n\nCalculate left side. When we move to `index 1`, `prefix_sum` should be `2`.\n```\ni: 1\nnum(= current number): 3\nprefix_sum = 2\n\nleft_sum = num * i - prefix_sum\n= 1 = 3 * 1 - 2\n```\n- Why `num * i - prefix_sum`?\n\nHow many numbers on the left of current number?\n\nThe answer is `1`. we only have `2` on the left side, so we need to multiply `current number` * `1`(= index) to calculate absolute value on the left side, because we need to subtract current number from each number on the left side.\n\n```\nnum * i = 3 * 1 = 3\n```\n`prefix_sum` is total of numbers we already met, which means total number of current left side. So if we subtract `prefix_sum` from `3`, we will get `left_sum`.\n```\nleft_sum = num * i - prefix_sum\n1 = 3 - 2\n```\nInput is \n```\n[2,3,5]\n i\n\nWhen i = 1, abosulute value of left side is 1.\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\n```\nLooks good.\n\nTo understand my idea easily, let me continue to calculate left side. In solution code, we calculate left side and right side in the same iteration.\n\n```\ni: 2\nnum(= current number): 5\nprefix_sum = 5 (= 2 + 3)\n\nleft_sum = num * i - prefix_sum\n= 5 = 5 * 2 - 5\n```\nAt `index 2`, we have two numbers(= `2` and `3`) on the left side of current index, so we need to subtract `5` from both numbers. That\'s why we need `5 * 2 = 10`.\n\nWe already met `2` and `3`, so current `prefix_sum` should be `5`. In the end,\n```\nleft_sum = 10 - 5\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\nLeft side is `5`(= `3 + 2`). Looks good.\n\nLet me calculate when i = 0\n\n```\ni: 0\nnum(= current number): 2\nprefix_sum = 0 (= no left number of current index)\n\nleft_sum = num * i - prefix_sum\n= 0 = 2 * 0 - 0\n\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\n```\nLooks good!\n\n### How to use suffix_sum\nWe initialize `suffix_sum` like this.\n```\nsuffix_sum = 10 (= sum(nums))\n```\nWe use `suffix_sum` to caculate `right_sum` of current index. `suffix_sum` is total number of right side including current number.\n\nHow many numbers do we have on the right side?\n\nSimply, we subtract current index from total length of input array.\n```\n[2,3,5]\n i\ntotal length: 3\nwhen i = 0, number of right side is 3 - 0 = 3 (= 2,3,5)\n\n[2,3,5]\n i\ntotal length: 3\nwhen i = 1, number of right side is 3 - 1 = 2 (= 3,5)\n\n[2,3,5]\n i\ntotal length: 3\nwhen i = 2, number of right side is 3 - 2 = 1 (= 5)\n```\nWe apply the same idea of the left side. We will subtract current number * length of right side from `suffix_sum`.\n\n```\n[2,3,5]\ni = 0\nnum(= current number): 2\nsuffix_sum = 10 (= 2 + 3 + 5)\n\nright_sum = suffix_sum - num * (len(nums) - i)\n= 10 - 2 * (3 - 0)\n= 4\n\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4\n```\nRight side is `1 + 3 = 4` Looks good! We start from `index 0`, so every time we move to next index, total of right side should be smaller. On the other hand left side should be bigger.\n\n```\n[2,3,5]\ni = 1\nnum(= current number): 3\nsuffix_sum = 8 (= 3 + 5)\n\nright_sum = suffix_sum - num * (len(nums) - i)\n= 8 - 3 * (3 - 1)\n= 2\n\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\n```\nRight side of `0` is `2`. Looks good!\n\n```\n[2,3,5]\ni = 2\nnum(= current number): 5\nsuffix_sum = 5 (= 5)\n\nright_sum = suffix_sum - num * (len(nums) - i)\n= 5 - 5 * (3 - 2)\n= 0\n\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\nRight side of `0` is `0`. Looks good!\n\nIn the end,\n\n```\ntotal_sum = left_sum + right_sum\n\nwhen index = 0\n4 = 0 + 4\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\n\nwhen index = 1\n3 = 1 + 2\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\n\nwhen index = 2\n5 = 5 + 0\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n\n```\n```\nOutput: [4,3,5]\n```\n\nEasy! \uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n---\n\n\n### Algorithm Overview:\n\nIn each iteration, we calculate left sum and right sum and add both as a result.\n\n### Detailed Explanation:\n\n1. **Initialize an empty list to store the result:**\n ```python\n res = []\n ```\n\n2. **Initialize variables for prefix and suffix sums:**\n ```python\n prefix_sum = 0\n suffix_sum = sum(nums)\n ```\n - `prefix_sum`: This variable is used to keep track of the sum of elements to the left of the current element.\n - `suffix_sum`: This variable is initialized as the sum of all elements in the array. It will be used to calculate the sum of elements to the right of the current element.\n\n3. **Iterate through each element in the array using `enumerate`:**\n ```python\n for i, num in enumerate(nums):\n ```\n - `i`: Represents the index of the current element.\n - `num`: Represents the value of the current element.\n\n4. **Calculate the sum of elements to the left of the current element (`left_sum`):**\n ```python\n left_sum = num * i - prefix_sum\n ```\n - This calculates the sum of elements to the left of the current element by multiplying the value of the current element (`num`) with its index (`i`) and subtracting the running sum of elements encountered so far (`prefix_sum`).\n\n5. **Calculate the sum of elements to the right of the current element (`right_sum`):**\n ```python\n right_sum = suffix_sum - num * (len(nums) - i)\n ```\n - This calculates the sum of elements to the right of the current element by subtracting the running sum of elements (`suffix_sum`) from the product of the value of the current element (`num`) and the count of elements to its right (`len(nums) - i`).\n\n6. **Calculate the total sum of absolute differences for the current element (`total_sum`):**\n ```python\n total_sum = left_sum + right_sum\n ```\n - This combines the left and right sums to get the total sum of absolute differences for the current element.\n\n7. **Append the total sum to the result list (`res`):**\n ```python\n res.append(total_sum)\n ```\n\n8. **Update the prefix sum and suffix sum for the next iteration:**\n ```python\n prefix_sum += num\n suffix_sum -= num\n ```\n - `prefix_sum` is updated by adding the value of the current element (`num`).\n - `suffix_sum` is updated by subtracting the value of the current element (`num`).\n\n9. **Return the final result list (`res`):**\n ```python\n return res\n ```\n\nThis algorithm efficiently calculates the sum of absolute differences for each element in the array by taking advantage of the sorted nature of the array and updating prefix and suffix sums during each iteration.\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\nExcept `res`.\n\n```python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n # Initialize an empty list to store the result\n res = []\n\n # Initialize variables for prefix and suffix sums\n prefix_sum = 0\n suffix_sum = sum(nums)\n\n # Iterate through each element in the array\n for i, num in enumerate(nums):\n # Calculate the sum of elements to the left of the current element\n left_sum = num * i - prefix_sum\n\n # Calculate the sum of elements to the right of the current element\n right_sum = suffix_sum - num * (len(nums) - i)\n\n # Calculate the total sum of absolute differences for the current element\n total_sum = left_sum + right_sum\n\n # Append the total sum to the result list\n res.append(total_sum)\n\n # Update the prefix sum and suffix sum for the next iteration\n prefix_sum += num\n suffix_sum -= num\n\n # Return the final result list\n return res \n```\n```javascript []\nvar getSumAbsoluteDifferences = function(nums) {\n let res = [];\n let prefixSum = 0;\n let suffixSum = nums.reduce((acc, num) => acc + num, 0);\n\n for (let i = 0; i < nums.length; i++) {\n let leftSum = nums[i] * i - prefixSum;\n let rightSum = suffixSum - nums[i] * (nums.length - i);\n let totalSum = leftSum + rightSum;\n\n res.push(totalSum);\n\n prefixSum += nums[i];\n suffixSum -= nums[i];\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int[] res = new int[nums.length];\n int prefixSum = 0;\n int suffixSum = 0;\n\n for (int num : nums) {\n suffixSum += num;\n }\n\n for (int i = 0; i < nums.length; i++) {\n int leftSum = nums[i] * i - prefixSum;\n int rightSum = suffixSum - nums[i] * (nums.length - i);\n int totalSum = leftSum + rightSum;\n\n res[i] = totalSum;\n\n prefixSum += nums[i];\n suffixSum -= nums[i];\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n vector<int> res;\n int prefixSum = 0;\n int suffixSum = 0;\n\n for (int num : nums) {\n suffixSum += num;\n }\n\n for (int i = 0; i < nums.size(); i++) {\n int leftSum = nums[i] * i - prefixSum;\n int rightSum = suffixSum - nums[i] * (nums.size() - i);\n int totalSum = leftSum + rightSum;\n\n res.push_back(totalSum);\n\n prefixSum += nums[i];\n suffixSum -= nums[i];\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/largest-submatrix-with-rearrangements/solutions/4331142/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/odAv92zWKqs\n\n\u25A0 Timeline of the video\n\n`0:05` How we can move columns\n`1:09` Calculate height\n`2:48` Calculate width\n`4:10` Let\'s make sure it works\n`5:40` Demonstrate how it works\n`7:44` Coding\n`9:59` Time Complexity and Space Complexity\n`10:35` Summary of the algorithm with my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-number-of-coins-you-can-get/solutions/4322538/video-give-me-4-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/HPzfCHfWPlY\n\n\u25A0 Timeline of the video\n`0:04` Two key points to solve this question\n`1:46` Demonstrate how it works\n`3:17` Coding\n`4:14` Time Complexity and Space Complexity\n`4:33` Summary of the algorithm with my solution code\n | 12 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
γVideoγGive me 10 minutes - How we think about a solution. | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # Intuition\nCalcuate left side and right side.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bwQh44GWME8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve this question\n`1:56` Calculate left total\n`6:32` Calculate right total\n`11:12` Create answers\n`11:51` Coding\n`14:14` Time Complexity and Space Complexity\n`14:39` Summary of the algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,217\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nThis is brute force solution.\n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n res = []\n\n for i in range(n):\n current_sum = 0\n\n for j in range(n):\n current_sum += abs(nums[i] - nums[j])\n\n res.append(current_sum)\n\n return res\n```\nBut I got `Time Limit Exceeded`. lol\n\nLook at Example 1.\n```\nInput: nums = [2,3,5]\n```\n```\nOutput: [4,3,5]\n\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\nLet\'s focus on this.\n```\n0 + 1 + 3 = 4\n1 + 0 + 2 = 3\n3 + 2 + 0 = 5\n```\nEach calculation has `0`. It means `current number` - `current number`. Look at positions for other numbers.\n```\n0 + 1 + 3 = 4\nWe have `1` and `3` on the right of `0`.\n\n1 + 0 + 2 = 3\nWe have `1` on the left of `0` and `2` on the right of `0`.\n\n3 + 2 + 0 = 5\nWe have `3` and `2` on the left of `0`.\n```\n\n---\n\n\u2B50\uFE0F Points\n\nWe should calculate left total and right total from 0 position, so that we will get the right answer.\n\n---\n\n- How we calculate both totals?\n\nLet\'s say we call left total `prefix` and right total `suffix`\n\n```\nInput: nums = [2,3,5]\n```\n\n```\nprefix_sum = 0\nsuffix_sum = 10 (= sum(nums))\n```\n### How to use prefix_sum\n`prefix_sum` is total of numbers we already met in the iteration.\n\nTo understand my idea easily, let me explain it when `index = 1`. In solution code, we start iteration from `index 0`. \n\nCalculate left side. When we move to `index 1`, `prefix_sum` should be `2`.\n```\ni: 1\nnum(= current number): 3\nprefix_sum = 2\n\nleft_sum = num * i - prefix_sum\n= 1 = 3 * 1 - 2\n```\n- Why `num * i - prefix_sum`?\n\nHow many numbers on the left of current number?\n\nThe answer is `1`. we only have `2` on the left side, so we need to multiply `current number` * `1`(= index) to calculate absolute value on the left side, because we need to subtract current number from each number on the left side.\n\n```\nnum * i = 3 * 1 = 3\n```\n`prefix_sum` is total of numbers we already met, which means total number of current left side. So if we subtract `prefix_sum` from `3`, we will get `left_sum`.\n```\nleft_sum = num * i - prefix_sum\n1 = 3 - 2\n```\nInput is \n```\n[2,3,5]\n i\n\nWhen i = 1, abosulute value of left side is 1.\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\n```\nLooks good.\n\nTo understand my idea easily, let me continue to calculate left side. In solution code, we calculate left side and right side in the same iteration.\n\n```\ni: 2\nnum(= current number): 5\nprefix_sum = 5 (= 2 + 3)\n\nleft_sum = num * i - prefix_sum\n= 5 = 5 * 2 - 5\n```\nAt `index 2`, we have two numbers(= `2` and `3`) on the left side of current index, so we need to subtract `5` from both numbers. That\'s why we need `5 * 2 = 10`.\n\nWe already met `2` and `3`, so current `prefix_sum` should be `5`. In the end,\n```\nleft_sum = 10 - 5\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\nLeft side is `5`(= `3 + 2`). Looks good.\n\nLet me calculate when i = 0\n\n```\ni: 0\nnum(= current number): 2\nprefix_sum = 0 (= no left number of current index)\n\nleft_sum = num * i - prefix_sum\n= 0 = 2 * 0 - 0\n\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\n```\nLooks good!\n\n### How to use suffix_sum\nWe initialize `suffix_sum` like this.\n```\nsuffix_sum = 10 (= sum(nums))\n```\nWe use `suffix_sum` to caculate `right_sum` of current index. `suffix_sum` is total number of right side including current number.\n\nHow many numbers do we have on the right side?\n\nSimply, we subtract current index from total length of input array.\n```\n[2,3,5]\n i\ntotal length: 3\nwhen i = 0, number of right side is 3 - 0 = 3 (= 2,3,5)\n\n[2,3,5]\n i\ntotal length: 3\nwhen i = 1, number of right side is 3 - 1 = 2 (= 3,5)\n\n[2,3,5]\n i\ntotal length: 3\nwhen i = 2, number of right side is 3 - 2 = 1 (= 5)\n```\nWe apply the same idea of the left side. We will subtract current number * length of right side from `suffix_sum`.\n\n```\n[2,3,5]\ni = 0\nnum(= current number): 2\nsuffix_sum = 10 (= 2 + 3 + 5)\n\nright_sum = suffix_sum - num * (len(nums) - i)\n= 10 - 2 * (3 - 0)\n= 4\n\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4\n```\nRight side is `1 + 3 = 4` Looks good! We start from `index 0`, so every time we move to next index, total of right side should be smaller. On the other hand left side should be bigger.\n\n```\n[2,3,5]\ni = 1\nnum(= current number): 3\nsuffix_sum = 8 (= 3 + 5)\n\nright_sum = suffix_sum - num * (len(nums) - i)\n= 8 - 3 * (3 - 1)\n= 2\n\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\n```\nRight side of `0` is `2`. Looks good!\n\n```\n[2,3,5]\ni = 2\nnum(= current number): 5\nsuffix_sum = 5 (= 5)\n\nright_sum = suffix_sum - num * (len(nums) - i)\n= 5 - 5 * (3 - 2)\n= 0\n\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\nRight side of `0` is `0`. Looks good!\n\nIn the end,\n\n```\ntotal_sum = left_sum + right_sum\n\nwhen index = 0\n4 = 0 + 4\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\n\nwhen index = 1\n3 = 1 + 2\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\n\nwhen index = 2\n5 = 5 + 0\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n\n```\n```\nOutput: [4,3,5]\n```\n\nEasy! \uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n---\n\n\n### Algorithm Overview:\n\nIn each iteration, we calculate left sum and right sum and add both as a result.\n\n### Detailed Explanation:\n\n1. **Initialize an empty list to store the result:**\n ```python\n res = []\n ```\n\n2. **Initialize variables for prefix and suffix sums:**\n ```python\n prefix_sum = 0\n suffix_sum = sum(nums)\n ```\n - `prefix_sum`: This variable is used to keep track of the sum of elements to the left of the current element.\n - `suffix_sum`: This variable is initialized as the sum of all elements in the array. It will be used to calculate the sum of elements to the right of the current element.\n\n3. **Iterate through each element in the array using `enumerate`:**\n ```python\n for i, num in enumerate(nums):\n ```\n - `i`: Represents the index of the current element.\n - `num`: Represents the value of the current element.\n\n4. **Calculate the sum of elements to the left of the current element (`left_sum`):**\n ```python\n left_sum = num * i - prefix_sum\n ```\n - This calculates the sum of elements to the left of the current element by multiplying the value of the current element (`num`) with its index (`i`) and subtracting the running sum of elements encountered so far (`prefix_sum`).\n\n5. **Calculate the sum of elements to the right of the current element (`right_sum`):**\n ```python\n right_sum = suffix_sum - num * (len(nums) - i)\n ```\n - This calculates the sum of elements to the right of the current element by subtracting the running sum of elements (`suffix_sum`) from the product of the value of the current element (`num`) and the count of elements to its right (`len(nums) - i`).\n\n6. **Calculate the total sum of absolute differences for the current element (`total_sum`):**\n ```python\n total_sum = left_sum + right_sum\n ```\n - This combines the left and right sums to get the total sum of absolute differences for the current element.\n\n7. **Append the total sum to the result list (`res`):**\n ```python\n res.append(total_sum)\n ```\n\n8. **Update the prefix sum and suffix sum for the next iteration:**\n ```python\n prefix_sum += num\n suffix_sum -= num\n ```\n - `prefix_sum` is updated by adding the value of the current element (`num`).\n - `suffix_sum` is updated by subtracting the value of the current element (`num`).\n\n9. **Return the final result list (`res`):**\n ```python\n return res\n ```\n\nThis algorithm efficiently calculates the sum of absolute differences for each element in the array by taking advantage of the sorted nature of the array and updating prefix and suffix sums during each iteration.\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\nExcept `res`.\n\n```python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n # Initialize an empty list to store the result\n res = []\n\n # Initialize variables for prefix and suffix sums\n prefix_sum = 0\n suffix_sum = sum(nums)\n\n # Iterate through each element in the array\n for i, num in enumerate(nums):\n # Calculate the sum of elements to the left of the current element\n left_sum = num * i - prefix_sum\n\n # Calculate the sum of elements to the right of the current element\n right_sum = suffix_sum - num * (len(nums) - i)\n\n # Calculate the total sum of absolute differences for the current element\n total_sum = left_sum + right_sum\n\n # Append the total sum to the result list\n res.append(total_sum)\n\n # Update the prefix sum and suffix sum for the next iteration\n prefix_sum += num\n suffix_sum -= num\n\n # Return the final result list\n return res \n```\n```javascript []\nvar getSumAbsoluteDifferences = function(nums) {\n let res = [];\n let prefixSum = 0;\n let suffixSum = nums.reduce((acc, num) => acc + num, 0);\n\n for (let i = 0; i < nums.length; i++) {\n let leftSum = nums[i] * i - prefixSum;\n let rightSum = suffixSum - nums[i] * (nums.length - i);\n let totalSum = leftSum + rightSum;\n\n res.push(totalSum);\n\n prefixSum += nums[i];\n suffixSum -= nums[i];\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int[] res = new int[nums.length];\n int prefixSum = 0;\n int suffixSum = 0;\n\n for (int num : nums) {\n suffixSum += num;\n }\n\n for (int i = 0; i < nums.length; i++) {\n int leftSum = nums[i] * i - prefixSum;\n int rightSum = suffixSum - nums[i] * (nums.length - i);\n int totalSum = leftSum + rightSum;\n\n res[i] = totalSum;\n\n prefixSum += nums[i];\n suffixSum -= nums[i];\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n vector<int> res;\n int prefixSum = 0;\n int suffixSum = 0;\n\n for (int num : nums) {\n suffixSum += num;\n }\n\n for (int i = 0; i < nums.size(); i++) {\n int leftSum = nums[i] * i - prefixSum;\n int rightSum = suffixSum - nums[i] * (nums.size() - i);\n int totalSum = leftSum + rightSum;\n\n res.push_back(totalSum);\n\n prefixSum += nums[i];\n suffixSum -= nums[i];\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/largest-submatrix-with-rearrangements/solutions/4331142/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/odAv92zWKqs\n\n\u25A0 Timeline of the video\n\n`0:05` How we can move columns\n`1:09` Calculate height\n`2:48` Calculate width\n`4:10` Let\'s make sure it works\n`5:40` Demonstrate how it works\n`7:44` Coding\n`9:59` Time Complexity and Space Complexity\n`10:35` Summary of the algorithm with my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-number-of-coins-you-can-get/solutions/4322538/video-give-me-4-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/HPzfCHfWPlY\n\n\u25A0 Timeline of the video\n`0:04` Two key points to solve this question\n`1:46` Demonstrate how it works\n`3:17` Coding\n`4:14` Time Complexity and Space Complexity\n`4:33` Summary of the algorithm with my solution code\n | 12 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
Python3 Solution | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | \n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n=len(nums)\n ans=[]\n total=0\n for num in nums:\n total+=abs(num-nums[0])\n ans.append(total)\n for idx in range(1,n):\n res=nums[idx]-nums[idx-1]\n total+=res*idx\n total-=res*(n-idx)\n ans.append(total)\n return ans \n``` | 5 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Python3 Solution | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | \n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n=len(nums)\n ans=[]\n total=0\n for num in nums:\n total+=abs(num-nums[0])\n ans.append(total)\n for idx in range(1,n):\n res=nums[idx]-nums[idx-1]\n total+=res*idx\n total-=res*(n-idx)\n ans.append(total)\n return ans \n``` | 5 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
β
β[C++/Java/Python/JavaScript] || Beats 99% || 2 Approaches || EXPLAINEDπ₯ | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1***\n1. **vector<int> getSumAbsoluteDifferences(vector<int>& nums):** A function that takes a vector of integers as input and returns a vector that contains the sum of absolute differences for each element of the input vector.\n\n1. **int n = nums.size();:** Determines the size of the input vector nums.\n\n1. **int A = 0, B = accumulate(nums.begin(), nums.end(), 0);:** Initializes two variables `A` and `B`. `A` starts at 0, while `B` is set to the sum of all elements in `nums`.\n\n1. **vector<int> ans(n, 0);:** Initializes a result vector `ans` of size `n`, filled with zeros.\n\n1. **#pragma unroll:** Compiler directive to suggest loop unrolling for optimization purposes.\n\n1. **for(int x : nums) { ... }:** Looping through each element `x` in the `nums` vector.\n\n1. **ans[i++] = (2 * i - n) * x + B - A;:** Calculates and assigns the sum of absolute differences based on the given formula to the `i`th position in the `ans` vector.\n\n1. **A += x;** and **B -= x;:** Updates the values of `A` and `B` by adding and subtracting the current element `x`, respectively.\n\n1. Returns the `ans` vector containing the sum of absolute differences for each element in the input vector `nums`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size();\n int A = 0, B = accumulate(nums.begin(), nums.end(), 0);\n vector<int> ans(n, 0);\n int i = 0;\n \n // Loop through the elements of the \'nums\' vector\n // Unrolls the loop for optimization\n #pragma unroll\n for(int x : nums){\n // Calculate and store the absolute differences based on the formula\n ans[i++] = (2 * i - n) * x + B - A;\n A += x;\n B -= x;\n }\n return ans; // Return the vector containing the sum absolute differences\n }\n};\n\n\n\n```\n```C []\n\nint* getSumAbsoluteDifferences(int* nums, int numsSize) {\n int n = numsSize;\n int A = 0, B = 0;\n int *ans = (int*)malloc(n * sizeof(int));\n\n for (int i = 0; i < n; i++) {\n B += nums[i];\n }\n\n int i = 0;\n for (int j = 0; j < n; j++) {\n ans[i] = (2 * i - n) * nums[j] + B - A;\n A += nums[j];\n B -= nums[j];\n i++;\n }\n\n return ans;\n}\n\n\n\n```\n```Java []\n\n\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n = nums.length;\n int A = 0, B = 0;\n for (int x : nums) {\n B += x;\n }\n\n int[] ans = new int[n];\n int i = 0;\n for (int x : nums) {\n ans[i] = (2 * i - n) * x + B - A;\n A += x;\n B -= x;\n i++;\n }\n return ans;\n }\n}\n\n\n```\n\n```python3 []\n\n\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n A = B = 0\n for x in nums:\n B += x\n\n ans = [0] * n\n i = 0\n for x in nums:\n ans[i] = (2 * i - n) * x + B - A\n A += x\n B -= x\n i += 1\n return ans\n\n\n\n```\n```javascript []\nfunction getSumAbsoluteDifferences(nums) {\n const n = nums.length;\n let A = 0, B = nums.reduce((acc, curr) => acc + curr, 0);\n const ans = [];\n\n let i = 0;\n for (const x of nums) {\n ans.push((2 * i - n) * x + B - A);\n A += x;\n B -= x;\n i++;\n }\n\n return ans;\n}\n\n```\n\n---\n\n#### ***Approach 2(Prefix Sum***\n\n\n1. **Prefix Sum Calculation:**\n\n - A prefix array is created to store the cumulative sum of elements in `nums` up to each index.\n - It helps in efficiently calculating the left and right sum for each element.\n1. **Iterating through Elements:**\n\n - For each element `nums[i]` in the input array:\n1. **Calculating Left and Right Sums:**\n\n - **leftSum:** The sum of elements to the left of the current element `nums[i]`.\n - **rightSum:** The sum of elements to the right of the current element `nums[i]`.\n1. **Count of Elements:**\n\n - **leftCount:** The count of elements to the left of the current element `nums[i]`.\n - **rightCount:** The count of elements to the right of the current element `nums[i]`.\n1. **Absolute Difference Sums:**\n\n - **leftTotal:** The sum of absolute differences for the left part based on leftSum and leftCount.\n - **rightTotal:** The sum of absolute differences for the right part based on rightSum and rightCount.\n1. **Total Sum of Absolute Differences:**\n\n - **leftTotal + rightTotal:** Summing the left and right absolute differences to get the total sum for the current element.\n1. **Result:**\n\n - The calculated sums are stored in the `ans` vector and returned as the final result.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size();\n \n // Calculate the prefix sum of the input array \'nums\'\n vector<int> prefix = {nums[0]};\n for (int i = 1; i < n; i++) {\n prefix.push_back(prefix[i - 1] + nums[i]);\n }\n \n vector<int> ans;\n for (int i = 0; i < n; i++) {\n // Calculate the sum of elements to the left and right of the current element\n int leftSum = prefix[i] - nums[i];\n int rightSum = prefix[n - 1] - prefix[i];\n \n // Calculate the count of elements to the left and right of the current element\n int leftCount = i;\n int rightCount = n - 1 - i;\n \n // Calculate the absolute difference sums for left and right parts\n int leftTotal = leftCount * nums[i] - leftSum;\n int rightTotal = rightSum - rightCount * nums[i];\n \n // Calculate the total sum of absolute differences for the current element\n ans.push_back(leftTotal + rightTotal);\n }\n \n return ans;\n }\n};\n```\n```C []\nint* getSumAbsoluteDifferences(int* nums, int numsSize) {\n int n = numsSize;\n int* prefix = (int*)malloc(n * sizeof(int));\n prefix[0] = nums[0];\n\n // Calculate prefix sums\n for (int i = 1; i < n; i++) {\n prefix[i] = prefix[i - 1] + nums[i];\n }\n\n int* ans = (int*)malloc(n * sizeof(int));\n\n for (int i = 0; i < n; i++) {\n int leftSum = prefix[i] - nums[i];\n int rightSum = prefix[n - 1] - prefix[i];\n \n int leftCount = i;\n int rightCount = n - 1 - i;\n \n int leftTotal = leftCount * nums[i] - leftSum;\n int rightTotal = rightSum - rightCount * nums[i];\n \n ans[i] = leftTotal + rightTotal;\n }\n\n return ans;\n}\n\n```\n```java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n = nums.length;\n int[] prefix = new int[n];\n prefix[0] = nums[0];\n for (int i = 1; i < n; i++) {\n prefix[i] = prefix[i - 1] + nums[i];\n }\n \n int[] ans = new int[n];\n for (int i = 0; i < n; i++) {\n int leftSum = prefix[i] - nums[i];\n int rightSum = prefix[n - 1] - prefix[i];\n \n int leftCount = i;\n int rightCount = n - 1 - i;\n \n int leftTotal = leftCount * nums[i] - leftSum;\n int rightTotal = rightSum - rightCount * nums[i];\n \n ans[i] = leftTotal + rightTotal;\n }\n \n return ans;\n }\n}\n```\n```python3 []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n prefix = [nums[0]]\n for i in range(1, n):\n prefix.append(prefix[-1] + nums[i])\n \n ans = []\n for i in range(len(nums)):\n left_sum = prefix[i] - nums[i]\n right_sum = prefix[-1] - prefix[i]\n \n left_count = i\n right_count = n - 1 - i\n \n left_total = left_count * nums[i] - left_sum\n right_total = right_sum - right_count * nums[i]\n\n ans.append(left_total + right_total)\n \n return ans\n```\n```javascript []\nfunction getSumAbsoluteDifferences(nums) {\n const n = nums.length;\n const prefix = [nums[0]];\n\n // Calculate prefix sums\n for (let i = 1; i < n; i++) {\n prefix.push(prefix[i - 1] + nums[i]);\n }\n\n const ans = [];\n\n for (let i = 0; i < n; i++) {\n const leftSum = prefix[i] - nums[i];\n const rightSum = prefix[n - 1] - prefix[i];\n \n const leftCount = i;\n const rightCount = n - 1 - i;\n \n const leftTotal = leftCount * nums[i] - leftSum;\n const rightTotal = rightSum - rightCount * nums[i];\n \n ans.push(leftTotal + rightTotal);\n }\n\n return ans;\n}\n\n```\n\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 9 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
β
β[C++/Java/Python/JavaScript] || Beats 99% || 2 Approaches || EXPLAINEDπ₯ | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1***\n1. **vector<int> getSumAbsoluteDifferences(vector<int>& nums):** A function that takes a vector of integers as input and returns a vector that contains the sum of absolute differences for each element of the input vector.\n\n1. **int n = nums.size();:** Determines the size of the input vector nums.\n\n1. **int A = 0, B = accumulate(nums.begin(), nums.end(), 0);:** Initializes two variables `A` and `B`. `A` starts at 0, while `B` is set to the sum of all elements in `nums`.\n\n1. **vector<int> ans(n, 0);:** Initializes a result vector `ans` of size `n`, filled with zeros.\n\n1. **#pragma unroll:** Compiler directive to suggest loop unrolling for optimization purposes.\n\n1. **for(int x : nums) { ... }:** Looping through each element `x` in the `nums` vector.\n\n1. **ans[i++] = (2 * i - n) * x + B - A;:** Calculates and assigns the sum of absolute differences based on the given formula to the `i`th position in the `ans` vector.\n\n1. **A += x;** and **B -= x;:** Updates the values of `A` and `B` by adding and subtracting the current element `x`, respectively.\n\n1. Returns the `ans` vector containing the sum of absolute differences for each element in the input vector `nums`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size();\n int A = 0, B = accumulate(nums.begin(), nums.end(), 0);\n vector<int> ans(n, 0);\n int i = 0;\n \n // Loop through the elements of the \'nums\' vector\n // Unrolls the loop for optimization\n #pragma unroll\n for(int x : nums){\n // Calculate and store the absolute differences based on the formula\n ans[i++] = (2 * i - n) * x + B - A;\n A += x;\n B -= x;\n }\n return ans; // Return the vector containing the sum absolute differences\n }\n};\n\n\n\n```\n```C []\n\nint* getSumAbsoluteDifferences(int* nums, int numsSize) {\n int n = numsSize;\n int A = 0, B = 0;\n int *ans = (int*)malloc(n * sizeof(int));\n\n for (int i = 0; i < n; i++) {\n B += nums[i];\n }\n\n int i = 0;\n for (int j = 0; j < n; j++) {\n ans[i] = (2 * i - n) * nums[j] + B - A;\n A += nums[j];\n B -= nums[j];\n i++;\n }\n\n return ans;\n}\n\n\n\n```\n```Java []\n\n\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n = nums.length;\n int A = 0, B = 0;\n for (int x : nums) {\n B += x;\n }\n\n int[] ans = new int[n];\n int i = 0;\n for (int x : nums) {\n ans[i] = (2 * i - n) * x + B - A;\n A += x;\n B -= x;\n i++;\n }\n return ans;\n }\n}\n\n\n```\n\n```python3 []\n\n\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n A = B = 0\n for x in nums:\n B += x\n\n ans = [0] * n\n i = 0\n for x in nums:\n ans[i] = (2 * i - n) * x + B - A\n A += x\n B -= x\n i += 1\n return ans\n\n\n\n```\n```javascript []\nfunction getSumAbsoluteDifferences(nums) {\n const n = nums.length;\n let A = 0, B = nums.reduce((acc, curr) => acc + curr, 0);\n const ans = [];\n\n let i = 0;\n for (const x of nums) {\n ans.push((2 * i - n) * x + B - A);\n A += x;\n B -= x;\n i++;\n }\n\n return ans;\n}\n\n```\n\n---\n\n#### ***Approach 2(Prefix Sum***\n\n\n1. **Prefix Sum Calculation:**\n\n - A prefix array is created to store the cumulative sum of elements in `nums` up to each index.\n - It helps in efficiently calculating the left and right sum for each element.\n1. **Iterating through Elements:**\n\n - For each element `nums[i]` in the input array:\n1. **Calculating Left and Right Sums:**\n\n - **leftSum:** The sum of elements to the left of the current element `nums[i]`.\n - **rightSum:** The sum of elements to the right of the current element `nums[i]`.\n1. **Count of Elements:**\n\n - **leftCount:** The count of elements to the left of the current element `nums[i]`.\n - **rightCount:** The count of elements to the right of the current element `nums[i]`.\n1. **Absolute Difference Sums:**\n\n - **leftTotal:** The sum of absolute differences for the left part based on leftSum and leftCount.\n - **rightTotal:** The sum of absolute differences for the right part based on rightSum and rightCount.\n1. **Total Sum of Absolute Differences:**\n\n - **leftTotal + rightTotal:** Summing the left and right absolute differences to get the total sum for the current element.\n1. **Result:**\n\n - The calculated sums are stored in the `ans` vector and returned as the final result.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n```C++ []\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n = nums.size();\n \n // Calculate the prefix sum of the input array \'nums\'\n vector<int> prefix = {nums[0]};\n for (int i = 1; i < n; i++) {\n prefix.push_back(prefix[i - 1] + nums[i]);\n }\n \n vector<int> ans;\n for (int i = 0; i < n; i++) {\n // Calculate the sum of elements to the left and right of the current element\n int leftSum = prefix[i] - nums[i];\n int rightSum = prefix[n - 1] - prefix[i];\n \n // Calculate the count of elements to the left and right of the current element\n int leftCount = i;\n int rightCount = n - 1 - i;\n \n // Calculate the absolute difference sums for left and right parts\n int leftTotal = leftCount * nums[i] - leftSum;\n int rightTotal = rightSum - rightCount * nums[i];\n \n // Calculate the total sum of absolute differences for the current element\n ans.push_back(leftTotal + rightTotal);\n }\n \n return ans;\n }\n};\n```\n```C []\nint* getSumAbsoluteDifferences(int* nums, int numsSize) {\n int n = numsSize;\n int* prefix = (int*)malloc(n * sizeof(int));\n prefix[0] = nums[0];\n\n // Calculate prefix sums\n for (int i = 1; i < n; i++) {\n prefix[i] = prefix[i - 1] + nums[i];\n }\n\n int* ans = (int*)malloc(n * sizeof(int));\n\n for (int i = 0; i < n; i++) {\n int leftSum = prefix[i] - nums[i];\n int rightSum = prefix[n - 1] - prefix[i];\n \n int leftCount = i;\n int rightCount = n - 1 - i;\n \n int leftTotal = leftCount * nums[i] - leftSum;\n int rightTotal = rightSum - rightCount * nums[i];\n \n ans[i] = leftTotal + rightTotal;\n }\n\n return ans;\n}\n\n```\n```java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n = nums.length;\n int[] prefix = new int[n];\n prefix[0] = nums[0];\n for (int i = 1; i < n; i++) {\n prefix[i] = prefix[i - 1] + nums[i];\n }\n \n int[] ans = new int[n];\n for (int i = 0; i < n; i++) {\n int leftSum = prefix[i] - nums[i];\n int rightSum = prefix[n - 1] - prefix[i];\n \n int leftCount = i;\n int rightCount = n - 1 - i;\n \n int leftTotal = leftCount * nums[i] - leftSum;\n int rightTotal = rightSum - rightCount * nums[i];\n \n ans[i] = leftTotal + rightTotal;\n }\n \n return ans;\n }\n}\n```\n```python3 []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n prefix = [nums[0]]\n for i in range(1, n):\n prefix.append(prefix[-1] + nums[i])\n \n ans = []\n for i in range(len(nums)):\n left_sum = prefix[i] - nums[i]\n right_sum = prefix[-1] - prefix[i]\n \n left_count = i\n right_count = n - 1 - i\n \n left_total = left_count * nums[i] - left_sum\n right_total = right_sum - right_count * nums[i]\n\n ans.append(left_total + right_total)\n \n return ans\n```\n```javascript []\nfunction getSumAbsoluteDifferences(nums) {\n const n = nums.length;\n const prefix = [nums[0]];\n\n // Calculate prefix sums\n for (let i = 1; i < n; i++) {\n prefix.push(prefix[i - 1] + nums[i]);\n }\n\n const ans = [];\n\n for (let i = 0; i < n; i++) {\n const leftSum = prefix[i] - nums[i];\n const rightSum = prefix[n - 1] - prefix[i];\n \n const leftCount = i;\n const rightCount = n - 1 - i;\n \n const leftTotal = leftCount * nums[i] - leftSum;\n const rightTotal = rightSum - rightCount * nums[i];\n \n ans.push(leftTotal + rightTotal);\n }\n\n return ans;\n}\n\n```\n\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 9 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
O(n) Linear time complexity using Python | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # **Solution by** [**Rockposedon**](https://leetcode.com/Rockposedon/)\n#\n## **Approach: PrefixSum & SuffixSum**\n#\n### Intuition\nThis solution utilizes the PrefixSum and SuffixSum techniques to efficiently calculate the sum of absolute differences for each element in the array. The key idea is to precompute the prefix sum and suffix sum arrays, which allows us to calculate the left and right sums for each element in linear time.\n#\n### Implementation\n1. Initialize arrays for prefix sum and suffix sum.\n2. Calculate the prefix sum by iterating through the array from left to right.\n3. Calculate the suffix sum by iterating through the array from right to left.\n4. Iterate through the array and calculate the left and right sums using the precomputed prefix and suffix sums.\n5. Assemble the total sum of absolute differences and return the result.\n#\n### Time Complexity\nThe time complexity of this solution is O(n), where n is the size of the input array. The use of prefix sum and suffix sum optimizes the computation of left and right sums.\n\n```python\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n prefix_sum = [0] * n\n suffix_sum = [0] * n\n\n # Calculate prefix sum\n prefix_sum[0] = nums[0]\n for i in range(1, n):\n prefix_sum[i] = prefix_sum[i - 1] + nums[i]\n\n # Calculate suffix sum\n suffix_sum[n - 1] = nums[n - 1]\n for i in range(n - 2, -1, -1):\n suffix_sum[i] = suffix_sum[i + 1] + nums[i]\n\n result = []\n for i in range(n):\n # Calculate left and right sums efficiently using prefix and suffix sums\n left_sum = i * nums[i] - prefix_sum[i]\n right_sum = suffix_sum[i] - (n - i - 1) * nums[i]\n\n # Calculate the total sum of absolute differences\n result.append(left_sum + right_sum)\n\n return result\n-----------------------------------------------------------------------------------------------------\n\n\t\t\t\tIf you find this solution helpful, consider giving it an upvote! \uD83D\uDC4D\n\t\t\t\t\n-----------------------------------------------------------------------------------------------------\n | 4 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
O(n) Linear time complexity using Python | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # **Solution by** [**Rockposedon**](https://leetcode.com/Rockposedon/)\n#\n## **Approach: PrefixSum & SuffixSum**\n#\n### Intuition\nThis solution utilizes the PrefixSum and SuffixSum techniques to efficiently calculate the sum of absolute differences for each element in the array. The key idea is to precompute the prefix sum and suffix sum arrays, which allows us to calculate the left and right sums for each element in linear time.\n#\n### Implementation\n1. Initialize arrays for prefix sum and suffix sum.\n2. Calculate the prefix sum by iterating through the array from left to right.\n3. Calculate the suffix sum by iterating through the array from right to left.\n4. Iterate through the array and calculate the left and right sums using the precomputed prefix and suffix sums.\n5. Assemble the total sum of absolute differences and return the result.\n#\n### Time Complexity\nThe time complexity of this solution is O(n), where n is the size of the input array. The use of prefix sum and suffix sum optimizes the computation of left and right sums.\n\n```python\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n prefix_sum = [0] * n\n suffix_sum = [0] * n\n\n # Calculate prefix sum\n prefix_sum[0] = nums[0]\n for i in range(1, n):\n prefix_sum[i] = prefix_sum[i - 1] + nums[i]\n\n # Calculate suffix sum\n suffix_sum[n - 1] = nums[n - 1]\n for i in range(n - 2, -1, -1):\n suffix_sum[i] = suffix_sum[i + 1] + nums[i]\n\n result = []\n for i in range(n):\n # Calculate left and right sums efficiently using prefix and suffix sums\n left_sum = i * nums[i] - prefix_sum[i]\n right_sum = suffix_sum[i] - (n - i - 1) * nums[i]\n\n # Calculate the total sum of absolute differences\n result.append(left_sum + right_sum)\n\n return result\n-----------------------------------------------------------------------------------------------------\n\n\t\t\t\tIf you find this solution helpful, consider giving it an upvote! \uD83D\uDC4D\n\t\t\t\t\n-----------------------------------------------------------------------------------------------------\n | 4 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
C++/Python Math sum||50ms Beats 100% | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet the non-decreasing sequence is given\n$$\na_0\\leq a_1\\leq\\cdots \\leq a_i\\leq \\cdots a_{n-1}\n$$\nConsider the computation\n$$\n\\sum_j|a_j-a_i|=\\sum_{i<j}a_j-a_i+\\sum_{j<i}a_i-a_j \\\\\n=\\sum_{i<j}a_j-(n-i-1)a_i+ia_i-\\sum_{j<i}a_j\\\\\n=\\sum_{i<j}a_j+(2i-n+1)a_i-\\sum_{j<i}a_j\n$$\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/FGDkETbwWHc?si=Ag7otErPwleFlz10](https://youtu.be/FGDkETbwWHc?si=Ag7otErPwleFlz10)\nLet A[i]=$\\sum_{j<i}a_j$, B[i]=$\\sum_{i<j}a_j$\nUse prefix sum & suffix sum to solve.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code 50ms Beats 100%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n=nums.size();\n nums.push_back(0);//Adding 0 for avoid of if-branch in the loop\n int A=0, B=accumulate(nums.begin()+1, nums.end(), 0);\n vector<int> ans(n, 0);\n #pragma unroll\n for(int i=0; i<n; i++){\n ans[i]=(2*i-n+1)*nums[i]+B-A;\n A+=nums[i];\n B-=nums[i+1];\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# A variant solution where B beginning with sum(nums)\n```C++ []\n\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n=nums.size();\n int A=0, B=accumulate(nums.begin(), nums.end(), 0);\n vector<int> ans(n, 0);\n int i=0;\n #pragma unroll\n for(int x: nums){\n ans[i++]=(2*i-n)*x+B-A;\n A+=x;\n B-=x;\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n=len(nums)\n A=0\n B=sum(nums)\n ans=[0]*n\n\n for i, x in enumerate(nums):\n ans[i]=(2*i-n)*x+B-A\n A+=x\n B-=x\n return ans\n```\n```Java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n=nums.length;\n int A=0;\n int B=Arrays.stream(nums).sum();\n int [] ans=new int[n];\n int i=0;\n for(int x : nums){\n ans[i]=(2*i-n)*x+B-A;\n A+=x;\n B-=x;\n i++;\n }\n return ans; \n }\n}\n```\n```C []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\n#pragma GCC optimize("O3")\nint* getSumAbsoluteDifferences(int* nums, int n, int* returnSize){\n *returnSize=n;\n int A=0;\n int B=0;\n #pragma unroll\n for(register i=0; i<n; i++)\n B+=nums[i];\n int *ans=(int*)malloc(sizeof(int)*n);\n #pragma unroll\n for(register i=0; i<n; i++){\n ans[i]=(2*i-n)*nums[i]+B-A;\n A+=nums[i];\n B-=nums[i];\n }\n return ans;\n}\n```\n | 17 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
C++/Python Math sum||50ms Beats 100% | sum-of-absolute-differences-in-a-sorted-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet the non-decreasing sequence is given\n$$\na_0\\leq a_1\\leq\\cdots \\leq a_i\\leq \\cdots a_{n-1}\n$$\nConsider the computation\n$$\n\\sum_j|a_j-a_i|=\\sum_{i<j}a_j-a_i+\\sum_{j<i}a_i-a_j \\\\\n=\\sum_{i<j}a_j-(n-i-1)a_i+ia_i-\\sum_{j<i}a_j\\\\\n=\\sum_{i<j}a_j+(2i-n+1)a_i-\\sum_{j<i}a_j\n$$\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/FGDkETbwWHc?si=Ag7otErPwleFlz10](https://youtu.be/FGDkETbwWHc?si=Ag7otErPwleFlz10)\nLet A[i]=$\\sum_{j<i}a_j$, B[i]=$\\sum_{i<j}a_j$\nUse prefix sum & suffix sum to solve.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code 50ms Beats 100%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n=nums.size();\n nums.push_back(0);//Adding 0 for avoid of if-branch in the loop\n int A=0, B=accumulate(nums.begin()+1, nums.end(), 0);\n vector<int> ans(n, 0);\n #pragma unroll\n for(int i=0; i<n; i++){\n ans[i]=(2*i-n+1)*nums[i]+B-A;\n A+=nums[i];\n B-=nums[i+1];\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# A variant solution where B beginning with sum(nums)\n```C++ []\n\nclass Solution {\npublic:\n vector<int> getSumAbsoluteDifferences(vector<int>& nums) {\n int n=nums.size();\n int A=0, B=accumulate(nums.begin(), nums.end(), 0);\n vector<int> ans(n, 0);\n int i=0;\n #pragma unroll\n for(int x: nums){\n ans[i++]=(2*i-n)*x+B-A;\n A+=x;\n B-=x;\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n=len(nums)\n A=0\n B=sum(nums)\n ans=[0]*n\n\n for i, x in enumerate(nums):\n ans[i]=(2*i-n)*x+B-A\n A+=x\n B-=x\n return ans\n```\n```Java []\nclass Solution {\n public int[] getSumAbsoluteDifferences(int[] nums) {\n int n=nums.length;\n int A=0;\n int B=Arrays.stream(nums).sum();\n int [] ans=new int[n];\n int i=0;\n for(int x : nums){\n ans[i]=(2*i-n)*x+B-A;\n A+=x;\n B-=x;\n i++;\n }\n return ans; \n }\n}\n```\n```C []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\n#pragma GCC optimize("O3")\nint* getSumAbsoluteDifferences(int* nums, int n, int* returnSize){\n *returnSize=n;\n int A=0;\n int B=0;\n #pragma unroll\n for(register i=0; i<n; i++)\n B+=nums[i];\n int *ans=(int*)malloc(sizeof(int)*n);\n #pragma unroll\n for(register i=0; i<n; i++){\n ans[i]=(2*i-n)*nums[i]+B-A;\n A+=nums[i];\n B-=nums[i];\n }\n return ans;\n}\n```\n | 17 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
Simple solution with Prefix Sum in Python3 | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Intuition\nHere we have:\n- `nums` as list of integers\n- our goal is to find sum of absolute differences in sorted array\n\nWe\'re going to use **Prefix Sum** to calculate `left` and `right` parts (the first is for **positive** diff, and the last if for **negative**).\n\n# Approach\n1. declare and fill `prefix`\n2. iterate over `nums`\n3. calculate `left` and `right` sum parts\n4. append sum to the `ans` and return it\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n prefix = [nums[0]]\n n = len(nums)\n\n for i in range(1, n): prefix.append(prefix[i - 1] + nums[i])\n\n ans = []\n \n for i in range(len(nums)):\n left = nums[i] * (i + 1) - prefix[i]\n right = prefix[-1] - prefix[i] - nums[i] * (n - i - 1)\n ans.append(left + right)\n\n return ans \n``` | 1 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Simple solution with Prefix Sum in Python3 | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Intuition\nHere we have:\n- `nums` as list of integers\n- our goal is to find sum of absolute differences in sorted array\n\nWe\'re going to use **Prefix Sum** to calculate `left` and `right` parts (the first is for **positive** diff, and the last if for **negative**).\n\n# Approach\n1. declare and fill `prefix`\n2. iterate over `nums`\n3. calculate `left` and `right` sum parts\n4. append sum to the `ans` and return it\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n prefix = [nums[0]]\n n = len(nums)\n\n for i in range(1, n): prefix.append(prefix[i - 1] + nums[i])\n\n ans = []\n \n for i in range(len(nums)):\n left = nums[i] * (i + 1) - prefix[i]\n right = prefix[-1] - prefix[i] - nums[i] * (n - i - 1)\n ans.append(left + right)\n\n return ans \n``` | 1 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
Math explained with inductive logic and code with descriptive variable names π 3οΈβ£.π and π | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Intuition\nThe way the problem is explained it is automatically $$O(n^2)$$ this should send off signal flairs that there will be a trick. If we re-examine the conditions provided, nums is a strictly increasing array of positive numbers. Is there some [sum?] way to use this information to reduce the time complexity?\n\n\nLuckily the initial example given is a good starting point to think about this. Here is the example again:\n```\nExample 1:\n\nInput: nums = [2,3,5]\nOutput: [4,3,5]\nExplanation: Assuming the arrays are 0-indexed, then\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\n\nLets pick on `result[1]`.\nresult[1]\n= |3-2| + |3-3| + |3-5|\n= 1 + 0 + 2 \n= 3\n<br/>\nSo what happens here?\n1. We subtract an element less than nums[1]\n2. We subtract an element equal to nums[1]\n3. We subtract an element greater than nums[1]\n** Note this is the only case where absolute value does anything. Here we acutally have to subtract nums[1] from the element to get the right value\n\nSince the array is strictly increasing we can say that elements to the left of i will always be less than nums[i], nums[i] == nums[i], and that all elements to the right of i will always be greater than nums[i].\n\n<br/>\nBy using a prefix sum array and a suffix sum array to keep track of the sum of elements of nums to the left and right of i respectively, we can generalize this to 3 cases:\n\n1. There are i elements to the left of i and they will always be less than nums[i]. This tells us that the absolute sum to the left of i is always nums[i] times the number of elements to the left of i minus the sum of elements left of i.\n*i.e.*\nleft_sum \n= (nums[i] - nums[i - 1]) + (nums[i] - nums[i - 2]) + ... + (nums[i] - nums[0])\n= (nums[i] + nums[i] + ... + nums[i]) - (nums[i - 1] + nums[i - 2] + ... + nums[0])\nleft_sum = nums[i] * i - prefix_sum[i]\n\n2. There is 1 element at i equal to nums[i]. This absolute sum is always 0\n\n3. There are n - i - 1 elements to the right of i and they will always be greater than nums[i]. The absolute sum to the right of i is always the sum of elements to right of i minus nums[i] times the number of elements to the right of i.\n*i.e.*\nright_sum \n= (nums[i + 1] - nums[i] ) + (nums[i + 2] - nums[i] ) + ... + (nums[n] - nums[i] )\n= (nums[i + 1] + nums[i - 2] + ... + nums[n]) - (nums[i] + nums[i] + ... + nums[i])\nright_sum = suffix_sum[i] - nums[i] * (n - i - 1)\n\nFinally we are left with combining the absolute sum from elements to the left of i, 0, and the absolute sum from elements to the right of i to get the absolute sum of i. We just repeat this process at each element of the array to construct our solution.\n\n# Approach\nInstead of constructing a new O(n) dictionary with prefix and suffix sums of nums (or even worse two lists), we can just use two pointers to keep track of the prefix and suffix sum at each time step.\n\nWe will have to be strategic with when we increment the pointers so that we aren\'t double counting the current index in the left and right sums.\n\nFrom there, the given intuition and the code with it\'s inline comments should be self explanatory. \n\n# Complexity\n- Time complexity: $$O(n)$$\nRequires two passes of nums: \nonce for the sum.\nonce for the construction of the absolute differences array\n\n- Space complexity: $$O(n)$$\nWe construct a new list of size n to hold absolute differences.\n\n# Code\n\n```python3 []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n # instead of building prefix and suffix sums, quick compute using pointers\n sum_to_left, sum_to_right = 0, sum(nums)\n\n # O(n) time and space complexity\n abs_diffs = []\n for index, num in enumerate(nums):\n\n # calculate abs diff sums for nums less than num\n left_abs_sum = (num * index) - sum_to_left\n sum_to_left += num\n\n # calculate abs diff sums for nums greater than num\n sum_to_right -= num\n right_elements = n - index - 1\n right_abs_sum = sum_to_right - (num * right_elements)\n\n abs_diffs.append(left_abs_sum + right_abs_sum)\n\n return abs_diffs\n\n```\n```ruby []\n# @param {Integer[]} nums\n# @return {Integer[]}\ndef get_sum_absolute_differences(nums)\n n = nums.length\n sum_to_left, sum_to_right = 0, nums.reduce(0, :+)\n\n abs_diffs = []\n nums.each_with_index do |num, index|\n left_abs_sum = (num * index) - sum_to_left\n\n sum_to_left += num\n sum_to_right -= num\n\n right_elements = n - index - 1\n right_abs_sum = sum_to_right - (num * right_elements)\n\n abs_diffs.append(left_abs_sum + right_abs_sum)\n end\n\n abs_diffs\nend\n\n```\n$$\\blacksquare$$ | 1 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Math explained with inductive logic and code with descriptive variable names π 3οΈβ£.π and π | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Intuition\nThe way the problem is explained it is automatically $$O(n^2)$$ this should send off signal flairs that there will be a trick. If we re-examine the conditions provided, nums is a strictly increasing array of positive numbers. Is there some [sum?] way to use this information to reduce the time complexity?\n\n\nLuckily the initial example given is a good starting point to think about this. Here is the example again:\n```\nExample 1:\n\nInput: nums = [2,3,5]\nOutput: [4,3,5]\nExplanation: Assuming the arrays are 0-indexed, then\nresult[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,\nresult[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,\nresult[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.\n```\n\nLets pick on `result[1]`.\nresult[1]\n= |3-2| + |3-3| + |3-5|\n= 1 + 0 + 2 \n= 3\n<br/>\nSo what happens here?\n1. We subtract an element less than nums[1]\n2. We subtract an element equal to nums[1]\n3. We subtract an element greater than nums[1]\n** Note this is the only case where absolute value does anything. Here we acutally have to subtract nums[1] from the element to get the right value\n\nSince the array is strictly increasing we can say that elements to the left of i will always be less than nums[i], nums[i] == nums[i], and that all elements to the right of i will always be greater than nums[i].\n\n<br/>\nBy using a prefix sum array and a suffix sum array to keep track of the sum of elements of nums to the left and right of i respectively, we can generalize this to 3 cases:\n\n1. There are i elements to the left of i and they will always be less than nums[i]. This tells us that the absolute sum to the left of i is always nums[i] times the number of elements to the left of i minus the sum of elements left of i.\n*i.e.*\nleft_sum \n= (nums[i] - nums[i - 1]) + (nums[i] - nums[i - 2]) + ... + (nums[i] - nums[0])\n= (nums[i] + nums[i] + ... + nums[i]) - (nums[i - 1] + nums[i - 2] + ... + nums[0])\nleft_sum = nums[i] * i - prefix_sum[i]\n\n2. There is 1 element at i equal to nums[i]. This absolute sum is always 0\n\n3. There are n - i - 1 elements to the right of i and they will always be greater than nums[i]. The absolute sum to the right of i is always the sum of elements to right of i minus nums[i] times the number of elements to the right of i.\n*i.e.*\nright_sum \n= (nums[i + 1] - nums[i] ) + (nums[i + 2] - nums[i] ) + ... + (nums[n] - nums[i] )\n= (nums[i + 1] + nums[i - 2] + ... + nums[n]) - (nums[i] + nums[i] + ... + nums[i])\nright_sum = suffix_sum[i] - nums[i] * (n - i - 1)\n\nFinally we are left with combining the absolute sum from elements to the left of i, 0, and the absolute sum from elements to the right of i to get the absolute sum of i. We just repeat this process at each element of the array to construct our solution.\n\n# Approach\nInstead of constructing a new O(n) dictionary with prefix and suffix sums of nums (or even worse two lists), we can just use two pointers to keep track of the prefix and suffix sum at each time step.\n\nWe will have to be strategic with when we increment the pointers so that we aren\'t double counting the current index in the left and right sums.\n\nFrom there, the given intuition and the code with it\'s inline comments should be self explanatory. \n\n# Complexity\n- Time complexity: $$O(n)$$\nRequires two passes of nums: \nonce for the sum.\nonce for the construction of the absolute differences array\n\n- Space complexity: $$O(n)$$\nWe construct a new list of size n to hold absolute differences.\n\n# Code\n\n```python3 []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n n = len(nums)\n # instead of building prefix and suffix sums, quick compute using pointers\n sum_to_left, sum_to_right = 0, sum(nums)\n\n # O(n) time and space complexity\n abs_diffs = []\n for index, num in enumerate(nums):\n\n # calculate abs diff sums for nums less than num\n left_abs_sum = (num * index) - sum_to_left\n sum_to_left += num\n\n # calculate abs diff sums for nums greater than num\n sum_to_right -= num\n right_elements = n - index - 1\n right_abs_sum = sum_to_right - (num * right_elements)\n\n abs_diffs.append(left_abs_sum + right_abs_sum)\n\n return abs_diffs\n\n```\n```ruby []\n# @param {Integer[]} nums\n# @return {Integer[]}\ndef get_sum_absolute_differences(nums)\n n = nums.length\n sum_to_left, sum_to_right = 0, nums.reduce(0, :+)\n\n abs_diffs = []\n nums.each_with_index do |num, index|\n left_abs_sum = (num * index) - sum_to_left\n\n sum_to_left += num\n sum_to_right -= num\n\n right_elements = n - index - 1\n right_abs_sum = sum_to_right - (num * right_elements)\n\n abs_diffs.append(left_abs_sum + right_abs_sum)\n end\n\n abs_diffs\nend\n\n```\n$$\\blacksquare$$ | 1 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
Prefix Sum Approach | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Code\n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n s,n=0,len(nums)\n ps,ans=[0]*n,[0]*n\n for i in range(n):\n s+=nums[i]\n ps[i]=s\n for i in range(n):\n ans[i] = s - 2*ps[i] - nums[i]*(n-1-i) + nums[i]*(i+1)\n return ans\n``` | 1 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Prefix Sum Approach | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Code\n```\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n s,n=0,len(nums)\n ps,ans=[0]*n,[0]*n\n for i in range(n):\n s+=nums[i]\n ps[i]=s\n for i in range(n):\n ans[i] = s - 2*ps[i] - nums[i]*(n-1-i) + nums[i]*(i+1)\n return ans\n``` | 1 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
Rust/Python/Go linear time/constant space with explanation | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Intuition\nLets look what be the result for the position `i`. We need to look at values before and after this one:\n\n1. Every value at position after `i` is $\\ge$ than `nums[i]` the result will be `sum(nums[i + 1:])` minus `nums[i]` multiplied by the number of items (which will be `len(nums) - i`).\n2. Every value at position before `i` is $\\le$ than `nums[i]` the result will be `nums[i]` multiplied by the number of items (which will be `i`) minus `sum(:nums[i])`\n\nNow you can just precalculate prefix/suffix sum and do this will give you a linear time solution (but will need to store two arrays for those prefix/suffix sum). But you can do better with constant time. \n\nIn one pass you calculate the total sum `s`. Now at every element you calculate current sum `curr_s` and then you calculate the value 1 as `s - curr_s - (len(nums) - i) * nums[i]` and the value 2 as `nums[i] * i - curr_s`. In total it will be `s - 2 * curr_s + nums[i] * (2 * i - len(nums))`\n\n# Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(1)$ not counting input/output\n\n# Code\n```Rust []\nimpl Solution {\n pub fn get_sum_absolute_differences(nums: Vec<i32>) -> Vec<i32> {\n let s: i32 = nums.iter().sum();\n let mut res = vec![0; nums.len()];\n\n let mut curr_s = 0;\n for i in 0 .. nums.len() {\n res[i] = s - 2 * curr_s + nums[i] * ((2 * i - nums.len()) as i32);\n curr_s += nums[i];\n }\n\n return res;\n }\n}\n```\n```Python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n prev, s1, s2, res = 0, sum(nums), 0, []\n for i, v in enumerate(nums):\n delta, prev = v - prev, v\n s1 -= delta * (len(nums) - i)\n s2 += delta * i\n \n res.append(s1 + s2)\n \n return res\n```\n```Go []\nfunc getSumAbsoluteDifferences(nums []int) []int {\n l := len(nums)\n prev, s, res := 0, 0, make([]int, l)\n for _, v := range nums {\n s += v\n }\n \n for i, v := range nums {\n delta := v - prev\n prev = v\n \n s += delta * (2 * i - l)\n res[i] = s\n }\n \n return res\n}\n``` | 1 | You are given an integer array `nums` sorted in **non-decreasing** order.
Build and return _an integer array_ `result` _with the same length as_ `nums` _such that_ `result[i]` _is equal to the **summation of absolute differences** between_ `nums[i]` _and all the other elements in the array._
In other words, `result[i]` is equal to `sum(|nums[i]-nums[j]|)` where `0 <= j < nums.length` and `j != i` (**0-indexed**).
**Example 1:**
**Input:** nums = \[2,3,5\]
**Output:** \[4,3,5\]
**Explanation:** Assuming the arrays are 0-indexed, then
result\[0\] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4,
result\[1\] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3,
result\[2\] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5.
**Example 2:**
**Input:** nums = \[1,4,6,8,10\]
**Output:** \[24,15,13,15,21\]
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= nums[i + 1] <= 104` | We need to try all possible divisions for the current row to get the max score. As calculating all possible divisions will lead us to calculate some sub-problems more than once, we need to think of dynamic programming. |
Rust/Python/Go linear time/constant space with explanation | sum-of-absolute-differences-in-a-sorted-array | 0 | 1 | # Intuition\nLets look what be the result for the position `i`. We need to look at values before and after this one:\n\n1. Every value at position after `i` is $\\ge$ than `nums[i]` the result will be `sum(nums[i + 1:])` minus `nums[i]` multiplied by the number of items (which will be `len(nums) - i`).\n2. Every value at position before `i` is $\\le$ than `nums[i]` the result will be `nums[i]` multiplied by the number of items (which will be `i`) minus `sum(:nums[i])`\n\nNow you can just precalculate prefix/suffix sum and do this will give you a linear time solution (but will need to store two arrays for those prefix/suffix sum). But you can do better with constant time. \n\nIn one pass you calculate the total sum `s`. Now at every element you calculate current sum `curr_s` and then you calculate the value 1 as `s - curr_s - (len(nums) - i) * nums[i]` and the value 2 as `nums[i] * i - curr_s`. In total it will be `s - 2 * curr_s + nums[i] * (2 * i - len(nums))`\n\n# Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(1)$ not counting input/output\n\n# Code\n```Rust []\nimpl Solution {\n pub fn get_sum_absolute_differences(nums: Vec<i32>) -> Vec<i32> {\n let s: i32 = nums.iter().sum();\n let mut res = vec![0; nums.len()];\n\n let mut curr_s = 0;\n for i in 0 .. nums.len() {\n res[i] = s - 2 * curr_s + nums[i] * ((2 * i - nums.len()) as i32);\n curr_s += nums[i];\n }\n\n return res;\n }\n}\n```\n```Python []\nclass Solution:\n def getSumAbsoluteDifferences(self, nums: List[int]) -> List[int]:\n prev, s1, s2, res = 0, sum(nums), 0, []\n for i, v in enumerate(nums):\n delta, prev = v - prev, v\n s1 -= delta * (len(nums) - i)\n s2 += delta * i\n \n res.append(s1 + s2)\n \n return res\n```\n```Go []\nfunc getSumAbsoluteDifferences(nums []int) []int {\n l := len(nums)\n prev, s, res := 0, 0, make([]int, l)\n for _, v := range nums {\n s += v\n }\n \n for i, v := range nums {\n delta := v - prev\n prev = v\n \n s += delta * (2 * i - l)\n res[i] = s\n }\n \n return res\n}\n``` | 1 | You are given an array `nums`βββ and an integer `k`βββββ. The XOR of a segment `[left, right]` where `left <= right` is the `XOR` of all the elements with indices between `left` and `right`, inclusive: `nums[left] XOR nums[left+1] XOR ... XOR nums[right]`.
Return _the minimum number of elements to change in the array_ such that the `XOR` of all segments of size `k`ββββββ is equal to zero.
**Example 1:**
**Input:** nums = \[1,2,0,3,0\], k = 1
**Output:** 3
**Explanation:** Modify the array from \[**1**,**2**,0,**3**,0\] to from \[**0**,**0**,0,**0**,0\].
**Example 2:**
**Input:** nums = \[3,4,5,2,1,7,3,4,7\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[3,4,**5**,**2**,**1**,7,3,4,7\] to \[3,4,**7**,**3**,**4**,7,3,4,7\].
**Example 3:**
**Input:** nums = \[1,2,4,1,2,5,1,2,6\], k = 3
**Output:** 3
**Explanation:** Modify the array from \[1,2,**4,**1,2,**5**,1,2,**6**\] to \[1,2,**3**,1,2,**3**,1,2,**3**\].
**Constraints:**
* `1 <= k <= nums.length <= 2000`
* `ββββββ0 <= nums[i] < 210` | Absolute difference is the same as max(a, b) - min(a, b). How can you use this fact with the fact that the array is sorted? For nums[i], the answer is (nums[i] - nums[0]) + (nums[i] - nums[1]) + ... + (nums[i] - nums[i-1]) + (nums[i+1] - nums[i]) + (nums[i+2] - nums[i]) + ... + (nums[n-1] - nums[i]). It can be simplified to (nums[i] * i - (nums[0] + nums[1] + ... + nums[i-1])) + ((nums[i+1] + nums[i+2] + ... + nums[n-1]) - nums[i] * (n-i-1)). One can build prefix and suffix sums to compute this quickly. |
Beats 99.38 % || PYTHON 3 || Explained | stone-game-vi | 0 | 1 | # Intuition\nIn this problem instead of picking/not Picking largest making sum we need to pick those stones by alice which can hurt bob more.\nSo we combine them and sort them in reverse order\n`why we can do sorting? Because in question its stated we can pick any stone (and not only from left most or right most)`\nNow alice will pick first highest combined effecting the bobPoints most (which is the total Sum of bob values) and then skip next point (which is to be picked by bob).\nAccording to our alicePoints and bobPoints return the ans.\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, a: List[int], b: List[int]) -> int:\n # hurt other enemy rather than self collecting to max\n combines = [(a[i] + b[i], a[i], b[i]) for i in range(len(a))]\n combines.sort(reverse=True) # why we can sort? -> because we can pick any stone we want\n bobPoints = sum(b)\n alicePoints = 0\n for i in range(0, len(a), 2):\n alicePoints += combines[i][1]\n bobPoints -= combines[i][2]\n if alicePoints > bobPoints:\n return 1\n elif alicePoints < bobPoints:\n return -1\n return 0\n \n\n``` | 3 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Beats 99.38 % || PYTHON 3 || Explained | stone-game-vi | 0 | 1 | # Intuition\nIn this problem instead of picking/not Picking largest making sum we need to pick those stones by alice which can hurt bob more.\nSo we combine them and sort them in reverse order\n`why we can do sorting? Because in question its stated we can pick any stone (and not only from left most or right most)`\nNow alice will pick first highest combined effecting the bobPoints most (which is the total Sum of bob values) and then skip next point (which is to be picked by bob).\nAccording to our alicePoints and bobPoints return the ans.\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, a: List[int], b: List[int]) -> int:\n # hurt other enemy rather than self collecting to max\n combines = [(a[i] + b[i], a[i], b[i]) for i in range(len(a))]\n combines.sort(reverse=True) # why we can sort? -> because we can pick any stone we want\n bobPoints = sum(b)\n alicePoints = 0\n for i in range(0, len(a), 2):\n alicePoints += combines[i][1]\n bobPoints -= combines[i][2]\n if alicePoints > bobPoints:\n return 1\n elif alicePoints < bobPoints:\n return -1\n return 0\n \n\n``` | 3 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
Python Easy understanding | stone-game-vi | 0 | 1 | Simple logic, greedy approach, sort based on maximum sum of pairs.\n* The best approach is not only to pick the stone with maximum value, but the one where you could hurt your opponent\'s chances by picking an optimal value.\n* So by picking a stone, you get x points and you affect bob\'s chances by -y points, so the impact inflicted by picking a given stone is a-(-b) = a+b. \n* So sorting based on sum, you get the maximum impact you could inflict.\n\nFor example, \nalice=[2,3] and bob=[5,3]\nNormally it would be nice for alice to pick 3 to increase her chances, but when she picks 2, she could hurt bob\'s chances by not allowing him to pick 5, so instead of selecting the maximum one, find the one where you could hurt your opponents chances(Greedy).\n```\nclass Solution:\n def stoneGameVI(self, alice: List[int], bob: List[int]) -> int:\n t=list(zip(alice,bob))\n t=sorted(t,key=lambda x: sum(x),reverse=True)\n al=sum([i[0] for i in t[::2]])\n bb=sum([i[1] for i in t[1::2]])\n if al>bb:\n return 1\n elif al<bb:\n return -1\n return 0\n``` | 15 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Python Easy understanding | stone-game-vi | 0 | 1 | Simple logic, greedy approach, sort based on maximum sum of pairs.\n* The best approach is not only to pick the stone with maximum value, but the one where you could hurt your opponent\'s chances by picking an optimal value.\n* So by picking a stone, you get x points and you affect bob\'s chances by -y points, so the impact inflicted by picking a given stone is a-(-b) = a+b. \n* So sorting based on sum, you get the maximum impact you could inflict.\n\nFor example, \nalice=[2,3] and bob=[5,3]\nNormally it would be nice for alice to pick 3 to increase her chances, but when she picks 2, she could hurt bob\'s chances by not allowing him to pick 5, so instead of selecting the maximum one, find the one where you could hurt your opponents chances(Greedy).\n```\nclass Solution:\n def stoneGameVI(self, alice: List[int], bob: List[int]) -> int:\n t=list(zip(alice,bob))\n t=sorted(t,key=lambda x: sum(x),reverse=True)\n al=sum([i[0] for i in t[::2]])\n bb=sum([i[1] for i in t[1::2]])\n if al>bb:\n return 1\n elif al<bb:\n return -1\n return 0\n``` | 15 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
Easy Python | 99% Speed | stone-game-vi | 0 | 1 | **Easy Python | 99% Speed**\n\nEasy Python algorithm, which can be derived by rephrasing the problem statement:\n\nInstead of taking turns starting from a situation where both players have zero score, we first consider that Bob has a maximum score of ```sum(B)```. As a result, Alice starts with an inmense loss ```-sum(B)```, and every stone ```A[i]``` she takes gives her a net gain ```A[i]+B[i]```, because she gains the value of the stone (```A[i]```) plus what she takes away from Bob\'s score ```B[i]```.\n\nThe algorithm then becomes very easy to program, because we can build an array with the gains for Alice ```G=A+B```, where we can sort the entries to find the upcoming optimal moves. Also, Bob in his turn will try to delete the biggest entries in this array, since they are the biggest gains for Alice.\n\nThe implementation of the program is thus very simple. It\'s incredible how easy a problem can become once you rephrase the question.\n\nI hope the explanation was helpful.\nCheers,\n\n\n```\nclass Solution:\n def stoneGameVI(self, A, B):\n G = [a+b for a,b in zip(A,B)]\n G.sort()\n L = len(A)\n d = -sum(B) + sum( G[i] for i in range(L-1,-1,-2) )\n return 1 if d>0 else ( -1 if d<0 else 0 )\n``` | 5 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Easy Python | 99% Speed | stone-game-vi | 0 | 1 | **Easy Python | 99% Speed**\n\nEasy Python algorithm, which can be derived by rephrasing the problem statement:\n\nInstead of taking turns starting from a situation where both players have zero score, we first consider that Bob has a maximum score of ```sum(B)```. As a result, Alice starts with an inmense loss ```-sum(B)```, and every stone ```A[i]``` she takes gives her a net gain ```A[i]+B[i]```, because she gains the value of the stone (```A[i]```) plus what she takes away from Bob\'s score ```B[i]```.\n\nThe algorithm then becomes very easy to program, because we can build an array with the gains for Alice ```G=A+B```, where we can sort the entries to find the upcoming optimal moves. Also, Bob in his turn will try to delete the biggest entries in this array, since they are the biggest gains for Alice.\n\nThe implementation of the program is thus very simple. It\'s incredible how easy a problem can become once you rephrase the question.\n\nI hope the explanation was helpful.\nCheers,\n\n\n```\nclass Solution:\n def stoneGameVI(self, A, B):\n G = [a+b for a,b in zip(A,B)]\n G.sort()\n L = len(A)\n d = -sum(B) + sum( G[i] for i in range(L-1,-1,-2) )\n return 1 if d>0 else ( -1 if d<0 else 0 )\n``` | 5 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
Greedy + Heep | stone-game-vi | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n values = [(-a - b, a, b) for a, b in zip(aliceValues, bobValues)]\n heapq.heapify(values)\n aliceScore = bobScore = 0\n while True:\n if values:\n aliceScore += heapq.heappop(values)[1]\n else:\n break\n\n if values:\n bobScore += heapq.heappop(values)[2]\n else:\n break\n \n if aliceScore > bobScore:\n return 1\n elif aliceScore < bobScore:\n return -1\n return 0\n``` | 1 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Greedy + Heep | stone-game-vi | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n values = [(-a - b, a, b) for a, b in zip(aliceValues, bobValues)]\n heapq.heapify(values)\n aliceScore = bobScore = 0\n while True:\n if values:\n aliceScore += heapq.heappop(values)[1]\n else:\n break\n\n if values:\n bobScore += heapq.heappop(values)[2]\n else:\n break\n \n if aliceScore > bobScore:\n return 1\n elif aliceScore < bobScore:\n return -1\n return 0\n``` | 1 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
python3 greedy | stone-game-vi | 0 | 1 | # Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n \n # intuition: stones are valued by individual points + the number of points the other person loses out on, so we can simply add the two scores in a new array to assign values\n values = [] # array of [value, index]\n for i in range(len(aliceValues)):\n values.append([aliceValues[i] + bobValues[i], i])\n\n # sort by value\n values = sorted(values, key=lambda x : x[0])\n\n # keep track of respective points, alice always goes first\n alice_points = 0\n bob_points = 0\n alice_turn = True\n\n # calculate points based on optimal play\n for i in range(len(values) - 1, -1, -1):\n stone_index = values[i][1]\n \n if alice_turn:\n alice_points += aliceValues[stone_index]\n \n else:\n bob_points += bobValues[stone_index]\n \n alice_turn = (not alice_turn)\n \n # return int according to spec\n if alice_points > bob_points:\n return 1\n elif bob_points > alice_points:\n return -1\n else:\n return 0\n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
python3 greedy | stone-game-vi | 0 | 1 | # Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n \n # intuition: stones are valued by individual points + the number of points the other person loses out on, so we can simply add the two scores in a new array to assign values\n values = [] # array of [value, index]\n for i in range(len(aliceValues)):\n values.append([aliceValues[i] + bobValues[i], i])\n\n # sort by value\n values = sorted(values, key=lambda x : x[0])\n\n # keep track of respective points, alice always goes first\n alice_points = 0\n bob_points = 0\n alice_turn = True\n\n # calculate points based on optimal play\n for i in range(len(values) - 1, -1, -1):\n stone_index = values[i][1]\n \n if alice_turn:\n alice_points += aliceValues[stone_index]\n \n else:\n bob_points += bobValues[stone_index]\n \n alice_turn = (not alice_turn)\n \n # return int according to spec\n if alice_points > bob_points:\n return 1\n elif bob_points > alice_points:\n return -1\n else:\n return 0\n``` | 0 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
Stone Game VI: Python Greedy | stone-game-vi | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLets say it is alice\'s turn and there are only two options available. Option 1 is to select the stone at index $$i$$ and option 2 is to select the stone at index $$j$$.\nAlice wants to win and knows the stone values for bob as well.\nAlice will select the stone at index $$i$$ if and only if\n$$aliceValue[i] - bobValue[j] > aliceValue[j] - bobValue[i]$$,\nthat is, selecting the stone at index $$i$$ (and leaving bob with only $$j$$) is better for Alice.\nRearranging the above inequality:\n$$aliceValue[i] + bobValue[i] > aliceValue[j] + bobValue[j]$$\nNote: The same equation can be arrived at by assuming that it was Bob\'s turn and the same 2 options were given to Bob.\nThus, we can conclude that irrespective of who\'s turn it is, it is optimal to select the stone from the available stones, at index with the greatest sum of aliceValue and bobValue.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBased on the above argument, we can solve the problem by following steps,\n1. Sort the arrays $$aliceValue$$ and $$bobValue$$ in the decreasing order of the sum of their elements at the original indices. Now in every turn $i$(0 based), the optimal choice would be to select the element at the $i^{th}$(0 based) index, as it would be the index where the sum of $aliceValue$ and $bobValue$ would be the greatest.\n2. Now, in the new arrangement, every even indexed stone will be the optimal choice for Alice, and odd indexed stone will be the optimal choice for Bob. \n# Complexity\n- Time complexity: The Bottleneck operation is sorting. Thus the time complexity is $$O(n.\\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n values = zip(aliceValues, bobValues)\n values = sorted(values, key = lambda x : -(x[0] + x[1]))\n alice_sum, bob_sum = sum([values[i][0] for i in range(0, len(values), 2)]), sum([values[i][1] for i in range(1, len(values), 2)])\n return 0 if alice_sum==bob_sum else int((alice_sum - bob_sum)/abs(alice_sum - bob_sum))\n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Stone Game VI: Python Greedy | stone-game-vi | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLets say it is alice\'s turn and there are only two options available. Option 1 is to select the stone at index $$i$$ and option 2 is to select the stone at index $$j$$.\nAlice wants to win and knows the stone values for bob as well.\nAlice will select the stone at index $$i$$ if and only if\n$$aliceValue[i] - bobValue[j] > aliceValue[j] - bobValue[i]$$,\nthat is, selecting the stone at index $$i$$ (and leaving bob with only $$j$$) is better for Alice.\nRearranging the above inequality:\n$$aliceValue[i] + bobValue[i] > aliceValue[j] + bobValue[j]$$\nNote: The same equation can be arrived at by assuming that it was Bob\'s turn and the same 2 options were given to Bob.\nThus, we can conclude that irrespective of who\'s turn it is, it is optimal to select the stone from the available stones, at index with the greatest sum of aliceValue and bobValue.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBased on the above argument, we can solve the problem by following steps,\n1. Sort the arrays $$aliceValue$$ and $$bobValue$$ in the decreasing order of the sum of their elements at the original indices. Now in every turn $i$(0 based), the optimal choice would be to select the element at the $i^{th}$(0 based) index, as it would be the index where the sum of $aliceValue$ and $bobValue$ would be the greatest.\n2. Now, in the new arrangement, every even indexed stone will be the optimal choice for Alice, and odd indexed stone will be the optimal choice for Bob. \n# Complexity\n- Time complexity: The Bottleneck operation is sorting. Thus the time complexity is $$O(n.\\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n values = zip(aliceValues, bobValues)\n values = sorted(values, key = lambda x : -(x[0] + x[1]))\n alice_sum, bob_sum = sum([values[i][0] for i in range(0, len(values), 2)]), sum([values[i][1] for i in range(1, len(values), 2)])\n return 0 if alice_sum==bob_sum else int((alice_sum - bob_sum)/abs(alice_sum - bob_sum))\n``` | 0 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
Python3: FT 100%: TC O(N+R), SC O(R): Counting Sort and Iteration | stone-game-vi | 0 | 1 | # Intuition\n\nThe usual game theory approach, of top-down DFS, will NOT work here: there are 1e5 plays, so you\'ll get TLE for certain.\n\nSo I thought about what it really means for Alice to win: she needs to have a sum of plays that is larger than Bob\'s sum: `aliceSum > bobSum`. Still hard, but now we\'ve reduced this to a sum which is potentially O(N).\n\nTo maximize this difference, Alice will try to maximize her score and *minimize* Bob\'s score, and vice-versa. This was the breakthrough.\n\nSuppose the sum of Bob\'s stones is `B`. When Alice picks index `i`, she will score `a[i]`, *and will deny `b[i]` to Bob*.\n\nThis is when I realized that `aliceSum - bobSum` is the same as\n```\n(sum of Alice\'s values for Alice\'s picks)\n - (B - (sum of Bob\'s values for Alice\'s picks))\n\n== (sum of Alice values) + (sum of Bob values) - B\n```\nwhere we\'ve rewritten Bob\'s score as (sum of Bob stones) - (Bob values for Alice\'s picks).\n\nPretty surprising, but neat. Alice picks the stones with the highest value of `a[i] + b[i]`.\n\nIf we repeat the logic for Bob, *Bob picks stones according to the same criterion*. The only difference is `-A` instead of `-B`, a constant offset.\n\n# Approach\n\nThe core of the algorithm is above.\n\nBut there are a couple of optimizations we can make.\n\nFirst, instead of literally sorting by `a[i] + b[i]`, we do a counting sort since the range of values is only [2, 200]. This lowers the sorting complexity to O(N) time and O(R) space where R is the range of values.\n\nSecond, instead of separately simulating all N plays, we know that there are `counts[200]` items with the max possible value. Alice plays first, so we can calculate how many copies of 200 that Alice gets, and how many Bob gets. We can also calculate whether Alice or Bob will be the first to get a copy of `counts[199]`. The math is a little annoying, but doable in a few minutes of careful thought. This way we avoid doing another O(N) loop, and instead reduce it to some math in an O(R) loop. N ~ 1e5 while R ~ 200 so this is a big time savings.\n\nThe combination of these is what results in the FT 100% achievement.\n* it was faster than about 98% just with counting sort\n* the conversion of a final O(N) loop to a final O(R) loop achieves the final speedup to FT 100%\n\n# Complexity\n- Time complexity: O(N+R) as written, O(N) sum of Bob values and a counting sort, then an O(R) final pass where R is the range of stone values.\n\n- Space complexity: O(R) for the counting sort buckets\n\n# Final Notes\n\nIn an interview, when you see a large number of elements but a small range of values, the answer almost always involves a counting sort of some kind.\n\nWhen it doesn\'t, it\'s a dynamic programming problem (e.g. knapsack problems)\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, a: List[int], b: List[int]) -> int:\n # alice, bob, alice, bob, etc.\n\n # remove one stone from the pile to score points\n # alice: attributes `aliceValues[i]` to stone i\n # bob: attributes `bobValues[i]` to stone i\n\n # there are 1e5 stones, so too many for the usual recursive solution\n # the values are in [1, 100] which may open up optimizations based on counting sorts\n\n # each player wants to score more than the other; so really the figure of merit at the end is having\n # a positive score differential over the opponent\n\n # if a pair has vales [5, 2] then Alice scores 5, and denies 2 to Bob\n # if a pair has values [1, 20] then Alice scores 1, and denies 20 to Bob\n\n # so [1, 100], [5, 6], [5, 6], ..: Alice should pick the first element. Fewest for her, but denies Bob a ton of points\n # what\'s best for Alice is worst for Bob and vice-versa\n\n # result is aliceSum - bobSum\n # aliceSum is sum of alicePicks\n # bobSum is B - bob values for alice\'s picks\n\n # so result is aliceSum - (B - bob values of alice\'s picks)\n # aliceValuesOfAlicePicks + bobValuesOfAlicePicks - B\n\n # so we can sort 0..i-1 by a[i] + b[i]\n # Bob picks according to the same approach as Alice actually, just with -A instead of -B\n\n # so we can do a counting sort by a[i]+b[i]\n\n N = len(a)\n B = sum(b)\n counts = [0]*203\n for i in range(N):\n counts[a[i] + b[i]] += 1\n\n while counts[-1] == 0: counts.pop()\n\n alice = -B\n player = 0\n for v in range(len(counts)-1, -1, -1):\n c = counts[v]\n # c//2 pairs of turns, Alice and Bob both get one copy of v for each pair\n # if c%2, then the next player up gets another copy\n # i.e. Alice gets another copy if player==0\n\n alice += v*(c//2)\n if c % 2 and player == 0:\n alice += v\n\n # update first player for next bucket\n player = (player + c) % 2\n\n if alice > 0:\n return 1\n elif alice < 0:\n return -1\n else:\n return 0\n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Python3: FT 100%: TC O(N+R), SC O(R): Counting Sort and Iteration | stone-game-vi | 0 | 1 | # Intuition\n\nThe usual game theory approach, of top-down DFS, will NOT work here: there are 1e5 plays, so you\'ll get TLE for certain.\n\nSo I thought about what it really means for Alice to win: she needs to have a sum of plays that is larger than Bob\'s sum: `aliceSum > bobSum`. Still hard, but now we\'ve reduced this to a sum which is potentially O(N).\n\nTo maximize this difference, Alice will try to maximize her score and *minimize* Bob\'s score, and vice-versa. This was the breakthrough.\n\nSuppose the sum of Bob\'s stones is `B`. When Alice picks index `i`, she will score `a[i]`, *and will deny `b[i]` to Bob*.\n\nThis is when I realized that `aliceSum - bobSum` is the same as\n```\n(sum of Alice\'s values for Alice\'s picks)\n - (B - (sum of Bob\'s values for Alice\'s picks))\n\n== (sum of Alice values) + (sum of Bob values) - B\n```\nwhere we\'ve rewritten Bob\'s score as (sum of Bob stones) - (Bob values for Alice\'s picks).\n\nPretty surprising, but neat. Alice picks the stones with the highest value of `a[i] + b[i]`.\n\nIf we repeat the logic for Bob, *Bob picks stones according to the same criterion*. The only difference is `-A` instead of `-B`, a constant offset.\n\n# Approach\n\nThe core of the algorithm is above.\n\nBut there are a couple of optimizations we can make.\n\nFirst, instead of literally sorting by `a[i] + b[i]`, we do a counting sort since the range of values is only [2, 200]. This lowers the sorting complexity to O(N) time and O(R) space where R is the range of values.\n\nSecond, instead of separately simulating all N plays, we know that there are `counts[200]` items with the max possible value. Alice plays first, so we can calculate how many copies of 200 that Alice gets, and how many Bob gets. We can also calculate whether Alice or Bob will be the first to get a copy of `counts[199]`. The math is a little annoying, but doable in a few minutes of careful thought. This way we avoid doing another O(N) loop, and instead reduce it to some math in an O(R) loop. N ~ 1e5 while R ~ 200 so this is a big time savings.\n\nThe combination of these is what results in the FT 100% achievement.\n* it was faster than about 98% just with counting sort\n* the conversion of a final O(N) loop to a final O(R) loop achieves the final speedup to FT 100%\n\n# Complexity\n- Time complexity: O(N+R) as written, O(N) sum of Bob values and a counting sort, then an O(R) final pass where R is the range of stone values.\n\n- Space complexity: O(R) for the counting sort buckets\n\n# Final Notes\n\nIn an interview, when you see a large number of elements but a small range of values, the answer almost always involves a counting sort of some kind.\n\nWhen it doesn\'t, it\'s a dynamic programming problem (e.g. knapsack problems)\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, a: List[int], b: List[int]) -> int:\n # alice, bob, alice, bob, etc.\n\n # remove one stone from the pile to score points\n # alice: attributes `aliceValues[i]` to stone i\n # bob: attributes `bobValues[i]` to stone i\n\n # there are 1e5 stones, so too many for the usual recursive solution\n # the values are in [1, 100] which may open up optimizations based on counting sorts\n\n # each player wants to score more than the other; so really the figure of merit at the end is having\n # a positive score differential over the opponent\n\n # if a pair has vales [5, 2] then Alice scores 5, and denies 2 to Bob\n # if a pair has values [1, 20] then Alice scores 1, and denies 20 to Bob\n\n # so [1, 100], [5, 6], [5, 6], ..: Alice should pick the first element. Fewest for her, but denies Bob a ton of points\n # what\'s best for Alice is worst for Bob and vice-versa\n\n # result is aliceSum - bobSum\n # aliceSum is sum of alicePicks\n # bobSum is B - bob values for alice\'s picks\n\n # so result is aliceSum - (B - bob values of alice\'s picks)\n # aliceValuesOfAlicePicks + bobValuesOfAlicePicks - B\n\n # so we can sort 0..i-1 by a[i] + b[i]\n # Bob picks according to the same approach as Alice actually, just with -A instead of -B\n\n # so we can do a counting sort by a[i]+b[i]\n\n N = len(a)\n B = sum(b)\n counts = [0]*203\n for i in range(N):\n counts[a[i] + b[i]] += 1\n\n while counts[-1] == 0: counts.pop()\n\n alice = -B\n player = 0\n for v in range(len(counts)-1, -1, -1):\n c = counts[v]\n # c//2 pairs of turns, Alice and Bob both get one copy of v for each pair\n # if c%2, then the next player up gets another copy\n # i.e. Alice gets another copy if player==0\n\n alice += v*(c//2)\n if c % 2 and player == 0:\n alice += v\n\n # update first player for next bucket\n player = (player + c) % 2\n\n if alice > 0:\n return 1\n elif alice < 0:\n return -1\n else:\n return 0\n``` | 0 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
Greedy Python Solution | stone-game-vi | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n #Alice wants the most, she get and the least bob gets\n\n Values = [(aliceValues[i] + bobValues[i], i) for i in range(len(aliceValues))]\n Values.sort(key = lambda x: x[0])\n AliceScore = 0\n BobScore = 0\n AliceTurn = True\n while Values:\n curr = Values.pop()\n if AliceTurn:\n AliceScore += aliceValues[curr[1]]\n AliceTurn = False\n else:\n BobScore += bobValues[curr[1]]\n AliceTurn = True\n \n if AliceScore == BobScore:\n return 0\n elif AliceScore > BobScore:\n return 1\n else:\n return -1\n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
Greedy Python Solution | stone-game-vi | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n #Alice wants the most, she get and the least bob gets\n\n Values = [(aliceValues[i] + bobValues[i], i) for i in range(len(aliceValues))]\n Values.sort(key = lambda x: x[0])\n AliceScore = 0\n BobScore = 0\n AliceTurn = True\n while Values:\n curr = Values.pop()\n if AliceTurn:\n AliceScore += aliceValues[curr[1]]\n AliceTurn = False\n else:\n BobScore += bobValues[curr[1]]\n AliceTurn = True\n \n if AliceScore == BobScore:\n return 0\n elif AliceScore > BobScore:\n return 1\n else:\n return -1\n``` | 0 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
5 line python solution (beat 88% runtime) | stone-game-vi | 0 | 1 | # Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n combinedArr = sorted(zip(aliceValues, bobValues), key = lambda x: -(x[0]+x[1]))\n alice = sum(aliceValues for aliceValues, bobValues in combinedArr[::2])\n bob = sum(bobValues for aliceValues, bobValues in combinedArr[1::2])\n if alice < bob: return -1\n return 0 if alice == bob else 1\n \n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
5 line python solution (beat 88% runtime) | stone-game-vi | 0 | 1 | # Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n combinedArr = sorted(zip(aliceValues, bobValues), key = lambda x: -(x[0]+x[1]))\n alice = sum(aliceValues for aliceValues, bobValues in combinedArr[::2])\n bob = sum(bobValues for aliceValues, bobValues in combinedArr[1::2])\n if alice < bob: return -1\n return 0 if alice == bob else 1\n \n``` | 0 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
An almost one line solution | stone-game-vi | 0 | 1 | # Intuition\n\nSuppose Alice selects a subset of stones $S$ and Bob the complement $S^c$. Then the difference of the value obtained by Alice and Bob is:\n$$\nv = \\sum_{i\\in S} a_i-\\sum_{j\\in S^c} b_j\n=\\sum_{i\\in S} (a_i+b_i) - B, \\quad \\text{where $B=\\sum_j b_j$ the total value of stones for Bob}.\n$$\nHere $a_i$ is the value of the $i$th stone for Alice and $b_i$ is the same for Bob.\n\nSo Alice goal is to select the most valuable stones, where the value measured by ($a_i+b_i$). Since Bob has the same goal, if they play rationally they will select the first available stone with the largest value. \n\nSo all we have to do is the sort the array with elements $(a_i+b_i)$ and sum every second term. Subtracting $B$ the total value of stones for Bob, gives the final standing.\n \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n\\log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n c = sorted((ai+bi for ai, bi in zip(aliceValues, bobValues)), reverse=True)\n val = sum(c[::2])-sum(bobValues)\n if val > 0:\n return 1\n if val < 0:\n return -1\n return 0\n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
There are `n` stones in a pile. On each player's turn, they can **remove** a stone from the pile and receive points based on the stone's value. Alice and Bob may **value the stones differently**.
You are given two integer arrays of length `n`, `aliceValues` and `bobValues`. Each `aliceValues[i]` and `bobValues[i]` represents how Alice and Bob, respectively, value the `ith` stone.
The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play **optimally**. Both players know the other's values.
Determine the result of the game, and:
* If Alice wins, return `1`.
* If Bob wins, return `-1`.
* If the game results in a draw, return `0`.
**Example 1:**
**Input:** aliceValues = \[1,3\], bobValues = \[2,1\]
**Output:** 1
**Explanation:**
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.
**Example 2:**
**Input:** aliceValues = \[1,2\], bobValues = \[3,1\]
**Output:** 0
**Explanation:**
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.
**Example 3:**
**Input:** aliceValues = \[2,4,3\], bobValues = \[1,6,7\]
**Output:** -1
**Explanation:**
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.
**Constraints:**
* `n == aliceValues.length == bobValues.length`
* `1 <= n <= 105`
* `1 <= aliceValues[i], bobValues[i] <= 100` | null |
An almost one line solution | stone-game-vi | 0 | 1 | # Intuition\n\nSuppose Alice selects a subset of stones $S$ and Bob the complement $S^c$. Then the difference of the value obtained by Alice and Bob is:\n$$\nv = \\sum_{i\\in S} a_i-\\sum_{j\\in S^c} b_j\n=\\sum_{i\\in S} (a_i+b_i) - B, \\quad \\text{where $B=\\sum_j b_j$ the total value of stones for Bob}.\n$$\nHere $a_i$ is the value of the $i$th stone for Alice and $b_i$ is the same for Bob.\n\nSo Alice goal is to select the most valuable stones, where the value measured by ($a_i+b_i$). Since Bob has the same goal, if they play rationally they will select the first available stone with the largest value. \n\nSo all we have to do is the sort the array with elements $(a_i+b_i)$ and sum every second term. Subtracting $B$ the total value of stones for Bob, gives the final standing.\n \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n\\log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVI(self, aliceValues: List[int], bobValues: List[int]) -> int:\n c = sorted((ai+bi for ai, bi in zip(aliceValues, bobValues)), reverse=True)\n val = sum(c[::2])-sum(bobValues)\n if val > 0:\n return 1\n if val < 0:\n return -1\n return 0\n``` | 0 | There is a garden of `n` flowers, and each flower has an integer beauty value. The flowers are arranged in a line. You are given an integer array `flowers` of size `n` and each `flowers[i]` represents the beauty of the `ith` flower.
A garden is **valid** if it meets these conditions:
* The garden has at least two flowers.
* The first and the last flower of the garden have the same beauty value.
As the appointed gardener, you have the ability to **remove** any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden **valid**. The beauty of the garden is the sum of the beauty of all the remaining flowers.
Return the maximum possible beauty of some **valid** garden after you have removed any (possibly none) flowers.
**Example 1:**
**Input:** flowers = \[1,2,3,1,2\]
**Output:** 8
**Explanation:** You can produce the valid garden \[2,3,1,2\] to have a total beauty of 2 + 3 + 1 + 2 = 8.
**Example 2:**
**Input:** flowers = \[100,1,1,-3,1\]
**Output:** 3
**Explanation:** You can produce the valid garden \[1,1,1\] to have a total beauty of 1 + 1 + 1 = 3.
**Example 3:**
**Input:** flowers = \[-1,-2,0,-1\]
**Output:** -2
**Explanation:** You can produce the valid garden \[-1,-1\] to have a total beauty of -1 + -1 = -2.
**Constraints:**
* `2 <= flowers.length <= 105`
* `-104 <= flowers[i] <= 104`
* It is possible to create a valid garden by removing some (possibly none) flowers. | When one takes the stone, they not only get the points, but they take them away from the other player too. Greedily choose the stone with the maximum aliceValues[i] + bobValues[i]. |
96/94 in speed and memory #2023 1st solution | delivering-boxes-from-storage-to-ports | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def boxDelivering(self, boxes: List[List[int]], portsCount: int, maxBoxes: int, maxWeight: int) -> int: \n num_boxes = len(boxes)\n left = -1 \n dp = [0 for _ in range(num_boxes)]\n res = 0\n for right in range(num_boxes): \n maxBoxes -= 1 \n maxWeight -= boxes[right][1]\n \n if right==left+1:\n res+=2 \n elif boxes[right][0] != boxes[right-1][0]:\n res+=1 \n \n while maxBoxes<0 or maxWeight<0 or (left<right-1 and dp[left]==dp[left+1]): \n left += 1 \n maxBoxes += 1 \n maxWeight += boxes[left][1]\n if boxes[left][0] != boxes[left+1][0]:\n res -= 1 \n \n dp[right] = dp[left] + res \n return dp[num_boxes-1]\n``` | 0 | You have the task of delivering some boxes from storage to their ports using only one ship. However, this ship has a **limit** on the **number of boxes** and the **total weight** that it can carry.
You are given an array `boxes`, where `boxes[i] = [portsββiβ, weighti]`, and three integers `portsCount`, `maxBoxes`, and `maxWeight`.
* `portsββi` is the port where you need to deliver the `ith` box and `weightsi` is the weight of the `ith` box.
* `portsCount` is the number of ports.
* `maxBoxes` and `maxWeight` are the respective box and weight limits of the ship.
The boxes need to be delivered **in the order they are given**. The ship will follow these steps:
* The ship will take some number of boxes from the `boxes` queue, not violating the `maxBoxes` and `maxWeight` constraints.
* For each loaded box **in order**, the ship will make a **trip** to the port the box needs to be delivered to and deliver it. If the ship is already at the correct port, no **trip** is needed, and the box can immediately be delivered.
* The ship then makes a return **trip** to storage to take more boxes from the queue.
The ship must end at storage after all the boxes have been delivered.
Return _the **minimum** number of **trips** the ship needs to make to deliver all boxes to their respective ports._
**Example 1:**
**Input:** boxes = \[\[1,1\],\[2,1\],\[1,1\]\], portsCount = 2, maxBoxes = 3, maxWeight = 3
**Output:** 4
**Explanation:** The optimal strategy is as follows:
- The ship takes all the boxes in the queue, goes to port 1, then port 2, then port 1 again, then returns to storage. 4 trips.
So the total number of trips is 4.
Note that the first and third boxes cannot be delivered together because the boxes need to be delivered in order (i.e. the second box needs to be delivered at port 2 before the third box).
**Example 2:**
**Input:** boxes = \[\[1,2\],\[3,3\],\[3,1\],\[3,1\],\[2,4\]\], portsCount = 3, maxBoxes = 3, maxWeight = 6
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first box, goes to port 1, then returns to storage. 2 trips.
- The ship takes the second, third and fourth boxes, goes to port 3, then returns to storage. 2 trips.
- The ship takes the fifth box, goes to port 2, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Example 3:**
**Input:** boxes = \[\[1,4\],\[1,2\],\[2,1\],\[2,1\],\[3,2\],\[3,4\]\], portsCount = 3, maxBoxes = 6, maxWeight = 7
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first and second boxes, goes to port 1, then returns to storage. 2 trips.
- The ship takes the third and fourth boxes, goes to port 2, then returns to storage. 2 trips.
- The ship takes the fifth and sixth boxes, goes to port 3, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Constraints:**
* `1 <= boxes.length <= 105`
* `1 <= portsCount, maxBoxes, maxWeight <= 105`
* `1 <= portsββi <= portsCount`
* `1 <= weightsi <= maxWeight` | Create an array dp where dp[i][j] is the min edit distance for the path starting at node i and compared to index j of the targetPath. Traverse the dp array to obtain a valid answer. |
python solution || dynamic programming + sliding window || faster than 55% | delivering-boxes-from-storage-to-ports | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach: dynamic programming + sliding window\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def boxDelivering(self, boxes: List[List[int]], portsCount: int, maxBoxes: int, maxWeight: int) -> int: \n num_boxes = len(boxes)\n left = -1 \n dp = [0 for _ in range(num_boxes)]\n res = 0\n for right in range(num_boxes): \n maxBoxes -= 1 \n maxWeight -= boxes[right][1]\n \n if right==left+1:\n res+=2 \n elif boxes[right][0] != boxes[right-1][0]:\n res+=1 \n \n while maxBoxes<0 or maxWeight<0 or (left<right-1 and dp[left]==dp[left+1]): \n left += 1 \n maxBoxes += 1 \n maxWeight += boxes[left][1]\n if boxes[left][0] != boxes[left+1][0]:\n res -= 1 \n \n dp[right] = dp[left] + res \n return dp[num_boxes-1] \n\n\n\n``` | 0 | You have the task of delivering some boxes from storage to their ports using only one ship. However, this ship has a **limit** on the **number of boxes** and the **total weight** that it can carry.
You are given an array `boxes`, where `boxes[i] = [portsββiβ, weighti]`, and three integers `portsCount`, `maxBoxes`, and `maxWeight`.
* `portsββi` is the port where you need to deliver the `ith` box and `weightsi` is the weight of the `ith` box.
* `portsCount` is the number of ports.
* `maxBoxes` and `maxWeight` are the respective box and weight limits of the ship.
The boxes need to be delivered **in the order they are given**. The ship will follow these steps:
* The ship will take some number of boxes from the `boxes` queue, not violating the `maxBoxes` and `maxWeight` constraints.
* For each loaded box **in order**, the ship will make a **trip** to the port the box needs to be delivered to and deliver it. If the ship is already at the correct port, no **trip** is needed, and the box can immediately be delivered.
* The ship then makes a return **trip** to storage to take more boxes from the queue.
The ship must end at storage after all the boxes have been delivered.
Return _the **minimum** number of **trips** the ship needs to make to deliver all boxes to their respective ports._
**Example 1:**
**Input:** boxes = \[\[1,1\],\[2,1\],\[1,1\]\], portsCount = 2, maxBoxes = 3, maxWeight = 3
**Output:** 4
**Explanation:** The optimal strategy is as follows:
- The ship takes all the boxes in the queue, goes to port 1, then port 2, then port 1 again, then returns to storage. 4 trips.
So the total number of trips is 4.
Note that the first and third boxes cannot be delivered together because the boxes need to be delivered in order (i.e. the second box needs to be delivered at port 2 before the third box).
**Example 2:**
**Input:** boxes = \[\[1,2\],\[3,3\],\[3,1\],\[3,1\],\[2,4\]\], portsCount = 3, maxBoxes = 3, maxWeight = 6
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first box, goes to port 1, then returns to storage. 2 trips.
- The ship takes the second, third and fourth boxes, goes to port 3, then returns to storage. 2 trips.
- The ship takes the fifth box, goes to port 2, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Example 3:**
**Input:** boxes = \[\[1,4\],\[1,2\],\[2,1\],\[2,1\],\[3,2\],\[3,4\]\], portsCount = 3, maxBoxes = 6, maxWeight = 7
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first and second boxes, goes to port 1, then returns to storage. 2 trips.
- The ship takes the third and fourth boxes, goes to port 2, then returns to storage. 2 trips.
- The ship takes the fifth and sixth boxes, goes to port 3, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Constraints:**
* `1 <= boxes.length <= 105`
* `1 <= portsCount, maxBoxes, maxWeight <= 105`
* `1 <= portsββi <= portsCount`
* `1 <= weightsi <= maxWeight` | Create an array dp where dp[i][j] is the min edit distance for the path starting at node i and compared to index j of the targetPath. Traverse the dp array to obtain a valid answer. |
[Python3] dp + greedy | delivering-boxes-from-storage-to-ports | 0 | 1 | \n```\nclass Solution:\n def boxDelivering(self, boxes: List[List[int]], portsCount: int, maxBoxes: int, maxWeight: int) -> int:\n dp = [0] + [inf]*len(boxes)\n trips = 2\n ii = 0\n for i in range(len(boxes)):\n maxWeight -= boxes[i][1]\n if i and boxes[i-1][0] != boxes[i][0]: trips += 1\n while maxBoxes < i - ii + 1 or maxWeight < 0 or ii < i and dp[ii] == dp[ii+1]:\n maxWeight += boxes[ii][1]\n if boxes[ii][0] != boxes[ii+1][0]: trips-=1\n ii += 1\n dp[i+1] = dp[ii] + trips\n return dp[-1] \n``` | 2 | You have the task of delivering some boxes from storage to their ports using only one ship. However, this ship has a **limit** on the **number of boxes** and the **total weight** that it can carry.
You are given an array `boxes`, where `boxes[i] = [portsββiβ, weighti]`, and three integers `portsCount`, `maxBoxes`, and `maxWeight`.
* `portsββi` is the port where you need to deliver the `ith` box and `weightsi` is the weight of the `ith` box.
* `portsCount` is the number of ports.
* `maxBoxes` and `maxWeight` are the respective box and weight limits of the ship.
The boxes need to be delivered **in the order they are given**. The ship will follow these steps:
* The ship will take some number of boxes from the `boxes` queue, not violating the `maxBoxes` and `maxWeight` constraints.
* For each loaded box **in order**, the ship will make a **trip** to the port the box needs to be delivered to and deliver it. If the ship is already at the correct port, no **trip** is needed, and the box can immediately be delivered.
* The ship then makes a return **trip** to storage to take more boxes from the queue.
The ship must end at storage after all the boxes have been delivered.
Return _the **minimum** number of **trips** the ship needs to make to deliver all boxes to their respective ports._
**Example 1:**
**Input:** boxes = \[\[1,1\],\[2,1\],\[1,1\]\], portsCount = 2, maxBoxes = 3, maxWeight = 3
**Output:** 4
**Explanation:** The optimal strategy is as follows:
- The ship takes all the boxes in the queue, goes to port 1, then port 2, then port 1 again, then returns to storage. 4 trips.
So the total number of trips is 4.
Note that the first and third boxes cannot be delivered together because the boxes need to be delivered in order (i.e. the second box needs to be delivered at port 2 before the third box).
**Example 2:**
**Input:** boxes = \[\[1,2\],\[3,3\],\[3,1\],\[3,1\],\[2,4\]\], portsCount = 3, maxBoxes = 3, maxWeight = 6
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first box, goes to port 1, then returns to storage. 2 trips.
- The ship takes the second, third and fourth boxes, goes to port 3, then returns to storage. 2 trips.
- The ship takes the fifth box, goes to port 2, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Example 3:**
**Input:** boxes = \[\[1,4\],\[1,2\],\[2,1\],\[2,1\],\[3,2\],\[3,4\]\], portsCount = 3, maxBoxes = 6, maxWeight = 7
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first and second boxes, goes to port 1, then returns to storage. 2 trips.
- The ship takes the third and fourth boxes, goes to port 2, then returns to storage. 2 trips.
- The ship takes the fifth and sixth boxes, goes to port 3, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Constraints:**
* `1 <= boxes.length <= 105`
* `1 <= portsCount, maxBoxes, maxWeight <= 105`
* `1 <= portsββi <= portsCount`
* `1 <= weightsi <= maxWeight` | Create an array dp where dp[i][j] is the min edit distance for the path starting at node i and compared to index j of the targetPath. Traverse the dp array to obtain a valid answer. |
Additional test case for easy debugging (read if test 39 fails) | delivering-boxes-from-storage-to-ports | 0 | 1 | This problem can be solved optimally via a sliding window approach, as explained by others. Something I got stuck on is the optimal unloading of boxes, to me this seems the crux of the problem. Unfortunately for me, my code was wrong only on test case 39 (80000 boxes). I have made a simpler example producing the same error and am posting it here for your convenience:\n```python\nboxes = [[1, 2], [3, 2], [3, 1], [3, 2], [5, 4]]\nportsCount = 6\nmaxBoxes = 5\nmaxWeight = 4\n\nExpected result: 7\n```\n\nIn case it helps, I am stating my wrong delivery logic (this is not a full tutorial, have a look at other posts for that):\n1. Fill the boat (= sliding window) with boxes until at least one of it\'s capacities (maxBoxes or maxWeight) is reached --> the next box does not fit anymore\n2. Make the smallest possible delivery to make the next box fit. This delivery is as small as possible for maximum flexibiliy: it is cheaper to transport the current box together with other boxes on the ship (extra cost 0 if the port is the same as the current last box on the ship, else extra cost of 1) than to start an additional delivery for this box (cost of 2).\n3. Assume I needed to deliver __x__ boxes to make room for the next box, then I would deliver all consecutive boxes after the __xth__ box that needed to be delivered to the same port as __x__.\n\nPoint 3 above makes a mistake: it assumes that, just because two consecutive boxes are delivered to the same port, it will always be cheapest to also deliver them together. This is untrue, as you\'ll see if you go through the example given above.\nConcretely: It may be cheaper to split a consecutive series of boxes delivered to the same port. If it is cheapest to deliver them together, then their delivery price will be exactly the same (as there is no extra cost for dropping additional boxes on a port the ship is alrady at).\nTherefore, we only deliver more boxes than necessary (more than __x__ in the rules above) if the additinal delivery is completely free, i.e. dp[x] == dp[x + 1].\n\nCorrect code, explicitly implementing what I outlined above in a separate (the second) while loop:\n```python\nclass Solution:\n def boxDelivering(self, boxes: List[List[int]], portsCount: int, maxBoxes: int, maxWeight: int) -> int:\n left = 0 # idx of the box to be delivered first during the next run -> left idx in sliding window\n ports_on_route = 0\n weight_on_ship = 0\n dp = [0]\n for right in range(len(boxes)):\n while weight_on_ship + boxes[right][1] > maxWeight or right - left == maxBoxes:\n # ship is full --> deliver boxes until there is enough space for the new box\n weight_on_ship -= boxes[left][1]\n ports_on_route -= boxes[left][0] != boxes[left + 1][0]\n left += 1\n \n while left < right and dp[left] == dp[left + 1]:\n\t\t\t # if some additional boxes can be delivered for free, deliver them as well\n\t\t\t # (there can\'t be a cheaper than free deliveray, plus we clear additional space on the boat)\n weight_on_ship -= boxes[left][1]\n ports_on_route -= boxes[left][0] != boxes[left + 1][0]\n left += 1\n\n # load next box\n weight_on_ship += boxes[right][1]\n if right == 0 or boxes[right - 1][0] != boxes[right][0]:\n ports_on_route += 1\n dp.append(dp[left] + ports_on_route + 1)\n \n return dp[-1]\n```\n\n | 1 | You have the task of delivering some boxes from storage to their ports using only one ship. However, this ship has a **limit** on the **number of boxes** and the **total weight** that it can carry.
You are given an array `boxes`, where `boxes[i] = [portsββiβ, weighti]`, and three integers `portsCount`, `maxBoxes`, and `maxWeight`.
* `portsββi` is the port where you need to deliver the `ith` box and `weightsi` is the weight of the `ith` box.
* `portsCount` is the number of ports.
* `maxBoxes` and `maxWeight` are the respective box and weight limits of the ship.
The boxes need to be delivered **in the order they are given**. The ship will follow these steps:
* The ship will take some number of boxes from the `boxes` queue, not violating the `maxBoxes` and `maxWeight` constraints.
* For each loaded box **in order**, the ship will make a **trip** to the port the box needs to be delivered to and deliver it. If the ship is already at the correct port, no **trip** is needed, and the box can immediately be delivered.
* The ship then makes a return **trip** to storage to take more boxes from the queue.
The ship must end at storage after all the boxes have been delivered.
Return _the **minimum** number of **trips** the ship needs to make to deliver all boxes to their respective ports._
**Example 1:**
**Input:** boxes = \[\[1,1\],\[2,1\],\[1,1\]\], portsCount = 2, maxBoxes = 3, maxWeight = 3
**Output:** 4
**Explanation:** The optimal strategy is as follows:
- The ship takes all the boxes in the queue, goes to port 1, then port 2, then port 1 again, then returns to storage. 4 trips.
So the total number of trips is 4.
Note that the first and third boxes cannot be delivered together because the boxes need to be delivered in order (i.e. the second box needs to be delivered at port 2 before the third box).
**Example 2:**
**Input:** boxes = \[\[1,2\],\[3,3\],\[3,1\],\[3,1\],\[2,4\]\], portsCount = 3, maxBoxes = 3, maxWeight = 6
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first box, goes to port 1, then returns to storage. 2 trips.
- The ship takes the second, third and fourth boxes, goes to port 3, then returns to storage. 2 trips.
- The ship takes the fifth box, goes to port 2, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Example 3:**
**Input:** boxes = \[\[1,4\],\[1,2\],\[2,1\],\[2,1\],\[3,2\],\[3,4\]\], portsCount = 3, maxBoxes = 6, maxWeight = 7
**Output:** 6
**Explanation:** The optimal strategy is as follows:
- The ship takes the first and second boxes, goes to port 1, then returns to storage. 2 trips.
- The ship takes the third and fourth boxes, goes to port 2, then returns to storage. 2 trips.
- The ship takes the fifth and sixth boxes, goes to port 3, then returns to storage. 2 trips.
So the total number of trips is 2 + 2 + 2 = 6.
**Constraints:**
* `1 <= boxes.length <= 105`
* `1 <= portsCount, maxBoxes, maxWeight <= 105`
* `1 <= portsββi <= portsCount`
* `1 <= weightsi <= maxWeight` | Create an array dp where dp[i][j] is the min edit distance for the path starting at node i and compared to index j of the targetPath. Traverse the dp array to obtain a valid answer. |
Except for the winner, each team loses exactly 1 game!||Math explains | count-of-matches-in-tournament | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExcept for the winner, each team loses exactly 1 game!\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Theorem.** The are n teams. It needs $n-1$ games to determine the winner.\n*Proof.*\nThe are n teams. 1 team is the champion, each of others loses exactly once, totally n-1 games. \nThe number of games is n-1. **Q.E.D.**\n\nIf $n=2^k$ for some integer $k$, it is easy to see that the answer is $n-1=2^0+2^1+\\cdots +2^{k-1}=2^k-1.$ That tournament is in fact like a **full & complete Binary Tree**!\n\nUsing this fact, not only a more arithmetic proof for Theorem can be established, but also a recursive solution is doable which is also fast & runs 0ms beating 100%!\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# C++ Code\n```\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n-1; \n }\n};\n```\n# Python\n```\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n-1\n \n```\n# Appproach using Recursion\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int bit=31-__builtin_clz(n);//bit-length(n)\n if (__builtin_popcount(n)==1) return n-1;//n=2^k \n return (1<<bit)+numberOfMatches(n-(1<<bit));\n }\n};\n``` | 9 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
Except for the winner, each team loses exactly 1 game!||Math explains | count-of-matches-in-tournament | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExcept for the winner, each team loses exactly 1 game!\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Theorem.** The are n teams. It needs $n-1$ games to determine the winner.\n*Proof.*\nThe are n teams. 1 team is the champion, each of others loses exactly once, totally n-1 games. \nThe number of games is n-1. **Q.E.D.**\n\nIf $n=2^k$ for some integer $k$, it is easy to see that the answer is $n-1=2^0+2^1+\\cdots +2^{k-1}=2^k-1.$ That tournament is in fact like a **full & complete Binary Tree**!\n\nUsing this fact, not only a more arithmetic proof for Theorem can be established, but also a recursive solution is doable which is also fast & runs 0ms beating 100%!\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# C++ Code\n```\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n-1; \n }\n};\n```\n# Python\n```\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n-1\n \n```\n# Appproach using Recursion\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int bit=31-__builtin_clz(n);//bit-length(n)\n if (__builtin_popcount(n)==1) return n-1;//n=2^k \n return (1<<bit)+numberOfMatches(n-(1<<bit));\n }\n};\n``` | 9 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
π₯ return N-1 ; ] | count-of-matches-in-tournament | 1 | 1 | \n**Upvote If You Like the IDEA**\n\nThere are `n` teams participating in the tournament.\nAfter each match `1` team is eliminated.\n`n-1` teams needs to be eliminated: hence `n-1` matches.\n\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n``` Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n-1\n```\n``` C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n``` JAVA []\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n\n# ORRRR\nMake `res = 0`\n- `res += (n // 2)`\n- `n = (n // 2) + 1` : if `n % 2 == 1`\n- `n = (n // 2)` : if `n % 2 == 0`\n- Repeat till `n` > 1\nO(log n)\n\n\n\n\n**UPVOTE IF HELPFuuL** | 72 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
π₯ return N-1 ; ] | count-of-matches-in-tournament | 1 | 1 | \n**Upvote If You Like the IDEA**\n\nThere are `n` teams participating in the tournament.\nAfter each match `1` team is eliminated.\n`n-1` teams needs to be eliminated: hence `n-1` matches.\n\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n``` Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n-1\n```\n``` C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n``` JAVA []\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n\n# ORRRR\nMake `res = 0`\n- `res += (n // 2)`\n- `n = (n // 2) + 1` : if `n % 2 == 1`\n- `n = (n // 2)` : if `n % 2 == 0`\n- Repeat till `n` > 1\nO(log n)\n\n\n\n\n**UPVOTE IF HELPFuuL** | 72 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
π₯π₯ SIMPLE MATH | MOST EASY SOLUTION | STEPWISE EXPLAINATION ππ₯ | count-of-matches-in-tournament | 1 | 1 | # Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\uD83D\uDD0D **Understanding the Problem:**\n - Given the number of teams `n` in a tournament with specific rules.\n - Teams are paired, and matches are played until a winner is decided.\n\n\uD83E\uDD14 **Approach:**\n 1. Initialize a variable `ans` to 0 to keep track of the total number of matches played.\n 2. Use a while loop until there is only one team left (i.e., `n != 1`).\n 3. Inside the loop:\n - If the current number of teams is odd (`n & 1` is true):\n - Add `(n / 2)` to `ans` because there are `(n - 1) / 2` matches played, and `(n / 2) + 1` teams advance.\n - Update `n` to `(n / 2) + 1` as mentioned in the rules.\n - If the current number of teams is even:\n - Add `(n / 2)` to `ans` because there are `n / 2` matches played, and `n / 2` teams advance.\n - Update `n` to `n / 2`.\n 4. Return the final value of `ans`.\n\n\uD83E\uDDD0 **Explanation:**\n - The loop continues until there is only one team left.\n - In each iteration, it checks if the number of teams is odd or even and updates the variables accordingly.\n - The total number of matches is accumulated in the `ans` variable.\n\n\uD83C\uDF89 **Conclusion:**\n - The provided code efficiently calculates the total number of matches played in the tournament based on the given rules.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int ans = 0;\n\n while(n != 1)\n {\n // odd\n if(n & 1)\n {\n ans += (n / 2);\n n = (n / 2) + 1;\n }\n else\n {\n ans += (n / 2);\n n = (n / 2);\n }\n }\n return ans;\n }\n};\n```\n\n | 4 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
π₯π₯ SIMPLE MATH | MOST EASY SOLUTION | STEPWISE EXPLAINATION ππ₯ | count-of-matches-in-tournament | 1 | 1 | # Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\uD83D\uDD0D **Understanding the Problem:**\n - Given the number of teams `n` in a tournament with specific rules.\n - Teams are paired, and matches are played until a winner is decided.\n\n\uD83E\uDD14 **Approach:**\n 1. Initialize a variable `ans` to 0 to keep track of the total number of matches played.\n 2. Use a while loop until there is only one team left (i.e., `n != 1`).\n 3. Inside the loop:\n - If the current number of teams is odd (`n & 1` is true):\n - Add `(n / 2)` to `ans` because there are `(n - 1) / 2` matches played, and `(n / 2) + 1` teams advance.\n - Update `n` to `(n / 2) + 1` as mentioned in the rules.\n - If the current number of teams is even:\n - Add `(n / 2)` to `ans` because there are `n / 2` matches played, and `n / 2` teams advance.\n - Update `n` to `n / 2`.\n 4. Return the final value of `ans`.\n\n\uD83E\uDDD0 **Explanation:**\n - The loop continues until there is only one team left.\n - In each iteration, it checks if the number of teams is odd or even and updates the variables accordingly.\n - The total number of matches is accumulated in the `ans` variable.\n\n\uD83C\uDF89 **Conclusion:**\n - The provided code efficiently calculates the total number of matches played in the tournament based on the given rules.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int ans = 0;\n\n while(n != 1)\n {\n // odd\n if(n & 1)\n {\n ans += (n / 2);\n n = (n / 2) + 1;\n }\n else\n {\n ans += (n / 2);\n n = (n / 2);\n }\n }\n return ans;\n }\n};\n```\n\n | 4 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
π―Fasterβ
π― Lesserβ
3 Methodsπ₯Simple Mathπ₯Iterative Solutionπ₯Recursive Solutionπ₯Visualized Tooπ₯ | count-of-matches-in-tournament | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 3 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe problem involves simulating a tournament with a specific set of rules and determining the total number of matches played until a winner is decided. The rules of the tournament are as follows:\n\n- If the current number of teams `n` is even, each team is paired with another team. This results in `n / 2` matches being played, and `n / 2` teams advancing to the next round.\n\n- If the current number of teams `n` is odd, one team randomly advances to the next round, and the remaining teams are paired. This results in `(n - 1) / 2` matches being played, and `(n - 1) / 2 + 1` teams advancing to the next round.\n\nThe goal is to calculate and return the total number of matches played in the tournament until a winner is decided.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering three different methods to solve this problem:\n1. Mathematical Formula \n2. Iterative Solution\n3. Recursive Solution\n\n# 1. Mathematical Formula: \n- Subtract 1 from the total number of teams to get the number of matches played in each round.\n\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(1)`\n\n- \uD83D\uDE80 Space Complexity: `O(1)`\n\n# Code\n```Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n```C []\nint numberOfMatches(int n) {\n return n - 1;\n}\n```\n# 2. Iterative Solution:\n- Initialize a variable matches to 0.\n- While the number of teams is greater than 1:\n - Add the floor division of the number of teams by 2 to matches.\n - Set the number of teams to the result of the floor division.\n- Return the value of matches.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(log n)`\n\n- \uD83D\uDE80 Space Complexity: `O(1)`\n# Code\n```Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n matches = 0\n while n > 1:\n matches += n // 2\n n = (n + 1) // 2\n return matches\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n int matches = 0;\n while (n > 1) {\n matches += n / 2;\n n = (n + 1) / 2;\n }\n return matches;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int matches = 0;\n while (n > 1) {\n matches += n / 2;\n n = (n + 1) / 2;\n }\n return matches;\n }\n};\n```\n```C []\nint numberOfMatches(int n) {\n int matches = 0;\n while (n > 1) {\n matches += n / 2;\n n = (n + 1) / 2;\n }\n return matches;\n}\n```\n# 3. Recursive Solution:\n- Base case: If the number of teams is 1, return 0.\n- Otherwise, return the floor division of the number of teams by 2 plus the result of the function called recursively with the new number of teams.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(log n)`\n\n- \uD83D\uDE80 Space Complexity: `O(log n)`\n\n# Code\n```Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n if n == 1:\n return 0\n return n // 2 + self.numberOfMatches(n // 2 + n % 2)\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n if (n == 1) {\n return 0;\n }\n return n / 2 + numberOfMatches(n / 2 + n % 2);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n if (n == 1) {\n return 0;\n }\n return n / 2 + numberOfMatches((n + 1) / 2);\n }\n};\n```\n```C []\nint numberOfMatches(int n) {\n if (n == 1) {\n return 0;\n }\n return n / 2 + numberOfMatches(n / 2 + n % 2);\n}\n```\n# \uD83C\uDFC6Conclusion: \nIn conclusion, the mathematical formula method is the most optimal solution for the `Count of Matches in Tournament` problem. It provides a direct and efficient way to calculate the total number of matches played based on the given rules. \n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 25 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
π―Fasterβ
π― Lesserβ
3 Methodsπ₯Simple Mathπ₯Iterative Solutionπ₯Recursive Solutionπ₯Visualized Tooπ₯ | count-of-matches-in-tournament | 1 | 1 | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 3 ways to solve this question with detailed explanation of each approach:\n\n# Problem Explaination: \nThe problem involves simulating a tournament with a specific set of rules and determining the total number of matches played until a winner is decided. The rules of the tournament are as follows:\n\n- If the current number of teams `n` is even, each team is paired with another team. This results in `n / 2` matches being played, and `n / 2` teams advancing to the next round.\n\n- If the current number of teams `n` is odd, one team randomly advances to the next round, and the remaining teams are paired. This results in `(n - 1) / 2` matches being played, and `(n - 1) / 2 + 1` teams advancing to the next round.\n\nThe goal is to calculate and return the total number of matches played in the tournament until a winner is decided.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering three different methods to solve this problem:\n1. Mathematical Formula \n2. Iterative Solution\n3. Recursive Solution\n\n# 1. Mathematical Formula: \n- Subtract 1 from the total number of teams to get the number of matches played in each round.\n\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(1)`\n\n- \uD83D\uDE80 Space Complexity: `O(1)`\n\n# Code\n```Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n```C []\nint numberOfMatches(int n) {\n return n - 1;\n}\n```\n# 2. Iterative Solution:\n- Initialize a variable matches to 0.\n- While the number of teams is greater than 1:\n - Add the floor division of the number of teams by 2 to matches.\n - Set the number of teams to the result of the floor division.\n- Return the value of matches.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(log n)`\n\n- \uD83D\uDE80 Space Complexity: `O(1)`\n# Code\n```Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n matches = 0\n while n > 1:\n matches += n // 2\n n = (n + 1) // 2\n return matches\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n int matches = 0;\n while (n > 1) {\n matches += n / 2;\n n = (n + 1) / 2;\n }\n return matches;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int matches = 0;\n while (n > 1) {\n matches += n / 2;\n n = (n + 1) / 2;\n }\n return matches;\n }\n};\n```\n```C []\nint numberOfMatches(int n) {\n int matches = 0;\n while (n > 1) {\n matches += n / 2;\n n = (n + 1) / 2;\n }\n return matches;\n}\n```\n# 3. Recursive Solution:\n- Base case: If the number of teams is 1, return 0.\n- Otherwise, return the floor division of the number of teams by 2 plus the result of the function called recursively with the new number of teams.\n# Complexity\n- \u23F1\uFE0F Time Complexity: `O(log n)`\n\n- \uD83D\uDE80 Space Complexity: `O(log n)`\n\n# Code\n```Python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n if n == 1:\n return 0\n return n // 2 + self.numberOfMatches(n // 2 + n % 2)\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n if (n == 1) {\n return 0;\n }\n return n / 2 + numberOfMatches(n / 2 + n % 2);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n if (n == 1) {\n return 0;\n }\n return n / 2 + numberOfMatches((n + 1) / 2);\n }\n};\n```\n```C []\nint numberOfMatches(int n) {\n if (n == 1) {\n return 0;\n }\n return n / 2 + numberOfMatches(n / 2 + n % 2);\n}\n```\n# \uD83C\uDFC6Conclusion: \nIn conclusion, the mathematical formula method is the most optimal solution for the `Count of Matches in Tournament` problem. It provides a direct and efficient way to calculate the total number of matches played based on the given rules. \n\n# \uD83D\uDCA1 I invite you to check out my profile for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 25 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
β
β[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINEDπ₯ | count-of-matches-in-tournament | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1()***\n1. **Variable Initialization:** Initialize the variable `ans` as 0, which will store the total number of matches played.\n\n1. **While Loop:** Execute a loop until the value of `n` becomes 1 (signifying the end of matches).\n\n1. **Odd Number Condition:** If the current value of `n` is `odd` (`n % 2 != 0`):\n\n- Increment `ans` by half of the value of `n` minus 1 (`(n - 1) / 2`).\n- Update the value of `n` to half of the original odd number plus 1 ((`n - 1) / 2 + 1`).\n1. **Even Number Condition:** If the current value of `n` is `even` (`n % 2 == 0`):\n\n- Increment `ans` by half of the current value of `n` (`n / 2`).\n- Update the value of `n` to half of the original even number (`n / 2`).\n1. **Return:** After the loop completes (when n becomes 1), return the total number of matches stored in `ans`.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int ans = 0; // Variable to store the number of matches\n \n while(n != 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if(n % 2 != 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if(n % 2 == 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n }\n};\n\n\n\n```\n```C []\nint numberOfMatches(int n) {\n int ans = 0; // Variable to store the number of matches\n \n while (n != 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if (n % 2 != 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if (n % 2 == 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n}\n\n\n\n\n```\n```Java []\n\nclass Solution {\n public int numberOfMatches(int n) {\n int ans = 0; // Variable to store the number of matches\n \n while (n != 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if (n % 2 != 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if (n % 2 == 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n ans = 0 # Variable to store the number of matches\n \n while n != 1: # Continue the loop until \'n\' becomes 1 (end of matches)\n if n % 2 != 0: # If \'n\' is odd\n ans += (n - 1) // 2 # Increment \'ans\' by (n - 1) // 2\n n = (n - 1) // 2 + 1 # Update \'n\' to ((n - 1) // 2) + 1\n if n % 2 == 0: # If \'n\' is even\n ans += n // 2 # Increment \'ans\' by n // 2\n n = n // 2 # Update \'n\' to n // 2\n \n return ans # Return the total number of matches\n\n\n\n```\n```javascript []\n\nfunction numberOfMatches(n) {\n let ans = 0; // Variable to store the number of matches\n \n while (n !== 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if (n % 2 !== 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if (n % 2 === 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n}\n\n\n```\n---\n#### ***Approach 2(Basic)***\n\n\n# Complexity\n- *Time complexity:*\n $$O(1)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n\n```\n```C []\n\nint numberOfMatches(int n) {\n return n - 1;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n\n\n```\n```javascript []\nfunction numberOfMatches(n) {\n return n - 1;\n}\n\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
β
β[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINEDπ₯ | count-of-matches-in-tournament | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1()***\n1. **Variable Initialization:** Initialize the variable `ans` as 0, which will store the total number of matches played.\n\n1. **While Loop:** Execute a loop until the value of `n` becomes 1 (signifying the end of matches).\n\n1. **Odd Number Condition:** If the current value of `n` is `odd` (`n % 2 != 0`):\n\n- Increment `ans` by half of the value of `n` minus 1 (`(n - 1) / 2`).\n- Update the value of `n` to half of the original odd number plus 1 ((`n - 1) / 2 + 1`).\n1. **Even Number Condition:** If the current value of `n` is `even` (`n % 2 == 0`):\n\n- Increment `ans` by half of the current value of `n` (`n / 2`).\n- Update the value of `n` to half of the original even number (`n / 2`).\n1. **Return:** After the loop completes (when n becomes 1), return the total number of matches stored in `ans`.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int ans = 0; // Variable to store the number of matches\n \n while(n != 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if(n % 2 != 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if(n % 2 == 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n }\n};\n\n\n\n```\n```C []\nint numberOfMatches(int n) {\n int ans = 0; // Variable to store the number of matches\n \n while (n != 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if (n % 2 != 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if (n % 2 == 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n}\n\n\n\n\n```\n```Java []\n\nclass Solution {\n public int numberOfMatches(int n) {\n int ans = 0; // Variable to store the number of matches\n \n while (n != 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if (n % 2 != 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if (n % 2 == 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n ans = 0 # Variable to store the number of matches\n \n while n != 1: # Continue the loop until \'n\' becomes 1 (end of matches)\n if n % 2 != 0: # If \'n\' is odd\n ans += (n - 1) // 2 # Increment \'ans\' by (n - 1) // 2\n n = (n - 1) // 2 + 1 # Update \'n\' to ((n - 1) // 2) + 1\n if n % 2 == 0: # If \'n\' is even\n ans += n // 2 # Increment \'ans\' by n // 2\n n = n // 2 # Update \'n\' to n // 2\n \n return ans # Return the total number of matches\n\n\n\n```\n```javascript []\n\nfunction numberOfMatches(n) {\n let ans = 0; // Variable to store the number of matches\n \n while (n !== 1) { // Continue the loop until \'n\' becomes 1 (end of matches)\n if (n % 2 !== 0) { // If \'n\' is odd\n ans += (n - 1) / 2; // Increment \'ans\' by (n - 1) / 2\n n = (n - 1) / 2 + 1; // Update \'n\' to ((n - 1) / 2) + 1\n }\n if (n % 2 === 0) { // If \'n\' is even\n ans += n / 2; // Increment \'ans\' by n / 2\n n = n / 2; // Update \'n\' to n / 2\n }\n }\n return ans; // Return the total number of matches\n}\n\n\n```\n---\n#### ***Approach 2(Basic)***\n\n\n# Complexity\n- *Time complexity:*\n $$O(1)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n\n```\n```C []\n\nint numberOfMatches(int n) {\n return n - 1;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n\n\n```\n```javascript []\nfunction numberOfMatches(n) {\n return n - 1;\n}\n\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
(^_^)Python3 and C++ Solutions(100% Beats C++ users)π | count-of-matches-in-tournament | 0 | 1 | # Solution in Python3\n```\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n counter = 0\n while n != 1:\n if n % 2 == 0:\n counter += n/2\n n = n/2\n else:\n counter += (n - 1) / 2\n n = (n - 1) / 2 + 1\n return int(counter)\n```\n# Solution in C++\n```\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int counter = 0;\n while ( n != 1){\n if ( n % 2 == 0){\n counter += n / 2;\n n = n/2;\n }else{\n counter += ( n - 1 )/2;\n n = ( n - 1 )/2 + 1;\n }\n }\n return counter;\n }\n};\n``` | 2 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
(^_^)Python3 and C++ Solutions(100% Beats C++ users)π | count-of-matches-in-tournament | 0 | 1 | # Solution in Python3\n```\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n counter = 0\n while n != 1:\n if n % 2 == 0:\n counter += n/2\n n = n/2\n else:\n counter += (n - 1) / 2\n n = (n - 1) / 2 + 1\n return int(counter)\n```\n# Solution in C++\n```\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n int counter = 0;\n while ( n != 1){\n if ( n % 2 == 0){\n counter += n / 2;\n n = n/2;\n }else{\n counter += ( n - 1 )/2;\n n = ( n - 1 )/2 + 1;\n }\n }\n return counter;\n }\n};\n``` | 2 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
β
Beginner Friendlyβ
Mastering Tournament Dynamics: A Comprehensive Guide to Match Counting Algorithms | count-of-matches-in-tournament | 1 | 1 | > \u2753**The way to solve this is DRY RUN and Observe that number of matches is one less than number of teams given**\n## \uD83D\uDCA1Approach 1: Recursive Approach - Brute Force\n\n### \u2728Explanation\nThis approach uses recursion to count the number of matches played. The base cases are when there is only one team, in which case no matches are played, or when there are two teams, in which case only one match is played. For any other number of teams, the function recursively calculates the number of matches for half of the teams and adds the result.\n\n### \uD83D\uDCDDDry Run\nLet\'s take an example with n = 4:\n- Teams: 4\n- Matches in the first round: 2 (Team 1 vs Team 2, Team 3 vs Team 4)\n- Matches in the second round: 1 (Winner of Match 1 vs Winner of Match 2)\n\nTotal matches: 3\n\n### \uD83D\uDD0DEdge Cases\n- For n = 1, no matches are played.\n- For n = 2, one match is played.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(2^n), where n is the number of teams.\n- Space Complexity: O(n), where n is the number of teams.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the approach\nclass Solution\n{\npublic:\n int numberOfMatches(int n)\n {\n if (n == 1 or n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + numberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + numberOfMatches(n / 2);\n }\n};\n```\n\n```java []\n// Java code block for the approach\nclass Solution {\n public int numberOfMatches(int n) {\n if (n == 1 || n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + numberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + numberOfMatches(n / 2);\n }\n}\n```\n\n```python []\n# Python code block for the approach\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n if n == 1 or n == 2:\n return n - 1\n if n % 2 == 1:\n return (n - 1) // 2 + self.numberOfMatches((n - 1) // 2 + 1)\n else:\n return n // 2 + self.numberOfMatches(n // 2)\n```\n\n```csharp []\n// C# code block for the approach\npublic class Solution {\n public int NumberOfMatches(int n) {\n if (n == 1 || n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + NumberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + NumberOfMatches(n / 2);\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the approach\nvar numberOfMatches = function(n) {\n if (n == 1 || n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + numberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + numberOfMatches(n / 2);\n};\n```\n\n\n\n---\n\n---\n\n## \uD83D\uDCA1Approach 2: Mathematical Formula\n\n### \u2728Explanation\nThis approach utilizes a mathematical formula to directly calculate the number of matches based on the number of teams. The formula is `n - 1`, where `n` is the number of teams.\n### $$totalNumber Of Matches = total Number Of Teams - 1 $$\n\n### \uD83D\uDCDDDry Run\nLet\'s take an example with n = 4:\n- Teams: 4\n\nTotal matches: 3\n\n### \uD83D\uDD0DEdge Cases\n- For n = 1, no matches are played.\n- For n = 2, one match is played.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(1).\n- Space Complexity: O(1).\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the approach\nclass Solution{\n public:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n\n```java []\n// Java code block for the approach\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n\n```python []\n# Python code block for the approach\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n```\n\n```csharp []\n// C# code block for the approach\npublic class Solution {\n public int NumberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the approach\nvar numberOfMatches = function(n) {\n return n - 1;\n};\n```\n\n---\n## \uD83D\uDCCA Analysis\n| Language | Runtime | Memory |\n|----------|---------|--------|\n| C++ | 0 ms | 0 MB |\n| Java | 0 ms | 0 MB |\n| Python | 0 ms | 0 MB |\n| C# | 0 ms | 0 MB |\n| JavaScript | 0 ms | 0 MB | \n---\n\n\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF* | 1 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
β
Beginner Friendlyβ
Mastering Tournament Dynamics: A Comprehensive Guide to Match Counting Algorithms | count-of-matches-in-tournament | 1 | 1 | > \u2753**The way to solve this is DRY RUN and Observe that number of matches is one less than number of teams given**\n## \uD83D\uDCA1Approach 1: Recursive Approach - Brute Force\n\n### \u2728Explanation\nThis approach uses recursion to count the number of matches played. The base cases are when there is only one team, in which case no matches are played, or when there are two teams, in which case only one match is played. For any other number of teams, the function recursively calculates the number of matches for half of the teams and adds the result.\n\n### \uD83D\uDCDDDry Run\nLet\'s take an example with n = 4:\n- Teams: 4\n- Matches in the first round: 2 (Team 1 vs Team 2, Team 3 vs Team 4)\n- Matches in the second round: 1 (Winner of Match 1 vs Winner of Match 2)\n\nTotal matches: 3\n\n### \uD83D\uDD0DEdge Cases\n- For n = 1, no matches are played.\n- For n = 2, one match is played.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(2^n), where n is the number of teams.\n- Space Complexity: O(n), where n is the number of teams.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the approach\nclass Solution\n{\npublic:\n int numberOfMatches(int n)\n {\n if (n == 1 or n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + numberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + numberOfMatches(n / 2);\n }\n};\n```\n\n```java []\n// Java code block for the approach\nclass Solution {\n public int numberOfMatches(int n) {\n if (n == 1 || n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + numberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + numberOfMatches(n / 2);\n }\n}\n```\n\n```python []\n# Python code block for the approach\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n if n == 1 or n == 2:\n return n - 1\n if n % 2 == 1:\n return (n - 1) // 2 + self.numberOfMatches((n - 1) // 2 + 1)\n else:\n return n // 2 + self.numberOfMatches(n // 2)\n```\n\n```csharp []\n// C# code block for the approach\npublic class Solution {\n public int NumberOfMatches(int n) {\n if (n == 1 || n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + NumberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + NumberOfMatches(n / 2);\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the approach\nvar numberOfMatches = function(n) {\n if (n == 1 || n == 2) return n - 1;\n if (n % 2 == 1)\n return (n - 1) / 2 + numberOfMatches((n - 1) / 2 + 1);\n else return n / 2 + numberOfMatches(n / 2);\n};\n```\n\n\n\n---\n\n---\n\n## \uD83D\uDCA1Approach 2: Mathematical Formula\n\n### \u2728Explanation\nThis approach utilizes a mathematical formula to directly calculate the number of matches based on the number of teams. The formula is `n - 1`, where `n` is the number of teams.\n### $$totalNumber Of Matches = total Number Of Teams - 1 $$\n\n### \uD83D\uDCDDDry Run\nLet\'s take an example with n = 4:\n- Teams: 4\n\nTotal matches: 3\n\n### \uD83D\uDD0DEdge Cases\n- For n = 1, no matches are played.\n- For n = 2, one match is played.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(1).\n- Space Complexity: O(1).\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the approach\nclass Solution{\n public:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n\n```java []\n// Java code block for the approach\nclass Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n\n```python []\n# Python code block for the approach\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n```\n\n```csharp []\n// C# code block for the approach\npublic class Solution {\n public int NumberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the approach\nvar numberOfMatches = function(n) {\n return n - 1;\n};\n```\n\n---\n## \uD83D\uDCCA Analysis\n| Language | Runtime | Memory |\n|----------|---------|--------|\n| C++ | 0 ms | 0 MB |\n| Java | 0 ms | 0 MB |\n| Python | 0 ms | 0 MB |\n| C# | 0 ms | 0 MB |\n| JavaScript | 0 ms | 0 MB | \n---\n\n\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF* | 1 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
πβ
π 100% beats || One line || Easy peasy || Java, Python, C#, Rust, Ruby, Go, C, C++, Php|| π₯π₯ | count-of-matches-in-tournament | 1 | 1 | \n\n\n# Intuition\nThe solution is based on the observation that, in each round of the tournament, one team is eliminated, except in the final round where the winner is decided. Therefore, the number of matches played until a winner is decided is equal to the number of teams minus one.\n\n# Approach\nThe approach is straightforward. We initialize a variable `matches` to 0 and then iterate through the tournament rounds. In each round, we eliminate one team and increment the `matches` counter. This process continues until there is only one team left as the winner.\n\n# Complexity\n- **Time complexity:** O(1)\n - The time complexity is constant as the solution involves a simple arithmetic operation (subtraction) regardless of the value of n.\n\n- **Space complexity:** O(1)\n - The space complexity is constant as there is no additional space used that depends on the input size.\n\n```python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n```\n```C# []\npublic class Solution {\n public int NumberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n```Rust []\nimpl Solution {\n pub fn number_of_matches(n: i32) -> i32 {\n n - 1\n }\n}\n```\n``` Php []\nclass Solution {\n function numberOfMatches($n) {\n return $n - 1;\n }\n}\n```\n```Ruby []\ndef number_of_matches(n)\n n - 1\nend\n```\n``` Go []\nfunc numberOfMatches(n int) int {\n return n - 1\n}\n```\n```C []\nint numberOfMatches(int n){\n return n - 1;\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n\n\n- Please upvote me !!! | 7 | You are given an integer `n`, the number of teams in a tournament that has strange rules:
* If the current number of teams is **even**, each team gets paired with another team. A total of `n / 2` matches are played, and `n / 2` teams advance to the next round.
* If the current number of teams is **odd**, one team randomly advances in the tournament, and the rest gets paired. A total of `(n - 1) / 2` matches are played, and `(n - 1) / 2 + 1` teams advance to the next round.
Return _the number of matches played in the tournament until a winner is decided._
**Example 1:**
**Input:** n = 7
**Output:** 6
**Explanation:** Details of the tournament:
- 1st Round: Teams = 7, Matches = 3, and 4 teams advance.
- 2nd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 3rd Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 3 + 2 + 1 = 6.
**Example 2:**
**Input:** n = 14
**Output:** 13
**Explanation:** Details of the tournament:
- 1st Round: Teams = 14, Matches = 7, and 7 teams advance.
- 2nd Round: Teams = 7, Matches = 3, and 4 teams advance.
- 3rd Round: Teams = 4, Matches = 2, and 2 teams advance.
- 4th Round: Teams = 2, Matches = 1, and 1 team is declared the winner.
Total number of matches = 7 + 3 + 2 + 1 = 13.
**Constraints:**
* `1 <= n <= 200` | null |
πβ
π 100% beats || One line || Easy peasy || Java, Python, C#, Rust, Ruby, Go, C, C++, Php|| π₯π₯ | count-of-matches-in-tournament | 1 | 1 | \n\n\n# Intuition\nThe solution is based on the observation that, in each round of the tournament, one team is eliminated, except in the final round where the winner is decided. Therefore, the number of matches played until a winner is decided is equal to the number of teams minus one.\n\n# Approach\nThe approach is straightforward. We initialize a variable `matches` to 0 and then iterate through the tournament rounds. In each round, we eliminate one team and increment the `matches` counter. This process continues until there is only one team left as the winner.\n\n# Complexity\n- **Time complexity:** O(1)\n - The time complexity is constant as the solution involves a simple arithmetic operation (subtraction) regardless of the value of n.\n\n- **Space complexity:** O(1)\n - The space complexity is constant as there is no additional space used that depends on the input size.\n\n```python []\nclass Solution:\n def numberOfMatches(self, n: int) -> int:\n return n - 1\n```\n```C# []\npublic class Solution {\n public int NumberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int numberOfMatches(int n) {\n return n - 1;\n }\n}\n```\n```Rust []\nimpl Solution {\n pub fn number_of_matches(n: i32) -> i32 {\n n - 1\n }\n}\n```\n``` Php []\nclass Solution {\n function numberOfMatches($n) {\n return $n - 1;\n }\n}\n```\n```Ruby []\ndef number_of_matches(n)\n n - 1\nend\n```\n``` Go []\nfunc numberOfMatches(n int) int {\n return n - 1\n}\n```\n```C []\nint numberOfMatches(int n){\n return n - 1;\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numberOfMatches(int n) {\n return n - 1;\n }\n};\n```\n\n\n- Please upvote me !!! | 7 | You are given an **even** integer `n`ββββββ. You initially have a permutation `perm` of size `n`ββ where `perm[i] == i`β **(0-indexed)**ββββ.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr`ββββ to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n`ββββββ is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
Very easy soln Just find max of given str | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # ONe liner Code very easy\n\n# Code\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max(map(int,n))\n``` | 1 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Very easy soln Just find max of given str | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # ONe liner Code very easy\n\n# Code\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max(map(int,n))\n``` | 1 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
[C++/Java/Python]- Easy One liner with explanation | partitioning-into-minimum-number-of-deci-binary-numbers | 1 | 1 | For this one, we would just rely on simple maths.\n> Example: **n = "153"**\n> \nNow let\'s break down each digit with required number of ones as we can use only `0` or `1` in deci-binaries.\n>**1** - 1 0 0 0 0 \n>**5** - 1 1 1 1 1\n>**3** - 1 1 1 0 0 \n> Added zero padding to the tail to align with max number of in `n`.\n> \nNow if you consider each above entry as an array, you can group digits at same index to form a number. Something like this:\n> **111 + 011 + 011 + 010 + 010 = 153**\n> \nSo in all you require `5` deci-binaries to form the required `153`.\n\nNow let\'s take another example:\n> **n = "3271"**\n> **3** - 1 1 1 0 0 0 0\n> **2** - 1 1 0 0 0 0 0\n> **7** - 1 1 1 1 1 1 1 \n> **1** - 1 0 0 0 0 0 0\n\nNow after grouping digits at same index:\n> **1111 + 1110 + 1010 + 0010 + 0010 + 0010 + 0010 = 3271**\n> \nHere we requred `7` deci-binaries.\n\nNow taking both the examples into account, we can observe the minimum number of deci-binaries required to create the required `n` is the max digit in the input `n`.\n\nBelow is my implementation based on above observation:\n**Python3**\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return int(max(n)) \n```\n\n**C++**\n```\nclass Solution {\npublic:\n int minPartitions(string n) {\n return *max_element(n.begin(), n.end()) - \'0\';\n }\n};\n```\n\n**Java**\n```\nclass Solution {\n public int minPartitions(String n) {\n int res = 0;\n for (int i = 0; i < n.length(); i++) {\n res = Math.max(res, n.charAt(i) - \'0\');\n }\n return res;\n }\n}\n```\n\nIf `len` is the length of the input string `n`,\n**Time - O(len)**\n**Space - O(1)**\n\n--- \n\n***Please upvote if you find it useful*** | 70 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.