title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[C++/Java/Python]- Easy One liner with explanation | partitioning-into-minimum-number-of-deci-binary-numbers | 1 | 1 | For this one, we would just rely on simple maths.\n> Example: **n = "153"**\n> \nNow let\'s break down each digit with required number of ones as we can use only `0` or `1` in deci-binaries.\n>**1** - 1 0 0 0 0 \n>**5** - 1 1 1 1 1\n>**3** - 1 1 1 0 0 \n> Added zero padding to the tail to align with max number of in `n`.\n> \nNow if you consider each above entry as an array, you can group digits at same index to form a number. Something like this:\n> **111 + 011 + 011 + 010 + 010 = 153**\n> \nSo in all you require `5` deci-binaries to form the required `153`.\n\nNow let\'s take another example:\n> **n = "3271"**\n> **3** - 1 1 1 0 0 0 0\n> **2** - 1 1 0 0 0 0 0\n> **7** - 1 1 1 1 1 1 1 \n> **1** - 1 0 0 0 0 0 0\n\nNow after grouping digits at same index:\n> **1111 + 1110 + 1010 + 0010 + 0010 + 0010 + 0010 = 3271**\n> \nHere we requred `7` deci-binaries.\n\nNow taking both the examples into account, we can observe the minimum number of deci-binaries required to create the required `n` is the max digit in the input `n`.\n\nBelow is my implementation based on above observation:\n**Python3**\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return int(max(n)) \n```\n\n**C++**\n```\nclass Solution {\npublic:\n int minPartitions(string n) {\n return *max_element(n.begin(), n.end()) - \'0\';\n }\n};\n```\n\n**Java**\n```\nclass Solution {\n public int minPartitions(String n) {\n int res = 0;\n for (int i = 0; i < n.length(); i++) {\n res = Math.max(res, n.charAt(i) - \'0\');\n }\n return res;\n }\n}\n```\n\nIf `len` is the length of the input string `n`,\n**Time - O(len)**\n**Space - O(1)**\n\n--- \n\n***Please upvote if you find it useful*** | 70 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Detailed Easiest Explanation of Solution | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | I was trying it hard for several days , then checked out the discussion group for some hints.\nI really got surprised by the one-liner solutions. I\'m just providing here the detailed explanation to the solution for others to get help from it.\n\n**In Python**\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max(n)\n```\n\n\n\n\n**If you find this helpful, please upvote to motivate me to do it regularly!! Thank You.**\n | 149 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Detailed Easiest Explanation of Solution | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | I was trying it hard for several days , then checked out the discussion group for some hints.\nI really got surprised by the one-liner solutions. I\'m just providing here the detailed explanation to the solution for others to get help from it.\n\n**In Python**\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max(n)\n```\n\n\n\n\n**If you find this helpful, please upvote to motivate me to do it regularly!! Thank You.**\n | 149 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python3 easy solution | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$, where n is the length of the input string n.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return int(max(n))\n``` | 2 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Python3 easy solution | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$, where n is the length of the input string n.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return int(max(n))\n``` | 2 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Beginner-friendly || Simple/tricky solution in Python3 and JavaScript/TypeScript | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a `n` string, that\'s a valid positive integer\n- our goal is to calculate, how many **deci-binary** integers it contains \n\nFollowing to the statement, **deci-binary** integer is that, which has only `1`-s and `0`-s as digits with **no leading zeroes**.\n\nInstead of thinking **HOW to find** this numbers, let\'s pay your attention at these notes.\n```\n# Example\nn = \'692\'\n\n# As always we can start from top to bottom like\ndigits = \'111\' => n = \'692\' - \'111\' == \'581\'...\n=> n = \'26\' => \'15\' => \'4\' ... => \'1\' \n# And we think that this will work.\n\n# Try to practice reducing an integer like in the task example =>\nn = \'82734\'\n# and y\'ll see, that this approach WON\'T lead us \n# to the optimal solution!\n\n# For this moment we can try to iterate vice-versa, i.e. bottom-up,\n# but with some trick\n\n# Consider an integer like 692 again and\nn = \'692\'\n\n# 1. break down the integer into digits 6-9-2 or 600 + 90 + 2 \n# and start from the least digit\n# 2. calculate HOW many numbers we can sum up to get\n# a current integer\n# 3. y\'ll find, that maximum count of integers you need\n# to sum up is THE LARGEST digit!\n```\n\n# Approach\n1. declare an `ans` variable\n2. iterate over `n` string\n3. define the maximum digits count and store in `ans`\n4. return `ans`\n\n# Complexity\n- Time complexity: **O(n)** to iterate over `n`\n- Space complexity: **O(1)**, we don\'t allocate extra space\n\n\n# Code in JavaScript/TypeScript\n```\nfunction minPartitions(n: string): number {\n let ans = 0\n\n for (let i = 0; i < n.length; i++) {\n ans = Math.max(ans, +n[i])\n }\n\n return ans\n};\n```\n\n# Code in Python3\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max([int(x) for x in n])\n``` | 2 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Beginner-friendly || Simple/tricky solution in Python3 and JavaScript/TypeScript | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a `n` string, that\'s a valid positive integer\n- our goal is to calculate, how many **deci-binary** integers it contains \n\nFollowing to the statement, **deci-binary** integer is that, which has only `1`-s and `0`-s as digits with **no leading zeroes**.\n\nInstead of thinking **HOW to find** this numbers, let\'s pay your attention at these notes.\n```\n# Example\nn = \'692\'\n\n# As always we can start from top to bottom like\ndigits = \'111\' => n = \'692\' - \'111\' == \'581\'...\n=> n = \'26\' => \'15\' => \'4\' ... => \'1\' \n# And we think that this will work.\n\n# Try to practice reducing an integer like in the task example =>\nn = \'82734\'\n# and y\'ll see, that this approach WON\'T lead us \n# to the optimal solution!\n\n# For this moment we can try to iterate vice-versa, i.e. bottom-up,\n# but with some trick\n\n# Consider an integer like 692 again and\nn = \'692\'\n\n# 1. break down the integer into digits 6-9-2 or 600 + 90 + 2 \n# and start from the least digit\n# 2. calculate HOW many numbers we can sum up to get\n# a current integer\n# 3. y\'ll find, that maximum count of integers you need\n# to sum up is THE LARGEST digit!\n```\n\n# Approach\n1. declare an `ans` variable\n2. iterate over `n` string\n3. define the maximum digits count and store in `ans`\n4. return `ans`\n\n# Complexity\n- Time complexity: **O(n)** to iterate over `n`\n- Space complexity: **O(1)**, we don\'t allocate extra space\n\n\n# Code in JavaScript/TypeScript\n```\nfunction minPartitions(n: string): number {\n let ans = 0\n\n for (let i = 0; i < n.length; i++) {\n ans = Math.max(ans, +n[i])\n }\n\n return ans\n};\n```\n\n# Code in Python3\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max([int(x) for x in n])\n``` | 2 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python3 || Beats 91.67% 🚀🚀|| One liner || Self explanatory. | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # **Note:**\n**Check the hint given in description to understand the solution.**\n# Code\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return int(max(n)) \n```\n**Please upvote if you find it helpful.** | 4 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Python3 || Beats 91.67% 🚀🚀|| One liner || Self explanatory. | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | # **Note:**\n**Check the hint given in description to understand the solution.**\n# Code\n```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return int(max(n)) \n```\n**Please upvote if you find it helpful.** | 4 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python - one line code | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | ```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max(n)\n``` | 2 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Python - one line code | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | ```\nclass Solution:\n def minPartitions(self, n: str) -> int:\n return max(n)\n``` | 2 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python3 || Can't believe this solution || 99 % Faster 🚀 | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | **Upvote and let others also see \uD83D\uDE02\uD83D\uDC4C\u2764\uFE0F**\n.\n\n* By observation we can say we only have deci-binary (0, 1) to sum up to given number n, we need atleast n[i] deci-binary numbers to sum up to n[i], where n[i] is the ith digit of given number.\n\n* Consider n="9", We need to add 1 for 9 times to get n so the largest number in the str will aslo be "9"\n\n* So when we pass str in our max fn it will take max char by comparing characters with ASCII Numbers, thus we get max number\n\n* ***Note: I can\'t figure out why on returning the max as sring its not giving error as return type is strictly integer. If you know then please let everyone know in comments*** \n\n\n.\n***Runtime: 31 ms, faster than 99.74% of Python3** online submissions for Partitioning Into Minimum Number Of Deci-Binary Numbers. **Memory Usage: 11.7 MB, less than 93.73% of Python3** online submissions for Partitioning Into Minimum Number Of Deci-Binary Numbers.*\n.\n```\nclass Solution:\n def minPartitions(self, n: str) -> int: \n return max(n)\n``` | 4 | A decimal number is called **deci-binary** if each of its digits is either `0` or `1` without any leading zeros. For example, `101` and `1100` are **deci-binary**, while `112` and `3001` are not.
Given a string `n` that represents a positive decimal integer, return _the **minimum** number of positive **deci-binary** numbers needed so that they sum up to_ `n`_._
**Example 1:**
**Input:** n = "32 "
**Output:** 3
**Explanation:** 10 + 11 + 11 = 32
**Example 2:**
**Input:** n = "82734 "
**Output:** 8
**Example 3:**
**Input:** n = "27346209830709182346 "
**Output:** 9
**Constraints:**
* `1 <= n.length <= 105`
* `n` consists of only digits.
* `n` does not contain any leading zeros and represents a positive integer. | Use a three-layer loop to check all possible patterns by iterating through all possible starting positions, all indexes less than m, and if the character at the index is repeated k times. |
Python3 || Can't believe this solution || 99 % Faster 🚀 | partitioning-into-minimum-number-of-deci-binary-numbers | 0 | 1 | **Upvote and let others also see \uD83D\uDE02\uD83D\uDC4C\u2764\uFE0F**\n.\n\n* By observation we can say we only have deci-binary (0, 1) to sum up to given number n, we need atleast n[i] deci-binary numbers to sum up to n[i], where n[i] is the ith digit of given number.\n\n* Consider n="9", We need to add 1 for 9 times to get n so the largest number in the str will aslo be "9"\n\n* So when we pass str in our max fn it will take max char by comparing characters with ASCII Numbers, thus we get max number\n\n* ***Note: I can\'t figure out why on returning the max as sring its not giving error as return type is strictly integer. If you know then please let everyone know in comments*** \n\n\n.\n***Runtime: 31 ms, faster than 99.74% of Python3** online submissions for Partitioning Into Minimum Number Of Deci-Binary Numbers. **Memory Usage: 11.7 MB, less than 93.73% of Python3** online submissions for Partitioning Into Minimum Number Of Deci-Binary Numbers.*\n.\n```\nclass Solution:\n def minPartitions(self, n: str) -> int: \n return max(n)\n``` | 4 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python 3 || 5 lines, recursion, prefix || T/M: 59% / 88% | stone-game-vii | 0 | 1 | I had trouble with TLE, even with `@lru_cache(None)`. Someone under the Discussion tab said resetting it to `2000` would help, and it did!\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n\n pref = list(accumulate(stones, initial = 0))\n \n @lru_cache(2000)\n def dp(l: int, r: int)->int:\n\n return 0 if l == r else max(pref[r ] - pref[l+1] - dp(l+1, r), \n pref[r-1] - pref[l ] - dp(l, r-1))\n\n return dp(0, len(stones))\n```\n[https://leetcode.com/problems/stone-game-vii/submissions/874367058/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*^2) / *O*(*N*log*N*).\n | 3 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
Python 3 || 5 lines, recursion, prefix || T/M: 59% / 88% | stone-game-vii | 0 | 1 | I had trouble with TLE, even with `@lru_cache(None)`. Someone under the Discussion tab said resetting it to `2000` would help, and it did!\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n\n pref = list(accumulate(stones, initial = 0))\n \n @lru_cache(2000)\n def dp(l: int, r: int)->int:\n\n return 0 if l == r else max(pref[r ] - pref[l+1] - dp(l+1, r), \n pref[r-1] - pref[l ] - dp(l, r-1))\n\n return dp(0, len(stones))\n```\n[https://leetcode.com/problems/stone-game-vii/submissions/874367058/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*^2) / *O*(*N*log*N*).\n | 3 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Time 100% and Memory 100% | stone-game-vii | 0 | 1 | # Intuition\nNotice that the difference of scores is the sum of all the stones that Bob takes, so for both Alice and Bob, their optimal strategy is to minimize their own sums of stones.\n\n# Approach\nUse dynamic programming from the last step to the first.\n\n# Complexity\n- Time complexity:\n$O(n^2)$\n\n- Space complexity:\n$O(n)$\n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n flag = 1\n lis = list(stones)\n for i in range(1,n):\n for j in range(n - i):\n if flag:\n lis[j] = max(lis[j],lis[j+1])\n else:\n lis[j] = min(lis[j] + stones[j + i],lis[j+1] + stones[j])\n flag ^= 1\n #print(lis)\n return lis[0] if not flag else sum(stones) - lis[0]\n \n``` | 1 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
Time 100% and Memory 100% | stone-game-vii | 0 | 1 | # Intuition\nNotice that the difference of scores is the sum of all the stones that Bob takes, so for both Alice and Bob, their optimal strategy is to minimize their own sums of stones.\n\n# Approach\nUse dynamic programming from the last step to the first.\n\n# Complexity\n- Time complexity:\n$O(n^2)$\n\n- Space complexity:\n$O(n)$\n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n n = len(stones)\n flag = 1\n lis = list(stones)\n for i in range(1,n):\n for j in range(n - i):\n if flag:\n lis[j] = max(lis[j],lis[j+1])\n else:\n lis[j] = min(lis[j] + stones[j + i],lis[j+1] + stones[j])\n flag ^= 1\n #print(lis)\n return lis[0] if not flag else sum(stones) - lis[0]\n \n``` | 1 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Recursion->Memoization->Tabulation | stone-game-vii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n```\nAlice Turn\n [5 3 1 4 2]\n A = 5 + 3 + 1 + 4 = 13 \nBob Turn\n [5 3 1 4]\n B = 3 + 1 + 4 = 8\nAlice Turn\n [3 1 4]\n A = 1 + 4 = 5\nBob Turn\n [1 4]\n B = 4 = 4\nResult\n A = 13 + 5 = 18\n - B = 8 + 4 = 12\n ------------------\n 6\n\n ---> 13 - 8 + 5 - 4 = 6\n can also be written as:\n ---> 13 -(8 - (5-(4)))\n 13 - 8 + (5-(4)) \n 13 - 8 + 5 - 4 = 6\nSo in recursive approach we will just keep subtracting the next Call\n```\n# Recursive Approach\n<!-- Describe your approach to solving the problem. -->\n```\ndef stoneGameVII(self, nums: List[int]) -> int:\n def f(start,end,total):\n if start>=end:return 0 //in recursion this line is not req. but converting this recursion to tabulation this is required\n if total == 0:\n return 0\n pickS = (total-nums[start]) - f(start+1,end,total-nums[start])\n pickE = (total-nums[end]) - f(start,end-1,total-nums[end])\n\n return max(pickS,pickE)\n return f(0,len(nums)-1,sum(nums))\n\n```\n\n# Memoization\n```\ndef stoneGameVII(self, nums: List[int]) -> int:\n def f(start,end,total,dp):\n if start>=end:return 0\n if total == 0:\n return 0\n if dp[start][end][total] != -1:return dp[start][end][total]\n pickS = (total-nums[start]) - f(start+1,end,total-nums[start],dp)\n pickE = (total-nums[end]) - f(start,end-1,total-nums[end],dp)\n\n dp[start][end][total] = max(pickS,pickE)\n return dp[start][end][total]\n\n n = len(nums)\n t = sum(nums)\n dp = [[[0]*(t+1) for _ in range(n+1)] for _ in range(n+1)]\n return f(0,n-1,t,dp)\n```\n\n# Tabulation\n```\nclass Solution:\n def stoneGameVII(self, nums: List[int]) -> int:\n n = len(nums)\n total = sum(nums)\n dp = [[0]*(n+1) for _ in range(n+1)]\n front = [0]*(n+1)\n back = [0]*(n+1)\n front[1] = nums[0]\n back[n-1] = nums[n-1]\n # Sum from start to end and end to start\n for i in range(1,n):\n front[i+1] = front[i] + nums[i]\n back[n-1-i] = back[n-i] + nums[n-i-1]\n # note front[0] = 0\n # back[n] = 0\n # for calculation purpose\n for start in range(n-1,-1,-1):\n for end in range(start+1,n,1):\n pickS = (total-(front[start+1]+back[end+1])) - dp[start+1][end]\n pickE = (total-(front[start]+back[end]))- dp[start][end-1]\n dp[start][end] = max(pickS,pickE)\n return dp[0][n-1]\n\n``` | 3 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
Recursion->Memoization->Tabulation | stone-game-vii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n```\nAlice Turn\n [5 3 1 4 2]\n A = 5 + 3 + 1 + 4 = 13 \nBob Turn\n [5 3 1 4]\n B = 3 + 1 + 4 = 8\nAlice Turn\n [3 1 4]\n A = 1 + 4 = 5\nBob Turn\n [1 4]\n B = 4 = 4\nResult\n A = 13 + 5 = 18\n - B = 8 + 4 = 12\n ------------------\n 6\n\n ---> 13 - 8 + 5 - 4 = 6\n can also be written as:\n ---> 13 -(8 - (5-(4)))\n 13 - 8 + (5-(4)) \n 13 - 8 + 5 - 4 = 6\nSo in recursive approach we will just keep subtracting the next Call\n```\n# Recursive Approach\n<!-- Describe your approach to solving the problem. -->\n```\ndef stoneGameVII(self, nums: List[int]) -> int:\n def f(start,end,total):\n if start>=end:return 0 //in recursion this line is not req. but converting this recursion to tabulation this is required\n if total == 0:\n return 0\n pickS = (total-nums[start]) - f(start+1,end,total-nums[start])\n pickE = (total-nums[end]) - f(start,end-1,total-nums[end])\n\n return max(pickS,pickE)\n return f(0,len(nums)-1,sum(nums))\n\n```\n\n# Memoization\n```\ndef stoneGameVII(self, nums: List[int]) -> int:\n def f(start,end,total,dp):\n if start>=end:return 0\n if total == 0:\n return 0\n if dp[start][end][total] != -1:return dp[start][end][total]\n pickS = (total-nums[start]) - f(start+1,end,total-nums[start],dp)\n pickE = (total-nums[end]) - f(start,end-1,total-nums[end],dp)\n\n dp[start][end][total] = max(pickS,pickE)\n return dp[start][end][total]\n\n n = len(nums)\n t = sum(nums)\n dp = [[[0]*(t+1) for _ in range(n+1)] for _ in range(n+1)]\n return f(0,n-1,t,dp)\n```\n\n# Tabulation\n```\nclass Solution:\n def stoneGameVII(self, nums: List[int]) -> int:\n n = len(nums)\n total = sum(nums)\n dp = [[0]*(n+1) for _ in range(n+1)]\n front = [0]*(n+1)\n back = [0]*(n+1)\n front[1] = nums[0]\n back[n-1] = nums[n-1]\n # Sum from start to end and end to start\n for i in range(1,n):\n front[i+1] = front[i] + nums[i]\n back[n-1-i] = back[n-i] + nums[n-i-1]\n # note front[0] = 0\n # back[n] = 0\n # for calculation purpose\n for start in range(n-1,-1,-1):\n for end in range(start+1,n,1):\n pickS = (total-(front[start+1]+back[end+1])) - dp[start+1][end]\n pickE = (total-(front[start]+back[end]))- dp[start][end-1]\n dp[start][end] = max(pickS,pickE)\n return dp[0][n-1]\n\n``` | 3 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
[Python3] Easy code with explanation - DP | stone-game-vii | 0 | 1 | The subproblem for the DP solution is that,\nFor n = 1, Alice or Bob picks the stone and nobody gets any score.\nFor n = 2, the person picks first stone and the score equals second stone or vice versa.\nso on....\n\nNow, that we have the subproblem how do we fill the DP table and fill it with what?\nI thought of 3 choice for entries into the DP table - Alice\'s score, Bob\'s score or **difference of their scores**.\nIt gets messy for the rest so I chose difference of their scores. After zeroing on that, what should be the size of the table?\nEach table entry dp[i][j] signifies the difference in scores between the ith stone and jth stone.\nNow that we know what i and j mean its obvious that we have to find the difference of scores between the 0th stone and nth stone.\n\nOkay, next question that arises is, how do we fill the table entry when its Bob\'s turn and when its Alice\'s turn?\nNote that: the difference of scores is : (sum of scores obtained by Alice) - (sum of scores obtained by Bob)\nWhen its **Bob\'s turn**, his target is to minimize the difference:\n**dp[i][j] = min(dp[i][j-1] - (score after removing jth stone), dp[i+1][j] - (score after removing ith stone))**\n\ndp[i][j] -> Difference in score between ith and jth stone\ndp[i][j-1] -> Difference in score between ith and j-1 th stone\ndp[i+1][j] -> Difference in score between i+1 th and j th stone\n\nThe intuition is to make the negative part larger to minimize the difference.\n\nWhen its **Alice\'s turn**, her target is to maximize the difference:\n**dp[i][j] = min(dp[i][j-1] + (score after removing jth stone), dp[i+1][j] + (score after removing ith stone))**\n\ndp[i][j] -> Difference in score between ith and jth stone\ndp[i][j-1] -> Difference in score between ith and j-1 th stone\ndp[i+1][j] -> Difference in score between i+1 th and j th stone\n\nThe intuition is to make the positive part larger to maximize the difference.\n\nIf even number of stones were removed from the array then the upcoming turn is Alice\'s and similary for Bob odd number of stones must be removed.\n\nThe direction left to right and bottom to top.\n\nExample of DP table for : 5,3,1,4,2\n\n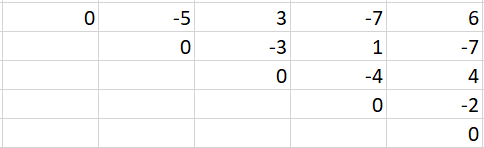\n\nRunning time: O(n^2)\nMemory : O(n^2)\n\nThis question is similar to: https://leetcode.com/problems/stone-game-vi/\n\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n dp = [[0 for _ in range(len(stones))] for _ in range(len(stones))] # dp table n x n\n run_sum = [0] # running sum -> sum [i..j] = run_sum[j] - run_sum[i]\n s = 0\n \n\t\t## Calculation of running sum\n for i in stones:\n s += i\n run_sum.append(s)\n\t\t\n n = len(stones) \n \n for k in range(1, n): # no. of stones left\n for i in range(0, n - k): # from each starting point\n remove_i_stone = (run_sum[i+k+1] - run_sum[i+1]) # score after removing i th stone\n remove_j_stone = (run_sum[i+k] - run_sum[i]) # score after removing j th stone\n \n if (n-(k+1))%2 == 0: # alice\'s move \n dp[i][i+k] = max(remove_i_stone + dp[i+1][i+k],\n remove_j_stone + dp[i][i+k-1])\n else: # bob\'s move\n dp[i][i+k] = min(-remove_i_stone + dp[i+1][i+k],\n - remove_j_stone + dp[i][i+k-1])\n \n return dp[0][n - 1]\n``` | 9 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
[Python3] Easy code with explanation - DP | stone-game-vii | 0 | 1 | The subproblem for the DP solution is that,\nFor n = 1, Alice or Bob picks the stone and nobody gets any score.\nFor n = 2, the person picks first stone and the score equals second stone or vice versa.\nso on....\n\nNow, that we have the subproblem how do we fill the DP table and fill it with what?\nI thought of 3 choice for entries into the DP table - Alice\'s score, Bob\'s score or **difference of their scores**.\nIt gets messy for the rest so I chose difference of their scores. After zeroing on that, what should be the size of the table?\nEach table entry dp[i][j] signifies the difference in scores between the ith stone and jth stone.\nNow that we know what i and j mean its obvious that we have to find the difference of scores between the 0th stone and nth stone.\n\nOkay, next question that arises is, how do we fill the table entry when its Bob\'s turn and when its Alice\'s turn?\nNote that: the difference of scores is : (sum of scores obtained by Alice) - (sum of scores obtained by Bob)\nWhen its **Bob\'s turn**, his target is to minimize the difference:\n**dp[i][j] = min(dp[i][j-1] - (score after removing jth stone), dp[i+1][j] - (score after removing ith stone))**\n\ndp[i][j] -> Difference in score between ith and jth stone\ndp[i][j-1] -> Difference in score between ith and j-1 th stone\ndp[i+1][j] -> Difference in score between i+1 th and j th stone\n\nThe intuition is to make the negative part larger to minimize the difference.\n\nWhen its **Alice\'s turn**, her target is to maximize the difference:\n**dp[i][j] = min(dp[i][j-1] + (score after removing jth stone), dp[i+1][j] + (score after removing ith stone))**\n\ndp[i][j] -> Difference in score between ith and jth stone\ndp[i][j-1] -> Difference in score between ith and j-1 th stone\ndp[i+1][j] -> Difference in score between i+1 th and j th stone\n\nThe intuition is to make the positive part larger to maximize the difference.\n\nIf even number of stones were removed from the array then the upcoming turn is Alice\'s and similary for Bob odd number of stones must be removed.\n\nThe direction left to right and bottom to top.\n\nExample of DP table for : 5,3,1,4,2\n\n\n\nRunning time: O(n^2)\nMemory : O(n^2)\n\nThis question is similar to: https://leetcode.com/problems/stone-game-vi/\n\n```\nclass Solution:\n def stoneGameVII(self, stones: List[int]) -> int:\n dp = [[0 for _ in range(len(stones))] for _ in range(len(stones))] # dp table n x n\n run_sum = [0] # running sum -> sum [i..j] = run_sum[j] - run_sum[i]\n s = 0\n \n\t\t## Calculation of running sum\n for i in stones:\n s += i\n run_sum.append(s)\n\t\t\n n = len(stones) \n \n for k in range(1, n): # no. of stones left\n for i in range(0, n - k): # from each starting point\n remove_i_stone = (run_sum[i+k+1] - run_sum[i+1]) # score after removing i th stone\n remove_j_stone = (run_sum[i+k] - run_sum[i]) # score after removing j th stone\n \n if (n-(k+1))%2 == 0: # alice\'s move \n dp[i][i+k] = max(remove_i_stone + dp[i+1][i+k],\n remove_j_stone + dp[i][i+k-1])\n else: # bob\'s move\n dp[i][i+k] = min(-remove_i_stone + dp[i+1][i+k],\n - remove_j_stone + dp[i][i+k-1])\n \n return dp[0][n - 1]\n``` | 9 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Python3, O(n*n) time O(n) space, bottom-up DP, no prefix, beats 97% | stone-game-vii | 0 | 1 | # Intuition\nThe intuition behind this solution is that the difference in scores between Alice and Bob is actually the sum of the values of the stones removed by Bob. This can be seen by considering each Alice + Bob turn in isolation (if the number of stones is odd, the last turn where only Alice removes a stone does not award her any points so it can be safely ignored). See for instance the explanation for the first A&B turn of the first test case:\n\n - Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = [5,3,1,4].\n- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = [3,1,4].\n\nDuring this A&B turn, the difference in scores has gone from $0-0=0$ to $13-8=5=5+3+1+4-(3+1+4)$, meaning that because the sums cancel out in this way, only the value of the stone removed by Bob has an impact on the difference between scores.\n\nLet\'s look at the second turn of this test case:\n- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = [1,4].\n- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = [4].\n\nDuring this turn, the difference in scores has gone from $13-8=5$ to $18-12=6$. The increase in the difference is thus $1=1+4-4$. The final difference in score is $6=5+1$, the sum of the values of the stones removed by Bob. Note how the last stone removed by Alice does not change the total difference in scores.\n\nThis intuition can be formalized by writing out the sums cleanly and canceling them out.\n\n# Approach\nBased on the intuition above, the problem reduces to maximizing/minimizing the value of the stones removed by Bob only.\n\nWe do so using a bottom-up DP approach: for each possible number of remaining stones >=1, we compute, for each possible list of remaining stones of this length, the value of the stones that Bob would remove from these stones assuming that A & B play optimally, taking into account whose turn it is.\n\nSuppose for instance that the initial stones are [1, 2, 3, 4]. Then for our first step, the possible lists of remaining stones (after Alice, then Bob, then Alice have played) is [1], [2], [3], and [4]. Then, since it is Bob\'s turn, he has to remove a stone from each list, so our initial dp is dp[1] = [1, 2, 3, 4], corresponding to the value of each stone removed by Bob.\n\nIf however our initial stones are [1, 2, 3], then in our first step, the possible list of stones are similarly [1], [2] and [3], but this time it\'s Alice\'s turn, meaning the value of stones removed by Bob from these lists is 0 for each. This means that our initial dp is dp[1] = [0, 0, 0].\n\nLet\'s know consider one step of the algorithm, i.e. how to go from x remaining stones to x+1 remaining stones. When it\'s Alice\'s turn, she will simply pick the stone which maximizes the value of the stones picked by Bob from the remaining stones, which we have computed in the previous step i.e. dp[x+1][i] = max(dp[x][i], dp[x][i+1]). When it\'s Bob\'s turn, he tries to minimize both the value of the stone he removes and the value of the stone he will have to remove in the future, i.e. dp[x+1][i] = min(dp[x][i] + stones[i + x], dp[x][i + 1] + stones[i]).\n\nThe final value is then dp[0] after having applied this algorithm len(stones) times.\n\nSince dp[x+1][i] only uses dp[x][i] and dp[x][i+1], if we compute dp[x+1][i] with increasing i, once we compute dp[x+1][i] we can discard the value of dp[x][i], meaning we can use a 1D array where we replace the value of dp[x][i] by dp[x+1][i] instead of a 2D array, allowing us to go from $O(n^2)$ to $O(n)$ space.\n\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, stones: list[int]) -> int:\n nb_stones = len(stones)\n if nb_stones % 2 == 0:\n dp = list(stones)\n for interval_length in range(1, nb_stones, 2):\n for i in range(nb_stones - interval_length):\n dp[i] = max(dp[i], dp[i + 1])\n for i in range(nb_stones - interval_length - 1):\n dp[i] = min(stones[i] + dp[i + 1], stones[i + interval_length + 1] + dp[i])\n dp[0] = max(dp[0], dp[1])\n else:\n dp = [0] * nb_stones\n for interval_length in range(1, nb_stones, 2):\n for i in range(nb_stones - interval_length):\n dp[i] = min(stones[i] + dp[i + 1], stones[i + interval_length] + dp[i])\n for i in range(nb_stones - interval_length - 1):\n dp[i] = max(dp[i], dp[i + 1])\n\n return dp[0]\n```\n\nSince we start from the bottom, and each step of the algorithm depends on whose turn this is, I needed to split the cases depending on whether Alice or Bob plays last. If someone finds out how to combine the two, it would be much appreciated! | 0 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
Python3, O(n*n) time O(n) space, bottom-up DP, no prefix, beats 97% | stone-game-vii | 0 | 1 | # Intuition\nThe intuition behind this solution is that the difference in scores between Alice and Bob is actually the sum of the values of the stones removed by Bob. This can be seen by considering each Alice + Bob turn in isolation (if the number of stones is odd, the last turn where only Alice removes a stone does not award her any points so it can be safely ignored). See for instance the explanation for the first A&B turn of the first test case:\n\n - Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = [5,3,1,4].\n- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = [3,1,4].\n\nDuring this A&B turn, the difference in scores has gone from $0-0=0$ to $13-8=5=5+3+1+4-(3+1+4)$, meaning that because the sums cancel out in this way, only the value of the stone removed by Bob has an impact on the difference between scores.\n\nLet\'s look at the second turn of this test case:\n- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = [1,4].\n- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = [4].\n\nDuring this turn, the difference in scores has gone from $13-8=5$ to $18-12=6$. The increase in the difference is thus $1=1+4-4$. The final difference in score is $6=5+1$, the sum of the values of the stones removed by Bob. Note how the last stone removed by Alice does not change the total difference in scores.\n\nThis intuition can be formalized by writing out the sums cleanly and canceling them out.\n\n# Approach\nBased on the intuition above, the problem reduces to maximizing/minimizing the value of the stones removed by Bob only.\n\nWe do so using a bottom-up DP approach: for each possible number of remaining stones >=1, we compute, for each possible list of remaining stones of this length, the value of the stones that Bob would remove from these stones assuming that A & B play optimally, taking into account whose turn it is.\n\nSuppose for instance that the initial stones are [1, 2, 3, 4]. Then for our first step, the possible lists of remaining stones (after Alice, then Bob, then Alice have played) is [1], [2], [3], and [4]. Then, since it is Bob\'s turn, he has to remove a stone from each list, so our initial dp is dp[1] = [1, 2, 3, 4], corresponding to the value of each stone removed by Bob.\n\nIf however our initial stones are [1, 2, 3], then in our first step, the possible list of stones are similarly [1], [2] and [3], but this time it\'s Alice\'s turn, meaning the value of stones removed by Bob from these lists is 0 for each. This means that our initial dp is dp[1] = [0, 0, 0].\n\nLet\'s know consider one step of the algorithm, i.e. how to go from x remaining stones to x+1 remaining stones. When it\'s Alice\'s turn, she will simply pick the stone which maximizes the value of the stones picked by Bob from the remaining stones, which we have computed in the previous step i.e. dp[x+1][i] = max(dp[x][i], dp[x][i+1]). When it\'s Bob\'s turn, he tries to minimize both the value of the stone he removes and the value of the stone he will have to remove in the future, i.e. dp[x+1][i] = min(dp[x][i] + stones[i + x], dp[x][i + 1] + stones[i]).\n\nThe final value is then dp[0] after having applied this algorithm len(stones) times.\n\nSince dp[x+1][i] only uses dp[x][i] and dp[x][i+1], if we compute dp[x+1][i] with increasing i, once we compute dp[x+1][i] we can discard the value of dp[x][i], meaning we can use a 1D array where we replace the value of dp[x][i] by dp[x+1][i] instead of a 2D array, allowing us to go from $O(n^2)$ to $O(n)$ space.\n\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, stones: list[int]) -> int:\n nb_stones = len(stones)\n if nb_stones % 2 == 0:\n dp = list(stones)\n for interval_length in range(1, nb_stones, 2):\n for i in range(nb_stones - interval_length):\n dp[i] = max(dp[i], dp[i + 1])\n for i in range(nb_stones - interval_length - 1):\n dp[i] = min(stones[i] + dp[i + 1], stones[i + interval_length + 1] + dp[i])\n dp[0] = max(dp[0], dp[1])\n else:\n dp = [0] * nb_stones\n for interval_length in range(1, nb_stones, 2):\n for i in range(nb_stones - interval_length):\n dp[i] = min(stones[i] + dp[i + 1], stones[i + interval_length] + dp[i])\n for i in range(nb_stones - interval_length - 1):\n dp[i] = max(dp[i], dp[i + 1])\n\n return dp[0]\n```\n\nSince we start from the bottom, and each step of the algorithm depends on whose turn this is, I needed to split the cases depending on whether Alice or Bob plays last. If someone finds out how to combine the two, it would be much appreciated! | 0 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
[Python] compact solution | stone-game-vii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n`c` is partial sum of original array `s` which gives us sum of points in an interval on `s`. In every turn, a player has two options which are pick the stone on the left `l` or on the right `r`. We should return `max` of these options. If there is one stone which `l == r`, we got no point because we pick the only stone. \n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, s):\n c = [0] + list(accumulate(s))\n @lru_cache(1000)\n def D(l,r):\n return l<r and max(c[r]-c[l+1]-D(l+1,r),c[r-1]-c[l]-D(l,r-1))\n return D(0,len(s))\n\n```\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: $$O(n^2)$$ - *without cache limit*\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 0 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, they can **remove** either the leftmost stone or the rightmost stone from the row and receive points equal to the **sum** of the remaining stones' values in the row. The winner is the one with the higher score when there are no stones left to remove.
Bob found that he will always lose this game (poor Bob, he always loses), so he decided to **minimize the score's difference**. Alice's goal is to **maximize the difference** in the score.
Given an array of integers `stones` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **difference** in Alice and Bob's score if they both play **optimally**._
**Example 1:**
**Input:** stones = \[5,3,1,4,2\]
**Output:** 6
**Explanation:**
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = \[5,3,1,4\].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = \[3,1,4\].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = \[1,4\].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = \[4\].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = \[\].
The score difference is 18 - 12 = 6.
**Example 2:**
**Input:** stones = \[7,90,5,1,100,10,10,2\]
**Output:** 122
**Constraints:**
* `n == stones.length`
* `2 <= n <= 1000`
* `1 <= stones[i] <= 1000` | Split the whole array into subarrays by zeroes since a subarray with positive product cannot contain any zero. If the subarray has even number of negative numbers, the whole subarray has positive product. Otherwise, we have two choices, either - remove the prefix till the first negative element in this subarray, or remove the suffix starting from the last negative element in this subarray. |
[Python] compact solution | stone-game-vii | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n`c` is partial sum of original array `s` which gives us sum of points in an interval on `s`. In every turn, a player has two options which are pick the stone on the left `l` or on the right `r`. We should return `max` of these options. If there is one stone which `l == r`, we got no point because we pick the only stone. \n\n# Code\n```\nclass Solution:\n def stoneGameVII(self, s):\n c = [0] + list(accumulate(s))\n @lru_cache(1000)\n def D(l,r):\n return l<r and max(c[r]-c[l+1]-D(l+1,r),c[r-1]-c[l]-D(l,r-1))\n return D(0,len(s))\n\n```\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: $$O(n^2)$$ - *without cache limit*\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 0 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
python with clean explanation with example(dp with sort) | maximum-height-by-stacking-cuboids | 0 | 1 | **a brief explanation on how code works:**\n consider example: [[50,45,20],[95,37,53],[45,23,12]]\n* at first we are assigning length of cubiods list to n (=3)\n* initializing dp arrray with 0 values of length n \n\t\t\t\t\t\tdp[3] = [0, 0, 0]\n* we are sorting the inner lists in order to get maximum height since it is given the cuboid can be rotated \n on running code the example becomes \n \n\t\t\t\t\t\t\t\t[[20,45,50] , [ 37,53,95] , [12,23,45]]\n* now we are sorting the cuboid\n then the above example .. \n\t \n\t\t\t\t\t\t\t\t [ [12,23,45], [20,45,50] , [ 37,53,95] ] (this sorting is based on element at 0th position in each inner list)\n*\twe intialize dp[i] value to the cuboid ( ith position ) height present.\n* now in for loop we check for length and height (since already width is in ascending order we dont check it)\n* now we enter to main line of code....\n \n\t\t\t\t dp[i] = max(dp[i],dp[j]+cuboids[i][2])\n to explain what happens at for loop\n \n\t\tat i =0 dp[0] = [45]\n it wont enter inner loop\n\t\t\t \n**next iteration**\n\t\t\t \n\t\tat i = 1 dp[1] = [ 50 ] dp = [45,50,0]\n for j in range(1):\n\t\t\t j=0\n\t\t\t\t dp[1] = max(50, 45 + 50 ) = 95\n**next iteration**\n\n\t\tat i = 2 dp[2] =[95] dp = [45 , 95 , 95]\n for j in range(2):\n\t\t\t\t at j = 0 dp [2] = max(95, 45+95) = 140\n\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\tdp = [45,95,140]\n\t\t\t\t\t\tat j = 1 dp [2] = max(140, 95+95) = 190\n\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\tdp = [45,95,190]\n\t\n* now returns max(dp) and the answer is 190\n\n**if there is any mistake in above explanation report me back (as i need to find my mistake while explanation)**\n\n**upvote if u like my explanation**\n\n```\nclass Solution:\n def maxHeight(self, cuboids: List[List[int]]) -> int:\n n = len(cuboids)\n \n dp = [0]*n\n for c in cuboids:\n c.sort()\n cuboids.sort()\n \n for i in range(n):\n dp[i] = cuboids[i][2]\n for j in range(i):\n if cuboids[j][1] <= cuboids[i][1] and cuboids[j][2] <= cuboids[i][2]:\n dp[i] = max(dp[i],dp[j]+cuboids[i][2])\n \n return max(dp)\n\t\t\n\n```\n\n\n\n | 0 | Given a binary tree `root` and a linked list with `head` as the first node.
Return True if all the elements in the linked list starting from the `head` correspond to some _downward path_ connected in the binary tree otherwise return False.
In this context downward path means a path that starts at some node and goes downwards.
**Example 1:**
**Input:** head = \[4,2,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Explanation:** Nodes in blue form a subpath in the binary Tree.
**Example 2:**
**Input:** head = \[1,4,2,6\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Example 3:**
**Input:** head = \[1,4,2,6,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** false
**Explanation:** There is no path in the binary tree that contains all the elements of the linked list from `head`.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 2500]`.
* The number of nodes in the list will be in the range `[1, 100]`.
* `1 <= Node.val <= 100` for each node in the linked list and binary tree. | Does the dynamic programming sound like the right algorithm after sorting? Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest? |
python with clean explanation with example(dp with sort) | maximum-height-by-stacking-cuboids | 0 | 1 | **a brief explanation on how code works:**\n consider example: [[50,45,20],[95,37,53],[45,23,12]]\n* at first we are assigning length of cubiods list to n (=3)\n* initializing dp arrray with 0 values of length n \n\t\t\t\t\t\tdp[3] = [0, 0, 0]\n* we are sorting the inner lists in order to get maximum height since it is given the cuboid can be rotated \n on running code the example becomes \n \n\t\t\t\t\t\t\t\t[[20,45,50] , [ 37,53,95] , [12,23,45]]\n* now we are sorting the cuboid\n then the above example .. \n\t \n\t\t\t\t\t\t\t\t [ [12,23,45], [20,45,50] , [ 37,53,95] ] (this sorting is based on element at 0th position in each inner list)\n*\twe intialize dp[i] value to the cuboid ( ith position ) height present.\n* now in for loop we check for length and height (since already width is in ascending order we dont check it)\n* now we enter to main line of code....\n \n\t\t\t\t dp[i] = max(dp[i],dp[j]+cuboids[i][2])\n to explain what happens at for loop\n \n\t\tat i =0 dp[0] = [45]\n it wont enter inner loop\n\t\t\t \n**next iteration**\n\t\t\t \n\t\tat i = 1 dp[1] = [ 50 ] dp = [45,50,0]\n for j in range(1):\n\t\t\t j=0\n\t\t\t\t dp[1] = max(50, 45 + 50 ) = 95\n**next iteration**\n\n\t\tat i = 2 dp[2] =[95] dp = [45 , 95 , 95]\n for j in range(2):\n\t\t\t\t at j = 0 dp [2] = max(95, 45+95) = 140\n\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\tdp = [45,95,140]\n\t\t\t\t\t\tat j = 1 dp [2] = max(140, 95+95) = 190\n\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\tdp = [45,95,190]\n\t\n* now returns max(dp) and the answer is 190\n\n**if there is any mistake in above explanation report me back (as i need to find my mistake while explanation)**\n\n**upvote if u like my explanation**\n\n```\nclass Solution:\n def maxHeight(self, cuboids: List[List[int]]) -> int:\n n = len(cuboids)\n \n dp = [0]*n\n for c in cuboids:\n c.sort()\n cuboids.sort()\n \n for i in range(n):\n dp[i] = cuboids[i][2]\n for j in range(i):\n if cuboids[j][1] <= cuboids[i][1] and cuboids[j][2] <= cuboids[i][2]:\n dp[i] = max(dp[i],dp[j]+cuboids[i][2])\n \n return max(dp)\n\t\t\n\n```\n\n\n\n | 0 | You are given an m x n binary grid grid where 1 represents land and 0 represents water. An island is a maximal 4-directionally (horizontal or vertical) connected group of 1's. The grid is said to be connected if we have exactly one island, otherwise is said disconnected. In one day, we are allowed to change any single land cell (1) into a water cell (0). Return the minimum number of days to disconnect the grid. | Return 0 if the grid is already disconnected. Return 1 if changing a single land to water disconnect the island. Otherwise return 2. We can disconnect the grid within at most 2 days. |
Python 3 | DP, Sort, O(N^2) | Explanation | maximum-height-by-stacking-cuboids | 0 | 1 | ### Explanation\n- Sort each cub\'s length, width, height from small to large\n- Sort cub by length, width, height from large to small\n- Initialize a 1-D dp array, `dp[i] = largest height if put cuboids[i] at the top`\n- Iterate over cuboids, from large to small; try get the largest height by putting itself on previous cube `cub[j] (j < i)`\n- Record height while iterating and return the maximum height\n- Time: `O(N*N)`\n- Space: `O(N)`\n### Implementation\n```\nclass Solution:\n def maxHeight(self, cuboids: List[List[int]]) -> int:\n cuboids = sorted([sorted(cub) for cub in cuboids], reverse=True) # sort LxWxH in cube, then sort cube reversely\n ok = lambda x, y: (x[0] >= y[0] and x[1] >= y[1] and x[2] >= y[2]) # make a lambda function to verify whether y can be put on top of x\n n = len(cuboids)\n dp = [cu[2] for cu in cuboids] # create dp array\n ans = max(dp)\n for i in range(1, n): # iterate over each cube\n for j in range(i): # compare with previous calculated cube\n if ok(cuboids[j], cuboids[i]): # update dp[i] if cube[i] can be put on top of cube[j]\n dp[i] = max(dp[i], dp[j] + cuboids[i][2]) # always get the maximum\n ans = max(ans, dp[i]) # record the largest value\n return ans\n``` | 7 | Given a binary tree `root` and a linked list with `head` as the first node.
Return True if all the elements in the linked list starting from the `head` correspond to some _downward path_ connected in the binary tree otherwise return False.
In this context downward path means a path that starts at some node and goes downwards.
**Example 1:**
**Input:** head = \[4,2,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Explanation:** Nodes in blue form a subpath in the binary Tree.
**Example 2:**
**Input:** head = \[1,4,2,6\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** true
**Example 3:**
**Input:** head = \[1,4,2,6,8\], root = \[1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3\]
**Output:** false
**Explanation:** There is no path in the binary tree that contains all the elements of the linked list from `head`.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 2500]`.
* The number of nodes in the list will be in the range `[1, 100]`.
* `1 <= Node.val <= 100` for each node in the linked list and binary tree. | Does the dynamic programming sound like the right algorithm after sorting? Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest? |
Python 3 | DP, Sort, O(N^2) | Explanation | maximum-height-by-stacking-cuboids | 0 | 1 | ### Explanation\n- Sort each cub\'s length, width, height from small to large\n- Sort cub by length, width, height from large to small\n- Initialize a 1-D dp array, `dp[i] = largest height if put cuboids[i] at the top`\n- Iterate over cuboids, from large to small; try get the largest height by putting itself on previous cube `cub[j] (j < i)`\n- Record height while iterating and return the maximum height\n- Time: `O(N*N)`\n- Space: `O(N)`\n### Implementation\n```\nclass Solution:\n def maxHeight(self, cuboids: List[List[int]]) -> int:\n cuboids = sorted([sorted(cub) for cub in cuboids], reverse=True) # sort LxWxH in cube, then sort cube reversely\n ok = lambda x, y: (x[0] >= y[0] and x[1] >= y[1] and x[2] >= y[2]) # make a lambda function to verify whether y can be put on top of x\n n = len(cuboids)\n dp = [cu[2] for cu in cuboids] # create dp array\n ans = max(dp)\n for i in range(1, n): # iterate over each cube\n for j in range(i): # compare with previous calculated cube\n if ok(cuboids[j], cuboids[i]): # update dp[i] if cube[i] can be put on top of cube[j]\n dp[i] = max(dp[i], dp[j] + cuboids[i][2]) # always get the maximum\n ans = max(ans, dp[i]) # record the largest value\n return ans\n``` | 7 | You are given an m x n binary grid grid where 1 represents land and 0 represents water. An island is a maximal 4-directionally (horizontal or vertical) connected group of 1's. The grid is said to be connected if we have exactly one island, otherwise is said disconnected. In one day, we are allowed to change any single land cell (1) into a water cell (0). Return the minimum number of days to disconnect the grid. | Return 0 if the grid is already disconnected. Return 1 if changing a single land to water disconnect the island. Otherwise return 2. We can disconnect the grid within at most 2 days. |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | daily-leads-and-partners | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef daily_leads_and_partners(daily_sales: pd.DataFrame) -> pd.DataFrame:\n return daily_sales.groupby(\n [\'date_id\', \'make_name\']\n ).nunique().reset_index().rename(columns={\n \'lead_id\': \'unique_leads\',\n \'partner_id\': \'unique_partners\',\n })\n```\n```SQL []\nSELECT date_id,\n make_name,\n count(DISTINCT lead_id) AS unique_leads,\n count(DISTINCT partner_id) AS unique_partners\n FROM DailySales\n GROUP BY date_id,\n make_name;\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n | 20 | Given an integer `n` (in base `10`) and a base `k`, return _the **sum** of the digits of_ `n` _**after** converting_ `n` _from base_ `10` _to base_ `k`.
After converting, each digit should be interpreted as a base `10` number, and the sum should be returned in base `10`.
**Example 1:**
**Input:** n = 34, k = 6
**Output:** 9
**Explanation:** 34 (base 10) expressed in base 6 is 54. 5 + 4 = 9.
**Example 2:**
**Input:** n = 10, k = 10
**Output:** 1
**Explanation:** n is already in base 10. 1 + 0 = 1.
**Constraints:**
* `1 <= n <= 100`
* `2 <= k <= 10` | null |
✅ Pandas Simple Step By Step Solution For Beginners 🔥💯 | daily-leads-and-partners | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n```\nimport pandas as pd\n\ndef daily_leads_and_partners(daily_sales: pd.DataFrame) -> pd.DataFrame:\n \n result = daily_sales.groupby([\'date_id\', \'make_name\']).nunique().reset_index()\n \n result.columns = [\'date_id\', \'make_name\', \'unique_leads\', \'unique_partners\']\n \n return result\n\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 2 | Given an integer `n` (in base `10`) and a base `k`, return _the **sum** of the digits of_ `n` _**after** converting_ `n` _from base_ `10` _to base_ `k`.
After converting, each digit should be interpreted as a base `10` number, and the sum should be returned in base `10`.
**Example 1:**
**Input:** n = 34, k = 6
**Output:** 9
**Explanation:** 34 (base 10) expressed in base 6 is 54. 5 + 4 = 9.
**Example 2:**
**Input:** n = 10, k = 10
**Output:** 1
**Explanation:** n is already in base 10. 1 + 0 = 1.
**Constraints:**
* `1 <= n <= 100`
* `2 <= k <= 10` | null |
Beginer Friendly solution Python3 Beat 92% O(n) | reformat-phone-number | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number, a, i = (number.replace(\' \', \'\').replace(\'-\', \'\')), \'\', 0\n n = len(number)\n while n > 0:\n if n > 4 or n == 3:\n j = i + 3\n if j != len(number): a += number[i:j] + \'-\'\n else: a += number[i:j] \n i = j\n n -= 3\n elif n == 4 or n == 2:\n j = i + 2\n if j != len(number): a += number[i:j] + \'-\'\n else: a += number[i:j] \n i = j\n n -= 2\n return a\n``` | 1 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Beginer Friendly solution Python3 Beat 92% O(n) | reformat-phone-number | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number, a, i = (number.replace(\' \', \'\').replace(\'-\', \'\')), \'\', 0\n n = len(number)\n while n > 0:\n if n > 4 or n == 3:\n j = i + 3\n if j != len(number): a += number[i:j] + \'-\'\n else: a += number[i:j] \n i = j\n n -= 3\n elif n == 4 or n == 2:\n j = i + 2\n if j != len(number): a += number[i:j] + \'-\'\n else: a += number[i:j] \n i = j\n n -= 2\n return a\n``` | 1 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
Python Easy to Understand | reformat-phone-number | 0 | 1 | # Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n res=[]\n new=""\n for i in number:\n if i!=" " and i!="-":\n res.append(i)\n n=len(res)\n while(n>4):\n s="".join(res[:3])\n res=res[3:]\n n-=3\n new=new+s+"-"\n if len(res)==3 or len(res)==2:\n new=new+"".join(res)\n if len(res)==4:\n s1="".join(res[:2])\n s2="".join(res[2:])\n new=new+s1+"-"+s2\n return new\n \n \n \n \n``` | 1 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Python Easy to Understand | reformat-phone-number | 0 | 1 | # Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n res=[]\n new=""\n for i in number:\n if i!=" " and i!="-":\n res.append(i)\n n=len(res)\n while(n>4):\n s="".join(res[:3])\n res=res[3:]\n n-=3\n new=new+s+"-"\n if len(res)==3 or len(res)==2:\n new=new+"".join(res)\n if len(res)==4:\n s1="".join(res[:2])\n s2="".join(res[2:])\n new=new+s1+"-"+s2\n return new\n \n \n \n \n``` | 1 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
Simple and Easy Python Code | reformat-phone-number | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(n)\n\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number = number.strip()\n no=\'\'\n\n for i in number:\n if i>=chr(48) and i <=chr(57):\n no=no+i\n \n number=no\n l,i = len(number),0\n no=\'\'\n\n while(i<len(number)): \n if l>4:\n no=no+number[i]+number[i+1]+number[i+2]\n no=no+\'-\'\n l-=3\n i+=3\n\n if l==3:\n no=no+number[i]+number[i+1]+number[i+2]\n l-=3\n i+=3\n\n if l==4 or l==2:\n no=no+number[i]+number[i+1]\n if l!=2:\n no=no+\'-\'\n l-=2\n i+=2\n return no\n``` | 2 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Simple and Easy Python Code | reformat-phone-number | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(n)\n\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number = number.strip()\n no=\'\'\n\n for i in number:\n if i>=chr(48) and i <=chr(57):\n no=no+i\n \n number=no\n l,i = len(number),0\n no=\'\'\n\n while(i<len(number)): \n if l>4:\n no=no+number[i]+number[i+1]+number[i+2]\n no=no+\'-\'\n l-=3\n i+=3\n\n if l==3:\n no=no+number[i]+number[i+1]+number[i+2]\n l-=3\n i+=3\n\n if l==4 or l==2:\n no=no+number[i]+number[i+1]\n if l!=2:\n no=no+\'-\'\n l-=2\n i+=2\n return no\n``` | 2 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
[Python3] string processing | reformat-phone-number | 0 | 1 | **Algo**\nCheck the special case of 4 letters remaining. \n\n**Implementation**\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number = number.replace("-", "").replace(" ", "") # removing - and space \n ans = []\n for i in range(0, len(number), 3): \n if len(number) - i != 4: ans.append(number[i:i+3])\n else: \n ans.extend([number[i:i+2], number[i+2:]])\n break \n return "-".join(ans)\n```\n\n**Analysis**\nTime complexity `O(N)`\nSpace complexity `O(N)` | 18 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
[Python3] string processing | reformat-phone-number | 0 | 1 | **Algo**\nCheck the special case of 4 letters remaining. \n\n**Implementation**\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number = number.replace("-", "").replace(" ", "") # removing - and space \n ans = []\n for i in range(0, len(number), 3): \n if len(number) - i != 4: ans.append(number[i:i+3])\n else: \n ans.extend([number[i:i+2], number[i+2:]])\n break \n return "-".join(ans)\n```\n\n**Analysis**\nTime complexity `O(N)`\nSpace complexity `O(N)` | 18 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
O(n) in Python | reformat-phone-number | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n num = number.replace(\' \', \'\').replace(\'-\', \'\')\n ans = \'\'\n while len(num) > 4:\n if ans:\n ans += \'-\'\n ans += num[0:3]\n num = num[3:]\n if len(num) == 4:\n if ans:\n ans += \'-\'\n ans += \'\'.join([num[0:2], \'-\', num[2:]])\n else:\n if ans:\n ans += \'-\'\n ans += \'\'.join(num[0:len(num)])\n return ans\n``` | 1 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
O(n) in Python | reformat-phone-number | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n num = number.replace(\' \', \'\').replace(\'-\', \'\')\n ans = \'\'\n while len(num) > 4:\n if ans:\n ans += \'-\'\n ans += num[0:3]\n num = num[3:]\n if len(num) == 4:\n if ans:\n ans += \'-\'\n ans += \'\'.join([num[0:2], \'-\', num[2:]])\n else:\n if ans:\n ans += \'-\'\n ans += \'\'.join(num[0:len(num)])\n return ans\n``` | 1 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
Python Solution using Minimal New Variables (+ Explanation for Logic) | reformat-phone-number | 0 | 1 | My first attempt at this problem utilized separating the string into an array and while that works, it\'s clearly not the intended solution. This function instead works by overwriting the existing string input and outputting the necessary values into another string to be returned. Leetcode keeps flip-flopping on just how effective of a solution this is, however I find it to be a fairly memory-efficient one that also is easy to follow and write (I\'ve included extensive comments to explain the process for anyone confused)\n\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n\t\t# Written by LeetCode user DyHorowitz\n # remove the unnecessary characters - we don\'t care about the dashes nor spaces\n number = number.replace(\'-\', \'\')\n number = number.replace(\' \', \'\')\n \n # set up a return string to store our answer into\n returnString = ""\n \n # So long as there are more than 4 digits in number,\n # we want to group the first 3 into our return string\n # followed by a dash, then remove those 3 from the initial string\n while len(number) > 4:\n returnString += number[0:3] + "-"\n number = number[3:]\n \n # If there are only three digits left, we just put them all into \n # the return string and are done\n if len(number) == 3:\n returnString += number[0:3]\n \n # A remainder of 4 or 2 will result in blocks of 2, so\n # we might as well combine these two possibilities \n # for the first part and save some computing time\n else:\n returnString += number[0:2]\n number = number[2:]\n \n # This is where we test if there were 4 or 2 digits \n # left over. If there were 2, then removing the last\n # 2 in the step above should leave us with a string\n # of length 0\n if len(number) > 0:\n returnString += "-" + number\n \n # Note that we only created ONE new variable in this entire function:\n # "returnString". By having \'number\' overwrite itself, we save\n # significantly on memory space (you could probably save even more)\n # by using recursion to avoid storing any variables, however\n # that may come at the cost of processing time\n return returnString\n``` | 2 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Python Solution using Minimal New Variables (+ Explanation for Logic) | reformat-phone-number | 0 | 1 | My first attempt at this problem utilized separating the string into an array and while that works, it\'s clearly not the intended solution. This function instead works by overwriting the existing string input and outputting the necessary values into another string to be returned. Leetcode keeps flip-flopping on just how effective of a solution this is, however I find it to be a fairly memory-efficient one that also is easy to follow and write (I\'ve included extensive comments to explain the process for anyone confused)\n\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n\t\t# Written by LeetCode user DyHorowitz\n # remove the unnecessary characters - we don\'t care about the dashes nor spaces\n number = number.replace(\'-\', \'\')\n number = number.replace(\' \', \'\')\n \n # set up a return string to store our answer into\n returnString = ""\n \n # So long as there are more than 4 digits in number,\n # we want to group the first 3 into our return string\n # followed by a dash, then remove those 3 from the initial string\n while len(number) > 4:\n returnString += number[0:3] + "-"\n number = number[3:]\n \n # If there are only three digits left, we just put them all into \n # the return string and are done\n if len(number) == 3:\n returnString += number[0:3]\n \n # A remainder of 4 or 2 will result in blocks of 2, so\n # we might as well combine these two possibilities \n # for the first part and save some computing time\n else:\n returnString += number[0:2]\n number = number[2:]\n \n # This is where we test if there were 4 or 2 digits \n # left over. If there were 2, then removing the last\n # 2 in the step above should leave us with a string\n # of length 0\n if len(number) > 0:\n returnString += "-" + number\n \n # Note that we only created ONE new variable in this entire function:\n # "returnString". By having \'number\' overwrite itself, we save\n # significantly on memory space (you could probably save even more)\n # by using recursion to avoid storing any variables, however\n # that may come at the cost of processing time\n return returnString\n``` | 2 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
Python Solution Easy To Read!! | reformat-phone-number | 0 | 1 | \n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n \n number = number.replace(" ","").replace("-","")\n phone: list = [number[index: index + 3] for index in range(0, len(number), 3)] \n \n if len(phone[-1]) == 1:\n phone[-2:] = [phone[-2][:-1], phone[-2][-1] + phone[-1]]\n \n return "-".join(phone)\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Python Solution Easy To Read!! | reformat-phone-number | 0 | 1 | \n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n \n number = number.replace(" ","").replace("-","")\n phone: list = [number[index: index + 3] for index in range(0, len(number), 3)] \n \n if len(phone[-1]) == 1:\n phone[-2:] = [phone[-2][:-1], phone[-2][-1] + phone[-1]]\n \n return "-".join(phone)\n``` | 0 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
Python solution | reformat-phone-number | 0 | 1 | ```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n numbers: str = "".join([number for number in number if number not in [" ", "-"]])\n packages: list[str] = []\n\n for i in range(0, len(numbers), 3):\n packages.append(numbers[i: i + 3])\n\n if len(packages[-1]) == 1:\n packages[-2:] = [packages[-2][:2], packages[-2][2] + packages[-1]]\n\n return "-".join(packages)\n\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Python solution | reformat-phone-number | 0 | 1 | ```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n numbers: str = "".join([number for number in number if number not in [" ", "-"]])\n packages: list[str] = []\n\n for i in range(0, len(numbers), 3):\n packages.append(numbers[i: i + 3])\n\n if len(packages[-1]) == 1:\n packages[-2:] = [packages[-2][:2], packages[-2][2] + packages[-1]]\n\n return "-".join(packages)\n\n``` | 0 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
Python3 Solution | reformat-phone-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number = number.replace(\'-\', \'\')\n number = number.replace(\' \', \'\')\n result = \'\'\n while True: \n if len(number) > 4: \n result += number[:3] + "-"\n number = number[3:]\n elif len(number) == 4: \n result += number[:2] + "-"\n result += number[2:]\n break\n else: \n result += number\n break \n return result \n\n``` | 0 | You are given a phone number as a string `number`. `number` consists of digits, spaces `' '`, and/or dashes `'-'`.
You would like to reformat the phone number in a certain manner. Firstly, **remove** all spaces and dashes. Then, **group** the digits from left to right into blocks of length 3 **until** there are 4 or fewer digits. The final digits are then grouped as follows:
* 2 digits: A single block of length 2.
* 3 digits: A single block of length 3.
* 4 digits: Two blocks of length 2 each.
The blocks are then joined by dashes. Notice that the reformatting process should **never** produce any blocks of length 1 and produce **at most** two blocks of length 2.
Return _the phone number after formatting._
**Example 1:**
**Input:** number = "1-23-45 6 "
**Output:** "123-456 "
**Explanation:** The digits are "123456 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456 ".
Joining the blocks gives "123-456 ".
**Example 2:**
**Input:** number = "123 4-567 "
**Output:** "123-45-67 "
**Explanation:** The digits are "1234567 ".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123 ".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45 " and "67 ".
Joining the blocks gives "123-45-67 ".
**Example 3:**
**Input:** number = "123 4-5678 "
**Output:** "123-456-78 "
**Explanation:** The digits are "12345678 ".
Step 1: The 1st block is "123 ".
Step 2: The 2nd block is "456 ".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78 ".
Joining the blocks gives "123-456-78 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits and the characters `'-'` and `' '`.
* There are at least **two** digits in `number`. | Use prefix sums to calculate the subarray sums. Suppose you know the remainder for the sum of the entire array. How does removing a subarray affect that remainder? What remainder does the subarray need to have in order to make the rest of the array sum up to be divisible by k? Use a map to keep track of the rightmost index for every prefix sum % p. |
Python3 Solution | reformat-phone-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformatNumber(self, number: str) -> str:\n number = number.replace(\'-\', \'\')\n number = number.replace(\' \', \'\')\n result = \'\'\n while True: \n if len(number) > 4: \n result += number[:3] + "-"\n number = number[3:]\n elif len(number) == 4: \n result += number[:2] + "-"\n result += number[2:]\n break\n else: \n result += number\n break \n return result \n\n``` | 0 | You are given `coordinates`, a string that represents the coordinates of a square of the chessboard. Below is a chessboard for your reference.
Return `true` _if the square is white, and_ `false` _if the square is black_.
The coordinate will always represent a valid chessboard square. The coordinate will always have the letter first, and the number second.
**Example 1:**
**Input:** coordinates = "a1 "
**Output:** false
**Explanation:** From the chessboard above, the square with coordinates "a1 " is black, so return false.
**Example 2:**
**Input:** coordinates = "h3 "
**Output:** true
**Explanation:** From the chessboard above, the square with coordinates "h3 " is white, so return true.
**Example 3:**
**Input:** coordinates = "c7 "
**Output:** false
**Constraints:**
* `coordinates.length == 2`
* `'a' <= coordinates[0] <= 'h'`
* `'1' <= coordinates[1] <= '8'` | Discard all the spaces and dashes. Use a while loop. While the string still has digits, check its length and see which rule to apply. |
✅ Python Easy 2 approaches | maximum-erasure-value | 0 | 1 | ## \u2714\uFE0F*Solution I - Two pointers using Counter*\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n counter=defaultdict(int) # track count of elements in the window\n res=i=tot=0\n\t\t\n for j in range(len(nums)):\n x=nums[j] \n tot+=x\n counter[x]+=1\n # adjust the left bound of sliding window until you get all unique elements\n while i < j and counter[x]>1: \n counter[nums[i]]-=1\n tot-=nums[i]\n i+=1\n \n res=max(res, tot) \n return res\n```\n\n## \u2714\uFE0F*Solution II - Two pointers using Visited*\n\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n seen=set() # track visited elements in the window\n res=i=tot=0\n for j in range(len(nums)):\n x=nums[j] \n\t\t\t # adjust the left bound of sliding window until you get all unique elements\n while i < j and x in seen: \n seen.remove(nums[i])\n tot-=nums[i]\n i+=1 \n tot+=x\n seen.add(x)\n res=max(res, tot) \n return res\n```\n\n**Time - O(n)**\n**Space - O(k)** - where` k` is number of unique elements in input `nums`.\n\n\n---\n\n\n***Please upvote if you find it useful*** | 18 | You are given an array of positive integers `nums` and want to erase a subarray containing **unique elements**. The **score** you get by erasing the subarray is equal to the **sum** of its elements.
Return _the **maximum score** you can get by erasing **exactly one** subarray._
An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
**Example 1:**
**Input:** nums = \[4,2,4,5,6\]
**Output:** 17
**Explanation:** The optimal subarray here is \[2,4,5,6\].
**Example 2:**
**Input:** nums = \[5,2,1,2,5,2,1,2,5\]
**Output:** 8
**Explanation:** The optimal subarray here is \[5,2,1\] or \[1,2,5\].
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | Indexes with higher frequencies should be bound with larger values |
✅ Python Easy 2 approaches | maximum-erasure-value | 0 | 1 | ## \u2714\uFE0F*Solution I - Two pointers using Counter*\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n counter=defaultdict(int) # track count of elements in the window\n res=i=tot=0\n\t\t\n for j in range(len(nums)):\n x=nums[j] \n tot+=x\n counter[x]+=1\n # adjust the left bound of sliding window until you get all unique elements\n while i < j and counter[x]>1: \n counter[nums[i]]-=1\n tot-=nums[i]\n i+=1\n \n res=max(res, tot) \n return res\n```\n\n## \u2714\uFE0F*Solution II - Two pointers using Visited*\n\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n seen=set() # track visited elements in the window\n res=i=tot=0\n for j in range(len(nums)):\n x=nums[j] \n\t\t\t # adjust the left bound of sliding window until you get all unique elements\n while i < j and x in seen: \n seen.remove(nums[i])\n tot-=nums[i]\n i+=1 \n tot+=x\n seen.add(x)\n res=max(res, tot) \n return res\n```\n\n**Time - O(n)**\n**Space - O(k)** - where` k` is number of unique elements in input `nums`.\n\n\n---\n\n\n***Please upvote if you find it useful*** | 18 | A sentence is a list of words that are separated by a single space with no leading or trailing spaces. For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters.
Two sentences `sentence1` and `sentence2` are **similar** if it is possible to insert an arbitrary sentence **(possibly empty)** inside one of these sentences such that the two sentences become equal. For example, `sentence1 = "Hello my name is Jane "` and `sentence2 = "Hello Jane "` can be made equal by inserting `"my name is "` between `"Hello "` and `"Jane "` in `sentence2`.
Given two sentences `sentence1` and `sentence2`, return `true` _if_ `sentence1` _and_ `sentence2` _are similar._ Otherwise, return `false`.
**Example 1:**
**Input:** sentence1 = "My name is Haley ", sentence2 = "My Haley "
**Output:** true
**Explanation:** sentence2 can be turned to sentence1 by inserting "name is " between "My " and "Haley ".
**Example 2:**
**Input:** sentence1 = "of ", sentence2 = "A lot of words "
**Output:** false
**Explanation:** No single sentence can be inserted inside one of the sentences to make it equal to the other.
**Example 3:**
**Input:** sentence1 = "Eating right now ", sentence2 = "Eating "
**Output:** true
**Explanation:** sentence2 can be turned to sentence1 by inserting "right now " at the end of the sentence.
**Constraints:**
* `1 <= sentence1.length, sentence2.length <= 100`
* `sentence1` and `sentence2` consist of lowercase and uppercase English letters and spaces.
* The words in `sentence1` and `sentence2` are separated by a single space. | The main point here is for the subarray to contain unique elements for each index. Only the first subarrays starting from that index have unique elements. This can be solved using the two pointers technique |
PrefixSum Array + Sliding Window || Easy Solution | maximum-erasure-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPrefixSum Array + Sliding Window \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use the concept of prefix sum array to currect our current window sum in case of repeating element.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int: \n \n # ans --> final answer\n # cur --> current window sum\n # start --> current window starting position\n \n ans = cur = start = 0 \n d = {} # stores previous(latest) position of element\n\n for i,j in enumerate(nums):\n if i > 0: nums[i] += nums[i-1] # making prefixSum array \n cur += j \n if j in d and d[j] >= start: # if element is present already in our current window \n ind = d[j] \n cur = cur - (nums[ind] - nums[start-1] if start != 0 else nums[ind]) # correction in current window sum\n start = ind + 1 # current window starting position gets changed\n\n d[j] = i \n ans = max(ans,cur)\n\n return ans\n``` | 2 | You are given an array of positive integers `nums` and want to erase a subarray containing **unique elements**. The **score** you get by erasing the subarray is equal to the **sum** of its elements.
Return _the **maximum score** you can get by erasing **exactly one** subarray._
An array `b` is called to be a subarray of `a` if it forms a contiguous subsequence of `a`, that is, if it is equal to `a[l],a[l+1],...,a[r]` for some `(l,r)`.
**Example 1:**
**Input:** nums = \[4,2,4,5,6\]
**Output:** 17
**Explanation:** The optimal subarray here is \[2,4,5,6\].
**Example 2:**
**Input:** nums = \[5,2,1,2,5,2,1,2,5\]
**Output:** 8
**Explanation:** The optimal subarray here is \[5,2,1\] or \[1,2,5\].
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | Indexes with higher frequencies should be bound with larger values |
PrefixSum Array + Sliding Window || Easy Solution | maximum-erasure-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPrefixSum Array + Sliding Window \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use the concept of prefix sum array to currect our current window sum in case of repeating element.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int: \n \n # ans --> final answer\n # cur --> current window sum\n # start --> current window starting position\n \n ans = cur = start = 0 \n d = {} # stores previous(latest) position of element\n\n for i,j in enumerate(nums):\n if i > 0: nums[i] += nums[i-1] # making prefixSum array \n cur += j \n if j in d and d[j] >= start: # if element is present already in our current window \n ind = d[j] \n cur = cur - (nums[ind] - nums[start-1] if start != 0 else nums[ind]) # correction in current window sum\n start = ind + 1 # current window starting position gets changed\n\n d[j] = i \n ans = max(ans,cur)\n\n return ans\n``` | 2 | A sentence is a list of words that are separated by a single space with no leading or trailing spaces. For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters.
Two sentences `sentence1` and `sentence2` are **similar** if it is possible to insert an arbitrary sentence **(possibly empty)** inside one of these sentences such that the two sentences become equal. For example, `sentence1 = "Hello my name is Jane "` and `sentence2 = "Hello Jane "` can be made equal by inserting `"my name is "` between `"Hello "` and `"Jane "` in `sentence2`.
Given two sentences `sentence1` and `sentence2`, return `true` _if_ `sentence1` _and_ `sentence2` _are similar._ Otherwise, return `false`.
**Example 1:**
**Input:** sentence1 = "My name is Haley ", sentence2 = "My Haley "
**Output:** true
**Explanation:** sentence2 can be turned to sentence1 by inserting "name is " between "My " and "Haley ".
**Example 2:**
**Input:** sentence1 = "of ", sentence2 = "A lot of words "
**Output:** false
**Explanation:** No single sentence can be inserted inside one of the sentences to make it equal to the other.
**Example 3:**
**Input:** sentence1 = "Eating right now ", sentence2 = "Eating "
**Output:** true
**Explanation:** sentence2 can be turned to sentence1 by inserting "right now " at the end of the sentence.
**Constraints:**
* `1 <= sentence1.length, sentence2.length <= 100`
* `sentence1` and `sentence2` consist of lowercase and uppercase English letters and spaces.
* The words in `sentence1` and `sentence2` are separated by a single space. | The main point here is for the subarray to contain unique elements for each index. Only the first subarrays starting from that index have unique elements. This can be solved using the two pointers technique |
Python Multiple Solution 1000 ms Fast solution | jump-game-vi | 0 | 1 | Using Deque:\n\n\t\t\n\tclass Solution:\n\t\tdef maxResult(self, nums: List[int], k: int) -> int:\n\t\t\tn = len(nums)\n\t\t\tdeq = deque([n-1])\n\t\t\tfor i in range(n-2, -1, -1):\n\t\t\t\tif deq[0] - i > k: deq.popleft()\n\t\t\t\tnums[i] += nums[deq[0]]\n\t\t\t\twhile len(deq) and nums[deq[-1]] <= nums[i]: deq.pop()\n\t\t\t\tdeq.append(i)\n\t\t\treturn nums[0]\n\t\t\t\n\t\t\t\nDeque Another approach: \n\n\tclass Solution:\n\t\tdef maxResult(self, A: List[int], k: int) -> int:\n\t\t\tlog = deque([(0, -k)])\n\t\t\tfor i, a in enumerate(A):\n\t\t\t\tif i - log[0][1] > k:\n\t\t\t\t\tlog.popleft()\n\t\t\t\ta += log[0][0]\n\t\t\t\twhile log and log[-1][0] <= a:\n\t\t\t\t\tlog.pop()\n\t\t\t\tlog.append((a, i))\n\t\t\treturn a\n\t\t\t\nHeap Approach:\n\n\t\t\timport heapq\n\n\t\t\tclass Solution:\n\t\t\t\tdef maxResult(self, nums: List[int], k: int) -> int:\n\t\t\t\t\tn = len(nums)\n\t\t\t\t\tD = [-float(\'inf\')] * (n)\n\t\t\t\t\theap = [(-nums[0], 0)]\n\t\t\t\t\tD[0] = nums[0] \n\t\t\t\t\tfor i in range(1,n):\n\t\t\t\t\t\t(maxValue, index) = heap[0] \n\t\t\t\t\t\twhile index < i - k:\n\t\t\t\t\t\t\theapq.heappop(heap)\n\t\t\t\t\t\t\t(maxValue, index) = heap[0]\n\n\t\t\t\t\t\tD[i] = -maxValue + nums[i]\n\t\t\t\t\t\theapq.heappush(heap, (-D[i], i))\n\n\t\t\t\t\treturn D[n-1] | 2 | You are given a **0-indexed** integer array `nums` and an integer `k`.
You are initially standing at index `0`. In one move, you can jump at most `k` steps forward without going outside the boundaries of the array. That is, you can jump from index `i` to any index in the range `[i + 1, min(n - 1, i + k)]` **inclusive**.
You want to reach the last index of the array (index `n - 1`). Your **score** is the **sum** of all `nums[j]` for each index `j` you visited in the array.
Return _the **maximum score** you can get_.
**Example 1:**
**Input:** nums = \[1,\-1,-2,4,-7,3\], k = 2
**Output:** 7
**Explanation:** You can choose your jumps forming the subsequence \[1,-1,4,3\] (underlined above). The sum is 7.
**Example 2:**
**Input:** nums = \[10,-5,-2,4,0,3\], k = 3
**Output:** 17
**Explanation:** You can choose your jumps forming the subsequence \[10,4,3\] (underlined above). The sum is 17.
**Example 3:**
**Input:** nums = \[1,-5,-20,4,-1,3,-6,-3\], k = 2
**Output:** 0
**Constraints:**
* `1 <= nums.length, k <= 105`
* `-104 <= nums[i] <= 104` | Try thinking in reverse. Given the grid, how can you tell if a colour was painted last? |
Python Multiple Solution 1000 ms Fast solution | jump-game-vi | 0 | 1 | Using Deque:\n\n\t\t\n\tclass Solution:\n\t\tdef maxResult(self, nums: List[int], k: int) -> int:\n\t\t\tn = len(nums)\n\t\t\tdeq = deque([n-1])\n\t\t\tfor i in range(n-2, -1, -1):\n\t\t\t\tif deq[0] - i > k: deq.popleft()\n\t\t\t\tnums[i] += nums[deq[0]]\n\t\t\t\twhile len(deq) and nums[deq[-1]] <= nums[i]: deq.pop()\n\t\t\t\tdeq.append(i)\n\t\t\treturn nums[0]\n\t\t\t\n\t\t\t\nDeque Another approach: \n\n\tclass Solution:\n\t\tdef maxResult(self, A: List[int], k: int) -> int:\n\t\t\tlog = deque([(0, -k)])\n\t\t\tfor i, a in enumerate(A):\n\t\t\t\tif i - log[0][1] > k:\n\t\t\t\t\tlog.popleft()\n\t\t\t\ta += log[0][0]\n\t\t\t\twhile log and log[-1][0] <= a:\n\t\t\t\t\tlog.pop()\n\t\t\t\tlog.append((a, i))\n\t\t\treturn a\n\t\t\t\nHeap Approach:\n\n\t\t\timport heapq\n\n\t\t\tclass Solution:\n\t\t\t\tdef maxResult(self, nums: List[int], k: int) -> int:\n\t\t\t\t\tn = len(nums)\n\t\t\t\t\tD = [-float(\'inf\')] * (n)\n\t\t\t\t\theap = [(-nums[0], 0)]\n\t\t\t\t\tD[0] = nums[0] \n\t\t\t\t\tfor i in range(1,n):\n\t\t\t\t\t\t(maxValue, index) = heap[0] \n\t\t\t\t\t\twhile index < i - k:\n\t\t\t\t\t\t\theapq.heappop(heap)\n\t\t\t\t\t\t\t(maxValue, index) = heap[0]\n\n\t\t\t\t\t\tD[i] = -maxValue + nums[i]\n\t\t\t\t\t\theapq.heappush(heap, (-D[i], i))\n\n\t\t\t\t\treturn D[n-1] | 2 | You are given an array `nums` that consists of non-negative integers. Let us define `rev(x)` as the reverse of the non-negative integer `x`. For example, `rev(123) = 321`, and `rev(120) = 21`. A pair of indices `(i, j)` is **nice** if it satisfies all of the following conditions:
* `0 <= i < j < nums.length`
* `nums[i] + rev(nums[j]) == nums[j] + rev(nums[i])`
Return _the number of nice pairs of indices_. Since that number can be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nums = \[42,11,1,97\]
**Output:** 2
**Explanation:** The two pairs are:
- (0,3) : 42 + rev(97) = 42 + 79 = 121, 97 + rev(42) = 97 + 24 = 121.
- (1,2) : 11 + rev(1) = 11 + 1 = 12, 1 + rev(11) = 1 + 11 = 12.
**Example 2:**
**Input:** nums = \[13,10,35,24,76\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | Let dp[i] be "the maximum score to reach the end starting at index i". The answer for dp[i] is nums[i] + max{dp[i+j]} for 1 <= j <= k. That gives an O(n*k) solution. Instead of checking every j for every i, keep track of the largest dp[i] values in a heap and calculate dp[i] from right to left. When the largest value in the heap is out of bounds of the current index, remove it and keep checking. |
Python (Simple Union Find) | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distanceLimitedPathsExist(self, n, edgeList, queries):\n dict1, n = defaultdict(int), len(queries)\n\n def find(x):\n if x not in dict1:\n return x\n else:\n if x != dict1[x]:\n dict1[x] = find(dict1[x])\n return dict1[x]\n\n def union(x,y):\n a, b = find(x), find(y)\n\n if a != b:\n dict1[b] = a\n\n edgeList.sort(key = lambda x: x[2])\n\n i, res = 0, [False]*n\n\n for limit, x, y, idx in sorted((q[2],q[0],q[1],i) for i,q in enumerate(queries)):\n while i < len(edgeList) and edgeList[i][2] < limit:\n union(edgeList[i][0],edgeList[i][1])\n i += 1\n res[idx] = find(x) == find(y)\n \n return res\n \n \n \n \n \n \n \n \n \n \n \n \n \n``` | 5 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Python (Simple Union Find) | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distanceLimitedPathsExist(self, n, edgeList, queries):\n dict1, n = defaultdict(int), len(queries)\n\n def find(x):\n if x not in dict1:\n return x\n else:\n if x != dict1[x]:\n dict1[x] = find(dict1[x])\n return dict1[x]\n\n def union(x,y):\n a, b = find(x), find(y)\n\n if a != b:\n dict1[b] = a\n\n edgeList.sort(key = lambda x: x[2])\n\n i, res = 0, [False]*n\n\n for limit, x, y, idx in sorted((q[2],q[0],q[1],i) for i,q in enumerate(queries)):\n while i < len(edgeList) and edgeList[i][2] < limit:\n union(edgeList[i][0],edgeList[i][1])\n i += 1\n res[idx] = find(x) == find(y)\n \n return res\n \n \n \n \n \n \n \n \n \n \n \n \n \n``` | 5 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Python3 beats 87.42% 🚀🚀 quibler7 | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Code\n```\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n parent = [i for i in range(n+1)]\n \n rank = [0 for i in range(n+1)]\n\n def find(parent, x):\n\n if parent[x] == x:\n return x\n parent[x] = find(parent, parent[x])\n return parent[x]\n\n def union(parent, a, b):\n\n a = find(parent, a)\n b = find(parent, b)\n\n if a == b:\n return \n\n if rank[a] < rank[b]:\n parent[a] = b\n elif rank[a] > rank[b]:\n parent[b] = a\n else:\n parent[b] = a\n rank[a] += 1\n \n edgeList.sort(key = lambda x: x[2])\n res = [0] * len(queries)\n queries = [[i, ch] for i, ch in enumerate(queries)]\n queries.sort(key = lambda x: x[1][2])\n \n ind = 0\n for i, (a, b, w) in queries:\n \n while ind < len(edgeList) and edgeList[ind][2] < w:\n union(parent, edgeList[ind][0], edgeList[ind][1])\n ind += 1\n \n res[i] = find(parent, a) == find(parent, b)\n return res\n``` | 2 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Python3 beats 87.42% 🚀🚀 quibler7 | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Code\n```\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n parent = [i for i in range(n+1)]\n \n rank = [0 for i in range(n+1)]\n\n def find(parent, x):\n\n if parent[x] == x:\n return x\n parent[x] = find(parent, parent[x])\n return parent[x]\n\n def union(parent, a, b):\n\n a = find(parent, a)\n b = find(parent, b)\n\n if a == b:\n return \n\n if rank[a] < rank[b]:\n parent[a] = b\n elif rank[a] > rank[b]:\n parent[b] = a\n else:\n parent[b] = a\n rank[a] += 1\n \n edgeList.sort(key = lambda x: x[2])\n res = [0] * len(queries)\n queries = [[i, ch] for i, ch in enumerate(queries)]\n queries.sort(key = lambda x: x[1][2])\n \n ind = 0\n for i, (a, b, w) in queries:\n \n while ind < len(edgeList) and edgeList[ind][2] < w:\n union(parent, edgeList[ind][0], edgeList[ind][1])\n ind += 1\n \n res[i] = find(parent, a) == find(parent, b)\n return res\n``` | 2 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Union Find python | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n``` | 1 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Union Find python | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n``` | 1 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Holy Moly !. Give it a try for this solution | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Hint 1\nForget about multiple edges between two nodes. They are just to confuse. If we want the weight to be less than limitlimitlimit, just check with the minimum weight. We can always traverse a\u2194ba \\leftrightarrow ba\u2194b via minimum weighted edge if minWeight<limitmin.\n\n# Hint 2\nNormal traversal from source to destination for each query will be TLE. What is the redundant work? If we could traverse 1\u22122\u22123\u22124 with limit=10, then we can also traverse from any source to destination pair in [1,2,3,4]with limit\u226510.\n\n# Hint 3\nSo, for a specific queries[i], assume there is a copy of the given graph but it has only those edges which has weight<limit. Then we can check if there is a path from source to destination, or in other words, whether source and destination belong to same component or not. What happens when we increase the limitlimitlimit?\n\n# Hint 4\nWhen we were able to traverse 1\u22122\u22123\u22124 with limit=10, suppose there was one edge 1\u21945 with weight=11, and we were not able to use it to reach 555. But if limitlimitlimit is increased to 12, then we can use it to go 1\u22125 and subsequently any source to destination pair in [1,2,3,4,5].\n\n# Hint 5\nWhen limit is increased, we can still use all the edges that were there in our copied graph. But we can use even more edges that has weight where oldLimit\u2264weight<newLimit. We can add these new edges that could not be used earlier, in our copied graph and check for a path again. To do this, we would like to have queries and edgeList sorted with weight or limit. But, before sorting queries, don\'t forget to store their original indices for final result array.\n\n# Hint 6\nLooks like we are still doing traversal in copied graph to check for path on same nodes again and again. How can we quickly check if two nodes belong to the same component in the copied graph? We can make Disjoint Sets of components and check for their parents (See [This](https://leetcode.com/discuss/general-discussion/1072418/Disjoint-Set-Union-(DSU)Union-Find-A-Complete-Guide/) if you want to learn DSU). For an increased limit, take union of those disjoint sets for those new edges.\n\n# Intuition & Approach\n\u2022 problem is to determine if there is a path between two nodes in an undirected graph such that each edge on the path has a distance strictly less than a given limit.\n\n\u2022 The input consists of the number of nodes, the edge list, and the queries.\n\n\u2022 The edge list is an array of arrays, where each sub-array represents an edge between two nodes and the distance between them.\n\n\u2022 The queries are an array of arrays, where each sub-array represents a query with two nodes and a limit.\n\n\u2022 The using the union-find algorithm to determine if there is a path between two nodes.\n\n\u2022 The union-find algorithm is used to group nodes into connected components.\n\n\u2022 First sorts the edges in the edge list by their distance in ascending order.\n\n\u2022 Then iterates over the sorted edges and performs a union operation on the nodes connected by the edge.\n\n\u2022 The union operation updates the parent and rank arrays to group the nodes into connected components.\n\n\u2022 Then iterates over the queries and checks if the two nodes are connected and if the distance between them is less than the given limit.\n\n\u2022 The isConnectedAndWithinLimit method uses the find method to determine if the two nodes are connected and if the distance between them is less than the given limit.\n\n\u2022 The find method uses the parent and weight arrays to find the root of the connected component and checks if the weight of the edge is less than the given limit.\n\n\u2022 The union method updates the parent, rank, and weight arrays to group the nodes into connected components and store the weight of the edge.\n\n\u2022 finally returns a boolean array where each element represents if there is a path between the two nodes in the corresponding query with edges less than the given limit.$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, size):\n self.parent = [i for i in range(size)]\n \n def union(self, a, b):\n self.parent[self.find(a)] = self.find(b)\n \n def find(self, a):\n if self.parent[a] != a:\n self.parent[a] = self.find(self.parent[a])\n return self.parent[a]\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n E = len(edgeList)\n Q = len(queries)\n uf = UnionFind(n)\n ans = [False] * Q\n for i in range(Q):\n queries[i].append(i)\n queries.sort(key=lambda x: x[2])\n edgeList.sort(key=lambda x: x[2])\n j = 0\n for i in range(Q):\n while j < E and edgeList[j][2] < queries[i][2]:\n uf.union(edgeList[j][0], edgeList[j][1])\n j += 1\n ans[queries[i][3]] = (uf.find(queries[i][0]) == uf.find(queries[i][1]))\n return ans\n\n\n"""\n# TLE and wrong ans\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n parents = defaultdict(lambda: None)\n sizes = defaultdict(int)\n \n def find(a):\n if a not in parents:\n parents[a] = a\n sizes[a] = 1\n return a\n\n root = a\n while parents[root] != root:\n root = parents[root]\n while parents[a] != a:\n nxt = parents[a]\n parents[a] = root\n a = nxt\n return root\n \n def union(a,b):\n roota = find(a)\n rootb = find(b)\n if roota == rootb:\n return\n if sizes[roota] > sizes[rootb]:\n sizes[roota] += sizes[rootb]\n sizes[rootb] = 0\n parents[rootb] = roota\n else:\n sizes[rootb] += sizes[roota]\n sizes[roota] = 0\n parents[roota] = rootb\n\n Q, E = len(queries), len(edgeList)\n\n #print(edgeList) \n edgeList.sort(key=lambda x: x[2])\n #print(edgeList)\n queries = sorted(((u,v,l,idx) for idx,(u,v,l) in enumerate(queries)), key=lambda x: x[2])\n #print(queries)\n\n res = [False] * Q\n e_idx = 0\n for p, q, l, i in queries:\n while e_idx < E and edgeList[e_idx][2] < l:\n u, v, _ = edgeList[e_idx]\n union(u, v)\n res[i] = find(p) == find(q)\n e_idx += 1\n return res\n"""\n``` | 1 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Holy Moly !. Give it a try for this solution | checking-existence-of-edge-length-limited-paths | 0 | 1 | # Hint 1\nForget about multiple edges between two nodes. They are just to confuse. If we want the weight to be less than limitlimitlimit, just check with the minimum weight. We can always traverse a\u2194ba \\leftrightarrow ba\u2194b via minimum weighted edge if minWeight<limitmin.\n\n# Hint 2\nNormal traversal from source to destination for each query will be TLE. What is the redundant work? If we could traverse 1\u22122\u22123\u22124 with limit=10, then we can also traverse from any source to destination pair in [1,2,3,4]with limit\u226510.\n\n# Hint 3\nSo, for a specific queries[i], assume there is a copy of the given graph but it has only those edges which has weight<limit. Then we can check if there is a path from source to destination, or in other words, whether source and destination belong to same component or not. What happens when we increase the limitlimitlimit?\n\n# Hint 4\nWhen we were able to traverse 1\u22122\u22123\u22124 with limit=10, suppose there was one edge 1\u21945 with weight=11, and we were not able to use it to reach 555. But if limitlimitlimit is increased to 12, then we can use it to go 1\u22125 and subsequently any source to destination pair in [1,2,3,4,5].\n\n# Hint 5\nWhen limit is increased, we can still use all the edges that were there in our copied graph. But we can use even more edges that has weight where oldLimit\u2264weight<newLimit. We can add these new edges that could not be used earlier, in our copied graph and check for a path again. To do this, we would like to have queries and edgeList sorted with weight or limit. But, before sorting queries, don\'t forget to store their original indices for final result array.\n\n# Hint 6\nLooks like we are still doing traversal in copied graph to check for path on same nodes again and again. How can we quickly check if two nodes belong to the same component in the copied graph? We can make Disjoint Sets of components and check for their parents (See [This](https://leetcode.com/discuss/general-discussion/1072418/Disjoint-Set-Union-(DSU)Union-Find-A-Complete-Guide/) if you want to learn DSU). For an increased limit, take union of those disjoint sets for those new edges.\n\n# Intuition & Approach\n\u2022 problem is to determine if there is a path between two nodes in an undirected graph such that each edge on the path has a distance strictly less than a given limit.\n\n\u2022 The input consists of the number of nodes, the edge list, and the queries.\n\n\u2022 The edge list is an array of arrays, where each sub-array represents an edge between two nodes and the distance between them.\n\n\u2022 The queries are an array of arrays, where each sub-array represents a query with two nodes and a limit.\n\n\u2022 The using the union-find algorithm to determine if there is a path between two nodes.\n\n\u2022 The union-find algorithm is used to group nodes into connected components.\n\n\u2022 First sorts the edges in the edge list by their distance in ascending order.\n\n\u2022 Then iterates over the sorted edges and performs a union operation on the nodes connected by the edge.\n\n\u2022 The union operation updates the parent and rank arrays to group the nodes into connected components.\n\n\u2022 Then iterates over the queries and checks if the two nodes are connected and if the distance between them is less than the given limit.\n\n\u2022 The isConnectedAndWithinLimit method uses the find method to determine if the two nodes are connected and if the distance between them is less than the given limit.\n\n\u2022 The find method uses the parent and weight arrays to find the root of the connected component and checks if the weight of the edge is less than the given limit.\n\n\u2022 The union method updates the parent, rank, and weight arrays to group the nodes into connected components and store the weight of the edge.\n\n\u2022 finally returns a boolean array where each element represents if there is a path between the two nodes in the corresponding query with edges less than the given limit.$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, size):\n self.parent = [i for i in range(size)]\n \n def union(self, a, b):\n self.parent[self.find(a)] = self.find(b)\n \n def find(self, a):\n if self.parent[a] != a:\n self.parent[a] = self.find(self.parent[a])\n return self.parent[a]\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n E = len(edgeList)\n Q = len(queries)\n uf = UnionFind(n)\n ans = [False] * Q\n for i in range(Q):\n queries[i].append(i)\n queries.sort(key=lambda x: x[2])\n edgeList.sort(key=lambda x: x[2])\n j = 0\n for i in range(Q):\n while j < E and edgeList[j][2] < queries[i][2]:\n uf.union(edgeList[j][0], edgeList[j][1])\n j += 1\n ans[queries[i][3]] = (uf.find(queries[i][0]) == uf.find(queries[i][1]))\n return ans\n\n\n"""\n# TLE and wrong ans\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n parents = defaultdict(lambda: None)\n sizes = defaultdict(int)\n \n def find(a):\n if a not in parents:\n parents[a] = a\n sizes[a] = 1\n return a\n\n root = a\n while parents[root] != root:\n root = parents[root]\n while parents[a] != a:\n nxt = parents[a]\n parents[a] = root\n a = nxt\n return root\n \n def union(a,b):\n roota = find(a)\n rootb = find(b)\n if roota == rootb:\n return\n if sizes[roota] > sizes[rootb]:\n sizes[roota] += sizes[rootb]\n sizes[rootb] = 0\n parents[rootb] = roota\n else:\n sizes[rootb] += sizes[roota]\n sizes[roota] = 0\n parents[roota] = rootb\n\n Q, E = len(queries), len(edgeList)\n\n #print(edgeList) \n edgeList.sort(key=lambda x: x[2])\n #print(edgeList)\n queries = sorted(((u,v,l,idx) for idx,(u,v,l) in enumerate(queries)), key=lambda x: x[2])\n #print(queries)\n\n res = [False] * Q\n e_idx = 0\n for p, q, l, i in queries:\n while e_idx < E and edgeList[e_idx][2] < l:\n u, v, _ = edgeList[e_idx]\n union(u, v)\n res[i] = find(p) == find(q)\n e_idx += 1\n return res\n"""\n``` | 1 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Python3 Solution | checking-existence-of-edge-length-limited-paths | 0 | 1 | \n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n``` | 1 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Python3 Solution | checking-existence-of-edge-length-limited-paths | 0 | 1 | \n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n``` | 1 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Python disjoint-set union | checking-existence-of-edge-length-limited-paths | 0 | 1 | ```python []\nclass DSU:\n def __init__(self, n):\n self.parent = list(range(n))\n self.rank = [0] * n\n\n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n x_root, y_root = self.find(x), self.find(y)\n if x_root == y_root:\n return\n if self.rank[x_root] < self.rank[y_root]:\n x_root, y_root = y_root, x_root\n self.parent[y_root] = x_root\n if self.rank[x_root] == self.rank[y_root]:\n self.rank[x_root] += 1\n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = [[i] + q for i, q in enumerate(queries)]\n queries.sort(key=lambda x: x[3])\n edges.sort(key=lambda x: x[2])\n dsu = DSU(n)\n res = [0] * len(queries)\n j = 0\n for i, u, v, lim in queries:\n while j < len(edges) and edges[j][2] < lim:\n p, q = edges[j][:2]\n dsu.union(p, q)\n j += 1\n res[i] = dsu.find(u) == dsu.find(v)\n return res\n\n``` | 1 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Python disjoint-set union | checking-existence-of-edge-length-limited-paths | 0 | 1 | ```python []\nclass DSU:\n def __init__(self, n):\n self.parent = list(range(n))\n self.rank = [0] * n\n\n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n x_root, y_root = self.find(x), self.find(y)\n if x_root == y_root:\n return\n if self.rank[x_root] < self.rank[y_root]:\n x_root, y_root = y_root, x_root\n self.parent[y_root] = x_root\n if self.rank[x_root] == self.rank[y_root]:\n self.rank[x_root] += 1\n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = [[i] + q for i, q in enumerate(queries)]\n queries.sort(key=lambda x: x[3])\n edges.sort(key=lambda x: x[2])\n dsu = DSU(n)\n res = [0] * len(queries)\n j = 0\n for i, u, v, lim in queries:\n while j < len(edges) and edges[j][2] < lim:\n p, q = edges[j][:2]\n dsu.union(p, q)\n j += 1\n res[i] = dsu.find(u) == dsu.find(v)\n return res\n\n``` | 1 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Image Explanation🏆- [Easiest & Complete Intuition] - C++/Java/Python | checking-existence-of-edge-length-limited-paths | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Checking Existence of Edge Length Limited Paths` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n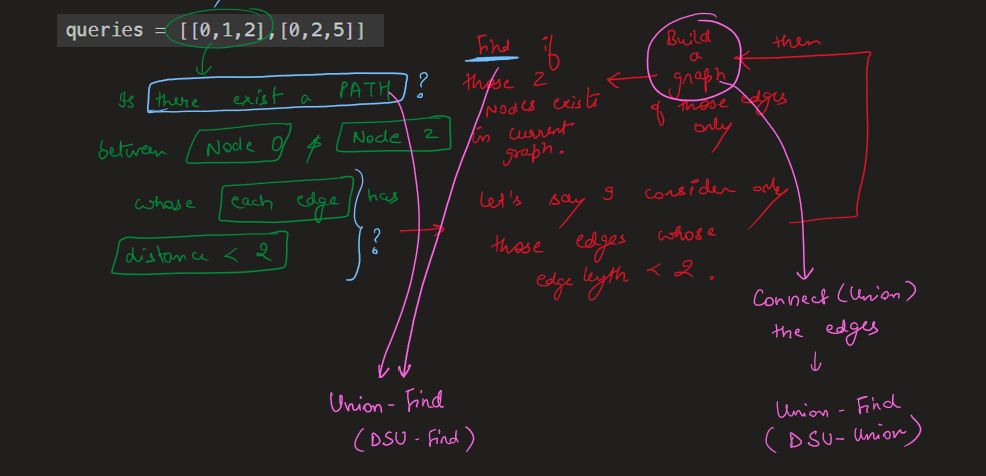\n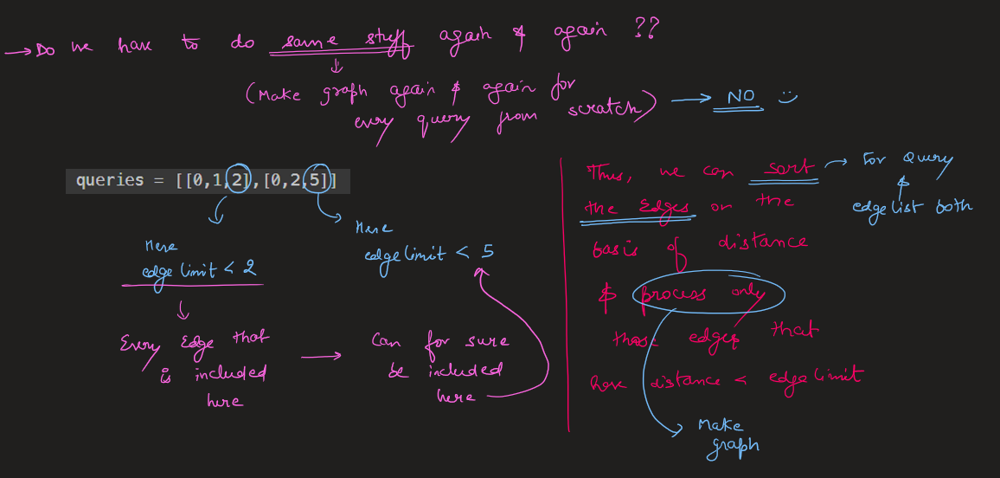\n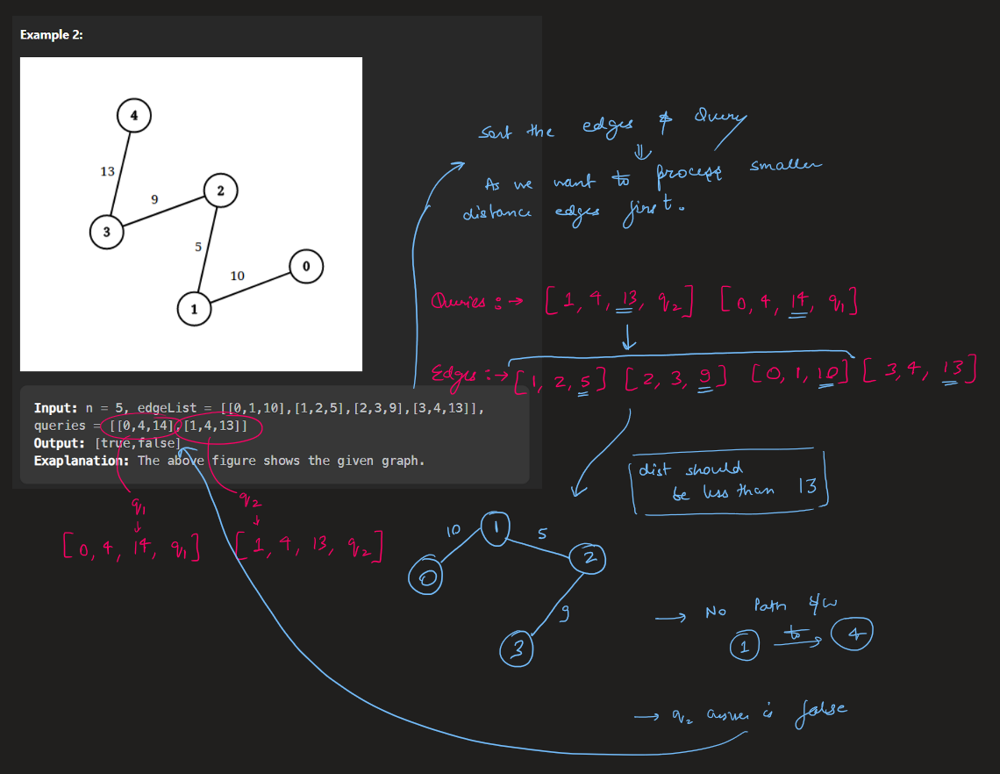\n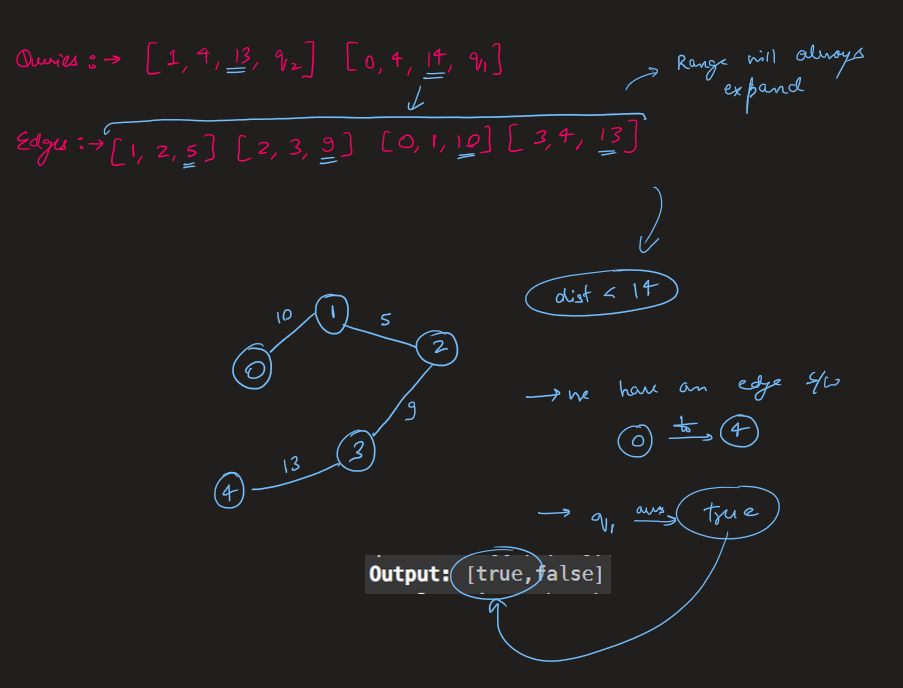\n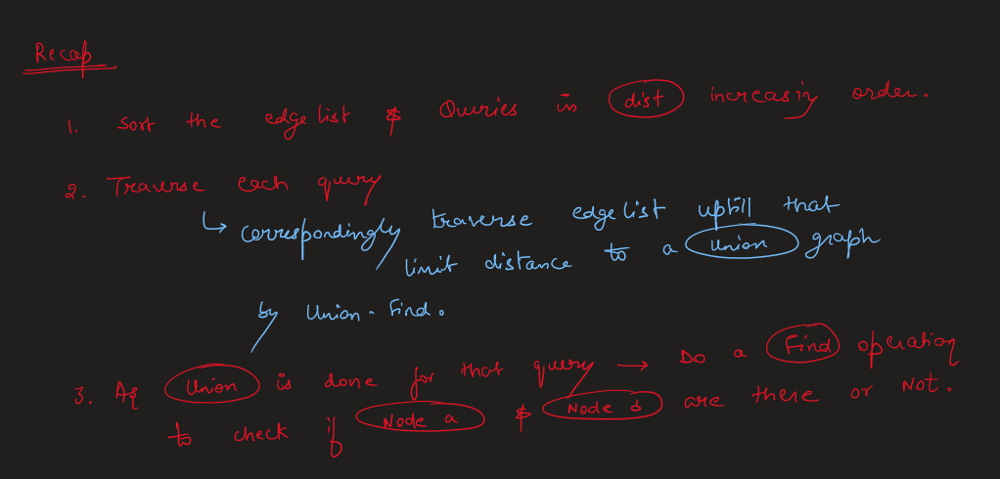\n\n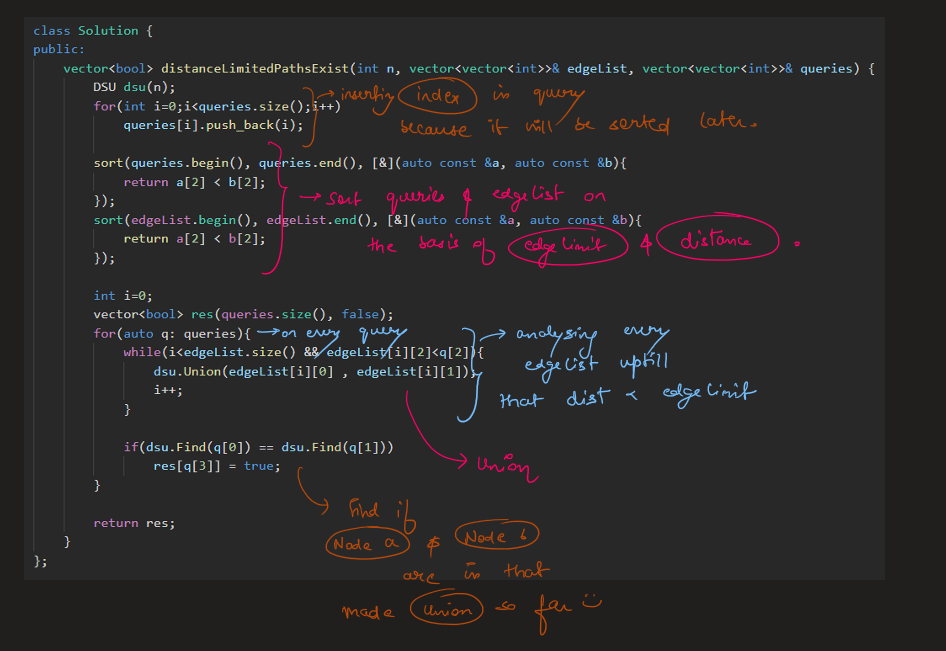\n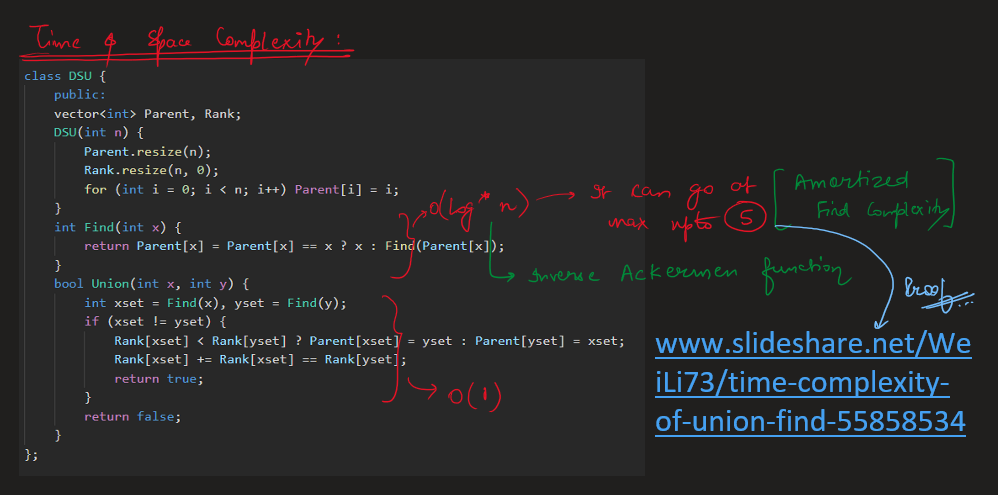\n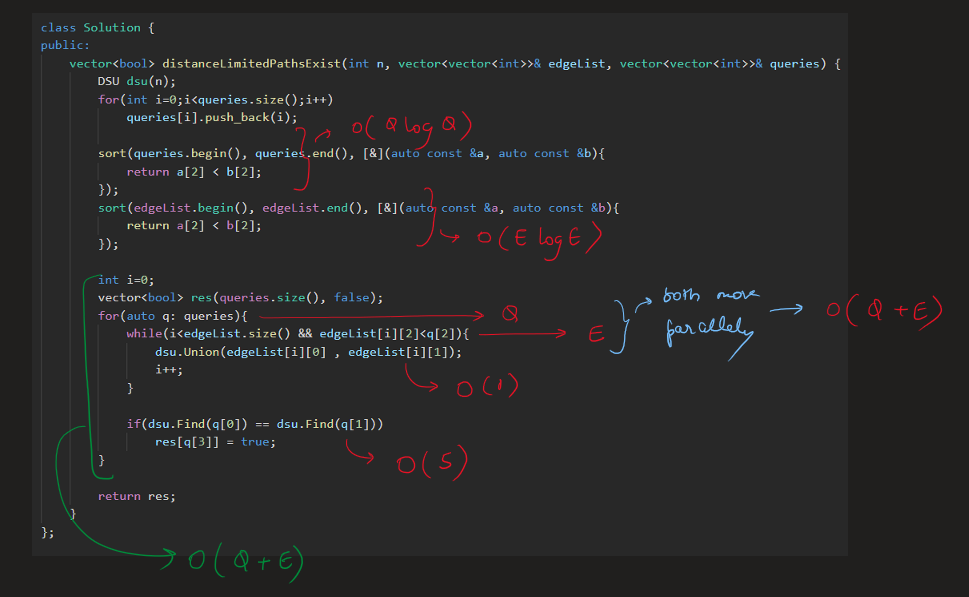\n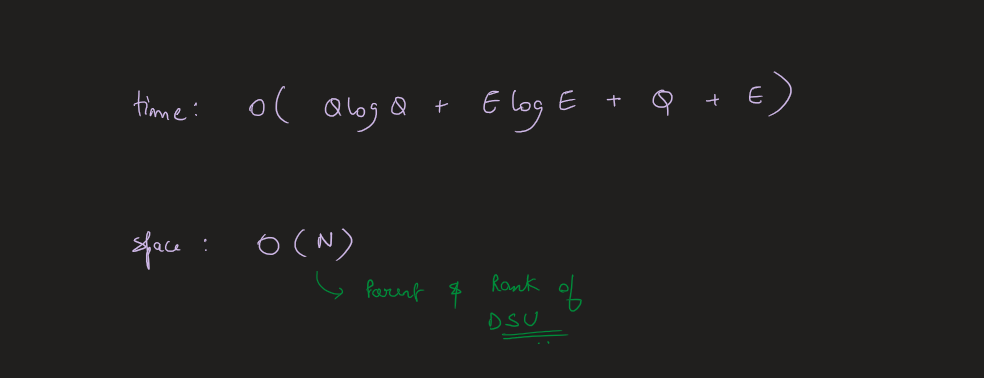\n\n\n# Code\n`Mark the DSU Code as the template [I always use this ONLY]`\n```C++ []\nclass DSU {\n public:\n vector<int> Parent, Rank;\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for (int i = 0; i < n; i++) Parent[i] = i;\n }\n int Find(int x) {\n return Parent[x] = Parent[x] == x ? x : Find(Parent[x]);\n }\n bool Union(int x, int y) {\n int xset = Find(x), yset = Find(y);\n if (xset != yset) {\n Rank[xset] < Rank[yset] ? Parent[xset] = yset : Parent[yset] = xset;\n Rank[xset] += Rank[xset] == Rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n DSU dsu(n);\n for(int i=0;i<queries.size();i++)\n queries[i].push_back(i);\n \n sort(queries.begin(), queries.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n sort(edgeList.begin(), edgeList.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n \n int i=0;\n vector<bool> res(queries.size(), false);\n for(auto q: queries){\n while(i<edgeList.size() && edgeList[i][2]<q[2]){\n dsu.Union(edgeList[i][0] , edgeList[i][1]);\n i++;\n }\n \n if(dsu.Find(q[0]) == dsu.Find(q[1]))\n res[q[3]] = true;\n }\n \n return res;\n }\n};\n```\n```Java []\nclass DSU {\n private int[] parent;\n private int[] rank;\n\n public DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n\n public int find(int x) {\n if (parent[x] == x) {\n return x;\n }\n return parent[x] = find(parent[x]);\n }\n\n public boolean union(int x, int y) {\n int xset = find(x), yset = find(y);\n if (xset != yset) {\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n } else {\n parent[yset] = xset;\n }\n if (rank[xset] == rank[yset]) {\n rank[xset]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n DSU dsu = new DSU(n);\n for (int i = 0; i < queries.length; i++) {\n queries[i] = new int[] { queries[i][0], queries[i][1], queries[i][2], i };\n }\n\n Arrays.sort(queries, (a, b) -> Integer.compare(a[2], b[2]));\n Arrays.sort(edgeList, (a, b) -> Integer.compare(a[2], b[2]));\n\n int i = 0;\n boolean[] res = new boolean[queries.length];\n for (int[] q : queries) {\n while (i < edgeList.length && edgeList[i][2] < q[2]) {\n dsu.union(edgeList[i][0], edgeList[i][1]);\n i++;\n }\n\n if (dsu.find(q[0]) == dsu.find(q[1])) {\n res[q[3]] = true;\n }\n }\n\n return res;\n }\n}\n```\n```Python []\nclass DSU:\n def __init__(self, n):\n self.parent = list(range(n))\n self.rank = [0] * n\n\n def find(self, x):\n if self.parent[x] == x:\n return x\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n xset, yset = self.find(x), self.find(y)\n if xset != yset:\n if self.rank[xset] < self.rank[yset]:\n self.parent[xset] = yset\n else:\n self.parent[yset] = xset\n if self.rank[xset] == self.rank[yset]:\n self.rank[xset] += 1\n return True\n return False\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n dsu = DSU(n)\n for i, q in enumerate(queries):\n queries[i].append(i)\n\n queries.sort(key=lambda q: q[2])\n edgeList.sort(key=lambda e: e[2])\n\n i = 0\n res = [False] * len(queries)\n for q in queries:\n while i < len(edgeList) and edgeList[i][2] < q[2]:\n dsu.union(edgeList[i][0], edgeList[i][1])\n i += 1\n\n if dsu.find(q[0]) == dsu.find(q[1]):\n res[q[3]] = True\n\n return res\n```\n | 87 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
Image Explanation🏆- [Easiest & Complete Intuition] - C++/Java/Python | checking-existence-of-edge-length-limited-paths | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Checking Existence of Edge Length Limited Paths` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n\n\n\n\n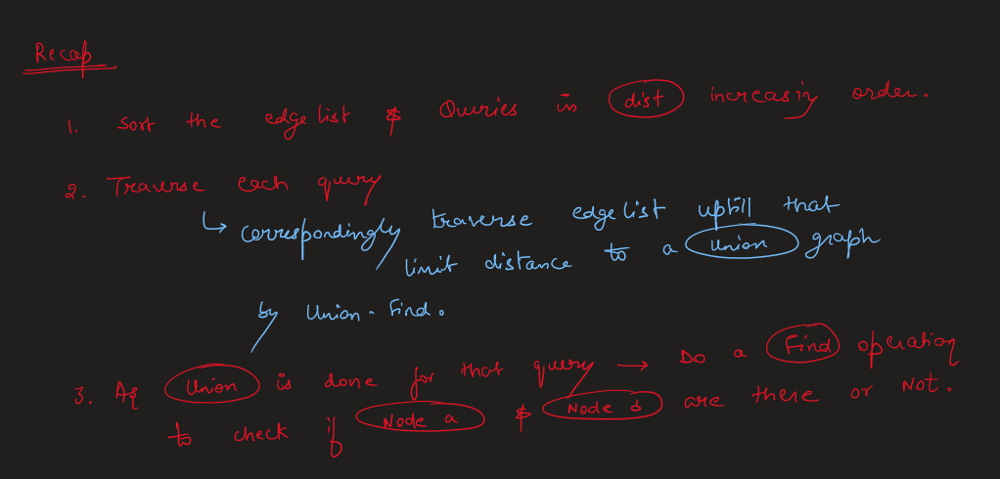\n\n\n\n\n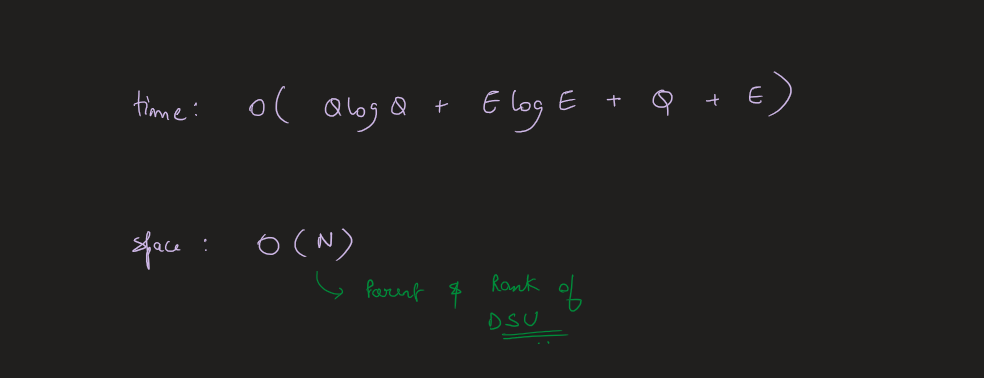\n\n\n# Code\n`Mark the DSU Code as the template [I always use this ONLY]`\n```C++ []\nclass DSU {\n public:\n vector<int> Parent, Rank;\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for (int i = 0; i < n; i++) Parent[i] = i;\n }\n int Find(int x) {\n return Parent[x] = Parent[x] == x ? x : Find(Parent[x]);\n }\n bool Union(int x, int y) {\n int xset = Find(x), yset = Find(y);\n if (xset != yset) {\n Rank[xset] < Rank[yset] ? Parent[xset] = yset : Parent[yset] = xset;\n Rank[xset] += Rank[xset] == Rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n DSU dsu(n);\n for(int i=0;i<queries.size();i++)\n queries[i].push_back(i);\n \n sort(queries.begin(), queries.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n sort(edgeList.begin(), edgeList.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n \n int i=0;\n vector<bool> res(queries.size(), false);\n for(auto q: queries){\n while(i<edgeList.size() && edgeList[i][2]<q[2]){\n dsu.Union(edgeList[i][0] , edgeList[i][1]);\n i++;\n }\n \n if(dsu.Find(q[0]) == dsu.Find(q[1]))\n res[q[3]] = true;\n }\n \n return res;\n }\n};\n```\n```Java []\nclass DSU {\n private int[] parent;\n private int[] rank;\n\n public DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n\n public int find(int x) {\n if (parent[x] == x) {\n return x;\n }\n return parent[x] = find(parent[x]);\n }\n\n public boolean union(int x, int y) {\n int xset = find(x), yset = find(y);\n if (xset != yset) {\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n } else {\n parent[yset] = xset;\n }\n if (rank[xset] == rank[yset]) {\n rank[xset]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n DSU dsu = new DSU(n);\n for (int i = 0; i < queries.length; i++) {\n queries[i] = new int[] { queries[i][0], queries[i][1], queries[i][2], i };\n }\n\n Arrays.sort(queries, (a, b) -> Integer.compare(a[2], b[2]));\n Arrays.sort(edgeList, (a, b) -> Integer.compare(a[2], b[2]));\n\n int i = 0;\n boolean[] res = new boolean[queries.length];\n for (int[] q : queries) {\n while (i < edgeList.length && edgeList[i][2] < q[2]) {\n dsu.union(edgeList[i][0], edgeList[i][1]);\n i++;\n }\n\n if (dsu.find(q[0]) == dsu.find(q[1])) {\n res[q[3]] = true;\n }\n }\n\n return res;\n }\n}\n```\n```Python []\nclass DSU:\n def __init__(self, n):\n self.parent = list(range(n))\n self.rank = [0] * n\n\n def find(self, x):\n if self.parent[x] == x:\n return x\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n xset, yset = self.find(x), self.find(y)\n if xset != yset:\n if self.rank[xset] < self.rank[yset]:\n self.parent[xset] = yset\n else:\n self.parent[yset] = xset\n if self.rank[xset] == self.rank[yset]:\n self.rank[xset] += 1\n return True\n return False\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n dsu = DSU(n)\n for i, q in enumerate(queries):\n queries[i].append(i)\n\n queries.sort(key=lambda q: q[2])\n edgeList.sort(key=lambda e: e[2])\n\n i = 0\n res = [False] * len(queries)\n for q in queries:\n while i < len(edgeList) and edgeList[i][2] < q[2]:\n dsu.union(edgeList[i][0], edgeList[i][1])\n i += 1\n\n if dsu.find(q[0]) == dsu.find(q[1]):\n res[q[3]] = True\n\n return res\n```\n | 87 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
✔💯 DAY 394 | Custom Union-Find | 100% 0ms | [PYTHON/JAVA/C++] | EXPLAINED | Approach 💫 | checking-existence-of-edge-length-limited-paths | 1 | 1 | # Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tproblem is to determine if there is a path between two nodes in an undirected graph such that each edge on the path has a distance strictly less than a given limit.\n##### \u2022\tThe input consists of the number of nodes, the edge list, and the queries.\n##### \u2022\tThe edge list is an array of arrays, where each sub-array represents an edge between two nodes and the distance between them.\n##### \u2022\tThe queries are an array of arrays, where each sub-array represents a query with two nodes and a limit.\n##### \u2022\tThe using the union-find algorithm to determine if there is a path between two nodes.\n##### \u2022\tThe union-find algorithm is used to group nodes into connected components.\n##### \u2022\tFirst sorts the edges in the edge list by their distance in ascending order.\n##### \u2022 Then iterates over the sorted edges and performs a union operation on the nodes connected by the edge.\n##### \u2022\tThe union operation updates the parent and rank arrays to group the nodes into connected components.\n##### \u2022\tThen iterates over the queries and checks if the two nodes are connected and if the distance between them is less than the given limit.\n##### \u2022\tThe isConnectedAndWithinLimit method uses the find method to determine if the two nodes are connected and if the distance between them is less than the given limit.\n##### \u2022\tThe find method uses the parent and weight arrays to find the root of the connected component and checks if the weight of the edge is less than the given limit.\n##### \u2022\tThe union method updates the parent, rank, and weight arrays to group the nodes into connected components and store the weight of the edge.\n##### \u2022\tfinally returns a boolean array where each element represents if there is a path between the two nodes in the corresponding query with edges less than the given limit.\n\n\n\n# Code\n```java []\nclass Solution {\n private int[] parent;\n private int[] rank;\n private int[] weight;\n public boolean[] distanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n // Initialize parent, rank, and weight arrays\n parent = new int[length];\n rank = new int[length];\n weight = new int[length];\n for (int i = 0; i < length ; i++) parent[i] = i;\n\n // Sort edges in the adjacency list by distance\n Arrays.sort(adjList, Comparator.comparingInt(a -> a[2]));\n // Group nodes into connected components using union-find algorithm\n for (int[] edge : adjList) unionByRank(edge[0], edge[1], edge[2]);\n\n // Initialize answer array\n boolean[] answer = new boolean[queries.length];\n // Check if there is a path between two nodes with distance less than the given limit for each query\n for (int i = 0 ; i < queries.length; i++)\n answer[i] = isConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2]);\n\n return answer;\n }\n\n // Check if there is a path between two nodes with distance less than the given limit\n public boolean isConnectedAndWithinLimit(int p, int q, int limit) {\n return find(p, limit) == find(q, limit);\n }\n\n // Find the root of the connected component for a node with distance less than the given limit\n private int find (int x, int limit) {\n while (x != parent[x]) {\n // If the weight of the edge is greater than or equal to the given limit, break out of the loop\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n // Union two nodes into the same connected component with the given limit as the weight of the edge\n private void unionByRank (int x, int y, int limit) {\n // Find the root of the connected component for each node\n int x_ref = find (x, Integer.MAX_VALUE);\n int y_ref = find (y, Integer.MAX_VALUE);\n if (x_ref != y_ref) {\n // If the rank of the root of x is less than the rank of the root of y, make y the parent of x\n if (rank[x_ref] < rank[y_ref]) {\n parent[x_ref] = y_ref;\n weight [x_ref] = limit;;\n } else {\n // Otherwise, make x the parent of y\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n // If the ranks of the roots are equal, increment the rank of the root of x\n if (rank[x_ref] == rank[y_ref]) {\n rank[x_ref]++;\n }\n }\n }\n }\n}\n```\n```python []\nclass Solution:\n def distanceLimitedPathsExist(self, length: int, adjList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n parent = [i for i in range(length)]\n rank = [0 for i in range(length)]\n weight = [0 for i in range(length)]\n\n adjList.sort(key=lambda x: x[2])\n for edge in adjList:\n self.unionByRank(edge[0], edge[1], edge[2], parent, rank, weight)\n\n answer = []\n for query in queries:\n answer.append(self.isConnectedAndWithinLimit(query[0], query[1], query[2], parent, weight))\n\n return answer\n\n def isConnectedAndWithinLimit(self, p: int, q: int, limit: int, parent: List[int], weight: List[int]) -> bool:\n return self.find(p, limit, parent, weight) == self.find(q, limit, parent, weight)\n\n def find(self, x: int, limit: int, parent: List[int], weight: List[int]) -> int:\n while x != parent[x]:\n if weight[x] >= limit:\n break\n x = parent[x]\n return x\n\n def unionByRank(self, x: int, y: int, limit: int, parent: List[int], rank: List[int], weight: List[int]) -> None:\n x_ref = self.find(x, float(\'inf\'), parent, weight)\n y_ref = self.find(y, float(\'inf\'), parent, weight)\n if x_ref != y_ref:\n if rank[x_ref] < rank[y_ref]:\n parent[x_ref] = y_ref\n weight[x_ref] = limit\n else:\n parent[y_ref] = x_ref\n weight[y_ref] = limit\n if rank[x_ref] == rank[y_ref]:\n rank[x_ref] += 1\n```\n\n```c++ []\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int length, vector<vector<int>>& adjList, vector<vector<int>>& queries) {\n vector<int> parent(length);\n vector<int> rank(length);\n vector<int> weight(length);\n for (int i = 0; i < length ; i++) parent[i] = i;\n\n sort(adjList.begin(), adjList.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[2] < b[2];\n });\n for (vector<int>& edge : adjList) unionByRank(edge[0], edge[1], edge[2], parent, rank, weight);\n\n vector<bool> answer;\n for (vector<int>& query : queries)\n answer.push_back(isConnectedAndWithinLimit(query[0], query[1], query[2], parent, weight));\n\n return answer;\n }\n\n bool isConnectedAndWithinLimit(int p, int q, int limit, vector<int>& parent, vector<int>& weight) {\n return find(p, limit, parent, weight) == find(q, limit, parent, weight);\n }\n\n int find(int x, int limit, vector<int>& parent, vector<int>& weight) {\n while (x != parent[x]) {\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n void unionByRank(int x, int y, int limit, vector<int>& parent, vector<int>& rank, vector<int>& weight) {\n int x_ref = find(x, INT_MAX, parent, weight);\n int y_ref = find(y, INT_MAX, parent, weight);\n if (x_ref != y_ref) {\n if (rank[x_ref] < rank[y_ref]) {\n parent[x_ref] = y_ref;\n weight[x_ref] = limit;\n } else {\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n if (rank[x_ref] == rank[y_ref]) {\n rank[x_ref]++;\n }\n }\n }\n }\n};\n```\n```csharp []\npublic class Solution {\n public bool[] DistanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n int[] parent = Enumerable.Range(0, length).ToArray();\n int[] rank = new int[length];\n int[] weight = new int[length];\n\n Array.Sort(adjList, (a, b) => a[2].CompareTo(b[2]));\n foreach (int[] edge in adjList) {\n Union(edge[0], edge[1], edge[2], parent, rank, weight);\n }\n\n bool[] answer = new bool[queries.Length];\n for (int i = 0; i < queries.Length; i++) {\n answer[i] = IsConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2], parent, weight);\n }\n\n return answer;\n }\n\n private bool IsConnectedAndWithinLimit(int p, int q, int limit, int[] parent, int[] weight) {\n return Find(p, limit, parent, weight) == Find(q, limit, parent, weight);\n }\n\n private int Find(int x, int limit, int[] parent, int[] weight) {\n while (x != parent[x]) {\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n private void Union(int x, int y, int limit, int[] parent, int[] rank, int[] weight) {\n int xRef = Find(x, int.MaxValue, parent, weight);\n int yRef = Find(y, int.MaxValue, parent, weight);\n if (xRef == yRef) {\n return;\n }\n if (rank[xRef] < rank[yRef]) {\n parent[xRef] = yRef;\n weight[xRef] = limit;\n } else {\n parent[yRef] = xRef;\n weight[yRef] = limit;\n if (rank[xRef] == rank[yRef]) {\n rank[xRef]++;\n }\n }\n }\n}\n```\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# 2nd union by size \n\n```java []\nclass Solution {\n private int[] parent;\n private int[] size;\n private int[] weight;\n public boolean[] distanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n // Initialize parent, size, and weight arrays\n parent = new int[length];\n size = new int[length];\n weight = new int[length];\n for (int i = 0; i < length ; i++) {\n parent[i] = i;\n size[i] = 1;\n }\n\n // Sort edges in the adjacency list by distance\n Arrays.sort(adjList, Comparator.comparingInt(a -> a[2]));\n // Group nodes into connected components using union-find algorithm\n for (int[] edge : adjList) unionBySize(edge[0], edge[1], edge[2]);\n\n // Initialize answer array\n boolean[] answer = new boolean[queries.length];\n // Check if there is a path between two nodes with distance less than the given limit for each query\n for (int i = 0 ; i < queries.length; i++)\n answer[i] = isConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2]);\n\n return answer;\n }\n\n // Check if there is a path between two nodes with distance less than the given limit\n public boolean isConnectedAndWithinLimit(int p, int q, int limit) {\n return find(p, limit) == find(q, limit);\n }\n\n // Find the root of the connected component for a node with distance less than the given limit\n private int find (int x, int limit) {\n while (x != parent[x]) {\n // If the weight of the edge is greater than or equal to the given limit, break out of the loop\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n // Union two nodes into the same connected component with the given limit as the weight of the edge\n private void unionBySize (int x, int y, int limit) {\n // Find the root of the connected component for each node\n int x_ref = find (x, Integer.MAX_VALUE);\n int y_ref = find (y, Integer.MAX_VALUE);\n if (x_ref != y_ref) {\n // If the size of the root of x is less than the size of the root of y, make y the parent of x\n if (size[x_ref] < size[y_ref]) {\n parent[x_ref] = y_ref;\n weight [x_ref] = limit;\n size[y_ref] += size[x_ref];\n } else {\n // Otherwise, make x the parent of y\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n size[x_ref] += size[y_ref];\n }\n }\n }\n}\n```\n# Complexity\n- Time complexity:\nSorting the adjacency list takes O(E log E) time, where E is the number of edges in the graph.\nThe union-find algorithm takes O(E \u03B1(V)) time, where \u03B1 is the inverse Ackermann function and V is the number of vertices in the graph. In practice, \u03B1(V) is a very small value, so we can consider the time complexity to be O(E).\nChecking if there is a path between two nodes with distance less than the given limit takes O(log V) time, where V is the number of vertices in the graph.\nWe perform this check for each query, so the total time complexity for all queries is O(Q log V), where Q is the number of queries.\nTherefore, the overall time complexity of the algorithm is O(E log E + Q log V).\n- Space Complexity:\nWe use three arrays of size V to store the parent, rank, and weight of each node in the graph, so the space complexity is O(V).\nWe also use a boolean array of size Q to store the answer for each query, so the space complexity is O(Q).\nTherefore, the overall space complexity of the algorithm is O(V + Q).\n\n\n# dry run \nFor the first: Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]\nOutput: [false,true]\n\n\nWe have 3 nodes and the following edges: (0,1) with weight 2, (1,2) with weight 4, (2,0) with weight 8, and (1,0) with weight 16.\nWe have 2 queries: (0,1) with limit 2 and (0,2) with limit 5.\nWe initialize the parent, rank, and weight arrays to [0, 1, 2] and [0, 0, 0].\nWe sort the edges in the adjacency list by distance: (0,1) with weight 2, (1,2) with weight 4, (2,0) with weight 8, and (1,0) with weight 16.\nWe group the nodes into connected components using the union-find algorithm. First, we union nodes 0 and 1 with weight 2, then we union nodes 1 and 2 with weight 4, and finally we union nodes 2 and 0 with weight 8. The resulting parent array is [0, 0, 0].\nFor the first query (0,1) with limit 2, we check if there is a path between nodes 0 and 1 with distance less than 2. We find the root of node 0 with limit 2, which is 0, and the root of node 1 with limit 2, which is 0. Since the roots are the same, we return true.\nFor the second query (0,2) with limit 5, we check if there is a path between nodes 0 and 2 with distance less than 5. We find the root of node 0 with limit 5, which is 0, and the root of node 2 with limit 5, which is 0. Since the roots are the same, we return true.\nTherefore, the output is [false, true].\n\nFor the second input:\nInput: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]\nOutput: [true,false]\n\nWe have 5 nodes and the following edges: (0,1) with weight 10, (1,2) with weight 5, (2,3) with weight 9, and (3,4) with weight 13.\nWe have 2 queries: (0,4) with limit 14 and (1,4) with limit 13.\nWe initialize the parent, rank, and weight arrays to [0, 1, 2, 3, 4] and [0, 0, 0, 0, 0].\nWe sort the edges in the adjacency list by distance: (1,2) with weight 5, (0,1) with weight 10, (2,3) with weight 9, and (3,4) with weight 13.\nWe group the nodes into connected components using the union-find algorithm. First, we union nodes 1 and 2 with weight 5, then we union nodes 0 and 1 with weight 10, then we union nodes 2 and 3 with weight 9, and finally we union nodes 3 and 4 with weight 13. The resulting parent array is [0, 0, 0, 2, 3].\nFor the first query (0,4) with limit 14, we check if there is a path between nodes 0 and 4 with distance less than 14. We find the root of node 0 with limit 14, which is 0, and the root of node 4 with limit 14, which is 3. Since the roots are not the same, we return false.\nFor the second query (1,4) with limit 13, we check if there is a path between nodes 1 and 4 with distance less than 13. We find the root of node 1 with limit 13, which is 0, and the root of node 4 with limit 13, which is 3. Since the roots are the same, we return true.\nTherefore, the output is [true, false].\n\n\n# FAQ \n\n# Why we want to merge the smaller tree into the larger tree?\n\nIn the Union-Find algorithm, the rank array is used to keep of the depth of each node in the tree. When performing the union operation, we want to merge the smaller tree into the larger tree to keep the depth of the tree as small as possible. This helps to improve the performance of the find operation, which is used to determine the root of the tree.\n\nIf we always merge the smaller tree into the larger tree, we can ensure that the depth of the tree does not increase significantly. This is because the depth of the tree is proportional to the logarithm of the number of nodes in the tree. By keeping the depth of the tree small, we can ensure that the find operation runs in O(log n) time, where n is the number of nodes in the tree.\n\nThe rank array is used to keep track of the depth of each node in the tree. When we merge two trees, we compare the rank of the root nodes of the two trees. If the rank of the root node of the first tree is less than the rank of the root node of the second tree, we make the root node of the first tree a child of the root node of the second tree. Otherwise, we make the root node of the second tree a child of the root node of the first tree. If the rank of the root nodes is the same, we arbitrarily choose one of the root nodes to be the parent and increment its rank by one.\n\nBy always merging the smaller tree into the larger tree, we can ensure that the depth of the tree does not increase significantly, which helps to improve the performance of the find operation.\n\n# How Path Compression will work in the Union-Find.\n\nPath is a technique used in the Union-Find algorithm to improve the performance the find operation The find operation is used to determine the root of the tree that a node belongs to. In the basic implementation of the Union-Find algorithm, the find operation traverses the tree from the node to the root to determine the root of the tree. This can take O(log n) time in the worst case, where n is the number of nodes in the tree.\n\nPath compression is a technique that can be used to reduce the depth of the tree during the find operation. When we perform the find operation on a node, we traverse the tree from the node to the root to determine the root of the tree. During this traversal, we can update the parent of each node along the path to the root to be the root itself. This can be done recursively or iteratively.\n\nBy updating the parent of each node along the path to the root to be the root itself, we can reduce the depth of the tree. This can help to improve the performance of the find operation, as subsequent find operations on the same node or its descendants will take less time.\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nhttps://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/solutions/3465024/day-394-union-find-100-0ms-python-java-c-explained-approach/\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A | 31 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
✔💯 DAY 394 | Custom Union-Find | 100% 0ms | [PYTHON/JAVA/C++] | EXPLAINED | Approach 💫 | checking-existence-of-edge-length-limited-paths | 1 | 1 | # Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tproblem is to determine if there is a path between two nodes in an undirected graph such that each edge on the path has a distance strictly less than a given limit.\n##### \u2022\tThe input consists of the number of nodes, the edge list, and the queries.\n##### \u2022\tThe edge list is an array of arrays, where each sub-array represents an edge between two nodes and the distance between them.\n##### \u2022\tThe queries are an array of arrays, where each sub-array represents a query with two nodes and a limit.\n##### \u2022\tThe using the union-find algorithm to determine if there is a path between two nodes.\n##### \u2022\tThe union-find algorithm is used to group nodes into connected components.\n##### \u2022\tFirst sorts the edges in the edge list by their distance in ascending order.\n##### \u2022 Then iterates over the sorted edges and performs a union operation on the nodes connected by the edge.\n##### \u2022\tThe union operation updates the parent and rank arrays to group the nodes into connected components.\n##### \u2022\tThen iterates over the queries and checks if the two nodes are connected and if the distance between them is less than the given limit.\n##### \u2022\tThe isConnectedAndWithinLimit method uses the find method to determine if the two nodes are connected and if the distance between them is less than the given limit.\n##### \u2022\tThe find method uses the parent and weight arrays to find the root of the connected component and checks if the weight of the edge is less than the given limit.\n##### \u2022\tThe union method updates the parent, rank, and weight arrays to group the nodes into connected components and store the weight of the edge.\n##### \u2022\tfinally returns a boolean array where each element represents if there is a path between the two nodes in the corresponding query with edges less than the given limit.\n\n\n\n# Code\n```java []\nclass Solution {\n private int[] parent;\n private int[] rank;\n private int[] weight;\n public boolean[] distanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n // Initialize parent, rank, and weight arrays\n parent = new int[length];\n rank = new int[length];\n weight = new int[length];\n for (int i = 0; i < length ; i++) parent[i] = i;\n\n // Sort edges in the adjacency list by distance\n Arrays.sort(adjList, Comparator.comparingInt(a -> a[2]));\n // Group nodes into connected components using union-find algorithm\n for (int[] edge : adjList) unionByRank(edge[0], edge[1], edge[2]);\n\n // Initialize answer array\n boolean[] answer = new boolean[queries.length];\n // Check if there is a path between two nodes with distance less than the given limit for each query\n for (int i = 0 ; i < queries.length; i++)\n answer[i] = isConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2]);\n\n return answer;\n }\n\n // Check if there is a path between two nodes with distance less than the given limit\n public boolean isConnectedAndWithinLimit(int p, int q, int limit) {\n return find(p, limit) == find(q, limit);\n }\n\n // Find the root of the connected component for a node with distance less than the given limit\n private int find (int x, int limit) {\n while (x != parent[x]) {\n // If the weight of the edge is greater than or equal to the given limit, break out of the loop\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n // Union two nodes into the same connected component with the given limit as the weight of the edge\n private void unionByRank (int x, int y, int limit) {\n // Find the root of the connected component for each node\n int x_ref = find (x, Integer.MAX_VALUE);\n int y_ref = find (y, Integer.MAX_VALUE);\n if (x_ref != y_ref) {\n // If the rank of the root of x is less than the rank of the root of y, make y the parent of x\n if (rank[x_ref] < rank[y_ref]) {\n parent[x_ref] = y_ref;\n weight [x_ref] = limit;;\n } else {\n // Otherwise, make x the parent of y\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n // If the ranks of the roots are equal, increment the rank of the root of x\n if (rank[x_ref] == rank[y_ref]) {\n rank[x_ref]++;\n }\n }\n }\n }\n}\n```\n```python []\nclass Solution:\n def distanceLimitedPathsExist(self, length: int, adjList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n parent = [i for i in range(length)]\n rank = [0 for i in range(length)]\n weight = [0 for i in range(length)]\n\n adjList.sort(key=lambda x: x[2])\n for edge in adjList:\n self.unionByRank(edge[0], edge[1], edge[2], parent, rank, weight)\n\n answer = []\n for query in queries:\n answer.append(self.isConnectedAndWithinLimit(query[0], query[1], query[2], parent, weight))\n\n return answer\n\n def isConnectedAndWithinLimit(self, p: int, q: int, limit: int, parent: List[int], weight: List[int]) -> bool:\n return self.find(p, limit, parent, weight) == self.find(q, limit, parent, weight)\n\n def find(self, x: int, limit: int, parent: List[int], weight: List[int]) -> int:\n while x != parent[x]:\n if weight[x] >= limit:\n break\n x = parent[x]\n return x\n\n def unionByRank(self, x: int, y: int, limit: int, parent: List[int], rank: List[int], weight: List[int]) -> None:\n x_ref = self.find(x, float(\'inf\'), parent, weight)\n y_ref = self.find(y, float(\'inf\'), parent, weight)\n if x_ref != y_ref:\n if rank[x_ref] < rank[y_ref]:\n parent[x_ref] = y_ref\n weight[x_ref] = limit\n else:\n parent[y_ref] = x_ref\n weight[y_ref] = limit\n if rank[x_ref] == rank[y_ref]:\n rank[x_ref] += 1\n```\n\n```c++ []\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int length, vector<vector<int>>& adjList, vector<vector<int>>& queries) {\n vector<int> parent(length);\n vector<int> rank(length);\n vector<int> weight(length);\n for (int i = 0; i < length ; i++) parent[i] = i;\n\n sort(adjList.begin(), adjList.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[2] < b[2];\n });\n for (vector<int>& edge : adjList) unionByRank(edge[0], edge[1], edge[2], parent, rank, weight);\n\n vector<bool> answer;\n for (vector<int>& query : queries)\n answer.push_back(isConnectedAndWithinLimit(query[0], query[1], query[2], parent, weight));\n\n return answer;\n }\n\n bool isConnectedAndWithinLimit(int p, int q, int limit, vector<int>& parent, vector<int>& weight) {\n return find(p, limit, parent, weight) == find(q, limit, parent, weight);\n }\n\n int find(int x, int limit, vector<int>& parent, vector<int>& weight) {\n while (x != parent[x]) {\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n void unionByRank(int x, int y, int limit, vector<int>& parent, vector<int>& rank, vector<int>& weight) {\n int x_ref = find(x, INT_MAX, parent, weight);\n int y_ref = find(y, INT_MAX, parent, weight);\n if (x_ref != y_ref) {\n if (rank[x_ref] < rank[y_ref]) {\n parent[x_ref] = y_ref;\n weight[x_ref] = limit;\n } else {\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n if (rank[x_ref] == rank[y_ref]) {\n rank[x_ref]++;\n }\n }\n }\n }\n};\n```\n```csharp []\npublic class Solution {\n public bool[] DistanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n int[] parent = Enumerable.Range(0, length).ToArray();\n int[] rank = new int[length];\n int[] weight = new int[length];\n\n Array.Sort(adjList, (a, b) => a[2].CompareTo(b[2]));\n foreach (int[] edge in adjList) {\n Union(edge[0], edge[1], edge[2], parent, rank, weight);\n }\n\n bool[] answer = new bool[queries.Length];\n for (int i = 0; i < queries.Length; i++) {\n answer[i] = IsConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2], parent, weight);\n }\n\n return answer;\n }\n\n private bool IsConnectedAndWithinLimit(int p, int q, int limit, int[] parent, int[] weight) {\n return Find(p, limit, parent, weight) == Find(q, limit, parent, weight);\n }\n\n private int Find(int x, int limit, int[] parent, int[] weight) {\n while (x != parent[x]) {\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n private void Union(int x, int y, int limit, int[] parent, int[] rank, int[] weight) {\n int xRef = Find(x, int.MaxValue, parent, weight);\n int yRef = Find(y, int.MaxValue, parent, weight);\n if (xRef == yRef) {\n return;\n }\n if (rank[xRef] < rank[yRef]) {\n parent[xRef] = yRef;\n weight[xRef] = limit;\n } else {\n parent[yRef] = xRef;\n weight[yRef] = limit;\n if (rank[xRef] == rank[yRef]) {\n rank[xRef]++;\n }\n }\n }\n}\n```\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# 2nd union by size \n\n```java []\nclass Solution {\n private int[] parent;\n private int[] size;\n private int[] weight;\n public boolean[] distanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n // Initialize parent, size, and weight arrays\n parent = new int[length];\n size = new int[length];\n weight = new int[length];\n for (int i = 0; i < length ; i++) {\n parent[i] = i;\n size[i] = 1;\n }\n\n // Sort edges in the adjacency list by distance\n Arrays.sort(adjList, Comparator.comparingInt(a -> a[2]));\n // Group nodes into connected components using union-find algorithm\n for (int[] edge : adjList) unionBySize(edge[0], edge[1], edge[2]);\n\n // Initialize answer array\n boolean[] answer = new boolean[queries.length];\n // Check if there is a path between two nodes with distance less than the given limit for each query\n for (int i = 0 ; i < queries.length; i++)\n answer[i] = isConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2]);\n\n return answer;\n }\n\n // Check if there is a path between two nodes with distance less than the given limit\n public boolean isConnectedAndWithinLimit(int p, int q, int limit) {\n return find(p, limit) == find(q, limit);\n }\n\n // Find the root of the connected component for a node with distance less than the given limit\n private int find (int x, int limit) {\n while (x != parent[x]) {\n // If the weight of the edge is greater than or equal to the given limit, break out of the loop\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n // Union two nodes into the same connected component with the given limit as the weight of the edge\n private void unionBySize (int x, int y, int limit) {\n // Find the root of the connected component for each node\n int x_ref = find (x, Integer.MAX_VALUE);\n int y_ref = find (y, Integer.MAX_VALUE);\n if (x_ref != y_ref) {\n // If the size of the root of x is less than the size of the root of y, make y the parent of x\n if (size[x_ref] < size[y_ref]) {\n parent[x_ref] = y_ref;\n weight [x_ref] = limit;\n size[y_ref] += size[x_ref];\n } else {\n // Otherwise, make x the parent of y\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n size[x_ref] += size[y_ref];\n }\n }\n }\n}\n```\n# Complexity\n- Time complexity:\nSorting the adjacency list takes O(E log E) time, where E is the number of edges in the graph.\nThe union-find algorithm takes O(E \u03B1(V)) time, where \u03B1 is the inverse Ackermann function and V is the number of vertices in the graph. In practice, \u03B1(V) is a very small value, so we can consider the time complexity to be O(E).\nChecking if there is a path between two nodes with distance less than the given limit takes O(log V) time, where V is the number of vertices in the graph.\nWe perform this check for each query, so the total time complexity for all queries is O(Q log V), where Q is the number of queries.\nTherefore, the overall time complexity of the algorithm is O(E log E + Q log V).\n- Space Complexity:\nWe use three arrays of size V to store the parent, rank, and weight of each node in the graph, so the space complexity is O(V).\nWe also use a boolean array of size Q to store the answer for each query, so the space complexity is O(Q).\nTherefore, the overall space complexity of the algorithm is O(V + Q).\n\n\n# dry run \nFor the first: Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]\nOutput: [false,true]\n\n\nWe have 3 nodes and the following edges: (0,1) with weight 2, (1,2) with weight 4, (2,0) with weight 8, and (1,0) with weight 16.\nWe have 2 queries: (0,1) with limit 2 and (0,2) with limit 5.\nWe initialize the parent, rank, and weight arrays to [0, 1, 2] and [0, 0, 0].\nWe sort the edges in the adjacency list by distance: (0,1) with weight 2, (1,2) with weight 4, (2,0) with weight 8, and (1,0) with weight 16.\nWe group the nodes into connected components using the union-find algorithm. First, we union nodes 0 and 1 with weight 2, then we union nodes 1 and 2 with weight 4, and finally we union nodes 2 and 0 with weight 8. The resulting parent array is [0, 0, 0].\nFor the first query (0,1) with limit 2, we check if there is a path between nodes 0 and 1 with distance less than 2. We find the root of node 0 with limit 2, which is 0, and the root of node 1 with limit 2, which is 0. Since the roots are the same, we return true.\nFor the second query (0,2) with limit 5, we check if there is a path between nodes 0 and 2 with distance less than 5. We find the root of node 0 with limit 5, which is 0, and the root of node 2 with limit 5, which is 0. Since the roots are the same, we return true.\nTherefore, the output is [false, true].\n\nFor the second input:\nInput: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]\nOutput: [true,false]\n\nWe have 5 nodes and the following edges: (0,1) with weight 10, (1,2) with weight 5, (2,3) with weight 9, and (3,4) with weight 13.\nWe have 2 queries: (0,4) with limit 14 and (1,4) with limit 13.\nWe initialize the parent, rank, and weight arrays to [0, 1, 2, 3, 4] and [0, 0, 0, 0, 0].\nWe sort the edges in the adjacency list by distance: (1,2) with weight 5, (0,1) with weight 10, (2,3) with weight 9, and (3,4) with weight 13.\nWe group the nodes into connected components using the union-find algorithm. First, we union nodes 1 and 2 with weight 5, then we union nodes 0 and 1 with weight 10, then we union nodes 2 and 3 with weight 9, and finally we union nodes 3 and 4 with weight 13. The resulting parent array is [0, 0, 0, 2, 3].\nFor the first query (0,4) with limit 14, we check if there is a path between nodes 0 and 4 with distance less than 14. We find the root of node 0 with limit 14, which is 0, and the root of node 4 with limit 14, which is 3. Since the roots are not the same, we return false.\nFor the second query (1,4) with limit 13, we check if there is a path between nodes 1 and 4 with distance less than 13. We find the root of node 1 with limit 13, which is 0, and the root of node 4 with limit 13, which is 3. Since the roots are the same, we return true.\nTherefore, the output is [true, false].\n\n\n# FAQ \n\n# Why we want to merge the smaller tree into the larger tree?\n\nIn the Union-Find algorithm, the rank array is used to keep of the depth of each node in the tree. When performing the union operation, we want to merge the smaller tree into the larger tree to keep the depth of the tree as small as possible. This helps to improve the performance of the find operation, which is used to determine the root of the tree.\n\nIf we always merge the smaller tree into the larger tree, we can ensure that the depth of the tree does not increase significantly. This is because the depth of the tree is proportional to the logarithm of the number of nodes in the tree. By keeping the depth of the tree small, we can ensure that the find operation runs in O(log n) time, where n is the number of nodes in the tree.\n\nThe rank array is used to keep track of the depth of each node in the tree. When we merge two trees, we compare the rank of the root nodes of the two trees. If the rank of the root node of the first tree is less than the rank of the root node of the second tree, we make the root node of the first tree a child of the root node of the second tree. Otherwise, we make the root node of the second tree a child of the root node of the first tree. If the rank of the root nodes is the same, we arbitrarily choose one of the root nodes to be the parent and increment its rank by one.\n\nBy always merging the smaller tree into the larger tree, we can ensure that the depth of the tree does not increase significantly, which helps to improve the performance of the find operation.\n\n# How Path Compression will work in the Union-Find.\n\nPath is a technique used in the Union-Find algorithm to improve the performance the find operation The find operation is used to determine the root of the tree that a node belongs to. In the basic implementation of the Union-Find algorithm, the find operation traverses the tree from the node to the root to determine the root of the tree. This can take O(log n) time in the worst case, where n is the number of nodes in the tree.\n\nPath compression is a technique that can be used to reduce the depth of the tree during the find operation. When we perform the find operation on a node, we traverse the tree from the node to the root to determine the root of the tree. During this traversal, we can update the parent of each node along the path to the root to be the root itself. This can be done recursively or iteratively.\n\nBy updating the parent of each node along the path to the root to be the root itself, we can reduce the depth of the tree. This can help to improve the performance of the find operation, as subsequent find operations on the same node or its descendants will take less time.\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nhttps://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/solutions/3465024/day-394-union-find-100-0ms-python-java-c-explained-approach/\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A | 31 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
[Python3] Union-Find | checking-existence-of-edge-length-limited-paths | 0 | 1 | **Algo**\nSort queries based on weight and sort edges based on weight as well. Scan through queries from lowest to highest weight and connect the edges whose weight strictly fall below this limit. Check if the queried nodes `p` and `q` are connected in Union-Find structure. If so, put `True` in the relevant position; otherwise put `False`. \n\n**Implementation**\n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n```\n\n**Analysis**\nTime complexity `O(NlogN) + O(MlogM)`\nSpace complexity `O(N)` | 108 | An undirected graph of `n` nodes is defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]` denotes an edge between nodes `ui` and `vi` with distance `disi`. Note that there may be **multiple** edges between two nodes.
Given an array `queries`, where `queries[j] = [pj, qj, limitj]`, your task is to determine for each `queries[j]` whether there is a path between `pj` and `qj` such that each edge on the path has a distance **strictly less than** `limitj` .
Return _a **boolean array**_ `answer`_, where_ `answer.length == queries.length` _and the_ `jth` _value of_ `answer` _is_ `true` _if there is a path for_ `queries[j]` _is_ `true`_, and_ `false` _otherwise_.
**Example 1:**
**Input:** n = 3, edgeList = \[\[0,1,2\],\[1,2,4\],\[2,0,8\],\[1,0,16\]\], queries = \[\[0,1,2\],\[0,2,5\]\]
**Output:** \[false,true\]
**Explanation:** The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1,10\],\[1,2,5\],\[2,3,9\],\[3,4,13\]\], queries = \[\[0,4,14\],\[1,4,13\]\]
**Output:** \[true,false\]
**Exaplanation:** The above figure shows the given graph.
**Constraints:**
* `2 <= n <= 105`
* `1 <= edgeList.length, queries.length <= 105`
* `edgeList[i].length == 3`
* `queries[j].length == 3`
* `0 <= ui, vi, pj, qj <= n - 1`
* `ui != vi`
* `pj != qj`
* `1 <= disi, limitj <= 109`
* There may be **multiple** edges between two nodes. | BruteForce, check all pairs and verify if they differ in one character. O(n^2 * m) where n is the number of words and m is the length of each string. O(m^2 * n), Use hashset, to insert all possible combinations adding a character "*". For example: If dict[i] = "abc", insert ("*bc", "a*c" and "ab*"). |
[Python3] Union-Find | checking-existence-of-edge-length-limited-paths | 0 | 1 | **Algo**\nSort queries based on weight and sort edges based on weight as well. Scan through queries from lowest to highest weight and connect the edges whose weight strictly fall below this limit. Check if the queried nodes `p` and `q` are connected in Union-Find structure. If so, put `True` in the relevant position; otherwise put `False`. \n\n**Implementation**\n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n```\n\n**Analysis**\nTime complexity `O(NlogN) + O(MlogM)`\nSpace complexity `O(N)` | 108 | There is a donuts shop that bakes donuts in batches of `batchSize`. They have a rule where they must serve **all** of the donuts of a batch before serving any donuts of the next batch. You are given an integer `batchSize` and an integer array `groups`, where `groups[i]` denotes that there is a group of `groups[i]` customers that will visit the shop. Each customer will get exactly one donut.
When a group visits the shop, all customers of the group must be served before serving any of the following groups. A group will be happy if they all get fresh donuts. That is, the first customer of the group does not receive a donut that was left over from the previous group.
You can freely rearrange the ordering of the groups. Return _the **maximum** possible number of happy groups after rearranging the groups._
**Example 1:**
**Input:** batchSize = 3, groups = \[1,2,3,4,5,6\]
**Output:** 4
**Explanation:** You can arrange the groups as \[6,2,4,5,1,3\]. Then the 1st, 2nd, 4th, and 6th groups will be happy.
**Example 2:**
**Input:** batchSize = 4, groups = \[1,3,2,5,2,2,1,6\]
**Output:** 4
**Constraints:**
* `1 <= batchSize <= 9`
* `1 <= groups.length <= 30`
* `1 <= groups[i] <= 109` | All the queries are given in advance. Is there a way you can reorder the queries to avoid repeated computations? |
Simple Python Solution using Counter | number-of-students-unable-to-eat-lunch | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can distribute sandwich, if there is any student who wants that sandwich.\nSo, we create a counter of students.\nAnd, iterate sandwiches, one by one and check if there is any student left who wants that sandwich.\n\nIf there is a student who wants that sandwich, we decrease counter by 1, else we return count of students which want other kind of sandwich\n\n# Code\n```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n student_count = Counter(students)\n for sandwich in sandwiches:\n if student_count[sandwich] > 0:\n student_count[sandwich] -= 1\n else:\n return student_count[not sandwich]\n return 0\n\n``` | 2 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Simple Python Solution using Counter | number-of-students-unable-to-eat-lunch | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can distribute sandwich, if there is any student who wants that sandwich.\nSo, we create a counter of students.\nAnd, iterate sandwiches, one by one and check if there is any student left who wants that sandwich.\n\nIf there is a student who wants that sandwich, we decrease counter by 1, else we return count of students which want other kind of sandwich\n\n# Code\n```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n student_count = Counter(students)\n for sandwich in sandwiches:\n if student_count[sandwich] > 0:\n student_count[sandwich] -= 1\n else:\n return student_count[not sandwich]\n return 0\n\n``` | 2 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Python Queue || easy || approach | number-of-students-unable-to-eat-lunch | 0 | 1 | ```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n count = 0\n while len(students) > count:\n if students[0] == sandwiches[0]:\n sandwiches.pop(0)\n count = 0\n else:\n students.append(students[0])\n count+=1\n\n students.pop(0)\n return len(students)\n\t\t\n#Upvote will be encouraging.\n``` | 23 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Python Queue || easy || approach | number-of-students-unable-to-eat-lunch | 0 | 1 | ```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n count = 0\n while len(students) > count:\n if students[0] == sandwiches[0]:\n sandwiches.pop(0)\n count = 0\n else:\n students.append(students[0])\n count+=1\n\n students.pop(0)\n return len(students)\n\t\t\n#Upvote will be encouraging.\n``` | 23 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Easy Approach | number-of-students-unable-to-eat-lunch | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n while(len(students)!=0):\n if(sandwiches[0] not in students):\n return(len(students))\n if(students[0]==sandwiches[0]):\n students.pop(0)\n sandwiches.pop(0)\n else:\n a=students.pop(0)\n students.append(a)\n return(len(students))\n\n \n``` | 5 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Easy Approach | number-of-students-unable-to-eat-lunch | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n while(len(students)!=0):\n if(sandwiches[0] not in students):\n return(len(students))\n if(students[0]==sandwiches[0]):\n students.pop(0)\n sandwiches.pop(0)\n else:\n a=students.pop(0)\n students.append(a)\n return(len(students))\n\n \n``` | 5 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Simple solution by using Deque DS | number-of-students-unable-to-eat-lunch | 0 | 1 | # Intuition\nThe task description clearly describes the path to resolve the problem.\n\n```\n# each student can take a sandwich \n# according to it\'s index (that\'s 1 OR 0)\n# from sandwiches stack\n\n# the simplest example and pseudocode\nsandwiches = [1, 0, 1]\nstudents = [0, 1, 1]\n\n# while sandwiches\n# i = 0 => student == students[i] == 0\n# student != sandwiches[0] => he goes to the end \n\nsandwiches = [1, 0, 1]\nstudents = [1, 1, 0]\n\n# i = 1 => student == students[i] == 1\n# student == sandwiches[0] => he eats the sandwich and leaves the q\n\nsandwiches = [0, 1]\nstudents = [1, 0]\n\n# and so on \n```\n\n# Approach\n1. convert list of `students` and `sandwiches` into `deque` (though it\'s not necessary because of small size of data)\n2. then check, if the student can eat the sandwich, that\'s in the top of the stack, or move the student to the end of the stack, or **if the q is STUCK**, and there\'re no available permutations i.e.\n```\n# nobody can eat 0-sandwich in the q\nsandwiches = [0, 1, 1]\nstudents = [1, 1, 1]\n``` \n3. return remained amount of students\n\n# Complexity\n- Time complexity: **O(n^2)** in the worst case, because of iterating `n * n` students at all \n\n- Space complexity: **O(n)** because of converting lists into `deques`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countStudents(self, students: list[int], sandwiches: list[int]) -> int:\n students = deque(students)\n sandwiches = deque(sandwiches)\n \n while sandwiches:\n student = students[0]\n \n if student == sandwiches[0]:\n students.popleft()\n sandwiches.popleft()\n else:\n if sandwiches[0] not in students:\n break\n\n students.popleft()\n students.append(student)\n\n return len(students)\n \n \n``` | 3 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Simple solution by using Deque DS | number-of-students-unable-to-eat-lunch | 0 | 1 | # Intuition\nThe task description clearly describes the path to resolve the problem.\n\n```\n# each student can take a sandwich \n# according to it\'s index (that\'s 1 OR 0)\n# from sandwiches stack\n\n# the simplest example and pseudocode\nsandwiches = [1, 0, 1]\nstudents = [0, 1, 1]\n\n# while sandwiches\n# i = 0 => student == students[i] == 0\n# student != sandwiches[0] => he goes to the end \n\nsandwiches = [1, 0, 1]\nstudents = [1, 1, 0]\n\n# i = 1 => student == students[i] == 1\n# student == sandwiches[0] => he eats the sandwich and leaves the q\n\nsandwiches = [0, 1]\nstudents = [1, 0]\n\n# and so on \n```\n\n# Approach\n1. convert list of `students` and `sandwiches` into `deque` (though it\'s not necessary because of small size of data)\n2. then check, if the student can eat the sandwich, that\'s in the top of the stack, or move the student to the end of the stack, or **if the q is STUCK**, and there\'re no available permutations i.e.\n```\n# nobody can eat 0-sandwich in the q\nsandwiches = [0, 1, 1]\nstudents = [1, 1, 1]\n``` \n3. return remained amount of students\n\n# Complexity\n- Time complexity: **O(n^2)** in the worst case, because of iterating `n * n` students at all \n\n- Space complexity: **O(n)** because of converting lists into `deques`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countStudents(self, students: list[int], sandwiches: list[int]) -> int:\n students = deque(students)\n sandwiches = deque(sandwiches)\n \n while sandwiches:\n student = students[0]\n \n if student == sandwiches[0]:\n students.popleft()\n sandwiches.popleft()\n else:\n if sandwiches[0] not in students:\n break\n\n students.popleft()\n students.append(student)\n\n return len(students)\n \n \n``` | 3 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
100% speed Python [No imports][Simple to understand / commented!] | number-of-students-unable-to-eat-lunch | 0 | 1 | Code: \n```\ndef countStu(stu,sand):\n while sand:\n if sand[0] in stu:\n stu.remove(sand[0])\n sand.pop(0)\n else:break\n return len(sand)\n```\n\nCommented Code:\n```\ndef countStu(stu,sand):\n\t# while there are still elements in sandwich list\n while sand:\n\t\t# check if the first element of sand is in the student list\n if sand[0] in stu:\n\t\t\t# remove the element from the student list\n stu.remove(sand[0])\n\t\t\t# remove the first element in the sandwich list\n sand.pop(0)\n\t\t# if the first element of sand isn\'t in the student list break the while loop\n else:break\n\t# after removing all the sandwiches that have a student to eat them, the length of sand is the\n\t# amount of uneaten sandwiches\n return len(sand)\n```\n | 30 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
100% speed Python [No imports][Simple to understand / commented!] | number-of-students-unable-to-eat-lunch | 0 | 1 | Code: \n```\ndef countStu(stu,sand):\n while sand:\n if sand[0] in stu:\n stu.remove(sand[0])\n sand.pop(0)\n else:break\n return len(sand)\n```\n\nCommented Code:\n```\ndef countStu(stu,sand):\n\t# while there are still elements in sandwich list\n while sand:\n\t\t# check if the first element of sand is in the student list\n if sand[0] in stu:\n\t\t\t# remove the element from the student list\n stu.remove(sand[0])\n\t\t\t# remove the first element in the sandwich list\n sand.pop(0)\n\t\t# if the first element of sand isn\'t in the student list break the while loop\n else:break\n\t# after removing all the sandwiches that have a student to eat them, the length of sand is the\n\t# amount of uneaten sandwiches\n return len(sand)\n```\n | 30 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Python using queue push pop | number-of-students-unable-to-eat-lunch | 0 | 1 | ```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n count = len(students)\n while(sandwiches and students and sandwiches[0] in students):\n if(sandwiches[0]!=students[0]):\n students.append(students[0])\n students.pop(0)\n else:\n students.pop(0)\n sandwiches.pop(0)\n count-=1\n return count\n``` | 3 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
Python using queue push pop | number-of-students-unable-to-eat-lunch | 0 | 1 | ```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n count = len(students)\n while(sandwiches and students and sandwiches[0] in students):\n if(sandwiches[0]!=students[0]):\n students.append(students[0])\n students.pop(0)\n else:\n students.pop(0)\n sandwiches.pop(0)\n count-=1\n return count\n``` | 3 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
[Python3] 32ms Brute Force Solution | number-of-students-unable-to-eat-lunch | 0 | 1 | ```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n curr = 0\n \n while students:\n if(students[0] == sandwiches[0]):\n curr = 0\n students.pop(0)\n sandwiches.pop(0)\n else:\n curr += 1\n students.append(students.pop(0))\n \n if(curr >= len(students)):\n break\n \n return len(students)\n``` | 11 | The school cafeteria offers circular and square sandwiches at lunch break, referred to by numbers `0` and `1` respectively. All students stand in a queue. Each student either prefers square or circular sandwiches.
The number of sandwiches in the cafeteria is equal to the number of students. The sandwiches are placed in a **stack**. At each step:
* If the student at the front of the queue **prefers** the sandwich on the top of the stack, they will **take it** and leave the queue.
* Otherwise, they will **leave it** and go to the queue's end.
This continues until none of the queue students want to take the top sandwich and are thus unable to eat.
You are given two integer arrays `students` and `sandwiches` where `sandwiches[i]` is the type of the `ith` sandwich in the stack (`i = 0` is the top of the stack) and `students[j]` is the preference of the `jth` student in the initial queue (`j = 0` is the front of the queue). Return _the number of students that are unable to eat._
**Example 1:**
**Input:** students = \[1,1,0,0\], sandwiches = \[0,1,0,1\]
**Output:** 0
**Explanation:**
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,0,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,0,1,1\].
- Front student takes the top sandwich and leaves the line making students = \[0,1,1\] and sandwiches = \[1,0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[1,1,0\].
- Front student takes the top sandwich and leaves the line making students = \[1,0\] and sandwiches = \[0,1\].
- Front student leaves the top sandwich and returns to the end of the line making students = \[0,1\].
- Front student takes the top sandwich and leaves the line making students = \[1\] and sandwiches = \[1\].
- Front student takes the top sandwich and leaves the line making students = \[\] and sandwiches = \[\].
Hence all students are able to eat.
**Example 2:**
**Input:** students = \[1,1,1,0,0,1\], sandwiches = \[1,0,0,0,1,1\]
**Output:** 3
**Constraints:**
* `1 <= students.length, sandwiches.length <= 100`
* `students.length == sandwiches.length`
* `sandwiches[i]` is `0` or `1`.
* `students[i]` is `0` or `1`. | Maintain the running sum and max value for repeated letters. |
[Python3] 32ms Brute Force Solution | number-of-students-unable-to-eat-lunch | 0 | 1 | ```\nclass Solution:\n def countStudents(self, students: List[int], sandwiches: List[int]) -> int:\n curr = 0\n \n while students:\n if(students[0] == sandwiches[0]):\n curr = 0\n students.pop(0)\n sandwiches.pop(0)\n else:\n curr += 1\n students.append(students.pop(0))\n \n if(curr >= len(students)):\n break\n \n return len(students)\n``` | 11 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Python Elegant & Short | One Pass | average-waiting-time | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n finish_time = -maxsize\n total_wait_time = 0\n\n for time, duration in customers:\n if time < finish_time:\n total_wait_time += finish_time - time + duration\n finish_time += duration\n else:\n total_wait_time += duration\n finish_time = time + duration\n\n return total_wait_time / len(customers)\n\n``` | 1 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Python Elegant & Short | One Pass | average-waiting-time | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n finish_time = -maxsize\n total_wait_time = 0\n\n for time, duration in customers:\n if time < finish_time:\n total_wait_time += finish_time - time + duration\n finish_time += duration\n else:\n total_wait_time += duration\n finish_time = time + duration\n\n return total_wait_time / len(customers)\n\n``` | 1 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
Beginner Friendly || Easy Understandable solution || Python 3 | average-waiting-time | 0 | 1 | \n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, arr: List[List[int]]) -> float:\n a=[[arr[0][0],arr[0][0]+arr[0][1]]]\n for i in range(1,len(arr)):\n if arr[i][0]>a[-1][1]:\n a.append([arr[i][0],arr[i][0]+arr[i][1]])\n else:\n a.append([a[-1][1],a[-1][1]+arr[i][1]])\n s=arr[0][1]\n \n for i in range(1,len(a)):\n s+=abs(arr[i][0]-a[i][1])\n \n return (s)/len(a)\n\n\n\n\n\n \n``` | 1 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Beginner Friendly || Easy Understandable solution || Python 3 | average-waiting-time | 0 | 1 | \n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, arr: List[List[int]]) -> float:\n a=[[arr[0][0],arr[0][0]+arr[0][1]]]\n for i in range(1,len(arr)):\n if arr[i][0]>a[-1][1]:\n a.append([arr[i][0],arr[i][0]+arr[i][1]])\n else:\n a.append([a[-1][1],a[-1][1]+arr[i][1]])\n s=arr[0][1]\n \n for i in range(1,len(a)):\n s+=abs(arr[i][0]-a[i][1])\n \n return (s)/len(a)\n\n\n\n\n\n \n``` | 1 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
Easy Approach | average-waiting-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n a=customers[0][0]\n wait=0\n for i in customers:\n \n if(a<i[0]):\n wait+=((i[0]+i[1])-i[0])\n a=i[0]+i[1]\n else:\n a+=i[1]\n wait+=(a-i[0])\n print(wait,a)\n return(wait/len(customers))\n\n\n``` | 3 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Easy Approach | average-waiting-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n a=customers[0][0]\n wait=0\n for i in customers:\n \n if(a<i[0]):\n wait+=((i[0]+i[1])-i[0])\n a=i[0]+i[1]\n else:\n a+=i[1]\n wait+=(a-i[0])\n print(wait,a)\n return(wait/len(customers))\n\n\n``` | 3 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
✅⬆️🔥 BEATS 100 % | 0ms | 3 lines | easy | proof | average-waiting-time | 1 | 1 | # UPVOTE please\n\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public double averageWaitingTime(int[][] C) {\n double an=0;\n int st=C[0][0];\n for (var v:C){\n st = (st>=v[0])? st+v[1] : v[0]+v[1];\n an+=(st-v[0]);\n }return an/C.length;\n }\n}\n``` | 2 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
✅⬆️🔥 BEATS 100 % | 0ms | 3 lines | easy | proof | average-waiting-time | 1 | 1 | # UPVOTE please\n\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public double averageWaitingTime(int[][] C) {\n double an=0;\n int st=C[0][0];\n for (var v:C){\n st = (st>=v[0])? st+v[1] : v[0]+v[1];\n an+=(st-v[0]);\n }return an/C.length;\n }\n}\n``` | 2 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
[Python3] Simple And Fast Solution | average-waiting-time | 0 | 1 | ```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n arr = []\n \n time = 0\n \n for i , j in customers:\n if(i > time):\n time = i + j\n else:\n time += j\n arr.append(time - i)\n \n return sum(arr) / len(arr)\n``` | 7 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
[Python3] Simple And Fast Solution | average-waiting-time | 0 | 1 | ```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n arr = []\n \n time = 0\n \n for i , j in customers:\n if(i > time):\n time = i + j\n else:\n time += j\n arr.append(time - i)\n \n return sum(arr) / len(arr)\n``` | 7 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
Easy Python solution (ACCEPTED) | average-waiting-time | 0 | 1 | **Explanation**\nFirstly, we get the initial customer arrival time as actual time, then go through all customers one by one with special logic. We add waiting to time to actual time. If the next arrival time is bigger than the current actual time, it means that customer ordered it when chef is free.\n**Complexity**\n\nTime ```O(N)```\nSpace ```O(1)```\n\n**Python:**\n```\ndef averageWaitingTime(self, customers: List[List[int]]) -> float:\n\xA0 \xA0 \xA0 \xA0 act = customers[0][0]\n\xA0 \xA0 \xA0 \xA0 wait = 0\n\xA0 \xA0 \xA0 \xA0 for item in customers:\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 if act<item[0]:\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 act = item[0]\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 act += item[1]\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 wait +=(act - item[0])\n\xA0 \xA0 \xA0 \xA0 return wait/len(customers)\n``` | 6 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Easy Python solution (ACCEPTED) | average-waiting-time | 0 | 1 | **Explanation**\nFirstly, we get the initial customer arrival time as actual time, then go through all customers one by one with special logic. We add waiting to time to actual time. If the next arrival time is bigger than the current actual time, it means that customer ordered it when chef is free.\n**Complexity**\n\nTime ```O(N)```\nSpace ```O(1)```\n\n**Python:**\n```\ndef averageWaitingTime(self, customers: List[List[int]]) -> float:\n\xA0 \xA0 \xA0 \xA0 act = customers[0][0]\n\xA0 \xA0 \xA0 \xA0 wait = 0\n\xA0 \xA0 \xA0 \xA0 for item in customers:\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 if act<item[0]:\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 act = item[0]\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 act += item[1]\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 wait +=(act - item[0])\n\xA0 \xA0 \xA0 \xA0 return wait/len(customers)\n``` | 6 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
brute force | average-waiting-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def averageWaitingTime(self, customers: List[List[int]]) -> float:\n start=customers[0][0]\n total=0\n for i in customers:\n if i[0]>start:\n total=total+i[1]\n start=i[0]+i[1]\n else:\n \n total=total+start+i[1]-i[0]\n start=start+i[1]\n return total/len(customers)\n\n\n\n\n\n\n\n \n``` | 0 | There is a restaurant with a single chef. You are given an array `customers`, where `customers[i] = [arrivali, timei]:`
* `arrivali` is the arrival time of the `ith` customer. The arrival times are sorted in **non-decreasing** order.
* `timei` is the time needed to prepare the order of the `ith` customer.
When a customer arrives, he gives the chef his order, and the chef starts preparing it once he is idle. The customer waits till the chef finishes preparing his order. The chef does not prepare food for more than one customer at a time. The chef prepares food for customers **in the order they were given in the input**.
Return _the **average** waiting time of all customers_. Solutions within `10-5` from the actual answer are considered accepted.
**Example 1:**
**Input:** customers = \[\[1,2\],\[2,5\],\[4,3\]\]
**Output:** 5.00000
**Explanation:**
1) The first customer arrives at time 1, the chef takes his order and starts preparing it immediately at time 1, and finishes at time 3, so the waiting time of the first customer is 3 - 1 = 2.
2) The second customer arrives at time 2, the chef takes his order and starts preparing it at time 3, and finishes at time 8, so the waiting time of the second customer is 8 - 2 = 6.
3) The third customer arrives at time 4, the chef takes his order and starts preparing it at time 8, and finishes at time 11, so the waiting time of the third customer is 11 - 4 = 7.
So the average waiting time = (2 + 6 + 7) / 3 = 5.
**Example 2:**
**Input:** customers = \[\[5,2\],\[5,4\],\[10,3\],\[20,1\]\]
**Output:** 3.25000
**Explanation:**
1) The first customer arrives at time 5, the chef takes his order and starts preparing it immediately at time 5, and finishes at time 7, so the waiting time of the first customer is 7 - 5 = 2.
2) The second customer arrives at time 5, the chef takes his order and starts preparing it at time 7, and finishes at time 11, so the waiting time of the second customer is 11 - 5 = 6.
3) The third customer arrives at time 10, the chef takes his order and starts preparing it at time 11, and finishes at time 14, so the waiting time of the third customer is 14 - 10 = 4.
4) The fourth customer arrives at time 20, the chef takes his order and starts preparing it immediately at time 20, and finishes at time 21, so the waiting time of the fourth customer is 21 - 20 = 1.
So the average waiting time = (2 + 6 + 4 + 1) / 4 = 3.25.
**Constraints:**
* `1 <= customers.length <= 105`
* `1 <= arrivali, timei <= 104`
* `arrivali <= arrivali+1` | Build the network instead of removing extra edges. Suppose you have the final graph (after removing extra edges). Consider the subgraph with only the edges that Alice can traverse. What structure does this subgraph have? How many edges are there? Use disjoint set union data structure for both Alice and Bob. Always use Type 3 edges first, and connect the still isolated ones using other edges. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.