title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n self.count = 0\n def fib(k):\n l = [0,1]\n for i in range(1,k+1):\n if l[-2]+l[-1]<k:\n l.append(l[-1] + l[-2])\n elif l[-2]+l[-1]==k:\n l.append(l[-1] + l[-2])\n self.count+=1\n k = k - l[-1]\n return k\n else:\n self.count+=1\n k = k - l[-1]\n return k\n while k>0:\n k = fib(k)\n if k==1:\n return self.count+1\n return self.count\n\n \n \n\n\n\n \n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python Solution using Greedy approach | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Approach\nInitially we will create a pre calculated fibonacci sequence and later on using greedy approach we will count the valid additions needed for achieving the value of `k`.\n\n# Complexity\n- Time complexity:\nThe number of iterations in this loop is proportional to the length of the arr list, which is $$O(n)$$.\n\n- Space complexity:\nThe list `arr` is proportional to the length of `arr` and since other variables (`k`, `a`, `b`, `counter`, `expected`, `ix`) use constant space, The space complexitiy is $$O(n)$$.\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n a = 0\n b = 1\n arr = [1]\n counter = 1\n\n while True:\n arr.append(a + b)\n a, b = b, a + b\n if a + b > k:\n break\n\n expected = arr[-1]\n for ix in range(len(arr) - 2, -1, -1):\n if (arr[ix] + expected) <= k:\n expected = arr[ix] + expected\n counter = counter + 1\n\n return counter\n```\n\n\nP.S. First ever post on leetcode, hope it helps you in anyway :-) | 0 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Python Solution using Greedy approach | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Approach\nInitially we will create a pre calculated fibonacci sequence and later on using greedy approach we will count the valid additions needed for achieving the value of `k`.\n\n# Complexity\n- Time complexity:\nThe number of iterations in this loop is proportional to the length of the arr list, which is $$O(n)$$.\n\n- Space complexity:\nThe list `arr` is proportional to the length of `arr` and since other variables (`k`, `a`, `b`, `counter`, `expected`, `ix`) use constant space, The space complexitiy is $$O(n)$$.\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n a = 0\n b = 1\n arr = [1]\n counter = 1\n\n while True:\n arr.append(a + b)\n a, b = b, a + b\n if a + b > k:\n break\n\n expected = arr[-1]\n for ix in range(len(arr) - 2, -1, -1):\n if (arr[ix] + expected) <= k:\n expected = arr[ix] + expected\n counter = counter + 1\n\n return counter\n```\n\n\nP.S. First ever post on leetcode, hope it helps you in anyway :-) | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python solution !!!98% Beat . | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFist find fibonacci numbers less than k ,append them in a list .List must be in increasing order.\n\n**Find the integer numbers whose sumation is equal to k**\nCheck the numbers from the last index of the list(which contains fibonacci numbers).Check the value of last index is less than k ,if True subtract the value from k than decrease the pointer and use a counter pointer .\nBest of LUCK !!!!\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n flist=[1]\n value=0\n while True and flist[-1]<k:\n flist.append(value+flist[-1])\n value=flist[-2]\n j=len(flist)-1\n count=0\n while j>=0 and k>0:\n if flist[j]<=k:\n k-=flist[j]\n count+=1\n j-=1\n return (count)\n \n``` | 0 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Python solution !!!98% Beat . | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFist find fibonacci numbers less than k ,append them in a list .List must be in increasing order.\n\n**Find the integer numbers whose sumation is equal to k**\nCheck the numbers from the last index of the list(which contains fibonacci numbers).Check the value of last index is less than k ,if True subtract the value from k than decrease the pointer and use a counter pointer .\nBest of LUCK !!!!\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n flist=[1]\n value=0\n while True and flist[-1]<k:\n flist.append(value+flist[-1])\n value=flist[-2]\n j=len(flist)-1\n count=0\n while j>=0 and k>0:\n if flist[j]<=k:\n k-=flist[j]\n count+=1\n j-=1\n return (count)\n \n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
A proof of the correctness for greedy, and comparison to other problems | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Approach\nThere are tons of good solutions posted by others, but I want to explain why greedy is correct for this problem, and compare to another one.\nFirst consider a variation of this question. Given a number K, choose a minimal amount of numbers amoung a *given list* instead of *Fibonacci sequence*. For example:\nK = 7, numbers = [1,3,4,5].\n(I guess this problem is in Leetcode but I forget the number. Anyone who remembers can add a comment.)\nIf use greedy for this problem, then you may end up with a solution 7 = 5 + 1 + 1, and your answer is 3. However, the minimal amount you can choose is 2, because 7 = 3 + 4.\nThe reason why greedy holds, is because the definition of Fibonacci sequence. Since f[i] = f[i-1] + f[i-2], choosing a larger number (if you can) would definitely reduce the amount of numbers you need. This is the intuition.\n\nAlso I can think of a formal proof using contradiction:\n1) If there exists $$i$$, such that $$f[i] = k$$, then the optimal solution is 1.\n2) If the optimal solution is not 1, meaning that you cannot directly find $$f[i] = k$$, then we can assume that the optimal solution is obtained by choosing $$f[i]$$ and $$f[j]$$. Assume this optimal solution is $$N$$. However, there exists a larger number $$f[p]$$, such that $$f[p] > f[i], f[j]$$, and also $$f[p] \\leq k$$. By choosing $$f[p]$$, $$k$$ reduces to $$k - f[p]$$. Note that $$f[p]$$ can be written as a sum of $$f[i]$$, $$f[j]$$ and some extra terms within the sequence. Therefore, by choosing $$f[p]$$, we don\'t need $$f[i], f[j]$$ anymore. Thus, the optimal solution becomes $$N - 1 < N$$, the original solution is no more the optimal one $$\\rightarrow$$ contradiction. \n\nTherefore, when there is a large number exists, the larger one should always be chosen. This proof does not hold for my problem, where the list is not a Fibonacci sequence. This is because choosing a larger number does not necessary eliminate smaller ones. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(f^{-1}(k))$$, $$f^{-1}$$ is the inversion of Fibonacci function, almost constant. \n\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n fNumber = [1,1]\n while fNumber[-1] < k:\n fNumber.append(fNumber[-1] + fNumber[-2])\n length = len(fNumber)\n cnt = 0\n for i in range(length - 1, -1, -1):\n while k >= fNumber[i]:\n k = k - fNumber[i]\n cnt += 1\n return cnt\n``` | 0 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
A proof of the correctness for greedy, and comparison to other problems | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Approach\nThere are tons of good solutions posted by others, but I want to explain why greedy is correct for this problem, and compare to another one.\nFirst consider a variation of this question. Given a number K, choose a minimal amount of numbers amoung a *given list* instead of *Fibonacci sequence*. For example:\nK = 7, numbers = [1,3,4,5].\n(I guess this problem is in Leetcode but I forget the number. Anyone who remembers can add a comment.)\nIf use greedy for this problem, then you may end up with a solution 7 = 5 + 1 + 1, and your answer is 3. However, the minimal amount you can choose is 2, because 7 = 3 + 4.\nThe reason why greedy holds, is because the definition of Fibonacci sequence. Since f[i] = f[i-1] + f[i-2], choosing a larger number (if you can) would definitely reduce the amount of numbers you need. This is the intuition.\n\nAlso I can think of a formal proof using contradiction:\n1) If there exists $$i$$, such that $$f[i] = k$$, then the optimal solution is 1.\n2) If the optimal solution is not 1, meaning that you cannot directly find $$f[i] = k$$, then we can assume that the optimal solution is obtained by choosing $$f[i]$$ and $$f[j]$$. Assume this optimal solution is $$N$$. However, there exists a larger number $$f[p]$$, such that $$f[p] > f[i], f[j]$$, and also $$f[p] \\leq k$$. By choosing $$f[p]$$, $$k$$ reduces to $$k - f[p]$$. Note that $$f[p]$$ can be written as a sum of $$f[i]$$, $$f[j]$$ and some extra terms within the sequence. Therefore, by choosing $$f[p]$$, we don\'t need $$f[i], f[j]$$ anymore. Thus, the optimal solution becomes $$N - 1 < N$$, the original solution is no more the optimal one $$\\rightarrow$$ contradiction. \n\nTherefore, when there is a large number exists, the larger one should always be chosen. This proof does not hold for my problem, where the list is not a Fibonacci sequence. This is because choosing a larger number does not necessary eliminate smaller ones. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(f^{-1}(k))$$, $$f^{-1}$$ is the inversion of Fibonacci function, almost constant. \n\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n fNumber = [1,1]\n while fNumber[-1] < k:\n fNumber.append(fNumber[-1] + fNumber[-2])\n length = len(fNumber)\n cnt = 0\n for i in range(length - 1, -1, -1):\n while k >= fNumber[i]:\n k = k - fNumber[i]\n cnt += 1\n return cnt\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python Simple Solution | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBecuase there is always an answer, we will just subtract the biggest Fibonacci number possible until we get k down to zero. We create a helper function to subtract the maximum number, then simply count how many times we do this.\n\nIn the helper funciton, we first check if we need to add more entries to fibs. After this, we search through fibs and return the biggest number that we can subtract from k (without it going less than 0)\n\n\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n\n fibs = [1,1,2]\n\n count = 0\n while k > 0 :\n k = self.subtractMaxFibNumber(k, fibs)\n count += 1\n\n return count\n \n\n def subtractMaxFibNumber(self, k, fibs) :\n # if we need to add more fib numbers, do it\n while fibs[-1] < k :\n fibs.append(fibs[-1] + fibs[-2])\n \n # subtract biggest fib number\n for x in fibs[::-1] :\n if x <= k :\n return k - x\n \n \n\n \n\n``` | 0 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Python Simple Solution | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBecuase there is always an answer, we will just subtract the biggest Fibonacci number possible until we get k down to zero. We create a helper function to subtract the maximum number, then simply count how many times we do this.\n\nIn the helper funciton, we first check if we need to add more entries to fibs. After this, we search through fibs and return the biggest number that we can subtract from k (without it going less than 0)\n\n\n# Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n\n fibs = [1,1,2]\n\n count = 0\n while k > 0 :\n k = self.subtractMaxFibNumber(k, fibs)\n count += 1\n\n return count\n \n\n def subtractMaxFibNumber(self, k, fibs) :\n # if we need to add more fib numbers, do it\n while fibs[-1] < k :\n fibs.append(fibs[-1] + fibs[-2])\n \n # subtract biggest fib number\n for x in fibs[::-1] :\n if x <= k :\n return k - x\n \n \n\n \n\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python sol. with utube video | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Code\n```\n# https://www.youtube.com/watch?v=w3zD7kyJE8U\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n fib=[1,1]\n a=b=1\n for i in range(3,100):\n c=a+b\n if c>10**9:\n break\n a=b\n b=c\n fib.append(c)\n # print(fib)\n fib=fib[::-1]\n res=0\n for i in fib:\n if i<=k:\n k-=i\n res+=1\n if k==0:\n return res\n return res\n``` | 0 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Python sol. with utube video | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Code\n```\n# https://www.youtube.com/watch?v=w3zD7kyJE8U\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n fib=[1,1]\n a=b=1\n for i in range(3,100):\n c=a+b\n if c>10**9:\n break\n a=b\n b=c\n fib.append(c)\n # print(fib)\n fib=fib[::-1]\n res=0\n for i in fib:\n if i<=k:\n k-=i\n res+=1\n if k==0:\n return res\n return res\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Simple solution with Backtracking in Python3 / TypeScript | the-k-th-lexicographical-string-of-all-happy-strings-of-length-n | 0 | 1 | # Intuition\nHere\'s a brief explanation of a problem:\n- there\'re `n` and `k` integers\n- our goal is to get `k` - th permutation of a **happy string** with length `n`\n\nA **happy string** consists with letters `abc`, that\'s formed as permutation.\nThe neighbours **can\'t be equal** such as `s[i] != s[i+1] (or s[i-1])`.\n\nThe approach is straightforward: append to the current permutation a **character**, if it follows the rules above.\n\n# Approach\n1. declare `ans`, that\'s the answer\n2. define `backtrack`, that accepts `path`\n3. since we\'re looking for a permutation at `k - 1` - th position, if `k == 0`, we\'ve founded it\n4. then check `len(path) == n` and store a current permutation to the `ans`\n5. otherwise iterate over `abc` and follow the rules above\n6. finally check, if the count of permutation is more than `k`, and return an empty string or `ans` \n\n# Complexity\n- Time complexity: **O(3^N)**, where **N** is the length of `abc` in worst-case scenario\n\n- Space complexity: **O(N)**, for recursive call stack\n\n# Code in Python3\n```\nclass Solution:\n def getHappyString(self, n: int, k: int) -> str:\n self.ans = \'\'\n\n def backtrack(path):\n nonlocal k\n\n if k == 0: return\n\n if len(path) == n:\n k -= 1\n self.ans = "".join(path)\n return\n\n for i in range(3):\n char = chr(97 + i)\n\n if not path or path[-1] != char:\n path.append(char)\n backtrack(path)\n path.pop()\n \n backtrack([])\n\n return self.ans if not k else \'\'\n```\n# Code in TypeScript\n```\nfunction getHappyString(n: number, k: number): string {\n let ans = \'\';\n\n const backtrack = (path: string[]): void => {\n if (k === 0) return;\n\n if (path.length === n) {\n k--;\n ans = path.join(\'\');\n return;\n }\n\n for (let i = 0; i < 3; i++) {\n const char = String.fromCharCode(\'a\'.charCodeAt(0) + i);\n\n if (path[path.length - 1] !== char) {\n path.push(char);\n backtrack(path);\n path.pop();\n }\n }\n };\n\n backtrack([]);\n\n return !k ? ans : \'\';\n}\n``` | 2 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
Python 3 || 9 lines, binary map w/example || T/M: 99% / 87% | the-k-th-lexicographical-string-of-all-happy-strings-of-length-n | 0 | 1 | ```\nclass Solution:\n def getHappyString(self, n: int, k: int) -> str:\n\n d = {\'a\':\'bc\',\'b\':\'ac\',\'c\':\'ab\'} # Example: n = 5, k = 20\n\n div,r = divmod(k-1,2**(n-1)) # div,r = divmod(19,16) = 1,3\n\n if div > 2: return \'\'\n prev = ans = \'abc\'[div] # prev = ans = \'b\'\n \n r = list(map(int,bin(r)[2:].rjust(n-1,\'0\'))) # r = map(int, \'0011\') = [0,0,1,1]\n \n for i in range(n-1): # i r[i] d[prev][r[i]] ans\n prev = d[prev][r[i]] --- --- --------- ------\n ans+= prev # \'b\'\n # 0 0 d[\'b\'][0] = \'a\' \'ba\' \n return ans # 1 0 d[\'a\'][0] = \'b\' \'bab\'\n # 2 1 d[\'b\'][1] = \'c\' \'babc\'\n # 3 1 d[\'c\'][1] = \'b\' \'babcb\'\n```\n[https://leetcode.com/problems/the-k-th-lexicographical-string-of-all-happy-strings-of-length-n/submissions/937031498/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 4 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
Python3 O(n) solution using math with clear explanation | the-k-th-lexicographical-string-of-all-happy-strings-of-length-n | 0 | 1 | let\'s consider n=3 and k=9\nThe lexicographical order of the strings are ["aba", "abc", "aca", "acb", "bab", "bac", "bca", "bcb", "cab", "cac", "cba", "cbc"]\n\nWe can observe that each element a,b,c has repeated 2**(n-1) times as the first character which is 4 in our case they are ["aba", "abc", "aca", "acb"], ["bab", "bac", "bca", "bcb"], ["cab", "cac", "cba", "cbc"]\n\nWe can also observe that total number of permutations are 3*(2**(n-1)) which 12 in our case.\n\n\n```\nfrom math import ceil\nclass Solution:\n def getHappyString(self, n: int, k: int) -> str:\n single_ele = 2**(n-1)\n if k>3*single_ele:\n return ""\n result = [\'a\',\'b\',\'c\'][ceil(k/single_ele)-1]\n while single_ele>1:\n k = (k-1)%single_ele +1\n single_ele = single_ele//2\n if result[-1]==\'a\':\n result+=[\'b\',\'c\'][ceil(k/single_ele)-1]\n elif result[-1]==\'b\':\n result+=[\'a\',\'c\'][ceil(k/single_ele)-1]\n else:\n result+=[\'a\',\'b\'][ceil(k/single_ele)-1]\n return result\n``` | 15 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
1st char to last | the-k-th-lexicographical-string-of-all-happy-strings-of-length-n | 0 | 1 | # Intuition\nYou could just generate all the cases by using python itertools.product, but that would take too long.\n\nIt seems you should be able to more or less go straight to the kth item.\n\n# Approach\nFirst figure out how many happy lists there are\n\nDraw on a whiteboard n=3 get a feel for it\n\n\n# Complexity\nO(n) we go down a list of n, just do division, arthimatic, dictionary lookup along the way\n\n- Space complexity:\nO(n) - to store the length of the kth happy string we find.\n\n# Code\n```\nclass Solution:\n def getHappyString(self, n: int, k: int) -> str:\n\n nxt_choices = dict(a=(\'b\', \'c\'), b=(\'a\', \'c\'), c=(\'a\', \'b\'))\n\n num_happy = 3 * (2**(n-1))\n\n kth_happy_string = ""\n\n k = k - 1\n if k >= num_happy:\n return kth_happy_string\n\n choices = [\'a\', \'b\', \'c\']\n block = 2**(n-1)\n while block >= 1:\n choice, k = k // block, k % block\n ch = choices[choice]\n kth_happy_string += ch\n choices = nxt_choices[ch]\n block //= 2\n\n return kth_happy_string\n \n``` | 0 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
Easy to understand Python3 solution | the-k-th-lexicographical-string-of-all-happy-strings-of-length-n | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getHappyString(self, n: int, k: int) -> str:\n digits = [\'a\', \'b\', \'c\']\n res, res2 = [], []\n\n for arr in list(itertools.product(digits, repeat=n)):\n res.append("".join(arr))\n\n for j,r in enumerate(res):\n check = False\n for i in range(1, len(r)):\n if r[i] == r[i-1]:\n check = True\n break\n if not check:\n res2.append(r)\n \n res2.sort()\n\n if k > len(res2):\n return ""\n \n return res2[k-1]\n``` | 0 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
Concise solution on python3 | the-k-th-lexicographical-string-of-all-happy-strings-of-length-n | 0 | 1 | \n# Code\n```\nclass Solution:\n def getHappyString(self, n: int, k: int) -> str:\n \n cnt = 0\n ans = ""\n def go(res):\n if len(res) == n:\n nonlocal cnt, ans\n cnt += 1\n if cnt == k:\n ans = res\n return\n\n if cnt >= k:\n return\n\n if not res:\n for char in \'abc\':\n go(char)\n else:\n for char in \'abc\':\n if char == res[-1]:\n continue\n go(res + char)\n\n\n go("")\n return ans\n\n``` | 0 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
Clean partition dp solution | restore-the-array | 0 | 1 | # Code\n```\nclass Solution:\n def numberOfArrays(self, s: str, k: int) -> int:\n\n n = len(s)\n mod = 10**9+7\n\n @lru_cache(None)\n def rec(i=0):\n\n if i==n :\n return 1\n \n if s[i]=="0":\n return 0\n \n res = 0\n curr = ""\n for x in range(i, n):\n curr += s[x]\n if int(curr)<=k:\n res += (rec(x+1)%mod)\n res %= mod\n else:\n break\n\n return res\n \n return rec()\n``` | 2 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
Image Explanation🏆- [Easiest & Concise] - C++/Java/Python | restore-the-array | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Restore The Array` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n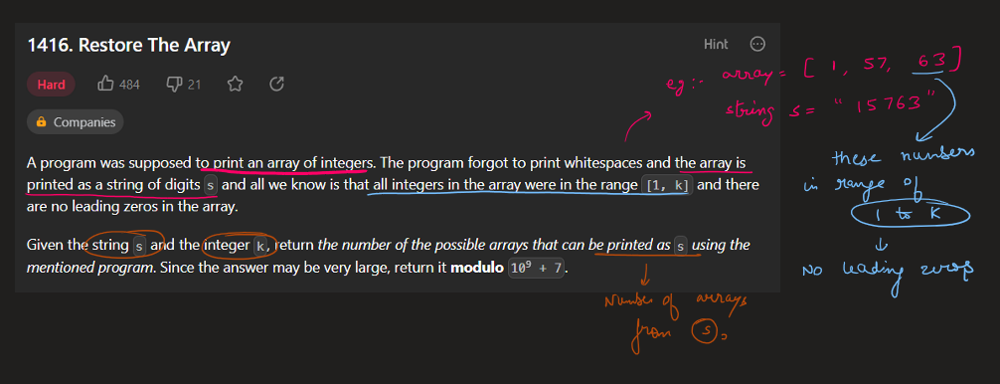\n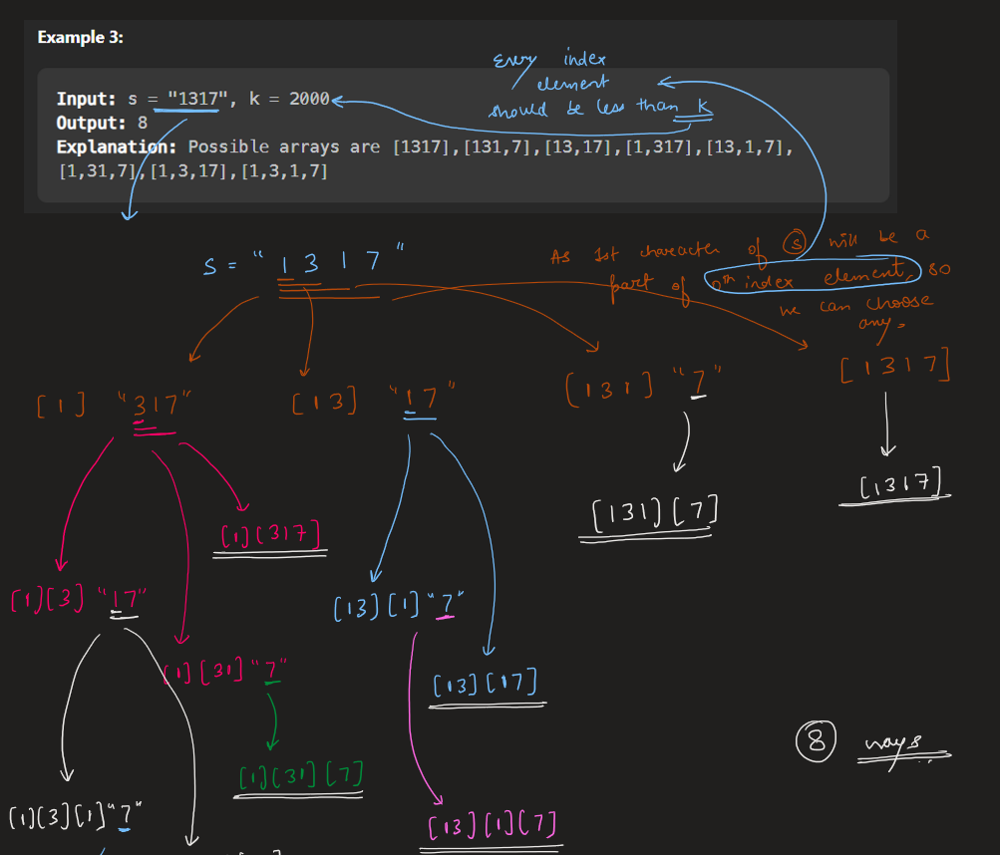\n\n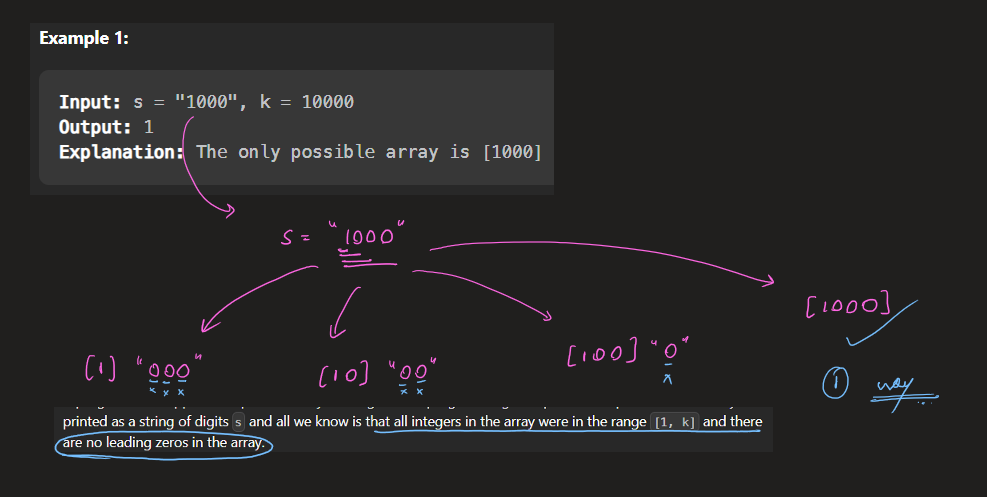\n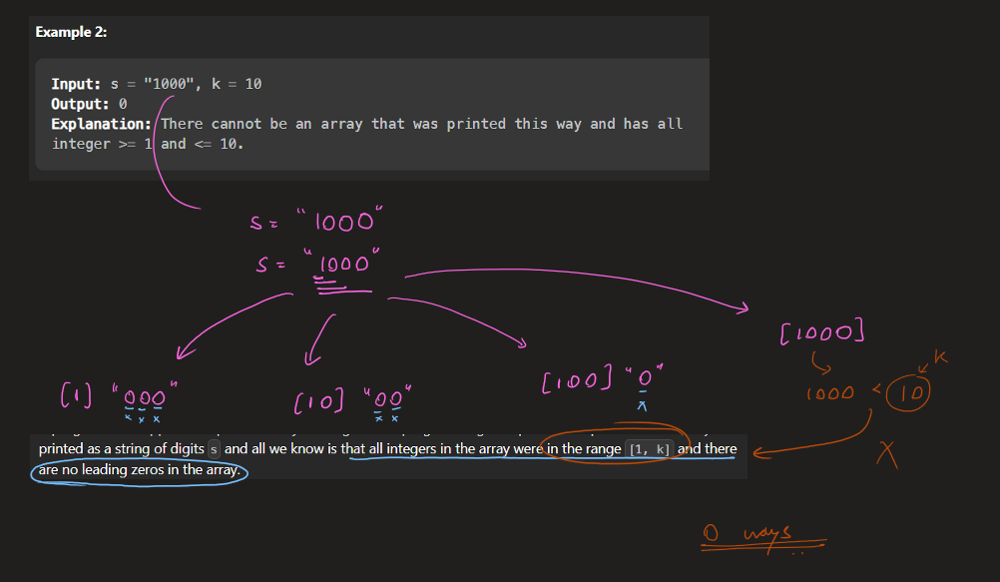\n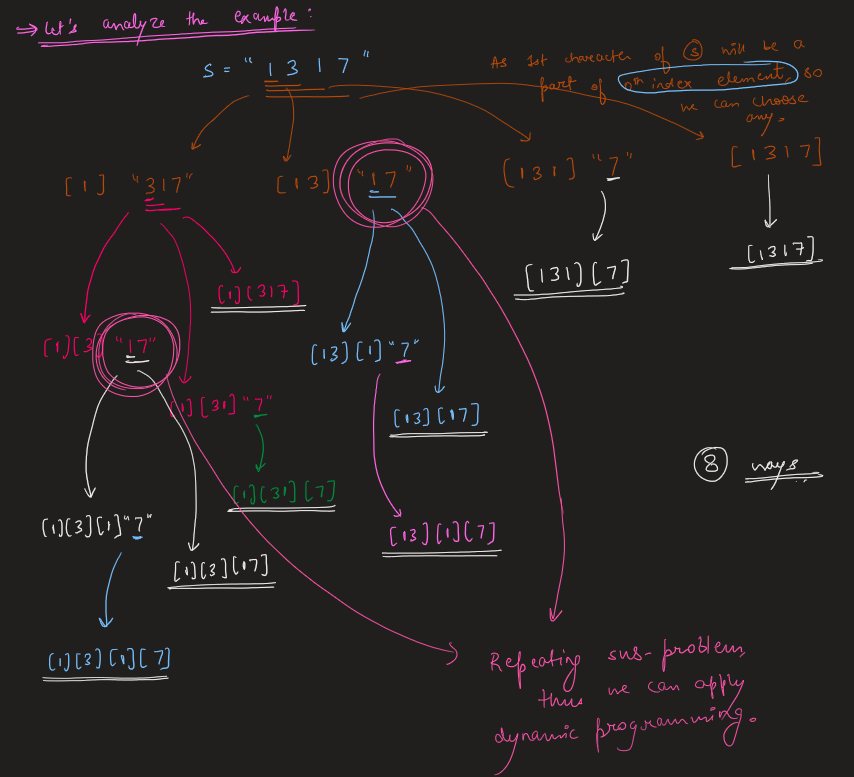\n\n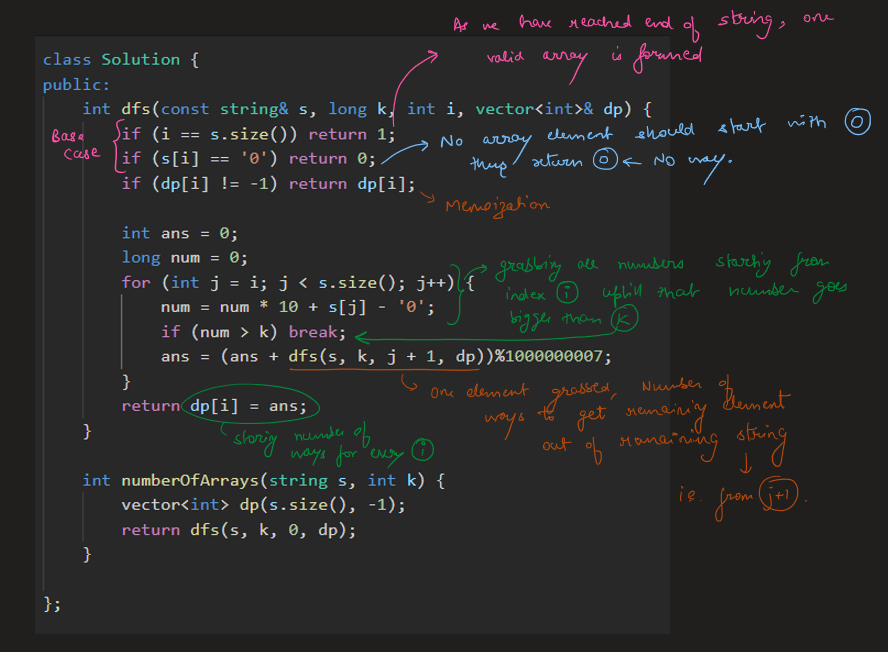\n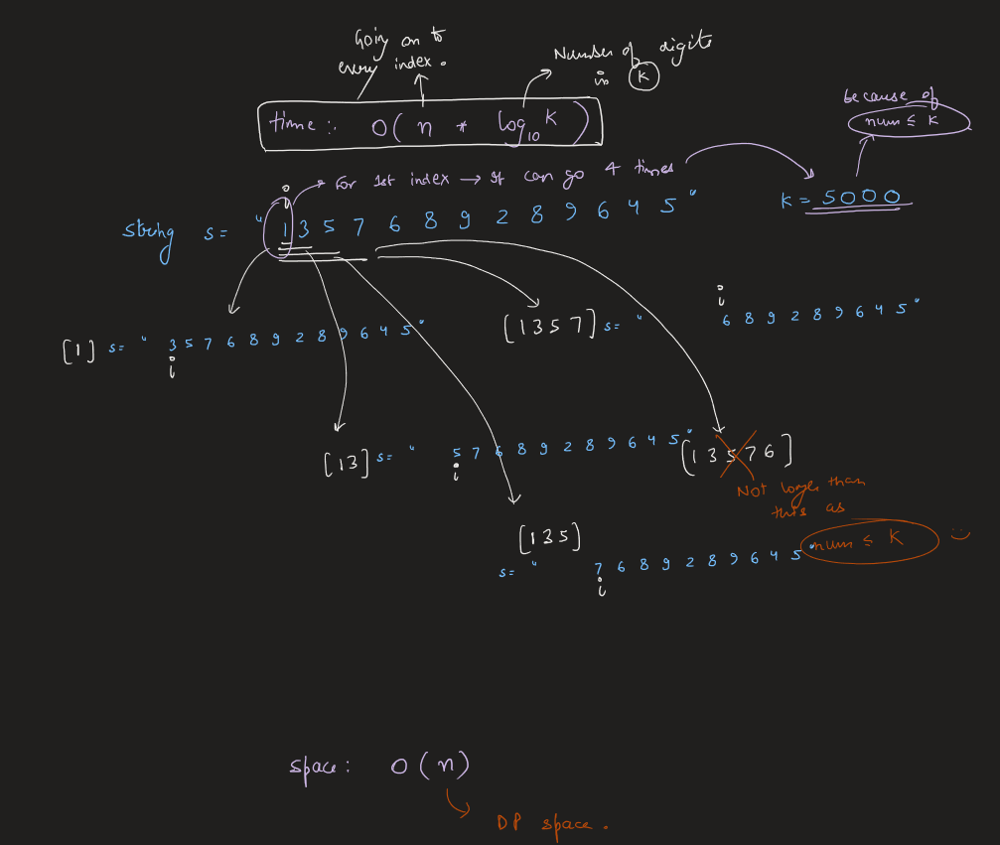\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int dfs(const string& s, long k, int i, vector<int>& dp) {\n if (i == s.size()) return 1;\n if (s[i] == \'0\') return 0;\n if (dp[i] != -1) return dp[i];\n\n int ans = 0;\n long num = 0;\n for (int j = i; j < s.size(); j++) {\n num = num * 10 + s[j] - \'0\';\n if (num > k) break;\n ans = (ans + dfs(s, k, j + 1, dp))%1000000007;\n }\n return dp[i] = ans;\n }\n\n int numberOfArrays(string s, int k) {\n vector<int> dp(s.size(), -1);\n return dfs(s, k, 0, dp);\n }\n};\n```\n```Java []\nclass Solution {\n public int dfs(String s, long k, int i, int[] dp) {\n if (i == s.length()) return 1;\n if (s.charAt(i) == \'0\') return 0;\n if (dp[i] != -1) return dp[i];\n\n int ans = 0;\n long num = 0;\n for (int j = i; j < s.length(); j++) {\n num = num * 10 + s.charAt(j) - \'0\';\n if (num > k) break;\n ans = (ans + dfs(s, k, j + 1, dp)) % 1000000007;\n }\n return dp[i] = ans;\n }\n\n public int numberOfArrays(String s, int k) {\n int[] dp = new int[s.length()];\n Arrays.fill(dp, -1);\n return dfs(s, k, 0, dp);\n }\n}\n```\n```Python []\nclass Solution:\n def dfs(self, s: str, k: int, i: int, dp: List[int]) -> int:\n if i == len(s):\n return 1\n if s[i] == \'0\':\n return 0\n if dp[i] != -1:\n return dp[i]\n\n ans = 0\n num = 0\n for j in range(i, len(s)):\n num = num * 10 + int(s[j])\n if num > k:\n break\n ans = (ans + self.dfs(s, k, j + 1, dp)) % 1000000007\n\n dp[i] = ans\n return ans\n\n def numberOfArrays(self, s: str, k: int) -> int:\n dp = [-1] * len(s)\n return self.dfs(s, k, 0, dp)\n```\n | 118 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
Pruned Bottom Up approach. | restore-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIts easy to think like, if you partioning from each index checking that the partion is valid(i.e., in the range [1,k] also it shouldn\'t start with a zero). Then your subproblem becomes the rest of the string.)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBut the going the above approach can consume a Time complexity ofO(N^2) but think of it minutely, that what is the max size of integer?.\nThats your homework. Here\'s my pruned Bottom Up Approach.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*32)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n def numberOfArrays(self, s: str, k: int) -> int:\n mod=10**9+7\n # Bottom Up Approach\n dp=[0 for _ in range(len(s)+1)]\n dp[len(s)]=1\n for i in range(len(s)-1,-1,-1):\n if s[i]==\'0\':\n continue\n for j in range(i,min(i+32,len(s))):\n if int(s[i:j+1])>k:\n break\n dp[i]+=dp[j+1]%mod\n return dp[0]%mod\n``` | 1 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
python3 , TopDown + Bottom Up | restore-the-array | 0 | 1 | # Intuition\nWe need to explore all the number in range starting with single digit possible number , 2 digits possible numbers and so on.\n\n\n# Code [TopDown]\n```\nclass Solution:\n def numberOfArrays(self, s: str, k: int) -> int:\n n = len(s)\n MOD = 1000000007\n dp = [-1]*n\n def count(i):\n if i >= n:\n return 1\n if dp[i] != -1:\n return dp[i]\n num = []\n c = 0\n for j in range(i,n):\n num = num + [s[j]]\n num_int = int("".join(num)) \n if num_int :\n if num_int <= k:\n c += count(j+1) %MOD\n else:\n break\n else:\n c = 0\n break\n dp[i] = c\n return dp[i]%MOD\n \n return count(0)\n\n```\n# Code [Bottom-UP]\n```\nclass Solution:\n def numberOfArrays(self, s: str, k: int) -> int:\n n = len(s)\n MOD = 1000000007\n dp = [-0]* (n+1)\n dp[n] = 1\n for i in range(n-1,-1,-1):\n num = []\n c = 0\n for j in range(i,n):\n num = num + [s[j]]\n num_int = int ("".join(num))\n \n if num_int :\n if num_int <= k:\n c += dp[j+1] %MOD\n else:\n break\n else:\n c = 0\n break\n dp[i] = c\n \n return dp[i]%MOD\n\n \n```\n | 1 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
✨ Linear time and near constant space | Details explanation | S: 100% M: 100% ✨ | restore-the-array | 0 | 1 | \n\n# Approach\nSimilar to Solution 3 of the Editorial but without the second loop.\n\n# Complexity\nn = len(s)\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(log_{10}{k})$$ ~ $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfArrays(self, s: str, k: int) -> int:\n mod = 10**9 + 7\n n = len(s)\n len_k = len(str(k))\n dp = deque([1, 1])\n \n subtract = False\n for i in range(1, n):\n start = max(0, i - len_k + 1)\n\n # Formula\n # dp[i] = sum(dp[j-1] for j in range(i - len_k + 1, i + 1) if s[j] != \'0\' and int(dp[j : i+1]) <= k)\n # dp[i - 1] = sum(dp[j-1] for j in range(i - len_k , i ) if s[j] != \'0\' and int(dp[j : i]) <= k)\n # => dp[i] = dp[i - 1] (step 1)\n # - dp[i - len_k - 1] if dp[i - len_k - 1] is included in dp[i-1] (step 2)\n # - dp[i - len_k] if int(dp[i - len_k + 1 : i + 1]) > k (step 3)\n # + dp[i - 1] if s[i] != \'0\' (step 4)\n \n # This way, there is no need for looping backward because dp[i] can be calculated \n # using dp[i - 1], dp[i - len_k] and dp[i - len_k - 1]\n\n # In order to save space, we don\'t need a dp array of size n but just need a window of size (len_k + 1).\n # Then dp[i] is dp_cur\n # dp[i - 1] is dp[-1]\n # dp[i - len_k] is dp[1]\n # dp[i - len_k - 1] is dp[0]\n \n dp_cur = dp[-1] # step 1\n \n if subtract:\n dp_cur -= dp[0] # step 2\n \n subtract = False\n if int(s[start : i + 1]) > k:\n dp_cur -= dp[1] # step 3\n elif len(dp) >= len_k and s[start] != \'0\':\n subtract = True # need to perform step 2 in the next iteration\n \n if s[i] != \'0\':\n dp_cur += dp[-1] # step 4\n \n dp_cur %= mod\n\n if len(dp) > len_k: # update the window\n dp.popleft()\n dp.append(dp_cur)\n\n return dp_cur\n \n```\n**Your upvote is highly appreciated!** | 1 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
python3 Solution | restore-the-array | 0 | 1 | \n```\nclass Solution:\n def numberOfArrays(self, s: str, k: int) -> int:\n n=len(s)\n mod=10**9+7\n dp=[0]*(n+1)\n dp[-1]=1\n for i in range(n-1,-1,-1):\n if s[i]==\'0\':\n continue\n\n num=0\n j=i\n while j<n and int(s[i:j+1])<=k:\n num+=dp[j+1]\n j+=1\n\n dp[i]=num%mod\n\n return dp[0] \n``` | 1 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
Python (Simple DP) | restore-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfArrays(self, s, k):\n n, mod = len(s), 10**9+7\n\n @lru_cache(None)\n def dfs(i):\n if i == 0:\n return 1\n\n total = 0\n\n for j in range(i-1,-1,-1):\n if s[j] == "0": continue\n elif int(s[j:i]) <= k:\n total += dfs(j)%mod\n elif int(s[j:i]) > k:\n break\n\n return total\n\n return dfs(n)%mod\n``` | 2 | A program was supposed to print an array of integers. The program forgot to print whitespaces and the array is printed as a string of digits `s` and all we know is that all integers in the array were in the range `[1, k]` and there are no leading zeros in the array.
Given the string `s` and the integer `k`, return _the number of the possible arrays that can be printed as_ `s` _using the mentioned program_. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "1000 ", k = 10000
**Output:** 1
**Explanation:** The only possible array is \[1000\]
**Example 2:**
**Input:** s = "1000 ", k = 10
**Output:** 0
**Explanation:** There cannot be an array that was printed this way and has all integer >= 1 and <= 10.
**Example 3:**
**Input:** s = "1317 ", k = 2000
**Output:** 8
**Explanation:** Possible arrays are \[1317\],\[131,7\],\[13,17\],\[1,317\],\[13,1,7\],\[1,31,7\],\[1,3,17\],\[1,3,1,7\]
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only digits and does not contain leading zeros.
* `1 <= k <= 109` | Try sorting nums. If nums is consecutive and sorted in ascending order, then nums[i] + 1 = nums[i + 1] for every i in the range 0 ≤ i < nums.length - 1. |
[Python] Clean solutions with explanation. O(N) Time and Space. | reformat-the-string | 0 | 1 | First we get lists of letters and digits seperately. \nThen we append the bigger list first. In this problem, i use flag to keep track of which one to append, this will make the code cleaner.\n**1st Solution**\n```python\nclass Solution:\n def reformat(self, s: str) -> str:\n letters = [c for c in s if c.isalpha()]\n digits = [c for c in s if c.isdigit()]\n if abs(len(letters) - len(digits)) > 1: return ""\n \n rv = []\n flag = len(letters) > len(digits)\n while letters or digits:\n rv.append(letters.pop() if flag else digits.pop())\n flag = not flag\n return rv\n```\n\n**Another** pythonic solution. Inspired from [post](https://leetcode.com/problems/reformat-the-string/discuss/586674/Python-Simple-solution)\nThe idea is to swap a and b such that `len(a) > len(b)`\n```python\n # Different Pythonic solution\n def reformat(self, s: str) -> str:\n a = [c for c in s if c.isalpha()]\n b = [c for c in s if c.isdigit()]\n if len(a) < len(b): a, b = b, a\n if len(a) - len(b) > 1: return ""\n \n rv = []\n while a:\n rv.append(a.pop())\n if b: rv.append(b.pop())\n return rv\n``` | 16 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Python3 Solution with separated lists | reformat-the-string | 0 | 1 | # Intuition\nSeparate list into letters and digits. If the length of the lists differ by more than 1, then return empty string (cannot create alternating new string)\n\nCreate flag to determine whether to start with digits or letters first (whichever list is longer)\n\n# Code\n```\nclass Solution:\n def getLettersAndDigits(self, s: str) -> tuple:\n letters = []\n digits = []\n for c in s:\n if c.isalpha():\n letters.append(c)\n elif c.isdigit():\n digits.append(c)\n return letters,digits\n\n def reformat(self, s: str) -> str:\n letters, digits = self.getLettersAndDigits(s)\n\n if abs(len(letters)-len(digits)) > 1:\n return \'\'\n \n digitStart = False\n \n if len(digits) > len(letters):\n digitStart = True\n \n res = \'\'\n for i in range(len(s)):\n if digitStart:\n res += digits.pop(0)\n else:\n res += letters.pop(0) \n digitStart = not digitStart\n\n return res\n\n\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Python solution | reformat-the-string | 0 | 1 | ```\nclass Solution:\n def reformat(self, s: str) -> str:\n alphabet: str = "abcdefghijklmnopqrstuvwxyz"\n digits: str = "1234567890"\n permutation: str = ""\n\n letters: list[str] = [letter for letter in s if letter in alphabet]\n numbers: list[str] = [number for number in s if number in digits]\n\n if len(letters) == len(numbers):\n for a,b in zip(letters, numbers):\n permutation += a + b\n return permutation\n \n elif len(letters) > len(numbers) and len(letters) - len(numbers) == 1:\n for a,b in zip(letters, numbers):\n permutation += a + b\n return permutation + letters[-1]\n \n elif len(numbers) > len(letters) and len(numbers) - len(letters) == 1:\n for a,b in zip(numbers, letters):\n permutation += a + b\n return permutation + numbers[-1]\n\n return ""\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
beats 94% uisng zip | reformat-the-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n \n if len(s) == 1:\n return s\n\n numeric = [x for x in s if x.isnumeric()]\n alpha = [x for x in s if x.isalpha()]\n\n if abs(len(alpha) - len(numeric)) > 1:\n return ""\n\n else:\n s_new =""\n if len(alpha) > len(numeric):\n s_new += \'\'.join([a + n for a, n in zip(alpha, numeric)])\n s_new += alpha[-1]\n \n elif len(numeric) > len(alpha):\n s_new +=numeric[-1]\n s_new += \'\'.join([a + n for a, n in zip(alpha, numeric)])\n else:\n s_new = \'\'.join([a + n for a, n in zip(alpha, numeric)])\n return s_new\n\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Python solution easy to understand | reformat-the-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n nums=[i for i in s if i.isnumeric()]\n s=[i for i in s if i.isalpha()]\n if len(nums)!=len(s) and len(nums)-1!=len(s) and len(nums)+1!=len(s):\n return ""\n else:\n if len(nums)==len(s):\n a=zip(nums,s)\n return "".join([j for i in list(a) for j in i]) \n \n elif len(nums)>len(s):\n a=zip(nums,s)\n a=[j for i in list(a) for j in i]\n a.append(nums[-1])\n return "".join(a)\n\n elif len(nums)<len(s):\n a=zip(s,nums)\n a=[j for i in list(a) for j in i]\n a.append(s[-1])\n return "".join(a)\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Alternating Characters and Digits in a String: Detailed Explanation Included | reformat-the-string | 0 | 1 | # Approach & Intuition:\n\nWhen given a string that contains both alphabetic and numeric characters, the goal is to reformat the string so that no two adjacent characters are of the same type and to alternate between letters and digits as much as possible. The core challenges here are determining the right order and ensuring that the reformatting is even possible given the character counts.\n\n## Step-by-Step Breakdown:\n\n1. **Separate Characters by Type**:\nThe first step involves segregating alphabetic and numeric characters into separate lists. This separation enables us to handle them individually and simplifies the logic for alternation.\n\n2. **Feasibility Check**:\nBefore attempting to interleave the characters, we need to check if a valid reformation is possible. If the difference in counts between alphabetic and numeric characters is more than 1, no such reformation can fulfill the alternating condition, and we return an empty string.\n\n3. **Determine Starting Character**:\nIf the reformation is possible, we determine whether to start with an alphabetic or numeric character. If they are equal, we start with an alphabetic character by default. If not, we start with the type that has an extra character.\n\n4. **Interleave Characters**:\nWith the starting character type decided, we interleave characters from each list, maintaining the order until one (or both) of the lists is exhausted. The iteration continues for the length of the shorter list to avoid index out-of-range errors.\n\n5. **Handle Extra Character**:\nAfter interleaving, if there\'s an extra character remaining in one of the lists (because one list was longer by exactly one), we append it to the result. This step ensures that the resultant string maintains the alternating pattern even when the counts are uneven.\n\n6. **Build and Return Result**:\nThroughout the process, we construct the resultant string by concatenating characters in the alternating order determined by the above steps. The final string is returned as the output of the function.\n\n## Intuitive Explanation:\n\nThink of the reformatting process as filling seats in two rows where one row is for letters and the other for numbers. Ideally, we want to alternate seats: a letter seat followed by a number seat, and so on. However, if we have an extra seat in one of the rows (say, one more letter than numbers), we\'ll need to start and end in that row to make sure no two same seats are next to each other. If the two rows have an equal number of seats, we\'ll start with a letter seat by convention. If the difference in the number of seats is more than one, then we simply can\'t alternate perfectly, and the function conveys this by returning an empty string, signaling that there\'s no way to arrange the seats as desired.\n\nBy following this logical flow, the solution adheres to the problem\'s requirements and efficiently builds a correctly reformatted string, if possible.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n # We check the lengths of the alpha and numeric arrays, because if one array has more \n # ... than 1 character than the other, we won\'t be able to find a permutation. \n # For e.g., consider this example: alpha = [\'a\', \'b\', \'c\'], numeric = [\'1\', \'2\', \'3\'] \n # ... We can create a permututation like this [\'a\', \'1\', \'b\', \'2\', \'c\', \'3\'] \n # ... since both sides have an equal amount of characters. But let\'s say we have 1\n # ... more numeric number than we have alphabets, then we can start off with the number\n # ... so that the insides hold the alphabets. For e.g. [\'1\', \'a\', \'2\', \'b\', \'3\', \'c\', \'4\']\n # But you\'ll notice that if we had just 1 more number, we won\'t be able to find a\n # permutation that fits the rules. Since wherever we put it, it would be next to a number.\n # So, the lists cannot have a difference of more than 1 from each other.\n alpha = []\n numeric = []\n result = ""\n\n # First we collect all the alpha and numeric characters separately\n for letter in s:\n if letter.isnumeric():\n numeric.append(letter)\n else:\n alpha.append(letter)\n\n alpha_len = len(alpha)\n numeric_len = len(numeric)\n # Lists cannot have a length difference of more than 1\n if abs(alpha_len - numeric_len) > 1:\n return result\n else:\n # Keeping track if one array has more characters than the other.\n # Also checking if alphabet comes first or not. It doesn\'t actually matter if we\n # ... track alphabet or numeric in this case. But the main idea is that we set\n # ... a standard so that we can start and end off with that type of character\n # ... in the permutation if there\'s more of that character. For e.g., if we have\n # ... 3 alphabets and 2 numbers, we can have a permutation like "a1b2c", but we\n # ... won\'t be able to start and end with a numeric number since we don\'t have \n # ... enough of them. \n alpha_has_extra = False\n numeric_has_extra = False\n\n if alpha_len > numeric_len:\n alpha_first = True\n alpha_has_extra = True\n elif alpha_len == numeric_len:\n alpha_first = True\n else:\n alpha_first = False\n numeric_has_extra = True\n\n # Get the minimum amount of iterations we can loop through the arrays with.\n # So that we don\'t go out of range if one array has more numbers than the other.\n iterations = min(alpha_len, numeric_len)\n for index in range(0, iterations, 1):\n # Based on whether the alphabet array is longer than numeric or not, we\n # ... decide the order of the characters in the permutation.\n if alpha_first:\n result += alpha[index] + numeric[index]\n else:\n result += numeric[index] + alpha[index]\n\n # Based on whether the alphabet or numeric list has a larger length than the other,\n # ... we make sure we collect the last element we didn\'t collect in the for loop above.\n # You can possibly also rewrite this solution using the zip() function instead to \n # ... simplify this process.\n if alpha_has_extra:\n result += alpha[iterations]\n elif numeric_has_extra:\n result += numeric[iterations]\n\n\n return result\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Len of list comprehension Python solution | reformat-the-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n a = [i for i in s if i.isdigit()]\n b = [j for j in s if j.isalpha()]\n if abs(len(a) - len(b)) > 1:\n return ""\n result = ""\n if len(a) == len(b):\n for k in range(len(a)):\n result += a[k] + b[k]\n elif len(a) > len(b):\n for k in range(len(a) - 1):\n result += a[k] + b[k]\n result += a[-1]\n else:\n for k in range(len(b) - 1):\n result += b[k] + a[k]\n result += b[-1]\n return result\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
reformat string | reformat-the-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n + m + k), where n is the length of the string s and m is the length of the shorter list among alpha and nums, and k is the length of the merged_list.\n- Space complexity:\nO(n), where n is the length of the string s.\n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n alpha = []\n nums = []\n merged_list = []\n for x in s:\n if x.isalpha():\n alpha.append(x)\n else:\n nums.append(x)\n if len(nums) == len(alpha) - 1:\n for i in range(len(nums)):\n merged_list.append(alpha[i])\n merged_list.append(nums[i])\n merged_list.append(alpha[-1])\n elif len(nums) == len(alpha) + 1:\n for j in range(len(alpha)):\n merged_list.append(nums[j])\n merged_list.append(alpha[j])\n merged_list.append(nums[-1])\n elif len(nums) == len(alpha):\n for j in range(len(alpha)):\n merged_list.append(nums[j])\n merged_list.append(alpha[j])\n \n if not merged_list:\n return \'\'\n return \'\'.join(merged_list)\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Interesting way to intentionally choose the array for consideration - Python3 | reformat-the-string | 0 | 1 | It just a smart way to overcome which array (digit or characters) is larger then we consider that array prior to the other by using index: -1, 0, 1. When applying absolute, we will always get 0 and 1!!\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n divide = [[], []]\n res = ""\n for c in s:\n divide[0 if c.isdigit() else 1].append(c)\n if abs(len(divide[0]) - len(divide[1])) > 1:\n return ""\n else:\n idx = 1 if len(divide[1]) > len(divide[0]) else 0\n if len(divide[0]) != len(divide[1]): res += divide[idx].pop(0)\n for i in range(0, len(divide[abs(idx - 1)])):\n res += (divide[abs(idx - 1)][i] + divide[idx][i])\n return res\n\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Python3 Naive Solution | reformat-the-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n \n digits=[]\n chrs=[]\n \n for ch in s:\n if ch.isdigit():\n digits.append(ch)\n else:\n chrs.append(ch)\n \n if abs(len(digits)-len(chrs))>=2:\n return ""\n \n \n ans=""\n \n while digits and chrs:\n if len(digits)>len(chrs):\n ans+=digits.pop()\n ans+=chrs.pop()\n else:\n ans+=chrs.pop()\n ans+=digits.pop()\n \n \n if digits:\n ans+=digits[0]\n if chrs:\n ans+=chrs[0]\n \n return ans\n \n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Easy Python Solution Using zip() || ✅✅✅ | reformat-the-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reformat(self, s: str) -> str:\n nums = [i for i in s if i.isdigit()]\n alp = [i for i in s if i.isalpha()]\n if len(nums)> 1+len(alp) or len(nums) + 1 < len(alp):\n return(\'\')\n if len(nums)==len(alp):\n return ("".join([i+j for i,j in zip(nums,alp)]))\n elif len(nums)+1 == len(alp):\n return ("".join([i+j for i,j in zip(alp,nums)])+alp[-1])\n else:\n return ("".join([i+j for i,j in zip(nums,alp)])+nums[-1])\n return \'\'\n``` | 0 | You are given an alphanumeric string `s`. (**Alphanumeric string** is a string consisting of lowercase English letters and digits).
You have to find a permutation of the string where no letter is followed by another letter and no digit is followed by another digit. That is, no two adjacent characters have the same type.
Return _the reformatted string_ or return **an empty string** if it is impossible to reformat the string.
**Example 1:**
**Input:** s = "a0b1c2 "
**Output:** "0a1b2c "
**Explanation:** No two adjacent characters have the same type in "0a1b2c ". "a0b1c2 ", "0a1b2c ", "0c2a1b " are also valid permutations.
**Example 2:**
**Input:** s = "leetcode "
**Output:** " "
**Explanation:** "leetcode " has only characters so we cannot separate them by digits.
**Example 3:**
**Input:** s = "1229857369 "
**Output:** " "
**Explanation:** "1229857369 " has only digits so we cannot separate them by characters.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | null |
Solution in Python3. Beats 100% of users with Python3 | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n1. We have the input as an array of arrays, where each item has three information to provide about the order : [[Customer_Name, Table_Number, Food_Item]]. \r\n2. The output should be in the form of an array of arrays which represents a table. The first item of the array contains the headings. The subsequent items contains details of the orders placed at each table.\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nWe need to build and return the output array. The problem can be broken into three parts:\r\n1. **Building the first item of output array (Heading)**\r\n2. **Building the structure other items of output array (Order Details)**\r\n3. **Updating Information about orders**\r\n\r\n##### **Building the first item of output array (Heading)**\r\nWe need to build a set with the Food Items. We will need to use a set as we do not want to add duplicates while traversing the orders(input) array. \r\nThis set is typecast into a list and then sorted alphabetically.\r\nWe also make a dictionary where items of this sorted array are entered as key with values starting from 1.\r\nWe append this array to our output array as the first element(Headings) after adding "Table" to the front of the the array.\r\n##### **Building the structure other items of output array (Order Details)**\r\nWe build a set of Table Numbers used. This set contains table numbers as a string value. We typecast the set into a list. The items are sorted using the integer value of items.\r\nWe also make a dictionary where items of this sorted array are entered as key with values starting from 1.\r\nWe now enter these orders into the output array as follows:\r\n- We build an array with "0" as value for length equal to number of food items ordered. Let\'s call this as "Temp".\r\n- We add items to output array as an array where the first item is a table number (taken from the sorted array of table numbers), and followed by the array "Temp" added to it.\r\n\r\n##### **Updating Information about orders**\r\nAt this stage our output array has the required structure. We have the Headings ready and the tables that eventually make orders are loaded with 0 orders as default value.\r\nNow, we traverse the input array(orders). We locate the correct element in our output array using our dictionaries, which provide values from the keys using the food item and table number specified in the input array.\r\nThe selected element in the output array will be a string. It is first typecasted into an integer, incremented, and the again typecasted into a string.\r\nAfter traversing the input array, our output array will be built and can be returned. \r\n\r\n# Complexity\r\n- Time complexity: O(n)\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n<!-- - Space complexity: -->\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n a=set()\r\n b=set()\r\n for i in orders:\r\n a.add(i[2])\r\n b.add(i[1])\r\n a=list(a)\r\n b=list(b)\r\n a=sorted(a)\r\n b=sorted(b,key=lambda x:int(x))\r\n dic_a={}\r\n dic_b={}\r\n c=1\r\n for i in a :\r\n dic_a[i]=c\r\n c+=1\r\n c=1\r\n for i in b:\r\n dic_b[i]=c\r\n c+=1\r\n output=[]\r\n output.append(["Table"]+a)\r\n\r\n crx=["0" for i in range(len(a))]\r\n for i in b:\r\n output.append([i]+crx)\r\n \r\n for i in orders:\r\n output[dic_b[i[1]]][dic_a[i[2]]]=int(output[dic_b[i[1]]][dic_a[i[2]]])\r\n output[dic_b[i[1]]][dic_a[i[2]]]+=1\r\n output[dic_b[i[1]]][dic_a[i[2]]]=str(output[dic_b[i[1]]][dic_a[i[2]]])\r\n \r\n return output\r\n``` | 2 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Python3 O(NlogN) solution with dictionaries (98.54% Runtime) | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\nUse a dictionary to store mappings of table -> menus\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n- Define a dictionary to store table -> menus mapping\r\n- Iteratively update the dictionary\r\n- Define an array for your answer and append schema row\r\n- Iteratively add corresponding menus per table with sorted order\r\n- Return your answer\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n d = {}\r\n menus = set()\r\n\r\n for _, tn, fi in orders:\r\n if tn not in d:\r\n d[tn] = {}\r\n\r\n if fi not in d[tn]:\r\n d[tn][fi] = 1\r\n else:\r\n d[tn][fi] += 1\r\n\r\n menus.add(fi)\r\n\r\n menus = sorted(list(menus))\r\n ans = [["Table"] + menus]\r\n\r\n for key in sorted([int(x) for x in list(d.keys())]):\r\n k = str(key)\r\n r = [k]\r\n \r\n for m in menus:\r\n if m not in d[k]:\r\n r.append("0")\r\n else:\r\n r.append(str(d[k][m]))\r\n\r\n ans.append(r)\r\n\r\n return ans\r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
✅ Easy Python Solution | HashMap | Sorting | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n hashMap = {}\r\n sortedFoodItems = []\r\n ans = []\r\n temp = [\'Table\']\r\n for order in orders:\r\n if order[2] not in sortedFoodItems:\r\n sortedFoodItems.append(order[2])\r\n sortedFoodItems.sort()\r\n\r\n for order in sortedFoodItems:\r\n temp.append(order)\r\n ans.append(temp)\r\n\r\n for order in orders:\r\n if int(order[1]) not in hashMap:\r\n hashMap[int(order[1])] = {}\r\n for item in sortedFoodItems:\r\n hashMap[int(order[1])][item] = 0\r\n hashMap[int(order[1])][order[2]] += 1\r\n \r\n hashMap = sorted(hashMap.items(), key = lambda x:x[0])\r\n\r\n for k,v in hashMap:\r\n temp = [str(k)]\r\n for item,quant in v.items():\r\n temp.append(str(quant))\r\n ans.append(temp)\r\n return ans\r\n \r\n\r\n \r\n\r\n\r\n\r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Beginner friendly | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n obj={}\r\n for order in orders:\r\n if order[1] not in obj:\r\n obj[order[1]]=[order[2]]\r\n else:\r\n obj[order[1]].append(order[2])\r\n items_list=[]\r\n table_no=[]\r\n for key,value in obj.items():\r\n items_list+=value\r\n table_no.append(int(key))\r\n k=list(set(items_list))\r\n k.sort()\r\n first_ind=[\'Table\']+k\r\n first=[]\r\n sub_list=[]\r\n table_no.sort()\r\n for i in table_no:\r\n sub_list.append(str(i))\r\n for j in k:\r\n c=obj[str(i)].count(j)\r\n sub_list.append(str(c))\r\n first.append(sub_list)\r\n sub_list=[]\r\n first=[first_ind]+first\r\n print(first)\r\n return first\r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Python Solution | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n d=dict()\r\n s=set()\r\n for i in orders:\r\n if int(i[1]) in d.keys():\r\n d1=d.get(int(i[1]))\r\n if(i[2] in d1.keys()):\r\n d1[i[2]]=d1.get(i[2])+1\r\n else:\r\n d1[i[2]]=1\r\n s.add(i[2])\r\n d[int(i[1])]=d1\r\n else:\r\n d[int(i[1])]={i[2]:1}\r\n s.add(i[2])\r\n \r\n res=[]\r\n l=[]\r\n l.append("Table")\r\n s=sorted(s)\r\n for i in (s):\r\n l.append(i)\r\n res.append(l)\r\n d=dict(sorted(d.items(),key=lambda x:x[0]))\r\n for x,y in d.items():\r\n l=[]\r\n l.append(str(x))\r\n for i in (s):\r\n if i in y.keys():\r\n l.append(str(y.get(i)))\r\n else:\r\n l.append(str(0))\r\n res.append(l)\r\n return res\r\n\r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Python 100%, very short code. Explanation line by line. | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Intuition\nIt\'s quite simple problem, if you are familiar with working with dataframes.\n\n# Approach\n1. Create sorted list of all items in menu\n2. Create dictionary of positions of all items in menu, so later when we go trough order, we will know where to put each item for each table.\n3. create dictionary where key is table, and value is list of `0` representing every potential item in menu.\n4. going trough all orders ( and there can be more than one order for one table ) we systematically add each item from menu to its place to coresponding table.\n5. finally creating output list - first we create list with "Table" followed by every item in menu.\n6. simply adding each table into output - first table number, followed by list of how many each item in menu was ordered for this table.\n\n# Code\n```\nclass Solution:\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\n menu = sorted(list(set(y for x in orders for y in x[2:])))\n menu = {x:i for i,x in enumerate(menu)}\n tables = {o[1]:[0]*len(menu) for o in orders}\n for o in orders:\n for item in o[2:]:\n tables[o[1]][menu[item]]+=1\n output = [["Table"] + list(menu.keys())]\n for t in sorted(tables.keys(), key = int):\n output.append([t] + [str(x) for x in tables[t]])\n return output\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Fast python3 solution using Hashmap and set | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Approach\r\nMy approach was to have a dictionary keep track of the number of each food served to each table. That is a dictionary with key, table number and value another dictionary with key, food and value number of orders.\r\n\r\nWe must however sort the orders list by table number so that we can compute the orders in increasing table number.\r\n\r\nA set must be created as well to have all the foods ordered. Each food will be added to the set when iterating over orders. It should then be type casted to a list and then sorted. This is because we will use this list as our header as well.\r\n\r\n# Complexity\r\nif N is the total number of different table numbers in orders and M is the total number of foods in orders,\r\n- Time complexity:\r\nO(N x M)\r\n\r\n- Space complexity:\r\nO(N x M)\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n orders.sort(key = lambda x:int(x[1]))\r\n orders_info = defaultdict(dict)\r\n foods = set()\r\n result = []\r\n\r\n for _,table_no,food in orders:\r\n orders_info[table_no][food] = orders_info[table_no].get(food,0) + 1\r\n foods.add(food)\r\n\r\n foods = sorted(list(foods))\r\n headers = ["Table"] + foods\r\n result.append(headers)\r\n\r\n for table_no in orders_info:\r\n row = [table_no]\r\n for food in foods:\r\n number_of_orders = str(orders_info[table_no].get(food,0))\r\n row.append(number_of_orders)\r\n result.append(row)\r\n\r\n return result\r\n\r\n \r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
python3 straight forward solution beats +90% | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n hm = {}\r\n itms = set()\r\n foods = {}\r\n for i in orders:\r\n itms.add(i[2])\r\n\r\n itms = sorted(itms)\r\n\r\n for k,itm in enumerate(itms):\r\n foods[itm] = k + 1\r\n\r\n for i in orders:\r\n temp = int(i[1])\r\n if temp in hm:\r\n hm[temp][foods[i[2]]] = str(int(hm[temp][foods[i[2]]]) + 1)\r\n else:\r\n hm[temp] = ["0"] * (len(itms) + 1)\r\n hm[temp][0] = i[1]\r\n hm[temp][foods[i[2]]] = str(1)\r\n\r\n res = [["Table"] + itms]\r\n\r\n for k in sorted(hm.keys()):\r\n res.append(hm[k])\r\n\r\n return res\r\n\r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Python Solution, hashmap O(N + TlogT + FlogF + T * F) | display-table-of-food-orders-in-a-restaurant | 0 | 1 | It\'s quit straightforward to use a hashmap to save meals that each table has.\nTime: O(N + TlogT + FlogF + T * F)\nN, T, F stands for amount of orders, tables and foods\nCost come from iterating orders and sorting tables and foods.\nAnd the last for takes T * F to dump the result.\nSpace: O(T * F)\n# Code\n```\nimport collections\nclass Solution:\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\n desk = collections.defaultdict(collections.Counter)\n meal = set()\n for _, table, food in orders:\n meal.add(food)\n desk[table][food] += 1\n foods = sorted(meal)\n result = [[\'Table\'] + [food for food in foods]]\n for table in sorted(desk, key=int):\n result.append([table] + [str(desk[table][food]) for food in foods])\n return result\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Easy to understand Python3 solution | display-table-of-food-orders-in-a-restaurant | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def displayTable(self, orders: List[List[str]]) -> List[List[str]]:\r\n d = {}\r\n\r\n for name, num, food in orders:\r\n if food in d:\r\n d[food][0].append(num)\r\n d[food][1] += 1\r\n d[food][0].sort()\r\n else:\r\n d[food] = [[num], 1]\r\n \r\n d = dict(sorted(d.items(), key= lambda x: x[0]))\r\n\r\n d_num = {}\r\n\r\n for name, num, food in orders:\r\n if num in d_num:\r\n check = True\r\n for f in d_num[num]:\r\n if f[0] == food:\r\n f[1] += 1\r\n check = False\r\n if check:\r\n d_num[num].append([food, 1])\r\n else:\r\n d_num[num] = [[food, 1]]\r\n\r\n d_num = dict(sorted(d_num.items(), key= lambda x: int(x[0])))\r\n\r\n output = [[\'Table\']]\r\n\r\n for k in d:\r\n output[0].append(k)\r\n \r\n for k in d_num:\r\n output.append([k])\r\n for food in output[0][1:]:\r\n check = False\r\n for f, c in d_num[k]:\r\n if food == f:\r\n output[-1].append(str(c))\r\n check = True\r\n if not check:\r\n output[-1].append("0")\r\n \r\n return output\r\n``` | 0 | Given the array `orders`, which represents the orders that customers have done in a restaurant. More specifically `orders[i]=[customerNamei,tableNumberi,foodItemi]` where `customerNamei` is the name of the customer, `tableNumberi` is the table customer sit at, and `foodItemi` is the item customer orders.
_Return the restaurant's "**display table**"_. The "**display table**" is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is "Table", followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
**Example 1:**
**Input:** orders = \[\[ "David ", "3 ", "Ceviche "\],\[ "Corina ", "10 ", "Beef Burrito "\],\[ "David ", "3 ", "Fried Chicken "\],\[ "Carla ", "5 ", "Water "\],\[ "Carla ", "5 ", "Ceviche "\],\[ "Rous ", "3 ", "Ceviche "\]\]
**Output:** \[\[ "Table ", "Beef Burrito ", "Ceviche ", "Fried Chicken ", "Water "\],\[ "3 ", "0 ", "2 ", "1 ", "0 "\],\[ "5 ", "0 ", "1 ", "0 ", "1 "\],\[ "10 ", "1 ", "0 ", "0 ", "0 "\]\]
**Explanation:**
The displaying table looks like:
**Table,Beef Burrito,Ceviche,Fried Chicken,Water**
3 ,0 ,2 ,1 ,0
5 ,0 ,1 ,0 ,1
10 ,1 ,0 ,0 ,0
For the table 3: David orders "Ceviche " and "Fried Chicken ", and Rous orders "Ceviche ".
For the table 5: Carla orders "Water " and "Ceviche ".
For the table 10: Corina orders "Beef Burrito ".
**Example 2:**
**Input:** orders = \[\[ "James ", "12 ", "Fried Chicken "\],\[ "Ratesh ", "12 ", "Fried Chicken "\],\[ "Amadeus ", "12 ", "Fried Chicken "\],\[ "Adam ", "1 ", "Canadian Waffles "\],\[ "Brianna ", "1 ", "Canadian Waffles "\]\]
**Output:** \[\[ "Table ", "Canadian Waffles ", "Fried Chicken "\],\[ "1 ", "2 ", "0 "\],\[ "12 ", "0 ", "3 "\]\]
**Explanation:**
For the table 1: Adam and Brianna order "Canadian Waffles ".
For the table 12: James, Ratesh and Amadeus order "Fried Chicken ".
**Example 3:**
**Input:** orders = \[\[ "Laura ", "2 ", "Bean Burrito "\],\[ "Jhon ", "2 ", "Beef Burrito "\],\[ "Melissa ", "2 ", "Soda "\]\]
**Output:** \[\[ "Table ", "Bean Burrito ", "Beef Burrito ", "Soda "\],\[ "2 ", "1 ", "1 ", "1 "\]\]
**Constraints:**
* `1 <= orders.length <= 5 * 10^4`
* `orders[i].length == 3`
* `1 <= customerNamei.length, foodItemi.length <= 20`
* `customerNamei` and `foodItemi` consist of lowercase and uppercase English letters and the space character.
* `tableNumberi` is a valid integer between `1` and `500`. | null |
Elegant and short, perfect for interview | minimum-number-of-frogs-croaking | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is somewhat similar to the famous problem of checking validity of braces. For example "(()())" is a valid sequence and "()(()" is invalid. The expected solution is to keep the number of open braces `num_open`. Increment the value, when we meed an open brace \'(\' and decrement the value, when we meet a closing brace \')\'. If you think about it, it\'s clear that either a negative value of `num_open` at any moment or a positive final value means the sequence is invalid.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of 2 types of braces expected to appear in the particular sequence: first \'(\' and then \')\', we have 5 types of chars expected to appear in the particular sequence. A \'c\' *must* be a previous to a \'r\'. A \'r\' *must* be a previous to an \'o\'. Etc.\nThere are two tricky parts here. Number one. To count only *simultaneous* croaks (target number of frogs) we need to treat \'k\' as previous to \'c\'.\nNumber two. At the end there must be a bunch of \'k\'s, which are our target number of frogs. That number of \'k\'s is the number of frogs which croaked *simultaneously*.\nThe fact that any incomplete sequence of \'croak\' makes the chole string invalid helps a lot to keep the logic simpler. Just keep deducting the "previous" character counts. If any count becomes negative, then the string is invalid. If any count besides the count of \'k\' is positive, then there are incomplete sequences, which makes the whole string invalid.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N) to process each character of the input string. We use Hash Map (Counter\\dictionary) with O(1) for all other operations.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1), because there are only 5 possible types of characters used as keys for the Hash Map (Counter\\dictionary).\n\n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n char_counter = Counter()\n prevs = {\n \'c\': \'k\',\n \'r\': \'c\',\n \'o\': \'r\',\n \'a\': \'o\',\n \'k\': \'a\',\n }\n\n for ch in croakOfFrogs:\n prev_ch = prevs[ch]\n if char_counter[prev_ch] > 0:\n char_counter[prev_ch] -= 1\n char_counter[ch] += 1\n elif ch == \'c\':\n char_counter[ch] += 1\n else:\n return -1\n \n for ch, val in char_counter.items():\n if ch != \'k\' and val > 0:\n return -1\n\n return char_counter[\'k\']\n``` | 2 | You are given the string `croakOfFrogs`, which represents a combination of the string `"croak "` from different frogs, that is, multiple frogs can croak at the same time, so multiple `"croak "` are mixed.
_Return the minimum number of_ different _frogs to finish all the croaks in the given string._
A valid `"croak "` means a frog is printing five letters `'c'`, `'r'`, `'o'`, `'a'`, and `'k'` **sequentially**. The frogs have to print all five letters to finish a croak. If the given string is not a combination of a valid `"croak "` return `-1`.
**Example 1:**
**Input:** croakOfFrogs = "croakcroak "
**Output:** 1
**Explanation:** One frog yelling "croak **"** twice.
**Example 2:**
**Input:** croakOfFrogs = "crcoakroak "
**Output:** 2
**Explanation:** The minimum number of frogs is two.
The first frog could yell "**cr**c**oak**roak ".
The second frog could yell later "cr**c**oak**roak** ".
**Example 3:**
**Input:** croakOfFrogs = "croakcrook "
**Output:** -1
**Explanation:** The given string is an invalid combination of "croak **"** from different frogs.
**Constraints:**
* `1 <= croakOfFrogs.length <= 105`
* `croakOfFrogs` is either `'c'`, `'r'`, `'o'`, `'a'`, or `'k'`. | null |
Elegant and short, perfect for interview | minimum-number-of-frogs-croaking | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is somewhat similar to the famous problem of checking validity of braces. For example "(()())" is a valid sequence and "()(()" is invalid. The expected solution is to keep the number of open braces `num_open`. Increment the value, when we meed an open brace \'(\' and decrement the value, when we meet a closing brace \')\'. If you think about it, it\'s clear that either a negative value of `num_open` at any moment or a positive final value means the sequence is invalid.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of 2 types of braces expected to appear in the particular sequence: first \'(\' and then \')\', we have 5 types of chars expected to appear in the particular sequence. A \'c\' *must* be a previous to a \'r\'. A \'r\' *must* be a previous to an \'o\'. Etc.\nThere are two tricky parts here. Number one. To count only *simultaneous* croaks (target number of frogs) we need to treat \'k\' as previous to \'c\'.\nNumber two. At the end there must be a bunch of \'k\'s, which are our target number of frogs. That number of \'k\'s is the number of frogs which croaked *simultaneously*.\nThe fact that any incomplete sequence of \'croak\' makes the chole string invalid helps a lot to keep the logic simpler. Just keep deducting the "previous" character counts. If any count becomes negative, then the string is invalid. If any count besides the count of \'k\' is positive, then there are incomplete sequences, which makes the whole string invalid.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N) to process each character of the input string. We use Hash Map (Counter\\dictionary) with O(1) for all other operations.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1), because there are only 5 possible types of characters used as keys for the Hash Map (Counter\\dictionary).\n\n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n char_counter = Counter()\n prevs = {\n \'c\': \'k\',\n \'r\': \'c\',\n \'o\': \'r\',\n \'a\': \'o\',\n \'k\': \'a\',\n }\n\n for ch in croakOfFrogs:\n prev_ch = prevs[ch]\n if char_counter[prev_ch] > 0:\n char_counter[prev_ch] -= 1\n char_counter[ch] += 1\n elif ch == \'c\':\n char_counter[ch] += 1\n else:\n return -1\n \n for ch, val in char_counter.items():\n if ch != \'k\' and val > 0:\n return -1\n\n return char_counter[\'k\']\n``` | 2 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Py O(n) Sol: Easy to Understand, Ask Doubt | minimum-number-of-frogs-croaking | 0 | 1 | ```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n c = r = o = a = k = max_frog_croak = present_frog_croak = 0\n # need to know, at particular point,\n # what are the max frog are croaking,\n\n for i, v in enumerate(croakOfFrogs):\n if v == \'c\':\n c += 1\n\t\t\t\t# c gives a signal for a frog\n present_frog_croak += 1\n elif v == \'r\':\n r += 1\n elif v == \'o\':\n o += 1\n elif v == \'a\':\n a += 1\n else:\n k += 1\n\t\t\t\t# frog stop croaking\n present_frog_croak -= 1\n\n max_frog_croak = max(max_frog_croak, present_frog_croak)\n # if any inoder occurs;\n if c < r or r < o or o < a or a < k:\n return -1\n\n # if all good, else -1\n if present_frog_croak == 0 and c == r and r == o and o == a and a == k:\n return max_frog_croak\n return -1\n\n``` | 30 | You are given the string `croakOfFrogs`, which represents a combination of the string `"croak "` from different frogs, that is, multiple frogs can croak at the same time, so multiple `"croak "` are mixed.
_Return the minimum number of_ different _frogs to finish all the croaks in the given string._
A valid `"croak "` means a frog is printing five letters `'c'`, `'r'`, `'o'`, `'a'`, and `'k'` **sequentially**. The frogs have to print all five letters to finish a croak. If the given string is not a combination of a valid `"croak "` return `-1`.
**Example 1:**
**Input:** croakOfFrogs = "croakcroak "
**Output:** 1
**Explanation:** One frog yelling "croak **"** twice.
**Example 2:**
**Input:** croakOfFrogs = "crcoakroak "
**Output:** 2
**Explanation:** The minimum number of frogs is two.
The first frog could yell "**cr**c**oak**roak ".
The second frog could yell later "cr**c**oak**roak** ".
**Example 3:**
**Input:** croakOfFrogs = "croakcrook "
**Output:** -1
**Explanation:** The given string is an invalid combination of "croak **"** from different frogs.
**Constraints:**
* `1 <= croakOfFrogs.length <= 105`
* `croakOfFrogs` is either `'c'`, `'r'`, `'o'`, `'a'`, or `'k'`. | null |
Py O(n) Sol: Easy to Understand, Ask Doubt | minimum-number-of-frogs-croaking | 0 | 1 | ```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n c = r = o = a = k = max_frog_croak = present_frog_croak = 0\n # need to know, at particular point,\n # what are the max frog are croaking,\n\n for i, v in enumerate(croakOfFrogs):\n if v == \'c\':\n c += 1\n\t\t\t\t# c gives a signal for a frog\n present_frog_croak += 1\n elif v == \'r\':\n r += 1\n elif v == \'o\':\n o += 1\n elif v == \'a\':\n a += 1\n else:\n k += 1\n\t\t\t\t# frog stop croaking\n present_frog_croak -= 1\n\n max_frog_croak = max(max_frog_croak, present_frog_croak)\n # if any inoder occurs;\n if c < r or r < o or o < a or a < k:\n return -1\n\n # if all good, else -1\n if present_frog_croak == 0 and c == r and r == o and o == a and a == k:\n return max_frog_croak\n return -1\n\n``` | 30 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
</> | minimum-number-of-frogs-croaking | 0 | 1 | \n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n Frogs = 0\n sounds = [0] * 5\n d = {\n "c" : 0,\n "r" : 1,\n "o" : 2,\n "a" : 3,\n "k" : 4\n }\n\n for s in croakOfFrogs:\n sounds[d[s]] += 1\n if s == "c":\n Frogs = max(Frogs, sounds[0] - sounds[-1])\n\n if not (sounds[0] >= sounds[1] >= sounds[2] >= sounds[3] >= sounds[4]):\n return -1\n\n if sounds[0] == sounds[-1]:\n return Frogs\n \n return -1\n\n\n\n \n\n \n \n\n``` | 1 | You are given the string `croakOfFrogs`, which represents a combination of the string `"croak "` from different frogs, that is, multiple frogs can croak at the same time, so multiple `"croak "` are mixed.
_Return the minimum number of_ different _frogs to finish all the croaks in the given string._
A valid `"croak "` means a frog is printing five letters `'c'`, `'r'`, `'o'`, `'a'`, and `'k'` **sequentially**. The frogs have to print all five letters to finish a croak. If the given string is not a combination of a valid `"croak "` return `-1`.
**Example 1:**
**Input:** croakOfFrogs = "croakcroak "
**Output:** 1
**Explanation:** One frog yelling "croak **"** twice.
**Example 2:**
**Input:** croakOfFrogs = "crcoakroak "
**Output:** 2
**Explanation:** The minimum number of frogs is two.
The first frog could yell "**cr**c**oak**roak ".
The second frog could yell later "cr**c**oak**roak** ".
**Example 3:**
**Input:** croakOfFrogs = "croakcrook "
**Output:** -1
**Explanation:** The given string is an invalid combination of "croak **"** from different frogs.
**Constraints:**
* `1 <= croakOfFrogs.length <= 105`
* `croakOfFrogs` is either `'c'`, `'r'`, `'o'`, `'a'`, or `'k'`. | null |
</> | minimum-number-of-frogs-croaking | 0 | 1 | \n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n Frogs = 0\n sounds = [0] * 5\n d = {\n "c" : 0,\n "r" : 1,\n "o" : 2,\n "a" : 3,\n "k" : 4\n }\n\n for s in croakOfFrogs:\n sounds[d[s]] += 1\n if s == "c":\n Frogs = max(Frogs, sounds[0] - sounds[-1])\n\n if not (sounds[0] >= sounds[1] >= sounds[2] >= sounds[3] >= sounds[4]):\n return -1\n\n if sounds[0] == sounds[-1]:\n return Frogs\n \n return -1\n\n\n\n \n\n \n \n\n``` | 1 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Python 3 | Greedy, Simulation, Clean code | Explanantion | minimum-number-of-frogs-croaking | 0 | 1 | # Explanation\n- Need to find the maximum number of "croak" ongoing at some time point `t`. \n\t- e.g. `crcoakroak`\n\t\t- `0123456789` - time\n\t\t- `cr*oak****` - first \n\t\t- `**c***roak` - second\n\t- At time 2,3,4,5, there are 2 "croak" ongoing at the same time, thus there will be 2 frogs needed\n- To simulate this, we can apply a greedy algorithm as follow\n\t- Create a dictionary `cnt` to count how many each letter is being prononciated currently\n\t- Greedy method is here:\n\t\t- If we see any char in `roak`, increase `cnt` for this char, and decrease its previous char, i.e.:\n\t\t\t- If current char is `r`, then we will do:\n\t\t\t\t- `cnt[\'r\'] += 1`\n\t\t\t\t- `cnt[\'c\'] -= 1`\n\t\t\t- If ever previous char fall below to zero, then meaning frog is croaking from the middle, not from the beginning, thus invalid, `return -1`.\n\t\t- At the same time, whenever `\'c\'` is met, we want to increase `cur` (current ongoing croaks)\n\t\t- If `\'k\'` is met, we want to decrease `cnt[\'k\']` and `cur` since there is no following letter after `\'k\'` and `"croak"` is finished\n\t\t- If any characters other than `"croak"` is met, then invalid, `return -1`\n\n# Implementation\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n cnt, s = collections.defaultdict(int), \'croak\' \n ans, cur, d = 0, 0, {c:i for i, c in enumerate(s)} # d: mapping for letter & its index\n for letter in croakOfFrogs: # iterate over the string\n if letter not in s: return -1 # if any letter other than "croak" is met, then invalid\n cnt[letter] += 1 # increase cnt for letter\n if letter == \'c\': cur += 1 # \'c\' is met, increase current ongoing croak `cur`\n elif cnt[s[d[letter]-1]] <= 0: return -1 # if previous character fall below to 0, return -1\n else: cnt[s[d[letter]-1]] -= 1 # otherwise, decrease cnt for previous character\n ans = max(ans, cur) # update answer using `cur`\n if letter == \'k\': # when \'k\' is met, decrease cnt and cur\n cnt[letter] -= 1\n cur -= 1\n return ans if not cur else -1 # return ans if current ongoing "croak" is 0\n``` | 6 | You are given the string `croakOfFrogs`, which represents a combination of the string `"croak "` from different frogs, that is, multiple frogs can croak at the same time, so multiple `"croak "` are mixed.
_Return the minimum number of_ different _frogs to finish all the croaks in the given string._
A valid `"croak "` means a frog is printing five letters `'c'`, `'r'`, `'o'`, `'a'`, and `'k'` **sequentially**. The frogs have to print all five letters to finish a croak. If the given string is not a combination of a valid `"croak "` return `-1`.
**Example 1:**
**Input:** croakOfFrogs = "croakcroak "
**Output:** 1
**Explanation:** One frog yelling "croak **"** twice.
**Example 2:**
**Input:** croakOfFrogs = "crcoakroak "
**Output:** 2
**Explanation:** The minimum number of frogs is two.
The first frog could yell "**cr**c**oak**roak ".
The second frog could yell later "cr**c**oak**roak** ".
**Example 3:**
**Input:** croakOfFrogs = "croakcrook "
**Output:** -1
**Explanation:** The given string is an invalid combination of "croak **"** from different frogs.
**Constraints:**
* `1 <= croakOfFrogs.length <= 105`
* `croakOfFrogs` is either `'c'`, `'r'`, `'o'`, `'a'`, or `'k'`. | null |
Python 3 | Greedy, Simulation, Clean code | Explanantion | minimum-number-of-frogs-croaking | 0 | 1 | # Explanation\n- Need to find the maximum number of "croak" ongoing at some time point `t`. \n\t- e.g. `crcoakroak`\n\t\t- `0123456789` - time\n\t\t- `cr*oak****` - first \n\t\t- `**c***roak` - second\n\t- At time 2,3,4,5, there are 2 "croak" ongoing at the same time, thus there will be 2 frogs needed\n- To simulate this, we can apply a greedy algorithm as follow\n\t- Create a dictionary `cnt` to count how many each letter is being prononciated currently\n\t- Greedy method is here:\n\t\t- If we see any char in `roak`, increase `cnt` for this char, and decrease its previous char, i.e.:\n\t\t\t- If current char is `r`, then we will do:\n\t\t\t\t- `cnt[\'r\'] += 1`\n\t\t\t\t- `cnt[\'c\'] -= 1`\n\t\t\t- If ever previous char fall below to zero, then meaning frog is croaking from the middle, not from the beginning, thus invalid, `return -1`.\n\t\t- At the same time, whenever `\'c\'` is met, we want to increase `cur` (current ongoing croaks)\n\t\t- If `\'k\'` is met, we want to decrease `cnt[\'k\']` and `cur` since there is no following letter after `\'k\'` and `"croak"` is finished\n\t\t- If any characters other than `"croak"` is met, then invalid, `return -1`\n\n# Implementation\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n cnt, s = collections.defaultdict(int), \'croak\' \n ans, cur, d = 0, 0, {c:i for i, c in enumerate(s)} # d: mapping for letter & its index\n for letter in croakOfFrogs: # iterate over the string\n if letter not in s: return -1 # if any letter other than "croak" is met, then invalid\n cnt[letter] += 1 # increase cnt for letter\n if letter == \'c\': cur += 1 # \'c\' is met, increase current ongoing croak `cur`\n elif cnt[s[d[letter]-1]] <= 0: return -1 # if previous character fall below to 0, return -1\n else: cnt[s[d[letter]-1]] -= 1 # otherwise, decrease cnt for previous character\n ans = max(ans, cur) # update answer using `cur`\n if letter == \'k\': # when \'k\' is met, decrease cnt and cur\n cnt[letter] -= 1\n cur -= 1\n return ans if not cur else -1 # return ans if current ongoing "croak" is 0\n``` | 6 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Monotonic sequence, quick | minimum-number-of-frogs-croaking | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nList record every word count, the list is decreasing sequence\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ncount[\'c\'] - count[\'k\'] == active_forg\nif pre word less cur word is invalid\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n d = [0] * 5\n res = 1\n dt = {k:i for i,k in enumerate(\'croak\')}\n for i in croakOfFrogs:\n ind = dt[i]\n d[ind] += 1\n if ind == 0:\n res = max(res, d[0] - d[-1])\n else:\n if d[ind-1] < d[ind]:\n return -1\n if d[-1] != d[0]:\n return -1\n return res\n \n\n\n \n``` | 0 | You are given the string `croakOfFrogs`, which represents a combination of the string `"croak "` from different frogs, that is, multiple frogs can croak at the same time, so multiple `"croak "` are mixed.
_Return the minimum number of_ different _frogs to finish all the croaks in the given string._
A valid `"croak "` means a frog is printing five letters `'c'`, `'r'`, `'o'`, `'a'`, and `'k'` **sequentially**. The frogs have to print all five letters to finish a croak. If the given string is not a combination of a valid `"croak "` return `-1`.
**Example 1:**
**Input:** croakOfFrogs = "croakcroak "
**Output:** 1
**Explanation:** One frog yelling "croak **"** twice.
**Example 2:**
**Input:** croakOfFrogs = "crcoakroak "
**Output:** 2
**Explanation:** The minimum number of frogs is two.
The first frog could yell "**cr**c**oak**roak ".
The second frog could yell later "cr**c**oak**roak** ".
**Example 3:**
**Input:** croakOfFrogs = "croakcrook "
**Output:** -1
**Explanation:** The given string is an invalid combination of "croak **"** from different frogs.
**Constraints:**
* `1 <= croakOfFrogs.length <= 105`
* `croakOfFrogs` is either `'c'`, `'r'`, `'o'`, `'a'`, or `'k'`. | null |
Monotonic sequence, quick | minimum-number-of-frogs-croaking | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nList record every word count, the list is decreasing sequence\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ncount[\'c\'] - count[\'k\'] == active_forg\nif pre word less cur word is invalid\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n d = [0] * 5\n res = 1\n dt = {k:i for i,k in enumerate(\'croak\')}\n for i in croakOfFrogs:\n ind = dt[i]\n d[ind] += 1\n if ind == 0:\n res = max(res, d[0] - d[-1])\n else:\n if d[ind-1] < d[ind]:\n return -1\n if d[-1] != d[0]:\n return -1\n return res\n \n\n\n \n``` | 0 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
Python3 - Easy to understand | minimum-number-of-frogs-croaking | 0 | 1 | # Approach\nThink of the problem as a state machine: frog A begins with "c" then transitions to "r" then transitions to "o" all the way to "k." If the input were to be always valid, we would only care about the maximum number of frogs concurrently croaking. In the context of the state machine, this is the number of frogs which have started but have not finished croaking. \n\nSince the input is not always perfect, we need to catch instances where "croak" is not spelled with the right letters ("crook") or when it\'s not spelled all the way ("croa"). The first case can be caught by checking for invalid intermediate state values (freq[ch] < 0) and the second can be caught by ensuring all frogs are in the "done" state at the end of the program.\n\n# Complexity\n- Time complexity: $$O(n)$$\nNote a constant speedup can be achieved by indexing into an array- this is less readable, so it is not presented here. The initial sum could also be avoided and handled in the main for loop.\n- Space complexity: $$O(1)$$\n\n\n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n cnt = sum(ch == \'c\' for ch in croakOfFrogs)\n tr = {"c": "r", "r": "o", "o": "a", "a": "k", "k": "done"} # State transition\n freq = {"c": cnt, "r": 0, "o": 0, "a": 0, "k": 0, "done": 0} # State\n max_croaking = 0 \n for ch in croakOfFrogs:\n freq[ch] -= 1\n if freq[ch] < 0:\n return -1\n freq[tr[ch]] += 1\n max_croaking = max(max_croaking, cnt - freq["c"] - freq["done"])\n\n return max_croaking if cnt == freq["done"] else -1\n``` | 0 | You are given the string `croakOfFrogs`, which represents a combination of the string `"croak "` from different frogs, that is, multiple frogs can croak at the same time, so multiple `"croak "` are mixed.
_Return the minimum number of_ different _frogs to finish all the croaks in the given string._
A valid `"croak "` means a frog is printing five letters `'c'`, `'r'`, `'o'`, `'a'`, and `'k'` **sequentially**. The frogs have to print all five letters to finish a croak. If the given string is not a combination of a valid `"croak "` return `-1`.
**Example 1:**
**Input:** croakOfFrogs = "croakcroak "
**Output:** 1
**Explanation:** One frog yelling "croak **"** twice.
**Example 2:**
**Input:** croakOfFrogs = "crcoakroak "
**Output:** 2
**Explanation:** The minimum number of frogs is two.
The first frog could yell "**cr**c**oak**roak ".
The second frog could yell later "cr**c**oak**roak** ".
**Example 3:**
**Input:** croakOfFrogs = "croakcrook "
**Output:** -1
**Explanation:** The given string is an invalid combination of "croak **"** from different frogs.
**Constraints:**
* `1 <= croakOfFrogs.length <= 105`
* `croakOfFrogs` is either `'c'`, `'r'`, `'o'`, `'a'`, or `'k'`. | null |
Python3 - Easy to understand | minimum-number-of-frogs-croaking | 0 | 1 | # Approach\nThink of the problem as a state machine: frog A begins with "c" then transitions to "r" then transitions to "o" all the way to "k." If the input were to be always valid, we would only care about the maximum number of frogs concurrently croaking. In the context of the state machine, this is the number of frogs which have started but have not finished croaking. \n\nSince the input is not always perfect, we need to catch instances where "croak" is not spelled with the right letters ("crook") or when it\'s not spelled all the way ("croa"). The first case can be caught by checking for invalid intermediate state values (freq[ch] < 0) and the second can be caught by ensuring all frogs are in the "done" state at the end of the program.\n\n# Complexity\n- Time complexity: $$O(n)$$\nNote a constant speedup can be achieved by indexing into an array- this is less readable, so it is not presented here. The initial sum could also be avoided and handled in the main for loop.\n- Space complexity: $$O(1)$$\n\n\n# Code\n```\nclass Solution:\n def minNumberOfFrogs(self, croakOfFrogs: str) -> int:\n cnt = sum(ch == \'c\' for ch in croakOfFrogs)\n tr = {"c": "r", "r": "o", "o": "a", "a": "k", "k": "done"} # State transition\n freq = {"c": cnt, "r": 0, "o": 0, "a": 0, "k": 0, "done": 0} # State\n max_croaking = 0 \n for ch in croakOfFrogs:\n freq[ch] -= 1\n if freq[ch] < 0:\n return -1\n freq[tr[ch]] += 1\n max_croaking = max(max_croaking, cnt - freq["c"] - freq["done"])\n\n return max_croaking if cnt == freq["done"] else -1\n``` | 0 | Given an array of integers `arr`, and three integers `a`, `b` and `c`. You need to find the number of good triplets.
A triplet `(arr[i], arr[j], arr[k])` is **good** if the following conditions are true:
* `0 <= i < j < k < arr.length`
* `|arr[i] - arr[j]| <= a`
* `|arr[j] - arr[k]| <= b`
* `|arr[i] - arr[k]| <= c`
Where `|x|` denotes the absolute value of `x`.
Return _the number of good triplets_.
**Example 1:**
**Input:** arr = \[3,0,1,1,9,7\], a = 7, b = 2, c = 3
**Output:** 4
**Explanation:** There are 4 good triplets: \[(3,0,1), (3,0,1), (3,1,1), (0,1,1)\].
**Example 2:**
**Input:** arr = \[1,1,2,2,3\], a = 0, b = 0, c = 1
**Output:** 0
**Explanation:** No triplet satisfies all conditions.
**Constraints:**
* `3 <= arr.length <= 100`
* `0 <= arr[i] <= 1000`
* `0 <= a, b, c <= 1000` | keep the frequency of all characters from "croak" using a hashmap. For each character in the given string, greedily match it to a possible "croak". |
EASY PYTHON SOLUTION USING SIMPLE DP | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | \n# Code\n```\nclass Solution:\n def dp(self,i,n,m,k,last,dct):\n if i==n:\n if k==0:\n return 1\n return 0\n if (i,k,last) in dct:\n return dct[(i,k,last)]\n val=0\n for j in range(1,m+1):\n if j<=last:\n val+=self.dp(i+1,n,m,k,last,dct)\n else:\n val+=self.dp(i+1,n,m,k-1,j,dct)\n dct[(i,k,last)]=val\n return val%1000000007\n\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n return self.dp(0,n,m,k,-1,{})%1000000007\n``` | 4 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
EASY PYTHON SOLUTION USING SIMPLE DP | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | \n# Code\n```\nclass Solution:\n def dp(self,i,n,m,k,last,dct):\n if i==n:\n if k==0:\n return 1\n return 0\n if (i,k,last) in dct:\n return dct[(i,k,last)]\n val=0\n for j in range(1,m+1):\n if j<=last:\n val+=self.dp(i+1,n,m,k,last,dct)\n else:\n val+=self.dp(i+1,n,m,k-1,j,dct)\n dct[(i,k,last)]=val\n return val%1000000007\n\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n return self.dp(0,n,m,k,-1,{})%1000000007\n``` | 4 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Python solution with optimize space and easy to understand | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves finding the number of ways to build an array arr with certain constraints while using dynamic programming.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitialize a 3D DP array dp where dp[i][j][cost] represents the number of ways to build an array of length i such that the maximum element is j and the search cost is cost.\n\nInitialize the base case dp[0][0][0] = 1 since there\'s one way to build an empty array.\n\nUse nested loops to iterate through the array length i, maximum element j, and search cost cost.\n\nUpdate dp[i][j][cost] by considering two cases:\n\nAdding a new element with value j to the array, which contributes to the search cost.\nNot adding a new element with value j to the array, which does not contribute to the search cost.\nCalculate the total number of ways to build the array by summing up dp[n][j][k] for all possible maximum elements j.\n\nReturn the result modulo 10^9 + 7 to handle large values.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * m * k)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n * m * k)\n# Code\n```\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n MOD = 10**9 + 7\n dp = [[[0] * (k + 1) for _ in range(m + 1)] for _ in range(n + 1)]\n dp[0][0][0] = 1\n \n for i in range(1, n + 1):\n for j in range(1, m + 1):\n for cost in range(1, k + 1):\n dp[i][j][cost] = (dp[i][j][cost] + dp[i - 1][j][cost] * j) % MOD\n for prev in range(j):\n dp[i][j][cost] = (dp[i][j][cost] + dp[i - 1][prev][cost - 1]) % MOD\n total_ways = sum(dp[n][j][k] for j in range(1, m + 1)) % MOD\n \n return total_ways\n\n``` | 2 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
Python solution with optimize space and easy to understand | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves finding the number of ways to build an array arr with certain constraints while using dynamic programming.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitialize a 3D DP array dp where dp[i][j][cost] represents the number of ways to build an array of length i such that the maximum element is j and the search cost is cost.\n\nInitialize the base case dp[0][0][0] = 1 since there\'s one way to build an empty array.\n\nUse nested loops to iterate through the array length i, maximum element j, and search cost cost.\n\nUpdate dp[i][j][cost] by considering two cases:\n\nAdding a new element with value j to the array, which contributes to the search cost.\nNot adding a new element with value j to the array, which does not contribute to the search cost.\nCalculate the total number of ways to build the array by summing up dp[n][j][k] for all possible maximum elements j.\n\nReturn the result modulo 10^9 + 7 to handle large values.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * m * k)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n * m * k)\n# Code\n```\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n MOD = 10**9 + 7\n dp = [[[0] * (k + 1) for _ in range(m + 1)] for _ in range(n + 1)]\n dp[0][0][0] = 1\n \n for i in range(1, n + 1):\n for j in range(1, m + 1):\n for cost in range(1, k + 1):\n dp[i][j][cost] = (dp[i][j][cost] + dp[i - 1][j][cost] * j) % MOD\n for prev in range(j):\n dp[i][j][cost] = (dp[i][j][cost] + dp[i - 1][prev][cost - 1]) % MOD\n total_ways = sum(dp[n][j][k] for j in range(1, m + 1)) % MOD\n \n return total_ways\n\n``` | 2 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Simple Solution || Beginner Friendly || Easy to Understand ✅ | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- We are given three integers `n, m, and k`.\n- We need to find the number of ways to build an array `arr` of `n` positive integers, each ranging from 1 to `m`, such that the "search_cost" of the array is equal to `k`.\n- "Search_cost" is defined as the number of elements in the array that are greater than all the elements to their left.\n- We use dynamic programming to solve this problem, creating a 3D array `dp` to store intermediate results.\n- `dp[i][cost][max_val]` represents the number of ways to build an array of length i+1 with a maximum value of `max_val+1` and a search cost of cost+1.\n- We initialize the base case where `i = 0`, and `cost = 0`, setting `dp[0][0][max_val]` to 1 for all possible `max_val`.\n- We iterate through the remaining values of `i`, `cost`, and `max_val`, calculating the number of ways to build the array based on the previous values in `dp`.\n- To calculate `dp[i][cost][max_val]`, we consider two cases:\n1. Adding `max_val+1` as the maximum element to the array.\n1. Not adding max_val+1 as the maximum element to the array.\n- We update `dp[i][cost][max_val]` accordingly and take care of the modulo operation to prevent overflow.\n- Finally, we sum up the values of `dp[n-1][k-1][max_val]` for all possible `max_val` to get the total number of arrays with the desired properties.\n- The result is returned as `(int) ans` after taking the modulo `10^9 + 7`.\n\n# Complexity\n- Time complexity: `O(n * m * k)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n * k * m)` \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numOfArrays(int n, int m, int k) {\n long[][][] dp = new long[n][k][m];\n long mod = 1000000007;\n Arrays.fill(dp[0][0], 1);\n \n for (int i = 1; i < n; i++) {\n for (int cost = 0; cost < Math.min(i + 1, k); cost++) {\n for (int max = 0; max < m; max++) {\n dp[i][cost][max] = (dp[i][cost][max] + (max + 1) * dp[i - 1][cost][max]) % mod;\n if (cost != 0) {\n long sum = 0;\n for (int prevMax = 0; prevMax < max; prevMax++) {\n sum += dp[i - 1][cost - 1][prevMax];\n sum %= mod;\n }\n dp[i][cost][max] = (dp[i][cost][max] + sum) % mod;\n }\n }\n }\n }\n long ans = 0;\n for (int max = 0; max < m; max++) {\n ans += dp[n - 1][k - 1][max];\n ans %= mod;\n }\n return (int) ans;\n }\n}\n```\n```python3 []\nclass Solution:\n def numOfArrays(self, n, m, k):\n if m < k: return 0\n dp = [[1] * m] + [[0] * m for _ in range(k - 1)]\n mod = 10 ** 9 + 7\n for _ in range(n - 1):\n for i in range(k - 1, -1, -1):\n cur = 0\n for j in range(m):\n dp[i][j] = (dp[i][j] * (j + 1) + cur) % mod\n if i: cur = (cur + dp[i - 1][j]) % mod\n return sum(dp[-1]) % mod\n```\n```python []\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n \n MOD = 10**9 + 7\n\n def helper(indx, curr_max, cost, m, dp):\n\n tpl = (indx, curr_max, cost)\n\n if tpl in dp:\n return dp[tpl]\n\n if indx == 1 and cost == 1:\n return 1\n elif indx == 1:\n return 0\n elif cost == 0:\n return 0\n \n numberWays = 0\n\n for j in range(1, m+1):\n if j <= curr_max:\n numberWays += helper(indx-1, curr_max, cost, m, dp)\n else:\n numberWays += helper(indx-1, j, cost-1, m, dp)\n dp[tpl] = numberWays % MOD\n\n return dp[tpl]\n\n ans = 0\n\n dp = {}\n\n for j in range(1, m+1):\n ans = (ans + helper(n, j, k, m, dp)) % MOD\n \n return ans\n```\n```C++ []\nclass Solution {\npublic:\n int dp[51][101][51], pre[51][101][51], mod = 1e9 + 7;\n \n int numOfArrays(int n, int m, int k) {\n for (int j = 0; j<= m; j++) {\n dp[1][j][1] = 1;\n pre[1][j][1] = j;\n }\n \n for (int len = 2; len <= n; len++) {\n for (int mx = 1; mx <= m; mx++) {\n for (int cost = 1; cost <=k; cost++) {\n /* In this first case, we can append any element from [1, mx] to the end of the array. */\n dp[len][mx][cost] = (1LL * mx * dp[len-1][mx][cost]) % mod;\n \n /* In this second case, we can append the element "mx" to the end of the array. \n for (int i = 1; i < mx; i++) dp[len][mx][cost] += ways[len - 1][i][cost - 1];*/\n dp[len][mx][cost] = (dp[len][mx][cost] + pre[len-1][mx-1][cost-1]) % mod;\\\n \n pre[len][mx][cost] = (pre[len][mx-1][cost] + dp[len][mx][cost]) % mod;\n }\n }\n }\n return pre[n][m][k];\n }\n};\n```\n```C []\nclass Solution {\npublic:\n int n,m,k,dp[55][105][55],mod=1e9+7;\n \n int sol(int id,int mx,int inv)\n {\n // cout<<id<<" "<<mx<<" "<<inv<<endl;\n if(id==n) return (inv==k);\n if(inv>k) return 0;\n \n long ans=dp[id][mx][inv];\n if(ans!=-1) return ans;\n ans=0;\n \n for(int l=1;l<=m;l++)\n {\n if(l<=mx) ans+=sol(id+1,mx,inv);\n else ans+=sol(id+1,l,inv+1);\n ans%=mod;\n }\n return dp[id][mx][inv]=ans;\n }\n \n int numOfArrays(int nn, int mm, int kk) \n {\n n=nn; m=mm; k=kk;\n memset(dp,-1,sizeof(dp));\n return sol(0,0,0);\n }\n};\n``` | 66 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
Simple Solution || Beginner Friendly || Easy to Understand ✅ | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- We are given three integers `n, m, and k`.\n- We need to find the number of ways to build an array `arr` of `n` positive integers, each ranging from 1 to `m`, such that the "search_cost" of the array is equal to `k`.\n- "Search_cost" is defined as the number of elements in the array that are greater than all the elements to their left.\n- We use dynamic programming to solve this problem, creating a 3D array `dp` to store intermediate results.\n- `dp[i][cost][max_val]` represents the number of ways to build an array of length i+1 with a maximum value of `max_val+1` and a search cost of cost+1.\n- We initialize the base case where `i = 0`, and `cost = 0`, setting `dp[0][0][max_val]` to 1 for all possible `max_val`.\n- We iterate through the remaining values of `i`, `cost`, and `max_val`, calculating the number of ways to build the array based on the previous values in `dp`.\n- To calculate `dp[i][cost][max_val]`, we consider two cases:\n1. Adding `max_val+1` as the maximum element to the array.\n1. Not adding max_val+1 as the maximum element to the array.\n- We update `dp[i][cost][max_val]` accordingly and take care of the modulo operation to prevent overflow.\n- Finally, we sum up the values of `dp[n-1][k-1][max_val]` for all possible `max_val` to get the total number of arrays with the desired properties.\n- The result is returned as `(int) ans` after taking the modulo `10^9 + 7`.\n\n# Complexity\n- Time complexity: `O(n * m * k)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n * k * m)` \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numOfArrays(int n, int m, int k) {\n long[][][] dp = new long[n][k][m];\n long mod = 1000000007;\n Arrays.fill(dp[0][0], 1);\n \n for (int i = 1; i < n; i++) {\n for (int cost = 0; cost < Math.min(i + 1, k); cost++) {\n for (int max = 0; max < m; max++) {\n dp[i][cost][max] = (dp[i][cost][max] + (max + 1) * dp[i - 1][cost][max]) % mod;\n if (cost != 0) {\n long sum = 0;\n for (int prevMax = 0; prevMax < max; prevMax++) {\n sum += dp[i - 1][cost - 1][prevMax];\n sum %= mod;\n }\n dp[i][cost][max] = (dp[i][cost][max] + sum) % mod;\n }\n }\n }\n }\n long ans = 0;\n for (int max = 0; max < m; max++) {\n ans += dp[n - 1][k - 1][max];\n ans %= mod;\n }\n return (int) ans;\n }\n}\n```\n```python3 []\nclass Solution:\n def numOfArrays(self, n, m, k):\n if m < k: return 0\n dp = [[1] * m] + [[0] * m for _ in range(k - 1)]\n mod = 10 ** 9 + 7\n for _ in range(n - 1):\n for i in range(k - 1, -1, -1):\n cur = 0\n for j in range(m):\n dp[i][j] = (dp[i][j] * (j + 1) + cur) % mod\n if i: cur = (cur + dp[i - 1][j]) % mod\n return sum(dp[-1]) % mod\n```\n```python []\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n \n MOD = 10**9 + 7\n\n def helper(indx, curr_max, cost, m, dp):\n\n tpl = (indx, curr_max, cost)\n\n if tpl in dp:\n return dp[tpl]\n\n if indx == 1 and cost == 1:\n return 1\n elif indx == 1:\n return 0\n elif cost == 0:\n return 0\n \n numberWays = 0\n\n for j in range(1, m+1):\n if j <= curr_max:\n numberWays += helper(indx-1, curr_max, cost, m, dp)\n else:\n numberWays += helper(indx-1, j, cost-1, m, dp)\n dp[tpl] = numberWays % MOD\n\n return dp[tpl]\n\n ans = 0\n\n dp = {}\n\n for j in range(1, m+1):\n ans = (ans + helper(n, j, k, m, dp)) % MOD\n \n return ans\n```\n```C++ []\nclass Solution {\npublic:\n int dp[51][101][51], pre[51][101][51], mod = 1e9 + 7;\n \n int numOfArrays(int n, int m, int k) {\n for (int j = 0; j<= m; j++) {\n dp[1][j][1] = 1;\n pre[1][j][1] = j;\n }\n \n for (int len = 2; len <= n; len++) {\n for (int mx = 1; mx <= m; mx++) {\n for (int cost = 1; cost <=k; cost++) {\n /* In this first case, we can append any element from [1, mx] to the end of the array. */\n dp[len][mx][cost] = (1LL * mx * dp[len-1][mx][cost]) % mod;\n \n /* In this second case, we can append the element "mx" to the end of the array. \n for (int i = 1; i < mx; i++) dp[len][mx][cost] += ways[len - 1][i][cost - 1];*/\n dp[len][mx][cost] = (dp[len][mx][cost] + pre[len-1][mx-1][cost-1]) % mod;\\\n \n pre[len][mx][cost] = (pre[len][mx-1][cost] + dp[len][mx][cost]) % mod;\n }\n }\n }\n return pre[n][m][k];\n }\n};\n```\n```C []\nclass Solution {\npublic:\n int n,m,k,dp[55][105][55],mod=1e9+7;\n \n int sol(int id,int mx,int inv)\n {\n // cout<<id<<" "<<mx<<" "<<inv<<endl;\n if(id==n) return (inv==k);\n if(inv>k) return 0;\n \n long ans=dp[id][mx][inv];\n if(ans!=-1) return ans;\n ans=0;\n \n for(int l=1;l<=m;l++)\n {\n if(l<=mx) ans+=sol(id+1,mx,inv);\n else ans+=sol(id+1,l,inv+1);\n ans%=mod;\n }\n return dp[id][mx][inv]=ans;\n }\n \n int numOfArrays(int nn, int mm, int kk) \n {\n n=nn; m=mm; k=kk;\n memset(dp,-1,sizeof(dp));\n return sol(0,0,0);\n }\n};\n``` | 66 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
JAVA and C++ Faster | Fastest In Python | Dynamic Programming | O(n*k*m) | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | \n\n# YouTube Video:\n[https://youtu.be/EwZ9yLxrYRg]()\n\n# Intuition:\n\n- To find the number of ways to construct the array `arr` satisfying the given conditions, we can use dynamic programming. We maintain a 3D array `dp`, where `dp[i][cost][max]` represents the number of ways to construct an array of length `i` with exactly `cost` search costs, where `max` is the maximum value in the last slot. We iterate through the slots of the array and calculate the possibilities based on the previous slot\'s values. Finally, we sum up the possibilities for the last slot with exactly `k` search costs and different maximum values.\n\n# Approach:\n\n1. Initialize a 3D array `dp` to store the number of ways.\n2. Fill the first slot of `dp` with 1, as there\'s only one way to fill it (with value 1).\n3. Iterate through the slots of the array, search costs, and maximum values, calculating the possibilities and storing them in `dp`.\n4. Sum up the possibilities for the last slot with exactly `k` search costs and different maximum values.\n5. Return the result modulo 10^9 + 7.\n\n**Complexity Analysis:**\n\n- Time Complexity: O(n * k * m), where `n` is the length of the array, `k` is the maximum search cost, and `m` is the maximum value allowed.\n- Space Complexity: O(n * k * m) for the dynamic programming table.\n---\n# Code\n<iframe src="https://leetcode.com/playground/cr8kZhGk/shared" frameBorder="0" width="1000" height="550"></iframe>\n\n---\n\n<!-- # Code\n```\nclass Solution {\n public int numOfArrays(int n, int m, int k) {\n long[][][] dp =new long[n][k][m];\n long mod = 1000000007;\n Arrays.fill(dp[0][0], 1);\n for (int i = 1;i<n;i++) {\n for (int cost = 0;cost <Math.min(i+1, k);cost++) {\n for (int max = 0;max < m;max++){\n long sum = 0;\n sum += dp[i-1][cost][max] * (max+1);\n \n if (cost != 0) {\n long[] arr = dp[i-1][cost-1];\n for (int prevMax = 0;prevMax < max; prevMax++) {\n sum += arr[prevMax];\n }\n }\n dp[i][cost][max] = sum %mod;\n }\n }\n }\n long ans = 0;\n for (int max = 0;max < m;max++) {\n ans += dp[n-1][k-1][max];\n ans %= mod;\n }\n return (int) ans;\n }\n}\n``` -->\n\n | 13 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
JAVA and C++ Faster | Fastest In Python | Dynamic Programming | O(n*k*m) | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | \n\n# YouTube Video:\n[https://youtu.be/EwZ9yLxrYRg]()\n\n# Intuition:\n\n- To find the number of ways to construct the array `arr` satisfying the given conditions, we can use dynamic programming. We maintain a 3D array `dp`, where `dp[i][cost][max]` represents the number of ways to construct an array of length `i` with exactly `cost` search costs, where `max` is the maximum value in the last slot. We iterate through the slots of the array and calculate the possibilities based on the previous slot\'s values. Finally, we sum up the possibilities for the last slot with exactly `k` search costs and different maximum values.\n\n# Approach:\n\n1. Initialize a 3D array `dp` to store the number of ways.\n2. Fill the first slot of `dp` with 1, as there\'s only one way to fill it (with value 1).\n3. Iterate through the slots of the array, search costs, and maximum values, calculating the possibilities and storing them in `dp`.\n4. Sum up the possibilities for the last slot with exactly `k` search costs and different maximum values.\n5. Return the result modulo 10^9 + 7.\n\n**Complexity Analysis:**\n\n- Time Complexity: O(n * k * m), where `n` is the length of the array, `k` is the maximum search cost, and `m` is the maximum value allowed.\n- Space Complexity: O(n * k * m) for the dynamic programming table.\n---\n# Code\n<iframe src="https://leetcode.com/playground/cr8kZhGk/shared" frameBorder="0" width="1000" height="550"></iframe>\n\n---\n\n<!-- # Code\n```\nclass Solution {\n public int numOfArrays(int n, int m, int k) {\n long[][][] dp =new long[n][k][m];\n long mod = 1000000007;\n Arrays.fill(dp[0][0], 1);\n for (int i = 1;i<n;i++) {\n for (int cost = 0;cost <Math.min(i+1, k);cost++) {\n for (int max = 0;max < m;max++){\n long sum = 0;\n sum += dp[i-1][cost][max] * (max+1);\n \n if (cost != 0) {\n long[] arr = dp[i-1][cost-1];\n for (int prevMax = 0;prevMax < max; prevMax++) {\n sum += arr[prevMax];\n }\n }\n dp[i][cost][max] = sum %mod;\n }\n }\n }\n long ans = 0;\n for (int max = 0;max < m;max++) {\n ans += dp[n-1][k-1][max];\n ans %= mod;\n }\n return (int) ans;\n }\n}\n``` -->\n\n | 13 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
✅ 90.27% Dynamic Programming Optimized | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | # Intuition\n\nUpon reading the problem, we\'re tasked with finding the number of arrays of length `n` with values in the range `[1, m]` such that the array has exactly `k` cost. The challenge is not only in understanding what constitutes this cost but also in devising an efficient algorithm to count these arrays given the constraints.\n\n## Live Coding & Explaining\nhttps://youtu.be/BmMJP_qVBXM?si=4qwN0ijOwMVIygC8\n\n# Approach\n\nThe problem can be tackled with dynamic programming, where we try to build the solution incrementally. We can break down the problem into sub-problems where we consider smaller arrays and try to determine the number of valid arrays we can form given a certain cost and maximum value. \n\nWe use the following states:\n- `i`: the length of the array.\n- `maxNum`: the maximum number in the array.\n- `cost`: the cost of the array.\n\nWe define `dp[i][maxNum][cost]` as the number of arrays of length `i` with a maximum value of `maxNum` and a cost of `cost`. To compute this, we consider two cases:\n\n1. The last number added to the array isn\'t a new maximum. In this case, it can be any number from 1 to `maxNum`, and the cost remains unchanged.\n2. The last number added is a new maximum. Here, the previous maximum could be any number from 1 to `maxNum - 1`, and the cost decreases by 1 since we\'ve added a new maximum.\n\nHowever, summing over possible maximums for each state would be inefficient. To accelerate this, we introduce a prefix sum array that keeps track of the sum of valid arrays for a given cost up to the current maximum.\n\n# Complexity\n\n- **Time complexity:** $$O(n \\times m \\times k)$$\n The main loop iterates `n` times. For each iteration, we consider `m` possible maximum values and `k` possible costs, making the time complexity cubic.\n\n- **Space complexity:** $$O(m \\times k)$$\n We use two 2D arrays, `dp` and `prefix`, each of size $$m \\times k$$, and two other arrays, `prevDp` and `prevPrefix`, for storing the previous state. Hence, the space complexity is quadratic.\n\n# Code\n``` Python []\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n mod = 10**9 + 7\n \n dp = [[0] * (k+1) for _ in range(m+1)]\n prefix = [[0] * (k+1) for _ in range(m+1)]\n prevDp = [[0] * (k+1) for _ in range(m+1)]\n prevPrefix = [[0] * (k+1) for _ in range(m+1)]\n \n for j in range(1, m+1):\n prevDp[j][1] = 1\n prevPrefix[j][1] = j\n \n for _ in range(2, n+1):\n dp = [[0] * (k+1) for _ in range(m+1)]\n prefix = [[0] * (k+1) for _ in range(m+1)]\n \n for maxNum in range(1, m+1):\n for cost in range(1, k+1):\n dp[maxNum][cost] = (maxNum * prevDp[maxNum][cost]) % mod\n \n if maxNum > 1 and cost > 1:\n dp[maxNum][cost] += prevPrefix[maxNum - 1][cost - 1]\n dp[maxNum][cost] %= mod\n \n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod\n \n prevDp, prevPrefix = [row[:] for row in dp], [row[:] for row in prefix]\n \n return prefix[m][k]\n```\n``` Go []\nfunc numOfArrays(n int, m int, k int) int {\n mod := int(1e9 + 7)\n\n dp := make([][]int, m+1)\n prefix := make([][]int, m+1)\n prevDp := make([][]int, m+1)\n prevPrefix := make([][]int, m+1)\n\n for i := range dp {\n dp[i] = make([]int, k+1)\n prefix[i] = make([]int, k+1)\n prevDp[i] = make([]int, k+1)\n prevPrefix[i] = make([]int, k+1)\n }\n\n for j := 1; j <= m; j++ {\n prevDp[j][1] = 1\n prevPrefix[j][1] = j\n }\n\n for i := 2; i <= n; i++ {\n for maxNum := 1; maxNum <= m; maxNum++ {\n for cost := 1; cost <= k; cost++ {\n dp[maxNum][cost] = (maxNum * prevDp[maxNum][cost]) % mod\n\n if maxNum > 1 && cost > 1 {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum-1][cost-1]) % mod\n }\n\n prefix[maxNum][cost] = (prefix[maxNum-1][cost] + dp[maxNum][cost]) % mod\n }\n }\n\n for j := 1; j <= m; j++ {\n copy(prevDp[j], dp[j])\n copy(prevPrefix[j], prefix[j])\n }\n }\n\n return prefix[m][k]\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_of_arrays(n: i32, m: i32, k: i32) -> i32 {\n const MOD: i32 = 1_000_000_007;\n\n let mut dp = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n let mut prefix = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n let mut prevDp = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n let mut prevPrefix = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n\n for j in 1..=m {\n prevDp[j as usize][1] = 1;\n prevPrefix[j as usize][1] = j;\n }\n\n for _ in 2..=n {\n for maxNum in 1..=m {\n for cost in 1..=k {\n dp[maxNum as usize][cost as usize] = \n ((maxNum as i64 * prevDp[maxNum as usize][cost as usize] as i64) % MOD as i64) as i32;\n \n if maxNum > 1 && cost > 1 {\n dp[maxNum as usize][cost as usize] = \n (dp[maxNum as usize][cost as usize] + prevPrefix[(maxNum-1) as usize][(cost-1) as usize]) % MOD;\n }\n\n prefix[maxNum as usize][cost as usize] = \n (prefix[(maxNum-1) as usize][cost as usize] + dp[maxNum as usize][cost as usize]) % MOD;\n }\n }\n\n prevDp = dp.clone();\n prevPrefix = prefix.clone();\n }\n\n prefix[m as usize][k as usize]\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numOfArrays(int n, int m, int k) {\n const int mod = 1e9 + 7;\n\n vector<vector<int>> dp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prefix(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevDp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevPrefix(m+1, vector<int>(k+1, 0));\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int _ = 2; _ <= n; _++) {\n dp.assign(m+1, vector<int>(k+1, 0));\n prefix.assign(m+1, vector<int>(k+1, 0));\n\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (static_cast<long long>(maxNum) * prevDp[maxNum][cost]) % mod;\n \n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n \n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n prevDp = dp;\n prevPrefix = prefix;\n }\n\n return prefix[m][k];\n }\n};\n```\n``` Java []\npublic class Solution {\n public int numOfArrays(int n, int m, int k) {\n final int mod = 1000000007;\n\n int[][] dp = new int[m+1][k+1];\n int[][] prefix = new int[m+1][k+1];\n int[][] prevDp = new int[m+1][k+1];\n int[][] prevPrefix = new int[m+1][k+1];\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int i = 2; i <= n; i++) {\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (int)(((long)maxNum * prevDp[maxNum][cost]) % mod);\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n for (int j = 1; j <= m; j++) {\n System.arraycopy(dp[j], 0, prevDp[j], 0, k+1);\n System.arraycopy(prefix[j], 0, prevPrefix[j], 0, k+1);\n }\n }\n\n return prefix[m][k];\n }\n}\n```\n``` JavaScript []\nvar numOfArrays = function(n, m, k){\n const mod = 1e9 + 7;\n\n let dp = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n let prefix = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n let prevDp = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n let prevPrefix = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n\n for (let j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (let _ = 2; _ <= n; _++) {\n dp = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n prefix = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n\n for (let maxNum = 1; maxNum <= m; maxNum++) {\n for (let cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (maxNum * prevDp[maxNum][cost]) % mod;\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n prevDp = dp;\n prevPrefix = prefix;\n }\n\n return prefix[m][k];\n }\n```\n``` PHP []\nclass Solution {\n function numOfArrays($n, $m, $k) {\n $mod = 1000000007;\n\n $dp = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n $prefix = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n $prevDp = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n $prevPrefix = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n\n for ($j = 1; $j <= $m; $j++) {\n $prevDp[$j][1] = 1;\n $prevPrefix[$j][1] = $j;\n }\n\n for ($i = 2; $i <= $n; $i++) {\n for ($maxNum = 1; $maxNum <= $m; $maxNum++) {\n for ($cost = 1; $cost <= $k; $cost++) {\n $dp[$maxNum][$cost] = ($maxNum * $prevDp[$maxNum][$cost]) % $mod;\n\n if ($maxNum > 1 && $cost > 1) {\n $dp[$maxNum][$cost] = ($dp[$maxNum][$cost] + $prevPrefix[$maxNum - 1][$cost - 1]) % $mod;\n }\n\n $prefix[$maxNum][$cost] = ($prefix[$maxNum - 1][$cost] + $dp[$maxNum][$cost]) % $mod;\n }\n }\n\n $prevDp = $dp;\n $prevPrefix = $prefix;\n }\n\n return $prefix[$m][$k];\n }\n}\n```\n``` C# []\npublic class Solution {\n public int NumOfArrays(int n, int m, int k) {\n const int mod = 1000000007;\n\n int[][] dp = new int[m+1][];\n int[][] prefix = new int[m+1][];\n int[][] prevDp = new int[m+1][];\n int[][] prevPrefix = new int[m+1][];\n\n for (int i = 0; i <= m; i++) {\n dp[i] = new int[k+1];\n prefix[i] = new int[k+1];\n prevDp[i] = new int[k+1];\n prevPrefix[i] = new int[k+1];\n }\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int i = 2; i <= n; i++) {\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (int)(((long)maxNum * prevDp[maxNum][cost]) % mod);\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n for (int j = 1; j <= m; j++) {\n Array.Copy(dp[j], prevDp[j], k+1);\n Array.Copy(prefix[j], prevPrefix[j], k+1);\n }\n }\n\n return prefix[m][k];\n }\n}\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|-----------|---------------------|-------------------|\n| Go | 3 | 2.4 |\n| Rust | 3 | 2.2 |\n| Java | 9 | 39.2 |\n| C++ | 16 | 7.4 |\n| C# | 26 | 26.8 |\n| PHP | 45 | 19.9 |\n| JavaScript| 94 | 49.4 |\n| Python3 | 153 | 16.8 |\n\n\n\n\n# Why does it work?\n\nThe approach works because at each stage we\'re considering all possible ways an array can be formed based on its last element. We\'re effectively breaking down the problem into smaller subproblems (smaller arrays) and using solutions to these subproblems to build solutions to larger ones.\n\n# Logic behind the solution\n\nThe logic is rooted in dynamic programming, where we leverage previously computed results to avoid redundant computations. The introduction of the prefix sum array is a common optimization technique in dynamic programming to quickly sum up results from prior states.\n\n# Naive vs. Optimized version\n\nThe naive approach would involve brute-forcing every possible array, calculating the cost for each one, and checking if it matches the desired cost. This approach would be factorial in time complexity and thus infeasible.\n\nOur current solution, on the other hand, is much more optimized. It avoids redundant calculations by storing and reusing prior results in the `dp` and `prefix` tables.\n\n# What we learned?\n\n- **Problem Decomposition:** We learned how to break down a seemingly complex problem into smaller, more manageable subproblems.\n \n- **Dynamic Programming:** This problem reinforced the utility of dynamic programming in solving problems where subproblems overlap.\n \n- **Optimization:** The use of prefix sums showcased how to optimize certain operations in dynamic programming to improve efficiency. | 75 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
✅ 90.27% Dynamic Programming Optimized | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | # Intuition\n\nUpon reading the problem, we\'re tasked with finding the number of arrays of length `n` with values in the range `[1, m]` such that the array has exactly `k` cost. The challenge is not only in understanding what constitutes this cost but also in devising an efficient algorithm to count these arrays given the constraints.\n\n## Live Coding & Explaining\nhttps://youtu.be/BmMJP_qVBXM?si=4qwN0ijOwMVIygC8\n\n# Approach\n\nThe problem can be tackled with dynamic programming, where we try to build the solution incrementally. We can break down the problem into sub-problems where we consider smaller arrays and try to determine the number of valid arrays we can form given a certain cost and maximum value. \n\nWe use the following states:\n- `i`: the length of the array.\n- `maxNum`: the maximum number in the array.\n- `cost`: the cost of the array.\n\nWe define `dp[i][maxNum][cost]` as the number of arrays of length `i` with a maximum value of `maxNum` and a cost of `cost`. To compute this, we consider two cases:\n\n1. The last number added to the array isn\'t a new maximum. In this case, it can be any number from 1 to `maxNum`, and the cost remains unchanged.\n2. The last number added is a new maximum. Here, the previous maximum could be any number from 1 to `maxNum - 1`, and the cost decreases by 1 since we\'ve added a new maximum.\n\nHowever, summing over possible maximums for each state would be inefficient. To accelerate this, we introduce a prefix sum array that keeps track of the sum of valid arrays for a given cost up to the current maximum.\n\n# Complexity\n\n- **Time complexity:** $$O(n \\times m \\times k)$$\n The main loop iterates `n` times. For each iteration, we consider `m` possible maximum values and `k` possible costs, making the time complexity cubic.\n\n- **Space complexity:** $$O(m \\times k)$$\n We use two 2D arrays, `dp` and `prefix`, each of size $$m \\times k$$, and two other arrays, `prevDp` and `prevPrefix`, for storing the previous state. Hence, the space complexity is quadratic.\n\n# Code\n``` Python []\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n mod = 10**9 + 7\n \n dp = [[0] * (k+1) for _ in range(m+1)]\n prefix = [[0] * (k+1) for _ in range(m+1)]\n prevDp = [[0] * (k+1) for _ in range(m+1)]\n prevPrefix = [[0] * (k+1) for _ in range(m+1)]\n \n for j in range(1, m+1):\n prevDp[j][1] = 1\n prevPrefix[j][1] = j\n \n for _ in range(2, n+1):\n dp = [[0] * (k+1) for _ in range(m+1)]\n prefix = [[0] * (k+1) for _ in range(m+1)]\n \n for maxNum in range(1, m+1):\n for cost in range(1, k+1):\n dp[maxNum][cost] = (maxNum * prevDp[maxNum][cost]) % mod\n \n if maxNum > 1 and cost > 1:\n dp[maxNum][cost] += prevPrefix[maxNum - 1][cost - 1]\n dp[maxNum][cost] %= mod\n \n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod\n \n prevDp, prevPrefix = [row[:] for row in dp], [row[:] for row in prefix]\n \n return prefix[m][k]\n```\n``` Go []\nfunc numOfArrays(n int, m int, k int) int {\n mod := int(1e9 + 7)\n\n dp := make([][]int, m+1)\n prefix := make([][]int, m+1)\n prevDp := make([][]int, m+1)\n prevPrefix := make([][]int, m+1)\n\n for i := range dp {\n dp[i] = make([]int, k+1)\n prefix[i] = make([]int, k+1)\n prevDp[i] = make([]int, k+1)\n prevPrefix[i] = make([]int, k+1)\n }\n\n for j := 1; j <= m; j++ {\n prevDp[j][1] = 1\n prevPrefix[j][1] = j\n }\n\n for i := 2; i <= n; i++ {\n for maxNum := 1; maxNum <= m; maxNum++ {\n for cost := 1; cost <= k; cost++ {\n dp[maxNum][cost] = (maxNum * prevDp[maxNum][cost]) % mod\n\n if maxNum > 1 && cost > 1 {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum-1][cost-1]) % mod\n }\n\n prefix[maxNum][cost] = (prefix[maxNum-1][cost] + dp[maxNum][cost]) % mod\n }\n }\n\n for j := 1; j <= m; j++ {\n copy(prevDp[j], dp[j])\n copy(prevPrefix[j], prefix[j])\n }\n }\n\n return prefix[m][k]\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_of_arrays(n: i32, m: i32, k: i32) -> i32 {\n const MOD: i32 = 1_000_000_007;\n\n let mut dp = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n let mut prefix = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n let mut prevDp = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n let mut prevPrefix = vec![vec![0; (k + 1) as usize]; (m + 1) as usize];\n\n for j in 1..=m {\n prevDp[j as usize][1] = 1;\n prevPrefix[j as usize][1] = j;\n }\n\n for _ in 2..=n {\n for maxNum in 1..=m {\n for cost in 1..=k {\n dp[maxNum as usize][cost as usize] = \n ((maxNum as i64 * prevDp[maxNum as usize][cost as usize] as i64) % MOD as i64) as i32;\n \n if maxNum > 1 && cost > 1 {\n dp[maxNum as usize][cost as usize] = \n (dp[maxNum as usize][cost as usize] + prevPrefix[(maxNum-1) as usize][(cost-1) as usize]) % MOD;\n }\n\n prefix[maxNum as usize][cost as usize] = \n (prefix[(maxNum-1) as usize][cost as usize] + dp[maxNum as usize][cost as usize]) % MOD;\n }\n }\n\n prevDp = dp.clone();\n prevPrefix = prefix.clone();\n }\n\n prefix[m as usize][k as usize]\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numOfArrays(int n, int m, int k) {\n const int mod = 1e9 + 7;\n\n vector<vector<int>> dp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prefix(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevDp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevPrefix(m+1, vector<int>(k+1, 0));\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int _ = 2; _ <= n; _++) {\n dp.assign(m+1, vector<int>(k+1, 0));\n prefix.assign(m+1, vector<int>(k+1, 0));\n\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (static_cast<long long>(maxNum) * prevDp[maxNum][cost]) % mod;\n \n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n \n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n prevDp = dp;\n prevPrefix = prefix;\n }\n\n return prefix[m][k];\n }\n};\n```\n``` Java []\npublic class Solution {\n public int numOfArrays(int n, int m, int k) {\n final int mod = 1000000007;\n\n int[][] dp = new int[m+1][k+1];\n int[][] prefix = new int[m+1][k+1];\n int[][] prevDp = new int[m+1][k+1];\n int[][] prevPrefix = new int[m+1][k+1];\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int i = 2; i <= n; i++) {\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (int)(((long)maxNum * prevDp[maxNum][cost]) % mod);\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n for (int j = 1; j <= m; j++) {\n System.arraycopy(dp[j], 0, prevDp[j], 0, k+1);\n System.arraycopy(prefix[j], 0, prevPrefix[j], 0, k+1);\n }\n }\n\n return prefix[m][k];\n }\n}\n```\n``` JavaScript []\nvar numOfArrays = function(n, m, k){\n const mod = 1e9 + 7;\n\n let dp = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n let prefix = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n let prevDp = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n let prevPrefix = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n\n for (let j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (let _ = 2; _ <= n; _++) {\n dp = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n prefix = Array.from({ length: m + 1 }, () => Array(k + 1).fill(0));\n\n for (let maxNum = 1; maxNum <= m; maxNum++) {\n for (let cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (maxNum * prevDp[maxNum][cost]) % mod;\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n prevDp = dp;\n prevPrefix = prefix;\n }\n\n return prefix[m][k];\n }\n```\n``` PHP []\nclass Solution {\n function numOfArrays($n, $m, $k) {\n $mod = 1000000007;\n\n $dp = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n $prefix = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n $prevDp = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n $prevPrefix = array_fill(0, $m+1, array_fill(0, $k+1, 0));\n\n for ($j = 1; $j <= $m; $j++) {\n $prevDp[$j][1] = 1;\n $prevPrefix[$j][1] = $j;\n }\n\n for ($i = 2; $i <= $n; $i++) {\n for ($maxNum = 1; $maxNum <= $m; $maxNum++) {\n for ($cost = 1; $cost <= $k; $cost++) {\n $dp[$maxNum][$cost] = ($maxNum * $prevDp[$maxNum][$cost]) % $mod;\n\n if ($maxNum > 1 && $cost > 1) {\n $dp[$maxNum][$cost] = ($dp[$maxNum][$cost] + $prevPrefix[$maxNum - 1][$cost - 1]) % $mod;\n }\n\n $prefix[$maxNum][$cost] = ($prefix[$maxNum - 1][$cost] + $dp[$maxNum][$cost]) % $mod;\n }\n }\n\n $prevDp = $dp;\n $prevPrefix = $prefix;\n }\n\n return $prefix[$m][$k];\n }\n}\n```\n``` C# []\npublic class Solution {\n public int NumOfArrays(int n, int m, int k) {\n const int mod = 1000000007;\n\n int[][] dp = new int[m+1][];\n int[][] prefix = new int[m+1][];\n int[][] prevDp = new int[m+1][];\n int[][] prevPrefix = new int[m+1][];\n\n for (int i = 0; i <= m; i++) {\n dp[i] = new int[k+1];\n prefix[i] = new int[k+1];\n prevDp[i] = new int[k+1];\n prevPrefix[i] = new int[k+1];\n }\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int i = 2; i <= n; i++) {\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (int)(((long)maxNum * prevDp[maxNum][cost]) % mod);\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n for (int j = 1; j <= m; j++) {\n Array.Copy(dp[j], prevDp[j], k+1);\n Array.Copy(prefix[j], prevPrefix[j], k+1);\n }\n }\n\n return prefix[m][k];\n }\n}\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|-----------|---------------------|-------------------|\n| Go | 3 | 2.4 |\n| Rust | 3 | 2.2 |\n| Java | 9 | 39.2 |\n| C++ | 16 | 7.4 |\n| C# | 26 | 26.8 |\n| PHP | 45 | 19.9 |\n| JavaScript| 94 | 49.4 |\n| Python3 | 153 | 16.8 |\n\n\n\n\n# Why does it work?\n\nThe approach works because at each stage we\'re considering all possible ways an array can be formed based on its last element. We\'re effectively breaking down the problem into smaller subproblems (smaller arrays) and using solutions to these subproblems to build solutions to larger ones.\n\n# Logic behind the solution\n\nThe logic is rooted in dynamic programming, where we leverage previously computed results to avoid redundant computations. The introduction of the prefix sum array is a common optimization technique in dynamic programming to quickly sum up results from prior states.\n\n# Naive vs. Optimized version\n\nThe naive approach would involve brute-forcing every possible array, calculating the cost for each one, and checking if it matches the desired cost. This approach would be factorial in time complexity and thus infeasible.\n\nOur current solution, on the other hand, is much more optimized. It avoids redundant calculations by storing and reusing prior results in the `dp` and `prefix` tables.\n\n# What we learned?\n\n- **Problem Decomposition:** We learned how to break down a seemingly complex problem into smaller, more manageable subproblems.\n \n- **Dynamic Programming:** This problem reinforced the utility of dynamic programming in solving problems where subproblems overlap.\n \n- **Optimization:** The use of prefix sums showcased how to optimize certain operations in dynamic programming to improve efficiency. | 75 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Python3 Solution | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | \n```\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n mod=10**9+7\n @lru_cache(None)\n def dp(i,h,k):\n if i==n and k==0:\n return 1\n if i==n or k<0:\n return 0\n return sum(dp(i+1,max(h,j),k-(j>h)) for j in range(1,m+1))%mod\n return dp(0,-1,k) \n \n``` | 1 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
Python3 Solution | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | \n```\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n mod=10**9+7\n @lru_cache(None)\n def dp(i,h,k):\n if i==n and k==0:\n return 1\n if i==n or k<0:\n return 0\n return sum(dp(i+1,max(h,j),k-(j>h)) for j in range(1,m+1))%mod\n return dp(0,-1,k) \n \n``` | 1 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
✅ Beats 92% || Dynamic Programming || Full Explanation || | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | # Intuition\n1. dp[i][j][k] denotes the number of ways to build an array of length i, with the maximum element j and cost k.\n2. dp[i][j][k] = dp[i-1][j][k]*j + sum(dp[i-1][x][k-1]) for x in range(1,j)\n3. return sum(dp[n][i][k] for i in range(1,m+1))%(10**9+7)\n\n\n# Approach\n1. The maximum element in the array can be from 1 to m.\n2. The cost of the array can be from 1 to k.\n3. We can build the array from left to right.\n4. If we want to build an array of length i, with the maximum element j and cost k, we can build it from an array of length i-1, with the maximum element j and cost k, and then append a new element to the end of the array.\n5. If we want to build an array of length i, with the maximum element j and cost k, we can build it from an array of length i-1, with the maximum element x and cost k-1, and then append a new element to the end of the array, where x is from 1 to j-1.\n6. We can use dynamic programming to solve this problem.\n7. dp[i][j][k] denotes the number of ways to build an array of length i, with the maximum element j and cost k.\n8. dp[i][j][k] = dp[i-1][j][k]*j + sum(dp[i-1][x][k-1]) for x in range(1,j)\n9. return sum(dp[n][i][k] for i in range(1,m+1))%(10**9+7)\n\n# Complexity\n- Time complexity : $$O(n*m*k)$$\n- Space complexity : $$O(n*m*k)$$\n\n# Code\n``` Python []\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n dp=[[[0 for _ in range(k+1)] for _ in range(m+1)] for _ in range(n+1)]\n for i in range(1,m+1):\n dp[1][i][1]=1\n for i in range(2,n+1):\n for j in range(1,m+1):\n for l in range(1,k+1):\n dp[i][j][l]+=dp[i-1][j][l]*j\n for x in range(1,j):\n dp[i][j][l]+=dp[i-1][x][l-1]\n return sum(dp[n][i][k] for i in range(1,m+1))%(10**9+7)\n```\n``` Java []\npublic class Solution {\n public int numOfArrays(int n, int m, int k) {\n final int mod = 1000000007;\n\n int[][] dp = new int[m+1][k+1];\n int[][] prefix = new int[m+1][k+1];\n int[][] prevDp = new int[m+1][k+1];\n int[][] prevPrefix = new int[m+1][k+1];\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int i = 2; i <= n; i++) {\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (int)(((long)maxNum * prevDp[maxNum][cost]) % mod);\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n for (int j = 1; j <= m; j++) {\n System.arraycopy(dp[j], 0, prevDp[j], 0, k+1);\n System.arraycopy(prefix[j], 0, prevPrefix[j], 0, k+1);\n }\n }\n\n return prefix[m][k];\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numOfArrays(int n, int m, int k) {\n const int mod = 1e9 + 7;\n\n vector<vector<int>> dp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prefix(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevDp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevPrefix(m+1, vector<int>(k+1, 0));\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int _ = 2; _ <= n; _++) {\n dp.assign(m+1, vector<int>(k+1, 0));\n prefix.assign(m+1, vector<int>(k+1, 0));\n\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (static_cast<long long>(maxNum) * prevDp[maxNum][cost]) % mod;\n \n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n \n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n prevDp = dp;\n prevPrefix = prefix;\n }\n\n return prefix[m][k];\n }\n};\n``` | 1 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
✅ Beats 92% || Dynamic Programming || Full Explanation || | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 1 | 1 | # Intuition\n1. dp[i][j][k] denotes the number of ways to build an array of length i, with the maximum element j and cost k.\n2. dp[i][j][k] = dp[i-1][j][k]*j + sum(dp[i-1][x][k-1]) for x in range(1,j)\n3. return sum(dp[n][i][k] for i in range(1,m+1))%(10**9+7)\n\n\n# Approach\n1. The maximum element in the array can be from 1 to m.\n2. The cost of the array can be from 1 to k.\n3. We can build the array from left to right.\n4. If we want to build an array of length i, with the maximum element j and cost k, we can build it from an array of length i-1, with the maximum element j and cost k, and then append a new element to the end of the array.\n5. If we want to build an array of length i, with the maximum element j and cost k, we can build it from an array of length i-1, with the maximum element x and cost k-1, and then append a new element to the end of the array, where x is from 1 to j-1.\n6. We can use dynamic programming to solve this problem.\n7. dp[i][j][k] denotes the number of ways to build an array of length i, with the maximum element j and cost k.\n8. dp[i][j][k] = dp[i-1][j][k]*j + sum(dp[i-1][x][k-1]) for x in range(1,j)\n9. return sum(dp[n][i][k] for i in range(1,m+1))%(10**9+7)\n\n# Complexity\n- Time complexity : $$O(n*m*k)$$\n- Space complexity : $$O(n*m*k)$$\n\n# Code\n``` Python []\nclass Solution:\n def numOfArrays(self, n: int, m: int, k: int) -> int:\n dp=[[[0 for _ in range(k+1)] for _ in range(m+1)] for _ in range(n+1)]\n for i in range(1,m+1):\n dp[1][i][1]=1\n for i in range(2,n+1):\n for j in range(1,m+1):\n for l in range(1,k+1):\n dp[i][j][l]+=dp[i-1][j][l]*j\n for x in range(1,j):\n dp[i][j][l]+=dp[i-1][x][l-1]\n return sum(dp[n][i][k] for i in range(1,m+1))%(10**9+7)\n```\n``` Java []\npublic class Solution {\n public int numOfArrays(int n, int m, int k) {\n final int mod = 1000000007;\n\n int[][] dp = new int[m+1][k+1];\n int[][] prefix = new int[m+1][k+1];\n int[][] prevDp = new int[m+1][k+1];\n int[][] prevPrefix = new int[m+1][k+1];\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int i = 2; i <= n; i++) {\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (int)(((long)maxNum * prevDp[maxNum][cost]) % mod);\n\n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n\n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n for (int j = 1; j <= m; j++) {\n System.arraycopy(dp[j], 0, prevDp[j], 0, k+1);\n System.arraycopy(prefix[j], 0, prevPrefix[j], 0, k+1);\n }\n }\n\n return prefix[m][k];\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int numOfArrays(int n, int m, int k) {\n const int mod = 1e9 + 7;\n\n vector<vector<int>> dp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prefix(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevDp(m+1, vector<int>(k+1, 0));\n vector<vector<int>> prevPrefix(m+1, vector<int>(k+1, 0));\n\n for (int j = 1; j <= m; j++) {\n prevDp[j][1] = 1;\n prevPrefix[j][1] = j;\n }\n\n for (int _ = 2; _ <= n; _++) {\n dp.assign(m+1, vector<int>(k+1, 0));\n prefix.assign(m+1, vector<int>(k+1, 0));\n\n for (int maxNum = 1; maxNum <= m; maxNum++) {\n for (int cost = 1; cost <= k; cost++) {\n dp[maxNum][cost] = (static_cast<long long>(maxNum) * prevDp[maxNum][cost]) % mod;\n \n if (maxNum > 1 && cost > 1) {\n dp[maxNum][cost] = (dp[maxNum][cost] + prevPrefix[maxNum - 1][cost - 1]) % mod;\n }\n \n prefix[maxNum][cost] = (prefix[maxNum - 1][cost] + dp[maxNum][cost]) % mod;\n }\n }\n\n prevDp = dp;\n prevPrefix = prefix;\n }\n\n return prefix[m][k];\n }\n};\n``` | 1 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Python || Documented and Simple Memoization Solution | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | ```\nfrom functools import cache\n\nMAX = 10 ** 9 + 7\n\n\nclass Solution:\n def numOfArrays(self, N: int, M: int, K: int) -> int:\n @cache\n def ways(n: int, m: int, k: int) -> int:\n """\n :param n:\n :param m:\n :param k:\n :return: number of ways an array (say A) can be constructed with constraints\n 1) len(A) == n\n 2) max(A) == m\n 3) search_cost(A) = k (definition of search_cost is in problem)\n """\n if n * m * k == 0: # same as: (n == 0 or m == 0 or k == 0)\n return 0\n elif n == k == 1:\n # length is 1 and cost is 1 then m will be the only number in the\n # array. So total number of ways an array can be constructed is 1\n return 1\n else:\n return (\n # let A be the one of the constructed arrays\n\n # case-1: k-th search_cost is NOT incurred at (n - 1)th index. It \n # means that m is already present in sub array A[:n - 1].\n # So last value in A could be any of [1, 2,..., m].\n ways(n - 1, m, k) * m\n\n +\n\n # case-2: k-th search_cost is incurred at (n - 1)th index. If means \n # that m is NOT in sub-array A[:n - 1]. So sub-array A[:n - 1] \n # which is of length (n - 1) should consist of k - 1 search_costs \n # and the largest value in A[:n - 1] could be any of [1, 2,..., m - 1]\n sum(ways(n - 1, mx, k - 1) for mx in range(1, m))\n ) % MAX\n\n # As maximum of constructed array can be any of [1, 2,..., m] so summing all the ways\n return sum(ways(N, mx, K) for mx in range(1, M + 1)) % MAX\n``` | 1 | You are given three integers `n`, `m` and `k`. Consider the following algorithm to find the maximum element of an array of positive integers:
You should build the array arr which has the following properties:
* `arr` has exactly `n` integers.
* `1 <= arr[i] <= m` where `(0 <= i < n)`.
* After applying the mentioned algorithm to `arr`, the value `search_cost` is equal to `k`.
Return _the number of ways_ to build the array `arr` under the mentioned conditions. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, m = 3, k = 1
**Output:** 6
**Explanation:** The possible arrays are \[1, 1\], \[2, 1\], \[2, 2\], \[3, 1\], \[3, 2\] \[3, 3\]
**Example 2:**
**Input:** n = 5, m = 2, k = 3
**Output:** 0
**Explanation:** There are no possible arrays that satisify the mentioned conditions.
**Example 3:**
**Input:** n = 9, m = 1, k = 1
**Output:** 1
**Explanation:** The only possible array is \[1, 1, 1, 1, 1, 1, 1, 1, 1\]
**Constraints:**
* `1 <= n <= 50`
* `1 <= m <= 100`
* `0 <= k <= n` | null |
Python || Documented and Simple Memoization Solution | build-array-where-you-can-find-the-maximum-exactly-k-comparisons | 0 | 1 | ```\nfrom functools import cache\n\nMAX = 10 ** 9 + 7\n\n\nclass Solution:\n def numOfArrays(self, N: int, M: int, K: int) -> int:\n @cache\n def ways(n: int, m: int, k: int) -> int:\n """\n :param n:\n :param m:\n :param k:\n :return: number of ways an array (say A) can be constructed with constraints\n 1) len(A) == n\n 2) max(A) == m\n 3) search_cost(A) = k (definition of search_cost is in problem)\n """\n if n * m * k == 0: # same as: (n == 0 or m == 0 or k == 0)\n return 0\n elif n == k == 1:\n # length is 1 and cost is 1 then m will be the only number in the\n # array. So total number of ways an array can be constructed is 1\n return 1\n else:\n return (\n # let A be the one of the constructed arrays\n\n # case-1: k-th search_cost is NOT incurred at (n - 1)th index. It \n # means that m is already present in sub array A[:n - 1].\n # So last value in A could be any of [1, 2,..., m].\n ways(n - 1, m, k) * m\n\n +\n\n # case-2: k-th search_cost is incurred at (n - 1)th index. If means \n # that m is NOT in sub-array A[:n - 1]. So sub-array A[:n - 1] \n # which is of length (n - 1) should consist of k - 1 search_costs \n # and the largest value in A[:n - 1] could be any of [1, 2,..., m - 1]\n sum(ways(n - 1, mx, k - 1) for mx in range(1, m))\n ) % MAX\n\n # As maximum of constructed array can be any of [1, 2,..., m] so summing all the ways\n return sum(ways(N, mx, K) for mx in range(1, M + 1)) % MAX\n``` | 1 | Given an integer array `arr` of **distinct** integers and an integer `k`.
A game will be played between the first two elements of the array (i.e. `arr[0]` and `arr[1]`). In each round of the game, we compare `arr[0]` with `arr[1]`, the larger integer wins and remains at position `0`, and the smaller integer moves to the end of the array. The game ends when an integer wins `k` consecutive rounds.
Return _the integer which will win the game_.
It is **guaranteed** that there will be a winner of the game.
**Example 1:**
**Input:** arr = \[2,1,3,5,4,6,7\], k = 2
**Output:** 5
**Explanation:** Let's see the rounds of the game:
Round | arr | winner | win\_count
1 | \[2,1,3,5,4,6,7\] | 2 | 1
2 | \[2,3,5,4,6,7,1\] | 3 | 1
3 | \[3,5,4,6,7,1,2\] | 5 | 1
4 | \[5,4,6,7,1,2,3\] | 5 | 2
So we can see that 4 rounds will be played and 5 is the winner because it wins 2 consecutive games.
**Example 2:**
**Input:** arr = \[3,2,1\], k = 10
**Output:** 3
**Explanation:** 3 will win the first 10 rounds consecutively.
**Constraints:**
* `2 <= arr.length <= 105`
* `1 <= arr[i] <= 106`
* `arr` contains **distinct** integers.
* `1 <= k <= 109` | Use dynamic programming approach. Build dp table where dp[a][b][c] is the number of ways you can start building the array starting from index a where the search_cost = c and the maximum used integer was b. Recursively, solve the small sub-problems first. Optimize your answer by stopping the search if you exceeded k changes. |
Just count, do sum and boomm | in O(n) time | python3 | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ncount \'0\' and \'1\'. Do sum conditionally.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst of all count how many one have the input sitring and store the result. again loop thorugh the string and check how many \'0\' and \'1\' have traversed. do the sum of remaining number of one and number of \'0\' we already traversed. if the sum is bigger than previous sum. update the sum. that\'s it. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n countOne = 0\n for ele in s:\n if ele == "1":\n countOne += 1\n\n\n zero = 0\n one = 0\n\n ans = 0\n for i, ele in enumerate(s):\n\n if i > 0:\n right1 = countOne - one\n print(zero, right1)\n if ans < zero + right1:\n ans = zero + right1\n\n if ele == "1":\n one += 1\n else:\n zero += 1\n return ans\n\n``` | 1 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
Just count, do sum and boomm | in O(n) time | python3 | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ncount \'0\' and \'1\'. Do sum conditionally.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst of all count how many one have the input sitring and store the result. again loop thorugh the string and check how many \'0\' and \'1\' have traversed. do the sum of remaining number of one and number of \'0\' we already traversed. if the sum is bigger than previous sum. update the sum. that\'s it. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n countOne = 0\n for ele in s:\n if ele == "1":\n countOne += 1\n\n\n zero = 0\n one = 0\n\n ans = 0\n for i, ele in enumerate(s):\n\n if i > 0:\n right1 = countOne - one\n print(zero, right1)\n if ans < zero + right1:\n ans = zero + right1\n\n if ele == "1":\n one += 1\n else:\n zero += 1\n return ans\n\n``` | 1 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
✅ PYTHON || Simple Beginner Solution | maximum-score-after-splitting-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n cnt = 0\n for i in range(1, len(s)):\n cnt = max(cnt, (s[:i].count(\'0\') + s[i:].count(\'1\')))\n return cnt\n\n``` | 1 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
✅ PYTHON || Simple Beginner Solution | maximum-score-after-splitting-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n cnt = 0\n for i in range(1, len(s)):\n cnt = max(cnt, (s[:i].count(\'0\') + s[i:].count(\'1\')))\n return cnt\n\n``` | 1 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
Python | Easy Solution✅ | maximum-score-after-splitting-a-string | 0 | 1 | ```\ndef maxScore(self, s: str) -> int:\n maxx = 0\n i=1\n while i <= len(s)-1:\n left = s[:i]\n right = s[i:]\n zero_count = left.count("0")\n one_count = right.count("1")\n maxx = max(maxx,(zero_count+one_count))\n i = i+1\n return maxx\n``` | 8 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
Python | Easy Solution✅ | maximum-score-after-splitting-a-string | 0 | 1 | ```\ndef maxScore(self, s: str) -> int:\n maxx = 0\n i=1\n while i <= len(s)-1:\n left = s[:i]\n right = s[i:]\n zero_count = left.count("0")\n one_count = right.count("1")\n maxx = max(maxx,(zero_count+one_count))\n i = i+1\n return maxx\n``` | 8 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
Linear time Python solution with explanation | maximum-score-after-splitting-a-string | 0 | 1 | ```\n# IDEA: on first pass count total number of 1s, on second pass keep track of how many 0s and 1s encountered so far\n# and calculate current score (subtract current 1s from total 1s and add current 0s), keep track of maximum\n# O(N) time, O(1) space\n#\nclass Solution:\n def maxScore(self, s: str) -> int:\n curr0, curr1, total1 = 0, 0, 0\n for c in s:\n if c == \'1\':\n total1 += 1\n \n maxScore = 0\n for c in s[:-1]:\n if c == \'0\':\n curr0 += 1\n else:\n curr1 += 1\n maxScore = max(maxScore, curr0 + total1 - curr1)\n \n return maxScore\n\t\t | 7 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
Linear time Python solution with explanation | maximum-score-after-splitting-a-string | 0 | 1 | ```\n# IDEA: on first pass count total number of 1s, on second pass keep track of how many 0s and 1s encountered so far\n# and calculate current score (subtract current 1s from total 1s and add current 0s), keep track of maximum\n# O(N) time, O(1) space\n#\nclass Solution:\n def maxScore(self, s: str) -> int:\n curr0, curr1, total1 = 0, 0, 0\n for c in s:\n if c == \'1\':\n total1 += 1\n \n maxScore = 0\n for c in s[:-1]:\n if c == \'0\':\n curr0 += 1\n else:\n curr1 += 1\n maxScore = max(maxScore, curr0 + total1 - curr1)\n \n return maxScore\n\t\t | 7 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
python one line solution | maximum-score-after-splitting-a-string | 0 | 1 | ```\nclass Solution:\n def maxScore(self, s: str) -> int:\n \n return max([s[:i].count(\'0\')+s[i:].count(\'1\') for i in range(1, len(s))])\n``` | 1 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
python one line solution | maximum-score-after-splitting-a-string | 0 | 1 | ```\nclass Solution:\n def maxScore(self, s: str) -> int:\n \n return max([s[:i].count(\'0\')+s[i:].count(\'1\') for i in range(1, len(s))])\n``` | 1 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
Python, two passes. Time: O(N) | maximum-score-after-splitting-a-string | 0 | 1 | ```\nclass Solution:\n def maxScore(self, s: str) -> int:\n score = 0 \n zeros = 0\n ones = s.count(\'1\') \n \n for i in range(len(s)-1):\n if s[i] == \'0\':\n zeros += 1\n else:\n ones -= 1\n score = max(score, ones + zeros)\n \n return score\n``` | 8 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
Python, two passes. Time: O(N) | maximum-score-after-splitting-a-string | 0 | 1 | ```\nclass Solution:\n def maxScore(self, s: str) -> int:\n score = 0 \n zeros = 0\n ones = s.count(\'1\') \n \n for i in range(len(s)-1):\n if s[i] == \'0\':\n zeros += 1\n else:\n ones -= 1\n score = max(score, ones + zeros)\n \n return score\n``` | 8 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
Beats 91.69% of users with Python3 | maximum-score-after-splitting-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n # straight forward approach\n # 41ms\n # Beats 65.17% of users with Python3\n """\n ret, n = 0, len(s)\n for i in range(1, n):\n a = s.count("0", 0, i)\n b = s.count("1", i, n)\n ret = max(ret, a+b)\n return ret\n """\n\n # can we refactoring to make On ??\n # 35ms\n # Beats 91.69% of users with Python3\n ret = zeros = ones = 0\n for num in s:\n ones += num == "1"\n \n for num in s[:-1]:\n zeros += num == "0"\n ones -= num == "1"\n \n ret = max(ret, ones + zeros)\n \n \n return ret\n``` | 0 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
Beats 91.69% of users with Python3 | maximum-score-after-splitting-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n # straight forward approach\n # 41ms\n # Beats 65.17% of users with Python3\n """\n ret, n = 0, len(s)\n for i in range(1, n):\n a = s.count("0", 0, i)\n b = s.count("1", i, n)\n ret = max(ret, a+b)\n return ret\n """\n\n # can we refactoring to make On ??\n # 35ms\n # Beats 91.69% of users with Python3\n ret = zeros = ones = 0\n for num in s:\n ones += num == "1"\n \n for num in s[:-1]:\n zeros += num == "0"\n ones -= num == "1"\n \n ret = max(ret, ones + zeros)\n \n \n return ret\n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
[Python | beats 95.96% in time | no need to count each time] | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnce you count the number of zeros in the left substring, and the number of ones in the right substring, you don\'t have to count them every time you make new substrings. All you need to do is check whether the new character moved from right to left is one or zero. If it is one, then you subtract from the previous score, since the score from the left substring does not change while the score from the right substring loses one. On the other hand, if it is one, you add one to the previous score, since the score from the left substring gets one while the score from the right substring does not change.\n\nFor instance, let `s = \'00111\'`. Initially, you split them into `left = \'0\'` and `right = \'0111\'`. Then your score from the left is 1 and score from the right is 3, so total 4. In the next split, you will move the second zero from right to the left, so that `left = \'00\'` and `right = \'111\'`. All you need to check is the character moved from right to left, `0`. Since it is zero, you add one to the previous score, thus 4 + 1 = 5. In fact, in the new substrings, the score from the left is 2, and the score from the right is 3, so that total score is 5.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Split `s` into `s[:1]` and `s[1:]\n2) calculate the initial `score`, and assign it to `maxScore`\n3) iterate through for loops, check whether each character is zero or one. If it is zero, add one to the `score`. If it is one, subtract one from the `score`.\n4) If the current score is bigger than `maxScore`, update the `maxScore`\n5) return `maxScore`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n left, right = s[:1], s[1:]\n score = left.count(\'0\')+right.count(\'1\')\n maxScore = score\n for i in range(1, len(s)-1):\n if s[i] == \'0\':\n score += 1\n else:\n score -= 1\n maxScore = max(maxScore, score)\n return maxScore\n \n``` | 0 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
[Python | beats 95.96% in time | no need to count each time] | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnce you count the number of zeros in the left substring, and the number of ones in the right substring, you don\'t have to count them every time you make new substrings. All you need to do is check whether the new character moved from right to left is one or zero. If it is one, then you subtract from the previous score, since the score from the left substring does not change while the score from the right substring loses one. On the other hand, if it is one, you add one to the previous score, since the score from the left substring gets one while the score from the right substring does not change.\n\nFor instance, let `s = \'00111\'`. Initially, you split them into `left = \'0\'` and `right = \'0111\'`. Then your score from the left is 1 and score from the right is 3, so total 4. In the next split, you will move the second zero from right to the left, so that `left = \'00\'` and `right = \'111\'`. All you need to check is the character moved from right to left, `0`. Since it is zero, you add one to the previous score, thus 4 + 1 = 5. In fact, in the new substrings, the score from the left is 2, and the score from the right is 3, so that total score is 5.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Split `s` into `s[:1]` and `s[1:]\n2) calculate the initial `score`, and assign it to `maxScore`\n3) iterate through for loops, check whether each character is zero or one. If it is zero, add one to the `score`. If it is one, subtract one from the `score`.\n4) If the current score is bigger than `maxScore`, update the `maxScore`\n5) return `maxScore`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n left, right = s[:1], s[1:]\n score = left.count(\'0\')+right.count(\'1\')\n maxScore = score\n for i in range(1, len(s)-1):\n if s[i] == \'0\':\n score += 1\n else:\n score -= 1\n maxScore = max(maxScore, score)\n return maxScore\n \n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
🐍🐍🐍 One line solution 🐍🐍🐍 | maximum-score-after-splitting-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n return max([s[:i].count(\'0\')+s[i:].count(\'1\') for i in range(1,len(s))])\n \n``` | 0 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
🐍🐍🐍 One line solution 🐍🐍🐍 | maximum-score-after-splitting-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n return max([s[:i].count(\'0\')+s[i:].count(\'1\') for i in range(1,len(s))])\n \n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
python simple solution | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n score = 0\n for i in range(1,len(s)):\n val = s[:i].count("0") + s[i:].count("1")\n if val > score:\n score = val\n return score\n \n``` | 0 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
python simple solution | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n score = 0\n for i in range(1,len(s)):\n val = s[:i].count("0") + s[i:].count("1")\n if val > score:\n score = val\n return score\n \n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
easy solution | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n a = []\n for i in range(len(s)-1):\n left = s[0:i+1]\n right = s[i+1:len(s)]\n sum_ = left.count(\'0\') + right.count(\'1\')\n a.append(sum_)\n return max(a)\n``` | 0 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
easy solution | maximum-score-after-splitting-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, s: str) -> int:\n a = []\n for i in range(len(s)-1):\n left = s[0:i+1]\n right = s[i+1:len(s)]\n sum_ = left.count(\'0\') + right.count(\'1\')\n a.append(sum_)\n return max(a)\n``` | 0 | You are given two **sorted** arrays of distinct integers `nums1` and `nums2.`
A **valid path** is defined as follows:
* Choose array `nums1` or `nums2` to traverse (from index-0).
* Traverse the current array from left to right.
* If you are reading any value that is present in `nums1` and `nums2` you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).
The **score** is defined as the sum of uniques values in a valid path.
Return _the maximum score you can obtain of all possible **valid paths**_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** nums1 = \[2,4,5,8,10\], nums2 = \[4,6,8,9\]
**Output:** 30
**Explanation:** Valid paths:
\[2,4,5,8,10\], \[2,4,5,8,9\], \[2,4,6,8,9\], \[2,4,6,8,10\], (starting from nums1)
\[4,6,8,9\], \[4,5,8,10\], \[4,5,8,9\], \[4,6,8,10\] (starting from nums2)
The maximum is obtained with the path in green **\[2,4,6,8,10\]**.
**Example 2:**
**Input:** nums1 = \[1,3,5,7,9\], nums2 = \[3,5,100\]
**Output:** 109
**Explanation:** Maximum sum is obtained with the path **\[1,3,5,100\]**.
**Example 3:**
**Input:** nums1 = \[1,2,3,4,5\], nums2 = \[6,7,8,9,10\]
**Output:** 40
**Explanation:** There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path \[6,7,8,9,10\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 107`
* `nums1` and `nums2` are strictly increasing. | Precompute a prefix sum of ones ('1'). Iterate from left to right counting the number of zeros ('0'), then use the precomputed prefix sum for counting ones ('1'). Update the answer. |
[Python3] O(n) - Clean and Simple Sliding Window Solution | maximum-points-you-can-obtain-from-cards | 0 | 1 | **Implementation**\n\n1. Calculate the sum of all cards and store it in total.\n\n2. Calculate the sum of the initial subarray of size `n - k` and store it in `subarray_sum`.\n\n3. Initialize `min_sum` to `subarray_sum`. This variable will track the overall minimum subarray sum we\'ve seen so far. After iterating over the array, `min_sum` will hold the smallest possible subarray score.\n\n4. Iterate through the array starting from index `remaining_length` and update `subarray_sum` by adding the current element and subtracting the element that\'s no longer included in this subarray.\n\n5. Update `min_sum` so that it\'s always keeping track of the global minimum so far.\n\n6. The answer at the end is `total - minSum`. This is equal to the maximum sum of `k` elements from the beginning and end of the array. \n\n**Code**\n```\nclass Solution:\n def maxScore(self, cardPoints: List[int], k: int) -> int:\n n = len(cardPoints)\n total = sum(cardPoints)\n \n remaining_length = n - k\n subarray_sum = sum(cardPoints[:remaining_length])\n \n min_sum = subarray_sum\n for i in range(remaining_length, n):\n # Update the sliding window sum to the subarray ending at index i\n subarray_sum += cardPoints[i]\n subarray_sum -= cardPoints[i - remaining_length]\n # Update min_sum to track the overall minimum sum so far\n min_sum = min(min_sum, subarray_sum)\n return total - min_sum\n```\n\nPlease upvote if you liked this solution!\n\nFor more in-depth details with an explanation of the **intution** and **time/space complexity analysis**, join our discord at **https://discord.gg/m9MRe9ZR**. | 42 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Python Solution | Sliding Window Approach | maximum-points-you-can-obtain-from-cards | 0 | 1 | ```\nclass Solution:\n def maxScore(self, cardPoints: List[int], k: int) -> int:\n if len(cardPoints) <= k:\n return sum(cardPoints)\n\n points = cardPoints[len(cardPoints) - k:] + cardPoints[:k]\n temp_sum = sum(points[:k])\n largest = temp_sum\n for i in range(len(points) - k):\n temp_sum -= (points[i] - points[i + k])\n largest = max(largest, temp_sum)\n return largest\n``` | 1 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Recursive + DP Solution | maximum-points-you-can-obtain-from-cards | 0 | 1 | **Recursive Solution :-**\n\n```\nclass Solution:\n def maxScore(self, cardPoints: List[int], k: int) -> int:\n n = len(cardPoints)\n if k == 1:\n return max(cardPoints[0], cardPoints[-1])\n \n maximumScore = max(cardPoints[0] + self.maxScore(cardPoints[1:], k - 1), cardPoints[n - 1] + self.maxScore(cardPoints[:n - 1], k - 1))\n return maximumScore\n```\n\n**DP Solution :-**\n```\nclass Solution:\n def maxScore(self, cardPoints: List[int], k: int) -> int:\n dpArray = [0 for i in range(k + 1)]\n \n dpArray[0] = sum(cardPoints[:k])\n \n for i in range(1, k + 1):\n dpArray[i] = dpArray[i - 1] - cardPoints[k - i] + cardPoints[-i]\n return max(dpArray)\n``` | 6 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
📌 Convert into maximum sum subarray of length k using sliding window | maximum-points-you-can-obtain-from-cards | 0 | 1 | ```\nclass Solution:\n def maxScore(self, cardPoints: List[int], k: int) -> int:\n length = len(cardPoints)\n s = sum(cardPoints[-k:])\n maximum = s\n j = length-k\n i=0\n while i!=j and j<length:\n s+=cardPoints[i]\n s-=cardPoints[j]\n i+=1\n j+=1\n maximum = max(s,maximum)\n return maximum\n``` | 6 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Python/JS/Java/Go/C++ O( k ) sliding window. [w/ Visualization] | maximum-points-you-can-obtain-from-cards | 1 | 1 | O( k ) sliding window solution\n\n---\n\n**Diagram & Visualization**:\n\n\n\n---\n\n**Implementation**:\n\nPython\n\n```\nclass Solution:\n def maxScore(self, cardPoints: List[int], k: int) -> int:\n \n size = len(cardPoints)\n left, right = k-1, size-1\n \n # Initial pick: take all k card from left hand side\n current_pick = sum(cardPoints[:k])\n max_point = current_pick\n \n # adjustment\n for _ in range(k):\n \n # left hand side discards one, and right hand side picks one more \n current_pick += ( cardPoints[right] - cardPoints[left] )\n \n # update max point\n max_point = max(max_point, current_pick)\n \n # update card index for both sides in adjustment\n left, right = left-1, right-1\n \n return max_point\n```\n\n---\n\nJava:\n\n```\nclass Solution {\n public int maxScore(int[] cardPoints, int k) {\n \n int size = cardPoints.length;\n int left = k-1, right=size-1;\n \n // Initial pick: pick all k crad from left hand side\n int currentPick = 0;\n \n for( int i = 0; i < k ; i++){\n currentPick += cardPoints[i];\n }\n \n int maxPoint = currentPick;\n \n // adjustment\n for( int i=0 ; i<k ; i++){\n \n //left hand side discards one, and right hand side picks on more\n currentPick += ( cardPoints[right] - cardPoints[left] );\n \n //update max point\n maxPoint = Math.max( maxPoint, currentPick);\n \n // update card index for both sides in adjustment\n left -= 1;\n right -= 1;\n }\n \n return maxPoint;\n }\n}\n```\n\n---\n\nJavascript:\n\n```\nvar maxScore = function(cardPoints, k) {\n let size = cardPoints.length;\n let [left, right] = [k-1, size-1];\n \n // Initial pick: take all k cards from left hand side\n let currentPick = cardPoints.slice(0,k).reduce( (x, y) => x+y, 0);\n let maxPoint = currentPick;\n \n // adjustment\n for(let i = 0 ; i < k ; i++ ){\n \n // left hand side discards one, and right hand side picks one more\n currentPick += ( cardPoints[right] - cardPoints[left] );\n \n // update max point\n maxPoint = Math.max( maxPoint, currentPick );\n \n // update card index for both sides in adjustment\n [left, right] = [left-1, right-1];\n \n }\n \n return maxPoint;\n};\n```\n\n---\n\nGo:\n\n```\nfunc max( x, y int) int {\n \n if x > y{\n return x\n \n }else{\n return y\n }\n}\n\nfunc maxScore(cardPoints []int, k int) int {\n\n size := len(cardPoints)\n left, right := k-1, size-1\n \n // Initial pick: take all k cards from left hand side\n currentPick := 0\n for _, card := range cardPoints[0:k]{\n currentPick += card\n }\n \n maxPoint := currentPick\n \n // Adjustment\n for i:=0 ; i < k ; i++{\n \n // left hand side discards one, and right hand side picks one more\n currentPick += ( cardPoints[right] - cardPoints[left] )\n \n // update max point\n maxPoint = max( maxPoint, currentPick)\n \n // update card index from both side in adjustment\n left, right = left-1, right-1\n \n }\n \n return maxPoint\n}\n```\n\n---\n\nC++\n\n```\nclass Solution {\npublic:\n int maxScore(vector<int>& cardPoints, int k) {\n \n size_t size = cardPoints.size();\n int left = k-1, right=size-1;\n \n // Initial pick: pick all k crad from left hand side\n int currentPick = accumulate( cardPoints.begin(), cardPoints.begin()+k, 0);\n int maxPoint = currentPick;\n \n // adjustment\n for( int i=0 ; i<k ; i++){\n \n //left hand side discards one, and right hand side picks on more\n currentPick += ( cardPoints[right] - cardPoints[left] );\n \n //update max point\n maxPoint = max( maxPoint, currentPick);\n \n // update card index for both sides in adjustment\n left -= 1;\n right -= 1;\n }\n \n return maxPoint;\n \n }\n};\n``` | 53 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.