title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Go/Python/JavaScript/Java O(n) time | O(n) space | destination-city | 1 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc destCity(paths [][]string) string {\n routes := make(map[string]int)\n\n for _,pair := range(paths){\n p := pair[0]\n q := pair[1]\n routes[p]+=1\n routes[q]+=0\n }\n\n for key,value := range(routes){\n if value == 0{\n return key\n }\n }\n \n return ""\n}\n```\n```python []\nclass Solution:\n def destCity(self, paths: List[List[str]]) -> str:\n routes = defaultdict(int)\n\n for p,q in paths:\n routes[p]+=1\n routes[q]+=0\n\n for key,value in routes.items():\n if value == 0:\n return key\n \n return ""\n```\n```javascript []\n/**\n * @param {string[][]} paths\n * @return {string}\n */\nvar destCity = function(paths) {\n let routes = new Map()\n\n for (let [p,q] of paths){\n if (!routes.has(p)){\n routes.set(p,0)\n }\n if (!routes.has(q)){\n routes.set(q,0)\n }\n routes.set(p,routes.get(p)+1)\n }\n\n for (let [key,value] of routes){\n if (value == 0){\n return key\n }\n }\n \n return ""\n};\n```\n```java []\nclass Solution {\n public String destCity(List<List<String>> paths) {\n HashMap<String,Integer> routes = new HashMap<>();\n\n for (List pair : paths){\n String p = pair.get(0).toString();\n String q = pair.get(1).toString();\n if (!routes.containsKey(p)){\n routes.put(p,0);\n }\n if (!routes.containsKey(q)){\n routes.put(q,0);\n }\n routes.put(p,routes.get(p)+1);\n }\n\n for (String key : routes.keySet()){\n int value = routes.get(key);\n if (value == 0){\n return key;\n }\n }\n \n return "";\n }\n}\n``` | 1 | You are given the array `paths`, where `paths[i] = [cityAi, cityBi]` means there exists a direct path going from `cityAi` to `cityBi`. _Return the destination city, that is, the city without any path outgoing to another city._
It is guaranteed that the graph of paths forms a line without any loop, therefore, there will be exactly one destination city.
**Example 1:**
**Input:** paths = \[\[ "London ", "New York "\],\[ "New York ", "Lima "\],\[ "Lima ", "Sao Paulo "\]\]
**Output:** "Sao Paulo "
**Explanation:** Starting at "London " city you will reach "Sao Paulo " city which is the destination city. Your trip consist of: "London " -> "New York " -> "Lima " -> "Sao Paulo ".
**Example 2:**
**Input:** paths = \[\[ "B ", "C "\],\[ "D ", "B "\],\[ "C ", "A "\]\]
**Output:** "A "
**Explanation:** All possible trips are:
"D " -> "B " -> "C " -> "A ".
"B " -> "C " -> "A ".
"C " -> "A ".
"A ".
Clearly the destination city is "A ".
**Example 3:**
**Input:** paths = \[\[ "A ", "Z "\]\]
**Output:** "Z "
**Constraints:**
* `1 <= paths.length <= 100`
* `paths[i].length == 2`
* `1 <= cityAi.length, cityBi.length <= 10`
* `cityAi != cityBi`
* All strings consist of lowercase and uppercase English letters and the space character. | Do BFS to find the kth level friends. Then collect movies saw by kth level friends and sort them accordingly. |
Go/Python/JavaScript/Java O(n) time | O(n) space | destination-city | 1 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc destCity(paths [][]string) string {\n routes := make(map[string]int)\n\n for _,pair := range(paths){\n p := pair[0]\n q := pair[1]\n routes[p]+=1\n routes[q]+=0\n }\n\n for key,value := range(routes){\n if value == 0{\n return key\n }\n }\n \n return ""\n}\n```\n```python []\nclass Solution:\n def destCity(self, paths: List[List[str]]) -> str:\n routes = defaultdict(int)\n\n for p,q in paths:\n routes[p]+=1\n routes[q]+=0\n\n for key,value in routes.items():\n if value == 0:\n return key\n \n return ""\n```\n```javascript []\n/**\n * @param {string[][]} paths\n * @return {string}\n */\nvar destCity = function(paths) {\n let routes = new Map()\n\n for (let [p,q] of paths){\n if (!routes.has(p)){\n routes.set(p,0)\n }\n if (!routes.has(q)){\n routes.set(q,0)\n }\n routes.set(p,routes.get(p)+1)\n }\n\n for (let [key,value] of routes){\n if (value == 0){\n return key\n }\n }\n \n return ""\n};\n```\n```java []\nclass Solution {\n public String destCity(List<List<String>> paths) {\n HashMap<String,Integer> routes = new HashMap<>();\n\n for (List pair : paths){\n String p = pair.get(0).toString();\n String q = pair.get(1).toString();\n if (!routes.containsKey(p)){\n routes.put(p,0);\n }\n if (!routes.containsKey(q)){\n routes.put(q,0);\n }\n routes.put(p,routes.get(p)+1);\n }\n\n for (String key : routes.keySet()){\n int value = routes.get(key);\n if (value == 0){\n return key;\n }\n }\n \n return "";\n }\n}\n``` | 1 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
🚀Unbeatable Python Mastery: Soaring above 97.12% in destination city Challenge! 🏆 #PythonMagic | destination-city | 0 | 1 | # Intuition\n\uD83E\uDDE0 **Intuition Behind the Dominant Python Solution**\n\n**Step 1:** \uD83D\uDCCD Begin by segregating the source and destination cities into separate lists. This ensures clarity in tracking city connections.\n\n**Step 2:** \uD83D\uDD17 Leverage the power of Python\'s `symmetric_difference()` method on sets. This nifty technique reveals the non-connecting cities with elegance.\n\n**Step 3:** \uD83C\uDFAF Navigate through the result array containing both destination and source cities. Employ a conditional check: If the current element is from the destination array, return it; otherwise, gracefully move on to the next city in the result array.\n\nThis strategic approach not only disentangles city connections efficiently but also showcases the finesse of Python\'s set operations. \uD83D\uDE80 Elevate your LeetCode game with this intuitive and high-achieving solution! \uD83C\uDFC5 #PythonWizardry #LeetCodeMastery\n\n# Approach\nCertainly! Here\'s an explanation of the approach for the provided code:\n\n1. **City Separation:**\n - Two lists, `st` and `dest`, are created to store the starting cities and destination cities, respectively.\n\n2. **Iterative Population:**\n - Loop through each entry in the `paths` list.\n - For each entry, add the first element (`paths[i][0]`) to the `st` list (starting city) and the second element (`paths[i][1]`) to the `dest` list (destination city).\n\n3. **Symmetric Difference:**\n - Utilize the `symmetric_difference()` method on sets formed from `dest` and `st`. This operation identifies the cities that are present in either `dest` or `st`, but not in both.\n\n4. **Conditional Return:**\n - Check if the first element (`res[0]`) of the result array is in the `dest` list.\n - If true, return the first element as the destination city.\n - If false, return the second element (`res[1]`) as the destination city.\n\n**Explanation:**\nThe strategy is to exploit set operations to efficiently find the non-connecting city. The symmetric difference reveals the city that is either the starting or destination city but not both. The conditional check ensures that the correct destination city is returned based on its presence in the `dest` list.\n\nThis approach not only simplifies the city separation process but also showcases the elegance of set operations in Python. \uD83C\uDF10\u2728 Elevate your LeetCode submissions with this concise and effective solution! #PythonMastery #LeetCodePro\n\n# Complexity\n- Time complexity:\nThe overall time complexity of the provided code is **O(n)**, where n is the number of entries in the `paths` list.\n\n- Space complexity:\n The space complexity of the provided code can be expressed as **O(n)**.`code`\n\n\n# Code\n```\nclass Solution:\n def destCity(self, paths: List[List[str]]) -> str:\n dest=[]\n st=[]\n for i in range(len(paths)):\n st.append(paths[i][0])\n dest.append(paths[i][1])\n res = list(set(dest).symmetric_difference(set(st)))\n if res[0] in dest:\n return res[0]\n else:\n return res[1]\n \n \n``` | 1 | You are given the array `paths`, where `paths[i] = [cityAi, cityBi]` means there exists a direct path going from `cityAi` to `cityBi`. _Return the destination city, that is, the city without any path outgoing to another city._
It is guaranteed that the graph of paths forms a line without any loop, therefore, there will be exactly one destination city.
**Example 1:**
**Input:** paths = \[\[ "London ", "New York "\],\[ "New York ", "Lima "\],\[ "Lima ", "Sao Paulo "\]\]
**Output:** "Sao Paulo "
**Explanation:** Starting at "London " city you will reach "Sao Paulo " city which is the destination city. Your trip consist of: "London " -> "New York " -> "Lima " -> "Sao Paulo ".
**Example 2:**
**Input:** paths = \[\[ "B ", "C "\],\[ "D ", "B "\],\[ "C ", "A "\]\]
**Output:** "A "
**Explanation:** All possible trips are:
"D " -> "B " -> "C " -> "A ".
"B " -> "C " -> "A ".
"C " -> "A ".
"A ".
Clearly the destination city is "A ".
**Example 3:**
**Input:** paths = \[\[ "A ", "Z "\]\]
**Output:** "Z "
**Constraints:**
* `1 <= paths.length <= 100`
* `paths[i].length == 2`
* `1 <= cityAi.length, cityBi.length <= 10`
* `cityAi != cityBi`
* All strings consist of lowercase and uppercase English letters and the space character. | Do BFS to find the kth level friends. Then collect movies saw by kth level friends and sort them accordingly. |
🚀Unbeatable Python Mastery: Soaring above 97.12% in destination city Challenge! 🏆 #PythonMagic | destination-city | 0 | 1 | # Intuition\n\uD83E\uDDE0 **Intuition Behind the Dominant Python Solution**\n\n**Step 1:** \uD83D\uDCCD Begin by segregating the source and destination cities into separate lists. This ensures clarity in tracking city connections.\n\n**Step 2:** \uD83D\uDD17 Leverage the power of Python\'s `symmetric_difference()` method on sets. This nifty technique reveals the non-connecting cities with elegance.\n\n**Step 3:** \uD83C\uDFAF Navigate through the result array containing both destination and source cities. Employ a conditional check: If the current element is from the destination array, return it; otherwise, gracefully move on to the next city in the result array.\n\nThis strategic approach not only disentangles city connections efficiently but also showcases the finesse of Python\'s set operations. \uD83D\uDE80 Elevate your LeetCode game with this intuitive and high-achieving solution! \uD83C\uDFC5 #PythonWizardry #LeetCodeMastery\n\n# Approach\nCertainly! Here\'s an explanation of the approach for the provided code:\n\n1. **City Separation:**\n - Two lists, `st` and `dest`, are created to store the starting cities and destination cities, respectively.\n\n2. **Iterative Population:**\n - Loop through each entry in the `paths` list.\n - For each entry, add the first element (`paths[i][0]`) to the `st` list (starting city) and the second element (`paths[i][1]`) to the `dest` list (destination city).\n\n3. **Symmetric Difference:**\n - Utilize the `symmetric_difference()` method on sets formed from `dest` and `st`. This operation identifies the cities that are present in either `dest` or `st`, but not in both.\n\n4. **Conditional Return:**\n - Check if the first element (`res[0]`) of the result array is in the `dest` list.\n - If true, return the first element as the destination city.\n - If false, return the second element (`res[1]`) as the destination city.\n\n**Explanation:**\nThe strategy is to exploit set operations to efficiently find the non-connecting city. The symmetric difference reveals the city that is either the starting or destination city but not both. The conditional check ensures that the correct destination city is returned based on its presence in the `dest` list.\n\nThis approach not only simplifies the city separation process but also showcases the elegance of set operations in Python. \uD83C\uDF10\u2728 Elevate your LeetCode submissions with this concise and effective solution! #PythonMastery #LeetCodePro\n\n# Complexity\n- Time complexity:\nThe overall time complexity of the provided code is **O(n)**, where n is the number of entries in the `paths` list.\n\n- Space complexity:\n The space complexity of the provided code can be expressed as **O(n)**.`code`\n\n\n# Code\n```\nclass Solution:\n def destCity(self, paths: List[List[str]]) -> str:\n dest=[]\n st=[]\n for i in range(len(paths)):\n st.append(paths[i][0])\n dest.append(paths[i][1])\n res = list(set(dest).symmetric_difference(set(st)))\n if res[0] in dest:\n return res[0]\n else:\n return res[1]\n \n \n``` | 1 | Given a wooden stick of length `n` units. The stick is labelled from `0` to `n`. For example, a stick of length **6** is labelled as follows:
Given an integer array `cuts` where `cuts[i]` denotes a position you should perform a cut at.
You should perform the cuts in order, you can change the order of the cuts as you wish.
The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.
Return _the minimum total cost_ of the cuts.
**Example 1:**
**Input:** n = 7, cuts = \[1,3,4,5\]
**Output:** 16
**Explanation:** Using cuts order = \[1, 3, 4, 5\] as in the input leads to the following scenario:
The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be \[3, 5, 1, 4\] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).
**Example 2:**
**Input:** n = 9, cuts = \[5,6,1,4,2\]
**Output:** 22
**Explanation:** If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order \[4, 6, 5, 2, 1\] has total cost = 22 which is the minimum possible.
**Constraints:**
* `2 <= n <= 106`
* `1 <= cuts.length <= min(n - 1, 100)`
* `1 <= cuts[i] <= n - 1`
* All the integers in `cuts` array are **distinct**. | Start in any city and use the path to move to the next city. Eventually, you will reach a city with no path outgoing, this is the destination city. |
Simple Python solution | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n a = []\n for i in range(len(nums)):\n if nums[i] == 1:\n a.append(i+1)\n return all((a[i+1]-a[i]) >= k+1 for i in range(len(a)-1))\n``` | 1 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
Python easy solution , beats 86% efficiency ✅✅🚀🚀 | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n count=k\n for i in nums:\n if i==1:\n if count<k:\n return False\n count=0\n else:\n count+=1\n return True \n``` | 1 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
[Python] i guess it's cheating but it works tho | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n n = k #\'<- the cheating line\n for i in nums:\n if i == 0:\n n += 1\n else:\n if n < k:\n return False\n n = 0\n return True\n```\n\n | 2 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
Only judge when 1 appears | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnly judge when 1 appear\n# Approach\n<!-- Describe your approach to solving the problem. -->\ni = first 1 index &\nnext 1 index must >= i + 1\nLoop for count(1) - 1 (last 1 have no next 1 to judge)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nonly go for count(1) times not all nums\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nNo\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n if 1 not in nums:\n return True\n else:\n oneCount = nums.count(1)\n i = nums.index(1)\n for i2 in range(oneCount-1):\n if nums.index(1,i+1) - nums.index(1,i)-1 < k :\n return False\n i = nums.index(1,i+1)\n return True\n``` | 0 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
Using string with separator solution (Explaned) | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Approach\nSeparate the string by k*"0" then we get an array of strings, if we encounter a string where the number of 1\'s is greater than 1, then there are not enough zeros between 1\'s and the condition is not met, then return false, otherwise if the strings in the array do not contain more than one 1 then there are enough zeros to fill the space between all 1\'s.\n\n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n if k == 0:\n return True\n nums = (\'\'.join(map(str,nums))).split(k*\'0\')\n for i in nums:\n if i.count(\'1\') > 1:\n return False\n return True\n```\n\n# PS\n\nObviously this solution is not intended to be fast, but it is very interesting :) | 0 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
My Solution :) BEATS 92.9% RUNTIME | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n if 1 not in nums:\n return True\n count = 0\n for i in range(nums.index(1)+1, len(nums)):\n if nums[i] == 1 and count < k:\n return False\n elif nums[i] == 1 and count >= k:\n count = 0\n else:\n count += 1\n return True\n``` | 0 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
check individual differences | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | Don\'t need to check differences of non-adjacent 1s. If two 1s i and jare correctly separated, then 1 k where index of k is j + n will definitely be greater than k. Therefore we just need to check the indices of inner 1s.\n\n\nOther hand, if two 1s aren\'t correctly separated, we can sniff that out first without having to check whether 3 1s spread across a non-valid distance is valid.\n\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n \n\n lastseen = -1\n\n for i,n in enumerate(nums):\n if n == 1:\n if lastseen == -1:\n lastseen = i\n else:\n if i - lastseen - 1 < k:\n return False\n lastseen = i \n\n return True\n``` | 0 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
Python | BruteForce Solution | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n ranging = [x for x in range(1, len(nums) + 1)]\n dictionary = dict(zip(ranging, nums))\n finding_1 = [key for key, value in dictionary.items() if value == 1]\n sliding = list()\n for i in range(len(finding_1)):\n if len(finding_1[i:i + 2]) == 2:\n difference = finding_1[i:i + 2][-1] - finding_1[i:i + 2][0]\n sliding.append(difference)\n\n answer = [x for x in sliding if x>k]\n if len(answer)== len(sliding):\n return True\n else:\n return False\n \n``` | 0 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
Solution | check-if-all-1s-are-at-least-length-k-places-away | 0 | 1 | # Approach\nIterate through the array and check each distance\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def kLengthApart(self, nums: List[int], k: int) -> bool:\n j = 0\n for x in nums:\n if j > 0 and x == 1:\n return False\n elif x == 1:\n j = k\n else:\n j -= 1\n return True\n \n``` | 0 | Given an binary array `nums` and an integer `k`, return `true` _if all_ `1`_'s are at least_ `k` _places away from each other, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[1,0,0,0,1,0,0,1\], k = 2
**Output:** true
**Explanation:** Each of the 1s are at least 2 places away from each other.
**Example 2:**
**Input:** nums = \[1,0,0,1,0,1\], k = 2
**Output:** false
**Explanation:** The second 1 and third 1 are only one apart from each other.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= k <= nums.length`
* `nums[i]` is `0` or `1` | Is dynamic programming suitable for this problem ? If we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome. |
C++ Solution with Easiest Explanation using Map (beats 83% runtime && 50% Memory) | longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1-> We can use window sliding and keep all the values in map that can tell us min and max value in that window.\n2-> If the range (i.e., max-min) is greater than limit then we need to delete element from the left of window that we can do using map in O(1).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1 -> keep inserting the values in map and keep increasing the size of window, until we found max-min>limit and Keep updating the size of window as answer.\n2-> If max-min>limit, then we can start deleting the values from map. This can be done by getting the left indexes of window and acces the value at that index and delete it from map.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nsince we are using map here, so complexity for map is O(Nlog(N));\nand we are traversing the array from 0-N then it\'ll take O(N);\n\nSo overall, **Time complexity: O(Nlog(N))**.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nsince we are using one extra map here, so **space complexity is O(N)**.\n\n# Code\n```\nclass Solution {\npublic:\n int longestSubarray(vector<int>& nums, int limit) {\n int ans=1,l=0,h=1,count=1;\n map<int,int> mp;\n mp[nums[l]]++;\n \n while(h<nums.size()){\n mp[nums[h]]++;\n count++; //counting the number of elements in map\n \n if(prev(mp.end())->first - mp.begin()->first <= limit){ // checking the diff \n ans=max(ans,count); // giving the size of subarray that may make our answer\n }else{\n // If diff is more than limit then we\'ll start deleting the indexes from left side until we get the max and minimum value such that diff is in range\n while(prev(mp.end())->first - mp.begin()->first > limit && l<h){\n if(mp[nums[l]]>1)mp[nums[l]]--;\n else mp.erase(nums[l]);\n count--;\n l++;\n }\n }\n h++;\n }\n return ans;\n }\n};\n``` | 2 | Given an array of integers `nums` and an integer `limit`, return the size of the longest **non-empty** subarray such that the absolute difference between any two elements of this subarray is less than or equal to `limit`_._
**Example 1:**
**Input:** nums = \[8,2,4,7\], limit = 4
**Output:** 2
**Explanation:** All subarrays are:
\[8\] with maximum absolute diff |8-8| = 0 <= 4.
\[8,2\] with maximum absolute diff |8-2| = 6 > 4.
\[8,2,4\] with maximum absolute diff |8-2| = 6 > 4.
\[8,2,4,7\] with maximum absolute diff |8-2| = 6 > 4.
\[2\] with maximum absolute diff |2-2| = 0 <= 4.
\[2,4\] with maximum absolute diff |2-4| = 2 <= 4.
\[2,4,7\] with maximum absolute diff |2-7| = 5 > 4.
\[4\] with maximum absolute diff |4-4| = 0 <= 4.
\[4,7\] with maximum absolute diff |4-7| = 3 <= 4.
\[7\] with maximum absolute diff |7-7| = 0 <= 4.
Therefore, the size of the longest subarray is 2.
**Example 2:**
**Input:** nums = \[10,1,2,4,7,2\], limit = 5
**Output:** 4
**Explanation:** The subarray \[2,4,7,2\] is the longest since the maximum absolute diff is |2-7| = 5 <= 5.
**Example 3:**
**Input:** nums = \[4,2,2,2,4,4,2,2\], limit = 0
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `0 <= limit <= 109` | null |
Brute Force - Two Heaps - Treemap - Monotonic Queue, should be well-explained | longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit | 0 | 1 | # Approach 1: Brute Force\nIn this approach, what I do is just create a max heap and a min heap for every number in the list and use nested for loop to find the valid "window "for every number and return the max one. \n\n# Complexity\n- Time complexity:\n$n^2log(n)$ because when pushing element to each heap, I need $log(n)$ time. \n\n- Space complexity:\n$O(n)$ to store numbers in two heaps. \n\n# Code\n```\nimport heapq\nclass Solution:\n def longestSubarray(self, nums: List[int], limit: int) -> int:\n # most instinct method\n max_length = 1\n for i in range(len(nums)):\n max_hq = [-nums[i]] # heapq in which the max is at the beginning\n min_hq = [nums[i]] # heapq in which the min is at the beginning\n \n for j in range(i + 1, len(nums)):\n # find max and min for every window and compare until the window is no longer valid\n if abs(-max_hq[0] - nums[j]) <= limit and abs(min_hq[0] - nums[j]) <= limit:\n heapq.heappush(max_hq, -nums[j])\n heapq.heappush(min_hq, nums[j])\n else:\n break # break when the window is no longer valid\n max_length = max(len(max_hq), max_length)\n return max_length\n```\n\n# Approach 2: Two Heaps\nDifferent to the brute force approach, this one is better in that we only have one "window" in the whole process. We only manipulate the left and right index of the window. \n\nWhat we did differently is that we try to slide the window forward while keeping numbers in the window is valid. \n\n# Complexity\n- Time complexity:\n$nlog(n)$ because when pushing element to each heap, I need $log(n)$ time and every element can only be pushed to the heap once. \n\n- Space complexity:\n$O(n)$ to store numbers in two heaps. \n\n# Code\n```\nimport heapq\nclass Solution:\n def longestSubarray(self, nums: List[int], limit: int) -> int:\n # most instinct method\n max_length = 1\n left = 0 # We want to have a sliding window so that we can know the length of the window (i.e. the possible solution, thus we named the start of the window "left")\n min_heap = [] # named min_heap because this heap\'s purpose is to find the minimum\n max_heap = [] # named max_heap because this heap\'s purpose is to find the maximum\n for right in range(len(nums)): # "right" is the right end of the window\n # first of all, we push the [right] element to both the min_heap and the max_heap\n # because we need to first "slide" the window \n # we also need the index information because we need to make sure our min and max is valid while we are sliding the window\n heapq.heappush(min_heap, (nums[right], right))\n heapq.heappush(max_heap, (-nums[right], right))\n\n # in this step, we need to retrieve the minimum element and the maximum element in the window range, \n # therefore, we need to make sure the maximum and the minimum are within window range (i.e. left <= index <= right)\n # thus we need to pop the minheap until we find the smallest element which is in the window\n # we also need to pop the maxheap until we find the largest element which is in the window\n while min_heap[0][1] < left:\n heapq.heappop(min_heap)\n while max_heap[0][1] < left:\n heapq.heappop(max_heap)\n\n # We find the minimum and the maximum in the window, we can check whether the window is valid or not\n if -max_heap[0][0] - min_heap[0][0] <= limit:\n # if it\'s valid, we can update the answer\n max_length = max(max_length, right - left + 1)\n else:\n # else we just move the left end of the window\n left += 1\n return max_length\n \n \n \n```\n\n# Approach 3: Treemap\nIn this approach, we still need to use the sliding window method, the difference between this method and the two heaps is that in this method, we keep the frequency of num in a treemap in order to retrieve the maximum and the minimum in the window. \n\nI think the most important part of solving a problem is to find the train of thought. As a matter of fact, this method is actually along the same direction with the two heaps method. In other words, you need to first set the left and right end of the window and then check if the maximum and the minimum in this window conform with the requirements. \u201CSeek common points while reserving difference\u201D. \n\n# Complexity\n- Time complexity: $O(nlogn)$ because of the operations of treemap. \n- Space complexity: $O(n)$ to create the treemap. \n\n# Code \n```\nimport sortedcontainers\nfrom sortedcontainers import SortedDict\nclass Solution:\n def longestSubarray(self, nums: List[int], limit: int) -> int: \n left = 0 # Set up the left end of the window\n num_to_freq = SortedDict() # Python version of treemap\n max_length = 1\n for right in range(len(nums)):\n if nums[right] not in num_to_freq:\n num_to_freq[nums[right]] = 0\n num_to_freq[nums[right]] += 1 # if the right end of the window is not in the treemap, add it to the treemap\n while num_to_freq.peekitem(index=-1)[0] - num_to_freq.peekitem(index=0)[0] > limit: \n # Check if the maximum and the minimum conform the requirement\n # If it\'s not, we pop the number at index left and update the left index. \n # Remember we cannot retrieve the frequency of start of the window and then minus the frequency \n # because we need to make sure our window is consecutive. It\'s necessary to pop one item each time. \n # If you are still confused, think about this case: [2,2,2,4,4,2,5,5,5,5,5,2]\n num_to_freq[nums[left]] -= 1 \n if num_to_freq[nums[left]] == 0:\n num_to_freq.pop(nums[left])\n left += 1\n \n max_length = max(max_length, right - left + 1) # if the maximum and the minimum conform the requirement, we update our result\n return max_length\n```\n\n# Approach 4: Two Monotonic Queue\nWe followed the same directions as the solutions before: we need to maintain a window and try to find the index of the valid maximum and the minimum within the window. \n\nThe difference is that we used two monotonic array to find the maximum and the minimum, which is different from the previous two cases, in which the built-in data structures find the max and the min for us, we need to maintain the monotonic array ourselves. \n\n# Complexity\n- Time Complexity: O(N), for each elements in the array, we only need to add and pop one time per element. \n- Space Complexity: O(N), we need to create two deques to store the two monotonic arrays. \n\n# Code\n```\nimport collections\nclass Solution:\n def longestSubarray(self, nums: List[int], limit: int) -> int:\n left = 0\n max_length = 1\n n = len(nums)\n # We defined the two monotonic array here, we named the increasing array "increasing_q" and the decreasing array "decreasing_q"\n increasing_q = collections.deque()\n decreasing_q = collections.deque() \n # Start sliding -_- ...\n for right in range(n):\n # remember we should always try to insert the value into the last of the monotonic arrays\n # For increasing_q, we need to check whether the last value of the monotonic array is larger than the right end of the window. If it is, then we need to pop the value until we find the one which is smaller than the right end of the window and insert the right end of the window at the last of the increasing monotonic array. \n # You cannot put the increasing_q[-1] >= nums[right] here because the limit might be 0 and in this case, we need to count the number of equal value.\n while increasing_q and increasing_q[-1] > nums[right]:\n increasing_q.pop()\n increasing_q.append(nums[right])\n\n # For decreasing_q, we need to check whether the last value of the monotonic array is smaller than the right end of the window. If it is, then we need to pop the value until we find the one which is larger than the right end of the window and insert the right end of the window at the last of the decreasing monotonic array. \n # You cannot put the decreasing_q[-1] <= nums[right] here because the limit might be 0 and in this case, we need to count the number of equal value.\n while decreasing_q and decreasing_q[-1] < nums[right]:\n decreasing_q.pop()\n decreasing_q.append(nums[right])\n\n # we need to check if the difference of the max and min in the current window is bigger than the limit or not, if it is, we need to do something and update our window. \n while decreasing_q[0] - increasing_q[0] > limit:\n # For decreasing_q, there are 3(actually I think there are only 2) cases here: \n # nums[left] is greater than decreasing_q[0], then it must have been popped before\n # nums[left] == decreasing_q[0], then pop it here\n # nums[left] is smaller than decreasing_q[0](which I think is impossible because we should always pop the bigger ones first to get the smaller ones so we haven\'t reached those nums which are smaller than decreasing_q[0] yet.) \n if decreasing_q[0] == nums[left]:\n decreasing_q.popleft()\n # For increasing_q, there are 3(actually I think there are only 2) cases here: \n # nums[left] is smaller than increasing_q[0], then it must have been popped before\n # nums[left] == increasing_q[0], then pop it here\n # nums[left] is greater than increasing_q[0](which I think is impossible because we should always pop the smaller ones first to get the bigger ones so we haven\'t reached those nums which are bigger than increasing_q[0] yet.) \n if increasing_q[0] == nums[left]:\n increasing_q.popleft()\n \n # We need to update the left here to forward our window so that it is more likely to be valid\n left += 1\n # window is valid \uD83D\uDE0A, update the max_length here. \n max_length = max(max_length, right - left + 1)\n return max_length\n \n```\n\n\n\n\n\n\n\n\n\n | 5 | Given an array of integers `nums` and an integer `limit`, return the size of the longest **non-empty** subarray such that the absolute difference between any two elements of this subarray is less than or equal to `limit`_._
**Example 1:**
**Input:** nums = \[8,2,4,7\], limit = 4
**Output:** 2
**Explanation:** All subarrays are:
\[8\] with maximum absolute diff |8-8| = 0 <= 4.
\[8,2\] with maximum absolute diff |8-2| = 6 > 4.
\[8,2,4\] with maximum absolute diff |8-2| = 6 > 4.
\[8,2,4,7\] with maximum absolute diff |8-2| = 6 > 4.
\[2\] with maximum absolute diff |2-2| = 0 <= 4.
\[2,4\] with maximum absolute diff |2-4| = 2 <= 4.
\[2,4,7\] with maximum absolute diff |2-7| = 5 > 4.
\[4\] with maximum absolute diff |4-4| = 0 <= 4.
\[4,7\] with maximum absolute diff |4-7| = 3 <= 4.
\[7\] with maximum absolute diff |7-7| = 0 <= 4.
Therefore, the size of the longest subarray is 2.
**Example 2:**
**Input:** nums = \[10,1,2,4,7,2\], limit = 5
**Output:** 4
**Explanation:** The subarray \[2,4,7,2\] is the longest since the maximum absolute diff is |2-7| = 5 <= 5.
**Example 3:**
**Input:** nums = \[4,2,2,2,4,4,2,2\], limit = 0
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `0 <= limit <= 109` | null |
Monotonic Queue Implementation | longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit | 0 | 1 | ```\nfrom collections import deque\n\nclass Solution:\n def longestSubarray(self, nums: List[int], limit: int) -> int:\n maxQueue = deque()\n minQueue = deque()\n \n length = len(nums)\n \n i = 0\n maxSize = 0\n \n for j, num in enumerate(nums):\n while maxQueue and maxQueue[-1] < num:\n maxQueue.pop()\n \n maxQueue.append(num)\n \n while minQueue and minQueue[-1] > num:\n minQueue.pop()\n \n minQueue.append(num)\n \n while maxQueue[0] - minQueue[0] > limit:\n if maxQueue[0] == nums[i]:\n maxQueue.popleft()\n if minQueue[0] == nums[i]:\n minQueue.popleft()\n \n i += 1\n maxSize = max(maxSize, j - i + 1)\n return maxSize\n``` | 2 | Given an array of integers `nums` and an integer `limit`, return the size of the longest **non-empty** subarray such that the absolute difference between any two elements of this subarray is less than or equal to `limit`_._
**Example 1:**
**Input:** nums = \[8,2,4,7\], limit = 4
**Output:** 2
**Explanation:** All subarrays are:
\[8\] with maximum absolute diff |8-8| = 0 <= 4.
\[8,2\] with maximum absolute diff |8-2| = 6 > 4.
\[8,2,4\] with maximum absolute diff |8-2| = 6 > 4.
\[8,2,4,7\] with maximum absolute diff |8-2| = 6 > 4.
\[2\] with maximum absolute diff |2-2| = 0 <= 4.
\[2,4\] with maximum absolute diff |2-4| = 2 <= 4.
\[2,4,7\] with maximum absolute diff |2-7| = 5 > 4.
\[4\] with maximum absolute diff |4-4| = 0 <= 4.
\[4,7\] with maximum absolute diff |4-7| = 3 <= 4.
\[7\] with maximum absolute diff |7-7| = 0 <= 4.
Therefore, the size of the longest subarray is 2.
**Example 2:**
**Input:** nums = \[10,1,2,4,7,2\], limit = 5
**Output:** 4
**Explanation:** The subarray \[2,4,7,2\] is the longest since the maximum absolute diff is |2-7| = 5 <= 5.
**Example 3:**
**Input:** nums = \[4,2,2,2,4,4,2,2\], limit = 0
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `0 <= limit <= 109` | null |
[Python3] | O(m * knlogkn) | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | ```\nclass Solution:\n def kthSmallest(self, mat: List[List[int]], k: int) -> int:\n row=len(mat)\n col=len(mat[0])\n temp=[i for i in mat[0]]\n for i in range(1,row):\n currSum=[]\n for j in range(col):\n for it in range(len(temp)):\n currSum.append(temp[it]+mat[i][j])\n currSum.sort()\n temp.clear()\n maxSize=min(k,len(currSum))\n for size in range(maxSize):\n temp.append(currSum[size])\n return temp[k-1]\n``` | 2 | You are given an `m x n` matrix `mat` that has its rows sorted in non-decreasing order and an integer `k`.
You are allowed to choose **exactly one element** from each row to form an array.
Return _the_ `kth` _smallest array sum among all possible arrays_.
**Example 1:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 5
**Output:** 7
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,2\], \[1,4\], \[3,2\], \[3,4\], \[1,6\]. Where the 5th sum is 7.
**Example 2:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 9
**Output:** 17
**Example 3:**
**Input:** mat = \[\[1,10,10\],\[1,4,5\],\[2,3,6\]\], k = 7
**Output:** 9
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,1,2\], \[1,1,3\], \[1,4,2\], \[1,4,3\], \[1,1,6\], \[1,5,2\], \[1,5,3\]. Where the 7th sum is 9.
**Constraints:**
* `m == mat.length`
* `n == mat.length[i]`
* `1 <= m, n <= 40`
* `1 <= mat[i][j] <= 5000`
* `1 <= k <= min(200, nm)`
* `mat[i]` is a non-decreasing array. | null |
[Python3] | O(m * knlogkn) | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | ```\nclass Solution:\n def kthSmallest(self, mat: List[List[int]], k: int) -> int:\n row=len(mat)\n col=len(mat[0])\n temp=[i for i in mat[0]]\n for i in range(1,row):\n currSum=[]\n for j in range(col):\n for it in range(len(temp)):\n currSum.append(temp[it]+mat[i][j])\n currSum.sort()\n temp.clear()\n maxSize=min(k,len(currSum))\n for size in range(maxSize):\n temp.append(currSum[size])\n return temp[k-1]\n``` | 2 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Simple python3 solution | Heap | 122 ms - faster than 84.54% solutions | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Complexity\n- Time complexity: $$O(k \\cdot m \\cdot max(n, \\log(k \\cdot m)))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k \\cdot m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nimport heapq\n\nclass Solution:\n def kthSmallest(self, mat: List[List[int]], k: int) -> int:\n m = len(mat)\n n = len(mat[0])\n\n _first_line_indexes = (0,) * m\n \n in_progress = {_first_line_indexes}\n h = [(sum(line[0] for line in mat), _first_line_indexes)]\n\n for _ in range(k - 1):\n current_sum, current_indexes = heapq.heappop(h)\n indexes_as_list = list(current_indexes)\n\n for i, (line, current_index) in enumerate(zip(mat, current_indexes)):\n if current_index == n - 1:\n continue\n \n indexes_as_list[i] += 1\n next_indexes = tuple(indexes_as_list)\n indexes_as_list[i] -= 1\n\n if next_indexes in in_progress:\n continue\n in_progress.add(next_indexes)\n\n next_sum = current_sum - line[current_index] + line[current_index + 1]\n heapq.heappush(h, (next_sum, next_indexes))\n\n return h[0][0]\n\n``` | 0 | You are given an `m x n` matrix `mat` that has its rows sorted in non-decreasing order and an integer `k`.
You are allowed to choose **exactly one element** from each row to form an array.
Return _the_ `kth` _smallest array sum among all possible arrays_.
**Example 1:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 5
**Output:** 7
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,2\], \[1,4\], \[3,2\], \[3,4\], \[1,6\]. Where the 5th sum is 7.
**Example 2:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 9
**Output:** 17
**Example 3:**
**Input:** mat = \[\[1,10,10\],\[1,4,5\],\[2,3,6\]\], k = 7
**Output:** 9
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,1,2\], \[1,1,3\], \[1,4,2\], \[1,4,3\], \[1,1,6\], \[1,5,2\], \[1,5,3\]. Where the 7th sum is 9.
**Constraints:**
* `m == mat.length`
* `n == mat.length[i]`
* `1 <= m, n <= 40`
* `1 <= mat[i][j] <= 5000`
* `1 <= k <= min(200, nm)`
* `mat[i]` is a non-decreasing array. | null |
Simple python3 solution | Heap | 122 ms - faster than 84.54% solutions | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Complexity\n- Time complexity: $$O(k \\cdot m \\cdot max(n, \\log(k \\cdot m)))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k \\cdot m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nimport heapq\n\nclass Solution:\n def kthSmallest(self, mat: List[List[int]], k: int) -> int:\n m = len(mat)\n n = len(mat[0])\n\n _first_line_indexes = (0,) * m\n \n in_progress = {_first_line_indexes}\n h = [(sum(line[0] for line in mat), _first_line_indexes)]\n\n for _ in range(k - 1):\n current_sum, current_indexes = heapq.heappop(h)\n indexes_as_list = list(current_indexes)\n\n for i, (line, current_index) in enumerate(zip(mat, current_indexes)):\n if current_index == n - 1:\n continue\n \n indexes_as_list[i] += 1\n next_indexes = tuple(indexes_as_list)\n indexes_as_list[i] -= 1\n\n if next_indexes in in_progress:\n continue\n in_progress.add(next_indexes)\n\n next_sum = current_sum - line[current_index] + line[current_index + 1]\n heapq.heappush(h, (next_sum, next_indexes))\n\n return h[0][0]\n\n``` | 0 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python - 2 lines | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Complexity\n- Time complexity:\n$$O(MN^2klogk)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, m, k):\n for r in range(1, len(m)): m[0] = sorted([a+b for a in m[0] for b in m[r][:]])[:k]\n return m[0][k-1]\n\n \n\n\n\n\n``` | 0 | You are given an `m x n` matrix `mat` that has its rows sorted in non-decreasing order and an integer `k`.
You are allowed to choose **exactly one element** from each row to form an array.
Return _the_ `kth` _smallest array sum among all possible arrays_.
**Example 1:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 5
**Output:** 7
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,2\], \[1,4\], \[3,2\], \[3,4\], \[1,6\]. Where the 5th sum is 7.
**Example 2:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 9
**Output:** 17
**Example 3:**
**Input:** mat = \[\[1,10,10\],\[1,4,5\],\[2,3,6\]\], k = 7
**Output:** 9
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,1,2\], \[1,1,3\], \[1,4,2\], \[1,4,3\], \[1,1,6\], \[1,5,2\], \[1,5,3\]. Where the 7th sum is 9.
**Constraints:**
* `m == mat.length`
* `n == mat.length[i]`
* `1 <= m, n <= 40`
* `1 <= mat[i][j] <= 5000`
* `1 <= k <= min(200, nm)`
* `mat[i]` is a non-decreasing array. | null |
Python - 2 lines | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Complexity\n- Time complexity:\n$$O(MN^2klogk)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, m, k):\n for r in range(1, len(m)): m[0] = sorted([a+b for a in m[0] for b in m[r][:]])[:k]\n return m[0][k-1]\n\n \n\n\n\n\n``` | 0 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
MinHeap with Backtracking | Commented and Explained | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFrom the problem description we have at most 40 rows and 40 columns, and from which we will select the 200th smallest at worst. This gives us bounds that make a minheap with backtracking set up possible for our implementation needs, as this means we will need to do at worst 200 * 40 * log (200 * 40) calculations by considering a backtracking over the rows and their respective indices. This lets us have a min heap that is growing at worst linearly, and as such maintains our space bounds in a range of 40*40 + 200 * 40, of which the secondary wins out in terms of growth rate potential. \n\nWhy 200 and why 40\'s? From description, k is bound to minimum of 200 and n^m. Of those two, 200 is the tighter bound since 40^40 vastly exceeds 200. Similarly, m and n of our matrix are bound to 40. This gives us a nice problem space to exploit with backtracking and heaps. \n\nHow to go about that though? The first question is, what is our minimal bound? \n\nOur minimal bound, for k = 1, meaning the smallest sum of row items, is in fact our value of the items in column 0 for each row in the matrix. \n\nOur maximal bound is the sum of the final item in each row \n\nOne way forward with this is to binarily search within these bounds by modifying the current sum towards the kth iteration, but that would require valuation of all sums in that range -> a costly process! \n\nTo do better, we can consider instead the idea of selecting different column indices for each row as we go along and building in order of the current best choice. This greedily lets us advance toward an answer which we can be assured is the cheapest via the idea of a cheapest path algorithm like djikstra\'s (which also works on this problem!) \n\nThen, after doing k selections, we arrive at the kth smallest, and can return our valuation. Approach provides details on the how. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up our minimal answer as kth_smallest as the sum of the first item in each row of the matrix. If k is 1, you\'re done, return the kth smallest. Otherwise, decrement k by 1 since you did a set already. \n\nOtherwise, we need a min heap of possible smallest sums for each row alteration, as wewll as the size of our rows and cols in our matrix \n\nWith those, we then move to set up for each row index and row in matrix \n- a row to col indices of 0\'s for all rows currently \n- set the current row (denoted by row index) in row to col indices to 1 \n- the new sum is the kth smallest minus the current rows 0 item plus the current rows 1 item \n- each of our nodes in our heap will store a new sum, a row index (which row is this based off of) and a current row to col indices \n- add the new node to heap \n\nWhen done with initial, heapify heap \n\nNow we need to get the kth smallest (so far we have the smallest) \nTo do so, loop in range k (remember offset earlier!) and \n- get current kth smallest sum, row index and row to col indices by popping from min heap \n- for row current and row in enumerate(matrix[row_index:], row_index) \n - we need the second argument in enumerate to not mess up our other claculations. This makes enumerate start counting from current row index instead of 0 \n - if we can move the current rows column index over 1 still \n - move it over 1 (increment row to col indices at row current by 1)\n - get new sum when you do (remove prior value from this row from kth smallest and add to kth smallest the value of the new position in the row current)\n - make a new node using this new sum, row current, and row to col indices as a list (heap will make it a tuple when you pop, watch that!)\n - push new node into the heap \n - move the current rows column index back 1 \n - otherwise, continue \n\nWhen done, return the kth smallest \n\n# Complexity\n- Time complexity : O(R * k log (R * k))\n - Takes O(R) to build the first kth smallest \n - Takes O(R) to build the first heap \n - Takes O(R log R) to build first min heap \n - For k times \n - do r log r work building the heap, where r is subset of R inclusive \n - builds up over k loops though, so log r * k instead of r \n - Total complexity is then O(2R + R log R + k * r log r*k) \n - At worst r is R \n - So O(R * k log (R * k))\n\n- Space complexity : O(R * k log (R * k))\n - Our heap at first holds only R log R items \n - However, over looping we add at most R * k log R * k items \n - So our size must match at least \n\n# Code\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int :\n # get smallest summation first \n kth_smallest = sum(row[0] for row in matrix)\n # if k is 1, this is the answer, return it \n if k == 1 : \n return kth_smallest\n else : \n k -= 1 \n\n # otherwise, we proceed to set up the following \n # a minimum heap of updates to the kth smallest sum \n min_heap = []\n # dimensions of our matrix \n rows = len(matrix)\n cols = len(matrix[0])\n # now we prefill the min heap of kth smallest sums \n for row_index, row in enumerate(matrix) : \n # set up row to col indices for each \n row_to_col_indices = [0] * rows\n # mark as if they use 1 instead \n row_to_col_indices[row_index] = 1\n # determine new sum \n new_sum = kth_smallest - row[0] + row[1]\n # make new node \n new_node = (new_sum, row_index, row_to_col_indices)\n # append \n min_heap.append(new_node)\n \n # heapify after first option \n heapq.heapify(min_heap) \n\n # we are determining the kth smallest, so we generate k - 1 options \n for option in range(k) : \n # get kth smallest, row index, and row to col indices from node in heappop \n kth_smallest, row_index, row_to_col_indices = heapq.heappop(min_heap)\n # uncommnt to view progression \n # print(f\'For the {option} smallest row sum, the value is {kth_smallest}\')\n # as we do, we consider each row current index and row in matrix from row index forward \n # where we will start row current at row index to maintain connection to set up (this is why row index is second argument) \n # without that, we would start at 0, and that would actually throw off our counting progressions \n for row_current, row in enumerate(matrix[row_index:], row_index) : \n # if row indices at row current + 1 is less than cols -> we can still go over a column in this rows column indices \n if row_to_col_indices[row_current] + 1 < cols : \n # move it over one \n row_to_col_indices[row_current] += 1\n # get new sum if you do (kth smallest needs to lose prior value of row at row indices at row current - 1 and gain row at row indices at row current) \n new_sum = kth_smallest - row[row_to_col_indices[row_current] - 1] + row[row_to_col_indices[row_current]]\n # this makes a new node with new sum, row current and a list cast of row indices \n new_node = (new_sum, row_current, list(row_to_col_indices))\n # push in the new node \n heapq.heappush(min_heap, new_node)\n # backtrack \n row_to_col_indices[row_current] -= 1 \n else : \n continue\n # return when done \n return kth_smallest\n \n``` | 0 | You are given an `m x n` matrix `mat` that has its rows sorted in non-decreasing order and an integer `k`.
You are allowed to choose **exactly one element** from each row to form an array.
Return _the_ `kth` _smallest array sum among all possible arrays_.
**Example 1:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 5
**Output:** 7
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,2\], \[1,4\], \[3,2\], \[3,4\], \[1,6\]. Where the 5th sum is 7.
**Example 2:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 9
**Output:** 17
**Example 3:**
**Input:** mat = \[\[1,10,10\],\[1,4,5\],\[2,3,6\]\], k = 7
**Output:** 9
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,1,2\], \[1,1,3\], \[1,4,2\], \[1,4,3\], \[1,1,6\], \[1,5,2\], \[1,5,3\]. Where the 7th sum is 9.
**Constraints:**
* `m == mat.length`
* `n == mat.length[i]`
* `1 <= m, n <= 40`
* `1 <= mat[i][j] <= 5000`
* `1 <= k <= min(200, nm)`
* `mat[i]` is a non-decreasing array. | null |
MinHeap with Backtracking | Commented and Explained | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFrom the problem description we have at most 40 rows and 40 columns, and from which we will select the 200th smallest at worst. This gives us bounds that make a minheap with backtracking set up possible for our implementation needs, as this means we will need to do at worst 200 * 40 * log (200 * 40) calculations by considering a backtracking over the rows and their respective indices. This lets us have a min heap that is growing at worst linearly, and as such maintains our space bounds in a range of 40*40 + 200 * 40, of which the secondary wins out in terms of growth rate potential. \n\nWhy 200 and why 40\'s? From description, k is bound to minimum of 200 and n^m. Of those two, 200 is the tighter bound since 40^40 vastly exceeds 200. Similarly, m and n of our matrix are bound to 40. This gives us a nice problem space to exploit with backtracking and heaps. \n\nHow to go about that though? The first question is, what is our minimal bound? \n\nOur minimal bound, for k = 1, meaning the smallest sum of row items, is in fact our value of the items in column 0 for each row in the matrix. \n\nOur maximal bound is the sum of the final item in each row \n\nOne way forward with this is to binarily search within these bounds by modifying the current sum towards the kth iteration, but that would require valuation of all sums in that range -> a costly process! \n\nTo do better, we can consider instead the idea of selecting different column indices for each row as we go along and building in order of the current best choice. This greedily lets us advance toward an answer which we can be assured is the cheapest via the idea of a cheapest path algorithm like djikstra\'s (which also works on this problem!) \n\nThen, after doing k selections, we arrive at the kth smallest, and can return our valuation. Approach provides details on the how. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up our minimal answer as kth_smallest as the sum of the first item in each row of the matrix. If k is 1, you\'re done, return the kth smallest. Otherwise, decrement k by 1 since you did a set already. \n\nOtherwise, we need a min heap of possible smallest sums for each row alteration, as wewll as the size of our rows and cols in our matrix \n\nWith those, we then move to set up for each row index and row in matrix \n- a row to col indices of 0\'s for all rows currently \n- set the current row (denoted by row index) in row to col indices to 1 \n- the new sum is the kth smallest minus the current rows 0 item plus the current rows 1 item \n- each of our nodes in our heap will store a new sum, a row index (which row is this based off of) and a current row to col indices \n- add the new node to heap \n\nWhen done with initial, heapify heap \n\nNow we need to get the kth smallest (so far we have the smallest) \nTo do so, loop in range k (remember offset earlier!) and \n- get current kth smallest sum, row index and row to col indices by popping from min heap \n- for row current and row in enumerate(matrix[row_index:], row_index) \n - we need the second argument in enumerate to not mess up our other claculations. This makes enumerate start counting from current row index instead of 0 \n - if we can move the current rows column index over 1 still \n - move it over 1 (increment row to col indices at row current by 1)\n - get new sum when you do (remove prior value from this row from kth smallest and add to kth smallest the value of the new position in the row current)\n - make a new node using this new sum, row current, and row to col indices as a list (heap will make it a tuple when you pop, watch that!)\n - push new node into the heap \n - move the current rows column index back 1 \n - otherwise, continue \n\nWhen done, return the kth smallest \n\n# Complexity\n- Time complexity : O(R * k log (R * k))\n - Takes O(R) to build the first kth smallest \n - Takes O(R) to build the first heap \n - Takes O(R log R) to build first min heap \n - For k times \n - do r log r work building the heap, where r is subset of R inclusive \n - builds up over k loops though, so log r * k instead of r \n - Total complexity is then O(2R + R log R + k * r log r*k) \n - At worst r is R \n - So O(R * k log (R * k))\n\n- Space complexity : O(R * k log (R * k))\n - Our heap at first holds only R log R items \n - However, over looping we add at most R * k log R * k items \n - So our size must match at least \n\n# Code\n```\nclass Solution:\n def kthSmallest(self, matrix: List[List[int]], k: int) -> int :\n # get smallest summation first \n kth_smallest = sum(row[0] for row in matrix)\n # if k is 1, this is the answer, return it \n if k == 1 : \n return kth_smallest\n else : \n k -= 1 \n\n # otherwise, we proceed to set up the following \n # a minimum heap of updates to the kth smallest sum \n min_heap = []\n # dimensions of our matrix \n rows = len(matrix)\n cols = len(matrix[0])\n # now we prefill the min heap of kth smallest sums \n for row_index, row in enumerate(matrix) : \n # set up row to col indices for each \n row_to_col_indices = [0] * rows\n # mark as if they use 1 instead \n row_to_col_indices[row_index] = 1\n # determine new sum \n new_sum = kth_smallest - row[0] + row[1]\n # make new node \n new_node = (new_sum, row_index, row_to_col_indices)\n # append \n min_heap.append(new_node)\n \n # heapify after first option \n heapq.heapify(min_heap) \n\n # we are determining the kth smallest, so we generate k - 1 options \n for option in range(k) : \n # get kth smallest, row index, and row to col indices from node in heappop \n kth_smallest, row_index, row_to_col_indices = heapq.heappop(min_heap)\n # uncommnt to view progression \n # print(f\'For the {option} smallest row sum, the value is {kth_smallest}\')\n # as we do, we consider each row current index and row in matrix from row index forward \n # where we will start row current at row index to maintain connection to set up (this is why row index is second argument) \n # without that, we would start at 0, and that would actually throw off our counting progressions \n for row_current, row in enumerate(matrix[row_index:], row_index) : \n # if row indices at row current + 1 is less than cols -> we can still go over a column in this rows column indices \n if row_to_col_indices[row_current] + 1 < cols : \n # move it over one \n row_to_col_indices[row_current] += 1\n # get new sum if you do (kth smallest needs to lose prior value of row at row indices at row current - 1 and gain row at row indices at row current) \n new_sum = kth_smallest - row[row_to_col_indices[row_current] - 1] + row[row_to_col_indices[row_current]]\n # this makes a new node with new sum, row current and a list cast of row indices \n new_node = (new_sum, row_current, list(row_to_col_indices))\n # push in the new node \n heapq.heappush(min_heap, new_node)\n # backtrack \n row_to_col_indices[row_current] -= 1 \n else : \n continue\n # return when done \n return kth_smallest\n \n``` | 0 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python Priority Queue | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | \n# Approach\nUse a priority queue to keep track of current sum and its indexes. Pop next element from the queue, we can push new m elements to the queue by increasing index at each row by 1\n\n# Complexity\n- Time complexity:\nO(log(m * n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m * n)\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, mat: List[List[int]], k: int) -> int:\n ROWS, COLS = len(mat), len(mat[0])\n seen = set()\n\n pq = [\n (\n sum(l[0] for l in mat),\n [0] * ROWS\n )\n ] # (val, [indexes])\n\n while k - 1:\n val, index_l = heapq.heappop(pq)\n k -= 1\n\n for i in range(ROWS):\n if index_l[i] + 1 == COLS:\n continue\n \n new_l = list(index_l)\n new_l[i] += 1\n t = tuple(new_l)\n if t in seen:\n continue\n \n new_val = val\n new_val -= mat[i][new_l[i] - 1]\n new_val += mat[i][new_l[i]]\n seen.add(t)\n heapq.heappush(pq, (new_val, new_l))\n\n return pq[0][0]\n\n\n``` | 0 | You are given an `m x n` matrix `mat` that has its rows sorted in non-decreasing order and an integer `k`.
You are allowed to choose **exactly one element** from each row to form an array.
Return _the_ `kth` _smallest array sum among all possible arrays_.
**Example 1:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 5
**Output:** 7
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,2\], \[1,4\], \[3,2\], \[3,4\], \[1,6\]. Where the 5th sum is 7.
**Example 2:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 9
**Output:** 17
**Example 3:**
**Input:** mat = \[\[1,10,10\],\[1,4,5\],\[2,3,6\]\], k = 7
**Output:** 9
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,1,2\], \[1,1,3\], \[1,4,2\], \[1,4,3\], \[1,1,6\], \[1,5,2\], \[1,5,3\]. Where the 7th sum is 9.
**Constraints:**
* `m == mat.length`
* `n == mat.length[i]`
* `1 <= m, n <= 40`
* `1 <= mat[i][j] <= 5000`
* `1 <= k <= min(200, nm)`
* `mat[i]` is a non-decreasing array. | null |
Python Priority Queue | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | \n# Approach\nUse a priority queue to keep track of current sum and its indexes. Pop next element from the queue, we can push new m elements to the queue by increasing index at each row by 1\n\n# Complexity\n- Time complexity:\nO(log(m * n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m * n)\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, mat: List[List[int]], k: int) -> int:\n ROWS, COLS = len(mat), len(mat[0])\n seen = set()\n\n pq = [\n (\n sum(l[0] for l in mat),\n [0] * ROWS\n )\n ] # (val, [indexes])\n\n while k - 1:\n val, index_l = heapq.heappop(pq)\n k -= 1\n\n for i in range(ROWS):\n if index_l[i] + 1 == COLS:\n continue\n \n new_l = list(index_l)\n new_l[i] += 1\n t = tuple(new_l)\n if t in seen:\n continue\n \n new_val = val\n new_val -= mat[i][new_l[i] - 1]\n new_val += mat[i][new_l[i]]\n seen.add(t)\n heapq.heappush(pq, (new_val, new_l))\n\n return pq[0][0]\n\n\n``` | 0 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
Python (Simple Dijkstra's algorithm) | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, mat, k):\n def func_(nums1,nums2):\n distance = collections.defaultdict(int)\n\n for i in range(len(nums1)):\n for j in range(len(nums2)):\n distance[(i,j)] = float("inf")\n\n distance[(0,0)] = 0\n\n stack = [(nums1[0]+nums2[0],0,0)]\n\n res = []\n\n while stack:\n total, i, j = heapq.heappop(stack)\n\n res.append(total)\n\n if len(res) == k:\n break\n\n if i+1<len(nums1) and distance[(i+1,j)] > nums1[i+1] + nums2[j]:\n distance[(i+1,j)] = nums1[i+1] + nums2[j]\n heapq.heappush(stack,(nums1[i+1]+nums2[j],i+1,j))\n\n if j+1<len(nums2) and distance[(i,j+1)] > nums1[i] + nums2[j+1]:\n distance[(i,j+1)] = nums1[i] + nums2[j+1]\n heapq.heappush(stack,(nums1[i]+nums2[j+1],i,j+1))\n\n return res\n\n result = mat[0]\n\n for i in mat[1:]:\n result = func_(result,i)\n\n return result[-1]\n\n \n \n\n\n\n\n\n\n\n``` | 0 | You are given an `m x n` matrix `mat` that has its rows sorted in non-decreasing order and an integer `k`.
You are allowed to choose **exactly one element** from each row to form an array.
Return _the_ `kth` _smallest array sum among all possible arrays_.
**Example 1:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 5
**Output:** 7
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,2\], \[1,4\], \[3,2\], \[3,4\], \[1,6\]. Where the 5th sum is 7.
**Example 2:**
**Input:** mat = \[\[1,3,11\],\[2,4,6\]\], k = 9
**Output:** 17
**Example 3:**
**Input:** mat = \[\[1,10,10\],\[1,4,5\],\[2,3,6\]\], k = 7
**Output:** 9
**Explanation:** Choosing one element from each row, the first k smallest sum are:
\[1,1,2\], \[1,1,3\], \[1,4,2\], \[1,4,3\], \[1,1,6\], \[1,5,2\], \[1,5,3\]. Where the 7th sum is 9.
**Constraints:**
* `m == mat.length`
* `n == mat.length[i]`
* `1 <= m, n <= 40`
* `1 <= mat[i][j] <= 5000`
* `1 <= k <= min(200, nm)`
* `mat[i]` is a non-decreasing array. | null |
Python (Simple Dijkstra's algorithm) | find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthSmallest(self, mat, k):\n def func_(nums1,nums2):\n distance = collections.defaultdict(int)\n\n for i in range(len(nums1)):\n for j in range(len(nums2)):\n distance[(i,j)] = float("inf")\n\n distance[(0,0)] = 0\n\n stack = [(nums1[0]+nums2[0],0,0)]\n\n res = []\n\n while stack:\n total, i, j = heapq.heappop(stack)\n\n res.append(total)\n\n if len(res) == k:\n break\n\n if i+1<len(nums1) and distance[(i+1,j)] > nums1[i+1] + nums2[j]:\n distance[(i+1,j)] = nums1[i+1] + nums2[j]\n heapq.heappush(stack,(nums1[i+1]+nums2[j],i+1,j))\n\n if j+1<len(nums2) and distance[(i,j+1)] > nums1[i] + nums2[j+1]:\n distance[(i,j+1)] = nums1[i] + nums2[j+1]\n heapq.heappush(stack,(nums1[i]+nums2[j+1],i,j+1))\n\n return res\n\n result = mat[0]\n\n for i in mat[1:]:\n result = func_(result,i)\n\n return result[-1]\n\n \n \n\n\n\n\n\n\n\n``` | 0 | Given an integer array `arr`, return `true` if there are three consecutive odd numbers in the array. Otherwise, return `false`.
**Example 1:**
**Input:** arr = \[2,6,4,1\]
**Output:** false
**Explanation:** There are no three consecutive odds.
**Example 2:**
**Input:** arr = \[1,2,34,3,4,5,7,23,12\]
**Output:** true
**Explanation:** \[5,7,23\] are three consecutive odds.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 1000` | Save all visited sums and corresponding indexes in a priority queue. Then, once you pop the smallest sum so far, you can quickly identify the next m candidates for smallest sum by incrementing each row index by 1. |
【Video】Give me 5 minutes - How we think about a solution | build-an-array-with-stack-operations | 1 | 1 | # Intuition\nThere is an answer in Example 1. lol\n\n---\n\n# Solution Video\n\nhttps://youtu.be/MCYiEw2zvNw\n\n\u25A0 Timeline of the video\n\n`0:04` Basic idea to solve this question\n`1:04` How do you operate each number from the steam of integers?\n`3:34` What operation we need for the two patterns\n`5:17` Coding\n`6:37` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,935\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\n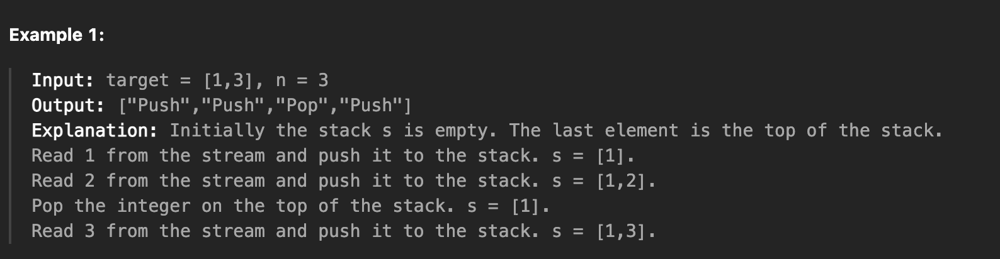\n\nLet me use Example 1 from description.\n\nWe need to build the target which means\n\n---\n\n\u2B50\uFE0F Points\n\n- All numbers we need are in the target input.\n\n- If a stream of the integers is greater than the last number in target, we don\'t have to care about them becuase they are out of the target range.\n\n---\n\nThat\'s why we iterate through the target input and record operations we do.\n\n- **How do you operate each number from the steam of integers.**\n\nOkay. let\'s think about each operation.\n\nWe have two patterns.\n\n---\n\n\u25A0 Key Points to Consider\n\n- A number from the steam is equal to current target number\n\n- A number from the steam is smaller than current target number\n\n\nThere is not possibility that a number from the steam is greater than current target number, because we have constrants.\n\n```\n1 <= n <= 100\n1 <= target[i] <= n\ntarget is strictly increasing.\n```\n\nIf target is including `1`, then the two number should be equal. After that, next target number should be greater than current target because the constrants say "target is strictly increasing.".\n\nLet\'s say the next target is `2`. The next number from the steam is also `2`. In that case they are equal.\n\nLet\'s say the next target is `3`. The next number from the steam is `2`. In that case a number from the steam is smaller than current target number. And next, they will be equal(`3` and `3`).\n\nAnd the next target number should be greater than `3`...\n\nThat\'s why we have only two cases above.\n\n---\n\n- A number from the steam is equal to current target number\n\nIn this case, simply, `"Push"`. No wonder.\n\n- A number from the steam is smaller than current target number\n\nLook at Example 1 in the description. After push `1`, the next target is `3`, a number from the steam is `2`. In that case, `Push` and `Pop`, so\n\n```\ncurrent: [1]\nPush: [1,2]\nPop: [1]\n```\nThat\'s because we don\'t need `2` as a target. Then `"Push"` for `3`.\n\n\n---\n\n\u2B50\uFE0F Points\n\nThe two numbers are equal \n\u2192 "Push"\n\nA number from the steam is smaller than current target number\n\u2192 "Push"&"Pop"\n\n---\n\nLet\'s see a real algorithm!\n\n##### Algorithm Overview:\n\nThe code constructs a target array using a stack-like approach, generating a sequence of "Push" and "Pop" operations to match the given target array.\n\n##### Detailed Explanation:\n\n1. Initialize an empty list `res` to store the stack operations.\n2. Initialize a variable `cur` to 1, which represents the current number.\n\n3. Iterate through the elements of the `target` array:\n - For each element `num` in the `target` array, you will perform the following steps.\n\n4. Inside the loop:\n - Use a `while` loop to check if the `cur` is less than the current element `num`.\n - If `cur` is less than `num`, it means we need to push elements from `cur` up to `num - 1` into the `res` list to simulate the stack operations.\n - Append "Push" and "Pop" into the `res` list to represent pushing and popping operations.\n - Increment `cur` by 1 to move to the next number.\n\n5. After the `while` loop:\n - Push the current number (`cur`) into the `res` list. This represents a "Push" operation.\n - Increment `cur` by 1 to move to the next number.\n\n6. Repeat steps 4 and 5 for all elements in the `target` array.\n\n7. Once all elements in the `target` array have been processed, return the `res` list, which contains the stack operations needed to build the target array.\n\nThe algorithm effectively simulates the stack operations required to construct the target array using the given instructions.\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n\n- Space complexity: $$O(n)$$\n\n\n\n```python []\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n res = [] # Initialize an empty result list\n cur = 1 # Initialize the current number to 1\n\n for num in target:\n while cur < num:\n # Push elements from 1 to num - 1 into the result list\n res.append("Push")\n res.append("Pop")\n cur += 1\n\n # Push the current number into the result list\n # Current number should be a target number right now\n res.append("Push")\n cur += 1\n\n return res \n```\n```javascript []\n/**\n * @param {number[]} target\n * @param {number} n\n * @return {string[]}\n */\nvar buildArray = function(target, n) {\n const result = []; // Initialize an empty result array\n let current = 1; // Initialize the current number to 1\n\n for (const num of target) {\n while (current < num) {\n // Push elements from 1 to num - 1 into the result array\n result.push("Push");\n result.push("Pop");\n current++;\n }\n\n // Push the current number into the result array\n // Current number should be a target number right now\n result.push("Push");\n current++;\n }\n\n return result; \n};\n```\n```java []\nclass Solution {\n public List<String> buildArray(int[] target, int n) {\n List<String> result = new ArrayList<>(); // Initialize an empty result list\n int current = 1; // Initialize the current number to 1\n\n for (int num : target) {\n while (current < num) {\n // Push elements from 1 to num - 1 into the result list\n result.add("Push");\n result.add("Pop");\n current++;\n }\n\n // Push the current number into the result list\n // Current number should be a target number right now\n result.add("Push");\n current++;\n }\n\n return result; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<string> buildArray(vector<int>& target, int n) {\n vector<string> result; // Initialize an empty result vector\n int current = 1; // Initialize the current number to 1\n\n for (int num : target) {\n while (current < num) {\n // Push elements from 1 to num - 1 into the result vector\n result.push_back("Push");\n result.push_back("Pop");\n current++;\n }\n\n // Push the current number into the result vector\n // Current number should be a target number right now\n result.push_back("Push");\n current++;\n }\n\n return result; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/seat-reservation-manager/solutions/4256920/video-give-me-5-minutes-bests-98-79-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/rgdtMOI5AKA\n\n\u25A0 Timeline of the video\n\n`0:04` Difficulty of Seat Reservation Manager\n`0:52` Two key points to solve Seat Reservation Manager\n`3:25` Coding\n`5:18` Time Complexity and Space Complexity\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-nodes-equal-to-average-of-subtree/solutions/4237404/video-give-me-8-minutes-how-we-think-about-a-solution-why-we-use-postorder-traversal/\n\nvideo\nhttps://youtu.be/MV6NpUXCfUU\n\n\u25A0 Timeline of the video\n`0:05` Which traversal do you use for this question?\n`1:55` How do you calculate information you need?\n`3:34` How to write Inorder, Preorder, Postorder\n`4:16` Coding\n`7:50` Time Complexity and Space Complexity | 7 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
【Video】Give me 5 minutes - How we think about a solution | build-an-array-with-stack-operations | 1 | 1 | # Intuition\nThere is an answer in Example 1. lol\n\n---\n\n# Solution Video\n\nhttps://youtu.be/MCYiEw2zvNw\n\n\u25A0 Timeline of the video\n\n`0:04` Basic idea to solve this question\n`1:04` How do you operate each number from the steam of integers?\n`3:34` What operation we need for the two patterns\n`5:17` Coding\n`6:37` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,935\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\n\n\nLet me use Example 1 from description.\n\nWe need to build the target which means\n\n---\n\n\u2B50\uFE0F Points\n\n- All numbers we need are in the target input.\n\n- If a stream of the integers is greater than the last number in target, we don\'t have to care about them becuase they are out of the target range.\n\n---\n\nThat\'s why we iterate through the target input and record operations we do.\n\n- **How do you operate each number from the steam of integers.**\n\nOkay. let\'s think about each operation.\n\nWe have two patterns.\n\n---\n\n\u25A0 Key Points to Consider\n\n- A number from the steam is equal to current target number\n\n- A number from the steam is smaller than current target number\n\n\nThere is not possibility that a number from the steam is greater than current target number, because we have constrants.\n\n```\n1 <= n <= 100\n1 <= target[i] <= n\ntarget is strictly increasing.\n```\n\nIf target is including `1`, then the two number should be equal. After that, next target number should be greater than current target because the constrants say "target is strictly increasing.".\n\nLet\'s say the next target is `2`. The next number from the steam is also `2`. In that case they are equal.\n\nLet\'s say the next target is `3`. The next number from the steam is `2`. In that case a number from the steam is smaller than current target number. And next, they will be equal(`3` and `3`).\n\nAnd the next target number should be greater than `3`...\n\nThat\'s why we have only two cases above.\n\n---\n\n- A number from the steam is equal to current target number\n\nIn this case, simply, `"Push"`. No wonder.\n\n- A number from the steam is smaller than current target number\n\nLook at Example 1 in the description. After push `1`, the next target is `3`, a number from the steam is `2`. In that case, `Push` and `Pop`, so\n\n```\ncurrent: [1]\nPush: [1,2]\nPop: [1]\n```\nThat\'s because we don\'t need `2` as a target. Then `"Push"` for `3`.\n\n\n---\n\n\u2B50\uFE0F Points\n\nThe two numbers are equal \n\u2192 "Push"\n\nA number from the steam is smaller than current target number\n\u2192 "Push"&"Pop"\n\n---\n\nLet\'s see a real algorithm!\n\n##### Algorithm Overview:\n\nThe code constructs a target array using a stack-like approach, generating a sequence of "Push" and "Pop" operations to match the given target array.\n\n##### Detailed Explanation:\n\n1. Initialize an empty list `res` to store the stack operations.\n2. Initialize a variable `cur` to 1, which represents the current number.\n\n3. Iterate through the elements of the `target` array:\n - For each element `num` in the `target` array, you will perform the following steps.\n\n4. Inside the loop:\n - Use a `while` loop to check if the `cur` is less than the current element `num`.\n - If `cur` is less than `num`, it means we need to push elements from `cur` up to `num - 1` into the `res` list to simulate the stack operations.\n - Append "Push" and "Pop" into the `res` list to represent pushing and popping operations.\n - Increment `cur` by 1 to move to the next number.\n\n5. After the `while` loop:\n - Push the current number (`cur`) into the `res` list. This represents a "Push" operation.\n - Increment `cur` by 1 to move to the next number.\n\n6. Repeat steps 4 and 5 for all elements in the `target` array.\n\n7. Once all elements in the `target` array have been processed, return the `res` list, which contains the stack operations needed to build the target array.\n\nThe algorithm effectively simulates the stack operations required to construct the target array using the given instructions.\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n\n- Space complexity: $$O(n)$$\n\n\n\n```python []\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n res = [] # Initialize an empty result list\n cur = 1 # Initialize the current number to 1\n\n for num in target:\n while cur < num:\n # Push elements from 1 to num - 1 into the result list\n res.append("Push")\n res.append("Pop")\n cur += 1\n\n # Push the current number into the result list\n # Current number should be a target number right now\n res.append("Push")\n cur += 1\n\n return res \n```\n```javascript []\n/**\n * @param {number[]} target\n * @param {number} n\n * @return {string[]}\n */\nvar buildArray = function(target, n) {\n const result = []; // Initialize an empty result array\n let current = 1; // Initialize the current number to 1\n\n for (const num of target) {\n while (current < num) {\n // Push elements from 1 to num - 1 into the result array\n result.push("Push");\n result.push("Pop");\n current++;\n }\n\n // Push the current number into the result array\n // Current number should be a target number right now\n result.push("Push");\n current++;\n }\n\n return result; \n};\n```\n```java []\nclass Solution {\n public List<String> buildArray(int[] target, int n) {\n List<String> result = new ArrayList<>(); // Initialize an empty result list\n int current = 1; // Initialize the current number to 1\n\n for (int num : target) {\n while (current < num) {\n // Push elements from 1 to num - 1 into the result list\n result.add("Push");\n result.add("Pop");\n current++;\n }\n\n // Push the current number into the result list\n // Current number should be a target number right now\n result.add("Push");\n current++;\n }\n\n return result; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<string> buildArray(vector<int>& target, int n) {\n vector<string> result; // Initialize an empty result vector\n int current = 1; // Initialize the current number to 1\n\n for (int num : target) {\n while (current < num) {\n // Push elements from 1 to num - 1 into the result vector\n result.push_back("Push");\n result.push_back("Pop");\n current++;\n }\n\n // Push the current number into the result vector\n // Current number should be a target number right now\n result.push_back("Push");\n current++;\n }\n\n return result; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/seat-reservation-manager/solutions/4256920/video-give-me-5-minutes-bests-98-79-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/rgdtMOI5AKA\n\n\u25A0 Timeline of the video\n\n`0:04` Difficulty of Seat Reservation Manager\n`0:52` Two key points to solve Seat Reservation Manager\n`3:25` Coding\n`5:18` Time Complexity and Space Complexity\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-nodes-equal-to-average-of-subtree/solutions/4237404/video-give-me-8-minutes-how-we-think-about-a-solution-why-we-use-postorder-traversal/\n\nvideo\nhttps://youtu.be/MV6NpUXCfUU\n\n\u25A0 Timeline of the video\n`0:05` Which traversal do you use for this question?\n`1:55` How do you calculate information you need?\n`3:34` How to write Inorder, Preorder, Postorder\n`4:16` Coding\n`7:50` Time Complexity and Space Complexity | 7 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || 2 Approaches || EXPLAINED🔥 | build-an-array-with-stack-operations | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Brute Force)***\n\n\n1. We initialize an empty vector of strings called `ans`, which will store the sequence of "`Push`" and "`Pop`" instructions.\n\n1. We also initialize an integer `i` to `1`, which represents the current number we\'re considering.\n\n1. We use a for loop to iterate through each element `a` in the `target` vector.\n\n1. Inside the loop, we use a while loop to check if `i` is less than `a`. If it is, we perform the following steps:\n\n - Add "`Push`" to the `ans` vector to simulate pushing the current number onto the stack.\n - Add "`Pop`" to the `ans` vector to simulate popping an element from the stack.\n - Increment `i` to move to the next number.\n1. After the while loop, we add "`Push`" to the `ans` vector to simulate pushing the next number onto the stack.\n\n1. Finally, we increment `i` to move to the next number.\n\n1. Repeat this process for each element in the `target` vector.\n\n1. Return the `ans` vector, which contains the sequence of "`Push`" and "`Pop`" instructions required to build the `target` array.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n vector<string> buildArray(vector<int>& target, int n) {\n vector<string> ans; // Initialize a vector of strings to store the result.\n int i = 1; // Initialize an integer \'i\' to represent the current number.\n\n // Iterate through each element \'a\' in the \'target\' vector.\n for (auto a : target) {\n // Check if \'i\' is less than \'a\' and perform the following steps if true:\n while (i < a) {\n ans.push_back("Push"); // Simulate pushing the current number onto the stack.\n ans.push_back("Pop"); // Simulate popping an element from the stack.\n i++; // Move to the next number.\n }\n\n ans.push_back("Push"); // Simulate pushing \'a\' onto the stack.\n i++; // Move to the next number.\n }\n\n return ans; // Return the \'ans\' vector containing the sequence of "Push" and "Pop" instructions.\n }\n};\n\n\n```\n```C []\n\n\n/**\n * Function to build an array with stack operations.\n * @param target: A vector containing the target array to be built.\n * @param n: An integer representing the size of the target array.\n * @return: A vector of strings containing the sequence of stack operations.\n */\nchar ** buildArray(int* target, int targetSize, int n, int* returnSize) {\n // Initialize a vector of strings to store the result.\n char **ans = (char **)malloc(2 * n * sizeof(char *));\n \n int i = 1; // Initialize an integer \'i\' to represent the current number.\n int idx = 0; // Initialize an index to track the position in the \'ans\' array.\n \n // Iterate through each element \'a\' in the \'target\' array.\n for (int j = 0; j < targetSize; j++) {\n int a = target[j];\n \n // Check if \'i\' is less than \'a\' and perform the following steps if true:\n while (i < a) {\n ans[idx++] = strdup("Push"); // Simulate pushing the current number onto the stack.\n ans[idx++] = strdup("Pop"); // Simulate popping an element from the stack.\n i++; // Move to the next number.\n }\n\n ans[idx++] = strdup("Push"); // Simulate pushing \'a\' onto the stack.\n i++; // Move to the next number.\n }\n \n *returnSize = idx; // Set the return size to the number of operations performed.\n return ans; // Return the \'ans\' array containing the sequence of stack operations.\n}\n\n\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<String> buildArray(int[] target, int n) {\n List<String> ans = new ArrayList<>();\n int i = 1;\n\n for (int a : target) {\n while (i < a) {\n ans.add("Push");\n ans.add("Pop");\n i++;\n }\n\n ans.add("Push");\n i++;\n }\n\n return ans;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def buildArray(self, target, n):\n ans = []\n i = 1\n\n for a in target:\n while i < a:\n ans.append("Push")\n ans.append("Pop")\n i += 1\n\n ans.append("Push")\n i += 1\n\n return ans\n\n\n```\n\n```javascript []\nvar buildArray = function (target, n) {\n let ans = [];\n let i = 1;\n\n for (let a of target) {\n while (i < a) {\n ans.push("Push");\n ans.push("Pop");\n i++;\n }\n\n ans.push("Push");\n i++;\n }\n\n return ans;\n};\n\n\n```\n\n---\n\n#### ***Approach 2 (2 pointer)***\n1. Create an empty vector `ans` to store the sequence of "`Push`" and "Pop" instructions.\n\n1. Initialize `temp` `to` 0, which will be used to track the current index in the `target` vector, and `i` to `1`, representing the current number to be pushed.\n\n1. Enter a while loop that continues until `temp` is less than the size of the target vector. This loop is used to iterate through the elements of the target vector.\n\n1. Inside the loop, check if the element at the current index in the `target` vector (`target[temp]`) is equal to `i`. This check compares the current number to be pushed (`i`) with the target number at index `temp`.\n\n1. If they are equal, it means that the current number should be pushed without popping. So, add "`Push`" to the `ans` vector and increment `temp` to move to the next `target` number in the target vector.\n\n1. If the numbers are not equal, it means that a number is skipped. In this case, add "`Push`" and "`Pop`" to the `ans` vector to simulate pushing and popping an element from the stack. No need to increment `temp` in this case.\n\n1. Increment `i` to move to the next number.\n\n1. Continue this process until all elements in the target vector have been processed.\n\n1. Finally, return the ans vector containing the sequence of "`Push`" and "`Pop`" instructions that, when executed, would transform an empty stack into the specified `target` array.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<string> buildArray(vector<int>& target, int n) {\n vector<string> ans; // Initialize a vector of strings to store the result.\n int temp = 0; // Initialize a temporary variable to keep track of the elements in the \'target\' array.\n int i = 1; // Initialize an integer \'i\' to represent the current number.\n\n // Continue the loop until all elements in the \'target\' array are processed.\n while (temp < target.size()) {\n if (target[temp] == i) {\n ans.push_back("Push"); // Simulate pushing the current number onto the stack.\n temp++; // Move to the next element in the \'target\' array.\n } else {\n ans.push_back("Push"); // Simulate pushing the current number onto the stack.\n ans.push_back("Pop"); // Simulate popping an element from the stack (even though it\'s not the target element).\n }\n i++; // Move to the next number.\n }\n\n return ans; // Return the \'ans\' vector containing the sequence of "Push" and "Pop" instructions.\n }\n};\n\n\n\n```\n```C []\n\n\n\nclass Solution {\npublic:\n std::vector<std::string> buildArray(std::vector<int>& target, int n) {\n std::vector<std::string> ans;\n int temp = 0;\n int i = 1;\n\n while (temp < target.size()) {\n if (target[temp] == i) {\n ans.push_back("Push");\n temp++;\n } else {\n ans.push_back("Push");\n ans.push_back("Pop");\n }\n i++;\n }\n\n return ans;\n }\n};\n\n\n\n```\n```Java []\n\n\nclass Solution {\n public List<String> buildArray(int[] target, int n) {\n List<String> ans = new ArrayList<>();\n int temp = 0;\n int i = 1;\n\n while (temp < target.length) {\n if (target[temp] == i) {\n ans.add("Push");\n temp++;\n } else {\n ans.add("Push");\n ans.add("Pop");\n }\n i++;\n }\n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def buildArray(self, target, n):\n ans = []\n temp = 0\n i = 1\n\n while temp < len(target):\n if target[temp] == i:\n ans.append("Push")\n temp += 1\n else:\n ans.append("Push")\n ans.append("Pop")\n i += 1\n\n return ans\n\n\n```\n\n```javascript []\nvar buildArray = function (target, n) {\n let ans = [];\n let temp = 0;\n let i = 1;\n\n while (temp < target.length) {\n if (target[temp] === i) {\n ans.push("Push");\n temp++;\n } else {\n ans.push("Push");\n ans.push("Pop");\n }\n i++;\n }\n\n return ans;\n};\n\n\n```\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 4 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || 2 Approaches || EXPLAINED🔥 | build-an-array-with-stack-operations | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Brute Force)***\n\n\n1. We initialize an empty vector of strings called `ans`, which will store the sequence of "`Push`" and "`Pop`" instructions.\n\n1. We also initialize an integer `i` to `1`, which represents the current number we\'re considering.\n\n1. We use a for loop to iterate through each element `a` in the `target` vector.\n\n1. Inside the loop, we use a while loop to check if `i` is less than `a`. If it is, we perform the following steps:\n\n - Add "`Push`" to the `ans` vector to simulate pushing the current number onto the stack.\n - Add "`Pop`" to the `ans` vector to simulate popping an element from the stack.\n - Increment `i` to move to the next number.\n1. After the while loop, we add "`Push`" to the `ans` vector to simulate pushing the next number onto the stack.\n\n1. Finally, we increment `i` to move to the next number.\n\n1. Repeat this process for each element in the `target` vector.\n\n1. Return the `ans` vector, which contains the sequence of "`Push`" and "`Pop`" instructions required to build the `target` array.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n vector<string> buildArray(vector<int>& target, int n) {\n vector<string> ans; // Initialize a vector of strings to store the result.\n int i = 1; // Initialize an integer \'i\' to represent the current number.\n\n // Iterate through each element \'a\' in the \'target\' vector.\n for (auto a : target) {\n // Check if \'i\' is less than \'a\' and perform the following steps if true:\n while (i < a) {\n ans.push_back("Push"); // Simulate pushing the current number onto the stack.\n ans.push_back("Pop"); // Simulate popping an element from the stack.\n i++; // Move to the next number.\n }\n\n ans.push_back("Push"); // Simulate pushing \'a\' onto the stack.\n i++; // Move to the next number.\n }\n\n return ans; // Return the \'ans\' vector containing the sequence of "Push" and "Pop" instructions.\n }\n};\n\n\n```\n```C []\n\n\n/**\n * Function to build an array with stack operations.\n * @param target: A vector containing the target array to be built.\n * @param n: An integer representing the size of the target array.\n * @return: A vector of strings containing the sequence of stack operations.\n */\nchar ** buildArray(int* target, int targetSize, int n, int* returnSize) {\n // Initialize a vector of strings to store the result.\n char **ans = (char **)malloc(2 * n * sizeof(char *));\n \n int i = 1; // Initialize an integer \'i\' to represent the current number.\n int idx = 0; // Initialize an index to track the position in the \'ans\' array.\n \n // Iterate through each element \'a\' in the \'target\' array.\n for (int j = 0; j < targetSize; j++) {\n int a = target[j];\n \n // Check if \'i\' is less than \'a\' and perform the following steps if true:\n while (i < a) {\n ans[idx++] = strdup("Push"); // Simulate pushing the current number onto the stack.\n ans[idx++] = strdup("Pop"); // Simulate popping an element from the stack.\n i++; // Move to the next number.\n }\n\n ans[idx++] = strdup("Push"); // Simulate pushing \'a\' onto the stack.\n i++; // Move to the next number.\n }\n \n *returnSize = idx; // Set the return size to the number of operations performed.\n return ans; // Return the \'ans\' array containing the sequence of stack operations.\n}\n\n\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public List<String> buildArray(int[] target, int n) {\n List<String> ans = new ArrayList<>();\n int i = 1;\n\n for (int a : target) {\n while (i < a) {\n ans.add("Push");\n ans.add("Pop");\n i++;\n }\n\n ans.add("Push");\n i++;\n }\n\n return ans;\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def buildArray(self, target, n):\n ans = []\n i = 1\n\n for a in target:\n while i < a:\n ans.append("Push")\n ans.append("Pop")\n i += 1\n\n ans.append("Push")\n i += 1\n\n return ans\n\n\n```\n\n```javascript []\nvar buildArray = function (target, n) {\n let ans = [];\n let i = 1;\n\n for (let a of target) {\n while (i < a) {\n ans.push("Push");\n ans.push("Pop");\n i++;\n }\n\n ans.push("Push");\n i++;\n }\n\n return ans;\n};\n\n\n```\n\n---\n\n#### ***Approach 2 (2 pointer)***\n1. Create an empty vector `ans` to store the sequence of "`Push`" and "Pop" instructions.\n\n1. Initialize `temp` `to` 0, which will be used to track the current index in the `target` vector, and `i` to `1`, representing the current number to be pushed.\n\n1. Enter a while loop that continues until `temp` is less than the size of the target vector. This loop is used to iterate through the elements of the target vector.\n\n1. Inside the loop, check if the element at the current index in the `target` vector (`target[temp]`) is equal to `i`. This check compares the current number to be pushed (`i`) with the target number at index `temp`.\n\n1. If they are equal, it means that the current number should be pushed without popping. So, add "`Push`" to the `ans` vector and increment `temp` to move to the next `target` number in the target vector.\n\n1. If the numbers are not equal, it means that a number is skipped. In this case, add "`Push`" and "`Pop`" to the `ans` vector to simulate pushing and popping an element from the stack. No need to increment `temp` in this case.\n\n1. Increment `i` to move to the next number.\n\n1. Continue this process until all elements in the target vector have been processed.\n\n1. Finally, return the ans vector containing the sequence of "`Push`" and "`Pop`" instructions that, when executed, would transform an empty stack into the specified `target` array.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<string> buildArray(vector<int>& target, int n) {\n vector<string> ans; // Initialize a vector of strings to store the result.\n int temp = 0; // Initialize a temporary variable to keep track of the elements in the \'target\' array.\n int i = 1; // Initialize an integer \'i\' to represent the current number.\n\n // Continue the loop until all elements in the \'target\' array are processed.\n while (temp < target.size()) {\n if (target[temp] == i) {\n ans.push_back("Push"); // Simulate pushing the current number onto the stack.\n temp++; // Move to the next element in the \'target\' array.\n } else {\n ans.push_back("Push"); // Simulate pushing the current number onto the stack.\n ans.push_back("Pop"); // Simulate popping an element from the stack (even though it\'s not the target element).\n }\n i++; // Move to the next number.\n }\n\n return ans; // Return the \'ans\' vector containing the sequence of "Push" and "Pop" instructions.\n }\n};\n\n\n\n```\n```C []\n\n\n\nclass Solution {\npublic:\n std::vector<std::string> buildArray(std::vector<int>& target, int n) {\n std::vector<std::string> ans;\n int temp = 0;\n int i = 1;\n\n while (temp < target.size()) {\n if (target[temp] == i) {\n ans.push_back("Push");\n temp++;\n } else {\n ans.push_back("Push");\n ans.push_back("Pop");\n }\n i++;\n }\n\n return ans;\n }\n};\n\n\n\n```\n```Java []\n\n\nclass Solution {\n public List<String> buildArray(int[] target, int n) {\n List<String> ans = new ArrayList<>();\n int temp = 0;\n int i = 1;\n\n while (temp < target.length) {\n if (target[temp] == i) {\n ans.add("Push");\n temp++;\n } else {\n ans.add("Push");\n ans.add("Pop");\n }\n i++;\n }\n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def buildArray(self, target, n):\n ans = []\n temp = 0\n i = 1\n\n while temp < len(target):\n if target[temp] == i:\n ans.append("Push")\n temp += 1\n else:\n ans.append("Push")\n ans.append("Pop")\n i += 1\n\n return ans\n\n\n```\n\n```javascript []\nvar buildArray = function (target, n) {\n let ans = [];\n let temp = 0;\n let i = 1;\n\n while (temp < target.length) {\n if (target[temp] === i) {\n ans.push("Push");\n temp++;\n } else {\n ans.push("Push");\n ans.push("Pop");\n }\n i++;\n }\n\n return ans;\n};\n\n\n```\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 4 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
Python one line | build-an-array-with-stack-operations | 0 | 1 | ```python []\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n return [\n x\n for i in range(1, target[-1] + 1)\n for x in ["Push"] + ["Pop"] * (i not in set(target))\n ]\n\n``` | 3 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
Python one line | build-an-array-with-stack-operations | 0 | 1 | ```python []\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n return [\n x\n for i in range(1, target[-1] + 1)\n for x in ["Push"] + ["Pop"] * (i not in set(target))\n ]\n\n``` | 3 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
✅ 99.80% Iterative Set Stack Simulation | build-an-array-with-stack-operations | 1 | 1 | # Intuition\nGiven a target list of numbers and a stream of numbers from 1 to $ n $, the goal is to simulate a stack to recreate the target list using just "Push" and "Pop" operations. The intuitive approach is to push each number from the stream onto the stack. If the number is not in the target list, we pop it off immediately. We continue this process until we\'ve constructed the target list in the stack.\n\n# Live Coding + Comments\nhttps://youtu.be/ortH58dpXlE?si=ST32gpGDy-QoorTr\n\n# Approach\n1. **Set Conversion**: Convert the target list to a set. This conversion allows us to check the existence of a number in the target list in constant time, $O(1)$. \n2. **Iterative Process**: Iterate through the numbers from 1 up to the last element of the target list.\n - If the current number is in the target set, we only "Push".\n - If the current number is not in the target set, we "Push" and then "Pop" immediately, indicating that the number is not required in the final stack.\n3. **Completion**: Once we\'ve reached the last number in the target list, we can be sure that we\'ve constructed the target list in the stack and stop our operations.\n\n# Complexity\n- **Time complexity**: $O(n)$. The iteration goes up to the last element of the target list, which could be as large as $n$. Each operation (push/pop) is $O(1)$.\n- **Space complexity**: $O(n)$. The combined space required for the `target_set` and the `result` list is linear with respect to $n$.\n\n---\n\n# Code\n``` Python []\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n target_set = set(target)\n result = []\n \n for i in range(1, target[-1] + 1):\n if i in target_set:\n result.append("Push")\n else:\n result.append("Push")\n result.append("Pop")\n \n return result\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<std::string> buildArray(std::vector<int>& target, int n) {\n std::unordered_set<int> target_set(target.begin(), target.end());\n std::vector<std::string> result;\n\n for (int i = 1; i <= target.back(); ++i) {\n if (target_set.find(i) != target_set.end()) {\n result.push_back("Push");\n } else {\n result.push_back("Push");\n result.push_back("Pop");\n }\n }\n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<String> buildArray(int[] target, int n) {\n HashSet<Integer> targetSet = new HashSet<>();\n for (int num : target) {\n targetSet.add(num);\n }\n\n List<String> result = new ArrayList<>();\n for (int i = 1; i <= target[target.length - 1]; i++) {\n if (targetSet.contains(i)) {\n result.add("Push");\n } else {\n result.add("Push");\n result.add("Pop");\n }\n }\n return result;\n }\n}\n```\n``` Go []\nfunc buildArray(target []int, n int) []string {\n targetSet := make(map[int]bool)\n for _, num := range target {\n targetSet[num] = true\n }\n\n var result []string\n for i := 1; i <= target[len(target)-1]; i++ {\n if targetSet[i] {\n result = append(result, "Push")\n } else {\n result = append(result, "Push")\n result = append(result, "Pop")\n }\n }\n return result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn build_array(target: Vec<i32>, n: i32) -> Vec<String> {\n let target_set: std::collections::HashSet<_> = target.iter().cloned().collect();\n let mut result = vec![];\n\n for i in 1..=*target.last().unwrap() {\n if target_set.contains(&i) {\n result.push("Push".to_string());\n } else {\n result.push("Push".to_string());\n result.push("Pop".to_string());\n }\n }\n result\n }\n}\n```\n``` PHP []\nclass Solution {\n\nfunction buildArray($target, $n) {\n $targetSet = array_flip($target);\n $result = [];\n\n for ($i = 1; $i <= end($target); $i++) {\n if (isset($targetSet[$i])) {\n $result[] = "Push";\n } else {\n $result[] = "Push";\n $result[] = "Pop";\n }\n }\n return $result;\n}\n\n}\n```\n``` JavaScript []\nfunction buildArray(target, n) {\n const targetSet = new Set(target);\n const result = [];\n\n for (let i = 1; i <= target[target.length - 1]; i++) {\n if (targetSet.has(i)) {\n result.push("Push");\n } else {\n result.push("Push");\n result.push("Pop");\n }\n }\n return result;\n}\n```\n``` C# []\npublic class Solution {\n public IList<string> BuildArray(int[] target, int n) {\n HashSet<int> targetSet = new HashSet<int>(target);\n List<string> result = new List<string>();\n\n for (int i = 1; i <= target[target.Length - 1]; i++) {\n if (targetSet.Contains(i)) {\n result.Add("Push");\n } else {\n result.Add("Push");\n result.Add("Pop");\n }\n }\n return result;\n }\n}\n```\n\n# Performance\n\n| Language | Execution Time (ms) | Memory (MB) |\n|------------|---------------------|-------------|\n| C++ | 0 ms | 8.4 MB |\n| Java | 0 ms | 42 MB |\n| Rust | 1 ms | 2.2 MB |\n| Go | 2 ms | 2.4 MB |\n| PHP | 11 ms | 18.9 MB |\n| Python3 | 26 ms | 16.2 MB |\n| JavaScript | 60 ms | 42.5 MB |\n| C# | 157 ms | 46 MB |\n\n\n\n\n# Why is it optimal?\nThis approach is optimal because:\n1. It avoids unnecessary iterations beyond the last element of the target list. This is significant especially when the last element of the target list is much smaller than $ n $.\n2. By converting the target list to a set, we are able to perform constant time lookups, ensuring that our solution is efficient.\n3. The solution leverages the properties of the stack and the strictly increasing nature of the target list to minimize the number of operations and achieve the desired result. | 15 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
✅ 99.80% Iterative Set Stack Simulation | build-an-array-with-stack-operations | 1 | 1 | # Intuition\nGiven a target list of numbers and a stream of numbers from 1 to $ n $, the goal is to simulate a stack to recreate the target list using just "Push" and "Pop" operations. The intuitive approach is to push each number from the stream onto the stack. If the number is not in the target list, we pop it off immediately. We continue this process until we\'ve constructed the target list in the stack.\n\n# Live Coding + Comments\nhttps://youtu.be/ortH58dpXlE?si=ST32gpGDy-QoorTr\n\n# Approach\n1. **Set Conversion**: Convert the target list to a set. This conversion allows us to check the existence of a number in the target list in constant time, $O(1)$. \n2. **Iterative Process**: Iterate through the numbers from 1 up to the last element of the target list.\n - If the current number is in the target set, we only "Push".\n - If the current number is not in the target set, we "Push" and then "Pop" immediately, indicating that the number is not required in the final stack.\n3. **Completion**: Once we\'ve reached the last number in the target list, we can be sure that we\'ve constructed the target list in the stack and stop our operations.\n\n# Complexity\n- **Time complexity**: $O(n)$. The iteration goes up to the last element of the target list, which could be as large as $n$. Each operation (push/pop) is $O(1)$.\n- **Space complexity**: $O(n)$. The combined space required for the `target_set` and the `result` list is linear with respect to $n$.\n\n---\n\n# Code\n``` Python []\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n target_set = set(target)\n result = []\n \n for i in range(1, target[-1] + 1):\n if i in target_set:\n result.append("Push")\n else:\n result.append("Push")\n result.append("Pop")\n \n return result\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<std::string> buildArray(std::vector<int>& target, int n) {\n std::unordered_set<int> target_set(target.begin(), target.end());\n std::vector<std::string> result;\n\n for (int i = 1; i <= target.back(); ++i) {\n if (target_set.find(i) != target_set.end()) {\n result.push_back("Push");\n } else {\n result.push_back("Push");\n result.push_back("Pop");\n }\n }\n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public List<String> buildArray(int[] target, int n) {\n HashSet<Integer> targetSet = new HashSet<>();\n for (int num : target) {\n targetSet.add(num);\n }\n\n List<String> result = new ArrayList<>();\n for (int i = 1; i <= target[target.length - 1]; i++) {\n if (targetSet.contains(i)) {\n result.add("Push");\n } else {\n result.add("Push");\n result.add("Pop");\n }\n }\n return result;\n }\n}\n```\n``` Go []\nfunc buildArray(target []int, n int) []string {\n targetSet := make(map[int]bool)\n for _, num := range target {\n targetSet[num] = true\n }\n\n var result []string\n for i := 1; i <= target[len(target)-1]; i++ {\n if targetSet[i] {\n result = append(result, "Push")\n } else {\n result = append(result, "Push")\n result = append(result, "Pop")\n }\n }\n return result\n}\n```\n``` Rust []\nimpl Solution {\n pub fn build_array(target: Vec<i32>, n: i32) -> Vec<String> {\n let target_set: std::collections::HashSet<_> = target.iter().cloned().collect();\n let mut result = vec![];\n\n for i in 1..=*target.last().unwrap() {\n if target_set.contains(&i) {\n result.push("Push".to_string());\n } else {\n result.push("Push".to_string());\n result.push("Pop".to_string());\n }\n }\n result\n }\n}\n```\n``` PHP []\nclass Solution {\n\nfunction buildArray($target, $n) {\n $targetSet = array_flip($target);\n $result = [];\n\n for ($i = 1; $i <= end($target); $i++) {\n if (isset($targetSet[$i])) {\n $result[] = "Push";\n } else {\n $result[] = "Push";\n $result[] = "Pop";\n }\n }\n return $result;\n}\n\n}\n```\n``` JavaScript []\nfunction buildArray(target, n) {\n const targetSet = new Set(target);\n const result = [];\n\n for (let i = 1; i <= target[target.length - 1]; i++) {\n if (targetSet.has(i)) {\n result.push("Push");\n } else {\n result.push("Push");\n result.push("Pop");\n }\n }\n return result;\n}\n```\n``` C# []\npublic class Solution {\n public IList<string> BuildArray(int[] target, int n) {\n HashSet<int> targetSet = new HashSet<int>(target);\n List<string> result = new List<string>();\n\n for (int i = 1; i <= target[target.Length - 1]; i++) {\n if (targetSet.Contains(i)) {\n result.Add("Push");\n } else {\n result.Add("Push");\n result.Add("Pop");\n }\n }\n return result;\n }\n}\n```\n\n# Performance\n\n| Language | Execution Time (ms) | Memory (MB) |\n|------------|---------------------|-------------|\n| C++ | 0 ms | 8.4 MB |\n| Java | 0 ms | 42 MB |\n| Rust | 1 ms | 2.2 MB |\n| Go | 2 ms | 2.4 MB |\n| PHP | 11 ms | 18.9 MB |\n| Python3 | 26 ms | 16.2 MB |\n| JavaScript | 60 ms | 42.5 MB |\n| C# | 157 ms | 46 MB |\n\n\n\n\n# Why is it optimal?\nThis approach is optimal because:\n1. It avoids unnecessary iterations beyond the last element of the target list. This is significant especially when the last element of the target list is much smaller than $ n $.\n2. By converting the target list to a set, we are able to perform constant time lookups, ensuring that our solution is efficient.\n3. The solution leverages the properties of the stack and the strictly increasing nature of the target list to minimize the number of operations and achieve the desired result. | 15 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
✅ Simulation Approach | 99.60% Faster | Nov Daily (Annoying desc -> Easy Q) ✅ | build-an-array-with-stack-operations | 0 | 1 | # Intuition\nWhen you first read the problems description, it makes like 0 sense. Once you look at some of the test cases and constraints though, this question becomes a lot easier. First we see that every time we want to keep a value we only add a single "Push" and any time we don\'t want to, we add "Push" "Pop" and second, we see that we\'re strictly increasing. This is key.\n\n# Approach\nNow that we know we\'re only increasing, we can iterate through the values 1 to n and check if the current value == the current value in target array, move i forward. If not, add and remove the value/show you did. Lastly check if i == len of target and return if so.\n\n# Complexity\n- Time & Space complexity:\n$$O(n)$$ where n is the largest value in the range given\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n # continue while len(stack) != len(target)\n # make a res array\n # make a pointer to first elem in target once n == pointer add\n\n res = []\n i = 0\n\n for curr in range(1, n+1):\n if curr == target[i]:\n res.append("Push")\n i += 1\n else:\n res.append("Push")\n res.append("Pop")\n if i == len(target): return res\n``` | 1 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
✅ Simulation Approach | 99.60% Faster | Nov Daily (Annoying desc -> Easy Q) ✅ | build-an-array-with-stack-operations | 0 | 1 | # Intuition\nWhen you first read the problems description, it makes like 0 sense. Once you look at some of the test cases and constraints though, this question becomes a lot easier. First we see that every time we want to keep a value we only add a single "Push" and any time we don\'t want to, we add "Push" "Pop" and second, we see that we\'re strictly increasing. This is key.\n\n# Approach\nNow that we know we\'re only increasing, we can iterate through the values 1 to n and check if the current value == the current value in target array, move i forward. If not, add and remove the value/show you did. Lastly check if i == len of target and return if so.\n\n# Complexity\n- Time & Space complexity:\n$$O(n)$$ where n is the largest value in the range given\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n # continue while len(stack) != len(target)\n # make a res array\n # make a pointer to first elem in target once n == pointer add\n\n res = []\n i = 0\n\n for curr in range(1, n+1):\n if curr == target[i]:\n res.append("Push")\n i += 1\n else:\n res.append("Push")\n res.append("Pop")\n if i == len(target): return res\n``` | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
Understandable python using stacks | build-an-array-with-stack-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n l=[]\n k=[]\n for i in range(1,n+1):\n if i in target:\n k.append(i)\n l.append("Push")\n if k==target:\n return l\n break \n else:\n l.append("Push")\n l.append("Pop") \n \n return l\n``` | 1 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
Understandable python using stacks | build-an-array-with-stack-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n l=[]\n k=[]\n for i in range(1,n+1):\n if i in target:\n k.append(i)\n l.append("Push")\n if k==target:\n return l\n break \n else:\n l.append("Push")\n l.append("Pop") \n \n return l\n``` | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
Beats 97.44% of other users🔥 | build-an-array-with-stack-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n list1=[x for x in range(1,n+1)]\n list2=[]\n list3=[]\n for i in range(len(list1)):\n list2.append("Push")\n list3.append(list1[i])\n if(list1[i] not in target):\n list2.append("Pop")\n list3.pop()\n elif(list3==target):\n break\n return list2\n\n \n``` | 1 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
Beats 97.44% of other users🔥 | build-an-array-with-stack-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n list1=[x for x in range(1,n+1)]\n list2=[]\n list3=[]\n for i in range(len(list1)):\n list2.append("Push")\n list3.append(list1[i])\n if(list1[i] not in target):\n list2.append("Pop")\n list3.pop()\n elif(list3==target):\n break\n return list2\n\n \n``` | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
understandable code | build-an-array-with-stack-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n l=[]\n for i in range(1,target[-1]+1):\n l.append("Push")\n if i not in target:\n l.append("Pop")\n return l\n``` | 1 | You are given an integer array `target` and an integer `n`.
You have an empty stack with the two following operations:
* **`"Push "`**: pushes an integer to the top of the stack.
* **`"Pop "`**: removes the integer on the top of the stack.
You also have a stream of the integers in the range `[1, n]`.
Use the two stack operations to make the numbers in the stack (from the bottom to the top) equal to `target`. You should follow the following rules:
* If the stream of the integers is not empty, pick the next integer from the stream and push it to the top of the stack.
* If the stack is not empty, pop the integer at the top of the stack.
* If, at any moment, the elements in the stack (from the bottom to the top) are equal to `target`, do not read new integers from the stream and do not do more operations on the stack.
Return _the stack operations needed to build_ `target` following the mentioned rules. If there are multiple valid answers, return **any of them**.
**Example 1:**
**Input:** target = \[1,3\], n = 3
**Output:** \[ "Push ", "Push ", "Pop ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Pop the integer on the top of the stack. s = \[1\].
Read 3 from the stream and push it to the stack. s = \[1,3\].
**Example 2:**
**Input:** target = \[1,2,3\], n = 3
**Output:** \[ "Push ", "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Read 3 from the stream and push it to the stack. s = \[1,2,3\].
**Example 3:**
**Input:** target = \[1,2\], n = 4
**Output:** \[ "Push ", "Push "\]
**Explanation:** Initially the stack s is empty. The last element is the top of the stack.
Read 1 from the stream and push it to the stack. s = \[1\].
Read 2 from the stream and push it to the stack. s = \[1,2\].
Since the stack (from the bottom to the top) is equal to target, we stop the stack operations.
The answers that read integer 3 from the stream are not accepted.
**Constraints:**
* `1 <= target.length <= 100`
* `1 <= n <= 100`
* `1 <= target[i] <= n`
* `target` is strictly increasing. | Check the bits one by one whether they need to be flipped. |
understandable code | build-an-array-with-stack-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildArray(self, target: List[int], n: int) -> List[str]:\n l=[]\n for i in range(1,target[-1]+1):\n l.append("Push")\n if i not in target:\n l.append("Pop")\n return l\n``` | 1 | In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has `n` empty baskets, the `ith` basket is at `position[i]`, Morty has `m` balls and needs to distribute the balls into the baskets such that the **minimum magnetic force** between any two balls is **maximum**.
Rick stated that magnetic force between two different balls at positions `x` and `y` is `|x - y|`.
Given the integer array `position` and the integer `m`. Return _the required force_.
**Example 1:**
**Input:** position = \[1,2,3,4,7\], m = 3
**Output:** 3
**Explanation:** Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs \[3, 3, 6\]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
**Example 2:**
**Input:** position = \[5,4,3,2,1,1000000000\], m = 2
**Output:** 999999999
**Explanation:** We can use baskets 1 and 1000000000.
**Constraints:**
* `n == position.length`
* `2 <= n <= 105`
* `1 <= position[i] <= 109`
* All integers in `position` are **distinct**.
* `2 <= m <= position.length` | Use “Push” for numbers to be kept in target array and [“Push”, “Pop”] for numbers to be discarded. |
O(n**2) straightforward python solution. | count-triplets-that-can-form-two-arrays-of-equal-xor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\na == b means a ^ b == 0\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\niterative two pointers, the first reprersent the start search position of a, the second represent the end search position of b. Then calculate bitwise XOR. If result in 0, that means we can start anywhere for b in between.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n**2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def countTriplets(self, arr: List[int]) -> int:\n n = len(arr)\n ans = 0\n\n for i in range(n):\n bitcount = arr[i]\n for j in range(i+1, n):\n bitcount ^= arr[j]\n if bitcount == 0:\n ans += (j-i)\n return ans\n``` | 0 | Given an array of integers `arr`.
We want to select three indices `i`, `j` and `k` where `(0 <= i < j <= k < arr.length)`.
Let's define `a` and `b` as follows:
* `a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]`
* `b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]`
Note that **^** denotes the **bitwise-xor** operation.
Return _the number of triplets_ (`i`, `j` and `k`) Where `a == b`.
**Example 1:**
**Input:** arr = \[2,3,1,6,7\]
**Output:** 4
**Explanation:** The triplets are (0,1,2), (0,2,2), (2,3,4) and (2,4,4)
**Example 2:**
**Input:** arr = \[1,1,1,1,1\]
**Output:** 10
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[i] <= 108` | As long as there are at least (n - 1) connections, there is definitely a way to connect all computers. Use DFS to determine the number of isolated computer clusters. |
O(n**2) straightforward python solution. | count-triplets-that-can-form-two-arrays-of-equal-xor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\na == b means a ^ b == 0\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\niterative two pointers, the first reprersent the start search position of a, the second represent the end search position of b. Then calculate bitwise XOR. If result in 0, that means we can start anywhere for b in between.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n**2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def countTriplets(self, arr: List[int]) -> int:\n n = len(arr)\n ans = 0\n\n for i in range(n):\n bitcount = arr[i]\n for j in range(i+1, n):\n bitcount ^= arr[j]\n if bitcount == 0:\n ans += (j-i)\n return ans\n``` | 0 | There are `n` oranges in the kitchen and you decided to eat some of these oranges every day as follows:
* Eat one orange.
* If the number of remaining oranges `n` is divisible by `2` then you can eat `n / 2` oranges.
* If the number of remaining oranges `n` is divisible by `3` then you can eat `2 * (n / 3)` oranges.
You can only choose one of the actions per day.
Given the integer `n`, return _the minimum number of days to eat_ `n` _oranges_.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2\*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
**Example 2:**
**Input:** n = 6
**Output:** 3
**Explanation:** You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2\*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
**Constraints:**
* `1 <= n <= 2 * 109` | We are searching for sub-array of length ≥ 2 and we need to split it to 2 non-empty arrays so that the xor of the first array is equal to the xor of the second array. This is equivalent to searching for sub-array with xor = 0. Keep the prefix xor of arr in another array, check the xor of all sub-arrays in O(n^2), if the xor of sub-array of length x is 0 add x-1 to the answer. |
😯 Intuitive & Readable: Recursive, OO + Functional, Depth-First Tree Traversal Edge Count [Python] | minimum-time-to-collect-all-apples-in-a-tree | 0 | 1 | <i><span style="color:dodgerblue">Please upvote if you find this post useful.</span> \uD83D\uDE4F</i>\n\n---\n\n# Intuition\n\nThe essence of this problem can be simply stated as:\n\n> Count the number of edges that need to be traversed to reach all apples.\n\nThe requirement to count the "time" including "coming back" simply requires doubling the number of edges found.\n\n# Approach\n\nThe problem can easily be broken down such that the solution for any node / subtree is a function of the results for its child nodes / subtrees.\n\nWhen looking at the root of any subtree, any immediate child which has an apple itself *or* any edges beneath it leading to apples, adds 1 to the total (counting the edge to the child), *as well as* the count of edges leading to apples in *the child\'s* subtree. Using this recursive definition of the count makes it relatively simple to write a recursive function defining the count for a subtree. I\'ve expressed this as a functional one-liner in Python using `for` comprehensions and `sum()`.\n\n(Note: At first the `Node` class had `children` instead of `neighbours`, and `count_edges_leading_to_apples()` was simpler due to not having the `from_node` parameter. However, one of the test cases connected a child in a non-child fashion from the perspective of the root (which is fine because, as the problem definition says, the tree is non-directional). That resulted in the need to store bi-directional edges, which then leads to needing the `from_node` parameter to avoid walking back up the tree.)\n\n# Complexity\n- Time complexity: $$O(n)$$ ~ I don\'t believe there\'s any way to avoid traversing the whole tree with this problem, as we need to know whether any leaf has an apple.\n\n- Space complexity: $$O(n)$$ ~ From the creation of `Node` objects with their `neighbours` lists.\n\n# Code\n```\n\nclass Node:\n has_apple: bool\n neighbours: List[\'Node\']\n\n def __init__(self, has_apple: bool):\n self.has_apple = has_apple\n self.neighbours = []\n\n def count_edges_leading_to_apples(self, from_node: Optional[\'Node\'] = None) -> int:\n return sum(\n (subtree_count + 1) if subtree_count != 0 or child.has_apple else 0\n for child, subtree_count in ((n, n.count_edges_leading_to_apples(self))\n for n in self.neighbours if n is not from_node)\n )\n\n\nclass Solution:\n def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:\n # Create a tree of bi-directionally connected Nodes:\n nodes = [Node(ha) for ha in hasApple]\n for a, b in edges:\n na, nb = nodes[a], nodes[b]\n na.neighbours.append(nb)\n nb.neighbours.append(na)\n\n # Calculate the count of edges from the root, x by 2 for "coming back"\n return nodes[0].count_edges_leading_to_apples() * 2\n\n```\n\nIf you find that functional implementation of `count_edges_leading_to_apples()` a little hard to read, here\'s the equivalent procedural version:\n```\n def count_edges_leading_to_apples(self, from_node: Optional[\'Node\'] = None) -> int:\n result = 0\n for child_node in self.neighbours:\n if child_node is not from_node:\n subtree_count = child_node.count_edges_leading_to_apples(from_node=self)\n if subtree_count != 0 or child_node.has_apple:\n result += subtree_count + 1\n return result\n``` | 4 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
FASTEST SIMPLE PYTHON SOLUTION || DFS TRAVERSAL | minimum-time-to-collect-all-apples-in-a-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(V+2E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(V+E)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dfs(self,node,grid,hasApple,visited):\n visited[node]=1\n ct=0\n for i in grid[node]:\n if visited[i]==1:\n continue\n x=self.dfs(i,grid,hasApple,visited)\n if x!=-1:\n ct+=x\n ct+=2\n if ct>0 or hasApple[node]==True:\n return ct\n return -1\n\n\n\n def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:\n grid=[[] for i in range(n)]\n for i, j in edges:\n grid[i].append(j)\n grid[j].append(i)\n visited=[0]*n\n x=self.dfs(0,grid,hasApple,visited)\n if x==-1:\n return 0\n return x\n\n``` | 3 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
✅ Easy python3 solution using DFS (beats 99% on time) ✅ | minimum-time-to-collect-all-apples-in-a-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition is to create a graph from the edges and not consider the input as a straight tree with all nodes in order.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst build the adjacency list from the edges. Then we use DFS to search for apples. For a node, we check all the children, if the result is > 0, then we just add 2 which is the cost to get to that node (we don\'t have to add it in the case of the root node). \n\nIf the cost is 0, it means that none of the children have apples, so we return 2 only if the node at which we are has an apple (also only if we are not at the root).\n\nWe ignore if a node $$N$$ has an apple in the case any of the children of the node $$N$$ also has an apple, since in that case we are sure to pass by the node $$N$$ and get its apple.\n# Complexity\n- Time complexity: $$O(n)$$ since we check $$n$$ nodes\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ because of the $$n$$ nodes that are kept in the recursive call stack\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:\n adj = {}\n\n for x, y in edges:\n if x not in adj:\n adj[x] = []\n if y not in adj:\n adj[y] = []\n adj[x].append(y)\n adj[y].append(x)\n \n def dfs(parent, val):\n c = 0\n\n for neighbour in adj[val]:\n if neighbour != parent:\n c += dfs(val, neighbour)\n\n if c > 0:\n return c + 2 if val > 0 else c\n \n if hasApple[val] and val > 0:\n return 2\n \n return 0\n\n c = dfs(None, 0)\n\n return c\n``` | 1 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
[Python3] [Beats 100%] Linear Time & Space w/ No Hashtable | minimum-time-to-collect-all-apples-in-a-tree | 0 | 1 | # Intuition\n1. Find out every node\'s parent node. \n2. Traverse from each apple upward to the nearest seen node.\n\n# Approach\n1. For every edge, if we have already seen the left vertex, then know that the right vertex must be its child. The same holds for the reverse. We then record that we have seen the right vertex.\n2. Traverse the parents array from the position of an apple until we find a node that has already been seen. This approach will both account for overlap between apples taking the same path, and also reduce runtime as we at most traverse the entire tree once.\n\n# Time Complexity\n1. The runtime for this section is $$O(n)$$ because we traverse edges once.\n2. The runtime for this section is $$O(n)$$ because the outer loop runs from $$1 \\to n$$ and the inner while loop can at most run for another $$O(n)$$ because of the aforementioned stopping once we reach a seen node.\n\n# Space Complexity\nThe memory consumed is $$O(n)$$ because we use two arrays of size $$n$$.\n\n# Code\n```Python\nclass Solution:\n def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:\n res: int = 0\n # edges.sort(key=lambda x: x[0]) not needed for the test cases\n # but is needed if the test cases included unsorted edges\n parents = [-1] * n\n seen = [False] * n\n seen[0] = True\n\n for a, b in edges:\n if seen[a] is True:\n parents[b] = a\n else:\n parents[a] = b\n\n seen[b] = True\n\n seen = [False] * n\n seen[0] = True\n\n for parent in range(1, n): # 0 contributes no time regardless\n if hasApple[parent] is False:\n continue\n \n res += 1\n seen[parent] = True\n parent = parents[parent]\n while not seen[parent]:\n res += 1\n seen[parent] = True\n parent = parents[parent]\n \n return 2 * res\n``` | 1 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
[Python] memorization and prefix sum; Explained | number-of-ways-of-cutting-a-pizza | 0 | 1 | The key to this problem is how to count the number of apples on the region we want to cut.\n\nWe can simply use the prefix sum that help to identify the number of apples between any two index.\n\nTherefore, we need to pre-process the input array, get the prefix sum horizatonally and vertically.\n\nWith the prefix sum array, we can create a dp funtion that get the number of cuts in the region (i, j) to (row - 1, col - 1)\n\n\n```\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n self.r = len(pizza)\n self.c = len(pizza[0])\n \n # Step 1, pre-process the apple array and get the prefix sum\n tot_apples = 0\n self.pfsum_row = []\n self.pfsum_col = []\n \n for i in range(self.r):\n pfr = 0\n pfs_r = [0] * self.c\n pfs_c = [0] * self.c\n for j in range(self.c):\n if i > 0:\n pfs_c[j] += self.pfsum_col[i - 1][j]\n if pizza[i][j] == \'A\':\n pfr += 1\n pfs_c[j] += 1\n tot_apples += 1\n pfs_r[j] = pfr\n self.pfsum_row.append(pfs_r)\n self.pfsum_col.append(pfs_c)\n \n if tot_apples < k:\n return 0\n \n if k == 1:\n return 1\n \n return self.getWays(0, 0, k) % (1000000007)\n \n \n @cache\n def getWays(self, i, j, k):\n if k == 1:\n # if only left one piece for cutting, we just need to check if there is any apple in the region\n found = False\n for c in range(j, self.c):\n apple_in_region = self.pfsum_col[self.r - 1][c]\n if i > 0:\n apple_in_region -= self.pfsum_col[i - 1][c]\n if apple_in_region:\n found = True\n break\n if found:\n return 1\n return 0\n else:\n # horizontally cut\n cannot_cut = True\n nr = i\n t_cnt = 0\n while nr < self.r - 1:\n # find the first row that we can start cutting\n while nr < self.r - 1 and cannot_cut:\n apple_in_region = self.pfsum_row[nr][self.c - 1]\n if j > 0:\n apple_in_region -= self.pfsum_row[nr][j - 1]\n if apple_in_region:\n cannot_cut = False\n else:\n nr += 1\n \n if nr < self.r - 1:\n t_cnt += self.getWays(nr + 1, j, k - 1)\n nr += 1\n \n # vertically cut\n cannot_cut = True\n nc = j\n while nc < self.c - 1:\n # find the first col that we can start cutting\n while nc < self. c - 1 and cannot_cut:\n apple_in_region = self.pfsum_col[self.r - 1][nc]\n if i > 0:\n apple_in_region -= self.pfsum_col[i - 1][nc]\n if apple_in_region:\n cannot_cut = False\n else:\n nc += 1\n \n if nc < self.c - 1:\n t_cnt += self.getWays(i, nc + 1, k - 1)\n nc += 1\n \n return t_cnt\n\n``` | 3 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Clean Code Python | number-of-ways-of-cutting-a-pizza | 0 | 1 | **Please Upvote**\n```\nMOD = 1000000007\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n \n m, n = len(pizza), len(pizza[0])\n \n @lru_cache(None)\n def dfs(k, i = 0, j = 0, res = 0):\n \n if not(0 <= i < m and 0 <= j < n): return 0\n\n for x, y in product(range(i, m),range(j, n)):\n if pizza[x][y] == "A":\n if not k : return 1\n res+= sum(dfs(k-1,X, j) for X in range(x+1, m))\n break\n\n for y,x in product(range(j, n), range(i, m)):\n if pizza[x][y] == "A": \n if not k: return 1\n res+= sum(dfs(k-1, i, Y) for Y in range(y+1, n))\n break\n \n return res % MOD\n \n\n return dfs(k-1) \n``` | 1 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Python 3 Recursion with Memoization | number-of-ways-of-cutting-a-pizza | 0 | 1 | The basic intuition is recursively cut the pizza as the problem requests. After each cut we apply recursively the cut function to the remaining pizza. \n\n### A few ways to reduce time complexity\n- Use memoization (LRU-Caches)\n- Use coordinates of top-left and bottom-right corners to represent current pizza. It is obvious that the remaining pizza will always be a rectangle. This avoids the costs of taking substrings and subarrays.\n- Use a prefix sum to quickly get the number of apples within a rectangular region. This avoids looping through the region.\n\n\n# Code\n```\nclass Solution:\n def ways(self, p: List[str], k: int) -> int:\n m, n = len(p), len(p[0])\n apples = [[0 for _ in range(n+1)] for _ in range(m+1)] \n # number of apples in (0,0) to (i,j)\n apples[1][1] = 0 if p[0][0] == \'.\' else 1\n for j in range(1,n):\n apples[1][j+1] = apples[1][j] if p[0][j] == \'.\' else apples[1][j] + 1\n for i in range(1,m):\n cur_apple = 0 if p[i][0] == \'.\' else 1\n apples[i+1][1] = apples[i][1] + cur_apple\n for j in range(1,n):\n if p[i][j] == \'A\': cur_apple += 1\n apples[i+1][j+1] = apples[i][j+1] + cur_apple\n\n def getApples(x,y,z,w):\n # get the number of apples within range\n # x,y: top-left coordinates of current pizza\n # z,w: bottom-right\n return apples[z+1][w+1] + apples[x][y] - apples[z+1][y] - apples[x][w+1]\n\n @lru_cache(None)\n def cut(c,x,y,z,w):\n # c: number of cuts already cut\n # x,y: top-left coordinates of current pizza\n # z,w: bottom-right\n if c == k - 1:\n return 1 if getApples(x,y,z,w) > 0 else 0\n\n r = 0\n # horizontal cuts\n i = x\n while i < z:\n if getApples(x,y,i,w) > 0: break\n i += 1\n while i < z:\n r += cut(c+1,i+1,y,z,w)\n i += 1\n # vertical cuts\n j = y\n while j < w:\n if getApples(x,y,z,j) > 0: break\n j += 1\n while j < w:\n r += cut(c+1,x,j+1,z,w)\n j += 1\n\n return r\n\n return cut(0,0,0,m-1,n-1)%(10**9+7)\n``` | 1 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
✅Python3✅ DP+PrefSum+Memoization | number-of-ways-of-cutting-a-pizza | 0 | 1 | We can use dynamic programming to solve this problem. Let\'s define dp[i][j][p] as the number of ways to cut the pizza of size (i+1) * (j+1) into p pieces such that every piece contains at least one apple. The base cases are dp[i][j][1] = 1 if there is at least one apple in the pizza[i][j], otherwise dp[i][j][1] = 0.\n\nFor p > 1, we can iterate over all possible cuts in horizontal and vertical directions. For each cut, we split the pizza into two pieces and recursively calculate the number of ways to cut each piece into (p-1) pieces. Then we sum the results for all possible cuts to get dp[i][j][p].\n\nThe final answer is given by dp[0][0][k]. We can calculate dp using a bottom-up approach and memoize the results using a dictionary to avoid recalculating the same subproblems.\n\n# Please Upvote \uD83D\uDE07\n## Python3\n```\nclass Solution:\n MOD = 10**9 + 7\n \n def ways(self, pizza: List[str], k: int) -> int:\n m, n = len(pizza), len(pizza[0])\n apple = [[0] * (n+1) for _ in range(m+1)]\n for i in range(m-1, -1, -1):\n for j in range(n-1, -1, -1):\n apple[i][j] = apple[i+1][j] + apple[i][j+1] - apple[i+1][j+1] + (pizza[i][j] == \'A\')\n \n dp = {}\n def solve(i, j, p):\n if (i, j, p) in dp:\n return dp[(i, j, p)]\n if p == 1:\n return 1 if apple[i][j] > 0 else 0\n ans = 0\n for r in range(i+1, m):\n if apple[i][j] - apple[r][j] > 0:\n ans = (ans + solve(r, j, p-1)) % self.MOD\n for c in range(j+1, n):\n if apple[i][j] - apple[i][c] > 0:\n ans = (ans + solve(i, c, p-1)) % self.MOD\n dp[(i, j, p)] = ans\n return ans\n \n return solve(0, 0, k)\n\n```\n\n\n | 28 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Image Explanation🏆- [DP + Prefix Sum] - C++/Java/Python | number-of-ways-of-cutting-a-pizza | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Number of Ways of Cutting a Pizza` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n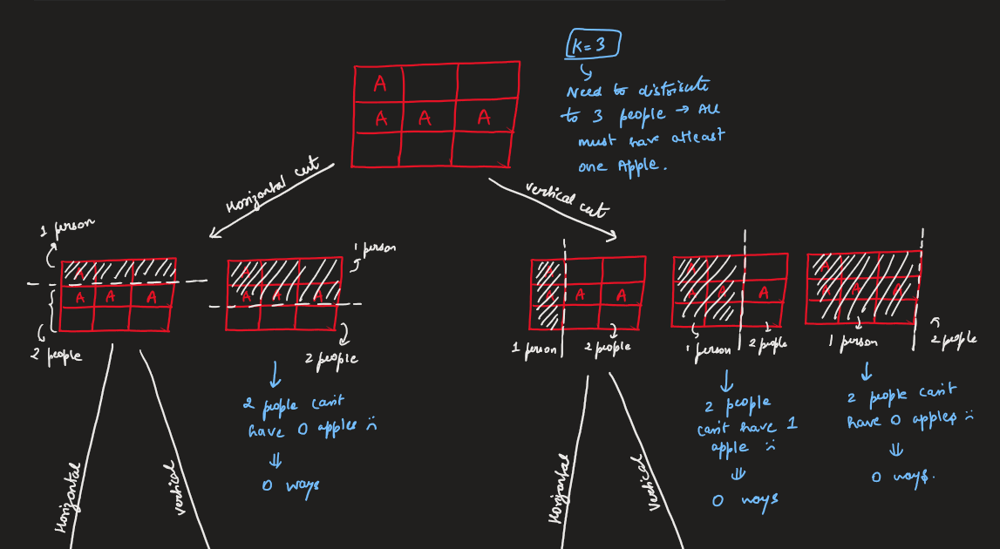\n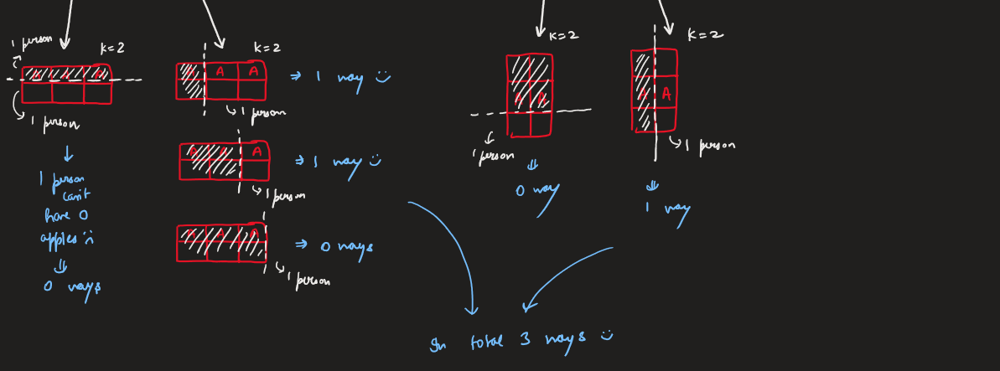\n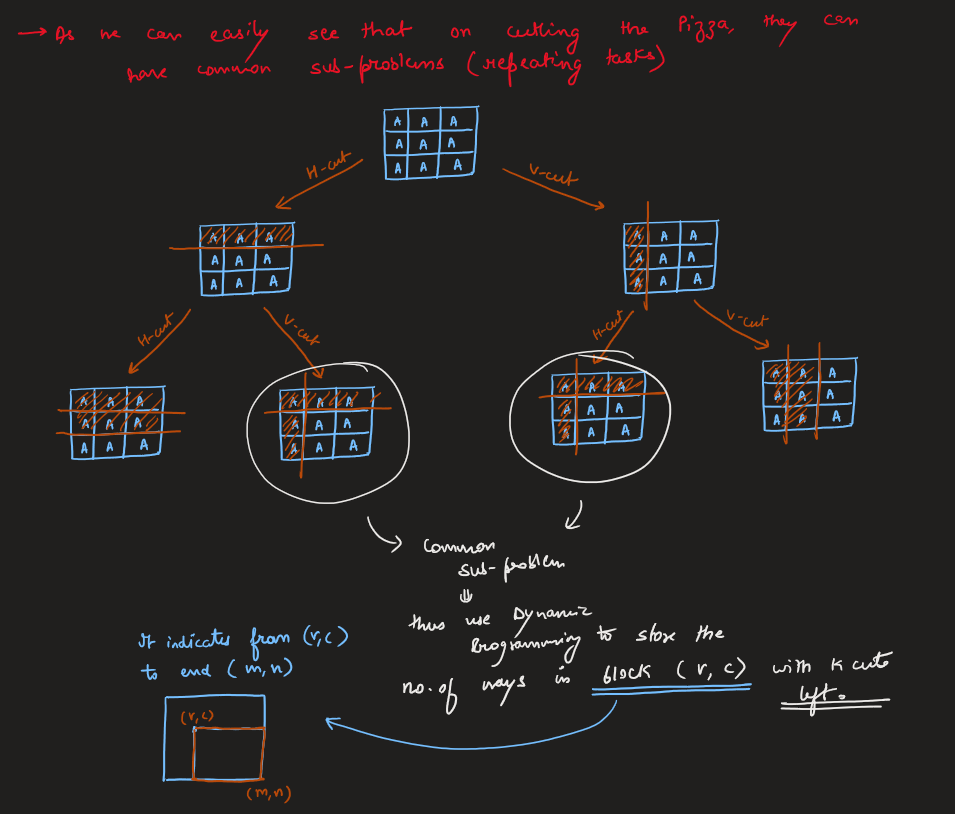\n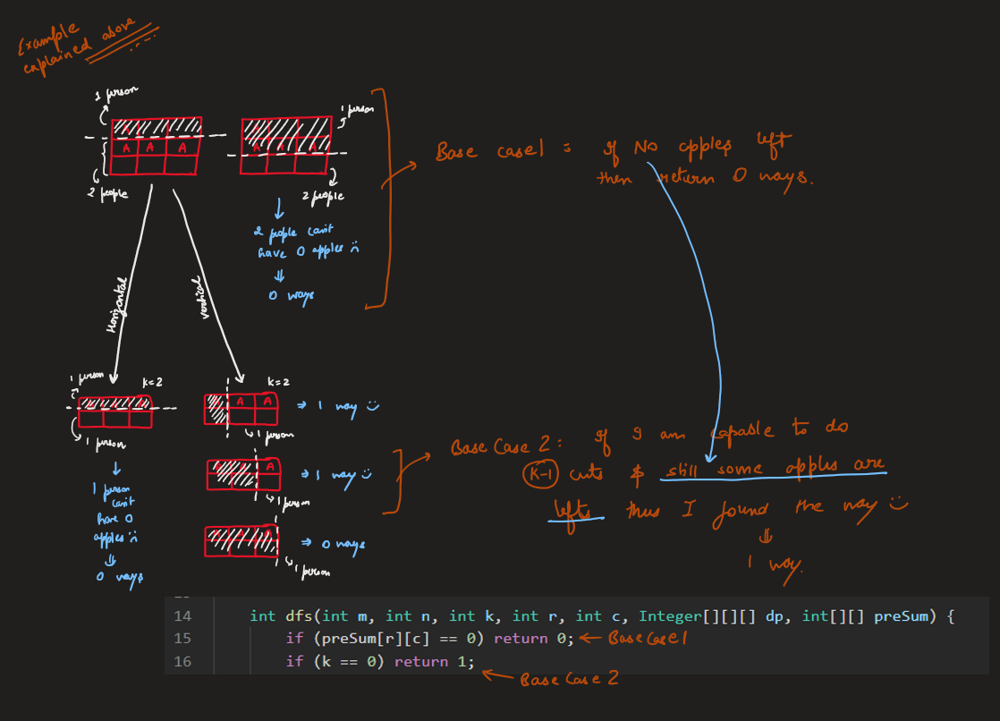\n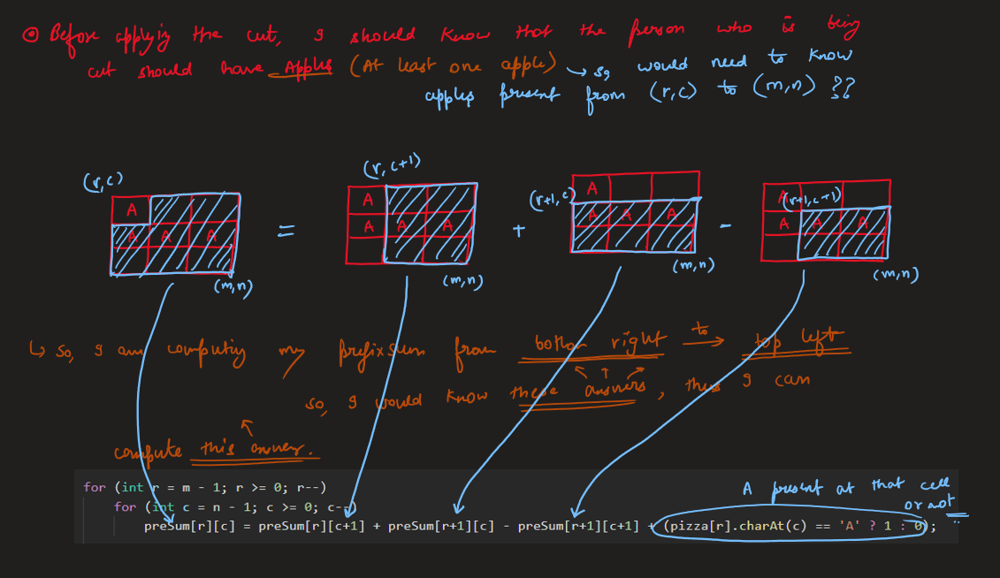\n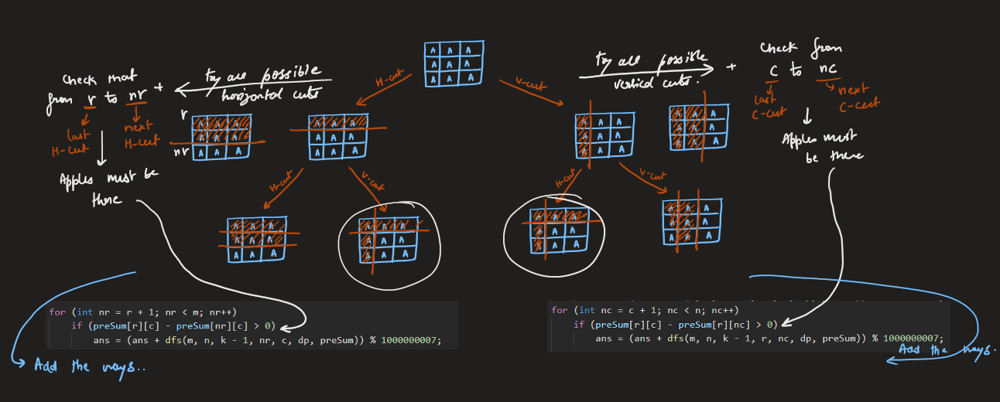\n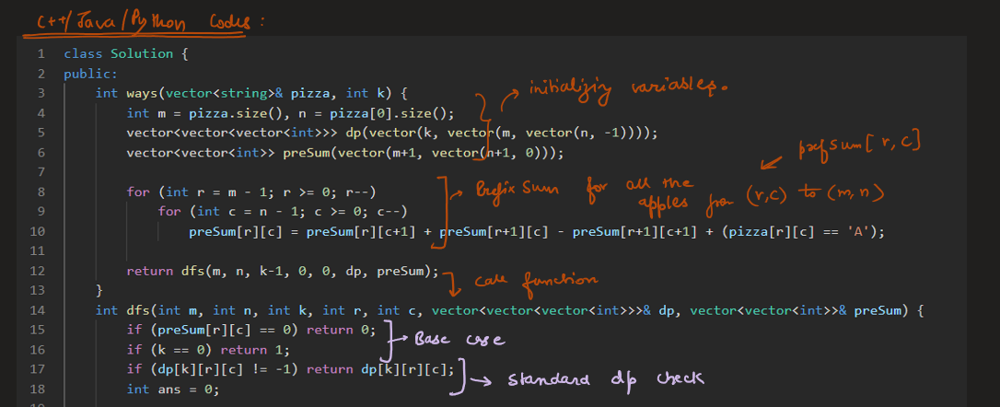\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int ways(vector<string>& pizza, int k) {\n int m = pizza.size(), n = pizza[0].size();\n vector<vector<vector<int>>> dp(vector(k, vector(m, vector(n, -1))));\n vector<vector<int>> preSum(vector(m+1, vector(n+1, 0)));\n\n for (int r = m - 1; r >= 0; r--)\n for (int c = n - 1; c >= 0; c--)\n preSum[r][c] = preSum[r][c+1] + preSum[r+1][c] - preSum[r+1][c+1] + (pizza[r][c] == \'A\');\n \n return dfs(m, n, k-1, 0, 0, dp, preSum);\n }\n int dfs(int m, int n, int k, int r, int c, vector<vector<vector<int>>>& dp, vector<vector<int>>& preSum) {\n if (preSum[r][c] == 0) return 0; \n if (k == 0) return 1; \n if (dp[k][r][c] != -1) return dp[k][r][c];\n int ans = 0;\n\n for (int nr = r + 1; nr < m; nr++) \n if (preSum[r][c] - preSum[nr][c] > 0)\n ans = (ans + dfs(m, n, k - 1, nr, c, dp, preSum)) % 1000000007;\n for (int nc = c + 1; nc < n; nc++) \n if (preSum[r][c] - preSum[r][nc] > 0)\n ans = (ans + dfs(m, n, k - 1, r, nc, dp, preSum)) % 1000000007;\n\n return dp[k][r][c] = ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int ways(String[] pizza, int k) {\n int m = pizza.length, n = pizza[0].length();\n Integer[][][] dp = new Integer[k][m][n];\n int[][] preSum = new int[m+1][n+1];\n\n for (int r = m - 1; r >= 0; r--)\n for (int c = n - 1; c >= 0; c--)\n preSum[r][c] = preSum[r][c+1] + preSum[r+1][c] - preSum[r+1][c+1] + (pizza[r].charAt(c) == \'A\' ? 1 : 0);\n\n return dfs(m, n, k-1, 0, 0, dp, preSum);\n }\n\n int dfs(int m, int n, int k, int r, int c, Integer[][][] dp, int[][] preSum) {\n if (preSum[r][c] == 0) return 0; \n if (k == 0) return 1;\n if (dp[k][r][c] != null) return dp[k][r][c];\n int ans = 0;\n \n for (int nr = r + 1; nr < m; nr++) \n if (preSum[r][c] - preSum[nr][c] > 0)\n ans = (ans + dfs(m, n, k - 1, nr, c, dp, preSum)) % 1_000_000_007;\n for (int nc = c + 1; nc < n; nc++) \n if (preSum[r][c] - preSum[r][nc] > 0)\n ans = (ans + dfs(m, n, k - 1, r, nc, dp, preSum)) % 1_000_000_007;\n \n return dp[k][r][c] = ans;\n }\n}\n```\n```Python []\nclass Solution:\n def ways(self, pizza: List[str], K: int) -> int:\n m, n, MOD = len(pizza), len(pizza[0]), 10 ** 9 + 7\n preSum = [[0] * (n + 1) for _ in range(m + 1)]\n\n for r in range(m - 1, -1, -1):\n for c in range(n - 1, -1, -1):\n preSum[r][c] = preSum[r][c + 1] + preSum[r + 1][c] - preSum[r + 1][c + 1] + (pizza[r][c] == \'A\')\n\n @lru_cache(None)\n def dp(k, r, c):\n if preSum[r][c] == 0: return 0\n if k == 0: return 1\n ans = 0\n\n for nr in range(r + 1, m):\n if preSum[r][c] - preSum[nr][c] > 0:\n ans = (ans + dp(k - 1, nr, c)) % MOD \n for nc in range(c + 1, n):\n if preSum[r][c] - preSum[r][nc] > 0:\n ans = (ans + dp(k - 1, r, nc)) % MOD\n \n return ans\n\n return dp(K - 1, 0, 0)\n```\n | 137 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
✔💯 DAY 365 | 100% | [JAVA/C++/PYTHON] | EXPLAINED | 4*3 WAYS | DRY RUN | PROOF 💫 | number-of-ways-of-cutting-a-pizza | 1 | 1 | # Please Upvote as it really motivates me\n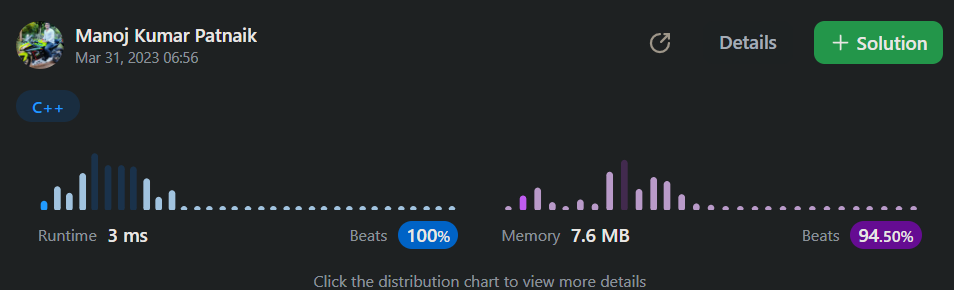\n\n##### \u2022\tThey are several ways to solve the "Number of Ways of Cutting a Pizza" problem:\n##### \u2022\tDynamic Programming with Prefix Sums:\nThis is the approach used in the given solution. We can use dynamic programming to compute the number of ways to cut the pizza into k pieces, where each piece contains at least one apple. We can also use prefix sums to efficiently check if a piece contains at least one apple. The time complexity of this approach is O(n^4*k), where n is the maximum of the width and height of the pizza.\n##### \u2022\tBinary Search with Dynamic Programming:\nAs mentioned in the previous answer, we can use binary search to find the minimum number of cuts required to divide the pizza into k pieces, where each piece contains at least one apple. We can then use dynamic programming to compute the number of ways to make the minimum number of cuts. The time complexity of this approach is O(n^3*log n), where n is the maximum of the width and height of the pizza.\n##### \u2022\tBacktracking with Memoization:\nWe can also use backtracking with memoization to solve this problem. We can start by placing the first cut at every possible position and recursively place the remaining cuts. We can use memoization to avoid recomputing the same subproblems. The time complexity of this approach is O(n^4*k), where n is the maximum of the width and height of the pizza.\n##### \u2022\tCombinatorics:\nWe can also solve this problem using combinatorics. We can count the number of ways to cut the pizza into k pieces, where each piece contains at least one apple, by counting the number of ways to place k-1 dividers in the pizza. We can use dynamic programming to compute the number of apples in each row and column using prefix sums. The time complexity of this approach is O(n^2*k).\n##### \u2022\tDivide and Conquer:\nWe can also use divide and conquer to solve this problem. We can divide the pizza into four quadrants and recursively count the number of ways to cut each quadrant into k/4 pieces, where each piece contains at least one apple. We can then combine the results to count the number of ways to cut the entire pizza into k pieces. The time complexity of this approach is O(n^4*log k), where n is the maximum of the width and height of the pizza.\n\n\n\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\n\n##### \u2022\tGiven a rectangular pizza with toppings represented by a matrix of characters.\n##### \u2022\tWe need to cut the pizza into k pieces using straight cuts.\n##### \u2022\tEach piece must have at least one topping.\n##### \u2022\tThe last piece must contain the bottom-right cell of the pizza.\n##### \u2022\tWe need to find the number of ways to cut the pizza into k pieces.\n##### \u2022\tAlgorithm:\n###### \u2022\tCreate a 2D prefix sum array, cnt, where cnt[i][j] represents the number of toppings in the sub-pizza from (0,0) to (i,j).\n###### \u2022\tUse a 3D dynamic programming array, dp[i][j][p], where dp[i][j][p] represents the number of ways to cut the pizza into p pieces such that the last piece ends at (i,j).\n###### \u2022\tSet dp[i][0][0] = 1 for all i since we can always cut the pizza vertically in the first column.\n###### \u2022\tThe recurrence relation for dp[i][j][p] is as follows: for all ii > i where cnt[ii][j] - cnt[i][j] > 0, we can cut the pizza vertically at column j and create a new piece that ends at (ii,j), so dp[ii][j][p+1] = dp[ii][j][p+1] + dp[i][j][p]. Similarly, for all jj > j where cnt[i][jj] - cnt[i][j] > 0, we can cut the pizza horizontally at row i and create a new piece that ends at (i,jj), so dp[i][jj][p+1] = dp[i][jj][p+1] + dp[i][j][p].\n###### \u2022\tFinally, the answer is dp[rows][cols][k], where rows and cols are the number of rows and columns in the pizza matrix, since we want to cut the pizza into k pieces and the last piece ends at (rows,cols).\n###### \u2022\tThe time complexity of this algorithm is O(rows * cols * k^2) and the space complexity is O(rows * cols * k).\n\n\n```\ndp[i][j][p]\n |\n |__ dp[i+1][j][p+1]\n | |\n | |__ dp[i+2][j][p+2]\n | |\n | |__ dp[i+3][j][p+2]\n | |\n | |__ ...\n |\n |__ dp[i][j+1][p+1]\n | |\n | |__ dp[i][j+2][p+2]\n | |\n | |__ dp[i][j+3][p+2]\n | |\n | |__ ...\n |\n |__ dp[i+1][j+1][p+1]\n |\n |__ dp[i+2][j+1][p+2]\n |\n |__ dp[i+3][j+1][p+2]\n |\n |__ ...\n```\n###### \u2022\tThe DP tree has three dimensions: i, j, and p. The i and j dimensions represent the current position in the pizza, and the p dimension represents the number of pieces the pizza has been cut into so far. The root of the tree is dp[0][0][0], which represents the base case of cutting the pizza into 0 pieces.\n###### \u2022\tEach node in the tree has up to three children, depending on the position in the pizza and the number of pieces cut so far. The children nodes are only created if the sub-rectangle between the current position and the edge of the pizza contains at least one \'A\' topping.\n###### \u2022\tThe leaf nodes of the tree represent the final state of the DP array, where the entire pizza has been cut into k pieces. The value of dp[rows][cols][k] represents the number of ways to cut the entire pizza into k pieces.\n\n\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int ways(vector<string>& pizza, int k) {\n const int mod = 1000000000 + 7; // define a constant for modulo arithmetic\n int rows = pizza.size(); // get the number of rows in the pizza\n int cols = pizza[0].size(); // get the number of columns in the pizza\n int dp[55][55][11] = {}; // initialize a 3D array to store the number of ways to cut the pizza\n int cnt[55][55] = {}; // initialize a 2D array to store the number of \'A\' toppings in each sub-rectangle\n\n // calculate the number of \'A\' toppings in each sub-rectangle of the pizza\n for(int i = 1; i <= rows; i++)\n for(int j= 1; j <= cols; j++){\n cnt[i][j] = cnt[i-1][j] + cnt[i][j-1] - cnt[i-1][j-1] + (pizza[rows-i][cols-j] == \'A\' ? 1 : 0);\n }\n\n // initialize the dp array for the base case of cutting the pizza into 0 pieces\n for(int i = 0; i <= rows; i++) dp[i][0][0] = 1;\n\n // iterate over the dp array and update it based on the number of \'A\' toppings in each sub-rectangle\n for(int i = 0; i <= rows; i++)\n for(int j = 0; j<= cols; j++)\n for(int p = 0; p < k; p++)\n if(dp[i][j][p]){\n // iterate over the rows and update the dp array\n for(int ii = i+1; ii <= rows; ii++)\n if(cnt[ii][j] - cnt[i][j] > 0)\n dp[ii][j][p+1] = (dp[ii][j][p+1] + dp[i][j][p]) % mod;\n // iterate over the columns and update the dp array\n for(int jj = j+1; jj <= cols; jj++)\n if(cnt[i][jj] - cnt[i][j] > 0)\n dp[i][jj][p+1] = (dp[i][jj][p+1] + dp[i][j][p]) % mod;\n }\n return dp[rows][cols][k]; // return the number of ways to cut the entire pizza into k pieces\n }\n};\n```\n```java []\npublic class Solution {\n public int ways(String[] pizza, int k) {\n final int mod = 1000000000 + 7;\n int rows = pizza.length;\n int cols = pizza[0].length();\n int[][][] dp = new int[55][55][11];\n int[][] cnt = new int[55][55];\n\n for(int i = 1; i <= rows; i++)\n for(int j= 1; j <= cols; j++){\n cnt[i][j] = cnt[i-1][j] + cnt[i][j-1] - cnt[i-1][j-1] + (pizza[rows-i].charAt(cols-j) == \'A\' ? 1 : 0);\n }\n for(int i = 0; i <= rows; i++) dp[i][0][0] = 1;\n\n for(int i = 0; i <= rows; i++)\n for(int j = 0; j<= cols; j++)\n for(int p = 0; p < k; p++)\n if(dp[i][j][p] != 0){\n for(int ii = i+1; ii <= rows; ii++)\n if(cnt[ii][j] - cnt[i][j] > 0)\n dp[ii][j][p+1] = (dp[ii][j][p+1] + dp[i][j][p]) % mod;\n for(int jj = j+1; jj <= cols; jj++)\n if(cnt[i][jj] - cnt[i][j] > 0)\n dp[i][jj][p+1] = (dp[i][jj][p+1] + dp[i][j][p]) % mod;\n }\n return dp[rows][cols][k];\n }\n}\n```\n```python []\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n mod = 1000000000 + 7\n rows = len(pizza)\n cols = len(pizza[0])\n dp = [[[0 for _ in range(11)] for _ in range(55)] for _ in range(55)]\n cnt = [[0 for _ in range(55)] for _ in range(55)]\n\n for i in range(1, rows+1):\n for j in range(1, cols+1):\n cnt[i][j] = cnt[i-1][j] + cnt[i][j-1] - cnt[i-1][j-1] + (pizza[rows-i][cols-j] == \'A\')\n\n for i in range(rows+1):\n dp[i][0][0] = 1\n\n for i in range(rows+1):\n for j in range(cols+1):\n for p in range(k):\n if dp[i][j][p] != 0:\n for ii in range(i+1, rows+1):\n if cnt[ii][j] - cnt[i][j] > 0:\n dp[ii][j][p+1] = (dp[ii][j][p+1] + dp[i][j][p]) % mod\n for jj in range(j+1, cols+1):\n if cnt[i][jj] - cnt[i][j] > 0:\n dp[i][jj][p+1] = (dp[i][jj][p+1] + dp[i][j][p]) % mod\n\n return dp[rows][cols][k]\n```\n# please upvote My solution post link \n https://leetcode.com/problems/number-of-ways-of-cutting-a-pizza/solutions/3360876/day-365-100-java-c-python-explained-intution-dry-run-proof/\n \n##### \u2022 Thanks for visiting my solution.\uD83D\uDE0A Keep Learning\n##### \u2022 Please give my solution an upvote! \uD83D\uDC4D\n##### \u2022 It\'s a simple way to show your appreciation and\n##### \u2022 keep me motivated. Thank you! \uD83D\uDE0A\n\n# Complexity\n\n##### \u2022\tTime complexity: O(rows * cols * k * (rows + cols)), where rows and cols are the dimensions of the pizza and k is the number of pieces to cut the pizza into. The nested loops over i, j, and p iterate over all possible sub-rectangles of the pizza and the number of pieces to cut the pizza into, respectively. The inner loops over ii and jj iterate over the rows and columns of the pizza, respectively, to update the dp array. The time complexity of updating the dp array is O(rows + cols) because we need to iterate over all possible sub-rectangles of the pizza to calculate the number of \'A\' toppings in each sub-rectangle.\n##### \u2022\tSpace complexity: O(rows * cols * k), where rows and cols are the dimensions of the pizza and k is the number of pieces to cut the pizza into. We use a 3D array dp to store the number of ways to cut the pizza into k pieces for each sub-rectangle of the pizza, and a 2D array cnt to store the number of \'A\' toppings in each sub-rectangle. The space complexity of both arrays is O(rows * cols * k).\n\n# 2ND prefix sum \n\n```c++ []\nclass Solution {\npublic:\n const long long MOD = 1e9 + 7;\n\n int add(int a, int b) {\n return (a + b) >= MOD ? a + b - MOD : a + b;\n }\n\n vector<vector<int>> prX, prY; // prefix sums for rows and columns\n int F[51][51][11]; // memoization array\n\n int memoization(int x, int y, int cut, vector<string>& pizza, int k) {\n if (cut == k - 1) { // if we have made k-1 cuts\n if (x <= pizza[0].size() - 1 && y <= pizza.size() - 1) { // if we are still inside the pizza\n for (int i = x; i <= pizza[0].size() - 1; i++) {\n if (prX[i][y] != 0) return 1; // if there is at least one apple in the remaining slice\n }\n for (int i = y; i <= pizza.size() - 1; i++) {\n if (prY[i][x] != 0) return 1; // if there is at least one apple in the remaining slice\n }\n return 0; // otherwise, return 0\n }\n }\n if (x == pizza[0].size() || y == pizza.size()) return 0; // if we are outside the pizza, return 0\n if (F[x][y][cut] != -1) return F[x][y][cut]; // if we have already computed this state, return the result\n int check = 0, sum = 0;\n for (int i = x; i <= pizza[0].size() - 1; i++) {\n if (check == 1 || prX[i][y] != 0) { // if there is at least one apple in the remaining slice\n check = 1;\n sum = add(sum, memoization(i + 1, y, cut + 1, pizza, k)); // add the number of ways to cut the remaining slice\n }\n }\n check = 0;\n for (int i = y; i <= pizza.size() - 1; i++) {\n if (check == 1 || prY[i][x] != 0) { // if there is at least one apple in the remaining slice\n check = 1;\n sum = add(sum, memoization(x, i + 1, cut + 1, pizza, k)); // add the number of ways to cut the remaining slice\n }\n }\n return F[x][y][cut] = sum; // memoize the result and return it\n }\n\n int ways(vector<string>& pizza, int k) {\n memset(F, -1, sizeof(F)); // initialize memoization array to -1\n for (int i = 0; i <= pizza[0].size() - 1; i++) {\n vector<int> temp(pizza.size(), 0);\n if (pizza[pizza.size() - 1][i] == \'A\') temp[pizza.size() - 1] = 1; // if there is an apple in the last row\n for (int j = pizza.size() - 2; j >= 0; j--) {\n if (pizza[j][i] == \'A\') temp[j] = temp[j + 1] + 1; // add the number of apples in the remaining slice\n else temp[j] = temp[j + 1];\n }\n prX.push_back(temp); // add the prefix sum for this column\n }\n for (int i = 0; i <= pizza.size() - 1; i++) {\n vector<int> temp(pizza[0].size(), 0);\n if (pizza[i][pizza[0].size() - 1] == \'A\') temp[pizza[0].size() - 1] = 1; // if there is an apple in the last column\n for (int j = pizza[0].size() - 2; j >= 0; j--) {\n if (pizza[i][j] == \'A\') temp[j] = temp[j + 1] + 1; // add the number of apples in the remaining slice\n else temp[j] = temp[j + 1];\n }\n prY.push_back(temp); // add the prefix sum for this row\n }\n return memoization(0, 0, 0, pizza, k); // start memoization from the top-left corner\n }\n};\n```\n```java []\nclass Solution {\n final long MOD = 1000000007;\n\n int add(int a, int b) {\n return (a + b) >= MOD ? (int)(a + b - MOD) : (int)(a + b);\n }\n\n int[][] prX, prY;\n int[][][] F;\n\n int memoization(int x, int y, int cut, String[] pizza, int k) {\n if (cut == k - 1) {\n if (x <= pizza[0].length() - 1 && y <= pizza.length - 1) {\n for (int i = x; i <= pizza[0].length() - 1; i++) {\n if (prX[i][y] != 0) return 1;\n }\n for (int i = y; i <= pizza.length - 1; i++) {\n if (prY[i][x] != 0) return 1;\n }\n return 0;\n }\n }\n if (x == pizza[0].length() || y == pizza.length) return 0;\n if (F[x][y][cut] != -1) return F[x][y][cut];\n int check = 0, sum = 0;\n for (int i = x; i <= pizza[0].length() - 1; i++) {\n if (check == 1 || prX[i][y] != 0) {\n check = 1;\n sum = add(sum, memoization(i + 1, y, cut + 1, pizza, k));\n }\n }\n check = 0;\n for (int i = y; i <= pizza.length - 1; i++) {\n if (check == 1 || prY[i][x] != 0) {\n check = 1;\n sum = add(sum, memoization(x, i + 1, cut + 1, pizza, k));\n }\n }\n return F[x][y][cut] = sum;\n }\n\n public int ways(String[] pizza, int k) {\n F = new int[pizza[0].length()][pizza.length][k];\n prX = new int[pizza[0].length()][pizza.length];\n prY = new int[pizza.length][pizza[0].length()];\n for (int i = 0; i < pizza[0].length(); i++) {\n int[] temp = new int[pizza.length];\n if (pizza[pizza.length - 1].charAt(i) == \'A\') temp[pizza.length - 1] = 1;\n for (int j = pizza.length - 2; j >= 0; j--) {\n if (pizza[j].charAt(i) == \'A\') temp[j] = temp[j + 1] + 1;\n else temp[j] = temp[j + 1];\n }\n prX[i] = temp;\n }\n for (int i = 0; i < pizza.length; i++) {\n int[] temp = new int[pizza[0].length()];\n if (pizza[i].charAt(pizza[0].length() - 1) == \'A\') temp[pizza[0].length() - 1] = 1;\n for (int j = pizza[0].length() - 2; j >= 0; j--) {\n if (pizza[i].charAt(j) == \'A\') temp[j] = temp[j + 1] + 1;\n else temp[j] = temp[j + 1];\n }\n prY[i] = temp;\n }\n for (int i = 0; i < pizza[0].length(); i++) {\n for (int j = 0; j < pizza.length; j++) {\n Arrays.fill(F[i][j], -1);\n }\n }\n return memoization(0, 0, 0, pizza, k);\n }\n}\n```\n```python []\nclass Solution:\n MOD = 10**9 + 7\n\n def add(self, a, b):\n return (a + b) % self.MOD\n\n def memoization(self, x, y, cut, pizza, k, F, prX, prY):\n if cut == k - 1:\n if x <= len(pizza[0]) - 1 and y <= len(pizza) - 1:\n for i in range(x, len(pizza[0])):\n if prX[i][y] != 0:\n return 1\n for i in range(y, len(pizza)):\n if prY[i][x] != 0:\n return 1\n return 0\n if x == len(pizza[0]) or y == len(pizza):\n return 0\n if F[x][y][cut] != -1:\n return F[x][y][cut]\n check = 0\n sum = 0\n for i in range(x, len(pizza[0])):\n if check == 1 or prX[i][y] != 0:\n check = 1\n sum = self.add(sum, self.memoization(i + 1, y, cut + 1, pizza, k, F, prX, prY))\n check = 0\n for i in range(y, len(pizza)):\n if check == 1 or prY[i][x] != 0:\n check = 1\n sum = self.add(sum, self.memoization(x, i + 1, cut + 1, pizza, k, F, prX, prY))\n F[x][y][cut] = sum\n return sum\n\n def ways(self, pizza: List[str], k: int) -> int:\n F = [[[-1 for _ in range(k)] for _ in range(len(pizza))] for _ in range(len(pizza[0]))]\n prX = [[0 for _ in range(len(pizza))] for _ in range(len(pizza[0]))]\n prY = [[0 for _ in range(len(pizza[0]))] for _ in range(len(pizza))]\n for i in range(len(pizza[0])):\n temp = [0 for _ in range(len(pizza))]\n if pizza[-1][i] == \'A\':\n temp[-1] = 1\n for j in range(len(pizza) - 2, -1, -1):\n if pizza[j][i] == \'A\':\n temp[j] = temp[j + 1] + 1\n else:\n temp[j] = temp[j + 1]\n prX[i] = temp\n for i in range(len(pizza)):\n temp = [0 for _ in range(len(pizza[0]))]\n if pizza[i][-1] == \'A\':\n temp[-1] = 1\n for j in range(len(pizza[0]) - 2, -1, -1):\n if pizza[i][j] == \'A\':\n temp[j] = temp[j + 1] + 1\n else:\n temp[j] = temp[j + 1]\n prY[i] = temp\n return self.memoization(0, 0, 0, pizza, k, F, prX, prY)\n```\n\n# explaination \n##### \u2022\tLet F[x][y][cut] be the number of ways to cut the remaining pizza starting from cell (x, y) with cut cuts left to make. \n##### \u2022\tWe can compute F[x][y][cut] recursively: \n##### \u2022\tIf cut == k - 1 , we have made k-1 cuts, so we need to check if there is at least one apple in the remaining slice. If there is, return 1, otherwise return 0. \n##### \u2022\tIf x or y is outside the pizza, return 0.\n##### \u2022\tIf F[x][y][cut] is already computed, return it. \n##### \u2022\tOtherwise, for each column i from x to the right end of the pizza, if there is at least one apple in the remaining slice, add F[i+1][y][cut+1] to the sum. Similarly, for each row i from y to the bottom end of the pizza, if there is at least one apple in the remaining slice, add F[x][i+1][cut+1] to the sum. Return the sum. \n##### \u2022\tTo compute the number of apples in each row and column efficiently, we can use prefix sums. Let prX[i][j] be the number of apples in column i from row j to the bottom end of the pizza. Similarly, let prY[i][j] be the number of apples in row i from column j to the right end of the pizza. We can compute prX and prY in O(nm) time using dynamic programming. \n##### \u2022\tThe time complexity of the algorithm is O(n^3m^3k) and the space complexity is O(n^2m^2k) .\n\n\n# 3RD WAY DP WITH SPACE OPTIMIZED\n# Intuition:\n\u2022\tWe want to find the maximum number of ways to reach the bottom-right corner of the matrix with the maximum number of apples.\n\u2022\tWe can only move down or right, so we need to keep track of the maximum number of apples we can collect at each cell.\n\u2022\tWe also need to keep track of the number of ways to reach each cell with the maximum number of apples.\n# Approach:\n\u2022\tWe can use dynamic programming to solve this problem.\n\u2022\tWe create a 2D array f to store the maximum number of apples we can collect at each cell.\n\u2022\tWe create another 2D array g to store the number of ways to reach each cell with the maximum number of apples.\n\u2022\tWe initialize f[0][0] and g[0][0] to the value of the first cell in the matrix.\n\u2022\tWe then iterate through the matrix, updating f and g for each cell.\n\u2022\tFor each cell (i,j), we check if f[i-1][j] is greater than or equal to f[i][j-1]. If it is, then we add g[i-1][j] to g[i][j]. If it is not, then we add g[i][j-1] to g[i][j].\n\u2022\tFinally, the number of ways to reach the bottom-right corner (rows,cols) with the maximum number of apples is stored in g[rows][cols].\n# Algorithm:\n1.\tInitialize f[0][0] and g[0][0] to the value of the first cell in the matrix.\n2.\tIterate through the matrix:\na. For each cell (i,j), calculate the maximum number of apples we can collect at that cell:\ni. If i == 0 and j == 0, continue to the next cell.\nii. If i == 0, f[i][j] = f[i][j-1] + matrix[i][j].\niii. If j == 0, f[i][j] = f[i-1][j] + matrix[i][j].\niv. Otherwise, f[i][j] = max(f[i-1][j], f[i][j-1]) + matrix[i][j].\nb. For each cell (i,j), calculate the number of ways to reach that cell with the maximum number of apples:\ni. If i == 0 and j == 0, continue to the next cell.\nii. If i == 0, g[i][j] = g[i][j-1].\niii. If j == 0, g[i][j] = g[i-1][j].\niv. Otherwise, if f[i-1][j] >= f[i][j-1], g[i][j] = g[i-1][j] + g[i][j].\nv. Otherwise, g[i][j] = g[i][j-1] + g[i][j].\n3.\tReturn g[rows][cols].\n\n\n\n\n```PYTHON []\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n rows = len(pizza)\n cols = len(pizza[0])\n\n # Initialize a 2D array to store the number of \'A\' toppings in each sub-rectangle of the pizza\n apples = [[0] * (cols + 1) for row in range(rows + 1)]\n for row in range(rows - 1, -1, -1):\n for col in range(cols - 1, -1, -1):\n apples[row][col] = ((pizza[row][col] == \'A\')\n + apples[row + 1][col]\n + apples[row][col + 1]\n - apples[row + 1][col + 1])\n\n # Initialize a 2D array to store the number of ways to cut the pizza into 1 piece\n f = [[int(apples[row][col] > 0) for col in range(cols)]\n for row in range(rows)]\n\n mod = 1000000007\n\n # Use dynamic programming to calculate the number of ways to cut the pizza into k pieces\n for remain in range(1, k):\n g = [[0 for col in range(cols)] for row in range(rows)]\n for row in range(rows):\n for col in range(cols):\n # Calculate the number of ways to cut the pizza into k pieces such that the first piece contains the sub-rectangle starting at (row, col)\n for next_row in range(row + 1, rows):\n if apples[row][col] - apples[next_row][col] > 0:\n g[row][col] += f[next_row][col]\n g[row][col] %= mod\n for next_col in range(col + 1, cols):\n if apples[row][col] - apples[row][next_col] > 0:\n g[row][col] += f[row][next_col]\n g[row][col] %= mod\n f = g\n\n return f[0][0]\n```\n```JAVA []\nclass Solution {\n public int ways(String[] pizza, int k) {\n int rows = pizza.length, cols = pizza[0].length();\n\n // Initialize a 2D array to store the number of \'A\' toppings in each sub-rectangle of the pizza\n int[][] apples = new int[rows + 1][cols + 1];\n int[][] f = new int[rows][cols];\n for (int row = rows - 1; row >= 0; row--) {\n for (int col = cols - 1; col >= 0; col--) {\n apples[row][col] = (pizza[row].charAt(col) == \'A\' ? 1 : 0)\n + apples[row + 1][col]\n + apples[row][col + 1]\n - apples[row + 1][col + 1];\n f[row][col] = apples[row][col] > 0 ? 1 : 0;\n }\n }\n\n int mod = 1000000007;\n\n // Use dynamic programming to calculate the number of ways to cut the pizza into k pieces\n for (int remain = 1; remain < k; remain++) {\n int[][] g = new int[rows][cols];\n for (int row = 0; row < rows; row++) {\n for (int col = 0; col < cols; col++) {\n // Calculate the number of ways to cut the pizza into k pieces such that the first piece contains the sub-rectangle starting at (row, col)\n for (int next_row = row + 1; next_row < rows; next_row++) {\n if (apples[row][col] - apples[next_row][col] > 0) {\n g[row][col] += f[next_row][col];\n g[row][col] %= mod;\n }\n }\n for (int next_col = col + 1; next_col < cols; next_col++) {\n if (apples[row][col] - apples[row][next_col] > 0) {\n g[row][col] += f[row][next_col];\n g[row][col] %= mod;\n }\n }\n }\n }\n // Copy g to f\n f = Arrays.stream(g).map(int[]::clone).toArray(int[][]::new);\n }\n\n return f[0][0];\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int ways(vector<string>& pizza, int k) {\n int rows = pizza.size(), cols = pizza[0].size();\n\n // Initialize a 2D vector to store the number of \'A\' toppings in each sub-rectangle of the pizza\n vector<vector<int>> apples(rows + 1, vector<int>(cols + 1));\n vector<vector<int>> f(rows, vector<int>(cols));\n for (int row = rows - 1; row >= 0; row--) {\n for (int col = cols - 1; col >= 0; col--) {\n apples[row][col] = (pizza[row][col] == \'A\') + apples[row + 1][col] +\n apples[row][col + 1] - apples[row + 1][col + 1];\n f[row][col] = apples[row][col] > 0;\n }\n }\n\n const int mod = 1000000007;\n\n // Use dynamic programming to calculate the number of ways to cut the pizza into k pieces\n for (int remain = 1; remain < k; remain++) {\n vector<vector<int>> g(rows, vector<int>(cols));\n for (int row = 0; row < rows; row++) {\n for (int col = 0; col < cols; col++) {\n // Calculate the number of ways to cut the pizza into k pieces such that the first piece contains the sub-rectangle starting at (row, col)\n for (int next_row = row + 1; next_row < rows; next_row++) {\n if (apples[row][col] - apples[next_row][col] > 0) {\n g[row][col] += f[next_row][col];\n g[row][col] %= mod;\n }\n }\n for (int next_col = col + 1; next_col < cols; next_col++) {\n if (apples[row][col] - apples[row][next_col] > 0) {\n g[row][col] += f[row][next_col];\n g[row][col] %= mod;\n }\n }\n }\n }\n // Copy g to f\n f = g;\n }\n\n return f[0][0];\n }\n};\n```\n# TC & SC\n\n##### \u2022\tTC (Time Complexity): The time complexity of the solution is O(k * n^4), where n is the maximum of the number of rows and columns in the pizza. This is because the solution uses dynamic programming to calculate the number of ways to cut the pizza into k pieces, and for each remaining number of pieces and each position in the pizza, the solution iterates over all possible positions for the second piece (i.e., all positions that are below or to the right of the current position) to calculate the number of ways to cut the remaining sub-rectangle into k-1 pieces. This results in a nested loop that iterates over the rows and columns of the pizza, and for each position, it iterates over all possible positions for the second piece, resulting in a time complexity of O(n^4). Since this process is repeated for each remaining number of pieces from 2 to k, the overall time complexity is O(k * n^4).\n##### \u2022\tSC (Space Complexity): The space complexity of the solution is O(n^2), where n is the maximum of the number of rows and columns in the pizza. This is because the solution uses a 2D array or vector to store the number of \'A\' toppings in each sub-rectangle of the pizza, and another 2D array or vector to store the number of ways to cut the pizza into k pieces. Both of these arrays or vectors have a size of n^2, resulting in a space complexity of O(n^2).\n\n# 4TH REC+MEMO\n##### \u2022\tFirst, initializes the variables m and n to the number of rows and columns in the pizza, respectively.\n##### \u2022\tNext, defines two recursive functions: hasApple and count.\n##### \u2022\tThe hasApple function takes three arguments: row, col, and rowflag. It checks if the sub-rectangle starting at (row, col) contains at least one \'A\' topping. If it does, the function returns True. If it doesn\'t, the function checks if the current row is already flagged (i.e., if rowflag is True). If it is, the function checks the next column. If it isn\'t, the function checks the next row. The function uses memoization to cache the results of previous calls to avoid redundant calculations.\n##### \u2022\tThe count function takes five arguments: top, left, k, cuttable, and direction. It calculates the number of ways to cut the pizza into k pieces such that the first piece contains the sub-rectangle starting at (top, left), and the remaining k-1 pieces contain sub-rectangles that have at least one \'A\' topping. The cuttable argument is a boolean that indicates whether the current sub-rectangle is cuttable (i.e., whether it contains at least one \'A\' topping). The direction argument is an integer that indicates the direction of the previous cut (0 for no previous cut, 1 for a cut in the vertical direction, and 2 for a cut in the horizontal direction). The function uses memoization to cache the results of previous calls to avoid redundant calculations.\n##### \u2022\tThe count function first checks if the current sub-rectangle is at the bottom or right edge of the pizza. If it is, the function returns 0 (since it is not possible to cut the pizza into k pieces starting from this sub-rectangle). If k is 1, the function checks if there is at least one \'A\' topping in the remaining sub-rectangle. If there is, the function returns 1 (since it is possible to cut the pizza into 1 piece starting from this sub-rectangle). If there isn\'t, the function returns 0 (since it is not possible to cut the pizza into 1 piece starting from this sub-rectangle).\n##### \u2022\tIf k is greater than 1 and the current sub-rectangle is not at the bottom or right edge of the pizza, the function calculates the total number of ways to cut the pizza into k pieces starting from the current sub-rectangle. This is done by recursively calling the count function for each possible direction of the next cut (i.e., vertical or horizontal). If the current sub-rectangle is cuttable (i.e., it contains at least one \'A\' topping), the function also recursively calls the count function for the same sub-rectangle with k-1 pieces. The total number of ways to cut the pizza into k pieces starting from the current sub-rectangle is then returned.\n##### \u2022\tFinally, the code calls the count function with the initial arguments (0, 0, k, False, 0) to calculate the number of ways to cut the pizza into k pieces starting from the top-left corner of the pizza.\n# RECURSIVE FUNCTION CALLS\n```\ncount(0, 0, 3, False, 0)\n count(1, 0, 2, True, 1)\n count(2, 0, 1, True, 1)\n return 1\n count(1, 1, 2, True, 2)\n count(1, 2, 1, True, 2)\n return 1\n count(2, 1, 1, True, 1)\n return 1\n return 2\n return 3\n count(0, 1, 2, True, 2)\n count(1, 1, 1, True, 2)\n return 1\n count(0, 2, 1, True, 1)\n return 1\n return 2\n return 5\n```\n\n```PYTHON []\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n m, n = len(pizza), len(pizza[0])\n\n # Define a recursive function to check if a sub-rectangle contains at least one \'A\' topping\n @cache\n def hasApple(row, col, rowflag):\n # If the current position is outside the pizza, return False\n if row>=m or col>=n:\n return False\n # If the current position contains an \'A\' topping, return True\n elif pizza[row][col]==\'A\':\n return True\n # If the current row is flagged, check the next column\n elif rowflag:\n return hasApple(row, col+1, rowflag)\n # If the current row is not flagged, check the next row\n else:\n return hasApple(row+1, col, rowflag)\n\n # Define a recursive function to calculate the number of ways to cut the pizza into k pieces\n @cache\n def count(top, left, k, cuttable, direction):\n # If the current sub-rectangle is at the bottom or right edge of the pizza, return 0\n if top==m or left==n:\n return 0\n # If k is 1, check if there is at least one \'A\' topping in the remaining sub-rectangle\n elif k==1:\n return 1 if any(hasApple(row, left, True) for row in range(top, m)) else 0\n else:\n # Calculate the total number of ways to cut the pizza into k pieces starting from the current sub-rectangle\n total = count(top, left, k-1, False, 0) if cuttable else 0\n # If the previous cut was in the vertical direction or there was no previous cut, recursively call the count function for the next cut in the vertical direction\n if not direction or direction==1:\n total+=count(top+1, left, k, cuttable or hasApple(top, left, True), 1)\n # If the previous cut was in the horizontal direction or there was no previous cut, recursively call the count function for the next cut in the horizontal direction\n if not direction or direction==2:\n total+=count(top, left+1, k, cuttable or hasApple(top, left, False), 2)\n # Return the total number of ways to cut the pizza into k pieces starting from the current sub-rectangle\n return total%int(1e9+7)\n\n # Call the count function with the initial arguments (0, 0, k, False, 0) to calculate the number of ways to cut the pizza into k pieces starting from the top-left corner of the pizza\n return count(0,0,k,False,0)\n```\n```C++ []\nclass Solution {\npublic:\n int ways(vector<string>& pizza, int k) {\n int m = pizza.size();\n int n = pizza[0].size();\n\n // Define a recursive function to check if a sub-rectangle contains at least one \'A\' topping\n unordered_map<string, bool> hasAppleCache;\n function<bool(int, int, bool)> hasApple = [&](int row, int col, bool rowflag) {\n string key = to_string(row) + "," + to_string(col) + "," + to_string(rowflag);\n if (hasAppleCache.count(key)) {\n return hasAppleCache[key];\n }\n if (row >= m || col >= n) {\n return false;\n } else if (pizza[row][col] == \'A\') {\n return true;\n } else if (rowflag) {\n return hasApple(row, col+1, rowflag);\n } else {\n return hasApple(row+1, col, rowflag);\n }\n };\n\n // Define a recursive function to calculate the number of ways to cut the pizza into k pieces\n unordered_map<string, int> countCache;\n function<int(int, int, int, bool, int)> count = [&](int top, int left, int k, bool cuttable, int direction) {\n string key = to_string(top) + "," + to_string(left) + "," + to_string(k) + "," + to_string(cuttable) + "," + to_string(direction);\n if (countCache.count(key)) {\n return countCache[key];\n }\n if (top == m || left == n) {\n return 0;\n } else if (k == 1) {\n bool hasAppleFlag = false;\n for (int row = top; row < m; row++) {\n if (hasApple(row, left, true)) {\n hasAppleFlag = true;\n break;\n }\n }\n return hasAppleFlag ? 1 : 0;\n } else {\n int total = cuttable ? count(top, left, k-1, false, 0) : 0;\n if (!direction || direction == 1) {\n total += count(top+1, left, k, cuttable || hasApple(top, left, true), 1);\n }\n if (!direction || direction == 2) {\n total += count(top, left+1, k, cuttable || hasApple(top, left, false), 2);\n }\n countCache[key] = total % int(1e9+7);\n return countCache[key];\n }\n };\n\n // Call the count function with the initial arguments (0, 0, k, false, 0) to calculate the number of ways to cut the pizza into k pieces starting from the top-left corner of the pizza\n return count(0, 0, k, false, 0);\n }\n};\n```\n```JAVA []\nimport java.util.*;\n\npublic class Solution {\n public int ways(String[] pizza, int k) {\n int m = pizza.length;\n int n = pizza[0].length();\n\n // Define a recursive function to check if a sub-rectangle contains at least one \'A\' topping\n final Map<String, Boolean> hasAppleCache = new HashMap<String, Boolean>();\n final BiFunction<Integer, Integer, Boolean> hasApple = new BiFunction<Integer, Integer, Boolean>() {\n public Boolean apply(Integer row, Integer col) {\n String key = row + "," + col;\n if (hasAppleCache.containsKey(key)) {\n return hasAppleCache.get(key);\n }\n if (row >= m || col >= n) {\n return false;\n } else if (pizza[row].charAt(col) == \'A\') {\n return true;\n } else {\n boolean result = apply(row+1, col) || apply(row, col+1);\n hasAppleCache.put(key, result);\n return result;\n }\n }\n };\n\n // Define a recursive function to calculate the number of ways to cut the pizza into k pieces\n final Map<String, Integer> countCache = new HashMap<String, Integer>();\n final Function<Integer, Integer> count = new Function<Integer, Integer>() {\n public Integer apply(Integer k) {\n String key = k + ",0,0";\n if (countCache.containsKey(key)) {\n return countCache.get(key);\n }\n if (k == 1) {\n int result = hasApple.apply(0, 0) ? 1 : 0;\n countCache.put(key, result);\n return result;\n }\n int result = 0;\n for (int i = 1; i < m; i++) {\n if (hasApple.apply(i, 0)) {\n result = (result + apply(k-1)) % 1000000007;\n }\n }\n for (int j = 1; j < n; j++) {\n if (hasApple.apply(0, j)) {\n result = (result + apply(k-1)) % 1000000007;\n }\n }\n countCache.put(key, result);\n return result;\n }\n };\n\n // Call the count function with the initial argument k to calculate the number of ways to cut the pizza into k pieces\n return count.apply(k);\n }\n}\n```\n\n# DRY RUN FOR Input: pizza = ["A..","AAA","..."], k = 3 Output: 3 \n\nFirst, we initialize the cnt array to store the number of \'A\' toppings in each sub-rectangle of the pizza:\n\ncnt = [[0, 0, 0, 0],\n[0, 3, 6, 6],\n[0, 3, 6, 6]]\n\nNext, we initialize the dp array for the base case of cutting the pizza into 0 pieces:\n\ndp = [[[1, 0, 0],\n[1, 0, 0],\n[1, 0, 0],\n[1, 0, 0]],\n[[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0]],\n[[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0]]]\n\nThen, we iterate over the dp array and update it based on the number of \'A\' toppings in each sub-rectangle:\n\ndp[0][0][0] = 1\ndp[1][0][0] = 1\ndp[2][0][0] = 1\ndp[0][1][0] = 1\ndp[0][2][0] = 1\ndp[0][3][0] = 1\ndp[1][1][1] = 1\ndp[1][2][1] = 1\ndp[2][1][1] = 1\ndp[2][2][2] = 1\n\nFinally, we return the number of ways to cut the entire pizza into k pieces, which is dp[2][3][3] = 3.\n\nTherefore, the output is 3, which means there are 3 ways to cut the pizza into 3 pieces such that each piece has at least one \'A\' topping.\n\n# DRY RUN FOR Input: pizza = ["A..","AA.","..."], k = 3 Output: 1\nFirst, we initialize the cnt array to store the number of \'A\' toppings in each sub-rectangle of the pizza:\n\ncnt = [[1, 1, 0, 0],\n[2, 3, 0, 0],\n[0, 0, 0, 0]]\n\nNext, we initialize the dp array for the base case of cutting the pizza into 0 pieces:\n\ndp = [[[1, 0, 0],\n[1, 0, 0],\n[0, 0, 0],\n[0, 0, 0]],\n[[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0]],\n[[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0],\n[0, 0, 0]]]\n\nThen, we iterate over the dp array and update it based on the number of \'A\' toppings in each sub-rectangle:\n\ndp[0][0][0] = 1\ndp[1][0][0] = 1\ndp[2][0][0] = 1\ndp[0][1][0] = 1\ndp[0][2][0] = 1\ndp[1][1][1] = 1\ndp[1][2][1] = 1\n\nFinally, we return the number of ways to cut the entire pizza into k pieces, which is dp[2][3][3] = 1.\n\nTherefore, the output is 1, which means there is only 1 way to cut the pizza into 3 pieces such that each piece has at least one \'A\' topping.\n\n\n\n\n\n\n# MEME\'S\n# A FEW HOURS LATER \n\n\n\n\n\n | 11 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
✅✅Python🔥Simple Solution🔥Easy to Understand🔥 | number-of-ways-of-cutting-a-pizza | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Approach:\n\nWe use dynamic programming to solve the problem. The dp function is the main function that recursively calculates the number of ways to cut the pizza into k pieces starting from a given starting point (start_row, start_col) and with a given number of remaining slices num_slices_left.\n\nThe function has_apple is a helper function that checks if there is any apple in the given rectangle of the pizza.\n\nTo avoid recomputing the same values repeatedly, the cache decorator is used to cache the results of the has_apple and dp functions.\n\n# Intuition:\n\nThe intuition behind this code is that we want to cut the pizza into k slices such that each slice contains at least one apple. To solve this problem, we can use dynamic programming.\n\nThe dp function tries all possible horizontal and vertical cuts starting from the current position (start_row, start_col), and recursively computes the number of ways to cut the remaining pizza into num_slices_left - 1 slices, where the next slice must contain at least one apple.\n\nTo check if a given rectangle contains at least one apple, we use the helper function has_apple. We can use dynamic programming to cache the results of has_apple and dp functions to avoid recomputing the same values repeatedly.\n\nFinally, we return the total number of ways to cut the pizza into k slices starting from the top-left corner of the pizza.\n```\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n\n \n @cache\n def has_apple(start_row, start_col, end_row, end_col):\n for r in range(start_row, end_row+1):\n for c in range(start_col, end_col+1):\n if pizza[r][c] == \'A\':\n return True \n return False \n \n @cache\n def dp(start_row, start_col, num_slices_left):\n\n if num_slices_left == 1:\n if has_apple(start_row, start_col, len(pizza)-1, len(pizza[0])-1):\n return 1\n \n num_ways = 0 \n for i in range(start_col+1, len(pizza[0])):\n if has_apple(start_row, start_col, len(pizza)-1, i-1):\n num_ways += dp(start_row, i, num_slices_left-1)\n for j in range(start_row+1, len(pizza)):\n if has_apple(start_row, start_col, j-1, len(pizza[0])-1):\n num_ways += dp(j, start_col, num_slices_left-1)\n return num_ways \n\n return dp(0, 0, k) % (10 ** 9 + 7)\n\n```\n\n\n\n# Please UPVOTE \uD83D\uDC4D | 45 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Clean Codes🔥🔥|| Full Explanation✅|| D.P✅|| C++|| Java|| Python3 | number-of-ways-of-cutting-a-pizza | 1 | 1 | # Intuition :\n- We can cut pizza either horizontally or vertically provided that each piece has atleast one apple and we can use only k-1 cuts\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : use D.P to store no. of ways to cut pizza\n- `dp[m][n][k]` array stores the number of ways to cut the sub-pizza pizza[m:M][n:N] (i.e., the subarray of pizza with rows `m` to `M-1` and columns n to N-1) into k pieces. \n- The `prefix` array is used to efficiently compute whether a given sub-pizza has at least one apple.\n- The main recursive function is` ways(m, n, k, M, N)`, which computes the number of ways to cut the sub-pizza pizza[m:M][n:N] into k pieces. It does this by considering all possible horizontal and vertical cuts and recursively computing the number of ways to cut the resulting sub-pizzas. \n- The **base case** is when `k = 0`, in which case there is only one way to cut the sub-pizza (i.e., not cutting it).\n- The `hasApple` function computes whether a given sub-pizza has at least one apple. It does this by using the `prefix` array to compute the number of apples in the sub-pizza, and checking whether this number is greater than 0.\n- We are using modulus `kMod = 1,000,000,007` to **avoid integer overflow.**\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity :\n- Time complexity : O(MNk\u22C5(M+N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(MNk)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n\n# Codes [C++ |Java |Python3] : With Comments\n```Java []\nclass Solution {\n private static final int kMod = 1_000_000_007;\n private int[][][] dp;\n private int[][] prefix;\n\n public int ways(String[] pizza, int k) {\n final int M = pizza.length;\n final int N = pizza[0].length();\n // dp[m][n][k] := # of ways to cut pizza[m:M][n:N] w/ k cuts\n dp = new int[M][N][k];\n for (int[][] A : dp)\n Arrays.stream(A).forEach(a -> Arrays.fill(a, -1));\n prefix = new int[M + 1][N + 1];\n\n for (int i = 0; i < M; ++i)\n for (int j = 0; j < N; ++j)\n prefix[i + 1][j + 1] = (pizza[i].charAt(j) == \'A\' ? 1 : 0) + prefix[i][j + 1] + prefix[i + 1][j] - prefix[i][j];\n\n return ways(0, 0, k - 1, M, N);\n }\n\n private int ways(int m, int n, int k, final int M, final int N) {\n if (k == 0)\n return 1;\n if (dp[m][n][k] >= 0)\n return dp[m][n][k];\n\n dp[m][n][k] = 0;\n\n for (int i = m + 1; i < M; ++i) // Cut horizontally\n if (hasApple(m, i, n, N) && hasApple(i, M, n, N))\n dp[m][n][k] = (dp[m][n][k] + ways(i, n, k - 1, M, N)) % kMod;\n\n for (int j = n + 1; j < N; ++j) // Cut vertically\n if (hasApple(m, M, n, j) && hasApple(m, M, j, N))\n dp[m][n][k] = (dp[m][n][k] + ways(m, j, k - 1, M, N)) % kMod;\n\n return dp[m][n][k];\n }\n // HasApple of pizza[row1..row2)[col1..col2)\n private boolean hasApple(int row1, int row2, int col1, int col2) {\n return (prefix[row2][col2] - prefix[row1][col2] - prefix[row2][col1] + prefix[row1][col1]) > 0;\n }\n}\n```\n```C++ []\nclass Solution {\n private:\n static constexpr int kMod = 1\'000\'000\'007;\n vector<vector<vector<int>>> dp;\n vector<vector<int>> prefix;\n\n public:\n int ways(vector<string>& pizza, int k) {\n const int M = pizza.size();\n const int N = pizza[0].size();\n // dp[m][n][k] := # of ways to cut pizza[m:M][n:N] w/ k cuts\n dp.resize(M, vector<vector<int>>(N, vector<int>(k, -1)));\n prefix.resize(M + 1, vector<int>(N + 1));\n\n for (int i = 0; i < M; ++i)\n for (int j = 0; j < N; ++j)\n prefix[i + 1][j + 1] = (pizza[i][j] == \'A\') + prefix[i][j + 1] +\n prefix[i + 1][j] - prefix[i][j];\n\n return ways(0, 0, k - 1, M, N);\n }\n\n int ways(int m, int n, int k, const int M, const int N) {\n if (k == 0)\n return 1;\n if (dp[m][n][k] >= 0)\n return dp[m][n][k];\n\n dp[m][n][k] = 0;\n\n for (int i = m + 1; i < M; ++i) // Cut horizontally\n if (hasApple(m, i, n, N) && hasApple(i, M, n, N))\n dp[m][n][k] = (dp[m][n][k] + ways(i, n, k - 1, M, N)) % kMod;\n\n for (int j = n + 1; j < N; ++j) // Cut vertically\n if (hasApple(m, M, n, j) && hasApple(m, M, j, N))\n dp[m][n][k] = (dp[m][n][k] + ways(m, j, k - 1, M, N)) % kMod;\n\n return dp[m][n][k];\n }\n // HasApple of pizza[row1..row2)[col1..col2)\n bool hasApple(int row1, int row2, int col1, int col2) {\n return (prefix[row2][col2] - prefix[row1][col2] - prefix[row2][col1] +\n prefix[row1][col1]) > 0;\n };\n};\n```\n```Python []\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n M = len(pizza)\n N = len(pizza[0])\n prefix = [[0] * (N + 1) for _ in range(M + 1)]\n\n for i in range(M):\n for j in range(N):\n prefix[i + 1][j + 1] = (pizza[i][j] == \'A\') + \\\n prefix[i][j + 1] + prefix[i + 1][j] - prefix[i][j]\n\n # Dp(m, n, k) := # of ways to cut pizza[m:M][n:N] w/ k cuts\n @functools.lru_cache(None)\n def dp(m: int, n: int, k: int) -> int:\n if k == 0:\n return 1\n\n ans = 0\n\n for i in range(m + 1, M): # Cut horizontally\n if hasApple(m, i, n, N) and hasApple(i, M, n, N):\n ans += dp(i, n, k - 1)\n\n for j in range(n + 1, N): # Cut vertically\n if hasApple(m, M, n, j) and hasApple(m, M, j, N):\n ans += dp(m, j, k - 1)\n\n return ans\n\n # HasApple of pizza[row1..row2)[col1..col2)\n def hasApple(row1: int, row2: int, col1: int, col2: int) -> bool:\n return (prefix[row2][col2] - prefix[row1][col2] -\n prefix[row2][col1] + prefix[row1][col1]) > 0\n\n return dp(0, 0, k - 1) % (10**9 + 7)\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 7 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Python DP code for reference | number-of-ways-of-cutting-a-pizza | 0 | 1 | Inspired by [this post](https://leetcode.com/problems/number-of-ways-of-cutting-a-pizza/solutions/623759/c-dp-cutting-with-picture-explanation/?orderBy=most_votes)\n```\nclass Solution:\n def ways(self, pizza: List[str], K: int) -> int:\n m,n = len(pizza),len(pizza[0])\n grid = [[0]*(n+1) for _ in range(0,(m+1))]\n # grid[i][j] tells the amount of apples in (i..m)(j..n) part\n # of matrix , To calcuate , we add right + left - inersecting part \n # + 1 if current cell is Apple\n for i in range(m-1,-1,-1):\n for j in range(n-1,-1,-1):\n grid[i][j]= grid[i+1][j]+grid[i][j+1] - \\\n grid[i+1][j+1] + (pizza[i][j] ==\'A\')\n\n # rec(r,c,k) , number of ways to do k slashes in this submatrix \n @lru_cache(None)\n def rec(r,c,k):\n if(k==K-1):\n # if K-1 slashes done, check if remaining part has some apples \n if(grid[r][c] > 0 ): return 1\n else: return 0\n mod = pow(10,9)+7\n res = 0\n\n # slashing along the rows, with constant column value \n # check if left and right part of the slash has happle\n # total - bottompart = Toppart , or that would mean that\n # Toppart has some apples , we later check if bottom has also has some \n for i in range(r,m):\n if(grid[r][c]-grid[i][c]>0 ):\n res += rec(i,c,k+1)\n\n for j in range(c,n):\n if(grid[r][c]-grid[r][j]>0 ):\n res += rec(r,j,k+1)\n \n return res%mod\n return rec(0,0,0)\n \n``` | 4 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
(Python) No need prefix, Just Check! | number-of-ways-of-cutting-a-pizza | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O (r * c * k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O (r * c * k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom functools import cache\n\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n\n # From (x1, y1) To (x2, y2)\n @cache\n def check (x1,y1,x2,y2):\n for r in range(x1, x2+1):\n for c in range(y1, y2+1):\n if pizza[r][c] == \'A\':\n return True \n return False \n \n @cache\n def dp (r, c, k):\n\n if k == 1 :\n if check (r, c, len(pizza)-1, len(pizza[0])-1):\n return 1\n \n cnt = 0 \n for i in range(c+1, len(pizza[0])):\n if check (r, c, len(pizza)-1, i-1):\n cnt += dp (r, i, k-1)\n for j in range(r+1, len(pizza)):\n if check (r, c, j-1, len(pizza[0])-1):\n cnt += dp (j, c, k-1)\n return cnt \n\n return dp(0,0,k) % (10 ** 9 + 7)\n\n \n``` | 10 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Python3 | Space Optimized Bottom-Up DP | O(k * r * c * (r + c)) Time, O(r * c) Space | number-of-ways-of-cutting-a-pizza | 0 | 1 | Please upvote if it helps!\n```\nclass Solution:\n def ways(self, pizza: List[str], k: int) -> int:\n rows, cols = len(pizza), len(pizza[0])\n \n # first, need way to query if a section contains an apple given a top left (r1, c1) and bottom right (r2, c2)\n # we can do this in constant time by keeping track of the number of apples above and to the left of any given cell\n apples = [[0] * cols for _ in range(rows)]\n for row in range(rows):\n apples_left = 0\n for col in range(cols):\n if pizza[row][col] == \'A\':\n apples_left += 1\n apples[row][col] = apples[row-1][col] + apples_left\n \n # query if there is an apple in this rectangle using the prefix sums\n def has_apple(r1, c1, r2 = rows-1, c2 = cols-1) -> bool:\n if r1 > r2 or c1 > c2:\n return False\n tot = apples[r2][c2]\n left_sub = apples[r2][c1-1] if c1 > 0 else 0\n up_sub = apples[r1-1][c2] if r1 > 0 else 0\n upleft_sub = apples[r1-1][c1-1] if r1 > 0 < c1 else 0\n in_rect = tot - left_sub - up_sub + upleft_sub\n return in_rect > 0\n \n # memory optimized dp, keep track of only one matrix of rows x cols\n # bc we only need to access the values at the previous number of cuts\n dp = [[1 if has_apple(r, c) else 0 for c in range(cols + 1)] for r in range(rows + 1)]\n \n for cuts in range(1, k):\n new_dp = [[0] * (cols + 1) for _ in range(rows + 1)]\n for row in range(rows-1, -1, -1):\n for col in range(cols-1, -1, -1):\n \n for r2 in range(row, rows):\n if has_apple(row, col, r2):\n new_dp[row][col] += dp[r2+1][col]\n \n for c2 in range(col, cols):\n if has_apple(row, col, rows-1, c2):\n new_dp[row][col] += dp[row][c2+1]\n dp = new_dp\n \n return dp[0][0] % (10**9 + 7) | 4 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
List usage O(N) solution | consecutive-characters | 1 | 1 | # Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Add the elements to the list and everytime u try to add the character just check the character that you are trying to add is equal to the present character if that is the case then increment the count and then store the value ..\n2. If the value is not equal make sure you that add the value back to the list so that the character might be useful for the next character..\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n def maxPower(self, s: str) -> int:\n c=1\n res=[s[0]]\n maxi=1\n for i in range(1,len(s)):\n if s[i]==res[-1]:\n #checking the consecutive or not...\n c+=1\n maxi=max(maxi,c)\n else:\n c=1\n res.append(s[i])\n return maxi\n\n``` | 1 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
List usage O(N) solution | consecutive-characters | 1 | 1 | # Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Add the elements to the list and everytime u try to add the character just check the character that you are trying to add is equal to the present character if that is the case then increment the count and then store the value ..\n2. If the value is not equal make sure you that add the value back to the list so that the character might be useful for the next character..\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n def maxPower(self, s: str) -> int:\n c=1\n res=[s[0]]\n maxi=1\n for i in range(1,len(s)):\n if s[i]==res[-1]:\n #checking the consecutive or not...\n c+=1\n maxi=max(maxi,c)\n else:\n c=1\n res.append(s[i])\n return maxi\n\n``` | 1 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Easy python solution | consecutive-characters | 0 | 1 | ```\ndef maxPower(self, s: str) -> int:\n c,ans = 1,1\n for i in range(len(s)-1):\n if s[i]==s[i+1]:\n c+=1\n ans=max(c,ans)\n else:\n c=1\n return ans\n``` | 8 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Easy python solution | consecutive-characters | 0 | 1 | ```\ndef maxPower(self, s: str) -> int:\n c,ans = 1,1\n for i in range(len(s)-1):\n if s[i]==s[i+1]:\n c+=1\n ans=max(c,ans)\n else:\n c=1\n return ans\n``` | 8 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Python ✅✅✅ || Faster than 99.60% || Memory Beats 97.63% | consecutive-characters | 0 | 1 | # Code\n```\nclass Solution:\n def maxPower(self, s):\n cnt = 0\n m = 0\n for i in range(1, len(s)):\n if (s[i-1] == s[i]): \n cnt += 1\n m = max(cnt, m)\n else: cnt = 0\n return m + 1\n```\n\n\n | 3 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Python ✅✅✅ || Faster than 99.60% || Memory Beats 97.63% | consecutive-characters | 0 | 1 | # Code\n```\nclass Solution:\n def maxPower(self, s):\n cnt = 0\n m = 0\n for i in range(1, len(s)):\n if (s[i-1] == s[i]): \n cnt += 1\n m = max(cnt, m)\n else: cnt = 0\n return m + 1\n```\n\n\n | 3 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Python O(n) by linear scan. [w/ Comment] | consecutive-characters | 0 | 1 | Python O(n) by linear scan.\n\n---\n\n```\nclass Solution:\n def maxPower(self, s: str) -> int:\n \n # the minimum value for consecutive is 1\n local_max, global_max = 1, 1\n \n # dummy char for initialization\n prev = \'#\'\n for char in s:\n \n if char == prev:\n \n # keeps consecutive, update local max\n local_max += 1\n \n # update global max length with latest one\n global_max = max( global_max, local_max )\n \n else:\n \n # lastest consective chars stops, reset local max\n local_max = 1\n \n # update previous char as current char for next iteration\n prev = char\n \n \n return global_max\n``` | 9 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Python O(n) by linear scan. [w/ Comment] | consecutive-characters | 0 | 1 | Python O(n) by linear scan.\n\n---\n\n```\nclass Solution:\n def maxPower(self, s: str) -> int:\n \n # the minimum value for consecutive is 1\n local_max, global_max = 1, 1\n \n # dummy char for initialization\n prev = \'#\'\n for char in s:\n \n if char == prev:\n \n # keeps consecutive, update local max\n local_max += 1\n \n # update global max length with latest one\n global_max = max( global_max, local_max )\n \n else:\n \n # lastest consective chars stops, reset local max\n local_max = 1\n \n # update previous char as current char for next iteration\n prev = char\n \n \n return global_max\n``` | 9 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Python Solution | 99% Faster | Simple Logic - Iterative Checking Based | consecutive-characters | 0 | 1 | ```\nclass Solution:\n def maxPower(self, s: str) -> int:\n if len(s) == 1:\n return 1\n count = 0\n i = 1\n ans = -inf\n while i < len(s):\n if s[i] == s[i-1]:\n count += 1\n ans = max(ans,count)\n else:\n count = 0\n i += 1\n \n return 1 if ans == -inf else ans + 1\n``` | 0 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Python Solution | 99% Faster | Simple Logic - Iterative Checking Based | consecutive-characters | 0 | 1 | ```\nclass Solution:\n def maxPower(self, s: str) -> int:\n if len(s) == 1:\n return 1\n count = 0\n i = 1\n ans = -inf\n while i < len(s):\n if s[i] == s[i-1]:\n count += 1\n ans = max(ans,count)\n else:\n count = 0\n i += 1\n \n return 1 if ans == -inf else ans + 1\n``` | 0 | You are given a string `s`. An **awesome** substring is a non-empty substring of `s` such that we can make any number of swaps in order to make it a palindrome.
Return _the length of the maximum length **awesome substring** of_ `s`.
**Example 1:**
**Input:** s = "3242415 "
**Output:** 5
**Explanation:** "24241 " is the longest awesome substring, we can form the palindrome "24142 " with some swaps.
**Example 2:**
**Input:** s = "12345678 "
**Output:** 1
**Example 3:**
**Input:** s = "213123 "
**Output:** 6
**Explanation:** "213123 " is the longest awesome substring, we can form the palindrome "231132 " with some swaps.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists only of digits. | Keep an array power where power[i] is the maximum power of the i-th character. The answer is max(power[i]). |
Easy | Python Solution | Hashmap | simplified-fractions | 0 | 1 | # Code\n```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n vis = {}\n ans = []\n for i in range(1, n+1):\n for j in range(i+1, n+1):\n if i/j not in vis:\n vis[i/j] = 1\n ans.append(f"{i}/{j}")\n return ans\n```\nDo upvote if you like the solution :) | 2 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
simple python solution | simplified-fractions | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n l=[]\n l2=[]\n for i in range(1,n+1):\n for j in range(i+1,n+1):\n if i/j not in l2:\n l2.append(i/j)\n l.append(str(i)+\'/\'+str(j))\n return l\n``` | 1 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Easy to understand Python3 solution | simplified-fractions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n res = []\n seen = set()\n\n for i in range(1, n+1):\n for j in range(i, n+1):\n if int(i/j) != i/j and i/j not in seen:\n seen.add(i/j)\n res.append(str(i) + \'/\' + str(j))\n \n return res\n \n``` | 0 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
easy solution using 2 loop | simplified-fractions | 0 | 1 | ## My solution\n```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n ans = []\n for i in range(1, n):\n for j in range(i+1, n+1):\n if gcd(i, j)==1: ans.append(f\'{i}/{j}\')\n return ans\n``` | 0 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Python | Brute Force GCD | simplified-fractions | 0 | 1 | # Code\n```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n res = [f"{n_}/{d_}" for d_ in range(2, n + 1) for n_ in range(1, d_) if gcd(n_, d_) == 1]\n return res\n``` | 0 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Python3 GCD | simplified-fractions | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n \n ans=[]\n \n for i in range(2,n+1):\n j=1\n \n while j<i:\n if gcd(i,j)==1:\n ans.append(str(j)+"/"+str(i))\n j+=1\n \n return ans\n \n``` | 0 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Simple python3 solution | 123 ms - faster than 100% solutions | simplified-fractions | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot n \\cdot log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nsee Euclidean algorithm\'s efficiency ([wiki](https://en.wikipedia.org/wiki/Euclidean_algorithm#Algorithmic_efficiency))\n\n- Space complexity: $$O(n \\cdot n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nfrom math import gcd\n\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n result = []\n for denominator in range(2, n + 1):\n for nominator in range(1, denominator):\n if gcd(nominator, denominator) == 1:\n current = f\'{nominator}/{denominator}\'\n result.append(current)\n return result\n\n``` | 0 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Python3 - Easy Solution | simplified-fractions | 0 | 1 | ```\nclass Solution:\n def simplifiedFractions(self, n: int) -> List[str]:\n output = []\n for denominator in range(1, n+1):\n for numerator in range(1, denominator):\n if math.gcd(denominator, numerator) == 1:\n output.append(f\'{numerator}/{denominator}\')\n \n return output\n``` | 0 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Solution Python Easy | count-good-nodes-in-binary-tree | 0 | 1 | # Intuition\nUse preorder to compare nodes from top to bottom.\n\n# Approach\nWhile traversing to the bottom, save the lower limit as the maximum node value in the path, and compare it to each node.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(h), (O(n) for skewed tree, O(log(n) for balanced tree)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n res = []\n\n def dfs(node, prev_max=float("-inf")):\n if not node:\n return None\n nonlocal res\n\n if prev_max<=node.val:\n res.append(node.val)\n\n prev_max = max(node.val, prev_max)\n\n if node.left:\n dfs(node.left, prev_max)\n \n if node.right:\n dfs(node.right, prev_max)\n \n dfs(root)\n return len(res)\n \n\n\n\n``` | 1 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
Solution Python Easy | count-good-nodes-in-binary-tree | 0 | 1 | # Intuition\nUse preorder to compare nodes from top to bottom.\n\n# Approach\nWhile traversing to the bottom, save the lower limit as the maximum node value in the path, and compare it to each node.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(h), (O(n) for skewed tree, O(log(n) for balanced tree)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n res = []\n\n def dfs(node, prev_max=float("-inf")):\n if not node:\n return None\n nonlocal res\n\n if prev_max<=node.val:\n res.append(node.val)\n\n prev_max = max(node.val, prev_max)\n\n if node.left:\n dfs(node.left, prev_max)\n \n if node.right:\n dfs(node.right, prev_max)\n \n dfs(root)\n return len(res)\n \n\n\n\n``` | 1 | Given a string `s` of lower and upper case English letters.
A good string is a string which doesn't have **two adjacent characters** `s[i]` and `s[i + 1]` where:
* `0 <= i <= s.length - 2`
* `s[i]` is a lower-case letter and `s[i + 1]` is the same letter but in upper-case or **vice-versa**.
To make the string good, you can choose **two adjacent** characters that make the string bad and remove them. You can keep doing this until the string becomes good.
Return _the string_ after making it good. The answer is guaranteed to be unique under the given constraints.
**Notice** that an empty string is also good.
**Example 1:**
**Input:** s = "leEeetcode "
**Output:** "leetcode "
**Explanation:** In the first step, either you choose i = 1 or i = 2, both will result "leEeetcode " to be reduced to "leetcode ".
**Example 2:**
**Input:** s = "abBAcC "
**Output:** " "
**Explanation:** We have many possible scenarios, and all lead to the same answer. For example:
"abBAcC " --> "aAcC " --> "cC " --> " "
"abBAcC " --> "abBA " --> "aA " --> " "
**Example 3:**
**Input:** s = "s "
**Output:** "s "
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only lower and upper case English letters. | Use DFS (Depth First Search) to traverse the tree, and constantly keep track of the current path maximum. |
Recursive approach✅ | O( n)✅ | (Step by step explanation)✅ | count-good-nodes-in-binary-tree | 0 | 1 | # Intuition\nThe problem asks to find the number of "good" nodes in a binary tree. A node is considered "good" if its value is greater than or equal to the maximum value in the path from the root to that node.\n\n# Approach\nThe approach is based on a depth-first search (DFS) traversal of the binary tree. We maintain the maximum value encountered in the path from the root to the current node. If the value of the current node is greater than or equal to this maximum value, the node is considered "good," and we increment the count of good nodes. We then recursively explore the left and right subtrees.\n\n1. **Initialization**: Start with the root of the binary tree.\n\n **Reason**: We begin the DFS traversal from the root.\n\n2. **DFS Traversal**: Use a recursive DFS traversal to explore the binary tree. For each node, check if it is a "good" node based on the maximum value encountered so far in the path from the root.\n\n **Reason**: DFS allows us to explore the tree and update the maximum value in the path.\n\n3. **Good Node Check**: Check if the value of the current node is greater than or equal to the maximum value encountered so far. If true, increment the count of good nodes.\n\n **Reason**: A node is considered "good" if its value is greater than or equal to the maximum value in the path.\n\n4. **Maximum Value Update**: Update the maximum value encountered so far by taking the maximum of the current node\'s value and the maximum value in the path.\n\n **Reason**: We need to track the maximum value in the path for the "good" node condition.\n\n5. **Recursive Exploration**: Recursively explore the left and right subtrees of the current node.\n\n **Reason**: Continue the DFS traversal to explore the entire binary tree.\n\n6. **Result**: The count of good nodes is the final result.\n\n **Reason**: We are asked to find the number of "good" nodes in the binary tree.\n\n# Complexity\n- **Time complexity**: O(n)\n - We visit each node once during the DFS traversal.\n- **Space complexity**: O(h)\n - The maximum depth of the recursion stack is the height of the binary tree. In the worst case, the space complexity is proportional to the height of the tree.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n good = [0]\n\n def dfs(root , max_val ):\n if root == None:\n return \n\n if root.val >= max_val:\n good[0] += 1\n\n max_val = max(max_val , root.val)\n\n dfs(root.left, max_val)\n dfs(root.right, max_val) \n\n\n dfs(root, float(\'-inf\')) \n return good[0]\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n int goodNodes(TreeNode* root) {\n int good = 0;\n dfs(root, INT_MIN, good);\n return good;\n }\n\n void dfs(TreeNode* root, int max_val, int& good) {\n if (root == NULL) {\n return;\n }\n\n if (root->val >= max_val) {\n good++;\n }\n\n max_val = max(max_val, root->val);\n\n dfs(root->left, max_val, good);\n dfs(root->right, max_val, good);\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n | 1 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
Recursive approach✅ | O( n)✅ | (Step by step explanation)✅ | count-good-nodes-in-binary-tree | 0 | 1 | # Intuition\nThe problem asks to find the number of "good" nodes in a binary tree. A node is considered "good" if its value is greater than or equal to the maximum value in the path from the root to that node.\n\n# Approach\nThe approach is based on a depth-first search (DFS) traversal of the binary tree. We maintain the maximum value encountered in the path from the root to the current node. If the value of the current node is greater than or equal to this maximum value, the node is considered "good," and we increment the count of good nodes. We then recursively explore the left and right subtrees.\n\n1. **Initialization**: Start with the root of the binary tree.\n\n **Reason**: We begin the DFS traversal from the root.\n\n2. **DFS Traversal**: Use a recursive DFS traversal to explore the binary tree. For each node, check if it is a "good" node based on the maximum value encountered so far in the path from the root.\n\n **Reason**: DFS allows us to explore the tree and update the maximum value in the path.\n\n3. **Good Node Check**: Check if the value of the current node is greater than or equal to the maximum value encountered so far. If true, increment the count of good nodes.\n\n **Reason**: A node is considered "good" if its value is greater than or equal to the maximum value in the path.\n\n4. **Maximum Value Update**: Update the maximum value encountered so far by taking the maximum of the current node\'s value and the maximum value in the path.\n\n **Reason**: We need to track the maximum value in the path for the "good" node condition.\n\n5. **Recursive Exploration**: Recursively explore the left and right subtrees of the current node.\n\n **Reason**: Continue the DFS traversal to explore the entire binary tree.\n\n6. **Result**: The count of good nodes is the final result.\n\n **Reason**: We are asked to find the number of "good" nodes in the binary tree.\n\n# Complexity\n- **Time complexity**: O(n)\n - We visit each node once during the DFS traversal.\n- **Space complexity**: O(h)\n - The maximum depth of the recursion stack is the height of the binary tree. In the worst case, the space complexity is proportional to the height of the tree.\n\n# Code\n\n\n<details open>\n <summary>Python Solution</summary>\n\n```python\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n good = [0]\n\n def dfs(root , max_val ):\n if root == None:\n return \n\n if root.val >= max_val:\n good[0] += 1\n\n max_val = max(max_val , root.val)\n\n dfs(root.left, max_val)\n dfs(root.right, max_val) \n\n\n dfs(root, float(\'-inf\')) \n return good[0]\n```\n</details>\n\n<details open>\n <summary>C++ Solution</summary>\n\n```cpp\nclass Solution {\npublic:\n int goodNodes(TreeNode* root) {\n int good = 0;\n dfs(root, INT_MIN, good);\n return good;\n }\n\n void dfs(TreeNode* root, int max_val, int& good) {\n if (root == NULL) {\n return;\n }\n\n if (root->val >= max_val) {\n good++;\n }\n\n max_val = max(max_val, root->val);\n\n dfs(root->left, max_val, good);\n dfs(root->right, max_val, good);\n }\n};\n```\n</details>\n\n# Please upvote the solution if you understood it.\n\n\n | 1 | Given a string `s` of lower and upper case English letters.
A good string is a string which doesn't have **two adjacent characters** `s[i]` and `s[i + 1]` where:
* `0 <= i <= s.length - 2`
* `s[i]` is a lower-case letter and `s[i + 1]` is the same letter but in upper-case or **vice-versa**.
To make the string good, you can choose **two adjacent** characters that make the string bad and remove them. You can keep doing this until the string becomes good.
Return _the string_ after making it good. The answer is guaranteed to be unique under the given constraints.
**Notice** that an empty string is also good.
**Example 1:**
**Input:** s = "leEeetcode "
**Output:** "leetcode "
**Explanation:** In the first step, either you choose i = 1 or i = 2, both will result "leEeetcode " to be reduced to "leetcode ".
**Example 2:**
**Input:** s = "abBAcC "
**Output:** " "
**Explanation:** We have many possible scenarios, and all lead to the same answer. For example:
"abBAcC " --> "aAcC " --> "cC " --> " "
"abBAcC " --> "abBA " --> "aA " --> " "
**Example 3:**
**Input:** s = "s "
**Output:** "s "
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only lower and upper case English letters. | Use DFS (Depth First Search) to traverse the tree, and constantly keep track of the current path maximum. |
🥇 C++ | PYTHON || EXPLAINED || ; ] | count-good-nodes-in-binary-tree | 0 | 1 | **UPVOTE IF HELPFuuL**\n\n**APPROACH**\n\nAny sort of traversal would work here.\nWhile traversing the tree, keep a variable that stores the maximum value till now in the path.\nCompare it with node value to decide whether it is a ood node or not.\n\n\n**BASE CASE**\n* Return ```0```, whenever ```root == NULL```\n\n**RECURSIVE CALL**\n* Call the funtion for both ```root->left``` and ```root->right``` and changing the max value to ```max(max_till_now,root->val)```\n\n**SELF-WORK**\n* Get answer recursively for next nodes.\n* If ```root->val > max_value_till_now``` increment the answer by one.\n\n**UPVOTE IF HELPFuuL**\n\n**C++**\n```\nclass Solution {\npublic:\n \n int solve(TreeNode* root,int hi){\n if (root){\n int k=solve(root->left, max(hi,root->val)) + solve(root->right, max(hi,root->val));\n if (root->val>=hi){\n k++;\n }\n return k;\n }\n return 0;\n }\n int goodNodes(TreeNode* root) {\n return solve(root,-10001);\n }\n};\n```\n**PYTHON**\n```\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n def solve(root,val):\n if root:\n k = solve(root.left, max(val,root.val)) + solve(root.right, max(val,root.val))\n if root.val >= val:\n k+=1\n return k\n return 0\n return solve(root,root.val)\n```\n\n | 66 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
🥇 C++ | PYTHON || EXPLAINED || ; ] | count-good-nodes-in-binary-tree | 0 | 1 | **UPVOTE IF HELPFuuL**\n\n**APPROACH**\n\nAny sort of traversal would work here.\nWhile traversing the tree, keep a variable that stores the maximum value till now in the path.\nCompare it with node value to decide whether it is a ood node or not.\n\n\n**BASE CASE**\n* Return ```0```, whenever ```root == NULL```\n\n**RECURSIVE CALL**\n* Call the funtion for both ```root->left``` and ```root->right``` and changing the max value to ```max(max_till_now,root->val)```\n\n**SELF-WORK**\n* Get answer recursively for next nodes.\n* If ```root->val > max_value_till_now``` increment the answer by one.\n\n**UPVOTE IF HELPFuuL**\n\n**C++**\n```\nclass Solution {\npublic:\n \n int solve(TreeNode* root,int hi){\n if (root){\n int k=solve(root->left, max(hi,root->val)) + solve(root->right, max(hi,root->val));\n if (root->val>=hi){\n k++;\n }\n return k;\n }\n return 0;\n }\n int goodNodes(TreeNode* root) {\n return solve(root,-10001);\n }\n};\n```\n**PYTHON**\n```\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n def solve(root,val):\n if root:\n k = solve(root.left, max(val,root.val)) + solve(root.right, max(val,root.val))\n if root.val >= val:\n k+=1\n return k\n return 0\n return solve(root,root.val)\n```\n\n | 66 | Given a string `s` of lower and upper case English letters.
A good string is a string which doesn't have **two adjacent characters** `s[i]` and `s[i + 1]` where:
* `0 <= i <= s.length - 2`
* `s[i]` is a lower-case letter and `s[i + 1]` is the same letter but in upper-case or **vice-versa**.
To make the string good, you can choose **two adjacent** characters that make the string bad and remove them. You can keep doing this until the string becomes good.
Return _the string_ after making it good. The answer is guaranteed to be unique under the given constraints.
**Notice** that an empty string is also good.
**Example 1:**
**Input:** s = "leEeetcode "
**Output:** "leetcode "
**Explanation:** In the first step, either you choose i = 1 or i = 2, both will result "leEeetcode " to be reduced to "leetcode ".
**Example 2:**
**Input:** s = "abBAcC "
**Output:** " "
**Explanation:** We have many possible scenarios, and all lead to the same answer. For example:
"abBAcC " --> "aAcC " --> "cC " --> " "
"abBAcC " --> "abBA " --> "aA " --> " "
**Example 3:**
**Input:** s = "s "
**Output:** "s "
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only lower and upper case English letters. | Use DFS (Depth First Search) to traverse the tree, and constantly keep track of the current path maximum. |
[Python 3] Extremely Simple 8 Line Recursive Solution, beats >99%. | count-good-nodes-in-binary-tree | 0 | 1 | # Intuition\nWhether a node is "good" or not is based on the node before it. This screams "recursion" to me, so I took a shot at it.\n\n# Approach\nWe want our function to return an int (the number of good nodes). We could implement this by dragging a counter through each function as a variable and incrementing it as we go, but if we can do it inline it would be better.\n\nTo accomplish this, we can use recursion to return the count of a nodes "good" children.\n\nTo perform the comparison and determine if something is a "good" node, we need to store the highest value so far. This can be passed as a parameter to our function.\n\nWe then need to satisfy three possible scenarios:\n\n1. End of a tree branch.\n2. Nodes which are "good".\n3. Nodes which are not "good".\n\nIf we\'re at the end of a branch of the tree, we can safely add zero to the count and return as a non-existent node could never be "good".\n\nIf we\'re not at the end of a branch, then we must be at a node. We can test this node against the highest value so far, and if it\'s "good" then we can return 1 + the value of its children. We can also pass this new highest value as a parameter to propagate it down the tree.\n\nIf it\'s not "good", then we just return the value of its children. We don\'t need to update the highest value, as the node must have been less if it\'s not "good".\n\n# Complexity\n- Time: $$O(n)$$\n\nWe perform only one operation for each node in the tree.\n\n- Space: $$O(n)$$\n\nAs we\'re using recursion, space usage is based on the number of children we\'re creating. This will be equal to the length of the input tree.\n\n\n\n\n# Code\n```\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n \n def dfs(node, prev_val):\n if not node:\n return 0\n elif node.val >= prev_val:\n return 1 + dfs(node.left, node.val) + dfs(node.right, node.val)\n else:\n return dfs(node.left, prev_val) + dfs(node.right, prev_val)\n\n return dfs(root, root.val)\n``` | 3 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
[Python 3] Extremely Simple 8 Line Recursive Solution, beats >99%. | count-good-nodes-in-binary-tree | 0 | 1 | # Intuition\nWhether a node is "good" or not is based on the node before it. This screams "recursion" to me, so I took a shot at it.\n\n# Approach\nWe want our function to return an int (the number of good nodes). We could implement this by dragging a counter through each function as a variable and incrementing it as we go, but if we can do it inline it would be better.\n\nTo accomplish this, we can use recursion to return the count of a nodes "good" children.\n\nTo perform the comparison and determine if something is a "good" node, we need to store the highest value so far. This can be passed as a parameter to our function.\n\nWe then need to satisfy three possible scenarios:\n\n1. End of a tree branch.\n2. Nodes which are "good".\n3. Nodes which are not "good".\n\nIf we\'re at the end of a branch of the tree, we can safely add zero to the count and return as a non-existent node could never be "good".\n\nIf we\'re not at the end of a branch, then we must be at a node. We can test this node against the highest value so far, and if it\'s "good" then we can return 1 + the value of its children. We can also pass this new highest value as a parameter to propagate it down the tree.\n\nIf it\'s not "good", then we just return the value of its children. We don\'t need to update the highest value, as the node must have been less if it\'s not "good".\n\n# Complexity\n- Time: $$O(n)$$\n\nWe perform only one operation for each node in the tree.\n\n- Space: $$O(n)$$\n\nAs we\'re using recursion, space usage is based on the number of children we\'re creating. This will be equal to the length of the input tree.\n\n\n\n\n# Code\n```\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n \n def dfs(node, prev_val):\n if not node:\n return 0\n elif node.val >= prev_val:\n return 1 + dfs(node.left, node.val) + dfs(node.right, node.val)\n else:\n return dfs(node.left, prev_val) + dfs(node.right, prev_val)\n\n return dfs(root, root.val)\n``` | 3 | Given a string `s` of lower and upper case English letters.
A good string is a string which doesn't have **two adjacent characters** `s[i]` and `s[i + 1]` where:
* `0 <= i <= s.length - 2`
* `s[i]` is a lower-case letter and `s[i + 1]` is the same letter but in upper-case or **vice-versa**.
To make the string good, you can choose **two adjacent** characters that make the string bad and remove them. You can keep doing this until the string becomes good.
Return _the string_ after making it good. The answer is guaranteed to be unique under the given constraints.
**Notice** that an empty string is also good.
**Example 1:**
**Input:** s = "leEeetcode "
**Output:** "leetcode "
**Explanation:** In the first step, either you choose i = 1 or i = 2, both will result "leEeetcode " to be reduced to "leetcode ".
**Example 2:**
**Input:** s = "abBAcC "
**Output:** " "
**Explanation:** We have many possible scenarios, and all lead to the same answer. For example:
"abBAcC " --> "aAcC " --> "cC " --> " "
"abBAcC " --> "abBA " --> "aA " --> " "
**Example 3:**
**Input:** s = "s "
**Output:** "s "
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only lower and upper case English letters. | Use DFS (Depth First Search) to traverse the tree, and constantly keep track of the current path maximum. |
BFS With MaxValue | Template of Similar Problems Python | count-good-nodes-in-binary-tree | 0 | 1 | From very First problem I used to apply BFS only so i have come up with this soln.\nevery Easy/Mediam level Tree Problems has same concept of travesal of tree and keep track of other parameter like path or sum etc... you can use Same template given hear or your Own..\n\n```\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n\t\n\t\tans = 0\n q = deque()\n\t\t\n q.append((root,-inf))\n \'\'\'perform bfs with track of maxval till perant node\'\'\'\t\n\n while q:\n node,maxval = q.popleft()\n\t\t\t \'\'\'if curr node has max or eqvalue till current max\'\'\'\n if node.val >= maxval: \n ans += 1\n\t\t\t\t\n if node.left: #new max update\n q.append((node.left,max(maxval,node.val)))\n \n if node.right:\n q.append((node.right,max(maxval,node.val)))\n \n return ans\n```\nhear listed a few problems you can do with same template..\n\n[112. Path Sum](https://leetcode.com/problems/path-sum/)\n```\ndef hasPathSum(self, root: TreeNode, sumT: int) -> bool:\n if not root:\n return False\n q = deque()\n q.append((root,0)) # track of path\n while q:\n node,value = q.popleft()\n print(value)\n if not node.left and not node.right:\n if sumT == value + node.val:\n return True\n if node.left:\n q.append((node.left,value+node.val))\n if node.right:\n q.append((node.right,value+node.val))\n return False\n```\n\n[100.Same Tree](https://leetcode.com/problems/same-tree/)\n```\nclass Solution:\n def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:\n queue = deque()\n queue.append(p)\n queue.append(q)\n while queue:\n node1= queue.popleft()\n node2 = queue.popleft()\n \n if not node1 and not node2: # track of same node you can define fun isMatch(n1,n2) and based on that track or return also\n continue\n \n if not node1 or not node2:\n return False\n \n if node1.val != node2.val:\n return False\n \n queue.append(node1.left)\n queue.append(node2.left)\n queue.append(node1.right)\n queue.append(node2.right)\n \n return True\n```\n[101.symmetric-tree](https://leetcode.com/problems/symmetric-tree/)\n```\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n# q = deque()\n# q.append(root)\n# q.append(root)\n# while q:\n# t1 = q.popleft()\n# t2 = q.popleft()\n \n# if not t1 and not t2:\n# continue\n# if not t1 or not t2:\n# return False\n# if t1.val != t2.val:\n# return False\n \n# q.append(t1.right)\n# q.append(t2.left)\n# q.append(t1.left)\n# q.append(t2.right)\n# return True\n```\n[102. Binary Tree Level Order Traversal](https://leetcode.com/problems/binary-tree-level-order-traversal/)\n```\ndef levelOrder(self, root: TreeNode) -> List[List[int]]:\n\n if not root:\n return []\n q=deque()\n q.append((root,1))\n answer = defaultdict(list) #track of level order nodes\n \n while q:\n node,depth= q.popleft()\n answer[depth].append(node.val)\n if node.left:\n q.append((node.left,depth+1))\n if node.right:\n q.append((node.right,depth+1))\n return answer.values()\n```\n[103. Binary Tree Zigzag Level Order Traversal](https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/)\n```\n def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:\n ans = defaultdict(list)\n if not root:\n return None\n q = deque()\n q.append((root,0))\n \n while q:\n node,depth = q.popleft()\n ans[depth].append(node.val)\n if node.left :\n q.append((node.left,depth+1))\n if node.right :\n q.append((node.right,depth+1))\n ct = 0 \n for i in ans:\n if ct % 2 :\n ans[i] = reversed(ans[i])\n ct+=1\n return ans.values()\n```\n\nAnd Many More [257. Binary Tree Paths](https://leetcode.com/problems/binary-tree-paths/) [404. Sum of Left Leaves](https://leetcode.com/problems/sum-of-left-leaves/) [1022. Sum of Root To Leaf Binary Numbers](https://leetcode.com/problems/sum-of-root-to-leaf-binary-numbers/)\n\nfor N-array tree\n[559. Maximum Depth of N-ary Tree](https://leetcode.com/problems/maximum-depth-of-n-ary-tree/)\n```\ndef maxDepth(self, root: \'Node\') -> int:\n \n\n \n if not root:\n return 0\n q=deque()\n maxdepth=-(math.inf)\n q.append((root,1))\n while q:\n node,depth = q.popleft()\n if not node.children:\n maxdepth=max(maxdepth,depth)\n \n for i in node.children:\n q.append((i,depth+1))\n \n return maxdepth\n```\n\nYou can also find By your self many more examples...by your own.. find and try to applay this kind of methods and thinks in that way also a bit.. thank you. happy coding. | 99 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
BFS With MaxValue | Template of Similar Problems Python | count-good-nodes-in-binary-tree | 0 | 1 | From very First problem I used to apply BFS only so i have come up with this soln.\nevery Easy/Mediam level Tree Problems has same concept of travesal of tree and keep track of other parameter like path or sum etc... you can use Same template given hear or your Own..\n\n```\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n\t\n\t\tans = 0\n q = deque()\n\t\t\n q.append((root,-inf))\n \'\'\'perform bfs with track of maxval till perant node\'\'\'\t\n\n while q:\n node,maxval = q.popleft()\n\t\t\t \'\'\'if curr node has max or eqvalue till current max\'\'\'\n if node.val >= maxval: \n ans += 1\n\t\t\t\t\n if node.left: #new max update\n q.append((node.left,max(maxval,node.val)))\n \n if node.right:\n q.append((node.right,max(maxval,node.val)))\n \n return ans\n```\nhear listed a few problems you can do with same template..\n\n[112. Path Sum](https://leetcode.com/problems/path-sum/)\n```\ndef hasPathSum(self, root: TreeNode, sumT: int) -> bool:\n if not root:\n return False\n q = deque()\n q.append((root,0)) # track of path\n while q:\n node,value = q.popleft()\n print(value)\n if not node.left and not node.right:\n if sumT == value + node.val:\n return True\n if node.left:\n q.append((node.left,value+node.val))\n if node.right:\n q.append((node.right,value+node.val))\n return False\n```\n\n[100.Same Tree](https://leetcode.com/problems/same-tree/)\n```\nclass Solution:\n def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:\n queue = deque()\n queue.append(p)\n queue.append(q)\n while queue:\n node1= queue.popleft()\n node2 = queue.popleft()\n \n if not node1 and not node2: # track of same node you can define fun isMatch(n1,n2) and based on that track or return also\n continue\n \n if not node1 or not node2:\n return False\n \n if node1.val != node2.val:\n return False\n \n queue.append(node1.left)\n queue.append(node2.left)\n queue.append(node1.right)\n queue.append(node2.right)\n \n return True\n```\n[101.symmetric-tree](https://leetcode.com/problems/symmetric-tree/)\n```\nclass Solution:\n def isSymmetric(self, root: TreeNode) -> bool:\n# q = deque()\n# q.append(root)\n# q.append(root)\n# while q:\n# t1 = q.popleft()\n# t2 = q.popleft()\n \n# if not t1 and not t2:\n# continue\n# if not t1 or not t2:\n# return False\n# if t1.val != t2.val:\n# return False\n \n# q.append(t1.right)\n# q.append(t2.left)\n# q.append(t1.left)\n# q.append(t2.right)\n# return True\n```\n[102. Binary Tree Level Order Traversal](https://leetcode.com/problems/binary-tree-level-order-traversal/)\n```\ndef levelOrder(self, root: TreeNode) -> List[List[int]]:\n\n if not root:\n return []\n q=deque()\n q.append((root,1))\n answer = defaultdict(list) #track of level order nodes\n \n while q:\n node,depth= q.popleft()\n answer[depth].append(node.val)\n if node.left:\n q.append((node.left,depth+1))\n if node.right:\n q.append((node.right,depth+1))\n return answer.values()\n```\n[103. Binary Tree Zigzag Level Order Traversal](https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/)\n```\n def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:\n ans = defaultdict(list)\n if not root:\n return None\n q = deque()\n q.append((root,0))\n \n while q:\n node,depth = q.popleft()\n ans[depth].append(node.val)\n if node.left :\n q.append((node.left,depth+1))\n if node.right :\n q.append((node.right,depth+1))\n ct = 0 \n for i in ans:\n if ct % 2 :\n ans[i] = reversed(ans[i])\n ct+=1\n return ans.values()\n```\n\nAnd Many More [257. Binary Tree Paths](https://leetcode.com/problems/binary-tree-paths/) [404. Sum of Left Leaves](https://leetcode.com/problems/sum-of-left-leaves/) [1022. Sum of Root To Leaf Binary Numbers](https://leetcode.com/problems/sum-of-root-to-leaf-binary-numbers/)\n\nfor N-array tree\n[559. Maximum Depth of N-ary Tree](https://leetcode.com/problems/maximum-depth-of-n-ary-tree/)\n```\ndef maxDepth(self, root: \'Node\') -> int:\n \n\n \n if not root:\n return 0\n q=deque()\n maxdepth=-(math.inf)\n q.append((root,1))\n while q:\n node,depth = q.popleft()\n if not node.children:\n maxdepth=max(maxdepth,depth)\n \n for i in node.children:\n q.append((i,depth+1))\n \n return maxdepth\n```\n\nYou can also find By your self many more examples...by your own.. find and try to applay this kind of methods and thinks in that way also a bit.. thank you. happy coding. | 99 | Given a string `s` of lower and upper case English letters.
A good string is a string which doesn't have **two adjacent characters** `s[i]` and `s[i + 1]` where:
* `0 <= i <= s.length - 2`
* `s[i]` is a lower-case letter and `s[i + 1]` is the same letter but in upper-case or **vice-versa**.
To make the string good, you can choose **two adjacent** characters that make the string bad and remove them. You can keep doing this until the string becomes good.
Return _the string_ after making it good. The answer is guaranteed to be unique under the given constraints.
**Notice** that an empty string is also good.
**Example 1:**
**Input:** s = "leEeetcode "
**Output:** "leetcode "
**Explanation:** In the first step, either you choose i = 1 or i = 2, both will result "leEeetcode " to be reduced to "leetcode ".
**Example 2:**
**Input:** s = "abBAcC "
**Output:** " "
**Explanation:** We have many possible scenarios, and all lead to the same answer. For example:
"abBAcC " --> "aAcC " --> "cC " --> " "
"abBAcC " --> "abBA " --> "aA " --> " "
**Example 3:**
**Input:** s = "s "
**Output:** "s "
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only lower and upper case English letters. | Use DFS (Depth First Search) to traverse the tree, and constantly keep track of the current path maximum. |
✅[Python] DFS Iterative, beats 88%✅ | count-good-nodes-in-binary-tree | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n# Intuition\nThe problem asks us to return the number of good nodes in a binary tree. A node is considered good if there are no nodes with a value greater than it in the path from root to that node. This means that we need to keep track of the maximum value we have seen so far while traversing from root to each node and compare it with the current node\'s value.\n\n# Approach\n1. We start by initializing a stack with a tuple containing the root node and negative infinity (i.e., `(root,float(\'-inf\'))`).\n2. We also initialize a variable `count` to keep track of the number of good nodes we have seen so far.\n3. We use a while loop to iterate over our stack until it is empty.\n4. For each iteration, we pop a tuple from our stack containing a node and the maximum value we have seen so far in its path from root (i.e., `node, maxNum = stack.pop()`).\n5. We then check if this node\'s value is greater than or equal to `maxNum`. If it is, we increment our `count` variable by 1 since this node is considered good.\n6. We update our `maxNum` variable by taking the maximum between `maxNum` and this node\'s value (i.e., `maxNum = max(maxNum,node.val)`).\n7. If this node has left or right children, we add them to our stack along with our updated `maxNum` value (i.e., `stack.append((node.left,maxNum))` and `stack.append((node.right,maxNum))`).\n8. Finally, after all nodes have been processed, we return our count variable which contains the number of good nodes in our binary tree.\n\n# Complexity\n- Time complexity: $$O(n)$$ where n is the number of nodes in the tree since we visit each node once.\n- Space complexity: $$O(n)$$ where n is also the number of nodes in tree since in worst case scenario when tree is skewed all n nodes will be stored on stack.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n stack = [(root,float(\'-inf\'))]\n count = 0\n while stack:\n node, maxNum = stack.pop()\n if node.val>=maxNum:\n count+=1\n maxNum = max(maxNum,node.val)\n if node.left:\n stack.append((node.left,maxNum))\n if node.right:\n stack.append((node.right,maxNum))\n return count\n``` | 14 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
✅[Python] DFS Iterative, beats 88%✅ | count-good-nodes-in-binary-tree | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n# Intuition\nThe problem asks us to return the number of good nodes in a binary tree. A node is considered good if there are no nodes with a value greater than it in the path from root to that node. This means that we need to keep track of the maximum value we have seen so far while traversing from root to each node and compare it with the current node\'s value.\n\n# Approach\n1. We start by initializing a stack with a tuple containing the root node and negative infinity (i.e., `(root,float(\'-inf\'))`).\n2. We also initialize a variable `count` to keep track of the number of good nodes we have seen so far.\n3. We use a while loop to iterate over our stack until it is empty.\n4. For each iteration, we pop a tuple from our stack containing a node and the maximum value we have seen so far in its path from root (i.e., `node, maxNum = stack.pop()`).\n5. We then check if this node\'s value is greater than or equal to `maxNum`. If it is, we increment our `count` variable by 1 since this node is considered good.\n6. We update our `maxNum` variable by taking the maximum between `maxNum` and this node\'s value (i.e., `maxNum = max(maxNum,node.val)`).\n7. If this node has left or right children, we add them to our stack along with our updated `maxNum` value (i.e., `stack.append((node.left,maxNum))` and `stack.append((node.right,maxNum))`).\n8. Finally, after all nodes have been processed, we return our count variable which contains the number of good nodes in our binary tree.\n\n# Complexity\n- Time complexity: $$O(n)$$ where n is the number of nodes in the tree since we visit each node once.\n- Space complexity: $$O(n)$$ where n is also the number of nodes in tree since in worst case scenario when tree is skewed all n nodes will be stored on stack.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def goodNodes(self, root: TreeNode) -> int:\n stack = [(root,float(\'-inf\'))]\n count = 0\n while stack:\n node, maxNum = stack.pop()\n if node.val>=maxNum:\n count+=1\n maxNum = max(maxNum,node.val)\n if node.left:\n stack.append((node.left,maxNum))\n if node.right:\n stack.append((node.right,maxNum))\n return count\n``` | 14 | Given a string `s` of lower and upper case English letters.
A good string is a string which doesn't have **two adjacent characters** `s[i]` and `s[i + 1]` where:
* `0 <= i <= s.length - 2`
* `s[i]` is a lower-case letter and `s[i + 1]` is the same letter but in upper-case or **vice-versa**.
To make the string good, you can choose **two adjacent** characters that make the string bad and remove them. You can keep doing this until the string becomes good.
Return _the string_ after making it good. The answer is guaranteed to be unique under the given constraints.
**Notice** that an empty string is also good.
**Example 1:**
**Input:** s = "leEeetcode "
**Output:** "leetcode "
**Explanation:** In the first step, either you choose i = 1 or i = 2, both will result "leEeetcode " to be reduced to "leetcode ".
**Example 2:**
**Input:** s = "abBAcC "
**Output:** " "
**Explanation:** We have many possible scenarios, and all lead to the same answer. For example:
"abBAcC " --> "aAcC " --> "cC " --> " "
"abBAcC " --> "abBA " --> "aA " --> " "
**Example 3:**
**Input:** s = "s "
**Output:** "s "
**Constraints:**
* `1 <= s.length <= 100`
* `s` contains only lower and upper case English letters. | Use DFS (Depth First Search) to traverse the tree, and constantly keep track of the current path maximum. |
Python - knapsack with repetitions, bottom up DP | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Intuition\nWithin combinatorial optimization there are 3 school models of knapsack: fractional (greedy solution, easiest), integer with repetitions and integer without repetitions (hardest). This is integer with repetitions, weigth/capacity is target and cost, value is number constructed. Items to pick as much as you can are digits from 1-9 and their costs as weight reduction element.\n\n\n# Complexity\n- Time complexity:\n$$O(TW)$$ - T is target, W is size of word in comparison char by char, loop that iterates are ignored as they are constant, 9. \n\n- Space complexity:\n$$O(T)$$\n\n# Code\n```\nclass Solution:\n def bigger(self, a, b):\n if len(a) != len(b): return len(a) > len(b)\n return a > b\n def largestNumber(self, cost, target):\n dp = [None] * (target + 1)\n dp[0] = \'\'\n for t in range(1, target + 1):\n for d in range(1, 10):\n c = cost[d-1]\n if t-c >= 0:\n if dp[t-c] is not None:\n candidate = dp[t-c] + str(d)\n if dp[t] is None or self.bigger(candidate, dp[t]):\n dp[t] = candidate\n\n return dp[target] if dp[target] else \'0\'\n\n\n\n \n \n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python - knapsack with repetitions, bottom up DP | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Intuition\nWithin combinatorial optimization there are 3 school models of knapsack: fractional (greedy solution, easiest), integer with repetitions and integer without repetitions (hardest). This is integer with repetitions, weigth/capacity is target and cost, value is number constructed. Items to pick as much as you can are digits from 1-9 and their costs as weight reduction element.\n\n\n# Complexity\n- Time complexity:\n$$O(TW)$$ - T is target, W is size of word in comparison char by char, loop that iterates are ignored as they are constant, 9. \n\n- Space complexity:\n$$O(T)$$\n\n# Code\n```\nclass Solution:\n def bigger(self, a, b):\n if len(a) != len(b): return len(a) > len(b)\n return a > b\n def largestNumber(self, cost, target):\n dp = [None] * (target + 1)\n dp[0] = \'\'\n for t in range(1, target + 1):\n for d in range(1, 10):\n c = cost[d-1]\n if t-c >= 0:\n if dp[t-c] is not None:\n candidate = dp[t-c] + str(d)\n if dp[t] is None or self.bigger(candidate, dp[t]):\n dp[t] = candidate\n\n return dp[target] if dp[target] else \'0\'\n\n\n\n \n \n``` | 0 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
Python | Easiest Solution Faster than 100% | Top Down Approach | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost: List[int], target: int) -> str:\n @lru_cache(None)\n def solve(target):\n if target < 0:\n return float(\'-inf\')\n if target == 0:\n return 0\n res = float(\'-inf\')\n for i in cost:\n res = max(res, 1+solve(target-i))\n return res\n temp = solve(target)\n if temp == float(\'-inf\'):return "0"\n ans = ""\n while target:\n mx, res = 0, 0\n for idx,i in enumerate(cost):\n temp = solve(target-i)\n if temp > mx:\n mx = temp\n res = idx+1\n elif temp == mx:\n res = max(res, idx+1)\n ans += str(res)\n target -= cost[res-1]\n return ans\n\n \n \n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python | Easiest Solution Faster than 100% | Top Down Approach | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost: List[int], target: int) -> str:\n @lru_cache(None)\n def solve(target):\n if target < 0:\n return float(\'-inf\')\n if target == 0:\n return 0\n res = float(\'-inf\')\n for i in cost:\n res = max(res, 1+solve(target-i))\n return res\n temp = solve(target)\n if temp == float(\'-inf\'):return "0"\n ans = ""\n while target:\n mx, res = 0, 0\n for idx,i in enumerate(cost):\n temp = solve(target-i)\n if temp > mx:\n mx = temp\n res = idx+1\n elif temp == mx:\n res = max(res, idx+1)\n ans += str(res)\n target -= cost[res-1]\n return ans\n\n \n \n``` | 0 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
DFS+Memo || both 2d + 1d DP || Unbounded knapsack | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost: List[int], target: int) -> str:\n\n\n dp = [-1]*(target+1) \n def dfs(t):\n\n if t==0: return 0 \n if t<0: return -inf \n\n if dp[t] != -1: return dp[t] \n\n \n dp[t] = max(dfs(t - c) * 10 + i + 1 for i, c in enumerate(cost))\n return dp[t] \n \n return str(max(0,dfs(target)))\n \n\n # 2D dP\n # dp = [[-1]*(target+1) for _ in range(len(cost)+1)]\n # def dfs(idx , t): \n\n \n # if t==0: return 0\n # if t<0 or idx==len(cost): return -inf \n\n # if dp[idx][t]!=-1: return dp[idx][t]\n \n \n # pick = (idx+1)+10*dfs(idx,t-cost[idx]) \n # npick = dfs(idx+1,t) \n \n # dp[idx][t] = max(pick,npick)\n # return dp[idx][t] \n \n \n # return str(max(0,dfs(0,target)))\n \n\n \n\n\n\n \n\n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
DFS+Memo || both 2d + 1d DP || Unbounded knapsack | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost: List[int], target: int) -> str:\n\n\n dp = [-1]*(target+1) \n def dfs(t):\n\n if t==0: return 0 \n if t<0: return -inf \n\n if dp[t] != -1: return dp[t] \n\n \n dp[t] = max(dfs(t - c) * 10 + i + 1 for i, c in enumerate(cost))\n return dp[t] \n \n return str(max(0,dfs(target)))\n \n\n # 2D dP\n # dp = [[-1]*(target+1) for _ in range(len(cost)+1)]\n # def dfs(idx , t): \n\n \n # if t==0: return 0\n # if t<0 or idx==len(cost): return -inf \n\n # if dp[idx][t]!=-1: return dp[idx][t]\n \n \n # pick = (idx+1)+10*dfs(idx,t-cost[idx]) \n # npick = dfs(idx+1,t) \n \n # dp[idx][t] = max(pick,npick)\n # return dp[idx][t] \n \n \n # return str(max(0,dfs(0,target)))\n \n\n \n\n\n\n \n\n``` | 0 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
Python (Simple DP) | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost, target):\n dict1 = collections.defaultdict(int)\n\n for i,j in enumerate(cost):\n dict1[i+1] = j\n\n @lru_cache(None)\n def dfs(total):\n if total == 0:\n return 0\n\n str1 = float("-inf")\n\n for j in range(1,10):\n if total - dict1[j] >= 0:\n str1 = max(str1,dfs(total-dict1[j])*10 + j)\n\n return str1\n\n res = dfs(target)\n\n return str(res) if res != float("-inf") else "0"\n\n\n\n\n\n\n\n\n \n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python (Simple DP) | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost, target):\n dict1 = collections.defaultdict(int)\n\n for i,j in enumerate(cost):\n dict1[i+1] = j\n\n @lru_cache(None)\n def dfs(total):\n if total == 0:\n return 0\n\n str1 = float("-inf")\n\n for j in range(1,10):\n if total - dict1[j] >= 0:\n str1 = max(str1,dfs(total-dict1[j])*10 + j)\n\n return str1\n\n res = dfs(target)\n\n return str(res) if res != float("-inf") else "0"\n\n\n\n\n\n\n\n\n \n``` | 0 | Given two positive integers `n` and `k`, the binary string `Sn` is formed as follows:
* `S1 = "0 "`
* `Si = Si - 1 + "1 " + reverse(invert(Si - 1))` for `i > 1`
Where `+` denotes the concatenation operation, `reverse(x)` returns the reversed string `x`, and `invert(x)` inverts all the bits in `x` (`0` changes to `1` and `1` changes to `0`).
For example, the first four strings in the above sequence are:
* `S1 = "0 "`
* `S2 = "0**1**1 "`
* `S3 = "011**1**001 "`
* `S4 = "0111001**1**0110001 "`
Return _the_ `kth` _bit_ _in_ `Sn`. It is guaranteed that `k` is valid for the given `n`.
**Example 1:**
**Input:** n = 3, k = 1
**Output:** "0 "
**Explanation:** S3 is "**0**111001 ".
The 1st bit is "0 ".
**Example 2:**
**Input:** n = 4, k = 11
**Output:** "1 "
**Explanation:** S4 is "0111001101**1**0001 ".
The 11th bit is "1 ".
**Constraints:**
* `1 <= n <= 20`
* `1 <= k <= 2n - 1` | Use dynamic programming to find the maximum digits to paint given a total cost. Build the largest number possible using this DP table. |
PYTHON SIMPLE DP ᓚᘏᗢ | form-largest-integer-with-digits-that-add-up-to-target | 0 | 1 | # Approach\ndp which is easy to see and read :) <3\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Code\n```\nclass Solution:\n def largestNumber(self, cost: List[int], target: int) -> str:\n dp=[""]*(target+1)\n for i in range(0,target+1):\n for j in range(1,10):\n if i+cost[j-1]<=target :\n if dp[i]=="" and i!=0:\n continue\n res="".join(sorted(dp[i]+str(j),reverse=True))\n if len(res)>len(dp[i+cost[j-1]]):\n dp[i+cost[j-1]]=res\n elif len(res)==len(dp[i+cost[j-1]]) and res>dp[i+cost[j-1]]:\n dp[i+cost[j-1]]=res\n return [dp[target],"0"][dp[target]==""]\n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.