title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python3] DP + Greedy approach + explanation | reducing-dishes | 0 | 1 | # Intuition\nWe need to maximaze the satisfaction usign formulae:\n```\nsum((i+1) * dish[i])\n```\nwith some of the dishes reduced. \nWe can have negative satisfaction dishes, which reduce the overall satisfaction, apart from they add time so that further positive-satisfaction dishes contribute more satisfaction. \n\nAlso we see that we will maximize overall satisfaction if we cook best dishes last, so that their time multiplied by satisfaction is maximized.\n\nWe can use a greedy approach to maximize satisfaction by reducing some negative-satisfaction dishes.\n\nNote that if we start adding dishes, we can have overall satisfaction calculated by formulae:\n\n```\nD(i) = s(0) * (i-1) + s(1) * (i-2) + ... + s(i) * 1 = s(0) * (i-2) + s(1) * (i-3) + ... + s(i-1) + (s(0) + s(1) + ... + s(i-1)) + s(i) = D(i-1) + ps(i-1) + s(i)\n```\n\nWhere ``ps(i)`` is partial sum of first ``i`` dishes (The best ones).\n\nHere we can apply dynamic programming to solve this.\n\n# Approach\n1. Sort ``satisfaction`` in descending order\n2. Calculate ``D(i)`` and maintaining partial sum ``ps`` and updating maximum satisfaction ``result``\n3. Return the ``result``\n\n# Complexity\n- Time complexity:\n$$O(n*log(n))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort(reverse=True)\n result, current, ps = 0, 0, 0\n n = len(satisfaction)\n for i in range(n):\n current += ps + satisfaction[i]\n ps += satisfaction[i]\n result = max(result, current)\n return result\n```\n\nShall you have any questions please don\'t hesitate to ask! \n\nAnd upvote if you like this approach! | 1 | We have a wooden plank of the length `n` **units**. Some ants are walking on the plank, each ant moves with a speed of **1 unit per second**. Some of the ants move to the **left**, the other move to the **right**.
When two ants moving in two **different** directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.
When an ant reaches **one end** of the plank at a time `t`, it falls out of the plank immediately.
Given an integer `n` and two integer arrays `left` and `right`, the positions of the ants moving to the left and the right, return _the moment when the last ant(s) fall out of the plank_.
**Example 1:**
**Input:** n = 4, left = \[4,3\], right = \[0,1\]
**Output:** 4
**Explanation:** In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).
**Example 2:**
**Input:** n = 7, left = \[\], right = \[0,1,2,3,4,5,6,7\]
**Output:** 7
**Explanation:** All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
**Example 3:**
**Input:** n = 7, left = \[0,1,2,3,4,5,6,7\], right = \[\]
**Output:** 7
**Explanation:** All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
**Constraints:**
* `1 <= n <= 104`
* `0 <= left.length <= n + 1`
* `0 <= left[i] <= n`
* `0 <= right.length <= n + 1`
* `0 <= right[i] <= n`
* `1 <= left.length + right.length <= n + 1`
* All values of `left` and `right` are unique, and each value can appear **only in one** of the two arrays. | Use dynamic programming to find the optimal solution by saving the previous best like-time coefficient and its corresponding element sum. If adding the current element to the previous best like-time coefficient and its corresponding element sum would increase the best like-time coefficient, then go ahead and add it. Otherwise, keep the previous best like-time coefficient. |
easy greedy solution without using DP | reducing-dishes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort()\n res = cnt = 0\n while satisfaction:\n cur = satisfaction.pop()\n if cur + cnt < 0: return res\n cnt += cur\n res += cnt\n return res\n``` | 1 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
easy greedy solution without using DP | reducing-dishes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort()\n res = cnt = 0\n while satisfaction:\n cur = satisfaction.pop()\n if cur + cnt < 0: return res\n cnt += cur\n res += cnt\n return res\n``` | 1 | We have a wooden plank of the length `n` **units**. Some ants are walking on the plank, each ant moves with a speed of **1 unit per second**. Some of the ants move to the **left**, the other move to the **right**.
When two ants moving in two **different** directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.
When an ant reaches **one end** of the plank at a time `t`, it falls out of the plank immediately.
Given an integer `n` and two integer arrays `left` and `right`, the positions of the ants moving to the left and the right, return _the moment when the last ant(s) fall out of the plank_.
**Example 1:**
**Input:** n = 4, left = \[4,3\], right = \[0,1\]
**Output:** 4
**Explanation:** In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).
**Example 2:**
**Input:** n = 7, left = \[\], right = \[0,1,2,3,4,5,6,7\]
**Output:** 7
**Explanation:** All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
**Example 3:**
**Input:** n = 7, left = \[0,1,2,3,4,5,6,7\], right = \[\]
**Output:** 7
**Explanation:** All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
**Constraints:**
* `1 <= n <= 104`
* `0 <= left.length <= n + 1`
* `0 <= left[i] <= n`
* `0 <= right.length <= n + 1`
* `0 <= right[i] <= n`
* `1 <= left.length + right.length <= n + 1`
* All values of `left` and `right` are unique, and each value can appear **only in one** of the two arrays. | Use dynamic programming to find the optimal solution by saving the previous best like-time coefficient and its corresponding element sum. If adding the current element to the previous best like-time coefficient and its corresponding element sum would increase the best like-time coefficient, then go ahead and add it. Otherwise, keep the previous best like-time coefficient. |
5 LINES || EASY SOLUTION USING || PREFIX SUM || PYTHON | reducing-dishes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort(reverse=True)\n n = len(satisfaction)\n result, prefix, sum_dishes = 0, 0, 0\n for i in range(n):\n prefix += satisfaction[i]\n sum_dishes += prefix\n result = max(result, sum_dishes)\n \n return result\n``` | 1 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
5 LINES || EASY SOLUTION USING || PREFIX SUM || PYTHON | reducing-dishes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort(reverse=True)\n n = len(satisfaction)\n result, prefix, sum_dishes = 0, 0, 0\n for i in range(n):\n prefix += satisfaction[i]\n sum_dishes += prefix\n result = max(result, sum_dishes)\n \n return result\n``` | 1 | We have a wooden plank of the length `n` **units**. Some ants are walking on the plank, each ant moves with a speed of **1 unit per second**. Some of the ants move to the **left**, the other move to the **right**.
When two ants moving in two **different** directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.
When an ant reaches **one end** of the plank at a time `t`, it falls out of the plank immediately.
Given an integer `n` and two integer arrays `left` and `right`, the positions of the ants moving to the left and the right, return _the moment when the last ant(s) fall out of the plank_.
**Example 1:**
**Input:** n = 4, left = \[4,3\], right = \[0,1\]
**Output:** 4
**Explanation:** In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).
**Example 2:**
**Input:** n = 7, left = \[\], right = \[0,1,2,3,4,5,6,7\]
**Output:** 7
**Explanation:** All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
**Example 3:**
**Input:** n = 7, left = \[0,1,2,3,4,5,6,7\], right = \[\]
**Output:** 7
**Explanation:** All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
**Constraints:**
* `1 <= n <= 104`
* `0 <= left.length <= n + 1`
* `0 <= left[i] <= n`
* `0 <= right.length <= n + 1`
* `0 <= right[i] <= n`
* `1 <= left.length + right.length <= n + 1`
* All values of `left` and `right` are unique, and each value can appear **only in one** of the two arrays. | Use dynamic programming to find the optimal solution by saving the previous best like-time coefficient and its corresponding element sum. If adding the current element to the previous best like-time coefficient and its corresponding element sum would increase the best like-time coefficient, then go ahead and add it. Otherwise, keep the previous best like-time coefficient. |
😍 C & Python Solution | detailed explained | reducing-dishes | 0 | 1 | # \uD83C\uDF40 Intuition\n## Sort the array in increasing (non-decreasing) order \uD83C\uDF4C\n- This is the base structure for maximum sum of ***like-time coefficient***\n## First, let have some mind experiment \uD83C\uDF4C\n- We know the lefter the index, the bigger the coefficient is...\n- Let\'s consider `[-9,-8,-1,0,5]`, and check the sum of ***like-time coefficient***\n- What can we see if we keep `index 4 ~ 4`, `index 3 ~ 4` ... `index 0 ~ 4`\n- ```\n 5 => 5\n ```\n- ```\n 5\n 0 + 5 => 10\n ```\n- ```\n 5\n 0 + 5\n -1 + 0 + 5 => 14\n ```\n- ```\n 5\n 0 + 5\n -1 + 0 + 5\n -8 + -1 + 0 + 5 => 10\n ```\n- ```\n 5\n 0 + 5\n -1 + 0 + 5\n -8 + -1 + 0 + 5\n -9 + -8 + -1 + 0 + 5 => -3\n ```\n- ```\n 5 => 5\n 0 + 5 => 10\n -1 + 0 + 5 => 14\n -8 + -1 + 0 + 5 => 10\n -9 + -8 + -1 + 0 + 5 => -3\n ```\n- Although negative value seem to decrease the max sum, we might increase the max sum after all, just see `index 3 ~ 4` and `index 2 ~ 4`\n## \uD83D\uDE1D **which is why I think this problem is hard**\n- Notice that, we can increment the coefficient of **all** its right part of the array (+1) if we add a new element to the left\n- Everytime we add a new element, we add all right elements again, therefore...\n\n## Whether delete a element is determined by: \uD83C\uDF4C\n- check if `(its value + sum of all its right values > 0)`\n - Yes: keep it\n - No: delete it\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# \uD83C\uDF40 Approach\n## Step 1:\n- Sort the array in non-decreasing order\n- Two variables\n - `rightSum` stores `sum of all its right values (including itself)`\n - `res` stores `sum of like-time coefficient`, which is the result return value\n - Keep in mind that, everytime we add a new element, `res += rightSum`\n## Step 2:\n- For loop, `i` from `last index` to `0`,\n - Each round, check if `(its value + sum of all its right values > 0)`\n - True: don\'t delete this element, and update `rightSum` and `res`\n - False: delete this element and all its left ones, return `res`\n<!-- Describe your approach to solving the problem. -->\n\n# \uD83C\uDF40 Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \uD83C\uDF40 Code\n``` C []\n// Quick sort sub-function\nvoid swap(int *a0, int *a1);\nint mid(int a, int b, int c);\nvoid quickSort(int *a, int x, int y);\n\n// Answer solution\nint maxSatisfaction(int* satisfaction, int satisfactionSize){\n // Step 1\n quickSort(satisfaction, 0, satisfactionSize - 1);\n int rightSum = 0;\n int res = 0;\n // Step 2\n for (int i = satisfactionSize - 1; i >= 0; i--)\n {\n if (satisfaction[i] + rightSum > 0)\n {\n rightSum += satisfaction[i];\n res += rightSum;\n }\n else\n {\n return res;\n }\n }\n return res;\n}\n\n// Below is quick sort sub-function\nvoid swap(int *a0, int *a1)\n{\n int t = *a0;\n *a0 = *a1;\n *a1 = t;\n return;\n}\n\nint mid(int a, int b, int c)\n{\n if (a <= b)\n {\n if (c <= a)\n return a;\n else if (b <= c)\n return b;\n return c;\n }\n else // b <= a\n {\n if (c <= b)\n return b;\n else if (a <= c)\n return a;\n return c;\n }\n}\n\nvoid quickSort(int *a, int x, int y)\n{\n // non-decreasing order\n // array, Quick Sort a[x] ~ a[y]\n if (x < y) // has at least 2 data to sort\n {\n // choose mid value as pivot key\n int pk = mid(a[x], a[(x + y) / 2], a[y]);\n if (pk == a[(x + y) / 2])\n swap(&a[x], &a[(x + y) / 2]);\n else if (pk == a[y])\n swap(&a[x], &a[y]);\n\n int i = x, j = y + 1;\n do // while (i < j)\n {\n do\n {\n i++;\n } while (a[i] < pk && i != y);\n do\n {\n j--;\n } while (a[j] > pk && j != x);\n if (i < j)\n {\n swap(&a[i], &a[j]);\n }\n } while (i < j);\n swap(&a[j], &a[x]);\n quickSort(a, x, j - 1);\n quickSort(a, j + 1, y);\n }\n return;\n}\n```\n``` Python3 []\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n # Step 1\n satisfaction.sort()\n rightSum = 0\n res = 0\n # Step 2\n for i in reversed(satisfaction):\n if i + rightSum > 0:\n rightSum += i\n res += rightSum\n else:\n return res\n return res\n```\n\nPlease upvote uwu | 1 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
😍 C & Python Solution | detailed explained | reducing-dishes | 0 | 1 | # \uD83C\uDF40 Intuition\n## Sort the array in increasing (non-decreasing) order \uD83C\uDF4C\n- This is the base structure for maximum sum of ***like-time coefficient***\n## First, let have some mind experiment \uD83C\uDF4C\n- We know the lefter the index, the bigger the coefficient is...\n- Let\'s consider `[-9,-8,-1,0,5]`, and check the sum of ***like-time coefficient***\n- What can we see if we keep `index 4 ~ 4`, `index 3 ~ 4` ... `index 0 ~ 4`\n- ```\n 5 => 5\n ```\n- ```\n 5\n 0 + 5 => 10\n ```\n- ```\n 5\n 0 + 5\n -1 + 0 + 5 => 14\n ```\n- ```\n 5\n 0 + 5\n -1 + 0 + 5\n -8 + -1 + 0 + 5 => 10\n ```\n- ```\n 5\n 0 + 5\n -1 + 0 + 5\n -8 + -1 + 0 + 5\n -9 + -8 + -1 + 0 + 5 => -3\n ```\n- ```\n 5 => 5\n 0 + 5 => 10\n -1 + 0 + 5 => 14\n -8 + -1 + 0 + 5 => 10\n -9 + -8 + -1 + 0 + 5 => -3\n ```\n- Although negative value seem to decrease the max sum, we might increase the max sum after all, just see `index 3 ~ 4` and `index 2 ~ 4`\n## \uD83D\uDE1D **which is why I think this problem is hard**\n- Notice that, we can increment the coefficient of **all** its right part of the array (+1) if we add a new element to the left\n- Everytime we add a new element, we add all right elements again, therefore...\n\n## Whether delete a element is determined by: \uD83C\uDF4C\n- check if `(its value + sum of all its right values > 0)`\n - Yes: keep it\n - No: delete it\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# \uD83C\uDF40 Approach\n## Step 1:\n- Sort the array in non-decreasing order\n- Two variables\n - `rightSum` stores `sum of all its right values (including itself)`\n - `res` stores `sum of like-time coefficient`, which is the result return value\n - Keep in mind that, everytime we add a new element, `res += rightSum`\n## Step 2:\n- For loop, `i` from `last index` to `0`,\n - Each round, check if `(its value + sum of all its right values > 0)`\n - True: don\'t delete this element, and update `rightSum` and `res`\n - False: delete this element and all its left ones, return `res`\n<!-- Describe your approach to solving the problem. -->\n\n# \uD83C\uDF40 Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \uD83C\uDF40 Code\n``` C []\n// Quick sort sub-function\nvoid swap(int *a0, int *a1);\nint mid(int a, int b, int c);\nvoid quickSort(int *a, int x, int y);\n\n// Answer solution\nint maxSatisfaction(int* satisfaction, int satisfactionSize){\n // Step 1\n quickSort(satisfaction, 0, satisfactionSize - 1);\n int rightSum = 0;\n int res = 0;\n // Step 2\n for (int i = satisfactionSize - 1; i >= 0; i--)\n {\n if (satisfaction[i] + rightSum > 0)\n {\n rightSum += satisfaction[i];\n res += rightSum;\n }\n else\n {\n return res;\n }\n }\n return res;\n}\n\n// Below is quick sort sub-function\nvoid swap(int *a0, int *a1)\n{\n int t = *a0;\n *a0 = *a1;\n *a1 = t;\n return;\n}\n\nint mid(int a, int b, int c)\n{\n if (a <= b)\n {\n if (c <= a)\n return a;\n else if (b <= c)\n return b;\n return c;\n }\n else // b <= a\n {\n if (c <= b)\n return b;\n else if (a <= c)\n return a;\n return c;\n }\n}\n\nvoid quickSort(int *a, int x, int y)\n{\n // non-decreasing order\n // array, Quick Sort a[x] ~ a[y]\n if (x < y) // has at least 2 data to sort\n {\n // choose mid value as pivot key\n int pk = mid(a[x], a[(x + y) / 2], a[y]);\n if (pk == a[(x + y) / 2])\n swap(&a[x], &a[(x + y) / 2]);\n else if (pk == a[y])\n swap(&a[x], &a[y]);\n\n int i = x, j = y + 1;\n do // while (i < j)\n {\n do\n {\n i++;\n } while (a[i] < pk && i != y);\n do\n {\n j--;\n } while (a[j] > pk && j != x);\n if (i < j)\n {\n swap(&a[i], &a[j]);\n }\n } while (i < j);\n swap(&a[j], &a[x]);\n quickSort(a, x, j - 1);\n quickSort(a, j + 1, y);\n }\n return;\n}\n```\n``` Python3 []\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n # Step 1\n satisfaction.sort()\n rightSum = 0\n res = 0\n # Step 2\n for i in reversed(satisfaction):\n if i + rightSum > 0:\n rightSum += i\n res += rightSum\n else:\n return res\n return res\n```\n\nPlease upvote uwu | 1 | We have a wooden plank of the length `n` **units**. Some ants are walking on the plank, each ant moves with a speed of **1 unit per second**. Some of the ants move to the **left**, the other move to the **right**.
When two ants moving in two **different** directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.
When an ant reaches **one end** of the plank at a time `t`, it falls out of the plank immediately.
Given an integer `n` and two integer arrays `left` and `right`, the positions of the ants moving to the left and the right, return _the moment when the last ant(s) fall out of the plank_.
**Example 1:**
**Input:** n = 4, left = \[4,3\], right = \[0,1\]
**Output:** 4
**Explanation:** In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).
**Example 2:**
**Input:** n = 7, left = \[\], right = \[0,1,2,3,4,5,6,7\]
**Output:** 7
**Explanation:** All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
**Example 3:**
**Input:** n = 7, left = \[0,1,2,3,4,5,6,7\], right = \[\]
**Output:** 7
**Explanation:** All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
**Constraints:**
* `1 <= n <= 104`
* `0 <= left.length <= n + 1`
* `0 <= left[i] <= n`
* `0 <= right.length <= n + 1`
* `0 <= right[i] <= n`
* `1 <= left.length + right.length <= n + 1`
* All values of `left` and `right` are unique, and each value can appear **only in one** of the two arrays. | Use dynamic programming to find the optimal solution by saving the previous best like-time coefficient and its corresponding element sum. If adding the current element to the previous best like-time coefficient and its corresponding element sum would increase the best like-time coefficient, then go ahead and add it. Otherwise, keep the previous best like-time coefficient. |
easy python solution | reducing-dishes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->o(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->o(1)\n\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort(reverse = True)\n presum ,res =0,0\n for dish in satisfaction:\n presum += dish\n if presum < 0:\n break\n res += presum\n return res\n``` | 1 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
easy python solution | reducing-dishes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->o(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->o(1)\n\n# Code\n```\nclass Solution:\n def maxSatisfaction(self, satisfaction: List[int]) -> int:\n satisfaction.sort(reverse = True)\n presum ,res =0,0\n for dish in satisfaction:\n presum += dish\n if presum < 0:\n break\n res += presum\n return res\n``` | 1 | We have a wooden plank of the length `n` **units**. Some ants are walking on the plank, each ant moves with a speed of **1 unit per second**. Some of the ants move to the **left**, the other move to the **right**.
When two ants moving in two **different** directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.
When an ant reaches **one end** of the plank at a time `t`, it falls out of the plank immediately.
Given an integer `n` and two integer arrays `left` and `right`, the positions of the ants moving to the left and the right, return _the moment when the last ant(s) fall out of the plank_.
**Example 1:**
**Input:** n = 4, left = \[4,3\], right = \[0,1\]
**Output:** 4
**Explanation:** In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).
**Example 2:**
**Input:** n = 7, left = \[\], right = \[0,1,2,3,4,5,6,7\]
**Output:** 7
**Explanation:** All ants are going to the right, the ant at index 0 needs 7 seconds to fall.
**Example 3:**
**Input:** n = 7, left = \[0,1,2,3,4,5,6,7\], right = \[\]
**Output:** 7
**Explanation:** All ants are going to the left, the ant at index 7 needs 7 seconds to fall.
**Constraints:**
* `1 <= n <= 104`
* `0 <= left.length <= n + 1`
* `0 <= left[i] <= n`
* `0 <= right.length <= n + 1`
* `0 <= right[i] <= n`
* `1 <= left.length + right.length <= n + 1`
* All values of `left` and `right` are unique, and each value can appear **only in one** of the two arrays. | Use dynamic programming to find the optimal solution by saving the previous best like-time coefficient and its corresponding element sum. If adding the current element to the previous best like-time coefficient and its corresponding element sum would increase the best like-time coefficient, then go ahead and add it. Otherwise, keep the previous best like-time coefficient. |
Beginner-friendly || Simple solution with Greedy in Python3/TypeScript | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a list of `nums`\n- our goal is to extract subsequence of `nums`, whose sum is **greater**, than a rest sum\n- if there\'re multiple solutions, return the subsequence with the **minimum size** and with **maximum total sum**\n\n# Approach\n1. sort `nums` in **descending** order\n2. initialize `ans` to store subsequence and `total` to track **prefix sum**\n3. calculate **prefix sum**\n4. initialize `curSum` to compare with `total`\n5. iterate over sorted `nums` and check `curSum > total`, if it\'s, then return `ans`, otherwise continue to increase the subsequence\n\n# Complexity\n- Time complexity: **O(n log n)**, to sort input\n\n- Space complexity: **O(k)**, to store subsequence `ans`\n\n# Code in Python3\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort(reverse=True)\n ans = []\n total = 0\n\n for num in nums:\n total += num\n\n curSum = 0\n\n for num in nums:\n total -= num\n curSum += num\n ans.append(num)\n\n if curSum > total: return ans\n```\n# Code in TypeScript\n```\nfunction minSubsequence(nums: number[]): number[] {\n nums.sort((a, b) => b - a)\n const ans = []\n let total = 0\n\n for (let i = 0; i < nums.length; i++) {\n total += nums[i]\n }\n\n let curSum = 0\n\n for (let i = 0; i < nums.length; i++) {\n total -= nums[i]\n curSum += nums[i]\n ans.push(nums[i])\n\n if (curSum > total) return ans\n }\n};\n``` | 1 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Beginner-friendly || Simple solution with Greedy in Python3/TypeScript | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a list of `nums`\n- our goal is to extract subsequence of `nums`, whose sum is **greater**, than a rest sum\n- if there\'re multiple solutions, return the subsequence with the **minimum size** and with **maximum total sum**\n\n# Approach\n1. sort `nums` in **descending** order\n2. initialize `ans` to store subsequence and `total` to track **prefix sum**\n3. calculate **prefix sum**\n4. initialize `curSum` to compare with `total`\n5. iterate over sorted `nums` and check `curSum > total`, if it\'s, then return `ans`, otherwise continue to increase the subsequence\n\n# Complexity\n- Time complexity: **O(n log n)**, to sort input\n\n- Space complexity: **O(k)**, to store subsequence `ans`\n\n# Code in Python3\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort(reverse=True)\n ans = []\n total = 0\n\n for num in nums:\n total += num\n\n curSum = 0\n\n for num in nums:\n total -= num\n curSum += num\n ans.append(num)\n\n if curSum > total: return ans\n```\n# Code in TypeScript\n```\nfunction minSubsequence(nums: number[]): number[] {\n nums.sort((a, b) => b - a)\n const ans = []\n let total = 0\n\n for (let i = 0; i < nums.length; i++) {\n total += nums[i]\n }\n\n let curSum = 0\n\n for (let i = 0; i < nums.length; i++) {\n total -= nums[i]\n curSum += nums[i]\n ans.push(nums[i])\n\n if (curSum > total) return ans\n }\n};\n``` | 1 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python Solution | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition \n JUET\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n EASY UNDERSTANDING \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- o(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n)\n- \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n ans=[]\n nums.sort()\n while sum(nums)>sum(ans):\n ans.append(nums.pop())\n if sum(nums)==sum(ans):\n ans.append(nums.pop())\n return ans\n``` | 1 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Python Solution | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition \n JUET\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n EASY UNDERSTANDING \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- o(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n)\n- \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n ans=[]\n nums.sort()\n while sum(nums)>sum(ans):\n ans.append(nums.pop())\n if sum(nums)==sum(ans):\n ans.append(nums.pop())\n return ans\n``` | 1 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Easy Python3 Codes | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Code1\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums=sorted(nums)[::-1]\n sum1,sum2=0,sum(nums)\n for i in range(len(nums)):\n sum1+=nums[i]\n sum2-=nums[i] \n if sum1>sum2:\n return nums[0:i+1]\n```\n# Code2\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums=sorted(nums)[::-1]\n for i in range(len(nums)+1):\n if sum(nums[0:i])>sum(nums[i:]):\n return nums[0:i]\n``` | 3 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Easy Python3 Codes | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Code1\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums=sorted(nums)[::-1]\n sum1,sum2=0,sum(nums)\n for i in range(len(nums)):\n sum1+=nums[i]\n sum2-=nums[i] \n if sum1>sum2:\n return nums[0:i+1]\n```\n# Code2\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums=sorted(nums)[::-1]\n for i in range(len(nums)+1):\n if sum(nums[0:i])>sum(nums[i:]):\n return nums[0:i]\n``` | 3 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Solution | minimum-subsequence-in-non-increasing-order | 0 | 1 | ```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n if (len(nums) == 1):\n return nums\n nums.sort()\n count = 0\n num = []\n l = len(nums)\n for i in range(1,l+1):\n count += nums[-i]\n num.append(nums[-i])\n if count > sum(nums[:l-i]):\n return (num)\n \n``` | 2 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Solution | minimum-subsequence-in-non-increasing-order | 0 | 1 | ```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n if (len(nums) == 1):\n return nums\n nums.sort()\n count = 0\n num = []\n l = len(nums)\n for i in range(1,l+1):\n count += nums[-i]\n num.append(nums[-i])\n if count > sum(nums[:l-i]):\n return (num)\n \n``` | 2 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python || O(n) Solution || Easily understandable | minimum-subsequence-in-non-increasing-order | 0 | 1 | This solution might not be the fastest but the code is simple enough to understand the underlying concept. Further optimization can be done to make it faster.\n\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n \n nums.sort()\n totalSum=sum(nums)\n currSum=0\n seq=[]\n \n for i in range(len(nums)-1,-1,-1):\n currSum+=nums[i]\n seq.append(nums[i])\n \n if(currSum>totalSum-currSum):\n return seq\n \n return seq\n``` | 1 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Python || O(n) Solution || Easily understandable | minimum-subsequence-in-non-increasing-order | 0 | 1 | This solution might not be the fastest but the code is simple enough to understand the underlying concept. Further optimization can be done to make it faster.\n\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n \n nums.sort()\n totalSum=sum(nums)\n currSum=0\n seq=[]\n \n for i in range(len(nums)-1,-1,-1):\n currSum+=nums[i]\n seq.append(nums[i])\n \n if(currSum>totalSum-currSum):\n return seq\n \n return seq\n``` | 1 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python3 simple solution | minimum-subsequence-in-non-increasing-order | 0 | 1 | ```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort()\n l = []\n while sum(l) <= sum(nums):\n l.append(nums.pop())\n return l\n```\nIf you like the solution, please vote for this. | 12 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Python3 simple solution | minimum-subsequence-in-non-increasing-order | 0 | 1 | ```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort()\n l = []\n while sum(l) <= sum(nums):\n l.append(nums.pop())\n return l\n```\nIf you like the solution, please vote for this. | 12 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python solution | runtime - 40ms beats 92% | minimum-subsequence-in-non-increasing-order | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n total = sum(nums)\n nums.sort(reverse = True)\n sub_sum, sub_seq = 0, []\n for x in nums:\n sub_sum += x\n total -= x\n sub_seq.append(x)\n if sub_sum > total:\n return sub_seq\n``` | 3 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Python solution | runtime - 40ms beats 92% | minimum-subsequence-in-non-increasing-order | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n total = sum(nums)\n nums.sort(reverse = True)\n sub_sum, sub_seq = 0, []\n for x in nums:\n sub_sum += x\n total -= x\n sub_seq.append(x)\n if sub_sum > total:\n return sub_seq\n``` | 3 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
#PYTHON Code using sort | minimum-subsequence-in-non-increasing-order | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n l=[]\n nums.sort(reverse=True)\n for i in range(len(nums)):\n if(sum(nums[:i+1])>(sum(nums)-sum(nums[:i+1]))):\n return nums[:i+1]\n``` | 0 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
#PYTHON Code using sort | minimum-subsequence-in-non-increasing-order | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n l=[]\n nums.sort(reverse=True)\n for i in range(len(nums)):\n if(sum(nums[:i+1])>(sum(nums)-sum(nums[:i+1]))):\n return nums[:i+1]\n``` | 0 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python solution | runtime - 47 ms beats - 97.65% 💯 | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort()\n l = 0\n r = len(nums) - 1\n sub_sum = 0\n sub_seq = []\n sub_seq_sum = 0\n while l<=r:\n sub_sum +=nums[l]\n while l<=r and sub_sum>=sub_seq_sum:\n sub_seq.append(nums[r])\n sub_seq_sum+=nums[r]\n r -=1\n l +=1\n return sub_seq\n\n \n``` | 0 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Python solution | runtime - 47 ms beats - 97.65% 💯 | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort()\n l = 0\n r = len(nums) - 1\n sub_sum = 0\n sub_seq = []\n sub_seq_sum = 0\n while l<=r:\n sub_sum +=nums[l]\n while l<=r and sub_sum>=sub_seq_sum:\n sub_seq.append(nums[r])\n sub_seq_sum+=nums[r]\n r -=1\n l +=1\n return sub_seq\n\n \n``` | 0 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
python made easy | beats 88% in memory | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\nsort the give list by descending\n\n# Approach\nsort the give list nums and then lopp through nums and pop and append the first element of nums to new list arr and check on each append whether sum(arr)>sum(nums) if yes then return the arr\n\n# Complexity\n- Time complexity:\nn\n\n- Space complexity:\n1\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n\n arr =[]\n nums.sort(reverse = True)\n\n for i in range(len(nums)):\n arr.append(nums.pop(0))\n if sum(arr) > sum(nums):\n return arr\n\n \n``` | 0 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
python made easy | beats 88% in memory | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\nsort the give list by descending\n\n# Approach\nsort the give list nums and then lopp through nums and pop and append the first element of nums to new list arr and check on each append whether sum(arr)>sum(nums) if yes then return the arr\n\n# Complexity\n- Time complexity:\nn\n\n- Space complexity:\n1\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n\n arr =[]\n nums.sort(reverse = True)\n\n for i in range(len(nums)):\n arr.append(nums.pop(0))\n if sum(arr) > sum(nums):\n return arr\n\n \n``` | 0 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Simple Python Code | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBy taking the sum of highest elements iteratively, we can minimize the loop iterations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo implement the above intuition, we will first sort the `nums` on `reverse` order. Then with iterations, we will increase the number of elements of the subsequence, and we will do it till the sum of that subsequence is not greater than the sum of other elements in the loop. In case, the sequence has only one element in it, we will return the whole sequence as a subsequence.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity of this function will be $$O(n)$$.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity of this function will be $$O(1)$$.\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort(reverse=True)\n r = len(nums)\n total = sum(nums)\n for n in range(r):\n subseq = nums[:n]\n sum_n = sum(subseq)\n if sum_n > total-sum_n:\n return subseq\n return nums\n \n``` | 0 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Simple Python Code | minimum-subsequence-in-non-increasing-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBy taking the sum of highest elements iteratively, we can minimize the loop iterations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo implement the above intuition, we will first sort the `nums` on `reverse` order. Then with iterations, we will increase the number of elements of the subsequence, and we will do it till the sum of that subsequence is not greater than the sum of other elements in the loop. In case, the sequence has only one element in it, we will return the whole sequence as a subsequence.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity of this function will be $$O(n)$$.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity of this function will be $$O(1)$$.\n\n# Code\n```\nclass Solution:\n def minSubsequence(self, nums: List[int]) -> List[int]:\n nums.sort(reverse=True)\n r = len(nums)\n total = sum(nums)\n for n in range(r):\n subseq = nums[:n]\n sum_n = sum(subseq)\n if sum_n > total-sum_n:\n return subseq\n return nums\n \n``` | 0 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
✔ Python3 Solution | One Line | number-of-steps-to-reduce-a-number-in-binary-representation-to-one | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def numSteps(self, s):\n return len(s) + s.rstrip(\'0\').count(\'0\') + 2 * (s.count(\'1\') != 1) - 1\n``` | 1 | Given the binary representation of an integer as a string `s`, return _the number of steps to reduce it to_ `1` _under the following rules_:
* If the current number is even, you have to divide it by `2`.
* If the current number is odd, you have to add `1` to it.
It is guaranteed that you can always reach one for all test cases.
**Example 1:**
**Input:** s = "1101 "
**Output:** 6
**Explanation:** "1101 " corressponds to number 13 in their decimal representation.
Step 1) 13 is odd, add 1 and obtain 14.
Step 2) 14 is even, divide by 2 and obtain 7.
Step 3) 7 is odd, add 1 and obtain 8.
Step 4) 8 is even, divide by 2 and obtain 4.
Step 5) 4 is even, divide by 2 and obtain 2.
Step 6) 2 is even, divide by 2 and obtain 1.
**Example 2:**
**Input:** s = "10 "
**Output:** 1
**Explanation:** "10 " corressponds to number 2 in their decimal representation.
Step 1) 2 is even, divide by 2 and obtain 1.
**Example 3:**
**Input:** s = "1 "
**Output:** 0
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of characters '0' or '1'
* `s[0] == '1'` | null |
✔ Python3 Solution | One Line | number-of-steps-to-reduce-a-number-in-binary-representation-to-one | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def numSteps(self, s):\n return len(s) + s.rstrip(\'0\').count(\'0\') + 2 * (s.count(\'1\') != 1) - 1\n``` | 1 | Given a string `s` of lowercase letters, you need to find the maximum number of **non-empty** substrings of `s` that meet the following conditions:
1. The substrings do not overlap, that is for any two substrings `s[i..j]` and `s[x..y]`, either `j < x` or `i > y` is true.
2. A substring that contains a certain character `c` must also contain all occurrences of `c`.
Find _the maximum number of substrings that meet the above conditions_. If there are multiple solutions with the same number of substrings, _return the one with minimum total length._ It can be shown that there exists a unique solution of minimum total length.
Notice that you can return the substrings in **any** order.
**Example 1:**
**Input:** s = "adefaddaccc "
**Output:** \[ "e ", "f ", "ccc "\]
**Explanation:** The following are all the possible substrings that meet the conditions:
\[
"adefaddaccc "
"adefadda ",
"ef ",
"e ",
"f ",
"ccc ",
\]
If we choose the first string, we cannot choose anything else and we'd get only 1. If we choose "adefadda ", we are left with "ccc " which is the only one that doesn't overlap, thus obtaining 2 substrings. Notice also, that it's not optimal to choose "ef " since it can be split into two. Therefore, the optimal way is to choose \[ "e ", "f ", "ccc "\] which gives us 3 substrings. No other solution of the same number of substrings exist.
**Example 2:**
**Input:** s = "abbaccd "
**Output:** \[ "d ", "bb ", "cc "\]
**Explanation:** Notice that while the set of substrings \[ "d ", "abba ", "cc "\] also has length 3, it's considered incorrect since it has larger total length.
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Read the string from right to left, if the string ends in '0' then the number is even otherwise it is odd. Simulate the steps described in the binary string. |
Why my Python solution failed on: "1111011110000011100000110001011011110010111001010111110001"? | number-of-steps-to-reduce-a-number-in-binary-representation-to-one | 0 | 1 | ```\nres = 0\nnum = int(s,2)\nwhile num != 1:\n\tif num % 2 == 0:\n\t\tnum = num / 2\n\telse:\n\t\tnum = num + 1\n\tres +=1\n\nreturn res\n```\n:-( | 8 | Given the binary representation of an integer as a string `s`, return _the number of steps to reduce it to_ `1` _under the following rules_:
* If the current number is even, you have to divide it by `2`.
* If the current number is odd, you have to add `1` to it.
It is guaranteed that you can always reach one for all test cases.
**Example 1:**
**Input:** s = "1101 "
**Output:** 6
**Explanation:** "1101 " corressponds to number 13 in their decimal representation.
Step 1) 13 is odd, add 1 and obtain 14.
Step 2) 14 is even, divide by 2 and obtain 7.
Step 3) 7 is odd, add 1 and obtain 8.
Step 4) 8 is even, divide by 2 and obtain 4.
Step 5) 4 is even, divide by 2 and obtain 2.
Step 6) 2 is even, divide by 2 and obtain 1.
**Example 2:**
**Input:** s = "10 "
**Output:** 1
**Explanation:** "10 " corressponds to number 2 in their decimal representation.
Step 1) 2 is even, divide by 2 and obtain 1.
**Example 3:**
**Input:** s = "1 "
**Output:** 0
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of characters '0' or '1'
* `s[0] == '1'` | null |
Why my Python solution failed on: "1111011110000011100000110001011011110010111001010111110001"? | number-of-steps-to-reduce-a-number-in-binary-representation-to-one | 0 | 1 | ```\nres = 0\nnum = int(s,2)\nwhile num != 1:\n\tif num % 2 == 0:\n\t\tnum = num / 2\n\telse:\n\t\tnum = num + 1\n\tres +=1\n\nreturn res\n```\n:-( | 8 | Given a string `s` of lowercase letters, you need to find the maximum number of **non-empty** substrings of `s` that meet the following conditions:
1. The substrings do not overlap, that is for any two substrings `s[i..j]` and `s[x..y]`, either `j < x` or `i > y` is true.
2. A substring that contains a certain character `c` must also contain all occurrences of `c`.
Find _the maximum number of substrings that meet the above conditions_. If there are multiple solutions with the same number of substrings, _return the one with minimum total length._ It can be shown that there exists a unique solution of minimum total length.
Notice that you can return the substrings in **any** order.
**Example 1:**
**Input:** s = "adefaddaccc "
**Output:** \[ "e ", "f ", "ccc "\]
**Explanation:** The following are all the possible substrings that meet the conditions:
\[
"adefaddaccc "
"adefadda ",
"ef ",
"e ",
"f ",
"ccc ",
\]
If we choose the first string, we cannot choose anything else and we'd get only 1. If we choose "adefadda ", we are left with "ccc " which is the only one that doesn't overlap, thus obtaining 2 substrings. Notice also, that it's not optimal to choose "ef " since it can be split into two. Therefore, the optimal way is to choose \[ "e ", "f ", "ccc "\] which gives us 3 substrings. No other solution of the same number of substrings exist.
**Example 2:**
**Input:** s = "abbaccd "
**Output:** \[ "d ", "bb ", "cc "\]
**Explanation:** Notice that while the set of substrings \[ "d ", "abba ", "cc "\] also has length 3, it's considered incorrect since it has larger total length.
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Read the string from right to left, if the string ends in '0' then the number is even otherwise it is odd. Simulate the steps described in the binary string. |
linear time constant space | longest-happy-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def longestDiverseString(self, a: int, b: int, c: int) -> str:\n res,maxHeap = "",[]\n for count,char in [(-a,"a"),(-b,"b"),(-c,"c")]:\n if count != 0:\n heapq.heappush(maxHeap,(count,char))\n\n while maxHeap:\n count,char = heapq.heappop(maxHeap)\n if len(res) > 1 and res[-1] == res[-2] == char:\n if not maxHeap:\n break\n \n count2,char2 = heapq.heappop(maxHeap)\n res += char2\n count2 += 1\n if count2:\n heapq.heappush(maxHeap,(count2,char2))\n\n else:\n res += char\n count += 1\n if count:\n heapq.heappush(maxHeap,(count,char))\n \n return res\n\n# worst time -- O(N)\n# space - O(1)\n``` | 1 | A string `s` is called **happy** if it satisfies the following conditions:
* `s` only contains the letters `'a'`, `'b'`, and `'c'`.
* `s` does not contain any of `"aaa "`, `"bbb "`, or `"ccc "` as a substring.
* `s` contains **at most** `a` occurrences of the letter `'a'`.
* `s` contains **at most** `b` occurrences of the letter `'b'`.
* `s` contains **at most** `c` occurrences of the letter `'c'`.
Given three integers `a`, `b`, and `c`, return _the **longest possible happy** string_. If there are multiple longest happy strings, return _any of them_. If there is no such string, return _the empty string_ `" "`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** a = 1, b = 1, c = 7
**Output:** "ccaccbcc "
**Explanation:** "ccbccacc " would also be a correct answer.
**Example 2:**
**Input:** a = 7, b = 1, c = 0
**Output:** "aabaa "
**Explanation:** It is the only correct answer in this case.
**Constraints:**
* `0 <= a, b, c <= 100`
* `a + b + c > 0` | null |
linear time constant space | longest-happy-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def longestDiverseString(self, a: int, b: int, c: int) -> str:\n res,maxHeap = "",[]\n for count,char in [(-a,"a"),(-b,"b"),(-c,"c")]:\n if count != 0:\n heapq.heappush(maxHeap,(count,char))\n\n while maxHeap:\n count,char = heapq.heappop(maxHeap)\n if len(res) > 1 and res[-1] == res[-2] == char:\n if not maxHeap:\n break\n \n count2,char2 = heapq.heappop(maxHeap)\n res += char2\n count2 += 1\n if count2:\n heapq.heappush(maxHeap,(count2,char2))\n\n else:\n res += char\n count += 1\n if count:\n heapq.heappush(maxHeap,(count,char))\n \n return res\n\n# worst time -- O(N)\n# space - O(1)\n``` | 1 | Given an integer `n`, return **any** array containing `n` **unique** integers such that they add up to `0`.
**Example 1:**
**Input:** n = 5
**Output:** \[-7,-1,1,3,4\]
**Explanation:** These arrays also are accepted \[-5,-1,1,2,3\] , \[-3,-1,2,-2,4\].
**Example 2:**
**Input:** n = 3
**Output:** \[-1,0,1\]
**Example 3:**
**Input:** n = 1
**Output:** \[0\]
**Constraints:**
* `1 <= n <= 1000` | Use a greedy approach. Use the letter with the maximum current limit that can be added without breaking the condition. |
Python3 Solution | stone-game-iii | 0 | 1 | \n```\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n=len(stoneValue)\n dp=[0]*(n+1)\n i=n-1\n \n while i>=0:\n ans=-1001\n ans=max(ans,stoneValue[i]-dp[i+1])\n \n if i+1<n:\n ans=max(ans,stoneValue[i]+stoneValue[i+1]-dp[i+2])\n \n if i+2<n:\n ans=max(ans,stoneValue[i]+stoneValue[i+1]+stoneValue[i+2]-dp[i+3])\n dp[i]=ans\n i-=1\n \n \n alice=dp[0]\n if alice>0:\n return "Alice"\n elif alice<0:\n return "Bob"\n else:\n return "Tie"\n``` | 2 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python Elegant & Short | O(n) | Top-Down DP | stone-game-iii | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def stoneGameIII(self, stone_value: List[int]) -> str:\n @cache\n def dp(i: int) -> int:\n take_one = stone_value[i] - dp(i + 1) \\\n if i <= n - 1 else 0\n take_two = stone_value[i] + stone_value[i + 1] - dp(i + 2) \\\n if i <= n - 2 else -maxsize\n take_three = stone_value[i] + stone_value[i + 1] + stone_value[i + 2] - dp(i + 3) \\\n if i <= n - 3 else -maxsize\n\n return max(take_one, take_three, take_two)\n\n n = len(stone_value)\n score = dp(0)\n\n return {\n score > 0: \'Alice\',\n score < 0: \'Bob\',\n }.get(True, \'Tie\')\n``` | 1 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python sol using Relative scores!! | stone-game-iii | 0 | 1 | # Code\n```\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n=len(stoneValue)\n\n @cache\n def dfs(idx):\n if idx>=n:\n return 0\n best=-10**20\n s=0\n for i in range(3):\n if (i+idx)>=n:\n break\n s+=stoneValue[i+idx]\n best=max(best,s-dfs(idx+i+1))\n return best\n\n relativeRes = dfs(0)\n return "Alice" if relativeRes>0 else ("Tie" if relativeRes==0 else "Bob")\n``` | 1 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
simple python code, beats 92.38% runtime. | stone-game-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n=len(stoneValue)\n dp=[0]*(n+1)\n i=n-1\n \n while i>=0:\n ans=-1001\n ans=max(ans,stoneValue[i]-dp[i+1])\n \n if i+1<n:\n ans=max(ans,stoneValue[i]+stoneValue[i+1]-dp[i+2])\n \n if i+2<n:\n ans=max(ans,stoneValue[i]+stoneValue[i+1]+stoneValue[i+2]-dp[i+3])\n dp[i]=ans\n i-=1\n \n \n alice=dp[0]\n if alice>0:\n return "Alice"\n elif alice<0:\n return "Bob"\n else:\n return "Tie"\n``` | 1 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
The evolution of solutions from naive to perfect one 🦊 🚀 | stone-game-iii | 0 | 1 | # Solution 1: Naive one\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\n- Use memoization with `@cache` in function `dp(l)`.\n- Drop usage of `if - else` with `min()` and `max()` and array.\n- `-1001` is used as the minimal value according to problem constrains.\n\n## Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n## Code\n```\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n = len(stoneValue)\n\n @cache\n def dp(l):\n if l >= n: return 0\n max_score = -1001\n R = min(l+3, n) + 1\n for r in range(l+1, R):\n score = sum(stoneValue[l:r]) - dp(r)\n max_score = max(max_score, score)\n\n return max_score\n\n winners = [\'Tie\', \'Alice\', \'Bob\']\n score = max(-1, min(dp(0), 1))\n return winners[score]\n```\n\n# Solution 2: Naive one + prefix sum\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\n- Use memoization with `@cache` in function `dp(l)`.\n- Drop usage of `if - else` with `min()` and `max()` and array.\n- Drop usage of function `sum()` with a prefix sum `prefix`.\n- `-1001` is used as the minimal value according to problem constrains.\n\n## Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n## Code\n```\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n = len(stoneValue)\n\n @cache\n def dp(l):\n if l >= n: return 0\n max_score = -1001\n\n prefix = 0\n for r in range(l, min(l+3, n)):\n prefix += stoneValue[r]\n max_score = max(max_score, prefix - dp(r+1))\n\n return max_score\n\n winners = [\'Tie\', \'Alice\', \'Bob\']\n score = max(-1, min(dp(0), 1))\n return winners[score]\n```\n# Solution 3: Explicit memoization\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\n- Use memoization explicitly with array `dp`.\n- Drop usage of `if - else` with `min()`, `max()`, and array `winners`.\n- Drop usage of function `sum()` with a prefix sum `prefix`.\n- `-1001` is used as the minimal value according to problem constrains.\n\n## Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n- Performance is slightly better than the previous solution\n\n\n## Code\n```\nfrom array import array\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n = len(stoneValue)\n dp = array(\'i\', [-1001]*n + [0])\n\n for l in range(n - 1, -1, -1):\n prefix = 0\n for r in range(l, min(l+3, n)):\n prefix += stoneValue[r]\n dp[l] = max(dp[l], prefix - dp[r+1])\n \n winners = [\'Tie\', \'Alice\', \'Bob\']\n score = max(-1, min(dp(0), 1))\n return winners[score]\n```\n\n# Solution 4: Explicit memoization of constant space\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\n- Use memoization explicitly with limited to size of 4 array `dp`.\n- Drop usage of `if - else` with `min()`, `max()`, and array `winners`.\n- Drop usage of function `sum()` with a prefix sum `prefix`.\n- `-1001` is used as the minimal value according to problem constrains.\n\n## Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- Performance is slightly better than the previous solution\n\n\n```\nfrom array import array\nclass Solution:\n def stoneGameIII(self, stoneValue: List[int]) -> str:\n n = len(stoneValue)\n dp = array(\'i\', [0]*4)\n\n for l in range(n-1, -1, -1):\n dp[l%4] = -1001 # to rewrite the previous value\n prefix = 0\n for r in range(l, min(l+3, n)):\n prefix += stoneValue[r]\n dp[l%4] = max(dp[l%4], prefix - dp[(r+1) % 4])\n \n winners = [\'Tie\', \'Alice\', \'Bob\']\n score = max(-1, min(dp[0], 1))\n return winners[score]\n``` | 3 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Beating 80% Python Easy Solution | stone-game-iii | 0 | 1 | \n\n# Code\n```\nclass Solution(object):\n def stoneGameIII(self, stoneValue):\n """\n :type stoneValue: List[int]\n :rtype: str\n """\n \n dp = [0 for _ in range(len(stoneValue))]\n if len(dp) >= 1:\n dp[-1] = stoneValue[-1]\n if len(dp) >= 2:\n dp[-2] = max(stoneValue[-1] + stoneValue[-2], stoneValue[-2] - dp[-1])\n if len(dp) >= 3:\n dp[-3] = max(stoneValue[-3] + stoneValue[-1] + stoneValue[-2], stoneValue[-3] - dp[-2], stoneValue[-3] + stoneValue[-2] - dp[-1])\n \n for i in range(len(stoneValue) - 4, -1, -1):\n \n dp[i] = max([sum(stoneValue[i: i + j]) - dp[i + j] for j in range(1, 4)])\n \n if dp[0] > 0:\n return "Alice"\n if dp[0] == 0:\n return "Tie"\n return "Bob"\n``` | 1 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python short and clean. Functional programming. | stone-game-iii | 0 | 1 | # Approach: Recursive DP\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is number of values.`\n\n# Code\n```python\nclass Solution:\n def stoneGameIII(self, values: list[int]) -> str:\n @cache\n def score(i: int) -> int:\n return (i < len(values)) and max(sum(values[i : j]) - score(j) for j in range(i + 1, i + 4))\n \n s = score(0)\n return \'Tie\' if s == 0 else (\'Alice\' if s > 0 else \'Bob\')\n\n\n``` | 2 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Image Explanation🏆- [Recursion->Memo->Bottom Up-> O(1) Space] - C++/Java/Python | stone-game-iii | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Stone Game III` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n\n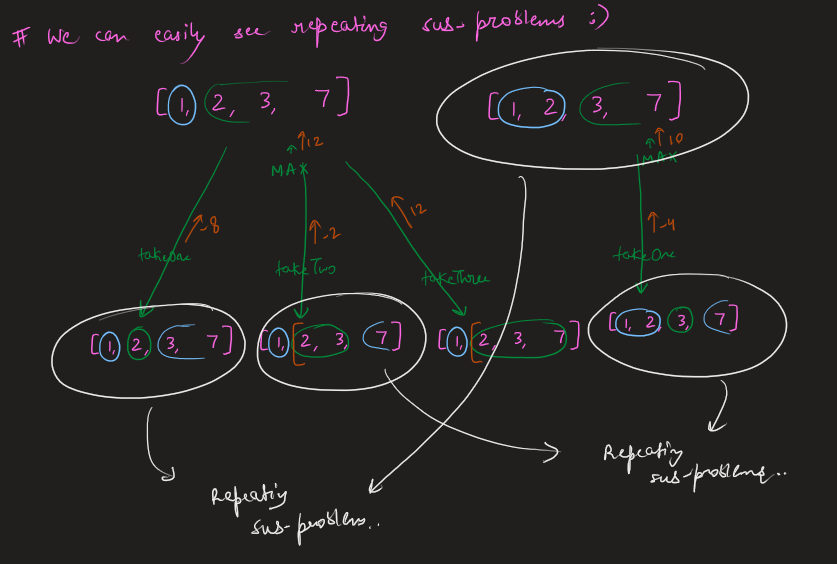\n\n\n\n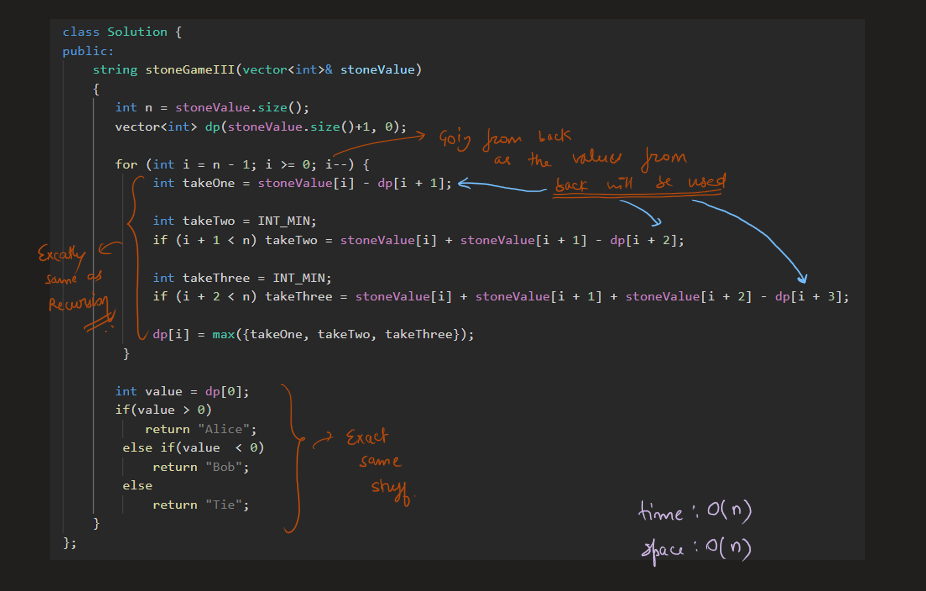\n\n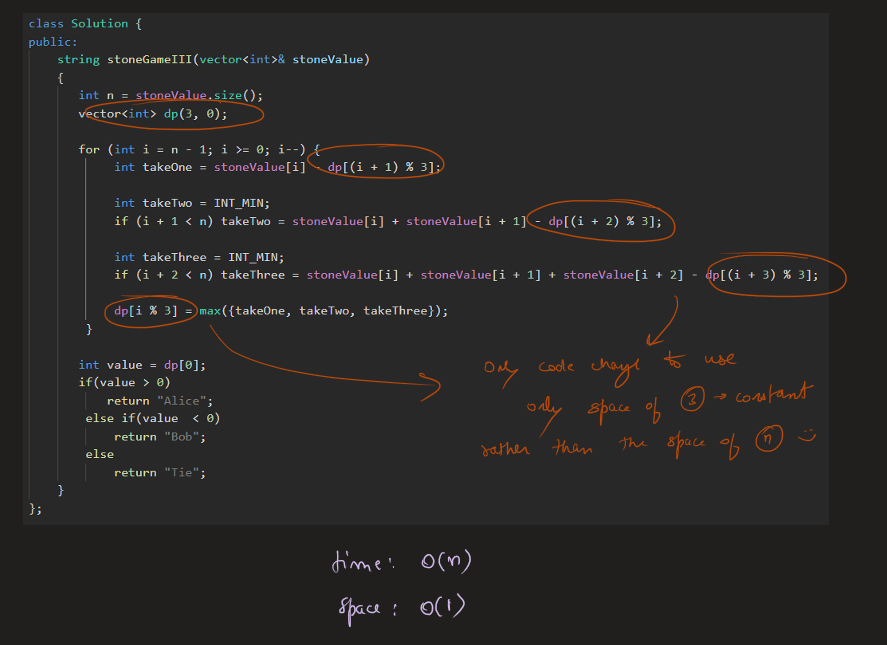\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n string stoneGameIII(vector<int>& stoneValue) \n {\n int n = stoneValue.size(); \n vector<int> dp(3, 0); \n\n for (int i = n - 1; i >= 0; i--) {\n int takeOne = stoneValue[i] - dp[(i + 1) % 3];\n\n int takeTwo = INT_MIN;\n if (i + 1 < n) takeTwo = stoneValue[i] + stoneValue[i + 1] - dp[(i + 2) % 3];\n\n int takeThree = INT_MIN;\n if (i + 2 < n) takeThree = stoneValue[i] + stoneValue[i + 1] + stoneValue[i + 2] - dp[(i + 3) % 3];\n\n dp[i % 3] = max({takeOne, takeTwo, takeThree});\n } \n\n int value = dp[0]; \n if(value > 0)\n return "Alice";\n else if(value < 0)\n return "Bob";\n else\n return "Tie";\n }\n};\n```\n```Java []\nclass Solution {\n public String stoneGameIII(int[] stoneValue) {\n int n = stoneValue.length;\n int[] dp = new int[3];\n\n for (int i = n - 1; i >= 0; i--) {\n int takeOne = stoneValue[i] - dp[(i + 1) % 3];\n\n int takeTwo = Integer.MIN_VALUE;\n if (i + 1 < n)\n takeTwo = stoneValue[i] + stoneValue[i + 1] - dp[(i + 2) % 3];\n\n int takeThree = Integer.MIN_VALUE;\n if (i + 2 < n)\n takeThree = stoneValue[i] + stoneValue[i + 1] + stoneValue[i + 2] - dp[(i + 3) % 3];\n\n dp[i % 3] = Math.max(Math.max(takeOne, takeTwo), takeThree);\n }\n\n int value = dp[0];\n if (value > 0)\n return "Alice";\n else if (value < 0)\n return "Bob";\n else\n return "Tie";\n }\n}\n```\n```Python []\nclass Solution:\n def stoneGameIII(self, stoneValue):\n n = len(stoneValue)\n dp = [0] * 3\n\n for i in range(n - 1, -1, -1):\n takeOne = stoneValue[i] - dp[(i + 1) % 3]\n\n takeTwo = float(\'-inf\')\n if i + 1 < n:\n takeTwo = stoneValue[i] + stoneValue[i + 1] - dp[(i + 2) % 3]\n\n takeThree = float(\'-inf\')\n if i + 2 < n:\n takeThree = stoneValue[i] + stoneValue[i + 1] + stoneValue[i + 2] - dp[(i + 3) % 3]\n\n dp[i % 3] = max(takeOne, takeTwo, takeThree)\n\n value = dp[0]\n if value > 0:\n return "Alice"\n elif value < 0:\n return "Bob"\n else:\n return "Tie"\n``` | 55 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | stone-game-iii | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n\n# Approach:\n\nThe optimized solution for the "Stone Game III" problem follows a dynamic programming approach. It utilizes a rolling array to store the dynamic programming values, eliminating the need for a memoization table. The approach involves iterating through the stone positions in reverse order and calculating the maximum score difference for each position.\n\n# Intuition:\n\nThe problem involves two players, Alice and Bob, who take turns picking stones from a sequence of stones. Each stone has a certain value associated with it. The goal is to maximize the score difference between Alice and Bob.\n\nTo approach this problem, we need to consider the choices available to the current player and the potential outcomes of those choices. The dynamic programming approach allows us to calculate the maximum score difference for each stone position based on the optimal choices made by both players.\n\n\n- We iterate through the stone positions in reverse order to ensure that we have the results for subsequent stones when calculating the current stone\'s score difference.\n- For each stone position, we consider three possible choices: taking one, two, or three stones.\n- We calculate the score difference for each choice by subtracting the opponent\'s score difference after the move.\n- We update the dynamic programming array, storing the maximum score difference for the current stone position.\n- After iterating through all stone positions, the maximum score difference is stored in the first element of the dynamic programming array.\n- Based on the value of the maximum score difference, we determine the winner (Alice, Bob, or a tie).\n\n```Python []\nclass Solution:\n def stoneGameIII(self, stoneValue):\n n = len(stoneValue)\n dp = [0] * 3\n\n for i in range(n - 1, -1, -1):\n take_one = stoneValue[i] - dp[(i + 1) % 3]\n take_two = float(\'-inf\')\n if i + 1 < n:\n take_two = stoneValue[i] + stoneValue[i + 1] - dp[(i + 2) % 3]\n take_three = float(\'-inf\')\n if i + 2 < n:\n take_three = stoneValue[i] + stoneValue[i + 1] + stoneValue[i + 2] - dp[(i + 3) % 3]\n\n dp[i % 3] = max(take_one, take_two, take_three)\n\n score_diff = dp[0]\n if score_diff > 0:\n return "Alice"\n elif score_diff < 0:\n return "Bob"\n else:\n return "Tie"\n\n```\n```Java []\nclass Solution {\n public String stoneGameIII(int[] stoneValue) {\n int n = stoneValue.length;\n int[] dp = new int[3];\n\n for (int i = n - 1; i >= 0; i--) {\n int takeOne = stoneValue[i] - dp[(i + 1) % 3];\n int takeTwo = Integer.MIN_VALUE;\n if (i + 1 < n) {\n takeTwo = stoneValue[i] + stoneValue[i + 1] - dp[(i + 2) % 3];\n }\n int takeThree = Integer.MIN_VALUE;\n if (i + 2 < n) {\n takeThree = stoneValue[i] + stoneValue[i + 1] + stoneValue[i + 2] - dp[(i + 3) % 3];\n }\n\n dp[i % 3] = Math.max(takeOne, Math.max(takeTwo, takeThree));\n }\n\n int scoreDiff = dp[0];\n if (scoreDiff > 0) {\n return "Alice";\n } else if (scoreDiff < 0) {\n return "Bob";\n } else {\n return "Tie";\n }\n }\n}\n```\n```C++ []\n\nclass Solution {\npublic:\n string stoneGameIII(vector<int>& stoneValue) {\n int n = stoneValue.size();\n vector<int> dp(3);\n\n for (int i = n - 1; i >= 0; i--) {\n int takeOne = stoneValue[i] - dp[(i + 1) % 3];\n int takeTwo = INT_MIN;\n if (i + 1 < n) {\n takeTwo = stoneValue[i] + stoneValue[i + 1] - dp[(i + 2) % 3];\n }\n int takeThree = INT_MIN;\n if (i + 2 < n) {\n takeThree = stoneValue[i] + stoneValue[i + 1] + stoneValue[i + 2] - dp[(i + 3) % 3];\n }\n\n dp[i % 3] = max(takeOne, max(takeTwo, takeThree));\n }\n\n int scoreDiff = dp[0];\n if (scoreDiff > 0) {\n return "Alice";\n } else if (scoreDiff < 0) {\n return "Bob";\n } else {\n return "Tie";\n }\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 19 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python3 Simple Code | string-matching-in-an-array | 0 | 1 | ```\narr = \' \'.join(words)\nsubStr = [i for i in words if arr.count(i) >= 2]\n \nreturn subStr\n\t\t | 95 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
Python3 Simple Code | string-matching-in-an-array | 0 | 1 | ```\narr = \' \'.join(words)\nsubStr = [i for i in words if arr.count(i) >= 2]\n \nreturn subStr\n\t\t | 95 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Simple Explained Solution🙂 | string-matching-in-an-array | 0 | 1 | # Approach\n 1. Initialize an empty list `ans` to store the **result**.\n 2. Iterate through the `words` list using a for loop along with their indices.\n 3. For each word, concatenate all other words in the list (except the current word) into a single string `other_words`.\n 4. Check if the current word is a substring of the `other_words` using the `in` operator.\n 5. If it is a substring, append the current word to the `ans` list.\n 6. Continue this process for all words in the list.\n 7. Return the `ans` list as the final result containing words that are substrings of other words in the list.\n\n\n# Code\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n ans = [] # we gonna store the results here\n\n for i, x in enumerate(words):\n # Join all words before and after the current word into a single string\n other_words = " ".join(words[:i] + words[i + 1:])\n # Example: words = ["mass","as","hero","superhero"]\n # other_words = "mass as hero superhero"\n\n # Check if the current word is a substring of other_words (any other words in words)\n if x in other_words:\n ans.append(x)\n\n return ans\n```\n\n | 4 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
Simple Explained Solution🙂 | string-matching-in-an-array | 0 | 1 | # Approach\n 1. Initialize an empty list `ans` to store the **result**.\n 2. Iterate through the `words` list using a for loop along with their indices.\n 3. For each word, concatenate all other words in the list (except the current word) into a single string `other_words`.\n 4. Check if the current word is a substring of the `other_words` using the `in` operator.\n 5. If it is a substring, append the current word to the `ans` list.\n 6. Continue this process for all words in the list.\n 7. Return the `ans` list as the final result containing words that are substrings of other words in the list.\n\n\n# Code\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n ans = [] # we gonna store the results here\n\n for i, x in enumerate(words):\n # Join all words before and after the current word into a single string\n other_words = " ".join(words[:i] + words[i + 1:])\n # Example: words = ["mass","as","hero","superhero"]\n # other_words = "mass as hero superhero"\n\n # Check if the current word is a substring of other_words (any other words in words)\n if x in other_words:\n ans.append(x)\n\n return ans\n```\n\n | 4 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Clean Python 3, suffix trie O(NlogN + N * S^2) | string-matching-in-an-array | 0 | 1 | Sort `words` with length first.\nThen add all suffix for each word to the trie after checking its existence in it.\n\nTime: `O(NlogN + N * S^2)`, where `S` is the max length of all words.\nNlogN for sorting and N * S^2 for build suffix trie.\n\nSpace: `O(N * S^2)` for suffix trie\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n def add(word: str):\n node = trie\n for c in word:\n node = node.setdefault(c, {})\n\n def get(word: str) -> bool:\n node = trie\n for c in word:\n if (node := node.get(c)) is None: return False\n return True\n\n words.sort(key=len, reverse=True)\n trie, result = {}, []\n for word in words:\n if get(word): result.append(word)\n for i in range(len(word)):\n add(word[i:])\n return result\n```\n\n--\nUpdate:\nThere is [another `O(N * S^2)` approach](https://leetcode.com/problems/string-matching-in-an-array/discuss/575916/Python-3-Crazy-Trie-Implementation-O(N*S2)) proposed by [`@serdes`](https://leetcode.com/serdes/).\nIt utilizes counting on trie nodes in suffix trie and can prevent to perform sorting at first.\nMy implementation by referring to this idea:\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n def add(word: str):\n node = trie\n for c in word:\n node = node.setdefault(c, {})\n node[\'#\'] = node.get(\'#\', 0) + 1\n\n def get(word: str) -> bool:\n node = trie\n for c in word:\n if (node := node.get(c)) is None: return False\n return node[\'#\'] > 1\n\n trie = {}\n for word in words:\n for i in range(len(word)):\n add(word[i:])\n return [word for word in words if get(word)]\n``` | 52 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
Clean Python 3, suffix trie O(NlogN + N * S^2) | string-matching-in-an-array | 0 | 1 | Sort `words` with length first.\nThen add all suffix for each word to the trie after checking its existence in it.\n\nTime: `O(NlogN + N * S^2)`, where `S` is the max length of all words.\nNlogN for sorting and N * S^2 for build suffix trie.\n\nSpace: `O(N * S^2)` for suffix trie\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n def add(word: str):\n node = trie\n for c in word:\n node = node.setdefault(c, {})\n\n def get(word: str) -> bool:\n node = trie\n for c in word:\n if (node := node.get(c)) is None: return False\n return True\n\n words.sort(key=len, reverse=True)\n trie, result = {}, []\n for word in words:\n if get(word): result.append(word)\n for i in range(len(word)):\n add(word[i:])\n return result\n```\n\n--\nUpdate:\nThere is [another `O(N * S^2)` approach](https://leetcode.com/problems/string-matching-in-an-array/discuss/575916/Python-3-Crazy-Trie-Implementation-O(N*S2)) proposed by [`@serdes`](https://leetcode.com/serdes/).\nIt utilizes counting on trie nodes in suffix trie and can prevent to perform sorting at first.\nMy implementation by referring to this idea:\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n def add(word: str):\n node = trie\n for c in word:\n node = node.setdefault(c, {})\n node[\'#\'] = node.get(\'#\', 0) + 1\n\n def get(word: str) -> bool:\n node = trie\n for c in word:\n if (node := node.get(c)) is None: return False\n return node[\'#\'] > 1\n\n trie = {}\n for word in words:\n for i in range(len(word)):\n add(word[i:])\n return [word for word in words if get(word)]\n``` | 52 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Python One Liner, Improved | Pre-computed Merged Sentence | string-matching-in-an-array | 0 | 1 | Pre-computed merged sentence (a) for faster iterations.\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n a = " ".join(words)\n return [w for w in words if a.count(w)>1]\n``` | 20 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
Python One Liner, Improved | Pre-computed Merged Sentence | string-matching-in-an-array | 0 | 1 | Pre-computed merged sentence (a) for faster iterations.\n```\nclass Solution:\n def stringMatching(self, words: List[str]) -> List[str]:\n a = " ".join(words)\n return [w for w in words if a.count(w)>1]\n``` | 20 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
use permutation | string-matching-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stringMatching(self, l):\n substring=[]\n for i in range(len(l)):\n fixed=l[i]\n remaining=l[:i]+l[i+1:]\n t=set([fixed for item in remaining if fixed in item])\n substring.append(\'\'.join(t))\n substring=[item for item in substring if len(item)>0]\n return substring\n\n \n``` | 0 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
use permutation | string-matching-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stringMatching(self, l):\n substring=[]\n for i in range(len(l)):\n fixed=l[i]\n remaining=l[:i]+l[i+1:]\n t=set([fixed for item in remaining if fixed in item])\n substring.append(\'\'.join(t))\n substring=[item for item in substring if len(item)>0]\n return substring\n\n \n``` | 0 | Given an array of integers `arr`, return _the number of subarrays with an **odd** sum_.
Since the answer can be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** arr = \[1,3,5\]
**Output:** 4
**Explanation:** All subarrays are \[\[1\],\[1,3\],\[1,3,5\],\[3\],\[3,5\],\[5\]\]
All sub-arrays sum are \[1,4,9,3,8,5\].
Odd sums are \[1,9,3,5\] so the answer is 4.
**Example 2:**
**Input:** arr = \[2,4,6\]
**Output:** 0
**Explanation:** All subarrays are \[\[2\],\[2,4\],\[2,4,6\],\[4\],\[4,6\],\[6\]\]
All sub-arrays sum are \[2,6,12,4,10,6\].
All sub-arrays have even sum and the answer is 0.
**Example 3:**
**Input:** arr = \[1,2,3,4,5,6,7\]
**Output:** 16
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 100` | Bruteforce to find if one string is substring of another or use KMP algorithm. |
Fenwick Tree | queries-on-a-permutation-with-key | 0 | 1 | # Intuition\nFenwick tree is also called BIT(binary index tree). Fenwick tree is good for getting prefixSum. How prefix sum helps with our problem?\nOur problem boils down to tracking the position of elements in the permutation. If we initilize the Fenwick tree leaves with 1 the prefix sum because the position in the permutation.\n\nTo facilitate elements moves, we initialize the tree with 2 * m elements, leaving the first half with 0\'s, the 2nd half with 1\'s. For every move we move an element from 2nd half to 1st half.\n\n# Complexity\n- Time complexity:\nlog(n)\n\n# Code\n```\nclass BITTree:\n def __init__(self, n):\n n = self._round(n)\n self.tree = [0] + [0] * n\n\n def _round(self, n):\n n -= 1\n n |= n >> 1\n n |= n >> 2\n n |= n >> 4\n n |= n >> 8\n n |= n >> 16\n n += 1\n return n\n\n def update(self, pos, delta):\n while pos < len(self.tree):\n self.tree[pos] += delta\n pos += pos & -pos\n\n def prefixSum(self, index):\n ans = 0\n while index != 0:\n ans += self.tree[index]\n index -= index & -index\n return ans\n\nclass Solution:\n def processQueries(self, queries: List[int], m: int) -> List[int]:\n r = []\n map = defaultdict(int)\n bt = BITTree(m << 1)\n for i in range(1, m+1):\n map[i] = i + m\n bt.update(map[i], 1)\n\n for q in queries:\n r.append(bt.prefixSum(map[q]) - 1)\n bt.update(map[q], -1)\n map[q] = m\n bt.update(map[q], 1)\n m -= 1\n return r\n\n``` | 1 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Fenwick Tree | queries-on-a-permutation-with-key | 0 | 1 | # Intuition\nFenwick tree is also called BIT(binary index tree). Fenwick tree is good for getting prefixSum. How prefix sum helps with our problem?\nOur problem boils down to tracking the position of elements in the permutation. If we initilize the Fenwick tree leaves with 1 the prefix sum because the position in the permutation.\n\nTo facilitate elements moves, we initialize the tree with 2 * m elements, leaving the first half with 0\'s, the 2nd half with 1\'s. For every move we move an element from 2nd half to 1st half.\n\n# Complexity\n- Time complexity:\nlog(n)\n\n# Code\n```\nclass BITTree:\n def __init__(self, n):\n n = self._round(n)\n self.tree = [0] + [0] * n\n\n def _round(self, n):\n n -= 1\n n |= n >> 1\n n |= n >> 2\n n |= n >> 4\n n |= n >> 8\n n |= n >> 16\n n += 1\n return n\n\n def update(self, pos, delta):\n while pos < len(self.tree):\n self.tree[pos] += delta\n pos += pos & -pos\n\n def prefixSum(self, index):\n ans = 0\n while index != 0:\n ans += self.tree[index]\n index -= index & -index\n return ans\n\nclass Solution:\n def processQueries(self, queries: List[int], m: int) -> List[int]:\n r = []\n map = defaultdict(int)\n bt = BITTree(m << 1)\n for i in range(1, m+1):\n map[i] = i + m\n bt.update(map[i], 1)\n\n for q in queries:\n r.append(bt.prefixSum(map[q]) - 1)\n bt.update(map[q], -1)\n map[q] = m\n bt.update(map[q], 1)\n m -= 1\n return r\n\n``` | 1 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
BRUTE FORCE || PYTHON || EASY UNDERSTANDING | queries-on-a-permutation-with-key | 0 | 1 | **90% FASTER || PYTHON || BEGINNER-FRIENDLY**\n*Upvote If you like the Solution*\n```\n ans=[]\n perm=[]\n \n for x in range(1,m+1):\n perm.append(x)\n for i in range(len(queries)):\n v=perm.index(queries[i])\n ans.append(v)\n cc=queries[i]\n perm.remove(cc)\n perm.insert(0,cc)\n return ans\n``` | 1 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
BRUTE FORCE || PYTHON || EASY UNDERSTANDING | queries-on-a-permutation-with-key | 0 | 1 | **90% FASTER || PYTHON || BEGINNER-FRIENDLY**\n*Upvote If you like the Solution*\n```\n ans=[]\n perm=[]\n \n for x in range(1,m+1):\n perm.append(x)\n for i in range(len(queries)):\n v=perm.index(queries[i])\n ans.append(v)\n cc=queries[i]\n perm.remove(cc)\n perm.insert(0,cc)\n return ans\n``` | 1 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
python very Simple Approch easy to understand code | queries-on-a-permutation-with-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def processQueries(self, queries: List[int], m: int) -> List[int]:\n arr=[]\n res=[]\n for i in range(m):\n arr.append(i+1)\n\n for i in range(len(queries)):\n ind=arr.index(queries[i])\n arr.pop(ind)\n res.append(ind)\n arr.insert(0,queries[i])\n return res\n``` | 3 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
python very Simple Approch easy to understand code | queries-on-a-permutation-with-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def processQueries(self, queries: List[int], m: int) -> List[int]:\n arr=[]\n res=[]\n for i in range(m):\n arr.append(i+1)\n\n for i in range(len(queries)):\n ind=arr.index(queries[i])\n arr.pop(ind)\n res.append(ind)\n arr.insert(0,queries[i])\n return res\n``` | 3 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
Solution | Python | queries-on-a-permutation-with-key | 0 | 1 | ```\nclass Solution: \n def processQueries(self, queries: List[int], m: int) -> List[int]:\n # create an empty list to hold result\n result = []\n \n # create the permutation\n mList = [x for x in range(1, m + 1)]\n \n # iterate over each element from queries\n for x in queries:\n # append the index of query value from the permutation\n result.append(mList.index(x))\n # remove the element from the permutataion\n mList.remove(x)\n # add the query element in the begining of the permutation\n mList.insert(0, x)\n \n # return the stored index result of queries\n return result\n```\n*Please comment if there is any better approach or any improvement in the solution* | 7 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Solution | Python | queries-on-a-permutation-with-key | 0 | 1 | ```\nclass Solution: \n def processQueries(self, queries: List[int], m: int) -> List[int]:\n # create an empty list to hold result\n result = []\n \n # create the permutation\n mList = [x for x in range(1, m + 1)]\n \n # iterate over each element from queries\n for x in queries:\n # append the index of query value from the permutation\n result.append(mList.index(x))\n # remove the element from the permutataion\n mList.remove(x)\n # add the query element in the begining of the permutation\n mList.insert(0, x)\n \n # return the stored index result of queries\n return result\n```\n*Please comment if there is any better approach or any improvement in the solution* | 7 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
Python3 O(N ^ 2) solution with an array (92.46% Runtime) | queries-on-a-permutation-with-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nIteratively reconstruct permutation array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Define a permutation array in range [1, m] (inclusive)\n- For each iteration get index of the query element & reconstruct permutation array\n- Store indexes for each query & return them\n\n# Complexity\n- Time complexity: O(N ^ 2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def processQueries(self, queries: List[int], m: int) -> List[int]:\n perm = [x for x in range(1, m+1)]\n ans = []\n for query in queries:\n i = perm.index(query)\n perm = [perm[i]] + perm[:i] + perm[i+1:]\n ans.append(i)\n\n return ans\n``` | 0 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Python3 O(N ^ 2) solution with an array (92.46% Runtime) | queries-on-a-permutation-with-key | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nIteratively reconstruct permutation array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Define a permutation array in range [1, m] (inclusive)\n- For each iteration get index of the query element & reconstruct permutation array\n- Store indexes for each query & return them\n\n# Complexity\n- Time complexity: O(N ^ 2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def processQueries(self, queries: List[int], m: int) -> List[int]:\n perm = [x for x in range(1, m+1)]\n ans = []\n for query in queries:\n i = perm.index(query)\n perm = [perm[i]] + perm[:i] + perm[i+1:]\n ans.append(i)\n\n return ans\n``` | 0 | You are given a string `s`.
A split is called **good** if you can split `s` into two non-empty strings `sleft` and `sright` where their concatenation is equal to `s` (i.e., `sleft + sright = s`) and the number of distinct letters in `sleft` and `sright` is the same.
Return _the number of **good splits** you can make in `s`_.
**Example 1:**
**Input:** s = "aacaba "
**Output:** 2
**Explanation:** There are 5 ways to split ` "aacaba "` and 2 of them are good.
( "a ", "acaba ") Left string and right string contains 1 and 3 different letters respectively.
( "aa ", "caba ") Left string and right string contains 1 and 3 different letters respectively.
( "aac ", "aba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aaca ", "ba ") Left string and right string contains 2 and 2 different letters respectively (good split).
( "aacab ", "a ") Left string and right string contains 3 and 1 different letters respectively.
**Example 2:**
**Input:** s = "abcd "
**Output:** 1
**Explanation:** Split the string as follows ( "ab ", "cd ").
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of only lowercase English letters. | Create the permutation P=[1,2,...,m], it could be a list for example. For each i, find the position of queries[i] with a simple scan over P and then move this to the beginning. |
One-liner code Python. | html-entity-parser | 0 | 1 | # One liner Code. Python.\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n return text.replace(\'"\', \'"\').replace(\'>\', \'>\').replace(\'<\', \'<\').replace(\''\', "\'").replace(\'&\', \'&\').replace(\'⁄\', \'/\')\n``` | 1 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
One-liner code Python. | html-entity-parser | 0 | 1 | # One liner Code. Python.\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n return text.replace(\'"\', \'"\').replace(\'>\', \'>\').replace(\'<\', \'<\').replace(\''\', "\'").replace(\'&\', \'&\').replace(\'⁄\', \'/\')\n``` | 1 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Python sol by replace and regex. 85%+ [w/ Hint ] | html-entity-parser | 0 | 1 | Python sol by replacement.\n\n---\n\n**Hint**:\n\nRemeber to put the & replacement on the last one, in order to avoid chain reaction replacement.\n\nFor example: \nshould be , instead of ">"\n\n---\n\n**Implementation** by string replacement:\n\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n \n html_symbol = [ \'"\', \''\', \'>\', \'<\', \'⁄\', \'&\']\n formal_symbol = [ \'"\', "\'", \'>\', \'<\', \'/\', \'&\']\n \n for html_sym, formal_sym in zip(html_symbol, formal_symbol):\n text = text.replace( html_sym , formal_sym )\n \n return text\n \n```\n\n---\n\n**Implementation** by regular expression:\n\n```\nimport re\nclass Solution:\n def entityParser(self, text: str) -> str:\n \n html_symbol = [ \'"\', \''\', \'>\', \'<\', \'⁄\', \'&\']\n formal_symbol = [ \'"\', "\'", \'>\', \'<\', \'/\', \'&\']\n \n for html_sym, formal_sym in zip(html_symbol, formal_symbol):\n text = re.sub( html_sym , formal_sym, text )\n \n return text\n```\n\n---\n\n\nReference:\n\n[1] [Python official docs about str.replace( ... )](https://docs.python.org/3/library/stdtypes.html#str.replace)\n\n[2] [Python official docs about re.sub( ... )](https://docs.python.org/3/library/re.html#re.sub)\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #1108 Defanging an IP Address](https://leetcode.com/problems/defanging-an-ip-address/) | 13 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Python sol by replace and regex. 85%+ [w/ Hint ] | html-entity-parser | 0 | 1 | Python sol by replacement.\n\n---\n\n**Hint**:\n\nRemeber to put the & replacement on the last one, in order to avoid chain reaction replacement.\n\nFor example: \nshould be , instead of ">"\n\n---\n\n**Implementation** by string replacement:\n\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n \n html_symbol = [ \'"\', \''\', \'>\', \'<\', \'⁄\', \'&\']\n formal_symbol = [ \'"\', "\'", \'>\', \'<\', \'/\', \'&\']\n \n for html_sym, formal_sym in zip(html_symbol, formal_symbol):\n text = text.replace( html_sym , formal_sym )\n \n return text\n \n```\n\n---\n\n**Implementation** by regular expression:\n\n```\nimport re\nclass Solution:\n def entityParser(self, text: str) -> str:\n \n html_symbol = [ \'"\', \''\', \'>\', \'<\', \'⁄\', \'&\']\n formal_symbol = [ \'"\', "\'", \'>\', \'<\', \'/\', \'&\']\n \n for html_sym, formal_sym in zip(html_symbol, formal_symbol):\n text = re.sub( html_sym , formal_sym, text )\n \n return text\n```\n\n---\n\n\nReference:\n\n[1] [Python official docs about str.replace( ... )](https://docs.python.org/3/library/stdtypes.html#str.replace)\n\n[2] [Python official docs about re.sub( ... )](https://docs.python.org/3/library/re.html#re.sub)\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #1108 Defanging an IP Address](https://leetcode.com/problems/defanging-an-ip-address/) | 13 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Python Simple Logic (48ms) | html-entity-parser | 0 | 1 | # Intuition\nJust think of string replace method.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nJust replace the all given html parsers.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n if text == "&gt;":\n return ">"\n text = text.replace(\'"\', \'"\')\n text = text.replace(\''\', "\'")\n text = text.replace(\'&\', \'&\')\n text = text.replace(\'>\', \'>\')\n text = text.replace(\'<\', \'<\')\n text = text.replace(\'⁄\', \'/\')\n return text\n``` | 1 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Python Simple Logic (48ms) | html-entity-parser | 0 | 1 | # Intuition\nJust think of string replace method.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nJust replace the all given html parsers.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n if text == "&gt;":\n return ">"\n text = text.replace(\'"\', \'"\')\n text = text.replace(\''\', "\'")\n text = text.replace(\'&\', \'&\')\n text = text.replace(\'>\', \'>\')\n text = text.replace(\'<\', \'<\')\n text = text.replace(\'⁄\', \'/\')\n return text\n``` | 1 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Python code using regex | html-entity-parser | 0 | 1 | ```\nentities = [(\'"\', \'\\"\'), (\''\', \'\\\'\'), (\'>\', \'>\'), (\'<\', \'<\'), (\'⁄\', \'/\'),(\'&\', \'&\')]\n \n for pat, repl in entities:\n\t text = re.sub(pat, repl,text)\n \n return text | 7 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Python code using regex | html-entity-parser | 0 | 1 | ```\nentities = [(\'"\', \'\\"\'), (\''\', \'\\\'\'), (\'>\', \'>\'), (\'<\', \'<\'), (\'⁄\', \'/\'),(\'&\', \'&\')]\n \n for pat, repl in entities:\n\t text = re.sub(pat, repl,text)\n \n return text | 7 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Python3 Map | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n dict= {\n """ : "\\"",\n "'" : "\'",\n "&" : "&",\n ">" : ">",\n "<" : "<",\n "⁄" : "/"\n}\n\n newans = \'\'\n i = 0\n\n while i < len(text):\n if text[i] == \'&\':\n idx = i\n while i < len(text) and text[i]!=\';\':\n i+=1\n if i <len(text) and text[i] ==\'&\':\n i = idx\n break\n \n if text[idx:i+1] in dict:\n newans+=dict[text[idx:i+1]]\n else:\n newans+=text[idx:i+1]\n else:\n \n newans+=text[i]\n i+=1\n\n return newans\n \n \n \n\n\n``` | 0 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Python3 Map | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n dict= {\n """ : "\\"",\n "'" : "\'",\n "&" : "&",\n ">" : ">",\n "<" : "<",\n "⁄" : "/"\n}\n\n newans = \'\'\n i = 0\n\n while i < len(text):\n if text[i] == \'&\':\n idx = i\n while i < len(text) and text[i]!=\';\':\n i+=1\n if i <len(text) and text[i] ==\'&\':\n i = idx\n break\n \n if text[idx:i+1] in dict:\n newans+=dict[text[idx:i+1]]\n else:\n newans+=text[idx:i+1]\n else:\n \n newans+=text[i]\n i+=1\n\n return newans\n \n \n \n\n\n``` | 0 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Describe your first thoughts on how solve problem .By using time complexity and Space complexity | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n return text.replace(\'"\', \'"\').replace(\'>\', \'>\').replace(\'<\', \'<\').replace(\''\', "\'").replace(\'&\', \'&\').replace(\'⁄\', \'/\')\n``` | 0 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Describe your first thoughts on how solve problem .By using time complexity and Space complexity | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n return text.replace(\'"\', \'"\').replace(\'>\', \'>\').replace(\'<\', \'<\').replace(\''\', "\'").replace(\'&\', \'&\').replace(\'⁄\', \'/\')\n``` | 0 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
HTML Entity Parser(Runtime 45ms Beats 100.00%) | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def entityParser(self, text: str) -> str:\n p=""\n p=text.replace("'","\'")\n \n \n \n text=p.replace(">",">")\n p=text.replace("<","<")\n text=p.replace("⁄","/")\n p=text.replace(""","\\"")\n text=p.replace("&","&")\n \n return text\n``` | 0 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
HTML Entity Parser(Runtime 45ms Beats 100.00%) | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def entityParser(self, text: str) -> str:\n p=""\n p=text.replace("'","\'")\n \n \n \n text=p.replace(">",">")\n p=text.replace("<","<")\n text=p.replace("⁄","/")\n p=text.replace(""","\\"")\n text=p.replace("&","&")\n \n return text\n``` | 0 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Simple Python one-liner Solution | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust perform replace operation\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\napply .replace() everytime\n\n# Complexity\n- Time complexity: $$O(n^2)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n return text.replace(""","\\"").replace("'","\'").replace(">",">").replace("<","<").replace("⁄","/").replace("&","&")\n``` | 0 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Simple Python one-liner Solution | html-entity-parser | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust perform replace operation\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\napply .replace() everytime\n\n# Complexity\n- Time complexity: $$O(n^2)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n return text.replace(""","\\"").replace("'","\'").replace(">",">").replace("<","<").replace("⁄","/").replace("&","&")\n``` | 0 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
Python | Using just String Manipulation | html-entity-parser | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n result = \'\'\n words = text.split(\'&\')\n print(words)\n for i in range(len(words)):\n if words[i].startswith(\'quot;\'):\n words[i] = \'\\"\' + words[i][5:]\n elif words[i].startswith(\'apos;\'):\n words[i] = \'\\\'\' + words[i][5:]\n elif words[i].startswith(\'amp;\'):\n words[i] = \'&\' + words[i][4:]\n elif words[i].startswith(\'gt;\'):\n words[i] = \'>\' + words[i][3:]\n elif words[i].startswith(\'lt;\'):\n words[i] = \'<\' + words[i][3:]\n elif words[i].startswith(\'frasl;\'):\n words[i] = \'/\' + words[i][6:]\n else:\n if i != 0:\n words[i] = \'&\' + words[i]\n return \'\'.join(words)\n\n \n\n\n \n \n\n\n``` | 0 | **HTML entity parser** is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
* **Quotation Mark:** the entity is `"` and symbol character is `"`.
* **Single Quote Mark:** the entity is `'` and symbol character is `'`.
* **Ampersand:** the entity is `&` and symbol character is `&`.
* **Greater Than Sign:** the entity is `>` and symbol character is `>`.
* **Less Than Sign:** the entity is `<` and symbol character is `<`.
* **Slash:** the entity is `⁄` and symbol character is `/`.
Given the input `text` string to the HTML parser, you have to implement the entity parser.
Return _the text after replacing the entities by the special characters_.
**Example 1:**
**Input:** text = "& is an HTML entity but &ambassador; is not. "
**Output:** "& is an HTML entity but &ambassador; is not. "
**Explanation:** The parser will replace the & entity by &
**Example 2:**
**Input:** text = "and I quote: "..." "
**Output:** "and I quote: \\ "...\\ " "
**Constraints:**
* `1 <= text.length <= 105`
* The string may contain any possible characters out of all the 256 ASCII characters. | null |
Python | Using just String Manipulation | html-entity-parser | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def entityParser(self, text: str) -> str:\n result = \'\'\n words = text.split(\'&\')\n print(words)\n for i in range(len(words)):\n if words[i].startswith(\'quot;\'):\n words[i] = \'\\"\' + words[i][5:]\n elif words[i].startswith(\'apos;\'):\n words[i] = \'\\\'\' + words[i][5:]\n elif words[i].startswith(\'amp;\'):\n words[i] = \'&\' + words[i][4:]\n elif words[i].startswith(\'gt;\'):\n words[i] = \'>\' + words[i][3:]\n elif words[i].startswith(\'lt;\'):\n words[i] = \'<\' + words[i][3:]\n elif words[i].startswith(\'frasl;\'):\n words[i] = \'/\' + words[i][6:]\n else:\n if i != 0:\n words[i] = \'&\' + words[i]\n return \'\'.join(words)\n\n \n\n\n \n \n\n\n``` | 0 | You are given an integer array `target`. You have an integer array `initial` of the same size as `target` with all elements initially zeros.
In one operation you can choose **any** subarray from `initial` and increment each value by one.
Return _the minimum number of operations to form a_ `target` _array from_ `initial`.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** target = \[1,2,3,2,1\]
**Output:** 3
**Explanation:** We need at least 3 operations to form the target array from the initial array.
\[**0,0,0,0,0**\] increment 1 from index 0 to 4 (inclusive).
\[1,**1,1,1**,1\] increment 1 from index 1 to 3 (inclusive).
\[1,2,**2**,2,1\] increment 1 at index 2.
\[1,2,3,2,1\] target array is formed.
**Example 2:**
**Input:** target = \[3,1,1,2\]
**Output:** 4
**Explanation:** \[**0,0,0,0**\] -> \[1,1,1,**1**\] -> \[**1**,1,1,2\] -> \[**2**,1,1,2\] -> \[3,1,1,2\]
**Example 3:**
**Input:** target = \[3,1,5,4,2\]
**Output:** 7
**Explanation:** \[**0,0,0,0,0**\] -> \[**1**,1,1,1,1\] -> \[**2**,1,1,1,1\] -> \[3,1,**1,1,1**\] -> \[3,1,**2,2**,2\] -> \[3,1,**3,3**,2\] -> \[3,1,**4**,4,2\] -> \[3,1,5,4,2\].
**Constraints:**
* `1 <= target.length <= 105`
* `1 <= target[i] <= 105` | Search the string for all the occurrences of the character '&'. For every '&' check if it matches an HTML entity by checking the ';' character and if entity found replace it in the answer. |
python super easy understand DP top down | number-of-ways-to-paint-n-3-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfWays(self, n: int) -> int:\n\n\n color = {"r", "y", "g"}\n @lru_cache(None)\n def dp(row, prev1, prev2, prev3):\n if row == n:\n return 1\n \n\n ans = 0\n \n for i in color:\n for j in color:\n for k in color:\n if i != j and j != k and i != prev1 and j != prev2 and k !=prev3:\n ans += dp(row+1, i, j, k)\n return ans \n \n\n return dp(0, "", "", "") % (10**9 + 7)\n``` | 1 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
dynamic programming, 32ms, beats 99.44% in Python | number-of-ways-to-paint-n-3-grid | 0 | 1 | ```\nclass Solution:\n def numOfWays(self, n: int) -> int:\n mod = 10 ** 9 + 7\n two_color, three_color = 6, 6\n for _ in range(n - 1):\n two_color, three_color = (two_color * 3 + three_color * 2) % mod, (two_color * 2 + three_color * 2) % mod\n return (two_color + three_color) % mod\n``` | 2 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
Math / Linear Time | number-of-ways-to-paint-n-3-grid | 0 | 1 | # Intuition\nEach of the 12 original grids (where n=1) can be divided into grids with two colors (ie: \'RGR\' which I call abas) or three colors (ie: "RGY\' aka abcs).\n\nEach aba can be followed by either 3 abas or 2 abcs, Each abc can be followed by either 2 abas or 2 abcs.\n\n# Approach\nLoop through + sum abas and abcs at the end.\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def numOfWays(self, n: int) -> int:\n MOD = 10**9 + 7\n\n # each of the og 6 aba\'s -> 3 aba\'s, 2 abc\'s\n # each of the og 6 abc\'s -> 2 aba\'s, 2 abc\'s\n abas, abcs = 6,6\n \n for _ in range(1,n): \n abas, abcs = abas * 3 + abcs * 2, abas * 2 + abcs * 2\n\n return (abas + abcs) % MOD\n\n \n``` | 0 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
Python| Prefix Sum | One Pass | 99.7% beats | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n val = psum = 0 \n for num in nums:\n psum += num\n val = min(val,psum)\n return abs(val) + 1\n``` | 1 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
Python| Prefix Sum | One Pass | 99.7% beats | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n val = psum = 0 \n for num in nums:\n psum += num\n val = min(val,psum)\n return abs(val) + 1\n``` | 1 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
🔥 EASY ONE LINE SOLUTION | PYTHON | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Approach\nFirst of all, we have to find prefix sums. There is the great `accumulate` function from `itertools` module.\n\n```python\naccumulate(nums)\n```\n\nNext step is to find the minimum prefix, so we use `min` function.\n\n```python\nmin(accumulate(nums))\n```\n\nFor example, if the minimum is $$-4$$, then we should return $$5$$, because $$5 - 4 = 1 > 0$$. So we just inverse the minimum and add $$1$$ to result.\n\n```python\n1 - min(accumulate(nums))\n```\n\nBut there is edge case - what if our minimum prefix is positive? Using this expression we can get non-positive number.\n\nThat is why we use `max` saying that our answer should be at least `1`.\n\n```python\nmax(1, 1 - min(accumulate))\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$, since `accumulate` function returns generator, not list\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n return max(1, 1 - min(accumulate(nums)))\n``` | 3 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
🔥 EASY ONE LINE SOLUTION | PYTHON | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Approach\nFirst of all, we have to find prefix sums. There is the great `accumulate` function from `itertools` module.\n\n```python\naccumulate(nums)\n```\n\nNext step is to find the minimum prefix, so we use `min` function.\n\n```python\nmin(accumulate(nums))\n```\n\nFor example, if the minimum is $$-4$$, then we should return $$5$$, because $$5 - 4 = 1 > 0$$. So we just inverse the minimum and add $$1$$ to result.\n\n```python\n1 - min(accumulate(nums))\n```\n\nBut there is edge case - what if our minimum prefix is positive? Using this expression we can get non-positive number.\n\nThat is why we use `max` saying that our answer should be at least `1`.\n\n```python\nmax(1, 1 - min(accumulate))\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$, since `accumulate` function returns generator, not list\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n return max(1, 1 - min(accumulate(nums)))\n``` | 3 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
✔Easy prefix sum solution in Python | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe maximum initial value will be 1 more than the minimum number obtained less than 1 at some step while adding the elements of array, so we have to find that non-positive number.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing **prefix sum** we will get the sum of all the elements upto that index. Then we will find the minimum non-positive value and return 1 more than the absolute value of it in order to ensure that the sum remains greater than or equal to 1. If no non-positive value is obtained then we will return 1.\n\n# Complexity\n- **Time complexity:**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n- **Space complexity:**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n for i in range(1,len(nums)):\n nums[i]+=nums[i-1]\n\n temp=min(nums)\n if temp>0:\n return 1\n else:\n return -temp+1\n``` | 2 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
✔Easy prefix sum solution in Python | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe maximum initial value will be 1 more than the minimum number obtained less than 1 at some step while adding the elements of array, so we have to find that non-positive number.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing **prefix sum** we will get the sum of all the elements upto that index. Then we will find the minimum non-positive value and return 1 more than the absolute value of it in order to ensure that the sum remains greater than or equal to 1. If no non-positive value is obtained then we will return 1.\n\n# Complexity\n- **Time complexity:**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n- **Space complexity:**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n for i in range(1,len(nums)):\n nums[i]+=nums[i-1]\n\n temp=min(nums)\n if temp>0:\n return 1\n else:\n return -temp+1\n``` | 2 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
95%+ O(n) solution || Python Simple Solution | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Intuition\nThe smallest initial value for the sum to not dip below 1 can be found by taking a look at the lowest point the sum gets while looping through the array. Find this minimum and then add 1, since the boundery is 1 and not 0.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse an aux array to keep track of the cumlative sum overtime as each iteration of the array happens. Once the entire array has been iterated though find this minimum value.\n\nIf the value is below 0 (i.e -4) then the min value for it to not dip below 1 would be 5. So take this minimum multiply by -1 and add 1 to it. \n\nIf at all points during the summation the sum stays positive just return 1 as that is the base case\n\n# Complexity\n- Time complexity: $$O(n)$$\n - Iterate once to get the clumlative array \n - Iterate once more to get the min value\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n - Use an aux array size n. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n\n\n currSum = 0\n culmSum = []\n\n for i in range(0,len(nums)):\n currSum += nums[i]\n culmSum.append(currSum)\n\n currMin = min(culmSum)\n\n if currMin <= 0:\n return (-1*currMin) + 1\n else:\n return 1\n``` | 2 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
95%+ O(n) solution || Python Simple Solution | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | # Intuition\nThe smallest initial value for the sum to not dip below 1 can be found by taking a look at the lowest point the sum gets while looping through the array. Find this minimum and then add 1, since the boundery is 1 and not 0.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse an aux array to keep track of the cumlative sum overtime as each iteration of the array happens. Once the entire array has been iterated though find this minimum value.\n\nIf the value is below 0 (i.e -4) then the min value for it to not dip below 1 would be 5. So take this minimum multiply by -1 and add 1 to it. \n\nIf at all points during the summation the sum stays positive just return 1 as that is the base case\n\n# Complexity\n- Time complexity: $$O(n)$$\n - Iterate once to get the clumlative array \n - Iterate once more to get the min value\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n - Use an aux array size n. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n\n\n currSum = 0\n culmSum = []\n\n for i in range(0,len(nums)):\n currSum += nums[i]\n culmSum.append(currSum)\n\n currMin = min(culmSum)\n\n if currMin <= 0:\n return (-1*currMin) + 1\n else:\n return 1\n``` | 2 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
Python Simplest Solution With Explanation | Beg to adv | Prefix sum | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | ```python\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n prefix_sum = 0 # taking this variable to store prefix sum\n min_start_value = 1 # as stated in the question min startValue shouldn`t be less then 1.\n \n for num in nums: # traversing through the provided list\n prefix_sum += num # calculating prefix sum\n min_start_value = max(min_start_value, 1-prefix_sum) # Taking max as value shouldnt be less them 1. Subtracting 1 to convert the negetives to positives.\n return min_start_value\n```\n\n```python\nValues of prefix_sum & min_start_values would be as follows for better understanding:-\nprefix_sum: 0,-3,-1,-4,0,2\nmin_start_value:1,4,4,5,5,5\n```\n\n***Found helpful, Do upvote !!*** | 6 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
Python Simplest Solution With Explanation | Beg to adv | Prefix sum | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | ```python\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n prefix_sum = 0 # taking this variable to store prefix sum\n min_start_value = 1 # as stated in the question min startValue shouldn`t be less then 1.\n \n for num in nums: # traversing through the provided list\n prefix_sum += num # calculating prefix sum\n min_start_value = max(min_start_value, 1-prefix_sum) # Taking max as value shouldnt be less them 1. Subtracting 1 to convert the negetives to positives.\n return min_start_value\n```\n\n```python\nValues of prefix_sum & min_start_values would be as follows for better understanding:-\nprefix_sum: 0,-3,-1,-4,0,2\nmin_start_value:1,4,4,5,5,5\n```\n\n***Found helpful, Do upvote !!*** | 6 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
2 Lines Easy Python Solution | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | This solution is not necessary the fastest one. But it is super easy and clean (at least I think so).\n\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n \n for i in range(1, len(nums)): nums[i] = nums[i] + nums[i - 1]\n \n return 1 if min(nums) >= 1 else abs(min(nums)) + 1\n``` | 5 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
2 Lines Easy Python Solution | minimum-value-to-get-positive-step-by-step-sum | 0 | 1 | This solution is not necessary the fastest one. But it is super easy and clean (at least I think so).\n\n```\nclass Solution:\n def minStartValue(self, nums: List[int]) -> int:\n \n for i in range(1, len(nums)): nums[i] = nums[i] + nums[i - 1]\n \n return 1 if min(nums) >= 1 else abs(min(nums)) + 1\n``` | 5 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k | 0 | 1 | # Code\n```\nclass Solution:\n def findMinFibonacciNumbers(self, k: int) -> int:\n self.count = 0\n def fib(k):\n l = [0,1]\n for i in range(1,k+1):\n if l[-2]+l[-1]<k:\n l.append(l[-1] + l[-2])\n elif l[-2]+l[-1]==k:\n l.append(l[-1] + l[-2])\n self.count+=1\n k = k - l[-1]\n return k\n else:\n self.count+=1\n k = k - l[-1]\n return k\n while k>0:\n k = fib(k)\n if k==1:\n return self.count+1\n return self.count\n\n \n \n\n\n\n \n``` | 0 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.