title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
SImple DP in python3 | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Code\n```\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n def place(l):\n a = ord(l) - ord(\'A\')\n return (a//6,a%6)\n places = {a:place(a) for a in \'ABCDEFGHIJKLMNOPQRSTUVWXYZ\'}\n def dist(a,b):\n if a == None:\n return 0\n return abs(place(a)[0] - place(b)[0])+abs(place(a)[1] - place(b)[1])\n @cache\n def dp(i,j,k):\n if k == len(word)-1:\n return 0\n else:\n return min(dist(i,word[k+1])+dp(word[k+1],j,k+1),dist(j,word[k+1])+dp(i,word[k+1],k+1))\n return dp(None,None,-1)\n\n \n\n \n``` | 0 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
Solution | minimum-distance-to-type-a-word-using-two-fingers | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minimumDistance(string word) {\n int n = word.length();\n int* dp = new int[n];\n dp[0] = 0;\n for (int w=1; w<n; w++) {\n int d = dist(word, w, w-1);\n dp[w] = dp[w-1] + d;\n\n for (int j=0; j<w-1; j++) {\n dp[w-1] = min(dp[w-1], dp[j] + dist(word, w, j));\n }\n for (int i=w-2; i>=0; i--) {\n dp[i] += d;\n }\n }\n int m = INT_MAX;\n for (int i=0; i<n; i++) {\n m = min(m, dp[i]);\n }\n return m;\n }\n int minimumDistance1(string word) {\n int n = word.length();\n map<pair<int, int>,int> dp;\n dp.insert({{-1, -1}, 0});\n for (int w=0; w<n; w++) {\n map<pair<int, int>,int> dp2;\n for (const auto& [lr, sum] : dp) {\n const auto& [l, r] = lr;\n insert_or_min(dp2, {w, r}, dist(word, w, l) + sum);\n insert_or_min(dp2, {w, l}, dist(word, w, r) + sum);\n }\n swap(dp, dp2);\n }\n int m = INT_MAX;\n for (const auto& [lr, sum] : dp) {\n m = min(m, sum);\n }\n return m;\n }\n void insert_or_min(map<pair<int, int>,int>& dp, const pair<int, int>& k, int v) {\n if (auto it=dp.find(k); it == dp.end()) {\n dp[k] = v;\n } else {\n dp[k] = min(dp[k], v);\n }\n }\n int dist(const string& word, int x, int y) {\n if (x == -1 || y == -1) return 0;\n char a = word[x];\n char b = word[y];\n return abs(horizontal(a) - horizontal(b))\n + abs(vertical(a) - vertical(b));\n }\n int horizontal(char a) {\n return (a - \'A\') % 6;\n }\n int vertical(char a) {\n return (a - \'A\') / 6;\n }\n};\n```\n\n```Python3 []\ngrid = [\n ["A", "B", "C", "D", "E", "F"],\n ["G", "H", "I", "J", "K", "L"],\n ["M", "N", "O", "P", "Q", "R"],\n ["S", "T", "U", "V", "W", "X"],\n ["Y", "Z"],\n]\ncoords = {}\nfor i in range(len(grid)):\n for j in range(len(grid[i])):\n coords[grid[i][j]] = (i, j)\ndists = {}\nfor c1, (i1, j1) in coords.items():\n for c2, (i2, j2) in coords.items():\n dists[(c1, c2)] = abs(i1 - i2) + abs(j1 - j2)\n\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n n = len(word)\n x = [{} for _ in range(n)]\n for i in reversed(range(n)):\n if i == n - 1:\n x[i][None] = 0\n else:\n \n d1 =dists[(word[i], word[i + 1])]\n for c, dist in x[i + 1].items():\n x[i][c] = d1 + x[i + 1][c]\n \n x[i][word[i+1]] = min(\n x[i].get(word[i+1], float("inf")),\n min(\n dist + (dists[(word[i], c)] if c is not None else 0)\n for c, dist in x[i + 1].items()\n )\n )\n return min(x[0].values())\n```\n\n```Java []\nclass Solution {\n public int minimumDistance(String word) {\n int[] keys = new int[word.length()];\n for (int i = 0; i < word.length(); i++) keys[i] = word.charAt(i) - \'A\';\n\n int[][] cost = new int[27][26];\n for (int i = 0; i < 26; i++) {\n for (int j = i; j < 26; j++) {\n cost[i][j] = Math.abs(i/6 - j/6) + Math.abs(i%6 - j%6);\n cost[j][i] = cost[i][j];\n }\n }\n int[] dp = new int[27];\n \n for (int i = keys.length - 1; i > 0; i--) {\n int dp_for_key_at_i_minus_1 = dp[keys[i - 1]];\n int cost_i_minus_1_to_i = cost[keys[i - 1]][keys[i]];\n for (int j = 0; j < 27; j++) {\n dp[j] = Math.min(\n dp_for_key_at_i_minus_1 + cost[j][keys[i]], \n dp[j] + cost_i_minus_1_to_i);\n }\n }\n return dp[26];\n }\n}\n``` | 0 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Solution | minimum-distance-to-type-a-word-using-two-fingers | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minimumDistance(string word) {\n int n = word.length();\n int* dp = new int[n];\n dp[0] = 0;\n for (int w=1; w<n; w++) {\n int d = dist(word, w, w-1);\n dp[w] = dp[w-1] + d;\n\n for (int j=0; j<w-1; j++) {\n dp[w-1] = min(dp[w-1], dp[j] + dist(word, w, j));\n }\n for (int i=w-2; i>=0; i--) {\n dp[i] += d;\n }\n }\n int m = INT_MAX;\n for (int i=0; i<n; i++) {\n m = min(m, dp[i]);\n }\n return m;\n }\n int minimumDistance1(string word) {\n int n = word.length();\n map<pair<int, int>,int> dp;\n dp.insert({{-1, -1}, 0});\n for (int w=0; w<n; w++) {\n map<pair<int, int>,int> dp2;\n for (const auto& [lr, sum] : dp) {\n const auto& [l, r] = lr;\n insert_or_min(dp2, {w, r}, dist(word, w, l) + sum);\n insert_or_min(dp2, {w, l}, dist(word, w, r) + sum);\n }\n swap(dp, dp2);\n }\n int m = INT_MAX;\n for (const auto& [lr, sum] : dp) {\n m = min(m, sum);\n }\n return m;\n }\n void insert_or_min(map<pair<int, int>,int>& dp, const pair<int, int>& k, int v) {\n if (auto it=dp.find(k); it == dp.end()) {\n dp[k] = v;\n } else {\n dp[k] = min(dp[k], v);\n }\n }\n int dist(const string& word, int x, int y) {\n if (x == -1 || y == -1) return 0;\n char a = word[x];\n char b = word[y];\n return abs(horizontal(a) - horizontal(b))\n + abs(vertical(a) - vertical(b));\n }\n int horizontal(char a) {\n return (a - \'A\') % 6;\n }\n int vertical(char a) {\n return (a - \'A\') / 6;\n }\n};\n```\n\n```Python3 []\ngrid = [\n ["A", "B", "C", "D", "E", "F"],\n ["G", "H", "I", "J", "K", "L"],\n ["M", "N", "O", "P", "Q", "R"],\n ["S", "T", "U", "V", "W", "X"],\n ["Y", "Z"],\n]\ncoords = {}\nfor i in range(len(grid)):\n for j in range(len(grid[i])):\n coords[grid[i][j]] = (i, j)\ndists = {}\nfor c1, (i1, j1) in coords.items():\n for c2, (i2, j2) in coords.items():\n dists[(c1, c2)] = abs(i1 - i2) + abs(j1 - j2)\n\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n n = len(word)\n x = [{} for _ in range(n)]\n for i in reversed(range(n)):\n if i == n - 1:\n x[i][None] = 0\n else:\n \n d1 =dists[(word[i], word[i + 1])]\n for c, dist in x[i + 1].items():\n x[i][c] = d1 + x[i + 1][c]\n \n x[i][word[i+1]] = min(\n x[i].get(word[i+1], float("inf")),\n min(\n dist + (dists[(word[i], c)] if c is not None else 0)\n for c, dist in x[i + 1].items()\n )\n )\n return min(x[0].values())\n```\n\n```Java []\nclass Solution {\n public int minimumDistance(String word) {\n int[] keys = new int[word.length()];\n for (int i = 0; i < word.length(); i++) keys[i] = word.charAt(i) - \'A\';\n\n int[][] cost = new int[27][26];\n for (int i = 0; i < 26; i++) {\n for (int j = i; j < 26; j++) {\n cost[i][j] = Math.abs(i/6 - j/6) + Math.abs(i%6 - j%6);\n cost[j][i] = cost[i][j];\n }\n }\n int[] dp = new int[27];\n \n for (int i = keys.length - 1; i > 0; i--) {\n int dp_for_key_at_i_minus_1 = dp[keys[i - 1]];\n int cost_i_minus_1_to_i = cost[keys[i - 1]][keys[i]];\n for (int j = 0; j < 27; j++) {\n dp[j] = Math.min(\n dp_for_key_at_i_minus_1 + cost[j][keys[i]], \n dp[j] + cost_i_minus_1_to_i);\n }\n }\n return dp[26];\n }\n}\n``` | 0 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
Cache | Simple | Fast | Python Solution | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Code\n```\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n def dist(pre,cur):\n if pre==None:\n return 0\n x1,y1 = divmod(ord(pre)-ord(\'A\'),6)\n x2,y2 = divmod(ord(cur)-ord(\'A\'),6)\n return abs(x1-x2) + abs(y1-y2)\n \n @lru_cache(None)\n def fingers(i,l,r):\n if i == len(word):\n return 0\n n1 = dist(l,word[i]) + fingers(i+1,word[i],r)\n n2 = dist(r,word[i]) + fingers(i+1,l,word[i])\n return min(n1,n2)\n \n return fingers(0,None,None)\n``` | 0 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Cache | Simple | Fast | Python Solution | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Code\n```\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n def dist(pre,cur):\n if pre==None:\n return 0\n x1,y1 = divmod(ord(pre)-ord(\'A\'),6)\n x2,y2 = divmod(ord(cur)-ord(\'A\'),6)\n return abs(x1-x2) + abs(y1-y2)\n \n @lru_cache(None)\n def fingers(i,l,r):\n if i == len(word):\n return 0\n n1 = dist(l,word[i]) + fingers(i+1,word[i],r)\n n2 = dist(r,word[i]) + fingers(i+1,l,word[i])\n return min(n1,n2)\n \n return fingers(0,None,None)\n``` | 0 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
Python DP with Reused Storage -- Time O(27N) beats 100%; Space O(4 * 27 N) beats 94% | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Code\n```\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n n = len(word)\n if n == 2: return 0\n dp01, dp02, dp11, dp12 = ([0] * 27 for _ in range(4))\n dm = divmod\n c = ord(word[-1]) - 0x41\n i = n - 1\n while i > 0:\n pc = ord(word[i-1]) - 0x41\n cx, cy = dm(c, 6)\n pcx, pcy = dm(pc, 6)\n dist = abs(cx - pcx) + abs(cy - pcy)\n for f in range(26):\n fx, fy = dm(f, 6)\n distf = abs(cx - fx) + abs(cy - fy)\n a1 = dist + dp01[f]\n a2 = distf + dp02[pc]\n dp11[f] = a1 if a1 < a2 else a2\n a1 = distf + dp01[pc]\n a2 = dist + dp02[f]\n dp12[f] = a1 if a1 < a2 else a2\n a1 = dp01[pc]\n a2 = dist + dp02[-1]\n dp12[-1] = a1 if a1 < a2 else a2\n a1 = dp02[pc]\n a2 = dist + dp01[-1]\n dp11[-1] = a1 if a1 < a2 else a2\n dp11, dp12, dp01, dp02 = dp01, dp02, dp11, dp12\n c = pc\n i -= 1\n a1 = dp01[-1]\n a2 = dp02[-1]\n return a1 if a1 < a2 else a2\n``` | 0 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Python DP with Reused Storage -- Time O(27N) beats 100%; Space O(4 * 27 N) beats 94% | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Code\n```\nclass Solution:\n def minimumDistance(self, word: str) -> int:\n n = len(word)\n if n == 2: return 0\n dp01, dp02, dp11, dp12 = ([0] * 27 for _ in range(4))\n dm = divmod\n c = ord(word[-1]) - 0x41\n i = n - 1\n while i > 0:\n pc = ord(word[i-1]) - 0x41\n cx, cy = dm(c, 6)\n pcx, pcy = dm(pc, 6)\n dist = abs(cx - pcx) + abs(cy - pcy)\n for f in range(26):\n fx, fy = dm(f, 6)\n distf = abs(cx - fx) + abs(cy - fy)\n a1 = dist + dp01[f]\n a2 = distf + dp02[pc]\n dp11[f] = a1 if a1 < a2 else a2\n a1 = distf + dp01[pc]\n a2 = dist + dp02[f]\n dp12[f] = a1 if a1 < a2 else a2\n a1 = dp01[pc]\n a2 = dist + dp02[-1]\n dp12[-1] = a1 if a1 < a2 else a2\n a1 = dp02[pc]\n a2 = dist + dp01[-1]\n dp11[-1] = a1 if a1 < a2 else a2\n dp11, dp12, dp01, dp02 = dp01, dp02, dp11, dp12\n c = pc\n i -= 1\n a1 = dp01[-1]\n a2 = dp02[-1]\n return a1 if a1 < a2 else a2\n``` | 0 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
Python (Simple DP) | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDistance(self, word):\n n = len(word)\n\n d1 = {"A":(0,0),"B":(0,1),"C":(0,2),"D":(0,3),"E":(0,4),"F":(0,5),"G":(1,0),"H":(1,1),"I":(1,2),"J":(1,3),"K":(1,4),"L":(1,5),"M":(2,0),"N":(2,1),"O":(2,2),"P":(2,3),"Q":(2,4),"R":(2,5),"S":(3,0),"T":(3,1),"U":(3,2),"V":(3,3),"W":(3,4),"X":(3,5),"Y":(4,0),"Z":(4,1)}\n\n @lru_cache(None)\n def dfs(i,j,k):\n if k >= n:\n return 0\n\n if i == -1:\n val1 = dfs(k,j,k+1)\n else:\n val1 = abs(d1[word[i]][0]-d1[word[k]][0]) + abs(d1[word[i]][1] - d1[word[k]][1]) + dfs(k,j,k+1)\n\n if j == -1:\n val2 = dfs(i,k,k+1)\n else:\n val2 = abs(d1[word[j]][0]-d1[word[k]][0]) + abs(d1[word[j]][1] - d1[word[k]][1]) + dfs(i,k,k+1)\n\n return min(val1,val2)\n\n return dfs(-1,-1,0)\n\n``` | 0 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Python (Simple DP) | minimum-distance-to-type-a-word-using-two-fingers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDistance(self, word):\n n = len(word)\n\n d1 = {"A":(0,0),"B":(0,1),"C":(0,2),"D":(0,3),"E":(0,4),"F":(0,5),"G":(1,0),"H":(1,1),"I":(1,2),"J":(1,3),"K":(1,4),"L":(1,5),"M":(2,0),"N":(2,1),"O":(2,2),"P":(2,3),"Q":(2,4),"R":(2,5),"S":(3,0),"T":(3,1),"U":(3,2),"V":(3,3),"W":(3,4),"X":(3,5),"Y":(4,0),"Z":(4,1)}\n\n @lru_cache(None)\n def dfs(i,j,k):\n if k >= n:\n return 0\n\n if i == -1:\n val1 = dfs(k,j,k+1)\n else:\n val1 = abs(d1[word[i]][0]-d1[word[k]][0]) + abs(d1[word[i]][1] - d1[word[k]][1]) + dfs(k,j,k+1)\n\n if j == -1:\n val2 = dfs(i,k,k+1)\n else:\n val2 = abs(d1[word[j]][0]-d1[word[k]][0]) + abs(d1[word[j]][1] - d1[word[k]][1]) + dfs(i,k,k+1)\n\n return min(val1,val2)\n\n return dfs(-1,-1,0)\n\n``` | 0 | Given an undirected tree consisting of `n` vertices numbered from `0` to `n-1`, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. _Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at **vertex 0** and coming back to this vertex._
The edges of the undirected tree are given in the array `edges`, where `edges[i] = [ai, bi]` means that exists an edge connecting the vertices `ai` and `bi`. Additionally, there is a boolean array `hasApple`, where `hasApple[i] = true` means that vertex `i` has an apple; otherwise, it does not have any apple.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,true,true,false\]
**Output:** 8
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 2:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,true,false,false,true,false\]
**Output:** 6
**Explanation:** The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
**Example 3:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], hasApple = \[false,false,false,false,false,false,false\]
**Output:** 0
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai < bi <= n - 1`
* `hasApple.length == n` | Use dynamic programming. dp[i][j][k]: smallest movements when you have one finger on i-th char and the other one on j-th char already having written k first characters from word. |
Easy Python Solution | maximum-69-number | 0 | 1 | # Complexity\nThe current complexity is $O(n^2)$ because of the for loop and the max function, but it can be brought done to $O(n)$ if we replace max with normal if condition to check if m<temp: m=temp\n# Code\n```\nclass Solution:\n def maximum69Number (self, num: int) -> int:\n m=num\n s=(str(num))\n for i in range(len(s)):\n if s[i]=="6":\n temp=(int(s[:i]+"9"+s[i+1:]))\n else:\n temp=(int(s[:i]+"6"+s[i+1:]))\n m=max(m,temp)\n return m\n``` | 2 | You are given a positive integer `num` consisting only of digits `6` and `9`.
Return _the maximum number you can get by changing **at most** one digit (_`6` _becomes_ `9`_, and_ `9` _becomes_ `6`_)_.
**Example 1:**
**Input:** num = 9669
**Output:** 9969
**Explanation:**
Changing the first digit results in 6669.
Changing the second digit results in 9969.
Changing the third digit results in 9699.
Changing the fourth digit results in 9666.
The maximum number is 9969.
**Example 2:**
**Input:** num = 9996
**Output:** 9999
**Explanation:** Changing the last digit 6 to 9 results in the maximum number.
**Example 3:**
**Input:** num = 9999
**Output:** 9999
**Explanation:** It is better not to apply any change.
**Constraints:**
* `1 <= num <= 104`
* `num` consists of only `6` and `9` digits. | null |
Easy Python Solution | maximum-69-number | 0 | 1 | # Complexity\nThe current complexity is $O(n^2)$ because of the for loop and the max function, but it can be brought done to $O(n)$ if we replace max with normal if condition to check if m<temp: m=temp\n# Code\n```\nclass Solution:\n def maximum69Number (self, num: int) -> int:\n m=num\n s=(str(num))\n for i in range(len(s)):\n if s[i]=="6":\n temp=(int(s[:i]+"9"+s[i+1:]))\n else:\n temp=(int(s[:i]+"6"+s[i+1:]))\n m=max(m,temp)\n return m\n``` | 2 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
Not a obtained solution | maximum-69-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximum69Number (self, num: int) -> int:\n res=0\n val=list(str(num))\n for i in range(len(val)):\n temp=list(str(num))\n if val[i]==\'6\':\n temp[i]="9"\n i_temp=int("".join(temp))\n if i_temp>res:\n res=i_temp\n return res\n\n``` | 1 | You are given a positive integer `num` consisting only of digits `6` and `9`.
Return _the maximum number you can get by changing **at most** one digit (_`6` _becomes_ `9`_, and_ `9` _becomes_ `6`_)_.
**Example 1:**
**Input:** num = 9669
**Output:** 9969
**Explanation:**
Changing the first digit results in 6669.
Changing the second digit results in 9969.
Changing the third digit results in 9699.
Changing the fourth digit results in 9666.
The maximum number is 9969.
**Example 2:**
**Input:** num = 9996
**Output:** 9999
**Explanation:** Changing the last digit 6 to 9 results in the maximum number.
**Example 3:**
**Input:** num = 9999
**Output:** 9999
**Explanation:** It is better not to apply any change.
**Constraints:**
* `1 <= num <= 104`
* `num` consists of only `6` and `9` digits. | null |
Not a obtained solution | maximum-69-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximum69Number (self, num: int) -> int:\n res=0\n val=list(str(num))\n for i in range(len(val)):\n temp=list(str(num))\n if val[i]==\'6\':\n temp[i]="9"\n i_temp=int("".join(temp))\n if i_temp>res:\n res=i_temp\n return res\n\n``` | 1 | Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
Return the number of **good** nodes in the binary tree.
**Example 1:**
**Input:** root = \[3,1,4,3,null,1,5\]
**Output:** 4
**Explanation:** Nodes in blue are **good**.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.
**Example 2:**
**Input:** root = \[3,3,null,4,2\]
**Output:** 3
**Explanation:** Node 2 -> (3, 3, 2) is not good, because "3 " is higher than it.
**Example 3:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** Root is considered as **good**.
**Constraints:**
* The number of nodes in the binary tree is in the range `[1, 10^5]`.
* Each node's value is between `[-10^4, 10^4]`. | Convert the number in an array of its digits. Brute force on every digit to get the maximum number. |
Python Elegant & Short | No loops | 1 line | print-words-vertically | 0 | 1 | ```\nfrom itertools import zip_longest\nfrom typing import Iterable\n\n\nclass Solution:\n def printVertically(self, s: str) -> Iterable[str]:\n return map(str.rstrip, map(\'\'.join, zip_longest(*s.split(), fillvalue=\' \')))\n\n``` | 1 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
Python Elegant & Short | No loops | 1 line | print-words-vertically | 0 | 1 | ```\nfrom itertools import zip_longest\nfrom typing import Iterable\n\n\nclass Solution:\n def printVertically(self, s: str) -> Iterable[str]:\n return map(str.rstrip, map(\'\'.join, zip_longest(*s.split(), fillvalue=\' \')))\n\n``` | 1 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python simple solution (92.9% Faster) | print-words-vertically | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n yo = s.split()\n max = 0\n for i in yo:\n if len(i)>max: max = len(i)\n m = {}\n for i in yo:\n for j in range(max):\n try:\n if j not in m:\n m[j] = i[j]\n else:\n m[j]+=i[j]\n except:\n if j not in m:\n m[j] = " "\n else:\n m[j]+=" "\n \n\n res = []\n for i in m:\n res.append(m[i].rstrip())\n return res\n \n``` | 1 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
Python simple solution (92.9% Faster) | print-words-vertically | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n yo = s.split()\n max = 0\n for i in yo:\n if len(i)>max: max = len(i)\n m = {}\n for i in yo:\n for j in range(max):\n try:\n if j not in m:\n m[j] = i[j]\n else:\n m[j]+=i[j]\n except:\n if j not in m:\n m[j] = " "\n else:\n m[j]+=" "\n \n\n res = []\n for i in m:\n res.append(m[i].rstrip())\n return res\n \n``` | 1 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python 3 Zip solution | print-words-vertically | 0 | 1 | \n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n a, b, words = [], [], s.split()\n max_length = len(max(words, key=len))\n for i in words:\n if len(i) < max_length:\n i = i + " " * (max_length - len(i)) \n a.append(i)\n for i in zip(*a):\n b.append(\'\'.join(i).rstrip())\n return b\n\n\n \n\n``` | 1 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
Python 3 Zip solution | print-words-vertically | 0 | 1 | \n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n a, b, words = [], [], s.split()\n max_length = len(max(words, key=len))\n for i in words:\n if len(i) < max_length:\n i = i + " " * (max_length - len(i)) \n a.append(i)\n for i in zip(*a):\n b.append(\'\'.join(i).rstrip())\n return b\n\n\n \n\n``` | 1 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python3 solution using try and except block | print-words-vertically | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n w=[]\n l=s.split()\n for i in range(len(sorted(s.split(),key=len,reverse=1)[0])):\n ss=""\n for j in range(len(s.split())):\n try:\n ss+=l[j][i]\n except:\n ss+=" "\n w.append(ss)\n return ["".join(i).rstrip() for i in w]\n\n``` | 1 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
Python3 solution using try and except block | print-words-vertically | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n w=[]\n l=s.split()\n for i in range(len(sorted(s.split(),key=len,reverse=1)[0])):\n ss=""\n for j in range(len(s.split())):\n try:\n ss+=l[j][i]\n except:\n ss+=" "\n w.append(ss)\n return ["".join(i).rstrip() for i in w]\n\n``` | 1 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Beats 90% || Python || Easy To Understand | print-words-vertically | 0 | 1 | # Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n s=list(s.split())\n\n max_len=0\n for ele in s:\n max_len=max(max_len,len(ele))\n\n for i in range(len(s)):\n if len(s[i])<max_len:\n s[i]=s[i]+" "*(max_len-len(s[i]))\n\n grid=[list(ele) for ele in s]\n\n result=[]\n for i in range(max_len):\n temp_str=""\n for j in range(len(grid)):\n temp_str+=grid[j][i]\n \n # removing the spaces that comes in last\n temp_str=temp_str.rstrip() \n result.append(temp_str)\n \n return result\n```\n\n | 2 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
Beats 90% || Python || Easy To Understand | print-words-vertically | 0 | 1 | # Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n s=list(s.split())\n\n max_len=0\n for ele in s:\n max_len=max(max_len,len(ele))\n\n for i in range(len(s)):\n if len(s[i])<max_len:\n s[i]=s[i]+" "*(max_len-len(s[i]))\n\n grid=[list(ele) for ele in s]\n\n result=[]\n for i in range(max_len):\n temp_str=""\n for j in range(len(grid)):\n temp_str+=grid[j][i]\n \n # removing the spaces that comes in last\n temp_str=temp_str.rstrip() \n result.append(temp_str)\n \n return result\n```\n\n | 2 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python3 Sloution . Beats 100% | print-words-vertically | 0 | 1 | \n\n# Approach\nfirst split the string and then collect all the values in the same index then strip all the trailling white spaces.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n\n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n temp = s.split()\n res = []\n\n l, k = 0, 0\n for i in temp:\n if (len(i) == l):\n k += 1\n elif (len(i) > l):\n k = 1\n l = len(i)\n for i in range(l):\n new = []\n for j in temp:\n\n if i < len(j):\n new.append(j[i])\n if (i + 1 == l):\n k -= 1\n if (k == 0):\n break\n elif (i >= len(j)):\n new.append(\' \')\n res.append("".join(new).rstrip())\n new = []\n return res \n``` | 0 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
Python3 Sloution . Beats 100% | print-words-vertically | 0 | 1 | \n\n# Approach\nfirst split the string and then collect all the values in the same index then strip all the trailling white spaces.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n\n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n temp = s.split()\n res = []\n\n l, k = 0, 0\n for i in temp:\n if (len(i) == l):\n k += 1\n elif (len(i) > l):\n k = 1\n l = len(i)\n for i in range(l):\n new = []\n for j in temp:\n\n if i < len(j):\n new.append(j[i])\n if (i + 1 == l):\n k -= 1\n if (k == 0):\n break\n elif (i >= len(j)):\n new.append(\' \')\n res.append("".join(new).rstrip())\n new = []\n return res \n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
cool python | print-words-vertically | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n x=s.split()\n y=max(list(map(len,x)))\n a=[]\n for i in range(y):\n m=\'\'\n for j in range(len(x)):\n if len(x[j])>i:\n m+=x[j][i]\n else:\n m+=\' \'\n for k in range(len(m)):\n m=m.removesuffix(\' \')\n a.append(m)\n return a\n\n``` | 0 | Given a string `s`. Return all the words vertically in the same order in which they appear in `s`.
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
Each word would be put on only one column and that in one column there will be only one word.
**Example 1:**
**Input:** s = "HOW ARE YOU "
**Output:** \[ "HAY ", "ORO ", "WEU "\]
**Explanation:** Each word is printed vertically.
"HAY "
"ORO "
"WEU "
**Example 2:**
**Input:** s = "TO BE OR NOT TO BE "
**Output:** \[ "TBONTB ", "OEROOE ", " T "\]
**Explanation:** Trailing spaces is not allowed.
"TBONTB "
"OEROOE "
" T "
**Example 3:**
**Input:** s = "CONTEST IS COMING "
**Output:** \[ "CIC ", "OSO ", "N M ", "T I ", "E N ", "S G ", "T "\]
**Constraints:**
* `1 <= s.length <= 200`
* `s` contains only upper case English letters.
* It's guaranteed that there is only one space between 2 words. | Use DFS. Traverse the path of the ball downwards until you reach the bottom or get stuck. |
cool python | print-words-vertically | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def printVertically(self, s: str) -> List[str]:\n x=s.split()\n y=max(list(map(len,x)))\n a=[]\n for i in range(y):\n m=\'\'\n for j in range(len(x)):\n if len(x[j])>i:\n m+=x[j][i]\n else:\n m+=\' \'\n for k in range(len(m)):\n m=m.removesuffix(\' \')\n a.append(m)\n return a\n\n``` | 0 | Given an array of integers `cost` and an integer `target`, return _the **maximum** integer you can paint under the following rules_:
* The cost of painting a digit `(i + 1)` is given by `cost[i]` (**0-indexed**).
* The total cost used must be equal to `target`.
* The integer does not have `0` digits.
Since the answer may be very large, return it as a string. If there is no way to paint any integer given the condition, return `"0 "`.
**Example 1:**
**Input:** cost = \[4,3,2,5,6,7,2,5,5\], target = 9
**Output:** "7772 "
**Explanation:** The cost to paint the digit '7' is 2, and the digit '2' is 3. Then cost( "7772 ") = 2\*3+ 3\*1 = 9. You could also paint "977 ", but "7772 " is the largest number.
**Digit cost**
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5
**Example 2:**
**Input:** cost = \[7,6,5,5,5,6,8,7,8\], target = 12
**Output:** "85 "
**Explanation:** The cost to paint the digit '8' is 7, and the digit '5' is 5. Then cost( "85 ") = 7 + 5 = 12.
**Example 3:**
**Input:** cost = \[2,4,6,2,4,6,4,4,4\], target = 5
**Output:** "0 "
**Explanation:** It is impossible to paint any integer with total cost equal to target.
**Constraints:**
* `cost.length == 9`
* `1 <= cost[i], target <= 5000` | Use the maximum length of words to determine the length of the returned answer. However, don't forget to remove trailing spaces. |
Python3 O(N) solution with DFS (99.65% Runtime) | delete-leaves-with-a-given-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n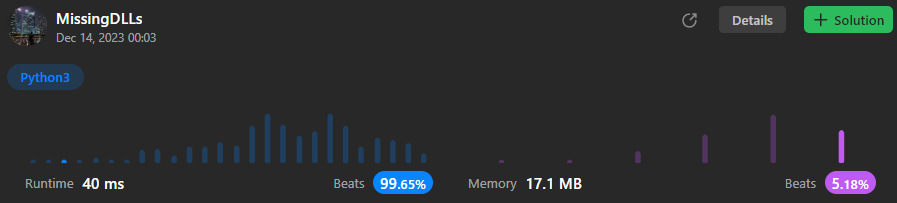\nUtilize depth first search with leaf node check and check if it become leaf node \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- You should consider:\n - If a node is leaf\n - If a node become leaf\n- You can easily solve the problem with depth first search with recursion\n - Define a base case (none check)\n - Check if current node is a leaf:\n - If current value == target, return None\n - Get left child node from recursion\n - Get right child node from recursion\n - Check if current node becomes a leaf:\n - If current value == target, return None\n - Return current node\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(logN)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def removeLeafNodes(self, root: Optional[TreeNode], target: int) -> Optional[TreeNode]:\n\n def dfs(node: TreeNode) -> TreeNode:\n if not node:\n return None\n\n if node.val == target and not node.left and not node.right:\n return None\n\n node.left = dfs(node.left)\n node.right = dfs(node.right)\n\n if node.val == target and not node.left and not node.right:\n return None\n\n return node\n\n return dfs(root)\n``` | 1 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
Python3 O(N) solution with DFS (99.65% Runtime) | delete-leaves-with-a-given-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nUtilize depth first search with leaf node check and check if it become leaf node \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- You should consider:\n - If a node is leaf\n - If a node become leaf\n- You can easily solve the problem with depth first search with recursion\n - Define a base case (none check)\n - Check if current node is a leaf:\n - If current value == target, return None\n - Get left child node from recursion\n - Get right child node from recursion\n - Check if current node becomes a leaf:\n - If current value == target, return None\n - Return current node\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(logN)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def removeLeafNodes(self, root: Optional[TreeNode], target: int) -> Optional[TreeNode]:\n\n def dfs(node: TreeNode) -> TreeNode:\n if not node:\n return None\n\n if node.val == target and not node.left and not node.right:\n return None\n\n node.left = dfs(node.left)\n node.right = dfs(node.right)\n\n if node.val == target and not node.left and not node.right:\n return None\n\n return node\n\n return dfs(root)\n``` | 1 | Given two integer arrays `startTime` and `endTime` and given an integer `queryTime`.
The `ith` student started doing their homework at the time `startTime[i]` and finished it at time `endTime[i]`.
Return _the number of students_ doing their homework at time `queryTime`. More formally, return the number of students where `queryTime` lays in the interval `[startTime[i], endTime[i]]` inclusive.
**Example 1:**
**Input:** startTime = \[1,2,3\], endTime = \[3,2,7\], queryTime = 4
**Output:** 1
**Explanation:** We have 3 students where:
The first student started doing homework at time 1 and finished at time 3 and wasn't doing anything at time 4.
The second student started doing homework at time 2 and finished at time 2 and also wasn't doing anything at time 4.
The third student started doing homework at time 3 and finished at time 7 and was the only student doing homework at time 4.
**Example 2:**
**Input:** startTime = \[4\], endTime = \[4\], queryTime = 4
**Output:** 1
**Explanation:** The only student was doing their homework at the queryTime.
**Constraints:**
* `startTime.length == endTime.length`
* `1 <= startTime.length <= 100`
* `1 <= startTime[i] <= endTime[i] <= 1000`
* `1 <= queryTime <= 1000` | Use the DFS to reconstruct the tree such that no leaf node is equal to the target. If the leaf node is equal to the target, return an empty object instead. |
python, >90%, short (6 lines) and easy, explained | delete-leaves-with-a-given-value | 0 | 1 | \n\n```\nclass Solution:\n def removeLeafNodes(self, root: TreeNode, target: int) -> TreeNode:\n if root:\n root.left = self.removeLeafNodes(root.left, target)\n root.right = self.removeLeafNodes(root.right, target) \n if root.val == target and not root.left and not root.right:\n root = None\n return root \n```\n\nOk, so the explanation. First let\'s see how many logical conditions we need to check?\n\n1. Is our root empty? if it is, there is not much we can do about it, we just return. Otherwise we try to traverse down the tree.\n2. Is it a leaf with root value == target? Then we prune it.\n\nSo somewhat surprisingly, we should be able to get it done with just two `if` statements! \n\nThe first `if` is really straightforward - return if root is empty:\n\n```\n if root:\n\t\t\t...\n return root \n```\n\nSo if root is not empty, we try to descend down first:\n\n```\n root.left = self.removeLeafNodes(root.left, target)\n root.right = self.removeLeafNodes(root.right, target) \n```\n\nand then we need to add our 2nd `if`:\n\n```\n if root.val == target and not root.left and not root.right:\n root = None\n```\n\nThat `if` checks if the val == target and if this node is a leaf (neither has root.left nor root.right) and prunes it if it\'s true.\n\nThat\'s it!\n\n\n\n\n | 36 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
python, >90%, short (6 lines) and easy, explained | delete-leaves-with-a-given-value | 0 | 1 | \n\n```\nclass Solution:\n def removeLeafNodes(self, root: TreeNode, target: int) -> TreeNode:\n if root:\n root.left = self.removeLeafNodes(root.left, target)\n root.right = self.removeLeafNodes(root.right, target) \n if root.val == target and not root.left and not root.right:\n root = None\n return root \n```\n\nOk, so the explanation. First let\'s see how many logical conditions we need to check?\n\n1. Is our root empty? if it is, there is not much we can do about it, we just return. Otherwise we try to traverse down the tree.\n2. Is it a leaf with root value == target? Then we prune it.\n\nSo somewhat surprisingly, we should be able to get it done with just two `if` statements! \n\nThe first `if` is really straightforward - return if root is empty:\n\n```\n if root:\n\t\t\t...\n return root \n```\n\nSo if root is not empty, we try to descend down first:\n\n```\n root.left = self.removeLeafNodes(root.left, target)\n root.right = self.removeLeafNodes(root.right, target) \n```\n\nand then we need to add our 2nd `if`:\n\n```\n if root.val == target and not root.left and not root.right:\n root = None\n```\n\nThat `if` checks if the val == target and if this node is a leaf (neither has root.left nor root.right) and prunes it if it\'s true.\n\nThat\'s it!\n\n\n\n\n | 36 | Given two integer arrays `startTime` and `endTime` and given an integer `queryTime`.
The `ith` student started doing their homework at the time `startTime[i]` and finished it at time `endTime[i]`.
Return _the number of students_ doing their homework at time `queryTime`. More formally, return the number of students where `queryTime` lays in the interval `[startTime[i], endTime[i]]` inclusive.
**Example 1:**
**Input:** startTime = \[1,2,3\], endTime = \[3,2,7\], queryTime = 4
**Output:** 1
**Explanation:** We have 3 students where:
The first student started doing homework at time 1 and finished at time 3 and wasn't doing anything at time 4.
The second student started doing homework at time 2 and finished at time 2 and also wasn't doing anything at time 4.
The third student started doing homework at time 3 and finished at time 7 and was the only student doing homework at time 4.
**Example 2:**
**Input:** startTime = \[4\], endTime = \[4\], queryTime = 4
**Output:** 1
**Explanation:** The only student was doing their homework at the queryTime.
**Constraints:**
* `startTime.length == endTime.length`
* `1 <= startTime.length <= 100`
* `1 <= startTime[i] <= endTime[i] <= 1000`
* `1 <= queryTime <= 1000` | Use the DFS to reconstruct the tree such that no leaf node is equal to the target. If the leaf node is equal to the target, return an empty object instead. |
2 solutions | DFS | Easy to understand | Faster | Python Solutions | delete-leaves-with-a-given-value | 0 | 1 | ```\n def dfs_second(self, root, target):\n def rec(node):\n if node:\n left = rec(node.left)\n right = rec(node.right)\n if not left and not right and node.val == target:\n return None\n node.left = left\n node.right = right\n return node\n return None\n return rec(root)\n \n \n def dfs_first(self, root, target):\n def rec(node, target):\n if node:\n left_leaf, match_left = rec(node.left, target)\n right_leaf, match_right = rec(node.right, target)\n if left_leaf and match_left: node.left = None\n if right_leaf and match_right: node.right = None\n return left_leaf and right_leaf and match_left and match_right, node.val == target\n return True, True\n\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38\n\n | 9 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
2 solutions | DFS | Easy to understand | Faster | Python Solutions | delete-leaves-with-a-given-value | 0 | 1 | ```\n def dfs_second(self, root, target):\n def rec(node):\n if node:\n left = rec(node.left)\n right = rec(node.right)\n if not left and not right and node.val == target:\n return None\n node.left = left\n node.right = right\n return node\n return None\n return rec(root)\n \n \n def dfs_first(self, root, target):\n def rec(node, target):\n if node:\n left_leaf, match_left = rec(node.left, target)\n right_leaf, match_right = rec(node.right, target)\n if left_leaf and match_left: node.left = None\n if right_leaf and match_right: node.right = None\n return left_leaf and right_leaf and match_left and match_right, node.val == target\n return True, True\n\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38\n\n | 9 | Given two integer arrays `startTime` and `endTime` and given an integer `queryTime`.
The `ith` student started doing their homework at the time `startTime[i]` and finished it at time `endTime[i]`.
Return _the number of students_ doing their homework at time `queryTime`. More formally, return the number of students where `queryTime` lays in the interval `[startTime[i], endTime[i]]` inclusive.
**Example 1:**
**Input:** startTime = \[1,2,3\], endTime = \[3,2,7\], queryTime = 4
**Output:** 1
**Explanation:** We have 3 students where:
The first student started doing homework at time 1 and finished at time 3 and wasn't doing anything at time 4.
The second student started doing homework at time 2 and finished at time 2 and also wasn't doing anything at time 4.
The third student started doing homework at time 3 and finished at time 7 and was the only student doing homework at time 4.
**Example 2:**
**Input:** startTime = \[4\], endTime = \[4\], queryTime = 4
**Output:** 1
**Explanation:** The only student was doing their homework at the queryTime.
**Constraints:**
* `startTime.length == endTime.length`
* `1 <= startTime.length <= 100`
* `1 <= startTime[i] <= endTime[i] <= 1000`
* `1 <= queryTime <= 1000` | Use the DFS to reconstruct the tree such that no leaf node is equal to the target. If the leaf node is equal to the target, return an empty object instead. |
⏰3 Minutes To Realise \\\ Greedy Approach \\\ Beats 99% | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | # Make sure that the following works\n**Simple algorithm O(n) space, time.**\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n arr = [0] * (n + 1)\n for idx, cur_radius in enumerate(ranges):\n if cur_radius == 0:\n continue\n \n left_border_idx = max(0, idx - cur_radius)\n arr[left_border_idx] = max(arr[left_border_idx], idx + cur_radius)\n\n right_border_of_watered_points = 0\n ans, watered_on_cur_step = 0, 0\n\n for idx, right_border in enumerate(arr):\n if idx > watered_on_cur_step:\n if right_border_of_watered_points <= watered_on_cur_step:\n return -1\n ans += 1\n watered_on_cur_step = right_border_of_watered_points\n\n right_border_of_watered_points = max(right_border_of_watered_points, right_border)\n\n return ans + (watered_on_cur_step < n)\n\n```\n\n# Approach\n1. It\'s necessary to realise that we should water segment but not dots only, so the example\n> n = 2, arr = [1, 0, 0, 1]\n\nshould return -1\n\n2. Let\'s make an `arr = [0] * (n + 1)` to store there the most remote right spot in line which can be covered with current spot with one fountain.\nSo we begin and fill the array:\n```\narr = [0] * (n + 1)\nfor idx, cur_radius in enumerate(ranges):\n if cur_radius == 0:\n continue\n # To write to arr[i] most remote right spot\n # we should return on current step to the most\n # remote left spot and write to \'there idx + cur_radius\'\n left_border_idx = max(0, idx - cur_radius)\n arr[left_border_idx] = max(arr[left_border_idx], idx + cur_radius)\n```\n3. After that we just count taps. `i` is i-th step on cycle.\n - **IDEA 1**: We will maintain `right_border_of_watered_points` variable which indicates the most right remote spot which can be watered by all meeted fountains on $$\\{0, 1, \\dots, i - 1\\}$$ steps.\n - **IDEA2**: We will increment number of needed taps \n - former right border of group less than `i`. Because we include the whole segment [0, i-1] and according to **2.** i-1 was the most right remote spot for previous group.\n```\nfor idx, right_border in enumerate(arr):\n if idx > right_border_of_group:\n ans += 1\n right_border_of_group = right_border_of_watered_points\n\n right_border_of_watered_points = max(right_border_of_watered_points, right_border)\n```\n4. When should we return -1?\nWhen on steps $$\\{0, \\dots, i-1\\}$$ we didn\'t meet fountain that was cover `i-th` dot. So we should upgrade or piece of code that was written in **3.**!\n```\nfor idx, right_border in enumerate(arr):\n if idx > right_border_of_group:\n # We didn\'t meet on steps 0, ... i-1 tap\n # that it\'s radius + (it\'s index) > i - 1.\n if right_border_of_watered_points <= right_border_of_group:\n return -1\n ans += 1\n right_border_of_group = right_border_of_watered_points\n\n right_border_of_watered_points = max(right_border_of_watered_points, right_border)\n```\n\n5. The last step is not to miss last increment of `answer\'s` variable: So just add 1 if `right_border_of_group` < `n`.\n\n.\n.\n.\n## Upvote if you quickly understood :) | 6 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
⏰3 Minutes To Realise \\\ Greedy Approach \\\ Beats 99% | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | # Make sure that the following works\n**Simple algorithm O(n) space, time.**\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n arr = [0] * (n + 1)\n for idx, cur_radius in enumerate(ranges):\n if cur_radius == 0:\n continue\n \n left_border_idx = max(0, idx - cur_radius)\n arr[left_border_idx] = max(arr[left_border_idx], idx + cur_radius)\n\n right_border_of_watered_points = 0\n ans, watered_on_cur_step = 0, 0\n\n for idx, right_border in enumerate(arr):\n if idx > watered_on_cur_step:\n if right_border_of_watered_points <= watered_on_cur_step:\n return -1\n ans += 1\n watered_on_cur_step = right_border_of_watered_points\n\n right_border_of_watered_points = max(right_border_of_watered_points, right_border)\n\n return ans + (watered_on_cur_step < n)\n\n```\n\n# Approach\n1. It\'s necessary to realise that we should water segment but not dots only, so the example\n> n = 2, arr = [1, 0, 0, 1]\n\nshould return -1\n\n2. Let\'s make an `arr = [0] * (n + 1)` to store there the most remote right spot in line which can be covered with current spot with one fountain.\nSo we begin and fill the array:\n```\narr = [0] * (n + 1)\nfor idx, cur_radius in enumerate(ranges):\n if cur_radius == 0:\n continue\n # To write to arr[i] most remote right spot\n # we should return on current step to the most\n # remote left spot and write to \'there idx + cur_radius\'\n left_border_idx = max(0, idx - cur_radius)\n arr[left_border_idx] = max(arr[left_border_idx], idx + cur_radius)\n```\n3. After that we just count taps. `i` is i-th step on cycle.\n - **IDEA 1**: We will maintain `right_border_of_watered_points` variable which indicates the most right remote spot which can be watered by all meeted fountains on $$\\{0, 1, \\dots, i - 1\\}$$ steps.\n - **IDEA2**: We will increment number of needed taps \n - former right border of group less than `i`. Because we include the whole segment [0, i-1] and according to **2.** i-1 was the most right remote spot for previous group.\n```\nfor idx, right_border in enumerate(arr):\n if idx > right_border_of_group:\n ans += 1\n right_border_of_group = right_border_of_watered_points\n\n right_border_of_watered_points = max(right_border_of_watered_points, right_border)\n```\n4. When should we return -1?\nWhen on steps $$\\{0, \\dots, i-1\\}$$ we didn\'t meet fountain that was cover `i-th` dot. So we should upgrade or piece of code that was written in **3.**!\n```\nfor idx, right_border in enumerate(arr):\n if idx > right_border_of_group:\n # We didn\'t meet on steps 0, ... i-1 tap\n # that it\'s radius + (it\'s index) > i - 1.\n if right_border_of_watered_points <= right_border_of_group:\n return -1\n ans += 1\n right_border_of_group = right_border_of_watered_points\n\n right_border_of_watered_points = max(right_border_of_watered_points, right_border)\n```\n\n5. The last step is not to miss last increment of `answer\'s` variable: So just add 1 if `right_border_of_group` < `n`.\n\n.\n.\n.\n## Upvote if you quickly understood :) | 6 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
[Python3][Stack] Easy Stack Solution beats 94% runtime. | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty stack called `range_stack` to keep track of the ranges being used.\n2. Initialize a variable `covered` to keep track of the total coverage achieved.\n3. Iterate through the given ranges. For each range, check if the current range can be extended to cover the garden.\n - If the current range overlaps with the last range in the `range_stack`, discard the range(s) from the `range_stack` that are no longer needed to extend the coverage.\n - If the current range does not overlap with the last range in the `range_stack`, add it to the `range_stack` and update the coverage.\n - If the total coverage becomes equal to or greater than `n`, return the number of taps used.\n4. If the entire garden is not covered after processing all ranges, return -1.\n.\n# Complexity\n- Time complexity:O(n)\n- The time complexity of this code depends on the number of ranges and the operations performed within the loops. The inner while loop that pops ranges from the `range_stack` runs in linear time O(m), where m is the number of taps in the `range_stack`. Since each tap can be added or removed at most once, the overall time complexity of the algorithm is O(n), where n is the number of ranges.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n- The space complexity is determined by the `range_stack`, which can hold at most all the ranges. Therefore, the space complexity is O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n range_stack = []\n covered = 0\n res = len(ranges) + 1\n for idx, range_ in enumerate(ranges):\n if range_stack and idx+range_ < range_stack[-1][1]:\n continue\n while range_stack and range_stack[-1][0] >= idx - range_:\n popped_range = range_stack.pop()\n covered -= popped_range[1] - popped_range[0]\n if not range_stack or range_stack[-1][1] < idx+range_:\n if not range_stack:\n left_point = max(idx-range_, 0)\n else:\n left_point = max([idx-range_, 0, range_stack[-1][1]])\n new_coverage = min(idx+range_, n)-left_point\n range_stack.append([left_point, min(idx+range_, n)])\n covered += new_coverage\n if covered >= n:\n res = min(res, len(range_stack)) \n return -1 if res == len(ranges) + 1 else res\n \n``` | 3 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
[Python3][Stack] Easy Stack Solution beats 94% runtime. | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty stack called `range_stack` to keep track of the ranges being used.\n2. Initialize a variable `covered` to keep track of the total coverage achieved.\n3. Iterate through the given ranges. For each range, check if the current range can be extended to cover the garden.\n - If the current range overlaps with the last range in the `range_stack`, discard the range(s) from the `range_stack` that are no longer needed to extend the coverage.\n - If the current range does not overlap with the last range in the `range_stack`, add it to the `range_stack` and update the coverage.\n - If the total coverage becomes equal to or greater than `n`, return the number of taps used.\n4. If the entire garden is not covered after processing all ranges, return -1.\n.\n# Complexity\n- Time complexity:O(n)\n- The time complexity of this code depends on the number of ranges and the operations performed within the loops. The inner while loop that pops ranges from the `range_stack` runs in linear time O(m), where m is the number of taps in the `range_stack`. Since each tap can be added or removed at most once, the overall time complexity of the algorithm is O(n), where n is the number of ranges.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n- The space complexity is determined by the `range_stack`, which can hold at most all the ranges. Therefore, the space complexity is O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n range_stack = []\n covered = 0\n res = len(ranges) + 1\n for idx, range_ in enumerate(ranges):\n if range_stack and idx+range_ < range_stack[-1][1]:\n continue\n while range_stack and range_stack[-1][0] >= idx - range_:\n popped_range = range_stack.pop()\n covered -= popped_range[1] - popped_range[0]\n if not range_stack or range_stack[-1][1] < idx+range_:\n if not range_stack:\n left_point = max(idx-range_, 0)\n else:\n left_point = max([idx-range_, 0, range_stack[-1][1]])\n new_coverage = min(idx+range_, n)-left_point\n range_stack.append([left_point, min(idx+range_, n)])\n covered += new_coverage\n if covered >= n:\n res = min(res, len(range_stack)) \n return -1 if res == len(ranges) + 1 else res\n \n``` | 3 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
Python3 👍||⚡95% faster beats, not dp 🔥|| clean solution || simple explain || | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | \n\n# Complexity\n- Time complexity: O (*N logN*)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O (*N*)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n ranges = sorted([(max(a-b,0),a+b) for a,b in enumerate(ranges) if b != 0]) # [(0, 3), (0, 5), (2, 11), (3, 13), (5,12)....]\n if not ranges or ranges[0][0]:\n return -1\n start,end = ranges[0]\n ct = 1\n cur_end = end\n for s,e in ranges:\n if s == start: # (start,end) (0,1) => (0,5)\n end = e\n elif s <= end: # (start,end)=(0,5) \n if e > cur_end: # (2,11) => (3,13) but not (3,13) =X=> (5,12)\n cur_end,cur_start = e, s \n else:\n if cur_end < s: # (cur_start,cur_end)=(3,13) but next (14,any)\n return -1\n else:\n start,end = cur_start, cur_end # change and count\n ct += 1\n if e > end:\n cur_end,cur_start = e, s\n if end >= n or cur_end>=n:\n return ct + (cur_end>=n)\n return -1\n``` | 2 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python3 👍||⚡95% faster beats, not dp 🔥|| clean solution || simple explain || | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | \n\n# Complexity\n- Time complexity: O (*N logN*)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O (*N*)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n ranges = sorted([(max(a-b,0),a+b) for a,b in enumerate(ranges) if b != 0]) # [(0, 3), (0, 5), (2, 11), (3, 13), (5,12)....]\n if not ranges or ranges[0][0]:\n return -1\n start,end = ranges[0]\n ct = 1\n cur_end = end\n for s,e in ranges:\n if s == start: # (start,end) (0,1) => (0,5)\n end = e\n elif s <= end: # (start,end)=(0,5) \n if e > cur_end: # (2,11) => (3,13) but not (3,13) =X=> (5,12)\n cur_end,cur_start = e, s \n else:\n if cur_end < s: # (cur_start,cur_end)=(3,13) but next (14,any)\n return -1\n else:\n start,end = cur_start, cur_end # change and count\n ct += 1\n if e > end:\n cur_end,cur_start = e, s\n if end >= n or cur_end>=n:\n return ct + (cur_end>=n)\n return -1\n``` | 2 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
Python3 Solution | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | \n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp=[0]+[n+2]*n\n for i,x in enumerate(ranges):\n for j in range(max(i-x+1,0),min(i+x,n)+1):\n dp[j]=min(dp[j],dp[max(0,i-x)]+1)\n\n return dp[n] if dp[n]<n+2 else -1 \n``` | 2 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python3 Solution | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | \n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp=[0]+[n+2]*n\n for i,x in enumerate(ranges):\n for j in range(max(i-x+1,0),min(i+x,n)+1):\n dp[j]=min(dp[j],dp[max(0,i-x)]+1)\n\n return dp[n] if dp[n]<n+2 else -1 \n``` | 2 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
Python Top Down and Bottom Up Solution | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | # Intuition\nThe problem can be solved using a dynamic programming approach with memoization. The idea is to work backwards from the end of the garden and determine the minimum number of taps needed to water each position, while considering the coverage of each tap.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$ \n\n# Code \n# Top Down\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n memo = {}\n\n def recur(ind):\n if ind <=0:return 0\n if ind in memo:return memo[ind]\n \n count = float(\'inf\')\n for i in range(ind,-1,-1):\n if ranges[i] > 0 and ranges[i] + i >= ind:\n count = min(count, 1 + recur(i - ranges[i]))\n \n memo[ind] = count\n return memo[ind]\n \n ans = recur(n)\n return -1 if ans >= float(\'inf\') else ans\n \n```\n\n# Bottom Up\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [float(\'inf\')] * (n + 1)\n dp[0] = 0\n\n for i in range(n+1):\n tap_start = max(0, i - ranges[i])\n tap_end = min(n, i + ranges[i])\n for j in range(tap_start,tap_end + 1):\n dp[j] = min(dp[j], 1+dp[tap_start])\n \n if dp[n] == float(\'inf\'):\n return -1\n \n return dp[n]\n``` | 1 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python Top Down and Bottom Up Solution | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | # Intuition\nThe problem can be solved using a dynamic programming approach with memoization. The idea is to work backwards from the end of the garden and determine the minimum number of taps needed to water each position, while considering the coverage of each tap.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$ \n\n# Code \n# Top Down\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n memo = {}\n\n def recur(ind):\n if ind <=0:return 0\n if ind in memo:return memo[ind]\n \n count = float(\'inf\')\n for i in range(ind,-1,-1):\n if ranges[i] > 0 and ranges[i] + i >= ind:\n count = min(count, 1 + recur(i - ranges[i]))\n \n memo[ind] = count\n return memo[ind]\n \n ans = recur(n)\n return -1 if ans >= float(\'inf\') else ans\n \n```\n\n# Bottom Up\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [float(\'inf\')] * (n + 1)\n dp[0] = 0\n\n for i in range(n+1):\n tap_start = max(0, i - ranges[i])\n tap_end = min(n, i + ranges[i])\n for j in range(tap_start,tap_end + 1):\n dp[j] = min(dp[j], 1+dp[tap_start])\n \n if dp[n] == float(\'inf\'):\n return -1\n \n return dp[n]\n``` | 1 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
Greedy Approach | Python/ JS Solution | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we have a one-dimensional garden represented by a line starting from point 0 and ending at point n. There are taps placed along this line at various points, and each tap has a coverage range that can water a specific area around it.\n\nYour goal is to determine the minimum number of taps you need to open in order to water the entire garden. If it\'s impossible to water the whole garden, you should return -1.\n\n### Explanation\n\nThis problem is considered a variation of the `452. Minimum Number of Arrows to Burst Balloons`. However, for this problem, instead of balloons, we have intervals represented by taps and their coverage range. The goal is to find the minimum number of "arrows" denoted as taps to open to burst all the "balloons" denoted as covering the entire garden\n\nSince, we want to cover the entire garden using as few taps as possible. We can greedily iterate through the taps in a specific order, trying to extend the coverage as much as possible with each selected tap. \n\n\n- Initialize the following: \n\n 1) Intervals list to store the range of the intervals denoted as start, end\n \n 2) current interval to keep track of the index of the interval currently being considered\n \n 3) farthest reach to keep track of the farthest point we have currently covered\n \n 3) taps used to count the number of taps used thus far\n\n- First iterate over each taps coverage range and calculate the interval boundaries as we append it to intervals:\n\n 1) max(0, i - r), ensures that the left boundary of the interval does not go below 0\n \n 2) min(n, i + r), ensure that the right boundary does not go beyond `n`\n \n- After find the interval boundaries, we must sort it based on their starting points. If two intervals have the same starting point, sort them based on their ending points in descending order. Sorting is a crucial step because it allows us to process the intervals in a sequential order, which is essential for the greedy approach used in this solution.\n\n- The core part of this solution is to continue iterating until `farthest reach` reaches or exceeds the gardens\' endpoint denoted as `n` as this indicate the entire garden has been covered.\n\n 1) We need to also keep track of the farthest point that have been covered using the taps thus far\n \n - So we create a variable called farthest covered and set it to the farthest reach thus far\n \n 2) The inner while loop iterates through the intervals starting from current interval and looks for the interval that covers the current farthest covered. \n \n - Update farthest reach to be the maximum of its current value and the right boundary of the interval denoted as `intervals[current interval][1]` as this will extends the coverage to the maximum\n \n - After finding the interval that covers the current farthest_covered, increment current interval to move onto the next interval for the next iteration\n \n 3) After the inner loop, we check if farthest covered is equal to farthest reach as this represents that we couldnt find an interval to cover the next point. \n \n - In this case, there is a gap in the coverage so we return -1\n \n 4) Otherwise, if an interval was found to extend the coverage, we increment `taps_used` to keep track of the number of taps used \n \n \n 5) After we have covered the entire garden, we return the total number of taps used to achieve the full garden coverage \n \n\n\n# Code\n**Python**\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n intervals = []\n\n for i, r in enumerate(ranges): intervals.append((max(0, i - r), min(n , i + r)))\n\n intervals.sort(key=lambda x: (x[0], -x[1]))\n\n current_interval = 0\n farthest_reach = 0\n taps_used = 0\n\n while farthest_reach < n:\n farthest_covered = farthest_reach\n while current_interval < len(intervals) and intervals[current_interval][0] <= farthest_covered:\n farthest_reach = max(farthest_reach, intervals[current_interval][1])\n current_interval += 1\n \n if farthest_reach == farthest_covered: return -1\n\n taps_used += 1\n\n return taps_used\n```\n\n**JavaScript**\n```\n/**\n * @param {number} n\n * @param {number[]} ranges\n * @return {number}\n */\nvar minTaps = function(n, ranges) {\n const intervals = []\n\n for (let i = 0; i <= n; i++){\n const [start, end] = [Math.max(0, i - ranges[i]), Math.min(n, i + ranges[i])];\n intervals.push([start, end]);\n }\n\n intervals.sort((a, b) => a[0] - b[0] || b[1] - a[1]);\n\n let currentInterval = 0\n let farthestReach = 0\n let tapsUsed = 0\n\n\n while(farthestReach < n){\n const farthestCovered = farthestReach\n while(currentInterval < intervals.length && intervals[currentInterval][0] <= farthestCovered){\n farthestReach = Math.max(farthestReach, intervals[currentInterval][1])\n currentInterval += 1\n }\n\n if(farthestCovered === farthestReach) return - 1\n tapsUsed += 1\n }\n\n return tapsUsed\n};\n```\n### Time Complexity: `O(nlogn)`\n### Space Complexity: `O(n)`\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n | 1 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Greedy Approach | Python/ JS Solution | minimum-number-of-taps-to-open-to-water-a-garden | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we have a one-dimensional garden represented by a line starting from point 0 and ending at point n. There are taps placed along this line at various points, and each tap has a coverage range that can water a specific area around it.\n\nYour goal is to determine the minimum number of taps you need to open in order to water the entire garden. If it\'s impossible to water the whole garden, you should return -1.\n\n### Explanation\n\nThis problem is considered a variation of the `452. Minimum Number of Arrows to Burst Balloons`. However, for this problem, instead of balloons, we have intervals represented by taps and their coverage range. The goal is to find the minimum number of "arrows" denoted as taps to open to burst all the "balloons" denoted as covering the entire garden\n\nSince, we want to cover the entire garden using as few taps as possible. We can greedily iterate through the taps in a specific order, trying to extend the coverage as much as possible with each selected tap. \n\n\n- Initialize the following: \n\n 1) Intervals list to store the range of the intervals denoted as start, end\n \n 2) current interval to keep track of the index of the interval currently being considered\n \n 3) farthest reach to keep track of the farthest point we have currently covered\n \n 3) taps used to count the number of taps used thus far\n\n- First iterate over each taps coverage range and calculate the interval boundaries as we append it to intervals:\n\n 1) max(0, i - r), ensures that the left boundary of the interval does not go below 0\n \n 2) min(n, i + r), ensure that the right boundary does not go beyond `n`\n \n- After find the interval boundaries, we must sort it based on their starting points. If two intervals have the same starting point, sort them based on their ending points in descending order. Sorting is a crucial step because it allows us to process the intervals in a sequential order, which is essential for the greedy approach used in this solution.\n\n- The core part of this solution is to continue iterating until `farthest reach` reaches or exceeds the gardens\' endpoint denoted as `n` as this indicate the entire garden has been covered.\n\n 1) We need to also keep track of the farthest point that have been covered using the taps thus far\n \n - So we create a variable called farthest covered and set it to the farthest reach thus far\n \n 2) The inner while loop iterates through the intervals starting from current interval and looks for the interval that covers the current farthest covered. \n \n - Update farthest reach to be the maximum of its current value and the right boundary of the interval denoted as `intervals[current interval][1]` as this will extends the coverage to the maximum\n \n - After finding the interval that covers the current farthest_covered, increment current interval to move onto the next interval for the next iteration\n \n 3) After the inner loop, we check if farthest covered is equal to farthest reach as this represents that we couldnt find an interval to cover the next point. \n \n - In this case, there is a gap in the coverage so we return -1\n \n 4) Otherwise, if an interval was found to extend the coverage, we increment `taps_used` to keep track of the number of taps used \n \n \n 5) After we have covered the entire garden, we return the total number of taps used to achieve the full garden coverage \n \n\n\n# Code\n**Python**\n```\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n intervals = []\n\n for i, r in enumerate(ranges): intervals.append((max(0, i - r), min(n , i + r)))\n\n intervals.sort(key=lambda x: (x[0], -x[1]))\n\n current_interval = 0\n farthest_reach = 0\n taps_used = 0\n\n while farthest_reach < n:\n farthest_covered = farthest_reach\n while current_interval < len(intervals) and intervals[current_interval][0] <= farthest_covered:\n farthest_reach = max(farthest_reach, intervals[current_interval][1])\n current_interval += 1\n \n if farthest_reach == farthest_covered: return -1\n\n taps_used += 1\n\n return taps_used\n```\n\n**JavaScript**\n```\n/**\n * @param {number} n\n * @param {number[]} ranges\n * @return {number}\n */\nvar minTaps = function(n, ranges) {\n const intervals = []\n\n for (let i = 0; i <= n; i++){\n const [start, end] = [Math.max(0, i - ranges[i]), Math.min(n, i + ranges[i])];\n intervals.push([start, end]);\n }\n\n intervals.sort((a, b) => a[0] - b[0] || b[1] - a[1]);\n\n let currentInterval = 0\n let farthestReach = 0\n let tapsUsed = 0\n\n\n while(farthestReach < n){\n const farthestCovered = farthestReach\n while(currentInterval < intervals.length && intervals[currentInterval][0] <= farthestCovered){\n farthestReach = Math.max(farthestReach, intervals[currentInterval][1])\n currentInterval += 1\n }\n\n if(farthestCovered === farthestReach) return - 1\n tapsUsed += 1\n }\n\n return tapsUsed\n};\n```\n### Time Complexity: `O(nlogn)`\n### Space Complexity: `O(n)`\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n | 1 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
✅ 99.5% Greedy with Dynamic + DP | minimum-number-of-taps-to-open-to-water-a-garden | 1 | 1 | # Interview Guide - Minimum Number of Taps to Open to Water a Garden\n\n## Problem Understanding\n\n### Description\nAt its core, this problem is a fascinating blend of interval merging and greedy optimization. You are provided with a one-dimensional garden and the ability to water certain intervals of it by opening taps located at different points. The goal is to water the entire garden with the minimum number of taps opened.\n\n---\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n- Garden Length: $$ 1 \\leq n \\leq 10^4 $$\n- Number of Taps: $$ n + 1 $$\n- Watering Range: $$ 0 \\leq \\text{ranges}[i] \\leq 100 $$\n\n### 2. Unveil the Significance of Intervals\nThe problem can be visualized as merging intervals. The operation to open a tap can be thought of as covering an interval within the garden. The challenge is to cover the entire garden with the least number of intervals. This applies to both the greedy and dynamic programming approaches.\n\n### 3. Algorithmic Approaches\nThis problem can be tackled using two different approaches: the Greedy Approach and the Dynamic Programming (DP) Approach.\n\n#### Greedy Approach in Context\nIn the greedy approach, the algorithm makes the best local choice at each decision point with the aim of finding a global optimum. In this problem, each tap you decide to open becomes a commitment to water a specific range in the garden. The greedy strategy here involves always picking the tap that extends your reach as far as possible. This approach is optimized for speed, aiming to solve the problem in the least amount of time.\n\n#### Dynamic Programming in Context\nDynamic Programming, on the other hand, builds the solution step by step. It uses an array to keep track of the minimum number of taps needed to water the garden up to each point. The DP approach is generally more flexible and can handle more complicated scenarios at the cost of potentially slower runtime for larger problem sizes.\n\n### 4. Key Concepts in Each Approach\n\n#### The Magic of "Farthest Reach" (Greedy)\nIn the greedy approach, the concept of "farthest reach" is crucial. As you move from the first to the last tap, this variable adapts dynamically, reflecting the furthest point that can be watered by any tap that intersects with the currently watered range. This dynamic updating is vital for deciding whether or not a new tap needs to be opened.\n\n#### The Power of Incremental Build-up (DP)\nIn the DP approach, the array essentially serves as a memoization table. Each element in the DP array signifies the minimum number of taps required to water the garden up to that point. This array gets updated iteratively as we consider each tap, forming the basis for the final solution.\n\n### 5. Importance of Ordered Intervals (Greedy)\nFor the greedy algorithm, it\'s beneficial to consider the taps in an ordered sequence, sorted by their starting points. This ordering helps make the local choices more straightforward and effective, thereby aiding in the search for a global optimum.\n\n### 6. Explain Your Thought Process\nRegardless of the approach, clear thinking and explanation are crucial. For the greedy approach, maintaining and updating the variable `far_can_reach` is key. In the DP approach, the DP array holds the minimum number of taps needed to water each point, and it\'s updated as we go through each tap.\n\n---\n\n# Live Coding & More\nhttps://youtu.be/UQ__VyptWPQ?si=NrC2tEc2X24SSCpZ\n\n---\n\n# Approach: Greedy Algorithm with Dynamic "Farthest Reach" Adjustment\n\n## Intuition and Logic Behind the Solution\nThe problem challenges us to water an entire one-dimensional garden using the fewest number of taps. Each tap has a range that it can water. The crux of our solution is to always choose the tap that allows us to water the farthest point in the garden that hasn\'t been watered yet.\n\n## Why Greedy?\nThe greedy approach works well in this situation because it aims to make the best local choices in the hope of reaching an optimal global solution. In this context, each local choice is to open a tap that extends our watering range as far as possible. By doing so, we minimize the total number of taps that need to be opened.\n\n## Step-by-step Explanation\n- **Initialization**: We initialize `end = 0`, `far_can_reach = 0`, and `cnt = 0`. Here, `end` represents the last point that can be watered by the previously considered taps, `far_can_reach` is the farthest point that can be watered by any tap considered so far, and `cnt` keeps track of the number of taps opened.\n \n- **Prepare the Ranges**: We prepare an array `arr` where the index represents the starting point, and the value at that index represents the farthest point that can be watered from that starting point.\n \n- **Main Algorithm**: We iterate through the array `arr`. If the current index `i` is greater than `end`, we update `end` to `far_can_reach` and increment `cnt` by 1. This is because we need to open a new tap to extend our reach.\n \n- **Check for Gaps**: If at any point we find that we can\'t extend our reach (`far_can_reach <= end`), we return -1.\n \n- **Count Taps**: `cnt` keeps track of the minimum number of taps we need to open.\n\n## Wrap-up\nThe function returns the minimum number of taps needed to water the entire garden. If it\'s not possible to water the whole garden, the function returns -1.\n\n## Complexity Analysis\n- **Time Complexity**: The algorithm runs in $$O(n)$$ time because it only needs to traverse the array `arr` once.\n \n- **Space Complexity**: The space complexity is $$O(n)$$ due to the additional array `arr`.\n\n---\n\n# Approach: Dynamic Programming with Local Optimization\n\n## Intuition and Logic Behind the Solution\nThe problem asks us to water the entire garden by opening the minimum number of taps. Unlike the greedy approach, which focuses on extending the range to be watered as far as possible, the dynamic programming approach calculates the minimum number of taps needed to water each point in the garden.\n\n## Why Dynamic Programming?\nDynamic programming (DP) is effective here because it allows us to build up a solution incrementally, using previously calculated results to inform future calculations. Each element in the DP array represents the minimum number of taps needed to water up to that point, which we update as we consider each tap in the garden. The DP approach is particularly useful when we need to make decisions that depend on previous choices, as is the case here.\n\n## Step-by-step Explanation\n- **Initialization**: Initialize an array `dp` of size `n+1` with `float(\'inf\')`, except for `dp[0]`, which is set to 0. This array will store the minimum number of taps needed to water up to each point.\n- **Iterate through Ranges**: Loop through the array `ranges`, which contains the range each tap can cover.\n - **Calculate Start and End**: For each tap at index `i`, calculate the start and end of the interval it can water.\n - **Update DP Array**: For each point `j` in the interval, update `dp[j]` to be the minimum of its current value and $$dp[\\text{start}] + 1$$.\n \n- **Check Feasibility**: If `dp[-1]` remains `float(\'inf\')`, then the garden can\'t be fully watered, and the function returns -1.\n\n## Wrap-up\nThe function returns `dp[-1]`, which holds the minimum number of taps needed to water the entire garden, or -1 if it\'s not possible to water the whole garden.\n\n## Complexity Analysis\n- **Time Complexity**: $$O(n^2)$$ due to the nested loop structure. For each tap, we potentially update $$O(n)$$ elements in the DP array.\n- **Space Complexity**: $$O(n)$$ for storing the DP array.\n\nThis DP approach provides an exact solution but may be slower than the greedy approach for large problem sizes. However, it is conceptually straightforward and builds a solid foundation for understanding more complex DP problems.\n\n---\n\n# Performance\n\n| Language | Approach | Runtime (ms) | Memory (MB) |\n|------------|----------|--------------|-------------|\n| Rust | Greedy | 2 | 2.2 |\n| Java | Greedy | 4 | 43.9 |\n| Go | Greedy | 7 | 5.5 |\n| C++ | Greedy | 10 | 14.6 |\n| PHP | Greedy | 32 | 20.8 |\n| JavaScript | Greedy | 71 | 43.8 |\n| C# | Greedy | 97 | 42.2 |\n| Python3 | Greedy | 112 | 16.8 |\n| Python3 | DP | 416 | 16.6 |\n\n\n\n# Code Greedy\n``` Python []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n arr = [0] * (n + 1)\n for i, r in enumerate(ranges):\n if r == 0:\n continue\n left = max(0, i - r)\n arr[left] = max(arr[left], i + r)\n\n end, far_can_reach, cnt = 0, 0, 0\n \n for i, reach in enumerate(arr):\n if i > end:\n if far_can_reach <= end:\n return -1\n end, cnt = far_can_reach, cnt + 1\n far_can_reach = max(far_can_reach, reach)\n\n return cnt + (end < n)\n\n```\n``` C++ []\nclass Solution {\npublic:\n int minTaps(int n, vector<int>& ranges) {\n vector<int> arr(n + 1, 0);\n for(int i = 0; i < ranges.size(); ++i) {\n if(ranges[i] == 0) continue;\n int left = max(0, i - ranges[i]);\n arr[left] = max(arr[left], i + ranges[i]);\n }\n \n int end = 0, far_can_reach = 0, cnt = 0;\n for(int i = 0; i <= n; ++i) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n ++cnt;\n }\n far_can_reach = max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n);\n }\n};\n```\n``` Rust []\nimpl Solution {\n pub fn min_taps(n: i32, ranges: Vec<i32>) -> i32 {\n let mut arr = vec![0; (n + 1) as usize];\n \n for i in 0..ranges.len() {\n if ranges[i] == 0 { continue; }\n let left = std::cmp::max(0, i as i32 - ranges[i]) as usize;\n arr[left] = std::cmp::max(arr[left], (i as i32 + ranges[i]) as usize);\n }\n \n let (mut end, mut far_can_reach, mut cnt) = (0, 0, 0);\n for i in 0..=n as usize {\n if i > end {\n if far_can_reach <= end { return -1; }\n end = far_can_reach;\n cnt += 1;\n }\n far_can_reach = std::cmp::max(far_can_reach, arr[i]);\n }\n \n cnt + if end < n as usize { 1 } else { 0 }\n }\n}\n```\n``` Go []\nfunc minTaps(n int, ranges []int) int {\n arr := make([]int, n+1)\n \n for i, r := range ranges {\n if r == 0 {\n continue\n }\n left := max(0, i - r)\n arr[left] = max(arr[left], i + r)\n }\n \n end, far_can_reach, cnt := 0, 0, 0\n for i := 0; i <= n; i++ {\n if i > end {\n if far_can_reach <= end {\n return -1\n }\n end = far_can_reach\n cnt++\n }\n far_can_reach = max(far_can_reach, arr[i])\n }\n \n if end < n {\n cnt++\n }\n return cnt\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` Java []\npublic class Solution {\n public int minTaps(int n, int[] ranges) {\n int[] arr = new int[n + 1];\n Arrays.fill(arr, 0);\n \n for(int i = 0; i < ranges.length; i++) {\n if(ranges[i] == 0) continue;\n int left = Math.max(0, i - ranges[i]);\n arr[left] = Math.max(arr[left], i + ranges[i]);\n }\n \n int end = 0, far_can_reach = 0, cnt = 0;\n for(int i = 0; i <= n; i++) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n cnt++;\n }\n far_can_reach = Math.max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n ? 1 : 0);\n }\n}\n```\n``` C# []\npublic class Solution {\n public int MinTaps(int n, int[] ranges) {\n int[] arr = new int[n + 1];\n Array.Fill(arr, 0);\n \n for(int i = 0; i < ranges.Length; i++) {\n if(ranges[i] == 0) continue;\n int left = Math.Max(0, i - ranges[i]);\n arr[left] = Math.Max(arr[left], i + ranges[i]);\n }\n \n int end = 0, far_can_reach = 0, cnt = 0;\n for(int i = 0; i <= n; i++) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n cnt++;\n }\n far_can_reach = Math.Max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n ? 1 : 0);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number[]} ranges\n * @return {number}\n */\nvar minTaps = function(n, ranges) {\n const arr = new Array(n + 1).fill(0);\n \n for(let i = 0; i < ranges.length; i++) {\n if(ranges[i] === 0) continue;\n const left = Math.max(0, i - ranges[i]);\n arr[left] = Math.max(arr[left], i + ranges[i]);\n }\n \n let end = 0, far_can_reach = 0, cnt = 0;\n for(let i = 0; i <= n; i++) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n cnt++;\n }\n far_can_reach = Math.max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n ? 1 : 0);\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @param Integer[] $ranges\n * @return Integer\n */\n function minTaps($n, $ranges) {\n $arr = array_fill(0, $n + 1, 0);\n \n foreach($ranges as $i => $r) {\n if($r === 0) continue;\n $left = max(0, $i - $r);\n $arr[$left] = max($arr[$left], $i + $r);\n }\n \n $end = 0; $far_can_reach = 0; $cnt = 0;\n for($i = 0; $i <= $n; $i++) {\n if($i > $end) {\n if($far_can_reach <= $end) return -1;\n $end = $far_can_reach;\n $cnt++;\n }\n $far_can_reach = max($far_can_reach, $arr[$i]);\n }\n \n return $cnt + ($end < $n ? 1 : 0);\n }\n}\n```\n\n# Code DP \n``` Python []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [float(\'inf\')] * (n + 1)\n dp[0] = 0\n \n for i, r in enumerate(ranges):\n start, end = max(0, i - r), min(n, i + r)\n for j in range(start + 1, end + 1):\n dp[j] = min(dp[j], dp[start] + 1)\n \n return dp[-1] if dp[-1] != float(\'inf\') else -1\n```\n\nEvery problem presents a new challenge and an opportunity to learn. Whether you\'re a beginner or an expert, each problem has something new to offer. So dive in, explore, and share your insights. Happy Coding! \uD83D\uDE80\uD83D\uDCA1\uD83C\uDF1F | 84 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
✅ 99.5% Greedy with Dynamic + DP | minimum-number-of-taps-to-open-to-water-a-garden | 1 | 1 | # Interview Guide - Minimum Number of Taps to Open to Water a Garden\n\n## Problem Understanding\n\n### Description\nAt its core, this problem is a fascinating blend of interval merging and greedy optimization. You are provided with a one-dimensional garden and the ability to water certain intervals of it by opening taps located at different points. The goal is to water the entire garden with the minimum number of taps opened.\n\n---\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n- Garden Length: $$ 1 \\leq n \\leq 10^4 $$\n- Number of Taps: $$ n + 1 $$\n- Watering Range: $$ 0 \\leq \\text{ranges}[i] \\leq 100 $$\n\n### 2. Unveil the Significance of Intervals\nThe problem can be visualized as merging intervals. The operation to open a tap can be thought of as covering an interval within the garden. The challenge is to cover the entire garden with the least number of intervals. This applies to both the greedy and dynamic programming approaches.\n\n### 3. Algorithmic Approaches\nThis problem can be tackled using two different approaches: the Greedy Approach and the Dynamic Programming (DP) Approach.\n\n#### Greedy Approach in Context\nIn the greedy approach, the algorithm makes the best local choice at each decision point with the aim of finding a global optimum. In this problem, each tap you decide to open becomes a commitment to water a specific range in the garden. The greedy strategy here involves always picking the tap that extends your reach as far as possible. This approach is optimized for speed, aiming to solve the problem in the least amount of time.\n\n#### Dynamic Programming in Context\nDynamic Programming, on the other hand, builds the solution step by step. It uses an array to keep track of the minimum number of taps needed to water the garden up to each point. The DP approach is generally more flexible and can handle more complicated scenarios at the cost of potentially slower runtime for larger problem sizes.\n\n### 4. Key Concepts in Each Approach\n\n#### The Magic of "Farthest Reach" (Greedy)\nIn the greedy approach, the concept of "farthest reach" is crucial. As you move from the first to the last tap, this variable adapts dynamically, reflecting the furthest point that can be watered by any tap that intersects with the currently watered range. This dynamic updating is vital for deciding whether or not a new tap needs to be opened.\n\n#### The Power of Incremental Build-up (DP)\nIn the DP approach, the array essentially serves as a memoization table. Each element in the DP array signifies the minimum number of taps required to water the garden up to that point. This array gets updated iteratively as we consider each tap, forming the basis for the final solution.\n\n### 5. Importance of Ordered Intervals (Greedy)\nFor the greedy algorithm, it\'s beneficial to consider the taps in an ordered sequence, sorted by their starting points. This ordering helps make the local choices more straightforward and effective, thereby aiding in the search for a global optimum.\n\n### 6. Explain Your Thought Process\nRegardless of the approach, clear thinking and explanation are crucial. For the greedy approach, maintaining and updating the variable `far_can_reach` is key. In the DP approach, the DP array holds the minimum number of taps needed to water each point, and it\'s updated as we go through each tap.\n\n---\n\n# Live Coding & More\nhttps://youtu.be/UQ__VyptWPQ?si=NrC2tEc2X24SSCpZ\n\n---\n\n# Approach: Greedy Algorithm with Dynamic "Farthest Reach" Adjustment\n\n## Intuition and Logic Behind the Solution\nThe problem challenges us to water an entire one-dimensional garden using the fewest number of taps. Each tap has a range that it can water. The crux of our solution is to always choose the tap that allows us to water the farthest point in the garden that hasn\'t been watered yet.\n\n## Why Greedy?\nThe greedy approach works well in this situation because it aims to make the best local choices in the hope of reaching an optimal global solution. In this context, each local choice is to open a tap that extends our watering range as far as possible. By doing so, we minimize the total number of taps that need to be opened.\n\n## Step-by-step Explanation\n- **Initialization**: We initialize `end = 0`, `far_can_reach = 0`, and `cnt = 0`. Here, `end` represents the last point that can be watered by the previously considered taps, `far_can_reach` is the farthest point that can be watered by any tap considered so far, and `cnt` keeps track of the number of taps opened.\n \n- **Prepare the Ranges**: We prepare an array `arr` where the index represents the starting point, and the value at that index represents the farthest point that can be watered from that starting point.\n \n- **Main Algorithm**: We iterate through the array `arr`. If the current index `i` is greater than `end`, we update `end` to `far_can_reach` and increment `cnt` by 1. This is because we need to open a new tap to extend our reach.\n \n- **Check for Gaps**: If at any point we find that we can\'t extend our reach (`far_can_reach <= end`), we return -1.\n \n- **Count Taps**: `cnt` keeps track of the minimum number of taps we need to open.\n\n## Wrap-up\nThe function returns the minimum number of taps needed to water the entire garden. If it\'s not possible to water the whole garden, the function returns -1.\n\n## Complexity Analysis\n- **Time Complexity**: The algorithm runs in $$O(n)$$ time because it only needs to traverse the array `arr` once.\n \n- **Space Complexity**: The space complexity is $$O(n)$$ due to the additional array `arr`.\n\n---\n\n# Approach: Dynamic Programming with Local Optimization\n\n## Intuition and Logic Behind the Solution\nThe problem asks us to water the entire garden by opening the minimum number of taps. Unlike the greedy approach, which focuses on extending the range to be watered as far as possible, the dynamic programming approach calculates the minimum number of taps needed to water each point in the garden.\n\n## Why Dynamic Programming?\nDynamic programming (DP) is effective here because it allows us to build up a solution incrementally, using previously calculated results to inform future calculations. Each element in the DP array represents the minimum number of taps needed to water up to that point, which we update as we consider each tap in the garden. The DP approach is particularly useful when we need to make decisions that depend on previous choices, as is the case here.\n\n## Step-by-step Explanation\n- **Initialization**: Initialize an array `dp` of size `n+1` with `float(\'inf\')`, except for `dp[0]`, which is set to 0. This array will store the minimum number of taps needed to water up to each point.\n- **Iterate through Ranges**: Loop through the array `ranges`, which contains the range each tap can cover.\n - **Calculate Start and End**: For each tap at index `i`, calculate the start and end of the interval it can water.\n - **Update DP Array**: For each point `j` in the interval, update `dp[j]` to be the minimum of its current value and $$dp[\\text{start}] + 1$$.\n \n- **Check Feasibility**: If `dp[-1]` remains `float(\'inf\')`, then the garden can\'t be fully watered, and the function returns -1.\n\n## Wrap-up\nThe function returns `dp[-1]`, which holds the minimum number of taps needed to water the entire garden, or -1 if it\'s not possible to water the whole garden.\n\n## Complexity Analysis\n- **Time Complexity**: $$O(n^2)$$ due to the nested loop structure. For each tap, we potentially update $$O(n)$$ elements in the DP array.\n- **Space Complexity**: $$O(n)$$ for storing the DP array.\n\nThis DP approach provides an exact solution but may be slower than the greedy approach for large problem sizes. However, it is conceptually straightforward and builds a solid foundation for understanding more complex DP problems.\n\n---\n\n# Performance\n\n| Language | Approach | Runtime (ms) | Memory (MB) |\n|------------|----------|--------------|-------------|\n| Rust | Greedy | 2 | 2.2 |\n| Java | Greedy | 4 | 43.9 |\n| Go | Greedy | 7 | 5.5 |\n| C++ | Greedy | 10 | 14.6 |\n| PHP | Greedy | 32 | 20.8 |\n| JavaScript | Greedy | 71 | 43.8 |\n| C# | Greedy | 97 | 42.2 |\n| Python3 | Greedy | 112 | 16.8 |\n| Python3 | DP | 416 | 16.6 |\n\n\n\n# Code Greedy\n``` Python []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n arr = [0] * (n + 1)\n for i, r in enumerate(ranges):\n if r == 0:\n continue\n left = max(0, i - r)\n arr[left] = max(arr[left], i + r)\n\n end, far_can_reach, cnt = 0, 0, 0\n \n for i, reach in enumerate(arr):\n if i > end:\n if far_can_reach <= end:\n return -1\n end, cnt = far_can_reach, cnt + 1\n far_can_reach = max(far_can_reach, reach)\n\n return cnt + (end < n)\n\n```\n``` C++ []\nclass Solution {\npublic:\n int minTaps(int n, vector<int>& ranges) {\n vector<int> arr(n + 1, 0);\n for(int i = 0; i < ranges.size(); ++i) {\n if(ranges[i] == 0) continue;\n int left = max(0, i - ranges[i]);\n arr[left] = max(arr[left], i + ranges[i]);\n }\n \n int end = 0, far_can_reach = 0, cnt = 0;\n for(int i = 0; i <= n; ++i) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n ++cnt;\n }\n far_can_reach = max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n);\n }\n};\n```\n``` Rust []\nimpl Solution {\n pub fn min_taps(n: i32, ranges: Vec<i32>) -> i32 {\n let mut arr = vec![0; (n + 1) as usize];\n \n for i in 0..ranges.len() {\n if ranges[i] == 0 { continue; }\n let left = std::cmp::max(0, i as i32 - ranges[i]) as usize;\n arr[left] = std::cmp::max(arr[left], (i as i32 + ranges[i]) as usize);\n }\n \n let (mut end, mut far_can_reach, mut cnt) = (0, 0, 0);\n for i in 0..=n as usize {\n if i > end {\n if far_can_reach <= end { return -1; }\n end = far_can_reach;\n cnt += 1;\n }\n far_can_reach = std::cmp::max(far_can_reach, arr[i]);\n }\n \n cnt + if end < n as usize { 1 } else { 0 }\n }\n}\n```\n``` Go []\nfunc minTaps(n int, ranges []int) int {\n arr := make([]int, n+1)\n \n for i, r := range ranges {\n if r == 0 {\n continue\n }\n left := max(0, i - r)\n arr[left] = max(arr[left], i + r)\n }\n \n end, far_can_reach, cnt := 0, 0, 0\n for i := 0; i <= n; i++ {\n if i > end {\n if far_can_reach <= end {\n return -1\n }\n end = far_can_reach\n cnt++\n }\n far_can_reach = max(far_can_reach, arr[i])\n }\n \n if end < n {\n cnt++\n }\n return cnt\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` Java []\npublic class Solution {\n public int minTaps(int n, int[] ranges) {\n int[] arr = new int[n + 1];\n Arrays.fill(arr, 0);\n \n for(int i = 0; i < ranges.length; i++) {\n if(ranges[i] == 0) continue;\n int left = Math.max(0, i - ranges[i]);\n arr[left] = Math.max(arr[left], i + ranges[i]);\n }\n \n int end = 0, far_can_reach = 0, cnt = 0;\n for(int i = 0; i <= n; i++) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n cnt++;\n }\n far_can_reach = Math.max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n ? 1 : 0);\n }\n}\n```\n``` C# []\npublic class Solution {\n public int MinTaps(int n, int[] ranges) {\n int[] arr = new int[n + 1];\n Array.Fill(arr, 0);\n \n for(int i = 0; i < ranges.Length; i++) {\n if(ranges[i] == 0) continue;\n int left = Math.Max(0, i - ranges[i]);\n arr[left] = Math.Max(arr[left], i + ranges[i]);\n }\n \n int end = 0, far_can_reach = 0, cnt = 0;\n for(int i = 0; i <= n; i++) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n cnt++;\n }\n far_can_reach = Math.Max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n ? 1 : 0);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number[]} ranges\n * @return {number}\n */\nvar minTaps = function(n, ranges) {\n const arr = new Array(n + 1).fill(0);\n \n for(let i = 0; i < ranges.length; i++) {\n if(ranges[i] === 0) continue;\n const left = Math.max(0, i - ranges[i]);\n arr[left] = Math.max(arr[left], i + ranges[i]);\n }\n \n let end = 0, far_can_reach = 0, cnt = 0;\n for(let i = 0; i <= n; i++) {\n if(i > end) {\n if(far_can_reach <= end) return -1;\n end = far_can_reach;\n cnt++;\n }\n far_can_reach = Math.max(far_can_reach, arr[i]);\n }\n \n return cnt + (end < n ? 1 : 0);\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @param Integer[] $ranges\n * @return Integer\n */\n function minTaps($n, $ranges) {\n $arr = array_fill(0, $n + 1, 0);\n \n foreach($ranges as $i => $r) {\n if($r === 0) continue;\n $left = max(0, $i - $r);\n $arr[$left] = max($arr[$left], $i + $r);\n }\n \n $end = 0; $far_can_reach = 0; $cnt = 0;\n for($i = 0; $i <= $n; $i++) {\n if($i > $end) {\n if($far_can_reach <= $end) return -1;\n $end = $far_can_reach;\n $cnt++;\n }\n $far_can_reach = max($far_can_reach, $arr[$i]);\n }\n \n return $cnt + ($end < $n ? 1 : 0);\n }\n}\n```\n\n# Code DP \n``` Python []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [float(\'inf\')] * (n + 1)\n dp[0] = 0\n \n for i, r in enumerate(ranges):\n start, end = max(0, i - r), min(n, i + r)\n for j in range(start + 1, end + 1):\n dp[j] = min(dp[j], dp[start] + 1)\n \n return dp[-1] if dp[-1] != float(\'inf\') else -1\n```\n\nEvery problem presents a new challenge and an opportunity to learn. Whether you\'re a beginner or an expert, each problem has something new to offer. So dive in, explore, and share your insights. Happy Coding! \uD83D\uDE80\uD83D\uDCA1\uD83C\uDF1F | 84 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
✅Easy Solution✅Python/C#/C++/Java/C🔥Clean Code🔥 | minimum-number-of-taps-to-open-to-water-a-garden | 1 | 1 | # Problem\n***\nThis problem involves finding the minimum number of taps that need to be open to water the entire garden. The garden is represented as a one-dimensional axis from 0 to n, and each tap can water a specific range around its location. The goal is to determine the minimum number of taps you need to turn on to ensure that the entire garden is watered.\n***\n# Solution\n1. Initialize a list dp of size (n + 1) to store the minimum number of taps needed to water each position.\n\n2. Initialize dp[0] to 0, because no taps are needed to water the starting position.\n\n3. Iterate through each tap location using the enumerate function. For each tap:\n**a**. Calculate the leftmost and rightmost positions that can be watered by the current tap. These positions are given by max(0, i - tap_range) and min(n, i + tap_range) respectively, where i is the current tap\'s position.\n**b**. Iterate through the positions that can be watered by the current tap (from left to right). For each position j, update dp[j] to be the minimum of its current value and dp[left] + 1. This means that if you can reach the current position j from the left position of the current tap, you update the minimum number of taps required to reach position j.\n\n4. After iterating through all taps, the value of dp[n] will represent the minimum number of taps required to water the entire garden. If dp[n] is still the initial maximum value (indicating that the garden couldn\'t be watered), return -1. Otherwise, return the value of dp[n].\n\nThe dynamic programming approach ensures that each position in the garden is reached using the minimum number of taps. By updating the dp array as taps are considered, the algorithm efficiently calculates the minimum number of taps required to water the entire garden.\n\n**Overall, the provided solution is a well-implemented approach to solving the given problem efficiently.**\n\n\n\n\n```Python3 []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [sys.maxsize] * (n + 1)\n\n dp[0] = 0\n\n for i, tap_range in enumerate(ranges):\n left = max(0, i - tap_range)\n right = min(n, i + tap_range)\n\n for j in range(left, right + 1):\n dp[j] = min(dp[j], dp[left] + 1)\n\n return dp[n] if dp[n] < sys.maxsize else -1\n```\n```python []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [sys.maxsize] * (n + 1)\n\n dp[0] = 0\n\n for i, tap_range in enumerate(ranges):\n left = max(0, i - tap_range)\n right = min(n, i + tap_range)\n\n for j in range(left, right + 1):\n dp[j] = min(dp[j], dp[left] + 1)\n\n return dp[n] if dp[n] < sys.maxsize else -1\n```\n```C# []\npublic class Solution {\n public int MinTaps(int n, int[] ranges) {\n int[] dp = new int[n + 1];\n for (int i = 1; i <= n; i++) {\n dp[i] = n + 2; // Set to a value larger than n + 1 to handle the all-zero ranges case\n }\n\n dp[0] = 0;\n\n for (int i = 0; i <= n; i++) {\n int tapRange = ranges[i];\n int left = Math.Max(0, i - tapRange);\n int right = Math.Min(n, i + tapRange);\n\n for (int j = left; j <= right; j++) {\n dp[j] = Math.Min(dp[j], dp[left] + 1);\n }\n }\n\n return dp[n] <= n + 1 ? dp[n] : -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minTaps(int n, std::vector<int>& ranges) {\n std::vector<int> dp(n + 1, n + 2); // Set to a value larger than n + 1 to handle the all-zero ranges case\n dp[0] = 0;\n\n for (int i = 0; i <= n; i++) {\n int tapRange = ranges[i];\n int left = std::max(0, i - tapRange);\n int right = std::min(n, i + tapRange);\n\n for (int j = left; j <= right; j++) {\n dp[j] = std::min(dp[j], dp[left] + 1);\n }\n }\n\n return dp[n] <= n + 1 ? dp[n] : -1;\n }\n};\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int minTaps(int n, int[] ranges) {\n int[] dp = new int[n + 1];\n Arrays.fill(dp, n + 2); // Set to a value larger than n + 1 to handle the all-zero ranges case\n dp[0] = 0;\n\n for (int i = 0; i <= n; i++) {\n int tapRange = ranges[i];\n int left = Math.max(0, i - tapRange);\n int right = Math.min(n, i + tapRange);\n\n for (int j = left; j <= right; j++) {\n dp[j] = Math.min(dp[j], dp[left] + 1);\n }\n }\n\n return dp[n] <= n + 1 ? dp[n] : -1;\n }\n}\n``` | 13 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
✅Easy Solution✅Python/C#/C++/Java/C🔥Clean Code🔥 | minimum-number-of-taps-to-open-to-water-a-garden | 1 | 1 | # Problem\n***\nThis problem involves finding the minimum number of taps that need to be open to water the entire garden. The garden is represented as a one-dimensional axis from 0 to n, and each tap can water a specific range around its location. The goal is to determine the minimum number of taps you need to turn on to ensure that the entire garden is watered.\n***\n# Solution\n1. Initialize a list dp of size (n + 1) to store the minimum number of taps needed to water each position.\n\n2. Initialize dp[0] to 0, because no taps are needed to water the starting position.\n\n3. Iterate through each tap location using the enumerate function. For each tap:\n**a**. Calculate the leftmost and rightmost positions that can be watered by the current tap. These positions are given by max(0, i - tap_range) and min(n, i + tap_range) respectively, where i is the current tap\'s position.\n**b**. Iterate through the positions that can be watered by the current tap (from left to right). For each position j, update dp[j] to be the minimum of its current value and dp[left] + 1. This means that if you can reach the current position j from the left position of the current tap, you update the minimum number of taps required to reach position j.\n\n4. After iterating through all taps, the value of dp[n] will represent the minimum number of taps required to water the entire garden. If dp[n] is still the initial maximum value (indicating that the garden couldn\'t be watered), return -1. Otherwise, return the value of dp[n].\n\nThe dynamic programming approach ensures that each position in the garden is reached using the minimum number of taps. By updating the dp array as taps are considered, the algorithm efficiently calculates the minimum number of taps required to water the entire garden.\n\n**Overall, the provided solution is a well-implemented approach to solving the given problem efficiently.**\n\n\n\n\n```Python3 []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [sys.maxsize] * (n + 1)\n\n dp[0] = 0\n\n for i, tap_range in enumerate(ranges):\n left = max(0, i - tap_range)\n right = min(n, i + tap_range)\n\n for j in range(left, right + 1):\n dp[j] = min(dp[j], dp[left] + 1)\n\n return dp[n] if dp[n] < sys.maxsize else -1\n```\n```python []\nclass Solution:\n def minTaps(self, n: int, ranges: List[int]) -> int:\n dp = [sys.maxsize] * (n + 1)\n\n dp[0] = 0\n\n for i, tap_range in enumerate(ranges):\n left = max(0, i - tap_range)\n right = min(n, i + tap_range)\n\n for j in range(left, right + 1):\n dp[j] = min(dp[j], dp[left] + 1)\n\n return dp[n] if dp[n] < sys.maxsize else -1\n```\n```C# []\npublic class Solution {\n public int MinTaps(int n, int[] ranges) {\n int[] dp = new int[n + 1];\n for (int i = 1; i <= n; i++) {\n dp[i] = n + 2; // Set to a value larger than n + 1 to handle the all-zero ranges case\n }\n\n dp[0] = 0;\n\n for (int i = 0; i <= n; i++) {\n int tapRange = ranges[i];\n int left = Math.Max(0, i - tapRange);\n int right = Math.Min(n, i + tapRange);\n\n for (int j = left; j <= right; j++) {\n dp[j] = Math.Min(dp[j], dp[left] + 1);\n }\n }\n\n return dp[n] <= n + 1 ? dp[n] : -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minTaps(int n, std::vector<int>& ranges) {\n std::vector<int> dp(n + 1, n + 2); // Set to a value larger than n + 1 to handle the all-zero ranges case\n dp[0] = 0;\n\n for (int i = 0; i <= n; i++) {\n int tapRange = ranges[i];\n int left = std::max(0, i - tapRange);\n int right = std::min(n, i + tapRange);\n\n for (int j = left; j <= right; j++) {\n dp[j] = std::min(dp[j], dp[left] + 1);\n }\n }\n\n return dp[n] <= n + 1 ? dp[n] : -1;\n }\n};\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int minTaps(int n, int[] ranges) {\n int[] dp = new int[n + 1];\n Arrays.fill(dp, n + 2); // Set to a value larger than n + 1 to handle the all-zero ranges case\n dp[0] = 0;\n\n for (int i = 0; i <= n; i++) {\n int tapRange = ranges[i];\n int left = Math.max(0, i - tapRange);\n int right = Math.min(n, i + tapRange);\n\n for (int j = left; j <= right; j++) {\n dp[j] = Math.min(dp[j], dp[left] + 1);\n }\n }\n\n return dp[n] <= n + 1 ? dp[n] : -1;\n }\n}\n``` | 13 | Given a sentence `text` (A _sentence_ is a string of space-separated words) in the following format:
* First letter is in upper case.
* Each word in `text` are separated by a single space.
Your task is to rearrange the words in text such that all words are rearranged in an increasing order of their lengths. If two words have the same length, arrange them in their original order.
Return the new text following the format shown above.
**Example 1:**
**Input:** text = "Leetcode is cool "
**Output:** "Is cool leetcode "
**Explanation:** There are 3 words, "Leetcode " of length 8, "is " of length 2 and "cool " of length 4.
Output is ordered by length and the new first word starts with capital letter.
**Example 2:**
**Input:** text = "Keep calm and code on "
**Output:** "On and keep calm code "
**Explanation:** Output is ordered as follows:
"On " 2 letters.
"and " 3 letters.
"keep " 4 letters in case of tie order by position in original text.
"calm " 4 letters.
"code " 4 letters.
**Example 3:**
**Input:** text = "To be or not to be "
**Output:** "To be or to be not "
**Constraints:**
* `text` begins with a capital letter and then contains lowercase letters and single space between words.
* `1 <= text.length <= 10^5` | Create intervals of the area covered by each tap, sort intervals by the left end. We need to cover the interval [0, n]. we can start with the first interval and out of all intervals that intersect with it we choose the one that covers the farthest point to the right. What if there is a gap between intervals that is not covered ? we should stop and return -1 as there is some interval that cannot be covered. |
Simple Python Solution | sort-the-matrix-diagonally | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing Hashmap\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:94.27%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:86.07%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n d=defaultdict(list)\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n d[i-j].append(mat[i][j])\n for i in d.values():\n i.sort()\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n v=d[i-j].pop(0)\n mat[i][j]=v\n return mat\n``` | 2 | A **matrix diagonal** is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the **matrix diagonal** starting from `mat[2][0]`, where `mat` is a `6 x 3` matrix, includes cells `mat[2][0]`, `mat[3][1]`, and `mat[4][2]`.
Given an `m x n` matrix `mat` of integers, sort each **matrix diagonal** in ascending order and return _the resulting matrix_.
**Example 1:**
**Input:** mat = \[\[3,3,1,1\],\[2,2,1,2\],\[1,1,1,2\]\]
**Output:** \[\[1,1,1,1\],\[1,2,2,2\],\[1,2,3,3\]\]
**Example 2:**
**Input:** mat = \[\[11,25,66,1,69,7\],\[23,55,17,45,15,52\],\[75,31,36,44,58,8\],\[22,27,33,25,68,4\],\[84,28,14,11,5,50\]\]
**Output:** \[\[5,17,4,1,52,7\],\[11,11,25,45,8,69\],\[14,23,25,44,58,15\],\[22,27,31,36,50,66\],\[84,28,75,33,55,68\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `1 <= mat[i][j] <= 100` | The first move keeps the parity of the element as it is. The second move changes the parity of the element. Since the first move is free, if all the numbers have the same parity, the answer would be zero. Find the minimum cost to make all the numbers have the same parity. |
Simple Python Solution | sort-the-matrix-diagonally | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing Hashmap\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:94.27%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:86.07%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n d=defaultdict(list)\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n d[i-j].append(mat[i][j])\n for i in d.values():\n i.sort()\n for i in range(len(mat)):\n for j in range(len(mat[0])):\n v=d[i-j].pop(0)\n mat[i][j]=v\n return mat\n``` | 2 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
[Python 3] Intuitive solution (sort each diagonal) | sort-the-matrix-diagonally | 0 | 1 | ```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n m = len(mat)\n n = len(mat[0])\n \n if m == 1 or n == 1:\n return mat\n \n # each column\n for j in range(n):\n self.sort(mat, 0, j, m, n)\n \n # each row\n for i in range(m):\n self.sort(mat, i, 0, m, n)\n \n return mat\n \n \n def sort(self, mat, i, j, m, n):\n values = []\n \n # loop through diagonal\n while(i < m and j < n):\n values.append(mat[i][j])\n \n i += 1\n j += 1\n \n values.sort()\n \n # substract because i and j out of range\n i -= 1\n j -= 1\n\n # fill diagonal in reversed order\n while(values):\n mat[i][j] = values.pop()\n i -= 1\n j -= 1 \n``` | 1 | A **matrix diagonal** is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the **matrix diagonal** starting from `mat[2][0]`, where `mat` is a `6 x 3` matrix, includes cells `mat[2][0]`, `mat[3][1]`, and `mat[4][2]`.
Given an `m x n` matrix `mat` of integers, sort each **matrix diagonal** in ascending order and return _the resulting matrix_.
**Example 1:**
**Input:** mat = \[\[3,3,1,1\],\[2,2,1,2\],\[1,1,1,2\]\]
**Output:** \[\[1,1,1,1\],\[1,2,2,2\],\[1,2,3,3\]\]
**Example 2:**
**Input:** mat = \[\[11,25,66,1,69,7\],\[23,55,17,45,15,52\],\[75,31,36,44,58,8\],\[22,27,33,25,68,4\],\[84,28,14,11,5,50\]\]
**Output:** \[\[5,17,4,1,52,7\],\[11,11,25,45,8,69\],\[14,23,25,44,58,15\],\[22,27,31,36,50,66\],\[84,28,75,33,55,68\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `1 <= mat[i][j] <= 100` | The first move keeps the parity of the element as it is. The second move changes the parity of the element. Since the first move is free, if all the numbers have the same parity, the answer would be zero. Find the minimum cost to make all the numbers have the same parity. |
[Python 3] Intuitive solution (sort each diagonal) | sort-the-matrix-diagonally | 0 | 1 | ```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n m = len(mat)\n n = len(mat[0])\n \n if m == 1 or n == 1:\n return mat\n \n # each column\n for j in range(n):\n self.sort(mat, 0, j, m, n)\n \n # each row\n for i in range(m):\n self.sort(mat, i, 0, m, n)\n \n return mat\n \n \n def sort(self, mat, i, j, m, n):\n values = []\n \n # loop through diagonal\n while(i < m and j < n):\n values.append(mat[i][j])\n \n i += 1\n j += 1\n \n values.sort()\n \n # substract because i and j out of range\n i -= 1\n j -= 1\n\n # fill diagonal in reversed order\n while(values):\n mat[i][j] = values.pop()\n i -= 1\n j -= 1 \n``` | 1 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
python3 | easy-understanding | explained | sort | sort-the-matrix-diagonally | 0 | 1 | ```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n lst = []\n n, m = len(mat), len(mat[0])\n \n # leftmost column\n for i in range(n):\n lst.append([i, 0])\n \n # rightmost row\n for i in range(m):\n lst.append([0, i])\n \n lst.pop(0)\n \n for x, y in lst:\n arr = []\n i, j = x, y\n \n # getting the diagonal elements\n while i < n and j < m:\n arr.append(mat[i][j])\n i, j = i+1, j+1\n \n arr.sort() # sort the elements\n \n i, j = x, y\n # setting the element in sorted order\n while i < n and j < m:\n mat[i][j] = arr.pop(0)\n i, j = i+1, j+1\n \n return mat\n``` | 2 | A **matrix diagonal** is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the **matrix diagonal** starting from `mat[2][0]`, where `mat` is a `6 x 3` matrix, includes cells `mat[2][0]`, `mat[3][1]`, and `mat[4][2]`.
Given an `m x n` matrix `mat` of integers, sort each **matrix diagonal** in ascending order and return _the resulting matrix_.
**Example 1:**
**Input:** mat = \[\[3,3,1,1\],\[2,2,1,2\],\[1,1,1,2\]\]
**Output:** \[\[1,1,1,1\],\[1,2,2,2\],\[1,2,3,3\]\]
**Example 2:**
**Input:** mat = \[\[11,25,66,1,69,7\],\[23,55,17,45,15,52\],\[75,31,36,44,58,8\],\[22,27,33,25,68,4\],\[84,28,14,11,5,50\]\]
**Output:** \[\[5,17,4,1,52,7\],\[11,11,25,45,8,69\],\[14,23,25,44,58,15\],\[22,27,31,36,50,66\],\[84,28,75,33,55,68\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `1 <= mat[i][j] <= 100` | The first move keeps the parity of the element as it is. The second move changes the parity of the element. Since the first move is free, if all the numbers have the same parity, the answer would be zero. Find the minimum cost to make all the numbers have the same parity. |
python3 | easy-understanding | explained | sort | sort-the-matrix-diagonally | 0 | 1 | ```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n lst = []\n n, m = len(mat), len(mat[0])\n \n # leftmost column\n for i in range(n):\n lst.append([i, 0])\n \n # rightmost row\n for i in range(m):\n lst.append([0, i])\n \n lst.pop(0)\n \n for x, y in lst:\n arr = []\n i, j = x, y\n \n # getting the diagonal elements\n while i < n and j < m:\n arr.append(mat[i][j])\n i, j = i+1, j+1\n \n arr.sort() # sort the elements\n \n i, j = x, y\n # setting the element in sorted order\n while i < n and j < m:\n mat[i][j] = arr.pop(0)\n i, j = i+1, j+1\n \n return mat\n``` | 2 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Python sorting one diag at a time | O(min(M,N)) space | explained | sort-the-matrix-diagonally | 0 | 1 | zip takes two lists A and B and turns them into a 2d list\nA = [1,2,3]\nB = [0,0,0]\nzip(A,B) will be [ (1,0), (2,0), (3,0) ]\n\nfor m=2 and n = 3\nstarting points will be [ (0,1), (1,0), (0,1), (0,2) ] \nwe use this zip function to make a list having starting rows and columns of all diagonals\nwe get the rest of the diagonal by incrementing both current row and current column\n\n```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n r,c = len(mat), len(mat[0])\n \n for sr,sc in list(zip(range(r-1,-1,-1),[0 for _ in range(r)])) + list(zip([0 for _ in range(c-1)],range(1,c))): \n diag = []\n i,j = sr, sc\n while j<c and i<r:\n bruh.append(mat[i][j])\n i+=1\n j+=1\n diag.sort()\n i,j = sr, sc\n count = 0\n while j<c and i<r:\n mat[i][j] = diag[count]\n count+=1\n i+=1\n j+=1\n\n return mat\n``` | 2 | A **matrix diagonal** is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the **matrix diagonal** starting from `mat[2][0]`, where `mat` is a `6 x 3` matrix, includes cells `mat[2][0]`, `mat[3][1]`, and `mat[4][2]`.
Given an `m x n` matrix `mat` of integers, sort each **matrix diagonal** in ascending order and return _the resulting matrix_.
**Example 1:**
**Input:** mat = \[\[3,3,1,1\],\[2,2,1,2\],\[1,1,1,2\]\]
**Output:** \[\[1,1,1,1\],\[1,2,2,2\],\[1,2,3,3\]\]
**Example 2:**
**Input:** mat = \[\[11,25,66,1,69,7\],\[23,55,17,45,15,52\],\[75,31,36,44,58,8\],\[22,27,33,25,68,4\],\[84,28,14,11,5,50\]\]
**Output:** \[\[5,17,4,1,52,7\],\[11,11,25,45,8,69\],\[14,23,25,44,58,15\],\[22,27,31,36,50,66\],\[84,28,75,33,55,68\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `1 <= mat[i][j] <= 100` | The first move keeps the parity of the element as it is. The second move changes the parity of the element. Since the first move is free, if all the numbers have the same parity, the answer would be zero. Find the minimum cost to make all the numbers have the same parity. |
Python sorting one diag at a time | O(min(M,N)) space | explained | sort-the-matrix-diagonally | 0 | 1 | zip takes two lists A and B and turns them into a 2d list\nA = [1,2,3]\nB = [0,0,0]\nzip(A,B) will be [ (1,0), (2,0), (3,0) ]\n\nfor m=2 and n = 3\nstarting points will be [ (0,1), (1,0), (0,1), (0,2) ] \nwe use this zip function to make a list having starting rows and columns of all diagonals\nwe get the rest of the diagonal by incrementing both current row and current column\n\n```\nclass Solution:\n def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:\n r,c = len(mat), len(mat[0])\n \n for sr,sc in list(zip(range(r-1,-1,-1),[0 for _ in range(r)])) + list(zip([0 for _ in range(c-1)],range(1,c))): \n diag = []\n i,j = sr, sc\n while j<c and i<r:\n bruh.append(mat[i][j])\n i+=1\n j+=1\n diag.sort()\n i,j = sr, sc\n count = 0\n while j<c and i<r:\n mat[i][j] = diag[count]\n count+=1\n i+=1\n j+=1\n\n return mat\n``` | 2 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Concise | Simple | Fast | Python Solution | reverse-subarray-to-maximize-array-value | 0 | 1 | # Code\n```\nclass Solution:\n def maxValueAfterReverse(self, nums: List[int]) -> int:\n originalValue, sz = 0, len(nums)\n for idx in range(sz - 1):\n originalValue += abs(nums[idx] - nums[idx + 1])\n finalValue = originalValue\n for idx in range(1, sz - 1):\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx + 1]) + abs(nums[idx + 1] - nums[0]))\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx - 1]) + abs(nums[idx - 1] - nums[sz - 1]))\n minimum, maximum = inf, -inf\n for idx in range(sz - 1):\n tempMin, tempMax = min(nums[idx], nums[idx + 1]), max(nums[idx], nums[idx + 1])\n if minimum < tempMin: finalValue = max(finalValue, originalValue + (tempMin - minimum) * 2)\n if tempMax < maximum: finalValue = max(finalValue, originalValue + (maximum - tempMax) * 2)\n minimum = min(minimum, tempMax)\n maximum = max(maximum, tempMin)\n return finalValue\n``` | 0 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Concise | Simple | Fast | Python Solution | reverse-subarray-to-maximize-array-value | 0 | 1 | # Code\n```\nclass Solution:\n def maxValueAfterReverse(self, nums: List[int]) -> int:\n originalValue, sz = 0, len(nums)\n for idx in range(sz - 1):\n originalValue += abs(nums[idx] - nums[idx + 1])\n finalValue = originalValue\n for idx in range(1, sz - 1):\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx + 1]) + abs(nums[idx + 1] - nums[0]))\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx - 1]) + abs(nums[idx - 1] - nums[sz - 1]))\n minimum, maximum = inf, -inf\n for idx in range(sz - 1):\n tempMin, tempMax = min(nums[idx], nums[idx + 1]), max(nums[idx], nums[idx + 1])\n if minimum < tempMin: finalValue = max(finalValue, originalValue + (tempMin - minimum) * 2)\n if tempMax < maximum: finalValue = max(finalValue, originalValue + (maximum - tempMax) * 2)\n minimum = min(minimum, tempMax)\n maximum = max(maximum, tempMin)\n return finalValue\n``` | 0 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
Python Linear Time Solution | Faster than 60% | reverse-subarray-to-maximize-array-value | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIn this problem we can use a math tool ... to say that ```abs(a - b)``` is a range, where ```a``` and ```b``` are some values in the array that are next to each other ```[num[0], ..., a, b, ..., nums[n - 1]]```. If we follow this line of thought and consider bunch of cases we can observe the current outcome, the code below.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def maxValueAfterReverse(self, nums: List[int]) -> int:\n originalValue, sz = 0, len(nums)\n for idx in range(sz - 1):\n originalValue += abs(nums[idx] - nums[idx + 1])\n finalValue = originalValue\n for idx in range(1, sz - 1):\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx + 1]) + abs(nums[idx + 1] - nums[0]))\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx - 1]) + abs(nums[idx - 1] - nums[sz - 1]))\n minimum, maximum = inf, -inf\n for idx in range(sz - 1):\n tempMin, tempMax = min(nums[idx], nums[idx + 1]), max(nums[idx], nums[idx + 1])\n if minimum < tempMin:\n finalValue = max(finalValue, originalValue + (tempMin - minimum) * 2)\n if tempMax < maximum:\n finalValue = max(finalValue, originalValue + (maximum - tempMax) * 2)\n minimum = min(minimum, tempMax)\n maximum = max(maximum, tempMin)\n return finalValue\n``` | 0 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Python Linear Time Solution | Faster than 60% | reverse-subarray-to-maximize-array-value | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIn this problem we can use a math tool ... to say that ```abs(a - b)``` is a range, where ```a``` and ```b``` are some values in the array that are next to each other ```[num[0], ..., a, b, ..., nums[n - 1]]```. If we follow this line of thought and consider bunch of cases we can observe the current outcome, the code below.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def maxValueAfterReverse(self, nums: List[int]) -> int:\n originalValue, sz = 0, len(nums)\n for idx in range(sz - 1):\n originalValue += abs(nums[idx] - nums[idx + 1])\n finalValue = originalValue\n for idx in range(1, sz - 1):\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx + 1]) + abs(nums[idx + 1] - nums[0]))\n finalValue = max(finalValue, originalValue - abs(nums[idx] - nums[idx - 1]) + abs(nums[idx - 1] - nums[sz - 1]))\n minimum, maximum = inf, -inf\n for idx in range(sz - 1):\n tempMin, tempMax = min(nums[idx], nums[idx + 1]), max(nums[idx], nums[idx + 1])\n if minimum < tempMin:\n finalValue = max(finalValue, originalValue + (tempMin - minimum) * 2)\n if tempMax < maximum:\n finalValue = max(finalValue, originalValue + (maximum - tempMax) * 2)\n minimum = min(minimum, tempMax)\n maximum = max(maximum, tempMin)\n return finalValue\n``` | 0 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
Super Easy Python | O(nlogn) | Beats 97.96% submissions | rank-transform-of-an-array | 0 | 1 | Upvote if you find it helpful :-) \n# Intuition\n1. Sort the input array and store its index\n2. Map that index with the value of the input array\n3. Use hashmap for $$O(1)$$ access time\n\n# Approach\n1. Create hashmap\n2. Sort unique elements using sorted and set functions\n3. update the arr or create new list and map the elements using hashmap\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n store = {}\n sort_arr = sorted(set(arr))\n\n for i in range(len(sort_arr)):\n store[sort_arr[i]] = i+1\n\n \n for i in range(len(arr)):\n arr[i] = store[arr[i]]\n \n return arr\n\n```\n\n\n | 0 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
Python3 || Beats 84.44% | rank-transform-of-an-array | 0 | 1 | # Please upvote if you find the solution helpful.\n\n# Code\n```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n d = {}\n f_lst=[]\n arr1 = sorted(list(set(arr)))\n for i in range(len(arr1)):\n d[arr1[i]] = i+1\n for i in arr:\n f_lst.append(d[i])\n return f_lst\n \n``` | 3 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
Easy Python Solution| Beats 95% Run Time | rank-transform-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n rank = {}\n cnt = 1\n for i in sorted(list(set(arr))):\n rank[i] = cnt\n cnt += 1\n #print(rank)\n return [rank[i] for i in arr]\n``` | 3 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
Python Easy Solution || Sorting || Hashmap | rank-transform-of-an-array | 0 | 1 | # Complexity\n- Time complexity:\nO(nlogn) \nBecause of sorting\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n dic={}\n lis=list(set(arr))\n lis.sort()\n for i in range(len(lis)):\n dic[lis[i]]=i\n for i in range(len(arr)):\n arr[i]=(dic[arr[i]]+1)\n return arr \n``` | 2 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
Easiest solution you ever find.#python3 | rank-transform-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n list1=[]\n x=sorted(set(arr))\n dict1={}\n for i in range(len(x)):\n dict1[x[i]]=i+1\n for j in arr:\n y=dict1[j]\n list1.append(y)\n return list1\n #please do upvote it will help alot to gain my love in coding\n\n```\n# consider upvoting if found helpful\n | 4 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
Python Easy Solution | rank-transform-of-an-array | 0 | 1 | ```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n \n arrx = [i for i in set(arr)]\n arrx.sort()\n \n hp={}\n for i in range(len(arrx)):\n if arrx[i] in hp:\n continue\n else:\n hp[arrx[i]] = i+1 \n \n print(hp) \n for j in range(len(arr)):\n arr[j] = hp[arr[j]]\n \n return arr\n \n``` | 1 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
1331. Rank Transform of an Array | using python| beats 95% | rank-transform-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayRankTransform(self, arr: List[int]) -> List[int]:\n rank = {}\n cnt = 1\n for i in sorted(list(set(arr))):\n rank[i] = cnt\n cnt += 1\n return [rank[i] for i in arr]\n``` | 1 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
✅ Python || 2 Easy || One liner | remove-palindromic-subsequences | 0 | 1 | The input `s` meets the following requirements:\n>s[i] is either \'a\' or \'b\'.\n>1 <= s.length <= 1000\n\nSo if you take this as a hint, you can observe there are only two possible outputs:\n1. if `s` is pallindrome, return `1`\n2. else return `2`. \n\nIf the `s` is not pallindrome, it will always be reduced to empty string in 2 steps.\n>eg: s=\'ababaab\'\n>ababaab -> bbb -> \'\' or ababaab -> aba -> \'\'\n\nSo taking this observation into account, the main component of our solution is to determine if a given input is pallindrome or not.\n\n1. ## **Reverse String**\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n return 1 if s == s[::-1] else 2\n```\n\nAnother variation by [darkHarry](https://leetcode.com/darkHarry/):\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n return int(s==s[::-1]) or 2\n```\n\n**Time - O(n)**\n**Space - O(n)** - space for reverse string\n\n---\n\n2. ## **Two pointers**\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n def zip_iter():\n i,j,n=0,len(s)-1,len(s)//2\n while i<=n:\n yield (s[i], s[j])\n i+=1\n j-=1\n \n return 1 if all(x==y for x,y in zip_iter()) else 2\n```\n\nA one-liner variation by [borkooo](https://leetcode.com/borkooo/).\n\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n return 2 - all(s[i] == s[~i] for i in range(len(s) // 2))\n```\n\n**Time - O(n)**\n**Space - O(1)**\n\n---\n\n***Please upvote if you find it useful*** | 48 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
Easiest solution O(1) complexity in python | remove-palindromic-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n count=0\n if s==s[::-1]:\n count+=1\n else:\n count+=2\n return count\n\n\n\n\n \n``` | 2 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
1 Line Super simple: return 1 if s==s[::-1] else 2 | remove-palindromic-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\naaa...aaa is palindrome. So as bbbb...bbb.\nWe can disassemble every string s as this form.\nSo maximum return value is 2\nIf and only if s is palindrome, it returns 1\n\n# Code\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n return 1 if s==s[::-1] else 2\n``` | 1 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
1-liner Python easy to understand | remove-palindromic-subsequences | 0 | 1 | Pay attention to the constraints! It says that s[i] is either \'a\' or \'b\', so we can have at most two cases, \n\n1) If the string already is palindrome then the result is 1 \n\n2) The string is not a palindrome, which is we can think of as removing all letters \'a\' and \'b\', resulting in 2.\n\nI really lost real time trying to solve in \'the other way\' until I realize this!\n\nThe running time is O(n), as it takes n steps to reverse the string to compare with the original to check whether it is a palindrome or not.\n\nHave a good day! \n# Code\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n return 1 if s[::-1] == s else 2\n \n``` | 1 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
remove-palindromic-subsequences | remove-palindromic-subsequences | 0 | 1 | # Code\n```\nclass Solution:\n def removePalindromeSub(self, s: str) -> int:\n if s=="":\n return 0\n elif s==s[::-1]:\n return 1\n return 2\n\n \n``` | 1 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
Python Easy Solution || Sorting | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n rating=[]\n res=[]\n for restro in restaurants:\n if (restro[3]<=maxPrice) and (restro[4]<=maxDistance):\n if (veganFriendly):\n if restro[2]==1:\n rating.append([restro[1],restro[0]])\n else:\n rating.append([restro[1],restro[0]])\n rating.sort()\n for i in rating:\n res.append(i[1])\n res.reverse()\n return res\n \n``` | 1 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Python Easy Solution || Sorting | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n rating=[]\n res=[]\n for restro in restaurants:\n if (restro[3]<=maxPrice) and (restro[4]<=maxDistance):\n if (veganFriendly):\n if restro[2]==1:\n rating.append([restro[1],restro[0]])\n else:\n rating.append([restro[1],restro[0]])\n rating.sort()\n for i in rating:\n res.append(i[1])\n res.reverse()\n return res\n \n``` | 1 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Easy Python Solution | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n restaurants.sort(key=itemgetter(1,0),reverse=True)\n lst=[]\n """for i in restaurants:\n print(i)"""\n for i in restaurants:\n if veganFriendly==0:\n if i[3]<=maxPrice and i[4]<=maxDistance:\n lst.append(i[0]) \n elif i[2]==veganFriendly and i[3]<=maxPrice and i[4]<=maxDistance:\n lst.append(i[0])\n return lst\n``` | 2 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Easy Python Solution | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n restaurants.sort(key=itemgetter(1,0),reverse=True)\n lst=[]\n """for i in restaurants:\n print(i)"""\n for i in restaurants:\n if veganFriendly==0:\n if i[3]<=maxPrice and i[4]<=maxDistance:\n lst.append(i[0]) \n elif i[2]==veganFriendly and i[3]<=maxPrice and i[4]<=maxDistance:\n lst.append(i[0])\n return lst\n``` | 2 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Python3 solution | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | ```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n def f(x):\n if (veganFriendly == 1 and x[2] == 1 and x[3] <= maxPrice and x[4] <= maxDistance) or (veganFriendly == 0 and x[3] <= maxPrice and x[4] <= maxDistance):\n return True\n else:\n return False\n y = list(filter(f,restaurants))\n y.sort(key=lambda a:a[0],reverse=True)\n y.sort(key=lambda a:a[1],reverse=True)\n return [i[0] for i in y]\n```\n**If you like this solution, please upvote for this** | 3 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Python3 solution | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | ```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n def f(x):\n if (veganFriendly == 1 and x[2] == 1 and x[3] <= maxPrice and x[4] <= maxDistance) or (veganFriendly == 0 and x[3] <= maxPrice and x[4] <= maxDistance):\n return True\n else:\n return False\n y = list(filter(f,restaurants))\n y.sort(key=lambda a:a[0],reverse=True)\n y.sort(key=lambda a:a[1],reverse=True)\n return [i[0] for i in y]\n```\n**If you like this solution, please upvote for this** | 3 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Simple python3 solution | Filter + Sorting | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot \\log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n data = [\n (rating, id_)\n for id_, rating, vegan, price, distance in restaurants\n if (\n vegan >= veganFriendly\n and price <= maxPrice\n and distance <= maxDistance\n )\n ]\n\n data.sort(reverse=True)\n return [\n id_\n for _, id_ in data\n ]\n\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Simple python3 solution | Filter + Sorting | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot \\log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n data = [\n (rating, id_)\n for id_, rating, vegan, price, distance in restaurants\n if (\n vegan >= veganFriendly\n and price <= maxPrice\n and distance <= maxDistance\n )\n ]\n\n data.sort(reverse=True)\n return [\n id_\n for _, id_ in data\n ]\n\n``` | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Easy to understand Python3 solution | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n res = []\n\n if veganFriendly:\n for r in restaurants:\n if r[2] == veganFriendly and r[3] <= maxPrice and r[4] <= maxDistance:\n res.append(r)\n else:\n for r in restaurants:\n if r[3] <= maxPrice and r[4] <= maxDistance:\n res.append(r)\n \n res = sorted(res, key=lambda x:(-x[1],-x[0]))\n\n return [i[0] for i in res]\n \n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Easy to understand Python3 solution | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n res = []\n\n if veganFriendly:\n for r in restaurants:\n if r[2] == veganFriendly and r[3] <= maxPrice and r[4] <= maxDistance:\n res.append(r)\n else:\n for r in restaurants:\n if r[3] <= maxPrice and r[4] <= maxDistance:\n res.append(r)\n \n res = sorted(res, key=lambda x:(-x[1],-x[0]))\n\n return [i[0] for i in res]\n \n``` | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Very east simple for beginners !!!! | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n res=[]\n a=[]\n for i in range(len(restaurants)):\n if veganFriendly==1:\n if restaurants[i][2]==veganFriendly and restaurants[i][3]<=maxPrice and restaurants[i][4]<= maxDistance:\n res.append([restaurants[i][0],restaurants[i][1]])\n else:\n if restaurants[i][3]<=maxPrice and restaurants[i][4]<= maxDistance:\n res.append([restaurants[i][0],restaurants[i][1]])\n res.sort(key=lambda x:x[0],reverse=True)\n res.sort(key=lambda x:x[1],reverse=True)\n for i in res:\n a.append(i[0])\n return a\n\n\n\n \n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Very east simple for beginners !!!! | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n res=[]\n a=[]\n for i in range(len(restaurants)):\n if veganFriendly==1:\n if restaurants[i][2]==veganFriendly and restaurants[i][3]<=maxPrice and restaurants[i][4]<= maxDistance:\n res.append([restaurants[i][0],restaurants[i][1]])\n else:\n if restaurants[i][3]<=maxPrice and restaurants[i][4]<= maxDistance:\n res.append([restaurants[i][0],restaurants[i][1]])\n res.sort(key=lambda x:x[0],reverse=True)\n res.sort(key=lambda x:x[1],reverse=True)\n for i in res:\n a.append(i[0])\n return a\n\n\n\n \n``` | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Python solution using sorting | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | ```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n res = []\n for restaurant in restaurants:\n if restaurant[2] >= veganFriendly and restaurant[3] <= maxPrice and restaurant[4] <= maxDistance:\n res.append(restaurant)\n\t\t# sort results based on rating and then based on id\n res.sort(key=lambda x:(-x[1], -x[0]))\n res = [i[0] for i in res]\n return res\n\t | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Python solution using sorting | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | ```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n res = []\n for restaurant in restaurants:\n if restaurant[2] >= veganFriendly and restaurant[3] <= maxPrice and restaurant[4] <= maxDistance:\n res.append(restaurant)\n\t\t# sort results based on rating and then based on id\n res.sort(key=lambda x:(-x[1], -x[0]))\n res = [i[0] for i in res]\n return res\n\t | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Beats 99.19%of users with Python3 | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | \n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n selectedRes = []\n\n if veganFriendly == 0:\n for i in range(len(restaurants)):\n if restaurants[i][3] <= maxPrice and restaurants[i][4] <= maxDistance:\n selectedRes.append([restaurants[i][0],restaurants[i][1]])\n #append only (id and rating)\n else:\n for i in range(len(restaurants)):\n if restaurants[i][2] == 1 and restaurants[i][3] <= maxPrice and restaurants[i][4] <= maxDistance:\n selectedRes.append([restaurants[i][0],restaurants[i][1]])\n #print(selectedRes)\n\n selectedRes.sort(key=lambda x:x[0], reverse=True)\n selectedRes.sort(key=lambda x:x[1], reverse=True)\n #print(selectedRes)\n finalRes = []\n for i in range(len(selectedRes)):\n finalRes.append(selectedRes[i][0])\n return(finalRes)\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Beats 99.19%of users with Python3 | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | \n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n selectedRes = []\n\n if veganFriendly == 0:\n for i in range(len(restaurants)):\n if restaurants[i][3] <= maxPrice and restaurants[i][4] <= maxDistance:\n selectedRes.append([restaurants[i][0],restaurants[i][1]])\n #append only (id and rating)\n else:\n for i in range(len(restaurants)):\n if restaurants[i][2] == 1 and restaurants[i][3] <= maxPrice and restaurants[i][4] <= maxDistance:\n selectedRes.append([restaurants[i][0],restaurants[i][1]])\n #print(selectedRes)\n\n selectedRes.sort(key=lambda x:x[0], reverse=True)\n selectedRes.sort(key=lambda x:x[1], reverse=True)\n #print(selectedRes)\n finalRes = []\n for i in range(len(selectedRes)):\n finalRes.append(selectedRes[i][0])\n return(finalRes)\n``` | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Python 1-Liner | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | ```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n return [\n id for id, _, is_vegan, price, distance in sorted(restaurants, key=lambda x: (-x[1], -x[0])) if \n ((veganFriendly and is_vegan) or not veganFriendly) and price <= maxPrice and distance <= maxDistance\n ]\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Python 1-Liner | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | ```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n return [\n id for id, _, is_vegan, price, distance in sorted(restaurants, key=lambda x: (-x[1], -x[0])) if \n ((veganFriendly and is_vegan) or not veganFriendly) and price <= maxPrice and distance <= maxDistance\n ]\n``` | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
[Python3] Easy way | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n ans= []\n for i in range(len(restaurants)):\n if restaurants[i][2] >= veganFriendly and restaurants[i][3] <= maxPrice and restaurants[i][4] <= maxDistance:\n ans.append(restaurants[i])\n\n ans.sort(key=lambda x:x[0], reverse=True)\n ans.sort(key=lambda x:x[1], reverse=True)\n \n return [x[0] for x in ans]\n\n\n\n\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
[Python3] Easy way | filter-restaurants-by-vegan-friendly-price-and-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def filterRestaurants(self, restaurants: List[List[int]], veganFriendly: int, maxPrice: int, maxDistance: int) -> List[int]:\n ans= []\n for i in range(len(restaurants)):\n if restaurants[i][2] >= veganFriendly and restaurants[i][3] <= maxPrice and restaurants[i][4] <= maxDistance:\n ans.append(restaurants[i])\n\n ans.sort(key=lambda x:x[0], reverse=True)\n ans.sort(key=lambda x:x[1], reverse=True)\n \n return [x[0] for x in ans]\n\n\n\n\n``` | 0 | Given a `sentence` that consists of some words separated by a **single space**, and a `searchWord`, check if `searchWord` is a prefix of any word in `sentence`.
Return _the index of the word in_ `sentence` _(**1-indexed**) where_ `searchWord` _is a prefix of this word_. If `searchWord` is a prefix of more than one word, return the index of the first word **(minimum index)**. If there is no such word return `-1`.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** sentence = "i love eating burger ", searchWord = "burg "
**Output:** 4
**Explanation:** "burg " is prefix of "burger " which is the 4th word in the sentence.
**Example 2:**
**Input:** sentence = "this problem is an easy problem ", searchWord = "pro "
**Output:** 2
**Explanation:** "pro " is prefix of "problem " which is the 2nd and the 6th word in the sentence, but we return 2 as it's the minimal index.
**Example 3:**
**Input:** sentence = "i am tired ", searchWord = "you "
**Output:** -1
**Explanation:** "you " is not a prefix of any word in the sentence.
**Constraints:**
* `1 <= sentence.length <= 100`
* `1 <= searchWord.length <= 10`
* `sentence` consists of lowercase English letters and spaces.
* `searchWord` consists of lowercase English letters. | Do the filtering and sort as said. Note that the id may not be the index in the array. |
Python || 98.46% Faster || Explained || Floyd Warshall || Dijkstra's | find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | 0 | 1 | **Brute Force Approach (Floyd Warshall) :**\n```\ndef findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n cost=[[float(\'inf\') if i!=j else 0 for j in range(n)] for i in range(n)]\n for u,v,d in edges:\n cost[u][v]=d\n cost[v][u]=d\n for via in range(n):\n for i in range(n):\n for j in range(n):\n cost[i][j]=min(cost[i][j],cost[i][via]+cost[via][j])\n d={}\n for i in range(n):\n c=0\n for j in range(n):\n if cost[i][j]<=distanceThreshold and i!=j:\n c+=1\n d[i]=c\n m1=min(d.values())\n m2=0\n for k,v in d.items():\n if m1==v:\n m2=max(m2,k)\n return m2\n```\n\n**Optimized Approach (Dijkstra\'s Algorithm) :**\n\n**Here we have applied dijkstra\'s algorithm for every node find the possible nodes which are less than the threshold value and then later on find the node with minimum no. of cities connected and with greatest element**\n```\ndef findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n adj={i:dict() for i in range(n)}\n for u,v,d in edges:\n adj[u][v]=d\n adj[v][u]=d\n cities=[0]*n\n for k in range(n):\n c=-1\n dist=[float(\'inf\')]*n\n dist[k]=0\n visited=[0]*n\n pq=[(0,k)]\n heapify(pq)\n while pq:\n d,node=heappop(pq)\n if d>distanceThreshold:\n break\n if visited[node]:\n continue\n visited[node]=1\n c+=1\n for v in adj[node]:\n if visited[v]==0 and d+adj[node][v]<dist[v]:\n dist[v]=d+adj[node][v]\n heappush(pq,(dist[v],v))\n cities[k]=c\n maxNode=0\n minDist=cities[0]\n for i in range(n):\n if cities[i]<=minDist and maxNode<i:\n maxNode=i\n minDist=cities[i]\n return maxNode\n```\n\n**An upvote will be encouraging** | 7 | There are `n` cities numbered from `0` to `n-1`. Given the array `edges` where `edges[i] = [fromi, toi, weighti]` represents a bidirectional and weighted edge between cities `fromi` and `toi`, and given the integer `distanceThreshold`.
Return the city with the smallest number of cities that are reachable through some path and whose distance is **at most** `distanceThreshold`, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities _**i**_ and _**j**_ is equal to the sum of the edges' weights along that path.
**Example 1:**
**Input:** n = 4, edges = \[\[0,1,3\],\[1,2,1\],\[1,3,4\],\[2,3,1\]\], distanceThreshold = 4
**Output:** 3
**Explanation:** The figure above describes the graph.
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> \[City 1, City 2\]
City 1 -> \[City 0, City 2, City 3\]
City 2 -> \[City 0, City 1, City 3\]
City 3 -> \[City 1, City 2\]
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
**Example 2:**
**Input:** n = 5, edges = \[\[0,1,2\],\[0,4,8\],\[1,2,3\],\[1,4,2\],\[2,3,1\],\[3,4,1\]\], distanceThreshold = 2
**Output:** 0
**Explanation:** The figure above describes the graph.
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> \[City 1\]
City 1 -> \[City 0, City 4\]
City 2 -> \[City 3, City 4\]
City 3 -> \[City 2, City 4\]
City 4 -> \[City 1, City 2, City 3\]
The city 0 has 1 neighboring city at a distanceThreshold = 2.
**Constraints:**
* `2 <= n <= 100`
* `1 <= edges.length <= n * (n - 1) / 2`
* `edges[i].length == 3`
* `0 <= fromi < toi < n`
* `1 <= weighti, distanceThreshold <= 10^4`
* All pairs `(fromi, toi)` are distinct. | null |
Python || 98.46% Faster || Explained || Floyd Warshall || Dijkstra's | find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | 0 | 1 | **Brute Force Approach (Floyd Warshall) :**\n```\ndef findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n cost=[[float(\'inf\') if i!=j else 0 for j in range(n)] for i in range(n)]\n for u,v,d in edges:\n cost[u][v]=d\n cost[v][u]=d\n for via in range(n):\n for i in range(n):\n for j in range(n):\n cost[i][j]=min(cost[i][j],cost[i][via]+cost[via][j])\n d={}\n for i in range(n):\n c=0\n for j in range(n):\n if cost[i][j]<=distanceThreshold and i!=j:\n c+=1\n d[i]=c\n m1=min(d.values())\n m2=0\n for k,v in d.items():\n if m1==v:\n m2=max(m2,k)\n return m2\n```\n\n**Optimized Approach (Dijkstra\'s Algorithm) :**\n\n**Here we have applied dijkstra\'s algorithm for every node find the possible nodes which are less than the threshold value and then later on find the node with minimum no. of cities connected and with greatest element**\n```\ndef findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n adj={i:dict() for i in range(n)}\n for u,v,d in edges:\n adj[u][v]=d\n adj[v][u]=d\n cities=[0]*n\n for k in range(n):\n c=-1\n dist=[float(\'inf\')]*n\n dist[k]=0\n visited=[0]*n\n pq=[(0,k)]\n heapify(pq)\n while pq:\n d,node=heappop(pq)\n if d>distanceThreshold:\n break\n if visited[node]:\n continue\n visited[node]=1\n c+=1\n for v in adj[node]:\n if visited[v]==0 and d+adj[node][v]<dist[v]:\n dist[v]=d+adj[node][v]\n heappush(pq,(dist[v],v))\n cities[k]=c\n maxNode=0\n minDist=cities[0]\n for i in range(n):\n if cities[i]<=minDist and maxNode<i:\n maxNode=i\n minDist=cities[i]\n return maxNode\n```\n\n**An upvote will be encouraging** | 7 | Given a string `s` and an integer `k`, return _the maximum number of vowel letters in any substring of_ `s` _with length_ `k`.
**Vowel letters** in English are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** s = "abciiidef ", k = 3
**Output:** 3
**Explanation:** The substring "iii " contains 3 vowel letters.
**Example 2:**
**Input:** s = "aeiou ", k = 2
**Output:** 2
**Explanation:** Any substring of length 2 contains 2 vowels.
**Example 3:**
**Input:** s = "leetcode ", k = 3
**Output:** 2
**Explanation:** "lee ", "eet " and "ode " contain 2 vowels.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= s.length` | Use Floyd-Warshall's algorithm to compute any-point to any-point distances. (Or can also do Dijkstra from every node due to the weights are non-negative). For each city calculate the number of reachable cities within the threshold, then search for the optimal city. |
ALL SOURCE SORTEST PATH | FLOYD ALGO | find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | 0 | 1 | \n# Code\n```\nclass Solution:\n def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n\n k = float("inf")\n cost = [[k for _ in range(n)] for _ in range(n)]\n \n for u, v, w in edges:\n cost[u][v] = cost[v][u] = w\n\n for i in range(n):\n for j in range(n):\n for k in range(n):\n cost[j][k] = min(cost[j][i] + cost[i][k], cost[j][k])\n\n ans = -1\n k = float("inf")\n\n for i in range(n):\n count = 0\n for j in range(n):\n if i != j and cost[i][j] <= distanceThreshold:\n count += 1\n\n if k >= count:\n ans = i\n k = count\n\n return ans\n\n\n\n\n\n \n``` | 4 | There are `n` cities numbered from `0` to `n-1`. Given the array `edges` where `edges[i] = [fromi, toi, weighti]` represents a bidirectional and weighted edge between cities `fromi` and `toi`, and given the integer `distanceThreshold`.
Return the city with the smallest number of cities that are reachable through some path and whose distance is **at most** `distanceThreshold`, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities _**i**_ and _**j**_ is equal to the sum of the edges' weights along that path.
**Example 1:**
**Input:** n = 4, edges = \[\[0,1,3\],\[1,2,1\],\[1,3,4\],\[2,3,1\]\], distanceThreshold = 4
**Output:** 3
**Explanation:** The figure above describes the graph.
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> \[City 1, City 2\]
City 1 -> \[City 0, City 2, City 3\]
City 2 -> \[City 0, City 1, City 3\]
City 3 -> \[City 1, City 2\]
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
**Example 2:**
**Input:** n = 5, edges = \[\[0,1,2\],\[0,4,8\],\[1,2,3\],\[1,4,2\],\[2,3,1\],\[3,4,1\]\], distanceThreshold = 2
**Output:** 0
**Explanation:** The figure above describes the graph.
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> \[City 1\]
City 1 -> \[City 0, City 4\]
City 2 -> \[City 3, City 4\]
City 3 -> \[City 2, City 4\]
City 4 -> \[City 1, City 2, City 3\]
The city 0 has 1 neighboring city at a distanceThreshold = 2.
**Constraints:**
* `2 <= n <= 100`
* `1 <= edges.length <= n * (n - 1) / 2`
* `edges[i].length == 3`
* `0 <= fromi < toi < n`
* `1 <= weighti, distanceThreshold <= 10^4`
* All pairs `(fromi, toi)` are distinct. | null |
ALL SOURCE SORTEST PATH | FLOYD ALGO | find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | 0 | 1 | \n# Code\n```\nclass Solution:\n def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n\n k = float("inf")\n cost = [[k for _ in range(n)] for _ in range(n)]\n \n for u, v, w in edges:\n cost[u][v] = cost[v][u] = w\n\n for i in range(n):\n for j in range(n):\n for k in range(n):\n cost[j][k] = min(cost[j][i] + cost[i][k], cost[j][k])\n\n ans = -1\n k = float("inf")\n\n for i in range(n):\n count = 0\n for j in range(n):\n if i != j and cost[i][j] <= distanceThreshold:\n count += 1\n\n if k >= count:\n ans = i\n k = count\n\n return ans\n\n\n\n\n\n \n``` | 4 | Given a string `s` and an integer `k`, return _the maximum number of vowel letters in any substring of_ `s` _with length_ `k`.
**Vowel letters** in English are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** s = "abciiidef ", k = 3
**Output:** 3
**Explanation:** The substring "iii " contains 3 vowel letters.
**Example 2:**
**Input:** s = "aeiou ", k = 2
**Output:** 2
**Explanation:** Any substring of length 2 contains 2 vowels.
**Example 3:**
**Input:** s = "leetcode ", k = 3
**Output:** 2
**Explanation:** "lee ", "eet " and "ode " contain 2 vowels.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= s.length` | Use Floyd-Warshall's algorithm to compute any-point to any-point distances. (Or can also do Dijkstra from every node due to the weights are non-negative). For each city calculate the number of reachable cities within the threshold, then search for the optimal city. |
Help Needed|| Leetcode Community | find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | 0 | 1 | ## Help Needed \n\nSomeone please point out where i am wrong :)\n\n```\nimport heapq\nfrom typing import List\nclass Solution:\n def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n # code here\n graph = [[] for _ in range(n)]\n for u, v, w in edges:\n graph[u].append((v, w))\n graph[v].append((u, w))\n \n \n ans = [float(\'inf\')] * n\n for city in range(n):\n pq = [(0, city)]\n while pq:\n dist, node = heapq.heappop(pq)\n if dist <= distanceThreshold:\n for adjnode, adjdis in graph[node]:\n if dist + adjdis < ans[adjnode]:\n ans[adjnode] = dist + adjdis\n heapq.heappush(pq, (dist + adjdis, adjnode))\n \n \n cntcity = n+1\n cityno = -1\n for i in range(n):\n c = 0\n for j in range(n):\n if ans[j] <= distanceThreshold:\n c += 1\n if c <= cntcity:\n cntcity = c\n cityno = i\n \n return cityno\n``` | 2 | There are `n` cities numbered from `0` to `n-1`. Given the array `edges` where `edges[i] = [fromi, toi, weighti]` represents a bidirectional and weighted edge between cities `fromi` and `toi`, and given the integer `distanceThreshold`.
Return the city with the smallest number of cities that are reachable through some path and whose distance is **at most** `distanceThreshold`, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities _**i**_ and _**j**_ is equal to the sum of the edges' weights along that path.
**Example 1:**
**Input:** n = 4, edges = \[\[0,1,3\],\[1,2,1\],\[1,3,4\],\[2,3,1\]\], distanceThreshold = 4
**Output:** 3
**Explanation:** The figure above describes the graph.
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> \[City 1, City 2\]
City 1 -> \[City 0, City 2, City 3\]
City 2 -> \[City 0, City 1, City 3\]
City 3 -> \[City 1, City 2\]
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
**Example 2:**
**Input:** n = 5, edges = \[\[0,1,2\],\[0,4,8\],\[1,2,3\],\[1,4,2\],\[2,3,1\],\[3,4,1\]\], distanceThreshold = 2
**Output:** 0
**Explanation:** The figure above describes the graph.
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> \[City 1\]
City 1 -> \[City 0, City 4\]
City 2 -> \[City 3, City 4\]
City 3 -> \[City 2, City 4\]
City 4 -> \[City 1, City 2, City 3\]
The city 0 has 1 neighboring city at a distanceThreshold = 2.
**Constraints:**
* `2 <= n <= 100`
* `1 <= edges.length <= n * (n - 1) / 2`
* `edges[i].length == 3`
* `0 <= fromi < toi < n`
* `1 <= weighti, distanceThreshold <= 10^4`
* All pairs `(fromi, toi)` are distinct. | null |
Help Needed|| Leetcode Community | find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance | 0 | 1 | ## Help Needed \n\nSomeone please point out where i am wrong :)\n\n```\nimport heapq\nfrom typing import List\nclass Solution:\n def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:\n # code here\n graph = [[] for _ in range(n)]\n for u, v, w in edges:\n graph[u].append((v, w))\n graph[v].append((u, w))\n \n \n ans = [float(\'inf\')] * n\n for city in range(n):\n pq = [(0, city)]\n while pq:\n dist, node = heapq.heappop(pq)\n if dist <= distanceThreshold:\n for adjnode, adjdis in graph[node]:\n if dist + adjdis < ans[adjnode]:\n ans[adjnode] = dist + adjdis\n heapq.heappush(pq, (dist + adjdis, adjnode))\n \n \n cntcity = n+1\n cityno = -1\n for i in range(n):\n c = 0\n for j in range(n):\n if ans[j] <= distanceThreshold:\n c += 1\n if c <= cntcity:\n cntcity = c\n cityno = i\n \n return cityno\n``` | 2 | Given a string `s` and an integer `k`, return _the maximum number of vowel letters in any substring of_ `s` _with length_ `k`.
**Vowel letters** in English are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** s = "abciiidef ", k = 3
**Output:** 3
**Explanation:** The substring "iii " contains 3 vowel letters.
**Example 2:**
**Input:** s = "aeiou ", k = 2
**Output:** 2
**Explanation:** Any substring of length 2 contains 2 vowels.
**Example 3:**
**Input:** s = "leetcode ", k = 3
**Output:** 2
**Explanation:** "lee ", "eet " and "ode " contain 2 vowels.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= s.length` | Use Floyd-Warshall's algorithm to compute any-point to any-point distances. (Or can also do Dijkstra from every node due to the weights are non-negative). For each city calculate the number of reachable cities within the threshold, then search for the optimal city. |
91% Faster Solution | minimum-difficulty-of-a-job-schedule | 0 | 1 | ```\nclass Solution:\n def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:\n jobCount = len(jobDifficulty) \n if jobCount < d:\n return -1\n\n @lru_cache(None)\n def topDown(jobIndex: int, remainDayCount: int) -> int:\n remainJobCount = jobCount - jobIndex\n if remainDayCount == 1:\n return max(jobDifficulty[jobIndex:])\n \n if remainJobCount == remainDayCount:\n return sum(jobDifficulty[jobIndex:])\n\n minDiff = float(\'inf\')\n maxToday = 0\n for i in range(jobIndex, jobCount - remainDayCount + 1):\n maxToday = max(maxToday, jobDifficulty[i])\n minDiff = min(minDiff, maxToday + topDown(i+1, remainDayCount-1))\n return minDiff\n\n return topDown(0, d)\n``` | 4 | You want to schedule a list of jobs in `d` days. Jobs are dependent (i.e To work on the `ith` job, you have to finish all the jobs `j` where `0 <= j < i`).
You have to finish **at least** one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the `d` days. The difficulty of a day is the maximum difficulty of a job done on that day.
You are given an integer array `jobDifficulty` and an integer `d`. The difficulty of the `ith` job is `jobDifficulty[i]`.
Return _the minimum difficulty of a job schedule_. If you cannot find a schedule for the jobs return `-1`.
**Example 1:**
**Input:** jobDifficulty = \[6,5,4,3,2,1\], d = 2
**Output:** 7
**Explanation:** First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7
**Example 2:**
**Input:** jobDifficulty = \[9,9,9\], d = 4
**Output:** -1
**Explanation:** If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
**Example 3:**
**Input:** jobDifficulty = \[1,1,1\], d = 3
**Output:** 3
**Explanation:** The schedule is one job per day. total difficulty will be 3.
**Constraints:**
* `1 <= jobDifficulty.length <= 300`
* `0 <= jobDifficulty[i] <= 1000`
* `1 <= d <= 10` | For a fixed number of candies c, how can you check if each child can get c candies? Use binary search to find the maximum c as the answer. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.