title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 3 (20ms) | Faster than 95% | Generating All Sequential Digits within Range | sequential-digits | 0 | 1 | ***Generating All Sequential Digits with help of of Array "a" and thus appending the required ones in Array "ans" which are within the range low and high :-***\n\n```\nclass Solution:\n def sequentialDigits(self, low: int, high: int) -> List[int]:\n l=len(str(low))\n h=len(str(high))\n ans=[]\n a=[12,23,34,45,56,67,78,89]\n t=0\n while l<=h:\n for i in a:\n for j in range(0,l-2):\n t=i%10\n if i==9:\n break\n i=int(str(i)+str(t+1))\n if i%10==0:\n break\n if i>=low and i<=high:\n ans.append(i)\n l+=1\n return ans\n``` | 3 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
[Python3] prefix sum & binary search | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | Algorithm: \nBuild a `(m+1)x(n+1)` matrix of prefix sums of given matrix where `prefix[i][j] = sum(mat[:i][:j])`. And search for maximum `k` such that `sum(mat[i:i+k][j:j+k])` not exceeding threshold. Notice:\n1) `prefix[i+1][j+1] = prefix[i][j+1] + prefix[i+1][j] - prefix[i][j] + mat[i][j]`. \n2) `sum(mat[i:i+k][j:j+k]) = prefix[i+k][j+k] - prefix[i][j+k] - prefix[i+k][j] + prefix[i][j]`. \n\nImplementation (100%): \n```\nfrom itertools import product\n\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n """\n prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + mat[i][j]\n """\n m, n = len(mat), len(mat[0])\n #build prefix sum \n prefix = [[0]*(n+1) for _ in range(m+1)]\n \n for i, j in product(range(m), range(n)):\n prefix[i+1][j+1] = prefix[i+1][j] + prefix[i][j+1] - prefix[i][j] + mat[i][j]\n \n def below(k): \n """reture true if there is such a sub-matrix of length k"""\n for i, j in product(range(m+1-k), range(n+1-k)):\n if prefix[i+k][j+k] - prefix[i][j+k] - prefix[i+k][j] + prefix[i][j] <= threshold: return True\n return False \n \n #binary search\n lo, hi = 1, min(m, n)\n while lo <= hi: \n mid = (lo + hi)//2\n if below(mid): lo = mid + 1\n else: hi = mid - 1\n \n return hi\n```\nAnalysis: \nTime complexity `O(MNlog(min(M,N))`\nSpace complexity `O(MN)` | 18 | Given a `m x n` matrix `mat` and an integer `threshold`, return _the maximum side-length of a square with a sum less than or equal to_ `threshold` _or return_ `0` _if there is no such square_.
**Example 1:**
**Input:** mat = \[\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\]\], threshold = 4
**Output:** 2
**Explanation:** The maximum side length of square with sum less than 4 is 2 as shown.
**Example 2:**
**Input:** mat = \[\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\]\], threshold = 1
**Output:** 0
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 300`
* `0 <= mat[i][j] <= 104`
* `0 <= threshold <= 105` | null |
[Python3] prefix sum & binary search | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | Algorithm: \nBuild a `(m+1)x(n+1)` matrix of prefix sums of given matrix where `prefix[i][j] = sum(mat[:i][:j])`. And search for maximum `k` such that `sum(mat[i:i+k][j:j+k])` not exceeding threshold. Notice:\n1) `prefix[i+1][j+1] = prefix[i][j+1] + prefix[i+1][j] - prefix[i][j] + mat[i][j]`. \n2) `sum(mat[i:i+k][j:j+k]) = prefix[i+k][j+k] - prefix[i][j+k] - prefix[i+k][j] + prefix[i][j]`. \n\nImplementation (100%): \n```\nfrom itertools import product\n\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n """\n prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + mat[i][j]\n """\n m, n = len(mat), len(mat[0])\n #build prefix sum \n prefix = [[0]*(n+1) for _ in range(m+1)]\n \n for i, j in product(range(m), range(n)):\n prefix[i+1][j+1] = prefix[i+1][j] + prefix[i][j+1] - prefix[i][j] + mat[i][j]\n \n def below(k): \n """reture true if there is such a sub-matrix of length k"""\n for i, j in product(range(m+1-k), range(n+1-k)):\n if prefix[i+k][j+k] - prefix[i][j+k] - prefix[i+k][j] + prefix[i][j] <= threshold: return True\n return False \n \n #binary search\n lo, hi = 1, min(m, n)\n while lo <= hi: \n mid = (lo + hi)//2\n if below(mid): lo = mid + 1\n else: hi = mid - 1\n \n return hi\n```\nAnalysis: \nTime complexity `O(MNlog(min(M,N))`\nSpace complexity `O(MN)` | 18 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
[ O(MN) ] Prefix Sum + Sliding Window. Beats 99% | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(MN)\n\n- Space complexity: O(MN)\n\n# Code\n```\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n m = len(mat)\n n = len(mat[0])\n matrix = [ [0]*(n+1) for _ in range(m+1) ]\n for i in range(m):\n sum_ = 0\n for j in range(n):\n sum_ += mat[i][j]\n matrix[i+1][j+1] = matrix[i][j+1] + sum_\n \n def calculateArea(i, j, l):\n return matrix[i+l][j+l] + matrix[i][j] - matrix[i][j+l] - matrix[i+l][j]\n \n s = min(m, n)\n ans = 0\n for i in range(m):\n for j in range(n):\n while ans < m-i and ans < n-j and calculateArea(i, j, ans+1) <= threshold:\n ans += 1\n if ans == s:\n return ans\n return ans\n\n\n\n\n\n \n``` | 0 | Given a `m x n` matrix `mat` and an integer `threshold`, return _the maximum side-length of a square with a sum less than or equal to_ `threshold` _or return_ `0` _if there is no such square_.
**Example 1:**
**Input:** mat = \[\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\]\], threshold = 4
**Output:** 2
**Explanation:** The maximum side length of square with sum less than 4 is 2 as shown.
**Example 2:**
**Input:** mat = \[\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\]\], threshold = 1
**Output:** 0
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 300`
* `0 <= mat[i][j] <= 104`
* `0 <= threshold <= 105` | null |
[ O(MN) ] Prefix Sum + Sliding Window. Beats 99% | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(MN)\n\n- Space complexity: O(MN)\n\n# Code\n```\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n m = len(mat)\n n = len(mat[0])\n matrix = [ [0]*(n+1) for _ in range(m+1) ]\n for i in range(m):\n sum_ = 0\n for j in range(n):\n sum_ += mat[i][j]\n matrix[i+1][j+1] = matrix[i][j+1] + sum_\n \n def calculateArea(i, j, l):\n return matrix[i+l][j+l] + matrix[i][j] - matrix[i][j+l] - matrix[i+l][j]\n \n s = min(m, n)\n ans = 0\n for i in range(m):\n for j in range(n):\n while ans < m-i and ans < n-j and calculateArea(i, j, ans+1) <= threshold:\n ans += 1\n if ans == s:\n return ans\n return ans\n\n\n\n\n\n \n``` | 0 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
Prefix Sum & Binary Search | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1.Add dummy row and column with value 0 for convenience.\n2.Compute prefix sum of mat.\n3.For a given side_length, square sum where the bottom right cell locates at (r, c) = mat[r][c] - mat[r-k][c] - mat[r][c-k] + mat[r-k][c-k].\n The test function returns True if there is a square with sum <= threshold.\n4.Since test function couldn\'t check square with side length 0, if test(1) is False, then every value > threshold, thus return 0.\n5.For a side length m, if test(m) is True, then test(sl) is True for all sl <= m, so we search for [m, inf) aiming for test(sl) is True.\nIf test(m) is False, then test(sl) is False for all sl >= m (i.e.test(sl) might not be False for sl < m), hence search for [l, m-1].\n6.If r = l+1 at the end of binary search, then we have no idea if test(r) is True or False, we could only assert that test(l) is True.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mn lg(min(m, n)))\nm:mat.length\nn:mat[0].length\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n def show():\n for r in range(len(mat)):\n for c in range(len(mat[0])):\n print(mat[r][c], end = \' \')\n print()\n \n def test(sl):#side_length\n for r in range(1, len(mat)-sl+1):\n for c in range(1, len(mat[0])-sl+1):\n if mat[r+sl-1][c+sl-1]-mat[r+sl-1][c-1]-mat[r-1][c+sl-1]+mat[r-1][c-1] <= threshold:\n return True\n \n return False\n \n mat = [[0 for _ in range(len(mat[0])+1)]] + [[0] + mat[r] for r in range(len(mat))]\n \n m, n = len(mat), len(mat[0])\n\n for r in range(m):\n for c in range(1, n):\n mat[r][c] += mat[r][c-1]\n \n for c in range(n):\n for r in range(1, m):\n mat[r][c] += mat[r-1][c]\n #show()\n \'\'\'\n for sl in range(1, min(m-1, n-1)+1):\n print(sl, test(sl))\n \'\'\'\n if not test(1):\n return 0\n\n l, r = 1, min(m-1, n-1)\n\n while l+1 < r:\n #print(l, r)\n m = (l+r)//2\n\n if test(m):\n l = m\n else:\n r = m-1\n \n if test(r):\n return r\n else:\n return l\n\n\n``` | 0 | Given a `m x n` matrix `mat` and an integer `threshold`, return _the maximum side-length of a square with a sum less than or equal to_ `threshold` _or return_ `0` _if there is no such square_.
**Example 1:**
**Input:** mat = \[\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\]\], threshold = 4
**Output:** 2
**Explanation:** The maximum side length of square with sum less than 4 is 2 as shown.
**Example 2:**
**Input:** mat = \[\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\]\], threshold = 1
**Output:** 0
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 300`
* `0 <= mat[i][j] <= 104`
* `0 <= threshold <= 105` | null |
Prefix Sum & Binary Search | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1.Add dummy row and column with value 0 for convenience.\n2.Compute prefix sum of mat.\n3.For a given side_length, square sum where the bottom right cell locates at (r, c) = mat[r][c] - mat[r-k][c] - mat[r][c-k] + mat[r-k][c-k].\n The test function returns True if there is a square with sum <= threshold.\n4.Since test function couldn\'t check square with side length 0, if test(1) is False, then every value > threshold, thus return 0.\n5.For a side length m, if test(m) is True, then test(sl) is True for all sl <= m, so we search for [m, inf) aiming for test(sl) is True.\nIf test(m) is False, then test(sl) is False for all sl >= m (i.e.test(sl) might not be False for sl < m), hence search for [l, m-1].\n6.If r = l+1 at the end of binary search, then we have no idea if test(r) is True or False, we could only assert that test(l) is True.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mn lg(min(m, n)))\nm:mat.length\nn:mat[0].length\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n def show():\n for r in range(len(mat)):\n for c in range(len(mat[0])):\n print(mat[r][c], end = \' \')\n print()\n \n def test(sl):#side_length\n for r in range(1, len(mat)-sl+1):\n for c in range(1, len(mat[0])-sl+1):\n if mat[r+sl-1][c+sl-1]-mat[r+sl-1][c-1]-mat[r-1][c+sl-1]+mat[r-1][c-1] <= threshold:\n return True\n \n return False\n \n mat = [[0 for _ in range(len(mat[0])+1)]] + [[0] + mat[r] for r in range(len(mat))]\n \n m, n = len(mat), len(mat[0])\n\n for r in range(m):\n for c in range(1, n):\n mat[r][c] += mat[r][c-1]\n \n for c in range(n):\n for r in range(1, m):\n mat[r][c] += mat[r-1][c]\n #show()\n \'\'\'\n for sl in range(1, min(m-1, n-1)+1):\n print(sl, test(sl))\n \'\'\'\n if not test(1):\n return 0\n\n l, r = 1, min(m-1, n-1)\n\n while l+1 < r:\n #print(l, r)\n m = (l+r)//2\n\n if test(m):\n l = m\n else:\n r = m-1\n \n if test(r):\n return r\n else:\n return l\n\n\n``` | 0 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
Solution | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxSideLength(vector<vector<int>>& mat, int threshold) {\n int row = mat.size(), col = mat.front().size();\n \n vector<vector<int>> psum(row, vector<int>(col, 0));\n psum[0][0] = mat[0][0];\n for (int i = 1; i < row; i++)\n psum[i][0] = psum[i - 1][0] + mat[i][0];\n \n for (int i = 1; i < col; i++) {\n psum[0][i] = psum[0][i - 1] + mat[0][i];\n }\n for (int i = 1; i < row; i++) {\n for (int j = 1; j < col; j++) {\n psum[i][j] = - psum[i - 1][j - 1] + psum[i - 1][j] + psum[i][j - 1] + mat[i][j];\n }\n }\n int res = 0;\n for (int i = 0; i < row; i++) {\n int sum = 0;\n int ptr = res;\n for (int j = 0; j < col; j++) {\n while (i + ptr < row && j + ptr < col) {\n int next_sum = psum[i + ptr][j + ptr];\n if (i != 0 && j != 0) {\n next_sum -= psum[i + ptr][j - 1];\n next_sum -= psum[i - 1][j + ptr];\n next_sum += psum[i - 1][j - 1];\n }\n else if (i != 0) {\n next_sum -= psum[i - 1][j + ptr];\n }\n else if (j != 0) {\n next_sum -= psum[i + ptr][j - 1];\n }\n if (next_sum <= threshold) sum = next_sum, ptr++;\n else break;\n }\n res = ptr;\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n m,n = len(mat),len(mat[0])\n for j in range(1,n): mat[0][j] += mat[0][j-1]\n for i in range(1,m):\n mat[i][0] += mat[i-1][0]\n for j in range(1,n):\n mat[i][j] += mat[i-1][j]+mat[i][j-1]-mat[i-1][j-1]\n for row in mat: row.append(0)\n mat.append([0]*n)\n leng = 1\n for i,j in product(range(m),range(n)):\n if i < leng-1 or j < leng-1: continue\n if mat[i][j]-mat[i-leng][j]-mat[i][j-leng] \\\n +mat[i-leng][j-leng] <= threshold:\n leng += 1\n return leng-1\n```\n\n```Java []\nclass Solution {\n public int maxSideLength(int[][] mat, int threshold) {\n int r = mat.length, c = mat[0].length;\n int[][] pre = new int[r+1][c+1];\n for (int i = 1; i <= r; i++) {\n for (int j = 1; j <= c; j++) {\n pre[i][j] = pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + mat[i-1][j-1];\n }\n }\n int res = 0, l = 0;\n for (int i = 0; i <= r; i++) {\n for (int j = 0; j <= c; j++) {\n while (i + l <= r && j + l <= c &&\n (pre[i+l][j+l]-pre[i+l][j]-pre[i][j+l]+pre[i][j] <= threshold)) {\n res = l++;\n }\n }\n }\n return res;\n }\n}\n``` | 0 | Given a `m x n` matrix `mat` and an integer `threshold`, return _the maximum side-length of a square with a sum less than or equal to_ `threshold` _or return_ `0` _if there is no such square_.
**Example 1:**
**Input:** mat = \[\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\]\], threshold = 4
**Output:** 2
**Explanation:** The maximum side length of square with sum less than 4 is 2 as shown.
**Example 2:**
**Input:** mat = \[\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\]\], threshold = 1
**Output:** 0
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 300`
* `0 <= mat[i][j] <= 104`
* `0 <= threshold <= 105` | null |
Solution | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxSideLength(vector<vector<int>>& mat, int threshold) {\n int row = mat.size(), col = mat.front().size();\n \n vector<vector<int>> psum(row, vector<int>(col, 0));\n psum[0][0] = mat[0][0];\n for (int i = 1; i < row; i++)\n psum[i][0] = psum[i - 1][0] + mat[i][0];\n \n for (int i = 1; i < col; i++) {\n psum[0][i] = psum[0][i - 1] + mat[0][i];\n }\n for (int i = 1; i < row; i++) {\n for (int j = 1; j < col; j++) {\n psum[i][j] = - psum[i - 1][j - 1] + psum[i - 1][j] + psum[i][j - 1] + mat[i][j];\n }\n }\n int res = 0;\n for (int i = 0; i < row; i++) {\n int sum = 0;\n int ptr = res;\n for (int j = 0; j < col; j++) {\n while (i + ptr < row && j + ptr < col) {\n int next_sum = psum[i + ptr][j + ptr];\n if (i != 0 && j != 0) {\n next_sum -= psum[i + ptr][j - 1];\n next_sum -= psum[i - 1][j + ptr];\n next_sum += psum[i - 1][j - 1];\n }\n else if (i != 0) {\n next_sum -= psum[i - 1][j + ptr];\n }\n else if (j != 0) {\n next_sum -= psum[i + ptr][j - 1];\n }\n if (next_sum <= threshold) sum = next_sum, ptr++;\n else break;\n }\n res = ptr;\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n m,n = len(mat),len(mat[0])\n for j in range(1,n): mat[0][j] += mat[0][j-1]\n for i in range(1,m):\n mat[i][0] += mat[i-1][0]\n for j in range(1,n):\n mat[i][j] += mat[i-1][j]+mat[i][j-1]-mat[i-1][j-1]\n for row in mat: row.append(0)\n mat.append([0]*n)\n leng = 1\n for i,j in product(range(m),range(n)):\n if i < leng-1 or j < leng-1: continue\n if mat[i][j]-mat[i-leng][j]-mat[i][j-leng] \\\n +mat[i-leng][j-leng] <= threshold:\n leng += 1\n return leng-1\n```\n\n```Java []\nclass Solution {\n public int maxSideLength(int[][] mat, int threshold) {\n int r = mat.length, c = mat[0].length;\n int[][] pre = new int[r+1][c+1];\n for (int i = 1; i <= r; i++) {\n for (int j = 1; j <= c; j++) {\n pre[i][j] = pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + mat[i-1][j-1];\n }\n }\n int res = 0, l = 0;\n for (int i = 0; i <= r; i++) {\n for (int j = 0; j <= c; j++) {\n while (i + l <= r && j + l <= c &&\n (pre[i+l][j+l]-pre[i+l][j]-pre[i][j+l]+pre[i][j] <= threshold)) {\n res = l++;\n }\n }\n }\n return res;\n }\n}\n``` | 0 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
Easy Presum with For Loop | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | # Approach\nPresum[:i][:j] store the sum of all elements in mat[:i][:j]\n\nSo the sum for the rectangle of `[i+length][j+length]` is\n```\nprefix[i+length][j+length] - prefix[i][j+length] - prefix[i+length][j]\n+ prefix[i][j]\n```\nThen iterate all possible squares with starting points of [i,j], if there is a square that satifies the length, then we plut one to the length and continue the search.\n\n# Code\n```\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n m, n = len(mat), len(mat[0])\n prefix = [[0]*(n+1) for _ in range(m+1)]\n \n for i, j in product(range(m), range(n)):\n prefix[i+1][j+1] = prefix[i+1][j] + prefix[i][j+1] - prefix[i][j] + mat[i][j]\n\n length = 0\n for i in range(m):\n for j in range(n):\n while i+length <= m and j + length <= n and prefix[i+length][j+length] - prefix[i][j+length] - prefix[i+length][j] + prefix[i][j] <= threshold:\n length += 1\n\n return length - 1\n\n\n``` | 0 | Given a `m x n` matrix `mat` and an integer `threshold`, return _the maximum side-length of a square with a sum less than or equal to_ `threshold` _or return_ `0` _if there is no such square_.
**Example 1:**
**Input:** mat = \[\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\],\[1,1,3,2,4,3,2\]\], threshold = 4
**Output:** 2
**Explanation:** The maximum side length of square with sum less than 4 is 2 as shown.
**Example 2:**
**Input:** mat = \[\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\],\[2,2,2,2,2\]\], threshold = 1
**Output:** 0
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 300`
* `0 <= mat[i][j] <= 104`
* `0 <= threshold <= 105` | null |
Easy Presum with For Loop | maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold | 0 | 1 | # Approach\nPresum[:i][:j] store the sum of all elements in mat[:i][:j]\n\nSo the sum for the rectangle of `[i+length][j+length]` is\n```\nprefix[i+length][j+length] - prefix[i][j+length] - prefix[i+length][j]\n+ prefix[i][j]\n```\nThen iterate all possible squares with starting points of [i,j], if there is a square that satifies the length, then we plut one to the length and continue the search.\n\n# Code\n```\nclass Solution:\n def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:\n m, n = len(mat), len(mat[0])\n prefix = [[0]*(n+1) for _ in range(m+1)]\n \n for i, j in product(range(m), range(n)):\n prefix[i+1][j+1] = prefix[i+1][j] + prefix[i][j+1] - prefix[i][j] + mat[i][j]\n\n length = 0\n for i in range(m):\n for j in range(n):\n while i+length <= m and j + length <= n and prefix[i+length][j+length] - prefix[i][j+length] - prefix[i+length][j] + prefix[i][j] <= threshold:\n length += 1\n\n return length - 1\n\n\n``` | 0 | Given an array of integers `nums`, you start with an initial **positive** value _startValue__._
In each iteration, you calculate the step by step sum of _startValue_ plus elements in `nums` (from left to right).
Return the minimum **positive** value of _startValue_ such that the step by step sum is never less than 1.
**Example 1:**
**Input:** nums = \[-3,2,-3,4,2\]
**Output:** 5
**Explanation:** If you choose startValue = 4, in the third iteration your step by step sum is less than 1.
**step by step sum**
**startValue = 4 | startValue = 5 | nums**
(4 **\-3** ) = 1 | (5 **\-3** ) = 2 | -3
(1 **+2** ) = 3 | (2 **+2** ) = 4 | 2
(3 **\-3** ) = 0 | (4 **\-3** ) = 1 | -3
(0 **+4** ) = 4 | (1 **+4** ) = 5 | 4
(4 **+2** ) = 6 | (5 **+2** ) = 7 | 2
**Example 2:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** Minimum start value should be positive.
**Example 3:**
**Input:** nums = \[1,-2,-3\]
**Output:** 5
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Store prefix sum of all grids in another 2D array. Try all possible solutions and if you cannot find one return -1. If x is a valid answer then any y < x is also valid answer. Use binary search to find answer. |
Dijkstra, Python 3 | shortest-path-in-a-grid-with-obstacles-elimination | 0 | 1 | ```\nimport heapq\nclass Solution:\n def shortestPath(self, grid: List[List[int]], k: int) -> int:\n ROW, COL = len(grid), len(grid[0])\n # Dijkstra\n steps = []\n heapq.heappush(steps, (0, 0, ROW-1, COL-1))\n found = set([(ROW-1, COL-1)])\n while steps:\n s, removed, r, c = heapq.heappop(steps)\n if r == 0 and c == 0:\n return s\n while steps and (r, c) in found:\n s, removed, r, c = heapq.heappop(steps)\n found.add((r, c))\n for rr, cc in (r-1,c), (r+1,c), (r,c-1), (r,c+1):\n if rr<0 or rr>=ROW or cc<0 or cc>=COL:\n continue\n if (rr, cc) in found:\n continue\n if grid[rr][cc] == 1 and removed == k:\n continue\n heapq.heappush(steps, (s+1, removed + grid[rr][cc], rr, cc))\n return -1\n\n``` | 1 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Dijkstra, Python 3 | shortest-path-in-a-grid-with-obstacles-elimination | 0 | 1 | ```\nimport heapq\nclass Solution:\n def shortestPath(self, grid: List[List[int]], k: int) -> int:\n ROW, COL = len(grid), len(grid[0])\n # Dijkstra\n steps = []\n heapq.heappush(steps, (0, 0, ROW-1, COL-1))\n found = set([(ROW-1, COL-1)])\n while steps:\n s, removed, r, c = heapq.heappop(steps)\n if r == 0 and c == 0:\n return s\n while steps and (r, c) in found:\n s, removed, r, c = heapq.heappop(steps)\n found.add((r, c))\n for rr, cc in (r-1,c), (r+1,c), (r,c-1), (r,c+1):\n if rr<0 or rr>=ROW or cc<0 or cc>=COL:\n continue\n if (rr, cc) in found:\n continue\n if grid[rr][cc] == 1 and removed == k:\n continue\n heapq.heappush(steps, (s+1, removed + grid[rr][cc], rr, cc))\n return -1\n\n``` | 1 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Simple solution using BFS traversal (58% Faster, 99.44% memory efficient) | shortest-path-in-a-grid-with-obstacles-elimination | 0 | 1 | ```\nimport heapq\nclass Solution:\n def shortestPath(self, grid: List[List[int]], k: int) -> int:\n m=len(grid)\n n=len(grid[0])\n visited=[[-1]*n for _ in range(m)]\n lst=[(0,-1*k,0,0)]\n visited[0][0]=1\n row=[-1,1,0,0]\n col=[0,0,-1,1]\n heapq.heapify(lst)\n while lst:\n steps,k,x,y=heapq.heappop(lst)\n k=-1*k\n # print(x,y,k)\n if x==m-1 and y==n-1:\n return steps\n for i in range(4):\n n_row=x+row[i]\n n_col=y+col[i]\n if n_row>=0 and n_row<m and n_col>=0 and n_col<n and k-grid[n_row][n_col]>=0:\n if visited[n_row][n_col]==-1 or (visited[n_row][n_col]!=-1 and (visited[n_row][n_col]<k)):\n heapq.heappush(lst,(steps+1,-1*(k-grid[n_row][n_col]),n_row,n_col))\n visited[n_row][n_col]=k-grid[n_row][n_col]\n return -1\n``` | 1 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Simple solution using BFS traversal (58% Faster, 99.44% memory efficient) | shortest-path-in-a-grid-with-obstacles-elimination | 0 | 1 | ```\nimport heapq\nclass Solution:\n def shortestPath(self, grid: List[List[int]], k: int) -> int:\n m=len(grid)\n n=len(grid[0])\n visited=[[-1]*n for _ in range(m)]\n lst=[(0,-1*k,0,0)]\n visited[0][0]=1\n row=[-1,1,0,0]\n col=[0,0,-1,1]\n heapq.heapify(lst)\n while lst:\n steps,k,x,y=heapq.heappop(lst)\n k=-1*k\n # print(x,y,k)\n if x==m-1 and y==n-1:\n return steps\n for i in range(4):\n n_row=x+row[i]\n n_col=y+col[i]\n if n_row>=0 and n_row<m and n_col>=0 and n_col<n and k-grid[n_row][n_col]>=0:\n if visited[n_row][n_col]==-1 or (visited[n_row][n_col]!=-1 and (visited[n_row][n_col]<k)):\n heapq.heappush(lst,(steps+1,-1*(k-grid[n_row][n_col]),n_row,n_col))\n visited[n_row][n_col]=k-grid[n_row][n_col]\n return -1\n``` | 1 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Dual BFS!!! | Beats 99.43%!!! | First Dual BFS Solution Posted in LeetCode!!! | shortest-path-in-a-grid-with-obstacles-elimination | 0 | 1 | [TOC]\n\n# Approach\nStart search from both sides.\n\nTo use dual BFS, we need to record the number of eliminated obstacles from both side, say `used`, seperately, because one coordinate can be reached from both sides, and for each side, there might be different path with different number of eliminated obstacles.\n\nSince we need to see whether a position is in the other queue, we can\'t use `(row, column, used)` as a state and put it into the queue and the set recording visited coordinates, say `visited`. So both queues and `visited` should be hashmaps, with coordinates as key and the number of eliminated obstacles as value.\n\n# Complexity\n- Time complexity: $O(N\u22C5K)$\nSame as normal BFS.\n\n- Space complexity: $O(N\u22C5K)$\nSame as normal BFS.\n\n# Code\n```\nclass Solution:\n def shortestPath(self, grid: List[List[int]], k: int) -> int:\n m, n = len(grid), len(grid[0])\n if k >= m + n - 2:\n return m + n - 2\n q1 = {(0, 0): 0}\n q2 = {(m - 1, n - 1): 0}\n step = 0\n visited1 = {}\n visited2 = {}\n while q1 and q2:\n if len(q1) > len(q2):\n q1, q2 = q2, q1\n visited1, visited2 = visited2, visited1\n queue = {}\n for row, col in q1:\n if (row, col) in q2:\n total_used = q1[(row, col)] + q2[(row, col)] - grid[row][col]\n if total_used <= k:\n return step\n visited1[(row, col)] = q1[(row, col)]\n for r, c in [(row - 1, col), (row + 1, col), (row, col - 1), (row, col + 1)]:\n if 0 <= r < m and 0 <= c < n:\n used = q1[(row, col)] + grid[r][c]\n if used <= k and ((r, c) not in visited1 or used < visited1[(r, c)]) and ((r, c) not in queue or used < queue[(r, c)]):\n queue[(r, c)] = used\n q1 = queue\n step += 1\n return -1\n``` | 1 | You are given an `m x n` integer matrix `grid` where each cell is either `0` (empty) or `1` (obstacle). You can move up, down, left, or right from and to an empty cell in **one step**.
Return _the minimum number of **steps** to walk from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)` _given that you can eliminate **at most**_ `k` _obstacles_. If it is not possible to find such walk return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0\],\[1,1,0\],\[0,0,0\],\[0,1,1\],\[0,0,0\]\], k = 1
**Output:** 6
**Explanation:**
The shortest path without eliminating any obstacle is 10.
The shortest path with one obstacle elimination at position (3,2) is 6. Such path is (0,0) -> (0,1) -> (0,2) -> (1,2) -> (2,2) -> **(3,2)** -> (4,2).
**Example 2:**
**Input:** grid = \[\[0,1,1\],\[1,1,1\],\[1,0,0\]\], k = 1
**Output:** -1
**Explanation:** We need to eliminate at least two obstacles to find such a walk.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 40`
* `1 <= k <= m * n`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Check every three consecutive numbers in the array for parity. |
Dual BFS!!! | Beats 99.43%!!! | First Dual BFS Solution Posted in LeetCode!!! | shortest-path-in-a-grid-with-obstacles-elimination | 0 | 1 | [TOC]\n\n# Approach\nStart search from both sides.\n\nTo use dual BFS, we need to record the number of eliminated obstacles from both side, say `used`, seperately, because one coordinate can be reached from both sides, and for each side, there might be different path with different number of eliminated obstacles.\n\nSince we need to see whether a position is in the other queue, we can\'t use `(row, column, used)` as a state and put it into the queue and the set recording visited coordinates, say `visited`. So both queues and `visited` should be hashmaps, with coordinates as key and the number of eliminated obstacles as value.\n\n# Complexity\n- Time complexity: $O(N\u22C5K)$\nSame as normal BFS.\n\n- Space complexity: $O(N\u22C5K)$\nSame as normal BFS.\n\n# Code\n```\nclass Solution:\n def shortestPath(self, grid: List[List[int]], k: int) -> int:\n m, n = len(grid), len(grid[0])\n if k >= m + n - 2:\n return m + n - 2\n q1 = {(0, 0): 0}\n q2 = {(m - 1, n - 1): 0}\n step = 0\n visited1 = {}\n visited2 = {}\n while q1 and q2:\n if len(q1) > len(q2):\n q1, q2 = q2, q1\n visited1, visited2 = visited2, visited1\n queue = {}\n for row, col in q1:\n if (row, col) in q2:\n total_used = q1[(row, col)] + q2[(row, col)] - grid[row][col]\n if total_used <= k:\n return step\n visited1[(row, col)] = q1[(row, col)]\n for r, c in [(row - 1, col), (row + 1, col), (row, col - 1), (row, col + 1)]:\n if 0 <= r < m and 0 <= c < n:\n used = q1[(row, col)] + grid[r][c]\n if used <= k and ((r, c) not in visited1 or used < visited1[(r, c)]) and ((r, c) not in queue or used < queue[(r, c)]):\n queue[(r, c)] = used\n q1 = queue\n step += 1\n return -1\n``` | 1 | Given an integer `k`, _return the minimum number of Fibonacci numbers whose sum is equal to_ `k`. The same Fibonacci number can be used multiple times.
The Fibonacci numbers are defined as:
* `F1 = 1`
* `F2 = 1`
* `Fn = Fn-1 + Fn-2` for `n > 2.`
It is guaranteed that for the given constraints we can always find such Fibonacci numbers that sum up to `k`.
**Example 1:**
**Input:** k = 7
**Output:** 2
**Explanation:** The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13, ...
For k = 7 we can use 2 + 5 = 7.
**Example 2:**
**Input:** k = 10
**Output:** 2
**Explanation:** For k = 10 we can use 2 + 8 = 10.
**Example 3:**
**Input:** k = 19
**Output:** 3
**Explanation:** For k = 19 we can use 1 + 5 + 13 = 19.
**Constraints:**
* `1 <= k <= 109` | Use BFS. BFS on (x,y,r) x,y is coordinate, r is remain number of obstacles you can remove. |
Simplest Python one-liner | find-numbers-with-even-number-of-digits | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findNumbers(self, nums: List[int]) -> int:\n return len([x for x in nums if len(str(x)) % 2 == 0])\n``` | 2 | Given an array `nums` of integers, return how many of them contain an **even number** of digits.
**Example 1:**
**Input:** nums = \[12,345,2,6,7896\]
**Output:** 2
**Explanation:**
12 contains 2 digits (even number of digits).
345 contains 3 digits (odd number of digits).
2 contains 1 digit (odd number of digits).
6 contains 1 digit (odd number of digits).
7896 contains 4 digits (even number of digits).
Therefore only 12 and 7896 contain an even number of digits.
**Example 2:**
**Input:** nums = \[555,901,482,1771\]
**Output:** 1
**Explanation:**
Only 1771 contains an even number of digits.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 105` | Find a formula for the number of apples inside a square with a side length L. Iterate over the possible lengths of the square until enough apples are collected. |
Python Simple Solution-O(n),O(n) | find-numbers-with-even-number-of-digits | 0 | 1 | # Intuition\n1)Task is to find out how many given numbers has even number of digits.\n2)Check the length of the integers after converting them into string format\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nBrute Force Approach : Convert the integers into string format and then check if the length is even or odd.If the length of the string is even it contains even number of digits else odd number of digits.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findNumbers(self, nums: List[int]) -> int:\n c=0 #To count the number of numbers having even number of digits\n l=[str(i) for i in nums] #Converting into string format\n for i in l:\n if len(i)%2==0: #Checking length(or number of digits) if even or odd\n c+=1\n return c\n \n``` | 1 | Given an array `nums` of integers, return how many of them contain an **even number** of digits.
**Example 1:**
**Input:** nums = \[12,345,2,6,7896\]
**Output:** 2
**Explanation:**
12 contains 2 digits (even number of digits).
345 contains 3 digits (odd number of digits).
2 contains 1 digit (odd number of digits).
6 contains 1 digit (odd number of digits).
7896 contains 4 digits (even number of digits).
Therefore only 12 and 7896 contain an even number of digits.
**Example 2:**
**Input:** nums = \[555,901,482,1771\]
**Output:** 1
**Explanation:**
Only 1771 contains an even number of digits.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 105` | Find a formula for the number of apples inside a square with a side length L. Iterate over the possible lengths of the square until enough apples are collected. |
Python 3 lightning fast one line solution | find-numbers-with-even-number-of-digits | 0 | 1 | ```\nclass Solution:\n def findNumbers(self, nums: List[int]) -> int:\n return len([x for x in nums if len(str(x)) % 2 == 0])\n``` | 32 | Given an array `nums` of integers, return how many of them contain an **even number** of digits.
**Example 1:**
**Input:** nums = \[12,345,2,6,7896\]
**Output:** 2
**Explanation:**
12 contains 2 digits (even number of digits).
345 contains 3 digits (odd number of digits).
2 contains 1 digit (odd number of digits).
6 contains 1 digit (odd number of digits).
7896 contains 4 digits (even number of digits).
Therefore only 12 and 7896 contain an even number of digits.
**Example 2:**
**Input:** nums = \[555,901,482,1771\]
**Output:** 1
**Explanation:**
Only 1771 contains an even number of digits.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 105` | Find a formula for the number of apples inside a square with a side length L. Iterate over the possible lengths of the square until enough apples are collected. |
1 Liner using map | find-numbers-with-even-number-of-digits | 0 | 1 | # Code\n```\nclass Solution:\n def findNumbers(self, nums: List[int]) -> int:\n return sum(not n&1 for n in map(len, map(str, nums)))\n``` | 3 | Given an array `nums` of integers, return how many of them contain an **even number** of digits.
**Example 1:**
**Input:** nums = \[12,345,2,6,7896\]
**Output:** 2
**Explanation:**
12 contains 2 digits (even number of digits).
345 contains 3 digits (odd number of digits).
2 contains 1 digit (odd number of digits).
6 contains 1 digit (odd number of digits).
7896 contains 4 digits (even number of digits).
Therefore only 12 and 7896 contain an even number of digits.
**Example 2:**
**Input:** nums = \[555,901,482,1771\]
**Output:** 1
**Explanation:**
Only 1771 contains an even number of digits.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 105` | Find a formula for the number of apples inside a square with a side length L. Iterate over the possible lengths of the square until enough apples are collected. |
Easy to understand Python Solution | divide-array-in-sets-of-k-consecutive-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def isPossibleDivide(self, nums: List[int], k: int) -> bool:\n nums.sort()\n count = Counter(nums)\n\n if len(nums)%k!=0:\n return False\n\n for num in nums:\n if count[num]:\n for n in range(num,num+k):\n if n in count:\n count[n]-=1 \n else:\n return False\n \n return True\n``` | 0 | Given an array of integers `nums` and a positive integer `k`, check whether it is possible to divide this array into sets of `k` consecutive numbers.
Return `true` _if it is possible_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[1,2,3,3,4,4,5,6\], k = 4
**Output:** true
**Explanation:** Array can be divided into \[1,2,3,4\] and \[3,4,5,6\].
**Example 2:**
**Input:** nums = \[3,2,1,2,3,4,3,4,5,9,10,11\], k = 3
**Output:** true
**Explanation:** Array can be divided into \[1,2,3\] , \[2,3,4\] , \[3,4,5\] and \[9,10,11\].
**Example 3:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Explanation:** Each array should be divided in subarrays of size 3.
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `1 <= nums[i] <= 109`
**Note:** This question is the same as 846: [https://leetcode.com/problems/hand-of-straights/](https://leetcode.com/problems/hand-of-straights/) | The queries must be answered efficiently to avoid time limit exceeded verdict. Use sparse table (dynamic programming application) to travel the tree upwards in a fast way. |
Easy to understand Python Solution | divide-array-in-sets-of-k-consecutive-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def isPossibleDivide(self, nums: List[int], k: int) -> bool:\n nums.sort()\n count = Counter(nums)\n\n if len(nums)%k!=0:\n return False\n\n for num in nums:\n if count[num]:\n for n in range(num,num+k):\n if n in count:\n count[n]-=1 \n else:\n return False\n \n return True\n``` | 0 | Given a string `s` of zeros and ones, _return the maximum score after splitting the string into two **non-empty** substrings_ (i.e. **left** substring and **right** substring).
The score after splitting a string is the number of **zeros** in the **left** substring plus the number of **ones** in the **right** substring.
**Example 1:**
**Input:** s = "011101 "
**Output:** 5
**Explanation:**
All possible ways of splitting s into two non-empty substrings are:
left = "0 " and right = "11101 ", score = 1 + 4 = 5
left = "01 " and right = "1101 ", score = 1 + 3 = 4
left = "011 " and right = "101 ", score = 1 + 2 = 3
left = "0111 " and right = "01 ", score = 1 + 1 = 2
left = "01110 " and right = "1 ", score = 2 + 1 = 3
**Example 2:**
**Input:** s = "00111 "
**Output:** 5
**Explanation:** When left = "00 " and right = "111 ", we get the maximum score = 2 + 3 = 5
**Example 3:**
**Input:** s = "1111 "
**Output:** 3
**Constraints:**
* `2 <= s.length <= 500`
* The string `s` consists of characters `'0'` and `'1'` only. | If the smallest number in the possible-to-split array is V, then numbers V+1, V+2, ... V+k-1 must contain there as well. You can iteratively find k sets and remove them from array until it becomes empty. Failure to do so would mean that array is unsplittable. |
Intuitive Python solution - using template | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Approach\n\nIn short, we record each VALID substrings and their occurrence and return their max occ. \n\nUsing sliding window template to solve this problem. Having left and right index. We update the occurrence of specific substring when it meets the conditions, and we need to shrink the window when its length is in the required range.\n\n\n# Code\n```python3\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n left = 0\n result = defaultdict(int)\n freqs = defaultdict(int)\n for right, num in enumerate(s):\n freqs[num] += 1\n while (right - left + 1) >= minSize and (right - left + 1) <= maxSize:\n if len(freqs) <= maxLetters:\n result[s[left:right + 1]] += 1\n freqs[s[left]] -= 1\n if not freqs[s[left]]:\n freqs.pop(s[left])\n left += 1\n \n return max(result.values()) if result else 0\n``` | 1 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
Intuitive Python solution - using template | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Approach\n\nIn short, we record each VALID substrings and their occurrence and return their max occ. \n\nUsing sliding window template to solve this problem. Having left and right index. We update the occurrence of specific substring when it meets the conditions, and we need to shrink the window when its length is in the required range.\n\n\n# Code\n```python3\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n left = 0\n result = defaultdict(int)\n freqs = defaultdict(int)\n for right, num in enumerate(s):\n freqs[num] += 1\n while (right - left + 1) >= minSize and (right - left + 1) <= maxSize:\n if len(freqs) <= maxLetters:\n result[s[left:right + 1]] += 1\n freqs[s[left]] -= 1\n if not freqs[s[left]]:\n freqs.pop(s[left])\n left += 1\n \n return max(result.values()) if result else 0\n``` | 1 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Use hashmap, only store subs which satisfy the maxLetters | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Intuition\nFirstly, you can ignore the maxSize. Why ?\nA window with repeated maxSize will always satisfy its prefix and minSize of that repeated maxSize substring would be a prefix. If we can already satisfy the prefix so why even bother moving any further. Also, with minSize, our substring size will be small and have greater possibility of having more of it occurence as len(s)/minSize > len(s)/maxSize. So by ignoring the maxSize you can easily solve this.\nWe create a counter of substring of length minSize and we check if it satisfy the maxLetters. If that window does then we add that to our counter. \nThen the answer would be the substring with the max count. \n\n# Complexity\n- Time complexity:\nO(n * minSize)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n\n subs = {0:0}\n\n for i in range(len(s)-minSize +1):\n\n sub = s[i:i+minSize]\n set_s = set(sub)\n if len(set_s) <= maxLetters:\n subs[sub] = subs.get(sub,0) + 1\n \n return max(subs.values())\n```\n\n# using two dics and no set for each substring\n\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n\n subs = {0:0}\n #rolling sub string count\n u = {}\n\n #we get the first substring count\n for i in range(minSize-1):\n l = s[i]\n u[l] = u.get(l,0) + 1 \n\n for i in range(len(s)-minSize +1):\n \n sub= s[ i : i+minSize]\n #get the last char of current sub and add to the rolling count \n last = sub[-1]\n\n # setting the last\n u[last] = u.get(last,0) + 1\n\n # keys\n set_s = u.keys()\n \n #condition \n if len(set_s) <= maxLetters:\n subs[sub] = subs.get(sub,0) + 1\n \n #now we remove the ith letter to get the the rolling count ready for the next sub\n u[s[i]] -= 1\n if u[s[i]] == 0:\n #takes O(1)\n del u[s[i]] \n \n return max(subs.values())\n``` | 1 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
Use hashmap, only store subs which satisfy the maxLetters | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Intuition\nFirstly, you can ignore the maxSize. Why ?\nA window with repeated maxSize will always satisfy its prefix and minSize of that repeated maxSize substring would be a prefix. If we can already satisfy the prefix so why even bother moving any further. Also, with minSize, our substring size will be small and have greater possibility of having more of it occurence as len(s)/minSize > len(s)/maxSize. So by ignoring the maxSize you can easily solve this.\nWe create a counter of substring of length minSize and we check if it satisfy the maxLetters. If that window does then we add that to our counter. \nThen the answer would be the substring with the max count. \n\n# Complexity\n- Time complexity:\nO(n * minSize)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n\n subs = {0:0}\n\n for i in range(len(s)-minSize +1):\n\n sub = s[i:i+minSize]\n set_s = set(sub)\n if len(set_s) <= maxLetters:\n subs[sub] = subs.get(sub,0) + 1\n \n return max(subs.values())\n```\n\n# using two dics and no set for each substring\n\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n\n subs = {0:0}\n #rolling sub string count\n u = {}\n\n #we get the first substring count\n for i in range(minSize-1):\n l = s[i]\n u[l] = u.get(l,0) + 1 \n\n for i in range(len(s)-minSize +1):\n \n sub= s[ i : i+minSize]\n #get the last char of current sub and add to the rolling count \n last = sub[-1]\n\n # setting the last\n u[last] = u.get(last,0) + 1\n\n # keys\n set_s = u.keys()\n \n #condition \n if len(set_s) <= maxLetters:\n subs[sub] = subs.get(sub,0) + 1\n \n #now we remove the ith letter to get the the rolling count ready for the next sub\n u[s[i]] -= 1\n if u[s[i]] == 0:\n #takes O(1)\n del u[s[i]] \n \n return max(subs.values())\n``` | 1 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Python 3 || 2 lines, Counter || T/M: 100% / 29% | maximum-number-of-occurrences-of-a-substring | 0 | 1 | Another`Counter`version for consideration. Two observations:\n- The`maxSize`parameter is a "red herring." I suspect it was added to make this problem a *Medium* rather than an *Easy*. For example, if the string`"abcdef"`has five occurrences, then so does`"abc"` Thus, if `minSize = 3`, then we only need check strings of length three.\n- There are some test cases in which no substring qualifies under the`maxLetters`constraint, so using the`default`parameter in`max`takes care of that.\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n\n c = Counter([s[i:i+minSize] for i in range(len(s)-minSize+1)])\n \n return max((c[substr] for substr in c\n if len(set(substr)) <= maxLetters), default = 0)\n```\n[https://leetcode.com/problems/maximum-number-of-occurrences-of-a-substring/submissions/932085530/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 4 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
Python 3 || 2 lines, Counter || T/M: 100% / 29% | maximum-number-of-occurrences-of-a-substring | 0 | 1 | Another`Counter`version for consideration. Two observations:\n- The`maxSize`parameter is a "red herring." I suspect it was added to make this problem a *Medium* rather than an *Easy*. For example, if the string`"abcdef"`has five occurrences, then so does`"abc"` Thus, if `minSize = 3`, then we only need check strings of length three.\n- There are some test cases in which no substring qualifies under the`maxLetters`constraint, so using the`default`parameter in`max`takes care of that.\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n\n c = Counter([s[i:i+minSize] for i in range(len(s)-minSize+1)])\n \n return max((c[substr] for substr in c\n if len(set(substr)) <= maxLetters), default = 0)\n```\n[https://leetcode.com/problems/maximum-number-of-occurrences-of-a-substring/submissions/932085530/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 4 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
✅ Python Hashmap Easy Approach ✅ | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n d = defaultdict(int)\n\n for i in range(0, len(s)-minSize+1):\n if len(set((t:=s[i:minSize+i]))) <= maxLetters: d[t] += 1\n\n return max(d.values()) if d else 0\n \n``` | 1 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
✅ Python Hashmap Easy Approach ✅ | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n d = defaultdict(int)\n\n for i in range(0, len(s)-minSize+1):\n if len(set((t:=s[i:minSize+i]))) <= maxLetters: d[t] += 1\n\n return max(d.values()) if d else 0\n \n``` | 1 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
python easy approach | maximum-number-of-occurrences-of-a-substring | 0 | 1 | ```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n s1 = []\n count ={}\n while minSize <= maxSize:\n for i in range(0,len(s)):\n if (i+ minSize) <=len(s) and len(set(s[i: i+ minSize])) <= maxLetters:\n s1.append(s[i: i+ minSize])\n minSize += 1 \n for i in s1:\n count[i] = count[i] + 1 if i in count else 1 \n return max(count.values()) if count else 0\n```\nPlease do upvote if you like this solution | 4 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
python easy approach | maximum-number-of-occurrences-of-a-substring | 0 | 1 | ```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n s1 = []\n count ={}\n while minSize <= maxSize:\n for i in range(0,len(s)):\n if (i+ minSize) <=len(s) and len(set(s[i: i+ minSize])) <= maxLetters:\n s1.append(s[i: i+ minSize])\n minSize += 1 \n for i in s1:\n count[i] = count[i] + 1 if i in count else 1 \n return max(count.values()) if count else 0\n```\nPlease do upvote if you like this solution | 4 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
[Python] O(n) simple solution using counter. | maximum-number-of-occurrences-of-a-substring | 0 | 1 | ```python\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n # count frequency of characters\n count = collections.Counter()\n \n # Check only for minSize\n for i in range(len(s) - minSize + 1):\n t = s[i : i+minSize]\n if len(set(t)) <= maxLetters:\n count[t] += 1\n \n return max(count.values()) if count else 0\n\t\t\n``` | 9 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
[Python] O(n) simple solution using counter. | maximum-number-of-occurrences-of-a-substring | 0 | 1 | ```python\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n # count frequency of characters\n count = collections.Counter()\n \n # Check only for minSize\n for i in range(len(s) - minSize + 1):\n t = s[i : i+minSize]\n if len(set(t)) <= maxLetters:\n count[t] += 1\n \n return max(count.values()) if count else 0\n\t\t\n``` | 9 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
You just have to focus on minSize | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Intuition\nUnderstand there is no need to check for maxSize.\n\n# Approach\nCheck for the occurance on minSize and add them to dictionary. Finally return the max value.\n\n# Complexity\n- Time complexity:\n The time complexity of this solution be O(N * K / M) where N = input size ; M = minSize and K = size of the dictionary. Here I\'m talking about average case. but in (worst case minSize becomes 1) then it will become O(N * K). **Correct me if wrong**\n\n- Space complexity:\n the space complexity be O(K); where k is the size of dictionary, which in worst case be equal to size of input[O(N)] but in average case will be less than O(len(s) - minSize + 1).**Correct me if wrong**\n\n# Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n \n count = collections.defaultdict(int)\n\n for i in range(len(s) - minSize + 1):\n substr = s[i:i+minSize]\n\n if substr in count:\n count[substr] += 1\n\n else:\n if len(set(substr)) <= maxLetters:\n count[substr] += 1\n \n return max(count.values()) if count else 0 \n\n\n \n \n \n``` | 0 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
You just have to focus on minSize | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Intuition\nUnderstand there is no need to check for maxSize.\n\n# Approach\nCheck for the occurance on minSize and add them to dictionary. Finally return the max value.\n\n# Complexity\n- Time complexity:\n The time complexity of this solution be O(N * K / M) where N = input size ; M = minSize and K = size of the dictionary. Here I\'m talking about average case. but in (worst case minSize becomes 1) then it will become O(N * K). **Correct me if wrong**\n\n- Space complexity:\n the space complexity be O(K); where k is the size of dictionary, which in worst case be equal to size of input[O(N)] but in average case will be less than O(len(s) - minSize + 1).**Correct me if wrong**\n\n# Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n \n count = collections.defaultdict(int)\n\n for i in range(len(s) - minSize + 1):\n substr = s[i:i+minSize]\n\n if substr in count:\n count[substr] += 1\n\n else:\n if len(set(substr)) <= maxLetters:\n count[substr] += 1\n \n return max(count.values()) if count else 0 \n\n\n \n \n \n``` | 0 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Python Easy to Understand and Efficient Sliding Window | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n frequency, visited = {}, {}\n for i in range(minSize):\n frequency[s[i]] = frequency.get(s[i], 0) + 1\n if len(frequency) <= maxLetters: visited[s[:minSize]] = 1\n l = 0\n for r in range(minSize, len(s)):\n frequency[s[r]] = frequency.get(s[r], 0) + 1\n frequency[s[l]] -= 1\n if frequency[s[l]] == 0:\n del frequency[s[l]]\n l += 1\n if len(frequency) <= maxLetters:\n visited[s[l:r + 1]] = visited.get(s[l:r + 1], 0) + 1\n return max(visited.values()) if len(visited) > 0 else 0\n \n\n \n\n \n``` | 0 | Given a string `s`, return the maximum number of ocurrences of **any** substring under the following rules:
* The number of unique characters in the substring must be less than or equal to `maxLetters`.
* The substring size must be between `minSize` and `maxSize` inclusive.
**Example 1:**
**Input:** s = "aababcaab ", maxLetters = 2, minSize = 3, maxSize = 4
**Output:** 2
**Explanation:** Substring "aab " has 2 ocurrences in the original string.
It satisfies the conditions, 2 unique letters and size 3 (between minSize and maxSize).
**Example 2:**
**Input:** s = "aaaa ", maxLetters = 1, minSize = 3, maxSize = 3
**Output:** 2
**Explanation:** Substring "aaa " occur 2 times in the string. It can overlap.
**Constraints:**
* `1 <= s.length <= 105`
* `1 <= maxLetters <= 26`
* `1 <= minSize <= maxSize <= min(26, s.length)`
* `s` consists of only lowercase English letters. | Count the frequency of letters in the given string. Find the letter than can make the minimum number of instances of the word "balloon". |
Python Easy to Understand and Efficient Sliding Window | maximum-number-of-occurrences-of-a-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:\n frequency, visited = {}, {}\n for i in range(minSize):\n frequency[s[i]] = frequency.get(s[i], 0) + 1\n if len(frequency) <= maxLetters: visited[s[:minSize]] = 1\n l = 0\n for r in range(minSize, len(s)):\n frequency[s[r]] = frequency.get(s[r], 0) + 1\n frequency[s[l]] -= 1\n if frequency[s[l]] == 0:\n del frequency[s[l]]\n l += 1\n if len(frequency) <= maxLetters:\n visited[s[l:r + 1]] = visited.get(s[l:r + 1], 0) + 1\n return max(visited.values()) if len(visited) > 0 else 0\n \n\n \n\n \n``` | 0 | There are several cards **arranged in a row**, and each card has an associated number of points. The points are given in the integer array `cardPoints`.
In one step, you can take one card from the beginning or from the end of the row. You have to take exactly `k` cards.
Your score is the sum of the points of the cards you have taken.
Given the integer array `cardPoints` and the integer `k`, return the _maximum score_ you can obtain.
**Example 1:**
**Input:** cardPoints = \[1,2,3,4,5,6,1\], k = 3
**Output:** 12
**Explanation:** After the first step, your score will always be 1. However, choosing the rightmost card first will maximize your total score. The optimal strategy is to take the three cards on the right, giving a final score of 1 + 6 + 5 = 12.
**Example 2:**
**Input:** cardPoints = \[2,2,2\], k = 2
**Output:** 4
**Explanation:** Regardless of which two cards you take, your score will always be 4.
**Example 3:**
**Input:** cardPoints = \[9,7,7,9,7,7,9\], k = 7
**Output:** 55
**Explanation:** You have to take all the cards. Your score is the sum of points of all cards.
**Constraints:**
* `1 <= cardPoints.length <= 105`
* `1 <= cardPoints[i] <= 104`
* `1 <= k <= cardPoints.length`
1\. The number of unique characters in the substring must not exceed k. 2. The substring must not contain more than one instance of the same character. 3. The length of the substring must not exceed the length of the original string. | Check out the constraints, (maxSize <=26). This means you can explore all substrings in O(n * 26). Find the Maximum Number of Occurrences of a Substring with bruteforce. |
Python, C++ Solution || modified BFS Solution easy to understand | maximum-candies-you-can-get-from-boxes | 0 | 1 | # Intuition\nWe check boxes in queue once every iteration, if no box get opened, then we finished the BFS.\n\nIn BFS, if a box is open, we do 4 things.\n1. opened += 1 to track if there has boxes opened or not in a iteration.\n2. add candy to ans.\n3. change the status of box to open if there\'s the key.\n4. append the boxes(from containedBoxes) into queue.\n# Code\n```Python []\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n ans = 0\n q = deque()\n\n for box in initialBoxes:\n q.append(box)\n \n while q:\n opened = 0\n n = len(q)\n for _ in range(n):\n box = q.popleft()\n if status[box] == 0:\n q.append(box)\n else:\n opened += 1\n ans += candies[box]\n for key in keys[box]:\n status[key] = 1\n for insideBox in containedBoxes[box]:\n q.append(insideBox)\n \n if opened == 0:\n break\n \n return ans\n \n\n```\n```C++ []\nclass Solution {\npublic:\n int maxCandies(vector<int>& status, vector<int>& candies, vector<vector<int>>& keys, vector<vector<int>>& containedBoxes, vector<int>& initialBoxes) {\n int ans = 0;\n queue<int> q;\n for (int box : initialBoxes) {\n q.push(box);\n }\n\n while (!q.empty()) {\n int opened = 0, n = q.size();\n while (n--) {\n int box = q.front(); q.pop();\n if (status[box] == 0) {\n q.push(box);\n } else {\n opened++;\n ans += candies[box];\n for (int key : keys[box]) {\n status[key] = 1;\n }\n for (int insideBox : containedBoxes[box]) {\n q.push(insideBox);\n }\n }\n }\n if (opened == 0) {\n break;\n }\n }\n\n return ans;\n }\n};\n``` | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Python, C++ Solution || modified BFS Solution easy to understand | maximum-candies-you-can-get-from-boxes | 0 | 1 | # Intuition\nWe check boxes in queue once every iteration, if no box get opened, then we finished the BFS.\n\nIn BFS, if a box is open, we do 4 things.\n1. opened += 1 to track if there has boxes opened or not in a iteration.\n2. add candy to ans.\n3. change the status of box to open if there\'s the key.\n4. append the boxes(from containedBoxes) into queue.\n# Code\n```Python []\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n ans = 0\n q = deque()\n\n for box in initialBoxes:\n q.append(box)\n \n while q:\n opened = 0\n n = len(q)\n for _ in range(n):\n box = q.popleft()\n if status[box] == 0:\n q.append(box)\n else:\n opened += 1\n ans += candies[box]\n for key in keys[box]:\n status[key] = 1\n for insideBox in containedBoxes[box]:\n q.append(insideBox)\n \n if opened == 0:\n break\n \n return ans\n \n\n```\n```C++ []\nclass Solution {\npublic:\n int maxCandies(vector<int>& status, vector<int>& candies, vector<vector<int>>& keys, vector<vector<int>>& containedBoxes, vector<int>& initialBoxes) {\n int ans = 0;\n queue<int> q;\n for (int box : initialBoxes) {\n q.push(box);\n }\n\n while (!q.empty()) {\n int opened = 0, n = q.size();\n while (n--) {\n int box = q.front(); q.pop();\n if (status[box] == 0) {\n q.push(box);\n } else {\n opened++;\n ans += candies[box];\n for (int key : keys[box]) {\n status[key] = 1;\n }\n for (int insideBox : containedBoxes[box]) {\n q.push(insideBox);\n }\n }\n }\n if (opened == 0) {\n break;\n }\n }\n\n return ans;\n }\n};\n``` | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
Python 3: Simple BFS | maximum-candies-you-can-get-from-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n \n # starting from the initial boxes\n # open? open the boxes that are open\n\n # for each state\n # start openeing boxes that are open (status == 0)\n # get the candies\n # get the keys\n \n # for the closed boxes\n # check if we have keys to the boxes\n # give two chances to check if we have keys\n n = len(status)\n key_col = set() # keys collected\n box_col = set()\n res = 0 # candies collected\n q = deque()\n opened = [False] * n\n for box in initialBoxes:\n box_col.add(box)\n if status[box] == 1:\n q.append(box)\n \n while q:\n # get the boxes (we have key or was open) and have the box\n box = q.popleft()\n opened[box] = True # mark opened as true\n res += candies[box]\n\n # update the boxes we collected\n for new_box in containedBoxes[box]:\n box_col.add(new_box)\n\n # visit the boxes that we originally had the keys and we can directly open\n if not opened[new_box] and (new_box in key_col or status[new_box] == 1):\n opened[new_box] = True\n q.append(new_box)\n\n # update the keys we collected\n for new_key in keys[box]:\n key_col.add(new_key)\n \n # visit the box that we originally had the box and wasn\'t opened before\n if not opened[new_key] and new_key in box_col and status[new_key] != 1:\n opened[new_key] = True\n q.append(new_key)\n return res\n\n``` | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Python 3: Simple BFS | maximum-candies-you-can-get-from-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n \n # starting from the initial boxes\n # open? open the boxes that are open\n\n # for each state\n # start openeing boxes that are open (status == 0)\n # get the candies\n # get the keys\n \n # for the closed boxes\n # check if we have keys to the boxes\n # give two chances to check if we have keys\n n = len(status)\n key_col = set() # keys collected\n box_col = set()\n res = 0 # candies collected\n q = deque()\n opened = [False] * n\n for box in initialBoxes:\n box_col.add(box)\n if status[box] == 1:\n q.append(box)\n \n while q:\n # get the boxes (we have key or was open) and have the box\n box = q.popleft()\n opened[box] = True # mark opened as true\n res += candies[box]\n\n # update the boxes we collected\n for new_box in containedBoxes[box]:\n box_col.add(new_box)\n\n # visit the boxes that we originally had the keys and we can directly open\n if not opened[new_box] and (new_box in key_col or status[new_box] == 1):\n opened[new_box] = True\n q.append(new_box)\n\n # update the keys we collected\n for new_key in keys[box]:\n key_col.add(new_key)\n \n # visit the box that we originally had the box and wasn\'t opened before\n if not opened[new_key] and new_key in box_col and status[new_key] != 1:\n opened[new_key] = True\n q.append(new_key)\n return res\n\n``` | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
Shortest BFS Code With Explanation | maximum-candies-you-can-get-from-boxes | 0 | 1 | 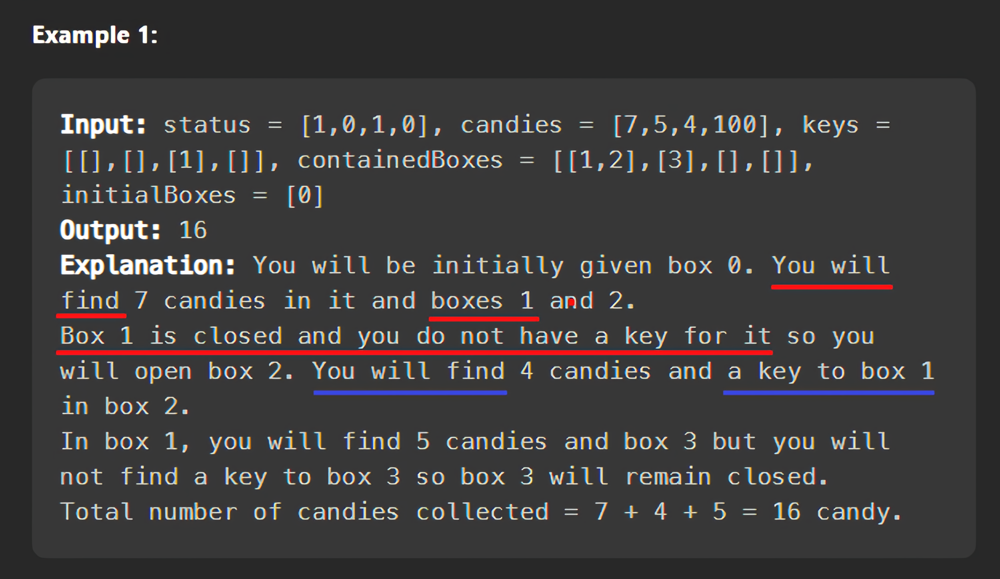\n\n```\nBox 1 initially was closed(0), but later when we found a key to open box 1 we opened it.\n\nThat means if we find hundred boxes which is closed but later when we found keys to open those\nhundred boxes, we open them then by going back to those boxes.\n```\n```\nThis is a simulation problem. As long as you can open a box, open it.\nWhen you open it: you get more keys and more boxes.\n\n```\n### Implementation\n```\nSo why not we go through \'keys\' and open every boxes at very first as if we find keys for those\nclosed boxes later, we\'ve to come back to those closed boxes to open them which is same as \nopening those closed boxes with keys at very first if keys for them available.\n\nNow riding on a Elon Mask rocket we just have go through every box (starting from initialBoxes)\nwhose status[i] is 1 and add the candie.\n```\n\n```CPP []\nclass Solution {\npublic:\n int maxCandies(vector<int>& status, vector<int>& candies, vector<vector<int>>& keys, vector<vector<int>>& containedBoxes, vector<int>& initialBoxes) \n {\n for(auto &arr: keys) // opened every box with available keys\n for(auto &k: arr)\n status[k] = 1;\n \n queue<int> q;\n for(auto &i: initialBoxes)\n if(status[i] == 1) q.push(i); // pushed only \'opened\' boxes\n int candie = 0, i;\n\n while(!q.empty()) // untill queue runs out all the \'opened\' boxes\n {\n i = q.front(); q.pop();\n candie += candies[i];\n for(auto &b: containedBoxes[i])\n if(status[b] == 1) q.push(b);\n }\n\n return candie;\n }\n};\n```\n```Python []\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n for k in chain(*keys): # opened every box with available keys\n status[k] = 1\n q, candie = deque([i for i in initialBoxes if status[i] == 1]), 0 # pushed only \'open\' boxes in q\n\n while q: # untill queue runs out all the \'opened\' boxes\n i = q.popleft()\n candie += candies[i]\n for b in containedBoxes[i]:\n if status[b] == 1:\n q.append(b)\n\n return candie\n```\n```\nTime complexity : O(n) probably\nSpace complexity : O(n) as we are storing n values in queue\n```\n\n### If the post was helpful an upvote will really be appreciated. Thank You. | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Shortest BFS Code With Explanation | maximum-candies-you-can-get-from-boxes | 0 | 1 | \n\n```\nBox 1 initially was closed(0), but later when we found a key to open box 1 we opened it.\n\nThat means if we find hundred boxes which is closed but later when we found keys to open those\nhundred boxes, we open them then by going back to those boxes.\n```\n```\nThis is a simulation problem. As long as you can open a box, open it.\nWhen you open it: you get more keys and more boxes.\n\n```\n### Implementation\n```\nSo why not we go through \'keys\' and open every boxes at very first as if we find keys for those\nclosed boxes later, we\'ve to come back to those closed boxes to open them which is same as \nopening those closed boxes with keys at very first if keys for them available.\n\nNow riding on a Elon Mask rocket we just have go through every box (starting from initialBoxes)\nwhose status[i] is 1 and add the candie.\n```\n\n```CPP []\nclass Solution {\npublic:\n int maxCandies(vector<int>& status, vector<int>& candies, vector<vector<int>>& keys, vector<vector<int>>& containedBoxes, vector<int>& initialBoxes) \n {\n for(auto &arr: keys) // opened every box with available keys\n for(auto &k: arr)\n status[k] = 1;\n \n queue<int> q;\n for(auto &i: initialBoxes)\n if(status[i] == 1) q.push(i); // pushed only \'opened\' boxes\n int candie = 0, i;\n\n while(!q.empty()) // untill queue runs out all the \'opened\' boxes\n {\n i = q.front(); q.pop();\n candie += candies[i];\n for(auto &b: containedBoxes[i])\n if(status[b] == 1) q.push(b);\n }\n\n return candie;\n }\n};\n```\n```Python []\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n for k in chain(*keys): # opened every box with available keys\n status[k] = 1\n q, candie = deque([i for i in initialBoxes if status[i] == 1]), 0 # pushed only \'open\' boxes in q\n\n while q: # untill queue runs out all the \'opened\' boxes\n i = q.popleft()\n candie += candies[i]\n for b in containedBoxes[i]:\n if status[b] == 1:\n q.append(b)\n\n return candie\n```\n```\nTime complexity : O(n) probably\nSpace complexity : O(n) as we are storing n values in queue\n```\n\n### If the post was helpful an upvote will really be appreciated. Thank You. | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
Simple Python3 BFS | maximum-candies-you-can-get-from-boxes | 0 | 1 | ```\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n queue = [i for i in initialBoxes if status[i] == 1]\n visited = set(queue)\n res = 0\n #haskeys = set([])\n nokeys = set([i for i in initialBoxes if status[i] == 0])\n for box in queue:\n res += candies[box]\n for key in keys[box]:\n status[key] = 1\n for nextbox in containedBoxes[box]:\n if nextbox not in visited:\n if status[nextbox] == 1:\n queue.append(nextbox)\n visited.add(nextbox)\n else:\n nokeys.add(nextbox)\n todelete = []\n for nextbox in nokeys:\n if status[nextbox] == 1:\n queue.append(nextbox)\n visited.add(nextbox) \n todelete.append(nextbox)\n for t in todelete:\n nokeys.remove(t)\n return res\n``` | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Simple Python3 BFS | maximum-candies-you-can-get-from-boxes | 0 | 1 | ```\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n queue = [i for i in initialBoxes if status[i] == 1]\n visited = set(queue)\n res = 0\n #haskeys = set([])\n nokeys = set([i for i in initialBoxes if status[i] == 0])\n for box in queue:\n res += candies[box]\n for key in keys[box]:\n status[key] = 1\n for nextbox in containedBoxes[box]:\n if nextbox not in visited:\n if status[nextbox] == 1:\n queue.append(nextbox)\n visited.add(nextbox)\n else:\n nokeys.add(nextbox)\n todelete = []\n for nextbox in nokeys:\n if status[nextbox] == 1:\n queue.append(nextbox)\n visited.add(nextbox) \n todelete.append(nextbox)\n for t in todelete:\n nokeys.remove(t)\n return res\n``` | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
Solution | maximum-candies-you-can-get-from-boxes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxCandies(vector<int>& status, vector<int>& candies, vector<vector<int>>& keys, vector<vector<int>>& containedBoxes, vector<int>& initialBoxes) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n int n = candies.size(), ans = 0;\n queue<int> q;\n\n for(int i: initialBoxes) q.push(i);\n\n while(!q.empty()){\n int top = q.front();\n q.pop();\n if(status[top]==0 && q.size()>0){\n q.push(top);\n continue;\n }\n else if (status[top]==0 && q.size()==0) return ans;\n else{\n ans += candies[top];\n for(int it: containedBoxes[top]) q.push(it);\n\n for(int it: keys[top]) status[it]=1;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n \n q = deque(initialBoxes)\n visited = set()\n res = 0\n while q:\n itr, opened = len(q), False\n while (itr):\n itr -= 1\n v = q.popleft()\n if status[v]:\n \n opened = True\n res += candies[v]\n visited.add(v)\n \n for x in keys[v]:\n status[x] = 1\n \n for x in containedBoxes[v]:\n if x not in visited:\n q.append(x)\n \n elif v not in visited:\n q.append(v)\n if not opened:\n return res\n return res\n```\n\n```Java []\nimport java.util.*;\n\nclass Solution {\n private int collected = 0;\n \n private void addKeysFromBoxes(int[] status, int[][] keys, int[] boxes) {\n for (int box : boxes) {\n for (int key : keys[box]) {\n status[key] = 1;\n }\n }\n }\n private void openBoxes(Queue<Integer> q, boolean[] visited, int[] status, int[] candies, int[] boxes) {\n for (int box : boxes) {\n if (!visited[box] && status[box] == 1) {\n q.offer(box);\n visited[box] = true;\n collected += candies[box];\n }\n }\n }\n public int maxCandies(int[] status, int[] candies, int[][] keys, int[][] containedBoxes, int[] initialBoxes) {\n Queue<Integer> q = new LinkedList<>();\n boolean[] visited = new boolean[status.length];\n \n addKeysFromBoxes(status, keys, initialBoxes);\n openBoxes(q, visited, status, candies, initialBoxes);\n \n while (!q.isEmpty()) {\n int box = q.poll();\n addKeysFromBoxes(status, keys, containedBoxes[box]);\n openBoxes(q, visited, status, candies, containedBoxes[box]);\n }\n return collected;\n }\n}\n``` | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Solution | maximum-candies-you-can-get-from-boxes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxCandies(vector<int>& status, vector<int>& candies, vector<vector<int>>& keys, vector<vector<int>>& containedBoxes, vector<int>& initialBoxes) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n int n = candies.size(), ans = 0;\n queue<int> q;\n\n for(int i: initialBoxes) q.push(i);\n\n while(!q.empty()){\n int top = q.front();\n q.pop();\n if(status[top]==0 && q.size()>0){\n q.push(top);\n continue;\n }\n else if (status[top]==0 && q.size()==0) return ans;\n else{\n ans += candies[top];\n for(int it: containedBoxes[top]) q.push(it);\n\n for(int it: keys[top]) status[it]=1;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n \n q = deque(initialBoxes)\n visited = set()\n res = 0\n while q:\n itr, opened = len(q), False\n while (itr):\n itr -= 1\n v = q.popleft()\n if status[v]:\n \n opened = True\n res += candies[v]\n visited.add(v)\n \n for x in keys[v]:\n status[x] = 1\n \n for x in containedBoxes[v]:\n if x not in visited:\n q.append(x)\n \n elif v not in visited:\n q.append(v)\n if not opened:\n return res\n return res\n```\n\n```Java []\nimport java.util.*;\n\nclass Solution {\n private int collected = 0;\n \n private void addKeysFromBoxes(int[] status, int[][] keys, int[] boxes) {\n for (int box : boxes) {\n for (int key : keys[box]) {\n status[key] = 1;\n }\n }\n }\n private void openBoxes(Queue<Integer> q, boolean[] visited, int[] status, int[] candies, int[] boxes) {\n for (int box : boxes) {\n if (!visited[box] && status[box] == 1) {\n q.offer(box);\n visited[box] = true;\n collected += candies[box];\n }\n }\n }\n public int maxCandies(int[] status, int[] candies, int[][] keys, int[][] containedBoxes, int[] initialBoxes) {\n Queue<Integer> q = new LinkedList<>();\n boolean[] visited = new boolean[status.length];\n \n addKeysFromBoxes(status, keys, initialBoxes);\n openBoxes(q, visited, status, candies, initialBoxes);\n \n while (!q.isEmpty()) {\n int box = q.poll();\n addKeysFromBoxes(status, keys, containedBoxes[box]);\n openBoxes(q, visited, status, candies, containedBoxes[box]);\n }\n return collected;\n }\n}\n``` | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
Deque | Fast | Python Solution | maximum-candies-you-can-get-from-boxes | 0 | 1 | \n# Code\n```\nfrom collections import deque\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n \n q = deque(initialBoxes)\n visited = set()\n res = 0\n while q:\n itr, opened = len(q), False # To detect cycle\n opened = False\n while (itr):\n itr -= 1\n v = q.popleft()\n if status[v]: # Open box, (key is available or is open)\n \n opened = True\n res += candies[v]\n visited.add(v)\n \n for x in keys[v]:\n status[x] = 1\n \n for x in containedBoxes[v]:\n if x not in visited:\n q.append(x)\n \n elif v not in visited: # Open when key is available\n q.append(v)\n if not opened:\n return res # Exit cycle detected\n return res\n``` | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Deque | Fast | Python Solution | maximum-candies-you-can-get-from-boxes | 0 | 1 | \n# Code\n```\nfrom collections import deque\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n \n q = deque(initialBoxes)\n visited = set()\n res = 0\n while q:\n itr, opened = len(q), False # To detect cycle\n opened = False\n while (itr):\n itr -= 1\n v = q.popleft()\n if status[v]: # Open box, (key is available or is open)\n \n opened = True\n res += candies[v]\n visited.add(v)\n \n for x in keys[v]:\n status[x] = 1\n \n for x in containedBoxes[v]:\n if x not in visited:\n q.append(x)\n \n elif v not in visited: # Open when key is available\n q.append(v)\n if not opened:\n return res # Exit cycle detected\n return res\n``` | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
Plain BFS Solution. 80.90% | maximum-candies-you-can-get-from-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n Problem is SIMPLE BFS with just one addition of keys and that works based on few conditions.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1) If we get any box with locked status we can store that box for future in case we might be able to unlock the box.\n 2) If we get the key just unlock the box for future use.\n\n# Complexity\n- Time complexity: $$O(V + E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n vis = set()\n noSet = set()\n totalCandies = 0\n for b in initialBoxes:\n if b not in vis and status[b]:\n que = [b]\n vis.add(b)\n while que:\n node = que.pop(0)\n totalCandies += candies[node]\n for k in keys[node]:\n if k in noSet and not status[k]:\n status[k] = 1\n que.append(k)\n noSet.discard(k)\n elif not status[k]:\n status[k] = 1\n for con in containedBoxes[node]:\n if con not in vis and status[con]:\n que.append(con)\n elif con not in vis and not status[con]:\n noSet.add(con)\n elif b not in vis and not status[b]:\n noSet.add(b)\n return totalCandies\n \n\n``` | 0 | You have `n` boxes labeled from `0` to `n - 1`. You are given four arrays: `status`, `candies`, `keys`, and `containedBoxes` where:
* `status[i]` is `1` if the `ith` box is open and `0` if the `ith` box is closed,
* `candies[i]` is the number of candies in the `ith` box,
* `keys[i]` is a list of the labels of the boxes you can open after opening the `ith` box.
* `containedBoxes[i]` is a list of the boxes you found inside the `ith` box.
You are given an integer array `initialBoxes` that contains the labels of the boxes you initially have. You can take all the candies in **any open box** and you can use the keys in it to open new boxes and you also can use the boxes you find in it.
Return _the maximum number of candies you can get following the rules above_.
**Example 1:**
**Input:** status = \[1,0,1,0\], candies = \[7,5,4,100\], keys = \[\[\],\[\],\[1\],\[\]\], containedBoxes = \[\[1,2\],\[3\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 16
**Explanation:** You will be initially given box 0. You will find 7 candies in it and boxes 1 and 2.
Box 1 is closed and you do not have a key for it so you will open box 2. You will find 4 candies and a key to box 1 in box 2.
In box 1, you will find 5 candies and box 3 but you will not find a key to box 3 so box 3 will remain closed.
Total number of candies collected = 7 + 4 + 5 = 16 candy.
**Example 2:**
**Input:** status = \[1,0,0,0,0,0\], candies = \[1,1,1,1,1,1\], keys = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], containedBoxes = \[\[1,2,3,4,5\],\[\],\[\],\[\],\[\],\[\]\], initialBoxes = \[0\]
**Output:** 6
**Explanation:** You have initially box 0. Opening it you can find boxes 1,2,3,4 and 5 and their keys.
The total number of candies will be 6.
**Constraints:**
* `n == status.length == candies.length == keys.length == containedBoxes.length`
* `1 <= n <= 1000`
* `status[i]` is either `0` or `1`.
* `1 <= candies[i] <= 1000`
* `0 <= keys[i].length <= n`
* `0 <= keys[i][j] < n`
* All values of `keys[i]` are **unique**.
* `0 <= containedBoxes[i].length <= n`
* `0 <= containedBoxes[i][j] < n`
* All values of `containedBoxes[i]` are unique.
* Each box is contained in one box at most.
* `0 <= initialBoxes.length <= n`
* `0 <= initialBoxes[i] < n` | Find all brackets in the string. Does the order of the reverse matter ? The order does not matter. |
Plain BFS Solution. 80.90% | maximum-candies-you-can-get-from-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n Problem is SIMPLE BFS with just one addition of keys and that works based on few conditions.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1) If we get any box with locked status we can store that box for future in case we might be able to unlock the box.\n 2) If we get the key just unlock the box for future use.\n\n# Complexity\n- Time complexity: $$O(V + E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:\n vis = set()\n noSet = set()\n totalCandies = 0\n for b in initialBoxes:\n if b not in vis and status[b]:\n que = [b]\n vis.add(b)\n while que:\n node = que.pop(0)\n totalCandies += candies[node]\n for k in keys[node]:\n if k in noSet and not status[k]:\n status[k] = 1\n que.append(k)\n noSet.discard(k)\n elif not status[k]:\n status[k] = 1\n for con in containedBoxes[node]:\n if con not in vis and status[con]:\n que.append(con)\n elif con not in vis and not status[con]:\n noSet.add(con)\n elif b not in vis and not status[b]:\n noSet.add(b)\n return totalCandies\n \n\n``` | 0 | Given a 2D integer array `nums`, return _all elements of_ `nums` _in diagonal order as shown in the below images_.
**Example 1:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,4,2,7,5,3,8,6,9\]
**Example 2:**
**Input:** nums = \[\[1,2,3,4,5\],\[6,7\],\[8\],\[9,10,11\],\[12,13,14,15,16\]\]
**Output:** \[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i].length <= 105`
* `1 <= sum(nums[i].length) <= 105`
* `1 <= nums[i][j] <= 105` | Use Breadth First Search (BFS) to traverse all possible boxes you can open. Only push to the queue the boxes the you have with their keys. |
real in place solution on python | replace-elements-with-greatest-element-on-right-side | 0 | 1 | # Approach\n1. for comfortable we need to start for the last elem, but we musn\'t use reversed or [::-1] becouse its create a new list. its not in place. We should not create any structure.\n2. We need to start loop for the last element.\n3. After that we comparable number with temporary max\n4. if number bigger than maximum, we change our maximum to this number. in first number it always well be -1 besouse we initialaized our maximum like -1\n5. m, arr[i] = arr[i]\nin this, we change maximum to our number if number is bigger than maximum, and, we change number to maximum. We do this becouse we need to change all on the right side form bigest number i.e. we change max and current number in 1 line\n6. if max bigger that current number we change that number to max\n7. return our arry\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def replaceElements(self, arr: List[int]) -> List[int]:\n m = -1\n for i in range(len(arr)-1,-1,-1):\n if arr[i]>m :\n m, arr[i] = arr[i], m\n else:\n arr[i] = m\n return arr\n \n \n# 1234\n# 4321\n# 1111\n# 14,33,2,3,6\n``` | 2 | Given an array `arr`, replace every element in that array with the greatest element among the elements to its right, and replace the last element with `-1`.
After doing so, return the array.
**Example 1:**
**Input:** arr = \[17,18,5,4,6,1\]
**Output:** \[18,6,6,6,1,-1\]
**Explanation:**
- index 0 --> the greatest element to the right of index 0 is index 1 (18).
- index 1 --> the greatest element to the right of index 1 is index 4 (6).
- index 2 --> the greatest element to the right of index 2 is index 4 (6).
- index 3 --> the greatest element to the right of index 3 is index 4 (6).
- index 4 --> the greatest element to the right of index 4 is index 5 (1).
- index 5 --> there are no elements to the right of index 5, so we put -1.
**Example 2:**
**Input:** arr = \[400\]
**Output:** \[-1\]
**Explanation:** There are no elements to the right of index 0.
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i] <= 105` | How to solve the problem for k=1 ? Use Kadane's algorithm for k=1. What are the possible cases for the answer ? The answer is the maximum between, the answer for k=1, the sum of the whole array multiplied by k, or the maximum suffix sum plus the maximum prefix sum plus (k-2) multiplied by the whole array sum for k > 1. |
Easy to Understand | Simple | Python Solution | replace-elements-with-greatest-element-on-right-side | 0 | 1 | ```\ndef replaceElements(self, arr: List[int]) -> List[int]:\n m = -1\n i = len(arr) -1 \n while i >= 0:\n temp = arr[i]\n arr[i] = m\n if temp > m:\n m = temp\n i-= 1\n return arr\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 47 | Given an array `arr`, replace every element in that array with the greatest element among the elements to its right, and replace the last element with `-1`.
After doing so, return the array.
**Example 1:**
**Input:** arr = \[17,18,5,4,6,1\]
**Output:** \[18,6,6,6,1,-1\]
**Explanation:**
- index 0 --> the greatest element to the right of index 0 is index 1 (18).
- index 1 --> the greatest element to the right of index 1 is index 4 (6).
- index 2 --> the greatest element to the right of index 2 is index 4 (6).
- index 3 --> the greatest element to the right of index 3 is index 4 (6).
- index 4 --> the greatest element to the right of index 4 is index 5 (1).
- index 5 --> there are no elements to the right of index 5, so we put -1.
**Example 2:**
**Input:** arr = \[400\]
**Output:** \[-1\]
**Explanation:** There are no elements to the right of index 0.
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i] <= 105` | How to solve the problem for k=1 ? Use Kadane's algorithm for k=1. What are the possible cases for the answer ? The answer is the maximum between, the answer for k=1, the sum of the whole array multiplied by k, or the maximum suffix sum plus the maximum prefix sum plus (k-2) multiplied by the whole array sum for k > 1. |
Python 3, simple For loop for suffix max approach, time complexity: O(n), Space complexity: O(1) | replace-elements-with-greatest-element-on-right-side | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt can be solved by suffix sum approach\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere we are storing previous maxvalue and replacing array element with the same if it is not last element. I am using 2 variables to determine if the element is grater than the maxele before changing its value to previous max element.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def replaceElements(self, arr: List[int]) -> List[int]:\n #ans = [0]*len(arr)\n maxele = -1\n for i in range(len(arr)-1,-1,-1):\n temp = maxele\n maxele = max(maxele,arr[i])\n arr[i] = temp\n \n return arr\n\n\n\n``` | 2 | Given an array `arr`, replace every element in that array with the greatest element among the elements to its right, and replace the last element with `-1`.
After doing so, return the array.
**Example 1:**
**Input:** arr = \[17,18,5,4,6,1\]
**Output:** \[18,6,6,6,1,-1\]
**Explanation:**
- index 0 --> the greatest element to the right of index 0 is index 1 (18).
- index 1 --> the greatest element to the right of index 1 is index 4 (6).
- index 2 --> the greatest element to the right of index 2 is index 4 (6).
- index 3 --> the greatest element to the right of index 3 is index 4 (6).
- index 4 --> the greatest element to the right of index 4 is index 5 (1).
- index 5 --> there are no elements to the right of index 5, so we put -1.
**Example 2:**
**Input:** arr = \[400\]
**Output:** \[-1\]
**Explanation:** There are no elements to the right of index 0.
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i] <= 105` | How to solve the problem for k=1 ? Use Kadane's algorithm for k=1. What are the possible cases for the answer ? The answer is the maximum between, the answer for k=1, the sum of the whole array multiplied by k, or the maximum suffix sum plus the maximum prefix sum plus (k-2) multiplied by the whole array sum for k > 1. |
Easy Python Solution | replace-elements-with-greatest-element-on-right-side | 0 | 1 | ```\nclass Solution:\n def replaceElements(self, arr: List[int]) -> List[int]:\n maxi=-1\n n=len(arr)\n for i in range(n-1, -1, -1):\n temp=arr[i]\n arr[i]=maxi\n maxi=max(maxi, temp)\n return arr\n``` | 1 | Given an array `arr`, replace every element in that array with the greatest element among the elements to its right, and replace the last element with `-1`.
After doing so, return the array.
**Example 1:**
**Input:** arr = \[17,18,5,4,6,1\]
**Output:** \[18,6,6,6,1,-1\]
**Explanation:**
- index 0 --> the greatest element to the right of index 0 is index 1 (18).
- index 1 --> the greatest element to the right of index 1 is index 4 (6).
- index 2 --> the greatest element to the right of index 2 is index 4 (6).
- index 3 --> the greatest element to the right of index 3 is index 4 (6).
- index 4 --> the greatest element to the right of index 4 is index 5 (1).
- index 5 --> there are no elements to the right of index 5, so we put -1.
**Example 2:**
**Input:** arr = \[400\]
**Output:** \[-1\]
**Explanation:** There are no elements to the right of index 0.
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i] <= 105` | How to solve the problem for k=1 ? Use Kadane's algorithm for k=1. What are the possible cases for the answer ? The answer is the maximum between, the answer for k=1, the sum of the whole array multiplied by k, or the maximum suffix sum plus the maximum prefix sum plus (k-2) multiplied by the whole array sum for k > 1. |
Simple Binary Search approach without Sorting. | sum-of-mutated-array-closest-to-target | 0 | 1 | # Intuition\nI thought of completing this problem without any extra space. So, the arrsum function I thought would take O(n) time to find arrsum. If I iterate through every possiblilty it will lead to O(N*N) .So, I used Binary Search therefore, O(N*logN).\n\n# Approach\nUse two Binary searches in the possible range (target/len(arr) and the maximum element of the array) you need to find the possible arrsum which is just below the target and the possible arrsum which is above the target then we will check the minimum number from these two possible answers.There is no use of Sorting in this approach :).\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findBestValue(self, arr: List[int], target: int) -> int:\n n,s,maxi=0,0,arr[0]\n for i in arr:\n s+=i\n n+=1\n if maxi<i:\n maxi=i\n if s==target:\n return maxi\n def arrsum(n):\n s=0\n for i in arr:\n if i<n:\n s+=i\n else:\n s+=n\n return s\n ans1,ans2=maxi,maxi\n i,j=target//n,maxi\n while i<=j:\n mid=(i+j)//2\n k=arrsum(mid)\n if k==target:\n return mid\n elif k>target:\n ans1=mid\n j=mid-1\n else:\n i=mid+1\n i,j=target//n,maxi\n while i<=j:\n mid=(i+j)//2\n k=arrsum(mid)\n if k==target:\n return mid\n elif k<target:\n ans2=mid\n i=mid+1\n else:\n j=mid-1\n m1,m2=abs(target-arrsum(ans1)),abs(target-arrsum(ans2))\n if m1==m2:\n return min(ans1,ans2)\n elif m1<m2:\n return ans1\n return ans2\n\n``` | 0 | Given an integer array `arr` and a target value `target`, return the integer `value` such that when we change all the integers larger than `value` in the given array to be equal to `value`, the sum of the array gets as close as possible (in absolute difference) to `target`.
In case of a tie, return the minimum such integer.
Notice that the answer is not neccesarilly a number from `arr`.
**Example 1:**
**Input:** arr = \[4,9,3\], target = 10
**Output:** 3
**Explanation:** When using 3 arr converts to \[3, 3, 3\] which sums 9 and that's the optimal answer.
**Example 2:**
**Input:** arr = \[2,3,5\], target = 10
**Output:** 5
**Example 3:**
**Input:** arr = \[60864,25176,27249,21296,20204\], target = 56803
**Output:** 11361
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i], target <= 105` | Use Tarjan's algorithm. |
Simple Binary Search approach without Sorting. | sum-of-mutated-array-closest-to-target | 0 | 1 | # Intuition\nI thought of completing this problem without any extra space. So, the arrsum function I thought would take O(n) time to find arrsum. If I iterate through every possiblilty it will lead to O(N*N) .So, I used Binary Search therefore, O(N*logN).\n\n# Approach\nUse two Binary searches in the possible range (target/len(arr) and the maximum element of the array) you need to find the possible arrsum which is just below the target and the possible arrsum which is above the target then we will check the minimum number from these two possible answers.There is no use of Sorting in this approach :).\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findBestValue(self, arr: List[int], target: int) -> int:\n n,s,maxi=0,0,arr[0]\n for i in arr:\n s+=i\n n+=1\n if maxi<i:\n maxi=i\n if s==target:\n return maxi\n def arrsum(n):\n s=0\n for i in arr:\n if i<n:\n s+=i\n else:\n s+=n\n return s\n ans1,ans2=maxi,maxi\n i,j=target//n,maxi\n while i<=j:\n mid=(i+j)//2\n k=arrsum(mid)\n if k==target:\n return mid\n elif k>target:\n ans1=mid\n j=mid-1\n else:\n i=mid+1\n i,j=target//n,maxi\n while i<=j:\n mid=(i+j)//2\n k=arrsum(mid)\n if k==target:\n return mid\n elif k<target:\n ans2=mid\n i=mid+1\n else:\n j=mid-1\n m1,m2=abs(target-arrsum(ans1)),abs(target-arrsum(ans2))\n if m1==m2:\n return min(ans1,ans2)\n elif m1<m2:\n return ans1\n return ans2\n\n``` | 0 | You are given an array `coordinates`, `coordinates[i] = [x, y]`, where `[x, y]` represents the coordinate of a point. Check if these points make a straight line in the XY plane.
**Example 1:**
**Input:** coordinates = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\],\[5,6\],\[6,7\]\]
**Output:** true
**Example 2:**
**Input:** coordinates = \[\[1,1\],\[2,2\],\[3,4\],\[4,5\],\[5,6\],\[7,7\]\]
**Output:** false
**Constraints:**
* `2 <= coordinates.length <= 1000`
* `coordinates[i].length == 2`
* `-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4`
* `coordinates` contains no duplicate point. | If you draw a graph with the value on one axis and the absolute difference between the target and the array sum, what will you get? That graph is uni-modal. Use ternary search on that graph to find the best value. |
[Python3] Sort & scan | sum-of-mutated-array-closest-to-target | 0 | 1 | Algorithm:\nSort the array in ascending order. \nAt each index `i`, compute the value to set `arr[i:]` to so that `sum(arr)` would be closest to `target`. If this value is smaller than `arr[i]`, return it; otherwise, return `arr[-1]`. \n\nImplementation (24ms, 100%):\n```\nclass Solution:\n def findBestValue(self, arr: List[int], target: int) -> int:\n arr.sort()\n s, n = 0, len(arr)\n \n for i in range(n):\n ans = round((target - s)/n)\n if ans <= arr[i]: return ans \n s += arr[i]\n n -= 1\n \n return arr[-1]\n```\n\nAnalysis:\nTime complexity `O(NlogN)`\nSpace complexity `O(1)` | 22 | Given an integer array `arr` and a target value `target`, return the integer `value` such that when we change all the integers larger than `value` in the given array to be equal to `value`, the sum of the array gets as close as possible (in absolute difference) to `target`.
In case of a tie, return the minimum such integer.
Notice that the answer is not neccesarilly a number from `arr`.
**Example 1:**
**Input:** arr = \[4,9,3\], target = 10
**Output:** 3
**Explanation:** When using 3 arr converts to \[3, 3, 3\] which sums 9 and that's the optimal answer.
**Example 2:**
**Input:** arr = \[2,3,5\], target = 10
**Output:** 5
**Example 3:**
**Input:** arr = \[60864,25176,27249,21296,20204\], target = 56803
**Output:** 11361
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i], target <= 105` | Use Tarjan's algorithm. |
[Python3] Sort & scan | sum-of-mutated-array-closest-to-target | 0 | 1 | Algorithm:\nSort the array in ascending order. \nAt each index `i`, compute the value to set `arr[i:]` to so that `sum(arr)` would be closest to `target`. If this value is smaller than `arr[i]`, return it; otherwise, return `arr[-1]`. \n\nImplementation (24ms, 100%):\n```\nclass Solution:\n def findBestValue(self, arr: List[int], target: int) -> int:\n arr.sort()\n s, n = 0, len(arr)\n \n for i in range(n):\n ans = round((target - s)/n)\n if ans <= arr[i]: return ans \n s += arr[i]\n n -= 1\n \n return arr[-1]\n```\n\nAnalysis:\nTime complexity `O(NlogN)`\nSpace complexity `O(1)` | 22 | You are given an array `coordinates`, `coordinates[i] = [x, y]`, where `[x, y]` represents the coordinate of a point. Check if these points make a straight line in the XY plane.
**Example 1:**
**Input:** coordinates = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\],\[5,6\],\[6,7\]\]
**Output:** true
**Example 2:**
**Input:** coordinates = \[\[1,1\],\[2,2\],\[3,4\],\[4,5\],\[5,6\],\[7,7\]\]
**Output:** false
**Constraints:**
* `2 <= coordinates.length <= 1000`
* `coordinates[i].length == 2`
* `-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4`
* `coordinates` contains no duplicate point. | If you draw a graph with the value on one axis and the absolute difference between the target and the array sum, what will you get? That graph is uni-modal. Use ternary search on that graph to find the best value. |
Python solution with video explanation | sum-of-mutated-array-closest-to-target | 0 | 1 | [https://www.youtube.com/watch?v=j0KejYpI_Mc&feature=youtu.be]\n```\nclass Solution:\n def findBestValue(self, arr: List[int], target: int) -> int:\n arr.sort()\n length = len(arr)\n \n for x in range(length):\n sol = round(target / length)\n if arr[x] >= sol:\n return sol\n target -= arr[x]\n length -= 1\n \n return arr[-1]\n```\n | 5 | Given an integer array `arr` and a target value `target`, return the integer `value` such that when we change all the integers larger than `value` in the given array to be equal to `value`, the sum of the array gets as close as possible (in absolute difference) to `target`.
In case of a tie, return the minimum such integer.
Notice that the answer is not neccesarilly a number from `arr`.
**Example 1:**
**Input:** arr = \[4,9,3\], target = 10
**Output:** 3
**Explanation:** When using 3 arr converts to \[3, 3, 3\] which sums 9 and that's the optimal answer.
**Example 2:**
**Input:** arr = \[2,3,5\], target = 10
**Output:** 5
**Example 3:**
**Input:** arr = \[60864,25176,27249,21296,20204\], target = 56803
**Output:** 11361
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i], target <= 105` | Use Tarjan's algorithm. |
Python solution with video explanation | sum-of-mutated-array-closest-to-target | 0 | 1 | [https://www.youtube.com/watch?v=j0KejYpI_Mc&feature=youtu.be]\n```\nclass Solution:\n def findBestValue(self, arr: List[int], target: int) -> int:\n arr.sort()\n length = len(arr)\n \n for x in range(length):\n sol = round(target / length)\n if arr[x] >= sol:\n return sol\n target -= arr[x]\n length -= 1\n \n return arr[-1]\n```\n | 5 | You are given an array `coordinates`, `coordinates[i] = [x, y]`, where `[x, y]` represents the coordinate of a point. Check if these points make a straight line in the XY plane.
**Example 1:**
**Input:** coordinates = \[\[1,2\],\[2,3\],\[3,4\],\[4,5\],\[5,6\],\[6,7\]\]
**Output:** true
**Example 2:**
**Input:** coordinates = \[\[1,1\],\[2,2\],\[3,4\],\[4,5\],\[5,6\],\[7,7\]\]
**Output:** false
**Constraints:**
* `2 <= coordinates.length <= 1000`
* `coordinates[i].length == 2`
* `-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4`
* `coordinates` contains no duplicate point. | If you draw a graph with the value on one axis and the absolute difference between the target and the array sum, what will you get? That graph is uni-modal. Use ternary search on that graph to find the best value. |
Python (Simple DP) | number-of-paths-with-max-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pathsWithMaxScore(self, board):\n matrix = []\n\n for i in board:\n matrix += [list(i)]\n\n m, n, mod = len(matrix), len(matrix[0]), 10**9+7\n\n @lru_cache(None)\n def dfs(i,j):\n if i >= m or j >= n or matrix[i][j] == "X":\n return (float("-inf"),0)\n\n if i == m-1 and j == n-1:\n return (0,1)\n\n op1 = dfs(i+1,j)\n op2 = dfs(i,j+1)\n op3 = dfs(i+1,j+1)\n\n score = int(matrix[i][j]) if matrix[i][j] != "E" else 0\n\n count, prev_score = 0, max(op1[0],op2[0],op3[0])\n\n if op1[0] == prev_score:\n count += op1[1]\n if op2[0] == prev_score:\n count += op2[1]\n if op3[0] == prev_score:\n count += op3[1]\n\n return (score + prev_score,count%mod)\n\n \n res = dfs(0,0)\n\n return [max(res[0],0),res[1]]\n\n \n \n``` | 1 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
Python (Simple DP) | number-of-paths-with-max-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pathsWithMaxScore(self, board):\n matrix = []\n\n for i in board:\n matrix += [list(i)]\n\n m, n, mod = len(matrix), len(matrix[0]), 10**9+7\n\n @lru_cache(None)\n def dfs(i,j):\n if i >= m or j >= n or matrix[i][j] == "X":\n return (float("-inf"),0)\n\n if i == m-1 and j == n-1:\n return (0,1)\n\n op1 = dfs(i+1,j)\n op2 = dfs(i,j+1)\n op3 = dfs(i+1,j+1)\n\n score = int(matrix[i][j]) if matrix[i][j] != "E" else 0\n\n count, prev_score = 0, max(op1[0],op2[0],op3[0])\n\n if op1[0] == prev_score:\n count += op1[1]\n if op2[0] == prev_score:\n count += op2[1]\n if op3[0] == prev_score:\n count += op3[1]\n\n return (score + prev_score,count%mod)\n\n \n res = dfs(0,0)\n\n return [max(res[0],0),res[1]]\n\n \n \n``` | 1 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
Python | DP | number-of-paths-with-max-score | 0 | 1 | # Complexity\n- Time complexity: O(n^2)\n- Space complexity: O(n^2)\n\n# Code\n```\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n n, m = len(board), len(board[0])\n\n dp = [[(float(\'-inf\'), 0)] * m for _ in range(n)]\n dp[0][0] = (0, 1)\n\n for i in range(n):\n for j in range(m):\n v = board[i][j]\n\n if v == \'X\' or v == \'E\':\n continue\n \n tp, tp_c = dp[i-1][j] if i > 0 else (float(\'-inf\'), 1)\n tl, tl_c = dp[i-1][j-1] if i > 0 and j > 0 else (float(\'-inf\'), 1)\n lf, lf_c = dp[i][j-1] if j > 0 else (float(\'-inf\'), 1)\n\n mx = max(tp, tl, lf)\n weight = (int(v) if v != "S" else 0)\n frq = 0\n for num, cnt in [(tp, tp_c), (tl, tl_c), (lf, lf_c)]:\n if num == mx:\n frq += cnt\n \n dp[i][j] = (mx+weight, frq)\n return [dp[-1][-1][0], dp[-1][-1][1] % (10**9 + 7)] if dp[-1][-1][0] != float(\'-inf\') else [0, 0]\n``` | 0 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
Python | DP | number-of-paths-with-max-score | 0 | 1 | # Complexity\n- Time complexity: O(n^2)\n- Space complexity: O(n^2)\n\n# Code\n```\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n n, m = len(board), len(board[0])\n\n dp = [[(float(\'-inf\'), 0)] * m for _ in range(n)]\n dp[0][0] = (0, 1)\n\n for i in range(n):\n for j in range(m):\n v = board[i][j]\n\n if v == \'X\' or v == \'E\':\n continue\n \n tp, tp_c = dp[i-1][j] if i > 0 else (float(\'-inf\'), 1)\n tl, tl_c = dp[i-1][j-1] if i > 0 and j > 0 else (float(\'-inf\'), 1)\n lf, lf_c = dp[i][j-1] if j > 0 else (float(\'-inf\'), 1)\n\n mx = max(tp, tl, lf)\n weight = (int(v) if v != "S" else 0)\n frq = 0\n for num, cnt in [(tp, tp_c), (tl, tl_c), (lf, lf_c)]:\n if num == mx:\n frq += cnt\n \n dp[i][j] = (mx+weight, frq)\n return [dp[-1][-1][0], dp[-1][-1][1] % (10**9 + 7)] if dp[-1][-1][0] != float(\'-inf\') else [0, 0]\n``` | 0 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
python, DP, intuitive | number-of-paths-with-max-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nstill studying, should be O(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nfrom functools import cache\nmod = 1000000007\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n @cache\n def DP(i,j):\n if board[i][j]=="X":\n return [0,0]\n if i==0 and j==0:\n return [0,1]\n \n if i==0:\n previous = DP(0, j-1)\n return [previous[0]+int(board[i][j]), previous[1]]\n if j==0:\n previous = DP(i-1, 0)\n return [previous[0]+int(board[i][j]), previous[1]]\n\n left = DP(i-1,j)\n up = DP(i,j-1)\n upleft=DP(i-1,j-1)\n\n val = max(left[0], up[0], upleft[0])\n count = 0\n if left[0]==val:\n count +=left[1]\n if up[0]==val:\n count +=up[1] \n if upleft[0]==val:\n count +=upleft[1] \n\n if i==len(board)-1 and j==len(board)-1 :\n if count ==0:\n val =0\n return [val, count%mod] \n return [val+int(board[i][j]), count%mod] \n\n return DP( len(board)-1,len(board)-1 )\n \n \n\n``` | 0 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
python, DP, intuitive | number-of-paths-with-max-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nstill studying, should be O(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nfrom functools import cache\nmod = 1000000007\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n @cache\n def DP(i,j):\n if board[i][j]=="X":\n return [0,0]\n if i==0 and j==0:\n return [0,1]\n \n if i==0:\n previous = DP(0, j-1)\n return [previous[0]+int(board[i][j]), previous[1]]\n if j==0:\n previous = DP(i-1, 0)\n return [previous[0]+int(board[i][j]), previous[1]]\n\n left = DP(i-1,j)\n up = DP(i,j-1)\n upleft=DP(i-1,j-1)\n\n val = max(left[0], up[0], upleft[0])\n count = 0\n if left[0]==val:\n count +=left[1]\n if up[0]==val:\n count +=up[1] \n if upleft[0]==val:\n count +=upleft[1] \n\n if i==len(board)-1 and j==len(board)-1 :\n if count ==0:\n val =0\n return [val, count%mod] \n return [val+int(board[i][j]), count%mod] \n\n return DP( len(board)-1,len(board)-1 )\n \n \n\n``` | 0 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
DP | 10 liner | Simple | Fast | Python Solution | number-of-paths-with-max-score | 0 | 1 | # Code\n```\nclass Solution:\n def pathsWithMaxScore(self, A):\n n, mod = len(A), 10**9 + 7\n dp = [[[-10**5, 0] for j in range(n + 1)] for i in range(n + 1)]\n dp[n - 1][n - 1] = [0, 1]\n for x in range(n)[::-1]:\n for y in range(n)[::-1]:\n if A[x][y] in \'XS\': continue\n for i, j in [[0, 1], [1, 0], [1, 1]]:\n if dp[x][y][0] < dp[x + i][y + j][0]: dp[x][y] = [dp[x + i][y + j][0], 0]\n if dp[x][y][0] == dp[x + i][y + j][0]: dp[x][y][1] += dp[x + i][y + j][1]\n dp[x][y][0] += int(A[x][y]) if x or y else 0\n return [dp[0][0][0] if dp[0][0][1] else 0, dp[0][0][1] % mod]\n``` | 0 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
DP | 10 liner | Simple | Fast | Python Solution | number-of-paths-with-max-score | 0 | 1 | # Code\n```\nclass Solution:\n def pathsWithMaxScore(self, A):\n n, mod = len(A), 10**9 + 7\n dp = [[[-10**5, 0] for j in range(n + 1)] for i in range(n + 1)]\n dp[n - 1][n - 1] = [0, 1]\n for x in range(n)[::-1]:\n for y in range(n)[::-1]:\n if A[x][y] in \'XS\': continue\n for i, j in [[0, 1], [1, 0], [1, 1]]:\n if dp[x][y][0] < dp[x + i][y + j][0]: dp[x][y] = [dp[x + i][y + j][0], 0]\n if dp[x][y][0] == dp[x + i][y + j][0]: dp[x][y][1] += dp[x + i][y + j][1]\n dp[x][y][0] += int(A[x][y]) if x or y else 0\n return [dp[0][0][0] if dp[0][0][1] else 0, dp[0][0][1] % mod]\n``` | 0 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
Solution | number-of-paths-with-max-score | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n typedef pair<int, int> pr;\n \n vector<int> pathsWithMaxScore(vector<string>& board) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n char n = board.size();\n \n board[0][0] = \'0\';\n \n pr tb[n][n], p = {0, 0};\n int mod = 1e9 + 7;\n \n tb[n - 1][n - 1] = {1, 1};\n \n for(char i = n - 2; i != -1; --i) {\n tb[i][n - 1] = (board[i][n - 1] == \'X\' || board[i + 1][n - 1] == \'X\') ? p : pr{tb[i + 1][n - 1].first + board[i][n - 1] - \'0\', tb[i + 1][n - 1].second};\n tb[n - 1][i] = (board[n - 1][i] == \'X\' || board[n - 1][i + 1] == \'X\') ? p : pr{tb[n - 1][i + 1].first + board[n - 1][i] - \'0\', tb[n - 1][i + 1].second};\n }\n \n pr R, D, RD;\n int M, sum;\n for(char i = n - 2; i != -1; --i) {\n auto &b = board[i];\n auto &t0 = tb[i];\n auto &t1 = tb[i + 1];\n for(char j = n - 2; j != -1; --j) {\n if(b[j] == \'X\')\n t0[j] = p;\n else {\n R = t0[j + 1];\n D = t1[j];\n RD = t1[j + 1];\n M = max(max(R.first, D.first), RD.first);\n \n sum = 0;\n if(R.first == M) sum = (sum + R.second) % mod;\n if(D.first == M) sum = (sum + D.second) % mod;\n if(RD.first == M) sum = (sum + RD.second) % mod;\n \n t0[j] = M ? pr{M + b[j] - \'0\', sum} : pr{0, 0};\n }\n }\n }\n \n return {max(0, tb[0][0].first - 1), tb[0][0].second};\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n n = len(board)\n dp = [[-math.inf]*n for _ in range(n)]\n count = [[0]*n for _ in range(n)]\n\n dp[-1][-1] = 0\n count[-1][-1] = 1\n for i in range(n-1, -1, -1):\n for j in range(n-1, -1, -1):\n if i == (n-1) and j == (n-1):\n continue\n \n if board[i][j] == \'X\':\n continue\n \n dp[i][j] = dp[i][j+1] if j+1 < n else -math.inf\n count[i][j] = count[i][j+1] if j+1 < n else 0\n\n tmp = dp[i+1][j] if i+1 < n else -math.inf\n if tmp > dp[i][j]:\n dp[i][j] = tmp\n count[i][j] = count[i+1][j] if i+1 < n else 0\n elif tmp == dp[i][j]:\n count[i][j] += count[i+1][j] if i+1 < n else 0\n \n tmp = dp[i+1][j+1] if i+1 < n and j+1 < n else -math.inf\n if tmp > dp[i][j]:\n dp[i][j] = tmp\n count[i][j] = count[i+1][j+1] if i+1 < n and j+1 < n else 0\n elif tmp == dp[i][j]:\n count[i][j] += count[i+1][j+1] if i+1 < n and j+1 < n else 0\n \n if i != 0 or j != 0:\n dp[i][j] += int(board[i][j])\n \n if dp[0][0] == -math.inf:\n return [0, 0]\n else:\n return [dp[0][0], count[0][0]%(10**9+7)]\n\n```\n\n```Java []\nclass Solution {\n public int[] pathsWithMaxScore(List<String> board) {\n int MOD = (int)(1e9 + 7);\n int n = board.size();\n int[][] sum = new int[n][n];\n int[][] cnt = new int[n][n];\n cnt[n-1][n-1] = 1;\n int[][] m = {{-1, 0}, {0, -1}, {-1, -1}};\n \n for(int i = n - 1; i >= 0; i--){\n for(int j = n - 1; j >= 0; j--){\n char val = board.get(i).charAt(j);\n if(val == \'X\' || val == \'S\'){\n continue; // sum, cnt = 0\n }\n \n int v = val - \'0\';\n int maxSum = 0;\n int maxCnt = 0;\n for(int k = 0; k < 3; k++){\n int r = i - m[k][0];\n int c = j - m[k][1];\n if(r >= n || c >= n)\n continue;\n if(sum[r][c] > maxSum){\n maxSum = sum[r][c];\n maxCnt = cnt[r][c];\n }\n else if(sum[r][c] == maxSum){\n maxCnt += cnt[r][c];\n }\n }\n if(val == \'E\')\n sum[i][j] = maxSum;\n else\n sum[i][j] = v + maxSum;\n cnt[i][j] = maxCnt % MOD;\n }\n }\n \n int[] ans = new int[2];\n ans[0] = sum[0][0];\n ans[1] = cnt[0][0];\n if(cnt[0][0] == 0)\n ans[0] = 0;\n return ans;\n }\n}\n```\n | 0 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
Solution | number-of-paths-with-max-score | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n typedef pair<int, int> pr;\n \n vector<int> pathsWithMaxScore(vector<string>& board) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n char n = board.size();\n \n board[0][0] = \'0\';\n \n pr tb[n][n], p = {0, 0};\n int mod = 1e9 + 7;\n \n tb[n - 1][n - 1] = {1, 1};\n \n for(char i = n - 2; i != -1; --i) {\n tb[i][n - 1] = (board[i][n - 1] == \'X\' || board[i + 1][n - 1] == \'X\') ? p : pr{tb[i + 1][n - 1].first + board[i][n - 1] - \'0\', tb[i + 1][n - 1].second};\n tb[n - 1][i] = (board[n - 1][i] == \'X\' || board[n - 1][i + 1] == \'X\') ? p : pr{tb[n - 1][i + 1].first + board[n - 1][i] - \'0\', tb[n - 1][i + 1].second};\n }\n \n pr R, D, RD;\n int M, sum;\n for(char i = n - 2; i != -1; --i) {\n auto &b = board[i];\n auto &t0 = tb[i];\n auto &t1 = tb[i + 1];\n for(char j = n - 2; j != -1; --j) {\n if(b[j] == \'X\')\n t0[j] = p;\n else {\n R = t0[j + 1];\n D = t1[j];\n RD = t1[j + 1];\n M = max(max(R.first, D.first), RD.first);\n \n sum = 0;\n if(R.first == M) sum = (sum + R.second) % mod;\n if(D.first == M) sum = (sum + D.second) % mod;\n if(RD.first == M) sum = (sum + RD.second) % mod;\n \n t0[j] = M ? pr{M + b[j] - \'0\', sum} : pr{0, 0};\n }\n }\n }\n \n return {max(0, tb[0][0].first - 1), tb[0][0].second};\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n n = len(board)\n dp = [[-math.inf]*n for _ in range(n)]\n count = [[0]*n for _ in range(n)]\n\n dp[-1][-1] = 0\n count[-1][-1] = 1\n for i in range(n-1, -1, -1):\n for j in range(n-1, -1, -1):\n if i == (n-1) and j == (n-1):\n continue\n \n if board[i][j] == \'X\':\n continue\n \n dp[i][j] = dp[i][j+1] if j+1 < n else -math.inf\n count[i][j] = count[i][j+1] if j+1 < n else 0\n\n tmp = dp[i+1][j] if i+1 < n else -math.inf\n if tmp > dp[i][j]:\n dp[i][j] = tmp\n count[i][j] = count[i+1][j] if i+1 < n else 0\n elif tmp == dp[i][j]:\n count[i][j] += count[i+1][j] if i+1 < n else 0\n \n tmp = dp[i+1][j+1] if i+1 < n and j+1 < n else -math.inf\n if tmp > dp[i][j]:\n dp[i][j] = tmp\n count[i][j] = count[i+1][j+1] if i+1 < n and j+1 < n else 0\n elif tmp == dp[i][j]:\n count[i][j] += count[i+1][j+1] if i+1 < n and j+1 < n else 0\n \n if i != 0 or j != 0:\n dp[i][j] += int(board[i][j])\n \n if dp[0][0] == -math.inf:\n return [0, 0]\n else:\n return [dp[0][0], count[0][0]%(10**9+7)]\n\n```\n\n```Java []\nclass Solution {\n public int[] pathsWithMaxScore(List<String> board) {\n int MOD = (int)(1e9 + 7);\n int n = board.size();\n int[][] sum = new int[n][n];\n int[][] cnt = new int[n][n];\n cnt[n-1][n-1] = 1;\n int[][] m = {{-1, 0}, {0, -1}, {-1, -1}};\n \n for(int i = n - 1; i >= 0; i--){\n for(int j = n - 1; j >= 0; j--){\n char val = board.get(i).charAt(j);\n if(val == \'X\' || val == \'S\'){\n continue; // sum, cnt = 0\n }\n \n int v = val - \'0\';\n int maxSum = 0;\n int maxCnt = 0;\n for(int k = 0; k < 3; k++){\n int r = i - m[k][0];\n int c = j - m[k][1];\n if(r >= n || c >= n)\n continue;\n if(sum[r][c] > maxSum){\n maxSum = sum[r][c];\n maxCnt = cnt[r][c];\n }\n else if(sum[r][c] == maxSum){\n maxCnt += cnt[r][c];\n }\n }\n if(val == \'E\')\n sum[i][j] = maxSum;\n else\n sum[i][j] = v + maxSum;\n cnt[i][j] = maxCnt % MOD;\n }\n }\n \n int[] ans = new int[2];\n ans[0] = sum[0][0];\n ans[1] = cnt[0][0];\n if(cnt[0][0] == 0)\n ans[0] = 0;\n return ans;\n }\n}\n```\n | 0 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
Python Bottom-up DP: 87% time, 51% space | number-of-paths-with-max-score | 0 | 1 | ```python []\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n MOD = 10 ** 9 + 7\n m = len(board)\n n = len(board[0])\n\n dp = [[[0, 0]] * (n + 1) for _ in range(m + 1)]\n dp[1][1] = [0, 1]\n for i in range(m + 1): dp[i][0] = [-math.inf, 0]\n\n for r in range(1, m + 1):\n for c in range(1, n + 1):\n if r == 1 and c == 1: continue\n\n val = board[r - 1][c - 1]\n if val == \'X\': \n dp[r][c] = [-math.inf, 0]\n continue\n val = 0 if val == \'S\' else int(val)\n\n maxi, paths = -math.inf, 0\n for rr, cc in [[-1, 0], [0, -1], [-1, -1]]:\n new_r = r + rr\n new_c = c + cc\n _sum = val + dp[new_r][new_c][0]\n if _sum == maxi: paths += dp[new_r][new_c][1]\n elif _sum > maxi:\n maxi = _sum\n paths = dp[new_r][new_c][1]\n dp[r][c] = [maxi, paths % MOD]\n\n return [0, 0] if dp[m][n][0] == -math.inf else dp[m][n]\n``` | 0 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
Python Bottom-up DP: 87% time, 51% space | number-of-paths-with-max-score | 0 | 1 | ```python []\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n MOD = 10 ** 9 + 7\n m = len(board)\n n = len(board[0])\n\n dp = [[[0, 0]] * (n + 1) for _ in range(m + 1)]\n dp[1][1] = [0, 1]\n for i in range(m + 1): dp[i][0] = [-math.inf, 0]\n\n for r in range(1, m + 1):\n for c in range(1, n + 1):\n if r == 1 and c == 1: continue\n\n val = board[r - 1][c - 1]\n if val == \'X\': \n dp[r][c] = [-math.inf, 0]\n continue\n val = 0 if val == \'S\' else int(val)\n\n maxi, paths = -math.inf, 0\n for rr, cc in [[-1, 0], [0, -1], [-1, -1]]:\n new_r = r + rr\n new_c = c + cc\n _sum = val + dp[new_r][new_c][0]\n if _sum == maxi: paths += dp[new_r][new_c][1]\n elif _sum > maxi:\n maxi = _sum\n paths = dp[new_r][new_c][1]\n dp[r][c] = [maxi, paths % MOD]\n\n return [0, 0] if dp[m][n][0] == -math.inf else dp[m][n]\n``` | 0 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
Easy Recursion + Memoization Python Solution | Faster than 97% | number-of-paths-with-max-score | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain 2 separate states in the DP: Max Score and number of paths with max score\n\n# Complexity\n- Time complexity: $$O(n * m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n * m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n MOD = 1000000007\n \n @cache\n def dp(row: int, col: int) -> Tuple[int]:\n numRows, numCols = len(board), len(board[0])\n if row >= numRows or col >= numCols or board[row][col] == \'X\':\n return(-inf, 0)\n score = ord(board[row][col]) - ord(\'0\')\n if board[row][col] == \'E\':\n score = 0\n if row == numRows - 1 and col == numCols - 1:\n return (0, 1)\n option1 = dp(row + 1, col)\n option2 = dp(row, col + 1)\n option3 = dp(row + 1, col + 1)\n count, ans = 0, score + max(option1[0], option2[0], option3[0])\n if score + option1[0] == ans: \n count = (count + option1[1]) % MOD\n if score + option2[0] == ans: \n count = (count + option2[1]) % MOD\n if score + option3[0] == ans:\n count = (count + option3[1]) % MOD\n return (ans, count % MOD)\n\n ans = dp(0, 0)\n return [max(ans[0], 0), ans[1]]\n``` | 0 | You are given a square `board` of characters. You can move on the board starting at the bottom right square marked with the character `'S'`.
You need to reach the top left square marked with the character `'E'`. The rest of the squares are labeled either with a numeric character `1, 2, ..., 9` or with an obstacle `'X'`. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.
Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, **taken modulo `10^9 + 7`**.
In case there is no path, return `[0, 0]`.
**Example 1:**
**Input:** board = \["E23","2X2","12S"\]
**Output:** \[7,1\]
**Example 2:**
**Input:** board = \["E12","1X1","21S"\]
**Output:** \[4,2\]
**Example 3:**
**Input:** board = \["E11","XXX","11S"\]
**Output:** \[0,0\]
**Constraints:**
* `2 <= board.length == board[i].length <= 100` | null |
Easy Recursion + Memoization Python Solution | Faster than 97% | number-of-paths-with-max-score | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain 2 separate states in the DP: Max Score and number of paths with max score\n\n# Complexity\n- Time complexity: $$O(n * m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n * m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def pathsWithMaxScore(self, board: List[str]) -> List[int]:\n MOD = 1000000007\n \n @cache\n def dp(row: int, col: int) -> Tuple[int]:\n numRows, numCols = len(board), len(board[0])\n if row >= numRows or col >= numCols or board[row][col] == \'X\':\n return(-inf, 0)\n score = ord(board[row][col]) - ord(\'0\')\n if board[row][col] == \'E\':\n score = 0\n if row == numRows - 1 and col == numCols - 1:\n return (0, 1)\n option1 = dp(row + 1, col)\n option2 = dp(row, col + 1)\n option3 = dp(row + 1, col + 1)\n count, ans = 0, score + max(option1[0], option2[0], option3[0])\n if score + option1[0] == ans: \n count = (count + option1[1]) % MOD\n if score + option2[0] == ans: \n count = (count + option2[1]) % MOD\n if score + option3[0] == ans:\n count = (count + option3[1]) % MOD\n return (ans, count % MOD)\n\n ans = dp(0, 0)\n return [max(ans[0], 0), ans[1]]\n``` | 0 | You are given a string s of length `n` containing only four kinds of characters: `'Q'`, `'W'`, `'E'`, and `'R'`.
A string is said to be **balanced** if each of its characters appears `n / 4` times where `n` is the length of the string.
Return _the minimum length of the substring that can be replaced with **any** other string of the same length to make_ `s` _**balanced**_. If s is already **balanced**, return `0`.
**Example 1:**
**Input:** s = "QWER "
**Output:** 0
**Explanation:** s is already balanced.
**Example 2:**
**Input:** s = "QQWE "
**Output:** 1
**Explanation:** We need to replace a 'Q' to 'R', so that "RQWE " (or "QRWE ") is balanced.
**Example 3:**
**Input:** s = "QQQW "
**Output:** 2
**Explanation:** We can replace the first "QQ " to "ER ".
**Constraints:**
* `n == s.length`
* `4 <= n <= 105`
* `n` is a multiple of `4`.
* `s` contains only `'Q'`, `'W'`, `'E'`, and `'R'`. | Use dynamic programming to find the path with the max score. Use another dynamic programming array to count the number of paths with max score. |
Easy Python soln | deepest-leaves-sum | 0 | 1 | # Easy python soln\n\n# Code\n```\nclass Solution(object):\n def deepestLeavesSum(self, root):\n if not root: return 0\n h=[0]\n def dfs(root,depth):\n h[0]=max(h[0],depth)\n if root.left: dfs(root.left,depth+1)\n if root.right: dfs(root.right,depth+1)\n dfs(root,0)\n ans=[0]\n def find(root,depth):\n if depth==h[0]:\n ans[0]+=root.val\n if root.left: find(root.left,depth+1)\n if root.right: find(root.right,depth+1)\n find(root,0)\n return ans[0]\n``` | 1 | Given the `root` of a binary tree, return _the sum of values of its deepest leaves_.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,6,7,null,null,null,null,8\]
**Output:** 15
**Example 2:**
**Input:** root = \[6,7,8,2,7,1,3,9,null,1,4,null,null,null,5\]
**Output:** 19
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `1 <= Node.val <= 100` | What's the optimal way to delete characters if three or more consecutive characters are equal? If three or more consecutive characters are equal, keep two of them and delete the rest. |
Easy Python soln | deepest-leaves-sum | 0 | 1 | # Easy python soln\n\n# Code\n```\nclass Solution(object):\n def deepestLeavesSum(self, root):\n if not root: return 0\n h=[0]\n def dfs(root,depth):\n h[0]=max(h[0],depth)\n if root.left: dfs(root.left,depth+1)\n if root.right: dfs(root.right,depth+1)\n dfs(root,0)\n ans=[0]\n def find(root,depth):\n if depth==h[0]:\n ans[0]+=root.val\n if root.left: find(root.left,depth+1)\n if root.right: find(root.right,depth+1)\n find(root,0)\n return ans[0]\n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Deepest leaves sum | deepest-leaves-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:\n l=defaultdict(list)\n def dls(node,h):\n if node is None:\n return\n l[h].append(node.val)\n dls(node.left,h+1)\n dls(node.right,h+1)\n dls(root,0)\n return sum(l[len(l)-1])\n``` | 2 | Given the `root` of a binary tree, return _the sum of values of its deepest leaves_.
**Example 1:**
**Input:** root = \[1,2,3,4,5,null,6,7,null,null,null,null,8\]
**Output:** 15
**Example 2:**
**Input:** root = \[6,7,8,2,7,1,3,9,null,1,4,null,null,null,5\]
**Output:** 19
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `1 <= Node.val <= 100` | What's the optimal way to delete characters if three or more consecutive characters are equal? If three or more consecutive characters are equal, keep two of them and delete the rest. |
Deepest leaves sum | deepest-leaves-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:\n l=defaultdict(list)\n def dls(node,h):\n if node is None:\n return\n l[h].append(node.val)\n dls(node.left,h+1)\n dls(node.right,h+1)\n dls(root,0)\n return sum(l[len(l)-1])\n``` | 2 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Simple solution in Python3 | find-n-unique-integers-sum-up-to-zero | 0 | 1 | # Intuition\nHere we have:\n- `n` as integer\n- and our goal is to create a list of integers, that sum up to `0`\n\nSince we could represent a final answer with **any valid combination** of integers, an algorithm is quite simple:\n- **define** a starting point as `mid = n // 2 or n >> 1`\n- **enumerate** `mid` count of integers to distribute them by **each sign (plus and minus)**\n- **distribute** them, while they\'re opposite to each other \n\n```\n# Example\nn = 5\nans = [2, -2, 1, -1, 0]\n```\n\n# Approach\n1. declare `ans` to store integers and `mid`\n2. iterate in range `mid`\n3. fill `ans` with integers\n4. when you have an **odd n**, simple add `0` to `ans`\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N/2)**, to distribute integers => **O(N)**\n- Space complexity: **O(N)**, to store them\n\n# Code\n```\nclass Solution:\n def sumZero(self, n: int) -> list[int]:\n ans = []\n mid = n >> 1\n\n for _ in range(mid):\n ans.append(mid)\n ans.append(-mid)\n mid -= 1\n \n if n & 1:\n ans.append(0)\n\n return ans\n``` | 1 | Given an integer `n`, return **any** array containing `n` **unique** integers such that they add up to `0`.
**Example 1:**
**Input:** n = 5
**Output:** \[-7,-1,1,3,4\]
**Explanation:** These arrays also are accepted \[-5,-1,1,2,3\] , \[-3,-1,2,-2,4\].
**Example 2:**
**Input:** n = 3
**Output:** \[-1,0,1\]
**Example 3:**
**Input:** n = 1
**Output:** \[0\]
**Constraints:**
* `1 <= n <= 1000` | Use a greedy approach. Use the letter with the maximum current limit that can be added without breaking the condition. |
Easy Peasy Python Solution ^_^ | find-n-unique-integers-sum-up-to-zero | 0 | 1 | # Intuition\nHere we get two cases:\nCase 1: \nIf number of elements is odd.\nWe will add a zero at the beginning and rest of the elements will be negative and postive integers of ceiling(n/2).\n\nCase 2:\nIf number of elements is even.\nWe will directly add the elements that will be negative and postive integers of ceiling(n/2).\n\n\n# Code\n```\nclass Solution:\n def sumZero(self, n: int) -> List[int]:\n ans=[]\n nums= int(n/2)\n if n%2!=0:\n ans.append(0)\n for i in range(1,nums+1):\n ans.append(i)\n ans.append(-i)\n return ans\n```\n\n\n | 5 | Given an integer `n`, return **any** array containing `n` **unique** integers such that they add up to `0`.
**Example 1:**
**Input:** n = 5
**Output:** \[-7,-1,1,3,4\]
**Explanation:** These arrays also are accepted \[-5,-1,1,2,3\] , \[-3,-1,2,-2,4\].
**Example 2:**
**Input:** n = 3
**Output:** \[-1,0,1\]
**Example 3:**
**Input:** n = 1
**Output:** \[0\]
**Constraints:**
* `1 <= n <= 1000` | Use a greedy approach. Use the letter with the maximum current limit that can be added without breaking the condition. |
Simple solution with Sorting in Python3 | all-elements-in-two-binary-search-trees | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'re two **Binary Search Trees(BST)** \n- the task is to **merge** their values in **sorted** ascending order and store them to list\n\n# Approach\n1. initialize an empty `nums` list to store the nodes\n2. create function `dfs` to iterate over trees, **the order of traversal doesn\'t matter**\n3. perform `dfs(root1), dfs(root2)`\n4. return `sorted(ans)`\n\n# Complexity\n- Time complexity: **O(nlogn)**, because of sorting\n\n- Space complexity: **O(n)**, because of storing `ans` with numbers\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n ans = []\n\n def dfs(node):\n if node:\n ans.append(node.val)\n dfs(node.left)\n dfs(node.right)\n\n dfs(root1)\n dfs(root2)\n\n return sorted(ans)\n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
All elements in two binary search trees | all-elements-in-two-binary-search-trees | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n l=list()\n def traversal(root):\n if root is None :\n return\n l.append(root.val)\n traversal(root.left)\n traversal(root.right)\n traversal(root1)\n traversal(root2)\n l.sort()\n return l\n\n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
simple iterative solution with simultaneous traversal of both the BSTs | all-elements-in-two-binary-search-trees | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n stack1, stack2, output = [], [], []\n\n while root1 or root2 or stack1 or stack2:\n # update both stacks\n # by going as far to the left as possible\n while root1:\n stack1.append(root1)\n root1 = root1.left\n while root2:\n stack2.append(root2)\n root2 = root2.left\n\n # add the smallest value into output,\n # pop it from the stack,\n # and then move one step right\n if not stack2 or stack1 and stack1[-1].val <= stack2[-1].val:\n root1 = stack1.pop()\n output.append(root1.val)\n root1 = root1.right\n else:\n root2 = stack2.pop()\n output.append(root2.val)\n root2 = root2.right\n\n return output\n \n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
✔️ [Python3] 6-LINES (╭ರ_ ⊙ ), Explained | all-elements-in-two-binary-search-trees | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe simplest way to solve this problem is to traverse two trees to form lists with sorted values, and then just merge them. For traversing BST we use recursive in-order DFS. We form sorted lists in descending order as it will allow us to avoid maintaining indexes when merging and just pop elements from lists. To merge lists, we compare elements and push the smallest ones to the result first. Leftovers from the merging are attached to the result.\n\nTime: **O(n)** - for DFS and merge sort\nSpace: **O(n)** - recursion stack and intermediate lists\n\n```\ndef getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n\tdef dfs(root):\n\t\tif not root: return []\n\t\treturn dfs(root.right) + [root.val] + dfs(root.left)\n\n\tel1, el2, res = dfs(root1), dfs(root2), [] \n\twhile el1 and el2: \n\t\tres.append(el1.pop() if el1[-1] < el2[-1] else el2.pop())\n\n\treturn res + list(reversed(el1 or el2))\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 32 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
python3 easy solution 3lines | all-elements-in-two-binary-search-trees | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n def help(root):\n if root:\n return help(root.left) + [root.val] + help(root.right)\n else:\n return []\n x = list(sorted(help(root1) + help(root2)))\n return x\n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
Why is Python generator-based inorder traversal so slow? | all-elements-in-two-binary-search-trees | 0 | 1 | The Python 3 solution below gets TLE for the last test case, both of whose trees are lopsided (each node has at most one child) and consist of 5000 nodes:\n```\nimport heapq\n\nclass Solution:\n def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n def gen(node):\n if node:\n yield from gen(node.left)\n yield node.val\n yield from gen(node.right)\n return list(heapq.merge(gen(root1), gen(root2)))\n```\nThat last test case alone needs ~2.6s to finish and almost all of the time was consumed by the generators. The Python 2 equivalent is just as slow. In comparison, the following solution blazes through that last test case in ~80 ms:\n```\nimport heapq\n\nclass Solution:\n def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:\n def listify(node, l):\n if node:\n listify(node.left, l)\n l.append(node.val)\n listify(node.right, l)\n l1, l2 = [], []\n listify(root1, l1)\n listify(root2, l2)\n return list(heapq.merge(l1, l2))\n```\n\nI decided to get to the bottom of the issue experimentally. Here is the timing result of running inorder traversal for a lopsided tree to create a list of values, using generator vs. simple append with `listify()`:\n\nx-axis is number of nodes, y-axis is traversal walltime in seconds. It seems that inorder traversal for a lopsided tree using generator is O(n^2)! Each level of nested generator results in constant overhead of yielding control from callee to caller, so for a nested generator the time complexity of yielding an item is O(d), d being the depth of nesting. O(n^2) time complexity for generator-based lopsided tree inorder traversal follows from that.\n\nFor completeness, here is the timing result of running inorder traversal for a balanced tree:\n\n\nIf all of the above is correct, the time complexity of generator-based inorder traversal for a balanced tree should be O(nlogn). It is hard to verify and distinguish from O(n) though, and the Jupyter Notebook kernal can\'t take it anymore \uD83E\uDD23\n\nThis exact problem was in fact mentioned in [PEP 380, Optimisations](https://www.python.org/dev/peps/pep-0380/#optimisations):\n>Using a specialised syntax opens up possibilities for optimisation when there is a long chain of generators. Such chains can arise, for instance, when recursively traversing a tree structure. The overhead of passing \\_\\_next\\_\\_() calls and yielded values down and up the chain can cause what ought to be an O(n) operation to become, in the worst case, O(n\\*\\*2).\n\nEvidently it hasn\'t been optimized away yet. | 37 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
Recursion and BFS | jump-game-iii | 0 | 1 | ### BFS\n\n```CPP []\nclass Solution {\npublic:\n bool canReach(vector<int>& arr, int start) \n {\n queue<int> q(deque<int>{start});\n int i = start, n = arr.size(), left_index, right_index;\n\n while(!q.empty() && arr[i] != 0)\n {\n i = q.front(), q.pop();\n left_index = i - arr[i], right_index = i + arr[i];\n if(left_index > -1 && arr[left_index] > -1)\n q.push(left_index);\n if(right_index < n && arr[right_index] > -1)\n q.push(right_index);\n arr[i] *= -1;\n }\n return arr[i] == 0;\n }\n};\n```\n```Python []\nclass Solution:\n def canReach(self, arr: List[int], start: int) -> bool:\n q, n, i = deque([start]), len(arr), start\n\n while q and arr[i] != 0:\n i = q.popleft()\n left_index, right_index = i-arr[i], i+arr[i]\n if left_index > -1 and arr[left_index] > -1:\n q.append(left_index)\n if right_index < n and arr[right_index] > -1:\n q.append(right_index)\n arr[i] *= -1\n\n return arr[i] == 0\n```\n```\nTime complexity : O(n)\nSpace complexity : O(n)\n```\n\n## Recursion\n```CPP []\nclass Solution {\npublic:\n bool canReach(vector<int>& arr, int start) \n {\n if(start < 0 || start >= arr.size() || arr[start] < 0)\n return false;\n arr[start] *= -1; \n return arr[start] == 0 || canReach(arr, start-arr[start]) || canReach(arr, start+arr[start]);\n }\n};\n```\n```\nTime complexity : O(n)\nSpace complexity : O(n)\n``` | 2 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
[Python3] backtracking | verbal-arithmetic-puzzle | 0 | 1 | \n```\nclass Solution:\n def isSolvable(self, words: List[str], result: str) -> bool:\n if max(map(len, words)) > len(result): return False # edge case \n \n words.append(result)\n digits = [0]*10 \n mp = {} # mapping from letter to digit \n \n def fn(i, j, val): \n """Find proper mapping for words[i][~j] and result[~j] via backtracking."""\n if j == len(result): return val == 0 # base condition \n if i == len(words): return val % 10 == 0 and fn(0, j+1, val//10)\n \n if j >= len(words[i]): return fn(i+1, j, val)\n if words[i][~j] in mp: \n if j and j+1 == len(words[i]) and mp[words[i][~j]] == 0: return # backtrack (no leading 0)\n if i+1 == len(words): return fn(i+1, j, val - mp[words[i][~j]])\n else: return fn(i+1, j, val + mp[words[i][~j]])\n else: \n for k, x in enumerate(digits): \n if not x and (k or j == 0 or j+1 < len(words[i])): \n mp[words[i][~j]] = k\n digits[k] = 1\n if i+1 == len(words) and fn(i+1, j, val-k): return True \n if i+1 < len(words) and fn(i+1, j, val+k): return True \n digits[k] = 0\n mp.pop(words[i][~j])\n \n return fn(0, 0, 0)\n``` | 7 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Python: Backtracking with Pruning | verbal-arithmetic-puzzle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSolvable(self, words: List[str], result: str) -> bool:\n max_len = 0\n for i in range(len(words)):\n words[i] = words[i][::-1]\n max_len= max(max_len, len(words[i]))\n\n result = result[::-1]\n if len(result) < max_len or len(result) - max_len > 1:\n return False\n\n def dfs(column: int, row: int, sum_so_far: int, mapping: Dict[str, int]) -> bool:\n if column == len(result):\n return not sum_so_far\n else:\n if row == len(words):\n # we need to process result[column]\n r = result[column]\n if not sum_so_far % 10 and len(result) > 1 and column == len(result) - 1:\n return False\n if r in mapping:\n if mapping[r] != sum_so_far % 10:\n return False\n else:\n return dfs(column + 1, 0, sum_so_far // 10, mapping)\n if sum_so_far % 10 in mapping.values():\n return False\n else:\n mapping[r] = sum_so_far % 10\n if dfs(column + 1, 0, sum_so_far // 10, mapping):\n return True\n else:\n del mapping[r]\n return False\n else:\n if column >= len(words[row]):\n return dfs(column, row + 1, sum_so_far, mapping)\n elif words[row][column] in mapping:\n if len(words[row]) > 1 and column == len(words[row]) - 1 and not mapping[words[row][column]]:\n return False\n return dfs(column, row + 1, sum_so_far + mapping[words[row][column]], mapping)\n else:\n for num in range(10):\n if num in mapping.values():\n continue\n if len(words[row]) > 1 and column == len(words[row]) - 1 and not num:\n continue \n mapping[words[row][column]] = num\n if dfs(column, row + 1, sum_so_far + num, mapping):\n return True\n else:\n del mapping[words[row][column]]\n return False\n\n return dfs(0, 0,0, {})\n``` | 0 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
python solution faster than 98% | verbal-arithmetic-puzzle | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nBacktracking\n\n\n# Code\n```\nclass Solution:\n def isSolvable(self, words: List[str], result: str) -> bool:\n head = set()\n num = dict()\n for word in words:\n for i in range(len(word)):\n if i == 0 and len(word) > 1:\n head.add(word[i])\n if word[i] not in num:\n num[word[i]] = 10 ** (len(word) - i - 1)\n else:\n num[word[i]] += 10 ** (len(word) - i - 1)\n num2 = dict()\n for i in range(len(result)):\n if i == 0 and len(result ) > 1:\n head.add(result[i])\n if result[i] not in num2:\n num2[result[i]] = 10 ** (len(result) - i - 1)\n else:\n num2[result[i]] += 10 ** (len(result) - i - 1)\n arr = list(set([i for i in num] + [i for i in num2]))\n arr.sort(key = lambda x: -(num[x] if x in num else 0) -(num2[x] if x in num2 else 0))\n suml, sumr = sum([num[i] for i in num]), sum([num2[i] for i in num2])\n s = [suml, sumr]\n left, right = 0, 0\n check = set()\n def backTrack(x, left, right):\n if len(check) == len(arr):\n if left == right:\n return True\n else:\n return False\n a = arr[x]\n if abs(left - right) > 9 * (max(s[0], s[1])):\n return False\n for i in range(10):\n if i in check:\n continue\n if i == 0 and a in head:\n continue\n s[0] = s[0] - num[a] if a in num else s[0]\n s[1] = s[1] - num2[a] if a in num2 else s[1]\n check.add(i)\n if backTrack(x + 1, left + num[a] * i if a in num else left, right + num2[a] * i if a in num2 else right):\n return True\n s[0] = s[0] + num[a] if a in num else s[0]\n s[1] = s[1] + num2[a] if a in num2 else s[1]\n check.remove(i)\n return False\n\n\n return backTrack(0, 0, 0)\n``` | 0 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Solution | verbal-arithmetic-puzzle | 1 | 1 | ```C++ []\nusing PCI = pair<char, int>;\n\nclass Solution {\nprivate:\n vector<PCI> weight;\n vector<int> suffix_sum_min, suffix_sum_max;\n vector<int> lead_zero;\n bool used[10];\npublic:\n int pow10(int x) {\n int ret = 1;\n for (int i = 0; i < x; ++i) {\n ret *= 10;\n }\n return ret;\n }\n bool dfs(int pos, int total) {\n if (pos == weight.size()) {\n return total == 0;\n }\n if (!(total + suffix_sum_min[pos] <= 0 && 0 <= total + suffix_sum_max[pos])) {\n return false;\n }\n for (int i = lead_zero[pos]; i < 10; ++i) {\n if (!used[i]) {\n used[i] = true;\n bool check = dfs(pos + 1, total + weight[pos].second * i);\n used[i] = false;\n if (check) {\n return true;\n }\n }\n }\n return false;\n }\n bool isSolvable(vector<string>& words, string result) {\n unordered_map<char, int> _weight;\n unordered_set<char> _lead_zero;\n for (const string& word: words) {\n for (int i = 0; i < word.size(); ++i) {\n _weight[word[i]] += pow10(word.size() - i - 1);\n }\n if (word.size() > 1) {\n _lead_zero.insert(word[0]);\n }\n }\n for (int i = 0; i < result.size(); ++i) {\n _weight[result[i]] -= pow10(result.size() - i - 1);\n }\n if (result.size() > 1) {\n _lead_zero.insert(result[0]);\n }\n weight = vector<PCI>(_weight.begin(), _weight.end());\n sort(weight.begin(), weight.end(), [](const PCI& u, const PCI& v) {\n return abs(u.second) > abs(v.second);\n });\n int n = weight.size();\n suffix_sum_min.resize(n);\n suffix_sum_max.resize(n);\n for (int i = 0; i < n; ++i) {\n vector<int> suffix_pos, suffix_neg;\n for (int j = i; j < n; ++j) {\n if (weight[j].second > 0) {\n suffix_pos.push_back(weight[j].second);\n }\n else if (weight[j].second < 0) {\n suffix_neg.push_back(weight[j].second);\n }\n }\n sort(suffix_pos.begin(), suffix_pos.end());\n sort(suffix_neg.begin(), suffix_neg.end());\n for (int j = 0; j < suffix_pos.size(); ++j) {\n suffix_sum_min[i] += (suffix_pos.size() - 1 - j) * suffix_pos[j];\n suffix_sum_max[i] += (10 - suffix_pos.size() + j) * suffix_pos[j];\n }\n for (int j = 0; j < suffix_neg.size(); ++j) {\n suffix_sum_min[i] += (9 - j) * suffix_neg[j];\n suffix_sum_max[i] += j * suffix_neg[j];\n }\n }\n lead_zero.resize(n);\n for (int i = 0; i < n; ++i) {\n lead_zero[i] = (_lead_zero.count(weight[i].first) ? 1 : 0);\n }\n memset(used, false, sizeof(used));\n return dfs(0, 0);\n }\n};\n```\n\n```Python3 []\nimport itertools\n\nclass Solution:\n def simplify(self, words, result):\n terms = {}\n nonzero_letters = set()\n\n def add_to_term(letter, amount):\n if letter not in terms:\n terms[letter] = 0\n terms[letter] += amount\n\n for word, sign in zip(words + [result], [1] * len(words) + [-1]):\n multiplier = 10**(len(word) - 1)\n first_letter = len(word) > 1\n for letter in word:\n if first_letter:\n nonzero_letters.add(letter)\n first_letter = False\n add_to_term(letter, multiplier * sign)\n multiplier //= 10\n \n terms = [(letter, term) for letter, term in sorted(terms.items(), key=lambda x: abs(x[1]), reverse=True) if term != 0]\n return terms, nonzero_letters\n\n def solve(self, terms, sum_so_far, available_digits, nonzero_letters) -> bool:\n if len(terms) == 0:\n return sum_so_far == 0\n\n lower_bound = sum_so_far\n available_digits_copy = sorted(available_digits)\n for letter, coeff in terms:\n lower_bound += coeff * available_digits_copy.pop(0 if coeff > 0 else -1)\n \n upper_bound = sum_so_far\n available_digits_copy = sorted(available_digits)\n for letter, coeff in terms:\n upper_bound += coeff * available_digits_copy.pop(0 if coeff < 0 else -1)\n \n if lower_bound <= 0 and upper_bound >= 0:\n return any([\n self.solve(terms[1:], sum_so_far + terms[0][1] * digit, available_digits - {digit}, nonzero_letters)\n for digit in available_digits - ({0} if terms[0][0] in nonzero_letters else set())\n ])\n else:\n return False\n\n def isSolvable(self, words, result: str) -> bool:\n terms, nonzero_letters = self.simplify(words, result)\n return self.solve(terms, 0, set(range(10)), nonzero_letters)\n```\n\n```Java []\nclass Solution {\n int[] c2N = new int[26];\n int[] n2C = new int[10];\n boolean[] not0 = new boolean[26];\n public boolean isSolvable(String[] words, String result) {\n int maxWord = 1;\n for (String word : words) {\n if (word.length() > 1) {\n not0[word.charAt(0) - \'A\'] = true;\n } \n maxWord = Math.max(maxWord, word.length());\n if (word.length() > result.length()) {\n return false;\n }\n }\n if (maxWord + 1 < result.length()) {\n return false;\n }\n if (result.length() > 1) {\n not0[result.charAt(0) - \'A\'] = true;\n }\n Arrays.fill(c2N, -1);\n Arrays.fill(n2C, -1);\n return dfs(words, result, 0, 0, 0);\n }\n public boolean dfs(String[] words, String result, int wordIdx, int pos, int x) {\n if (pos == result.length()) {\n return x == 0;\n }\n if (wordIdx == words.length) {\n int sum = x;\n for (String word : words) {\n if (word.length() > pos) {\n sum += c2N[word.charAt(word.length() - 1 - pos) - \'A\'];\n }\n }\n int num = sum % 10;\n char c = result.charAt(result.length() - 1 - pos);\n if (c2N[c - \'A\'] != -1) {\n if (c2N[c - \'A\'] == num) {\n return dfs(words, result, 0, pos + 1, sum / 10);\n }\n return false; \n } else {\n if (n2C[num] != -1) {\n return false;\n }\n c2N[c - \'A\'] = num;\n n2C[num] = (int) c;\n boolean check = dfs(words, result, 0, pos + 1, sum / 10);\n if (check) {\n return true;\n }\n n2C[num] = -1;\n c2N[c - \'A\'] = -1;\n return false;\n }\n } else {\n String word = words[wordIdx];\n if (word.length() <= pos) {\n return dfs(words, result, wordIdx + 1, pos, x);\n } else {\n char c = word.charAt(word.length() - 1 - pos);\n if (c2N[c - \'A\'] != -1) {\n return dfs(words, result, wordIdx + 1, pos, x);\n } else {\n if (not0[c - \'A\']) {\n for (int i = 1; i < 10; i++) {\n if (n2C[i] == -1) {\n n2C[i] = c;\n c2N[c - \'A\'] = i;\n boolean check = dfs(words, result, wordIdx + 1, pos, x);\n if (check) {\n return true;\n }\n c2N[c - \'A\'] = -1;\n n2C[i] = -1;\n }\n }\n } else {\n for (int i = 0; i < 10; i++) {\n if (n2C[i] == -1) {\n n2C[i] = c;\n c2N[c - \'A\'] = i;\n boolean check = dfs(words, result, wordIdx + 1, pos, x);\n if (check) {\n return true;\n }\n c2N[c - \'A\'] = -1;\n n2C[i] = -1;\n }\n }\n }\n }\n }\n }\n return false;\n }\n}\n``` | 0 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Fast | Python Solution | verbal-arithmetic-puzzle | 0 | 1 | # Code\n```\nclass Solution:\n def isSolvable(self, words: List[str], result: str) -> bool:\n if max(map(len, words)) > len(result): return False # edge case \n \n words.append(result)\n digits = [0]*10 \n mp = {} # mapping from letter to digit \n \n def fn(i, j, val): \n """Find proper mapping for words[i][~j] and result[~j] via backtracking."""\n if j == len(result): return val == 0 # base condition \n if i == len(words): return val % 10 == 0 and fn(0, j+1, val//10)\n \n if j >= len(words[i]): return fn(i+1, j, val)\n if words[i][~j] in mp: \n if j and j+1 == len(words[i]) and mp[words[i][~j]] == 0: return # backtrack (no leading 0)\n if i+1 == len(words): return fn(i+1, j, val - mp[words[i][~j]])\n else: return fn(i+1, j, val + mp[words[i][~j]])\n else: \n for k, x in enumerate(digits): \n if not x and (k or j == 0 or j+1 < len(words[i])): \n mp[words[i][~j]] = k\n digits[k] = 1\n if i+1 == len(words) and fn(i+1, j, val-k): return True \n if i+1 < len(words) and fn(i+1, j, val+k): return True \n digits[k] = 0\n mp.pop(words[i][~j])\n \n return fn(0, 0, 0)\n``` | 0 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Backtracking with Cuts in Python, faster than 85% | verbal-arithmetic-puzzle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExploring all the $$N!$$ permutations can be too slow. This solution simulates the additive arithmetic that guesses the value of each alphabet from the least significant column to the most significant column. Of course, the carry should be handled when shift to every next column. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFollowing the order from the least significant column to the most significant column, the backtracking can be done in the typical manner. Notice the leading alphabets that should not be zero. \n\n\n# Code\n```\nclass Solution:\n def isSolvable(self, words: List[str], result: str) -> bool:\n var = {}\n digits = set()\n \n def check(column, carry):\n s = sum((var[w[-1-column]] for w in words if len(w) > column)) + carry\n c = result[-1-column]\n if c in var:\n if var[c] != s % 10:\n return -1, False\n else:\n return s // 10, False\n if s % 10 == 0 and c in leadings:\n return -1, False\n if s % 10 in digits:\n return -1, False\n var[c] = s % 10\n digits.add(s % 10)\n return s // 10, c\n\n def dfs(column, word_id, carry):\n reset = False\n if word_id >= len(words):\n carry, reset = check(column, carry)\n if carry < 0:\n return False\n word_id = 0\n column += 1\n if column >= len(result):\n if carry == 0:\n return True\n elif len(words[word_id]) <= column or words[word_id][-1-column] in var:\n if dfs(column, word_id+1, carry):\n return True\n else:\n c = words[word_id][-1-column]\n for d in range(10):\n if (d in digits) or (d == 0 and c in leadings):\n continue\n digits.add(d)\n var[c] = d\n if dfs(column, word_id+1, carry):\n return True\n digits.remove(d)\n del var[c]\n if reset != False:\n digits.remove(var[reset])\n del var[reset]\n return False\n\n leadings = set([w[0] for w in words + [result] if len(w) > 1])\n if any(len(w) > len(result) for w in words):\n return False\n return dfs(0, 0, 0)\n\n``` | 0 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Similar to Ye15 Solution with more Comments for easier understanding! | verbal-arithmetic-puzzle | 0 | 1 | # Code\n```python []\nclass Solution:\n def isSolvable(self, words: List[str], result: str) -> bool:\n if max(map(len, words)) > len(result): # If any of the words are bigger than the result, it will be impossible to solve\n return False\n # Add the result to the list, this way we will only subtract values when it comes to the result word.\n # Thus at every index, if the total is zero, then for that letter index the formulat is correct\n words = [word[::-1] for word in words] + [result[::-1]]\n values = {} #Mapping from letter to values\n nums = [0] * 10\n\n # i: word index, j: ltr index, total: total current Sum\n def dfs(i, j, total):\n if j == len(result): # Reached end of the indecies for ltrs in all words (END)\n return total % 10 == 0 # Checking to see if the total for the current character is correct or not \n if i == len(words): # Checked ltr at index j for all the words\n return total % 10 == 0 and dfs(0, j + 1, total // 10)\n \n if j >= len(words[i]):\n return dfs(i + 1, j, total)\n\n if words[i][j] in values:\n if values[words[i][j]] == 0 and j == len(words[i]) - 1:\n return False\n if i == len(words) - 1:\n return dfs(i + 1, j, total - values[words[i][j]])\n else:\n return dfs(i + 1, j, total + values[words[i][j]])\n else:\n for val, isUsed in enumerate(nums):\n if not isUsed and (val != 0 or j == 0 or j < len(words[i]) - 1):\n values[words[i][j]] = val\n nums[val] = True\n\n if i == len(words) - 1 and dfs(i + 1, j, total - values[words[i][j]]):\n return True\n elif i < len(words) - 1 and dfs(i + 1, j, total + values[words[i][j]]):\n return True\n \n values.pop(words[i][j])\n nums[val] = False\n\n return dfs(0, 0, 0)\n \n``` | 1 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Python Soln | Best for Interview | decrypt-string-from-alphabet-to-integer-mapping | 0 | 1 | 1. Starting from `i=0`, check if `s[i+2]==\'#\'`\n2. If yes, then `s[i: i+2]` is a character\n3. Else, `s[i]` is a character\n```\ndef freqAlphabets(self, s: str) -> str:\n\tres = []\n\ti = 0\n\n\twhile i < len(s):\n\t\tif i + 2 < len(s) and s[i + 2] == \'#\':\n\t\t\tval = int(s[i: i + 2])\n\t\t\tres.append(chr(val + 96)) # chr(65 - 90) is \'A\' to \'Z\', chr(97 - 122) is \'a\' to \'z\'\n\t\t\ti += 3\n\t\telse:\n\t\t\tres.append(chr(int(s[i]) + 96))\n\t\t\ti += 1\n\n\treturn \'\'.join(res)\n \n```\n\n\n | 68 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
Python Soln | Best for Interview | decrypt-string-from-alphabet-to-integer-mapping | 0 | 1 | 1. Starting from `i=0`, check if `s[i+2]==\'#\'`\n2. If yes, then `s[i: i+2]` is a character\n3. Else, `s[i]` is a character\n```\ndef freqAlphabets(self, s: str) -> str:\n\tres = []\n\ti = 0\n\n\twhile i < len(s):\n\t\tif i + 2 < len(s) and s[i + 2] == \'#\':\n\t\t\tval = int(s[i: i + 2])\n\t\t\tres.append(chr(val + 96)) # chr(65 - 90) is \'A\' to \'Z\', chr(97 - 122) is \'a\' to \'z\'\n\t\t\ti += 3\n\t\telse:\n\t\t\tres.append(chr(int(s[i]) + 96))\n\t\t\ti += 1\n\n\treturn \'\'.join(res)\n \n```\n\n\n | 68 | There are `n` people and `40` types of hats labeled from `1` to `40`.
Given a 2D integer array `hats`, where `hats[i]` is a list of all hats preferred by the `ith` person.
Return _the number of ways that the `n` people wear different hats to each other_.
Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** hats = \[\[3,4\],\[4,5\],\[5\]\]
**Output:** 1
**Explanation:** There is only one way to choose hats given the conditions.
First person choose hat 3, Second person choose hat 4 and last one hat 5.
**Example 2:**
**Input:** hats = \[\[3,5,1\],\[3,5\]\]
**Output:** 4
**Explanation:** There are 4 ways to choose hats:
(3,5), (5,3), (1,3) and (1,5)
**Example 3:**
**Input:** hats = \[\[1,2,3,4\],\[1,2,3,4\],\[1,2,3,4\],\[1,2,3,4\]\]
**Output:** 24
**Explanation:** Each person can choose hats labeled from 1 to 4.
Number of Permutations of (1,2,3,4) = 24.
**Constraints:**
* `n == hats.length`
* `1 <= n <= 10`
* `1 <= hats[i].length <= 40`
* `1 <= hats[i][j] <= 40`
* `hats[i]` contains a list of **unique** integers. | Scan from right to left, in each step of the scanning check whether there is a trailing "#" 2 indexes away. |
Python 3 (two lines) (beats 100%) (16 ms) (With Explanation) | decrypt-string-from-alphabet-to-integer-mapping | 0 | 1 | - Start from letter z (two digit numbers) and work backwords to avoid any confusion or inteference with one digit numbers. After replacing all two digit (hashtag based) numbers, we know that the remaining numbers will be simple one digit replacements.\n- Note that ord(\'a\') is 97 which means that chr(97) is \'a\'. This allows us to easily create a character based on its number in the alphabet. For example, \'a\' is the first letter in the alphabet. It has an index of 1 and chr(96 + 1) is \'a\'.\n\n```\nclass Solution:\n def freqAlphabets(self, s: str) -> str:\n for i in range(26,0,-1): s = s.replace(str(i)+\'#\'*(i>9),chr(96+i))\n return s\n \n\t\t\n\t\t\n- Junaid Mansuri\n- Chicago, IL | 138 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.