title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python Math | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nO(2)\n\n# Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:\n if tomatoSlices < 2*cheeseSlices: return [] # not enough tomato\n elif tomatoSlices % 2: return [] # uneven tomato\n\n j = (tomatoSlices//2 - cheeseSlices) \n s = (2*cheeseSlices - tomatoSlices//2) \n\n if j < 0 or s < 0: return []\n return [j, s]\n\n\n \n``` | 0 | You are given a circle represented as `(radius, xCenter, yCenter)` and an axis-aligned rectangle represented as `(x1, y1, x2, y2)`, where `(x1, y1)` are the coordinates of the bottom-left corner, and `(x2, y2)` are the coordinates of the top-right corner of the rectangle.
Return `true` _if the circle and rectangle are overlapped otherwise return_ `false`. In other words, check if there is **any** point `(xi, yi)` that belongs to the circle and the rectangle at the same time.
**Example 1:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
**Output:** true
**Explanation:** Circle and rectangle share the point (1,0).
**Example 2:**
**Input:** radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
**Output:** false
**Example 3:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
**Output:** true
**Constraints:**
* `1 <= radius <= 2000`
* `-104 <= xCenter, yCenter <= 104`
* `-104 <= x1 < x2 <= 104`
* `-104 <= y1 < y2 <= 104` | Can we have an answer if the number of tomatoes is odd ? If we have answer will be there multiple answers or just one answer ? Let us define number of jumbo burgers as X and number of small burgers as Y
We have to find an x and y in this equation 1. 4X + 2Y = tomato 2. X + Y = cheese |
Python 3 | Solution | one-liner | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:\n\n return [tomatoSlices//2 - cheeseSlices, 2*cheeseSlices - tomatoSlices//2] if (tomatoSlices - 2*cheeseSlices)%2 == 0 and (tomatoSlices - 2*cheeseSlices) >= 0 and (2*cheeseSlices - tomatoSlices//2) >= 0 else []\n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Python 3 | Solution | one-liner | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:\n\n return [tomatoSlices//2 - cheeseSlices, 2*cheeseSlices - tomatoSlices//2] if (tomatoSlices - 2*cheeseSlices)%2 == 0 and (tomatoSlices - 2*cheeseSlices) >= 0 and (2*cheeseSlices - tomatoSlices//2) >= 0 else []\n``` | 0 | You are given a circle represented as `(radius, xCenter, yCenter)` and an axis-aligned rectangle represented as `(x1, y1, x2, y2)`, where `(x1, y1)` are the coordinates of the bottom-left corner, and `(x2, y2)` are the coordinates of the top-right corner of the rectangle.
Return `true` _if the circle and rectangle are overlapped otherwise return_ `false`. In other words, check if there is **any** point `(xi, yi)` that belongs to the circle and the rectangle at the same time.
**Example 1:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
**Output:** true
**Explanation:** Circle and rectangle share the point (1,0).
**Example 2:**
**Input:** radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
**Output:** false
**Example 3:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
**Output:** true
**Constraints:**
* `1 <= radius <= 2000`
* `-104 <= xCenter, yCenter <= 104`
* `-104 <= x1 < x2 <= 104`
* `-104 <= y1 < y2 <= 104` | Can we have an answer if the number of tomatoes is odd ? If we have answer will be there multiple answers or just one answer ? Let us define number of jumbo burgers as X and number of small burgers as Y
We have to find an x and y in this equation 1. 4X + 2Y = tomato 2. X + Y = cheese |
Python exercise in solving linear equations | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLetting T = ```tomatoSlices``` and C = ```cheeseSlices```, we have the equations:\n T = tomatoSlices; C = cheeseSlices\n T - ( 4*J + 2*S ) = 0\n C - ( 1*J + 1*S ) = 0\n T = 4*J + 2*S\n C = 1*J + 1*S\n T - 2*C = 2*J\n T - 4*C = -2*S\n T / 2 - C = J\n - T / 2 + 2 * C = S\nWe also need two validity checks: First, T must be even because it\'s divided by two, and Second, both S and J must be non-negative\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nImplement the last two equations and add logic for the validity checks.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ because there is no dependence in the size of the input (a pair of scalars )\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ because the only temporary variables are scalars.\n# Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:\n T = tomatoSlices; C = cheeseSlices\n # T - ( 4*J + 2*S ) = 0\n # C - ( 1*J + 1*S ) = 0\n # T = 4*J + 2*S\n # C = 1*J + 1*S\n # T - 2*C = 2*J\n # T - 4*C = -2*S\n if T % 2 == 1:\n return []\n else:\n J = ( T - 2 * C ) // 2\n S = - ( T - 4 * C ) // 2\n if J >= 0 and S >= 0:\n return [ J, S ]\n else:\n return []\n\n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Python exercise in solving linear equations | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLetting T = ```tomatoSlices``` and C = ```cheeseSlices```, we have the equations:\n T = tomatoSlices; C = cheeseSlices\n T - ( 4*J + 2*S ) = 0\n C - ( 1*J + 1*S ) = 0\n T = 4*J + 2*S\n C = 1*J + 1*S\n T - 2*C = 2*J\n T - 4*C = -2*S\n T / 2 - C = J\n - T / 2 + 2 * C = S\nWe also need two validity checks: First, T must be even because it\'s divided by two, and Second, both S and J must be non-negative\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nImplement the last two equations and add logic for the validity checks.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ because there is no dependence in the size of the input (a pair of scalars )\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ because the only temporary variables are scalars.\n# Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:\n T = tomatoSlices; C = cheeseSlices\n # T - ( 4*J + 2*S ) = 0\n # C - ( 1*J + 1*S ) = 0\n # T = 4*J + 2*S\n # C = 1*J + 1*S\n # T - 2*C = 2*J\n # T - 4*C = -2*S\n if T % 2 == 1:\n return []\n else:\n J = ( T - 2 * C ) // 2\n S = - ( T - 4 * C ) // 2\n if J >= 0 and S >= 0:\n return [ J, S ]\n else:\n return []\n\n``` | 0 | You are given a circle represented as `(radius, xCenter, yCenter)` and an axis-aligned rectangle represented as `(x1, y1, x2, y2)`, where `(x1, y1)` are the coordinates of the bottom-left corner, and `(x2, y2)` are the coordinates of the top-right corner of the rectangle.
Return `true` _if the circle and rectangle are overlapped otherwise return_ `false`. In other words, check if there is **any** point `(xi, yi)` that belongs to the circle and the rectangle at the same time.
**Example 1:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
**Output:** true
**Explanation:** Circle and rectangle share the point (1,0).
**Example 2:**
**Input:** radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
**Output:** false
**Example 3:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
**Output:** true
**Constraints:**
* `1 <= radius <= 2000`
* `-104 <= xCenter, yCenter <= 104`
* `-104 <= x1 < x2 <= 104`
* `-104 <= y1 < y2 <= 104` | Can we have an answer if the number of tomatoes is odd ? If we have answer will be there multiple answers or just one answer ? Let us define number of jumbo burgers as X and number of small burgers as Y
We have to find an x and y in this equation 1. 4X + 2Y = tomato 2. X + Y = cheese |
mind blown logic using DP in python3 | count-square-submatrices-with-all-ones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport numpy\nclass Solution:\n def countSquares(self, matrix: List[List[int]]) -> int:\n dp=[[0 for i in range(len(matrix[0]))] for j in range(len(matrix))]\n for row in range(len(matrix)):\n for col in range(len(matrix[0])):\n if matrix[row][col]==0:\n continue\n if row==0:\n dp[row][col]=1\n elif col==0:\n dp[row][col]=1\n else:\n minimum=min(dp[row-1][col],dp[row][col-1],dp[row-1][col-1])\n dp[row][col]=minimum+1\n return sum(numpy.concatenate(dp))\n\n``` | 2 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
mind blown logic using DP in python3 | count-square-submatrices-with-all-ones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport numpy\nclass Solution:\n def countSquares(self, matrix: List[List[int]]) -> int:\n dp=[[0 for i in range(len(matrix[0]))] for j in range(len(matrix))]\n for row in range(len(matrix)):\n for col in range(len(matrix[0])):\n if matrix[row][col]==0:\n continue\n if row==0:\n dp[row][col]=1\n elif col==0:\n dp[row][col]=1\n else:\n minimum=min(dp[row-1][col],dp[row][col-1],dp[row-1][col-1])\n dp[row][col]=minimum+1\n return sum(numpy.concatenate(dp))\n\n``` | 2 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
DP with figure explanation | count-square-submatrices-with-all-ones | 0 | 1 | 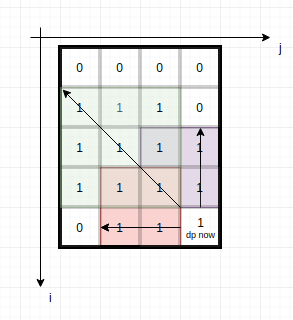\n\n----\n----\n## ## Explanation\n\n `dp[i][j]` represent edge length of the biggest square whose lower right corner element is `matrix[i][j]`. Also there are `dp[i][j]` squares whose lower right corner element are `matrix[i][j]`. The answer of count-square-submatrices-with-all-ones is sum of all `dp[i][j]`.\n\nAs Figure, **the square edge length** ( whose lower right corner element is `matrix[i][j]` ) is not greater than `the minimum of three arrows + 1`. \n\nFortunately it can be equal to when `matrix[i][j]==1`. On this condition `dp[i][j]=the minimum of three arrows + 1`;\n\nAnd when `matrix[i][j]==0` , `dp[i][j]=0`.\n\nSo\n\n```py\nif matrix[i][j]==1 : \n if i!=0 and j!=0: \n dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])+1\n else: \n dp[i][j] = 0 + 1\nelse:\n dp[i][j] = 0\n```\n\nIn the 3rd line, each `dp[i][j]` is reused for 3 times.\nIf you think there are too many coincidences, please read next paragraph.\nNow we can write a top-down recursive algorithm:\n\n----\n\n### ### A top-down DP\n\ntime O(m*n), space O(m*n)\n\n```py\nclass Solution(object):\n def countSquares(self, matrix):\n m, n = len(matrix), len(matrix[0])\n\n @cache # memorize\n def dp(i,j):\n if matrix[i][j]==1 : \n if i!=0 and j!=0:\n return min(dp(i-1,j), dp(i,j-1), dp(i-1,j-1))+1\n else:\n return 0+1\n else:\n return 0\n \n return sum(dp(i,j) for i in range(m) for j in range(n))\n```\n\nAfter wrtie this we know the call order of the dp function, then we can change it to bottom-up, make sure each dp(i,j) is calculated before dp(i,j+1) and dp(i+1,j) and dp(i+1,j+1). That\'s the classic iteration order: from left to right and from up to down.\n\n---\n\n### ### A bottom-up DP\n\ntime O(m*n), space O(m*n)\n\nHere in order to easily process border condition, use `dp[i+1][j+1]` save edge length of the biggest square whose lower right corner element is `matrix[i][j]`.\n\n```py\nclass Solution(object):\n def countSquares(self, matrix):\n m, n = len(matrix), len(matrix[0])\n dp = [[0] * (n+1) for _ in range(m+1)] # new int[m+1][n+1];\n ans = 0\n for i in range(m):\n for j in range(n):\n if matrix[i][j]:\n dp[i+1][j+1] = min(dp[i][j+1], dp[i+1][j], dp[i][j]) + 1\n ans += dp[i+1][j+1]\n return ans\n```\n\n----\n----\n\n## ## P.S. \n\nThe same problem: https://leetcode.com/problems/maximal-square/\nsimilar: https://leetcode.com/problems/minimum-path-sum/\nextend: https://leetcode.com/problems/count-fertile-pyramids-in-a-land\nharder(still can use one dp): https://codeforces.com/contest/1393/problem/D\n\nMore about top-down and bottom-up \nhttps://leetcode.com/explore/learn/card/recursion-i/\nhttps://leetcode.com/explore/learn/card/recursion-ii/\n | 154 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
DP with figure explanation | count-square-submatrices-with-all-ones | 0 | 1 | \n\n----\n----\n## ## Explanation\n\n `dp[i][j]` represent edge length of the biggest square whose lower right corner element is `matrix[i][j]`. Also there are `dp[i][j]` squares whose lower right corner element are `matrix[i][j]`. The answer of count-square-submatrices-with-all-ones is sum of all `dp[i][j]`.\n\nAs Figure, **the square edge length** ( whose lower right corner element is `matrix[i][j]` ) is not greater than `the minimum of three arrows + 1`. \n\nFortunately it can be equal to when `matrix[i][j]==1`. On this condition `dp[i][j]=the minimum of three arrows + 1`;\n\nAnd when `matrix[i][j]==0` , `dp[i][j]=0`.\n\nSo\n\n```py\nif matrix[i][j]==1 : \n if i!=0 and j!=0: \n dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])+1\n else: \n dp[i][j] = 0 + 1\nelse:\n dp[i][j] = 0\n```\n\nIn the 3rd line, each `dp[i][j]` is reused for 3 times.\nIf you think there are too many coincidences, please read next paragraph.\nNow we can write a top-down recursive algorithm:\n\n----\n\n### ### A top-down DP\n\ntime O(m*n), space O(m*n)\n\n```py\nclass Solution(object):\n def countSquares(self, matrix):\n m, n = len(matrix), len(matrix[0])\n\n @cache # memorize\n def dp(i,j):\n if matrix[i][j]==1 : \n if i!=0 and j!=0:\n return min(dp(i-1,j), dp(i,j-1), dp(i-1,j-1))+1\n else:\n return 0+1\n else:\n return 0\n \n return sum(dp(i,j) for i in range(m) for j in range(n))\n```\n\nAfter wrtie this we know the call order of the dp function, then we can change it to bottom-up, make sure each dp(i,j) is calculated before dp(i,j+1) and dp(i+1,j) and dp(i+1,j+1). That\'s the classic iteration order: from left to right and from up to down.\n\n---\n\n### ### A bottom-up DP\n\ntime O(m*n), space O(m*n)\n\nHere in order to easily process border condition, use `dp[i+1][j+1]` save edge length of the biggest square whose lower right corner element is `matrix[i][j]`.\n\n```py\nclass Solution(object):\n def countSquares(self, matrix):\n m, n = len(matrix), len(matrix[0])\n dp = [[0] * (n+1) for _ in range(m+1)] # new int[m+1][n+1];\n ans = 0\n for i in range(m):\n for j in range(n):\n if matrix[i][j]:\n dp[i+1][j+1] = min(dp[i][j+1], dp[i+1][j], dp[i][j]) + 1\n ans += dp[i+1][j+1]\n return ans\n```\n\n----\n----\n\n## ## P.S. \n\nThe same problem: https://leetcode.com/problems/maximal-square/\nsimilar: https://leetcode.com/problems/minimum-path-sum/\nextend: https://leetcode.com/problems/count-fertile-pyramids-in-a-land\nharder(still can use one dp): https://codeforces.com/contest/1393/problem/D\n\nMore about top-down and bottom-up \nhttps://leetcode.com/explore/learn/card/recursion-i/\nhttps://leetcode.com/explore/learn/card/recursion-ii/\n | 154 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
Superb Logic Python3 ---->DP | count-square-submatrices-with-all-ones | 0 | 1 | # Dynamic Programming\n```\nclass Solution:\n def countSquares(self, matrix: List[List[int]]) -> int:\n row=len(matrix)\n col=len(matrix[0])\n dp=[[0]*col for i in range(row)]\n for i in range(row):\n for j in range(col):\n if (i==0 or j==0) and matrix[i][j]==1:\n dp[i][j]=1\n for i in range(1,row):\n for j in range(1,col):\n if matrix[i][j]==1:\n dp[i][j]=1+min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])\n ans=0\n for rows in dp:\n ans+=sum(rows)\n return ans\n``` \n# please upvote me it would encourage me alot\n\n\t | 7 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Superb Logic Python3 ---->DP | count-square-submatrices-with-all-ones | 0 | 1 | # Dynamic Programming\n```\nclass Solution:\n def countSquares(self, matrix: List[List[int]]) -> int:\n row=len(matrix)\n col=len(matrix[0])\n dp=[[0]*col for i in range(row)]\n for i in range(row):\n for j in range(col):\n if (i==0 or j==0) and matrix[i][j]==1:\n dp[i][j]=1\n for i in range(1,row):\n for j in range(1,col):\n if matrix[i][j]==1:\n dp[i][j]=1+min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])\n ans=0\n for rows in dp:\n ans+=sum(rows)\n return ans\n``` \n# please upvote me it would encourage me alot\n\n\t | 7 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
Py | Easy solution | Best Approch 💯 ✅ | count-square-submatrices-with-all-ones | 0 | 1 | ```\nclass Solution:\n def countSquares(self, arr: List[List[int]]) -> int:\n n=len(arr)\n m=len(arr[0])\n dp=[[0 for i in range(m)]for j in range(n)]\n for i in range(n):\n dp[i][0]=arr[i][0]\n for j in range(m):\n dp[0][j]=arr[0][j]\n for i in range(1,n):\n for j in range(1,m):\n if arr[i][j]==1:\n dp[i][j]= 1+min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])\n else:\n dp[i][j]=0\n \n ans=0\n for i in range(n):\n ans+=sum(dp[i])\n return ans\n``` | 1 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Py | Easy solution | Best Approch 💯 ✅ | count-square-submatrices-with-all-ones | 0 | 1 | ```\nclass Solution:\n def countSquares(self, arr: List[List[int]]) -> int:\n n=len(arr)\n m=len(arr[0])\n dp=[[0 for i in range(m)]for j in range(n)]\n for i in range(n):\n dp[i][0]=arr[i][0]\n for j in range(m):\n dp[0][j]=arr[0][j]\n for i in range(1,n):\n for j in range(1,m):\n if arr[i][j]==1:\n dp[i][j]= 1+min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])\n else:\n dp[i][j]=0\n \n ans=0\n for i in range(n):\n ans+=sum(dp[i])\n return ans\n``` | 1 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
Python || DP || Tabulation || Explained | count-square-submatrices-with-all-ones | 0 | 1 | **Intuition:**\n\nFollowing the tabulation method, we will first create a 2D dp array of the same size as the given 2D matrix. And in the dp array, dp[i][j] will signify, how many squares end at the cell (i, j) i.e. for how many squares the rightmost bottom cell is (i, j).\nFor example, consider the following matrix:\n\n 1 1\n 1 1\n\nFor the given matrix, the dp array will be the following:\n \n 1 1 \n 1 2\n\nFor the above matrix, dp[0][0] stores 1, whereas dp[1][1] stores 2. For cell (0, 0), there is only 1 square(i.e. the cell itself) that ends at (0,0). But for cell (1,1), there is a square of size 1 i.e. the cell itself and there is also a square of size 2 (i.e. the whole matrix) that end at cell (1,1).\n\nSimilarly, let\u2019s try it for the following 3X3 matrix:\n\n[[1 1 1], [[1 1 1],\n [1 1 1], [1 2 2],\n [1 1 1]] [1 2 3]]\n\nNow, to get the final answer, we will just add all the values of the cells and the total sum will be our final answer. So, for the 2X2 matrix, the answer is (1+1+1+2) = 5 squares and for the 3X3 matrix, the answer is (1+1+1+1+2+2+1+2+3) = 14 squares.\n\nNow, it\u2019s time to discuss how to fill the values of the dp array:\n\nIf we carefully observe, for the first row and for the first column, each cell (i, j), itself will be the one and only square(if cell(i, j) contains 1) that ends at that particular cell i.e. (i, j). So, for the first row and first column, we will just copy the values of the matrix as it is to the dp array. \nNow, to fill the other cells, we will check the following:\nIf the cell contains 1, we will have to check its three adjacent cells i.e. (i-1, j), (i-1, j-1), and (i, j-1). We will first figure out the minimum number of squares that end at these adjacent cells. And while filling the value for cell(i, j) we will add 1 with that minimum value as the cell (i, j) itself is a square. The formula will be the following:dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) +1\nOtherwise, if the cell(i, j) contains 0, we will also set the value of dp[i][j] as 0.\n\n```\nclass Solution:\n def countSquares(self, matrix: List[List[int]]) -> int:\n m,n=len(matrix),len(matrix[0])\n dp=[[0 for j in range(n)] for i in range(m)]\n for i in range(m): #First column and row will remain same as in original matrix\n dp[i][0]=matrix[i][0]\n for j in range(n):\n dp[0][j]=matrix[0][j]\n for i in range(1,m):\n for j in range(1,n):\n if matrix[i][j]==0:\n dp[i][j]=0\n else:\n dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])\n ans=0\n for i in range(m):\n for j in range(n):\n ans+=dp[i][j]\n print(dp)\n return ans \n```\n**An upvote will be encouraging** | 2 | Given a `m * n` matrix of ones and zeros, return how many **square** submatrices have all ones.
**Example 1:**
**Input:** matrix =
\[
\[0,1,1,1\],
\[1,1,1,1\],
\[0,1,1,1\]
\]
**Output:** 15
**Explanation:**
There are **10** squares of side 1.
There are **4** squares of side 2.
There is **1** square of side 3.
Total number of squares = 10 + 4 + 1 = **15**.
**Example 2:**
**Input:** matrix =
\[
\[1,0,1\],
\[1,1,0\],
\[1,1,0\]
\]
**Output:** 7
**Explanation:**
There are **6** squares of side 1.
There is **1** square of side 2.
Total number of squares = 6 + 1 = **7**.
**Constraints:**
* `1 <= arr.length <= 300`
* `1 <= arr[0].length <= 300`
* `0 <= arr[i][j] <= 1` | A number is a multiple of three if and only if its sum of digits is a multiple of three. Use dynamic programming. To find the maximum number, try to maximize the number of digits of the number. Sort the digits in descending order to find the maximum number. |
Python || DP || Tabulation || Explained | count-square-submatrices-with-all-ones | 0 | 1 | **Intuition:**\n\nFollowing the tabulation method, we will first create a 2D dp array of the same size as the given 2D matrix. And in the dp array, dp[i][j] will signify, how many squares end at the cell (i, j) i.e. for how many squares the rightmost bottom cell is (i, j).\nFor example, consider the following matrix:\n\n 1 1\n 1 1\n\nFor the given matrix, the dp array will be the following:\n \n 1 1 \n 1 2\n\nFor the above matrix, dp[0][0] stores 1, whereas dp[1][1] stores 2. For cell (0, 0), there is only 1 square(i.e. the cell itself) that ends at (0,0). But for cell (1,1), there is a square of size 1 i.e. the cell itself and there is also a square of size 2 (i.e. the whole matrix) that end at cell (1,1).\n\nSimilarly, let\u2019s try it for the following 3X3 matrix:\n\n[[1 1 1], [[1 1 1],\n [1 1 1], [1 2 2],\n [1 1 1]] [1 2 3]]\n\nNow, to get the final answer, we will just add all the values of the cells and the total sum will be our final answer. So, for the 2X2 matrix, the answer is (1+1+1+2) = 5 squares and for the 3X3 matrix, the answer is (1+1+1+1+2+2+1+2+3) = 14 squares.\n\nNow, it\u2019s time to discuss how to fill the values of the dp array:\n\nIf we carefully observe, for the first row and for the first column, each cell (i, j), itself will be the one and only square(if cell(i, j) contains 1) that ends at that particular cell i.e. (i, j). So, for the first row and first column, we will just copy the values of the matrix as it is to the dp array. \nNow, to fill the other cells, we will check the following:\nIf the cell contains 1, we will have to check its three adjacent cells i.e. (i-1, j), (i-1, j-1), and (i, j-1). We will first figure out the minimum number of squares that end at these adjacent cells. And while filling the value for cell(i, j) we will add 1 with that minimum value as the cell (i, j) itself is a square. The formula will be the following:dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) +1\nOtherwise, if the cell(i, j) contains 0, we will also set the value of dp[i][j] as 0.\n\n```\nclass Solution:\n def countSquares(self, matrix: List[List[int]]) -> int:\n m,n=len(matrix),len(matrix[0])\n dp=[[0 for j in range(n)] for i in range(m)]\n for i in range(m): #First column and row will remain same as in original matrix\n dp[i][0]=matrix[i][0]\n for j in range(n):\n dp[0][j]=matrix[0][j]\n for i in range(1,m):\n for j in range(1,n):\n if matrix[i][j]==0:\n dp[i][j]=0\n else:\n dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])\n ans=0\n for i in range(m):\n for j in range(n):\n ans+=dp[i][j]\n print(dp)\n return ans \n```\n**An upvote will be encouraging** | 2 | A chef has collected data on the `satisfaction` level of his `n` dishes. Chef can cook any dish in 1 unit of time.
**Like-time coefficient** of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. `time[i] * satisfaction[i]`.
Return _the maximum sum of **like-time coefficient** that the chef can obtain after dishes preparation_.
Dishes can be prepared in **any** order and the chef can discard some dishes to get this maximum value.
**Example 1:**
**Input:** satisfaction = \[-1,-8,0,5,-9\]
**Output:** 14
**Explanation:** After Removing the second and last dish, the maximum total **like-time coefficient** will be equal to (-1\*1 + 0\*2 + 5\*3 = 14).
Each dish is prepared in one unit of time.
**Example 2:**
**Input:** satisfaction = \[4,3,2\]
**Output:** 20
**Explanation:** Dishes can be prepared in any order, (2\*1 + 3\*2 + 4\*3 = 20)
**Example 3:**
**Input:** satisfaction = \[-1,-4,-5\]
**Output:** 0
**Explanation:** People do not like the dishes. No dish is prepared.
**Constraints:**
* `n == satisfaction.length`
* `1 <= n <= 500`
* `-1000 <= satisfaction[i] <= 1000` | Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0). Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer. |
Easy DP Solution | palindrome-partitioning-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def palindromePartition(self, S, K):\n N = len(S)\n dp = [[N] * (N + 1) for _ in range(K + 1)]\n dp[0][0] = 0\n for i in range(2 * N - 1):\n c = 0\n l = i // 2\n r = l + (i & 1)\n while 0 <= l and r < N:\n if S[l] != S[r]: c += 1\n for i in range(K):\n dp[i + 1][r + 1] = min(dp[i + 1][r + 1], dp[i][l] + c)\n l -= 1\n r += 1\n return dp[-1][-1]\n``` | 0 | You are given a string `s` containing lowercase letters and an integer `k`. You need to :
* First, change some characters of `s` to other lowercase English letters.
* Then divide `s` into `k` non-empty disjoint substrings such that each substring is a palindrome.
Return _the minimal number of characters that you need to change to divide the string_.
**Example 1:**
**Input:** s = "abc ", k = 2
**Output:** 1
**Explanation:** You can split the string into "ab " and "c ", and change 1 character in "ab " to make it palindrome.
**Example 2:**
**Input:** s = "aabbc ", k = 3
**Output:** 0
**Explanation:** You can split the string into "aa ", "bb " and "c ", all of them are palindrome.
**Example 3:**
**Input:** s = "leetcode ", k = 8
**Output:** 0
**Constraints:**
* `1 <= k <= s.length <= 100`.
* `s` only contains lowercase English letters. | null |
Easy DP Solution | palindrome-partitioning-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def palindromePartition(self, S, K):\n N = len(S)\n dp = [[N] * (N + 1) for _ in range(K + 1)]\n dp[0][0] = 0\n for i in range(2 * N - 1):\n c = 0\n l = i // 2\n r = l + (i & 1)\n while 0 <= l and r < N:\n if S[l] != S[r]: c += 1\n for i in range(K):\n dp[i + 1][r + 1] = min(dp[i + 1][r + 1], dp[i][l] + c)\n l -= 1\n r += 1\n return dp[-1][-1]\n``` | 0 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
python super easy DP top down | palindrome-partitioning-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def palindromePartition(self, s: str, k: int) -> int:\n\n \n def min_steps(s):\n l = 0\n r = len(s)-1\n ans = 0\n while l < r:\n if s[l] != s[r]:\n ans +=1\n l +=1\n r -=1\n return ans\n\n\n @lru_cache(None)\n def dp(i, k):\n if i == len(s):\n if k == 0:\n return 0\n return float("inf")\n if k == 0:\n return float("inf")\n ans = float("inf")\n for j in range(i, len(s)):\n ans = min(ans, min_steps(s[i:j+1]) + dp(j+1, k-1))\n return ans\n \n return dp(0, k)\n \n \n\n\n\n``` | 0 | You are given a string `s` containing lowercase letters and an integer `k`. You need to :
* First, change some characters of `s` to other lowercase English letters.
* Then divide `s` into `k` non-empty disjoint substrings such that each substring is a palindrome.
Return _the minimal number of characters that you need to change to divide the string_.
**Example 1:**
**Input:** s = "abc ", k = 2
**Output:** 1
**Explanation:** You can split the string into "ab " and "c ", and change 1 character in "ab " to make it palindrome.
**Example 2:**
**Input:** s = "aabbc ", k = 3
**Output:** 0
**Explanation:** You can split the string into "aa ", "bb " and "c ", all of them are palindrome.
**Example 3:**
**Input:** s = "leetcode ", k = 8
**Output:** 0
**Constraints:**
* `1 <= k <= s.length <= 100`.
* `s` only contains lowercase English letters. | null |
python super easy DP top down | palindrome-partitioning-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def palindromePartition(self, s: str, k: int) -> int:\n\n \n def min_steps(s):\n l = 0\n r = len(s)-1\n ans = 0\n while l < r:\n if s[l] != s[r]:\n ans +=1\n l +=1\n r -=1\n return ans\n\n\n @lru_cache(None)\n def dp(i, k):\n if i == len(s):\n if k == 0:\n return 0\n return float("inf")\n if k == 0:\n return float("inf")\n ans = float("inf")\n for j in range(i, len(s)):\n ans = min(ans, min_steps(s[i:j+1]) + dp(j+1, k-1))\n return ans\n \n return dp(0, k)\n \n \n\n\n\n``` | 0 | Given the array `nums`, obtain a subsequence of the array whose sum of elements is **strictly greater** than the sum of the non included elements in such subsequence.
If there are multiple solutions, return the subsequence with **minimum size** and if there still exist multiple solutions, return the subsequence with the **maximum total sum** of all its elements. A subsequence of an array can be obtained by erasing some (possibly zero) elements from the array.
Note that the solution with the given constraints is guaranteed to be **unique**. Also return the answer sorted in **non-increasing** order.
**Example 1:**
**Input:** nums = \[4,3,10,9,8\]
**Output:** \[10,9\]
**Explanation:** The subsequences \[10,9\] and \[10,8\] are minimal such that the sum of their elements is strictly greater than the sum of elements not included. However, the subsequence \[10,9\] has the maximum total sum of its elements.
**Example 2:**
**Input:** nums = \[4,4,7,6,7\]
**Output:** \[7,7,6\]
**Explanation:** The subsequence \[7,7\] has the sum of its elements equal to 14 which is not strictly greater than the sum of elements not included (14 = 4 + 4 + 6). Therefore, the subsequence \[7,6,7\] is the minimal satisfying the conditions. Note the subsequence has to be returned in non-decreasing order.
**Constraints:**
* `1 <= nums.length <= 500`
* `1 <= nums[i] <= 100` | For each substring calculate the minimum number of steps to make it palindrome and store it in a table. Create a dp(pos, cnt) which means the minimum number of characters changed for the suffix of s starting on pos splitting the suffix on cnt chunks. |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | students-and-examinations | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef students_and_examinations(students: pd.DataFrame, subjects: pd.DataFrame, examinations: pd.DataFrame) -> pd.DataFrame:\n return pd.merge(\n left=pd.merge(\n students, subjects, how=\'cross\',\n ).sort_values(\n by=[\'student_id\', \'subject_name\']\n ),\n right=examinations.groupby(\n [\'student_id\', \'subject_name\'],\n ).agg(\n attended_exams=(\'subject_name\', \'count\')\n ).reset_index(),\n how=\'left\',\n on=[\'student_id\', \'subject_name\'],\n ).fillna(0)[\n [\'student_id\', \'student_name\', \'subject_name\', \'attended_exams\']\n ]\n```\n```SQL []\nSELECT\n Students.student_id,\n Students.student_name,\n Subjects.subject_name,\n count(Examinations.subject_name) AS attended_exams\n FROM Students\n JOIN Subjects\n LEFT JOIN Examinations\n ON Students.student_id = Examinations.student_id\n AND Subjects.subject_name = Examinations.subject_name\nGROUP BY Students.student_id,\n Subjects.subject_name\nORDER BY student_id,\n subject_name;\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n | 38 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
🔥 Pandas Step by Step and Concise Solution For Beginners 💯 | students-and-examinations | 0 | 1 | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n```\nimport pandas as pd\n\ndef students_and_examinations(students: pd.DataFrame, subjects: pd.DataFrame, examinations: pd.DataFrame) -> pd.DataFrame:\n \n df1 = students.merge(subjects, how=\'cross\')\n \n df2 = examinations.groupby([\'student_id\', \'subject_name\']).agg(\n attended_exams=(\'subject_name\', \'count\')\n ).reset_index()\n \n result = df1.merge(df2, on=[\'student_id\',\'subject_name\'], how=\'left\').sort_values(by = [\'student_id\', \'subject_name\'])\n \n return result.fillna(0)[[\'student_id\', \'student_name\', \'subject_name\', \'attended_exams\']]\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 7 | A **happy string** is a string that:
* consists only of letters of the set `['a', 'b', 'c']`.
* `s[i] != s[i + 1]` for all values of `i` from `1` to `s.length - 1` (string is 1-indexed).
For example, strings **"abc ", "ac ", "b "** and **"abcbabcbcb "** are all happy strings and strings **"aa ", "baa "** and **"ababbc "** are not happy strings.
Given two integers `n` and `k`, consider a list of all happy strings of length `n` sorted in lexicographical order.
Return _the kth string_ of this list or return an **empty string** if there are less than `k` happy strings of length `n`.
**Example 1:**
**Input:** n = 1, k = 3
**Output:** "c "
**Explanation:** The list \[ "a ", "b ", "c "\] contains all happy strings of length 1. The third string is "c ".
**Example 2:**
**Input:** n = 1, k = 4
**Output:** " "
**Explanation:** There are only 3 happy strings of length 1.
**Example 3:**
**Input:** n = 3, k = 9
**Output:** "cab "
**Explanation:** There are 12 different happy string of length 3 \[ "aba ", "abc ", "aca ", "acb ", "bab ", "bac ", "bca ", "bcb ", "cab ", "cac ", "cba ", "cbc "\]. You will find the 9th string = "cab "
**Constraints:**
* `1 <= n <= 10`
* `1 <= k <= 100` | null |
Python simple code | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | \n# Code\n```\nclass Solution:\n def subtractProductAndSum(self, n: int) -> int:\n s = 0\n mult = 1\n\n while n > 0:\n digit = n%10\n s += digit\n mult *= digit\n n = n//10\n\n return mult-s\n\n \n``` | 1 | Given an integer number `n`, return the difference between the product of its digits and the sum of its digits.
**Example 1:**
**Input:** n = 234
**Output:** 15
**Explanation:**
Product of digits = 2 \* 3 \* 4 = 24
Sum of digits = 2 + 3 + 4 = 9
Result = 24 - 9 = 15
**Example 2:**
**Input:** n = 4421
**Output:** 21
**Explanation:**
Product of digits = 4 \* 4 \* 2 \* 1 = 32
Sum of digits = 4 + 4 + 2 + 1 = 11
Result = 32 - 11 = 21
**Constraints:**
* `1 <= n <= 10^5` | Since we can rearrange the substring, all we care about is the frequency of each character in that substring. How to find the character frequencies efficiently ? As a preprocess, calculate the accumulate frequency of all characters for all prefixes of the string. How to check if a substring can be changed to a palindrome given its characters frequency ? Count the number of odd frequencies, there can be at most one odd frequency in a palindrome. |
Python simple code | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | \n# Code\n```\nclass Solution:\n def subtractProductAndSum(self, n: int) -> int:\n s = 0\n mult = 1\n\n while n > 0:\n digit = n%10\n s += digit\n mult *= digit\n n = n//10\n\n return mult-s\n\n \n``` | 1 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Solution of subtract the product and sum of digits of an integer problem | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | # Approach\n- Solved using simple loop\n- We iterate over a number and multiply and sum the digits of the number\n\n# Complexity\n- Time complexity:\n$$0(n)$$ - as we are iterating over n elements.\n\n# Code\n```\nclass Solution:\n def subtractProductAndSum(self, n: int) -> int:\n product_d, sum_d = 1, 0\n for digit in str(n):\n product_d *= int(digit)\n sum_d += int(digit)\n return product_d - sum_d\n\n``` | 1 | Given an integer number `n`, return the difference between the product of its digits and the sum of its digits.
**Example 1:**
**Input:** n = 234
**Output:** 15
**Explanation:**
Product of digits = 2 \* 3 \* 4 = 24
Sum of digits = 2 + 3 + 4 = 9
Result = 24 - 9 = 15
**Example 2:**
**Input:** n = 4421
**Output:** 21
**Explanation:**
Product of digits = 4 \* 4 \* 2 \* 1 = 32
Sum of digits = 4 + 4 + 2 + 1 = 11
Result = 32 - 11 = 21
**Constraints:**
* `1 <= n <= 10^5` | Since we can rearrange the substring, all we care about is the frequency of each character in that substring. How to find the character frequencies efficiently ? As a preprocess, calculate the accumulate frequency of all characters for all prefixes of the string. How to check if a substring can be changed to a palindrome given its characters frequency ? Count the number of odd frequencies, there can be at most one odd frequency in a palindrome. |
Solution of subtract the product and sum of digits of an integer problem | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | # Approach\n- Solved using simple loop\n- We iterate over a number and multiply and sum the digits of the number\n\n# Complexity\n- Time complexity:\n$$0(n)$$ - as we are iterating over n elements.\n\n# Code\n```\nclass Solution:\n def subtractProductAndSum(self, n: int) -> int:\n product_d, sum_d = 1, 0\n for digit in str(n):\n product_d *= int(digit)\n sum_d += int(digit)\n return product_d - sum_d\n\n``` | 1 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python | Easy Solution✅ | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | ```\ndef subtractProductAndSum(self, n: int) -> int:\n prod = 1 # n =234\n sums = 0\n while n != 0: # 1st loop 2nd loop 3rd loop \n last = n % 10 # last = 4 3 2\n prod *= last # prod = 1*4 = 4 4*3 = 12 12*2 = 24\n sums += last # sums = 0+4 = 4 4+3 = 7 7+2 = 9\n n =n//10 # n = 23 2 0\n return prod - sums # 24 - 9 = 15\n``` | 25 | Given an integer number `n`, return the difference between the product of its digits and the sum of its digits.
**Example 1:**
**Input:** n = 234
**Output:** 15
**Explanation:**
Product of digits = 2 \* 3 \* 4 = 24
Sum of digits = 2 + 3 + 4 = 9
Result = 24 - 9 = 15
**Example 2:**
**Input:** n = 4421
**Output:** 21
**Explanation:**
Product of digits = 4 \* 4 \* 2 \* 1 = 32
Sum of digits = 4 + 4 + 2 + 1 = 11
Result = 32 - 11 = 21
**Constraints:**
* `1 <= n <= 10^5` | Since we can rearrange the substring, all we care about is the frequency of each character in that substring. How to find the character frequencies efficiently ? As a preprocess, calculate the accumulate frequency of all characters for all prefixes of the string. How to check if a substring can be changed to a palindrome given its characters frequency ? Count the number of odd frequencies, there can be at most one odd frequency in a palindrome. |
Python | Easy Solution✅ | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | ```\ndef subtractProductAndSum(self, n: int) -> int:\n prod = 1 # n =234\n sums = 0\n while n != 0: # 1st loop 2nd loop 3rd loop \n last = n % 10 # last = 4 3 2\n prod *= last # prod = 1*4 = 4 4*3 = 12 12*2 = 24\n sums += last # sums = 0+4 = 4 4+3 = 7 7+2 = 9\n n =n//10 # n = 23 2 0\n return prod - sums # 24 - 9 = 15\n``` | 25 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python one-liner using eval function (28ms, 14MB) | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | Solution is relatively straightforward. You just have to make sure to cast `n` to be a string.\n\n```Python\ndef subtractProductAndSum(n)t:\n return eval(\'*\'.join(str(n))) - eval(\'+\'.join(str(n)))\n```\n\nThe time complexity of this solution is O(n) due to the two `join` operations.\n\n### Edit\nAs somebody said in the comments section, it\'s worth noting that the `eval` function of Python isn\'t safe. For those of you curious why, there\'s a great [Stack Overflow question](https://stackoverflow.com/questions/35804961/python-eval-is-it-still-dangerous-if-i-disable-builtins-and-attribute-access) and also an [in-depth blog post](https://nedbatchelder.com/blog/201206/eval_really_is_dangerous.html).\n\nIt\'s worth noting that if you use the `eval` function during an interview, the interviewers may ask you if you\'re aware of the security implications.\n\nHappy coding! | 68 | Given an integer number `n`, return the difference between the product of its digits and the sum of its digits.
**Example 1:**
**Input:** n = 234
**Output:** 15
**Explanation:**
Product of digits = 2 \* 3 \* 4 = 24
Sum of digits = 2 + 3 + 4 = 9
Result = 24 - 9 = 15
**Example 2:**
**Input:** n = 4421
**Output:** 21
**Explanation:**
Product of digits = 4 \* 4 \* 2 \* 1 = 32
Sum of digits = 4 + 4 + 2 + 1 = 11
Result = 32 - 11 = 21
**Constraints:**
* `1 <= n <= 10^5` | Since we can rearrange the substring, all we care about is the frequency of each character in that substring. How to find the character frequencies efficiently ? As a preprocess, calculate the accumulate frequency of all characters for all prefixes of the string. How to check if a substring can be changed to a palindrome given its characters frequency ? Count the number of odd frequencies, there can be at most one odd frequency in a palindrome. |
Python one-liner using eval function (28ms, 14MB) | subtract-the-product-and-sum-of-digits-of-an-integer | 0 | 1 | Solution is relatively straightforward. You just have to make sure to cast `n` to be a string.\n\n```Python\ndef subtractProductAndSum(n)t:\n return eval(\'*\'.join(str(n))) - eval(\'+\'.join(str(n)))\n```\n\nThe time complexity of this solution is O(n) due to the two `join` operations.\n\n### Edit\nAs somebody said in the comments section, it\'s worth noting that the `eval` function of Python isn\'t safe. For those of you curious why, there\'s a great [Stack Overflow question](https://stackoverflow.com/questions/35804961/python-eval-is-it-still-dangerous-if-i-disable-builtins-and-attribute-access) and also an [in-depth blog post](https://nedbatchelder.com/blog/201206/eval_really_is_dangerous.html).\n\nIt\'s worth noting that if you use the `eval` function during an interview, the interviewers may ask you if you\'re aware of the security implications.\n\nHappy coding! | 68 | Alice and Bob continue their games with piles of stones. There are several stones **arranged in a row**, and each stone has an associated value which is an integer given in the array `stoneValue`.
Alice and Bob take turns, with Alice starting first. On each player's turn, that player can take `1`, `2`, or `3` stones from the **first** remaining stones in the row.
The score of each player is the sum of the values of the stones taken. The score of each player is `0` initially.
The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.
Assume Alice and Bob **play optimally**.
Return `"Alice "` _if Alice will win,_ `"Bob "` _if Bob will win, or_ `"Tie "` _if they will end the game with the same score_.
**Example 1:**
**Input:** values = \[1,2,3,7\]
**Output:** "Bob "
**Explanation:** Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.
**Example 2:**
**Input:** values = \[1,2,3,-9\]
**Output:** "Alice "
**Explanation:** Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. In the next move, Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. In the next move, Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.
**Example 3:**
**Input:** values = \[1,2,3,6\]
**Output:** "Tie "
**Explanation:** Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.
**Constraints:**
* `1 <= stoneValue.length <= 5 * 104`
* `-1000 <= stoneValue[i] <= 1000` | How to compute all digits of the number ? Use modulus operator (%) to compute the last digit. Generalise modulus operator idea to compute all digits. |
Python ( dict ) and C++ ( map ) | hashtable with greedy | group-the-people-given-the-group-size-they-belong-to | 0 | 1 | ```CPP []\nclass Solution {\npublic:\n vector<vector<int>> groupThePeople(vector<int>& gS) {\n map<int,vector<int>>m;\n int i = 0;\n for(auto &sz: gS) m[sz].push_back(i++);\n vector<vector<int>>ans;\n for(auto &i: m){\n vector<int>temp;\n for(int j = 0; j < i.second.size(); ++j) {\n if(temp.size() == i.first){\n ans.push_back(temp);\n temp.clear();\n }\n temp.push_back(i.second[j]);\n }\n ans.push_back(temp);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def groupThePeople(self, groupSizes: List[int]) -> List[List[int]]:\n dic = defaultdict(list) \n for i in range(len(groupSizes)):\n dic[groupSizes[i]].append(i)\n ans = []\n for grp, arr in dic.items():\n l1 = [];\n for k in range(len(arr)):\n if len(l1) == grp:\n ans.append(l1)\n l1 = []\n l1.append(arr[k])\n ans.append(l1)\n return ans\n```\n\n | 2 | There are `n` people that are split into some unknown number of groups. Each person is labeled with a **unique ID** from `0` to `n - 1`.
You are given an integer array `groupSizes`, where `groupSizes[i]` is the size of the group that person `i` is in. For example, if `groupSizes[1] = 3`, then person `1` must be in a group of size `3`.
Return _a list of groups such that each person `i` is in a group of size `groupSizes[i]`_.
Each person should appear in **exactly one group**, and every person must be in a group. If there are multiple answers, **return any of them**. It is **guaranteed** that there will be **at least one** valid solution for the given input.
**Example 1:**
**Input:** groupSizes = \[3,3,3,3,3,1,3\]
**Output:** \[\[5\],\[0,1,2\],\[3,4,6\]\]
**Explanation:**
The first group is \[5\]. The size is 1, and groupSizes\[5\] = 1.
The second group is \[0,1,2\]. The size is 3, and groupSizes\[0\] = groupSizes\[1\] = groupSizes\[2\] = 3.
The third group is \[3,4,6\]. The size is 3, and groupSizes\[3\] = groupSizes\[4\] = groupSizes\[6\] = 3.
Other possible solutions are \[\[2,1,6\],\[5\],\[0,4,3\]\] and \[\[5\],\[0,6,2\],\[4,3,1\]\].
**Example 2:**
**Input:** groupSizes = \[2,1,3,3,3,2\]
**Output:** \[\[1\],\[0,5\],\[2,3,4\]\]
**Constraints:**
* `groupSizes.length == n`
* `1 <= n <= 500`
* `1 <= groupSizes[i] <= n` | Exploit the fact that the length of the puzzle is only 7. Use bit-masks to represent the word and puzzle strings. For each puzzle, count the number of words whose bit-mask is a sub-mask of the puzzle's bit-mask. |
Python3 👍||⚡94% faster beats, only 10 lines🔥|| clean solution || | group-the-people-given-the-group-size-they-belong-to | 0 | 1 | \n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def groupThePeople(self, groupSizes: List[int]) -> List[List[int]]:\n map = defaultdict(list)\n for i,g in enumerate(groupSizes):\n map[g].append(i)\n ans = []\n for g_key in map.keys():\n for div in range(len(map[g_key])//g_key):\n ans.append(map[g_key][g_key*div:g_key*(1+div)])\n return ans\n\n \n``` | 2 | There are `n` people that are split into some unknown number of groups. Each person is labeled with a **unique ID** from `0` to `n - 1`.
You are given an integer array `groupSizes`, where `groupSizes[i]` is the size of the group that person `i` is in. For example, if `groupSizes[1] = 3`, then person `1` must be in a group of size `3`.
Return _a list of groups such that each person `i` is in a group of size `groupSizes[i]`_.
Each person should appear in **exactly one group**, and every person must be in a group. If there are multiple answers, **return any of them**. It is **guaranteed** that there will be **at least one** valid solution for the given input.
**Example 1:**
**Input:** groupSizes = \[3,3,3,3,3,1,3\]
**Output:** \[\[5\],\[0,1,2\],\[3,4,6\]\]
**Explanation:**
The first group is \[5\]. The size is 1, and groupSizes\[5\] = 1.
The second group is \[0,1,2\]. The size is 3, and groupSizes\[0\] = groupSizes\[1\] = groupSizes\[2\] = 3.
The third group is \[3,4,6\]. The size is 3, and groupSizes\[3\] = groupSizes\[4\] = groupSizes\[6\] = 3.
Other possible solutions are \[\[2,1,6\],\[5\],\[0,4,3\]\] and \[\[5\],\[0,6,2\],\[4,3,1\]\].
**Example 2:**
**Input:** groupSizes = \[2,1,3,3,3,2\]
**Output:** \[\[1\],\[0,5\],\[2,3,4\]\]
**Constraints:**
* `groupSizes.length == n`
* `1 <= n <= 500`
* `1 <= groupSizes[i] <= n` | Exploit the fact that the length of the puzzle is only 7. Use bit-masks to represent the word and puzzle strings. For each puzzle, count the number of words whose bit-mask is a sub-mask of the puzzle's bit-mask. |
simple python3 solution (list comprehension, python list slicing) | group-the-people-given-the-group-size-they-belong-to | 0 | 1 | # Intuition\nJust track the person index and his belong **groupsize** then later he has to be grouped into a group with other person with same **groupsize** while maintaining each group size by using python list *slicing* method.\n\n# Complexity\n- Time complexity:\nO(n): one loop is to go through the __groupSizes__ list for creating the dictionary, another loop is to go through the dictionary for building the result.\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def groupThePeople(self, groupSizes: List[int]) -> List[List[int]]:\n dic,res = {},[]\n for person, groupsize in enumerate(groupSizes):\n dic[groupsize] = dic.get(groupsize, []) + [person] \n for key, lst in dic.items():\n groups = [lst[i:i+key] for i in range(0,len(lst),key)]\n res.extend(groups)\n return res\n\n-----------------------------------------------------------------\nclass Solution:\n def groupThePeople(self, groupSizes: List[int]) -> List[List[int]]:\n dic = {}\n for person, groupsize in enumerate(groupSizes):\n dic[groupsize] = dic.get(groupsize, []) + [person] \n return [lst[i:i+key] for key, lst in dic.items() for i in range(0,len(lst),key)]\n\n``` | 2 | There are `n` people that are split into some unknown number of groups. Each person is labeled with a **unique ID** from `0` to `n - 1`.
You are given an integer array `groupSizes`, where `groupSizes[i]` is the size of the group that person `i` is in. For example, if `groupSizes[1] = 3`, then person `1` must be in a group of size `3`.
Return _a list of groups such that each person `i` is in a group of size `groupSizes[i]`_.
Each person should appear in **exactly one group**, and every person must be in a group. If there are multiple answers, **return any of them**. It is **guaranteed** that there will be **at least one** valid solution for the given input.
**Example 1:**
**Input:** groupSizes = \[3,3,3,3,3,1,3\]
**Output:** \[\[5\],\[0,1,2\],\[3,4,6\]\]
**Explanation:**
The first group is \[5\]. The size is 1, and groupSizes\[5\] = 1.
The second group is \[0,1,2\]. The size is 3, and groupSizes\[0\] = groupSizes\[1\] = groupSizes\[2\] = 3.
The third group is \[3,4,6\]. The size is 3, and groupSizes\[3\] = groupSizes\[4\] = groupSizes\[6\] = 3.
Other possible solutions are \[\[2,1,6\],\[5\],\[0,4,3\]\] and \[\[5\],\[0,6,2\],\[4,3,1\]\].
**Example 2:**
**Input:** groupSizes = \[2,1,3,3,3,2\]
**Output:** \[\[1\],\[0,5\],\[2,3,4\]\]
**Constraints:**
* `groupSizes.length == n`
* `1 <= n <= 500`
* `1 <= groupSizes[i] <= n` | Exploit the fact that the length of the puzzle is only 7. Use bit-masks to represent the word and puzzle strings. For each puzzle, count the number of words whose bit-mask is a sub-mask of the puzzle's bit-mask. |
Python short and clean. Functional programming. | group-the-people-given-the-group-size-they-belong-to | 0 | 1 | # Approach\n1. Create a HashMap called `groups` that maps from `group_size` to list of `people_ids` belonging to that group.\n\n2. For each `group_size` in `groups`, divide the `people_ids` sequence into sub sequences of length `group_size`.\nThis can be done either while inserting to `groups` or as a seperate operation later.\n\n3. `chain` all the sub sequences from `groups` and return.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is length of group_sizes`.\n\n# Code\nImperative:\n```python\nclass Solution:\n def groupThePeople(self, group_sizes: list[int]) -> list[list[int]]:\n groups = defaultdict(lambda: [[]])\n for i, s in enumerate(group_sizes):\n if len(groups[s][-1]) == s: groups[s].append([])\n groups[s][-1].append(i)\n \n return list(chain.from_iterable(groups.values()))\n\n\n```\n\nDeclarative and Functional:\n```python\nclass Solution:\n def groupThePeople(self, group_sizes: list[int]) -> list[list[int]]:\n T = TypeVar(\'T\')\n def divide(xs: Sequence[T], k: int) -> Iterator[Sequence[T]]:\n """Divide sequence xs into smaller sequence of length k"""\n return (xs[i : i + k] for i in range(ceil(len(xs) / k)))\n \n groups = reduce(\n lambda a, x: a[x[1]].append(x[0]) or a,\n enumerate(group_sizes),\n defaultdict(list),\n )\n\n return list(chain.from_iterable((divide(xs, g) for g, xs in groups.items())))\n\n\n``` | 1 | There are `n` people that are split into some unknown number of groups. Each person is labeled with a **unique ID** from `0` to `n - 1`.
You are given an integer array `groupSizes`, where `groupSizes[i]` is the size of the group that person `i` is in. For example, if `groupSizes[1] = 3`, then person `1` must be in a group of size `3`.
Return _a list of groups such that each person `i` is in a group of size `groupSizes[i]`_.
Each person should appear in **exactly one group**, and every person must be in a group. If there are multiple answers, **return any of them**. It is **guaranteed** that there will be **at least one** valid solution for the given input.
**Example 1:**
**Input:** groupSizes = \[3,3,3,3,3,1,3\]
**Output:** \[\[5\],\[0,1,2\],\[3,4,6\]\]
**Explanation:**
The first group is \[5\]. The size is 1, and groupSizes\[5\] = 1.
The second group is \[0,1,2\]. The size is 3, and groupSizes\[0\] = groupSizes\[1\] = groupSizes\[2\] = 3.
The third group is \[3,4,6\]. The size is 3, and groupSizes\[3\] = groupSizes\[4\] = groupSizes\[6\] = 3.
Other possible solutions are \[\[2,1,6\],\[5\],\[0,4,3\]\] and \[\[5\],\[0,6,2\],\[4,3,1\]\].
**Example 2:**
**Input:** groupSizes = \[2,1,3,3,3,2\]
**Output:** \[\[1\],\[0,5\],\[2,3,4\]\]
**Constraints:**
* `groupSizes.length == n`
* `1 <= n <= 500`
* `1 <= groupSizes[i] <= n` | Exploit the fact that the length of the puzzle is only 7. Use bit-masks to represent the word and puzzle strings. For each puzzle, count the number of words whose bit-mask is a sub-mask of the puzzle's bit-mask. |
Python3, C++ | Brute-force -> Optimal | Full Explanation | find-the-smallest-divisor-given-a-threshold | 0 | 1 | ### Find the Smallest Divisor Given a Threshold\n\nGiven an array of integers `nums` and an integer `threshold`, we will choose a positive integer `divisor`, divide all the array by it, and sum the division\'s result. Find the **smallest** `divisor` such that the result mentioned above is less than or equal to `threshold`.\n\nEach result of the division is rounded to the nearest integer greater than or equal to that element. (For example: `7/3 = 3` and `10/2 = 5`).\n\n- Approach\n - Brute-force\n - Answer lies between `1` and `max(nums)` as dividing by `1` will give max sum and dividing by `max(nums)` will give minimum sum\n - For every integer in range 1 to `max(nums)` check if the sum after division\u2019s result is \u2264 threshold\n - Time Complexity: $O(n * max(nums))$\n - Space Complexity: $O(1)$\n - Optimal\n - Binary Search answer between `1` and `max(nums)`\n - Time Complexity: $O(n * log(max(nums)))$\n - Space Complexity: $O(1)$\n\n```python\n# Python3\n# Brute-force Solution\nfrom math import ceil\nclass Solution:\n def smallestDivisor(self, nums: List[int], threshold: int) -> int:\n rng = max(nums)\n for i in range(1, rng+1):\n if sum(ceil(j / i) for j in nums) <= threshold:\n return i\n return -1\n```\n\n```python\n# Python3\n# Optimal Solution\nfrom math import ceil\nclass Solution:\n def smallestDivisor(self, nums: List[int], threshold: int) -> int:\n l = 1\n r = max(nums)\n\n while l <= r:\n mid = (l + r) // 2\n if sum(ceil(j / mid) for j in nums) <= threshold:\n r = mid - 1\n else:\n l = mid + 1\n return l\n```\n\n```cpp\n// C++\n// Optimal Solution\nclass Solution {\npublic:\n int smallestDivisor(vector<int>& nums, int threshold) {\n int l = 1, r = nums[0];\n for (int i = 0; i < nums.size(); i++) {\n r = max(r, nums[i]);\n }\n while (l <= r) {\n int mid = l + (r - l) / 2;\n long long int sum = 0;\n for (int i = 0; i < nums.size(); i++) {\n sum += ceil((double)nums[i]/(double)mid);\n }\n if (sum <= threshold) {\n r = mid - 1;\n }\n else {\n l = mid + 1;\n }\n }\n return l;\n }\n};\n``` | 1 | Given an array of integers `nums` and an integer `threshold`, we will choose a positive integer `divisor`, divide all the array by it, and sum the division's result. Find the **smallest** `divisor` such that the result mentioned above is less than or equal to `threshold`.
Each result of the division is rounded to the nearest integer greater than or equal to that element. (For example: `7/3 = 3` and `10/2 = 5`).
The test cases are generated so that there will be an answer.
**Example 1:**
**Input:** nums = \[1,2,5,9\], threshold = 6
**Output:** 5
**Explanation:** We can get a sum to 17 (1+2+5+9) if the divisor is 1.
If the divisor is 4 we can get a sum of 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).
**Example 2:**
**Input:** nums = \[44,22,33,11,1\], threshold = 5
**Output:** 44
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 106`
* `nums.length <= threshold <= 106` | Handle the conversions of day, month and year separately. Notice that days always have a two-word ending, so if you erase the last two characters of this days you'll get the number. |
Python3, C++ | Brute-force -> Optimal | Full Explanation | find-the-smallest-divisor-given-a-threshold | 0 | 1 | ### Find the Smallest Divisor Given a Threshold\n\nGiven an array of integers `nums` and an integer `threshold`, we will choose a positive integer `divisor`, divide all the array by it, and sum the division\'s result. Find the **smallest** `divisor` such that the result mentioned above is less than or equal to `threshold`.\n\nEach result of the division is rounded to the nearest integer greater than or equal to that element. (For example: `7/3 = 3` and `10/2 = 5`).\n\n- Approach\n - Brute-force\n - Answer lies between `1` and `max(nums)` as dividing by `1` will give max sum and dividing by `max(nums)` will give minimum sum\n - For every integer in range 1 to `max(nums)` check if the sum after division\u2019s result is \u2264 threshold\n - Time Complexity: $O(n * max(nums))$\n - Space Complexity: $O(1)$\n - Optimal\n - Binary Search answer between `1` and `max(nums)`\n - Time Complexity: $O(n * log(max(nums)))$\n - Space Complexity: $O(1)$\n\n```python\n# Python3\n# Brute-force Solution\nfrom math import ceil\nclass Solution:\n def smallestDivisor(self, nums: List[int], threshold: int) -> int:\n rng = max(nums)\n for i in range(1, rng+1):\n if sum(ceil(j / i) for j in nums) <= threshold:\n return i\n return -1\n```\n\n```python\n# Python3\n# Optimal Solution\nfrom math import ceil\nclass Solution:\n def smallestDivisor(self, nums: List[int], threshold: int) -> int:\n l = 1\n r = max(nums)\n\n while l <= r:\n mid = (l + r) // 2\n if sum(ceil(j / mid) for j in nums) <= threshold:\n r = mid - 1\n else:\n l = mid + 1\n return l\n```\n\n```cpp\n// C++\n// Optimal Solution\nclass Solution {\npublic:\n int smallestDivisor(vector<int>& nums, int threshold) {\n int l = 1, r = nums[0];\n for (int i = 0; i < nums.size(); i++) {\n r = max(r, nums[i]);\n }\n while (l <= r) {\n int mid = l + (r - l) / 2;\n long long int sum = 0;\n for (int i = 0; i < nums.size(); i++) {\n sum += ceil((double)nums[i]/(double)mid);\n }\n if (sum <= threshold) {\n r = mid - 1;\n }\n else {\n l = mid + 1;\n }\n }\n return l;\n }\n};\n``` | 1 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
Simple Binary Search Approach in Python | find-the-smallest-divisor-given-a-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n Binary Search \n\n# Complexity\n- Time complexity: O( log( max(array) ) )\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) constant space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestDivisor(self, nums: List[int], threshold: int) -> int:\n start = 1\n end = max(nums)\n ans = -1\n while start<=end:\n mid = (start+end)//2\n sum = 0\n for ele in nums:\n sum += math.ceil(ele/mid)\n if sum <= threshold:\n ans = mid\n end = mid - 1\n else:\n start = mid + 1\n print(mid,start,end)\n return ans\n\n``` | 4 | Given an array of integers `nums` and an integer `threshold`, we will choose a positive integer `divisor`, divide all the array by it, and sum the division's result. Find the **smallest** `divisor` such that the result mentioned above is less than or equal to `threshold`.
Each result of the division is rounded to the nearest integer greater than or equal to that element. (For example: `7/3 = 3` and `10/2 = 5`).
The test cases are generated so that there will be an answer.
**Example 1:**
**Input:** nums = \[1,2,5,9\], threshold = 6
**Output:** 5
**Explanation:** We can get a sum to 17 (1+2+5+9) if the divisor is 1.
If the divisor is 4 we can get a sum of 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).
**Example 2:**
**Input:** nums = \[44,22,33,11,1\], threshold = 5
**Output:** 44
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 106`
* `nums.length <= threshold <= 106` | Handle the conversions of day, month and year separately. Notice that days always have a two-word ending, so if you erase the last two characters of this days you'll get the number. |
Simple Binary Search Approach in Python | find-the-smallest-divisor-given-a-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n Binary Search \n\n# Complexity\n- Time complexity: O( log( max(array) ) )\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) constant space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestDivisor(self, nums: List[int], threshold: int) -> int:\n start = 1\n end = max(nums)\n ans = -1\n while start<=end:\n mid = (start+end)//2\n sum = 0\n for ele in nums:\n sum += math.ceil(ele/mid)\n if sum <= threshold:\n ans = mid\n end = mid - 1\n else:\n start = mid + 1\n print(mid,start,end)\n return ans\n\n``` | 4 | Given an array of string `words`, return _all strings in_ `words` _that is a **substring** of another word_. You can return the answer in **any order**.
A **substring** is a contiguous sequence of characters within a string
**Example 1:**
**Input:** words = \[ "mass ", "as ", "hero ", "superhero "\]
**Output:** \[ "as ", "hero "\]
**Explanation:** "as " is substring of "mass " and "hero " is substring of "superhero ".
\[ "hero ", "as "\] is also a valid answer.
**Example 2:**
**Input:** words = \[ "leetcode ", "et ", "code "\]
**Output:** \[ "et ", "code "\]
**Explanation:** "et ", "code " are substring of "leetcode ".
**Example 3:**
**Input:** words = \[ "blue ", "green ", "bu "\]
**Output:** \[\]
**Explanation:** No string of words is substring of another string.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 30`
* `words[i]` contains only lowercase English letters.
* All the strings of `words` are **unique**. | Examine every possible number for solution. Choose the largest of them. Use binary search to reduce the time complexity. |
Python BFS & Bit operation | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | \nclass Solution:\n\n def minFlips(self, mat: List[List[int]]) -> int:\n m,n=len(mat),len(mat[0])\n def convert_to_bit(M):\n start=0\n for i in range(m):\n for j in range(n):\n start|=M[i][j]<<(i*n+j)\n return start\n init=convert_to_bit(mat)\n Q=deque([(0,init)])\n seen={init}\n while Q:\n step,curr=Q.popleft()\n if curr==0:\n return step\n for r in range(m):\n for c in range(n):\n temp=curr\n for dr,dc in [(0,0),(1,0),(-1,0),(0,1),(0,-1)]:\n nr,nc=r+dr,c+dc\n if 0<=nr<m and 0<=nc<n:\n temp^=1<<(nr*n+nc)\n if temp not in seen:\n \n Q.append((step+1,temp))\n seen.add(temp)\n \n return -1\n \n | 3 | Given a `m x n` binary matrix `mat`. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing `1` to `0` and `0` to `1`). A pair of cells are called neighbors if they share one edge.
Return the _minimum number of steps_ required to convert `mat` to a zero matrix or `-1` if you cannot.
A **binary matrix** is a matrix with all cells equal to `0` or `1` only.
A **zero matrix** is a matrix with all cells equal to `0`.
**Example 1:**
**Input:** mat = \[\[0,0\],\[0,1\]\]
**Output:** 3
**Explanation:** One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.
**Example 2:**
**Input:** mat = \[\[0\]\]
**Output:** 0
**Explanation:** Given matrix is a zero matrix. We do not need to change it.
**Example 3:**
**Input:** mat = \[\[1,0,0\],\[1,0,0\]\]
**Output:** -1
**Explanation:** Given matrix cannot be a zero matrix.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 3`
* `mat[i][j]` is either `0` or `1`. | Find the divisors of each element in the array. You only need to loop to the square root of a number to find its divisors. |
Python BFS & Bit operation | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | \nclass Solution:\n\n def minFlips(self, mat: List[List[int]]) -> int:\n m,n=len(mat),len(mat[0])\n def convert_to_bit(M):\n start=0\n for i in range(m):\n for j in range(n):\n start|=M[i][j]<<(i*n+j)\n return start\n init=convert_to_bit(mat)\n Q=deque([(0,init)])\n seen={init}\n while Q:\n step,curr=Q.popleft()\n if curr==0:\n return step\n for r in range(m):\n for c in range(n):\n temp=curr\n for dr,dc in [(0,0),(1,0),(-1,0),(0,1),(0,-1)]:\n nr,nc=r+dr,c+dc\n if 0<=nr<m and 0<=nc<n:\n temp^=1<<(nr*n+nc)\n if temp not in seen:\n \n Q.append((step+1,temp))\n seen.add(temp)\n \n return -1\n \n | 3 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
BFS + Bit manipulation Python3 Solution | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | ```\nclass Solution:\n \n def getFlattnedIndex(self, row: int, col: int, cols: int) -> int:\n return row*cols + col\n \n \n def getNeighbors(self, row: int, col: int, mat: List[List[int]]) -> List[Tuple[int]]:\n \n nbrs = []\n directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n \n for x, y in directions:\n new_row, new_col = row+x, col+y\n if 0 <= new_row < len(mat) and 0 <= new_col < len(mat[0]):\n nbrs.append((new_row, new_col))\n \n return nbrs\n \n \n def flip(self, index: int, prev_bits: List[int], nbrs: Dict[int, int]) -> None:\n bits = prev_bits[::]\n bits[index] += 1\n bits[index] %= 2\n \n for i in nbrs[index]:\n bits[i] += 1\n bits[i] %= 2\n \n return bits\n \n \n def getMinFlips(self, bits: List[int], nbrs: Dict[int, int], visited: Set[int]) -> int:\n \n min_flips = 0\n queue = deque()\n visited = set()\n queue.append(bits)\n \n while queue:\n queue_len = len(queue)\n for _ in range(queue_len):\n curr = queue.popleft()\n num = int("".join([str(d) for d in curr]), 2)\n if num == 0:\n return min_flips\n \n if num in visited:\n continue\n visited.add(num)\n \n for i in range(len(curr)):\n nbr = self.flip(i, curr, nbrs)\n queue.append(nbr)\n \n min_flips += 1\n \n return -1\n \n \n # O(2^(m+n)) time, m -> rows, n -> cols\n # O(2^(m+n)) space,\n # Approach: bit masking, bfs, \n def minFlips(self, mat: List[List[int]]) -> int:\n ROWS, COLS = len(mat), len(mat[0])\n bits = []\n nbrs = defaultdict(list)\n \n for row in range(ROWS):\n for col in range(COLS):\n bits.append(mat[row][col])\n \n index = self.getFlattnedIndex(row, col, COLS)\n for nbr_row, nbr_col in self.getNeighbors(row, col, mat):\n nbrs[index].append(self.getFlattnedIndex(nbr_row, nbr_col, COLS))\n \n return self.getMinFlips(bits, nbrs, set())\n``` | 0 | Given a `m x n` binary matrix `mat`. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing `1` to `0` and `0` to `1`). A pair of cells are called neighbors if they share one edge.
Return the _minimum number of steps_ required to convert `mat` to a zero matrix or `-1` if you cannot.
A **binary matrix** is a matrix with all cells equal to `0` or `1` only.
A **zero matrix** is a matrix with all cells equal to `0`.
**Example 1:**
**Input:** mat = \[\[0,0\],\[0,1\]\]
**Output:** 3
**Explanation:** One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.
**Example 2:**
**Input:** mat = \[\[0\]\]
**Output:** 0
**Explanation:** Given matrix is a zero matrix. We do not need to change it.
**Example 3:**
**Input:** mat = \[\[1,0,0\],\[1,0,0\]\]
**Output:** -1
**Explanation:** Given matrix cannot be a zero matrix.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 3`
* `mat[i][j]` is either `0` or `1`. | Find the divisors of each element in the array. You only need to loop to the square root of a number to find its divisors. |
BFS + Bit manipulation Python3 Solution | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | ```\nclass Solution:\n \n def getFlattnedIndex(self, row: int, col: int, cols: int) -> int:\n return row*cols + col\n \n \n def getNeighbors(self, row: int, col: int, mat: List[List[int]]) -> List[Tuple[int]]:\n \n nbrs = []\n directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n \n for x, y in directions:\n new_row, new_col = row+x, col+y\n if 0 <= new_row < len(mat) and 0 <= new_col < len(mat[0]):\n nbrs.append((new_row, new_col))\n \n return nbrs\n \n \n def flip(self, index: int, prev_bits: List[int], nbrs: Dict[int, int]) -> None:\n bits = prev_bits[::]\n bits[index] += 1\n bits[index] %= 2\n \n for i in nbrs[index]:\n bits[i] += 1\n bits[i] %= 2\n \n return bits\n \n \n def getMinFlips(self, bits: List[int], nbrs: Dict[int, int], visited: Set[int]) -> int:\n \n min_flips = 0\n queue = deque()\n visited = set()\n queue.append(bits)\n \n while queue:\n queue_len = len(queue)\n for _ in range(queue_len):\n curr = queue.popleft()\n num = int("".join([str(d) for d in curr]), 2)\n if num == 0:\n return min_flips\n \n if num in visited:\n continue\n visited.add(num)\n \n for i in range(len(curr)):\n nbr = self.flip(i, curr, nbrs)\n queue.append(nbr)\n \n min_flips += 1\n \n return -1\n \n \n # O(2^(m+n)) time, m -> rows, n -> cols\n # O(2^(m+n)) space,\n # Approach: bit masking, bfs, \n def minFlips(self, mat: List[List[int]]) -> int:\n ROWS, COLS = len(mat), len(mat[0])\n bits = []\n nbrs = defaultdict(list)\n \n for row in range(ROWS):\n for col in range(COLS):\n bits.append(mat[row][col])\n \n index = self.getFlattnedIndex(row, col, COLS)\n for nbr_row, nbr_col in self.getNeighbors(row, col, mat):\n nbrs[index].append(self.getFlattnedIndex(nbr_row, nbr_col, COLS))\n \n return self.getMinFlips(bits, nbrs, set())\n``` | 0 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Python Hard | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | ```\nclass Solution:\n def minFlips(self, mat: List[List[int]]) -> int:\n \'\'\'\n try bfs + heap\n \'\'\'\n directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n M, N = len(mat), len(mat[0])\n h = []\n\n seen = set()\n\n heapq.heappush(h, (0, mat))\n\n while h:\n\n\n\n amt, cur = heapq.heappop(h)\n\n\n s = ""\n for i in range(M):\n for j in range(N):\n s += str(cur[i][j])\n\n\n\n\n if s in seen:\n continue\n\n\n check = True\n\n for char in s:\n if char == "1":\n check = False\n break\n \n if check:\n return amt\n\n\n \n \n seen.add(s)\n\n for i in range(M):\n for j in range(N):\n\n\n\n cur[i][j] ^= 1\n\n for dx, dy in directions:\n nx, ny = i + dx, j + dy\n\n if 0 <= nx < M and 0 <= ny < N:\n cur[nx][ny] ^= 1\n\n heapq.heappush(h, (amt + 1, deepcopy(cur)))\n\n cur[i][j] ^= 1\n\n for dx, dy in directions:\n nx, ny = i + dx, j + dy\n\n if 0 <= nx < M and 0 <= ny < N:\n cur[nx][ny] ^= 1\n\n \n\n\n\n return -1\n\n \n``` | 0 | Given a `m x n` binary matrix `mat`. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing `1` to `0` and `0` to `1`). A pair of cells are called neighbors if they share one edge.
Return the _minimum number of steps_ required to convert `mat` to a zero matrix or `-1` if you cannot.
A **binary matrix** is a matrix with all cells equal to `0` or `1` only.
A **zero matrix** is a matrix with all cells equal to `0`.
**Example 1:**
**Input:** mat = \[\[0,0\],\[0,1\]\]
**Output:** 3
**Explanation:** One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.
**Example 2:**
**Input:** mat = \[\[0\]\]
**Output:** 0
**Explanation:** Given matrix is a zero matrix. We do not need to change it.
**Example 3:**
**Input:** mat = \[\[1,0,0\],\[1,0,0\]\]
**Output:** -1
**Explanation:** Given matrix cannot be a zero matrix.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 3`
* `mat[i][j]` is either `0` or `1`. | Find the divisors of each element in the array. You only need to loop to the square root of a number to find its divisors. |
Python Hard | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | ```\nclass Solution:\n def minFlips(self, mat: List[List[int]]) -> int:\n \'\'\'\n try bfs + heap\n \'\'\'\n directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n M, N = len(mat), len(mat[0])\n h = []\n\n seen = set()\n\n heapq.heappush(h, (0, mat))\n\n while h:\n\n\n\n amt, cur = heapq.heappop(h)\n\n\n s = ""\n for i in range(M):\n for j in range(N):\n s += str(cur[i][j])\n\n\n\n\n if s in seen:\n continue\n\n\n check = True\n\n for char in s:\n if char == "1":\n check = False\n break\n \n if check:\n return amt\n\n\n \n \n seen.add(s)\n\n for i in range(M):\n for j in range(N):\n\n\n\n cur[i][j] ^= 1\n\n for dx, dy in directions:\n nx, ny = i + dx, j + dy\n\n if 0 <= nx < M and 0 <= ny < N:\n cur[nx][ny] ^= 1\n\n heapq.heappush(h, (amt + 1, deepcopy(cur)))\n\n cur[i][j] ^= 1\n\n for dx, dy in directions:\n nx, ny = i + dx, j + dy\n\n if 0 <= nx < M and 0 <= ny < N:\n cur[nx][ny] ^= 1\n\n \n\n\n\n return -1\n\n \n``` | 0 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Python3 - Bitwise operations | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def minFlips(self, mat: List[List[int]]) -> int:\n mx, nx = len(mat), len(mat[0])\n bv = 1\n m = defaultdict(int)\n \n c = 0\n for i in range(mx):\n for j in range(nx):\n m[(i, j)] = bv\n \n if mat[i][j]:\n c += bv\n bv *= 2\n if c == 0:\n return 0\n f = set()\n for i in range(mx):\n for j in range(nx):\n f.add(m[(i,j)] + m[(i+1,j)] + m[(i-1,j)] + m[(i,j+1)] + m[(i,j-1)])\n mvs = [999 for i in range(bv)]\n mvs[c] = 0\n moves = {c}\n while moves:\n c = moves.pop()\n k = mvs[c]\n for i in f:\n if mvs[c ^ i] > k + 1:\n moves.add(c^i)\n mvs[c^i] = 1 + k\n if mvs[0] < 999:\n return mvs[0]\n return -1\n \n\n \n``` | 0 | Given a `m x n` binary matrix `mat`. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing `1` to `0` and `0` to `1`). A pair of cells are called neighbors if they share one edge.
Return the _minimum number of steps_ required to convert `mat` to a zero matrix or `-1` if you cannot.
A **binary matrix** is a matrix with all cells equal to `0` or `1` only.
A **zero matrix** is a matrix with all cells equal to `0`.
**Example 1:**
**Input:** mat = \[\[0,0\],\[0,1\]\]
**Output:** 3
**Explanation:** One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.
**Example 2:**
**Input:** mat = \[\[0\]\]
**Output:** 0
**Explanation:** Given matrix is a zero matrix. We do not need to change it.
**Example 3:**
**Input:** mat = \[\[1,0,0\],\[1,0,0\]\]
**Output:** -1
**Explanation:** Given matrix cannot be a zero matrix.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 3`
* `mat[i][j]` is either `0` or `1`. | Find the divisors of each element in the array. You only need to loop to the square root of a number to find its divisors. |
Python3 - Bitwise operations | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def minFlips(self, mat: List[List[int]]) -> int:\n mx, nx = len(mat), len(mat[0])\n bv = 1\n m = defaultdict(int)\n \n c = 0\n for i in range(mx):\n for j in range(nx):\n m[(i, j)] = bv\n \n if mat[i][j]:\n c += bv\n bv *= 2\n if c == 0:\n return 0\n f = set()\n for i in range(mx):\n for j in range(nx):\n f.add(m[(i,j)] + m[(i+1,j)] + m[(i-1,j)] + m[(i,j+1)] + m[(i,j-1)])\n mvs = [999 for i in range(bv)]\n mvs[c] = 0\n moves = {c}\n while moves:\n c = moves.pop()\n k = mvs[c]\n for i in f:\n if mvs[c ^ i] > k + 1:\n moves.add(c^i)\n mvs[c^i] = 1 + k\n if mvs[0] < 999:\n return mvs[0]\n return -1\n \n\n \n``` | 0 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Concise solution on Python3 | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def minFlips(self, mat: List[List[int]]) -> int:\n\n n = len(mat)\n m = len(mat[0])\n\n def ins(i, j):\n return 0 <= i < n and 0 <= j < m\n\n def swipe(i, j):\n mat[i][j] ^= 1\n\n if ins(i-1, j):\n mat[i-1][j] ^= 1\n\n if ins(i+1, j):\n mat[i+1][j] ^= 1\n\n if ins(i, j-1):\n mat[i][j-1] ^= 1\n\n if ins(i, j+1):\n mat[i][j+1] ^= 1\n\n def check():\n for i in range(n):\n for j in range(m):\n if mat[i][j] == 1:\n return False\n return True\n\n def go(i, j, cnt):\n if j == m:\n i += 1\n j = 0\n\n if i == n:\n if check():\n nonlocal ans\n ans = min(ans, cnt)\n return\n\n # do not swipe\n go(i, j+1, cnt)\n\n # do swipe\n swipe(i, j)\n go(i, j+1, cnt+1)\n swipe(i, j)\n\n\n ans = float(\'inf\')\n go(0, 0, 0)\n\n return ans if ans != float(\'inf\') else -1\n\n``` | 0 | Given a `m x n` binary matrix `mat`. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing `1` to `0` and `0` to `1`). A pair of cells are called neighbors if they share one edge.
Return the _minimum number of steps_ required to convert `mat` to a zero matrix or `-1` if you cannot.
A **binary matrix** is a matrix with all cells equal to `0` or `1` only.
A **zero matrix** is a matrix with all cells equal to `0`.
**Example 1:**
**Input:** mat = \[\[0,0\],\[0,1\]\]
**Output:** 3
**Explanation:** One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.
**Example 2:**
**Input:** mat = \[\[0\]\]
**Output:** 0
**Explanation:** Given matrix is a zero matrix. We do not need to change it.
**Example 3:**
**Input:** mat = \[\[1,0,0\],\[1,0,0\]\]
**Output:** -1
**Explanation:** Given matrix cannot be a zero matrix.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 3`
* `mat[i][j]` is either `0` or `1`. | Find the divisors of each element in the array. You only need to loop to the square root of a number to find its divisors. |
Concise solution on Python3 | minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def minFlips(self, mat: List[List[int]]) -> int:\n\n n = len(mat)\n m = len(mat[0])\n\n def ins(i, j):\n return 0 <= i < n and 0 <= j < m\n\n def swipe(i, j):\n mat[i][j] ^= 1\n\n if ins(i-1, j):\n mat[i-1][j] ^= 1\n\n if ins(i+1, j):\n mat[i+1][j] ^= 1\n\n if ins(i, j-1):\n mat[i][j-1] ^= 1\n\n if ins(i, j+1):\n mat[i][j+1] ^= 1\n\n def check():\n for i in range(n):\n for j in range(m):\n if mat[i][j] == 1:\n return False\n return True\n\n def go(i, j, cnt):\n if j == m:\n i += 1\n j = 0\n\n if i == n:\n if check():\n nonlocal ans\n ans = min(ans, cnt)\n return\n\n # do not swipe\n go(i, j+1, cnt)\n\n # do swipe\n swipe(i, j)\n go(i, j+1, cnt+1)\n swipe(i, j)\n\n\n ans = float(\'inf\')\n go(0, 0, 0)\n\n return ans if ans != float(\'inf\') else -1\n\n``` | 0 | Given the array `queries` of positive integers between `1` and `m`, you have to process all `queries[i]` (from `i=0` to `i=queries.length-1`) according to the following rules:
* In the beginning, you have the permutation `P=[1,2,3,...,m]`.
* For the current `i`, find the position of `queries[i]` in the permutation `P` (**indexing from 0**) and then move this at the beginning of the permutation `P.` Notice that the position of `queries[i]` in `P` is the result for `queries[i]`.
Return an array containing the result for the given `queries`.
**Example 1:**
**Input:** queries = \[3,1,2,1\], m = 5
**Output:** \[2,1,2,1\]
**Explanation:** The queries are processed as follow:
For i=0: queries\[i\]=3, P=\[1,2,3,4,5\], position of 3 in P is **2**, then we move 3 to the beginning of P resulting in P=\[3,1,2,4,5\].
For i=1: queries\[i\]=1, P=\[3,1,2,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,3,2,4,5\].
For i=2: queries\[i\]=2, P=\[1,3,2,4,5\], position of 2 in P is **2**, then we move 2 to the beginning of P resulting in P=\[2,1,3,4,5\].
For i=3: queries\[i\]=1, P=\[2,1,3,4,5\], position of 1 in P is **1**, then we move 1 to the beginning of P resulting in P=\[1,2,3,4,5\].
Therefore, the array containing the result is \[2,1,2,1\].
**Example 2:**
**Input:** queries = \[4,1,2,2\], m = 4
**Output:** \[3,1,2,0\]
**Example 3:**
**Input:** queries = \[7,5,5,8,3\], m = 8
**Output:** \[6,5,0,7,5\]
**Constraints:**
* `1 <= m <= 10^3`
* `1 <= queries.length <= m`
* `1 <= queries[i] <= m` | Flipping same index two times is like not flipping it at all. Each index can be flipped one time. Try all possible combinations. O(2^(n*m)). |
Python super-simple and easy solution | iterator-for-combination | 0 | 1 | ```\nclass CombinationIterator:\n def __init__(self, characters: str, combinationLength: int):\n self.allCombinations = list(combinations(characters, combinationLength))\n self.count = 0\n\n def next(self) -> str:\n self.count += 1\n return "".join(self.allCombinations[self.count-1])\n \n def hasNext(self) -> bool:\n return self.count < len(self.allCombinations)\n\n``` | 7 | Design the `CombinationIterator` class:
* `CombinationIterator(string characters, int combinationLength)` Initializes the object with a string `characters` of **sorted distinct** lowercase English letters and a number `combinationLength` as arguments.
* `next()` Returns the next combination of length `combinationLength` in **lexicographical order**.
* `hasNext()` Returns `true` if and only if there exists a next combination.
**Example 1:**
**Input**
\[ "CombinationIterator ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[ "abc ", 2\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, "ab ", true, "ac ", true, "bc ", false\]
**Explanation**
CombinationIterator itr = new CombinationIterator( "abc ", 2);
itr.next(); // return "ab "
itr.hasNext(); // return True
itr.next(); // return "ac "
itr.hasNext(); // return True
itr.next(); // return "bc "
itr.hasNext(); // return False
**Constraints:**
* `1 <= combinationLength <= characters.length <= 15`
* All the characters of `characters` are **unique**.
* At most `104` calls will be made to `next` and `hasNext`.
* It is guaranteed that all calls of the function `next` are valid. | Use dynamic programming. Let dp[i] be the solution for the prefix of the array that ends at index i, if the element at index i is in the subsequence. dp[i] = nums[i] + max(0, dp[i-k], dp[i-k+1], ..., dp[i-1]) Use a heap with the sliding window technique to optimize the dp. |
Simple python solution for iterator if combination | iterator-for-combination | 0 | 1 | 1) Create a list of combinations using binary numbers.\n\te.g. In "abc", there are two possibilities for each character x : include it or not \n\t\t\tTherefore, we may have [1,0,1] or [0,1,1] or [1,1,0] or [0,0,0] or [1,1,1],etc \n\t\t\t\n2) Check if number of ones in each possible binary list is equal to combination length or not. If yes,\n\n3) Use the indices of one in the list to produce a substring and append it to a final list\n\n4) Sort the final list \n\n5) Create an iterator and end position of list of substrings in constructor and increment it in **next** method. \n\n6) Check if iterator irrived at end of list in **hasNext** method\n\n\n\n\n\n```\nclass CombinationIterator:\n\n def __init__(self, characters: str, combinationLength: int):\n l=[]\n chars=list(characters)\n N=2**len(characters)\n for i in range(N):\n nums=list(str(bin(i)).replace(\'0b\',\'\').zfill(len(chars)))\n if(list(nums).count(\'1\')==combinationLength):\n ans = [int(nums[j]) * chars[j] for j in range(len(chars))]\n final=\'\'.join(ans)\n l.append(final)\n l.sort()\n self.p=l\n self.itr=0\n self.end=len(l)\n \n\n def next(self) -> str:\n i=self.itr\n x=self.p[i]\n i+=1\n self.itr=i\n return(x)\n\n def hasNext(self) -> bool:\n return(self.itr<self.end)\n\n\n# Your CombinationIterator object will be instantiated and called as such:\n# obj = CombinationIterator(characters, combinationLength)\n# param_1 = obj.next()\n# param_2 = obj.hasNext()\n``` | 6 | Design the `CombinationIterator` class:
* `CombinationIterator(string characters, int combinationLength)` Initializes the object with a string `characters` of **sorted distinct** lowercase English letters and a number `combinationLength` as arguments.
* `next()` Returns the next combination of length `combinationLength` in **lexicographical order**.
* `hasNext()` Returns `true` if and only if there exists a next combination.
**Example 1:**
**Input**
\[ "CombinationIterator ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[ "abc ", 2\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, "ab ", true, "ac ", true, "bc ", false\]
**Explanation**
CombinationIterator itr = new CombinationIterator( "abc ", 2);
itr.next(); // return "ab "
itr.hasNext(); // return True
itr.next(); // return "ac "
itr.hasNext(); // return True
itr.next(); // return "bc "
itr.hasNext(); // return False
**Constraints:**
* `1 <= combinationLength <= characters.length <= 15`
* All the characters of `characters` are **unique**.
* At most `104` calls will be made to `next` and `hasNext`.
* It is guaranteed that all calls of the function `next` are valid. | Use dynamic programming. Let dp[i] be the solution for the prefix of the array that ends at index i, if the element at index i is in the subsequence. dp[i] = nums[i] + max(0, dp[i-k], dp[i-k+1], ..., dp[i-1]) Use a heap with the sliding window technique to optimize the dp. |
Python || Backtracking | iterator-for-combination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse backtracking (comb method from the code) to find all the combinations of length combinationLength from characters. As you find next, pop from the list.\n\n\n# Code\n```\nclass CombinationIterator:\n def __init__(self, characters: str, combinationLength: int):\n self.characters = characters\n self.combinationLength = combinationLength\n self.combMap = defaultdict(list)\n self.combMap[self.characters] = self.comb(self.characters, self.combinationLength)\n\n def next(self) -> str:\n nextE = self.combMap[self.characters][0]\n self.combMap[self.characters].pop(0)\n return nextE\n\n def hasNext(self) -> bool:\n return True if len(self.combMap[self.characters])>0 else False\n \n def comb(self, s, length):\n res = []\n def backtrack(i,cur):\n if len(cur)==length:\n res.append(cur)\n return\n \n for j in range(i, len(s)):\n cur = cur+s[j]\n backtrack(j+1, cur)\n cur = cur[:-1]\n backtrack(0,"")\n return res \n\n# Your CombinationIterator object will be instantiated and called as such:\n# obj = CombinationIterator(characters, combinationLength)\n# param_1 = obj.next()\n# param_2 = obj.hasNext()\n``` | 0 | Design the `CombinationIterator` class:
* `CombinationIterator(string characters, int combinationLength)` Initializes the object with a string `characters` of **sorted distinct** lowercase English letters and a number `combinationLength` as arguments.
* `next()` Returns the next combination of length `combinationLength` in **lexicographical order**.
* `hasNext()` Returns `true` if and only if there exists a next combination.
**Example 1:**
**Input**
\[ "CombinationIterator ", "next ", "hasNext ", "next ", "hasNext ", "next ", "hasNext "\]
\[\[ "abc ", 2\], \[\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, "ab ", true, "ac ", true, "bc ", false\]
**Explanation**
CombinationIterator itr = new CombinationIterator( "abc ", 2);
itr.next(); // return "ab "
itr.hasNext(); // return True
itr.next(); // return "ac "
itr.hasNext(); // return True
itr.next(); // return "bc "
itr.hasNext(); // return False
**Constraints:**
* `1 <= combinationLength <= characters.length <= 15`
* All the characters of `characters` are **unique**.
* At most `104` calls will be made to `next` and `hasNext`.
* It is guaranteed that all calls of the function `next` are valid. | Use dynamic programming. Let dp[i] be the solution for the prefix of the array that ends at index i, if the element at index i is in the subsequence. dp[i] = nums[i] + max(0, dp[i-k], dp[i-k+1], ..., dp[i-1]) Use a heap with the sliding window technique to optimize the dp. |
C++/Python frequency count vs Binary search||0ms Beats 100% | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n3 different kinds of soultion arte provided.\n1 is very naive, solved this with counting frequency for each number; no hash table is used.\nThe 2nd approach uses binary search if the possible target \n`int x[5]={arr[0], arr[n/4], arr[n/2], arr[3*n/4], arr[n-1]};`\nnot hit.\n\nBoth solutions have the same speed with different TC.\n\nThe 3rd approach uses C code by sliding window with running time 7ms.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn English subtitles if necessary]\n[https://youtu.be/nzVIomp9qSg?si=F-B65MLzQqrHhsq1](https://youtu.be/nzVIomp9qSg?si=F-B65MLzQqrHhsq1)\nTo shrink the searching range, define the array for specific indices\n```\nint q[5]={0, n/4, n/2, 3*n/4, n-1};\n```\nThe binary searching part is as follows:\n```\n//If not found, proceed the binary search\nfor (int i=1; i<4; i++){\n int r=upper_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin()-1;\n int l=lower_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin();\n if (r-l+1>n/4) return x[i];\n }\n```\nPython code is also provided.\n\nThanks to @Sergei, C++ using Binary search is revised to reduce the number of iterations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(100001)$$\n# revised C++ Code using Binary search runs in 0ms Beats 100%\n```C++ []\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size();\n if (n<4) //There is exactly one integer occurs more than 25%\n return arr[0];\n int x[5]={arr[0], arr[n/4], arr[n/2], arr[3*n/4], arr[n-1]};\n for (int i=0; i<4; i++)\n if (x[i]==x[i+1]) return x[i];\n\n //If not found, proceed the binary search\n int q[5]={0, n/4, n/2, 3*n/4, n-1};\n for (int i=1; i<3; i++){\n int r=upper_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin()-1;\n int l=lower_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin();\n if (r-l+1>n/4) return x[i];\n }\n \n return x[3];\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n=len(arr)\n if n<4: return arr[0]\n q=[0, n//4, n//2, 3*n//4, n-1]\n x=[arr[0], arr[q[1]], arr[q[2]], arr[q[3]], arr[-1]]\n for i in range(4):\n if x[i]==x[i+1]: return x[i]\n print("binary search")\n for i in range(1,4):\n a=arr[q[i-1]:q[i+1]+1]\n r=bisect.bisect_right(a, x[i])-1\n l=bisect.bisect_left(a, x[i])\n if (r-l+1>n//4): return x[i]\n return -1\n \n```\n\n# Code using Frequency count 3 ms Beats 98.94%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size(), q=n/4;\n int freq[100001]={0};\n for(int x: arr){\n freq[x]++;\n if (freq[x]>q) return x;\n }\n return -1;\n }\n};\n```\n# C code using sliding window runing 7ms\n```\n#pragma GCC optimize("O3", "unroll-loops")\nint findSpecialInteger(int* arr, int n) {\n int q=n/4;\n for(register int i=0; i<n-q; i++){\n if (arr[i]==arr[i+q])\n return arr[i];\n }\n return -1;\n}\n``` | 11 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
C++/Python frequency count vs Binary search||0ms Beats 100% | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n3 different kinds of soultion arte provided.\n1 is very naive, solved this with counting frequency for each number; no hash table is used.\nThe 2nd approach uses binary search if the possible target \n`int x[5]={arr[0], arr[n/4], arr[n/2], arr[3*n/4], arr[n-1]};`\nnot hit.\n\nBoth solutions have the same speed with different TC.\n\nThe 3rd approach uses C code by sliding window with running time 7ms.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn English subtitles if necessary]\n[https://youtu.be/nzVIomp9qSg?si=F-B65MLzQqrHhsq1](https://youtu.be/nzVIomp9qSg?si=F-B65MLzQqrHhsq1)\nTo shrink the searching range, define the array for specific indices\n```\nint q[5]={0, n/4, n/2, 3*n/4, n-1};\n```\nThe binary searching part is as follows:\n```\n//If not found, proceed the binary search\nfor (int i=1; i<4; i++){\n int r=upper_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin()-1;\n int l=lower_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin();\n if (r-l+1>n/4) return x[i];\n }\n```\nPython code is also provided.\n\nThanks to @Sergei, C++ using Binary search is revised to reduce the number of iterations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(100001)$$\n# revised C++ Code using Binary search runs in 0ms Beats 100%\n```C++ []\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size();\n if (n<4) //There is exactly one integer occurs more than 25%\n return arr[0];\n int x[5]={arr[0], arr[n/4], arr[n/2], arr[3*n/4], arr[n-1]};\n for (int i=0; i<4; i++)\n if (x[i]==x[i+1]) return x[i];\n\n //If not found, proceed the binary search\n int q[5]={0, n/4, n/2, 3*n/4, n-1};\n for (int i=1; i<3; i++){\n int r=upper_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin()-1;\n int l=lower_bound(arr.begin()+q[i-1], arr.begin()+q[i+1]+1, x[i])-arr.begin();\n if (r-l+1>n/4) return x[i];\n }\n \n return x[3];\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n=len(arr)\n if n<4: return arr[0]\n q=[0, n//4, n//2, 3*n//4, n-1]\n x=[arr[0], arr[q[1]], arr[q[2]], arr[q[3]], arr[-1]]\n for i in range(4):\n if x[i]==x[i+1]: return x[i]\n print("binary search")\n for i in range(1,4):\n a=arr[q[i-1]:q[i+1]+1]\n r=bisect.bisect_right(a, x[i])-1\n l=bisect.bisect_left(a, x[i])\n if (r-l+1>n//4): return x[i]\n return -1\n \n```\n\n# Code using Frequency count 3 ms Beats 98.94%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n=arr.size(), q=n/4;\n int freq[100001]={0};\n for(int x: arr){\n freq[x]++;\n if (freq[x]>q) return x;\n }\n return -1;\n }\n};\n```\n# C code using sliding window runing 7ms\n```\n#pragma GCC optimize("O3", "unroll-loops")\nint findSpecialInteger(int* arr, int n) {\n int q=n/4;\n for(register int i=0; i<n-q; i++){\n if (arr[i]==arr[i+q])\n return arr[i];\n }\n return -1;\n}\n``` | 11 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
【Video】Give me 5 minutes - 2 solutions - How we think about a solution | element-appearing-more-than-25-in-sorted-array | 1 | 1 | # Intuition\nCalculate quarter length of input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\nWhen I added the second solution, it exceeded five minutes. lol\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,409\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\n### Solution 1\n\nThe description say "more than 25%", that means length of target number should be at least `quarter` of length of input array.\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\n```\n```[]\n9 // 4 = 2\n```\n\n---\n\n\u2B50\uFE0F Points\n\nIf the number two steps ahead is the same as the current number, it can be considered as 25%.\n\nBe careful, we need to include the current number because 2 / 9 = 0.22222...not more than 25%. If we include the current number, 3 / 9 = 0.33333...\n\nOne more point is that we don\'t have to iterate all numbers in input array, because we compare the current number and the number in current index + quarter, so number of max iteration should be `total length of input array - quarter`.\n\n---\n\nLet\'s see one by one\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\n```\nAt index = 0\n\nif arr[i] == arr[i + quarter]:\nif 1 == 2 \u2192 false\n\ni + quarter = 2\n```\n```\nAt index = 1\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 3\n```\n```\nAt index = 2\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 4\n```\n```\nAt index = 3\n\nif arr[i] == arr[i + quarter]:\nif 6 == 6 \u2192 true\n\ni + quarter = 5\n```\n```\nOutput: 6\n```\n\nEasy!\uD83D\uDE06\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(n - quarter)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n quarter = n // 4\n\n for i in range(n - quarter):\n if arr[i] == arr[i + quarter]:\n return arr[i]\n```\n```javascript []\nvar findSpecialInteger = function(arr) {\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n for (let i = 0; i < n - quarter; i++) {\n if (arr[i] === arr[i + quarter]) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1; \n }\n};\n```\n\n# Step by step Algorithm\n\n1. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n2. **Loop through the array:**\n ```python\n for i in range(n - quarter):\n ```\n - The loop iterates through the array indices from 0 to `(n - quarter - 1)`. This ensures that there are at least `quarter` elements remaining in the array for each iteration.\n\n3. **Check if the next element is the same:**\n ```python\n if arr[i] == arr[i + quarter]:\n ```\n - For each iteration, it checks whether the element at the current index (`i`) is equal to the element two steps ahead (`i + quarter`).\n - If the condition is true, it means the current element is repeated in the next `quarter` elements, which corresponds to 25% of the array.\n\n4. **Return the special integer:**\n ```python\n return arr[i]\n ```\n - If the condition in the `if` statement is satisfied, the function returns the special integer (`arr[i]`).\n\nIn summary, the algorithm iterates through the array, comparing each element with the one current index + quarter steps ahead. If a match is found, it returns the special integer. This logic assumes that such a special integer always exists based on the problem statement.\n\n\n---\n\n# Solution 2 - Binary Search\n\nMy second solution is to use binary search to find leftmost current number and rightmost current number. The title says "Sorted Array", so we can easliy imagine we have binary search solution. lol\n\nI think we have 3 points.\n\n---\n\n\u2B50\uFE0F Points\n\n1. We can start from index that is equal to quarter\n2. Number of iteration should be number of possible candidate element\n3. Even If we find the target number by binary search, we should continue it\n\n---\n\n### 1. We can start from index that is equal to quarter\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nIn this case, we can start from index 2. If the number at index 0 is answer, index 2 is the same number as index 0. In other words, if leftmost index is not 0 when we execute binary search to find the number at index 2, index 0 is not answer. We don\'t have to start from index 0. We can start from index which is equal to quarter.\n\n\n### 2. Number of iteration should be number of possible candidate element\n\nIf current number is answer number we should return, there is the same number in current index + quarter. **In other words, if not, we don\'t have to care about numbers between current index and current index + quarter - 1.** They are not answer definitely, so we can move forward by number of quarter.\n\nThe number in current index + quarter should be the next target number. There is possibility that the number is answer number we should return. That\'s why I say "current index + quarter - 1".\n\nFor example\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nLet\'s say we are at index 2.\n```\ncurrent number is 2 (= index 2)\nthe number in current index + quarter is 4 (= index 4)\n```\nThey are different numbers, so from index 2 to index 3, there is not answer number. We can jump into index 4(the next candicate) in this case.(Index 3 is 6, but in the end, we know that 6 is answer. We can find it in the next interation, because next candidate is 6).\n\n- How we can know current index + quarter is different number?\n\nWe can calcuate like this\n\n```\nrightmost index - leftmost index + 1 > quarter\n```\nIf we meet this condition, that is answer, if not, Go to the next candidate. `+1` is to get real length because we use index numbers for the calculation. If rightmost and leftmost is the same index(Let\'s say 0), length should 1, because there is a number at index 0.\n\n### 3. Even If we find the target number by binary search, we should continue it\n\nUsually, when we execute binary search, we stop when we find the target number, but in this question, we need to find leftmost index and rightmost index, so even if we find the target number, the number is not always leftmost or righmost index. That\'s why we continue if we meet this condition.\n\n```\nwhile left <= right:\n```\n\nIf we find target number when we find leftmost index, move left, because leftmost is on the left side.\n\n```\nright = mid - 1\n```\n\nIf we find target number when we find rightmost index, move right, because rightmost is on the right side.\n\n```\nleft = mid + 1\n```\n\nEasy\uD83D\uDE06\nLet\'s see a real algorithm!\n\nIf you are not familar with typical binary search, I have a video for you.\n\nhttps://youtu.be/gVLvNe_SNc0\n\n\n---\n\n# Complexity\n- Time complexity: $$O(c log n)$$\n`n` is length of input array\n`c` is number of candidates\n```\nc = (n - qurater) / qurater\n```\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n \n n = len(arr)\n quarter = n // 4\n\n # Handle the case where quarter is zero\n if quarter == 0:\n return arr[0] if n > 0 else None\n\n # Check every possible candidate element\n for i in range(quarter, n, quarter):\n # Use binary search to find the first and last occurrence of the candidate element\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n\n # Check if the frequency is greater than 25%\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n```\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n function binarySearch(target, isFirst) {\n let left = 0;\n let right = arr.length - 1;\n let result = -1;\n\n while (left <= right) {\n let mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] === target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n }\n\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n // Handle the case where quarter is zero\n if (quarter === 0) {\n return n > 0 ? arr[0] : null;\n }\n\n // Check every possible candidate element\n for (let i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n const leftOccurrence = binarySearch(arr[i], true);\n const rightOccurrence = binarySearch(arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1;\n }\n\n private int binarySearch(int[] arr, int target, boolean isFirst) {\n int left = 0;\n int right = arr.length - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1; \n }\n\nprivate:\n int binarySearch(const vector<int>& arr, int target, bool isFirst) {\n int left = 0;\n int right = arr.size() - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n};\n```\n# Step by step algorithm\n\n1. **Binary Search Function:**\n ```python\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n ```\n - This is a binary search function that finds either the first or the last occurrence of the `target` in the `arr` array based on the `is_first` parameter.\n\n2. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n3. **Handling the Case Where Quarter is Zero:**\n ```python\n if quarter == 0:\n return arr[0] if n > 0 else None\n ```\n - If `quarter` is zero, it means the array has fewer than 4 elements. The function returns the first element if the array is not empty; otherwise, it returns `None`.\n\n4. **Checking Every Possible Candidate Element:**\n ```python\n for i in range(quarter, n, quarter):\n ```\n - The loop iterates through the array indices from `quarter` to `n - 1` with a step of `quarter`.\n\n5. **Using Binary Search to Find Occurrences:**\n ```python\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n ```\n - For each candidate element, it uses the binary search function to find the first and last occurrences.\n\n6. **Checking Frequency and Returning Result:**\n ```python\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n ```\n - It checks if the frequency of the candidate element is greater than 25%. If true, it returns the candidate element as the result.\n\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/transpose-matrix/solutions/4384180/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n\n | 78 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
【Video】Give me 5 minutes - 2 solutions - How we think about a solution | element-appearing-more-than-25-in-sorted-array | 1 | 1 | # Intuition\nCalculate quarter length of input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\nWhen I added the second solution, it exceeded five minutes. lol\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,409\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\n### Solution 1\n\nThe description say "more than 25%", that means length of target number should be at least `quarter` of length of input array.\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\n```\n```[]\n9 // 4 = 2\n```\n\n---\n\n\u2B50\uFE0F Points\n\nIf the number two steps ahead is the same as the current number, it can be considered as 25%.\n\nBe careful, we need to include the current number because 2 / 9 = 0.22222...not more than 25%. If we include the current number, 3 / 9 = 0.33333...\n\nOne more point is that we don\'t have to iterate all numbers in input array, because we compare the current number and the number in current index + quarter, so number of max iteration should be `total length of input array - quarter`.\n\n---\n\nLet\'s see one by one\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\n```\nAt index = 0\n\nif arr[i] == arr[i + quarter]:\nif 1 == 2 \u2192 false\n\ni + quarter = 2\n```\n```\nAt index = 1\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 3\n```\n```\nAt index = 2\n\nif arr[i] == arr[i + quarter]:\nif 2 == 6 \u2192 false\n\ni + quarter = 4\n```\n```\nAt index = 3\n\nif arr[i] == arr[i + quarter]:\nif 6 == 6 \u2192 true\n\ni + quarter = 5\n```\n```\nOutput: 6\n```\n\nEasy!\uD83D\uDE06\nLet\'s see a real algorithm!\n\n---\n\n# Complexity\n- Time complexity: $$O(n - quarter)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n = len(arr)\n quarter = n // 4\n\n for i in range(n - quarter):\n if arr[i] == arr[i + quarter]:\n return arr[i]\n```\n```javascript []\nvar findSpecialInteger = function(arr) {\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n for (let i = 0; i < n - quarter; i++) {\n if (arr[i] === arr[i + quarter]) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n for (int i = 0; i < n - quarter; i++) {\n if (arr[i] == arr[i + quarter]) {\n return arr[i];\n }\n }\n\n return -1; \n }\n};\n```\n\n# Step by step Algorithm\n\n1. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n2. **Loop through the array:**\n ```python\n for i in range(n - quarter):\n ```\n - The loop iterates through the array indices from 0 to `(n - quarter - 1)`. This ensures that there are at least `quarter` elements remaining in the array for each iteration.\n\n3. **Check if the next element is the same:**\n ```python\n if arr[i] == arr[i + quarter]:\n ```\n - For each iteration, it checks whether the element at the current index (`i`) is equal to the element two steps ahead (`i + quarter`).\n - If the condition is true, it means the current element is repeated in the next `quarter` elements, which corresponds to 25% of the array.\n\n4. **Return the special integer:**\n ```python\n return arr[i]\n ```\n - If the condition in the `if` statement is satisfied, the function returns the special integer (`arr[i]`).\n\nIn summary, the algorithm iterates through the array, comparing each element with the one current index + quarter steps ahead. If a match is found, it returns the special integer. This logic assumes that such a special integer always exists based on the problem statement.\n\n\n---\n\n# Solution 2 - Binary Search\n\nMy second solution is to use binary search to find leftmost current number and rightmost current number. The title says "Sorted Array", so we can easliy imagine we have binary search solution. lol\n\nI think we have 3 points.\n\n---\n\n\u2B50\uFE0F Points\n\n1. We can start from index that is equal to quarter\n2. Number of iteration should be number of possible candidate element\n3. Even If we find the target number by binary search, we should continue it\n\n---\n\n### 1. We can start from index that is equal to quarter\n\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nIn this case, we can start from index 2. If the number at index 0 is answer, index 2 is the same number as index 0. In other words, if leftmost index is not 0 when we execute binary search to find the number at index 2, index 0 is not answer. We don\'t have to start from index 0. We can start from index which is equal to quarter.\n\n\n### 2. Number of iteration should be number of possible candidate element\n\nIf current number is answer number we should return, there is the same number in current index + quarter. **In other words, if not, we don\'t have to care about numbers between current index and current index + quarter - 1.** They are not answer definitely, so we can move forward by number of quarter.\n\nThe number in current index + quarter should be the next target number. There is possibility that the number is answer number we should return. That\'s why I say "current index + quarter - 1".\n\nFor example\n```\nInput: arr = [1,2,2,6,6,6,6,7,10]\nquarter = 2\n```\nLet\'s say we are at index 2.\n```\ncurrent number is 2 (= index 2)\nthe number in current index + quarter is 4 (= index 4)\n```\nThey are different numbers, so from index 2 to index 3, there is not answer number. We can jump into index 4(the next candicate) in this case.(Index 3 is 6, but in the end, we know that 6 is answer. We can find it in the next interation, because next candidate is 6).\n\n- How we can know current index + quarter is different number?\n\nWe can calcuate like this\n\n```\nrightmost index - leftmost index + 1 > quarter\n```\nIf we meet this condition, that is answer, if not, Go to the next candidate. `+1` is to get real length because we use index numbers for the calculation. If rightmost and leftmost is the same index(Let\'s say 0), length should 1, because there is a number at index 0.\n\n### 3. Even If we find the target number by binary search, we should continue it\n\nUsually, when we execute binary search, we stop when we find the target number, but in this question, we need to find leftmost index and rightmost index, so even if we find the target number, the number is not always leftmost or righmost index. That\'s why we continue if we meet this condition.\n\n```\nwhile left <= right:\n```\n\nIf we find target number when we find leftmost index, move left, because leftmost is on the left side.\n\n```\nright = mid - 1\n```\n\nIf we find target number when we find rightmost index, move right, because rightmost is on the right side.\n\n```\nleft = mid + 1\n```\n\nEasy\uD83D\uDE06\nLet\'s see a real algorithm!\n\nIf you are not familar with typical binary search, I have a video for you.\n\nhttps://youtu.be/gVLvNe_SNc0\n\n\n---\n\n# Complexity\n- Time complexity: $$O(c log n)$$\n`n` is length of input array\n`c` is number of candidates\n```\nc = (n - qurater) / qurater\n```\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n```python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n \n n = len(arr)\n quarter = n // 4\n\n # Handle the case where quarter is zero\n if quarter == 0:\n return arr[0] if n > 0 else None\n\n # Check every possible candidate element\n for i in range(quarter, n, quarter):\n # Use binary search to find the first and last occurrence of the candidate element\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n\n # Check if the frequency is greater than 25%\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n```\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar findSpecialInteger = function(arr) {\n function binarySearch(target, isFirst) {\n let left = 0;\n let right = arr.length - 1;\n let result = -1;\n\n while (left <= right) {\n let mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] === target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n }\n\n const n = arr.length;\n const quarter = Math.floor(n / 4);\n\n // Handle the case where quarter is zero\n if (quarter === 0) {\n return n > 0 ? arr[0] : null;\n }\n\n // Check every possible candidate element\n for (let i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n const leftOccurrence = binarySearch(arr[i], true);\n const rightOccurrence = binarySearch(arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n};\n```\n```java []\nclass Solution {\n public int findSpecialInteger(int[] arr) {\n int n = arr.length;\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1;\n }\n\n private int binarySearch(int[] arr, int target, boolean isFirst) {\n int left = 0;\n int right = arr.length - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int findSpecialInteger(vector<int>& arr) {\n int n = arr.size();\n int quarter = n / 4;\n\n // Handle the case where quarter is zero\n if (quarter == 0) {\n return n > 0 ? arr[0] : -1;\n }\n\n // Check every possible candidate element\n for (int i = quarter; i < n; i += quarter) {\n // Use binary search to find the first and last occurrence of the candidate element\n int leftOccurrence = binarySearch(arr, arr[i], true);\n int rightOccurrence = binarySearch(arr, arr[i], false);\n\n // Check if the frequency is greater than 25%\n if (rightOccurrence - leftOccurrence + 1 > quarter) {\n return arr[i];\n }\n }\n\n return -1; \n }\n\nprivate:\n int binarySearch(const vector<int>& arr, int target, bool isFirst) {\n int left = 0;\n int right = arr.size() - 1;\n int result = -1;\n\n while (left <= right) {\n int mid = (left + right) / 2;\n\n if (arr[mid] == target) {\n result = mid;\n if (isFirst) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n return result;\n } \n};\n```\n# Step by step algorithm\n\n1. **Binary Search Function:**\n ```python\n def binary_search(target, is_first):\n left, right = 0, len(arr) - 1\n result = -1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == target:\n result = mid\n if is_first:\n right = mid - 1\n else:\n left = mid + 1\n elif arr[mid] < target:\n left = mid + 1\n else:\n right = mid - 1\n\n return result\n ```\n - This is a binary search function that finds either the first or the last occurrence of the `target` in the `arr` array based on the `is_first` parameter.\n\n2. **Initialization:**\n ```python\n n = len(arr)\n quarter = n // 4\n ```\n - `n` is assigned the length of the input array `arr`.\n - `quarter` is calculated as one-fourth of the length of the array `arr` using integer division (`//`), ensuring it\'s an integer.\n\n3. **Handling the Case Where Quarter is Zero:**\n ```python\n if quarter == 0:\n return arr[0] if n > 0 else None\n ```\n - If `quarter` is zero, it means the array has fewer than 4 elements. The function returns the first element if the array is not empty; otherwise, it returns `None`.\n\n4. **Checking Every Possible Candidate Element:**\n ```python\n for i in range(quarter, n, quarter):\n ```\n - The loop iterates through the array indices from `quarter` to `n - 1` with a step of `quarter`.\n\n5. **Using Binary Search to Find Occurrences:**\n ```python\n left_occurrence = binary_search(arr[i], True)\n right_occurrence = binary_search(arr[i], False)\n ```\n - For each candidate element, it uses the binary search function to find the first and last occurrences.\n\n6. **Checking Frequency and Returning Result:**\n ```python\n if right_occurrence - left_occurrence + 1 > quarter:\n return arr[i]\n ```\n - It checks if the frequency of the candidate element is greater than 25%. If true, it returns the candidate element as the result.\n\n\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-product-of-two-elements-in-an-array/solutions/4392747/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/transpose-matrix/solutions/4384180/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n\n | 78 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Simple approach without use of hashmap and extra libraries! | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the array elements are sorted whenever in the loop ith element equals i+len(arr)//4 th element. We will return the element.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n for i in range(len(arr) - len(arr)//4):\n if arr[i] == arr[i + len(arr)//4]:\n return arr[i]\n\n``` | 3 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
Simple approach without use of hashmap and extra libraries! | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the array elements are sorted whenever in the loop ith element equals i+len(arr)//4 th element. We will return the element.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n for i in range(len(arr) - len(arr)//4):\n if arr[i] == arr[i + len(arr)//4]:\n return arr[i]\n\n``` | 3 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
⭐One-Liner Hack in 🐍|| Two Approaches ||😐Beats 75.32%😐⭐ | element-appearing-more-than-25-in-sorted-array | 0 | 1 | \n# Code\n```py\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return next(i for i in arr if arr.count(i) / len(arr) > 0.25)\n```\n ---\n\n\n# Code\n```py\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return statistics.mode(arr)\n```\n---\n\n_If you like the solution, promote it. Thank You._\n \n--- | 3 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
⭐One-Liner Hack in 🐍|| Two Approaches ||😐Beats 75.32%😐⭐ | element-appearing-more-than-25-in-sorted-array | 0 | 1 | \n# Code\n```py\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return next(i for i in arr if arr.count(i) / len(arr) > 0.25)\n```\n ---\n\n\n# Code\n```py\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n return statistics.mode(arr)\n```\n---\n\n_If you like the solution, promote it. Thank You._\n \n--- | 3 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Beats 97% very Easy | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n threshold = len(arr) // 4\n \n for i in range(len(arr)):\n if arr[i] == arr[i + threshold]:\n return arr[i]\n \n return -1 # If not found\n``` | 8 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
Beats 97% very Easy | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n threshold = len(arr) // 4\n \n for i in range(len(arr)):\n if arr[i] == arr[i + threshold]:\n return arr[i]\n \n return -1 # If not found\n``` | 8 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Best and Easy Approach...... || Beginners friendly...🔥🔥🔥 | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty dictionary \'arr2\' to store the count of occurrences for each unique element in the input array.\n2. Iterate through each element i in the input array arr.\n3. If i is already a key in \'arr2\', increment its count.\n4. If i is not a key in \'arr2\', add it to the dictionary with a count of 1.\n5. Retrieve the keys and values from the dictionary using list(arr2.keys()) and list(arr2.values()), respectively.\n6. Find the maximum count (maxval) from the values.\n7. Find the index of the maximum count in the values list (index = Val.index(maxval)).\n8. Return the element at the corresponding index in the keys list (keyVal[index]).\nNote: The code is essentially finding the element with the highest count in the array\n\n# Complexity\n- Time complexity:- O(N) -> where N is the number of elements in the array. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N) -> the number of unique elements in the input array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n arr2 = {}\n count = 0\n for i in arr:\n if i in arr2:\n arr2[i] += 1\n else:\n arr2[i] = 1\n keyVal = list(arr2.keys())\n Val = list(arr2.values())\n maxval = max(Val)\n index = Val.index(maxval)\n return keyVal[index]\n \n \n``` | 2 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
Best and Easy Approach...... || Beginners friendly...🔥🔥🔥 | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty dictionary \'arr2\' to store the count of occurrences for each unique element in the input array.\n2. Iterate through each element i in the input array arr.\n3. If i is already a key in \'arr2\', increment its count.\n4. If i is not a key in \'arr2\', add it to the dictionary with a count of 1.\n5. Retrieve the keys and values from the dictionary using list(arr2.keys()) and list(arr2.values()), respectively.\n6. Find the maximum count (maxval) from the values.\n7. Find the index of the maximum count in the values list (index = Val.index(maxval)).\n8. Return the element at the corresponding index in the keys list (keyVal[index]).\nNote: The code is essentially finding the element with the highest count in the array\n\n# Complexity\n- Time complexity:- O(N) -> where N is the number of elements in the array. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N) -> the number of unique elements in the input array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n arr2 = {}\n count = 0\n for i in arr:\n if i in arr2:\n arr2[i] += 1\n else:\n arr2[i] = 1\n keyVal = list(arr2.keys())\n Val = list(arr2.values())\n maxval = max(Val)\n index = Val.index(maxval)\n return keyVal[index]\n \n \n``` | 2 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
✅✅Majority Element in Array🔥🔥 | element-appearing-more-than-25-in-sorted-array | 1 | 1 | # Intuition\nThe problem seems to ask for finding a "special" integer, which appears more than 25% of the time in the given array. The approach appears to use a dictionary to count the occurrences of each element and then iterate through the dictionary to find the element that meets the criteria.\n\n# Approach\n1. Check if the array length is less than 2, return the only element.\n2. Initialize variables, including a dictionary to store the count of each element and a variable to store the result.\n3. Iterate through the array, updating the dictionary with element counts.\n4. Iterate through the dictionary to find the element that appears more than 25% of the time.\n5. Return the result.\n\n# Complexity\n- **Time complexity:** O(n), where n is the length of the input array. The code iterates through the array once and then iterates through the dictionary, both operations taking linear time.\n- **Space complexity:** O(n), where n is the length of the input array. The dictionary stores counts for each unique element in the array.\n\n# Code\n```csharp []\npublic class Solution {\n public int FindSpecialInteger(int[] arr)\n {\n if (arr.Length < 2){\n return arr[0];\n }\n int result = 0;\n int percent = (int)(arr.Length * 0.25);\n Dictionary<int, int> dc = new Dictionary<int, int>();\n foreach (int i in arr)\n {\n if (dc.ContainsKey(i))\n {\n dc[i]++;\n }\n else {\n dc[i] = 1;\n }\n }\n\n foreach (int key in dc.Keys)\n {\n if (dc[key] > percent)\n {\n result = key;\n }\n }\n\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int findSpecialInteger(int[] arr) {\n if (arr.length < 2) {\n return arr[0];\n }\n int result = 0;\n int percent = (int) (arr.length * 0.25);\n Map<Integer, Integer> map = new HashMap<>();\n \n for (int i : arr) {\n map.put(i, map.getOrDefault(i, 0) + 1);\n }\n\n for (int key : map.keySet()) {\n if (map.get(key) > percent) {\n result = key;\n }\n }\n\n return result;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_special_integer(arr: Vec<i32>) -> i32 {\n if arr.len() < 2 {\n return arr[0];\n }\n let mut result = 0;\n let percent = (arr.len() as f32 * 0.25) as usize;\n let mut map = HashMap::new();\n\n for &i in &arr {\n *map.entry(i).or_insert(0) += 1;\n }\n\n for (&key, &count) in &map {\n if count > percent {\n result = key;\n }\n }\n\n result\n }\n}\n```\n```Go []\nfunc findSpecialInteger(arr []int) int {\n\tif len(arr) < 2 {\n\t\treturn arr[0]\n\t}\n\tresult := 0\n\tpercent := int(float64(len(arr)) * 0.25)\n\tcountMap := make(map[int]int)\n\n\tfor _, i := range arr {\n\t\tcountMap[i]++\n\t}\n\n\tfor key, count := range countMap {\n\t\tif count > percent {\n\t\t\tresult = key\n\t\t}\n\t}\n\n\treturn result\n}\n```\n```Python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n if len(arr) < 2:\n return arr[0]\n result = 0\n percent = int(len(arr) * 0.25)\n count_map = {}\n\n for i in arr:\n count_map[i] = count_map.get(i, 0) + 1\n\n for key, count in count_map.items():\n if count > percent:\n result = key\n\n return result\n```\n\n\n\n- Please upvote me !!! | 11 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
✅✅Majority Element in Array🔥🔥 | element-appearing-more-than-25-in-sorted-array | 1 | 1 | # Intuition\nThe problem seems to ask for finding a "special" integer, which appears more than 25% of the time in the given array. The approach appears to use a dictionary to count the occurrences of each element and then iterate through the dictionary to find the element that meets the criteria.\n\n# Approach\n1. Check if the array length is less than 2, return the only element.\n2. Initialize variables, including a dictionary to store the count of each element and a variable to store the result.\n3. Iterate through the array, updating the dictionary with element counts.\n4. Iterate through the dictionary to find the element that appears more than 25% of the time.\n5. Return the result.\n\n# Complexity\n- **Time complexity:** O(n), where n is the length of the input array. The code iterates through the array once and then iterates through the dictionary, both operations taking linear time.\n- **Space complexity:** O(n), where n is the length of the input array. The dictionary stores counts for each unique element in the array.\n\n# Code\n```csharp []\npublic class Solution {\n public int FindSpecialInteger(int[] arr)\n {\n if (arr.Length < 2){\n return arr[0];\n }\n int result = 0;\n int percent = (int)(arr.Length * 0.25);\n Dictionary<int, int> dc = new Dictionary<int, int>();\n foreach (int i in arr)\n {\n if (dc.ContainsKey(i))\n {\n dc[i]++;\n }\n else {\n dc[i] = 1;\n }\n }\n\n foreach (int key in dc.Keys)\n {\n if (dc[key] > percent)\n {\n result = key;\n }\n }\n\n return result;\n }\n}\n```\n``` Java []\npublic class Solution {\n public int findSpecialInteger(int[] arr) {\n if (arr.length < 2) {\n return arr[0];\n }\n int result = 0;\n int percent = (int) (arr.length * 0.25);\n Map<Integer, Integer> map = new HashMap<>();\n \n for (int i : arr) {\n map.put(i, map.getOrDefault(i, 0) + 1);\n }\n\n for (int key : map.keySet()) {\n if (map.get(key) > percent) {\n result = key;\n }\n }\n\n return result;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_special_integer(arr: Vec<i32>) -> i32 {\n if arr.len() < 2 {\n return arr[0];\n }\n let mut result = 0;\n let percent = (arr.len() as f32 * 0.25) as usize;\n let mut map = HashMap::new();\n\n for &i in &arr {\n *map.entry(i).or_insert(0) += 1;\n }\n\n for (&key, &count) in &map {\n if count > percent {\n result = key;\n }\n }\n\n result\n }\n}\n```\n```Go []\nfunc findSpecialInteger(arr []int) int {\n\tif len(arr) < 2 {\n\t\treturn arr[0]\n\t}\n\tresult := 0\n\tpercent := int(float64(len(arr)) * 0.25)\n\tcountMap := make(map[int]int)\n\n\tfor _, i := range arr {\n\t\tcountMap[i]++\n\t}\n\n\tfor key, count := range countMap {\n\t\tif count > percent {\n\t\t\tresult = key\n\t\t}\n\t}\n\n\treturn result\n}\n```\n```Python []\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n if len(arr) < 2:\n return arr[0]\n result = 0\n percent = int(len(arr) * 0.25)\n count_map = {}\n\n for i in arr:\n count_map[i] = count_map.get(i, 0) + 1\n\n for key, count in count_map.items():\n if count > percent:\n result = key\n\n return result\n```\n\n\n\n- Please upvote me !!! | 11 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Easiest Solution || Python | element-appearing-more-than-25-in-sorted-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n= len(arr)\n threshold= n//4\n\n candidate=arr[0]\n count = 1\n for i in range(1,n):\n if arr[i] == candidate:\n count+=1\n else:\n count = 1\n candidate = arr[i]\n if count > threshold:\n return candidate\n return arr[0]\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
Easiest Solution || Python | element-appearing-more-than-25-in-sorted-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n n= len(arr)\n threshold= n//4\n\n candidate=arr[0]\n count = 1\n for i in range(1,n):\n if arr[i] == candidate:\n count+=1\n else:\n count = 1\n candidate = arr[i]\n if count > threshold:\n return candidate\n return arr[0]\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79** | 1 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Using Counter in python | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->Linear O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->Constant O(1)\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n count=Counter(arr)\n n=len(arr)\n for keys, values in count.items():\n if values>n/4:\n return keys\n \n``` | 1 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
Using Counter in python | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->Linear O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->Constant O(1)\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n count=Counter(arr)\n n=len(arr)\n for keys, values in count.items():\n if values>n/4:\n return keys\n \n``` | 1 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Solution of element appearing more than 25 in sorted array problem | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Approach\n1. Step one: Compare the current number (`arr[idx]`) with the previous number (`cur_number`)\n- If they are equal, increment the count `count`.\n- If they are not equal, reset the count `count` to 1.\n2. Step two: Check if the count `count` is greater than 25% of the \narray size (`0.25 * len(arr)`)\n3. Step three: return this nimber\n\n# Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n\n- Space complexity:\n$$0(1)$$ - as no extra space is requried\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n count = 0\n cur_number = arr[0]\n for idx in range(len(arr)):\n if cur_number == arr[idx]:\n count += 1\n else:\n count = 1\n if count > 0.25 * len(arr):\n return cur_number\n cur_number = arr[idx] \n``` | 1 | Given an integer array **sorted** in non-decreasing order, there is exactly one integer in the array that occurs more than 25% of the time, return that integer.
**Example 1:**
**Input:** arr = \[1,2,2,6,6,6,6,7,10\]
**Output:** 6
**Example 2:**
**Input:** arr = \[1,1\]
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 105` | Find the distance between the two stops if the bus moved in clockwise or counterclockwise directions. |
Solution of element appearing more than 25 in sorted array problem | element-appearing-more-than-25-in-sorted-array | 0 | 1 | # Approach\n1. Step one: Compare the current number (`arr[idx]`) with the previous number (`cur_number`)\n- If they are equal, increment the count `count`.\n- If they are not equal, reset the count `count` to 1.\n2. Step two: Check if the count `count` is greater than 25% of the \narray size (`0.25 * len(arr)`)\n3. Step three: return this nimber\n\n# Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n\n- Space complexity:\n$$0(1)$$ - as no extra space is requried\n\n# Code\n```\nclass Solution:\n def findSpecialInteger(self, arr: List[int]) -> int:\n count = 0\n cur_number = arr[0]\n for idx in range(len(arr)):\n if cur_number == arr[idx]:\n count += 1\n else:\n count = 1\n if count > 0.25 * len(arr):\n return cur_number\n cur_number = arr[idx] \n``` | 1 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
✔️ [Python3] SORTING 👀, Explained | remove-covered-intervals | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nAs for almost all problems related to intervals, we have to sort them first by the starting position. The next problem is how to define whether an interval is covered? After the sorting, we know that the start of every subsequent interval is greater or equal to all previous interval starts but we can\'t say the same about ends. \nFirst of all, we don\'t need to remember the end positions of all previous intervals, and only keep track of the longest interval seen before. If the end of the current interval lies in the range of some long previous interval that means it is covered. Second of all, we need to handle an edge case when the starts of some intervals are the same and the trick with the longest interval won\'t work. For example, there are might be a case like this `[[1,2],[1,4],[3,4]]`:\n```\n__\n____\n ____\n```\nFor that we can make sure that in case of a tie, the sorting function puts a longer interval in the first place:\n```\n____\n__\n ____\n```\n\n*For reference: https://www.programiz.com/python-programming/methods/built-in/sorted*\n\nTime: **O(Nlog(N))** - sorting\nSpace: **O(N)** - sorting\n\nRuntime: 100 ms, faster than **78.70%** of Python3 online submissions for Remove Covered Intervals.\nMemory Usage: 14.5 MB, less than **86.23%** of Python3 online submissions for Remove Covered Intervals.\n\n```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n res, longest = len(intervals), 0\n srtd = sorted(intervals, key = lambda i: (i[0], -i[1]))\n \n for _, end in srtd:\n if end <= longest:\n res -= 1\n else:\n longest = end\n \n return res\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 49 | Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
Return _the number of remaining intervals_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[3,6\],\[2,8\]\]
**Output:** 2
**Explanation:** Interval \[3,6\] is covered by \[2,8\], therefore it is removed.
**Example 2:**
**Input:** intervals = \[\[1,4\],\[2,3\]\]
**Output:** 1
**Constraints:**
* `1 <= intervals.length <= 1000`
* `intervals[i].length == 2`
* `0 <= li < ri <= 105`
* All the given intervals are **unique**. | How to solve this problem if no deletions are allowed ? Try deleting each element and find the maximum subarray sum to both sides of that element. To do that efficiently, use the idea of Kadane's algorithm. |
✔️ [Python3] SORTING 👀, Explained | remove-covered-intervals | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nAs for almost all problems related to intervals, we have to sort them first by the starting position. The next problem is how to define whether an interval is covered? After the sorting, we know that the start of every subsequent interval is greater or equal to all previous interval starts but we can\'t say the same about ends. \nFirst of all, we don\'t need to remember the end positions of all previous intervals, and only keep track of the longest interval seen before. If the end of the current interval lies in the range of some long previous interval that means it is covered. Second of all, we need to handle an edge case when the starts of some intervals are the same and the trick with the longest interval won\'t work. For example, there are might be a case like this `[[1,2],[1,4],[3,4]]`:\n```\n__\n____\n ____\n```\nFor that we can make sure that in case of a tie, the sorting function puts a longer interval in the first place:\n```\n____\n__\n ____\n```\n\n*For reference: https://www.programiz.com/python-programming/methods/built-in/sorted*\n\nTime: **O(Nlog(N))** - sorting\nSpace: **O(N)** - sorting\n\nRuntime: 100 ms, faster than **78.70%** of Python3 online submissions for Remove Covered Intervals.\nMemory Usage: 14.5 MB, less than **86.23%** of Python3 online submissions for Remove Covered Intervals.\n\n```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n res, longest = len(intervals), 0\n srtd = sorted(intervals, key = lambda i: (i[0], -i[1]))\n \n for _, end in srtd:\n if end <= longest:\n res -= 1\n else:\n longest = end\n \n return res\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 49 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Python Simple Solution Explained (video + code) (Fastest) | remove-covered-intervals | 0 | 1 | [](https://www.youtube.com/watch?v=emPnw5m2nN0)\nhttps://www.youtube.com/watch?v=emPnw5m2nN0\n```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n intervals = sorted(intervals, key = lambda x : (x[0], -x[1]))\n \n res = 0\n ending = 0\n \n for _, end in intervals:\n if end > ending:\n res += 1\n ending = end\n \n return res\n``` | 14 | Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
Return _the number of remaining intervals_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[3,6\],\[2,8\]\]
**Output:** 2
**Explanation:** Interval \[3,6\] is covered by \[2,8\], therefore it is removed.
**Example 2:**
**Input:** intervals = \[\[1,4\],\[2,3\]\]
**Output:** 1
**Constraints:**
* `1 <= intervals.length <= 1000`
* `intervals[i].length == 2`
* `0 <= li < ri <= 105`
* All the given intervals are **unique**. | How to solve this problem if no deletions are allowed ? Try deleting each element and find the maximum subarray sum to both sides of that element. To do that efficiently, use the idea of Kadane's algorithm. |
Python Simple Solution Explained (video + code) (Fastest) | remove-covered-intervals | 0 | 1 | [](https://www.youtube.com/watch?v=emPnw5m2nN0)\nhttps://www.youtube.com/watch?v=emPnw5m2nN0\n```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n intervals = sorted(intervals, key = lambda x : (x[0], -x[1]))\n \n res = 0\n ending = 0\n \n for _, end in intervals:\n if end > ending:\n res += 1\n ending = end\n \n return res\n``` | 14 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
[ Python ] ✔✔ Simple Python Solution By Sorting the List 🔥✌ | remove-covered-intervals | 0 | 1 | # If It is Useful to Understand Please Upvote Me \uD83D\uDE4F\uD83D\uDE4F\n\tclass Solution:\n\t\tdef removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n\n\t\t\tintervals=sorted(intervals)\n\n\t\t\ti=0\n\t\t\twhile i<len(intervals)-1:\n\n\t\t\t\t\ta,b = intervals[i]\n\t\t\t\t\tp,q = intervals[i+1]\n\n\t\t\t\t\tif a <= p and q <= b:\n\t\t\t\t\t\tintervals.remove(intervals[i+1])\n\t\t\t\t\t\ti=i-1\n\n\t\t\t\t\telif p <= a and b <= q:\n\t\t\t\t\t\tintervals.remove(intervals[i])\n\t\t\t\t\t\ti=i-1\n\n\t\t\t\t\ti=i+1\n\t\t\treturn len(intervals)\n\n | 10 | Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
Return _the number of remaining intervals_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[3,6\],\[2,8\]\]
**Output:** 2
**Explanation:** Interval \[3,6\] is covered by \[2,8\], therefore it is removed.
**Example 2:**
**Input:** intervals = \[\[1,4\],\[2,3\]\]
**Output:** 1
**Constraints:**
* `1 <= intervals.length <= 1000`
* `intervals[i].length == 2`
* `0 <= li < ri <= 105`
* All the given intervals are **unique**. | How to solve this problem if no deletions are allowed ? Try deleting each element and find the maximum subarray sum to both sides of that element. To do that efficiently, use the idea of Kadane's algorithm. |
[ Python ] ✔✔ Simple Python Solution By Sorting the List 🔥✌ | remove-covered-intervals | 0 | 1 | # If It is Useful to Understand Please Upvote Me \uD83D\uDE4F\uD83D\uDE4F\n\tclass Solution:\n\t\tdef removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n\n\t\t\tintervals=sorted(intervals)\n\n\t\t\ti=0\n\t\t\twhile i<len(intervals)-1:\n\n\t\t\t\t\ta,b = intervals[i]\n\t\t\t\t\tp,q = intervals[i+1]\n\n\t\t\t\t\tif a <= p and q <= b:\n\t\t\t\t\t\tintervals.remove(intervals[i+1])\n\t\t\t\t\t\ti=i-1\n\n\t\t\t\t\telif p <= a and b <= q:\n\t\t\t\t\t\tintervals.remove(intervals[i])\n\t\t\t\t\t\ti=i-1\n\n\t\t\t\t\ti=i+1\n\t\t\treturn len(intervals)\n\n | 10 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Python3 || brute force - 40% Faster | remove-covered-intervals | 0 | 1 | ```\nclass Solution:\n def removeCoveredIntervals(self, new: List[List[int]]) -> int:\n arr=[]\n for i in range(len(new)):\n for j in range(len(new)):\n if i!=j and new[j][0] <= new[i][0] and new[i][1] <= new[j][1]:\n arr.append(new[i])\n break\n return len(new)-len(arr)\n``` | 3 | Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
Return _the number of remaining intervals_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[3,6\],\[2,8\]\]
**Output:** 2
**Explanation:** Interval \[3,6\] is covered by \[2,8\], therefore it is removed.
**Example 2:**
**Input:** intervals = \[\[1,4\],\[2,3\]\]
**Output:** 1
**Constraints:**
* `1 <= intervals.length <= 1000`
* `intervals[i].length == 2`
* `0 <= li < ri <= 105`
* All the given intervals are **unique**. | How to solve this problem if no deletions are allowed ? Try deleting each element and find the maximum subarray sum to both sides of that element. To do that efficiently, use the idea of Kadane's algorithm. |
Python3 || brute force - 40% Faster | remove-covered-intervals | 0 | 1 | ```\nclass Solution:\n def removeCoveredIntervals(self, new: List[List[int]]) -> int:\n arr=[]\n for i in range(len(new)):\n for j in range(len(new)):\n if i!=j and new[j][0] <= new[i][0] and new[i][1] <= new[j][1]:\n arr.append(new[i])\n break\n return len(new)-len(arr)\n``` | 3 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Python 3 (90ms) | Sorted Matrix Solution | Easy to Understand | remove-covered-intervals | 0 | 1 | ```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n intervals = sorted(intervals, key = lambda x : (x[0], -x[1]))\n res = 0\n ending = 0\n for _, end in intervals:\n if end > ending:\n res += 1\n ending = end\n return res\n``` | 3 | Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
Return _the number of remaining intervals_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[3,6\],\[2,8\]\]
**Output:** 2
**Explanation:** Interval \[3,6\] is covered by \[2,8\], therefore it is removed.
**Example 2:**
**Input:** intervals = \[\[1,4\],\[2,3\]\]
**Output:** 1
**Constraints:**
* `1 <= intervals.length <= 1000`
* `intervals[i].length == 2`
* `0 <= li < ri <= 105`
* All the given intervals are **unique**. | How to solve this problem if no deletions are allowed ? Try deleting each element and find the maximum subarray sum to both sides of that element. To do that efficiently, use the idea of Kadane's algorithm. |
Python 3 (90ms) | Sorted Matrix Solution | Easy to Understand | remove-covered-intervals | 0 | 1 | ```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n intervals = sorted(intervals, key = lambda x : (x[0], -x[1]))\n res = 0\n ending = 0\n for _, end in intervals:\n if end > ending:\n res += 1\n ending = end\n return res\n``` | 3 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Python | Faster than 99% | Using Dict. | remove-covered-intervals | 0 | 1 | The idea is to keep a track of the highest ending time for every starting time and storing it as a key.\nEx - [[1,2],[1,4],[2,6]]\nwe would store : {1:4 , 2:6}\nWe only need the max ones becuase the ones lesser than that will be included in the highest one anyway.\n\nLike in our example, [1,2] is in [1,4] that\'s why we don\'t need it.\n\nthen we just use the dictionary to find out any other matching intervals and return ans.\n```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n d=dict() \n high=-1\n ans=0\n totalIntervals = len(intervals)\n\t\t\n for i in range(len(intervals)):\n if intervals[i][0] in d.keys():\n if d[intervals[i][0]]< intervals[i][1]:\n d[intervals[i][0]] = intervals[i][1]\n else:\n d[intervals[i][0]] = intervals[i][1]\n for i in sorted(d):\n if d[i] > high:\n high = d[i]\n ans+=1\n return ans\n \n \n \n \n``` | 6 | Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
Return _the number of remaining intervals_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[3,6\],\[2,8\]\]
**Output:** 2
**Explanation:** Interval \[3,6\] is covered by \[2,8\], therefore it is removed.
**Example 2:**
**Input:** intervals = \[\[1,4\],\[2,3\]\]
**Output:** 1
**Constraints:**
* `1 <= intervals.length <= 1000`
* `intervals[i].length == 2`
* `0 <= li < ri <= 105`
* All the given intervals are **unique**. | How to solve this problem if no deletions are allowed ? Try deleting each element and find the maximum subarray sum to both sides of that element. To do that efficiently, use the idea of Kadane's algorithm. |
Python | Faster than 99% | Using Dict. | remove-covered-intervals | 0 | 1 | The idea is to keep a track of the highest ending time for every starting time and storing it as a key.\nEx - [[1,2],[1,4],[2,6]]\nwe would store : {1:4 , 2:6}\nWe only need the max ones becuase the ones lesser than that will be included in the highest one anyway.\n\nLike in our example, [1,2] is in [1,4] that\'s why we don\'t need it.\n\nthen we just use the dictionary to find out any other matching intervals and return ans.\n```\nclass Solution:\n def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:\n d=dict() \n high=-1\n ans=0\n totalIntervals = len(intervals)\n\t\t\n for i in range(len(intervals)):\n if intervals[i][0] in d.keys():\n if d[intervals[i][0]]< intervals[i][1]:\n d[intervals[i][0]] = intervals[i][1]\n else:\n d[intervals[i][0]] = intervals[i][1]\n for i in sorted(d):\n if d[i] > high:\n high = d[i]\n ans+=1\n return ans\n \n \n \n \n``` | 6 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
python easy DP beats 98.27% | minimum-falling-path-sum-ii | 0 | 1 | \n\n```\ndef minFallingPathSum(self, g: List[List[int]]) -> int:\n l=len(g)\n for i in range(1,l):\n temp = sorted(g[i-1])\n for j in range(l):\n if g[i-1][j] == temp[0]:\n g[i][j] += temp[1]\n else:\n g[i][j] += temp[0]\n return min(g[-1])\n``` | 1 | Given an `n x n` integer matrix `grid`, return _the minimum sum of a **falling path with non-zero shifts**_.
A **falling path with non-zero shifts** is a choice of exactly one element from each row of `grid` such that no two elements chosen in adjacent rows are in the same column.
**Example 1:**
**Input:** arr = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** 13
**Explanation:**
The possible falling paths are:
\[1,5,9\], \[1,5,7\], \[1,6,7\], \[1,6,8\],
\[2,4,8\], \[2,4,9\], \[2,6,7\], \[2,6,8\],
\[3,4,8\], \[3,4,9\], \[3,5,7\], \[3,5,9\]
The falling path with the smallest sum is \[1,5,7\], so the answer is 13.
**Example 2:**
**Input:** grid = \[\[7\]\]
**Output:** 7
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 200`
* `-99 <= grid[i][j] <= 99` | Sum up the number of days for the years before the given year. Handle the case of a leap year. Find the number of days for each month of the given year. |
python easy DP beats 98.27% | minimum-falling-path-sum-ii | 0 | 1 | \n\n```\ndef minFallingPathSum(self, g: List[List[int]]) -> int:\n l=len(g)\n for i in range(1,l):\n temp = sorted(g[i-1])\n for j in range(l):\n if g[i-1][j] == temp[0]:\n g[i][j] += temp[1]\n else:\n g[i][j] += temp[0]\n return min(g[-1])\n``` | 1 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
🐍 Python3 Clean Solution using DP | minimum-falling-path-sum-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def minFallingPathSum(self, grid: List[List[int]]) -> int:\n N = len(grid)\n DP = grid[0]\n\n for i in range(1, N):\n indx1 = DP.index(min(DP))\n indx2 = DP.index(min(DP[:indx1] + DP[indx1+1:]))\n for j in range(N):\n if j != indx1:\n grid[i][j] += DP[indx1]\n else:\n grid[i][j] += DP[indx2]\n DP = grid[i]\n\n return min(DP)\n\n``` | 1 | Given an `n x n` integer matrix `grid`, return _the minimum sum of a **falling path with non-zero shifts**_.
A **falling path with non-zero shifts** is a choice of exactly one element from each row of `grid` such that no two elements chosen in adjacent rows are in the same column.
**Example 1:**
**Input:** arr = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** 13
**Explanation:**
The possible falling paths are:
\[1,5,9\], \[1,5,7\], \[1,6,7\], \[1,6,8\],
\[2,4,8\], \[2,4,9\], \[2,6,7\], \[2,6,8\],
\[3,4,8\], \[3,4,9\], \[3,5,7\], \[3,5,9\]
The falling path with the smallest sum is \[1,5,7\], so the answer is 13.
**Example 2:**
**Input:** grid = \[\[7\]\]
**Output:** 7
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 200`
* `-99 <= grid[i][j] <= 99` | Sum up the number of days for the years before the given year. Handle the case of a leap year. Find the number of days for each month of the given year. |
🐍 Python3 Clean Solution using DP | minimum-falling-path-sum-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def minFallingPathSum(self, grid: List[List[int]]) -> int:\n N = len(grid)\n DP = grid[0]\n\n for i in range(1, N):\n indx1 = DP.index(min(DP))\n indx2 = DP.index(min(DP[:indx1] + DP[indx1+1:]))\n for j in range(N):\n if j != indx1:\n grid[i][j] += DP[indx1]\n else:\n grid[i][j] += DP[indx2]\n DP = grid[i]\n\n return min(DP)\n\n``` | 1 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
hi | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhi\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nlinear\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n r=""\n while(head):\n r+=str(head.val)\n head=head.next\n return int(r,2)\n\n \n```\n\nhi | 0 | Given `head` which is a reference node to a singly-linked list. The value of each node in the linked list is either `0` or `1`. The linked list holds the binary representation of a number.
Return the _decimal value_ of the number in the linked list.
The **most significant bit** is at the head of the linked list.
**Example 1:**
**Input:** head = \[1,0,1\]
**Output:** 5
**Explanation:** (101) in base 2 = (5) in base 10
**Example 2:**
**Input:** head = \[0\]
**Output:** 0
**Constraints:**
* The Linked List is not empty.
* Number of nodes will not exceed `30`.
* Each node's value is either `0` or `1`. | Use dynamic programming. The state would be the index in arr1 and the index of the previous element in arr2 after sorting it and removing duplicates. |
hi | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhi\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nlinear\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n r=""\n while(head):\n r+=str(head.val)\n head=head.next\n return int(r,2)\n\n \n```\n\nhi | 0 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
Nurbek | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n p = head\n ans = \'\'\n while p != None:\n ans += str(p.val)\n p = p.next\n return int(ans,2)\n``` | 0 | Given `head` which is a reference node to a singly-linked list. The value of each node in the linked list is either `0` or `1`. The linked list holds the binary representation of a number.
Return the _decimal value_ of the number in the linked list.
The **most significant bit** is at the head of the linked list.
**Example 1:**
**Input:** head = \[1,0,1\]
**Output:** 5
**Explanation:** (101) in base 2 = (5) in base 10
**Example 2:**
**Input:** head = \[0\]
**Output:** 0
**Constraints:**
* The Linked List is not empty.
* Number of nodes will not exceed `30`.
* Each node's value is either `0` or `1`. | Use dynamic programming. The state would be the index in arr1 and the index of the previous element in arr2 after sorting it and removing duplicates. |
Nurbek | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n p = head\n ans = \'\'\n while p != None:\n ans += str(p.val)\n p = p.next\n return int(ans,2)\n``` | 0 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
[Python] Simple. 20ms. | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | Read the binary number from MSB to LSB\n```\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n answer = 0\n while head: \n answer = 2*answer + head.val \n head = head.next \n return answer \n``` | 244 | Given `head` which is a reference node to a singly-linked list. The value of each node in the linked list is either `0` or `1`. The linked list holds the binary representation of a number.
Return the _decimal value_ of the number in the linked list.
The **most significant bit** is at the head of the linked list.
**Example 1:**
**Input:** head = \[1,0,1\]
**Output:** 5
**Explanation:** (101) in base 2 = (5) in base 10
**Example 2:**
**Input:** head = \[0\]
**Output:** 0
**Constraints:**
* The Linked List is not empty.
* Number of nodes will not exceed `30`.
* Each node's value is either `0` or `1`. | Use dynamic programming. The state would be the index in arr1 and the index of the previous element in arr2 after sorting it and removing duplicates. |
[Python] Simple. 20ms. | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | Read the binary number from MSB to LSB\n```\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n answer = 0\n while head: \n answer = 2*answer + head.val \n head = head.next \n return answer \n``` | 244 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
simple python solution. | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst find the length of the linked list then compute the number using loop\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n n = head\n c=0\n while n:\n c+=1\n n = n.next\n d=0\n n = head\n for i in range(c-1,-1,-1):\n d+=n.val * (2**i)\n n = n.next\n return d\n``` | 2 | Given `head` which is a reference node to a singly-linked list. The value of each node in the linked list is either `0` or `1`. The linked list holds the binary representation of a number.
Return the _decimal value_ of the number in the linked list.
The **most significant bit** is at the head of the linked list.
**Example 1:**
**Input:** head = \[1,0,1\]
**Output:** 5
**Explanation:** (101) in base 2 = (5) in base 10
**Example 2:**
**Input:** head = \[0\]
**Output:** 0
**Constraints:**
* The Linked List is not empty.
* Number of nodes will not exceed `30`.
* Each node's value is either `0` or `1`. | Use dynamic programming. The state would be the index in arr1 and the index of the previous element in arr2 after sorting it and removing duplicates. |
simple python solution. | convert-binary-number-in-a-linked-list-to-integer | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst find the length of the linked list then compute the number using loop\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def getDecimalValue(self, head: ListNode) -> int:\n n = head\n c=0\n while n:\n c+=1\n n = n.next\n d=0\n n = head\n for i in range(c-1,-1,-1):\n d+=n.val * (2**i)\n n = n.next\n return d\n``` | 2 | You have a `grid` of size `n x 3` and you want to paint each cell of the grid with exactly one of the three colors: **Red**, **Yellow,** or **Green** while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).
Given `n` the number of rows of the grid, return _the number of ways_ you can paint this `grid`. As the answer may grow large, the answer **must be** computed modulo `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 12
**Explanation:** There are 12 possible way to paint the grid as shown.
**Example 2:**
**Input:** n = 5000
**Output:** 30228214
**Constraints:**
* `n == grid.length`
* `1 <= n <= 5000` | Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value. You can solve the problem in O(1) memory using bits operation. use shift left operation ( << ) and or operation ( | ) to get the decimal value in one operation. |
Simple Brute Force Approach | sequential-digits | 0 | 1 | # Intuition\nThe constraints make us think that thi sproblem should be solved with the help of converting the low and high to stirngs.\n\n# Approach\nCalculate the length of low and high and then run a loop from lowest length to greatest length.\nfor each length there can be only certain possibilites \nFor ex.- For length 5 there can be\n[12345,23456,34567,45678,56789]\nhere we can see the last number starts from 5 that is 11-len(of that iteration.)\nfor each start we then make the number by by incrementing the last digit by one till the length is reached and then check if it lies between the range of low and high. \n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:easy\n\n# Code\n```\nclass Solution:\n def sequentialDigits(self, low: int, high: int) -> List[int]:\n l = len(str(low))\n h = len(str(high))\n ans = []\n for i in range(l,h+1):\n for j in range(1,11-i):\n t = str(j)\n for k in range(i-1):\n t+=str(int(t[-1])+1)\n if int(t)<=high and int(t)>=low:\n ans.append(int(t))\n ans.sort()\n return ans\n\n``` | 1 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
Easy to Solve By python | sequential-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sequentialDigits(self, low, high):\n out = []\n queue = deque(range(1,10))\n while queue:\n elem = queue.popleft()\n if low <= elem <= high:\n out.append(elem)\n last = elem % 10\n if last < 9: queue.append(elem*10 + last + 1)\n \n return out\n``` | 1 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
Python - math oriented | sequential-digits | 0 | 1 | # Intuition\n\nI didn\'t even consider using strings to solve this :). Oops.\n\nStarted by thinking of the properties we can leverage:\n- we can group the answers into # of digits (2, 3, etc)\n- we have a fixed initial value for each number of digits (12, 123, 1234 etc)\n- we have a fixed increment for each number of digits (11, 111, 1111, etc)\n- for each number of digits, we can only incrment until the last digit gets to 9\n\n# Approach\n\n- Loop over each number of digits we need to consider\n - Start with a base value (e.g. 123), save it, and keep adding the increment (e.g. 111) until we go out of range (e.g. 789 is the last for three digits)\n\n# Complexity\n- Time complexity:\n\nO(n) where n is # high digits - # low digits + 1\n\nEach pass through a digit length < 10 actions, so we have O(10*n) => O(n)\n\n- Space complexity:\n\nO(n) for the answers array. Lookups for increments and starting points are O(1)\n\n\n# Code\n```\nclass Solution:\n def sequentialDigits(self, low: int, high: int) -> List[int]:\n num_digits_low = int(log(low)//log(10)) + 1 \n num_digits_hi = int(log(high)//log(10)) + 1\n\n bases = [12,123,1234,12345,123456,1234567,12345678,123456789]\n increment = [11,111,1111,11111,111111,1111111,11111111,1111111111]\n answers = []\n\n for digits in range(num_digits_low, num_digits_hi+1):\n value = bases[digits-2]\n num_attempts = 10 - (value % 10)\n # for each attempt, we add 1, 1, 11, 111, etc\n for _ in range(num_attempts):\n if low <= value <= high:\n answers.append(value)\n value += increment[digits-2] \n\n return answers \n\n \n``` | 0 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
✔️ [Python3] ( ͡- ͜ʖ ͡-) ( ͡° ͜ʖ ͡°) ( ͡ʘ ͜ʖ ͡ʘ) LOG10, Explained | sequential-digits | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe main observation here is that all numbers in the result can be formed from the simple tuple `(1, 2, 3, 4, 5, 6, 7, 8, 9)` using a sliding window. What windows we should use? The range of window widths can be derived from the input `low` and `high`. Since the resulting numbers should be in the range `[low, high]`, the minimum window width should be equal to the number of digits in the `low` and the maximum to the number of digits in the `high`. The formula for the number of digits in the positive integer is `floor(log10(n))+1`. \n\nSo our algorithm iterates over all possible window widths and, for every window, slides it over the digits `(1, 2, ...)` forming numbers for the result. Every number must be checked for occurrence in the interval `[low, high]`. For example, if we have `low=199` and `high=200` the algorithm will form numbers like `123, 234, 345, 456, 567, 678, 789` which are all out of the range.\n\nTime: **O(log10(N))** - scan\nSpace: **O(1)** - nothing stored\n\nRuntime: 32 ms, faster than **62.30%** of Python3 online submissions for Sequential Digits.\nMemory Usage: 14.2 MB, less than **80.16%** of Python3 online submissions for Sequential Digits.\n\n```\ndef sequentialDigits(self, low: int, high: int) -> List[int]:\n\tres = list()\n\n\tfor window in range(floor(log10(low)) + 1, floor(log10(high)) + 2):\n\t\tfor start in range(10 - window):\n\t\t\tnumber = 0\n\t\t\tfor i in range(start, start + window):\n\t\t\t\tnumber = number * 10 + i + 1\n\n\t\t\tif low <= number <= high: \n\t\t\t\tres.append(number)\n\n\treturn res\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 18 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
BFS solution in Python, Time: O(1), Space: O(1) | sequential-digits | 0 | 1 | start from 1 ~ 9, and then increase by multiplying by 10 and adding last_num + 1. (last_num = num % 10)\n\nIn this solution, you don\'t even need to sort at the end.\n\n**Time: O(1)**, since you need to check at most `81` values. `(Start num: 1 ~ 9) * (At most 9 digits) = 81`\n**Space: O(1)**, since you store at most `9` numbers in the queue.\n\n```\nfrom collections import deque\n\nclass Solution:\n def sequentialDigits(self, low: int, high: int) -> List[int]:\n queue = deque(range(1, 10))\n res = []\n while queue:\n u = queue.popleft()\n if low <= u <= high:\n res.append(u)\n elif high < u:\n continue\n \n last_num = u % 10\n if last_num != 9:\n queue.append(u * 10 + last_num + 1)\n \n return res\n``` | 16 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
Python Super_Super easy #Simplest question 100% faster | sequential-digits | 0 | 1 | ```\n#(please upvote if you like the solution)\nclass Solution:\n def sequentialDigits(self, low: int, high: int) -> List[int]:\n s=\'123456789\'\n ans=[]\n for i in range(len(s)):\n for j in range(i+1,len(s)):\n st=int(s[i:j+1])\n if(st>=low and st<=high):\n ans.append(st)\n ans.sort() \n return ans \n \n``` | 29 | An integer has _sequential digits_ if and only if each digit in the number is one more than the previous digit.
Return a **sorted** list of all the integers in the range `[low, high]` inclusive that have sequential digits.
**Example 1:**
**Input:** low = 100, high = 300
**Output:** \[123,234\]
**Example 2:**
**Input:** low = 1000, high = 13000
**Output:** \[1234,2345,3456,4567,5678,6789,12345\]
**Constraints:**
* `10 <= low <= high <= 10^9` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.