title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Intuitive Python Recursive Solution With Explanation | find-elements-in-a-contaminated-binary-tree | 0 | 1 | # Intuition\nWe can just depth first search the tree and recover the values.\n\n# Approach\nDepth first search the tree and recover the values. Add the values we have recovered to a set for $O(1)$ lookup with `find` method.\n\n# Complexity\n- Time complexity:\n$$O(n)$$, $n$ being the number the nodes in the tree. We depth first search the tree, visiting each node once.\n\n- Space complexity:\n$$O(n)$$, maintain set of values we recovered.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n\n def __init__(self, root: Optional[TreeNode]):\n self.root = root\n self.values = set()\n self.recover(root, 0)\n\n def recover(self, node: Optional[TreeNode], val: int) -> None:\n if not node:\n return\n node.val = val\n self.values.add(val)\n self.recover(node.left, 2*val+1)\n self.recover(node.right, 2*val+2)\n\n def find(self, target: int) -> bool:\n return target in self.values\n\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Easy python solution using BFS | Beats 84.70% in memory | find-elements-in-a-contaminated-binary-tree | 0 | 1 | # Intuition\nrecover the nodes of the tree using BFS and store it in a `list`. return `true` if target in list else `false`. \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```py\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n\n def __init__(self, root: Optional[TreeNode]):\n self.root = root \n self.tree = []\n self.recover(root)\n\n def recover(self, root) : \n q = deque()\n q.append((root, -1, 0))\n\n while q : \n node, parent, pointer = q.pop()\n if parent == -1 : \n self.tree.append(0)\n parent = 0 \n else :\n if pointer == 1 : \n self.tree.append(parent*2 + 1)\n parent = parent*2 + 1\n elif pointer == -1 : \n self.tree.append(parent*2 + 2)\n parent = parent*2 + 2\n\n if node.left :\n q.append((node.left, parent, 1))\n\n if node.right : \n q.append((node.right, parent, -1))\n\n \n def find(self, target: int) -> bool:\n return target in self.tree \n\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
[Python] Greedy, heap | greatest-sum-divisible-by-three | 0 | 1 | # Intuition\nIn order to maximize sum divisible by 3, we need to minimize sum of items, which give the same remainder as the whole array sum.\n\n# Approach\n1. Check whole array sum remainder.\n- If it is ``0`` then return whole array sum\n- Otherwise check the remainder - either ``1`` or ``2``\n2. Build two min-heaps for each of the remainders of size ``2``\n3. Check different cases for each remainder:\n- ``1`` is either smallest remainder-1 value or sum of two smallest remainder-2 values\n- ``2`` is either smallest remainder-2 value or sum of two smallest remainder-1 values\n\n# Complexity\n- Time complexity:\n$$O(n*log(n))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxSumDivThree(self, nums: List[int]) -> int:\n s = sum(nums)\n r = s % 3\n if r == 0:\n return s\n h1, h2 = [], []\n for v in nums:\n if v % 3 == 1:\n if len(h1) < 2:\n heapq.heappush(h1, -v)\n elif v < -h1[0]:\n heapq.heappop(h1)\n heapq.heappush(h1, -v)\n elif v % 3 == 2:\n if len(h2) < 2:\n heapq.heappush(h2, -v)\n elif v < -h2[0]:\n heapq.heappop(h2)\n heapq.heappush(h2, -v)\n\n r11, r12 = -heapq.heappop(h1) if h1 else s, -heapq.heappop(h1) if h1 else s\n r21, r22 = -heapq.heappop(h2) if h2 else s, -heapq.heappop(h2) if h2 else s\n\n if r == 1:\n return s - min(r12, r11, r21+r22)\n\n return s - min(r11 + r12, r22, r21) | 1 | Given an integer array `nums`, return _the **maximum possible sum** of elements of the array such that it is divisible by three_.
**Example 1:**
**Input:** nums = \[3,6,5,1,8\]
**Output:** 18
**Explanation:** Pick numbers 3, 6, 1 and 8 their sum is 18 (maximum sum divisible by 3).
**Example 2:**
**Input:** nums = \[4\]
**Output:** 0
**Explanation:** Since 4 is not divisible by 3, do not pick any number.
**Example 3:**
**Input:** nums = \[1,2,3,4,4\]
**Output:** 12
**Explanation:** Pick numbers 1, 3, 4 and 4 their sum is 12 (maximum sum divisible by 3).
**Constraints:**
* `1 <= nums.length <= 4 * 104`
* `1 <= nums[i] <= 104` | What's special about a majority element ? A majority element appears more than half the length of the array number of times. If we tried a random index of the array, what's the probability that this index has a majority element ? It's more than 50% if that array has a majority element. Try a random index for a proper number of times so that the probability of not finding the answer tends to zero. |
[Python] Greedy, heap | greatest-sum-divisible-by-three | 0 | 1 | # Intuition\nIn order to maximize sum divisible by 3, we need to minimize sum of items, which give the same remainder as the whole array sum.\n\n# Approach\n1. Check whole array sum remainder.\n- If it is ``0`` then return whole array sum\n- Otherwise check the remainder - either ``1`` or ``2``\n2. Build two min-heaps for each of the remainders of size ``2``\n3. Check different cases for each remainder:\n- ``1`` is either smallest remainder-1 value or sum of two smallest remainder-2 values\n- ``2`` is either smallest remainder-2 value or sum of two smallest remainder-1 values\n\n# Complexity\n- Time complexity:\n$$O(n*log(n))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxSumDivThree(self, nums: List[int]) -> int:\n s = sum(nums)\n r = s % 3\n if r == 0:\n return s\n h1, h2 = [], []\n for v in nums:\n if v % 3 == 1:\n if len(h1) < 2:\n heapq.heappush(h1, -v)\n elif v < -h1[0]:\n heapq.heappop(h1)\n heapq.heappush(h1, -v)\n elif v % 3 == 2:\n if len(h2) < 2:\n heapq.heappush(h2, -v)\n elif v < -h2[0]:\n heapq.heappop(h2)\n heapq.heappush(h2, -v)\n\n r11, r12 = -heapq.heappop(h1) if h1 else s, -heapq.heappop(h1) if h1 else s\n r21, r22 = -heapq.heappop(h2) if h2 else s, -heapq.heappop(h2) if h2 else s\n\n if r == 1:\n return s - min(r12, r11, r21+r22)\n\n return s - min(r11 + r12, r22, r21) | 1 | There is a pizza with `3n` slices of varying size, you and your friends will take slices of pizza as follows:
* You will pick **any** pizza slice.
* Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
* Your friend Bob will pick the next slice in the clockwise direction of your pick.
* Repeat until there are no more slices of pizzas.
Given an integer array `slices` that represent the sizes of the pizza slices in a clockwise direction, return _the maximum possible sum of slice sizes that you can pick_.
**Example 1:**
**Input:** slices = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.
**Example 2:**
**Input:** slices = \[8,9,8,6,1,1\]
**Output:** 16
**Explanation:** Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.
**Constraints:**
* `3 * n == slices.length`
* `1 <= slices.length <= 500`
* `1 <= slices[i] <= 1000` | Represent the state as DP[pos][mod]: maximum possible sum starting in the position "pos" in the array where the current sum modulo 3 is equal to mod. |
Python3 Greedy Linear Time | greatest-sum-divisible-by-three | 0 | 1 | In this approach, the goal will be to sum up the entire list, and subtract only what needs to be subtracted to make the sum divisible by 3.\n\nThere are 3 situations regarding the sum:\n**It is divisible by 3:** We are done already, just return the sum\n**Leaves a remainder of 1:** Subtract the smallest number that leaves a remainder of 1, or the 2 smallest numbers which leave a remainder of 2- whichever one leaves the larger sum.\n**Leaves a remainder of 2:** Subtract the smallest number that leaves a remainder of 2, or the 2 smallest numbers which leave a remainder of 1- whichever one leaves the larger sum.\n\n```\ndef maxSumDivThree(self, nums: List[int]) -> int:\n\ttotal = sum(nums)\n\tif total%3 == 0:\n\t\treturn total\n\n\trem1_min = [10000, 10000] # Smallest 2 numbers leaving remainder of 1\n\trem2_min = [10000, 10000] # Smallest 2 numbers leaving remainder of 2\n\tfor num in nums:\n\t\tif num % 3 == 1:\n\t\t\tif num < rem1_min[0]:\n\t\t\t\trem1_min[0], rem1_min[1] = num, rem1_min[0]\n\t\t\telif num < rem1_min[1]:\n\t\t\t\trem1_min[1] = num\n\t\telif num % 3 == 2:\n\t\t\tif num < rem2_min[0]:\n\t\t\t\trem2_min[0], rem2_min[1] = num, rem2_min[0]\n\t\t\telif num < rem2_min[1]:\n\t\t\t\trem2_min[1] = num\n\n\tif total%3 == 1:\n\t\treturn total - min(rem1_min[0], sum(rem2_min))\n\tif total%3 == 2:\n\t\treturn total - min(rem2_min[0], sum(rem1_min)) | 2 | Given an integer array `nums`, return _the **maximum possible sum** of elements of the array such that it is divisible by three_.
**Example 1:**
**Input:** nums = \[3,6,5,1,8\]
**Output:** 18
**Explanation:** Pick numbers 3, 6, 1 and 8 their sum is 18 (maximum sum divisible by 3).
**Example 2:**
**Input:** nums = \[4\]
**Output:** 0
**Explanation:** Since 4 is not divisible by 3, do not pick any number.
**Example 3:**
**Input:** nums = \[1,2,3,4,4\]
**Output:** 12
**Explanation:** Pick numbers 1, 3, 4 and 4 their sum is 12 (maximum sum divisible by 3).
**Constraints:**
* `1 <= nums.length <= 4 * 104`
* `1 <= nums[i] <= 104` | What's special about a majority element ? A majority element appears more than half the length of the array number of times. If we tried a random index of the array, what's the probability that this index has a majority element ? It's more than 50% if that array has a majority element. Try a random index for a proper number of times so that the probability of not finding the answer tends to zero. |
Python3 Greedy Linear Time | greatest-sum-divisible-by-three | 0 | 1 | In this approach, the goal will be to sum up the entire list, and subtract only what needs to be subtracted to make the sum divisible by 3.\n\nThere are 3 situations regarding the sum:\n**It is divisible by 3:** We are done already, just return the sum\n**Leaves a remainder of 1:** Subtract the smallest number that leaves a remainder of 1, or the 2 smallest numbers which leave a remainder of 2- whichever one leaves the larger sum.\n**Leaves a remainder of 2:** Subtract the smallest number that leaves a remainder of 2, or the 2 smallest numbers which leave a remainder of 1- whichever one leaves the larger sum.\n\n```\ndef maxSumDivThree(self, nums: List[int]) -> int:\n\ttotal = sum(nums)\n\tif total%3 == 0:\n\t\treturn total\n\n\trem1_min = [10000, 10000] # Smallest 2 numbers leaving remainder of 1\n\trem2_min = [10000, 10000] # Smallest 2 numbers leaving remainder of 2\n\tfor num in nums:\n\t\tif num % 3 == 1:\n\t\t\tif num < rem1_min[0]:\n\t\t\t\trem1_min[0], rem1_min[1] = num, rem1_min[0]\n\t\t\telif num < rem1_min[1]:\n\t\t\t\trem1_min[1] = num\n\t\telif num % 3 == 2:\n\t\t\tif num < rem2_min[0]:\n\t\t\t\trem2_min[0], rem2_min[1] = num, rem2_min[0]\n\t\t\telif num < rem2_min[1]:\n\t\t\t\trem2_min[1] = num\n\n\tif total%3 == 1:\n\t\treturn total - min(rem1_min[0], sum(rem2_min))\n\tif total%3 == 2:\n\t\treturn total - min(rem2_min[0], sum(rem1_min)) | 2 | There is a pizza with `3n` slices of varying size, you and your friends will take slices of pizza as follows:
* You will pick **any** pizza slice.
* Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
* Your friend Bob will pick the next slice in the clockwise direction of your pick.
* Repeat until there are no more slices of pizzas.
Given an integer array `slices` that represent the sizes of the pizza slices in a clockwise direction, return _the maximum possible sum of slice sizes that you can pick_.
**Example 1:**
**Input:** slices = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.
**Example 2:**
**Input:** slices = \[8,9,8,6,1,1\]
**Output:** 16
**Explanation:** Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.
**Constraints:**
* `3 * n == slices.length`
* `1 <= slices.length <= 500`
* `1 <= slices[i] <= 1000` | Represent the state as DP[pos][mod]: maximum possible sum starting in the position "pos" in the array where the current sum modulo 3 is equal to mod. |
Python Very Easy Solution | greatest-sum-divisible-by-three | 0 | 1 | # Complexity\n- Time complexity\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumDivThree(self, nums: List[int]) -> int:\n dp = [0] * 3\n for v in nums:\n a, b, c = dp[0] + v, dp[1] + v, dp[2] + v\n dp[a % 3] = max(dp[a % 3], a)\n dp[b % 3] = max(dp[b % 3], b)\n dp[c % 3] = max(dp[c % 3], c)\n return dp[0]\n``` | 1 | Given an integer array `nums`, return _the **maximum possible sum** of elements of the array such that it is divisible by three_.
**Example 1:**
**Input:** nums = \[3,6,5,1,8\]
**Output:** 18
**Explanation:** Pick numbers 3, 6, 1 and 8 their sum is 18 (maximum sum divisible by 3).
**Example 2:**
**Input:** nums = \[4\]
**Output:** 0
**Explanation:** Since 4 is not divisible by 3, do not pick any number.
**Example 3:**
**Input:** nums = \[1,2,3,4,4\]
**Output:** 12
**Explanation:** Pick numbers 1, 3, 4 and 4 their sum is 12 (maximum sum divisible by 3).
**Constraints:**
* `1 <= nums.length <= 4 * 104`
* `1 <= nums[i] <= 104` | What's special about a majority element ? A majority element appears more than half the length of the array number of times. If we tried a random index of the array, what's the probability that this index has a majority element ? It's more than 50% if that array has a majority element. Try a random index for a proper number of times so that the probability of not finding the answer tends to zero. |
Python Very Easy Solution | greatest-sum-divisible-by-three | 0 | 1 | # Complexity\n- Time complexity\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumDivThree(self, nums: List[int]) -> int:\n dp = [0] * 3\n for v in nums:\n a, b, c = dp[0] + v, dp[1] + v, dp[2] + v\n dp[a % 3] = max(dp[a % 3], a)\n dp[b % 3] = max(dp[b % 3], b)\n dp[c % 3] = max(dp[c % 3], c)\n return dp[0]\n``` | 1 | There is a pizza with `3n` slices of varying size, you and your friends will take slices of pizza as follows:
* You will pick **any** pizza slice.
* Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
* Your friend Bob will pick the next slice in the clockwise direction of your pick.
* Repeat until there are no more slices of pizzas.
Given an integer array `slices` that represent the sizes of the pizza slices in a clockwise direction, return _the maximum possible sum of slice sizes that you can pick_.
**Example 1:**
**Input:** slices = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.
**Example 2:**
**Input:** slices = \[8,9,8,6,1,1\]
**Output:** 16
**Explanation:** Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.
**Constraints:**
* `3 * n == slices.length`
* `1 <= slices.length <= 500`
* `1 <= slices[i] <= 1000` | Represent the state as DP[pos][mod]: maximum possible sum starting in the position "pos" in the array where the current sum modulo 3 is equal to mod. |
[Python 3] 0-1 BFS clean code | minimum-moves-to-move-a-box-to-their-target-location | 0 | 1 | \tclass Solution:\n\t\tdef minPushBox(self, grid: List[List[str]]) -> int:\n\t\t\tn,m=len(grid),len(grid[0])\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(m):\n\t\t\t\t\tif grid[i][j]==\'S\':\n\t\t\t\t\t\tplayer=[i,j]\n\t\t\t\t\telif grid[i][j]==\'T\':\n\t\t\t\t\t\ttarget=[i,j]\n\t\t\t\t\telif grid[i][j]==\'B\':\n\t\t\t\t\t\tbox=[i,j]\n\t\t\tq=deque([[player[0],player[1],box[0],box[1],0]])\n\t\t\tvis=set([(player[0],player[1],box[0],box[1])])\n\t\t\twhile q:\n\t\t\t\ti,j,bi,bj,steps=q.pop()\n\t\t\t\tif [bi,bj]==target:\n\t\t\t\t\treturn steps\n\t\t\t\tfor dx,dy in [(0,1),(1,0),(-1,0),(0,-1)]:\n\t\t\t\t\tx,y=i+dx,j+dy\n\t\t\t\t\tif 0<=x<n and 0<=y<m and grid[x][y]!=\'#\':\n\t\t\t\t\t\tif (x,y)==(bi,bj):\n\t\t\t\t\t\t\tif 0<=bi+dx<n and 0<=bj+dy<m and grid[bi+dx][bj+dy]!=\'#\':\n\t\t\t\t\t\t\t\tif not (x,y,bi+dx,bj+dy) in vis:\n\t\t\t\t\t\t\t\t\tvis.add((x,y,bi+dx,bj+dy))\n\t\t\t\t\t\t\t\t\tq.appendleft([x,y,bi+dx,bj+dy,steps+1])\n\t\t\t\t\t\telif (x,y,bi,bj) not in vis:\n\t\t\t\t\t\t\tvis.add((x,y,bi,bj))\n\t\t\t\t\t\t\tq.append([x,y,bi,bj,steps])\n\t\t\treturn -1 | 1 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Beats 100/95 in speed and memory , simple code using Java | minimum-moves-to-move-a-box-to-their-target-location | 0 | 1 | \n# Code\n```\nclass Solution:\n def minPushBox(self, grid):\n free = set()\n \n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == "#": continue\n if grid[i][j] == "S": sx,sy = i,j\n if grid[i][j] == "B": bx,by = i,j\n if grid[i][j] == "T": tx,ty = i,j\n free.add((i,j))\n \n stack, visited = [(0,sx,sy,bx,by)], {(sx,sy,bx,by)}\n \n while stack:\n t, si, sj, bi, bj = heappop(stack)\n \n if (bi,bj) == (tx,ty): return t\n \n for d in [(1,0),(-1,0),(0,1),(0,-1)]:\n if (si+d[0],sj+d[1]) == (bi,bj) and (bi+d[0],bj+d[1]) in free and (si+d[0],sj+d[1],bi+d[0],bj+d[1]) not in visited:\n visited.add((si+d[0],sj+d[1],bi+d[0],bj+d[1]))\n heappush(stack,(t+1,si+d[0],sj+d[1],bi+d[0],bj+d[1]))\n elif (si+d[0],sj+d[1]) in free and (si+d[0],sj+d[1]) != (bi,bj) and (si+d[0],sj+d[1],bi,bj) not in visited:\n visited.add((si+d[0],sj+d[1],bi,bj))\n heappush(stack,(t,si+d[0],sj+d[1],bi,bj))\n \n return -1\n \n \n\n\n\n\n\n\n\n\n\n \n\n \n\n\n\n \n\n\n\n``` | 0 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Solution | minimum-moves-to-move-a-box-to-their-target-location | 1 | 1 | ```C++ []\ntypedef pair<int, int> PII;\n\nstruct Node {\n PII b_pos;\n PII p_pos;\n int steps;\n Node(PII b_pos_, PII p_pos_, int step) : b_pos(b_pos_), p_pos(p_pos_), steps(step) {}\n};\nclass Solution {\npublic:\n int dx[4] = {0, 1, 0, -1};\n int dy[4] = {1, 0, -1, 0};\n int row = 0, col = 0;\n PII target_pos;\n\n int minPushBox(vector<vector<char>>& grid) {\n row = grid.size(), col = grid[0].size();\n PII box_pos, player_pos;\n for(int i = 0; i<row; i++) {\n for(int j = 0; j<col; j++) {\n if(grid[i][j] == \'T\') {\n target_pos.first = i, target_pos.second = j;\n } else if(grid[i][j] == \'B\') {\n box_pos.first = i, box_pos.second = j;\n } else if(grid[i][j] == \'S\') {\n player_pos.first = i, player_pos.second = j;\n }\n }\n }\n auto can_get = [&](PII player_pos_func, PII box_pos_func, PII tar_pos) -> bool {\n if(player_pos_func.first == tar_pos.first && player_pos_func.second == tar_pos.second) return true;\n queue<PII> que;\n que.push(player_pos_func);\n bool sta[25][25];\n memset(sta, false, sizeof sta);\n sta[player_pos_func.first][player_pos_func.second] = true;\n while(que.size()) {\n auto cur_player_pos = que.front();\n que.pop();\n int cur_p_x = cur_player_pos.first, cur_p_y = cur_player_pos.second;\n for(int i = 0; i<4; i++) {\n int x = cur_p_x + dx[i], y = cur_p_y + dy[i];\n if(x<0 || x>=row || y<0 || y>=col || grid[x][y] == \'#\' || sta[x][y]) continue;\n if(x == box_pos_func.first && y == box_pos_func.second) continue;\n if(x == tar_pos.first && y == tar_pos.second) return true;\n que.push({x, y});\n sta[x][y] = true;\n }\n }\n return false;\n };\n queue<Node> q;\n q.push({box_pos, player_pos, 0});\n bool st[25][25][25][25];\n memset(st, false, sizeof st);\n while(q.size()) {\n auto cur = q.front();\n q.pop();\n PII cur_box_pos = cur.b_pos, cur_player_pos = cur.p_pos;\n int cur_step = cur.steps;\n for(int i = 0; i<4; i++) {\n int box_next_x = cur_box_pos.first + dx[i], box_next_y = cur_box_pos.second + dy[i];\n if(box_next_x<0 || box_next_x>=row || box_next_y<0 || box_next_y>=col || grid[box_next_x][box_next_y] == \'#\') {\n continue;\n }\n int player_next_x, player_next_y;\n if(dx[i] == 0) {\n player_next_x = cur_box_pos.first, player_next_y = cur_box_pos.second - dy[i];\n }\n if(dy[i] == 0) {\n player_next_x = cur_box_pos.first - dx[i], player_next_y = cur_box_pos.second;\n }\n if(player_next_x<0 || player_next_x>=row || player_next_y<0 || player_next_y>=col || grid[player_next_x][player_next_y] == \'#\') {\n continue;\n }\n if(st[cur_box_pos.first][cur_box_pos.second][player_next_x][player_next_y]) continue;\n if(!can_get(cur_player_pos, cur_box_pos, {player_next_x, player_next_y})) {\n continue;\n }\n if(box_next_x == target_pos.first && box_next_y == target_pos.second) return cur_step + 1;\n q.push({{box_next_x, box_next_y}, cur_box_pos, cur_step+1});\n st[cur_box_pos.first][cur_box_pos.second][player_next_x][player_next_y] = true;\n }\n }\n return -1;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n\n R = len(grid)\n C = len(grid[0])\n maze = [[\'#\']*(C+2)]\n\n for r in range(1,R+1):\n maze.append([\'#\'])\n str = grid[r-1]\n for c in range(1,C+1): \n match str[c-1]:\n case \'B\':\n Box = (r,c)\n case \'S\':\n Source = (r,c)\n case \'T\':\n Target = (r,c)\n\n if(str[c-1] == \'#\'):\n maze[r].append(\'#\')\n else:\n maze[r].append(\'.\')\n\n maze[r].append(\'#\')\n\n maze.append(maze[0])\n\n layer = 0\n layermap = [[0]*(C+2) for _ in range(R+2)]\n ways = [[1,0], [0,1], [-1,0], [0,-1]]\n\n def reachable(source, target, layer):\n buffer = deque([source])\n\n while buffer:\n pos = buffer.popleft()\n\n if(pos == target):\n return True\n\n next = [(pos[0]-1, pos[1]), (pos[0], pos[1]-1), (pos[0]+1, pos[1]), (pos[0], pos[1]+1)]\n\n for r, c in next:\n if(maze[r][c] == \'.\' and layermap[r][c] != layer):\n layermap[r][c] = layer\n buffer.append((r,c))\n \n return False\n\n maxstep = 400\n steped = [[[0]*4 for _ in range(C+2)] for _ in range(R+2)]\n buffer = deque([(Box, Source, 0)])\n\n while buffer:\n box, source, step = buffer.popleft()\n\n if(box == Target):\n maxstep = step\n break\n if(step > maxstep):\n break\n\n new_boxes = [(box[0]+1, box[1]), (box[0], box[1]+1), (box[0]-1, box[1]), (box[0], box[1]-1)]\n new_sources = [(box[0]-1, box[1]), (box[0], box[1]-1), (box[0]+1, box[1]), (box[0], box[1]+1)]\n w = 0\n\n for push_to, push_from in zip(new_boxes, new_sources):\n if(maze[push_to[0]][push_to[1]] == \'.\' and maze[push_from[0]][push_from[1]] == \'.\' and steped[push_to[0]][push_to[1]][w] == 0):\n maze[box[0]][box[1]] = \'#\'\n layer += 1\n\n if(reachable(source, push_from, layer)):\n steped[push_to[0]][push_to[1]][w] = step+1\n buffer.append((push_to, box, step+1))\n\n maze[box[0]][box[1]] = \'.\'\n\n w += 1\n\n if(maxstep == 400):\n return -1\n \n return maxstep\n```\n\n```Java []\nclass Solution {\n char[][] grid;\n int m, n;\n int[][] DIRS = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n boolean[][] reachable; \n\n public int minPushBox(char[][] grid) {\n this.grid = grid;\n m = grid.length;\n n = grid[0].length;\n int step = 0;\n boolean[][][] visited = new boolean[m][n][4];\n reachable = new boolean[m][n];\n\n Deque<int[]> boxQ = new LinkedList<>();\n Deque<int[]> playerQ = new LinkedList<>();\n int[] targetLoc = new int[2];\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'B\') boxQ.offer(new int[]{i, j});\n if (grid[i][j] == \'T\') targetLoc = new int[]{i, j};\n if (grid[i][j] == \'S\') playerQ.offer(new int[]{i, j});\n }\n }\n while (!boxQ.isEmpty()) {\n int size = boxQ.size();\n while (size-- > 0) {\n int[] boxLoc = boxQ.poll();\n int[] playerLoc = playerQ.poll();\n if (boxLoc[0] == targetLoc[0] && boxLoc[1] == targetLoc[1])\n return step;\n\n for (int d = 0; d < 4; d++) {\n if (visited[boxLoc[0]][boxLoc[1]][d]) continue;\n int[] dir = DIRS[d];\n int newPlayerR = boxLoc[0] - dir[0], newPlayerC = boxLoc[1] - dir[1];\n if (newPlayerR < 0 || newPlayerR >= m || newPlayerC < 0 || newPlayerC >= n\n || grid[newPlayerR][newPlayerC] == \'#\')\n continue;\n int newBoxR = boxLoc[0] + dir[0], newBoxC = boxLoc[1] + dir[1];\n if (newBoxR < 0 || newBoxR >= m || newBoxC < 0 || newBoxC >= n\n || grid[newBoxR][newBoxC] == \'#\')\n continue;\n if (!reachable(newPlayerR, newPlayerC, boxLoc, playerLoc))\n continue;\n\n visited[boxLoc[0]][boxLoc[1]][d] = true;\n boxQ.offer(new int[]{newBoxR, newBoxC});\n playerQ.offer(new int[]{newPlayerR, newPlayerC});\n }\n }\n step++;\n }\n return -1;\n }\n private boolean reachable(int targetR, int targetC, int[] boxLoc, int[] playerLoc) {\n if (reachable[targetR][targetC]){\n return true;\n }\n Deque<int[]> queue = new LinkedList<>();\n queue.offer(playerLoc);\n boolean[][] visited = new boolean[m][n];\n visited[boxLoc[0]][boxLoc[1]] = true;\n\n while (!queue.isEmpty()) {\n int[] curr = queue.poll();\n if (curr[0] == targetR && curr[1] == targetC){\n reachable[targetR][targetC] = true;\n return true;\n }\n for (int[] d : DIRS) {\n int r = curr[0] + d[0], c = curr[1] + d[1];\n if (r < 0 || r >= m || c < 0 || c >= n || visited[r][c] || grid[r][c] == \'#\')\n continue;\n queue.offer(new int[]{r, c});\n visited[r][c] = true;\n }\n }\n return false;\n }\n}\n``` | 0 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Clean | Fast | Python Solution | minimum-moves-to-move-a-box-to-their-target-location | 0 | 1 | # Code\n```\nclass Solution:\n\tdef minPushBox(self, grid: List[List[str]]) -> int:\n\t\tn,m=len(grid),len(grid[0])\n\t\tfor i in range(n):\n\t\t\tfor j in range(m):\n\t\t\t\tif grid[i][j]==\'S\':\n\t\t\t\t\tplayer=[i,j]\n\t\t\t\telif grid[i][j]==\'T\':\n\t\t\t\t\ttarget=[i,j]\n\t\t\t\telif grid[i][j]==\'B\':\n\t\t\t\t\tbox=[i,j]\n\t\tq=deque([[player[0],player[1],box[0],box[1],0]])\n\t\tvis=set([(player[0],player[1],box[0],box[1])])\n\t\twhile q:\n\t\t\ti,j,bi,bj,steps=q.pop()\n\t\t\tif [bi,bj]==target:\n\t\t\t\treturn steps\n\t\t\tfor dx,dy in [(0,1),(1,0),(-1,0),(0,-1)]:\n\t\t\t\tx,y=i+dx,j+dy\n\t\t\t\tif 0<=x<n and 0<=y<m and grid[x][y]!=\'#\':\n\t\t\t\t\tif (x,y)==(bi,bj):\n\t\t\t\t\t\tif 0<=bi+dx<n and 0<=bj+dy<m and grid[bi+dx][bj+dy]!=\'#\':\n\t\t\t\t\t\t\tif not (x,y,bi+dx,bj+dy) in vis:\n\t\t\t\t\t\t\t\tvis.add((x,y,bi+dx,bj+dy))\n\t\t\t\t\t\t\t\tq.appendleft([x,y,bi+dx,bj+dy,steps+1])\n\t\t\t\t\telif (x,y,bi,bj) not in vis:\n\t\t\t\t\t\tvis.add((x,y,bi,bj))\n\t\t\t\t\t\tq.append([x,y,bi,bj,steps])\n\t\treturn -1\n``` | 0 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Python (Simple Dijkstra's algorithm) | minimum-moves-to-move-a-box-to-their-target-location | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid):\n free = set()\n \n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == "#": continue\n if grid[i][j] == "S": sx,sy = i,j\n if grid[i][j] == "B": bx,by = i,j\n if grid[i][j] == "T": tx,ty = i,j\n free.add((i,j))\n \n stack, visited = [(0,sx,sy,bx,by)], {(sx,sy,bx,by)}\n \n while stack:\n t, si, sj, bi, bj = heappop(stack)\n \n if (bi,bj) == (tx,ty): return t\n \n for d in [(1,0),(-1,0),(0,1),(0,-1)]:\n if (si+d[0],sj+d[1]) == (bi,bj) and (bi+d[0],bj+d[1]) in free and (si+d[0],sj+d[1],bi+d[0],bj+d[1]) not in visited:\n visited.add((si+d[0],sj+d[1],bi+d[0],bj+d[1]))\n heappush(stack,(t+1,si+d[0],sj+d[1],bi+d[0],bj+d[1]))\n elif (si+d[0],sj+d[1]) in free and (si+d[0],sj+d[1]) != (bi,bj) and (si+d[0],sj+d[1],bi,bj) not in visited:\n visited.add((si+d[0],sj+d[1],bi,bj))\n heappush(stack,(t,si+d[0],sj+d[1],bi,bj))\n \n return -1\n \n \n\n\n\n\n\n\n\n\n\n \n\n \n\n\n\n \n\n\n\n\n``` | 0 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Python Simple BFS Solution, Faster than 90% | minimum-moves-to-move-a-box-to-their-target-location | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Check whether the box can be shifted to the new position(up, down, left, right)\n2. For it to be shifted to the new position the person has to be in a corresponding position.\n3. So, we check if the person can travel from his old position to his corresponding new position(using another BFS).\n4. If the person can travel to his new position than the box can be shifted, otherwise the box cannot be shifted.\n5. We repeat steps 1-4 until we reach the target or it is not possible to move the box anymore.\n\n\n# Code\n```\nclass Solution:\n def checkValid(self, grid: List[List[int]], numRows: int, numCols: int, row: int, col: int) -> bool:\n return 0 <= row < numRows and 0 <= col < numCols and grid[row][col] != \'#\'\n \n def minPushBox(self, grid: List[List[str]]) -> int:\n numRows, numCols = len(grid), len(grid[0])\n for row in range(numRows):\n for col in range(numCols):\n if grid[row][col] == "T":\n target = (row, col)\n if grid[row][col] == "B":\n box = (row, col)\n if grid[row][col] == "S":\n person = (row, col)\n \n def check(curr, dest, box):\n queue, visited = deque([curr]), set()\n while queue:\n pos = queue.popleft()\n if pos == dest: return True\n new_pos = [(pos[0] + 1, pos[1]), (pos[0] - 1, pos[1]), (pos[0], pos[1] + 1), (pos[0], pos[1] - 1)]\n for newRow, newCol in new_pos:\n if self.checkValid(grid, numRows, numCols, newRow, newCol) and (newRow, newCol) not in visited and (newRow, newCol) != box:\n visited.add((newRow, newCol))\n queue.append((newRow, newCol))\n return False\n \n queue, visited = deque([(0, box, person)]), {box + person}\n while queue:\n dist, box, person = queue.popleft()\n if box == target:\n return dist\n boxCoord = [(box[0] + 1, box[1]), (box[0] - 1, box[1]), (box[0], box[1] + 1), (box[0], box[1] - 1)]\n personCoord = [(box[0] - 1, box[1]), (box[0] + 1, box[1]), (box[0], box[1] - 1), (box[0], box[1] + 1)]\n for newBoxCoord, newPersonCoord in zip(boxCoord, personCoord): \n if self.checkValid(grid, numRows, numCols, newBoxCoord[0], newBoxCoord[1]) and newBoxCoord + box not in visited:\n if self.checkValid(grid, numRows, numCols, newPersonCoord[0], newPersonCoord[1]) and check(person, newPersonCoord, box):\n visited.add(newBoxCoord + box)\n queue.append((dist + 1, newBoxCoord, box))\n return -1\n``` | 0 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
python bfs + dfs | minimum-moves-to-move-a-box-to-their-target-location | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid) -> int:\n def gen_next(x, y):\n for dx, dy in [(0, -1), (0, 1), (1, 0), (-1, 0)]:\n new_x = x + dx\n new_y = y + dy\n if 0 <= new_x < len(grid) and 0 <= new_y < len(grid[0]):\n yield new_x, new_y\n\n def find_people_pos(x, y, box_pos):\n visited.add((x, y))\n for new_x, new_y in gen_next(x, y):\n if grid[new_x][new_y] == "." and (new_x, new_y) != box_pos and (new_x, new_y) not in visited:\n find_people_pos(new_x, new_y, box_pos)\n\n def compute_push_pos(new_box_pos, original_pos):\n return 2 * original_pos[0] - new_box_pos[0], 2 * original_pos[1] - new_box_pos[1]\n\n q = deque([])\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == "T":\n target_pos = i, j\n grid[i][j] = "."\n elif grid[i][j] == "B":\n grid[i][j] = "."\n box_pos = i, j\n elif grid[i][j] == "S":\n people_pos = i, j\n grid[i][j] = "."\n if box_pos == target_pos:\n return 0\n\n q.append((box_pos, 0, people_pos))\n box_visited = set()\n while len(q) > 0:\n (x, y), cnt, people_pos = q.popleft()\n visited = set()\n find_people_pos(people_pos[0], people_pos[1], (x,y))\n for new_box_pos in gen_next(x, y):\n \n if (new_box_pos, (x,y)) in box_visited or grid[new_box_pos[0]][new_box_pos[1]] == "#":\n continue\n push_pos = compute_push_pos(new_box_pos, (x, y))\n if push_pos in visited:\n if new_box_pos == target_pos:\n return cnt + 1\n q.append((new_box_pos, cnt + 1, (x,y)))\n box_visited.add((new_box_pos, (x, y)))\n\n return -1\n\n``` | 0 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Simple approach by using abs() | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n totalTime = 0\n\n for i in range(1, len(points)):\n\n previousPoint = points[i - 1]\n currentPoint = points[i]\n\n xDistance = abs(currentPoint[0] - previousPoint[0])\n yDistance = abs(currentPoint[1] - previousPoint[1])\n\n totalTime += max(xDistance, yDistance)\n\n return totalTime\n\n \n``` | 7 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Simple approach by using abs() | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n totalTime = 0\n\n for i in range(1, len(points)):\n\n previousPoint = points[i - 1]\n currentPoint = points[i]\n\n xDistance = abs(currentPoint[0] - previousPoint[0])\n yDistance = abs(currentPoint[1] - previousPoint[1])\n\n totalTime += max(xDistance, yDistance)\n\n return totalTime\n\n \n``` | 7 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
✅ One Line Solution | minimum-time-visiting-all-points | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code #1\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, p: List[List[int]]) -> int:\n return sum(max(abs(x1-x2), abs(y1-y2)) for (x1, y1), (x2, y2) in zip(p, p[1:]))\n```\n\n# Code #2\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, p: List[List[int]]) -> int:\n return sum(max(abs(p[i][0]-p[i-1][0]), abs(p[i][1]-p[i-1][1])) for i in range(1, len(p)))\n``` | 3 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
✅ One Line Solution | minimum-time-visiting-all-points | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$.\n\n# Code #1\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, p: List[List[int]]) -> int:\n return sum(max(abs(x1-x2), abs(y1-y2)) for (x1, y1), (x2, y2) in zip(p, p[1:]))\n```\n\n# Code #2\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, p: List[List[int]]) -> int:\n return sum(max(abs(p[i][0]-p[i-1][0]), abs(p[i][1]-p[i-1][1])) for i in range(1, len(p)))\n``` | 3 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
✅☑[C++/Java/Python/JavaScript] || Easy Solution || EXPLAINED🔥 | minimum-time-visiting-all-points | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n1. **minTimeToVisitAllPoints Function:**\n\n - This function calculates the minimum time required to visit all points given a vector of points.\n1. **Total Time Calculation:**\n\n - It initializes the `ans` variable to keep track of the total time.\n - It iterates through the points starting from the second point (index 1) to compare consecutive points.\n - For each pair of consecutive points, it calculates the absolute differences in x and y coordinates (`diffx` and `diffy`).\n - It adds the maximum of these differences (`max(diffx, diffy)`) to the total time `ans`.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n // Function to calculate the minimum time to visit all points\n int minTimeToVisitAllPoints(vector<vector<int>>& points) {\n int ans = 0; // Variable to store the total time taken\n int n = points.size(); // Get the number of points\n\n // Iterate through the points starting from the second point\n for (int i = 1; i < n; ++i) {\n // Calculate the absolute differences in x and y coordinates between consecutive points\n int diffx = abs(points[i][0] - points[i - 1][0]);\n int diffy = abs(points[i][1] - points[i - 1][1]);\n\n // Add the maximum difference between x and y coordinates to the total time\n ans += max(diffx, diffy);\n }\n return ans; // Return the total time taken to visit all points\n }\n};\n\n\n```\n```C []\n\n\n\nint minTimeToVisitAllPoints(int** points, int pointsSize, int* pointsColSize) {\n int ans = 0;\n int n = pointsSize;\n\n for (int i = 1; i < n; ++i) {\n int diffx = abs(points[i][0] - points[i - 1][0]);\n int diffy = abs(points[i][1] - points[i - 1][1]);\n\n ans += diffx > diffy ? diffx : diffy;\n }\n\n return ans;\n}\n\n\n\n```\n```Java []\nimport java.util.List;\n\npublic class Solution {\n public int minTimeToVisitAllPoints(int[][] points) {\n int ans = 0;\n int n = points.length;\n\n for (int i = 1; i < n; ++i) {\n int diffx = Math.abs(points[i][0] - points[i - 1][0]);\n int diffy = Math.abs(points[i][1] - points[i - 1][1]);\n ans += Math.max(diffx, diffy);\n }\n return ans;\n }\n\n \n}\n\n\n\n```\n```python3 []\n\nclass Solution:\n def minTimeToVisitAllPoints(self, points):\n ans = 0\n n = len(points)\n\n for i in range(1, n):\n diffx = abs(points[i][0] - points[i - 1][0])\n diffy = abs(points[i][1] - points[i - 1][1])\n ans += max(diffx, diffy)\n \n return ans\n\n```\n```javascript []\nvar minTimeToVisitAllPoints = function(points) {\n let ans = 0;\n const n = points.length;\n\n for (let i = 1; i < n; ++i) {\n const diffx = Math.abs(points[i][0] - points[i - 1][0]);\n const diffy = Math.abs(points[i][1] - points[i - 1][1]);\n\n ans += Math.max(diffx, diffy);\n }\n\n return ans;\n};\n\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 5 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
✅☑[C++/Java/Python/JavaScript] || Easy Solution || EXPLAINED🔥 | minimum-time-visiting-all-points | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n1. **minTimeToVisitAllPoints Function:**\n\n - This function calculates the minimum time required to visit all points given a vector of points.\n1. **Total Time Calculation:**\n\n - It initializes the `ans` variable to keep track of the total time.\n - It iterates through the points starting from the second point (index 1) to compare consecutive points.\n - For each pair of consecutive points, it calculates the absolute differences in x and y coordinates (`diffx` and `diffy`).\n - It adds the maximum of these differences (`max(diffx, diffy)`) to the total time `ans`.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n // Function to calculate the minimum time to visit all points\n int minTimeToVisitAllPoints(vector<vector<int>>& points) {\n int ans = 0; // Variable to store the total time taken\n int n = points.size(); // Get the number of points\n\n // Iterate through the points starting from the second point\n for (int i = 1; i < n; ++i) {\n // Calculate the absolute differences in x and y coordinates between consecutive points\n int diffx = abs(points[i][0] - points[i - 1][0]);\n int diffy = abs(points[i][1] - points[i - 1][1]);\n\n // Add the maximum difference between x and y coordinates to the total time\n ans += max(diffx, diffy);\n }\n return ans; // Return the total time taken to visit all points\n }\n};\n\n\n```\n```C []\n\n\n\nint minTimeToVisitAllPoints(int** points, int pointsSize, int* pointsColSize) {\n int ans = 0;\n int n = pointsSize;\n\n for (int i = 1; i < n; ++i) {\n int diffx = abs(points[i][0] - points[i - 1][0]);\n int diffy = abs(points[i][1] - points[i - 1][1]);\n\n ans += diffx > diffy ? diffx : diffy;\n }\n\n return ans;\n}\n\n\n\n```\n```Java []\nimport java.util.List;\n\npublic class Solution {\n public int minTimeToVisitAllPoints(int[][] points) {\n int ans = 0;\n int n = points.length;\n\n for (int i = 1; i < n; ++i) {\n int diffx = Math.abs(points[i][0] - points[i - 1][0]);\n int diffy = Math.abs(points[i][1] - points[i - 1][1]);\n ans += Math.max(diffx, diffy);\n }\n return ans;\n }\n\n \n}\n\n\n\n```\n```python3 []\n\nclass Solution:\n def minTimeToVisitAllPoints(self, points):\n ans = 0\n n = len(points)\n\n for i in range(1, n):\n diffx = abs(points[i][0] - points[i - 1][0])\n diffy = abs(points[i][1] - points[i - 1][1])\n ans += max(diffx, diffy)\n \n return ans\n\n```\n```javascript []\nvar minTimeToVisitAllPoints = function(points) {\n let ans = 0;\n const n = points.length;\n\n for (let i = 1; i < n; ++i) {\n const diffx = Math.abs(points[i][0] - points[i - 1][0]);\n const diffy = Math.abs(points[i][1] - points[i - 1][1]);\n\n ans += Math.max(diffx, diffy);\n }\n\n return ans;\n};\n\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 5 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
1️⃣Liner.py | minimum-time-visiting-all-points | 0 | 1 | \n\n# Code\n```py\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n return sum([max(abs(points[i-1][0]-points[i][0]),abs(points[i-1][1]-points[i][1])) for i in range(1,len(points))])\n```\n | 4 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
1️⃣Liner.py | minimum-time-visiting-all-points | 0 | 1 | \n\n# Code\n```py\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n return sum([max(abs(points[i-1][0]-points[i][0]),abs(points[i-1][1]-points[i][1])) for i in range(1,len(points))])\n```\n | 4 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
Beats 83% | Python 3 | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n time=0\n for i in range(len(points)-1):\n current_point = points[i]\n next_point = points[i+1]\n\n xd = abs(next_point[0] - current_point[0])\n yd = abs(next_point[1] - current_point[1])\n\n time += max(xd,yd)\n return time\n\n \n``` | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Beats 83% | Python 3 | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n time=0\n for i in range(len(points)-1):\n current_point = points[i]\n next_point = points[i+1]\n\n xd = abs(next_point[0] - current_point[0])\n yd = abs(next_point[1] - current_point[1])\n\n time += max(xd,yd)\n return time\n\n \n``` | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
Python | One Liner | O(n) / O(1) | minimum-time-visiting-all-points | 0 | 1 | # Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n return sum(max(abs(points[i][0] - points[i-1][0]), abs(points[i][1] - points[i-1][1])) for i in range(1, len(points)))\n\n\n``` | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Python | One Liner | O(n) / O(1) | minimum-time-visiting-all-points | 0 | 1 | # Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n return sum(max(abs(points[i][0] - points[i-1][0]), abs(points[i][1] - points[i-1][1])) for i in range(1, len(points)))\n\n\n``` | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
Easy to read solution. TC = On, SC = O1 | minimum-time-visiting-all-points | 1 | 1 | # Intuition\nWhen solving this problem, it\'s essential to make the most of diagonal movement. \n\n# Approach\nFor example, when moving from point [1,1] to [3,4], First calculate the differences in both `x` and `y` coordinates: `dx = 3 - 1 = 2` and `dy = 4 - 1 = 3`. You can move diagonally for the minimum of these two values, which is 2 times in this case. After these diagonal moves, you have one remaining vertical move to reach [3,4], because the difference in y-coordinate is still 1 after accounting for the diagonal moves. **The total time for each segment is the maximum of dx and dy**, as this combines diagonal movement with any remaining horizontal or vertical movement needed.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O1\n\n# Code\n\n<iframe src="https://leetcode.com/playground/SQmkav97/shared" frameBorder="0" width="100%" height="450"></iframe>\n | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Easy to read solution. TC = On, SC = O1 | minimum-time-visiting-all-points | 1 | 1 | # Intuition\nWhen solving this problem, it\'s essential to make the most of diagonal movement. \n\n# Approach\nFor example, when moving from point [1,1] to [3,4], First calculate the differences in both `x` and `y` coordinates: `dx = 3 - 1 = 2` and `dy = 4 - 1 = 3`. You can move diagonally for the minimum of these two values, which is 2 times in this case. After these diagonal moves, you have one remaining vertical move to reach [3,4], because the difference in y-coordinate is still 1 after accounting for the diagonal moves. **The total time for each segment is the maximum of dx and dy**, as this combines diagonal movement with any remaining horizontal or vertical movement needed.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O1\n\n# Code\n\n<iframe src="https://leetcode.com/playground/SQmkav97/shared" frameBorder="0" width="100%" height="450"></iframe>\n | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
【Video】Give me 5 minutes - How we think about a solution | minimum-time-visiting-all-points | 1 | 1 | # Intuition\nWe can move diagonally.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/3i7JVvaKX5M\n\n\u25A0 Timeline of the video\n\n`0:05` Think about distance of two points with a simple example\n`1:37` Demonstrate how it works\n`3:31` Make sure important points\n`5:09` Coding\n`6:26` Time Complexity and Space Complexity\n`6:36` Step by step algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,357\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nLet\'s think about a simple case.\n\n\n\nStart point is bottom left of `red` and goal point is top right of `blue`. we can move only 4 corners of each cell(top left, top right, bottom left and bottom right). In this case, how many seconds do we need?\n\nThe answer is `2` seconds.\n\n---\nIf we move `bottom left of red` \u2192 `top right of red` \u2192 `top right of blue`, we need 2 seconds.\n\nOther path need more seconds. For example, \n`bottom left of red` \u2192 `bottom right of red` \u2192 `bottom right of yellow` \u2192 `top right of yellow` \u2192 `top right of blue`\n\nWe need 4 seconds.\n\n---\n\nHow about this?\n\n\n\nAgain start point is bottom left of `red` and goal point is top right of `blue`. In this case, how many seconds do we need?\n\n---\n\nOne of paths for minimum seconds should be `bottom left of red` \u2192 `top right of red` \u2192 `top right of orange` \u2192 `top right of blue`\n\nOther path need more seconds. For example, \n`bottom left of red` \u2192 `bottom right of red` \u2192 `bottom right of yellow` \u2192 `top right of yellow` \u2192 `top right of orange` \u2192 `top right of blue`\n\nWe need 5 seconds.\n\n---\n\n- Why these happen?\n\nThat\'s because we can move diagonally, that means we can move vertically and horizontally at the same time. We can save seconds.\n\nIn other words, \n\n---\n\n\u2B50\uFE0F Points\n\nMoving the same distance as the greater difference between the horizontal coordinates (x-axis) or vertical coordinates (y-axis) of two points is sufficient. \n\n---\n\nIn the second example above, we move 3 points vertically and 2 points horizontally. So we need to move 3 times to reach the goal point(= top right of blue).\n\nLet\'s see the example in the description.\n\n```\nInput: points = [[1,1],[3,4],[-1,0]]\n```\nSince we need to take greater difference between 2 points, we start from index 1. We use absolute value.\n\n```\nabs(3 - 1) vs abs(4 - 1) (= horizontal distance vs vertical distance)\n= 2 vs 3\n= 3 seconds\n```\nNext 2 points\n```\nabs(-1 - 3) vs abs(0 - 4) (= horizontal distance vs vertical distance)\n= 4 vs 4\n= 4 seconds\n```\nTotal seconds should be\n```\nOutput: 7 (seconds)\n```\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm.\n\n---\n\n**Algorithm Overview:**\n\nThe algorithm calculates the minimum time required to visit all points on a 2D plane. It iterates through the given list of points and accumulates the maximum difference in horizontal or vertical coordinates between consecutive points.\n\n**Detailed Explanation:**\n\n1. **Initialize Result Variable:**\n ```python\n res = 0\n ```\n - `res` is initialized to 0. This variable will store the accumulated minimum time to visit all points.\n\n2. **Iterate through Points:**\n ```python\n for i in range(1, len(points)):\n ```\n - The algorithm uses a for loop to iterate through the points starting from index 1 (since there is no need to calculate the distance for the first point).\n\n3. **Calculate Horizontal and Vertical Differences:**\n ```python\n res += max(abs(points[i][0] - points[i - 1][0]), \n abs(points[i][1] - points[i - 1][1]))\n ```\n - For each pair of consecutive points, the algorithm calculates the absolute differences in horizontal and vertical coordinates.\n - `abs(points[i][0] - points[i - 1][0])` calculates the absolute horizontal difference.\n - `abs(points[i][1] - points[i - 1][1])` calculates the absolute vertical difference.\n\n4. **Accumulate Maximum Difference:**\n ```python\n res += max(...)\n ```\n - The algorithm adds the maximum of the horizontal and vertical differences to the `res` variable. This ensures that the accumulated time represents the maximum distance traveled in either the horizontal or vertical direction between consecutive points.\n\n5. **Return Result:**\n ```python\n return res\n ```\n - The final result, representing the minimum time to visit all points, is returned.\n\nOverall, the algorithm efficiently calculates the minimum time required to visit all points by considering the maximum difference in either the horizontal or vertical direction between consecutive points.\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\nn is the number of points in the input array. The loop iterates through the points array once, and each iteration involves constant time operations.\n\n- Space complexity: $$O(1)$$\n\n```python []\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n res = 0\n\n for i in range(1, len(points)):\n res += max(abs(points[i][0] - points[i - 1][0]),\n abs(points[i][1] - points[i - 1][1]))\n\n return res\n```\n```javascript []\n/**\n * @param {number[][]} points\n * @return {number}\n */\nvar minTimeToVisitAllPoints = function(points) {\n let res = 0;\n\n for (let i = 1; i < points.length; i++) {\n res += Math.max(\n Math.abs(points[i][0] - points[i - 1][0]),\n Math.abs(points[i][1] - points[i - 1][1])\n );\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int minTimeToVisitAllPoints(int[][] points) {\n int res = 0;\n\n for (int i = 1; i < points.length; i++) {\n res += Math.max(\n Math.abs(points[i][0] - points[i - 1][0]),\n Math.abs(points[i][1] - points[i - 1][1])\n );\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minTimeToVisitAllPoints(vector<vector<int>>& points) {\n int res = 0;\n\n for (int i = 1; i < points.size(); i++) {\n res += max(\n abs(points[i][0] - points[i - 1][0]),\n abs(points[i][1] - points[i - 1][1])\n );\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-words-that-can-be-formed-by-characters/solutions/4354470/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/6LrW0uIlqX8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve "Find Words That Can Be Formed by Characters"\n`3:48` What if we have extra character when specific character was already 0 in HashMap?\n`4:17` Coding\n`7:45` Time Complexity and Space Complexity\n`8:17` Step by step algorithm with my solution code\n | 17 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
【Video】Give me 5 minutes - How we think about a solution | minimum-time-visiting-all-points | 1 | 1 | # Intuition\nWe can move diagonally.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/3i7JVvaKX5M\n\n\u25A0 Timeline of the video\n\n`0:05` Think about distance of two points with a simple example\n`1:37` Demonstrate how it works\n`3:31` Make sure important points\n`5:09` Coding\n`6:26` Time Complexity and Space Complexity\n`6:36` Step by step algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,357\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nLet\'s think about a simple case.\n\n\n\nStart point is bottom left of `red` and goal point is top right of `blue`. we can move only 4 corners of each cell(top left, top right, bottom left and bottom right). In this case, how many seconds do we need?\n\nThe answer is `2` seconds.\n\n---\nIf we move `bottom left of red` \u2192 `top right of red` \u2192 `top right of blue`, we need 2 seconds.\n\nOther path need more seconds. For example, \n`bottom left of red` \u2192 `bottom right of red` \u2192 `bottom right of yellow` \u2192 `top right of yellow` \u2192 `top right of blue`\n\nWe need 4 seconds.\n\n---\n\nHow about this?\n\n\n\nAgain start point is bottom left of `red` and goal point is top right of `blue`. In this case, how many seconds do we need?\n\n---\n\nOne of paths for minimum seconds should be `bottom left of red` \u2192 `top right of red` \u2192 `top right of orange` \u2192 `top right of blue`\n\nOther path need more seconds. For example, \n`bottom left of red` \u2192 `bottom right of red` \u2192 `bottom right of yellow` \u2192 `top right of yellow` \u2192 `top right of orange` \u2192 `top right of blue`\n\nWe need 5 seconds.\n\n---\n\n- Why these happen?\n\nThat\'s because we can move diagonally, that means we can move vertically and horizontally at the same time. We can save seconds.\n\nIn other words, \n\n---\n\n\u2B50\uFE0F Points\n\nMoving the same distance as the greater difference between the horizontal coordinates (x-axis) or vertical coordinates (y-axis) of two points is sufficient. \n\n---\n\nIn the second example above, we move 3 points vertically and 2 points horizontally. So we need to move 3 times to reach the goal point(= top right of blue).\n\nLet\'s see the example in the description.\n\n```\nInput: points = [[1,1],[3,4],[-1,0]]\n```\nSince we need to take greater difference between 2 points, we start from index 1. We use absolute value.\n\n```\nabs(3 - 1) vs abs(4 - 1) (= horizontal distance vs vertical distance)\n= 2 vs 3\n= 3 seconds\n```\nNext 2 points\n```\nabs(-1 - 3) vs abs(0 - 4) (= horizontal distance vs vertical distance)\n= 4 vs 4\n= 4 seconds\n```\nTotal seconds should be\n```\nOutput: 7 (seconds)\n```\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm.\n\n---\n\n**Algorithm Overview:**\n\nThe algorithm calculates the minimum time required to visit all points on a 2D plane. It iterates through the given list of points and accumulates the maximum difference in horizontal or vertical coordinates between consecutive points.\n\n**Detailed Explanation:**\n\n1. **Initialize Result Variable:**\n ```python\n res = 0\n ```\n - `res` is initialized to 0. This variable will store the accumulated minimum time to visit all points.\n\n2. **Iterate through Points:**\n ```python\n for i in range(1, len(points)):\n ```\n - The algorithm uses a for loop to iterate through the points starting from index 1 (since there is no need to calculate the distance for the first point).\n\n3. **Calculate Horizontal and Vertical Differences:**\n ```python\n res += max(abs(points[i][0] - points[i - 1][0]), \n abs(points[i][1] - points[i - 1][1]))\n ```\n - For each pair of consecutive points, the algorithm calculates the absolute differences in horizontal and vertical coordinates.\n - `abs(points[i][0] - points[i - 1][0])` calculates the absolute horizontal difference.\n - `abs(points[i][1] - points[i - 1][1])` calculates the absolute vertical difference.\n\n4. **Accumulate Maximum Difference:**\n ```python\n res += max(...)\n ```\n - The algorithm adds the maximum of the horizontal and vertical differences to the `res` variable. This ensures that the accumulated time represents the maximum distance traveled in either the horizontal or vertical direction between consecutive points.\n\n5. **Return Result:**\n ```python\n return res\n ```\n - The final result, representing the minimum time to visit all points, is returned.\n\nOverall, the algorithm efficiently calculates the minimum time required to visit all points by considering the maximum difference in either the horizontal or vertical direction between consecutive points.\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\nn is the number of points in the input array. The loop iterates through the points array once, and each iteration involves constant time operations.\n\n- Space complexity: $$O(1)$$\n\n```python []\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n res = 0\n\n for i in range(1, len(points)):\n res += max(abs(points[i][0] - points[i - 1][0]),\n abs(points[i][1] - points[i - 1][1]))\n\n return res\n```\n```javascript []\n/**\n * @param {number[][]} points\n * @return {number}\n */\nvar minTimeToVisitAllPoints = function(points) {\n let res = 0;\n\n for (let i = 1; i < points.length; i++) {\n res += Math.max(\n Math.abs(points[i][0] - points[i - 1][0]),\n Math.abs(points[i][1] - points[i - 1][1])\n );\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int minTimeToVisitAllPoints(int[][] points) {\n int res = 0;\n\n for (int i = 1; i < points.length; i++) {\n res += Math.max(\n Math.abs(points[i][0] - points[i - 1][0]),\n Math.abs(points[i][1] - points[i - 1][1])\n );\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minTimeToVisitAllPoints(vector<vector<int>>& points) {\n int res = 0;\n\n for (int i = 1; i < points.size(); i++) {\n res += max(\n abs(points[i][0] - points[i - 1][0]),\n abs(points[i][1] - points[i - 1][1])\n );\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-words-that-can-be-formed-by-characters/solutions/4354470/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/6LrW0uIlqX8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve "Find Words That Can Be Formed by Characters"\n`3:48` What if we have extra character when specific character was already 0 in HashMap?\n`4:17` Coding\n`7:45` Time Complexity and Space Complexity\n`8:17` Step by step algorithm with my solution code\n | 17 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
Easy python solution for beginners | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) ->int:\n s=0\n for i in range(len(points)-1):\n a=points[i]\n b=points[i+1]\n max1=max(a[0],b[0])\n min1=min(a[0],b[0])\n max2=max(a[1],b[1])\n min2=min(a[1],b[1])\n c=max((max1-min1),(max2-min2)) \n s+=c \n return (s)\n\n \n``` | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Easy python solution for beginners | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) ->int:\n s=0\n for i in range(len(points)-1):\n a=points[i]\n b=points[i+1]\n max1=max(a[0],b[0])\n min1=min(a[0],b[0])\n max2=max(a[1],b[1])\n min2=min(a[1],b[1])\n c=max((max1-min1),(max2-min2)) \n s+=c \n return (s)\n\n \n``` | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
🔥🔥🔥BEATS 100% CODERS🔥🔥🔥by PRODONiK✅✅✅ | minimum-time-visiting-all-points | 1 | 1 | # Intuition\nThe problem involves calculating the minimum time to visit all points in a 2D array (`points`). The initial intuition might involve considering the distances between consecutive points and determining the time required to travel from one point to another.\n\n# Approach\nThe code uses a straightforward approach by iterating through the array of points. For each pair of consecutive points, it calculates the horizontal and vertical distances (absolute differences in x and y coordinates) and takes the maximum of the two. This maximum represents the time required to travel from one point to the next, considering both horizontal and vertical movements. The result is accumulated, providing the total minimum time to visit all points.\n\n# Complexity\n- Time complexity: O(n)\n The time complexity is linear, where `n` is the number of points. The algorithm iterates through the array once, performing constant-time operations for each pair of consecutive points.\n\n- Space complexity: O(1)\n The space complexity is constant, as the algorithm uses only a constant amount of additional space for variables (`result` and loop counters).\n\n# Code\n```java []\nclass Solution {\n public int minTimeToVisitAllPoints(int[][] points) {\n int result = 0;\n for (int i = 0; i < points.length - 1; i++) {\n result += Math.max(Math.abs(points[i][0] - points[i + 1][0]), Math.abs(points[i][1] - points[i + 1][1]));\n }\n return result;\n }\n}\n```\n```C# []\npublic class Solution {\n public int MinTimeToVisitAllPoints(int[][] points) {\n int result = 0;\n for (int i = 0; i < points.Length - 1; i++) {\n result += Math.Max(Math.Abs(points[i][0] - points[i + 1][0]), Math.Abs(points[i][1] - points[i + 1][1]));\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minTimeToVisitAllPoints(std::vector<std::vector<int>>& points) {\n int result = 0;\n for (int i = 0; i < points.size() - 1; i++) {\n result += std::max(std::abs(points[i][0] - points[i + 1][0]), std::abs(points[i][1] - points[i + 1][1]));\n }\n return result;\n }\n};\n```\n```Python []\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n result = 0\n for i in range(len(points) - 1):\n result += max(abs(points[i][0] - points[i + 1][0]), abs(points[i][1] - points[i + 1][1]))\n return result\n```\n```Ruby []\nclass Solution\n def min_time_to_visit_all_points(points)\n result = 0\n (0...points.length - 1).each do |i|\n result += [points[i][0] - points[i + 1][0]].abs, [points[i][1] - points[i + 1][1]].abs].max\n end\n result\n end\nend\n | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
🔥🔥🔥BEATS 100% CODERS🔥🔥🔥by PRODONiK✅✅✅ | minimum-time-visiting-all-points | 1 | 1 | # Intuition\nThe problem involves calculating the minimum time to visit all points in a 2D array (`points`). The initial intuition might involve considering the distances between consecutive points and determining the time required to travel from one point to another.\n\n# Approach\nThe code uses a straightforward approach by iterating through the array of points. For each pair of consecutive points, it calculates the horizontal and vertical distances (absolute differences in x and y coordinates) and takes the maximum of the two. This maximum represents the time required to travel from one point to the next, considering both horizontal and vertical movements. The result is accumulated, providing the total minimum time to visit all points.\n\n# Complexity\n- Time complexity: O(n)\n The time complexity is linear, where `n` is the number of points. The algorithm iterates through the array once, performing constant-time operations for each pair of consecutive points.\n\n- Space complexity: O(1)\n The space complexity is constant, as the algorithm uses only a constant amount of additional space for variables (`result` and loop counters).\n\n# Code\n```java []\nclass Solution {\n public int minTimeToVisitAllPoints(int[][] points) {\n int result = 0;\n for (int i = 0; i < points.length - 1; i++) {\n result += Math.max(Math.abs(points[i][0] - points[i + 1][0]), Math.abs(points[i][1] - points[i + 1][1]));\n }\n return result;\n }\n}\n```\n```C# []\npublic class Solution {\n public int MinTimeToVisitAllPoints(int[][] points) {\n int result = 0;\n for (int i = 0; i < points.Length - 1; i++) {\n result += Math.Max(Math.Abs(points[i][0] - points[i + 1][0]), Math.Abs(points[i][1] - points[i + 1][1]));\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minTimeToVisitAllPoints(std::vector<std::vector<int>>& points) {\n int result = 0;\n for (int i = 0; i < points.size() - 1; i++) {\n result += std::max(std::abs(points[i][0] - points[i + 1][0]), std::abs(points[i][1] - points[i + 1][1]));\n }\n return result;\n }\n};\n```\n```Python []\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n result = 0\n for i in range(len(points) - 1):\n result += max(abs(points[i][0] - points[i + 1][0]), abs(points[i][1] - points[i + 1][1]))\n return result\n```\n```Ruby []\nclass Solution\n def min_time_to_visit_all_points(points)\n result = 0\n (0...points.length - 1).each do |i|\n result += [points[i][0] - points[i + 1][0]].abs, [points[i][1] - points[i + 1][1]].abs].max\n end\n result\n end\nend\n | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
Python, multiple liners but better readability and explain | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n\nConsidering two points with the distances x_dist and y_dist between them, the travel time is calculated as the sum of the minimum of x_dist and y_dist, along with the absolute difference between x_dist and y_dist.\n\n# Code\n```python\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n def travel_time(src: List[int], dest: List[int]) -> int:\n distance_x = abs(src[0] - dest[0])\n distance_y = abs(src[1] - dest[1])\n return min(distance_x, distance_y) + abs(distance_x - distance_y)\n \n res = 0\n for i in range(len(points)-1):\n res += travel_time(points[i], points[i+1])\n return res\n``` | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Python, multiple liners but better readability and explain | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n\nConsidering two points with the distances x_dist and y_dist between them, the travel time is calculated as the sum of the minimum of x_dist and y_dist, along with the absolute difference between x_dist and y_dist.\n\n# Code\n```python\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n def travel_time(src: List[int], dest: List[int]) -> int:\n distance_x = abs(src[0] - dest[0])\n distance_y = abs(src[1] - dest[1])\n return min(distance_x, distance_y) + abs(distance_x - distance_y)\n \n res = 0\n for i in range(len(points)-1):\n res += travel_time(points[i], points[i+1])\n return res\n``` | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
Best and Simple Solution | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBest and Fast code using simple Python and basic Knowledge\n\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize Variables:\n\nlength: This variable is used to keep track of the total time (or distance) it takes to visit all the points.\n- Loop Through Points:\n\nThe code uses a for loop to iterate through each pair of consecutive points in the given list (points).\n- Calculate Maximum Distance:\n\n. For each pair of points, the code calculates the maximum distance to travel between them. It does this by finding the maximum of the absolute differences in their x-coordinates and y-coordinates.\n. The abs function is used to ensure that the differences are positive, as we\'re interested in distances.\n- Update Total Time:\n\nThe maximum distance calculated for each pair is then added to the total time (length).\n- Return Total Time:\n\nOnce the loop has gone through all pairs of points, the function returns the total time (length), which represents the minimum time needed to visit all the points in the given order.\n\n\n\nIn simpler terms, the code calculates the total time it takes to move from one point to the next for each pair of consecutive points in the given list. The maximum distance, considering both x and y coordinates, is used to determine the time it takes to travel between each pair. The total time is then returned as the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n length = 0\n\n for i in range(len(points)-1):\n val = max(abs(points[i+1][0]-points[i][0]), abs(points[i+1][1]-points[i][1]))\n length += val\n\n return(length)\n \n \n```\n# Explanatino with example \n\n\n**points = [[1,1],[3,4],[-1,0]]\nlength=0**\n\nDistance between (3,4) and (1,1)-->\n\nval = max (abs(3-1),abs(4-1))\n max (2,3)\n 3//\n\nlength=length+val\n 0+3\n 3//\n\nDistance between (3,4) and (-1,0)-->\n\nval = max (abs(-1-3),abs(0-4))\n max (4,4)\n 4//\n\nlength=length+val\n 3+4\n 7//\n\n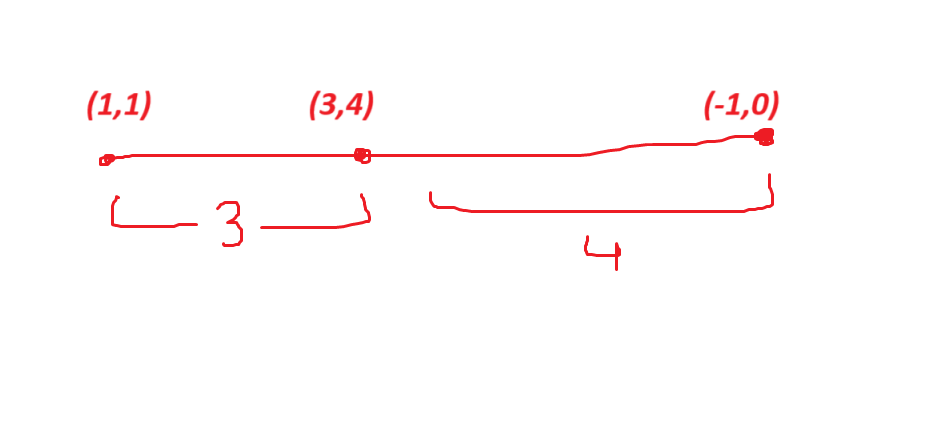\n\n\n\n | 1 | On a 2D plane, there are `n` points with integer coordinates `points[i] = [xi, yi]`. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
You can move according to these rules:
* In `1` second, you can either:
* move vertically by one unit,
* move horizontally by one unit, or
* move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
* You have to visit the points in the same order as they appear in the array.
* You are allowed to pass through points that appear later in the order, but these do not count as visits.
**Example 1:**
**Input:** points = \[\[1,1\],\[3,4\],\[-1,0\]\]
**Output:** 7
**Explanation:** One optimal path is **\[1,1\]** -> \[2,2\] -> \[3,3\] -> **\[3,4\]** \-> \[2,3\] -> \[1,2\] -> \[0,1\] -> **\[-1,0\]**
Time from \[1,1\] to \[3,4\] = 3 seconds
Time from \[3,4\] to \[-1,0\] = 4 seconds
Total time = 7 seconds
**Example 2:**
**Input:** points = \[\[3,2\],\[-2,2\]\]
**Output:** 5
**Constraints:**
* `points.length == n`
* `1 <= n <= 100`
* `points[i].length == 2`
* `-1000 <= points[i][0], points[i][1] <= 1000` | null |
Best and Simple Solution | minimum-time-visiting-all-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBest and Fast code using simple Python and basic Knowledge\n\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize Variables:\n\nlength: This variable is used to keep track of the total time (or distance) it takes to visit all the points.\n- Loop Through Points:\n\nThe code uses a for loop to iterate through each pair of consecutive points in the given list (points).\n- Calculate Maximum Distance:\n\n. For each pair of points, the code calculates the maximum distance to travel between them. It does this by finding the maximum of the absolute differences in their x-coordinates and y-coordinates.\n. The abs function is used to ensure that the differences are positive, as we\'re interested in distances.\n- Update Total Time:\n\nThe maximum distance calculated for each pair is then added to the total time (length).\n- Return Total Time:\n\nOnce the loop has gone through all pairs of points, the function returns the total time (length), which represents the minimum time needed to visit all the points in the given order.\n\n\n\nIn simpler terms, the code calculates the total time it takes to move from one point to the next for each pair of consecutive points in the given list. The maximum distance, considering both x and y coordinates, is used to determine the time it takes to travel between each pair. The total time is then returned as the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:\n length = 0\n\n for i in range(len(points)-1):\n val = max(abs(points[i+1][0]-points[i][0]), abs(points[i+1][1]-points[i][1]))\n length += val\n\n return(length)\n \n \n```\n# Explanatino with example \n\n\n**points = [[1,1],[3,4],[-1,0]]\nlength=0**\n\nDistance between (3,4) and (1,1)-->\n\nval = max (abs(3-1),abs(4-1))\n max (2,3)\n 3//\n\nlength=length+val\n 0+3\n 3//\n\nDistance between (3,4) and (-1,0)-->\n\nval = max (abs(-1-3),abs(0-4))\n max (4,4)\n 4//\n\nlength=length+val\n 3+4\n 7//\n\n\n\n\n\n | 1 | There are `n` soldiers standing in a line. Each soldier is assigned a **unique** `rating` value.
You have to form a team of 3 soldiers amongst them under the following rules:
* Choose 3 soldiers with index (`i`, `j`, `k`) with rating (`rating[i]`, `rating[j]`, `rating[k]`).
* A team is valid if: (`rating[i] < rating[j] < rating[k]`) or (`rating[i] > rating[j] > rating[k]`) where (`0 <= i < j < k < n`).
Return the number of teams you can form given the conditions. (soldiers can be part of multiple teams).
**Example 1:**
**Input:** rating = \[2,5,3,4,1\]
**Output:** 3
**Explanation:** We can form three teams given the conditions. (2,3,4), (5,4,1), (5,3,1).
**Example 2:**
**Input:** rating = \[2,1,3\]
**Output:** 0
**Explanation:** We can't form any team given the conditions.
**Example 3:**
**Input:** rating = \[1,2,3,4\]
**Output:** 4
**Constraints:**
* `n == rating.length`
* `3 <= n <= 1000`
* `1 <= rating[i] <= 105`
* All the integers in `rating` are **unique**.
In one second, you can either: - Move vertically by one unit, - Move horizontally by one unit, or - Move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in one second). You have to visit the points in the same order as they appear in the array. You are allowed to pass through points, but they do not count as visited unless you stop on them. | To walk from point A to point B there will be an optimal strategy to walk ? Advance in diagonal as possible then after that go in straight line. Repeat the process until visiting all the points. |
[Python 3] Check rows and cols sum || beats 98% || 401ms 🥷🏼 | count-servers-that-communicate | 0 | 1 | ```python3 []\nclass Solution:\n def countServers(self, grid: List[List[int]]) -> int:\n rows = list(map(sum, grid))\n cols = list(map(sum, zip(*grid)))\n \n res = 0\n for i, j in product(range(len(grid)), range(len(grid[0]))):\n if grid[i][j] == 1 and (rows[i] > 1 or cols[j] > 1):\n res += 1\n\n return res\n```\n\n | 4 | You are given a map of a server center, represented as a `m * n` integer matrix `grid`, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.
Return the number of servers that communicate with any other server.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 0
**Explanation:** No servers can communicate with others.
**Example 2:**
**Input:** grid = \[\[1,0\],\[1,1\]\]
**Output:** 3
**Explanation:** All three servers can communicate with at least one other server.
**Example 3:**
**Input:** grid = \[\[1,1,0,0\],\[0,0,1,0\],\[0,0,1,0\],\[0,0,0,1\]\]
**Output:** 4
**Explanation:** The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 250`
* `1 <= n <= 250`
* `grid[i][j] == 0 or 1` | Convert the linked list into an array. While you can find a non-empty subarray with sum = 0, erase it. Convert the array into a linked list. |
[Python 3] Check rows and cols sum || beats 98% || 401ms 🥷🏼 | count-servers-that-communicate | 0 | 1 | ```python3 []\nclass Solution:\n def countServers(self, grid: List[List[int]]) -> int:\n rows = list(map(sum, grid))\n cols = list(map(sum, zip(*grid)))\n \n res = 0\n for i, j in product(range(len(grid)), range(len(grid[0]))):\n if grid[i][j] == 1 and (rows[i] > 1 or cols[j] > 1):\n res += 1\n\n return res\n```\n\n | 4 | An underground railway system is keeping track of customer travel times between different stations. They are using this data to calculate the average time it takes to travel from one station to another.
Implement the `UndergroundSystem` class:
* `void checkIn(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks in at the station `stationName` at time `t`.
* A customer can only be checked into one place at a time.
* `void checkOut(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks out from the station `stationName` at time `t`.
* `double getAverageTime(string startStation, string endStation)`
* Returns the average time it takes to travel from `startStation` to `endStation`.
* The average time is computed from all the previous traveling times from `startStation` to `endStation` that happened **directly**, meaning a check in at `startStation` followed by a check out from `endStation`.
* The time it takes to travel from `startStation` to `endStation` **may be different** from the time it takes to travel from `endStation` to `startStation`.
* There will be at least one customer that has traveled from `startStation` to `endStation` before `getAverageTime` is called.
You may assume all calls to the `checkIn` and `checkOut` methods are consistent. If a customer checks in at time `t1` then checks out at time `t2`, then `t1 < t2`. All events happen in chronological order.
**Example 1:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkIn ", "checkIn ", "checkOut ", "checkOut ", "checkOut ", "getAverageTime ", "getAverageTime ", "checkIn ", "getAverageTime ", "checkOut ", "getAverageTime "\]
\[\[\],\[45, "Leyton ",3\],\[32, "Paradise ",8\],\[27, "Leyton ",10\],\[45, "Waterloo ",15\],\[27, "Waterloo ",20\],\[32, "Cambridge ",22\],\[ "Paradise ", "Cambridge "\],\[ "Leyton ", "Waterloo "\],\[10, "Leyton ",24\],\[ "Leyton ", "Waterloo "\],\[10, "Waterloo ",38\],\[ "Leyton ", "Waterloo "\]\]
**Output**
\[null,null,null,null,null,null,null,14.00000,11.00000,null,11.00000,null,12.00000\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(45, "Leyton ", 3);
undergroundSystem.checkIn(32, "Paradise ", 8);
undergroundSystem.checkIn(27, "Leyton ", 10);
undergroundSystem.checkOut(45, "Waterloo ", 15); // Customer 45 "Leyton " -> "Waterloo " in 15-3 = 12
undergroundSystem.checkOut(27, "Waterloo ", 20); // Customer 27 "Leyton " -> "Waterloo " in 20-10 = 10
undergroundSystem.checkOut(32, "Cambridge ", 22); // Customer 32 "Paradise " -> "Cambridge " in 22-8 = 14
undergroundSystem.getAverageTime( "Paradise ", "Cambridge "); // return 14.00000. One trip "Paradise " -> "Cambridge ", (14) / 1 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000. Two trips "Leyton " -> "Waterloo ", (10 + 12) / 2 = 11
undergroundSystem.checkIn(10, "Leyton ", 24);
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000
undergroundSystem.checkOut(10, "Waterloo ", 38); // Customer 10 "Leyton " -> "Waterloo " in 38-24 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 12.00000. Three trips "Leyton " -> "Waterloo ", (10 + 12 + 14) / 3 = 12
**Example 2:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime "\]
\[\[\],\[10, "Leyton ",3\],\[10, "Paradise ",8\],\[ "Leyton ", "Paradise "\],\[5, "Leyton ",10\],\[5, "Paradise ",16\],\[ "Leyton ", "Paradise "\],\[2, "Leyton ",21\],\[2, "Paradise ",30\],\[ "Leyton ", "Paradise "\]\]
**Output**
\[null,null,null,5.00000,null,null,5.50000,null,null,6.66667\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(10, "Leyton ", 3);
undergroundSystem.checkOut(10, "Paradise ", 8); // Customer 10 "Leyton " -> "Paradise " in 8-3 = 5
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.00000, (5) / 1 = 5
undergroundSystem.checkIn(5, "Leyton ", 10);
undergroundSystem.checkOut(5, "Paradise ", 16); // Customer 5 "Leyton " -> "Paradise " in 16-10 = 6
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.50000, (5 + 6) / 2 = 5.5
undergroundSystem.checkIn(2, "Leyton ", 21);
undergroundSystem.checkOut(2, "Paradise ", 30); // Customer 2 "Leyton " -> "Paradise " in 30-21 = 9
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 6.66667, (5 + 6 + 9) / 3 = 6.66667
**Constraints:**
* `1 <= id, t <= 106`
* `1 <= stationName.length, startStation.length, endStation.length <= 10`
* All strings consist of uppercase and lowercase English letters and digits.
* There will be at most `2 * 104` calls **in total** to `checkIn`, `checkOut`, and `getAverageTime`.
* Answers within `10-5` of the actual value will be accepted. | Store number of computer in each row and column. Count all servers that are not isolated. |
Python, simple, fast with full explanation | count-servers-that-communicate | 0 | 1 | ```\nclass Solution:\n def countServers(self, grid: List[List[int]]) -> int:\n rows = len(grid)\n cols = len(grid[0])\n \n # Check the input: size of the grid. If it is 0 then exit\n if not (cols and rows):\n return 0\n\n connected = 0 # store number of connected computers \n points=[] # store coordinates of all the computers \n comps_per_row = [0] * rows # store number of computers in given row\n comps_per_col = [0] * cols # store number of computers in given column\n \n for row_i in range(rows):\n for col_i in range(cols):\n if grid[row_i][col_i]: # checking if given cell is not 0\n points.append((row_i,col_i)) # add coordinated to the set\n comps_per_row[row_i]+=1 # increase nimber of computers in a given row\n comps_per_col[col_i]+=1 # increase nimber of computers in a given column \n \n # iterate through all computers\n for row_i,col_i in points:\n # is there more than 1 computer in given row or column\n if comps_per_row[row_i]>1 or comps_per_col[col_i]>1 :\n # if yes, then computer is connected, count him \n connected += 1 \n \n return connected\n```\nRuntime: **484 ms**, faster than **98.61%** of Python3 online submissions for Count Servers that Communicate.\nMemory Usage: **14.3 MB**, less than **100.00%** of Python3 online submissions for Count Servers that Communicate. | 44 | You are given a map of a server center, represented as a `m * n` integer matrix `grid`, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.
Return the number of servers that communicate with any other server.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 0
**Explanation:** No servers can communicate with others.
**Example 2:**
**Input:** grid = \[\[1,0\],\[1,1\]\]
**Output:** 3
**Explanation:** All three servers can communicate with at least one other server.
**Example 3:**
**Input:** grid = \[\[1,1,0,0\],\[0,0,1,0\],\[0,0,1,0\],\[0,0,0,1\]\]
**Output:** 4
**Explanation:** The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 250`
* `1 <= n <= 250`
* `grid[i][j] == 0 or 1` | Convert the linked list into an array. While you can find a non-empty subarray with sum = 0, erase it. Convert the array into a linked list. |
Python, simple, fast with full explanation | count-servers-that-communicate | 0 | 1 | ```\nclass Solution:\n def countServers(self, grid: List[List[int]]) -> int:\n rows = len(grid)\n cols = len(grid[0])\n \n # Check the input: size of the grid. If it is 0 then exit\n if not (cols and rows):\n return 0\n\n connected = 0 # store number of connected computers \n points=[] # store coordinates of all the computers \n comps_per_row = [0] * rows # store number of computers in given row\n comps_per_col = [0] * cols # store number of computers in given column\n \n for row_i in range(rows):\n for col_i in range(cols):\n if grid[row_i][col_i]: # checking if given cell is not 0\n points.append((row_i,col_i)) # add coordinated to the set\n comps_per_row[row_i]+=1 # increase nimber of computers in a given row\n comps_per_col[col_i]+=1 # increase nimber of computers in a given column \n \n # iterate through all computers\n for row_i,col_i in points:\n # is there more than 1 computer in given row or column\n if comps_per_row[row_i]>1 or comps_per_col[col_i]>1 :\n # if yes, then computer is connected, count him \n connected += 1 \n \n return connected\n```\nRuntime: **484 ms**, faster than **98.61%** of Python3 online submissions for Count Servers that Communicate.\nMemory Usage: **14.3 MB**, less than **100.00%** of Python3 online submissions for Count Servers that Communicate. | 44 | An underground railway system is keeping track of customer travel times between different stations. They are using this data to calculate the average time it takes to travel from one station to another.
Implement the `UndergroundSystem` class:
* `void checkIn(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks in at the station `stationName` at time `t`.
* A customer can only be checked into one place at a time.
* `void checkOut(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks out from the station `stationName` at time `t`.
* `double getAverageTime(string startStation, string endStation)`
* Returns the average time it takes to travel from `startStation` to `endStation`.
* The average time is computed from all the previous traveling times from `startStation` to `endStation` that happened **directly**, meaning a check in at `startStation` followed by a check out from `endStation`.
* The time it takes to travel from `startStation` to `endStation` **may be different** from the time it takes to travel from `endStation` to `startStation`.
* There will be at least one customer that has traveled from `startStation` to `endStation` before `getAverageTime` is called.
You may assume all calls to the `checkIn` and `checkOut` methods are consistent. If a customer checks in at time `t1` then checks out at time `t2`, then `t1 < t2`. All events happen in chronological order.
**Example 1:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkIn ", "checkIn ", "checkOut ", "checkOut ", "checkOut ", "getAverageTime ", "getAverageTime ", "checkIn ", "getAverageTime ", "checkOut ", "getAverageTime "\]
\[\[\],\[45, "Leyton ",3\],\[32, "Paradise ",8\],\[27, "Leyton ",10\],\[45, "Waterloo ",15\],\[27, "Waterloo ",20\],\[32, "Cambridge ",22\],\[ "Paradise ", "Cambridge "\],\[ "Leyton ", "Waterloo "\],\[10, "Leyton ",24\],\[ "Leyton ", "Waterloo "\],\[10, "Waterloo ",38\],\[ "Leyton ", "Waterloo "\]\]
**Output**
\[null,null,null,null,null,null,null,14.00000,11.00000,null,11.00000,null,12.00000\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(45, "Leyton ", 3);
undergroundSystem.checkIn(32, "Paradise ", 8);
undergroundSystem.checkIn(27, "Leyton ", 10);
undergroundSystem.checkOut(45, "Waterloo ", 15); // Customer 45 "Leyton " -> "Waterloo " in 15-3 = 12
undergroundSystem.checkOut(27, "Waterloo ", 20); // Customer 27 "Leyton " -> "Waterloo " in 20-10 = 10
undergroundSystem.checkOut(32, "Cambridge ", 22); // Customer 32 "Paradise " -> "Cambridge " in 22-8 = 14
undergroundSystem.getAverageTime( "Paradise ", "Cambridge "); // return 14.00000. One trip "Paradise " -> "Cambridge ", (14) / 1 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000. Two trips "Leyton " -> "Waterloo ", (10 + 12) / 2 = 11
undergroundSystem.checkIn(10, "Leyton ", 24);
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000
undergroundSystem.checkOut(10, "Waterloo ", 38); // Customer 10 "Leyton " -> "Waterloo " in 38-24 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 12.00000. Three trips "Leyton " -> "Waterloo ", (10 + 12 + 14) / 3 = 12
**Example 2:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime "\]
\[\[\],\[10, "Leyton ",3\],\[10, "Paradise ",8\],\[ "Leyton ", "Paradise "\],\[5, "Leyton ",10\],\[5, "Paradise ",16\],\[ "Leyton ", "Paradise "\],\[2, "Leyton ",21\],\[2, "Paradise ",30\],\[ "Leyton ", "Paradise "\]\]
**Output**
\[null,null,null,5.00000,null,null,5.50000,null,null,6.66667\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(10, "Leyton ", 3);
undergroundSystem.checkOut(10, "Paradise ", 8); // Customer 10 "Leyton " -> "Paradise " in 8-3 = 5
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.00000, (5) / 1 = 5
undergroundSystem.checkIn(5, "Leyton ", 10);
undergroundSystem.checkOut(5, "Paradise ", 16); // Customer 5 "Leyton " -> "Paradise " in 16-10 = 6
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.50000, (5 + 6) / 2 = 5.5
undergroundSystem.checkIn(2, "Leyton ", 21);
undergroundSystem.checkOut(2, "Paradise ", 30); // Customer 2 "Leyton " -> "Paradise " in 30-21 = 9
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 6.66667, (5 + 6 + 9) / 3 = 6.66667
**Constraints:**
* `1 <= id, t <= 106`
* `1 <= stationName.length, startStation.length, endStation.length <= 10`
* All strings consist of uppercase and lowercase English letters and digits.
* There will be at most `2 * 104` calls **in total** to `checkIn`, `checkOut`, and `getAverageTime`.
* Answers within `10-5` of the actual value will be accepted. | Store number of computer in each row and column. Count all servers that are not isolated. |
85% TC and 78% SC easy python solution | count-servers-that-communicate | 0 | 1 | ```\ndef countServers(self, grid: List[List[int]]) -> int:\n\tm, n = len(grid), len(grid[0])\n\trows = [0] * m\n\tcols = [0] * n\n\tfor i in range(m):\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j]):\n\t\t\t\trows[i] += 1\n\t\t\t\tcols[j] += 1\n\tans = 0\n\tfor i in range(m):\n\t\tif(rows[i] > 1):\n\t\t\tans += rows[i]\n\t\t\tcontinue\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j] and cols[j] > 1):\n\t\t\t\tans += 1\n\treturn ans\n``` | 1 | You are given a map of a server center, represented as a `m * n` integer matrix `grid`, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.
Return the number of servers that communicate with any other server.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 0
**Explanation:** No servers can communicate with others.
**Example 2:**
**Input:** grid = \[\[1,0\],\[1,1\]\]
**Output:** 3
**Explanation:** All three servers can communicate with at least one other server.
**Example 3:**
**Input:** grid = \[\[1,1,0,0\],\[0,0,1,0\],\[0,0,1,0\],\[0,0,0,1\]\]
**Output:** 4
**Explanation:** The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 250`
* `1 <= n <= 250`
* `grid[i][j] == 0 or 1` | Convert the linked list into an array. While you can find a non-empty subarray with sum = 0, erase it. Convert the array into a linked list. |
85% TC and 78% SC easy python solution | count-servers-that-communicate | 0 | 1 | ```\ndef countServers(self, grid: List[List[int]]) -> int:\n\tm, n = len(grid), len(grid[0])\n\trows = [0] * m\n\tcols = [0] * n\n\tfor i in range(m):\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j]):\n\t\t\t\trows[i] += 1\n\t\t\t\tcols[j] += 1\n\tans = 0\n\tfor i in range(m):\n\t\tif(rows[i] > 1):\n\t\t\tans += rows[i]\n\t\t\tcontinue\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j] and cols[j] > 1):\n\t\t\t\tans += 1\n\treturn ans\n``` | 1 | An underground railway system is keeping track of customer travel times between different stations. They are using this data to calculate the average time it takes to travel from one station to another.
Implement the `UndergroundSystem` class:
* `void checkIn(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks in at the station `stationName` at time `t`.
* A customer can only be checked into one place at a time.
* `void checkOut(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks out from the station `stationName` at time `t`.
* `double getAverageTime(string startStation, string endStation)`
* Returns the average time it takes to travel from `startStation` to `endStation`.
* The average time is computed from all the previous traveling times from `startStation` to `endStation` that happened **directly**, meaning a check in at `startStation` followed by a check out from `endStation`.
* The time it takes to travel from `startStation` to `endStation` **may be different** from the time it takes to travel from `endStation` to `startStation`.
* There will be at least one customer that has traveled from `startStation` to `endStation` before `getAverageTime` is called.
You may assume all calls to the `checkIn` and `checkOut` methods are consistent. If a customer checks in at time `t1` then checks out at time `t2`, then `t1 < t2`. All events happen in chronological order.
**Example 1:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkIn ", "checkIn ", "checkOut ", "checkOut ", "checkOut ", "getAverageTime ", "getAverageTime ", "checkIn ", "getAverageTime ", "checkOut ", "getAverageTime "\]
\[\[\],\[45, "Leyton ",3\],\[32, "Paradise ",8\],\[27, "Leyton ",10\],\[45, "Waterloo ",15\],\[27, "Waterloo ",20\],\[32, "Cambridge ",22\],\[ "Paradise ", "Cambridge "\],\[ "Leyton ", "Waterloo "\],\[10, "Leyton ",24\],\[ "Leyton ", "Waterloo "\],\[10, "Waterloo ",38\],\[ "Leyton ", "Waterloo "\]\]
**Output**
\[null,null,null,null,null,null,null,14.00000,11.00000,null,11.00000,null,12.00000\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(45, "Leyton ", 3);
undergroundSystem.checkIn(32, "Paradise ", 8);
undergroundSystem.checkIn(27, "Leyton ", 10);
undergroundSystem.checkOut(45, "Waterloo ", 15); // Customer 45 "Leyton " -> "Waterloo " in 15-3 = 12
undergroundSystem.checkOut(27, "Waterloo ", 20); // Customer 27 "Leyton " -> "Waterloo " in 20-10 = 10
undergroundSystem.checkOut(32, "Cambridge ", 22); // Customer 32 "Paradise " -> "Cambridge " in 22-8 = 14
undergroundSystem.getAverageTime( "Paradise ", "Cambridge "); // return 14.00000. One trip "Paradise " -> "Cambridge ", (14) / 1 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000. Two trips "Leyton " -> "Waterloo ", (10 + 12) / 2 = 11
undergroundSystem.checkIn(10, "Leyton ", 24);
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000
undergroundSystem.checkOut(10, "Waterloo ", 38); // Customer 10 "Leyton " -> "Waterloo " in 38-24 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 12.00000. Three trips "Leyton " -> "Waterloo ", (10 + 12 + 14) / 3 = 12
**Example 2:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime "\]
\[\[\],\[10, "Leyton ",3\],\[10, "Paradise ",8\],\[ "Leyton ", "Paradise "\],\[5, "Leyton ",10\],\[5, "Paradise ",16\],\[ "Leyton ", "Paradise "\],\[2, "Leyton ",21\],\[2, "Paradise ",30\],\[ "Leyton ", "Paradise "\]\]
**Output**
\[null,null,null,5.00000,null,null,5.50000,null,null,6.66667\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(10, "Leyton ", 3);
undergroundSystem.checkOut(10, "Paradise ", 8); // Customer 10 "Leyton " -> "Paradise " in 8-3 = 5
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.00000, (5) / 1 = 5
undergroundSystem.checkIn(5, "Leyton ", 10);
undergroundSystem.checkOut(5, "Paradise ", 16); // Customer 5 "Leyton " -> "Paradise " in 16-10 = 6
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.50000, (5 + 6) / 2 = 5.5
undergroundSystem.checkIn(2, "Leyton ", 21);
undergroundSystem.checkOut(2, "Paradise ", 30); // Customer 2 "Leyton " -> "Paradise " in 30-21 = 9
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 6.66667, (5 + 6 + 9) / 3 = 6.66667
**Constraints:**
* `1 <= id, t <= 106`
* `1 <= stationName.length, startStation.length, endStation.length <= 10`
* All strings consist of uppercase and lowercase English letters and digits.
* There will be at most `2 * 104` calls **in total** to `checkIn`, `checkOut`, and `getAverageTime`.
* Answers within `10-5` of the actual value will be accepted. | Store number of computer in each row and column. Count all servers that are not isolated. |
Python Union Find. Fast and easy to understand. | count-servers-that-communicate | 0 | 1 | # Code\n```\nclass Solution:\n def countServers(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n uf = {}\n computer = []\n for i in range(m):\n for j in range(n):\n if grid[i][j]:\n # story the column and row in 1 dimension\n computer.append((i, j + m))\n\n def find(x):\n if x not in uf:\n uf[x] = x\n if uf[x] != x:\n uf[x] = find(uf[x])\n return uf[x]\n\n def union(x, y):\n root_x = find(x)\n root_y = find(y)\n uf[root_x] = root_y\n\n for x, y in computer:\n union(x, y)\n \n counter = collections.Counter([find(i) for i, _ in computer])\n return sum([i if i > 1 else 0 for i in counter.values()])\n\n \n\n \n\n\n``` | 2 | You are given a map of a server center, represented as a `m * n` integer matrix `grid`, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.
Return the number of servers that communicate with any other server.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 0
**Explanation:** No servers can communicate with others.
**Example 2:**
**Input:** grid = \[\[1,0\],\[1,1\]\]
**Output:** 3
**Explanation:** All three servers can communicate with at least one other server.
**Example 3:**
**Input:** grid = \[\[1,1,0,0\],\[0,0,1,0\],\[0,0,1,0\],\[0,0,0,1\]\]
**Output:** 4
**Explanation:** The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can't communicate with any other server.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 250`
* `1 <= n <= 250`
* `grid[i][j] == 0 or 1` | Convert the linked list into an array. While you can find a non-empty subarray with sum = 0, erase it. Convert the array into a linked list. |
Python Union Find. Fast and easy to understand. | count-servers-that-communicate | 0 | 1 | # Code\n```\nclass Solution:\n def countServers(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n uf = {}\n computer = []\n for i in range(m):\n for j in range(n):\n if grid[i][j]:\n # story the column and row in 1 dimension\n computer.append((i, j + m))\n\n def find(x):\n if x not in uf:\n uf[x] = x\n if uf[x] != x:\n uf[x] = find(uf[x])\n return uf[x]\n\n def union(x, y):\n root_x = find(x)\n root_y = find(y)\n uf[root_x] = root_y\n\n for x, y in computer:\n union(x, y)\n \n counter = collections.Counter([find(i) for i, _ in computer])\n return sum([i if i > 1 else 0 for i in counter.values()])\n\n \n\n \n\n\n``` | 2 | An underground railway system is keeping track of customer travel times between different stations. They are using this data to calculate the average time it takes to travel from one station to another.
Implement the `UndergroundSystem` class:
* `void checkIn(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks in at the station `stationName` at time `t`.
* A customer can only be checked into one place at a time.
* `void checkOut(int id, string stationName, int t)`
* A customer with a card ID equal to `id`, checks out from the station `stationName` at time `t`.
* `double getAverageTime(string startStation, string endStation)`
* Returns the average time it takes to travel from `startStation` to `endStation`.
* The average time is computed from all the previous traveling times from `startStation` to `endStation` that happened **directly**, meaning a check in at `startStation` followed by a check out from `endStation`.
* The time it takes to travel from `startStation` to `endStation` **may be different** from the time it takes to travel from `endStation` to `startStation`.
* There will be at least one customer that has traveled from `startStation` to `endStation` before `getAverageTime` is called.
You may assume all calls to the `checkIn` and `checkOut` methods are consistent. If a customer checks in at time `t1` then checks out at time `t2`, then `t1 < t2`. All events happen in chronological order.
**Example 1:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkIn ", "checkIn ", "checkOut ", "checkOut ", "checkOut ", "getAverageTime ", "getAverageTime ", "checkIn ", "getAverageTime ", "checkOut ", "getAverageTime "\]
\[\[\],\[45, "Leyton ",3\],\[32, "Paradise ",8\],\[27, "Leyton ",10\],\[45, "Waterloo ",15\],\[27, "Waterloo ",20\],\[32, "Cambridge ",22\],\[ "Paradise ", "Cambridge "\],\[ "Leyton ", "Waterloo "\],\[10, "Leyton ",24\],\[ "Leyton ", "Waterloo "\],\[10, "Waterloo ",38\],\[ "Leyton ", "Waterloo "\]\]
**Output**
\[null,null,null,null,null,null,null,14.00000,11.00000,null,11.00000,null,12.00000\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(45, "Leyton ", 3);
undergroundSystem.checkIn(32, "Paradise ", 8);
undergroundSystem.checkIn(27, "Leyton ", 10);
undergroundSystem.checkOut(45, "Waterloo ", 15); // Customer 45 "Leyton " -> "Waterloo " in 15-3 = 12
undergroundSystem.checkOut(27, "Waterloo ", 20); // Customer 27 "Leyton " -> "Waterloo " in 20-10 = 10
undergroundSystem.checkOut(32, "Cambridge ", 22); // Customer 32 "Paradise " -> "Cambridge " in 22-8 = 14
undergroundSystem.getAverageTime( "Paradise ", "Cambridge "); // return 14.00000. One trip "Paradise " -> "Cambridge ", (14) / 1 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000. Two trips "Leyton " -> "Waterloo ", (10 + 12) / 2 = 11
undergroundSystem.checkIn(10, "Leyton ", 24);
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 11.00000
undergroundSystem.checkOut(10, "Waterloo ", 38); // Customer 10 "Leyton " -> "Waterloo " in 38-24 = 14
undergroundSystem.getAverageTime( "Leyton ", "Waterloo "); // return 12.00000. Three trips "Leyton " -> "Waterloo ", (10 + 12 + 14) / 3 = 12
**Example 2:**
**Input**
\[ "UndergroundSystem ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime ", "checkIn ", "checkOut ", "getAverageTime "\]
\[\[\],\[10, "Leyton ",3\],\[10, "Paradise ",8\],\[ "Leyton ", "Paradise "\],\[5, "Leyton ",10\],\[5, "Paradise ",16\],\[ "Leyton ", "Paradise "\],\[2, "Leyton ",21\],\[2, "Paradise ",30\],\[ "Leyton ", "Paradise "\]\]
**Output**
\[null,null,null,5.00000,null,null,5.50000,null,null,6.66667\]
**Explanation**
UndergroundSystem undergroundSystem = new UndergroundSystem();
undergroundSystem.checkIn(10, "Leyton ", 3);
undergroundSystem.checkOut(10, "Paradise ", 8); // Customer 10 "Leyton " -> "Paradise " in 8-3 = 5
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.00000, (5) / 1 = 5
undergroundSystem.checkIn(5, "Leyton ", 10);
undergroundSystem.checkOut(5, "Paradise ", 16); // Customer 5 "Leyton " -> "Paradise " in 16-10 = 6
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 5.50000, (5 + 6) / 2 = 5.5
undergroundSystem.checkIn(2, "Leyton ", 21);
undergroundSystem.checkOut(2, "Paradise ", 30); // Customer 2 "Leyton " -> "Paradise " in 30-21 = 9
undergroundSystem.getAverageTime( "Leyton ", "Paradise "); // return 6.66667, (5 + 6 + 9) / 3 = 6.66667
**Constraints:**
* `1 <= id, t <= 106`
* `1 <= stationName.length, startStation.length, endStation.length <= 10`
* All strings consist of uppercase and lowercase English letters and digits.
* There will be at most `2 * 104` calls **in total** to `checkIn`, `checkOut`, and `getAverageTime`.
* Answers within `10-5` of the actual value will be accepted. | Store number of computer in each row and column. Count all servers that are not isolated. |
C#, Go, Python | Two approaches | search-suggestions-system | 0 | 1 | # Code\n\n## Option 1\n``` csharp [one]\npublic class Solution {\n public IList<IList<string>> SuggestedProducts(string[] products, string searchWord) {\n var result = new List<IList<string>>();\n var previouse = products.OrderBy(it => it).ToList();\n for (var i = 0; i < searchWord.Length; i++)\n {\n var temp = new List<string>();\n foreach (var product in previouse)\n {\n if (product.Length > i && product[i] == searchWord[i])\n {\n temp.Add(product);\n }\n }\n\n previouse = temp;\n result.Add(temp.Take(3).ToArray());\n }\n\n return result;\n }\n}\n```\n\n``` go [one]\nfunc suggestedProducts(products []string, searchWord string) [][]string {\n sort.Strings(products)\n\n result := [][]string{}\n previous := products\n for i := 0; i < len(searchWord); i++ {\n temp := []string{}\n for _, product := range previous {\n if len(product) > i && product[i] == searchWord[i] {\n temp = append(temp, product)\n }\n }\n\n previous = temp\n if len(temp) <= 3 {\n result = append(result, temp)\n } else {\n result = append(result, temp[:3])\n }\n }\n\n return result\n}\n```\n\n``` python [one]\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort()\n\n result = []\n previous = products\n for i in range(len(searchWord)):\n temp = []\n for product in previous:\n if len(product) > i and product[i] == searchWord[i]:\n temp.append(product)\n\n previous = temp\n result.append(temp[:3])\n\n return result\n```\n\n## Option 2 (Trie)\n``` csharp [two]\npublic class Solution {\n public IList<IList<string>> SuggestedProducts(string[] products, string searchWord) {\n var root = new Node();\n\n foreach (var product in products.OrderBy(it => it))\n {\n var current = root;\n foreach (var ch in product)\n {\n current = current.Children[ch - \'a\'] ??= new Node();\n current.Words.Add(product);\n }\n }\n\n var result = new List<IList<string>>();\n var node = root;\n foreach (var ch in searchWord)\n {\n node = node?.Children[ch - \'a\'];\n result.Add(node is null ? Array.Empty<string>() : node.Words.Take(3).ToArray());\n }\n\n return result;\n }\n\n class Node\n {\n public HashSet<string> Words = new HashSet<string>();\n public Node?[] Children { get; } = new Node?[26];\n };\n}\n```\n\n``` go [two]\nfunc suggestedProducts(products []string, searchWord string) [][]string {\n sort.Strings(products)\n\n root := &Trie{}\n result := [][]string{}\n\n for _, product := range products {\n current := root\n for _, ch := range product {\n if current.children[ch - \'a\'] != nil {\n current = current.children[ch - \'a\']\n } else {\n current.children[ch - \'a\'] = &Trie{}\n current = current.children[ch - \'a\']\n }\n current.words = append(current.words, product)\n }\n }\n\n node := root\n for _, ch := range searchWord {\n if node != nil && node.children[ch - \'a\'] != nil {\n node = node.children[ch - \'a\']\n if len(node.words) <= 3 {\n result = append(result, node.words)\n } else {\n result = append(result, node.words[:3])\n }\n } else {\n node = nil\n result = append(result, []string{})\n } \n }\n\n return result\n}\n\ntype Trie struct {\n children [26]*Trie\n words []string\n}\n```\n\n``` python [two]\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n root = Trie()\n\n products.sort()\n for product in products:\n current = root\n for ch in product:\n if ch in current.children:\n current = current.children[ch] \n else:\n current.children[ch] = Trie()\n current = current.children[ch]\n current.words.append(product)\n \n result = []\n node = root\n for ch in searchWord:\n node = node.children[ch] if node and ch in node.children else None\n result.append(node.words[:3] if node else [])\n\n return result\n \nclass Trie:\n def __init__(self) -> None:\n self.children = {}\n self.words = []\n``` | 2 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
C#, Go, Python | Two approaches | search-suggestions-system | 0 | 1 | # Code\n\n## Option 1\n``` csharp [one]\npublic class Solution {\n public IList<IList<string>> SuggestedProducts(string[] products, string searchWord) {\n var result = new List<IList<string>>();\n var previouse = products.OrderBy(it => it).ToList();\n for (var i = 0; i < searchWord.Length; i++)\n {\n var temp = new List<string>();\n foreach (var product in previouse)\n {\n if (product.Length > i && product[i] == searchWord[i])\n {\n temp.Add(product);\n }\n }\n\n previouse = temp;\n result.Add(temp.Take(3).ToArray());\n }\n\n return result;\n }\n}\n```\n\n``` go [one]\nfunc suggestedProducts(products []string, searchWord string) [][]string {\n sort.Strings(products)\n\n result := [][]string{}\n previous := products\n for i := 0; i < len(searchWord); i++ {\n temp := []string{}\n for _, product := range previous {\n if len(product) > i && product[i] == searchWord[i] {\n temp = append(temp, product)\n }\n }\n\n previous = temp\n if len(temp) <= 3 {\n result = append(result, temp)\n } else {\n result = append(result, temp[:3])\n }\n }\n\n return result\n}\n```\n\n``` python [one]\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort()\n\n result = []\n previous = products\n for i in range(len(searchWord)):\n temp = []\n for product in previous:\n if len(product) > i and product[i] == searchWord[i]:\n temp.append(product)\n\n previous = temp\n result.append(temp[:3])\n\n return result\n```\n\n## Option 2 (Trie)\n``` csharp [two]\npublic class Solution {\n public IList<IList<string>> SuggestedProducts(string[] products, string searchWord) {\n var root = new Node();\n\n foreach (var product in products.OrderBy(it => it))\n {\n var current = root;\n foreach (var ch in product)\n {\n current = current.Children[ch - \'a\'] ??= new Node();\n current.Words.Add(product);\n }\n }\n\n var result = new List<IList<string>>();\n var node = root;\n foreach (var ch in searchWord)\n {\n node = node?.Children[ch - \'a\'];\n result.Add(node is null ? Array.Empty<string>() : node.Words.Take(3).ToArray());\n }\n\n return result;\n }\n\n class Node\n {\n public HashSet<string> Words = new HashSet<string>();\n public Node?[] Children { get; } = new Node?[26];\n };\n}\n```\n\n``` go [two]\nfunc suggestedProducts(products []string, searchWord string) [][]string {\n sort.Strings(products)\n\n root := &Trie{}\n result := [][]string{}\n\n for _, product := range products {\n current := root\n for _, ch := range product {\n if current.children[ch - \'a\'] != nil {\n current = current.children[ch - \'a\']\n } else {\n current.children[ch - \'a\'] = &Trie{}\n current = current.children[ch - \'a\']\n }\n current.words = append(current.words, product)\n }\n }\n\n node := root\n for _, ch := range searchWord {\n if node != nil && node.children[ch - \'a\'] != nil {\n node = node.children[ch - \'a\']\n if len(node.words) <= 3 {\n result = append(result, node.words)\n } else {\n result = append(result, node.words[:3])\n }\n } else {\n node = nil\n result = append(result, []string{})\n } \n }\n\n return result\n}\n\ntype Trie struct {\n children [26]*Trie\n words []string\n}\n```\n\n``` python [two]\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n root = Trie()\n\n products.sort()\n for product in products:\n current = root\n for ch in product:\n if ch in current.children:\n current = current.children[ch] \n else:\n current.children[ch] = Trie()\n current = current.children[ch]\n current.words.append(product)\n \n result = []\n node = root\n for ch in searchWord:\n node = node.children[ch] if node and ch in node.children else None\n result.append(node.words[:3] if node else [])\n\n return result\n \nclass Trie:\n def __init__(self) -> None:\n self.children = {}\n self.words = []\n``` | 2 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
✅ 90.51% Binary Search Unleashed | search-suggestions-system | 0 | 1 | # **Intuition**\nThe problem revolves around finding product suggestions as we type each character of a search word. One of the immediate observations is that if the products list was sorted, our task of finding the lexicographically smallest products would become easier. Given a prefix from the search word, we would need to find its position in the sorted list and then simply take the next few words as suggestions.\n\n## Live Coding & More \nhttps://youtu.be/ePH2hNLO2Ms?si=Wvd7rebpj2wPRdhf\n\n# **Approach**\n\n1. **Sorting Products**: The first step is to sort our products list. This ensures that our suggestions are lexicographically ordered.\n\n2. **Prefix Iteration**: For every prefix of the search word (starting from the first character and increasing in length), we try to find its position in the sorted list of products.\n\n3. **Binary Search**: Instead of a linear search, which would take O(n) time for every prefix, we employ binary search. This reduces our search time for each prefix to O(log n). We use the `bisect_left` function from Python\'s bisect module to accomplish this.\n\n4. **Collect Suggestions**: Once we have the starting position of our prefix in the sorted list, the next few products (up to 3) which also have this prefix are added as our suggestions for that prefix.\n\n5. **Result Compilation**: We add the suggestions for each prefix to our result list.\n\n# **Complexity**\n\n- **Time complexity**: $O(n \\log n)$ for sorting the products. For each prefix of the search word, our binary search takes $O(\\log n)$. Thus, the overall complexity becomes $O(n \\log n + m \\log n)$, where $n$ is the number of products and $m$ is the length of the search word.\n\n- **Space complexity**: $O(n)$ to store the sorted list of products. We also use additional space for the result, but this is dependent on the length of the search word and is thus $O(m)$, making the overall space complexity $O(n + m)$.\n\n# Code\n``` Python []\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n # Sort the product list \n sorted_products = sorted(products) \n result = [] \n\n # Iterate over each prefix of the searchWord \n for i in range(1, len(searchWord) + 1): \n prefix = searchWord[:i] \n\n # Find the starting position of the prefix in sorted products \n idx = bisect_left(sorted_products, prefix) \n suggestions = [] \n\n # Collect up to 3 products as suggestions \n for j in range(idx, min(idx + 3, len(sorted_products))): \n if sorted_products[j].startswith(prefix): \n suggestions.append(sorted_products[j]) \n\n result.append(suggestions) \n\n return result \n \n```\n\n\nBy leveraging the power of sorting and binary search, we have created an efficient solution for this problem. This approach also showcases the versatility of binary search beyond simple number finding problems. | 4 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
✅ 90.51% Binary Search Unleashed | search-suggestions-system | 0 | 1 | # **Intuition**\nThe problem revolves around finding product suggestions as we type each character of a search word. One of the immediate observations is that if the products list was sorted, our task of finding the lexicographically smallest products would become easier. Given a prefix from the search word, we would need to find its position in the sorted list and then simply take the next few words as suggestions.\n\n## Live Coding & More \nhttps://youtu.be/ePH2hNLO2Ms?si=Wvd7rebpj2wPRdhf\n\n# **Approach**\n\n1. **Sorting Products**: The first step is to sort our products list. This ensures that our suggestions are lexicographically ordered.\n\n2. **Prefix Iteration**: For every prefix of the search word (starting from the first character and increasing in length), we try to find its position in the sorted list of products.\n\n3. **Binary Search**: Instead of a linear search, which would take O(n) time for every prefix, we employ binary search. This reduces our search time for each prefix to O(log n). We use the `bisect_left` function from Python\'s bisect module to accomplish this.\n\n4. **Collect Suggestions**: Once we have the starting position of our prefix in the sorted list, the next few products (up to 3) which also have this prefix are added as our suggestions for that prefix.\n\n5. **Result Compilation**: We add the suggestions for each prefix to our result list.\n\n# **Complexity**\n\n- **Time complexity**: $O(n \\log n)$ for sorting the products. For each prefix of the search word, our binary search takes $O(\\log n)$. Thus, the overall complexity becomes $O(n \\log n + m \\log n)$, where $n$ is the number of products and $m$ is the length of the search word.\n\n- **Space complexity**: $O(n)$ to store the sorted list of products. We also use additional space for the result, but this is dependent on the length of the search word and is thus $O(m)$, making the overall space complexity $O(n + m)$.\n\n# Code\n``` Python []\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n # Sort the product list \n sorted_products = sorted(products) \n result = [] \n\n # Iterate over each prefix of the searchWord \n for i in range(1, len(searchWord) + 1): \n prefix = searchWord[:i] \n\n # Find the starting position of the prefix in sorted products \n idx = bisect_left(sorted_products, prefix) \n suggestions = [] \n\n # Collect up to 3 products as suggestions \n for j in range(idx, min(idx + 3, len(sorted_products))): \n if sorted_products[j].startswith(prefix): \n suggestions.append(sorted_products[j]) \n\n result.append(suggestions) \n\n return result \n \n```\n\n\nBy leveraging the power of sorting and binary search, we have created an efficient solution for this problem. This approach also showcases the versatility of binary search beyond simple number finding problems. | 4 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
Beats 96.8 % || Python Explained | search-suggestions-system | 0 | 1 | # Intuition\nSo, basically instead of searching the complete list again and again for each character rather trim ur products array.\nSort ur array lexiographically.\nKeep popping out elements from first whose first char doesnt match with to be searchedWord.\nSimilarly do it from back.\n`why? Because it can be so that u found suppose \'m\' starting words which occurance is only one and u didnt check any further thus removing from back all those non-m starting words is also important`\nafter triming now ur product array consists of only those words which start with given first letter and keep shortening the array similarly and add first 3 (if there are) suggestions into ur ans. \n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort()\n ans = []\n for i in range(len(searchWord)):\n while products and (i > len(products[0]) - 1 or searchWord[i] != products[0][i]):\n products.pop(0)\n while products and (i > len(products[-1]) - 1 or searchWord[i] != products[-1][i]):\n products.pop()\n ans.append(products[:3])\n # print(ans)\n return ans\n \n\n\n \n``` | 1 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
Beats 96.8 % || Python Explained | search-suggestions-system | 0 | 1 | # Intuition\nSo, basically instead of searching the complete list again and again for each character rather trim ur products array.\nSort ur array lexiographically.\nKeep popping out elements from first whose first char doesnt match with to be searchedWord.\nSimilarly do it from back.\n`why? Because it can be so that u found suppose \'m\' starting words which occurance is only one and u didnt check any further thus removing from back all those non-m starting words is also important`\nafter triming now ur product array consists of only those words which start with given first letter and keep shortening the array similarly and add first 3 (if there are) suggestions into ur ans. \n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort()\n ans = []\n for i in range(len(searchWord)):\n while products and (i > len(products[0]) - 1 or searchWord[i] != products[0][i]):\n products.pop(0)\n while products and (i > len(products[-1]) - 1 or searchWord[i] != products[-1][i]):\n products.pop()\n ans.append(products[:3])\n # print(ans)\n return ans\n \n\n\n \n``` | 1 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
Python Easy 2 Approaches | search-suggestions-system | 0 | 1 | The solution that I have implemented is brute force. With each iteration, I will update the list of available words using `indices`.\n\n## **Example**\n```\n# sort the products\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] \nsearchWord = "mouse"\n```\n\nAfter each iteration, the contents of products will look like this.\n\n```\n# After match \'m\'\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Common prefix = \u2018m\u2019\nres[0]=["mobile","moneypot","monitor"]\n\n# After match \'mo\'\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"]\nres[1]=["mobile","moneypot","monitor"]\n\n# After match \'mou\'\nproducts = ["mouse","mousepad"]\nres[2]=["mouse","mousepad"]\n\n# After match \'mous\'\nproducts = ["mouse","mousepad"]\nres[3]=["mouse","mousepad"]\n\n# After match \'mous\')\nproducts = ["mouse","mousepad"]\nres[4]=["mouse","mousepad"]\n```\n\n\n```\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort()\n n=len(products)\n indices=[i for i in range(n)]\n res=[]\n for idx, c in enumerate(searchWord):\n indices = [i for i in indices if len(products[i])>idx and products[i][idx] == c] \n res.append(products[i] for i in indices[:3]) \n return res \n```\n\nIf `n` is the length of `products` and `m` is length of `searchWord`, then\n**Time - O(nlogn + n.m)** - Sorting requires `O(nlogn)` \n**Space - O(N)** - If you exclude the output array, then the space required is for storing `indices`. \n\n---\n\nAs the `products` list is sorted, we can also use **Binary search** to find the lower bound of our desired list. Following is **binary search variant**:\n\n```\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort() \n prefix=\'\'\n res=[]\n i=0\n for c in searchWord:\n prefix+=c\n i=bisect_left(products, prefix,i)\n res.append([w for w in products[i:i+3] if w.startswith(prefix)]) \n return res \n```\n\nIf `n` is the length of `products` and `m` is length of `searchWord`, then\n**Time - O(nlogn + mlogn)** - Sorting requires `O(nlogn)` and `O(logn)` is for binary search the `products` for a `prefix`.\n**Space - O(1)** \n\n--- \n\n***Please upvote if you find it useful*** | 29 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
Python Easy 2 Approaches | search-suggestions-system | 0 | 1 | The solution that I have implemented is brute force. With each iteration, I will update the list of available words using `indices`.\n\n## **Example**\n```\n# sort the products\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] \nsearchWord = "mouse"\n```\n\nAfter each iteration, the contents of products will look like this.\n\n```\n# After match \'m\'\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Common prefix = \u2018m\u2019\nres[0]=["mobile","moneypot","monitor"]\n\n# After match \'mo\'\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"]\nres[1]=["mobile","moneypot","monitor"]\n\n# After match \'mou\'\nproducts = ["mouse","mousepad"]\nres[2]=["mouse","mousepad"]\n\n# After match \'mous\'\nproducts = ["mouse","mousepad"]\nres[3]=["mouse","mousepad"]\n\n# After match \'mous\')\nproducts = ["mouse","mousepad"]\nres[4]=["mouse","mousepad"]\n```\n\n\n```\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort()\n n=len(products)\n indices=[i for i in range(n)]\n res=[]\n for idx, c in enumerate(searchWord):\n indices = [i for i in indices if len(products[i])>idx and products[i][idx] == c] \n res.append(products[i] for i in indices[:3]) \n return res \n```\n\nIf `n` is the length of `products` and `m` is length of `searchWord`, then\n**Time - O(nlogn + n.m)** - Sorting requires `O(nlogn)` \n**Space - O(N)** - If you exclude the output array, then the space required is for storing `indices`. \n\n---\n\nAs the `products` list is sorted, we can also use **Binary search** to find the lower bound of our desired list. Following is **binary search variant**:\n\n```\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n products.sort() \n prefix=\'\'\n res=[]\n i=0\n for c in searchWord:\n prefix+=c\n i=bisect_left(products, prefix,i)\n res.append([w for w in products[i:i+3] if w.startswith(prefix)]) \n return res \n```\n\nIf `n` is the length of `products` and `m` is length of `searchWord`, then\n**Time - O(nlogn + mlogn)** - Sorting requires `O(nlogn)` and `O(logn)` is for binary search the `products` for a `prefix`.\n**Space - O(1)** \n\n--- \n\n***Please upvote if you find it useful*** | 29 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
Simple Easy Approach | search-suggestions-system | 0 | 1 | ```\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n product = []\n for i in range(len(searchWord)):\n p = []\n for prod in products:\n if prod.startswith(searchWord[:i+1]):\n p.append(prod)\n p = sorted(p)[:3]\n product.append(p)\n return product\n``` | 4 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
Simple Easy Approach | search-suggestions-system | 0 | 1 | ```\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n product = []\n for i in range(len(searchWord)):\n p = []\n for prod in products:\n if prod.startswith(searchWord[:i+1]):\n p.append(prod)\n p = sorted(p)[:3]\n product.append(p)\n return product\n``` | 4 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
[Python] A simple approach without using Trie | search-suggestions-system | 0 | 1 | # Solution\n\nUse sort and list comprehension.\n\n```python\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n list_ = []\n products.sort()\n for i, c in enumerate(searchWord):\n products = [ p for p in products if len(p) > i and p[i] == c ]\n list_.append(products[:3])\n return list_\n```\n\nUse sort and filter.\n\n```python\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n list_ = []\n products.sort()\n for i, c in enumerate(searchWord):\n products = list(filter(lambda p: p[i] == c if len(p) > i else False, products))\n list_.append(products[:3])\n return list_\n```\n\n\n---\n\n\n\n# Explanation\n\n(This section is the same as the reply below.)\n\nThe problem asks us to return a list of lists of suggested products, which means the list at index i contains products that have the same common prefix. So, we can generate results by filtering products based on the typing of the user in each iteration. For example\n\n```python\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Sorted\nsearchWord = "mouse"\n\n# After typing \u2018m\u2019 (i=0, c=\u2018m\u2019)\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Common prefix = \u2018m\u2019\nlist_[0]=["mobile","moneypot","monitor"]\n\n# After typing \u2018o\u2019 (i=1, c=\u2018o\u2019)\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Common prefix = \u2018mo\u2019\nlist_[1]=["mobile","moneypot","monitor"]\n\n# After typing \u2018u\u2019 (i=2, c=\u2018u\u2019)\nproducts = ["mouse","mousepad"] # Common prefix = \u2018mou\u2019\nlist_[2]=["mouse","mousepad"]\n\n# After typing \u2018s\u2019 (i=3, c=\u2018s\u2019)\nproducts = ["mouse","mousepad"] # Common prefix = \u2018mous\u2019\nlist_[3]=["mouse","mousepad"]\n\n# After typing \u2018e\u2019 (i=4, c=\u2018e\u2019)\nproducts = ["mouse","mousepad"] # Common prefix = \u2018mouse\u2019\nlist_[4]=["mouse","mousepad"]\n```\n\n\n---\n\n\n\n# Complexity\n\n## Definition\n- `N` is the number of products.\n- `M` is the average length of product names.\n- `L` is the length of the search word.\n\n## Constraint\n- `N`: 1 <= products.length <= 1000\n- `M`: 1 <= products[i].length <= 3000\n- `L`: 1 <= searchWord.length <= 1000\n\n## Time\n- Sorting: `O(MN logN)`. (String comparison is `O(M)`.)\n- Loop and filter: `O(LN)`. Loop L times in the outer loop(i.e. for-loop) and N times in the inner loop(i.e. list comprehension). Every filter condition completes in `O(1)`.\n\nThe N times loop occurs when all products share the same prefixes of the search word. In this worst case, the 2-pointers approach can reduce the inner loop complexity. However, please notice that the time complexity of the sorting dominates the loop and filter.\n\n## Space\n- Sorting: `O(MN)`. Python\'s built-in sort is Timsort. | 44 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
[Python] A simple approach without using Trie | search-suggestions-system | 0 | 1 | # Solution\n\nUse sort and list comprehension.\n\n```python\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n list_ = []\n products.sort()\n for i, c in enumerate(searchWord):\n products = [ p for p in products if len(p) > i and p[i] == c ]\n list_.append(products[:3])\n return list_\n```\n\nUse sort and filter.\n\n```python\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n list_ = []\n products.sort()\n for i, c in enumerate(searchWord):\n products = list(filter(lambda p: p[i] == c if len(p) > i else False, products))\n list_.append(products[:3])\n return list_\n```\n\n\n---\n\n\n\n# Explanation\n\n(This section is the same as the reply below.)\n\nThe problem asks us to return a list of lists of suggested products, which means the list at index i contains products that have the same common prefix. So, we can generate results by filtering products based on the typing of the user in each iteration. For example\n\n```python\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Sorted\nsearchWord = "mouse"\n\n# After typing \u2018m\u2019 (i=0, c=\u2018m\u2019)\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Common prefix = \u2018m\u2019\nlist_[0]=["mobile","moneypot","monitor"]\n\n# After typing \u2018o\u2019 (i=1, c=\u2018o\u2019)\nproducts = ["mobile","moneypot","monitor","mouse","mousepad"] # Common prefix = \u2018mo\u2019\nlist_[1]=["mobile","moneypot","monitor"]\n\n# After typing \u2018u\u2019 (i=2, c=\u2018u\u2019)\nproducts = ["mouse","mousepad"] # Common prefix = \u2018mou\u2019\nlist_[2]=["mouse","mousepad"]\n\n# After typing \u2018s\u2019 (i=3, c=\u2018s\u2019)\nproducts = ["mouse","mousepad"] # Common prefix = \u2018mous\u2019\nlist_[3]=["mouse","mousepad"]\n\n# After typing \u2018e\u2019 (i=4, c=\u2018e\u2019)\nproducts = ["mouse","mousepad"] # Common prefix = \u2018mouse\u2019\nlist_[4]=["mouse","mousepad"]\n```\n\n\n---\n\n\n\n# Complexity\n\n## Definition\n- `N` is the number of products.\n- `M` is the average length of product names.\n- `L` is the length of the search word.\n\n## Constraint\n- `N`: 1 <= products.length <= 1000\n- `M`: 1 <= products[i].length <= 3000\n- `L`: 1 <= searchWord.length <= 1000\n\n## Time\n- Sorting: `O(MN logN)`. (String comparison is `O(M)`.)\n- Loop and filter: `O(LN)`. Loop L times in the outer loop(i.e. for-loop) and N times in the inner loop(i.e. list comprehension). Every filter condition completes in `O(1)`.\n\nThe N times loop occurs when all products share the same prefixes of the search word. In this worst case, the 2-pointers approach can reduce the inner loop complexity. However, please notice that the time complexity of the sorting dominates the loop and filter.\n\n## Space\n- Sorting: `O(MN)`. Python\'s built-in sort is Timsort. | 44 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
Python 3 | Two Methods (Sort, Trie) | Explanation | search-suggestions-system | 0 | 1 | ### Approach \\#1. Sort + Binary Search\n- Sort `A`\n- For each prefix, do binary search\n- Get 3 words from the index and check if it matches the prefix\n```\nclass Solution:\n def suggestedProducts(self, A: List[str], searchWord: str) -> List[List[str]]:\n A.sort()\n res, cur = [], \'\'\n for c in searchWord:\n cur += c\n i = bisect.bisect_left(A, cur)\n res.append([w for w in A[i:i+3] if w.startswith(cur)])\n return res\n```\n### Approach \\#2. Trie\n- Pretty standard Trie\n- Add word to trie while maintain a list of `words` of length 3 for each prefix\n- Search each prefix and return \n```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.words = list()\n self.n = 0\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def add_word(self, word):\n node = self.root\n for c in word:\n if c not in node.children: node.children[c] = TrieNode()\n node = node.children[c] \n if node.n < 3:\n node.words.append(word)\n node.n += 1\n \n def find_word_by_prefix(self, prefix):\n node = self.root\n for c in prefix:\n if c not in node.children: return \'\'\n node = node.children[c] \n return node.words\n \nclass Solution:\n def suggestedProducts(self, A: List[str], searchWord: str) -> List[List[str]]:\n A.sort()\n trie = Trie()\n for word in A: trie.add_word(word)\n ans, cur = [], \'\'\n for c in searchWord:\n cur += c \n ans.append(trie.find_word_by_prefix(cur))\n return ans \n```\n### Approach \\#2.1 Trie (alternative)\nTo save some time, it\'s not necessary to search prefix from beginning. Use a static variable to search only current state.\n```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.words = list()\n self.n = 0\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n self.node = self.root\n \n def add_word(self, word):\n node = self.root\n for c in word:\n if c not in node.children:\n node.children[c] = TrieNode()\n node = node.children[c] \n if node.n < 3:\n node.words.append(word)\n node.n += 1\n \n def find_word_by_prefix(self, c):\n if self.node and c in self.node.children: \n self.node = self.node.children[c] \n return self.node.words\n else: \n self.node = None \n return []\n \n \nclass Solution:\n def suggestedProducts(self, A: List[str], searchWord: str) -> List[List[str]]:\n A.sort()\n trie = Trie()\n for word in A: trie.add_word(word)\n return [trie.find_word_by_prefix(c) for c in searchWord]\n``` | 30 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
Python 3 | Two Methods (Sort, Trie) | Explanation | search-suggestions-system | 0 | 1 | ### Approach \\#1. Sort + Binary Search\n- Sort `A`\n- For each prefix, do binary search\n- Get 3 words from the index and check if it matches the prefix\n```\nclass Solution:\n def suggestedProducts(self, A: List[str], searchWord: str) -> List[List[str]]:\n A.sort()\n res, cur = [], \'\'\n for c in searchWord:\n cur += c\n i = bisect.bisect_left(A, cur)\n res.append([w for w in A[i:i+3] if w.startswith(cur)])\n return res\n```\n### Approach \\#2. Trie\n- Pretty standard Trie\n- Add word to trie while maintain a list of `words` of length 3 for each prefix\n- Search each prefix and return \n```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.words = list()\n self.n = 0\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def add_word(self, word):\n node = self.root\n for c in word:\n if c not in node.children: node.children[c] = TrieNode()\n node = node.children[c] \n if node.n < 3:\n node.words.append(word)\n node.n += 1\n \n def find_word_by_prefix(self, prefix):\n node = self.root\n for c in prefix:\n if c not in node.children: return \'\'\n node = node.children[c] \n return node.words\n \nclass Solution:\n def suggestedProducts(self, A: List[str], searchWord: str) -> List[List[str]]:\n A.sort()\n trie = Trie()\n for word in A: trie.add_word(word)\n ans, cur = [], \'\'\n for c in searchWord:\n cur += c \n ans.append(trie.find_word_by_prefix(cur))\n return ans \n```\n### Approach \\#2.1 Trie (alternative)\nTo save some time, it\'s not necessary to search prefix from beginning. Use a static variable to search only current state.\n```\nclass TrieNode:\n def __init__(self):\n self.children = dict()\n self.words = list()\n self.n = 0\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n self.node = self.root\n \n def add_word(self, word):\n node = self.root\n for c in word:\n if c not in node.children:\n node.children[c] = TrieNode()\n node = node.children[c] \n if node.n < 3:\n node.words.append(word)\n node.n += 1\n \n def find_word_by_prefix(self, c):\n if self.node and c in self.node.children: \n self.node = self.node.children[c] \n return self.node.words\n else: \n self.node = None \n return []\n \n \nclass Solution:\n def suggestedProducts(self, A: List[str], searchWord: str) -> List[List[str]]:\n A.sort()\n trie = Trie()\n for word in A: trie.add_word(word)\n return [trie.find_word_by_prefix(c) for c in searchWord]\n``` | 30 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
Python Trie Solution. Industry Level Code | search-suggestions-system | 0 | 1 | ```\nclass TreeNode:\n def __init__(self):\n self.children = [None]*26\n self.words = []\nclass Trie:\n def __init__(self):\n self.root = TreeNode()\n def _getIndex(self,ch):\n return ord(ch)-ord(\'a\')\n def insert(self,word):\n cur_node = self.root\n for ch in word:\n index = self._getIndex(ch)\n if cur_node.children[index] is None:\n cur_node.children[index] =TreeNode()\n cur_node = cur_node.children[index]\n cur_node.words.append(word)\n return\n def search(self,word):\n cur_node = self.root\n for ch in word:\n index = self._getIndex(ch)\n if cur_node.children[index] is None:\n return False\n cur_node = cur_node.children[index]\n return cur_node.words\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n root = Trie()\n for word in products:\n root.insert(word)\n res = []\n for i in range(len(searchWord)):\n tmp = root.search(searchWord[:i+1])\n if tmp:\n res.append(sorted(tmp)[:3])\n else:\n res.append([])\n return res\n``` | 11 | You are given an array of strings `products` and a string `searchWord`.
Design a system that suggests at most three product names from `products` after each character of `searchWord` is typed. Suggested products should have common prefix with `searchWord`. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return _a list of lists of the suggested products after each character of_ `searchWord` _is typed_.
**Example 1:**
**Input:** products = \[ "mobile ", "mouse ", "moneypot ", "monitor ", "mousepad "\], searchWord = "mouse "
**Output:** \[\[ "mobile ", "moneypot ", "monitor "\],\[ "mobile ", "moneypot ", "monitor "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\],\[ "mouse ", "mousepad "\]\]
**Explanation:** products sorted lexicographically = \[ "mobile ", "moneypot ", "monitor ", "mouse ", "mousepad "\].
After typing m and mo all products match and we show user \[ "mobile ", "moneypot ", "monitor "\].
After typing mou, mous and mouse the system suggests \[ "mouse ", "mousepad "\].
**Example 2:**
**Input:** products = \[ "havana "\], searchWord = "havana "
**Output:** \[\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\],\[ "havana "\]\]
**Explanation:** The only word "havana " will be always suggested while typing the search word.
**Constraints:**
* `1 <= products.length <= 1000`
* `1 <= products[i].length <= 3000`
* `1 <= sum(products[i].length) <= 2 * 104`
* All the strings of `products` are **unique**.
* `products[i]` consists of lowercase English letters.
* `1 <= searchWord.length <= 1000`
* `searchWord` consists of lowercase English letters. | null |
Python Trie Solution. Industry Level Code | search-suggestions-system | 0 | 1 | ```\nclass TreeNode:\n def __init__(self):\n self.children = [None]*26\n self.words = []\nclass Trie:\n def __init__(self):\n self.root = TreeNode()\n def _getIndex(self,ch):\n return ord(ch)-ord(\'a\')\n def insert(self,word):\n cur_node = self.root\n for ch in word:\n index = self._getIndex(ch)\n if cur_node.children[index] is None:\n cur_node.children[index] =TreeNode()\n cur_node = cur_node.children[index]\n cur_node.words.append(word)\n return\n def search(self,word):\n cur_node = self.root\n for ch in word:\n index = self._getIndex(ch)\n if cur_node.children[index] is None:\n return False\n cur_node = cur_node.children[index]\n return cur_node.words\nclass Solution:\n def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:\n root = Trie()\n for word in products:\n root.insert(word)\n res = []\n for i in range(len(searchWord)):\n tmp = root.search(searchWord[:i+1])\n if tmp:\n res.append(sorted(tmp)[:3])\n else:\n res.append([])\n return res\n``` | 11 | Given the strings `s1` and `s2` of size `n` and the string `evil`, return _the number of **good** strings_.
A **good** string has size `n`, it is alphabetically greater than or equal to `s1`, it is alphabetically smaller than or equal to `s2`, and it does not contain the string `evil` as a substring. Since the answer can be a huge number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 2, s1 = "aa ", s2 = "da ", evil = "b "
**Output:** 51
**Explanation:** There are 25 good strings starting with 'a': "aa ", "ac ", "ad ",..., "az ". Then there are 25 good strings starting with 'c': "ca ", "cc ", "cd ",..., "cz " and finally there is one good string starting with 'd': "da ".
**Example 2:**
**Input:** n = 8, s1 = "leetcode ", s2 = "leetgoes ", evil = "leet "
**Output:** 0
**Explanation:** All strings greater than or equal to s1 and smaller than or equal to s2 start with the prefix "leet ", therefore, there is not any good string.
**Example 3:**
**Input:** n = 2, s1 = "gx ", s2 = "gz ", evil = "x "
**Output:** 2
**Constraints:**
* `s1.length == n`
* `s2.length == n`
* `s1 <= s2`
* `1 <= n <= 500`
* `1 <= evil.length <= 50`
* All strings consist of lowercase English letters. | Brute force is a good choice because length of the string is ≤ 1000. Binary search the answer. Use Trie data structure to store the best three matching. Traverse the Trie. |
【Video】Give me 10 minutes - How we think abou a solution - Python, JavaScript, Java, C++ | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\nWe only care about steps / 2\n\n---\n\n# Solution Video\n\nhttps://youtu.be/uC0nI4E7ozw\n\n\u25A0 Timeline of the video\n`0:04` How we think about a solution\n`0:05` Two key points to solve this question\n`0:21` Explain the first key point\n`1:28` Explain the second key point\n`2:36` Break down and explain real algorithms\n`6:09` Demonstrate how it works\n`10:17` Coding\n`12:58` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,714\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nThis is a very simple solution. First of all, we have to come back to start position `index 0`, so the first thing that I came up with right after I read description is this.\n\n\n---\n\n\u2B50\uFE0F Points\n\nWe can move half length of input `steps` at most because we need some steps to go back to start position. In other words we don\'t have to care about input length of array greater than `steps / 2`.\n\n\n---\n\n- How we can calculate number of ways to each position.\n\nThis is also simple idea. The description says "you can move 1 position to the left, 1 position to the right in the array, or stay in the same place".\n\n\n---\n\n\u2B50\uFE0F Points\nCalculation of number of ways for current position is simply\n```\ncurrent position = a[postion] + a[postion - 1] + a[postion + 1]\n\na: array\nposition: stay\nposition - 1: from left side\nposition + 1: from righ side\n\n```\n\n---\n\nSince we need to keep current number of ways so far, seems like we can use dynamic programing.\n\n- How it works\n\nLet\'s see the key points with simple concrete example.\n\n```\nInput: steps = 2, arrLen = 4\n```\n\nFirst of all, we take max position where we can go by\n\n```\nmin(steps // 2 + 1, arrLen)\n= min(2 // 2 + 1, 4)\n= 2\n\n```\n- **why +1?**\n\nThe reason why we need `+1` is simply, this example gives us `2` steps, so we need `2` positions to calculate ways.\n\nWe start from `index 1`(we consider index 1 as start position(index 0) in arrays for dynamic programming). In that case, we can move until `index 2` which is half of steps, so we need `index 2` to check the ways.\n\n- **Why we start from `index 1`?**\n\nActually you can start from `index 0` but if you start from `index 1`, you don\'t have to check out of bounds in the loop.\n\n\nLook at these Python code.\n\n```\ncur_ways = [0] * (max_position + 2)\nnext_ways = [0] * (max_position + 2)\n```\n\nThat\'s because we will calcuate total of `stay`, `left`, `right` positions, so having two extra position enables us to write code easy. we don\'t have to check out of bounds in the loop.\n\n```\n0,1,2,3\n```\nIn this case, we really need `index 1` and `index 2` and we added `index 0` and `index 3` as extra `2` positions.\n\nSo, when we calculate start position(index 1), we can simply calculate \n\n```\nindex 0 + index 1 + index 2\n```\n\nNo need if statement or something.\n\n`index 3` is also the same idea when we calculate `index 2` and both sides of indices are always `0`, so they prevent out of bounds and doesn\'t affect result of calculation.\n\n---\n\n\u2B50\uFE0F Points\n\n- Having two extra positions will prevent us from out of bounds\n- the extra splace always 0 value, so they don\'t affect results of calculation.\n\n---\n\nWe will create two arrays(`cur_ways`, `next_ways`) and will update `next_ways`, then swap `next_ways` with `cur_ways`, because (current) next ways is the next current ways.\n\nWe check all positions from 1 to `max_position` by number of steps. I print `next_ways` variable. The first number is position(`pos`). \n\n\n\nIn the end if we have \n\n```\nInput: steps = 2, arrLen = 4\n```\n\n`next_way` will be updated like that, so we should return `2` at `index1`.\n\nI think the two ways are \n```\n"stay", "stay"\n"right", "left"\n\n```\nWe can\'t go "left", "right", because that is out of bounds. The description says "The pointer should not be placed outside the array at any time".\n\nLet\'s see a real algorithm!\n\n\n### Algorithm Overview:\nThe algorithm employs dynamic programming to calculate the number of ways to reach the starting position after a specified number of steps on an array of tiles.\n\n### Detailed Explanation:\n1. **Initialization**:\n - Calculate the maximum position (`max_position`) based on the minimum of half the steps plus one and the array length. This restricts the position within the array.\n - Initialize arrays `cur_ways` and `next_ways` of length `(max_position + 2)` and fill them with zeros. These arrays store the number of ways to reach each position.\n - Set `cur_ways[1]` to 1 since there\'s one way to start at position 1.\n - Define a variable `mod` to store the modulo value (`10^9 + 7`) for overflow prevention.\n\n2. **Dynamic Programming**:\n - Iterate through the steps, decrementing the count with each iteration.\n - For each step:\n - Iterate through each position from `1` to `max_position`.\n - Update `next_ways[pos]` using the rule: the sum of the number of ways from the previous step at the current position, the previous position, and the next position, all modulo `mod` to prevent overflow.\n - Swap `cur_ways` and `next_ways` to update the current ways for the next step.\n\n3. **Return Result**:\n - After the iterations, return the number of ways to reach the first position (`cur_ways[1]`) after the specified number of steps. This represents the total number of ways to reach the starting position.\n\n# Complexity\n- Time complexity: O(steps * min(steps // 2 + 1, arrLen))\n\n- Space complexity: O(steps)\n\n\n```python []\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n max_position = min(steps // 2 + 1, arrLen)\n cur_ways = [0] * (max_position + 2)\n next_ways = [0] * (max_position + 2)\n cur_ways[1] = 1\n mod = 10 ** 9 + 7\n\n while steps > 0:\n for pos in range(1, max_position + 1):\n next_ways[pos] = (cur_ways[pos] + cur_ways[pos - 1] + cur_ways[pos + 1]) % mod\n\n cur_ways, next_ways = next_ways, cur_ways\n steps -= 1\n\n return cur_ways[1] \n```\n```javascript []\nvar numWays = function(steps, arrLen) {\n const maxPosition = Math.min(Math.floor(steps / 2) + 1, arrLen);\n let curWays = new Array(maxPosition + 2).fill(0);\n let nextWays = new Array(maxPosition + 2).fill(0);\n curWays[1] = 1;\n const mod = 10 ** 9 + 7;\n\n while (steps > 0) {\n for (let pos = 1; pos <= maxPosition; pos++) {\n nextWays[pos] = (curWays[pos] + curWays[pos - 1] + curWays[pos + 1]) % mod;\n }\n\n // Swap arrays using a temporary variable\n let temp = curWays;\n curWays = nextWays;\n nextWays = temp;\n steps--;\n }\n\n return curWays[1]; \n};\n```\n```java []\nclass Solution {\n public int numWays(int steps, int arrLen) {\n int maxPosition = Math.min(steps / 2 + 1, arrLen);\n int[] curWays = new int[maxPosition + 2];\n int[] nextWays = new int[maxPosition + 2];\n curWays[1] = 1;\n int mod = 1000000007;\n\n while (steps > 0) {\n for (int pos = 1; pos <= maxPosition; pos++) {\n nextWays[pos] = (int)(((long)curWays[pos] + curWays[pos - 1] + curWays[pos + 1]) % mod);\n }\n\n int[] temp = curWays;\n curWays = nextWays;\n nextWays = temp;\n steps--;\n }\n\n return curWays[1]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numWays(int steps, int arrLen) {\n int maxPosition = min(steps / 2 + 1, arrLen);\n vector<int> curWays(maxPosition + 2, 0);\n vector<int> nextWays(maxPosition + 2, 0);\n curWays[1] = 1;\n const int mod = 1000000007;\n\n while (steps > 0) {\n for (int pos = 1; pos <= maxPosition; pos++) {\n nextWays[pos] = ((long)curWays[pos] + curWays[pos - 1] + curWays[pos + 1]) % mod;\n }\n\n swap(curWays, nextWays);\n steps--;\n }\n\n return curWays[1]; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 My next post and video for daily coding challenge\n\npost\nhttps://leetcode.com/problems/pascals-triangle-ii/solutions/4173366/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/1162hVzZ3sM\n\n\u25A0 Timeline of the video\n`0:04` Key point to solve this question\n`0:05` Two key points to solve this question\n`0:16` Actually there is a formula for Pascal\'s Triangle\n`0:32` Explain basic idea and the key point\n`2:38` Demonstrate real algorithms\n`6:39` Coding\n`7:43` Time Complexity and Space Complexity\n\n\u25A0 My previous post and video for daily coding challenge\n\npost\nhttps://leetcode.com/problems/min-cost-climbing-stairs/solutions/4162780/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/LopoDDa4dLY\n\n\u25A0 Timeline of the video\n\n`0:00` Read the question of Min Cost Climbing Stairs\n`1:43` Explain a basic idea to solve Min Cost Climbing Stairs\n`6:03` Coding\n`8:21` Summarize the algorithm of Min Cost Climbing Stairs\n\n | 36 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
🚩📈Beats 99.70% |🔥Easy and Optimised O(sqrt(n)) Approach | 📈Explained in detail | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea behind this solution is to recognize that as the number of steps increases, the number of ways to reach the starting position at index 0 forms a bell curve. This bell curve reaches its peak at the midpoint and then starts to decrease symmetrically. Since moving left or right by one step is symmetric, the number of ways to reach index 0 is determined by the number of ways to reach positions up to the midpoint.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a constant `MOD` to 1000000007, which will be used for taking the modulo of intermediate and final results.\n2. Calculate the `maxPosition`, which represents the maximum position that can be reached without going out of bounds. This is determined as the minimum of `steps / 2` and `arrLen - 1`.\n3. Initialize a vector `dp` of size `maxPosition + 1` to keep track of the number of ways to reach each position.\n4. Initialize `dp[0]` to 1, representing that there is one way to stay at index 0 after 0 steps.\n5. Use an iterative approach to calculate the number of ways to reach each position for each step. For each step, update the number of ways for each position based on the previous step\'s values.\n6. Return `dp[0]`, which represents the number of ways to stay at index 0 after `steps` steps.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(sqrt(n)), where n is the number of steps. The loop iterates for each step, and for each step, it updates all positions up to the `maxPosition`, which is sqrt(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(maxPosition), which is O(sqrt(n)). This is because we only store the number of ways for positions up to the `maxPosition`.\n# Code\n```\nclass Solution {\npublic:\n int numWays(int steps, int arrLen) {\n int MOD = 1000000007;\n int maxPosition = min(steps / 2, arrLen - 1);\n vector<long long> dp(maxPosition + 1, 0);\n dp[0] = 1;\n\n for (int i = 1; i <= steps; i++) {\n vector<long long> new_dp(maxPosition + 1, 0);\n for (int j = 0; j <= maxPosition; j++) {\n new_dp[j] = dp[j];\n if (j > 0)\n new_dp[j] = (new_dp[j] + dp[j - 1]) % MOD;\n if (j < maxPosition)\n new_dp[j] = (new_dp[j] + dp[j + 1]) % MOD;\n }\n dp = new_dp;\n }\n return dp[0];\n }\n};\n\n``` | 3 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Beats 100%🔥Memory & Runtime🦄7 Lines🔮1D DP✅Python 3 | number-of-ways-to-stay-in-the-same-place-after-some-steps | 0 | 1 | \n<!--  -->\n\n\n\n# Complexity\n- Time complexity: `O (arrlen * steps)`\n- Space complexity: `O (n)`\n\n# Code\n```Python []\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n n = min(steps//2 + 1, arrLen)\n dp = [1] + [0]*n\n for _ in range(steps):\n prev=0\n for i in range(n):\n dp[i], prev =(prev + dp[i] + dp[i + 1]), dp[i]\n return dp[0] % (10**9+7)\n```\n\n\n> \n\n> _"catphrase"_ | 3 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Dynamic Programming Staircase || Beginner Friendly || Easy To Understand || Python || Beats 100 % || | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | # BEATS 100%\n\n\n# Intuition\n\n\nImagine you are standing at the beginning of a long staircase. You want to reach the top, but you can only take one or two steps at a time. How many different ways can you reach the top?\n\nThe number of ways to reach the top of the staircase depends on the number of ways to reach the previous step and the next step. This can be modeled using a dynamic programming recurrence relation.\n\n# Approach\n\nThe following algorithm is used to calculate the number of ways to reach the top of the staircase:\n\n1. **Define a modulo constant** to prevent integer overflow.\n2. **Calculate the maximum possible position** on the staircase that can be reached.\n3. **Initialize an array** to store the number of ways to reach each position on the staircase.\n4. **Set the base case:** There is one way to stay at the initial position.\n5. **Iterate through the number of steps taken:**\n * Set a variable `left` to 0.\n * Iterate through possible positions on the staircase, considering bounds:\n * Calculate the number of ways to reach the current position `j` using the dynamic programming recurrence relation and considering the `left` value.\n * Update `left` and `ways[j]`.\n6. **Return the value of `ways[0]`,** which represents the number of ways to reach the top of the staircase.\n\n# Complexity\n\n* **Time complexity:** $O(n)$\n* **Space complexity:** $O(n)$\n\nwhere $n$ is the number of steps taken.\n\n# Code\n\n```python\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n # Define a modulo constant to prevent integer overflow\n modulo = 1000000007\n\n # Calculate the maximum possible position on the staircase that can be reached\n max_len = min(arrLen, 1 + steps // 2)\n\n # Initialize an array to store the number of ways to reach each position on the staircase\n ways = [0] * (max_len + 1)\n\n # Set the base case: There is one way to stay at the initial position\n ways[0] = 1\n\n # Iterate through the number of steps taken\n for i in range(steps):\n left = 0\n\n # Iterate through possible positions on the staircase, considering bounds\n for j in range(min(max_len, i + 2, steps - i + 3)):\n # Calculate the number of ways to reach the current position `j`\n # using the dynamic programming recurrence relation and considering the `left` value\n left, ways[j] = ways[j], (ways[j] + left + ways[j + 1]) % modulo\n\n # The `ways[0]` value represents the number of ways to reach the top of the staircase\n return ways[0]\n```\n# RUBY\n```\ndef num_ways(steps, max_position)\n @max = max_position - 1\n @memo = Array.new(max_position) { {} }\n ways(0, steps) % 1000000007\nend\n\ndef ways(current_position, remaining_steps)\n return (current_position == 0 ? 1 : 0) if remaining_steps == 0\n return @memo[current_position][remaining_steps] if @memo[current_position][remaining_steps]\n\n total = ways(current_position, remaining_steps - 1)\n total += ways(current_position - 1, remaining_steps - 1) unless current_position == 0\n total += ways(current_position + 1, remaining_steps - 1) unless current_position == @max\n\n @memo[current_position][remaining_steps] = total\nend\n\n```\n\n# C++\n```\nconst int MOD = 1e9 + 7;\n\nconst int maxPositions = 250 + 3;\nconst int maxSteps = 500 + 3;\n\nclass Solution {\npublic:\n int dp[maxSteps][maxPositions];\n\n int calculateWays(int currentPosition, int remainingSteps, int maxPosition) {\n if (remainingSteps == 0)\n return dp[remainingSteps][currentPosition] = (currentPosition == 0) ? 1 : 0;\n\n if (dp[remainingSteps][currentPosition] != -1)\n return dp[remainingSteps][currentPosition];\n\n int ways = 0;\n for (int dir = -1; dir <= 1; dir++) {\n int nextPosition = currentPosition + dir;\n\n if (nextPosition >= remainingSteps)\n continue;\n\n if (nextPosition >= 0 && nextPosition < maxPosition) {\n ways += calculateWays(nextPosition, remainingSteps - 1, maxPosition);\n ways %= MOD;\n }\n }\n\n return dp[remainingSteps][currentPosition] = ways;\n }\n\n int numWays(int steps, int maxPosition) {\n memset(dp, -1, sizeof(dp));\n return calculateWays(0, steps, maxPosition);\n }\n};\n\n```\n# Java\n```\nclass Solution {\n public int numWays(int steps, int arrLen) {\n if (arrLen == 1) {\n return 1;\n }\n \n arrLen = Math.min(steps / 2 + 1, arrLen);\n long modulo = 1_000_000_007;\n\n long[] current = new long[arrLen];\n current[0] = 1;\n current[1] = 1;\n long[] next = new long[arrLen];\n\n for (int i = 2; i <= steps; i++) {\n int maxPos = Math.min(i + 1, arrLen);\n next[0] = (current[0] + current[1]) % modulo;\n for (int j = 1; j < maxPos - 1; j++) {\n next[j] = (current[j - 1] + current[j] + current[j + 1]) % modulo;\n }\n next[maxPos - 1] = (current[maxPos - 2] + current[maxPos - 1]) % modulo;\n\n long[] temp = current;\n current = next;\n next = temp;\n }\n\n return (int) current[0];\n }\n}\n\n```\n\n# JavaScript\n```\nvar numWays = function(numSteps, arrayLength) {\n // Define a modulus value for taking the modulo operation to avoid overflow.\n const mod = 1000000007;\n\n // Calculate the maximum position the pointer can reach, which is the minimum of numSteps/2 and arrayLength - 1.\n const maxPosition = Math.min(Math.floor(numSteps / 2), arrayLength - 1);\n\n // Create a 2D array dp to store the number of ways to reach a specific position at each step.\n const dp = new Array(numSteps + 1).fill().map(() => new Array(maxPosition + 1).fill(0));\n\n // Initialize the number of ways to stay at position 0 after 0 steps to 1.\n dp[0][0] = 1;\n\n // Loop through the number of steps.\n for (let i = 1; i <= numSteps; i++) {\n for (let j = 0; j <= maxPosition; j++) {\n // Initialize the number of ways to stay at the current position with the number of ways to stay at the same position in the previous step.\n dp[i][j] = dp[i - 1][j];\n\n // If the current position is greater than 0, add the number of ways to reach it by moving left.\n if (j > 0) {\n dp[i][j] = (dp[i][j] + dp[i - 1][j - 1]) % mod;\n }\n\n // If the current position is less than the maximum position, add the number of ways to reach it by moving right.\n if (j < maxPosition) {\n dp[i][j] = (dp[i][j] + dp[i - 1][j + 1]) % mod;\n }\n }\n }\n\n // The final result is stored in dp[numSteps][0], representing the number of ways to reach the initial position after taking \'numSteps\' steps.\n return dp[numSteps][0];\n};\n\n\n```\n# PHP\n```\nclass Solution {\n function numWays($numSteps, $arrayLength) {\n // Define a modulus value for taking the modulo operation to avoid overflow.\n $mod = 1000000007;\n \n // Calculate the maximum position the pointer can reach, which is the minimum of numSteps/2 and arrayLength - 1.\n $maxPosition = min($numSteps / 2, $arrayLength - 1);\n \n // Create a 2D array dp to store the number of ways to reach a specific position at each step.\n $dp = array_fill(0, $numSteps + 1, array_fill(0, $maxPosition + 1, 0));\n \n // Initialize the number of ways to stay at position 0 after 0 steps to 1.\n $dp[0][0] = 1;\n \n // Loop through the number of steps.\n for ($i = 1; $i <= $numSteps; $i++) {\n for ($j = 0; $j <= $maxPosition; $j++) {\n // Initialize the number of ways to stay at the current position with the number of ways to stay at the same position in the previous step.\n $dp[$i][$j] = $dp[$i - 1][$j];\n \n // If the current position is greater than 0, add the number of ways to reach it by moving left.\n if ($j > 0) {\n $dp[$i][$j] = ($dp[$i][$j] + $dp[$i - 1][$j - 1]) % $mod;\n }\n \n // If the current position is less than the maximum position, add the number of ways to reach it by moving right.\n if ($j < $maxPosition) {\n $dp[$i][$j] = ($dp[$i][$j] + $dp[$i - 1][$j + 1]) % $mod;\n }\n }\n }\n \n // The final result is stored in dp[numSteps][0], representing the number of ways to reach the initial position after taking \'numSteps\' steps.\n return $dp[$numSteps][0];\n }\n}\n\n``` | 29 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Beats 99% | Optimised Solution Using Dynamic Programming | Easy O(steps * maxPosition) Solution | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to count the number of ways to stay at index 0 in an array of length arrLen after taking steps steps. You can move one step to the left, one step to the right, or stay in the same place at each step. To solve this problem, dynamic programming can be used to keep track of the number of ways to reach each position at each step.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a constant `MOD` for taking the result modulo 10^9 + 7, a variable `maxPosition` as the maximum position to avoid going out of bounds, and a vector `dp` to keep track of the number of ways to reach each position.\n\n2. Initialize `dp[0]` to 1 because initially, you are at position 0 after 0 steps.\n\n3. Use a nested loop to iterate for each step from 1 to `steps`.\n\n4. Inside the nested loop, create a new vector `new_dp` to store the updated values for the number of ways.\n\n5. Iterate for each position j from 0 to `maxPosition`.\n\n6. Update `new_dp[j]` by considering three possibilities:\n\n7. Stay in the same place, which is `dp[j]`.\n\n8. Move one step to the left if `j > 0`, which is `dp[j - 1]`.\n\n9. Move one step to the right if `j < maxPosition`, which is `dp[j + 1]`.\n\n10. Update `dp` to be equal to `new_dp` for the next iteration.\n\n11. After all iterations, the result is stored in `dp[0]`, which represents the number of ways to stay at index 0 after `steps` steps.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(steps * maxPosition), where `steps` is the input number of steps and `maxPosition` is the minimum of `steps / 2` and `arrLen - 1`. In the worst case, this solution has a time complexity of O(steps * min(steps/2, arrLen)).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this solution is O(maxPosition) to store the dynamic programming array `dp` and `new_dp`.\n# Code\n```\nclass Solution {\npublic:\n int numWays(int steps, int arrLen) {\n int MOD = 1000000007;\n int maxPosition = min(steps / 2, arrLen - 1);\n vector<long long> dp(maxPosition + 1, 0);\n dp[0] = 1;\n\n for (int i = 1; i <= steps; i++) {\n vector<long long> new_dp(maxPosition + 1, 0);\n for (int j = 0; j <= maxPosition; j++) {\n new_dp[j] = dp[j];\n if (j > 0)\n new_dp[j] = (new_dp[j] + dp[j - 1]) % MOD;\n if (j < maxPosition)\n new_dp[j] = (new_dp[j] + dp[j + 1]) % MOD;\n }\n dp = new_dp;\n }\n return dp[0];\n }\n};\n``` | 3 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
✅☑[C++/C/Java/Python/JavaScript] || 3 Approaches || EXPLAINED🔥 | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### *Approach 1(Top Down DP)*\n\n1. **Class Definition:** The code defines a class called Solution.\n\n1. **Member Variables:**\n\n - **memo:** A 2D vector to store the memoization table for dynamic programming.\n - **MOD:** A constant for the modulo operation.\n - **arrLen:** A variable to store the minimum of `arrLen` and `steps`.\n1. **dp Function:**\n\n - This is a recursive function that calculates the number of ways to reach a certain state (index and remaining steps).\n - It takes two arguments: `curr` (current index) and `remain` (remaining steps).\n - **Base case:**\n - If there are no remaining steps (`remain == 0`), it checks if the current index is at position 0 (`curr == 0`). If true, it returns 1 (indicating a valid way); otherwise, it returns 0.\n - **Memoization:**\n - It checks if the result for the current state ( ) is already stored in the `memo` table. If found, it returns the memoized result.\n - **Recursive Computation:**\n - It computes the result by recursively calling `dp` for three possible scenarios:\n - Moving to the same position (`dp(curr, remain - 1)`).\n - Moving one step to the left (`dp(curr - 1, remain - 1)`), if it\'s a valid move (checking if `curr > 0`).\n - Moving one step to the right (`dp(curr + 1, remain - 1)`), if it\'s a valid move (checking if `curr < arrLen - 1`).\n - It calculates the sum of these scenarios while considering the modulo operation with `MOD`.\n - Finally, it stores the computed result in the `memo` table and returns it.\n1. **numWays Function:**\n\n - This function is the entry point for calculating the number of ways.\n - It takes two arguments: `steps` (total steps allowed) and `arrLen` (the length of the array).\n - It first sets `arrLen` to the minimum of `arrLen` and `steps`.\n - It initializes the `memo` table as a 2D vector with dimensions `[arrLen][steps + 1]`, filled with `-1` to indicate that no values have been computed yet.\n - It calls the `dp` function with initial arguments (`0, steps`) to start the recursive computation.\n - The result is the number of ways to reach the index 0 within `steps` steps.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n\u22C5min(n,m))$$\n \n\n- *Space complexity:*\n $$O(n\u22C5min(n,m))$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n vector<vector<int>> memo;\n int MOD = 1e9 + 7;\n int arrLen;\n \n int dp(int curr, int remain) {\n if (remain == 0) {\n if (curr == 0) {\n return 1;\n }\n \n return 0;\n }\n \n if (memo[curr][remain] != -1) {\n return memo[curr][remain];\n }\n\n int ans = dp(curr, remain - 1);\n if (curr > 0) {\n ans = (ans + dp(curr - 1, remain - 1)) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + dp(curr + 1, remain - 1)) % MOD;\n }\n \n memo[curr][remain] = ans;\n return ans;\n }\n \n int numWays(int steps, int arrLen) {\n arrLen = min(arrLen, steps);\n this->arrLen = arrLen;\n memo = vector(arrLen, vector(steps + 1, -1));\n return dp(0, steps);\n }\n};\n\n```\n\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nint MOD = 1000000007;\n\nint **memo;\nint arrLen;\n\nint dp(int curr, int remain) {\n if (remain == 0) {\n if (curr == 0) {\n return 1;\n }\n return 0;\n }\n\n if (memo[curr][remain] != -1) {\n return memo[curr][remain];\n }\n\n int ans = dp(curr, remain - 1);\n if (curr > 0) {\n ans = (ans + dp(curr - 1, remain - 1)) % MOD;\n }\n\n if (curr < arrLen - 1) {\n ans = (ans + dp(curr + 1, remain - 1)) % MOD;\n }\n\n memo[curr][remain] = ans;\n return ans;\n}\n\nint numWays(int steps, int arrLen) {\n arrLen = arrLen < steps ? arrLen : steps;\n memo = (int **)malloc(arrLen * sizeof(int *));\n for (int i = 0; i < arrLen; i++) {\n memo[i] = (int *)malloc((steps + 1) * sizeof(int));\n for (int j = 0; j <= steps; j++) {\n memo[i][j] = -1;\n }\n }\n\n int result = dp(0, steps);\n\n // Clean up memory\n for (int i = 0; i < arrLen; i++) {\n free(memo[i]);\n }\n free(memo);\n\n return result;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n int[][] memo;\n int MOD = (int) 1e9 + 7;\n int arrLen;\n \n public int dp(int curr, int remain) {\n if (remain == 0) {\n if (curr == 0) {\n return 1;\n }\n \n return 0;\n }\n \n if (memo[curr][remain] != -1) {\n return memo[curr][remain];\n }\n\n int ans = dp(curr, remain - 1);\n if (curr > 0) {\n ans = (ans + dp(curr - 1, remain - 1)) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + dp(curr + 1, remain - 1)) % MOD;\n }\n \n memo[curr][remain] = ans;\n return ans;\n }\n \n public int numWays(int steps, int arrLen) {\n arrLen = Math.min(arrLen, steps);\n this.arrLen = arrLen;\n memo = new int[arrLen][steps + 1];\n for (int[] row : memo) {\n Arrays.fill(row, -1);\n }\n \n return dp(0, steps);\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n @cache\n def dp(curr, remain):\n if remain == 0:\n if curr == 0:\n return 1\n \n return 0\n \n ans = dp(curr, remain - 1)\n if curr > 0:\n ans = (ans + dp(curr - 1, remain - 1)) % MOD\n \n if curr < arrLen - 1:\n ans = (ans + dp(curr + 1, remain - 1)) % MOD\n \n return ans\n \n MOD = 10 ** 9 + 7\n return dp(0, steps)\n\n```\n\n\n```javascript []\n\n```\n\n\n---\n\n#### *Approach 2(Bottom Up DP)*\n\n1. **numWays Function:**\n\n - This function calculates the number of ways to reach index 0 in an array with a given number of steps while following specific rules.\n1. **Variables:**\n\n - **MOD:** A constant for the modulo operation.\n - **arrLen:** It\'s set to the minimum of arrLen and steps.\n - **dp:** A 2D vector to store dynamic programming results.\n1. **Initialization:**\n\n - The code initializes `dp` as a 2D vector of dimensions `[arrLen][steps + 1]` and initializes all values to 0, except for `dp[0][0]`, which is set to 1 (starting point).\n1. **Dynamic Programming Loop:**\n\n - The function uses a nested loop to compute the dynamic programming results.\n - The outer loop iterates from `remain = 1` to `steps`, representing the remaining steps.\n - The inner loop iterates in reverse order from `curr = arrLen - 1` down to `0`, representing the current position.\n1. **Calculating ans:**\n\n - `ans` is a variable to store the number of ways to reach the current position (`curr`) with the given number of remaining steps (`remain`).\n - Initially, it\'s set to the value from the previous step `dp[curr][remain - 1]`.\n1. **Checking Valid Moves:**\n\n - It checks two possible moves:\n - Moving one step to the left if `curr > 0`, and adds `dp[curr - 1][remain - 1]` to ans.\n - Moving one step to the right if `curr < arrLen - 1`, and adds `dp[curr + 1][remain - 1]` to `ans`.\n1. **Modulo Operation:**\n\n - After updating `ans`, it applies the modulo operation with `MOD` to prevent integer overflow.\n1. **Updating dp Table:**\n\n- The calculated `ans` is stored in the `dp` table for the current position `curr` and remaining steps `remain`.\n1. **Return Result:**\n\nThe final result is the number of ways to reach index 0 `(dp[0][steps])`.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n\u22C5min(n,m))$$\n \n\n- *Space complexity:*\n $$O(n\u22C5min(n,m))$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numWays(int steps, int arrLen) {\n int MOD = 1e9 + 7;\n arrLen = min(arrLen, steps);\n vector<vector<int>> dp(arrLen, vector(steps + 1, 0));\n dp[0][0] = 1;\n \n for (int remain = 1; remain <= steps; remain++) {\n for (int curr = arrLen - 1; curr >= 0; curr--) {\n int ans = dp[curr][remain - 1];\n \n if (curr > 0) {\n ans = (ans + dp[curr - 1][remain - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + dp[curr + 1][remain - 1]) % MOD;\n }\n \n dp[curr][remain] = ans;\n }\n }\n \n return dp[0][steps];\n }\n};\n```\n\n\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\nint min(int a, int b) {\n return (a < b) ? a : b;\n}\n\nint numWays(int steps, int arrLen) {\n int MOD = 1000000007;\n arrLen = min(arrLen, steps);\n int dp[arrLen][steps + 1];\n \n for (int i = 0; i < arrLen; i++) {\n for (int j = 0; j <= steps; j++) {\n dp[i][j] = 0;\n }\n }\n \n dp[0][0] = 1;\n \n for (int remain = 1; remain <= steps; remain++) {\n for (int curr = arrLen - 1; curr >= 0; curr--) {\n int ans = dp[curr][remain - 1];\n \n if (curr > 0) {\n ans = (ans + dp[curr - 1][remain - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + dp[curr + 1][remain - 1]) % MOD;\n }\n \n dp[curr][remain] = ans;\n }\n }\n \n return dp[0][steps];\n}\n\nint main() {\n int steps = 3;\n int arrLen = 2;\n int result = numWays(steps, arrLen);\n printf("Number of ways: %d\\n", result);\n return 0;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public int numWays(int steps, int arrLen) {\n int MOD = (int) 1e9 + 7;\n arrLen = Math.min(arrLen, steps);\n int[][] dp = new int[arrLen][steps + 1];\n dp[0][0] = 1;\n \n for (int remain = 1; remain <= steps; remain++) {\n for (int curr = arrLen - 1; curr >= 0; curr--) {\n int ans = dp[curr][remain - 1];\n \n if (curr > 0) {\n ans = (ans + dp[curr - 1][remain - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + dp[curr + 1][remain - 1]) % MOD;\n }\n \n dp[curr][remain] = ans;\n }\n }\n \n return dp[0][steps];\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n MOD = 10 ** 9 + 7\n arrLen = min(arrLen, steps)\n dp = [[0] * (steps + 1) for _ in range(arrLen)]\n dp[0][0] = 1\n \n for remain in range(1, steps + 1):\n for curr in range(arrLen - 1, -1, -1):\n ans = dp[curr][remain - 1]\n \n if curr > 0:\n ans = (ans + dp[curr - 1][remain - 1]) % MOD\n \n if curr < arrLen - 1:\n ans = (ans + dp[curr + 1][remain - 1]) % MOD\n \n dp[curr][remain] = ans\n \n return dp[0][steps]\n```\n\n\n```javascript []\nfunction numWays(steps, arrLen) {\n const MOD = 1000000007;\n arrLen = Math.min(arrLen, steps);\n const dp = new Array(arrLen).fill(0).map(() => new Array(steps + 1).fill(0));\n \n dp[0][0] = 1;\n \n for (let remain = 1; remain <= steps; remain++) {\n for (let curr = arrLen - 1; curr >= 0; curr--) {\n let ans = dp[curr][remain - 1];\n \n if (curr > 0) {\n ans = (ans + dp[curr - 1][remain - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + dp[curr + 1][remain - 1]) % MOD;\n }\n \n dp[curr][remain] = ans;\n }\n }\n \n return dp[0][steps];\n}\n\nconst steps = 3;\nconst arrLen = 2;\nconst result = numWays(steps, arrLen);\nconsole.log("Number of ways:", result);\n\n```\n\n\n---\n#### *Approach 3(Space Optimized DP)*\n\n1. The function `numWays` takes two parameters: `steps`, which represents the total number of steps allowed, and `arrLen`, which is the length of the array.\n\n1. It defines the constant `MOD` to be 1e9 + 7, which is used to perform modulo operations to prevent integer overflow.\n\n1. To ensure that `arrLen` does not exceed the number of steps available, it sets `arrLen` to the minimum of `arrLen` and `steps`.\n\n1. It initializes two vectors, `dp` and `prevDp`, both of size `arrLen`, to keep track of dynamic programming values.\n\n1. The `prevDp` vector is initialized with a single element set to 1. This represents the starting point where there\'s only one way to reach index 0 (no steps taken).\n\n1. It enters a loop that iterates through the number of remaining steps, from 1 up to `steps`.\n\n1. Inside the loop, it reinitializes the `dp` vector to all 0s. This vector represents the dynamic programming values for the current number of remaining steps.\n\n1. It then enters a nested loop that iterates through each possible index `curr` in the range from `arrLen - 1` down to 0. This represents considering the array length and the possible positions at each step.\n\n1. For each `curr`, it calculates the number of ways to reach that position in the current step (`remain`). It uses the dynamic programming values from the previous step (`prevDp`) to calculate this. The calculation takes into account the possibilities of staying in the same position or moving one step left or right if those positions are within bounds.\n\n1. The computed value is stored in the `dp[curr]` vector for the current step.\n\n1. After completing the inner loop, the `prevDp` vector is updated with the values from the `dp` vector. This is done to prepare for the next iteration of the loop.\n\n1. Once the loop finishes, the final result is in the `dp[0]` element of the vector, which represents the number of ways to reach index 0 within the given number of steps.\n\n1. The function returns this value as the answer.\n\n# Complexity\n- *Time complexity:*\n $$O(n\u22C5min(n,m))$$\n \n\n- *Space complexity:*\n $$O(min(n,m))$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numWays(int steps, int arrLen) {\n int MOD = 1e9 + 7;\n arrLen = min(arrLen, steps);\n vector<int> dp(arrLen, 0);\n vector<int> prevDp(arrLen, 0);\n prevDp[0] = 1;\n \n for (int remain = 1; remain <= steps; remain++) {\n dp = vector(arrLen, 0);\n \n for (int curr = arrLen - 1; curr >= 0; curr--) {\n int ans = prevDp[curr];\n \n if (curr > 0) {\n ans = (ans + prevDp[curr - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + prevDp[curr + 1]) % MOD;\n }\n \n dp[curr] = ans;\n }\n \n prevDp = dp;\n }\n \n return dp[0];\n }\n};\n```\n\n\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <stdbool.h>\n\nint numWays(int steps, int arrLen) {\n int MOD = 1000000007;\n arrLen = arrLen < steps ? arrLen : steps;\n \n int* dp = (int*)malloc(arrLen * sizeof(int));\n int* prevDp = (int*)malloc(arrLen * sizeof(int));\n \n for (int i = 0; i < arrLen; i++) {\n dp[i] = 0;\n prevDp[i] = 0;\n }\n \n prevDp[0] = 1;\n \n for (int remain = 1; remain <= steps; remain++) {\n for (int curr = arrLen - 1; curr >= 0; curr--) {\n int ans = prevDp[curr];\n \n if (curr > 0) {\n ans = (ans + prevDp[curr - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + prevDp[curr + 1]) % MOD;\n }\n \n dp[curr] = ans;\n }\n \n // Swap dp and prevDp arrays for the next iteration\n int* temp = dp;\n dp = prevDp;\n prevDp = temp;\n }\n \n int result = dp[0];\n \n free(dp);\n free(prevDp);\n \n return result;\n}\n\nint main() {\n int steps = 3;\n int arrLen = 2;\n \n int ways = numWays(steps, arrLen);\n \n printf("Number of Ways: %d\\n", ways);\n \n return 0;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public int numWays(int steps, int arrLen) {\n int MOD = (int) 1e9 + 7;\n arrLen = Math.min(arrLen, steps);\n int[] dp = new int[arrLen];\n int[] prevDp = new int[arrLen];\n prevDp[0] = 1;\n \n for (int remain = 1; remain <= steps; remain++) {\n dp = new int[arrLen];\n \n for (int curr = arrLen - 1; curr >= 0; curr--) {\n int ans = prevDp[curr];\n if (curr > 0) {\n ans = (ans + prevDp[curr - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + prevDp[curr + 1]) % MOD;\n }\n \n dp[curr] = ans;\n }\n \n prevDp = dp;\n }\n \n return dp[0];\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n MOD = 10 ** 9 + 7\n arrLen = min(arrLen, steps)\n dp = [0] * (arrLen)\n prevDp = [0] * (arrLen)\n prevDp[0] = 1\n \n for remain in range(1, steps + 1):\n dp = [0] * (arrLen)\n \n for curr in range(arrLen - 1, -1, -1):\n ans = prevDp[curr]\n \n if curr > 0:\n ans = (ans + prevDp[curr - 1]) % MOD\n \n if curr < arrLen - 1:\n ans = (ans + prevDp[curr + 1]) % MOD\n \n dp[curr] = ans\n \n prevDp = dp\n \n return dp[0]\n```\n\n\n```javascript []\nfunction numWays(steps, arrLen) {\n const MOD = 1000000007;\n arrLen = Math.min(arrLen, steps);\n \n let dp = new Array(arrLen).fill(0);\n let prevDp = new Array(arrLen).fill(0);\n \n prevDp[0] = 1;\n \n for (let remain = 1; remain <= steps; remain++) {\n for (let curr = arrLen - 1; curr >= 0; curr--) {\n let ans = prevDp[curr];\n \n if (curr > 0) {\n ans = (ans + prevDp[curr - 1]) % MOD;\n }\n \n if (curr < arrLen - 1) {\n ans = (ans + prevDp[curr + 1]) % MOD;\n }\n \n dp[curr] = ans;\n }\n \n // Swap dp and prevDp arrays for the next iteration\n [dp, prevDp] = [prevDp, dp];\n }\n \n return dp[0];\n}\n\nconst steps = 3;\nconst arrLen = 2;\n\nconst ways = numWays(steps, arrLen);\nconsole.log("Number of Ways: " + ways);\n\n```\n\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Python3 Solution | number-of-ways-to-stay-in-the-same-place-after-some-steps | 0 | 1 | \n\n```\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n mod=10**9+7\n n=min(arrLen,steps//2+1)\n ways=[1]+[0]*(n-1)\n for step in range(steps):\n ways=[sum(ways[max(0,i-1):i+2])%mod for i in range(min(step+2,steps-step,n))]\n return ways[0] \n``` | 2 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Python 36ms no caching :) | number-of-ways-to-stay-in-the-same-place-after-some-steps | 0 | 1 | This is very similar to all the other DP approaches here.\n\nThe technique with using a `prev` variable that starts at `0` is one I found from this nice solution: https://leetcode.com/problems/number-of-ways-to-stay-in-the-same-place-after-some-steps/solutions/4169508/beats-99-44-7-lines-1d-dp-python-3/\n\nHowever, there is another optimisation that I don\'t see many solutions using (I haven\'t found any! Not even the official editorial does any of this! But I don\'t understand how to search for solutions very well, so maybe I missed them).\n\nNamely, say $$f(n, k)$$ is the number of ways to get from $$0$$ to $$n$$ in $$k$$ steps. This is also the number of ways to get from $$n$$ to $$0$$, by symmetry. Therefore,\n\n$$\\displaystyle f(0, k_1 + k_2) = \\sum_n f(n, k_1)f(n, k_2)$$.\n\nThis can be viewed as a special case of the fact that the number of ways to get from $$a$$ to $$b$$ is an entry in the $$k$$th power of the adjacency matrix, which is symmetric.\n\nIn particular, this means that we can get away with only calculating half the steps! This ought to make the solution roughly twice as fast for very large inputs.\n\nNow since we are doing `steps // 2` iterations on `dp`, which has length roughly `steps // 2`, we can save another factor of roughly 2 in the worst case by not iterating over all of `dp` every time (see the `islice`).\n\nLastly, in the case where `arrLen` is too big, the question is actually just to compute the `steps`th Motzkin number, which is a well-understood problem - we can do that in linear time.\n\nIn general to scale this up to much larger inputs, you would have to reduce modulo $$p$$ at each stage, and calculate multiplicative inverses modulo $$p$$ in the Motzkin number calculation. However the inputs seem to be small enough that this doesn\'t really save time - a very rough asymptotic for the Motzkin numbers is $$3^n$$, so for $n = 500$ the numbers we\'re working with will have roughly 800 bits, and most of the test cases will be much less than that. This is still well within Python\'s capabilities to handle. Technically this means that in this implementation, the Motzkin calculation takes quadratic time and the main calculation takes cubic time, but this is easy to fix if you\'re interested in larger inputs.\n\nThere is some literature on the combinatorics of these numbers `numWays(m, n)`. As I mentioned, in the case `n >= m // 2 + 1`, it\'s just the `m`th Motzkin number. For some small, fixed values of `n`, there are some useful known recurrences. For `n = 3, 4, 5, 6, 7`, the sequence appears in the OEIS:\n- 3: https://oeis.org/A024537\n- 4: https://oeis.org/A005207\n- 5: https://oeis.org/A094286\n- 6: https://oeis.org/A094287\n- 7: https://oeis.org/A094288\n\nParticularly `n = 3, 4` have some funny recurrences and relations to other famous sequences. (These recurrences won\'t make anything particularly faster, since for small `n`, the size of `dp` is small, so it\'s effectively a linear recurrence involving a small number of terms anyway). In the last 3, a general formula is mentioned, in terms of trigonometric functions, which is derived from the linear algebra of the adjacency matrix (which is a tridiagonal Toeplitz matrix). This formula is equation (4) in https://cs.uwaterloo.ca/journals/JIS/VOL18/Felsner/felsner2.html. This paper refers to these numbers as "bounded Motzkin numbers".\n\nSadly I don\'t see a way to use this theory to make the code substantially faster!\n\n# Code\n```python\nP = 10 ** 9 + 7\n\n# compute nth Motzkin number modulo p\n# we could easily just cache all the Motzkin numbers to make this O(1)\n# but it\'s already linear time anyway so who cares\ndef motz(n):\n a, b = 1, 1\n for k in range(2, n + 1):\n # we could work modulo p in each step, but actually\n # the test cases are all small enough that this doesn\'t save time\n a, b = b, ((2 * k + 1) * b + (3 * k - 3) * a) // (k + 2)\n return b % P\n\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n if arrLen >= steps // 2 + 1:\n return motz(steps)\n dp = [0] * (arrLen + 1)\n dp[0] = 1\n for j in range(steps // 2):\n prev = 0\n for i, (dpi, dpni) in islice(enumerate(pairwise(dp)), j + 2):\n dp[i] += prev + dpni\n prev = dpi\n if steps & 1:\n total = 0\n prev = 0\n for i, (dpi, dpni) in enumerate(pairwise(dp)):\n total += dpi * (prev + dpi + dpni)\n prev = dpi\n return total % P\n else:\n return sum(map((2).__rpow__, dp)) % P\n```\n\nI did some timings comparing a few different approaches on much larger inputs (up to $$\\mathrm{steps} = 10^7$$ in the case `arrLen >= steps // 2 + 1`, and up to $$\\mathrm{steps} = 6000$$ on CPython and up to $$\\mathrm{steps} = 10^5$$ on PyPy in the case `arrLen < steps // 2 + 1`). These timings can be found [here](https://gist.github.com/goedel-gang/1f551222cad67292db24d78483c6b3e1). I produced some graphs as well, which you can find at that link. Here I attach the two most important ones:\n\n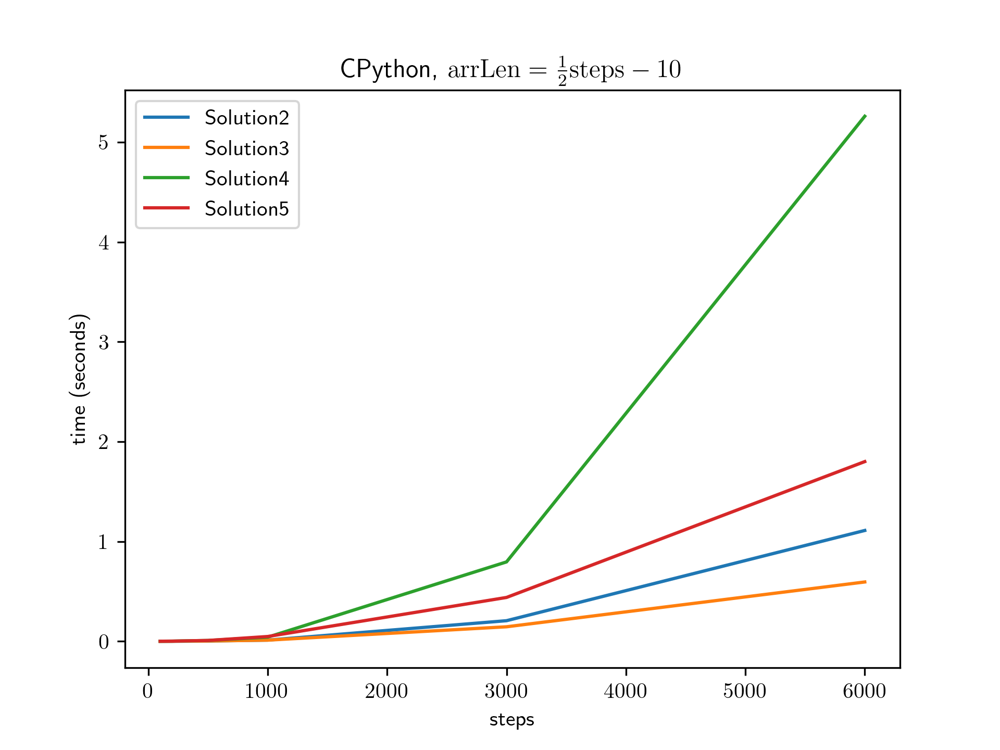\n\n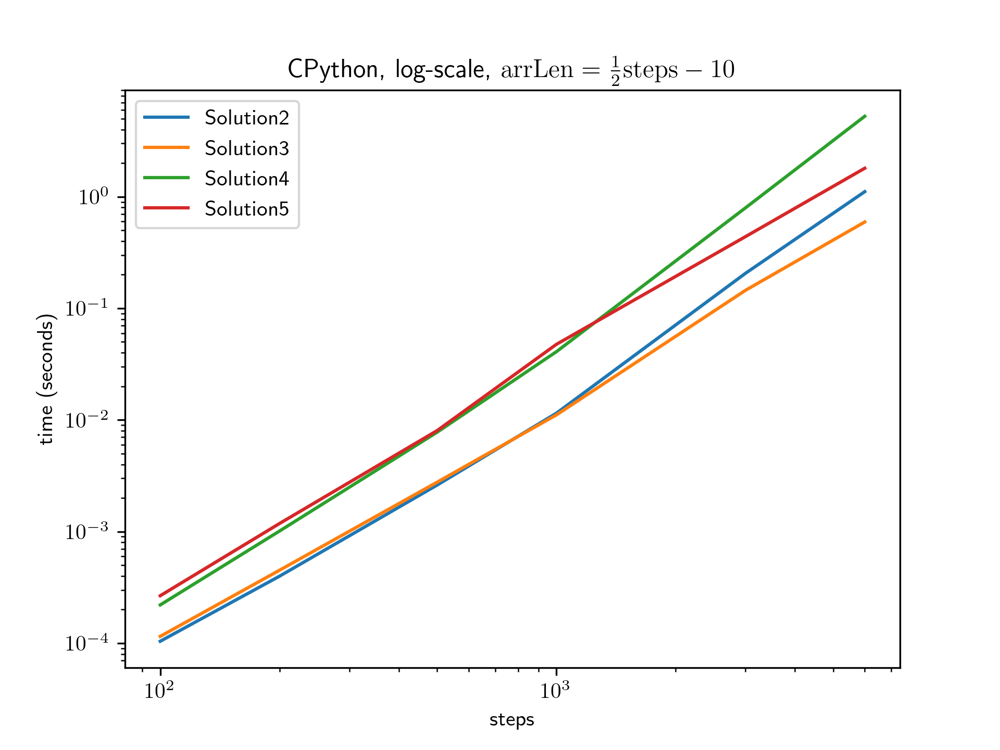\n\n\n\nThe blue line is my solution with no reduction modulo $$p$$ at each stage, and the orange line is my solution with reduction modulo $$p$$ at each stage.\n\nThe green line is the solution from the other post I linked, and the red line is that solution with reduction modulo $$p$$ at each stage.\n\nThis is a logarithmic scale, so the blue and orange lines are pretty fast! My predicted improvement of a factor of about 4 seems to be correct.\n\nLastly, here is a cheeky C implementation for the C enjoyers out there :)\n```C\n#include <sys/param.h>\n\nint numWays(int steps, int arrLen){\n arrLen = MIN(arrLen, steps / 2 + 1);\n int P = 1000000007;\n long *dp = (long *)calloc(arrLen + 1, sizeof(long));\n long prev, tmp, total;\n dp[0] = 1;\n for (int j = 0; j < steps / 2; j++) {\n prev = 0;\n for (int i = 0; i < j + 2 && i < arrLen; i++) {\n tmp = dp[i];\n dp[i] += prev + dp[i + 1];\n dp[i] %= P;\n prev = tmp;\n }\n }\n total = 0;\n if (steps & 1) {\n prev = 0;\n for (int i = 0; i < arrLen; i++) {\n total += (dp[i] * (prev + dp[i] + dp[i + 1])) % P;\n prev = dp[i];\n }\n } else {\n for (int i = 0; i < arrLen; i++) {\n total += (dp[i] * dp[i]) % P;\n }\n }\n free(dp);\n return total % P;\n}\n``` | 1 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Mastering Dynamic Programming: Counting Ways to Reach a Position in an Array | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | # Counting Ways to Reach a Position in an Array\n\n## Approach 1: Recursion\n\n### Explanation\nIn this approach, we\'ll use a recursive function to explore all possible ways to reach a specific position in an array after a given number of steps. The key idea is to consider three options at each step: staying in the current position, moving one step to the right, or moving one step to the left. We\'ll use recursion to explore all these possibilities.\n\n### Dry Run\nLet\'s consider an example: we want to find the number of ways to reach position 2 in an array after 3 steps. We\'ll start with `Recursion_Solution(3, arrLen, 2)`.\n\n1. At step 3, we have 3 options:\n - Stay in the current position: `Recursion_Solution(2, arrLen, 2)`\n - Move one step to the right: `Recursion_Solution(2, arrLen, 3)`\n - Move one step to the left: `Recursion_Solution(2, arrLen, 1)`\n\n2. We continue this process, exploring all possibilities until we reach the base cases:\n - If steps = 0 and pos = 0, return 1.\n - If steps = 0 and pos is not 0, return 0.\n - If steps become negative or pos goes out of bounds, return 0.\n\n3. The total count of ways to reach position 2 after 3 steps is the sum of all possibilities.\n\n### Edge Cases\n- We need to handle cases where the number of steps becomes negative or the position goes out of bounds.\n\n### Complexity Analysis\n- Time Complexity: O(3^steps) in the worst case, where "steps" is the number of steps.\n- Space Complexity: O(steps) for the recursion stack.\n\n### Codes : \n```cpp []\nstatic int MOD = 1e9 + 7;\nclass Solution\n{\n public:\n int Recursion_Solution(int steps, int arrLen, int pos)\n {\n if (steps == 0 and pos == 0) return 1;\n if (steps == 0 and pos != 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n return (Recursion_Solution(steps - 1, arrLen, pos) % MOD // stay\n + Recursion_Solution(steps - 1, arrLen, pos + 1) % MOD // right\n + Recursion_Solution(steps - 1, arrLen, pos - 1) % MOD); // left\n }\n\n int numWays(int steps, int arrLen)\n {\n return Recursion_Solution(steps, arrLen, 0);\n }\n};\n```\n\n```java []\nclass Solution {\n private static final int MOD = 1000000007;\n\n public int Recursion_Solution(int steps, int arrLen, int pos) {\n if (steps == 0 && pos == 0) return 1;\n if (steps == 0 && pos != 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n return (Recursion_Solution(steps - 1, arrLen, pos) % MOD // stay\n + Recursion_Solution(steps - 1, arrLen, pos + 1) % MOD // right\n + Recursion_Solution(steps - 1, arrLen, pos - 1) % MOD); // left\n }\n\n public int numWays(int steps, int arrLen) {\n return Recursion_Solution(steps, arrLen, 0);\n }\n}\n```\n\n\n```python []\nMOD = 10**9 + 7\n\nclass Solution:\n def Recursion_Solution(self, steps, arrLen, pos):\n if steps == 0 and pos == 0:\n return 1\n if steps == 0 and pos != 0:\n return 0\n if steps < 0 or pos < 0 or pos >= arrLen:\n return 0\n return (self.Recursion_Solution(steps - 1, arrLen, pos) % MOD # stay\n + self.Recursion_Solution(steps - 1, arrLen, pos + 1) % MOD # right\n + self.Recursion_Solution(steps - 1, arrLen, pos - 1) % MOD) # left\n\n def numWays(self, steps, arrLen):\n return self.Recursion_Solution(steps, arrLen, 0)\n```\n\n\n```javascript []\ncvar MOD = 1000000007;\n\nvar Recursion_Solution = function (steps, arrLen, pos) {\n if (steps === 0 && pos === 0) return 1;\n if (steps === 0 && pos !== 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n return (\n (Recursion_Solution(steps - 1, arrLen, pos) % MOD) + // stay\n (Recursion_Solution(steps - 1, arrLen, pos + 1) % MOD) + // right\n (Recursion_Solution(steps - 1, arrLen, pos - 1) % MOD)\n ); // left\n};\n\nvar numWays = function (steps, arrLen) {\n return Recursion_Solution(steps, arrLen, 0);\n};\n\n```\n\n```csharp []\npublic class Solution {\n private static int MOD = 1000000007;\n\n public int Recursion_Solution(int steps, int arrLen, int pos) {\n if (steps == 0 && pos == 0) return 1;\n if (steps == 0 && pos != 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n return (Recursion_Solution(steps - 1, arrLen, pos) % MOD // stay\n + Recursion_Solution(steps - 1, arrLen, pos + 1) % MOD // right\n + Recursion_Solution(steps - 1, arrLen, pos - 1) % MOD); // left\n }\n\n public int NumWays(int steps, int arrLen) {\n return Recursion_Solution(steps, arrLen, 0);\n }\n}\n```\n\n\n---\n\n## Approach 2: Top-Down Dynamic Programming\n\n### Explanation\nIn this approach, we\'ll use top-down dynamic programming to solve the problem. We\'ll maintain a 2D array `dp` to store the number of ways to reach a specific position in the array. We\'ll use recursion to calculate these values based on three possible moves: stay, move right, and move left. We\'ll apply modular arithmetic to handle large numbers.\n\n### Dry Run\nLet\'s run a dry run example to illustrate how the approach works.\n\nFor `steps = 3` and `arrLen = 2`, the `dp` array might look like this:\n\n```\n[[1, 0, -1], // Step 0\n [1, -1, -1], // Step 1\n [1, -1, -1]] // Step 2\n```\n\nHere, we start at position 0, and after 3 steps, we have 1 way to reach position 0.\n\n### Edge Cases\n- If `steps` is 0 and `pos` is 0, return 1.\n- If `steps` is 0 and `pos` is not 0, return 0.\n- If `steps` is negative or `pos` is out of bounds, return 0.\n\n### Complexity Analysis\n- Time Complexity: O(steps * min(steps, min(steps,arrLen))) as we fill the `dp` array.\n- Space Complexity: O(steps * min(steps, min(steps,arrLen))) for the `dp` array.\n\n### Codes \n\n```cpp []\nstatic int MOD = 1e9 + 7;\n\nclass Solution {\npublic:\n int TopDown(int steps, int arrLen, int pos, vector<vector<int>>& dp) {\n if (steps == 0 && pos == 0) return 1;\n if (steps == 0 && pos != 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n if (dp[steps][pos] != -1) return dp[steps][pos];\n return dp[steps][pos] = ((TopDown(steps - 1, arrLen, pos, dp) % MOD // stay\n + TopDown(steps - 1, arrLen, pos + 1, dp) % MOD) % MOD // right\n + TopDown(steps - 1, arrLen, pos - 1, dp) % MOD) % MOD; // left\n }\n\n int numWays(int steps, int arrLen) {\n vector<vector<int>> dp(steps + 1, vector<int>(steps+2, -1));\n return TopDown(steps, arrLen, 0, dp);\n }\n};\n```\n\n\n```java []\nclass Solution {\n private static final int MOD = 1000000007;\n\n public int TopDown(int steps, int arrLen, int pos, int[][] dp) {\n if (steps == 0 && pos == 0) return 1;\n if (steps == 0 && pos != 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n if (dp[steps][pos] != -1) return dp[steps][pos];\n return dp[steps][pos] = ((TopDown(steps - 1, arrLen, pos, dp) % MOD // stay\n + TopDown(steps - 1, arrLen, pos + 1, dp) % MOD) % MOD // right\n + TopDown(steps - 1, arrLen, pos - 1, dp) % MOD) % MOD; // left\n }\n\n public int numWays(int steps, int arrLen) {\n int[][] dp = new int[steps + 1][steps+2];\n for (int[] row : dp) Arrays.fill(row, -1);\n return TopDown(steps, arrLen, 0, dp);\n }\n}\n```\n\n\n```python []\nMOD = 10**9 + 7\n\nclass Solution:\n def TopDown(self, steps, arrLen, pos, dp):\n if steps == 0 and pos == 0:\n return 1\n if steps == 0 and pos != 0:\n return 0\n if steps < 0 or pos < 0 or pos >= arrLen:\n return 0\n if dp[steps][pos] != -1:\n return dp[steps][pos]\n dp[steps][pos] = ((self.TopDown(steps - 1, arrLen, pos, dp) % MOD # stay\n + self.TopDown(steps - 1, arrLen, pos + 1, dp) % MOD) % MOD # right\n + self.TopDown(steps - 1, arrLen\n\n, pos - 1, dp) % MOD) % MOD # left\n return dp[steps][pos]\n\n def numWays(self, steps, arrLen):\n dp = [[-1 for _ in range(steps + 2)] for _ in range(steps + 1)]\n return self.TopDown(steps, arrLen, 0, dp)\n```\n\n\n```javascript []\n\nvar MOD = 1000000007;\n\nvar TopDown = function (steps, arrLen, pos, dp) {\n if (steps === 0 && pos === 0) return 1;\n if (steps === 0 && pos !== 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n if (dp[steps][pos] !== -1) return dp[steps][pos];\n dp[steps][pos] =\n ((((TopDown(steps - 1, arrLen, pos, dp) % MOD) + // stay\n (TopDown(steps - 1, arrLen, pos + 1, dp) % MOD)) %\n MOD) + // right\n (TopDown(steps - 1, arrLen, pos - 1, dp) % MOD)) %\n MOD; // left\n return dp[steps][pos];\n};\n\nvar numWays = function (steps, arrLen) {\n const dp = Array.from({ length: steps + 1 }, () => Array(steps + 2).fill(-1));\n return TopDown(steps, arrLen, 0, dp);\n};\n\n\n```\n\n\n\n```csharp []\nppublic class Solution {\n private const int MOD = 1000000007;\n\n public int TopDown(int steps, int arrLen, int pos, int[][] dp) {\n if (steps == 0 && pos == 0) return 1;\n if (steps == 0 && pos != 0) return 0;\n if (steps < 0 || pos < 0 || pos >= arrLen) return 0;\n if (dp[steps][pos] != -1) return dp[steps][pos];\n dp[steps][pos] = ((TopDown(steps - 1, arrLen, pos, dp) % MOD // stay\n + TopDown(steps - 1, arrLen, pos + 1, dp) % MOD) % MOD // right\n + TopDown(steps - 1, arrLen, pos - 1, dp) % MOD) % MOD; // left\n return dp[steps][pos];\n }\n\n public int NumWays(int steps, int arrLen) {\n int[][] dp = new int[steps + 1][];\n for (int i = 0; i <= steps; i++) {\n dp[i] = new int[steps + 2]; \n for (int j = 0; j < steps + 2; j++) {\n dp[i][j] = -1;\n }\n }\n return TopDown(steps, arrLen, 0, dp);\n }\n}\n\n```\n\n---\n\n\n\n## Approach 3: Bottom-Up Dynamic Programming\n\n### Explanation\n\nThe problem asks us to find the number of ways to stay in the same place after some steps. We can solve this problem using dynamic programming.\n\nIn the dynamic programming approach, we maintain a 2D array `dp` where `dp[i][j]` represents the number of ways to be at position `j` after taking `i` steps. We initialize `dp[0][0]` to 1, as there is one way to be at position 0 after 0 steps.\n\nWe then iterate through the number of steps and positions, filling in the `dp` array according to the three possible movements: stay in the same place, move one step to the right, and move one step to the left. We use modular arithmetic with a constant `MOD` to prevent overflow.\n\nThe final answer is found in `dp[steps][0]`, which represents the number of ways to be at position 0 after taking `steps` steps.\n\n### Dry Run\n\nLet\'s dry run the code with `steps = 3` and `arrLen = 2`:\n\n1. Initialize the `dp` array:\n ```\n dp = [[1, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]]\n ```\n\n2. Fill in the `dp` array:\n - After 1 step, `dp[1][0] = dp[0][0] = 1`\n - After 1 step, `dp[1][1] = dp[0][0] + dp[0][1] = 1`\n - After 1 step, `dp[1][2] = dp[0][1] = 1`\n\n - After 2 steps, `dp[2][0] = dp[1][0] + dp[1][1] = 2`\n - After 2 steps, `dp[2][1] = dp[1][0] + dp[1][1] + dp[1][2] = 3`\n - After 2 steps, `dp[2][2] = dp[1][1] + dp[1][2] = 2`\n\n - After 3 steps, `dp[3][0] = dp[2][0] + dp[2][1] = 5`\n - After 3 steps, `dp[3][1] = dp[2][0] + dp[2][1] + dp[2][2] = 7`\n - After 3 steps, `dp[3][2] = dp[2][1] + dp[2][2] = 5`\n\n3. The final answer is `dp[3][0] = 5`, which is the number of ways to be at position 0 after taking 3 steps.\n\n### Edge Cases\n\n- When `steps` is 0, the number of ways to stay in the same place is 1.\n- When `arrLen` is 1, there is only one position, so the answer is 1 regardless of the number of steps.\n\n### Complexity Analysis\n\n- Time Complexity: O(steps * arrLen)\n- Space Complexity: O(steps * arrLen)\n\n\n# **Codes :**\n\n```cpp []\nclass Solution {\npublic:\n int numWays(int steps, int arrLen) {\n static const int MOD = 1000000007;\n vector<vector<long long>> dp(steps + 1, vector<long long>(min(steps, arrLen) + 2, 0));\n dp[0][0] = 1;\n\n for (int step = 1; step <= steps; step++) {\n for (int pos = 0; pos < min(steps, arrLen); pos++) {\n dp[step][pos] = (((dp[step - 1][pos]) % MOD // stay\n + dp[step - 1][pos + 1] % MOD) % MOD // right\n + (pos > 0 ? dp[step - 1][pos - 1] : 0)) % MOD; // left\n }\n }\n return dp[steps][0];\n }\n};\n```\n\n```java []\npublic class Solution {\n private static final int MOD = 1000000007;\n\n public int numWays(int steps, int arrLen) {\n int[][] dp = new int[steps + 1][Math.min(steps, arrLen) + 2];\n dp[0][0] = 1;\n\n for (int step = 1; step <= steps; step++) {\n for (int pos = 0; pos < Math.min(steps, arrLen); pos++) {\n dp[step][pos] = (((dp[step - 1][pos] % MOD) // stay\n + (dp[step - 1][pos + 1] % MOD)) % MOD // right\n + ((pos > 0) ? (dp[step - 1][pos - 1] % MOD) : 0)) % MOD; // left\n }\n }\n return dp[steps][0];\n }\n}\n```\n\n\n\n```python []\nMOD = 10**9 + 7\n\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n dp = [[0] * (min(steps, arrLen) + 2) for _ in range(steps + 1)]\n dp[0][0] = 1\n\n for step in range(1, steps + 1):\n for pos in range(min(steps, arrLen)):\n dp[step][pos] = ((dp[step - 1][pos] + dp[step - 1][pos + 1]) % MOD + (dp[step - 1][pos - 1] if pos > 0 else 0)) % MOD\n\n return dp[steps][0]\n```\n\n\n```javascript []\nvar numWays = function (steps, arrLen) {\n const MOD = 10 ** 9 + 7;\n let dp = Array.from({ length: steps + 1 }, () => Array(Math.min(steps, arrLen) + 2).fill(0));\n dp[0][0] = 1;\n\n for (let step = 1; step <= steps; step++) {\n for (let pos = 0; pos < Math.min(steps, arrLen); pos++) {\n dp[step][pos] = ((dp[step - 1][pos] + dp[step - 1][pos + 1]) % MOD + (pos > 0 ? dp[step - 1][pos - 1] : 0)) % MOD;\n }\n }\n return dp[steps][0];\n};\n\n```\n\n```csharp []\npublic class Solution {\n public int NumWays(int steps, int arrLen) {\n const int MOD = 1000000007;\n long[][] dp = new long[steps + 1][];\n for (int i = 0; i <= steps; i++) {\n dp[i] = new long[Math.Min(steps, arrLen) + 2];\n for (int j = 0; j < Math.Min(steps, arrLen) + 2; j++) {\n dp[i][j] = 0;\n }\n }\n dp[0][0] = 1;\n\n for (int step = 1; step <= steps; step++) {\n for (int pos = 0; pos < Math.Min(steps, arrLen); pos++) {\n dp[step][pos] = ((dp[step - 1][pos] + dp[step - 1][pos + 1]) % MOD + (pos > 0 ? dp[step - 1][pos - 1] : 0)) % MOD;\n }\n }\n return (int)dp[steps][0];\n }\n}\n```\n---\n\n## Analysis of Code in Different Languages : \n\n\n\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| C++ | 27 | 36 |\n| Java | 17 | 43.4 |\n| Python | 303 | 22 |\n| JavaScript | 55 | 48.3 |\n| C# | 27 | 36 |\n\n\n---\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n\n\n | 2 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
🔥 Easy solution | Python 3 🔥| | number-of-ways-to-stay-in-the-same-place-after-some-steps | 0 | 1 | # Intuition\nNumber of Ways to Stay in the Same Place After Some Steps\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize constants and variables:\n\n 1. MOD is set to 10^9 + 7, which is used for taking the modulus of the result to avoid integer overflow.\n 1. Calculate maxPosition as the minimum of arrLen - 1 and steps // 2. This is because you can only move arrLen - 1 steps at most.\n1. Create a 2D list dp of size (steps + 1) x (maxPosition + 1). dp[i][j] represents the number of ways to reach position j after i steps.\n\n1. Initialize dp[0][0] to 1 since there\'s one way to be at position 0 after 0 steps.\n\n1. Use a nested loop to iterate through each step from 1 to steps and each position from 0 to maxPosition.\n\n1. Update dp[i][j] as follows:\n\n 1. Set dp[i][j] to dp[i - 1][j], which represents staying in the same position (not moving).\n 1. If j > 0, add dp[i - 1][j - 1] to dp[i][j], which represents moving one step to the left.\n 1. If j < maxPosition, add dp[i - 1][j + 1] to dp[i][j], which represents moving one step to the right.\n 1. Take the modulus MOD of each addition to prevent overflow.\n1. After the loops, the final result is stored in dp[steps][0], which represents the number of ways to reach position 0 after steps steps.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity her e, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n MOD = 10**9 + 7\n maxPosition = min(arrLen - 1, steps // 2)\n dp = [[0] * (maxPosition + 1) for _ in range(steps + 1)]\n dp[0][0] = 1\n\n for i in range(1, steps + 1):\n for j in range(maxPosition + 1):\n dp[i][j] = dp[i - 1][j]\n if j > 0:\n dp[i][j] = (dp[i][j] + dp[i - 1][j - 1]) % MOD\n if j < maxPosition:\n dp[i][j] = (dp[i][j] + dp[i - 1][j + 1]) % MOD\n\n return dp[steps][0]\n \n``` | 1 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
python | number-of-ways-to-stay-in-the-same-place-after-some-steps | 0 | 1 | ```\nclass Solution:\n def numWays(self, steps: int, arrLen: int) -> int:\n modulo = 1000000007\n max_len = min(arrLen, 1 + steps // 2)\n ways = [0] * (max_len + 1)\n ways[0] = 1\n for i in range(steps):\n left = 0\n for j in range(min(max_len, i + 2, steps - i + 3)):\n left, ways[j] = ways[j], (ways[j] + left + ways[j + 1]) % modulo\n return ways[0]\n``` | 1 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
Easy Solution | Recursion-> Memoization-> Tabulation | Python Solution | Easy Explanation | number-of-ways-to-stay-in-the-same-place-after-some-steps | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to break down the problem into smaller subproblems. At each step, you can make three possible moves, so you explore all three options and recursively calculate the number of ways to reach the destination. The memoization ensures that you don\'t recompute the same subproblem multiple times, making the solution more efficient. By building up the results from smaller steps and positions, you eventually get the total number of ways to reach the destination position after a certain number of steps.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Recursion (TLE):**\n - This approach uses a recursive function to explore all possible paths from the current position, considering left, stay, and right moves.\n - It applies memoization to store previously computed results to avoid redundant calculations, which helps improve performance.\n - However, this approach may lead to Time Limit Exceeded (TLE) errors for larger inputs because it has an exponential time complexity of O(3^steps).\n\n2. **Memoization:**\n - Similar to the recursive approach, it uses memoization to avoid recomputation of the same subproblems.\n - The memoization table `dp` stores the number of ways to reach a specific position with a specific number of steps.\n - This approach has a better time complexity than pure recursion but can still have performance issues for large inputs. Its time complexity is O(steps * arrLen).\n\n3. **Tabulation:**\n - This approach uses dynamic programming with a 2D table `dp` to iteratively compute the number of ways to reach each position at each step.\n - The base case is initialized in `dp[0][0] = 1`, and then the table is filled in a bottom-up manner.\n - The final result is obtained from `dp[steps][0]`, representing the number of ways to reach the destination (position 0) after taking `steps` steps.\n - This approach is the most efficient one, with a time complexity of O(steps * arrLen) and is preferred for solving this problem.\n\nThe Tabulation approach is the most efficient and recommended one for this problem, as it has a better time complexity and is less likely to encounter performance issues for large inputs. It essentially breaks down the problem into smaller subproblems and builds the solution iteratively, making it more scalable.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. Time Complexity for Approach 1: O(3^steps) - Exponential\n2. Time Complexity for Approach 2: O(steps * arrLen) \n3. Time Complexity for Approach 3: O(steps * arrLen)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. Space Complexity for Approach 1: Stack Space \n2. Space Complexity for Approach 2: O(steps * arrLen)+ Stack Space \n3. Space Complexity for Approach 3: O(steps * arrLen)\n# Code\n# Recursion (TLE)\n```\nclass Solution:\n def helper(self,step, position,arrLen):\n mod = 10**9+7\n if position <0 or position>=arrLen:\n return 0\n if step == 0:\n return 1 if position == 0 else 0\n\n if dp[step][position]!=-1:\n return dp[step][position]\n # Calculate the number of ways recursively\n ways = 0\n \n ways = (ways+self.helper(step - 1, position - 1,arrLen))%mod\n ways = (ways+self.helper(step - 1, position,arrLen))%mod\n ways = (ways+self.helper(step - 1, position + 1,arrLen))%mod\n\n return ways\n \n\n def numWays(self, steps: int, arrLen: int) -> int:\n return self.helper(steps,0,arrLen) \n```\n\n\n# Memoization\n```\nclass Solution:\n def helper(self,step, position,arrLen,dp):\n mod = 10**9+7\n if position <0 or position>=arrLen:\n return 0\n if step == 0:\n return 1 if position == 0 else 0\n\n if dp[step][position]!=-1:\n return dp[step][position]\n # Calculate the number of ways recursively\n ways = 0\n \n ways = (ways+self.helper(step - 1, position - 1,arrLen,dp))%mod\n ways = (ways+self.helper(step - 1, position,arrLen,dp))%mod\n ways = (ways+self.helper(step - 1, position + 1,arrLen,dp))%mod\n\n dp[step][position] =ways\n\n return dp[step][position]\n\n \n\n def numWays(self, steps: int, arrLen: int) -> int:\n m = steps\n n = min(steps//2+1,arrLen)\n dp = [[-1]*n for i in range(m+1)]\n return self.helper(steps,0,n,dp)\n\n \n```\n\n# Tabulation\n\n```\n def numWays(self, steps: int, arrLen: int) -> int:\n n = min(steps//2+1,arrLen)\n m= steps\n dp = [[0]*n for i in range(m+1)]\n dp[0][0]=1\n mod = 10**9+7\n for i in range(1,m+1):\n for j in range(n):\n dp[i][j]=dp[i-1][j]\n if j>0:\n dp[i][j] +=dp[i-1][j-1]\n if j<n-1:\n dp[i][j]+=dp[i-1][j+1]\n return dp[m][0]%mod\n\n```\n\n\nFor better understanding of approach and intuition you can watch out this video. Hope it helps you out.\n\nhttps://youtu.be/ZgN7e9oqRtw\n\nPlease upvote if you understood the solution. | 1 | You have a pointer at index `0` in an array of size `arrLen`. At each step, you can move 1 position to the left, 1 position to the right in the array, or stay in the same place (The pointer should not be placed outside the array at any time).
Given two integers `steps` and `arrLen`, return the number of ways such that your pointer is still at index `0` after **exactly** `steps` steps. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** steps = 3, arrLen = 2
**Output:** 4
**Explanation:** There are 4 differents ways to stay at index 0 after 3 steps.
Right, Left, Stay
Stay, Right, Left
Right, Stay, Left
Stay, Stay, Stay
**Example 2:**
**Input:** steps = 2, arrLen = 4
**Output:** 2
**Explanation:** There are 2 differents ways to stay at index 0 after 2 steps
Right, Left
Stay, Stay
**Example 3:**
**Input:** steps = 4, arrLen = 2
**Output:** 8
**Constraints:**
* `1 <= steps <= 500`
* `1 <= arrLen <= 106` | null |
🔥 [Python 3] 2 solutions, beats 90% 🥷🏼 | find-winner-on-a-tic-tac-toe-game | 0 | 1 | ```python3 []\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n winner = None\n matrix = [[0 for _ in range(3)] for _ in range(3)]\n\n # use 1 for the first player move, 5 \u2014 the second player\n # winner sum on row/col/diagonal == 3(1+1+1) or 15(5+5+5)\n for i, (x, y) in enumerate(moves):\n matrix[x][y] = 5 if i & 1 else 1\n \n def checkWin(s):\n nonlocal winner\n if winner: return\n if s == 3: winner = \'A\'\n if s == 15: winner = \'B\'\n\n def checkRows():\n for row in matrix: checkWin(sum(row))\n\n def checkCols():\n for col in zip(*matrix): checkWin(sum(col))\n\n def checkDiagonal1():\n checkWin(matrix[0][0] + matrix[1][1] + matrix[2][2]) \n\n def checkDiagonal2():\n checkWin(matrix[0][2] + matrix[1][1] + matrix[2][0])\n\n checkRows()\n checkCols()\n checkDiagonal1()\n checkDiagonal2()\n\n return winner or (\'Draw\' if len(moves) == 9 else \'Pending\')\n```\n```python3 []\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n matrix = [[0 for _ in range(3)] for _ in range(3)]\n\n #fill matrix with moves add 1 for the first player and 5 for the second\n for i, move in enumerate(moves):\n matrix[move[0]][move[1]] = 5 if i % 2 else 1\n\n res = {1: \'A\', 5: \'B\'}\n #check rows\n for row in matrix:\n S = sum(row)\n if S in (3, 15):\n return res[S // 3]\n #check columns\n for col in zip(*matrix):\n S = sum(col)\n if S in (3, 15):\n return res[S // 3]\n #check main diagonal\n S = matrix[0][0] + matrix[1][1] + matrix[2][2]\n if S in (3, 15):\n return res[S // 3]\n #check second diagonal\n S = matrix[0][2] + matrix[1][1] + matrix[2][0]\n if S in (3, 15):\n return res[S // 3]\n\n return \'Draw\' if len(moves) == 9 else \'Pending\'\n```\np.s. Obviously you can check is there the winner after each of methods calls: `checkRows`, `checkCols`, `checkDiagonal1`, it will be faster, but less readable imho.\n\n | 8 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
🔥 [Python 3] 2 solutions, beats 90% 🥷🏼 | find-winner-on-a-tic-tac-toe-game | 0 | 1 | ```python3 []\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n winner = None\n matrix = [[0 for _ in range(3)] for _ in range(3)]\n\n # use 1 for the first player move, 5 \u2014 the second player\n # winner sum on row/col/diagonal == 3(1+1+1) or 15(5+5+5)\n for i, (x, y) in enumerate(moves):\n matrix[x][y] = 5 if i & 1 else 1\n \n def checkWin(s):\n nonlocal winner\n if winner: return\n if s == 3: winner = \'A\'\n if s == 15: winner = \'B\'\n\n def checkRows():\n for row in matrix: checkWin(sum(row))\n\n def checkCols():\n for col in zip(*matrix): checkWin(sum(col))\n\n def checkDiagonal1():\n checkWin(matrix[0][0] + matrix[1][1] + matrix[2][2]) \n\n def checkDiagonal2():\n checkWin(matrix[0][2] + matrix[1][1] + matrix[2][0])\n\n checkRows()\n checkCols()\n checkDiagonal1()\n checkDiagonal2()\n\n return winner or (\'Draw\' if len(moves) == 9 else \'Pending\')\n```\n```python3 []\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n matrix = [[0 for _ in range(3)] for _ in range(3)]\n\n #fill matrix with moves add 1 for the first player and 5 for the second\n for i, move in enumerate(moves):\n matrix[move[0]][move[1]] = 5 if i % 2 else 1\n\n res = {1: \'A\', 5: \'B\'}\n #check rows\n for row in matrix:\n S = sum(row)\n if S in (3, 15):\n return res[S // 3]\n #check columns\n for col in zip(*matrix):\n S = sum(col)\n if S in (3, 15):\n return res[S // 3]\n #check main diagonal\n S = matrix[0][0] + matrix[1][1] + matrix[2][2]\n if S in (3, 15):\n return res[S // 3]\n #check second diagonal\n S = matrix[0][2] + matrix[1][1] + matrix[2][0]\n if S in (3, 15):\n return res[S // 3]\n\n return \'Draw\' if len(moves) == 9 else \'Pending\'\n```\np.s. Obviously you can check is there the winner after each of methods calls: `checkRows`, `checkCols`, `checkDiagonal1`, it will be faster, but less readable imho.\n\n | 8 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
[Java/Python/C++] 0ms, short and simple, all 8 ways to win in one array | find-winner-on-a-tic-tac-toe-game | 0 | 1 | There are 8 ways to win for each player:\n - 3 columns\n - 3 rows\n - 2 diagonals\n \nPlayers make moves one by one so all odd moves are for player A, even for B.\nNow we just need to track if we reach 3 in any line for any of the players.\nOne array keeps all ways to win for each player:\n - 0,1,2 - for rows\n - 3,4,5 - for cols\n - 6 - for diagonal top left - bottom right\n - 7 - for diagonal top right - bottom left\n\nJava, 0 ms\n```\n public String tictactoe(int[][] moves) {\n int[] A = new int[8], B = new int[8]; // 3 rows, 3 cols, 2 diagonals\n for(int i=0;i<moves.length;i++) {\n int r=moves[i][0], c=moves[i][1];\n int[] player = (i%2==0)?A:B;\n player[r]++;\n player[c+3]++;\n if(r==c) player[6]++;\n if(r==2-c) player[7]++;\n }\n for(int i=0;i<8;i++) {\n if(A[i]==3) return "A";\n if(B[i]==3) return "B";\n }\n return moves.length==9 ? "Draw":"Pending";\n }\n```\n\nC++, 0 ms\n ```\n string tictactoe(vector<vector<int>>& moves) {\n vector<int> A(8,0), B(8,0); // 3 rows, 3 cols, 2 diagonals\n for(int i=0; i<moves.size(); i++) {\n int r=moves[i][0], c=moves[i][1];\n vector<int>& player = (i%2==0)?A:B;\n player[r]++;\n player[c+3]++; \n if(r==c) player[6]++;\n if(r==2-c) player[7]++;\n }\n for(int i=0; i<8; i++) {\n if(A[i]==3) return "A";\n if(B[i]==3) return "B";\n }\n return moves.size()==9 ? "Draw":"Pending";\n }\n```\n\nPython, 24 ms, beats 100%\n```\n def tictactoe(self, moves: List[List[int]]) -> str:\n A=[0]*8\n B=[0]*8\n for i in range(len(moves)):\n r,c=moves[i]\n player = A if i%2==0 else B\n player[r] += 1\n player[c+3] += 1\n if r==c:\n player[6] += 1\n if r==2-c:\n player[7] += 1\n for i in range(8):\n if A[i]==3:\n return "A"\n if B[i]==3:\n return "B"\n \n return "Draw" if len(moves) == 9 else "Pending"\n``` | 164 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
[Java/Python/C++] 0ms, short and simple, all 8 ways to win in one array | find-winner-on-a-tic-tac-toe-game | 0 | 1 | There are 8 ways to win for each player:\n - 3 columns\n - 3 rows\n - 2 diagonals\n \nPlayers make moves one by one so all odd moves are for player A, even for B.\nNow we just need to track if we reach 3 in any line for any of the players.\nOne array keeps all ways to win for each player:\n - 0,1,2 - for rows\n - 3,4,5 - for cols\n - 6 - for diagonal top left - bottom right\n - 7 - for diagonal top right - bottom left\n\nJava, 0 ms\n```\n public String tictactoe(int[][] moves) {\n int[] A = new int[8], B = new int[8]; // 3 rows, 3 cols, 2 diagonals\n for(int i=0;i<moves.length;i++) {\n int r=moves[i][0], c=moves[i][1];\n int[] player = (i%2==0)?A:B;\n player[r]++;\n player[c+3]++;\n if(r==c) player[6]++;\n if(r==2-c) player[7]++;\n }\n for(int i=0;i<8;i++) {\n if(A[i]==3) return "A";\n if(B[i]==3) return "B";\n }\n return moves.length==9 ? "Draw":"Pending";\n }\n```\n\nC++, 0 ms\n ```\n string tictactoe(vector<vector<int>>& moves) {\n vector<int> A(8,0), B(8,0); // 3 rows, 3 cols, 2 diagonals\n for(int i=0; i<moves.size(); i++) {\n int r=moves[i][0], c=moves[i][1];\n vector<int>& player = (i%2==0)?A:B;\n player[r]++;\n player[c+3]++; \n if(r==c) player[6]++;\n if(r==2-c) player[7]++;\n }\n for(int i=0; i<8; i++) {\n if(A[i]==3) return "A";\n if(B[i]==3) return "B";\n }\n return moves.size()==9 ? "Draw":"Pending";\n }\n```\n\nPython, 24 ms, beats 100%\n```\n def tictactoe(self, moves: List[List[int]]) -> str:\n A=[0]*8\n B=[0]*8\n for i in range(len(moves)):\n r,c=moves[i]\n player = A if i%2==0 else B\n player[r] += 1\n player[c+3] += 1\n if r==c:\n player[6] += 1\n if r==2-c:\n player[7] += 1\n for i in range(8):\n if A[i]==3:\n return "A"\n if B[i]==3:\n return "B"\n \n return "Draw" if len(moves) == 9 else "Pending"\n``` | 164 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Python Short, Optimized and Interview Friendly Solution | find-winner-on-a-tic-tac-toe-game | 0 | 1 | * Instead of harcoding 3 all over the place. Solve for n * n grid and set n = 3 in the beginning. That way the code is scalable and there will just be a one line change if the interviewer asks your for a 4x4 grid.\n* Storing the rows and cols as array of size n + 2 variables for diagonals and reverse diagonal. This requires less memory O(2n + 2) instead of O(n^2)\n* Also checking if a player has won or not takes O(1) time as I have to check 4 variables.\n* The logic is to increment(Player A) and decrement(Player B) the row, col and the 2 diagonal variables depending on who played and which row, col was played.\n* After every move, we need to check if the value of the row, col, or the diagonal variables is 3 or -3. Whoever played in that turn is the winner.\n\nTime Complexity for every move check: O(1)\nSpace Complexity: O(n)\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n n = 3\n rows, cols = [0] * n, [0] * n\n diag1 = diag2 = 0\n for index, move in enumerate(moves):\n i, j = move\n sign = 1 if index % 2 == 0 else -1\n rows[i] += sign\n cols[j] += sign\n if i == j:\n diag1 += sign\n if i + j == n-1:\n diag2 += sign\n if abs(rows[i]) == n or abs(cols[j]) == n or abs(diag1) == n or abs(diag2) == n:\n return \'A\' if sign == 1 else \'B\'\n return "Draw" if len(moves) == (n * n) else \'Pending\' | 111 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python Short, Optimized and Interview Friendly Solution | find-winner-on-a-tic-tac-toe-game | 0 | 1 | * Instead of harcoding 3 all over the place. Solve for n * n grid and set n = 3 in the beginning. That way the code is scalable and there will just be a one line change if the interviewer asks your for a 4x4 grid.\n* Storing the rows and cols as array of size n + 2 variables for diagonals and reverse diagonal. This requires less memory O(2n + 2) instead of O(n^2)\n* Also checking if a player has won or not takes O(1) time as I have to check 4 variables.\n* The logic is to increment(Player A) and decrement(Player B) the row, col and the 2 diagonal variables depending on who played and which row, col was played.\n* After every move, we need to check if the value of the row, col, or the diagonal variables is 3 or -3. Whoever played in that turn is the winner.\n\nTime Complexity for every move check: O(1)\nSpace Complexity: O(n)\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n n = 3\n rows, cols = [0] * n, [0] * n\n diag1 = diag2 = 0\n for index, move in enumerate(moves):\n i, j = move\n sign = 1 if index % 2 == 0 else -1\n rows[i] += sign\n cols[j] += sign\n if i == j:\n diag1 += sign\n if i + j == n-1:\n diag2 += sign\n if abs(rows[i]) == n or abs(cols[j]) == n or abs(diag1) == n or abs(diag2) == n:\n return \'A\' if sign == 1 else \'B\'\n return "Draw" if len(moves) == (n * n) else \'Pending\' | 111 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Python/C++ solution beats 100% w printing Board | find-winner-on-a-tic-tac-toe-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo design a Tic Tac Toe game, you have to at first judge who wins. Use "012345678" to denote the positions in board.\n\nThere are exactly 8 lines to observe; \n$$\n\\{\n \\{0, 1, 2\\},\\{3, 4, 5\\},\\{6, 7, 8\\},\\\\\n \\{0, 3, 6\\},\\{1, 4, 7\\},\\{2, 5, 8\\},\\\\\n \\{0, 4, 8\\},\\{2, 4, 6\\}\\};\n$$\neach line L has 3 elements, say x0, x1, x2, which are using number 0, 1 or 2 denoting its status:\n 1 for player \'X\', 2 for player \'O\' and 0 for none.\n\nConsider the judge function \n$$\nf(x_0, x_1, x_2)=x_0x_1+x_1x_2+x_2x_0\n$$\nif $f=3$ then player \'X\' wins, if $f=12$ then player \'O\' wins, otherwise check all other lines.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[https://youtu.be/7g-E3d_Oja4](https://youtu.be/7g-E3d_Oja4)\n```\nX12\n3X5\nOOX\n=====\n"A"\n\n-------\nXXO\nXO5\nO78\n=====\n"B"\n\n-------\nXXO\nOOX\nXOX\n=====\n"Draw"\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code beats 100% 0 ms\n```\nclass Solution {\npublic:\n int Lines[8][3]={\n {0, 1, 2},{3, 4, 5},{6, 7, 8},\n {0, 3, 6},{1, 4, 7},{2, 5, 8},\n {0, 4, 8},{2, 4, 6}};\n char Board[10]="012345678";\n int check_win(){\n for(int* l: Lines){\n int x0=(Board[l[0]]==\'X\')?1:(Board[l[0]]==\'O\')?2:0;\n int x1=(Board[l[1]]==\'X\')?1:(Board[l[1]]==\'O\')?2:0;\n int x2=(Board[l[2]]==\'X\')?1:(Board[l[2]]==\'O\')?2:0;\n // cout<<l[0]<<l[1]<<l[2]<<"-->"<<x0<<x1<<x2<<endl;\n int result=x0*x1+x1*x2+x2*x1;\n if (result==3) return 1;\n else if (result==12) return 2;\n }\n //cout<<"==========\\n";\n return 0;\n }\n void print(){\n for(int i=0; i<3; i++){\n for(int j=0; j<3; j++){\n cout<<Board[3*i+j];\n }\n cout<<endl; \n }\n cout<<"=====\\n";\n }\n string tictactoe(vector<vector<int>>& moves) {\n int n=moves.size();\n for(int i=0; i<n; i++){\n int idx=3*moves[i][0]+moves[i][1];\n if (i&1) Board[idx]=\'O\';\n else Board[idx]=\'X\';\n }\n // print();\n if (check_win()==1) return "A";\n else if (check_win()==2) return "B";\n if (n==9) return "Draw";\n else return "Pending";\n } \n};\n```\n# Python solution\n\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n Lines = [[0, 1, 2], [3, 4, 5], [6, 7, 8], [0, 3, 6], [1, 4, 7], [2, 5, 8], [0, 4, 8], [2, 4, 6]]\n Board = [0] * 9 \n def check_win():\n for L in Lines:\n x0, x1, x2 = Board[L[0]], Board[L[1]], Board[L[2]]\n res = x0*x1+x1*x2+x2*x0\n if res == 3:\n return 1\n elif res == 12:\n return 2\n return 0\n\n n = len(moves)\n for i in range(n):\n a, b = moves[i]\n idx = 3 * a + b\n if i % 2 == 1:\n Board[idx] = 2\n else:\n Board[idx] = 1\n\n if check_win() == 1:\n return \'A\'\n elif check_win() == 2:\n return \'B\'\n if n == 9:\n return "Draw"\n else:\n return "Pending"\n``` | 3 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python/C++ solution beats 100% w printing Board | find-winner-on-a-tic-tac-toe-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo design a Tic Tac Toe game, you have to at first judge who wins. Use "012345678" to denote the positions in board.\n\nThere are exactly 8 lines to observe; \n$$\n\\{\n \\{0, 1, 2\\},\\{3, 4, 5\\},\\{6, 7, 8\\},\\\\\n \\{0, 3, 6\\},\\{1, 4, 7\\},\\{2, 5, 8\\},\\\\\n \\{0, 4, 8\\},\\{2, 4, 6\\}\\};\n$$\neach line L has 3 elements, say x0, x1, x2, which are using number 0, 1 or 2 denoting its status:\n 1 for player \'X\', 2 for player \'O\' and 0 for none.\n\nConsider the judge function \n$$\nf(x_0, x_1, x_2)=x_0x_1+x_1x_2+x_2x_0\n$$\nif $f=3$ then player \'X\' wins, if $f=12$ then player \'O\' wins, otherwise check all other lines.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[https://youtu.be/7g-E3d_Oja4](https://youtu.be/7g-E3d_Oja4)\n```\nX12\n3X5\nOOX\n=====\n"A"\n\n-------\nXXO\nXO5\nO78\n=====\n"B"\n\n-------\nXXO\nOOX\nXOX\n=====\n"Draw"\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code beats 100% 0 ms\n```\nclass Solution {\npublic:\n int Lines[8][3]={\n {0, 1, 2},{3, 4, 5},{6, 7, 8},\n {0, 3, 6},{1, 4, 7},{2, 5, 8},\n {0, 4, 8},{2, 4, 6}};\n char Board[10]="012345678";\n int check_win(){\n for(int* l: Lines){\n int x0=(Board[l[0]]==\'X\')?1:(Board[l[0]]==\'O\')?2:0;\n int x1=(Board[l[1]]==\'X\')?1:(Board[l[1]]==\'O\')?2:0;\n int x2=(Board[l[2]]==\'X\')?1:(Board[l[2]]==\'O\')?2:0;\n // cout<<l[0]<<l[1]<<l[2]<<"-->"<<x0<<x1<<x2<<endl;\n int result=x0*x1+x1*x2+x2*x1;\n if (result==3) return 1;\n else if (result==12) return 2;\n }\n //cout<<"==========\\n";\n return 0;\n }\n void print(){\n for(int i=0; i<3; i++){\n for(int j=0; j<3; j++){\n cout<<Board[3*i+j];\n }\n cout<<endl; \n }\n cout<<"=====\\n";\n }\n string tictactoe(vector<vector<int>>& moves) {\n int n=moves.size();\n for(int i=0; i<n; i++){\n int idx=3*moves[i][0]+moves[i][1];\n if (i&1) Board[idx]=\'O\';\n else Board[idx]=\'X\';\n }\n // print();\n if (check_win()==1) return "A";\n else if (check_win()==2) return "B";\n if (n==9) return "Draw";\n else return "Pending";\n } \n};\n```\n# Python solution\n\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n Lines = [[0, 1, 2], [3, 4, 5], [6, 7, 8], [0, 3, 6], [1, 4, 7], [2, 5, 8], [0, 4, 8], [2, 4, 6]]\n Board = [0] * 9 \n def check_win():\n for L in Lines:\n x0, x1, x2 = Board[L[0]], Board[L[1]], Board[L[2]]\n res = x0*x1+x1*x2+x2*x0\n if res == 3:\n return 1\n elif res == 12:\n return 2\n return 0\n\n n = len(moves)\n for i in range(n):\n a, b = moves[i]\n idx = 3 * a + b\n if i % 2 == 1:\n Board[idx] = 2\n else:\n Board[idx] = 1\n\n if check_win() == 1:\n return \'A\'\n elif check_win() == 2:\n return \'B\'\n if n == 9:\n return "Draw"\n else:\n return "Pending"\n``` | 3 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Python 3 solution with comments | find-winner-on-a-tic-tac-toe-game | 0 | 1 | ```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n # keep track of the "net score" of each row/col/diagonal\n # player A adds 1 to the "net score" of each row/col/diagonal they play in,\n # player B subtracts 1\n # scores[0], scores[1] and scores[2] are for rows 0, 1 and 2\n # scores[3], scores[4] and scores[5] are for cols 0, 1 and 2\n # scores[6] and scores[7] are for the forward and backward diagonal\n scores = [0] * 8\n for i, (row, col) in enumerate(moves):\n if i % 2 == 0: # player A is playing\n x = 1\n else: # player B is playing\n x = -1\n scores[row] += x\n scores[col + 3] += x\n if row == col:\n scores[6] += x\n if 2 - row == col:\n scores[7] += x\n for score in scores:\n if score == 3:\n return \'A\'\n elif score == -3:\n return \'B\'\n return \'Draw\' if len(moves) == 9 else \'Pending\' | 19 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python 3 solution with comments | find-winner-on-a-tic-tac-toe-game | 0 | 1 | ```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n # keep track of the "net score" of each row/col/diagonal\n # player A adds 1 to the "net score" of each row/col/diagonal they play in,\n # player B subtracts 1\n # scores[0], scores[1] and scores[2] are for rows 0, 1 and 2\n # scores[3], scores[4] and scores[5] are for cols 0, 1 and 2\n # scores[6] and scores[7] are for the forward and backward diagonal\n scores = [0] * 8\n for i, (row, col) in enumerate(moves):\n if i % 2 == 0: # player A is playing\n x = 1\n else: # player B is playing\n x = -1\n scores[row] += x\n scores[col + 3] += x\n if row == col:\n scores[6] += x\n if 2 - row == col:\n scores[7] += x\n for score in scores:\n if score == 3:\n return \'A\'\n elif score == -3:\n return \'B\'\n return \'Draw\' if len(moves) == 9 else \'Pending\' | 19 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Python3 | find-winner-on-a-tic-tac-toe-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n\n board = [[\' \' for _ in range(3)] for _ in range(3)]\n player_moves = {\'A\': [], \'B\': []}\n win_combinations = [[[i, j] for j in range(3)] for i in range(3)] + \\\n [[[j, i] for j in range(3)] for i in range(3)] + \\\n [[[i, i] for i in range(3)]] + \\\n [[[i, 2-i] for i in range(3)]]\n\n for i, move in enumerate(moves):\n player = \'A\' if i % 2 == 0 else \'B\'\n player_moves[player].append(move)\n board[move[0]][move[1]] = \'X\' if player == \'A\' else \'O\'\n\n for combo in win_combinations:\n if all(m in player_moves[player] for m in combo):\n return player\n\n if i == 8:\n return "Draw"\n\n return "Pending"\n \n \n``` | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python3 | find-winner-on-a-tic-tac-toe-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n\n board = [[\' \' for _ in range(3)] for _ in range(3)]\n player_moves = {\'A\': [], \'B\': []}\n win_combinations = [[[i, j] for j in range(3)] for i in range(3)] + \\\n [[[j, i] for j in range(3)] for i in range(3)] + \\\n [[[i, i] for i in range(3)]] + \\\n [[[i, 2-i] for i in range(3)]]\n\n for i, move in enumerate(moves):\n player = \'A\' if i % 2 == 0 else \'B\'\n player_moves[player].append(move)\n board[move[0]][move[1]] = \'X\' if player == \'A\' else \'O\'\n\n for combo in win_combinations:\n if all(m in player_moves[player] for m in combo):\n return player\n\n if i == 8:\n return "Draw"\n\n return "Pending"\n \n \n``` | 1 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Python elegant and short, based on bitmasks | find-winner-on-a-tic-tac-toe-game | 0 | 1 | \n WIN_MASKS = {7, 56, 73, 84, 146, 273, 292, 448}\n\n def tictactoe(self, moves: List[List[int]]) -> str:\n cross_mask = zero_mask = 0\n\n for ind, (r, c) in enumerate(moves):\n if ind & 1:\n zero_mask |= 1 << 3 * r + c\n else:\n cross_mask |= 1 << 3 * r + c\n\n for mask in self.WIN_MASKS:\n if mask & cross_mask == mask:\n return \'A\'\n if mask & zero_mask == mask:\n return \'B\'\n\n return "Draw" if len(moves) == 9 else "Pending"\n | 3 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python elegant and short, based on bitmasks | find-winner-on-a-tic-tac-toe-game | 0 | 1 | \n WIN_MASKS = {7, 56, 73, 84, 146, 273, 292, 448}\n\n def tictactoe(self, moves: List[List[int]]) -> str:\n cross_mask = zero_mask = 0\n\n for ind, (r, c) in enumerate(moves):\n if ind & 1:\n zero_mask |= 1 << 3 * r + c\n else:\n cross_mask |= 1 << 3 * r + c\n\n for mask in self.WIN_MASKS:\n if mask & cross_mask == mask:\n return \'A\'\n if mask & zero_mask == mask:\n return \'B\'\n\n return "Draw" if len(moves) == 9 else "Pending"\n | 3 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
FAST but long code || is there a shorter way? || Explained | find-winner-on-a-tic-tac-toe-game | 0 | 1 | # Intuition\nYou can just try all possibilities. I used ifs for the diagonals and nested loops for the rows and columns.\n\n# Approach\nThis is slow. This post must be one of my worst. Ok, I\'ll get started.\n- creating the grid\n - create an empty grid first\n - loop over `moves` starting from index `0` and skipping by `2`\n - > A wins, **they always play first**.\n - same for B except you start at index `1`\n- check the diagonals\n - check diagonal from left to right\n - if they are equal but not `" "`\n - and again for right to left\n- check each row and column\n - the best way to loop is to start from the loop for the columns and **then** nest the loop for the rows\n - keep a list for the column items\n - now for the rows. \n - while you are loop over the rows, keep track of if there is **an empty cell** in the matrix.\n - this will be used to tell if the game is `pending` or it is a `draw` when you didn\'t find a winner\n - check if the row includes a winner. if so, return any item in the row, this is the winner.\n - then, check if the column inclues a winner. if so, return any item in the column.\n- finally, we are done with the loops! If there was a space, aka, if `isSpace` is `True`, return `"Pending"`\n- otherwise, return `"Draw"`\n\n# Complexity\n- Time complexity: $$O(n) + O(n^2)$$\n\n- Space complexity: still don\'t know\n\n# Code\n```\nclass Solution:\n def tictactoe(self, moves):\n grid = [[" ", " ", " "], \n [" ", " ", " "], \n [" ", " ", " "]]\n for m in moves[0::2]: grid[m[0]][m[1]] = "A"\n for m in moves[1::2]: grid[m[0]][m[1]] = "B"\n \n if grid[0][2] == grid[1][1] == grid[2][0] != " ":\n return grid[0][2]\n \n elif grid[0][0] == grid[1][1] == grid[2][2] != " ":\n return grid[0][0]\n \n isSpace = False\n for c in range(3):\n colItms = []\n for r in range(3):\n if grid[r][c] == " ":\n isSpace = True\n colItms.append(grid[r][c])\n if len(set(grid[r])) == 1 and grid[r][0] != " ":\n return grid[r][0]\n if colItms[0] != " " and len(set(colItms)) == 1:\n return colItms[0]\n if isSpace: return "Pending"\n return "Draw"\n```\n\nmy computer just got really slow!!\n### if u found this helpful, plz upvote! | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
FAST but long code || is there a shorter way? || Explained | find-winner-on-a-tic-tac-toe-game | 0 | 1 | # Intuition\nYou can just try all possibilities. I used ifs for the diagonals and nested loops for the rows and columns.\n\n# Approach\nThis is slow. This post must be one of my worst. Ok, I\'ll get started.\n- creating the grid\n - create an empty grid first\n - loop over `moves` starting from index `0` and skipping by `2`\n - > A wins, **they always play first**.\n - same for B except you start at index `1`\n- check the diagonals\n - check diagonal from left to right\n - if they are equal but not `" "`\n - and again for right to left\n- check each row and column\n - the best way to loop is to start from the loop for the columns and **then** nest the loop for the rows\n - keep a list for the column items\n - now for the rows. \n - while you are loop over the rows, keep track of if there is **an empty cell** in the matrix.\n - this will be used to tell if the game is `pending` or it is a `draw` when you didn\'t find a winner\n - check if the row includes a winner. if so, return any item in the row, this is the winner.\n - then, check if the column inclues a winner. if so, return any item in the column.\n- finally, we are done with the loops! If there was a space, aka, if `isSpace` is `True`, return `"Pending"`\n- otherwise, return `"Draw"`\n\n# Complexity\n- Time complexity: $$O(n) + O(n^2)$$\n\n- Space complexity: still don\'t know\n\n# Code\n```\nclass Solution:\n def tictactoe(self, moves):\n grid = [[" ", " ", " "], \n [" ", " ", " "], \n [" ", " ", " "]]\n for m in moves[0::2]: grid[m[0]][m[1]] = "A"\n for m in moves[1::2]: grid[m[0]][m[1]] = "B"\n \n if grid[0][2] == grid[1][1] == grid[2][0] != " ":\n return grid[0][2]\n \n elif grid[0][0] == grid[1][1] == grid[2][2] != " ":\n return grid[0][0]\n \n isSpace = False\n for c in range(3):\n colItms = []\n for r in range(3):\n if grid[r][c] == " ":\n isSpace = True\n colItms.append(grid[r][c])\n if len(set(grid[r])) == 1 and grid[r][0] != " ":\n return grid[r][0]\n if colItms[0] != " " and len(set(colItms)) == 1:\n return colItms[0]\n if isSpace: return "Pending"\n return "Draw"\n```\n\nmy computer just got really slow!!\n### if u found this helpful, plz upvote! | 1 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
[Python3] memo scores | find-winner-on-a-tic-tac-toe-game | 0 | 1 | For each player, we use a list `score` of 8 elements with below meaning \n0-2 : number of characters placed at each row \n3-5 : number of characters placed at each column\n6 : number of characters placed at diagonal \n7 : number of characters placed at anti-diagonal\nto keep track of his/her winning status. \n\nHere, "A" and "B" correspond to the two rows of `score`. \n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n score = [[0]*8 for _ in range(2)]\n \n for p, (i, j) in enumerate(moves):\n p %= 2\n score[p][i] += 1\n score[p][3+j] += 1\n if i == j: score[p][6] += 1\n if i+j == 2: score[p][7] += 1\n if any(x == 3 for x in score[p]): return "AB"[p]\n \n return "Pending" if len(moves) < 9 else "Draw"\n``` | 16 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
[Python3] memo scores | find-winner-on-a-tic-tac-toe-game | 0 | 1 | For each player, we use a list `score` of 8 elements with below meaning \n0-2 : number of characters placed at each row \n3-5 : number of characters placed at each column\n6 : number of characters placed at diagonal \n7 : number of characters placed at anti-diagonal\nto keep track of his/her winning status. \n\nHere, "A" and "B" correspond to the two rows of `score`. \n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n score = [[0]*8 for _ in range(2)]\n \n for p, (i, j) in enumerate(moves):\n p %= 2\n score[p][i] += 1\n score[p][3+j] += 1\n if i == j: score[p][6] += 1\n if i+j == 2: score[p][7] += 1\n if any(x == 3 for x in score[p]): return "AB"[p]\n \n return "Pending" if len(moves) < 9 else "Draw"\n``` | 16 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Python - 30ms Solution - Easy | find-winner-on-a-tic-tac-toe-game | 0 | 1 | 30ms code- Easy To understand...\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n if len(moves)<5:\n return"Pending"\n grid=[[0,0,0],[0,0,0],[0,0,0]]\n for i in range(len(moves)):\n if i%2:\n grid[moves[i][0]][moves[i][1]]= "B"\n else:\n grid[moves[i][0]][moves[i][1]]="A"\n for i in range(len(grid)):\n if grid[i][0] == grid[i][1] == grid[i][2] and grid[i][0] != 0:\n return grid[i][0]\n elif grid[0][i] == grid[1][i] == grid[2][i] and grid[0][i] != 0:\n return grid[0][i]\n elif i == 0 and grid[i][i] == grid[i+1][i+1] == grid[i+2][i+2] and grid[i][i] != 0:\n return grid[i][i]\n elif i == 2 and grid[i][0] == grid[i-1][i-1] == grid[0][i] and grid[i][0] != 0:\n return grid[i][0]\n return "Draw" if len(moves) == 9 else "Pending"\n \n```\nthank you guys | 1 | **Tic-tac-toe** is played by two players `A` and `B` on a `3 x 3` grid. The rules of Tic-Tac-Toe are:
* Players take turns placing characters into empty squares `' '`.
* The first player `A` always places `'X'` characters, while the second player `B` always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never on filled ones.
* The game ends when there are **three** of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
Given a 2D integer array `moves` where `moves[i] = [rowi, coli]` indicates that the `ith` move will be played on `grid[rowi][coli]`. return _the winner of the game if it exists_ (`A` or `B`). In case the game ends in a draw return `"Draw "`. If there are still movements to play return `"Pending "`.
You can assume that `moves` is valid (i.e., it follows the rules of **Tic-Tac-Toe**), the grid is initially empty, and `A` will play first.
**Example 1:**
**Input:** moves = \[\[0,0\],\[2,0\],\[1,1\],\[2,1\],\[2,2\]\]
**Output:** "A "
**Explanation:** A wins, they always play first.
**Example 2:**
**Input:** moves = \[\[0,0\],\[1,1\],\[0,1\],\[0,2\],\[1,0\],\[2,0\]\]
**Output:** "B "
**Explanation:** B wins.
**Example 3:**
**Input:** moves = \[\[0,0\],\[1,1\],\[2,0\],\[1,0\],\[1,2\],\[2,1\],\[0,1\],\[0,2\],\[2,2\]\]
**Output:** "Draw "
**Explanation:** The game ends in a draw since there are no moves to make.
**Constraints:**
* `1 <= moves.length <= 9`
* `moves[i].length == 2`
* `0 <= rowi, coli <= 2`
* There are no repeated elements on `moves`.
* `moves` follow the rules of tic tac toe. | Find the parent of each node. A valid tree must have nodes with only one parent and exactly one node with no parent. |
Python - 30ms Solution - Easy | find-winner-on-a-tic-tac-toe-game | 0 | 1 | 30ms code- Easy To understand...\n```\nclass Solution:\n def tictactoe(self, moves: List[List[int]]) -> str:\n if len(moves)<5:\n return"Pending"\n grid=[[0,0,0],[0,0,0],[0,0,0]]\n for i in range(len(moves)):\n if i%2:\n grid[moves[i][0]][moves[i][1]]= "B"\n else:\n grid[moves[i][0]][moves[i][1]]="A"\n for i in range(len(grid)):\n if grid[i][0] == grid[i][1] == grid[i][2] and grid[i][0] != 0:\n return grid[i][0]\n elif grid[0][i] == grid[1][i] == grid[2][i] and grid[0][i] != 0:\n return grid[0][i]\n elif i == 0 and grid[i][i] == grid[i+1][i+1] == grid[i+2][i+2] and grid[i][i] != 0:\n return grid[i][i]\n elif i == 2 and grid[i][0] == grid[i-1][i-1] == grid[0][i] and grid[i][0] != 0:\n return grid[i][0]\n return "Draw" if len(moves) == 9 else "Pending"\n \n```\nthank you guys | 1 | Given a string `s` and an integer `k`, return `true` _if you can use all the characters in_ `s` _to construct_ `k` _palindrome strings or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "annabelle ", k = 2
**Output:** true
**Explanation:** You can construct two palindromes using all characters in s.
Some possible constructions "anna " + "elble ", "anbna " + "elle ", "anellena " + "b "
**Example 2:**
**Input:** s = "leetcode ", k = 3
**Output:** false
**Explanation:** It is impossible to construct 3 palindromes using all the characters of s.
**Example 3:**
**Input:** s = "true ", k = 4
**Output:** true
**Explanation:** The only possible solution is to put each character in a separate string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `1 <= k <= 105` | It's straightforward to check if A or B won or not, check for each row/column/diag if all the three are the same. Then if no one wins, the game is a draw iff the board is full, i.e. moves.length = 9 otherwise is pending. |
Alternative Solution Binary Search | Explained | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\nWell you can do this problem in many linear way but i tried to do this in binary search for a better understanding of binary Search algorithm.\nSo what are the left and right limits? Its the 0 and the max Jumbo burger we can create from given tomatoes(t).\nFind the remaining tomatoes left for making small burgers after making jumbo burgers, if it is equal to number of cheese(c) given return it as ans.\nNow suppose the total no of Jumbo + small burger < required Burger\n-> We are making more Jumbo than required shift right pointer\nelse:\nshift left pointer\n# Code\n```\nclass Solution:\n def numOfBurgers(self, t: int, c: int) -> List[int]:\n if t % 2 != 0: # its odd then 1 tomato will always be remaining\n return []\n totalJumbo = t // 4\n left = 0\n right = totalJumbo\n while left < right:\n mid = (left + right) // 2\n remaining = t - (4 * mid)\n totalSmall = remaining / 2\n burgerPossible = mid + totalSmall\n if burgerPossible == c:\n return [mid, int(totalSmall)]\n elif (burgerPossible) < c: # we are making more jumbo reduce it \n right = mid\n else:\n left = mid + 1\n remaining = t - (4 * left)\n Small = remaining / 2\n if left + Small == c:\n return [left, int(Small)]\n return []\n``` | 1 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Alternative Solution Binary Search | Explained | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\nWell you can do this problem in many linear way but i tried to do this in binary search for a better understanding of binary Search algorithm.\nSo what are the left and right limits? Its the 0 and the max Jumbo burger we can create from given tomatoes(t).\nFind the remaining tomatoes left for making small burgers after making jumbo burgers, if it is equal to number of cheese(c) given return it as ans.\nNow suppose the total no of Jumbo + small burger < required Burger\n-> We are making more Jumbo than required shift right pointer\nelse:\nshift left pointer\n# Code\n```\nclass Solution:\n def numOfBurgers(self, t: int, c: int) -> List[int]:\n if t % 2 != 0: # its odd then 1 tomato will always be remaining\n return []\n totalJumbo = t // 4\n left = 0\n right = totalJumbo\n while left < right:\n mid = (left + right) // 2\n remaining = t - (4 * mid)\n totalSmall = remaining / 2\n burgerPossible = mid + totalSmall\n if burgerPossible == c:\n return [mid, int(totalSmall)]\n elif (burgerPossible) < c: # we are making more jumbo reduce it \n right = mid\n else:\n left = mid + 1\n remaining = t - (4 * left)\n Small = remaining / 2\n if left + Small == c:\n return [left, int(Small)]\n return []\n``` | 1 | You are given a circle represented as `(radius, xCenter, yCenter)` and an axis-aligned rectangle represented as `(x1, y1, x2, y2)`, where `(x1, y1)` are the coordinates of the bottom-left corner, and `(x2, y2)` are the coordinates of the top-right corner of the rectangle.
Return `true` _if the circle and rectangle are overlapped otherwise return_ `false`. In other words, check if there is **any** point `(xi, yi)` that belongs to the circle and the rectangle at the same time.
**Example 1:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
**Output:** true
**Explanation:** Circle and rectangle share the point (1,0).
**Example 2:**
**Input:** radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
**Output:** false
**Example 3:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
**Output:** true
**Constraints:**
* `1 <= radius <= 2000`
* `-104 <= xCenter, yCenter <= 104`
* `-104 <= x1 < x2 <= 104`
* `-104 <= y1 < y2 <= 104` | Can we have an answer if the number of tomatoes is odd ? If we have answer will be there multiple answers or just one answer ? Let us define number of jumbo burgers as X and number of small burgers as Y
We have to find an x and y in this equation 1. 4X + 2Y = tomato 2. X + Y = cheese |
Pure Maths | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices, cheeseSlices):\n val = (tomatoSlices - 2*cheeseSlices)\n\n if val >= 0 and val%2 == 0 and cheeseSlices-val//2 >= 0:\n return [val//2,cheeseSlices-val//2]\n\n return list()\n\n\n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Pure Maths | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices, cheeseSlices):\n val = (tomatoSlices - 2*cheeseSlices)\n\n if val >= 0 and val%2 == 0 and cheeseSlices-val//2 >= 0:\n return [val//2,cheeseSlices-val//2]\n\n return list()\n\n\n``` | 0 | You are given a circle represented as `(radius, xCenter, yCenter)` and an axis-aligned rectangle represented as `(x1, y1, x2, y2)`, where `(x1, y1)` are the coordinates of the bottom-left corner, and `(x2, y2)` are the coordinates of the top-right corner of the rectangle.
Return `true` _if the circle and rectangle are overlapped otherwise return_ `false`. In other words, check if there is **any** point `(xi, yi)` that belongs to the circle and the rectangle at the same time.
**Example 1:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
**Output:** true
**Explanation:** Circle and rectangle share the point (1,0).
**Example 2:**
**Input:** radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
**Output:** false
**Example 3:**
**Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
**Output:** true
**Constraints:**
* `1 <= radius <= 2000`
* `-104 <= xCenter, yCenter <= 104`
* `-104 <= x1 < x2 <= 104`
* `-104 <= y1 < y2 <= 104` | Can we have an answer if the number of tomatoes is odd ? If we have answer will be there multiple answers or just one answer ? Let us define number of jumbo burgers as X and number of small burgers as Y
We have to find an x and y in this equation 1. 4X + 2Y = tomato 2. X + Y = cheese |
Python Math | number-of-burgers-with-no-waste-of-ingredients | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nO(2)\n\n# Code\n```\nclass Solution:\n def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:\n if tomatoSlices < 2*cheeseSlices: return [] # not enough tomato\n elif tomatoSlices % 2: return [] # uneven tomato\n\n j = (tomatoSlices//2 - cheeseSlices) \n s = (2*cheeseSlices - tomatoSlices//2) \n\n if j < 0 or s < 0: return []\n return [j, s]\n\n\n \n``` | 0 | Given two integers `tomatoSlices` and `cheeseSlices`. The ingredients of different burgers are as follows:
* **Jumbo Burger:** `4` tomato slices and `1` cheese slice.
* **Small Burger:** `2` Tomato slices and `1` cheese slice.
Return `[total_jumbo, total_small]` so that the number of remaining `tomatoSlices` equal to `0` and the number of remaining `cheeseSlices` equal to `0`. If it is not possible to make the remaining `tomatoSlices` and `cheeseSlices` equal to `0` return `[]`.
**Example 1:**
**Input:** tomatoSlices = 16, cheeseSlices = 7
**Output:** \[1,6\]
**Explantion:** To make one jumbo burger and 6 small burgers we need 4\*1 + 2\*6 = 16 tomato and 1 + 6 = 7 cheese.
There will be no remaining ingredients.
**Example 2:**
**Input:** tomatoSlices = 17, cheeseSlices = 4
**Output:** \[\]
**Explantion:** There will be no way to use all ingredients to make small and jumbo burgers.
**Example 3:**
**Input:** tomatoSlices = 4, cheeseSlices = 17
**Output:** \[\]
**Explantion:** Making 1 jumbo burger there will be 16 cheese remaining and making 2 small burgers there will be 15 cheese remaining.
**Constraints:**
* `0 <= tomatoSlices, cheeseSlices <= 107` | Find the divisors of n+1 and n+2. To find the divisors of a number, you only need to iterate to the square root of that number. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.