title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Sliding Window,PrefixSum Approach | count-number-of-nice-subarrays | 0 | 1 | ```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n prefixsum=0\n dic=defaultdict(int)\n dic[0]=1\n ans=0\n for i in nums:\n if i%2==1:\n prefixsum+=1\n ans+=dic[prefixsum-k]\n dic[prefixsum]+=1\n return ans\n```\n# please upvote me it would encourage me alot\n | 6 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Sliding Window,PrefixSum Approach | count-number-of-nice-subarrays | 0 | 1 | ```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n prefixsum=0\n dic=defaultdict(int)\n dic[0]=1\n ans=0\n for i in nums:\n if i%2==1:\n prefixsum+=1\n ans+=dic[prefixsum-k]\n dic[prefixsum]+=1\n return ans\n```\n# please upvote me it would encourage me alot\n | 6 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
USING QUEUE || python Explained | count-number-of-nice-subarrays | 0 | 1 | # Intuition\r\nIn your queue store the index of all odd elements.\r\nNow acc to question each subarray must have only k odd elements so we have to design our window limits such that there are only k odd\r\n**So what must be the boundaries?**\r\n`window start = curr Index`\r\n`atleast window End = min k odd from window start i.e q[k-1]`\r\nNow upto where we can extend the end of our window? Untill and unless we find next odd element index i.e q[k]\r\n`window maxLimit = q[k]`\r\nso the `no of subarrays which can be formed = window max Limit - atleast window end`\r\nand increment ur curr index\r\nif ur currIndex > q[0] -> pop out the index as we calculated all possible sub arrays for it\r\n\r\nNow the only base case here is what if the odd number sits at the end of the array so we can still make one subarray from it\r\n**so add len(arr) to queue at end and this will be the maxWindowLimit for the last subarray if possible**\r\n\r\nThis might not be the best solution space optimization wise but many sliding window problems for counting subarrays can be solved with similar pattern approach.\r\n\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n q = deque()\r\n n = len(nums)\r\n for i in range(len(nums)):\r\n if nums[i] % 2 != 0:\r\n q.append(i)\r\n q.append(n) # for the subarray can be formed by odd ele at last index\r\n i = 0\r\n subarrays = 0\r\n while len(q) > k:\r\n minWindowLen = q[k-1]\r\n nextWindow = q[k]\r\n subarrays += nextWindow - minWindowLen\r\n if i == q[0]:\r\n q.popleft()\r\n i += 1\r\n return subarrays\r\n \r\n\r\n\r\n``` | 1 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
USING QUEUE || python Explained | count-number-of-nice-subarrays | 0 | 1 | # Intuition\r\nIn your queue store the index of all odd elements.\r\nNow acc to question each subarray must have only k odd elements so we have to design our window limits such that there are only k odd\r\n**So what must be the boundaries?**\r\n`window start = curr Index`\r\n`atleast window End = min k odd from window start i.e q[k-1]`\r\nNow upto where we can extend the end of our window? Untill and unless we find next odd element index i.e q[k]\r\n`window maxLimit = q[k]`\r\nso the `no of subarrays which can be formed = window max Limit - atleast window end`\r\nand increment ur curr index\r\nif ur currIndex > q[0] -> pop out the index as we calculated all possible sub arrays for it\r\n\r\nNow the only base case here is what if the odd number sits at the end of the array so we can still make one subarray from it\r\n**so add len(arr) to queue at end and this will be the maxWindowLimit for the last subarray if possible**\r\n\r\nThis might not be the best solution space optimization wise but many sliding window problems for counting subarrays can be solved with similar pattern approach.\r\n\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n q = deque()\r\n n = len(nums)\r\n for i in range(len(nums)):\r\n if nums[i] % 2 != 0:\r\n q.append(i)\r\n q.append(n) # for the subarray can be formed by odd ele at last index\r\n i = 0\r\n subarrays = 0\r\n while len(q) > k:\r\n minWindowLen = q[k-1]\r\n nextWindow = q[k]\r\n subarrays += nextWindow - minWindowLen\r\n if i == q[0]:\r\n q.popleft()\r\n i += 1\r\n return subarrays\r\n \r\n\r\n\r\n``` | 1 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
Python - Two pointer | count-number-of-nice-subarrays | 0 | 1 | ```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n right ,left = 0,0\n ans = 0 \n odd_cnt = 0\n ans = 0\n cur_sub_cnt = 0\n for right in range(len(nums)):\n \n if nums[right]%2 == 1:\n odd_cnt += 1\n cur_sub_cnt = 0\n \n while odd_cnt == k:\n if nums[left]%2 == 1:\n odd_cnt -= 1\n cur_sub_cnt += 1\n left += 1\n \n ans += cur_sub_cnt\n \n return ans \n``` | 36 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Python - Two pointer | count-number-of-nice-subarrays | 0 | 1 | ```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n right ,left = 0,0\n ans = 0 \n odd_cnt = 0\n ans = 0\n cur_sub_cnt = 0\n for right in range(len(nums)):\n \n if nums[right]%2 == 1:\n odd_cnt += 1\n cur_sub_cnt = 0\n \n while odd_cnt == k:\n if nums[left]%2 == 1:\n odd_cnt -= 1\n cur_sub_cnt += 1\n left += 1\n \n ans += cur_sub_cnt\n \n return ans \n``` | 36 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
Easy sliding widow | Beats 100 % | count-number-of-nice-subarrays | 0 | 1 | \r\n# Code\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n odd_count = 0\r\n res = 0\r\n i = 0\r\n count = 0\r\n for ele in nums:\r\n if ele % 2 == 1:\r\n odd_count += 1\r\n count = 0\r\n\r\n while odd_count==k:\r\n if nums[i] % 2 == 1:\r\n odd_count -= 1\r\n i += 1\r\n count += 1\r\n \r\n res += count\r\n return res\r\n``` | 1 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Easy sliding widow | Beats 100 % | count-number-of-nice-subarrays | 0 | 1 | \r\n# Code\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n odd_count = 0\r\n res = 0\r\n i = 0\r\n count = 0\r\n for ele in nums:\r\n if ele % 2 == 1:\r\n odd_count += 1\r\n count = 0\r\n\r\n while odd_count==k:\r\n if nums[i] % 2 == 1:\r\n odd_count -= 1\r\n i += 1\r\n count += 1\r\n \r\n res += count\r\n return res\r\n``` | 1 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
easy peasy python solution with explanation | count-number-of-nice-subarrays | 0 | 1 | \t# Just keep count of the current odd number.\n\t# Look in the dictionary if we can find (currendOds - k), \n\t# if it exisits that means I can get an subarray with k odds.\n\t# Also keep count of number of different types of odds too,\n\t# because for K =1 , [2,2,1] is a valid list, so does, [2,1] and [1].\n\t\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n\t\t\tdic = { 0: 1 }\n\t\t\tcnt = res = 0\n\t\t\tfor idx, num in enumerate(nums):\n\t\t\t\tif num % 2 == 1:\n\t\t\t\t\tcnt += 1\n\n\t\t\t\tif cnt - k in dic:\n\t\t\t\t\tres += dic[cnt-k]\n\n\t\t\t\tdic[cnt] = dic.get(cnt, 0) + 1\n\n\t\t\treturn res | 31 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
easy peasy python solution with explanation | count-number-of-nice-subarrays | 0 | 1 | \t# Just keep count of the current odd number.\n\t# Look in the dictionary if we can find (currendOds - k), \n\t# if it exisits that means I can get an subarray with k odds.\n\t# Also keep count of number of different types of odds too,\n\t# because for K =1 , [2,2,1] is a valid list, so does, [2,1] and [1].\n\t\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n\t\t\tdic = { 0: 1 }\n\t\t\tcnt = res = 0\n\t\t\tfor idx, num in enumerate(nums):\n\t\t\t\tif num % 2 == 1:\n\t\t\t\t\tcnt += 1\n\n\t\t\t\tif cnt - k in dic:\n\t\t\t\t\tres += dic[cnt-k]\n\n\t\t\t\tdic[cnt] = dic.get(cnt, 0) + 1\n\n\t\t\treturn res | 31 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
Python | Sliding window with comments for explanation | count-number-of-nice-subarrays | 0 | 1 | ```python\nclass Solution:\n\tdef numberOfSubarrays(self, arr, k):\n\t\t# the difference gives the exact K elements count\n\t\treturn self.atMostKElements(arr, k) - self.atMostKElements(arr, k-1)\n\n\tdef atMostKElements(self, arr, k):\n\t\ti, j = 0, 0\n\t\tres, curr_window_count = 0, 0\n\t\tfor j in range(len(arr)):\n\t\t\t# the {condition} which increases the curr_window_count. Different for different problems\n\t\t\tif arr[j]%2 != 0: curr_window_count += 1\n\n\t\t\t# check if the window is valid. If its invalid, make it valid by shortening the left pointer.\n\t\t\t# Valid is when curr_window_count <= k (at most K elements)\n\t\t\tif curr_window_count > k:\n\t\t\t\twhile curr_window_count > k:\n\t\t\t\t\t# this condition will be specific to the problem\n\t\t\t\t\tif arr[i]%2 != 0: curr_window_count -= 1\n\t\t\t\t\ti += 1\n\n\t\t\t# total nos of elements in the valid window is added to the res. \n\t\t\t# eg: [1, 2, 3], if this is the valid window, then [3], [2,3], [1,2,3] are all valid for solving at most K elements problem.\n\t\t\tres += j-i+1\n\t\t\tj += 1\n\t\treturn res\n``` | 1 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Python | Sliding window with comments for explanation | count-number-of-nice-subarrays | 0 | 1 | ```python\nclass Solution:\n\tdef numberOfSubarrays(self, arr, k):\n\t\t# the difference gives the exact K elements count\n\t\treturn self.atMostKElements(arr, k) - self.atMostKElements(arr, k-1)\n\n\tdef atMostKElements(self, arr, k):\n\t\ti, j = 0, 0\n\t\tres, curr_window_count = 0, 0\n\t\tfor j in range(len(arr)):\n\t\t\t# the {condition} which increases the curr_window_count. Different for different problems\n\t\t\tif arr[j]%2 != 0: curr_window_count += 1\n\n\t\t\t# check if the window is valid. If its invalid, make it valid by shortening the left pointer.\n\t\t\t# Valid is when curr_window_count <= k (at most K elements)\n\t\t\tif curr_window_count > k:\n\t\t\t\twhile curr_window_count > k:\n\t\t\t\t\t# this condition will be specific to the problem\n\t\t\t\t\tif arr[i]%2 != 0: curr_window_count -= 1\n\t\t\t\t\ti += 1\n\n\t\t\t# total nos of elements in the valid window is added to the res. \n\t\t\t# eg: [1, 2, 3], if this is the valid window, then [3], [2,3], [1,2,3] are all valid for solving at most K elements problem.\n\t\t\tres += j-i+1\n\t\t\tj += 1\n\t\treturn res\n``` | 1 | You are given a string `s`. Reorder the string using the following algorithm:
1. Pick the **smallest** character from `s` and **append** it to the result.
2. Pick the **smallest** character from `s` which is greater than the last appended character to the result and **append** it.
3. Repeat step 2 until you cannot pick more characters.
4. Pick the **largest** character from `s` and **append** it to the result.
5. Pick the **largest** character from `s` which is smaller than the last appended character to the result and **append** it.
6. Repeat step 5 until you cannot pick more characters.
7. Repeat the steps from 1 to 6 until you pick all characters from `s`.
In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.
Return _the result string after sorting_ `s` _with this algorithm_.
**Example 1:**
**Input:** s = "aaaabbbbcccc "
**Output:** "abccbaabccba "
**Explanation:** After steps 1, 2 and 3 of the first iteration, result = "abc "
After steps 4, 5 and 6 of the first iteration, result = "abccba "
First iteration is done. Now s = "aabbcc " and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc "
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba "
**Example 2:**
**Input:** s = "rat "
**Output:** "art "
**Explanation:** The word "rat " becomes "art " after re-ordering it with the mentioned algorithm.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | After replacing each even by zero and every odd by one can we use prefix sum to find answer ? Can we use two pointers to count number of sub-arrays ? Can we store indices of odd numbers and for each k indices count number of sub-arrays contains them ? |
Simple solution with Stack in Python3 / TypeScript | minimum-remove-to-make-valid-parentheses | 0 | 1 | # Intuition\nHere we have:\n- a string `s`\n- our goal is to **remove** minimum count of parentheses to make string **valid**\n\nAccording to the description a string is **valid**, if it meets conditions such that for **each open par** exists **closed par**.\n\nTo be short: for each par we need to store an index into `stack`, each time **open par** meets **closed par**, we can **pop** from `stack` and this pair considered as a **valid** one.\n\n# Approach\n1. declare `stack` and `ans`\n2. iterate over `s`\n3. check for **open par** and **push** it onto `stack`\n4. otherwise check, if the last par in stack **exists**, **pop** it, otherwise this par is **invalid** one\n5. iterate over all **invalid pars** of `stack` an replace them by empty string\n6. return `ans`\n\n# Complexity\n- Time complexity: **O(N)**, twice iterating over `s` and `stack` in worst-case scenario\n\n- Space complexity: **O(N)**, the same.\n\n# Code in Python3\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n ans = list(s)\n\n for i, char in enumerate(s):\n if char == \'(\': stack.append(i)\n elif char == \')\':\n if stack and s[stack[-1]] == \'(\': stack.pop()\n else: stack.append(i)\n\n for i in range(len(stack)): \n ans[stack[i]] = \'\'\n\n return \'\'.join(ans)\n```\n# Code in TypeScript\n```\nfunction minRemoveToMakeValid(s: string): string {\n const stack = [];\n const ans = s.split(\'\');\n\n for (let i = 0; i < s.length; i++) {\n const char = s[i];\n\n if (char === \'(\') {\n stack.push(i);\n } else if (char === \')\') {\n if (stack.length && s[stack[stack.length - 1]] === \'(\') {\n stack.pop();\n } else stack.push(i);\n }\n }\n\n for (let i = 0; i < stack.length; i++) ans[stack[i]] = \'\';\n\n return ans.join(\'\');\n}\n``` | 1 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
Simple solution with Stack in Python3 / TypeScript | minimum-remove-to-make-valid-parentheses | 0 | 1 | # Intuition\nHere we have:\n- a string `s`\n- our goal is to **remove** minimum count of parentheses to make string **valid**\n\nAccording to the description a string is **valid**, if it meets conditions such that for **each open par** exists **closed par**.\n\nTo be short: for each par we need to store an index into `stack`, each time **open par** meets **closed par**, we can **pop** from `stack` and this pair considered as a **valid** one.\n\n# Approach\n1. declare `stack` and `ans`\n2. iterate over `s`\n3. check for **open par** and **push** it onto `stack`\n4. otherwise check, if the last par in stack **exists**, **pop** it, otherwise this par is **invalid** one\n5. iterate over all **invalid pars** of `stack` an replace them by empty string\n6. return `ans`\n\n# Complexity\n- Time complexity: **O(N)**, twice iterating over `s` and `stack` in worst-case scenario\n\n- Space complexity: **O(N)**, the same.\n\n# Code in Python3\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n ans = list(s)\n\n for i, char in enumerate(s):\n if char == \'(\': stack.append(i)\n elif char == \')\':\n if stack and s[stack[-1]] == \'(\': stack.pop()\n else: stack.append(i)\n\n for i in range(len(stack)): \n ans[stack[i]] = \'\'\n\n return \'\'.join(ans)\n```\n# Code in TypeScript\n```\nfunction minRemoveToMakeValid(s: string): string {\n const stack = [];\n const ans = s.split(\'\');\n\n for (let i = 0; i < s.length; i++) {\n const char = s[i];\n\n if (char === \'(\') {\n stack.push(i);\n } else if (char === \')\') {\n if (stack.length && s[stack[stack.length - 1]] === \'(\') {\n stack.pop();\n } else stack.push(i);\n }\n }\n\n for (let i = 0; i < stack.length; i++) ans[stack[i]] = \'\';\n\n return ans.join(\'\');\n}\n``` | 1 | Implement a SnapshotArray that supports the following interface: | Use a list of lists, adding both the element and the snap_id to each index. |
Super simple Python solution with explanation. Faster than 100%, Memory Usage less than 100% | minimum-remove-to-make-valid-parentheses | 0 | 1 | 1. Convert string to list, because String is an immutable data structure in Python and it\'s much easier and memory-efficient to deal with a list for this task.\n2. Iterate through list\n3. Keep track of indices with open parentheses in the stack. In other words, when we come across open parenthesis we add an index to the stack.\n4. When we come across close parenthesis we pop an element from the stack. If the stack is empty we replace current list element with an empty string\n5. After iteration, we replace all indices we have in the stack with empty strings, because we don\'t have close parentheses for them.\n6. Convert list to string and return\n\n```\ndef minRemoveToMakeValid(self, s: str) -> str:\n s = list(s)\n stack = []\n for i, char in enumerate(s):\n if char == \'(\':\n stack.append(i)\n elif char == \')\':\n if stack:\n stack.pop()\n else:\n s[i] = \'\'\n while stack:\n s[stack.pop()] = \'\'\n return \'\'.join(s)\n```\n\nTime complexity is O(n)\nMemory complexity is O(n) | 483 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
Super simple Python solution with explanation. Faster than 100%, Memory Usage less than 100% | minimum-remove-to-make-valid-parentheses | 0 | 1 | 1. Convert string to list, because String is an immutable data structure in Python and it\'s much easier and memory-efficient to deal with a list for this task.\n2. Iterate through list\n3. Keep track of indices with open parentheses in the stack. In other words, when we come across open parenthesis we add an index to the stack.\n4. When we come across close parenthesis we pop an element from the stack. If the stack is empty we replace current list element with an empty string\n5. After iteration, we replace all indices we have in the stack with empty strings, because we don\'t have close parentheses for them.\n6. Convert list to string and return\n\n```\ndef minRemoveToMakeValid(self, s: str) -> str:\n s = list(s)\n stack = []\n for i, char in enumerate(s):\n if char == \'(\':\n stack.append(i)\n elif char == \')\':\n if stack:\n stack.pop()\n else:\n s[i] = \'\'\n while stack:\n s[stack.pop()] = \'\'\n return \'\'.join(s)\n```\n\nTime complexity is O(n)\nMemory complexity is O(n) | 483 | Implement a SnapshotArray that supports the following interface: | Use a list of lists, adding both the element and the snap_id to each index. |
Python || 95.62% Faster || Stack || Easy | minimum-remove-to-make-valid-parentheses | 0 | 1 | ```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s=list(s)\n st=[]\n for i in range(len(s)):\n if s[i]==\'(\':\n st.append(i)\n elif s[i]==\')\':\n if st:\n st.pop()\n else:\n s[i]=\'\'\n for i in st:\n s[i]=\'\'\n return \'\'.join(s)\n```\n**An upvote will be encouraging** | 1 | Given the string `s`, return the size of the longest substring containing each vowel an even number of times. That is, 'a', 'e', 'i', 'o', and 'u' must appear an even number of times.
**Example 1:**
**Input:** s = "eleetminicoworoep "
**Output:** 13
**Explanation:** The longest substring is "leetminicowor " which contains two each of the vowels: **e**, **i** and **o** and zero of the vowels: **a** and **u**.
**Example 2:**
**Input:** s = "leetcodeisgreat "
**Output:** 5
**Explanation:** The longest substring is "leetc " which contains two e's.
**Example 3:**
**Input:** s = "bcbcbc "
**Output:** 6
**Explanation:** In this case, the given string "bcbcbc " is the longest because all vowels: **a**, **e**, **i**, **o** and **u** appear zero times.
**Constraints:**
* `1 <= s.length <= 5 x 10^5`
* `s` contains only lowercase English letters.
It is the empty string, or It can be written as AB (A concatenated with B), where A and B are valid strings, or It can be written as (A), where A is a valid string. | Each prefix of a balanced parentheses has a number of open parentheses greater or equal than closed parentheses, similar idea with each suffix. Check the array from left to right, remove characters that do not meet the property mentioned above, same idea in backward way. |
Python || 95.62% Faster || Stack || Easy | minimum-remove-to-make-valid-parentheses | 0 | 1 | ```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s=list(s)\n st=[]\n for i in range(len(s)):\n if s[i]==\'(\':\n st.append(i)\n elif s[i]==\')\':\n if st:\n st.pop()\n else:\n s[i]=\'\'\n for i in st:\n s[i]=\'\'\n return \'\'.join(s)\n```\n**An upvote will be encouraging** | 1 | Implement a SnapshotArray that supports the following interface: | Use a list of lists, adding both the element and the snap_id to each index. |
Hand Written Easy Explanation with Bézout's Lemma | check-if-it-is-a-good-array | 0 | 1 | \n\n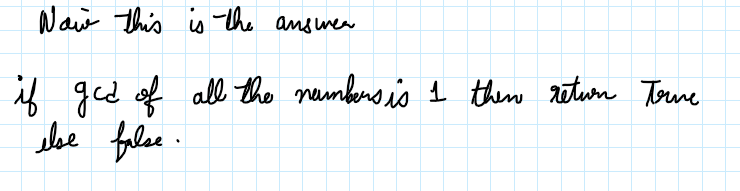\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n ans=nums[0]\n for i in range (1,len(nums)):\n ans=math.gcd(ans,nums[i])\n return ans==1\n```\n\nPlease Upvote the solution is you like it. | 2 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
Hand Written Easy Explanation with Bézout's Lemma | check-if-it-is-a-good-array | 0 | 1 | \n\n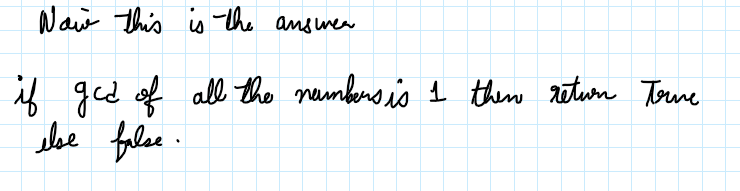\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n ans=nums[0]\n for i in range (1,len(nums)):\n ans=math.gcd(ans,nums[i])\n return ans==1\n```\n\nPlease Upvote the solution is you like it. | 2 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
Simple setwise coprimality check | check-if-it-is-a-good-array | 0 | 1 | # Intuition\nWe need to determine if the numbers are setwise coprime.\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return functools.reduce(math.gcd, nums) == 1\n``` | 0 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
Simple setwise coprimality check | check-if-it-is-a-good-array | 0 | 1 | # Intuition\nWe need to determine if the numbers are setwise coprime.\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return functools.reduce(math.gcd, nums) == 1\n``` | 0 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
0 Line Solution | check-if-it-is-a-good-array | 0 | 1 | # Description\nThe entire code is ran inline for the Solution\'s Function leading to a 2 line solution (0 added lines).\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool: return bool(functools.reduce(math.gcd, nums) == 1)\n``` | 0 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
0 Line Solution | check-if-it-is-a-good-array | 0 | 1 | # Description\nThe entire code is ran inline for the Solution\'s Function leading to a 2 line solution (0 added lines).\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool: return bool(functools.reduce(math.gcd, nums) == 1)\n``` | 0 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
my own solution | check-if-it-is-a-good-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n if nums == [1]:\n return True\n elif len(nums) == 1:\n return False\n else:\n gcd1=math.gcd(nums[0],nums[1])\n if len(nums)==2:\n return gcd1==1\n else:\n for i in range(2,len(nums)):\n gcd1 = math.gcd(gcd1,nums[i])\n if gcd1 == 1:\n return True\n else:\n return False\n \n \n``` | 0 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
my own solution | check-if-it-is-a-good-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n if nums == [1]:\n return True\n elif len(nums) == 1:\n return False\n else:\n gcd1=math.gcd(nums[0],nums[1])\n if len(nums)==2:\n return gcd1==1\n else:\n for i in range(2,len(nums)):\n gcd1 = math.gcd(gcd1,nums[i])\n if gcd1 == 1:\n return True\n else:\n return False\n \n \n``` | 0 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
1250. Check If It Is a Good Array | check-if-it-is-a-good-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd, nums) == 1\n``` | 0 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
1250. Check If It Is a Good Array | check-if-it-is-a-good-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd, nums) == 1\n``` | 0 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
Simple Approach Using GCD property | check-if-it-is-a-good-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFrom gcd property we know , ax + by = gcd(a,b) , if a and b are coprime then gcd(a,b) == 1.\nNow in this arry we need to find a subset whose gcd is equal to 1 , and it is always optimal to check the gcd of whole array , if we have the gcd equal to 1 then its possible otherwise its not possilbe\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N log(max(nums)))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n from math import gcd\n gc = 0\n for num in nums:\n gc = gcd(gc,num)\n if gc == 1:\n return True\n return False\n \n``` | 0 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
Simple Approach Using GCD property | check-if-it-is-a-good-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFrom gcd property we know , ax + by = gcd(a,b) , if a and b are coprime then gcd(a,b) == 1.\nNow in this arry we need to find a subset whose gcd is equal to 1 , and it is always optimal to check the gcd of whole array , if we have the gcd equal to 1 then its possible otherwise its not possilbe\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N log(max(nums)))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n from math import gcd\n gc = 0\n for num in nums:\n gc = gcd(gc,num)\n if gc == 1:\n return True\n return False\n \n``` | 0 | You are given the `root` of a binary tree.
A ZigZag path for a binary tree is defined as follow:
* Choose **any** node in the binary tree and a direction (right or left).
* If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
* Change the direction from right to left or from left to right.
* Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return _the longest **ZigZag** path contained in that tree_.
**Example 1:**
**Input:** root = \[1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1\]
**Output:** 3
**Explanation:** Longest ZigZag path in blue nodes (right -> left -> right).
**Example 2:**
**Input:** root = \[1,1,1,null,1,null,null,1,1,null,1\]
**Output:** 4
**Explanation:** Longest ZigZag path in blue nodes (left -> right -> left -> right).
**Example 3:**
**Input:** root = \[1\]
**Output:** 0
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5 * 104]`.
* `1 <= Node.val <= 100` | Eq. ax+by=1 has solution x, y if gcd(a,b) = 1. Can you generalize the formula?. Check Bézout's lemma. |
97% Runtime 80% Memory The simpliest solution | cells-with-odd-values-in-a-matrix | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(m*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:\n rows,cols = [0]*m,[0]*n\n \n for r,c in indices: rows[r] += 1; cols[c] += 1\n \n return sum(\n 1\n for r in rows\n for c in cols\n if (r + c) % 2\n )\n \n``` | 0 | There is an `m x n` matrix that is initialized to all `0`'s. There is also a 2D array `indices` where each `indices[i] = [ri, ci]` represents a **0-indexed location** to perform some increment operations on the matrix.
For each location `indices[i]`, do **both** of the following:
1. Increment **all** the cells on row `ri`.
2. Increment **all** the cells on column `ci`.
Given `m`, `n`, and `indices`, return _the **number of odd-valued cells** in the matrix after applying the increment to all locations in_ `indices`.
**Example 1:**
**Input:** m = 2, n = 3, indices = \[\[0,1\],\[1,1\]\]
**Output:** 6
**Explanation:** Initial matrix = \[\[0,0,0\],\[0,0,0\]\].
After applying first increment it becomes \[\[1,2,1\],\[0,1,0\]\].
The final matrix is \[\[1,3,1\],\[1,3,1\]\], which contains 6 odd numbers.
**Example 2:**
**Input:** m = 2, n = 2, indices = \[\[1,1\],\[0,0\]\]
**Output:** 0
**Explanation:** Final matrix = \[\[2,2\],\[2,2\]\]. There are no odd numbers in the final matrix.
**Constraints:**
* `1 <= m, n <= 50`
* `1 <= indices.length <= 100`
* `0 <= ri < m`
* `0 <= ci < n`
**Follow up:** Could you solve this in `O(n + m + indices.length)` time with only `O(n + m)` extra space? | How to detect if there is impossible to perform the replacement? Only when the length = 1. Change the first non 'a' character to 'a'. What if the string has only 'a'? Change the last character to 'b'. |
Python | O(n*m+indices) | Easy | Hashing | cells-with-odd-values-in-a-matrix | 0 | 1 | ```\nclass Solution:\n def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:\n dict_ = {} #List to keep track of total increase row and column wise\n dict_[\'col\'] = [0]*n\n dict_[\'row\'] = [0]*m\n for idx in range(len(indices)):\n dict_[\'row\'][indices[idx][0]] += 1\n dict_[\'col\'][indices[idx][1]] += 1\n count_odd = 0\n for row in range(m):\n for col in range(n):\n if (dict_[\'row\'][row] + dict_[\'col\'][col])&1 == 1: #if total increase is odd\n count_odd += 1\n return count_odd\n``` | 0 | There is an `m x n` matrix that is initialized to all `0`'s. There is also a 2D array `indices` where each `indices[i] = [ri, ci]` represents a **0-indexed location** to perform some increment operations on the matrix.
For each location `indices[i]`, do **both** of the following:
1. Increment **all** the cells on row `ri`.
2. Increment **all** the cells on column `ci`.
Given `m`, `n`, and `indices`, return _the **number of odd-valued cells** in the matrix after applying the increment to all locations in_ `indices`.
**Example 1:**
**Input:** m = 2, n = 3, indices = \[\[0,1\],\[1,1\]\]
**Output:** 6
**Explanation:** Initial matrix = \[\[0,0,0\],\[0,0,0\]\].
After applying first increment it becomes \[\[1,2,1\],\[0,1,0\]\].
The final matrix is \[\[1,3,1\],\[1,3,1\]\], which contains 6 odd numbers.
**Example 2:**
**Input:** m = 2, n = 2, indices = \[\[1,1\],\[0,0\]\]
**Output:** 0
**Explanation:** Final matrix = \[\[2,2\],\[2,2\]\]. There are no odd numbers in the final matrix.
**Constraints:**
* `1 <= m, n <= 50`
* `1 <= indices.length <= 100`
* `0 <= ri < m`
* `0 <= ci < n`
**Follow up:** Could you solve this in `O(n + m + indices.length)` time with only `O(n + m)` extra space? | How to detect if there is impossible to perform the replacement? Only when the length = 1. Change the first non 'a' character to 'a'. What if the string has only 'a'? Change the last character to 'b'. |
Simple Python Greedy O(n) Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n \n n = len(colsum)\n matrix = [[0] * n for _ in range(2)]\n if upper + lower != sum(colsum): return []\n\n for i in range(n):\n if colsum[i] == 2:\n matrix[0][i] = 1\n matrix[1][i] = 1\n upper -= 1\n lower -= 1\n elif colsum[i] == 1:\n if lower <= upper:\n matrix[0][i] = 1\n upper -= 1\n else:\n matrix[1][i] = 1\n lower -= 1\n \n if upper > 0 or lower > 0:\n return []\n \n return matrix\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Simple Python Greedy O(n) Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n \n n = len(colsum)\n matrix = [[0] * n for _ in range(2)]\n if upper + lower != sum(colsum): return []\n\n for i in range(n):\n if colsum[i] == 2:\n matrix[0][i] = 1\n matrix[1][i] = 1\n upper -= 1\n lower -= 1\n elif colsum[i] == 1:\n if lower <= upper:\n matrix[0][i] = 1\n upper -= 1\n else:\n matrix[1][i] = 1\n lower -= 1\n \n if upper > 0 or lower > 0:\n return []\n \n return matrix\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Simple and clear python3 solutions | 524 ms - faster than 94.4% solutions | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ (only for answer)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n if upper > n or lower > n:\n return []\n\n deuces = sum(1 for elem in colsum if elem == 2)\n if upper < deuces or lower < deuces:\n return []\n\n if upper + lower != sum(colsum):\n return []\n \n result = [[0] * n for _ in range(2)]\n upper -= deuces\n lower -= deuces\n\n for i, s in enumerate(colsum):\n if s == 2:\n result[0][i] = 1\n result[1][i] = 1\n elif s == 1:\n if upper:\n result[0][i] = 1\n upper -= 1\n else:\n result[1][i] = 1\n lower -= 1\n\n return result\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Simple and clear python3 solutions | 524 ms - faster than 94.4% solutions | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ (only for answer)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n if upper > n or lower > n:\n return []\n\n deuces = sum(1 for elem in colsum if elem == 2)\n if upper < deuces or lower < deuces:\n return []\n\n if upper + lower != sum(colsum):\n return []\n \n result = [[0] * n for _ in range(2)]\n upper -= deuces\n lower -= deuces\n\n for i, s in enumerate(colsum):\n if s == 2:\n result[0][i] = 1\n result[1][i] = 1\n elif s == 1:\n if upper:\n result[0][i] = 1\n upper -= 1\n else:\n result[1][i] = 1\n lower -= 1\n\n return result\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Python Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSome tricky edge cases should to be considered carefully.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n arr=[]\n for i in range(2):\n p=[]\n for j in range(len(colsum)):\n p.append(0)\n arr.append(p)\n if lower+upper<sum(colsum):\n return []\n if (lower==len(colsum) or upper==len(colsum)) or (lower==0 or upper==0):\n return []\n k=0\n if upper==lower:\n for i in range(len(colsum)):\n if colsum[i]==2:\n arr[0][i]=1 \n arr[1][i]=1 \n upper-=1 \n lower-=1 \n for i in range(len(colsum)):\n if colsum[i]==1:\n if k%2==0 :\n arr[0][i]=1 \n arr[1][i]=0\n upper-=1 \n \n elif k%2!=0 :\n arr[0][i]=0\n arr[1][i]=1 \n lower-=1 \n k+=1\n if colsum[i]==0:\n arr[0][i]=0\n arr[1][i]=0\n else:\n for i in range(len(colsum)):\n if colsum[i]==2:\n arr[0][i]=1 \n arr[1][i]=1 \n upper-=1 \n lower-=1 \n for i in range(len(colsum)):\n if colsum[i]==1:\n if upper>0 and arr[0][i]+arr[1][i]<colsum[i]:\n arr[0][i]=1\n upper-=1 \n elif lower>0 and arr[0][i]+arr[1][i]<colsum[i]:\n arr[1][i]=1 \n lower-=1 \n print(lower,upper)\n if upper!=0 or lower!=0:\n return []\n else:\n return arr\n\n \n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Python Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSome tricky edge cases should to be considered carefully.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n arr=[]\n for i in range(2):\n p=[]\n for j in range(len(colsum)):\n p.append(0)\n arr.append(p)\n if lower+upper<sum(colsum):\n return []\n if (lower==len(colsum) or upper==len(colsum)) or (lower==0 or upper==0):\n return []\n k=0\n if upper==lower:\n for i in range(len(colsum)):\n if colsum[i]==2:\n arr[0][i]=1 \n arr[1][i]=1 \n upper-=1 \n lower-=1 \n for i in range(len(colsum)):\n if colsum[i]==1:\n if k%2==0 :\n arr[0][i]=1 \n arr[1][i]=0\n upper-=1 \n \n elif k%2!=0 :\n arr[0][i]=0\n arr[1][i]=1 \n lower-=1 \n k+=1\n if colsum[i]==0:\n arr[0][i]=0\n arr[1][i]=0\n else:\n for i in range(len(colsum)):\n if colsum[i]==2:\n arr[0][i]=1 \n arr[1][i]=1 \n upper-=1 \n lower-=1 \n for i in range(len(colsum)):\n if colsum[i]==1:\n if upper>0 and arr[0][i]+arr[1][i]<colsum[i]:\n arr[0][i]=1\n upper-=1 \n elif lower>0 and arr[0][i]+arr[1][i]<colsum[i]:\n arr[1][i]=1 \n lower-=1 \n print(lower,upper)\n if upper!=0 or lower!=0:\n return []\n else:\n return arr\n\n \n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Solution | reconstruct-a-2-row-binary-matrix | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& c) {\n vector<vector<int>> res(2,vector<int>(c.size(),0));\n int count=0;\n for(auto &el:c) count+=el==2;\n for(int i=0;i<c.size();i++){\n if(c[i]==2){\n if(upper==0 || lower==0) return {};\n upper--,lower--;\n res[0][i]=1,res[1][i]=1;\n count--;\n }else if(c[i]==1){\n if(upper==0 && lower==0) return {};\n if(upper>0 && count<upper) res[0][i]=1,upper--;\n else if(lower>0 && count<lower) res[1][i]=1,lower--;\n else return {};\n }\n }\n if(upper || lower) return {};\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n \n s, n = sum(colsum), len(colsum)\n if upper + lower != s: return []\n u, d = [0] * n, [0] * n\n for i in range(n):\n if colsum[i] == 2 and upper > 0 and lower > 0:\n u[i] = d[i] = 1\n upper, lower = upper-1, lower-1\n elif colsum[i] == 1: \n if upper > 0 and upper >= lower:\n u[i], upper = 1, upper-1\n elif lower > 0 and lower >= upper:\n d[i], lower = 1, lower-1\n else: return [] \n elif not colsum[i]: continue\n else: return []\n return [u, d] \n```\n\n```Java []\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int[][] ans=new int[2][colsum.length];\n for(int j=0;j<colsum.length;j++)\n {\n if(colsum[j]==2)\n {\n ans[0][j]=1;\n ans[1][j]=1;\n lower-=1;\n upper-=1;\n }\n else if(colsum[j]==0)\n {\n ans[0][j]=0;\n ans[1][j]=0;\n }\n else\n {\n if(upper>=lower)\n {\n ans[0][j]=1;\n ans[1][j]=0;\n upper-=1;\n }\n else\n {\n ans[0][j]=0;\n ans[1][j]=1;\n lower-=1;\n }\n } \n }\n return lower == 0 && upper == 0 ? new ArrayList(Arrays.asList(ans[0], ans[1])) : new ArrayList();\n }\n}\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Solution | reconstruct-a-2-row-binary-matrix | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& c) {\n vector<vector<int>> res(2,vector<int>(c.size(),0));\n int count=0;\n for(auto &el:c) count+=el==2;\n for(int i=0;i<c.size();i++){\n if(c[i]==2){\n if(upper==0 || lower==0) return {};\n upper--,lower--;\n res[0][i]=1,res[1][i]=1;\n count--;\n }else if(c[i]==1){\n if(upper==0 && lower==0) return {};\n if(upper>0 && count<upper) res[0][i]=1,upper--;\n else if(lower>0 && count<lower) res[1][i]=1,lower--;\n else return {};\n }\n }\n if(upper || lower) return {};\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n \n s, n = sum(colsum), len(colsum)\n if upper + lower != s: return []\n u, d = [0] * n, [0] * n\n for i in range(n):\n if colsum[i] == 2 and upper > 0 and lower > 0:\n u[i] = d[i] = 1\n upper, lower = upper-1, lower-1\n elif colsum[i] == 1: \n if upper > 0 and upper >= lower:\n u[i], upper = 1, upper-1\n elif lower > 0 and lower >= upper:\n d[i], lower = 1, lower-1\n else: return [] \n elif not colsum[i]: continue\n else: return []\n return [u, d] \n```\n\n```Java []\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int[][] ans=new int[2][colsum.length];\n for(int j=0;j<colsum.length;j++)\n {\n if(colsum[j]==2)\n {\n ans[0][j]=1;\n ans[1][j]=1;\n lower-=1;\n upper-=1;\n }\n else if(colsum[j]==0)\n {\n ans[0][j]=0;\n ans[1][j]=0;\n }\n else\n {\n if(upper>=lower)\n {\n ans[0][j]=1;\n ans[1][j]=0;\n upper-=1;\n }\n else\n {\n ans[0][j]=0;\n ans[1][j]=1;\n lower-=1;\n }\n } \n }\n return lower == 0 && upper == 0 ? new ArrayList(Arrays.asList(ans[0], ans[1])) : new ArrayList();\n }\n}\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Runtime 667 ms Beats 83.48% Memory 26.7 MB Beats 20.87% | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if upper+lower!=sum(colsum) :return []\n arr=[\n [0 for i in range(len(colsum))],\n [0 for i in range(len(colsum))]\n ]\n for i in range(len(colsum)):\n if colsum[i]==2:\n arr[0][i]=1\n arr[1][i]=1\n upper-=1\n lower-=1\n for i in range(len(colsum)):\n if lower<0 or upper<0:return []\n if colsum[i]==1:\n if upper>0:\n arr[0][i]=1\n arr[1][i]=0\n upper-=1\n else:\n arr[0][i]=0\n arr[1][i]=1\n lower-=1\n return arr\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Runtime 667 ms Beats 83.48% Memory 26.7 MB Beats 20.87% | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if upper+lower!=sum(colsum) :return []\n arr=[\n [0 for i in range(len(colsum))],\n [0 for i in range(len(colsum))]\n ]\n for i in range(len(colsum)):\n if colsum[i]==2:\n arr[0][i]=1\n arr[1][i]=1\n upper-=1\n lower-=1\n for i in range(len(colsum)):\n if lower<0 or upper<0:return []\n if colsum[i]==1:\n if upper>0:\n arr[0][i]=1\n arr[1][i]=0\n upper-=1\n else:\n arr[0][i]=0\n arr[1][i]=1\n lower-=1\n return arr\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Clean | Concise | Fast | 4 Lines | Python Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n upper_list = [0 for _ in range(n)]\n lower_list = [0 for _ in range(n)]\n \n for i, v in enumerate(colsum):\n if v == 1:\n if upper > lower:\n upper_list[i] = 1\n upper -= 1\n else: \n lower_list[i] = 1\n lower -= 1\n elif v == 2: \n upper_list[i] = lower_list[i] = 1\n upper, lower = upper - 1, lower - 1\n \n return [upper_list, lower_list] if upper == lower == 0 else []\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Clean | Concise | Fast | 4 Lines | Python Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n upper_list = [0 for _ in range(n)]\n lower_list = [0 for _ in range(n)]\n \n for i, v in enumerate(colsum):\n if v == 1:\n if upper > lower:\n upper_list[i] = 1\n upper -= 1\n else: \n lower_list[i] = 1\n lower -= 1\n elif v == 2: \n upper_list[i] = lower_list[i] = 1\n upper, lower = upper - 1, lower - 1\n \n return [upper_list, lower_list] if upper == lower == 0 else []\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Simple 3 Case Iterator on Columns | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\nThe fact that this is binary helps us.\n\n# Approach\nHandle each column, and split it into the 0, 1, 2 bucket.\n## Case: 0\nFor 0, it\'s easy. Neither row has an entry, we can proceed.\n\n## Case: 2 (we\'ll come back to 1)\nFor 2, we simply check if we have already reached our limits, and exit with the "null case" if so. This is because we\'re confident that we\'ve made the best choices we can up until this point.\n\n## Case: 1\nFor case 1, we have a choice to make -- add an entry to the top line, or the bottom line? To make this choice, we keep a running total of the sum for each row. Then, we decide to add entries to only the row that is furthest from reaching its desired sum total.\n\n# Complexity\n- Time complexity: O(N)\n\n\n- Space complexity: O(2N)\n\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n # 2-row binary matrix\n # upper row sum -> upper\n # lower row sum -> lower\n # sum of elements in each column -> colsum\n # Get original matrix\n full_sum = upper + lower \n\n ret = [[0 for x in range(len(colsum))] for y in (1,2)]\n\n cursums = [0, 0]\n\n for ci, csum in enumerate(colsum):\n # If 0, nothing to do\n if csum == 0:\n continue\n # If 1, we have to make some decisions\n elif csum == 1:\n # First we must check if we\'re at either of our limits, and return a failure case.\n if cursums[0] >= upper:\n if cursums[1] >= lower:\n return []\n # If we no longer have a choice to pick this one, we pick the other one\n else:\n ret[1][ci] += 1\n cursums[1] += 1\n \n elif cursums[1] >= lower:\n # not strictly necessary\n if cursums[0] >= upper:\n return []\n # If we no longer have a choice to pick this one, we pick the other one\n else:\n ret[0][ci] += 1\n cursums[0] += 1\n else:\n # Since we can choose, we pick whichever one has the lowest running sum.\n if ((upper - cursums[0]) > (lower - cursums[1])):\n ret[0][ci] += 1\n cursums[0] += 1\n else:\n ret[1][ci] += 1\n cursums[1] += 1\n\n # If 2, both are populated.\n elif csum == 2:\n # Fail if we\'re over limit.\n if cursums[0] >= upper or cursums[1] >= lower:\n return []\n \n # Increment.\n cursums[0] += 1\n cursums[1] += 1\n ret[0][ci] += 1\n ret[1][ci] += 1\n \n if upper != cursums[0] or lower != cursums[1]:\n return []\n else:\n return ret\n \n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Simple 3 Case Iterator on Columns | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\nThe fact that this is binary helps us.\n\n# Approach\nHandle each column, and split it into the 0, 1, 2 bucket.\n## Case: 0\nFor 0, it\'s easy. Neither row has an entry, we can proceed.\n\n## Case: 2 (we\'ll come back to 1)\nFor 2, we simply check if we have already reached our limits, and exit with the "null case" if so. This is because we\'re confident that we\'ve made the best choices we can up until this point.\n\n## Case: 1\nFor case 1, we have a choice to make -- add an entry to the top line, or the bottom line? To make this choice, we keep a running total of the sum for each row. Then, we decide to add entries to only the row that is furthest from reaching its desired sum total.\n\n# Complexity\n- Time complexity: O(N)\n\n\n- Space complexity: O(2N)\n\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n # 2-row binary matrix\n # upper row sum -> upper\n # lower row sum -> lower\n # sum of elements in each column -> colsum\n # Get original matrix\n full_sum = upper + lower \n\n ret = [[0 for x in range(len(colsum))] for y in (1,2)]\n\n cursums = [0, 0]\n\n for ci, csum in enumerate(colsum):\n # If 0, nothing to do\n if csum == 0:\n continue\n # If 1, we have to make some decisions\n elif csum == 1:\n # First we must check if we\'re at either of our limits, and return a failure case.\n if cursums[0] >= upper:\n if cursums[1] >= lower:\n return []\n # If we no longer have a choice to pick this one, we pick the other one\n else:\n ret[1][ci] += 1\n cursums[1] += 1\n \n elif cursums[1] >= lower:\n # not strictly necessary\n if cursums[0] >= upper:\n return []\n # If we no longer have a choice to pick this one, we pick the other one\n else:\n ret[0][ci] += 1\n cursums[0] += 1\n else:\n # Since we can choose, we pick whichever one has the lowest running sum.\n if ((upper - cursums[0]) > (lower - cursums[1])):\n ret[0][ci] += 1\n cursums[0] += 1\n else:\n ret[1][ci] += 1\n cursums[1] += 1\n\n # If 2, both are populated.\n elif csum == 2:\n # Fail if we\'re over limit.\n if cursums[0] >= upper or cursums[1] >= lower:\n return []\n \n # Increment.\n cursums[0] += 1\n cursums[1] += 1\n ret[0][ci] += 1\n ret[1][ci] += 1\n \n if upper != cursums[0] or lower != cursums[1]:\n return []\n else:\n return ret\n \n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Python easy solution with explanation O(n) | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Approach\n\n1. Create required 2D matrix filled with 0\'s\n2. \'top\' and \'bot\' are counts of 1\'s in top and bottom rows. They are initialised as a number of 2\'s in colsum.\n3. Go over colsum: If val == 2: make top and bottom values 1. If val == 1 make either top or bottom value 1 (checking if limit is not exceeded)\n4. Lastly check if counts match \'upper\' and \'lower\' values given. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n\n res = [[0 for _ in colsum] for _ in range(2)]\n top = bot = colsum.count(2)\n for i,val in enumerate(colsum):\n if val == 2: res[0][i],res[1][i] = 1,1\n if val == 1:\n if top < upper: res[0][i],top = 1,top+1\n elif bot < lower: res[1][i],bot = 1,bot+1\n else: return [] \n\n return res if top == upper and bot == lower else []\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Python easy solution with explanation O(n) | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Approach\n\n1. Create required 2D matrix filled with 0\'s\n2. \'top\' and \'bot\' are counts of 1\'s in top and bottom rows. They are initialised as a number of 2\'s in colsum.\n3. Go over colsum: If val == 2: make top and bottom values 1. If val == 1 make either top or bottom value 1 (checking if limit is not exceeded)\n4. Lastly check if counts match \'upper\' and \'lower\' values given. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n\n res = [[0 for _ in colsum] for _ in range(2)]\n top = bot = colsum.count(2)\n for i,val in enumerate(colsum):\n if val == 2: res[0][i],res[1][i] = 1,1\n if val == 1:\n if top < upper: res[0][i],top = 1,top+1\n elif bot < lower: res[1][i],bot = 1,bot+1\n else: return [] \n\n return res if top == upper and bot == lower else []\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
O(n) python solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem statement is to reconstruct a matrix given the upper and lower row sums and the sum of each column. The idea is to start with the columns that have a sum of 2 and place one 1 in the upper row and one 1 in the lower row. Then, iterate through the remaining columns with a sum of 1 and place the 1 in the remaining available row (either upper or lower).\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to iterate through the colsum list and first, handle the columns with a sum of 2 by placing 1 in both upper and lower rows. Then, iterate through the remaining columns with a sum of 1 and place the 1 in the remaining available row (either upper or lower). If at any point the number of 1\'s placed in the upper or lower row exceeds the respective upper or lower row sum, return an empty list, as the matrix cannot be reconstructed. Finally, check if all upper and lower row sum has been exhausted and return the matrix, else return an empty list.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n a = [0] * len(colsum)\n b = [0] * len(colsum)\n for i in range(len(colsum)):\n if colsum[i] == 2:\n a[i] = 1\n b[i] = 1\n upper -= 1\n lower -= 1\n if upper < 0 or lower < 0:\n return []\n for i in range(len(colsum)):\n if colsum[i] == 1:\n if upper > 0:\n a[i] = 1\n upper -= 1\n elif lower > 0:\n b[i] = 1\n lower -= 1\n else:\n return []\n return [a, b] if upper == 0 and lower == 0 else []\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
O(n) python solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem statement is to reconstruct a matrix given the upper and lower row sums and the sum of each column. The idea is to start with the columns that have a sum of 2 and place one 1 in the upper row and one 1 in the lower row. Then, iterate through the remaining columns with a sum of 1 and place the 1 in the remaining available row (either upper or lower).\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to iterate through the colsum list and first, handle the columns with a sum of 2 by placing 1 in both upper and lower rows. Then, iterate through the remaining columns with a sum of 1 and place the 1 in the remaining available row (either upper or lower). If at any point the number of 1\'s placed in the upper or lower row exceeds the respective upper or lower row sum, return an empty list, as the matrix cannot be reconstructed. Finally, check if all upper and lower row sum has been exhausted and return the matrix, else return an empty list.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n a = [0] * len(colsum)\n b = [0] * len(colsum)\n for i in range(len(colsum)):\n if colsum[i] == 2:\n a[i] = 1\n b[i] = 1\n upper -= 1\n lower -= 1\n if upper < 0 or lower < 0:\n return []\n for i in range(len(colsum)):\n if colsum[i] == 1:\n if upper > 0:\n a[i] = 1\n upper -= 1\n elif lower > 0:\n b[i] = 1\n lower -= 1\n else:\n return []\n return [a, b] if upper == 0 and lower == 0 else []\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Simple to understand Python O(n) Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\nFirst I place all the "forced entries" into the solution array. These "forced entries" are when the colsum is either 0 or 2. If the colsum is 0, then clearly both the upper and lower values must be 0. If colsum is 2, then cleary both the upper and lower values must be 1. As such, these values are forced. If the colsum is 1, then this represents a "choice" we must make later. So, the basic outline is: First, go through the colsum and add the "forced entries". Second, determine if there is a solution. Finally, if there is a solution, use a greedy based approach to make all the remaining choices.\n\n# Complexity\n- Time complexity:\nTwo passes of O(n) each, resulting in O(n)\n\n- Space complexity:\nEverything is done inplace, resulting in O(n) total place and O(1) extra space.\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n choices = 0\n\n solution = []\n solution.append([0 for i in range(n)])\n solution.append([0 for i in range(n)])\n #This creates our empty binary matrix that will become our solution\n\n #Now, go through the array and fill in all the current information we have\n \n for i in range(n):\n #If the colsum is 0, both must be zero\n if colsum[i] == 0:\n solution[0][i] = 0\n solution[0][i] = 0\n #If the colsum is 2, then they both must be 1\n elif colsum[i] == 2:\n solution[0][i] = 1\n solution[1][i] = 1\n\n #Since we are inputting 1\'s into our solution, the remaining 1\'s can be reduced\n upper += -1\n lower += -1\n else:\n #In this case, colsum[i] == 1 and so there is a choice\n choices += 1\n \n #If number of forced entries has already excited the total number of entrices, it is impossible\n if lower < 0 or upper < 0:\n return []\n #The number of chioces has to equal the sum of upper or lower now that the known \n #Information has been added, otherwise it is impossible\n if choices != upper + lower:\n return []\n\n #The first pass took O(n) time\n #Now, for each remaining column, we can freely decide whether the upper or lower gets the 1\\\n #The way we will decide this is by choosing the larger of upper and lower\n #This will ensure that both reach zero by the end\n for i in range(n):\n if colsum[i] == 1:\n if lower > upper: \n #If lower is bigger, reduce it\n solution[0][i] = 0\n solution[1][i] = 1\n\n lower += -1\n else:\n #Otherwise, lower is smaller or the same, so reduce upper\n solution[0][i] = 1\n solution[1][i] = 0\n\n upper += -1\n \n #This pass also takes O(n) time, for a final time of O(n)\n return solution\n\n\n\n``` | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Simple to understand Python O(n) Solution | reconstruct-a-2-row-binary-matrix | 0 | 1 | # Intuition\nFirst I place all the "forced entries" into the solution array. These "forced entries" are when the colsum is either 0 or 2. If the colsum is 0, then clearly both the upper and lower values must be 0. If colsum is 2, then cleary both the upper and lower values must be 1. As such, these values are forced. If the colsum is 1, then this represents a "choice" we must make later. So, the basic outline is: First, go through the colsum and add the "forced entries". Second, determine if there is a solution. Finally, if there is a solution, use a greedy based approach to make all the remaining choices.\n\n# Complexity\n- Time complexity:\nTwo passes of O(n) each, resulting in O(n)\n\n- Space complexity:\nEverything is done inplace, resulting in O(n) total place and O(1) extra space.\n\n# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n choices = 0\n\n solution = []\n solution.append([0 for i in range(n)])\n solution.append([0 for i in range(n)])\n #This creates our empty binary matrix that will become our solution\n\n #Now, go through the array and fill in all the current information we have\n \n for i in range(n):\n #If the colsum is 0, both must be zero\n if colsum[i] == 0:\n solution[0][i] = 0\n solution[0][i] = 0\n #If the colsum is 2, then they both must be 1\n elif colsum[i] == 2:\n solution[0][i] = 1\n solution[1][i] = 1\n\n #Since we are inputting 1\'s into our solution, the remaining 1\'s can be reduced\n upper += -1\n lower += -1\n else:\n #In this case, colsum[i] == 1 and so there is a choice\n choices += 1\n \n #If number of forced entries has already excited the total number of entrices, it is impossible\n if lower < 0 or upper < 0:\n return []\n #The number of chioces has to equal the sum of upper or lower now that the known \n #Information has been added, otherwise it is impossible\n if choices != upper + lower:\n return []\n\n #The first pass took O(n) time\n #Now, for each remaining column, we can freely decide whether the upper or lower gets the 1\\\n #The way we will decide this is by choosing the larger of upper and lower\n #This will ensure that both reach zero by the end\n for i in range(n):\n if colsum[i] == 1:\n if lower > upper: \n #If lower is bigger, reduce it\n solution[0][i] = 0\n solution[1][i] = 1\n\n lower += -1\n else:\n #Otherwise, lower is smaller or the same, so reduce upper\n solution[0][i] = 1\n solution[1][i] = 0\n\n upper += -1\n \n #This pass also takes O(n) time, for a final time of O(n)\n return solution\n\n\n\n``` | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Easy to Understand | reconstruct-a-2-row-binary-matrix | 0 | 1 | \tclass Solution:\n\t\tdef reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n\t\t\tbm = [[0 for _ in range(len(colsum))] for i in range(2)]\n\t\t\tfor i in range(len(colsum)):\n\t\t\t\tif colsum[i]==2:\n\t\t\t\t\tcolsum[i]=0\n\t\t\t\t\tupper-=1\n\t\t\t\t\tlower-=1\n\t\t\t\t\tbm[0][i]=1\n\t\t\t\t\tbm[1][i]=1\n\n\t\t\tfor i in range(len(colsum)):\n\t\t\t\tif colsum[i]>0 and upper>0:\n\t\t\t\t\tbm[0][i]=1\n\t\t\t\t\tupper-=1\n\t\t\t\t\tcolsum[i]-=1\n\t\t\tfor i in range(len(colsum)):\n\t\t\t\tif colsum[i]>0 and lower>0:\n\t\t\t\t\tbm[1][i]=1\n\t\t\t\t\tlower-=1\n\t\t\t\t\tcolsum[i]-=1\n\t\t\tif upper!=0 or lower!=0 or sum(colsum)!=0:\n\t\t\t\treturn []\n\t\t\treturn bm\n | 0 | Given the following details of a matrix with `n` columns and `2` rows :
* The matrix is a binary matrix, which means each element in the matrix can be `0` or `1`.
* The sum of elements of the 0-th(upper) row is given as `upper`.
* The sum of elements of the 1-st(lower) row is given as `lower`.
* The sum of elements in the i-th column(0-indexed) is `colsum[i]`, where `colsum` is given as an integer array with length `n`.
Your task is to reconstruct the matrix with `upper`, `lower` and `colsum`.
Return it as a 2-D integer array.
If there are more than one valid solution, any of them will be accepted.
If no valid solution exists, return an empty 2-D array.
**Example 1:**
**Input:** upper = 2, lower = 1, colsum = \[1,1,1\]
**Output:** \[\[1,1,0\],\[0,0,1\]\]
**Explanation:** \[\[1,0,1\],\[0,1,0\]\], and \[\[0,1,1\],\[1,0,0\]\] are also correct answers.
**Example 2:**
**Input:** upper = 2, lower = 3, colsum = \[2,2,1,1\]
**Output:** \[\]
**Example 3:**
**Input:** upper = 5, lower = 5, colsum = \[2,1,2,0,1,0,1,2,0,1\]
**Output:** \[\[1,1,1,0,1,0,0,1,0,0\],\[1,0,1,0,0,0,1,1,0,1\]\]
**Constraints:**
* `1 <= colsum.length <= 10^5`
* `0 <= upper, lower <= colsum.length`
* `0 <= colsum[i] <= 2` | Use a data structure to store all values of each diagonal. How to index the data structure with the id of the diagonal? All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j. |
Easy to Understand | reconstruct-a-2-row-binary-matrix | 0 | 1 | \tclass Solution:\n\t\tdef reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n\t\t\tbm = [[0 for _ in range(len(colsum))] for i in range(2)]\n\t\t\tfor i in range(len(colsum)):\n\t\t\t\tif colsum[i]==2:\n\t\t\t\t\tcolsum[i]=0\n\t\t\t\t\tupper-=1\n\t\t\t\t\tlower-=1\n\t\t\t\t\tbm[0][i]=1\n\t\t\t\t\tbm[1][i]=1\n\n\t\t\tfor i in range(len(colsum)):\n\t\t\t\tif colsum[i]>0 and upper>0:\n\t\t\t\t\tbm[0][i]=1\n\t\t\t\t\tupper-=1\n\t\t\t\t\tcolsum[i]-=1\n\t\t\tfor i in range(len(colsum)):\n\t\t\t\tif colsum[i]>0 and lower>0:\n\t\t\t\t\tbm[1][i]=1\n\t\t\t\t\tlower-=1\n\t\t\t\t\tcolsum[i]-=1\n\t\t\tif upper!=0 or lower!=0 or sum(colsum)!=0:\n\t\t\t\treturn []\n\t\t\treturn bm\n | 0 | Given two binary trees `original` and `cloned` and given a reference to a node `target` in the original tree.
The `cloned` tree is a **copy of** the `original` tree.
Return _a reference to the same node_ in the `cloned` tree.
**Note** that you are **not allowed** to change any of the two trees or the `target` node and the answer **must be** a reference to a node in the `cloned` tree.
**Example 1:**
**Input:** tree = \[7,4,3,null,null,6,19\], target = 3
**Output:** 3
**Explanation:** In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
**Example 2:**
**Input:** tree = \[7\], target = 7
**Output:** 7
**Example 3:**
**Input:** tree = \[8,null,6,null,5,null,4,null,3,null,2,null,1\], target = 4
**Output:** 4
**Constraints:**
* The number of nodes in the `tree` is in the range `[1, 104]`.
* The values of the nodes of the `tree` are unique.
* `target` node is a node from the `original` tree and is not `null`.
**Follow up:** Could you solve the problem if repeated values on the tree are allowed? | You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row. Fill 0 and 2 first, then fill 1 in the upper row or lower row in turn but be careful about exhausting permitted 1s in each row. |
Simple dfs solution!! | number-of-closed-islands | 0 | 1 | # Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n vis=defaultdict(lambda:False)\n n=len(grid)\n m=len(grid[0])\n \'\'\'\n \'\'\'\n def dfs(x,y):\n vis[(x,y)]=True\n isedge=True\n for i,j in ((x+1,y),(x-1,y),(x,y+1),(x,y-1)):\n if 0<=i<n and 0<=j<m:\n if not vis[(i,j)] and (not grid[i][j]):\n isedge=(dfs(i,j) and isedge)\n else:\n isedge=(False and isedge)\n return isedge\n res=0\n for i in range(n):\n for j in range(m):\n if not vis[(i,j)] and (not grid[i][j]):\n if dfs(i,j):\n res+=1\n # print(vis)\n return res\n\n``` | 2 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Simple dfs solution!! | number-of-closed-islands | 0 | 1 | # Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n vis=defaultdict(lambda:False)\n n=len(grid)\n m=len(grid[0])\n \'\'\'\n \'\'\'\n def dfs(x,y):\n vis[(x,y)]=True\n isedge=True\n for i,j in ((x+1,y),(x-1,y),(x,y+1),(x,y-1)):\n if 0<=i<n and 0<=j<m:\n if not vis[(i,j)] and (not grid[i][j]):\n isedge=(dfs(i,j) and isedge)\n else:\n isedge=(False and isedge)\n return isedge\n res=0\n for i in range(n):\n for j in range(m):\n if not vis[(i,j)] and (not grid[i][j]):\n if dfs(i,j):\n res+=1\n # print(vis)\n return res\n\n``` | 2 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Easy & Clear Solution Python 3 DFS | number-of-closed-islands | 0 | 1 | \n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n def dfs(i,j,newval):\n if grid[i][j]==0:\n grid[i][j]=2\n if i<len(grid)-1 : dfs(i+1,j,newval)\n if i >0 : dfs(i-1,j,newval)\n if j<len(grid[0])-1 : dfs(i,j+1,newval)\n if j>0 : dfs(i,j-1,newval)\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if i==0 or j==0 or i==len(grid)-1 or j == len(grid[0])-1:\n if grid[i][j]==0:\n dfs(i,j,2)\n res=0\n for i in range(1,len(grid)-1):\n for j in range(1,len(grid[0])-1):\n if grid[i][j]==0:\n res+=1\n dfs(i,j,2)\n return res\n``` | 5 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Easy & Clear Solution Python 3 DFS | number-of-closed-islands | 0 | 1 | \n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n def dfs(i,j,newval):\n if grid[i][j]==0:\n grid[i][j]=2\n if i<len(grid)-1 : dfs(i+1,j,newval)\n if i >0 : dfs(i-1,j,newval)\n if j<len(grid[0])-1 : dfs(i,j+1,newval)\n if j>0 : dfs(i,j-1,newval)\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if i==0 or j==0 or i==len(grid)-1 or j == len(grid[0])-1:\n if grid[i][j]==0:\n dfs(i,j,2)\n res=0\n for i in range(1,len(grid)-1):\n for j in range(1,len(grid[0])-1):\n if grid[i][j]==0:\n res+=1\n dfs(i,j,2)\n return res\n``` | 5 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Super easy edge-in dfs // Beats 97% | number-of-closed-islands | 0 | 1 | # Intuition\nIf the island touches the edge of the board, it will not be a closed island. So, if we find all those islands by starting from the outside-in, the number of remaining islands will be the answer!\n\n# Approach\nGo around the outside and perform dfs for all the 0s found and replace with 2. Then go through the board and replace all cases of an island with 2s as well and add to the overall answer.\n\n# Complexity\n- Time complexity:\nO(m + n)\n\n- Space complexity:\nO(m + n)\n\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n \n ans = 0\n\n def dfs(x, y):\n if x < 0 or x >= len(grid) or y < 0 or y >= len(grid[0]) or grid[x][y] != 0: \n return\n \n grid[x][y] = 2\n \n dfs(x, y+1)\n dfs(x, y-1)\n dfs(x-1, y)\n dfs(x+1, y)\n\n for x in range(len(grid)):\n dfs(x, 0)\n dfs(x, len(grid[0])-1)\n\n for y in range(len(grid[0])):\n dfs(0, y)\n dfs(len(grid)-1, y)\n\n for x in range(len(grid)):\n for y in range(len(grid[0])):\n if grid[x][y] == 0:\n dfs(x, y)\n ans += 1\n\n return ans\n```\n\n\nUpvote would be great if this helped!\n\n | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Super easy edge-in dfs // Beats 97% | number-of-closed-islands | 0 | 1 | # Intuition\nIf the island touches the edge of the board, it will not be a closed island. So, if we find all those islands by starting from the outside-in, the number of remaining islands will be the answer!\n\n# Approach\nGo around the outside and perform dfs for all the 0s found and replace with 2. Then go through the board and replace all cases of an island with 2s as well and add to the overall answer.\n\n# Complexity\n- Time complexity:\nO(m + n)\n\n- Space complexity:\nO(m + n)\n\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n \n ans = 0\n\n def dfs(x, y):\n if x < 0 or x >= len(grid) or y < 0 or y >= len(grid[0]) or grid[x][y] != 0: \n return\n \n grid[x][y] = 2\n \n dfs(x, y+1)\n dfs(x, y-1)\n dfs(x-1, y)\n dfs(x+1, y)\n\n for x in range(len(grid)):\n dfs(x, 0)\n dfs(x, len(grid[0])-1)\n\n for y in range(len(grid[0])):\n dfs(0, y)\n dfs(len(grid)-1, y)\n\n for x in range(len(grid)):\n for y in range(len(grid[0])):\n if grid[x][y] == 0:\n dfs(x, y)\n ans += 1\n\n return ans\n```\n\n\nUpvote would be great if this helped!\n\n | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Beats 100% runtime. Easy to understand | number-of-closed-islands | 0 | 1 | \n\nhttps://leetcode.com/problems/number-of-closed-islands/submissions/1052991341/\n\n# Intuition\nAt first we need to except all islands, that have land on a border of a grip. Then count all remaining ones\n\n# Approach\n1. Loop only through first and last rows and columns of a grid and find land pieces there.\n 1) If such was found, start BFS and mark all its land elements \n(In my case, I changed their value to 2).\n2. Loop through the remaining columns and rows and find pieces of land, that wasn\'t marked in the first step. \n 1) If such found, start BFS again on them. When BFS finishes, the island will be marked in another way in order not to come here again in the loop (In my case, I changed their value to 3).\n 2) Add 1 to the counter after the end of a BFS\n\n\n\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n len1,len2=len(grid),len(grid[0])\n ways=[(1,0),(0,1),(-1,0),(0,-1)]\n check1,check2=[0,len1-1],[0,len2-1]\n que=deque()\n count=0\n for i in range(len1):\n temp=check2 if i not in check1 else range(len2)\n for j in temp:\n if not grid[i][j]:\n grid[i][j]=2\n que.append((i,j))\n while que:\n x,y=que.popleft()\n for dx,dy in ways:\n new_x=x+dx\n new_y=y+dy\n if 0<=new_x<len1 and 0<=new_y<len2 and grid[new_x][new_y]==0:\n grid[new_x][new_y]=2\n que.append((new_x,new_y))\n for i in range(1,len1-1):\n for j in range(1,len2-1):\n if not grid[i][j]:\n grid[i][j]=3\n que.append((i,j))\n while que:\n x,y=que.popleft()\n for dx,dy in ways:\n new_x=x+dx\n new_y=y+dy\n if grid[new_x][new_y]==0:\n grid[new_x][new_y]=3\n que.append((new_x,new_y))\n count+=1\n return count\n\n\n\n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Beats 100% runtime. Easy to understand | number-of-closed-islands | 0 | 1 | \n\nhttps://leetcode.com/problems/number-of-closed-islands/submissions/1052991341/\n\n# Intuition\nAt first we need to except all islands, that have land on a border of a grip. Then count all remaining ones\n\n# Approach\n1. Loop only through first and last rows and columns of a grid and find land pieces there.\n 1) If such was found, start BFS and mark all its land elements \n(In my case, I changed their value to 2).\n2. Loop through the remaining columns and rows and find pieces of land, that wasn\'t marked in the first step. \n 1) If such found, start BFS again on them. When BFS finishes, the island will be marked in another way in order not to come here again in the loop (In my case, I changed their value to 3).\n 2) Add 1 to the counter after the end of a BFS\n\n\n\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n len1,len2=len(grid),len(grid[0])\n ways=[(1,0),(0,1),(-1,0),(0,-1)]\n check1,check2=[0,len1-1],[0,len2-1]\n que=deque()\n count=0\n for i in range(len1):\n temp=check2 if i not in check1 else range(len2)\n for j in temp:\n if not grid[i][j]:\n grid[i][j]=2\n que.append((i,j))\n while que:\n x,y=que.popleft()\n for dx,dy in ways:\n new_x=x+dx\n new_y=y+dy\n if 0<=new_x<len1 and 0<=new_y<len2 and grid[new_x][new_y]==0:\n grid[new_x][new_y]=2\n que.append((new_x,new_y))\n for i in range(1,len1-1):\n for j in range(1,len2-1):\n if not grid[i][j]:\n grid[i][j]=3\n que.append((i,j))\n while que:\n x,y=que.popleft()\n for dx,dy in ways:\n new_x=x+dx\n new_y=y+dy\n if grid[new_x][new_y]==0:\n grid[new_x][new_y]=3\n que.append((new_x,new_y))\n count+=1\n return count\n\n\n\n``` | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Python DFS O(n) code for reference | number-of-closed-islands | 0 | 1 | ```\n1. Mark all the connected 0\'s as 1\'s, and see if we can reach out of bounds. \n if we can then return False, since we shouldn\'t count it. \n2. If A is True , then in (A or B or C ) B and C will not be checked\n3. If A is False , then in (A and B and C ) B and C will not be checked \n\n```\n\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n m,n,res = len(grid),len(grid[0]),0\n def dfs(i,j):\n nonlocal grid \n if(i<0 or j<0 or i>=m or j>=n ):\n return False \n elif(grid[i][j] == 1):\n return True\n grid[i][j] = 1\n ans = True \n ans = dfs(i+1,j) and ans \n ans = dfs(i-1,j) and ans \n ans = dfs(i,j+1) and ans \n ans = dfs(i,j-1) and ans \n return ans\n \n for i in range(m):\n for j in range(n):\n if(grid[i][j] != 1 and dfs(i,j)):\n res += 1\n return res \n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Python DFS O(n) code for reference | number-of-closed-islands | 0 | 1 | ```\n1. Mark all the connected 0\'s as 1\'s, and see if we can reach out of bounds. \n if we can then return False, since we shouldn\'t count it. \n2. If A is True , then in (A or B or C ) B and C will not be checked\n3. If A is False , then in (A and B and C ) B and C will not be checked \n\n```\n\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n m,n,res = len(grid),len(grid[0]),0\n def dfs(i,j):\n nonlocal grid \n if(i<0 or j<0 or i>=m or j>=n ):\n return False \n elif(grid[i][j] == 1):\n return True\n grid[i][j] = 1\n ans = True \n ans = dfs(i+1,j) and ans \n ans = dfs(i-1,j) and ans \n ans = dfs(i,j+1) and ans \n ans = dfs(i,j-1) and ans \n return ans\n \n for i in range(m):\n for j in range(n):\n if(grid[i][j] != 1 and dfs(i,j)):\n res += 1\n return res \n``` | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Easy and Simple approach || Python|| Beginner | number-of-closed-islands | 0 | 1 | You can use vis and dic or instead make the element we are visiting 1 as we don\'t care about it any further.\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n dic={}\n vis=[]\n def fun(i,j):\n if i<0 or j<0 or i>=len(grid) or j>=len(grid[0]):\n return False\n #You can use vis and dic or instead make the element we are visiting 1 as we don\'t care about it any further.\n if [i,j] in vis:\n return True\n if grid[i][j]==1:\n return True\n vis.append([i,j])\n dic[i,j]=fun(i+1,j) and fun(i-1,j) and fun(i,j+1) and fun(i,j-1)\n return dic[i,j]\n c=0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if (i,j) not in dic and grid[i][j]==0 and fun(i,j):\n c+=1\n vis=[]\n return c\n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Easy and Simple approach || Python|| Beginner | number-of-closed-islands | 0 | 1 | You can use vis and dic or instead make the element we are visiting 1 as we don\'t care about it any further.\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n dic={}\n vis=[]\n def fun(i,j):\n if i<0 or j<0 or i>=len(grid) or j>=len(grid[0]):\n return False\n #You can use vis and dic or instead make the element we are visiting 1 as we don\'t care about it any further.\n if [i,j] in vis:\n return True\n if grid[i][j]==1:\n return True\n vis.append([i,j])\n dic[i,j]=fun(i+1,j) and fun(i-1,j) and fun(i,j+1) and fun(i,j-1)\n return dic[i,j]\n c=0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if (i,j) not in dic and grid[i][j]==0 and fun(i,j):\n c+=1\n vis=[]\n return c\n``` | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Python O(m * n) Time Solution - Line By Line Explanation and Comments - Thought Process Explained | number-of-closed-islands | 0 | 1 | # Intuition\nSince an island can only be enclosed if there are water along all the 4 sides. The reverse is also true - An island is not enclosed if any of the cells touches the boundary.\n\nGoing by this logic we need to find all the cells that are 4-directionally connected and if any of those cells touch the boundry, i.e. - `if row == 0 or col == 0 or row == len(grid)-1 or col == len(grid[0])-1` then do not count those subsection of cells as "closed island".\n\n\n# Approach\nLoop over the `grid` and for every cell that has `0` start a Breadth First Search.\nMaintain a `count` variable to keep track of number of "closed" islands.\n```\ncount = 0\nfor row in range(len(grid)):\n for col in range(len(grid[row])):\n if grid[row][col] == 0:\n count += bfs((row, col), grid)\n else:\n grid[row][col] = -1\nreturn count\n```\n\nPerform a `Breadth First Search` from that position, maintain a queue of "discovered" nodes.\n```\ndef bfs(pos, grid):\n to_return = 1\n queue = [pos]\n```\nWhile there are nodes in the `queue`. Keep popping nodes \n```\nwhile queue:\n row, col = queue.pop()\n```\n\nIf the current `row` or `col` is out of bounds move on to the next cell\n```\n if row == -1 or col == -1 or row == len(grid) or col == len(grid[0]):\n continue\n```\n\nWe will mark our visited cells as `-1`, Also since our "water" cells are `1`.\nWe can simply check if current `grid[row][col] != 0` (already visited or water cell), if so mark it as `-1` and move on to the next cell from our `queue`.\n```\n if grid[row][col] != 0:\n grid[row][col] = -1\n continue\n``` \n\nOtherwise the current cell is "island" also mark the cell as `-1`. \n```\n grid[row][col] = -1 # Mark as visited\n```\n\nNote: This might look redundant as the previous check also updates to cell to `-1`, but note we should only update cells after checking the value of the cell, and since the `if` block stops at a `continue` we have a follow up code to update `grid[row][col]` to `-1` when the cell is a `0` so we can continue adding the next group of cells.\n\nCheck if we our current `island` cell is at the boundary - \n```\nif row == 0 or col == 0 or row == len(grid)-1 or col == len(grid[0])-1:\n to_return = 0\n```\nIf so set `to_return` to `0`. Recall at the beginning we had `to_return` set to `1` since we start with the assumption that the current group of cells is a "closed island".\n\nNote: We don\'t necessarily have to return back to the caller once we have discovered that the island is not a "closed island" but rather we can continue to explore as many cells as we can and keep marking them as `-1`\n\nAdd cells from `row-1`, `row+1`, `col-1`, `col+1`.\n```\n queue.append((row-1, col))\n queue.append((row+1, col))\n queue.append((row, col-1))\n queue.append((row, col+1))\n```\n\nFinally return `to_return`.\n\nOnce we return to the caller, based on the value of `to_return` from `bfs` we will increment the `count` by `1` or keep it same by adding `0`\n```\ncount += bfs((row, col), grid)\n```\n\nReturn `count` as our final answer.\n\n\n# Complexity\n- Time complexity:\nO(m * n) Since we go over all the cells atleast once.\n- Space complexity:\nO(m * n) Since our queue can take atmost O(m * n) space in our `bfs`\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n def bfs(pos, grid):\n to_return = 1\n queue = [pos]\n while queue:\n row, col = queue.pop()\n if row == -1 or col == -1 or row == len(grid) or col == len(grid[0]): # If out of bounds don\'t consider\n continue\n if grid[row][col] != 0: # Mark and move on if not an island\n grid[row][col] = -1 # Mark as visited\n continue\n grid[row][col] = -1 # Mark as visited\n if row == 0 or col == 0 or row == len(grid)-1 or col == len(grid[0])-1: # If border and island (0)\n to_return = 0\n queue.append((row-1, col))\n queue.append((row+1, col))\n queue.append((row, col-1))\n queue.append((row, col+1))\n return to_return\n count = 0\n for row in range(len(grid)):\n for col in range(len(grid[row])):\n if grid[row][col] == 0:\n count += bfs((row, col), grid)\n else:\n grid[row][col] = -1\n return count\n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Python O(m * n) Time Solution - Line By Line Explanation and Comments - Thought Process Explained | number-of-closed-islands | 0 | 1 | # Intuition\nSince an island can only be enclosed if there are water along all the 4 sides. The reverse is also true - An island is not enclosed if any of the cells touches the boundary.\n\nGoing by this logic we need to find all the cells that are 4-directionally connected and if any of those cells touch the boundry, i.e. - `if row == 0 or col == 0 or row == len(grid)-1 or col == len(grid[0])-1` then do not count those subsection of cells as "closed island".\n\n\n# Approach\nLoop over the `grid` and for every cell that has `0` start a Breadth First Search.\nMaintain a `count` variable to keep track of number of "closed" islands.\n```\ncount = 0\nfor row in range(len(grid)):\n for col in range(len(grid[row])):\n if grid[row][col] == 0:\n count += bfs((row, col), grid)\n else:\n grid[row][col] = -1\nreturn count\n```\n\nPerform a `Breadth First Search` from that position, maintain a queue of "discovered" nodes.\n```\ndef bfs(pos, grid):\n to_return = 1\n queue = [pos]\n```\nWhile there are nodes in the `queue`. Keep popping nodes \n```\nwhile queue:\n row, col = queue.pop()\n```\n\nIf the current `row` or `col` is out of bounds move on to the next cell\n```\n if row == -1 or col == -1 or row == len(grid) or col == len(grid[0]):\n continue\n```\n\nWe will mark our visited cells as `-1`, Also since our "water" cells are `1`.\nWe can simply check if current `grid[row][col] != 0` (already visited or water cell), if so mark it as `-1` and move on to the next cell from our `queue`.\n```\n if grid[row][col] != 0:\n grid[row][col] = -1\n continue\n``` \n\nOtherwise the current cell is "island" also mark the cell as `-1`. \n```\n grid[row][col] = -1 # Mark as visited\n```\n\nNote: This might look redundant as the previous check also updates to cell to `-1`, but note we should only update cells after checking the value of the cell, and since the `if` block stops at a `continue` we have a follow up code to update `grid[row][col]` to `-1` when the cell is a `0` so we can continue adding the next group of cells.\n\nCheck if we our current `island` cell is at the boundary - \n```\nif row == 0 or col == 0 or row == len(grid)-1 or col == len(grid[0])-1:\n to_return = 0\n```\nIf so set `to_return` to `0`. Recall at the beginning we had `to_return` set to `1` since we start with the assumption that the current group of cells is a "closed island".\n\nNote: We don\'t necessarily have to return back to the caller once we have discovered that the island is not a "closed island" but rather we can continue to explore as many cells as we can and keep marking them as `-1`\n\nAdd cells from `row-1`, `row+1`, `col-1`, `col+1`.\n```\n queue.append((row-1, col))\n queue.append((row+1, col))\n queue.append((row, col-1))\n queue.append((row, col+1))\n```\n\nFinally return `to_return`.\n\nOnce we return to the caller, based on the value of `to_return` from `bfs` we will increment the `count` by `1` or keep it same by adding `0`\n```\ncount += bfs((row, col), grid)\n```\n\nReturn `count` as our final answer.\n\n\n# Complexity\n- Time complexity:\nO(m * n) Since we go over all the cells atleast once.\n- Space complexity:\nO(m * n) Since our queue can take atmost O(m * n) space in our `bfs`\n# Code\n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n def bfs(pos, grid):\n to_return = 1\n queue = [pos]\n while queue:\n row, col = queue.pop()\n if row == -1 or col == -1 or row == len(grid) or col == len(grid[0]): # If out of bounds don\'t consider\n continue\n if grid[row][col] != 0: # Mark and move on if not an island\n grid[row][col] = -1 # Mark as visited\n continue\n grid[row][col] = -1 # Mark as visited\n if row == 0 or col == 0 or row == len(grid)-1 or col == len(grid[0])-1: # If border and island (0)\n to_return = 0\n queue.append((row-1, col))\n queue.append((row+1, col))\n queue.append((row, col-1))\n queue.append((row, col+1))\n return to_return\n count = 0\n for row in range(len(grid)):\n for col in range(len(grid[row])):\n if grid[row][col] == 0:\n count += bfs((row, col), grid)\n else:\n grid[row][col] = -1\n return count\n``` | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Python Elegant & Short | DFS | number-of-closed-islands | 0 | 1 | # Complexity\n- Time complexity: $$O(n*m)$$\n- Space complexity: $$O(n*m)$$\n\n# Code\n```\nclass Solution:\n LAND = 0\n WATER = 1\n\n def closedIsland(self, grid: List[List[int]]) -> int:\n n, m = len(grid), len(grid[0])\n\n for row in range(n):\n self.water_island(row, 0, grid)\n self.water_island(row, m - 1, grid)\n\n for col in range(m):\n self.water_island( 0, col, grid)\n self.water_island(n - 1, col, grid)\n\n closed = 0\n for row in range(1, n - 1):\n for col in range(1, m - 1):\n if grid[row][col] == self.LAND:\n self.water_island(row, col, grid)\n closed += 1\n\n return closed\n\n @classmethod\n def water_island(cls, row: int, col: int, grid: List[List[int]]):\n if cls.in_bounds(row, col, grid) and grid[row][col] == cls.LAND:\n grid[row][col] = cls.WATER\n cls.water_island(row - 1, col, grid)\n cls.water_island(row + 1, col, grid)\n cls.water_island(row, col - 1, grid)\n cls.water_island(row, col + 1, grid)\n\n @staticmethod\n def in_bounds(row: int, col: int, grid: List[List[int]]) -> bool:\n return 0 <= row < len(grid) and 0 <= col < len(grid[0])\n\n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Python Elegant & Short | DFS | number-of-closed-islands | 0 | 1 | # Complexity\n- Time complexity: $$O(n*m)$$\n- Space complexity: $$O(n*m)$$\n\n# Code\n```\nclass Solution:\n LAND = 0\n WATER = 1\n\n def closedIsland(self, grid: List[List[int]]) -> int:\n n, m = len(grid), len(grid[0])\n\n for row in range(n):\n self.water_island(row, 0, grid)\n self.water_island(row, m - 1, grid)\n\n for col in range(m):\n self.water_island( 0, col, grid)\n self.water_island(n - 1, col, grid)\n\n closed = 0\n for row in range(1, n - 1):\n for col in range(1, m - 1):\n if grid[row][col] == self.LAND:\n self.water_island(row, col, grid)\n closed += 1\n\n return closed\n\n @classmethod\n def water_island(cls, row: int, col: int, grid: List[List[int]]):\n if cls.in_bounds(row, col, grid) and grid[row][col] == cls.LAND:\n grid[row][col] = cls.WATER\n cls.water_island(row - 1, col, grid)\n cls.water_island(row + 1, col, grid)\n cls.water_island(row, col - 1, grid)\n cls.water_island(row, col + 1, grid)\n\n @staticmethod\n def in_bounds(row: int, col: int, grid: List[List[int]]) -> bool:\n return 0 <= row < len(grid) and 0 <= col < len(grid[0])\n\n``` | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Python - BFS | number-of-closed-islands | 0 | 1 | \n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n def is_closed(pos):\n if grid[pos[0]][pos[1]]:\n return 0\n stack = [pos]\n is_closed_state = 1\n while stack:\n i, j = stack.pop()\n grid[i][j] = 1\n for x, y in dirs:\n nx, ny = i + x, j + y\n if not (-1 < nx < m and -1 < ny < n):\n is_closed_state = 0\n continue\n if grid[nx][ny]:\n continue\n stack.append((nx, ny))\n return is_closed_state\n \n count = 0\n m, n = len(grid), len(grid[0])\n dirs = ((1, 0), (0, 1), (-1, 0), (0, -1))\n return sum(map(is_closed, product(range(m), range(n))))\n\n\n \n \n``` | 1 | Given a 2D `grid` consists of `0s` (land) and `1s` (water). An _island_ is a maximal 4-directionally connected group of `0s` and a _closed island_ is an island **totally** (all left, top, right, bottom) surrounded by `1s.`
Return the number of _closed islands_.
**Example 1:**
**Input:** grid = \[\[1,1,1,1,1,1,1,0\],\[1,0,0,0,0,1,1,0\],\[1,0,1,0,1,1,1,0\],\[1,0,0,0,0,1,0,1\],\[1,1,1,1,1,1,1,0\]\]
**Output:** 2
**Explanation:**
Islands in gray are closed because they are completely surrounded by water (group of 1s).
**Example 2:**
**Input:** grid = \[\[0,0,1,0,0\],\[0,1,0,1,0\],\[0,1,1,1,0\]\]
**Output:** 1
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1,1,1\],
\[1,0,0,0,0,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,1,0,1,0,1\],
\[1,0,1,1,1,0,1\],
\[1,0,0,0,0,0,1\],
\[1,1,1,1,1,1,1\]\]
**Output:** 2
**Constraints:**
* `1 <= grid.length, grid[0].length <= 100`
* `0 <= grid[i][j] <=1` | Traverse the tree to find the max depth. Traverse the tree again to compute the sum required. |
Python - BFS | number-of-closed-islands | 0 | 1 | \n```\nclass Solution:\n def closedIsland(self, grid: List[List[int]]) -> int:\n def is_closed(pos):\n if grid[pos[0]][pos[1]]:\n return 0\n stack = [pos]\n is_closed_state = 1\n while stack:\n i, j = stack.pop()\n grid[i][j] = 1\n for x, y in dirs:\n nx, ny = i + x, j + y\n if not (-1 < nx < m and -1 < ny < n):\n is_closed_state = 0\n continue\n if grid[nx][ny]:\n continue\n stack.append((nx, ny))\n return is_closed_state\n \n count = 0\n m, n = len(grid), len(grid[0])\n dirs = ((1, 0), (0, 1), (-1, 0), (0, -1))\n return sum(map(is_closed, product(range(m), range(n))))\n\n\n \n \n``` | 1 | Given an `m x n` matrix of **distinct** numbers, return _all **lucky numbers** in the matrix in **any** order_.
A **lucky number** is an element of the matrix such that it is the minimum element in its row and maximum in its column.
**Example 1:**
**Input:** matrix = \[\[3,7,8\],\[9,11,13\],\[15,16,17\]\]
**Output:** \[15\]
**Explanation:** 15 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 2:**
**Input:** matrix = \[\[1,10,4,2\],\[9,3,8,7\],\[15,16,17,12\]\]
**Output:** \[12\]
**Explanation:** 12 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Example 3:**
**Input:** matrix = \[\[7,8\],\[1,2\]\]
**Output:** \[7\]
**Explanation:** 7 is the only lucky number since it is the minimum in its row and the maximum in its column.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= n, m <= 50`
* `1 <= matrix[i][j] <= 105`.
* All elements in the matrix are distinct. | Exclude connected group of 0s on the corners because they are not closed island. Return number of connected component of 0s on the grid. |
Backtrack Code and 9 Liner Code Explained | maximum-score-words-formed-by-letters | 0 | 1 | # Explanation:\n```\n/*\n\nwe will check for all words (from 0 to n-1)\nfor every Index we have 2 choises\n --can we consider our current index\n --> if we consider to choose current index we need\n to update letters and check for next index\n --should we skip and check for next\n --> if we consider to skip letters will not get\n updated simply check for next\n\n*/\n```\n\n# Backtrack Code\n```\n// dic - A dictionary/list that will keep current count or letters\n// total - keep record to MAX\n// ind - index\n// mydict - count of letter at the beginning\n\ndef maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n self.maxx = 0\n def f(ind,dic,total):\n if ind == len(words):return\n for i in range(ind,len(words)):\n state = True\n res = 0\n // check if we can create the word\n for each in words[i]:\n if each in dic:\n dic[each] -= 1\n res += score[ord(each)-97]\n if dic[each]<0:\n state = False\n else:\n state = False\n // if state = True we can create and check for next\n if state:\n self.maxx = max(self.maxx,total+res)\n // check for next index i.e currentInd = i so i+1\n f(i+1,dic,total+res)\n // if we dont pick we need back our deleted letters\n // adding in the deleted letters\n for each in words[i]:\n if each in dic:\n dic[each] += 1\n mydic = {}\n for each in letters:\n if each in mydic:\n mydic[each] += 1\n else:\n mydic[each] = 1\n f(0,mydic,0)\n return self.maxx\n```\n# Simplyfing Code\n```\n\n# Rather than creating dictionary we will update the letter itself\n# Convert letters from LIST->STRING\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n def f(ind,letterS):\n if ind == len(words):return 0\n // we will create a copy so we dont need to add again\n copy = letterS\n res = 0\n for each in words[ind]:\n // if current letter is not in copy\n // we cannot create this word so skip\n if each not in copy:return f(ind+1,letterS)\n res += score[ord(each)-97]\n copy = copy.replace(each,\'\',1)\n // if we reach this point\n // then we have 2 choice to pick or notPick\n // notPick pick\n // \u25BC \u25BC\n return max(f(ind+1,letterS),res + f(ind+1,copy))\n return f(0,\'\'.join(letters))\n``` | 1 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
Backtrack Code and 9 Liner Code Explained | maximum-score-words-formed-by-letters | 0 | 1 | # Explanation:\n```\n/*\n\nwe will check for all words (from 0 to n-1)\nfor every Index we have 2 choises\n --can we consider our current index\n --> if we consider to choose current index we need\n to update letters and check for next index\n --should we skip and check for next\n --> if we consider to skip letters will not get\n updated simply check for next\n\n*/\n```\n\n# Backtrack Code\n```\n// dic - A dictionary/list that will keep current count or letters\n// total - keep record to MAX\n// ind - index\n// mydict - count of letter at the beginning\n\ndef maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n self.maxx = 0\n def f(ind,dic,total):\n if ind == len(words):return\n for i in range(ind,len(words)):\n state = True\n res = 0\n // check if we can create the word\n for each in words[i]:\n if each in dic:\n dic[each] -= 1\n res += score[ord(each)-97]\n if dic[each]<0:\n state = False\n else:\n state = False\n // if state = True we can create and check for next\n if state:\n self.maxx = max(self.maxx,total+res)\n // check for next index i.e currentInd = i so i+1\n f(i+1,dic,total+res)\n // if we dont pick we need back our deleted letters\n // adding in the deleted letters\n for each in words[i]:\n if each in dic:\n dic[each] += 1\n mydic = {}\n for each in letters:\n if each in mydic:\n mydic[each] += 1\n else:\n mydic[each] = 1\n f(0,mydic,0)\n return self.maxx\n```\n# Simplyfing Code\n```\n\n# Rather than creating dictionary we will update the letter itself\n# Convert letters from LIST->STRING\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n def f(ind,letterS):\n if ind == len(words):return 0\n // we will create a copy so we dont need to add again\n copy = letterS\n res = 0\n for each in words[ind]:\n // if current letter is not in copy\n // we cannot create this word so skip\n if each not in copy:return f(ind+1,letterS)\n res += score[ord(each)-97]\n copy = copy.replace(each,\'\',1)\n // if we reach this point\n // then we have 2 choice to pick or notPick\n // notPick pick\n // \u25BC \u25BC\n return max(f(ind+1,letterS),res + f(ind+1,copy))\n return f(0,\'\'.join(letters))\n``` | 1 | Design a stack that supports increment operations on its elements.
Implement the `CustomStack` class:
* `CustomStack(int maxSize)` Initializes the object with `maxSize` which is the maximum number of elements in the stack.
* `void push(int x)` Adds `x` to the top of the stack if the stack has not reached the `maxSize`.
* `int pop()` Pops and returns the top of the stack or `-1` if the stack is empty.
* `void inc(int k, int val)` Increments the bottom `k` elements of the stack by `val`. If there are less than `k` elements in the stack, increment all the elements in the stack.
**Example 1:**
**Input**
\[ "CustomStack ", "push ", "push ", "pop ", "push ", "push ", "push ", "increment ", "increment ", "pop ", "pop ", "pop ", "pop "\]
\[\[3\],\[1\],\[2\],\[\],\[2\],\[3\],\[4\],\[5,100\],\[2,100\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,2,null,null,null,null,null,103,202,201,-1\]
**Explanation**
CustomStack stk = new CustomStack(3); // Stack is Empty \[\]
stk.push(1); // stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.pop(); // return 2 --> Return top of the stack 2, stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.push(3); // stack becomes \[1, 2, 3\]
stk.push(4); // stack still \[1, 2, 3\], Do not add another elements as size is 4
stk.increment(5, 100); // stack becomes \[101, 102, 103\]
stk.increment(2, 100); // stack becomes \[201, 202, 103\]
stk.pop(); // return 103 --> Return top of the stack 103, stack becomes \[201, 202\]
stk.pop(); // return 202 --> Return top of the stack 202, stack becomes \[201\]
stk.pop(); // return 201 --> Return top of the stack 201, stack becomes \[\]
stk.pop(); // return -1 --> Stack is empty return -1.
**Constraints:**
* `1 <= maxSize, x, k <= 1000`
* `0 <= val <= 100`
* At most `1000` calls will be made to each method of `increment`, `push` and `pop` each separately. | Note that words.length is small. This means you can iterate over every subset of words (2^N). |
Python | Short & Easy 6 lines | Counter | maximum-score-words-formed-by-letters | 0 | 1 | # Code\n```\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n \n def bckt(i, counts):\n if i == len(words): return 0\n word = Counter(words[i])\n if word == word & counts:\n curr = sum([score[ord(c) - ord("a")] * word[c] for c in word])\n return max(curr + bckt(i + 1 , counts - word), bckt(i + 1, counts))\n return bckt(i + 1, counts)\n\n return bckt(0, Counter(letters))\n``` | 2 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
Python | Short & Easy 6 lines | Counter | maximum-score-words-formed-by-letters | 0 | 1 | # Code\n```\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n \n def bckt(i, counts):\n if i == len(words): return 0\n word = Counter(words[i])\n if word == word & counts:\n curr = sum([score[ord(c) - ord("a")] * word[c] for c in word])\n return max(curr + bckt(i + 1 , counts - word), bckt(i + 1, counts))\n return bckt(i + 1, counts)\n\n return bckt(0, Counter(letters))\n``` | 2 | Design a stack that supports increment operations on its elements.
Implement the `CustomStack` class:
* `CustomStack(int maxSize)` Initializes the object with `maxSize` which is the maximum number of elements in the stack.
* `void push(int x)` Adds `x` to the top of the stack if the stack has not reached the `maxSize`.
* `int pop()` Pops and returns the top of the stack or `-1` if the stack is empty.
* `void inc(int k, int val)` Increments the bottom `k` elements of the stack by `val`. If there are less than `k` elements in the stack, increment all the elements in the stack.
**Example 1:**
**Input**
\[ "CustomStack ", "push ", "push ", "pop ", "push ", "push ", "push ", "increment ", "increment ", "pop ", "pop ", "pop ", "pop "\]
\[\[3\],\[1\],\[2\],\[\],\[2\],\[3\],\[4\],\[5,100\],\[2,100\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,2,null,null,null,null,null,103,202,201,-1\]
**Explanation**
CustomStack stk = new CustomStack(3); // Stack is Empty \[\]
stk.push(1); // stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.pop(); // return 2 --> Return top of the stack 2, stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.push(3); // stack becomes \[1, 2, 3\]
stk.push(4); // stack still \[1, 2, 3\], Do not add another elements as size is 4
stk.increment(5, 100); // stack becomes \[101, 102, 103\]
stk.increment(2, 100); // stack becomes \[201, 202, 103\]
stk.pop(); // return 103 --> Return top of the stack 103, stack becomes \[201, 202\]
stk.pop(); // return 202 --> Return top of the stack 202, stack becomes \[201\]
stk.pop(); // return 201 --> Return top of the stack 201, stack becomes \[\]
stk.pop(); // return -1 --> Stack is empty return -1.
**Constraints:**
* `1 <= maxSize, x, k <= 1000`
* `0 <= val <= 100`
* At most `1000` calls will be made to each method of `increment`, `push` and `pop` each separately. | Note that words.length is small. This means you can iterate over every subset of words (2^N). |
Solved using Python Counters | maximum-score-words-formed-by-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs the hint suggests, there are few enough ```words``` that we can exhaustively enumerate its possible subsets, scoring each and keeping track of the maximum score. This implies that we will calculate attributes of each one of the ```words``` multiple times during the recursive depth-first traversal of the space of subsets, so it may be desirable to calculate these once, up front. The attributes of each word are (1) What is the score for the word and (2) what does the word "cost" in terms of consuming the ```letters```.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince the attributes both depend on the number and indentity of the letters making up each word, we will use one of my favorite Python constructs, the ```Counter``` (see https://docs.python.org/3/library/collections.html#collections.Counter). \n\nFirst, we calculate the score for each of the ```words``` by mapping the ```scoreWord``` method over them. We also calculate, using several ```Counter```s, the number of each character in both ```letters``` and each of the ```words```.\n\nNext, we perform a recursive depth-first search over the possible subsets of ```words```, using ```Counter```s several ways: First, we determine whether the remaining ```letters``` can cover the next word being considered with the method ```is_enough```. Then, for the recursion, part of the state is the number of unconsumed ```letters```, which get decremented for the word we are trying. We can do this very conveniently with ```Counter```s using their ```update``` and ```subtract``` methods. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time for the first part of the program, which ```map```s over ```letters``` and ```words```, is proportional to the number and length of ```words```. The time for the second part, enumerating and scoring the subsets of ```words```, is proportional to the number of subsets, which is 2 ^ |words|, which dominates the time, so the overall time complexity is $$O(2^n)$$; as noted in the hint, this is acceptable since $$n$$ is limited to 16.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe storage used, besides the arguments and the return value, consists mainly of a number of ```Counters```; each consists of up to 26 letter:count pairs, so the overall storage is $$O(1)$$.\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n self.words = words\n self.word_scores = list( map( lambda word: self.scoreWord( word, score ), words ) )\n self.word_letter_counts = list( map( Counter, words ) )\n maxScore = self.maxScoreRec( 0, Counter( letters ) ) # First arg. is index into "words"\n return maxScore\n\n def maxScoreRec( self, index, letter_counter ):\n result = 0\n if index == len( self.words ):\n result = 0\n else:\n # Try skipping "words[index]"\n result = max( result, self.maxScoreRec( index + 1, letter_counter ) )\n # Try using "words[index]"\n if self.enough_letters( letter_counter, self.word_letter_counts[ index ] ):\n self.subtract_count( letter_counter, self.word_letter_counts[ index ] )\n result = max( result, \n self.word_scores[ index ] +\n self.maxScoreRec( index + 1, letter_counter ) )\n self.add_count( letter_counter, self.word_letter_counts[ index ] )\n return result\n\n def scoreWord( self, word, score ):\n return sum( map( lambda letter: score[ ord( letter ) - ord( \'a\' ) ], word ) )\n\n def enough_letters( self, letter_counter, word_letter_count ):\n for letter in word_letter_count:\n if letter_counter[ letter ] < word_letter_count[ letter ]:\n return False\n return True\n\n def subtract_count( self, letter_counter, word_letter_count ):\n letter_counter.subtract( word_letter_count )\n\n def add_count( self, letter_counter, word_letter_count ):\n letter_counter.update( word_letter_count )\n``` | 1 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
Solved using Python Counters | maximum-score-words-formed-by-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs the hint suggests, there are few enough ```words``` that we can exhaustively enumerate its possible subsets, scoring each and keeping track of the maximum score. This implies that we will calculate attributes of each one of the ```words``` multiple times during the recursive depth-first traversal of the space of subsets, so it may be desirable to calculate these once, up front. The attributes of each word are (1) What is the score for the word and (2) what does the word "cost" in terms of consuming the ```letters```.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince the attributes both depend on the number and indentity of the letters making up each word, we will use one of my favorite Python constructs, the ```Counter``` (see https://docs.python.org/3/library/collections.html#collections.Counter). \n\nFirst, we calculate the score for each of the ```words``` by mapping the ```scoreWord``` method over them. We also calculate, using several ```Counter```s, the number of each character in both ```letters``` and each of the ```words```.\n\nNext, we perform a recursive depth-first search over the possible subsets of ```words```, using ```Counter```s several ways: First, we determine whether the remaining ```letters``` can cover the next word being considered with the method ```is_enough```. Then, for the recursion, part of the state is the number of unconsumed ```letters```, which get decremented for the word we are trying. We can do this very conveniently with ```Counter```s using their ```update``` and ```subtract``` methods. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time for the first part of the program, which ```map```s over ```letters``` and ```words```, is proportional to the number and length of ```words```. The time for the second part, enumerating and scoring the subsets of ```words```, is proportional to the number of subsets, which is 2 ^ |words|, which dominates the time, so the overall time complexity is $$O(2^n)$$; as noted in the hint, this is acceptable since $$n$$ is limited to 16.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe storage used, besides the arguments and the return value, consists mainly of a number of ```Counters```; each consists of up to 26 letter:count pairs, so the overall storage is $$O(1)$$.\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n self.words = words\n self.word_scores = list( map( lambda word: self.scoreWord( word, score ), words ) )\n self.word_letter_counts = list( map( Counter, words ) )\n maxScore = self.maxScoreRec( 0, Counter( letters ) ) # First arg. is index into "words"\n return maxScore\n\n def maxScoreRec( self, index, letter_counter ):\n result = 0\n if index == len( self.words ):\n result = 0\n else:\n # Try skipping "words[index]"\n result = max( result, self.maxScoreRec( index + 1, letter_counter ) )\n # Try using "words[index]"\n if self.enough_letters( letter_counter, self.word_letter_counts[ index ] ):\n self.subtract_count( letter_counter, self.word_letter_counts[ index ] )\n result = max( result, \n self.word_scores[ index ] +\n self.maxScoreRec( index + 1, letter_counter ) )\n self.add_count( letter_counter, self.word_letter_counts[ index ] )\n return result\n\n def scoreWord( self, word, score ):\n return sum( map( lambda letter: score[ ord( letter ) - ord( \'a\' ) ], word ) )\n\n def enough_letters( self, letter_counter, word_letter_count ):\n for letter in word_letter_count:\n if letter_counter[ letter ] < word_letter_count[ letter ]:\n return False\n return True\n\n def subtract_count( self, letter_counter, word_letter_count ):\n letter_counter.subtract( word_letter_count )\n\n def add_count( self, letter_counter, word_letter_count ):\n letter_counter.update( word_letter_count )\n``` | 1 | Design a stack that supports increment operations on its elements.
Implement the `CustomStack` class:
* `CustomStack(int maxSize)` Initializes the object with `maxSize` which is the maximum number of elements in the stack.
* `void push(int x)` Adds `x` to the top of the stack if the stack has not reached the `maxSize`.
* `int pop()` Pops and returns the top of the stack or `-1` if the stack is empty.
* `void inc(int k, int val)` Increments the bottom `k` elements of the stack by `val`. If there are less than `k` elements in the stack, increment all the elements in the stack.
**Example 1:**
**Input**
\[ "CustomStack ", "push ", "push ", "pop ", "push ", "push ", "push ", "increment ", "increment ", "pop ", "pop ", "pop ", "pop "\]
\[\[3\],\[1\],\[2\],\[\],\[2\],\[3\],\[4\],\[5,100\],\[2,100\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,2,null,null,null,null,null,103,202,201,-1\]
**Explanation**
CustomStack stk = new CustomStack(3); // Stack is Empty \[\]
stk.push(1); // stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.pop(); // return 2 --> Return top of the stack 2, stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.push(3); // stack becomes \[1, 2, 3\]
stk.push(4); // stack still \[1, 2, 3\], Do not add another elements as size is 4
stk.increment(5, 100); // stack becomes \[101, 102, 103\]
stk.increment(2, 100); // stack becomes \[201, 202, 103\]
stk.pop(); // return 103 --> Return top of the stack 103, stack becomes \[201, 202\]
stk.pop(); // return 202 --> Return top of the stack 202, stack becomes \[201\]
stk.pop(); // return 201 --> Return top of the stack 201, stack becomes \[\]
stk.pop(); // return -1 --> Stack is empty return -1.
**Constraints:**
* `1 <= maxSize, x, k <= 1000`
* `0 <= val <= 100`
* At most `1000` calls will be made to each method of `increment`, `push` and `pop` each separately. | Note that words.length is small. This means you can iterate over every subset of words (2^N). |
Python solution Beats 98%. Commented code w/ explanation | maximum-score-words-formed-by-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is to use a backtracking approach to solve this problem. We can check all possible combinations of words and check if they can be made with the given letters and what the score would be.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI will use a backtracking approach where I will start with the first word and check if it can be made with the given letters. If it can, I will add the score of the word to the current sum and move on to the next word. If it can\'t, I will skip the word and move on to the next one. I will also keep track of the count of each letter in the letters list to check if the current word can be made. I will also keep track of the maximum score that can be achieved and return that at the end.\n# Complexity\n- Time complexity: O$$(2^N * N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n def backtrack(index, letter_count, curr_sum):\n # if index is past the length of words array\n # then return the current sum\n if index == len(words):\n self.ans = max(self.ans, curr_sum)\n return\n \n # the current word\n word = words[index]\n \n # create a new letter count array\n # as we need to restore the old \n # letter count\n temp = letter_count[:]\n \n # find the sum of the current word\n # if the current word can be made\n # using the current letter count\n curr_word_sum = 0\n valid = True\n for c in word:\n if letter_count[ord(c)-97] == 0:\n valid = False\n break\n curr_word_sum += score[ord(c)-97]\n letter_count[ord(c)-97] -= 1\n \n # if the current word can be made\n # then check if the current word with\n # the current sum can give a better\n # result\n if valid:\n backtrack(index+1, letter_count, curr_sum+curr_word_sum)\n \n # reset the letter count\n letter_count = temp[:]\n \n # skip the current word\n backtrack(index+1, letter_count, curr_sum)\n \n \n # create an array to store the \n # count of each letter\n letter_count = [0]*26\n for c in letters:\n letter_count[ord(c)-97] += 1\n \n self.ans = 0\n backtrack(0, letter_count, 0)\n return self.ans\n``` | 3 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
Python solution Beats 98%. Commented code w/ explanation | maximum-score-words-formed-by-letters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is to use a backtracking approach to solve this problem. We can check all possible combinations of words and check if they can be made with the given letters and what the score would be.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI will use a backtracking approach where I will start with the first word and check if it can be made with the given letters. If it can, I will add the score of the word to the current sum and move on to the next word. If it can\'t, I will skip the word and move on to the next one. I will also keep track of the count of each letter in the letters list to check if the current word can be made. I will also keep track of the maximum score that can be achieved and return that at the end.\n# Complexity\n- Time complexity: O$$(2^N * N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n def backtrack(index, letter_count, curr_sum):\n # if index is past the length of words array\n # then return the current sum\n if index == len(words):\n self.ans = max(self.ans, curr_sum)\n return\n \n # the current word\n word = words[index]\n \n # create a new letter count array\n # as we need to restore the old \n # letter count\n temp = letter_count[:]\n \n # find the sum of the current word\n # if the current word can be made\n # using the current letter count\n curr_word_sum = 0\n valid = True\n for c in word:\n if letter_count[ord(c)-97] == 0:\n valid = False\n break\n curr_word_sum += score[ord(c)-97]\n letter_count[ord(c)-97] -= 1\n \n # if the current word can be made\n # then check if the current word with\n # the current sum can give a better\n # result\n if valid:\n backtrack(index+1, letter_count, curr_sum+curr_word_sum)\n \n # reset the letter count\n letter_count = temp[:]\n \n # skip the current word\n backtrack(index+1, letter_count, curr_sum)\n \n \n # create an array to store the \n # count of each letter\n letter_count = [0]*26\n for c in letters:\n letter_count[ord(c)-97] += 1\n \n self.ans = 0\n backtrack(0, letter_count, 0)\n return self.ans\n``` | 3 | Design a stack that supports increment operations on its elements.
Implement the `CustomStack` class:
* `CustomStack(int maxSize)` Initializes the object with `maxSize` which is the maximum number of elements in the stack.
* `void push(int x)` Adds `x` to the top of the stack if the stack has not reached the `maxSize`.
* `int pop()` Pops and returns the top of the stack or `-1` if the stack is empty.
* `void inc(int k, int val)` Increments the bottom `k` elements of the stack by `val`. If there are less than `k` elements in the stack, increment all the elements in the stack.
**Example 1:**
**Input**
\[ "CustomStack ", "push ", "push ", "pop ", "push ", "push ", "push ", "increment ", "increment ", "pop ", "pop ", "pop ", "pop "\]
\[\[3\],\[1\],\[2\],\[\],\[2\],\[3\],\[4\],\[5,100\],\[2,100\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,2,null,null,null,null,null,103,202,201,-1\]
**Explanation**
CustomStack stk = new CustomStack(3); // Stack is Empty \[\]
stk.push(1); // stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.pop(); // return 2 --> Return top of the stack 2, stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.push(3); // stack becomes \[1, 2, 3\]
stk.push(4); // stack still \[1, 2, 3\], Do not add another elements as size is 4
stk.increment(5, 100); // stack becomes \[101, 102, 103\]
stk.increment(2, 100); // stack becomes \[201, 202, 103\]
stk.pop(); // return 103 --> Return top of the stack 103, stack becomes \[201, 202\]
stk.pop(); // return 202 --> Return top of the stack 202, stack becomes \[201\]
stk.pop(); // return 201 --> Return top of the stack 201, stack becomes \[\]
stk.pop(); // return -1 --> Stack is empty return -1.
**Constraints:**
* `1 <= maxSize, x, k <= 1000`
* `0 <= val <= 100`
* At most `1000` calls will be made to each method of `increment`, `push` and `pop` each separately. | Note that words.length is small. This means you can iterate over every subset of words (2^N). |
✅ || easiest solution to understand ||100% runtime (32 ms)|| python || Explanation and comments || | maximum-score-words-formed-by-letters | 0 | 1 | \n \n \n \n # This problem is quite similiar to classic dp problems\n # where we have two options \n # 1. = choose that word if possible ( if it is following all conditions ) and go forward \n # 2. = If not possible to choose just go forward\n \n # return maximum of all options you choosed .\n \n \n def abhi(n,letter):\n \n if n==len(words):return 0\n \n ans =0 # thie will calculate score of current word\n \n copy = letter \n \n for i in words[n]:\n \n if i not in copy:return abhi(n+1, letter) # if this word has a letter which is not\n # available just move forward \n \n copy = copy.replace(i,\'\',1)\n \n ans+= score[ord(i)-97]\n \n # if the current word has all its letter available on letter\n \n return max( abhi(n+1, letter) , ans+abhi(n+1, copy))\n # max(not choosing , choosing that word) # two choices\n \n return abhi(0,\'\'.join(letters))\n\n\nif you like solution and it helps you **Kindly upvote !!** | 9 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
✅ || easiest solution to understand ||100% runtime (32 ms)|| python || Explanation and comments || | maximum-score-words-formed-by-letters | 0 | 1 | \n \n \n \n # This problem is quite similiar to classic dp problems\n # where we have two options \n # 1. = choose that word if possible ( if it is following all conditions ) and go forward \n # 2. = If not possible to choose just go forward\n \n # return maximum of all options you choosed .\n \n \n def abhi(n,letter):\n \n if n==len(words):return 0\n \n ans =0 # thie will calculate score of current word\n \n copy = letter \n \n for i in words[n]:\n \n if i not in copy:return abhi(n+1, letter) # if this word has a letter which is not\n # available just move forward \n \n copy = copy.replace(i,\'\',1)\n \n ans+= score[ord(i)-97]\n \n # if the current word has all its letter available on letter\n \n return max( abhi(n+1, letter) , ans+abhi(n+1, copy))\n # max(not choosing , choosing that word) # two choices\n \n return abhi(0,\'\'.join(letters))\n\n\nif you like solution and it helps you **Kindly upvote !!** | 9 | Design a stack that supports increment operations on its elements.
Implement the `CustomStack` class:
* `CustomStack(int maxSize)` Initializes the object with `maxSize` which is the maximum number of elements in the stack.
* `void push(int x)` Adds `x` to the top of the stack if the stack has not reached the `maxSize`.
* `int pop()` Pops and returns the top of the stack or `-1` if the stack is empty.
* `void inc(int k, int val)` Increments the bottom `k` elements of the stack by `val`. If there are less than `k` elements in the stack, increment all the elements in the stack.
**Example 1:**
**Input**
\[ "CustomStack ", "push ", "push ", "pop ", "push ", "push ", "push ", "increment ", "increment ", "pop ", "pop ", "pop ", "pop "\]
\[\[3\],\[1\],\[2\],\[\],\[2\],\[3\],\[4\],\[5,100\],\[2,100\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,2,null,null,null,null,null,103,202,201,-1\]
**Explanation**
CustomStack stk = new CustomStack(3); // Stack is Empty \[\]
stk.push(1); // stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.pop(); // return 2 --> Return top of the stack 2, stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.push(3); // stack becomes \[1, 2, 3\]
stk.push(4); // stack still \[1, 2, 3\], Do not add another elements as size is 4
stk.increment(5, 100); // stack becomes \[101, 102, 103\]
stk.increment(2, 100); // stack becomes \[201, 202, 103\]
stk.pop(); // return 103 --> Return top of the stack 103, stack becomes \[201, 202\]
stk.pop(); // return 202 --> Return top of the stack 202, stack becomes \[201\]
stk.pop(); // return 201 --> Return top of the stack 201, stack becomes \[\]
stk.pop(); // return -1 --> Stack is empty return -1.
**Constraints:**
* `1 <= maxSize, x, k <= 1000`
* `0 <= val <= 100`
* At most `1000` calls will be made to each method of `increment`, `push` and `pop` each separately. | Note that words.length is small. This means you can iterate over every subset of words (2^N). |
75% Tc and 78% Sc easy python solution | maximum-score-words-formed-by-letters | 0 | 1 | ```\ndef maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n\tdef solve(i, d):\n\t\tif(i == len(words)): return 0\n\t\tt = solve(i+1, d)\n\t\tcurr_count = Counter(words[i])\n\t\tfor c in curr_count:\n\t\t\tif(c not in d or curr_count[c] > d[c]):\n\t\t\t\treturn t\n\t\tnew_d = d.copy()\n\t\ty = 0\n\t\tfor c in curr_count:\n\t\t\tnew_d[c] -= curr_count[c]\n\t\t\ty += curr_count[c] * score[ord(c)-97]\n\t\tt = max(t, solve(i+1, new_d) + y)\n\t\treturn t\n\n\tdic = Counter(letters) \n\treturn solve(0, dic)\n``` | 1 | Given a list of `words`, list of single `letters` (might be repeating) and `score` of every character.
Return the maximum score of **any** valid set of words formed by using the given letters (`words[i]` cannot be used two or more times).
It is not necessary to use all characters in `letters` and each letter can only be used once. Score of letters `'a'`, `'b'`, `'c'`, ... ,`'z'` is given by `score[0]`, `score[1]`, ... , `score[25]` respectively.
**Example 1:**
**Input:** words = \[ "dog ", "cat ", "dad ", "good "\], letters = \[ "a ", "a ", "c ", "d ", "d ", "d ", "g ", "o ", "o "\], score = \[1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** 23
**Explanation:**
Score a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad " (5+1+5) and "good " (3+2+2+5) with a score of 23.
Words "dad " and "dog " only get a score of 21.
**Example 2:**
**Input:** words = \[ "xxxz ", "ax ", "bx ", "cx "\], letters = \[ "z ", "a ", "b ", "c ", "x ", "x ", "x "\], score = \[4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10\]
**Output:** 27
**Explanation:**
Score a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax " (4+5), "bx " (4+5) and "cx " (4+5) with a score of 27.
Word "xxxz " only get a score of 25.
**Example 3:**
**Input:** words = \[ "leetcode "\], letters = \[ "l ", "e ", "t ", "c ", "o ", "d "\], score = \[0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0\]
**Output:** 0
**Explanation:**
Letter "e " can only be used once.
**Constraints:**
* `1 <= words.length <= 14`
* `1 <= words[i].length <= 15`
* `1 <= letters.length <= 100`
* `letters[i].length == 1`
* `score.length == 26`
* `0 <= score[i] <= 10`
* `words[i]`, `letters[i]` contains only lower case English letters. | What's the score after reversing a sub-array [L, R] ? It's the score without reversing it + abs(a[R] - a[L-1]) + abs(a[L] - a[R+1]) - abs(a[L] - a[L-1]) - abs(a[R] - a[R+1]) How to maximize that formula given that abs(x - y) = max(x - y, y - x) ? This can be written as max(max(a[R] - a[L - 1], a[L - 1] - a[R]) + max(a[R + 1] - a[L], a[L] - a[R + 1]) - value(L) - value(R + 1)) over all L < R where value(i) = abs(a[i] - a[i-1]) This can be divided into 4 cases. |
75% Tc and 78% Sc easy python solution | maximum-score-words-formed-by-letters | 0 | 1 | ```\ndef maxScoreWords(self, words: List[str], letters: List[str], score: List[int]) -> int:\n\tdef solve(i, d):\n\t\tif(i == len(words)): return 0\n\t\tt = solve(i+1, d)\n\t\tcurr_count = Counter(words[i])\n\t\tfor c in curr_count:\n\t\t\tif(c not in d or curr_count[c] > d[c]):\n\t\t\t\treturn t\n\t\tnew_d = d.copy()\n\t\ty = 0\n\t\tfor c in curr_count:\n\t\t\tnew_d[c] -= curr_count[c]\n\t\t\ty += curr_count[c] * score[ord(c)-97]\n\t\tt = max(t, solve(i+1, new_d) + y)\n\t\treturn t\n\n\tdic = Counter(letters) \n\treturn solve(0, dic)\n``` | 1 | Design a stack that supports increment operations on its elements.
Implement the `CustomStack` class:
* `CustomStack(int maxSize)` Initializes the object with `maxSize` which is the maximum number of elements in the stack.
* `void push(int x)` Adds `x` to the top of the stack if the stack has not reached the `maxSize`.
* `int pop()` Pops and returns the top of the stack or `-1` if the stack is empty.
* `void inc(int k, int val)` Increments the bottom `k` elements of the stack by `val`. If there are less than `k` elements in the stack, increment all the elements in the stack.
**Example 1:**
**Input**
\[ "CustomStack ", "push ", "push ", "pop ", "push ", "push ", "push ", "increment ", "increment ", "pop ", "pop ", "pop ", "pop "\]
\[\[3\],\[1\],\[2\],\[\],\[2\],\[3\],\[4\],\[5,100\],\[2,100\],\[\],\[\],\[\],\[\]\]
**Output**
\[null,null,null,2,null,null,null,null,null,103,202,201,-1\]
**Explanation**
CustomStack stk = new CustomStack(3); // Stack is Empty \[\]
stk.push(1); // stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.pop(); // return 2 --> Return top of the stack 2, stack becomes \[1\]
stk.push(2); // stack becomes \[1, 2\]
stk.push(3); // stack becomes \[1, 2, 3\]
stk.push(4); // stack still \[1, 2, 3\], Do not add another elements as size is 4
stk.increment(5, 100); // stack becomes \[101, 102, 103\]
stk.increment(2, 100); // stack becomes \[201, 202, 103\]
stk.pop(); // return 103 --> Return top of the stack 103, stack becomes \[201, 202\]
stk.pop(); // return 202 --> Return top of the stack 202, stack becomes \[201\]
stk.pop(); // return 201 --> Return top of the stack 201, stack becomes \[\]
stk.pop(); // return -1 --> Stack is empty return -1.
**Constraints:**
* `1 <= maxSize, x, k <= 1000`
* `0 <= val <= 100`
* At most `1000` calls will be made to each method of `increment`, `push` and `pop` each separately. | Note that words.length is small. This means you can iterate over every subset of words (2^N). |
Very Simple Solution | shift-2d-grid | 1 | 1 | ```\n// Please upvote if you like my solution :)\nvoid reverse(vector<int> &nums,int start,int end){\n for(int i=start,j=end;i<j;i++,j--){\n swap(nums[i],nums[j]);\n }\n }\n vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {\n int ro = grid.size();\n int col = grid[0].size();\n vector<int> v;\n for(auto &gri:grid){\n for(auto &val:gri){\n v.push_back(val);\n }\n }\n k = k % v.size();\n reverse(v,0,v.size()-k-1);\n reverse(v,v.size()-k,v.size()-1);\n reverse(v,0,v.size()-1);\n int vec = 0;\n for(int i=0;i<ro;i++){\n for(int j=0;j<col;j++){\n grid[i][j] = v[vec];\n vec++;\n }\n }\n return grid;\n }\n// Please upvote if you like my solution :)\n``` | 14 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Very Simple Solution | shift-2d-grid | 1 | 1 | ```\n// Please upvote if you like my solution :)\nvoid reverse(vector<int> &nums,int start,int end){\n for(int i=start,j=end;i<j;i++,j--){\n swap(nums[i],nums[j]);\n }\n }\n vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {\n int ro = grid.size();\n int col = grid[0].size();\n vector<int> v;\n for(auto &gri:grid){\n for(auto &val:gri){\n v.push_back(val);\n }\n }\n k = k % v.size();\n reverse(v,0,v.size()-k-1);\n reverse(v,v.size()-k,v.size()-1);\n reverse(v,0,v.size()-1);\n int vec = 0;\n for(int i=0;i<ro;i++){\n for(int j=0;j<col;j++){\n grid[i][j] = v[vec];\n vec++;\n }\n }\n return grid;\n }\n// Please upvote if you like my solution :)\n``` | 14 | A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
_Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as \[3,3\] and \[3,4\]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
**Example 1:**
**Input:** n = 3, reservedSeats = \[\[1,2\],\[1,3\],\[1,8\],\[2,6\],\[3,1\],\[3,10\]\]
**Output:** 4
**Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
**Example 2:**
**Input:** n = 2, reservedSeats = \[\[2,1\],\[1,8\],\[2,6\]\]
**Output:** 2
**Example 3:**
**Input:** n = 4, reservedSeats = \[\[4,3\],\[1,4\],\[4,6\],\[1,7\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 10^9`
* `1 <= reservedSeats.length <= min(10*n, 10^4)`
* `reservedSeats[i].length == 2`
* `1 <= reservedSeats[i][0] <= n`
* `1 <= reservedSeats[i][1] <= 10`
* All `reservedSeats[i]` are distinct. | Simulate step by step. move grid[i][j] to grid[i][j+1]. handle last column of the grid. Put the matrix row by row to a vector. take k % vector.length and move last k of the vector to the beginning. put the vector to the matrix back the same way. |
Python3: 2 simple approaches with explanations (by creating a vector) | shift-2d-grid | 0 | 1 | # **Algorithm:**\n1) put the matrix row by row to a vector.\n2) rotate the vector k times.\n3) put the vector to the matrix back the same way.\n\nThe **second step** is the same as problem [#189 (Rotate an Array)](https://leetcode.com/problems/rotate-array/), and can be solved in many ways, but here we consider **two approaches** that are simple and have reasonable time and space complexities: \n**(a) direct shift approach**\n**(b) reverse approach**\n\nAs an example of **Approach (a)**, imagine we want to rotate the vector [1, 2, 3, 4, 5, 6, 7] for k = 3 times. We just need to add these two subsets of the vector, respectively: last k elements and first len(vec)-k elements:\n[5, 6, 7] + [1, 2, 3, 4] = [5, 6, 7, 1, 2, 3, 4]\n\nAn example of **Approach (b)**:\nreverse all elements : [7, 6, 5, 4, 3, 2, 1]\nreverse first k elements : [5, 6, 7, 4, 3, 2, 1]\nreverse last len(vec)-k elements : [5, 6, 7, 1, 2, 3, 4]\n\nAlthough approach (a) seems simpler, it take additional space (needs an extra vector in addition to the vector created in step 1). Approach (b) might need extra code lines, but does not take additional space.\n\n# **Python3 codes:**\n\n**Approach (a), direct shift:**\n```\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n #dimensions:\n\t\tNR = len(grid)\n NC = len(grid[0])\n vec = [0] * NR * NC #initialize the vector.\n #If k is greater than the length of vector, \n\t\t#the shift will repeat itself in a cycle; \n\t\t#hence, we only care about the remainder.\n k = k % (NR * NC) \n \n\t\t#step 1: put the matrix row by row to the vector.\n for i in range(NR):\n for j in range(NC):\n vec[i * NC + j] = grid[i][j]\n\t\t\t\t\n #step 2: rotate vector k times by direct shift approach\n vec = vec[-k:] + vec[:-k]\n\t\t\n # step 3: put vector to matrix back the same way\n for i in range(NR):\n for j in range(NC):\n grid[i][j] = vec[i * NC + j]\n return grid\n```\n\n\n**Approach (b), reverse method**: (Note that only step 2 has changed):\n```\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n # dimensions:\n NR = len(grid)\n NC = len(grid[0])\n vec = [0] * NR * NC #initialize the vector.\n # If k is greater than the length of vector, \n\t\t# the shift will repeat itself in a cycle; \n\t\t# hence, we only care about the remainder.\n k = k % (NR * NC)\n\t\t\n #step 1: put the matrix row by row to the vector.\n for i in range(NR):\n for j in range(NC):\n vec[i * NC + j] = grid[i][j]\n\t\t\t\t\n #step 2: rotate vector k times by reverse approach.\n self.Rev(vec, 0, NR * NC - 1) #reverse all elements.\n self.Rev(vec, 0, k-1) #reverse first k elements.\n self.Rev(vec, k, NR * NC - 1) #revere last len(vec)-k elements. \n \n #step 3: put the vector to the matrix back the same way.\n for i in range(NR):\n for j in range(NC):\n grid[i][j] = vec[i * NC + j]\n return grid\n\t\t\n # This function returns the reverse a subset of the vector,\n\t# bound by "left" and "right" elements\n def Rev(self, vec, left, right):\n while left < right:\n vec[left], vec[right] = vec[right], vec[left]\n left += 1 \n right -= 1\n``` | 28 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Python3: 2 simple approaches with explanations (by creating a vector) | shift-2d-grid | 0 | 1 | # **Algorithm:**\n1) put the matrix row by row to a vector.\n2) rotate the vector k times.\n3) put the vector to the matrix back the same way.\n\nThe **second step** is the same as problem [#189 (Rotate an Array)](https://leetcode.com/problems/rotate-array/), and can be solved in many ways, but here we consider **two approaches** that are simple and have reasonable time and space complexities: \n**(a) direct shift approach**\n**(b) reverse approach**\n\nAs an example of **Approach (a)**, imagine we want to rotate the vector [1, 2, 3, 4, 5, 6, 7] for k = 3 times. We just need to add these two subsets of the vector, respectively: last k elements and first len(vec)-k elements:\n[5, 6, 7] + [1, 2, 3, 4] = [5, 6, 7, 1, 2, 3, 4]\n\nAn example of **Approach (b)**:\nreverse all elements : [7, 6, 5, 4, 3, 2, 1]\nreverse first k elements : [5, 6, 7, 4, 3, 2, 1]\nreverse last len(vec)-k elements : [5, 6, 7, 1, 2, 3, 4]\n\nAlthough approach (a) seems simpler, it take additional space (needs an extra vector in addition to the vector created in step 1). Approach (b) might need extra code lines, but does not take additional space.\n\n# **Python3 codes:**\n\n**Approach (a), direct shift:**\n```\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n #dimensions:\n\t\tNR = len(grid)\n NC = len(grid[0])\n vec = [0] * NR * NC #initialize the vector.\n #If k is greater than the length of vector, \n\t\t#the shift will repeat itself in a cycle; \n\t\t#hence, we only care about the remainder.\n k = k % (NR * NC) \n \n\t\t#step 1: put the matrix row by row to the vector.\n for i in range(NR):\n for j in range(NC):\n vec[i * NC + j] = grid[i][j]\n\t\t\t\t\n #step 2: rotate vector k times by direct shift approach\n vec = vec[-k:] + vec[:-k]\n\t\t\n # step 3: put vector to matrix back the same way\n for i in range(NR):\n for j in range(NC):\n grid[i][j] = vec[i * NC + j]\n return grid\n```\n\n\n**Approach (b), reverse method**: (Note that only step 2 has changed):\n```\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n # dimensions:\n NR = len(grid)\n NC = len(grid[0])\n vec = [0] * NR * NC #initialize the vector.\n # If k is greater than the length of vector, \n\t\t# the shift will repeat itself in a cycle; \n\t\t# hence, we only care about the remainder.\n k = k % (NR * NC)\n\t\t\n #step 1: put the matrix row by row to the vector.\n for i in range(NR):\n for j in range(NC):\n vec[i * NC + j] = grid[i][j]\n\t\t\t\t\n #step 2: rotate vector k times by reverse approach.\n self.Rev(vec, 0, NR * NC - 1) #reverse all elements.\n self.Rev(vec, 0, k-1) #reverse first k elements.\n self.Rev(vec, k, NR * NC - 1) #revere last len(vec)-k elements. \n \n #step 3: put the vector to the matrix back the same way.\n for i in range(NR):\n for j in range(NC):\n grid[i][j] = vec[i * NC + j]\n return grid\n\t\t\n # This function returns the reverse a subset of the vector,\n\t# bound by "left" and "right" elements\n def Rev(self, vec, left, right):\n while left < right:\n vec[left], vec[right] = vec[right], vec[left]\n left += 1 \n right -= 1\n``` | 28 | A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
_Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as \[3,3\] and \[3,4\]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
**Example 1:**
**Input:** n = 3, reservedSeats = \[\[1,2\],\[1,3\],\[1,8\],\[2,6\],\[3,1\],\[3,10\]\]
**Output:** 4
**Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
**Example 2:**
**Input:** n = 2, reservedSeats = \[\[2,1\],\[1,8\],\[2,6\]\]
**Output:** 2
**Example 3:**
**Input:** n = 4, reservedSeats = \[\[4,3\],\[1,4\],\[4,6\],\[1,7\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 10^9`
* `1 <= reservedSeats.length <= min(10*n, 10^4)`
* `reservedSeats[i].length == 2`
* `1 <= reservedSeats[i][0] <= n`
* `1 <= reservedSeats[i][1] <= 10`
* All `reservedSeats[i]` are distinct. | Simulate step by step. move grid[i][j] to grid[i][j+1]. handle last column of the grid. Put the matrix row by row to a vector. take k % vector.length and move last k of the vector to the beginning. put the vector to the matrix back the same way. |
Beats 99.43% #python3 | shift-2d-grid | 0 | 1 | # Approach\nFirst of all accessing each list of grid through index, popping the last element and inserting it to the starting of next list. \n\nFinally, accessing the last list popping the last element and inserting it to the first list. \n\n\n# Code\n```\nclass Solution:\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n def shift(grid):\n for i in range(len(grid) - 1):\n grid[i + 1].insert(0, grid[i].pop())\n grid[0].insert(0, grid[-1].pop())\n return grid\n for i in range(k):\n shift(grid)\n return grid\n``` | 1 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Beats 99.43% #python3 | shift-2d-grid | 0 | 1 | # Approach\nFirst of all accessing each list of grid through index, popping the last element and inserting it to the starting of next list. \n\nFinally, accessing the last list popping the last element and inserting it to the first list. \n\n\n# Code\n```\nclass Solution:\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n def shift(grid):\n for i in range(len(grid) - 1):\n grid[i + 1].insert(0, grid[i].pop())\n grid[0].insert(0, grid[-1].pop())\n return grid\n for i in range(k):\n shift(grid)\n return grid\n``` | 1 | A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
_Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as \[3,3\] and \[3,4\]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
**Example 1:**
**Input:** n = 3, reservedSeats = \[\[1,2\],\[1,3\],\[1,8\],\[2,6\],\[3,1\],\[3,10\]\]
**Output:** 4
**Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
**Example 2:**
**Input:** n = 2, reservedSeats = \[\[2,1\],\[1,8\],\[2,6\]\]
**Output:** 2
**Example 3:**
**Input:** n = 4, reservedSeats = \[\[4,3\],\[1,4\],\[4,6\],\[1,7\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 10^9`
* `1 <= reservedSeats.length <= min(10*n, 10^4)`
* `reservedSeats[i].length == 2`
* `1 <= reservedSeats[i][0] <= n`
* `1 <= reservedSeats[i][1] <= 10`
* All `reservedSeats[i]` are distinct. | Simulate step by step. move grid[i][j] to grid[i][j+1]. handle last column of the grid. Put the matrix row by row to a vector. take k % vector.length and move last k of the vector to the beginning. put the vector to the matrix back the same way. |
⭐ Just Flatten and Rotate the Array | shift-2d-grid | 0 | 1 | **OBSERVATION:**\nIf we trace the path of any number/index as we do the operation multiple times we find that the number is merely traversing the matrix row-wise. Take 1 for example and look at its path.\n\n1. This gives us an idea to flatten out the array and rotate it k times to get the final matrix in Row Major Order. \n2. One other thing to notice is that after M X N number of operations, the resulting matrix is the original matrix. Hence we can update k as **`k = k % ( m * n )`.** \n3. The rotation algorithm can be practiced from [Leetcode 189. Rotate Array](https://leetcode.com/problems/rotate-array/).\n\n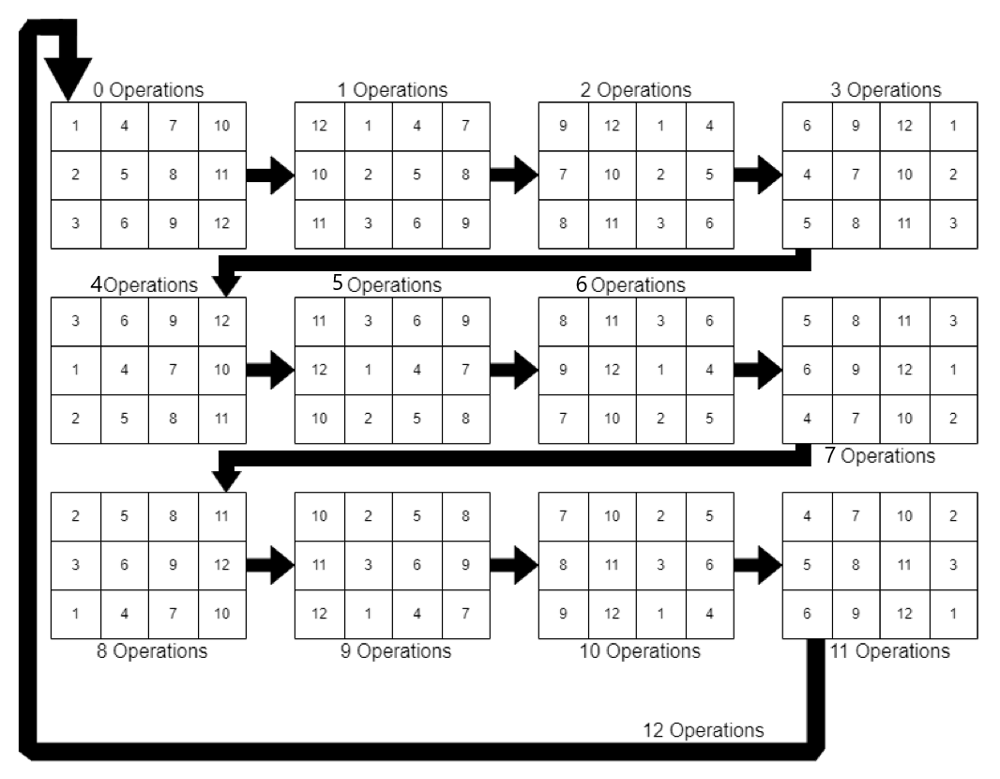\n\n**STEPS:**\n1. Flatten out the array.\n2. Rotate the array k times.\n3. Resulting list is a Row Major representation of our answer array. So convert this 1d Array to 2d Matrix.\n\n\n**CODE:**\n```\nclass Solution:\n def rotate(self, nums: List[int], k: int) -> None: # From Leetcode Problem 189. Rotate Array\n n = len(nums)\n k = k % n\n nums[:] = nums[n - k:] + nums[:n - k]\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n m, n = len(grid), len(grid[0])\n arr = [i for sublist in grid for i in sublist] # Flatten out the array\n self.rotate(arr,k) # Rotate the array \n grid = [[arr[i*n+j] for j in range(n)] for i in range(m)] # Convert Flattened output to 2d Matrix\n return grid # Return 2d Result\n```\n**NOTE:** \n**`grid = [[arr[i*n+j] for j in range(n)] for i in range(m)]`** is just a shorter way for doing the following:\n```\ngrid = []\nfor i in range(m):\n temp = []\n for j in range(n):\n temp.append(arr[i*n+j])\n grid.append(temp)\n``` | 7 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
⭐ Just Flatten and Rotate the Array | shift-2d-grid | 0 | 1 | **OBSERVATION:**\nIf we trace the path of any number/index as we do the operation multiple times we find that the number is merely traversing the matrix row-wise. Take 1 for example and look at its path.\n\n1. This gives us an idea to flatten out the array and rotate it k times to get the final matrix in Row Major Order. \n2. One other thing to notice is that after M X N number of operations, the resulting matrix is the original matrix. Hence we can update k as **`k = k % ( m * n )`.** \n3. The rotation algorithm can be practiced from [Leetcode 189. Rotate Array](https://leetcode.com/problems/rotate-array/).\n\n\n\n**STEPS:**\n1. Flatten out the array.\n2. Rotate the array k times.\n3. Resulting list is a Row Major representation of our answer array. So convert this 1d Array to 2d Matrix.\n\n\n**CODE:**\n```\nclass Solution:\n def rotate(self, nums: List[int], k: int) -> None: # From Leetcode Problem 189. Rotate Array\n n = len(nums)\n k = k % n\n nums[:] = nums[n - k:] + nums[:n - k]\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n m, n = len(grid), len(grid[0])\n arr = [i for sublist in grid for i in sublist] # Flatten out the array\n self.rotate(arr,k) # Rotate the array \n grid = [[arr[i*n+j] for j in range(n)] for i in range(m)] # Convert Flattened output to 2d Matrix\n return grid # Return 2d Result\n```\n**NOTE:** \n**`grid = [[arr[i*n+j] for j in range(n)] for i in range(m)]`** is just a shorter way for doing the following:\n```\ngrid = []\nfor i in range(m):\n temp = []\n for j in range(n):\n temp.append(arr[i*n+j])\n grid.append(temp)\n``` | 7 | A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
_Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as \[3,3\] and \[3,4\]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
**Example 1:**
**Input:** n = 3, reservedSeats = \[\[1,2\],\[1,3\],\[1,8\],\[2,6\],\[3,1\],\[3,10\]\]
**Output:** 4
**Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
**Example 2:**
**Input:** n = 2, reservedSeats = \[\[2,1\],\[1,8\],\[2,6\]\]
**Output:** 2
**Example 3:**
**Input:** n = 4, reservedSeats = \[\[4,3\],\[1,4\],\[4,6\],\[1,7\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 10^9`
* `1 <= reservedSeats.length <= min(10*n, 10^4)`
* `reservedSeats[i].length == 2`
* `1 <= reservedSeats[i][0] <= n`
* `1 <= reservedSeats[i][1] <= 10`
* All `reservedSeats[i]` are distinct. | Simulate step by step. move grid[i][j] to grid[i][j+1]. handle last column of the grid. Put the matrix row by row to a vector. take k % vector.length and move last k of the vector to the beginning. put the vector to the matrix back the same way. |
✅✅✅ python solution using simple methods | just 8 lines | shift-2d-grid | 0 | 1 | # Code\n```\nclass Solution:\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n n, m = len(grid), len(grid[0])\n k%=n*m\n new_grid = [[False for j in range(m)] for i in range(n)]\n for i in range(n):\n for j in range(m):\n i0, j0 = ((i*m+j+k)//m)%n, (i*m+j+k)%m\n new_grid[i0][j0]=grid[i][j] \n return new_grid\n``` | 4 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
✅✅✅ python solution using simple methods | just 8 lines | shift-2d-grid | 0 | 1 | # Code\n```\nclass Solution:\n def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:\n n, m = len(grid), len(grid[0])\n k%=n*m\n new_grid = [[False for j in range(m)] for i in range(n)]\n for i in range(n):\n for j in range(m):\n i0, j0 = ((i*m+j+k)//m)%n, (i*m+j+k)%m\n new_grid[i0][j0]=grid[i][j] \n return new_grid\n``` | 4 | A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
_Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as \[3,3\] and \[3,4\]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
**Example 1:**
**Input:** n = 3, reservedSeats = \[\[1,2\],\[1,3\],\[1,8\],\[2,6\],\[3,1\],\[3,10\]\]
**Output:** 4
**Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
**Example 2:**
**Input:** n = 2, reservedSeats = \[\[2,1\],\[1,8\],\[2,6\]\]
**Output:** 2
**Example 3:**
**Input:** n = 4, reservedSeats = \[\[4,3\],\[1,4\],\[4,6\],\[1,7\]\]
**Output:** 4
**Constraints:**
* `1 <= n <= 10^9`
* `1 <= reservedSeats.length <= min(10*n, 10^4)`
* `reservedSeats[i].length == 2`
* `1 <= reservedSeats[i][0] <= n`
* `1 <= reservedSeats[i][1] <= 10`
* All `reservedSeats[i]` are distinct. | Simulate step by step. move grid[i][j] to grid[i][j+1]. handle last column of the grid. Put the matrix row by row to a vector. take k % vector.length and move last k of the vector to the beginning. put the vector to the matrix back the same way. |
Python Special Way for find() without HashSet O(1) Space O(logn) Time | find-elements-in-a-contaminated-binary-tree | 0 | 1 | It\'s obvious to use `BFS` for the initial part. However, a lot of people use HashSet(`set()` in python) to pre-store all the values in the initial part, which may cause MLE when the values are huge. There is a special way to implement `find()` that costs O(1) in space and O(logn) in time. \n\nFirstly, let\'s see what a complete tree will look like in this problem: \n\n\nIt\'s very easy to find that numbers in each layer range from `[2^i-1,2^(i+1)-2]`\nwhat if we add 1 to each number? Then it should range from `[2^i, 2^(i+1)-1]`\nSee? the binary of all numbers in each layer should be: `100..00` to `111...11`\n\nHence we could discover that maybe we could use the `binary number` of `target+1` to find a path:\n\n\n\nI\'m not proficient in English, so I would prefer to show my code here to explain my idea:\n\n```python\ndef find(self, target: int) -> bool:\n\t\tbinary = bin(target+1)[3:] # remove the useless first `1`\n index = 0\n root = self.root # use a new pointer `root` to traverse the tree\n while root and index <= len(binary): # traverse the binary number from left to right\n if root.val == target:\n return True\n if binary[index] == \'0\': # if it\'s 0, we have to go left\n root = root.left\n else: # if it\'s 1, we have to go right\n root = root.right\n index += 1\n return False\n``` | 131 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Simple solution with Depth-First Search + HashSet in Python3 | find-elements-in-a-contaminated-binary-tree | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a **Binary Tree**, all of its values equal to `-1`\n- our goal is to **recover** all nodes by changing values according to the schema\n\n```py\n# Example\ntree = TreeNode(-1, None, TreeNode(-1, TreeNode(-1)))\n\n# The original values in left parentheses and \n# restored in right ones \n# (-1) => (0)\n# \\ \\\n# (-1) => (2)\n# / /\n# (-1)=> (5)\n\n# The formulae to calculate value for a particular node\n# is the following (for root.val == 0)\n# node.left.val = parentNode.val * 2 + 1 \n# node.right.val = parentNode.val * 2 + 2\n \n```\n\n# Approach \n1. define a `set`, that\'ll store all of the traversed values from `root` to quick search inside `find` method\n2. define `recover` function to recover the values of a tree\n3. if there\'s no `node` return `None`\n4. if the `left` or `right` children exist, change the values according to the schema and store the values inside `self.set`\n5. implement the `find` method with checking value in `self.set`\n\n# Complexity\n- Time complexity: **O(n)**, because of iterating over `root`\n\n- Space complexity: **O(n)**, because of recursive call stack and storing all the values inside `self.set`\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n def recover(self, node):\n if not node: \n return node\n\n node.val = 0\n \n def dfs(node, val = 0):\n if not node:\n return \n if node.left:\n node.left.val = val * 2 + 1\n self.set.add(node.left.val)\n dfs(node.left, node.left.val)\n if node.right:\n node.right.val = val * 2 + 2\n self.set.add(node.right.val)\n dfs(node.right, node.right.val)\n\n dfs(node)\n\n def __init__(self, root: Optional[TreeNode]):\n self.set = {0}\n self.recover(root)\n self.root = root\n\n def find(self, target: int) -> bool:\n return target in self.set\n \n\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 1 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Easy Python Solution | Faster than 99% (76 ms) | Comments | find-elements-in-a-contaminated-binary-tree | 0 | 1 | # Easy Python Solution | Faster than 99% (76 ms) | With Comments\n\n**Runtime: 76 ms, faster than 99.13% of Python3 online submissions for Find Elements in a Contaminated Binary Tree.\nMemory Usage: 17.9 MB**\n\n```\nclass FindElements:\n \n def dfs(self, node, val):\n if node:\n self.store[val] = 1 # adding the value of node to hashmap\n if node.left:\n vl = (2 * val) + 1 # correcting the value of left node\n self.dfs(node.left,vl) # left sub tree traversal\n if node.right:\n vr = (2* val) + 2 # correcting the value of right node\n self.dfs(node.right, vr) # right sub tree traversal\n\n def __init__(self, root: TreeNode):\n self.store = {} # hashmap for storing the corrected node values. And searching the values.\n self.dfs(root, 0) # Traversing the incorrect tree and saving correct values on the way\n\n def find(self, target: int) -> bool:\n\t\t# checking if the target value exists in O(1) time\n if self.store.get(target, None) is not None:\n return True\n else:\n return False\n```\n\n\n | 2 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Easy to understand python BFS solution | find-elements-in-a-contaminated-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverse the tree using BFS, and store all the values of the nodes in a set. Then find whether the \'target\' exists in the set or not.\n# Complexity\n- Time complexity: O(n) => where \'n\' is the number of nodes\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(h) => where \'h\' is the height of the tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n\n def __init__(self, root: Optional[TreeNode]):\n self.s = set()\n q = deque()\n q.append((root, 0))\n while q:\n for _ in range(len(q)):\n node, val = q.popleft()\n self.s.add(val)\n if node.left:\n q.append((node.left, 2*val+1))\n if node.right:\n q.append((node.right, 2*val+2))\n\n def find(self, target: int) -> bool:\n return target in self.s\n \n\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Python3 O(N) solution with preorder traversal (100% Runtime) | find-elements-in-a-contaminated-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nUse preorder to assign values & use a dictionary for constant time existence check\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- If you use preorder traversal, you can assign correct values very easy:\n - Parent\'s value = x\n - Left child\'s value = 2 * x + 1\n - Right child\'s value = 2 * x + 2\n- During preorder traversal, update your dictionary to store existence info of the value\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n\n def __init__(self, root: Optional[TreeNode]):\n self.d = {}\n\n def preorder(node: TreeNode, x: int):\n if not node:\n return\n\n node.val = x\n self.d[x] = True\n preorder(node.left, 2 * x + 1)\n preorder(node.right, 2 * x + 2)\n\n self.root = root\n preorder(self.root, 0)\n \n def find(self, target: int) -> bool:\n return target in self.d\n \n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Extremely short solution in Python 3, using generator and set | find-elements-in-a-contaminated-binary-tree | 0 | 1 | ```python\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n\n def __init__(self, root: Optional[TreeNode]):\n \n def gen(n: TreeNode, v=0):\n if not n:\n return\n yield v\n if n.left:\n yield from gen(n.left, 2 * v + 1)\n if n.right:\n yield from gen(n.right, 2 * v + 2)\n\n self.vals = set(gen(root))\n \n\n def find(self, target: int) -> bool:\n return target in self.vals\n \n\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.