title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
🚀🔥Leetcode 1218 | Python Solution + Video Tutorial 🎯🐍 | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\nhttps://youtu.be/Ho7uSMTguCU\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n dp = {}\n ans = 1\n for item in arr:\n val = 1\n if item - difference in dp:\n val += dp[item-difference]\n ans = max(ans, val)\n dp[item] = val\n \n return ans\n \n``` | 8 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
[Python] it's all about expectations (explained) | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | The key idea here is to maintain a dictionary with:\n1. **keys** being the numbers that we *expect* to encounter in order to increase subsequence, and \n2. the respective **values** representing lengths of currently constructed subsequences.\n\nEvery time we hit one of the expected numbers `n`, we increase the subsequence by updating the `n+d`-th entry of the dictionary. Notice that multiple subsequences of different length sharing some number may be present. To prevent overwriting of large subsequence length by a smaller value, we store a maximal of these (`max(...)`). \n\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], d: int) -> int:\n\n subseqs = {}\n for n in arr:\n cnt_prev = subseqs.get(n, 0)\n cnt_next = subseqs.get(n+d,0)\n subseqs[n+d] = max(cnt_prev + 1, cnt_next)\n \n return max(subseqs.values())\n``` | 7 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
[Python] it's all about expectations (explained) | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | The key idea here is to maintain a dictionary with:\n1. **keys** being the numbers that we *expect* to encounter in order to increase subsequence, and \n2. the respective **values** representing lengths of currently constructed subsequences.\n\nEvery time we hit one of the expected numbers `n`, we increase the subsequence by updating the `n+d`-th entry of the dictionary. Notice that multiple subsequences of different length sharing some number may be present. To prevent overwriting of large subsequence length by a smaller value, we store a maximal of these (`max(...)`). \n\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], d: int) -> int:\n\n subseqs = {}\n for n in arr:\n cnt_prev = subseqs.get(n, 0)\n cnt_next = subseqs.get(n+d,0)\n subseqs[n+d] = max(cnt_prev + 1, cnt_next)\n \n return max(subseqs.values())\n``` | 7 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
4 Line Python || HashMap + DP || Two Sum Variation | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\nMain Intuition comes from problem "Two Sum"\n\n# Approach\nSimply Hash previously seen values and the count of ongoing AP Length\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n map = {}\n for val in arr:\n map[val] = map.get(val - difference, 0) + 1\n return max(map.values())\n \n\n\n``` | 5 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
4 Line Python || HashMap + DP || Two Sum Variation | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\nMain Intuition comes from problem "Two Sum"\n\n# Approach\nSimply Hash previously seen values and the count of ongoing AP Length\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n map = {}\n for val in arr:\n map[val] = map.get(val - difference, 0) + 1\n return max(map.values())\n \n\n\n``` | 5 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Easiest python solution using Default Dict best approach for begginers | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is to use a dynamic programming approach to calculate the length of subsequences ending at each element of the array. By keeping track of the lengths of subsequences, we can determine the longest subsequence with the required difference.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code aims to find the length of the longest subsequence in the given arr list, where the difference between consecutive elements is equal to dif. The approach used is dynamic programming.\n\n- Create a defaultdict lengths to store the lengths of subsequences. The defaultdict is initialized with a default value of 0.\n- Iterate over the elements of the arr list.\n- For each element num, calculate the length of the subsequence ending at num by adding 1 to the length of the subsequence ending at num - dif. Store this value in lengths[num].\n- After iterating over all elements, find the maximum value in the lengths dictionary, which represents the length of the longest subsequence.\n- Return the maximum length.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nUpvote appreciated , Thanks!\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def longestSubsequence(self, arr: List[int], dif: int) -> int:\n # Create a defaultdict to store the lengths of subsequences\n lengths = defaultdict(lambda: 0)\n \n # Iterate over the array elements\n for num in arr:\n # Calculate the length of the subsequence ending at the current element\n lengths[num] = lengths[num - dif] + 1\n\n # Return the maximum length of subsequences\n return max(lengths.values())\n\n``` | 4 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Easiest python solution using Default Dict best approach for begginers | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is to use a dynamic programming approach to calculate the length of subsequences ending at each element of the array. By keeping track of the lengths of subsequences, we can determine the longest subsequence with the required difference.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code aims to find the length of the longest subsequence in the given arr list, where the difference between consecutive elements is equal to dif. The approach used is dynamic programming.\n\n- Create a defaultdict lengths to store the lengths of subsequences. The defaultdict is initialized with a default value of 0.\n- Iterate over the elements of the arr list.\n- For each element num, calculate the length of the subsequence ending at num by adding 1 to the length of the subsequence ending at num - dif. Store this value in lengths[num].\n- After iterating over all elements, find the maximum value in the lengths dictionary, which represents the length of the longest subsequence.\n- Return the maximum length.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nUpvote appreciated , Thanks!\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def longestSubsequence(self, arr: List[int], dif: int) -> int:\n # Create a defaultdict to store the lengths of subsequences\n lengths = defaultdict(lambda: 0)\n \n # Iterate over the array elements\n for num in arr:\n # Calculate the length of the subsequence ending at the current element\n lengths[num] = lengths[num - dif] + 1\n\n # Return the maximum length of subsequences\n return max(lengths.values())\n\n``` | 4 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
[Python, Java] Elegant & Short | DP | HashMap | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n\n```python []\nclass Solution:\n def longestSubsequence(self, nums: List[int], difference: int) -> int:\n dp = defaultdict(int)\n\n for num in nums:\n dp[num] = dp[num - difference] + 1\n\n return max(dp.values())\n```\n\n```java []\nclass Solution {\n public int longestSubsequence(int[] numbers, int difference) {\n Map<Integer, Integer> dp = new HashMap<>();\n\n for (int num : numbers)\n dp.put(num, dp.getOrDefault(num - difference, 0) + 1);\n\n return dp.values().stream().max(Comparator.naturalOrder()).get();\n }\n}\n```\n | 3 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
[Python, Java] Elegant & Short | DP | HashMap | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n\n```python []\nclass Solution:\n def longestSubsequence(self, nums: List[int], difference: int) -> int:\n dp = defaultdict(int)\n\n for num in nums:\n dp[num] = dp[num - difference] + 1\n\n return max(dp.values())\n```\n\n```java []\nclass Solution {\n public int longestSubsequence(int[] numbers, int difference) {\n Map<Integer, Integer> dp = new HashMap<>();\n\n for (int num : numbers)\n dp.put(num, dp.getOrDefault(num - difference, 0) + 1);\n\n return dp.values().stream().max(Comparator.naturalOrder()).get();\n }\n}\n```\n | 3 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | longest-arithmetic-subsequence-of-given-difference | 1 | 1 | # Intuition\nUse Dynamic Programming to store the longest length of subsequence at each number.\n\n# Solution Video\nPlease subscribe to my channel from here. I have 222 LeetCode videos as of July 15th, 2023.\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/Yi2hGxQsL6Y\n\n# Please Upvote!!\n\n---\n\n# Approach\nThis is based on Python code. Here\'s a step-by-step algorithm for the provided code:\n\n1. Create an empty dictionary `dp` to store the length of the longest subsequence for each number encountered.\n2. Initialize `max_length` to 0, which will keep track of the maximum subsequence length seen so far.\n3. Iterate through each number `n` in the `arr` list:\n a. Check if `n - difference` exists as a key in the `dp` dictionary.\n b. If the key exists:\n - Set `dp[n]` to be equal to `dp[n - difference] + 1`, indicating that the subsequence length of `n` is one greater than the subsequence length of `n - difference`.\n c. If the key doesn\'t exist:\n - Set `dp[n]` to 1, indicating that the subsequence length of `n` is 1, as it is the first occurrence of `n` in the sequence.\n d. Update `max_length` by taking the maximum value between `max_length` and `dp[n]`.\n4. Return `max_length`, which represents the length of the longest arithmetic subsequence with the given difference.\n\n# Complexity\n- Time complexity: O(n)\nn is the length of the input list arr. This is because we iterate through the arr list once, performing a constant-time operation for each element.\n\n- Space complexity: O(n)\nn is the length of the input list arr. This is because we use a dictionary dp to store the longest subsequence length for each number encountered. In the worst case scenario, where all elements in arr are distinct, the dictionary will have a size of n.\n\n```python []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n dp = {}\n max_length = 0\n\n for n in arr:\n if n - difference in dp:\n dp[n] = dp[n - difference] + 1\n else:\n dp[n] = 1\n \n max_length = max(max_length, dp[n])\n \n return max_length\n```\n```javascript []\n/**\n * @param {number[]} arr\n * @param {number} difference\n * @return {number}\n */\nvar longestSubsequence = function(arr, difference) {\n let dp = {};\n let max_length = 0;\n\n for (let n of arr) {\n if (n - difference in dp) {\n dp[n] = dp[n - difference] + 1;\n } else {\n dp[n] = 1;\n }\n \n max_length = Math.max(max_length, dp[n]);\n }\n \n return max_length; \n};\n```\n```java []\nclass Solution {\n public int longestSubsequence(int[] arr, int difference) {\n Map<Integer, Integer> dp = new HashMap<>();\n int maxLength = 0;\n\n for (int n : arr) {\n if (dp.containsKey(n - difference)) {\n dp.put(n, dp.get(n - difference) + 1);\n } else {\n dp.put(n, 1);\n }\n\n maxLength = Math.max(maxLength, dp.get(n));\n }\n\n return maxLength; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int longestSubsequence(vector<int>& arr, int difference) {\n std::unordered_map<int, int> dp;\n int maxLength = 0;\n\n for (int n : arr) {\n if (dp.count(n - difference)) {\n dp[n] = dp[n - difference] + 1;\n } else {\n dp[n] = 1;\n }\n\n maxLength = std::max(maxLength, dp[n]);\n }\n\n return maxLength; \n }\n};\n```\n | 6 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | longest-arithmetic-subsequence-of-given-difference | 1 | 1 | # Intuition\nUse Dynamic Programming to store the longest length of subsequence at each number.\n\n# Solution Video\nPlease subscribe to my channel from here. I have 222 LeetCode videos as of July 15th, 2023.\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/Yi2hGxQsL6Y\n\n# Please Upvote!!\n\n---\n\n# Approach\nThis is based on Python code. Here\'s a step-by-step algorithm for the provided code:\n\n1. Create an empty dictionary `dp` to store the length of the longest subsequence for each number encountered.\n2. Initialize `max_length` to 0, which will keep track of the maximum subsequence length seen so far.\n3. Iterate through each number `n` in the `arr` list:\n a. Check if `n - difference` exists as a key in the `dp` dictionary.\n b. If the key exists:\n - Set `dp[n]` to be equal to `dp[n - difference] + 1`, indicating that the subsequence length of `n` is one greater than the subsequence length of `n - difference`.\n c. If the key doesn\'t exist:\n - Set `dp[n]` to 1, indicating that the subsequence length of `n` is 1, as it is the first occurrence of `n` in the sequence.\n d. Update `max_length` by taking the maximum value between `max_length` and `dp[n]`.\n4. Return `max_length`, which represents the length of the longest arithmetic subsequence with the given difference.\n\n# Complexity\n- Time complexity: O(n)\nn is the length of the input list arr. This is because we iterate through the arr list once, performing a constant-time operation for each element.\n\n- Space complexity: O(n)\nn is the length of the input list arr. This is because we use a dictionary dp to store the longest subsequence length for each number encountered. In the worst case scenario, where all elements in arr are distinct, the dictionary will have a size of n.\n\n```python []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n dp = {}\n max_length = 0\n\n for n in arr:\n if n - difference in dp:\n dp[n] = dp[n - difference] + 1\n else:\n dp[n] = 1\n \n max_length = max(max_length, dp[n])\n \n return max_length\n```\n```javascript []\n/**\n * @param {number[]} arr\n * @param {number} difference\n * @return {number}\n */\nvar longestSubsequence = function(arr, difference) {\n let dp = {};\n let max_length = 0;\n\n for (let n of arr) {\n if (n - difference in dp) {\n dp[n] = dp[n - difference] + 1;\n } else {\n dp[n] = 1;\n }\n \n max_length = Math.max(max_length, dp[n]);\n }\n \n return max_length; \n};\n```\n```java []\nclass Solution {\n public int longestSubsequence(int[] arr, int difference) {\n Map<Integer, Integer> dp = new HashMap<>();\n int maxLength = 0;\n\n for (int n : arr) {\n if (dp.containsKey(n - difference)) {\n dp.put(n, dp.get(n - difference) + 1);\n } else {\n dp.put(n, 1);\n }\n\n maxLength = Math.max(maxLength, dp.get(n));\n }\n\n return maxLength; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int longestSubsequence(vector<int>& arr, int difference) {\n std::unordered_map<int, int> dp;\n int maxLength = 0;\n\n for (int n : arr) {\n if (dp.count(n - difference)) {\n dp[n] = dp[n - difference] + 1;\n } else {\n dp[n] = 1;\n }\n\n maxLength = std::max(maxLength, dp[n]);\n }\n\n return maxLength; \n }\n};\n```\n | 6 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
✔️ Python || Short solution || Detailed explanation || DP | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\nLet\'s say the next element for the subsequence will be: `arr[i] + difference`.\nWhen we go through array we need to store this next elements, because if we will met them, than we can add them to subsequence. \n# Approach\n\nLet\'s create a hashtable (dict) with the next structure:\n - key \u2013 next value for a subsequence which we are looking for\n - value \u2013 current length of that subsequence\n \nGoing through the `arr` and check:\n1. If *we haven\u2019t* met the subsequence with the same **next** element as the next element for **current number**, than:\n\t- Either just set 1 to this value (if **current number** wasn\u2019t **next element** for some previous subsequence). \n\n\t- Or add 1 to the length of subsequence for witch one **our current number** was **next**.\n\n1. If we already *met* the subsequence with the same **next** element then we pick that one which will have maximal length (i.e. based on the same logic as in the first paragraph or keep the value witch we have before).\n\nAnd finally pick the subsequence of maximal length.\n\n***To make it simpler let\'s just look at the example \u21163:***\n\n`arr = [1,5,7,8,5,3,4,2,1], difference = -2`\n\nAt the begining our *dict*(`count`) to store `next_` element is empty.\n\nStep one(*case 1.1 from the explanation above*):\n\n next_ = arr[0] + difference = -1 --> count[next_] = 1 \n i.e. count == {-1: 1}\n\nStep two(*case 1.1*):\n\n next_ = arr[1] + difference = 3 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 1}\nStep three(*case 1.1*):\n\n next_ = arr[2] + difference = 5 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 1, 5: 1}\n\nStep four(*case 1.1*):\n\n next_ = arr[3] + difference = 6 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 1, 5: 1, 6: 1}\n\nStep five(*case 2*):\n\n next_ = arr[4] + difference = 3 --> count[next_] = count[arr[4]] + 1 = count[5] + 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1}\n\nStep six(*case 1.2*):\n\n next_ = arr[5] + difference = 1 --> count[next_] = count[arr[5]] + 1 = count[3] + 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1, 1: 3}\n\nStep seven(*case 1.1*):\n\n next_ = arr[6] + difference = 2 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1, 2: 1}\n\nStep eight(*case 1.2*):\n\n next_ = arr[7] + difference = 0 --> count[next_] = count[2] + 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1, 2: 1, 0: 2}\n\nStep nine(*case 2*):\n\n next_ = arr[8] + difference = -1 --> count[next_] = max(count[-1], count[1] + 1) = max(1, 3 + 1) \n i.e. count == {-1: 4, 3: 2, 5: 1, 6: 1, 2: 1}\n\n\n\n# Complexity\nN == len(arr)\n- Time complexity:\n O(N)\n\n- Space complexity:\n O(N)\n\n***Please upvote if you liked the solution :)***\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n count = {}\n for num in arr:\n next_ = num + difference\n if next_ not in count:\n count[next_] = count.get(num, 0) + 1\n else:\n count[next_] = max(count[next_], count.get(num, 0) + 1)\n return max(count.values())\n```\n\n | 2 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
✔️ Python || Short solution || Detailed explanation || DP | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\nLet\'s say the next element for the subsequence will be: `arr[i] + difference`.\nWhen we go through array we need to store this next elements, because if we will met them, than we can add them to subsequence. \n# Approach\n\nLet\'s create a hashtable (dict) with the next structure:\n - key \u2013 next value for a subsequence which we are looking for\n - value \u2013 current length of that subsequence\n \nGoing through the `arr` and check:\n1. If *we haven\u2019t* met the subsequence with the same **next** element as the next element for **current number**, than:\n\t- Either just set 1 to this value (if **current number** wasn\u2019t **next element** for some previous subsequence). \n\n\t- Or add 1 to the length of subsequence for witch one **our current number** was **next**.\n\n1. If we already *met* the subsequence with the same **next** element then we pick that one which will have maximal length (i.e. based on the same logic as in the first paragraph or keep the value witch we have before).\n\nAnd finally pick the subsequence of maximal length.\n\n***To make it simpler let\'s just look at the example \u21163:***\n\n`arr = [1,5,7,8,5,3,4,2,1], difference = -2`\n\nAt the begining our *dict*(`count`) to store `next_` element is empty.\n\nStep one(*case 1.1 from the explanation above*):\n\n next_ = arr[0] + difference = -1 --> count[next_] = 1 \n i.e. count == {-1: 1}\n\nStep two(*case 1.1*):\n\n next_ = arr[1] + difference = 3 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 1}\nStep three(*case 1.1*):\n\n next_ = arr[2] + difference = 5 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 1, 5: 1}\n\nStep four(*case 1.1*):\n\n next_ = arr[3] + difference = 6 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 1, 5: 1, 6: 1}\n\nStep five(*case 2*):\n\n next_ = arr[4] + difference = 3 --> count[next_] = count[arr[4]] + 1 = count[5] + 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1}\n\nStep six(*case 1.2*):\n\n next_ = arr[5] + difference = 1 --> count[next_] = count[arr[5]] + 1 = count[3] + 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1, 1: 3}\n\nStep seven(*case 1.1*):\n\n next_ = arr[6] + difference = 2 --> count[next_] = 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1, 2: 1}\n\nStep eight(*case 1.2*):\n\n next_ = arr[7] + difference = 0 --> count[next_] = count[2] + 1 \n i.e. count == {-1: 1, 3: 2, 5: 1, 6: 1, 2: 1, 0: 2}\n\nStep nine(*case 2*):\n\n next_ = arr[8] + difference = -1 --> count[next_] = max(count[-1], count[1] + 1) = max(1, 3 + 1) \n i.e. count == {-1: 4, 3: 2, 5: 1, 6: 1, 2: 1}\n\n\n\n# Complexity\nN == len(arr)\n- Time complexity:\n O(N)\n\n- Space complexity:\n O(N)\n\n***Please upvote if you liked the solution :)***\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n count = {}\n for num in arr:\n next_ = num + difference\n if next_ not in count:\n count[next_] = count.get(num, 0) + 1\n else:\n count[next_] = max(count[next_], count.get(num, 0) + 1)\n return max(count.values())\n```\n\n | 2 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
🔥Memoization(✅) + Bottom UP || 🔥[C++,JAVA,🐍] || ✅DP + Hashing⭐ | longest-arithmetic-subsequence-of-given-difference | 1 | 1 | ### Connect with me on LinkedIN : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n# Approach(For BottomUP)\n\n1. Initialize a variable `ans` to 0. This variable will store the length of the longest subsequence.\n2. Create an unordered map `mp`. This map will store the count of subsequences ending at each element of `arr`.\n3. Iterate over `arr` in reverse order, starting from the last element.\n4. For each element `arr[i]`, update the count of subsequences ending at `arr[i]` in `mp`. The count is obtained by adding 1 to the count of subsequences ending at `arr[i] + difference` (if it exists in `mp`).\n5. Update `ans` by taking the maximum between its current value and the count of subsequences ending at `arr[i]`. This ensures that `ans` always stores the length of the longest subsequence found so far.\n6. After the iteration is complete, `ans` will contain the length of the longest subsequence with the given difference.\n7. Return `ans`.\n\n## Overall, the code efficiently calculates the length of the longest subsequence with a given difference using dynamic programming and a map to store intermediate results.\n\n# Complexity\n```\n- Time complexity:\nO(n) for BottomUP\nO(nlogn) for TopDown/Memoization\n```\n```\n- Space complexity:\nO(n)\n```\n\n# Code\n## An Upvote will be encouraging as it motivates me to post such more solutions\uD83E\uDD17\u2B50\n\n## Bottom UP Approach:-\n```C++ []\nclass Solution {\npublic:\n int longestSubsequence(std::vector<int>& arr, int difference) {\n int n = arr.size(); // Get the size of the input vector \'arr\'\n int ans = 0; // Initialize the variable \'ans\' to store the length of the longest subsequence\n unordered_map<int, int> mp; // Create an unordered map \'mp\' to store the counts of subsequences\n \n for (int i = n - 1; i >= 0; i--) { // Iterate over the elements of \'arr\' in reverse order\n // Calculate the count of subsequences ending at \'arr[i]\' by adding 1 to the count of subsequences ending at \'arr[i] + difference\' (if it exists in \'mp\')\n mp[arr[i]] = mp[arr[i] + difference] + 1;\n ans = max(ans, mp[arr[i]]); // Update \'ans\' by taking the maximum between its current value and the count of subsequences ending at \'arr[i]\'\n }\n \n return ans; // Return the length of the longest subsequence\n }\n}; \n\n//OR\n\nclass Solution {\npublic:\n int longestSubsequence(vector<int>& arr, int difference) {\n int n = arr.size(), maxi = 0;\n unordered_map<int,int> mp;\n for(auto it : arr){\n int x = it - difference;\n mp[it] = mp[x] + 1;\n maxi = max(maxi,mp[it]);\n }\n return maxi;\n }\n};\n\n```\n```JAVA []\nclass Solution {\n public int longestSubsequence(int[] arr, int difference) {\n int n = arr.length; // Get the length of the input array \'arr\'\n int ans = 0; // Initialize the variable \'ans\' to store the length of the longest subsequence\n Map<Integer, Integer> mp = new HashMap<>(); // Create a HashMap \'mp\' to store the counts of subsequences\n \n for (int i = n - 1; i >= 0; i--) { // Iterate over the elements of \'arr\' in reverse order\n // Calculate the count of subsequences ending at \'arr[i]\' by adding 1 to the count of subsequences ending at \'arr[i] + difference\' (if it exists in \'mp\')\n mp.put(arr[i], mp.getOrDefault(arr[i] + difference, 0) + 1);\n ans = Math.max(ans, mp.get(arr[i])); // Update \'ans\' by taking the maximum between its current value and the count of subsequences ending at \'arr[i]\'\n }\n \n return ans; // Return the length of the longest subsequence\n }\n}\n\n```\n```python3 []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n n = len(arr) # Get the length of the input list \'arr\'\n ans = 0 # Initialize the variable \'ans\' to store the length of the longest subsequence\n mp = defaultdict(int) # Create a defaultdict \'mp\' to store the counts of subsequences\n \n for i in range(n - 1, -1, -1): # Iterate over the elements of \'arr\' in reverse order\n # Calculate the count of subsequences ending at \'arr[i]\' by adding 1 to the count of subsequences ending at \'arr[i] + difference\' (if it exists in \'mp\')\n mp[arr[i]] = mp[arr[i] + difference] + 1\n ans = max(ans, mp[arr[i]]) # Update \'ans\' by taking the maximum between its current value and the count of subsequences ending at \'arr[i]\'\n \n return ans # Return the length of the longest subsequence\n\n```\n## TopDown/Memoization Code in C++(Accepted\u2705) :-\n```\nclass Solution {\npublic:\n int dp[100001];\n unordered_map<int,vector<int>> mp;\n int helper(int ind, vector<int>& arr, int diff, int n){\n if(ind == n)\n return 0;\n if(dp[ind] != -1)\n return dp[ind];\n int maxi = 0; \n int curr_ele = arr[ind], req_ele = curr_ele + diff;\n if(mp.find(req_ele) != mp.end()){\n auto vec = mp[req_ele];\n int x = upper_bound(vec.begin(),vec.end(),ind) - vec.begin();\n if(x != vec.size())\n maxi = max(maxi,1 + helper(vec[x],arr,diff,n));\n }\n return dp[ind] = maxi;\n }\n int longestSubsequence(vector<int>& arr, int difference) {\n int n = arr.size(), ans = 0;\n for(int i=0;i<n;i++)\n mp[arr[i]].push_back(i);\n memset(dp,-1,sizeof(dp));\n for(int i=0;i<n;i++)\n ans = max(ans,helper(i,arr,difference,n));\n return ans + 1;\n }\n};\n```\n\n | 2 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
🔥Memoization(✅) + Bottom UP || 🔥[C++,JAVA,🐍] || ✅DP + Hashing⭐ | longest-arithmetic-subsequence-of-given-difference | 1 | 1 | ### Connect with me on LinkedIN : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n# Approach(For BottomUP)\n\n1. Initialize a variable `ans` to 0. This variable will store the length of the longest subsequence.\n2. Create an unordered map `mp`. This map will store the count of subsequences ending at each element of `arr`.\n3. Iterate over `arr` in reverse order, starting from the last element.\n4. For each element `arr[i]`, update the count of subsequences ending at `arr[i]` in `mp`. The count is obtained by adding 1 to the count of subsequences ending at `arr[i] + difference` (if it exists in `mp`).\n5. Update `ans` by taking the maximum between its current value and the count of subsequences ending at `arr[i]`. This ensures that `ans` always stores the length of the longest subsequence found so far.\n6. After the iteration is complete, `ans` will contain the length of the longest subsequence with the given difference.\n7. Return `ans`.\n\n## Overall, the code efficiently calculates the length of the longest subsequence with a given difference using dynamic programming and a map to store intermediate results.\n\n# Complexity\n```\n- Time complexity:\nO(n) for BottomUP\nO(nlogn) for TopDown/Memoization\n```\n```\n- Space complexity:\nO(n)\n```\n\n# Code\n## An Upvote will be encouraging as it motivates me to post such more solutions\uD83E\uDD17\u2B50\n\n## Bottom UP Approach:-\n```C++ []\nclass Solution {\npublic:\n int longestSubsequence(std::vector<int>& arr, int difference) {\n int n = arr.size(); // Get the size of the input vector \'arr\'\n int ans = 0; // Initialize the variable \'ans\' to store the length of the longest subsequence\n unordered_map<int, int> mp; // Create an unordered map \'mp\' to store the counts of subsequences\n \n for (int i = n - 1; i >= 0; i--) { // Iterate over the elements of \'arr\' in reverse order\n // Calculate the count of subsequences ending at \'arr[i]\' by adding 1 to the count of subsequences ending at \'arr[i] + difference\' (if it exists in \'mp\')\n mp[arr[i]] = mp[arr[i] + difference] + 1;\n ans = max(ans, mp[arr[i]]); // Update \'ans\' by taking the maximum between its current value and the count of subsequences ending at \'arr[i]\'\n }\n \n return ans; // Return the length of the longest subsequence\n }\n}; \n\n//OR\n\nclass Solution {\npublic:\n int longestSubsequence(vector<int>& arr, int difference) {\n int n = arr.size(), maxi = 0;\n unordered_map<int,int> mp;\n for(auto it : arr){\n int x = it - difference;\n mp[it] = mp[x] + 1;\n maxi = max(maxi,mp[it]);\n }\n return maxi;\n }\n};\n\n```\n```JAVA []\nclass Solution {\n public int longestSubsequence(int[] arr, int difference) {\n int n = arr.length; // Get the length of the input array \'arr\'\n int ans = 0; // Initialize the variable \'ans\' to store the length of the longest subsequence\n Map<Integer, Integer> mp = new HashMap<>(); // Create a HashMap \'mp\' to store the counts of subsequences\n \n for (int i = n - 1; i >= 0; i--) { // Iterate over the elements of \'arr\' in reverse order\n // Calculate the count of subsequences ending at \'arr[i]\' by adding 1 to the count of subsequences ending at \'arr[i] + difference\' (if it exists in \'mp\')\n mp.put(arr[i], mp.getOrDefault(arr[i] + difference, 0) + 1);\n ans = Math.max(ans, mp.get(arr[i])); // Update \'ans\' by taking the maximum between its current value and the count of subsequences ending at \'arr[i]\'\n }\n \n return ans; // Return the length of the longest subsequence\n }\n}\n\n```\n```python3 []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n n = len(arr) # Get the length of the input list \'arr\'\n ans = 0 # Initialize the variable \'ans\' to store the length of the longest subsequence\n mp = defaultdict(int) # Create a defaultdict \'mp\' to store the counts of subsequences\n \n for i in range(n - 1, -1, -1): # Iterate over the elements of \'arr\' in reverse order\n # Calculate the count of subsequences ending at \'arr[i]\' by adding 1 to the count of subsequences ending at \'arr[i] + difference\' (if it exists in \'mp\')\n mp[arr[i]] = mp[arr[i] + difference] + 1\n ans = max(ans, mp[arr[i]]) # Update \'ans\' by taking the maximum between its current value and the count of subsequences ending at \'arr[i]\'\n \n return ans # Return the length of the longest subsequence\n\n```\n## TopDown/Memoization Code in C++(Accepted\u2705) :-\n```\nclass Solution {\npublic:\n int dp[100001];\n unordered_map<int,vector<int>> mp;\n int helper(int ind, vector<int>& arr, int diff, int n){\n if(ind == n)\n return 0;\n if(dp[ind] != -1)\n return dp[ind];\n int maxi = 0; \n int curr_ele = arr[ind], req_ele = curr_ele + diff;\n if(mp.find(req_ele) != mp.end()){\n auto vec = mp[req_ele];\n int x = upper_bound(vec.begin(),vec.end(),ind) - vec.begin();\n if(x != vec.size())\n maxi = max(maxi,1 + helper(vec[x],arr,diff,n));\n }\n return dp[ind] = maxi;\n }\n int longestSubsequence(vector<int>& arr, int difference) {\n int n = arr.size(), ans = 0;\n for(int i=0;i<n;i++)\n mp[arr[i]].push_back(i);\n memset(dp,-1,sizeof(dp));\n for(int i=0;i<n;i++)\n ans = max(ans,helper(i,arr,difference,n));\n return ans + 1;\n }\n};\n```\n\n | 2 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Simple C++/Python with unordered_map/dict | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse hash table to record dp[x]=maximal length of the arithmetic progression ending at the number x.\nThe crucial recurrence is: dp[x]=1+dp[x-difference]\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a loop to iterate.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n\n```C++ []\n\nclass Solution {\npublic:\n unordered_map<int, int> dp;\n \n int longestSubsequence(vector<int>& arr, int difference) {\n int ans = 0;\n \n for (int x : arr) {\n if (dp.count(x - difference))\n dp[x] = dp[x - difference] + 1;\n else\n dp[x] = 1;\n \n ans = max(ans, dp[x]);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n ans=0\n dp={}\n for x in arr:\n if x-difference in dp:\n dp[x]=dp[x-difference]+1\n else:\n dp[x]=1\n ans=max(ans, dp[x])\n return ans\n```\n | 2 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Simple C++/Python with unordered_map/dict | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse hash table to record dp[x]=maximal length of the arithmetic progression ending at the number x.\nThe crucial recurrence is: dp[x]=1+dp[x-difference]\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a loop to iterate.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n\n```C++ []\n\nclass Solution {\npublic:\n unordered_map<int, int> dp;\n \n int longestSubsequence(vector<int>& arr, int difference) {\n int ans = 0;\n \n for (int x : arr) {\n if (dp.count(x - difference))\n dp[x] = dp[x - difference] + 1;\n else\n dp[x] = 1;\n \n ans = max(ans, dp[x]);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n ans=0\n dp={}\n for x in arr:\n if x-difference in dp:\n dp[x]=dp[x-difference]+1\n else:\n dp[x]=1\n ans=max(ans, dp[x])\n return ans\n```\n | 2 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Easy solution with time complexity O(n) | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Complexity\n\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n d = defaultdict(int)\n for n in arr:\n d[n] = d[n - difference] + 1\n\n return max(d.values())\n``` | 1 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Easy solution with time complexity O(n) | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Complexity\n\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n d = defaultdict(int)\n for n in arr:\n d[n] = d[n - difference] + 1\n\n return max(d.values())\n``` | 1 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Python3 👍||⚡98/93 faster beats,only 4 lines 🔥|| clean solution || | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n times = defaultdict(int)\n for num in arr:\n times[num] = times[num-difference]+1\n return max(times.values())\n``` | 1 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Python3 👍||⚡98/93 faster beats,only 4 lines 🔥|| clean solution || | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n times = defaultdict(int)\n for num in arr:\n times[num] = times[num-difference]+1\n return max(times.values())\n``` | 1 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Go/Python O(n) time | O(n) space | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc longestSubsequence(arr []int, difference int) int {\n dp := make(map[int]int)\n answer := 1\n for _,item := range(arr){\n dp[item] = dp[item-difference]+1\n answer = max(answer,dp[item])\n }\n return answer\n}\n\nfunc max(a,b int) int{\n if a > b{\n return a\n }\n return b\n}\n```\n```python []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n dp = defaultdict(int)\n answer = 1\n for item in arr:\n dp[item] = dp[item-difference]+1\n answer = max(answer,dp[item])\n return answer\n``` | 1 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Go/Python O(n) time | O(n) space | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc longestSubsequence(arr []int, difference int) int {\n dp := make(map[int]int)\n answer := 1\n for _,item := range(arr){\n dp[item] = dp[item-difference]+1\n answer = max(answer,dp[item])\n }\n return answer\n}\n\nfunc max(a,b int) int{\n if a > b{\n return a\n }\n return b\n}\n```\n```python []\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n dp = defaultdict(int)\n answer = 1\n for item in arr:\n dp[item] = dp[item-difference]+1\n answer = max(answer,dp[item])\n return answer\n``` | 1 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Dict.py | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], dif: int) -> int:\n m={}\n mx=0\n for i in range(len(arr)):\n val=arr[i]\n if val-dif in m:\n m[val]=m[val-dif]+1\n else:\n m[val]=1\n mx=max(mx,m[val])\n return mx\n``` | 1 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Dict.py | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], dif: int) -> int:\n m={}\n mx=0\n for i in range(len(arr)):\n val=arr[i]\n if val-dif in m:\n m[val]=m[val-dif]+1\n else:\n m[val]=1\n mx=max(mx,m[val])\n return mx\n``` | 1 | You are given an integer array `nums`. The _value_ of this array is defined as the sum of `|nums[i] - nums[i + 1]|` for all `0 <= i < nums.length - 1`.
You are allowed to select any subarray of the given array and reverse it. You can perform this operation **only once**.
Find maximum possible value of the final array.
**Example 1:**
**Input:** nums = \[2,3,1,5,4\]
**Output:** 10
**Explanation:** By reversing the subarray \[3,1,5\] the array becomes \[2,5,1,3,4\] whose value is 10.
**Example 2:**
**Input:** nums = \[2,4,9,24,2,1,10\]
**Output:** 68
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `-105 <= nums[i] <= 105` | Use dynamic programming. Let dp[i] be the maximum length of a subsequence of the given difference whose last element is i. dp[i] = 1 + dp[i-k] |
Fast DFS with back-tracking | path-with-maximum-gold | 0 | 1 | # Intuition\n- Given the requirements, it\'s a classical and straight forward back-tracking question.\n- Most of the solutions are not making a somewhat SAFE assumption given the current set of test cases that we\'re likely to start at the boundary and spiral down inwards. \n- I added that logic and voila it passed the test cases (in _pickStart)\n\n\n# Complexity\n- Time complexity: 4^\\*(N*M)\n- Space complexity: O(N*M)\n\n# Code\n```python3\nclass Solution:\n def getMaximumGold(self, grid: List[List[int]]) -> int:\n\n def helper(i, j, visited): \n # base cases\n if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == 0 or visited[i][j]:\n return 1e-9\n\n # Choices\n # Marking the cell as visited and mutating the grid\n \n visited[i][j] = 1\n gold_here = grid[i][j]\n grid[i][j] = 0\n\n u = helper(i + 1, j, visited)\n d = helper(i - 1, j, visited)\n l = helper(i, j + 1, visited)\n r = helper(i, j - 1, visited)\n\n # Unchoose and reset the grid\n visited[i][j] = 0\n grid[i][j] = gold_here\n\n return max(u, d, l, r) + gold_here\n\n if not grid: return 0\n elif not grid[0]:return 0\n\n maxsum = 0\n res = {}\n \n def pickStart(i: int, j: int):\n direction = 0\n for _i, _j in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):\n if 0 <= _i < len(grid) and 0 <= _j < len(grid[0]) and grid[_i][_j]:\n direction += 1\n return direction <= 2\n \n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] and pickStart(i, j):\n visited = [[0 for x in range(len(grid[0]))] for y in range(len(grid))]\n\n _sum = helper(i, j, visited)\n maxsum = max(maxsum, _sum)\n res[_sum] = (i, j)\n \n return int(maxsum)\n | 0 | In a gold mine `grid` of size `m x n`, each cell in this mine has an integer representing the amount of gold in that cell, `0` if it is empty.
Return the maximum amount of gold you can collect under the conditions:
* Every time you are located in a cell you will collect all the gold in that cell.
* From your position, you can walk one step to the left, right, up, or down.
* You can't visit the same cell more than once.
* Never visit a cell with `0` gold.
* You can start and stop collecting gold from **any** position in the grid that has some gold.
**Example 1:**
**Input:** grid = \[\[0,6,0\],\[5,8,7\],\[0,9,0\]\]
**Output:** 24
**Explanation:**
\[\[0,6,0\],
\[5,8,7\],
\[0,9,0\]\]
Path to get the maximum gold, 9 -> 8 -> 7.
**Example 2:**
**Input:** grid = \[\[1,0,7\],\[2,0,6\],\[3,4,5\],\[0,3,0\],\[9,0,20\]\]
**Output:** 28
**Explanation:**
\[\[1,0,7\],
\[2,0,6\],
\[3,4,5\],
\[0,3,0\],
\[9,0,20\]\]
Path to get the maximum gold, 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 15`
* `0 <= grid[i][j] <= 100`
* There are at most **25** cells containing gold. | Make a new array A of +1/-1s corresponding to if hours[i] is > 8 or not. The goal is to find the longest subarray with positive sum. Using prefix sums (PrefixSum[i+1] = A[0] + A[1] + ... + A[i]), you need to find for each j, the smallest i < j with PrefixSum[i] + 1 == PrefixSum[j]. |
Fast DFS with back-tracking | path-with-maximum-gold | 0 | 1 | # Intuition\n- Given the requirements, it\'s a classical and straight forward back-tracking question.\n- Most of the solutions are not making a somewhat SAFE assumption given the current set of test cases that we\'re likely to start at the boundary and spiral down inwards. \n- I added that logic and voila it passed the test cases (in _pickStart)\n\n\n# Complexity\n- Time complexity: 4^\\*(N*M)\n- Space complexity: O(N*M)\n\n# Code\n```python3\nclass Solution:\n def getMaximumGold(self, grid: List[List[int]]) -> int:\n\n def helper(i, j, visited): \n # base cases\n if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == 0 or visited[i][j]:\n return 1e-9\n\n # Choices\n # Marking the cell as visited and mutating the grid\n \n visited[i][j] = 1\n gold_here = grid[i][j]\n grid[i][j] = 0\n\n u = helper(i + 1, j, visited)\n d = helper(i - 1, j, visited)\n l = helper(i, j + 1, visited)\n r = helper(i, j - 1, visited)\n\n # Unchoose and reset the grid\n visited[i][j] = 0\n grid[i][j] = gold_here\n\n return max(u, d, l, r) + gold_here\n\n if not grid: return 0\n elif not grid[0]:return 0\n\n maxsum = 0\n res = {}\n \n def pickStart(i: int, j: int):\n direction = 0\n for _i, _j in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):\n if 0 <= _i < len(grid) and 0 <= _j < len(grid[0]) and grid[_i][_j]:\n direction += 1\n return direction <= 2\n \n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] and pickStart(i, j):\n visited = [[0 for x in range(len(grid[0]))] for y in range(len(grid))]\n\n _sum = helper(i, j, visited)\n maxsum = max(maxsum, _sum)\n res[_sum] = (i, j)\n \n return int(maxsum)\n | 0 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
[Python3] DFS | path-with-maximum-gold | 0 | 1 | ```\nclass Solution:\n def getMaximumGold(self, grid: List[List[int]]) -> int:\n def dfs(i, j, v):\n seen.add((i, j))\n dp[i][j] = max(dp[i][j], v)\n for x, y in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):\n if 0 <= x < m and 0 <= y < n and grid[x][y] and (x, y) not in seen:\n dfs(x, y, v + grid[x][y])\n seen.discard((i, j))\n m, n = len(grid), len(grid[0])\n dp = [[0] * n for _ in range(m)]\n for i in range(m):\n for j in range(n):\n if grid[i][j]:\n seen = set()\n dfs(i, j, grid[i][j])\n return max(c for row in dp for c in row)\n``` | 27 | In a gold mine `grid` of size `m x n`, each cell in this mine has an integer representing the amount of gold in that cell, `0` if it is empty.
Return the maximum amount of gold you can collect under the conditions:
* Every time you are located in a cell you will collect all the gold in that cell.
* From your position, you can walk one step to the left, right, up, or down.
* You can't visit the same cell more than once.
* Never visit a cell with `0` gold.
* You can start and stop collecting gold from **any** position in the grid that has some gold.
**Example 1:**
**Input:** grid = \[\[0,6,0\],\[5,8,7\],\[0,9,0\]\]
**Output:** 24
**Explanation:**
\[\[0,6,0\],
\[5,8,7\],
\[0,9,0\]\]
Path to get the maximum gold, 9 -> 8 -> 7.
**Example 2:**
**Input:** grid = \[\[1,0,7\],\[2,0,6\],\[3,4,5\],\[0,3,0\],\[9,0,20\]\]
**Output:** 28
**Explanation:**
\[\[1,0,7\],
\[2,0,6\],
\[3,4,5\],
\[0,3,0\],
\[9,0,20\]\]
Path to get the maximum gold, 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 15`
* `0 <= grid[i][j] <= 100`
* There are at most **25** cells containing gold. | Make a new array A of +1/-1s corresponding to if hours[i] is > 8 or not. The goal is to find the longest subarray with positive sum. Using prefix sums (PrefixSum[i+1] = A[0] + A[1] + ... + A[i]), you need to find for each j, the smallest i < j with PrefixSum[i] + 1 == PrefixSum[j]. |
[Python3] DFS | path-with-maximum-gold | 0 | 1 | ```\nclass Solution:\n def getMaximumGold(self, grid: List[List[int]]) -> int:\n def dfs(i, j, v):\n seen.add((i, j))\n dp[i][j] = max(dp[i][j], v)\n for x, y in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):\n if 0 <= x < m and 0 <= y < n and grid[x][y] and (x, y) not in seen:\n dfs(x, y, v + grid[x][y])\n seen.discard((i, j))\n m, n = len(grid), len(grid[0])\n dp = [[0] * n for _ in range(m)]\n for i in range(m):\n for j in range(n):\n if grid[i][j]:\n seen = set()\n dfs(i, j, grid[i][j])\n return max(c for row in dp for c in row)\n``` | 27 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
✅⬆️⬆️🔥🔥100% | 0MS | FASTER | CONCISE | DFS | PROOF ⬆️⬆️⬆️⬆️🔥🙌 | path-with-maximum-gold | 1 | 1 | # UPVOTE PLS\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# 5*5=25 possiblities use as accumulator & update flag\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:O(N2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic int getMaximumGold(int[][] G) {\n int max=0,m=G.length,n=G[0].length;\n for(int r=0;r<m;r++)\n for(int c=0;c<n;c++)\n if(G[r][c]!=0)\n max=Math.max(max,dfs(G,m,n,r,c,0));\n return max;\n }\n int D[]={0,1,0,-1,0};\n boolean flag=false;\n public int dfs(int[][] G,int m,int n,int r,int c,int used){\n if(used==25) flag=true; //max possibility\n if(r<0 || r==m || c<0 || c==n || G[r][c]==0)return 0;\n int orignal=G[r][c],max=0;\n G[r][c]=0;//mark as visted \n for(int i=0;i<4;i++)\n if(!flag)\n max=Math.max(max,dfs(G,m,n,r+D[i],c+D[i+1],used+1));\n G[r][c]=orignal;//backtrack\n return max+orignal;\n}\n\n``` | 3 | In a gold mine `grid` of size `m x n`, each cell in this mine has an integer representing the amount of gold in that cell, `0` if it is empty.
Return the maximum amount of gold you can collect under the conditions:
* Every time you are located in a cell you will collect all the gold in that cell.
* From your position, you can walk one step to the left, right, up, or down.
* You can't visit the same cell more than once.
* Never visit a cell with `0` gold.
* You can start and stop collecting gold from **any** position in the grid that has some gold.
**Example 1:**
**Input:** grid = \[\[0,6,0\],\[5,8,7\],\[0,9,0\]\]
**Output:** 24
**Explanation:**
\[\[0,6,0\],
\[5,8,7\],
\[0,9,0\]\]
Path to get the maximum gold, 9 -> 8 -> 7.
**Example 2:**
**Input:** grid = \[\[1,0,7\],\[2,0,6\],\[3,4,5\],\[0,3,0\],\[9,0,20\]\]
**Output:** 28
**Explanation:**
\[\[1,0,7\],
\[2,0,6\],
\[3,4,5\],
\[0,3,0\],
\[9,0,20\]\]
Path to get the maximum gold, 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 15`
* `0 <= grid[i][j] <= 100`
* There are at most **25** cells containing gold. | Make a new array A of +1/-1s corresponding to if hours[i] is > 8 or not. The goal is to find the longest subarray with positive sum. Using prefix sums (PrefixSum[i+1] = A[0] + A[1] + ... + A[i]), you need to find for each j, the smallest i < j with PrefixSum[i] + 1 == PrefixSum[j]. |
✅⬆️⬆️🔥🔥100% | 0MS | FASTER | CONCISE | DFS | PROOF ⬆️⬆️⬆️⬆️🔥🙌 | path-with-maximum-gold | 1 | 1 | # UPVOTE PLS\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# 5*5=25 possiblities use as accumulator & update flag\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:O(N2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic int getMaximumGold(int[][] G) {\n int max=0,m=G.length,n=G[0].length;\n for(int r=0;r<m;r++)\n for(int c=0;c<n;c++)\n if(G[r][c]!=0)\n max=Math.max(max,dfs(G,m,n,r,c,0));\n return max;\n }\n int D[]={0,1,0,-1,0};\n boolean flag=false;\n public int dfs(int[][] G,int m,int n,int r,int c,int used){\n if(used==25) flag=true; //max possibility\n if(r<0 || r==m || c<0 || c==n || G[r][c]==0)return 0;\n int orignal=G[r][c],max=0;\n G[r][c]=0;//mark as visted \n for(int i=0;i<4;i++)\n if(!flag)\n max=Math.max(max,dfs(G,m,n,r+D[i],c+D[i+1],used+1));\n G[r][c]=orignal;//backtrack\n return max+orignal;\n}\n\n``` | 3 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
Python3 | Backtracking | path-with-maximum-gold | 0 | 1 | Not a very very fast solution (the runtime is about 5xxx ms) but it may help you understand a pattern easily. \n\n```\nclass Solution:\n def getMaximumGold(self, grid: List[List[int]]) -> int: \n m, n = len(grid), len(grid[0])\n \n def helper(i, j, visited):\n if i < 0 or i >= m or j < 0 or j >= n or grid[i][j] == 0 or (i,j) in visited:\n return 0\n visited.add((i,j))\n d = helper(i+1, j, visited)\n u = helper(i-1, j, visited)\n r = helper(i, j+1, visited)\n l = helper(i, j-1, visited) \n visited.discard((i,j))\n return grid[i][j] + max(d, u, r, l)\n \n max_gold = 0\n for i in range(m):\n for j in range(n):\n if grid[i][j]:\n max_gold = max(max_gold, helper(i, j, set()))\n \n return max_gold\n```\n\n | 1 | In a gold mine `grid` of size `m x n`, each cell in this mine has an integer representing the amount of gold in that cell, `0` if it is empty.
Return the maximum amount of gold you can collect under the conditions:
* Every time you are located in a cell you will collect all the gold in that cell.
* From your position, you can walk one step to the left, right, up, or down.
* You can't visit the same cell more than once.
* Never visit a cell with `0` gold.
* You can start and stop collecting gold from **any** position in the grid that has some gold.
**Example 1:**
**Input:** grid = \[\[0,6,0\],\[5,8,7\],\[0,9,0\]\]
**Output:** 24
**Explanation:**
\[\[0,6,0\],
\[5,8,7\],
\[0,9,0\]\]
Path to get the maximum gold, 9 -> 8 -> 7.
**Example 2:**
**Input:** grid = \[\[1,0,7\],\[2,0,6\],\[3,4,5\],\[0,3,0\],\[9,0,20\]\]
**Output:** 28
**Explanation:**
\[\[1,0,7\],
\[2,0,6\],
\[3,4,5\],
\[0,3,0\],
\[9,0,20\]\]
Path to get the maximum gold, 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 15`
* `0 <= grid[i][j] <= 100`
* There are at most **25** cells containing gold. | Make a new array A of +1/-1s corresponding to if hours[i] is > 8 or not. The goal is to find the longest subarray with positive sum. Using prefix sums (PrefixSum[i+1] = A[0] + A[1] + ... + A[i]), you need to find for each j, the smallest i < j with PrefixSum[i] + 1 == PrefixSum[j]. |
Python3 | Backtracking | path-with-maximum-gold | 0 | 1 | Not a very very fast solution (the runtime is about 5xxx ms) but it may help you understand a pattern easily. \n\n```\nclass Solution:\n def getMaximumGold(self, grid: List[List[int]]) -> int: \n m, n = len(grid), len(grid[0])\n \n def helper(i, j, visited):\n if i < 0 or i >= m or j < 0 or j >= n or grid[i][j] == 0 or (i,j) in visited:\n return 0\n visited.add((i,j))\n d = helper(i+1, j, visited)\n u = helper(i-1, j, visited)\n r = helper(i, j+1, visited)\n l = helper(i, j-1, visited) \n visited.discard((i,j))\n return grid[i][j] + max(d, u, r, l)\n \n max_gold = 0\n for i in range(m):\n for j in range(n):\n if grid[i][j]:\n max_gold = max(max_gold, helper(i, j, set()))\n \n return max_gold\n```\n\n | 1 | Given an array of integers `arr`, replace each element with its rank.
The rank represents how large the element is. The rank has the following rules:
* Rank is an integer starting from 1.
* The larger the element, the larger the rank. If two elements are equal, their rank must be the same.
* Rank should be as small as possible.
**Example 1:**
**Input:** arr = \[40,10,20,30\]
**Output:** \[4,1,2,3\]
**Explanation**: 40 is the largest element. 10 is the smallest. 20 is the second smallest. 30 is the third smallest.
**Example 2:**
**Input:** arr = \[100,100,100\]
**Output:** \[1,1,1\]
**Explanation**: Same elements share the same rank.
**Example 3:**
**Input:** arr = \[37,12,28,9,100,56,80,5,12\]
**Output:** \[5,3,4,2,8,6,7,1,3\]
**Constraints:**
* `0 <= arr.length <= 105`
* `-109 <= arr[i] <= 109`
\- Every time you are in a cell you will collect all the gold in that cell. - From your position, you can walk one step to the left, right, up, or down. - You can't visit the same cell more than once. - Never visit a cell with 0 gold. - You can start and stop collecting gold from any position in the grid that has some gold. | Use recursion to try all such paths and find the one with the maximum value. |
✅ Beats 97.08% 🔥 || 2 Approaches of DP || | count-vowels-permutation | 1 | 1 | # Approach 1: Tabulation with O(n) Space\n\n\n# Intuition :\n**If we know the number of strings of length n - 1, for each of the vowels ending in each of the vowels, then we can know the number of strings of length n. For example, if we know the number of strings ending in a, e, and i of length n - 1, then we know the number of strings ending in a, e, i, o, u of length n. The answer will be the sum of these strings. We can use dynamic programming to store the number of strings of length n ending in each vowel.**\n\n# Algorithm :\n1. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. We can compute dp[i][j] from dp[i - 1][*] in O(1) time.\n2. The answer will be the sum of dp[n - 1][*].\n3. We can improve the space complexity to O(1) by using only 5 variables to store the current row of dp.\n4. We can improve the time complexity to O(n) by using matrix multiplication to compute dp[i] from dp[i - 1].\n\n# Complexity Analysis :\n- Time Complexity: ***O(n)***, where n is the input number. We can compute dp[i] from dp[i - 1] in O(1) time.\n- Space Complexity: ***O(n)***.\n\n# Code \n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 10 ** 9 + 7\n dp = [[0] * 5 for _ in range(n)]\n for i in range(5):\n dp[0][i] = 1\n for i in range(1, n):\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD\n dp[i][3] = dp[i - 1][2]\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD\n return sum(dp[-1]) % MOD\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1e9 + 7;\n vector<vector<long long>> dp(n, vector<long long>(5, 0));\n \n for (int i = 0; i < 5; ++i) {\n dp[0][i] = 1;\n }\n \n for (int i = 1; i < n; ++i) {\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD;\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD;\n dp[i][3] = dp[i - 1][2];\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD;\n }\n \n long long total = 0;\n for (int i = 0; i < 5; ++i) {\n total = (total + dp[n - 1][i]) % MOD;\n }\n \n return total;\n }\n};\n```\n``` Java []\nclass Solution {\n public int countVowelPermutation(int n) {\n final int MOD = (int) 1e9 + 7;\n long[][] dp = new long[n][5];\n \n for (int i = 0; i < 5; ++i) {\n dp[0][i] = 1;\n }\n \n for (int i = 1; i < n; ++i) {\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD;\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD;\n dp[i][3] = dp[i - 1][2];\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD;\n }\n \n long total = 0;\n for (int i = 0; i < 5; ++i) {\n total = (total + dp[n - 1][i]) % MOD;\n }\n \n return (int) total;\n }\n}\n```\n\n#### \u2705 Both the time and space complexity of the above approach can be improved. We can use only 5 variables to store the current row of dp. We can also use matrix multiplication to compute dp[i] from dp[i - 1]. \n\n# Approach 2: Tabulation with O(1) Space\n\n\n# Difference between Approach 1 and Approach 2 :\n- In Approach 1, we use dp[i][j] to denote the number of strings of length i that ends with the j-th vowel. We can compute dp[i][j] from dp[i - 1][*] in O(1) time.\n- In Approach 2, we use dp[j] to denote the number of strings of length i that ends with the j-th vowel. We can compute dp[j] from dp[*] in O(1) time.\n\n# Algorithm :\n1. Let dp[j] be the number of strings of length i that ends with the j-th vowel. We can compute dp[j] from dp[*] in O(1) time.\n2. The answer will be the sum of dp[*].\n3. We can improve the space complexity to O(1) by using only 5 variables to store the current row of dp.\n4. We can improve the time complexity to O(n) by using matrix multiplication to compute dp[i] from dp[i - 1].\n\n# Complexity Analysis :\n- Time Complexity: ***O(n)***, where n is the input number. We can compute dp[i] from dp[i - 1] in O(1) time.\n- Space Complexity: ***O(n)***.\n# Code\n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 10 ** 9 + 7\n a_count = e_count = i_count = o_count = u_count = 1\n for _ in range(1, n):\n a_count, e_count, i_count, o_count, u_count = \\\n (e_count + i_count + u_count) % MOD, \\\n (a_count + i_count) % MOD, \\\n (e_count + o_count) % MOD, \\\n i_count, \\\n (i_count + o_count) % MOD\n return (a_count + e_count + i_count + o_count + u_count) % MOD\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1e9 + 7;\n long long a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (int _ = 1; _ < n; ++_) {\n long long new_a = (e_count + i_count + u_count) % MOD;\n long long new_e = (a_count + i_count) % MOD;\n long long new_i = (e_count + o_count) % MOD;\n long long new_o = i_count;\n long long new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n long long total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return static_cast<int>(total);\n }\n};\n```\n``` Java []\nclass Solution {\n public int countVowelPermutation(int n) {\n final int MOD = (int) 1e9 + 7;\n long a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (int i = 1; i < n; ++i) {\n long new_a = (e_count + i_count + u_count) % MOD;\n long new_e = (a_count + i_count) % MOD;\n long new_i = (e_count + o_count) % MOD;\n long new_o = i_count;\n long new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n long total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return (int) total;\n }\n}\n```\n``` JavaScipt []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countVowelPermutation = function(n) {\n const MOD = 1e9 + 7;\n let a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (let i = 1; i < n; ++i) {\n const new_a = (e_count + i_count + u_count) % MOD;\n const new_e = (a_count + i_count) % MOD;\n const new_i = (e_count + o_count) % MOD;\n const new_o = i_count;\n const new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n const total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return total;\n};\n```\n``` TypeScript []\nfunction countVowelPermutation(n: number): number {\nconst MOD = 1e9 + 7;\n let a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (let i = 1; i < n; ++i) {\n const new_a = (e_count + i_count + u_count) % MOD;\n const new_e = (a_count + i_count) % MOD;\n const new_i = (e_count + o_count) % MOD;\n const new_o = i_count;\n const new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n const total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return total;\n};\n```\n``` C# []\npublic class Solution {\n public int CountVowelPermutation(int n) {\n const int MOD = 1000000007;\n long a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (int i = 1; i < n; ++i) {\n long new_a = (e_count + i_count + u_count) % MOD;\n long new_e = (a_count + i_count) % MOD;\n long new_i = (e_count + o_count) % MOD;\n long new_o = i_count;\n long new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n long total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return (int)total;\n }\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @return Integer\n */\n function countVowelPermutation($n) {\n $MOD = 1000000007;\n $a_count = $e_count = $i_count = $o_count = $u_count = 1;\n \n for ($i = 1; $i < $n; ++$i) {\n $new_a = ($e_count + $i_count + $u_count) % $MOD;\n $new_e = ($a_count + $i_count) % $MOD;\n $new_i = ($e_count + $o_count) % $MOD;\n $new_o = $i_count;\n $new_u = ($i_count + $o_count) % $MOD;\n \n $a_count = $new_a;\n $e_count = $new_e;\n $i_count = $new_i;\n $o_count = $new_o;\n $u_count = $new_u;\n }\n \n $total = ($a_count + $e_count + $i_count + $o_count + $u_count) % $MOD;\n \n return $total;\n }\n}\n```\n``` Kotlin []\nclass Solution {\n fun countVowelPermutation(n: Int): Int {\n val MOD = 1_000_000_007\n var aCount = 1L\n var eCount = 1L\n var iCount = 1L\n var oCount = 1L\n var uCount = 1L\n\n for (i in 1 until n) {\n val newA = (eCount + iCount + uCount) % MOD\n val newE = (aCount + iCount) % MOD\n val newI = (eCount + oCount) % MOD\n val newO = iCount\n val newU = (iCount + oCount) % MOD\n\n aCount = newA\n eCount = newE\n iCount = newI\n oCount = newO\n uCount = newU\n }\n\n return ((aCount + eCount + iCount + oCount + uCount) % MOD).toInt()\n }\n}\n```\n\n# Please UpVote \u2B06\uFE0F if this healps you\n\n\n | 6 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
✅ Beats 97.08% 🔥 || 2 Approaches of DP || | count-vowels-permutation | 1 | 1 | # Approach 1: Tabulation with O(n) Space\n\n\n# Intuition :\n**If we know the number of strings of length n - 1, for each of the vowels ending in each of the vowels, then we can know the number of strings of length n. For example, if we know the number of strings ending in a, e, and i of length n - 1, then we know the number of strings ending in a, e, i, o, u of length n. The answer will be the sum of these strings. We can use dynamic programming to store the number of strings of length n ending in each vowel.**\n\n# Algorithm :\n1. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. We can compute dp[i][j] from dp[i - 1][*] in O(1) time.\n2. The answer will be the sum of dp[n - 1][*].\n3. We can improve the space complexity to O(1) by using only 5 variables to store the current row of dp.\n4. We can improve the time complexity to O(n) by using matrix multiplication to compute dp[i] from dp[i - 1].\n\n# Complexity Analysis :\n- Time Complexity: ***O(n)***, where n is the input number. We can compute dp[i] from dp[i - 1] in O(1) time.\n- Space Complexity: ***O(n)***.\n\n# Code \n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 10 ** 9 + 7\n dp = [[0] * 5 for _ in range(n)]\n for i in range(5):\n dp[0][i] = 1\n for i in range(1, n):\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD\n dp[i][3] = dp[i - 1][2]\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD\n return sum(dp[-1]) % MOD\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1e9 + 7;\n vector<vector<long long>> dp(n, vector<long long>(5, 0));\n \n for (int i = 0; i < 5; ++i) {\n dp[0][i] = 1;\n }\n \n for (int i = 1; i < n; ++i) {\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD;\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD;\n dp[i][3] = dp[i - 1][2];\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD;\n }\n \n long long total = 0;\n for (int i = 0; i < 5; ++i) {\n total = (total + dp[n - 1][i]) % MOD;\n }\n \n return total;\n }\n};\n```\n``` Java []\nclass Solution {\n public int countVowelPermutation(int n) {\n final int MOD = (int) 1e9 + 7;\n long[][] dp = new long[n][5];\n \n for (int i = 0; i < 5; ++i) {\n dp[0][i] = 1;\n }\n \n for (int i = 1; i < n; ++i) {\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD;\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD;\n dp[i][3] = dp[i - 1][2];\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD;\n }\n \n long total = 0;\n for (int i = 0; i < 5; ++i) {\n total = (total + dp[n - 1][i]) % MOD;\n }\n \n return (int) total;\n }\n}\n```\n\n#### \u2705 Both the time and space complexity of the above approach can be improved. We can use only 5 variables to store the current row of dp. We can also use matrix multiplication to compute dp[i] from dp[i - 1]. \n\n# Approach 2: Tabulation with O(1) Space\n\n\n# Difference between Approach 1 and Approach 2 :\n- In Approach 1, we use dp[i][j] to denote the number of strings of length i that ends with the j-th vowel. We can compute dp[i][j] from dp[i - 1][*] in O(1) time.\n- In Approach 2, we use dp[j] to denote the number of strings of length i that ends with the j-th vowel. We can compute dp[j] from dp[*] in O(1) time.\n\n# Algorithm :\n1. Let dp[j] be the number of strings of length i that ends with the j-th vowel. We can compute dp[j] from dp[*] in O(1) time.\n2. The answer will be the sum of dp[*].\n3. We can improve the space complexity to O(1) by using only 5 variables to store the current row of dp.\n4. We can improve the time complexity to O(n) by using matrix multiplication to compute dp[i] from dp[i - 1].\n\n# Complexity Analysis :\n- Time Complexity: ***O(n)***, where n is the input number. We can compute dp[i] from dp[i - 1] in O(1) time.\n- Space Complexity: ***O(n)***.\n# Code\n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 10 ** 9 + 7\n a_count = e_count = i_count = o_count = u_count = 1\n for _ in range(1, n):\n a_count, e_count, i_count, o_count, u_count = \\\n (e_count + i_count + u_count) % MOD, \\\n (a_count + i_count) % MOD, \\\n (e_count + o_count) % MOD, \\\n i_count, \\\n (i_count + o_count) % MOD\n return (a_count + e_count + i_count + o_count + u_count) % MOD\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1e9 + 7;\n long long a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (int _ = 1; _ < n; ++_) {\n long long new_a = (e_count + i_count + u_count) % MOD;\n long long new_e = (a_count + i_count) % MOD;\n long long new_i = (e_count + o_count) % MOD;\n long long new_o = i_count;\n long long new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n long long total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return static_cast<int>(total);\n }\n};\n```\n``` Java []\nclass Solution {\n public int countVowelPermutation(int n) {\n final int MOD = (int) 1e9 + 7;\n long a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (int i = 1; i < n; ++i) {\n long new_a = (e_count + i_count + u_count) % MOD;\n long new_e = (a_count + i_count) % MOD;\n long new_i = (e_count + o_count) % MOD;\n long new_o = i_count;\n long new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n long total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return (int) total;\n }\n}\n```\n``` JavaScipt []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countVowelPermutation = function(n) {\n const MOD = 1e9 + 7;\n let a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (let i = 1; i < n; ++i) {\n const new_a = (e_count + i_count + u_count) % MOD;\n const new_e = (a_count + i_count) % MOD;\n const new_i = (e_count + o_count) % MOD;\n const new_o = i_count;\n const new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n const total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return total;\n};\n```\n``` TypeScript []\nfunction countVowelPermutation(n: number): number {\nconst MOD = 1e9 + 7;\n let a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (let i = 1; i < n; ++i) {\n const new_a = (e_count + i_count + u_count) % MOD;\n const new_e = (a_count + i_count) % MOD;\n const new_i = (e_count + o_count) % MOD;\n const new_o = i_count;\n const new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n const total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return total;\n};\n```\n``` C# []\npublic class Solution {\n public int CountVowelPermutation(int n) {\n const int MOD = 1000000007;\n long a_count = 1, e_count = 1, i_count = 1, o_count = 1, u_count = 1;\n \n for (int i = 1; i < n; ++i) {\n long new_a = (e_count + i_count + u_count) % MOD;\n long new_e = (a_count + i_count) % MOD;\n long new_i = (e_count + o_count) % MOD;\n long new_o = i_count;\n long new_u = (i_count + o_count) % MOD;\n \n a_count = new_a;\n e_count = new_e;\n i_count = new_i;\n o_count = new_o;\n u_count = new_u;\n }\n \n long total = (a_count + e_count + i_count + o_count + u_count) % MOD;\n \n return (int)total;\n }\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @return Integer\n */\n function countVowelPermutation($n) {\n $MOD = 1000000007;\n $a_count = $e_count = $i_count = $o_count = $u_count = 1;\n \n for ($i = 1; $i < $n; ++$i) {\n $new_a = ($e_count + $i_count + $u_count) % $MOD;\n $new_e = ($a_count + $i_count) % $MOD;\n $new_i = ($e_count + $o_count) % $MOD;\n $new_o = $i_count;\n $new_u = ($i_count + $o_count) % $MOD;\n \n $a_count = $new_a;\n $e_count = $new_e;\n $i_count = $new_i;\n $o_count = $new_o;\n $u_count = $new_u;\n }\n \n $total = ($a_count + $e_count + $i_count + $o_count + $u_count) % $MOD;\n \n return $total;\n }\n}\n```\n``` Kotlin []\nclass Solution {\n fun countVowelPermutation(n: Int): Int {\n val MOD = 1_000_000_007\n var aCount = 1L\n var eCount = 1L\n var iCount = 1L\n var oCount = 1L\n var uCount = 1L\n\n for (i in 1 until n) {\n val newA = (eCount + iCount + uCount) % MOD\n val newE = (aCount + iCount) % MOD\n val newI = (eCount + oCount) % MOD\n val newO = iCount\n val newU = (iCount + oCount) % MOD\n\n aCount = newA\n eCount = newE\n iCount = newI\n oCount = newO\n uCount = newU\n }\n\n return ((aCount + eCount + iCount + oCount + uCount) % MOD).toInt()\n }\n}\n```\n\n# Please UpVote \u2B06\uFE0F if this healps you\n\n\n | 6 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | count-vowels-permutation | 1 | 1 | # Intuition\nJust follow the rules lol\n\n---\n\n# Solution Video\n\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,860\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nThis question is a very simple. We just follow the rules in the description.\n\n---\n\n\u25A0 Rules\n\n\u2460 Each vowel `\'a\'` may only be followed by an `\'e\'`.\n\u2461 Each vowel `\'e\'` may only be followed by an `\'a\'` or an `\'i\'`.\n\u2462 Each vowel `\'i\'` may not be followed by another `\'i\'`.\n\u2463 Each vowel `\'o\'` may only be followed by an `\'i\'` or a `\'u\'`.\n\u2464 Each vowel `\'u\'` may only be followed by an `\'a\'`.\n\n---\n\nConvert the rules to a diagram below. Regarding \u2462 Each vowel `\'i\'` may not be followed by another `\'i\'`, in other word following character may be `\'a\'`,`\'e\'`,`\'o\'`,`\'u\'`.\n\n\n\n- How do you count strings with length of `n`? \n\nNow we have organized the information. All we have to do is to count all indegrees(arrows pointing toward each node) for each character.\n\nLet\'s see an example and think about `n = 3`.\n\nIn that case, how many indgrees do you have about `\'a\'`? It\'s `3`(`\'e\'`,`\'i\'`,`\'u\'`).\n\nWe can create characters `\'ea\'`,`\'ia\'`,`\'ua\'`. If `n = 2`, we have `3` strings with end of `\'a\'`.\n\nBut this example is `n = 3`, let\'s move to the next characters from `\'a\'`. We have a rule.\n\n---\n\n\u2460 Each vowel `\'a\'` may only be followed by an `\'e\'`.\n\n---\n\nAt end of `\'a\'`, we have `3` strings, when we add `\'e\'` to the characters we can create `\'eae\'`,`\'iae\'`,`\'uae\'`. At end of `\'e\'`, we can create `3` characters from `\'a\'`. \n\nPlus\n\n`\'e\'` has another indgree from `\'i\'` and the same caculation happens at each character at the same time, so we must have total number of strings ending at `\'i\'`.\n\nIn summary, at end of `\'e\'`, total number of strings we can create is `3`(from `\'a\'`) + total numbers from `\'i\'`. That\'s the total number of strings which is length of `3` ending at `\'e\'`.\n\nWe calculate total numbers for each vowel. Let me skip other parts.\n\nAt last, just add total numbers from `5` vowels and return the answer.\n\nEasy \uD83D\uDE06\nLet\'s see a real algorithm!\n\n\n---\n\n\n\n**Algorithm Overview:**\n\nThe code calculates the count of valid permutations of vowels (\'a\', \'e\', \'i\', \'o\', \'u\') of length `n` according to specific rules, while keeping track of counts for each vowel. The code uses dynamic programming to update these counts iteratively.\n\n**Detailed Explanation:**\n\n1. Check the base case: If `n` is equal to 1, return 5. This is because for `n = 1`, there are only 5 single-character permutations (\'a\', \'e\', \'i\', \'o\', \'u\'), and these are the initial values for the counts of each vowel.\n\n2. Initialize variables: Create variables `a`, `e`, `i`, `o`, and `u` and set their initial values to 1. These variables represent the counts of permutations ending with each vowel (\'a\', \'e\', \'i\', \'o\', \'u\'). Initialize the `mod` variable to 10^9 + 7, which is used for taking the modulo to prevent integer overflow.\n\n3. Calculate the count of permutations for `n > 1`:\n - Enter a loop from `2` to `n` (inclusive). This loop iterates from 2 to `n` to calculate the counts for each `n` starting from `n = 2`.\n\n4. Update counts based on the rules for each vowel:\n - Calculate `new_a` by adding counts that are valid according to the rules. For \'a\', it can be followed by \'e\', \'i\', or \'u\'. So, `new_a` is calculated as `(e + i + u) % mod`.\n - Calculate `new_e` for \'e\' by considering that it can be followed by \'a\' or \'i\'. So, `new_e` is calculated as `(a + i) % mod`.\n - Calculate `new_i` for \'i\' by considering that it can be followed by \'e\' or \'o\'. So, `new_i` is calculated as `(e + o) % mod`.\n - Calculate `new_o` for \'o\', which can be followed by \'i\'. So, `new_o` is set to the value of `i`.\n - Calculate `new_u` for \'u\' by considering that it can be followed by \'a\' or \'o\'. So, `new_u` is calculated as `(a + o) % mod`.\n\n5. Update counts for the next iteration:\n - Update the counts for \'a\', \'e\', \'i\', \'o\', and \'u\' with their respective `new_a`, `new_e`, `new_i`, `new_o`, and `new_u` values. This step prepares the counts for the next iteration (for `n + 1`).\n\n6. Return the total count: After the loop is complete (for `n` iterations), the code returns the total count of valid permutations by adding the counts of \'a\', \'e\', \'i\', \'o\', and \'u\', and taking the modulo `mod`.\n\nThis algorithm uses dynamic programming to efficiently calculate the count of valid permutations for a given value of `n` while adhering to the specified rules.\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\nThe time complexity of the code is $$O(n)$$. This is because there is a loop that iterates from 2 to n, and the core calculation inside the loop takes constant time. Therefore, the overall time complexity is linear in terms of n.\n\n- Space complexity: O(1)\nThis is because it uses a constant amount of additional space regardless of the input n. The code only uses a fixed number of integer variables (a, e, i, o, u, and mod) to keep track of counts and constants. It does not use any data structures that grow with the input size, and it does not create any lists or arrays. Hence, the space complexity is constant.\n\n```python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n # Base case: there are 5 single character permutations (A, E, I, O, U) for n=1\n if n == 1:\n return 5\n # Initialize variables for each vowel count, and set the modulo value \n a = e = i = o = u = 1\n mod = 10**9 + 7\n\n # Calculate the count of permutations for n > 1\n for _ in range(2, n + 1):\n # Update counts based on the rules for each vowel\n new_a = (e + u + i) % mod\n new_e = (a + i) % mod\n new_i = (e + o) % mod\n new_o = i\n new_u = (i + o) % mod\n # Update counts for the next iteration\n a, e, i, o, u = new_a, new_e, new_i, new_o, new_u\n\n return (a + e + i + o + u) % mod \n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countVowelPermutation = function(n) {\n if (n === 1) {\n return 5;\n }\n\n let a = 1, e = 1, i = 1, o = 1, u = 1;\n const mod = 1000000007;\n\n for (let step = 2; step <= n; step++) {\n const newA = (e + u + i) % mod;\n const newE = (a + i) % mod;\n const newI = (e + o) % mod;\n const newO = i;\n const newU = (i + o) % mod;\n\n a = newA;\n e = newE;\n i = newI;\n o = newO;\n u = newU;\n }\n\n return (a + e + i + o + u) % mod; \n};\n```\n```java []\nclass Solution {\n public int countVowelPermutation(int n) {\n if (n == 1) {\n return 5;\n }\n\n long a = 1, e = 1, i = 1, o = 1, u = 1;\n long mod = 1000000007L;\n\n for (int step = 2; step <= n; step++) {\n long newA = (e + u + i) % mod;\n long newE = (a + i) % mod;\n long newI = (e + o) % mod;\n long newO = i;\n long newU = (i + o) % mod;\n\n a = newA;\n e = newE;\n i = newI;\n o = newO;\n u = newU;\n }\n\n return (int)((a + e + i + o + u) % mod); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n if (n == 1) {\n return 5;\n }\n\n long long a = 1, e = 1, i = 1, o = 1, u = 1;\n long long mod = 1000000007LL;\n\n for (int step = 2; step <= n; step++) {\n long long newA = (e + u + i) % mod;\n long long newE = (a + i) % mod;\n long long newI = (e + o) % mod;\n long long newO = i;\n long long newU = (i + o) % mod;\n\n a = newA;\n e = newE;\n i = newI;\n o = newO;\n u = newU;\n }\n\n return (a + e + i + o + u) % mod; \n }\n};\n```\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/sort-integers-by-the-number-of-1-bits/solutions/4225041/video-give-me-10-minutes-using-heap-without-build-in-function-such-as-sort-or-bit-count/\n\nvideo\nhttps://youtu.be/oqV8Ai0_UWA\n\n\u25A0 Timeline\n`0:05` Solution code with build-in function\n`0:26` Two difficulties to solve the question\n`0:41` How do you count 1 bits?\n`1:05` Understanding to count 1 bits with an example\n`3:02` How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n`5:29` Coding\n`7:54` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/longest-palindromic-substring/solutions/4213031/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/aMH1eomKCmE\n\n\u25A0 Timeline of the video\n`0:04` How did you find longest palindromic substring?\n`0:59` What is start point?\n`1:44` Demonstrate how it works with odd case\n`4:36` How do you calculate length of palindrome we found?\n`7:35` Will you pass all test cases?\n`7:53` Consider even case\n`9:03` How to deal with even case\n`11:26` Coding\n`14:52` Explain how to calculate range of palindrome substring\n`17:18` Time Complexity and Space Complexity\n | 12 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | count-vowels-permutation | 1 | 1 | # Intuition\nJust follow the rules lol\n\n---\n\n# Solution Video\n\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,860\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nThis question is a very simple. We just follow the rules in the description.\n\n---\n\n\u25A0 Rules\n\n\u2460 Each vowel `\'a\'` may only be followed by an `\'e\'`.\n\u2461 Each vowel `\'e\'` may only be followed by an `\'a\'` or an `\'i\'`.\n\u2462 Each vowel `\'i\'` may not be followed by another `\'i\'`.\n\u2463 Each vowel `\'o\'` may only be followed by an `\'i\'` or a `\'u\'`.\n\u2464 Each vowel `\'u\'` may only be followed by an `\'a\'`.\n\n---\n\nConvert the rules to a diagram below. Regarding \u2462 Each vowel `\'i\'` may not be followed by another `\'i\'`, in other word following character may be `\'a\'`,`\'e\'`,`\'o\'`,`\'u\'`.\n\n\n\n- How do you count strings with length of `n`? \n\nNow we have organized the information. All we have to do is to count all indegrees(arrows pointing toward each node) for each character.\n\nLet\'s see an example and think about `n = 3`.\n\nIn that case, how many indgrees do you have about `\'a\'`? It\'s `3`(`\'e\'`,`\'i\'`,`\'u\'`).\n\nWe can create characters `\'ea\'`,`\'ia\'`,`\'ua\'`. If `n = 2`, we have `3` strings with end of `\'a\'`.\n\nBut this example is `n = 3`, let\'s move to the next characters from `\'a\'`. We have a rule.\n\n---\n\n\u2460 Each vowel `\'a\'` may only be followed by an `\'e\'`.\n\n---\n\nAt end of `\'a\'`, we have `3` strings, when we add `\'e\'` to the characters we can create `\'eae\'`,`\'iae\'`,`\'uae\'`. At end of `\'e\'`, we can create `3` characters from `\'a\'`. \n\nPlus\n\n`\'e\'` has another indgree from `\'i\'` and the same caculation happens at each character at the same time, so we must have total number of strings ending at `\'i\'`.\n\nIn summary, at end of `\'e\'`, total number of strings we can create is `3`(from `\'a\'`) + total numbers from `\'i\'`. That\'s the total number of strings which is length of `3` ending at `\'e\'`.\n\nWe calculate total numbers for each vowel. Let me skip other parts.\n\nAt last, just add total numbers from `5` vowels and return the answer.\n\nEasy \uD83D\uDE06\nLet\'s see a real algorithm!\n\n\n---\n\n\n\n**Algorithm Overview:**\n\nThe code calculates the count of valid permutations of vowels (\'a\', \'e\', \'i\', \'o\', \'u\') of length `n` according to specific rules, while keeping track of counts for each vowel. The code uses dynamic programming to update these counts iteratively.\n\n**Detailed Explanation:**\n\n1. Check the base case: If `n` is equal to 1, return 5. This is because for `n = 1`, there are only 5 single-character permutations (\'a\', \'e\', \'i\', \'o\', \'u\'), and these are the initial values for the counts of each vowel.\n\n2. Initialize variables: Create variables `a`, `e`, `i`, `o`, and `u` and set their initial values to 1. These variables represent the counts of permutations ending with each vowel (\'a\', \'e\', \'i\', \'o\', \'u\'). Initialize the `mod` variable to 10^9 + 7, which is used for taking the modulo to prevent integer overflow.\n\n3. Calculate the count of permutations for `n > 1`:\n - Enter a loop from `2` to `n` (inclusive). This loop iterates from 2 to `n` to calculate the counts for each `n` starting from `n = 2`.\n\n4. Update counts based on the rules for each vowel:\n - Calculate `new_a` by adding counts that are valid according to the rules. For \'a\', it can be followed by \'e\', \'i\', or \'u\'. So, `new_a` is calculated as `(e + i + u) % mod`.\n - Calculate `new_e` for \'e\' by considering that it can be followed by \'a\' or \'i\'. So, `new_e` is calculated as `(a + i) % mod`.\n - Calculate `new_i` for \'i\' by considering that it can be followed by \'e\' or \'o\'. So, `new_i` is calculated as `(e + o) % mod`.\n - Calculate `new_o` for \'o\', which can be followed by \'i\'. So, `new_o` is set to the value of `i`.\n - Calculate `new_u` for \'u\' by considering that it can be followed by \'a\' or \'o\'. So, `new_u` is calculated as `(a + o) % mod`.\n\n5. Update counts for the next iteration:\n - Update the counts for \'a\', \'e\', \'i\', \'o\', and \'u\' with their respective `new_a`, `new_e`, `new_i`, `new_o`, and `new_u` values. This step prepares the counts for the next iteration (for `n + 1`).\n\n6. Return the total count: After the loop is complete (for `n` iterations), the code returns the total count of valid permutations by adding the counts of \'a\', \'e\', \'i\', \'o\', and \'u\', and taking the modulo `mod`.\n\nThis algorithm uses dynamic programming to efficiently calculate the count of valid permutations for a given value of `n` while adhering to the specified rules.\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\nThe time complexity of the code is $$O(n)$$. This is because there is a loop that iterates from 2 to n, and the core calculation inside the loop takes constant time. Therefore, the overall time complexity is linear in terms of n.\n\n- Space complexity: O(1)\nThis is because it uses a constant amount of additional space regardless of the input n. The code only uses a fixed number of integer variables (a, e, i, o, u, and mod) to keep track of counts and constants. It does not use any data structures that grow with the input size, and it does not create any lists or arrays. Hence, the space complexity is constant.\n\n```python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n # Base case: there are 5 single character permutations (A, E, I, O, U) for n=1\n if n == 1:\n return 5\n # Initialize variables for each vowel count, and set the modulo value \n a = e = i = o = u = 1\n mod = 10**9 + 7\n\n # Calculate the count of permutations for n > 1\n for _ in range(2, n + 1):\n # Update counts based on the rules for each vowel\n new_a = (e + u + i) % mod\n new_e = (a + i) % mod\n new_i = (e + o) % mod\n new_o = i\n new_u = (i + o) % mod\n # Update counts for the next iteration\n a, e, i, o, u = new_a, new_e, new_i, new_o, new_u\n\n return (a + e + i + o + u) % mod \n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countVowelPermutation = function(n) {\n if (n === 1) {\n return 5;\n }\n\n let a = 1, e = 1, i = 1, o = 1, u = 1;\n const mod = 1000000007;\n\n for (let step = 2; step <= n; step++) {\n const newA = (e + u + i) % mod;\n const newE = (a + i) % mod;\n const newI = (e + o) % mod;\n const newO = i;\n const newU = (i + o) % mod;\n\n a = newA;\n e = newE;\n i = newI;\n o = newO;\n u = newU;\n }\n\n return (a + e + i + o + u) % mod; \n};\n```\n```java []\nclass Solution {\n public int countVowelPermutation(int n) {\n if (n == 1) {\n return 5;\n }\n\n long a = 1, e = 1, i = 1, o = 1, u = 1;\n long mod = 1000000007L;\n\n for (int step = 2; step <= n; step++) {\n long newA = (e + u + i) % mod;\n long newE = (a + i) % mod;\n long newI = (e + o) % mod;\n long newO = i;\n long newU = (i + o) % mod;\n\n a = newA;\n e = newE;\n i = newI;\n o = newO;\n u = newU;\n }\n\n return (int)((a + e + i + o + u) % mod); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n if (n == 1) {\n return 5;\n }\n\n long long a = 1, e = 1, i = 1, o = 1, u = 1;\n long long mod = 1000000007LL;\n\n for (int step = 2; step <= n; step++) {\n long long newA = (e + u + i) % mod;\n long long newE = (a + i) % mod;\n long long newI = (e + o) % mod;\n long long newO = i;\n long long newU = (i + o) % mod;\n\n a = newA;\n e = newE;\n i = newI;\n o = newO;\n u = newU;\n }\n\n return (a + e + i + o + u) % mod; \n }\n};\n```\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/sort-integers-by-the-number-of-1-bits/solutions/4225041/video-give-me-10-minutes-using-heap-without-build-in-function-such-as-sort-or-bit-count/\n\nvideo\nhttps://youtu.be/oqV8Ai0_UWA\n\n\u25A0 Timeline\n`0:05` Solution code with build-in function\n`0:26` Two difficulties to solve the question\n`0:41` How do you count 1 bits?\n`1:05` Understanding to count 1 bits with an example\n`3:02` How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n`5:29` Coding\n`7:54` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/longest-palindromic-substring/solutions/4213031/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/aMH1eomKCmE\n\n\u25A0 Timeline of the video\n`0:04` How did you find longest palindromic substring?\n`0:59` What is start point?\n`1:44` Demonstrate how it works with odd case\n`4:36` How do you calculate length of palindrome we found?\n`7:35` Will you pass all test cases?\n`7:53` Consider even case\n`9:03` How to deal with even case\n`11:26` Coding\n`14:52` Explain how to calculate range of palindrome substring\n`17:18` Time Complexity and Space Complexity\n | 12 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
🚀 100% || Easy Iterative Approach || Explained Intuition 🚀 | count-vowels-permutation | 1 | 1 | # Porblem Description\nGiven an integer `n`, The task is to **determine** the number of **valid** strings of length `n` that can be formed based on a specific set of **rules**. \n\n- The rules for forming these strings are as follows:\n - Each character in the string must be a lowercase vowel, which includes \'a\', \'e\', \'i\', \'o\', and \'u\'.\n - \'a\' may **only** be followed by \'e\'.\n - \'e\' may **only** be followed by \'a\' or \'i\'.\n - \'i\' may **not be** followed by another \'i\'.\n - \'o\' may **only** be followed by \'i\' or \'u\'.\n - \'u\' may **only** be followed by \'a\'.\n \nThe task is to **count** how many valid strings of length `n` can be created following these rules. As the answer may potentially be a large number, return it modulo `10^9 + 7`.\n\n- **Constraints:**\n - $1 <= n <= 2 * 10^4$\n\n---\n\n\n# Intuition\n\nHi There, \uD83D\uDC4B\n\nLet\'s deep dive\uD83E\uDD3F into our today\'s problem.\nThe task today is to calculate how many **valid** strings of length `n` can we have based on some **rules**. and the interesting that all of the strings consists only of **voweld** letters.\uD83D\uDE00\n\nFirst things first, let\'s check our **saviour** all the time, **Brute Force**\uD83D\uDCAA. We can **loop** of all the string that consists of vowels and see how many of them are **valid** according to our rules.\nUnfortunately, It will give us TLE since we have about $5^N$ strings we sill have to check on.\uD83D\uDE22\n\nCan we something more **optimized** ?\uD83E\uDD14\nWhy don\'t we change our **perspective** a little bit.\uD83D\uDC40\nSince we have only `5 letters` in our strings why don\'t we track the number of strings that ends with these letters according to the rules !\uD83E\uDD28\nDidn\'t get it ? No problem\uD83D\uDE05\nLet\'s see the rules in simpler form.\n\n \n\n\n\n\nWe draw our rules in **Tree** form to make it easier.\nI said before we want to change our **perspective**. How can we change it\u2753\n**Instead** of check all the strings and see who is following the rules and since we have only `5 letters` in our strings. why don\'t we traverse these trees and count number of leaves for each letter.\uD83E\uDD28\n\nLet\'s see how:\n```\nn = 1\nWe have 5 asnwers\na, e, o, i, u\n```\n```\nn = 2\nWe have 10 asnwers\nae, ei, ea, ua, oi, ou, ie, iu, io, ia\n```\n```\nn = 3\nWe have 19 asnwers\naei, aea, eie, eiu, eio, eia, eae, uae.....\n```\nWe can see in each `n` we traverse the trees for one more level and see the number of **leaves** ends with each vowel.\n\n\n\nLike the tree above we can start with one letter and traverse the tree level by level and see the number of leaves in the `n-th` level.\uD83E\uDD29\n\n**How can we maintain this?**\nActually, It\'s easy. By looping for `n` iterations and in each iterations for each vowel that we can end with in our leaves, we **sum** the number of leaves that can **precede** the current vowel and maintain the rules from the **previous** iterations.\n- So we will have:\n - `a = e + u + i`\n - `e = a + i`\n - `i = e + o`\n - `o = i`\n - `u = o + i`\n - \nEach rule of the new rules means that a **specific** vowel is **sum** of other vowels that can **precede** it according to the rules.\n**i.e.** `a` only can be preceded by `e`, `u` or `i` and `e` only can be preceded by `a` or `i` and so on.\nAnd we can check these new rules from the trees that we made from the first rules we have.\u2714\u2705\n\n**Does this consider Dynamic Programming?**\nYes, we can say that not using an array is considered as **DP** since it has the **core of DP** which is **caching** the results that we will use it later instead of re-calculate it again even if it was one variable.\uD83E\uDD29\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n# Approach\n1. Initialize variables `prevA`, `prevE`, `prevI`, `prevO`, and `prevU` to 1 to represent the counts of strings ends with vowels `a`, `e`, `i`, `o`, and `u` respectively.\n2. Use a loop to iterate from `length = 2` to `n` based on the given rules and track how many strings ends with specific vowels:\n - Inside the loop, calculate the next values for each vowel based on the rules and store them in `nextA`, `nextE`, `nextI`, `nextO`, and `nextU`.\n - Update the previous counts `prevA`, `prevE`, `prevI`, `prevO`, and `prevU` with their respective next values.\n3. After the loop, return the sum of all vowel counts (`prevA`, `prevE`, `prevI`, `prevO`, `prevU`) modulo `mod` as the final result.\n\n\n# Complexity\n- **Time complexity:**$O(N)$\nSince we are only using one loop with size `N` and all of our operations are constant time.\n- **Space complexity:**$O(1)$\nSince we are only storing constant space variables.\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n long long prevA = 1, prevE = 1, prevI = 1, prevO = 1, prevU = 1;\n int mod = 1e9 + 7; // Modulo value to handle large numbers\n\n for (int length = 2; length <= n; length++) {\n // Calculate the next values for each vowel following the rules\n long long nextA = (prevE + prevU + prevI) % mod; // \'a\' can be preceded by \'e\', \'u\', or \'i\'\n long long nextE = (prevA + prevI) % mod; // \'e\' can be preceded by \'a\' or \'i\'\n long long nextI = (prevE + prevO) % mod; // \'i\' can be preceded by \'e\' or\'o\'\n long long nextO = prevI; // \'o\' can only be preceded by \'i\'\n long long nextU = (prevO + prevI) % mod; // \'u\' can be preceded by \'o\' or \'i\'\n\n // Update the previous values for the next iteration\n prevA = nextA;\n prevE = nextE;\n prevI = nextI;\n prevO = nextO;\n prevU = nextU;\n }\n\n // Return the sum of all vowel counts modulo the defined value\n return (prevA + prevE + prevI + prevO + prevU) % mod;\n }\n};\n\n```\n```Java []\npublic class Solution {\n public int countVowelPermutation(int n) {\n long prevA = 1, prevE = 1, prevI = 1, prevO = 1, prevU = 1;\n int mod = 1000000007; // Modulo value to handle large numbers\n\n for (int length = 2; length <= n; length++) {\n // Calculate the next values for each vowel following the rules\n long nextA = (prevE + prevU + prevI) % mod; // \'a\' can be preceded by \'e\', \'u\', or \'i\'\n long nextE = (prevA + prevI) % mod; // \'e\' can be preceded by \'a\' or \'i\'\n long nextI = (prevE + prevO) % mod; // \'i\' can be preceded by \'e\' or \'o\'\n long nextO = prevI; // \'o\' can only be preceded by \'i\'\n long nextU = (prevO + prevI) % mod; // \'u\' can be preceded by \'o\' or \'i\'\n\n // Update the previous values for the next iteration\n prevA = nextA;\n prevE = nextE;\n prevI = nextI;\n prevO = nextO;\n prevU = nextU;\n }\n\n // Return the sum of all vowel counts modulo the defined value\n return (int) ((prevA + prevE + prevI + prevO + prevU) % mod);\n }\n}\n```\n```Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n prevA, prevE, prevI, prevO, prevU = 1, 1, 1, 1, 1\n mod = 10**9 + 7 # Modulo value to handle large numbers\n\n for length in range(2, n + 1):\n # Calculate the next values for each vowel following the rules\n nextA = (prevE + prevU + prevI) % mod # \'a\' can be preceded by \'e\', \'u\', or \'i\'\n nextE = (prevA + prevI) % mod # \'e\' can be preceded by \'a\' or \'i\'\n nextI = (prevE + prevO) % mod # \'i\' can be preceded by \'e\' or \'o\'\n nextO = prevI # \'o\' can only be preceded by \'i\'\n nextU = (prevO + prevI) % mod # \'u\' can be preceded by \'o\' or \'i\'\n\n # Update the previous values for the next iteration\n prevA, prevE, prevI, prevO, prevU = nextA, nextE, nextI, nextO, nextU\n\n # Return the sum of all vowel counts modulo the defined value\n return (prevA + prevE + prevI + prevO + prevU) % mod\n```\n```C []\nint countVowelPermutation(int n) {\n long long prevA = 1, prevE = 1, prevI = 1, prevO = 1, prevU = 1;\n int mod = 1000000007; // Modulo value to handle large numbers\n\n for (int length = 2; length <= n; length++) {\n // Calculate the next values for each vowel following the rules\n long long nextA = (prevE + prevU + prevI) % mod; // \'a\' can be preceded by \'e\', \'u\', or \'i\'\n long long nextE = (prevA + prevI) % mod; // \'e\' can be preceded by \'a\' or \'i\'\n long long nextI = (prevE + prevO) % mod; // \'i\' can be preceded by \'e\' or \'o\'\n long long nextO = prevI; // \'o\' can only be preceded by \'i\'\n long long nextU = (prevO + prevI) % mod; // \'u\' can be preceded by \'o\' or \'i\'\n\n // Update the previous values for the next iteration\n prevA = nextA;\n prevE = nextE;\n prevI = nextI;\n prevO = nextO;\n prevU = nextU;\n }\n\n // Return the sum of all vowel counts modulo the defined value\n return (int)((prevA + prevE + prevI + prevO + prevU) % mod);\n}\n```\n\n\n\n\n\n | 32 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
🚀 100% || Easy Iterative Approach || Explained Intuition 🚀 | count-vowels-permutation | 1 | 1 | # Porblem Description\nGiven an integer `n`, The task is to **determine** the number of **valid** strings of length `n` that can be formed based on a specific set of **rules**. \n\n- The rules for forming these strings are as follows:\n - Each character in the string must be a lowercase vowel, which includes \'a\', \'e\', \'i\', \'o\', and \'u\'.\n - \'a\' may **only** be followed by \'e\'.\n - \'e\' may **only** be followed by \'a\' or \'i\'.\n - \'i\' may **not be** followed by another \'i\'.\n - \'o\' may **only** be followed by \'i\' or \'u\'.\n - \'u\' may **only** be followed by \'a\'.\n \nThe task is to **count** how many valid strings of length `n` can be created following these rules. As the answer may potentially be a large number, return it modulo `10^9 + 7`.\n\n- **Constraints:**\n - $1 <= n <= 2 * 10^4$\n\n---\n\n\n# Intuition\n\nHi There, \uD83D\uDC4B\n\nLet\'s deep dive\uD83E\uDD3F into our today\'s problem.\nThe task today is to calculate how many **valid** strings of length `n` can we have based on some **rules**. and the interesting that all of the strings consists only of **voweld** letters.\uD83D\uDE00\n\nFirst things first, let\'s check our **saviour** all the time, **Brute Force**\uD83D\uDCAA. We can **loop** of all the string that consists of vowels and see how many of them are **valid** according to our rules.\nUnfortunately, It will give us TLE since we have about $5^N$ strings we sill have to check on.\uD83D\uDE22\n\nCan we something more **optimized** ?\uD83E\uDD14\nWhy don\'t we change our **perspective** a little bit.\uD83D\uDC40\nSince we have only `5 letters` in our strings why don\'t we track the number of strings that ends with these letters according to the rules !\uD83E\uDD28\nDidn\'t get it ? No problem\uD83D\uDE05\nLet\'s see the rules in simpler form.\n\n \n\n\n\n\nWe draw our rules in **Tree** form to make it easier.\nI said before we want to change our **perspective**. How can we change it\u2753\n**Instead** of check all the strings and see who is following the rules and since we have only `5 letters` in our strings. why don\'t we traverse these trees and count number of leaves for each letter.\uD83E\uDD28\n\nLet\'s see how:\n```\nn = 1\nWe have 5 asnwers\na, e, o, i, u\n```\n```\nn = 2\nWe have 10 asnwers\nae, ei, ea, ua, oi, ou, ie, iu, io, ia\n```\n```\nn = 3\nWe have 19 asnwers\naei, aea, eie, eiu, eio, eia, eae, uae.....\n```\nWe can see in each `n` we traverse the trees for one more level and see the number of **leaves** ends with each vowel.\n\n\n\nLike the tree above we can start with one letter and traverse the tree level by level and see the number of leaves in the `n-th` level.\uD83E\uDD29\n\n**How can we maintain this?**\nActually, It\'s easy. By looping for `n` iterations and in each iterations for each vowel that we can end with in our leaves, we **sum** the number of leaves that can **precede** the current vowel and maintain the rules from the **previous** iterations.\n- So we will have:\n - `a = e + u + i`\n - `e = a + i`\n - `i = e + o`\n - `o = i`\n - `u = o + i`\n - \nEach rule of the new rules means that a **specific** vowel is **sum** of other vowels that can **precede** it according to the rules.\n**i.e.** `a` only can be preceded by `e`, `u` or `i` and `e` only can be preceded by `a` or `i` and so on.\nAnd we can check these new rules from the trees that we made from the first rules we have.\u2714\u2705\n\n**Does this consider Dynamic Programming?**\nYes, we can say that not using an array is considered as **DP** since it has the **core of DP** which is **caching** the results that we will use it later instead of re-calculate it again even if it was one variable.\uD83E\uDD29\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n# Approach\n1. Initialize variables `prevA`, `prevE`, `prevI`, `prevO`, and `prevU` to 1 to represent the counts of strings ends with vowels `a`, `e`, `i`, `o`, and `u` respectively.\n2. Use a loop to iterate from `length = 2` to `n` based on the given rules and track how many strings ends with specific vowels:\n - Inside the loop, calculate the next values for each vowel based on the rules and store them in `nextA`, `nextE`, `nextI`, `nextO`, and `nextU`.\n - Update the previous counts `prevA`, `prevE`, `prevI`, `prevO`, and `prevU` with their respective next values.\n3. After the loop, return the sum of all vowel counts (`prevA`, `prevE`, `prevI`, `prevO`, `prevU`) modulo `mod` as the final result.\n\n\n# Complexity\n- **Time complexity:**$O(N)$\nSince we are only using one loop with size `N` and all of our operations are constant time.\n- **Space complexity:**$O(1)$\nSince we are only storing constant space variables.\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n long long prevA = 1, prevE = 1, prevI = 1, prevO = 1, prevU = 1;\n int mod = 1e9 + 7; // Modulo value to handle large numbers\n\n for (int length = 2; length <= n; length++) {\n // Calculate the next values for each vowel following the rules\n long long nextA = (prevE + prevU + prevI) % mod; // \'a\' can be preceded by \'e\', \'u\', or \'i\'\n long long nextE = (prevA + prevI) % mod; // \'e\' can be preceded by \'a\' or \'i\'\n long long nextI = (prevE + prevO) % mod; // \'i\' can be preceded by \'e\' or\'o\'\n long long nextO = prevI; // \'o\' can only be preceded by \'i\'\n long long nextU = (prevO + prevI) % mod; // \'u\' can be preceded by \'o\' or \'i\'\n\n // Update the previous values for the next iteration\n prevA = nextA;\n prevE = nextE;\n prevI = nextI;\n prevO = nextO;\n prevU = nextU;\n }\n\n // Return the sum of all vowel counts modulo the defined value\n return (prevA + prevE + prevI + prevO + prevU) % mod;\n }\n};\n\n```\n```Java []\npublic class Solution {\n public int countVowelPermutation(int n) {\n long prevA = 1, prevE = 1, prevI = 1, prevO = 1, prevU = 1;\n int mod = 1000000007; // Modulo value to handle large numbers\n\n for (int length = 2; length <= n; length++) {\n // Calculate the next values for each vowel following the rules\n long nextA = (prevE + prevU + prevI) % mod; // \'a\' can be preceded by \'e\', \'u\', or \'i\'\n long nextE = (prevA + prevI) % mod; // \'e\' can be preceded by \'a\' or \'i\'\n long nextI = (prevE + prevO) % mod; // \'i\' can be preceded by \'e\' or \'o\'\n long nextO = prevI; // \'o\' can only be preceded by \'i\'\n long nextU = (prevO + prevI) % mod; // \'u\' can be preceded by \'o\' or \'i\'\n\n // Update the previous values for the next iteration\n prevA = nextA;\n prevE = nextE;\n prevI = nextI;\n prevO = nextO;\n prevU = nextU;\n }\n\n // Return the sum of all vowel counts modulo the defined value\n return (int) ((prevA + prevE + prevI + prevO + prevU) % mod);\n }\n}\n```\n```Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n prevA, prevE, prevI, prevO, prevU = 1, 1, 1, 1, 1\n mod = 10**9 + 7 # Modulo value to handle large numbers\n\n for length in range(2, n + 1):\n # Calculate the next values for each vowel following the rules\n nextA = (prevE + prevU + prevI) % mod # \'a\' can be preceded by \'e\', \'u\', or \'i\'\n nextE = (prevA + prevI) % mod # \'e\' can be preceded by \'a\' or \'i\'\n nextI = (prevE + prevO) % mod # \'i\' can be preceded by \'e\' or \'o\'\n nextO = prevI # \'o\' can only be preceded by \'i\'\n nextU = (prevO + prevI) % mod # \'u\' can be preceded by \'o\' or \'i\'\n\n # Update the previous values for the next iteration\n prevA, prevE, prevI, prevO, prevU = nextA, nextE, nextI, nextO, nextU\n\n # Return the sum of all vowel counts modulo the defined value\n return (prevA + prevE + prevI + prevO + prevU) % mod\n```\n```C []\nint countVowelPermutation(int n) {\n long long prevA = 1, prevE = 1, prevI = 1, prevO = 1, prevU = 1;\n int mod = 1000000007; // Modulo value to handle large numbers\n\n for (int length = 2; length <= n; length++) {\n // Calculate the next values for each vowel following the rules\n long long nextA = (prevE + prevU + prevI) % mod; // \'a\' can be preceded by \'e\', \'u\', or \'i\'\n long long nextE = (prevA + prevI) % mod; // \'e\' can be preceded by \'a\' or \'i\'\n long long nextI = (prevE + prevO) % mod; // \'i\' can be preceded by \'e\' or \'o\'\n long long nextO = prevI; // \'o\' can only be preceded by \'i\'\n long long nextU = (prevO + prevI) % mod; // \'u\' can be preceded by \'o\' or \'i\'\n\n // Update the previous values for the next iteration\n prevA = nextA;\n prevE = nextE;\n prevI = nextI;\n prevO = nextO;\n prevU = nextU;\n }\n\n // Return the sum of all vowel counts modulo the defined value\n return (int)((prevA + prevE + prevI + prevO + prevU) % mod);\n}\n```\n\n\n\n\n\n | 32 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
Python3 Solution | count-vowels-permutation | 0 | 1 | \n```\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n mod=10**9+7\n dp=[[],[1,1,1,1,1]]\n a,e,i,o,u=0,1,2,3,4\n for j in range(2,n+1):\n dp.append([0,0,0,0,0])\n dp[j][a]=(dp[j-1][e]+dp[j-1][i]+dp[j-1][u])\n dp[j][e]=(dp[j-1][a]+dp[j-1][i])%mod\n dp[j][i]=(dp[j-1][e]+dp[j-1][o])%mod\n dp[j][o]=dp[j-1][i]\n dp[j][u]=dp[j-1][i]+dp[j-1][o]\n\n return sum(dp[n])%mod \n``` | 3 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
Python3 Solution | count-vowels-permutation | 0 | 1 | \n```\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n mod=10**9+7\n dp=[[],[1,1,1,1,1]]\n a,e,i,o,u=0,1,2,3,4\n for j in range(2,n+1):\n dp.append([0,0,0,0,0])\n dp[j][a]=(dp[j-1][e]+dp[j-1][i]+dp[j-1][u])\n dp[j][e]=(dp[j-1][a]+dp[j-1][i])%mod\n dp[j][i]=(dp[j-1][e]+dp[j-1][o])%mod\n dp[j][o]=dp[j-1][i]\n dp[j][u]=dp[j-1][i]+dp[j-1][o]\n\n return sum(dp[n])%mod \n``` | 3 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
🔥🚀Beats 100% | 🚩Basic Simple Math Approach | 🧭Time - O(n), Space O(1) | 🔥Optimised Approach | count-vowels-permutation | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis solution is based on a mathematical approach to count the number of valid strings of length \'n\' that can be formed using the given vowel rules. The idea is to iteratively calculate the number of valid strings for each vowel at each length. By updating the counts for each vowel based on the rules, we can find the total count of valid strings of length \'n\' that follow the rules.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize variables \'a\', \'e\', \'i\', \'o\', and \'u\' to 1. These 2. variables will represent the count of valid strings ending with each vowel at length 1.\n3. Iterate from length 2 to \'n\':\n- Calculate the new count for each vowel based on the following rules:\n- \'a\' can be followed by \'e\', \'u\', or \'i\'.\n- \'e\' can be followed by \'a\' or \'i\'.\n- \'i\' can be followed by \'e\' or \'o\'.\n- \'o\' can be followed by \'i\'.\n- \'u\' can be followed by \'a\' or \'i\'.\n4. Update the counts for \'a\', \'e\', \'i\', \'o\', and \'u\' with the new counts.\n5. Calculate the total count by summing up \'a\', \'e\', \'i\', \'o\', and \'u\'.\n6. Return the total count modulo 10^9 + 7 as the answer.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n) because we iterate through the range from 2 to \'n\' once, updating the counts for each vowel at each length.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as we use a constant amount of extra space to store the counts for each vowel and a few additional variables.\n\n\n---\n\n\n```C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1000000007;\n long long a = 1, e = 1, i = 1, o = 1, u = 1;\n\n for (int len = 2; len <= n; len++) {\n long long new_a = (e + u + i) % MOD;\n long long new_e = (a + i) % MOD;\n long long new_i = (e + o) % MOD;\n long long new_o = (i) % MOD;\n long long new_u = (o + i) % MOD;\n\n a = new_a;\n e = new_e;\n i = new_i;\n o = new_o;\n u = new_u;\n }\n\n long long count = (a + e + i + o + u) % MOD;\n return static_cast<int>(count);\n }\n};\n```\n```Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 1000000007\n a = e = i = o = u = 1\n\n for length in range(2, n + 1):\n new_a = (e + u + i) % MOD\n new_e = (a + i) % MOD\n new_i = (e + o) % MOD\n new_o = i % MOD\n new_u = (o + i) % MOD\n\n a, e, i, o, u = new_a, new_e, new_i, new_o, new_u\n\n count = (a + e + i + o + u) % MOD\n return int(count)\n\n```\n```Java []\nclass Solution {\n public int countVowelPermutation(int n) {\n final int MOD = 1000000007;\n long a = 1, e = 1, i = 1, o = 1, u = 1;\n\n for (int len = 2; len <= n; len++) {\n long new_a = (e + u + i) % MOD;\n long new_e = (a + i) % MOD;\n long new_i = (e + o) % MOD;\n long new_o = (i) % MOD;\n long new_u = (o + i) % MOD;\n\n a = new_a;\n e = new_e;\n i = new_i;\n o = new_o;\n u = new_u;\n }\n\n long count = (a + e + i + o + u) % MOD;\n return (int) count;\n }\n}\n\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countVowelPermutation = function(n) {\n const MOD = 1000000007;\n let a = 1, e = 1, i = 1, o = 1, u = 1;\n\n for (let len = 2; len <= n; len++) {\n const new_a = (e + u + i) % MOD;\n const new_e = (a + i) % MOD;\n const new_i = (e + o) % MOD;\n const new_o = i % MOD;\n const new_u = (o + i) % MOD;\n\n a = new_a;\n e = new_e;\n i = new_i;\n o = new_o;\n u = new_u;\n }\n\n const count = (a + e + i + o + u) % MOD;\n return count;\n};\n```\n```PHP []\nclass Solution {\n function countVowelPermutation($n) {\n $MOD = 1000000007;\n $a = 1;\n $e = 1;\n $i = 1;\n $o = 1;\n $u = 1;\n\n for ($len = 2; $len <= $n; $len++) {\n $new_a = ($e + $u + $i) % $MOD;\n $new_e = ($a + $i) % $MOD;\n $new_i = ($e + $o) % $MOD;\n $new_o = $i % $MOD;\n $new_u = ($o + $i) % $MOD;\n\n $a = $new_a;\n $e = $new_e;\n $i = $new_i;\n $o = $new_o;\n $u = $new_u;\n }\n\n $count = ($a + $e + $i + $o + $u) % $MOD;\n return intval($count);\n }\n}\n\n```\n | 5 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
🔥🚀Beats 100% | 🚩Basic Simple Math Approach | 🧭Time - O(n), Space O(1) | 🔥Optimised Approach | count-vowels-permutation | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis solution is based on a mathematical approach to count the number of valid strings of length \'n\' that can be formed using the given vowel rules. The idea is to iteratively calculate the number of valid strings for each vowel at each length. By updating the counts for each vowel based on the rules, we can find the total count of valid strings of length \'n\' that follow the rules.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize variables \'a\', \'e\', \'i\', \'o\', and \'u\' to 1. These 2. variables will represent the count of valid strings ending with each vowel at length 1.\n3. Iterate from length 2 to \'n\':\n- Calculate the new count for each vowel based on the following rules:\n- \'a\' can be followed by \'e\', \'u\', or \'i\'.\n- \'e\' can be followed by \'a\' or \'i\'.\n- \'i\' can be followed by \'e\' or \'o\'.\n- \'o\' can be followed by \'i\'.\n- \'u\' can be followed by \'a\' or \'i\'.\n4. Update the counts for \'a\', \'e\', \'i\', \'o\', and \'u\' with the new counts.\n5. Calculate the total count by summing up \'a\', \'e\', \'i\', \'o\', and \'u\'.\n6. Return the total count modulo 10^9 + 7 as the answer.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n) because we iterate through the range from 2 to \'n\' once, updating the counts for each vowel at each length.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as we use a constant amount of extra space to store the counts for each vowel and a few additional variables.\n\n\n---\n\n\n```C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1000000007;\n long long a = 1, e = 1, i = 1, o = 1, u = 1;\n\n for (int len = 2; len <= n; len++) {\n long long new_a = (e + u + i) % MOD;\n long long new_e = (a + i) % MOD;\n long long new_i = (e + o) % MOD;\n long long new_o = (i) % MOD;\n long long new_u = (o + i) % MOD;\n\n a = new_a;\n e = new_e;\n i = new_i;\n o = new_o;\n u = new_u;\n }\n\n long long count = (a + e + i + o + u) % MOD;\n return static_cast<int>(count);\n }\n};\n```\n```Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 1000000007\n a = e = i = o = u = 1\n\n for length in range(2, n + 1):\n new_a = (e + u + i) % MOD\n new_e = (a + i) % MOD\n new_i = (e + o) % MOD\n new_o = i % MOD\n new_u = (o + i) % MOD\n\n a, e, i, o, u = new_a, new_e, new_i, new_o, new_u\n\n count = (a + e + i + o + u) % MOD\n return int(count)\n\n```\n```Java []\nclass Solution {\n public int countVowelPermutation(int n) {\n final int MOD = 1000000007;\n long a = 1, e = 1, i = 1, o = 1, u = 1;\n\n for (int len = 2; len <= n; len++) {\n long new_a = (e + u + i) % MOD;\n long new_e = (a + i) % MOD;\n long new_i = (e + o) % MOD;\n long new_o = (i) % MOD;\n long new_u = (o + i) % MOD;\n\n a = new_a;\n e = new_e;\n i = new_i;\n o = new_o;\n u = new_u;\n }\n\n long count = (a + e + i + o + u) % MOD;\n return (int) count;\n }\n}\n\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar countVowelPermutation = function(n) {\n const MOD = 1000000007;\n let a = 1, e = 1, i = 1, o = 1, u = 1;\n\n for (let len = 2; len <= n; len++) {\n const new_a = (e + u + i) % MOD;\n const new_e = (a + i) % MOD;\n const new_i = (e + o) % MOD;\n const new_o = i % MOD;\n const new_u = (o + i) % MOD;\n\n a = new_a;\n e = new_e;\n i = new_i;\n o = new_o;\n u = new_u;\n }\n\n const count = (a + e + i + o + u) % MOD;\n return count;\n};\n```\n```PHP []\nclass Solution {\n function countVowelPermutation($n) {\n $MOD = 1000000007;\n $a = 1;\n $e = 1;\n $i = 1;\n $o = 1;\n $u = 1;\n\n for ($len = 2; $len <= $n; $len++) {\n $new_a = ($e + $u + $i) % $MOD;\n $new_e = ($a + $i) % $MOD;\n $new_i = ($e + $o) % $MOD;\n $new_o = $i % $MOD;\n $new_u = ($o + $i) % $MOD;\n\n $a = $new_a;\n $e = $new_e;\n $i = $new_i;\n $o = $new_o;\n $u = $new_u;\n }\n\n $count = ($a + $e + $i + $o + $u) % $MOD;\n return intval($count);\n }\n}\n\n```\n | 5 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
✅ 98.55% DP Transition Matrix | count-vowels-permutation | 1 | 1 | # Intuition\n\nThe essence of this problem lies in the transitions between vowels and how they form sequences. Given the constraints, not every vowel can follow every other vowel. This forms a sort of directed graph where each vowel points to the vowels it can be followed by. As we\'re tasked with counting the number of valid sequences, our intuition guides us to explore paths in this graph, starting from each vowel and expanding based on the transitions allowed.\n\n# Live Coding & Logic\nhttps://youtu.be/RmGsEWLpAXs?si=XZ0NY_M142ufcerB\n\n# Logic Behind the Solution\n\n1. **Understanding Transitions**: The entire problem revolves around transitions. For a given vowel, the next character in the sequence can only be certain vowels. For instance, the vowel \'a\' can only be followed by \'e\'. This forms the backbone of our dynamic programming approach. By understanding these transitions, we can determine the number of sequences of length $ n $ ending in a particular vowel.\n\n2. **Recursive Nature of Problem**: If we want to find the number of sequences of length $ n $ ending in vowel \'a\', we don\'t need to consider all possible sequences of length $ n-1 $. Instead, we only need to know the number of sequences of length $ n-1 $ ending in vowels that can precede \'a\'. This recursive nature, combined with transitions, is what makes dynamic programming apt for this problem.\n\n3. **State Maintenance**: At each step (or length), we maintain the counts of sequences ending in each vowel. This forms the state of our dynamic programming solution. As we proceed, we update these counts based on the previous state and the transitions allowed.\n\n4. **Linear Time Complexity**: By maintaining state and ensuring that we only consider valid transitions, we ensure that our solution runs in linear time. At each step, we\'re essentially doing constant work, updating counts for 5 vowels.\n\n# Approach\n\n1. **Transition Matrix**: First, we need to understand the transition for each vowel. We can build this based on the rules provided:\n\n - \'a\' can only be followed by \'e\'\n - \'e\' can be followed by \'a\' or \'i\'\n - \'i\' cannot be followed by another \'i\'\n - \'o\' can be followed by \'i\' or \'u\'\n - \'u\' can only be followed by \'a\'\n\n2. **Dynamic Programming**: We maintain a dynamic programming array for each vowel which will store the count of strings ending with that vowel for a particular length.\n\n - For $n = 1$, all vowels have a count of 1.\n - For each subsequent length, the count for each vowel is updated based on the previous counts of the other vowels.\n - For example, the count of strings of length $i$ ending with \'a\' will be equal to the count of strings of length $i-1$ ending with \'e\', because \'a\' can only be followed by \'e\'.\n\n3. **Modulo Operation**: Since the answer can be large, we use modulo $10^9 + 7$ at each step to keep the numbers manageable.\n\n4. **Final Answer**: The final answer will be the sum of counts of all vowels for length $n$.\n\n# Complexity\n\n- **Time complexity**: $O(n)$\n - We iterate through the numbers from 1 to $n$ once, updating the count for each vowel in constant time.\n\n- **Space complexity**: $O(1)$\n - We are using a fixed amount of space regardless of the value of $n$ since we only maintain counts for the 5 vowels.\n\n# Code\n\n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 10**9 + 7\n \n a, e, i, o, u = 1, 1, 1, 1, 1\n \n for _ in range(1, n):\n a_next = e\n e_next = (a + i) % MOD\n i_next = (a + e + o + u) % MOD\n o_next = (i + u) % MOD\n u_next = a\n \n a, e, i, o, u = a_next, e_next, i_next, o_next, u_next\n \n return (a + e + i + o + u) % MOD\n```\n``` Go []\nfunc countVowelPermutation(n int) int {\n const MOD = 1e9 + 7;\n \n a, e, i, o, u := 1, 1, 1, 1, 1\n \n for j := 1; j < n; j++ {\n a_next := e\n e_next := (a + i) % MOD\n i_next := (a + e + o + u) % MOD\n o_next := (i + u) % MOD\n u_next := a\n \n a, e, i, o, u = a_next, e_next, i_next, o_next, u_next\n }\n \n return (a + e + i + o + u) % MOD\n}\n```\n``` Rust []\nimpl Solution {\n pub fn count_vowel_permutation(n: i32) -> i32 {\n const MOD: i64 = 1e9 as i64 + 7;\n \n let mut a = 1;\n let mut e = 1;\n let mut i = 1;\n let mut o = 1;\n let mut u = 1;\n \n for _ in 1..n {\n let a_next = e;\n let e_next = (a + i) % MOD;\n let i_next = (a + e + o + u) % MOD;\n let o_next = (i + u) % MOD;\n let u_next = a;\n \n a = a_next;\n e = e_next;\n i = i_next;\n o = o_next;\n u = u_next;\n }\n \n ((a + e + i + o + u) % MOD) as i32\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1e9 + 7;\n \n long long a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (int j = 1; j < n; j++) {\n long long a_next = e;\n long long e_next = (a + i) % MOD;\n long long i_next = (a + e + o + u) % MOD;\n long long o_next = (i + u) % MOD;\n long long u_next = a;\n \n a = a_next, e = e_next, i = i_next, o = o_next, u = u_next;\n }\n \n return (a + e + i + o + u) % MOD;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int countVowelPermutation(int n) {\n final int MOD = 1000000007;\n \n long a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (int j = 1; j < n; j++) {\n long a_next = e;\n long e_next = (a + i) % MOD;\n long i_next = (a + e + o + u) % MOD;\n long o_next = (i + u) % MOD;\n long u_next = a;\n \n a = a_next;\n e = e_next;\n i = i_next;\n o = o_next;\n u = u_next;\n }\n \n return (int)((a + e + i + o + u) % MOD);\n }\n}\n```\n``` PHP []\nclass Solution {\n function countVowelPermutation($n) {\n $MOD = 1000000007;\n \n $a = $e = $i = $o = $u = 1;\n \n for ($j = 1; $j < $n; $j++) {\n $a_next = $e;\n $e_next = ($a + $i) % $MOD;\n $i_next = ($a + $e + $o + $u) % $MOD;\n $o_next = ($i + $u) % $MOD;\n $u_next = $a;\n \n $a = $a_next;\n $e = $e_next;\n $i = $i_next;\n $o = $o_next;\n $u = $u_next;\n }\n \n return ($a + $e + $i + $o + $u) % $MOD;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int CountVowelPermutation(int n) {\n const int MOD = 1000000007;\n \n long a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (int j = 1; j < n; j++) {\n long a_next = e;\n long e_next = (a + i) % MOD;\n long i_next = (a + e + o + u) % MOD;\n long o_next = (i + u) % MOD;\n long u_next = a;\n \n a = a_next;\n e = e_next;\n i = i_next;\n o = o_next;\n u = u_next;\n }\n \n return (int)((a + e + i + o + u) % MOD);\n }\n}\n```\n```JavaScript []\nvar countVowelPermutation = function(n) {\n const MOD = 1e9 + 7;\n \n let a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (let j = 1; j < n; j++) {\n let a_next = e;\n let e_next = (a + i) % MOD;\n let i_next = (a + e + o + u) % MOD;\n let o_next = (i + u) % MOD;\n let u_next = a;\n \n a = a_next, e = e_next, i = i_next, o = o_next, u = u_next;\n }\n \n return (a + e + i + o + u) % MOD;\n }\n```\n\n# Performance\n| Language | Time (ms) | Memory (MB) |\n|------------|-----------|-------------|\n| Rust | 1 ms | 2.2 MB |\n| Go | 2 ms | 1.9 MB |\n| C++ | 3 ms | 6.2 MB |\n| Java | 5 ms | 39.7 MB |\n| PHP | 17 ms | 18.8 MB |\n| C# | 20 ms | 26.7 MB |\n| JavaScript | 54 ms | 43.5 MB |\n| Python3 | 72 ms | 16.2 MB |\n\n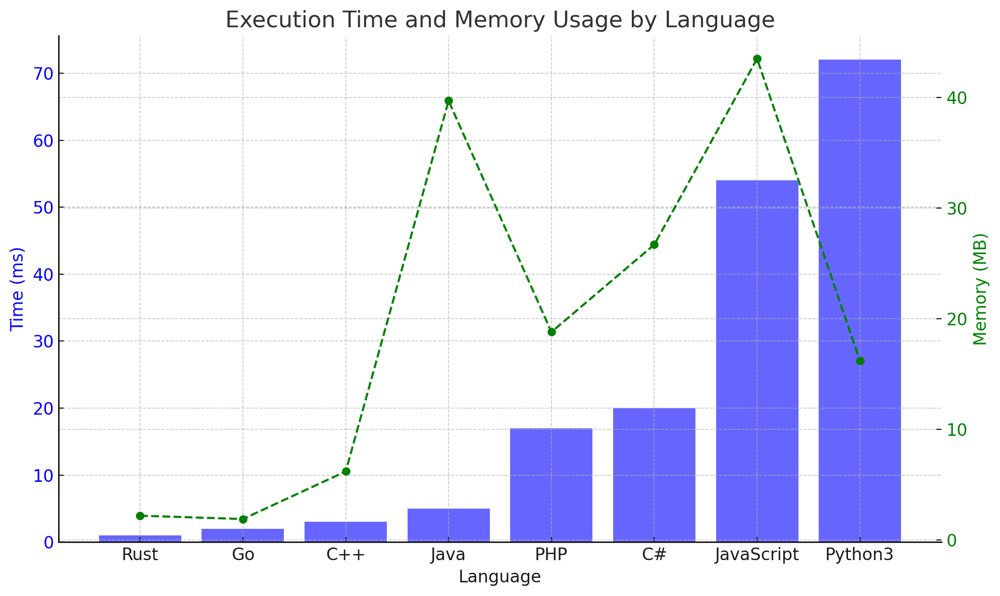\n\n# Why It Works ?\n\nThe given solution works primarily because of the transition rules provided and the state maintenance approach. By ensuring we only ever consider valid transitions and by utilizing previous results (counts for sequences of length $ n-1 $), we efficiently determine the counts for sequences of length $ n $. \n\n# Why It\'s Optimal ?\n\nThe solution leverages the power of dynamic programming. Instead of brute-forcing all possible sequences (which would be exponential in nature), the solution smartly reuses previously computed results, ensuring that the solution is linear in terms of time complexity. Additionally, since we\'re only maintaining counts for 5 vowels regardless of the length $ n $, our space complexity remains constant. This combination of linear time and constant space is what makes the solution optimal.\n\n# What We Have Learned ?\n\nThis problem teaches us the importance of recognizing patterns and formulating transition states in dynamic programming problems. By understanding the possible transitions for each vowel, we can optimize the solution to compute the counts in linear time. This is a classic example of how dynamic programming can turn a potentially exponential problem into a linear one.\n | 88 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
✅ 98.55% DP Transition Matrix | count-vowels-permutation | 1 | 1 | # Intuition\n\nThe essence of this problem lies in the transitions between vowels and how they form sequences. Given the constraints, not every vowel can follow every other vowel. This forms a sort of directed graph where each vowel points to the vowels it can be followed by. As we\'re tasked with counting the number of valid sequences, our intuition guides us to explore paths in this graph, starting from each vowel and expanding based on the transitions allowed.\n\n# Live Coding & Logic\nhttps://youtu.be/RmGsEWLpAXs?si=XZ0NY_M142ufcerB\n\n# Logic Behind the Solution\n\n1. **Understanding Transitions**: The entire problem revolves around transitions. For a given vowel, the next character in the sequence can only be certain vowels. For instance, the vowel \'a\' can only be followed by \'e\'. This forms the backbone of our dynamic programming approach. By understanding these transitions, we can determine the number of sequences of length $ n $ ending in a particular vowel.\n\n2. **Recursive Nature of Problem**: If we want to find the number of sequences of length $ n $ ending in vowel \'a\', we don\'t need to consider all possible sequences of length $ n-1 $. Instead, we only need to know the number of sequences of length $ n-1 $ ending in vowels that can precede \'a\'. This recursive nature, combined with transitions, is what makes dynamic programming apt for this problem.\n\n3. **State Maintenance**: At each step (or length), we maintain the counts of sequences ending in each vowel. This forms the state of our dynamic programming solution. As we proceed, we update these counts based on the previous state and the transitions allowed.\n\n4. **Linear Time Complexity**: By maintaining state and ensuring that we only consider valid transitions, we ensure that our solution runs in linear time. At each step, we\'re essentially doing constant work, updating counts for 5 vowels.\n\n# Approach\n\n1. **Transition Matrix**: First, we need to understand the transition for each vowel. We can build this based on the rules provided:\n\n - \'a\' can only be followed by \'e\'\n - \'e\' can be followed by \'a\' or \'i\'\n - \'i\' cannot be followed by another \'i\'\n - \'o\' can be followed by \'i\' or \'u\'\n - \'u\' can only be followed by \'a\'\n\n2. **Dynamic Programming**: We maintain a dynamic programming array for each vowel which will store the count of strings ending with that vowel for a particular length.\n\n - For $n = 1$, all vowels have a count of 1.\n - For each subsequent length, the count for each vowel is updated based on the previous counts of the other vowels.\n - For example, the count of strings of length $i$ ending with \'a\' will be equal to the count of strings of length $i-1$ ending with \'e\', because \'a\' can only be followed by \'e\'.\n\n3. **Modulo Operation**: Since the answer can be large, we use modulo $10^9 + 7$ at each step to keep the numbers manageable.\n\n4. **Final Answer**: The final answer will be the sum of counts of all vowels for length $n$.\n\n# Complexity\n\n- **Time complexity**: $O(n)$\n - We iterate through the numbers from 1 to $n$ once, updating the count for each vowel in constant time.\n\n- **Space complexity**: $O(1)$\n - We are using a fixed amount of space regardless of the value of $n$ since we only maintain counts for the 5 vowels.\n\n# Code\n\n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 10**9 + 7\n \n a, e, i, o, u = 1, 1, 1, 1, 1\n \n for _ in range(1, n):\n a_next = e\n e_next = (a + i) % MOD\n i_next = (a + e + o + u) % MOD\n o_next = (i + u) % MOD\n u_next = a\n \n a, e, i, o, u = a_next, e_next, i_next, o_next, u_next\n \n return (a + e + i + o + u) % MOD\n```\n``` Go []\nfunc countVowelPermutation(n int) int {\n const MOD = 1e9 + 7;\n \n a, e, i, o, u := 1, 1, 1, 1, 1\n \n for j := 1; j < n; j++ {\n a_next := e\n e_next := (a + i) % MOD\n i_next := (a + e + o + u) % MOD\n o_next := (i + u) % MOD\n u_next := a\n \n a, e, i, o, u = a_next, e_next, i_next, o_next, u_next\n }\n \n return (a + e + i + o + u) % MOD\n}\n```\n``` Rust []\nimpl Solution {\n pub fn count_vowel_permutation(n: i32) -> i32 {\n const MOD: i64 = 1e9 as i64 + 7;\n \n let mut a = 1;\n let mut e = 1;\n let mut i = 1;\n let mut o = 1;\n let mut u = 1;\n \n for _ in 1..n {\n let a_next = e;\n let e_next = (a + i) % MOD;\n let i_next = (a + e + o + u) % MOD;\n let o_next = (i + u) % MOD;\n let u_next = a;\n \n a = a_next;\n e = e_next;\n i = i_next;\n o = o_next;\n u = u_next;\n }\n \n ((a + e + i + o + u) % MOD) as i32\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1e9 + 7;\n \n long long a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (int j = 1; j < n; j++) {\n long long a_next = e;\n long long e_next = (a + i) % MOD;\n long long i_next = (a + e + o + u) % MOD;\n long long o_next = (i + u) % MOD;\n long long u_next = a;\n \n a = a_next, e = e_next, i = i_next, o = o_next, u = u_next;\n }\n \n return (a + e + i + o + u) % MOD;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int countVowelPermutation(int n) {\n final int MOD = 1000000007;\n \n long a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (int j = 1; j < n; j++) {\n long a_next = e;\n long e_next = (a + i) % MOD;\n long i_next = (a + e + o + u) % MOD;\n long o_next = (i + u) % MOD;\n long u_next = a;\n \n a = a_next;\n e = e_next;\n i = i_next;\n o = o_next;\n u = u_next;\n }\n \n return (int)((a + e + i + o + u) % MOD);\n }\n}\n```\n``` PHP []\nclass Solution {\n function countVowelPermutation($n) {\n $MOD = 1000000007;\n \n $a = $e = $i = $o = $u = 1;\n \n for ($j = 1; $j < $n; $j++) {\n $a_next = $e;\n $e_next = ($a + $i) % $MOD;\n $i_next = ($a + $e + $o + $u) % $MOD;\n $o_next = ($i + $u) % $MOD;\n $u_next = $a;\n \n $a = $a_next;\n $e = $e_next;\n $i = $i_next;\n $o = $o_next;\n $u = $u_next;\n }\n \n return ($a + $e + $i + $o + $u) % $MOD;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int CountVowelPermutation(int n) {\n const int MOD = 1000000007;\n \n long a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (int j = 1; j < n; j++) {\n long a_next = e;\n long e_next = (a + i) % MOD;\n long i_next = (a + e + o + u) % MOD;\n long o_next = (i + u) % MOD;\n long u_next = a;\n \n a = a_next;\n e = e_next;\n i = i_next;\n o = o_next;\n u = u_next;\n }\n \n return (int)((a + e + i + o + u) % MOD);\n }\n}\n```\n```JavaScript []\nvar countVowelPermutation = function(n) {\n const MOD = 1e9 + 7;\n \n let a = 1, e = 1, i = 1, o = 1, u = 1;\n \n for (let j = 1; j < n; j++) {\n let a_next = e;\n let e_next = (a + i) % MOD;\n let i_next = (a + e + o + u) % MOD;\n let o_next = (i + u) % MOD;\n let u_next = a;\n \n a = a_next, e = e_next, i = i_next, o = o_next, u = u_next;\n }\n \n return (a + e + i + o + u) % MOD;\n }\n```\n\n# Performance\n| Language | Time (ms) | Memory (MB) |\n|------------|-----------|-------------|\n| Rust | 1 ms | 2.2 MB |\n| Go | 2 ms | 1.9 MB |\n| C++ | 3 ms | 6.2 MB |\n| Java | 5 ms | 39.7 MB |\n| PHP | 17 ms | 18.8 MB |\n| C# | 20 ms | 26.7 MB |\n| JavaScript | 54 ms | 43.5 MB |\n| Python3 | 72 ms | 16.2 MB |\n\n\n\n# Why It Works ?\n\nThe given solution works primarily because of the transition rules provided and the state maintenance approach. By ensuring we only ever consider valid transitions and by utilizing previous results (counts for sequences of length $ n-1 $), we efficiently determine the counts for sequences of length $ n $. \n\n# Why It\'s Optimal ?\n\nThe solution leverages the power of dynamic programming. Instead of brute-forcing all possible sequences (which would be exponential in nature), the solution smartly reuses previously computed results, ensuring that the solution is linear in terms of time complexity. Additionally, since we\'re only maintaining counts for 5 vowels regardless of the length $ n $, our space complexity remains constant. This combination of linear time and constant space is what makes the solution optimal.\n\n# What We Have Learned ?\n\nThis problem teaches us the importance of recognizing patterns and formulating transition states in dynamic programming problems. By understanding the possible transitions for each vowel, we can optimize the solution to compute the counts in linear time. This is a classic example of how dynamic programming can turn a potentially exponential problem into a linear one.\n | 88 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
2D DP solution in Python by Akash Sinha | count-vowels-permutation | 0 | 1 | # Intuition\nLooking at the problem statement, the first thing which comes to mind is go for a recursive solution based on the constraints of alphabets.\n\n# Approach\n def f(s,n):\n if(n==0):\n return 1\n elif(s==\'\'):\n return f(\'a\',n-1)+f(\'e\',n-1)+f(\'i\',n-1)+f(\'o\',n-1)+f(\'u\',n-1) \n else:\n if(s==\'a\'):\n return f(\'e\',n-1)\n elif(s==\'e\'):\n return f(\'a\',n-1)+f(\'i\',n-1)\n elif(s==\'i\'):\n return f(\'a\',n-1,)+f(\'e\',n-1)+f(\'o\',n-1)+f(\'u\',n-1)\n elif(s==\'o\'):\n return f(\'i\',n-1)+f(\'u\',n-1)\n else:\n return f(\'a\',n-1)\n return f(\'\',n)%(1000000007)\n\nThis is a recusive solution. But this solution will give a Time Limit Exceed error as its time complexity will be O(4^n). \nSo here comes the concept of Dynamic Programming(DP), as here during this recursion we can understand there will be many repetitive recursive calls. So using DP we can solve this problem by using extra memory.\n\nHere we can see that our recursive function has 2 arguments, one is the previous character s and other is length of remaining string n. So we use a 2D DP. But we know there are only 5 possible characters i.e. vowels, So the shape of our dp memory will be 5*n. \n\nWe use a map/dictionary to map the vowels to values from 0 to 4 respectively so that these vowels\' values can be used as an index of our 2D dp list. \n\nIn this way we can solve the problem efficiently within the time limit. Below is the recursive solution code using DP.\n\n# Complexity\n- Time complexity:\nO(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity:\nO(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n def f(s,n,dp,d):\n if(n==0):\n return 1\n elif(s==\'\'):\n return f(\'a\',n-1,dp,d)+f(\'e\',n-1,dp,d)+f(\'i\',n-1,dp,d)+f(\'o\',n-1,dp,d)+f(\'u\',n-1,dp,d) \n elif(dp[d[s]][n]!=-1):\n return dp[d[s]][n]\n else:\n if(s==\'a\'):\n dp[d[s]][n]=f(\'e\',n-1,dp,d)\n elif(s==\'e\'):\n dp[d[s]][n]=f(\'a\',n-1,dp,d)+f(\'i\',n-1,dp,d)\n elif(s==\'i\'):\n dp[d[s]][n]=f(\'a\',n-1,dp,d)+f(\'e\',n-1,dp,d)+f(\'o\',n-1,dp,d)+f(\'u\',n-1,dp,d)\n elif(s==\'o\'):\n dp[d[s]][n]=f(\'i\',n-1,dp,d)+f(\'u\',n-1,dp,d)\n else:\n dp[d[s]][n]=f(\'a\',n-1,dp,d)\n return dp[d[s]][n]\n from collections import defaultdict\n dp=[[-1 for j in range(n)] for i in range(5)]\n d=defaultdict(int)\n d[\'a\']=0\n d[\'e\']=1\n d[\'i\']=2\n d[\'o\']=3\n d[\'u\']=4\n return f(\'\',n,dp,d)%((10**9)+7)\n``` | 2 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
2D DP solution in Python by Akash Sinha | count-vowels-permutation | 0 | 1 | # Intuition\nLooking at the problem statement, the first thing which comes to mind is go for a recursive solution based on the constraints of alphabets.\n\n# Approach\n def f(s,n):\n if(n==0):\n return 1\n elif(s==\'\'):\n return f(\'a\',n-1)+f(\'e\',n-1)+f(\'i\',n-1)+f(\'o\',n-1)+f(\'u\',n-1) \n else:\n if(s==\'a\'):\n return f(\'e\',n-1)\n elif(s==\'e\'):\n return f(\'a\',n-1)+f(\'i\',n-1)\n elif(s==\'i\'):\n return f(\'a\',n-1,)+f(\'e\',n-1)+f(\'o\',n-1)+f(\'u\',n-1)\n elif(s==\'o\'):\n return f(\'i\',n-1)+f(\'u\',n-1)\n else:\n return f(\'a\',n-1)\n return f(\'\',n)%(1000000007)\n\nThis is a recusive solution. But this solution will give a Time Limit Exceed error as its time complexity will be O(4^n). \nSo here comes the concept of Dynamic Programming(DP), as here during this recursion we can understand there will be many repetitive recursive calls. So using DP we can solve this problem by using extra memory.\n\nHere we can see that our recursive function has 2 arguments, one is the previous character s and other is length of remaining string n. So we use a 2D DP. But we know there are only 5 possible characters i.e. vowels, So the shape of our dp memory will be 5*n. \n\nWe use a map/dictionary to map the vowels to values from 0 to 4 respectively so that these vowels\' values can be used as an index of our 2D dp list. \n\nIn this way we can solve the problem efficiently within the time limit. Below is the recursive solution code using DP.\n\n# Complexity\n- Time complexity:\nO(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity:\nO(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n def f(s,n,dp,d):\n if(n==0):\n return 1\n elif(s==\'\'):\n return f(\'a\',n-1,dp,d)+f(\'e\',n-1,dp,d)+f(\'i\',n-1,dp,d)+f(\'o\',n-1,dp,d)+f(\'u\',n-1,dp,d) \n elif(dp[d[s]][n]!=-1):\n return dp[d[s]][n]\n else:\n if(s==\'a\'):\n dp[d[s]][n]=f(\'e\',n-1,dp,d)\n elif(s==\'e\'):\n dp[d[s]][n]=f(\'a\',n-1,dp,d)+f(\'i\',n-1,dp,d)\n elif(s==\'i\'):\n dp[d[s]][n]=f(\'a\',n-1,dp,d)+f(\'e\',n-1,dp,d)+f(\'o\',n-1,dp,d)+f(\'u\',n-1,dp,d)\n elif(s==\'o\'):\n dp[d[s]][n]=f(\'i\',n-1,dp,d)+f(\'u\',n-1,dp,d)\n else:\n dp[d[s]][n]=f(\'a\',n-1,dp,d)\n return dp[d[s]][n]\n from collections import defaultdict\n dp=[[-1 for j in range(n)] for i in range(5)]\n d=defaultdict(int)\n d[\'a\']=0\n d[\'e\']=1\n d[\'i\']=2\n d[\'o\']=3\n d[\'u\']=4\n return f(\'\',n,dp,d)%((10**9)+7)\n``` | 2 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
✅☑[C++/Java/Python/JavaScript] || EXPLAINED🔥 | count-vowels-permutation | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n1. The countVowelPermutation function is the main entry point to calculate the number of valid permutations of vowels for a given length `n`.\n\n1. The `mp` unordered_map stores information about possible vowel transitions. For each vowel `prev`, it lists the next possible vowels.\n\n1. The helper function recursively calculates the number of valid permutations given the current length `i` and the last vowel `prev`. It uses memoization to avoid redundant calculations.\n\n1. If `i` exceeds `n`, the function returns the count based on the last vowel `prev` following the given rules.\n\n1. The function recursively explores all possible vowel transitions from `prev` to the next vowel using `mp`, and it accumulates the counts.\n\n1. The memoization table `dp` is used to store already computed results, which improves the efficiency of the algorithm.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n#include <vector>\n#include <unordered_map>\n\nclass Solution {\n unordered_map<int, vector<int>> mp;\n int MOD = 1e9 + 7;\n\npublic:\n int helper(int n, int i, char prev, vector<vector<long long>>& dp) {\n // If we\'ve reached the required length \'n\', return the count based on the last vowel \'prev\'.\n if (i > n) {\n switch (prev) {\n case \'a\': return 1;\n case \'e\': return 2;\n case \'i\': return 4;\n case \'o\': return 2;\n case \'u\': return 1;\n default: return 5;\n }\n }\n\n int idx = prev - \'a\';\n if (dp[i][idx] != -1) {\n return dp[i][idx];\n }\n\n long long ans = 0;\n for (auto next : mp[prev]) {\n ans += (helper(n, i + 1, next, dp) % MOD);\n }\n return dp[i][idx] = ans % MOD;\n }\n\n int countVowelPermutation(int n) {\n // Define the possible vowel transitions in the \'mp\' map.\n mp[\'c\'] = { \'a\', \'e\', \'i\', \'o\', \'u\' };\n mp[\'a\'] = { \'e\' };\n mp[\'e\'] = { \'a\', \'i\' };\n mp[\'i\'] = { \'a\', \'e\', \'o\', \'u\' };\n mp[\'o\'] = { \'i\', \'u\' };\n mp[\'u\'] = { \'a\' };\n\n // Create a memoization table \'dp\' with -1 values to store computed results.\n vector<vector<long long>> dp(n + 2, vector<long long>(27, -1));\n\n // Start the helper function with initial parameters and return the result.\n return helper(n, 1, \'c\', dp);\n }\n};\n\n```\n\n\n```C []\n#include <vector>\n#include <unordered_map>\n\nclass Solution {\n std::unordered_map<int, std::vector<int>> mp;\n int MOD = 1e9 + 7;\n\npublic:\n int helper(int n, int i, char prev, std::vector<std::vector<long long>>& dp) {\n if (i > n) {\n switch (prev) {\n case \'a\': return 1;\n case \'e\': return 2;\n case \'i\': return 4;\n case \'o\': return 2;\n case \'u\': return 1;\n default: return 5;\n }\n }\n\n int idx = prev - \'a\';\n if (dp[i][idx] != -1) {\n return dp[i][idx];\n }\n\n long long ans = 0;\n for (auto next : mp[prev]) {\n ans += (helper(n, i + 1, next, dp) % MOD);\n }\n return dp[i][idx] = ans % MOD;\n }\n\n int countVowelPermutation(int n) {\n mp[\'c\'] = { \'a\', \'e\', \'i\', \'o\', \'u\' };\n mp[\'a\'] = { \'e\' };\n mp[\'e\'] = { \'a\', \'i\' };\n mp[\'i\'] = { \'a\', \'e\', \'o\', \'u\' };\n mp[\'o\'] = { \'i\', \'u\' };\n mp[\'u\'] = { \'a\' };\n\n std::vector<std::vector<long long>> dp(n + 2, std::vector<long long>(27, -1));\n\n return helper(n, 1, \'c\', dp);\n }\n};\n\n\n\n```\n\n```Java []\nimport java.util.*;\n\nclass Solution {\n private Map<Character, List<Character>> mp = new HashMap<>();\n private int MOD = 1000000007;\n\n public int helper(int n, int i, char prev, long[][] dp) {\n if (i > n) {\n switch (prev) {\n case \'a\': return 1;\n case \'e\': return 2;\n case \'i\': return 4;\n case \'o\': return 2;\n case \'u\': return 1;\n default: return 5;\n }\n }\n\n int idx = prev - \'a\';\n if (dp[i][idx] != -1) {\n return (int) dp[i][idx];\n }\n\n long ans = 0;\n for (char next : mp.get(prev)) {\n ans += helper(n, i + 1, next, dp);\n ans %= MOD;\n }\n dp[i][idx] = ans;\n\n return (int) ans;\n }\n\n public int countVowelPermutation(int n) {\n mp.put(\'c\', Arrays.asList(\'a\', \'e\', \'i\', \'o\', \'u\'));\n mp.put(\'a\', Arrays.asList(\'e\'));\n mp.put(\'e\', Arrays.asList(\'a\', \'i\'));\n mp.put(\'i\', Arrays.asList(\'a\', \'e\', \'o\', \'u\'));\n mp.put(\'o\', Arrays.asList(\'i\', \'u\'));\n mp.put(\'u\', Arrays.asList(\'a\'));\n\n long[][] dp = new long[n + 2][27];\n for (long[] row : dp) {\n Arrays.fill(row, -1);\n }\n\n return helper(n, 1, \'c\', dp);\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def __init__(self):\n self.mp = {\'c\': [\'a\', \'e\', \'i\', \'o\', \'u\'], \'a\': [\'e\'], \'e\': [\'a\', \'i\'], \'i\': [\'a\', \'e\', \'o\', \'u\'], \'o\': [\'i\', \'u\'], \'u\': [\'a\']}\n self.MOD = 10**9 + 7\n\n def helper(self, n, i, prev, dp):\n if i > n:\n if prev == \'a\':\n return 1\n elif prev == \'e\':\n return 2\n elif prev == \'i\':\n return 4\n elif prev == \'o\':\n return 2\n elif prev == \'u\':\n return 1\n else:\n return 5\n\n idx = ord(prev) - ord(\'a\')\n if dp[i][idx] != -1:\n return dp[i][idx]\n\n ans = 0\n for next_char in self.mp[prev]:\n ans += self.helper(n, i + 1, next_char, dp)\n ans %= self.MOD\n dp[i][idx] = ans\n\n return ans\n\n def countVowelPermutation(self, n: int) -> int:\n dp = [[-1] * 27 for _ in range(n + 2)]\n return self.helper(n, 1, \'c\', dp)\n\n\n\n```\n```javascript []\nclass Solution {\n constructor() {\n this.mp = {\n \'c\': [\'a\', \'e\', \'i\', \'o\', \'u\'],\n \'a\': [\'e\'],\n \'e\': [\'a\', \'i\'],\n \'i\': [\'a\', \'e\', \'o\', \'u\'],\n \'o\': [\'i\', \'u\'],\n \'u\': [\'a\']\n };\n this.MOD = 1000000007;\n }\n\n helper(n, i, prev, dp) {\n if (i > n) {\n switch (prev) {\n case \'a\':\n return 1;\n case \'e\':\n return 2;\n case \'i\':\n return 4;\n case \'o\':\n return 2;\n case \'u\':\n return 1;\n default:\n return 5;\n }\n }\n\n const idx = prev.charCodeAt(0) - \'a\'.charCodeAt(0);\n if (dp[i][idx] !== -1) {\n return dp[i][idx];\n }\n\n let ans = 0;\n for (const next of this.mp[prev]) {\n ans += this.helper(n, i + 1, next, dp);\n ans %= this.MOD;\n \n\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
✅☑[C++/Java/Python/JavaScript] || EXPLAINED🔥 | count-vowels-permutation | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n1. The countVowelPermutation function is the main entry point to calculate the number of valid permutations of vowels for a given length `n`.\n\n1. The `mp` unordered_map stores information about possible vowel transitions. For each vowel `prev`, it lists the next possible vowels.\n\n1. The helper function recursively calculates the number of valid permutations given the current length `i` and the last vowel `prev`. It uses memoization to avoid redundant calculations.\n\n1. If `i` exceeds `n`, the function returns the count based on the last vowel `prev` following the given rules.\n\n1. The function recursively explores all possible vowel transitions from `prev` to the next vowel using `mp`, and it accumulates the counts.\n\n1. The memoization table `dp` is used to store already computed results, which improves the efficiency of the algorithm.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n#include <vector>\n#include <unordered_map>\n\nclass Solution {\n unordered_map<int, vector<int>> mp;\n int MOD = 1e9 + 7;\n\npublic:\n int helper(int n, int i, char prev, vector<vector<long long>>& dp) {\n // If we\'ve reached the required length \'n\', return the count based on the last vowel \'prev\'.\n if (i > n) {\n switch (prev) {\n case \'a\': return 1;\n case \'e\': return 2;\n case \'i\': return 4;\n case \'o\': return 2;\n case \'u\': return 1;\n default: return 5;\n }\n }\n\n int idx = prev - \'a\';\n if (dp[i][idx] != -1) {\n return dp[i][idx];\n }\n\n long long ans = 0;\n for (auto next : mp[prev]) {\n ans += (helper(n, i + 1, next, dp) % MOD);\n }\n return dp[i][idx] = ans % MOD;\n }\n\n int countVowelPermutation(int n) {\n // Define the possible vowel transitions in the \'mp\' map.\n mp[\'c\'] = { \'a\', \'e\', \'i\', \'o\', \'u\' };\n mp[\'a\'] = { \'e\' };\n mp[\'e\'] = { \'a\', \'i\' };\n mp[\'i\'] = { \'a\', \'e\', \'o\', \'u\' };\n mp[\'o\'] = { \'i\', \'u\' };\n mp[\'u\'] = { \'a\' };\n\n // Create a memoization table \'dp\' with -1 values to store computed results.\n vector<vector<long long>> dp(n + 2, vector<long long>(27, -1));\n\n // Start the helper function with initial parameters and return the result.\n return helper(n, 1, \'c\', dp);\n }\n};\n\n```\n\n\n```C []\n#include <vector>\n#include <unordered_map>\n\nclass Solution {\n std::unordered_map<int, std::vector<int>> mp;\n int MOD = 1e9 + 7;\n\npublic:\n int helper(int n, int i, char prev, std::vector<std::vector<long long>>& dp) {\n if (i > n) {\n switch (prev) {\n case \'a\': return 1;\n case \'e\': return 2;\n case \'i\': return 4;\n case \'o\': return 2;\n case \'u\': return 1;\n default: return 5;\n }\n }\n\n int idx = prev - \'a\';\n if (dp[i][idx] != -1) {\n return dp[i][idx];\n }\n\n long long ans = 0;\n for (auto next : mp[prev]) {\n ans += (helper(n, i + 1, next, dp) % MOD);\n }\n return dp[i][idx] = ans % MOD;\n }\n\n int countVowelPermutation(int n) {\n mp[\'c\'] = { \'a\', \'e\', \'i\', \'o\', \'u\' };\n mp[\'a\'] = { \'e\' };\n mp[\'e\'] = { \'a\', \'i\' };\n mp[\'i\'] = { \'a\', \'e\', \'o\', \'u\' };\n mp[\'o\'] = { \'i\', \'u\' };\n mp[\'u\'] = { \'a\' };\n\n std::vector<std::vector<long long>> dp(n + 2, std::vector<long long>(27, -1));\n\n return helper(n, 1, \'c\', dp);\n }\n};\n\n\n\n```\n\n```Java []\nimport java.util.*;\n\nclass Solution {\n private Map<Character, List<Character>> mp = new HashMap<>();\n private int MOD = 1000000007;\n\n public int helper(int n, int i, char prev, long[][] dp) {\n if (i > n) {\n switch (prev) {\n case \'a\': return 1;\n case \'e\': return 2;\n case \'i\': return 4;\n case \'o\': return 2;\n case \'u\': return 1;\n default: return 5;\n }\n }\n\n int idx = prev - \'a\';\n if (dp[i][idx] != -1) {\n return (int) dp[i][idx];\n }\n\n long ans = 0;\n for (char next : mp.get(prev)) {\n ans += helper(n, i + 1, next, dp);\n ans %= MOD;\n }\n dp[i][idx] = ans;\n\n return (int) ans;\n }\n\n public int countVowelPermutation(int n) {\n mp.put(\'c\', Arrays.asList(\'a\', \'e\', \'i\', \'o\', \'u\'));\n mp.put(\'a\', Arrays.asList(\'e\'));\n mp.put(\'e\', Arrays.asList(\'a\', \'i\'));\n mp.put(\'i\', Arrays.asList(\'a\', \'e\', \'o\', \'u\'));\n mp.put(\'o\', Arrays.asList(\'i\', \'u\'));\n mp.put(\'u\', Arrays.asList(\'a\'));\n\n long[][] dp = new long[n + 2][27];\n for (long[] row : dp) {\n Arrays.fill(row, -1);\n }\n\n return helper(n, 1, \'c\', dp);\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def __init__(self):\n self.mp = {\'c\': [\'a\', \'e\', \'i\', \'o\', \'u\'], \'a\': [\'e\'], \'e\': [\'a\', \'i\'], \'i\': [\'a\', \'e\', \'o\', \'u\'], \'o\': [\'i\', \'u\'], \'u\': [\'a\']}\n self.MOD = 10**9 + 7\n\n def helper(self, n, i, prev, dp):\n if i > n:\n if prev == \'a\':\n return 1\n elif prev == \'e\':\n return 2\n elif prev == \'i\':\n return 4\n elif prev == \'o\':\n return 2\n elif prev == \'u\':\n return 1\n else:\n return 5\n\n idx = ord(prev) - ord(\'a\')\n if dp[i][idx] != -1:\n return dp[i][idx]\n\n ans = 0\n for next_char in self.mp[prev]:\n ans += self.helper(n, i + 1, next_char, dp)\n ans %= self.MOD\n dp[i][idx] = ans\n\n return ans\n\n def countVowelPermutation(self, n: int) -> int:\n dp = [[-1] * 27 for _ in range(n + 2)]\n return self.helper(n, 1, \'c\', dp)\n\n\n\n```\n```javascript []\nclass Solution {\n constructor() {\n this.mp = {\n \'c\': [\'a\', \'e\', \'i\', \'o\', \'u\'],\n \'a\': [\'e\'],\n \'e\': [\'a\', \'i\'],\n \'i\': [\'a\', \'e\', \'o\', \'u\'],\n \'o\': [\'i\', \'u\'],\n \'u\': [\'a\']\n };\n this.MOD = 1000000007;\n }\n\n helper(n, i, prev, dp) {\n if (i > n) {\n switch (prev) {\n case \'a\':\n return 1;\n case \'e\':\n return 2;\n case \'i\':\n return 4;\n case \'o\':\n return 2;\n case \'u\':\n return 1;\n default:\n return 5;\n }\n }\n\n const idx = prev.charCodeAt(0) - \'a\'.charCodeAt(0);\n if (dp[i][idx] !== -1) {\n return dp[i][idx];\n }\n\n let ans = 0;\n for (const next of this.mp[prev]) {\n ans += this.helper(n, i + 1, next, dp);\n ans %= this.MOD;\n \n\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
Dyamic programming, constant space solution, EXPLAINED | count-vowels-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen you think about solving this question brute force you will be forced to find all ways in which we can construct a string of length \'n\'. When we think of finding all ways of something, dynamic programming comes to mind.\nTherefore, we observe according to the rules provided there are only a few ways that our string ends in the 5 vowels:\n\'a\' : e, i, u\n\'e\' : a, i\n\'i\' : e, o\n\'o\' : i\n\'u\' : i, o\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNow, a string of length 1 will only have 1 vowel to end with, then using our rules we calculate for length 2. If we have the number of permutations for a string of length 2, we can use the values to calculate the number of permutations of length 3, and so on.\nSo we use 2 arrays of length 5 to store the current and previous length of permutations.\nWe will iterate till n to make sure n is included in our calculations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> Time complexity is O(n) as we are iterating only once.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(1)\nWe have a constant space complexity as we only need the current and previous row.\n\n# Code\n```\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n prev = [1,1,1,1,1]\n\n a, e, i, o, u = 0,1,2,3,4\n mod = 10**9 + 7\n\n for j in range(1,n):\n cur = [0,0,0,0,0]\n cur[a] = (prev[e] + prev[i] + prev[u])%mod\n cur[e] = (prev[a] + prev[i])%mod\n cur[i] = (prev[e] + prev[o])%mod\n cur[o] = (prev[i])%mod\n cur[u] = (prev[i] + prev[o])%mod\n prev = cur\n \n return sum(prev)%mod\n``` | 1 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
Dyamic programming, constant space solution, EXPLAINED | count-vowels-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen you think about solving this question brute force you will be forced to find all ways in which we can construct a string of length \'n\'. When we think of finding all ways of something, dynamic programming comes to mind.\nTherefore, we observe according to the rules provided there are only a few ways that our string ends in the 5 vowels:\n\'a\' : e, i, u\n\'e\' : a, i\n\'i\' : e, o\n\'o\' : i\n\'u\' : i, o\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNow, a string of length 1 will only have 1 vowel to end with, then using our rules we calculate for length 2. If we have the number of permutations for a string of length 2, we can use the values to calculate the number of permutations of length 3, and so on.\nSo we use 2 arrays of length 5 to store the current and previous length of permutations.\nWe will iterate till n to make sure n is included in our calculations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> Time complexity is O(n) as we are iterating only once.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(1)\nWe have a constant space complexity as we only need the current and previous row.\n\n# Code\n```\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n prev = [1,1,1,1,1]\n\n a, e, i, o, u = 0,1,2,3,4\n mod = 10**9 + 7\n\n for j in range(1,n):\n cur = [0,0,0,0,0]\n cur[a] = (prev[e] + prev[i] + prev[u])%mod\n cur[e] = (prev[a] + prev[i])%mod\n cur[i] = (prev[e] + prev[o])%mod\n cur[o] = (prev[i])%mod\n cur[u] = (prev[i] + prev[o])%mod\n prev = cur\n \n return sum(prev)%mod\n``` | 1 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
🔥99% Beats DP & 🔥100% Beats🔥 Matrix Exponentiation | 🔥 Explained Intuition & Approach | | count-vowels-permutation | 1 | 1 | # 1st Method : Bottom-Up Dynamic Programming \uD83D\uDD25\n## Intuition \uD83D\uDE80:\nThe problem asks you to count the number of valid strings of length `n` using the given rules for vowel transitions. You can think of this as a dynamic programming problem where you calculate the number of valid strings of different lengths and build up to the desired length `n`. The approach involves using a bottom-up dynamic programming approach to compute the counts efficiently.\n\n## Approach \uD83D\uDE80:\n1. Define a constant `MOD` to handle modular arithmetic to avoid integer overflow.\n\n2. Initialize five variables: `countA`, `countE`, `countI`, `countO`, and `countU`, each representing the count of valid strings of length 1 ending with the respective vowel (\'a\', \'e\', \'i\', \'o\', \'u\').\n\n3. Use a for loop to iterate from `length = 1` to `n - 1` because we already have the counts for length 1, and we want to calculate the counts for lengths 2 to `n`.\n\n4. Inside the loop, calculate the counts for each vowel for the next length based on the counts for the current length. The transitions are based on the given rules:\n - `countA` for the next length is the count of strings ending with \'e\'.\n - `countE` for the next length is the count of strings ending with \'a\' or \'i\'.\n - `countI` for the next length is the count of strings ending with \'a\', \'e\', \'o\', or \'u\'.\n - `countO` for the next length is the count of strings ending with \'i\' or \'u\'.\n - `countU` for the next length is the count of strings ending with \'a\'.\n\n5. Update the variables `countA`, `countE`, `countI`, `countO`, and `countU` with the newly calculated counts for the next length.\n\n6. After the loop, the variables contain the counts of valid strings of length `n` ending with each vowel.\n\n7. Calculate the total count of valid strings for length `n` by summing up the counts for all vowels and take the result modulo `MOD`.\n\n8. Return the total count as an integer.\n\nThe approach uses dynamic programming to efficiently compute the counts for different string lengths, following the rules for vowel transitions, and calculates the final result for length `n`.\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9Time complexity: O(n)\n1. The loop from `length = 1` to `n - 1` iterates `n` times.\n2. Inside the loop, there are constant time calculations for each vowel transition.\n3. Therefore, the time complexity is O(n).\n\n### \uD83C\uDFF9Space complexity: O(1)\n1. The space complexity is determined by the variables used to store counts for each vowel. There are five variables (`countA`, `countE`, `countI`, `countO`, and `countU`) that store the counts for each iteration of the loop.\n2. Since the loop iterates up to `n - 1`, the space complexity is O(1), which is constant, because the number of variables used does not depend on the input size.\n\nSo, the time complexity is O(n), and the space complexity is O(1) for the given code.\n## \u2712\uFE0FCode\n``` Java []\npublic class Solution {\n public int countVowelPermutation(int n) {\n final int MOD = 1000000007;\n \n long countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n \n for (int length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n long nextCountA = countE;\n long nextCountE = (countA + countI) % MOD;\n long nextCountI = (countA + countE + countO + countU) % MOD;\n long nextCountO = (countI + countU) % MOD;\n long nextCountU = countA;\n \n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n \n // Calculate the total count of valid strings for length n\n long totalCount = (countA + countE + countI + countO + countU) % MOD;\n \n return (int) totalCount;\n }\n}\n\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1000000007;\n\n // Initialize counts for each vowel for length 1\n long countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n\n // Iterate from length 1 to n - 1\n for (int length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n long nextCountA = countE;\n long nextCountE = (countA + countI) % MOD;\n long nextCountI = (countA + countE + countO + countU) % MOD;\n long nextCountO = (countI + countU) % MOD;\n long nextCountU = countA;\n\n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n\n // Calculate the total count of valid strings for length n\n long totalCount = (countA + countE + countI + countO + countU) % MOD;\n\n return static_cast<int>(totalCount);\n }\n};\n```\n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 1000000007\n\n # Initialize counts for each vowel for length 1\n countA = 1\n countE = 1\n countI = 1\n countO = 1\n countU = 1\n\n # Iterate from length 1 to n - 1\n for length in range(1, n):\n # Calculate the next counts for each vowel based on the previous counts\n nextCountA = countE\n nextCountE = (countA + countI) % MOD\n nextCountI = (countA + countE + countO + countU) % MOD\n nextCountO = (countI + countU) % MOD\n nextCountU = countA\n\n # Update the counts with the newly calculated values for the next length\n countA = nextCountA\n countE = nextCountE\n countI = nextCountI\n countO = nextCountO\n countU = nextCountU\n\n # Calculate the total count of valid strings for length n\n totalCount = (countA + countE + countI + countO + countU) % MOD\n\n return int(totalCount)\n```\n``` JavaScript []\nvar countVowelPermutation = function(n) {\n const MOD = 1000000007;\n \n let countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n \n for (let length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n let nextCountA = countE;\n let nextCountE = (countA + countI) % MOD;\n let nextCountI = (countA + countE + countO + countU) % MOD;\n let nextCountO = (countI + countU) % MOD;\n let nextCountU = countA;\n \n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n \n // Calculate the total count of valid strings for length n\n let totalCount = (countA + countE + countI + countO + countU) % MOD;\n \n return totalCount;\n};\n```\n``` C# []\npublic class Solution {\n public int CountVowelPermutation(int n) {\n const int MOD = 1000000007;\n \n long countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n \n for (int length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n long nextCountA = countE;\n long nextCountE = (countA + countI) % MOD;\n long nextCountI = (countA + countE + countO + countU) % MOD;\n long nextCountO = (countI + countU) % MOD;\n long nextCountU = countA;\n \n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n \n // Calculate the total count of valid strings for length n\n long totalCount = (countA + countE + countI + countO + countU) % MOD;\n \n return (int)totalCount;\n }\n}\n```\n``` PHP []\nclass Solution {\n function countVowelPermutation($n) {\n // Define the modulo constant\n $MOD = 1000000007;\n\n // Initialize counts for vowels \'a\', \'e\', \'i\', \'o\', and \'u\'\n $countA = 1;\n $countE = 1;\n $countI = 1;\n $countO = 1;\n $countU = 1;\n\n // Iterate from length 1 to n - 1\n for ($length = 1; $length < $n; $length++) {\n // Calculate the next counts for each vowel based on the previous counts\n $nextCountA = $countE;\n $nextCountE = ($countA + $countI) % $MOD;\n $nextCountI = ($countA + $countE + $countO + $countU) % $MOD;\n $nextCountO = ($countI + $countU) % $MOD;\n $nextCountU = $countA;\n\n // Update the counts with the newly calculated values for the next length\n $countA = $nextCountA;\n $countE = $nextCountE;\n $countI = $nextCountI;\n $countO = $nextCountO;\n $countU = $nextCountU;\n }\n\n // Calculate the total count of valid strings for length n\n $totalCount = ($countA + $countE + $countI + $countO + $countU) % $MOD;\n\n return (int)$totalCount;\n }\n}\n```\n``` Kotlin []\nclass Solution {\n fun countVowelPermutation(n: Int): Int {\n // Define the modulo constant\n val MOD = 1000000007\n\n // Initialize counts for vowels \'a\', \'e\', \'i\', \'o\', and \'u\'\n var countA = 1L\n var countE = 1L\n var countI = 1L\n var countO = 1L\n var countU = 1L\n\n // Iterate from length 1 to n - 1\n for (length in 1 until n) {\n // Calculate the next counts for each vowel based on the previous counts\n val nextCountA = countE\n val nextCountE = (countA + countI) % MOD\n val nextCountI = (countA + countE + countO + countU) % MOD\n val nextCountO = (countI + countU) % MOD\n val nextCountU = countA\n\n // Update the counts with the newly calculated values for the next length\n countA = nextCountA\n countE = nextCountE\n countI = nextCountI\n countO = nextCountO\n countU = nextCountU\n }\n\n // Calculate the total count of valid strings for length n\n val totalCount = (countA + countE + countI + countO + countU) % MOD\n\n return totalCount.toInt()\n }\n}\n```\n\n\n---\n\n# 2nd Method : Matrix Exponentiation \uD83D\uDD25\n\n## Intuition \uD83D\uDE80:\nThe problem asks us to count the number of valid strings of length `n` using lowercase vowels (\'a\', \'e\', \'i\', \'o\', \'u\') following specific rules. To solve this efficiently, the code employs a matrix exponentiation approach, which is a dynamic programming technique. The code uses matrices to represent the state transitions between vowels and computes the count of valid strings based on these transitions. The matrix exponentiation method optimizes this process by raising the transition matrix to the power of `n - 1` to calculate the count.\n\n## Approach \uD83D\uDE80:\n\n1. **Initialize the Count Matrix:** A 1x5 matrix `count` is initialized to represent the count of each vowel (\'a\', \'e\', \'i\', \'o\', \'u\') at the beginning. This matrix starts with all counts as 1.\n\n2. **Transition Matrix \'base\':** If `n` is greater than 1, a transition matrix `base` is defined. This matrix represents the valid transitions between vowels based on the problem rules. It\'s a 5x5 matrix where each element indicates whether a transition between two vowels is valid.\n\n3. **Matrix Exponentiation:** The code uses a matrix exponentiation approach to calculate the transition matrix raised to the power of `n - 1`. The `matrixPow` function is a recursive function that optimizes matrix exponentiation by using divide-and-conquer to calculate the matrix raised to a power efficiently.\n\n4. **Matrix Multiplication:** The `matrixMul` function is used for matrix multiplication. It multiplies two matrices and calculates the result with modulo M to avoid integer overflow.\n\n5. **Final Count:** The code then multiplies the initial `count` matrix with the result of matrix exponentiation to get the final matrix `finalMatrix`, which represents the count of valid strings of length `n`. The final answer is obtained by summing up the values in the first row of `finalMatrix`.\n\n6. **Modulo Operation:** To ensure the result does not exceed the modulo value `M`, the code takes the modulo of the result.\n\n7. **Return Result:** The code returns the final result as an integer.\n\nThe approach uses matrix operations to efficiently compute the count of valid strings while following the given rules. It leverages dynamic programming and matrix exponentiation to optimize the computation, making it much faster than naive approaches.\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9Time Complexity: O(log(n) * k^3)\n- `countVowelPermutation(int n)`: The main function iterates to calculate the final result, but the most time-consuming part is the matrix exponentiation and matrix multiplication.\n - Matrix Exponentiation (`matrixPow`) has a time complexity of O(log(n)).\n - Matrix Multiplication (`matrixMul`) has a time complexity of O(k^3), where k is the dimension of the matrices, in this case, k is 5 (for the 5 vowels). The matrix multiplication is called log(n) times in the exponentiation function.\n- Overall, the time complexity is O(log(n) * k^3), where k is a constant (5 in this case).\n\n### \uD83C\uDFF9Space Complexity: O(1)\n- The space complexity is determined by the data structures used in the code:\n - `count` and `finalMatrix` are 2D arrays of size 1x5, which is constant.\n - The recursive function `matrixPow` creates several 2D arrays for intermediate calculations, but their combined space usage is also bounded by a constant.\n - `matrixMul` uses additional space for temporary arrays, but again, this space is bounded by a constant.\n- Therefore, the space complexity is O(1), as the space usage does not depend on the input value `n`.\n\n\n\n\n\n\n## Code \u2712\uFE0F\n``` Java []\nclass Solution {\n private static final int M = 1_000_000_007;\n\n public int countVowelPermutation(int n) {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n long[][] count = {{1, 1, 1, 1, 1}};\n long[][] finalMatrix;\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n if (n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n long[][] base = {\n {0, 1, 1, 0, 1},\n {1, 0, 1, 0, 0},\n {0, 1, 0, 1, 0},\n {0, 0, 1, 0, 0},\n {0, 0, 1, 1, 0}\n };\n\n // Calculate the final matrix by raising the base matrix to the power (n - 1).\n finalMatrix = matrixMul(count, matrixPow(base, n - 1));\n } else {\n finalMatrix = count; // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo M.\n long result = 0;\n for (long l : finalMatrix[0]) {\n result += l;\n }\n result %= M;\n return Math.toIntExact(result);\n }\n\n // Function to calculate the matrix raised to a power using a recursive approach.\n private long[][] matrixPow(long[][] base, int pow) {\n if (pow == 1) {\n return base;\n }\n if (pow == 2) {\n return matrixMul(base, base);\n }\n long[][] matrixPow = matrixPow(base, pow / 2);\n long[][] matrix = matrixMul(matrixPow, matrixPow);\n if (pow % 2 == 0) {\n return matrix;\n } else {\n return matrixMul(matrix, base);\n }\n }\n\n // Function to perform matrix multiplication.\n private long[][] matrixMul(long[][] a, long[][] b) {\n int ai = a.length;\n int bi = b.length;\n int bj = b[0].length;\n long[][] result = new long[ai][bj];\n for (int i = 0; i < ai; i++) {\n for (int j = 0; j < bj; j++) {\n long sum = 0;\n for (int k = 0; k < bi; k++) {\n sum += a[i][k] * b[k][j];\n sum %= M;\n }\n result[i][j] = sum;\n }\n }\n return result;\n }\n}\n```\n``` C++ []\nclass Solution {\nprivate:\n static const int M = 1\'000\'000\'007;\n\npublic:\n int countVowelPermutation(int n) {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n std::vector<std::vector<long>> count = {{1, 1, 1, 1, 1}};\n std::vector<std::vector<long>> finalMatrix;\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n if (n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n std::vector<std::vector<long>> base = {\n {0, 1, 1, 0, 1},\n {1, 0, 1, 0, 0},\n {0, 1, 0, 1, 0},\n {0, 0, 1, 0, 0},\n {0, 0, 1, 1, 0}\n };\n\n // Calculate the final matrix by raising the base matrix to the power (n - 1).\n finalMatrix = matrixPow(base, n - 1);\n finalMatrix = matrixMul(count, finalMatrix);\n } else {\n finalMatrix = count; // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo M.\n long result = 0;\n for (long l : finalMatrix[0]) {\n result += l;\n }\n result %= M;\n return static_cast<int>(result);\n }\n\nprivate:\n // Function to calculate the matrix raised to a power using a recursive approach.\n std::vector<std::vector<long>> matrixPow(const std::vector<std::vector<long>>& base, int pow) {\n if (pow == 1) {\n return base;\n }\n if (pow == 2) {\n return matrixMul(base, base);\n }\n std::vector<std::vector<long>> matrixPowResult = matrixPow(base, pow / 2);\n std::vector<std::vector<long>> matrix = matrixMul(matrixPowResult, matrixPowResult);\n if (pow % 2 == 0) {\n return matrix;\n } else {\n return matrixMul(matrix, base);\n }\n }\n\n // Function to perform matrix multiplication.\n std::vector<std::vector<long>> matrixMul(const std::vector<std::vector<long>>& a, const std::vector<std::vector<long>>& b) {\n int ai = a.size();\n int bi = b.size();\n int bj = b[0].size();\n std::vector<std::vector<long>> result(ai, std::vector<long>(bj, 0));\n for (int i = 0; i < ai; i++) {\n for (int j = 0; j < bj; j++) {\n long sum = 0;\n for (int k = 0; k < bi; k++) {\n sum += a[i][k] * b[k][j];\n sum %= M;\n }\n result[i][j] = sum;\n }\n }\n return result;\n }\n};\n\n```\n``` Python []\nclass Solution:\n M = 1_000_000_007\n\n def countVowelPermutation(self, n: int) -> int:\n # Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n count = [[1, 1, 1, 1, 1]]\n finalMatrix = []\n\n # If n is greater than 1, perform matrix operations to calculate the count.\n if n > 1:\n # Define the base transition matrix that represents the vowel transitions.\n base = [\n [0, 1, 1, 0, 1],\n [1, 0, 1, 0, 0],\n [0, 1, 0, 1, 0],\n [0, 0, 1, 0, 0],\n [0, 0, 1, 1, 0]\n ]\n\n # Calculate the final matrix by raising the base matrix to the power (n - 1).\n finalMatrix = self.matrixMul(count, self.matrixPow(base, n - 1))\n else:\n finalMatrix = count # If n is 1, the result is the same as the initial count matrix.\n\n # Calculate the result by summing up the values in the finalMatrix and taking the modulo M.\n result = 0\n for l in finalMatrix[0]:\n result += l\n result %= self.M\n return int(result)\n\n # Function to calculate the matrix raised to a power using a recursive approach.\n def matrixPow(self, base, pow):\n if pow == 1:\n return base\n if pow == 2:\n return self.matrixMul(base, base)\n matrixPow = self.matrixPow(base, pow // 2)\n matrix = self.matrixMul(matrixPow, matrixPow)\n if pow % 2 == 0:\n return matrix\n else:\n return self.matrixMul(matrix, base)\n\n # Function to perform matrix multiplication.\n def matrixMul(self, a, b):\n ai = len(a)\n bi = len(b)\n bj = len(b[0])\n result = [[0 for _ in range(bj)] for _ in range(ai)]\n for i in range(ai):\n for j in range(bj):\n sum = 0\n for k in range(bi):\n sum += a[i][k] * b[k][j]\n sum %= self.M\n result[i][j] = sum\n return result\n```\n``` JavaScript []\nvar countVowelPermutation = function(n) {\n const MOD = 1000000007;\n \n // Initialize a 2D DP array to store counts for each vowel ending at position i.\n // dp[i][j] represents the count of strings of length (i + 1) ending with vowel j.\n const dp = new Array(n).fill(0).map(() => new Array(5).fill(0));\n \n // Initialize the base case: strings of length 1 ending with each vowel are 1.\n for (let j = 0; j < 5; j++) {\n dp[0][j] = 1;\n }\n \n // Fill the DP table for strings of length 2 to n.\n for (let i = 1; i < n; i++) {\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD; // \'a\' can follow \'e\', \'i\', or \'u\'\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD; // \'e\' can follow \'a\' or \'i\'\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD; // \'i\' can follow \'e\' or \'o\'\n dp[i][3] = dp[i - 1][2]; // \'o\' can only follow \'i\'\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD; // \'u\' can follow \'i\' or \'o\'\n }\n \n // Calculate the sum of all counts for strings of length n ending with each vowel.\n let result = 0;\n for (let j = 0; j < 5; j++) {\n result = (result + dp[n - 1][j]) % MOD;\n }\n \n return result;\n};\n\nconst n = 144;\nconsole.log(countVowelPermutation(n)); // Output: 18208803\n```\n``` PHP []\ntime limit exceed\nclass Solution {\n const MOD = 1000000007;\n\n function countVowelPermutation($n) {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n $count = array(array(1, 1, 1, 1, 1));\n $finalMatrix = array();\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n if ($n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n $base = array(\n array(0, 1, 1, 0, 1),\n array(1, 0, 1, 0, 0),\n array(0, 1, 0, 1, 0),\n array(0, 0, 1, 0, 0),\n array(0, 0, 1, 1, 0)\n );\n\n // Calculate the final matrix by raising the base matrix to the power ($n - 1).\n $finalMatrix = $this->matrixMul($count, $this->matrixPow($base, $n - 1));\n } else {\n $finalMatrix = $count; // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo MOD.\n $result = 0;\n foreach ($finalMatrix[0] as $value) {\n $result += $value;\n $result %= self::MOD;\n }\n return $result;\n }\n\n // Function to calculate the matrix raised to a power using a recursive approach.\n function matrixPow($base, $pow) {\n if ($pow == 1) {\n return $base;\n }\n if ($pow == 2) {\n return $this->matrixMul($base, $base);\n }\n $matrixPow = $this->matrixPow($base, $pow / 2);\n $matrix = $this->matrixMul($matrixPow, $matrixPow);\n if ($pow % 2 == 0) {\n return $matrix;\n } else {\n return $this->matrixMul($matrix, $base);\n }\n }\n\n // Function to perform matrix multiplication.\n function matrixMul($a, $b) {\n $ai = count($a);\n $bi = count($b);\n $bj = count($b[0]);\n $result = array();\n\n for ($i = 0; $i < $ai; $i++) {\n for ($j = 0; $j < $bj; $j++) {\n $sum = 0;\n for ($k = 0; $k < $bi; $k++) {\n $sum += $a[$i][$k] * $b[$k][$j];\n $sum %= self::MOD;\n }\n $result[$i][$j] = $sum;\n }\n }\n return $result;\n }\n}\n\n```\n``` Kotlin []\nclass Solution {\n companion object {\n const val MOD = 1_000_000_007\n }\n\n fun countVowelPermutation(n: Int): Int {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n val count = arrayOf(longArrayOf(1, 1, 1, 1, 1))\n val finalMatrix: Array<LongArray>\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n finalMatrix = if (n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n val base = arrayOf(\n longArrayOf(0, 1, 1, 0, 1),\n longArrayOf(1, 0, 1, 0, 0),\n longArrayOf(0, 1, 0, 1, 0),\n longArrayOf(0, 0, 1, 0, 0),\n longArrayOf(0, 0, 1, 1, 0)\n )\n\n // Calculate the final matrix by raising the base matrix to the power (n - 1).\n matrixMul(count, matrixPow(base, n - 1))\n } else {\n count // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo MOD.\n var result: Long = 0\n for (value in finalMatrix[0]) {\n result += value\n result %= MOD\n }\n return result.toInt()\n }\n\n // Function to calculate the matrix raised to a power using a recursive approach.\n private fun matrixPow(base: Array<LongArray>, pow: Int): Array<LongArray> {\n return when {\n pow == 1 -> base\n pow == 2 -> matrixMul(base, base)\n else -> {\n val matrixPow = matrixPow(base, pow / 2)\n val matrix = matrixMul(matrixPow, matrixPow)\n if (pow % 2 == 0) matrix else matrixMul(matrix, base)\n }\n }\n }\n\n // Function to perform matrix multiplication.\n private fun matrixMul(a: Array<LongArray>, b: Array<LongArray>): Array<LongArray> {\n val ai = a.size\n val bi = b.size\n val bj = b[0].size\n val result = Array(ai) { LongArray(bj) }\n\n for (i in 0 until ai) {\n for (j in 0 until bj) {\n var sum: Long = 0\n for (k in 0 until bi) {\n sum += a[i][k] * b[k][j]\n sum %= MOD\n }\n result[i][j] = sum\n }\n }\n return result\n }\n}\n\n```\n\n\n# Up Vote Guys\n | 43 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
🔥99% Beats DP & 🔥100% Beats🔥 Matrix Exponentiation | 🔥 Explained Intuition & Approach | | count-vowels-permutation | 1 | 1 | # 1st Method : Bottom-Up Dynamic Programming \uD83D\uDD25\n## Intuition \uD83D\uDE80:\nThe problem asks you to count the number of valid strings of length `n` using the given rules for vowel transitions. You can think of this as a dynamic programming problem where you calculate the number of valid strings of different lengths and build up to the desired length `n`. The approach involves using a bottom-up dynamic programming approach to compute the counts efficiently.\n\n## Approach \uD83D\uDE80:\n1. Define a constant `MOD` to handle modular arithmetic to avoid integer overflow.\n\n2. Initialize five variables: `countA`, `countE`, `countI`, `countO`, and `countU`, each representing the count of valid strings of length 1 ending with the respective vowel (\'a\', \'e\', \'i\', \'o\', \'u\').\n\n3. Use a for loop to iterate from `length = 1` to `n - 1` because we already have the counts for length 1, and we want to calculate the counts for lengths 2 to `n`.\n\n4. Inside the loop, calculate the counts for each vowel for the next length based on the counts for the current length. The transitions are based on the given rules:\n - `countA` for the next length is the count of strings ending with \'e\'.\n - `countE` for the next length is the count of strings ending with \'a\' or \'i\'.\n - `countI` for the next length is the count of strings ending with \'a\', \'e\', \'o\', or \'u\'.\n - `countO` for the next length is the count of strings ending with \'i\' or \'u\'.\n - `countU` for the next length is the count of strings ending with \'a\'.\n\n5. Update the variables `countA`, `countE`, `countI`, `countO`, and `countU` with the newly calculated counts for the next length.\n\n6. After the loop, the variables contain the counts of valid strings of length `n` ending with each vowel.\n\n7. Calculate the total count of valid strings for length `n` by summing up the counts for all vowels and take the result modulo `MOD`.\n\n8. Return the total count as an integer.\n\nThe approach uses dynamic programming to efficiently compute the counts for different string lengths, following the rules for vowel transitions, and calculates the final result for length `n`.\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9Time complexity: O(n)\n1. The loop from `length = 1` to `n - 1` iterates `n` times.\n2. Inside the loop, there are constant time calculations for each vowel transition.\n3. Therefore, the time complexity is O(n).\n\n### \uD83C\uDFF9Space complexity: O(1)\n1. The space complexity is determined by the variables used to store counts for each vowel. There are five variables (`countA`, `countE`, `countI`, `countO`, and `countU`) that store the counts for each iteration of the loop.\n2. Since the loop iterates up to `n - 1`, the space complexity is O(1), which is constant, because the number of variables used does not depend on the input size.\n\nSo, the time complexity is O(n), and the space complexity is O(1) for the given code.\n## \u2712\uFE0FCode\n``` Java []\npublic class Solution {\n public int countVowelPermutation(int n) {\n final int MOD = 1000000007;\n \n long countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n \n for (int length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n long nextCountA = countE;\n long nextCountE = (countA + countI) % MOD;\n long nextCountI = (countA + countE + countO + countU) % MOD;\n long nextCountO = (countI + countU) % MOD;\n long nextCountU = countA;\n \n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n \n // Calculate the total count of valid strings for length n\n long totalCount = (countA + countE + countI + countO + countU) % MOD;\n \n return (int) totalCount;\n }\n}\n\n```\n``` C++ []\nclass Solution {\npublic:\n int countVowelPermutation(int n) {\n const int MOD = 1000000007;\n\n // Initialize counts for each vowel for length 1\n long countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n\n // Iterate from length 1 to n - 1\n for (int length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n long nextCountA = countE;\n long nextCountE = (countA + countI) % MOD;\n long nextCountI = (countA + countE + countO + countU) % MOD;\n long nextCountO = (countI + countU) % MOD;\n long nextCountU = countA;\n\n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n\n // Calculate the total count of valid strings for length n\n long totalCount = (countA + countE + countI + countO + countU) % MOD;\n\n return static_cast<int>(totalCount);\n }\n};\n```\n``` Python []\nclass Solution:\n def countVowelPermutation(self, n: int) -> int:\n MOD = 1000000007\n\n # Initialize counts for each vowel for length 1\n countA = 1\n countE = 1\n countI = 1\n countO = 1\n countU = 1\n\n # Iterate from length 1 to n - 1\n for length in range(1, n):\n # Calculate the next counts for each vowel based on the previous counts\n nextCountA = countE\n nextCountE = (countA + countI) % MOD\n nextCountI = (countA + countE + countO + countU) % MOD\n nextCountO = (countI + countU) % MOD\n nextCountU = countA\n\n # Update the counts with the newly calculated values for the next length\n countA = nextCountA\n countE = nextCountE\n countI = nextCountI\n countO = nextCountO\n countU = nextCountU\n\n # Calculate the total count of valid strings for length n\n totalCount = (countA + countE + countI + countO + countU) % MOD\n\n return int(totalCount)\n```\n``` JavaScript []\nvar countVowelPermutation = function(n) {\n const MOD = 1000000007;\n \n let countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n \n for (let length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n let nextCountA = countE;\n let nextCountE = (countA + countI) % MOD;\n let nextCountI = (countA + countE + countO + countU) % MOD;\n let nextCountO = (countI + countU) % MOD;\n let nextCountU = countA;\n \n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n \n // Calculate the total count of valid strings for length n\n let totalCount = (countA + countE + countI + countO + countU) % MOD;\n \n return totalCount;\n};\n```\n``` C# []\npublic class Solution {\n public int CountVowelPermutation(int n) {\n const int MOD = 1000000007;\n \n long countA = 1, countE = 1, countI = 1, countO = 1, countU = 1;\n \n for (int length = 1; length < n; length++) {\n // Calculate the next counts for each vowel based on the previous counts\n long nextCountA = countE;\n long nextCountE = (countA + countI) % MOD;\n long nextCountI = (countA + countE + countO + countU) % MOD;\n long nextCountO = (countI + countU) % MOD;\n long nextCountU = countA;\n \n // Update the counts with the newly calculated values for the next length\n countA = nextCountA;\n countE = nextCountE;\n countI = nextCountI;\n countO = nextCountO;\n countU = nextCountU;\n }\n \n // Calculate the total count of valid strings for length n\n long totalCount = (countA + countE + countI + countO + countU) % MOD;\n \n return (int)totalCount;\n }\n}\n```\n``` PHP []\nclass Solution {\n function countVowelPermutation($n) {\n // Define the modulo constant\n $MOD = 1000000007;\n\n // Initialize counts for vowels \'a\', \'e\', \'i\', \'o\', and \'u\'\n $countA = 1;\n $countE = 1;\n $countI = 1;\n $countO = 1;\n $countU = 1;\n\n // Iterate from length 1 to n - 1\n for ($length = 1; $length < $n; $length++) {\n // Calculate the next counts for each vowel based on the previous counts\n $nextCountA = $countE;\n $nextCountE = ($countA + $countI) % $MOD;\n $nextCountI = ($countA + $countE + $countO + $countU) % $MOD;\n $nextCountO = ($countI + $countU) % $MOD;\n $nextCountU = $countA;\n\n // Update the counts with the newly calculated values for the next length\n $countA = $nextCountA;\n $countE = $nextCountE;\n $countI = $nextCountI;\n $countO = $nextCountO;\n $countU = $nextCountU;\n }\n\n // Calculate the total count of valid strings for length n\n $totalCount = ($countA + $countE + $countI + $countO + $countU) % $MOD;\n\n return (int)$totalCount;\n }\n}\n```\n``` Kotlin []\nclass Solution {\n fun countVowelPermutation(n: Int): Int {\n // Define the modulo constant\n val MOD = 1000000007\n\n // Initialize counts for vowels \'a\', \'e\', \'i\', \'o\', and \'u\'\n var countA = 1L\n var countE = 1L\n var countI = 1L\n var countO = 1L\n var countU = 1L\n\n // Iterate from length 1 to n - 1\n for (length in 1 until n) {\n // Calculate the next counts for each vowel based on the previous counts\n val nextCountA = countE\n val nextCountE = (countA + countI) % MOD\n val nextCountI = (countA + countE + countO + countU) % MOD\n val nextCountO = (countI + countU) % MOD\n val nextCountU = countA\n\n // Update the counts with the newly calculated values for the next length\n countA = nextCountA\n countE = nextCountE\n countI = nextCountI\n countO = nextCountO\n countU = nextCountU\n }\n\n // Calculate the total count of valid strings for length n\n val totalCount = (countA + countE + countI + countO + countU) % MOD\n\n return totalCount.toInt()\n }\n}\n```\n\n\n---\n\n# 2nd Method : Matrix Exponentiation \uD83D\uDD25\n\n## Intuition \uD83D\uDE80:\nThe problem asks us to count the number of valid strings of length `n` using lowercase vowels (\'a\', \'e\', \'i\', \'o\', \'u\') following specific rules. To solve this efficiently, the code employs a matrix exponentiation approach, which is a dynamic programming technique. The code uses matrices to represent the state transitions between vowels and computes the count of valid strings based on these transitions. The matrix exponentiation method optimizes this process by raising the transition matrix to the power of `n - 1` to calculate the count.\n\n## Approach \uD83D\uDE80:\n\n1. **Initialize the Count Matrix:** A 1x5 matrix `count` is initialized to represent the count of each vowel (\'a\', \'e\', \'i\', \'o\', \'u\') at the beginning. This matrix starts with all counts as 1.\n\n2. **Transition Matrix \'base\':** If `n` is greater than 1, a transition matrix `base` is defined. This matrix represents the valid transitions between vowels based on the problem rules. It\'s a 5x5 matrix where each element indicates whether a transition between two vowels is valid.\n\n3. **Matrix Exponentiation:** The code uses a matrix exponentiation approach to calculate the transition matrix raised to the power of `n - 1`. The `matrixPow` function is a recursive function that optimizes matrix exponentiation by using divide-and-conquer to calculate the matrix raised to a power efficiently.\n\n4. **Matrix Multiplication:** The `matrixMul` function is used for matrix multiplication. It multiplies two matrices and calculates the result with modulo M to avoid integer overflow.\n\n5. **Final Count:** The code then multiplies the initial `count` matrix with the result of matrix exponentiation to get the final matrix `finalMatrix`, which represents the count of valid strings of length `n`. The final answer is obtained by summing up the values in the first row of `finalMatrix`.\n\n6. **Modulo Operation:** To ensure the result does not exceed the modulo value `M`, the code takes the modulo of the result.\n\n7. **Return Result:** The code returns the final result as an integer.\n\nThe approach uses matrix operations to efficiently compute the count of valid strings while following the given rules. It leverages dynamic programming and matrix exponentiation to optimize the computation, making it much faster than naive approaches.\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9Time Complexity: O(log(n) * k^3)\n- `countVowelPermutation(int n)`: The main function iterates to calculate the final result, but the most time-consuming part is the matrix exponentiation and matrix multiplication.\n - Matrix Exponentiation (`matrixPow`) has a time complexity of O(log(n)).\n - Matrix Multiplication (`matrixMul`) has a time complexity of O(k^3), where k is the dimension of the matrices, in this case, k is 5 (for the 5 vowels). The matrix multiplication is called log(n) times in the exponentiation function.\n- Overall, the time complexity is O(log(n) * k^3), where k is a constant (5 in this case).\n\n### \uD83C\uDFF9Space Complexity: O(1)\n- The space complexity is determined by the data structures used in the code:\n - `count` and `finalMatrix` are 2D arrays of size 1x5, which is constant.\n - The recursive function `matrixPow` creates several 2D arrays for intermediate calculations, but their combined space usage is also bounded by a constant.\n - `matrixMul` uses additional space for temporary arrays, but again, this space is bounded by a constant.\n- Therefore, the space complexity is O(1), as the space usage does not depend on the input value `n`.\n\n\n\n\n\n\n## Code \u2712\uFE0F\n``` Java []\nclass Solution {\n private static final int M = 1_000_000_007;\n\n public int countVowelPermutation(int n) {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n long[][] count = {{1, 1, 1, 1, 1}};\n long[][] finalMatrix;\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n if (n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n long[][] base = {\n {0, 1, 1, 0, 1},\n {1, 0, 1, 0, 0},\n {0, 1, 0, 1, 0},\n {0, 0, 1, 0, 0},\n {0, 0, 1, 1, 0}\n };\n\n // Calculate the final matrix by raising the base matrix to the power (n - 1).\n finalMatrix = matrixMul(count, matrixPow(base, n - 1));\n } else {\n finalMatrix = count; // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo M.\n long result = 0;\n for (long l : finalMatrix[0]) {\n result += l;\n }\n result %= M;\n return Math.toIntExact(result);\n }\n\n // Function to calculate the matrix raised to a power using a recursive approach.\n private long[][] matrixPow(long[][] base, int pow) {\n if (pow == 1) {\n return base;\n }\n if (pow == 2) {\n return matrixMul(base, base);\n }\n long[][] matrixPow = matrixPow(base, pow / 2);\n long[][] matrix = matrixMul(matrixPow, matrixPow);\n if (pow % 2 == 0) {\n return matrix;\n } else {\n return matrixMul(matrix, base);\n }\n }\n\n // Function to perform matrix multiplication.\n private long[][] matrixMul(long[][] a, long[][] b) {\n int ai = a.length;\n int bi = b.length;\n int bj = b[0].length;\n long[][] result = new long[ai][bj];\n for (int i = 0; i < ai; i++) {\n for (int j = 0; j < bj; j++) {\n long sum = 0;\n for (int k = 0; k < bi; k++) {\n sum += a[i][k] * b[k][j];\n sum %= M;\n }\n result[i][j] = sum;\n }\n }\n return result;\n }\n}\n```\n``` C++ []\nclass Solution {\nprivate:\n static const int M = 1\'000\'000\'007;\n\npublic:\n int countVowelPermutation(int n) {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n std::vector<std::vector<long>> count = {{1, 1, 1, 1, 1}};\n std::vector<std::vector<long>> finalMatrix;\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n if (n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n std::vector<std::vector<long>> base = {\n {0, 1, 1, 0, 1},\n {1, 0, 1, 0, 0},\n {0, 1, 0, 1, 0},\n {0, 0, 1, 0, 0},\n {0, 0, 1, 1, 0}\n };\n\n // Calculate the final matrix by raising the base matrix to the power (n - 1).\n finalMatrix = matrixPow(base, n - 1);\n finalMatrix = matrixMul(count, finalMatrix);\n } else {\n finalMatrix = count; // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo M.\n long result = 0;\n for (long l : finalMatrix[0]) {\n result += l;\n }\n result %= M;\n return static_cast<int>(result);\n }\n\nprivate:\n // Function to calculate the matrix raised to a power using a recursive approach.\n std::vector<std::vector<long>> matrixPow(const std::vector<std::vector<long>>& base, int pow) {\n if (pow == 1) {\n return base;\n }\n if (pow == 2) {\n return matrixMul(base, base);\n }\n std::vector<std::vector<long>> matrixPowResult = matrixPow(base, pow / 2);\n std::vector<std::vector<long>> matrix = matrixMul(matrixPowResult, matrixPowResult);\n if (pow % 2 == 0) {\n return matrix;\n } else {\n return matrixMul(matrix, base);\n }\n }\n\n // Function to perform matrix multiplication.\n std::vector<std::vector<long>> matrixMul(const std::vector<std::vector<long>>& a, const std::vector<std::vector<long>>& b) {\n int ai = a.size();\n int bi = b.size();\n int bj = b[0].size();\n std::vector<std::vector<long>> result(ai, std::vector<long>(bj, 0));\n for (int i = 0; i < ai; i++) {\n for (int j = 0; j < bj; j++) {\n long sum = 0;\n for (int k = 0; k < bi; k++) {\n sum += a[i][k] * b[k][j];\n sum %= M;\n }\n result[i][j] = sum;\n }\n }\n return result;\n }\n};\n\n```\n``` Python []\nclass Solution:\n M = 1_000_000_007\n\n def countVowelPermutation(self, n: int) -> int:\n # Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n count = [[1, 1, 1, 1, 1]]\n finalMatrix = []\n\n # If n is greater than 1, perform matrix operations to calculate the count.\n if n > 1:\n # Define the base transition matrix that represents the vowel transitions.\n base = [\n [0, 1, 1, 0, 1],\n [1, 0, 1, 0, 0],\n [0, 1, 0, 1, 0],\n [0, 0, 1, 0, 0],\n [0, 0, 1, 1, 0]\n ]\n\n # Calculate the final matrix by raising the base matrix to the power (n - 1).\n finalMatrix = self.matrixMul(count, self.matrixPow(base, n - 1))\n else:\n finalMatrix = count # If n is 1, the result is the same as the initial count matrix.\n\n # Calculate the result by summing up the values in the finalMatrix and taking the modulo M.\n result = 0\n for l in finalMatrix[0]:\n result += l\n result %= self.M\n return int(result)\n\n # Function to calculate the matrix raised to a power using a recursive approach.\n def matrixPow(self, base, pow):\n if pow == 1:\n return base\n if pow == 2:\n return self.matrixMul(base, base)\n matrixPow = self.matrixPow(base, pow // 2)\n matrix = self.matrixMul(matrixPow, matrixPow)\n if pow % 2 == 0:\n return matrix\n else:\n return self.matrixMul(matrix, base)\n\n # Function to perform matrix multiplication.\n def matrixMul(self, a, b):\n ai = len(a)\n bi = len(b)\n bj = len(b[0])\n result = [[0 for _ in range(bj)] for _ in range(ai)]\n for i in range(ai):\n for j in range(bj):\n sum = 0\n for k in range(bi):\n sum += a[i][k] * b[k][j]\n sum %= self.M\n result[i][j] = sum\n return result\n```\n``` JavaScript []\nvar countVowelPermutation = function(n) {\n const MOD = 1000000007;\n \n // Initialize a 2D DP array to store counts for each vowel ending at position i.\n // dp[i][j] represents the count of strings of length (i + 1) ending with vowel j.\n const dp = new Array(n).fill(0).map(() => new Array(5).fill(0));\n \n // Initialize the base case: strings of length 1 ending with each vowel are 1.\n for (let j = 0; j < 5; j++) {\n dp[0][j] = 1;\n }\n \n // Fill the DP table for strings of length 2 to n.\n for (let i = 1; i < n; i++) {\n dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % MOD; // \'a\' can follow \'e\', \'i\', or \'u\'\n dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD; // \'e\' can follow \'a\' or \'i\'\n dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % MOD; // \'i\' can follow \'e\' or \'o\'\n dp[i][3] = dp[i - 1][2]; // \'o\' can only follow \'i\'\n dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % MOD; // \'u\' can follow \'i\' or \'o\'\n }\n \n // Calculate the sum of all counts for strings of length n ending with each vowel.\n let result = 0;\n for (let j = 0; j < 5; j++) {\n result = (result + dp[n - 1][j]) % MOD;\n }\n \n return result;\n};\n\nconst n = 144;\nconsole.log(countVowelPermutation(n)); // Output: 18208803\n```\n``` PHP []\ntime limit exceed\nclass Solution {\n const MOD = 1000000007;\n\n function countVowelPermutation($n) {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n $count = array(array(1, 1, 1, 1, 1));\n $finalMatrix = array();\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n if ($n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n $base = array(\n array(0, 1, 1, 0, 1),\n array(1, 0, 1, 0, 0),\n array(0, 1, 0, 1, 0),\n array(0, 0, 1, 0, 0),\n array(0, 0, 1, 1, 0)\n );\n\n // Calculate the final matrix by raising the base matrix to the power ($n - 1).\n $finalMatrix = $this->matrixMul($count, $this->matrixPow($base, $n - 1));\n } else {\n $finalMatrix = $count; // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo MOD.\n $result = 0;\n foreach ($finalMatrix[0] as $value) {\n $result += $value;\n $result %= self::MOD;\n }\n return $result;\n }\n\n // Function to calculate the matrix raised to a power using a recursive approach.\n function matrixPow($base, $pow) {\n if ($pow == 1) {\n return $base;\n }\n if ($pow == 2) {\n return $this->matrixMul($base, $base);\n }\n $matrixPow = $this->matrixPow($base, $pow / 2);\n $matrix = $this->matrixMul($matrixPow, $matrixPow);\n if ($pow % 2 == 0) {\n return $matrix;\n } else {\n return $this->matrixMul($matrix, $base);\n }\n }\n\n // Function to perform matrix multiplication.\n function matrixMul($a, $b) {\n $ai = count($a);\n $bi = count($b);\n $bj = count($b[0]);\n $result = array();\n\n for ($i = 0; $i < $ai; $i++) {\n for ($j = 0; $j < $bj; $j++) {\n $sum = 0;\n for ($k = 0; $k < $bi; $k++) {\n $sum += $a[$i][$k] * $b[$k][$j];\n $sum %= self::MOD;\n }\n $result[$i][$j] = $sum;\n }\n }\n return $result;\n }\n}\n\n```\n``` Kotlin []\nclass Solution {\n companion object {\n const val MOD = 1_000_000_007\n }\n\n fun countVowelPermutation(n: Int): Int {\n // Initialize a count matrix with one row representing the counts of \'a\', \'e\', \'i\', \'o\', and \'u\'.\n val count = arrayOf(longArrayOf(1, 1, 1, 1, 1))\n val finalMatrix: Array<LongArray>\n\n // If n is greater than 1, perform matrix operations to calculate the count.\n finalMatrix = if (n > 1) {\n // Define the base transition matrix that represents the vowel transitions.\n val base = arrayOf(\n longArrayOf(0, 1, 1, 0, 1),\n longArrayOf(1, 0, 1, 0, 0),\n longArrayOf(0, 1, 0, 1, 0),\n longArrayOf(0, 0, 1, 0, 0),\n longArrayOf(0, 0, 1, 1, 0)\n )\n\n // Calculate the final matrix by raising the base matrix to the power (n - 1).\n matrixMul(count, matrixPow(base, n - 1))\n } else {\n count // If n is 1, the result is the same as the initial count matrix.\n }\n\n // Calculate the result by summing up the values in the finalMatrix and taking the modulo MOD.\n var result: Long = 0\n for (value in finalMatrix[0]) {\n result += value\n result %= MOD\n }\n return result.toInt()\n }\n\n // Function to calculate the matrix raised to a power using a recursive approach.\n private fun matrixPow(base: Array<LongArray>, pow: Int): Array<LongArray> {\n return when {\n pow == 1 -> base\n pow == 2 -> matrixMul(base, base)\n else -> {\n val matrixPow = matrixPow(base, pow / 2)\n val matrix = matrixMul(matrixPow, matrixPow)\n if (pow % 2 == 0) matrix else matrixMul(matrix, base)\n }\n }\n }\n\n // Function to perform matrix multiplication.\n private fun matrixMul(a: Array<LongArray>, b: Array<LongArray>): Array<LongArray> {\n val ai = a.size\n val bi = b.size\n val bj = b[0].size\n val result = Array(ai) { LongArray(bj) }\n\n for (i in 0 until ai) {\n for (j in 0 until bj) {\n var sum: Long = 0\n for (k in 0 until bi) {\n sum += a[i][k] * b[k][j]\n sum %= MOD\n }\n result[i][j] = sum\n }\n }\n return result\n }\n}\n\n```\n\n\n# Up Vote Guys\n | 43 | You are given a string `s` consisting **only** of letters `'a'` and `'b'`. In a single step you can remove one **palindromic subsequence** from `s`.
Return _the **minimum** number of steps to make the given string empty_.
A string is a **subsequence** of a given string if it is generated by deleting some characters of a given string without changing its order. Note that a subsequence does **not** necessarily need to be contiguous.
A string is called **palindrome** if is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "ababa "
**Output:** 1
**Explanation:** s is already a palindrome, so its entirety can be removed in a single step.
**Example 2:**
**Input:** s = "abb "
**Output:** 2
**Explanation:** "abb " -> "bb " -> " ".
Remove palindromic subsequence "a " then "bb ".
**Example 3:**
**Input:** s = "baabb "
**Output:** 2
**Explanation:** "baabb " -> "b " -> " ".
Remove palindromic subsequence "baab " then "b ".
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'a'` or `'b'`. | Use dynamic programming. Let dp[i][j] be the number of strings of length i that ends with the j-th vowel. Deduce the recurrence from the given relations between vowels. |
Shortest solution, enjoy | split-a-string-in-balanced-strings | 0 | 1 | \n# Code\n```\nclass Solution:\n def balancedStringSplit(self, s: str) -> int:\n count, ans = 0, 0\n\n for char in s:\n count += 1 if char == \'R\' else -1\n ans += count == 0\n\n return ans\n\n```\nplease upvote :D | 4 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Python3 O(N) - Stack Greedy Algorithm Approach beats 99.9% | split-a-string-in-balanced-strings | 0 | 1 | ```\nclass Solution:\n def balancedStringSplit(self, s: str) -> int:\n stack, result = [], 0\n \n for char in s: \n if stack == []:\n stack.append(char)\n result += 1\n elif char == stack[-1]:\n stack.append(char)\n else:\n # []\n stack.pop()\n \n return result\n``` | 3 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Python one-line (99.31%) | split-a-string-in-balanced-strings | 0 | 1 | Summary of algo:\n1) set a flag to zero and loop through characters in string;\n2) if char is `R`, add flag by 1; if char is `L`, subtract 1 from flag;\n3) add 1 to counter whenever flag is 0.\nOne-line implementation utilizing accumulate function is below. \n```\nfrom itertools import accumulate\n\nclass Solution:\n def balancedStringSplit(self, s: str) -> int:\n return list(accumulate(1 if c == "R" else -1 for c in s)).count(0)\n```\n\nEdited on 3/2/2021\n```\nclass Solution:\n def balancedStringSplit(self, s: str) -> int:\n ans = prefix = 0\n for c in s: \n prefix += 1 if c == "R" else -1\n if not prefix: ans += 1\n return ans \n``` | 44 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
Python 3 (three lines) (beats 100.00 %) | split-a-string-in-balanced-strings | 0 | 1 | _Six Line Version:_\n```\nclass Solution:\n def balancedStringSplit(self, S: str) -> int:\n m = c = 0\n for s in S:\n if s == \'L\': c += 1\n if s == \'R\': c -= 1\n if c == 0: m += 1\n return m\n\n\n```\n_Three Line Version:_\n```\nclass Solution:\n def balancedStringSplit(self, S: str) -> int:\n m, c, D = 0, 0, {\'L\':1, \'R\':-1}\n for s in S: c, m = c + D[s], m + (c == 0)\n return m\n\t\t\n\t\t\n- Junaid Mansuri | 42 | **Balanced** strings are those that have an equal quantity of `'L'` and `'R'` characters.
Given a **balanced** string `s`, split it into some number of substrings such that:
* Each substring is balanced.
Return _the **maximum** number of balanced strings you can obtain._
**Example 1:**
**Input:** s = "RLRRLLRLRL "
**Output:** 4
**Explanation:** s can be split into "RL ", "RRLL ", "RL ", "RL ", each substring contains same number of 'L' and 'R'.
**Example 2:**
**Input:** s = "RLRRRLLRLL "
**Output:** 2
**Explanation:** s can be split into "RL ", "RRRLLRLL ", each substring contains same number of 'L' and 'R'.
Note that s cannot be split into "RL ", "RR ", "RL ", "LR ", "LL ", because the 2nd and 5th substrings are not balanced.
**Example 3:**
**Input:** s = "LLLLRRRR "
**Output:** 1
**Explanation:** s can be split into "LLLLRRRR ".
**Constraints:**
* `2 <= s.length <= 1000`
* `s[i]` is either `'L'` or `'R'`.
* `s` is a **balanced** string. | Divide the array in four parts [1 - 25%] [25 - 50 %] [50 - 75 %] [75% - 100%] The answer should be in one of the ends of the intervals. In order to check which is element is the answer we can count the frequency with binarySearch. |
python || easy to understand || with comments || begineer friendly | queens-that-can-attack-the-king | 0 | 1 | ```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n board = [[\'\' for i in range(8)] for j in range(8)]\n ans = []\n \n # marking queens position on board\n for queen in queens:\n board[queen[0]][queen[1]] = \'Q\'\n \n # marking kings position on board\n board[king[0]][king[1]] = \'K\'\n \n for queen in queens:\n # function to check if a queen can target to king on board or not\n if self.canTarget(queen,king,board):\n ans.append(queen)\n return ans\n \n \n \n def canTarget(self,queen,king,board):\n q_x,q_y = queen[0],queen[1]\n \n # right side\n for i in range(q_y+1,8):\n if board[q_x][i] == \'K\':\n return True\n elif board[q_x][i] == \'Q\':\n break\n \n # left side\n for i in range(q_y-1,-1,-1):\n if board[q_x][i] == \'K\':\n return True\n elif board[q_x][i] == \'Q\':\n break\n \n # lower side\n for i in range(q_x+1,8):\n if board[i][q_y] == \'K\':\n return True\n elif board[i][q_y] == \'Q\':\n break\n \n # upper side\n for i in range(q_x-1,-1,-1):\n if board[i][q_y] == \'K\':\n return True\n elif board[i][q_y] == \'Q\':\n break\n \n # right down diagonal\n i,j = q_x+1,q_y+1\n while i<8 and j<8:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i += 1\n j += 1\n \n # left down diagonal\n i,j = q_x+1,q_y-1\n while i<8 and j>=0:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i += 1\n j -= 1\n \n # right up diagonal\n i,j = q_x-1,q_y+1\n while i>=0 and j<8:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i -= 1\n j += 1\n \n # left up diagonal\n i,j = q_x-1,q_y-1\n while i>=0 and j>=0:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i -= 1\n j -= 1\n \n # otherwise\n return False\n``` | 1 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
python || easy to understand || with comments || begineer friendly | queens-that-can-attack-the-king | 0 | 1 | ```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n board = [[\'\' for i in range(8)] for j in range(8)]\n ans = []\n \n # marking queens position on board\n for queen in queens:\n board[queen[0]][queen[1]] = \'Q\'\n \n # marking kings position on board\n board[king[0]][king[1]] = \'K\'\n \n for queen in queens:\n # function to check if a queen can target to king on board or not\n if self.canTarget(queen,king,board):\n ans.append(queen)\n return ans\n \n \n \n def canTarget(self,queen,king,board):\n q_x,q_y = queen[0],queen[1]\n \n # right side\n for i in range(q_y+1,8):\n if board[q_x][i] == \'K\':\n return True\n elif board[q_x][i] == \'Q\':\n break\n \n # left side\n for i in range(q_y-1,-1,-1):\n if board[q_x][i] == \'K\':\n return True\n elif board[q_x][i] == \'Q\':\n break\n \n # lower side\n for i in range(q_x+1,8):\n if board[i][q_y] == \'K\':\n return True\n elif board[i][q_y] == \'Q\':\n break\n \n # upper side\n for i in range(q_x-1,-1,-1):\n if board[i][q_y] == \'K\':\n return True\n elif board[i][q_y] == \'Q\':\n break\n \n # right down diagonal\n i,j = q_x+1,q_y+1\n while i<8 and j<8:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i += 1\n j += 1\n \n # left down diagonal\n i,j = q_x+1,q_y-1\n while i<8 and j>=0:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i += 1\n j -= 1\n \n # right up diagonal\n i,j = q_x-1,q_y+1\n while i>=0 and j<8:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i -= 1\n j += 1\n \n # left up diagonal\n i,j = q_x-1,q_y-1\n while i>=0 and j>=0:\n if board[i][j] == \'K\':\n return True\n elif board[i][j] == \'Q\':\n break\n i -= 1\n j -= 1\n \n # otherwise\n return False\n``` | 1 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
Easy Python Code | Long But Easy Approach ✔ | queens-that-can-attack-the-king | 0 | 1 | Python3 Solution\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n l=[]\n #to traverse in straight left of king\'s position\n for i in range(king[1],-1,-1):\n if [king[0],i] in queens:\n l.append([king[0],i])\n break\n #to traverse in straight right of king\'s position\n for i in range(king[1],8,1):\n if [king[0],i] in queens:\n l.append([king[0],i])\n break\n #to traverse staright above king\'s position\n for i in range(king[0],-1,-1):\n if [i,king[1]] in queens:\n l.append([i,king[1]])\n break\n #to traverse straight down king\'s position\n for i in range(king[0],8,1):\n if [i,king[1]] in queens:\n l.append([i,king[1]])\n break\n \n \n #to traverse diagonally right down from king\'s position\n for i in range(1,8):\n if [king[0]+i,king[1]+i] in queens:\n l.append([king[0]+i,king[1]+i])\n break\n if king[0]+i>7 or king[1]+i>7:\n break\n #to traverse diagonally left up from king\'s position\n for i in range(1,8):\n if [king[0]-i,king[1]-i] in queens:\n l.append([king[0]-i,king[1]-i])\n break\n if king[0]-i<0 or king[1]-i<0:\n break\n #to traverse diagonally right up from king\'s position \n for i in range(1,8):\n if [king[0]-i,king[1]+i] in queens:\n l.append([king[0]-i,king[1]+i])\n break\n if king[0]-i<0 or king[1]+i>7:\n break\n #to traverse diagonally left down from king\'s position\n for i in range(1,8):\n if [king[0]+i,king[1]-i] in queens:\n l.append([king[0]+i,king[1]-i]) \n break \n if king[0]+i>7 or king[1]-i<0:\n break \n\n #below code is performed to remove duplicates and then return\n ans=[]\n for i in l:\n if i not in ans:\n ans.append(i)\n return ans\n\n``` | 2 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Easy Python Code | Long But Easy Approach ✔ | queens-that-can-attack-the-king | 0 | 1 | Python3 Solution\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n l=[]\n #to traverse in straight left of king\'s position\n for i in range(king[1],-1,-1):\n if [king[0],i] in queens:\n l.append([king[0],i])\n break\n #to traverse in straight right of king\'s position\n for i in range(king[1],8,1):\n if [king[0],i] in queens:\n l.append([king[0],i])\n break\n #to traverse staright above king\'s position\n for i in range(king[0],-1,-1):\n if [i,king[1]] in queens:\n l.append([i,king[1]])\n break\n #to traverse straight down king\'s position\n for i in range(king[0],8,1):\n if [i,king[1]] in queens:\n l.append([i,king[1]])\n break\n \n \n #to traverse diagonally right down from king\'s position\n for i in range(1,8):\n if [king[0]+i,king[1]+i] in queens:\n l.append([king[0]+i,king[1]+i])\n break\n if king[0]+i>7 or king[1]+i>7:\n break\n #to traverse diagonally left up from king\'s position\n for i in range(1,8):\n if [king[0]-i,king[1]-i] in queens:\n l.append([king[0]-i,king[1]-i])\n break\n if king[0]-i<0 or king[1]-i<0:\n break\n #to traverse diagonally right up from king\'s position \n for i in range(1,8):\n if [king[0]-i,king[1]+i] in queens:\n l.append([king[0]-i,king[1]+i])\n break\n if king[0]-i<0 or king[1]+i>7:\n break\n #to traverse diagonally left down from king\'s position\n for i in range(1,8):\n if [king[0]+i,king[1]-i] in queens:\n l.append([king[0]+i,king[1]-i]) \n break \n if king[0]+i>7 or king[1]-i<0:\n break \n\n #below code is performed to remove duplicates and then return\n ans=[]\n for i in l:\n if i not in ans:\n ans.append(i)\n return ans\n\n``` | 2 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
100% faster | Moving each direction separately | Python | queens-that-can-attack-the-king | 0 | 1 | \n```\nclass Solution(object):\n def queensAttacktheKing(self, queens, king):\n ans = []\n for i in range(king[0] - 1, -1, -1):\n if [i, king[1]] in queens:\n ans.append([i, king[1]])\n break\n c1, c2 = king[0] - 1, king[1] - 1\n while c1 >= 0 and c2 >= 0:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1 -= 1\n c2 -= 1\n for i in range(king[1] - 1, -1, -1):\n if [king[0], i] in queens:\n ans.append([king[0], i])\n break\n for i in range(king[1] + 1, 8):\n if [king[0], i] in queens:\n ans.append([king[0], i])\n break\n c1, c2 = king[0] - 1, king[1] + 1\n while -1 < c1 and 8 > c2:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1, c2 = c1 - 1, c2 + 1\n c1, c2 = king[0] + 1, king[1] - 1\n while 8 > c1 and -1 < c2:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1 += 1\n c2 -= 1\n for i in range(king[0], 8):\n if [i, king[1]] in queens:\n ans.append([i, king[1]])\n break\n c1, c2 = king[0] + 1, king[1] + 1\n while 8 > c1 and 8 > c2:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1, c2 = c1 + 1, c2 + 1\n return ans\n```\n | 2 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
100% faster | Moving each direction separately | Python | queens-that-can-attack-the-king | 0 | 1 | \n```\nclass Solution(object):\n def queensAttacktheKing(self, queens, king):\n ans = []\n for i in range(king[0] - 1, -1, -1):\n if [i, king[1]] in queens:\n ans.append([i, king[1]])\n break\n c1, c2 = king[0] - 1, king[1] - 1\n while c1 >= 0 and c2 >= 0:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1 -= 1\n c2 -= 1\n for i in range(king[1] - 1, -1, -1):\n if [king[0], i] in queens:\n ans.append([king[0], i])\n break\n for i in range(king[1] + 1, 8):\n if [king[0], i] in queens:\n ans.append([king[0], i])\n break\n c1, c2 = king[0] - 1, king[1] + 1\n while -1 < c1 and 8 > c2:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1, c2 = c1 - 1, c2 + 1\n c1, c2 = king[0] + 1, king[1] - 1\n while 8 > c1 and -1 < c2:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1 += 1\n c2 -= 1\n for i in range(king[0], 8):\n if [i, king[1]] in queens:\n ans.append([i, king[1]])\n break\n c1, c2 = king[0] + 1, king[1] + 1\n while 8 > c1 and 8 > c2:\n if [c1, c2] in queens:\n ans.append([c1, c2])\n break\n c1, c2 = c1 + 1, c2 + 1\n return ans\n```\n | 2 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
Python3 simple O(N) solution with DFS (99.47% Runtime) | queens-that-can-attack-the-king | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nUtilize recursive depth first search to find all 8 directions\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initiailize a dictionary to store coordinates for queens\n- Define a recursive DFS function with delta arguments for direction\n- Perform DFS on 8 directions with delta variables and collect first encountered queen\'s coordinate on that direction\n- Return collected all valid queen coordinates\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n q = {(x,y) for x,y in queens}\n ans = []\n\n def dfs(y: int, x: int, dy: int, dx: int):\n if y < 0 or x < 0 or y >= 8 or x >= 8:\n return \n\n if (x,y) in q:\n ans.append([x,y])\n return\n\n dfs(y+dy, x+dx, dy, dx)\n\n for dy, dx in [(0, 1), (0, -1), (1, 0), (-1, 0), (1, 1), (-1, -1), (1, -1), (-1, 1)]:\n dfs(king[1]+dy, king[0]+dx, dy, dx)\n\n return ans\n``` | 0 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Python3 simple O(N) solution with DFS (99.47% Runtime) | queens-that-can-attack-the-king | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nUtilize recursive depth first search to find all 8 directions\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initiailize a dictionary to store coordinates for queens\n- Define a recursive DFS function with delta arguments for direction\n- Perform DFS on 8 directions with delta variables and collect first encountered queen\'s coordinate on that direction\n- Return collected all valid queen coordinates\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIf this solution is similar to yours or helpful, upvote me if you don\'t mind\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n q = {(x,y) for x,y in queens}\n ans = []\n\n def dfs(y: int, x: int, dy: int, dx: int):\n if y < 0 or x < 0 or y >= 8 or x >= 8:\n return \n\n if (x,y) in q:\n ans.append([x,y])\n return\n\n dfs(y+dy, x+dx, dy, dx)\n\n for dy, dx in [(0, 1), (0, -1), (1, 0), (-1, 0), (1, 1), (-1, -1), (1, -1), (-1, 1)]:\n dfs(king[1]+dy, king[0]+dx, dy, dx)\n\n return ans\n``` | 0 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
python3, sparse board beats 99.5% | queens-that-can-attack-the-king | 0 | 1 | # Intuition\na relevant queen must be either\n- in the same diagonal as the king \n- have the same x or same y position as the king\n\nin addition to that you need to check, if any other queen is standing between the queen and the king. So you need to move the queen forward, towards the king and check if it is stepping on another queen\n \n# Approach\nA sparse board representing the other queens turns out to be very fast.\n\n# Complexity\n- Time complexity:\nO(n*m*k) where n m is the size of the board and k is the number of queens\n\n- Space complexity:\nO(k) where k is the number of queens\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], k: List[int]) -> List[List[int]]:\n\n board = Solution.initBoard(queens)\n ret = []\n\n for q in queens:\n if q[0] == k[0]:\n dir_x = 0\n dir_y = 1 if q[1]<k[1] else -1 \n elif q[1] == k[1]:\n dir_y = 0\n dir_x = 1 if q[0]<k[0] else -1 \n elif abs(q[0]-k[0]) == abs(q[1] - k[1]):\n dir_x = 1 if q[0]<k[0] else -1 \n dir_y = 1 if q[1]<k[1] else -1 \n else:\n continue \n\n\n q_x = q[0]\n q_y = q[1]\n \n can_eat = True\n while True:\n q_x += dir_x\n q_y += dir_y\n\n if q_x in board and q_y in board[q_x]:\n can_eat = False\n break\n\n if q_x == k[0] and q_y == k[1]:\n break\n\n if can_eat:\n ret.append(q)\n\n return ret\n\n\n def initBoard(queens):\n board = {}\n\n for q in queens:\n mp = board.setdefault(q[0],{})\n mp[q[1]] = 1\n\n return board\n\n \n\n \n \n``` | 0 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
python3, sparse board beats 99.5% | queens-that-can-attack-the-king | 0 | 1 | # Intuition\na relevant queen must be either\n- in the same diagonal as the king \n- have the same x or same y position as the king\n\nin addition to that you need to check, if any other queen is standing between the queen and the king. So you need to move the queen forward, towards the king and check if it is stepping on another queen\n \n# Approach\nA sparse board representing the other queens turns out to be very fast.\n\n# Complexity\n- Time complexity:\nO(n*m*k) where n m is the size of the board and k is the number of queens\n\n- Space complexity:\nO(k) where k is the number of queens\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], k: List[int]) -> List[List[int]]:\n\n board = Solution.initBoard(queens)\n ret = []\n\n for q in queens:\n if q[0] == k[0]:\n dir_x = 0\n dir_y = 1 if q[1]<k[1] else -1 \n elif q[1] == k[1]:\n dir_y = 0\n dir_x = 1 if q[0]<k[0] else -1 \n elif abs(q[0]-k[0]) == abs(q[1] - k[1]):\n dir_x = 1 if q[0]<k[0] else -1 \n dir_y = 1 if q[1]<k[1] else -1 \n else:\n continue \n\n\n q_x = q[0]\n q_y = q[1]\n \n can_eat = True\n while True:\n q_x += dir_x\n q_y += dir_y\n\n if q_x in board and q_y in board[q_x]:\n can_eat = False\n break\n\n if q_x == k[0] and q_y == k[1]:\n break\n\n if can_eat:\n ret.append(q)\n\n return ret\n\n\n def initBoard(queens):\n board = {}\n\n for q in queens:\n mp = board.setdefault(q[0],{})\n mp[q[1]] = 1\n\n return board\n\n \n\n \n \n``` | 0 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
✅BFS || python | queens-that-can-attack-the-king | 0 | 1 | # Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n ans=[]\n d={}\n for l in queens:\n d[(l[0],l[1])]=1\n q=[]\n q.append([king[0],king[1],0,1])\n q.append([king[0],king[1],0,-1])\n q.append([king[0],king[1],1,0])\n q.append([king[0],king[1],-1,0])\n q.append([king[0],king[1],1,1])\n q.append([king[0],king[1],1,-1])\n q.append([king[0],king[1],-1,1])\n q.append([king[0],king[1],-1,-1])\n while(len(q)!=0):\n i,j,id,jd=q.pop()\n if(i<0 or j<0 or i==8 or j==8):continue\n if(d.get((i,j),0)):\n ans.append([i,j])\n else:\n q.append([i+id,j+jd,id,jd])\n return ans\n \n``` | 0 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
✅BFS || python | queens-that-can-attack-the-king | 0 | 1 | # Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n ans=[]\n d={}\n for l in queens:\n d[(l[0],l[1])]=1\n q=[]\n q.append([king[0],king[1],0,1])\n q.append([king[0],king[1],0,-1])\n q.append([king[0],king[1],1,0])\n q.append([king[0],king[1],-1,0])\n q.append([king[0],king[1],1,1])\n q.append([king[0],king[1],1,-1])\n q.append([king[0],king[1],-1,1])\n q.append([king[0],king[1],-1,-1])\n while(len(q)!=0):\n i,j,id,jd=q.pop()\n if(i<0 or j<0 or i==8 or j==8):continue\n if(d.get((i,j),0)):\n ans.append([i,j])\n else:\n q.append([i+id,j+jd,id,jd])\n return ans\n \n``` | 0 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
Easy to understand Python3 solution | queens-that-can-attack-the-king | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n rows, cols, diag1, diag2 = [],[],[],[]\n\n for i in range(len(queens)):\n if queens[i][0] == king[0]:\n rows.append([queens[i][0],queens[i][1]])\n if queens[i][1] == king[1]:\n cols.append([queens[i][0],queens[i][1]])\n diff0 = king[0] - queens[i][0]\n diff1 = king[1] - queens[i][1]\n\n if diff0 == diff1:\n diag1.append([queens[i][0],queens[i][1]])\n if diff0 == -1 * diff1 or diff1 == -1 * diff0:\n diag2.append([queens[i][0],queens[i][1]])\n\n \n print(rows)\n print(cols)\n print(diag1)\n print(diag2)\n\n res = []\n\n\n if len(rows) > 0:\n check = False\n\n for c in range(king[1]+1,9):\n for i,row in enumerate(rows):\n if row[1] == c:\n res.append(row)\n check = True\n break\n if check:\n break\n\n check = False\n for c in range(king[1]-1, -1, -1):\n check = False\n for i,row in enumerate(rows):\n if row[1] == c:\n res.append(row)\n check = True\n break\n if check:\n break\n \n if len(cols) > 0:\n check = False\n\n for c in range(king[0]+1,9):\n for i,col in enumerate(cols):\n if col[0] == c:\n res.append(col)\n check = True\n break\n if check:\n break\n\n check = False\n for c in range(king[0]-1, -1, -1):\n for i,col in enumerate(cols):\n if col[0] == c:\n res.append(col)\n check = True\n break\n if check:\n break\n\n if len(diag1) > 0:\n check = False\n\n for r in range(king[0]+1,9):\n for i,d1 in enumerate(diag1):\n if d1[0] == r:\n res.append(d1)\n check = True\n break\n if check:\n break\n\n check = False\n for r in range(king[0]-1, -1, -1):\n for i,d1 in enumerate(diag1):\n if d1[0] == r:\n res.append(d1)\n check = True\n break\n if check:\n break\n\n if len(diag2) > 0:\n check = False\n\n for r in range(king[0]+1,9):\n for i,d2 in enumerate(diag2):\n if d2[0] == r:\n res.append(d2)\n check = True\n break\n if check:\n break\n\n check = False\n for r in range(king[0]-1, -1, -1):\n for i,d2 in enumerate(diag2):\n if d2[0] == r:\n res.append(d2)\n check = True\n break\n if check:\n break\n \n return res\n``` | 0 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Easy to understand Python3 solution | queens-that-can-attack-the-king | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n rows, cols, diag1, diag2 = [],[],[],[]\n\n for i in range(len(queens)):\n if queens[i][0] == king[0]:\n rows.append([queens[i][0],queens[i][1]])\n if queens[i][1] == king[1]:\n cols.append([queens[i][0],queens[i][1]])\n diff0 = king[0] - queens[i][0]\n diff1 = king[1] - queens[i][1]\n\n if diff0 == diff1:\n diag1.append([queens[i][0],queens[i][1]])\n if diff0 == -1 * diff1 or diff1 == -1 * diff0:\n diag2.append([queens[i][0],queens[i][1]])\n\n \n print(rows)\n print(cols)\n print(diag1)\n print(diag2)\n\n res = []\n\n\n if len(rows) > 0:\n check = False\n\n for c in range(king[1]+1,9):\n for i,row in enumerate(rows):\n if row[1] == c:\n res.append(row)\n check = True\n break\n if check:\n break\n\n check = False\n for c in range(king[1]-1, -1, -1):\n check = False\n for i,row in enumerate(rows):\n if row[1] == c:\n res.append(row)\n check = True\n break\n if check:\n break\n \n if len(cols) > 0:\n check = False\n\n for c in range(king[0]+1,9):\n for i,col in enumerate(cols):\n if col[0] == c:\n res.append(col)\n check = True\n break\n if check:\n break\n\n check = False\n for c in range(king[0]-1, -1, -1):\n for i,col in enumerate(cols):\n if col[0] == c:\n res.append(col)\n check = True\n break\n if check:\n break\n\n if len(diag1) > 0:\n check = False\n\n for r in range(king[0]+1,9):\n for i,d1 in enumerate(diag1):\n if d1[0] == r:\n res.append(d1)\n check = True\n break\n if check:\n break\n\n check = False\n for r in range(king[0]-1, -1, -1):\n for i,d1 in enumerate(diag1):\n if d1[0] == r:\n res.append(d1)\n check = True\n break\n if check:\n break\n\n if len(diag2) > 0:\n check = False\n\n for r in range(king[0]+1,9):\n for i,d2 in enumerate(diag2):\n if d2[0] == r:\n res.append(d2)\n check = True\n break\n if check:\n break\n\n check = False\n for r in range(king[0]-1, -1, -1):\n for i,d2 in enumerate(diag2):\n if d2[0] == r:\n res.append(d2)\n check = True\n break\n if check:\n break\n \n return res\n``` | 0 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
Easy 10 Line Code |||| Must see | queens-that-can-attack-the-king | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n row,col,left=[king],[king],[king]\n final=[]\n for i in queens:\n if i[0]+i[1]==king[0]+king[1]:\n left.append(i)\n if i[0]==king[0]:\n col.append(i)\n if i[1]==king[1]:\n row.append(i)\n left.sort()\n row.sort()\n col.sort()\n if len(row)>1 and (row[0]==king or row[-1]==king):\n if row[0]==king:\n final.append(row[1])\n else:\n final.append(row[-2])\n elif len(row)>1:\n for k in range(len(row)):\n if row[k]==king:\n final.append(row[k-1])\n final.append(row[k+1])\n break\n if len(col)>1 and (col[0]==king or col[-1]==king):\n if col[0]==king:\n final.append(col[1])\n else:\n final.append(col[-2])\n elif len(col)>1:\n for k in range(len(col)):\n if col[k]==king:\n final.append(col[k-1])\n final.append(col[k+1])\n break\n if len(left)>1 and (left[0]==king or left[-1]==king):\n if left[0]==king:\n final.append(left[1])\n else:\n final.append(left[-2])\n elif len(left)>1:\n for k in range(len(left)):\n if left[k]==king:\n final.append(left[k-1])\n final.append(left[k+1])\n break\n \n right=[king]\n a = min(king[1],king[0])\n i,j=king[0]-a,king[1]-a\n while(i<8 and j<8):\n if [i,j] in queens:\n right.append([i,j])\n i=i+1\n j=j+1\n right.sort()\n if len(right)>1 and (right[0]==king or right[-1]==king):\n if right[0]==king:\n final.append(right[1])\n else:\n final.append(right[-2])\n elif len(right)>1:\n for k in range(len(right)):\n if right[k]==king:\n final.append(right[k-1])\n final.append(right[k+1])\n break\n return final\n``` | 0 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
Easy 10 Line Code |||| Must see | queens-that-can-attack-the-king | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n row,col,left=[king],[king],[king]\n final=[]\n for i in queens:\n if i[0]+i[1]==king[0]+king[1]:\n left.append(i)\n if i[0]==king[0]:\n col.append(i)\n if i[1]==king[1]:\n row.append(i)\n left.sort()\n row.sort()\n col.sort()\n if len(row)>1 and (row[0]==king or row[-1]==king):\n if row[0]==king:\n final.append(row[1])\n else:\n final.append(row[-2])\n elif len(row)>1:\n for k in range(len(row)):\n if row[k]==king:\n final.append(row[k-1])\n final.append(row[k+1])\n break\n if len(col)>1 and (col[0]==king or col[-1]==king):\n if col[0]==king:\n final.append(col[1])\n else:\n final.append(col[-2])\n elif len(col)>1:\n for k in range(len(col)):\n if col[k]==king:\n final.append(col[k-1])\n final.append(col[k+1])\n break\n if len(left)>1 and (left[0]==king or left[-1]==king):\n if left[0]==king:\n final.append(left[1])\n else:\n final.append(left[-2])\n elif len(left)>1:\n for k in range(len(left)):\n if left[k]==king:\n final.append(left[k-1])\n final.append(left[k+1])\n break\n \n right=[king]\n a = min(king[1],king[0])\n i,j=king[0]-a,king[1]-a\n while(i<8 and j<8):\n if [i,j] in queens:\n right.append([i,j])\n i=i+1\n j=j+1\n right.sort()\n if len(right)>1 and (right[0]==king or right[-1]==king):\n if right[0]==king:\n final.append(right[1])\n else:\n final.append(right[-2])\n elif len(right)>1:\n for k in range(len(right)):\n if right[k]==king:\n final.append(right[k-1])\n final.append(right[k+1])\n break\n return final\n``` | 0 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
a 13-lines readable solution with clear comment | queens-that-can-attack-the-king | 0 | 1 | # Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n # define directions\n dirs = [(-1, -1), (0, -1), (1, -1), (-1, 0), (1, 0), (-1, 1), (0, 1), (1, 1)]\n\n # set has faster search performance than list\n qs = {(q[0], q[1]) for q in queens}\n ans = []\n\n # traverse all directions\n for r, c in dirs:\n\n # initial point of current direction\n nr, nc = king[0] + r, king[1] + c\n\n # if the point still on the board, we start to move further on this direction\n while nr >= 0 and nc >= 0 and nr <= 7 and nc <= 7:\n # if we find answer on this direction, exit\n if (nr, nc) in qs:\n ans.append([nr, nc])\n break\n # move to next point on this direction\n nr += r\n nc += c\n\n return ans\n``` | 0 | On a **0-indexed** `8 x 8` chessboard, there can be multiple black queens ad one white king.
You are given a 2D integer array `queens` where `queens[i] = [xQueeni, yQueeni]` represents the position of the `ith` black queen on the chessboard. You are also given an integer array `king` of length `2` where `king = [xKing, yKing]` represents the position of the white king.
Return _the coordinates of the black queens that can directly attack the king_. You may return the answer in **any order**.
**Example 1:**
**Input:** queens = \[\[0,1\],\[1,0\],\[4,0\],\[0,4\],\[3,3\],\[2,4\]\], king = \[0,0\]
**Output:** \[\[0,1\],\[1,0\],\[3,3\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Example 2:**
**Input:** queens = \[\[0,0\],\[1,1\],\[2,2\],\[3,4\],\[3,5\],\[4,4\],\[4,5\]\], king = \[3,3\]
**Output:** \[\[2,2\],\[3,4\],\[4,4\]\]
**Explanation:** The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
**Constraints:**
* `1 <= queens.length < 64`
* `queens[i].length == king.length == 2`
* `0 <= xQueeni, yQueeni, xKing, yKing < 8`
* All the given positions are **unique**. | How to check if an interval is covered by another? Compare each interval to all others and check if it is covered by any interval. |
a 13-lines readable solution with clear comment | queens-that-can-attack-the-king | 0 | 1 | # Code\n```\nclass Solution:\n def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:\n # define directions\n dirs = [(-1, -1), (0, -1), (1, -1), (-1, 0), (1, 0), (-1, 1), (0, 1), (1, 1)]\n\n # set has faster search performance than list\n qs = {(q[0], q[1]) for q in queens}\n ans = []\n\n # traverse all directions\n for r, c in dirs:\n\n # initial point of current direction\n nr, nc = king[0] + r, king[1] + c\n\n # if the point still on the board, we start to move further on this direction\n while nr >= 0 and nc >= 0 and nr <= 7 and nc <= 7:\n # if we find answer on this direction, exit\n if (nr, nc) in qs:\n ans.append([nr, nc])\n break\n # move to next point on this direction\n nr += r\n nc += c\n\n return ans\n``` | 0 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
✔ Python3 Solution | O(n) Time & Space | DP | dice-roll-simulation | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Solution 1\n```\nclass Solution:\n def dieSimulator(self, n, A):\n dp = [[0] * 7 for _ in range(n + 1)]\n dp[0][-1] = 1\n for i in range(1, n + 1):\n for j in range(6):\n dp[i][j] = dp[i - 1][-1]\n if i > A[j]: dp[i][j] -= dp[i - A[j] - 1][-1] - dp[i - A[j] - 1][j]\n dp[i][-1] = sum(dp[i]) % (10 ** 9 + 7)\n return dp[-1][-1]\n```\n\n# Solution 2\n```\nclass Solution:\n def dieSimulator(self, n, A):\n dp = [[0] * 6 + [1]]\n for i in range(n):\n dp.append([dp[i][-1] - (dp[i - A[j]][-1] - dp[i - A[j]][j] if i >= A[j] else 0) for j in range(6)])\n dp[-1].append(sum(dp[-1]) % (10 ** 9 + 7))\n return dp[-1][-1]\n``` | 3 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
✔ Python3 Solution | O(n) Time & Space | DP | dice-roll-simulation | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Solution 1\n```\nclass Solution:\n def dieSimulator(self, n, A):\n dp = [[0] * 7 for _ in range(n + 1)]\n dp[0][-1] = 1\n for i in range(1, n + 1):\n for j in range(6):\n dp[i][j] = dp[i - 1][-1]\n if i > A[j]: dp[i][j] -= dp[i - A[j] - 1][-1] - dp[i - A[j] - 1][j]\n dp[i][-1] = sum(dp[i]) % (10 ** 9 + 7)\n return dp[-1][-1]\n```\n\n# Solution 2\n```\nclass Solution:\n def dieSimulator(self, n, A):\n dp = [[0] * 6 + [1]]\n for i in range(n):\n dp.append([dp[i][-1] - (dp[i - A[j]][-1] - dp[i - A[j]][j] if i >= A[j] else 0) for j in range(6)])\n dp[-1].append(sum(dp[-1]) % (10 ** 9 + 7))\n return dp[-1][-1]\n``` | 3 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python 3: TC O(N), SC O(N): Dynamic Programming with "rollMax Correction" | dice-roll-simulation | 0 | 1 | # Intuition\n\nMy first attempt (commented out) was a VERY brute-force top-down DFS solution. It works, but is fairly slow. Vastly slower than this solution. The reason is it\'s not very clever about avoiding the max sequence length.\n\nSo I looked at some other solutions and didn\'t understand for a while.\n\nHere\'s the major insight:\n\nFirst, suppose we know the number of *valid* sequences of `r` rolls that end with `k = 1..6`. We\'ll call it `dp[r][k]`, not to be confused with the equally glorious DPRK.\n\nThe total number of ways to end with `k` after `r` rolls are:\n* we can do `r-1` rolls that end with 1, then roll `k`: `dp[r-1][1]`\n* or we can do `r-1` rolls ending with 2, then roll `k`: `dp[r-1][1]`\n* and so on\n\n**So the total ways is `dp[r][k] = dp[r-1][1] + .. + dp[r-1][6]`. To simplify that, let\'s call that sum of `dp[r][*] == s[r]`. `s` for "sum."**\n\nBut this total includes rolling `k` `rollMax[k]+1` times in a row. So **we need to correct for (i.e. subtract) the ways to roll `k` `rollMax[k]+1` times in a row.**\n\nNow here\'s the trick: how many ways can you do `r` rolls where the last `rollMax[k]+1` are all `k`?\n\nLooks hard, but the answer is actually very similar to the total ways formula. Let `f = r-(rollMax[k]+1)`, the number of rolls before rolling `rollMax[k]+1` `k`\'s in a row. The ways to do `r` rolls ending with `rollMax[k]+1` `k`\'s in a row is:\n* **do `f` rolls, ending with any number EXCEPT `k`**\n * `s[f] - dp[f][k]`\n* **then roll `rollMax[k]+1` `k`\'s in a row:** there\'s `1` way: all `k`\'s\n* so the total number of invalid sequences is `s[f] - dp[f][k]`\n\n**And thus the answer is `dp[r][k] = s[r-1] - (s[f] - dp[f][k])`.** This is all ways, minus all invalid ways.\n\n# Approach\n\nWe could (and probably should) have separate tables for `dp[r][k]` and `s[r]`. But I was inspired by the solutions to be really clever and store everything in one table.\n\nMoreover, the `k` above are 1-indexed, but the `rollMax` array is 0-indexed.\n\nSo I did the following, inspired by other solutions:\n* make `dp[r][k]` the ways to end `r` rolls with `k+1`\n* make `dp[r][6]` be `s[r]`, the sum of `dp[r][0] + .. + dp[r][5]`\n\nThe last detail is what happens when `f == 0`, or `r == rollMax[k]+1`. Then if you\'re not careful, the correction subtracts 0 instead of 1\n* the first row of the table is all zeros because you can\'t roll 0 dice\n* but there is really 1 way to roll all `k`\'s\n\nThe subtraction is fixed by making a quick hack to the table: `dp[0][-1] = 1`. This way the `-(s[f] - dp[f][k])` correction is `-1` when `f == 0`.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Possible Space Optimization\n\nWe know that we only need to go back `rollMax[k]+1` rows to get the correction. So we really only need about `max(rollMax)` rows in the table.\n\nAn easy-ish way to do it would be to make a table with about `max(rollMax)+2` rows, and have a pointer to the current index in that shorter table. Then we can use modular arithmetic to get the index of `r` in the shorter table.\n\nIn other words, basically make the table be a ring buffer of rows.\n\n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n # # # no more than rollMax consec. times\n\n # # # probably a DP question...\n # # # suppose I know C[k], the count of sequences with k consecutive ones\n\n # # # then from C[k] we can roll\n # # # 1 in one way: -> C[k+1]\n # # # !1 in five ways -> C[0]\n\n # # # and so C[k] after the roll is the sum of C[k-1] for k >= 1\n # # # and C[0] = 5*sum(C[k]) for all k\n\n # # # we can be REALLY clever and do some in-place stuff\n # # # but here we\'ll just "toggle" a prev/curr state\n # # BIG = 10**9+7\n # # prev = [0]*(rollMax+1)\n # # prev[0] = 5\n # # prev[1] = 1 # state after 1 roll\n # # curr = [0]*(rollMax+1)\n # # for _ in range(n-1):\n # # for k in range(1, rollMax+1):\n # # curr[k] = prev[k-1] # only one way: ...1{k-1} -[1]-> ...1{k}\n # # curr[0] = 5*sum(prev) % BIG # for any number of trailing 1s, we can roll 2..6 to get 0 trailing\n\n # # curr, prev = prev, curr\n\n # # return sum(prev) % BIG\n\n\n # ##### oh no... it\'s a separate max for each number!!\n # ## DP would be really annoying, but doable - relatively giant table\n # # with all number of trailing counts for each die. Oof.\n\n # m1, m2, m3, m4, m5, m6 = rollMax\n # BIG = 10**9 + 7\n\n # # actual number of states is lower, there are 1..mk missing from any one k\n # # so the complexity is O(S*n) where s = sum(rollMax)\n\n # # top-down DFS makes this a LOT easier\n # @cache\n # def ways(n: int, r1: int, r2: int, r3: int, r4: int, r5: int, r6: int) -> int:\n # """Returns ways to roll `n` dice given we can roll rk more rolls of k"""\n\n # if n == 1:\n # return bool(r1) + bool(r2) + bool(r3) + bool(r4) + bool(r5) + bool(r6)\n\n # ans = 0\n # if r1: ans += ways(n-1, r1-1, m2, m3, m4, m5, m6)\n # if r2: ans += ways(n-1, m1, r2-1, m3, m4, m5, m6)\n # if r3: ans += ways(n-1, m1, m2, r3-1, m4, m5, m6)\n # if r4: ans += ways(n-1, m1, m2, m3, r4-1, m5, m6)\n # if r5: ans += ways(n-1, m1, m2, m3, m4, r5-1, m6)\n # if r6: ans += ways(n-1, m1, m2, m3, m4, m5, r6-1)\n # return ans % BIG\n\n # return ways(n, m1, m2, m3, m4, m5, m6)\n\n # Something about\n # > suppose we want to avoid rolling more than 3 6\'s in a row\n # > and we\'re looking at roll 8\n # > then we can apparently determine all the valid ways just from the ways to\n # roll sequences with any number of each number\n\n # dp[r][k] is number of sequences after r rolls that end with k\n\n # dp[r][k] = dp[r-1][0] + .. + dp[r-1][5] == dp[r][-1]; store sum of each row in last element\n # is mostly right, but it includes (possibly) 3-in-a-row sixes\n # ways to get 1 6 in a roll after r: roll r-1 times, then add a 6 to each non-six-terminated squence:\n # dp[r][5] = dp[r-1][0] + .. + dp[r-1][4] = dp[r-1][-1] - dp[r-1][5]\n # ways to get 2 6 in a roll after r: roll r-2 times, ending with another number, then roll 6 twice:\n # dp[r-2][-1] - dp[r-2][5]\n # ways to roll k+1 in row: dp[r-k-1][-1] - dp[r-k-1][5]\n\n BIG = 10**9 + 7\n\n dp = [[0]*7 for _ in range(n+1)]\n for k in range(6):\n dp[1][k] = 1\n dp[1][-1] = 6\n dp[0][-1] = 1 # FIX, see below, this way the "rollMax" correction\n # is correct for f==0\n\n for r in range(2, n+1):\n for k in range(6):\n dp[r][k] = dp[r-1][-1]\n if r > rollMax[k]:\n # subtract off ways to roll rollMax[k]+1 rolls of k in a row\n # the ways to do that are\n # roll r-(rollMax+1) of anything *except* k\n # then roll k rollMax+1 times in a row\n\n # FIX: if f == 0 we subtracted 0 before\n # but that\'s wrong of course because there\'s 1 way\n # to roll all k\'s. So we set dp[0][-1] to 1 as a kind of guard element\n f = r-rollMax[k]-1\n dp[r][k] -= (dp[f][-1] - dp[f][k])\n\n dp[r][-1] += dp[r][k]\n\n dp[r][-1] %= BIG\n\n return dp[n][-1]\n``` | 0 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
Python 3: TC O(N), SC O(N): Dynamic Programming with "rollMax Correction" | dice-roll-simulation | 0 | 1 | # Intuition\n\nMy first attempt (commented out) was a VERY brute-force top-down DFS solution. It works, but is fairly slow. Vastly slower than this solution. The reason is it\'s not very clever about avoiding the max sequence length.\n\nSo I looked at some other solutions and didn\'t understand for a while.\n\nHere\'s the major insight:\n\nFirst, suppose we know the number of *valid* sequences of `r` rolls that end with `k = 1..6`. We\'ll call it `dp[r][k]`, not to be confused with the equally glorious DPRK.\n\nThe total number of ways to end with `k` after `r` rolls are:\n* we can do `r-1` rolls that end with 1, then roll `k`: `dp[r-1][1]`\n* or we can do `r-1` rolls ending with 2, then roll `k`: `dp[r-1][1]`\n* and so on\n\n**So the total ways is `dp[r][k] = dp[r-1][1] + .. + dp[r-1][6]`. To simplify that, let\'s call that sum of `dp[r][*] == s[r]`. `s` for "sum."**\n\nBut this total includes rolling `k` `rollMax[k]+1` times in a row. So **we need to correct for (i.e. subtract) the ways to roll `k` `rollMax[k]+1` times in a row.**\n\nNow here\'s the trick: how many ways can you do `r` rolls where the last `rollMax[k]+1` are all `k`?\n\nLooks hard, but the answer is actually very similar to the total ways formula. Let `f = r-(rollMax[k]+1)`, the number of rolls before rolling `rollMax[k]+1` `k`\'s in a row. The ways to do `r` rolls ending with `rollMax[k]+1` `k`\'s in a row is:\n* **do `f` rolls, ending with any number EXCEPT `k`**\n * `s[f] - dp[f][k]`\n* **then roll `rollMax[k]+1` `k`\'s in a row:** there\'s `1` way: all `k`\'s\n* so the total number of invalid sequences is `s[f] - dp[f][k]`\n\n**And thus the answer is `dp[r][k] = s[r-1] - (s[f] - dp[f][k])`.** This is all ways, minus all invalid ways.\n\n# Approach\n\nWe could (and probably should) have separate tables for `dp[r][k]` and `s[r]`. But I was inspired by the solutions to be really clever and store everything in one table.\n\nMoreover, the `k` above are 1-indexed, but the `rollMax` array is 0-indexed.\n\nSo I did the following, inspired by other solutions:\n* make `dp[r][k]` the ways to end `r` rolls with `k+1`\n* make `dp[r][6]` be `s[r]`, the sum of `dp[r][0] + .. + dp[r][5]`\n\nThe last detail is what happens when `f == 0`, or `r == rollMax[k]+1`. Then if you\'re not careful, the correction subtracts 0 instead of 1\n* the first row of the table is all zeros because you can\'t roll 0 dice\n* but there is really 1 way to roll all `k`\'s\n\nThe subtraction is fixed by making a quick hack to the table: `dp[0][-1] = 1`. This way the `-(s[f] - dp[f][k])` correction is `-1` when `f == 0`.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Possible Space Optimization\n\nWe know that we only need to go back `rollMax[k]+1` rows to get the correction. So we really only need about `max(rollMax)` rows in the table.\n\nAn easy-ish way to do it would be to make a table with about `max(rollMax)+2` rows, and have a pointer to the current index in that shorter table. Then we can use modular arithmetic to get the index of `r` in the shorter table.\n\nIn other words, basically make the table be a ring buffer of rows.\n\n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n # # # no more than rollMax consec. times\n\n # # # probably a DP question...\n # # # suppose I know C[k], the count of sequences with k consecutive ones\n\n # # # then from C[k] we can roll\n # # # 1 in one way: -> C[k+1]\n # # # !1 in five ways -> C[0]\n\n # # # and so C[k] after the roll is the sum of C[k-1] for k >= 1\n # # # and C[0] = 5*sum(C[k]) for all k\n\n # # # we can be REALLY clever and do some in-place stuff\n # # # but here we\'ll just "toggle" a prev/curr state\n # # BIG = 10**9+7\n # # prev = [0]*(rollMax+1)\n # # prev[0] = 5\n # # prev[1] = 1 # state after 1 roll\n # # curr = [0]*(rollMax+1)\n # # for _ in range(n-1):\n # # for k in range(1, rollMax+1):\n # # curr[k] = prev[k-1] # only one way: ...1{k-1} -[1]-> ...1{k}\n # # curr[0] = 5*sum(prev) % BIG # for any number of trailing 1s, we can roll 2..6 to get 0 trailing\n\n # # curr, prev = prev, curr\n\n # # return sum(prev) % BIG\n\n\n # ##### oh no... it\'s a separate max for each number!!\n # ## DP would be really annoying, but doable - relatively giant table\n # # with all number of trailing counts for each die. Oof.\n\n # m1, m2, m3, m4, m5, m6 = rollMax\n # BIG = 10**9 + 7\n\n # # actual number of states is lower, there are 1..mk missing from any one k\n # # so the complexity is O(S*n) where s = sum(rollMax)\n\n # # top-down DFS makes this a LOT easier\n # @cache\n # def ways(n: int, r1: int, r2: int, r3: int, r4: int, r5: int, r6: int) -> int:\n # """Returns ways to roll `n` dice given we can roll rk more rolls of k"""\n\n # if n == 1:\n # return bool(r1) + bool(r2) + bool(r3) + bool(r4) + bool(r5) + bool(r6)\n\n # ans = 0\n # if r1: ans += ways(n-1, r1-1, m2, m3, m4, m5, m6)\n # if r2: ans += ways(n-1, m1, r2-1, m3, m4, m5, m6)\n # if r3: ans += ways(n-1, m1, m2, r3-1, m4, m5, m6)\n # if r4: ans += ways(n-1, m1, m2, m3, r4-1, m5, m6)\n # if r5: ans += ways(n-1, m1, m2, m3, m4, r5-1, m6)\n # if r6: ans += ways(n-1, m1, m2, m3, m4, m5, r6-1)\n # return ans % BIG\n\n # return ways(n, m1, m2, m3, m4, m5, m6)\n\n # Something about\n # > suppose we want to avoid rolling more than 3 6\'s in a row\n # > and we\'re looking at roll 8\n # > then we can apparently determine all the valid ways just from the ways to\n # roll sequences with any number of each number\n\n # dp[r][k] is number of sequences after r rolls that end with k\n\n # dp[r][k] = dp[r-1][0] + .. + dp[r-1][5] == dp[r][-1]; store sum of each row in last element\n # is mostly right, but it includes (possibly) 3-in-a-row sixes\n # ways to get 1 6 in a roll after r: roll r-1 times, then add a 6 to each non-six-terminated squence:\n # dp[r][5] = dp[r-1][0] + .. + dp[r-1][4] = dp[r-1][-1] - dp[r-1][5]\n # ways to get 2 6 in a roll after r: roll r-2 times, ending with another number, then roll 6 twice:\n # dp[r-2][-1] - dp[r-2][5]\n # ways to roll k+1 in row: dp[r-k-1][-1] - dp[r-k-1][5]\n\n BIG = 10**9 + 7\n\n dp = [[0]*7 for _ in range(n+1)]\n for k in range(6):\n dp[1][k] = 1\n dp[1][-1] = 6\n dp[0][-1] = 1 # FIX, see below, this way the "rollMax" correction\n # is correct for f==0\n\n for r in range(2, n+1):\n for k in range(6):\n dp[r][k] = dp[r-1][-1]\n if r > rollMax[k]:\n # subtract off ways to roll rollMax[k]+1 rolls of k in a row\n # the ways to do that are\n # roll r-(rollMax+1) of anything *except* k\n # then roll k rollMax+1 times in a row\n\n # FIX: if f == 0 we subtracted 0 before\n # but that\'s wrong of course because there\'s 1 way\n # to roll all k\'s. So we set dp[0][-1] to 1 as a kind of guard element\n f = r-rollMax[k]-1\n dp[r][k] -= (dp[f][-1] - dp[f][k])\n\n dp[r][-1] += dp[r][k]\n\n dp[r][-1] %= BIG\n\n return dp[n][-1]\n``` | 0 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
SImple DP in python3 from front to rear, O(n*max(rollMax)) | dice-roll-simulation | 0 | 1 | # Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n @cache\n def dp(pos,last,lc):\n res = 0\n if pos > n:\n return 1 #exit case\n for i in range(1,7):\n if i !=last:\n res += dp(pos+1,i,1)\n elif lc + 1 <= rollMax[i-1]:\n res += dp(pos+1,i,lc+1)\n return res % (10**9+7)\n return dp(1,None,0) % (10**9+7)\n\n\n \n \n``` | 0 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
SImple DP in python3 from front to rear, O(n*max(rollMax)) | dice-roll-simulation | 0 | 1 | # Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n @cache\n def dp(pos,last,lc):\n res = 0\n if pos > n:\n return 1 #exit case\n for i in range(1,7):\n if i !=last:\n res += dp(pos+1,i,1)\n elif lc + 1 <= rollMax[i-1]:\n res += dp(pos+1,i,lc+1)\n return res % (10**9+7)\n return dp(1,None,0) % (10**9+7)\n\n\n \n \n``` | 0 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python 3: DP Bottom Up, Tabular solution | dice-roll-simulation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n\n # let dp[i][j] be number of the cases when,\n # the it is (i + 1)th roll of dice was thrown\n # the last roll was j(0 ~ len(rollMax))\n \n mod = 10 ** 9 + 7\n faces = len(rollMax)\n dp = [[0] * (faces + 1) for _ in range(n + 1)] # last col to aggregate the sum of the combs\n\n # set base case\n dp[0][faces] = 1\n for j in range(faces):\n dp[1][j] = 1\n dp[1][faces] = faces\n\n for i in range(2, n + 1):\n total = 0\n for j in range(faces):\n for m in range(1, min(i + 1, rollMax[j] + 1)): # i = 3, rollMax[j] = 2, -> 1\n # currently ending with A is sum of, given that maximum 3 in the row;\n # AAXA - 1st back is not A\n # AXAA - 2nd back is not A(after that whatever comes)\n # XAAA - 3rd back is not A(after that whatever comes)\n dp[i][j] += (dp[i - m][faces] - dp[i - m][j]) % mod\n total += dp[i][j] % mod\n\n # agregate\n dp[i][faces] = total % mod\n return dp[n][faces]\n``` | 0 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
Python 3: DP Bottom Up, Tabular solution | dice-roll-simulation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n\n # let dp[i][j] be number of the cases when,\n # the it is (i + 1)th roll of dice was thrown\n # the last roll was j(0 ~ len(rollMax))\n \n mod = 10 ** 9 + 7\n faces = len(rollMax)\n dp = [[0] * (faces + 1) for _ in range(n + 1)] # last col to aggregate the sum of the combs\n\n # set base case\n dp[0][faces] = 1\n for j in range(faces):\n dp[1][j] = 1\n dp[1][faces] = faces\n\n for i in range(2, n + 1):\n total = 0\n for j in range(faces):\n for m in range(1, min(i + 1, rollMax[j] + 1)): # i = 3, rollMax[j] = 2, -> 1\n # currently ending with A is sum of, given that maximum 3 in the row;\n # AAXA - 1st back is not A\n # AXAA - 2nd back is not A(after that whatever comes)\n # XAAA - 3rd back is not A(after that whatever comes)\n dp[i][j] += (dp[i - m][faces] - dp[i - m][j]) % mod\n total += dp[i][j] % mod\n\n # agregate\n dp[i][faces] = total % mod\n return dp[n][faces]\n``` | 0 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Fast and space efficient solution | dice-roll-simulation | 0 | 1 | \n# Code\n```\nP = 1_000_000_007\n\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n states = [[0]*(min(mr, n)-1)+[1] for mr in rollMax]\n totals = [1]*len(rollMax)\n total = len(rollMax)\n indices = [0]*len(rollMax)\n for _ in range(n-1):\n new_total = 0\n for i, (state, x) in enumerate(zip(states, totals)):\n idx = indices[i]\n totals[i] = total - state[idx]\n totals[i] %= P\n new_total += totals[i]\n state[idx] = total - x\n indices[i] = (idx+1) % len(state)\n total = new_total % P\n return total\n\n``` | 0 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
Fast and space efficient solution | dice-roll-simulation | 0 | 1 | \n# Code\n```\nP = 1_000_000_007\n\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n states = [[0]*(min(mr, n)-1)+[1] for mr in rollMax]\n totals = [1]*len(rollMax)\n total = len(rollMax)\n indices = [0]*len(rollMax)\n for _ in range(n-1):\n new_total = 0\n for i, (state, x) in enumerate(zip(states, totals)):\n idx = indices[i]\n totals[i] = total - state[idx]\n totals[i] %= P\n new_total += totals[i]\n state[idx] = total - x\n indices[i] = (idx+1) % len(state)\n total = new_total % P\n return total\n\n``` | 0 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Dictionary DP for Space Savings | Commented and Explained | dice-roll-simulation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor any given valuation of a probability table of this nature, we care only about the appropriate prior valuations that have an impact on our current valuation. Due to this, we can memoize the results in a lookup dictionary table for rows and sides as needed. As such, we can record these and when we find we need them, go look them up. Though we do end up using the entire space, we won\'t end up calling on all of it, thus making some redundancy that could be utilized by others later on. \n\nThis also lets us limit the value storage in a non-lookup feature in one dimension. This could be useful if we find that we want to limit our on site storage for rolls and want our offsite lookup that can be much larger. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up the modulo value \nSet up rolls as an array of 1\'s with a 6 at the end for a total of 7 items\nSet prior total to 6 \nSet a prior rolls dictionary of dictionaries\nFor col in range 7 \n- set prior rolls at 0 at col to rolls at col \n\nFor r as the rth roll in range 1 to n \n- set running total to 0 \n- for s as side in range 6 \n - set roll count to r - rollMax[s] - 1 (this is the amount for this side for this roll, aka roll count) \n - if roll count >= 0 \n - rolls[s] is prior total - (prior rolls at roll count at 6 - prior rolls at roll count at side), ie, prior total minus prior rolls at roll counts total minus the contribution for this side there \n - otherwise, rolls at s is prior total - (roll count == -1) to account for off by one issues \n - increment running total by rolls at s \n - prior rolls at r at s is rolls at s \n- rolls[-1] is running total mod mod \n- prior rolls at r at 6 is rolls at -1 \n- prior total is rolls at -1 \n\nreturn rolls at -1 when done \n\n# Complexity\n- Time complexity : O(R)\n - O(R) as R > s which is 6 \n\n- Space complexity : O(R)\n - O(R) as R > s which is 6 \n\n\n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int :\n # build modulo for later use \n mod = 10**9 + 7\n # probabilities of each side for roll in range n \n # with total probability at the end \n rolls = [1, 1, 1, 1, 1, 1, 6]\n prior_total = 6\n # store only as many prior rolls as you need \n prior_rolls = collections.defaultdict(dict)\n # set up initial \n for col in range(7) : \n prior_rolls[0][col] = rolls[col]\n # for each roll you could make \n for r in range(1, n) : \n # build the running total from 0 \n running_total = 0 \n # for each side you could land on \n for s in range(6) : \n # get the roll count as r - rollmax for side - 1 \n roll_count = r - rollMax[s] - 1\n # if roll count >= 0 \n if roll_count >= 0 : \n # set rolls at roll at side to prior rolls at roll count sum minus prior rolls at roll count side \n rolls[s] = prior_total - (prior_rolls[roll_count][6] - prior_rolls[roll_count][s])\n else : \n # otherwise, rolls at roll for side is prior total - 1 if roll count is -1 \n rolls[s] = prior_total - (roll_count == -1)\n # update running total and store prior rolls for roll at side \n running_total += rolls[s]\n prior_rolls[r][s] = rolls[s]\n # get sum of roll count mod modulo value for roll sum \n rolls[-1] = running_total % mod\n # store for prior rolls and update prior total \n prior_rolls[r][6] = rolls[-1]\n prior_total = rolls[-1]\n # return rolls at -1 \n return rolls[-1]\n``` | 0 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
Dictionary DP for Space Savings | Commented and Explained | dice-roll-simulation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor any given valuation of a probability table of this nature, we care only about the appropriate prior valuations that have an impact on our current valuation. Due to this, we can memoize the results in a lookup dictionary table for rows and sides as needed. As such, we can record these and when we find we need them, go look them up. Though we do end up using the entire space, we won\'t end up calling on all of it, thus making some redundancy that could be utilized by others later on. \n\nThis also lets us limit the value storage in a non-lookup feature in one dimension. This could be useful if we find that we want to limit our on site storage for rolls and want our offsite lookup that can be much larger. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up the modulo value \nSet up rolls as an array of 1\'s with a 6 at the end for a total of 7 items\nSet prior total to 6 \nSet a prior rolls dictionary of dictionaries\nFor col in range 7 \n- set prior rolls at 0 at col to rolls at col \n\nFor r as the rth roll in range 1 to n \n- set running total to 0 \n- for s as side in range 6 \n - set roll count to r - rollMax[s] - 1 (this is the amount for this side for this roll, aka roll count) \n - if roll count >= 0 \n - rolls[s] is prior total - (prior rolls at roll count at 6 - prior rolls at roll count at side), ie, prior total minus prior rolls at roll counts total minus the contribution for this side there \n - otherwise, rolls at s is prior total - (roll count == -1) to account for off by one issues \n - increment running total by rolls at s \n - prior rolls at r at s is rolls at s \n- rolls[-1] is running total mod mod \n- prior rolls at r at 6 is rolls at -1 \n- prior total is rolls at -1 \n\nreturn rolls at -1 when done \n\n# Complexity\n- Time complexity : O(R)\n - O(R) as R > s which is 6 \n\n- Space complexity : O(R)\n - O(R) as R > s which is 6 \n\n\n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int :\n # build modulo for later use \n mod = 10**9 + 7\n # probabilities of each side for roll in range n \n # with total probability at the end \n rolls = [1, 1, 1, 1, 1, 1, 6]\n prior_total = 6\n # store only as many prior rolls as you need \n prior_rolls = collections.defaultdict(dict)\n # set up initial \n for col in range(7) : \n prior_rolls[0][col] = rolls[col]\n # for each roll you could make \n for r in range(1, n) : \n # build the running total from 0 \n running_total = 0 \n # for each side you could land on \n for s in range(6) : \n # get the roll count as r - rollmax for side - 1 \n roll_count = r - rollMax[s] - 1\n # if roll count >= 0 \n if roll_count >= 0 : \n # set rolls at roll at side to prior rolls at roll count sum minus prior rolls at roll count side \n rolls[s] = prior_total - (prior_rolls[roll_count][6] - prior_rolls[roll_count][s])\n else : \n # otherwise, rolls at roll for side is prior total - 1 if roll count is -1 \n rolls[s] = prior_total - (roll_count == -1)\n # update running total and store prior rolls for roll at side \n running_total += rolls[s]\n prior_rolls[r][s] = rolls[s]\n # get sum of roll count mod modulo value for roll sum \n rolls[-1] = running_total % mod\n # store for prior rolls and update prior total \n prior_rolls[r][6] = rolls[-1]\n prior_total = rolls[-1]\n # return rolls at -1 \n return rolls[-1]\n``` | 0 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python3 Easy Solution | dice-roll-simulation | 0 | 1 | \n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n MOD = 10 ** 9 + 7\n \n @lru_cache(None)\n def func(idx, prevNum, prevNumFreq):\n if idx == n:\n return 1\n \n ans = 0\n for i in range(1, 7):\n if i == prevNum:\n if prevNumFreq < rollMax[i - 1]:\n ans += func(idx + 1, i, prevNumFreq + 1)\n \n else:\n ans += func(idx + 1, i, 1)\n \n return ans % MOD\n \n return func(0, 0, 0)\n``` | 0 | A die simulator generates a random number from `1` to `6` for each roll. You introduced a constraint to the generator such that it cannot roll the number `i` more than `rollMax[i]` (**1-indexed**) consecutive times.
Given an array of integers `rollMax` and an integer `n`, return _the number of distinct sequences that can be obtained with exact_ `n` _rolls_. Since the answer may be too large, return it **modulo** `109 + 7`.
Two sequences are considered different if at least one element differs from each other.
**Example 1:**
**Input:** n = 2, rollMax = \[1,1,2,2,2,3\]
**Output:** 34
**Explanation:** There will be 2 rolls of die, if there are no constraints on the die, there are 6 \* 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.
**Example 2:**
**Input:** n = 2, rollMax = \[1,1,1,1,1,1\]
**Output:** 30
**Example 3:**
**Input:** n = 3, rollMax = \[1,1,1,2,2,3\]
**Output:** 181
**Constraints:**
* `1 <= n <= 5000`
* `rollMax.length == 6`
* `1 <= rollMax[i] <= 15` | How to build the graph of the cities? Connect city i with all its multiples 2*i, 3*i, ... Answer the queries using union-find data structure. |
Python3 Easy Solution | dice-roll-simulation | 0 | 1 | \n# Code\n```\nclass Solution:\n def dieSimulator(self, n: int, rollMax: List[int]) -> int:\n MOD = 10 ** 9 + 7\n \n @lru_cache(None)\n def func(idx, prevNum, prevNumFreq):\n if idx == n:\n return 1\n \n ans = 0\n for i in range(1, 7):\n if i == prevNum:\n if prevNumFreq < rollMax[i - 1]:\n ans += func(idx + 1, i, prevNumFreq + 1)\n \n else:\n ans += func(idx + 1, i, 1)\n \n return ans % MOD\n \n return func(0, 0, 0)\n``` | 0 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python easy to read and understand | hash table | maximum-equal-frequency | 0 | 1 | ```\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n cnt, freq, maxfreq, ans = collections.defaultdict(int), collections.defaultdict(int), 0, 0\n for i, num in enumerate(nums):\n cnt[num] = cnt.get(num, 0) + 1\n freq[cnt[num]] += 1\n freq[cnt[num]-1] -= 1\n maxfreq = max(maxfreq, cnt[num])\n if maxfreq == 1:\n ans = i+1\n elif maxfreq*freq[maxfreq] == i:\n ans = i+1\n elif (maxfreq-1)*(freq[maxfreq-1]+1) == i:\n ans = i+1\n return ans | 1 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
Python easy to read and understand | hash table | maximum-equal-frequency | 0 | 1 | ```\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n cnt, freq, maxfreq, ans = collections.defaultdict(int), collections.defaultdict(int), 0, 0\n for i, num in enumerate(nums):\n cnt[num] = cnt.get(num, 0) + 1\n freq[cnt[num]] += 1\n freq[cnt[num]-1] -= 1\n maxfreq = max(maxfreq, cnt[num])\n if maxfreq == 1:\n ans = i+1\n elif maxfreq*freq[maxfreq] == i:\n ans = i+1\n elif (maxfreq-1)*(freq[maxfreq-1]+1) == i:\n ans = i+1\n return ans | 1 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
1224. Maximum Equal Frequency | maximum-equal-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n cnt = Counter()\n ccnt = Counter()\n ans = mx = 0\n for i, v in enumerate(nums, 1):\n if v in cnt:\n ccnt[cnt[v]] -= 1\n cnt[v] += 1\n mx = max(mx, cnt[v])\n ccnt[cnt[v]] += 1\n if mx == 1:\n ans = i\n elif ccnt[mx] * mx + ccnt[mx - 1] * (mx - 1) == i and ccnt[mx] == 1:\n ans = i\n elif ccnt[mx] * mx + 1 == i and ccnt[1] == 1:\n ans = i\n return ans\n\n``` | 0 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
1224. Maximum Equal Frequency | maximum-equal-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n cnt = Counter()\n ccnt = Counter()\n ans = mx = 0\n for i, v in enumerate(nums, 1):\n if v in cnt:\n ccnt[cnt[v]] -= 1\n cnt[v] += 1\n mx = max(mx, cnt[v])\n ccnt[cnt[v]] += 1\n if mx == 1:\n ans = i\n elif ccnt[mx] * mx + ccnt[mx - 1] * (mx - 1) == i and ccnt[mx] == 1:\n ans = i\n elif ccnt[mx] * mx + 1 == i and ccnt[1] == 1:\n ans = i\n return ans\n\n``` | 0 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Python 3 | Solution | Beats 91.14% in runtime | maximum-equal-frequency | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n\n D = defaultdict(int)\n\n for x in nums:\n D[x] += 1\n\n l = len(nums)\n d = len(D)\n m = min(list(D.values()))\n\n for i, x in enumerate(nums[::-1]): \n \n if m*d + 1 == l or len(set(D.keys())) == 1:\n return l\n\n if m == 1:\n\n if d == 1:\n return 2\n\n arr = list(D.values())\n number = (l - 1)/(d - 1)\n if number == float(round(number)):\n number = int(number)\n\n\n if (len(set(arr)) == 2 and number in set(arr)) or (len(set(arr)) == 1 and 1 in set(arr)):\n return l\n \n D[x] -= 1\n\n if D[x] == 0:\n del D[x]\n d -= 1\n\n m = min(D.values())\n l -= 1\n\n return len(nums) - i\n\n``` | 0 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
Python 3 | Solution | Beats 91.14% in runtime | maximum-equal-frequency | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n\n D = defaultdict(int)\n\n for x in nums:\n D[x] += 1\n\n l = len(nums)\n d = len(D)\n m = min(list(D.values()))\n\n for i, x in enumerate(nums[::-1]): \n \n if m*d + 1 == l or len(set(D.keys())) == 1:\n return l\n\n if m == 1:\n\n if d == 1:\n return 2\n\n arr = list(D.values())\n number = (l - 1)/(d - 1)\n if number == float(round(number)):\n number = int(number)\n\n\n if (len(set(arr)) == 2 and number in set(arr)) or (len(set(arr)) == 1 and 1 in set(arr)):\n return l\n \n D[x] -= 1\n\n if D[x] == 0:\n del D[x]\n d -= 1\n\n m = min(D.values())\n l -= 1\n\n return len(nums) - i\n\n``` | 0 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Python - double counting trick | maximum-equal-frequency | 0 | 1 | # Intuition\nA bit different approach, more logic deduction then coding.\nCollect frequencies and count of frequencies, double counting (count of counts).\nThere are 4 cases when problem requirements are satisfied:\n#### A: single frequency\n1. if frequency is 1, it doesn\'t matter how many time it appears, when you remove one item you are either left with empty or a bunch of ones, all same.\n2. if you have 1 frequency that appears once, by removing one item, freqeuency is replaced with one lower frequency.\n#### B: two frequencies\n3. if bigger frequency appears once and and difference between bigger and smaller is 1, then by removing 1 bigger item, it can be reduced to smaller\n4. if either frequency is 1 and it appears once, it can be removed completly \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxEqualFreq(self, A: List[int]) -> int:\n count_frequencies, frequencies, result = Counter(), Counter(), 1\n\n def update_frequencies(v):\n if frequencies[v] > 0: \n count_frequencies[frequencies[v]] -= 1\n if count_frequencies[frequencies[v]] == 0: del count_frequencies[frequencies[v]]\n frequencies[v] +=1\n count_frequencies[frequencies[v]] += 1\n\n def single_reducable_frequency():\n if len(count_frequencies) == 1:\n frequency = list(count_frequencies)[0]\n if frequency == 1 or count_frequencies[frequency] == 1: return True \n return False \n \n def double_reducable_frequency():\n if len(count_frequencies) == 2:\n a, b = list(count_frequencies)\n if count_frequencies[max(a, b)] == 1 and max(a, b) - min(a, b) == 1: return True\n if (a == count_frequencies[a] == 1) or (b == count_frequencies[b] == 1): return True\n return False\n\n for i, v in enumerate(A):\n update_frequencies(v)\n if single_reducable_frequency(): result = i + 1\n if double_reducable_frequency(): result = i + 1\n return result \n``` | 0 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
Python - double counting trick | maximum-equal-frequency | 0 | 1 | # Intuition\nA bit different approach, more logic deduction then coding.\nCollect frequencies and count of frequencies, double counting (count of counts).\nThere are 4 cases when problem requirements are satisfied:\n#### A: single frequency\n1. if frequency is 1, it doesn\'t matter how many time it appears, when you remove one item you are either left with empty or a bunch of ones, all same.\n2. if you have 1 frequency that appears once, by removing one item, freqeuency is replaced with one lower frequency.\n#### B: two frequencies\n3. if bigger frequency appears once and and difference between bigger and smaller is 1, then by removing 1 bigger item, it can be reduced to smaller\n4. if either frequency is 1 and it appears once, it can be removed completly \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxEqualFreq(self, A: List[int]) -> int:\n count_frequencies, frequencies, result = Counter(), Counter(), 1\n\n def update_frequencies(v):\n if frequencies[v] > 0: \n count_frequencies[frequencies[v]] -= 1\n if count_frequencies[frequencies[v]] == 0: del count_frequencies[frequencies[v]]\n frequencies[v] +=1\n count_frequencies[frequencies[v]] += 1\n\n def single_reducable_frequency():\n if len(count_frequencies) == 1:\n frequency = list(count_frequencies)[0]\n if frequency == 1 or count_frequencies[frequency] == 1: return True \n return False \n \n def double_reducable_frequency():\n if len(count_frequencies) == 2:\n a, b = list(count_frequencies)\n if count_frequencies[max(a, b)] == 1 and max(a, b) - min(a, b) == 1: return True\n if (a == count_frequencies[a] == 1) or (b == count_frequencies[b] == 1): return True\n return False\n\n for i, v in enumerate(A):\n update_frequencies(v)\n if single_reducable_frequency(): result = i + 1\n if double_reducable_frequency(): result = i + 1\n return result \n``` | 0 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Python Easy Solution | maximum-equal-frequency | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxEqualFreq(self, A):\n count = collections.Counter()\n freq = [0 for _ in range(len(A) + 1)]\n res = 0\n for n, a in enumerate(A, 1):\n freq[count[a]] -= 1\n freq[count[a] + 1] += 1\n c = count[a] = count[a] + 1\n if freq[c] * c == n and n < len(A):\n res = n + 1\n d = n - freq[c] * c\n if d in [c + 1, 1] and freq[d] == 1:\n res = n\n return res\n``` | 0 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
Python Easy Solution | maximum-equal-frequency | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxEqualFreq(self, A):\n count = collections.Counter()\n freq = [0 for _ in range(len(A) + 1)]\n res = 0\n for n, a in enumerate(A, 1):\n freq[count[a]] -= 1\n freq[count[a] + 1] += 1\n c = count[a] = count[a] + 1\n if freq[c] * c == n and n < len(A):\n res = n + 1\n d = n - freq[c] * c\n if d in [c + 1, 1] and freq[d] == 1:\n res = n\n return res\n``` | 0 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Frequency Distribution - Clean code | maximum-equal-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe question states\n> every number that has appeared in it will have the same number of occurrences\n\nThis is a clear sign that at the core of the problem we need to keep track of the frequency of the frequencies of each number (call this `freq_dist`). To do this, we must keep track of the frequency of each number (call this num_freq`). \n\nA list will satisfy the constraints of the problem if it passes one of three cases:\n1. All the numbers have a frequency of 1\n2. A single number has a frequency of 1. The rest have a frequency of `max_num_freq`\n3. A single number has a frequency of `max_num_freq`. The rest have a frequency of `max_num_freq - 1`\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n* Enumerate the list. We are focused on the length so we will start with a count of 1.\n * We have seen a new number. Thus, we want to update our frequencies.\n * We have want to increment `num_freq`. This means that the `freq_dist` record associated with this number will be one too high. Thus, decrement it.\n * Now, we can increment the `num_freq` of this number.\n * Increment the `freq_dist` to reflect the change of `num_freq`\n * Finally, update `max_num_freq` to reflect the changes\n * Now that we have updated our `freq_dist` table, we can check if it satisfies our criteria. If the criteria is satisfied then we will save the new length to return at the end.\n * Case 1 can be evaluated by checking of the `max_num_freq` is 1.\n * Case 2 and 3 can be evaluated by using our `freq_dist` to translate our criteria into a arithmetic formula `freq_dist[single_appears] == 1 and (rest_appear * freq_dist[rest_appear] == total_size - single_appears) `\n\n# Complexity\n- Time complexity `O(n)`:\n - We are passing through the input list one time which is `O(n)`\n\n- Space complexity `O(n)`:\n - `num_freq` will store a frequency for each number in the input list. Thus, `O(n)`\n - `freq_dist` will store a frequency for every frequency in `num_freq`. This can certainly not exceed `O(n)` values. Thus, `O(n)`\n\n# Code\n```\n# On each iteration, check if the frequency distribution satisfies the constraints\n\nfrom collections import defaultdict\n\nclass Solution:\n def maxEqualFreq(self, nums: List[int]) -> int:\n num_freq = collections.defaultdict(int) # frequency of numbers\n freq_dist = collections.defaultdict(int) # distribution of frequencies\n max_num_freq = 0 # max count of numbers\n res = 0 \n\n def equation(single_appears, rest_appear, total_size):\n return freq_dist[single_appears] == 1 and (rest_appear * freq_dist[rest_appear] == total_size - single_appears) \n\n def isSatisfied(total_size):\n case_1 = (max_num_freq == 1) # All appear once.\n case_2 = equation(1, max_num_freq, total_size) # single appears once. Rest appear max_num_freq. \n case_3 = equation(max_num_freq, max_num_freq - 1, total_size) # single appears max_num_freq. Rest appear max_num_freq-1\n \n return case_1 or case_2 or case_3\n\n for length, num in enumerate(nums, 1):\n # We have a new number\n # First, decrement the freq_dist since this is now out of date\n freq_dist[num_freq[num]] -= 1\n\n # Now, increment the num_freq of this number. Remember to update the new freq_dist\n num_freq[num] += 1 \n freq_dist[num_freq[num]] += 1\n\n # Update the new max_num_freq\n max_num_freq = max(max_num_freq, num_freq[num])\n \n if isSatisfied(length):\n res = length\n return res\n\n``` | 0 | Given an array `nums` of positive integers, return the longest possible length of an array prefix of `nums`, such that it is possible to remove **exactly one** element from this prefix so that every number that has appeared in it will have the same number of occurrences.
If after removing one element there are no remaining elements, it's still considered that every appeared number has the same number of ocurrences (0).
**Example 1:**
**Input:** nums = \[2,2,1,1,5,3,3,5\]
**Output:** 7
**Explanation:** For the subarray \[2,2,1,1,5,3,3\] of length 7, if we remove nums\[4\] = 5, we will get \[2,2,1,1,3,3\], so that each number will appear exactly twice.
**Example 2:**
**Input:** nums = \[1,1,1,2,2,2,3,3,3,4,4,4,5\]
**Output:** 13
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Use dynamic programming. Let dp[i][j] be the answer for the first i rows such that column j is chosen from row i. Use the concept of cumulative array to optimize the complexity of the solution. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.