title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
python approach o(n) | k-concatenation-maximum-sum | 0 | 1 | ### sorry if my explanation isn\'t good enough but i tried my best\n# Approach\n## can be done comparing that two cases (scenarios)\n## the first case\n- we take max contineous elements from the first array\n- ommitting the first negative ones\n- we take max continous elements from the last array\n- ommitting the last negative ones\n- and take sum of the (remaining) k-2 arays as they are and sum that all\n\n## the second case \n- that if we take kadane of array for\n- at least two times to get the best sum\n- ex [1, -7, 5] k = 3\n- best case to take [5] from first\n- [1] from second and ommit the rest of the second array and the whole last array\n- if repeated k = 50 it will give the same result if concatenated the array for 50 times and computed the kadane\n- so best to optimize and copmute kadane for two only\n- and compare it with first case\n\n## the first case can be computed with help of kadane \n- for example [-1,2,-1], k = 3\n- [2,-1], [-1 , 2, -1] [-1,2]\n- so we ommitted the first negative and last negative to get the max\n- to get around that to simplify computing it will be like as\n- we added all arrays as they are and get last kadane\n- [2,-1], [-1 , 2, -1] [-1,2]\n- will be by using last technique\n- [-1,2,-1], [-1 , 2, -1] [2] it is the same but computed easily\n- we will ommitt the all arrays if sum of one is negative\n# Complexity\n- Time complexity: o(n)\n- Space complexity: o(1)\n# Code\n```\nclass Solution:\n def kConcatenationMaxSum(self, arr: List[int], k: int) -> int:\n md = 1000000007\n\n def kadane(arr, k):\n curr_sum = 0\n max_sum = 0\n for i in range(min(k, 2)):\n for j in range(len(arr)):\n curr_sum = max(curr_sum + arr[j], 0)\n max_sum = max(max_sum, curr_sum)\n return max_sum\n\n first_case = kadane(arr, 1) + max(sum(arr)*(k-1), 0)\n second_case = kadane(arr, k)\n return max(first_case, second_case) % md\n\n # the max contactenated kadane\n # can be done by either two cases and comparing that two cases\n # ### the first case\n # we take max contineous elements from the first array\n # ommitting the first negative ones\n # we take max continous elements from the last array\n # ommitting the last negative ones\n # and take sum of the k-2 arays as they are and sum that all\n\n # ### the second case \n # that if we take kadane of array for\n # at least two times to get the best sum\n # ex [1, -7, 5] k = 3\n # best case to take [5] from first\n # [1] from second and ommit the last array\n # if repeated k = 50 it will give the same result\n # so best to optimize and copmute kadane for two only\n # and compare with first case\n\n # the first case can also be done by kadane \n # for example [-1,2,-1], k = 3\n # [2,-1], [-1 , 2, -1] [-1,2]\n # so we ommitted the first negative and last negative to get the max\n # to get around that to simplify computing it will be like as\n # we added all arrays as they are and get last kadane\n # [2,-1], [-1 , 2, -1] [-1,2]\n # will be by using last technique\n # [-1,2,-1], [-1 , 2, -1] [2] it is the same but computed easily\n # we will ommitt the all arrays if sum of one is negative\n \n\n \n``` | 0 | Given an integer array `arr` and an integer `k`, modify the array by repeating it `k` times.
For example, if `arr = [1, 2]` and `k = 3` then the modified array will be `[1, 2, 1, 2, 1, 2]`.
Return the maximum sub-array sum in the modified array. Note that the length of the sub-array can be `0` and its sum in that case is `0`.
As the answer can be very large, return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[1,2\], k = 3
**Output:** 9
**Example 2:**
**Input:** arr = \[1,-2,1\], k = 5
**Output:** 2
**Example 3:**
**Input:** arr = \[-1,-2\], k = 7
**Output:** 0
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= k <= 105`
* `-104 <= arr[i] <= 104` | Find all synonymous groups of words. Use union-find data structure. By backtracking, generate all possible statements. |
python approach o(n) | k-concatenation-maximum-sum | 0 | 1 | ### sorry if my explanation isn\'t good enough but i tried my best\n# Approach\n## can be done comparing that two cases (scenarios)\n## the first case\n- we take max contineous elements from the first array\n- ommitting the first negative ones\n- we take max continous elements from the last array\n- ommitting the last negative ones\n- and take sum of the (remaining) k-2 arays as they are and sum that all\n\n## the second case \n- that if we take kadane of array for\n- at least two times to get the best sum\n- ex [1, -7, 5] k = 3\n- best case to take [5] from first\n- [1] from second and ommit the rest of the second array and the whole last array\n- if repeated k = 50 it will give the same result if concatenated the array for 50 times and computed the kadane\n- so best to optimize and copmute kadane for two only\n- and compare it with first case\n\n## the first case can be computed with help of kadane \n- for example [-1,2,-1], k = 3\n- [2,-1], [-1 , 2, -1] [-1,2]\n- so we ommitted the first negative and last negative to get the max\n- to get around that to simplify computing it will be like as\n- we added all arrays as they are and get last kadane\n- [2,-1], [-1 , 2, -1] [-1,2]\n- will be by using last technique\n- [-1,2,-1], [-1 , 2, -1] [2] it is the same but computed easily\n- we will ommitt the all arrays if sum of one is negative\n# Complexity\n- Time complexity: o(n)\n- Space complexity: o(1)\n# Code\n```\nclass Solution:\n def kConcatenationMaxSum(self, arr: List[int], k: int) -> int:\n md = 1000000007\n\n def kadane(arr, k):\n curr_sum = 0\n max_sum = 0\n for i in range(min(k, 2)):\n for j in range(len(arr)):\n curr_sum = max(curr_sum + arr[j], 0)\n max_sum = max(max_sum, curr_sum)\n return max_sum\n\n first_case = kadane(arr, 1) + max(sum(arr)*(k-1), 0)\n second_case = kadane(arr, k)\n return max(first_case, second_case) % md\n\n # the max contactenated kadane\n # can be done by either two cases and comparing that two cases\n # ### the first case\n # we take max contineous elements from the first array\n # ommitting the first negative ones\n # we take max continous elements from the last array\n # ommitting the last negative ones\n # and take sum of the k-2 arays as they are and sum that all\n\n # ### the second case \n # that if we take kadane of array for\n # at least two times to get the best sum\n # ex [1, -7, 5] k = 3\n # best case to take [5] from first\n # [1] from second and ommit the last array\n # if repeated k = 50 it will give the same result\n # so best to optimize and copmute kadane for two only\n # and compare with first case\n\n # the first case can also be done by kadane \n # for example [-1,2,-1], k = 3\n # [2,-1], [-1 , 2, -1] [-1,2]\n # so we ommitted the first negative and last negative to get the max\n # to get around that to simplify computing it will be like as\n # we added all arrays as they are and get last kadane\n # [2,-1], [-1 , 2, -1] [-1,2]\n # will be by using last technique\n # [-1,2,-1], [-1 , 2, -1] [2] it is the same but computed easily\n # we will ommitt the all arrays if sum of one is negative\n \n\n \n``` | 0 | Given an array `arr`, replace every element in that array with the greatest element among the elements to its right, and replace the last element with `-1`.
After doing so, return the array.
**Example 1:**
**Input:** arr = \[17,18,5,4,6,1\]
**Output:** \[18,6,6,6,1,-1\]
**Explanation:**
- index 0 --> the greatest element to the right of index 0 is index 1 (18).
- index 1 --> the greatest element to the right of index 1 is index 4 (6).
- index 2 --> the greatest element to the right of index 2 is index 4 (6).
- index 3 --> the greatest element to the right of index 3 is index 4 (6).
- index 4 --> the greatest element to the right of index 4 is index 5 (1).
- index 5 --> there are no elements to the right of index 5, so we put -1.
**Example 2:**
**Input:** arr = \[400\]
**Output:** \[-1\]
**Explanation:** There are no elements to the right of index 0.
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i] <= 105` | How to solve the problem for k=1 ? Use Kadane's algorithm for k=1. What are the possible cases for the answer ? The answer is the maximum between, the answer for k=1, the sum of the whole array multiplied by k, or the maximum suffix sum plus the maximum prefix sum plus (k-2) multiplied by the whole array sum for k > 1. |
Python || 92.21% Faster || Tarjan's Algorithm || Explained ||DFS | critical-connections-in-a-network | 0 | 1 | ```\nclass Solution:\n def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:\n def dfs(sv,parent,c):\n visited[sv]=1\n time[sv]=low[sv]=c\n c+=1\n for u in adj[sv]:\n if u==parent:\n continue\n if visited[u]==0:\n dfs(u,sv,c)\n low[sv]=min(low[sv],low[u])\n#if lowest insertion of adjacent node is greater than insertion time of the current node then we can say that there is a bridge\n if low[u]>time[sv]: \n bridges.append([sv,u])\n else:\n low[sv]=min(low[sv],low[u])\n \n #DFS time insertion\n time=[0 for i in range(n)] \n #min lowest time insertion of adjacent nodes apart from parent nodes\n low=[0 for i in range(n)] \n adj=[[] for i in range(n)]\n visited=[0 for i in range(n)]\n bridges=[]\n for u,v in connections:\n adj[u].append(v)\n adj[v].append(u)\n c=1\n dfs(0,-1,c)\n return bridges\n```\n\n**An upvote will be encouraging**\n | 1 | There are `n` servers numbered from `0` to `n - 1` connected by undirected server-to-server `connections` forming a network where `connections[i] = [ai, bi]` represents a connection between servers `ai` and `bi`. Any server can reach other servers directly or indirectly through the network.
A _critical connection_ is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
**Example 1:**
**Input:** n = 4, connections = \[\[0,1\],\[1,2\],\[2,0\],\[1,3\]\]
**Output:** \[\[1,3\]\]
**Explanation:** \[\[3,1\]\] is also accepted.
**Example 2:**
**Input:** n = 2, connections = \[\[0,1\]\]
**Output:** \[\[0,1\]\]
**Constraints:**
* `2 <= n <= 105`
* `n - 1 <= connections.length <= 105`
* `0 <= ai, bi <= n - 1`
* `ai != bi`
* There are no repeated connections. | After dividing the array into K+1 sub-arrays, you will pick the sub-array with the minimum sum. Divide the sub-array into K+1 sub-arrays such that the minimum sub-array sum is as maximum as possible. Use binary search with greedy check. |
Python || 92.21% Faster || Tarjan's Algorithm || Explained ||DFS | critical-connections-in-a-network | 0 | 1 | ```\nclass Solution:\n def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:\n def dfs(sv,parent,c):\n visited[sv]=1\n time[sv]=low[sv]=c\n c+=1\n for u in adj[sv]:\n if u==parent:\n continue\n if visited[u]==0:\n dfs(u,sv,c)\n low[sv]=min(low[sv],low[u])\n#if lowest insertion of adjacent node is greater than insertion time of the current node then we can say that there is a bridge\n if low[u]>time[sv]: \n bridges.append([sv,u])\n else:\n low[sv]=min(low[sv],low[u])\n \n #DFS time insertion\n time=[0 for i in range(n)] \n #min lowest time insertion of adjacent nodes apart from parent nodes\n low=[0 for i in range(n)] \n adj=[[] for i in range(n)]\n visited=[0 for i in range(n)]\n bridges=[]\n for u,v in connections:\n adj[u].append(v)\n adj[v].append(u)\n c=1\n dfs(0,-1,c)\n return bridges\n```\n\n**An upvote will be encouraging**\n | 1 | Given an integer array `arr` and a target value `target`, return the integer `value` such that when we change all the integers larger than `value` in the given array to be equal to `value`, the sum of the array gets as close as possible (in absolute difference) to `target`.
In case of a tie, return the minimum such integer.
Notice that the answer is not neccesarilly a number from `arr`.
**Example 1:**
**Input:** arr = \[4,9,3\], target = 10
**Output:** 3
**Explanation:** When using 3 arr converts to \[3, 3, 3\] which sums 9 and that's the optimal answer.
**Example 2:**
**Input:** arr = \[2,3,5\], target = 10
**Output:** 5
**Example 3:**
**Input:** arr = \[60864,25176,27249,21296,20204\], target = 56803
**Output:** 11361
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i], target <= 105` | Use Tarjan's algorithm. |
Simple - Intuitive Explanation - Beats 99% in theory as well as compute 😉[PYTHON] | critical-connections-in-a-network | 0 | 1 | # **Points to remember**\n1. About the **START**:\n\t* It\'s a continuous graph - there is a START vertex - we chose this and every other vertex can be visited/discovered by just doing Depth First Traversal from START\n\t* With respect to START every vertex will be visited/discovered/explored in the process of DFTraversal - If the graph was a straight line with no back-paths/bypass/shortcuts/cycle each node would be discovered linearly in time for e.g. if graph looked like **A**-B-C-D where we chose A to be the start 0-1-2-3 will be the respective discovery time.\n\n2. About **any other NODE** in the graph:\n\t* For any node let\'s call all its **neighbors (except parent)** its **children** and this current node to be the **parent**.\n\t* Every **parent** expects it\'s children to be **discovered later than themselves** as the parent blindly expects that the only connection with the child is of his. This parent is the only one to guide this child - That\'s what every parent expects and they do their best.\n\t* If the **expectaion meets the reality** can we say that there is no cycle (no bypass or back path from **uncle/aunt** or any **grandparent** to the child node)? \n\t* **If** expectation meets reality then its a **critical edge** - No one except the parent is there to guide this child - sure it\'s critical.\n\t* **Else** there exists other connections may be from an uncle or aunt or may be from a grandparent and that makes the connection between the parent and child not so critical.\n\n3. About **low** a.k.a **low-links** or think of them **as the distance of a single node or a cycle from START** (if there is a cycle, all nodes in the cycle will have the same low value as the node which is the entry point of the cycle - entry point w.r.t the start node)\n\n\t* **low** or **rank** are nothing but the distance from the start - a cycle is grouped and represented by all nodes in that cycle having the same low value.\n\t* Again assume if the graph is linear - a single line of nodes - the low/rank of every node will just be the discovery time of that node e.g. A-B-C-D if **A is the start** 0-1-2-3 will be the lows.\n\t* JUST FOR ILLUSTRATION - But if there is a bypass/back path or a shortcut A-**B**-C-D-**B** (here **B** is same node - I just cant draw a loop here - Please imagine \uD83D\uDE1D) then the lows would be 0-1-1-1-1 as B-C-D-B is a cycle and is grouped by all of the individual nodes having same low as the exepcted (as well as actual - it\'s same for **B**) dicovery time of **B** from the start. \n\t\n# **Critical Key**\nThe intuition is in points 2 and 3 and **use of backpropagation (return) of the low[node]** to tell the parent that what it **expects** is either right or wrong. The parent can then make the decision to add the edge (parent, child) as critical or not.\n\n1. If **expectaion meets the reality** or **actual_discovery_time_of_child >= expected_discovery_time_of_child** then the edge is critical as **no uncle or aunt or grandparent** are able to reach the child faster then the current parent.\n2. Else there is a backpath or other parent/uncle/grandparent is also conencted to the child.\n\n\n```python\n\nclass Solution:\n def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:\n \n # node is index, neighbors are in the list\n graph = [[] for i in range(n)]\n \n # build graph\n for n1, n2 in connections:\n graph[n1].append(n2)\n graph[n2].append(n1)\n \n # min_discovery_time of nodes at respective indices from start node\n # 1. default to max which is the depth of continuous graph\n lows = [n] * n\n \n # critical edges \n critical = []\n \n # args: node, node discovery_time in dfs, parent of this node\n def dfs(node, discovery_time, parent):\n \n # if the low is not yet discovered for this node\n if lows[node] == n:\n \n # 2. default it to the depth or discovery time of this node\n lows[node] = discovery_time\n \n # iterate over neighbors\n for neighbor in graph[node]:\n \n # all neighbors except parent\n if neighbor != parent:\n \n expected_discovery_time_of_child = discovery_time + 1\n actual_discovery_time_of_child = dfs(neighbor, expected_discovery_time_of_child, node)\n \n # nothing wrong - parent got what was expected => no back path\n # this step is skipped if there is a back path\n if actual_discovery_time_of_child >= expected_discovery_time_of_child:\n critical.append((node, neighbor))\n \n # low will be equal to discovery time of this node or discovery time of child\n # whichever one is minm\n # if its discovery time of child - then there is a backpath\n lows[node] = min(lows[node], actual_discovery_time_of_child)\n \n\n # return low of this node discovered previously or during this call \n return lows[node]\n \n dfs(n-1, 0, -1)\n \n return critical \n```\n\n\nLet me know if there\'s any typo/mistake or any thing is missing!!\n\nLove \u2764\uFE0F and **UPVOTE** for everyone to read - \u270C\uFE0FI\'ll add more explanations if you guys find this simple enough.. | 87 | There are `n` servers numbered from `0` to `n - 1` connected by undirected server-to-server `connections` forming a network where `connections[i] = [ai, bi]` represents a connection between servers `ai` and `bi`. Any server can reach other servers directly or indirectly through the network.
A _critical connection_ is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
**Example 1:**
**Input:** n = 4, connections = \[\[0,1\],\[1,2\],\[2,0\],\[1,3\]\]
**Output:** \[\[1,3\]\]
**Explanation:** \[\[3,1\]\] is also accepted.
**Example 2:**
**Input:** n = 2, connections = \[\[0,1\]\]
**Output:** \[\[0,1\]\]
**Constraints:**
* `2 <= n <= 105`
* `n - 1 <= connections.length <= 105`
* `0 <= ai, bi <= n - 1`
* `ai != bi`
* There are no repeated connections. | After dividing the array into K+1 sub-arrays, you will pick the sub-array with the minimum sum. Divide the sub-array into K+1 sub-arrays such that the minimum sub-array sum is as maximum as possible. Use binary search with greedy check. |
Simple - Intuitive Explanation - Beats 99% in theory as well as compute 😉[PYTHON] | critical-connections-in-a-network | 0 | 1 | # **Points to remember**\n1. About the **START**:\n\t* It\'s a continuous graph - there is a START vertex - we chose this and every other vertex can be visited/discovered by just doing Depth First Traversal from START\n\t* With respect to START every vertex will be visited/discovered/explored in the process of DFTraversal - If the graph was a straight line with no back-paths/bypass/shortcuts/cycle each node would be discovered linearly in time for e.g. if graph looked like **A**-B-C-D where we chose A to be the start 0-1-2-3 will be the respective discovery time.\n\n2. About **any other NODE** in the graph:\n\t* For any node let\'s call all its **neighbors (except parent)** its **children** and this current node to be the **parent**.\n\t* Every **parent** expects it\'s children to be **discovered later than themselves** as the parent blindly expects that the only connection with the child is of his. This parent is the only one to guide this child - That\'s what every parent expects and they do their best.\n\t* If the **expectaion meets the reality** can we say that there is no cycle (no bypass or back path from **uncle/aunt** or any **grandparent** to the child node)? \n\t* **If** expectation meets reality then its a **critical edge** - No one except the parent is there to guide this child - sure it\'s critical.\n\t* **Else** there exists other connections may be from an uncle or aunt or may be from a grandparent and that makes the connection between the parent and child not so critical.\n\n3. About **low** a.k.a **low-links** or think of them **as the distance of a single node or a cycle from START** (if there is a cycle, all nodes in the cycle will have the same low value as the node which is the entry point of the cycle - entry point w.r.t the start node)\n\n\t* **low** or **rank** are nothing but the distance from the start - a cycle is grouped and represented by all nodes in that cycle having the same low value.\n\t* Again assume if the graph is linear - a single line of nodes - the low/rank of every node will just be the discovery time of that node e.g. A-B-C-D if **A is the start** 0-1-2-3 will be the lows.\n\t* JUST FOR ILLUSTRATION - But if there is a bypass/back path or a shortcut A-**B**-C-D-**B** (here **B** is same node - I just cant draw a loop here - Please imagine \uD83D\uDE1D) then the lows would be 0-1-1-1-1 as B-C-D-B is a cycle and is grouped by all of the individual nodes having same low as the exepcted (as well as actual - it\'s same for **B**) dicovery time of **B** from the start. \n\t\n# **Critical Key**\nThe intuition is in points 2 and 3 and **use of backpropagation (return) of the low[node]** to tell the parent that what it **expects** is either right or wrong. The parent can then make the decision to add the edge (parent, child) as critical or not.\n\n1. If **expectaion meets the reality** or **actual_discovery_time_of_child >= expected_discovery_time_of_child** then the edge is critical as **no uncle or aunt or grandparent** are able to reach the child faster then the current parent.\n2. Else there is a backpath or other parent/uncle/grandparent is also conencted to the child.\n\n\n```python\n\nclass Solution:\n def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:\n \n # node is index, neighbors are in the list\n graph = [[] for i in range(n)]\n \n # build graph\n for n1, n2 in connections:\n graph[n1].append(n2)\n graph[n2].append(n1)\n \n # min_discovery_time of nodes at respective indices from start node\n # 1. default to max which is the depth of continuous graph\n lows = [n] * n\n \n # critical edges \n critical = []\n \n # args: node, node discovery_time in dfs, parent of this node\n def dfs(node, discovery_time, parent):\n \n # if the low is not yet discovered for this node\n if lows[node] == n:\n \n # 2. default it to the depth or discovery time of this node\n lows[node] = discovery_time\n \n # iterate over neighbors\n for neighbor in graph[node]:\n \n # all neighbors except parent\n if neighbor != parent:\n \n expected_discovery_time_of_child = discovery_time + 1\n actual_discovery_time_of_child = dfs(neighbor, expected_discovery_time_of_child, node)\n \n # nothing wrong - parent got what was expected => no back path\n # this step is skipped if there is a back path\n if actual_discovery_time_of_child >= expected_discovery_time_of_child:\n critical.append((node, neighbor))\n \n # low will be equal to discovery time of this node or discovery time of child\n # whichever one is minm\n # if its discovery time of child - then there is a backpath\n lows[node] = min(lows[node], actual_discovery_time_of_child)\n \n\n # return low of this node discovered previously or during this call \n return lows[node]\n \n dfs(n-1, 0, -1)\n \n return critical \n```\n\n\nLet me know if there\'s any typo/mistake or any thing is missing!!\n\nLove \u2764\uFE0F and **UPVOTE** for everyone to read - \u270C\uFE0FI\'ll add more explanations if you guys find this simple enough.. | 87 | Given an integer array `arr` and a target value `target`, return the integer `value` such that when we change all the integers larger than `value` in the given array to be equal to `value`, the sum of the array gets as close as possible (in absolute difference) to `target`.
In case of a tie, return the minimum such integer.
Notice that the answer is not neccesarilly a number from `arr`.
**Example 1:**
**Input:** arr = \[4,9,3\], target = 10
**Output:** 3
**Explanation:** When using 3 arr converts to \[3, 3, 3\] which sums 9 and that's the optimal answer.
**Example 2:**
**Input:** arr = \[2,3,5\], target = 10
**Output:** 5
**Example 3:**
**Input:** arr = \[60864,25176,27249,21296,20204\], target = 56803
**Output:** 11361
**Constraints:**
* `1 <= arr.length <= 104`
* `1 <= arr[i], target <= 105` | Use Tarjan's algorithm. |
Python 3 -> O(n log n) time and O(n) space using sort() & dictionary | minimum-absolute-difference | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\nI almost thought I won\'t be able to solve this problem. But after thinking about using dictionary, I started figuring out.\n\nApproach:\n1. To find the minimum difference among numbers, we have to subtract ith number with all the remaining numbers. This will be O(n^2) time complexity. Can we do anything in O(n log n)? Then I thought about sorting. sort() sorts in-place whereas sorted returns iterable of sorted array without modifying the array.\n2. Sorting can help me find diffirence between 2 numbers next to each other and if that\'s the minimum, then we know we are on the right track. Now we have to return the list of pairs that match this difference.\n3. What can we use to store this list and then retrieve in O(1) time? This is where dictionary came into the solution.\n\n```\ndef minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n\tminDiff = math.inf\n\tdic = collections.defaultdict(list)\n\tarr.sort() #O(n log n) time\n\t\n\tfor i in range(len(arr)-1): #O(n) time\n\t\tdiff = arr[i+1] - arr[i]\n\t\tdic[diff].append([arr[i], arr[i+1]]) #O(n) space if all the pairs have the same minimum difference\n\t\tminDiff = min(minDiff, diff)\n\treturn dic[minDiff]\n```\n\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 84 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
Python 3 -> O(n log n) time and O(n) space using sort() & dictionary | minimum-absolute-difference | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\nI almost thought I won\'t be able to solve this problem. But after thinking about using dictionary, I started figuring out.\n\nApproach:\n1. To find the minimum difference among numbers, we have to subtract ith number with all the remaining numbers. This will be O(n^2) time complexity. Can we do anything in O(n log n)? Then I thought about sorting. sort() sorts in-place whereas sorted returns iterable of sorted array without modifying the array.\n2. Sorting can help me find diffirence between 2 numbers next to each other and if that\'s the minimum, then we know we are on the right track. Now we have to return the list of pairs that match this difference.\n3. What can we use to store this list and then retrieve in O(1) time? This is where dictionary came into the solution.\n\n```\ndef minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n\tminDiff = math.inf\n\tdic = collections.defaultdict(list)\n\tarr.sort() #O(n log n) time\n\t\n\tfor i in range(len(arr)-1): #O(n) time\n\t\tdiff = arr[i+1] - arr[i]\n\t\tdic[diff].append([arr[i], arr[i+1]]) #O(n) space if all the pairs have the same minimum difference\n\t\tminDiff = min(minDiff, diff)\n\treturn dic[minDiff]\n```\n\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 84 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
easy python solution | minimum-absolute-difference | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort() # Sort the array in ascending order\n min_diff = float(\'inf\') # Initialize the minimum difference to infinity\n result = []\n\n # Calculate the minimum difference\n for i in range(1, len(arr)):\n diff = arr[i] - arr[i-1]\n if diff < min_diff:\n min_diff = diff\n\n # Find pairs with the minimum difference\n for i in range(1, len(arr)):\n diff = arr[i] - arr[i-1]\n if diff == min_diff:\n result.append([arr[i-1], arr[i]])\n\n return result\n\n``` | 1 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
easy python solution | minimum-absolute-difference | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort() # Sort the array in ascending order\n min_diff = float(\'inf\') # Initialize the minimum difference to infinity\n result = []\n\n # Calculate the minimum difference\n for i in range(1, len(arr)):\n diff = arr[i] - arr[i-1]\n if diff < min_diff:\n min_diff = diff\n\n # Find pairs with the minimum difference\n for i in range(1, len(arr)):\n diff = arr[i] - arr[i-1]\n if diff == min_diff:\n result.append([arr[i-1], arr[i]])\n\n return result\n\n``` | 1 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
✅ Beats 96.10% Solutions, ✅ Easy to understand Python solution by ✅ BOLT CODING ✅ | minimum-absolute-difference | 0 | 1 | Solution is pretty simple -- > we are using 2 loops , one to find the minimum absolute difference and 2nd to map which two differences match the minimum difference.\n\n# Complexity\n- Time complexity: O(nlog(n)) ---> as we are using only a single loop to find minimum difference and to append into list\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) ---> using a list of size n-1 (worst case)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n m = 100000000\n arr.sort()\n for i in range(len(arr)-1):\n z = arr[i+1] - arr[i]\n if z<m:\n m = z\n l = []\n for i in range(len(arr)-1):\n if arr[i+1]-arr[i] == m:\n l.append([arr[i], arr[i+1]])\n return l\n\n```\n\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 2 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
✅ Beats 96.10% Solutions, ✅ Easy to understand Python solution by ✅ BOLT CODING ✅ | minimum-absolute-difference | 0 | 1 | Solution is pretty simple -- > we are using 2 loops , one to find the minimum absolute difference and 2nd to map which two differences match the minimum difference.\n\n# Complexity\n- Time complexity: O(nlog(n)) ---> as we are using only a single loop to find minimum difference and to append into list\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) ---> using a list of size n-1 (worst case)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n m = 100000000\n arr.sort()\n for i in range(len(arr)-1):\n z = arr[i+1] - arr[i]\n if z<m:\n m = z\n l = []\n for i in range(len(arr)-1):\n if arr[i+1]-arr[i] == m:\n l.append([arr[i], arr[i+1]])\n return l\n\n```\n\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 2 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
Beats 100% (292ms), sort + single scan in Python | minimum-absolute-difference | 0 | 1 | Time complexity: sort dominates, and it\'s O(NlogN)\nSpace complexity: depends on how you implement sort, but it\'s typically O(N)\n\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort()\n res = []\n min_diff_so_far = float(\'inf\')\n for val0, val1 in zip(arr, arr[1:]):\n diff = val1 - val0\n if diff < min_diff_so_far:\n min_diff_so_far = diff\n res = [(val0, val1)]\n elif diff == min_diff_so_far:\n res.append((val0, val1))\n \n return res\n``` | 4 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
Beats 100% (292ms), sort + single scan in Python | minimum-absolute-difference | 0 | 1 | Time complexity: sort dominates, and it\'s O(NlogN)\nSpace complexity: depends on how you implement sort, but it\'s typically O(N)\n\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort()\n res = []\n min_diff_so_far = float(\'inf\')\n for val0, val1 in zip(arr, arr[1:]):\n diff = val1 - val0\n if diff < min_diff_so_far:\n min_diff_so_far = diff\n res = [(val0, val1)]\n elif diff == min_diff_so_far:\n res.append((val0, val1))\n \n return res\n``` | 4 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
Easy to Understand | Faster | Simple | Python Solution | minimum-absolute-difference | 0 | 1 | ```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort()\n m = float(\'inf\')\n out = []\n for i in range(1, len(arr)):\n prev = arr[i - 1]\n curr = abs(prev - arr[i])\n if curr < m:\n out = [[prev, arr[i]]]\n m = curr\n elif curr == m: out.append([prev, arr[i]])\n return out\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 17 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
Easy to Understand | Faster | Simple | Python Solution | minimum-absolute-difference | 0 | 1 | ```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort()\n m = float(\'inf\')\n out = []\n for i in range(1, len(arr)):\n prev = arr[i - 1]\n curr = abs(prev - arr[i])\n if curr < m:\n out = [[prev, arr[i]]]\n m = curr\n elif curr == m: out.append([prev, arr[i]])\n return out\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 17 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
✅✅✅ 98.98% faster python solution | minimum-absolute-difference | 0 | 1 | \n# Code\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n l = len(arr)\n arr.sort()\n answer = [[arr[0], arr[1]]]\n difference = arr[1]-arr[0]\n for i in range(2, l):\n if arr[i] - arr[i-1]==difference: answer.append([arr[i-1], arr[i]])\n elif arr[i] - arr[i-1]<difference: \n answer = [[arr[i-1], arr[i]]]\n difference = arr[i] - arr[i-1]\n return answer\n``` | 2 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
✅✅✅ 98.98% faster python solution | minimum-absolute-difference | 0 | 1 | \n# Code\n```\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n l = len(arr)\n arr.sort()\n answer = [[arr[0], arr[1]]]\n difference = arr[1]-arr[0]\n for i in range(2, l):\n if arr[i] - arr[i-1]==difference: answer.append([arr[i-1], arr[i]])\n elif arr[i] - arr[i-1]<difference: \n answer = [[arr[i-1], arr[i]]]\n difference = arr[i] - arr[i-1]\n return answer\n``` | 2 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
Both CPP and Python | minimum-absolute-difference | 0 | 1 | \n```CPP []\nclass Solution \n{\npublic:\n vector<vector<int>> minimumAbsDifference(vector<int>& arr) \n {\n sort(arr.begin(),arr.end());\n \n int m = INT_MAX;\n for(int i=0;i<arr.size()-1;i++)\n m = min(m,arr[i+1]-arr[i]);\n\n vector<vector<int>> ans;\n for(int i=0;i<arr.size()-1;i++)\n if(arr[i+1]-arr[i] == m)\n ans.push_back({arr[i],arr[i+1]});\n \n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort()\n m = min(arr[i+1]-arr[i] for i in range(len(arr)-1))\n return [[arr[i], arr[i+1]] for i in range(len(arr)-1) if arr[i+1]-arr[i] == m]\n```\n```Complexity\nTime complexity : O(nlogn)\nSpace complexity : O(n)\n``` | 2 | Given an array of **distinct** integers `arr`, find all pairs of elements with the minimum absolute difference of any two elements.
Return a list of pairs in ascending order(with respect to pairs), each pair `[a, b]` follows
* `a, b` are from `arr`
* `a < b`
* `b - a` equals to the minimum absolute difference of any two elements in `arr`
**Example 1:**
**Input:** arr = \[4,2,1,3\]
**Output:** \[\[1,2\],\[2,3\],\[3,4\]\]
**Explanation:** The minimum absolute difference is 1. List all pairs with difference equal to 1 in ascending order.
**Example 2:**
**Input:** arr = \[1,3,6,10,15\]
**Output:** \[\[1,3\]\]
**Example 3:**
**Input:** arr = \[3,8,-10,23,19,-4,-14,27\]
**Output:** \[\[-14,-10\],\[19,23\],\[23,27\]\]
**Constraints:**
* `2 <= arr.length <= 105`
* `-106 <= arr[i] <= 106` | Solve the problem for every interval alone. Divide the problem into cases according to the position of the two intervals. |
Both CPP and Python | minimum-absolute-difference | 0 | 1 | \n```CPP []\nclass Solution \n{\npublic:\n vector<vector<int>> minimumAbsDifference(vector<int>& arr) \n {\n sort(arr.begin(),arr.end());\n \n int m = INT_MAX;\n for(int i=0;i<arr.size()-1;i++)\n m = min(m,arr[i+1]-arr[i]);\n\n vector<vector<int>> ans;\n for(int i=0;i<arr.size()-1;i++)\n if(arr[i+1]-arr[i] == m)\n ans.push_back({arr[i],arr[i+1]});\n \n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:\n arr.sort()\n m = min(arr[i+1]-arr[i] for i in range(len(arr)-1))\n return [[arr[i], arr[i+1]] for i in range(len(arr)-1) if arr[i+1]-arr[i] == m]\n```\n```Complexity\nTime complexity : O(nlogn)\nSpace complexity : O(n)\n``` | 2 | Given an array of non-negative integers `arr`, you are initially positioned at `start` index of the array. When you are at index `i`, you can jump to `i + arr[i]` or `i - arr[i]`, check if you can reach to **any** index with value 0.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 5
**Output:** true
**Explanation:**
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
**Example 2:**
**Input:** arr = \[4,2,3,0,3,1,2\], start = 0
**Output:** true
**Explanation:**
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3
**Example 3:**
**Input:** arr = \[3,0,2,1,2\], start = 2
**Output:** false
**Explanation:** There is no way to reach at index 1 with value 0.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] < arr.length`
* `0 <= start < arr.length`
a, b are from arr a < b b - a equals to the minimum absolute difference of any two elements in arr | Find the minimum absolute difference between two elements in the array. The minimum absolute difference must be a difference between two consecutive elements in the sorted array. |
Math | ugly-number-iii | 0 | 1 | Here we count the occurence of number which are multiple of a,b,c which are less than equal to val. \nThe main principle used here is\n> **The principle of inclusion and exclusion (PIE)** is a counting technique that computes the number of elements that satisfy at least one of several properties while guaranteeing that elements satisfying more than one property are not counted twice.\n\nAn underlying idea behind PIE is that summing the number of elements that satisfy at least one of two categories and subtracting the overlap prevents double counting.\n\nSimple Formula is $$ n(A \u222A B \u222A C) = n(A) + n(B) + n(C) - n(A \u2229 B) - n(A \u2229 C) - n(B \u2229 C) + n(A \u2229 B \u2229 C) $$\n\nIt is visually easy to prove this point (See the image ) - \n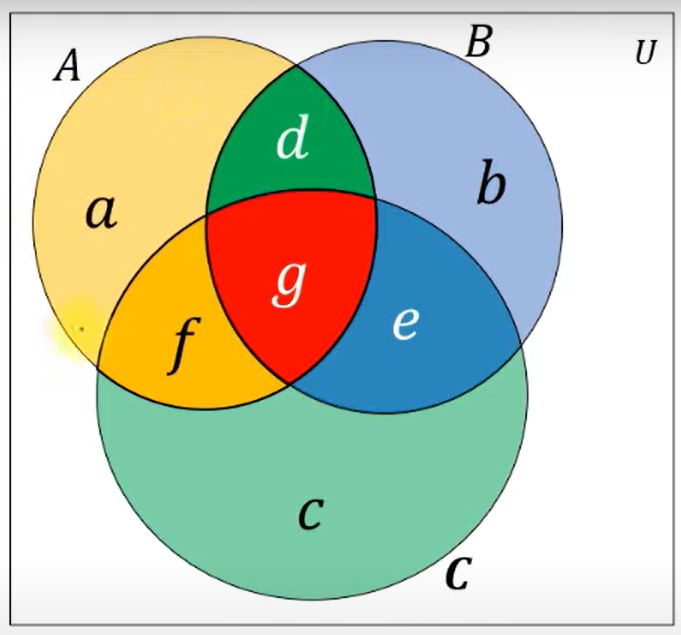\n\nA+B+C = (a+d+g+f) + (d+b+g+e) + (f+g+e+c) - (d+g) - (f+g) - (g+e) + (g)\n\nHere we have to add common part of A,B,C (i.e g) because g is added 3 times and is also subtracted 3 times \n\n>Tip: LCM(a,b) = GCD(a,b) / (a*b) is True but it is not guranteed that\nLCM(a,b,c) = GCD(a,b,c) / (a*b*c). But it is guranteed that LCM(a,b,c)=LCM(a, LCM(b,c) ) !!\n\n# Code\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n low = min(a,b,c)\n high = 2*10**9\n\n def feasible(val):\n result = val//a + val//b + val//c - val//lcm(a,b) - val//lcm(b,c) - val//lcm(a,c) + val//lcm(a,b,c)\n return result>=n\n \n while low<high:\n mid = low+high>>1\n if feasible(mid):\n high = mid\n else:\n low= mid+1\n return low\n``` | 4 | An **ugly number** is a positive integer that is divisible by `a`, `b`, or `c`.
Given four integers `n`, `a`, `b`, and `c`, return the `nth` **ugly number**.
**Example 1:**
**Input:** n = 3, a = 2, b = 3, c = 5
**Output:** 4
**Explanation:** The ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10... The 3rd is 4.
**Example 2:**
**Input:** n = 4, a = 2, b = 3, c = 4
**Output:** 6
**Explanation:** The ugly numbers are 2, 3, 4, 6, 8, 9, 10, 12... The 4th is 6.
**Example 3:**
**Input:** n = 5, a = 2, b = 11, c = 13
**Output:** 10
**Explanation:** The ugly numbers are 2, 4, 6, 8, 10, 11, 12, 13... The 5th is 10.
**Constraints:**
* `1 <= n, a, b, c <= 109`
* `1 <= a * b * c <= 1018`
* It is guaranteed that the result will be in range `[1, 2 * 109]`. | Traverse the tree using depth first search. Find for every node the sum of values of its sub-tree. Traverse the tree again from the root and return once you reach a node with zero sum of values in its sub-tree. |
Math | ugly-number-iii | 0 | 1 | Here we count the occurence of number which are multiple of a,b,c which are less than equal to val. \nThe main principle used here is\n> **The principle of inclusion and exclusion (PIE)** is a counting technique that computes the number of elements that satisfy at least one of several properties while guaranteeing that elements satisfying more than one property are not counted twice.\n\nAn underlying idea behind PIE is that summing the number of elements that satisfy at least one of two categories and subtracting the overlap prevents double counting.\n\nSimple Formula is $$ n(A \u222A B \u222A C) = n(A) + n(B) + n(C) - n(A \u2229 B) - n(A \u2229 C) - n(B \u2229 C) + n(A \u2229 B \u2229 C) $$\n\nIt is visually easy to prove this point (See the image ) - \n\n\nA+B+C = (a+d+g+f) + (d+b+g+e) + (f+g+e+c) - (d+g) - (f+g) - (g+e) + (g)\n\nHere we have to add common part of A,B,C (i.e g) because g is added 3 times and is also subtracted 3 times \n\n>Tip: LCM(a,b) = GCD(a,b) / (a*b) is True but it is not guranteed that\nLCM(a,b,c) = GCD(a,b,c) / (a*b*c). But it is guranteed that LCM(a,b,c)=LCM(a, LCM(b,c) ) !!\n\n# Code\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n low = min(a,b,c)\n high = 2*10**9\n\n def feasible(val):\n result = val//a + val//b + val//c - val//lcm(a,b) - val//lcm(b,c) - val//lcm(a,c) + val//lcm(a,b,c)\n return result>=n\n \n while low<high:\n mid = low+high>>1\n if feasible(mid):\n high = mid\n else:\n low= mid+1\n return low\n``` | 4 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
[Python3] inconsistent definition of "ugly numbers" | ugly-number-iii | 0 | 1 | The term "ugly number" seems to reflect a poorly-defined concept. Upon Googling it, I can only find it in a few places such as LC, GFG, etc. Even in the few posts on LC, the concept varies. For example, in [263. Ugly Number](https://leetcode.com/problems/ugly-number/), an ugly number is a positive integer whose only factors are 2, 3 and 5, but 1 is treated as an ugly number. This definition is consistent with that of [264. Ugly Number II](https://leetcode.com/problems/ugly-number-ii/). But in [1201. Ugly Number III](https://leetcode.com/problems/ugly-number-iii/), ugly number becomes positive integers divisible by given factors (let\'s still use 2, 3, 5 unless stated otherwise), and 1 is not considered ugly any more. \n\nLet\'s refer to the definition in 263 and 264 "Def 1" and the definition in 1201 "Def 2". Under Def 1, the first few ugly numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, ... while under Def 2 the first few ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, ... . The similarity is obvious at first glance. But if you look deeper, a fundamental difference can be revealed. Namely, under Def 1, ugly number is self-generated, i.e. large ugly numbers are generated by multiplying factors with small ugly numbers. Because of this, ugly numbers become rarer as number becomes larger. However, under Def 2, ugly numbers are periodic. The pattern repeats when least common multiple is reached. \n\nTo reflect the "self-generating" property of ugly number under Def 1, 263 and 264 can be solved using dynamic programming. For example, this [post](https://leetcode.com/problems/ugly-number/discuss/719320/Python3-4-line-concise) and this [post](https://leetcode.com/problems/ugly-number-ii/discuss/720034/Python3-7-line-dp) implement the solution using top-down approach. But 1201 needs to be solved in a completely different way. In the spirit of this difference, I think it is more confusing than helpful to put 1201 in the ugly number series. It is probably clearer if this is treated as a completely independent problem. \n\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n # inclusion-exclusion principle\n ab = a*b//gcd(a, b)\n bc = b*c//gcd(b, c)\n ca = c*a//gcd(c, a)\n abc = ab*c//gcd(ab, c)\n \n lo, hi = 1, n*min(a, b, c)\n while lo < hi: \n mid = lo + hi >> 1\n if mid//a + mid//b + mid//c - mid//ab - mid//bc - mid//ca + mid//abc < n: lo = mid + 1\n else: hi = mid \n return lo \n``` | 39 | An **ugly number** is a positive integer that is divisible by `a`, `b`, or `c`.
Given four integers `n`, `a`, `b`, and `c`, return the `nth` **ugly number**.
**Example 1:**
**Input:** n = 3, a = 2, b = 3, c = 5
**Output:** 4
**Explanation:** The ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10... The 3rd is 4.
**Example 2:**
**Input:** n = 4, a = 2, b = 3, c = 4
**Output:** 6
**Explanation:** The ugly numbers are 2, 3, 4, 6, 8, 9, 10, 12... The 4th is 6.
**Example 3:**
**Input:** n = 5, a = 2, b = 11, c = 13
**Output:** 10
**Explanation:** The ugly numbers are 2, 4, 6, 8, 10, 11, 12, 13... The 5th is 10.
**Constraints:**
* `1 <= n, a, b, c <= 109`
* `1 <= a * b * c <= 1018`
* It is guaranteed that the result will be in range `[1, 2 * 109]`. | Traverse the tree using depth first search. Find for every node the sum of values of its sub-tree. Traverse the tree again from the root and return once you reach a node with zero sum of values in its sub-tree. |
[Python3] inconsistent definition of "ugly numbers" | ugly-number-iii | 0 | 1 | The term "ugly number" seems to reflect a poorly-defined concept. Upon Googling it, I can only find it in a few places such as LC, GFG, etc. Even in the few posts on LC, the concept varies. For example, in [263. Ugly Number](https://leetcode.com/problems/ugly-number/), an ugly number is a positive integer whose only factors are 2, 3 and 5, but 1 is treated as an ugly number. This definition is consistent with that of [264. Ugly Number II](https://leetcode.com/problems/ugly-number-ii/). But in [1201. Ugly Number III](https://leetcode.com/problems/ugly-number-iii/), ugly number becomes positive integers divisible by given factors (let\'s still use 2, 3, 5 unless stated otherwise), and 1 is not considered ugly any more. \n\nLet\'s refer to the definition in 263 and 264 "Def 1" and the definition in 1201 "Def 2". Under Def 1, the first few ugly numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, ... while under Def 2 the first few ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, ... . The similarity is obvious at first glance. But if you look deeper, a fundamental difference can be revealed. Namely, under Def 1, ugly number is self-generated, i.e. large ugly numbers are generated by multiplying factors with small ugly numbers. Because of this, ugly numbers become rarer as number becomes larger. However, under Def 2, ugly numbers are periodic. The pattern repeats when least common multiple is reached. \n\nTo reflect the "self-generating" property of ugly number under Def 1, 263 and 264 can be solved using dynamic programming. For example, this [post](https://leetcode.com/problems/ugly-number/discuss/719320/Python3-4-line-concise) and this [post](https://leetcode.com/problems/ugly-number-ii/discuss/720034/Python3-7-line-dp) implement the solution using top-down approach. But 1201 needs to be solved in a completely different way. In the spirit of this difference, I think it is more confusing than helpful to put 1201 in the ugly number series. It is probably clearer if this is treated as a completely independent problem. \n\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n # inclusion-exclusion principle\n ab = a*b//gcd(a, b)\n bc = b*c//gcd(b, c)\n ca = c*a//gcd(c, a)\n abc = ab*c//gcd(ab, c)\n \n lo, hi = 1, n*min(a, b, c)\n while lo < hi: \n mid = lo + hi >> 1\n if mid//a + mid//b + mid//c - mid//ab - mid//bc - mid//ca + mid//abc < n: lo = mid + 1\n else: hi = mid \n return lo \n``` | 39 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
PYTHON | BRUTE FORCE TO OPTIMZIED SOL | FULL DETAILED EXPLANATION| | ugly-number-iii | 0 | 1 | \n# EXPLANATION BRUTE FORCE\n```\nBrute force is trying each number from 1 untill we get our nth ugly number\nNow we can improve this approach by using the idea that we need to get the nth ugly number which is divisible by a,b,or c\n\nSo we make a list of size 3 "times = [1,1,1]" having all values as 1 indicating the current number \nusing number a,b,c, respectively\n\nNow we find the smallest number which will be minimum of \n( times[0] * a, times[1] * b , times[c] * c )\n\nTHE smallest one can also occur by more than 1 source that is 2,3 may collide at 6\nso we traverse the list and compare the smallest with times[0]*a , times[1]*b and times[2]*c and if smallest is equal to it we increment times[i] by 1 making the number its next occurence\n\n```\n\n\n# CODE ( UNOPTIMIZED / BRUTE FORCE + )\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n times = [1,1,1]\n smallest = inf\n while n != 0:\n smallest = min ( times[0]*a,times[1]*b,times[2]*c)\n if times[0]*a == smallest: times[0] += 1\n if times[1]*b == smallest: times[1] += 1\n if times[2]*c == smallest: times[2] += 1\n n -= 1\n return smallest\n```\n\n# EXPLANATION BINARY SEARCH + VENN DIAGRAM\n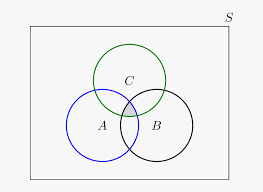\n\na \u2229 b \u2229 c = a \u222A b + a \u222A c + b \u222A c - a \u2229 b - a \u2229 c - b \u2229 c + a \u2229 b \u2229 c\n\n```\nLets say we have a = 2 , b = 3, c = 5 , n = 10\nNow the number must lie between the first occurence = min(a,b,c) i.e. 2\nand the n th occurence in case of no collision = min(a,b,c) * n i.e. 20\nas 2 , 4, 6 , 8 ,10 ,12 , 14 , 16 18 ,20 will lead to 10th ugly number is b,c do not collide\n\nNow since we know the range ... how can we decide to choose the left half or the right half\n... The main logic of binary search\n\nSee if we get to know the count of ugly numbers till mid we can decide which way to walk\n\nSO the question is how to find the count\n\n\nSay numbers a = 2 , b = 3 , c = 5 , n = 10\nlow = 2\nhigh = 20\nmid = 11\n\nNow we need to find the count of ugly numbers till 11........\nremember the formula\na \u2229 b \u2229 c = a \u222A b + a \u222A c + b \u222A c - a \u2229 b - a \u2229 c - b \u2229 c + a \u2229 b \u2229 c\n\nhow many 2s will occur till 11 = 11 // 2 = 5 ( 2,4,6,8,10)\nhow many 3s will occur till 11 = 11 // 3 = 3 ( 3,6,9)\nhow many 5s will occur till 11 = 11 // 5 = 2 ( 5,10)\nnow 2,3 may collide so we count them as\n11 // (lcm 2,3) = 11 // 6 = 1 (6)\nnow 2,5 may collide so we count them as\n11 // (lcm 2,5) = 11 // 10 = 1(10)\nnow 3,5 may collide so we count them as\n11 // (lcm 3,5) = 11 // 15 = 0 \nnow we may have count collision of (2,3) and (2,5) but it should be counted once as (2,3,5)\nso we have to add 11 // (lcm 2,3,5) = 11// 30 = 0\n\nSo according to our formula total count = 5 + 3 + 2 - 1 - 1 - 0 + 0 = 8\n(2,4,6,8,10) + ( 3,6,9) + (5,10) - (6) - (10) - ( ) + ( ) = (2,3,4,5,6,8,9,10)\n\nNow since the count is 8 and we need 10th ugly number we should go right\n\n\n\n\nTO GET LCM of two numbers:\n\tLCM(a,b) * HCF(a,b) = a*b\n\t\nTO GET LCM of three numbers:\n\tLCM(a,b,c) = a*b*c*HCF(a,b,c) // HCF(a,b) * HCF(b,c) * HCF(a,c)\n```\n# CODE ( BINARY SEARCH )\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n a,b,c = sorted((a,b,c))\n ans = inf\n def hcf(a,b):\n if a %b == 0: return b\n return hcf(b , a % b)\n p,q,r= hcf(a,b),hcf(b,c),hcf(a,c)\n s = hcf(r,b)\n x1 = (a*b) // p\n x2 = (b*c) // q \n x3 = (a*c) // r\n x4 = (a * b * c * s)// (p * q * r )\n low,high = a , a *n\n while low <= high:\n mid = (low + high)//2\n times = mid//a + mid//b + mid//c - mid//x1 - mid//x2 - mid//x3 + mid//x4\n if times < n : low = mid + 1\n elif times == n:\n ans = min(ans,mid)\n high = mid - 1\n else: high = mid - 1\n return ans\n``` | 4 | An **ugly number** is a positive integer that is divisible by `a`, `b`, or `c`.
Given four integers `n`, `a`, `b`, and `c`, return the `nth` **ugly number**.
**Example 1:**
**Input:** n = 3, a = 2, b = 3, c = 5
**Output:** 4
**Explanation:** The ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10... The 3rd is 4.
**Example 2:**
**Input:** n = 4, a = 2, b = 3, c = 4
**Output:** 6
**Explanation:** The ugly numbers are 2, 3, 4, 6, 8, 9, 10, 12... The 4th is 6.
**Example 3:**
**Input:** n = 5, a = 2, b = 11, c = 13
**Output:** 10
**Explanation:** The ugly numbers are 2, 4, 6, 8, 10, 11, 12, 13... The 5th is 10.
**Constraints:**
* `1 <= n, a, b, c <= 109`
* `1 <= a * b * c <= 1018`
* It is guaranteed that the result will be in range `[1, 2 * 109]`. | Traverse the tree using depth first search. Find for every node the sum of values of its sub-tree. Traverse the tree again from the root and return once you reach a node with zero sum of values in its sub-tree. |
PYTHON | BRUTE FORCE TO OPTIMZIED SOL | FULL DETAILED EXPLANATION| | ugly-number-iii | 0 | 1 | \n# EXPLANATION BRUTE FORCE\n```\nBrute force is trying each number from 1 untill we get our nth ugly number\nNow we can improve this approach by using the idea that we need to get the nth ugly number which is divisible by a,b,or c\n\nSo we make a list of size 3 "times = [1,1,1]" having all values as 1 indicating the current number \nusing number a,b,c, respectively\n\nNow we find the smallest number which will be minimum of \n( times[0] * a, times[1] * b , times[c] * c )\n\nTHE smallest one can also occur by more than 1 source that is 2,3 may collide at 6\nso we traverse the list and compare the smallest with times[0]*a , times[1]*b and times[2]*c and if smallest is equal to it we increment times[i] by 1 making the number its next occurence\n\n```\n\n\n# CODE ( UNOPTIMIZED / BRUTE FORCE + )\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n times = [1,1,1]\n smallest = inf\n while n != 0:\n smallest = min ( times[0]*a,times[1]*b,times[2]*c)\n if times[0]*a == smallest: times[0] += 1\n if times[1]*b == smallest: times[1] += 1\n if times[2]*c == smallest: times[2] += 1\n n -= 1\n return smallest\n```\n\n# EXPLANATION BINARY SEARCH + VENN DIAGRAM\n\n\na \u2229 b \u2229 c = a \u222A b + a \u222A c + b \u222A c - a \u2229 b - a \u2229 c - b \u2229 c + a \u2229 b \u2229 c\n\n```\nLets say we have a = 2 , b = 3, c = 5 , n = 10\nNow the number must lie between the first occurence = min(a,b,c) i.e. 2\nand the n th occurence in case of no collision = min(a,b,c) * n i.e. 20\nas 2 , 4, 6 , 8 ,10 ,12 , 14 , 16 18 ,20 will lead to 10th ugly number is b,c do not collide\n\nNow since we know the range ... how can we decide to choose the left half or the right half\n... The main logic of binary search\n\nSee if we get to know the count of ugly numbers till mid we can decide which way to walk\n\nSO the question is how to find the count\n\n\nSay numbers a = 2 , b = 3 , c = 5 , n = 10\nlow = 2\nhigh = 20\nmid = 11\n\nNow we need to find the count of ugly numbers till 11........\nremember the formula\na \u2229 b \u2229 c = a \u222A b + a \u222A c + b \u222A c - a \u2229 b - a \u2229 c - b \u2229 c + a \u2229 b \u2229 c\n\nhow many 2s will occur till 11 = 11 // 2 = 5 ( 2,4,6,8,10)\nhow many 3s will occur till 11 = 11 // 3 = 3 ( 3,6,9)\nhow many 5s will occur till 11 = 11 // 5 = 2 ( 5,10)\nnow 2,3 may collide so we count them as\n11 // (lcm 2,3) = 11 // 6 = 1 (6)\nnow 2,5 may collide so we count them as\n11 // (lcm 2,5) = 11 // 10 = 1(10)\nnow 3,5 may collide so we count them as\n11 // (lcm 3,5) = 11 // 15 = 0 \nnow we may have count collision of (2,3) and (2,5) but it should be counted once as (2,3,5)\nso we have to add 11 // (lcm 2,3,5) = 11// 30 = 0\n\nSo according to our formula total count = 5 + 3 + 2 - 1 - 1 - 0 + 0 = 8\n(2,4,6,8,10) + ( 3,6,9) + (5,10) - (6) - (10) - ( ) + ( ) = (2,3,4,5,6,8,9,10)\n\nNow since the count is 8 and we need 10th ugly number we should go right\n\n\n\n\nTO GET LCM of two numbers:\n\tLCM(a,b) * HCF(a,b) = a*b\n\t\nTO GET LCM of three numbers:\n\tLCM(a,b,c) = a*b*c*HCF(a,b,c) // HCF(a,b) * HCF(b,c) * HCF(a,c)\n```\n# CODE ( BINARY SEARCH )\n```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n a,b,c = sorted((a,b,c))\n ans = inf\n def hcf(a,b):\n if a %b == 0: return b\n return hcf(b , a % b)\n p,q,r= hcf(a,b),hcf(b,c),hcf(a,c)\n s = hcf(r,b)\n x1 = (a*b) // p\n x2 = (b*c) // q \n x3 = (a*c) // r\n x4 = (a * b * c * s)// (p * q * r )\n low,high = a , a *n\n while low <= high:\n mid = (low + high)//2\n times = mid//a + mid//b + mid//c - mid//x1 - mid//x2 - mid//x3 + mid//x4\n if times < n : low = mid + 1\n elif times == n:\n ans = min(ans,mid)\n high = mid - 1\n else: high = mid - 1\n return ans\n``` | 4 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
Python Medium | ugly-number-iii | 0 | 1 | ```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n\n\n lcm1 = math.lcm(a, b, c)\n lcm2 = math.lcm(a, b)\n lcm3 = math.lcm(a, c)\n lcm4 = math.lcm(b, c)\n\n l, r = min(a, b, c), max(a, b, c) * n\n\n\n while l < r:\n mid = (l + r) // 2\n\n if (mid // a) + (mid // b) + (mid // c) - (mid // lcm2) - (mid // lcm3) - (mid // lcm4) + (mid // lcm1) < n:\n l = mid + 1\n\n else:\n r = mid\n\n\n\n \n\n return l\n\n \n``` | 0 | An **ugly number** is a positive integer that is divisible by `a`, `b`, or `c`.
Given four integers `n`, `a`, `b`, and `c`, return the `nth` **ugly number**.
**Example 1:**
**Input:** n = 3, a = 2, b = 3, c = 5
**Output:** 4
**Explanation:** The ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10... The 3rd is 4.
**Example 2:**
**Input:** n = 4, a = 2, b = 3, c = 4
**Output:** 6
**Explanation:** The ugly numbers are 2, 3, 4, 6, 8, 9, 10, 12... The 4th is 6.
**Example 3:**
**Input:** n = 5, a = 2, b = 11, c = 13
**Output:** 10
**Explanation:** The ugly numbers are 2, 4, 6, 8, 10, 11, 12, 13... The 5th is 10.
**Constraints:**
* `1 <= n, a, b, c <= 109`
* `1 <= a * b * c <= 1018`
* It is guaranteed that the result will be in range `[1, 2 * 109]`. | Traverse the tree using depth first search. Find for every node the sum of values of its sub-tree. Traverse the tree again from the root and return once you reach a node with zero sum of values in its sub-tree. |
Python Medium | ugly-number-iii | 0 | 1 | ```\nclass Solution:\n def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:\n\n\n lcm1 = math.lcm(a, b, c)\n lcm2 = math.lcm(a, b)\n lcm3 = math.lcm(a, c)\n lcm4 = math.lcm(b, c)\n\n l, r = min(a, b, c), max(a, b, c) * n\n\n\n while l < r:\n mid = (l + r) // 2\n\n if (mid // a) + (mid // b) + (mid // c) - (mid // lcm2) - (mid // lcm3) - (mid // lcm4) + (mid // lcm1) < n:\n l = mid + 1\n\n else:\n r = mid\n\n\n\n \n\n return l\n\n \n``` | 0 | Given an equation, represented by `words` on the left side and the `result` on the right side.
You need to check if the equation is solvable under the following rules:
* Each character is decoded as one digit (0 - 9).
* No two characters can map to the same digit.
* Each `words[i]` and `result` are decoded as one number **without** leading zeros.
* Sum of numbers on the left side (`words`) will equal to the number on the right side (`result`).
Return `true` _if the equation is solvable, otherwise return_ `false`.
**Example 1:**
**Input:** words = \[ "SEND ", "MORE "\], result = "MONEY "
**Output:** true
**Explanation:** Map 'S'-> 9, 'E'->5, 'N'->6, 'D'->7, 'M'->1, 'O'->0, 'R'->8, 'Y'->'2'
Such that: "SEND " + "MORE " = "MONEY " , 9567 + 1085 = 10652
**Example 2:**
**Input:** words = \[ "SIX ", "SEVEN ", "SEVEN "\], result = "TWENTY "
**Output:** true
**Explanation:** Map 'S'-> 6, 'I'->5, 'X'->0, 'E'->8, 'V'->7, 'N'->2, 'T'->1, 'W'->'3', 'Y'->4
Such that: "SIX " + "SEVEN " + "SEVEN " = "TWENTY " , 650 + 68782 + 68782 = 138214
**Example 3:**
**Input:** words = \[ "LEET ", "CODE "\], result = "POINT "
**Output:** false
**Explanation:** There is no possible mapping to satisfy the equation, so we return false.
Note that two different characters cannot map to the same digit.
**Constraints:**
* `2 <= words.length <= 5`
* `1 <= words[i].length, result.length <= 7`
* `words[i], result` contain only uppercase English letters.
* The number of different characters used in the expression is at most `10`. | Write a function f(k) to determine how many ugly numbers smaller than k. As f(k) is non-decreasing, try binary search. Find all ugly numbers in [1, LCM(a, b, c)] (LCM is Least Common Multiple). Use inclusion-exclusion principle to expand the result. |
✔️ [Python3] UNION-FIND (❁´▽`❁)*✲゚*, Explained | smallest-string-with-swaps | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe main idea here is to represent the string as a graph (indexes are nodes and pairs are edges). We can swap characters only if they connected with an edge. Since we can swap chars any amount of time within formed by edges groups, any char in such a group can be placed to any place within the group. That means we can simply sort chars within every group, and resulting string will be the lexicographically smallest one. So we do it in three steps:\n\n1. Form groups using Union-Find data structure\n2. Convert union-find to a hashmap with chars and indexes as values\n3. Sort chars and indeses for every groups and form the result\n\nTime: **O(nlogn)**\nSpace: **O(n)**\n\nRuntime: 749 ms, faster than **82.09%** of Python3 online submissions for Smallest String With Swaps.\nMemory Usage: 50.3 MB, less than **93.45%** of Python3 online submissions for Smallest String With Swaps.\n\n```\nclass Solution:\n def union(self, a, b):\n self.parent[self.find(a)] = self.find(b)\n\t\t\n def find(self, a):\n if self.parent[a] != a:\n self.parent[a] = self.find(self.parent[a])\n\n return self.parent[a]\n \n def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:\n\t\t# 1. Union-Find\n self.parent = list(range(len(s)))\n for a, b in pairs:\n self.union(a, b)\n\n\t\t# 2. Grouping\n group = defaultdict(lambda: ([], [])) \n for i, ch in enumerate(s):\n parent = self.find(i)\n group[parent][0].append(i)\n group[parent][1].append(ch)\n\n\t\t# 3. Sorting\n res = [\'\'] * len(s)\n for ids, chars in group.values():\n ids.sort()\n chars.sort()\n for ch, i in zip(chars, ids):\n res[i] = ch\n \n return \'\'.join(res)\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 67 | You are given a string `s`, and an array of pairs of indices in the string `pairs` where `pairs[i] = [a, b]` indicates 2 indices(0-indexed) of the string.
You can swap the characters at any pair of indices in the given `pairs` **any number of times**.
Return the lexicographically smallest string that `s` can be changed to after using the swaps.
**Example 1:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\]\]
**Output:** "bacd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[1\] and s\[2\], s = "bacd "
**Example 2:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\],\[0,2\]\]
**Output:** "abcd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[0\] and s\[2\], s = "acbd "
Swap s\[1\] and s\[2\], s = "abcd "
**Example 3:**
**Input:** s = "cba ", pairs = \[\[0,1\],\[1,2\]\]
**Output:** "abc "
**Explaination:**
Swap s\[0\] and s\[1\], s = "bca "
Swap s\[1\] and s\[2\], s = "bac "
Swap s\[0\] and s\[1\], s = "abc "
**Constraints:**
* `1 <= s.length <= 10^5`
* `0 <= pairs.length <= 10^5`
* `0 <= pairs[i][0], pairs[i][1] < s.length`
* `s` only contains lower case English letters. | Use dynamic programming. Let dp[i][j] be the solution for the sub-array from index i to index j. Notice that if we have S[i] == S[j] one transition could be just dp(i + 1, j + 1) because in the last turn we would have a palindrome and we can extend this palindrome from both sides, the other transitions are not too difficult to deduce. |
[Python] Modified Disjoint Set Union with Explanation | smallest-string-with-swaps | 0 | 1 | ### Introduction\n\nGiven a string `s`, we need to find the minimum lexicographical arrangement of the characters in `s`, with the limitation that swaps in `s` are restricted to defined swaps between two indexes as per `pairs` (0-indexed).\n\nSince index pairs may overlap, it is important to know the full list of indexes that can swap among one another before we determine the minimum lexicographical arrangement. Hence, this problem can be broken down into two distinct parts:\n\n1. Determining the group(s) of indexes that can swap among one another.\n2. Obtaining the minimum lexicographical arrangement of characters per group.\n\nEach group of indexes is distinct by definition; if two groups of indexes contained the same index, then all the indexes in both groups can swap among one another. Hence, we can say that each group of indexes is **a disjoint set**. Then, to merge two groups together (because they share an index), we will require a union operation between the disjoint sets. This algorithm is thus commonly referred to as **Disjoint Set Union (DSU), or Union-Find**.\n\n---\n\n### Part 1: Implementing DSU\n\nWe can start with a standard implementation of a weighted DSU. This data structure allows for union-find operations to be performed in O(logn) time, where `n` is the number of nodes in the DSU. For a full, detailed explanation of implementing the weighted DSU, I recommend [this HackerEarth article](https://www.hackerearth.com/practice/notes/disjoint-set-union-union-find/) which is beginner-friendly and easy to understand.\n\n```python\nclass WeightedUnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n))\n self.size = [1]*n\n\n def _root(self, node: int) -> int:\n # Obtains the root node of the given node\n while self.parent[node] != node:\n self.parent[node] = self.parent[self.parent[node]] # perform path compression\n node = self.parent[node] # traverse up the tree\n return node\n\n def find(self, node1: int, node2: int) -> bool:\n # Determines if node1 and node2 are present in the same disjoint set\n return self._root(node1) == self._root(node2)\n\n def union(self, node1: int, node2: int) -> None:\n # Performs union operation for the disjoint sets containing node1 and node2 respectively\n root1, root2 = self._root(node1), self._root(node2)\n if root1 == root2: # the two nodes are already in the same disjoint set\n return\n elif self.size[root1] < self.size[root2]: # ensure that root1 is the larger tree\n root1, root2 = root2, root1\n self.parent[root2] = root1 # set root node of root2 to root1\n self.size[root1] += self.size[root2] # increase size of root1 tree by size of root2 subtree\n```\n\nThe problem with this implementation for this problem is that we still have no way of easily identifying each group of indexes. We could try to iterate through each index and find all the indexes that have the same root, but that will take too long.\n\n---\n\n### Part 2: Modifying DSU\n\nThe solution is to store the full list of indexes that is rooted in a given index, instead of simply storing the sizes of the tree. This way, we get the additional functionality of knowing\n\n1. which nodes are roots of the disjoint set(s) that exist, and\n2. the full list of nodes in each disjoint set.\n\n```python\nclass WeightedUnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n))\n self.group = [set([i]) for i in range(n)] # store full list of nodes in disjoint set\n \n def _root(self, node: int) -> int:\n while self.parent[node] != node:\n self.parent[node] = self.parent[self.parent[node]]\n node = self.parent[node]\n return node\n \n def find(self, node1: int, node2: int) -> bool:\n return self._root(node1) == self._root(node2)\n \n def union(self, node1: int, node2: int) -> None:\n root1, root2 = self._root(node1), self._root(node2)\n if len(self.group[root1]) < len(self.group[root2]):\n root1, root2 = root2, root1\n self.parent[root2] = root1\n self.group[root1] |= self.group[root2] # add all nodes in root2 to root1\n```\n\n---\n\n### Part 3: Determining minimum lexicographical arrangement\n\nFinally, we are ready to tackle this problem. By iterating through all the root nodes in our DSU class, we can perform the following sequence:\n\n1. Obtain all the nodes in the tree rooted by the given root node.\n2. Obtain all the characters in `s` if its index is found in the obtained disjoint set.\n3. Sort the obtained characters by ascending lexicographical order.\n4. Insert the sorted characters in order of the indexes in the disjoint set.\n\nThe full code is as follows:\n\n```python\nclass WeightedUnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n))\n self.group = [set([i]) for i in range(n)]\n \n def _root(self, node: int) -> int:\n while self.parent[node] != node:\n self.parent[node] = self.parent[self.parent[node]]\n node = self.parent[node]\n return node\n \n def find(self, node1: int, node2: int) -> bool:\n return self._root(node1) == self._root(node2)\n \n def union(self, node1: int, node2: int) -> None:\n root1, root2 = self._root(node1), self._root(node2)\n if len(self.group[root1]) < len(self.group[root2]):\n root1, root2 = root2, root1\n self.parent[root2] = root1\n self.group[root1] |= self.group[root2]\n\nclass Solution:\n def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:\n uf = WeightedUnionFind((l := len(s)))\n for a, b in pairs:\n uf.union(a, b)\n res = [\'\']*l\n for root in [i for i, node in enumerate(uf.parent) if node == i]:\n for i, ch in zip(sorted(uf.group[root]), sorted(s[i] for i in uf.group[root])):\n res[i] = ch\n return \'\'.join(res)\n```\n\n**TC: O(max(m, n)logn)**, where `m` is the number of `pairs` and `n` is the length of the given string `s`, due to the nested sorting / union-find algorithm. The TC of the union function may be worse than O(logn) if the set union operation `|=` is required to merge sets of large sizes (I think it should be O(n) worst case, in which case the overall TC is roughly O(n<sup>2</sup>), but it\'s quite complicated).\n**SC: O(n<sup>2</sup>)**; `uf.group` will have many duplicates if the graph is more connected than disjoint.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 7 | You are given a string `s`, and an array of pairs of indices in the string `pairs` where `pairs[i] = [a, b]` indicates 2 indices(0-indexed) of the string.
You can swap the characters at any pair of indices in the given `pairs` **any number of times**.
Return the lexicographically smallest string that `s` can be changed to after using the swaps.
**Example 1:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\]\]
**Output:** "bacd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[1\] and s\[2\], s = "bacd "
**Example 2:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\],\[0,2\]\]
**Output:** "abcd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[0\] and s\[2\], s = "acbd "
Swap s\[1\] and s\[2\], s = "abcd "
**Example 3:**
**Input:** s = "cba ", pairs = \[\[0,1\],\[1,2\]\]
**Output:** "abc "
**Explaination:**
Swap s\[0\] and s\[1\], s = "bca "
Swap s\[1\] and s\[2\], s = "bac "
Swap s\[0\] and s\[1\], s = "abc "
**Constraints:**
* `1 <= s.length <= 10^5`
* `0 <= pairs.length <= 10^5`
* `0 <= pairs[i][0], pairs[i][1] < s.length`
* `s` only contains lower case English letters. | Use dynamic programming. Let dp[i][j] be the solution for the sub-array from index i to index j. Notice that if we have S[i] == S[j] one transition could be just dp(i + 1, j + 1) because in the last turn we would have a palindrome and we can extend this palindrome from both sides, the other transitions are not too difficult to deduce. |
python3 explained | smallest-string-with-swaps | 0 | 1 | ```\nclass UnionFind:\n def __init__(self, size):\n self.root = [i for i in range(size)]\n self.rank = [1] * size\n def find(self, x):\n if x == self.root[x]:\n return x\n self.root[x] = self.find(self.root[x])\n return self.root[x]\n def union(self, x, y):\n rootX = self.find(x)\n rootY = self.find(y)\n if rootX != rootY:\n if self.rank[rootX] > self.rank[rootY]:\n self.root[rootY] = rootX\n elif self.rank[rootX] < self.rank[rootY]:\n self.root[rootX] = rootY\n else:\n self.root[rootY] = rootX\n self.rank[rootX] += 1\n def connected(self, x, y):\n return self.find(x) == self.find(y)\n\nclass Solution:\n def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]):\n N=len(s)\n DSU=UnionFind(N)\n for x,y in pairs:\n DSU.union(x,y)\n parent=[DSU.find(i) for i in range(N)]\n dict=defaultdict(deque)\n for i in range(N):\n dict[parent[i]].append(s[i])\n for key in dict:\n dict[key]=deque(sorted(dict[key]))\n ans=""\n for i in range(N):\n dict_key=parent[i]\n ans+=dict[dict_key].popleft()\n return ans\n """\n hint---->any number of times.\n from these words we conclude that we can swap any numbers of time\n \xA0 \xA0so we will form union fromeach pair in \xA0pairs.\n \xA0 \xA0eg. s = "dcab", pairs = [[0,3],[1,2]]\n \xA0 \xA0there will be two union .\n \xA0 0:[0,3]\n 1:[1,2]\n \xA0 \xA0so in one union we can swap any number of times,we will make unions using union-find .\n after union operation,parent array will look like this [0,1,1,0]\n after each union is formed we will make dictionary where value will \n store character values of indexes in every union [here there are two union with parent 0 and 1] and parent as keys.\n i have used dictionary of deque which i will explain below.\n from above example\n 0:[d,b] 0->d ,3->b\n 1:[c,a] 1->c,2->a\n after this we will sort each value in dictionary\n 0:[b,d]\n 1:[c,a]\n the reason of using deque is that after we iterate through parent array we have to get\n the first char in each values in dictionary of perticular union,so every time i will pop from\n left,which is also minimum of that group.\n """\n | 19 | You are given a string `s`, and an array of pairs of indices in the string `pairs` where `pairs[i] = [a, b]` indicates 2 indices(0-indexed) of the string.
You can swap the characters at any pair of indices in the given `pairs` **any number of times**.
Return the lexicographically smallest string that `s` can be changed to after using the swaps.
**Example 1:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\]\]
**Output:** "bacd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[1\] and s\[2\], s = "bacd "
**Example 2:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\],\[0,2\]\]
**Output:** "abcd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[0\] and s\[2\], s = "acbd "
Swap s\[1\] and s\[2\], s = "abcd "
**Example 3:**
**Input:** s = "cba ", pairs = \[\[0,1\],\[1,2\]\]
**Output:** "abc "
**Explaination:**
Swap s\[0\] and s\[1\], s = "bca "
Swap s\[1\] and s\[2\], s = "bac "
Swap s\[0\] and s\[1\], s = "abc "
**Constraints:**
* `1 <= s.length <= 10^5`
* `0 <= pairs.length <= 10^5`
* `0 <= pairs[i][0], pairs[i][1] < s.length`
* `s` only contains lower case English letters. | Use dynamic programming. Let dp[i][j] be the solution for the sub-array from index i to index j. Notice that if we have S[i] == S[j] one transition could be just dp(i + 1, j + 1) because in the last turn we would have a palindrome and we can extend this palindrome from both sides, the other transitions are not too difficult to deduce. |
Clean Python DFS | O( n log n ) | smallest-string-with-swaps | 0 | 1 | **Clean Python DFS | O( n log n )**\n\nThe code below presents a clean Python DFS solution for this problem. The algorithm works as follows:\n\n1. The initial idea is that each pair of swappable letters in "pairs" can be treated as an edge in a (undirected) graph. This works because, in the limit case, we could do bubble sort across connected letters.\n\n2. We then go one step further and treat each index s[i] as a node, and convert the array "pairs" into a dictionary "d" of connected nodes.\n\n3. While our dictionary "d" has entries, we choose one element in "d" and visit all connected nodes, returning a list of detected points. We sort this list, and place the results back in our final string/array. Since each node can only be visited once, this process has a linear time complexity of O(E), where E is the number of edges in our graph ( E = len(pairs) ).\n\n4. Once all nodes have been visited, we exit our function and return the final string, with all its connected sections sorted .\n\nI hope the explanation was helpful. The code below achieves a top Speed rating.\n\nCheers,\n\n```\nclass Solution:\n def smallestStringWithSwaps(self, s, pairs):\n d = defaultdict(list)\n for a,b in pairs:\n d[a].append(b)\n d[b].append(a)\n #\n def dfs(x,A):\n if x in d:\n A.append(x)\n for y in d.pop(x):\n dfs(y,A)\n #\n s = list(s)\n while d:\n x = next(iter(d))\n A = []\n dfs(x,A)\n A = sorted(A)\n B = sorted([ s[i] for i in A ])\n for i,b in enumerate(B):\n s[A[i]] = b\n return \'\'.join(s)\n``` | 18 | You are given a string `s`, and an array of pairs of indices in the string `pairs` where `pairs[i] = [a, b]` indicates 2 indices(0-indexed) of the string.
You can swap the characters at any pair of indices in the given `pairs` **any number of times**.
Return the lexicographically smallest string that `s` can be changed to after using the swaps.
**Example 1:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\]\]
**Output:** "bacd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[1\] and s\[2\], s = "bacd "
**Example 2:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\],\[0,2\]\]
**Output:** "abcd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[0\] and s\[2\], s = "acbd "
Swap s\[1\] and s\[2\], s = "abcd "
**Example 3:**
**Input:** s = "cba ", pairs = \[\[0,1\],\[1,2\]\]
**Output:** "abc "
**Explaination:**
Swap s\[0\] and s\[1\], s = "bca "
Swap s\[1\] and s\[2\], s = "bac "
Swap s\[0\] and s\[1\], s = "abc "
**Constraints:**
* `1 <= s.length <= 10^5`
* `0 <= pairs.length <= 10^5`
* `0 <= pairs[i][0], pairs[i][1] < s.length`
* `s` only contains lower case English letters. | Use dynamic programming. Let dp[i][j] be the solution for the sub-array from index i to index j. Notice that if we have S[i] == S[j] one transition could be just dp(i + 1, j + 1) because in the last turn we would have a palindrome and we can extend this palindrome from both sides, the other transitions are not too difficult to deduce. |
[Python3] Union-find + Priority Queue (Heap). Easy to understand | smallest-string-with-swaps | 0 | 1 | Method 1: Union-find + sort\nTC: O(nlogn)\nSC: O(n)\n```\nclass UnionFind:\n def __init__(self, size: int):\n self.root = [i for i in range(size)]\n self.rank = [1 for _ in range(size)]\n \n def find(self, x: int) -> int:\n if x == self.root[x]:\n return x\n \n self.root[x] = self.find(self.root[x])\n return self.root[x]\n \n def union(self, x: int, y: int) -> None:\n root_x, root_y = self.find(x), self.find(y)\n if root_x != root_y:\n if self.rank[root_x] > self.rank[root_y]:\n self.root[root_y] = root_x\n elif self.rank[root_x] < self.rank[root_y]:\n self.root[root_x] = root_y\n else:\n self.root[root_y] = root_x\n self.rank[root_x] += 1\n \n def connected(self, x: int, y: int) -> bool:\n return self.find(x) == self.find(y)\n\nclass Solution:\n def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:\n n = len(s)\n uf = UnionFind(n)\n for x, y in pairs:\n uf.union(x, y)\n \n alias = defaultdict(list)\n for i in range(n):\n root = uf.find(i)\n alias[root].append(s[i])\n for i in alias:\n alias[i].sort(reverse=True)\n \n res = []\n for i in range(n):\n res.append(alias[uf.find(i)].pop())\n \n return \'\'.join(res)\n```\n\nMethod 2: Union-find + priority queue\nTC: O(nlogk)\nSC: O(n)\n```\nclass UnionFind:\n def __init__(self, size: int):\n self.root = [i for i in range(size)]\n self.rank = [1 for _ in range(size)]\n \n def find(self, x: int) -> int:\n if x == self.root[x]:\n return x\n \n self.root[x] = self.find(self.root[x])\n return self.root[x]\n \n def union(self, x: int, y: int) -> None:\n root_x, root_y = self.find(x), self.find(y)\n if root_x != root_y:\n if self.rank[root_x] > self.rank[root_y]:\n self.root[root_y] = root_x\n elif self.rank[root_x] < self.rank[root_y]:\n self.root[root_x] = root_y\n else:\n self.root[root_y] = root_x\n self.rank[root_x] += 1\n \n def connected(self, x: int, y: int) -> bool:\n return self.find(x) == self.find(y)\n\nclass Solution:\n def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:\n n = len(s)\n uf = UnionFind(n)\n for x, y in pairs:\n uf.union(x, y)\n \n alias = defaultdict(list)\n for i in range(n):\n root = uf.find(i)\n heappush(alias[root], s[i])\n \n res = []\n for i in range(n):\n res.append(heappop(alias[uf.find(i)]))\n \n return \'\'.join(res)\n```\n | 10 | You are given a string `s`, and an array of pairs of indices in the string `pairs` where `pairs[i] = [a, b]` indicates 2 indices(0-indexed) of the string.
You can swap the characters at any pair of indices in the given `pairs` **any number of times**.
Return the lexicographically smallest string that `s` can be changed to after using the swaps.
**Example 1:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\]\]
**Output:** "bacd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[1\] and s\[2\], s = "bacd "
**Example 2:**
**Input:** s = "dcab ", pairs = \[\[0,3\],\[1,2\],\[0,2\]\]
**Output:** "abcd "
**Explaination:**
Swap s\[0\] and s\[3\], s = "bcad "
Swap s\[0\] and s\[2\], s = "acbd "
Swap s\[1\] and s\[2\], s = "abcd "
**Example 3:**
**Input:** s = "cba ", pairs = \[\[0,1\],\[1,2\]\]
**Output:** "abc "
**Explaination:**
Swap s\[0\] and s\[1\], s = "bca "
Swap s\[1\] and s\[2\], s = "bac "
Swap s\[0\] and s\[1\], s = "abc "
**Constraints:**
* `1 <= s.length <= 10^5`
* `0 <= pairs.length <= 10^5`
* `0 <= pairs[i][0], pairs[i][1] < s.length`
* `s` only contains lower case English letters. | Use dynamic programming. Let dp[i][j] be the solution for the sub-array from index i to index j. Notice that if we have S[i] == S[j] one transition could be just dp(i + 1, j + 1) because in the last turn we would have a palindrome and we can extend this palindrome from both sides, the other transitions are not too difficult to deduce. |
🔥🔥🔥🔥🔥Easy Solution | JS | TS | Java | C++ | Python 🔥🔥🔥🔥🔥 | sort-items-by-groups-respecting-dependencies | 1 | 1 | ---\n\n\n---\n**Intuition:**\nTo solve this problem, we need to perform a topological sort considering the constraints from both the `group` and `beforeItems` arrays. The items within the same group should be adjacent in the sorted list, and the ordering of items given in the `beforeItems` array should be respected.\n\n**Approach:**\n1. First, we\'ll construct a directed graph where nodes represent items and directed edges represent the "before" relationships given in the `beforeItems` array. We\'ll also keep track of the in-degrees (number of incoming edges) for each node.\n\n2. We\'ll create a separate graph for groups, where nodes represent groups and directed edges represent the "before" relationships between groups based on the items\' relationships.\n\n3. Next, we\'ll find the topological order of the groups using a modified version of Kahn\'s algorithm. While finding the topological order of groups, we\'ll also consider the constraints from the `group` array.\n\n4. For each group in the topological order:\n - Find the items within that group and sort them based on the constraints given in the `beforeItems` array. This can be done using a priority queue.\n - Append the sorted items to the final sorted list.\n\n5. If at any point, while constructing the topological order or sorting the items within a group, we encounter a cycle or any invalid ordering, we\'ll return an empty list as there\'s no valid solution.\n\n**Complexity:**\n- Constructing the graph takes O(n + m) time, where n is the number of items and m is the number of groups.\n- Constructing the topological order of groups takes O(n + m) time.\n- Sorting the items within each group takes O(n log n) time in total.\n- Overall, the time complexity is O(n log n).\n\nThe space complexity is O(n + m) for storing the graphs and related data structures.\n\nRemember that this is a complex problem with multiple steps involved, so make sure to understand each step before implementing it in code.\n\n# Code\n\n```javascript []\nconst initializeGraph = (n) => { let G = []; for (let i = 0; i < n; i++) { G.push([]); } return G; };\nconst initializeGraphSet = (n) => { let G = []; for (let i = 0; i < n; i++) { G.push(new Set()); } return G; };\n\nconst sortItems = (n, m, group, beforeItems) => {\n for (let i = 0; i < n; i++) {\n if (group[i] == -1) {\n group[i] = m++;\n }\n }\n let gg = initializeGraphSet(m); // graph group\n let gi = initializeGraphSet(n); // graph item\n let indegreeGG = Array(m).fill(0);\n let indegreeGI = Array(n).fill(0);\n let res = [];\n for (let i = 0; i < n; i++) {\n let to = group[i];\n for (const x of beforeItems[i]) {\n let from = group[x];\n if (from != to && !gg[from].has(to)) {\n gg[from].add(to);\n indegreeGG[to]++;\n }\n if (!gi[x].has(i)) {\n gi[x].add(i);\n indegreeGI[i]++;\n }\n }\n }\n let ggOrder = topologicalSort(gg, indegreeGG);\n let giOrder = topologicalSort(gi, indegreeGI);\n if (ggOrder.length == 0 || giOrder.length == 0) return [];\n let group2Item = initializeGraph(m);\n for (const item of giOrder) group2Item[group[item]].push(item);\n for (const group_id of ggOrder) {\n for (const item of group2Item[group_id]) {\n res.push(item);\n }\n }\n return res;\n};\n\nconst topologicalSort = (g, indegree) => {\n let res = [], q = [], len = indegree.length;\n for (let i = 0; i < len; i++) {\n if (indegree[i] == 0) q.push(i);\n }\n while (q.length) {\n let cur = q.shift();\n res.push(cur);\n for (const child of g[cur]) {\n if (--indegree[child] == 0) q.push(child);\n }\n }\n for (let i = 0; i < len; i++) {\n if (indegree[i] > 0) return [];\n }\n return res;\n};\n```\n```Typescript []\n/*\nThe idea is to combine nodes and groups.\n\nWe add group nodes and make beetween group relations.\n*/\n\nfunction sortItems(n: number, m: number, group: number[], beforeItems: number[][]): number[] {\n // create empty graph for nodes and groups (n + m);\n const graph = new Map<number, Set<number>>();\n for (let i = 0; i < n + m; i++) {\n graph.set(i, new Set());\n }\n\n const indegrees = new Array(n + m).fill(0);\n for (let i = 0; i < beforeItems.length; i++) {\n const items = beforeItems[i];\n const currGroup = n + group[i]; // group index started with offset;\n\n // Relation between group and current node \n if (group[i] !== -1) {\n graph.get(currGroup).add(i);\n indegrees[i]++;\n }\n\n // two types of relation 1) between nodes inside of the group 2) between the groups\n for (const item of items) {\n const itemGroup = n + group[item];\n if (currGroup === itemGroup || group[i] === -1 || group[item] === -1) {\n graph.get(item).add(i);\n indegrees[i]++;\n } else {\n if (!graph.get(itemGroup).has(currGroup)) {\n graph.get(itemGroup).add(currGroup);\n indegrees[currGroup]++;\n }\n }\n }\n }\n\n // Typical topological sort\n const zeroInDegree = [];\n for (let i = 0; i < indegrees.length; i++) {\n if (!indegrees[i]) {\n zeroInDegree.push(i)\n }\n }\n\n const map = new Map<number, number[]>();\n // keep groups order\n const pushToMap = (item: number ) => {\n if (group[item] === -1) {\n map.set(item + n, [item])\n return;\n } \n if (map.has(group[item])) {\n map.get(group[item]).push(item); \n } else {\n map.set(group[item], [item]);\n }\n }\n\n let count = 0;\n while (zeroInDegree.length) {\n const curr = zeroInDegree.shift();\n if (curr < n) {\n count++;\n pushToMap(curr);\n }\n \n for (const neighbor of graph.get(curr)) {\n indegrees[neighbor]--;\n if (!indegrees[neighbor]) {\n zeroInDegree.push(neighbor);\n }\n }\n }\n\n // Hadle cases with cycles\n if (count !== n) {\n return [];\n }\n\n return [].concat(...map.values());\n};\n```\n```Java []\nclass Solution {\n public int[] sortItems(int n, int m, int[] grp, List<List<Integer>> beforeItems) {\n int[] ans = new int[n];\n \n // Create data structures to store relationships between items and groups\n Map<Integer, Map<Integer, Set<Integer>>> itemMap = new HashMap<>();\n Map<Integer, Set<Integer>> grpMap = new HashMap<>();\n \n // Assign unique group IDs to items with no group\n for (int i = 0; i < n; i++) {\n if (grp[i] == -1) {\n grp[i] = m++;\n }\n }\n \n // Initialize the maps for groups and items\n for (int i = 0; i < m; i++) {\n grpMap.put(i, new HashSet<>());\n itemMap.put(i, new HashMap<>());\n }\n \n // Initialize intra-group relationships\n for (int i = 0; i < n; i++) {\n itemMap.get(grp[i]).put(i, new HashSet<>());\n }\n \n // Populate relationships between items based on beforeItems\n for (int i = 0; i < beforeItems.size(); i++) {\n for (int item : beforeItems.get(i)) {\n if (grp[i] == grp[item]) {\n // Within the same group, add relationship to intra-group map\n itemMap.get(grp[i]).get(item).add(i);\n } else {\n // Between different groups, add relationship to inter-group map\n grpMap.get(grp[item]).add(grp[i]);\n }\n }\n }\n \n int j = 0;\n // Perform topological sorting on groups and items within each group\n for (int g : topSort(grpMap)) {\n for (int item : topSort(itemMap.get(g))) {\n ans[j++] = item;\n }\n }\n \n // Return the sorted items or an empty array if sorting is not possible\n return j < ans.length ? new int[]{} : ans;\n }\n\n // Topological sorting function\n private int[] topSort(Map<Integer, Set<Integer>> map) {\n Map<Integer, Integer> indg = new HashMap<>();\n \n // Calculate in-degrees of nodes\n for (Set<Integer> values : map.values()) {\n for (int m : values) {\n indg.merge(m, 1, Integer::sum);\n }\n }\n \n Queue<Integer> queue = new ArrayDeque<>();\n \n // Initialize the queue with nodes having in-degree 0\n for (int key : map.keySet()) {\n if (!indg.containsKey(key)) {\n queue.offer(key);\n }\n }\n \n int j = 0;\n int[] ans = new int[map.size()];\n \n // Perform topological sorting\n while (!queue.isEmpty()) {\n int cur = queue.poll();\n ans[j++] = cur;\n \n // Update in-degrees and enqueue nodes with in-degree 0\n for (int next : map.get(cur)) {\n if (indg.merge(next, -1, Integer::sum) == 0) {\n queue.offer(next);\n }\n }\n }\n \n // Return the sorted array or an empty array if sorting is not possible\n return j == ans.length ? ans : new int[]{};\n }\n}\n```\n```Python3 []\nclass Solution:\n def has_cycle(self, graph, cur_node, visited, result):\n if visited[cur_node] == 1:\n return False\n if visited[cur_node] == 2:\n return True\n visited[cur_node] = 2\n for next_node in graph[cur_node]:\n if self.has_cycle(graph, next_node, visited, result):\n return True\n visited[cur_node] = 1\n result.append(cur_node)\n return False\n\n def sortItems(self, n: int, m: int, group: List[int],\n beforeItems: List[List[int]]) -> List[int]:\n # Map between group_id and item_ids\n group_items_map = defaultdict(list)\n # Visited for items in each group. Will be used later\n visited_item = defaultdict(dict)\n for i in range(n):\n # Assign no-group items to a new group\n if group[i] == -1:\n group[i] = m\n m += 1\n group_items_map[group[i]].append(i)\n visited_item[group[i]][i] = 0\n\n # key - group_id : value - next_groups\n graph_group = defaultdict(set)\n # key - group_id : value - {key - item_id : value: next_items}\n graph_item = {i: defaultdict(list) for i in range(m)}\n\n # Create graph for items and groups\n for item_after, before_items in enumerate(beforeItems):\n for item_before in before_items:\n group_before = group[item_before]\n group_after = group[item_after]\n\n # If two items belong to different groups,\n # add a dependency between groups\n # Otherwise, add a dependency between items in the same group\n if group_before != group_after:\n graph_group[group_before].add(group_after)\n else:\n graph_item[group_before][item_before].append(item_after)\n\n # Use DFS to find group order\n visited_group = [0] * m\n group_order = []\n for group_id in range(m):\n if self.has_cycle(graph_group, group_id,\n visited_group, group_order):\n return []\n\n # Use DFS to find item order in each group\n full_item_order = []\n for group_id in group_order:\n for item_id in group_items_map[group_id]:\n if self.has_cycle(graph_item[group_id], item_id,\n visited_item[group_id], full_item_order):\n return []\n return full_item_order[::-1]\n```\n```C++ []\nclass Solution {\npublic:\n // Topological Sort\n vector<int> topologicalSort(vector<unordered_set<int> >& graph, vector<int>& indegree) {\n vector<int> order;\n int processed = 0, n = graph.size();\n \n queue<int> q;\n // Add 0 indegree nodes\n for(int node = 0; node < n; node++) \n if(indegree[node] == 0)\n q.emplace(node);\n \n while(!q.empty()) {\n auto node = q.front();\n q.pop();\n \n // process the node\n ++processed;\n order.emplace_back(node);\n \n // Remove its dependence\n for(auto neighbor: graph[node]) {\n --indegree[neighbor];\n if(indegree[neighbor] == 0)\n q.emplace(neighbor);\n }\n }\n \n return processed < n ? vector<int>{} : order;\n }\n \n vector<int> sortItems(int n, int m, vector<int>& group, vector<vector<int>>& beforeItems) {\n // Each node without a group will be self contained in a new group with only itself\n // Set the new group id for each isolated node\n for(int node = 0; node < n; node++)\n if(group[node] == -1)\n group[node] = m++;\n \n // We create two graphs, one for the groups and another for the actual nodes\n vector<unordered_set<int> > group_graph(m), node_graph(n);\n // Stores the indegree for: Amongst Groups and nodes respectively\n vector<int> group_indegree(m, 0), node_indegree(n, 0);\n \n // Create cyclic graph for group and individual nodes\n for(auto node = 0; node < n; node++) {\n // Group to which the current node belongs\n int dst_group = group[node];\n // Source Groups on which the current node has a dependency\n for(auto src_node: beforeItems[node]) {\n int src_group = group[src_node];\n // check if the dependency is inter group or intra group\n // It is inter group dependency, make sure that the same dst_group was not seen\n // before, otherwise indegree will get additional 1, same logic for the node_graph\n if(dst_group != src_group && !group_graph[src_group].count(dst_group)) {\n group_graph[src_group].emplace(dst_group);\n ++group_indegree[dst_group];\n }\n \n // Add the dependency amongst the nodes\n if(!node_graph[src_node].count(node)) {\n node_graph[src_node].emplace(node);\n ++node_indegree[node];\n }\n }\n }\n \n // Perform topological sort at a node level \n vector<int> ordered_nodes = topologicalSort(node_graph, node_indegree);\n // Perform topological sort at a group level\n vector<int> ordered_groups = topologicalSort(group_graph, group_indegree);\n // Overall order of nodes\n vector<int> order;\n \n // For each group, put the ordered nodes after topological sort\n vector<vector<int> > group_ordered_nodes(m);\n for(auto node: ordered_nodes)\n group_ordered_nodes[group[node]].emplace_back(node);\n \n // Now that within each group, all the nodes are ordered.\n // Using the topological sort info about the groups, just put the nodes in that order\n for(auto group: ordered_groups) \n for(auto node: group_ordered_nodes[group])\n order.emplace_back(node);\n \n return order;\n }\n};\n```\n---\n\n\n---\n\n``` | 6 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
🔥🔥🔥🔥🔥Easy Solution | JS | TS | Java | C++ | Python 🔥🔥🔥🔥🔥 | sort-items-by-groups-respecting-dependencies | 1 | 1 | ---\n\n\n---\n**Intuition:**\nTo solve this problem, we need to perform a topological sort considering the constraints from both the `group` and `beforeItems` arrays. The items within the same group should be adjacent in the sorted list, and the ordering of items given in the `beforeItems` array should be respected.\n\n**Approach:**\n1. First, we\'ll construct a directed graph where nodes represent items and directed edges represent the "before" relationships given in the `beforeItems` array. We\'ll also keep track of the in-degrees (number of incoming edges) for each node.\n\n2. We\'ll create a separate graph for groups, where nodes represent groups and directed edges represent the "before" relationships between groups based on the items\' relationships.\n\n3. Next, we\'ll find the topological order of the groups using a modified version of Kahn\'s algorithm. While finding the topological order of groups, we\'ll also consider the constraints from the `group` array.\n\n4. For each group in the topological order:\n - Find the items within that group and sort them based on the constraints given in the `beforeItems` array. This can be done using a priority queue.\n - Append the sorted items to the final sorted list.\n\n5. If at any point, while constructing the topological order or sorting the items within a group, we encounter a cycle or any invalid ordering, we\'ll return an empty list as there\'s no valid solution.\n\n**Complexity:**\n- Constructing the graph takes O(n + m) time, where n is the number of items and m is the number of groups.\n- Constructing the topological order of groups takes O(n + m) time.\n- Sorting the items within each group takes O(n log n) time in total.\n- Overall, the time complexity is O(n log n).\n\nThe space complexity is O(n + m) for storing the graphs and related data structures.\n\nRemember that this is a complex problem with multiple steps involved, so make sure to understand each step before implementing it in code.\n\n# Code\n\n```javascript []\nconst initializeGraph = (n) => { let G = []; for (let i = 0; i < n; i++) { G.push([]); } return G; };\nconst initializeGraphSet = (n) => { let G = []; for (let i = 0; i < n; i++) { G.push(new Set()); } return G; };\n\nconst sortItems = (n, m, group, beforeItems) => {\n for (let i = 0; i < n; i++) {\n if (group[i] == -1) {\n group[i] = m++;\n }\n }\n let gg = initializeGraphSet(m); // graph group\n let gi = initializeGraphSet(n); // graph item\n let indegreeGG = Array(m).fill(0);\n let indegreeGI = Array(n).fill(0);\n let res = [];\n for (let i = 0; i < n; i++) {\n let to = group[i];\n for (const x of beforeItems[i]) {\n let from = group[x];\n if (from != to && !gg[from].has(to)) {\n gg[from].add(to);\n indegreeGG[to]++;\n }\n if (!gi[x].has(i)) {\n gi[x].add(i);\n indegreeGI[i]++;\n }\n }\n }\n let ggOrder = topologicalSort(gg, indegreeGG);\n let giOrder = topologicalSort(gi, indegreeGI);\n if (ggOrder.length == 0 || giOrder.length == 0) return [];\n let group2Item = initializeGraph(m);\n for (const item of giOrder) group2Item[group[item]].push(item);\n for (const group_id of ggOrder) {\n for (const item of group2Item[group_id]) {\n res.push(item);\n }\n }\n return res;\n};\n\nconst topologicalSort = (g, indegree) => {\n let res = [], q = [], len = indegree.length;\n for (let i = 0; i < len; i++) {\n if (indegree[i] == 0) q.push(i);\n }\n while (q.length) {\n let cur = q.shift();\n res.push(cur);\n for (const child of g[cur]) {\n if (--indegree[child] == 0) q.push(child);\n }\n }\n for (let i = 0; i < len; i++) {\n if (indegree[i] > 0) return [];\n }\n return res;\n};\n```\n```Typescript []\n/*\nThe idea is to combine nodes and groups.\n\nWe add group nodes and make beetween group relations.\n*/\n\nfunction sortItems(n: number, m: number, group: number[], beforeItems: number[][]): number[] {\n // create empty graph for nodes and groups (n + m);\n const graph = new Map<number, Set<number>>();\n for (let i = 0; i < n + m; i++) {\n graph.set(i, new Set());\n }\n\n const indegrees = new Array(n + m).fill(0);\n for (let i = 0; i < beforeItems.length; i++) {\n const items = beforeItems[i];\n const currGroup = n + group[i]; // group index started with offset;\n\n // Relation between group and current node \n if (group[i] !== -1) {\n graph.get(currGroup).add(i);\n indegrees[i]++;\n }\n\n // two types of relation 1) between nodes inside of the group 2) between the groups\n for (const item of items) {\n const itemGroup = n + group[item];\n if (currGroup === itemGroup || group[i] === -1 || group[item] === -1) {\n graph.get(item).add(i);\n indegrees[i]++;\n } else {\n if (!graph.get(itemGroup).has(currGroup)) {\n graph.get(itemGroup).add(currGroup);\n indegrees[currGroup]++;\n }\n }\n }\n }\n\n // Typical topological sort\n const zeroInDegree = [];\n for (let i = 0; i < indegrees.length; i++) {\n if (!indegrees[i]) {\n zeroInDegree.push(i)\n }\n }\n\n const map = new Map<number, number[]>();\n // keep groups order\n const pushToMap = (item: number ) => {\n if (group[item] === -1) {\n map.set(item + n, [item])\n return;\n } \n if (map.has(group[item])) {\n map.get(group[item]).push(item); \n } else {\n map.set(group[item], [item]);\n }\n }\n\n let count = 0;\n while (zeroInDegree.length) {\n const curr = zeroInDegree.shift();\n if (curr < n) {\n count++;\n pushToMap(curr);\n }\n \n for (const neighbor of graph.get(curr)) {\n indegrees[neighbor]--;\n if (!indegrees[neighbor]) {\n zeroInDegree.push(neighbor);\n }\n }\n }\n\n // Hadle cases with cycles\n if (count !== n) {\n return [];\n }\n\n return [].concat(...map.values());\n};\n```\n```Java []\nclass Solution {\n public int[] sortItems(int n, int m, int[] grp, List<List<Integer>> beforeItems) {\n int[] ans = new int[n];\n \n // Create data structures to store relationships between items and groups\n Map<Integer, Map<Integer, Set<Integer>>> itemMap = new HashMap<>();\n Map<Integer, Set<Integer>> grpMap = new HashMap<>();\n \n // Assign unique group IDs to items with no group\n for (int i = 0; i < n; i++) {\n if (grp[i] == -1) {\n grp[i] = m++;\n }\n }\n \n // Initialize the maps for groups and items\n for (int i = 0; i < m; i++) {\n grpMap.put(i, new HashSet<>());\n itemMap.put(i, new HashMap<>());\n }\n \n // Initialize intra-group relationships\n for (int i = 0; i < n; i++) {\n itemMap.get(grp[i]).put(i, new HashSet<>());\n }\n \n // Populate relationships between items based on beforeItems\n for (int i = 0; i < beforeItems.size(); i++) {\n for (int item : beforeItems.get(i)) {\n if (grp[i] == grp[item]) {\n // Within the same group, add relationship to intra-group map\n itemMap.get(grp[i]).get(item).add(i);\n } else {\n // Between different groups, add relationship to inter-group map\n grpMap.get(grp[item]).add(grp[i]);\n }\n }\n }\n \n int j = 0;\n // Perform topological sorting on groups and items within each group\n for (int g : topSort(grpMap)) {\n for (int item : topSort(itemMap.get(g))) {\n ans[j++] = item;\n }\n }\n \n // Return the sorted items or an empty array if sorting is not possible\n return j < ans.length ? new int[]{} : ans;\n }\n\n // Topological sorting function\n private int[] topSort(Map<Integer, Set<Integer>> map) {\n Map<Integer, Integer> indg = new HashMap<>();\n \n // Calculate in-degrees of nodes\n for (Set<Integer> values : map.values()) {\n for (int m : values) {\n indg.merge(m, 1, Integer::sum);\n }\n }\n \n Queue<Integer> queue = new ArrayDeque<>();\n \n // Initialize the queue with nodes having in-degree 0\n for (int key : map.keySet()) {\n if (!indg.containsKey(key)) {\n queue.offer(key);\n }\n }\n \n int j = 0;\n int[] ans = new int[map.size()];\n \n // Perform topological sorting\n while (!queue.isEmpty()) {\n int cur = queue.poll();\n ans[j++] = cur;\n \n // Update in-degrees and enqueue nodes with in-degree 0\n for (int next : map.get(cur)) {\n if (indg.merge(next, -1, Integer::sum) == 0) {\n queue.offer(next);\n }\n }\n }\n \n // Return the sorted array or an empty array if sorting is not possible\n return j == ans.length ? ans : new int[]{};\n }\n}\n```\n```Python3 []\nclass Solution:\n def has_cycle(self, graph, cur_node, visited, result):\n if visited[cur_node] == 1:\n return False\n if visited[cur_node] == 2:\n return True\n visited[cur_node] = 2\n for next_node in graph[cur_node]:\n if self.has_cycle(graph, next_node, visited, result):\n return True\n visited[cur_node] = 1\n result.append(cur_node)\n return False\n\n def sortItems(self, n: int, m: int, group: List[int],\n beforeItems: List[List[int]]) -> List[int]:\n # Map between group_id and item_ids\n group_items_map = defaultdict(list)\n # Visited for items in each group. Will be used later\n visited_item = defaultdict(dict)\n for i in range(n):\n # Assign no-group items to a new group\n if group[i] == -1:\n group[i] = m\n m += 1\n group_items_map[group[i]].append(i)\n visited_item[group[i]][i] = 0\n\n # key - group_id : value - next_groups\n graph_group = defaultdict(set)\n # key - group_id : value - {key - item_id : value: next_items}\n graph_item = {i: defaultdict(list) for i in range(m)}\n\n # Create graph for items and groups\n for item_after, before_items in enumerate(beforeItems):\n for item_before in before_items:\n group_before = group[item_before]\n group_after = group[item_after]\n\n # If two items belong to different groups,\n # add a dependency between groups\n # Otherwise, add a dependency between items in the same group\n if group_before != group_after:\n graph_group[group_before].add(group_after)\n else:\n graph_item[group_before][item_before].append(item_after)\n\n # Use DFS to find group order\n visited_group = [0] * m\n group_order = []\n for group_id in range(m):\n if self.has_cycle(graph_group, group_id,\n visited_group, group_order):\n return []\n\n # Use DFS to find item order in each group\n full_item_order = []\n for group_id in group_order:\n for item_id in group_items_map[group_id]:\n if self.has_cycle(graph_item[group_id], item_id,\n visited_item[group_id], full_item_order):\n return []\n return full_item_order[::-1]\n```\n```C++ []\nclass Solution {\npublic:\n // Topological Sort\n vector<int> topologicalSort(vector<unordered_set<int> >& graph, vector<int>& indegree) {\n vector<int> order;\n int processed = 0, n = graph.size();\n \n queue<int> q;\n // Add 0 indegree nodes\n for(int node = 0; node < n; node++) \n if(indegree[node] == 0)\n q.emplace(node);\n \n while(!q.empty()) {\n auto node = q.front();\n q.pop();\n \n // process the node\n ++processed;\n order.emplace_back(node);\n \n // Remove its dependence\n for(auto neighbor: graph[node]) {\n --indegree[neighbor];\n if(indegree[neighbor] == 0)\n q.emplace(neighbor);\n }\n }\n \n return processed < n ? vector<int>{} : order;\n }\n \n vector<int> sortItems(int n, int m, vector<int>& group, vector<vector<int>>& beforeItems) {\n // Each node without a group will be self contained in a new group with only itself\n // Set the new group id for each isolated node\n for(int node = 0; node < n; node++)\n if(group[node] == -1)\n group[node] = m++;\n \n // We create two graphs, one for the groups and another for the actual nodes\n vector<unordered_set<int> > group_graph(m), node_graph(n);\n // Stores the indegree for: Amongst Groups and nodes respectively\n vector<int> group_indegree(m, 0), node_indegree(n, 0);\n \n // Create cyclic graph for group and individual nodes\n for(auto node = 0; node < n; node++) {\n // Group to which the current node belongs\n int dst_group = group[node];\n // Source Groups on which the current node has a dependency\n for(auto src_node: beforeItems[node]) {\n int src_group = group[src_node];\n // check if the dependency is inter group or intra group\n // It is inter group dependency, make sure that the same dst_group was not seen\n // before, otherwise indegree will get additional 1, same logic for the node_graph\n if(dst_group != src_group && !group_graph[src_group].count(dst_group)) {\n group_graph[src_group].emplace(dst_group);\n ++group_indegree[dst_group];\n }\n \n // Add the dependency amongst the nodes\n if(!node_graph[src_node].count(node)) {\n node_graph[src_node].emplace(node);\n ++node_indegree[node];\n }\n }\n }\n \n // Perform topological sort at a node level \n vector<int> ordered_nodes = topologicalSort(node_graph, node_indegree);\n // Perform topological sort at a group level\n vector<int> ordered_groups = topologicalSort(group_graph, group_indegree);\n // Overall order of nodes\n vector<int> order;\n \n // For each group, put the ordered nodes after topological sort\n vector<vector<int> > group_ordered_nodes(m);\n for(auto node: ordered_nodes)\n group_ordered_nodes[group[node]].emplace_back(node);\n \n // Now that within each group, all the nodes are ordered.\n // Using the topological sort info about the groups, just put the nodes in that order\n for(auto group: ordered_groups) \n for(auto node: group_ordered_nodes[group])\n order.emplace_back(node);\n \n return order;\n }\n};\n```\n---\n\n\n---\n\n``` | 6 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
Python3 Solution | sort-items-by-groups-respecting-dependencies | 0 | 1 | \n```\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n for i in range(n):\n if group[i]==-1:\n group[i]=i+m\n\n graph0={}\n seen0=[0]*(m+n)\n graph1={}\n seen1=[0]*n\n\n for i,x in enumerate(beforeItems):\n for j in x:\n if group[j]!=group[i]:\n graph0.setdefault(group[j],[]).append(group[i])\n seen0[group[i]]+=1\n\n graph1.setdefault(j,[]).append(i)\n seen1[i]+=1\n\n def fn(graph,seen):\n N=len(seen)\n ans=[]\n stack=[k for k in range(N) if seen[k]==0 ]\n while stack:\n n=stack.pop()\n ans.append(n)\n for s in graph.get(n,[]):\n seen[s]-=1\n if seen[s]==0:\n stack.append(s)\n return ans\n\n top0=fn(graph0,seen0)\n a=len(top0)\n b=len(seen0) \n if a!=b:\n return []\n\n top1=fn(graph1,seen1)\n c=len(top1)\n d=len(seen1)\n if c!=d:\n return []\n map0={x:i for i,x in enumerate(top0)}\n map1={x:i for i,x in enumerate(top1)} \n return sorted( range(n),key=lambda x:(map0[group[x]],map1[x]))\n``` | 4 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
Python3 Solution | sort-items-by-groups-respecting-dependencies | 0 | 1 | \n```\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n for i in range(n):\n if group[i]==-1:\n group[i]=i+m\n\n graph0={}\n seen0=[0]*(m+n)\n graph1={}\n seen1=[0]*n\n\n for i,x in enumerate(beforeItems):\n for j in x:\n if group[j]!=group[i]:\n graph0.setdefault(group[j],[]).append(group[i])\n seen0[group[i]]+=1\n\n graph1.setdefault(j,[]).append(i)\n seen1[i]+=1\n\n def fn(graph,seen):\n N=len(seen)\n ans=[]\n stack=[k for k in range(N) if seen[k]==0 ]\n while stack:\n n=stack.pop()\n ans.append(n)\n for s in graph.get(n,[]):\n seen[s]-=1\n if seen[s]==0:\n stack.append(s)\n return ans\n\n top0=fn(graph0,seen0)\n a=len(top0)\n b=len(seen0) \n if a!=b:\n return []\n\n top1=fn(graph1,seen1)\n c=len(top1)\n d=len(seen1)\n if c!=d:\n return []\n map0={x:i for i,x in enumerate(top0)}\n map1={x:i for i,x in enumerate(top1)} \n return sorted( range(n),key=lambda x:(map0[group[x]],map1[x]))\n``` | 4 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
🚒 🚒 Two Level Topological Sorting 🕸️🕸️✅ | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Intuition\nTo solve this problem, topological sorting should be done at two levels, one topological sorting to sort the `groups`, and the other to sort the `items` with in a `group`.\n\n# Approach\n1. Assign unique groups to the items that are not part of any group to maintain consistency. i.e assign `group[item_id]` with unique `group_id` where ever it is `-1`.\n2. Using `beforeItems` create a topological graph to represent dependency b/w different `groups` represented with an adjacency list, also calculate `indegree` of each `group` w.r.t the graph.\n3. Similaly create a topological dependency graph represented in adjacency list between all the `items` by considering only the dependencies b/w the `items` with in the same `group`. Also calculate indegree of each item w.r.t the graph.\n4. Perform [topological sorting](https://www.hackerearth.com/practice/algorithms/graphs/topological-sort/tutorial/) on the `groups` using the dependency graph created in `#2`.\n5. Based on the topological order of `groups` in `#4`, perform topological sorting on `items` using the dependency graph and its indegree created in `#3` with in each `group`.\n6. If there is a cyclic dependency in either of the dependency graphs `#2` or `#3`, fail fast and return an empty list. To check if there is a cyclic dependency in a graph - if the indegree of any of the node in graph is non-zero after performing topological sorting.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass CyclicDependencyException(Exception):\n "Raised when there is a cyclic dependecy in graph"\n pass\n\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n\n # 1. Fill item to group mapping to create new groups for items non in any group\n def create_and_fill_groups():\n nonlocal m\n for i in range(n):\n if group[i] == -1:\n group[i] = m\n m += 1\n return m\n \n def get_items_in_group():\n nonlocal m\n items_in_group = [ [] for _ in range(m)]\n for i in range(n):\n items_in_group[group[i]].append(i)\n return items_in_group\n \n # 2. Create adjacency list from beforeItems[] also calculate indegree\n def get_adjacency_list_from_beforeItems(): \n nonlocal m, n\n group_indegree = [0] * m\n group_adj = [ set() for _ in range(m)]\n group_item_adj = []\n item_adj = [ [] for _ in range(n)]\n item_indegree = [0] * n\n\n for i in range(n):\n for beforeItem in beforeItems[i]:\n if group[beforeItem] == group[i]:\n item_adj[beforeItem].append(i)\n item_indegree[i] += 1\n else:\n if group[i] not in group_adj[group[beforeItem]]:\n group_adj[group[beforeItem]].add(group[i])\n group_indegree[group[i]] += 1\n \n return item_adj, item_indegree, group_adj, group_indegree\n \n\n def get_topological_order_of_items_in_group(items: List[int]) -> List[int]:\n queue = []\n items_topological_order = []\n\n for i in items:\n if item_indegree[i] == 0:\n queue.append(i)\n \n while len(queue):\n new_queue = []\n for item in queue:\n items_topological_order.append(item)\n for after_item in item_adj[item]:\n item_indegree[after_item] -= 1\n if item_indegree[after_item] == 0:\n new_queue.append(after_item)\n queue = new_queue\n \n for item in items:\n if item_indegree[item] != 0:\n raise CyclicDependencyException\n \n return items_topological_order\n\n # 3. Perform topological sorting based on groups\n def get_topological_order(items_in_group: List[List[int]]):\n nonlocal m\n queue = []\n for group_id in range(m):\n if group_indegree[group_id] == 0:\n queue.append(group_id)\n\n topological_order = []\n while len(queue):\n new_queue = []\n for group_id in queue:\n try:\n # topological order of items with in group\n items_topological_order = get_topological_order_of_items_in_group(items_in_group[group_id])\n except CyclicDependencyException:\n # fail fast and return empty list if items with in group have cyclic dependency\n return []\n topological_order.extend(items_topological_order)\n for after_group_id in group_adj[group_id]:\n group_indegree[after_group_id] -= 1\n if group_indegree[after_group_id] == 0:\n new_queue.append(after_group_id)\n queue = new_queue\n \n for group_id in range(m):\n if group_indegree[group_id] != 0:\n # fail fast and return empty list if groups have cyclic dependency \n return []\n return topological_order\n\n create_and_fill_groups()\n item_adj, item_indegree, group_adj, group_indegree = get_adjacency_list_from_beforeItems()\n items_in_group = get_items_in_group()\n\n return get_topological_order(items_in_group)\n\n\n\n``` | 1 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
🚒 🚒 Two Level Topological Sorting 🕸️🕸️✅ | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Intuition\nTo solve this problem, topological sorting should be done at two levels, one topological sorting to sort the `groups`, and the other to sort the `items` with in a `group`.\n\n# Approach\n1. Assign unique groups to the items that are not part of any group to maintain consistency. i.e assign `group[item_id]` with unique `group_id` where ever it is `-1`.\n2. Using `beforeItems` create a topological graph to represent dependency b/w different `groups` represented with an adjacency list, also calculate `indegree` of each `group` w.r.t the graph.\n3. Similaly create a topological dependency graph represented in adjacency list between all the `items` by considering only the dependencies b/w the `items` with in the same `group`. Also calculate indegree of each item w.r.t the graph.\n4. Perform [topological sorting](https://www.hackerearth.com/practice/algorithms/graphs/topological-sort/tutorial/) on the `groups` using the dependency graph created in `#2`.\n5. Based on the topological order of `groups` in `#4`, perform topological sorting on `items` using the dependency graph and its indegree created in `#3` with in each `group`.\n6. If there is a cyclic dependency in either of the dependency graphs `#2` or `#3`, fail fast and return an empty list. To check if there is a cyclic dependency in a graph - if the indegree of any of the node in graph is non-zero after performing topological sorting.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass CyclicDependencyException(Exception):\n "Raised when there is a cyclic dependecy in graph"\n pass\n\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n\n # 1. Fill item to group mapping to create new groups for items non in any group\n def create_and_fill_groups():\n nonlocal m\n for i in range(n):\n if group[i] == -1:\n group[i] = m\n m += 1\n return m\n \n def get_items_in_group():\n nonlocal m\n items_in_group = [ [] for _ in range(m)]\n for i in range(n):\n items_in_group[group[i]].append(i)\n return items_in_group\n \n # 2. Create adjacency list from beforeItems[] also calculate indegree\n def get_adjacency_list_from_beforeItems(): \n nonlocal m, n\n group_indegree = [0] * m\n group_adj = [ set() for _ in range(m)]\n group_item_adj = []\n item_adj = [ [] for _ in range(n)]\n item_indegree = [0] * n\n\n for i in range(n):\n for beforeItem in beforeItems[i]:\n if group[beforeItem] == group[i]:\n item_adj[beforeItem].append(i)\n item_indegree[i] += 1\n else:\n if group[i] not in group_adj[group[beforeItem]]:\n group_adj[group[beforeItem]].add(group[i])\n group_indegree[group[i]] += 1\n \n return item_adj, item_indegree, group_adj, group_indegree\n \n\n def get_topological_order_of_items_in_group(items: List[int]) -> List[int]:\n queue = []\n items_topological_order = []\n\n for i in items:\n if item_indegree[i] == 0:\n queue.append(i)\n \n while len(queue):\n new_queue = []\n for item in queue:\n items_topological_order.append(item)\n for after_item in item_adj[item]:\n item_indegree[after_item] -= 1\n if item_indegree[after_item] == 0:\n new_queue.append(after_item)\n queue = new_queue\n \n for item in items:\n if item_indegree[item] != 0:\n raise CyclicDependencyException\n \n return items_topological_order\n\n # 3. Perform topological sorting based on groups\n def get_topological_order(items_in_group: List[List[int]]):\n nonlocal m\n queue = []\n for group_id in range(m):\n if group_indegree[group_id] == 0:\n queue.append(group_id)\n\n topological_order = []\n while len(queue):\n new_queue = []\n for group_id in queue:\n try:\n # topological order of items with in group\n items_topological_order = get_topological_order_of_items_in_group(items_in_group[group_id])\n except CyclicDependencyException:\n # fail fast and return empty list if items with in group have cyclic dependency\n return []\n topological_order.extend(items_topological_order)\n for after_group_id in group_adj[group_id]:\n group_indegree[after_group_id] -= 1\n if group_indegree[after_group_id] == 0:\n new_queue.append(after_group_id)\n queue = new_queue\n \n for group_id in range(m):\n if group_indegree[group_id] != 0:\n # fail fast and return empty list if groups have cyclic dependency \n return []\n return topological_order\n\n create_and_fill_groups()\n item_adj, item_indegree, group_adj, group_indegree = get_adjacency_list_from_beforeItems()\n items_in_group = get_items_in_group()\n\n return get_topological_order(items_in_group)\n\n\n\n``` | 1 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
Python toposort | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Intuition\nToposort it. Return [] if failed.\nSort each groups first then sort all groups.\n\n# Code\n```\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n\n # Transform group definition\n group = [ g - (g==-1) * i for i, g in enumerate(group)]\n\n # Collect group items\n G = defaultdict(list)\n for i, g in enumerate(group):\n G[g] += [i]\n \n def toposorted(items, outEdges, inEdgeCount, transform = lambda x: [x]):\n done = set()\n sortedList = []\n while True:\n findAny = False\n for item in items:\n if item in done:\n continue\n if inEdgeCount[item] == 0:\n findAny = True\n for outEdge in outEdges[item]:\n inEdgeCount[outEdge] -= 1\n sortedList += transform(item)\n done |= set([item])\n if len(done) == len(items):\n return sortedList\n if findAny == False:\n return []\n\n # Resolve toposort for each groups\n sortedGroups = {}\n beforeGroups = defaultdict(list)\n for g, items in G.items():\n outEdges = defaultdict(list)\n inEdgeCount = defaultdict(int)\n for item in items:\n for beforeItem in beforeItems[item]:\n if beforeItem in items:\n outEdges[beforeItem] += [item]\n inEdgeCount[item] += 1\n else:\n beforeGroups[g] += [group[beforeItem]]\n sortedList = toposorted(items, outEdges, inEdgeCount)\n if not sortedList:\n return []\n sortedGroups[g] = sortedList\n\n # Resolve toposort between groups\n group = frozenset(group)\n outEdges = defaultdict(list)\n inEdgeCount = defaultdict(int)\n for g in group:\n for beforeGroup in beforeGroups[g]:\n outEdges[beforeGroup] += [g]\n inEdgeCount[g] += 1\n return toposorted(group, outEdges, inEdgeCount, lambda x: sortedGroups[x])\n\n\n\n``` | 1 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
Python toposort | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Intuition\nToposort it. Return [] if failed.\nSort each groups first then sort all groups.\n\n# Code\n```\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n\n # Transform group definition\n group = [ g - (g==-1) * i for i, g in enumerate(group)]\n\n # Collect group items\n G = defaultdict(list)\n for i, g in enumerate(group):\n G[g] += [i]\n \n def toposorted(items, outEdges, inEdgeCount, transform = lambda x: [x]):\n done = set()\n sortedList = []\n while True:\n findAny = False\n for item in items:\n if item in done:\n continue\n if inEdgeCount[item] == 0:\n findAny = True\n for outEdge in outEdges[item]:\n inEdgeCount[outEdge] -= 1\n sortedList += transform(item)\n done |= set([item])\n if len(done) == len(items):\n return sortedList\n if findAny == False:\n return []\n\n # Resolve toposort for each groups\n sortedGroups = {}\n beforeGroups = defaultdict(list)\n for g, items in G.items():\n outEdges = defaultdict(list)\n inEdgeCount = defaultdict(int)\n for item in items:\n for beforeItem in beforeItems[item]:\n if beforeItem in items:\n outEdges[beforeItem] += [item]\n inEdgeCount[item] += 1\n else:\n beforeGroups[g] += [group[beforeItem]]\n sortedList = toposorted(items, outEdges, inEdgeCount)\n if not sortedList:\n return []\n sortedGroups[g] = sortedList\n\n # Resolve toposort between groups\n group = frozenset(group)\n outEdges = defaultdict(list)\n inEdgeCount = defaultdict(int)\n for g in group:\n for beforeGroup in beforeGroups[g]:\n outEdges[beforeGroup] += [g]\n inEdgeCount[g] += 1\n return toposorted(group, outEdges, inEdgeCount, lambda x: sortedGroups[x])\n\n\n\n``` | 1 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
Python | Easy to Understand | Dependency Nodes | Two-Level Topological Sort | Optimal | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Python | Easy to Understand | Dependency Nodes | Two-Level Topological Sort | Optimal\n```\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n def topo_sort(points, pre, suc):\n order = []\n sources = [p for p in points if not pre[p]]\n while sources:\n s = sources.pop()\n order.append(s)\n for u in suc[s]:\n pre[u].remove(s)\n if not pre[u]:\n sources.append(u)\n return order if len(order) == len(points) else []\n \n # find the group of each item\n group2item = collections.defaultdict(set)\n for i in range(n):\n if group[i] == -1:\n group[i] = m\n m += 1\n group2item[group[i]].add(i)\n # find the relationships between the groups and each items in the same group\n t_pre, t_suc = collections.defaultdict(set), collections.defaultdict(set)\n g_pre, g_suc = collections.defaultdict(set), collections.defaultdict(set)\n for i in range(n):\n for j in beforeItems[i]:\n if group[i] == group[j]:\n t_pre[i].add(j)\n t_suc[j].add(i)\n else:\n g_pre[group[i]].add(group[j])\n g_suc[group[j]].add(group[i])\n # topological sort the groups\n groups_order = topo_sort([i for i in group2item], g_pre, g_suc)\n # topological sort the items in each group\n t_order = []\n for i in groups_order:\n items = group2item[i]\n i_order = topo_sort(items, t_pre, t_suc)\n if len(i_order) != len(items):\n return []\n t_order += i_order\n return t_order if len(t_order) == n else []\n``` | 1 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
Python | Easy to Understand | Dependency Nodes | Two-Level Topological Sort | Optimal | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Python | Easy to Understand | Dependency Nodes | Two-Level Topological Sort | Optimal\n```\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n def topo_sort(points, pre, suc):\n order = []\n sources = [p for p in points if not pre[p]]\n while sources:\n s = sources.pop()\n order.append(s)\n for u in suc[s]:\n pre[u].remove(s)\n if not pre[u]:\n sources.append(u)\n return order if len(order) == len(points) else []\n \n # find the group of each item\n group2item = collections.defaultdict(set)\n for i in range(n):\n if group[i] == -1:\n group[i] = m\n m += 1\n group2item[group[i]].add(i)\n # find the relationships between the groups and each items in the same group\n t_pre, t_suc = collections.defaultdict(set), collections.defaultdict(set)\n g_pre, g_suc = collections.defaultdict(set), collections.defaultdict(set)\n for i in range(n):\n for j in beforeItems[i]:\n if group[i] == group[j]:\n t_pre[i].add(j)\n t_suc[j].add(i)\n else:\n g_pre[group[i]].add(group[j])\n g_suc[group[j]].add(group[i])\n # topological sort the groups\n groups_order = topo_sort([i for i in group2item], g_pre, g_suc)\n # topological sort the items in each group\n t_order = []\n for i in groups_order:\n items = group2item[i]\n i_order = topo_sort(items, t_pre, t_suc)\n if len(i_order) != len(items):\n return []\n t_order += i_order\n return t_order if len(t_order) == n else []\n``` | 1 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
python 100% faster | two topological sort | simple code | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Approach\nIf we ignore the condition that elements of the same group must be together it is a classical problem solvable with topological sorting, now to add the other constraint we can make two separate networks and then run a topological sorting for each graph.\n\nThe first network will be a set of $m$ disjoint graphs in which each graph represents a group and there can only be edges between elements that share a group, of course the edges are given by the constraints $beforeItems$.\n\nThe second network will be for groups, now we treat each node of a group as equal.\n\n# Complexity\n- Time complexity:\n- $O(E+V)$ $V$ is the number of nodes and $E$ is the number of edges, in this problem $E = \\sum beforeItems[i].length$ \nAnd $V = max(n,m+#itemsWithoutGroup)$ since we assign a unique group to each element without a group to simplify the code and not have to deal with special cases\n\n\n# Code\n```python\nclass Solution:\n def topologicalSort(self,N,graph,inDegree):\n q = deque()\n for i in range(N):\n if inDegree[i]== 0:\n q.append(i)\n\n order = []\n while q: \n u = q.popleft()\n order.append(u)\n for v in graph[u]:\n inDegree[v]-=1 \n if inDegree[v]==0:\n q.append(v)\n\n return order\n\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n # Order inside a group\n graph = [[]for _ in range(n)]\n inDegree = [0]*n\n\n # For items that don\'t have group we assign an unique group, this allows simpler implementation\n for i in range(n):\n if group[i]==-1:\n group[i] = m\n m+=1\n\n orderByGroup = [[]for _ in range(m+1)]\n\n for i in range(n):\n for before in beforeItems[i]:\n if group[before] == group[i]:\n graph[before].append(i)\n inDegree[i]+=1\n\n\n order = self.topologicalSort(n,graph,inDegree)\n for u in order:\n orderByGroup[group[u]].append(u)\n\n #Order between groups\n graph = [[]for _ in range(m+1)]\n inDegree = [0]*(m+1)\n for i in range(n):\n for before in beforeItems[i]:\n if group[before] != group[i]:\n graph[group[before]].append(group[i])\n inDegree[group[i]]+=1\n\n order = self.topologicalSort(m+1,graph,inDegree)\n ans = []\n for group in order: \n ans+=orderByGroup[group]\n\n if len(ans)!=n: ans = []\n return ans\n \n\n \n\n \n\n\n``` | 1 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
python 100% faster | two topological sort | simple code | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Approach\nIf we ignore the condition that elements of the same group must be together it is a classical problem solvable with topological sorting, now to add the other constraint we can make two separate networks and then run a topological sorting for each graph.\n\nThe first network will be a set of $m$ disjoint graphs in which each graph represents a group and there can only be edges between elements that share a group, of course the edges are given by the constraints $beforeItems$.\n\nThe second network will be for groups, now we treat each node of a group as equal.\n\n# Complexity\n- Time complexity:\n- $O(E+V)$ $V$ is the number of nodes and $E$ is the number of edges, in this problem $E = \\sum beforeItems[i].length$ \nAnd $V = max(n,m+#itemsWithoutGroup)$ since we assign a unique group to each element without a group to simplify the code and not have to deal with special cases\n\n\n# Code\n```python\nclass Solution:\n def topologicalSort(self,N,graph,inDegree):\n q = deque()\n for i in range(N):\n if inDegree[i]== 0:\n q.append(i)\n\n order = []\n while q: \n u = q.popleft()\n order.append(u)\n for v in graph[u]:\n inDegree[v]-=1 \n if inDegree[v]==0:\n q.append(v)\n\n return order\n\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n # Order inside a group\n graph = [[]for _ in range(n)]\n inDegree = [0]*n\n\n # For items that don\'t have group we assign an unique group, this allows simpler implementation\n for i in range(n):\n if group[i]==-1:\n group[i] = m\n m+=1\n\n orderByGroup = [[]for _ in range(m+1)]\n\n for i in range(n):\n for before in beforeItems[i]:\n if group[before] == group[i]:\n graph[before].append(i)\n inDegree[i]+=1\n\n\n order = self.topologicalSort(n,graph,inDegree)\n for u in order:\n orderByGroup[group[u]].append(u)\n\n #Order between groups\n graph = [[]for _ in range(m+1)]\n inDegree = [0]*(m+1)\n for i in range(n):\n for before in beforeItems[i]:\n if group[before] != group[i]:\n graph[group[before]].append(group[i])\n inDegree[group[i]]+=1\n\n order = self.topologicalSort(m+1,graph,inDegree)\n ans = []\n for group in order: \n ans+=orderByGroup[group]\n\n if len(ans)!=n: ans = []\n return ans\n \n\n \n\n \n\n\n``` | 1 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
✅ 97.18% 2-Approaches Topological Sorting | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Problem Understanding\n\nIn the "Sort Items by Groups Respecting Dependencies" problem, we are given `n` items each belonging to one of `m` groups or to no group at all. Each item might have dependencies, which are other items that need to come before it in a sorted order. The task is to return a sorted list of items such that items from the same group are adjacent and the dependencies between items are respected.\n\nFor instance, given `n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]`, the output should be `[6,3,4,1,5,2,0,7]`.\n\n**Input**: `n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]`\n**Output**: `[6,3,4,1,5,2,0,7]`\n\n---\n\n# Live Coding\nhttps://youtu.be/5aG9GUpBOMI\n\n# Performance Comparison:\n\n| Version | Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|---------|----------|--------------|------------------|-------------|-----------------|\n| Kahn\'s Approach | Python | 345 ms | 97.18% | 33.1 MB | 96.61% |\n| Two-tier | Python | 373 ms | 81.36% | 57.8 MB | 5.8% |\n\nThe table clearly shows the improvement in performance using the 2nd Kahn Approach.\n\n---\n\n# Approach: Topological Sorting\n\nTo solve the "Sort Items by Groups Respecting Dependencies" problem, we leverage topological sorting. The challenge requires a two-tier topological sort: first on the groups and then on the items within each group.\n\n## Key Data Structures:\n- **Deque**: Efficiently handles nodes without predecessors (in-degree of 0) during the topological sort.\n- **DefaultDict**: Manages relationships, mapping items to groups, and tracking predecessors and successors.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - **`group_to_items`**: A defaultdict mapping groups to their respective items.\n - **`new_group`**: A counter initialized to `m` to assign unique group numbers to ungrouped items.\n - **`intra_pred`, `intra_succ`, `inter_pred`, `inter_succ`**: Defaultdicts to manage intra-group and inter-group dependencies.\n\n2. **Assigning Groups and Mapping Items**:\n - Iterate over all items.\n - If an item doesn\'t belong to any group (`group[item] == -1`), assign it a new unique group.\n - Map the item to its respective group in `group_to_items`.\n\n3. **Constructing Dependency Relationships**:\n - Iterate over all items.\n - For each item, check its `beforeItems` dependencies.\n - If a dependency belongs to the same group, it\'s an intra-group dependency. Update `intra_pred` and `intra_succ`.\n - If a dependency belongs to a different group, it\'s an inter-group dependency. Update `inter_pred` and `inter_succ`.\n\n4. **Topological Sort**:\n - **On Groups**:\n - Using `group_to_items`, perform a topological sort on the groups based on inter-group dependencies.\n - If the sort fails (due to a cycle or any other reason), return an empty list.\n - **On Items within Groups**:\n - For each sorted group, perform a topological sort on its items based on intra-group dependencies.\n - If the sort fails for any group, return an empty list.\n - If successful, append the sorted items of the group to the `items_order` list.\n\n5. **Return Result**:\n - After processing all groups and their items, return the `items_order` list.\n\nThis approach ensures that the topological sort respects both the group-level and item-level dependencies, providing a solution that aligns with the problem\'s requirements.\n\n---\n\n# Complexity:\n\n**Time Complexity:**\n- **Adjacency List Construction**: $$ O(n^2) $$ due to potential item dependencies in `beforeItems`.\n- **Topological Sort (Items)**: $$ O(n^2) $$ as every vertex and edge might be visited/processed.\n- **Topological Sort (Groups)**: $$ O(n^2) $$ as there can be up to $$ n $$ groups.\n- **Overall**: $$ O(n^2) $$.\n\n**Space Complexity:**\n- **Adjacency Lists**: $$ O(n^2) $$ in the worst case for items and groups.\n- **In-degree Storage**: $$ O(n) $$ for items and groups.\n- **Stack in Topological Sort**: $$ O(n) $$ for items or groups.\n- **Overall**: Dominated by adjacency lists, so $$ O(n^2) $$.\n\n---\n\n# Code - Two-tier\n``` Python []\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n \n def topologicalSort(nodes, pred, succ):\n order, no_pred = [], deque(node for node in nodes if not pred[node])\n while no_pred:\n node = no_pred.popleft()\n order.append(node)\n for s in succ[node]:\n pred[s].discard(node)\n if not pred[s]:\n no_pred.append(s)\n return order if len(order) == len(nodes) else []\n \n group_to_items, new_group = defaultdict(set), m\n for item in range(n):\n if group[item] == -1: group[item] = new_group; new_group += 1\n group_to_items[group[item]].add(item)\n \n intra_pred, intra_succ, inter_pred, inter_succ = defaultdict(set), defaultdict(set), defaultdict(set), defaultdict(set)\n for item in range(n):\n for before in beforeItems[item]:\n if group[item] == group[before]:\n intra_pred[item].add(before)\n intra_succ[before].add(item)\n else:\n inter_pred[group[item]].add(group[before])\n inter_succ[group[before]].add(group[item])\n \n groups_order = topologicalSort(list(group_to_items.keys()), inter_pred, inter_succ)\n if not groups_order: return []\n \n items_order = []\n for grp in groups_order:\n order = topologicalSort(group_to_items[grp], intra_pred, intra_succ)\n if not order: return []\n items_order.extend(order)\n \n return items_order\n\n```\n\n# Approach: Topological Sorting using Kahn\'s Algorithm\n\nTo solve the "Sort Items by Groups Respecting Dependencies" problem, we utilize Kahn\'s topological sorting algorithm. The challenge requires a two-tier topological sort: first on the groups and then on the items within each group. \n\nFor more insights on Kahn\'s algorithm, refer to the [Wikipedia page on Topological Sorting](https://en.wikipedia.org/wiki/Topological_sorting#Kahn\'s_algorithm).\n\n## Implementation:\n\n### `topologicalSort` function:\n\nThis function is an implementation of Kahn\'s algorithm. It sorts the nodes of a graph based on their dependencies.\n\n**Parameters**:\n- `successors`: An adjacency list representing nodes\' relationships.\n- `predecessors_count`: A list where each entry indicates the number of predecessors (or incoming edges) for the respective node.\n- `num_nodes`: Total number of nodes to be sorted.\n\n**Workflow**:\n1. Initialize the `order` list to store the sorted nodes.\n2. Identify nodes with no incoming edges (no predecessors) and add them to a deque.\n3. While the deque is not empty:\n - Dequeue a node and append it to the `order` list.\n - For every successor of the current node, decrement its predecessor count.\n - If a successor node has no remaining predecessors, enqueue it.\n4. Return the `order` list if all nodes are sorted; otherwise, return an empty list indicating the presence of a cycle.\n\n### `sortItems` function:\n\nThis function sorts items based on their group dependencies and intra-group dependencies.\n\n**Parameters**:\n- `n`: Number of items.\n- `m`: Number of groups.\n- `group`: A list indicating the group of each item.\n- `beforeItems`: A list of dependencies for each item.\n\n**Workflow**:\n1. Assign items with no group to their unique groups.\n2. Create adjacency lists for items and groups (`successors_item` and `successors_group`).\n3. Populate the adjacency lists and update the predecessor counts based on the dependencies provided in `beforeItems`.\n4. Call `topologicalSort` for groups and items to get their respective orders (`groups_order` and `items_order`).\n5. If either of the orders is empty (indicating a cycle), return an empty list.\n6. Arrange items based on the sorted order of their groups.\n7. Return the final sorted order of items.\n\n---\n\n**Time Complexity**:\nThe overall time complexity of the implementation is $$O(|V| + |E|)$$, where $$|V|$$ is the number of vertices (or nodes) and $$|E|$$ is the number of edges (or relationships). This accounts for the linear time complexity of Kahn\'s algorithm, which is applied separately for both items and groups.\n\n**Space Complexity**:\nThe space complexity is dominated by the adjacency lists and predecessor counts, resulting in a complexity of $$O(|V| + |E|)$$.\n\n# Code - Kahn\'s\n``` Python []\nclass Solution:\n def topologicalSort(self, successors: List[List[int]], predecessors_count: List[int], num_nodes: int) -> List[int]:\n order = []\n nodes_with_no_predecessors = deque(node for node in range(num_nodes) if not predecessors_count[node])\n \n while nodes_with_no_predecessors:\n node = nodes_with_no_predecessors.popleft()\n order.append(node)\n for successor in successors[node]:\n predecessors_count[successor] -= 1\n if not predecessors_count[successor]:\n nodes_with_no_predecessors.append(successor)\n \n return order if len(order) == num_nodes else []\n\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n for item in range(n):\n if group[item] == -1: \n group[item] = m\n m += 1\n \n successors_group, successors_item = [[] for _ in range(m)], [[] for _ in range(n)]\n predecessors_count_group, predecessors_count_item = [0] * m, [0] * n\n \n for item in range(n):\n current_group = group[item]\n for before in beforeItems[item]:\n before_group = group[before]\n if current_group == before_group:\n successors_item[before].append(item)\n predecessors_count_item[item] += 1\n else:\n successors_group[before_group].append(current_group)\n predecessors_count_group[current_group] += 1\n \n groups_order = self.topologicalSort(successors_group, predecessors_count_group, m)\n items_order = self.topologicalSort(successors_item, predecessors_count_item, n)\n \n if not groups_order or not items_order:\n return []\n \n items_grouped = [[] for _ in range(m)]\n for item in items_order:\n items_grouped[group[item]].append(item)\n \n result = []\n for grp in groups_order:\n result.extend(items_grouped[grp])\n \n return result\n\n```\n\nThis problem beautifully showcases the power of topological sorting in organizing items based on dependencies. Mastering such foundational algorithms can greatly simplify complex tasks! \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB\n | 28 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
✅ 97.18% 2-Approaches Topological Sorting | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Problem Understanding\n\nIn the "Sort Items by Groups Respecting Dependencies" problem, we are given `n` items each belonging to one of `m` groups or to no group at all. Each item might have dependencies, which are other items that need to come before it in a sorted order. The task is to return a sorted list of items such that items from the same group are adjacent and the dependencies between items are respected.\n\nFor instance, given `n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]`, the output should be `[6,3,4,1,5,2,0,7]`.\n\n**Input**: `n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]`\n**Output**: `[6,3,4,1,5,2,0,7]`\n\n---\n\n# Live Coding\nhttps://youtu.be/5aG9GUpBOMI\n\n# Performance Comparison:\n\n| Version | Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|---------|----------|--------------|------------------|-------------|-----------------|\n| Kahn\'s Approach | Python | 345 ms | 97.18% | 33.1 MB | 96.61% |\n| Two-tier | Python | 373 ms | 81.36% | 57.8 MB | 5.8% |\n\nThe table clearly shows the improvement in performance using the 2nd Kahn Approach.\n\n---\n\n# Approach: Topological Sorting\n\nTo solve the "Sort Items by Groups Respecting Dependencies" problem, we leverage topological sorting. The challenge requires a two-tier topological sort: first on the groups and then on the items within each group.\n\n## Key Data Structures:\n- **Deque**: Efficiently handles nodes without predecessors (in-degree of 0) during the topological sort.\n- **DefaultDict**: Manages relationships, mapping items to groups, and tracking predecessors and successors.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - **`group_to_items`**: A defaultdict mapping groups to their respective items.\n - **`new_group`**: A counter initialized to `m` to assign unique group numbers to ungrouped items.\n - **`intra_pred`, `intra_succ`, `inter_pred`, `inter_succ`**: Defaultdicts to manage intra-group and inter-group dependencies.\n\n2. **Assigning Groups and Mapping Items**:\n - Iterate over all items.\n - If an item doesn\'t belong to any group (`group[item] == -1`), assign it a new unique group.\n - Map the item to its respective group in `group_to_items`.\n\n3. **Constructing Dependency Relationships**:\n - Iterate over all items.\n - For each item, check its `beforeItems` dependencies.\n - If a dependency belongs to the same group, it\'s an intra-group dependency. Update `intra_pred` and `intra_succ`.\n - If a dependency belongs to a different group, it\'s an inter-group dependency. Update `inter_pred` and `inter_succ`.\n\n4. **Topological Sort**:\n - **On Groups**:\n - Using `group_to_items`, perform a topological sort on the groups based on inter-group dependencies.\n - If the sort fails (due to a cycle or any other reason), return an empty list.\n - **On Items within Groups**:\n - For each sorted group, perform a topological sort on its items based on intra-group dependencies.\n - If the sort fails for any group, return an empty list.\n - If successful, append the sorted items of the group to the `items_order` list.\n\n5. **Return Result**:\n - After processing all groups and their items, return the `items_order` list.\n\nThis approach ensures that the topological sort respects both the group-level and item-level dependencies, providing a solution that aligns with the problem\'s requirements.\n\n---\n\n# Complexity:\n\n**Time Complexity:**\n- **Adjacency List Construction**: $$ O(n^2) $$ due to potential item dependencies in `beforeItems`.\n- **Topological Sort (Items)**: $$ O(n^2) $$ as every vertex and edge might be visited/processed.\n- **Topological Sort (Groups)**: $$ O(n^2) $$ as there can be up to $$ n $$ groups.\n- **Overall**: $$ O(n^2) $$.\n\n**Space Complexity:**\n- **Adjacency Lists**: $$ O(n^2) $$ in the worst case for items and groups.\n- **In-degree Storage**: $$ O(n) $$ for items and groups.\n- **Stack in Topological Sort**: $$ O(n) $$ for items or groups.\n- **Overall**: Dominated by adjacency lists, so $$ O(n^2) $$.\n\n---\n\n# Code - Two-tier\n``` Python []\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n \n def topologicalSort(nodes, pred, succ):\n order, no_pred = [], deque(node for node in nodes if not pred[node])\n while no_pred:\n node = no_pred.popleft()\n order.append(node)\n for s in succ[node]:\n pred[s].discard(node)\n if not pred[s]:\n no_pred.append(s)\n return order if len(order) == len(nodes) else []\n \n group_to_items, new_group = defaultdict(set), m\n for item in range(n):\n if group[item] == -1: group[item] = new_group; new_group += 1\n group_to_items[group[item]].add(item)\n \n intra_pred, intra_succ, inter_pred, inter_succ = defaultdict(set), defaultdict(set), defaultdict(set), defaultdict(set)\n for item in range(n):\n for before in beforeItems[item]:\n if group[item] == group[before]:\n intra_pred[item].add(before)\n intra_succ[before].add(item)\n else:\n inter_pred[group[item]].add(group[before])\n inter_succ[group[before]].add(group[item])\n \n groups_order = topologicalSort(list(group_to_items.keys()), inter_pred, inter_succ)\n if not groups_order: return []\n \n items_order = []\n for grp in groups_order:\n order = topologicalSort(group_to_items[grp], intra_pred, intra_succ)\n if not order: return []\n items_order.extend(order)\n \n return items_order\n\n```\n\n# Approach: Topological Sorting using Kahn\'s Algorithm\n\nTo solve the "Sort Items by Groups Respecting Dependencies" problem, we utilize Kahn\'s topological sorting algorithm. The challenge requires a two-tier topological sort: first on the groups and then on the items within each group. \n\nFor more insights on Kahn\'s algorithm, refer to the [Wikipedia page on Topological Sorting](https://en.wikipedia.org/wiki/Topological_sorting#Kahn\'s_algorithm).\n\n## Implementation:\n\n### `topologicalSort` function:\n\nThis function is an implementation of Kahn\'s algorithm. It sorts the nodes of a graph based on their dependencies.\n\n**Parameters**:\n- `successors`: An adjacency list representing nodes\' relationships.\n- `predecessors_count`: A list where each entry indicates the number of predecessors (or incoming edges) for the respective node.\n- `num_nodes`: Total number of nodes to be sorted.\n\n**Workflow**:\n1. Initialize the `order` list to store the sorted nodes.\n2. Identify nodes with no incoming edges (no predecessors) and add them to a deque.\n3. While the deque is not empty:\n - Dequeue a node and append it to the `order` list.\n - For every successor of the current node, decrement its predecessor count.\n - If a successor node has no remaining predecessors, enqueue it.\n4. Return the `order` list if all nodes are sorted; otherwise, return an empty list indicating the presence of a cycle.\n\n### `sortItems` function:\n\nThis function sorts items based on their group dependencies and intra-group dependencies.\n\n**Parameters**:\n- `n`: Number of items.\n- `m`: Number of groups.\n- `group`: A list indicating the group of each item.\n- `beforeItems`: A list of dependencies for each item.\n\n**Workflow**:\n1. Assign items with no group to their unique groups.\n2. Create adjacency lists for items and groups (`successors_item` and `successors_group`).\n3. Populate the adjacency lists and update the predecessor counts based on the dependencies provided in `beforeItems`.\n4. Call `topologicalSort` for groups and items to get their respective orders (`groups_order` and `items_order`).\n5. If either of the orders is empty (indicating a cycle), return an empty list.\n6. Arrange items based on the sorted order of their groups.\n7. Return the final sorted order of items.\n\n---\n\n**Time Complexity**:\nThe overall time complexity of the implementation is $$O(|V| + |E|)$$, where $$|V|$$ is the number of vertices (or nodes) and $$|E|$$ is the number of edges (or relationships). This accounts for the linear time complexity of Kahn\'s algorithm, which is applied separately for both items and groups.\n\n**Space Complexity**:\nThe space complexity is dominated by the adjacency lists and predecessor counts, resulting in a complexity of $$O(|V| + |E|)$$.\n\n# Code - Kahn\'s\n``` Python []\nclass Solution:\n def topologicalSort(self, successors: List[List[int]], predecessors_count: List[int], num_nodes: int) -> List[int]:\n order = []\n nodes_with_no_predecessors = deque(node for node in range(num_nodes) if not predecessors_count[node])\n \n while nodes_with_no_predecessors:\n node = nodes_with_no_predecessors.popleft()\n order.append(node)\n for successor in successors[node]:\n predecessors_count[successor] -= 1\n if not predecessors_count[successor]:\n nodes_with_no_predecessors.append(successor)\n \n return order if len(order) == num_nodes else []\n\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n for item in range(n):\n if group[item] == -1: \n group[item] = m\n m += 1\n \n successors_group, successors_item = [[] for _ in range(m)], [[] for _ in range(n)]\n predecessors_count_group, predecessors_count_item = [0] * m, [0] * n\n \n for item in range(n):\n current_group = group[item]\n for before in beforeItems[item]:\n before_group = group[before]\n if current_group == before_group:\n successors_item[before].append(item)\n predecessors_count_item[item] += 1\n else:\n successors_group[before_group].append(current_group)\n predecessors_count_group[current_group] += 1\n \n groups_order = self.topologicalSort(successors_group, predecessors_count_group, m)\n items_order = self.topologicalSort(successors_item, predecessors_count_item, n)\n \n if not groups_order or not items_order:\n return []\n \n items_grouped = [[] for _ in range(m)]\n for item in items_order:\n items_grouped[group[item]].append(item)\n \n result = []\n for grp in groups_order:\n result.extend(items_grouped[grp])\n \n return result\n\n```\n\nThis problem beautifully showcases the power of topological sorting in organizing items based on dependencies. Mastering such foundational algorithms can greatly simplify complex tasks! \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB\n | 28 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
2x Kahn's Algorithm, explained! (Python3 | 97.8% S, 99.6% M) | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Intuition\n\nWe want to order by precedence and also order by grouping. This type of ordering is similar to course schedule prerequisite problems, so I got the idea of using topological sort from that. \n\nFor topological sort, we can use DFS or kahn\'s algorithm, but I chose kahn\'s algorithm since its more intuitive.\n\nI did take a look at the editorial afterwards and while we both use kahn\'s algorithm twice, mine does it a little different since it\'s nested within each other instead.\n\n# Approach\n\nBased on the problem, it seems like grouping takes precedence over the before prerequisites. \n\nSo in order to determine which group to go first, **apply kahn\'s algorithm on the groups first**. We count each group\'s indegrees from external groups, aka internal indegrees from nodes within the group to other nodes in the group don\'t count.\n\n Use a queue to keep track of the ordering of groups / append a list of the nodes from that group once the group\'s external indegree count is 0.\n\nOnce we have a group to process in the group queue, we can **apply kahn\'s algorithm on the nodes within that group** to determine an internal ordering within that group. Make sure that its able to reach all nodes in the group, aka there are no cycles. Also update other group\'s external indegrees as you do this so we can add new groups to the group queue as we go along.\n\nOnce a group is processed, add it to our final solution. In the very end, check that our final solution covers all nodes / groups.\n\n# Complexity\n- Time complexity:\nO(V + E)\n\n- Space complexity:\nO(V + E)\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n # topological sorting via kahn\'s algorithm\n # apply kahn\'s algorithm on groups with 0 external indegrees, try determine ordering within group\n grouping = [[] for _ in range(m)]\n for ind, g in enumerate(group):\n if g != -1:\n grouping[g].append(ind)\n\n adj_list = [[] for _ in range(n)]\n in_degrees = [0] * n # indegrees of a node\n group_indegrees = [0] * m # external indegrees of group\n\n for node, before_list in enumerate(beforeItems):\n for before in before_list:\n adj_list[before].append(node)\n in_degrees[node] += 1\n if group[node] != -1 and group[node] != group[before]: # external indegree\n group_indegrees[group[node]] += 1\n\n sol = []\n\n queue = deque()\n\n for node, degrees in enumerate(in_degrees):\n if not degrees and group[node] == -1:\n queue.append([node])\n \n for g, degrees in enumerate(group_indegrees):\n if not degrees:\n queue.append(grouping[g])\n \n while queue:\n g = queue.popleft()\n group_sorted = []\n\n kahn_queue = deque()\n for node in g:\n if not in_degrees[node]:\n kahn_queue.append(node)\n \n while kahn_queue:\n node = kahn_queue.popleft()\n group_sorted.append(node)\n for neighbor in adj_list[node]:\n in_degrees[neighbor] -= 1\n neighbor_group = group[neighbor]\n if neighbor_group == -1: # neighbor has no group\n if not in_degrees[neighbor]:\n queue.append([neighbor])\n elif group[node] != neighbor_group: # different group\n group_indegrees[neighbor_group] -= 1\n if not group_indegrees[neighbor_group]: # group indegrees 0 \n queue.append(grouping[neighbor_group])\n else: # same group \n if not in_degrees[neighbor]:\n kahn_queue.append(neighbor)\n \n if len(group_sorted) != len(g):\n return []\n \n sol += group_sorted\n\n return sol if len(sol) == n else []\n \n\n \n \n\n\n \n\n\n\n \n\n\n``` | 1 | There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`\-th item belongs to and it's equal to `-1` if the `i`\-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
* The items that belong to the same group are next to each other in the sorted list.
* There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`\-th item in the sorted array (to the left of the `i`\-th item).
Return any solution if there is more than one solution and return an **empty list** if there is no solution.
**Example 1:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3,6\],\[\],\[\],\[\]\]
**Output:** \[6,3,4,1,5,2,0,7\]
**Example 2:**
**Input:** n = 8, m = 2, group = \[-1,-1,1,0,0,1,0,-1\], beforeItems = \[\[\],\[6\],\[5\],\[6\],\[3\],\[\],\[4\],\[\]\]
**Output:** \[\]
**Explanation:** This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
**Constraints:**
* `1 <= m <= n <= 3 * 104`
* `group.length == beforeItems.length == n`
* `-1 <= group[i] <= m - 1`
* `0 <= beforeItems[i].length <= n - 1`
* `0 <= beforeItems[i][j] <= n - 1`
* `i != beforeItems[i][j]`
* `beforeItems[i]` does not contain duplicates elements. | null |
2x Kahn's Algorithm, explained! (Python3 | 97.8% S, 99.6% M) | sort-items-by-groups-respecting-dependencies | 0 | 1 | # Intuition\n\nWe want to order by precedence and also order by grouping. This type of ordering is similar to course schedule prerequisite problems, so I got the idea of using topological sort from that. \n\nFor topological sort, we can use DFS or kahn\'s algorithm, but I chose kahn\'s algorithm since its more intuitive.\n\nI did take a look at the editorial afterwards and while we both use kahn\'s algorithm twice, mine does it a little different since it\'s nested within each other instead.\n\n# Approach\n\nBased on the problem, it seems like grouping takes precedence over the before prerequisites. \n\nSo in order to determine which group to go first, **apply kahn\'s algorithm on the groups first**. We count each group\'s indegrees from external groups, aka internal indegrees from nodes within the group to other nodes in the group don\'t count.\n\n Use a queue to keep track of the ordering of groups / append a list of the nodes from that group once the group\'s external indegree count is 0.\n\nOnce we have a group to process in the group queue, we can **apply kahn\'s algorithm on the nodes within that group** to determine an internal ordering within that group. Make sure that its able to reach all nodes in the group, aka there are no cycles. Also update other group\'s external indegrees as you do this so we can add new groups to the group queue as we go along.\n\nOnce a group is processed, add it to our final solution. In the very end, check that our final solution covers all nodes / groups.\n\n# Complexity\n- Time complexity:\nO(V + E)\n\n- Space complexity:\nO(V + E)\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:\n # topological sorting via kahn\'s algorithm\n # apply kahn\'s algorithm on groups with 0 external indegrees, try determine ordering within group\n grouping = [[] for _ in range(m)]\n for ind, g in enumerate(group):\n if g != -1:\n grouping[g].append(ind)\n\n adj_list = [[] for _ in range(n)]\n in_degrees = [0] * n # indegrees of a node\n group_indegrees = [0] * m # external indegrees of group\n\n for node, before_list in enumerate(beforeItems):\n for before in before_list:\n adj_list[before].append(node)\n in_degrees[node] += 1\n if group[node] != -1 and group[node] != group[before]: # external indegree\n group_indegrees[group[node]] += 1\n\n sol = []\n\n queue = deque()\n\n for node, degrees in enumerate(in_degrees):\n if not degrees and group[node] == -1:\n queue.append([node])\n \n for g, degrees in enumerate(group_indegrees):\n if not degrees:\n queue.append(grouping[g])\n \n while queue:\n g = queue.popleft()\n group_sorted = []\n\n kahn_queue = deque()\n for node in g:\n if not in_degrees[node]:\n kahn_queue.append(node)\n \n while kahn_queue:\n node = kahn_queue.popleft()\n group_sorted.append(node)\n for neighbor in adj_list[node]:\n in_degrees[neighbor] -= 1\n neighbor_group = group[neighbor]\n if neighbor_group == -1: # neighbor has no group\n if not in_degrees[neighbor]:\n queue.append([neighbor])\n elif group[node] != neighbor_group: # different group\n group_indegrees[neighbor_group] -= 1\n if not group_indegrees[neighbor_group]: # group indegrees 0 \n queue.append(grouping[neighbor_group])\n else: # same group \n if not in_degrees[neighbor]:\n kahn_queue.append(neighbor)\n \n if len(group_sorted) != len(g):\n return []\n \n sol += group_sorted\n\n return sol if len(sol) == n else []\n \n\n \n \n\n\n \n\n\n\n \n\n\n``` | 1 | You are given a string `s` formed by digits and `'#'`. We want to map `s` to English lowercase characters as follows:
* Characters (`'a'` to `'i'`) are represented by (`'1'` to `'9'`) respectively.
* Characters (`'j'` to `'z'`) are represented by (`'10#'` to `'26#'`) respectively.
Return _the string formed after mapping_.
The test cases are generated so that a unique mapping will always exist.
**Example 1:**
**Input:** s = "10#11#12 "
**Output:** "jkab "
**Explanation:** "j " -> "10# " , "k " -> "11# " , "a " -> "1 " , "b " -> "2 ".
**Example 2:**
**Input:** s = "1326# "
**Output:** "acz "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of digits and the `'#'` letter.
* `s` will be a valid string such that mapping is always possible. | Think of it as a graph problem. We need to find a topological order on the dependency graph. Build two graphs, one for the groups and another for the items. |
simple solution with dynamic levels + references | design-skiplist | 0 | 1 | Info that helped me to solve this problem:\n- https://leetcode.com/problems/design-skiplist/discuss/698146/Things-that-helped-me-solve-this-problem\n- https://cw.fel.cvut.cz/old/_media/courses/a4b36acm/maraton2015skiplist.pdf\n- https://cglab.ca/~morin/teaching/5408/refs/p90b.pdf\n\nFollowing implementation is pretty straightforward. It is possible to cut lines amount here and there but I left it this way so it would be easier to quickly understand how it works.\n\n```\nimport random\n\n\nclass ListNode:\n __slots__ = (\'val\', \'next\', \'down\')\n\n def __init__(self, val):\n self.val = val\n self.next = None\n self.down = None\n\n\nclass Skiplist:\n def __init__(self):\n # sentinel nodes to keep code simple\n node = ListNode(float(\'-inf\'))\n node.next = ListNode(float(\'inf\'))\n self.levels = [node]\n\n def search(self, target: int) -> bool:\n level = self.levels[-1]\n while level:\n node = level\n while node.next.val < target:\n node = node.next\n if node.next.val == target:\n return True\n level = node.down\n return False\n\n def add(self, num: int) -> None:\n stack = []\n level = self.levels[-1]\n while level:\n node = level\n while node.next.val < num:\n node = node.next\n stack.append(node)\n level = node.down\n\n heads = True\n down = None\n while stack and heads:\n prev = stack.pop()\n node = ListNode(num)\n node.next = prev.next\n node.down = down\n prev.next = node\n down = node\n # flip a coin to stop or continue with the next level\n heads = random.randint(0, 1)\n\n # add a new level if we got to the top with heads\n if not stack and heads:\n node = ListNode(float(\'-inf\'))\n node.next = ListNode(num)\n node.down = self.levels[-1]\n node.next.next = ListNode(float(\'inf\'))\n node.next.down = down\n self.levels.append(node)\n\n def erase(self, num: int) -> bool:\n stack = []\n level = self.levels[-1]\n while level:\n node = level\n while node.next.val < num:\n node = node.next\n if node.next.val == num:\n stack.append(node)\n level = node.down\n\n if not stack:\n return False\n\n for node in stack:\n node.next = node.next.next\n\n # remove the top level if it\'s empty\n while len(self.levels) > 1 and self.levels[-1].next.next is None:\n self.levels.pop()\n\n return True\n\n``` | 11 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
simple solution with dynamic levels + references | design-skiplist | 0 | 1 | Info that helped me to solve this problem:\n- https://leetcode.com/problems/design-skiplist/discuss/698146/Things-that-helped-me-solve-this-problem\n- https://cw.fel.cvut.cz/old/_media/courses/a4b36acm/maraton2015skiplist.pdf\n- https://cglab.ca/~morin/teaching/5408/refs/p90b.pdf\n\nFollowing implementation is pretty straightforward. It is possible to cut lines amount here and there but I left it this way so it would be easier to quickly understand how it works.\n\n```\nimport random\n\n\nclass ListNode:\n __slots__ = (\'val\', \'next\', \'down\')\n\n def __init__(self, val):\n self.val = val\n self.next = None\n self.down = None\n\n\nclass Skiplist:\n def __init__(self):\n # sentinel nodes to keep code simple\n node = ListNode(float(\'-inf\'))\n node.next = ListNode(float(\'inf\'))\n self.levels = [node]\n\n def search(self, target: int) -> bool:\n level = self.levels[-1]\n while level:\n node = level\n while node.next.val < target:\n node = node.next\n if node.next.val == target:\n return True\n level = node.down\n return False\n\n def add(self, num: int) -> None:\n stack = []\n level = self.levels[-1]\n while level:\n node = level\n while node.next.val < num:\n node = node.next\n stack.append(node)\n level = node.down\n\n heads = True\n down = None\n while stack and heads:\n prev = stack.pop()\n node = ListNode(num)\n node.next = prev.next\n node.down = down\n prev.next = node\n down = node\n # flip a coin to stop or continue with the next level\n heads = random.randint(0, 1)\n\n # add a new level if we got to the top with heads\n if not stack and heads:\n node = ListNode(float(\'-inf\'))\n node.next = ListNode(num)\n node.down = self.levels[-1]\n node.next.next = ListNode(float(\'inf\'))\n node.next.down = down\n self.levels.append(node)\n\n def erase(self, num: int) -> bool:\n stack = []\n level = self.levels[-1]\n while level:\n node = level\n while node.next.val < num:\n node = node.next\n if node.next.val == num:\n stack.append(node)\n level = node.down\n\n if not stack:\n return False\n\n for node in stack:\n node.next = node.next.next\n\n # remove the top level if it\'s empty\n while len(self.levels) > 1 and self.levels[-1].next.next is None:\n self.levels.pop()\n\n return True\n\n``` | 11 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
[Python3] skiplist | design-skiplist | 0 | 1 | \n```\nclass ListNode: \n def __init__(self, val, cnt=1, next=None, down=None): \n self.val = val\n self.cnt = cnt\n self.next = next\n self.down = down\n\n \nclass Skiplist:\n\n def __init__(self):\n self.head = ListNode(-inf)\n self.p = 1/4 \n \n def search(self, target: int) -> bool:\n node = self.head \n while node and node.val < target: \n if node.next and node.next.val <= target: node = node.next \n else: node = node.down \n return node\n\n def add(self, num: int) -> None:\n node = self.head \n stack = []\n while node and node.val < num: \n if node.next and node.next.val <= num: node = node.next \n else: \n stack.append(node)\n node = node.down\n if node: \n while node: \n node.cnt += 1\n node = node.down \n else: \n prev = None\n while True: \n if stack: \n node = stack.pop()\n node.next = prev = ListNode(num, down=prev, next=node.next)\n else: \n self.head = ListNode(-inf, down=self.head)\n self.head.next = prev = ListNode(num, down=prev)\n if random.random() >= self.p: break \n\n def erase(self, num: int) -> bool:\n node = self.head \n stack = []\n ans = False\n while node: \n if node.next and node.next.val < num: node = node.next\n else: \n stack.append(node)\n node = node.down \n while stack: \n node = stack.pop()\n if node.next and node.next.val == num: \n ans = True\n if node.next.cnt > 1: node.next.cnt -= 1\n else: node.next = node.next.next \n else: break \n return ans \n``` | 5 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
[Python3] skiplist | design-skiplist | 0 | 1 | \n```\nclass ListNode: \n def __init__(self, val, cnt=1, next=None, down=None): \n self.val = val\n self.cnt = cnt\n self.next = next\n self.down = down\n\n \nclass Skiplist:\n\n def __init__(self):\n self.head = ListNode(-inf)\n self.p = 1/4 \n \n def search(self, target: int) -> bool:\n node = self.head \n while node and node.val < target: \n if node.next and node.next.val <= target: node = node.next \n else: node = node.down \n return node\n\n def add(self, num: int) -> None:\n node = self.head \n stack = []\n while node and node.val < num: \n if node.next and node.next.val <= num: node = node.next \n else: \n stack.append(node)\n node = node.down\n if node: \n while node: \n node.cnt += 1\n node = node.down \n else: \n prev = None\n while True: \n if stack: \n node = stack.pop()\n node.next = prev = ListNode(num, down=prev, next=node.next)\n else: \n self.head = ListNode(-inf, down=self.head)\n self.head.next = prev = ListNode(num, down=prev)\n if random.random() >= self.p: break \n\n def erase(self, num: int) -> bool:\n node = self.head \n stack = []\n ans = False\n while node: \n if node.next and node.next.val < num: node = node.next\n else: \n stack.append(node)\n node = node.down \n while stack: \n node = stack.pop()\n if node.next and node.next.val == num: \n ans = True\n if node.next.cnt > 1: node.next.cnt -= 1\n else: node.next = node.next.next \n else: break \n return ans \n``` | 5 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Python 3: Clean Implementation, Next/Down Convention | design-skiplist | 0 | 1 | # Intuition\n\nThe gif is a bit misleading; the core parts of a skiplist are\n* the skiplist has `levels` linked lists\n* each list has a subset of the values in the list below it (about half usually)\n* for each node in a higher list (subset), it has a pointer to the corresponding node in the next level down\n * so if level 2 has nodes for `b` and `e`\n * and level one has nodes for `a`, `b`, `c`, `d`, `e`, `f`\n * then there\'s a link from level2(`b`) -> level1(`b`) for example\n\nSo the stacks aren\'t literal stacks (although you can implement the list like this, it\'s not recommended); they\'re really linked lists. The "stacks" are *vertical* linked lists with the `down` pointers, where the top of the stack has `top.down == second`, and `second.down == third`, etc.\n\nSo each level is a horizontal linked list with the `node.next` pointers, and each "stack" is a vertical linked list with the `node.down` pointers.\n\nLast note: if a stack has height `h`, the top of the stack is at level `h`, and it has a node in each of the lower levels. So if the node exists in level `h`, it has a `node.down` child, and `node.down` is in the listin level `h-1 > 0`\n\n## Implementation Alternatives\n\n**Next/down**\n * each node has a `next` (or `right`) pointer, and a `down` pointer\n * in other words, the nodes define a singly linked list in both directions\n * this is the minimum memory overhead solution\n * it\'s still reasonable to implement, as long as you\'re careful about keeping track of linked list pointers\n * **this is the implementation I used**\n\n**Connect four**\n * each node has `up`, `down`, `left`, `right`\n * in other words, the nodes define a doubly linked list in both directions\n * this has almost twice as much memory overhead as Next/Down (double the number of pointers, but not double the number of Node objects)\n * this simplifies deletion logic in each level becuase we don\'t have to worry about overshooting; we can use the `left` pointer to move back and forth. We can also delete `node` from a list by setting `node.left.right = node.right`, etc.\n\n**T series**\n * each node has `down`, `left`, `right`\n * in **Connect four** we don\'t actually ever use the `up` pointer\n * similarly this increases overhead, but simplifies the code\n\n**Literal stacks**\n * you can store nodes that have a `self.stack: List[Node]`\n * this is a literal interpretation of the gif\n * you only store one node per entry which is nice\n * but the insert and delete logic is more complicated, because you need the prior node in each level of the stack to be inserted and deleted\n\n# Approach\n\n## Navigation in a Skiplist\n\nFollowing the gif, you can the expected position of a node as follows:\n* **start with the very top-left of the skiplist**, which I call `root`\n * this is the special node before all real nodes in the list at the height of `self.levels`\n* **move as far right as you can in the current level without overshooting the value**\n * if the next node is the target value, you have found the top of a "stack" for this node\n * otherwise, we don\'t know if the value is in the skiplist\n * the value might be missing entirely\n * or maybe the value just isn\'t part of this levels subset\n * **if you didn\'t find the target value, descend one level and repeat**\n* keep going until you find the value, or `curr` is `None`, which means we failed to find the value in the bottom layer with all the values.\n\nWe always have `curr` be the last node *before* the target. This is because our nodes only have `next` (right) and `down` pointers. So if we ever advance too far right, we can\'t go back because we don\'t have a left pointer. We\'d have to do a O(log(N)) scan from `root` again.\n\n## Insertion\n\nThe gif is misleading; in the next/down convention you must choose the height of the "stack" to insert before doing the inserts. The reason is that we don\'t have `up` and `left` pointers, so you can only navigate down and right from the root. Therefore we can\'t insert the node at level 1 first, then decide to insert it at higher levels - we\'d have to re-traverse the skiplist to find the node again.\n\nAnyway, it\'s mostly the same as find. The difference is\n* at the highest height, create a node\n* record this node, I call it `above`, so when we insert a new `node` in the next level, we can set `above.down = node`. (this is the usual "how to append a node to a linked list)\n* at all lower levels, repeat this find-and-insert logic. Set `above.down = node`, and set `above=node`.\n\nWhen `curr` is empty, i.e. there is no next level to insert at, return.\n\n## Deletion\n\nFirst, we follow the find process until we find a copy of the node. We search from the top left. Let `top = curr.next` be the top of the stack to delete.\n\n**In each subsequent level we delete `top` in particular.** Otherwise we\'ll be haphazardly deleting nodes from different "stacks"/vertical chains.\n\nSo for each level once we\'ve found `top`:\n* the top of the loop has the property that `curr.next == top`\n* delete `top`:\n * set `curr.next = curr.next.next` (or `top.next`) to bypass `top`; Python\'s GC will delete `top` later at its leisure\n * set `top = top.next` to find the new top of the remaining stack\n* navigate to the next level\n * move `curr = curr.down` to move down to the next level\n * move `curr` right until `curr.next == top`\n* repeat this until `top` is `None`, meaning we deleted the whole stack of nodes\n\n# Complexity\n- Time complexity: $O(\\log{N})$ for each operation with high probability\n - bottom level has all $N$ nodes\n - next level has an expected value of $N/2$ nodes\n - so there are about $O(\\log{N})$ levels\n - when we find an arbitrary value:\n - iterating through the top level, with one node, effectively partitions the nodes into 2 partitions\n - the next level, with about twice as many nodes, is about 4 partitions\n - so iterating in the top list moves in an average of N/2 elements\n - the second level moves over N/4 elements on average\n - between nodes of the top level, there are about 2 nodes in this level\n - the third level moves over N/8 on average\n - another ~2 nodes between nodes of the prior level\n - so we can move to any position in the list in about O(1) moves per level.\n - therefore over all $\\log{N}$ levels we do $O(\\log{N})$ moves\n - same logic for adding and deleting nodes, which are mostly the same as finding values, but with O(1) operations per level to handle the add and delete\n\n- Space complexity: $O(N)$\n - the bottom level has all N values\n - the next level has about N/2 values\n - third level has about N/4 values\n - total expected number of nodes is N*(1+1/2+1/4+...) = 2N\n\n# Code\n```\nclass Skiplist:\n\n class Node:\n def __init__(self, v: int):\n self.v = v # TODO: make this a pointer so we don\'t overallocate up to self.levels times :(\n self.next = None\n self.down = None\n\n def __init__(self):\n self.levels = 1\n self.root = self.Node(0) # top-left node; guard pattern\n self.last = self.root # bottom-left node; guard pattern\n\n def search(self, target: int) -> bool:\n curr = self.root\n while curr:\n # advance left at current level without overshooting\n while curr.next and curr.next.v < target:\n curr = curr.next\n \n if curr.next and curr.next.v == target:\n return True\n \n # not found at this level; descend to next level\n # which is more detailed\n curr = curr.down\n\n return False\n \n\n def add(self, num: int) -> None:\n # gif is misleading: for next-down pointers you need to know up front!\n height = 1\n while randrange(2): # 0 or 1, 50/50\n height += 1\n\n # augment height and max stack height\n while self.levels < height:\n topleft = self.Node(0)\n topleft.down = self.root\n self.root = topleft\n self.levels += 1\n\n curr = self.root\n above = None # so we remember node in prior (higher) level of the new stack\n for l in range(self.levels, 0, -1):\n # go as far left as we can without overshooting the value to add\n while curr.next and curr.next.v < num:\n curr = curr.next\n\n # insert new node in front of all others with the same key\n if l <= height:\n # have: curr -> next\n # want: curr -> n -> next\n n = self.Node(num)\n n.next = curr.next\n curr.next = n\n if above: above.down = n\n above = n\n\n curr = curr.down\n\n\n def erase(self, num: int) -> bool:\n curr = self.root # last node before `num` in each level\n top = None\n while curr:\n while curr.next and curr.next.v < num:\n curr = curr.next\n\n if curr.next and curr.next.v == num:\n top = curr.next\n break\n\n curr = curr.down\n\n if top is None: return False # not found\n\n while True:\n # curr -> top\n curr.next = curr.next.next\n top = top.down\n if top is None: break # stack is totally deleted\n\n # reposition curr so it\'s the node immediately before top\n curr = curr.down\n while curr.next != top:\n curr = curr.next\n\n # we may of removed the tallest stack; delete any empty levels\n while self.levels > 1 and self.root.next == None:\n self.levels -= 1\n self.root = self.root.down\n\n return True\n\n \n\n\n# Your Skiplist object will be instantiated and called as such:\n# obj = Skiplist()\n# param_1 = obj.search(target)\n# obj.add(num)\n# param_3 = obj.erase(num)\n``` | 0 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
Python 3: Clean Implementation, Next/Down Convention | design-skiplist | 0 | 1 | # Intuition\n\nThe gif is a bit misleading; the core parts of a skiplist are\n* the skiplist has `levels` linked lists\n* each list has a subset of the values in the list below it (about half usually)\n* for each node in a higher list (subset), it has a pointer to the corresponding node in the next level down\n * so if level 2 has nodes for `b` and `e`\n * and level one has nodes for `a`, `b`, `c`, `d`, `e`, `f`\n * then there\'s a link from level2(`b`) -> level1(`b`) for example\n\nSo the stacks aren\'t literal stacks (although you can implement the list like this, it\'s not recommended); they\'re really linked lists. The "stacks" are *vertical* linked lists with the `down` pointers, where the top of the stack has `top.down == second`, and `second.down == third`, etc.\n\nSo each level is a horizontal linked list with the `node.next` pointers, and each "stack" is a vertical linked list with the `node.down` pointers.\n\nLast note: if a stack has height `h`, the top of the stack is at level `h`, and it has a node in each of the lower levels. So if the node exists in level `h`, it has a `node.down` child, and `node.down` is in the listin level `h-1 > 0`\n\n## Implementation Alternatives\n\n**Next/down**\n * each node has a `next` (or `right`) pointer, and a `down` pointer\n * in other words, the nodes define a singly linked list in both directions\n * this is the minimum memory overhead solution\n * it\'s still reasonable to implement, as long as you\'re careful about keeping track of linked list pointers\n * **this is the implementation I used**\n\n**Connect four**\n * each node has `up`, `down`, `left`, `right`\n * in other words, the nodes define a doubly linked list in both directions\n * this has almost twice as much memory overhead as Next/Down (double the number of pointers, but not double the number of Node objects)\n * this simplifies deletion logic in each level becuase we don\'t have to worry about overshooting; we can use the `left` pointer to move back and forth. We can also delete `node` from a list by setting `node.left.right = node.right`, etc.\n\n**T series**\n * each node has `down`, `left`, `right`\n * in **Connect four** we don\'t actually ever use the `up` pointer\n * similarly this increases overhead, but simplifies the code\n\n**Literal stacks**\n * you can store nodes that have a `self.stack: List[Node]`\n * this is a literal interpretation of the gif\n * you only store one node per entry which is nice\n * but the insert and delete logic is more complicated, because you need the prior node in each level of the stack to be inserted and deleted\n\n# Approach\n\n## Navigation in a Skiplist\n\nFollowing the gif, you can the expected position of a node as follows:\n* **start with the very top-left of the skiplist**, which I call `root`\n * this is the special node before all real nodes in the list at the height of `self.levels`\n* **move as far right as you can in the current level without overshooting the value**\n * if the next node is the target value, you have found the top of a "stack" for this node\n * otherwise, we don\'t know if the value is in the skiplist\n * the value might be missing entirely\n * or maybe the value just isn\'t part of this levels subset\n * **if you didn\'t find the target value, descend one level and repeat**\n* keep going until you find the value, or `curr` is `None`, which means we failed to find the value in the bottom layer with all the values.\n\nWe always have `curr` be the last node *before* the target. This is because our nodes only have `next` (right) and `down` pointers. So if we ever advance too far right, we can\'t go back because we don\'t have a left pointer. We\'d have to do a O(log(N)) scan from `root` again.\n\n## Insertion\n\nThe gif is misleading; in the next/down convention you must choose the height of the "stack" to insert before doing the inserts. The reason is that we don\'t have `up` and `left` pointers, so you can only navigate down and right from the root. Therefore we can\'t insert the node at level 1 first, then decide to insert it at higher levels - we\'d have to re-traverse the skiplist to find the node again.\n\nAnyway, it\'s mostly the same as find. The difference is\n* at the highest height, create a node\n* record this node, I call it `above`, so when we insert a new `node` in the next level, we can set `above.down = node`. (this is the usual "how to append a node to a linked list)\n* at all lower levels, repeat this find-and-insert logic. Set `above.down = node`, and set `above=node`.\n\nWhen `curr` is empty, i.e. there is no next level to insert at, return.\n\n## Deletion\n\nFirst, we follow the find process until we find a copy of the node. We search from the top left. Let `top = curr.next` be the top of the stack to delete.\n\n**In each subsequent level we delete `top` in particular.** Otherwise we\'ll be haphazardly deleting nodes from different "stacks"/vertical chains.\n\nSo for each level once we\'ve found `top`:\n* the top of the loop has the property that `curr.next == top`\n* delete `top`:\n * set `curr.next = curr.next.next` (or `top.next`) to bypass `top`; Python\'s GC will delete `top` later at its leisure\n * set `top = top.next` to find the new top of the remaining stack\n* navigate to the next level\n * move `curr = curr.down` to move down to the next level\n * move `curr` right until `curr.next == top`\n* repeat this until `top` is `None`, meaning we deleted the whole stack of nodes\n\n# Complexity\n- Time complexity: $O(\\log{N})$ for each operation with high probability\n - bottom level has all $N$ nodes\n - next level has an expected value of $N/2$ nodes\n - so there are about $O(\\log{N})$ levels\n - when we find an arbitrary value:\n - iterating through the top level, with one node, effectively partitions the nodes into 2 partitions\n - the next level, with about twice as many nodes, is about 4 partitions\n - so iterating in the top list moves in an average of N/2 elements\n - the second level moves over N/4 elements on average\n - between nodes of the top level, there are about 2 nodes in this level\n - the third level moves over N/8 on average\n - another ~2 nodes between nodes of the prior level\n - so we can move to any position in the list in about O(1) moves per level.\n - therefore over all $\\log{N}$ levels we do $O(\\log{N})$ moves\n - same logic for adding and deleting nodes, which are mostly the same as finding values, but with O(1) operations per level to handle the add and delete\n\n- Space complexity: $O(N)$\n - the bottom level has all N values\n - the next level has about N/2 values\n - third level has about N/4 values\n - total expected number of nodes is N*(1+1/2+1/4+...) = 2N\n\n# Code\n```\nclass Skiplist:\n\n class Node:\n def __init__(self, v: int):\n self.v = v # TODO: make this a pointer so we don\'t overallocate up to self.levels times :(\n self.next = None\n self.down = None\n\n def __init__(self):\n self.levels = 1\n self.root = self.Node(0) # top-left node; guard pattern\n self.last = self.root # bottom-left node; guard pattern\n\n def search(self, target: int) -> bool:\n curr = self.root\n while curr:\n # advance left at current level without overshooting\n while curr.next and curr.next.v < target:\n curr = curr.next\n \n if curr.next and curr.next.v == target:\n return True\n \n # not found at this level; descend to next level\n # which is more detailed\n curr = curr.down\n\n return False\n \n\n def add(self, num: int) -> None:\n # gif is misleading: for next-down pointers you need to know up front!\n height = 1\n while randrange(2): # 0 or 1, 50/50\n height += 1\n\n # augment height and max stack height\n while self.levels < height:\n topleft = self.Node(0)\n topleft.down = self.root\n self.root = topleft\n self.levels += 1\n\n curr = self.root\n above = None # so we remember node in prior (higher) level of the new stack\n for l in range(self.levels, 0, -1):\n # go as far left as we can without overshooting the value to add\n while curr.next and curr.next.v < num:\n curr = curr.next\n\n # insert new node in front of all others with the same key\n if l <= height:\n # have: curr -> next\n # want: curr -> n -> next\n n = self.Node(num)\n n.next = curr.next\n curr.next = n\n if above: above.down = n\n above = n\n\n curr = curr.down\n\n\n def erase(self, num: int) -> bool:\n curr = self.root # last node before `num` in each level\n top = None\n while curr:\n while curr.next and curr.next.v < num:\n curr = curr.next\n\n if curr.next and curr.next.v == num:\n top = curr.next\n break\n\n curr = curr.down\n\n if top is None: return False # not found\n\n while True:\n # curr -> top\n curr.next = curr.next.next\n top = top.down\n if top is None: break # stack is totally deleted\n\n # reposition curr so it\'s the node immediately before top\n curr = curr.down\n while curr.next != top:\n curr = curr.next\n\n # we may of removed the tallest stack; delete any empty levels\n while self.levels > 1 and self.root.next == None:\n self.levels -= 1\n self.root = self.root.down\n\n return True\n\n \n\n\n# Your Skiplist object will be instantiated and called as such:\n# obj = Skiplist()\n# param_1 = obj.search(target)\n# obj.add(num)\n# param_3 = obj.erase(num)\n``` | 0 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Super simple defaultdict solution that beats 100% | design-skiplist | 1 | 1 | # Code\n```\nclass Skiplist:\n\n def __init__(self):\n self.skiplist = defaultdict(int)\n\n def search(self, target: int) -> bool:\n return self.skiplist[target] > 0\n\n def add(self, num: int) -> None:\n self.skiplist[num] += 1\n\n def erase(self, num: int) -> bool:\n if self.skiplist[num] > 0:\n self.skiplist[num] -= 1\n return True\n return False\n\n``` | 0 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
Super simple defaultdict solution that beats 100% | design-skiplist | 1 | 1 | # Code\n```\nclass Skiplist:\n\n def __init__(self):\n self.skiplist = defaultdict(int)\n\n def search(self, target: int) -> bool:\n return self.skiplist[target] > 0\n\n def add(self, num: int) -> None:\n self.skiplist[num] += 1\n\n def erase(self, num: int) -> bool:\n if self.skiplist[num] > 0:\n self.skiplist[num] -= 1\n return True\n return False\n\n``` | 0 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
(Python3) Readable version (hopefully) | design-skiplist | 0 | 1 | \n```\nfrom random import getrandbits\n\n\nclass SkipNode:\n __slots__ = "prev", "next", "child", "value"\n\n def __init__(self, prev=None, next=None, child=None, value=-float("inf")):\n self.prev = prev\n self.next = next\n self.child = child\n self.value = value\n if next:\n next.prev = self\n\n def insert(self, value, child=None):\n self.next = SkipNode(self, self.next, child, value)\n return self.next\n\n def unlink(self):\n prev, next = self.prev, self.next\n prev.next = next\n if next:\n next.prev = prev\n if child := self.child:\n child.unlink()\n\n\nclass Skiplist:\n __slots__ = ("roots",)\n\n def __init__(self):\n self.roots = [SkipNode()]\n\n def search(self, target: int) -> bool:\n return self._search(target)[0]\n\n def _search(self, target):\n node = self.roots[-1]\n found = False\n chain = []\n\n while node:\n if node.value == target:\n chain.append(node)\n found = True\n break\n\n if (next := node.next) and next.value <= target:\n node = next\n else:\n chain.append(node)\n node = node.child\n\n return found, chain\n\n def add(self, num: int) -> None:\n chain = self._search(num)[1]\n node = chain[-1]\n\n while child := node.child:\n chain.append(child)\n node = child\n\n chain.pop()\n chain = iter(reversed(chain))\n node = node.insert(num)\n\n while getrandbits(1):\n if not (prev := next(chain, None)):\n prev = SkipNode(child=self.roots[-1])\n self.roots.append(prev)\n\n node = prev.insert(num, node)\n\n def erase(self, num: int) -> bool:\n found, chain = self._search(num)\n if not found:\n return False\n\n chain[-1].unlink()\n\n roots = self.roots\n while len(roots) > 1 and not roots[-1].next:\n roots.pop()\n\n return True\n``` | 0 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
(Python3) Readable version (hopefully) | design-skiplist | 0 | 1 | \n```\nfrom random import getrandbits\n\n\nclass SkipNode:\n __slots__ = "prev", "next", "child", "value"\n\n def __init__(self, prev=None, next=None, child=None, value=-float("inf")):\n self.prev = prev\n self.next = next\n self.child = child\n self.value = value\n if next:\n next.prev = self\n\n def insert(self, value, child=None):\n self.next = SkipNode(self, self.next, child, value)\n return self.next\n\n def unlink(self):\n prev, next = self.prev, self.next\n prev.next = next\n if next:\n next.prev = prev\n if child := self.child:\n child.unlink()\n\n\nclass Skiplist:\n __slots__ = ("roots",)\n\n def __init__(self):\n self.roots = [SkipNode()]\n\n def search(self, target: int) -> bool:\n return self._search(target)[0]\n\n def _search(self, target):\n node = self.roots[-1]\n found = False\n chain = []\n\n while node:\n if node.value == target:\n chain.append(node)\n found = True\n break\n\n if (next := node.next) and next.value <= target:\n node = next\n else:\n chain.append(node)\n node = node.child\n\n return found, chain\n\n def add(self, num: int) -> None:\n chain = self._search(num)[1]\n node = chain[-1]\n\n while child := node.child:\n chain.append(child)\n node = child\n\n chain.pop()\n chain = iter(reversed(chain))\n node = node.insert(num)\n\n while getrandbits(1):\n if not (prev := next(chain, None)):\n prev = SkipNode(child=self.roots[-1])\n self.roots.append(prev)\n\n node = prev.insert(num, node)\n\n def erase(self, num: int) -> bool:\n found, chain = self._search(num)\n if not found:\n return False\n\n chain[-1].unlink()\n\n roots = self.roots\n while len(roots) > 1 and not roots[-1].next:\n roots.pop()\n\n return True\n``` | 0 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Simple to understand solution with level lists!!! + 2 solutions | design-skiplist | 0 | 1 | \n```\nclass ListNode:\n def __init__(self, val=0, counter= 1, next=[]):\n self.val = val\n self.counter = counter\n self.next = next\n\nclass Skiplist:\n def __init__(self):\n self.max_level = 1 \n self.max_length = 1\n self.length_list = 0\n self.tail = ListNode(val= inf)\n self.head = ListNode(val= -inf, next= [self.tail])\n\n def search(self, target: int) -> bool:\n node = self.head\n for i in range(len(self.head.next)-1, -1, -1):\n while node.next[i].val <= target:\n node = node.next[i]\n if node.val == target:\n return True\n return False \n\n # generated random namber of levels in the range [0, max_level]\n def random_level(self):\n level = 0\n # max_level = log(length_list, 2)\n if self.length_list > self.max_length:\n self.max_level += 1\n self.max_length *= 2 \n while random.random() < 0.5 and level < self.max_level:\n level += 1 \n yield\n\n def add(self, num: int) -> None:\n node = self.head\n stack = []\n for i in range(len(self.head.next)-1, -1, -1): \n while node.next[i].val <= num:\n node = node.next[i]\n #if "num" is found in the list, increase the count of "num"s and exit \n if node.val == num: \n node.counter += 1\n return\n stack.append((node, i))\n #insert "num" in lowest level\n prev_node, i = stack.pop()\n node = ListNode(val= num, next=[prev_node.next[i]])\n prev_node.next[i] = node\n self.length_list += 1 #increase length list\n \n for _ in self.random_level():\n if stack:\n #insert duplicate "num" in exists level\n prev_node, i = stack.pop()\n node.next.append(prev_node.next[i])\n prev_node.next[i] = node\n else:\n #create new level with duplicate "num"\n self.head.next.append(node)\n node.next.append(self.tail)\n\n def erase(self, num: int) -> bool: \n node = self.head\n flag = False #if finded "num" then "flag" = True\n for i in range(len(self.head.next)-1, -1, -1): \n while node.next[i].val < num:\n node = node.next[i]\n if node.next[i].val == num:\n if flag:\n node.next[i] = node.next[i].next[i] #erase "num" in "i"-level\n else:\n node.next[i].counter -= 1 #reduce the count of "num"s\n if node.next[i].counter > 0: \n return True \n node.next[i] = node.next[i].next[i]\n flag = True \n if flag:\n #remove the top level if it\'s empty\n while self.head.next[-1] == self.tail and len(self.head.next) > 1:\n self.head.next.pop()\n self.length_list -= 1 #reduce length list\n return flag \n```\n# One more solution\n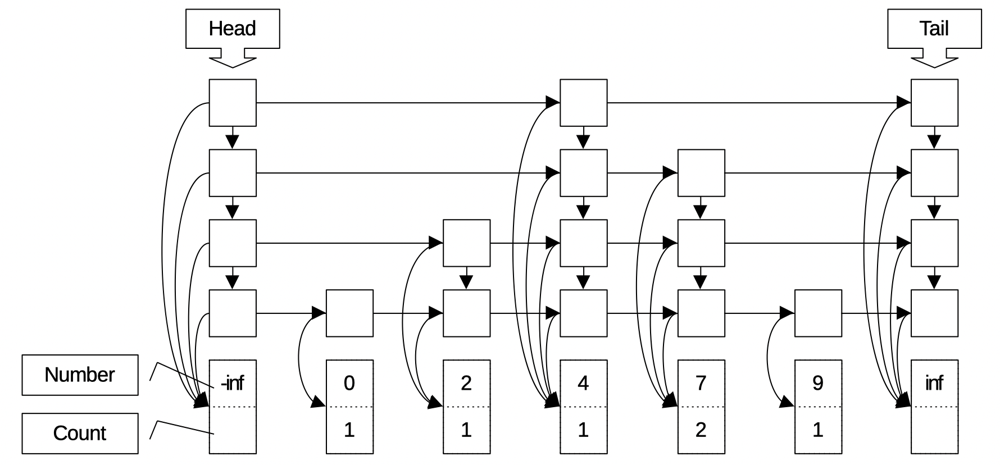\n```\nclass ValueNode:\n def __init__(self, num= 0, counter= 1):\n self.num = num\n self.counter = counter\n\nclass ListNode:\n def __init__(self, value= None, down = None, next= None):\n self.value = value\n self.down = down\n self.next = next\n\nclass Skiplist:\n def __init__(self):\n self.max_level = 1\n self.max_length = 1\n self.length_list = 0\n self.tail = ListNode(value= ValueNode(num= inf))\n self.head = ListNode(value= ValueNode(num= -inf), next= self.tail) \n\n def search(self, target: int) -> bool:\n node = self.head\n while node:\n while node.next.value.num <= target: \n node = node.next\n if node.value.num == target:\n return True \n node = node.down \n return False\n\n def random_level(self):\n level = 0\n if self.length_list > self.max_length:\n self.max_level += 1\n self.max_length *= 2 \n while random.random() < 0.5 and level < self.max_level:\n level += 1 \n yield\n\n def add(self, num: int) -> None:\n node = self.head\n stack = []\n while node:\n while node.next.value.num <= num: \n node = node.next \n if node.value.num == num: \n node.value.counter += 1\n return\n stack.append(node)\n node = node.down\n prev_node = stack.pop()\n node = ListNode(value= ValueNode(num= num))\n node.next = prev_node.next\n prev_node.next = node\n self.length_list += 1 \n for _ in self.random_level():\n new_node = ListNode(value= node.value, down= node)\n if stack:\n prev_node = stack.pop()\n new_node.next = prev_node.next\n prev_node.next = new_node \n else:\n self.head = ListNode(value= self.head.value, down= self.head, next= new_node)\n new_node.next = ListNode(value= self.tail.value, down= self.tail)\n self.tail = new_node.next\n node = new_node\n \n def erase(self, num: int) -> bool:\n node = self.head\n flag = False\n while node:\n while node.next.value.num < num: \n node = node.next \n if node.next.value.num == num:\n if flag:\n node.next = node.next.next\n else:\n node.next.value.counter -= 1\n if node.next.value.counter > 0:\n return True\n node.next = node.next.next\n flag = True \n node = node.down \n if flag:\n while self.head.next == self.tail and self.head.down:\n self.head = self.head.down\n self.tail = self.tail.down\n self.length_list -= 1\n return flag \n```\n# Solution with recursion\n```\nclass ListNode:\n def __init__(self, val= 0, next= None, down = None):\n self.val = val\n self.next = next\n self.down = down\n\nclass Skiplist:\n def __init__(self):\n self.head = ListNode(val= -inf) \n \n def searchRec(self, node, target): \n while node.next and node.next.val <= target: \n node = node.next \n if node.down == None: \n return node.val \n return self.searchRec(node.down, target)\n \n def search(self, target: int) -> bool:\n return self.searchRec(self.head, target) == target\n\n def addRec(self, node, num):\n while node.next and node.next.val < num:\n node = node.next \n if node.down == None:\n downNode = None\n else:\n downNode = self.addRec(node.down, num)\n if downNode != None or node.down == None:\n node.next = ListNode(val= num, next= node.next, down= downNode)\n if random.random() < 0.5:\n return node.next\n return None \n \n def add(self, num: int) -> None:\n node = self.addRec(self.head, num)\n if node != None:\n newNode = ListNode(val= -inf, down=self.head)\n newNode.next = ListNode(val= num, down= node)\n self.head = newNode\n \n def eraseRec(self, node, num):\n flag = False\n while node.next and node.next.val < num:\n node = node.next\n if node.down != None:\n flag = self.eraseRec(node.down, num)\n if node.next and node.next.val == num:\n node.next = node.next.next\n return True\n return flag\n \n def erase(self, num: int) -> bool:\n return self.eraseRec(self.head, num)\n``` | 0 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
Simple to understand solution with level lists!!! + 2 solutions | design-skiplist | 0 | 1 | \n```\nclass ListNode:\n def __init__(self, val=0, counter= 1, next=[]):\n self.val = val\n self.counter = counter\n self.next = next\n\nclass Skiplist:\n def __init__(self):\n self.max_level = 1 \n self.max_length = 1\n self.length_list = 0\n self.tail = ListNode(val= inf)\n self.head = ListNode(val= -inf, next= [self.tail])\n\n def search(self, target: int) -> bool:\n node = self.head\n for i in range(len(self.head.next)-1, -1, -1):\n while node.next[i].val <= target:\n node = node.next[i]\n if node.val == target:\n return True\n return False \n\n # generated random namber of levels in the range [0, max_level]\n def random_level(self):\n level = 0\n # max_level = log(length_list, 2)\n if self.length_list > self.max_length:\n self.max_level += 1\n self.max_length *= 2 \n while random.random() < 0.5 and level < self.max_level:\n level += 1 \n yield\n\n def add(self, num: int) -> None:\n node = self.head\n stack = []\n for i in range(len(self.head.next)-1, -1, -1): \n while node.next[i].val <= num:\n node = node.next[i]\n #if "num" is found in the list, increase the count of "num"s and exit \n if node.val == num: \n node.counter += 1\n return\n stack.append((node, i))\n #insert "num" in lowest level\n prev_node, i = stack.pop()\n node = ListNode(val= num, next=[prev_node.next[i]])\n prev_node.next[i] = node\n self.length_list += 1 #increase length list\n \n for _ in self.random_level():\n if stack:\n #insert duplicate "num" in exists level\n prev_node, i = stack.pop()\n node.next.append(prev_node.next[i])\n prev_node.next[i] = node\n else:\n #create new level with duplicate "num"\n self.head.next.append(node)\n node.next.append(self.tail)\n\n def erase(self, num: int) -> bool: \n node = self.head\n flag = False #if finded "num" then "flag" = True\n for i in range(len(self.head.next)-1, -1, -1): \n while node.next[i].val < num:\n node = node.next[i]\n if node.next[i].val == num:\n if flag:\n node.next[i] = node.next[i].next[i] #erase "num" in "i"-level\n else:\n node.next[i].counter -= 1 #reduce the count of "num"s\n if node.next[i].counter > 0: \n return True \n node.next[i] = node.next[i].next[i]\n flag = True \n if flag:\n #remove the top level if it\'s empty\n while self.head.next[-1] == self.tail and len(self.head.next) > 1:\n self.head.next.pop()\n self.length_list -= 1 #reduce length list\n return flag \n```\n# One more solution\n\n```\nclass ValueNode:\n def __init__(self, num= 0, counter= 1):\n self.num = num\n self.counter = counter\n\nclass ListNode:\n def __init__(self, value= None, down = None, next= None):\n self.value = value\n self.down = down\n self.next = next\n\nclass Skiplist:\n def __init__(self):\n self.max_level = 1\n self.max_length = 1\n self.length_list = 0\n self.tail = ListNode(value= ValueNode(num= inf))\n self.head = ListNode(value= ValueNode(num= -inf), next= self.tail) \n\n def search(self, target: int) -> bool:\n node = self.head\n while node:\n while node.next.value.num <= target: \n node = node.next\n if node.value.num == target:\n return True \n node = node.down \n return False\n\n def random_level(self):\n level = 0\n if self.length_list > self.max_length:\n self.max_level += 1\n self.max_length *= 2 \n while random.random() < 0.5 and level < self.max_level:\n level += 1 \n yield\n\n def add(self, num: int) -> None:\n node = self.head\n stack = []\n while node:\n while node.next.value.num <= num: \n node = node.next \n if node.value.num == num: \n node.value.counter += 1\n return\n stack.append(node)\n node = node.down\n prev_node = stack.pop()\n node = ListNode(value= ValueNode(num= num))\n node.next = prev_node.next\n prev_node.next = node\n self.length_list += 1 \n for _ in self.random_level():\n new_node = ListNode(value= node.value, down= node)\n if stack:\n prev_node = stack.pop()\n new_node.next = prev_node.next\n prev_node.next = new_node \n else:\n self.head = ListNode(value= self.head.value, down= self.head, next= new_node)\n new_node.next = ListNode(value= self.tail.value, down= self.tail)\n self.tail = new_node.next\n node = new_node\n \n def erase(self, num: int) -> bool:\n node = self.head\n flag = False\n while node:\n while node.next.value.num < num: \n node = node.next \n if node.next.value.num == num:\n if flag:\n node.next = node.next.next\n else:\n node.next.value.counter -= 1\n if node.next.value.counter > 0:\n return True\n node.next = node.next.next\n flag = True \n node = node.down \n if flag:\n while self.head.next == self.tail and self.head.down:\n self.head = self.head.down\n self.tail = self.tail.down\n self.length_list -= 1\n return flag \n```\n# Solution with recursion\n```\nclass ListNode:\n def __init__(self, val= 0, next= None, down = None):\n self.val = val\n self.next = next\n self.down = down\n\nclass Skiplist:\n def __init__(self):\n self.head = ListNode(val= -inf) \n \n def searchRec(self, node, target): \n while node.next and node.next.val <= target: \n node = node.next \n if node.down == None: \n return node.val \n return self.searchRec(node.down, target)\n \n def search(self, target: int) -> bool:\n return self.searchRec(self.head, target) == target\n\n def addRec(self, node, num):\n while node.next and node.next.val < num:\n node = node.next \n if node.down == None:\n downNode = None\n else:\n downNode = self.addRec(node.down, num)\n if downNode != None or node.down == None:\n node.next = ListNode(val= num, next= node.next, down= downNode)\n if random.random() < 0.5:\n return node.next\n return None \n \n def add(self, num: int) -> None:\n node = self.addRec(self.head, num)\n if node != None:\n newNode = ListNode(val= -inf, down=self.head)\n newNode.next = ListNode(val= num, down= node)\n self.head = newNode\n \n def eraseRec(self, node, num):\n flag = False\n while node.next and node.next.val < num:\n node = node.next\n if node.down != None:\n flag = self.eraseRec(node.down, num)\n if node.next and node.next.val == num:\n node.next = node.next.next\n return True\n return flag\n \n def erase(self, num: int) -> bool:\n return self.eraseRec(self.head, num)\n``` | 0 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Super simple defaultdict Python solution that beats 100% | design-skiplist | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Skiplist:\n\n def __init__(self):\n self.skiplist = defaultdict(int)\n \n\n def search(self, target: int) -> bool:\n return self.skiplist[target] > 0\n \n\n def add(self, num: int) -> None:\n self.skiplist[num] += 1\n \n\n def erase(self, num: int) -> bool:\n if self.skiplist[num] > 0:\n self.skiplist[num] -= 1\n return True\n return False\n \n\n\n# Your Skiplist object will be instantiated and called as such:\n# obj = Skiplist()\n# param_1 = obj.search(target)\n# obj.add(num)\n# param_3 = obj.erase(num)\n``` | 0 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
Super simple defaultdict Python solution that beats 100% | design-skiplist | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Skiplist:\n\n def __init__(self):\n self.skiplist = defaultdict(int)\n \n\n def search(self, target: int) -> bool:\n return self.skiplist[target] > 0\n \n\n def add(self, num: int) -> None:\n self.skiplist[num] += 1\n \n\n def erase(self, num: int) -> bool:\n if self.skiplist[num] > 0:\n self.skiplist[num] -= 1\n return True\n return False\n \n\n\n# Your Skiplist object will be instantiated and called as such:\n# obj = Skiplist()\n# param_1 = obj.search(target)\n# obj.add(num)\n# param_3 = obj.erase(num)\n``` | 0 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Design skiplist | design-skiplist | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Skiplist:\n\n def __init__(self):\n self.skiplist=[]\n\n def search(self, target: int) -> bool:\n if target in self.skiplist:\n return True\n return False\n\n def add(self, num: int) -> None:\n self.skiplist.append(num)\n\n def erase(self, num: int) -> bool:\n if num in self.skiplist:\n self.skiplist.remove(num)\n return True\n return False\n\n\n# Your Skiplist object will be instantiated and called as such:\n# obj = Skiplist()\n# param_1 = obj.search(target)\n# obj.add(num)\n# param_3 = obj.erase(num)\n``` | 0 | Design a **Skiplist** without using any built-in libraries.
A **skiplist** is a data structure that takes `O(log(n))` time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.
For example, we have a Skiplist containing `[30,40,50,60,70,90]` and we want to add `80` and `45` into it. The Skiplist works this way:
Artyom Kalinin \[CC BY-SA 3.0\], via [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Skip_list_add_element-en.gif "Artyom Kalinin [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons")
You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than `O(n)`. It can be proven that the average time complexity for each operation is `O(log(n))` and space complexity is `O(n)`.
See more about Skiplist: [https://en.wikipedia.org/wiki/Skip\_list](https://en.wikipedia.org/wiki/Skip_list)
Implement the `Skiplist` class:
* `Skiplist()` Initializes the object of the skiplist.
* `bool search(int target)` Returns `true` if the integer `target` exists in the Skiplist or `false` otherwise.
* `void add(int num)` Inserts the value `num` into the SkipList.
* `bool erase(int num)` Removes the value `num` from the Skiplist and returns `true`. If `num` does not exist in the Skiplist, do nothing and return `false`. If there exist multiple `num` values, removing any one of them is fine.
Note that duplicates may exist in the Skiplist, your code needs to handle this situation.
**Example 1:**
**Input**
\[ "Skiplist ", "add ", "add ", "add ", "search ", "add ", "search ", "erase ", "erase ", "search "\]
\[\[\], \[1\], \[2\], \[3\], \[0\], \[4\], \[1\], \[0\], \[1\], \[1\]\]
**Output**
\[null, null, null, null, false, null, true, false, true, false\]
**Explanation**
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0); // return False, 0 is not in skiplist.
skiplist.erase(1); // return True
skiplist.search(1); // return False, 1 has already been erased.
**Constraints:**
* `0 <= num, target <= 2 * 104`
* At most `5 * 104` calls will be made to `search`, `add`, and `erase`. | null |
Design skiplist | design-skiplist | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Skiplist:\n\n def __init__(self):\n self.skiplist=[]\n\n def search(self, target: int) -> bool:\n if target in self.skiplist:\n return True\n return False\n\n def add(self, num: int) -> None:\n self.skiplist.append(num)\n\n def erase(self, num: int) -> bool:\n if num in self.skiplist:\n self.skiplist.remove(num)\n return True\n return False\n\n\n# Your Skiplist object will be instantiated and called as such:\n# obj = Skiplist()\n# param_1 = obj.search(target)\n# obj.add(num)\n# param_3 = obj.erase(num)\n``` | 0 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Simple Python 1 liner | unique-number-of-occurrences | 0 | 1 | \n# Code\n```\nclass Solution:\n def uniqueOccurrences(self, arr: List[int]) -> bool:\n return len(set(Counter(arr).values())) == len(Counter(arr).values())\n``` | 2 | Given an array of integers `arr`, return `true` _if the number of occurrences of each value in the array is **unique** or_ `false` _otherwise_.
**Example 1:**
**Input:** arr = \[1,2,2,1,1,3\]
**Output:** true
**Explanation:** The value 1 has 3 occurrences, 2 has 2 and 3 has 1. No two values have the same number of occurrences.
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** false
**Example 3:**
**Input:** arr = \[-3,0,1,-3,1,1,1,-3,10,0\]
**Output:** true
**Constraints:**
* `1 <= arr.length <= 1000`
* `-1000 <= arr[i] <= 1000` | null |
Simple Python 1 liner | unique-number-of-occurrences | 0 | 1 | \n# Code\n```\nclass Solution:\n def uniqueOccurrences(self, arr: List[int]) -> bool:\n return len(set(Counter(arr).values())) == len(Counter(arr).values())\n``` | 2 | There are `n` computers numbered from `0` to `n - 1` connected by ethernet cables `connections` forming a network where `connections[i] = [ai, bi]` represents a connection between computers `ai` and `bi`. Any computer can reach any other computer directly or indirectly through the network.
You are given an initial computer network `connections`. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.
Return _the minimum number of times you need to do this in order to make all the computers connected_. If it is not possible, return `-1`.
**Example 1:**
**Input:** n = 4, connections = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 1
**Explanation:** Remove cable between computer 1 and 2 and place between computers 1 and 3.
**Example 2:**
**Input:** n = 6, connections = \[\[0,1\],\[0,2\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 2
**Example 3:**
**Input:** n = 6, connections = \[\[0,1\],\[0,2\],\[0,3\],\[1,2\]\]
**Output:** -1
**Explanation:** There are not enough cables.
**Constraints:**
* `1 <= n <= 105`
* `1 <= connections.length <= min(n * (n - 1) / 2, 105)`
* `connections[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated connections.
* No two computers are connected by more than one cable. | Find the number of occurrences of each element in the array using a hash map. Iterate through the hash map and check if there is a repeated value. |
Take it easy ! | unique-number-of-occurrences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal appears to be checking whether the number of occurrences of each element in the given list (arr) is unique.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach involves iterating through each element in the list (arr) and counting the occurrences of each element using the count() method. The counts are stored in a new list (c). Finally, the code compares the length of the set of counts (set(c)) with the length of the set of unique elements in the original list (set(arr)). If these lengths are equal, it implies that the occurrences of each element are unique, and the function returns True; otherwise, it returns False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe count operation for each element involves iterating through the entire list, leading to a time complexity of O(n^2), where n is the length of the input list arr.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n), where n is the length of the input list arr, as an additional list (c) is used to store the counts.\n\n\n# Code\n```\nclass Solution:\n def uniqueOccurrences(self, arr: List[int]) -> bool:\n c = []\n for i in arr:\n c.append(arr.count(i))\n return len(set(c)) == len(set(arr))\n\n\n``` | 1 | Given an array of integers `arr`, return `true` _if the number of occurrences of each value in the array is **unique** or_ `false` _otherwise_.
**Example 1:**
**Input:** arr = \[1,2,2,1,1,3\]
**Output:** true
**Explanation:** The value 1 has 3 occurrences, 2 has 2 and 3 has 1. No two values have the same number of occurrences.
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** false
**Example 3:**
**Input:** arr = \[-3,0,1,-3,1,1,1,-3,10,0\]
**Output:** true
**Constraints:**
* `1 <= arr.length <= 1000`
* `-1000 <= arr[i] <= 1000` | null |
Take it easy ! | unique-number-of-occurrences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal appears to be checking whether the number of occurrences of each element in the given list (arr) is unique.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach involves iterating through each element in the list (arr) and counting the occurrences of each element using the count() method. The counts are stored in a new list (c). Finally, the code compares the length of the set of counts (set(c)) with the length of the set of unique elements in the original list (set(arr)). If these lengths are equal, it implies that the occurrences of each element are unique, and the function returns True; otherwise, it returns False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe count operation for each element involves iterating through the entire list, leading to a time complexity of O(n^2), where n is the length of the input list arr.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n), where n is the length of the input list arr, as an additional list (c) is used to store the counts.\n\n\n# Code\n```\nclass Solution:\n def uniqueOccurrences(self, arr: List[int]) -> bool:\n c = []\n for i in arr:\n c.append(arr.count(i))\n return len(set(c)) == len(set(arr))\n\n\n``` | 1 | There are `n` computers numbered from `0` to `n - 1` connected by ethernet cables `connections` forming a network where `connections[i] = [ai, bi]` represents a connection between computers `ai` and `bi`. Any computer can reach any other computer directly or indirectly through the network.
You are given an initial computer network `connections`. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.
Return _the minimum number of times you need to do this in order to make all the computers connected_. If it is not possible, return `-1`.
**Example 1:**
**Input:** n = 4, connections = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 1
**Explanation:** Remove cable between computer 1 and 2 and place between computers 1 and 3.
**Example 2:**
**Input:** n = 6, connections = \[\[0,1\],\[0,2\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 2
**Example 3:**
**Input:** n = 6, connections = \[\[0,1\],\[0,2\],\[0,3\],\[1,2\]\]
**Output:** -1
**Explanation:** There are not enough cables.
**Constraints:**
* `1 <= n <= 105`
* `1 <= connections.length <= min(n * (n - 1) / 2, 105)`
* `connections[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated connections.
* No two computers are connected by more than one cable. | Find the number of occurrences of each element in the array using a hash map. Iterate through the hash map and check if there is a repeated value. |
Python3|| O(N^2)||Runtime 61 ms Beats 64.37% Memory 14.1 MB Beats 32.48% | unique-number-of-occurrences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniqueOccurrences(self, arr: List[int]) -> bool:\n dit={}\n for i in range(len(arr)):\n if arr[i] in dit:\n dit[arr[i]]+=1\n else:\n dit[arr[i]]=1\n ans=[]\n for i, j in enumerate(dit):\n if dit[j] in ans:\n return False\n else:\n ans.append(dit[j])\n return True\n \n``` | 1 | Given an array of integers `arr`, return `true` _if the number of occurrences of each value in the array is **unique** or_ `false` _otherwise_.
**Example 1:**
**Input:** arr = \[1,2,2,1,1,3\]
**Output:** true
**Explanation:** The value 1 has 3 occurrences, 2 has 2 and 3 has 1. No two values have the same number of occurrences.
**Example 2:**
**Input:** arr = \[1,2\]
**Output:** false
**Example 3:**
**Input:** arr = \[-3,0,1,-3,1,1,1,-3,10,0\]
**Output:** true
**Constraints:**
* `1 <= arr.length <= 1000`
* `-1000 <= arr[i] <= 1000` | null |
Python3|| O(N^2)||Runtime 61 ms Beats 64.37% Memory 14.1 MB Beats 32.48% | unique-number-of-occurrences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniqueOccurrences(self, arr: List[int]) -> bool:\n dit={}\n for i in range(len(arr)):\n if arr[i] in dit:\n dit[arr[i]]+=1\n else:\n dit[arr[i]]=1\n ans=[]\n for i, j in enumerate(dit):\n if dit[j] in ans:\n return False\n else:\n ans.append(dit[j])\n return True\n \n``` | 1 | There are `n` computers numbered from `0` to `n - 1` connected by ethernet cables `connections` forming a network where `connections[i] = [ai, bi]` represents a connection between computers `ai` and `bi`. Any computer can reach any other computer directly or indirectly through the network.
You are given an initial computer network `connections`. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.
Return _the minimum number of times you need to do this in order to make all the computers connected_. If it is not possible, return `-1`.
**Example 1:**
**Input:** n = 4, connections = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 1
**Explanation:** Remove cable between computer 1 and 2 and place between computers 1 and 3.
**Example 2:**
**Input:** n = 6, connections = \[\[0,1\],\[0,2\],\[0,3\],\[1,2\],\[1,3\]\]
**Output:** 2
**Example 3:**
**Input:** n = 6, connections = \[\[0,1\],\[0,2\],\[0,3\],\[1,2\]\]
**Output:** -1
**Explanation:** There are not enough cables.
**Constraints:**
* `1 <= n <= 105`
* `1 <= connections.length <= min(n * (n - 1) / 2, 105)`
* `connections[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated connections.
* No two computers are connected by more than one cable. | Find the number of occurrences of each element in the array using a hash map. Iterate through the hash map and check if there is a repeated value. |
[Python3] Sliding Window - Two ways to implement - Easy to Understand | get-equal-substrings-within-budget | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n res = 0\n i = j = cost = 0\n while j < len(s):\n cost += abs(ord(s[j]) - ord(t[j]))\n while cost > maxCost:\n cost -= abs(ord(s[i]) - ord(t[i]))\n i += 1\n res = max(res, j - i + 1)\n j += 1\n return res\n```\n\n\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n res = 0\n i = j = cost = 0\n while j < len(s):\n cost += abs(ord(s[j]) - ord(t[j]))\n if cost > maxCost:\n cost -= abs(ord(s[i]) - ord(t[i]))\n i += 1\n j += 1\n return j - i\n``` | 4 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
Python || Easy Clean Solution. Sliding Window. | get-equal-substrings-within-budget | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n left = ans = curr = 0\n for i in range(len(s)):\n curr += abs(ord(s[i]) - ord(t[i]))\n while curr > maxCost:\n curr -= abs(ord(s[left]) - ord(t[left]))\n left += 1\n ans = max(ans, i - left + 1)\n return ans\n```\n\n | 4 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
PYTHON | SLIDING WINDOW | O(n) | WELL EXPLAINED | EASY | | get-equal-substrings-within-budget | 0 | 1 | # EXPLANATION\nThe idea is very simple we keep a sliding window which will contain the substring which we \ncan convert using maxCost\n\nNow the idea of sliding window is \n1. increase the window from right\n2. decrease the window from left when we cannot increase further\n\nwe use the same idea for our sliding window \n\n\n# CODE\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n cost,start,ans = 0,0,0\n for i in range(n):\n diff = abs(ord(s[i]) - ord(t[i]))\n if cost + diff <= maxCost:\n # we can increase our sliding window\n cost += diff\n else:\n # we are unable to increase our sliding window\n ans = max(ans,i - start)\n while True:\n cost -= abs(ord(s[start]) - ord(t[start]))\n start += 1\n if cost + diff <= maxCost: break\n if cost + diff > maxCost: start = i + 1\n else: cost += diff\n \n ans = max(ans,n - start)\n return ans\n``` | 1 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
Clean, easy to understand solution: prefix sum + sliding window | get-equal-substrings-within-budget | 0 | 1 | # Intuition\nI started calculating the cost at each step in a for loop, then I realized I could stop checking the items directly and focus on the costs. That gave me the idea to use a prefix sum.\n\n# Approach\n1. Calculate each cost and add it to a separate array\n2. Using that array, calculate the prefix sum and save it in another array\n3. Iterate over that array checking the cost at each step with a sliding window.\n4. If the cost is too high, reduce the window size\n5. Return the largest window size seen.\n\n# Complexity\n- Time complexity:\nO(n), the time to traverse the input.\nI actually traverse the input 3 times but it\'s linear so the total is still O(n)\n\n- Space complexity:\n O(n) for the prefix sum array and costs array.\n\n **$$CAVEAT$$**: You can get rid of this if you calculate the prefix sum directly in the for loop, but calculating it separately is cleaner to understand the problem.\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n left = 0\n ans = float(\'-inf\')\n\n costs = []\n for i, j in zip(s, t):\n price = abs(ord(i) - ord(j))\n costs.append(price)\n \n # Calculate the prefix sum so we can know the cost of\n # a subarray in O(1)\n cumulative_costs = [costs[0]]\n for k in range(1, len(costs)):\n cumulative_costs.append(cumulative_costs[-1] + costs[k])\n \n for right in range(len(cumulative_costs)):\n substring_cost = cumulative_costs[right] - cumulative_costs[left] + costs[left]\n while left < right and substring_cost > maxCost:\n left += 1\n substring_cost = cumulative_costs[right] - cumulative_costs[left] + costs[left]\n if substring_cost <= maxCost:\n ans = max(ans, right - left + 1)\n \n return ans if ans != float(\'-inf\') else 0\n``` | 0 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
Fastest Python3 Sliding Window Solution | get-equal-substrings-within-budget | 0 | 1 | # Intuition\nConvert the problem to: Find Longest Subarray with Sum Less than K\n\n# Approach\nFirst calculate an array diff: store the differences between all entries.\nThen, find the longest subarray of diff with sum less than maxCost\nUse classic sliding window approach.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n), may reduce to O(1) without calculating diff array. It is faster and more intuitive with diff array.\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n diff = [abs(ord(s[i]) - ord(t[i])) for i in range(len(s))]\n l = 0\n ans = cost = 0\n for r in range(len(diff)):\n cost += diff[r]\n if cost > maxCost:\n cost -= diff[l]\n l += 1\n ans = max(ans, r - l + 1)\n return ans\n\n``` | 0 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
Simple Python Approach Beats 95.8% | get-equal-substrings-within-budget | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCreating a list with the differences between each character\'s ascii value\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSimple two pointer approach\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2n) = O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n differenceList = [abs(ord(a)-ord(b)) for a,b in zip(s,t)]\n startind, endind, maxCount, currCount = -1, -1, 0, 0\n while endind < len(t)-1:\n endind += 1\n currCount += differenceList[endind]\n while currCount > maxCost:\n startind += 1\n currCount -= differenceList[startind]\n if endind - startind > maxCount:\n maxCount = endind - startind\n return maxCount\n``` | 0 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
Python3 | get-equal-substrings-within-budget | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n # if maxCost==0:\n # return 1\n \n l=0\n r=0\n maxs=0\n sums=0\n while r<len(s):\n sums+=(abs(ord(s[r])-ord(t[r])))\n\n while sums>maxCost:\n sums-=(abs(ord(s[l])-ord(t[l])))\n l+=1\n \n maxs=max(maxs,r-l+1)\n r+=1\n return maxs\n``` | 0 | You are given two strings `s` and `t` of the same length and an integer `maxCost`.
You want to change `s` to `t`. Changing the `ith` character of `s` to `ith` character of `t` costs `|s[i] - t[i]|` (i.e., the absolute difference between the ASCII values of the characters).
Return _the maximum length of a substring of_ `s` _that can be changed to be the same as the corresponding substring of_ `t` _with a cost less than or equal to_ `maxCost`. If there is no substring from `s` that can be changed to its corresponding substring from `t`, return `0`.
**Example 1:**
**Input:** s = "abcd ", t = "bcdf ", maxCost = 3
**Output:** 3
**Explanation:** "abc " of s can change to "bcd ".
That costs 3, so the maximum length is 3.
**Example 2:**
**Input:** s = "abcd ", t = "cdef ", maxCost = 3
**Output:** 1
**Explanation:** Each character in s costs 2 to change to character in t, so the maximum length is 1.
**Example 3:**
**Input:** s = "abcd ", t = "acde ", maxCost = 0
**Output:** 1
**Explanation:** You cannot make any change, so the maximum length is 1.
**Constraints:**
* `1 <= s.length <= 105`
* `t.length == s.length`
* `0 <= maxCost <= 106`
* `s` and `t` consist of only lowercase English letters. | null |
✅Python 2D Stack implementation Easy + Accurate + Concise✅ | remove-all-adjacent-duplicates-in-string-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06\n# Code\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str:\n stack = []\n count = 1\n for i in s:\n if stack and stack[-1][0]==i:\n stack[-1][1]+=1\n if stack[-1][1]==k:\n stack.pop()\n else:\n stack.append([i,1])\n ans = \'\'\n for i in stack:\n ans+=i[0]*i[1]\n return ans\n```\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06 | 4 | You are given a string `s` and an integer `k`, a `k` **duplicate removal** consists of choosing `k` adjacent and equal letters from `s` and removing them, causing the left and the right side of the deleted substring to concatenate together.
We repeatedly make `k` **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It is guaranteed that the answer is **unique**.
**Example 1:**
**Input:** s = "abcd ", k = 2
**Output:** "abcd "
**Explanation:** There's nothing to delete.
**Example 2:**
**Input:** s = "deeedbbcccbdaa ", k = 3
**Output:** "aa "
**Explanation:**
First delete "eee " and "ccc ", get "ddbbbdaa "
Then delete "bbb ", get "dddaa "
Finally delete "ddd ", get "aa "
**Example 3:**
**Input:** s = "pbbcggttciiippooaais ", k = 2
**Output:** "ps "
**Constraints:**
* `1 <= s.length <= 105`
* `2 <= k <= 104`
* `s` only contains lowercase English letters. | null |
✅Python 2D Stack implementation Easy + Accurate + Concise✅ | remove-all-adjacent-duplicates-in-string-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06\n# Code\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str:\n stack = []\n count = 1\n for i in s:\n if stack and stack[-1][0]==i:\n stack[-1][1]+=1\n if stack[-1][1]==k:\n stack.pop()\n else:\n stack.append([i,1])\n ans = \'\'\n for i in stack:\n ans+=i[0]*i[1]\n return ans\n```\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06 | 4 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
✅ Python Simple One Pass Solution | remove-all-adjacent-duplicates-in-string-ii | 0 | 1 | Once you have identified that **stack** solves this problem (this took me like 30mins to figure out :)...), the logic is quite straightforward. We just need to track consecutive occurences of a character. If **count** matches **k**, we pop the element from stack.\n\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str: \n stck = [[\'$\', 0]] # a placeholder to mark stack is empty. This eliminates the need to do an empty check later\n \n for c in s:\n if stck[-1][0] == c:\n stck[-1][1]+=1 # update occurences count of top element if it matches current character\n if stck[-1][1] == k:\n stck.pop()\n else:\n stck.append([c, 1]) \n \n return \'\'.join(c * cnt for c, cnt in stck)\n \n```\n \n**Time = O(N)** - single iteration of input string\n**Space = O(N)** - for stack\n\nI have initialzed the **stack** with `[\'$\', 0]` placeholder. I am using `$` because the input string will only have lower case alphabets. I did this to remove the stack empty check. If you don\'t need this, you can just do the following:\n\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str: \n stck = [] \n \n for c in s: \n if stck and stck[-1][0] == c: # check if stack is not empty\n stck[-1][1]+=1\n if stck[-1][1] == k:\n stck.pop()\n else:\n stck.append([c, 1]) \n \n return \'\'.join(c * cnt for c, cnt in stck) \n```\n\n---\n***Please upvote if you find it useful*** | 96 | You are given a string `s` and an integer `k`, a `k` **duplicate removal** consists of choosing `k` adjacent and equal letters from `s` and removing them, causing the left and the right side of the deleted substring to concatenate together.
We repeatedly make `k` **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It is guaranteed that the answer is **unique**.
**Example 1:**
**Input:** s = "abcd ", k = 2
**Output:** "abcd "
**Explanation:** There's nothing to delete.
**Example 2:**
**Input:** s = "deeedbbcccbdaa ", k = 3
**Output:** "aa "
**Explanation:**
First delete "eee " and "ccc ", get "ddbbbdaa "
Then delete "bbb ", get "dddaa "
Finally delete "ddd ", get "aa "
**Example 3:**
**Input:** s = "pbbcggttciiippooaais ", k = 2
**Output:** "ps "
**Constraints:**
* `1 <= s.length <= 105`
* `2 <= k <= 104`
* `s` only contains lowercase English letters. | null |
✅ Python Simple One Pass Solution | remove-all-adjacent-duplicates-in-string-ii | 0 | 1 | Once you have identified that **stack** solves this problem (this took me like 30mins to figure out :)...), the logic is quite straightforward. We just need to track consecutive occurences of a character. If **count** matches **k**, we pop the element from stack.\n\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str: \n stck = [[\'$\', 0]] # a placeholder to mark stack is empty. This eliminates the need to do an empty check later\n \n for c in s:\n if stck[-1][0] == c:\n stck[-1][1]+=1 # update occurences count of top element if it matches current character\n if stck[-1][1] == k:\n stck.pop()\n else:\n stck.append([c, 1]) \n \n return \'\'.join(c * cnt for c, cnt in stck)\n \n```\n \n**Time = O(N)** - single iteration of input string\n**Space = O(N)** - for stack\n\nI have initialzed the **stack** with `[\'$\', 0]` placeholder. I am using `$` because the input string will only have lower case alphabets. I did this to remove the stack empty check. If you don\'t need this, you can just do the following:\n\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str: \n stck = [] \n \n for c in s: \n if stck and stck[-1][0] == c: # check if stack is not empty\n stck[-1][1]+=1\n if stck[-1][1] == k:\n stck.pop()\n else:\n stck.append([c, 1]) \n \n return \'\'.join(c * cnt for c, cnt in stck) \n```\n\n---\n***Please upvote if you find it useful*** | 96 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Python || 98.58% Faster || Stack || O(n) Solution | remove-all-adjacent-duplicates-in-string-ii | 0 | 1 | ```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str:\n a=[]\n for i in s:\n if a and a[-1][0]==i:\n a[-1][1]+=1\n if a[-1][1]==k: a.pop()\n else: a.append([i,1])\n return \'\'.join(key*value for key, value in a) \n```\n\n**An upvote will be encouraging** | 7 | You are given a string `s` and an integer `k`, a `k` **duplicate removal** consists of choosing `k` adjacent and equal letters from `s` and removing them, causing the left and the right side of the deleted substring to concatenate together.
We repeatedly make `k` **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It is guaranteed that the answer is **unique**.
**Example 1:**
**Input:** s = "abcd ", k = 2
**Output:** "abcd "
**Explanation:** There's nothing to delete.
**Example 2:**
**Input:** s = "deeedbbcccbdaa ", k = 3
**Output:** "aa "
**Explanation:**
First delete "eee " and "ccc ", get "ddbbbdaa "
Then delete "bbb ", get "dddaa "
Finally delete "ddd ", get "aa "
**Example 3:**
**Input:** s = "pbbcggttciiippooaais ", k = 2
**Output:** "ps "
**Constraints:**
* `1 <= s.length <= 105`
* `2 <= k <= 104`
* `s` only contains lowercase English letters. | null |
Python || 98.58% Faster || Stack || O(n) Solution | remove-all-adjacent-duplicates-in-string-ii | 0 | 1 | ```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str:\n a=[]\n for i in s:\n if a and a[-1][0]==i:\n a[-1][1]+=1\n if a[-1][1]==k: a.pop()\n else: a.append([i,1])\n return \'\'.join(key*value for key, value in a) \n```\n\n**An upvote will be encouraging** | 7 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | remove-all-adjacent-duplicates-in-string-ii | 1 | 1 | # My youtube channel - KeetCode(Ex-Amazon)\nI create 147 videos for leetcode questions as of April 15, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**Remove All Adjacent Duplicates in String \u2161 video**\nhttps://qr.paps.jp/F6L00\n\n**My youtube channel - KeetCode(Ex-Amazon)**\nhttps://qr.paps.jp/q2r7Z\n\n\n\n\n---\n\n\n\n# Intuition\nAn important point to solve this question is that how we count k length adjacent characters and delete them. To solve the question, I use stack.\n\n# Approach\nThe method first checks if the length of the input string is less than k. If it is, then it simply returns the input string as it is.\n\nIt then creates an empty list called st(stack) which will be used to store the characters and their occurrence counts.\n\nThe method then iterates over each character in the input string. For each character, it checks if the stack st is non-empty and if the current character is equal to the last character on the stack (i.e., st[-1][0]). If both conditions are true, then it increments the occurrence count of the last character on the stack by 1. If this count becomes equal to k, then the last character on the stack is popped from the stack.\n\nIf the current character is not equal to the last character on the stack or if the stack is empty, then the current character and its occurrence count 1 are added to the stack as a new list [c, 1].\n\nOnce all the characters in the input string have been processed, the method creates an empty string called res which will be used to store the final output.\n\nIt then iterates over each list in the stack st and adds the character multiplied by its occurrence count to the res string.\n\nFinally, the method returns the res string as the final output.\n\n\n# Complexity\n- Time complexity: O(n)\nWe iterate through all characters one by one. \n\n- Space complexity: O(n)\nThe worst case is when all characters are unique. In that case, we need to put all characters into stack.\n\n# Python\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str:\n if len(s) < k:\n return s\n \n st = []\n\n for c in s:\n if st and c == st[-1][0]:\n st[-1][-1] += 1\n\n if st[-1][-1] == k:\n st.pop()\n else:\n st.append([c, 1])\n \n res = ""\n for char, count in st:\n res += char * count\n \n return res\n```\n\n# JavaScript\n```\n/**\n * @param {string} s\n * @param {number} k\n * @return {string}\n */\nvar removeDuplicates = function(s, k) {\n if (s.length < k) {\n return s;\n }\n\n const st = [];\n\n for (const c of s) {\n if (st.length && c === st[st.length - 1][0]) {\n st[st.length - 1][1]++;\n\n if (st[st.length - 1][1] === k) {\n st.pop();\n }\n } else {\n st.push([c, 1]);\n }\n }\n\n let res = "";\n for (const [char, count] of st) {\n res += char.repeat(count);\n }\n\n return res; \n};\n```\n\n# Java\n```\nclass Solution {\n public String removeDuplicates(String s, int k) {\n if (s.length() < k) {\n return s;\n }\n\n List<int[]> st = new ArrayList<>();\n\n for (char c : s.toCharArray()) {\n if (!st.isEmpty() && c == st.get(st.size() - 1)[0]) {\n st.get(st.size() - 1)[1]++;\n\n if (st.get(st.size() - 1)[1] == k) {\n st.remove(st.size() - 1);\n }\n } else {\n st.add(new int[] {c, 1});\n }\n }\n\n StringBuilder res = new StringBuilder();\n for (int[] pair : st) {\n for (int i = 0; i < pair[1]; i++) {\n res.append((char) pair[0]);\n }\n }\n\n return res.toString(); \n }\n}\n```\n\n# C++\n```\nclass Solution {\npublic:\n string removeDuplicates(string s, int k) {\n if (s.length() < k) {\n return s;\n }\n\n std::vector<std::pair<char, int>> st;\n\n for (char c : s) {\n if (!st.empty() && c == st.back().first) {\n st.back().second++;\n\n if (st.back().second == k) {\n st.pop_back();\n }\n } else {\n st.emplace_back(c, 1);\n }\n }\n\n std::string res;\n for (const auto& [char_val, count] : st) {\n res.append(count, char_val);\n }\n\n return res; \n }\n};\n``` | 1 | You are given a string `s` and an integer `k`, a `k` **duplicate removal** consists of choosing `k` adjacent and equal letters from `s` and removing them, causing the left and the right side of the deleted substring to concatenate together.
We repeatedly make `k` **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It is guaranteed that the answer is **unique**.
**Example 1:**
**Input:** s = "abcd ", k = 2
**Output:** "abcd "
**Explanation:** There's nothing to delete.
**Example 2:**
**Input:** s = "deeedbbcccbdaa ", k = 3
**Output:** "aa "
**Explanation:**
First delete "eee " and "ccc ", get "ddbbbdaa "
Then delete "bbb ", get "dddaa "
Finally delete "ddd ", get "aa "
**Example 3:**
**Input:** s = "pbbcggttciiippooaais ", k = 2
**Output:** "ps "
**Constraints:**
* `1 <= s.length <= 105`
* `2 <= k <= 104`
* `s` only contains lowercase English letters. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | remove-all-adjacent-duplicates-in-string-ii | 1 | 1 | # My youtube channel - KeetCode(Ex-Amazon)\nI create 147 videos for leetcode questions as of April 15, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**Remove All Adjacent Duplicates in String \u2161 video**\nhttps://qr.paps.jp/F6L00\n\n**My youtube channel - KeetCode(Ex-Amazon)**\nhttps://qr.paps.jp/q2r7Z\n\n\n\n\n---\n\n\n\n# Intuition\nAn important point to solve this question is that how we count k length adjacent characters and delete them. To solve the question, I use stack.\n\n# Approach\nThe method first checks if the length of the input string is less than k. If it is, then it simply returns the input string as it is.\n\nIt then creates an empty list called st(stack) which will be used to store the characters and their occurrence counts.\n\nThe method then iterates over each character in the input string. For each character, it checks if the stack st is non-empty and if the current character is equal to the last character on the stack (i.e., st[-1][0]). If both conditions are true, then it increments the occurrence count of the last character on the stack by 1. If this count becomes equal to k, then the last character on the stack is popped from the stack.\n\nIf the current character is not equal to the last character on the stack or if the stack is empty, then the current character and its occurrence count 1 are added to the stack as a new list [c, 1].\n\nOnce all the characters in the input string have been processed, the method creates an empty string called res which will be used to store the final output.\n\nIt then iterates over each list in the stack st and adds the character multiplied by its occurrence count to the res string.\n\nFinally, the method returns the res string as the final output.\n\n\n# Complexity\n- Time complexity: O(n)\nWe iterate through all characters one by one. \n\n- Space complexity: O(n)\nThe worst case is when all characters are unique. In that case, we need to put all characters into stack.\n\n# Python\n```\nclass Solution:\n def removeDuplicates(self, s: str, k: int) -> str:\n if len(s) < k:\n return s\n \n st = []\n\n for c in s:\n if st and c == st[-1][0]:\n st[-1][-1] += 1\n\n if st[-1][-1] == k:\n st.pop()\n else:\n st.append([c, 1])\n \n res = ""\n for char, count in st:\n res += char * count\n \n return res\n```\n\n# JavaScript\n```\n/**\n * @param {string} s\n * @param {number} k\n * @return {string}\n */\nvar removeDuplicates = function(s, k) {\n if (s.length < k) {\n return s;\n }\n\n const st = [];\n\n for (const c of s) {\n if (st.length && c === st[st.length - 1][0]) {\n st[st.length - 1][1]++;\n\n if (st[st.length - 1][1] === k) {\n st.pop();\n }\n } else {\n st.push([c, 1]);\n }\n }\n\n let res = "";\n for (const [char, count] of st) {\n res += char.repeat(count);\n }\n\n return res; \n};\n```\n\n# Java\n```\nclass Solution {\n public String removeDuplicates(String s, int k) {\n if (s.length() < k) {\n return s;\n }\n\n List<int[]> st = new ArrayList<>();\n\n for (char c : s.toCharArray()) {\n if (!st.isEmpty() && c == st.get(st.size() - 1)[0]) {\n st.get(st.size() - 1)[1]++;\n\n if (st.get(st.size() - 1)[1] == k) {\n st.remove(st.size() - 1);\n }\n } else {\n st.add(new int[] {c, 1});\n }\n }\n\n StringBuilder res = new StringBuilder();\n for (int[] pair : st) {\n for (int i = 0; i < pair[1]; i++) {\n res.append((char) pair[0]);\n }\n }\n\n return res.toString(); \n }\n}\n```\n\n# C++\n```\nclass Solution {\npublic:\n string removeDuplicates(string s, int k) {\n if (s.length() < k) {\n return s;\n }\n\n std::vector<std::pair<char, int>> st;\n\n for (char c : s) {\n if (!st.empty() && c == st.back().first) {\n st.back().second++;\n\n if (st.back().second == k) {\n st.pop_back();\n }\n } else {\n st.emplace_back(c, 1);\n }\n }\n\n std::string res;\n for (const auto& [char_val, count] : st) {\n res.append(count, char_val);\n }\n\n return res; \n }\n};\n``` | 1 | You have a keyboard layout as shown above in the **X-Y** plane, where each English uppercase letter is located at some coordinate.
* For example, the letter `'A'` is located at coordinate `(0, 0)`, the letter `'B'` is located at coordinate `(0, 1)`, the letter `'P'` is located at coordinate `(2, 3)` and the letter `'Z'` is located at coordinate `(4, 1)`.
Given the string `word`, return _the minimum total **distance** to type such string using only two fingers_.
The **distance** between coordinates `(x1, y1)` and `(x2, y2)` is `|x1 - x2| + |y1 - y2|`.
**Note** that the initial positions of your two fingers are considered free so do not count towards your total distance, also your two fingers do not have to start at the first letter or the first two letters.
**Example 1:**
**Input:** word = "CAKE "
**Output:** 3
**Explanation:** Using two fingers, one optimal way to type "CAKE " is:
Finger 1 on letter 'C' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'C' to letter 'A' = 2
Finger 2 on letter 'K' -> cost = 0
Finger 2 on letter 'E' -> cost = Distance from letter 'K' to letter 'E' = 1
Total distance = 3
**Example 2:**
**Input:** word = "HAPPY "
**Output:** 6
**Explanation:** Using two fingers, one optimal way to type "HAPPY " is:
Finger 1 on letter 'H' -> cost = 0
Finger 1 on letter 'A' -> cost = Distance from letter 'H' to letter 'A' = 2
Finger 2 on letter 'P' -> cost = 0
Finger 2 on letter 'P' -> cost = Distance from letter 'P' to letter 'P' = 0
Finger 1 on letter 'Y' -> cost = Distance from letter 'A' to letter 'Y' = 4
Total distance = 6
**Constraints:**
* `2 <= word.length <= 300`
* `word` consists of uppercase English letters. | Use a stack to store the characters, when there are k same characters, delete them. To make it more efficient, use a pair to store the value and the count of each character. |
Python || BFS | minimum-moves-to-reach-target-with-rotations | 0 | 1 | deque is defined as follows- \n(snake head x corrdinate, snake head y corrdinate, direction, iteration number)\nTime Complexity - O(n^2)\n\n```\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n n=len(grid)\n seen=set()\n dq=deque()\n dq.append((0,1,"r",0))\n seen.add((0,1,"r"))\n while dq:\n i,j,pos,val=dq.popleft()\n if i==n-1 and j==n-1 and pos=="r": return val \n #move right\n if j+1<n and grid[i][j+1]==0 and (i,j+1,pos) not in seen:\n if pos=="r" or pos=="d" and grid[i-1][j+1]==0:\n dq.append((i,j+1,pos,val+1))\n seen.add((i,j+1,pos))\n #move down\n if i+1<n and grid[i+1][j]==0 and (i+1,j,pos) not in seen:\n if pos=="d" or pos=="r" and grid[i+1][j-1]==0:\n dq.append((i+1,j,pos,val+1))\n seen.add((i+1,j,pos))\n #change dir to down if curr is right\n if pos=="r" and j-1>=0 and i+1<n and grid[i+1][j]==grid[i+1][j-1]==0 and (i+1,j-1,"d") not in seen:\n dq.append((i+1,j-1,"d",val+1))\n seen.add((i+1,j-1,"d"))\n #change dir to right if curr is down\n if pos=="d" and i-1>=0 and j+1<n and grid[i-1][j+1]==grid[i][j+1]==0 and (i-1,j+1,"r") not in seen:\n dq.append((i-1,j+1,"r",val+1))\n seen.add((i-1,j+1,"r"))\n return -1\n``` | 1 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Standard BFS in python3, not quite a hard one | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Code\n```\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n n = len(grid)\n queue = [(0,1,0,0)]\n seen = set([(0,1,0)])\n for i,j,direc,step in queue:\n if (i,j,direc) == (n-1,n-1,0):\n return step\n if direc == 0:\n if j < n - 1 and grid[i][j+1] != 1 and (i,j+1,0) not in seen:\n seen.add((i,j+1,0))\n queue.append((i,j+1,0,step+1))\n if i < n - 1 and grid[i+1][j] != 1 and grid[i+1][j-1] != 1 and (i+1,j-1,1) not in seen:\n seen.add((i+1,j-1,1))\n queue.append((i+1,j-1,1,step+1))\n if i < n - 1 and grid[i+1][j-1]!=1 and grid[i+1][j] != 1 and (i+1,j,0) not in seen:\n seen.add((i+1,j,0))\n queue.append((i+1,j,0,step+1))\n else:\n if i < n - 1 and grid[i+1][j] != 1 and (i+1,j,1) not in seen:\n seen.add((i+1,j,1))\n queue.append((i+1,j,1,step+1))\n if j < n - 1 and grid[i][j+1] != 1 and grid[i-1][j+1] != 1 and (i-1,j+1,0) not in seen:\n seen.add((i-1,j+1,0))\n queue.append((i-1,j+1,0,step+1))\n if j < n - 1 and grid[i][j+1]!=1 and grid[i-1][j+1] != 1 and (i,j+1,1) not in seen:\n seen.add((i,j+1,1))\n queue.append((i,j+1,1,step+1))\n return -1\n \n\n\n\n \n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
DP but saving time and memory at the same time | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Code\n```\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n n = len(grid)\n h = []\n for i in grid[0][1:]:\n if i == 0:\n h.append(0)\n else:\n h += [float(\'INF\')] * (n - 1 - len(h))\n break\n\n v = [float(\'INF\')]\n for i in range(n-1):\n if grid[1][i] == 0:\n v.append(v[-1])\n if grid[0][i+1] == 0 and grid[1][i+1] == 0:\n v[-1] = min(v[-1], h[i] + 1)\n else:\n v.append(float(\'INF\'))\n v.pop(0)\n\n grid.append([1] * n)\n\n for i in range(1,n):\n j = 0\n if grid[i][0] == 1:\n h[0],v[0] = float(\'INF\'), float(\'INF\')\n else:\n if grid[i][1] == 0 and grid[i+1][0] == 0:\n if grid[i+1][1] == 0:\n if h[j] < v[j]:\n v[j] = h[j] + 1\n elif v[j] < h[j]:\n h[j] = v[j] + 1\n elif grid[i][1] == 0:\n v[j] = float(\'INF\')\n elif grid[i+1][j] == 0:\n h[j] = float(\'INF\')\n else:\n h[j],v[j] = float(\'INF\'),float(\'INF\')\n \n for j in range(1,n - 1):\n if grid[i][j] == 1:\n h[j],v[j] = float(\'INF\'), float(\'INF\')\n continue\n if grid[i][j + 1] == 0 and grid[i+1][j] == 0:\n h[j] = min(h[j],h[j-1])\n v[j] = min(v[j],v[j-1])\n if grid[i+1][j+1] == 0:\n if h[j] < v[j]:\n v[j] = h[j] + 1\n elif v[j] < h[j]:\n h[j] = v[j] + 1\n elif grid[i][j + 1] == 0:\n h[j] = min(h[j],h[j-1])\n v[j] = float(\'INF\')\n elif grid[i+1][j] == 0:\n v[j] = min(v[j],v[j-1])\n h[j] = float(\'INF\')\n else:\n h[j],v[j] = float(\'INF\'),float(\'INF\')\n \n res = h[-1] + n * 2 - 3\n return res if res < float(\'INF\') else -1\n\n\n\n\n\n\n\n\n \n\n\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
✅3d dp solution || python | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Intuition\n please use bfs approach,my solution works but not optimize.\n\n# Code\n```\nclass Solution:\n\n def check(self,dp,grid,i,j,k,n):\n if(i==n-1 and j==n-1 and k==0):return 0\n if(min(i,j)<0 or max(i,j)>=n or grid[i][j]==1 or grid[i][j]==-1):return n*n\n # print(i,j,k,dp[i][j][k],"------")\n if(dp[i][j][k]!=-1):return dp[i][j][k]\n ans=n*n\n pre=grid[i][j]\n grid[i][j]=-1\n if(k==0):\n if(i+1<n and grid[i+1][j-1]!=1 and grid[i+1][j]!=1):\n ans=min(ans,self.check(dp,grid,i+1,j,k,n)+1)\n ans=min(ans,self.check(dp,grid,i+1,j-1,k^1,n)+1)\n ans=min(ans,self.check(dp,grid,i,j+1,k,n)+1)\n else:\n ans=min(ans,self.check(dp,grid,i+1,j,k,n)+1)\n if(j+1<n and grid[i-1][j+1]!=1 and grid[i][j+1]!=1):\n ans=min(ans,self.check(dp,grid,i,j+1,k,n)+1)\n ans=min(ans,self.check(dp,grid,i-1,j+1,k^1,n)+1)\n dp[i][j][k]=ans\n grid[i][j]=pre\n # print(i,j,k,dp[i][j][k])\n return dp[i][j][k]\n\n def minimumMoves(self, grid: List[List[int]]) -> int:\n n=len(grid)\n dp=[[[-1 for k in range(2)] for i in range(n)] for j in range(n)]\n ans=self.check(dp,grid,0,1,0,n)\n if(ans>=n*n):return -1\n return ans\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Super Fast And Readable Python Solution Using Breadth First Search | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Intuition\nThis looks like a variation of the basic path planning problem where we must navigate a grid with obstacles. These are classically solved with breadth first search BFS as BFS reveals the shortest path to a node the very first time you reach it.\n\nThe twist here is that we have a snake that takes up two squares instead of the usual one. This slightly complicates the graph representation of the problem.\n\n# Approach\nWe create a graph as follows:\n* A vertex V is a triple of the form (row, column, orientation) where orientation is 0 if the snake is horizontal and 1 if the snake is vertical. As an example (3, 5, 0) means that the snake is taking up grid positions (3, 5) and (3, 6) and (3, 5, 1) means that the snake is taking up grid positions (3, 5) and (4, 5).\n* A directed edge exists between two vertices V1 and V2 if it is possible to go from V1 to V2 with a single move (right, down, clockwise rotation, or counter-clockwise rotation).\n* The resulting graph G can be more easily represented by its two subgraphs GH and GV with each consisting of horizontally- and vertically-oriented vertices. We create two matrices Hnodes and Vnodes to store the minimum distance to each node. A sentinel value of infinity (inf) is used to represent nodes that have not been reached yet. If a node remains infinity after the algorithm terminates, then it is unreachable via the allowed moves.\n* Now apply a BFS traversal of G using a queue.\n\nNote that as of this writing, this solution was the fastest running submission and also the submission using the least memory.\n\n\n# Complexity\n- Time complexity:\n$O(n^2)$ where $n$ is the length of the side of the square grid. Note that general BFS can be much slower, especially for densely connected graphs; however, we take advantage of the fact the local connectedness topology.\n\n- Space complexity:\n$O(n^2)$ from the matrices we used to store distances.\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n inf = 10000\n N = len(grid)\n Hnodes = [[inf for col in range(N-1)] for row in range(N)]\n Vnodes = [[inf for col in range(N)] for row in range(N-1)]\n nodeQueue = deque()\n\n # Starting position\n Hnodes[0][0] = 0\n nodeQueue.append((0, 0, 0)) # row, col, orientation\n\n while len(nodeQueue) > 0:\n node = nodeQueue.popleft()\n row = node[0]\n col = node[1]\n orientation = node[2]\n # horizontal case\n if orientation == 0:\n minMoves = Hnodes[row][col]\n # move right case\n if col + 2 < N and grid[row][col + 2] == 0 and Hnodes[row][col + 1] == inf:\n Hnodes[row][col + 1] = minMoves + 1\n nodeQueue.append((row, col + 1, 0))\n # move down case or rotate clockwise case\n if row + 1 < N and grid[row + 1][col] == 0 and grid[row + 1][col + 1] == 0:\n # move down\n if Hnodes[row + 1][col] == inf:\n Hnodes[row + 1][col] = minMoves + 1\n nodeQueue.append((row + 1, col, 0))\n # rotate clockwise\n if Vnodes[row][col] == inf:\n Vnodes[row][col] = minMoves + 1\n nodeQueue.append((row, col, 1))\n # vertical case\n else:\n minMoves = Vnodes[row][col]\n # move down case\n if row + 2 < N and grid[row + 2][col] == 0 and Vnodes[row + 1][col] == inf:\n Vnodes[row + 1][col] = minMoves + 1\n nodeQueue.append((row + 1, col, 1))\n # move right or rotate counter clockwise case\n if col + 1 < N and grid[row][col + 1] == 0 and grid[row + 1][col + 1] == 0:\n # move right\n if Vnodes[row][col + 1] == inf:\n Vnodes[row][col + 1] = minMoves + 1\n nodeQueue.append((row, col + 1, 1))\n # rotate counter clockwise\n if Hnodes[row][col] == inf:\n Hnodes[row][col] = minMoves + 1\n nodeQueue.append((row, col, 0))\n\n minDist = Hnodes[N - 1][N - 2]\n return minDist if minDist < inf else -1\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Easy to Understand | Faster | Simple | Python Solution | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Code\n```\nclass Solution:\n def minimumMoves(self, G: List[List[int]]) -> int:\n \tN, I, DP = len(G)-1, math.inf, [[math.inf]*2 for i in range(len(G)+1)]\n \tDP[N-1][0] = I if 1 in [G[N][N],G[N][N-1]] else 0\n \tfor j in range(N-2,-1,-1): DP[j][0] = (DP[j+1][0] + 1) if G[N][j] == 0 else I\n \tfor i,j in itertools.product(range(N-1,-1,-1),range(N,-1,-1)):\n \t\tn = [G[i][j],G[i][min(j+1,N)],G[min(i+1,N)][j],G[min(i+1,N)][min(j+1,N)]]\n \t\tDP[j][0], DP[j][1] = min(1+DP[j+1][0],1+DP[j][0]), min(1+DP[j+1][1],1+DP[j][1])\n \t\tif 1 not in n: DP[j][0], DP[j][1] = min(DP[j][0],2+DP[j+1][1],1+DP[j][1]), min(DP[j][1],2+DP[j+1][0],1+DP[j][0])\n \t\tif 1 in [n[0],n[1]]: DP[j][0] = I\n \t\tif 1 in [n[0],n[2]]: DP[j][1] = I\n \treturn -1 if DP[0][0] == I else DP[0][0]\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Time: O(n2)O(n2) Space: O(n2)O(n2) | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom enum import IntEnum\n\n\nclass Pos(IntEnum):\n kHorizontal = 0\n kVertical = 1\n\n\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n n = len(grid)\n ans = 0\n # State of (x, y, pos)\n # Pos := 0 (horizontal) // 1 (vertical)\n q = collections.deque([(0, 0, Pos.kHorizontal)])\n seen = {(0, 0, Pos.kHorizontal)}\n\n def canMoveRight(x: int, y: int, pos: Pos) -> bool:\n if pos == Pos.kHorizontal:\n return y + 2 < n and not grid[x][y + 2]\n return y + 1 < n and not grid[x][y + 1] and not grid[x + 1][y + 1]\n\n def canMoveDown(x: int, y: int, pos: Pos) -> bool:\n if pos == Pos.kVertical:\n return x + 2 < n and not grid[x + 2][y]\n return x + 1 < n and not grid[x + 1][y] and not grid[x + 1][y + 1]\n\n def canRotateClockwise(x: int, y: int, pos: Pos) -> bool:\n return pos == Pos.kHorizontal and x + 1 < n and \\\n not grid[x + 1][y + 1] and not grid[x + 1][y]\n\n def canRotateCounterclockwise(x: int, y: int, pos: Pos) -> bool:\n return pos == Pos.kVertical and y + 1 < n and \\\n not grid[x + 1][y + 1] and not grid[x][y + 1]\n\n while q:\n for _ in range(len(q)):\n x, y, pos = q.popleft()\n if x == n - 1 and y == n - 2 and pos == Pos.kHorizontal:\n return ans\n if canMoveRight(x, y, pos) and (x, y + 1, pos) not in seen:\n q.append((x, y + 1, pos))\n seen.add((x, y + 1, pos))\n if canMoveDown(x, y, pos) and (x + 1, y, pos) not in seen:\n q.append((x + 1, y, pos))\n seen.add((x + 1, y, pos))\n newPos = Pos.kVertical if pos == Pos.kHorizontal else Pos.kHorizontal\n if (canRotateClockwise(x, y, pos) or canRotateCounterclockwise(x, y, pos)) and \\\n (x, y, newPos) not in seen:\n q.append((x, y, newPos))\n seen.add((x, y, newPos))\n ans += 1\n\n return -1\n\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Python (Simple Dijkstra's algorithm) | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumMoves(self, grid):\n n = len(grid)\n dict1, stack = {(0,0,0,1):0}, [(0,0,0,0,1)]\n\n while stack:\n steps,i,j,ii,jj = heappop(stack)\n if i == n-1 and j == n-2 and ii == n-1 and jj == n-1: return steps\n if ii+1 < n and grid[i+1][j] == grid[ii+1][jj] == 0 and steps + 1 < dict1.get((i+1,j,ii+1,jj),float("inf")):\n heappush(stack,(steps+1,i+1,j,ii+1,jj))\n dict1[(i+1,j,ii+1,jj)] = steps + 1\n if jj+1 < n and grid[i][j+1] == grid[ii][jj+1] == 0 and steps + 1 < dict1.get((i,j+1,ii,jj+1),float("inf")):\n heappush(stack,(steps+1,i,j+1,ii,jj+1))\n dict1[(i,j+1,ii,jj+1)] = steps + 1\n if i == ii and ii+1 < n and grid[i+1][j] == grid[i+1][jj] == 0 and steps + 1 < dict1.get((i,j,i+1,j),float("inf")):\n heappush(stack,(steps+1,i,j,i+1,j))\n dict1[(i,j,i+1,j)] = steps + 1\n if j == jj and jj+1 < n and grid[i][j+1] == grid[ii][jj+1] == 0 and steps + 1 < dict1.get((i,j,i,j+1),float("inf")):\n heappush(stack,(steps+1,i,j,i,j+1))\n dict1[(i,j,i,j+1)] = steps + 1\n\n return -1\n \n\n\n\n\n\n\n\n \n\n\n\n\n \n\n\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Python Straight BFS Solution | Easy to Understand | minimum-moves-to-reach-target-with-rotations | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nJust have right, down, clockwise and counter-clockwise as directions in the direction array and run a BFS\n\n# Code\n```\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n side, queue = len(grid), deque([[(0, 0), (0, 1), 0]])\n visited = {((0, 0), (0, 1))}\n directions = [[(0, 1), (0, 1)], [(1, 0), (1, 0)], \n [(0, 0), (1, -1)], [(0, 0), (-1, 1)]]\n\n def validate(row1: int, col1: int, row2: int, col2: int, dirIndex: int) -> bool:\n if not (0 <= row1 < side and 0 <= col1 < side and 0 <= row2 < side and 0 <= col2 < side):\n return False\n if grid[row1][col1] != 0 or grid[row2][col2] != 0:\n return False\n if dirIndex >= 2: # Edge Case 1\n if grid[row1 + 1][col1 + 1] == 1:\n return False\n return True\n \n while queue:\n (row1, col1), (row2, col2), step = queue.popleft()\n if row1 == side - 1 and col1 == side - 2 and row2 == side - 1 and col2 == side - 1:\n return step\n for dirIndex in range(len(directions)):\n if dirIndex == 2:\n if row1 != row2:\n continue\n if dirIndex == 3:\n if col1 != col2:\n continue\n (drow1, dcol1), (drow2, dcol2) = directions[dirIndex]\n newRow1, newCol1 = row1 + drow1, col1 + dcol1\n newRow2, newCol2 = row2 + drow2, col2 + dcol2\n if validate(newRow1, newCol1, newRow2, newCol2, dirIndex) and ((newRow1, newCol1), (newRow2, newCol2)) not in visited:\n visited.add(((newRow1, newCol1), (newRow2, newCol2)))\n queue.append(((newRow1, newCol1), (newRow2, newCol2), step + 1))\n return -1\n``` | 0 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Python 3 (BFS, DFS, and DP) (With Explanation) (beats 100.00%) | minimum-moves-to-reach-target-with-rotations | 0 | 1 | (Note to Reader: It will be helpful to have the code at the bottom visible separately on your screen while reading this explanation)\n\n_**BFS Explanation:**_\n\nThis program uses a BFS approach starting out from the top left corner. The program starts by saving the first position of the snake into list S. You do not need to know three pieces of information to know precisely where the snake is. From the three pieces of information (location of the snake\'s head, location of the snake\'s tail, and its orientation), you really only need to know two pieces of information. In this porgram, we only look at the position of the snake\'s tail and its orientation (horizontal = \'h\', or vertical = \'v\').\n\nThe program starts by finding the size of the square grid and stores the value as N which is important because we do not want the snake to go out of bounds. The starting location of the snake is put inside the list S. The snake\'s tail starts at (0,0) and its orientation is horizontal. Thus S contains the tuple (0,0,\'h\'). T is initialized as an empty list. In each iteration of the while loop, T will contain the new positions that the snake can go to based on the entire set of current positions it is at, which is stored in S. So the list S contains all of the snakes current positions after c moves and the list T will contain all of the snakes permissible positions after c + 1 moves. The variable c is the number of moves the snake has made thus far and c is initialized to 0 since the snake has not moved yet. The set V is a set which will contain all the previously visited positions of the snake, where the positions are encoded into tuples of length 3.\n\nThe while loop will continue as long as there are new positions for the snake to go and the snake has not reached its destination. Note that the destination position is (N-1,N-2,\'h\') as given in the problem description. If there are no new positions for the snake to go and the destination has not been reached, the while loop will end and -1 is returned. The for loop iterates through every current position of the snake which is in the list S. Remember that in a BFS search you expand outward from the starting point. So you can imagine that S contains the outer expanding front of all the places that the snake could have gotten to after c moves. As the for loop iterates through S, if it finds a point in S that the snake has already visited, that point is ignored as there is no point in going in that direction again. This step is essential as otherwise the snake could potentially go in circles. An example of this is that the snake can just go clockwise, counter clockwise, clockwise, counter clockwise, over and over and over. This will cause an exponential increase in the size of S which can slow things down tremendously.\n\nProvided that the position we are currently analyzing in S has not been visited, the program continues onto the next line. This position tuple is stored in _i_ from the for loop. If the position tuple _i_ equals the destination tuple, the program returns c. Since we want the shortest path, there is no point in searching after the first path to the destination is reached as it can only have a larger c. For ease of coding, the row and column positions of the snake\'s tail are called _a_ and _b_ respectively and the orientation is stored as the letter _o_. We also add the position tuple to the set of visited tuples so that we do not visit it again in the future.\n\nThe next part of the code looks at where the snake can move given its current location. The first if statement examines the possible next moves if the snake is currently in a horizontal position. Recall that (a,b) is the location of the snake\'s tail. The next if statement (inside the first one) sees if the snake can move to the right horizontally. This requires checking to make sure that the snake\'s head isn\'t at the right edge of the grid and that there is an open space ahead of the snake\'s head. If both conditions hold, the new location of the snake\'s tail is added to T. Recall that T is the list of all the new potential locations that the snake can go to in move c + 1. The next if statement checks to see if there are a horizontal pair of zeros directly under the horizontally oriented snake and that the snake is not on the bottom edge of the grid. If these conditions hold then the snake has two permissible moves. It can move down, maintaining its horizontal position, or it can rotate clockwise. These lead to two new positions which are added to the growing list T. Note that when the snake rotates, its orientation changes.\n\nThe next if statement examines the possible next moves if the snake is currently in a vertical position. In a similar fashion it checks to see if the snake is at the right or bottom edge of the grid or if there are open spaces for it to move. If there are, it will add the new locations to T.\n\nAfter all of the new potential locations have been added to T, the list S is overwritten by the list T and list T is emptied. The count of the number of moves, stored in c, is increased by 1. The while loop then continues with a new list S to iterate through in the for loop. If during a for loop, as the program iterates through S, not a single new permissible position can be found, then nothing will be appended to the empty list T. If T stays empty, then S will be overwritten by it and the while loop which only runs if S is nonempty will stop and -1 will be returned.\n\n_**BFS Code:**_ (beats 100.00%) ( 270 ms )\n```\nclass Solution:\n def minimumMoves(self, G: List[List[int]]) -> int:\n \tN, S, T, V, c = len(G), [(0, 0, \'h\')], [], set(), 0\n \twhile S:\n \t\tfor i in S:\n \t\t\tif i in V: continue\n \t\t\tif i == (N-1, N-2, \'h\'): return c\n \t\t\t(a, b, o), _ = i, V.add(i)\n\t \t\tif o == \'h\':\n \t\t\t\tif b + 2 != N and G[a][b+2] == 0: T.append((a, b+1, o))\n \t\t\t\tif a + 1 != N and G[a+1][b] == 0 and G[a+1][b+1] == 0: T.append((a+1, b, o)), T.append((a, b, \'v\'))\n \t\t\telif o == \'v\':\n \t\t\t\tif a + 2 != N and G[a+2][b] == 0: T.append((a+1, b, o))\n \t\t\t\tif b + 1 != N and G[a][b+1] == 0 and G[a+1][b+1] == 0: T.append((a, b+1, o)), T.append((a, b, \'h\'))\n \t\tS, T, c = T, [], c + 1\n \treturn -1\n\t\t\n\t\t\n\t\t\n\t\t\n```\n_**DFS Code:**_ (Time Limit Exceeded on Test Case 12 / 42 ) (A 20 x 20 Grid takes too long with DFS)\n```\nclass Solution:\n def minimumMoves(self, G: List[List[int]]) -> int:\n \tN, V, M, self.t, self.m = len(G), set(), collections.defaultdict(int), 0, math.inf\n \tprint(N)\n \tdef dfs(a,b,o):\n \t\tif (a,b,o) in V or M[(a,b,o)] == 2 or self.t > self.m: return\n \t\tif (a,b,o) == (N-1,N-2,\'h\'):\n \t\t\tself.m = min(self.m,self.t)\n \t\t\tfor i in V: M[i] = 1\n \t\t\treturn\n \t\tself.t, _ = self.t + 1, V.add((a,b,o))\n \t\tif o == \'h\':\n \t\t\tif b + 2 != N and G[a][b+2] == 0: dfs(a, b+1, o)\n \t\t\tif a + 1 != N and G[a+1][b] == 0 and G[a+1][b+1] == 0: dfs(a+1, b, o), dfs(a, b, \'v\')\n \t\telif o == \'v\':\n \t\t\tif a + 2 != N and G[a+2][b] == 0: dfs(a+1, b, o)\n \t\t\tif b + 1 != N and G[a][b+1] == 0 and G[a+1][b+1] == 0: dfs(a, b+1, o), dfs(a, b, \'h\')\n \t\tif M[(a,b,o)] == 0: M[(a,b,o)] = 2\n \t\tself.t, _ = self.t - 1, V.remove((a,b,o))\n \tdfs(0,0,\'h\')\n \treturn -1 if self.m == math.inf else self.m\n\n\n```\n_**DP Code:**_ (beats ~50%) ( 420 ms )\n```\nclass Solution:\n def minimumMoves(self, G: List[List[int]]) -> int:\n \tN, I, DP = len(G)-1, math.inf, [[math.inf]*2 for i in range(len(G)+1)]\n \tDP[N-1][0] = I if 1 in [G[N][N],G[N][N-1]] else 0\n \tfor j in range(N-2,-1,-1): DP[j][0] = (DP[j+1][0] + 1) if G[N][j] == 0 else I\n \tfor i,j in itertools.product(range(N-1,-1,-1),range(N,-1,-1)):\n \t\tn = [G[i][j],G[i][min(j+1,N)],G[min(i+1,N)][j],G[min(i+1,N)][min(j+1,N)]]\n \t\tDP[j][0], DP[j][1] = min(1+DP[j+1][0],1+DP[j][0]), min(1+DP[j+1][1],1+DP[j][1])\n \t\tif 1 not in n: DP[j][0], DP[j][1] = min(DP[j][0],2+DP[j+1][1],1+DP[j][1]), min(DP[j][1],2+DP[j+1][0],1+DP[j][0])\n \t\tif 1 in [n[0],n[1]]: DP[j][0] = I\n \t\tif 1 in [n[0],n[2]]: DP[j][1] = I\n \treturn -1 if DP[0][0] == I else DP[0][0]\n\t\t\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com | 9 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
[Python3] Dijkstra's algo | minimum-moves-to-reach-target-with-rotations | 0 | 1 | \n```\nclass Solution:\n def minimumMoves(self, grid: List[List[int]]) -> int:\n n = len(grid)\n dist = {(0, 0, 0, 1): 0}\n pq = [(0, 0, 0, 0, 1)]\n while pq: \n x, i, j, ii, jj = heappop(pq)\n if i == n-1 and j == n-2 and ii == n-1 and jj == n-1: return x\n if ii+1 < n and grid[i+1][j] == grid[ii+1][jj] == 0 and x+1 < dist.get((i+1, j, ii+1, jj), inf): \n heappush(pq, (x+1, i+1, j, ii+1, jj))\n dist[i+1, j, ii+1, jj] = x + 1\n if jj+1 < n and grid[i][j+1] == grid[ii][jj+1] == 0 and x+1 < dist.get((i, j+1, ii, jj+1), inf): \n heappush(pq, (x+1, i, j+1, ii, jj+1))\n dist[i, j+1, ii, jj+1] = x + 1\n if i == ii and ii+1 < n and grid[i+1][j] == grid[i+1][jj] == 0 and x+1 < dist.get((i, j, i+1, j), inf): \n heappush(pq, (x+1, i, j, i+1, j))\n dist[i, j, i+1, j] = x + 1\n if j == jj and jj+1 < n and grid[i][j+1] == grid[ii][j+1] == 0 and x+1 < dist.get((i, j, i, j+1), inf): \n heappush(pq, (x+1, i, j, i, j+1))\n dist[i, j, i, j+1] = x + 1\n return -1 \n``` | 2 | In an `n*n` grid, there is a snake that spans 2 cells and starts moving from the top left corner at `(0, 0)` and `(0, 1)`. The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at `(n-1, n-2)` and `(n-1, n-1)`.
In one move the snake can:
* Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
* Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from `(r, c)` and `(r, c+1)` to `(r, c)` and `(r+1, c)`.
* Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from `(r, c)` and `(r+1, c)` to `(r, c)` and `(r, c+1)`.
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[0,0,0,0,0,1\],
\[1,1,0,0,1,0\],
\[0,0,0,0,1,1\],
\[0,0,1,0,1,0\],
\[0,1,1,0,0,0\],
\[0,1,1,0,0,0\]\]
**Output:** 11
**Explanation:**
One possible solution is \[right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down\].
**Example 2:**
**Input:** grid = \[\[0,0,1,1,1,1\],
\[0,0,0,0,1,1\],
\[1,1,0,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,1\],
\[1,1,1,0,0,0\]\]
**Output:** 9
**Constraints:**
* `2 <= n <= 100`
* `0 <= grid[i][j] <= 1`
* It is guaranteed that the snake starts at empty cells. | Sort the given array. Remove the first and last 5% of the sorted array. |
Beats 100% || Full Explained || [Java/Python3/C++/JavaScript] | minimum-cost-to-move-chips-to-the-same-position | 1 | 1 | # Intuition\n1. Shift all the chips to neighbouring odd and even positon respectively, as the cost of moving chips to 2 position is 0.\n - So all the odd chips can be placed at a given odd position with 0 cost and same for even chips.\n - Distance between two odd place is 2 and distance between two even place is 2.\n2. `[2,2,2,3,5]` 1st 2nd and 3rd chips are at postion 2, and 4th chips at position 3 and 5th at position 5. We can move 5th to position 3 with 0 cost since distance is 2 in between them and to travel 2 distance cost is 0, and so now 5th and 3rd chips are at positon 3. Now chips are at 2 and 3 positona and to move one positon it cost is 1, so answer will be 1.\n\n# Approach\n1. **Observation:**\n - Chips at odd positions move to position 1 at zero cost.\n - Chips at even positions move to position 2 at zero cost.\n2. **Conclusion:**\n - All chips are now at positions 1 and 2.\n3. **Cost Analysis:**\n -Shifting chips between positions costs 1 per chip.\n4. **Optimal Approach:**\n -Compare chip counts at positions 1 and 2.\n - Move chips from the position with the lower count to the other position.\n - Minimize cost by moving fewer chips.\n5. **Example:**\n - If 5 chips are at position 1 and 8 chips at position 2:\n - Move 5 chips from position 1 to 2 at a cost of 5.\nTotal cost is minimized.\n6. **Final Observation:**\n - Count chips at odd and even positions.\n - The answer is the minimum of the two counts.\n\n`This adjusted strategy emphasizes moving chips from the position with the lower count to reduce the overall cost of consolidation.`\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```Java []\nclass Solution {\n public int minCostToMoveChips(int[] position) {\n int even = 0;\n int odd = 0;\n\n for(int chips : position) {\n if(chips % 2 == 0) {\n even++;\n }\n else {\n odd++;\n }\n }\n return Math.min(even, odd);\n }\n}\n```\n```python3 []\ndef minCostToMoveChips(self, chips: List[int]) -> int:\n even_parity = 0\n odd_parity = 0\n for chip in chips:\n if chip % 2 == 0:\n even_parity += 1\n else:\n odd_parity += 1\n return min(even_parity, odd_parity)\n```\n```C++ []\nclass Solution {\npublic:\n int minCostToMoveChips(vector<int>& chips) {\n int even=0,odd=0;\n for(int i=0;i<chips.size();i++){\n if(chips[i]%2==0)\n even++;\n else\n odd++;\n }\n if(even>odd)\n return odd;\n return even;\n \n }\n};\n```\n```JavaScript []\nfunction minCostToMoveChips(chips) {\n let evenParity = 0;\n let oddParity = 0;\n\n for (let chip of chips) {\n if (chip % 2 === 0) {\n evenParity += 1;\n } else {\n oddParity += 1;\n }\n }\n\n return Math.min(evenParity, oddParity);\n}\n\n```\n | 4 | We have `n` chips, where the position of the `ith` chip is `position[i]`.
We need to move all the chips to **the same position**. In one step, we can change the position of the `ith` chip from `position[i]` to:
* `position[i] + 2` or `position[i] - 2` with `cost = 0`.
* `position[i] + 1` or `position[i] - 1` with `cost = 1`.
Return _the minimum cost_ needed to move all the chips to the same position.
**Example 1:**
**Input:** position = \[1,2,3\]
**Output:** 1
**Explanation:** First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.
**Example 2:**
**Input:** position = \[2,2,2,3,3\]
**Output:** 2
**Explanation:** We can move the two chips at position 3 to position 2. Each move has cost = 1. The total cost = 2.
**Example 3:**
**Input:** position = \[1,1000000000\]
**Output:** 1
**Constraints:**
* `1 <= position.length <= 100`
* `1 <= position[i] <= 10^9` | Using a hashmap, we can map the values of arr2 to their position in arr2. After, we can use a custom sorting function. |
Beats 100% || Full Explained || [Java/Python3/C++/JavaScript] | minimum-cost-to-move-chips-to-the-same-position | 1 | 1 | # Intuition\n1. Shift all the chips to neighbouring odd and even positon respectively, as the cost of moving chips to 2 position is 0.\n - So all the odd chips can be placed at a given odd position with 0 cost and same for even chips.\n - Distance between two odd place is 2 and distance between two even place is 2.\n2. `[2,2,2,3,5]` 1st 2nd and 3rd chips are at postion 2, and 4th chips at position 3 and 5th at position 5. We can move 5th to position 3 with 0 cost since distance is 2 in between them and to travel 2 distance cost is 0, and so now 5th and 3rd chips are at positon 3. Now chips are at 2 and 3 positona and to move one positon it cost is 1, so answer will be 1.\n\n# Approach\n1. **Observation:**\n - Chips at odd positions move to position 1 at zero cost.\n - Chips at even positions move to position 2 at zero cost.\n2. **Conclusion:**\n - All chips are now at positions 1 and 2.\n3. **Cost Analysis:**\n -Shifting chips between positions costs 1 per chip.\n4. **Optimal Approach:**\n -Compare chip counts at positions 1 and 2.\n - Move chips from the position with the lower count to the other position.\n - Minimize cost by moving fewer chips.\n5. **Example:**\n - If 5 chips are at position 1 and 8 chips at position 2:\n - Move 5 chips from position 1 to 2 at a cost of 5.\nTotal cost is minimized.\n6. **Final Observation:**\n - Count chips at odd and even positions.\n - The answer is the minimum of the two counts.\n\n`This adjusted strategy emphasizes moving chips from the position with the lower count to reduce the overall cost of consolidation.`\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```Java []\nclass Solution {\n public int minCostToMoveChips(int[] position) {\n int even = 0;\n int odd = 0;\n\n for(int chips : position) {\n if(chips % 2 == 0) {\n even++;\n }\n else {\n odd++;\n }\n }\n return Math.min(even, odd);\n }\n}\n```\n```python3 []\ndef minCostToMoveChips(self, chips: List[int]) -> int:\n even_parity = 0\n odd_parity = 0\n for chip in chips:\n if chip % 2 == 0:\n even_parity += 1\n else:\n odd_parity += 1\n return min(even_parity, odd_parity)\n```\n```C++ []\nclass Solution {\npublic:\n int minCostToMoveChips(vector<int>& chips) {\n int even=0,odd=0;\n for(int i=0;i<chips.size();i++){\n if(chips[i]%2==0)\n even++;\n else\n odd++;\n }\n if(even>odd)\n return odd;\n return even;\n \n }\n};\n```\n```JavaScript []\nfunction minCostToMoveChips(chips) {\n let evenParity = 0;\n let oddParity = 0;\n\n for (let chip of chips) {\n if (chip % 2 === 0) {\n evenParity += 1;\n } else {\n oddParity += 1;\n }\n }\n\n return Math.min(evenParity, oddParity);\n}\n\n```\n | 4 | A **matrix diagonal** is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the **matrix diagonal** starting from `mat[2][0]`, where `mat` is a `6 x 3` matrix, includes cells `mat[2][0]`, `mat[3][1]`, and `mat[4][2]`.
Given an `m x n` matrix `mat` of integers, sort each **matrix diagonal** in ascending order and return _the resulting matrix_.
**Example 1:**
**Input:** mat = \[\[3,3,1,1\],\[2,2,1,2\],\[1,1,1,2\]\]
**Output:** \[\[1,1,1,1\],\[1,2,2,2\],\[1,2,3,3\]\]
**Example 2:**
**Input:** mat = \[\[11,25,66,1,69,7\],\[23,55,17,45,15,52\],\[75,31,36,44,58,8\],\[22,27,33,25,68,4\],\[84,28,14,11,5,50\]\]
**Output:** \[\[5,17,4,1,52,7\],\[11,11,25,45,8,69\],\[14,23,25,44,58,15\],\[22,27,31,36,50,66\],\[84,28,75,33,55,68\]\]
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 100`
* `1 <= mat[i][j] <= 100` | The first move keeps the parity of the element as it is. The second move changes the parity of the element. Since the first move is free, if all the numbers have the same parity, the answer would be zero. Find the minimum cost to make all the numbers have the same parity. |
🚀🔥Leetcode 1218 | Python Solution + Video Tutorial 🎯🐍 | longest-arithmetic-subsequence-of-given-difference | 0 | 1 | # Intuition\nhttps://youtu.be/Ho7uSMTguCU\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nclass Solution:\n def longestSubsequence(self, arr: List[int], difference: int) -> int:\n dp = {}\n ans = 1\n for item in arr:\n val = 1\n if item - difference in dp:\n val += dp[item-difference]\n ans = max(ans, val)\n dp[item] = val\n \n return ans\n \n``` | 8 | Given an integer array `arr` and an integer `difference`, return the length of the longest subsequence in `arr` which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals `difference`.
A **subsequence** is a sequence that can be derived from `arr` by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[1,2,3,4\], difference = 1
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[1,2,3,4\].
**Example 2:**
**Input:** arr = \[1,3,5,7\], difference = 1
**Output:** 1
**Explanation:** The longest arithmetic subsequence is any single element.
**Example 3:**
**Input:** arr = \[1,5,7,8,5,3,4,2,1\], difference = -2
**Output:** 4
**Explanation:** The longest arithmetic subsequence is \[7,5,3,1\].
**Constraints:**
* `1 <= arr.length <= 105`
* `-104 <= arr[i], difference <= 104`
The node of a binary tree is a leaf if and only if it has no children. The depth of the node of a binary tree is the number of nodes along the path from the root node down to the node itself. | Do a postorder traversal. Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far). The final node marked will be the correct answer. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.