title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
91% Faster Solution | minimum-difficulty-of-a-job-schedule | 0 | 1 | ```\nclass Solution:\n def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:\n jobCount = len(jobDifficulty) \n if jobCount < d:\n return -1\n\n @lru_cache(None)\n def topDown(jobIndex: int, remainDayCount: int) -> int:\n remainJobCount = jobCount - jobIndex\n if remainDayCount == 1:\n return max(jobDifficulty[jobIndex:])\n \n if remainJobCount == remainDayCount:\n return sum(jobDifficulty[jobIndex:])\n\n minDiff = float(\'inf\')\n maxToday = 0\n for i in range(jobIndex, jobCount - remainDayCount + 1):\n maxToday = max(maxToday, jobDifficulty[i])\n minDiff = min(minDiff, maxToday + topDown(i+1, remainDayCount-1))\n return minDiff\n\n return topDown(0, d)\n``` | 4 | Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be **pseudo-palindromic** if at least one permutation of the node values in the path is a palindrome.
_Return the number of **pseudo-palindromic** paths going from the root node to leaf nodes._
**Example 1:**
**Input:** root = \[2,3,1,3,1,null,1\]
**Output:** 2
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path \[2,3,3\], the green path \[2,1,1\], and the path \[2,3,1\]. Among these paths only red path and green path are pseudo-palindromic paths since the red path \[2,3,3\] can be rearranged in \[3,2,3\] (palindrome) and the green path \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 2:**
**Input:** root = \[2,1,1,1,3,null,null,null,null,null,1\]
**Output:** 1
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path \[2,1,1\], the path \[2,1,3,1\], and the path \[2,1\]. Among these paths only the green path is pseudo-palindromic since \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 3:**
**Input:** root = \[9\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 9` | Use DP. Try to cut the array into d non-empty sub-arrays. Try all possible cuts for the array. Use dp[i][j] where DP states are i the index of the last cut and j the number of remaining cuts. Complexity is O(n * n * d). |
python3 | dp | dfs | memoziation | minimum-difficulty-of-a-job-schedule | 0 | 1 | ```\nclass Solution:\n def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:\n \n n = len(jobDifficulty)\n @lru_cache(None)\n def dfs(index, remaining_days):\n \n if remaining_days == 0:\n if index == n: return 0\n else: return sys.maxsize\n if index == n:\n if remaining_days == 0: return 0\n else: return sys.maxsize\n \n ans = sys.maxsize\n count_max = 0\n for i in range(index, n):\n count_max = max(count_max, jobDifficulty[i])\n ans = min(ans, count_max + dfs(i+1, remaining_days-1)) \n return ans\n \n if n < d: return -1\n return dfs(0, d)\n``` | 2 | You want to schedule a list of jobs in `d` days. Jobs are dependent (i.e To work on the `ith` job, you have to finish all the jobs `j` where `0 <= j < i`).
You have to finish **at least** one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the `d` days. The difficulty of a day is the maximum difficulty of a job done on that day.
You are given an integer array `jobDifficulty` and an integer `d`. The difficulty of the `ith` job is `jobDifficulty[i]`.
Return _the minimum difficulty of a job schedule_. If you cannot find a schedule for the jobs return `-1`.
**Example 1:**
**Input:** jobDifficulty = \[6,5,4,3,2,1\], d = 2
**Output:** 7
**Explanation:** First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7
**Example 2:**
**Input:** jobDifficulty = \[9,9,9\], d = 4
**Output:** -1
**Explanation:** If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
**Example 3:**
**Input:** jobDifficulty = \[1,1,1\], d = 3
**Output:** 3
**Explanation:** The schedule is one job per day. total difficulty will be 3.
**Constraints:**
* `1 <= jobDifficulty.length <= 300`
* `0 <= jobDifficulty[i] <= 1000`
* `1 <= d <= 10` | For a fixed number of candies c, how can you check if each child can get c candies? Use binary search to find the maximum c as the answer. |
python3 | dp | dfs | memoziation | minimum-difficulty-of-a-job-schedule | 0 | 1 | ```\nclass Solution:\n def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:\n \n n = len(jobDifficulty)\n @lru_cache(None)\n def dfs(index, remaining_days):\n \n if remaining_days == 0:\n if index == n: return 0\n else: return sys.maxsize\n if index == n:\n if remaining_days == 0: return 0\n else: return sys.maxsize\n \n ans = sys.maxsize\n count_max = 0\n for i in range(index, n):\n count_max = max(count_max, jobDifficulty[i])\n ans = min(ans, count_max + dfs(i+1, remaining_days-1)) \n return ans\n \n if n < d: return -1\n return dfs(0, d)\n``` | 2 | Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be **pseudo-palindromic** if at least one permutation of the node values in the path is a palindrome.
_Return the number of **pseudo-palindromic** paths going from the root node to leaf nodes._
**Example 1:**
**Input:** root = \[2,3,1,3,1,null,1\]
**Output:** 2
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path \[2,3,3\], the green path \[2,1,1\], and the path \[2,3,1\]. Among these paths only red path and green path are pseudo-palindromic paths since the red path \[2,3,3\] can be rearranged in \[3,2,3\] (palindrome) and the green path \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 2:**
**Input:** root = \[2,1,1,1,3,null,null,null,null,null,1\]
**Output:** 1
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path \[2,1,1\], the path \[2,1,3,1\], and the path \[2,1\]. Among these paths only the green path is pseudo-palindromic since \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 3:**
**Input:** root = \[9\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 9` | Use DP. Try to cut the array into d non-empty sub-arrays. Try all possible cuts for the array. Use dp[i][j] where DP states are i the index of the last cut and j the number of remaining cuts. Complexity is O(n * n * d). |
EASY PYTHON SOLUTION USING DP | minimum-difficulty-of-a-job-schedule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,jobDifficulty,d,n,mx,dct):\n if i>=n:\n if d>0:\n return float("infinity")\n return mx\n if (i,d,mx) in dct:\n return dct[(i,d,mx)]\n x=self.dp(i+1,jobDifficulty,d-1,n,0,dct)+max(mx,jobDifficulty[i])\n y=self.dp(i+1,jobDifficulty,d,n,max(mx,jobDifficulty[i]),dct)\n dct[(i,d,mx)]=min(x,y)\n return min(x,y)\n def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:\n n=len(jobDifficulty)\n if n<d:\n return -1\n return self.dp(0,jobDifficulty,d,n,0,{})\n\n \n``` | 1 | You want to schedule a list of jobs in `d` days. Jobs are dependent (i.e To work on the `ith` job, you have to finish all the jobs `j` where `0 <= j < i`).
You have to finish **at least** one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the `d` days. The difficulty of a day is the maximum difficulty of a job done on that day.
You are given an integer array `jobDifficulty` and an integer `d`. The difficulty of the `ith` job is `jobDifficulty[i]`.
Return _the minimum difficulty of a job schedule_. If you cannot find a schedule for the jobs return `-1`.
**Example 1:**
**Input:** jobDifficulty = \[6,5,4,3,2,1\], d = 2
**Output:** 7
**Explanation:** First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7
**Example 2:**
**Input:** jobDifficulty = \[9,9,9\], d = 4
**Output:** -1
**Explanation:** If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
**Example 3:**
**Input:** jobDifficulty = \[1,1,1\], d = 3
**Output:** 3
**Explanation:** The schedule is one job per day. total difficulty will be 3.
**Constraints:**
* `1 <= jobDifficulty.length <= 300`
* `0 <= jobDifficulty[i] <= 1000`
* `1 <= d <= 10` | For a fixed number of candies c, how can you check if each child can get c candies? Use binary search to find the maximum c as the answer. |
EASY PYTHON SOLUTION USING DP | minimum-difficulty-of-a-job-schedule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,jobDifficulty,d,n,mx,dct):\n if i>=n:\n if d>0:\n return float("infinity")\n return mx\n if (i,d,mx) in dct:\n return dct[(i,d,mx)]\n x=self.dp(i+1,jobDifficulty,d-1,n,0,dct)+max(mx,jobDifficulty[i])\n y=self.dp(i+1,jobDifficulty,d,n,max(mx,jobDifficulty[i]),dct)\n dct[(i,d,mx)]=min(x,y)\n return min(x,y)\n def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:\n n=len(jobDifficulty)\n if n<d:\n return -1\n return self.dp(0,jobDifficulty,d,n,0,{})\n\n \n``` | 1 | Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be **pseudo-palindromic** if at least one permutation of the node values in the path is a palindrome.
_Return the number of **pseudo-palindromic** paths going from the root node to leaf nodes._
**Example 1:**
**Input:** root = \[2,3,1,3,1,null,1\]
**Output:** 2
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path \[2,3,3\], the green path \[2,1,1\], and the path \[2,3,1\]. Among these paths only red path and green path are pseudo-palindromic paths since the red path \[2,3,3\] can be rearranged in \[3,2,3\] (palindrome) and the green path \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 2:**
**Input:** root = \[2,1,1,1,3,null,null,null,null,null,1\]
**Output:** 1
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path \[2,1,1\], the path \[2,1,3,1\], and the path \[2,1\]. Among these paths only the green path is pseudo-palindromic since \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 3:**
**Input:** root = \[9\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 9` | Use DP. Try to cut the array into d non-empty sub-arrays. Try all possible cuts for the array. Use dp[i][j] where DP states are i the index of the last cut and j the number of remaining cuts. Complexity is O(n * n * d). |
Python 3 Memoized and Tabulated Solution (Credits: Striver DP Series) | minimum-difficulty-of-a-job-schedule | 0 | 1 | **The Problem is Same as Partition Array For max Sum, So You can Refer To Striver\'s DP Series for the Solution of that problem.\nIn This You Just need to minimize the Sum instead of max and keep track of no of remaining days rest is just the same.**\n```\nclass Solution1: # Memoized Solution\n def minDifficulty(self, arr: List[int], d: int) -> int:\n if d>len(arr): return -1\n n = len(arr)\n dp = [[-1 for i in range(d+1)] for j in range(n)]\n def f(ind,d):\n if ind==n: return float(\'inf\')\n if d==1: # if we have only one day then we just take max of all remaining jobs\n return max(arr[ind:])\n if dp[ind][d]!=-1: return dp[ind][d]\n ans = float(\'inf\')\n mx = float(\'-inf\')\n s = 0\n for i in range(ind,n):\n mx = max(mx,arr[i])\n s=mx+f(i+1,d-1)\n ans = min(ans,s)\n dp[ind][d] = ans\n return dp[ind][d]\n return f(0,d)\nclass Solution: # Tabulation version\n def minDifficulty(self, arr: List[int], d: int) -> int:\n if d>len(arr): return -1\n n = len(arr)\n dp = [[0 for i in range(d+1)] for j in range(n+1)]\n for i in range(d+1): # Base Cases\n dp[n][i] = float(\'inf\')\n for i in range(n): # Base Case\n dp[i][1]=max(arr[i:])\n for ind in range(n-1,-1,-1):\n for days in range(2,d+1):\n ans = float(\'inf\')\n mx = float(\'-inf\')\n s = 0\n for i in range(ind,n):\n mx = max(mx,arr[i])\n s=mx+dp[i+1][days-1]\n ans = min(ans,s)\n dp[ind][days] = ans\n return dp[0][d]\n```\n**Please Upvote if You like this solution.**\n | 2 | You want to schedule a list of jobs in `d` days. Jobs are dependent (i.e To work on the `ith` job, you have to finish all the jobs `j` where `0 <= j < i`).
You have to finish **at least** one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the `d` days. The difficulty of a day is the maximum difficulty of a job done on that day.
You are given an integer array `jobDifficulty` and an integer `d`. The difficulty of the `ith` job is `jobDifficulty[i]`.
Return _the minimum difficulty of a job schedule_. If you cannot find a schedule for the jobs return `-1`.
**Example 1:**
**Input:** jobDifficulty = \[6,5,4,3,2,1\], d = 2
**Output:** 7
**Explanation:** First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7
**Example 2:**
**Input:** jobDifficulty = \[9,9,9\], d = 4
**Output:** -1
**Explanation:** If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
**Example 3:**
**Input:** jobDifficulty = \[1,1,1\], d = 3
**Output:** 3
**Explanation:** The schedule is one job per day. total difficulty will be 3.
**Constraints:**
* `1 <= jobDifficulty.length <= 300`
* `0 <= jobDifficulty[i] <= 1000`
* `1 <= d <= 10` | For a fixed number of candies c, how can you check if each child can get c candies? Use binary search to find the maximum c as the answer. |
Python 3 Memoized and Tabulated Solution (Credits: Striver DP Series) | minimum-difficulty-of-a-job-schedule | 0 | 1 | **The Problem is Same as Partition Array For max Sum, So You can Refer To Striver\'s DP Series for the Solution of that problem.\nIn This You Just need to minimize the Sum instead of max and keep track of no of remaining days rest is just the same.**\n```\nclass Solution1: # Memoized Solution\n def minDifficulty(self, arr: List[int], d: int) -> int:\n if d>len(arr): return -1\n n = len(arr)\n dp = [[-1 for i in range(d+1)] for j in range(n)]\n def f(ind,d):\n if ind==n: return float(\'inf\')\n if d==1: # if we have only one day then we just take max of all remaining jobs\n return max(arr[ind:])\n if dp[ind][d]!=-1: return dp[ind][d]\n ans = float(\'inf\')\n mx = float(\'-inf\')\n s = 0\n for i in range(ind,n):\n mx = max(mx,arr[i])\n s=mx+f(i+1,d-1)\n ans = min(ans,s)\n dp[ind][d] = ans\n return dp[ind][d]\n return f(0,d)\nclass Solution: # Tabulation version\n def minDifficulty(self, arr: List[int], d: int) -> int:\n if d>len(arr): return -1\n n = len(arr)\n dp = [[0 for i in range(d+1)] for j in range(n+1)]\n for i in range(d+1): # Base Cases\n dp[n][i] = float(\'inf\')\n for i in range(n): # Base Case\n dp[i][1]=max(arr[i:])\n for ind in range(n-1,-1,-1):\n for days in range(2,d+1):\n ans = float(\'inf\')\n mx = float(\'-inf\')\n s = 0\n for i in range(ind,n):\n mx = max(mx,arr[i])\n s=mx+dp[i+1][days-1]\n ans = min(ans,s)\n dp[ind][days] = ans\n return dp[0][d]\n```\n**Please Upvote if You like this solution.**\n | 2 | Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be **pseudo-palindromic** if at least one permutation of the node values in the path is a palindrome.
_Return the number of **pseudo-palindromic** paths going from the root node to leaf nodes._
**Example 1:**
**Input:** root = \[2,3,1,3,1,null,1\]
**Output:** 2
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path \[2,3,3\], the green path \[2,1,1\], and the path \[2,3,1\]. Among these paths only red path and green path are pseudo-palindromic paths since the red path \[2,3,3\] can be rearranged in \[3,2,3\] (palindrome) and the green path \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 2:**
**Input:** root = \[2,1,1,1,3,null,null,null,null,null,1\]
**Output:** 1
**Explanation:** The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path \[2,1,1\], the path \[2,1,3,1\], and the path \[2,1\]. Among these paths only the green path is pseudo-palindromic since \[2,1,1\] can be rearranged in \[1,2,1\] (palindrome).
**Example 3:**
**Input:** root = \[9\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 9` | Use DP. Try to cut the array into d non-empty sub-arrays. Try all possible cuts for the array. Use dp[i][j] where DP states are i the index of the last cut and j the number of remaining cuts. Complexity is O(n * n * d). |
Python 3 || 1 line, w/ explanation || T/S: 98% / 94% | the-k-weakest-rows-in-a-matrix | 0 | 1 | Here\'s the plan:\n\n- We sort all `x`in `range(len(nums))` using the sum of the xth row as the key. (We could also sort on the rows themselves--`key = lambda x: mat[x]`-- but sorting on integer seems to be more efficient)\n\n- We return the initial`k`elements of this sorted range.\n```\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], \n k: int) -> list[int]:\n\n return sorted(range(len(mat)), \n key = lambda x: sum(mat[x]))[:k]\n```\n[https://leetcode.com/problems/the-k-weakest-rows-in-a-matrix/submissions/1052196417/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*MN* + *M*log*M*) and space complexity is *O*(*MN*), in which *M* ~ `len(mat)` and *N* ~ `len(mat[0]`).\n\'\'\' | 6 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Python 3 || 1 line, w/ explanation || T/S: 98% / 94% | the-k-weakest-rows-in-a-matrix | 0 | 1 | Here\'s the plan:\n\n- We sort all `x`in `range(len(nums))` using the sum of the xth row as the key. (We could also sort on the rows themselves--`key = lambda x: mat[x]`-- but sorting on integer seems to be more efficient)\n\n- We return the initial`k`elements of this sorted range.\n```\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], \n k: int) -> list[int]:\n\n return sorted(range(len(mat)), \n key = lambda x: sum(mat[x]))[:k]\n```\n[https://leetcode.com/problems/the-k-weakest-rows-in-a-matrix/submissions/1052196417/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*MN* + *M*log*M*) and space complexity is *O*(*MN*), in which *M* ~ `len(mat)` and *N* ~ `len(mat[0]`).\n\'\'\' | 6 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
【Video】Beats 97.49% - Simple Heap solution - Python, JavaScript, Java, C++ | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Intuition\nUsing min heap with data like (soldiers, index). This Python solution beats 97%.\n\n\n\n\n---\n\n# Solution Video\n\nhttps://youtu.be/mv8FvPlQxtM\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,363\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\nThis is based on Python. Other might be different a bit.\n\n### Algorithm Overview:\n\n1. Create an empty min heap to store tuples of (soldiers count, row index).\n2. Iterate through each row in the matrix.\n3. Count the number of soldiers in each row and insert the tuple (soldiers count, row index) into the min heap.\n4. Retrieve the k weakest rows from the min heap.\n5. Return the indices of the k weakest rows.\n\n### Detailed Explanation:\n\n1. Create an empty min heap (`min_heap`) to store tuples of (soldiers count, row index).\n\n2. Iterate through each row in the matrix:\n\n ```python\n for i, row in enumerate(mat):\n ```\n\n3. Count the number of soldiers in each row:\n\n ```python\n soldiers_count = 0\n for j in range(len(row)):\n if row[j] == 1:\n soldiers_count += 1\n else:\n break\n ```\n\n4. Push a tuple (soldiers count, row index) into the min heap (`min_heap`):\n\n ```python\n heapq.heappush(min_heap, (soldiers_count, i))\n ```\n\n5. Retrieve the k weakest rows from the min heap:\n\n ```python\n weakest_rows = [heapq.heappop(min_heap)[1] for _ in range(k)]\n ```\n\n6. Return the indices of the k weakest rows:\n\n ```python\n return weakest_rows\n ```\n\nThe algorithm calculates the number of soldiers in each row and uses a min heap to efficiently find the k weakest rows based on the soldiers count. The min heap allows us to extract the smallest soldiers count and its corresponding row index. The result is a list of indices representing the k weakest rows.\n\n# How it works\n\nLet me explain how it works with Example 1.\n```\nInput: mat = \n[[1,1,0,0,0],\n [1,1,1,1,0],\n [1,0,0,0,0],\n [1,1,0,0,0],\n [1,1,1,1,1]], \n\nk = 3\n```\n\nStep 3 in Detailed Explanation, we check each row one by one and count number of 1.\n\n```\n[1,1,0,0,0] \u2192 (2, 0) (number of 1, index of row)\n[1,1,1,1,0] \u2192 (4, 1)\n[1,0,0,0,0] \u2192 (1, 2)\n[1,1,0,0,0] \u2192 (2, 3)\n[1,1,1,1,1] \u2192 (5, 4)\n\n```\nStep 4 in Detailed Explanation, `min_heap` has these data.\n```\nmin_heap = [(1, 2), (2, 3), (2, 0), (4, 1), (5, 4)]\n```\nNow, we can access the weakest row very easily.\n\nStep 5 in Detailed Explanation, pop data[1] k times from Heap, so we can get index number.\n\n```\nmin_heap = [(1, 2), (2, 3), (2, 0), (4, 1), (5, 4)]\npop 2 from (1, 2)\nk = 1\n```\n```\nmin_heap = [(2, 0), (2, 3), (4, 1), (5, 4)]\npop 0 from (2, 0)\nk = 2\n```\n```\nmin_heap = [(2, 3), (4, 1), (5, 4)]\npop 3 from (2, 3)\nk = 3\n```\n```\nmin_heap = [(4, 1), (5, 4)]\n```\nNow `k = 3`, so we finish iteration.\n\n```\nOutput: [2,0,3]\n```\n\n# Complexity\n\n### Time Complexity\n\n1. **Loop over the Rows (Outer Loop)**:\n The outer loop iterates through each row of the matrix. It will run `n` times, where `n` is the number of rows in the matrix. This contributes O(n) to the time complexity.\n\n2. **Loop over Columns (Inner Loop)**:\n The inner loop goes through each element in a row. In the worst case, it can go up to the number of columns in the matrix. Let\'s denote this as m (the maximum number of columns in a row). This contributes O(m) to the time complexity.\n\n3. **Push and Pop Operations on the Min Heap**:\n Pushing an element into a min heap and popping the top element each takes logarithmic time in the size of the heap, which can have at most n elements. So, these operations combined contribute O(log n).\n\nPutting it all together, the overall time complexity is O(n * m) for the loop over rows and columns, plus O(k * log n) for the heap operations, where n is the number of rows and m is the maximum number of columns in a row.\n\nTherefore, the **total time complexity** is O(n * m + k * log n).\n\n### Space Complexity\n\n1. **min_heap**:\n The min heap can contain at most n elements, each being a tuple of size 2 (soldiers_count, row index). Therefore, the space required for the min heap is O(n).\n\n2. **weakest_rows**:\n The weakest_rows list can contain at most k elements, where k is the input parameter. Therefore, the space required for this list is O(k).\n\n3. **i, row, soldiers_count, j**:\n These variables are integers and do not depend on the input size. They take up a constant amount of space.\n\nPutting it all together, the **total space complexity** is O(n + k), which simplifies to O(max(n, k)) since either n or k could be larger.\n\n```python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n min_heap = []\n\n for i, row in enumerate(mat):\n soldiers_count = 0\n\n for j in range(len(row)):\n if row[j] == 1:\n soldiers_count += 1\n else:\n break\n \n heapq.heappush(min_heap, (soldiers_count, i))\n \n weakest_rows = [heapq.heappop(min_heap)[1] for _ in range(k)]\n\n return weakest_rows\n```\n```javascript []\n/**\n * @param {number[][]} mat\n * @param {number} k\n * @return {number[]}\n */\nvar kWeakestRows = function(mat, k) {\n let rowStrengthSet = new Set();\n\n for (let rowIndex = 0; rowIndex < mat.length; rowIndex++) {\n let oneCount = 0;\n\n for (let colIndex = 0; colIndex < mat[rowIndex].length; colIndex++) {\n if (mat[rowIndex][colIndex] === 1) {\n oneCount++;\n } else {\n break;\n }\n }\n\n rowStrengthSet.add([oneCount, rowIndex]);\n }\n\n const sortedRows = Array.from(rowStrengthSet);\n sortedRows.sort((a, b) => a[0] - b[0]);\n\n let weakestRowIndices = [];\n for (let i = 0; i < k; i++) {\n weakestRowIndices.push(sortedRows[i][1]);\n }\n\n return weakestRowIndices; \n};\n```\n```java []\nclass Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> {\n int strengthA = a[0];\n int strengthB = b[0];\n if (strengthA != strengthB) {\n return Integer.compare(strengthA, strengthB);\n } else {\n return Integer.compare(a[1], b[1]);\n }\n });\n\n for (int i = 0; i < mat.length; i++) {\n int soldiersCount = 0;\n\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1) {\n soldiersCount++;\n } else {\n break;\n }\n }\n\n minHeap.offer(new int[]{soldiersCount, i});\n }\n\n int[] weakestRows = new int[k];\n for (int i = 0; i < k; i++) {\n weakestRows[i] = minHeap.poll()[1];\n }\n\n return weakestRows; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> minHeap;\n\n for (int i = 0; i < mat.size(); i++) {\n int soldiersCount = 0;\n\n for (int j = 0; j < mat[i].size(); j++) {\n if (mat[i][j] == 1) {\n soldiersCount++;\n } else {\n break;\n }\n }\n\n minHeap.push({soldiersCount, i});\n }\n\n std::vector<int> weakestRows(k);\n for (int i = 0; i < k; i++) {\n weakestRows[i] = minHeap.top().second;\n minHeap.pop();\n }\n\n return weakestRows; \n }\n};\n```\n\nThank you for reading. Please upvote the post and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 19, 2023\nhttps://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/solutions/4066549/how-we-think-about-a-solution-on-time-o1-space-python-javascript-java-c/\n\nHave a nice day! | 23 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
【Video】Beats 97.49% - Simple Heap solution - Python, JavaScript, Java, C++ | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Intuition\nUsing min heap with data like (soldiers, index). This Python solution beats 97%.\n\n\n\n\n---\n\n# Solution Video\n\nhttps://youtu.be/mv8FvPlQxtM\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,363\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\nThis is based on Python. Other might be different a bit.\n\n### Algorithm Overview:\n\n1. Create an empty min heap to store tuples of (soldiers count, row index).\n2. Iterate through each row in the matrix.\n3. Count the number of soldiers in each row and insert the tuple (soldiers count, row index) into the min heap.\n4. Retrieve the k weakest rows from the min heap.\n5. Return the indices of the k weakest rows.\n\n### Detailed Explanation:\n\n1. Create an empty min heap (`min_heap`) to store tuples of (soldiers count, row index).\n\n2. Iterate through each row in the matrix:\n\n ```python\n for i, row in enumerate(mat):\n ```\n\n3. Count the number of soldiers in each row:\n\n ```python\n soldiers_count = 0\n for j in range(len(row)):\n if row[j] == 1:\n soldiers_count += 1\n else:\n break\n ```\n\n4. Push a tuple (soldiers count, row index) into the min heap (`min_heap`):\n\n ```python\n heapq.heappush(min_heap, (soldiers_count, i))\n ```\n\n5. Retrieve the k weakest rows from the min heap:\n\n ```python\n weakest_rows = [heapq.heappop(min_heap)[1] for _ in range(k)]\n ```\n\n6. Return the indices of the k weakest rows:\n\n ```python\n return weakest_rows\n ```\n\nThe algorithm calculates the number of soldiers in each row and uses a min heap to efficiently find the k weakest rows based on the soldiers count. The min heap allows us to extract the smallest soldiers count and its corresponding row index. The result is a list of indices representing the k weakest rows.\n\n# How it works\n\nLet me explain how it works with Example 1.\n```\nInput: mat = \n[[1,1,0,0,0],\n [1,1,1,1,0],\n [1,0,0,0,0],\n [1,1,0,0,0],\n [1,1,1,1,1]], \n\nk = 3\n```\n\nStep 3 in Detailed Explanation, we check each row one by one and count number of 1.\n\n```\n[1,1,0,0,0] \u2192 (2, 0) (number of 1, index of row)\n[1,1,1,1,0] \u2192 (4, 1)\n[1,0,0,0,0] \u2192 (1, 2)\n[1,1,0,0,0] \u2192 (2, 3)\n[1,1,1,1,1] \u2192 (5, 4)\n\n```\nStep 4 in Detailed Explanation, `min_heap` has these data.\n```\nmin_heap = [(1, 2), (2, 3), (2, 0), (4, 1), (5, 4)]\n```\nNow, we can access the weakest row very easily.\n\nStep 5 in Detailed Explanation, pop data[1] k times from Heap, so we can get index number.\n\n```\nmin_heap = [(1, 2), (2, 3), (2, 0), (4, 1), (5, 4)]\npop 2 from (1, 2)\nk = 1\n```\n```\nmin_heap = [(2, 0), (2, 3), (4, 1), (5, 4)]\npop 0 from (2, 0)\nk = 2\n```\n```\nmin_heap = [(2, 3), (4, 1), (5, 4)]\npop 3 from (2, 3)\nk = 3\n```\n```\nmin_heap = [(4, 1), (5, 4)]\n```\nNow `k = 3`, so we finish iteration.\n\n```\nOutput: [2,0,3]\n```\n\n# Complexity\n\n### Time Complexity\n\n1. **Loop over the Rows (Outer Loop)**:\n The outer loop iterates through each row of the matrix. It will run `n` times, where `n` is the number of rows in the matrix. This contributes O(n) to the time complexity.\n\n2. **Loop over Columns (Inner Loop)**:\n The inner loop goes through each element in a row. In the worst case, it can go up to the number of columns in the matrix. Let\'s denote this as m (the maximum number of columns in a row). This contributes O(m) to the time complexity.\n\n3. **Push and Pop Operations on the Min Heap**:\n Pushing an element into a min heap and popping the top element each takes logarithmic time in the size of the heap, which can have at most n elements. So, these operations combined contribute O(log n).\n\nPutting it all together, the overall time complexity is O(n * m) for the loop over rows and columns, plus O(k * log n) for the heap operations, where n is the number of rows and m is the maximum number of columns in a row.\n\nTherefore, the **total time complexity** is O(n * m + k * log n).\n\n### Space Complexity\n\n1. **min_heap**:\n The min heap can contain at most n elements, each being a tuple of size 2 (soldiers_count, row index). Therefore, the space required for the min heap is O(n).\n\n2. **weakest_rows**:\n The weakest_rows list can contain at most k elements, where k is the input parameter. Therefore, the space required for this list is O(k).\n\n3. **i, row, soldiers_count, j**:\n These variables are integers and do not depend on the input size. They take up a constant amount of space.\n\nPutting it all together, the **total space complexity** is O(n + k), which simplifies to O(max(n, k)) since either n or k could be larger.\n\n```python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n min_heap = []\n\n for i, row in enumerate(mat):\n soldiers_count = 0\n\n for j in range(len(row)):\n if row[j] == 1:\n soldiers_count += 1\n else:\n break\n \n heapq.heappush(min_heap, (soldiers_count, i))\n \n weakest_rows = [heapq.heappop(min_heap)[1] for _ in range(k)]\n\n return weakest_rows\n```\n```javascript []\n/**\n * @param {number[][]} mat\n * @param {number} k\n * @return {number[]}\n */\nvar kWeakestRows = function(mat, k) {\n let rowStrengthSet = new Set();\n\n for (let rowIndex = 0; rowIndex < mat.length; rowIndex++) {\n let oneCount = 0;\n\n for (let colIndex = 0; colIndex < mat[rowIndex].length; colIndex++) {\n if (mat[rowIndex][colIndex] === 1) {\n oneCount++;\n } else {\n break;\n }\n }\n\n rowStrengthSet.add([oneCount, rowIndex]);\n }\n\n const sortedRows = Array.from(rowStrengthSet);\n sortedRows.sort((a, b) => a[0] - b[0]);\n\n let weakestRowIndices = [];\n for (let i = 0; i < k; i++) {\n weakestRowIndices.push(sortedRows[i][1]);\n }\n\n return weakestRowIndices; \n};\n```\n```java []\nclass Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> {\n int strengthA = a[0];\n int strengthB = b[0];\n if (strengthA != strengthB) {\n return Integer.compare(strengthA, strengthB);\n } else {\n return Integer.compare(a[1], b[1]);\n }\n });\n\n for (int i = 0; i < mat.length; i++) {\n int soldiersCount = 0;\n\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1) {\n soldiersCount++;\n } else {\n break;\n }\n }\n\n minHeap.offer(new int[]{soldiersCount, i});\n }\n\n int[] weakestRows = new int[k];\n for (int i = 0; i < k; i++) {\n weakestRows[i] = minHeap.poll()[1];\n }\n\n return weakestRows; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> minHeap;\n\n for (int i = 0; i < mat.size(); i++) {\n int soldiersCount = 0;\n\n for (int j = 0; j < mat[i].size(); j++) {\n if (mat[i][j] == 1) {\n soldiersCount++;\n } else {\n break;\n }\n }\n\n minHeap.push({soldiersCount, i});\n }\n\n std::vector<int> weakestRows(k);\n for (int i = 0; i < k; i++) {\n weakestRows[i] = minHeap.top().second;\n minHeap.pop();\n }\n\n return weakestRows; \n }\n};\n```\n\nThank you for reading. Please upvote the post and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 19, 2023\nhttps://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/solutions/4066549/how-we-think-about-a-solution-on-time-o1-space-python-javascript-java-c/\n\nHave a nice day! | 23 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
Binary Search, Sorting, Priority Queue + bonus 1 liner | the-k-weakest-rows-in-a-matrix | 0 | 1 | \n# Code\nPQ:\n```\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; \n vector<int> res;\n for(int i = 0; i < mat.size(); ++i) {\n pq.push({accumulate(begin(mat[i]), end(mat[i]), 0), i});\n }\n while(k--) res.push_back(pq.top().second), pq.pop();\n return res;\n }\n};\n```\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n arr = [(sum(mat[i]),i) for i in range(len(mat))]\n heapq.heapify(arr)\n res = []\n for _ in range(k):\n _,row = heapq.heappop(arr)\n res.append(row)\n return res\n```\nBS:\n```\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n int n= mat.size();\n int m = mat[0].size();\n vector<int> res;\n vector<pair<int,int>> pa;\n for(int i = 0;i<n;i++)\n {\n int val = lower_bound(mat[i].begin(),mat[i].end(),0,greater<int>())-mat[i].begin();\n pa.push_back({val,i});\n }\n sort(pa.begin(),pa.end());\n for(int i=0;i<k;i++)\n {\n res.push_back(pa[i].second);\n }\n return res;\n\n }\n};\n```\nSorting:\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n arr = [(sum(mat[i]),i) for i in range(len(mat))]\n arr.sort()\n return [arr[i][1] for i in range(k)]\n```\nWhich can be done in one line:\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n return [sorted([(sum(mat[i]),i) for i in range(len(mat))])[i][1] for i in range(k)]\n\n``` | 2 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Binary Search, Sorting, Priority Queue + bonus 1 liner | the-k-weakest-rows-in-a-matrix | 0 | 1 | \n# Code\nPQ:\n```\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; \n vector<int> res;\n for(int i = 0; i < mat.size(); ++i) {\n pq.push({accumulate(begin(mat[i]), end(mat[i]), 0), i});\n }\n while(k--) res.push_back(pq.top().second), pq.pop();\n return res;\n }\n};\n```\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n arr = [(sum(mat[i]),i) for i in range(len(mat))]\n heapq.heapify(arr)\n res = []\n for _ in range(k):\n _,row = heapq.heappop(arr)\n res.append(row)\n return res\n```\nBS:\n```\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n int n= mat.size();\n int m = mat[0].size();\n vector<int> res;\n vector<pair<int,int>> pa;\n for(int i = 0;i<n;i++)\n {\n int val = lower_bound(mat[i].begin(),mat[i].end(),0,greater<int>())-mat[i].begin();\n pa.push_back({val,i});\n }\n sort(pa.begin(),pa.end());\n for(int i=0;i<k;i++)\n {\n res.push_back(pa[i].second);\n }\n return res;\n\n }\n};\n```\nSorting:\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n arr = [(sum(mat[i]),i) for i in range(len(mat))]\n arr.sort()\n return [arr[i][1] for i in range(k)]\n```\nWhich can be done in one line:\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n return [sorted([(sum(mat[i]),i) for i in range(len(mat))])[i][1] for i in range(k)]\n\n``` | 2 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
✅ 98.41% Sorting & Min-Heap & Binary Search | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Comprehensive Guide to Solving "The K Weakest Rows in a Matrix"\n\n## Introduction & Problem Statement\n\nIn today\'s journey through the realm of matrices, we aim to identify the k weakest rows based on the number of soldiers. Each row in the matrix represents a combination of soldiers (1\'s) and civilians (0\'s). The soldiers always appear to the left of civilians, making it a unique and intriguing challenge. Our mission is to order the rows from weakest (least number of soldiers) to strongest and return the indices of the first k rows.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Matrix Representation**:\n The given matrix is binary, consisting only of 0\'s and 1\'s. Each row represents soldiers followed by civilians.\n\n2. **Row Weakness Definition**:\n A row is considered weaker than another based on two conditions:\n - The number of soldiers in the row.\n - The index of the row (in case of a tie in the number of soldiers).\n\n3. **Constraints**: \n - Matrix dimensions: $$ 2 \\leq n, m \\leq 100 $$\n - $$ 1 \\leq k \\leq m $$\n\n### Strategies to Tackle the Problem\n\nThree main strategies can be employed to solve this problem:\n\n1. **Sorting**: Count the soldiers in each row and then sort rows based on the count and index.\n2. **Min-Heap**: Use a heap to keep track of the k weakest rows as we traverse through the matrix.\n3. **Binary Search**: Since each row is sorted (all 1\'s followed by all 0\'s), we can use binary search to efficiently count the soldiers in each row.\n\n---\n\n## Live Coding 3 Approaches\nhttps://youtu.be/Ha4_QWrnGw8?si=Q14r0QrKO7gBGP-S\n\n## Delving Deeper into the Strategies\n\n### 1. Sorting Approach\n\n**Logic**:\n- Traverse through the matrix and calculate the strength of each row (number of soldiers).\n- Pair each strength with its row index.\n- Sort the pairs based on strength and index.\n- Return the indices of the first k pairs.\n\n**Pros**:\n- Simple and straightforward.\n- Directly uses Python\'s built-in sorting for efficiency.\n\n**Cons**:\n- Iterates through the entire matrix even if $$ k $$ is very small.\n\n# Code #1 Sorting\n``` Python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n row_strength = [(sum(row), i) for i, row in enumerate(mat)]\n row_strength.sort(key=lambda x: (x[0], x[1]))\n return [row[1] for row in row_strength[:k]]\n```\n``` Go []\nfunc kWeakestRows(mat [][]int, k int) []int {\n type RowStrength struct {\n strength, index int\n }\n \n rowStrengths := make([]RowStrength, len(mat))\n \n for i, row := range mat {\n strength := 0\n for _, val := range row {\n strength += val\n }\n rowStrengths[i] = RowStrength{strength, i}\n }\n \n sort.Slice(rowStrengths, func(i, j int) bool {\n if rowStrengths[i].strength == rowStrengths[j].strength {\n return rowStrengths[i].index < rowStrengths[j].index\n }\n return rowStrengths[i].strength < rowStrengths[j].strength\n })\n \n result := make([]int, k)\n for i := 0; i < k; i++ {\n result[i] = rowStrengths[i].index\n }\n \n return result\n}\n```\n``` Rust []\nuse std::cmp::Ordering;\n\nimpl Solution {\n pub fn k_weakest_rows(mat: Vec<Vec<i32>>, k: i32) -> Vec<i32> {\n let mut row_strengths: Vec<(i32, i32)> = mat.iter().enumerate().map(|(i, row)| {\n (row.iter().sum(), i as i32)\n }).collect();\n \n row_strengths.sort_by(|a, b| {\n match a.0.cmp(&b.0) {\n Ordering::Equal => a.1.cmp(&b.1),\n other => other,\n }\n });\n \n row_strengths.into_iter().map(|(_, i)| i).take(k as usize).collect()\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n vector<pair<int, int>> rowStrengths;\n for (int i = 0; i < mat.size(); ++i) {\n int strength = accumulate(mat[i].begin(), mat[i].end(), 0);\n rowStrengths.push_back({strength, i});\n }\n \n sort(rowStrengths.begin(), rowStrengths.end());\n \n vector<int> result;\n for (int i = 0; i < k; ++i) {\n result.push_back(rowStrengths[i].second);\n }\n \n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n int[][] rowStrengths = new int[mat.length][2];\n \n for (int i = 0; i < mat.length; ++i) {\n int strength = 0;\n for (int val : mat[i]) {\n strength += val;\n }\n rowStrengths[i][0] = strength;\n rowStrengths[i][1] = i;\n }\n \n Arrays.sort(rowStrengths, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n \n int[] result = new int[k];\n for (int i = 0; i < k; ++i) {\n result[i] = rowStrengths[i][1];\n }\n \n return result;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] KWeakestRows(int[][] mat, int k) {\n var rowStrengths = mat.Select((row, i) => new { Strength = row.Sum(), Index = i })\n .OrderBy(x => x.Strength)\n .ThenBy(x => x.Index)\n .Take(k)\n .Select(x => x.Index)\n .ToArray();\n return rowStrengths;\n }\n}\n```\n``` JavaScript []\nvar kWeakestRows = function(mat, k) {\n let rowStrengths = mat.map((row, i) => [row.reduce((a, b) => a + b, 0), i]);\n rowStrengths.sort((a, b) => a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]);\n return rowStrengths.slice(0, k).map(([_, i]) => i);\n};\n```\n``` PHP []\nclass Solution {\n\n function kWeakestRows($mat, $k) {\n $rowStrengths = [];\n foreach ($mat as $i => $row) {\n $strength = array_sum($row);\n $rowStrengths[] = [$strength, $i];\n }\n \n usort($rowStrengths, function($a, $b) {\n return $a[0] <=> $b[0] ?: $a[1] <=> $b[1];\n });\n \n return array_slice(array_column($rowStrengths, 1), 0, $k);\n }\n}\n```\n\n### 2. Min-Heap Approach\n\n**Logic**:\n- Utilize a min-heap to maintain the `k` weakest rows while iterating through the matrix.\n- For each row, calculate its strength (the sum of its elements, representing the number of soldiers) and push this value into the heap.\n- Whenever the heap size grows beyond $$ k $$, remove the strongest row from the heap.\n- At the end of the traversal, the heap will contain the `k` weakest rows, which can then be extracted and returned.\n\n**Pros**:\n- This approach is particularly efficient when dealing with large matrices, especially when $$ k $$ is small relative to the number of rows.\n- Makes optimal use of Python\'s `heapq` library for efficient heap operations, ensuring that both `heap.push()` and `heap.pop()` operations are fast.\n\n**Cons**:\n- The heap-based approach adds a bit more complexity to the code compared to a straightforward sorting method, but it generally offers better performance for this problem.\n\n# Code #2 Min-Heap\n``` Python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n heap = []\n for i, row in enumerate(mat):\n strength = sum(row)\n heapq.heappush(heap, (-strength, -i))\n if len(heap) > k:\n heapq.heappop(heap)\n return [-i for _, i in sorted(heap, reverse=True)]\n```\n\n### 3. Binary Search and Heap Approach\n\n**Logic**:\n- Each row in the matrix is sorted such that all 1\'s appear to the left of all 0\'s. This allows us to use binary search to quickly find the number of soldiers (1\'s) in each row.\n- We use a heap data structure to efficiently find the weakest rows. For each row, we calculate its strength (number of soldiers) using binary search and then push this information into a min-heap. \n- Finally, we extract the `k` smallest elements from the heap, which correspond to the `k` weakest rows.\n\n**Pros**:\n- The binary search allows for efficient computation of the strength of each row, which is particularly useful when the number of soldiers varies significantly across rows.\n- The heap data structure ensures that we can efficiently find the `k` weakest rows without sorting the entire array, thus saving computational resources.\n\n**Cons**:\n- Although the binary search optimizes the row strength calculation, the overall time complexity can still be influenced by the time it takes to build and manipulate the heap. However, this is generally more efficient than sorting the entire array.\n \n# Code #3 Binary Search + Heap Approach\n``` Python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n def binarySearch(arr):\n left, right = 0, len(arr) - 1\n while left <= right:\n mid = (left + right) // 2\n if arr[mid] == 1:\n left = mid + 1\n else:\n right = mid - 1\n return left\n\n queue = [(binarySearch(row), idx) for idx, row in enumerate(mat)]\n heapq.heapify(queue)\n\n return [idx for _, idx in heapq.nsmallest(k, queue)]\n```\n\n\n\n## Time and Space Complexity\n\n### 1. Sorting Approach:\n- **Time Complexity**: $$O(m \\log m)$$\n - Here, `m` is the number of rows. Sorting an array of length `m` will take $$O(m \\log m)$$ time.\n- **Space Complexity**: $$O(m)$$\n - We need additional space for storing the strengths and indices, which will be of length `m`.\n\n### 2. Min-Heap Approach:\n- **Time Complexity**: $$O(m \\log k)$$\n - Pushing an element into a heap of size `k` takes $$O(\\log k)$$ time. We do this `m` times, so the total time is $$O(m \\log k)$$.\n- **Space Complexity**: $$O(k)$$\n - The heap will store `k` elements at most, so the space complexity is $$O(k)$$.\n\n### 3. Binary Search and Heap Approach:\n- **Time Complexity**: $$O(m \\log n + m \\log m)$$\n - Binary search on each row to find the number of soldiers will take $$O(\\log n)$$ time for each row, resulting in $$O(m \\log n)$$ for all rows. Building and manipulating the heap will take $$O(m \\log m)$$ time.\n- **Space Complexity**: $$O(m)$$\n - We need additional space for the heap to store the strengths and indices, which will be of length `m`.\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) | Version |\n|-------------|-----------|-------------|--------------------|\n| Rust | 0 | 2.2 | Sort |\n| Java | 2 | 44.4 | Sort |\n| C++ | 8 | 11.1 | Sort |\n| Go | 11 | 4.9 | Sort |\n| PHP | 32 | 20.8 | Sort |\n| JavaScript | 57 | 43.5 | Sort |\n| Python3 | 93 | 16.8 | Sort |\n| Python3 | 93 | 16.6 | Heap |\n| Python3 | 98 | 16.8 | Binary Search |\n| C# | 133 | 46.7 | Sort |\n\n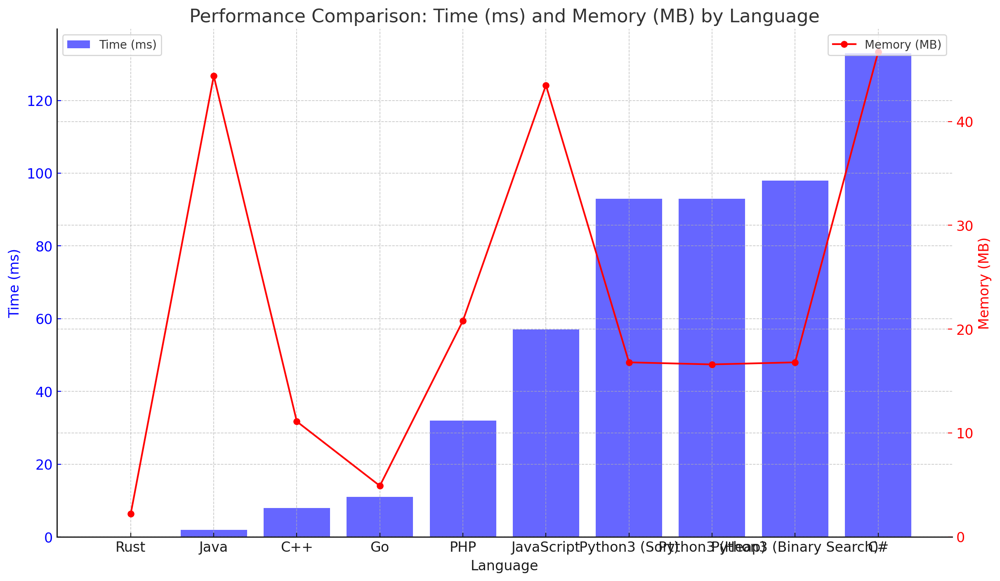\n\n\n## Conclusion\n\nEach of the strategies presented has its own merits. Depending on the specific requirements and constraints of the application, one approach might be preferred over the others. Whether you\'re a beginner or an expert, understanding these strategies will surely enhance your problem-solving skills. Happy coding!\n\n\n\n | 78 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
✅ 98.41% Sorting & Min-Heap & Binary Search | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Comprehensive Guide to Solving "The K Weakest Rows in a Matrix"\n\n## Introduction & Problem Statement\n\nIn today\'s journey through the realm of matrices, we aim to identify the k weakest rows based on the number of soldiers. Each row in the matrix represents a combination of soldiers (1\'s) and civilians (0\'s). The soldiers always appear to the left of civilians, making it a unique and intriguing challenge. Our mission is to order the rows from weakest (least number of soldiers) to strongest and return the indices of the first k rows.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Matrix Representation**:\n The given matrix is binary, consisting only of 0\'s and 1\'s. Each row represents soldiers followed by civilians.\n\n2. **Row Weakness Definition**:\n A row is considered weaker than another based on two conditions:\n - The number of soldiers in the row.\n - The index of the row (in case of a tie in the number of soldiers).\n\n3. **Constraints**: \n - Matrix dimensions: $$ 2 \\leq n, m \\leq 100 $$\n - $$ 1 \\leq k \\leq m $$\n\n### Strategies to Tackle the Problem\n\nThree main strategies can be employed to solve this problem:\n\n1. **Sorting**: Count the soldiers in each row and then sort rows based on the count and index.\n2. **Min-Heap**: Use a heap to keep track of the k weakest rows as we traverse through the matrix.\n3. **Binary Search**: Since each row is sorted (all 1\'s followed by all 0\'s), we can use binary search to efficiently count the soldiers in each row.\n\n---\n\n## Live Coding 3 Approaches\nhttps://youtu.be/Ha4_QWrnGw8?si=Q14r0QrKO7gBGP-S\n\n## Delving Deeper into the Strategies\n\n### 1. Sorting Approach\n\n**Logic**:\n- Traverse through the matrix and calculate the strength of each row (number of soldiers).\n- Pair each strength with its row index.\n- Sort the pairs based on strength and index.\n- Return the indices of the first k pairs.\n\n**Pros**:\n- Simple and straightforward.\n- Directly uses Python\'s built-in sorting for efficiency.\n\n**Cons**:\n- Iterates through the entire matrix even if $$ k $$ is very small.\n\n# Code #1 Sorting\n``` Python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n row_strength = [(sum(row), i) for i, row in enumerate(mat)]\n row_strength.sort(key=lambda x: (x[0], x[1]))\n return [row[1] for row in row_strength[:k]]\n```\n``` Go []\nfunc kWeakestRows(mat [][]int, k int) []int {\n type RowStrength struct {\n strength, index int\n }\n \n rowStrengths := make([]RowStrength, len(mat))\n \n for i, row := range mat {\n strength := 0\n for _, val := range row {\n strength += val\n }\n rowStrengths[i] = RowStrength{strength, i}\n }\n \n sort.Slice(rowStrengths, func(i, j int) bool {\n if rowStrengths[i].strength == rowStrengths[j].strength {\n return rowStrengths[i].index < rowStrengths[j].index\n }\n return rowStrengths[i].strength < rowStrengths[j].strength\n })\n \n result := make([]int, k)\n for i := 0; i < k; i++ {\n result[i] = rowStrengths[i].index\n }\n \n return result\n}\n```\n``` Rust []\nuse std::cmp::Ordering;\n\nimpl Solution {\n pub fn k_weakest_rows(mat: Vec<Vec<i32>>, k: i32) -> Vec<i32> {\n let mut row_strengths: Vec<(i32, i32)> = mat.iter().enumerate().map(|(i, row)| {\n (row.iter().sum(), i as i32)\n }).collect();\n \n row_strengths.sort_by(|a, b| {\n match a.0.cmp(&b.0) {\n Ordering::Equal => a.1.cmp(&b.1),\n other => other,\n }\n });\n \n row_strengths.into_iter().map(|(_, i)| i).take(k as usize).collect()\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n vector<pair<int, int>> rowStrengths;\n for (int i = 0; i < mat.size(); ++i) {\n int strength = accumulate(mat[i].begin(), mat[i].end(), 0);\n rowStrengths.push_back({strength, i});\n }\n \n sort(rowStrengths.begin(), rowStrengths.end());\n \n vector<int> result;\n for (int i = 0; i < k; ++i) {\n result.push_back(rowStrengths[i].second);\n }\n \n return result;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n int[][] rowStrengths = new int[mat.length][2];\n \n for (int i = 0; i < mat.length; ++i) {\n int strength = 0;\n for (int val : mat[i]) {\n strength += val;\n }\n rowStrengths[i][0] = strength;\n rowStrengths[i][1] = i;\n }\n \n Arrays.sort(rowStrengths, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n \n int[] result = new int[k];\n for (int i = 0; i < k; ++i) {\n result[i] = rowStrengths[i][1];\n }\n \n return result;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] KWeakestRows(int[][] mat, int k) {\n var rowStrengths = mat.Select((row, i) => new { Strength = row.Sum(), Index = i })\n .OrderBy(x => x.Strength)\n .ThenBy(x => x.Index)\n .Take(k)\n .Select(x => x.Index)\n .ToArray();\n return rowStrengths;\n }\n}\n```\n``` JavaScript []\nvar kWeakestRows = function(mat, k) {\n let rowStrengths = mat.map((row, i) => [row.reduce((a, b) => a + b, 0), i]);\n rowStrengths.sort((a, b) => a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]);\n return rowStrengths.slice(0, k).map(([_, i]) => i);\n};\n```\n``` PHP []\nclass Solution {\n\n function kWeakestRows($mat, $k) {\n $rowStrengths = [];\n foreach ($mat as $i => $row) {\n $strength = array_sum($row);\n $rowStrengths[] = [$strength, $i];\n }\n \n usort($rowStrengths, function($a, $b) {\n return $a[0] <=> $b[0] ?: $a[1] <=> $b[1];\n });\n \n return array_slice(array_column($rowStrengths, 1), 0, $k);\n }\n}\n```\n\n### 2. Min-Heap Approach\n\n**Logic**:\n- Utilize a min-heap to maintain the `k` weakest rows while iterating through the matrix.\n- For each row, calculate its strength (the sum of its elements, representing the number of soldiers) and push this value into the heap.\n- Whenever the heap size grows beyond $$ k $$, remove the strongest row from the heap.\n- At the end of the traversal, the heap will contain the `k` weakest rows, which can then be extracted and returned.\n\n**Pros**:\n- This approach is particularly efficient when dealing with large matrices, especially when $$ k $$ is small relative to the number of rows.\n- Makes optimal use of Python\'s `heapq` library for efficient heap operations, ensuring that both `heap.push()` and `heap.pop()` operations are fast.\n\n**Cons**:\n- The heap-based approach adds a bit more complexity to the code compared to a straightforward sorting method, but it generally offers better performance for this problem.\n\n# Code #2 Min-Heap\n``` Python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n heap = []\n for i, row in enumerate(mat):\n strength = sum(row)\n heapq.heappush(heap, (-strength, -i))\n if len(heap) > k:\n heapq.heappop(heap)\n return [-i for _, i in sorted(heap, reverse=True)]\n```\n\n### 3. Binary Search and Heap Approach\n\n**Logic**:\n- Each row in the matrix is sorted such that all 1\'s appear to the left of all 0\'s. This allows us to use binary search to quickly find the number of soldiers (1\'s) in each row.\n- We use a heap data structure to efficiently find the weakest rows. For each row, we calculate its strength (number of soldiers) using binary search and then push this information into a min-heap. \n- Finally, we extract the `k` smallest elements from the heap, which correspond to the `k` weakest rows.\n\n**Pros**:\n- The binary search allows for efficient computation of the strength of each row, which is particularly useful when the number of soldiers varies significantly across rows.\n- The heap data structure ensures that we can efficiently find the `k` weakest rows without sorting the entire array, thus saving computational resources.\n\n**Cons**:\n- Although the binary search optimizes the row strength calculation, the overall time complexity can still be influenced by the time it takes to build and manipulate the heap. However, this is generally more efficient than sorting the entire array.\n \n# Code #3 Binary Search + Heap Approach\n``` Python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n def binarySearch(arr):\n left, right = 0, len(arr) - 1\n while left <= right:\n mid = (left + right) // 2\n if arr[mid] == 1:\n left = mid + 1\n else:\n right = mid - 1\n return left\n\n queue = [(binarySearch(row), idx) for idx, row in enumerate(mat)]\n heapq.heapify(queue)\n\n return [idx for _, idx in heapq.nsmallest(k, queue)]\n```\n\n\n\n## Time and Space Complexity\n\n### 1. Sorting Approach:\n- **Time Complexity**: $$O(m \\log m)$$\n - Here, `m` is the number of rows. Sorting an array of length `m` will take $$O(m \\log m)$$ time.\n- **Space Complexity**: $$O(m)$$\n - We need additional space for storing the strengths and indices, which will be of length `m`.\n\n### 2. Min-Heap Approach:\n- **Time Complexity**: $$O(m \\log k)$$\n - Pushing an element into a heap of size `k` takes $$O(\\log k)$$ time. We do this `m` times, so the total time is $$O(m \\log k)$$.\n- **Space Complexity**: $$O(k)$$\n - The heap will store `k` elements at most, so the space complexity is $$O(k)$$.\n\n### 3. Binary Search and Heap Approach:\n- **Time Complexity**: $$O(m \\log n + m \\log m)$$\n - Binary search on each row to find the number of soldiers will take $$O(\\log n)$$ time for each row, resulting in $$O(m \\log n)$$ for all rows. Building and manipulating the heap will take $$O(m \\log m)$$ time.\n- **Space Complexity**: $$O(m)$$\n - We need additional space for the heap to store the strengths and indices, which will be of length `m`.\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) | Version |\n|-------------|-----------|-------------|--------------------|\n| Rust | 0 | 2.2 | Sort |\n| Java | 2 | 44.4 | Sort |\n| C++ | 8 | 11.1 | Sort |\n| Go | 11 | 4.9 | Sort |\n| PHP | 32 | 20.8 | Sort |\n| JavaScript | 57 | 43.5 | Sort |\n| Python3 | 93 | 16.8 | Sort |\n| Python3 | 93 | 16.6 | Heap |\n| Python3 | 98 | 16.8 | Binary Search |\n| C# | 133 | 46.7 | Sort |\n\n\n\n\n## Conclusion\n\nEach of the strategies presented has its own merits. Depending on the specific requirements and constraints of the application, one approach might be preferred over the others. Whether you\'re a beginner or an expert, understanding these strategies will surely enhance your problem-solving skills. Happy coding!\n\n\n\n | 78 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
Python 3 || Brute | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n hashm=[]\n for i in range(len(mat)):\n hashm.append([mat[i].count(1),i])\n hashm.sort()\n res=[]\n for i in range(k):\n res.append(hashm[i][1])\n return res\n \n``` | 2 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Python 3 || Brute | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n hashm=[]\n for i in range(len(mat)):\n hashm.append([mat[i].count(1),i])\n hashm.sort()\n res=[]\n for i in range(k):\n res.append(hashm[i][1])\n return res\n \n``` | 2 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
✅98.65%🔥Min-Heap & Sorting 🔥2 linear code🔥Py/C/C#/C++/Java | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Problem\n**The problem statement describes a binary matrix where 1\'s represent soldiers and 0\'s represent civilians. The task is to find the k weakest rows in the matrix based on the following criteria:**\n\n###### **1.** A row i is weaker than a row j if the number of soldiers in row i is less than the number of soldiers in row j.\n\n###### **2.** If both rows have the same number of soldiers, row i is weaker than row j if i < j (i.e., the row index i is smaller than j).\n\n---\n\n# Solution\n**The provided Python solution implements this by using a list comprehension to create a list of tuples. Each tuple contains two elements: the row index (i) and the count of soldiers in that row (sum(row)). Then, it sorts this list of tuples based on two criteria:**\n\n###### **1.** First, it sorts by the count of soldiers (x[1]) in ascending order.\n\n###### **2.** If two rows have the same count of soldiers, it sorts by the row index (x[0]) in ascending order.\n\n###### ***This sorting effectively arranges the rows in increasing order of weakness.***\n\n##### ***Finally, it extracts the row indices of the k weakest rows by taking the first k elements from the sorted list of tuples and returns these row indices as a list.***\n\n\n\n\n```Python3 []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n # Create a list of tuples containing row index and soldier count, then sort it\n rows_count = sorted(((i, sum(row)) for i, row in enumerate(mat)), key=lambda x: (x[1], x[0]))\n # Extract the row indices of the k weakest rows\n return [x[0] for x in rows_count[:k]]\n\n```\n```python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n # Create a list of tuples containing row index and soldier count, then sort it\n rows_count = sorted(((i, sum(row)) for i, row in enumerate(mat)), key=lambda x: (x[1], x[0]))\n # Extract the row indices of the k weakest rows\n return [x[0] for x in rows_count[:k]]\n\n```\n```C# []\npublic class Solution\n{\n public int[] KWeakestRows(int[][] mat, int k)\n {\n var rowsCount = mat\n .Select((row, index) => new { Index = index, Count = row.Count(soldier => soldier == 1) })\n .OrderBy(row => row.Count)\n .ThenBy(row => row.Index)\n .Take(k)\n .Select(row => row.Index)\n .ToArray();\n\n return rowsCount;\n }\n}\n```\n```C++ []\nstruct RowInfo {\n int index;\n int count;\n};\nbool compare(const RowInfo &a, const RowInfo &b) {\n if (a.count != b.count) {\n return a.count < b.count;\n }\n return a.index < b.index;\n}\n\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n int matSize = mat.size();\n int matColSize = mat[0].size();\n \n vector<RowInfo> rows(matSize);\n for (int i = 0; i < matSize; i++) {\n rows[i].index = i;\n rows[i].count = 0;\n for (int j = 0; j < matColSize; j++) {\n rows[i].count += mat[i][j];\n }\n }\n\n sort(rows.begin(), rows.end(), compare);\n\n vector<int> result(k);\n for (int i = 0; i < k; i++) {\n result[i] = rows[i].index;\n }\n\n return result;\n }\n};\n\n```\n```C []\nstruct RowInfo {\n int index;\n int count;\n};\n\nint compare(const void *a, const void *b) {\n struct RowInfo *rowA = (struct RowInfo *)a;\n struct RowInfo *rowB = (struct RowInfo *)b;\n if (rowA->count != rowB->count) {\n return rowA->count - rowB->count;\n }\n return rowA->index - rowB->index;\n}\n\nint* kWeakestRows(int** mat, int matSize, int* matColSize, int k, int* returnSize) {\n struct RowInfo* rows = (struct RowInfo*)malloc(matSize * sizeof(struct RowInfo));\n for (int i = 0; i < matSize; i++) {\n rows[i].index = i;\n rows[i].count = 0;\n for (int j = 0; j < *matColSize; j++) {\n rows[i].count += mat[i][j];\n }\n }\n qsort(rows, matSize, sizeof(struct RowInfo), compare);\n int* result = (int*)malloc(k * sizeof(int));\n for (int i = 0; i < k; i++) {\n result[i] = rows[i].index;\n }\n *returnSize = k;\n\n free(rows);\n return result;\n}\n\n```\n```Java []\nclass RowInfo implements Comparable<RowInfo> {\n int index;\n int count;\n\n public RowInfo(int index, int count) {\n this.index = index;\n this.count = count;\n }\n\n @Override\n public int compareTo(RowInfo other) {\n if (this.count != other.count) {\n return Integer.compare(this.count, other.count);\n }\n return Integer.compare(this.index, other.index);\n }\n}\n\nclass Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n int matSize = mat.length;\n int matColSize = mat[0].length;\n \n RowInfo[] rows = new RowInfo[matSize];\n for (int i = 0; i < matSize; i++) {\n int count = 0;\n for (int j = 0; j < matColSize; j++) {\n count += mat[i][j];\n }\n rows[i] = new RowInfo(i, count);\n }\n\n Arrays.sort(rows);\n\n int[] result = new int[k];\n for (int i = 0; i < k; i++) {\n result[i] = rows[i].index;\n }\n\n return result;\n }\n}\n\n```\n | 14 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
✅98.65%🔥Min-Heap & Sorting 🔥2 linear code🔥Py/C/C#/C++/Java | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Problem\n**The problem statement describes a binary matrix where 1\'s represent soldiers and 0\'s represent civilians. The task is to find the k weakest rows in the matrix based on the following criteria:**\n\n###### **1.** A row i is weaker than a row j if the number of soldiers in row i is less than the number of soldiers in row j.\n\n###### **2.** If both rows have the same number of soldiers, row i is weaker than row j if i < j (i.e., the row index i is smaller than j).\n\n---\n\n# Solution\n**The provided Python solution implements this by using a list comprehension to create a list of tuples. Each tuple contains two elements: the row index (i) and the count of soldiers in that row (sum(row)). Then, it sorts this list of tuples based on two criteria:**\n\n###### **1.** First, it sorts by the count of soldiers (x[1]) in ascending order.\n\n###### **2.** If two rows have the same count of soldiers, it sorts by the row index (x[0]) in ascending order.\n\n###### ***This sorting effectively arranges the rows in increasing order of weakness.***\n\n##### ***Finally, it extracts the row indices of the k weakest rows by taking the first k elements from the sorted list of tuples and returns these row indices as a list.***\n\n\n\n\n```Python3 []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n # Create a list of tuples containing row index and soldier count, then sort it\n rows_count = sorted(((i, sum(row)) for i, row in enumerate(mat)), key=lambda x: (x[1], x[0]))\n # Extract the row indices of the k weakest rows\n return [x[0] for x in rows_count[:k]]\n\n```\n```python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n # Create a list of tuples containing row index and soldier count, then sort it\n rows_count = sorted(((i, sum(row)) for i, row in enumerate(mat)), key=lambda x: (x[1], x[0]))\n # Extract the row indices of the k weakest rows\n return [x[0] for x in rows_count[:k]]\n\n```\n```C# []\npublic class Solution\n{\n public int[] KWeakestRows(int[][] mat, int k)\n {\n var rowsCount = mat\n .Select((row, index) => new { Index = index, Count = row.Count(soldier => soldier == 1) })\n .OrderBy(row => row.Count)\n .ThenBy(row => row.Index)\n .Take(k)\n .Select(row => row.Index)\n .ToArray();\n\n return rowsCount;\n }\n}\n```\n```C++ []\nstruct RowInfo {\n int index;\n int count;\n};\nbool compare(const RowInfo &a, const RowInfo &b) {\n if (a.count != b.count) {\n return a.count < b.count;\n }\n return a.index < b.index;\n}\n\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n int matSize = mat.size();\n int matColSize = mat[0].size();\n \n vector<RowInfo> rows(matSize);\n for (int i = 0; i < matSize; i++) {\n rows[i].index = i;\n rows[i].count = 0;\n for (int j = 0; j < matColSize; j++) {\n rows[i].count += mat[i][j];\n }\n }\n\n sort(rows.begin(), rows.end(), compare);\n\n vector<int> result(k);\n for (int i = 0; i < k; i++) {\n result[i] = rows[i].index;\n }\n\n return result;\n }\n};\n\n```\n```C []\nstruct RowInfo {\n int index;\n int count;\n};\n\nint compare(const void *a, const void *b) {\n struct RowInfo *rowA = (struct RowInfo *)a;\n struct RowInfo *rowB = (struct RowInfo *)b;\n if (rowA->count != rowB->count) {\n return rowA->count - rowB->count;\n }\n return rowA->index - rowB->index;\n}\n\nint* kWeakestRows(int** mat, int matSize, int* matColSize, int k, int* returnSize) {\n struct RowInfo* rows = (struct RowInfo*)malloc(matSize * sizeof(struct RowInfo));\n for (int i = 0; i < matSize; i++) {\n rows[i].index = i;\n rows[i].count = 0;\n for (int j = 0; j < *matColSize; j++) {\n rows[i].count += mat[i][j];\n }\n }\n qsort(rows, matSize, sizeof(struct RowInfo), compare);\n int* result = (int*)malloc(k * sizeof(int));\n for (int i = 0; i < k; i++) {\n result[i] = rows[i].index;\n }\n *returnSize = k;\n\n free(rows);\n return result;\n}\n\n```\n```Java []\nclass RowInfo implements Comparable<RowInfo> {\n int index;\n int count;\n\n public RowInfo(int index, int count) {\n this.index = index;\n this.count = count;\n }\n\n @Override\n public int compareTo(RowInfo other) {\n if (this.count != other.count) {\n return Integer.compare(this.count, other.count);\n }\n return Integer.compare(this.index, other.index);\n }\n}\n\nclass Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n int matSize = mat.length;\n int matColSize = mat[0].length;\n \n RowInfo[] rows = new RowInfo[matSize];\n for (int i = 0; i < matSize; i++) {\n int count = 0;\n for (int j = 0; j < matColSize; j++) {\n count += mat[i][j];\n }\n rows[i] = new RowInfo(i, count);\n }\n\n Arrays.sort(rows);\n\n int[] result = new int[k];\n for (int i = 0; i < k; i++) {\n result[i] = rows[i].index;\n }\n\n return result;\n }\n}\n\n```\n | 14 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
✔98.90% Beats C++ || Easy to understand 📈✨|| Commented Code Explanation || 3Beginner😉😎 | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Intuition\n- The code is designed to find the k weakest rows in a binary matrix. A "weakest" row is determined by the number of ones it contains. \n- The code calculates the number of ones in each row, then uses a set to store pairs of (count of ones, row index). \n- Finally, it extracts the k weakest rows from the set and returns them as a vector.\n\n# Approach\n1. Initialize a set s to store pairs of (count of ones in a row, row index).\n1. Iterate through each row of the matrix mat:\n - Count the number of ones in the current row and store it in the count variable.\n - Insert a pair of (count, row index) into the set s.\n1. Initialize an empty vector v to store the k weakest row indices.\n1. Iterate through the set s to extract the k weakest rows:\n - Push the row index (second element of the pair) into the vector v.\n1. Return the vector v containing the k weakest row indices.\n\n# Complexity\n- Time complexity:\n - O(m * n)\n\n **Explanation**\n1. The outer loop iterates through each row of the matrix, which takes `O(m)` time, where m is the number of rows.\n1. The inner loop iterates through each element in a row, which takes O(n) time on average, where n is the number of columns.\n1. Since we are iterating through all elements of the matrix, the overall time complexity for counting ones is` O(m * n)`.\n1. Inserting pairs into the set takes O(log k) time, and we do this for all m rows, so it\'s `O(m * log k)`.\n1. Extracting the k weakest rows from the set takes O(k * log k) time.\n1. Therefore, the total time complexity is O(m * n + m * log k + k * log k), and the most `significant term is O(m * n)`.\n\n- Space complexity:\n **O(m)**\n\n**Explanation**\n- The set s stores pairs for each row, so it can have a maximum of m elements.\n- The vector v stores the k weakest row indices.\n1. `The space complexity is O(m + k)`, but as k is usually much smaller than m, the dominant term `is O(m)`.\n**In summary, the code efficiently finds the k weakest rows in a binary matrix with a time complexity of O(m * n) and a space complexity of O(m).**\n\n# PLEASE UPVOTE\u2728\uD83D\uDE0D\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n // Create a set to store pairs of (count of ones in a row, row index)\n set<pair<int,int>>s;\n\n // Iterate through each row of the matrix\n for(int i=0;i<mat.size();i++) {\n int count=0;\n \n // Count the number of ones in the current row\n for(int j=0;j<mat[i].size();j++) {\n if(mat[i][j]==1) {\n count++;\n }\n }\n \n // Insert a pair of count and row index into the set\n s.insert({count,i});\n }\n\n // Create a vector to store the k weakest row indices\n vector<int>v;\n\n // Iterate through the set to extract the k weakest rows\n for(auto x=begin(s);k>0;k--,x++) {\n v.push_back(x->second);\n }\n\n // Return the vector containing the k weakest row indices\n return v;\n }\n};\n\n```\n# JAVA\n```\nimport java.util.*;\n\nclass Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n // Create a list to store pairs of (count of ones in a row, row index)\n List<Pair<Integer, Integer>> list = new ArrayList<>();\n\n // Iterate through each row of the matrix\n for (int i = 0; i < mat.length; i++) {\n int count = 0;\n\n // Count the number of ones in the current row\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1) {\n count++;\n }\n }\n\n // Add a pair of count and row index to the list\n list.add(new Pair<>(count, i));\n }\n\n // Sort the list based on the count of ones\n Collections.sort(list, (a, b) -> a.getKey() - b.getKey());\n\n // Create an array to store the k weakest row indices\n int[] result = new int[k];\n\n // Iterate through the sorted list to extract the k weakest rows\n for (int i = 0; i < k; i++) {\n result[i] = list.get(i).getValue();\n }\n\n // Return the array containing the k weakest row indices\n return result;\n }\n}\n\n```\n# PYTHON\n```\nclass Solution:\n def kWeakestRows(self, mat, k):\n # Create a list to store tuples of (count of ones in a row, row index)\n s = []\n\n # Iterate through each row of the matrix\n for i in range(len(mat)):\n count = 0\n\n # Count the number of ones in the current row\n for j in range(len(mat[i])):\n if mat[i][j] == 1:\n count += 1\n\n # Append a tuple of count and row index to the list\n s.append((count, i))\n\n # Sort the list based on the count of ones\n s.sort()\n\n # Create a list to store the k weakest row indices\n v = []\n\n # Iterate through the sorted list to extract the k weakest rows\n for x in s[:k]:\n v.append(x[1])\n\n # Return the list containing the k weakest row indices\n return v\n\n```\n# JAVASCRIPT\n```\nclass Solution {\n kWeakestRows(mat, k) {\n // Create a set to store pairs of (count of ones in a row, row index)\n let s = new Set();\n\n // Iterate through each row of the matrix\n for (let i = 0; i < mat.length; i++) {\n let count = 0;\n\n // Count the number of ones in the current row\n for (let j = 0; j < mat[i].length; j++) {\n if (mat[i][j] === 1) {\n count++;\n }\n }\n\n // Insert a pair of count and row index into the set\n s.add([count, i]);\n }\n\n // Create an array to store the k weakest row indices\n let v = [];\n\n // Convert the set to an array and sort it based on the count of ones\n let sortedArray = Array.from(s);\n sortedArray.sort((a, b) => a[0] - b[0]);\n\n // Iterate through the sorted array to extract the k weakest rows\n for (let i = 0; i < k; i++) {\n v.push(sortedArray[i][1]);\n }\n\n // Return the array containing the k weakest row indices\n return v;\n }\n}\n\n```\n# PLEASE UPVOTE\u2728\uD83D\uDE0D | 11 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
✔98.90% Beats C++ || Easy to understand 📈✨|| Commented Code Explanation || 3Beginner😉😎 | the-k-weakest-rows-in-a-matrix | 1 | 1 | # Intuition\n- The code is designed to find the k weakest rows in a binary matrix. A "weakest" row is determined by the number of ones it contains. \n- The code calculates the number of ones in each row, then uses a set to store pairs of (count of ones, row index). \n- Finally, it extracts the k weakest rows from the set and returns them as a vector.\n\n# Approach\n1. Initialize a set s to store pairs of (count of ones in a row, row index).\n1. Iterate through each row of the matrix mat:\n - Count the number of ones in the current row and store it in the count variable.\n - Insert a pair of (count, row index) into the set s.\n1. Initialize an empty vector v to store the k weakest row indices.\n1. Iterate through the set s to extract the k weakest rows:\n - Push the row index (second element of the pair) into the vector v.\n1. Return the vector v containing the k weakest row indices.\n\n# Complexity\n- Time complexity:\n - O(m * n)\n\n **Explanation**\n1. The outer loop iterates through each row of the matrix, which takes `O(m)` time, where m is the number of rows.\n1. The inner loop iterates through each element in a row, which takes O(n) time on average, where n is the number of columns.\n1. Since we are iterating through all elements of the matrix, the overall time complexity for counting ones is` O(m * n)`.\n1. Inserting pairs into the set takes O(log k) time, and we do this for all m rows, so it\'s `O(m * log k)`.\n1. Extracting the k weakest rows from the set takes O(k * log k) time.\n1. Therefore, the total time complexity is O(m * n + m * log k + k * log k), and the most `significant term is O(m * n)`.\n\n- Space complexity:\n **O(m)**\n\n**Explanation**\n- The set s stores pairs for each row, so it can have a maximum of m elements.\n- The vector v stores the k weakest row indices.\n1. `The space complexity is O(m + k)`, but as k is usually much smaller than m, the dominant term `is O(m)`.\n**In summary, the code efficiently finds the k weakest rows in a binary matrix with a time complexity of O(m * n) and a space complexity of O(m).**\n\n# PLEASE UPVOTE\u2728\uD83D\uDE0D\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {\n // Create a set to store pairs of (count of ones in a row, row index)\n set<pair<int,int>>s;\n\n // Iterate through each row of the matrix\n for(int i=0;i<mat.size();i++) {\n int count=0;\n \n // Count the number of ones in the current row\n for(int j=0;j<mat[i].size();j++) {\n if(mat[i][j]==1) {\n count++;\n }\n }\n \n // Insert a pair of count and row index into the set\n s.insert({count,i});\n }\n\n // Create a vector to store the k weakest row indices\n vector<int>v;\n\n // Iterate through the set to extract the k weakest rows\n for(auto x=begin(s);k>0;k--,x++) {\n v.push_back(x->second);\n }\n\n // Return the vector containing the k weakest row indices\n return v;\n }\n};\n\n```\n# JAVA\n```\nimport java.util.*;\n\nclass Solution {\n public int[] kWeakestRows(int[][] mat, int k) {\n // Create a list to store pairs of (count of ones in a row, row index)\n List<Pair<Integer, Integer>> list = new ArrayList<>();\n\n // Iterate through each row of the matrix\n for (int i = 0; i < mat.length; i++) {\n int count = 0;\n\n // Count the number of ones in the current row\n for (int j = 0; j < mat[i].length; j++) {\n if (mat[i][j] == 1) {\n count++;\n }\n }\n\n // Add a pair of count and row index to the list\n list.add(new Pair<>(count, i));\n }\n\n // Sort the list based on the count of ones\n Collections.sort(list, (a, b) -> a.getKey() - b.getKey());\n\n // Create an array to store the k weakest row indices\n int[] result = new int[k];\n\n // Iterate through the sorted list to extract the k weakest rows\n for (int i = 0; i < k; i++) {\n result[i] = list.get(i).getValue();\n }\n\n // Return the array containing the k weakest row indices\n return result;\n }\n}\n\n```\n# PYTHON\n```\nclass Solution:\n def kWeakestRows(self, mat, k):\n # Create a list to store tuples of (count of ones in a row, row index)\n s = []\n\n # Iterate through each row of the matrix\n for i in range(len(mat)):\n count = 0\n\n # Count the number of ones in the current row\n for j in range(len(mat[i])):\n if mat[i][j] == 1:\n count += 1\n\n # Append a tuple of count and row index to the list\n s.append((count, i))\n\n # Sort the list based on the count of ones\n s.sort()\n\n # Create a list to store the k weakest row indices\n v = []\n\n # Iterate through the sorted list to extract the k weakest rows\n for x in s[:k]:\n v.append(x[1])\n\n # Return the list containing the k weakest row indices\n return v\n\n```\n# JAVASCRIPT\n```\nclass Solution {\n kWeakestRows(mat, k) {\n // Create a set to store pairs of (count of ones in a row, row index)\n let s = new Set();\n\n // Iterate through each row of the matrix\n for (let i = 0; i < mat.length; i++) {\n let count = 0;\n\n // Count the number of ones in the current row\n for (let j = 0; j < mat[i].length; j++) {\n if (mat[i][j] === 1) {\n count++;\n }\n }\n\n // Insert a pair of count and row index into the set\n s.add([count, i]);\n }\n\n // Create an array to store the k weakest row indices\n let v = [];\n\n // Convert the set to an array and sort it based on the count of ones\n let sortedArray = Array.from(s);\n sortedArray.sort((a, b) => a[0] - b[0]);\n\n // Iterate through the sorted array to extract the k weakest rows\n for (let i = 0; i < k; i++) {\n v.push(sortedArray[i][1]);\n }\n\n // Return the array containing the k weakest row indices\n return v;\n }\n}\n\n```\n# PLEASE UPVOTE\u2728\uD83D\uDE0D | 11 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
🔥🔥 Python 3 | Beats 91.08% Runtime and 70.8% Memory | Min Heap Solution 🔥🔥 | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(nlogn) Time\n\n- Space complexity:\nO(n) Memory\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n\n arr = []\n for i in range(len(mat)):\n heapq.heappush(arr, (sum(mat[i]), i))\n\n ret = []\n while k > 0:\n node, i = heapq.heappop(arr)\n ret.append(i)\n k -= 1\n\n return ret\n\n\n\n\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
🔥🔥 Python 3 | Beats 91.08% Runtime and 70.8% Memory | Min Heap Solution 🔥🔥 | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(nlogn) Time\n\n- Space complexity:\nO(n) Memory\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n\n arr = []\n for i in range(len(mat)):\n heapq.heappush(arr, (sum(mat[i]), i))\n\n ret = []\n while k > 0:\n node, i = heapq.heappop(arr)\n ret.append(i)\n k -= 1\n\n return ret\n\n\n\n\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
One row Solution Python | the-k-weakest-rows-in-a-matrix | 0 | 1 | \n# Complexity\n- Time complexity: $$O(n log (n))$$\n\n# Code\n```python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n return [\n x[0] for x in sorted(enumerate(map(sum, mat)), key=lambda x: x[::-1])\n ][:k]\n\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
One row Solution Python | the-k-weakest-rows-in-a-matrix | 0 | 1 | \n# Complexity\n- Time complexity: $$O(n log (n))$$\n\n# Code\n```python []\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n return [\n x[0] for x in sorted(enumerate(map(sum, mat)), key=lambda x: x[::-1])\n ][:k]\n\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
Python 1-liners. 2 solutions. Functional programming. | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Approach 1: Sum and Sort\n1. Find the `soldiers` for each row `x` by summing over `mat[x]`.\n\n2. Sort the `soldiers` for each index from `0` to `m` and return the first `k` indices.\n\n# Complexity\n- Time complexity: $$O(m \\cdot n + m \\cdot log_2(m))$$\n\n- Space complexity: $$O(m)$$\n\nwhere,\n`m x n is the dimensions of mat`,\n`k is as number of weakest rows to be found`.\n\n# Code\n```python\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], k: int) -> list[int]:\n return sorted(range(len(mat)), key=lambda x: sum(mat[x]))[:k]\n \n```\n\n---\n# Approach 2: BinarySearch and Heap\n1. While finding `soldiers` for each row `x`, the $$O(n)$$ summation can be replaced by $$O(log_2(n))$$ BinarySearch over `mat[x]`.\n\n2. The $$O(m \\cdot log_2(m))$$ operation of sorting the `soldiers` for each index can be replaced by $$O(k \\cdot log_2(m))$$ operation of using heap to find the `k` smallest indexed `soldiers`.\n\n# Complexity\n- Time complexity: $$O(m \\cdot log_2(n) + k \\cdot log_2(m))$$\n\n- Space complexity: $$O(m)$$\n\nwhere,\n`m x n is the dimensions of mat`,\n`k is as number of weakest rows to be found`.\n\n# Code\nMultiliner:\n```python\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], k: int) -> list[int]:\n soldiers = tuple(bisect_right(row, -1, key=neg) for row in mat)\n return heapq.nsmallest(k, range(len(mat)), key=soldiers.__getitem__)\n\n\n```\n\nSame as 1-liner:\n```python\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], k: int) -> list[int]:\n return nsmallest(k, range(len(mat)),\n key=tuple(bisect_right(row, -1, key=neg) for row in mat).__getitem__,\n )\n\n\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Python 1-liners. 2 solutions. Functional programming. | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Approach 1: Sum and Sort\n1. Find the `soldiers` for each row `x` by summing over `mat[x]`.\n\n2. Sort the `soldiers` for each index from `0` to `m` and return the first `k` indices.\n\n# Complexity\n- Time complexity: $$O(m \\cdot n + m \\cdot log_2(m))$$\n\n- Space complexity: $$O(m)$$\n\nwhere,\n`m x n is the dimensions of mat`,\n`k is as number of weakest rows to be found`.\n\n# Code\n```python\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], k: int) -> list[int]:\n return sorted(range(len(mat)), key=lambda x: sum(mat[x]))[:k]\n \n```\n\n---\n# Approach 2: BinarySearch and Heap\n1. While finding `soldiers` for each row `x`, the $$O(n)$$ summation can be replaced by $$O(log_2(n))$$ BinarySearch over `mat[x]`.\n\n2. The $$O(m \\cdot log_2(m))$$ operation of sorting the `soldiers` for each index can be replaced by $$O(k \\cdot log_2(m))$$ operation of using heap to find the `k` smallest indexed `soldiers`.\n\n# Complexity\n- Time complexity: $$O(m \\cdot log_2(n) + k \\cdot log_2(m))$$\n\n- Space complexity: $$O(m)$$\n\nwhere,\n`m x n is the dimensions of mat`,\n`k is as number of weakest rows to be found`.\n\n# Code\nMultiliner:\n```python\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], k: int) -> list[int]:\n soldiers = tuple(bisect_right(row, -1, key=neg) for row in mat)\n return heapq.nsmallest(k, range(len(mat)), key=soldiers.__getitem__)\n\n\n```\n\nSame as 1-liner:\n```python\nclass Solution:\n def kWeakestRows(self, mat: list[list[int]], k: int) -> list[int]:\n return nsmallest(k, range(len(mat)),\n key=tuple(bisect_right(row, -1, key=neg) for row in mat).__getitem__,\n )\n\n\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
Python3 oneline 95% | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n return sorted(range(len(mat)), key = lambda x: sum(mat[x]))[:k]\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Python3 oneline 95% | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n return sorted(range(len(mat)), key = lambda x: sum(mat[x]))[:k]\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
[Python3] Easy to understand | Modified bucket sort approach | Linear Time | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(m x n)\n\n- Space complexity:\nO( max(m, n) )\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n counts = collections.defaultdict(int)\n\n # Create a hashmap with { rowIdx : soldier count }\n for row in range(len(mat)):\n soldierCount = 0\n for col in range(len(mat[0])):\n if mat[row][col] == 1:\n soldierCount += 1\n counts[row] = soldierCount\n \n # Create an arar of arrays\n # Each index here will act as soldier count. \n # As value we will add the rowIdx\n buckets = [ [] for __ in range(len(mat[0]) + 1) ]\n for key, val in counts.items():\n buckets[val].append(key)\n \n res = []\n\n for bucket in buckets:\n for val in bucket:\n if k == 0:\n break\n res.append(val)\n k -= 1\n\n return res\n\n\n\n\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
[Python3] Easy to understand | Modified bucket sort approach | Linear Time | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(m x n)\n\n- Space complexity:\nO( max(m, n) )\n\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n counts = collections.defaultdict(int)\n\n # Create a hashmap with { rowIdx : soldier count }\n for row in range(len(mat)):\n soldierCount = 0\n for col in range(len(mat[0])):\n if mat[row][col] == 1:\n soldierCount += 1\n counts[row] = soldierCount\n \n # Create an arar of arrays\n # Each index here will act as soldier count. \n # As value we will add the rowIdx\n buckets = [ [] for __ in range(len(mat[0]) + 1) ]\n for key, val in counts.items():\n buckets[val].append(key)\n \n res = []\n\n for bucket in buckets:\n for val in bucket:\n if k == 0:\n break\n res.append(val)\n k -= 1\n\n return res\n\n\n\n\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
Python3 Solution | the-k-weakest-rows-in-a-matrix | 0 | 1 | \n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n ans=[]\n n=len(mat)\n for i in range(n):\n ans.append([mat[i].count(1),i])\n\n ans.sort() \n return [i[1] for i in ans[:k]]\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Python3 Solution | the-k-weakest-rows-in-a-matrix | 0 | 1 | \n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n ans=[]\n n=len(mat)\n for i in range(n):\n ans.append([mat[i].count(1),i])\n\n ans.sort() \n return [i[1] for i in ans[:k]]\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
Simple Python Solution || Beats 99.07%📶 || HashMap✅ | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\nBuilding a **hash table** for number of ones in each row.\n\n# Approach\n1. Decalre a Hash Table with key as row index and value of each key as no of ones in each row.\n\n2. Sorting the hash table with key as values.\n\n3. Returning the top k elements from the sorted list.\n# Complexity\n- Time complexity:\n$$O(n*logn)$$\n\n- Space complexity:\n$$O(n)$$\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n d={}\n k1=0\n for i in mat:\n d[k1]=sum(i)\n k1+=1\n return list(sorted(d,key=lambda x:d[x]))[:k]\n``` | 1 | You are given an `m x n` binary matrix `mat` of `1`'s (representing soldiers) and `0`'s (representing civilians). The soldiers are positioned **in front** of the civilians. That is, all the `1`'s will appear to the **left** of all the `0`'s in each row.
A row `i` is **weaker** than a row `j` if one of the following is true:
* The number of soldiers in row `i` is less than the number of soldiers in row `j`.
* Both rows have the same number of soldiers and `i < j`.
Return _the indices of the_ `k` _**weakest** rows in the matrix ordered from weakest to strongest_.
**Example 1:**
**Input:** mat =
\[\[1,1,0,0,0\],
\[1,1,1,1,0\],
\[1,0,0,0,0\],
\[1,1,0,0,0\],
\[1,1,1,1,1\]\],
k = 3
**Output:** \[2,0,3\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 2
- Row 1: 4
- Row 2: 1
- Row 3: 2
- Row 4: 5
The rows ordered from weakest to strongest are \[2,0,3,1,4\].
**Example 2:**
**Input:** mat =
\[\[1,0,0,0\],
\[1,1,1,1\],
\[1,0,0,0\],
\[1,0,0,0\]\],
k = 2
**Output:** \[0,2\]
**Explanation:**
The number of soldiers in each row is:
- Row 0: 1
- Row 1: 4
- Row 2: 1
- Row 3: 1
The rows ordered from weakest to strongest are \[0,2,3,1\].
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `2 <= n, m <= 100`
* `1 <= k <= m`
* `matrix[i][j]` is either 0 or 1. | null |
Simple Python Solution || Beats 99.07%📶 || HashMap✅ | the-k-weakest-rows-in-a-matrix | 0 | 1 | # Intuition\nBuilding a **hash table** for number of ones in each row.\n\n# Approach\n1. Decalre a Hash Table with key as row index and value of each key as no of ones in each row.\n\n2. Sorting the hash table with key as values.\n\n3. Returning the top k elements from the sorted list.\n# Complexity\n- Time complexity:\n$$O(n*logn)$$\n\n- Space complexity:\n$$O(n)$$\n# Code\n```\nclass Solution:\n def kWeakestRows(self, mat: List[List[int]], k: int) -> List[int]:\n d={}\n k1=0\n for i in mat:\n d[k1]=sum(i)\n k1+=1\n return list(sorted(d,key=lambda x:d[x]))[:k]\n``` | 1 | You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
**Input:** grid = \[\[3,1,1\],\[2,5,1\],\[1,5,5\],\[2,1,1\]\]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
**Input:** grid = \[\[1,0,0,0,0,0,1\],\[2,0,0,0,0,3,0\],\[2,0,9,0,0,0,0\],\[0,3,0,5,4,0,0\],\[1,0,2,3,0,0,6\]\]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100` | Sort the matrix row indexes by the number of soldiers and then row indexes. |
👾C#, Java, Python3,JavaScript Solution | reduce-array-size-to-the-half | 1 | 1 | See all the code :**\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/)\u2B50**\n\nExample :\n\n**C# Solution - Dictionary + Linq (Sort by dict value)**\n```\n\t\t//0. half number\n int mid = arr.Length/2;\n \n //1. init dict\n Dictionary<int,int> dict = new Dictionary<int,int>();\n \n foreach(var i in arr)\n {\n if (!dict.ContainsKey(i))\n {\n dict.Add(i, 1);\n }\n else\n {\n dict[i] = dict[i]+1;\n }\n }\n \n //2. check > order by dict value(count)\n var sortedDict = from entry in dict orderby entry.Value descending select entry.Value;\n \n int res = 0;\n foreach(var s in sortedDict)\n {\n if (s>mid)\n { \n return res == 0 ? 1 : res+1;\n }\n else if (s<mid)\n {\n mid -= s;\n res +=1;\n }\n else //s == mid\n {\n return res+1;\n }\n }\n \n return res;\n```\n\nCount each integers first and store in dictionary, than sort it by value.\n\n\n**If you got any problem about the explanation or you need other programming language solution, please feel free to let me know (leave comment or messenger me).**\n\nThanks!\n\n**\uD83E\uDDE1See more LeetCode solution : [Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)** | 3 | You are given an integer array `arr`. You can choose a set of integers and remove all the occurrences of these integers in the array.
Return _the minimum size of the set so that **at least** half of the integers of the array are removed_.
**Example 1:**
**Input:** arr = \[3,3,3,3,5,5,5,2,2,7\]
**Output:** 2
**Explanation:** Choosing {3,7} will make the new array \[5,5,5,2,2\] which has size 5 (i.e equal to half of the size of the old array).
Possible sets of size 2 are {3,5},{3,2},{5,2}.
Choosing set {2,7} is not possible as it will make the new array \[3,3,3,3,5,5,5\] which has a size greater than half of the size of the old array.
**Example 2:**
**Input:** arr = \[7,7,7,7,7,7\]
**Output:** 1
**Explanation:** The only possible set you can choose is {7}. This will make the new array empty.
**Constraints:**
* `2 <= arr.length <= 105`
* `arr.length` is even.
* `1 <= arr[i] <= 105` | null |
👾C#, Java, Python3,JavaScript Solution | reduce-array-size-to-the-half | 1 | 1 | See all the code :**\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/)\u2B50**\n\nExample :\n\n**C# Solution - Dictionary + Linq (Sort by dict value)**\n```\n\t\t//0. half number\n int mid = arr.Length/2;\n \n //1. init dict\n Dictionary<int,int> dict = new Dictionary<int,int>();\n \n foreach(var i in arr)\n {\n if (!dict.ContainsKey(i))\n {\n dict.Add(i, 1);\n }\n else\n {\n dict[i] = dict[i]+1;\n }\n }\n \n //2. check > order by dict value(count)\n var sortedDict = from entry in dict orderby entry.Value descending select entry.Value;\n \n int res = 0;\n foreach(var s in sortedDict)\n {\n if (s>mid)\n { \n return res == 0 ? 1 : res+1;\n }\n else if (s<mid)\n {\n mid -= s;\n res +=1;\n }\n else //s == mid\n {\n return res+1;\n }\n }\n \n return res;\n```\n\nCount each integers first and store in dictionary, than sort it by value.\n\n\n**If you got any problem about the explanation or you need other programming language solution, please feel free to let me know (leave comment or messenger me).**\n\nThanks!\n\n**\uD83E\uDDE1See more LeetCode solution : [Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)** | 3 | Given the array of integers `nums`, you will choose two different indices `i` and `j` of that array. _Return the maximum value of_ `(nums[i]-1)*(nums[j]-1)`.
**Example 1:**
**Input:** nums = \[3,4,5,2\]
**Output:** 12
**Explanation:** If you choose the indices i=1 and j=2 (indexed from 0), you will get the maximum value, that is, (nums\[1\]-1)\*(nums\[2\]-1) = (4-1)\*(5-1) = 3\*4 = 12.
**Example 2:**
**Input:** nums = \[1,5,4,5\]
**Output:** 16
**Explanation:** Choosing the indices i=1 and j=3 (indexed from 0), you will get the maximum value of (5-1)\*(5-1) = 16.
**Example 3:**
**Input:** nums = \[3,7\]
**Output:** 12
**Constraints:**
* `2 <= nums.length <= 500`
* `1 <= nums[i] <= 10^3` | Count the frequency of each integer in the array. Start with an empty set, add to the set the integer with the maximum frequency. Keep Adding the integer with the max frequency until you remove at least half of the integers. |
Python Easy Solution | reduce-array-size-to-the-half | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSetSize(self, arr: List[int]) -> int:\n counts = Counter(arr)\n selected = set()\n\n sorted_counts = sorted(counts.items(), key=lambda x: x[1], reverse=True)\n removed_count = 0\n\n for num, freq in sorted_counts:\n selected.add(num)\n\n removed_count += freq\n if removed_count >= len(arr) // 2:\n break\n\n return len(selected)\n``` | 3 | You are given an integer array `arr`. You can choose a set of integers and remove all the occurrences of these integers in the array.
Return _the minimum size of the set so that **at least** half of the integers of the array are removed_.
**Example 1:**
**Input:** arr = \[3,3,3,3,5,5,5,2,2,7\]
**Output:** 2
**Explanation:** Choosing {3,7} will make the new array \[5,5,5,2,2\] which has size 5 (i.e equal to half of the size of the old array).
Possible sets of size 2 are {3,5},{3,2},{5,2}.
Choosing set {2,7} is not possible as it will make the new array \[3,3,3,3,5,5,5\] which has a size greater than half of the size of the old array.
**Example 2:**
**Input:** arr = \[7,7,7,7,7,7\]
**Output:** 1
**Explanation:** The only possible set you can choose is {7}. This will make the new array empty.
**Constraints:**
* `2 <= arr.length <= 105`
* `arr.length` is even.
* `1 <= arr[i] <= 105` | null |
Python Easy Solution | reduce-array-size-to-the-half | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSetSize(self, arr: List[int]) -> int:\n counts = Counter(arr)\n selected = set()\n\n sorted_counts = sorted(counts.items(), key=lambda x: x[1], reverse=True)\n removed_count = 0\n\n for num, freq in sorted_counts:\n selected.add(num)\n\n removed_count += freq\n if removed_count >= len(arr) // 2:\n break\n\n return len(selected)\n``` | 3 | Given the array of integers `nums`, you will choose two different indices `i` and `j` of that array. _Return the maximum value of_ `(nums[i]-1)*(nums[j]-1)`.
**Example 1:**
**Input:** nums = \[3,4,5,2\]
**Output:** 12
**Explanation:** If you choose the indices i=1 and j=2 (indexed from 0), you will get the maximum value, that is, (nums\[1\]-1)\*(nums\[2\]-1) = (4-1)\*(5-1) = 3\*4 = 12.
**Example 2:**
**Input:** nums = \[1,5,4,5\]
**Output:** 16
**Explanation:** Choosing the indices i=1 and j=3 (indexed from 0), you will get the maximum value of (5-1)\*(5-1) = 16.
**Example 3:**
**Input:** nums = \[3,7\]
**Output:** 12
**Constraints:**
* `2 <= nums.length <= 500`
* `1 <= nums[i] <= 10^3` | Count the frequency of each integer in the array. Start with an empty set, add to the set the integer with the maximum frequency. Keep Adding the integer with the max frequency until you remove at least half of the integers. |
[Python] - Hashmap and Heap - O(N) but optimal | reduce-array-size-to-the-half | 0 | 1 | My thought process regarding the solution was the following:\n\n1) We need some informations about the count of numbers \n2) We need to somehow sort the count of number as we need to subtract numbers with the highest count first to reach an optimal solution\n3) We might not need all of the counts, in the best case just the upper x -> heap!\n\nThe solution should be faster on average, as the cost of heappop is log(K). K beeing the amount of unique numbers in the array (keys of counter). In the worst Case we would then have K* log(K) complexity from the loop. But K beeing a maximum of N (N the length of the array), we are already bound by the O(N) complexity of making the counter.\n\nIn the best case we only have M* log(K), where M < K < N.\nSorting all the keys without using the heap would result into K* log(K) all the time. We have a change that M (the result of the exercise) is smaller than K.\n\n```\nfrom heapq import heapify, heappop\n\nclass Solution:\n def minSetSize(self, arr: List[int]) -> int:\n \n # count the amount of occurences\n cn = Counter(arr)\n \n # heapify the counter (minus for maxheap)\n cn = [-value for value in cn.values()]\n heapify(cn)\n \n # get the amount of numbers we need to forget\n amount = len(arr)//2 + len(arr) % 2\n counter = 0\n while amount > 0:\n amount += heappop(cn)\n counter += 1\n return counter\n``` | 2 | You are given an integer array `arr`. You can choose a set of integers and remove all the occurrences of these integers in the array.
Return _the minimum size of the set so that **at least** half of the integers of the array are removed_.
**Example 1:**
**Input:** arr = \[3,3,3,3,5,5,5,2,2,7\]
**Output:** 2
**Explanation:** Choosing {3,7} will make the new array \[5,5,5,2,2\] which has size 5 (i.e equal to half of the size of the old array).
Possible sets of size 2 are {3,5},{3,2},{5,2}.
Choosing set {2,7} is not possible as it will make the new array \[3,3,3,3,5,5,5\] which has a size greater than half of the size of the old array.
**Example 2:**
**Input:** arr = \[7,7,7,7,7,7\]
**Output:** 1
**Explanation:** The only possible set you can choose is {7}. This will make the new array empty.
**Constraints:**
* `2 <= arr.length <= 105`
* `arr.length` is even.
* `1 <= arr[i] <= 105` | null |
[Python] - Hashmap and Heap - O(N) but optimal | reduce-array-size-to-the-half | 0 | 1 | My thought process regarding the solution was the following:\n\n1) We need some informations about the count of numbers \n2) We need to somehow sort the count of number as we need to subtract numbers with the highest count first to reach an optimal solution\n3) We might not need all of the counts, in the best case just the upper x -> heap!\n\nThe solution should be faster on average, as the cost of heappop is log(K). K beeing the amount of unique numbers in the array (keys of counter). In the worst Case we would then have K* log(K) complexity from the loop. But K beeing a maximum of N (N the length of the array), we are already bound by the O(N) complexity of making the counter.\n\nIn the best case we only have M* log(K), where M < K < N.\nSorting all the keys without using the heap would result into K* log(K) all the time. We have a change that M (the result of the exercise) is smaller than K.\n\n```\nfrom heapq import heapify, heappop\n\nclass Solution:\n def minSetSize(self, arr: List[int]) -> int:\n \n # count the amount of occurences\n cn = Counter(arr)\n \n # heapify the counter (minus for maxheap)\n cn = [-value for value in cn.values()]\n heapify(cn)\n \n # get the amount of numbers we need to forget\n amount = len(arr)//2 + len(arr) % 2\n counter = 0\n while amount > 0:\n amount += heappop(cn)\n counter += 1\n return counter\n``` | 2 | Given the array of integers `nums`, you will choose two different indices `i` and `j` of that array. _Return the maximum value of_ `(nums[i]-1)*(nums[j]-1)`.
**Example 1:**
**Input:** nums = \[3,4,5,2\]
**Output:** 12
**Explanation:** If you choose the indices i=1 and j=2 (indexed from 0), you will get the maximum value, that is, (nums\[1\]-1)\*(nums\[2\]-1) = (4-1)\*(5-1) = 3\*4 = 12.
**Example 2:**
**Input:** nums = \[1,5,4,5\]
**Output:** 16
**Explanation:** Choosing the indices i=1 and j=3 (indexed from 0), you will get the maximum value of (5-1)\*(5-1) = 16.
**Example 3:**
**Input:** nums = \[3,7\]
**Output:** 12
**Constraints:**
* `2 <= nums.length <= 500`
* `1 <= nums[i] <= 10^3` | Count the frequency of each integer in the array. Start with an empty set, add to the set the integer with the maximum frequency. Keep Adding the integer with the max frequency until you remove at least half of the integers. |
👾C#, Java, Python3,JavaScript Solution | reduce-array-size-to-the-half | 1 | 1 | See all the code :**\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/)\u2B50**\n\nExample :\n\n**C# Solution - Dictionary + Linq (Sort by dict value)**\n```\n\t\t//0. half number\n int mid = arr.Length/2;\n \n //1. init dict\n Dictionary<int,int> dict = new Dictionary<int,int>();\n \n foreach(var i in arr)\n {\n if (!dict.ContainsKey(i))\n {\n dict.Add(i, 1);\n }\n else\n {\n dict[i] = dict[i]+1;\n }\n }\n \n //2. check > order by dict value(count)\n var sortedDict = from entry in dict orderby entry.Value descending select entry.Value;\n \n int res = 0;\n foreach(var s in sortedDict)\n {\n if (s>mid)\n { \n return res == 0 ? 1 : res+1;\n }\n else if (s<mid)\n {\n mid -= s;\n res +=1;\n }\n else //s == mid\n {\n return res+1;\n }\n }\n \n return res;\n```\n\nCount each integers first and store in dictionary, than sort it by value.\n\n\n**If you got any problem about the explanation or you need other programming language solution, please feel free to let me know (leave comment or messenger me).**\n\nThanks!\n\n**\uD83E\uDDE1See more LeetCode solution : [Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)** | 2 | You are given an integer array `arr`. You can choose a set of integers and remove all the occurrences of these integers in the array.
Return _the minimum size of the set so that **at least** half of the integers of the array are removed_.
**Example 1:**
**Input:** arr = \[3,3,3,3,5,5,5,2,2,7\]
**Output:** 2
**Explanation:** Choosing {3,7} will make the new array \[5,5,5,2,2\] which has size 5 (i.e equal to half of the size of the old array).
Possible sets of size 2 are {3,5},{3,2},{5,2}.
Choosing set {2,7} is not possible as it will make the new array \[3,3,3,3,5,5,5\] which has a size greater than half of the size of the old array.
**Example 2:**
**Input:** arr = \[7,7,7,7,7,7\]
**Output:** 1
**Explanation:** The only possible set you can choose is {7}. This will make the new array empty.
**Constraints:**
* `2 <= arr.length <= 105`
* `arr.length` is even.
* `1 <= arr[i] <= 105` | null |
👾C#, Java, Python3,JavaScript Solution | reduce-array-size-to-the-half | 1 | 1 | See all the code :**\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-1338-reduce-array-size-to-the-half-solution-and-explanation-en/)\u2B50**\n\nExample :\n\n**C# Solution - Dictionary + Linq (Sort by dict value)**\n```\n\t\t//0. half number\n int mid = arr.Length/2;\n \n //1. init dict\n Dictionary<int,int> dict = new Dictionary<int,int>();\n \n foreach(var i in arr)\n {\n if (!dict.ContainsKey(i))\n {\n dict.Add(i, 1);\n }\n else\n {\n dict[i] = dict[i]+1;\n }\n }\n \n //2. check > order by dict value(count)\n var sortedDict = from entry in dict orderby entry.Value descending select entry.Value;\n \n int res = 0;\n foreach(var s in sortedDict)\n {\n if (s>mid)\n { \n return res == 0 ? 1 : res+1;\n }\n else if (s<mid)\n {\n mid -= s;\n res +=1;\n }\n else //s == mid\n {\n return res+1;\n }\n }\n \n return res;\n```\n\nCount each integers first and store in dictionary, than sort it by value.\n\n\n**If you got any problem about the explanation or you need other programming language solution, please feel free to let me know (leave comment or messenger me).**\n\nThanks!\n\n**\uD83E\uDDE1See more LeetCode solution : [Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)** | 2 | Given the array of integers `nums`, you will choose two different indices `i` and `j` of that array. _Return the maximum value of_ `(nums[i]-1)*(nums[j]-1)`.
**Example 1:**
**Input:** nums = \[3,4,5,2\]
**Output:** 12
**Explanation:** If you choose the indices i=1 and j=2 (indexed from 0), you will get the maximum value, that is, (nums\[1\]-1)\*(nums\[2\]-1) = (4-1)\*(5-1) = 3\*4 = 12.
**Example 2:**
**Input:** nums = \[1,5,4,5\]
**Output:** 16
**Explanation:** Choosing the indices i=1 and j=3 (indexed from 0), you will get the maximum value of (5-1)\*(5-1) = 16.
**Example 3:**
**Input:** nums = \[3,7\]
**Output:** 12
**Constraints:**
* `2 <= nums.length <= 500`
* `1 <= nums[i] <= 10^3` | Count the frequency of each integer in the array. Start with an empty set, add to the set the integer with the maximum frequency. Keep Adding the integer with the max frequency until you remove at least half of the integers. |
recursion does the job | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\ndef tsum(root):\n if(root==None):\n return 0\n x= root.val+tsum(root.left)+tsum(root.right)\n return x\ndef fun(root,sm,mx):\n if(root==None):\n return 0\n a=fun(root.left,sm,mx)\n b=fun(root.right,sm,mx)\n mx[0]=max(mx[0],a*(sm-a),b*(sm-b))\n return a+b+root.val\n \nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n mx=[0]\n sm=tsum(root)\n memo={}\n fun(root,sm,mx)\n return mx[0]%(10**9+7)\n``` | 6 | Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return _the maximum product of the sums of the two subtrees_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that you need to maximize the answer before taking the mod and not after taking it.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 110
**Explanation:** Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11\*10)
**Example 2:**
**Input:** root = \[1,null,2,3,4,null,null,5,6\]
**Output:** 90
**Explanation:** Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15\*6)
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5 * 104]`.
* `1 <= Node.val <= 104` | null |
recursion does the job | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\ndef tsum(root):\n if(root==None):\n return 0\n x= root.val+tsum(root.left)+tsum(root.right)\n return x\ndef fun(root,sm,mx):\n if(root==None):\n return 0\n a=fun(root.left,sm,mx)\n b=fun(root.right,sm,mx)\n mx[0]=max(mx[0],a*(sm-a),b*(sm-b))\n return a+b+root.val\n \nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n mx=[0]\n sm=tsum(root)\n memo={}\n fun(root,sm,mx)\n return mx[0]%(10**9+7)\n``` | 6 | You are given a rectangular cake of size `h x w` and two arrays of integers `horizontalCuts` and `verticalCuts` where:
* `horizontalCuts[i]` is the distance from the top of the rectangular cake to the `ith` horizontal cut and similarly, and
* `verticalCuts[j]` is the distance from the left of the rectangular cake to the `jth` vertical cut.
Return _the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays_ `horizontalCuts` _and_ `verticalCuts`. Since the answer can be a large number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** h = 5, w = 4, horizontalCuts = \[1,2,4\], verticalCuts = \[1,3\]
**Output:** 4
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
**Example 2:**
**Input:** h = 5, w = 4, horizontalCuts = \[3,1\], verticalCuts = \[1\]
**Output:** 6
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
**Example 3:**
**Input:** h = 5, w = 4, horizontalCuts = \[3\], verticalCuts = \[3\]
**Output:** 9
**Constraints:**
* `2 <= h, w <= 109`
* `1 <= horizontalCuts.length <= min(h - 1, 105)`
* `1 <= verticalCuts.length <= min(w - 1, 105)`
* `1 <= horizontalCuts[i] < h`
* `1 <= verticalCuts[i] < w`
* All the elements in `horizontalCuts` are distinct.
* All the elements in `verticalCuts` are distinct. | If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node. |
Clean and Easy and Fast Python3 Code 🌴 | maximum-product-of-splitted-binary-tree | 0 | 1 | > Python3 Code\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n def dfs(node):\n if node:\n dfs(node.left)\n dfs(node.right)\n if node.left and node.right:\n node.val += node.left.val + node.right.val\n elif node.left and not node.right:\n node.val += node.left.val\n elif node.right:\n node.val += node.right.val\n dfs(root)\n\n ans, val = 0, root.val\n def f(node):\n nonlocal ans\n if node:\n ans = max(ans, (val - node.val) * node.val)\n f(node.left)\n f(node.right)\n f(root)\n return ans % 1000000007\n``` | 1 | Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return _the maximum product of the sums of the two subtrees_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that you need to maximize the answer before taking the mod and not after taking it.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 110
**Explanation:** Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11\*10)
**Example 2:**
**Input:** root = \[1,null,2,3,4,null,null,5,6\]
**Output:** 90
**Explanation:** Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15\*6)
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5 * 104]`.
* `1 <= Node.val <= 104` | null |
Clean and Easy and Fast Python3 Code 🌴 | maximum-product-of-splitted-binary-tree | 0 | 1 | > Python3 Code\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n def dfs(node):\n if node:\n dfs(node.left)\n dfs(node.right)\n if node.left and node.right:\n node.val += node.left.val + node.right.val\n elif node.left and not node.right:\n node.val += node.left.val\n elif node.right:\n node.val += node.right.val\n dfs(root)\n\n ans, val = 0, root.val\n def f(node):\n nonlocal ans\n if node:\n ans = max(ans, (val - node.val) * node.val)\n f(node.left)\n f(node.right)\n f(root)\n return ans % 1000000007\n``` | 1 | You are given a rectangular cake of size `h x w` and two arrays of integers `horizontalCuts` and `verticalCuts` where:
* `horizontalCuts[i]` is the distance from the top of the rectangular cake to the `ith` horizontal cut and similarly, and
* `verticalCuts[j]` is the distance from the left of the rectangular cake to the `jth` vertical cut.
Return _the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays_ `horizontalCuts` _and_ `verticalCuts`. Since the answer can be a large number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** h = 5, w = 4, horizontalCuts = \[1,2,4\], verticalCuts = \[1,3\]
**Output:** 4
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
**Example 2:**
**Input:** h = 5, w = 4, horizontalCuts = \[3,1\], verticalCuts = \[1\]
**Output:** 6
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
**Example 3:**
**Input:** h = 5, w = 4, horizontalCuts = \[3\], verticalCuts = \[3\]
**Output:** 9
**Constraints:**
* `2 <= h, w <= 109`
* `1 <= horizontalCuts.length <= min(h - 1, 105)`
* `1 <= verticalCuts.length <= min(w - 1, 105)`
* `1 <= horizontalCuts[i] < h`
* `1 <= verticalCuts[i] < w`
* All the elements in `horizontalCuts` are distinct.
* All the elements in `verticalCuts` are distinct. | If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node. |
Python: 85% Faster | O(n) Time complexity | Smallest difference from half of sum | DFS | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBreak the edge above node where current sum and half of sum have smallest difference.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n # Function to calculate sum of whole tree.\n def sum(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n return root.val+self.sum(root.left)+self.sum(root.right)\n # Function to calculate sum upto the current node using DFS.\n def currentsum(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n else:\n self.cur=root.val+self.currentsum(root.left)+self.currentsum(root.right)\n #Check for the smallest difference from half of sum\n self.min=min(self.min,abs(self.sum-self.cur))\n return self.cur\n\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n #Calculating half of sum\n self.sum=self.sum(root)/2\n self.min=self.sum\n self.cur=0\n self.currentsum(root)\n #Coming back to the current sum where difference is minimum\n self.min=self.min+self.sum\n return int(self.min*(self.sum*2-self.min)%(10**9+7))\n```\nUpvote if you understood the approach. Let me know if you need any help. | 1 | Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return _the maximum product of the sums of the two subtrees_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that you need to maximize the answer before taking the mod and not after taking it.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 110
**Explanation:** Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11\*10)
**Example 2:**
**Input:** root = \[1,null,2,3,4,null,null,5,6\]
**Output:** 90
**Explanation:** Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15\*6)
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5 * 104]`.
* `1 <= Node.val <= 104` | null |
Python: 85% Faster | O(n) Time complexity | Smallest difference from half of sum | DFS | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBreak the edge above node where current sum and half of sum have smallest difference.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n # Function to calculate sum of whole tree.\n def sum(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n return root.val+self.sum(root.left)+self.sum(root.right)\n # Function to calculate sum upto the current node using DFS.\n def currentsum(self, root: Optional[TreeNode]) -> int:\n if not root:\n return 0\n else:\n self.cur=root.val+self.currentsum(root.left)+self.currentsum(root.right)\n #Check for the smallest difference from half of sum\n self.min=min(self.min,abs(self.sum-self.cur))\n return self.cur\n\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n #Calculating half of sum\n self.sum=self.sum(root)/2\n self.min=self.sum\n self.cur=0\n self.currentsum(root)\n #Coming back to the current sum where difference is minimum\n self.min=self.min+self.sum\n return int(self.min*(self.sum*2-self.min)%(10**9+7))\n```\nUpvote if you understood the approach. Let me know if you need any help. | 1 | You are given a rectangular cake of size `h x w` and two arrays of integers `horizontalCuts` and `verticalCuts` where:
* `horizontalCuts[i]` is the distance from the top of the rectangular cake to the `ith` horizontal cut and similarly, and
* `verticalCuts[j]` is the distance from the left of the rectangular cake to the `jth` vertical cut.
Return _the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays_ `horizontalCuts` _and_ `verticalCuts`. Since the answer can be a large number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** h = 5, w = 4, horizontalCuts = \[1,2,4\], verticalCuts = \[1,3\]
**Output:** 4
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
**Example 2:**
**Input:** h = 5, w = 4, horizontalCuts = \[3,1\], verticalCuts = \[1\]
**Output:** 6
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
**Example 3:**
**Input:** h = 5, w = 4, horizontalCuts = \[3\], verticalCuts = \[3\]
**Output:** 9
**Constraints:**
* `2 <= h, w <= 109`
* `1 <= horizontalCuts.length <= min(h - 1, 105)`
* `1 <= verticalCuts.length <= min(w - 1, 105)`
* `1 <= horizontalCuts[i] < h`
* `1 <= verticalCuts[i] < w`
* All the elements in `horizontalCuts` are distinct.
* All the elements in `verticalCuts` are distinct. | If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node. |
Backtracking to find sub tree sum | maximum-product-of-splitted-binary-tree | 0 | 1 | Find sub tree sums of all nodes and then the find max product.\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n self.sub_sums = []\n self.dfs(root)\n tree_sum = max(self.sub_sums)\n max_prod = 0\n for s in self.sub_sums:\n max_prod = max(max_prod, (tree_sum - s) * s)\n return max_prod % (10 ** 9 + 7)\n\n def dfs(self, node):\n s = node.val\n if node.left:\n s += self.dfs(node.left)\n if node.right:\n s += self.dfs(node.right)\n self.sub_sums.append(s)\n return s\n``` | 1 | Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return _the maximum product of the sums of the two subtrees_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that you need to maximize the answer before taking the mod and not after taking it.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 110
**Explanation:** Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11\*10)
**Example 2:**
**Input:** root = \[1,null,2,3,4,null,null,5,6\]
**Output:** 90
**Explanation:** Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15\*6)
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5 * 104]`.
* `1 <= Node.val <= 104` | null |
Backtracking to find sub tree sum | maximum-product-of-splitted-binary-tree | 0 | 1 | Find sub tree sums of all nodes and then the find max product.\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n self.sub_sums = []\n self.dfs(root)\n tree_sum = max(self.sub_sums)\n max_prod = 0\n for s in self.sub_sums:\n max_prod = max(max_prod, (tree_sum - s) * s)\n return max_prod % (10 ** 9 + 7)\n\n def dfs(self, node):\n s = node.val\n if node.left:\n s += self.dfs(node.left)\n if node.right:\n s += self.dfs(node.right)\n self.sub_sums.append(s)\n return s\n``` | 1 | You are given a rectangular cake of size `h x w` and two arrays of integers `horizontalCuts` and `verticalCuts` where:
* `horizontalCuts[i]` is the distance from the top of the rectangular cake to the `ith` horizontal cut and similarly, and
* `verticalCuts[j]` is the distance from the left of the rectangular cake to the `jth` vertical cut.
Return _the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays_ `horizontalCuts` _and_ `verticalCuts`. Since the answer can be a large number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** h = 5, w = 4, horizontalCuts = \[1,2,4\], verticalCuts = \[1,3\]
**Output:** 4
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
**Example 2:**
**Input:** h = 5, w = 4, horizontalCuts = \[3,1\], verticalCuts = \[1\]
**Output:** 6
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
**Example 3:**
**Input:** h = 5, w = 4, horizontalCuts = \[3\], verticalCuts = \[3\]
**Output:** 9
**Constraints:**
* `2 <= h, w <= 109`
* `1 <= horizontalCuts.length <= min(h - 1, 105)`
* `1 <= verticalCuts.length <= min(w - 1, 105)`
* `1 <= horizontalCuts[i] < h`
* `1 <= verticalCuts[i] < w`
* All the elements in `horizontalCuts` are distinct.
* All the elements in `verticalCuts` are distinct. | If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node. |
Easy, Clean, Recursive Python3 Solution🔥🐍 | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can see in the question that we would need to find two such subtrees of the given subtree such that the product of their separate sums is maximum.\nTo do so, we need to know the sum of each subtree. That is waht we are doing in this solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nEach subtree is a binary tree in itself, so basically while calculating the sum of a subtree we have a big problem which can be broken down into smaller simpler problems and hence, we use recursion.\nIn a single pass, we are able to calculate the sum of each subtree as well as the total sum of the subtree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ where n is the number of nodes\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(number of subtrees)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n sums = [] # A class variable to store the sums of all the possible sub-trees\n\n #followinng function recursively calculates the sum of each subtree and\n #also stores the sum of each subtree in the class variable sums\n\n def sumTree(self, root):\n if not root: return 0 #base case for recursion, as a None node would have no value and hence, would return a sum 0 to its parent\n s = root.val + self.sumTree(root.right) + self.sumTree(root.left)\n Solution.sums.append(s)\n return s\n\n\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n mod = 10**9+7\n Solution.sums.clear()#to flush any existing values that the class variable might be storing, as we need an empty list for each\n #new object created for the Solution class\n total = self.sumTree(root) #the total sum of the subtree\n mx = 0\n for i in Solution.sums:\n mx = max(mx,i*(total-i))\n return mx%mod\n``` | 2 | Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return _the maximum product of the sums of the two subtrees_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that you need to maximize the answer before taking the mod and not after taking it.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 110
**Explanation:** Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11\*10)
**Example 2:**
**Input:** root = \[1,null,2,3,4,null,null,5,6\]
**Output:** 90
**Explanation:** Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15\*6)
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5 * 104]`.
* `1 <= Node.val <= 104` | null |
Easy, Clean, Recursive Python3 Solution🔥🐍 | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can see in the question that we would need to find two such subtrees of the given subtree such that the product of their separate sums is maximum.\nTo do so, we need to know the sum of each subtree. That is waht we are doing in this solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nEach subtree is a binary tree in itself, so basically while calculating the sum of a subtree we have a big problem which can be broken down into smaller simpler problems and hence, we use recursion.\nIn a single pass, we are able to calculate the sum of each subtree as well as the total sum of the subtree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ where n is the number of nodes\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(number of subtrees)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n sums = [] # A class variable to store the sums of all the possible sub-trees\n\n #followinng function recursively calculates the sum of each subtree and\n #also stores the sum of each subtree in the class variable sums\n\n def sumTree(self, root):\n if not root: return 0 #base case for recursion, as a None node would have no value and hence, would return a sum 0 to its parent\n s = root.val + self.sumTree(root.right) + self.sumTree(root.left)\n Solution.sums.append(s)\n return s\n\n\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n mod = 10**9+7\n Solution.sums.clear()#to flush any existing values that the class variable might be storing, as we need an empty list for each\n #new object created for the Solution class\n total = self.sumTree(root) #the total sum of the subtree\n mx = 0\n for i in Solution.sums:\n mx = max(mx,i*(total-i))\n return mx%mod\n``` | 2 | You are given a rectangular cake of size `h x w` and two arrays of integers `horizontalCuts` and `verticalCuts` where:
* `horizontalCuts[i]` is the distance from the top of the rectangular cake to the `ith` horizontal cut and similarly, and
* `verticalCuts[j]` is the distance from the left of the rectangular cake to the `jth` vertical cut.
Return _the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays_ `horizontalCuts` _and_ `verticalCuts`. Since the answer can be a large number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** h = 5, w = 4, horizontalCuts = \[1,2,4\], verticalCuts = \[1,3\]
**Output:** 4
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
**Example 2:**
**Input:** h = 5, w = 4, horizontalCuts = \[3,1\], verticalCuts = \[1\]
**Output:** 6
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
**Example 3:**
**Input:** h = 5, w = 4, horizontalCuts = \[3\], verticalCuts = \[3\]
**Output:** 9
**Constraints:**
* `2 <= h, w <= 109`
* `1 <= horizontalCuts.length <= min(h - 1, 105)`
* `1 <= verticalCuts.length <= min(w - 1, 105)`
* `1 <= horizontalCuts[i] < h`
* `1 <= verticalCuts[i] < w`
* All the elements in `horizontalCuts` are distinct.
* All the elements in `verticalCuts` are distinct. | If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node. |
Python | Visitor Pattern | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n\nI assume that you already know the solution: compute all subtree sums and find the best product of `(tree_sum - subtree_sum) * subtree_sum`. The purpose of this post is to discuss the implementation.\n\n# Approach\n\nYour initial approach may look something like this:\n\n```py\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n subtree_sum: dict[Optional[TreeNode], int] = {None: 0}\n\n def depth_first_search(node: Optional[TreeNode]):\n if node is not None:\n subtree_sum[node] = node.val\n for child in node.left, node.right:\n depth_first_search(child)\n subtree_sum[node] += subtree_sum[child]\n\n depth_first_search(root)\n tree_sum = subtree_sum[root]\n\n return max(subtree_sum * (tree_sum - subtree_sum)\n for subtree_sum in subtree_sum.values()) % (10**9 + 7)\n```\n\n- The main issue is that this code is hardly reusable - anyone willing to compute subtree sums for a different purpose wouldn\'t be able to do so without essentially copying the implementation of `depth_first_search`.\n- Another issue is that there is no encapsulation: `subtree_sum` mapping is just a plain old variable on its own. It makes it hard to ensure consistency, especially while copy-pasting and modifying the code.\n\nOne way to address these issues would be to pass `subtree_sum` mapping as a parameter to `depth_first_search` and to move `depth_first_search` out of the `Solution` class:\n\n```py\ndef depth_first_search(node: Optional[TreeNode],\n subtree_sum: dict[Optional[TreeNode], int]):\n if node is not None:\n subtree_sum[node] = node.val\n for child in node.left, node.right:\n depth_first_search(child, subtree_sum)\n subtree_sum[node] += subtree_sum[child]\n\n\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n subtree_sum: dict[Optional[TreeNode], int] = {None: 0}\n depth_first_search(root, subtree_sum)\n tree_sum = subtree_sum[root]\n\n return max(subtree_sum * (tree_sum - subtree_sum)\n for subtree_sum in subtree_sum.values()) % (10**9 + 7)\n```\n\nThis is better, but not ideal. Namely, `depth_first_search` violates Single Responsibility principle. Indeed, it both traverses the tree and computes subtree sums. These can be further separated with a usage of a Visitor pattern. \n\nThe idea behind Visitor pattern is to separate the traversal and problem-specific logic. It accomplishes this ambitious goal by introducing _event points_ into `depth_first_search`:\n\n```py\ndef depth_first_search(root: Optional[TreeNode], visitor: Visitor):\n visitor.before_vertex(root)\n if root is not None:\n for child in root.left, root.right:\n visitor.before_edge(root, child)\n depth_first_search(child, visitor)\n visitor.after_edge(root, child)\n visitor.after_vertex(root)\n```\n\nHere `Visitor` is an abstract base class which defines several event points: before and after each vertex and edge:\n\n```py\nfrom abc import ABC\n\nclass Visitor(ABC):\n def before_vertex(self, node: Optional[TreeNode]) -> None:\n pass\n\n def after_vertex(self, node: Optional[TreeNode]) -> None:\n pass\n\n def before_edge(self, node: TreeNode, child: Optional[TreeNode]) -> None:\n pass\n\n def after_edge(self, node: TreeNode, child: Optional[TreeNode]) -> None:\n pass\n```\n\nTo modify the behaviour for a specific problem, one inherits from `Visitor` and redefines some subset of method, like so:\n```py\nclass SubtreeSumVisitor(Visitor):\n def __init__(self):\n self.subtree_sum: dict[Optional[TreeNode], int] = {None: 0}\n\n def before_vertex(self, node: Optional[TreeNode]) -> None:\n if node is not None:\n self.subtree_sum[node] = node.val\n\n def after_edge(self, node: TreeNode, child: Optional[TreeNode]) -> None:\n self.subtree_sum[node] += self.subtree_sum[child]\n```\n\nThis approach allows to reuse both a problem-specific visitor class and a generic problem-agnostic depth first search function. It has also been used in the [boost C++ libraries](https://www.boost.org/doc/libs/1_80_0/libs/graph/doc/depth_first_search.html) for a long time.\n\n# Complexity\n\n- Time complexity: $$O(n)$$.\n- Space complexity: $$O(n)$$.\n\n# Code\n\nMain code using the above snippets:\n```py\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n visitor = SubtreeSumVisitor()\n depth_first_search(root, visitor)\n tree_sum = visitor.subtree_sum[root]\n return max(subtree_sum * (tree_sum - subtree_sum)\n for subtree_sum in visitor.subtree_sum.values()) % (10**9 + 7)\n```\n\n[Full submission link](https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/submissions/857409844/). | 1 | Given the `root` of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return _the maximum product of the sums of the two subtrees_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that you need to maximize the answer before taking the mod and not after taking it.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** 110
**Explanation:** Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11\*10)
**Example 2:**
**Input:** root = \[1,null,2,3,4,null,null,5,6\]
**Output:** 90
**Explanation:** Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15\*6)
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5 * 104]`.
* `1 <= Node.val <= 104` | null |
Python | Visitor Pattern | maximum-product-of-splitted-binary-tree | 0 | 1 | # Intuition\n\nI assume that you already know the solution: compute all subtree sums and find the best product of `(tree_sum - subtree_sum) * subtree_sum`. The purpose of this post is to discuss the implementation.\n\n# Approach\n\nYour initial approach may look something like this:\n\n```py\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n subtree_sum: dict[Optional[TreeNode], int] = {None: 0}\n\n def depth_first_search(node: Optional[TreeNode]):\n if node is not None:\n subtree_sum[node] = node.val\n for child in node.left, node.right:\n depth_first_search(child)\n subtree_sum[node] += subtree_sum[child]\n\n depth_first_search(root)\n tree_sum = subtree_sum[root]\n\n return max(subtree_sum * (tree_sum - subtree_sum)\n for subtree_sum in subtree_sum.values()) % (10**9 + 7)\n```\n\n- The main issue is that this code is hardly reusable - anyone willing to compute subtree sums for a different purpose wouldn\'t be able to do so without essentially copying the implementation of `depth_first_search`.\n- Another issue is that there is no encapsulation: `subtree_sum` mapping is just a plain old variable on its own. It makes it hard to ensure consistency, especially while copy-pasting and modifying the code.\n\nOne way to address these issues would be to pass `subtree_sum` mapping as a parameter to `depth_first_search` and to move `depth_first_search` out of the `Solution` class:\n\n```py\ndef depth_first_search(node: Optional[TreeNode],\n subtree_sum: dict[Optional[TreeNode], int]):\n if node is not None:\n subtree_sum[node] = node.val\n for child in node.left, node.right:\n depth_first_search(child, subtree_sum)\n subtree_sum[node] += subtree_sum[child]\n\n\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n subtree_sum: dict[Optional[TreeNode], int] = {None: 0}\n depth_first_search(root, subtree_sum)\n tree_sum = subtree_sum[root]\n\n return max(subtree_sum * (tree_sum - subtree_sum)\n for subtree_sum in subtree_sum.values()) % (10**9 + 7)\n```\n\nThis is better, but not ideal. Namely, `depth_first_search` violates Single Responsibility principle. Indeed, it both traverses the tree and computes subtree sums. These can be further separated with a usage of a Visitor pattern. \n\nThe idea behind Visitor pattern is to separate the traversal and problem-specific logic. It accomplishes this ambitious goal by introducing _event points_ into `depth_first_search`:\n\n```py\ndef depth_first_search(root: Optional[TreeNode], visitor: Visitor):\n visitor.before_vertex(root)\n if root is not None:\n for child in root.left, root.right:\n visitor.before_edge(root, child)\n depth_first_search(child, visitor)\n visitor.after_edge(root, child)\n visitor.after_vertex(root)\n```\n\nHere `Visitor` is an abstract base class which defines several event points: before and after each vertex and edge:\n\n```py\nfrom abc import ABC\n\nclass Visitor(ABC):\n def before_vertex(self, node: Optional[TreeNode]) -> None:\n pass\n\n def after_vertex(self, node: Optional[TreeNode]) -> None:\n pass\n\n def before_edge(self, node: TreeNode, child: Optional[TreeNode]) -> None:\n pass\n\n def after_edge(self, node: TreeNode, child: Optional[TreeNode]) -> None:\n pass\n```\n\nTo modify the behaviour for a specific problem, one inherits from `Visitor` and redefines some subset of method, like so:\n```py\nclass SubtreeSumVisitor(Visitor):\n def __init__(self):\n self.subtree_sum: dict[Optional[TreeNode], int] = {None: 0}\n\n def before_vertex(self, node: Optional[TreeNode]) -> None:\n if node is not None:\n self.subtree_sum[node] = node.val\n\n def after_edge(self, node: TreeNode, child: Optional[TreeNode]) -> None:\n self.subtree_sum[node] += self.subtree_sum[child]\n```\n\nThis approach allows to reuse both a problem-specific visitor class and a generic problem-agnostic depth first search function. It has also been used in the [boost C++ libraries](https://www.boost.org/doc/libs/1_80_0/libs/graph/doc/depth_first_search.html) for a long time.\n\n# Complexity\n\n- Time complexity: $$O(n)$$.\n- Space complexity: $$O(n)$$.\n\n# Code\n\nMain code using the above snippets:\n```py\nclass Solution:\n def maxProduct(self, root: Optional[TreeNode]) -> int:\n visitor = SubtreeSumVisitor()\n depth_first_search(root, visitor)\n tree_sum = visitor.subtree_sum[root]\n return max(subtree_sum * (tree_sum - subtree_sum)\n for subtree_sum in visitor.subtree_sum.values()) % (10**9 + 7)\n```\n\n[Full submission link](https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/submissions/857409844/). | 1 | You are given a rectangular cake of size `h x w` and two arrays of integers `horizontalCuts` and `verticalCuts` where:
* `horizontalCuts[i]` is the distance from the top of the rectangular cake to the `ith` horizontal cut and similarly, and
* `verticalCuts[j]` is the distance from the left of the rectangular cake to the `jth` vertical cut.
Return _the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays_ `horizontalCuts` _and_ `verticalCuts`. Since the answer can be a large number, return this **modulo** `109 + 7`.
**Example 1:**
**Input:** h = 5, w = 4, horizontalCuts = \[1,2,4\], verticalCuts = \[1,3\]
**Output:** 4
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
**Example 2:**
**Input:** h = 5, w = 4, horizontalCuts = \[3,1\], verticalCuts = \[1\]
**Output:** 6
**Explanation:** The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
**Example 3:**
**Input:** h = 5, w = 4, horizontalCuts = \[3\], verticalCuts = \[3\]
**Output:** 9
**Constraints:**
* `2 <= h, w <= 109`
* `1 <= horizontalCuts.length <= min(h - 1, 105)`
* `1 <= verticalCuts.length <= min(w - 1, 105)`
* `1 <= horizontalCuts[i] < h`
* `1 <= verticalCuts[i] < w`
* All the elements in `horizontalCuts` are distinct.
* All the elements in `verticalCuts` are distinct. | If we know the sum of a subtree, the answer is max( (total_sum - subtree_sum) * subtree_sum) in each node. |
Intuitive Topological Sort || Python || O(n*d) | jump-game-v | 0 | 1 | # Intuition\nThe idea is we construct a topological order (using monotonic stack) and take the length of the longest path.\n\n\n# Complexity\n- Time complexity:\nO(n*d)\n\n- Space complexity:\nO(n*d)\n\n# Code\n```\nclass Solution:\n def maxJumps(self, arr: List[int], d: int) -> int:\n \n\n \n graph = defaultdict(list)\n indegree = defaultdict(int)\n \n \n # connect nodes if prev_val < cur_val and cur_index - prev_index <= d\n stack = []\n for ind, num in enumerate(arr):\n \n while stack and ind - stack[-1] <= d and arr[stack[-1]] < num:\n popped = stack.pop()\n graph[ind].append(popped)\n indegree[popped] += 1\n \n stack.append(ind)\n \n # perform the same operation backwards from the end\n stack = []\n for ind in range(len(arr) - 1, -1, -1):\n num = arr[ind]\n while stack and stack[-1] - ind <= d and arr[stack[-1]] < num: \n popped = stack.pop()\n graph[ind].append(popped)\n indegree[popped] += 1\n \n stack.append(ind)\n \n \n # topological sorting\n queue = deque()\n for node in range(len(arr)):\n if not indegree[node]:\n queue.append(node)\n \n jumps = 0\n while queue:\n for _ in range(len(queue)):\n cur = queue.popleft()\n \n for neigh in graph[cur]:\n indegree[neigh] -= 1\n if not indegree[neigh]:\n queue.append(neigh)\n \n jumps += 1\n \n \n return jumps\n \n \n``` | 2 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
Intuitive Topological Sort || Python || O(n*d) | jump-game-v | 0 | 1 | # Intuition\nThe idea is we construct a topological order (using monotonic stack) and take the length of the longest path.\n\n\n# Complexity\n- Time complexity:\nO(n*d)\n\n- Space complexity:\nO(n*d)\n\n# Code\n```\nclass Solution:\n def maxJumps(self, arr: List[int], d: int) -> int:\n \n\n \n graph = defaultdict(list)\n indegree = defaultdict(int)\n \n \n # connect nodes if prev_val < cur_val and cur_index - prev_index <= d\n stack = []\n for ind, num in enumerate(arr):\n \n while stack and ind - stack[-1] <= d and arr[stack[-1]] < num:\n popped = stack.pop()\n graph[ind].append(popped)\n indegree[popped] += 1\n \n stack.append(ind)\n \n # perform the same operation backwards from the end\n stack = []\n for ind in range(len(arr) - 1, -1, -1):\n num = arr[ind]\n while stack and stack[-1] - ind <= d and arr[stack[-1]] < num: \n popped = stack.pop()\n graph[ind].append(popped)\n indegree[popped] += 1\n \n stack.append(ind)\n \n \n # topological sorting\n queue = deque()\n for node in range(len(arr)):\n if not indegree[node]:\n queue.append(node)\n \n jumps = 0\n while queue:\n for _ in range(len(queue)):\n cur = queue.popleft()\n \n for neigh in graph[cur]:\n indegree[neigh] -= 1\n if not indegree[neigh]:\n queue.append(neigh)\n \n jumps += 1\n \n \n return jumps\n \n \n``` | 2 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
Easy, Explained Python Soln. time: O(n*d) space:O(n) | jump-game-v | 0 | 1 | My solution with Explanation...\nwe Can use even less space if we store dp = [0]*N and when its value is updated it will alway be greater than 0.\nthere by seen (set) can be removed. \nreplacing \nif indx in seen: -> if dp[indx] \nHope it makes Sense. \nfeel free to comment. Networking helps \n\n\n# space complexity : O(n)\n# Time complexity : O(n*d)\n# where n is lenght of array/nums and "d" is the value of d.\n\n```\nclass Solution:\n def maxJumps(self, nums: List[int], d: int) -> int:\n N = len(nums)\n seen = set() # seen for lookup, to memoize\n dp = [1]*N # stores the values of jump we can make from Ith index in DP. # minimum being 1 jump (i.e its self)\n \n def recursion(indx):\n # if we have indx in seen return its value dp[indx].\n if indx in seen:\n return dp[indx]\n # base case if indx is out of range we cant jump. return 0\n if indx<0 or indx >= N:\n return 0\n \n # tempR : all the jumps we can make to the right side of indx\n # tempL : all the jumps we can make to the left side of indx\n tempR,tempL= 0,0\n curr = nums[indx] # height of current indx so we only jump allowed jump \n # i.e nums[i] < curr <- allowed if curr =< nums[i] break(jump not allowed)\n \n #max jump we can make to the right Side are stored in tempR, \n for i in range(indx+1, min(indx+d+1,N) ):\n if nums[i] < curr:\n tempR = max(tempR, recursion(i)) # store max jumps in right\n else:\n break\n for i in range(indx-1, max(-1,indx-d-1) , -1): \n if nums[i] < curr:\n tempL = max(tempL, recursion(i)) # store max jumps in left\n else:\n break\n # update dp[indx] by (1 + maxjumps( right, left)) ( 1 becoz it can jump on itself)\n dp[indx] = max(tempR,tempL) + 1 \n seen.add(indx) # as Indx calculated, can use its value next time, so added to seen\n return dp[indx]\n \n \n # for all indices we check how many jumps we can make\n for i in range(N): \n if i not in seen: # if ith index is not in seen then we have comupted its jumps.\n recursion(i)\n return max(dp) # returns the max jumps\n\t\t\n``` | 1 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
Easy, Explained Python Soln. time: O(n*d) space:O(n) | jump-game-v | 0 | 1 | My solution with Explanation...\nwe Can use even less space if we store dp = [0]*N and when its value is updated it will alway be greater than 0.\nthere by seen (set) can be removed. \nreplacing \nif indx in seen: -> if dp[indx] \nHope it makes Sense. \nfeel free to comment. Networking helps \n\n\n# space complexity : O(n)\n# Time complexity : O(n*d)\n# where n is lenght of array/nums and "d" is the value of d.\n\n```\nclass Solution:\n def maxJumps(self, nums: List[int], d: int) -> int:\n N = len(nums)\n seen = set() # seen for lookup, to memoize\n dp = [1]*N # stores the values of jump we can make from Ith index in DP. # minimum being 1 jump (i.e its self)\n \n def recursion(indx):\n # if we have indx in seen return its value dp[indx].\n if indx in seen:\n return dp[indx]\n # base case if indx is out of range we cant jump. return 0\n if indx<0 or indx >= N:\n return 0\n \n # tempR : all the jumps we can make to the right side of indx\n # tempL : all the jumps we can make to the left side of indx\n tempR,tempL= 0,0\n curr = nums[indx] # height of current indx so we only jump allowed jump \n # i.e nums[i] < curr <- allowed if curr =< nums[i] break(jump not allowed)\n \n #max jump we can make to the right Side are stored in tempR, \n for i in range(indx+1, min(indx+d+1,N) ):\n if nums[i] < curr:\n tempR = max(tempR, recursion(i)) # store max jumps in right\n else:\n break\n for i in range(indx-1, max(-1,indx-d-1) , -1): \n if nums[i] < curr:\n tempL = max(tempL, recursion(i)) # store max jumps in left\n else:\n break\n # update dp[indx] by (1 + maxjumps( right, left)) ( 1 becoz it can jump on itself)\n dp[indx] = max(tempR,tempL) + 1 \n seen.add(indx) # as Indx calculated, can use its value next time, so added to seen\n return dp[indx]\n \n \n # for all indices we check how many jumps we can make\n for i in range(N): \n if i not in seen: # if ith index is not in seen then we have comupted its jumps.\n recursion(i)\n return max(dp) # returns the max jumps\n\t\t\n``` | 1 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
✔ Python3 Solution | DP | O(nd) | jump-game-v | 0 | 1 | # Complexity\n- Time complexity: $$O(nd)$$\n- Space complexity: $$O(n)$$\n\n# Solution 1\n```\nclass Solution:\n def maxJumps(self, A, d):\n n = len(A)\n dp = [1] * n\n for i in sorted(range(n), key = lambda x: -A[x]):\n for x in range(i - 1, max(0, i - d) - 1, -1):\n if A[x] >= A[i]: break\n dp[x] = max(dp[x], dp[i] + 1)\n for x in range(i + 1, min(n, i + d + 1)):\n if A[x] >= A[i]: break\n dp[x] = max(dp[x], dp[i] + 1)\n return max(dp)\n```\n\n# Solution 2\n```\nclass Solution:\n def maxJumps(self, A, d):\n n = len(A)\n dp = [1] * n\n for i in sorted(range(n), key = lambda x: -A[x]):\n for rng in (range(i - 1, max(0, i - d) - 1, -1), range(i + 1, min(n, i + d + 1))):\n for x in rng:\n if A[x] >= A[i]: break\n dp[x] = max(dp[x], dp[i] + 1)\n return max(dp)\n``` | 3 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
✔ Python3 Solution | DP | O(nd) | jump-game-v | 0 | 1 | # Complexity\n- Time complexity: $$O(nd)$$\n- Space complexity: $$O(n)$$\n\n# Solution 1\n```\nclass Solution:\n def maxJumps(self, A, d):\n n = len(A)\n dp = [1] * n\n for i in sorted(range(n), key = lambda x: -A[x]):\n for x in range(i - 1, max(0, i - d) - 1, -1):\n if A[x] >= A[i]: break\n dp[x] = max(dp[x], dp[i] + 1)\n for x in range(i + 1, min(n, i + d + 1)):\n if A[x] >= A[i]: break\n dp[x] = max(dp[x], dp[i] + 1)\n return max(dp)\n```\n\n# Solution 2\n```\nclass Solution:\n def maxJumps(self, A, d):\n n = len(A)\n dp = [1] * n\n for i in sorted(range(n), key = lambda x: -A[x]):\n for rng in (range(i - 1, max(0, i - d) - 1, -1), range(i + 1, min(n, i + d + 1))):\n for x in rng:\n if A[x] >= A[i]: break\n dp[x] = max(dp[x], dp[i] + 1)\n return max(dp)\n``` | 3 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
📌📌 Well-Coded and Easy Explanation || Use of Memoization 🐍 | jump-game-v | 0 | 1 | ## IDEA:\nFor each index i, run search starting from i left and right up to d steps. This way, we can easily detect if arr[j] is blocking further jumps.\n\n**So, we stop the search when we encounter j where arr[i] <= arr[j].**\n\nTo prevent re-computations, we need to memoise max jumps for every index in dp.\n\n****\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n\t\tdef maxJumps(self, arr: List[int], d: int) -> int:\n\n\t\t\tdp = defaultdict(int)\n\t\t\tdef dfs(i):\n\t\t\t\tif i in dp: return dp[i]\n\t\t\t\tm_path = 0\n\t\t\t\tfor j in range(i+1,i+d+1):\n\t\t\t\t\tif j>=len(arr) or arr[j]>=arr[i]: break\n\t\t\t\t\tm_path = max(m_path,dfs(j))\n\n\t\t\t\tfor j in range(i-1,i-d-1,-1):\n\t\t\t\t\tif j<0 or arr[j]>=arr[i]: break\n\t\t\t\t\tm_path = max(m_path,dfs(j))\n\t\t\t\tdp[i] = m_path+1\n\t\t\t\treturn m_path+1\n\n\t\t\tres = 0\n\t\t\tfor i in range(len(arr)):\n\t\t\t\tres = max(res,dfs(i))\n\t\t\treturn res\n\t\n**Feel free to ask if you have any doubt !!** \uD83E\uDD17\n### Thanks & Upvote if you got any help !! \uD83E\uDD1E | 6 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
📌📌 Well-Coded and Easy Explanation || Use of Memoization 🐍 | jump-game-v | 0 | 1 | ## IDEA:\nFor each index i, run search starting from i left and right up to d steps. This way, we can easily detect if arr[j] is blocking further jumps.\n\n**So, we stop the search when we encounter j where arr[i] <= arr[j].**\n\nTo prevent re-computations, we need to memoise max jumps for every index in dp.\n\n****\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n\t\tdef maxJumps(self, arr: List[int], d: int) -> int:\n\n\t\t\tdp = defaultdict(int)\n\t\t\tdef dfs(i):\n\t\t\t\tif i in dp: return dp[i]\n\t\t\t\tm_path = 0\n\t\t\t\tfor j in range(i+1,i+d+1):\n\t\t\t\t\tif j>=len(arr) or arr[j]>=arr[i]: break\n\t\t\t\t\tm_path = max(m_path,dfs(j))\n\n\t\t\t\tfor j in range(i-1,i-d-1,-1):\n\t\t\t\t\tif j<0 or arr[j]>=arr[i]: break\n\t\t\t\t\tm_path = max(m_path,dfs(j))\n\t\t\t\tdp[i] = m_path+1\n\t\t\t\treturn m_path+1\n\n\t\t\tres = 0\n\t\t\tfor i in range(len(arr)):\n\t\t\t\tres = max(res,dfs(i))\n\t\t\treturn res\n\t\n**Feel free to ask if you have any doubt !!** \uD83E\uDD17\n### Thanks & Upvote if you got any help !! \uD83E\uDD1E | 6 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
Very Clear Python - DFS + Memoisation | jump-game-v | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe most nodes you can visit from a starting node is one more than the most you can reach from any other valid node. I.e., `f(x) = 1 + f(y)` for `y in [x-d, x+d]`.\n\nThe \'trick\' is to expand outwards from the starting node. As soon as you reach a node greater than the starting node you can stop checking, as all subsequent nodes will be invalid.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*d)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ as we may add all nodes to the stack before reaching the base case\n\n# Code\n```\nclass Solution:\n def maxJumps(self, arr: List[int], d: int) -> int:\n \n @cache\n def dfs(idx):\n start = max(0, idx - d)\n end = min(len(arr), idx + d + 1)\n\n most = 0\n\n for i in range(idx-1, start-1, -1):\n if arr[i] >= arr[idx]:\n break\n \n most = max(most, 1 + dfs(i))\n\n for i in range(idx+1, end):\n if arr[i] >= arr[idx]:\n break\n\n most = max(most, 1 + dfs(i))\n\n return most\n\n ans = 0\n for i in range(len(arr)):\n ans = max(dfs(i), ans)\n return ans + 1\n``` | 0 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
Very Clear Python - DFS + Memoisation | jump-game-v | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe most nodes you can visit from a starting node is one more than the most you can reach from any other valid node. I.e., `f(x) = 1 + f(y)` for `y in [x-d, x+d]`.\n\nThe \'trick\' is to expand outwards from the starting node. As soon as you reach a node greater than the starting node you can stop checking, as all subsequent nodes will be invalid.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*d)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ as we may add all nodes to the stack before reaching the base case\n\n# Code\n```\nclass Solution:\n def maxJumps(self, arr: List[int], d: int) -> int:\n \n @cache\n def dfs(idx):\n start = max(0, idx - d)\n end = min(len(arr), idx + d + 1)\n\n most = 0\n\n for i in range(idx-1, start-1, -1):\n if arr[i] >= arr[idx]:\n break\n \n most = max(most, 1 + dfs(i))\n\n for i in range(idx+1, end):\n if arr[i] >= arr[idx]:\n break\n\n most = max(most, 1 + dfs(i))\n\n return most\n\n ans = 0\n for i in range(len(arr)):\n ans = max(dfs(i), ans)\n return ans + 1\n``` | 0 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
Very Simple Dp in py3 | jump-game-v | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxJumps(self, arr: List[int], d: int) -> int:\n n = len(arr)\n @cache\n def dp(i):\n res = 0\n for j in range(i-1,max(0,i-d)-1,-1):\n if arr[j]>=arr[i]:break\n res = max(dp(j),res)\n for j in range(i+1,min(n,i+d+1)):\n if arr[j]>=arr[i]:break\n res = max(dp(j),res)\n return 1+res\n \n return max(dp(i) for i in range(n))\n\n \n``` | 0 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
Very Simple Dp in py3 | jump-game-v | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxJumps(self, arr: List[int], d: int) -> int:\n n = len(arr)\n @cache\n def dp(i):\n res = 0\n for j in range(i-1,max(0,i-d)-1,-1):\n if arr[j]>=arr[i]:break\n res = max(dp(j),res)\n for j in range(i+1,min(n,i+d+1)):\n if arr[j]>=arr[i]:break\n res = max(dp(j),res)\n return 1+res\n \n return max(dp(i) for i in range(n))\n\n \n``` | 0 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
✅ 🔥 Python3 || ⚡easy solution | jump-game-v | 0 | 1 | ```\nclass Solution:\n def maxJumps(self, nums: List[int], d: int) -> int:\n N = len(nums)\n seen = set()\n dp = [1] * N\n\n def recursion(indx):\n if indx in seen:\n return dp[indx]\n if indx < 0 or indx >= N:\n return 0\n\n tempR, tempL = 0, 0\n curr = nums[indx]\n\n for i in range(indx + 1, min(indx + d + 1, N)):\n if nums[i] < curr:\n tempR = max(tempR, recursion(i))\n else:\n break\n for i in range(indx - 1, max(-1, indx - d - 1), -1):\n if nums[i] < curr:\n tempL = max(tempL, recursion(i))\n else:\n break\n\n dp[indx] = max(tempR, tempL) + 1\n seen.add(indx)\n return dp[indx]\n\n for i in range(N):\n if i not in seen:\n recursion(i)\n return max(dp)\n\n``` | 0 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
✅ 🔥 Python3 || ⚡easy solution | jump-game-v | 0 | 1 | ```\nclass Solution:\n def maxJumps(self, nums: List[int], d: int) -> int:\n N = len(nums)\n seen = set()\n dp = [1] * N\n\n def recursion(indx):\n if indx in seen:\n return dp[indx]\n if indx < 0 or indx >= N:\n return 0\n\n tempR, tempL = 0, 0\n curr = nums[indx]\n\n for i in range(indx + 1, min(indx + d + 1, N)):\n if nums[i] < curr:\n tempR = max(tempR, recursion(i))\n else:\n break\n for i in range(indx - 1, max(-1, indx - d - 1), -1):\n if nums[i] < curr:\n tempL = max(tempL, recursion(i))\n else:\n break\n\n dp[indx] = max(tempR, tempL) + 1\n seen.add(indx)\n return dp[indx]\n\n for i in range(N):\n if i not in seen:\n recursion(i)\n return max(dp)\n\n``` | 0 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
DP SIMPLE ALGORITHM | jump-game-v | 0 | 1 | \n# Code\n```\nclass Solution:\n global arr\n global d \n\n\n\n def maxJumps(self, arr: List[int], d: int) -> int:\n #attempt jumps from every index\n @cache\n def dfs(index):\n #left compute\n rv = 1\n for i in range(index-1, max(-1, index - d-1), -1):\n if arr[i] >= arr[index]: break\n rv = max(rv, 1 + dfs(i))\n #right compute\n for i in range(index+1, min(len(arr), index + d + 1)):\n if arr[i] >= arr[index]: break\n rv = max(rv, 1 + dfs(i))\n return rv\n res = 0\n for i in range(len(arr)):\n res = max(res, dfs(i))\n return res\n \n``` | 0 | Given an array of integers `arr` and an integer `d`. In one step you can jump from index `i` to index:
* `i + x` where: `i + x < arr.length` and `0 < x <= d`.
* `i - x` where: `i - x >= 0` and `0 < x <= d`.
In addition, you can only jump from index `i` to index `j` if `arr[i] > arr[j]` and `arr[i] > arr[k]` for all indices `k` between `i` and `j` (More formally `min(i, j) < k < max(i, j)`).
You can choose any index of the array and start jumping. Return _the maximum number of indices_ you can visit.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[6,4,14,6,8,13,9,7,10,6,12\], d = 2
**Output:** 4
**Explanation:** You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.
**Example 2:**
**Input:** arr = \[3,3,3,3,3\], d = 3
**Output:** 1
**Explanation:** You can start at any index. You always cannot jump to any index.
**Example 3:**
**Input:** arr = \[7,6,5,4,3,2,1\], d = 1
**Output:** 7
**Explanation:** Start at index 0. You can visit all the indicies.
**Constraints:**
* `1 <= arr.length <= 1000`
* `1 <= arr[i] <= 105`
* `1 <= d <= arr.length` | null |
DP SIMPLE ALGORITHM | jump-game-v | 0 | 1 | \n# Code\n```\nclass Solution:\n global arr\n global d \n\n\n\n def maxJumps(self, arr: List[int], d: int) -> int:\n #attempt jumps from every index\n @cache\n def dfs(index):\n #left compute\n rv = 1\n for i in range(index-1, max(-1, index - d-1), -1):\n if arr[i] >= arr[index]: break\n rv = max(rv, 1 + dfs(i))\n #right compute\n for i in range(index+1, min(len(arr), index + d + 1)):\n if arr[i] >= arr[index]: break\n rv = max(rv, 1 + dfs(i))\n return rv\n res = 0\n for i in range(len(arr)):\n res = max(res, dfs(i))\n return res\n \n``` | 0 | There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.
This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city `0`. Return the **minimum** number of edges changed.
It's **guaranteed** that each city can reach city `0` after reorder.
**Example 1:**
**Input:** n = 6, connections = \[\[0,1\],\[1,3\],\[2,3\],\[4,0\],\[4,5\]\]
**Output:** 3
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 2:**
**Input:** n = 5, connections = \[\[1,0\],\[1,2\],\[3,2\],\[3,4\]\]
**Output:** 2
**Explanation:** Change the direction of edges show in red such that each node can reach the node 0 (capital).
**Example 3:**
**Input:** n = 3, connections = \[\[1,0\],\[2,0\]\]
**Output:** 0
**Constraints:**
* `2 <= n <= 5 * 104`
* `connections.length == n - 1`
* `connections[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi` | Use dynamic programming. dp[i] is max jumps you can do starting from index i. Answer is max(dp[i]). dp[i] = 1 + max (dp[j]) where j is all indices you can reach from i. |
Efficient Movie Analysis Approach | movie-rating | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to devide the problem into two separate tasks, each focusing on one aspect: finding the high-rated movie and finding the user who wrote the most reviews. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. ##### Filtering by Month:\n\n - Create conditions `cond_one` and `cond_two` to filter movie ratings for a specific month (in this case, February 2020).\n - Apply the conditions to the `movie_rating` DataFrame to obtain data for the target month.\n2. ##### Calculating Average Ratings by Movie:\n\n - Group the filtered data by `\'movie_id\'` and calculate the mean rating for each movie.\n - Create a DataFrame `avg_rating_by_movie` containing movie IDs and their corresponding average ratings.\n3. ##### Identifying Movies with Highest Average Rating:\n\n - Filter movies with the highest average rating from the DataFrame obtained in step 2 `highest_avg_rating_movies`.\n4. ##### Merging with Movie Information:\n\n - Merge the result with the movies DataFrame to obtain additional movie details such as the title.\n - Select the lexicographically smallest movie name from the sorted results.\n5. ##### Determining Reviews per User:\n\n - Group the original movie_rating DataFrame by user ID and count the number of reviews each user has written `reviews_per_user`.\n6. ##### Identifying Users with Most Reviews:\n\n - Filter users with the maximum number of reviews from the DataFrame obtained in step 5 `most_reviews_users`.\n7. ##### Merging with User Information:\n\n - Merge the result with the users DataFrame to obtain additional user details such as the name.\n - Select the lexicographically smallest user name from the sorted results.\n8. ##### Creating the Final DataFrame:\n\n - Construct a DataFrame with the selected user and movie names and return it as the final result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(M log M + U log U)$$, where $$M$$ is the number of unique movies, and $$U$$ is the number of unique users.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N + M + U)$$, where $$N$$ is the number of rows in `movie_rating`, $$M$$ is the number of unique movies, and $$U$$ is the number of unique users.\n# Runtime & Memory\n\n\n# Code\n```\nimport pandas as pd\n\n\ndef movie_rating(\n movies: pd.DataFrame, users: pd.DataFrame, movie_rating: pd.DataFrame\n) -> pd.DataFrame:\n """\n Analyzes movie ratings and user reviews to find the lexicographically smallest movie name\n with the highest average rating in a specific month, identifies the user with the most reviews.\n\n Parameters:\n - movies (pd.DataFrame): DataFrame containing movie information.\n - users (pd.DataFrame): DataFrame containing user information.\n - movie_rating (pd.DataFrame): DataFrame containing movie ratings and reviews.\n\n Returns:\n - pd.DataFrame: DataFrame containing the results (user name and movie name).\n """\n\n # Create filtering conditions for the specific month\n cond_one = movie_rating["created_at"].dt.year == 2020\n cond_two = movie_rating["created_at"].dt.month == 2\n\n # Filter movies by month and calculate the average rating\n avg_rating_by_movie = (\n movie_rating[cond_one & cond_two]\n .groupby("movie_id", sort=False)["rating"]\n .agg("mean")\n .reset_index()\n )\n\n # Filter movies with the highest average rating\n highest_avg_rating_movies = avg_rating_by_movie[\n avg_rating_by_movie["rating"] == avg_rating_by_movie["rating"].max()\n ]\n\n # Merge with movies to get the movie name(s) and filter the needed columns\n result_movies = highest_avg_rating_movies.merge(movies, on="movie_id")[\n ["rating", "title"]\n ]\n\n # Sort movies to get the lexicographically smallest movie name\n selected_movie = (\n result_movies.sort_values(by="title", ascending=True).head(1)["title"].values[0]\n )\n\n # Get the number of reviews each \'user_id\' wrote\n reviews_per_user = (\n movie_rating.groupby("user_id", sort=False)["user_id"]\n .count()\n .reset_index(name="reviews")\n )\n\n # Filter user(s) with the most reviews written\n most_reviews_users = reviews_per_user[\n reviews_per_user["reviews"] == reviews_per_user["reviews"].max()\n ]\n\n # Merge with users to get the user name(s) and sort them to get one user\n selected_user = (\n most_reviews_users.merge(users, on="user_id")[["name"]]\n .sort_values(by="name")\n .head(1)\n .values[0][0]\n )\n\n # Create a DataFrame to return\n return pd.DataFrame({"results": [selected_user, selected_movie]})\n\n``` | 0 | Given an array `nums`. We define a running sum of an array as `runningSum[i] = sum(nums[0]...nums[i])`.
Return the running sum of `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[1,3,6,10\]
**Explanation:** Running sum is obtained as follows: \[1, 1+2, 1+2+3, 1+2+3+4\].
**Example 2:**
**Input:** nums = \[1,1,1,1,1\]
**Output:** \[1,2,3,4,5\]
**Explanation:** Running sum is obtained as follows: \[1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1\].
**Example 3:**
**Input:** nums = \[3,1,2,10,1\]
**Output:** \[3,4,6,16,17\]
**Constraints:**
* `1 <= nums.length <= 1000`
* `-10^6 <= nums[i] <= 10^6` | null |
Python Elegant & Short | O(1) | Recursive / Iterative / Bit Manipulation | number-of-steps-to-reduce-a-number-to-zero | 0 | 1 | ## Recursive solution\n\n```\nclass Solution:\n """\n Time: O(log(n))\n Memory: O(log(n))\n """\n\n def numberOfSteps(self, num: int) -> int:\n if num == 0:\n return 0\n return 1 + self.numberOfSteps(num - 1 if num & 1 else num >> 1)\n```\n\n## Iterative solution\n\n```\nclass Solution:\n """\n Time: O(log(n))\n Memory: O(1)\n """\n\n def numberOfSteps(self, num: int) -> int:\n steps = 0\n\n while num != 0:\n steps += 1\n if num & 1:\n num -= 1\n else:\n num >>= 1\n\n return steps\n```\n\n## Bit Manipulation solution\n\n```\nclass Solution:\n """\n Time: O(1)\n Memory: O(1)\n """\n\n def numberOfSteps(self, num: int) -> int:\n if num == 0:\n return 0\n return num.bit_length() - 1 + num.bit_count()\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 217 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
Python Elegant & Short | O(1) | Recursive / Iterative / Bit Manipulation | number-of-steps-to-reduce-a-number-to-zero | 0 | 1 | ## Recursive solution\n\n```\nclass Solution:\n """\n Time: O(log(n))\n Memory: O(log(n))\n """\n\n def numberOfSteps(self, num: int) -> int:\n if num == 0:\n return 0\n return 1 + self.numberOfSteps(num - 1 if num & 1 else num >> 1)\n```\n\n## Iterative solution\n\n```\nclass Solution:\n """\n Time: O(log(n))\n Memory: O(1)\n """\n\n def numberOfSteps(self, num: int) -> int:\n steps = 0\n\n while num != 0:\n steps += 1\n if num & 1:\n num -= 1\n else:\n num >>= 1\n\n return steps\n```\n\n## Bit Manipulation solution\n\n```\nclass Solution:\n """\n Time: O(1)\n Memory: O(1)\n """\n\n def numberOfSteps(self, num: int) -> int:\n if num == 0:\n return 0\n return num.bit_length() - 1 + num.bit_count()\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 217 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
simple beginner friendly solutions | number-of-steps-to-reduce-a-number-to-zero | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nusing while loop and recursion\n\n# Complexity\n- Time complexity: $$O(logN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code 1\n```\nclass Solution:\n def numberOfSteps(self, n: int) -> int:\n is = 0\n while n > 0:\n if n % 2==0:\n else:\n n -= 1\n s += 1\n return s\n```\n\n# Code 2\n```\nclass Solution:\n def numberOfSteps(self, n: int) -> int:\n if n == 0:\n return 0\n if n % 2==0:\n return 1 + self.numberOfSteps(n//2)\n else:\n return 1 + self.numberOfSteps(n-1)\n``` | 1 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
simple beginner friendly solutions | number-of-steps-to-reduce-a-number-to-zero | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nusing while loop and recursion\n\n# Complexity\n- Time complexity: $$O(logN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code 1\n```\nclass Solution:\n def numberOfSteps(self, n: int) -> int:\n is = 0\n while n > 0:\n if n % 2==0:\n else:\n n -= 1\n s += 1\n return s\n```\n\n# Code 2\n```\nclass Solution:\n def numberOfSteps(self, n: int) -> int:\n if n == 0:\n return 0\n if n % 2==0:\n return 1 + self.numberOfSteps(n//2)\n else:\n return 1 + self.numberOfSteps(n-1)\n``` | 1 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Beats 94.19% || Number of steps to reduce a number to zero | number-of-steps-to-reduce-a-number-to-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfSteps(self, n: int) -> int:\n step=0\n while n!=0:\n if n%2==0:\n n/=2\n step+=1\n else:\n n-=1\n step+=1\n return step\n``` | 3 | Given an integer `num`, return _the number of steps to reduce it to zero_.
In one step, if the current number is even, you have to divide it by `2`, otherwise, you have to subtract `1` from it.
**Example 1:**
**Input:** num = 14
**Output:** 6
**Explanation:**
Step 1) 14 is even; divide by 2 and obtain 7.
Step 2) 7 is odd; subtract 1 and obtain 6.
Step 3) 6 is even; divide by 2 and obtain 3.
Step 4) 3 is odd; subtract 1 and obtain 2.
Step 5) 2 is even; divide by 2 and obtain 1.
Step 6) 1 is odd; subtract 1 and obtain 0.
**Example 2:**
**Input:** num = 8
**Output:** 4
**Explanation:**
Step 1) 8 is even; divide by 2 and obtain 4.
Step 2) 4 is even; divide by 2 and obtain 2.
Step 3) 2 is even; divide by 2 and obtain 1.
Step 4) 1 is odd; subtract 1 and obtain 0.
**Example 3:**
**Input:** num = 123
**Output:** 12
**Constraints:**
* `0 <= num <= 106` | Check 8 directions around the King. Find the nearest queen in each direction. |
Beats 94.19% || Number of steps to reduce a number to zero | number-of-steps-to-reduce-a-number-to-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfSteps(self, n: int) -> int:\n step=0\n while n!=0:\n if n%2==0:\n n/=2\n step+=1\n else:\n n-=1\n step+=1\n return step\n``` | 3 | Given a rectangular pizza represented as a `rows x cols` matrix containing the following characters: `'A'` (an apple) and `'.'` (empty cell) and given the integer `k`. You have to cut the pizza into `k` pieces using `k-1` cuts.
For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.
_Return the number of ways of cutting the pizza such that each piece contains **at least** one apple._ Since the answer can be a huge number, return this modulo 10^9 + 7.
**Example 1:**
**Input:** pizza = \[ "A.. ", "AAA ", "... "\], k = 3
**Output:** 3
**Explanation:** The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.
**Example 2:**
**Input:** pizza = \[ "A.. ", "AA. ", "... "\], k = 3
**Output:** 1
**Example 3:**
**Input:** pizza = \[ "A.. ", "A.. ", "... "\], k = 1
**Output:** 1
**Constraints:**
* `1 <= rows, cols <= 50`
* `rows == pizza.length`
* `cols == pizza[i].length`
* `1 <= k <= 10`
* `pizza` consists of characters `'A'` and `'.'` only. | Simulate the process to get the final answer. |
Python3 Easy Solution. Beats 97.53%. O(n) | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first, I used the sum() function for every subarray and divided it by k but then I realized, the time complexity would be better if we were just doing 2 computations per subarray so I created a running sum which can be easily calculated.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialize a running sum to take the runtime down by a little bit. Then we initialize our left ptr and result variable.\nWe itterate through the whole array with our right pointer and \nfind the average of each subarray of length K. \nIf the average is >= threshold we increment res by 1.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n res = 0\n runSum = sum(arr[:k-1])\n l = 0\n for r in range(k-1, len(arr)):\n runSum += arr[r]\n if runSum//k >= threshold:\n res += 1\n runSum -= arr[l]\n l+=1\n return res\n``` | 1 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Easy | Python Solution | Prefix Sum | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | # Code\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n\n currLen = 0\n currSum = 0\n ans = 0\n\n for i in range(0, len(arr)):\n\n if currLen == k:\n\n if currSum >= threshold:\n ans += 1\n\n currSum = currSum - (arr[i-k]/k)\n currLen -= 1\n\n currSum += (arr[i]/k)\n currLen += 1\n\n if currSum >= threshold:\n ans += 1\n \n return ans\n\n\n```\nDo upvote if you like the Solution :) | 1 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
easy python 2 pointers solution. DO UPVOTE!!! | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n res = 0\n cur_sum = sum(arr[:k - 1])\n \n for l in range(len(arr) - k + 1):\n cur_sum += arr[l + k - 1]\n if cur_sum >= k * threshold:\n res += 1\n cur_sum -= arr[l]\n \n return res\n``` | 1 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python Solution | Easy Approach ✅ | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | ```\ncount = 0\ncurrent_sum = sum(arr[:k]) # 1-st window\nif current_sum / k >= float(threshold): # check for 1-st window\n\tcount += 1\n\nfor i in range(len(arr) - k):\n\tcurrent_sum += (-1) * arr[i] + arr[i + k] # subtract 1-st element of current window & add the k-th\n\tif current_sum / k >= float(threshold):\n\t\tcount += 1\nreturn count\n``` | 2 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
🔥 [Python3] Easy, beats 99% 🔥 | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | ```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n res, s = 0, 0\n threshold = threshold * k\n s = sum(arr[:k-1])\n\n for r in range(k-1, len(arr)):\n s += arr[r]\n if s >= threshold: res +=1\n s -= arr[r-k+1]\n\n return res\n``` | 5 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
[Python 3] Sliding window - Fixed size approach | O(N) Time | O(1) Space | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | # Intuition\nThe question asks us to do something in a subarray of size `k`. This is quite standard with **Sliding Window** - *fixed size* problems, where `k` is the fixed size of the window.\n\n### What is a Sliding Window of fixed size ?\n> The fixed-size sliding window technique is a computer science algorithm that uses a predefined window size that remains constant throughout the problem-solving process. The window size is usually stated in the problem, for example, "find the highest sum of three contiguous numbers in the following array". The window size will be three, and the action will be summing and comparing. \n> \n> The fixed-size sliding window technique is often used to deal with problems involving subarrays of a fixed size. These problems may include finding the maximum or minimum sum of consecutive `k` elements in an array. \n\n\n# Approach\nThe idea behind having a fixed sliding window is to maintain two pointers that are k apart from each other and fit a certain constraint.\n1. Keep two pointers `l` and `r`\n\n2. Expand the window until we get a window size `k`. We can do this by moving `r` towards right until we get a size `k` - you can do this either by a `while` loop or a regular `for` loop. At each point of expanding the window, we will add the current value to our running sum\n\n3. Close the window once we have window of size `k`, that is `l - r > k`. While closing the window, that is incrementing left pointer by 1, we will also remove that value from the running sum\n\n4. Once we get a running sum equal to threshold, we increment our result counter by 1\n\n# Complexity\n- Time complexity:\nO(N) - N being number of elements in arr\n\n- Space complexity:\nO(1) - Because we only use three additional variables\n\n# Code\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n leftIdx, subarraySum, subarrayCount = 0, 0, 0\n\n for rightIdx in range(len(arr)):\n\n # close window\n if rightIdx - leftIdx + 1 > k:\n subarraySum -= arr[leftIdx]\n leftIdx += 1\n\n # open window\n subarraySum += arr[rightIdx]\n if ((rightIdx - leftIdx + 1) == k) and (subarraySum / k) >= threshold:\n subarrayCount += 1\n return subarrayCount\n \n```\n\n#### Note:\nPlease leave a comment if you think something is incorrect. \n\n\uD83D\uDC4D **Upvote if you like the approach.** \n\nThank you.\n | 5 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python3 simple and easy solution || sliding window | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | # Code\n```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n count = 0\n # avg >= threshold , avg = sum(subarray) / k >= threshold\n # thus, sum(subarray) >= k * threshold\n target = k * threshold \n\n curr = 0\n for i in range(k - 1):\n curr += arr[i]\n\n for i in range(k - 1, len(arr)):\n curr += arr[i]\n if curr >= target:\n count += 1\n curr -= arr[i - k + 1]\n \n return count\n``` | 2 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Python || 91.78%Faster || Sliding Window || O(N) Solution | number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold | 0 | 1 | ```\nclass Solution:\n def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:\n c,j,n=0,0,len(arr)\n s=sum(arr[:k])\n if s>=k*threshold:\n c=1\n for i in range(k,n):\n s+=arr[i]-arr[j]\n if s>=k*threshold:\n c+=1\n j+=1\n return c\n```\n\n**Upvote if you like the solution or ask if there is any query** | 2 | Given an array of integers `arr` and two integers `k` and `threshold`, return _the number of sub-arrays of size_ `k` _and average greater than or equal to_ `threshold`.
**Example 1:**
**Input:** arr = \[2,2,2,2,5,5,5,8\], k = 3, threshold = 4
**Output:** 3
**Explanation:** Sub-arrays \[2,5,5\],\[5,5,5\] and \[5,5,8\] have averages 4, 5 and 6 respectively. All other sub-arrays of size 3 have averages less than 4 (the threshold).
**Example 2:**
**Input:** arr = \[11,13,17,23,29,31,7,5,2,3\], k = 3, threshold = 5
**Output:** 6
**Explanation:** The first 6 sub-arrays of size 3 have averages greater than 5. Note that averages are not integers.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 104`
* `1 <= k <= arr.length`
* `0 <= threshold <= 104` | Think on Dynamic Programming. DP(pos, last) which means we are at the position pos having as last the last character seen. |
Easiest Array Solution (Beats 90%) | angle-between-hands-of-a-clock | 0 | 1 | # Code\n```\nclass Solution:\n def angleClock(self, hour: int, minutes: int) -> float:\n hour = hour % 12\n poss = [abs((((hour * 5) + (5 * (minutes / 60))) * 6) - minutes * 6), abs((360 - (((hour * 5) + (5 * (minutes / 60))) * 6)) + (360 - minutes * 6)), abs(((((hour * 5) + (5 * (minutes / 60))) * 6)) + (360 - minutes * 6)), abs((360 - (((hour * 5) + (5 * (minutes / 60))) * 6)) + (minutes * 6))]\n return min(poss)\n``` | 1 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Easiest Array Solution (Beats 90%) | angle-between-hands-of-a-clock | 0 | 1 | # Code\n```\nclass Solution:\n def angleClock(self, hour: int, minutes: int) -> float:\n hour = hour % 12\n poss = [abs((((hour * 5) + (5 * (minutes / 60))) * 6) - minutes * 6), abs((360 - (((hour * 5) + (5 * (minutes / 60))) * 6)) + (360 - minutes * 6)), abs(((((hour * 5) + (5 * (minutes / 60))) * 6)) + (360 - minutes * 6)), abs((360 - (((hour * 5) + (5 * (minutes / 60))) * 6)) + (minutes * 6))]\n return min(poss)\n``` | 1 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
[Java/Python/C++] Simple Math on Clock angles | angle-between-hands-of-a-clock | 1 | 1 | **Basic Unitary Method**\n(Credits - @rajcm)\n\n**Hour Hand**\nIn 12 hours Hour hand complete whole circle and cover 360\xB0\nSo, 1 hour = 360\xB0 / 12 = 30\xB0\n\nSince 1 hours = 30\xB0\nIn 1 minute, hours hand rotate -> 30\xB0 / 60 = 0.5\xB0\nSo total angle because of minutes by hour hand is `minutes/60 * 30` or `minutes * 0.5`\n\n**Minute Hand**\nIn 60 minutes Minute Hand completes whole circle and cover 360\xB0.\nSo, 1 minute -> 360\xB0 / 60 = 6\xB0\n\n<br><br>\n\n**Java**\n```\nclass Solution {\n public double angleClock(int hour, int minutes) {\n \n // Degree covered by hour hand (hour area + minutes area)\n double h = (hour%12 * 30) + ((double)minutes/60 * 30);\n \n // Degree covered by minute hand (Each minute = 6 degree)\n double m = minutes * 6;\n \n // Absolute angle between them\n double angle = Math.abs(m - h);\n \n // If the angle is obtuse (>180), convert it to acute (0<=x<=180)\n if (angle > 180) angle = 360.0 - angle;\n \n return angle;\n }\n}\n```\n<br><br>\n\n**Python**\n\n```\nclass Solution:\n def angleClock(self, hour: int, minutes: int) -> float:\n \n # Degree covered by hour hand (hour area + minutes area)\n h = (hour%12 * 30) + (minutes/60 * 30)\n \n # Degree covered by minute hand (Each minute = 6 degree)\n m = minutes * 6\n \n # Absolute angle between them\n angle = abs(m - h)\n \n # If the angle is obtuse (>180), convert it to acute (0<=x<=180)\n if angle > 180:\n angle = 360.0 - angle\n \n return (angle)\n```\n\n**C++**\nCredits : [MichaelZ](https://leetcode.com/michaelz/)\nThanks for the C++ code.\n```\ndouble angleClock(int hour, int minutes) {\n double minute=minutes*6, hr=hour*30+(double)minutes/2, diff=abs(hr-minute);\n return min(diff, 360-diff);\n }\n```\t\n\nPlease upvote if you found this useful.\nIf you have any queries, please post in comment section.\nThank you | 170 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
[Java/Python/C++] Simple Math on Clock angles | angle-between-hands-of-a-clock | 1 | 1 | **Basic Unitary Method**\n(Credits - @rajcm)\n\n**Hour Hand**\nIn 12 hours Hour hand complete whole circle and cover 360\xB0\nSo, 1 hour = 360\xB0 / 12 = 30\xB0\n\nSince 1 hours = 30\xB0\nIn 1 minute, hours hand rotate -> 30\xB0 / 60 = 0.5\xB0\nSo total angle because of minutes by hour hand is `minutes/60 * 30` or `minutes * 0.5`\n\n**Minute Hand**\nIn 60 minutes Minute Hand completes whole circle and cover 360\xB0.\nSo, 1 minute -> 360\xB0 / 60 = 6\xB0\n\n<br><br>\n\n**Java**\n```\nclass Solution {\n public double angleClock(int hour, int minutes) {\n \n // Degree covered by hour hand (hour area + minutes area)\n double h = (hour%12 * 30) + ((double)minutes/60 * 30);\n \n // Degree covered by minute hand (Each minute = 6 degree)\n double m = minutes * 6;\n \n // Absolute angle between them\n double angle = Math.abs(m - h);\n \n // If the angle is obtuse (>180), convert it to acute (0<=x<=180)\n if (angle > 180) angle = 360.0 - angle;\n \n return angle;\n }\n}\n```\n<br><br>\n\n**Python**\n\n```\nclass Solution:\n def angleClock(self, hour: int, minutes: int) -> float:\n \n # Degree covered by hour hand (hour area + minutes area)\n h = (hour%12 * 30) + (minutes/60 * 30)\n \n # Degree covered by minute hand (Each minute = 6 degree)\n m = minutes * 6\n \n # Absolute angle between them\n angle = abs(m - h)\n \n # If the angle is obtuse (>180), convert it to acute (0<=x<=180)\n if angle > 180:\n angle = 360.0 - angle\n \n return (angle)\n```\n\n**C++**\nCredits : [MichaelZ](https://leetcode.com/michaelz/)\nThanks for the C++ code.\n```\ndouble angleClock(int hour, int minutes) {\n double minute=minutes*6, hr=hour*30+(double)minutes/2, diff=abs(hr-minute);\n return min(diff, 360-diff);\n }\n```\t\n\nPlease upvote if you found this useful.\nIf you have any queries, please post in comment section.\nThank you | 170 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Python - Easiest to understand! Comments - Clear and Concise | angle-between-hands-of-a-clock | 0 | 1 | **Solution**:\n```\nclass Solution:\n def angleClock(self, h, m):\n # Convert the hour hand to another minute hand\n m2 = (h%12 + m/60)*5\n \n # Calculate the difference between the two minute hands\n diff = abs(m-m2)\n \n # Convert the difference to an angle\n ang = diff*(360/60)\n \n # Return the smallest angle\n return min(360-ang, ang)\n``` | 2 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Python - Easiest to understand! Comments - Clear and Concise | angle-between-hands-of-a-clock | 0 | 1 | **Solution**:\n```\nclass Solution:\n def angleClock(self, h, m):\n # Convert the hour hand to another minute hand\n m2 = (h%12 + m/60)*5\n \n # Calculate the difference between the two minute hands\n diff = abs(m-m2)\n \n # Convert the difference to an angle\n ang = diff*(360/60)\n \n # Return the smallest angle\n return min(360-ang, ang)\n``` | 2 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Python one line solution based on aptitude formula | angle-between-hands-of-a-clock | 0 | 1 | ```\nclass Solution:\n def angleClock(self, hour: int, minutes: int) -> float:\n return min(abs(30*hour-5.5*minutes),360-abs(30*hour-5.5*minutes))\n \n``` | 2 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Python one line solution based on aptitude formula | angle-between-hands-of-a-clock | 0 | 1 | ```\nclass Solution:\n def angleClock(self, hour: int, minutes: int) -> float:\n return min(abs(30*hour-5.5*minutes),360-abs(30*hour-5.5*minutes))\n \n``` | 2 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Angle Between Hands of a Clock python solution | angle-between-hands-of-a-clock | 0 | 1 | def angleClock(self, hour: int, minutes: int) -> float:\n \n """\n As hour clock move by (360/12) is per hour + ((360/12)/60) per minutes\n """\n hours_degree = (360/12)*hour+(360/720)*minutes\n minute_degree = (360/60)*minutes\n res = abs(hours_degree-minute_degree)\n if res > 180:\n return 360-res\n return res | 1 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Angle Between Hands of a Clock python solution | angle-between-hands-of-a-clock | 0 | 1 | def angleClock(self, hour: int, minutes: int) -> float:\n \n """\n As hour clock move by (360/12) is per hour + ((360/12)/60) per minutes\n """\n hours_degree = (360/12)*hour+(360/720)*minutes\n minute_degree = (360/60)*minutes\n res = abs(hours_degree-minute_degree)\n if res > 180:\n return 360-res\n return res | 1 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
Solution | Python | angle-between-hands-of-a-clock | 0 | 1 | # Intuition\n- This is a tricky problem, here any `division` of whole `whole` numbers will be evealuated to `floor` division. \n*In Python 2.x, the division of two integers returns an integer result (floor division) instead of a float.*\nMaybe the author wanted to pay respect or whatever.\nSo:\n - You can try `return 1 / 2 ` and see `0` \n - That\'s why you need to divide by a `float` number\n\n\n\n- Also, the function `abs` Returns the absolute value of the argument.\n\n# Detailed Code\n```\nclass Solution(object):\n def angleClock(self, hour, minutes):\n """\n 1 hour = 30\n 1 minute = 6\n """\n if hour == 12:\n hour = 0\n hand_one_angle = hour * 30 + (minutes / 2.0)\n\n hand_two_angle = minutes * 6\n\n angle = hand_one_angle - hand_two_angle\n angle = abs(angle) \n\n return angle if angle <= 180 else 360 - angle\n```\n# Short code\n```\nclass Solution(object):\n def angleClock(self, hour, minutes):\n if hour == 12:\n hour = 0\n\n angle = abs(hour * 30 + (minutes / 2.0) - minutes * 6)\n return angle if angle <= 180 else 360 - angle\n``` | 1 | Given two numbers, `hour` and `minutes`, return _the smaller angle (in degrees) formed between the_ `hour` _and the_ `minute` _hand_.
Answers within `10-5` of the actual value will be accepted as correct.
**Example 1:**
**Input:** hour = 12, minutes = 30
**Output:** 165
**Example 2:**
**Input:** hour = 3, minutes = 30
**Output:** 75
**Example 3:**
**Input:** hour = 3, minutes = 15
**Output:** 7.5
**Constraints:**
* `1 <= hour <= 12`
* `0 <= minutes <= 59` | Keep track of the min and max frequencies. The number to be eliminated must have a frequency of 1, same as the others or the same +1. |
Solution | Python | angle-between-hands-of-a-clock | 0 | 1 | # Intuition\n- This is a tricky problem, here any `division` of whole `whole` numbers will be evealuated to `floor` division. \n*In Python 2.x, the division of two integers returns an integer result (floor division) instead of a float.*\nMaybe the author wanted to pay respect or whatever.\nSo:\n - You can try `return 1 / 2 ` and see `0` \n - That\'s why you need to divide by a `float` number\n\n\n\n- Also, the function `abs` Returns the absolute value of the argument.\n\n# Detailed Code\n```\nclass Solution(object):\n def angleClock(self, hour, minutes):\n """\n 1 hour = 30\n 1 minute = 6\n """\n if hour == 12:\n hour = 0\n hand_one_angle = hour * 30 + (minutes / 2.0)\n\n hand_two_angle = minutes * 6\n\n angle = hand_one_angle - hand_two_angle\n angle = abs(angle) \n\n return angle if angle <= 180 else 360 - angle\n```\n# Short code\n```\nclass Solution(object):\n def angleClock(self, hour, minutes):\n if hour == 12:\n hour = 0\n\n angle = abs(hour * 30 + (minutes / 2.0) - minutes * 6)\n return angle if angle <= 180 else 360 - angle\n``` | 1 | The **power** of the string is the maximum length of a non-empty substring that contains only one unique character.
Given a string `s`, return _the **power** of_ `s`.
**Example 1:**
**Input:** s = "leetcode "
**Output:** 2
**Explanation:** The substring "ee " is of length 2 with the character 'e' only.
**Example 2:**
**Input:** s = "abbcccddddeeeeedcba "
**Output:** 5
**Explanation:** The substring "eeeee " is of length 5 with the character 'e' only.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters. | The tricky part is determining how the minute hand affects the position of the hour hand. Calculate the angles separately then find the difference. |
📌📌Python3 || ⚡623 ms, faster than 98.86% of Python3 | jump-game-iv | 0 | 1 | \n```\ndef minJumps(self, arr: List[int]) -> int:\n if len(arr) == 1: return 0\n dict = collections.defaultdict(list)\n for i , n in enumerate(arr): dict[n].append(i)\n\n N = len(arr) \n visited = {0, N - 1}\n s1, s2 = {0}, {N - 1}\n step = 0\n while s1:\n if len(s1) > len(s2): s1, s2 = s2, s1\n\n s3 = set()\n while s1:\n i = s1.pop()\n for n in [i - 1, i + 1] + dict[arr[i]]:\n if n in s2: return step + 1\n if n in visited: continue\n if not 0 <= n < N: continue\n visited.add(n)\n s3.add(n)\n del dict[arr[i]]\n\n s1 = s3\n if s1: step = step + 1\n return -1\n```\nThe given code is for finding the minimum number of jumps required to reach the end of an array of integers, where each integer represents the maximum number of steps that can be taken forward from that position.\n\nHere\'s a stepwise explanation of the code:\n\n1. First, check if the length of the given array is 1, then return 0 as there is no need to jump in this case.\n1. Create a dictionary to store the indices of all the occurrences of each element in the array.\n1. Initialize two sets s1 and s2 with the starting and ending indices of the array, respectively.\n1. Initialize a variable step to 0 to keep track of the number of jumps required.\n1. While s1 is not empty, do the following:\n\t1. If the length of s1 is greater than s2, swap them so that s1 always contains the smaller set.\n\t1. Create a new set s3 to store the indices that can be reached from s1 in one jump.\n\t1. For each index i in s1, do the following:\n\t\t1. For each index j that can be reached from i in one jump (i.e., i-1, i+1, and all the indices in the dictionary that have the same value as arr[i]), do the following:\n\t\t\t1. If j is in s2, return step+1 as we have reached the end.\n\t\t\t1. If j is already visited, skip to the next index. \n\t\t\t1. \tIf j is not within the range of the array, skip to the next index. \n\t\t\t1. \tOtherwise, add j to the set s3 and mark it as visited. \n\t\t1. \tRemove the key-value pair corresponding to arr[i] from the dictionary.\n\t1. Set s1 to s3 and increment the variable step by 1.\n1. If we have not returned in the while loop, return -1 as it means that we have not reached the end of the array. | 2 | Given an array of integers `arr`, you are initially positioned at the first index of the array.
In one step you can jump from index `i` to index:
* `i + 1` where: `i + 1 < arr.length`.
* `i - 1` where: `i - 1 >= 0`.
* `j` where: `arr[i] == arr[j]` and `i != j`.
Return _the minimum number of steps_ to reach the **last index** of the array.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[100,-23,-23,404,100,23,23,23,3,404\]
**Output:** 3
**Explanation:** You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.
**Example 2:**
**Input:** arr = \[7\]
**Output:** 0
**Explanation:** Start index is the last index. You do not need to jump.
**Example 3:**
**Input:** arr = \[7,6,9,6,9,6,9,7\]
**Output:** 1
**Explanation:** You can jump directly from index 0 to index 7 which is last index of the array.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `-108 <= arr[i] <= 108` | Intuitively performing all shift operations is acceptable due to the constraints. You may notice that left shift cancels the right shift, so count the total left shift times (may be negative if the final result is right shift), and perform it once. |
📌📌Python3 || ⚡623 ms, faster than 98.86% of Python3 | jump-game-iv | 0 | 1 | \n```\ndef minJumps(self, arr: List[int]) -> int:\n if len(arr) == 1: return 0\n dict = collections.defaultdict(list)\n for i , n in enumerate(arr): dict[n].append(i)\n\n N = len(arr) \n visited = {0, N - 1}\n s1, s2 = {0}, {N - 1}\n step = 0\n while s1:\n if len(s1) > len(s2): s1, s2 = s2, s1\n\n s3 = set()\n while s1:\n i = s1.pop()\n for n in [i - 1, i + 1] + dict[arr[i]]:\n if n in s2: return step + 1\n if n in visited: continue\n if not 0 <= n < N: continue\n visited.add(n)\n s3.add(n)\n del dict[arr[i]]\n\n s1 = s3\n if s1: step = step + 1\n return -1\n```\nThe given code is for finding the minimum number of jumps required to reach the end of an array of integers, where each integer represents the maximum number of steps that can be taken forward from that position.\n\nHere\'s a stepwise explanation of the code:\n\n1. First, check if the length of the given array is 1, then return 0 as there is no need to jump in this case.\n1. Create a dictionary to store the indices of all the occurrences of each element in the array.\n1. Initialize two sets s1 and s2 with the starting and ending indices of the array, respectively.\n1. Initialize a variable step to 0 to keep track of the number of jumps required.\n1. While s1 is not empty, do the following:\n\t1. If the length of s1 is greater than s2, swap them so that s1 always contains the smaller set.\n\t1. Create a new set s3 to store the indices that can be reached from s1 in one jump.\n\t1. For each index i in s1, do the following:\n\t\t1. For each index j that can be reached from i in one jump (i.e., i-1, i+1, and all the indices in the dictionary that have the same value as arr[i]), do the following:\n\t\t\t1. If j is in s2, return step+1 as we have reached the end.\n\t\t\t1. If j is already visited, skip to the next index. \n\t\t\t1. \tIf j is not within the range of the array, skip to the next index. \n\t\t\t1. \tOtherwise, add j to the set s3 and mark it as visited. \n\t\t1. \tRemove the key-value pair corresponding to arr[i] from the dictionary.\n\t1. Set s1 to s3 and increment the variable step by 1.\n1. If we have not returned in the while loop, return -1 as it means that we have not reached the end of the array. | 2 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.