title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
BFS Using Queue | jump-game-iv | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n\n # set pos[x][0] = True as unvisited indicator\n pos = collections.defaultdict(lambda: [True])\n\n # Store positions i based on value x=arr[i]\n # reverse is essential as we are finding shortest path backward\n for i, x in reversed(list(enumerate(arr))):\n pos[x].append(i)\n\n # res = result table, q = BFS queue\n n = len(arr)\n res = list(range(n-1, -1, -1))\n q = collections.deque()\n\n # start the search backward\n for k in range(n-1, -1, -1):\n q.append(k)\n while q:\n i = q.popleft()\n if pos[arr[i]][0]: # if unvisited\n pos[arr[i]][0] = False\n\n # create jump portal for all positions with same value\n for j in pos[arr[i]][1:]:\n res[j] = min(res[j], res[i]+1)\n q.append(j)\n\n # add adjcent posisitons to queue\n for j in pos[arr[i]][1:]:\n if j > 0:\n res[j-1] = min(res[j-1], res[j]+1)\n q.append(j-1)\n if j < n-1:\n res[j+1] = min(res[j+1], res[j]+1)\n q.append(j+1)\n return res[0]\n \n``` | 1 | Given an array of integers `arr`, you are initially positioned at the first index of the array.
In one step you can jump from index `i` to index:
* `i + 1` where: `i + 1 < arr.length`.
* `i - 1` where: `i - 1 >= 0`.
* `j` where: `arr[i] == arr[j]` and `i != j`.
Return _the minimum number of steps_ to reach the **last index** of the array.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[100,-23,-23,404,100,23,23,23,3,404\]
**Output:** 3
**Explanation:** You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.
**Example 2:**
**Input:** arr = \[7\]
**Output:** 0
**Explanation:** Start index is the last index. You do not need to jump.
**Example 3:**
**Input:** arr = \[7,6,9,6,9,6,9,7\]
**Output:** 1
**Explanation:** You can jump directly from index 0 to index 7 which is last index of the array.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `-108 <= arr[i] <= 108` | Intuitively performing all shift operations is acceptable due to the constraints. You may notice that left shift cancels the right shift, so count the total left shift times (may be negative if the final result is right shift), and perform it once. |
BFS Using Queue | jump-game-iv | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n\n # set pos[x][0] = True as unvisited indicator\n pos = collections.defaultdict(lambda: [True])\n\n # Store positions i based on value x=arr[i]\n # reverse is essential as we are finding shortest path backward\n for i, x in reversed(list(enumerate(arr))):\n pos[x].append(i)\n\n # res = result table, q = BFS queue\n n = len(arr)\n res = list(range(n-1, -1, -1))\n q = collections.deque()\n\n # start the search backward\n for k in range(n-1, -1, -1):\n q.append(k)\n while q:\n i = q.popleft()\n if pos[arr[i]][0]: # if unvisited\n pos[arr[i]][0] = False\n\n # create jump portal for all positions with same value\n for j in pos[arr[i]][1:]:\n res[j] = min(res[j], res[i]+1)\n q.append(j)\n\n # add adjcent posisitons to queue\n for j in pos[arr[i]][1:]:\n if j > 0:\n res[j-1] = min(res[j-1], res[j]+1)\n q.append(j-1)\n if j < n-1:\n res[j+1] = min(res[j+1], res[j]+1)\n q.append(j+1)\n return res[0]\n \n``` | 1 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
✔️✔️✔️ BFS - beats 94% - Python 3 - Solution 🔥🔥🔥 | jump-game-iv | 0 | 1 | \n\n# Approach\nThis code finds the minimum number of jumps needed to reach the end of an array by performing a breadth-first search. It uses a dictionary to store indices of elements with the same value, a queue to track indices to visit, and a set to track visited indices. It returns the number of steps required to reach the end.\n\n# Complexity\n- Time complexity: **O(N)**\n- Not 100% sure about that one. If you think it\'s different, please write down below. \n\n\n\n---\n\n\n\n- Space complexity: **O(N)**\n\n\n\n# Code\n```\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n edges, n = defaultdict(list), len(arr)\n for i in range(n):\n edges[arr[i]].append(i)\n queue, visited, steps = deque([0]), set([0]), 0\n while queue:\n for _ in range(len(queue)):\n idx = queue.popleft()\n if idx == n-1:\n return steps\n for new_idx in [idx-1, idx+1] + edges.pop(arr[idx], []):\n if 0 <= new_idx < n and new_idx not in visited:\n if new_idx == n-1:\n return steps + 1\n queue.append(new_idx)\n visited.add(new_idx)\n steps += 1\n\n``` | 1 | Given an array of integers `arr`, you are initially positioned at the first index of the array.
In one step you can jump from index `i` to index:
* `i + 1` where: `i + 1 < arr.length`.
* `i - 1` where: `i - 1 >= 0`.
* `j` where: `arr[i] == arr[j]` and `i != j`.
Return _the minimum number of steps_ to reach the **last index** of the array.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[100,-23,-23,404,100,23,23,23,3,404\]
**Output:** 3
**Explanation:** You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.
**Example 2:**
**Input:** arr = \[7\]
**Output:** 0
**Explanation:** Start index is the last index. You do not need to jump.
**Example 3:**
**Input:** arr = \[7,6,9,6,9,6,9,7\]
**Output:** 1
**Explanation:** You can jump directly from index 0 to index 7 which is last index of the array.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `-108 <= arr[i] <= 108` | Intuitively performing all shift operations is acceptable due to the constraints. You may notice that left shift cancels the right shift, so count the total left shift times (may be negative if the final result is right shift), and perform it once. |
✔️✔️✔️ BFS - beats 94% - Python 3 - Solution 🔥🔥🔥 | jump-game-iv | 0 | 1 | \n\n# Approach\nThis code finds the minimum number of jumps needed to reach the end of an array by performing a breadth-first search. It uses a dictionary to store indices of elements with the same value, a queue to track indices to visit, and a set to track visited indices. It returns the number of steps required to reach the end.\n\n# Complexity\n- Time complexity: **O(N)**\n- Not 100% sure about that one. If you think it\'s different, please write down below. \n\n\n\n---\n\n\n\n- Space complexity: **O(N)**\n\n\n\n# Code\n```\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n edges, n = defaultdict(list), len(arr)\n for i in range(n):\n edges[arr[i]].append(i)\n queue, visited, steps = deque([0]), set([0]), 0\n while queue:\n for _ in range(len(queue)):\n idx = queue.popleft()\n if idx == n-1:\n return steps\n for new_idx in [idx-1, idx+1] + edges.pop(arr[idx], []):\n if 0 <= new_idx < n and new_idx not in visited:\n if new_idx == n-1:\n return steps + 1\n queue.append(new_idx)\n visited.add(new_idx)\n steps += 1\n\n``` | 1 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Clean Codes🔥🔥|| Full Explanation✅|| Breadth First Search✅|| C++|| Java|| Python3 | jump-game-iv | 1 | 1 | # Intuition :\n- We ha ve to find the minimum number of jumps needed to reach the last index of an array. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- The idea is to use a **Breadth First Search** approach to explore all the possible paths starting from the first index.\n\n---\n\n\n\n# Steps needed to solve the Problem :\n\n ***\u27A1\uFE0FStep 1: Initialize data structures***\n- The first step is to initialize few data structures that will be used later in the algorithm. \n- Create a map to store the indices of each value in the input array, a queue to store the indices of the current nodes to be visited, and a boolean array to mark whether each index has been seen before:\n```\nfinal int n = arr.length;\n\n// Initialize a map to store the indices of each value in the array\nMap<Integer, List<Integer>> graph = new HashMap<>();\n\n// Initialize a queue with the first index and mark it as seen\nQueue<Integer> q = new ArrayDeque<>(Arrays.asList(0));\n\n// Initialize a boolean array to keep track of visited indices\nboolean[] seen = new boolean[n];\nseen[0] = true;\n\n```\n***\u27A1\uFE0FStep 2: Build the graph***\n- Next step is to build a graph that represents the relationships between the elements in the input array. And loop through the array and add each index to the list of indices for its corresponding value in the map:\n```\nfor (int i = 0; i < n; ++i) \n{\n // Add the current index to the list of indices for its corresponding value\n graph.putIfAbsent(arr[i], new ArrayList<>());\n graph.get(arr[i]).add(i);\n}\n\n```\n***\u27A1\uFE0FStep 3: BFS Algorithm***\n- Now, in this step enter a loop that performs a BFS algorithm to find the minimum number of jumps needed to reach the end of the array.\n- At each iteration of the loop, dequeue the next node from the queue, check if it\'s the last index of the array, and mark it as visited.\n- Then add the adjacent nodes to the list of indices for their corresponding value in the map, and enqueue any adjacent nodes that have not been visited yet:\n```\nfor (int steps = 0; !q.isEmpty(); ++steps) \n{\n // Iterate over all the nodes at the current level of the BFS\n for (int sz = q.size(); sz > 0; --sz) \n {\n // Dequeue the next node and check if it\'s the last index of the array\n final int i = q.poll();\n if (i == n - 1)\n return steps;\n seen[i] = true;\n final int u = arr[i];\n // Add the adjacent nodes to the list of indices for their corresponding value\n if (i + 1 < n)\n graph.get(u).add(i + 1);\n if (i - 1 >= 0)\n graph.get(u).add(i - 1);\n // Iterate over all the adjacent nodes and enqueue them if they haven\'t been seen yet\n for (final int v : graph.get(u)) \n {\n if (seen[v])\n continue;\n q.offer(v);\n }\n // Clear the list of indices for the current node value to avoid revisiting it\n graph.get(u).clear();\n }\n}\n\n```\n***\u27A1\uFE0FStep 4: Return the minimum number of jumps***\n- If the end of the array is reached, return the number of steps it took to get there. Otherwise, throw an error:\n```\n// If the last index is not reached, throw an exception\nthrow new IllegalArgumentException();\n\n```\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity :\n- Time complexity : O(N+K)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(N+K)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n***Let\'s Code it Up .\nThere may be minor syntax difference in C++ and Python***\n# Codes [C++ |Java |Python3] : With Comments\n```C++ []\nclass Solution {\npublic:\n int minJumps(vector<int>& arr) {\n const int n = arr.size();\n // {a: indices}\n unordered_map<int, vector<int>> graph;\n // Initialize queue with first index and mark as seen\n queue<int> q{{0}};\n vector<bool> seen(n);\n seen[0] = true;\n\n // Create graph where keys are elements and values are their indices in arr\n for (int i = 0; i < n; ++i)\n graph[arr[i]].push_back(i);\n\n // BFS\n for (int steps = 0; !q.empty(); ++steps) {\n // Process all nodes at current level\n for (int sz = q.size(); sz > 0; --sz) {\n const int i = q.front();\n q.pop();\n // If last index is reached, return number of steps\n if (i == n - 1)\n return steps;\n seen[i] = true;\n const int u = arr[i];\n // Add adjacent indices to graph\n if (i + 1 < n)\n graph[u].push_back(i + 1);\n if (i - 1 >= 0)\n graph[u].push_back(i - 1);\n // Process all adjacent nodes\n for (const int v : graph[u]) {\n if (seen[v])\n continue;\n q.push(v);\n }\n // Clear indices in graph to avoid revisiting\n graph[u].clear();\n }\n }\n // Should never reach here\n throw;\n }\n};\n```\n```Java []\nclass Solution \n{\n public int minJumps(int[] arr) \n {\n final int n = arr.length;\n // {a: indices}\n Map<Integer, List<Integer>> graph = new HashMap<>();\n // Initialize a map to store the indices of each value in the array\n Queue<Integer> q = new ArrayDeque<>(Arrays.asList(0));\n // Initialize a queue with the first index and mark it as seen\n boolean[] seen = new boolean[n];\n seen[0] = true;\n\n for (int i = 0; i < n; ++i) \n {\n // Add the current index to the list of indices for its corresponding value\n graph.putIfAbsent(arr[i], new ArrayList<>());\n graph.get(arr[i]).add(i);\n }\n\n for (int steps = 0; !q.isEmpty(); ++steps) \n {\n // Iterate over all the nodes at the current level of the BFS\n for (int sz = q.size(); sz > 0; --sz) \n {\n // Dequeue the next node and check if it\'s the last index of the array\n final int i = q.poll();\n if (i == n - 1)\n return steps;\n seen[i] = true;\n final int u = arr[i];\n // Add the adjacent nodes to the list of indices for their corresponding value\n if (i + 1 < n)\n graph.get(u).add(i + 1);\n if (i - 1 >= 0)\n graph.get(u).add(i - 1);\n // Iterate over all the adjacent nodes and enqueue them if they haven\'t been seen yet\n for (final int v : graph.get(u)) \n {\n if (seen[v])\n continue;\n q.offer(v);\n }\n // Clear the list of indices for the current node value to avoid revisiting it\n graph.get(u).clear();\n }\n }\n // If the last index is not reached, throw an exception\n throw new IllegalArgumentException();\n }\n}\n```\n```Python []\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n n = len(arr)\n # {num: indices}\n graph = collections.defaultdict(list)\n steps = 0\n q = collections.deque([0])\n seen = {0}\n\n # Create graph where keys are elements and values are their indices in arr\n for i, a in enumerate(arr):\n graph[a].append(i)\n\n # BFS\n while q:\n # Process all nodes at current level\n for _ in range(len(q)):\n i = q.popleft()\n # If last index is reached, return number of steps\n if i == n - 1:\n return steps\n seen.add(i)\n u = arr[i]\n # Add adjacent indices to graph\n if i + 1 < n:\n graph[u].append(i + 1)\n if i - 1 >= 0:\n graph[u].append(i - 1)\n # Process all adjacent nodes\n for v in graph[u]:\n if v in seen:\n continue\n q.append(v)\n # Clear indices in graph to avoid revisiting\n graph[u].clear()\n steps += 1\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 18 | Given an array of integers `arr`, you are initially positioned at the first index of the array.
In one step you can jump from index `i` to index:
* `i + 1` where: `i + 1 < arr.length`.
* `i - 1` where: `i - 1 >= 0`.
* `j` where: `arr[i] == arr[j]` and `i != j`.
Return _the minimum number of steps_ to reach the **last index** of the array.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[100,-23,-23,404,100,23,23,23,3,404\]
**Output:** 3
**Explanation:** You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.
**Example 2:**
**Input:** arr = \[7\]
**Output:** 0
**Explanation:** Start index is the last index. You do not need to jump.
**Example 3:**
**Input:** arr = \[7,6,9,6,9,6,9,7\]
**Output:** 1
**Explanation:** You can jump directly from index 0 to index 7 which is last index of the array.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `-108 <= arr[i] <= 108` | Intuitively performing all shift operations is acceptable due to the constraints. You may notice that left shift cancels the right shift, so count the total left shift times (may be negative if the final result is right shift), and perform it once. |
Clean Codes🔥🔥|| Full Explanation✅|| Breadth First Search✅|| C++|| Java|| Python3 | jump-game-iv | 1 | 1 | # Intuition :\n- We ha ve to find the minimum number of jumps needed to reach the last index of an array. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- The idea is to use a **Breadth First Search** approach to explore all the possible paths starting from the first index.\n\n---\n\n\n\n# Steps needed to solve the Problem :\n\n ***\u27A1\uFE0FStep 1: Initialize data structures***\n- The first step is to initialize few data structures that will be used later in the algorithm. \n- Create a map to store the indices of each value in the input array, a queue to store the indices of the current nodes to be visited, and a boolean array to mark whether each index has been seen before:\n```\nfinal int n = arr.length;\n\n// Initialize a map to store the indices of each value in the array\nMap<Integer, List<Integer>> graph = new HashMap<>();\n\n// Initialize a queue with the first index and mark it as seen\nQueue<Integer> q = new ArrayDeque<>(Arrays.asList(0));\n\n// Initialize a boolean array to keep track of visited indices\nboolean[] seen = new boolean[n];\nseen[0] = true;\n\n```\n***\u27A1\uFE0FStep 2: Build the graph***\n- Next step is to build a graph that represents the relationships between the elements in the input array. And loop through the array and add each index to the list of indices for its corresponding value in the map:\n```\nfor (int i = 0; i < n; ++i) \n{\n // Add the current index to the list of indices for its corresponding value\n graph.putIfAbsent(arr[i], new ArrayList<>());\n graph.get(arr[i]).add(i);\n}\n\n```\n***\u27A1\uFE0FStep 3: BFS Algorithm***\n- Now, in this step enter a loop that performs a BFS algorithm to find the minimum number of jumps needed to reach the end of the array.\n- At each iteration of the loop, dequeue the next node from the queue, check if it\'s the last index of the array, and mark it as visited.\n- Then add the adjacent nodes to the list of indices for their corresponding value in the map, and enqueue any adjacent nodes that have not been visited yet:\n```\nfor (int steps = 0; !q.isEmpty(); ++steps) \n{\n // Iterate over all the nodes at the current level of the BFS\n for (int sz = q.size(); sz > 0; --sz) \n {\n // Dequeue the next node and check if it\'s the last index of the array\n final int i = q.poll();\n if (i == n - 1)\n return steps;\n seen[i] = true;\n final int u = arr[i];\n // Add the adjacent nodes to the list of indices for their corresponding value\n if (i + 1 < n)\n graph.get(u).add(i + 1);\n if (i - 1 >= 0)\n graph.get(u).add(i - 1);\n // Iterate over all the adjacent nodes and enqueue them if they haven\'t been seen yet\n for (final int v : graph.get(u)) \n {\n if (seen[v])\n continue;\n q.offer(v);\n }\n // Clear the list of indices for the current node value to avoid revisiting it\n graph.get(u).clear();\n }\n}\n\n```\n***\u27A1\uFE0FStep 4: Return the minimum number of jumps***\n- If the end of the array is reached, return the number of steps it took to get there. Otherwise, throw an error:\n```\n// If the last index is not reached, throw an exception\nthrow new IllegalArgumentException();\n\n```\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity :\n- Time complexity : O(N+K)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(N+K)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n***Let\'s Code it Up .\nThere may be minor syntax difference in C++ and Python***\n# Codes [C++ |Java |Python3] : With Comments\n```C++ []\nclass Solution {\npublic:\n int minJumps(vector<int>& arr) {\n const int n = arr.size();\n // {a: indices}\n unordered_map<int, vector<int>> graph;\n // Initialize queue with first index and mark as seen\n queue<int> q{{0}};\n vector<bool> seen(n);\n seen[0] = true;\n\n // Create graph where keys are elements and values are their indices in arr\n for (int i = 0; i < n; ++i)\n graph[arr[i]].push_back(i);\n\n // BFS\n for (int steps = 0; !q.empty(); ++steps) {\n // Process all nodes at current level\n for (int sz = q.size(); sz > 0; --sz) {\n const int i = q.front();\n q.pop();\n // If last index is reached, return number of steps\n if (i == n - 1)\n return steps;\n seen[i] = true;\n const int u = arr[i];\n // Add adjacent indices to graph\n if (i + 1 < n)\n graph[u].push_back(i + 1);\n if (i - 1 >= 0)\n graph[u].push_back(i - 1);\n // Process all adjacent nodes\n for (const int v : graph[u]) {\n if (seen[v])\n continue;\n q.push(v);\n }\n // Clear indices in graph to avoid revisiting\n graph[u].clear();\n }\n }\n // Should never reach here\n throw;\n }\n};\n```\n```Java []\nclass Solution \n{\n public int minJumps(int[] arr) \n {\n final int n = arr.length;\n // {a: indices}\n Map<Integer, List<Integer>> graph = new HashMap<>();\n // Initialize a map to store the indices of each value in the array\n Queue<Integer> q = new ArrayDeque<>(Arrays.asList(0));\n // Initialize a queue with the first index and mark it as seen\n boolean[] seen = new boolean[n];\n seen[0] = true;\n\n for (int i = 0; i < n; ++i) \n {\n // Add the current index to the list of indices for its corresponding value\n graph.putIfAbsent(arr[i], new ArrayList<>());\n graph.get(arr[i]).add(i);\n }\n\n for (int steps = 0; !q.isEmpty(); ++steps) \n {\n // Iterate over all the nodes at the current level of the BFS\n for (int sz = q.size(); sz > 0; --sz) \n {\n // Dequeue the next node and check if it\'s the last index of the array\n final int i = q.poll();\n if (i == n - 1)\n return steps;\n seen[i] = true;\n final int u = arr[i];\n // Add the adjacent nodes to the list of indices for their corresponding value\n if (i + 1 < n)\n graph.get(u).add(i + 1);\n if (i - 1 >= 0)\n graph.get(u).add(i - 1);\n // Iterate over all the adjacent nodes and enqueue them if they haven\'t been seen yet\n for (final int v : graph.get(u)) \n {\n if (seen[v])\n continue;\n q.offer(v);\n }\n // Clear the list of indices for the current node value to avoid revisiting it\n graph.get(u).clear();\n }\n }\n // If the last index is not reached, throw an exception\n throw new IllegalArgumentException();\n }\n}\n```\n```Python []\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n n = len(arr)\n # {num: indices}\n graph = collections.defaultdict(list)\n steps = 0\n q = collections.deque([0])\n seen = {0}\n\n # Create graph where keys are elements and values are their indices in arr\n for i, a in enumerate(arr):\n graph[a].append(i)\n\n # BFS\n while q:\n # Process all nodes at current level\n for _ in range(len(q)):\n i = q.popleft()\n # If last index is reached, return number of steps\n if i == n - 1:\n return steps\n seen.add(i)\n u = arr[i]\n # Add adjacent indices to graph\n if i + 1 < n:\n graph[u].append(i + 1)\n if i - 1 >= 0:\n graph[u].append(i - 1)\n # Process all adjacent nodes\n for v in graph[u]:\n if v in seen:\n continue\n q.append(v)\n # Clear indices in graph to avoid revisiting\n graph[u].clear()\n steps += 1\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 18 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Python3 Solution ||Faster than 56% ||BFS|| Bahut TEZ | jump-game-iv | 0 | 1 | ```\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n h={}\n for i,e in enumerate(arr):\n if e not in h:\n h[e] = []\n h[e].append(i)\n q = [(0,0)]\n while q:\n n,d = q.pop(0)\n if n == len(arr)-1:\n return d\n if n+1 == len(arr)-1:\n return d+1\n if n+1 < len(arr) and h.get(arr[n+1]):\n q.append((n+1,d+1))\n if n-1 >= 0 and h.get(arr[n-1]):\n q.append((n-1,d+1))\n for i in h[arr[n]]:\n if i != n:\n q.append((i,d+1))\n if i == len(arr)-1:\n return d+1\n h[arr[n]] = [] | 4 | Given an array of integers `arr`, you are initially positioned at the first index of the array.
In one step you can jump from index `i` to index:
* `i + 1` where: `i + 1 < arr.length`.
* `i - 1` where: `i - 1 >= 0`.
* `j` where: `arr[i] == arr[j]` and `i != j`.
Return _the minimum number of steps_ to reach the **last index** of the array.
Notice that you can not jump outside of the array at any time.
**Example 1:**
**Input:** arr = \[100,-23,-23,404,100,23,23,23,3,404\]
**Output:** 3
**Explanation:** You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.
**Example 2:**
**Input:** arr = \[7\]
**Output:** 0
**Explanation:** Start index is the last index. You do not need to jump.
**Example 3:**
**Input:** arr = \[7,6,9,6,9,6,9,7\]
**Output:** 1
**Explanation:** You can jump directly from index 0 to index 7 which is last index of the array.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `-108 <= arr[i] <= 108` | Intuitively performing all shift operations is acceptable due to the constraints. You may notice that left shift cancels the right shift, so count the total left shift times (may be negative if the final result is right shift), and perform it once. |
Python3 Solution ||Faster than 56% ||BFS|| Bahut TEZ | jump-game-iv | 0 | 1 | ```\nclass Solution:\n def minJumps(self, arr: List[int]) -> int:\n h={}\n for i,e in enumerate(arr):\n if e not in h:\n h[e] = []\n h[e].append(i)\n q = [(0,0)]\n while q:\n n,d = q.pop(0)\n if n == len(arr)-1:\n return d\n if n+1 == len(arr)-1:\n return d+1\n if n+1 < len(arr) and h.get(arr[n+1]):\n q.append((n+1,d+1))\n if n-1 >= 0 and h.get(arr[n-1]):\n q.append((n-1,d+1))\n for i in h[arr[n]]:\n if i != n:\n q.append((i,d+1))\n if i == len(arr)-1:\n return d+1\n h[arr[n]] = [] | 4 | Given an integer `n`, return _a list of all **simplified** fractions between_ `0` _and_ `1` _(exclusive) such that the denominator is less-than-or-equal-to_ `n`. You can return the answer in **any order**.
**Example 1:**
**Input:** n = 2
**Output:** \[ "1/2 "\]
**Explanation:** "1/2 " is the only unique fraction with a denominator less-than-or-equal-to 2.
**Example 2:**
**Input:** n = 3
**Output:** \[ "1/2 ", "1/3 ", "2/3 "\]
**Example 3:**
**Input:** n = 4
**Output:** \[ "1/2 ", "1/3 ", "1/4 ", "2/3 ", "3/4 "\]
**Explanation:** "2/4 " is not a simplified fraction because it can be simplified to "1/2 ".
**Constraints:**
* `1 <= n <= 100` | Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j]. Start bfs from node 0 and keep distance. The answer is the distance when you reach node n-1. |
Python3 || Simple Binary Search approach | check-if-n-and-its-double-exist | 0 | 1 | \n# Code\n```\nclass Solution:\n def checkIfExist(self, arr: List[int]) -> bool:\n arr.sort()\n for i in range(len(arr)):\n product = arr[i]*2\n lo,hi = 0,len(arr)-1\n while lo<=hi:\n mid = (lo+hi)//2\n if arr[mid]==product and mid!= i:\n return True\n elif arr[mid]<product:\n lo+=1\n else:\n hi-=1\n return False\n```\n**Hope you find it helpful!** | 21 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
Haven't Seen this Solution Yet | Easy! | Python | check-if-n-and-its-double-exist | 0 | 1 | I am checking if `2*i` or `i/2` exists in `tmp`. I would note the \n`(i%2 == 0 and i/2 in tmp)` as we want to make sure our answer is a whole number, other no point in putting it in the array.\n# Code\n```\nclass Solution:\n def checkIfExist(self, arr: List[int]) -> bool:\n tmp = set()\n\n for i in arr:\n if 2*i in tmp or (i%2 == 0 and i/2 in tmp):\n return True\n tmp.add(i)\n \n \n``` | 1 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
4 LINES || PYTHON SOLUTION || USING SETS|| 40 MS||EASY | check-if-n-and-its-double-exist | 0 | 1 | ```\nclass Solution:\n def checkIfExist(self, arr: List[int]) -> bool:\n if arr.count(0) > 1: return 1\n S = set(arr) - {0}\n for i in arr:\n if 2*i in S: return 1\n return 0\n | 3 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
Easy O(n) solution with HashMap | check-if-n-and-its-double-exist | 0 | 1 | # Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def checkIfExist(self, arr: List[int]) -> bool:\n ans = set()\n\n for n in arr:\n if n in ans:\n return True\n\n ans.add(n * 2)\n\n # We can skip non integers values\n if n % 2 == 0:\n ans.add(int(n / 2))\n\n return False\n``` | 1 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
PYTHON || O( n logn ) || Binary Search | check-if-n-and-its-double-exist | 0 | 1 | Sort the array -> **n logn**\n\nIterate each element and search for its double usig binary search -> **n * log n**\n\n**OVERALL COMPLEXITY = O ( n logn )**\n\n```\nclass Solution:\n def checkIfExist(self, arr: List[int]) -> bool:\n arr.sort()\n n=len(arr)\n for i in range(n):\n k=arr[i]\n \n # binary search for negatives\n if k<0:\n lo=0\n hi=i\n while lo<hi:\n mid=(lo+hi)//2\n \n if arr[mid]==(2*k):\n return True\n elif arr[mid]<(2*k):\n lo=mid+1\n else:\n hi=mid\n \n # binary seach for non negatives\n else:\n lo=i+1\n hi=n\n while lo<hi:\n mid=(lo+hi)//2\n \n if arr[mid]==(k*2):\n return True\n elif arr[mid]<(k*2):\n lo=mid+1\n else:\n hi=mid\n \n return False\n``` | 5 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
python3, beat 85% ; 5 lines code | check-if-n-and-its-double-exist | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkIfExist(self, arr: List[int]) -> bool:\n l = len(arr)\n for i in range(l-1):\n if arr[i] * 2 in arr[0:i] + arr[i+1:] or arr[i] / 2 in arr[0:i]+ arr[i+1:]:\n return True\n return False\n\n\n \n``` | 2 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
Easy Solution in python | using Counter | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n cnt1=Counter(s)\n cnt2=Counter(t)\n sm=0\n for i,j in cnt2.items():\n if i in cnt1 and j>cnt1[i]:\n sm+=abs(j-cnt1[i])\n elif i not in cnt1:\n sm+=j\n return sm\n``` | 3 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
[Python 3] 1 line with Counter || beats 99% || 104ms 🥷🏼 | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | ```python3 []\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n return (Counter(s) - Counter(t)).total()\n```\n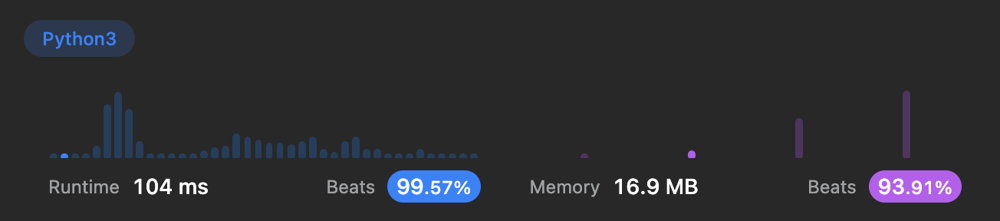\n\n[2186. Minimum Number of Steps to Make Two Strings Anagram II](https://leetcode.com/problems/minimum-number-of-steps-to-make-two-strings-anagram-ii/description/)\n```python3 []\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n cnt1, cnt2 = Counter(s), Counter(t)\n return (cnt1-cnt2).total() + (cnt2-cnt1).total()\n``` | 5 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
Python easy solution with explanation o(n) time and space: faster 97% | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | ##### Idea: the strings are equal in length \n* ##### Replacing is the only operation \n* ##### Find how many characters t and s shares \n* ##### And the remining would be the needed replacment \n\t1. * ##### count the letter occurance in the s \n\t1. * ##### iterate over t and when you get same letter as in s, substract it from s\n##### \n##### return the remaining number of letters in s\n\n```\n import collections \n memo = collections.defaultdict(int)\n # saving the number of occurance of characters in s\n for char in s:\n memo[char] += 1\n\t\t\t\n count = 0\n for char in t:\n if memo[char]:\n memo[char] -=1 # if char in t is also in memo, substract that from the counted number\n else:\n count += 1\n # return count #or\n return sum(memo.values())\n```\n\n##### IF this helps, please don\'t forget to upvote | 33 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
PYTHON SOLUTION - HASHMAP || EXPLAINED✔ | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | ```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n d1={}\n d2={}\n c=0\n #frequency of s\n for i in s:\n if i in d1:\n d1[i]+=1\n else:\n d1[i]=1\n #frequency of t \n for i in t:\n if i in d2:\n d2[i]+=1\n else:\n d2[i]=1\n #count the characters if s\'s characters not present in t\n #and if present and frequency of s\'s characters are greater than that of t\'s then store their\n #frequency diff(coz only those need to replace from t)\n for i in d1.keys():\n if i in d2:\n if d1[i]>d2[i]:\n c+=d1[i]-d2[i]\n else:\n c+=d1[i]\n return c\n \n```\n**PLEASE UPVOTE IF YOU FOUND THE SOLUTION HELPFUL** | 4 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
Very Easy one-liner Python Solution | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | \n\n# Approach\nAdd the differences in the frequencies of characters in t and s.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n return sum((Counter(t)-Counter(s)).values())\n``` | 2 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
Python || easy solution || beat~99% || using counter | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | # if you like the solution, Please upvote!!\n\tclass Solution:\n\t\tdef minSteps(self, s: str, t: str) -> int:\n\n\t\t\tcommon = Counter(s) & Counter(t)\n\t\t\tcount = sum(common.values())\n\n\t\t\treturn len(s) - count | 5 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
78% TC and 79% SC easy python solution | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | ```\ndef minSteps(self, s: str, t: str) -> int:\n\ts = Counter(s)\n\tt = Counter(t)\n\tans = 0\n\tfor i in t:\n\t\tif(i not in s):\n\t\t\tans += t[i]\n\t\telif(t[i] > s[i]):\n\t\t\tans += t[i]-s[i]\n\treturn ans\n``` | 2 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
Python solution | minimum-number-of-steps-to-make-two-strings-anagram | 0 | 1 | Delete the common characters in s and t; Number of remaining characters in t is the answer. \n\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n for ch in s:\n\t\t # Find and replace only one occurence of this character in t\n t = t.replace(ch, \'\', 1)\n \n return len(t)\n```\t | 19 | You are given two strings of the same length `s` and `t`. In one step you can choose **any character** of `t` and replace it with **another character**.
Return _the minimum number of steps_ to make `t` an anagram of `s`.
An **Anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "bab ", t = "aba "
**Output:** 1
**Explanation:** Replace the first 'a' in t with b, t = "bba " which is anagram of s.
**Example 2:**
**Input:** s = "leetcode ", t = "practice "
**Output:** 5
**Explanation:** Replace 'p', 'r', 'a', 'i' and 'c' from t with proper characters to make t anagram of s.
**Example 3:**
**Input:** s = "anagram ", t = "mangaar "
**Output:** 0
**Explanation:** "anagram " and "mangaar " are anagrams.
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `s.length == t.length`
* `s` and `t` consist of lowercase English letters only. | This problem can be broken down into two parts: finding the cycle, and finding the distance between each node and the cycle. How can we find the cycle? We can use DFS and keep track of the nodes we’ve seen, and the order that we see them in. Once we see a node we’ve already visited, we know that the cycle contains the node that was seen twice and all the nodes that we visited in between. Now that we know which nodes are part of the cycle, how can we find the distances? We can run a multi-source BFS starting from the nodes in the cycle and expanding outward. |
[Python3] linear scan | tweet-counts-per-frequency | 0 | 1 | Algorithm:\nScan through the time for a given `tweetName` and add the count in the corresponding interval. \n\nImplementation: \n```\nclass TweetCounts:\n\n def __init__(self):\n self.tweets = dict()\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n self.tweets.setdefault(tweetName, []).append(time)\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n if freq == "minute": seconds = 60 \n elif freq == "hour": seconds = 3600\n else: seconds = 86400\n \n ans = [0] * ((endTime - startTime)//seconds + 1)\n for t in self.tweets[tweetName]:\n if startTime <= t <= endTime: ans[(t-startTime)//seconds] += 1\n return ans \n```\nAnalysis:\nTime complexity `O(N)`\nSpace complexity `O(N)` | 39 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
[Python3] linear scan | tweet-counts-per-frequency | 0 | 1 | Algorithm:\nScan through the time for a given `tweetName` and add the count in the corresponding interval. \n\nImplementation: \n```\nclass TweetCounts:\n\n def __init__(self):\n self.tweets = dict()\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n self.tweets.setdefault(tweetName, []).append(time)\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n if freq == "minute": seconds = 60 \n elif freq == "hour": seconds = 3600\n else: seconds = 86400\n \n ans = [0] * ((endTime - startTime)//seconds + 1)\n for t in self.tweets[tweetName]:\n if startTime <= t <= endTime: ans[(t-startTime)//seconds] += 1\n return ans \n```\nAnalysis:\nTime complexity `O(N)`\nSpace complexity `O(N)` | 39 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Easy to Read Python Solution | tweet-counts-per-frequency | 0 | 1 | ```\nclass TweetCounts:\n\n def __init__(self):\n self.dict = {}\n \n\n def recordTweet(self, tweetName: str, time: int) -> None:\n if(tweetName not in self.dict):\n self.dict[tweetName] = [time]\n else:\n self.dict[tweetName].append(time)\n \n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n times = self.dict[tweetName]\n \n size = 0 \n secs = 0\n \n if(freq == \'minute\'):\n secs = 60\n size = (endTime - startTime) / 60 + 1\n if(freq == \'hour\'):\n secs = 3600\n size = (endTime - startTime) / 3600 + 1\n if(freq == \'day\'):\n secs = 86400\n size = (endTime - startTime) / 86400 + 1\n \n r = [0] * int(size)\n \n for i in times:\n if(startTime <= i and i <= endTime):\n index = int((i-startTime)/secs)\n r[index] += 1\n\n return r\n``` | 21 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Easy to Read Python Solution | tweet-counts-per-frequency | 0 | 1 | ```\nclass TweetCounts:\n\n def __init__(self):\n self.dict = {}\n \n\n def recordTweet(self, tweetName: str, time: int) -> None:\n if(tweetName not in self.dict):\n self.dict[tweetName] = [time]\n else:\n self.dict[tweetName].append(time)\n \n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n times = self.dict[tweetName]\n \n size = 0 \n secs = 0\n \n if(freq == \'minute\'):\n secs = 60\n size = (endTime - startTime) / 60 + 1\n if(freq == \'hour\'):\n secs = 3600\n size = (endTime - startTime) / 3600 + 1\n if(freq == \'day\'):\n secs = 86400\n size = (endTime - startTime) / 86400 + 1\n \n r = [0] * int(size)\n \n for i in times:\n if(startTime <= i and i <= endTime):\n index = int((i-startTime)/secs)\n r[index] += 1\n\n return r\n``` | 21 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Clean Python bisect solution | tweet-counts-per-frequency | 0 | 1 | ```\nimport bisect\nclass TweetCounts:\n FREQS = {\n \'minute\': 60,\n \'hour\': 60 * 60,\n \'day\': 60 * 60 * 24\n }\n\n def __init__(self):\n self.tweets = defaultdict(list)\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n bisect.insort(self.tweets[tweetName], time)\n \n def bucket(self, timeDelta, intervalTime):\n return (timeDelta // intervalTime)\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n tweets = self.tweets[tweetName]\n if not tweets:\n return []\n\n interval = self.FREQS[freq]\n output = [0] * (self.bucket((endTime-startTime), interval) + 1)\n start = bisect.bisect_left(tweets, startTime)\n end = bisect.bisect_right(tweets, endTime)\n\n for i in range(start, end):\n output[self.bucket(tweets[i]-startTime,interval)] += 1\n return output\n```\n\nThe tripping points of this problem are mainly:\n* keeping the times sorted, or deciding to sort on each query\n* figuring out how many buckets should be in the output\n* which bucket each time interval falls into\n\nLet\'s approach each individually.\n\n**Maintaining Sorted Tweet Times**\nMaintaining sorted lists means O(logN) insertion time for each new element (overall, O(NlogN) when N elements are added total). This is versus sorting for each query, which is O(NlogN) for each query - so for M queries, this costs M * NlogN.\n\nMaintaining a sorted input also means there is no need to iterate through every single item in `tweets`, as we can use binary search to find the start and end indices.\n\n**How many buckets for the output?**\nThere is at least one bucket, even if the total amount of time is less than our time interval. For example, if we want a per-minute frequency but only look at 30 seconds, that\'s still one (parital) bucket. If we wanted 90 seconds and a per-minute frequency, that\'s one full bucket (0-59 seconds) and one partial bucket (60-90). If we end the time interval exactly on the end of a bucket, like 119 seconds, we get 2 full buckets and no partial buckets (0-59, 60-119).\n\nThe answer of "how many buckets" boils down to "how many times can I fit all or part of the interval in seconds, into the total timespan in seconds? One way to calculate this is to divide the total timespan by the intervals, and take the ceiling. Since `math.ceil()` will always round up to the next natural integer, it accounts for the case where there is a parital interval as well as only whole intervals.\n\n**Which bucket should I increment for a given time?**\n\nIn some similar "bucketing" problems, it\'s possible to iterate over the elements themselves, and when a condition is reached that means the nexk bucket should be started, to append the current (now completed) bucket to the output, and reset it to 0/[]. However, in our case, we might have a jump between one time and the next that skips over an interval entirely. Consider this more trivial example:\n\n```\nnums = [1,2,3,9,10,11]\ninterval = 5\n# the goal is to group numbers into intervals of 5 (1-indexed), like this:\n# expected = [[1,2,3], [9,10], [11]]\n\n# we might be tempted to write:\n# note: THIS CODE IS WRONG for this problem!\nnext_interval = (1 + interval) # 6\ncurr_bucket = []\noutput = []\nfor item in nums:\n if item >= next_interval:\n\t output.append(curr_bucket)\n\t\tcurr_bucket = [item]\n\t\tnext_interval += interval\n\telse:\n\t curr_bucket.append(item)\noutput.append(curr_bucket)\nreturn output\n```\n\nThis works, because there is at least one element in each bucket. But what about this input:\n\n```\nnums = [1,2,3,4,5,34, 70]\nexpected = [[1,2,3,4,5], [34]]\n```\nThe code would get to 34, notice that it\'s greater than `6`, and reset `next_interval` to `11`. Now, the state is:\n```\nnext_interval = 11\nitem = 34\ncurr_bucket = [34]\noutput = [[1,2,3,4,5]]\n```\n\nOn the next iteration, we would have:\n```\nnext_interval = 11\nitem = 70\ncurr_bucket = [34, 70]\noutput = [[1,2,3,4,5]]\n```\n\nIn other words, `next_interval` has not kept up with how far we are into the possible values in `nums`. We\'ll never reach 11 because we\'ve already passed it. Instead of assuming we have at least one item for each bucket we want to populate, we should instead calculate which bucket it belongs to.\n\nIn the solution, there is a method used to do this calculation. For the case where we need to figure out how many buckets we need, we realize that for our `output` array, the "first" bucket will actually be at `index=0` - so if we calculate the last possible value in our input set\'s bucket *index*, that gives us a way to find the total length of the output array by adding 1.\n\n*Note: this does not work exactly like this in Python2, as Py2 handles division differently. To make it work in Python2, convert the numerator to a float, e.g. `float(totaltimespan) / interval`. Alternately, use `from __future__ import division` See [1]*\n\n\n\n\n[1] https://python-history.blogspot.com/2009/03/problem-with-integer-division.html\n | 5 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Clean Python bisect solution | tweet-counts-per-frequency | 0 | 1 | ```\nimport bisect\nclass TweetCounts:\n FREQS = {\n \'minute\': 60,\n \'hour\': 60 * 60,\n \'day\': 60 * 60 * 24\n }\n\n def __init__(self):\n self.tweets = defaultdict(list)\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n bisect.insort(self.tweets[tweetName], time)\n \n def bucket(self, timeDelta, intervalTime):\n return (timeDelta // intervalTime)\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n tweets = self.tweets[tweetName]\n if not tweets:\n return []\n\n interval = self.FREQS[freq]\n output = [0] * (self.bucket((endTime-startTime), interval) + 1)\n start = bisect.bisect_left(tweets, startTime)\n end = bisect.bisect_right(tweets, endTime)\n\n for i in range(start, end):\n output[self.bucket(tweets[i]-startTime,interval)] += 1\n return output\n```\n\nThe tripping points of this problem are mainly:\n* keeping the times sorted, or deciding to sort on each query\n* figuring out how many buckets should be in the output\n* which bucket each time interval falls into\n\nLet\'s approach each individually.\n\n**Maintaining Sorted Tweet Times**\nMaintaining sorted lists means O(logN) insertion time for each new element (overall, O(NlogN) when N elements are added total). This is versus sorting for each query, which is O(NlogN) for each query - so for M queries, this costs M * NlogN.\n\nMaintaining a sorted input also means there is no need to iterate through every single item in `tweets`, as we can use binary search to find the start and end indices.\n\n**How many buckets for the output?**\nThere is at least one bucket, even if the total amount of time is less than our time interval. For example, if we want a per-minute frequency but only look at 30 seconds, that\'s still one (parital) bucket. If we wanted 90 seconds and a per-minute frequency, that\'s one full bucket (0-59 seconds) and one partial bucket (60-90). If we end the time interval exactly on the end of a bucket, like 119 seconds, we get 2 full buckets and no partial buckets (0-59, 60-119).\n\nThe answer of "how many buckets" boils down to "how many times can I fit all or part of the interval in seconds, into the total timespan in seconds? One way to calculate this is to divide the total timespan by the intervals, and take the ceiling. Since `math.ceil()` will always round up to the next natural integer, it accounts for the case where there is a parital interval as well as only whole intervals.\n\n**Which bucket should I increment for a given time?**\n\nIn some similar "bucketing" problems, it\'s possible to iterate over the elements themselves, and when a condition is reached that means the nexk bucket should be started, to append the current (now completed) bucket to the output, and reset it to 0/[]. However, in our case, we might have a jump between one time and the next that skips over an interval entirely. Consider this more trivial example:\n\n```\nnums = [1,2,3,9,10,11]\ninterval = 5\n# the goal is to group numbers into intervals of 5 (1-indexed), like this:\n# expected = [[1,2,3], [9,10], [11]]\n\n# we might be tempted to write:\n# note: THIS CODE IS WRONG for this problem!\nnext_interval = (1 + interval) # 6\ncurr_bucket = []\noutput = []\nfor item in nums:\n if item >= next_interval:\n\t output.append(curr_bucket)\n\t\tcurr_bucket = [item]\n\t\tnext_interval += interval\n\telse:\n\t curr_bucket.append(item)\noutput.append(curr_bucket)\nreturn output\n```\n\nThis works, because there is at least one element in each bucket. But what about this input:\n\n```\nnums = [1,2,3,4,5,34, 70]\nexpected = [[1,2,3,4,5], [34]]\n```\nThe code would get to 34, notice that it\'s greater than `6`, and reset `next_interval` to `11`. Now, the state is:\n```\nnext_interval = 11\nitem = 34\ncurr_bucket = [34]\noutput = [[1,2,3,4,5]]\n```\n\nOn the next iteration, we would have:\n```\nnext_interval = 11\nitem = 70\ncurr_bucket = [34, 70]\noutput = [[1,2,3,4,5]]\n```\n\nIn other words, `next_interval` has not kept up with how far we are into the possible values in `nums`. We\'ll never reach 11 because we\'ve already passed it. Instead of assuming we have at least one item for each bucket we want to populate, we should instead calculate which bucket it belongs to.\n\nIn the solution, there is a method used to do this calculation. For the case where we need to figure out how many buckets we need, we realize that for our `output` array, the "first" bucket will actually be at `index=0` - so if we calculate the last possible value in our input set\'s bucket *index*, that gives us a way to find the total length of the output array by adding 1.\n\n*Note: this does not work exactly like this in Python2, as Py2 handles division differently. To make it work in Python2, convert the numerator to a float, e.g. `float(totaltimespan) / interval`. Alternately, use `from __future__ import division` See [1]*\n\n\n\n\n[1] https://python-history.blogspot.com/2009/03/problem-with-integer-division.html\n | 5 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Python. Beats 99% of solutions. Best data structures (Ordered lists and binary searches) | tweet-counts-per-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWith this problem, I was definitely aiming for a really nice solution but was blown away when my solution came in the top 1%. I was aiming to ensure that I kept things ordered where possible and possibly aimed for a bit of a production solution, but it\'s fairly readable. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nI keep the recorded_tweets in a defaultdictionary mapping tweetNames to tweet times. I also I endeavour to keep these tweetTimes sorted in order to ensure that we can find the relevant tweets as fast as possible.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**recordTweet** and maintaining the ordered lists: It takes $$O(n)$$ to insert a new element into an ordered list. We can find the insertion location in $$O(log(n))$$ however, the insertion is expensive and takes $$O(n)$$. Let me know if you can maintain this structure in $$O(log(n))$$.\n**getTweetCountsPerFrequency**:\nWe can find the list in $$O(1)$$ using the hashmap, then finding the starting index in $$O(log(n))$$. Then it takes an additional $$O(k)$$ where k is the length of the times for this tweetName to find all the relevant times and record their frequencies. Whilst the theoretical time complexity is not greater as we may need to search all the elements, in practice, this solution will be much much faster as seen by the incredible runtime.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ where n is the number of inputs. Any solution will require any info that is stored in this solution to be stored somehow.\n# Code\n```\nfrom collections import defaultdict\nfrom bisect import insort, bisect_left\nfrom math import ceil\nclass TweetCounts:\n\n def __init__(self):\n self.recorded_tweets = defaultdict(list)\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n insort(self.recorded_tweets[tweetName], time) \n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n \n delta_t = 0\n match freq:\n case "minute":\n delta_t = 60\n case "hour":\n delta_t = 3600\n case "day":\n delta_t = 86400\n r = (endTime-startTime) / delta_t\n if r.is_integer():\n num_slots = int(r+1)\n else:\n num_slots = ceil(r)\n frequencies = [0] * num_slots\n times = self.recorded_tweets[tweetName]\n starting_index = bisect_left(times, startTime)\n cur_index = starting_index\n if starting_index == len(times):\n return frequencies\n cur_time = times[starting_index]\n while cur_time <= endTime and cur_index < len(times):\n time_slot = (cur_time - startTime) // delta_t\n \n frequencies[time_slot] += 1\n cur_index += 1\n if cur_index == len(times):\n break\n cur_time = times[cur_index]\n return frequencies\n\n\n\n\n\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Python. Beats 99% of solutions. Best data structures (Ordered lists and binary searches) | tweet-counts-per-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWith this problem, I was definitely aiming for a really nice solution but was blown away when my solution came in the top 1%. I was aiming to ensure that I kept things ordered where possible and possibly aimed for a bit of a production solution, but it\'s fairly readable. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nI keep the recorded_tweets in a defaultdictionary mapping tweetNames to tweet times. I also I endeavour to keep these tweetTimes sorted in order to ensure that we can find the relevant tweets as fast as possible.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**recordTweet** and maintaining the ordered lists: It takes $$O(n)$$ to insert a new element into an ordered list. We can find the insertion location in $$O(log(n))$$ however, the insertion is expensive and takes $$O(n)$$. Let me know if you can maintain this structure in $$O(log(n))$$.\n**getTweetCountsPerFrequency**:\nWe can find the list in $$O(1)$$ using the hashmap, then finding the starting index in $$O(log(n))$$. Then it takes an additional $$O(k)$$ where k is the length of the times for this tweetName to find all the relevant times and record their frequencies. Whilst the theoretical time complexity is not greater as we may need to search all the elements, in practice, this solution will be much much faster as seen by the incredible runtime.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ where n is the number of inputs. Any solution will require any info that is stored in this solution to be stored somehow.\n# Code\n```\nfrom collections import defaultdict\nfrom bisect import insort, bisect_left\nfrom math import ceil\nclass TweetCounts:\n\n def __init__(self):\n self.recorded_tweets = defaultdict(list)\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n insort(self.recorded_tweets[tweetName], time) \n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n \n delta_t = 0\n match freq:\n case "minute":\n delta_t = 60\n case "hour":\n delta_t = 3600\n case "day":\n delta_t = 86400\n r = (endTime-startTime) / delta_t\n if r.is_integer():\n num_slots = int(r+1)\n else:\n num_slots = ceil(r)\n frequencies = [0] * num_slots\n times = self.recorded_tweets[tweetName]\n starting_index = bisect_left(times, startTime)\n cur_index = starting_index\n if starting_index == len(times):\n return frequencies\n cur_time = times[starting_index]\n while cur_time <= endTime and cur_index < len(times):\n time_slot = (cur_time - startTime) // delta_t\n \n frequencies[time_slot] += 1\n cur_index += 1\n if cur_index == len(times):\n break\n cur_time = times[cur_index]\n return frequencies\n\n\n\n\n\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Concise Python: SortedList + BinarySearch | tweet-counts-per-frequency | 0 | 1 | # Intuition\nsimulate the timeline fo the tweet records\n# Approach\nUse hashmap + sortedlist to \n\n# Complexity\n- Time complexity:\nadd record O(log(n))\ncountChunkFreq O(klog(n)) k = (endTime - startTime) / chunkSize\n\n- Space complexity:\nO(n) (n = number of records)\n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass TweetCounts:\n def __init__(self):\n self.chunks = {\'minute\': 60,\n \'hour\' : 60 * 60,\n \'day\' : 60 * 60 * 24\n }\n\n self.records = dict()\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n\n if tweetName not in self.records:\n self.records[tweetName] = SortedList()\n self.records[tweetName].add(time)\n \n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n ans = []\n if tweetName not in self.records:\n return ans\n\n chunk = self.chunks[freq]\n\n timeline = self.records[tweetName]\n startIndex = timeline.bisect_left(startTime)\n currChunk = startTime\n while currChunk <= endTime:\n nextIndex = timeline.bisect_left(min(currChunk + chunk, endTime + 1))\n ans.append(nextIndex - startIndex)\n startIndex = nextIndex\n currChunk = currChunk + chunk\n \n return ans\n \n\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Concise Python: SortedList + BinarySearch | tweet-counts-per-frequency | 0 | 1 | # Intuition\nsimulate the timeline fo the tweet records\n# Approach\nUse hashmap + sortedlist to \n\n# Complexity\n- Time complexity:\nadd record O(log(n))\ncountChunkFreq O(klog(n)) k = (endTime - startTime) / chunkSize\n\n- Space complexity:\nO(n) (n = number of records)\n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass TweetCounts:\n def __init__(self):\n self.chunks = {\'minute\': 60,\n \'hour\' : 60 * 60,\n \'day\' : 60 * 60 * 24\n }\n\n self.records = dict()\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n\n if tweetName not in self.records:\n self.records[tweetName] = SortedList()\n self.records[tweetName].add(time)\n \n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n ans = []\n if tweetName not in self.records:\n return ans\n\n chunk = self.chunks[freq]\n\n timeline = self.records[tweetName]\n startIndex = timeline.bisect_left(startTime)\n currChunk = startTime\n while currChunk <= endTime:\n nextIndex = timeline.bisect_left(min(currChunk + chunk, endTime + 1))\n ans.append(nextIndex - startIndex)\n startIndex = nextIndex\n currChunk = currChunk + chunk\n \n return ans\n \n\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Real World Optimized | Commented and Explained | tweet-counts-per-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want a map of a tweetName to a dictionary of time frequencies\nWe want to be able to do chunk sizes of seconds based on different larger intervals \nWe want to be able to determine an interval based on an ending and start time per chunk size \n\nIf we set all of these up in the initialization process, we can then do a linear scan over the appropriate tweets and allow for easy upgrading in the future \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up tweets to record as a map of tweetNames to dictionary of time frequencies. This way, as a tweet comes in, we can mark for that tweetName at that tweetTime the incidence of that tweet. This allows for realworld parallel scaling, where many of the same tweets may be arriving at the same or different timings. This could in turn be optimized by having time serve as a time pointer to a universal time object, which would in turn lower this from a necessary string to float mapping to int to a necessary string to pointer mapping to int pointer. Similarly, we can optimize by taking the string and doing encoding to shorten the bits related to it in lossless compression. This would eventually lead to a significant memory and thus time optimization. \n\nSet up seconds as a map of second intervals that are not seconds to the chunk size. This means we have second -> 1, minute -> 60, hour -> 60 * 60, day -> 60 * 60 * 24, week -> 60 * 60 * 24 * 7. Again this could be optimized, but for little gain as it is only done on init. Combinations of these could allow for more customized features as well. \n\nSet up a get interval inline function that is given an ending, starting, and chunk size and then returns the interval per chunk size result (ending - starting) per chunk_size in integer division format. \n\nBy keeping this as an inline function, the owners control over it is increased and thus maintained well. \n\nWe then record tweets by having the following checking process \n- If tweetName in self.tweets \n - if time in self.tweets[tweetName] \n - self.tweets[tweetName][time] += 1 \n - else self.tweets[tweetName][time] = 1 \n- else self.tweets[tweetName][time] = 1 \n\nTo getTweetCountsPerFrequency then \n- get chunksize from self.seconds with default set to a day (could be changed, but day works for the test cases used here) \n- answer is a list of 0s of size of the get interval function using endTime, startTime and now calculated chunksize \n- the time keys are the set of self.tweets at tweetName keys \n- the viable keys are those keys in tweet time keys that are in interval \n- for key in viable keys then, \n - get interval of key, startTime, chunksize \n - answer at this interval is updated by self.tweets at tweetName at key (avoids multiple loopings therein) \n- when loop concludes, return answer \n\n# Time Complexity \n- For init, O(1). \n- For recordTweet, O(2 bools, one set or one addition) \n- For getTweetCountsPerFrequency \n - get chunksize is O(1) \n - get interval is a subtraction, addition and division cost \n - get tweet_time_keys as a set is O(T) where T is the number of timekeys at the tweetName \n - viable keys then takes O(T) as well \n - answer updates then takes O(t) where t is subset of T as these are viable times \n - during which we need to do a subtraction, division, and access step \n - total then is O(1) + O(-, /, +) + O(T) + O(T) + O(t) * (-, /, @)\n - total then is O(2T + tc), where c == (-, /, @)\n\n# Space Complexity \n- For each tweetName \n - We store a dictionary of times \n - which point to integers \n - In total then O(D * I), where D is the dictionary of tweetNames and I is the set of time intervals is stored \n - All other storage is less than this by necessity and so is subsumed \n\n# Code\n```\nclass TweetCounts:\n\n def __init__(self):\n self.tweets = collections.defaultdict(dict)\n self.seconds = {\'minute\':60, \'hour\':(60*60), \'day\':(60*60*24)}\n self.get_interval = lambda ending, starting, chunk_size : (ending-starting)//chunk_size\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n if tweetName in self.tweets : \n if time in self.tweets[tweetName] : \n self.tweets[tweetName][time] += 1 \n else : \n self.tweets[tweetName][time] = 1 \n else : \n self.tweets[tweetName][time] = 1\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n chunk_size = self.seconds.get(freq, 86400)\n answer = [0] * (self.get_interval(endTime, startTime, chunk_size) + 1)\n tweet_time_keys = set(self.tweets[tweetName].keys())\n viable_keys = [key for key in tweet_time_keys if startTime <= key <= endTime]\n for key in viable_keys : \n answer[self.get_interval(key, startTime, chunk_size)] += self.tweets[tweetName][key]\n return answer\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Real World Optimized | Commented and Explained | tweet-counts-per-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want a map of a tweetName to a dictionary of time frequencies\nWe want to be able to do chunk sizes of seconds based on different larger intervals \nWe want to be able to determine an interval based on an ending and start time per chunk size \n\nIf we set all of these up in the initialization process, we can then do a linear scan over the appropriate tweets and allow for easy upgrading in the future \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up tweets to record as a map of tweetNames to dictionary of time frequencies. This way, as a tweet comes in, we can mark for that tweetName at that tweetTime the incidence of that tweet. This allows for realworld parallel scaling, where many of the same tweets may be arriving at the same or different timings. This could in turn be optimized by having time serve as a time pointer to a universal time object, which would in turn lower this from a necessary string to float mapping to int to a necessary string to pointer mapping to int pointer. Similarly, we can optimize by taking the string and doing encoding to shorten the bits related to it in lossless compression. This would eventually lead to a significant memory and thus time optimization. \n\nSet up seconds as a map of second intervals that are not seconds to the chunk size. This means we have second -> 1, minute -> 60, hour -> 60 * 60, day -> 60 * 60 * 24, week -> 60 * 60 * 24 * 7. Again this could be optimized, but for little gain as it is only done on init. Combinations of these could allow for more customized features as well. \n\nSet up a get interval inline function that is given an ending, starting, and chunk size and then returns the interval per chunk size result (ending - starting) per chunk_size in integer division format. \n\nBy keeping this as an inline function, the owners control over it is increased and thus maintained well. \n\nWe then record tweets by having the following checking process \n- If tweetName in self.tweets \n - if time in self.tweets[tweetName] \n - self.tweets[tweetName][time] += 1 \n - else self.tweets[tweetName][time] = 1 \n- else self.tweets[tweetName][time] = 1 \n\nTo getTweetCountsPerFrequency then \n- get chunksize from self.seconds with default set to a day (could be changed, but day works for the test cases used here) \n- answer is a list of 0s of size of the get interval function using endTime, startTime and now calculated chunksize \n- the time keys are the set of self.tweets at tweetName keys \n- the viable keys are those keys in tweet time keys that are in interval \n- for key in viable keys then, \n - get interval of key, startTime, chunksize \n - answer at this interval is updated by self.tweets at tweetName at key (avoids multiple loopings therein) \n- when loop concludes, return answer \n\n# Time Complexity \n- For init, O(1). \n- For recordTweet, O(2 bools, one set or one addition) \n- For getTweetCountsPerFrequency \n - get chunksize is O(1) \n - get interval is a subtraction, addition and division cost \n - get tweet_time_keys as a set is O(T) where T is the number of timekeys at the tweetName \n - viable keys then takes O(T) as well \n - answer updates then takes O(t) where t is subset of T as these are viable times \n - during which we need to do a subtraction, division, and access step \n - total then is O(1) + O(-, /, +) + O(T) + O(T) + O(t) * (-, /, @)\n - total then is O(2T + tc), where c == (-, /, @)\n\n# Space Complexity \n- For each tweetName \n - We store a dictionary of times \n - which point to integers \n - In total then O(D * I), where D is the dictionary of tweetNames and I is the set of time intervals is stored \n - All other storage is less than this by necessity and so is subsumed \n\n# Code\n```\nclass TweetCounts:\n\n def __init__(self):\n self.tweets = collections.defaultdict(dict)\n self.seconds = {\'minute\':60, \'hour\':(60*60), \'day\':(60*60*24)}\n self.get_interval = lambda ending, starting, chunk_size : (ending-starting)//chunk_size\n\n def recordTweet(self, tweetName: str, time: int) -> None:\n if tweetName in self.tweets : \n if time in self.tweets[tweetName] : \n self.tweets[tweetName][time] += 1 \n else : \n self.tweets[tweetName][time] = 1 \n else : \n self.tweets[tweetName][time] = 1\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n chunk_size = self.seconds.get(freq, 86400)\n answer = [0] * (self.get_interval(endTime, startTime, chunk_size) + 1)\n tweet_time_keys = set(self.tweets[tweetName].keys())\n viable_keys = [key for key in tweet_time_keys if startTime <= key <= endTime]\n for key in viable_keys : \n answer[self.get_interval(key, startTime, chunk_size)] += self.tweets[tweetName][key]\n return answer\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Python 3 using binary search | tweet-counts-per-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TweetCounts:\n\n def __init__(self):\n self.tweets = defaultdict(list)\n # Frequency to time\n self.freq = {\n \'minute\': 59,\n \'hour\': 3599,\n \'day\': 86399\n }\n \n def recordTweet(self, tweetName: str, time: int) -> None:\n # Using binary search to insert new occurrence for each tweet\n m = bisect.bisect(self.tweets[tweetName], time)\n self.tweets[tweetName].insert(m, time)\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n # Store the result\n result = []\n interval = self.freq[freq]\n cur_time = startTime\n\n # For each interval, find the number of occurrences for the tweet\n while cur_time <= endTime:\n end_cur_interval = min(cur_time + interval, endTime)\n\n\n i = bisect.bisect_left(self.tweets[tweetName], cur_time)\n j = bisect.bisect(self.tweets[tweetName], end_cur_interval)\n \n result.append(j-i)\n cur_time = end_cur_interval + 1\n return result\n\n\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Python 3 using binary search | tweet-counts-per-frequency | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TweetCounts:\n\n def __init__(self):\n self.tweets = defaultdict(list)\n # Frequency to time\n self.freq = {\n \'minute\': 59,\n \'hour\': 3599,\n \'day\': 86399\n }\n \n def recordTweet(self, tweetName: str, time: int) -> None:\n # Using binary search to insert new occurrence for each tweet\n m = bisect.bisect(self.tweets[tweetName], time)\n self.tweets[tweetName].insert(m, time)\n\n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n # Store the result\n result = []\n interval = self.freq[freq]\n cur_time = startTime\n\n # For each interval, find the number of occurrences for the tweet\n while cur_time <= endTime:\n end_cur_interval = min(cur_time + interval, endTime)\n\n\n i = bisect.bisect_left(self.tweets[tweetName], cur_time)\n j = bisect.bisect(self.tweets[tweetName], end_cur_interval)\n \n result.append(j-i)\n cur_time = end_cur_interval + 1\n return result\n\n\n\n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Binary Search python3 Solution | tweet-counts-per-frequency | 0 | 1 | ```\n\nclass TweetCounts:\n \n # O(1) time,\n # O(1) space,\n # Approach: hashtable, \n def __init__(self):\n self.records = defaultdict(list)\n self.time_mapping = {"minute": 59, "hour": 3599, "day": 86399}\n\n \n # O(1) time,\n # O(1) space,\n # Approach: hashtable, \n def recordTweet(self, tweetName: str, time: int) -> None:\n self.records[tweetName].append(time)\n \n def binarySearch(self, target, intervals):\n lo, hi = 0, len(intervals)-1\n \n if target < intervals[lo][0] or target > intervals[hi][1]:\n return hi+1\n \n while lo <= hi:\n mid = (lo+hi)//2\n \n if target >= intervals[mid][0] and target <= intervals[mid][1]:\n return mid\n elif target > intervals[mid][1]:\n lo = mid+1\n else:\n hi = mid-1\n \n \n # O(len(records[tweetName]) * log(len(intervals))) time,\n # O(len(intervals)) space,\n # Approach: binary search, \n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n ans = []\n intervals = []\n curr_interval = self.time_mapping[freq]\n curr_start = startTime\n curr_end = min(startTime+curr_interval, endTime)\n \n while curr_start <= endTime:\n ans.append(0)\n intervals.append((curr_start, curr_end))\n curr_start = curr_end + 1\n curr_end = min(curr_start+curr_interval, endTime)\n \n for record_time in self.records[tweetName]:\n interval_index = self.binarySearch(record_time, intervals)\n if interval_index < len(intervals):\n ans[interval_index] += 1\n \n return ans\n \n \n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | A social media company is trying to monitor activity on their site by analyzing the number of tweets that occur in select periods of time. These periods can be partitioned into smaller **time chunks** based on a certain frequency (every **minute**, **hour**, or **day**).
For example, the period `[10, 10000]` (in **seconds**) would be partitioned into the following **time chunks** with these frequencies:
* Every **minute** (60-second chunks): `[10,69]`, `[70,129]`, `[130,189]`, `...`, `[9970,10000]`
* Every **hour** (3600-second chunks): `[10,3609]`, `[3610,7209]`, `[7210,10000]`
* Every **day** (86400-second chunks): `[10,10000]`
Notice that the last chunk may be shorter than the specified frequency's chunk size and will always end with the end time of the period (`10000` in the above example).
Design and implement an API to help the company with their analysis.
Implement the `TweetCounts` class:
* `TweetCounts()` Initializes the `TweetCounts` object.
* `void recordTweet(String tweetName, int time)` Stores the `tweetName` at the recorded `time` (in **seconds**).
* `List getTweetCountsPerFrequency(String freq, String tweetName, int startTime, int endTime)` Returns a list of integers representing the number of tweets with `tweetName` in each **time chunk** for the given period of time `[startTime, endTime]` (in **seconds**) and frequency `freq`.
* `freq` is one of `"minute "`, `"hour "`, or `"day "` representing a frequency of every **minute**, **hour**, or **day** respectively.
**Example:**
**Input**
\[ "TweetCounts ", "recordTweet ", "recordTweet ", "recordTweet ", "getTweetCountsPerFrequency ", "getTweetCountsPerFrequency ", "recordTweet ", "getTweetCountsPerFrequency "\]
\[\[\],\[ "tweet3 ",0\],\[ "tweet3 ",60\],\[ "tweet3 ",10\],\[ "minute ", "tweet3 ",0,59\],\[ "minute ", "tweet3 ",0,60\],\[ "tweet3 ",120\],\[ "hour ", "tweet3 ",0,210\]\]
**Output**
\[null,null,null,null,\[2\],\[2,1\],null,\[4\]\]
**Explanation**
TweetCounts tweetCounts = new TweetCounts();
tweetCounts.recordTweet( "tweet3 ", 0); // New tweet "tweet3 " at time 0
tweetCounts.recordTweet( "tweet3 ", 60); // New tweet "tweet3 " at time 60
tweetCounts.recordTweet( "tweet3 ", 10); // New tweet "tweet3 " at time 10
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 59); // return \[2\]; chunk \[0,59\] had 2 tweets
tweetCounts.getTweetCountsPerFrequency( "minute ", "tweet3 ", 0, 60); // return \[2,1\]; chunk \[0,59\] had 2 tweets, chunk \[60,60\] had 1 tweet
tweetCounts.recordTweet( "tweet3 ", 120); // New tweet "tweet3 " at time 120
tweetCounts.getTweetCountsPerFrequency( "hour ", "tweet3 ", 0, 210); // return \[4\]; chunk \[0,210\] had 4 tweets
**Constraints:**
* `0 <= time, startTime, endTime <= 109`
* `0 <= endTime - startTime <= 104`
* There will be at most `104` calls **in total** to `recordTweet` and `getTweetCountsPerFrequency`. | null |
Binary Search python3 Solution | tweet-counts-per-frequency | 0 | 1 | ```\n\nclass TweetCounts:\n \n # O(1) time,\n # O(1) space,\n # Approach: hashtable, \n def __init__(self):\n self.records = defaultdict(list)\n self.time_mapping = {"minute": 59, "hour": 3599, "day": 86399}\n\n \n # O(1) time,\n # O(1) space,\n # Approach: hashtable, \n def recordTweet(self, tweetName: str, time: int) -> None:\n self.records[tweetName].append(time)\n \n def binarySearch(self, target, intervals):\n lo, hi = 0, len(intervals)-1\n \n if target < intervals[lo][0] or target > intervals[hi][1]:\n return hi+1\n \n while lo <= hi:\n mid = (lo+hi)//2\n \n if target >= intervals[mid][0] and target <= intervals[mid][1]:\n return mid\n elif target > intervals[mid][1]:\n lo = mid+1\n else:\n hi = mid-1\n \n \n # O(len(records[tweetName]) * log(len(intervals))) time,\n # O(len(intervals)) space,\n # Approach: binary search, \n def getTweetCountsPerFrequency(self, freq: str, tweetName: str, startTime: int, endTime: int) -> List[int]:\n ans = []\n intervals = []\n curr_interval = self.time_mapping[freq]\n curr_start = startTime\n curr_end = min(startTime+curr_interval, endTime)\n \n while curr_start <= endTime:\n ans.append(0)\n intervals.append((curr_start, curr_end))\n curr_start = curr_end + 1\n curr_end = min(curr_start+curr_interval, endTime)\n \n for record_time in self.records[tweetName]:\n interval_index = self.binarySearch(record_time, intervals)\n if interval_index < len(intervals):\n ans[interval_index] += 1\n \n return ans\n \n \n# Your TweetCounts object will be instantiated and called as such:\n# obj = TweetCounts()\n# obj.recordTweet(tweetName,time)\n# param_2 = obj.getTweetCountsPerFrequency(freq,tweetName,startTime,endTime)\n``` | 0 | Given the array `nums` consisting of `2n` elements in the form `[x1,x2,...,xn,y1,y2,...,yn]`.
_Return the array in the form_ `[x1,y1,x2,y2,...,xn,yn]`.
**Example 1:**
**Input:** nums = \[2,5,1,3,4,7\], n = 3
**Output:** \[2,3,5,4,1,7\]
**Explanation:** Since x1\=2, x2\=5, x3\=1, y1\=3, y2\=4, y3\=7 then the answer is \[2,3,5,4,1,7\].
**Example 2:**
**Input:** nums = \[1,2,3,4,4,3,2,1\], n = 4
**Output:** \[1,4,2,3,3,2,4,1\]
**Example 3:**
**Input:** nums = \[1,1,2,2\], n = 2
**Output:** \[1,2,1,2\]
**Constraints:**
* `1 <= n <= 500`
* `nums.length == 2n`
* `1 <= nums[i] <= 10^3` | null |
Python Easy Solution | Bitmask DP | Faster than 65% | maximum-students-taking-exam | 0 | 1 | # Code\n```python []\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int:\n numRows, numCols = len(seats), len(seats[0])\n\n def check(col: int, prevMask: int) -> bool:\n if col <= 0:\n if prevMask & (1 << (col + 1)):\n return False\n elif col >= numCols - 1:\n if prevMask & (1 << (col - 1)):\n return False\n else:\n if prevMask & (1 << (col - 1)) or prevMask & (1 << (col + 1)):\n return False\n return True\n\n @cache\n def solve(row: int, col: int, prevMask: int, mask: int) -> int:\n if row >= numRows:\n return 0\n if col == numCols:\n return solve(row + 1, 0, mask, 0)\n ans = 0\n if seats[row][col] == \'.\' and check(col, prevMask):\n if col == 0:\n ans = 1 + solve(row, col + 1, prevMask, mask | (1 << (col)))\n elif not (mask & (1 << (col - 1))):\n ans = 1 + solve(row, col + 1, prevMask, mask | (1 << (col)))\n ans = max(ans, solve(row, col + 1, prevMask, mask))\n return ans\n\n return solve(0, 0, 0, 0)\n``` | 2 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
[python] BitMask the seats, previous row state, and the current row state | maximum-students-taking-exam | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPut everythng into bitmask for easy comparisons. \nnew_mask & seat_mask[row] == 0. check if seats are not broken\n(mask << 1) & new_mask == (mask >> 1) & new_mask == 0. check if seats top left and top right are not cheatable. \n(new_mask << 1) & new_mask == 0. check if you are next to anybody. \n\n# Complexity\n- Time complexity: $$o(n * 2^m * 2^m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nonly n * 2^m states. each state takes 2^m to solve. \n\n- Space complexity: $$o(n * 2^m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nonly n * 2^m states.\n\n# Code\n```\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int:\n n, m = len(seats), len(seats[0])\n seat_mask = []\n\n for i in seats:\n seat_mask.append(int(\'\'.join(i).replace(\'.\', \'0\').replace(\'#\',\'1\'), 2))\n\n @cache\n def dfs(row, mask): # mask refers to previous row state\n if row == -1:\n return 0\n res = 0\n for new_mask in range(1 << m):\n if new_mask & seat_mask[row] == \\\n (mask << 1) & new_mask == (mask >> 1) & new_mask == \\\n (new_mask << 1) & new_mask == 0: \n res = max(res, new_mask.bit_count() + dfs(row - 1, new_mask))\n return res\n \n return dfs(n-1, 0)\n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
DFS + bitmask with memoization in python3 | maximum-students-taking-exam | 0 | 1 | This is basically a backtracking question. First bitmask question I solved myself...\n\n# Code\n```\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int:\n m = len(seats)\n n = len(seats[0])\n self.res = 0\n @cache \n def dp(i,premask,j,currmask,stu):\n if i == m:\n self.res = max(stu,self.res)\n return \n if j == n:\n dp(i+1,currmask,0,0,stu)\n return \n possible = seats[i][j] == \'.\' \n if j > 0:\n possible = possible and ((premask >> (j-1) & 1) == 0) and ((currmask >> (j-1)) & 1 ==0)\n if j < n-1:\n possible = possible and ((premask >> (j+1)) & 1 == 0)\n if possible:\n dp(i,premask,j+1,currmask | (1<<j),stu+1)\n dp(i,premask,j+1,currmask,stu)\n dp(0,0,0,0,0)\n return self.res\n \n \n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
Python 95% + intuition | maximum-students-taking-exam | 0 | 1 | # Intuition\nWe start with a brute force approach. This involves recursively backtracking over the entire set of states and choosing to place or not place children in seats. This will result in a cost of about O(2^(mn)).\n\nWhen it comes to recursive problems, a good question is to ask: is it possible to memoize, bounding the number of states? To do this, we need independent subproblems: specifically, later recursive calls should be self-sufficient, not having to regard previous states. \n\nTo create such independent subproblems, notice how we know when we place a student at some state, the seats to their left and right as well as bottom left and bottom right can no longer be occupied. This means if we selectively only visit valid seats later, we don\'t have to worry about whether we placed a student at this current state or not. This means we can memoize our solution.\n\nSo that\'s exactly what we\'ll do!\n\n# Approach\nUsing bitmasks to track the available seating for the next row, we will recursively backtrack through the states and place children in seats. This way, starting from a row, we can memoize our recursive calls.\n\n# Complexity\n- Time complexity:\nO((4^m))*m*n) - we track two bitmasks for the current row and the next row, as well as the current location (i,j). \n\n- Space complexity:\nO((4^m))*m*n) - number of cached states\n\n# Code\n```\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int:\n initial = ~((~0)<<len(seats[0]))\n # reset b for each row\n # rb is current row. cb is the next row\n @lru_cache(None)\n def dfs(i,j,rb,cb):\n if i == len(seats):\n return 0\n if j == len(seats[0]):\n return dfs(i+1,0,cb,initial)\n \n res = dfs(i,j+1,rb,cb)\n if rb & (1<<j) and seats[i][j] == ".":\n leftb = ~(1<<(j-1)) if j > 0 else ~0\n crb = rb & ~(1<<(j+1)) & leftb & ~(1<<j)\n ccb = cb & ~(1<<(j+1)) & leftb\n res = max(res, dfs(i,j+1,crb,ccb)+1)\n return res\n # indices are flipped (i.e. j @ 0 is to the rightmost bit)\n return dfs(0,0,initial,initial)\n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
Primal Dual Solution | Commented and Explained | maximum-students-taking-exam | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are asked to find how many students we can maximally seat. We can instead consider what is the minimal number of seats that have an invalid placement. From this, we can then take our total number of seats and reduce it by the total of invalid placement seats to get the number of maximal placement. This is a similar problem to the originally hungarian algorithm, found here : https://en.wikipedia.org/wiki/Hungarian_algorithm\n\nPrimal Dual type solutions have more on them here : https://en.wikipedia.org/wiki/Duality_(optimization)\n\nIt can be seen that we have a strict qualification condition in that we obviously could use all seats if no seats led to a possibility of cheating, and if there is a chance of cheating for a seat, we necessarily will lose some seats by inference. This lets us use the primal dual approach succesfully. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAt the start, set up the rows, cols, number of seats in total, the nodes visited originally (all -1 for dimensions of seats), and seat matching matrix (all -1 for dimensions of seats) \n\nThen we set up a dfs progression function to find if a seat is cheatable or not \nIn this function, we are givin a row and col contained within a given node. Then, using the row and col in the node \n- If any of our neighbors either left or right or diagonally forward or back are a valid seat in bounds and that is not yet visited \n - visit that node at the neighbor positions \n - if seat matching at the given location is -1 or a dfs off of the seat matching matrix at nr nc using nodes visited now updated is True,\n - mark this location in seat matching as the nr, nc \n - return True -> this implies we could cheat here \n- If all neighbors attempted to visit but did not progress, return False, this is a safe seat \n\nFor the hungarian algorithm, we will be finding the total number of invalid chairs (ones that we can cheat from) To do so \n- In col major order with col steps of 2 and row steps of 1 to avoid overcounting\n - if seats at row col is a seat \n - set up a fresh nodes visited \n - if dfs using row, col and new nodes visited is True \n - increment our number of invalid seats by 1 \n - reset the nodes visited originally after \n- When done, return number of invalid chairs \n\nWe can optimally seat the number of total chairs minus the total number of invalid chairs. Return this valuation. \n\n# Complexity\n- Time complexity : O(R * C)\n - We visit all chairs to get the value of the number of chairs \n - This dominates time complexity overall, so O(R * C) where R is rows and C is columns \n\n- Space complexity : O(R * C) \n - recursively we could at worst match time complexity for progression overall valid spaces. This would result in O(R * C) space complexity \n - We also use this in our number of seats, nodes visited, seat matching, etc. So this is also conditioned on that. \n\n# Code\n```\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int :\n # set up the rows, cols, number of seats, nodes visited originally, and the seat matching matrix to start \n self.rows = len(seats)\n self.cols = len(seats[0])\n self.number_of_seats = sum([sum([int(seat == ".") for seat in row]) for row in seats])\n self.nodes_visited_originally = [[-1] * self.cols for _ in range(self.rows)]\n seat_matching_matrix = [[-1] * self.cols for _ in range(self.rows)]\n \n # set up a dfs progression \n def dfs(node, nodes_visited) :\n # get row and col from node \n row, col = node \n # consider directions in those left and right, forward and backward diagonal \n for nr, nc in [[row, col+1], [row, col-1], [row+1, col+1], [row+1, col-1], [row-1, col+1], [row-1, col-1]] :\n # if in bounds, valid, and not visited \n if ((0 <= nr < self.rows) and (0 <= nc < self.cols)) and seats[nr][nc] == "." and nodes_visited[nr][nc] == -1 : \n # visit it \n nodes_visited[nr][nc] = 1\n # if we have a seat matching matrix of -1 or dfs on seat matching matrix nr nc is true \n if seat_matching_matrix[nr][nc] == -1 or dfs(seat_matching_matrix[nr][nc], nodes_visited) :\n # match it and return True \n seat_matching_matrix[nr][nc] = (row, col) \n return True \n # return False \n return False \n \n # set up hungarian algorithm \n def hungarian_algorithm() : \n # overall result of the optimization \n result = 0 \n # col major order in steps of 2 to not overcount \n for col in range(0, self.cols, 2) : \n # row major order in steps of 1 \n for row in range(0, self.rows) :\n # if we have a seat to consider \n if seats[row][col] == "." : \n # set up fresh nodes visited \n nodes_visited = self.nodes_visited_originally\n # if successful, increment result \n if dfs((row, col), nodes_visited) : \n result += 1\n # then reset nodes visited originally \n self.nodes_visited_originally = [[-1]*self.cols for _ in range(self.rows)]\n # return when done \n return result \n\n # get the number of invalid chairs \n number_of_invalid_chairs = hungarian_algorithm()\n # you can only seat as many students as you have less the number of invalid chairs \n return self.number_of_seats - number_of_invalid_chairs \n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
DP bitmask python3 | maximum-students-taking-exam | 0 | 1 | # Intuition\nplain back-tracking\nO(2^(n*n)) TLE\n```\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int:\n def can_place(i, j):\n if seats[i][j]==\'#\':\n return False\n for x, y in [(i, j-1), (i, j+1), (i-1,j+1), (i-1, j-1)]:\n if 0<=x<len(seats) and 0<=y<len(seats[0]) and seats[x][y]==\'S\':\n return False\n return True\n def place(i, j, count):\n if i==len(seats)-1 and j==len(seats[0]):\n place.max = max(place.max, count)\n return\n if j==len(seats[0]):\n place(i+1, 0, count)\n return\n if can_place(i, j):\n seats[i][j] = \'S\'\n place(i, j+1, count+1)\n seats[i][j] = \'.\'\n place(i, j+1, count)\n place.max = 0\n place(0, 0, 0)\n return place.max\n```\n\nbut we can do better we only need to memorize previous and current row state , we can use two bitmask for that.\n(O(m*n*2^m*2^n))\n```\nclass Solution:\n def maxStudents(self, seats: List[List[str]]) -> int:\n def can_place(i, j, prev_mask, cur_mask):\n if seats[i][j]==\'#\':\n return False\n for y in [j+1, j-1]:\n if 0<=y<len(seats[0]) and (prev_mask&1<<y or cur_mask&1<<y):\n return False\n return True\n memo = {}\n def place(i, j, prev_mask, cur_mask):\n key= (i, j, prev_mask, cur_mask) \n if key in memo:\n return memo[key]\n if i==len(seats)-1 and j==len(seats[0]):\n return 0\n if j==len(seats[0]):\n return place(i+1, 0, cur_mask, 0)\n max_ = 0 \n if can_place(i, j, prev_mask, cur_mask):\n max_ = max(1+place(i, j+1, prev_mask, cur_mask|1<<j),max_)\n max_ = max(place(i, j+1, prev_mask, cur_mask), max_)\n memo[key] = max_\n return max_\n res = place(0, 0, 0, 0)\n return res\n\n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
Short solution with memoization in Python, with explanation | maximum-students-taking-exam | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor every seat, we have two choices: to assign or not to assign a student. To assign a student, the seat should be not broken and no students assigned in its four neighboring seats (i.e., left, right, upper-left, and upper-right). The input size is quite small so we can explore all possible assignments with dynamic programming. The existing assignment of the front row and the current row can be represented in two integers with bit mask. \nFinally I implement the algorithm with memoization, which is slower but very easy to write and read. \n\n\n# Complexity\n- Time complexity: $$O(nm2^{m})$$, where $$n$$ is the number of rows and $$m$$ is the size of each row. \n\n# Code\n```\nclass Solution:\n @cache\n def dp(self, i, j, front, current):\n if j >= self.m:\n i += 1\n j = 0\n front, current = current, 0\n if i >= self.n:\n return 0\n ans = self.dp(i, j + 1, front, current)\n if (self.seats[i][j] == \'.\' \n and (j == 0 or (current & (1 << (j-1)) == 0)) \n and (j == 0 or (front & (1 << (j-1)) == 0)) \n and (j == self.m - 1 or (front & (1 << (j+1)) == 0))):\n ans = max(ans, self.dp(i, j + 2, front, current | (1 << j)) + 1)\n return ans\n \n def maxStudents(self, seats: List[List[str]]) -> int:\n self.seats = seats\n self.n, self.m = len(seats), len(seats[0])\n return self.dp(0, 0, 0, 0)\n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
Recursive Bitmask DP with Memoization | Python | maximum-students-taking-exam | 0 | 1 | # Intuition\nThe ```mask``` that has been used in this solution is for a row, mask of a row shows the seats that has a student on them(1 if there is a student on a seat and 0 otherwise)\n\nwe are filling rows from last to first(from ```m-1``` to 0). ```dfs(row, index, curr_mask, prev_mask)``` return the number of maximum students to have a seat for rows from number 1 to number```row``` under the condition that the previous row(row with number ```row + 1```) has a mask of ```prev_mask```.\n\n# Code\n```\nfrom typing import List\n\n\nclass Solution:\n\tdef maxStudents(self, seats: List[List[str]]) -> int:\n\t\tm, n = len(seats), len(seats[0])\n\t\tmem = dict()\n\n\t\tdef dfs(row, index, curr_mask, prev_mask):\n\t\t\tif row == -1:\n\t\t\t\treturn 0\n\n\t\t\tif (row, curr_mask, prev_mask) in mem:\n\t\t\t\treturn mem[(row, curr_mask, prev_mask)]\n\n\t\t\tif index == n:\n\t\t\t\tmem[(row, curr_mask, prev_mask)] = curr_mask.bit_count() + dfs(row - 1, 0, 0, curr_mask)\n\t\t\t\treturn mem[(row, curr_mask, prev_mask)]\n\n\t\t\tans = dfs(row, index + 1, curr_mask, prev_mask)\n\t\t\tcurr_mask |= 1 << (n - 1 - index)\n\t\t\tif (\n\t\t\t\t\tseats[row][index] != \'#\' and\n\t\t\t\t\tcurr_mask & prev_mask >> 1 == 0 and\n\t\t\t\t\tcurr_mask & prev_mask << 1 == 0 and\n\t\t\t\t\tcurr_mask & curr_mask >> 1 == 0 and\n\t\t\t\t\tcurr_mask & curr_mask << 1 == 0\n\t\t\t):\n\t\t\t\tans = max(ans, dfs(row, index + 1, curr_mask, prev_mask))\n\t\t\tcurr_mask ^= 1 << (n - 1 - index)\n\t\t\tmem[(row, curr_mask, prev_mask)] = ans\n\t\t\treturn ans\n\n\t\treturn dfs(m - 1, 0, 0, 0)\n\n``` | 0 | Given a `m * n` matrix `seats` that represent seats distributions in a classroom. If a seat is broken, it is denoted by `'#'` character otherwise it is denoted by a `'.'` character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the **maximum** number of students that can take the exam together without any cheating being possible..
Students must be placed in seats in good condition.
**Example 1:**
**Input:** seats = \[\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ ". ", "# ", "# ", "# ", "# ", ". "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\]\]
**Output:** 4
**Explanation:** Teacher can place 4 students in available seats so they don't cheat on the exam.
**Example 2:**
**Input:** seats = \[\[ ". ", "# "\],
\[ "# ", "# "\],
\[ "# ", ". "\],
\[ "# ", "# "\],
\[ ". ", "# "\]\]
**Output:** 3
**Explanation:** Place all students in available seats.
**Example 3:**
**Input:** seats = \[\[ "# ", ". ", "**.** ", ". ", "# "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "**.** ", ". ", "# ", ". ", "**.** "\],
\[ "**.** ", "# ", "**.** ", "# ", "**.** "\],
\[ "# ", ". ", "**.** ", ". ", "# "\]\]
**Output:** 10
**Explanation:** Place students in available seats in column 1, 3 and 5.
**Constraints:**
* `seats` contains only characters `'.' and``'#'.`
* `m == seats.length`
* `n == seats[i].length`
* `1 <= m <= 8`
* `1 <= n <= 8` | If there're only 2 points, return true. Check if all other points lie on the line defined by the first 2 points. Use cross product to check collinearity. |
Brute force simple solution in python. | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n count=0\n for i in grid:\n for j in range(len(i)):\n if i[j]<0:\n count+=1\n return count\n``` | 1 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
Brute force simple solution in python. | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n count=0\n for i in grid:\n for j in range(len(i)):\n if i[j]<0:\n count+=1\n return count\n``` | 1 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
izi | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n c = 0\n for i in grid:\n for j in i:\n if j < 0:\n c += 1\n return c\n``` | 0 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
izi | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n c = 0\n for i in grid:\n for j in i:\n if j < 0:\n c += 1\n return c\n``` | 0 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Python 3: (Easy) modificated Binary search | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n\n\n def binary_search(row):\n low = 0\n high = len(row)-1\n \n while low <= high: \n mid = (low+high)//2\n guess = row[mid]\n \n if guess < 0:\n high = mid - 1\n \n else:\n low = mid + 1\n \n return len(row) - low\n \n negative_count = 0\n\n for row in grid:\n negative_count += binary_search(row) \n return negative_count\n\n\n\n``` | 0 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
Python 3: (Easy) modificated Binary search | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n\n\n def binary_search(row):\n low = 0\n high = len(row)-1\n \n while low <= high: \n mid = (low+high)//2\n guess = row[mid]\n \n if guess < 0:\n high = mid - 1\n \n else:\n low = mid + 1\n \n return len(row) - low\n \n negative_count = 0\n\n for row in grid:\n negative_count += binary_search(row) \n return negative_count\n\n\n\n``` | 0 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Solution that is 99% better in speed and memory | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n number_negative_num = 0\n for lst in grid:\n number_negative_num += len(list(filter(lambda x: x < 0, lst)))\n return number_negative_num\n``` | 1 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
Solution that is 99% better in speed and memory | count-negative-numbers-in-a-sorted-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n number_negative_num = 0\n for lst in grid:\n number_negative_num += len(list(filter(lambda x: x < 0, lst)))\n return number_negative_num\n``` | 1 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
C++ O(N) 4 LINES Solution 🔥Beats 100%🔥NO Binary Search | count-negative-numbers-in-a-sorted-matrix | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStart!\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Start from the bottom of the row (it will -ve);\n- NO need to check column if the first element is -ve;(sorted)\n- move up directly, if first is +ve then check the Column ;\n- as soon as the -ve found ,minus the index with the lenght of \ncolumn ,no need to check later on number if -ve found (sorted)\n- Done !! repeat it till 0 index;\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int countNegatives(vector<vector<int>>& grid) {\n // int count=0;\n // int l=grid.size();\n \n // for(int i=0;i<l;i++)\n // { int b=grid[i].size();\n // for(int j=0;j<b;j++)\n // {\n // if(grid[i][j]<0)\n // {\n // count++;\n // }\n // }\n // }return count;\n int n=grid.size(), m=grid[0].size(),r=n-1,c=0,count=0;\n while(r>=0&&c<m)\n {\n if(grid[r][c]<0) \n {\n --r;\n count+=m-c;\n }\n else\n ++c;\n\n }return count;\n }\n};\n```\n\n | 8 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
C++ O(N) 4 LINES Solution 🔥Beats 100%🔥NO Binary Search | count-negative-numbers-in-a-sorted-matrix | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStart!\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Start from the bottom of the row (it will -ve);\n- NO need to check column if the first element is -ve;(sorted)\n- move up directly, if first is +ve then check the Column ;\n- as soon as the -ve found ,minus the index with the lenght of \ncolumn ,no need to check later on number if -ve found (sorted)\n- Done !! repeat it till 0 index;\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int countNegatives(vector<vector<int>>& grid) {\n // int count=0;\n // int l=grid.size();\n \n // for(int i=0;i<l;i++)\n // { int b=grid[i].size();\n // for(int j=0;j<b;j++)\n // {\n // if(grid[i][j]<0)\n // {\n // count++;\n // }\n // }\n // }return count;\n int n=grid.size(), m=grid[0].size(),r=n-1,c=0,count=0;\n while(r>=0&&c<m)\n {\n if(grid[r][c]<0) \n {\n --r;\n count+=m-c;\n }\n else\n ++c;\n\n }return count;\n }\n};\n```\n\n | 8 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Bruteforce Easiest Solution C++ 🔥 | count-negative-numbers-in-a-sorted-matrix | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSTART\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust trivese in each row and column and done\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N^2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int countNegatives(vector<vector<int>>& grid) {\n int count=0;\n int l=grid.size();\n \n for(int i=0;i<l;i++)\n { int b=grid[i].size();\n for(int j=0;j<b;j++)\n {\n if(grid[i][j]<0)\n {\n count++;\n }\n }\n }return count;\n \n }\n};\n```\n\n | 3 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
Bruteforce Easiest Solution C++ 🔥 | count-negative-numbers-in-a-sorted-matrix | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSTART\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust trivese in each row and column and done\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N^2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int countNegatives(vector<vector<int>>& grid) {\n int count=0;\n int l=grid.size();\n \n for(int i=0;i<l;i++)\n { int b=grid[i].size();\n for(int j=0;j<b;j++)\n {\n if(grid[i][j]<0)\n {\n count++;\n }\n }\n }return count;\n \n }\n};\n```\n\n | 3 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Simple Solution with both Brute Force and Optimal approaches in three languages | count-negative-numbers-in-a-sorted-matrix | 1 | 1 | # Brute Force\n## Intuition\nBrute force approach is easy just go through the matrix and find the number is less than zero or not ,if less than zero then increase your count variable.\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is same as I discussed in intution section \n\n## Complexity\n- Time complexity: $$O(n*m)$$\n \n- Space complexity: $$O(1)$$\n\n\n# Code\n\n```c++ []\nclass Solution {\npublic:\n int countNegatives(vector<vector<int>>& grid) {\n int count=0;\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[i].size();j++){\n if(grid[i][j]<0) count++;\n }\n }\n return count;\n }\n};\n```\n```java []\nclass Solution {\n public int countNegatives(int[][] grid) {\n int count=0;\n for(int i[]:grid){\n for(int x:i){\n if(x<0) count++;\n }\n }\n return count;\n }\n}\n```\n```python []\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n count=0\n for i in range(len(grid)):\n for j in range(len(grid[i])):\n if grid[i][j]<0:\n count+=1\n return count \n```\n\n\n\n\n# Optimal approach\n## Intuition\nIn the question they told us that the matrix is sorted in non-increasing order both row-wise and column-wise, so we can apply binarysearch here.\n## Approach\n<!-- Describe your approach to solving the problem. -->\n1. First of all we go through row-wise,means take rows one by one and in that row we apply binary search.\n2. Then find the mid value of the row if the value is less than zero then all the values,on the right side of the mid value ,should be less than zero and the number of values will be (end-mid+1).After that we do binarysearch on the left side of the mid value.\n\n3. and if the mid value is not less than zero than do the binary search on the right side of the mid value.\n4. Lastly return the count of negative number in the given matrix.\n\n## Complexity\n- Time complexity: let suppose row size=m and column size n then T.C will be $$O(m*logn)$$\n \n- Space complexity: $$O(1)$$\n\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int binarySearch(vector<vector<int>>& grid,int start,int end,int row){\n if(start>end) return 0;\n int mid=start+(end-start)/2;\n\n if(grid[row][mid]<0){\n return (end-mid+1)+binarySearch(grid,start,mid-1,row);\n }\n return binarySearch(grid,mid+1,end,row);\n }\n int countNegatives(vector<vector<int>>& grid) {\n int count=0;\n for(int i=0;i<grid.size();i++){\n count+=binarySearch(grid,0,grid[i].size()-1,i);\n }\n return count;\n }\n};\n```\n```java []\nclass Solution {\n public int binarySearch(int[][] grid,int start,int end,int row){\n if(start>end) return 0;\n int mid=start+(end-start)/2;\n\n if(grid[row][mid]<0){\n return (end-mid+1)+binarySearch(grid,start,mid-1,row);\n }\n return binarySearch(grid,mid+1,end,row);\n }\n public int countNegatives(int[][] grid) {\n int count=0;\n for(int i=0;i<grid.length;i++){\n count+=binarySearch(grid,0,grid[i].length-1,i);\n }\n return count;\n }\n}\n```\n```python []\nclass Solution:\n def binarySearch(self,grid: List[List[int]],st,en,r):\n if st>en:return 0\n mid=st+(en-st)//2\n if grid[r][mid]<0:\n return en-mid+1+self.binarySearch(grid,st,mid-1,r)\n return self.binarySearch(grid,mid+1,en,r)\n def countNegatives(self, grid: List[List[int]]) -> int:\n count=0\n for i in range(len(grid)):\n count+=self.binarySearch(grid,0,len(grid[i])-1,i)\n return count \n```\n\n\n\n\n\n\n | 3 | Given a `m x n` matrix `grid` which is sorted in non-increasing order both row-wise and column-wise, return _the number of **negative** numbers in_ `grid`.
**Example 1:**
**Input:** grid = \[\[4,3,2,-1\],\[3,2,1,-1\],\[1,1,-1,-2\],\[-1,-1,-2,-3\]\]
**Output:** 8
**Explanation:** There are 8 negatives number in the matrix.
**Example 2:**
**Input:** grid = \[\[3,2\],\[1,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `-100 <= grid[i][j] <= 100`
**Follow up:** Could you find an `O(n + m)` solution? | Use 2-pointers algorithm to make sure all amount of characters outside the 2 pointers are smaller or equal to n/4. That means you need to count the amount of each letter and make sure the amount is enough. |
Simple Solution with both Brute Force and Optimal approaches in three languages | count-negative-numbers-in-a-sorted-matrix | 1 | 1 | # Brute Force\n## Intuition\nBrute force approach is easy just go through the matrix and find the number is less than zero or not ,if less than zero then increase your count variable.\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is same as I discussed in intution section \n\n## Complexity\n- Time complexity: $$O(n*m)$$\n \n- Space complexity: $$O(1)$$\n\n\n# Code\n\n```c++ []\nclass Solution {\npublic:\n int countNegatives(vector<vector<int>>& grid) {\n int count=0;\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[i].size();j++){\n if(grid[i][j]<0) count++;\n }\n }\n return count;\n }\n};\n```\n```java []\nclass Solution {\n public int countNegatives(int[][] grid) {\n int count=0;\n for(int i[]:grid){\n for(int x:i){\n if(x<0) count++;\n }\n }\n return count;\n }\n}\n```\n```python []\nclass Solution:\n def countNegatives(self, grid: List[List[int]]) -> int:\n count=0\n for i in range(len(grid)):\n for j in range(len(grid[i])):\n if grid[i][j]<0:\n count+=1\n return count \n```\n\n\n\n\n# Optimal approach\n## Intuition\nIn the question they told us that the matrix is sorted in non-increasing order both row-wise and column-wise, so we can apply binarysearch here.\n## Approach\n<!-- Describe your approach to solving the problem. -->\n1. First of all we go through row-wise,means take rows one by one and in that row we apply binary search.\n2. Then find the mid value of the row if the value is less than zero then all the values,on the right side of the mid value ,should be less than zero and the number of values will be (end-mid+1).After that we do binarysearch on the left side of the mid value.\n\n3. and if the mid value is not less than zero than do the binary search on the right side of the mid value.\n4. Lastly return the count of negative number in the given matrix.\n\n## Complexity\n- Time complexity: let suppose row size=m and column size n then T.C will be $$O(m*logn)$$\n \n- Space complexity: $$O(1)$$\n\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int binarySearch(vector<vector<int>>& grid,int start,int end,int row){\n if(start>end) return 0;\n int mid=start+(end-start)/2;\n\n if(grid[row][mid]<0){\n return (end-mid+1)+binarySearch(grid,start,mid-1,row);\n }\n return binarySearch(grid,mid+1,end,row);\n }\n int countNegatives(vector<vector<int>>& grid) {\n int count=0;\n for(int i=0;i<grid.size();i++){\n count+=binarySearch(grid,0,grid[i].size()-1,i);\n }\n return count;\n }\n};\n```\n```java []\nclass Solution {\n public int binarySearch(int[][] grid,int start,int end,int row){\n if(start>end) return 0;\n int mid=start+(end-start)/2;\n\n if(grid[row][mid]<0){\n return (end-mid+1)+binarySearch(grid,start,mid-1,row);\n }\n return binarySearch(grid,mid+1,end,row);\n }\n public int countNegatives(int[][] grid) {\n int count=0;\n for(int i=0;i<grid.length;i++){\n count+=binarySearch(grid,0,grid[i].length-1,i);\n }\n return count;\n }\n}\n```\n```python []\nclass Solution:\n def binarySearch(self,grid: List[List[int]],st,en,r):\n if st>en:return 0\n mid=st+(en-st)//2\n if grid[r][mid]<0:\n return en-mid+1+self.binarySearch(grid,st,mid-1,r)\n return self.binarySearch(grid,mid+1,en,r)\n def countNegatives(self, grid: List[List[int]]) -> int:\n count=0\n for i in range(len(grid)):\n count+=self.binarySearch(grid,0,len(grid[i])-1,i)\n return count \n```\n\n\n\n\n\n\n | 3 | Implement the class `SubrectangleQueries` which receives a `rows x cols` rectangle as a matrix of integers in the constructor and supports two methods:
1. `updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)`
* Updates all values with `newValue` in the subrectangle whose upper left coordinate is `(row1,col1)` and bottom right coordinate is `(row2,col2)`.
2. `getValue(int row, int col)`
* Returns the current value of the coordinate `(row,col)` from the rectangle.
**Example 1:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue ", "getValue "\]
\[\[\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]\],\[0,2\],\[0,0,3,2,5\],\[0,2\],\[3,1\],\[3,0,3,2,10\],\[3,1\],\[0,2\]\]
**Output**
\[null,1,null,5,5,null,10,5\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,2,1\],\[4,3,4\],\[3,2,1\],\[1,1,1\]\]);
// The initial rectangle (4x3) looks like:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // return 5
subrectangleQueries.getValue(3, 1); // return 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// After this update the rectangle looks like:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // return 10
subrectangleQueries.getValue(0, 2); // return 5
**Example 2:**
**Input**
\[ "SubrectangleQueries ", "getValue ", "updateSubrectangle ", "getValue ", "getValue ", "updateSubrectangle ", "getValue "\]
\[\[\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]\],\[0,0\],\[0,0,2,2,100\],\[0,0\],\[2,2\],\[1,1,2,2,20\],\[2,2\]\]
**Output**
\[null,1,null,100,100,null,20\]
**Explanation**
SubrectangleQueries subrectangleQueries = new SubrectangleQueries(\[\[1,1,1\],\[2,2,2\],\[3,3,3\]\]);
subrectangleQueries.getValue(0, 0); // return 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // return 100
subrectangleQueries.getValue(2, 2); // return 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // return 20
**Constraints:**
* There will be at most `500` operations considering both methods: `updateSubrectangle` and `getValue`.
* `1 <= rows, cols <= 100`
* `rows == rectangle.length`
* `cols == rectangle[i].length`
* `0 <= row1 <= row2 < rows`
* `0 <= col1 <= col2 < cols`
* `1 <= newValue, rectangle[i][j] <= 10^9`
* `0 <= row < rows`
* `0 <= col < cols` | Use binary search for optimization or simply brute force. |
Python3 97% solution | product-of-the-last-k-numbers | 0 | 1 | ```python\nclass ProductOfNumbers:\n def __init__(self):\n self.data = []\n self.product = 1\n\n def add(self, num: int) -> None:\n if num != 0:\n self.product *= num\n self.data.append(self.product)\n else:\n self.data = []\n self.product = 1\n\n def getProduct(self, k: int) -> int:\n if len(self.data) < k:\n return 0\n if len(self.data) == k:\n return self.data[-1]\n else:\n return int(self.data[-1] / self.data[-1-k])\n``` | 29 | Design an algorithm that accepts a stream of integers and retrieves the product of the last `k` integers of the stream.
Implement the `ProductOfNumbers` class:
* `ProductOfNumbers()` Initializes the object with an empty stream.
* `void add(int num)` Appends the integer `num` to the stream.
* `int getProduct(int k)` Returns the product of the last `k` numbers in the current list. You can assume that always the current list has at least `k` numbers.
The test cases are generated so that, at any time, the product of any contiguous sequence of numbers will fit into a single 32-bit integer without overflowing.
**Example:**
**Input**
\[ "ProductOfNumbers ", "add ", "add ", "add ", "add ", "add ", "getProduct ", "getProduct ", "getProduct ", "add ", "getProduct "\]
\[\[\],\[3\],\[0\],\[2\],\[5\],\[4\],\[2\],\[3\],\[4\],\[8\],\[2\]\]
**Output**
\[null,null,null,null,null,null,20,40,0,null,32\]
**Explanation**
ProductOfNumbers productOfNumbers = new ProductOfNumbers();
productOfNumbers.add(3); // \[3\]
productOfNumbers.add(0); // \[3,0\]
productOfNumbers.add(2); // \[3,0,2\]
productOfNumbers.add(5); // \[3,0,2,5\]
productOfNumbers.add(4); // \[3,0,2,5,4\]
productOfNumbers.getProduct(2); // return 20. The product of the last 2 numbers is 5 \* 4 = 20
productOfNumbers.getProduct(3); // return 40. The product of the last 3 numbers is 2 \* 5 \* 4 = 40
productOfNumbers.getProduct(4); // return 0. The product of the last 4 numbers is 0 \* 2 \* 5 \* 4 = 0
productOfNumbers.add(8); // \[3,0,2,5,4,8\]
productOfNumbers.getProduct(2); // return 32. The product of the last 2 numbers is 4 \* 8 = 32
**Constraints:**
* `0 <= num <= 100`
* `1 <= k <= 4 * 104`
* At most `4 * 104` calls will be made to `add` and `getProduct`.
* The product of the stream at any point in time will fit in a **32-bit** integer. | Think on DP. Sort the elements by starting time, then define the dp[i] as the maximum profit taking elements from the suffix starting at i. Use binarySearch (lower_bound/upper_bound on C++) to get the next index for the DP transition. |
Python3 97% solution | product-of-the-last-k-numbers | 0 | 1 | ```python\nclass ProductOfNumbers:\n def __init__(self):\n self.data = []\n self.product = 1\n\n def add(self, num: int) -> None:\n if num != 0:\n self.product *= num\n self.data.append(self.product)\n else:\n self.data = []\n self.product = 1\n\n def getProduct(self, k: int) -> int:\n if len(self.data) < k:\n return 0\n if len(self.data) == k:\n return self.data[-1]\n else:\n return int(self.data[-1] / self.data[-1-k])\n``` | 29 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
87% beats. very easy | product-of-the-last-k-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.products = []\n self.product = 1\n \n\n def add(self, num: int) -> None:\n if num:\n self.product *= num\n self.products.append(self.product)\n else:\n self.products = []\n self.product = 1\n\n def getProduct(self, k: int) -> int:\n if len(self.products)< k:\n return 0\n elif k == len(self.products):\n return self.product\n else:\n return int(self.products[-1]/self.products[-1-k])\n \n\n\n# Your ProductOfNumbers object will be instantiated and called as such:\n# obj = ProductOfNumbers()\n# obj.add(num)\n# param_2 = obj.getProduct(k)\n``` | 4 | Design an algorithm that accepts a stream of integers and retrieves the product of the last `k` integers of the stream.
Implement the `ProductOfNumbers` class:
* `ProductOfNumbers()` Initializes the object with an empty stream.
* `void add(int num)` Appends the integer `num` to the stream.
* `int getProduct(int k)` Returns the product of the last `k` numbers in the current list. You can assume that always the current list has at least `k` numbers.
The test cases are generated so that, at any time, the product of any contiguous sequence of numbers will fit into a single 32-bit integer without overflowing.
**Example:**
**Input**
\[ "ProductOfNumbers ", "add ", "add ", "add ", "add ", "add ", "getProduct ", "getProduct ", "getProduct ", "add ", "getProduct "\]
\[\[\],\[3\],\[0\],\[2\],\[5\],\[4\],\[2\],\[3\],\[4\],\[8\],\[2\]\]
**Output**
\[null,null,null,null,null,null,20,40,0,null,32\]
**Explanation**
ProductOfNumbers productOfNumbers = new ProductOfNumbers();
productOfNumbers.add(3); // \[3\]
productOfNumbers.add(0); // \[3,0\]
productOfNumbers.add(2); // \[3,0,2\]
productOfNumbers.add(5); // \[3,0,2,5\]
productOfNumbers.add(4); // \[3,0,2,5,4\]
productOfNumbers.getProduct(2); // return 20. The product of the last 2 numbers is 5 \* 4 = 20
productOfNumbers.getProduct(3); // return 40. The product of the last 3 numbers is 2 \* 5 \* 4 = 40
productOfNumbers.getProduct(4); // return 0. The product of the last 4 numbers is 0 \* 2 \* 5 \* 4 = 0
productOfNumbers.add(8); // \[3,0,2,5,4,8\]
productOfNumbers.getProduct(2); // return 32. The product of the last 2 numbers is 4 \* 8 = 32
**Constraints:**
* `0 <= num <= 100`
* `1 <= k <= 4 * 104`
* At most `4 * 104` calls will be made to `add` and `getProduct`.
* The product of the stream at any point in time will fit in a **32-bit** integer. | Think on DP. Sort the elements by starting time, then define the dp[i] as the maximum profit taking elements from the suffix starting at i. Use binarySearch (lower_bound/upper_bound on C++) to get the next index for the DP transition. |
87% beats. very easy | product-of-the-last-k-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.products = []\n self.product = 1\n \n\n def add(self, num: int) -> None:\n if num:\n self.product *= num\n self.products.append(self.product)\n else:\n self.products = []\n self.product = 1\n\n def getProduct(self, k: int) -> int:\n if len(self.products)< k:\n return 0\n elif k == len(self.products):\n return self.product\n else:\n return int(self.products[-1]/self.products[-1-k])\n \n\n\n# Your ProductOfNumbers object will be instantiated and called as such:\n# obj = ProductOfNumbers()\n# obj.add(num)\n# param_2 = obj.getProduct(k)\n``` | 4 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
Python solution. With explanation. BEATS 99% | product-of-the-last-k-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is to use a list to store the numbers that have been added, and use the last k elements of the list to calculate the product. However, I also need to consider the case where a zero is added to the list, which would make the product of the last k elements 0.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach is to use a list to store the numbers that have been added, as well as a count of the number of zeroes that have been added, and their respective indices. When a new number is added, I will check if it is a zero and update the zero count and index accordingly. When getting the product of the last k elements, I will check if there are any zeroes in the list and if the last k elements contain any of them. If they do, I will return 0, otherwise I will return the product of the last k elements.\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.numbers = [1]\n self.zero = 0\n self.zero_index = []\n self.last_zero = 0\n\n def add(self, num: int) -> None:\n if num == 0:\n self.zero += 1\n self.zero_index.append(len(self.numbers))\n self.last_zero = len(self.numbers)\n self.numbers.append(1)\n else:\n self.numbers.append(self.numbers[-1] * num)\n\n def getProduct(self, k: int) -> int:\n if self.zero == 0:\n return self.numbers[-1] // self.numbers[-k - 1]\n else:\n if len(self.numbers) - k - 1 < self.zero_index[-1]:\n return 0\n else:\n return self.numbers[-1] // self.numbers[-k - 1]\n\n# Your ProductOfNumbers object will be instantiated and called as such:\n# obj = ProductOfNumbers()\n# obj.add(num)\n# param_2 = obj.getProduct(k)\n``` | 3 | Design an algorithm that accepts a stream of integers and retrieves the product of the last `k` integers of the stream.
Implement the `ProductOfNumbers` class:
* `ProductOfNumbers()` Initializes the object with an empty stream.
* `void add(int num)` Appends the integer `num` to the stream.
* `int getProduct(int k)` Returns the product of the last `k` numbers in the current list. You can assume that always the current list has at least `k` numbers.
The test cases are generated so that, at any time, the product of any contiguous sequence of numbers will fit into a single 32-bit integer without overflowing.
**Example:**
**Input**
\[ "ProductOfNumbers ", "add ", "add ", "add ", "add ", "add ", "getProduct ", "getProduct ", "getProduct ", "add ", "getProduct "\]
\[\[\],\[3\],\[0\],\[2\],\[5\],\[4\],\[2\],\[3\],\[4\],\[8\],\[2\]\]
**Output**
\[null,null,null,null,null,null,20,40,0,null,32\]
**Explanation**
ProductOfNumbers productOfNumbers = new ProductOfNumbers();
productOfNumbers.add(3); // \[3\]
productOfNumbers.add(0); // \[3,0\]
productOfNumbers.add(2); // \[3,0,2\]
productOfNumbers.add(5); // \[3,0,2,5\]
productOfNumbers.add(4); // \[3,0,2,5,4\]
productOfNumbers.getProduct(2); // return 20. The product of the last 2 numbers is 5 \* 4 = 20
productOfNumbers.getProduct(3); // return 40. The product of the last 3 numbers is 2 \* 5 \* 4 = 40
productOfNumbers.getProduct(4); // return 0. The product of the last 4 numbers is 0 \* 2 \* 5 \* 4 = 0
productOfNumbers.add(8); // \[3,0,2,5,4,8\]
productOfNumbers.getProduct(2); // return 32. The product of the last 2 numbers is 4 \* 8 = 32
**Constraints:**
* `0 <= num <= 100`
* `1 <= k <= 4 * 104`
* At most `4 * 104` calls will be made to `add` and `getProduct`.
* The product of the stream at any point in time will fit in a **32-bit** integer. | Think on DP. Sort the elements by starting time, then define the dp[i] as the maximum profit taking elements from the suffix starting at i. Use binarySearch (lower_bound/upper_bound on C++) to get the next index for the DP transition. |
Python solution. With explanation. BEATS 99% | product-of-the-last-k-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is to use a list to store the numbers that have been added, and use the last k elements of the list to calculate the product. However, I also need to consider the case where a zero is added to the list, which would make the product of the last k elements 0.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach is to use a list to store the numbers that have been added, as well as a count of the number of zeroes that have been added, and their respective indices. When a new number is added, I will check if it is a zero and update the zero count and index accordingly. When getting the product of the last k elements, I will check if there are any zeroes in the list and if the last k elements contain any of them. If they do, I will return 0, otherwise I will return the product of the last k elements.\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.numbers = [1]\n self.zero = 0\n self.zero_index = []\n self.last_zero = 0\n\n def add(self, num: int) -> None:\n if num == 0:\n self.zero += 1\n self.zero_index.append(len(self.numbers))\n self.last_zero = len(self.numbers)\n self.numbers.append(1)\n else:\n self.numbers.append(self.numbers[-1] * num)\n\n def getProduct(self, k: int) -> int:\n if self.zero == 0:\n return self.numbers[-1] // self.numbers[-k - 1]\n else:\n if len(self.numbers) - k - 1 < self.zero_index[-1]:\n return 0\n else:\n return self.numbers[-1] // self.numbers[-k - 1]\n\n# Your ProductOfNumbers object will be instantiated and called as such:\n# obj = ProductOfNumbers()\n# obj.add(num)\n# param_2 = obj.getProduct(k)\n``` | 3 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
[Python3] - Easy to Understand Prefix Product | product-of-the-last-k-numbers | 0 | 1 | This approach is similar to the one for prefix sum, where we keep a list of all the products up to index = i:\ne.g. If the given input of numbers is: ```[3, 4, 5]```, the prefix product list that we keep will be: ```[3, 3x4, 3x4x5] => [3, 12, 60]```\n\nEvery time we are fed with a zero, say at index i, we know that if the k is the range where it contains index i, the product will always be zero:\n\ne.g Given input: ```[3, 0, 2, 5, 4]``` , when ```k >= 4```, the product is always 0.\n\nTherefore, whenever we see a zero, we could discard the product list we have kept so far.\n\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.products = [] # containing the prefix producr\n\n def add(self, num: int) -> None:\n if num == 0:\n self.products = [] # discard product list so far\n else:\n if self.products: \n self.products.append(self.products[-1] * num) # if product list not empty, \n\t\t\t\t # calculate the prefix product \n else:\n self.products.append(num)\n \n def getProduct(self, k: int) -> int:\n if len(self.products) == k:\n return self.products[-1]\n elif len(self.products) > k:\n return self.products[-1] // self.products[len(self.products) - k - 1]\n else:\n return 0\n```\n\n | 4 | Design an algorithm that accepts a stream of integers and retrieves the product of the last `k` integers of the stream.
Implement the `ProductOfNumbers` class:
* `ProductOfNumbers()` Initializes the object with an empty stream.
* `void add(int num)` Appends the integer `num` to the stream.
* `int getProduct(int k)` Returns the product of the last `k` numbers in the current list. You can assume that always the current list has at least `k` numbers.
The test cases are generated so that, at any time, the product of any contiguous sequence of numbers will fit into a single 32-bit integer without overflowing.
**Example:**
**Input**
\[ "ProductOfNumbers ", "add ", "add ", "add ", "add ", "add ", "getProduct ", "getProduct ", "getProduct ", "add ", "getProduct "\]
\[\[\],\[3\],\[0\],\[2\],\[5\],\[4\],\[2\],\[3\],\[4\],\[8\],\[2\]\]
**Output**
\[null,null,null,null,null,null,20,40,0,null,32\]
**Explanation**
ProductOfNumbers productOfNumbers = new ProductOfNumbers();
productOfNumbers.add(3); // \[3\]
productOfNumbers.add(0); // \[3,0\]
productOfNumbers.add(2); // \[3,0,2\]
productOfNumbers.add(5); // \[3,0,2,5\]
productOfNumbers.add(4); // \[3,0,2,5,4\]
productOfNumbers.getProduct(2); // return 20. The product of the last 2 numbers is 5 \* 4 = 20
productOfNumbers.getProduct(3); // return 40. The product of the last 3 numbers is 2 \* 5 \* 4 = 40
productOfNumbers.getProduct(4); // return 0. The product of the last 4 numbers is 0 \* 2 \* 5 \* 4 = 0
productOfNumbers.add(8); // \[3,0,2,5,4,8\]
productOfNumbers.getProduct(2); // return 32. The product of the last 2 numbers is 4 \* 8 = 32
**Constraints:**
* `0 <= num <= 100`
* `1 <= k <= 4 * 104`
* At most `4 * 104` calls will be made to `add` and `getProduct`.
* The product of the stream at any point in time will fit in a **32-bit** integer. | Think on DP. Sort the elements by starting time, then define the dp[i] as the maximum profit taking elements from the suffix starting at i. Use binarySearch (lower_bound/upper_bound on C++) to get the next index for the DP transition. |
[Python3] - Easy to Understand Prefix Product | product-of-the-last-k-numbers | 0 | 1 | This approach is similar to the one for prefix sum, where we keep a list of all the products up to index = i:\ne.g. If the given input of numbers is: ```[3, 4, 5]```, the prefix product list that we keep will be: ```[3, 3x4, 3x4x5] => [3, 12, 60]```\n\nEvery time we are fed with a zero, say at index i, we know that if the k is the range where it contains index i, the product will always be zero:\n\ne.g Given input: ```[3, 0, 2, 5, 4]``` , when ```k >= 4```, the product is always 0.\n\nTherefore, whenever we see a zero, we could discard the product list we have kept so far.\n\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.products = [] # containing the prefix producr\n\n def add(self, num: int) -> None:\n if num == 0:\n self.products = [] # discard product list so far\n else:\n if self.products: \n self.products.append(self.products[-1] * num) # if product list not empty, \n\t\t\t\t # calculate the prefix product \n else:\n self.products.append(num)\n \n def getProduct(self, k: int) -> int:\n if len(self.products) == k:\n return self.products[-1]\n elif len(self.products) > k:\n return self.products[-1] // self.products[len(self.products) - k - 1]\n else:\n return 0\n```\n\n | 4 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
Easy Python Code in O(n) | product-of-the-last-k-numbers | 0 | 1 | # Code\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.p = []\n self.prod = 1\n\n def add(self, num: int) -> None:\n if(num != 0):\n self.prod *= num\n self.p.append(self.prod)\n else:\n self.p = []\n self.prod = 1\n \n\n def getProduct(self, k: int) -> int:\n if(len(self.p) == k):\n return self.p[-1]\n elif(len(self.p) < k):\n return 0\n else:\n if(self.p[-k-1] != 0):\n return int(self.p[-1] / self.p[-k-1])\n \n\n\n# Your ProductOfNumbers object will be instantiated and called as such:\n# obj = ProductOfNumbers()\n# obj.add(num)\n# param_2 = obj.getProduct(k)\n```\n\n# Explanation\n\nThe constructor (__init__) initializes two empty lists: self.p and self.prod. self.p will store the product of all numbers in the stream so far, while self.prod will store the product of the last k numbers in the stream.\n\nThe add() method appends the new number (num) to the stream. If num is not equal to 0, the product of all numbers in the stream so far is updated by multiplying it with num. The product of the last k numbers in the stream is also updated by appending the new product to self.p.\n\nThe getProduct() method returns the product of the last k numbers in the stream. If the length of the stream is less than k, the method returns 0. Otherwise, the method returns the quotient of the product of all numbers in the stream so far and the product of the first k-1 numbers in the stream. | 0 | Design an algorithm that accepts a stream of integers and retrieves the product of the last `k` integers of the stream.
Implement the `ProductOfNumbers` class:
* `ProductOfNumbers()` Initializes the object with an empty stream.
* `void add(int num)` Appends the integer `num` to the stream.
* `int getProduct(int k)` Returns the product of the last `k` numbers in the current list. You can assume that always the current list has at least `k` numbers.
The test cases are generated so that, at any time, the product of any contiguous sequence of numbers will fit into a single 32-bit integer without overflowing.
**Example:**
**Input**
\[ "ProductOfNumbers ", "add ", "add ", "add ", "add ", "add ", "getProduct ", "getProduct ", "getProduct ", "add ", "getProduct "\]
\[\[\],\[3\],\[0\],\[2\],\[5\],\[4\],\[2\],\[3\],\[4\],\[8\],\[2\]\]
**Output**
\[null,null,null,null,null,null,20,40,0,null,32\]
**Explanation**
ProductOfNumbers productOfNumbers = new ProductOfNumbers();
productOfNumbers.add(3); // \[3\]
productOfNumbers.add(0); // \[3,0\]
productOfNumbers.add(2); // \[3,0,2\]
productOfNumbers.add(5); // \[3,0,2,5\]
productOfNumbers.add(4); // \[3,0,2,5,4\]
productOfNumbers.getProduct(2); // return 20. The product of the last 2 numbers is 5 \* 4 = 20
productOfNumbers.getProduct(3); // return 40. The product of the last 3 numbers is 2 \* 5 \* 4 = 40
productOfNumbers.getProduct(4); // return 0. The product of the last 4 numbers is 0 \* 2 \* 5 \* 4 = 0
productOfNumbers.add(8); // \[3,0,2,5,4,8\]
productOfNumbers.getProduct(2); // return 32. The product of the last 2 numbers is 4 \* 8 = 32
**Constraints:**
* `0 <= num <= 100`
* `1 <= k <= 4 * 104`
* At most `4 * 104` calls will be made to `add` and `getProduct`.
* The product of the stream at any point in time will fit in a **32-bit** integer. | Think on DP. Sort the elements by starting time, then define the dp[i] as the maximum profit taking elements from the suffix starting at i. Use binarySearch (lower_bound/upper_bound on C++) to get the next index for the DP transition. |
Easy Python Code in O(n) | product-of-the-last-k-numbers | 0 | 1 | # Code\n```\nclass ProductOfNumbers:\n\n def __init__(self):\n self.p = []\n self.prod = 1\n\n def add(self, num: int) -> None:\n if(num != 0):\n self.prod *= num\n self.p.append(self.prod)\n else:\n self.p = []\n self.prod = 1\n \n\n def getProduct(self, k: int) -> int:\n if(len(self.p) == k):\n return self.p[-1]\n elif(len(self.p) < k):\n return 0\n else:\n if(self.p[-k-1] != 0):\n return int(self.p[-1] / self.p[-k-1])\n \n\n\n# Your ProductOfNumbers object will be instantiated and called as such:\n# obj = ProductOfNumbers()\n# obj.add(num)\n# param_2 = obj.getProduct(k)\n```\n\n# Explanation\n\nThe constructor (__init__) initializes two empty lists: self.p and self.prod. self.p will store the product of all numbers in the stream so far, while self.prod will store the product of the last k numbers in the stream.\n\nThe add() method appends the new number (num) to the stream. If num is not equal to 0, the product of all numbers in the stream so far is updated by multiplying it with num. The product of the last k numbers in the stream is also updated by appending the new product to self.p.\n\nThe getProduct() method returns the product of the last k numbers in the stream. If the length of the stream is less than k, the method returns 0. Otherwise, the method returns the quotient of the product of all numbers in the stream so far and the product of the first k-1 numbers in the stream. | 0 | You are given an array of integers `arr` and an integer `target`.
You have to find **two non-overlapping sub-arrays** of `arr` each with a sum equal `target`. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is **minimum**.
Return _the minimum sum of the lengths_ of the two required sub-arrays, or return `-1` if you cannot find such two sub-arrays.
**Example 1:**
**Input:** arr = \[3,2,2,4,3\], target = 3
**Output:** 2
**Explanation:** Only two sub-arrays have sum = 3 (\[3\] and \[3\]). The sum of their lengths is 2.
**Example 2:**
**Input:** arr = \[7,3,4,7\], target = 7
**Output:** 2
**Explanation:** Although we have three non-overlapping sub-arrays of sum = 7 (\[7\], \[3,4\] and \[7\]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.
**Example 3:**
**Input:** arr = \[4,3,2,6,2,3,4\], target = 6
**Output:** -1
**Explanation:** We have only one sub-array of sum = 6.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i] <= 1000`
* `1 <= target <= 108` | Keep all prefix products of numbers in an array, then calculate the product of last K elements in O(1) complexity. When a zero number is added, clean the array of prefix products. |
Simple and optimal python3 solution | 871 ms - faster than 99% solutions | maximum-number-of-events-that-can-be-attended | 0 | 1 | <!--# Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!--# Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n \\cdot log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nimport heapq\n\n\nclass Solution:\n def maxEvents(self, events: List[List[int]]) -> int:\n events.sort()\n\n # only for no duplication `while` after `for`\n events.append([float(\'inf\'), float(\'inf\')])\n\n result = 0\n h = []\n current_day = 0\n\n for start, end in events:\n while h and current_day < start:\n prev_end = heapq.heappop(h)\n if prev_end >= current_day:\n result += 1\n current_day += 1\n \n current_day = start\n heapq.heappush(h, end)\n \n return result\n\n``` | 1 | You are given an array of `events` where `events[i] = [startDayi, endDayi]`. Every event `i` starts at `startDayi` and ends at `endDayi`.
You can attend an event `i` at any day `d` where `startTimei <= d <= endTimei`. You can only attend one event at any time `d`.
Return _the maximum number of events you can attend_.
**Example 1:**
**Input:** events = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.
**Example 2:**
**Input:** events= \[\[1,2\],\[2,3\],\[3,4\],\[1,2\]\]
**Output:** 4
**Constraints:**
* `1 <= events.length <= 105`
* `events[i].length == 2`
* `1 <= startDayi <= endDayi <= 105` | null |
Simple and optimal python3 solution | 871 ms - faster than 99% solutions | maximum-number-of-events-that-can-be-attended | 0 | 1 | <!--# Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!--# Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n \\cdot log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nimport heapq\n\n\nclass Solution:\n def maxEvents(self, events: List[List[int]]) -> int:\n events.sort()\n\n # only for no duplication `while` after `for`\n events.append([float(\'inf\'), float(\'inf\')])\n\n result = 0\n h = []\n current_day = 0\n\n for start, end in events:\n while h and current_day < start:\n prev_end = heapq.heappop(h)\n if prev_end >= current_day:\n result += 1\n current_day += 1\n \n current_day = start\n heapq.heappush(h, end)\n \n return result\n\n``` | 1 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
[Python] Faster than 90%, Low-space, Simple, Min-Heap, Explained | maximum-number-of-events-that-can-be-attended | 0 | 1 | Please feel free to ask questions or give suggestions. **Upvote** if you liked the solution.\n**Idea**:\n1. Sort events by startDay.\n2. Keep track of endDays for started events in a min-heap based on current day.\n3. Greedily attend started event with lowest endDay. Move to the next viable day. \n4. Repeat steps 2 and 3 while there is some unstarted event.\n4. When all events have started, repeat step 3 until there are no started events remaining.\n```\ndef maxEvents(self, events: List[List[int]]) -> int:\n\tn = len(events)\n\t# Sort by startDay(needed), endDay (minimizes number of swaps when pushing in heap)\n\tevents.sort()\n\n\t# Min-heap that stores endDay for started events\n\tstarted = []\n\tcount = i = 0\n\t# First day an event starts\n\tcurr_day = events[0][0]\n\t# While some event hasn\'t been added to heap\n\twhile i<n:\n\t\t# Add all events that start on curr_day\n\t\twhile i<n and events[i][0]==curr_day:\n\t\t\theappush(started, events[i][1])\n\t\t\ti += 1\n\n\t\t# Attend started event that ends earliest\n\t\theappop(started)\n\t\tcount += 1\n\t\tcurr_day += 1\n\t\t\n\t\t# Remove all expired events\n\t\twhile started and started[0]<curr_day: heappop(started)\n\t\t# If no started events left, move to the next startDay\n\t\tif i<n and not started: curr_day = events[i][0]\n\n\t# Events that started that are still left in heap\n\twhile started:\n\t\t# Non-expired started event that ends earliest\n\t\tif heappop(started)>=curr_day:\n\t\t\tcurr_day += 1\n\t\t\tcount += 1\n\n\treturn count\n```\n**Worst-case Time Complexity**: O(nlogn)\n**Worst-case Space Complexity**: O(n) | 23 | You are given an array of `events` where `events[i] = [startDayi, endDayi]`. Every event `i` starts at `startDayi` and ends at `endDayi`.
You can attend an event `i` at any day `d` where `startTimei <= d <= endTimei`. You can only attend one event at any time `d`.
Return _the maximum number of events you can attend_.
**Example 1:**
**Input:** events = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.
**Example 2:**
**Input:** events= \[\[1,2\],\[2,3\],\[3,4\],\[1,2\]\]
**Output:** 4
**Constraints:**
* `1 <= events.length <= 105`
* `events[i].length == 2`
* `1 <= startDayi <= endDayi <= 105` | null |
[Python] Faster than 90%, Low-space, Simple, Min-Heap, Explained | maximum-number-of-events-that-can-be-attended | 0 | 1 | Please feel free to ask questions or give suggestions. **Upvote** if you liked the solution.\n**Idea**:\n1. Sort events by startDay.\n2. Keep track of endDays for started events in a min-heap based on current day.\n3. Greedily attend started event with lowest endDay. Move to the next viable day. \n4. Repeat steps 2 and 3 while there is some unstarted event.\n4. When all events have started, repeat step 3 until there are no started events remaining.\n```\ndef maxEvents(self, events: List[List[int]]) -> int:\n\tn = len(events)\n\t# Sort by startDay(needed), endDay (minimizes number of swaps when pushing in heap)\n\tevents.sort()\n\n\t# Min-heap that stores endDay for started events\n\tstarted = []\n\tcount = i = 0\n\t# First day an event starts\n\tcurr_day = events[0][0]\n\t# While some event hasn\'t been added to heap\n\twhile i<n:\n\t\t# Add all events that start on curr_day\n\t\twhile i<n and events[i][0]==curr_day:\n\t\t\theappush(started, events[i][1])\n\t\t\ti += 1\n\n\t\t# Attend started event that ends earliest\n\t\theappop(started)\n\t\tcount += 1\n\t\tcurr_day += 1\n\t\t\n\t\t# Remove all expired events\n\t\twhile started and started[0]<curr_day: heappop(started)\n\t\t# If no started events left, move to the next startDay\n\t\tif i<n and not started: curr_day = events[i][0]\n\n\t# Events that started that are still left in heap\n\twhile started:\n\t\t# Non-expired started event that ends earliest\n\t\tif heappop(started)>=curr_day:\n\t\t\tcurr_day += 1\n\t\t\tcount += 1\n\n\treturn count\n```\n**Worst-case Time Complexity**: O(nlogn)\n**Worst-case Space Complexity**: O(n) | 23 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
[Python3] Heap | maximum-number-of-events-that-can-be-attended | 0 | 1 | ```\nclass Solution:\n def maxEvents(self, events: List[List[int]]) -> int:\n # 1. person can only attend one event per day, even if there are multiple events on that day.\n # 2. if there are multiple events happen at one day,\n # person attend the event ends close to current day.\n #. so we need a data structure hold all the event happend today,\n # and sorted ascedningly. minimum heap is the data structure we need.\n \n """\n [[1,1],[1,2],[2,2],[3,4],[4,4]]\n day one events: [1,1] [1,2]\n events today: heap = [1,2]\n events expire today: none,heap = [1,2]\n events attend: 1, heap = [2]\n day two events: [1,2],[2,2]\n events today: heap = [2,2]\n events expire today:none, heap = [2,2]\n events attend: 2 heap = [2]\n day three events: [2,2][3,4]\n events today: heap = [2,4]\n events expire today;[1,2] heap = [4]\n events attend:3 heap = []\n """\n events = sorted(events,key = lambda x:(x[0],x[1])) \n #determine the number of days has events\n n = 0\n for i in range(len(events)):\n n = max(n,events[i][1])\n \n attended = 0\n day = 0\n eventIdx = 0\n heap =[]\n \n \n for day in range(1, n + 1):\n #step 1: Add all the events ending time to the heap that start today\n while eventIdx < len(events) and events[eventIdx][0] == day:\n heappush(heap,events[eventIdx][1])\n eventIdx += 1\n \n #step 2: Remove the events expired today\n while heap and heap[0] < day:\n heappop(heap)\n \n #step 3: event that can be attended today,only one event per day. \n if heap:\n heappop(heap)\n attended += 1\n \n return attended\n``` | 8 | You are given an array of `events` where `events[i] = [startDayi, endDayi]`. Every event `i` starts at `startDayi` and ends at `endDayi`.
You can attend an event `i` at any day `d` where `startTimei <= d <= endTimei`. You can only attend one event at any time `d`.
Return _the maximum number of events you can attend_.
**Example 1:**
**Input:** events = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.
**Example 2:**
**Input:** events= \[\[1,2\],\[2,3\],\[3,4\],\[1,2\]\]
**Output:** 4
**Constraints:**
* `1 <= events.length <= 105`
* `events[i].length == 2`
* `1 <= startDayi <= endDayi <= 105` | null |
[Python3] Heap | maximum-number-of-events-that-can-be-attended | 0 | 1 | ```\nclass Solution:\n def maxEvents(self, events: List[List[int]]) -> int:\n # 1. person can only attend one event per day, even if there are multiple events on that day.\n # 2. if there are multiple events happen at one day,\n # person attend the event ends close to current day.\n #. so we need a data structure hold all the event happend today,\n # and sorted ascedningly. minimum heap is the data structure we need.\n \n """\n [[1,1],[1,2],[2,2],[3,4],[4,4]]\n day one events: [1,1] [1,2]\n events today: heap = [1,2]\n events expire today: none,heap = [1,2]\n events attend: 1, heap = [2]\n day two events: [1,2],[2,2]\n events today: heap = [2,2]\n events expire today:none, heap = [2,2]\n events attend: 2 heap = [2]\n day three events: [2,2][3,4]\n events today: heap = [2,4]\n events expire today;[1,2] heap = [4]\n events attend:3 heap = []\n """\n events = sorted(events,key = lambda x:(x[0],x[1])) \n #determine the number of days has events\n n = 0\n for i in range(len(events)):\n n = max(n,events[i][1])\n \n attended = 0\n day = 0\n eventIdx = 0\n heap =[]\n \n \n for day in range(1, n + 1):\n #step 1: Add all the events ending time to the heap that start today\n while eventIdx < len(events) and events[eventIdx][0] == day:\n heappush(heap,events[eventIdx][1])\n eventIdx += 1\n \n #step 2: Remove the events expired today\n while heap and heap[0] < day:\n heappop(heap)\n \n #step 3: event that can be attended today,only one event per day. \n if heap:\n heappop(heap)\n attended += 1\n \n return attended\n``` | 8 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
📌📌 Well-Coded & Explained || Heap || For Beignners 🐍 | maximum-number-of-events-that-can-be-attended | 0 | 1 | ## IDEA :\n1. Person can only attend one event per day, even if there are multiple events on that day.\n2. if there are multiple events happen at one day, then person attend the event that ends close to current day. so we need a data structure hold all the event happend today, and sorted ascedningly. \n\n3. Minimum heap is the data structure we need.\n\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n def maxEvents(self, events: List[List[int]]) -> int:\n \n m = 0\n for eve in events:\n m = max(m,eve[1])\n \n events.sort(key = lambda x:(x[0],x[1]))\n heap = []\n res = 0\n event_ind = 0\n \n n = len(events)\n for day in range(1,m+1):\n # Pushing all the events in heap that starts Today\n while event_ind<n and events[event_ind][0]==day:\n heapq.heappush(heap,events[event_ind][1])\n event_ind += 1\n \n # Poping all the events in heap that ends Today\n while heap and heap[0]<day:\n heapq.heappop(heap)\n \n # If any event is there which can be attended today then pop it and add it to res count.\n if heap:\n heapq.heappop(heap)\n res+=1\n \n return res\n\n### Thanks and Upvote If you like the Idea or Explaination!! \uD83E\uDD1E | 13 | You are given an array of `events` where `events[i] = [startDayi, endDayi]`. Every event `i` starts at `startDayi` and ends at `endDayi`.
You can attend an event `i` at any day `d` where `startTimei <= d <= endTimei`. You can only attend one event at any time `d`.
Return _the maximum number of events you can attend_.
**Example 1:**
**Input:** events = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.
**Example 2:**
**Input:** events= \[\[1,2\],\[2,3\],\[3,4\],\[1,2\]\]
**Output:** 4
**Constraints:**
* `1 <= events.length <= 105`
* `events[i].length == 2`
* `1 <= startDayi <= endDayi <= 105` | null |
📌📌 Well-Coded & Explained || Heap || For Beignners 🐍 | maximum-number-of-events-that-can-be-attended | 0 | 1 | ## IDEA :\n1. Person can only attend one event per day, even if there are multiple events on that day.\n2. if there are multiple events happen at one day, then person attend the event that ends close to current day. so we need a data structure hold all the event happend today, and sorted ascedningly. \n\n3. Minimum heap is the data structure we need.\n\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n def maxEvents(self, events: List[List[int]]) -> int:\n \n m = 0\n for eve in events:\n m = max(m,eve[1])\n \n events.sort(key = lambda x:(x[0],x[1]))\n heap = []\n res = 0\n event_ind = 0\n \n n = len(events)\n for day in range(1,m+1):\n # Pushing all the events in heap that starts Today\n while event_ind<n and events[event_ind][0]==day:\n heapq.heappush(heap,events[event_ind][1])\n event_ind += 1\n \n # Poping all the events in heap that ends Today\n while heap and heap[0]<day:\n heapq.heappop(heap)\n \n # If any event is there which can be attended today then pop it and add it to res count.\n if heap:\n heapq.heappop(heap)\n res+=1\n \n return res\n\n### Thanks and Upvote If you like the Idea or Explaination!! \uD83E\uDD1E | 13 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Python3 solution with detailed explanation | maximum-number-of-events-that-can-be-attended | 0 | 1 | When I first tried to solve this problem, a bunch of `for` loops came to my mind where I\'d probably go over the `events` and add them to a list called `visited` and go forward until there\'s no further `event` in the `events`. [@bharadwaj6](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/discuss/510353/OUTDATED-Python3-greedy-100-no-heap-and-easy-to-read)\'s code (below, solution 1) does the exact same thing. However, if you run this code it will return the LTE (limit time exceeded) error. It sorts the `events` based on ending date, goes over `events` list (basically goes over the days each event is happening in) and add it to a `set()` in case that day has not been filled yet. Note that the `break` statement prevents addition of more than one day for a particular event (`break` statement stops current loop, see [this](https://www.tutorialspoint.com/python/python_break_statement.htm)). Can you understand this? Note that at first, we `sort` the `events` based on the last day of each event. \n\nExercise: Try to do these tasks! `sort` based on first day, last day, first day and then last day, last day and then first day (you can do this like: `events = sorted(events, key=lambda x: (x[1], x[0]))`) ! and check whether you would `return` correct output. Also, read [kaiwensun](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/discuss/510262/Detailed-analysisLet-me-lead-you-to-the-solution-step-by-step)\'s explanation about why choosing based on end date always works. \n\n```\n# Solution 1\ndef maxEvents(self, events: List[List[int]]) -> int:\n events = sorted(events, key=lambda x: x[1])\n visited = set()\n for s, e in events:\n for t in range(s, e+1):\n if t not in visited:\n visited.add(t)\n break\n return len(visited)\n```\n\nSince the above code is not working for this problem, I use a [priority queue](https://www.***.org/priority-queue-set-1-introduction/), and [kaiwensun](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/discuss/510262/Detailed-analysisLet-me-lead-you-to-the-solution-step-by-step)\'s solution. Something I don\'t like about the solution is importing the `heapq` module. I wasn\'t able to find a better solution except for implementing it from scratch, which is stupid for an interview question. \n\nIntuition? We use a priority queue, add events with starting day of today and remove events with ending day of today. Then, we attend an event that end sooner in the heap. Make sense? No? Keep reading! \n\n```\n# Solution 2: it use `import heapq`\nimport heapq\nclass Solution(object):\n def maxEvents(self, events):\n events = sorted(events, key = lambda x:x[0]) #1\n total_days = max(event[1] for event in events) #2\n min_heap = [] #3\n day, cnt, event_id = 1, 0, 0 #4\n \n \n while day <= total_days: #5\n\t\t # if no events are available to attend today, let time flies to the next available event.\n if event_id < len(events) and not min_heap: #6\n day = events[event_id][0] #7\n\t\t\t\n\t\t\t# all events starting from today are newly available. add them to the heap.\n while event_id < len(events) and events[event_id][0] <= day: #8\n heapq.heappush(min_heap, events[event_id][1]) #9\n event_id += 1 #10\n\n\t\t\t# if the event at heap top already ended, then discard it.\n while min_heap and min_heap[0] < day: #11\n heapq.heappop(min_heap) #12\n\n\t\t\t# attend the event that will end the earliest\n if min_heap: #13\n heapq.heappop(min_heap) #14 \n cnt += 1 #15\n elif event_id >= len(events): #16\n break # no more events to attend. so stop early to save time.\n day += 1 #17\n return cnt #18\n```\n\nThe outer `while` loop (line `#5`) takes care of `day` we\'re in. We start at `day = 1` (line `#4`) and update the `day` in line `#17` after doing some other stuff along the way. It\'s important to note that we\'re doing all the stuff between lines `#5` and `#16` on the same day. There are some notes I\'d like to mention about the solution before delving into it. 1) We define `min_heap` (line `#3`) as an array which will be used to `push` (for example line `#9`) or `pop` (for example line `#12` and `#14`) elements to or from. 2) We `push` end day of an event to the `min_heap` (line `#9`), and will `pop` it once the end day is passed by our day timer (variable `day`, line `#12`). 3) We add one to the counter (variable `cnt`, line `#15`) when there\'s something in the `min_heap` on a particular `day` and `pop` it from `min_heap` (line `#14`) since we\'re done with that day. \n\n\nThe solution: We first `sort` based on the starting day of each event (line `#1`)\n\n`total_days` is calculated based maximum ending day of `events` (line `#2`, we loop over all the events after sorting, and find an event with the maximum ending day). \n\nIn line `#3`, we initialize the `min_heap` as an array. \n\nLine `#4`: `day` keeps the day we\'re in, `cnt` keeps track of the number of events we\'ve already attended, and `event_id` keeps track of events being pushed into `min_heap` (line `#10`). `event_id` helps to `break` the loop after line `#16` (we don\'t get into this in the example shown below). \n\nLine `#5`: It\'s the outter `while` loop I already talked before. \n\nStarting now, I feel like following an example would make things easier. Say `events = [[1,4],[4,4],[2,2],[3,4],[1,1]]`. After sorting it\'d be `[[1, 1], [1, 4], [2, 2], [3, 4], [4, 4]]`, right? With `total_days = 4`. \n\nIn line `#6`, `event_id = 0`, `day = 1`. We go into the `while` loop of line `#6`, `day` re-assigns to `1`. Can you see why we have this line? Imagine after sorting, the first event has a starting day of 2 instead of 1, then, `day` gets updated to 2. Or if there is a gap between starting days of events. Lines `#6` and `#7` always get activated in the first pass of the outter `while` loop except if the `events` array is either empty of we just have one event. If we had more than one event, then these two lines would run for sure at first. So, after line `#7`, `day = 1` in this example. \n\n---- Day 1\nWe move to line `#8` (it\'s safe to change `<=` to `==` in line `#8`, but doesn\'t matter) and add the ending day of this event to `min_heal` in line `#9`. At this point, `min_heap = [1]`. We added the event with index `0` to `min_heap`. So, we update `event_id` (line `#10`). `event_id = 1` now. `min_heap` is not empty but its head (`min_heap[0]`) is 1. Note here that we don\'t go out of this `while` loop just yet. Since, we updated the `event_id` to be 1. Line `#8` gets checked again and guess what? In this example, `event_id = 1` also satisfies the criterion (event 1 also has a starting day of 1, similar to event 0). So, another event gets pushed into `min_heap` and `min_heap = [1,4]`. After all this, `event_id = 2` now. Then, we pass lines `#11` and `#12`. These two lines try to get rid of outdated events. For example, if you had three events like [[1,2],[1,2],[1,2]], you cannot attend all, right? After you assing the first two to day 1 and day 2, then in day 3, ending of your last event is less than day timer, therefore, it gets popped out of `min_heap`. Now it\'s the part we update `cnt`, our output. Line `#13` makes sure `min_heap` is not empty. If it\'s empty, then there\'s nothing to attend then, we move on. But, if it\'s not empty (which is not here since `min_heap = [1,4]`), then we updated `cnt` by 1 (line `#15`), we get rid of the event with minimum ending date (which is at the root of the heap we\'re dealing with, since it\'s a min heap. Check this out: [min heap](https://www.***.org/binary-heap/))) event. Makes sense? Now `min_heap = [4]`. After this, we go to the next day (line `#17`). `day = 2`. \n\n--- Day 2\nSimilar to day one. We don\'t get into line `#7` since `min_heap` is not empty now. We go into line `#9` and add `[2]` to the `min_heap`. Now, it\'s `min_heap = [2,4]`. We then go to line `#13`, pop `2` out and update `cnt` by one. Now, `min_heap = [4]` again and `cnt = 2`. We update `day` and go to day 3. `day = 3`. \n\n----Day 3\nAfter line `#10`, `min_heap = [4,4]` (note that ending date gets added to the heap) and `event_id = 3`. Note than `event_id` can be maximum of 4 or line `#16` gets activated and breaks the `while` loop. Again line `#14` and popping `[4]` this time, updating `cnt` to `3`. We do to the last day. `day = 4`. \n\n---Day 4.\nAfter line `#10`, `min_heap = [4,4]` again and `event_id = 4`. Again line `#14` and popping `[4]` this time, updating `cnt` to `4`. and `day = 4`, right? It\'s over (line `#5`, `day = 5` which is not `<=` of `total_days = 4`). We cannot allocate anymore event although we still have one more in the `min_heap` to attend.\n\n\nSo, the answer is 4. \n\n\nWere you able to follow? To wrapp up, we go and see whether there\'s an event in a day, we add it to the heap (we add more if there are more than one with the same starting day), we go and pop the root of heap, update the events attended, and do this for the total days we have to attend events. \n\n\n=================================================================\nFinal note: please let me know if you spot any typo/error/ etc. \n\nFinal note 2: I find explaining stuff in the simplest form instructive. I suggest you do the same in case you\'re having hard time understanding something. \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n | 17 | You are given an array of `events` where `events[i] = [startDayi, endDayi]`. Every event `i` starts at `startDayi` and ends at `endDayi`.
You can attend an event `i` at any day `d` where `startTimei <= d <= endTimei`. You can only attend one event at any time `d`.
Return _the maximum number of events you can attend_.
**Example 1:**
**Input:** events = \[\[1,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.
**Example 2:**
**Input:** events= \[\[1,2\],\[2,3\],\[3,4\],\[1,2\]\]
**Output:** 4
**Constraints:**
* `1 <= events.length <= 105`
* `events[i].length == 2`
* `1 <= startDayi <= endDayi <= 105` | null |
Python3 solution with detailed explanation | maximum-number-of-events-that-can-be-attended | 0 | 1 | When I first tried to solve this problem, a bunch of `for` loops came to my mind where I\'d probably go over the `events` and add them to a list called `visited` and go forward until there\'s no further `event` in the `events`. [@bharadwaj6](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/discuss/510353/OUTDATED-Python3-greedy-100-no-heap-and-easy-to-read)\'s code (below, solution 1) does the exact same thing. However, if you run this code it will return the LTE (limit time exceeded) error. It sorts the `events` based on ending date, goes over `events` list (basically goes over the days each event is happening in) and add it to a `set()` in case that day has not been filled yet. Note that the `break` statement prevents addition of more than one day for a particular event (`break` statement stops current loop, see [this](https://www.tutorialspoint.com/python/python_break_statement.htm)). Can you understand this? Note that at first, we `sort` the `events` based on the last day of each event. \n\nExercise: Try to do these tasks! `sort` based on first day, last day, first day and then last day, last day and then first day (you can do this like: `events = sorted(events, key=lambda x: (x[1], x[0]))`) ! and check whether you would `return` correct output. Also, read [kaiwensun](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/discuss/510262/Detailed-analysisLet-me-lead-you-to-the-solution-step-by-step)\'s explanation about why choosing based on end date always works. \n\n```\n# Solution 1\ndef maxEvents(self, events: List[List[int]]) -> int:\n events = sorted(events, key=lambda x: x[1])\n visited = set()\n for s, e in events:\n for t in range(s, e+1):\n if t not in visited:\n visited.add(t)\n break\n return len(visited)\n```\n\nSince the above code is not working for this problem, I use a [priority queue](https://www.***.org/priority-queue-set-1-introduction/), and [kaiwensun](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/discuss/510262/Detailed-analysisLet-me-lead-you-to-the-solution-step-by-step)\'s solution. Something I don\'t like about the solution is importing the `heapq` module. I wasn\'t able to find a better solution except for implementing it from scratch, which is stupid for an interview question. \n\nIntuition? We use a priority queue, add events with starting day of today and remove events with ending day of today. Then, we attend an event that end sooner in the heap. Make sense? No? Keep reading! \n\n```\n# Solution 2: it use `import heapq`\nimport heapq\nclass Solution(object):\n def maxEvents(self, events):\n events = sorted(events, key = lambda x:x[0]) #1\n total_days = max(event[1] for event in events) #2\n min_heap = [] #3\n day, cnt, event_id = 1, 0, 0 #4\n \n \n while day <= total_days: #5\n\t\t # if no events are available to attend today, let time flies to the next available event.\n if event_id < len(events) and not min_heap: #6\n day = events[event_id][0] #7\n\t\t\t\n\t\t\t# all events starting from today are newly available. add them to the heap.\n while event_id < len(events) and events[event_id][0] <= day: #8\n heapq.heappush(min_heap, events[event_id][1]) #9\n event_id += 1 #10\n\n\t\t\t# if the event at heap top already ended, then discard it.\n while min_heap and min_heap[0] < day: #11\n heapq.heappop(min_heap) #12\n\n\t\t\t# attend the event that will end the earliest\n if min_heap: #13\n heapq.heappop(min_heap) #14 \n cnt += 1 #15\n elif event_id >= len(events): #16\n break # no more events to attend. so stop early to save time.\n day += 1 #17\n return cnt #18\n```\n\nThe outer `while` loop (line `#5`) takes care of `day` we\'re in. We start at `day = 1` (line `#4`) and update the `day` in line `#17` after doing some other stuff along the way. It\'s important to note that we\'re doing all the stuff between lines `#5` and `#16` on the same day. There are some notes I\'d like to mention about the solution before delving into it. 1) We define `min_heap` (line `#3`) as an array which will be used to `push` (for example line `#9`) or `pop` (for example line `#12` and `#14`) elements to or from. 2) We `push` end day of an event to the `min_heap` (line `#9`), and will `pop` it once the end day is passed by our day timer (variable `day`, line `#12`). 3) We add one to the counter (variable `cnt`, line `#15`) when there\'s something in the `min_heap` on a particular `day` and `pop` it from `min_heap` (line `#14`) since we\'re done with that day. \n\n\nThe solution: We first `sort` based on the starting day of each event (line `#1`)\n\n`total_days` is calculated based maximum ending day of `events` (line `#2`, we loop over all the events after sorting, and find an event with the maximum ending day). \n\nIn line `#3`, we initialize the `min_heap` as an array. \n\nLine `#4`: `day` keeps the day we\'re in, `cnt` keeps track of the number of events we\'ve already attended, and `event_id` keeps track of events being pushed into `min_heap` (line `#10`). `event_id` helps to `break` the loop after line `#16` (we don\'t get into this in the example shown below). \n\nLine `#5`: It\'s the outter `while` loop I already talked before. \n\nStarting now, I feel like following an example would make things easier. Say `events = [[1,4],[4,4],[2,2],[3,4],[1,1]]`. After sorting it\'d be `[[1, 1], [1, 4], [2, 2], [3, 4], [4, 4]]`, right? With `total_days = 4`. \n\nIn line `#6`, `event_id = 0`, `day = 1`. We go into the `while` loop of line `#6`, `day` re-assigns to `1`. Can you see why we have this line? Imagine after sorting, the first event has a starting day of 2 instead of 1, then, `day` gets updated to 2. Or if there is a gap between starting days of events. Lines `#6` and `#7` always get activated in the first pass of the outter `while` loop except if the `events` array is either empty of we just have one event. If we had more than one event, then these two lines would run for sure at first. So, after line `#7`, `day = 1` in this example. \n\n---- Day 1\nWe move to line `#8` (it\'s safe to change `<=` to `==` in line `#8`, but doesn\'t matter) and add the ending day of this event to `min_heal` in line `#9`. At this point, `min_heap = [1]`. We added the event with index `0` to `min_heap`. So, we update `event_id` (line `#10`). `event_id = 1` now. `min_heap` is not empty but its head (`min_heap[0]`) is 1. Note here that we don\'t go out of this `while` loop just yet. Since, we updated the `event_id` to be 1. Line `#8` gets checked again and guess what? In this example, `event_id = 1` also satisfies the criterion (event 1 also has a starting day of 1, similar to event 0). So, another event gets pushed into `min_heap` and `min_heap = [1,4]`. After all this, `event_id = 2` now. Then, we pass lines `#11` and `#12`. These two lines try to get rid of outdated events. For example, if you had three events like [[1,2],[1,2],[1,2]], you cannot attend all, right? After you assing the first two to day 1 and day 2, then in day 3, ending of your last event is less than day timer, therefore, it gets popped out of `min_heap`. Now it\'s the part we update `cnt`, our output. Line `#13` makes sure `min_heap` is not empty. If it\'s empty, then there\'s nothing to attend then, we move on. But, if it\'s not empty (which is not here since `min_heap = [1,4]`), then we updated `cnt` by 1 (line `#15`), we get rid of the event with minimum ending date (which is at the root of the heap we\'re dealing with, since it\'s a min heap. Check this out: [min heap](https://www.***.org/binary-heap/))) event. Makes sense? Now `min_heap = [4]`. After this, we go to the next day (line `#17`). `day = 2`. \n\n--- Day 2\nSimilar to day one. We don\'t get into line `#7` since `min_heap` is not empty now. We go into line `#9` and add `[2]` to the `min_heap`. Now, it\'s `min_heap = [2,4]`. We then go to line `#13`, pop `2` out and update `cnt` by one. Now, `min_heap = [4]` again and `cnt = 2`. We update `day` and go to day 3. `day = 3`. \n\n----Day 3\nAfter line `#10`, `min_heap = [4,4]` (note that ending date gets added to the heap) and `event_id = 3`. Note than `event_id` can be maximum of 4 or line `#16` gets activated and breaks the `while` loop. Again line `#14` and popping `[4]` this time, updating `cnt` to `3`. We do to the last day. `day = 4`. \n\n---Day 4.\nAfter line `#10`, `min_heap = [4,4]` again and `event_id = 4`. Again line `#14` and popping `[4]` this time, updating `cnt` to `4`. and `day = 4`, right? It\'s over (line `#5`, `day = 5` which is not `<=` of `total_days = 4`). We cannot allocate anymore event although we still have one more in the `min_heap` to attend.\n\n\nSo, the answer is 4. \n\n\nWere you able to follow? To wrapp up, we go and see whether there\'s an event in a day, we add it to the heap (we add more if there are more than one with the same starting day), we go and pop the root of heap, update the events attended, and do this for the total days we have to attend events. \n\n\n=================================================================\nFinal note: please let me know if you spot any typo/error/ etc. \n\nFinal note 2: I find explaining stuff in the simplest form instructive. I suggest you do the same in case you\'re having hard time understanding something. \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n | 17 | Given the array `houses` where `houses[i]` is the location of the `ith` house along a street and an integer `k`, allocate `k` mailboxes in the street.
Return _the **minimum** total distance between each house and its nearest mailbox_.
The test cases are generated so that the answer fits in a 32-bit integer.
**Example 1:**
**Input:** houses = \[1,4,8,10,20\], k = 3
**Output:** 5
**Explanation:** Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
**Example 2:**
**Input:** houses = \[2,3,5,12,18\], k = 2
**Output:** 9
**Explanation:** Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
**Constraints:**
* `1 <= k <= houses.length <= 100`
* `1 <= houses[i] <= 104`
* All the integers of `houses` are **unique**. | Sort the events by the start time and in case of tie by the end time in ascending order. Loop over the sorted events. Attend as much as you can and keep the last day occupied. When you try to attend new event keep in mind the first day you can attend a new event in. |
Python Easy Solution || Less Line Of Code || Heapify | construct-target-array-with-multiple-sums | 0 | 1 | **Please Upvote If you find Useful**\n```\nclass Solution:\n\tdef isPossible(self, target: List[int]) -> bool:\n\n\t\theapq._heapify_max(target)\n\t\ts = sum(target)\n\n\t\twhile target[0] != 1:\n\t\t\tsub = s - target[0]\n\t\t\tif sub == 0: return False\n\t\t\tn = max((target[0] - 1) // sub, 1)\n\t\t\ts -= n * sub\n\t\t\ttarget0 = target[0] - n * sub\n\t\t\tif target0 < 1: return False\n\t\t\theapq._heapreplace_max(target, target0)\n\n\t\treturn True\n\t``` | 14 | You are given an array `target` of n integers. From a starting array `arr` consisting of `n` 1's, you may perform the following procedure :
* let `x` be the sum of all elements currently in your array.
* choose index `i`, such that `0 <= i < n` and set the value of `arr` at index `i` to `x`.
* You may repeat this procedure as many times as needed.
Return `true` _if it is possible to construct the_ `target` _array from_ `arr`_, otherwise, return_ `false`.
**Example 1:**
**Input:** target = \[9,3,5\]
**Output:** true
**Explanation:** Start with arr = \[1, 1, 1\]
\[1, 1, 1\], sum = 3 choose index 1
\[1, 3, 1\], sum = 5 choose index 2
\[1, 3, 5\], sum = 9 choose index 0
\[9, 3, 5\] Done
**Example 2:**
**Input:** target = \[1,1,1,2\]
**Output:** false
**Explanation:** Impossible to create target array from \[1,1,1,1\].
**Example 3:**
**Input:** target = \[8,5\]
**Output:** true
**Constraints:**
* `n == target.length`
* `1 <= n <= 5 * 104`
* `1 <= target[i] <= 109` | Count the number of times a player loses while iterating through the matches. |
Bucket sort vs sort with Lambda->1 line||0ms Beats 100% | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDefine the lambda function as the third parameter in sort function\n```\n [](int x, int y){\n if (__builtin_popcount(x)==__builtin_popcount(y))\n return x<y;\n else \n return __builtin_popcount(x)<__builtin_popcount(y);\n }\n```\n[https://youtu.be/dCV4xtEsY1E?si=IIau2Sx_pUaHAzDx](https://youtu.be/dCV4xtEsY1E?si=IIau2Sx_pUaHAzDx)\nPython code can be written used sorted in one line with lambda function.\n\nAn implemenation using bucket sort is also provided. Each bucket `B[bit_count]` contains the elements with Hamming weight=bit_count. The computing for Hamming weight uses Brian Kerninghan\'s Algorithm.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse GCC `__builtin_popcount`, or in a more standard way `bitset` to count bits, i.e Hamming weight.\n\nUse O3 optimization.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(1)$\nbucket sort: $O(n)$\n# Code\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), \n [](int x, int y){\n if (__builtin_popcount(x)==__builtin_popcount(y))\n return x<y;\n else \n return __builtin_popcount(x)<__builtin_popcount(y);\n });\n return arr;\n }\n};\n```\n# Code using bitset\n```\n sort(arr.begin(), arr.end(), \n [](int x, int y){\n if (bitset<31>(x).count()==bitset<31>(y).count())\n return x<y;\n else \n return bitset<31>(x).count()<bitset<31>(y).count();\n });\n return arr;\n```\n# Python code 1 line\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr, key=lambda x: [x.bit_count(), x])\n \n```\n# Code using Bucket Sort & Brian Kerninghan\'s Algorithm\n```\n//Bucket sort & Brian Kerninghan\'s Algorithm\nclass Solution {\npublic:\n int HammingWeight(int x){//Brian Kerninghan\'s Algorithm\n int wt=0;\n while(x>0)\n x&=(x-1), wt++;\n return wt;\n }\n vector<int> sortByBits(vector<int>& arr) {\n vector<vector<int>> B(32);\n #pragma unroll\n for(int x :arr)\n B[HammingWeight(x)].push_back(x);\n #pragma unroll\n for (auto& b: B)\n sort(b.begin(), b.end());\n int count=0;\n #pragma unroll\n for(int i=0; i<32; i++)\n for(int x: B[i])\n arr[count++]=x;\n return arr;\n }\n};\n```\n | 7 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Bucket sort vs sort with Lambda->1 line||0ms Beats 100% | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDefine the lambda function as the third parameter in sort function\n```\n [](int x, int y){\n if (__builtin_popcount(x)==__builtin_popcount(y))\n return x<y;\n else \n return __builtin_popcount(x)<__builtin_popcount(y);\n }\n```\n[https://youtu.be/dCV4xtEsY1E?si=IIau2Sx_pUaHAzDx](https://youtu.be/dCV4xtEsY1E?si=IIau2Sx_pUaHAzDx)\nPython code can be written used sorted in one line with lambda function.\n\nAn implemenation using bucket sort is also provided. Each bucket `B[bit_count]` contains the elements with Hamming weight=bit_count. The computing for Hamming weight uses Brian Kerninghan\'s Algorithm.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse GCC `__builtin_popcount`, or in a more standard way `bitset` to count bits, i.e Hamming weight.\n\nUse O3 optimization.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(1)$\nbucket sort: $O(n)$\n# Code\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), \n [](int x, int y){\n if (__builtin_popcount(x)==__builtin_popcount(y))\n return x<y;\n else \n return __builtin_popcount(x)<__builtin_popcount(y);\n });\n return arr;\n }\n};\n```\n# Code using bitset\n```\n sort(arr.begin(), arr.end(), \n [](int x, int y){\n if (bitset<31>(x).count()==bitset<31>(y).count())\n return x<y;\n else \n return bitset<31>(x).count()<bitset<31>(y).count();\n });\n return arr;\n```\n# Python code 1 line\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr, key=lambda x: [x.bit_count(), x])\n \n```\n# Code using Bucket Sort & Brian Kerninghan\'s Algorithm\n```\n//Bucket sort & Brian Kerninghan\'s Algorithm\nclass Solution {\npublic:\n int HammingWeight(int x){//Brian Kerninghan\'s Algorithm\n int wt=0;\n while(x>0)\n x&=(x-1), wt++;\n return wt;\n }\n vector<int> sortByBits(vector<int>& arr) {\n vector<vector<int>> B(32);\n #pragma unroll\n for(int x :arr)\n B[HammingWeight(x)].push_back(x);\n #pragma unroll\n for (auto& b: B)\n sort(b.begin(), b.end());\n int count=0;\n #pragma unroll\n for(int i=0; i<32; i++)\n for(int x: B[i])\n arr[count++]=x;\n return arr;\n }\n};\n```\n | 7 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
Python sort using lambda | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe simply pass the soring criteria in the lambda function for the key used for sorting.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMake use of inbuilt sort method.\n\n# Complexity\n- Time complexity: $O(n * log_2(n))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n arr.sort(key = lambda x: (x.bit_count(), x))\n return arr\n```\n\n**Please upvote if you like the solution. Have a great day!** | 4 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Python sort using lambda | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe simply pass the soring criteria in the lambda function for the key used for sorting.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMake use of inbuilt sort method.\n\n# Complexity\n- Time complexity: $O(n * log_2(n))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n arr.sort(key = lambda x: (x.bit_count(), x))\n return arr\n```\n\n**Please upvote if you like the solution. Have a great day!** | 4 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
✅ 89.93% Sort Bit | sort-integers-by-the-number-of-1-bits | 1 | 1 | # Intuition\nUpon reading the problem, our first observation is that the sorting criteria is twofold:\n1. First, by the count of 1\'s in the binary representation.\n2. If there\'s a tie, by the actual integer value.\n\nGiven this, we can leverage Python\'s built-in sorting mechanism which supports multi-criteria sorting using a tuple as the key.\n\n# Live Coding \nhttps://youtu.be/GQ0vpiPA2Cg?si=1CsU0oMNHyatlK59\n\n# Approach\nOur approach is straightforward:\n1. Convert each number into its binary representation using the `bin()` function.\n2. Count the number of 1\'s using the `count(\'1\')` method.\n3. Sort the numbers first by the count of 1\'s and then by the number itself.\n\nPython\'s `sorted` function will use the first element of the tuple for sorting and if there\'s a tie, it\'ll use the second element.\n\n# Complexity\n- **Time complexity:** The time complexity of the `sorted` function is $$O(n \\log n)$$, where $n$ is the length of the array. Counting the 1\'s in the binary representation of each number can be done in $O(m)$ time, where $m$ is the maximum number of bits needed to represent any number in the list. Thus, the overall time complexity is $O(n \\log n \\times m)$.\n \n- **Space complexity:** The space complexity of the `sorted` function is $O(n)$, as it returns a new sorted list.\n\n# Code\n```Python []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr, key=lambda x: (bin(x).count(\'1\'), x))\n```\n``` Rust []\nimpl Solution {\n pub fn sort_by_bits(mut arr: Vec<i32>) -> Vec<i32> {\n arr.sort_by_key(|&x| (x.count_ones(), x));\n arr\n }\n}\n```\n``` Go []\nimport (\n\t"sort"\n\t"math/bits"\n)\n\nfunc sortByBits(arr []int) []int {\n\tsort.Slice(arr, func(i, j int) bool {\n\t\tcountI := bits.OnesCount(uint(arr[i]))\n\t\tcountJ := bits.OnesCount(uint(arr[j]))\n\t\treturn countI < countJ || (countI == countJ && arr[i] < arr[j])\n\t})\n\treturn arr\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), [](int a, int b) {\n int countA = __builtin_popcount(a);\n int countB = __builtin_popcount(b);\n return (countA == countB) ? a < b : countA < countB;\n });\n return arr;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int[] sortByBits(int[] arr) {\n Integer[] boxedArray = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n Arrays.sort(boxedArray, (a, b) -> {\n int countA = Integer.bitCount(a);\n int countB = Integer.bitCount(b);\n return countA == countB ? a - b : countA - countB;\n });\n return Arrays.stream(boxedArray).mapToInt(Integer::intValue).toArray();\n }\n}\n```\n``` PHP []\nclass Solution {\n\n function sortByBits($arr) {\n usort($arr, function($a, $b) {\n $countA = substr_count(decbin($a), \'1\');\n $countB = substr_count(decbin($b), \'1\');\n return $countA == $countB ? $a - $b : $countA - $countB;\n });\n return $arr;\n }\n}\n```\n``` JavaScript []\nvar sortByBits = function(arr) {\n return arr.sort((a, b) => {\n let countA = a.toString(2).split(\'\').filter(bit => bit === \'1\').length;\n let countB = b.toString(2).split(\'\').filter(bit => bit === \'1\').length;\n return countA - countB || a - b;\n });\n};\n```\n``` C# []\npublic class Solution {\n public int[] SortByBits(int[] arr) {\n return arr.OrderBy(x => CountOnes(x)).ThenBy(x => x).ToArray();\n }\n\n private int CountOnes(int x) {\n int count = 0;\n while (x != 0) {\n count += x & 1;\n x >>= 1;\n }\n return count;\n }\n}\n```\n\n# Performance\n\n| Language | Time (ms) | Memory (MB) |\n|------------|-----------|-------------|\n| Rust | 3 | 2.2 |\n| C++ | 6 | 10.4 |\n| Go | 6 | 3.4 |\n| Java | 10 | 43.9 |\n| PHP | 41 | 19.2 |\n| Python3 | 62 | 16.2 |\n| JavaScript | 126 | 48.7 |\n| C# | 136 | 45.1 |\n\n\n | 41 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
✅ 89.93% Sort Bit | sort-integers-by-the-number-of-1-bits | 1 | 1 | # Intuition\nUpon reading the problem, our first observation is that the sorting criteria is twofold:\n1. First, by the count of 1\'s in the binary representation.\n2. If there\'s a tie, by the actual integer value.\n\nGiven this, we can leverage Python\'s built-in sorting mechanism which supports multi-criteria sorting using a tuple as the key.\n\n# Live Coding \nhttps://youtu.be/GQ0vpiPA2Cg?si=1CsU0oMNHyatlK59\n\n# Approach\nOur approach is straightforward:\n1. Convert each number into its binary representation using the `bin()` function.\n2. Count the number of 1\'s using the `count(\'1\')` method.\n3. Sort the numbers first by the count of 1\'s and then by the number itself.\n\nPython\'s `sorted` function will use the first element of the tuple for sorting and if there\'s a tie, it\'ll use the second element.\n\n# Complexity\n- **Time complexity:** The time complexity of the `sorted` function is $$O(n \\log n)$$, where $n$ is the length of the array. Counting the 1\'s in the binary representation of each number can be done in $O(m)$ time, where $m$ is the maximum number of bits needed to represent any number in the list. Thus, the overall time complexity is $O(n \\log n \\times m)$.\n \n- **Space complexity:** The space complexity of the `sorted` function is $O(n)$, as it returns a new sorted list.\n\n# Code\n```Python []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr, key=lambda x: (bin(x).count(\'1\'), x))\n```\n``` Rust []\nimpl Solution {\n pub fn sort_by_bits(mut arr: Vec<i32>) -> Vec<i32> {\n arr.sort_by_key(|&x| (x.count_ones(), x));\n arr\n }\n}\n```\n``` Go []\nimport (\n\t"sort"\n\t"math/bits"\n)\n\nfunc sortByBits(arr []int) []int {\n\tsort.Slice(arr, func(i, j int) bool {\n\t\tcountI := bits.OnesCount(uint(arr[i]))\n\t\tcountJ := bits.OnesCount(uint(arr[j]))\n\t\treturn countI < countJ || (countI == countJ && arr[i] < arr[j])\n\t})\n\treturn arr\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), [](int a, int b) {\n int countA = __builtin_popcount(a);\n int countB = __builtin_popcount(b);\n return (countA == countB) ? a < b : countA < countB;\n });\n return arr;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int[] sortByBits(int[] arr) {\n Integer[] boxedArray = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n Arrays.sort(boxedArray, (a, b) -> {\n int countA = Integer.bitCount(a);\n int countB = Integer.bitCount(b);\n return countA == countB ? a - b : countA - countB;\n });\n return Arrays.stream(boxedArray).mapToInt(Integer::intValue).toArray();\n }\n}\n```\n``` PHP []\nclass Solution {\n\n function sortByBits($arr) {\n usort($arr, function($a, $b) {\n $countA = substr_count(decbin($a), \'1\');\n $countB = substr_count(decbin($b), \'1\');\n return $countA == $countB ? $a - $b : $countA - $countB;\n });\n return $arr;\n }\n}\n```\n``` JavaScript []\nvar sortByBits = function(arr) {\n return arr.sort((a, b) => {\n let countA = a.toString(2).split(\'\').filter(bit => bit === \'1\').length;\n let countB = b.toString(2).split(\'\').filter(bit => bit === \'1\').length;\n return countA - countB || a - b;\n });\n};\n```\n``` C# []\npublic class Solution {\n public int[] SortByBits(int[] arr) {\n return arr.OrderBy(x => CountOnes(x)).ThenBy(x => x).ToArray();\n }\n\n private int CountOnes(int x) {\n int count = 0;\n while (x != 0) {\n count += x & 1;\n x >>= 1;\n }\n return count;\n }\n}\n```\n\n# Performance\n\n| Language | Time (ms) | Memory (MB) |\n|------------|-----------|-------------|\n| Rust | 3 | 2.2 |\n| C++ | 6 | 10.4 |\n| Go | 6 | 3.4 |\n| Java | 10 | 43.9 |\n| PHP | 41 | 19.2 |\n| Python3 | 62 | 16.2 |\n| JavaScript | 126 | 48.7 |\n| C# | 136 | 45.1 |\n\n\n | 41 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
✅1 Liner (sorting only)✅ | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06\n# Code\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n # we also need to sort the list with its value because \n # what if the numbers of 1\'s are equal in different elements\n # of list, So we have to maintain the order\n arr.sort(key= lambda x : (bin(x).count(\'1\'),x))\n return arr\n \n```\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06 | 3 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
✅1 Liner (sorting only)✅ | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06\n# Code\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n # we also need to sort the list with its value because \n # what if the numbers of 1\'s are equal in different elements\n # of list, So we have to maintain the order\n arr.sort(key= lambda x : (bin(x).count(\'1\'),x))\n return arr\n \n```\n\u2B06**PLEASE UPVOTE IF IT HELPS**\u2B06 | 3 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
✅☑[C++/Java/Python/JavaScript] || Beats 95% || 3 Approaches || EXPLAINED🔥 | sort-integers-by-the-number-of-1-bits | 1 | 1 | \n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Built-in function)***\n1. **Static Comparison Function:** The code defines a static comparison function named `compare`. This function takes two integers, `a` and `b`, as input parameters and returns a boolean value indicating whether `a` should come before `b` in the sorted array.\n\n1. **Counting Set Bits:** Within the `compare` function, the `__builtin_popcount` function is used to count the number of set bits (1s) in the binary representation of `a` and `b`. This count represents the number of set bits in each integer, which is a key factor for sorting.\n\n1. **Comparing Based on Set Bits Count:** The `compare` function compares `a` and `b` based on their set bits count. If the count of set bits in `a` is equal to the count of set bits in `b`, it uses a secondary comparison based on the integer values. This means that if two numbers have the same number of set bits, they are sorted in ascending order based on their actual values.\n\n1. **Sorting the Array:** The main function `sortByBits` takes an input array `arr` and sorts it using the `compare` function as the custom sorting criterion. The `sort` function from the C++ Standard Library is used to sort the array in place.\n\n1. **Returning the Sorted Array:** The sorted array, now sorted based on the set bits count and secondary value comparison, is returned as the result.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or O(logn)\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n static bool compare(int a, int b) {\n if (__builtin_popcount(a) == __builtin_popcount(b)) {\n return a < b;\n }\n \n return __builtin_popcount(a) < __builtin_popcount(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n\n -----------or-------------\n\n\n\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), [](int a, int b) {\n int countA = __builtin_popcount(a);\n int countB = __builtin_popcount(b);\n return countA == countB ? a < b : countA < countB;\n });\n return arr;\n }\n};\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\nint countSetBits(int num) {\n int count = 0;\n while (num) {\n count += num & 1;\n num >>= 1;\n }\n return count;\n}\n\nint compare(const void* a, const void* b) {\n int intA = *(int*)a;\n int intB = *(int*)b;\n\n int countA = countSetBits(intA);\n int countB = countSetBits(intB);\n\n if (countA == countB) {\n return (intA < intB) ? -1 : (intA > intB) ? 1 : 0;\n } else {\n return (countA < countB) ? -1 : 1;\n }\n}\n\nint* sortByBits(int* arr, int arrSize, int* returnSize) {\n qsort(arr, arrSize, sizeof(int), compare);\n *returnSize = arrSize;\n return arr;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Integer[] nums = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n Comparator<Integer> comparator = new CustomComparator();\n Arrays.sort(nums, comparator);\n return Arrays.stream(nums).mapToInt(Integer::intValue).toArray();\n }\n}\n\nclass CustomComparator implements Comparator<Integer> {\n @Override\n public int compare(Integer a, Integer b) {\n if (Integer.bitCount(a) == Integer.bitCount(b)) {\n return a - b;\n }\n \n return Integer.bitCount(a) - Integer.bitCount(b);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n arr.sort(key = lambda num: (num.bit_count(), num))\n return arr\n\n```\n\n```javascript []\nfunction countSetBits(num) {\n let count = 0;\n while (num) {\n count += num & 1;\n num >>= 1;\n }\n return count;\n}\n\nfunction compare(a, b) {\n let countA = countSetBits(a);\n let countB = countSetBits(b);\n\n if (countA === countB) {\n return a - b;\n } else {\n return countA - countB;\n }\n}\n\nfunction sortByBits(arr) {\n return arr.sort(compare);\n}\n\n\n```\n\n---\n#### ***Approach 2 (Bits Manipulation)***\n1. **findWeight Function:**\n\n - This static function calculates and returns the number of set bits (1s) in a given integer `num`. It uses a bit manipulation approach to count the set bits.\n - It initializes `mask` to 1, which represents the current bit being checked, and `weight` to 0.\n - It enters a loop that continues while `num` is greater than 0.\n - Inside the loop, it checks if the least significant bit of `num` is set (i.e., `num & mask` is greater than 0). If true, it increments the `weight` and clears the bit by performing a bitwise XOR operation on `num` with `mask`.\n - It then shifts the `mask` left by one bit to check the next bit.\n - This process continues until all bits of `num` have been counted, and the final `weight` is returned.\n1. **compare Function:**\n\n - This static function compares two integers `a` and `b` based on their set bit counts (weights) and values.\n - It first calls the `findWeight` function for `a` and `b` to get their respective weights.\n - If the weights are equal, it compares the values of `a` and `b`. If `a` is less than `b`, it returns `true`; otherwise, it returns `false`.\n - If the weights are not equal, it compares the weights directly. If the weight of `a` is less than the weight of `b`, it returns `true`; otherwise, it returns `false`.\n1. **sortByBits Function:**\n\n - This function takes an input vector of integers `arr` and sorts it using the `compare` function as the custom sorting criterion.\n - It uses the `sort` function from the C++ Standard Template Library (STL) to sort the `arr` vector in-place.\n - The `compare` function is used to determine the relative order of elements during sorting, which first considers the weight and then the value of the integers.\n - After sorting, the sorted vector is returned.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or O(logn)\n \n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n static int findWeight(int num) {\n int mask = 1;\n int weight = 0;\n \n while (num > 0) {\n if ((num & mask) > 0) {\n weight++;\n num ^= mask;\n }\n \n mask <<= 1;\n }\n \n return weight;\n }\n \n static bool compare(int a, int b) {\n if (findWeight(a) == findWeight(b)) {\n return a < b;\n }\n \n return findWeight(a) < findWeight(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n\nint findWeight(int num) {\n int mask = 1;\n int weight = 0;\n\n while (num > 0) {\n if ((num & mask) > 0) {\n weight++;\n num ^= mask;\n }\n\n mask <<= 1;\n }\n\n return weight;\n}\n\nint compare(const void* a, const void* b) {\n int intA = *((int*)a);\n int intB = *((int*)b);\n int weightA = findWeight(intA);\n int weightB = findWeight(intB);\n\n if (weightA == weightB) {\n return (intA - intB);\n }\n\n return (weightA - weightB);\n}\n\nvoid sortByBits(int arr[], int size) {\n qsort(arr, size, sizeof(int), compare);\n}\n\nint main() {\n int arr[] = {3, 7, 1, 2, 4, 5, 6, 8};\n int size = sizeof(arr) / sizeof(arr[0]);\n\n sortByBits(arr, size);\n\n for (int i = 0; i < size; i++) {\n printf("%d ", arr[i]);\n }\n\n return 0;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Integer[] nums = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n Comparator<Integer> comparator = new CustomComparator();\n Arrays.sort(nums, comparator);\n return Arrays.stream(nums).mapToInt(Integer::intValue).toArray();\n }\n}\n\nclass CustomComparator implements Comparator<Integer> {\n private int findWeight(int num) {\n int mask = 1;\n int weight = 0;\n \n while (num > 0) {\n if ((num & mask) > 0) {\n weight++;\n num ^= mask;\n }\n \n mask <<= 1;\n }\n \n return weight;\n }\n \n @Override\n public int compare(Integer a, Integer b) {\n if (findWeight(a) == findWeight(b)) {\n return a - b;\n }\n \n return findWeight(a) - findWeight(b);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n def find_weight(num):\n mask = 1\n weight = 0\n \n while num:\n if num & mask:\n weight += 1\n num ^= mask\n \n mask <<= 1\n \n return weight\n \n arr.sort(key = lambda num: (find_weight(num), num))\n return arr\n\n```\n\n```javascript []\nfunction findWeight(num) {\n let mask = 1;\n let weight = 0;\n\n while (num > 0) {\n if (num & mask) {\n weight++;\n num ^= mask;\n }\n\n mask <<= 1;\n }\n\n return weight;\n}\n\nfunction sortByBits(arr) {\n return arr.sort((a, b) => {\n const weightA = findWeight(a);\n const weightB = findWeight(b);\n\n if (weightA === weightB) {\n return a - b;\n }\n\n return weightA - weightB;\n });\n}\n\nconst arr = [3, 7, 1, 2, 4, 5, 6, 8];\nconst sortedArr = sortByBits(arr);\nconsole.log(sortedArr);\n\n\n```\n\n---\n\n#### ***Approach 3 (Brian Kerninghan\'s Algorithm)***\n1. **findWeight** Function:\n\n - `findWeight` is a static function that calculates the weight (number of set bits) in an integer.\n - It initializes a variable `weight` to 0.\n - It enters a loop that continues until the integer `num` becomes 0.\n - Inside the loop, it increments `weight` by 1 and clears the least significant set bit of `num` using the expression `num &= (num - 1)`. This operation effectively counts and removes the least significant set bit in each iteration.\n1. **compare** Function:\n\n - `compare` is another static function used as a custom comparison function for sorting integers.\n - It takes two integers `a` and `b` as input and compares them based on their weights and values.\n - If the weights of `a` and `b` are equal, it returns `true` if `a` is less than `b`, indicating that the integers are sorted by their values.\n - If the weights are not equal, it returns `true` if the weight of `a` is less than the weight of `b`, indicating that the integers are sorted by their weights first.\n1. **sortByBits** Method:\n\n - `sortByBits` is a method of the `Solution` class that takes a reference to a vector of integers `arr`.\n - Inside the method, it uses the `std::sort` function to sort the elements of the vector `arr` based on the custom comparison function `compare`.\n - The result is a sorted vector that first groups integers by their weights and then by their values if the weights are equal.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or O(logn)\n \n \n\n\n# Code\n```C++ []\n\n-class Solution {\npublic:\n static int findWeight(int num) {\n int weight = 0;\n \n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n \n return weight;\n }\n \n static bool compare(int a, int b) {\n if (findWeight(a) == findWeight(b)) {\n return a < b;\n }\n \n return findWeight(a) < findWeight(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\n// Function to calculate the weight (number of set bits) in an integer.\nint findWeight(int num) {\n int weight = 0;\n \n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n \n return weight;\n}\n\n// Custom comparison function for sorting integers.\nint compare(const void *a, const void *b) {\n int intA = *(int*)a;\n int intB = *(int*)b;\n \n int weightA = findWeight(intA);\n int weightB = findWeight(intB);\n \n if (weightA == weightB) {\n return (intA - intB);\n }\n \n return (weightA - weightB);\n}\n\n// Function to sort an array of integers by their weights and values.\nvoid sortByBits(int* arr, int arrSize) {\n qsort(arr, arrSize, sizeof(int), compare);\n}\n\nint main() {\n int arr[] = {5, 2, 8, 3, 1, 4, 6};\n int arrSize = sizeof(arr) / sizeof(arr[0]);\n\n // Sort the array using the custom comparison function.\n sortByBits(arr, arrSize);\n\n // Print the sorted array.\n for (int i = 0; i < arrSize; i++) {\n printf("%d ", arr[i]);\n }\n printf("\\n");\n\n return 0;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\npublic:\n static int findWeight(int num) {\n int weight = 0;\n \n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n \n return weight;\n }\n \n static bool compare(int a, int b) {\n if (findWeight(a) == findWeight(b)) {\n return a < b;\n }\n \n return findWeight(a) < findWeight(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n```\n```python3 []\n\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n def find_weight(num):\n weight = 0\n \n while num:\n weight += 1\n num &= (num - 1)\n \n return weight\n \n arr.sort(key = lambda num: (find_weight(num), num))\n return arr\n```\n\n```javascript []\nclass Solution {\n static findWeight(num) {\n let weight = 0;\n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n return weight;\n }\n\n static compare(a, b) {\n if (Solution.findWeight(a) === Solution.findWeight(b)) {\n return a - b;\n }\n return Solution.findWeight(a) - Solution.findWeight(b);\n }\n\n sortByBits(arr) {\n arr.sort(Solution.compare);\n return arr;\n }\n}\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
✅☑[C++/Java/Python/JavaScript] || Beats 95% || 3 Approaches || EXPLAINED🔥 | sort-integers-by-the-number-of-1-bits | 1 | 1 | \n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Built-in function)***\n1. **Static Comparison Function:** The code defines a static comparison function named `compare`. This function takes two integers, `a` and `b`, as input parameters and returns a boolean value indicating whether `a` should come before `b` in the sorted array.\n\n1. **Counting Set Bits:** Within the `compare` function, the `__builtin_popcount` function is used to count the number of set bits (1s) in the binary representation of `a` and `b`. This count represents the number of set bits in each integer, which is a key factor for sorting.\n\n1. **Comparing Based on Set Bits Count:** The `compare` function compares `a` and `b` based on their set bits count. If the count of set bits in `a` is equal to the count of set bits in `b`, it uses a secondary comparison based on the integer values. This means that if two numbers have the same number of set bits, they are sorted in ascending order based on their actual values.\n\n1. **Sorting the Array:** The main function `sortByBits` takes an input array `arr` and sorts it using the `compare` function as the custom sorting criterion. The `sort` function from the C++ Standard Library is used to sort the array in place.\n\n1. **Returning the Sorted Array:** The sorted array, now sorted based on the set bits count and secondary value comparison, is returned as the result.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or O(logn)\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n static bool compare(int a, int b) {\n if (__builtin_popcount(a) == __builtin_popcount(b)) {\n return a < b;\n }\n \n return __builtin_popcount(a) < __builtin_popcount(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n\n -----------or-------------\n\n\n\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), [](int a, int b) {\n int countA = __builtin_popcount(a);\n int countB = __builtin_popcount(b);\n return countA == countB ? a < b : countA < countB;\n });\n return arr;\n }\n};\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\nint countSetBits(int num) {\n int count = 0;\n while (num) {\n count += num & 1;\n num >>= 1;\n }\n return count;\n}\n\nint compare(const void* a, const void* b) {\n int intA = *(int*)a;\n int intB = *(int*)b;\n\n int countA = countSetBits(intA);\n int countB = countSetBits(intB);\n\n if (countA == countB) {\n return (intA < intB) ? -1 : (intA > intB) ? 1 : 0;\n } else {\n return (countA < countB) ? -1 : 1;\n }\n}\n\nint* sortByBits(int* arr, int arrSize, int* returnSize) {\n qsort(arr, arrSize, sizeof(int), compare);\n *returnSize = arrSize;\n return arr;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Integer[] nums = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n Comparator<Integer> comparator = new CustomComparator();\n Arrays.sort(nums, comparator);\n return Arrays.stream(nums).mapToInt(Integer::intValue).toArray();\n }\n}\n\nclass CustomComparator implements Comparator<Integer> {\n @Override\n public int compare(Integer a, Integer b) {\n if (Integer.bitCount(a) == Integer.bitCount(b)) {\n return a - b;\n }\n \n return Integer.bitCount(a) - Integer.bitCount(b);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n arr.sort(key = lambda num: (num.bit_count(), num))\n return arr\n\n```\n\n```javascript []\nfunction countSetBits(num) {\n let count = 0;\n while (num) {\n count += num & 1;\n num >>= 1;\n }\n return count;\n}\n\nfunction compare(a, b) {\n let countA = countSetBits(a);\n let countB = countSetBits(b);\n\n if (countA === countB) {\n return a - b;\n } else {\n return countA - countB;\n }\n}\n\nfunction sortByBits(arr) {\n return arr.sort(compare);\n}\n\n\n```\n\n---\n#### ***Approach 2 (Bits Manipulation)***\n1. **findWeight Function:**\n\n - This static function calculates and returns the number of set bits (1s) in a given integer `num`. It uses a bit manipulation approach to count the set bits.\n - It initializes `mask` to 1, which represents the current bit being checked, and `weight` to 0.\n - It enters a loop that continues while `num` is greater than 0.\n - Inside the loop, it checks if the least significant bit of `num` is set (i.e., `num & mask` is greater than 0). If true, it increments the `weight` and clears the bit by performing a bitwise XOR operation on `num` with `mask`.\n - It then shifts the `mask` left by one bit to check the next bit.\n - This process continues until all bits of `num` have been counted, and the final `weight` is returned.\n1. **compare Function:**\n\n - This static function compares two integers `a` and `b` based on their set bit counts (weights) and values.\n - It first calls the `findWeight` function for `a` and `b` to get their respective weights.\n - If the weights are equal, it compares the values of `a` and `b`. If `a` is less than `b`, it returns `true`; otherwise, it returns `false`.\n - If the weights are not equal, it compares the weights directly. If the weight of `a` is less than the weight of `b`, it returns `true`; otherwise, it returns `false`.\n1. **sortByBits Function:**\n\n - This function takes an input vector of integers `arr` and sorts it using the `compare` function as the custom sorting criterion.\n - It uses the `sort` function from the C++ Standard Template Library (STL) to sort the `arr` vector in-place.\n - The `compare` function is used to determine the relative order of elements during sorting, which first considers the weight and then the value of the integers.\n - After sorting, the sorted vector is returned.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or O(logn)\n \n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n static int findWeight(int num) {\n int mask = 1;\n int weight = 0;\n \n while (num > 0) {\n if ((num & mask) > 0) {\n weight++;\n num ^= mask;\n }\n \n mask <<= 1;\n }\n \n return weight;\n }\n \n static bool compare(int a, int b) {\n if (findWeight(a) == findWeight(b)) {\n return a < b;\n }\n \n return findWeight(a) < findWeight(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n\nint findWeight(int num) {\n int mask = 1;\n int weight = 0;\n\n while (num > 0) {\n if ((num & mask) > 0) {\n weight++;\n num ^= mask;\n }\n\n mask <<= 1;\n }\n\n return weight;\n}\n\nint compare(const void* a, const void* b) {\n int intA = *((int*)a);\n int intB = *((int*)b);\n int weightA = findWeight(intA);\n int weightB = findWeight(intB);\n\n if (weightA == weightB) {\n return (intA - intB);\n }\n\n return (weightA - weightB);\n}\n\nvoid sortByBits(int arr[], int size) {\n qsort(arr, size, sizeof(int), compare);\n}\n\nint main() {\n int arr[] = {3, 7, 1, 2, 4, 5, 6, 8};\n int size = sizeof(arr) / sizeof(arr[0]);\n\n sortByBits(arr, size);\n\n for (int i = 0; i < size; i++) {\n printf("%d ", arr[i]);\n }\n\n return 0;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Integer[] nums = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n Comparator<Integer> comparator = new CustomComparator();\n Arrays.sort(nums, comparator);\n return Arrays.stream(nums).mapToInt(Integer::intValue).toArray();\n }\n}\n\nclass CustomComparator implements Comparator<Integer> {\n private int findWeight(int num) {\n int mask = 1;\n int weight = 0;\n \n while (num > 0) {\n if ((num & mask) > 0) {\n weight++;\n num ^= mask;\n }\n \n mask <<= 1;\n }\n \n return weight;\n }\n \n @Override\n public int compare(Integer a, Integer b) {\n if (findWeight(a) == findWeight(b)) {\n return a - b;\n }\n \n return findWeight(a) - findWeight(b);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n def find_weight(num):\n mask = 1\n weight = 0\n \n while num:\n if num & mask:\n weight += 1\n num ^= mask\n \n mask <<= 1\n \n return weight\n \n arr.sort(key = lambda num: (find_weight(num), num))\n return arr\n\n```\n\n```javascript []\nfunction findWeight(num) {\n let mask = 1;\n let weight = 0;\n\n while (num > 0) {\n if (num & mask) {\n weight++;\n num ^= mask;\n }\n\n mask <<= 1;\n }\n\n return weight;\n}\n\nfunction sortByBits(arr) {\n return arr.sort((a, b) => {\n const weightA = findWeight(a);\n const weightB = findWeight(b);\n\n if (weightA === weightB) {\n return a - b;\n }\n\n return weightA - weightB;\n });\n}\n\nconst arr = [3, 7, 1, 2, 4, 5, 6, 8];\nconst sortedArr = sortByBits(arr);\nconsole.log(sortedArr);\n\n\n```\n\n---\n\n#### ***Approach 3 (Brian Kerninghan\'s Algorithm)***\n1. **findWeight** Function:\n\n - `findWeight` is a static function that calculates the weight (number of set bits) in an integer.\n - It initializes a variable `weight` to 0.\n - It enters a loop that continues until the integer `num` becomes 0.\n - Inside the loop, it increments `weight` by 1 and clears the least significant set bit of `num` using the expression `num &= (num - 1)`. This operation effectively counts and removes the least significant set bit in each iteration.\n1. **compare** Function:\n\n - `compare` is another static function used as a custom comparison function for sorting integers.\n - It takes two integers `a` and `b` as input and compares them based on their weights and values.\n - If the weights of `a` and `b` are equal, it returns `true` if `a` is less than `b`, indicating that the integers are sorted by their values.\n - If the weights are not equal, it returns `true` if the weight of `a` is less than the weight of `b`, indicating that the integers are sorted by their weights first.\n1. **sortByBits** Method:\n\n - `sortByBits` is a method of the `Solution` class that takes a reference to a vector of integers `arr`.\n - Inside the method, it uses the `std::sort` function to sort the elements of the vector `arr` based on the custom comparison function `compare`.\n - The result is a sorted vector that first groups integers by their weights and then by their values if the weights are equal.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$ or O(logn)\n \n \n\n\n# Code\n```C++ []\n\n-class Solution {\npublic:\n static int findWeight(int num) {\n int weight = 0;\n \n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n \n return weight;\n }\n \n static bool compare(int a, int b) {\n if (findWeight(a) == findWeight(b)) {\n return a < b;\n }\n \n return findWeight(a) < findWeight(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\n// Function to calculate the weight (number of set bits) in an integer.\nint findWeight(int num) {\n int weight = 0;\n \n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n \n return weight;\n}\n\n// Custom comparison function for sorting integers.\nint compare(const void *a, const void *b) {\n int intA = *(int*)a;\n int intB = *(int*)b;\n \n int weightA = findWeight(intA);\n int weightB = findWeight(intB);\n \n if (weightA == weightB) {\n return (intA - intB);\n }\n \n return (weightA - weightB);\n}\n\n// Function to sort an array of integers by their weights and values.\nvoid sortByBits(int* arr, int arrSize) {\n qsort(arr, arrSize, sizeof(int), compare);\n}\n\nint main() {\n int arr[] = {5, 2, 8, 3, 1, 4, 6};\n int arrSize = sizeof(arr) / sizeof(arr[0]);\n\n // Sort the array using the custom comparison function.\n sortByBits(arr, arrSize);\n\n // Print the sorted array.\n for (int i = 0; i < arrSize; i++) {\n printf("%d ", arr[i]);\n }\n printf("\\n");\n\n return 0;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\npublic:\n static int findWeight(int num) {\n int weight = 0;\n \n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n \n return weight;\n }\n \n static bool compare(int a, int b) {\n if (findWeight(a) == findWeight(b)) {\n return a < b;\n }\n \n return findWeight(a) < findWeight(b);\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n\n```\n```python3 []\n\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n def find_weight(num):\n weight = 0\n \n while num:\n weight += 1\n num &= (num - 1)\n \n return weight\n \n arr.sort(key = lambda num: (find_weight(num), num))\n return arr\n```\n\n```javascript []\nclass Solution {\n static findWeight(num) {\n let weight = 0;\n while (num > 0) {\n weight++;\n num &= (num - 1);\n }\n return weight;\n }\n\n static compare(a, b) {\n if (Solution.findWeight(a) === Solution.findWeight(b)) {\n return a - b;\n }\n return Solution.findWeight(a) - Solution.findWeight(b);\n }\n\n sortByBits(arr) {\n arr.sort(Solution.compare);\n return arr;\n }\n}\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
🚀 96.58% || Built-in Functions & Brian Kerninghan's Algorithm || Explained Intuition 🚀 | sort-integers-by-the-number-of-1-bits | 1 | 1 | # Problem Description\n\nGiven an integer array, **arrange** the integers in **ascending** order based on the **count** of `1s` in their **binary** representation. \nIn case of a **tie** (two or more integers with the **same** number of 1s), sort them in `ascending numerical order`. Return the **sorted** array.\n\n- Constraints:\n - `1 <= arr.length <= 500`\n - `0 <= arr[i] <= 10e4`\n\n---\n\n\n\n# Intuition\n\nHi there,\uD83D\uDE00\n\nLet\'s take a look\uD83D\uDC40 on our today\'s problem.\n\n- We are required today to sort a list of integers based on some rules:\n - **Ascending** order based on the **count** of `1s` in their **binary** representation. \n - If there\'s a tie, sort in `ascending numerical order`.\n\nSeems easy !\uD83D\uDE80\nEasiest solution to do here is to use **built-in sorting** funtion in the language that you use **instead** of implementing sorting algorithm from the scratch, then we will use a **comparator** to specify the **rules** of the sorting that we want.\n\nGreat now we are on a solid ground.\uD83E\uDDCD\u200D\u2642\uFE0F\uD83E\uDDCD\u200D\u2640\uFE0F\n- How we **specify** the comparator ?\uD83E\uDD14\n - Make **comparator** class or function based on your language.\n - **Count** number of one bits when comparing two integers. \n - **Compare** them based on **number** of ones bits\n - If number of one bits is **equal** then compare them based on **numerical** order.\n\nThis was straight forward !\uD83D\uDCAA\nNow, how to count number of one bits in any integer ?\uD83E\uDD14\nThis is the neat part.\uD83E\uDD2F\n\nThere are many ways to do that but we will discuss two interesting approaches which are using **Built-in Functions** based on the language you are using or using **Brian Kerninghan\'s Algorithm**.\n\n- For using **Built-in Functions**, Many languages have their own functions to count the number of one bits in the binary representation in any integer:\n - For **C++**, It uses `__builtin_popcount()` the great part here that it is not a built-in function in **C++** itself\uD83E\uDD28 but it is built-in function in **GCC** compiler of **C++**. It tries to use CPU `specific instructions` to count number of one bits since modern CPUs can count it in **one cycle**.\uD83E\uDD2F\n - For **Java**, It uses `Integer.bitCount()` which does some operations internally to calculate the number of one bits.\n - For **Python**, It uses `bin()` which loops over all bits of the integer and count its `1\'s`.\n - Unfortunately, **C** does not have built-in function.\uD83D\uDE14\n\n\nIs there another way than using built-in functions?\uD83E\uDD14\nActually there are. There are many algorithms one of them is **Brian Kerninghan\'s Algorithm**.\uD83E\uDD29\nWhat does this algorithm do?\nIt only loops over the one\'s in the binary representation of an integer not over all the bits.\u2753\n```\nEX: Integer = 9\nBinary Representation = 1001\nIt will only loop for two iterations.\n``` \n\nHow does it work?\uD83E\uDD14\nFor eavery **two consecutive** numbers, we are sure that there are `(n - 1)` `1\'s` which are **common** between the two numbers where `n` is the total number of `1\'s` in the **larger** number.\nLet\'s see this example for number `11`.\n\n\nThe algorithm utilizes this observation and loop according to it.\n\n### Note about space complexity.\n\n- The **space complexity** depends on the **implementation** of the Sorting algorithm in each language:\n - Within the realm of **Java**, `Arrays.sort()` using variant of quick sort called `Dual-Pivot Quicksort`, featuring a space complexity denoted as `O(log(N))`.\n - In the domain of **C++**, the `sort()` function within the Standard Template Library (STL) blends Quick Sort, Heap Sort, and Insertion Sort Called `Intro Sort` exhibiting a space complexity of `O(log(N))`.\n - In **Python**, the `sort()` function using the `Timsort algorithm`, and its space complexity in the worst-case scenario is `O(N)`.\n - In **C**, `qsort()` function uses internally `Quick Sort` algorithm, and its space complexity is `O(log(N))` since it is calling `O(log(N))` stack frames.\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n\n# Approach\n## 1. Built-in Functions\n1. Define a custom comparison function `compare` that takes two integers, `a` and `b`.\n2. Inside the `compare` function, count the number of set bits (1s) in the binary representations of `a` and `b` using the build-in function - `__builtin_popcount` in case if C++ -:\n - If the number of set bits is the **same** for `a` and `b`, compare them numerically by checking if `a` is **less** than `b`.\n - If the set bit counts are different, sort the integers in **ascending** order based on the number of set bits.\n3. **Sort** the elements of the array using the `compare` function and return the sorted vector.\n\n## Complexity\n- **Time complexity:** $O(N * log(N))$\nThe sorting algotirhm takes it self $O(N * log(N))$ and to compute its complexuty using custom comparator it should be `N * log(N) * comparator_time` but since the comparator is counting bits in numbers that have fixed number of bits which is `31` bits -since there\'s reserverd bit for the sign- then we can consider it as a constant. So total complexity is $O(N * log(N))$.\nWhere `N` is number of elements in the vector to be sorted.\n- **Space complexity:** $O(N) or O(log(N))$\nThe space complexity depends on the implementation of the sorting algorithm in each programming language.\n\n\n---\n\n## 2. Brian Kerninghan\'s Algorithm\n1. Implement a function `countBits` that calculates the **number** of set bits (1s) in the binary representation of a number using **Brian Kerninghan\'s Algorithm**.\n2. Inside the `compare` function, count the number of set bits (1s) in the binary representations of `a` and `b` using `countBits` function :\n - If the number of set bits is the **same** for `a` and `b`, compare them numerically by checking if `a` is **less** than `b`.\n - If the set bit counts are different, sort the integers in **ascending** order based on the number of set bits.\n3. **Sort** the elements of the array using the `compare` function and return the sorted vector.\n\n\n\n## Complexity\n- **Time complexity:** $O(N * log(N))$\nThe sorting algotirhm takes it self $O(N * log(N))$ and to compute its complexuty using custom comparator it should be `N * log(N) * comparator_time` but since the comparator is counting bits in numbers that have fixed number of bits which is `31` bits -since there\'s reserverd bit for the sign- then we can consider it as a constant. So total complexity is $O(N * log(N))$.\nWhere `N` is number of elements in the vector to be sorted.\n- **Space complexity:** $O(N) or O(log(N))$\nThe space complexity depends on the implementation of the sorting algorithm in each programming language.\n\n---\n\n\n\n# Code\n## 1. Built-in Functions\n```C++ []\nclass Solution {\npublic:\n static bool compare(int a, int b) {\n // Calculate the number of set bits (1s) in the binary representation of a and b\n int bitCountA = __builtin_popcount(a);\n int bitCountB = __builtin_popcount(b);\n\n // If the number of set bits is the same for a and b, compare them numerically\n if (bitCountA == bitCountB) {\n return a < b;\n }\n \n // Sort by the number of set bits in ascending order\n return bitCountA < bitCountB;\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n // Use the compare function to sort the vector\n sort(arr.begin(), arr.end(), compare);\n \n // Return the sorted vector\n return arr;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n // Convert the input integer array to Integer objects for sorting\n Integer[] integerArr = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n\n // Create a custom comparator to sort by bit count and then numerically\n Comparator<Integer> comparator = new BitCountComparator();\n\n // Sort the array using the custom comparator\n Arrays.sort(integerArr, comparator);\n\n // Convert the sorted array back to primitive integers\n int[] sortedArr = Arrays.stream(integerArr).mapToInt(Integer::intValue).toArray();\n\n return sortedArr;\n }\n}\n\nclass BitCountComparator implements Comparator<Integer> {\n @Override\n public int compare(Integer a, Integer b) {\n // Compare based on the count of set bits (1s) in the binary representation\n int bitCountA = Integer.bitCount(a);\n int bitCountB = Integer.bitCount(b);\n\n if (bitCountA == bitCountB) {\n // If bit counts are the same, compare numerically\n return a - b;\n } else {\n // Sort by the number of set bits in ascending order\n return bitCountA - bitCountB;\n }\n }\n}\n```\n```Python []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n # Define a custom comparison key function for sorting\n def custom_sort_key(num):\n # Calculate the number of set bits (1s) in the binary representation of num\n bit_count = bin(num).count(\'1\')\n return (bit_count, num)\n\n # Sort the input list using the custom comparison key function\n arr.sort(key=custom_sort_key)\n\n # Return the sorted list\n return arr\n```\n\n---\n\n## 2. Brian Kerninghan\'s Algorithm\n```C++ []\nclass Solution {\npublic:\n // Count the number of set bits (1s) in the binary representation of a number.\n static int countBits(int num) {\n int count = 0;\n \n while (num > 0) {\n count++;\n num &= (num - 1); // Clear the least significant set bit.\n }\n \n return count;\n }\n \n static bool compare(int a, int b) {\n int bitCountA = countBits(a);\n int bitCountB = countBits(b);\n \n if (bitCountA == bitCountB) {\n return a < b; // If set bit counts are equal, compare numerically.\n }\n \n return bitCountA < bitCountB; // Sort by the set bit count in ascending order.\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n // Convert the input array to an array of Integer objects for sorting\n Integer[] nums = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n\n // Create a custom comparator for sorting based on bit counts and numerical values\n Comparator<Integer> comparator = new BitCountComparator();\n\n // Sort the array using the custom comparator\n Arrays.sort(nums, comparator);\n\n // Convert the sorted Integer array back to a primitive int array\n return Arrays.stream(nums).mapToInt(Integer::intValue).toArray();\n }\n}\n\nclass BitCountComparator implements Comparator<Integer> {\n private int findBitCount(int num) {\n // Count the number of set bits (1s) in the binary representation of num\n int count = 0;\n\n while (num > 0) {\n count ++;\n num &= (num - 1);\n }\n\n return count ;\n }\n\n @Override\n public int compare(Integer a, Integer b) {\n int bitCountA = findBitCount(a);\n int bitCountB = findBitCount(b);\n\n if (bitCountA == bitCountB) {\n return a - b; // If bit counts are the same, compare numerically.\n }\n\n return bitCountA - bitCountB; // Sort by the bit count in ascending order.\n }\n}\n```\n```Python []\nclass Solution:\n def countBits(num):\n count = 0\n \n while num > 0:\n count += 1\n num &= (num - 1) # Clear the least significant set bit.\n \n return count\n\n def sortByBits(self, arr):\n arr.sort(key = lambda num: (Solution.countBits(num), num))\n return arr\n```\n```C []\nint countBits(int num) {\n int count = 0;\n\n while (num > 0) {\n count++;\n num &= (num - 1); // Clear the least significant set bit.\n }\n\n return count;\n}\n\n// Custom comparison function for sorting.\nint compare(const void *a, const void *b) {\n int intA = *((int *)a);\n int intB = *((int *)b);\n \n int bitCountA = countBits(intA);\n int bitCountB = countBits(intB);\n\n if (bitCountA == bitCountB) {\n return intA - intB; // If set bit counts are equal, compare numerically.\n }\n\n return bitCountA - bitCountB; // Sort by the set bit count in ascending order.\n}\n\nint* sortByBits(int* arr, int arrSize, int* returnSize) {\n // Allocate memory for the sorted array\n int* sortedArr = (int*)malloc(arrSize * sizeof(int));\n\n if (sortedArr == NULL) {\n // Memory allocation failed\n *returnSize = 0; // Set the size to 0 to indicate an error\n return NULL;\n }\n\n // Copy the original array to the new one\n for (int i = 0; i < arrSize; i++) {\n sortedArr[i] = arr[i];\n }\n\n // Sort the array using the custom comparator\n qsort(sortedArr, arrSize, sizeof(int), compare);\n\n *returnSize = arrSize; // Set the return size\n\n return sortedArr;\n}\n\n```\n\n\n\n\n\n | 88 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
🚀 96.58% || Built-in Functions & Brian Kerninghan's Algorithm || Explained Intuition 🚀 | sort-integers-by-the-number-of-1-bits | 1 | 1 | # Problem Description\n\nGiven an integer array, **arrange** the integers in **ascending** order based on the **count** of `1s` in their **binary** representation. \nIn case of a **tie** (two or more integers with the **same** number of 1s), sort them in `ascending numerical order`. Return the **sorted** array.\n\n- Constraints:\n - `1 <= arr.length <= 500`\n - `0 <= arr[i] <= 10e4`\n\n---\n\n\n\n# Intuition\n\nHi there,\uD83D\uDE00\n\nLet\'s take a look\uD83D\uDC40 on our today\'s problem.\n\n- We are required today to sort a list of integers based on some rules:\n - **Ascending** order based on the **count** of `1s` in their **binary** representation. \n - If there\'s a tie, sort in `ascending numerical order`.\n\nSeems easy !\uD83D\uDE80\nEasiest solution to do here is to use **built-in sorting** funtion in the language that you use **instead** of implementing sorting algorithm from the scratch, then we will use a **comparator** to specify the **rules** of the sorting that we want.\n\nGreat now we are on a solid ground.\uD83E\uDDCD\u200D\u2642\uFE0F\uD83E\uDDCD\u200D\u2640\uFE0F\n- How we **specify** the comparator ?\uD83E\uDD14\n - Make **comparator** class or function based on your language.\n - **Count** number of one bits when comparing two integers. \n - **Compare** them based on **number** of ones bits\n - If number of one bits is **equal** then compare them based on **numerical** order.\n\nThis was straight forward !\uD83D\uDCAA\nNow, how to count number of one bits in any integer ?\uD83E\uDD14\nThis is the neat part.\uD83E\uDD2F\n\nThere are many ways to do that but we will discuss two interesting approaches which are using **Built-in Functions** based on the language you are using or using **Brian Kerninghan\'s Algorithm**.\n\n- For using **Built-in Functions**, Many languages have their own functions to count the number of one bits in the binary representation in any integer:\n - For **C++**, It uses `__builtin_popcount()` the great part here that it is not a built-in function in **C++** itself\uD83E\uDD28 but it is built-in function in **GCC** compiler of **C++**. It tries to use CPU `specific instructions` to count number of one bits since modern CPUs can count it in **one cycle**.\uD83E\uDD2F\n - For **Java**, It uses `Integer.bitCount()` which does some operations internally to calculate the number of one bits.\n - For **Python**, It uses `bin()` which loops over all bits of the integer and count its `1\'s`.\n - Unfortunately, **C** does not have built-in function.\uD83D\uDE14\n\n\nIs there another way than using built-in functions?\uD83E\uDD14\nActually there are. There are many algorithms one of them is **Brian Kerninghan\'s Algorithm**.\uD83E\uDD29\nWhat does this algorithm do?\nIt only loops over the one\'s in the binary representation of an integer not over all the bits.\u2753\n```\nEX: Integer = 9\nBinary Representation = 1001\nIt will only loop for two iterations.\n``` \n\nHow does it work?\uD83E\uDD14\nFor eavery **two consecutive** numbers, we are sure that there are `(n - 1)` `1\'s` which are **common** between the two numbers where `n` is the total number of `1\'s` in the **larger** number.\nLet\'s see this example for number `11`.\n\n\nThe algorithm utilizes this observation and loop according to it.\n\n### Note about space complexity.\n\n- The **space complexity** depends on the **implementation** of the Sorting algorithm in each language:\n - Within the realm of **Java**, `Arrays.sort()` using variant of quick sort called `Dual-Pivot Quicksort`, featuring a space complexity denoted as `O(log(N))`.\n - In the domain of **C++**, the `sort()` function within the Standard Template Library (STL) blends Quick Sort, Heap Sort, and Insertion Sort Called `Intro Sort` exhibiting a space complexity of `O(log(N))`.\n - In **Python**, the `sort()` function using the `Timsort algorithm`, and its space complexity in the worst-case scenario is `O(N)`.\n - In **C**, `qsort()` function uses internally `Quick Sort` algorithm, and its space complexity is `O(log(N))` since it is calling `O(log(N))` stack frames.\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n\n# Approach\n## 1. Built-in Functions\n1. Define a custom comparison function `compare` that takes two integers, `a` and `b`.\n2. Inside the `compare` function, count the number of set bits (1s) in the binary representations of `a` and `b` using the build-in function - `__builtin_popcount` in case if C++ -:\n - If the number of set bits is the **same** for `a` and `b`, compare them numerically by checking if `a` is **less** than `b`.\n - If the set bit counts are different, sort the integers in **ascending** order based on the number of set bits.\n3. **Sort** the elements of the array using the `compare` function and return the sorted vector.\n\n## Complexity\n- **Time complexity:** $O(N * log(N))$\nThe sorting algotirhm takes it self $O(N * log(N))$ and to compute its complexuty using custom comparator it should be `N * log(N) * comparator_time` but since the comparator is counting bits in numbers that have fixed number of bits which is `31` bits -since there\'s reserverd bit for the sign- then we can consider it as a constant. So total complexity is $O(N * log(N))$.\nWhere `N` is number of elements in the vector to be sorted.\n- **Space complexity:** $O(N) or O(log(N))$\nThe space complexity depends on the implementation of the sorting algorithm in each programming language.\n\n\n---\n\n## 2. Brian Kerninghan\'s Algorithm\n1. Implement a function `countBits` that calculates the **number** of set bits (1s) in the binary representation of a number using **Brian Kerninghan\'s Algorithm**.\n2. Inside the `compare` function, count the number of set bits (1s) in the binary representations of `a` and `b` using `countBits` function :\n - If the number of set bits is the **same** for `a` and `b`, compare them numerically by checking if `a` is **less** than `b`.\n - If the set bit counts are different, sort the integers in **ascending** order based on the number of set bits.\n3. **Sort** the elements of the array using the `compare` function and return the sorted vector.\n\n\n\n## Complexity\n- **Time complexity:** $O(N * log(N))$\nThe sorting algotirhm takes it self $O(N * log(N))$ and to compute its complexuty using custom comparator it should be `N * log(N) * comparator_time` but since the comparator is counting bits in numbers that have fixed number of bits which is `31` bits -since there\'s reserverd bit for the sign- then we can consider it as a constant. So total complexity is $O(N * log(N))$.\nWhere `N` is number of elements in the vector to be sorted.\n- **Space complexity:** $O(N) or O(log(N))$\nThe space complexity depends on the implementation of the sorting algorithm in each programming language.\n\n---\n\n\n\n# Code\n## 1. Built-in Functions\n```C++ []\nclass Solution {\npublic:\n static bool compare(int a, int b) {\n // Calculate the number of set bits (1s) in the binary representation of a and b\n int bitCountA = __builtin_popcount(a);\n int bitCountB = __builtin_popcount(b);\n\n // If the number of set bits is the same for a and b, compare them numerically\n if (bitCountA == bitCountB) {\n return a < b;\n }\n \n // Sort by the number of set bits in ascending order\n return bitCountA < bitCountB;\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n // Use the compare function to sort the vector\n sort(arr.begin(), arr.end(), compare);\n \n // Return the sorted vector\n return arr;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n // Convert the input integer array to Integer objects for sorting\n Integer[] integerArr = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n\n // Create a custom comparator to sort by bit count and then numerically\n Comparator<Integer> comparator = new BitCountComparator();\n\n // Sort the array using the custom comparator\n Arrays.sort(integerArr, comparator);\n\n // Convert the sorted array back to primitive integers\n int[] sortedArr = Arrays.stream(integerArr).mapToInt(Integer::intValue).toArray();\n\n return sortedArr;\n }\n}\n\nclass BitCountComparator implements Comparator<Integer> {\n @Override\n public int compare(Integer a, Integer b) {\n // Compare based on the count of set bits (1s) in the binary representation\n int bitCountA = Integer.bitCount(a);\n int bitCountB = Integer.bitCount(b);\n\n if (bitCountA == bitCountB) {\n // If bit counts are the same, compare numerically\n return a - b;\n } else {\n // Sort by the number of set bits in ascending order\n return bitCountA - bitCountB;\n }\n }\n}\n```\n```Python []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n # Define a custom comparison key function for sorting\n def custom_sort_key(num):\n # Calculate the number of set bits (1s) in the binary representation of num\n bit_count = bin(num).count(\'1\')\n return (bit_count, num)\n\n # Sort the input list using the custom comparison key function\n arr.sort(key=custom_sort_key)\n\n # Return the sorted list\n return arr\n```\n\n---\n\n## 2. Brian Kerninghan\'s Algorithm\n```C++ []\nclass Solution {\npublic:\n // Count the number of set bits (1s) in the binary representation of a number.\n static int countBits(int num) {\n int count = 0;\n \n while (num > 0) {\n count++;\n num &= (num - 1); // Clear the least significant set bit.\n }\n \n return count;\n }\n \n static bool compare(int a, int b) {\n int bitCountA = countBits(a);\n int bitCountB = countBits(b);\n \n if (bitCountA == bitCountB) {\n return a < b; // If set bit counts are equal, compare numerically.\n }\n \n return bitCountA < bitCountB; // Sort by the set bit count in ascending order.\n }\n \n vector<int> sortByBits(vector<int>& arr) {\n sort(arr.begin(), arr.end(), compare);\n return arr;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n // Convert the input array to an array of Integer objects for sorting\n Integer[] nums = Arrays.stream(arr).boxed().toArray(Integer[]::new);\n\n // Create a custom comparator for sorting based on bit counts and numerical values\n Comparator<Integer> comparator = new BitCountComparator();\n\n // Sort the array using the custom comparator\n Arrays.sort(nums, comparator);\n\n // Convert the sorted Integer array back to a primitive int array\n return Arrays.stream(nums).mapToInt(Integer::intValue).toArray();\n }\n}\n\nclass BitCountComparator implements Comparator<Integer> {\n private int findBitCount(int num) {\n // Count the number of set bits (1s) in the binary representation of num\n int count = 0;\n\n while (num > 0) {\n count ++;\n num &= (num - 1);\n }\n\n return count ;\n }\n\n @Override\n public int compare(Integer a, Integer b) {\n int bitCountA = findBitCount(a);\n int bitCountB = findBitCount(b);\n\n if (bitCountA == bitCountB) {\n return a - b; // If bit counts are the same, compare numerically.\n }\n\n return bitCountA - bitCountB; // Sort by the bit count in ascending order.\n }\n}\n```\n```Python []\nclass Solution:\n def countBits(num):\n count = 0\n \n while num > 0:\n count += 1\n num &= (num - 1) # Clear the least significant set bit.\n \n return count\n\n def sortByBits(self, arr):\n arr.sort(key = lambda num: (Solution.countBits(num), num))\n return arr\n```\n```C []\nint countBits(int num) {\n int count = 0;\n\n while (num > 0) {\n count++;\n num &= (num - 1); // Clear the least significant set bit.\n }\n\n return count;\n}\n\n// Custom comparison function for sorting.\nint compare(const void *a, const void *b) {\n int intA = *((int *)a);\n int intB = *((int *)b);\n \n int bitCountA = countBits(intA);\n int bitCountB = countBits(intB);\n\n if (bitCountA == bitCountB) {\n return intA - intB; // If set bit counts are equal, compare numerically.\n }\n\n return bitCountA - bitCountB; // Sort by the set bit count in ascending order.\n}\n\nint* sortByBits(int* arr, int arrSize, int* returnSize) {\n // Allocate memory for the sorted array\n int* sortedArr = (int*)malloc(arrSize * sizeof(int));\n\n if (sortedArr == NULL) {\n // Memory allocation failed\n *returnSize = 0; // Set the size to 0 to indicate an error\n return NULL;\n }\n\n // Copy the original array to the new one\n for (int i = 0; i < arrSize; i++) {\n sortedArr[i] = arr[i];\n }\n\n // Sort the array using the custom comparator\n qsort(sortedArr, arrSize, sizeof(int), compare);\n\n *returnSize = arrSize; // Set the return size\n\n return sortedArr;\n}\n\n```\n\n\n\n\n\n | 88 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
【Video】Give me 10 minutes - Using Heap without build-in function such as sort or bit count | sort-integers-by-the-number-of-1-bits | 1 | 1 | # Intuition\nUsing Heap\n\n---\n\n# Solution Video\n\nhttps://youtu.be/oqV8Ai0_UWA\n\n\u25A0 Timeline\n`0:05` Solution code with build-in function\n`0:26` Two difficulties to solve the question\n`0:41` How do you count 1 bits?\n`1:05` Understanding to count 1 bits with an example\n`3:02` How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n`5:29` Coding\n`7:54` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,893\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n\n# Approach\n\n## How we think about a solution\n\nI think we can solve this question with the solution code below.\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n arr.sort(key = lambda num: (num.bit_count(), num))\n return arr \n```\n\nBut this question is asking you about "Sort Integers by The Number of 1 Bits", so I thought we should avoid build-in function such as `sort` or `bit_count`.\n\nI\'ll show you a solution code without build-in function.\n\nI think there are two difficuties to solve this quesiton. \n\n---\n\n\u25A0 Two difficulties\n\n- How do you count 1 bits?\n\n- How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n\n---\n\n- How do you count 1 bits?\n\nFirst of all, look at this.\n\n\nLeft: decimal\nRight: binary\n\nAcutually, there is well known algorithm to count bits.\n\n---\n\nThe fundamental idea of the algorithm is to count the number of bits using bitwise operations. Specifically, for an integer num that you want to count the bits of, you repetitively apply a bitwise AND operation between `num` and `(num - 1)`.\n\nBy continuing this operation, one set bit at a time is cleared in num, and the count of the bitwise AND operations performed in between becomes the count of set bits, which is the number of bits in the binary representation of the integer.\n\n---\n\nBut I forgot the name of person who found it. lol \u2190 This is "Brian Kerninghan\'s Algorithm".\n\nI think it\'s worth remembering.\n\nLet\'s see a concrete example.\n\n```\nnum = 7\ncount = 0\n```\nCalculate this. Just in case \n\nIf we use bitwise AND operator(`&`)...\nWhen both numbers are `1` \u2192 `1`\nOtherwise \u2192 `0`\n\n```\n7 & 6\n\u2193\n111\n110\n---\n110\n\ncount = 1\n```\n```\n6 & 5 (= 6 is coming from previous result 110)\n\u2193\n110\n101\n---\n100\n\ncount = 2\n```\n```\n4 & 3 (= 4 is coming from previous result 100)\n\u2193\n100\n 11\n---\n000\n\ncount = 3\n```\nWhen we reach `0`, we stop calculation.\n\n```\ncount = 3 (= 7 has `111`).\n```\n\nSeems like we can use the algorithm.\n\n\n---\n\n\n- How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n\nThe second difficulty is what if we have the same number of 1 bits?\n\n\n---\n\n\u2B50\uFE0F Points\n\nMy idea is to use `heap`, more precisely `min heap`.\n\n---\n\n```\nInput: [7,6,5]\n```\n\nAs you can see examples in description, we need to return output in ascending order.\n\nThe first priority of sorting data is number of ones, so we should have data like this.\n\n```\n(ones, n)\n\nones: number of 1\nn: current number\n```\n\nWhen we have `(3, 7)`,`(2, 6)`,`(2, 5)`, we can take them with this order.\n\n```\n(2, 5)\n(2, 6)\n(3, 7)\n```\nEasy! we don\'t need number of bits, so just access index `1`.\n\nLet\'s see a real algorithm!\n\n\n---\n\n\n**Algorithm Overview:**\n\nThe algorithm leverages the min-heap data structure to efficiently sort elements based on their number of set bits and original values. This ensures that elements with fewer set bits appear first, and in case of a tie, the original values are used for comparison.\n\nThis is based on Python. Other languages might be different a bit.\n\n**Detailed Explanation:**\n\n1. The `count_ones` function counts the number of set bits in an integer using the bitwise operation `num &= (num - 1)` until `num` becomes zero. The count of set bits is maintained and returned.\n\n2. The `one_list` list will store pairs (tuples) of the number of set bits and the original values. It will be used for sorting based on the number of set bits and the original values.\n\n3. The `for` loop iterates through each element in the input list `arr`. For each element `n`:\n - The `count_ones` function is called to count the number of set bits in `n`.\n - The pair of (number of set bits, original value) is created as a tuple and appended to the `one_list` list.\n\n4. The `heapify` function from the `heapq` module is called to convert the `one_list` list into a min-heap (priority queue). This step ensures that elements with fewer set bits are at the top of the heap, making it easy to pop the smallest elements.\n\n5. An empty list `res` is initialized to store the sorted values.\n\n6. The `while` loop continues until the `one_list` heap is not empty:\n - The `heapq.heappop(one_list)` function is used to pop the smallest element (based on the number of set bits and the original value) from the heap.\n - The original value (the second element in the tuple) of the popped element is appended to the `res` list.\n\n7. The loop continues to pop and append values until the `one_list` heap is empty.\n\n8. Finally, the sorted list `res` is returned as the result.\n\n\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n\n- Space complexity: $$O(n)$$\n\n```python []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n\n def count_ones(num):\n count = 0\n while num:\n num &= (num - 1)\n count += 1\n return count\n\n one_list = []\n for n in arr:\n ones = count_ones(n)\n one_list.append((ones, n))\n\n heapq.heapify(one_list)\n res = []\n\n while one_list:\n res.append(heapq.heappop(one_list)[1])\n\n return res \n```\n```java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Comparator<Integer> customComparator = (a, b) -> {\n int onesA = countOnes(a);\n int onesB = countOnes(b);\n if (onesA != onesB) {\n return onesA - onesB;\n }\n return a - b;\n };\n\n PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(customComparator);\n for (int n : arr) {\n priorityQueue.offer(n);\n }\n\n int[] res = new int[arr.length];\n int i = 0;\n while (!priorityQueue.isEmpty()) {\n res[i] = priorityQueue.poll();\n i++;\n }\n\n return res;\n }\n\n private int countOnes(int num) {\n int count = 0;\n while (num > 0) {\n num &= (num - 1);\n count++;\n }\n return count;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n auto customComparator = [this](int a, int b) {\n int onesA = countOnes(a);\n int onesB = countOnes(b);\n if (onesA != onesB) {\n return onesA > onesB;\n }\n return a > b;\n };\n\n priority_queue<int, vector<int>, decltype(customComparator)> priorityQueue(customComparator);\n for (int n : arr) {\n priorityQueue.push(n);\n }\n\n vector<int> res;\n while (!priorityQueue.empty()) {\n res.push_back(priorityQueue.top());\n priorityQueue.pop();\n }\n\n return res;\n }\n\n int countOnes(int num) {\n int count = 0;\n while (num) {\n num &= (num - 1);\n count++;\n }\n return count;\n } \n};\n```\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-the-original-array-of-prefix-xor/solutions/4228796/video-give-me-5-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/ck4dJURKAlA\n\n\u25A0 Timeline of the video\n`0:05` Solution code with build-in function\n`0:06` quick recap of XOR calculation\n`0:28` Demonstrate how to solve the question\n`1:37` How you keep the original previous number\n`2:29` Continue to demonstrate how to solve the question\n`3:59` Coding\n`4:43` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-vowels-permutation/solutions/4218427/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity | 21 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
【Video】Give me 10 minutes - Using Heap without build-in function such as sort or bit count | sort-integers-by-the-number-of-1-bits | 1 | 1 | # Intuition\nUsing Heap\n\n---\n\n# Solution Video\n\nhttps://youtu.be/oqV8Ai0_UWA\n\n\u25A0 Timeline\n`0:05` Solution code with build-in function\n`0:26` Two difficulties to solve the question\n`0:41` How do you count 1 bits?\n`1:05` Understanding to count 1 bits with an example\n`3:02` How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n`5:29` Coding\n`7:54` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,893\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n\n# Approach\n\n## How we think about a solution\n\nI think we can solve this question with the solution code below.\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n arr.sort(key = lambda num: (num.bit_count(), num))\n return arr \n```\n\nBut this question is asking you about "Sort Integers by The Number of 1 Bits", so I thought we should avoid build-in function such as `sort` or `bit_count`.\n\nI\'ll show you a solution code without build-in function.\n\nI think there are two difficuties to solve this quesiton. \n\n---\n\n\u25A0 Two difficulties\n\n- How do you count 1 bits?\n\n- How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n\n---\n\n- How do you count 1 bits?\n\nFirst of all, look at this.\n\n\nLeft: decimal\nRight: binary\n\nAcutually, there is well known algorithm to count bits.\n\n---\n\nThe fundamental idea of the algorithm is to count the number of bits using bitwise operations. Specifically, for an integer num that you want to count the bits of, you repetitively apply a bitwise AND operation between `num` and `(num - 1)`.\n\nBy continuing this operation, one set bit at a time is cleared in num, and the count of the bitwise AND operations performed in between becomes the count of set bits, which is the number of bits in the binary representation of the integer.\n\n---\n\nBut I forgot the name of person who found it. lol \u2190 This is "Brian Kerninghan\'s Algorithm".\n\nI think it\'s worth remembering.\n\nLet\'s see a concrete example.\n\n```\nnum = 7\ncount = 0\n```\nCalculate this. Just in case \n\nIf we use bitwise AND operator(`&`)...\nWhen both numbers are `1` \u2192 `1`\nOtherwise \u2192 `0`\n\n```\n7 & 6\n\u2193\n111\n110\n---\n110\n\ncount = 1\n```\n```\n6 & 5 (= 6 is coming from previous result 110)\n\u2193\n110\n101\n---\n100\n\ncount = 2\n```\n```\n4 & 3 (= 4 is coming from previous result 100)\n\u2193\n100\n 11\n---\n000\n\ncount = 3\n```\nWhen we reach `0`, we stop calculation.\n\n```\ncount = 3 (= 7 has `111`).\n```\n\nSeems like we can use the algorithm.\n\n\n---\n\n\n- How do you keep numbers in ascending order when multiple numbers have the same number of 1 bits?\n\nThe second difficulty is what if we have the same number of 1 bits?\n\n\n---\n\n\u2B50\uFE0F Points\n\nMy idea is to use `heap`, more precisely `min heap`.\n\n---\n\n```\nInput: [7,6,5]\n```\n\nAs you can see examples in description, we need to return output in ascending order.\n\nThe first priority of sorting data is number of ones, so we should have data like this.\n\n```\n(ones, n)\n\nones: number of 1\nn: current number\n```\n\nWhen we have `(3, 7)`,`(2, 6)`,`(2, 5)`, we can take them with this order.\n\n```\n(2, 5)\n(2, 6)\n(3, 7)\n```\nEasy! we don\'t need number of bits, so just access index `1`.\n\nLet\'s see a real algorithm!\n\n\n---\n\n\n**Algorithm Overview:**\n\nThe algorithm leverages the min-heap data structure to efficiently sort elements based on their number of set bits and original values. This ensures that elements with fewer set bits appear first, and in case of a tie, the original values are used for comparison.\n\nThis is based on Python. Other languages might be different a bit.\n\n**Detailed Explanation:**\n\n1. The `count_ones` function counts the number of set bits in an integer using the bitwise operation `num &= (num - 1)` until `num` becomes zero. The count of set bits is maintained and returned.\n\n2. The `one_list` list will store pairs (tuples) of the number of set bits and the original values. It will be used for sorting based on the number of set bits and the original values.\n\n3. The `for` loop iterates through each element in the input list `arr`. For each element `n`:\n - The `count_ones` function is called to count the number of set bits in `n`.\n - The pair of (number of set bits, original value) is created as a tuple and appended to the `one_list` list.\n\n4. The `heapify` function from the `heapq` module is called to convert the `one_list` list into a min-heap (priority queue). This step ensures that elements with fewer set bits are at the top of the heap, making it easy to pop the smallest elements.\n\n5. An empty list `res` is initialized to store the sorted values.\n\n6. The `while` loop continues until the `one_list` heap is not empty:\n - The `heapq.heappop(one_list)` function is used to pop the smallest element (based on the number of set bits and the original value) from the heap.\n - The original value (the second element in the tuple) of the popped element is appended to the `res` list.\n\n7. The loop continues to pop and append values until the `one_list` heap is empty.\n\n8. Finally, the sorted list `res` is returned as the result.\n\n\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n\n- Space complexity: $$O(n)$$\n\n```python []\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n\n def count_ones(num):\n count = 0\n while num:\n num &= (num - 1)\n count += 1\n return count\n\n one_list = []\n for n in arr:\n ones = count_ones(n)\n one_list.append((ones, n))\n\n heapq.heapify(one_list)\n res = []\n\n while one_list:\n res.append(heapq.heappop(one_list)[1])\n\n return res \n```\n```java []\nclass Solution {\n public int[] sortByBits(int[] arr) {\n Comparator<Integer> customComparator = (a, b) -> {\n int onesA = countOnes(a);\n int onesB = countOnes(b);\n if (onesA != onesB) {\n return onesA - onesB;\n }\n return a - b;\n };\n\n PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(customComparator);\n for (int n : arr) {\n priorityQueue.offer(n);\n }\n\n int[] res = new int[arr.length];\n int i = 0;\n while (!priorityQueue.isEmpty()) {\n res[i] = priorityQueue.poll();\n i++;\n }\n\n return res;\n }\n\n private int countOnes(int num) {\n int count = 0;\n while (num > 0) {\n num &= (num - 1);\n count++;\n }\n return count;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> sortByBits(vector<int>& arr) {\n auto customComparator = [this](int a, int b) {\n int onesA = countOnes(a);\n int onesB = countOnes(b);\n if (onesA != onesB) {\n return onesA > onesB;\n }\n return a > b;\n };\n\n priority_queue<int, vector<int>, decltype(customComparator)> priorityQueue(customComparator);\n for (int n : arr) {\n priorityQueue.push(n);\n }\n\n vector<int> res;\n while (!priorityQueue.empty()) {\n res.push_back(priorityQueue.top());\n priorityQueue.pop();\n }\n\n return res;\n }\n\n int countOnes(int num) {\n int count = 0;\n while (num) {\n num &= (num - 1);\n count++;\n }\n return count;\n } \n};\n```\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-the-original-array-of-prefix-xor/solutions/4228796/video-give-me-5-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/ck4dJURKAlA\n\n\u25A0 Timeline of the video\n`0:05` Solution code with build-in function\n`0:06` quick recap of XOR calculation\n`0:28` Demonstrate how to solve the question\n`1:37` How you keep the original previous number\n`2:29` Continue to demonstrate how to solve the question\n`3:59` Coding\n`4:43` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-vowels-permutation/solutions/4218427/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity | 21 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
Python3 Solution | sort-integers-by-the-number-of-1-bits | 0 | 1 | \n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr,key=lambda x:(bin(x).count("1"),x))\n``` | 1 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Python3 Solution | sort-integers-by-the-number-of-1-bits | 0 | 1 | \n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr,key=lambda x:(bin(x).count("1"),x))\n``` | 1 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
Simple one line solution | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nUse the built-in sorting mechanism, but specify a custom function to sort based on the given criteria.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nConvert each integer to its binary representation, then sort the list based on a tuple, where the first element is the number of $$1$$\'s in the binary string, and the second is the number itself. While sorting tuples in python, the first element is considered first, and if that isn\'t conclusive then the next elements are considered.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n$$O(n\\log(n)\\log(k))$$ where $$n$$ is the length of the list and $$k$$ largest integer in the list.\n\nThe sorting algorithm is $$O(n\\log(n))$$, but the ```bin(x).count(\'1\')``` is $$O(\\log(x))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n$$O(n)$$\n\nbecause we are creating a new list of the same length as ```arr```\n\n# Code\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr, key=lambda x: (bin(x).count(\'1\'), x))\n``` | 1 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Simple one line solution | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nUse the built-in sorting mechanism, but specify a custom function to sort based on the given criteria.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nConvert each integer to its binary representation, then sort the list based on a tuple, where the first element is the number of $$1$$\'s in the binary string, and the second is the number itself. While sorting tuples in python, the first element is considered first, and if that isn\'t conclusive then the next elements are considered.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n$$O(n\\log(n)\\log(k))$$ where $$n$$ is the length of the list and $$k$$ largest integer in the list.\n\nThe sorting algorithm is $$O(n\\log(n))$$, but the ```bin(x).count(\'1\')``` is $$O(\\log(x))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n$$O(n)$$\n\nbecause we are creating a new list of the same length as ```arr```\n\n# Code\n```\nclass Solution:\n def sortByBits(self, arr: List[int]) -> List[int]:\n return sorted(arr, key=lambda x: (bin(x).count(\'1\'), x))\n``` | 1 | Given two arrays `nums1` and `nums2`.
Return the maximum dot product between **non-empty** subsequences of nums1 and nums2 with the same length.
A subsequence of a array is a new array which is formed from the original array by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, `[2,3,5]` is a subsequence of `[1,2,3,4,5]` while `[1,5,3]` is not).
**Example 1:**
**Input:** nums1 = \[2,1,-2,5\], nums2 = \[3,0,-6\]
**Output:** 18
**Explanation:** Take subsequence \[2,-2\] from nums1 and subsequence \[3,-6\] from nums2.
Their dot product is (2\*3 + (-2)\*(-6)) = 18.
**Example 2:**
**Input:** nums1 = \[3,-2\], nums2 = \[2,-6,7\]
**Output:** 21
**Explanation:** Take subsequence \[3\] from nums1 and subsequence \[7\] from nums2.
Their dot product is (3\*7) = 21.
**Example 3:**
**Input:** nums1 = \[-1,-1\], nums2 = \[1,1\]
**Output:** -1
**Explanation:** Take subsequence \[-1\] from nums1 and subsequence \[1\] from nums2.
Their dot product is -1.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `-1000 <= nums1[i], nums2[i] <= 1000` | Simulate the problem. Count the number of 1's in the binary representation of each integer. Sort by the number of 1's ascending and by the value in case of tie. |
Python 1L / Rust 2-3 L / Go a lot. | sort-integers-by-the-number-of-1-bits | 0 | 1 | # Intuition\nAll you need is to count the number of ones, create tules of `(cnt, v)` and then do sorting. Many languages allow to do this in one line\n\n# Complexity\n- Time complexity: $O(n \\log n)$\n- Space complexity: $O(n)$\n\n# Code\n```Rust []\nimpl Solution {\n pub fn sort_by_bits(arr: Vec<i32>) -> Vec<i32> {\n let mut data: Vec<(u32, i32)> = arr.iter().map(|v| (v.count_ones(), *v)).collect();\n data.sort_unstable();\n return data.iter().map(|v| v.1).collect();\n }\n}\n```\n```Rust []\nimpl Solution {\n pub fn sort_by_bits(mut arr: Vec<i32>) -> Vec<i32> {\n arr.sort_unstable_by(|a, b| a.count_ones().cmp(&b.count_ones()).then(a.cmp(b)));\n return arr;\n }\n}\n```\n```python []\nclass Solution:\n def sortByBits(self, arr):\n return sorted(arr, key=lambda v: (bin(v).count(\'1\'), v)) \n```\n```Go []\nimport "math/bits"\nimport "fmt"\nimport "sort"\n\ntype num_bit struct {\n num int\n bit int\n}\n\nfunc sortByBits(arr []int) []int {\n data := make([]num_bit, len(arr), len(arr))\n \n for pos, v := range(arr) {\n data[pos] = num_bit{v, bits.OnesCount16(uint16(v))}\n }\n \n sort.Slice(data, func(i, j int) bool {\n if data[i].bit < data[j].bit {\n return true\n }\n if data[i].bit > data[j].bit {\n return false\n }\n return data[i].num < data[j].num\n })\n \n out := make([]int, len(arr), len(arr))\n for pos, v := range(data) {\n out[pos] = v.num\n }\n return out\n}\n```\n | 1 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.