title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python short and clean. DP. Bitmask. Functional programming. | smallest-sufficient-team | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution Approach 2](https://leetcode.com/problems/smallest-sufficient-team/editorial/) but written functionally.\n\n# Complexity\n- Time complexity: $$O(2^k \\cdot n \\cdot log(n))$$\n (Note: $$log(n)$$ is for `int.bit_count()`)\n\n- Space complexity: $$O(2^k)$$\n\nwhere,\n`n is number of people`,\n`k is number of req_skills`.\n\n# Code\n```python\nclass Solution:\n def smallestSufficientTeam(self, req_skills: list[str], people: list[list[str]]) -> list[int]:\n n, k = len(people), len(req_skills)\n\n masks = lambda: accumulate(repeat(1), lshift)\n skill_to_mask = dict(zip(req_skills, masks()))\n person_skills_m = [reduce(or_, map(skill_to_mask.get, skills), 0) for skills in people]\n \n @cache\n def smallest_team_m(req_skills_m: int) -> int:\n rem_skills_m = map(lambda m: req_skills_m & ~m, person_skills_m)\n filtered = (x for x in zip(masks(), rem_skills_m) if x[1] != req_skills_m)\n teams = (p_m | smallest_team_m(rem_m) for p_m, rem_m in filtered)\n return min(teams, key=int.bit_count) if req_skills_m else 0\n \n team_m = smallest_team_m((1 << k) - 1)\n selector = map(int, bin(team_m)[:1:-1])\n return list(compress(range(n), selector))\n\n\n``` | 1 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
Bottom-up + Bitmask | Python / JS Solution | smallest-sufficient-team | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we have you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.\n\nEach person in the `people` list has a set of skills represented as a list. Our objective is to form a team that covers all required skills such that for every required skill in `req_skills`, there will be at least one person on the team who has that skil.\n\nThus, we need to find a `sufficient team of the smallest possible size`\n\n## Explanation\n\nSince we want to find the smallest sufficient team that covers all the required skills, we can use `bottom-up DP / bitmask` to help us explore all possible combinations of teams and their skills efficiently. As a result, we can find the smallest sufficient team without having to consider all possible subsets of people directly. \n\n\n### DP (Bottom-up)\nUsing `DP`, we will use a single array to keep track of the best team we can form for each possbile set of covered skills.\n\nAs we iterate `people`, we will be considering whether we should include a person in the team which will lead to a better solution than what we have encountered thus far. If so, we update `dp` only when we find a better team that covers more skills with the smallest possible size\n\n\n### Bitmask\nThe main part of this solution is to use bitmask to represent each persons skills, where each bit will correspond to whether the person has the corresponding skill or not. To do that, we will be using bitwise shifting / OR operator to manipulate set of skills efficiently as possible.\n\nAs we iterate through the people and their skills, we will use bitwise OR operation to combine the person\'s skills with the existing set of covered skills for each team. This allows us to check if the newly formed team covers more skills or not\n\n\n1) Initialize:\n \n - A dictionary denoted as `bit skills` to map each required skills to its corresponding bitmask using bitwise shifting, allowing us to efficiently represent the skills possessed by each person and perform bitwise operations on them.\n \n - To calculate all the required skills combined, we will use bitwise shifting operations. For example, if `required_skills` has `X` amount of skills, then `target_skills = (1 << X) - 1`. This will help create bitmask with all `1` at positions `0` to `X - 1`\n \n - Use a single dp array to track the best team for each set of covered skills. The dp array has a size of `target_skills + 1` to accommodate all possible sets of covered skills from 0 to target_skills. We initialize the dp array with null for each element. The null value indicates that a specific set of covered skills has not been reached yet and, thus, doesn\'t have a team.\n \n2) We iterate over people, and for each person in `people`, we calculate the `bitmask` of each person denoted as `person_bitmask` \n\n - iterate through the dp array and check each element represented by covered_skills and only process elements that are not null, as they represent sets of covered skills that have been reached so far.\n \n - For each valid covered_skills, we calculate a new bitmask new_skills by performing a bitwise `OR` operation with the person_bitmask. This gives us a bitmask representing the set of skills that would be covered if we add the current person to the team with covered_skills.\n \n - If new_skills is different from covered_skills, it means the new team has additional covered skills compared to the current covered_skills. \n \n - We then check if the `dp[new_skills]` element is null or if the new team size `length of dp[covered_skills] + 1` is smaller than the previously recorded team size for the same new_skills. \n \n - If any of these conditions are met, it indicates a better team, and we update the dp array with the new team.\n\n3) Once we return `dp[target_skills]`, this will guarantee there will be a sufficient small team covering all the required skills\n\n\n# Code\n\n**Python**\n\n```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n\n bit_skills = {}\n for i, skill in enumerate(req_skills): bit_skills[skill] = 1 << i\n \n target_skills = (1 << len(req_skills)) - 1\n dp = [None] * (target_skills + 1)\n dp[0] = []\n\n for i, person_skills in enumerate(people):\n person_bitmask = sum(bit_skills[skill] for skill in person_skills)\n for covered_skills, team in enumerate(dp):\n if team is None: continue\n new_skills = covered_skills | person_bitmask\n if new_skills == covered_skills: continue\n if dp[new_skills] is None or len(dp[new_skills]) > len(team) + 1 : dp[new_skills] = team + [i]\n\n return dp[target_skills]\n```\n\n**JavaScript**\n```\n/**\n * @param {string[]} req_skills\n * @param {string[][]} people\n * @return {number[]}\n */\nvar smallestSufficientTeam = function(req_skills, people) {\n const skill_to_bit = req_skills.reduce((acc, skill, i) => {\n acc[skill] = 1 << i;\n return acc;\n }, {});\n\n const target_skills = (1 << req_skills.length) - 1;\n const dp = new Array(target_skills + 1).fill(null);\n dp[0] = [];\n\n for (let i = 0; i < people.length; i++) {\n const person_skills = people[i];\n const person_bitmask = person_skills.reduce((acc, skill) => {\n return acc | skill_to_bit[skill];\n }, 0);\n\n for (let covered_skills = 0; covered_skills <= target_skills; covered_skills++) {\n if (dp[covered_skills] === null) continue;\n\n const new_skills = covered_skills | person_bitmask;\n if (dp[new_skills] === null || dp[new_skills].length > dp[covered_skills].length + 1) {\n dp[new_skills] = [...dp[covered_skills], i];\n }\n }\n }\n\n return dp[target_skills];\n};\n\n```\n\n### Time Complexity: O(n*m*2^m)\n### Space Complexity: O(2^m)\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n | 12 | In a project, you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.
Consider a sufficient team: a set of people such that for every required skill in `req_skills`, there is at least one person in the team who has that skill. We can represent these teams by the index of each person.
* For example, `team = [0, 1, 3]` represents the people with skills `people[0]`, `people[1]`, and `people[3]`.
Return _any sufficient team of the smallest possible size, represented by the index of each person_. You may return the answer in **any order**.
It is **guaranteed** an answer exists.
**Example 1:**
**Input:** req\_skills = \["java","nodejs","reactjs"\], people = \[\["java"\],\["nodejs"\],\["nodejs","reactjs"\]\]
**Output:** \[0,2\]
**Example 2:**
**Input:** req\_skills = \["algorithms","math","java","reactjs","csharp","aws"\], people = \[\["algorithms","math","java"\],\["algorithms","math","reactjs"\],\["java","csharp","aws"\],\["reactjs","csharp"\],\["csharp","math"\],\["aws","java"\]\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= req_skills.length <= 16`
* `1 <= req_skills[i].length <= 16`
* `req_skills[i]` consists of lowercase English letters.
* All the strings of `req_skills` are **unique**.
* `1 <= people.length <= 60`
* `0 <= people[i].length <= 16`
* `1 <= people[i][j].length <= 16`
* `people[i][j]` consists of lowercase English letters.
* All the strings of `people[i]` are **unique**.
* Every skill in `people[i]` is a skill in `req_skills`.
* It is guaranteed a sufficient team exists. | What if you think of a tree hierarchy for the files?. A path is a node in the tree. Use a hash table to store the valid paths along with their values. |
Bottom-up + Bitmask | Python / JS Solution | smallest-sufficient-team | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we have you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.\n\nEach person in the `people` list has a set of skills represented as a list. Our objective is to form a team that covers all required skills such that for every required skill in `req_skills`, there will be at least one person on the team who has that skil.\n\nThus, we need to find a `sufficient team of the smallest possible size`\n\n## Explanation\n\nSince we want to find the smallest sufficient team that covers all the required skills, we can use `bottom-up DP / bitmask` to help us explore all possible combinations of teams and their skills efficiently. As a result, we can find the smallest sufficient team without having to consider all possible subsets of people directly. \n\n\n### DP (Bottom-up)\nUsing `DP`, we will use a single array to keep track of the best team we can form for each possbile set of covered skills.\n\nAs we iterate `people`, we will be considering whether we should include a person in the team which will lead to a better solution than what we have encountered thus far. If so, we update `dp` only when we find a better team that covers more skills with the smallest possible size\n\n\n### Bitmask\nThe main part of this solution is to use bitmask to represent each persons skills, where each bit will correspond to whether the person has the corresponding skill or not. To do that, we will be using bitwise shifting / OR operator to manipulate set of skills efficiently as possible.\n\nAs we iterate through the people and their skills, we will use bitwise OR operation to combine the person\'s skills with the existing set of covered skills for each team. This allows us to check if the newly formed team covers more skills or not\n\n\n1) Initialize:\n \n - A dictionary denoted as `bit skills` to map each required skills to its corresponding bitmask using bitwise shifting, allowing us to efficiently represent the skills possessed by each person and perform bitwise operations on them.\n \n - To calculate all the required skills combined, we will use bitwise shifting operations. For example, if `required_skills` has `X` amount of skills, then `target_skills = (1 << X) - 1`. This will help create bitmask with all `1` at positions `0` to `X - 1`\n \n - Use a single dp array to track the best team for each set of covered skills. The dp array has a size of `target_skills + 1` to accommodate all possible sets of covered skills from 0 to target_skills. We initialize the dp array with null for each element. The null value indicates that a specific set of covered skills has not been reached yet and, thus, doesn\'t have a team.\n \n2) We iterate over people, and for each person in `people`, we calculate the `bitmask` of each person denoted as `person_bitmask` \n\n - iterate through the dp array and check each element represented by covered_skills and only process elements that are not null, as they represent sets of covered skills that have been reached so far.\n \n - For each valid covered_skills, we calculate a new bitmask new_skills by performing a bitwise `OR` operation with the person_bitmask. This gives us a bitmask representing the set of skills that would be covered if we add the current person to the team with covered_skills.\n \n - If new_skills is different from covered_skills, it means the new team has additional covered skills compared to the current covered_skills. \n \n - We then check if the `dp[new_skills]` element is null or if the new team size `length of dp[covered_skills] + 1` is smaller than the previously recorded team size for the same new_skills. \n \n - If any of these conditions are met, it indicates a better team, and we update the dp array with the new team.\n\n3) Once we return `dp[target_skills]`, this will guarantee there will be a sufficient small team covering all the required skills\n\n\n# Code\n\n**Python**\n\n```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n\n bit_skills = {}\n for i, skill in enumerate(req_skills): bit_skills[skill] = 1 << i\n \n target_skills = (1 << len(req_skills)) - 1\n dp = [None] * (target_skills + 1)\n dp[0] = []\n\n for i, person_skills in enumerate(people):\n person_bitmask = sum(bit_skills[skill] for skill in person_skills)\n for covered_skills, team in enumerate(dp):\n if team is None: continue\n new_skills = covered_skills | person_bitmask\n if new_skills == covered_skills: continue\n if dp[new_skills] is None or len(dp[new_skills]) > len(team) + 1 : dp[new_skills] = team + [i]\n\n return dp[target_skills]\n```\n\n**JavaScript**\n```\n/**\n * @param {string[]} req_skills\n * @param {string[][]} people\n * @return {number[]}\n */\nvar smallestSufficientTeam = function(req_skills, people) {\n const skill_to_bit = req_skills.reduce((acc, skill, i) => {\n acc[skill] = 1 << i;\n return acc;\n }, {});\n\n const target_skills = (1 << req_skills.length) - 1;\n const dp = new Array(target_skills + 1).fill(null);\n dp[0] = [];\n\n for (let i = 0; i < people.length; i++) {\n const person_skills = people[i];\n const person_bitmask = person_skills.reduce((acc, skill) => {\n return acc | skill_to_bit[skill];\n }, 0);\n\n for (let covered_skills = 0; covered_skills <= target_skills; covered_skills++) {\n if (dp[covered_skills] === null) continue;\n\n const new_skills = covered_skills | person_bitmask;\n if (dp[new_skills] === null || dp[new_skills].length > dp[covered_skills].length + 1) {\n dp[new_skills] = [...dp[covered_skills], i];\n }\n }\n }\n\n return dp[target_skills];\n};\n\n```\n\n### Time Complexity: O(n*m*2^m)\n### Space Complexity: O(2^m)\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n | 12 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
Python3 Solution | smallest-sufficient-team | 0 | 1 | \n```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n m=len(req_skills)\n n=len(people)\n skill_index={v:i for i,v in enumerate(req_skills)}\n cand=[]\n for skills in people:\n val=0\n for skill in skills:\n val |=1<<skill_index[skill]\n\n cand.append(val)\n\n @cache\n def fn(i,mask):\n if mask==0:\n return []\n\n if i==n:\n return [0]*100\n\n if not (mask & cand[i]):\n return fn(i+1,mask)\n\n return min(fn(i+1,mask),[i]+fn(i+1,mask &~cand[i]),key=len)\n\n return fn(0,(1<<m)-1) \n``` | 5 | In a project, you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.
Consider a sufficient team: a set of people such that for every required skill in `req_skills`, there is at least one person in the team who has that skill. We can represent these teams by the index of each person.
* For example, `team = [0, 1, 3]` represents the people with skills `people[0]`, `people[1]`, and `people[3]`.
Return _any sufficient team of the smallest possible size, represented by the index of each person_. You may return the answer in **any order**.
It is **guaranteed** an answer exists.
**Example 1:**
**Input:** req\_skills = \["java","nodejs","reactjs"\], people = \[\["java"\],\["nodejs"\],\["nodejs","reactjs"\]\]
**Output:** \[0,2\]
**Example 2:**
**Input:** req\_skills = \["algorithms","math","java","reactjs","csharp","aws"\], people = \[\["algorithms","math","java"\],\["algorithms","math","reactjs"\],\["java","csharp","aws"\],\["reactjs","csharp"\],\["csharp","math"\],\["aws","java"\]\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= req_skills.length <= 16`
* `1 <= req_skills[i].length <= 16`
* `req_skills[i]` consists of lowercase English letters.
* All the strings of `req_skills` are **unique**.
* `1 <= people.length <= 60`
* `0 <= people[i].length <= 16`
* `1 <= people[i][j].length <= 16`
* `people[i][j]` consists of lowercase English letters.
* All the strings of `people[i]` are **unique**.
* Every skill in `people[i]` is a skill in `req_skills`.
* It is guaranteed a sufficient team exists. | What if you think of a tree hierarchy for the files?. A path is a node in the tree. Use a hash table to store the valid paths along with their values. |
Python3 Solution | smallest-sufficient-team | 0 | 1 | \n```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n m=len(req_skills)\n n=len(people)\n skill_index={v:i for i,v in enumerate(req_skills)}\n cand=[]\n for skills in people:\n val=0\n for skill in skills:\n val |=1<<skill_index[skill]\n\n cand.append(val)\n\n @cache\n def fn(i,mask):\n if mask==0:\n return []\n\n if i==n:\n return [0]*100\n\n if not (mask & cand[i]):\n return fn(i+1,mask)\n\n return min(fn(i+1,mask),[i]+fn(i+1,mask &~cand[i]),key=len)\n\n return fn(0,(1<<m)-1) \n``` | 5 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
🚀 [VIDEO] Faster than 90%🔥| ❗Long Explanation❗ | 2-D DP + BITMASK | Clean Code | smallest-sufficient-team | 1 | 1 | # \uD83C\uDF1F Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nMy initial intuition for solving this problem is to use a dynamic programming approach. Since we need to find the smallest sufficient team, it seems logical to consider all possible combinations of people and skills. By using a dynamic programming table to keep track of the skills covered by each team, we can gradually build up the solution.\n\nhttps://youtu.be/RJnReFN_nJE\n\n# \uD83D\uDCA1 Approach\n<!-- Describe your approach to solving the problem. -->\n\nHere is the approach I would take to solve the "Smallest Sufficient Team" problem:\n\n1. First, I would create a skill mapping that maps each skill to its corresponding index. This mapping will help us represent skills using bitmasks later on.\n\n2. Next, I would initialize a dynamic programming table called `dp` with one entry: 0, representing no skills covered and no team members selected.\n\n3. Then, I would iterate over each person in the `people` list. For each person, I would create a bitmask to represent their skills. This bitmask will have a 1 in the positions corresponding to the skills they possess.\n\n4. Within the person iteration, I would iterate over the existing teams in the `dp` table. For each team, I would combine the skills of the current person with the team\'s skills using the bitwise OR operator. If the new combined skills cover more skills or have a smaller size than the existing team, I would update the team in the `dp` table.\n\n5. Finally, I would return the team from the `dp` table that covers all the required skills. The required skills are represented by a bitmask where all the skill positions have a 1.\n\n# \u23F0 Complexity\n- Time complexity: \nThe time complexity of this approach is O(N * (2^M)), where N is the number of people and M is the number of required skills. This is because we iterate over each person (N) and for each person, we iterate over the existing teams (2^M) in the `dp` table.\n\n- Space complexity: \nThe space complexity is O(2^M) as we need to store the dynamic programming table `dp` that can have up to 2^M entries, where M is the number of required skills.\n\n# \uD83D\uDCDD Code\n```Python []\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n # Map skills to their indices\n skill_map = {skill: i for i, skill in enumerate(req_skills)}\n n = len(req_skills)\n # dp bitmask representing the skills covered by each team\n dp = {0: []}\n for i, person in enumerate(people):\n # Bitmask representing the skills of the current person\n person_skill_mask = 0\n for skill in person:\n # Set the corresponding bit for each skill\n person_skill_mask |= (1 << skill_map[skill])\n # Iterate over existing teams\n for skill_mask, team in list(dp.items()):\n # Combine the skills of the current person with the existing team\n new_mask = skill_mask | person_skill_mask\n if new_mask not in dp or len(dp[new_mask]) > len(team) + 1:\n # Update the team if it covers more skills or has a smaller size\n dp[new_mask] = team + [i]\n # Return the team that covers all the required skills\n return dp[(1 << n) - 1]\n```\n``` JavaScript []\nvar smallestSufficientTeam = function(req_skills, people) {\n let skill_map = {};\n let n = req_skills.length;\n for (let i = 0; i < n; ++i) {\n skill_map[req_skills[i]] = i;\n }\n\n let dp = [];\n dp[0] = [];\n\n for (let i = 0; i < people.length; ++i) {\n let person_skill_mask = 0;\n for (let skill of people[i]) {\n person_skill_mask |= (1 << skill_map[skill]);\n }\n\n for (let skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if ((dp[skill_mask] === undefined || dp[skill_mask].length == 0) && skill_mask != 0) continue;\n let new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask] === undefined || dp[new_mask].length > dp[skill_mask].length + 1) {\n dp[new_mask] = [...dp[skill_mask], i];\n }\n }\n }\n\n return dp[(1 << n) - 1]; \n};\n```\n``` Java []\nclass Solution {\n public int[] smallestSufficientTeam(String[] req_skills, List<List<String>> people) {\n Map<String, Integer> skill_map = new HashMap<>();\n int n = req_skills.length;\n for (int i = 0; i < n; ++i) {\n skill_map.put(req_skills[i], i);\n }\n \n List<Integer>[] dp = new ArrayList[1 << n];\n dp[0] = new ArrayList<>();\n\n for (int i = 0; i < people.size(); ++i) {\n int person_skill_mask = 0;\n for (String skill : people.get(i)) {\n person_skill_mask |= (1 << skill_map.get(skill));\n }\n\n for (int skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if (dp[skill_mask] == null && skill_mask != 0) continue;\n int new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask] == null || dp[new_mask].size() > dp[skill_mask].size() + 1) {\n dp[new_mask] = new ArrayList<>(dp[skill_mask]);\n dp[new_mask].add(i);\n }\n }\n }\n\n int[] res = new int[dp[(1 << n) - 1].size()];\n for (int i = 0; i < res.length; i++) {\n res[i] = dp[(1 << n) - 1].get(i);\n }\n return res;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] SmallestSufficientTeam(string[] req_skills, IList<IList<string>> people) {\n Dictionary<string, int> skill_map = new Dictionary<string, int>();\n int n = req_skills.Length;\n for (int i = 0; i < n; ++i) {\n skill_map[req_skills[i]] = i;\n }\n\n List<int>[] dp = new List<int>[1 << n];\n dp[0] = new List<int>();\n\n for (int i = 0; i < people.Count; ++i) {\n int person_skill_mask = 0;\n foreach (string skill in people[i]) {\n person_skill_mask |= (1 << skill_map[skill]);\n }\n\n for (int skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if (dp[skill_mask] == null && skill_mask != 0) continue;\n int new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask] == null || dp[new_mask].Count > dp[skill_mask].Count + 1) {\n dp[new_mask] = new List<int>(dp[skill_mask]);\n dp[new_mask].Add(i);\n }\n }\n }\n\n return dp[(1 << n) - 1].ToArray();\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> smallestSufficientTeam(std::vector<std::string>& req_skills, std::vector<std::vector<std::string>>& people) {\n std::unordered_map<std::string, int> skill_map;\n int n = req_skills.size();\n for (int i = 0; i < n; ++i) {\n skill_map[req_skills[i]] = i;\n }\n\n std::vector<std::vector<int>> dp(1 << n);\n dp[0] = std::vector<int>();\n\n for (int i = 0; i < people.size(); ++i) {\n if (people[i].empty()) continue; // Skip people with no skills\n\n int person_skill_mask = 0;\n for (const std::string& skill : people[i]) {\n person_skill_mask |= (1 << skill_map[skill]);\n }\n\n for (int skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if (dp[skill_mask].empty() && skill_mask != 0) continue;\n int new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask].empty() || dp[new_mask].size() > dp[skill_mask].size() + 1) {\n dp[new_mask] = dp[skill_mask];\n dp[new_mask].push_back(i);\n }\n }\n }\n\n return dp[(1 << n) - 1];\n }\n};\n``` | 1 | In a project, you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.
Consider a sufficient team: a set of people such that for every required skill in `req_skills`, there is at least one person in the team who has that skill. We can represent these teams by the index of each person.
* For example, `team = [0, 1, 3]` represents the people with skills `people[0]`, `people[1]`, and `people[3]`.
Return _any sufficient team of the smallest possible size, represented by the index of each person_. You may return the answer in **any order**.
It is **guaranteed** an answer exists.
**Example 1:**
**Input:** req\_skills = \["java","nodejs","reactjs"\], people = \[\["java"\],\["nodejs"\],\["nodejs","reactjs"\]\]
**Output:** \[0,2\]
**Example 2:**
**Input:** req\_skills = \["algorithms","math","java","reactjs","csharp","aws"\], people = \[\["algorithms","math","java"\],\["algorithms","math","reactjs"\],\["java","csharp","aws"\],\["reactjs","csharp"\],\["csharp","math"\],\["aws","java"\]\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= req_skills.length <= 16`
* `1 <= req_skills[i].length <= 16`
* `req_skills[i]` consists of lowercase English letters.
* All the strings of `req_skills` are **unique**.
* `1 <= people.length <= 60`
* `0 <= people[i].length <= 16`
* `1 <= people[i][j].length <= 16`
* `people[i][j]` consists of lowercase English letters.
* All the strings of `people[i]` are **unique**.
* Every skill in `people[i]` is a skill in `req_skills`.
* It is guaranteed a sufficient team exists. | What if you think of a tree hierarchy for the files?. A path is a node in the tree. Use a hash table to store the valid paths along with their values. |
🚀 [VIDEO] Faster than 90%🔥| ❗Long Explanation❗ | 2-D DP + BITMASK | Clean Code | smallest-sufficient-team | 1 | 1 | # \uD83C\uDF1F Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nMy initial intuition for solving this problem is to use a dynamic programming approach. Since we need to find the smallest sufficient team, it seems logical to consider all possible combinations of people and skills. By using a dynamic programming table to keep track of the skills covered by each team, we can gradually build up the solution.\n\nhttps://youtu.be/RJnReFN_nJE\n\n# \uD83D\uDCA1 Approach\n<!-- Describe your approach to solving the problem. -->\n\nHere is the approach I would take to solve the "Smallest Sufficient Team" problem:\n\n1. First, I would create a skill mapping that maps each skill to its corresponding index. This mapping will help us represent skills using bitmasks later on.\n\n2. Next, I would initialize a dynamic programming table called `dp` with one entry: 0, representing no skills covered and no team members selected.\n\n3. Then, I would iterate over each person in the `people` list. For each person, I would create a bitmask to represent their skills. This bitmask will have a 1 in the positions corresponding to the skills they possess.\n\n4. Within the person iteration, I would iterate over the existing teams in the `dp` table. For each team, I would combine the skills of the current person with the team\'s skills using the bitwise OR operator. If the new combined skills cover more skills or have a smaller size than the existing team, I would update the team in the `dp` table.\n\n5. Finally, I would return the team from the `dp` table that covers all the required skills. The required skills are represented by a bitmask where all the skill positions have a 1.\n\n# \u23F0 Complexity\n- Time complexity: \nThe time complexity of this approach is O(N * (2^M)), where N is the number of people and M is the number of required skills. This is because we iterate over each person (N) and for each person, we iterate over the existing teams (2^M) in the `dp` table.\n\n- Space complexity: \nThe space complexity is O(2^M) as we need to store the dynamic programming table `dp` that can have up to 2^M entries, where M is the number of required skills.\n\n# \uD83D\uDCDD Code\n```Python []\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n # Map skills to their indices\n skill_map = {skill: i for i, skill in enumerate(req_skills)}\n n = len(req_skills)\n # dp bitmask representing the skills covered by each team\n dp = {0: []}\n for i, person in enumerate(people):\n # Bitmask representing the skills of the current person\n person_skill_mask = 0\n for skill in person:\n # Set the corresponding bit for each skill\n person_skill_mask |= (1 << skill_map[skill])\n # Iterate over existing teams\n for skill_mask, team in list(dp.items()):\n # Combine the skills of the current person with the existing team\n new_mask = skill_mask | person_skill_mask\n if new_mask not in dp or len(dp[new_mask]) > len(team) + 1:\n # Update the team if it covers more skills or has a smaller size\n dp[new_mask] = team + [i]\n # Return the team that covers all the required skills\n return dp[(1 << n) - 1]\n```\n``` JavaScript []\nvar smallestSufficientTeam = function(req_skills, people) {\n let skill_map = {};\n let n = req_skills.length;\n for (let i = 0; i < n; ++i) {\n skill_map[req_skills[i]] = i;\n }\n\n let dp = [];\n dp[0] = [];\n\n for (let i = 0; i < people.length; ++i) {\n let person_skill_mask = 0;\n for (let skill of people[i]) {\n person_skill_mask |= (1 << skill_map[skill]);\n }\n\n for (let skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if ((dp[skill_mask] === undefined || dp[skill_mask].length == 0) && skill_mask != 0) continue;\n let new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask] === undefined || dp[new_mask].length > dp[skill_mask].length + 1) {\n dp[new_mask] = [...dp[skill_mask], i];\n }\n }\n }\n\n return dp[(1 << n) - 1]; \n};\n```\n``` Java []\nclass Solution {\n public int[] smallestSufficientTeam(String[] req_skills, List<List<String>> people) {\n Map<String, Integer> skill_map = new HashMap<>();\n int n = req_skills.length;\n for (int i = 0; i < n; ++i) {\n skill_map.put(req_skills[i], i);\n }\n \n List<Integer>[] dp = new ArrayList[1 << n];\n dp[0] = new ArrayList<>();\n\n for (int i = 0; i < people.size(); ++i) {\n int person_skill_mask = 0;\n for (String skill : people.get(i)) {\n person_skill_mask |= (1 << skill_map.get(skill));\n }\n\n for (int skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if (dp[skill_mask] == null && skill_mask != 0) continue;\n int new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask] == null || dp[new_mask].size() > dp[skill_mask].size() + 1) {\n dp[new_mask] = new ArrayList<>(dp[skill_mask]);\n dp[new_mask].add(i);\n }\n }\n }\n\n int[] res = new int[dp[(1 << n) - 1].size()];\n for (int i = 0; i < res.length; i++) {\n res[i] = dp[(1 << n) - 1].get(i);\n }\n return res;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int[] SmallestSufficientTeam(string[] req_skills, IList<IList<string>> people) {\n Dictionary<string, int> skill_map = new Dictionary<string, int>();\n int n = req_skills.Length;\n for (int i = 0; i < n; ++i) {\n skill_map[req_skills[i]] = i;\n }\n\n List<int>[] dp = new List<int>[1 << n];\n dp[0] = new List<int>();\n\n for (int i = 0; i < people.Count; ++i) {\n int person_skill_mask = 0;\n foreach (string skill in people[i]) {\n person_skill_mask |= (1 << skill_map[skill]);\n }\n\n for (int skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if (dp[skill_mask] == null && skill_mask != 0) continue;\n int new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask] == null || dp[new_mask].Count > dp[skill_mask].Count + 1) {\n dp[new_mask] = new List<int>(dp[skill_mask]);\n dp[new_mask].Add(i);\n }\n }\n }\n\n return dp[(1 << n) - 1].ToArray();\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<int> smallestSufficientTeam(std::vector<std::string>& req_skills, std::vector<std::vector<std::string>>& people) {\n std::unordered_map<std::string, int> skill_map;\n int n = req_skills.size();\n for (int i = 0; i < n; ++i) {\n skill_map[req_skills[i]] = i;\n }\n\n std::vector<std::vector<int>> dp(1 << n);\n dp[0] = std::vector<int>();\n\n for (int i = 0; i < people.size(); ++i) {\n if (people[i].empty()) continue; // Skip people with no skills\n\n int person_skill_mask = 0;\n for (const std::string& skill : people[i]) {\n person_skill_mask |= (1 << skill_map[skill]);\n }\n\n for (int skill_mask = 0; skill_mask < (1 << n); ++skill_mask) {\n if (dp[skill_mask].empty() && skill_mask != 0) continue;\n int new_mask = skill_mask | person_skill_mask;\n if (dp[new_mask].empty() || dp[new_mask].size() > dp[skill_mask].size() + 1) {\n dp[new_mask] = dp[skill_mask];\n dp[new_mask].push_back(i);\n }\n }\n }\n\n return dp[(1 << n) - 1];\n }\n};\n``` | 1 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
[Python3] Easy to understand. No DP, no bitmask | smallest-sufficient-team | 0 | 1 | ```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n n = len(req_skills)\n # 1. Assign indexes for each skill string\n skills = {\n skill: i for i, skill in enumerate(req_skills)\n }\n # 2. Create sets with skill indexes for each person\n people = [(i, {skills[skill] for skill in person}) for i, person in enumerate(people)]\n # 3. Sort people by length of skillset\n people.sort(key=lambda x: len(x[1]))\n\n valid_people = []\n # 4. Iterate over people list and check if person\'s skill set \n # is a subset of other person\'s skill set. If it is, ignore it,\n # otherwise, add it to `valid_people` list\n for idx, person in enumerate(people):\n i, skillset = person\n is_valid = True\n\n for j, s in people[idx + 1:]:\n if skillset.issubset(s):\n is_valid = False\n break\n\n if is_valid:\n valid_people.append((i, skillset))\n\n m = len(valid_people)\n # 5. BFS: init deque with combinations of length 1 for every valid person index\n d = deque([((i,)) for i in range(m)])\n\n while d:\n idxs = d.popleft()\n # Receive skill set for current combination of people\n skillset = set().union(*[valid_people[i][1] for i in idxs])\n\n # 6. Check if current combination of people contains all the skills.\n # If it does, return it as our answer.\n # Since we\'re using BFS and go from shortest to longest combination,\n # this combination is guaranteed to be the right answer.\n if len(skillset) == n:\n return [valid_people[i][0] for i in idxs]\n\n # Iterate for all the remaining people in `valid_people`\n for i in range(idxs[-1] + 1, m):\n # Check if we\'ll gain new skills by adding this person to combination.\n # If we won\'t, there\'s no point in adding such a combination to deque.\n if valid_people[i][1] - skillset:\n d.append((idxs + (i, )))\n\n``` | 2 | In a project, you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.
Consider a sufficient team: a set of people such that for every required skill in `req_skills`, there is at least one person in the team who has that skill. We can represent these teams by the index of each person.
* For example, `team = [0, 1, 3]` represents the people with skills `people[0]`, `people[1]`, and `people[3]`.
Return _any sufficient team of the smallest possible size, represented by the index of each person_. You may return the answer in **any order**.
It is **guaranteed** an answer exists.
**Example 1:**
**Input:** req\_skills = \["java","nodejs","reactjs"\], people = \[\["java"\],\["nodejs"\],\["nodejs","reactjs"\]\]
**Output:** \[0,2\]
**Example 2:**
**Input:** req\_skills = \["algorithms","math","java","reactjs","csharp","aws"\], people = \[\["algorithms","math","java"\],\["algorithms","math","reactjs"\],\["java","csharp","aws"\],\["reactjs","csharp"\],\["csharp","math"\],\["aws","java"\]\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= req_skills.length <= 16`
* `1 <= req_skills[i].length <= 16`
* `req_skills[i]` consists of lowercase English letters.
* All the strings of `req_skills` are **unique**.
* `1 <= people.length <= 60`
* `0 <= people[i].length <= 16`
* `1 <= people[i][j].length <= 16`
* `people[i][j]` consists of lowercase English letters.
* All the strings of `people[i]` are **unique**.
* Every skill in `people[i]` is a skill in `req_skills`.
* It is guaranteed a sufficient team exists. | What if you think of a tree hierarchy for the files?. A path is a node in the tree. Use a hash table to store the valid paths along with their values. |
[Python3] Easy to understand. No DP, no bitmask | smallest-sufficient-team | 0 | 1 | ```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n n = len(req_skills)\n # 1. Assign indexes for each skill string\n skills = {\n skill: i for i, skill in enumerate(req_skills)\n }\n # 2. Create sets with skill indexes for each person\n people = [(i, {skills[skill] for skill in person}) for i, person in enumerate(people)]\n # 3. Sort people by length of skillset\n people.sort(key=lambda x: len(x[1]))\n\n valid_people = []\n # 4. Iterate over people list and check if person\'s skill set \n # is a subset of other person\'s skill set. If it is, ignore it,\n # otherwise, add it to `valid_people` list\n for idx, person in enumerate(people):\n i, skillset = person\n is_valid = True\n\n for j, s in people[idx + 1:]:\n if skillset.issubset(s):\n is_valid = False\n break\n\n if is_valid:\n valid_people.append((i, skillset))\n\n m = len(valid_people)\n # 5. BFS: init deque with combinations of length 1 for every valid person index\n d = deque([((i,)) for i in range(m)])\n\n while d:\n idxs = d.popleft()\n # Receive skill set for current combination of people\n skillset = set().union(*[valid_people[i][1] for i in idxs])\n\n # 6. Check if current combination of people contains all the skills.\n # If it does, return it as our answer.\n # Since we\'re using BFS and go from shortest to longest combination,\n # this combination is guaranteed to be the right answer.\n if len(skillset) == n:\n return [valid_people[i][0] for i in idxs]\n\n # Iterate for all the remaining people in `valid_people`\n for i in range(idxs[-1] + 1, m):\n # Check if we\'ll gain new skills by adding this person to combination.\n # If we won\'t, there\'s no point in adding such a combination to deque.\n if valid_people[i][1] - skillset:\n d.append((idxs + (i, )))\n\n``` | 2 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
am i stupid for thinking bfs? [python 3 bfs solution] | smallest-sufficient-team | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ni thought it was bfs because it said minimum number of people. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ni started off with a convert function, traversed the graph using a bfs function and marking things visited using a bitmask\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n convert = {key:idx for idx, key in enumerate(req_skills)}\n\n n, m = len(req_skills), len(people)\n end_mask = 2 ** n - 1\n visit = set()\n\n for idx, i in enumerate(people):\n temp = 0\n for j in range(len(i)):\n temp += (1 << convert[i[j]])\n people[idx] = temp\n \n q = [(0, [])]\n while q:\n mask, arr = q.pop()\n if mask == end_mask:\n return arr\n for idx, skill in enumerate(people):\n new_mask = mask | skill\n if new_mask not in visit:\n visit.add(new_mask)\n q.insert(0, (new_mask, arr + [idx]))\n\n``` | 2 | In a project, you have a list of required skills `req_skills`, and a list of people. The `ith` person `people[i]` contains a list of skills that the person has.
Consider a sufficient team: a set of people such that for every required skill in `req_skills`, there is at least one person in the team who has that skill. We can represent these teams by the index of each person.
* For example, `team = [0, 1, 3]` represents the people with skills `people[0]`, `people[1]`, and `people[3]`.
Return _any sufficient team of the smallest possible size, represented by the index of each person_. You may return the answer in **any order**.
It is **guaranteed** an answer exists.
**Example 1:**
**Input:** req\_skills = \["java","nodejs","reactjs"\], people = \[\["java"\],\["nodejs"\],\["nodejs","reactjs"\]\]
**Output:** \[0,2\]
**Example 2:**
**Input:** req\_skills = \["algorithms","math","java","reactjs","csharp","aws"\], people = \[\["algorithms","math","java"\],\["algorithms","math","reactjs"\],\["java","csharp","aws"\],\["reactjs","csharp"\],\["csharp","math"\],\["aws","java"\]\]
**Output:** \[1,2\]
**Constraints:**
* `1 <= req_skills.length <= 16`
* `1 <= req_skills[i].length <= 16`
* `req_skills[i]` consists of lowercase English letters.
* All the strings of `req_skills` are **unique**.
* `1 <= people.length <= 60`
* `0 <= people[i].length <= 16`
* `1 <= people[i][j].length <= 16`
* `people[i][j]` consists of lowercase English letters.
* All the strings of `people[i]` are **unique**.
* Every skill in `people[i]` is a skill in `req_skills`.
* It is guaranteed a sufficient team exists. | What if you think of a tree hierarchy for the files?. A path is a node in the tree. Use a hash table to store the valid paths along with their values. |
am i stupid for thinking bfs? [python 3 bfs solution] | smallest-sufficient-team | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ni thought it was bfs because it said minimum number of people. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ni started off with a convert function, traversed the graph using a bfs function and marking things visited using a bitmask\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestSufficientTeam(self, req_skills: List[str], people: List[List[str]]) -> List[int]:\n convert = {key:idx for idx, key in enumerate(req_skills)}\n\n n, m = len(req_skills), len(people)\n end_mask = 2 ** n - 1\n visit = set()\n\n for idx, i in enumerate(people):\n temp = 0\n for j in range(len(i)):\n temp += (1 << convert[i[j]])\n people[idx] = temp\n \n q = [(0, [])]\n while q:\n mask, arr = q.pop()\n if mask == end_mask:\n return arr\n for idx, skill in enumerate(people):\n new_mask = mask | skill\n if new_mask not in visit:\n visit.add(new_mask)\n q.insert(0, (new_mask, arr + [idx]))\n\n``` | 2 | Given an integer `n`, your task is to count how many strings of length `n` can be formed under the following rules:
* Each character is a lower case vowel (`'a'`, `'e'`, `'i'`, `'o'`, `'u'`)
* Each vowel `'a'` may only be followed by an `'e'`.
* Each vowel `'e'` may only be followed by an `'a'` or an `'i'`.
* Each vowel `'i'` **may not** be followed by another `'i'`.
* Each vowel `'o'` may only be followed by an `'i'` or a `'u'`.
* Each vowel `'u'` may only be followed by an `'a'.`
Since the answer may be too large, return it modulo `10^9 + 7.`
**Example 1:**
**Input:** n = 1
**Output:** 5
**Explanation:** All possible strings are: "a ", "e ", "i " , "o " and "u ".
**Example 2:**
**Input:** n = 2
**Output:** 10
**Explanation:** All possible strings are: "ae ", "ea ", "ei ", "ia ", "ie ", "io ", "iu ", "oi ", "ou " and "ua ".
**Example 3:**
**Input:** n = 5
**Output:** 68
**Constraints:**
* `1 <= n <= 2 * 10^4` | Do a bitmask DP. For each person, for each set of skills, we can update our understanding of a minimum set of people needed to perform this set of skills. |
PYTHON DICTIONARY solution with explanation (252ms) | number-of-equivalent-domino-pairs | 0 | 1 | ```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n \n #Keep track of the dominoes with a dictionary\n\t\t#counter[ DOMINO ] = COUNT\n counter = defaultdict( int );\n \n #Total will be the total number of pairs\n total = 0;\n \n #Go through all of the dominoes\n for i in range( len ( dominoes ) ):\n #Check the pair at the index\n pair = dominoes[ i ];\n \n #Pull the two values\n first = pair[ 0 ];\n second = pair[ 1 ];\n \n #Sort them by value\n\t\t\t#This way, the reversed matches will go into the same count\n smaller = min ( first, second );\n bigger = max( first, second );\n \n #Reassemble into tuple\n\t\t\t#This will act as our key for each domino\n pair_sorted = ( smaller, bigger );\n \n #If the current domino is already in our counter\n #Add to the total the previous matches\n \n #That is\n #If we have already added matching dominoes\n #Our current one will match with all the previous\n if pair_sorted in counter:\n total += counter[ pair_sorted ];\n \n #Lastly, we increment the count of the current\n counter [ pair_sorted ] += 1;\n \n \n return total;\n``` | 6 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
PYTHON DICTIONARY solution with explanation (252ms) | number-of-equivalent-domino-pairs | 0 | 1 | ```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n \n #Keep track of the dominoes with a dictionary\n\t\t#counter[ DOMINO ] = COUNT\n counter = defaultdict( int );\n \n #Total will be the total number of pairs\n total = 0;\n \n #Go through all of the dominoes\n for i in range( len ( dominoes ) ):\n #Check the pair at the index\n pair = dominoes[ i ];\n \n #Pull the two values\n first = pair[ 0 ];\n second = pair[ 1 ];\n \n #Sort them by value\n\t\t\t#This way, the reversed matches will go into the same count\n smaller = min ( first, second );\n bigger = max( first, second );\n \n #Reassemble into tuple\n\t\t\t#This will act as our key for each domino\n pair_sorted = ( smaller, bigger );\n \n #If the current domino is already in our counter\n #Add to the total the previous matches\n \n #That is\n #If we have already added matching dominoes\n #Our current one will match with all the previous\n if pair_sorted in counter:\n total += counter[ pair_sorted ];\n \n #Lastly, we increment the count of the current\n counter [ pair_sorted ] += 1;\n \n \n return total;\n``` | 6 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
[python3] dictionary count | number-of-equivalent-domino-pairs | 0 | 1 | * Use a dictionary to count how many times an intrinsic domino appeared. Here we define intrinsic domino as a sorted domino. By sort the list, we can easily identify the intrinsic domino. Use the intrinsic domino as key, the intrinsic domino frequency as value, store the information we need in a dictionary.\n```\nExample:\nindex 0 1 2 3\ninput = [[1,2],[2,1],[1,2],[1,2]]\nd = { [1,2] : 4}\nThe number of equivalent domino pairs of the input will be 4 * 3 / 2 = 6\n index index\npair 1 : 0 [1,2] and 1 [2,1]\npair 2 : 0 [1,2] and 2 [1,2]\npair 3 : 0 [1,2] and 3 [1,2]\npair 4 : 1 [2,1] and 0 [1,2]\npair 5 : 1 [2,1] and 2 [1,2]\npair 6 : 1 [2,1] and 3 [1,2]\npair 7 : 2 [1,2] and 0 [1,2]\npair 8 : 2 [1,2] and 1 [1,2]\npair 9 : 2 [1,2] and 3 [1,2]\npair 10 : 3 [1,2] and 0 [1,2]\npair 11 : 3 [1,2] and 1 [1,2]\npair 12 : 3 [1,2] and 2 [1,2]\n\napparently, \npair 1 (index 0, 1) and pair 4 (index 1,0) are considered the same pair. \npair 2 (index 0, 2) and pair 7 (index 2,0) are considered the same pair. \npair 3 (index 0, 3) and pair 10 (index 3,0) are considered the same pair. \npair 5 (index 1, 2) and pair 8 (index 2,1) are considered the same pair. \npair 6 (index 1, 3) and pair 11 (index 3,1) are considered the same pair. \npair 9 (index 2, 3) and pair 12 (index 3,2) are considered the same pair. \n\n\n \n```\n* Calculate how many pairs of Equivalent domino:\nFor each domino, the number of pairs = n*(n-1)//2, \nwhere n is the domino frequency.\nExplanation:\n\tFor the first domino in the pair, we have n options, \n\tFor the second domino in the pair, we have (n - 1) options. \n\tSince the order of domino in the pair doesn\'t matter, which means\n```\nPair 1 : [1,2],[2,1]\nPair 2 : [2,1],[1,2]\nare considered the same pair.\n```\nWe need to divide by 2 to eliminate the duplicate.\n```\nimport collections\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n # step 1: count the dominoes\n d = {}\n for domi in dominoes:\n p = tuple(sorted(domi))\n if p in d:\n d[p] += 1\n else:\n d[p] = 1\n # step 2: caculate the pairs. for each pair, number of pairs = n*(n-1)//2\n c = 0\n for n in d.values():\n s = n*(n-1)//2\n c += s\n return c\n```\n**Complexity Analysis**\n* Time complexity: O(n)\nDictionary takes O(1) to store. \nTo generate the dictionary takes n*O(1) and calculate pairs takes O(n), the total time complexity is O(n), where n is the length of the input list.\n* Space complexity: O(n)\nAt worst case (every item in the input list appeared once), the algorithm needs a dictionary which it\'s size equals the length of the list, where n is the length of the input list.\n | 23 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
[python3] dictionary count | number-of-equivalent-domino-pairs | 0 | 1 | * Use a dictionary to count how many times an intrinsic domino appeared. Here we define intrinsic domino as a sorted domino. By sort the list, we can easily identify the intrinsic domino. Use the intrinsic domino as key, the intrinsic domino frequency as value, store the information we need in a dictionary.\n```\nExample:\nindex 0 1 2 3\ninput = [[1,2],[2,1],[1,2],[1,2]]\nd = { [1,2] : 4}\nThe number of equivalent domino pairs of the input will be 4 * 3 / 2 = 6\n index index\npair 1 : 0 [1,2] and 1 [2,1]\npair 2 : 0 [1,2] and 2 [1,2]\npair 3 : 0 [1,2] and 3 [1,2]\npair 4 : 1 [2,1] and 0 [1,2]\npair 5 : 1 [2,1] and 2 [1,2]\npair 6 : 1 [2,1] and 3 [1,2]\npair 7 : 2 [1,2] and 0 [1,2]\npair 8 : 2 [1,2] and 1 [1,2]\npair 9 : 2 [1,2] and 3 [1,2]\npair 10 : 3 [1,2] and 0 [1,2]\npair 11 : 3 [1,2] and 1 [1,2]\npair 12 : 3 [1,2] and 2 [1,2]\n\napparently, \npair 1 (index 0, 1) and pair 4 (index 1,0) are considered the same pair. \npair 2 (index 0, 2) and pair 7 (index 2,0) are considered the same pair. \npair 3 (index 0, 3) and pair 10 (index 3,0) are considered the same pair. \npair 5 (index 1, 2) and pair 8 (index 2,1) are considered the same pair. \npair 6 (index 1, 3) and pair 11 (index 3,1) are considered the same pair. \npair 9 (index 2, 3) and pair 12 (index 3,2) are considered the same pair. \n\n\n \n```\n* Calculate how many pairs of Equivalent domino:\nFor each domino, the number of pairs = n*(n-1)//2, \nwhere n is the domino frequency.\nExplanation:\n\tFor the first domino in the pair, we have n options, \n\tFor the second domino in the pair, we have (n - 1) options. \n\tSince the order of domino in the pair doesn\'t matter, which means\n```\nPair 1 : [1,2],[2,1]\nPair 2 : [2,1],[1,2]\nare considered the same pair.\n```\nWe need to divide by 2 to eliminate the duplicate.\n```\nimport collections\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n # step 1: count the dominoes\n d = {}\n for domi in dominoes:\n p = tuple(sorted(domi))\n if p in d:\n d[p] += 1\n else:\n d[p] = 1\n # step 2: caculate the pairs. for each pair, number of pairs = n*(n-1)//2\n c = 0\n for n in d.values():\n s = n*(n-1)//2\n c += s\n return c\n```\n**Complexity Analysis**\n* Time complexity: O(n)\nDictionary takes O(1) to store. \nTo generate the dictionary takes n*O(1) and calculate pairs takes O(n), the total time complexity is O(n), where n is the length of the input list.\n* Space complexity: O(n)\nAt worst case (every item in the input list appeared once), the algorithm needs a dictionary which it\'s size equals the length of the list, where n is the length of the input list.\n | 23 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
dictionary!! | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n counter={}\n total=0\n for i in range(len(dominoes)):\n first=dominoes[i][0]\n second=dominoes[i][1]\n pair_sorted=(min(first, second), max(first, second))\n if pair_sorted in counter:\n total+=counter[pair_sorted]\n else:\n counter[pair_sorted]=0\n counter[pair_sorted]+=1\n return total\n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
dictionary!! | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n counter={}\n total=0\n for i in range(len(dominoes)):\n first=dominoes[i][0]\n second=dominoes[i][1]\n pair_sorted=(min(first, second), max(first, second))\n if pair_sorted in counter:\n total+=counter[pair_sorted]\n else:\n counter[pair_sorted]=0\n counter[pair_sorted]+=1\n return total\n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
number-of-equivalent-domino-pairs | number-of-equivalent-domino-pairs | 0 | 1 | # Code\n```\nclass Solution:\n def numEquivDominoPairs(self, t: List[List[int]]) -> int:\n d = {}\n for i in range(len(t)):\n a = tuple(sorted(t[i]))\n if a not in d:\n d[a] = 1\n else:\n d[a]+=1\n count = 0\n print(d)\n for i in d:\n if d[i]>1:\n count+= (d[i]*(d[i] - 1))//2\n return count\n\n \n\n \n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
number-of-equivalent-domino-pairs | number-of-equivalent-domino-pairs | 0 | 1 | # Code\n```\nclass Solution:\n def numEquivDominoPairs(self, t: List[List[int]]) -> int:\n d = {}\n for i in range(len(t)):\n a = tuple(sorted(t[i]))\n if a not in d:\n d[a] = 1\n else:\n d[a]+=1\n count = 0\n print(d)\n for i in d:\n if d[i]>1:\n count+= (d[i]*(d[i] - 1))//2\n return count\n\n \n\n \n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Python O(n) solution | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Using Dictionary\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n d = dict()\n count = 0\n for i in range(0, len(dominoes), 1):\n if (dominoes[i][0], dominoes[i][1]) in d:\n count += len(d[(dominoes[i][0], dominoes[i][1])])\n d[(dominoes[i][0], dominoes[i][1])].append(i)\n elif (dominoes[i][1], dominoes[i][0]) in d:\n count += len(d[(dominoes[i][1], dominoes[i][0])])\n d[(dominoes[i][1], dominoes[i][0])].append(i)\n else: \n d[(dominoes[i][0], dominoes[i][1])] = list()\n d[(dominoes[i][0], dominoes[i][1])].append(i)\n return count\n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
Python O(n) solution | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Using Dictionary\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n d = dict()\n count = 0\n for i in range(0, len(dominoes), 1):\n if (dominoes[i][0], dominoes[i][1]) in d:\n count += len(d[(dominoes[i][0], dominoes[i][1])])\n d[(dominoes[i][0], dominoes[i][1])].append(i)\n elif (dominoes[i][1], dominoes[i][0]) in d:\n count += len(d[(dominoes[i][1], dominoes[i][0])])\n d[(dominoes[i][1], dominoes[i][0])].append(i)\n else: \n d[(dominoes[i][0], dominoes[i][1])] = list()\n d[(dominoes[i][0], dominoes[i][1])].append(i)\n return count\n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Python Simple Solution Without using dictionary | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to compare two dominoes which can be either exactly equal or there are equal after rotating one of the domino.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst instead of checking for both exactly equal and equal after rotation, I have sorted all the dominoes so we can direclty check for the exact equality.\n\nAfter that I have sorted the whole dominoes list. \n\nI have run a loop to check the count of each domino and added to the ans as (count*count-1)//2, since we need count of pairs.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n count=0\n for i in range(0,len(dominoes)):\n dominoes[i].sort()\n dominoes.sort()\n k=0\n for i in range(0,len(dominoes)):\n if i>0:\n if dominoes[i]==dominoes[i-1]:\n continue\n else:\n count+=(i-k)*(i-k-1)//2\n k=i\n count+=(len(dominoes)-k)*(len(dominoes)-k-1)//2\n return count\n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
Python Simple Solution Without using dictionary | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to compare two dominoes which can be either exactly equal or there are equal after rotating one of the domino.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst instead of checking for both exactly equal and equal after rotation, I have sorted all the dominoes so we can direclty check for the exact equality.\n\nAfter that I have sorted the whole dominoes list. \n\nI have run a loop to check the count of each domino and added to the ans as (count*count-1)//2, since we need count of pairs.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n count=0\n for i in range(0,len(dominoes)):\n dominoes[i].sort()\n dominoes.sort()\n k=0\n for i in range(0,len(dominoes)):\n if i>0:\n if dominoes[i]==dominoes[i-1]:\n continue\n else:\n count+=(i-k)*(i-k-1)//2\n k=i\n count+=(len(dominoes)-k)*(len(dominoes)-k-1)//2\n return count\n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Python Simple Solution!! | number-of-equivalent-domino-pairs | 0 | 1 | \n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n \n occurrences: dict = {}\n count: int = 0\n \n for pair in dominoes:\n a, b = sorted(pair)\n occurrences[f"{a}{b}"] = occurrences.get(f"{a}{b}", 0) + 1\n\n for _, value in occurrences.items():\n count += value * (value - 1) // 2 \n return count\n \n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
Python Simple Solution!! | number-of-equivalent-domino-pairs | 0 | 1 | \n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n \n occurrences: dict = {}\n count: int = 0\n \n for pair in dominoes:\n a, b = sorted(pair)\n occurrences[f"{a}{b}"] = occurrences.get(f"{a}{b}", 0) + 1\n\n for _, value in occurrences.items():\n count += value * (value - 1) // 2 \n return count\n \n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Python solution | number-of-equivalent-domino-pairs | 0 | 1 | ```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n couples, pairs = {}, 0\n\n for couple in dominoes:\n couple = f"{sorted(couple)}"\n couples[couple] = couples.get(couple, 0) + 1\n \n for _, value in couples.items():\n pairs += value * (value - 1) // 2\n \n return pairs\n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
Python solution | number-of-equivalent-domino-pairs | 0 | 1 | ```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n couples, pairs = {}, 0\n\n for couple in dominoes:\n couple = f"{sorted(couple)}"\n couples[couple] = couples.get(couple, 0) + 1\n \n for _, value in couples.items():\n pairs += value * (value - 1) // 2\n \n return pairs\n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Python3: find the number of combinations for each pair. T/M 90/59 | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nFirst, we need to count the number of equal dominoes, where n is the number of dominoes. \nSecond, we need to find the number of combinations 2 from n for each pair and sum them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor the firt step, I used this line to ensure that dominoes [x, y] and [y, x] are count as equal:`count[(min(a, b), max(a, b))] += 1`\nI saw that other folks used `tuple(sorted(x, y))`. Not sure which approach is better, would be happy to discuss. \n\nFor the second step we need to find the number of combinations for each pair and sum them. The [common formula](https://en.wikipedia.org/wiki/Combination) for k combinations from n is n! / ((n - k)! * k!). As we need the number of pairs, k = 2. So, we can simplify n * (n - 1) / 2. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n # find the number of pairs\n count = defaultdict(int)\n for a, b in dominoes:\n count[(min(a, b), max(a, b))] += 1\n\n # calculate total sum of the combinations\n return sum(n * (n - 1) // 2 for n in count.values())\n \n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
Python3: find the number of combinations for each pair. T/M 90/59 | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nFirst, we need to count the number of equal dominoes, where n is the number of dominoes. \nSecond, we need to find the number of combinations 2 from n for each pair and sum them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor the firt step, I used this line to ensure that dominoes [x, y] and [y, x] are count as equal:`count[(min(a, b), max(a, b))] += 1`\nI saw that other folks used `tuple(sorted(x, y))`. Not sure which approach is better, would be happy to discuss. \n\nFor the second step we need to find the number of combinations for each pair and sum them. The [common formula](https://en.wikipedia.org/wiki/Combination) for k combinations from n is n! / ((n - k)! * k!). As we need the number of pairs, k = 2. So, we can simplify n * (n - 1) / 2. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n # find the number of pairs\n count = defaultdict(int)\n for a, b in dominoes:\n count[(min(a, b), max(a, b))] += 1\n\n # calculate total sum of the combinations\n return sum(n * (n - 1) // 2 for n in count.values())\n \n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Python solution: O(n) time and space | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst let\'s try to find out how many equal pairs we have, knowing that (a, b) == (b, a). Then for each count, see how many indices i<j we need to add to the final solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a dictionary using the ordered pairs (a,b) a<b as keys and count how many equal pairs we have. \n\nThen for each count, compute how many different pairs we can form, that is, the combinations (count, 2). The result is the answer we are looing for.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nfrom collections import defaultdict\nfrom math import comb\n\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n dp = defaultdict(int)\n for a, b in dominoes:\n # order the pairs, as (a,b) == (b,a)\n a, b = (a, b) if a < b else (b, a)\n dp[(a,b)] += 1\n pairs = 0\n for p in dp.values():\n # note: comb(1,2) == 0\n pairs += comb(p, 2)\n return pairs\n \n``` | 0 | Given a list of `dominoes`, `dominoes[i] = [a, b]` is **equivalent to** `dominoes[j] = [c, d]` if and only if either (`a == c` and `b == d`), or (`a == d` and `b == c`) - that is, one domino can be rotated to be equal to another domino.
Return _the number of pairs_ `(i, j)` _for which_ `0 <= i < j < dominoes.length`_, and_ `dominoes[i]` _is **equivalent to**_ `dominoes[j]`.
**Example 1:**
**Input:** dominoes = \[\[1,2\],\[2,1\],\[3,4\],\[5,6\]\]
**Output:** 1
**Example 2:**
**Input:** dominoes = \[\[1,2\],\[1,2\],\[1,1\],\[1,2\],\[2,2\]\]
**Output:** 3
**Constraints:**
* `1 <= dominoes.length <= 4 * 104`
* `dominoes[i].length == 2`
* `1 <= dominoes[i][j] <= 9` | Use a stack to process everything greedily. |
Python solution: O(n) time and space | number-of-equivalent-domino-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst let\'s try to find out how many equal pairs we have, knowing that (a, b) == (b, a). Then for each count, see how many indices i<j we need to add to the final solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a dictionary using the ordered pairs (a,b) a<b as keys and count how many equal pairs we have. \n\nThen for each count, compute how many different pairs we can form, that is, the combinations (count, 2). The result is the answer we are looing for.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nfrom collections import defaultdict\nfrom math import comb\n\nclass Solution:\n def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:\n dp = defaultdict(int)\n for a, b in dominoes:\n # order the pairs, as (a,b) == (b,a)\n a, b = (a, b) if a < b else (b, a)\n dp[(a,b)] += 1\n pairs = 0\n for p in dp.values():\n # note: comb(1,2) == 0\n pairs += comb(p, 2)\n return pairs\n \n``` | 0 | `n` passengers board an airplane with exactly `n` seats. The first passenger has lost the ticket and picks a seat randomly. But after that, the rest of the passengers will:
* Take their own seat if it is still available, and
* Pick other seats randomly when they find their seat occupied
Return _the probability that the_ `nth` _person gets his own seat_.
**Example 1:**
**Input:** n = 1
**Output:** 1.00000
**Explanation:** The first person can only get the first seat.
**Example 2:**
**Input:** n = 2
**Output:** 0.50000
**Explanation:** The second person has a probability of 0.5 to get the second seat (when first person gets the first seat).
**Constraints:**
* `1 <= n <= 105` | For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent. You can keep track of what you've seen using a hashmap. |
Using BFS Alternating Path Length | shortest-path-with-alternating-colors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thoughts on solving this problem are to use a breadth-first search approach where we explore all the neighbors of each node. We need to keep track of the distances from node 0, alternating between red and blue distances. We also need to keep track of which nodes we have already visited to avoid visiting the same node multiple times. The result will be an array of the minimum alternating distances from node 0 to every other node in the graph, or -1 if such a path doesn\'t exist.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach I would take to solve this problem is to use a breadth-first search (BFS) algorithm. BFS is a good choice because it ensures that we visit all nodes at the same distance from node 0 before visiting nodes at a greater distance. This way, we can find the shortest distance from node 0 to every other node in the graph.\n\nIn this solution, we will keep two distances for each node: the distance from node 0 using only red edges, and the distance from node 0 using only blue edges. We will start with node 0 having a red distance of 0 and all other nodes having a red distance of -1.\n\nWe will use two queues to keep track of the nodes to visit: one for nodes that we can reach using only red edges, and one for nodes that we can reach using only blue edges. We will start with node 0 in the red queue.\n\nIn each iteration of the algorithm, we will check which of the two queues has nodes and process the nodes in that queue. If the red queue has nodes, we will update the blue distances of the neighboring nodes using the blue edges and add them to the blue queue. If the blue queue has nodes, we will update the red distances of the neighboring nodes using the red edges and add them to the red queue. This process continues until both queues are empty.\n\nFinally, for each node, we will find the minimum of its red and blue distances, and set the result for that node to be the minimum if both distances are not -1, or the maximum of the two distances if one of them is -1. This will give us the shortest alternating distance from node 0 to each node in the graph, or -1 if such a path doesn\'t exist.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(N + R + B), meaning it takes time proportional to the number of nodes, red edges, and blue edges in the graph. As the size of the graph increases, the amount of time required to find the shortest alternating distances from node 0 to all other nodes will also increase, but not faster than a linear rate. This is because we process one node from either the red queue or the blue queue per iteration, and add at most one node to each queue, with a total of N iterations.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this solution is O(N + R + B). This means it grows linearly with the size of the graph, using memory proportional to the number of nodes, red edges, and blue edges. This is due to the need for two arrays for distances, and two queues for processing the red and blue edges, which can each contain up to N nodes.\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n red_graph = {i: [] for i in range(n)}\n blue_graph = {i: [] for i in range(n)}\n\n for a,b in redEdges:\n red_graph[a].append(b)\n \n for u,v in blueEdges:\n blue_graph[u].append(v)\n \n red_dist = [-1] * n\n blue_dist = [-1] * n\n\n red_dist[0] = 0\n blue_dist[0] = 0\n\n red_queue = deque([0])\n blue_queue = deque([0])\n\n while red_queue or blue_queue:\n if red_queue:\n node = red_queue.popleft()\n for neighbor in blue_graph[node]:\n if blue_dist[neighbor] == -1:\n blue_dist[neighbor] = red_dist[node] + 1\n blue_queue.append(neighbor)\n if blue_queue:\n node = blue_queue.popleft()\n for neighbor in red_graph[node]:\n if red_dist[neighbor] == -1:\n red_dist[neighbor] = blue_dist[node] + 1\n red_queue.append(neighbor)\n \n result = [0] * n\n for i in range(n):\n if red_dist[i] == -1 or blue_dist[i] == -1:\n result[i] = max(red_dist[i], blue_dist[i])\n else:\n result[i] = min(red_dist[i], blue_dist[i])\n return result\n``` | 2 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
python bfs beats 95% | shortest-path-with-alternating-colors | 0 | 1 | - Use a hashmap to store all the edges and their colours\n- NO edge is travelled twice: during bfs, for each edge travelled, add the edge to a set\n- Only proceed with bfs for an edge if the colour it took to reach the current node, is different from the colour of the edge\n\n\n```\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n hm, seen, edges = collections.defaultdict(list), collections.defaultdict(int), set()\n for f, t in redEdges: hm[f].append(tuple([t, 0]))\n for f, t in blueEdges: hm[f].append(tuple([t, 1]))\n ans = [0]\n q = deque()\n q.append([0, -1, 0])\n while q:\n node, prev_colour, prev_dist = q.popleft()\n if node not in seen: seen[node] = prev_dist\n else:\n if prev_dist < seen[node]: seen[node] = prev_dist\n for next_node, next_colour in hm[node]:\n if prev_colour!=next_colour and (node, next_node, next_colour) not in edges:\n q.append([next_node, next_colour, prev_dist+1])\n edges.add((node, next_node, next_colour))\n for i in range(1, n):\n if i not in seen: ans.append(-1)\n else: ans.append(seen[i])\n return ans\n \n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
🗓️ Daily LeetCoding Challenge February, Day 11 [BFS SOLUTION] | shortest-path-with-alternating-colors | 1 | 1 | # Intuition \nuse BFS traversal with mindset of traversing..starting in two ways possible [RED&BLUE] . for that take a queue in which first element represents NODE and second represents COLOR. add into the queue with both red and blue. if started with RED , next we have to find BLUE one. vice-versa RED.\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ntraverse other elements starting with 1 and if any edge present as opposite of color that we current have then mark it as visited in visited set and calculate the length also "that how many steps that we have move"[level] and take the MINIMUM one. \nin the end check if any value in res array is INTEGER.MAX if it is that means we can\'t find a path to that node from 0.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] shortestAlternatingPaths(int n, int[][] redEdges, int[][] blueEdges) {\n int[][] g=new int[n][n];\n buildGraph(g,n,redEdges,blueEdges);\n Queue<int[]>q=new LinkedList<>();\n q.offer(new int[]{0,1});\n q.offer(new int[]{0,-1});\n int len=0;\n int[] res=new int[n];\n Arrays.fill(res,Integer.MAX_VALUE);\n res[0]=0;\n Set<String>visited=new HashSet<>();\n while(!q.isEmpty()){\n int qSize=q.size();\n len++;\n while(qSize-->0){\n int[] cur=q.poll();\n int node=cur[0];\n int color=cur[1];\n int oppoColor=-color;\n for(int j=1;j<n;j++){\n if(g[node][j]==oppoColor || g[node][j]==0){\n if(!visited.add(j+"visited with"+oppoColor)){\n continue;\n }\n q.offer(new int[]{j,oppoColor});\n res[j]=Math.min(res[j],len);\n }\n }\n }\n }\n for(int i=1;i<n;i++){\n if(res[i]==Integer.MAX_VALUE){\n res[i]=-1;\n }\n }\n return res;\n }\n private void buildGraph(int[][] g,int n, int[][] redEdges,int[][] blueEdges){\n for(int i=0;i<n;i++){\n Arrays.fill(g[i],-n);\n }\n for(int[] e:redEdges){\n int from=e[0];\n int to=e[1];\n g[from][to]=1;\n }\n for(int[] e:blueEdges){\n int from=e[0];\n int to=e[1];\n if(g[from][to]==1){\n g[from][to]=0;\n }else{\n g[from][to]=-1;\n }\n }\n }\n}\n```\n\n\n\n\n\n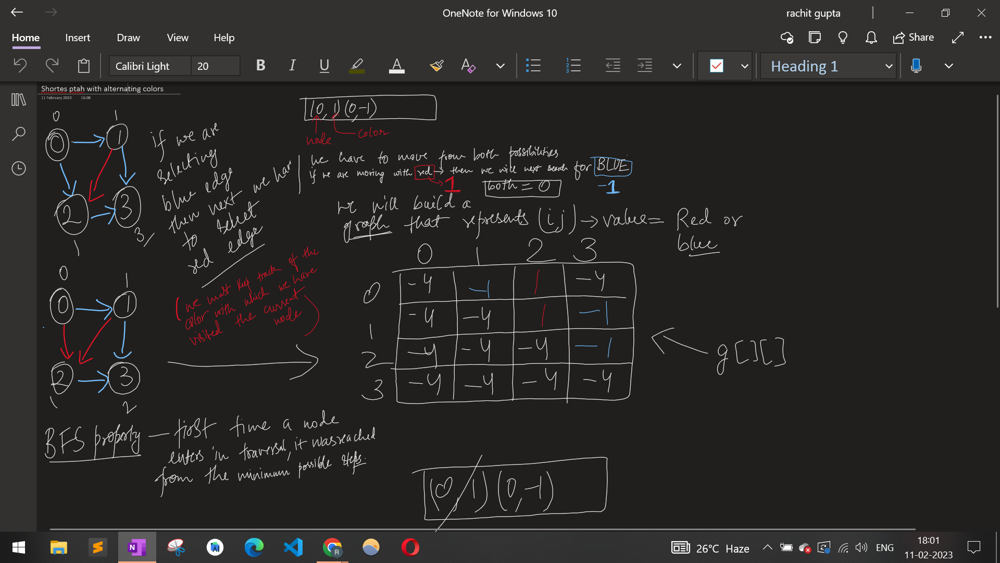\n\n\n# **PELASE UPVOTE ** if this finds useful for you ...\n\n\n\n\n | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
Python BFS solution | shortest-path-with-alternating-colors | 0 | 1 | ```\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n red = defaultdict(list)\n blue = defaultdict(list)\n for s, d in redEdges:\n red[s].append(d)\n for s, d in blueEdges:\n blue[s].append(d)\n c_map = [red, blue]\n\n bfs = []\n visited = set()\n if 0 in red:\n bfs.append((0,1,0))\n visited.add((1,0))\n if 0 in blue:\n bfs.append((0,0,0))\n visited.add((0,0))\n\n result = defaultdict(int)\n result[0] = 0\n while bfs:\n dist, color, node = bfs.pop(0)\n if node not in result: result[node] = dist\n next_color = int(not color)\n for next_node in c_map[next_color][node]:\n next_entry = (dist+1, next_color, next_node)\n visited_entry = (next_color, next_node)\n if visited_entry in visited: continue\n visited.add(visited_entry)\n bfs.append(next_entry)\n return [result[i] if i in result else -1 for i in range(n)]\n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
EASY PYTHON SOLUTION || BFS APPROACH | shortest-path-with-alternating-colors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N*K)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N*K)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n lst=[-1]*n\n grid=[[] for i in range(n)]\n vr=[-1]*n\n vb=[-1]*n\n for i,j in redEdges:\n grid[i].append((j,True))\n \n for i,j in blueEdges:\n grid[i].append((j,False))\n\n queue=[(0,0,True),(0,0,False)]\n vb[0]=1\n vr[0]=1\n while queue:\n d,x,flg=queue.pop(0)\n if lst[x]==-1:\n lst[x]=d\n for to,fg2 in grid[x]:\n if flg!=fg2:\n if (fg2==False and vb[to]==-1):\n queue.append((d+1,to,fg2))\n vb[to]=1\n elif (fg2==True and vr[to]==-1):\n queue.append((d+1,to,fg2))\n vr[to]=1\n return lst\n \n\n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
python - clean BFS - 90% | shortest-path-with-alternating-colors | 0 | 1 | \n# Code\n```\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n connections = defaultdict(list)\n for a, b in redEdges:\n connections[a].append((b, \'red\'))\n for a, b in blueEdges:\n connections[a].append((b, \'blue\'))\n\n distances = [math.inf] * n\n queue = deque([(0, \'red\', 0), (0, \'blue\', 0)])\n visited = set()\n while queue:\n node, color, level = queue.popleft()\n\n if (node, color) in visited:\n continue\n visited.add((node, color))\n\n distances[node] = min(distances[node], level)\n\n for next_node, next_color in connections[node]:\n if next_color != color:\n queue.append((next_node, next_color, level + 1))\n\n return [-1 if x == math.inf else x for x in distances]\n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
Python short and clean. BFS | shortest-path-with-alternating-colors | 0 | 1 | # Approach\nExtend the classic `BFS` from `source` node to all nodes into `(source, color)` to all nodes, making sure to `flip` colors on each step. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def shortestAlternatingPaths(self, n: int, red_edges: list[list[int]], blue_edges: list[list[int]]) -> list[int]:\n RED, BLUE = -1, +1\n flip = lambda color: -color # Flips color between RED and BLUE\n\n # Types declaration\n Color = RED | BLUE\n Node = int\n RedNodes = dict[RED , list[Node]]\n BlueNodes = dict[BLUE, list[Node]]\n ColoredGraph = dict[Node, tuple[RedNodes, BlueNodes]]\n Distances = dict[Node, int]\n\n def shortest_dist(graph: ColoredGraph, src: Node) -> Distances:\n """Finds shortest dist from src to all other nodes"""\n queue = deque(((src, RED, 0), (src, BLUE, 0))) # (source node, previous edge color, distance)\n seen = {(src, RED), (src, BLUE)}\n dists = {i: inf for i in graph}; dists[0] = 0\n\n while queue:\n node, prev_color, dist = queue.popleft()\n next_color = flip(prev_color)\n\n for nbr in filter(lambda nbr: (nbr, next_color) not in seen, graph[node][next_color]):\n queue.append((nbr, next_color, dist + 1))\n seen.add((nbr, next_color))\n dists[nbr] = min(dists[nbr], dist + 1)\n \n return dists\n \n g: ColoredGraph = {i: {RED: [], BLUE: []} for i in range(n)}\n for u, v in red_edges: g[u][RED].append(v)\n for u, v in blue_edges: g[u][BLUE].append(v)\n\n dists: Distances = shortest_dist(g, 0)\n return [-1 if dists[i] == inf else dists[i] for i in range(n)]\n\n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
[Python] Simple BFS and tracking visited color; Explained | shortest-path-with-alternating-colors | 0 | 1 | This is a simple BFS problem with a speical handling of picking different path color in each step.\n\nStep 1: Build two graphs based on the edge color;\nStep 2: BFS traverse each node, and check the steps for each node. We update the path length when we found a shorter path.\n\nTwo things we need to handle in this special problem:\n(1) we need to track both the node and the edge color we have visited. This is because we can visite the same node with different edge color\n(2) we run BFS twice as we can start with different colors\n\n\n```\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n # BFS to search the shortest path from 0 to other nodes\n self.G = []\n for i in [0, 1]:\n self.G.append(collections.defaultdict(set))\n \n for e0, e1 in redEdges:\n self.G[0][e0].add(e1)\n \n for e0, e1 in blueEdges:\n self.G[1][e0].add(e1)\n \n ans = [-1] * n\n visited = set()\n queue = collections.deque([(0, 0, 0)])\n # loop 1 start from a red edge\n while queue:\n node, color, step = queue.popleft()\n if (ans[node] == -1) or (ans[node] > step):\n ans[node] = step\n \n visited.add((node, color))\n next_color = (color + 1) % 2\n for nn in self.G[next_color][node]:\n if (nn, next_color) not in visited:\n queue.append((nn, next_color, step + 1))\n \n # loop 2 start from a blue edge\n visited = set()\n queue = collections.deque([(0, 1, 0)])\n while queue:\n node, color, step = queue.popleft()\n if (ans[node] == -1) or (ans[node] > step):\n ans[node] = step\n \n visited.add((node, color))\n next_color = (color + 1) % 2\n for nn in self.G[next_color][node]:\n if (nn, next_color) not in visited:\n queue.append((nn, next_color, step + 1))\n \n return ans\n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
simple & easy bfs solution in python | shortest-path-with-alternating-colors | 0 | 1 | \n# Code\n```\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n # Adjacent creation\n adj = [list() for _ in range(n)]\n\n for red_edge in redEdges:\n adj[red_edge[0]].append((red_edge[1], 0))\n\n for blue_edge in blueEdges:\n adj[blue_edge[0]].append((blue_edge[1], 1))\n\n # Initialization\n ans = [-1] * n\n visited = [[False, False] for _ in range(n)]\n queue = [(0, 0, -1)]\n ans[0] = 0\n\n # BFS\n while queue:\n node, dist, prev_color = queue.pop(0)\n\n for neighbor, col in adj[node]:\n if not visited[neighbor][col] and col != prev_color:\n visited[neighbor][col] = True\n queue.append((neighbor, dist + 1, col))\n if ans[neighbor] == -1:\n ans[neighbor] = dist + 1\n return ans\n``` | 3 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
Python || Breadth-First Search 🔥 | shortest-path-with-alternating-colors | 0 | 1 | # Code\n```\nclass Solution:\n def shortestAlternatingPaths(self, n, red_edges, blue_edges):\n graph = [[[], []] for i in range(n)]\n for i, j in red_edges:\n graph[i][0].append(j)\n for i, j in blue_edges:\n graph[i][1].append(j)\n ans = [[0, 0]] + [[n * 2, n * 2] for i in range(n - 1)]\n search = [[0, 0], [0,1]]\n for i, c in search:\n for j in graph[i][c]:\n if ans[j][c] == n * 2:\n ans[j][c] = ans[i][1 - c] + 1\n search.append([j, 1 - c])\n nums = []\n for x in map(min, ans):\n if x < n * 2:\n nums.append(x)\n else:\n nums.append(-1)\n return nums\n``` | 1 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
7ms (Beats 99.99%)🔥🔥|| Full Explanation✅|| Breadth First Search✅|| C++|| Java|| Python3 | shortest-path-with-alternating-colors | 1 | 1 | # Intuition :\n- Here we are given a graph with two types of edges (red and blue), the goal is to find the shortest path from node 0 to every other node such that no two consecutive edges have the same color.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Explanation to Approach :\n- So we are using a breadth-first search (BFS) algorithm to traverse the graph, keeping track of the distance from node 0 to every other node and the previous edge color. \n- The graph is represented as an adjacency list, where graph[u] is a list of pairs (v, edgeColor) representing an edge from node u to node v with color edgeColor.\n- The BFS algorithm starts from node 0 and adds node v to the queue if it is not visited yet or if the color of the edge from u to v is different from the previous edge color. \n- The distance from node 0 to node v is incremented in each step. \n- The ans array is updated with the minimum distance found so far to each node. If a node is visited again, its distance in ans is not updated.\n- The algorithm terminates when the queue is empty, meaning that all reachable nodes have been visited. \n- If a node is not visited, its distance in ans remains -1, indicating that it is not reachable from node 0.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity :\n- Time complexity : O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] with Comments :\n```C++ []\nenum class Color { kInit, kRed, kBlue };\n\nclass Solution {\n public:\n vector<int> shortestAlternatingPaths(int n, vector<vector<int>>& redEdges,\n vector<vector<int>>& blueEdges) {\n vector<int> ans(n, -1);\n vector<vector<pair<int, Color>>> graph(n); // graph[u] := [(v, edgeColor)]\n queue<pair<int, Color>> q{{{0, Color::kInit}}}; // [(u, prevColor)]\n\n for (const vector<int>& edge : redEdges) {\n const int u = edge[0];\n const int v = edge[1];\n graph[u].emplace_back(v, Color::kRed);\n }\n\n for (const vector<int>& edge : blueEdges) {\n const int u = edge[0];\n const int v = edge[1];\n graph[u].emplace_back(v, Color::kBlue);\n }\n\n for (int step = 0; !q.empty(); ++step)\n for (int sz = q.size(); sz > 0; --sz) {\n const auto [u, prevColor] = q.front();\n q.pop();\n ans[u] = ans[u] == -1 ? step : ans[u];\n for (auto& [v, edgeColor] : graph[u]) {\n if (v == -1 || edgeColor == prevColor)\n continue;\n q.emplace(v, edgeColor);\n v = -1; // Mark (u, v) as used.\n }\n }\n\n return ans;\n }\n};\n```\n```Java []\nenum Color { kInit, kRed, kBlue }\n\nclass Solution {\n public int[] shortestAlternatingPaths(int n, int[][] redEdges, int[][] blueEdges) {\n int[] ans = new int[n];\n Arrays.fill(ans, -1);\n // graph[u] := [(v, edgeColor)]\n List<Pair<Integer, Color>>[] graph = new List[n];\n // [(u, prevColor)]\n Queue<Pair<Integer, Color>> q = new ArrayDeque<>(Arrays.asList(new Pair<>(0, Color.kInit)));\n\n for (int i = 0; i < n; ++i)\n graph[i] = new ArrayList<>();\n\n for (int[] edge : redEdges) {\n final int u = edge[0];\n final int v = edge[1];\n graph[u].add(new Pair<>(v, Color.kRed));\n }\n\n for (int[] edge : blueEdges) {\n final int u = edge[0];\n final int v = edge[1];\n graph[u].add(new Pair<>(v, Color.kBlue));\n }\n\n for (int step = 0; !q.isEmpty(); ++step)\n for (int sz = q.size(); sz > 0; --sz) {\n final int u = q.peek().getKey();\n Color prevColor = q.poll().getValue();\n ans[u] = ans[u] == -1 ? step : ans[u];\n for (int i = 0; i < graph[u].size(); ++i) {\n Pair<Integer, Color> node = graph[u].get(i);\n final int v = node.getKey();\n Color edgeColor = node.getValue();\n if (v == -1 || edgeColor == prevColor)\n continue;\n q.add(new Pair<>(v, edgeColor));\n // Mark (u, v) as used.\n graph[u].set(i, new Pair<>(-1, edgeColor));\n }\n }\n\n return ans;\n }\n}\n```\n```Python3 []\nfrom enum import Enum\n\nclass Color(Enum):\n kInit = 0\n kRed = 1\n kBlue = 2\n\nclass Solution:\n def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:\n ans = [-1] * n\n graph = [[] for _ in range(n)] # graph[u] := [(v, edgeColor)]\n q = collections.deque([(0, Color.kInit)]) # [(u, prevColor)]\n\n for u, v in redEdges:\n graph[u].append((v, Color.kRed))\n\n for u, v in blueEdges:\n graph[u].append((v, Color.kBlue))\n\n step = 0\n while q:\n for _ in range(len(q)):\n u, prevColor = q.popleft()\n if ans[u] == -1:\n ans[u] = step\n for i, (v, edgeColor) in enumerate(graph[u]):\n if v == -1 or edgeColor == prevColor:\n continue\n q.append((v, edgeColor))\n graph[u][i] = (-1, edgeColor) # Mark (u, v) as used.\n step += 1\n\n return ans\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n | 66 | You are given an integer `n`, the number of nodes in a directed graph where the nodes are labeled from `0` to `n - 1`. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.
You are given two arrays `redEdges` and `blueEdges` where:
* `redEdges[i] = [ai, bi]` indicates that there is a directed red edge from node `ai` to node `bi` in the graph, and
* `blueEdges[j] = [uj, vj]` indicates that there is a directed blue edge from node `uj` to node `vj` in the graph.
Return an array `answer` of length `n`, where each `answer[x]` is the length of the shortest path from node `0` to node `x` such that the edge colors alternate along the path, or `-1` if such a path does not exist.
**Example 1:**
**Input:** n = 3, redEdges = \[\[0,1\],\[1,2\]\], blueEdges = \[\]
**Output:** \[0,1,-1\]
**Example 2:**
**Input:** n = 3, redEdges = \[\[0,1\]\], blueEdges = \[\[2,1\]\]
**Output:** \[0,1,-1\]
**Constraints:**
* `1 <= n <= 100`
* `0 <= redEdges.length, blueEdges.length <= 400`
* `redEdges[i].length == blueEdges[j].length == 2`
* `0 <= ai, bi, uj, vj < n` | Instead of adding a character, try deleting a character to form a chain in reverse. For each word in order of length, for each word2 which is word with one character removed, length[word2] = max(length[word2], length[word] + 1). |
Simple DP Solution | Easy - To - Understand 🚀🚀 | minimum-cost-tree-from-leaf-values | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n int mctFromLeafValuesRec(vector<int>& arr,map<pair<int,int>,int>& maxi,int left,int right)\n {\n // Base Case -- Leaf Node\n if(left == right)\n return 0;\n \n int ans = INT_MAX;\n for(int i = left; i < right; i++)\n {\n ans = min(ans, maxi[{left,i}] * maxi[{i+1,right}] + mctFromLeafValuesRec(arr,maxi,left,i) + mctFromLeafValuesRec(arr,maxi,i+1,right));\n }\n\n return ans;\n }\n\n // TC - O(N*3) and SC - O(N*2)\n int mctFromLeafValuesMem(vector<int>& arr,map<pair<int,int>,int>& maxi,int left,int right,vector<vector<int>>& dp)\n {\n // Base Case -- Leaf Node\n if(left == right)\n return 0;\n if(dp[left][right] != -1)\n return dp[left][right];\n \n int ans = INT_MAX;\n for(int i = left; i < right; i++)\n {\n ans = min(ans, maxi[{left,i}] * maxi[{i+1,right}] + mctFromLeafValuesMem(arr,maxi,left,i,dp) + mctFromLeafValuesMem(arr,maxi,i+1,right,dp));\n }\n\n dp[left][right] = ans;\n return dp[left][right];\n }\n\n // TC - O(N*3) and SC - O(N*2)\n int mctFromLeafValuesTab(vector<int>& arr,map<pair<int,int>,int>& maxi)\n {\n int n = arr.size();\n vector<vector<int>> dp(n+1,vector<int>(n+1,0));\n\n for(int left = n - 1; left >= 0; left--)\n {\n for(int right = 0; right <= n - 1; right++)\n {\n // Invalid Range\n if(left >= right)\n continue;\n \n int ans = INT_MAX;\n for(int i = left; i < right; i++)\n {\n ans = min(ans, maxi[{left,i}] * maxi[{i+1,right}] + dp[left][i] + dp[i+1][right]);\n }\n\n dp[left][right] = ans;\n }\n }\n return dp[0][n-1];\n }\n\n int mctFromLeafValues(vector<int>& arr) {\n map<pair<int,int>,int> maxi;\n int n = arr.size();\n\n for(int i = 0; i < n; i++)\n {\n maxi[{i,i}] = arr[i];\n for(int j = i + 1; j < n; j++)\n {\n maxi[{i,j}] = max(arr[j],maxi[{i,j-1}]);\n }\n }\n\n // 1. Recursion\n // return mctFromLeafValuesRec(arr,maxi,0,n-1);\n\n // 2. Top Down Approach\n // vector<vector<int>> dp(n+1,vector<int>(n+1,-1));\n // return mctFromLeafValuesMem(arr,maxi,0,n-1,dp);\n\n // 3. Bottom Up Approach\n return mctFromLeafValuesTab(arr,maxi);\n }\n};\n``` | 2 | Given an array `arr` of positive integers, consider all binary trees such that:
* Each node has either `0` or `2` children;
* The values of `arr` correspond to the values of each **leaf** in an in-order traversal of the tree.
* The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return _the smallest possible sum of the values of each non-leaf node_. It is guaranteed this sum fits into a **32-bit** integer.
A node is a **leaf** if and only if it has zero children.
**Example 1:**
**Input:** arr = \[6,2,4\]
**Output:** 32
**Explanation:** There are two possible trees shown.
The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
**Example 2:**
**Input:** arr = \[4,11\]
**Output:** 44
**Constraints:**
* `2 <= arr.length <= 40`
* `1 <= arr[i] <= 15`
* It is guaranteed that the answer fits into a **32-bit** signed integer (i.e., it is less than 231). | Think of the final answer as a sum of weights with + or - sign symbols infront of each weight. Actually, all sums with 1 of each sign symbol are possible. Use dynamic programming: for every possible sum with N stones, those sums +x or -x is possible with N+1 stones, where x is the value of the newest stone. (This overcounts sums that are all positive or all negative, but those don't matter.) |
[RZ] Summary of all the solutions I have learned from Discuss in Python | minimum-cost-tree-from-leaf-values | 0 | 1 | **1. Dynamic programming approach**\nWe are given a list of all the leaf nodes values for certain binary trees, but we do not know which leaf nodes belong to left subtree and which leaf nodes belong to right subtree. Since the given leaf nodes are result of inorder traversal, we know there will be pivots that divide arr into left and right, nodes in the left build left subtree and nodes in the right build right subtree. For each subtree, if we know the minimum sum, we can use it to build the result of the parent tree, so the problem can be divided into subproblems, and we have the following general transition equation (res(i, j) means the minimum non-leaf nodes sum with leaf nodes from arr[i] to arr[j]):\n\n```\nfor k from i to j\n res(i, j) = min(res(i, k) + res(k + 1, j) + max(arr[i] ... arr[k]) * max(arr[k + 1] ... arr[j]))\n```\n\n**Top down code with memorization ---> O(n ^ 3)**\n```\nclass Solution:\n def mctFromLeafValues(self, arr: List[int]) -> int:\n return self.helper(arr, 0, len(arr) - 1, {})\n \n def helper(self, arr, l, r, cache):\n if (l, r) in cache:\n return cache[(l, r)]\n if l >= r:\n return 0\n \n res = float(\'inf\')\n for i in range(l, r):\n rootVal = max(arr[l:i+1]) * max(arr[i+1:r+1])\n res = min(res, rootVal + self.helper(arr, l, i, cache) + self.helper(arr, i + 1, r, cache))\n \n cache[(l, r)] = res\n return res\n```\n\n**Bottom up code ---> O(n ^ 3)**\n```\nclass Solution:\n def mctFromLeafValues(self, arr: List[int]) -> int:\n n = len(arr)\n dp = [[float(\'inf\') for _ in range(n)] for _ in range(n)]\n for i in range(n):\n dp[i][i] = 0\n \n for l in range(2, n + 1):\n for i in range(n - l + 1):\n j = i + l - 1\n for k in range(i, j):\n rootVal = max(arr[i:k+1]) * max(arr[k+1:j+1])\n dp[i][j] = min(dp[i][j], rootVal + dp[i][k] + dp[k + 1][j])\n return dp[0][n - 1]\n```\n\n**2. Greedy approach ---> O(n ^ 2)**\nAbove approach is kind of like brute force since we calculate and compare the results all possible pivots. To achieve a better time complexity, one important observation is that when we build each level of the binary tree, it is the max left leaf node and max right lead node that are being used, so we would like to put big leaf nodes close to the root. Otherwise, taking the leaf node with max value in the array as an example, if its level is deep, for each level above it, its value will be used to calculate the non-leaf node value, which will result in a big total sum.\n\nWith above observation, the greedy approach is to find the smallest value in the array, use it and its smaller neighbor to build a non-leaf node, then we can safely delete it from the array since it has a smaller value than its neightbor so it will never be used again. Repeat this process until there is only one node left in the array (which means we cannot build a new level any more)\n\n```\nclass Solution:\n def mctFromLeafValues(self, arr: List[int]) -> int:\n res = 0\n while len(arr) > 1:\n index = arr.index(min(arr))\n if 0 < index < len(arr) - 1:\n res += arr[index] * min(arr[index - 1], arr[index + 1])\n else:\n res += arr[index] * (arr[index + 1] if index == 0 else arr[index - 1])\n arr.pop(index)\n return res\n```\n\n**3. Monotonic stack approach ---> O(n)**\nIn the greedy approach of 2), every time we delete the current minimum value, we need to start over and find the next smallest value again, so repeated operations are more or less involved. To further accelerate it, one observation is that for each leaf node in the array, when it becomes the minimum value in the remaining array, its left and right neighbors will be the first bigger value in the original array to its left and right. This observation is a clue of a possible monotonic stack solution as follows.\n\n```\nclass Solution:\n def mctFromLeafValues(self, arr: List[int]) -> int:\n stack = [float(\'inf\')]\n res = 0\n for num in arr:\n while stack and stack[-1] <= num:\n cur = stack.pop()\n if stack:\n res += cur * min(stack[-1], num)\n stack.append(num)\n while len(stack) > 2:\n res += stack.pop() * stack[-1]\n return res\n``` | 440 | Given an array `arr` of positive integers, consider all binary trees such that:
* Each node has either `0` or `2` children;
* The values of `arr` correspond to the values of each **leaf** in an in-order traversal of the tree.
* The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return _the smallest possible sum of the values of each non-leaf node_. It is guaranteed this sum fits into a **32-bit** integer.
A node is a **leaf** if and only if it has zero children.
**Example 1:**
**Input:** arr = \[6,2,4\]
**Output:** 32
**Explanation:** There are two possible trees shown.
The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
**Example 2:**
**Input:** arr = \[4,11\]
**Output:** 44
**Constraints:**
* `2 <= arr.length <= 40`
* `1 <= arr[i] <= 15`
* It is guaranteed that the answer fits into a **32-bit** signed integer (i.e., it is less than 231). | Think of the final answer as a sum of weights with + or - sign symbols infront of each weight. Actually, all sums with 1 of each sign symbol are possible. Use dynamic programming: for every possible sum with N stones, those sums +x or -x is possible with N+1 stones, where x is the value of the newest stone. (This overcounts sums that are all positive or all negative, but those don't matter.) |
📌📌 Greedy-Approach || 97% faster || Well-Explained 🐍 | minimum-cost-tree-from-leaf-values | 0 | 1 | ## IDEA :\n**The key idea is to choose the minimum value leaf node and combine it with its neighbour which gives minimum product.**\n\nExample Taken from https://leetcode.com/swapnilsingh421\narr = [5,2,3,4]\n\'\'\'\n\n\t\t ( ) p1 \t\t \t\t\t\t\t ( ) p1\n\t\t / \\ \t\t\t\t\t\t / \\\n\t\t5 ( ) p2\t\t\t\t\t\tp2 ( ) ( ) p3\n\t\t\t / \\ \t\t\t\t\t\t\t / \\\t / \\\n\t\t p3 ( ) 4 \t\t\t\t\t\t 5 2 3 4\t\n\t\t / \\\n\t\t 2 3\n\n* Consider node 2 which has minimum value , it has 2 options.\n\n* Combine with 3 as in first diagram or combine with 5 as in second diagram. So it will go for that option which gives minimum product that is 2*3 < 2*5.\n\n* So it choose 1st diagram and p3 = 6 . Now we remove the node 2 from array as to compute value for node p2 only node 3 is required because 3>2 and we want max of left leaf node and max of right leaf node So only greater node proceeds.\n* Array becomes [5,3,4] . Again we find minimum and repeat the process.\n\n**Implementation :**\n\'\'\'\n\n\tclass Solution:\n def mctFromLeafValues(self, arr: List[int]) -> int:\n \n arr = [float(\'inf\')] + arr + [float(\'inf\')]\n n, res = len(arr), 0\n \n while n>3:\n mi = min(arr)\n ind = arr.index(mi)\n \n if arr[ind-1]<arr[ind+1]:\n res+=arr[ind-1]*arr[ind]\n else:\n res+=arr[ind+1]*arr[ind]\n \n arr.remove(mi)\n n = len(arr)\n \n return res\n\n**Thanks & Upvote If you like the Idea!!** \uD83E\uDD1E | 23 | Given an array `arr` of positive integers, consider all binary trees such that:
* Each node has either `0` or `2` children;
* The values of `arr` correspond to the values of each **leaf** in an in-order traversal of the tree.
* The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return _the smallest possible sum of the values of each non-leaf node_. It is guaranteed this sum fits into a **32-bit** integer.
A node is a **leaf** if and only if it has zero children.
**Example 1:**
**Input:** arr = \[6,2,4\]
**Output:** 32
**Explanation:** There are two possible trees shown.
The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
**Example 2:**
**Input:** arr = \[4,11\]
**Output:** 44
**Constraints:**
* `2 <= arr.length <= 40`
* `1 <= arr[i] <= 15`
* It is guaranteed that the answer fits into a **32-bit** signed integer (i.e., it is less than 231). | Think of the final answer as a sum of weights with + or - sign symbols infront of each weight. Actually, all sums with 1 of each sign symbol are possible. Use dynamic programming: for every possible sum with N stones, those sums +x or -x is possible with N+1 stones, where x is the value of the newest stone. (This overcounts sums that are all positive or all negative, but those don't matter.) |
PYTHON | EXPLAINED WITH PICTURES | DP | TABULATION | INTUITIVE | | minimum-cost-tree-from-leaf-values | 0 | 1 | # EXPLANATION\n\n\nThe idea is very simple:\n\nGiven an array : We can break the array into two subarrays :\nexample arr is (2,3,4,5) \nwhich can be broken as:\n1. (2) (3,4,5)\n2. (2,3) (4,5)\n3. (2,3,4) (5)\n\nNow we recursively find the answer for the subarray until we reach the base case\n\nwhen arr.size = 1: we return 0\n\n\n\n# CODE\n```\nclass Solution:\n def mctFromLeafValues(self, arr: List[int]) -> int:\n n = len(arr)\n d = {}\n def findMax(start,end):\n if (start,end) in d: return d[(start,end)]\n maxx = start\n for i in range(start+1,end+1):\n if arr[maxx] < arr[i] : maxx = i\n d[(start,end)] = arr[maxx]\n return arr[maxx]\n \n dp = [[float(\'inf\') for i in range(n)] for j in range(n)]\n for gap in range(n):\n for row in range(n - gap):\n col = row + gap\n if gap == 0:\n dp[row][col] = 0\n elif gap == 1:\n dp[row][col] = arr[row] * arr[col]\n else:\n for k in range(row,col):\n val = dp[row][k] + findMax(row,k) * findMax(k+1,col) + dp[k+1][col]\n if val < dp[row][col]: dp[row][col] = val\n \n\n return dp[0][-1]\n \n``` | 2 | Given an array `arr` of positive integers, consider all binary trees such that:
* Each node has either `0` or `2` children;
* The values of `arr` correspond to the values of each **leaf** in an in-order traversal of the tree.
* The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return _the smallest possible sum of the values of each non-leaf node_. It is guaranteed this sum fits into a **32-bit** integer.
A node is a **leaf** if and only if it has zero children.
**Example 1:**
**Input:** arr = \[6,2,4\]
**Output:** 32
**Explanation:** There are two possible trees shown.
The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
**Example 2:**
**Input:** arr = \[4,11\]
**Output:** 44
**Constraints:**
* `2 <= arr.length <= 40`
* `1 <= arr[i] <= 15`
* It is guaranteed that the answer fits into a **32-bit** signed integer (i.e., it is less than 231). | Think of the final answer as a sum of weights with + or - sign symbols infront of each weight. Actually, all sums with 1 of each sign symbol are possible. Use dynamic programming: for every possible sum with N stones, those sums +x or -x is possible with N+1 stones, where x is the value of the newest stone. (This overcounts sums that are all positive or all negative, but those don't matter.) |
Easy Python and Beats 96% along with explanation | maximum-of-absolute-value-expression | 0 | 1 | # Code\n```\nclass Solution:\n def maxAbsValExpr(self, arr1: List[int], arr2: List[int]) -> int:\n \'\'\'\n |a1[i]-a1[j]| + |a2[i]-a2[j]| + |i-j|\n total 2(+ or -)**(no. of modules) == 2**3 cases\n\n --> a1[i]-a1[j]+a2[i]-a2[j]+i-j\n == (a1[i]+a2[i]+i) - (a1[j]+a2[j]+j)\n\n --> a1[i]-a1[j]+a2[i]-a2[j]-i-j\n == (a1[i]+a2[i]-i) - (a1[j]+a2[j]-j)\n \n ...etc\n \'\'\'\n val1,val2,val3,val4=[],[],[],[]\n for i in range(len(arr1)):\n val1.append(i+arr1[i]+arr2[i])\n val2.append(i+arr1[i]-arr2[i])\n val3.append(i-arr1[i]+arr2[i])\n val4.append(i-arr1[i]-arr2[i])\n ans=0\n ans=max(ans,max(val1)-min(val1))\n ans=max(ans,max(val2)-min(val2))\n ans=max(ans,max(val3)-min(val3))\n ans=max(ans,max(val4)-min(val4))\n return ans\n``` | 3 | Given two arrays of integers with equal lengths, return the maximum value of:
`|arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j|`
where the maximum is taken over all `0 <= i, j < arr1.length`.
**Example 1:**
**Input:** arr1 = \[1,2,3,4\], arr2 = \[-1,4,5,6\]
**Output:** 13
**Example 2:**
**Input:** arr1 = \[1,-2,-5,0,10\], arr2 = \[0,-2,-1,-7,-4\]
**Output:** 20
**Constraints:**
* `2 <= arr1.length == arr2.length <= 40000`
* `-10^6 <= arr1[i], arr2[i] <= 10^6` | What if we divide the string into substrings containing only one distinct character with maximal lengths? Now that you have sub-strings with only one distinct character, Try to come up with a formula that counts the number of its sub-strings. Alternatively, Observe that the constraints are small so you can use brute force. |
Python 3 | O(n)/O(1) | maximum-of-absolute-value-expression | 0 | 1 | ```\nclass Solution:\n def maxAbsValExpr(self, arr1: List[int], arr2: List[int]) -> int:\n minA = minB = minC = minD = math.inf\n maxA = maxB = maxC = maxD = -math.inf\n\n for i, (num1, num2) in enumerate(zip(arr1, arr2)):\n minA = min(minA, i + num1 + num2)\n maxA = max(maxA, i + num1 + num2)\n minB = min(minB, i + num1 - num2)\n maxB = max(maxB, i + num1 - num2)\n minC = min(minC, i - num1 + num2)\n maxC = max(maxC, i - num1 + num2)\n minD = min(minD, i - num1 - num2)\n maxD = max(maxD, i - num1 - num2)\n \n return max(maxA - minA, maxB - minB,\n maxC - minC, maxD - minD) | 2 | Given two arrays of integers with equal lengths, return the maximum value of:
`|arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j|`
where the maximum is taken over all `0 <= i, j < arr1.length`.
**Example 1:**
**Input:** arr1 = \[1,2,3,4\], arr2 = \[-1,4,5,6\]
**Output:** 13
**Example 2:**
**Input:** arr1 = \[1,-2,-5,0,10\], arr2 = \[0,-2,-1,-7,-4\]
**Output:** 20
**Constraints:**
* `2 <= arr1.length == arr2.length <= 40000`
* `-10^6 <= arr1[i], arr2[i] <= 10^6` | What if we divide the string into substrings containing only one distinct character with maximal lengths? Now that you have sub-strings with only one distinct character, Try to come up with a formula that counts the number of its sub-strings. Alternatively, Observe that the constraints are small so you can use brute force. |
Python3: TC O(n) SC O(1), Very Clear with Derivation | maximum-of-absolute-value-expression | 0 | 1 | # Intuition\n\nIn simpler versions of this problem where you want the maximum difference, we can do the following:\n* rewrite the score of a pair in terms of `j` terms and `i` terms\n* for each `j`, compute the `j` terms\n* add/subtract the cumulative min/max of the `i` terms.\n\nIn this case the formula is more complicated.\n\nI definitely needed the hint. I consider this a **HARD** problem because you NEED the clever absolute value insight. If you don\'t get it, you\'re doomed on this problem. IMO any problem that requires a clever non-standard insight counts as hard.\n\n# Approach\n\nFirst I take the convention that i < j for a pair. Usually helps with these problems.\n\nNext I used the LC hints of\n```\n|A| = max(A, -A)\n|A|+|B| = max(A+B, A-B, -A+B, -A-B)\n```\n\nTo rewrite |A|+|B|+j-i as the max of four different quantities.\n\nEach quantity is\n* some function of the current index `j`\n* and a cumulative minimum of earlier indices `i`\n\nSo the algorithm becomes this for each j:\n1. compute the 4 terms\n2. use the corresponding cumulative minimum of the 4 i terms over all i < j to get the best solution involving `j`\n3. update the cumulative minima to prepare for the next iteration with `j\' = j+1`\n\n# Complexity\n- Time complexity: O(N), we do O(1) work per iteration\n\n- Space complexity: O(1), we just need 4 cumulative minima\n\n# Code\n```\nclass Solution:\n def maxAbsValExpr(self, A: List[int], B: List[int]) -> int:\n \n # Definitely needed the LC hint.\n\n # LC hint: |A|+|B| == max(A+B, A-B, -A+B, -A-B)\n # Follows from |A| = max(A, -A). With two absolute values, there are 4 cases.\n\n # So if we plug in A and B, for i < j the score of a pair\n # is max of the following four:\n # A[j]-A[i]+B[j]-B[i]+j-i = A[j]+B[j]+j - (A[i]+B[i]+i)\n # A[j]-A[i]-B[j]+B[i]+j-i = A[j]-B[j]+j - (A[i]-B[i]+i)\n # -A[j]+A[i]+B[j]-B[i]+j-i =-A[j]+B[j]+j - (-A[i]+B[i]+i)\n # -A[j]+A[i]-B[j]+B[i]+j-i =-A[j]-B[j]+j - (-A[i]-B[i]+i)\n # ------------ --------------\n # current index subtract lowest\n # value we\'ve seen\n # over all i < j\n # (cumulative min)\n\n pp = A[0]+B[0] # cumulative min +-A[i] +-B[i] + i for i <\n pm = A[0]-B[0]\n mp = -A[0]+B[0]\n mm = -A[0]-B[0]\n best = 0\n for j in range(1, len(A)):\n ppj = A[j]+B[j]+j\n pmj = A[j]-B[j]+j\n mpj = -A[j]+B[j]+j\n mmj = -A[j]-B[j]+j\n\n best = max(best, ppj-pp, pmj-pm, mpj-mp, mmj-mm)\n\n pp = min(pp, ppj)\n pm = min(pm, pmj)\n mp = min(mp, mpj)\n mm = min(mm, mmj)\n\n return best\n``` | 0 | Given two arrays of integers with equal lengths, return the maximum value of:
`|arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j|`
where the maximum is taken over all `0 <= i, j < arr1.length`.
**Example 1:**
**Input:** arr1 = \[1,2,3,4\], arr2 = \[-1,4,5,6\]
**Output:** 13
**Example 2:**
**Input:** arr1 = \[1,-2,-5,0,10\], arr2 = \[0,-2,-1,-7,-4\]
**Output:** 20
**Constraints:**
* `2 <= arr1.length == arr2.length <= 40000`
* `-10^6 <= arr1[i], arr2[i] <= 10^6` | What if we divide the string into substrings containing only one distinct character with maximal lengths? Now that you have sub-strings with only one distinct character, Try to come up with a formula that counts the number of its sub-strings. Alternatively, Observe that the constraints are small so you can use brute force. |
Expansion | maximum-of-absolute-value-expression | 0 | 1 | # Intuition\nExpand the expression.\n\n# Approach\nRemove the mod and expand the expression, and check all possible expressions. Return the maximum value possible among all possible expressions.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$ \n\n# Code\n```\nclass Solution:\n def maxAbsValExpr(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n mx1, mx2, mx3, mx4 = -10**7, -10**7, -10**7, -10**7\n mn1, mn2, mn3, mn4 = 10**7, 10**7, 10**7, 10**7\n for i in range(n):\n X1 = i + A[i] + B[i]\n X2 = i - A[i] - B[i]\n X3 = i + A[i] - B[i]\n X4 = i - A[i] + B[i]\n mx1, mx2, mx3, mx4 = max(mx1, X1), max(mx2, X2), max(mx3, X3), max(mx4, X4)\n mn1, mn2, mn3, mn4 = min(mn1, X1), min(mn2, X2), min(mn3, X3), min(mn4, X4)\n return max(mx1-mn1, mx2-mn2, mx3-mn3, mx4-mn4)\n``` | 0 | Given two arrays of integers with equal lengths, return the maximum value of:
`|arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j|`
where the maximum is taken over all `0 <= i, j < arr1.length`.
**Example 1:**
**Input:** arr1 = \[1,2,3,4\], arr2 = \[-1,4,5,6\]
**Output:** 13
**Example 2:**
**Input:** arr1 = \[1,-2,-5,0,10\], arr2 = \[0,-2,-1,-7,-4\]
**Output:** 20
**Constraints:**
* `2 <= arr1.length == arr2.length <= 40000`
* `-10^6 <= arr1[i], arr2[i] <= 10^6` | What if we divide the string into substrings containing only one distinct character with maximal lengths? Now that you have sub-strings with only one distinct character, Try to come up with a formula that counts the number of its sub-strings. Alternatively, Observe that the constraints are small so you can use brute force. |
Python Elegant & Short | O(n) | 1-Pass | alphabet-board-path | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n MAPPING = {\n ltr: (i // 5, i % 5)\n for i, ltr in enumerate(ascii_lowercase)\n }\n\n def alphabetBoardPath(self, target: str) -> str:\n x, y = 0, 0\n path = \'\'\n\n for c in target:\n n_x, n_y = self.MAPPING[c]\n\n if n_y < y:\n path += \'L\' * (y - n_y)\n if n_x < x:\n path += \'U\' * (x - n_x)\n if n_x > x:\n path += \'D\' * (n_x - x)\n if n_y > y:\n path += \'R\' * (n_y - y)\n\n path += \'!\'\n x, y = n_x, n_y\n\n return path\n``` | 2 | On an alphabet board, we start at position `(0, 0)`, corresponding to character `board[0][0]`.
Here, `board = [ "abcde ", "fghij ", "klmno ", "pqrst ", "uvwxy ", "z "]`, as shown in the diagram below.
We may make the following moves:
* `'U'` moves our position up one row, if the position exists on the board;
* `'D'` moves our position down one row, if the position exists on the board;
* `'L'` moves our position left one column, if the position exists on the board;
* `'R'` moves our position right one column, if the position exists on the board;
* `'!'` adds the character `board[r][c]` at our current position `(r, c)` to the answer.
(Here, the only positions that exist on the board are positions with letters on them.)
Return a sequence of moves that makes our answer equal to `target` in the minimum number of moves. You may return any path that does so.
**Example 1:**
**Input:** target = "leet"
**Output:** "DDR!UURRR!!DDD!"
**Example 2:**
**Input:** target = "code"
**Output:** "RR!DDRR!UUL!R!"
**Constraints:**
* `1 <= target.length <= 100`
* `target` consists only of English lowercase letters. | Say the store owner uses their power in minute 1 to X and we have some answer A. If they instead use their power from minute 2 to X+1, we only have to use data from minutes 1, 2, X and X+1 to update our answer A. |
Python Elegant & Short | O(n) | 1-Pass | alphabet-board-path | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n MAPPING = {\n ltr: (i // 5, i % 5)\n for i, ltr in enumerate(ascii_lowercase)\n }\n\n def alphabetBoardPath(self, target: str) -> str:\n x, y = 0, 0\n path = \'\'\n\n for c in target:\n n_x, n_y = self.MAPPING[c]\n\n if n_y < y:\n path += \'L\' * (y - n_y)\n if n_x < x:\n path += \'U\' * (x - n_x)\n if n_x > x:\n path += \'D\' * (n_x - x)\n if n_y > y:\n path += \'R\' * (n_y - y)\n\n path += \'!\'\n x, y = n_x, n_y\n\n return path\n``` | 2 | Given 2 integers `n` and `start`. Your task is return **any** permutation `p` of `(0,1,2.....,2^n -1)` such that :
* `p[0] = start`
* `p[i]` and `p[i+1]` differ by only one bit in their binary representation.
* `p[0]` and `p[2^n -1]` must also differ by only one bit in their binary representation.
**Example 1:**
**Input:** n = 2, start = 3
**Output:** \[3,2,0,1\]
**Explanation:** The binary representation of the permutation is (11,10,00,01).
All the adjacent element differ by one bit. Another valid permutation is \[3,1,0,2\]
**Example 2:**
**Input:** n = 3, start = 2
**Output:** \[2,6,7,5,4,0,1,3\]
**Explanation:** The binary representation of the permutation is (010,110,111,101,100,000,001,011).
**Constraints:**
* `1 <= n <= 16`
* `0 <= start < 2 ^ n` | Create a hashmap from letter to position on the board. Now for each letter, try moving there in steps, where at each step you check if it is inside the boundaries of the board. |
python || 7 lines, w/ comments || T/M: 95% / 99% | alphabet-board-path | 0 | 1 | ```\nclass Solution:\n def alphabetBoardPath(self, target: str) -> str:\n \n rTrgt, cTrgt, ans = 0, 0, \'\' # <-- initialize some stuff\n f = lambda x: (abs(x)+x)//2 # <-- f returns the appropriate coefficient for\n # computing the path for each target element\n \n for ch in target:\n rCurr, cCurr = rTrgt, cTrgt # <-- update current position on board\n rTrgt, cTrgt = divmod(ord(ch)-97, 5) # <-- determine the 2D coordinates for target\n \n\n r, c = rTrgt - rCurr, cTrgt - cCurr # <-- row, col displacements when moving from \n # current to target\n\n ans+= f(-r)*"U"+f(-c)*"L"+f(c)*\'R\'+f(r)*\'D\'+"!" # <-- increments ans with directions to the target\n```\n[https://leetcode.com/submissions/detail/837045447/](http://)\n\nI could be wrong, but I think it\'s *O*(*n*) / *O*(*n*) | 5 | On an alphabet board, we start at position `(0, 0)`, corresponding to character `board[0][0]`.
Here, `board = [ "abcde ", "fghij ", "klmno ", "pqrst ", "uvwxy ", "z "]`, as shown in the diagram below.
We may make the following moves:
* `'U'` moves our position up one row, if the position exists on the board;
* `'D'` moves our position down one row, if the position exists on the board;
* `'L'` moves our position left one column, if the position exists on the board;
* `'R'` moves our position right one column, if the position exists on the board;
* `'!'` adds the character `board[r][c]` at our current position `(r, c)` to the answer.
(Here, the only positions that exist on the board are positions with letters on them.)
Return a sequence of moves that makes our answer equal to `target` in the minimum number of moves. You may return any path that does so.
**Example 1:**
**Input:** target = "leet"
**Output:** "DDR!UURRR!!DDD!"
**Example 2:**
**Input:** target = "code"
**Output:** "RR!DDRR!UUL!R!"
**Constraints:**
* `1 <= target.length <= 100`
* `target` consists only of English lowercase letters. | Say the store owner uses their power in minute 1 to X and we have some answer A. If they instead use their power from minute 2 to X+1, we only have to use data from minutes 1, 2, X and X+1 to update our answer A. |
python || 7 lines, w/ comments || T/M: 95% / 99% | alphabet-board-path | 0 | 1 | ```\nclass Solution:\n def alphabetBoardPath(self, target: str) -> str:\n \n rTrgt, cTrgt, ans = 0, 0, \'\' # <-- initialize some stuff\n f = lambda x: (abs(x)+x)//2 # <-- f returns the appropriate coefficient for\n # computing the path for each target element\n \n for ch in target:\n rCurr, cCurr = rTrgt, cTrgt # <-- update current position on board\n rTrgt, cTrgt = divmod(ord(ch)-97, 5) # <-- determine the 2D coordinates for target\n \n\n r, c = rTrgt - rCurr, cTrgt - cCurr # <-- row, col displacements when moving from \n # current to target\n\n ans+= f(-r)*"U"+f(-c)*"L"+f(c)*\'R\'+f(r)*\'D\'+"!" # <-- increments ans with directions to the target\n```\n[https://leetcode.com/submissions/detail/837045447/](http://)\n\nI could be wrong, but I think it\'s *O*(*n*) / *O*(*n*) | 5 | Given 2 integers `n` and `start`. Your task is return **any** permutation `p` of `(0,1,2.....,2^n -1)` such that :
* `p[0] = start`
* `p[i]` and `p[i+1]` differ by only one bit in their binary representation.
* `p[0]` and `p[2^n -1]` must also differ by only one bit in their binary representation.
**Example 1:**
**Input:** n = 2, start = 3
**Output:** \[3,2,0,1\]
**Explanation:** The binary representation of the permutation is (11,10,00,01).
All the adjacent element differ by one bit. Another valid permutation is \[3,1,0,2\]
**Example 2:**
**Input:** n = 3, start = 2
**Output:** \[2,6,7,5,4,0,1,3\]
**Explanation:** The binary representation of the permutation is (010,110,111,101,100,000,001,011).
**Constraints:**
* `1 <= n <= 16`
* `0 <= start < 2 ^ n` | Create a hashmap from letter to position on the board. Now for each letter, try moving there in steps, where at each step you check if it is inside the boundaries of the board. |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | alphabet-board-path | 0 | 1 | \n# Code\n```\nclass Solution:\n def alphabetBoardPath(self, target: str) -> str:\n i = j = 0\n ans = []\n for c in target:\n diff = ord(c) - ord(\'a\')\n row, col = divmod(diff, 5)\n while i > row:\n i -= 1\n ans.append(\'U\')\n while j > col:\n j -= 1\n ans.append(\'L\')\n while i < row:\n i += 1\n ans.append(\'D\')\n while j < col:\n j += 1\n ans.append(\'R\')\n ans.append(\'!\') \n return \'\'.join(ans) \n``` | 1 | On an alphabet board, we start at position `(0, 0)`, corresponding to character `board[0][0]`.
Here, `board = [ "abcde ", "fghij ", "klmno ", "pqrst ", "uvwxy ", "z "]`, as shown in the diagram below.
We may make the following moves:
* `'U'` moves our position up one row, if the position exists on the board;
* `'D'` moves our position down one row, if the position exists on the board;
* `'L'` moves our position left one column, if the position exists on the board;
* `'R'` moves our position right one column, if the position exists on the board;
* `'!'` adds the character `board[r][c]` at our current position `(r, c)` to the answer.
(Here, the only positions that exist on the board are positions with letters on them.)
Return a sequence of moves that makes our answer equal to `target` in the minimum number of moves. You may return any path that does so.
**Example 1:**
**Input:** target = "leet"
**Output:** "DDR!UURRR!!DDD!"
**Example 2:**
**Input:** target = "code"
**Output:** "RR!DDRR!UUL!R!"
**Constraints:**
* `1 <= target.length <= 100`
* `target` consists only of English lowercase letters. | Say the store owner uses their power in minute 1 to X and we have some answer A. If they instead use their power from minute 2 to X+1, we only have to use data from minutes 1, 2, X and X+1 to update our answer A. |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | alphabet-board-path | 0 | 1 | \n# Code\n```\nclass Solution:\n def alphabetBoardPath(self, target: str) -> str:\n i = j = 0\n ans = []\n for c in target:\n diff = ord(c) - ord(\'a\')\n row, col = divmod(diff, 5)\n while i > row:\n i -= 1\n ans.append(\'U\')\n while j > col:\n j -= 1\n ans.append(\'L\')\n while i < row:\n i += 1\n ans.append(\'D\')\n while j < col:\n j += 1\n ans.append(\'R\')\n ans.append(\'!\') \n return \'\'.join(ans) \n``` | 1 | Given 2 integers `n` and `start`. Your task is return **any** permutation `p` of `(0,1,2.....,2^n -1)` such that :
* `p[0] = start`
* `p[i]` and `p[i+1]` differ by only one bit in their binary representation.
* `p[0]` and `p[2^n -1]` must also differ by only one bit in their binary representation.
**Example 1:**
**Input:** n = 2, start = 3
**Output:** \[3,2,0,1\]
**Explanation:** The binary representation of the permutation is (11,10,00,01).
All the adjacent element differ by one bit. Another valid permutation is \[3,1,0,2\]
**Example 2:**
**Input:** n = 3, start = 2
**Output:** \[2,6,7,5,4,0,1,3\]
**Explanation:** The binary representation of the permutation is (010,110,111,101,100,000,001,011).
**Constraints:**
* `1 <= n <= 16`
* `0 <= start < 2 ^ n` | Create a hashmap from letter to position on the board. Now for each letter, try moving there in steps, where at each step you check if it is inside the boundaries of the board. |
Python | O(N) | without BFS | Faster than 90% | Less space than 100% | alphabet-board-path | 0 | 1 | ```\nclass Solution:\n def alphabetBoardPath(self, target: str):\n size = 5\n curx, cury = 0, 0\n offset = ord(\'a\')\n ans = \'\'\n \n for i in target:\n row = (ord(i)-offset)//size\n col = (ord(i)-offset)%size\n \n if curx > col: ans += \'L\'*(curx-col)\n if row > cury: ans += \'D\'*(row-cury)\n if cury > row: ans += \'U\'*(cury-row) \n if col > curx: ans += \'R\'*(col-curx)\n \n ans += \'!\'\n curx, cury = col, row\n \n return ans\n``` | 10 | On an alphabet board, we start at position `(0, 0)`, corresponding to character `board[0][0]`.
Here, `board = [ "abcde ", "fghij ", "klmno ", "pqrst ", "uvwxy ", "z "]`, as shown in the diagram below.
We may make the following moves:
* `'U'` moves our position up one row, if the position exists on the board;
* `'D'` moves our position down one row, if the position exists on the board;
* `'L'` moves our position left one column, if the position exists on the board;
* `'R'` moves our position right one column, if the position exists on the board;
* `'!'` adds the character `board[r][c]` at our current position `(r, c)` to the answer.
(Here, the only positions that exist on the board are positions with letters on them.)
Return a sequence of moves that makes our answer equal to `target` in the minimum number of moves. You may return any path that does so.
**Example 1:**
**Input:** target = "leet"
**Output:** "DDR!UURRR!!DDD!"
**Example 2:**
**Input:** target = "code"
**Output:** "RR!DDRR!UUL!R!"
**Constraints:**
* `1 <= target.length <= 100`
* `target` consists only of English lowercase letters. | Say the store owner uses their power in minute 1 to X and we have some answer A. If they instead use their power from minute 2 to X+1, we only have to use data from minutes 1, 2, X and X+1 to update our answer A. |
Python | O(N) | without BFS | Faster than 90% | Less space than 100% | alphabet-board-path | 0 | 1 | ```\nclass Solution:\n def alphabetBoardPath(self, target: str):\n size = 5\n curx, cury = 0, 0\n offset = ord(\'a\')\n ans = \'\'\n \n for i in target:\n row = (ord(i)-offset)//size\n col = (ord(i)-offset)%size\n \n if curx > col: ans += \'L\'*(curx-col)\n if row > cury: ans += \'D\'*(row-cury)\n if cury > row: ans += \'U\'*(cury-row) \n if col > curx: ans += \'R\'*(col-curx)\n \n ans += \'!\'\n curx, cury = col, row\n \n return ans\n``` | 10 | Given 2 integers `n` and `start`. Your task is return **any** permutation `p` of `(0,1,2.....,2^n -1)` such that :
* `p[0] = start`
* `p[i]` and `p[i+1]` differ by only one bit in their binary representation.
* `p[0]` and `p[2^n -1]` must also differ by only one bit in their binary representation.
**Example 1:**
**Input:** n = 2, start = 3
**Output:** \[3,2,0,1\]
**Explanation:** The binary representation of the permutation is (11,10,00,01).
All the adjacent element differ by one bit. Another valid permutation is \[3,1,0,2\]
**Example 2:**
**Input:** n = 3, start = 2
**Output:** \[2,6,7,5,4,0,1,3\]
**Explanation:** The binary representation of the permutation is (010,110,111,101,100,000,001,011).
**Constraints:**
* `1 <= n <= 16`
* `0 <= start < 2 ^ n` | Create a hashmap from letter to position on the board. Now for each letter, try moving there in steps, where at each step you check if it is inside the boundaries of the board. |
python runtime O(n) space O(n) using hash map | alphabet-board-path | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alphabetBoardPath(self, target: str) -> str:\n \n\n\n p = {}\n board = ["abcde", "fghij", "klmno", "pqrst", "uvwxy", "z"]\n for i in range(len(board)):\n for j in range(len(board[i])):\n p[board[i][j]] = (i, j)\n\n prev = (0, 0)\n ans = ""\n for s in target:\n y, x = p[s]\n prev_y, prev_x = prev\n if s == "z":\n if prev_x == 0:\n ans += "D" * (y-prev_y)\n \n else:\n ans += "D" * (4-prev_y)\n ans += "L" * (prev_x-x) + "D"\n else:\n \n if prev_y > y:\n ans += "U" * abs(prev_y-y)\n elif prev_y < y:\n ans += "D" * abs(prev_y-y)\n \n if prev_x > x:\n ans += "L" * abs(prev_x-x)\n elif prev_x < x:\n ans += "R" * abs(prev_x-x)\n ans += "!"\n prev = (y, x)\n\n return ans \n \n\n``` | 0 | On an alphabet board, we start at position `(0, 0)`, corresponding to character `board[0][0]`.
Here, `board = [ "abcde ", "fghij ", "klmno ", "pqrst ", "uvwxy ", "z "]`, as shown in the diagram below.
We may make the following moves:
* `'U'` moves our position up one row, if the position exists on the board;
* `'D'` moves our position down one row, if the position exists on the board;
* `'L'` moves our position left one column, if the position exists on the board;
* `'R'` moves our position right one column, if the position exists on the board;
* `'!'` adds the character `board[r][c]` at our current position `(r, c)` to the answer.
(Here, the only positions that exist on the board are positions with letters on them.)
Return a sequence of moves that makes our answer equal to `target` in the minimum number of moves. You may return any path that does so.
**Example 1:**
**Input:** target = "leet"
**Output:** "DDR!UURRR!!DDD!"
**Example 2:**
**Input:** target = "code"
**Output:** "RR!DDRR!UUL!R!"
**Constraints:**
* `1 <= target.length <= 100`
* `target` consists only of English lowercase letters. | Say the store owner uses their power in minute 1 to X and we have some answer A. If they instead use their power from minute 2 to X+1, we only have to use data from minutes 1, 2, X and X+1 to update our answer A. |
python runtime O(n) space O(n) using hash map | alphabet-board-path | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alphabetBoardPath(self, target: str) -> str:\n \n\n\n p = {}\n board = ["abcde", "fghij", "klmno", "pqrst", "uvwxy", "z"]\n for i in range(len(board)):\n for j in range(len(board[i])):\n p[board[i][j]] = (i, j)\n\n prev = (0, 0)\n ans = ""\n for s in target:\n y, x = p[s]\n prev_y, prev_x = prev\n if s == "z":\n if prev_x == 0:\n ans += "D" * (y-prev_y)\n \n else:\n ans += "D" * (4-prev_y)\n ans += "L" * (prev_x-x) + "D"\n else:\n \n if prev_y > y:\n ans += "U" * abs(prev_y-y)\n elif prev_y < y:\n ans += "D" * abs(prev_y-y)\n \n if prev_x > x:\n ans += "L" * abs(prev_x-x)\n elif prev_x < x:\n ans += "R" * abs(prev_x-x)\n ans += "!"\n prev = (y, x)\n\n return ans \n \n\n``` | 0 | Given 2 integers `n` and `start`. Your task is return **any** permutation `p` of `(0,1,2.....,2^n -1)` such that :
* `p[0] = start`
* `p[i]` and `p[i+1]` differ by only one bit in their binary representation.
* `p[0]` and `p[2^n -1]` must also differ by only one bit in their binary representation.
**Example 1:**
**Input:** n = 2, start = 3
**Output:** \[3,2,0,1\]
**Explanation:** The binary representation of the permutation is (11,10,00,01).
All the adjacent element differ by one bit. Another valid permutation is \[3,1,0,2\]
**Example 2:**
**Input:** n = 3, start = 2
**Output:** \[2,6,7,5,4,0,1,3\]
**Explanation:** The binary representation of the permutation is (010,110,111,101,100,000,001,011).
**Constraints:**
* `1 <= n <= 16`
* `0 <= start < 2 ^ n` | Create a hashmap from letter to position on the board. Now for each letter, try moving there in steps, where at each step you check if it is inside the boundaries of the board. |
✔ Python3 Solution | O(n * m * min(n, m)) | largest-1-bordered-square | 0 | 1 | # Complexity\n- Time complexity: $$O(n * m * min(n, m))$$\n- Space complexity: $$O(n * m)$$\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, A):\n n, m, ans = len(A), len(A[0]), 0\n H, V = [row[:] for row in A], [row[:] for row in A]\n for i in range(n):\n for j in range(m):\n if i and H[i][j]: H[i][j] += H[i - 1][j]\n if j and V[i][j]: V[i][j] += V[i][j - 1]\n for i in range(n):\n for j in range(m):\n for k in range(min(H[i][j], V[i][j]), ans, -1):\n if V[i - k + 1][j] >= k and H[i][j - k + 1] >= k:\n ans = k\n break\n return ans * ans\n``` | 2 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
✔ Python3 Solution | O(n * m * min(n, m)) | largest-1-bordered-square | 0 | 1 | # Complexity\n- Time complexity: $$O(n * m * min(n, m))$$\n- Space complexity: $$O(n * m)$$\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, A):\n n, m, ans = len(A), len(A[0]), 0\n H, V = [row[:] for row in A], [row[:] for row in A]\n for i in range(n):\n for j in range(m):\n if i and H[i][j]: H[i][j] += H[i - 1][j]\n if j and V[i][j]: V[i][j] += V[i][j - 1]\n for i in range(n):\n for j in range(m):\n for k in range(min(H[i][j], V[i][j]), ans, -1):\n if V[i - k + 1][j] >= k and H[i][j - k + 1] >= k:\n ans = k\n break\n return ans * ans\n``` | 2 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Python3: FT 100%: TC O(M^2 N), SC O(M N): Mostly DP with a Few Optimizations | largest-1-bordered-square | 0 | 1 | # Intuition\n\nFor most problems involving squares or sides in grids, we usually need to know the number of consecutive ones. We can do this with O(M N) DP.\n\nIn this case, 1-bordered squares mean we need to find cells with a specific number of consecutive 1s down and to the right. So we\'re probably on the right track.\n\nIn more detail: to form a 1-bordered region of size `k x k` with the upper-left corner at `r, c` we need\n* at `r, c`: `k` consecutive 1\'s going down\n* at `r, c`: `k` consecutive 1\'s going right\n* at `r+k-1, c`: `k` consecutive 1\'s going right\n* at `r, c+k-1`: `k` consecutive 1\'s going down\n\nHere\'s some ASCII art:\n```a\n (r,c) k ones\n \\ --------->\n k | 1 1 1 1 |\nones | 1 1 | k ones\n | 1 1 |\n | 1 1 1 1 V\n ------------>\n k ones\n```\n\nAt `r,c`:\n* suppose we have `D` 1s going down\n* and we have `R` 1s going right\n* then the largest *square* we can form has side length `min(D,R)`\n* so we know the largest side length to check\n\nWe can use DP to get the consecutive ones in both directions. Then we can iterate over the grid and find the largest square with each upper-left coordinate. The best answer is the max square size over all (r,c) starting locations (i.e. all O(M N) choices for the upper-left).\n\n# Approach\n\n## Consecutive Ones Down and Left\n\nA (somewhat) common DP operation for grids is getting the number of consecutive ones in some direction. This shows up in a lot of "skyline" problems too, or places where you need to quickly get information about consecutive elements meeting some criterion.\n\nFor consecutive ones going right:\n* if the right-most element is 0, the count is zero\n* if the right-most element is 1, the count is one\n* for each r < R-1\n * if the current element is 1, the count is 1 plus the number of consecutive ones starting one element to the right: we take the `k` 1\'s off to the right, and add 1 for the current element\n * if the current element is 0, the count is 0\n\nSome more ASCII art to explain what we\'re doing:\n```\nrow: 0 1 1 1 0 0 1 1 0 1 1 1 1 0\nconsecutive ones to right: 0 3 2 1 0 0 2 1 0 4 3 2 1 0\n```\n\nThe same logic applies to consecutive ones downward, but with rows/columns flipped. Same idea, just be careful about R vs. C.\n\n## Main Loop\n\nFor all `r,c` coordinates, we can find the max edge length using `min(down[r][c], right[r][c])`. Any edge longer than that will have a zero along at least one edge, or go out of bounds.\n\nThen for each possible side length `l`, we check\n* if we go the bottom-left corner, are there `l` ones to the right?\n* if we go to the top-right corner, are there `l` ones going down?\n\nIf the answer to both is yes, then we have a square of side length `l`.\n\n## Optimizations\n\nWe want the cumulative max over all starting locations. Therefore we only care about improving the current max.\n\n### Early Break in R/C Loops\n\nIf we\'re at (r,c) and the current best side length is `best`, then a new best square would end at least at `r+best+1-1, c+best+1-1 == r+best, c+best`.\n\nIf those coordinates are out of bounds, we can\'t possibly improve on the best. So I added an early `break` statement to the outermost loop (rows), and adjusted the upper bound of the inner loop (cols).\n\n### Try Longest First\n\nSince we want the maximum, we don\'t care about *all* the edge lengths we can form at `r,c` - we just want the max. So I iterate from the longest length downward, and break if/when we get a length. This way we look at the fewest squares possible.\n\n### Only Try Larger Squares\n\nSimilar to "Try Longest First," we know that the only squares that can improve the current `best` have side length `best+1` or longer.\n\nSo I only check lengths from `longest` to `best+1` in descending order. If we find a square, we know this is a new best (because we *only* consider lengths that will be a new best) so we set `best = l` directly.\n\n# Complexity\n- Time complexity: O(M^2 N)\n - M is the shorter axis\n - N is the longer axis\n - analysis: we do O(M N) iterations, over most upper-left coordintes `r, c`. In each iteration, we look at longest possible edge length, which is O(M). So we do O(M M N) work total.\n - the `down` and `left` DP grids only take O(M N)\n\n- Space complexity: O(M N) because we form `down` and `right` DP grids\n\nIn practice I think the complexity is typically lot lower because we only iterate over lengths from `min(down[r][c], right[r][c])` down to `best+1`\n* for early r,c coordinates, usually one axis will have many fewer consecutive ones than the other. The worst case would be a lot of downward and rightward lines of 1s\n* for later r,c coordinates, the current best increases so the number of side lengths we check decreases\n* for very late r,c coordintes, given the current best, we skip checking late r and c values entirely\n\nSo the effective size of the grid decreases over time, and the range of the loop decreases over time. If there\'s a large rectangle early then the "Only Try Larger Rectangles" optimization means we don\'t actually iterate over any candidate squares at all.\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n R = len(grid)\n C = len(grid[0])\n\n # want largest square subgrid: min(R,C) side length\n # max(R,C)-min(R,C)+1 different offsets in other direction\n\n # Reread problem, a lot easier than I thought (we\'re not counting\n # number of 1-bordered squares in the largest square) - we want\n # the size of the largest 1-bordered square\n\n # the grid already gives us the size of 1x1 squares\n # DP?\n # for x 1 1 1 1 1\n # 1 1\n # 1 1\n # 1 1 1 1 4x4\n\n # if we knew\n # x has 6 left and 4 down ones, including x\n # So max grid size at x is 4x4\n # We can look at right[x + (3,0)] -> get 4\n # and look at down[x + (0,3)] -> get 4\n # so we have a 4x4\n\n # For a MxN grid, the max number of 1s at any cell would be O(M) down and O(N) right\n # for each one we\'d do O(min(M,N)) ops\n # so if shorter axis is M and longer is N, then we\'d do O(MN) iterations, and O(M) ops per iteration\n \n # Can we go faster? I don\'t think so, but I have no proof.\n\n # foo[r][c] is number of consec. 1s, including (r,c), right/down starting at (r,c)\n right = [[0]*C for _ in range(R)]\n down = [[0]*C for _ in range(R)]\n\n for r in range(R):\n right[r][C-1] = grid[r][C-1]\n for c in range(C-2, -1, -1):\n if grid[r][c]:\n right[r][c] = right[r][c+1] + 1\n # else: leave it zero\n\n for c in range(C):\n down[R-1][c] = grid[R-1][c]\n for r in range(R-2, -1, -1):\n if grid[r][c]:\n down[r][c] = down[r+1][c] + 1\n\n L = min(R,C)\n best = 0\n for r in range(R):\n # break early if we can\'t improve on the best; new best would need row index >= r+(best+1)-1\n if r+best >= R: break\n for c in range(C-best):\n longest = min(down[r][c], right[r][c])\n # only candidates > best can change the answer\n for l in range(longest, best, -1):\n if right[r+l-1][c] >= l and down[r][c+l-1] >= l:\n best = l\n break\n \n return best**2 # FIX: area, not side length\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Python3: FT 100%: TC O(M^2 N), SC O(M N): Mostly DP with a Few Optimizations | largest-1-bordered-square | 0 | 1 | # Intuition\n\nFor most problems involving squares or sides in grids, we usually need to know the number of consecutive ones. We can do this with O(M N) DP.\n\nIn this case, 1-bordered squares mean we need to find cells with a specific number of consecutive 1s down and to the right. So we\'re probably on the right track.\n\nIn more detail: to form a 1-bordered region of size `k x k` with the upper-left corner at `r, c` we need\n* at `r, c`: `k` consecutive 1\'s going down\n* at `r, c`: `k` consecutive 1\'s going right\n* at `r+k-1, c`: `k` consecutive 1\'s going right\n* at `r, c+k-1`: `k` consecutive 1\'s going down\n\nHere\'s some ASCII art:\n```a\n (r,c) k ones\n \\ --------->\n k | 1 1 1 1 |\nones | 1 1 | k ones\n | 1 1 |\n | 1 1 1 1 V\n ------------>\n k ones\n```\n\nAt `r,c`:\n* suppose we have `D` 1s going down\n* and we have `R` 1s going right\n* then the largest *square* we can form has side length `min(D,R)`\n* so we know the largest side length to check\n\nWe can use DP to get the consecutive ones in both directions. Then we can iterate over the grid and find the largest square with each upper-left coordinate. The best answer is the max square size over all (r,c) starting locations (i.e. all O(M N) choices for the upper-left).\n\n# Approach\n\n## Consecutive Ones Down and Left\n\nA (somewhat) common DP operation for grids is getting the number of consecutive ones in some direction. This shows up in a lot of "skyline" problems too, or places where you need to quickly get information about consecutive elements meeting some criterion.\n\nFor consecutive ones going right:\n* if the right-most element is 0, the count is zero\n* if the right-most element is 1, the count is one\n* for each r < R-1\n * if the current element is 1, the count is 1 plus the number of consecutive ones starting one element to the right: we take the `k` 1\'s off to the right, and add 1 for the current element\n * if the current element is 0, the count is 0\n\nSome more ASCII art to explain what we\'re doing:\n```\nrow: 0 1 1 1 0 0 1 1 0 1 1 1 1 0\nconsecutive ones to right: 0 3 2 1 0 0 2 1 0 4 3 2 1 0\n```\n\nThe same logic applies to consecutive ones downward, but with rows/columns flipped. Same idea, just be careful about R vs. C.\n\n## Main Loop\n\nFor all `r,c` coordinates, we can find the max edge length using `min(down[r][c], right[r][c])`. Any edge longer than that will have a zero along at least one edge, or go out of bounds.\n\nThen for each possible side length `l`, we check\n* if we go the bottom-left corner, are there `l` ones to the right?\n* if we go to the top-right corner, are there `l` ones going down?\n\nIf the answer to both is yes, then we have a square of side length `l`.\n\n## Optimizations\n\nWe want the cumulative max over all starting locations. Therefore we only care about improving the current max.\n\n### Early Break in R/C Loops\n\nIf we\'re at (r,c) and the current best side length is `best`, then a new best square would end at least at `r+best+1-1, c+best+1-1 == r+best, c+best`.\n\nIf those coordinates are out of bounds, we can\'t possibly improve on the best. So I added an early `break` statement to the outermost loop (rows), and adjusted the upper bound of the inner loop (cols).\n\n### Try Longest First\n\nSince we want the maximum, we don\'t care about *all* the edge lengths we can form at `r,c` - we just want the max. So I iterate from the longest length downward, and break if/when we get a length. This way we look at the fewest squares possible.\n\n### Only Try Larger Squares\n\nSimilar to "Try Longest First," we know that the only squares that can improve the current `best` have side length `best+1` or longer.\n\nSo I only check lengths from `longest` to `best+1` in descending order. If we find a square, we know this is a new best (because we *only* consider lengths that will be a new best) so we set `best = l` directly.\n\n# Complexity\n- Time complexity: O(M^2 N)\n - M is the shorter axis\n - N is the longer axis\n - analysis: we do O(M N) iterations, over most upper-left coordintes `r, c`. In each iteration, we look at longest possible edge length, which is O(M). So we do O(M M N) work total.\n - the `down` and `left` DP grids only take O(M N)\n\n- Space complexity: O(M N) because we form `down` and `right` DP grids\n\nIn practice I think the complexity is typically lot lower because we only iterate over lengths from `min(down[r][c], right[r][c])` down to `best+1`\n* for early r,c coordinates, usually one axis will have many fewer consecutive ones than the other. The worst case would be a lot of downward and rightward lines of 1s\n* for later r,c coordinates, the current best increases so the number of side lengths we check decreases\n* for very late r,c coordintes, given the current best, we skip checking late r and c values entirely\n\nSo the effective size of the grid decreases over time, and the range of the loop decreases over time. If there\'s a large rectangle early then the "Only Try Larger Rectangles" optimization means we don\'t actually iterate over any candidate squares at all.\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n R = len(grid)\n C = len(grid[0])\n\n # want largest square subgrid: min(R,C) side length\n # max(R,C)-min(R,C)+1 different offsets in other direction\n\n # Reread problem, a lot easier than I thought (we\'re not counting\n # number of 1-bordered squares in the largest square) - we want\n # the size of the largest 1-bordered square\n\n # the grid already gives us the size of 1x1 squares\n # DP?\n # for x 1 1 1 1 1\n # 1 1\n # 1 1\n # 1 1 1 1 4x4\n\n # if we knew\n # x has 6 left and 4 down ones, including x\n # So max grid size at x is 4x4\n # We can look at right[x + (3,0)] -> get 4\n # and look at down[x + (0,3)] -> get 4\n # so we have a 4x4\n\n # For a MxN grid, the max number of 1s at any cell would be O(M) down and O(N) right\n # for each one we\'d do O(min(M,N)) ops\n # so if shorter axis is M and longer is N, then we\'d do O(MN) iterations, and O(M) ops per iteration\n \n # Can we go faster? I don\'t think so, but I have no proof.\n\n # foo[r][c] is number of consec. 1s, including (r,c), right/down starting at (r,c)\n right = [[0]*C for _ in range(R)]\n down = [[0]*C for _ in range(R)]\n\n for r in range(R):\n right[r][C-1] = grid[r][C-1]\n for c in range(C-2, -1, -1):\n if grid[r][c]:\n right[r][c] = right[r][c+1] + 1\n # else: leave it zero\n\n for c in range(C):\n down[R-1][c] = grid[R-1][c]\n for r in range(R-2, -1, -1):\n if grid[r][c]:\n down[r][c] = down[r+1][c] + 1\n\n L = min(R,C)\n best = 0\n for r in range(R):\n # break early if we can\'t improve on the best; new best would need row index >= r+(best+1)-1\n if r+best >= R: break\n for c in range(C-best):\n longest = min(down[r][c], right[r][c])\n # only candidates > best can change the answer\n for l in range(longest, best, -1):\n if right[r+l-1][c] >= l and down[r][c+l-1] >= l:\n best = l\n break\n \n return best**2 # FIX: area, not side length\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
92% FASTER || BOTTOM-UP DP || count row, col | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n\n m, n = len(grid), len(grid[0])\n res = 0\n col = [[0]*(n+1) for _ in range(m+1)]\n row = [[0]*(n+1) for _ in range(m+1)]\n\n for i in range(1, m+1):\n for j in range(1, n+1):\n if grid[i-1][j-1] != 0:\n row[i][j] = row[i-1][j] + 1\n col[i][j] = col[i][j-1] + 1\n \n\n x = min(col[i][j], row[i][j])\n \n for k in range(x, res, -1):\n if k <= min(col[i-k+1][j], row[i][j-k+1]):\n res = max(1, res, k)\n \n \n \n \n return res**2\n\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
92% FASTER || BOTTOM-UP DP || count row, col | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n\n m, n = len(grid), len(grid[0])\n res = 0\n col = [[0]*(n+1) for _ in range(m+1)]\n row = [[0]*(n+1) for _ in range(m+1)]\n\n for i in range(1, m+1):\n for j in range(1, n+1):\n if grid[i-1][j-1] != 0:\n row[i][j] = row[i-1][j] + 1\n col[i][j] = col[i][j-1] + 1\n \n\n x = min(col[i][j], row[i][j])\n \n for k in range(x, res, -1):\n if k <= min(col[i-k+1][j], row[i][j-k+1]):\n res = max(1, res, k)\n \n \n \n \n return res**2\n\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Brute Force: O(N*M*min(N, M)^2), O(1) | largest-1-bordered-square | 0 | 1 | # Intuition\nJust write a brute force algorithm. Treat the start row and start col as the **top left edge** of the square, then search for 1ns on its sides until we have an invalid square. Kinda suprised this passed as this can be O(N^4)\n\n\n\n# Code\n### Time Complexity: $$O(N * M * min(N, M)^2)$$\n### Space Complexity: $$O(1)$$\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n N,M = len(grid), len(grid[0])\n largest_square = 0\n for start_r in range(N):\n for start_c in range(M):\n for i in range(0, min(M-start_c, N-start_r)):\n valid_square = True\n if not (grid[start_r][start_c+i] and grid[start_r+i][start_c]):\n valid_square = False\n break\n for j in range(0, i+1):\n if not (grid[start_r+i][start_c+i-j] and grid[start_r+i-j][start_c+i]):\n valid_square = False\n break\n if valid_square:\n largest_square = max(largest_square, (i+1)*(i+1))\n return largest_square\n\n\n\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Brute Force: O(N*M*min(N, M)^2), O(1) | largest-1-bordered-square | 0 | 1 | # Intuition\nJust write a brute force algorithm. Treat the start row and start col as the **top left edge** of the square, then search for 1ns on its sides until we have an invalid square. Kinda suprised this passed as this can be O(N^4)\n\n\n\n# Code\n### Time Complexity: $$O(N * M * min(N, M)^2)$$\n### Space Complexity: $$O(1)$$\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n N,M = len(grid), len(grid[0])\n largest_square = 0\n for start_r in range(N):\n for start_c in range(M):\n for i in range(0, min(M-start_c, N-start_r)):\n valid_square = True\n if not (grid[start_r][start_c+i] and grid[start_r+i][start_c]):\n valid_square = False\n break\n for j in range(0, i+1):\n if not (grid[start_r+i][start_c+i-j] and grid[start_r+i-j][start_c+i]):\n valid_square = False\n break\n if valid_square:\n largest_square = max(largest_square, (i+1)*(i+1))\n return largest_square\n\n\n\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
[Python3] Prefix Sum Solution | largest-1-bordered-square | 0 | 1 | # Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n\n horiPrefix = [[0 for j in range(n)] for i in range(m)]\n vertiPrefix = [[0 for j in range(n)] for i in range(m)]\n\n for i in range(m):\n for j in range(n):\n if grid[i][j]==1:\n horiPrefix[i][j] = (horiPrefix[i][j-1] if j-1>=0 else 0) + grid[i][j]\n\n for j in range(n):\n for i in range(m):\n if grid[i][j]==1:\n vertiPrefix[i][j] = (vertiPrefix[i-1][j] if i-1>=0 else 0) + grid[i][j]\n \n ans = 0\n for i in range(m):\n for j in range(n):\n possibleLen = min(i,j)+1\n for l in range(1, possibleLen+1):\n if horiPrefix[i][j]>=l and vertiPrefix[i][j]>=l and horiPrefix[i-l+1][j]>=l and vertiPrefix[i][j-l+1]>=l:\n ans = max(ans, l*l)\n \n return ans\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
[Python3] Prefix Sum Solution | largest-1-bordered-square | 0 | 1 | # Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n\n horiPrefix = [[0 for j in range(n)] for i in range(m)]\n vertiPrefix = [[0 for j in range(n)] for i in range(m)]\n\n for i in range(m):\n for j in range(n):\n if grid[i][j]==1:\n horiPrefix[i][j] = (horiPrefix[i][j-1] if j-1>=0 else 0) + grid[i][j]\n\n for j in range(n):\n for i in range(m):\n if grid[i][j]==1:\n vertiPrefix[i][j] = (vertiPrefix[i-1][j] if i-1>=0 else 0) + grid[i][j]\n \n ans = 0\n for i in range(m):\n for j in range(n):\n possibleLen = min(i,j)+1\n for l in range(1, possibleLen+1):\n if horiPrefix[i][j]>=l and vertiPrefix[i][j]>=l and horiPrefix[i-l+1][j]>=l and vertiPrefix[i][j-l+1]>=l:\n ans = max(ans, l*l)\n \n return ans\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | largest-1-bordered-square | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, A):\n m, n = len(A), len(A[0])\n res = 0\n top, left = [a[:] for a in A], [a[:] for a in A]\n for i in range(m):\n for j in range(n):\n if A[i][j]:\n if i: top[i][j] = top[i - 1][j] + 1\n if j: left[i][j] = left[i][j - 1] + 1\n for r in range(min(m, n), 0, -1):\n for i in range(m - r + 1):\n for j in range(n - r + 1):\n if min(top[i + r - 1][j], top[i + r - 1][j + r - 1], left[i]\n [j + r - 1], left[i + r - 1][j + r - 1]) >= r:\n return r * r\n return 0\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | largest-1-bordered-square | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, A):\n m, n = len(A), len(A[0])\n res = 0\n top, left = [a[:] for a in A], [a[:] for a in A]\n for i in range(m):\n for j in range(n):\n if A[i][j]:\n if i: top[i][j] = top[i - 1][j] + 1\n if j: left[i][j] = left[i][j - 1] + 1\n for r in range(min(m, n), 0, -1):\n for i in range(m - r + 1):\n for j in range(n - r + 1):\n if min(top[i + r - 1][j], top[i + r - 1][j + r - 1], left[i]\n [j + r - 1], left[i + r - 1][j + r - 1]) >= r:\n return r * r\n return 0\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Python3 || Beats 100% || Easy Solution | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n maxi = 0\n rows = len(grid)\n cols = len(grid[0])\n\n hor = [[0]*cols for _ in range(rows)]\n ver = [[0]*cols for _ in range(rows)]\n\n # Auxilliary Horizontal and Vertical DP\n\n for i in range(rows):\n for j in range(cols):\n\n if grid[i][j] == 1:\n if j == 0:\n hor[i][j] = hor[i][j] = 1\n else:\n hor[i][j] = hor[i][j-1] + 1\n \n if i == 0:\n ver[i][j] = 1\n else:\n ver[i][j] = ver[i-1][j] + 1\n \n # for i in range(rows):\n # for j in range(cols):\n # print(hor[i][j],sep=\' \',end=\'\')\n # print() \n \n # print()\n\n # for i in range(rows):\n # for j in range(cols):\n # print(ver[i][j],sep=\' \',end=\'\')\n # print()\n\n\n for i in range(rows-1,-1,-1):\n for j in range(cols-1,-1,-1):\n small = min(ver[i][j], hor[i][j])\n\n while(small > maxi):\n if ver[i][j - small + 1] >= small and hor[i - small + 1][j] >= small:\n maxi = small\n # If above conition is not true then decrement small\n small-=1\n\n return (maxi*maxi)\n \n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Python3 || Beats 100% || Easy Solution | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n maxi = 0\n rows = len(grid)\n cols = len(grid[0])\n\n hor = [[0]*cols for _ in range(rows)]\n ver = [[0]*cols for _ in range(rows)]\n\n # Auxilliary Horizontal and Vertical DP\n\n for i in range(rows):\n for j in range(cols):\n\n if grid[i][j] == 1:\n if j == 0:\n hor[i][j] = hor[i][j] = 1\n else:\n hor[i][j] = hor[i][j-1] + 1\n \n if i == 0:\n ver[i][j] = 1\n else:\n ver[i][j] = ver[i-1][j] + 1\n \n # for i in range(rows):\n # for j in range(cols):\n # print(hor[i][j],sep=\' \',end=\'\')\n # print() \n \n # print()\n\n # for i in range(rows):\n # for j in range(cols):\n # print(ver[i][j],sep=\' \',end=\'\')\n # print()\n\n\n for i in range(rows-1,-1,-1):\n for j in range(cols-1,-1,-1):\n small = min(ver[i][j], hor[i][j])\n\n while(small > maxi):\n if ver[i][j - small + 1] >= small and hor[i - small + 1][j] >= small:\n maxi = small\n # If above conition is not true then decrement small\n small-=1\n\n return (maxi*maxi)\n \n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Python Easy DP Solution | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDynamic Programming should be used to calculate efficiently\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialise 2 DP grids, ```top``` and ```left``` to store number of 1s on top of the cell and on left of the cell respectively. Then, we iterate over the grid, trying all sides from maximum possible side to side length 1\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n numRows, numCols = len(grid), len(grid[0])\n top, left = [row[:] for row in grid], [row[:] for row in grid]\n for row in range(numRows):\n for col in range(numCols):\n if grid[row][col]:\n if row: top[row][col] = top[row - 1][col] + 1\n if col: left[row][col] = left[row][col - 1] + 1\n for side in range(min(numRows, numCols), 0, -1):\n for row in range(numRows - side + 1):\n for col in range(numCols - side + 1):\n if min(top[row + side - 1][col], top[row + side - 1][col + side - 1], left[row][col + side - 1], left[row + side - 1][col + side - 1]) >= side:\n return side * side\n return 0\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Python Easy DP Solution | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDynamic Programming should be used to calculate efficiently\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialise 2 DP grids, ```top``` and ```left``` to store number of 1s on top of the cell and on left of the cell respectively. Then, we iterate over the grid, trying all sides from maximum possible side to side length 1\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n numRows, numCols = len(grid), len(grid[0])\n top, left = [row[:] for row in grid], [row[:] for row in grid]\n for row in range(numRows):\n for col in range(numCols):\n if grid[row][col]:\n if row: top[row][col] = top[row - 1][col] + 1\n if col: left[row][col] = left[row][col - 1] + 1\n for side in range(min(numRows, numCols), 0, -1):\n for row in range(numRows - side + 1):\n for col in range(numCols - side + 1):\n if min(top[row + side - 1][col], top[row + side - 1][col + side - 1], left[row][col + side - 1], left[row + side - 1][col + side - 1]) >= side:\n return side * side\n return 0\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Python easy to read and understand | dp | largest-1-bordered-square | 0 | 1 | ```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n left = [[0 for _ in range(n)] for _ in range(m)]\n top = [[0 for _ in range(n)] for _ in range(m)]\n \n for i in range(m):\n for j in range(n):\n left[i][j] = grid[i][j]\n top[i][j] = grid[i][j]\n \n for i in range(m):\n for j in range(1, n):\n if grid[i][j] == 1:\n left[i][j] += left[i][j-1]\n \n for j in range(n):\n for i in range(1, m):\n if grid[i][j] == 1:\n top[i][j] += top[i-1][j]\n \n res = 0\n for i in range(m):\n for j in range(n):\n mn = min(left[i][j], top[i][j])\n while mn > 0:\n if left[i-mn+1][j] >= mn and top[i][j-mn+1] >= mn:\n res = max(res, mn)\n break\n mn -= 1\n \n return res*res | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Python easy to read and understand | dp | largest-1-bordered-square | 0 | 1 | ```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n left = [[0 for _ in range(n)] for _ in range(m)]\n top = [[0 for _ in range(n)] for _ in range(m)]\n \n for i in range(m):\n for j in range(n):\n left[i][j] = grid[i][j]\n top[i][j] = grid[i][j]\n \n for i in range(m):\n for j in range(1, n):\n if grid[i][j] == 1:\n left[i][j] += left[i][j-1]\n \n for j in range(n):\n for i in range(1, m):\n if grid[i][j] == 1:\n top[i][j] += top[i-1][j]\n \n res = 0\n for i in range(m):\n for j in range(n):\n mn = min(left[i][j], top[i][j])\n while mn > 0:\n if left[i-mn+1][j] >= mn and top[i][j-mn+1] >= mn:\n res = max(res, mn)\n break\n mn -= 1\n \n return res*res | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Python (Simple DP) | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid):\n n, m = len(grid), len(grid[0])\n\n top, left = [i[:] for i in grid], [i[:] for i in grid]\n\n for i in range(n):\n for j in range(m):\n if grid[i][j] == 1:\n if i: top[i][j] = top[i-1][j] + 1\n if j: left[i][j] = left[i][j-1] + 1\n\n\n for r in range(min(m,n),0,-1):\n for i in range(n-r+1):\n for j in range(m-r+1):\n if min(top[i+r-1][j],top[i+r-1][j+r-1],left[i][j+r-1],left[i+r-1][j+r-1]) >= r:\n return r*r\n\n return 0\n\n\n \n\n\n\n\n \n\n\n\n\n\n\n \n\n\n\n\n\n \n\n \n\n\n\n\n\n\n\n \n\n\n\n``` | 0 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Python (Simple DP) | largest-1-bordered-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid):\n n, m = len(grid), len(grid[0])\n\n top, left = [i[:] for i in grid], [i[:] for i in grid]\n\n for i in range(n):\n for j in range(m):\n if grid[i][j] == 1:\n if i: top[i][j] = top[i-1][j] + 1\n if j: left[i][j] = left[i][j-1] + 1\n\n\n for r in range(min(m,n),0,-1):\n for i in range(n-r+1):\n for j in range(m-r+1):\n if min(top[i+r-1][j],top[i+r-1][j+r-1],left[i][j+r-1],left[i+r-1][j+r-1]) >= r:\n return r*r\n\n return 0\n\n\n \n\n\n\n\n \n\n\n\n\n\n\n \n\n\n\n\n\n \n\n \n\n\n\n\n\n\n\n \n\n\n\n``` | 0 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
Python 3 | Prefix-sum, DP, O(N^3) | Explanation | largest-1-bordered-square | 0 | 1 | - Implementation as __*hint*__ section suggested\n- See below comments for more detail\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n dp = [[(0, 0)] * (n) for _ in range((m))] \n for i in range(m): # calculate prefix-sum as `hint` section suggested\n for j in range(n):\n if not grid[i][j]:\n continue\n dp[i][j] = (dp[i][j][0] + dp[i-1][j][0] + 1, dp[i][j][1] + dp[i][j-1][1] + 1)\n for win in range(min(m, n)-1, -1, -1): # for each window size\n for i in range(m-win): # for each x-axis\n for j in range(n-win): # for each y-axis\n if not grid[i][j]: continue # determine whether square of (i, j), (i+win, j+win) is 1-boarded\n x1, y1 = dp[i+win][j+win] # bottom-right corner\n x2, y2 = dp[i][j+win] # upper-right corner\n x3, y3 = dp[i+win][j] # bottom-left corner\n x4, y4 = dp[i][j] # upper-left corner\n if y1 - y3 == x1 - x2 == y2 - y4 == x3 - x4 == win:\n return (win+1) * (win+1)\n return 0\n``` | 3 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
Python 3 | Prefix-sum, DP, O(N^3) | Explanation | largest-1-bordered-square | 0 | 1 | - Implementation as __*hint*__ section suggested\n- See below comments for more detail\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n dp = [[(0, 0)] * (n) for _ in range((m))] \n for i in range(m): # calculate prefix-sum as `hint` section suggested\n for j in range(n):\n if not grid[i][j]:\n continue\n dp[i][j] = (dp[i][j][0] + dp[i-1][j][0] + 1, dp[i][j][1] + dp[i][j-1][1] + 1)\n for win in range(min(m, n)-1, -1, -1): # for each window size\n for i in range(m-win): # for each x-axis\n for j in range(n-win): # for each y-axis\n if not grid[i][j]: continue # determine whether square of (i, j), (i+win, j+win) is 1-boarded\n x1, y1 = dp[i+win][j+win] # bottom-right corner\n x2, y2 = dp[i][j+win] # upper-right corner\n x3, y3 = dp[i+win][j] # bottom-left corner\n x4, y4 = dp[i][j] # upper-left corner\n if y1 - y3 == x1 - x2 == y2 - y4 == x3 - x4 == win:\n return (win+1) * (win+1)\n return 0\n``` | 3 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
python, dp, faster than 98+% | largest-1-bordered-square | 0 | 1 | If anyone doesn\'t understand my solution, comment.\n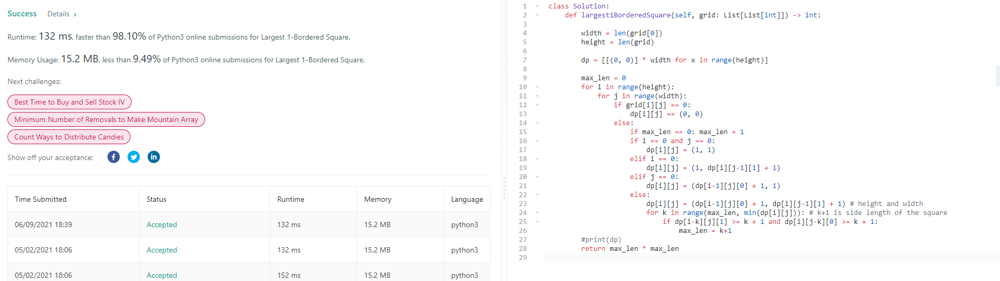\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n width = len(grid[0])\n height = len(grid)\n \n dp = [[(0, 0)] * width for x in range(height)]\n \n max_len = 0\n for i in range(height):\n for j in range(width):\n if grid[i][j] == 0:\n dp[i][j] == (0, 0)\n else:\n if max_len == 0: max_len = 1\n if i == 0 and j == 0: \n dp[i][j] = (1, 1)\n elif i == 0:\n dp[i][j] = (1, dp[i][j-1][1] + 1)\n elif j == 0:\n dp[i][j] = (dp[i-1][j][0] + 1, 1)\n else:\n dp[i][j] = (dp[i-1][j][0] + 1, dp[i][j-1][1] + 1) # height and width\n for k in range(max_len, min(dp[i][j])): # k+1 is side length of the square\n if dp[i-k][j][1] >= k + 1 and dp[i][j-k][0] >= k + 1:\n max_len = k+1\n #print(dp)\n return max_len * max_len\n```\nThe image below maybe help you understand the magic.\n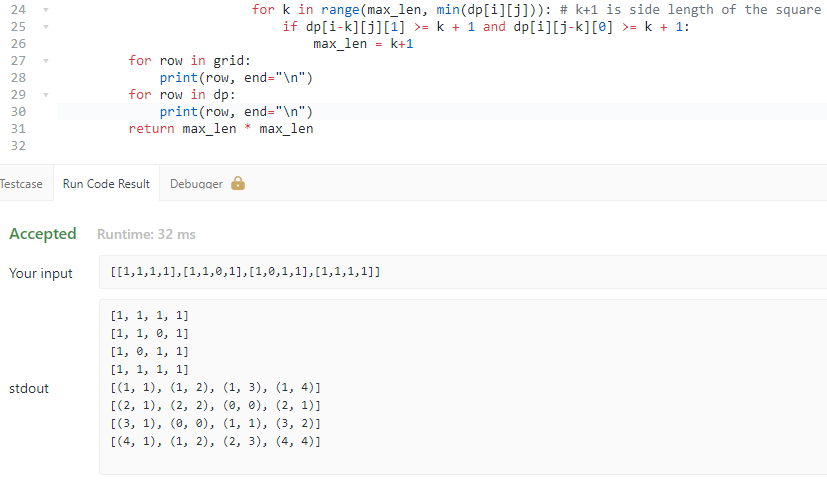\n | 3 | Given a 2D `grid` of `0`s and `1`s, return the number of elements in the largest **square** subgrid that has all `1`s on its **border**, or `0` if such a subgrid doesn't exist in the `grid`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 9
**Example 2:**
**Input:** grid = \[\[1,1,0,0\]\]
**Output:** 1
**Constraints:**
* `1 <= grid.length <= 100`
* `1 <= grid[0].length <= 100`
* `grid[i][j]` is `0` or `1` | You need to swap two values, one larger than the other. Where is the larger one located? |
python, dp, faster than 98+% | largest-1-bordered-square | 0 | 1 | If anyone doesn\'t understand my solution, comment.\n\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n width = len(grid[0])\n height = len(grid)\n \n dp = [[(0, 0)] * width for x in range(height)]\n \n max_len = 0\n for i in range(height):\n for j in range(width):\n if grid[i][j] == 0:\n dp[i][j] == (0, 0)\n else:\n if max_len == 0: max_len = 1\n if i == 0 and j == 0: \n dp[i][j] = (1, 1)\n elif i == 0:\n dp[i][j] = (1, dp[i][j-1][1] + 1)\n elif j == 0:\n dp[i][j] = (dp[i-1][j][0] + 1, 1)\n else:\n dp[i][j] = (dp[i-1][j][0] + 1, dp[i][j-1][1] + 1) # height and width\n for k in range(max_len, min(dp[i][j])): # k+1 is side length of the square\n if dp[i-k][j][1] >= k + 1 and dp[i][j-k][0] >= k + 1:\n max_len = k+1\n #print(dp)\n return max_len * max_len\n```\nThe image below maybe help you understand the magic.\n\n | 3 | You are given an array of strings `arr`. A string `s` is formed by the **concatenation** of a **subsequence** of `arr` that has **unique characters**.
Return _the **maximum** possible length_ of `s`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** arr = \[ "un ", "iq ", "ue "\]
**Output:** 4
**Explanation:** All the valid concatenations are:
- " "
- "un "
- "iq "
- "ue "
- "uniq " ( "un " + "iq ")
- "ique " ( "iq " + "ue ")
Maximum length is 4.
**Example 2:**
**Input:** arr = \[ "cha ", "r ", "act ", "ers "\]
**Output:** 6
**Explanation:** Possible longest valid concatenations are "chaers " ( "cha " + "ers ") and "acters " ( "act " + "ers ").
**Example 3:**
**Input:** arr = \[ "abcdefghijklmnopqrstuvwxyz "\]
**Output:** 26
**Explanation:** The only string in arr has all 26 characters.
**Constraints:**
* `1 <= arr.length <= 16`
* `1 <= arr[i].length <= 26`
* `arr[i]` contains only lowercase English letters. | For each square, know how many ones are up, left, down, and right of this square. You can find it in O(N^2) using dynamic programming. Now for each square ( O(N^3) ), we can evaluate whether that square is 1-bordered in O(1). |
EASY PYTHON SOLUTION USING DP | stone-game-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,nums,m,turn,dct):\n if i>=len(nums):\n return 0\n if (i,m,turn) in dct:\n return dct[(i,m,turn)]\n mx=0\n if turn:\n for j in range(1,(2*m)+1):\n x=self.dp(i+j,nums,max(m,j),False,dct)+sum(nums[i:i+j])\n mx=max(mx,x)\n dct[(i,m,turn)]=mx\n return mx\n else:\n mn=float("infinity")\n for j in range(1,(2*m)+1):\n y=self.dp(i+j,nums,max(m,j),True,dct)\n # print(y)\n mn=min(mn,y)\n dct[(i,m,turn)]=mn\n return mn\n \n\n def stoneGameII(self, piles: List[int]) -> int:\n n=len(piles)\n return self.dp(0,piles,1,True,{})\n``` | 4 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
EASY PYTHON SOLUTION USING DP | stone-game-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,nums,m,turn,dct):\n if i>=len(nums):\n return 0\n if (i,m,turn) in dct:\n return dct[(i,m,turn)]\n mx=0\n if turn:\n for j in range(1,(2*m)+1):\n x=self.dp(i+j,nums,max(m,j),False,dct)+sum(nums[i:i+j])\n mx=max(mx,x)\n dct[(i,m,turn)]=mx\n return mx\n else:\n mn=float("infinity")\n for j in range(1,(2*m)+1):\n y=self.dp(i+j,nums,max(m,j),True,dct)\n # print(y)\n mn=min(mn,y)\n dct[(i,m,turn)]=mn\n return mn\n \n\n def stoneGameII(self, piles: List[int]) -> int:\n n=len(piles)\n return self.dp(0,piles,1,True,{})\n``` | 4 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
[Python3] See this post if you are frustrating with cryptic codes. | stone-game-ii | 0 | 1 | ```\nfrom functools import cache\n\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n \n\t\t# Constants\n ALICE = 1 # To represent current turn.\n BOB = -1 # To represent current turn.\n N = len(piles)\n \n\t\t# Helpers\n @cache\n def max_piles_from(idx, m, turn): # Returns alice\'s gain from the given state.\n if idx == N:\n return 0\n\t\t\n # Note: We need to maximize alice\'s gain in alice\'s turn, minimize alice\'s gain in bob\'s turn.\n localMax = 0\n localMin = float(\'inf\')\n turnSum = 0\n \n\t\t\t# Try all choices.\n for x in range(1, min(2*m, N-idx) + 1): # harvesting index\'s upper is N-1.\n harvesting_idx = idx + x - 1\n turnSum += piles[harvesting_idx]\n next_m = max(m, x)\n \n current_turn_gain = turnSum if turn == ALICE else 0\n future_gain = max_piles_from(harvesting_idx+1, next_m, -turn) # Switching turn by multipling -1.\n \n localMax = max(localMax, current_turn_gain + future_gain)\n localMin = min(localMin, current_turn_gain + future_gain)\n \n return localMax if turn == ALICE else localMin\n \n # Main\n return max_piles_from(0, 1, ALICE)\n``` | 2 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
[Python3] See this post if you are frustrating with cryptic codes. | stone-game-ii | 0 | 1 | ```\nfrom functools import cache\n\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n \n\t\t# Constants\n ALICE = 1 # To represent current turn.\n BOB = -1 # To represent current turn.\n N = len(piles)\n \n\t\t# Helpers\n @cache\n def max_piles_from(idx, m, turn): # Returns alice\'s gain from the given state.\n if idx == N:\n return 0\n\t\t\n # Note: We need to maximize alice\'s gain in alice\'s turn, minimize alice\'s gain in bob\'s turn.\n localMax = 0\n localMin = float(\'inf\')\n turnSum = 0\n \n\t\t\t# Try all choices.\n for x in range(1, min(2*m, N-idx) + 1): # harvesting index\'s upper is N-1.\n harvesting_idx = idx + x - 1\n turnSum += piles[harvesting_idx]\n next_m = max(m, x)\n \n current_turn_gain = turnSum if turn == ALICE else 0\n future_gain = max_piles_from(harvesting_idx+1, next_m, -turn) # Switching turn by multipling -1.\n \n localMax = max(localMax, current_turn_gain + future_gain)\n localMin = min(localMin, current_turn_gain + future_gain)\n \n return localMax if turn == ALICE else localMin\n \n # Main\n return max_piles_from(0, 1, ALICE)\n``` | 2 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
Python3 Solution | stone-game-ii | 0 | 1 | \n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n def dp(i,m):\n if (i,m) in memo:\n return memo[(i,m)]\n if i>n-1:\n return 0\n ans=-sys.maxsize\n if n-i<2*m:\n ans=pre_sum[n-1]-pre_sum[i-1]\n else:\n for k in range(1,2*m+1):\n ans=max(ans,pre_sum[min(i+k-1,n-1)]-pre_sum[i-1]-dp(i+k,max(m,k)))\n \n memo[(i,m)]=ans\n return ans\n memo={}\n n=len(piles)\n pre_sum={-1:0}\n \n for i,p in enumerate(piles):\n pre_sum[i]=p+pre_sum[i-1]\n \n max_winning_scores=dp(0,1)\n \n return (pre_sum[n-1]+max_winning_scores)//2\n``` | 1 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
Python3 Solution | stone-game-ii | 0 | 1 | \n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n def dp(i,m):\n if (i,m) in memo:\n return memo[(i,m)]\n if i>n-1:\n return 0\n ans=-sys.maxsize\n if n-i<2*m:\n ans=pre_sum[n-1]-pre_sum[i-1]\n else:\n for k in range(1,2*m+1):\n ans=max(ans,pre_sum[min(i+k-1,n-1)]-pre_sum[i-1]-dp(i+k,max(m,k)))\n \n memo[(i,m)]=ans\n return ans\n memo={}\n n=len(piles)\n pre_sum={-1:0}\n \n for i,p in enumerate(piles):\n pre_sum[i]=p+pre_sum[i-1]\n \n max_winning_scores=dp(0,1)\n \n return (pre_sum[n-1]+max_winning_scores)//2\n``` | 1 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
Beating 84.33% Python Easy Solution | stone-game-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n @lru_cache(None)\n def play(i, m):\n s = sum(piles[i:])\n if i + 2 * m >= len(piles):\n return s\n return s - min(play(i + x, max(m, x)) for x in range(1, 2 * m + 1))\n return play(0, 1)\n``` | 1 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
Beating 84.33% Python Easy Solution | stone-game-ii | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n @lru_cache(None)\n def play(i, m):\n s = sum(piles[i:])\n if i + 2 * m >= len(piles):\n return s\n return s - min(play(i + x, max(m, x)) for x in range(1, 2 * m + 1))\n return play(0, 1)\n``` | 1 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
The best solutions you can find here 🦊 🚀 | stone-game-ii | 0 | 1 | # Option 1:\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n n = len(piles)\n\n @cache\n def dp(l, M=1):\n min_stones = left_stones = sum(piles[l:])\n \n R = min(l + 2*M, n) + 1\n for r in range(l+1, R):\n stones = dp(r, max(M, r - l))\n min_stones = min(min_stones, stones)\n \n return left_stones - min_stones\n\n return dp(0)\n```\n\n# Option 2: Option 1 + suffix sum of piles\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n n = len(piles)\n piles.append(0)\n for i in range(n-1, -1, -1):\n piles[i] += piles[i+1]\n\n @cache\n def dp(l, M=1):\n min_stones = left_stones = piles[l]\n\n R = min(l + 2*M, n) + 1\n for r in range(l+1, R):\n stones = dp(r, max(M, r - l))\n min_stones = min(min_stones, stones)\n \n return left_stones - min_stones\n\n return dp(0)\n``` | 3 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
The best solutions you can find here 🦊 🚀 | stone-game-ii | 0 | 1 | # Option 1:\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n n = len(piles)\n\n @cache\n def dp(l, M=1):\n min_stones = left_stones = sum(piles[l:])\n \n R = min(l + 2*M, n) + 1\n for r in range(l+1, R):\n stones = dp(r, max(M, r - l))\n min_stones = min(min_stones, stones)\n \n return left_stones - min_stones\n\n return dp(0)\n```\n\n# Option 2: Option 1 + suffix sum of piles\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n n = len(piles)\n piles.append(0)\n for i in range(n-1, -1, -1):\n piles[i] += piles[i+1]\n\n @cache\n def dp(l, M=1):\n min_stones = left_stones = piles[l]\n\n R = min(l + 2*M, n) + 1\n for r in range(l+1, R):\n stones = dp(r, max(M, r - l))\n min_stones = min(min_stones, stones)\n \n return left_stones - min_stones\n\n return dp(0)\n``` | 3 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
Image Explanation🏆- [Recursion Tree] [Recursion->Memo->Bottom Up + Suffix Sums] - C++/Java/Python | stone-game-ii | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Stone Game II` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n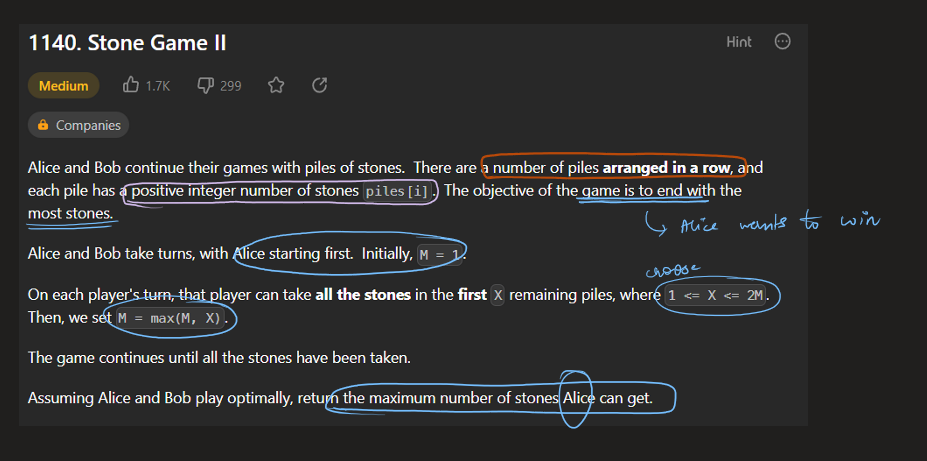\n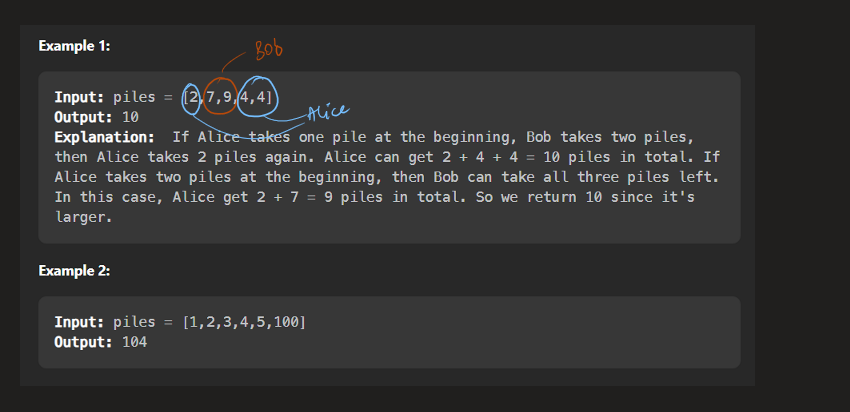\n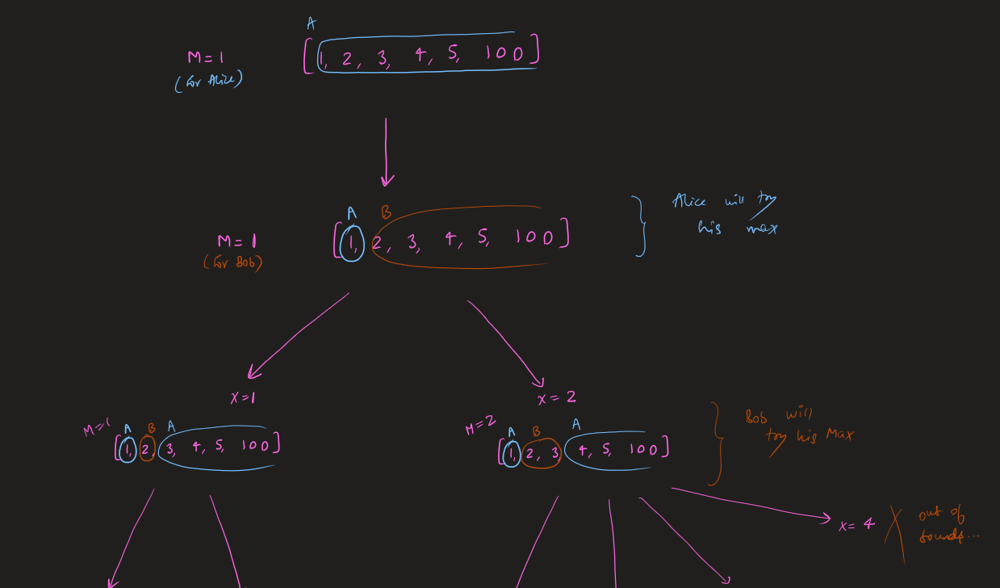\n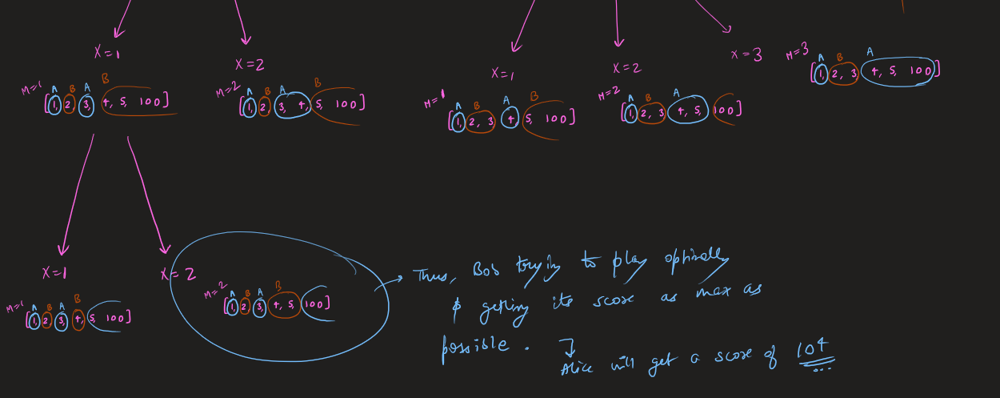\n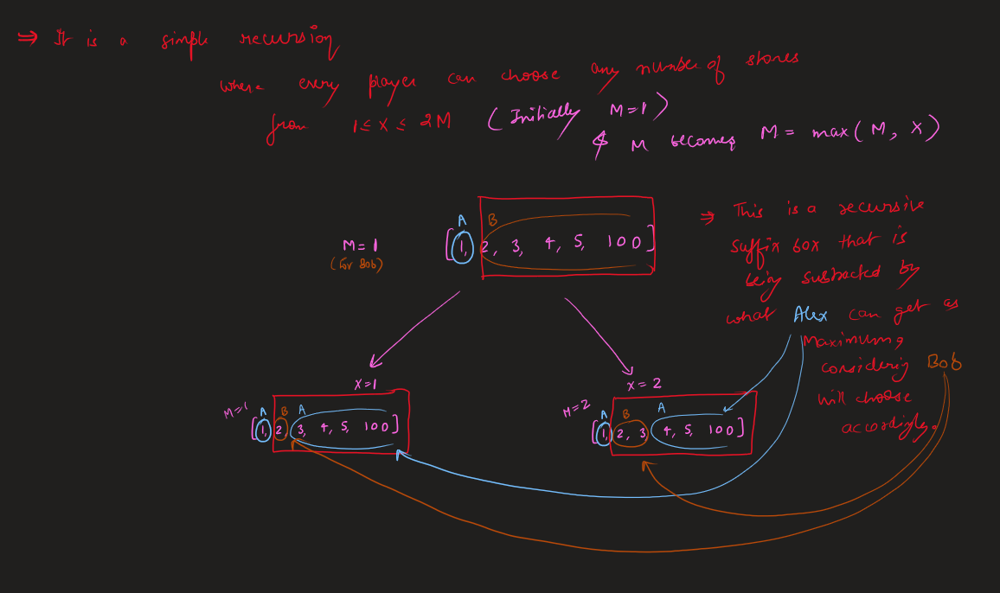\n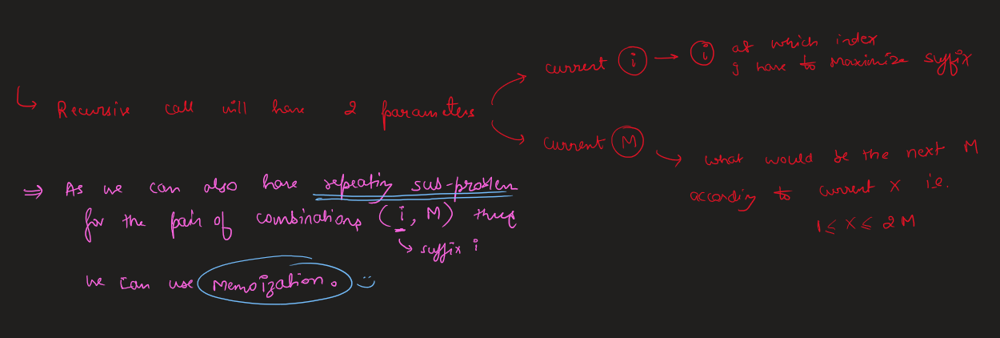\n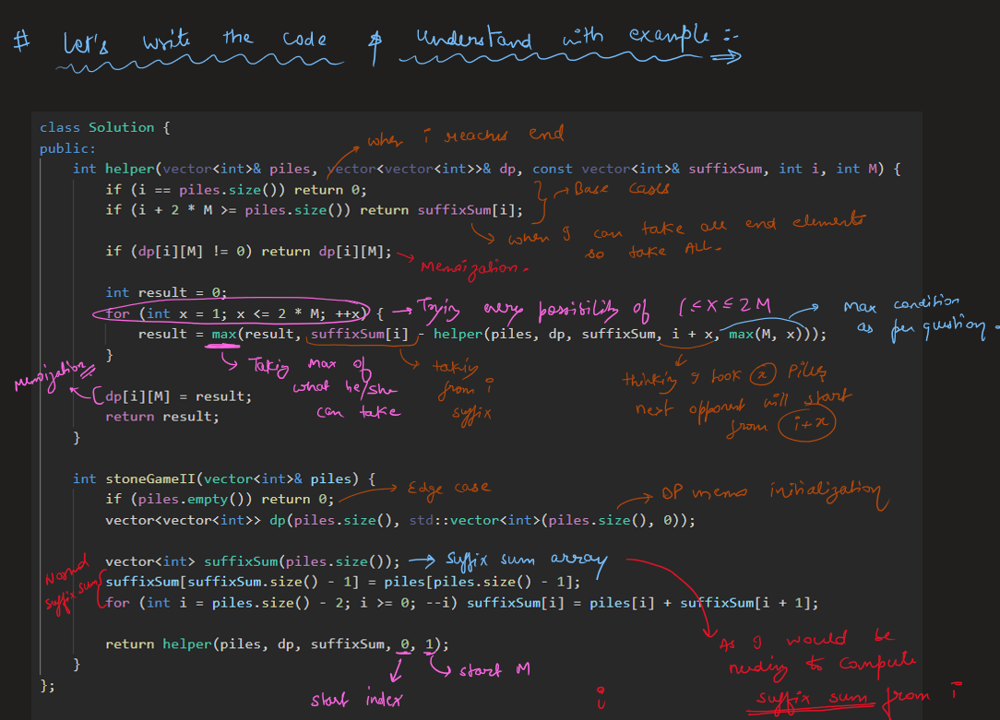\n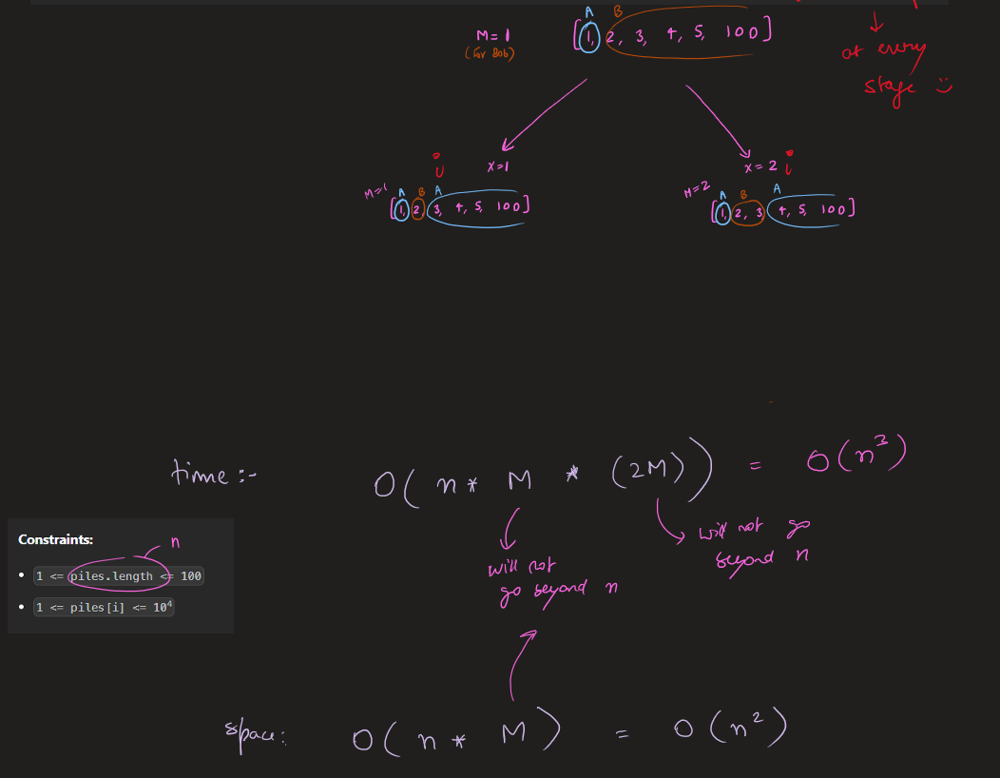\n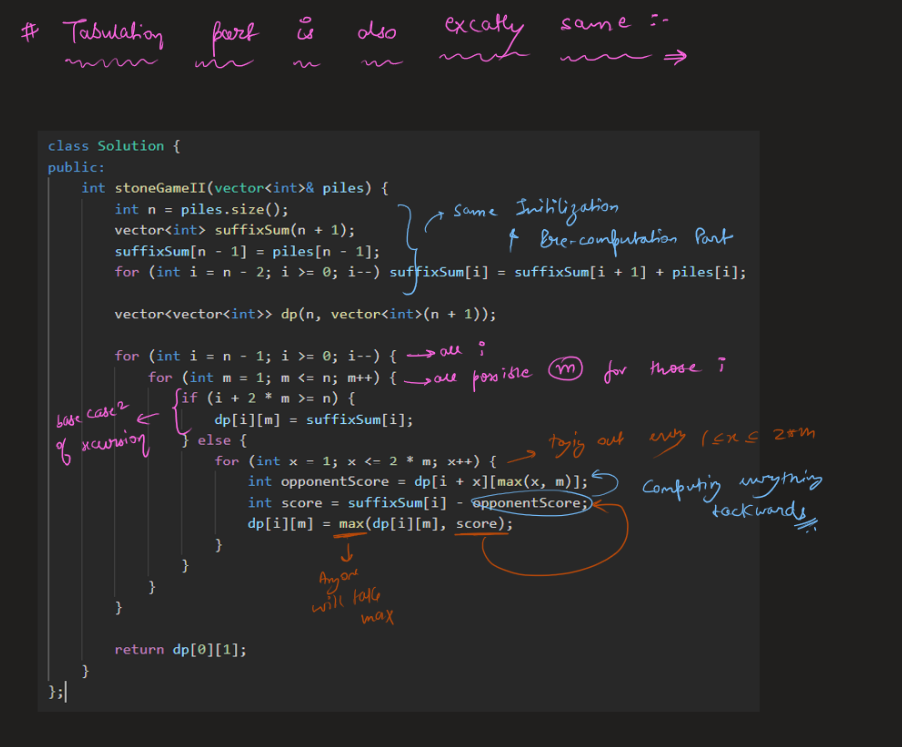\n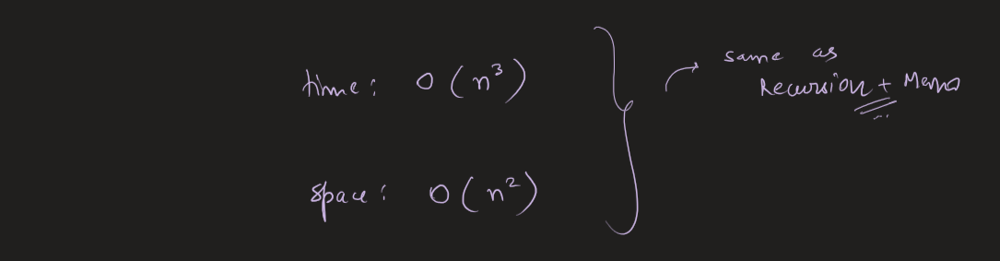\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int helper(vector<int>& piles, vector<vector<int>>& dp, const vector<int>& suffixSum, int i, int M) {\n if (i == piles.size()) return 0; \n if (i + 2 * M >= piles.size()) return suffixSum[i]; \n if (dp[i][M] != 0) return dp[i][M];\n int result = 0;\n for (int x = 1; x <= 2 * M; ++x) {\n result = max(result, suffixSum[i] - helper(piles, dp, suffixSum, i + x, max(M, x)));\n }\n dp[i][M] = result;\n return result;\n }\n int stoneGameII(vector<int>& piles) {\n if (piles.empty()) return 0;\n vector<vector<int>> dp(piles.size(), std::vector<int>(piles.size(), 0));\n vector<int> suffixSum(piles.size());\n suffixSum[suffixSum.size() - 1] = piles[piles.size() - 1];\n for (int i = piles.size() - 2; i >= 0; --i) suffixSum[i] = piles[i] + suffixSum[i + 1];\n return helper(piles, dp, suffixSum, 0, 1);\n }\n};\n```\n```Java []\nclass Solution {\n public int helper(int[] piles, int[][] dp, int[] suffixSum, int i, int M) {\n if (i == piles.length) return 0;\n if (i + 2 * M >= piles.length) return suffixSum[i];\n\n if (dp[i][M] != 0) return dp[i][M];\n\n int result = 0;\n for (int x = 1; x <= 2 * M; ++x) {\n result = Math.max(result, suffixSum[i] - helper(piles, dp, suffixSum, i + x, Math.max(M, x)));\n }\n\n dp[i][M] = result;\n return result;\n }\n\n public int stoneGameII(int[] piles) {\n if (piles.length == 0) return 0;\n int[][] dp = new int[piles.length][piles.length];\n\n int[] suffixSum = new int[piles.length];\n suffixSum[suffixSum.length - 1] = piles[piles.length - 1];\n for (int i = piles.length - 2; i >= 0; --i) suffixSum[i] = piles[i] + suffixSum[i + 1];\n\n return helper(piles, dp, suffixSum, 0, 1);\n }\n}\n```\n```Python []\nclass Solution:\n def helper(self, piles, dp, suffixSum, i, M):\n if i == len(piles):\n return 0\n if i + 2 * M >= len(piles):\n return suffixSum[i]\n\n if dp[i][M] != 0:\n return dp[i][M]\n\n result = 0\n for x in range(1, 2 * M + 1):\n result = max(result, suffixSum[i] - self.helper(piles, dp, suffixSum, i + x, max(M, x)))\n\n dp[i][M] = result\n return result\n\n def stoneGameII(self, piles):\n if not piles:\n return 0\n dp = [[0] * len(piles) for _ in range(len(piles))]\n\n suffixSum = [0] * len(piles)\n suffixSum[-1] = piles[-1]\n for i in range(len(piles) - 2, -1, -1):\n suffixSum[i] = piles[i] + suffixSum[i + 1]\n\n return self.helper(piles, dp, suffixSum, 0, 1)\n``` | 64 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
Image Explanation🏆- [Recursion Tree] [Recursion->Memo->Bottom Up + Suffix Sums] - C++/Java/Python | stone-game-ii | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Stone Game II` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n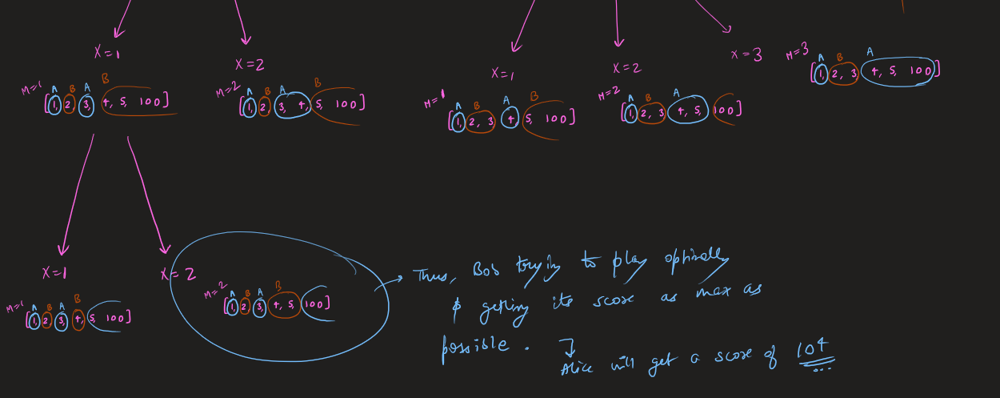\n\n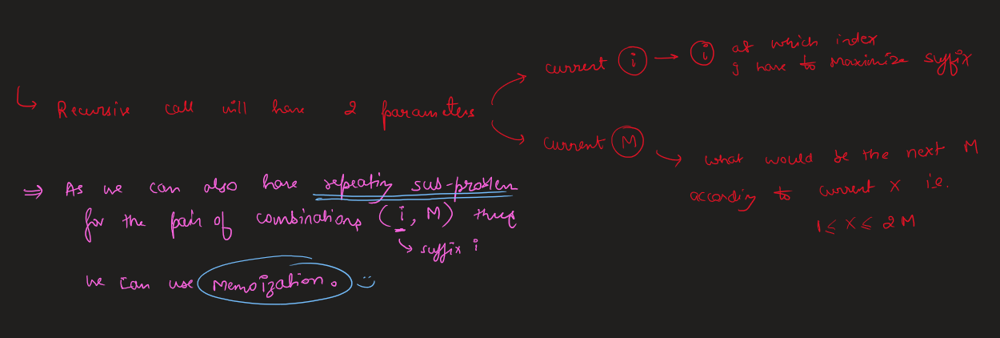\n\n\n\n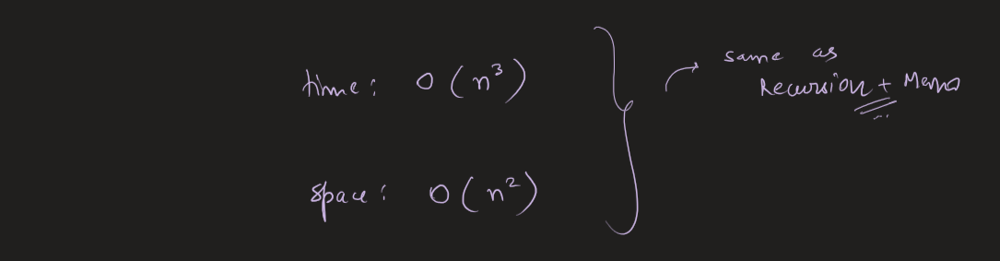\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int helper(vector<int>& piles, vector<vector<int>>& dp, const vector<int>& suffixSum, int i, int M) {\n if (i == piles.size()) return 0; \n if (i + 2 * M >= piles.size()) return suffixSum[i]; \n if (dp[i][M] != 0) return dp[i][M];\n int result = 0;\n for (int x = 1; x <= 2 * M; ++x) {\n result = max(result, suffixSum[i] - helper(piles, dp, suffixSum, i + x, max(M, x)));\n }\n dp[i][M] = result;\n return result;\n }\n int stoneGameII(vector<int>& piles) {\n if (piles.empty()) return 0;\n vector<vector<int>> dp(piles.size(), std::vector<int>(piles.size(), 0));\n vector<int> suffixSum(piles.size());\n suffixSum[suffixSum.size() - 1] = piles[piles.size() - 1];\n for (int i = piles.size() - 2; i >= 0; --i) suffixSum[i] = piles[i] + suffixSum[i + 1];\n return helper(piles, dp, suffixSum, 0, 1);\n }\n};\n```\n```Java []\nclass Solution {\n public int helper(int[] piles, int[][] dp, int[] suffixSum, int i, int M) {\n if (i == piles.length) return 0;\n if (i + 2 * M >= piles.length) return suffixSum[i];\n\n if (dp[i][M] != 0) return dp[i][M];\n\n int result = 0;\n for (int x = 1; x <= 2 * M; ++x) {\n result = Math.max(result, suffixSum[i] - helper(piles, dp, suffixSum, i + x, Math.max(M, x)));\n }\n\n dp[i][M] = result;\n return result;\n }\n\n public int stoneGameII(int[] piles) {\n if (piles.length == 0) return 0;\n int[][] dp = new int[piles.length][piles.length];\n\n int[] suffixSum = new int[piles.length];\n suffixSum[suffixSum.length - 1] = piles[piles.length - 1];\n for (int i = piles.length - 2; i >= 0; --i) suffixSum[i] = piles[i] + suffixSum[i + 1];\n\n return helper(piles, dp, suffixSum, 0, 1);\n }\n}\n```\n```Python []\nclass Solution:\n def helper(self, piles, dp, suffixSum, i, M):\n if i == len(piles):\n return 0\n if i + 2 * M >= len(piles):\n return suffixSum[i]\n\n if dp[i][M] != 0:\n return dp[i][M]\n\n result = 0\n for x in range(1, 2 * M + 1):\n result = max(result, suffixSum[i] - self.helper(piles, dp, suffixSum, i + x, max(M, x)))\n\n dp[i][M] = result\n return result\n\n def stoneGameII(self, piles):\n if not piles:\n return 0\n dp = [[0] * len(piles) for _ in range(len(piles))]\n\n suffixSum = [0] * len(piles)\n suffixSum[-1] = piles[-1]\n for i in range(len(piles) - 2, -1, -1):\n suffixSum[i] = piles[i] + suffixSum[i + 1]\n\n return self.helper(piles, dp, suffixSum, 0, 1)\n``` | 64 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
Python short and clean. Functional programming. | stone-game-ii | 0 | 1 | # Approach: Recursive DP\n\n# Complexity\n- Time complexity: $$O(n ^ 3)$$\n\n- Space complexity: $$O(n ^ 2)$$\n\nwhere, `n is number of piles.`\n\n# Code\n```python\nclass Solution:\n def stoneGameII(self, piles: list[int]) -> int:\n suffix_sums = tuple(reversed(tuple(accumulate(reversed(piles)))))\n\n @cache\n def score(i: int, m: int) -> int:\n return (i < len(piles)) and max(suffix_sums[i] - score(i + x, max(m, x)) for x in range(1, 2 * m + 1))\n \n return score(0, 1)\n\n\n``` | 2 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
Python short and clean. Functional programming. | stone-game-ii | 0 | 1 | # Approach: Recursive DP\n\n# Complexity\n- Time complexity: $$O(n ^ 3)$$\n\n- Space complexity: $$O(n ^ 2)$$\n\nwhere, `n is number of piles.`\n\n# Code\n```python\nclass Solution:\n def stoneGameII(self, piles: list[int]) -> int:\n suffix_sums = tuple(reversed(tuple(accumulate(reversed(piles)))))\n\n @cache\n def score(i: int, m: int) -> int:\n return (i < len(piles)) and max(suffix_sums[i] - score(i + x, max(m, x)) for x in range(1, 2 * m + 1))\n \n return score(0, 1)\n\n\n``` | 2 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
[python] DP Thought process explained | stone-game-ii | 0 | 1 | This was a really tough problem for me. It is so easy in the end when you got the idea, but it was pretty hard to get there (at least for me). So I\'m going to share here how I\'ve got to the optimal bottom-up DP solution for this task.\n\nThe first step was to write the straightforward top-down solution.\nThe basic idea is that on each step\n* if we\'re Alex (turn == True) then we try to pick up to `2 * M` piles and pass the turn to Lee\n* if we\'re Lee (turn == False) then we also try to pick up to `2 * M` piles and pass the turn to Alex\n\nWhile doing that\n* if we\'re Alex we try to minimize our opponent\'s (Lee) sum during next their turns\n* if we\'re Lee we try to minimize what Alex got during their turns\n\nThen we return both Lee\'s and Alex\'s sums (`sum_alex` and `sum_lee`) to reuse this information up in the call stack.\n\nThis logic brings us to the following solution (you\'ll find the snippet with `_suffix_sum` method in the end [1], since it is used in every solution here, and no reason to repeat it every time):\n\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n suffix_sum = self._suffix_sum(piles)\n\n @lru_cache(None)\n def dfs(pile: int, M: int, turn: bool) -> Tuple[int, int]:\n # turn: true - alex, false - lee\n sum_alex, sum_lee = suffix_sum[pile], suffix_sum[pile]\n\n for next_pile in range(pile + 1, min(pile + 2 * M + 1, len(piles) + 1)):\n sum_alex_next, sum_lee_next = dfs(\n next_pile, max(M, next_pile - pile), not turn\n )\n range_sum = suffix_sum[pile] - suffix_sum[next_pile]\n\n if turn:\n if sum_lee_next < sum_lee:\n sum_alex = sum_alex_next + range_sum\n sum_lee = sum_lee_next\n else:\n if sum_alex_next < sum_alex:\n sum_alex = sum_alex_next\n sum_lee = sum_lee_next + range_sum\n\n return sum_alex, sum_lee\n\n return dfs(0, 1, True)[0]\n```\nWhen the code is finished we see that the signature of the recursion function depends only on 3 arguments: `pile`, `M` and `turn`. So if there are repetitions we just cache them. And this is our first Top-Down DP soluiton.\n\nBut most of the solutions are different from this one. More conscise and don\'t use `turn` argument. So we can do better than this.\nThere is a very simple concept that I was missing and it took a while for me to figure it out.\nLet\'s look at modified Top-Down solution and then I\'ll explain how it works.\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n suffix_sum = self._suffix_sum(piles)\n\n @lru_cache(None)\n def dfs(pile: int, M: int) -> int:\n sum_next_player = suffix_sum[pile]\n\n for next_pile in range(pile + 1, min(pile + 2 * M + 1, len(piles) + 1)):\n sum_next_player = min(\n sum_next_player, dfs(next_pile, max(M, next_pile - pile))\n )\n\n sum_player = suffix_sum[pile] - sum_next_player\n\n return sum_player\n\n return dfs(0, 1)\n```\nAs you see it is almost the same, but just a bit shorter.\nSo the basic idea here is that there is no reason to have separate `sum_alex` and `sum_lee` variables, because they both sum up to `suffix_sum[pile]`\nHere is an example (`X` - we haven\'t desided yet, `A` - taken by Alex, `L` - taken by Lee)\n```\nXXXXXXXXXXAALAAALLLAALA\n ^\n\t\t pile\n```\nFrom this you can see that in order to calculate the number of piles taken by this player so far we just substract the number of the piles taken by another player from the total number of piles up to the current pile position.\nThe next important thing to notice is that minimizing sum for the one player leads to maximising it for another and vice versa.\nThis leads us to conclusion that we can do the same with just a single variable `sum_next_player`.\nThe alrorightm now looks the following way:\n* We\'re trying to pick up to `2 * M` piles from the current position and pass the turn to the next player\n* We\'re getting back from the next player the maximum sum they were able to get and trying to minimize it\n* Now when we found the minimum sum for the other player that also means we found the maximum sum for us, so return it\n\nThat\'s how we got to the nice and short Top-Down DP solution.\nThe only thing left - convert it to Bottom-Up solution to make the interviewer happy. And here is it\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n suffix_sum = self._suffix_sum(piles)\n\n dp = [[0] * (len(piles) + 1) for _ in range(len(piles) + 1)]\n\n for pile in reversed(range(len(piles))):\n for M in reversed(range(len(piles))):\n sum_next_player = suffix_sum[pile]\n\n for next_pile in range(pile + 1, min(pile + 2 * M + 1, len(piles) + 1)):\n sum_next_player = min(\n sum_next_player, dp[next_pile][max(M, next_pile - pile)]\n )\n\n sum_player = suffix_sum[pile] - sum_next_player\n\n dp[pile][M] = sum_player\n\n return dp[0][1]\n```\nAs you may see the Bottom-Up solution looks almost exactly the same in terms of the logic. And this is basically how I like to approach the conversion. Just take the Top-Down solution and convert it line-by-line to Bottom-Up. It usually works pretty well. The only difference you may spot in the body of the cycle is that we call `dp` table instead of `dfs` recursive function and that is about it.\n\nAnd this is everything I wanted to cover in this article, thank you for reading this far.\n\n[1] `_suffix_sum` method definition\n```\nclass Solution:\n @staticmethod\n def _suffix_sum(piles: List[int]) -> List[int]:\n suffix_sum = [0]\n\n for pile in reversed(piles):\n suffix_sum.append(suffix_sum[-1] + pile)\n\n suffix_sum.reverse()\n\n return suffix_sum\n``` | 43 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
[python] DP Thought process explained | stone-game-ii | 0 | 1 | This was a really tough problem for me. It is so easy in the end when you got the idea, but it was pretty hard to get there (at least for me). So I\'m going to share here how I\'ve got to the optimal bottom-up DP solution for this task.\n\nThe first step was to write the straightforward top-down solution.\nThe basic idea is that on each step\n* if we\'re Alex (turn == True) then we try to pick up to `2 * M` piles and pass the turn to Lee\n* if we\'re Lee (turn == False) then we also try to pick up to `2 * M` piles and pass the turn to Alex\n\nWhile doing that\n* if we\'re Alex we try to minimize our opponent\'s (Lee) sum during next their turns\n* if we\'re Lee we try to minimize what Alex got during their turns\n\nThen we return both Lee\'s and Alex\'s sums (`sum_alex` and `sum_lee`) to reuse this information up in the call stack.\n\nThis logic brings us to the following solution (you\'ll find the snippet with `_suffix_sum` method in the end [1], since it is used in every solution here, and no reason to repeat it every time):\n\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n suffix_sum = self._suffix_sum(piles)\n\n @lru_cache(None)\n def dfs(pile: int, M: int, turn: bool) -> Tuple[int, int]:\n # turn: true - alex, false - lee\n sum_alex, sum_lee = suffix_sum[pile], suffix_sum[pile]\n\n for next_pile in range(pile + 1, min(pile + 2 * M + 1, len(piles) + 1)):\n sum_alex_next, sum_lee_next = dfs(\n next_pile, max(M, next_pile - pile), not turn\n )\n range_sum = suffix_sum[pile] - suffix_sum[next_pile]\n\n if turn:\n if sum_lee_next < sum_lee:\n sum_alex = sum_alex_next + range_sum\n sum_lee = sum_lee_next\n else:\n if sum_alex_next < sum_alex:\n sum_alex = sum_alex_next\n sum_lee = sum_lee_next + range_sum\n\n return sum_alex, sum_lee\n\n return dfs(0, 1, True)[0]\n```\nWhen the code is finished we see that the signature of the recursion function depends only on 3 arguments: `pile`, `M` and `turn`. So if there are repetitions we just cache them. And this is our first Top-Down DP soluiton.\n\nBut most of the solutions are different from this one. More conscise and don\'t use `turn` argument. So we can do better than this.\nThere is a very simple concept that I was missing and it took a while for me to figure it out.\nLet\'s look at modified Top-Down solution and then I\'ll explain how it works.\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n suffix_sum = self._suffix_sum(piles)\n\n @lru_cache(None)\n def dfs(pile: int, M: int) -> int:\n sum_next_player = suffix_sum[pile]\n\n for next_pile in range(pile + 1, min(pile + 2 * M + 1, len(piles) + 1)):\n sum_next_player = min(\n sum_next_player, dfs(next_pile, max(M, next_pile - pile))\n )\n\n sum_player = suffix_sum[pile] - sum_next_player\n\n return sum_player\n\n return dfs(0, 1)\n```\nAs you see it is almost the same, but just a bit shorter.\nSo the basic idea here is that there is no reason to have separate `sum_alex` and `sum_lee` variables, because they both sum up to `suffix_sum[pile]`\nHere is an example (`X` - we haven\'t desided yet, `A` - taken by Alex, `L` - taken by Lee)\n```\nXXXXXXXXXXAALAAALLLAALA\n ^\n\t\t pile\n```\nFrom this you can see that in order to calculate the number of piles taken by this player so far we just substract the number of the piles taken by another player from the total number of piles up to the current pile position.\nThe next important thing to notice is that minimizing sum for the one player leads to maximising it for another and vice versa.\nThis leads us to conclusion that we can do the same with just a single variable `sum_next_player`.\nThe alrorightm now looks the following way:\n* We\'re trying to pick up to `2 * M` piles from the current position and pass the turn to the next player\n* We\'re getting back from the next player the maximum sum they were able to get and trying to minimize it\n* Now when we found the minimum sum for the other player that also means we found the maximum sum for us, so return it\n\nThat\'s how we got to the nice and short Top-Down DP solution.\nThe only thing left - convert it to Bottom-Up solution to make the interviewer happy. And here is it\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n suffix_sum = self._suffix_sum(piles)\n\n dp = [[0] * (len(piles) + 1) for _ in range(len(piles) + 1)]\n\n for pile in reversed(range(len(piles))):\n for M in reversed(range(len(piles))):\n sum_next_player = suffix_sum[pile]\n\n for next_pile in range(pile + 1, min(pile + 2 * M + 1, len(piles) + 1)):\n sum_next_player = min(\n sum_next_player, dp[next_pile][max(M, next_pile - pile)]\n )\n\n sum_player = suffix_sum[pile] - sum_next_player\n\n dp[pile][M] = sum_player\n\n return dp[0][1]\n```\nAs you may see the Bottom-Up solution looks almost exactly the same in terms of the logic. And this is basically how I like to approach the conversion. Just take the Top-Down solution and convert it line-by-line to Bottom-Up. It usually works pretty well. The only difference you may spot in the body of the cycle is that we call `dp` table instead of `dfs` recursive function and that is about it.\n\nAnd this is everything I wanted to cover in this article, thank you for reading this far.\n\n[1] `_suffix_sum` method definition\n```\nclass Solution:\n @staticmethod\n def _suffix_sum(piles: List[int]) -> List[int]:\n suffix_sum = [0]\n\n for pile in reversed(piles):\n suffix_sum.append(suffix_sum[-1] + pile)\n\n suffix_sum.reverse()\n\n return suffix_sum\n``` | 43 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.