title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Easy Python Game Theory DP solution 2D | stone-game-ii | 0 | 1 | # Intuition\nEach player at any point of the game will the stones he collects at this round and the number of stones left minus the max number of stones the other player can get.\n```\nF(M, i) = max(sum(pile[i:i + x]) + postfix[i+1] - F(max(M, x), i + x))\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: N^2\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: N^2\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n postfix = [0 for _ in piles]\n csum = 0\n for i in range(len(piles)-1 , -1, -1):\n csum += piles[i]\n postfix[i] = csum\n @functools.cache\n def dp(M, c):\n if 2 * M >= len(piles) - c:\n return sum(piles[c:])\n else:\n val = 0\n cmax = 0\n for i in range(c, min(len(piles), c + 2* M)):\n val += piles[i]\n cmax = max(val + postfix[i + 1] - dp(max(i - c + 1, M), i + 1), cmax)\n return cmax\n\n return dp(1, 0)\n\n\n\n``` | 1 | Alice and Bob continue their games with piles of stones. There are a number of piles **arranged in a row**, and each pile has a positive integer number of stones `piles[i]`. The objective of the game is to end with the most stones.
Alice and Bob take turns, with Alice starting first. Initially, `M = 1`.
On each player's turn, that player can take **all the stones** in the **first** `X` remaining piles, where `1 <= X <= 2M`. Then, we set `M = max(M, X)`.
The game continues until all the stones have been taken.
Assuming Alice and Bob play optimally, return the maximum number of stones Alice can get.
**Example 1:**
**Input:** piles = \[2,7,9,4,4\]
**Output:** 10
**Explanation:** If Alice takes one pile at the beginning, Bob takes two piles, then Alice takes 2 piles again. Alice can get 2 + 4 + 4 = 10 piles in total. If Alice takes two piles at the beginning, then Bob can take all three piles left. In this case, Alice get 2 + 7 = 9 piles in total. So we return 10 since it's larger.
**Example 2:**
**Input:** piles = \[1,2,3,4,5,100\]
**Output:** 104
**Constraints:**
* `1 <= piles.length <= 100`
* `1 <= piles[i] <= 104` | We want to always choose the most common or second most common element to write next. What data structure allows us to query this effectively? |
Easy Python Game Theory DP solution 2D | stone-game-ii | 0 | 1 | # Intuition\nEach player at any point of the game will the stones he collects at this round and the number of stones left minus the max number of stones the other player can get.\n```\nF(M, i) = max(sum(pile[i:i + x]) + postfix[i+1] - F(max(M, x), i + x))\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: N^2\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: N^2\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameII(self, piles: List[int]) -> int:\n postfix = [0 for _ in piles]\n csum = 0\n for i in range(len(piles)-1 , -1, -1):\n csum += piles[i]\n postfix[i] = csum\n @functools.cache\n def dp(M, c):\n if 2 * M >= len(piles) - c:\n return sum(piles[c:])\n else:\n val = 0\n cmax = 0\n for i in range(c, min(len(piles), c + 2* M)):\n val += piles[i]\n cmax = max(val + postfix[i + 1] - dp(max(i - c + 1, M), i + 1), cmax)\n return cmax\n\n return dp(1, 0)\n\n\n\n``` | 1 | Given a rectangle of size `n` x `m`, return _the minimum number of integer-sided squares that tile the rectangle_.
**Example 1:**
**Input:** n = 2, m = 3
**Output:** 3
**Explanation:** `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
**Example 2:**
**Input:** n = 5, m = 8
**Output:** 5
**Example 3:**
**Input:** n = 11, m = 13
**Output:** 6
**Constraints:**
* `1 <= n, m <= 13` | Use dynamic programming: the states are (i, m) for the answer of piles[i:] and that given m. |
Dynamic Programming Solution for Longest Common Subsequence Problem | longest-common-subsequence | 0 | 1 | # Intuition\nThe problem requires finding the length of the longest common subsequence (LCS) between two given strings, text1 and text2. A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.\n\nTo solve this problem, we can use dynamic programming. We\'ll create a 2D matrix, dp, where dp[i][j] represents the length of the LCS between the first i characters of text1 and the first j characters of text2.\n\n# Approach\n\n 1. Initialize a 2D matrix, dp, with dimensions (m + 1) x (n + 1) (where m is the length of text1 and n is the length of text2). Initialize all values in dp to 0.\n 2. Iterate through text1 from index 1 to m (both inclusive), and for each character text1[i - 1]:\n 3. Iterate through text2 from index 1 to n (both inclusive), and for each character text2[j - 1]:\n 4. If text1[i - 1] is equal to text2[j - 1], update dp[i][j] as dp[i - 1][j - 1] + 1. This means the current characters match, so the LCS length increases by 1.\n 5. Otherwise, take the maximum of dp[i - 1][j] (the LCS length without considering text1[i - 1]) and dp[i][j - 1] (the LCS length without considering text2[j - 1]), and assign it to dp[i][j]. This handles the case when the current characters don\'t match, so we need to consider the LCS length without one of the characters.\n 6. Finally, return dp[m][n], which represents the length of the LCS between text1 and text2.\n\n\n# Complexity\n- Time complexity:\n607ms\nBeats 96.42%of users with Python3\n\n- Space complexity:\n41.61mb\nBeats 74.89%of users with Python3\n\n# Code\n```\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n m = len(text1)\n n = len(text2)\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if text1[i - 1] == text2[j - 1]:\n dp[i][j] = dp[i - 1][j - 1] + 1\n else:\n dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])\n\n return dp[m][n]\n\n``` | 1 | Given two strings `text1` and `text2`, return _the length of their longest **common subsequence**._ If there is no **common subsequence**, return `0`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
A **common subsequence** of two strings is a subsequence that is common to both strings.
**Example 1:**
**Input:** text1 = "abcde ", text2 = "ace "
**Output:** 3
**Explanation:** The longest common subsequence is "ace " and its length is 3.
**Example 2:**
**Input:** text1 = "abc ", text2 = "abc "
**Output:** 3
**Explanation:** The longest common subsequence is "abc " and its length is 3.
**Example 3:**
**Input:** text1 = "abc ", text2 = "def "
**Output:** 0
**Explanation:** There is no such common subsequence, so the result is 0.
**Constraints:**
* `1 <= text1.length, text2.length <= 1000`
* `text1` and `text2` consist of only lowercase English characters. | Notice that each row has no duplicates. Is counting the frequency of elements enough to find the answer? Use a data structure to count the frequency of elements. Find an element whose frequency equals the number of rows. |
Dynamic Programming Solution for Longest Common Subsequence Problem | longest-common-subsequence | 0 | 1 | # Intuition\nThe problem requires finding the length of the longest common subsequence (LCS) between two given strings, text1 and text2. A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.\n\nTo solve this problem, we can use dynamic programming. We\'ll create a 2D matrix, dp, where dp[i][j] represents the length of the LCS between the first i characters of text1 and the first j characters of text2.\n\n# Approach\n\n 1. Initialize a 2D matrix, dp, with dimensions (m + 1) x (n + 1) (where m is the length of text1 and n is the length of text2). Initialize all values in dp to 0.\n 2. Iterate through text1 from index 1 to m (both inclusive), and for each character text1[i - 1]:\n 3. Iterate through text2 from index 1 to n (both inclusive), and for each character text2[j - 1]:\n 4. If text1[i - 1] is equal to text2[j - 1], update dp[i][j] as dp[i - 1][j - 1] + 1. This means the current characters match, so the LCS length increases by 1.\n 5. Otherwise, take the maximum of dp[i - 1][j] (the LCS length without considering text1[i - 1]) and dp[i][j - 1] (the LCS length without considering text2[j - 1]), and assign it to dp[i][j]. This handles the case when the current characters don\'t match, so we need to consider the LCS length without one of the characters.\n 6. Finally, return dp[m][n], which represents the length of the LCS between text1 and text2.\n\n\n# Complexity\n- Time complexity:\n607ms\nBeats 96.42%of users with Python3\n\n- Space complexity:\n41.61mb\nBeats 74.89%of users with Python3\n\n# Code\n```\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n m = len(text1)\n n = len(text2)\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if text1[i - 1] == text2[j - 1]:\n dp[i][j] = dp[i - 1][j - 1] + 1\n else:\n dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])\n\n return dp[m][n]\n\n``` | 1 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
[Java/Python 3] Two DP codes of O(mn) & O(min(m, n)) spaces w/ picture and analysis | longest-common-subsequence | 1 | 1 | **Update:**\n**Q & A:**\n\nQ1: What is the difference between `[[0] * m] * n` and `[[0] * m for _ in range(n)]`? Why does the former update all the rows of that column when I try to update one particular cell ?\nA1: `[[0] * m] * n` creates `n` references to the exactly same list objet: `[0] * m`; In contrast: `[[0] * m for _ in range(n)]` creates `n` different list objects that have same value of `[0] * m`.\n\n**End of Q & A**\n\n\n----\n\n\nPlease refer to my solution [Java/Python 3 2 Clean DP codes of O(m * n) & O(min(m, n)) space w/ breif explanation and analysis](https://leetcode.com/problems/max-dot-product-of-two-subsequences/discuss/649858/JavaPython-3-2-Clean-DP-codes-of-O(mn)-and-O(min(m-n))-space-w-breif-explanation-and-analysis.) of a similar problem: [1458. Max Dot Product of Two Subsequences](https://leetcode.com/problems/max-dot-product-of-two-subsequences/description/)\n\nMore similar LCS problems:\n[1092. Shortest Common Supersequence](https://leetcode.com/problems/shortest-common-supersequence/) and [Solution](https://leetcode.com/problems/shortest-common-supersequence/discuss/312757/JavaPython-3-O(mn)-clean-DP-code-w-picture-comments-and-analysis.)\n[1062. Longest Repeating Substring](https://leetcode.com/problems/longest-repeating-substring/) (Premium).\n[516. Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/)\n[1312. Minimum Insertion Steps to Make a String Palindrome](https://leetcode.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/discuss/470709/JavaPython-3-DP-longest-common-subsequence-w-brief-explanation-and-analysis)\n\n----\n\nFind LCS;\nLet `X` be `\u201CXMJYAUZ\u201D` and `Y` be `\u201CMZJAWXU\u201D`. The longest common subsequence between `X` and `Y` is `\u201CMJAU\u201D`. The following table shows the lengths of the longest common subsequences between prefixes of `X` and `Y`. The `ith` row and `jth` column shows the length of the LCS between `X_{1..i}` and `Y_{1..j}`.\n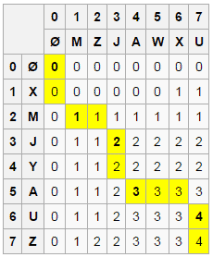\nyou can refer to [here](https://en.m.wikipedia.org/wiki/Longest_common_subsequence_problem) for more details.\n\n\n**Method 1:**\n\n```java\n public int longestCommonSubsequence(String s1, String s2) {\n int[][] dp = new int[s1.length() + 1][s2.length() + 1];\n for (int i = 0; i < s1.length(); ++i)\n for (int j = 0; j < s2.length(); ++j)\n if (s1.charAt(i) == s2.charAt(j)) dp[i + 1][j + 1] = 1 + dp[i][j];\n else dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]);\n return dp[s1.length()][s2.length()];\n }\n```\n```python\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]\n for i, c in enumerate(text1):\n for j, d in enumerate(text2):\n dp[i + 1][j + 1] = 1 + dp[i][j] if c == d else max(dp[i][j + 1], dp[i + 1][j])\n return dp[-1][-1]\n```\n**Analysis:**\n\nTime & space: O(m * n)\n\n---\n\n**Method 2:**\n\n***Space Optimization***\n\ncredit to **@FunBam** for the following picture.\n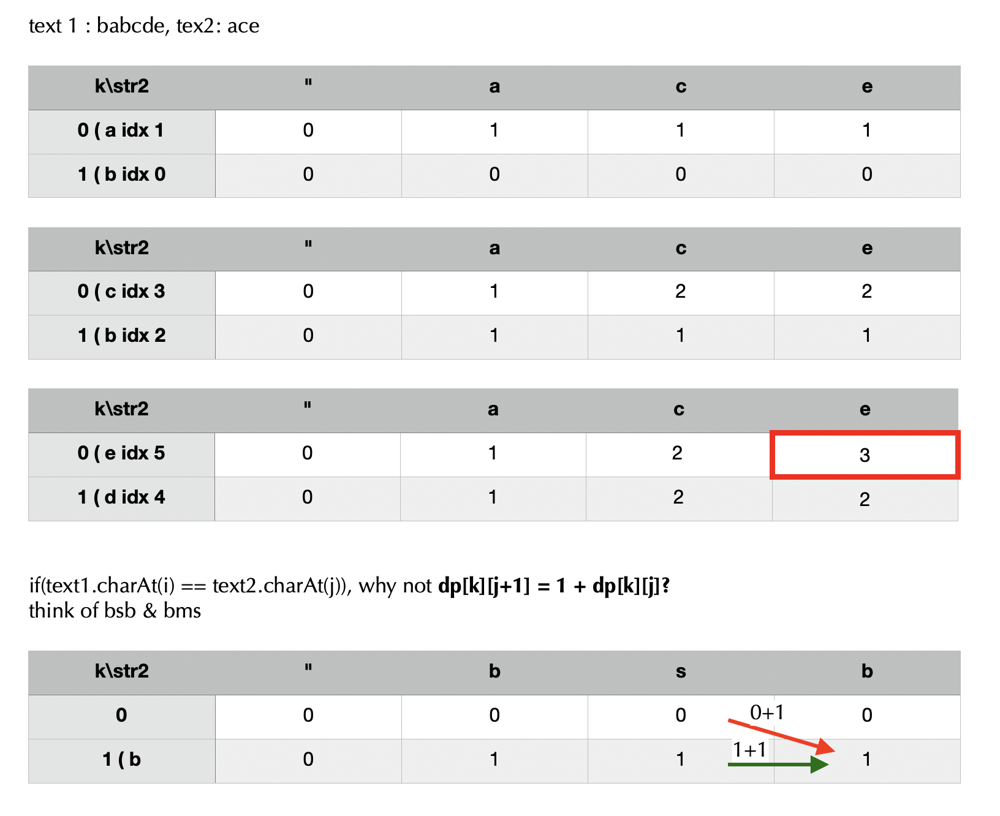\n\n\nObviously, the code in method 1 only needs information of previous row to update current row. So we just use a **two-row** 2D array to save and update the matching results for chars in `s1` and `s2`.\n\nNote: use `k ^ 1` and `k ^= 1` to switch between `dp[0] (row 0)` and `dp[1] (row 1)`.\n\n```java\n public int longestCommonSubsequence(String s1, String s2) {\n int m = s1.length(), n = s2.length();\n if (m < n) return longestCommonSubsequence(s2, s1);\n int[][] dp = new int[2][n + 1];\n for (int i = 0, k = 1; i < m; ++i, k ^= 1)\n for (int j = 0; j < n; ++j)\n if (s1.charAt(i) == s2.charAt(j)) dp[k][j + 1] = 1 + dp[k ^ 1][j];\n else dp[k][j + 1] = Math.max(dp[k ^ 1][j + 1], dp[k][j]);\n return dp[m % 2][n];\n }\n```\nNote: use `1 - i % 2` and `i % 2` to switch between `dp[0] (row 0)` and `dp[1] (row 1)`.\n```python\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n m, n = len(text1), len(text2)\n if m < n:\n tex1, tex2 = text2, text1\n dp = [[0] * (n + 1) for _ in range(2)]\n for i, c in enumerate(text1):\n for j, d in enumerate(text2):\n dp[1 - i % 2][j + 1] = 1 + dp[i % 2][j] if c == d else max(dp[i % 2][j + 1], dp[1 - i % 2][j])\n return dp[m % 2][-1]\n```\n***Further Space Optimization to save half space*** - credit to **@survive and @lenchen1112**.\n\nObviously, the above code in method 2 only needs information of previous and current columns of previous row to update current row. So we just use a **1-row** 1D array and `2` variables to save and update the matching results for chars in `text1` and `text2`.\n\n```java\n public int longestCommonSubsequence(String text1, String text2) {\n int m = text1.length(), n = text2.length();\n if (m < n) {\n return longestCommonSubsequence(text2, text1);\n }\n int[] dp = new int[n + 1];\n for (int i = 0; i < text1.length(); ++i) {\n for (int j = 0, prevRow = 0, prevRowPrevCol = 0; j < text2.length(); ++j) {\n prevRowPrevCol = prevRow;\n prevRow = dp[j + 1];\n dp[j + 1] = text1.charAt(i) == text2.charAt(j) ? prevRowPrevCol + 1 : Math.max(dp[j], prevRow);\n }\n }\n return dp[n];\n }\n```\n```python\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n m, n = map(len, (text1, text2))\n if m < n:\n tex1, tex2 = text2, text1\n dp = [0] * (n + 1)\n for c in text1:\n prevRow, prevRowPrevCol = 0, 0\n for j, d in enumerate(text2):\n prevRow, prevRowPrevCol = dp[j + 1], prevRow\n dp[j + 1] = prevRowPrevCol + 1 if c == d else max(dp[j], prevRow)\n return dp[-1]\n```\n\n**Analysis:**\n\n Time: O(m * n). space: O(min(m, n)).\n | 286 | Given two strings `text1` and `text2`, return _the length of their longest **common subsequence**._ If there is no **common subsequence**, return `0`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
A **common subsequence** of two strings is a subsequence that is common to both strings.
**Example 1:**
**Input:** text1 = "abcde ", text2 = "ace "
**Output:** 3
**Explanation:** The longest common subsequence is "ace " and its length is 3.
**Example 2:**
**Input:** text1 = "abc ", text2 = "abc "
**Output:** 3
**Explanation:** The longest common subsequence is "abc " and its length is 3.
**Example 3:**
**Input:** text1 = "abc ", text2 = "def "
**Output:** 0
**Explanation:** There is no such common subsequence, so the result is 0.
**Constraints:**
* `1 <= text1.length, text2.length <= 1000`
* `text1` and `text2` consist of only lowercase English characters. | Notice that each row has no duplicates. Is counting the frequency of elements enough to find the answer? Use a data structure to count the frequency of elements. Find an element whose frequency equals the number of rows. |
[Java/Python 3] Two DP codes of O(mn) & O(min(m, n)) spaces w/ picture and analysis | longest-common-subsequence | 1 | 1 | **Update:**\n**Q & A:**\n\nQ1: What is the difference between `[[0] * m] * n` and `[[0] * m for _ in range(n)]`? Why does the former update all the rows of that column when I try to update one particular cell ?\nA1: `[[0] * m] * n` creates `n` references to the exactly same list objet: `[0] * m`; In contrast: `[[0] * m for _ in range(n)]` creates `n` different list objects that have same value of `[0] * m`.\n\n**End of Q & A**\n\n\n----\n\n\nPlease refer to my solution [Java/Python 3 2 Clean DP codes of O(m * n) & O(min(m, n)) space w/ breif explanation and analysis](https://leetcode.com/problems/max-dot-product-of-two-subsequences/discuss/649858/JavaPython-3-2-Clean-DP-codes-of-O(mn)-and-O(min(m-n))-space-w-breif-explanation-and-analysis.) of a similar problem: [1458. Max Dot Product of Two Subsequences](https://leetcode.com/problems/max-dot-product-of-two-subsequences/description/)\n\nMore similar LCS problems:\n[1092. Shortest Common Supersequence](https://leetcode.com/problems/shortest-common-supersequence/) and [Solution](https://leetcode.com/problems/shortest-common-supersequence/discuss/312757/JavaPython-3-O(mn)-clean-DP-code-w-picture-comments-and-analysis.)\n[1062. Longest Repeating Substring](https://leetcode.com/problems/longest-repeating-substring/) (Premium).\n[516. Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/)\n[1312. Minimum Insertion Steps to Make a String Palindrome](https://leetcode.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/discuss/470709/JavaPython-3-DP-longest-common-subsequence-w-brief-explanation-and-analysis)\n\n----\n\nFind LCS;\nLet `X` be `\u201CXMJYAUZ\u201D` and `Y` be `\u201CMZJAWXU\u201D`. The longest common subsequence between `X` and `Y` is `\u201CMJAU\u201D`. The following table shows the lengths of the longest common subsequences between prefixes of `X` and `Y`. The `ith` row and `jth` column shows the length of the LCS between `X_{1..i}` and `Y_{1..j}`.\n\nyou can refer to [here](https://en.m.wikipedia.org/wiki/Longest_common_subsequence_problem) for more details.\n\n\n**Method 1:**\n\n```java\n public int longestCommonSubsequence(String s1, String s2) {\n int[][] dp = new int[s1.length() + 1][s2.length() + 1];\n for (int i = 0; i < s1.length(); ++i)\n for (int j = 0; j < s2.length(); ++j)\n if (s1.charAt(i) == s2.charAt(j)) dp[i + 1][j + 1] = 1 + dp[i][j];\n else dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]);\n return dp[s1.length()][s2.length()];\n }\n```\n```python\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]\n for i, c in enumerate(text1):\n for j, d in enumerate(text2):\n dp[i + 1][j + 1] = 1 + dp[i][j] if c == d else max(dp[i][j + 1], dp[i + 1][j])\n return dp[-1][-1]\n```\n**Analysis:**\n\nTime & space: O(m * n)\n\n---\n\n**Method 2:**\n\n***Space Optimization***\n\ncredit to **@FunBam** for the following picture.\n\n\n\nObviously, the code in method 1 only needs information of previous row to update current row. So we just use a **two-row** 2D array to save and update the matching results for chars in `s1` and `s2`.\n\nNote: use `k ^ 1` and `k ^= 1` to switch between `dp[0] (row 0)` and `dp[1] (row 1)`.\n\n```java\n public int longestCommonSubsequence(String s1, String s2) {\n int m = s1.length(), n = s2.length();\n if (m < n) return longestCommonSubsequence(s2, s1);\n int[][] dp = new int[2][n + 1];\n for (int i = 0, k = 1; i < m; ++i, k ^= 1)\n for (int j = 0; j < n; ++j)\n if (s1.charAt(i) == s2.charAt(j)) dp[k][j + 1] = 1 + dp[k ^ 1][j];\n else dp[k][j + 1] = Math.max(dp[k ^ 1][j + 1], dp[k][j]);\n return dp[m % 2][n];\n }\n```\nNote: use `1 - i % 2` and `i % 2` to switch between `dp[0] (row 0)` and `dp[1] (row 1)`.\n```python\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n m, n = len(text1), len(text2)\n if m < n:\n tex1, tex2 = text2, text1\n dp = [[0] * (n + 1) for _ in range(2)]\n for i, c in enumerate(text1):\n for j, d in enumerate(text2):\n dp[1 - i % 2][j + 1] = 1 + dp[i % 2][j] if c == d else max(dp[i % 2][j + 1], dp[1 - i % 2][j])\n return dp[m % 2][-1]\n```\n***Further Space Optimization to save half space*** - credit to **@survive and @lenchen1112**.\n\nObviously, the above code in method 2 only needs information of previous and current columns of previous row to update current row. So we just use a **1-row** 1D array and `2` variables to save and update the matching results for chars in `text1` and `text2`.\n\n```java\n public int longestCommonSubsequence(String text1, String text2) {\n int m = text1.length(), n = text2.length();\n if (m < n) {\n return longestCommonSubsequence(text2, text1);\n }\n int[] dp = new int[n + 1];\n for (int i = 0; i < text1.length(); ++i) {\n for (int j = 0, prevRow = 0, prevRowPrevCol = 0; j < text2.length(); ++j) {\n prevRowPrevCol = prevRow;\n prevRow = dp[j + 1];\n dp[j + 1] = text1.charAt(i) == text2.charAt(j) ? prevRowPrevCol + 1 : Math.max(dp[j], prevRow);\n }\n }\n return dp[n];\n }\n```\n```python\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n m, n = map(len, (text1, text2))\n if m < n:\n tex1, tex2 = text2, text1\n dp = [0] * (n + 1)\n for c in text1:\n prevRow, prevRowPrevCol = 0, 0\n for j, d in enumerate(text2):\n prevRow, prevRowPrevCol = dp[j + 1], prevRow\n dp[j + 1] = prevRowPrevCol + 1 if c == d else max(dp[j], prevRow)\n return dp[-1]\n```\n\n**Analysis:**\n\n Time: O(m * n). space: O(min(m, n)).\n | 286 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
Solution | longest-common-subsequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestCommonSubsequence(string text1, string text2) {\n int n = text1.size();\n int m = text2.size();\n \n int t[n+1][m+1];\n \n for(int i=0;i<n+1;i++)\n {\n t[i][0] = 0;\n }\n \n for(int i=1;i<m+1;i++)\n {\n t[0][i] = 0;\n }\n \n for(int i=1;i< n+1; i++)\n {\n for(int j =1; j<m+1;j++)\n {\n if(text1[i-1] == text2[j-1]) t[i][j] = 1 + t[i-1][j-1];\n else t[i][j] = max(t[i-1][j], t[i][j-1]);\n }\n }\n \n return t[n][m]; \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n l = len(text1)\n cache = [0] * l\n for let in text2:\n cnt = 0\n for i in range(l):\n if cnt < cache[i]:\n cnt = cache[i]\n elif let == text1[i]:\n cache[i] = cnt + 1\n return max(cache)\n```\n\n```Java []\nclass Solution {\n public int longestCommonSubsequence(String text1, String text2) {\n if (text2.length() > text1.length()) {\n return longestCommonSubsequence(text2, text1);\n }\n char[] t1 = text1.toCharArray();\n char[] t2 = text2.toCharArray();\n int[] prev = new int[t2.length + 1];\n int[] curr = new int[t2.length + 1];\n\n for (int pos1 = t1.length - 1; pos1 >= 0; pos1--) {\n for (int pos2 = t2.length - 1; pos2 >= 0; pos2--) {\n if (t1[pos1] == t2[pos2]) {\n curr[pos2] = 1 + prev[pos2 + 1];\n } else {\n curr[pos2] = Math.max(prev[pos2], curr[pos2 + 1]);\n }\n }\n int[] temp = prev;\n prev = curr;\n curr = temp;\n }\n\n return prev[0];\n }\n}\n```\n | 2 | Given two strings `text1` and `text2`, return _the length of their longest **common subsequence**._ If there is no **common subsequence**, return `0`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
A **common subsequence** of two strings is a subsequence that is common to both strings.
**Example 1:**
**Input:** text1 = "abcde ", text2 = "ace "
**Output:** 3
**Explanation:** The longest common subsequence is "ace " and its length is 3.
**Example 2:**
**Input:** text1 = "abc ", text2 = "abc "
**Output:** 3
**Explanation:** The longest common subsequence is "abc " and its length is 3.
**Example 3:**
**Input:** text1 = "abc ", text2 = "def "
**Output:** 0
**Explanation:** There is no such common subsequence, so the result is 0.
**Constraints:**
* `1 <= text1.length, text2.length <= 1000`
* `text1` and `text2` consist of only lowercase English characters. | Notice that each row has no duplicates. Is counting the frequency of elements enough to find the answer? Use a data structure to count the frequency of elements. Find an element whose frequency equals the number of rows. |
Solution | longest-common-subsequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestCommonSubsequence(string text1, string text2) {\n int n = text1.size();\n int m = text2.size();\n \n int t[n+1][m+1];\n \n for(int i=0;i<n+1;i++)\n {\n t[i][0] = 0;\n }\n \n for(int i=1;i<m+1;i++)\n {\n t[0][i] = 0;\n }\n \n for(int i=1;i< n+1; i++)\n {\n for(int j =1; j<m+1;j++)\n {\n if(text1[i-1] == text2[j-1]) t[i][j] = 1 + t[i-1][j-1];\n else t[i][j] = max(t[i-1][j], t[i][j-1]);\n }\n }\n \n return t[n][m]; \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str) -> int:\n l = len(text1)\n cache = [0] * l\n for let in text2:\n cnt = 0\n for i in range(l):\n if cnt < cache[i]:\n cnt = cache[i]\n elif let == text1[i]:\n cache[i] = cnt + 1\n return max(cache)\n```\n\n```Java []\nclass Solution {\n public int longestCommonSubsequence(String text1, String text2) {\n if (text2.length() > text1.length()) {\n return longestCommonSubsequence(text2, text1);\n }\n char[] t1 = text1.toCharArray();\n char[] t2 = text2.toCharArray();\n int[] prev = new int[t2.length + 1];\n int[] curr = new int[t2.length + 1];\n\n for (int pos1 = t1.length - 1; pos1 >= 0; pos1--) {\n for (int pos2 = t2.length - 1; pos2 >= 0; pos2--) {\n if (t1[pos1] == t2[pos2]) {\n curr[pos2] = 1 + prev[pos2 + 1];\n } else {\n curr[pos2] = Math.max(prev[pos2], curr[pos2 + 1]);\n }\n }\n int[] temp = prev;\n prev = curr;\n curr = temp;\n }\n\n return prev[0];\n }\n}\n```\n | 2 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
Python very detailed solution with explanation and walkthrough step by step. | longest-common-subsequence | 0 | 1 | **Why might we want to solve the longest common subsequence problem?**\n\n> File comparison. The Unix program "diff" is used to compare two different versions of the same file, to determine what changes have been made to the file. It works by finding a longest common subsequence of the lines of the two files; any line in the subsequence has not been changed, so what it displays is the remaining set of lines that have changed. In this instance of the problem we should think of each line of a file as being a single complicated character in a string.\n> \n\n### Solution\n\n#### 1. Recursive solution\n```python\n class Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n return self.helper(s1, s2, 0, 0)\n \n def helper(self, s1, s2, i, j):\n if i == len(s1) or j == len(s2):\n return 0\n if s1[i] == s2[j]:\n return 1 + self.helper(s1, s2, i + 1, j + 1)\n else:\n return max(self.helper(s1, s2, i+1, j), self.helper(s1, s2, i, j + 1))\n```\n\nIf the two strings have no matching characters, so the last line always gets executed, the the time bounds are binomial coefficients, which (if m=n) are close to 2^n.\n\n```\n\t\t\t\t\t\t\tlcs("AXYT", "AYZX")\n / \\\n lcs("AXY", "AYZX") lcs("AXYT", "AYZ")\n / \\ / \\ \n lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")\n```\n\n#### 2. Recursive solution with Memoization\n\n```python\n class Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n m = len(s1)\n n = len(s2)\n memo = [[-1 for _ in range(n + 1)] for _ in range(m + 1)]\n return self.helper(s1, s2, 0, 0, memo)\n \n def helper(self, s1, s2, i, j, memo):\n if memo[i][j] < 0:\n if i == len(s1) or j == len(s2):\n memo[i][j] = 0\n elif s1[i] == s2[j]:\n memo[i][j] = 1 + self.helper(s1, s2, i + 1, j + 1, memo)\n else:\n memo[i][j] = max(\n self.helper(s1, s2, i + 1, j, memo),\n self.helper(s1, s2, i, j + 1, memo),\n )\n return memo[i][j]\n```\n\nTime analysis: each call to subproblem takes constant time. We call it once from the main routine, and at most twice every time we fill in an entry of array L. There are (m+1)(n+1) entries, so the total number of calls is at most 2(m+1)(n+1)+1 and the time is O(mn).\n\nAs usual, this is a worst case analysis. The time might sometimes better, if not all array entries get filled out. For instance if the two strings match exactly, we\'ll only fill in diagonal entries and the algorithm will be fast.\n\n#### 3. Bottom up dynamic programming\n\nWe can view the code above as just being a slightly smarter way of doing the original recursive algorithm, saving work by not repeating subproblem computations. But it can also be thought of as a way of computing the entries in the array L. The recursive algorithm controls what order we fill them in, but we\'d get the same results if we filled them in in some other order. We might as well use something simpler, like a nested loop, that visits the array systematically. The only thing we have to worry about is that when we fill in a cell L[i,j], we need to already know the values it depends on, namely in this case L[i+1,j], L[i,j+1], and L[i+1,j+1]. For this reason we\'ll traverse the array backwards, from the last row working up to the first and from the last column working up to the first.\n\n```python\n\n class Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n m = len(s1)\n n = len(s2)\n memo = [[0 for _ in range(n + 1)] for _ in range(m + 1)]\n \n for row in range(1, m + 1):\n for col in range(1, n + 1):\n if s1[row - 1] == s2[col - 1]:\n memo[row][col] = 1 + memo[row - 1][col - 1]\n else:\n memo[row][col] = max(memo[row][col - 1], memo[row - 1][col])\n \n return memo[m][n]\n```\n\nAdvantages of this method include the fact that iteration is usually faster than recursion, we save three if statements per iteration since we don\'t need to test whether L[i,j], L[i+1,j], and L[i,j+1] have already been computed (we know in advance that the answers will be no, yes, and yes). One disadvantage over memoizing is that this fills in the entire array even when it might be possible to solve the problem by looking at only a fraction of the array\'s cells.\n\nTime complexity: O(mn) and Space complexity: O(mn)\n\n#### 4. Reduced space complexity\n\n```python\nclass Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n m = len(s1)\n n = len(s2)\n if m < n:\n return self.longestCommonSubsequence(s2, s1)\n memo = [[0 for _ in range(n + 1)] for _ in range(2)]\n\n for i in range(m):\n for j in range(n):\n if s1[i] == s2[j]:\n memo[1 - i % 2][j + 1] = 1 + memo[i % 2][j]\n else:\n memo[1 - i % 2][j + 1] = max(memo[1 - i % 2][j], memo[i % 2][j + 1])\n\n return memo[m % 2][n]\n```\n\nTime complexity: O(mn) ans Space comlexity: O(min(m, n))\n\nReference: https://www.ics.uci.edu/~eppstein/161/960229.html | 207 | Given two strings `text1` and `text2`, return _the length of their longest **common subsequence**._ If there is no **common subsequence**, return `0`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
A **common subsequence** of two strings is a subsequence that is common to both strings.
**Example 1:**
**Input:** text1 = "abcde ", text2 = "ace "
**Output:** 3
**Explanation:** The longest common subsequence is "ace " and its length is 3.
**Example 2:**
**Input:** text1 = "abc ", text2 = "abc "
**Output:** 3
**Explanation:** The longest common subsequence is "abc " and its length is 3.
**Example 3:**
**Input:** text1 = "abc ", text2 = "def "
**Output:** 0
**Explanation:** There is no such common subsequence, so the result is 0.
**Constraints:**
* `1 <= text1.length, text2.length <= 1000`
* `text1` and `text2` consist of only lowercase English characters. | Notice that each row has no duplicates. Is counting the frequency of elements enough to find the answer? Use a data structure to count the frequency of elements. Find an element whose frequency equals the number of rows. |
Python very detailed solution with explanation and walkthrough step by step. | longest-common-subsequence | 0 | 1 | **Why might we want to solve the longest common subsequence problem?**\n\n> File comparison. The Unix program "diff" is used to compare two different versions of the same file, to determine what changes have been made to the file. It works by finding a longest common subsequence of the lines of the two files; any line in the subsequence has not been changed, so what it displays is the remaining set of lines that have changed. In this instance of the problem we should think of each line of a file as being a single complicated character in a string.\n> \n\n### Solution\n\n#### 1. Recursive solution\n```python\n class Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n return self.helper(s1, s2, 0, 0)\n \n def helper(self, s1, s2, i, j):\n if i == len(s1) or j == len(s2):\n return 0\n if s1[i] == s2[j]:\n return 1 + self.helper(s1, s2, i + 1, j + 1)\n else:\n return max(self.helper(s1, s2, i+1, j), self.helper(s1, s2, i, j + 1))\n```\n\nIf the two strings have no matching characters, so the last line always gets executed, the the time bounds are binomial coefficients, which (if m=n) are close to 2^n.\n\n```\n\t\t\t\t\t\t\tlcs("AXYT", "AYZX")\n / \\\n lcs("AXY", "AYZX") lcs("AXYT", "AYZ")\n / \\ / \\ \n lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")\n```\n\n#### 2. Recursive solution with Memoization\n\n```python\n class Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n m = len(s1)\n n = len(s2)\n memo = [[-1 for _ in range(n + 1)] for _ in range(m + 1)]\n return self.helper(s1, s2, 0, 0, memo)\n \n def helper(self, s1, s2, i, j, memo):\n if memo[i][j] < 0:\n if i == len(s1) or j == len(s2):\n memo[i][j] = 0\n elif s1[i] == s2[j]:\n memo[i][j] = 1 + self.helper(s1, s2, i + 1, j + 1, memo)\n else:\n memo[i][j] = max(\n self.helper(s1, s2, i + 1, j, memo),\n self.helper(s1, s2, i, j + 1, memo),\n )\n return memo[i][j]\n```\n\nTime analysis: each call to subproblem takes constant time. We call it once from the main routine, and at most twice every time we fill in an entry of array L. There are (m+1)(n+1) entries, so the total number of calls is at most 2(m+1)(n+1)+1 and the time is O(mn).\n\nAs usual, this is a worst case analysis. The time might sometimes better, if not all array entries get filled out. For instance if the two strings match exactly, we\'ll only fill in diagonal entries and the algorithm will be fast.\n\n#### 3. Bottom up dynamic programming\n\nWe can view the code above as just being a slightly smarter way of doing the original recursive algorithm, saving work by not repeating subproblem computations. But it can also be thought of as a way of computing the entries in the array L. The recursive algorithm controls what order we fill them in, but we\'d get the same results if we filled them in in some other order. We might as well use something simpler, like a nested loop, that visits the array systematically. The only thing we have to worry about is that when we fill in a cell L[i,j], we need to already know the values it depends on, namely in this case L[i+1,j], L[i,j+1], and L[i+1,j+1]. For this reason we\'ll traverse the array backwards, from the last row working up to the first and from the last column working up to the first.\n\n```python\n\n class Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n m = len(s1)\n n = len(s2)\n memo = [[0 for _ in range(n + 1)] for _ in range(m + 1)]\n \n for row in range(1, m + 1):\n for col in range(1, n + 1):\n if s1[row - 1] == s2[col - 1]:\n memo[row][col] = 1 + memo[row - 1][col - 1]\n else:\n memo[row][col] = max(memo[row][col - 1], memo[row - 1][col])\n \n return memo[m][n]\n```\n\nAdvantages of this method include the fact that iteration is usually faster than recursion, we save three if statements per iteration since we don\'t need to test whether L[i,j], L[i+1,j], and L[i,j+1] have already been computed (we know in advance that the answers will be no, yes, and yes). One disadvantage over memoizing is that this fills in the entire array even when it might be possible to solve the problem by looking at only a fraction of the array\'s cells.\n\nTime complexity: O(mn) and Space complexity: O(mn)\n\n#### 4. Reduced space complexity\n\n```python\nclass Solution:\n def longestCommonSubsequence(self, s1: str, s2: str) -> int:\n m = len(s1)\n n = len(s2)\n if m < n:\n return self.longestCommonSubsequence(s2, s1)\n memo = [[0 for _ in range(n + 1)] for _ in range(2)]\n\n for i in range(m):\n for j in range(n):\n if s1[i] == s2[j]:\n memo[1 - i % 2][j + 1] = 1 + memo[i % 2][j]\n else:\n memo[1 - i % 2][j + 1] = max(memo[1 - i % 2][j], memo[i % 2][j + 1])\n\n return memo[m % 2][n]\n```\n\nTime complexity: O(mn) ans Space comlexity: O(min(m, n))\n\nReference: https://www.ics.uci.edu/~eppstein/161/960229.html | 207 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
Python (96% beats) || Tabulation || DP || Memorization || Optimize Way + 2D Matrix way | longest-common-subsequence | 0 | 1 | Try this also Similar to LCS:\n[516. Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/solutions/4122315/python-9972-beats-tabulation-memorization-lcs/)\n[583. Delete Operation for Two Strings](https://leetcode.com/problems/delete-operation-for-two-strings/solutions/4122272/python-9964-beats-tabulation-dp-using-lcs/)\n\n# Code\n> # Optimize Way\n```\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str):\n l1 = len(text1)\n l2 = len(text2)\n\n prev = [0 for j in range(l2+1)] \n\n for i in range(1,l1+1):\n curr = [0 for x in range(l2+1)] \n for j in range(1,l2+1):\n if text1[i-1] == text2[j-1]:\n curr[j] = prev[j-1] + 1\n else:\n curr[j] = max(curr[j-1], prev[j])\n \n prev = curr\n\n return curr[l2]\n\n\n```\n\n> # Simple Way 2D Matrix - not optimize\n```\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str):\n l1 = len(text1)\n l2 = len(text2)\n\n dp = [[0 for j in range(l2+1)] for i in range(l1+1)]\n\n for i in range(1,l1+1):\n for j in range(1,l2+1):\n if text1[i-1] == text2[j-1]:\n dp[i][j] = dp[i-1][j-1] + 1\n else:\n dp[i][j] = max(dp[i-1][j], dp[i][j-1])\n\n return dp[l1][l2]\n\n\n```\n\n# Your upvote is my motivation!\n\n. | 6 | Given two strings `text1` and `text2`, return _the length of their longest **common subsequence**._ If there is no **common subsequence**, return `0`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
A **common subsequence** of two strings is a subsequence that is common to both strings.
**Example 1:**
**Input:** text1 = "abcde ", text2 = "ace "
**Output:** 3
**Explanation:** The longest common subsequence is "ace " and its length is 3.
**Example 2:**
**Input:** text1 = "abc ", text2 = "abc "
**Output:** 3
**Explanation:** The longest common subsequence is "abc " and its length is 3.
**Example 3:**
**Input:** text1 = "abc ", text2 = "def "
**Output:** 0
**Explanation:** There is no such common subsequence, so the result is 0.
**Constraints:**
* `1 <= text1.length, text2.length <= 1000`
* `text1` and `text2` consist of only lowercase English characters. | Notice that each row has no duplicates. Is counting the frequency of elements enough to find the answer? Use a data structure to count the frequency of elements. Find an element whose frequency equals the number of rows. |
Python (96% beats) || Tabulation || DP || Memorization || Optimize Way + 2D Matrix way | longest-common-subsequence | 0 | 1 | Try this also Similar to LCS:\n[516. Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/solutions/4122315/python-9972-beats-tabulation-memorization-lcs/)\n[583. Delete Operation for Two Strings](https://leetcode.com/problems/delete-operation-for-two-strings/solutions/4122272/python-9964-beats-tabulation-dp-using-lcs/)\n\n# Code\n> # Optimize Way\n```\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str):\n l1 = len(text1)\n l2 = len(text2)\n\n prev = [0 for j in range(l2+1)] \n\n for i in range(1,l1+1):\n curr = [0 for x in range(l2+1)] \n for j in range(1,l2+1):\n if text1[i-1] == text2[j-1]:\n curr[j] = prev[j-1] + 1\n else:\n curr[j] = max(curr[j-1], prev[j])\n \n prev = curr\n\n return curr[l2]\n\n\n```\n\n> # Simple Way 2D Matrix - not optimize\n```\nclass Solution:\n def longestCommonSubsequence(self, text1: str, text2: str):\n l1 = len(text1)\n l2 = len(text2)\n\n dp = [[0 for j in range(l2+1)] for i in range(l1+1)]\n\n for i in range(1,l1+1):\n for j in range(1,l2+1):\n if text1[i-1] == text2[j-1]:\n dp[i][j] = dp[i-1][j-1] + 1\n else:\n dp[i][j] = max(dp[i-1][j], dp[i][j-1])\n\n return dp[l1][l2]\n\n\n```\n\n# Your upvote is my motivation!\n\n. | 6 | Given an array `nums` of positive integers. Your task is to select some subset of `nums`, multiply each element by an integer and add all these numbers. The array is said to be **good** if you can obtain a sum of `1` from the array by any possible subset and multiplicand.
Return `True` if the array is **good** otherwise return `False`.
**Example 1:**
**Input:** nums = \[12,5,7,23\]
**Output:** true
**Explanation:** Pick numbers 5 and 7.
5\*3 + 7\*(-2) = 1
**Example 2:**
**Input:** nums = \[29,6,10\]
**Output:** true
**Explanation:** Pick numbers 29, 6 and 10.
29\*1 + 6\*(-3) + 10\*(-1) = 1
**Example 3:**
**Input:** nums = \[3,6\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 10^5`
* `1 <= nums[i] <= 10^9` | Try dynamic programming.
DP[i][j] represents the longest common subsequence of text1[0 ... i] & text2[0 ... j]. DP[i][j] = DP[i - 1][j - 1] + 1 , if text1[i] == text2[j]
DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]) , otherwise |
80% TC and 76% SC easy python solution | decrease-elements-to-make-array-zigzag | 0 | 1 | ```\ndef movesToMakeZigzag(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tif(n == 1):\n\t\treturn 0\n\tt1 = t2 = 0\n\tfor i in range(n):\n\t\t# for t1\n\t\tif(i % 2):\n\t\t\tif(i == n-1):\n\t\t\t\tt1 += max(0, nums[i] - nums[i-1] + 1)\n\t\t\telse:\n\t\t\t\tt1 += max(0, nums[i] - min(nums[i+1], nums[i-1]) + 1)\n\n\t\t# for t2\n\t\telse:\n\t\t\tif(i == 0):\n\t\t\t\tt2 += max(0, nums[i] - nums[i+1] + 1)\n\t\t\telif(i == n-1):\n\t\t\t\tt2 += max(0, nums[i] - nums[i-1] + 1)\n\t\t\telse:\n\t\t\t\tt2 += max(0, nums[i] - min(nums[i+1], nums[i-1]) + 1)\n\treturn min(t1, t2)\n``` | 1 | Given an array `nums` of integers, a _move_ consists of choosing any element and **decreasing it by 1**.
An array `A` is a _zigzag array_ if either:
* Every even-indexed element is greater than adjacent elements, ie. `A[0] > A[1] < A[2] > A[3] < A[4] > ...`
* OR, every odd-indexed element is greater than adjacent elements, ie. `A[0] < A[1] > A[2] < A[3] > A[4] < ...`
Return the minimum number of moves to transform the given array `nums` into a zigzag array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** We can decrease 2 to 0 or 3 to 1.
**Example 2:**
**Input:** nums = \[9,6,1,6,2\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | What if we model this problem as a graph problem? A house is a node and a pipe is a weighted edge. How to represent building wells in the graph model? Add a virtual node, connect it to houses with edges weighted by the costs to build wells in these houses. The problem is now reduced to a Minimum Spanning Tree problem. |
80% TC and 76% SC easy python solution | decrease-elements-to-make-array-zigzag | 0 | 1 | ```\ndef movesToMakeZigzag(self, nums: List[int]) -> int:\n\tn = len(nums)\n\tif(n == 1):\n\t\treturn 0\n\tt1 = t2 = 0\n\tfor i in range(n):\n\t\t# for t1\n\t\tif(i % 2):\n\t\t\tif(i == n-1):\n\t\t\t\tt1 += max(0, nums[i] - nums[i-1] + 1)\n\t\t\telse:\n\t\t\t\tt1 += max(0, nums[i] - min(nums[i+1], nums[i-1]) + 1)\n\n\t\t# for t2\n\t\telse:\n\t\t\tif(i == 0):\n\t\t\t\tt2 += max(0, nums[i] - nums[i+1] + 1)\n\t\t\telif(i == n-1):\n\t\t\t\tt2 += max(0, nums[i] - nums[i-1] + 1)\n\t\t\telse:\n\t\t\t\tt2 += max(0, nums[i] - min(nums[i+1], nums[i-1]) + 1)\n\treturn min(t1, t2)\n``` | 1 | You are given two strings `s1` and `s2` of equal length consisting of letters `"x "` and `"y "` **only**. Your task is to make these two strings equal to each other. You can swap any two characters that belong to **different** strings, which means: swap `s1[i]` and `s2[j]`.
Return the minimum number of swaps required to make `s1` and `s2` equal, or return `-1` if it is impossible to do so.
**Example 1:**
**Input:** s1 = "xx ", s2 = "yy "
**Output:** 1
**Explanation:** Swap s1\[0\] and s2\[1\], s1 = "yx ", s2 = "yx ".
**Example 2:**
**Input:** s1 = "xy ", s2 = "yx "
**Output:** 2
**Explanation:** Swap s1\[0\] and s2\[0\], s1 = "yy ", s2 = "xx ".
Swap s1\[0\] and s2\[1\], s1 = "xy ", s2 = "xy ".
Note that you cannot swap s1\[0\] and s1\[1\] to make s1 equal to "yx ", cause we can only swap chars in different strings.
**Example 3:**
**Input:** s1 = "xx ", s2 = "xy "
**Output:** -1
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1.length == s2.length`
* `s1, s2` only contain `'x'` or `'y'`. | Do each case (even indexed is greater, odd indexed is greater) separately. In say the even case, you should decrease each even-indexed element until it is lower than its immediate neighbors. |
Python3: TC O(N), SC O(1): DP | decrease-elements-to-make-array-zigzag | 0 | 1 | # Intuition\n\nUsually a sequence problem can be solved starting at index `i` if you know the answer for `i+1`. This is because you can have the answer for `i+1:`, and then prepend `i`.\n\nIn this case there are two choices for prepending `i` to a zigzag sequence formed from `i+1`:\n1. up case: decrease `nums[i]` if needed, then prepend to the down-up sequence from i+1\n 1. cost is `decreaseAmount + dncost`, where `dncost` is the amount needed to make i+1: into a down-up-down-... zigzag\n2. dn case: decrease `nums[i+1]` if needed, then prepend to the up-down-up.. zigzag from i+1\n 1. cost is `decreaseAmount + upcost`, same as (1)\n 2. we may have decreased `nums[i+1]` already to make an up-down sequence (see (1)), so we should refer to value AFTER we did that decrement, not before. We can record this post-decrement value as `upval`, i.e. the first element in the up-down-up.. zigzag\n 3. `upval` we know is less than the next value, because we made a zigzag with the up-down-up.. pattern by definition. So we can decrease it even more to prepend i to make a down-up-down zigzag. I had a bug originally where I moved *all* the elements down, but that\'s not necessary. Just decrease `upval`\n\n# Approach\n\nThe hardest part of this problem is dealing with a combination of "index hell" and "up/down vs down/up hell" and "upval/dnval vs nums[i] vs nums[i+1]" hell.\n\nLots of tricky edge cases to get right. My first several submissions had bugs in them.\n\nI don\'t know of a good way to avoid these in an interview. In fact, under time pressure and with someone staring at you, it seems MORE likely to get bugs.\n\nSo maybe a better way to go is to use O(N) extra space instead of O(1) so that the indexing and state keeping is a bit simpler to start, then refine the solution if you have time... but then the interviewer might think that you *can\'t* optimize the space complexity and think you\'re a worse coder than you are. But if you try and have some bugs, then you\'ll lose points for that too. I guess you can\'t win :(\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N), we do O(1) work for each of O(N) elements\n\n- Space complexity: O(1), a couple of scalars\n\n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, nums: List[int]) -> int:\n # can only decrease elements to make zigzag\n # two states: given i, next element is larger\n # next element is smaller\n\n # suppose we know the cost to make i:end zigzag for i:\n \n # then cost[i],up is\n # if nums[i] < nums[i+1] AFTER zz stuff, cost is cost[i+1][dn], can prepend nums[i] -up-> nums[i+1], then down from there\n # if nums[i] >= nums[i+1] " ", cost is nums[i]-nums[i+1]+1 to decrease nums[i], then modified nums[i] -up-> nums[i+1] -dn->..\n \n # cost[i],dn is\n # if nums[i] > nums[i+1][up]: it\'s free to append\n # else nums[i] < nums[i+1][up]: decrement the N-i-1 later numbers by nums[i+1][up]-nums[i]+1, then prepend\n\n\n N = len(nums)\n upcost = 0 # to make dn zigzag starting from next element\n dncost = 0 # to make up zigzag starting from next element\n upval = nums[-1] # i+1 after zigzag modifications for i+1 -> up\n dnval = nums[-1] # i+1 -> dn\n\n for i in range(N-2, -1, -1):\n # i -> up\n if nums[i] < dnval:\n # i -> up -> i+1 -> dn .. requires no further operations\n new_upcost = dncost\n new_upval = nums[i]\n else:\n new_upval = dnval-1\n new_upcost = nums[i]-new_upval + dncost\n\n # i -> dn\n if nums[i] <= upval:\n # drag rest of numbers down <-- WRONG\n # FIX: for up cost, upval just needs to be less than later elements\n # if we decrease upval (further), then it\'s still less. So no need to change later elements.\n new_dncost = (upval-nums[i]+1) + upcost\n new_dnval = nums[i]\n # dnval doesn\'t change, can\'t increase it\n else:\n # nums[i] -> dn -> nums[i+1] -> up is free\n new_dncost = upcost\n new_dnval = nums[i]\n\n dncost = new_dncost\n upcost = new_upcost\n upval = new_upval\n dnval = new_dnval\n\n # TODO: simplifications are possible, but at the cost of not being intuitive\n # dnval is always nums[i+1] so all dnval accesses can be changed, and all updates elided\n # \n\n # print(f"i={i}: {upcost=}, {dncost=}")\n\n return min(upcost, dncost)\n``` | 0 | Given an array `nums` of integers, a _move_ consists of choosing any element and **decreasing it by 1**.
An array `A` is a _zigzag array_ if either:
* Every even-indexed element is greater than adjacent elements, ie. `A[0] > A[1] < A[2] > A[3] < A[4] > ...`
* OR, every odd-indexed element is greater than adjacent elements, ie. `A[0] < A[1] > A[2] < A[3] > A[4] < ...`
Return the minimum number of moves to transform the given array `nums` into a zigzag array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** We can decrease 2 to 0 or 3 to 1.
**Example 2:**
**Input:** nums = \[9,6,1,6,2\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | What if we model this problem as a graph problem? A house is a node and a pipe is a weighted edge. How to represent building wells in the graph model? Add a virtual node, connect it to houses with edges weighted by the costs to build wells in these houses. The problem is now reduced to a Minimum Spanning Tree problem. |
Python3: TC O(N), SC O(1): DP | decrease-elements-to-make-array-zigzag | 0 | 1 | # Intuition\n\nUsually a sequence problem can be solved starting at index `i` if you know the answer for `i+1`. This is because you can have the answer for `i+1:`, and then prepend `i`.\n\nIn this case there are two choices for prepending `i` to a zigzag sequence formed from `i+1`:\n1. up case: decrease `nums[i]` if needed, then prepend to the down-up sequence from i+1\n 1. cost is `decreaseAmount + dncost`, where `dncost` is the amount needed to make i+1: into a down-up-down-... zigzag\n2. dn case: decrease `nums[i+1]` if needed, then prepend to the up-down-up.. zigzag from i+1\n 1. cost is `decreaseAmount + upcost`, same as (1)\n 2. we may have decreased `nums[i+1]` already to make an up-down sequence (see (1)), so we should refer to value AFTER we did that decrement, not before. We can record this post-decrement value as `upval`, i.e. the first element in the up-down-up.. zigzag\n 3. `upval` we know is less than the next value, because we made a zigzag with the up-down-up.. pattern by definition. So we can decrease it even more to prepend i to make a down-up-down zigzag. I had a bug originally where I moved *all* the elements down, but that\'s not necessary. Just decrease `upval`\n\n# Approach\n\nThe hardest part of this problem is dealing with a combination of "index hell" and "up/down vs down/up hell" and "upval/dnval vs nums[i] vs nums[i+1]" hell.\n\nLots of tricky edge cases to get right. My first several submissions had bugs in them.\n\nI don\'t know of a good way to avoid these in an interview. In fact, under time pressure and with someone staring at you, it seems MORE likely to get bugs.\n\nSo maybe a better way to go is to use O(N) extra space instead of O(1) so that the indexing and state keeping is a bit simpler to start, then refine the solution if you have time... but then the interviewer might think that you *can\'t* optimize the space complexity and think you\'re a worse coder than you are. But if you try and have some bugs, then you\'ll lose points for that too. I guess you can\'t win :(\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N), we do O(1) work for each of O(N) elements\n\n- Space complexity: O(1), a couple of scalars\n\n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, nums: List[int]) -> int:\n # can only decrease elements to make zigzag\n # two states: given i, next element is larger\n # next element is smaller\n\n # suppose we know the cost to make i:end zigzag for i:\n \n # then cost[i],up is\n # if nums[i] < nums[i+1] AFTER zz stuff, cost is cost[i+1][dn], can prepend nums[i] -up-> nums[i+1], then down from there\n # if nums[i] >= nums[i+1] " ", cost is nums[i]-nums[i+1]+1 to decrease nums[i], then modified nums[i] -up-> nums[i+1] -dn->..\n \n # cost[i],dn is\n # if nums[i] > nums[i+1][up]: it\'s free to append\n # else nums[i] < nums[i+1][up]: decrement the N-i-1 later numbers by nums[i+1][up]-nums[i]+1, then prepend\n\n\n N = len(nums)\n upcost = 0 # to make dn zigzag starting from next element\n dncost = 0 # to make up zigzag starting from next element\n upval = nums[-1] # i+1 after zigzag modifications for i+1 -> up\n dnval = nums[-1] # i+1 -> dn\n\n for i in range(N-2, -1, -1):\n # i -> up\n if nums[i] < dnval:\n # i -> up -> i+1 -> dn .. requires no further operations\n new_upcost = dncost\n new_upval = nums[i]\n else:\n new_upval = dnval-1\n new_upcost = nums[i]-new_upval + dncost\n\n # i -> dn\n if nums[i] <= upval:\n # drag rest of numbers down <-- WRONG\n # FIX: for up cost, upval just needs to be less than later elements\n # if we decrease upval (further), then it\'s still less. So no need to change later elements.\n new_dncost = (upval-nums[i]+1) + upcost\n new_dnval = nums[i]\n # dnval doesn\'t change, can\'t increase it\n else:\n # nums[i] -> dn -> nums[i+1] -> up is free\n new_dncost = upcost\n new_dnval = nums[i]\n\n dncost = new_dncost\n upcost = new_upcost\n upval = new_upval\n dnval = new_dnval\n\n # TODO: simplifications are possible, but at the cost of not being intuitive\n # dnval is always nums[i+1] so all dnval accesses can be changed, and all updates elided\n # \n\n # print(f"i={i}: {upcost=}, {dncost=}")\n\n return min(upcost, dncost)\n``` | 0 | You are given two strings `s1` and `s2` of equal length consisting of letters `"x "` and `"y "` **only**. Your task is to make these two strings equal to each other. You can swap any two characters that belong to **different** strings, which means: swap `s1[i]` and `s2[j]`.
Return the minimum number of swaps required to make `s1` and `s2` equal, or return `-1` if it is impossible to do so.
**Example 1:**
**Input:** s1 = "xx ", s2 = "yy "
**Output:** 1
**Explanation:** Swap s1\[0\] and s2\[1\], s1 = "yx ", s2 = "yx ".
**Example 2:**
**Input:** s1 = "xy ", s2 = "yx "
**Output:** 2
**Explanation:** Swap s1\[0\] and s2\[0\], s1 = "yy ", s2 = "xx ".
Swap s1\[0\] and s2\[1\], s1 = "xy ", s2 = "xy ".
Note that you cannot swap s1\[0\] and s1\[1\] to make s1 equal to "yx ", cause we can only swap chars in different strings.
**Example 3:**
**Input:** s1 = "xx ", s2 = "xy "
**Output:** -1
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1.length == s2.length`
* `s1, s2` only contain `'x'` or `'y'`. | Do each case (even indexed is greater, odd indexed is greater) separately. In say the even case, you should decrease each even-indexed element until it is lower than its immediate neighbors. |
O(n) solution that beats 98% | decrease-elements-to-make-array-zigzag | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, nums: List[int]) -> int:\n \n n = len(nums)\n\n def check(start):\n t = 0\n for i in range(start, n, 2):\n has_left = i > 0\n has_right = i < n - 1\n smallest_neighbor = 0\n if has_left and has_right:\n smallest_neighbor = min(nums[i-1], nums[i+1])\n elif has_left:\n smallest_neighbor = nums[i-1]\n elif has_right:\n smallest_neighbor = nums[i+1]\n if smallest_neighbor <= nums[i]:\n t += nums[i] - smallest_neighbor + 1\n return t\n\n return min(check(0), check(1))\n``` | 0 | Given an array `nums` of integers, a _move_ consists of choosing any element and **decreasing it by 1**.
An array `A` is a _zigzag array_ if either:
* Every even-indexed element is greater than adjacent elements, ie. `A[0] > A[1] < A[2] > A[3] < A[4] > ...`
* OR, every odd-indexed element is greater than adjacent elements, ie. `A[0] < A[1] > A[2] < A[3] > A[4] < ...`
Return the minimum number of moves to transform the given array `nums` into a zigzag array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** We can decrease 2 to 0 or 3 to 1.
**Example 2:**
**Input:** nums = \[9,6,1,6,2\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | What if we model this problem as a graph problem? A house is a node and a pipe is a weighted edge. How to represent building wells in the graph model? Add a virtual node, connect it to houses with edges weighted by the costs to build wells in these houses. The problem is now reduced to a Minimum Spanning Tree problem. |
O(n) solution that beats 98% | decrease-elements-to-make-array-zigzag | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, nums: List[int]) -> int:\n \n n = len(nums)\n\n def check(start):\n t = 0\n for i in range(start, n, 2):\n has_left = i > 0\n has_right = i < n - 1\n smallest_neighbor = 0\n if has_left and has_right:\n smallest_neighbor = min(nums[i-1], nums[i+1])\n elif has_left:\n smallest_neighbor = nums[i-1]\n elif has_right:\n smallest_neighbor = nums[i+1]\n if smallest_neighbor <= nums[i]:\n t += nums[i] - smallest_neighbor + 1\n return t\n\n return min(check(0), check(1))\n``` | 0 | You are given two strings `s1` and `s2` of equal length consisting of letters `"x "` and `"y "` **only**. Your task is to make these two strings equal to each other. You can swap any two characters that belong to **different** strings, which means: swap `s1[i]` and `s2[j]`.
Return the minimum number of swaps required to make `s1` and `s2` equal, or return `-1` if it is impossible to do so.
**Example 1:**
**Input:** s1 = "xx ", s2 = "yy "
**Output:** 1
**Explanation:** Swap s1\[0\] and s2\[1\], s1 = "yx ", s2 = "yx ".
**Example 2:**
**Input:** s1 = "xy ", s2 = "yx "
**Output:** 2
**Explanation:** Swap s1\[0\] and s2\[0\], s1 = "yy ", s2 = "xx ".
Swap s1\[0\] and s2\[1\], s1 = "xy ", s2 = "xy ".
Note that you cannot swap s1\[0\] and s1\[1\] to make s1 equal to "yx ", cause we can only swap chars in different strings.
**Example 3:**
**Input:** s1 = "xx ", s2 = "xy "
**Output:** -1
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1.length == s2.length`
* `s1, s2` only contain `'x'` or `'y'`. | Do each case (even indexed is greater, odd indexed is greater) separately. In say the even case, you should decrease each even-indexed element until it is lower than its immediate neighbors. |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | decrease-elements-to-make-array-zigzag | 0 | 1 | \n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, A):\n A = [float(\'inf\')] + A + [float(\'inf\')]\n res = [0, 0]\n for i in range(1, len(A) - 1):\n res[i % 2] += max(0, A[i] - min(A[i - 1], A[i + 1]) + 1)\n return min(res)\n``` | 0 | Given an array `nums` of integers, a _move_ consists of choosing any element and **decreasing it by 1**.
An array `A` is a _zigzag array_ if either:
* Every even-indexed element is greater than adjacent elements, ie. `A[0] > A[1] < A[2] > A[3] < A[4] > ...`
* OR, every odd-indexed element is greater than adjacent elements, ie. `A[0] < A[1] > A[2] < A[3] > A[4] < ...`
Return the minimum number of moves to transform the given array `nums` into a zigzag array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** We can decrease 2 to 0 or 3 to 1.
**Example 2:**
**Input:** nums = \[9,6,1,6,2\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | What if we model this problem as a graph problem? A house is a node and a pipe is a weighted edge. How to represent building wells in the graph model? Add a virtual node, connect it to houses with edges weighted by the costs to build wells in these houses. The problem is now reduced to a Minimum Spanning Tree problem. |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | decrease-elements-to-make-array-zigzag | 0 | 1 | \n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, A):\n A = [float(\'inf\')] + A + [float(\'inf\')]\n res = [0, 0]\n for i in range(1, len(A) - 1):\n res[i % 2] += max(0, A[i] - min(A[i - 1], A[i + 1]) + 1)\n return min(res)\n``` | 0 | You are given two strings `s1` and `s2` of equal length consisting of letters `"x "` and `"y "` **only**. Your task is to make these two strings equal to each other. You can swap any two characters that belong to **different** strings, which means: swap `s1[i]` and `s2[j]`.
Return the minimum number of swaps required to make `s1` and `s2` equal, or return `-1` if it is impossible to do so.
**Example 1:**
**Input:** s1 = "xx ", s2 = "yy "
**Output:** 1
**Explanation:** Swap s1\[0\] and s2\[1\], s1 = "yx ", s2 = "yx ".
**Example 2:**
**Input:** s1 = "xy ", s2 = "yx "
**Output:** 2
**Explanation:** Swap s1\[0\] and s2\[0\], s1 = "yy ", s2 = "xx ".
Swap s1\[0\] and s2\[1\], s1 = "xy ", s2 = "xy ".
Note that you cannot swap s1\[0\] and s1\[1\] to make s1 equal to "yx ", cause we can only swap chars in different strings.
**Example 3:**
**Input:** s1 = "xx ", s2 = "xy "
**Output:** -1
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1.length == s2.length`
* `s1, s2` only contain `'x'` or `'y'`. | Do each case (even indexed is greater, odd indexed is greater) separately. In say the even case, you should decrease each even-indexed element until it is lower than its immediate neighbors. |
Python Simple O(n) Solution | Faster than 80% | decrease-elements-to-make-array-zigzag | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nJust calculate moves if we fix elements at odd indices and moves if we fix elements at even indices and return the minimum of both\n\n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, nums: List[int]) -> int:\n if len(nums) == 1: return 0\n oddMoves = evenMoves = 0\n for idx in range(1, len(nums), 2):\n minimum = 0\n if idx + 1 < len(nums):\n minimum = min(nums[idx - 1], nums[idx + 1])\n else:\n minimum = nums[idx - 1] \n if minimum <= nums[idx]:\n oddMoves += nums[idx] - minimum + 1\n if nums[0] >= nums[1]:\n evenMoves += (nums[0] - nums[1] + 1)\n for idx in range(2, len(nums), 2):\n minimum = 0\n if idx + 1 < len(nums):\n minimum = min(nums[idx - 1], nums[idx + 1])\n else:\n minimum = nums[idx - 1] \n if minimum <= nums[idx]:\n evenMoves += nums[idx] - minimum + 1\n return min(oddMoves, evenMoves)\n``` | 0 | Given an array `nums` of integers, a _move_ consists of choosing any element and **decreasing it by 1**.
An array `A` is a _zigzag array_ if either:
* Every even-indexed element is greater than adjacent elements, ie. `A[0] > A[1] < A[2] > A[3] < A[4] > ...`
* OR, every odd-indexed element is greater than adjacent elements, ie. `A[0] < A[1] > A[2] < A[3] > A[4] < ...`
Return the minimum number of moves to transform the given array `nums` into a zigzag array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** We can decrease 2 to 0 or 3 to 1.
**Example 2:**
**Input:** nums = \[9,6,1,6,2\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | What if we model this problem as a graph problem? A house is a node and a pipe is a weighted edge. How to represent building wells in the graph model? Add a virtual node, connect it to houses with edges weighted by the costs to build wells in these houses. The problem is now reduced to a Minimum Spanning Tree problem. |
Python Simple O(n) Solution | Faster than 80% | decrease-elements-to-make-array-zigzag | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nJust calculate moves if we fix elements at odd indices and moves if we fix elements at even indices and return the minimum of both\n\n# Code\n```\nclass Solution:\n def movesToMakeZigzag(self, nums: List[int]) -> int:\n if len(nums) == 1: return 0\n oddMoves = evenMoves = 0\n for idx in range(1, len(nums), 2):\n minimum = 0\n if idx + 1 < len(nums):\n minimum = min(nums[idx - 1], nums[idx + 1])\n else:\n minimum = nums[idx - 1] \n if minimum <= nums[idx]:\n oddMoves += nums[idx] - minimum + 1\n if nums[0] >= nums[1]:\n evenMoves += (nums[0] - nums[1] + 1)\n for idx in range(2, len(nums), 2):\n minimum = 0\n if idx + 1 < len(nums):\n minimum = min(nums[idx - 1], nums[idx + 1])\n else:\n minimum = nums[idx - 1] \n if minimum <= nums[idx]:\n evenMoves += nums[idx] - minimum + 1\n return min(oddMoves, evenMoves)\n``` | 0 | You are given two strings `s1` and `s2` of equal length consisting of letters `"x "` and `"y "` **only**. Your task is to make these two strings equal to each other. You can swap any two characters that belong to **different** strings, which means: swap `s1[i]` and `s2[j]`.
Return the minimum number of swaps required to make `s1` and `s2` equal, or return `-1` if it is impossible to do so.
**Example 1:**
**Input:** s1 = "xx ", s2 = "yy "
**Output:** 1
**Explanation:** Swap s1\[0\] and s2\[1\], s1 = "yx ", s2 = "yx ".
**Example 2:**
**Input:** s1 = "xy ", s2 = "yx "
**Output:** 2
**Explanation:** Swap s1\[0\] and s2\[0\], s1 = "yy ", s2 = "xx ".
Swap s1\[0\] and s2\[1\], s1 = "xy ", s2 = "xy ".
Note that you cannot swap s1\[0\] and s1\[1\] to make s1 equal to "yx ", cause we can only swap chars in different strings.
**Example 3:**
**Input:** s1 = "xx ", s2 = "xy "
**Output:** -1
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1.length == s2.length`
* `s1, s2` only contain `'x'` or `'y'`. | Do each case (even indexed is greater, odd indexed is greater) separately. In say the even case, you should decrease each even-indexed element until it is lower than its immediate neighbors. |
Python 3 || 12 lines, w/ explanation and example || T/M: 90%/93% | binary-tree-coloring-game | 0 | 1 | The problem reduces to whether any of the three subgraphs with edges to node `x` have at least `(n+1)//2` nodes.\n\nHere\'s the plan:\n- Traverse the tree with `dfs` recursively.\n- For each `node`, rewrite `node.val` with the count of nodes in its subtree.\n- Evaluate whether `node` is x, and if so, determine whether one of its neighbors is greater than `(n+1)//2`.\n- Return `True` if so, of if either child returns `True`. If not, return `False`\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n\n most = (n+1)//2\n\n def dfs(node):\n if not node: return False\n\n if dfs(node.left) or dfs(node.right): return True\n is_x = node.val == x\n \n l = node.left .val if node.left else 0\n r = node.right.val if node.right else 0\n\n if is_x and (l >= most or r >= most): return True\n\n node.val = 1 + l + r\n\n if is_x: return node.val < most\n\n return False\n\n return dfs(root)\n```\n[https://leetcode.com/problems/binary-tree-coloring-game/submissions/868289785/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1). | 4 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
Python 3 || 12 lines, w/ explanation and example || T/M: 90%/93% | binary-tree-coloring-game | 0 | 1 | The problem reduces to whether any of the three subgraphs with edges to node `x` have at least `(n+1)//2` nodes.\n\nHere\'s the plan:\n- Traverse the tree with `dfs` recursively.\n- For each `node`, rewrite `node.val` with the count of nodes in its subtree.\n- Evaluate whether `node` is x, and if so, determine whether one of its neighbors is greater than `(n+1)//2`.\n- Return `True` if so, of if either child returns `True`. If not, return `False`\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n\n most = (n+1)//2\n\n def dfs(node):\n if not node: return False\n\n if dfs(node.left) or dfs(node.right): return True\n is_x = node.val == x\n \n l = node.left .val if node.left else 0\n r = node.right.val if node.right else 0\n\n if is_x and (l >= most or r >= most): return True\n\n node.val = 1 + l + r\n\n if is_x: return node.val < most\n\n return False\n\n return dfs(root)\n```\n[https://leetcode.com/problems/binary-tree-coloring-game/submissions/868289785/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1). | 4 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Python, DFS | binary-tree-coloring-game | 0 | 1 | # Intuition\nWe have 3 different ways to choose the element that will beat opponent.\n1. Choose left sub-tree of opponent node\n2. Choose right sub-tree of opponent node\n3. Choose parent of opponent node\n\nThen we should calculate amount of nodes in left and right sub-trees. If one of them grater than sum of others - we can win.\n\nAnother edge case when opponent choose root. In this case we can win only if amount of left and right sub-trees are different.\n\n# Complexity\n- Time complexity:\nO(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root, n: int, x: int) -> bool:\n\n def calculateNodes(node):\n if not node:\n return 0\n \n result = 1\n \n if node.left:\n result += calculateNodes(node.left)\n if node.right:\n result += calculateNodes(node.right)\n\n return result\n\n if root.val == x:\n return calculateNodes(root.left) != calculateNodes(root.right)\n\n def dfs(node):\n if node.val == x:\n a = calculateNodes(node.left)\n b = calculateNodes(node.right)\n c = n - (a + b + 1)\n\n return a > b + c or b > a + c or c > a + b\n\n if node.left:\n result = dfs(node.left)\n if result != None:\n return result\n if node.right:\n result = dfs(node.right)\n if result != None:\n return result\n\n return None\n\n return dfs(root)\n``` | 2 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
Python, DFS | binary-tree-coloring-game | 0 | 1 | # Intuition\nWe have 3 different ways to choose the element that will beat opponent.\n1. Choose left sub-tree of opponent node\n2. Choose right sub-tree of opponent node\n3. Choose parent of opponent node\n\nThen we should calculate amount of nodes in left and right sub-trees. If one of them grater than sum of others - we can win.\n\nAnother edge case when opponent choose root. In this case we can win only if amount of left and right sub-trees are different.\n\n# Complexity\n- Time complexity:\nO(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root, n: int, x: int) -> bool:\n\n def calculateNodes(node):\n if not node:\n return 0\n \n result = 1\n \n if node.left:\n result += calculateNodes(node.left)\n if node.right:\n result += calculateNodes(node.right)\n\n return result\n\n if root.val == x:\n return calculateNodes(root.left) != calculateNodes(root.right)\n\n def dfs(node):\n if node.val == x:\n a = calculateNodes(node.left)\n b = calculateNodes(node.right)\n c = n - (a + b + 1)\n\n return a > b + c or b > a + c or c > a + b\n\n if node.left:\n result = dfs(node.left)\n if result != None:\n return result\n if node.right:\n result = dfs(node.right)\n if result != None:\n return result\n\n return None\n\n return dfs(root)\n``` | 2 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Python 3 | DFS | One pass & Three pass | Explanation | binary-tree-coloring-game | 0 | 1 | ### Intuition\n- When first player chose a node `x`, then there are 3 branches left there for second player to choose (left subtree of `x`, right subtree of `x`, parent end of `x`. \n- For the second player, to ensure a win, we need to make sure that there is one branch that dominate the sum of the other 2 branches. As showed at below.\n\t- left + right < parent\n\t- parent + right < left\n\t- parent + left < right\n### Three-pass solution\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n first = None\n def count(node):\n nonlocal first\n total = 0\n if node: \n if node.val == x: first = node\n total += count(node.left) + count(node.right) + 1\n return total\n \n s = count(root) # Get total number of nodes, and x node (first player\'s choice)\n l = count(first.left) # Number of nodes on left branch \n r = count(first.right) # Number of nodes on right branch \n p = s-l-r-1 # Number of nodes on parent branch (anything else other than node, left subtree of node or right subtree of node)\n return l+r < p or l+p < r or r+p < l\n```\n\n### One-pass solution\n- Once you understand the idea of three-pass solution, it\'s pretty easy to modify the code to a one-pass solution\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n l = r = 0\n def count(node):\n nonlocal l, r\n total = 0\n if node: \n l_count, r_count = count(node.left), count(node.right)\n if node.val == x: \n l, r = l_count, r_count\n total += l_count + r_count + 1\n return total\n s = count(root) \n p = s-l-r-1 \n return l+r < p or l+p < r or r+p < l\n``` | 14 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
Python 3 | DFS | One pass & Three pass | Explanation | binary-tree-coloring-game | 0 | 1 | ### Intuition\n- When first player chose a node `x`, then there are 3 branches left there for second player to choose (left subtree of `x`, right subtree of `x`, parent end of `x`. \n- For the second player, to ensure a win, we need to make sure that there is one branch that dominate the sum of the other 2 branches. As showed at below.\n\t- left + right < parent\n\t- parent + right < left\n\t- parent + left < right\n### Three-pass solution\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n first = None\n def count(node):\n nonlocal first\n total = 0\n if node: \n if node.val == x: first = node\n total += count(node.left) + count(node.right) + 1\n return total\n \n s = count(root) # Get total number of nodes, and x node (first player\'s choice)\n l = count(first.left) # Number of nodes on left branch \n r = count(first.right) # Number of nodes on right branch \n p = s-l-r-1 # Number of nodes on parent branch (anything else other than node, left subtree of node or right subtree of node)\n return l+r < p or l+p < r or r+p < l\n```\n\n### One-pass solution\n- Once you understand the idea of three-pass solution, it\'s pretty easy to modify the code to a one-pass solution\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n l = r = 0\n def count(node):\n nonlocal l, r\n total = 0\n if node: \n l_count, r_count = count(node.left), count(node.right)\n if node.val == x: \n l, r = l_count, r_count\n total += l_count + r_count + 1\n return total\n s = count(root) \n p = s-l-r-1 \n return l+r < p or l+p < r or r+p < l\n``` | 14 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Iterative BFS, python with my explanation | binary-tree-coloring-game | 0 | 1 | There are three "zones" in the tree:\n1. Left subtree under Red\n2. Right subtree under Red\n3. The remainder of the tree "above" Red\n\nBlue can pick the left child, right child, or parent of Red to control zones 1, 2, or 3, respectivley.\n\nTherefore we count the number of nodes in two of the zones. The third zone is simply n - sum(the other two zones) -1\n\nIf one of the zones is larger than the other two combined (plus 1 for the Red node), then we (Blue) can control it and win the game. Otherwise we lose :(\n\nSo I utilized a BFS to iterativley count Zone 3 first , leaving aside Red and its subtree(s) for the next BFS. Comments below:\n\n```python\nfrom collections import deque\ndef btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n\toutside_red, red_ltree, red_rtree = 0, 0, 0\n\tred_node = None\n\tq = deque([root])\n\twhile len(q):\n\t\tcurr_node = q.pop()\n\t\tif curr_node.val ==x:\n\t\t\t# we won\'t append any children this go-around\n\t\t\tred_node = curr_node\n\t\telse:\n\t\t\toutside_red += 1\n\t\t\tq.extendleft([x for x in [curr_node.left, curr_node.right] if x])\n\t#now check left subtree. If it\'s empty that makes our job easier because red_rtree = n-outside_red-1\n\tif red_node.left:\n\t\tq.append(red_node.left)\n\t\twhile len(q):\n\t\t\tcurr_node = q.pop()\n\t\t\tred_ltree +=1\n\t\t\tq.extend([x for x in [curr_node.left, curr_node.right] if x])\n\telse:\n\t\tred_ltree = 0\n\tred_rtree = n - outside_red - red_ltree - 1\n\t[low, med, high] = sorted([outside_red, red_ltree, red_rtree])\n\treturn high > med+low+1\n\t\t``` | 11 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
Iterative BFS, python with my explanation | binary-tree-coloring-game | 0 | 1 | There are three "zones" in the tree:\n1. Left subtree under Red\n2. Right subtree under Red\n3. The remainder of the tree "above" Red\n\nBlue can pick the left child, right child, or parent of Red to control zones 1, 2, or 3, respectivley.\n\nTherefore we count the number of nodes in two of the zones. The third zone is simply n - sum(the other two zones) -1\n\nIf one of the zones is larger than the other two combined (plus 1 for the Red node), then we (Blue) can control it and win the game. Otherwise we lose :(\n\nSo I utilized a BFS to iterativley count Zone 3 first , leaving aside Red and its subtree(s) for the next BFS. Comments below:\n\n```python\nfrom collections import deque\ndef btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n\toutside_red, red_ltree, red_rtree = 0, 0, 0\n\tred_node = None\n\tq = deque([root])\n\twhile len(q):\n\t\tcurr_node = q.pop()\n\t\tif curr_node.val ==x:\n\t\t\t# we won\'t append any children this go-around\n\t\t\tred_node = curr_node\n\t\telse:\n\t\t\toutside_red += 1\n\t\t\tq.extendleft([x for x in [curr_node.left, curr_node.right] if x])\n\t#now check left subtree. If it\'s empty that makes our job easier because red_rtree = n-outside_red-1\n\tif red_node.left:\n\t\tq.append(red_node.left)\n\t\twhile len(q):\n\t\t\tcurr_node = q.pop()\n\t\t\tred_ltree +=1\n\t\t\tq.extend([x for x in [curr_node.left, curr_node.right] if x])\n\telse:\n\t\tred_ltree = 0\n\tred_rtree = n - outside_red - red_ltree - 1\n\t[low, med, high] = sorted([outside_red, red_ltree, red_rtree])\n\treturn high > med+low+1\n\t\t``` | 11 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
PYTHON SOL | LINEAR TIME | EXPLAINED WITH PICTURE | EASY | TRAVERSING | | binary-tree-coloring-game | 0 | 1 | # TIME AND SPACE COMPLEXITY\nRuntime: 36 ms, faster than 89.14% of Python3 online submissions for Binary Tree Coloring Game.\nMemory Usage: 14 MB, less than 52.72% of Python3 online submissions for Binary Tree Coloring Game.\n\n\n# EXPLANATION\n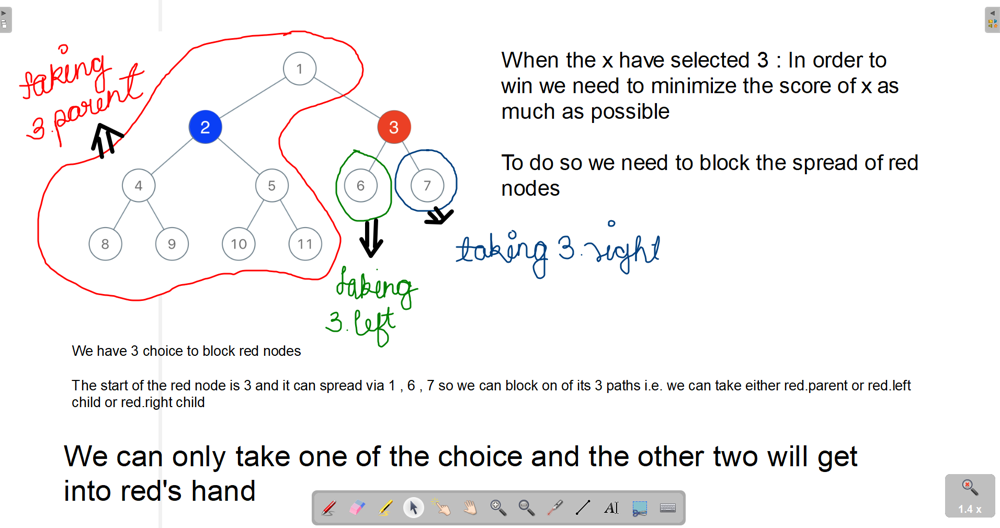\n\n# CODE\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findParent(self,node,par = None):\n if node:\n self.parent[node.val] = par\n self.findParent(node.left,node)\n self.findParent(node.right,node)\n \n def traverse(self,node,done):\n if node:\n if node in done: return 0\n done[node] = True\n a = self.traverse(self.parent[node.val],done)\n b = self.traverse(node.left,done)\n c = self.traverse(node.right,done)\n return a + b + c + 1\n return 0\n \n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n self.parent = {}\n self.findParent(root)\n parent = self.parent[x]\n node = root if root.val == x else parent.left if parent and parent.left and parent.left.val == x else parent.right\n up = self.traverse(parent,{node:True})\n left = self.traverse(node.left,{node:True})\n right = self.traverse(node.right,{node:True})\n return (up > left + right) or (left > up + right) or (right > up + left)\n```\n | 1 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
PYTHON SOL | LINEAR TIME | EXPLAINED WITH PICTURE | EASY | TRAVERSING | | binary-tree-coloring-game | 0 | 1 | # TIME AND SPACE COMPLEXITY\nRuntime: 36 ms, faster than 89.14% of Python3 online submissions for Binary Tree Coloring Game.\nMemory Usage: 14 MB, less than 52.72% of Python3 online submissions for Binary Tree Coloring Game.\n\n\n# EXPLANATION\n\n\n# CODE\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findParent(self,node,par = None):\n if node:\n self.parent[node.val] = par\n self.findParent(node.left,node)\n self.findParent(node.right,node)\n \n def traverse(self,node,done):\n if node:\n if node in done: return 0\n done[node] = True\n a = self.traverse(self.parent[node.val],done)\n b = self.traverse(node.left,done)\n c = self.traverse(node.right,done)\n return a + b + c + 1\n return 0\n \n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n self.parent = {}\n self.findParent(root)\n parent = self.parent[x]\n node = root if root.val == x else parent.left if parent and parent.left and parent.left.val == x else parent.right\n up = self.traverse(parent,{node:True})\n left = self.traverse(node.left,{node:True})\n right = self.traverse(node.right,{node:True})\n return (up > left + right) or (left > up + right) or (right > up + left)\n```\n | 1 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Single Pass, easy and clear solution T/M: 80%/83% | binary-tree-coloring-game | 0 | 1 | ```\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n self.ans = True\n def f(a,b,c): return not (a+b<c or a+c<b or b+c<a)\n \n def count(root):\n if not root: return 0\n l, r = count(root.left), count(root.right)\n if root.val == x: return f(l,r,n-l-r-1)\n return l+r+1\n \n def find(root):\n if not root: return\n if root.val == x and count(root): self.ans = False\n find(root.left)\n find(root.right)\n \n find(root)\n return self.ans\n``` | 0 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
Single Pass, easy and clear solution T/M: 80%/83% | binary-tree-coloring-game | 0 | 1 | ```\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n self.ans = True\n def f(a,b,c): return not (a+b<c or a+c<b or b+c<a)\n \n def count(root):\n if not root: return 0\n l, r = count(root.left), count(root.right)\n if root.val == x: return f(l,r,n-l-r-1)\n return l+r+1\n \n def find(root):\n if not root: return\n if root.val == x and count(root): self.ans = False\n find(root.left)\n find(root.right)\n \n find(root)\n return self.ans\n``` | 0 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
Easy and modular python solution | binary-tree-coloring-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition for the problem comes from the fact that in this game, we are trying to limit the area that player 1 can conquer through his/her turn. In order to limit the area, we must place the y directly as a neighbour to the x since the player 1 can only conquer uncoloured nodes. In doing so thre can be two things that the player 2 can do:\n1. The player 2 can place it as the parent of player 1\'s x, limiting him/her from moving up the tree. \n2. The player 2 can place y in the subtree of x, limiting him/her from moving down the tree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each case:\n1. In the first case, simply compare if the size of the tree excluding x is greater than the size of subtree at x\n2. In the second case, the player can place y in the larger subtree, hence the size of the larger subtree must be larger than the size of the smaller subtree + the size of the tree excluding subtree rooted at x\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n def treeSize (root):\n if not root:\n return 0\n return 1 + treeSize(root.left) + treeSize(root.right)\n \n def exclTreeSize(root, x):\n if not root:\n return 0\n if root.val == x:\n return 0\n return 1 + exclTreeSize(root.left, x) + exclTreeSize(root.right, x)\n \n def findNode(root, x):\n if not root:\n return None\n if root.val == x:\n return root\n return findNode(root.left, x) or findNode(root.right, x)\n\n # if choosing to place y in the parent of x\n node = findNode(root, x)\n exclTreeSize = exclTreeSize(root, x)\n if exclTreeSize > treeSize(node):\n return True\n \n # if choosing to place y in the larger subtree of x\n leftSubtree = treeSize(node.left)\n rightSubtree = treeSize(node.right)\n if max(leftSubtree, rightSubtree) > (min(leftSubtree, rightSubtree) + exclTreeSize):\n return True\n return False\n \n \n\n``` | 0 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
Easy and modular python solution | binary-tree-coloring-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition for the problem comes from the fact that in this game, we are trying to limit the area that player 1 can conquer through his/her turn. In order to limit the area, we must place the y directly as a neighbour to the x since the player 1 can only conquer uncoloured nodes. In doing so thre can be two things that the player 2 can do:\n1. The player 2 can place it as the parent of player 1\'s x, limiting him/her from moving up the tree. \n2. The player 2 can place y in the subtree of x, limiting him/her from moving down the tree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each case:\n1. In the first case, simply compare if the size of the tree excluding x is greater than the size of subtree at x\n2. In the second case, the player can place y in the larger subtree, hence the size of the larger subtree must be larger than the size of the smaller subtree + the size of the tree excluding subtree rooted at x\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n def treeSize (root):\n if not root:\n return 0\n return 1 + treeSize(root.left) + treeSize(root.right)\n \n def exclTreeSize(root, x):\n if not root:\n return 0\n if root.val == x:\n return 0\n return 1 + exclTreeSize(root.left, x) + exclTreeSize(root.right, x)\n \n def findNode(root, x):\n if not root:\n return None\n if root.val == x:\n return root\n return findNode(root.left, x) or findNode(root.right, x)\n\n # if choosing to place y in the parent of x\n node = findNode(root, x)\n exclTreeSize = exclTreeSize(root, x)\n if exclTreeSize > treeSize(node):\n return True\n \n # if choosing to place y in the larger subtree of x\n leftSubtree = treeSize(node.left)\n rightSubtree = treeSize(node.right)\n if max(leftSubtree, rightSubtree) > (min(leftSubtree, rightSubtree) + exclTreeSize):\n return True\n return False\n \n \n\n``` | 0 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
BFS | binary-tree-coloring-game | 0 | 1 | # Intuition\nWe try to choose the neighbor of the node our opponent choose since if we choose one step further, our opponent obtains one more node, which is not a wise choice. \n\nIf the first player choose the root node, then we could win if subtrees rooted at root.left or root.right has more than a half of nodes.\n\nElse, After finding node where node.val == x level by level, we have at most three choices:\n1.We choose parent of node if number of nodes of subtree rooted at node is less than half of the whole tree.\n2.We choose its children if number_of_nodes(node.child) > number_of_nodes(root) / 2.\n3.Otherwise we lose.\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n def node_of_subtree(node):\n if not node:\n return 0\n \n return 1 + node_of_subtree(node.left) + node_of_subtree(node.right)\n \n if x == root.val:\n return node_of_subtree(root.left) > n//2 or node_of_subtree(root.right) > n//2 \n\n q = [root]\n \n while q:\n #print([x.val for x in q])\n p = q\n q = []\n\n for node in p:\n if node.val == x:\n return node_of_subtree(node) <= n//2 or node_of_subtree(node.left) > n//2 or node_of_subtree(node.right) > n//2\n\n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n \n \n\n\n``` | 0 | Two players play a turn based game on a binary tree. We are given the `root` of this binary tree, and the number of nodes `n` in the tree. `n` is odd, and each node has a distinct value from `1` to `n`.
Initially, the first player names a value `x` with `1 <= x <= n`, and the second player names a value `y` with `1 <= y <= n` and `y != x`. The first player colors the node with value `x` red, and the second player colors the node with value `y` blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an **uncolored** neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a `y` to ensure you win the game, return `true`. If it is not possible, return `false`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6,7,8,9,10,11\], n = 11, x = 3
**Output:** true
**Explanation:** The second player can choose the node with value 2.
**Example 2:**
**Input:** root = \[1,2,3\], n = 3, x = 1
**Output:** false
**Constraints:**
* The number of nodes in the tree is `n`.
* `1 <= x <= n <= 100`
* `n` is odd.
* 1 <= Node.val <= n
* All the values of the tree are **unique**. | Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time.
Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window. |
BFS | binary-tree-coloring-game | 0 | 1 | # Intuition\nWe try to choose the neighbor of the node our opponent choose since if we choose one step further, our opponent obtains one more node, which is not a wise choice. \n\nIf the first player choose the root node, then we could win if subtrees rooted at root.left or root.right has more than a half of nodes.\n\nElse, After finding node where node.val == x level by level, we have at most three choices:\n1.We choose parent of node if number of nodes of subtree rooted at node is less than half of the whole tree.\n2.We choose its children if number_of_nodes(node.child) > number_of_nodes(root) / 2.\n3.Otherwise we lose.\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n def node_of_subtree(node):\n if not node:\n return 0\n \n return 1 + node_of_subtree(node.left) + node_of_subtree(node.right)\n \n if x == root.val:\n return node_of_subtree(root.left) > n//2 or node_of_subtree(root.right) > n//2 \n\n q = [root]\n \n while q:\n #print([x.val for x in q])\n p = q\n q = []\n\n for node in p:\n if node.val == x:\n return node_of_subtree(node) <= n//2 or node_of_subtree(node.left) > n//2 or node_of_subtree(node.right) > n//2\n\n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n \n \n\n\n``` | 0 | Given an array of integers `nums` and an integer `k`. A continuous subarray is called **nice** if there are `k` odd numbers on it.
Return _the number of **nice** sub-arrays_.
**Example 1:**
**Input:** nums = \[1,1,2,1,1\], k = 3
**Output:** 2
**Explanation:** The only sub-arrays with 3 odd numbers are \[1,1,2,1\] and \[1,2,1,1\].
**Example 2:**
**Input:** nums = \[2,4,6\], k = 1
**Output:** 0
**Explanation:** There is no odd numbers in the array.
**Example 3:**
**Input:** nums = \[2,2,2,1,2,2,1,2,2,2\], k = 2
**Output:** 16
**Constraints:**
* `1 <= nums.length <= 50000`
* `1 <= nums[i] <= 10^5`
* `1 <= k <= nums.length` | The best move y must be immediately adjacent to x, since it locks out that subtree. Can you count each of (up to) 3 different subtrees neighboring x? |
EASY PYTHON SOLUTION USING BINARY SEARCH || 2-D ARRAY | snapshot-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n*n*2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass SnapshotArray:\n def bs(self,lt,rt,tr,lst):\n ps=0\n while lt<=rt:\n mid=(lt+rt)//2\n if lst[mid][1]<=tr:\n ps=mid\n lt=mid+1\n else:\n rt=mid-1\n return ps\n\n\n def __init__(self, length: int):\n self.lst=[0]*length\n self._id=0\n self.nums=[[(0,0)] for _ in range(length)]\n \n\n def set(self, index: int, val: int) -> None:\n self.lst[index]=val\n if self.nums[index][-1][1]==self._id:\n self.nums[index][-1]=(val,self._id)\n elif self.nums[index][-1][1]<self._id:\n self.nums[index].append((val,self._id))\n \n\n def snap(self) -> int:\n x=self._id\n self._id+=1\n return x\n \n\n def get(self, index: int, snap_id: int) -> int:\n x=self.bs(0,len(self.nums[index])-1,snap_id,self.nums[index])\n return self.nums[index][x][0]\n\n \n\n\n# Your SnapshotArray object will be instantiated and called as such:\n# obj = SnapshotArray(length)\n# obj.set(index,val)\n# param_2 = obj.snap()\n# param_3 = obj.get(index,snap_id)\n``` | 3 | Implement a SnapshotArray that supports the following interface:
* `SnapshotArray(int length)` initializes an array-like data structure with the given length. **Initially, each element equals 0**.
* `void set(index, val)` sets the element at the given `index` to be equal to `val`.
* `int snap()` takes a snapshot of the array and returns the `snap_id`: the total number of times we called `snap()` minus `1`.
* `int get(index, snap_id)` returns the value at the given `index`, at the time we took the snapshot with the given `snap_id`
**Example 1:**
**Input:** \[ "SnapshotArray ", "set ", "snap ", "set ", "get "\]
\[\[3\],\[0,5\],\[\],\[0,6\],\[0,0\]\]
**Output:** \[null,null,0,null,5\]
**Explanation:**
SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3
snapshotArr.set(0,5); // Set array\[0\] = 5
snapshotArr.snap(); // Take a snapshot, return snap\_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0); // Get the value of array\[0\] with snap\_id = 0, return 5
**Constraints:**
* `1 <= length <= 5 * 104`
* `0 <= index < length`
* `0 <= val <= 109`
* `0 <= snap_id <` (the total number of times we call `snap()`)
* At most `5 * 104` calls will be made to `set`, `snap`, and `get`. | The greatest common divisor must be a prefix of each string, so we can try all prefixes. |
Python3 Solution | snapshot-array | 0 | 1 | \n```\nclass SnapshotArray:\n\n def __init__(self, length: int):\n self.array=[[[-1,0]] for _ in range(length)]\n self.snap_id=0\n \n \n\n def set(self, index: int, val: int) -> None:\n self.array[index].append([self.snap_id,val])\n\n def snap(self) -> int:\n self.snap_id+=1\n return self.snap_id-1\n \n\n def get(self, index: int, snap_id: int) -> int:\n i=bisect.bisect(self.array[index],[snap_id+1])-1\n return self.array[index][i][1] \n\n\n# Your SnapshotArray object will be instantiated and called as such:\n# obj = SnapshotArray(length)\n# obj.set(index,val)\n# param_2 = obj.snap()\n# param_3 = obj.get(index,snap_id)\n``` | 1 | Implement a SnapshotArray that supports the following interface:
* `SnapshotArray(int length)` initializes an array-like data structure with the given length. **Initially, each element equals 0**.
* `void set(index, val)` sets the element at the given `index` to be equal to `val`.
* `int snap()` takes a snapshot of the array and returns the `snap_id`: the total number of times we called `snap()` minus `1`.
* `int get(index, snap_id)` returns the value at the given `index`, at the time we took the snapshot with the given `snap_id`
**Example 1:**
**Input:** \[ "SnapshotArray ", "set ", "snap ", "set ", "get "\]
\[\[3\],\[0,5\],\[\],\[0,6\],\[0,0\]\]
**Output:** \[null,null,0,null,5\]
**Explanation:**
SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3
snapshotArr.set(0,5); // Set array\[0\] = 5
snapshotArr.snap(); // Take a snapshot, return snap\_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0); // Get the value of array\[0\] with snap\_id = 0, return 5
**Constraints:**
* `1 <= length <= 5 * 104`
* `0 <= index < length`
* `0 <= val <= 109`
* `0 <= snap_id <` (the total number of times we call `snap()`)
* At most `5 * 104` calls will be made to `set`, `snap`, and `get`. | The greatest common divisor must be a prefix of each string, so we can try all prefixes. |
Python Solution Using dictionary || Easy to understand | snapshot-array | 0 | 1 | ```\nclass SnapshotArray:\n\n def __init__(self, length: int):\n self.id = 0\n\t\t# to store current elm as index: val pair\n self.arr = {}\n\t\t# to store self.id: self.arr pairs i.e. snaps\n self._snap = {}\n\n def set(self, index: int, val: int) -> None:\n\t\t# set the value of index\n self.arr[index] = val\n\n def snap(self) -> int:\n\t\t# deep copy of dictionary\n self._snap[self.id] = dict(self.arr)\n\t\t# increment the id\n self.id += 1\n\t\t# return id-1\n return self.id-1\n\n def get(self, index: int, snap_id: int) -> int:\n\t\t# default value 0 will be return if index not in the snapshot dict\n return self._snap[snap_id].get(index,0)\n\n\n# Your SnapshotArray object will be instantiated and called as such:\n# obj = SnapshotArray(length)\n# obj.set(index,val)\n# param_2 = obj.snap()\n# param_3 = obj.get(index,snap_id)\n``` | 1 | Implement a SnapshotArray that supports the following interface:
* `SnapshotArray(int length)` initializes an array-like data structure with the given length. **Initially, each element equals 0**.
* `void set(index, val)` sets the element at the given `index` to be equal to `val`.
* `int snap()` takes a snapshot of the array and returns the `snap_id`: the total number of times we called `snap()` minus `1`.
* `int get(index, snap_id)` returns the value at the given `index`, at the time we took the snapshot with the given `snap_id`
**Example 1:**
**Input:** \[ "SnapshotArray ", "set ", "snap ", "set ", "get "\]
\[\[3\],\[0,5\],\[\],\[0,6\],\[0,0\]\]
**Output:** \[null,null,0,null,5\]
**Explanation:**
SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3
snapshotArr.set(0,5); // Set array\[0\] = 5
snapshotArr.snap(); // Take a snapshot, return snap\_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0); // Get the value of array\[0\] with snap\_id = 0, return 5
**Constraints:**
* `1 <= length <= 5 * 104`
* `0 <= index < length`
* `0 <= val <= 109`
* `0 <= snap_id <` (the total number of times we call `snap()`)
* At most `5 * 104` calls will be made to `set`, `snap`, and `get`. | The greatest common divisor must be a prefix of each string, so we can try all prefixes. |
✅Simple Java✔ || C++✔ ||Python✔ || Easy To Understand | snapshot-array | 1 | 1 | # Please Vote up :))\n**For this problem we need to optimize on space so we can\'t tradeoff memory for time. If you save the whole array for every snapshot there will be "Memory limit exceeded" error.\n\nEssentially we are interested only in history of changes for the index, and it could be only few changes of one index. This means we need to lookup effectively value by index and save only those that changed. We can use Map for this, use index as key, value as a value.\n\nWe keep such map for every snapshot, each consequence change will override previous value but this is perfectly fine - we care only about last value. We keep maps in a list, index of the element is a snapshot index.\n\nOn value lookup we start scanning list elements starting from the passed snapshot_id back to 0. Return first value for the index that we found - this means the most recent change up to this snapshot_id. If we haven\'t found anything it means there were no changes and we can return initial value which is 0 for all elements.\n\nO(1) for set - lookup for the map is O(1), put to the map is O(1) (average).\nO(snap_id) for get() - we can potentially search up to snap_id snapshots (maps in our list), then O(1) for the lookup by index.\nO(length^2) for space - we can save every element in map, then change every element for every snapshot**\n\n# Approach\nHere\'s a brief explanation of the approach:\n\n The array variable is initialized as a list of lists, where each element represents the history of a specific index. Each history entry is a tuple (snap_id, value) that records the value at that index and the snapshot ID when it was set.\n\n The set method appends a new history entry to the corresponding index in the array, using the current snap_id and the provided value.\n\n The snap method increments the snap_id and returns the previous snap_id, which represents the total number of snapshots taken minus 1.\n\n The get method searches for the closest snapshot index in the history of the specified index using binary search. It then returns the value recorded at that snapshot index.\n\nThis implementation provides efficient snapshots by only storing the changed values at each index and using binary search for retrieval, resulting in O(log N) time complexity for the get method, where N is the number of snapshots taken.\n\n\n\n# JAVA Code\n```\nclass SnapshotArray {\n TreeMap<Integer, Integer>[] Tm;\n int snap_id = 0;\n public SnapshotArray(int length) {\n Tm = new TreeMap[length];\n for (int i = 0; i < length; i++) {\n Tm[i] = new TreeMap<Integer, Integer>();\n Tm[i].put(0, 0);\n }\n }\n\n public void set(int index, int val) {\n Tm[index].put(snap_id, val);\n }\n\n public int snap() {\n return snap_id++;\n }\n\n public int get(int index, int snap_id) {\n return Tm[index].floorEntry(snap_id).getValue();\n }\n}\n\n\n```\n\n\n\n\n# C++ Code\n\n\n```\nclass SnapshotArray {\n vector<vector<pair<int, int>>>updates;\n int curSnap;\n\npublic:\n SnapshotArray(int length) {\n updates.resize(length);\n curSnap = 0;\n }\n\n void set(int index, int val) {\n if (!updates[index].empty() && updates[index].back().first == curSnap)\n updates[index].back().second = val;\n else\n updates[index].push_back({curSnap, val});\n }\n\n int snap() {\n curSnap++;\n return curSnap - 1;\n }\n\n int get(int index, int snap_id) {\n int idx = upper_bound(updates[index].begin(), updates[index].end(), make_pair(snap_id,INT_MAX)) - updates[index].begin();\n if (idx == 0) return 0;\n return updates[index][idx - 1].second;\n }\n};\n\n```\n\n\n# Python Code\n\n\n```\nclass SnapshotArray:\n\n def __init__(self, length: int):\n self.cur_id = 0\n self.curVals = [0] * length\n self.snapIdArr = [[-1] for _ in range(length)]\n self.arrVal = [[0] for _ in range(length)]\n self.modified = set()\n\n def set(self, index: int, val: int) -> None:\n if val == self.arrVal[index][-1]:\n if index in self.modified: self.modified.remove(index)\n return\n self.curVals[index] = val\n if index not in self.modified: self.modified.add(index)\n\n def snap(self) -> int:\n for idx in self.modified:\n self.snapIdArr[idx].append(self.cur_id)\n self.arrVal[idx].append(self.curVals[idx])\n self.modified.clear()\n self.cur_id += 1\n return self.cur_id - 1\n\n def get(self, index: int, snap_id: int) -> int:\n arr = self.snapIdArr[index]\n l, r = 0, len(arr)\n while l < r:\n m = (l + r) // 2\n if arr[m] <= snap_id:\n l = m + 1\n else: r = m\n return self.arrVal[index][l-1]\n\n\n\n``` | 74 | Implement a SnapshotArray that supports the following interface:
* `SnapshotArray(int length)` initializes an array-like data structure with the given length. **Initially, each element equals 0**.
* `void set(index, val)` sets the element at the given `index` to be equal to `val`.
* `int snap()` takes a snapshot of the array and returns the `snap_id`: the total number of times we called `snap()` minus `1`.
* `int get(index, snap_id)` returns the value at the given `index`, at the time we took the snapshot with the given `snap_id`
**Example 1:**
**Input:** \[ "SnapshotArray ", "set ", "snap ", "set ", "get "\]
\[\[3\],\[0,5\],\[\],\[0,6\],\[0,0\]\]
**Output:** \[null,null,0,null,5\]
**Explanation:**
SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3
snapshotArr.set(0,5); // Set array\[0\] = 5
snapshotArr.snap(); // Take a snapshot, return snap\_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0); // Get the value of array\[0\] with snap\_id = 0, return 5
**Constraints:**
* `1 <= length <= 5 * 104`
* `0 <= index < length`
* `0 <= val <= 109`
* `0 <= snap_id <` (the total number of times we call `snap()`)
* At most `5 * 104` calls will be made to `set`, `snap`, and `get`. | The greatest common divisor must be a prefix of each string, so we can try all prefixes. |
Easy | Python Solution | Two Pointers | longest-chunked-palindrome-decomposition | 0 | 1 | # Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n left = 0\n right = len(text)-1\n temp1 = ""\n temp2 = ""\n count = 0\n while left < right:\n temp1 += text[left]\n temp2 += text[right]\n if temp1 == temp2[::-1]:\n count += 2\n temp1 = ""\n temp2 = ""\n left += 1\n right -= 1\n else:\n left += 1\n right -= 1\n if left == right and len(temp1) == 0:\n count += 1\n if len(temp1) != 0:\n count += 1\n return count\n```\nDo upvote if you like the solution :) | 3 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
Close to O(n) Python, Rabin Karp Algorithm with two pointer technique with explanation (~40ms) | longest-chunked-palindrome-decomposition | 0 | 1 | [Important edit: I stand corrected. This algorithm isn\'t actually O(n), technically it\'s O(n^2). But in practice, it\'s very close to O(n), and will achieve substantially better performance than the more traditional O(n^2) approaches. In terms of real world performance/ progamming competitions, just pick a good big prime number and it\'ll scale more like an O(n) algorithm, achieving the ultimate objective of fastness. :-) Thanks to those who pointed out the incorrectness in my analysis!]\n\nThe Rabin-Karp algorithm seems perfect for this situation, so it is the approach I took.\n\nhttps://en.wikipedia.org/wiki/Rabin%E2%80%93Karp_algorithm\n\nSee code comments for an explanation of how it works. In essence, we keep track of a hash of the current substring at the start and the end of the string. **After the code I provide a few examples of the math and the ideas in the algorithm.**\n\nThis algorithm is **O(n)**, as we are only processing each character once, and we\'re not doing costly string comparing operations (remember, comparing 2 strings of length n has a cost of O(n), which would bring an algorithm depending on it up to O(n^2)). \n\n```py\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n \n\t\t# Used a prime number generator on the internet to grab a prime number to use.\n magic_prime = 32416189573\n \n\t\t# Standard 2 pointer technique variables.\n low = 0\n high = len(text) - 1\n \n\t\t# These are the hash tracking variables.\n\t\tcur_low_hash = 0\n cur_high_hash = 0\n cur_hash_length = 0\n \n\t\t# This is the number of parts we\'ve found, i.e. the k value we need to return.\n\t\tk = 0\n \n while low < high:\n \n\t\t\t# To put the current letter onto our low hash (i.e. the one that goes forward from\n\t\t\t# the start of the string, we shift up the existing hash by multiplying by the base\n\t\t\t# of 26, and then adding on the new character by converting it to a number from 0 - 25.\n cur_low_hash *= 26 # Shift up by the base of 26.\n cur_low_hash += ord(text[low]) - 97 # Take away 97 so that it\'s between 0 and 25.\n \n\t\t\t\n\t\t\t# The high one, i.e. the one backwards from the end is a little more complex, as we want the \n\t\t\t# hash to represent the characters in forward order, not backwards. If we did the exact same\n\t\t\t# thing we did for low, the string abc would be represented as cba, which is not right.\t\n\t\t\t\n\t\t\t# Start by getting the character\'s 0 - 25 number.\n\t\t\thigh_char = ord(text[high]) - 97\n\t\t\t\n\t\t\t# The third argument to pow is modular arithmetic. It says to give the answer modulo the\n\t\t\t# magic prime (more on that below). Just pretend it isn\'t doing that for now if it confuses you. \n # What we\'re doing is making an int that puts the high character at the top, and then the \n\t\t\t# existing hash at the bottom.\n\t\t\tcur_high_hash = (high_char * pow(26, cur_hash_length, magic_prime)) + cur_high_hash \n \n\t\t\t# Mathematically, we can safely do this. Impressive, huh? I\'m not going to go into here, but\n\t\t\t# I recommend studying up on modular arithmetic if you\'re confused.\n\t\t\t# The algorithm would be correct without doing this, BUT it\'d be very slow as the numbers could\n\t\t\t# become tens of thousands of bits long. The problem with that of course is that comparing the\n\t\t\t# numbers would no longer be O(1) constant. So we need to keep them small.\n\t\t\tcur_low_hash %= magic_prime \n cur_high_hash %= magic_prime\n \n\t\t\t# And now some standard 2 pointer technique stuff.\n low += 1\n high -= 1\n cur_hash_length += 1\n \n\t\t\t# This piece of code checks if we currently have a match.\n # This is actually probabilistic, i.e. it is possible to get false positives.\n # For correctness, we should be verifying that this is actually correct.\n # We would do this by ensuring the characters in each hash (using\n\t\t\t# the low, high, and length variables we\'ve been tracking) are\n\t\t\t# actually the same. But here I didn\'t bother as I figured Leetcode\n\t\t\t# would not have a test case that broke my specific prime.\n\t\t\tif cur_low_hash == cur_high_hash:\n k += 2 # We have just added 2 new strings to k.\n # And reset our hashing variables.\n\t\t\t\tcur_low_hash = 0\n cur_high_hash = 0\n cur_hash_length = 0\n \n\t\t# At the end, there are a couple of edge cases we need to address....\n\t\t# The first is if there is a middle character left.\n\t\t# The second is a non-paired off string in the middle.\n if (cur_hash_length == 0 and low == high) or cur_hash_length > 0:\n k += 1\n \n return k\n```\n\n# Representing a number as an integer.\nWe can represent a string of lower case letters as a base-26 number. Each letter is assigned a value from 0 to 25, and then each letter is the string is converted into its number and multiplied by a power of the base, based on its position. The numbers are then added together. For example, the string "cat":\nc = 2\na = 0\nt = 19\n\nnumber_for("cat") => (26 ^ 2) * 2 + (26 ^ 1) * 0 + (26 ^ 0) * 19\n\nThis is very much like how numbers are converted from base 2 to base 10.\n\n# Keeping track of rolling hashes.\nThe good thing about representing strings as a number is that it\'s very easy to add and remove characters from each end of the string, allowing us to maintain a "rolling hash" in O(n) time.\n\nSo say we have the string "foxyfox".\'\nf = 5\no = 14\nx = 23\ny = 24\n\nThe low hash will build up as follows.\n\nFirst letter: f\nlower_hash = 5\n\nSecond letter: o\nSo we multiply lower_hash by 26 and then add 14 (the number for "o").\n5 * 26 = 130\n130 + 14 = 144\nSo we now have lower_hash = 144\n\nThird letter: x\nSo we multply lower_hash by 26 and then add 23 (the number for "x").\n144 * 26 = 3744\n3744 + 23 = 3767\nSo now we have lower_hash = 3767\n\nAnd at the same time, the high hash is building up.\n\nFirst letter: x\nhigh_hash = 23\n\nSecond letter: o\nBecause we want the o "above" the x in the hash, we need to do this a bit differently to before.\n14 * (26 ** 1) = 364 ("Slide up" the new number making room for the old below).\n364 + 23 = 387 (Add the old hash on)\nhigh_hash = 387\n\nThird letter: f\n5 * (26 ** 2) = 3380 (Slide up the new number)\n3380 + 387 = 3767\n\nNow you might notice that when we add f->o->x onto the low high, and x->o->f onto the high hash, we end up with the same value: 3767. This is good, because it tells us we have a match. And it could be done in O(n) time.\n\n# Throwing modular arithmetic in\nThere is one problem with this approach though. What if the strings are *massive*. How many bits are there in a 1000 letter string? We are multiplying by 26 for every letter, so that is 26^1000, a very massive number. Comparing 2 numbers of this size is NOT O(1) anymore. \n\nIt turns out that we can take it modulo a large prime number at each step of the algorithm. I\'m not going to go into that here, but I recommend reading up on modular arithmetic if you\'re confused.\n# Resolving the potential bug\nSo there is one potential problem. It\'s possible for the hashes to be equal even if the strings weren\'t. This is more likely to happen with a smaller prime number.\n\nFor example, if our prime was 7, then that would mean the hash could only ever be 0, 1, 2, 3, 4, 5, or 6. "a" would be 0, and so would "h", so the algorithm would give a false positive match.\n\nWith a much higher prime number, it becomes increasingly less likely. This is how I protected against it in the contest.\n\nBut the correct way would be, each time we get a match, to also check the actual strings. As long as we are getting far fewer false positives than true positives, it will still be O(n) overall. A high enough prime will keep the number of false positives low.\n\nWith lots of collisons though, it will become O(n^2). Think about what would happen if our prime was 2.\n\nThis is a classic hashing collision problem. | 36 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
Python3 FT 80%: Repeatedly Check if Prefix == Suffix | longest-chunked-palindrome-decomposition | 0 | 1 | # Intuition\n\nThe problem can be reworded to\n* find the smallest prefix of `m` that is a suffix of `text`\n* remove these two fragments\n* repeat until the string is empty\n* how many fragments do you remove?\n\nIn this problem I guessed that the greedy solution was optimal, with the intuition that\n* if it wasn\'t the problem gets a LOT harder\n* and if a longer prefix and suffix match, then there are probably multiple matches\n\nSo we can brute-force simulate this problem. The complexity is O(N^2) which is acceptable given N ~ 1000.\n\n## Is Greedy Always Right?\n\nFortunately my guess was right; Lee215\'s answer has a longer proof. But here\'s a sketch. Suppose there\'s a longer prefix and suffix of the string that match like this:\n```\ntext = xyz......xyz\n```\nwhere `x`, `y`, `z` can be individual characters or substrings. `y` can be empty. And suppose there\'s a shorter prefix that matches.\n* "a shorter prefix that matches" means that `x == z`\n* so we really matched `xyx....xyx`\n * clearly there\'s a first match with the first and last x\n * that leaves `yx...xy`, where clearly the `y` matches (if `y` is nonempty)\n * and that leaves `x...x`, which obviously also has a match\n * so from one longer match we get 2-3 shorter matches with exactly the same characters\n\nTherefore any longer match produces 2-3 shorter matches among the same characters. Therefore it\'s *never* optimal to pick a longer prefix, and thus *always* optimal to pick the shortest prefix.\n\nIf there were "dangling characters" that remained it would be a different story, but here we showed that you get strictly more matches per character if you match shorter prefixes.\n\n# Approach\n\nFirst I wrote a helper function. It brute-force finds the smallest m where the first m characters match the last m characters among remaining characters at indices i..j.\n\nThis is good practice in NOT making many string copies; using indices to refer to the original string is generally a lot faster.\n\nThe only gotcha is to note that you only have two separate fragments if the length `m` of the next match at most half the remaining characters. This is because the text fragments can\'t be overlapping.\n\n# Complexity\n- Time complexity: O(N^2)\n - for a worst-case fragment we have to consider O(N) values before getting the shortest prefix length `m` ~ O(N)\n - and for each prefix length we tried, we compared most of the `m` characters\n - that gives us O(N^2) operations per iteration\n - but if we find prefixes of length O(N), then obviously there can\'t be more than O(1) matches of length O(N) (because O(1*N) = O(N); if there were more matches like O(log(N)) matches of size O(N) we\'d get a total length of O(N log(N)) - a contradiction!)\n - so in the worst case we do O(1 N^2) work\n - in the other extreme where we find a lot of O(1) matches, we do O(1) work for each of O(N) iterations - even better\n\n- Space complexity: O(1): just a bunch of indices and iteration\n\n# Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n # partition text into k substrings with the following properties\n # nonempty\n # text is the concatenation of the partitions\n # s_1 == s_k\n # s_2 == s_{k-1}\n # .. and so on\n\n # What\'s the max value of k?\n\n # we want the shortest strings then, and the order means we\n # process the first and last m chars of the remaining string\n # the middle is a "free space"\n\n # so let\'s assume greedy works\n\n # brute force: start with i = 0 and j = N-1,\n # then iterate with m = 1 .. until we find a shortest string where text[i:i+m] == text[j-m+1:j+1]\n\n def shortest(i: int, j: int) -> int:\n """Returns shortest length m where text[i:i+m] == text[j-m+1:j+1]"""\n\n for m in range(1, (j-i+1)//2+1):\n if all(text[i+a] == text[j-m+1+a] for a in range(m)):\n return m\n\n return j-i+1\n\n N = len(text)\n\n i = 0\n j = N-1\n ans = 0\n while i <= j:\n m = shortest(i, j)\n if m < j-i+1:\n i += m\n j -= m\n ans += 2\n else:\n ans += 1\n break\n\n return ans\n``` | 0 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
String Slicing | longest-chunked-palindrome-decomposition | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n text = text.strip()\n count = 0 \n if len(text) == 1:\n count += 1\n for i in range(len(text)//2):\n if text[:i+1] == text[len(text)-1-i:]:\n count += 2\n if len(text) >= 2:\n count += self.longestDecomposition(text[i+1:len(text)-i-1])\n break\n else:\n count += 1\n if (i+1)*2 >= len(text) -1:\n count += 1\n return count\n\n#case 1 even and pair, case 2 odd and pair +1, case 3 odd +1\n\n``` | 0 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
python super easy to understand dp top down + two pointer | longest-chunked-palindrome-decomposition | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n\n @functools.lru_cache(None)\n def dp(i, j):\n if i == j:\n return 1\n if i > j:\n return 0\n \n x = i\n y = j\n ans = 1\n while x < y:\n if text[i:x+1] == text[y:j+1]:\n ans = max(ans, 2 + dp(x+1, y-1))\n x +=1\n y -=1\n return ans\n return dp(0, len(text)-1)\n\n``` | 0 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
Solution using Two Pointers and Maximized Chunking with Example Walkthrough | longest-chunked-palindrome-decomposition | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe "Longest Chunked Palindrome Decomposition" problem challenges us to split a given string into as many substrings as possible, with each substring being a palindrome (a string that reads the same forwards and backwards). The task is to find the maximum number of such palindromic substrings that can be formed from the given string.\n\n## Example Walkthrough\n\nLet\'s illustrate the algorithm with an example:\n\n**Input**: "ghiabcdefhelloadamhelloabcdefghi"\n\n1. Initialize `i` and `j` at the beginning and end of the string, respectively.\n2. Start with `i = 1` and `j = 31`.\n\nInside the loop:\n- Compare `"g"` `(text[0:1])` with `"i"` `(text[31:32])`. They are not equal, so increment `i` and decrement `j`.\n\nNext:\n- Compare `"gh"` (text[0:2]) with `"hi"` (text[30:32]). They are not equal, so again increment `i` and decrement `j`.\n\nContinue this process until we find matching substrings:\n- `"ghi"` (text[0:3]) matches `"ghi"` (text[30:32]).\n- Append `"ghi"` and `"ghi"` to `lst`.\n- Update `start` to 3 i.e. `i` and `end` to 30 i.e. `j`.\n- Increment `i` and decrement `j`.\n\nRepeat this process until the loop ends, capturing all palindrome chunks.\n\nIn this case, the output will be `lst` with the following chunks: `["ghi", "abcdef", "hello", "hello", "abcdef", "ghi"].`\n\nThe concatenation of these chunks doesn\'t form the original string as it omits the substring `"adam"`, so the length is 6. To include the substring `"adam"`, return `length + 1`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can employ a two-pointer technique. Here\'s a step-by-step breakdown of the approach:\n\n1. Initialize two pointers, `i` and `j`, at the start and end of the input string, respectively.\n\n2. Create an empty list `lst` to store the palindrome chunks.\n\n3. Enter a loop that continues as long as `i` is less than or equal to `j`.\n\n4. Inside the loop, compare the substrings `text[start:i]` and `text[j:end]`. If they are not equal, increment `i` (moving from left to right) and decrement `j` (moving from right to left).\n\n5. If the substrings are equal, this means we\'ve found a palindrome chunk. Add both substrings to the `lst`, update `start` and `end` to new values, and increment `i` and decrement `j` to continue searching for the next chunk.\n\n6. After the loop, check if the concatenation of all the substrings in `lst` is equal to the original `text`. If it is, return the length of `lst`, which represents the largest possible value of `k`. Otherwise, return the length of `lst` plus 1, indicating that there\'s one additional chunk.\n\n# Complexity\n- Time complexity: O(n) - We iterate through each character in the string once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) - We store the palindrome chunks in a list, which can have up to `n/2` elements.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n start = 0\n end = len(text)\n \n i = start + 1\n j = end - 1\n \n lst = list()\n\n while i <= j: \n if text[start:i] != text[j:end]:\n i += 1\n j -= 1\n else:\n lst.append(text[start:i])\n lst.append(text[j:end])\n \n start = i\n end = j\n \n i += 1\n j -= 1\n\n if len(\'\'.join(lst)) == len(text):\n return len(lst)\n else:\n return len(lst) + 1\n``` | 0 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
{Not hard} beats 97.41% | longest-chunked-palindrome-decomposition | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n low = 0\n high = len(text)-1\n ans=0\n while high-low>0:\n if text[:low+1]==text[high:]:\n ans += 2\n text=text[low+1:high]\n low=0\n high=len(text)-1\n continue\n low +=1\n high -=1\n if len(text)>0:\n ans +=1\n return ans \n``` | 0 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
Longest Chunked Palindrome Decomposition || O(n) || Easy Solution | longest-chunked-palindrome-decomposition | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nitrate 1 side check other side \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestDecomposition(self, text: str) -> int:\n l=0\n r=1\n n=len(text)\n res=0\n while r<=n//2:\n print(text[l:r])\n if (l==0 and text[l:r]==text[-r:]) or text[l:r]==text[-r:-l]:\n res+=2\n l=r\n r+=1\n else:\n r+=1\n s=text[l:-l]\n print(s)\n if l==0:\n s=text\n \n if len(s)==1 or s[::-1]!=s:\n res+=1\n \n \n return res\n \n \n \n\n``` | 0 | You are given a string `text`. You should split it to k substrings `(subtext1, subtext2, ..., subtextk)` such that:
* `subtexti` is a **non-empty** string.
* The concatenation of all the substrings is equal to `text` (i.e., `subtext1 + subtext2 + ... + subtextk == text`).
* `subtexti == subtextk - i + 1` for all valid values of `i` (i.e., `1 <= i <= k`).
Return the largest possible value of `k`.
**Example 1:**
**Input:** text = "ghiabcdefhelloadamhelloabcdefghi "
**Output:** 7
**Explanation:** We can split the string on "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi) ".
**Example 2:**
**Input:** text = "merchant "
**Output:** 1
**Explanation:** We can split the string on "(merchant) ".
**Example 3:**
**Input:** text = "antaprezatepzapreanta "
**Output:** 11
**Explanation:** We can split the string on "(a)(nt)(a)(pre)(za)(tep)(za)(pre)(a)(nt)(a) ".
**Constraints:**
* `1 <= text.length <= 1000`
* `text` consists only of lowercase English characters. | Flipping a subset of columns is like doing a bitwise XOR of some number K onto each row. We want rows X with X ^ K = all 0s or all 1s. This is the same as X = X^K ^K = (all 0s or all 1s) ^ K, so we want to count rows that have opposite bits set. For example, if K = 1, then we count rows X = (00000...001, or 1111....110). |
Easy Python Solution | Gregorian calendar | Beginner Friendly | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The function aims to calculate the day of the year given a date in the format \'YYYY-MM-DD\'.\n- It considers leap years and non-leap years, adjusting the number of days in February accordingly.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The code first defines a function isLeap to check if a given year is a leap year.\n- Then, based on whether the input year is a leap year or not, it selects the corresponding list of days in each month.\n- If the month is January, it directly returns the day.\n- Otherwise, it calculates the day of the year by summing up the days in the preceding months and adding the day of the given date.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(1) because the calculation involves simple arithmetic operations and accessing elements in fixed-size lists.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as the size of the input does not affect the space usage, and the lists used are of constant size.\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n # Function to check if a given year is a leap year\n def isLeap(year):\n if year % 100 == 0:\n if year % 400 == 0:\n return True\n return False\n elif year % 4 == 0:\n return True\n return False\n\n # List of days in each month for non-leap and leap years\n if isLeap(int(date[:4])):\n days_in_month = [31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n else:\n days_in_month = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n\n # If the month is January, return the day directly\n if date[5:7] == \'01\':\n return int(date[-2:])\n \n # Calculate the day of the year by summing up days in preceding months and adding the day\n return sum(days_in_month[0:int(date[5:7]) - 1]) + int(date[-2:])\n\n```\n---\n# ***Please upvote if you like and understand the solution***\n\n\n\n | 4 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Easy Python Solution | Gregorian calendar | Beginner Friendly | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The function aims to calculate the day of the year given a date in the format \'YYYY-MM-DD\'.\n- It considers leap years and non-leap years, adjusting the number of days in February accordingly.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The code first defines a function isLeap to check if a given year is a leap year.\n- Then, based on whether the input year is a leap year or not, it selects the corresponding list of days in each month.\n- If the month is January, it directly returns the day.\n- Otherwise, it calculates the day of the year by summing up the days in the preceding months and adding the day of the given date.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(1) because the calculation involves simple arithmetic operations and accessing elements in fixed-size lists.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as the size of the input does not affect the space usage, and the lists used are of constant size.\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n # Function to check if a given year is a leap year\n def isLeap(year):\n if year % 100 == 0:\n if year % 400 == 0:\n return True\n return False\n elif year % 4 == 0:\n return True\n return False\n\n # List of days in each month for non-leap and leap years\n if isLeap(int(date[:4])):\n days_in_month = [31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n else:\n days_in_month = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n\n # If the month is January, return the day directly\n if date[5:7] == \'01\':\n return int(date[-2:])\n \n # Calculate the day of the year by summing up days in preceding months and adding the day\n return sum(days_in_month[0:int(date[5:7]) - 1]) + int(date[-2:])\n\n```\n---\n# ***Please upvote if you like and understand the solution***\n\n\n\n | 4 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
✅✅✅ Easy and faster than 99% solution | day-of-the-year | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n y,m,d = map(int, date.split(\'-\'))\n if (y%400==0 or (y%100!=0 and y%4==0)) and m>2: d+=1\n months = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n for i in range(1, m):\n d+=months[i-1]\n return d\n \n``` | 1 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
✅✅✅ Easy and faster than 99% solution | day-of-the-year | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n y,m,d = map(int, date.split(\'-\'))\n if (y%400==0 or (y%100!=0 and y%4==0)) and m>2: d+=1\n months = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n for i in range(1, m):\n d+=months[i-1]\n return d\n \n``` | 1 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
very easy solution for python 3 with comments | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n # we first make a list of days in a year when a specific\n # month ends\n list_year=[0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334]\n\n day=int(date[-2:])\n year=int(date[:4])\n month=int(date[5:7])\n\n # if year is leap and february is gone, add an extra day \n if year%4==0 and year!=1900 and month>2 :\n day+=1\n\n #return days of specific month + date\n return list_year[month-1]+day\n``` | 16 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
very easy solution for python 3 with comments | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n # we first make a list of days in a year when a specific\n # month ends\n list_year=[0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334]\n\n day=int(date[-2:])\n year=int(date[:4])\n month=int(date[5:7])\n\n # if year is leap and february is gone, add an extra day \n if year%4==0 and year!=1900 and month>2 :\n day+=1\n\n #return days of specific month + date\n return list_year[month-1]+day\n``` | 16 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Easy | Python Solution | String Manipulation | day-of-the-year | 0 | 1 | # Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n cal = {\n 1 : 31,\n 2 : 28,\n 3 : 31,\n 4 : 30,\n 5 : 31, \n 6 : 30, \n 7 : 31,\n 8 : 31, \n 9 : 30,\n 10 : 31,\n 11 : 30,\n 12 : 31\n }\n\n def isLeap(year):\n leap = False\n if (year % 400 == 0) and (year % 100 == 0):\n leap = True \n\n if (year % 4 == 0) and (year % 100 != 0):\n leap = True\n return leap\n\n year = int(date[:4])\n month = int(date[5:7])\n day = int(date[8:])\n leap = 0\n\n ans = 0\n if month > 2 and isLeap(year):\n leap = 1\n\n for i in range(1, month):\n ans += cal[i]\n return ans+leap+day\n\n```\nDo upvote if you like the solution :) | 2 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Easy | Python Solution | String Manipulation | day-of-the-year | 0 | 1 | # Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n cal = {\n 1 : 31,\n 2 : 28,\n 3 : 31,\n 4 : 30,\n 5 : 31, \n 6 : 30, \n 7 : 31,\n 8 : 31, \n 9 : 30,\n 10 : 31,\n 11 : 30,\n 12 : 31\n }\n\n def isLeap(year):\n leap = False\n if (year % 400 == 0) and (year % 100 == 0):\n leap = True \n\n if (year % 4 == 0) and (year % 100 != 0):\n leap = True\n return leap\n\n year = int(date[:4])\n month = int(date[5:7])\n day = int(date[8:])\n leap = 0\n\n ans = 0\n if month > 2 and isLeap(year):\n leap = 1\n\n for i in range(1, month):\n ans += cal[i]\n return ans+leap+day\n\n```\nDo upvote if you like the solution :) | 2 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
python 3 easy solution easy to under stand | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, a: str) -> int:\n if a == "1900-05-02":\n return 122\n b=(a[:4])\n c=(a[5:7])\n d=(a[8:10])\n print(b,c,d)\n s=0\n if int(b)%4!=0:\n f=[31,28,31,30,31,30,31,31,30,31,30,31]\n for i in range(int(c)-1):\n s=s+f[i]\n return(s+int(d))\n else:\n s=0\n f=[31,29,31,30,31,30,31,31,30,31,30,31]\n for i in range(int(c)-1):\n s=s+f[i]\n return(s+int(d))\n``` | 1 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
python 3 easy solution easy to under stand | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, a: str) -> int:\n if a == "1900-05-02":\n return 122\n b=(a[:4])\n c=(a[5:7])\n d=(a[8:10])\n print(b,c,d)\n s=0\n if int(b)%4!=0:\n f=[31,28,31,30,31,30,31,31,30,31,30,31]\n for i in range(int(c)-1):\n s=s+f[i]\n return(s+int(d))\n else:\n s=0\n f=[31,29,31,30,31,30,31,31,30,31,30,31]\n for i in range(int(c)-1):\n s=s+f[i]\n return(s+int(d))\n``` | 1 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Beats 86.32% || Day of the year | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n month=[31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n y,m,d=map(int,date.split("-"))\n if (y%400==0 or (y%100!=0 and y%4==0))and m>2:d+=1\n for i in range(1,m):\n d+=month[i-1]\n return d\n``` | 2 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Beats 86.32% || Day of the year | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n month=[31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n y,m,d=map(int,date.split("-"))\n if (y%400==0 or (y%100!=0 and y%4==0))and m>2:d+=1\n for i in range(1,m):\n d+=month[i-1]\n return d\n``` | 2 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Python 3 - Four liner - Simple Solution | day-of-the-year | 0 | 1 | ```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n y, m, d = map(int, date.split(\'-\'))\n days = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n if (y % 400) == 0 or ((y % 4 == 0) and (y % 100 != 0)): days[1] = 29\n return d + sum(days[:m-1])\n``` | 36 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Python 3 - Four liner - Simple Solution | day-of-the-year | 0 | 1 | ```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n y, m, d = map(int, date.split(\'-\'))\n days = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n if (y % 400) == 0 or ((y % 4 == 0) and (y % 100 != 0)): days[1] = 29\n return d + sum(days[:m-1])\n``` | 36 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
One line solution in Python | day-of-the-year | 0 | 1 | \n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n\n return datetime.date.fromisoformat(date).timetuple().tm_yday\n``` | 2 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
One line solution in Python | day-of-the-year | 0 | 1 | \n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n\n return datetime.date.fromisoformat(date).timetuple().tm_yday\n``` | 2 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Python - Easy Solution | day-of-the-year | 0 | 1 | \tclass Solution:\n\t\tdef dayOfYear(self, date: str) -> int:\n\t\t\tmap={\n\t\t\t\t0:0,\n\t\t\t\t1:31,\n\t\t\t\t2:28,\n\t\t\t\t3:31,\n\t\t\t\t4:30,\n\t\t\t\t5:31,\n\t\t\t\t6:30,\n\t\t\t\t7:31,\n\t\t\t\t8:31,\n\t\t\t\t9:30,\n\t\t\t\t10:31,\n\t\t\t\t11:30,\n\t\t\t\t12:31 \n\t\t\t}\n\n\t\t\tyear=int(date.split(\'-\')[0])\n\t\t\tmonth=date.split(\'-\')[1]\n\t\t\tday=date.split(\'-\')[2]\n\n\t\t\tdays=0\n\t\t\tfor x in range(0,int(month)):\n\t\t\t\tdays+=map.get(int(x))\n\n\t\t\tif not year % 400:\n\t\t\t\tis_leap_year = True\n\t\t\telif not year % 100:\n\t\t\t\tis_leap_year = False\n\t\t\telif not year % 4:\n\t\t\t\tis_leap_year = True\n\t\t\telse:\n\t\t\t\tis_leap_year = False\n\n\t\t\tif is_leap_year and int(month)>2:\n\t\t\t\treturn days+int(day)+1\n\t\t\telse:\n\t\t\t\treturn days+int(day) | 1 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Python - Easy Solution | day-of-the-year | 0 | 1 | \tclass Solution:\n\t\tdef dayOfYear(self, date: str) -> int:\n\t\t\tmap={\n\t\t\t\t0:0,\n\t\t\t\t1:31,\n\t\t\t\t2:28,\n\t\t\t\t3:31,\n\t\t\t\t4:30,\n\t\t\t\t5:31,\n\t\t\t\t6:30,\n\t\t\t\t7:31,\n\t\t\t\t8:31,\n\t\t\t\t9:30,\n\t\t\t\t10:31,\n\t\t\t\t11:30,\n\t\t\t\t12:31 \n\t\t\t}\n\n\t\t\tyear=int(date.split(\'-\')[0])\n\t\t\tmonth=date.split(\'-\')[1]\n\t\t\tday=date.split(\'-\')[2]\n\n\t\t\tdays=0\n\t\t\tfor x in range(0,int(month)):\n\t\t\t\tdays+=map.get(int(x))\n\n\t\t\tif not year % 400:\n\t\t\t\tis_leap_year = True\n\t\t\telif not year % 100:\n\t\t\t\tis_leap_year = False\n\t\t\telif not year % 4:\n\t\t\t\tis_leap_year = True\n\t\t\telse:\n\t\t\t\tis_leap_year = False\n\n\t\t\tif is_leap_year and int(month)>2:\n\t\t\t\treturn days+int(day)+1\n\t\t\telse:\n\t\t\t\treturn days+int(day) | 1 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
My banging solution | day-of-the-year | 0 | 1 | # Intuition\nI thought I just need to check for leap years and then add the days from the months before the one in the date. After that just add the days of the current month in the date.\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n months = [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n year, month, day = date.split(\'-\')\n year, month, day = int(year), int(month), int(day)\n days = 0\n if year % 4 == 0:\n if year % 100 != 0 or year % 400 == 0:\n months[2] = 29\n for mon in months[:month]:\n days += mon\n return days + day\n \n\n \n``` | 1 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
My banging solution | day-of-the-year | 0 | 1 | # Intuition\nI thought I just need to check for leap years and then add the days from the months before the one in the date. After that just add the days of the current month in the date.\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n months = [0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n year, month, day = date.split(\'-\')\n year, month, day = int(year), int(month), int(day)\n days = 0\n if year % 4 == 0:\n if year % 100 != 0 or year % 400 == 0:\n months[2] = 29\n for mon in months[:month]:\n days += mon\n return days + day\n \n\n \n``` | 1 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Python 3 -> 88% faster | day-of-the-year | 0 | 1 | ```\ndef dayOfYear(self, date: str) -> int:\n dates = date.split(\'-\')\n year, month, day = int(dates[0]), int(dates[1]), int(dates[2])\n \n months = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n countDays = 0\n i = 0\n\t\t\n while i < month - 1:\n countDays += months[i]\n i += 1\n\t\t\t\n if i>=2 and year%4==0 and year>1900:\n countDays += 1\n\t\t\t\n countDays += day\n return countDays\n``` | 7 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Python 3 -> 88% faster | day-of-the-year | 0 | 1 | ```\ndef dayOfYear(self, date: str) -> int:\n dates = date.split(\'-\')\n year, month, day = int(dates[0]), int(dates[1]), int(dates[2])\n \n months = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n countDays = 0\n i = 0\n\t\t\n while i < month - 1:\n countDays += months[i]\n i += 1\n\t\t\t\n if i>=2 and year%4==0 and year>1900:\n countDays += 1\n\t\t\t\n countDays += day\n return countDays\n``` | 7 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
O(1) solution using hashmap in Python | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen I first approached this problem, my initial idea was to utilize hashmaps to tackle the task.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used in the dayOfYear method is as follows:\n\nCreate a dictionary myDict to map each month to the cumulative day count up to the end of that month in a non-leap year.\n\nExtract the year from the input date string.\n\nCheck if the year is a leap year:\n\nIf the year is divisible by 4 and not divisible by 100, or it is divisible by 400, then it\'s a leap year. This is in accordance with the rules of the Gregorian calendar.\nCalculate the day of the year based on whether it\'s a leap year and the day of the month:\n\nIf it\'s a leap year and the month is after February, add 1 to the result to account for the extra day in a leap year.\nOtherwise, return the day number as per the non-leap year.\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n\n # Define a dictionary to map month to the day number in a non-leap year\n myDict = {"01":0, "02":31, "03":59, "04":90,"05":120,"06":151,\n "07":181,"08":212,"09":243,"10":273,"11":304,"12":334}\n # retreive the year from the string\n year = int(date[:4])\n\n # Check the condition for leap Year\n if year%4 == 0 and (year % 100 != 0 or year % 400 == 0) and int(date[5:7]) > 2:\n # If it\'s a leap year and the month is after February, add 1 to the result\n return myDict[date[5:7]] + int(date[8:]) + 1\n else:\n # Otherwise, return the day number as per the non-leap year\n return myDict[date[5:7]] + int(date[8:])\n \n \n \n``` | 0 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
O(1) solution using hashmap in Python | day-of-the-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen I first approached this problem, my initial idea was to utilize hashmaps to tackle the task.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used in the dayOfYear method is as follows:\n\nCreate a dictionary myDict to map each month to the cumulative day count up to the end of that month in a non-leap year.\n\nExtract the year from the input date string.\n\nCheck if the year is a leap year:\n\nIf the year is divisible by 4 and not divisible by 100, or it is divisible by 400, then it\'s a leap year. This is in accordance with the rules of the Gregorian calendar.\nCalculate the day of the year based on whether it\'s a leap year and the day of the month:\n\nIf it\'s a leap year and the month is after February, add 1 to the result to account for the extra day in a leap year.\nOtherwise, return the day number as per the non-leap year.\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n\n # Define a dictionary to map month to the day number in a non-leap year\n myDict = {"01":0, "02":31, "03":59, "04":90,"05":120,"06":151,\n "07":181,"08":212,"09":243,"10":273,"11":304,"12":334}\n # retreive the year from the string\n year = int(date[:4])\n\n # Check the condition for leap Year\n if year%4 == 0 and (year % 100 != 0 or year % 400 == 0) and int(date[5:7]) > 2:\n # If it\'s a leap year and the month is after February, add 1 to the result\n return myDict[date[5:7]] + int(date[8:]) + 1\n else:\n # Otherwise, return the day number as per the non-leap year\n return myDict[date[5:7]] + int(date[8:])\n \n \n \n``` | 0 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Clean Python code easy to understand 🔥🔥🔥| PYTHON | EASY | day-of-the-year | 0 | 1 | # Intuition\nfetch the date, year, month from the format using slicing. Aftwards check the given year is leap or not if it is a leap year then follow the days of month of that year. Add it to noOfDays variable.\n\n\n# Approach\ncreate a function leap year to check whether the year is leap or not.\nUse sum in built function to get the sum of the sliced days of month array.\n\n# Complexity\n- Time complexity:\nusing Sum in built function it will iterate over the array so Worst case TC will be O(N)\n\n- Space complexity:\n2O(N) which means O(N).\n\n# Code\n```\nclass Solution:\n def isLeap(self, y):\n year = int(y)\n if (year % 400 == 0) or ((year % 4 == 0) and (year % 100 != 0)):\n return 1\n else:\n return 0\n\n def dayOfYear(self, date: str) -> int:\n year = date[:4]\n month = date[5:7]\n day = date[8:10]\n noOfDays = 0\n\n if self.isLeap(year):\n daysOfMonth = [31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n noOfDays += sum(daysOfMonth[:int(month)-1])\n else:\n daysOfMonth = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n noOfDays += sum(daysOfMonth[:int(month)-1])\n\n noOfDays += int(day)\n return noOfDays\n```\n\nUPVOTE! | 0 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Clean Python code easy to understand 🔥🔥🔥| PYTHON | EASY | day-of-the-year | 0 | 1 | # Intuition\nfetch the date, year, month from the format using slicing. Aftwards check the given year is leap or not if it is a leap year then follow the days of month of that year. Add it to noOfDays variable.\n\n\n# Approach\ncreate a function leap year to check whether the year is leap or not.\nUse sum in built function to get the sum of the sliced days of month array.\n\n# Complexity\n- Time complexity:\nusing Sum in built function it will iterate over the array so Worst case TC will be O(N)\n\n- Space complexity:\n2O(N) which means O(N).\n\n# Code\n```\nclass Solution:\n def isLeap(self, y):\n year = int(y)\n if (year % 400 == 0) or ((year % 4 == 0) and (year % 100 != 0)):\n return 1\n else:\n return 0\n\n def dayOfYear(self, date: str) -> int:\n year = date[:4]\n month = date[5:7]\n day = date[8:10]\n noOfDays = 0\n\n if self.isLeap(year):\n daysOfMonth = [31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n noOfDays += sum(daysOfMonth[:int(month)-1])\n else:\n daysOfMonth = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]\n noOfDays += sum(daysOfMonth[:int(month)-1])\n\n noOfDays += int(day)\n return noOfDays\n```\n\nUPVOTE! | 0 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Python3: Slow but Reliable: Use datetime | day-of-the-year | 0 | 1 | # Intuition\n\nWhen handling date and time types, it\'s rarely the "correct" answer to handle conversions yourself.\n\nInstead, use the painstakingly writted and debugged stuff your system provides for you already!\n\nIf I\'m an interviewer, and someone starts busting out leap year modular arithmetic stuff, it\'s a red flag. It\'s the equivalent of an interviewer saying "hey find the phone numbers in this string," and someone starts knocking out an elaborate DP solution instead of saying the magic word "regex."\n\n# Approach\n\n## Getting a Date\n\nWe have a date, so we want to first get a `date` or `datetime` object.\n\n`datetime.strptime` ("string parse time," as opposed to `strftime` which is "string format time") parses a date.\n\n**Note:** it would be better to use a `date` instead. But I couldn\'t find something like `date.strptime` so I just used a `datetime` instead. (this is a mild sin, see below!)\n\n## Getting Another Date\n\nThen we want the first day of the same year: `datetime(year=d.year, 1, 1)` for Jan 1 on that year.\n\n## Getting the Number of Days\n\nMost languages have a type that represents a time difference. In python, that time is `timedelta`. In Java, it\'s `Duration`. The name varies from each language and framework to the next.\n\n# Quick Primer on Times\n\nTime and date handling in most langauges is a Kafkaesque nightmare, which is a real shame because datetime stuff is a major source of bugs in production software. Especially financial trading software like the kind I used to work on.\n\n## The Kinds of Times\n\nThere are three major categories:\n* **absolute times:** the most popular is epoch time, the number of seconds that have elapsed since 1970-01-01 at 00:00 in the UTC-0 time zone.\n * **absolute**: all users in all time zones agree on when exactly an event with this timestamp occurred\n * **time zone agnostic**: does not change based on time zone\n * commonly represented as an integer or float\n* **zoned date times**: a combination of a specific date and time, like 1970-01-01 at 00:00, and a time zone, like UTC-0\n * **absolute**: all users in all time zones agree when this occurrs\n * **time zone aware**: if you move to a different time zone, the date-time part changes. Examples of the same time:\n * 1970-01-01 at 00:00 in UTC-0\n * 1969-12-31 at 19:00 in Eastern Standard Time (UTC-5)\n * 1969-12-31 at 20:00 in Eastern Daylight Time (UTC-4)\n * 1970-01-01 at 01:00 in UTC+1\n * so clearly the time depends on the zone\n * warning: not all zones are integer multiples of an hour!!\n* **local date times**: a date and time WITHOUT a time zone attached\n * **relative**: time time e.g. "4 pm" occurs depends on your time zone\n * **time zone unaware**: there\'s no zone, so nothing changes as you change zones\n\n## The Kinds of Information\n\nThere are two common formats:\n* **date only**: something that represents \'YYYY-mm-dd\'\n* **date time**: something that represents a date AND an intraday time like 01:23:45.123456789\n * the gold standard for the time part is to include nanoseconds\n * Python\'s `datetime` only supports microseconds for whatever reason\n * some formats only support *millisecond* resolution\n\n### When to Use Dates vs Date-Times and Zones\n\n**Use the type contains ONLY the information you have and need.**\n\nIncluding extraneous fields (i.e. using a date-time where the time fields are set to midnight) and/or a time zone when it\'s not relevant is risky because it opens you up to bugs.\n\nBug I\'ve seen in production that caused problems:\n* someone created a zoned date time in January: e.g. `2021-01-01T00:00/America_NewYork`\n * America_NewYork is UTC-5 this time of year\n* then they created another zoned date time in July: e.g. `2021-07-01T00:00/America_NewYork`\n * this is UTC-4 this time of year\n* then they subtracted and got the number of days\n * the result is one off!!\n * because the first date is `2021-01-01T05:00Z`\n * and the second date is `2021-07-01T04:00Z`\n * so the time difference is *one hour short* of the right number of days. They were expecting `n` days, but the actual result for the time difference is `n-1` days and 23 hours. Oof.\n\nThe result of this bug was joining data to the wrong day, such that most of the days of the year had the expected `n` day difference, but some data straddling the "spring forward" EST -> EDT transition were off by a day and therefore were missing data (long story!).\n\nBut in this problem, making zone-*unaware* date-times and subtracting them doesn\'t give you this problem.\n\n# Code\n```\nfrom datetime import datetime, timedelta\n\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n # brute force: compute leap years, do calendar math yourself\n # smarter: use date stuff\n\n d = datetime.strptime(date, r\'%Y-%m-%d\')\n startOfYear = datetime(year=d.year, month=1, day=1)\n\n delta = d-startOfYear\n return delta.days + 1\n``` | 0 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Python3: Slow but Reliable: Use datetime | day-of-the-year | 0 | 1 | # Intuition\n\nWhen handling date and time types, it\'s rarely the "correct" answer to handle conversions yourself.\n\nInstead, use the painstakingly writted and debugged stuff your system provides for you already!\n\nIf I\'m an interviewer, and someone starts busting out leap year modular arithmetic stuff, it\'s a red flag. It\'s the equivalent of an interviewer saying "hey find the phone numbers in this string," and someone starts knocking out an elaborate DP solution instead of saying the magic word "regex."\n\n# Approach\n\n## Getting a Date\n\nWe have a date, so we want to first get a `date` or `datetime` object.\n\n`datetime.strptime` ("string parse time," as opposed to `strftime` which is "string format time") parses a date.\n\n**Note:** it would be better to use a `date` instead. But I couldn\'t find something like `date.strptime` so I just used a `datetime` instead. (this is a mild sin, see below!)\n\n## Getting Another Date\n\nThen we want the first day of the same year: `datetime(year=d.year, 1, 1)` for Jan 1 on that year.\n\n## Getting the Number of Days\n\nMost languages have a type that represents a time difference. In python, that time is `timedelta`. In Java, it\'s `Duration`. The name varies from each language and framework to the next.\n\n# Quick Primer on Times\n\nTime and date handling in most langauges is a Kafkaesque nightmare, which is a real shame because datetime stuff is a major source of bugs in production software. Especially financial trading software like the kind I used to work on.\n\n## The Kinds of Times\n\nThere are three major categories:\n* **absolute times:** the most popular is epoch time, the number of seconds that have elapsed since 1970-01-01 at 00:00 in the UTC-0 time zone.\n * **absolute**: all users in all time zones agree on when exactly an event with this timestamp occurred\n * **time zone agnostic**: does not change based on time zone\n * commonly represented as an integer or float\n* **zoned date times**: a combination of a specific date and time, like 1970-01-01 at 00:00, and a time zone, like UTC-0\n * **absolute**: all users in all time zones agree when this occurrs\n * **time zone aware**: if you move to a different time zone, the date-time part changes. Examples of the same time:\n * 1970-01-01 at 00:00 in UTC-0\n * 1969-12-31 at 19:00 in Eastern Standard Time (UTC-5)\n * 1969-12-31 at 20:00 in Eastern Daylight Time (UTC-4)\n * 1970-01-01 at 01:00 in UTC+1\n * so clearly the time depends on the zone\n * warning: not all zones are integer multiples of an hour!!\n* **local date times**: a date and time WITHOUT a time zone attached\n * **relative**: time time e.g. "4 pm" occurs depends on your time zone\n * **time zone unaware**: there\'s no zone, so nothing changes as you change zones\n\n## The Kinds of Information\n\nThere are two common formats:\n* **date only**: something that represents \'YYYY-mm-dd\'\n* **date time**: something that represents a date AND an intraday time like 01:23:45.123456789\n * the gold standard for the time part is to include nanoseconds\n * Python\'s `datetime` only supports microseconds for whatever reason\n * some formats only support *millisecond* resolution\n\n### When to Use Dates vs Date-Times and Zones\n\n**Use the type contains ONLY the information you have and need.**\n\nIncluding extraneous fields (i.e. using a date-time where the time fields are set to midnight) and/or a time zone when it\'s not relevant is risky because it opens you up to bugs.\n\nBug I\'ve seen in production that caused problems:\n* someone created a zoned date time in January: e.g. `2021-01-01T00:00/America_NewYork`\n * America_NewYork is UTC-5 this time of year\n* then they created another zoned date time in July: e.g. `2021-07-01T00:00/America_NewYork`\n * this is UTC-4 this time of year\n* then they subtracted and got the number of days\n * the result is one off!!\n * because the first date is `2021-01-01T05:00Z`\n * and the second date is `2021-07-01T04:00Z`\n * so the time difference is *one hour short* of the right number of days. They were expecting `n` days, but the actual result for the time difference is `n-1` days and 23 hours. Oof.\n\nThe result of this bug was joining data to the wrong day, such that most of the days of the year had the expected `n` day difference, but some data straddling the "spring forward" EST -> EDT transition were off by a day and therefore were missing data (long story!).\n\nBut in this problem, making zone-*unaware* date-times and subtracting them doesn\'t give you this problem.\n\n# Code\n```\nfrom datetime import datetime, timedelta\n\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n # brute force: compute leap years, do calendar math yourself\n # smarter: use date stuff\n\n d = datetime.strptime(date, r\'%Y-%m-%d\')\n startOfYear = datetime(year=d.year, month=1, day=1)\n\n delta = d-startOfYear\n return delta.days + 1\n``` | 0 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
Wins 94.87% , Day of the Year easy solution | day-of-the-year | 0 | 1 | """#For example, 1600 and 2000 are leap years because they are divisible by 400. However, #1700, 1800, and 1900 are not leap years because they are not divisible by 400.\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n calender1=[31,28,31,30,31,30,31,31,30,31,30,31]\n calender2=[31,29,31,30,31,30,31,31,30,31,30,31]\n year=int(date[0:4])\n month=int(date[5:7])\n days=int(date[8::])\n if year%4==0 and (year%100!=0 or year%400==0):\n main_calender=calender2\n else:\n main_calender=calender1\n month_sum=sum(main_calender[:month-1])\n return(month_sum+days)""" | 0 | Given a string `date` representing a [Gregorian calendar](https://en.wikipedia.org/wiki/Gregorian_calendar) date formatted as `YYYY-MM-DD`, return _the day number of the year_.
**Example 1:**
**Input:** date = "2019-01-09 "
**Output:** 9
**Explanation:** Given date is the 9th day of the year in 2019.
**Example 2:**
**Input:** date = "2019-02-10 "
**Output:** 41
**Constraints:**
* `date.length == 10`
* `date[4] == date[7] == '-'`, and all other `date[i]`'s are digits
* `date` represents a calendar date between Jan 1st, 1900 and Dec 31th, 2019. | null |
Wins 94.87% , Day of the Year easy solution | day-of-the-year | 0 | 1 | """#For example, 1600 and 2000 are leap years because they are divisible by 400. However, #1700, 1800, and 1900 are not leap years because they are not divisible by 400.\nclass Solution:\n def dayOfYear(self, date: str) -> int:\n calender1=[31,28,31,30,31,30,31,31,30,31,30,31]\n calender2=[31,29,31,30,31,30,31,31,30,31,30,31]\n year=int(date[0:4])\n month=int(date[5:7])\n days=int(date[8::])\n if year%4==0 and (year%100!=0 or year%400==0):\n main_calender=calender2\n else:\n main_calender=calender1\n month_sum=sum(main_calender[:month-1])\n return(month_sum+days)""" | 0 | Given a 2D `grid` of size `m x n` and an integer `k`. You need to shift the `grid` `k` times.
In one shift operation:
* Element at `grid[i][j]` moves to `grid[i][j + 1]`.
* Element at `grid[i][n - 1]` moves to `grid[i + 1][0]`.
* Element at `grid[m - 1][n - 1]` moves to `grid[0][0]`.
Return the _2D grid_ after applying shift operation `k` times.
**Example 1:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 1
**Output:** \[\[9,1,2\],\[3,4,5\],\[6,7,8\]\]
**Example 2:**
**Input:** `grid` = \[\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\],\[12,0,21,13\]\], k = 4
**Output:** \[\[12,0,21,13\],\[3,8,1,9\],\[19,7,2,5\],\[4,6,11,10\]\]
**Example 3:**
**Input:** `grid` = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\], k = 9
**Output:** \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m <= 50`
* `1 <= n <= 50`
* `-1000 <= grid[i][j] <= 1000`
* `0 <= k <= 100` | Have a integer array of how many days there are per month. February gets one extra day if its a leap year. Then, we can manually count the ordinal as day + (number of days in months before this one). |
😎Python3! As short as it gets! [T:96%] O(n*target) | number-of-dice-rolls-with-target-sum | 0 | 1 | Enjoy:\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n MOD = 1000 * 1000 * 1000 + 7 \n dp = defaultdict(int)\n dp[0] = 1 \n for c in range(n):\n sm = defaultdict(int)\n for i in range(target+1):\n sm[i] = sm[i-1] + dp[i]\n for i in range(target+1):\n dp[i] = (sm[i-1] - sm[i-k-1]) % MOD\n return dp[target]\n```\n`dp` is the dynamic-programming table and `sm` is a presum array to calculate sum of segments in `dp`. | 4 | You have `n` dice, and each die has `k` faces numbered from `1` to `k`.
Given three integers `n`, `k`, and `target`, return _the number of possible ways (out of the_ `kn` _total ways)_ _to roll the dice, so the sum of the face-up numbers equals_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, k = 6, target = 3
**Output:** 1
**Explanation:** You throw one die with 6 faces.
There is only one way to get a sum of 3.
**Example 2:**
**Input:** n = 2, k = 6, target = 7
**Output:** 6
**Explanation:** You throw two dice, each with 6 faces.
There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
**Example 3:**
**Input:** n = 30, k = 30, target = 500
**Output:** 222616187
**Explanation:** The answer must be returned modulo 109 + 7.
**Constraints:**
* `1 <= n, k <= 30`
* `1 <= target <= 1000` | null |
😎Python3! As short as it gets! [T:96%] O(n*target) | number-of-dice-rolls-with-target-sum | 0 | 1 | Enjoy:\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n MOD = 1000 * 1000 * 1000 + 7 \n dp = defaultdict(int)\n dp[0] = 1 \n for c in range(n):\n sm = defaultdict(int)\n for i in range(target+1):\n sm[i] = sm[i-1] + dp[i]\n for i in range(target+1):\n dp[i] = (sm[i-1] - sm[i-k-1]) % MOD\n return dp[target]\n```\n`dp` is the dynamic-programming table and `sm` is a presum array to calculate sum of segments in `dp`. | 4 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
86.7% Faster Solution || DP | number-of-dice-rolls-with-target-sum | 0 | 1 | ```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n mod = 10**9+7\n dp = [[0]*(target + 1) for _ in range(n + 1)]\n dp[0][0] = 1\n if target < 1 or target > n*k: return 0\n for x in range(1, n + 1):\n for y in range(1, k + 1):\n for z in range(y, target + 1):\n dp[x][z] = (dp[x][z] + dp[x-1][z-y]) % mod\n return dp[-1][-1]\n``` | 2 | You have `n` dice, and each die has `k` faces numbered from `1` to `k`.
Given three integers `n`, `k`, and `target`, return _the number of possible ways (out of the_ `kn` _total ways)_ _to roll the dice, so the sum of the face-up numbers equals_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, k = 6, target = 3
**Output:** 1
**Explanation:** You throw one die with 6 faces.
There is only one way to get a sum of 3.
**Example 2:**
**Input:** n = 2, k = 6, target = 7
**Output:** 6
**Explanation:** You throw two dice, each with 6 faces.
There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
**Example 3:**
**Input:** n = 30, k = 30, target = 500
**Output:** 222616187
**Explanation:** The answer must be returned modulo 109 + 7.
**Constraints:**
* `1 <= n, k <= 30`
* `1 <= target <= 1000` | null |
86.7% Faster Solution || DP | number-of-dice-rolls-with-target-sum | 0 | 1 | ```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n mod = 10**9+7\n dp = [[0]*(target + 1) for _ in range(n + 1)]\n dp[0][0] = 1\n if target < 1 or target > n*k: return 0\n for x in range(1, n + 1):\n for y in range(1, k + 1):\n for z in range(y, target + 1):\n dp[x][z] = (dp[x][z] + dp[x-1][z-y]) % mod\n return dp[-1][-1]\n``` | 2 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
✅[Python C++] ⏱90% Fast || Easy || Recursion + Bottom-Up | number-of-dice-rolls-with-target-sum | 0 | 1 | We can fix one die with any number `f`(f<k=number of faces) and from remaining `n-1` dices we can make the target = `targert-f`\n\n**Python**\n\n1. Recursive Solution using memorisation(`@lru_cache`)\n```\nclass Solution:\n @lru_cache(maxsize=None)\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n if n==1:\n return int(0<target<=k)\n \n ans=0\n for i in range(1,k+1):\n ans+=self.numRollsToTarget(n-1,k,target-i)\n return ans%(10**9+7)\n```\n\n2. Bottom Up Approach\n\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n \n mod=10**9+7\n if target < n or target > n * k:\n return 0\n \n dp=[[0 for _ in range(target+1)] for _ in range(n+1)]\n dp[0][0]=1\n \n for i in range(1,n+1):\n for j in range(1,target+1):\n for x in range(1,k+1):\n if j-x>=0:\n dp[i][j]=(dp[i][j]%mod+dp[i-1][j-x]%mod)%mod\n \n return dp[n][target]\n```\n\n**=================================**\n**C++**\n\n```\nclass Solution {\npublic:\n int numRollsToTarget(int n, int k, int target) {\n int mod=1000000007;\n if (target < n or target > n * k)\n return 0;\n \n vector<vector<int>> dp(n+1,vector<int>(target+1,0));\n dp[0][0]=1;\n \n for(int i=1;i<=n;i++)\n for(int j=1;j<=target;j++)\n for(int x=1;x<=k;x++)\n if(j-x>=0)\n dp[i][j]=(dp[i][j]%mod+dp[i-1][j-x]%mod)%mod;\n return dp[n][target];\n \n }\n};\n``` | 2 | You have `n` dice, and each die has `k` faces numbered from `1` to `k`.
Given three integers `n`, `k`, and `target`, return _the number of possible ways (out of the_ `kn` _total ways)_ _to roll the dice, so the sum of the face-up numbers equals_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, k = 6, target = 3
**Output:** 1
**Explanation:** You throw one die with 6 faces.
There is only one way to get a sum of 3.
**Example 2:**
**Input:** n = 2, k = 6, target = 7
**Output:** 6
**Explanation:** You throw two dice, each with 6 faces.
There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
**Example 3:**
**Input:** n = 30, k = 30, target = 500
**Output:** 222616187
**Explanation:** The answer must be returned modulo 109 + 7.
**Constraints:**
* `1 <= n, k <= 30`
* `1 <= target <= 1000` | null |
✅[Python C++] ⏱90% Fast || Easy || Recursion + Bottom-Up | number-of-dice-rolls-with-target-sum | 0 | 1 | We can fix one die with any number `f`(f<k=number of faces) and from remaining `n-1` dices we can make the target = `targert-f`\n\n**Python**\n\n1. Recursive Solution using memorisation(`@lru_cache`)\n```\nclass Solution:\n @lru_cache(maxsize=None)\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n if n==1:\n return int(0<target<=k)\n \n ans=0\n for i in range(1,k+1):\n ans+=self.numRollsToTarget(n-1,k,target-i)\n return ans%(10**9+7)\n```\n\n2. Bottom Up Approach\n\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n \n mod=10**9+7\n if target < n or target > n * k:\n return 0\n \n dp=[[0 for _ in range(target+1)] for _ in range(n+1)]\n dp[0][0]=1\n \n for i in range(1,n+1):\n for j in range(1,target+1):\n for x in range(1,k+1):\n if j-x>=0:\n dp[i][j]=(dp[i][j]%mod+dp[i-1][j-x]%mod)%mod\n \n return dp[n][target]\n```\n\n**=================================**\n**C++**\n\n```\nclass Solution {\npublic:\n int numRollsToTarget(int n, int k, int target) {\n int mod=1000000007;\n if (target < n or target > n * k)\n return 0;\n \n vector<vector<int>> dp(n+1,vector<int>(target+1,0));\n dp[0][0]=1;\n \n for(int i=1;i<=n;i++)\n for(int j=1;j<=target;j++)\n for(int x=1;x<=k;x++)\n if(j-x>=0)\n dp[i][j]=(dp[i][j]%mod+dp[i-1][j-x]%mod)%mod;\n return dp[n][target];\n \n }\n};\n``` | 2 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
python dp solution | number-of-dice-rolls-with-target-sum | 0 | 1 | ```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n def func(i,n,k,tr,dic):\n if i==n and tr==0:\n return 1\n if i>=n or tr<=0:\n return 0\n if (i,tr) in dic:\n return dic[(i,tr)]\n sm=0\n for j in range(1,k+1):\n # print(i+1,tr-j)\n sm+=func(i+1,n,k,tr-j,dic)\n dic[(i,tr)]=sm\n return sm\n return func(0,n,k,target,{})%1000000007\n``` | 2 | You have `n` dice, and each die has `k` faces numbered from `1` to `k`.
Given three integers `n`, `k`, and `target`, return _the number of possible ways (out of the_ `kn` _total ways)_ _to roll the dice, so the sum of the face-up numbers equals_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, k = 6, target = 3
**Output:** 1
**Explanation:** You throw one die with 6 faces.
There is only one way to get a sum of 3.
**Example 2:**
**Input:** n = 2, k = 6, target = 7
**Output:** 6
**Explanation:** You throw two dice, each with 6 faces.
There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
**Example 3:**
**Input:** n = 30, k = 30, target = 500
**Output:** 222616187
**Explanation:** The answer must be returned modulo 109 + 7.
**Constraints:**
* `1 <= n, k <= 30`
* `1 <= target <= 1000` | null |
python dp solution | number-of-dice-rolls-with-target-sum | 0 | 1 | ```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n def func(i,n,k,tr,dic):\n if i==n and tr==0:\n return 1\n if i>=n or tr<=0:\n return 0\n if (i,tr) in dic:\n return dic[(i,tr)]\n sm=0\n for j in range(1,k+1):\n # print(i+1,tr-j)\n sm+=func(i+1,n,k,tr-j,dic)\n dic[(i,tr)]=sm\n return sm\n return func(0,n,k,target,{})%1000000007\n``` | 2 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
O(target*n*k) using Memorize Dynamic Programming | number-of-dice-rolls-with-target-sum | 0 | 1 | **Main Idea**:\n+ Applying memorize dynamic programming as follows:\n```\ndp[target][n] = sum(\n dp[target - ki][n-1] where target-ki>=0, n>=1\n)\ndp[target][n] = 0 when target==0 or target>k\ndp[target][n] = 1 when n = 1 and 1<=target<=k\n```\n\n**Code**:\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n """\n x1 + x2 + ... + xn = target\n 1<=xi<=k\n dp[target][6] = sum(dp[target-xi][5]) with 1<=xi<=k and target-xi>=0\n """\n # print("n, k, target:", n, k, target)\n mod = 10**9 + 7\n dp = [[None] * n for _ in range(target+1)]\n \n def fsol(vsum, ndice):\n if dp[vsum][ndice-1] is None:\n # print("+ ", (vsum, ndice), dp[vsum][ndice-1])\n if vsum==0:\n dp[vsum][ndice-1] = 0\n elif ndice==1:\n dp[vsum][ndice-1] = 1 if 1<=vsum and vsum<=k else 0\n else:\n total = 0\n for ki in range(1, k+1):\n if vsum-ki>=0:\n total = (total + fsol(vsum-ki, ndice-1))%mod\n dp[vsum][ndice-1] = total\n pass\n return dp[vsum][ndice-1]%mod\n \n ans = fsol(target, n)%mod\n # print("ans:", ans)\n # print("=" * 20, "\\n")\n return ans\n``` | 1 | You have `n` dice, and each die has `k` faces numbered from `1` to `k`.
Given three integers `n`, `k`, and `target`, return _the number of possible ways (out of the_ `kn` _total ways)_ _to roll the dice, so the sum of the face-up numbers equals_ `target`. Since the answer may be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, k = 6, target = 3
**Output:** 1
**Explanation:** You throw one die with 6 faces.
There is only one way to get a sum of 3.
**Example 2:**
**Input:** n = 2, k = 6, target = 7
**Output:** 6
**Explanation:** You throw two dice, each with 6 faces.
There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
**Example 3:**
**Input:** n = 30, k = 30, target = 500
**Output:** 222616187
**Explanation:** The answer must be returned modulo 109 + 7.
**Constraints:**
* `1 <= n, k <= 30`
* `1 <= target <= 1000` | null |
O(target*n*k) using Memorize Dynamic Programming | number-of-dice-rolls-with-target-sum | 0 | 1 | **Main Idea**:\n+ Applying memorize dynamic programming as follows:\n```\ndp[target][n] = sum(\n dp[target - ki][n-1] where target-ki>=0, n>=1\n)\ndp[target][n] = 0 when target==0 or target>k\ndp[target][n] = 1 when n = 1 and 1<=target<=k\n```\n\n**Code**:\n```\nclass Solution:\n def numRollsToTarget(self, n: int, k: int, target: int) -> int:\n """\n x1 + x2 + ... + xn = target\n 1<=xi<=k\n dp[target][6] = sum(dp[target-xi][5]) with 1<=xi<=k and target-xi>=0\n """\n # print("n, k, target:", n, k, target)\n mod = 10**9 + 7\n dp = [[None] * n for _ in range(target+1)]\n \n def fsol(vsum, ndice):\n if dp[vsum][ndice-1] is None:\n # print("+ ", (vsum, ndice), dp[vsum][ndice-1])\n if vsum==0:\n dp[vsum][ndice-1] = 0\n elif ndice==1:\n dp[vsum][ndice-1] = 1 if 1<=vsum and vsum<=k else 0\n else:\n total = 0\n for ki in range(1, k+1):\n if vsum-ki>=0:\n total = (total + fsol(vsum-ki, ndice-1))%mod\n dp[vsum][ndice-1] = total\n pass\n return dp[vsum][ndice-1]%mod\n \n ans = fsol(target, n)%mod\n # print("ans:", ans)\n # print("=" * 20, "\\n")\n return ans\n``` | 1 | A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an `m x n` grid of characters `grid` where each element is a wall, floor, or box.
Your task is to move the box `'B'` to the target position `'T'` under the following rules:
* The character `'S'` represents the player. The player can move up, down, left, right in `grid` if it is a floor (empty cell).
* The character `'.'` represents the floor which means a free cell to walk.
* The character `'#'` represents the wall which means an obstacle (impossible to walk there).
* There is only one box `'B'` and one target cell `'T'` in the `grid`.
* The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a **push**.
* The player cannot walk through the box.
Return _the minimum number of **pushes** to move the box to the target_. If there is no way to reach the target, return `-1`.
**Example 1:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", ". ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 3
**Explanation:** We return only the number of times the box is pushed.
**Example 2:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", "# ", "# ", "# ", "# "\],
\[ "# ", ". ", ". ", "B ", ". ", "# "\],
\[ "# ", "# ", "# ", "# ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** -1
**Example 3:**
**Input:** grid = \[\[ "# ", "# ", "# ", "# ", "# ", "# "\],
\[ "# ", "T ", ". ", ". ", "# ", "# "\],
\[ "# ", ". ", "# ", "B ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", ". ", "# "\],
\[ "# ", ". ", ". ", ". ", "S ", "# "\],
\[ "# ", "# ", "# ", "# ", "# ", "# "\]\]
**Output:** 5
**Explanation:** push the box down, left, left, up and up.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid` contains only characters `'.'`, `'#'`, `'S'`, `'T'`, or `'B'`.
* There is only one character `'S'`, `'B'`, and `'T'` in the `grid`. | Use dynamic programming. The states are how many dice are remaining, and what sum total you have rolled so far. |
Python 3 || 9 lines, groupby, w/ example || T/M: 95% / 15% | swap-for-longest-repeated-character-substring | 0 | 1 | ```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int: # Example: text = "babbab"\n\n c = Counter(text) # c = {\'a\':2, \'b\':4}\n\n ch, ct = zip(*[(k, sum(1 for _ in g)) # ch = (\'b\',\'a\',\'b\',\'a\',\'b\')\n for k, g in groupby(text)]) # ct = ( 1 , 1 , 2 , 1 , 1 )\n\n n = len(ch)\n \n ans = max(ct[i]+(ct[i]<c[ch[i]]) for i in range(n)) # ans = max (2 , 2, 3, 2, 2 ) = 3\n\n for i in range(1, n-1): # i sm+(sm<c[ch[i-1]]) ans\n # \u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\n if ch[i-1] == ch[i+1] and ct[i] == 1: # 0 3\n sm = ct[i-1]+ct[i+1] # 1 3 + (3 < 4) = 4 4\n ans = max(ans, sm + (sm < c[ch[i-1]])) # 2 4\n # 3 3 + (3 < 4) = 4 4\n return ans # 4 4 <\u2013\u2013 return\n```\n[https://leetcode.com/problems/swap-for-longest-repeated-character-substring/submissions/860807955/](http://)\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(*N*). | 6 | You are given a string `text`. You can swap two of the characters in the `text`.
Return _the length of the longest substring with repeated characters_.
**Example 1:**
**Input:** text = "ababa "
**Output:** 3
**Explanation:** We can swap the first 'b' with the last 'a', or the last 'b' with the first 'a'. Then, the longest repeated character substring is "aaa " with length 3.
**Example 2:**
**Input:** text = "aaabaaa "
**Output:** 6
**Explanation:** Swap 'b' with the last 'a' (or the first 'a'), and we get longest repeated character substring "aaaaaa " with length 6.
**Example 3:**
**Input:** text = "aaaaa "
**Output:** 5
**Explanation:** No need to swap, longest repeated character substring is "aaaaa " with length is 5.
**Constraints:**
* `1 <= text.length <= 2 * 104`
* `text` consist of lowercase English characters only. | Split the string into words, then look at adjacent triples of words. |
Python 3 || 9 lines, groupby, w/ example || T/M: 95% / 15% | swap-for-longest-repeated-character-substring | 0 | 1 | ```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int: # Example: text = "babbab"\n\n c = Counter(text) # c = {\'a\':2, \'b\':4}\n\n ch, ct = zip(*[(k, sum(1 for _ in g)) # ch = (\'b\',\'a\',\'b\',\'a\',\'b\')\n for k, g in groupby(text)]) # ct = ( 1 , 1 , 2 , 1 , 1 )\n\n n = len(ch)\n \n ans = max(ct[i]+(ct[i]<c[ch[i]]) for i in range(n)) # ans = max (2 , 2, 3, 2, 2 ) = 3\n\n for i in range(1, n-1): # i sm+(sm<c[ch[i-1]]) ans\n # \u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\n if ch[i-1] == ch[i+1] and ct[i] == 1: # 0 3\n sm = ct[i-1]+ct[i+1] # 1 3 + (3 < 4) = 4 4\n ans = max(ans, sm + (sm < c[ch[i-1]])) # 2 4\n # 3 3 + (3 < 4) = 4 4\n return ans # 4 4 <\u2013\u2013 return\n```\n[https://leetcode.com/problems/swap-for-longest-repeated-character-substring/submissions/860807955/](http://)\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(*N*). | 6 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Python, very easy to understand approach | swap-for-longest-repeated-character-substring | 0 | 1 | # Intuition\nidea is simple we can have only two characaters in a window and one should have freq = 1\n\n# Approach\nif size of window ==2 we try to see if current freq of\ncharacter (other than 1 freq character) is less than that of total freq of that character if yes we can replace this char with 1 freq char if not we shrink window\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n c = Counter(text)\n l = 0\n r = len(text)-1\n start = 0\n res = 0\n m = {}\n maxi = 0\n while l<=r:\n if text[l] in m:\n m[text[l]]+=1\n else:\n m[text[l]]=1\n le = len(m)\n while le>2:\n m[text[start]]-=1\n if m[text[start]]==0:\n m.pop(text[start])\n start+=1\n le = len(m)\n mini = float(\'inf\')\n for ch in m:\n mini = min(mini, m[ch])\n while mini>1 and le>1:\n m[text[start]]-=1\n if m[text[start]]==0:\n m.pop(text[start])\n start+=1\n le = len(m)\n for ch in m:\n mini = min(mini, m[ch])\n if le>1:\n ch1, ch2 = None, None\n for ch in m:\n if not ch1:\n ch1 = ch\n else:\n ch2 = ch\n if mini==m[ch1]:\n if m[ch2]<c[ch2]:\n res = max(res, l-start+1)\n else:\n res = max(res, m[ch2])\n else:\n if m[ch1]<c[ch1]:\n res = max(res, l-start+1)\n else:\n res = max(res, m[ch1])\n else:\n for ch in m:\n res = max(res, m[ch])\n l+=1\n return res\n\n\n\n``` | 0 | You are given a string `text`. You can swap two of the characters in the `text`.
Return _the length of the longest substring with repeated characters_.
**Example 1:**
**Input:** text = "ababa "
**Output:** 3
**Explanation:** We can swap the first 'b' with the last 'a', or the last 'b' with the first 'a'. Then, the longest repeated character substring is "aaa " with length 3.
**Example 2:**
**Input:** text = "aaabaaa "
**Output:** 6
**Explanation:** Swap 'b' with the last 'a' (or the first 'a'), and we get longest repeated character substring "aaaaaa " with length 6.
**Example 3:**
**Input:** text = "aaaaa "
**Output:** 5
**Explanation:** No need to swap, longest repeated character substring is "aaaaa " with length is 5.
**Constraints:**
* `1 <= text.length <= 2 * 104`
* `text` consist of lowercase English characters only. | Split the string into words, then look at adjacent triples of words. |
Python, very easy to understand approach | swap-for-longest-repeated-character-substring | 0 | 1 | # Intuition\nidea is simple we can have only two characaters in a window and one should have freq = 1\n\n# Approach\nif size of window ==2 we try to see if current freq of\ncharacter (other than 1 freq character) is less than that of total freq of that character if yes we can replace this char with 1 freq char if not we shrink window\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n c = Counter(text)\n l = 0\n r = len(text)-1\n start = 0\n res = 0\n m = {}\n maxi = 0\n while l<=r:\n if text[l] in m:\n m[text[l]]+=1\n else:\n m[text[l]]=1\n le = len(m)\n while le>2:\n m[text[start]]-=1\n if m[text[start]]==0:\n m.pop(text[start])\n start+=1\n le = len(m)\n mini = float(\'inf\')\n for ch in m:\n mini = min(mini, m[ch])\n while mini>1 and le>1:\n m[text[start]]-=1\n if m[text[start]]==0:\n m.pop(text[start])\n start+=1\n le = len(m)\n for ch in m:\n mini = min(mini, m[ch])\n if le>1:\n ch1, ch2 = None, None\n for ch in m:\n if not ch1:\n ch1 = ch\n else:\n ch2 = ch\n if mini==m[ch1]:\n if m[ch2]<c[ch2]:\n res = max(res, l-start+1)\n else:\n res = max(res, m[ch2])\n else:\n if m[ch1]<c[ch1]:\n res = max(res, l-start+1)\n else:\n res = max(res, m[ch1])\n else:\n for ch in m:\n res = max(res, m[ch])\n l+=1\n return res\n\n\n\n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Python 3 run length encoding + Check Triplets | swap-for-longest-repeated-character-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n run_len_coded = []\n\n cnt = 1\n\n #also keep the count of largest block\n ans = float(\'-inf\')\n count = collections.Counter(text)\n for i in range(1, len(text)):\n if text[i]!= text[i-1]:\n #reset the counter\n ans = max(ans ,cnt )\n \n if cnt < count[text[i-1]]:\n ans = max(ans , cnt+1)\n \n run_len_coded.append((text[i-1] , cnt))\n cnt=1\n \n else:\n cnt+=1\n\n ans = max(ans , cnt)\n if cnt < count[text[-1]]:\n ans = max(ans , cnt+1)\n run_len_coded.append((text[-1],cnt))\n\n\n\n\n #at momebnt we have largest that is already present without any swap\n #swap can be done if between 2 blocks there is a single a length block ans\n #we have more 2 adjacent chars left before or after the \n\n #Formally we can merge them in following consditons\n\n # if arr[i-1] == arr[i+1] and len(arr[i])==1 and count(arr[i-1]) > len(arr[i-1])+len(arr[i]) \n\n #examining edges cases , exploration\n #aaabaaacaazhfjdaa\n #another edge case\n #aaaafjofrja #ans we will have to check this case as well\n\n for i in range(0, len(run_len_coded)-2):\n #first check the case for last or first append\n \n \n #check the merge condition\n if run_len_coded[i][0] == run_len_coded[i+2][0] and run_len_coded[i+1][1]== 1:\n if run_len_coded[i][1] + run_len_coded[i+2][1] == count[run_len_coded[i][0]]:\n \n ans = max(ans , run_len_coded[i][1] +run_len_coded[i+2][1])\n elif run_len_coded[i][1] + run_len_coded[i+2][1] < count[run_len_coded[i][0]]:\n ans = max(ans , run_len_coded[i][1] +run_len_coded[i+2][1]+1)\n \n \n \n\n\n return(ans)\n \n``` | 0 | You are given a string `text`. You can swap two of the characters in the `text`.
Return _the length of the longest substring with repeated characters_.
**Example 1:**
**Input:** text = "ababa "
**Output:** 3
**Explanation:** We can swap the first 'b' with the last 'a', or the last 'b' with the first 'a'. Then, the longest repeated character substring is "aaa " with length 3.
**Example 2:**
**Input:** text = "aaabaaa "
**Output:** 6
**Explanation:** Swap 'b' with the last 'a' (or the first 'a'), and we get longest repeated character substring "aaaaaa " with length 6.
**Example 3:**
**Input:** text = "aaaaa "
**Output:** 5
**Explanation:** No need to swap, longest repeated character substring is "aaaaa " with length is 5.
**Constraints:**
* `1 <= text.length <= 2 * 104`
* `text` consist of lowercase English characters only. | Split the string into words, then look at adjacent triples of words. |
Python 3 run length encoding + Check Triplets | swap-for-longest-repeated-character-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n run_len_coded = []\n\n cnt = 1\n\n #also keep the count of largest block\n ans = float(\'-inf\')\n count = collections.Counter(text)\n for i in range(1, len(text)):\n if text[i]!= text[i-1]:\n #reset the counter\n ans = max(ans ,cnt )\n \n if cnt < count[text[i-1]]:\n ans = max(ans , cnt+1)\n \n run_len_coded.append((text[i-1] , cnt))\n cnt=1\n \n else:\n cnt+=1\n\n ans = max(ans , cnt)\n if cnt < count[text[-1]]:\n ans = max(ans , cnt+1)\n run_len_coded.append((text[-1],cnt))\n\n\n\n\n #at momebnt we have largest that is already present without any swap\n #swap can be done if between 2 blocks there is a single a length block ans\n #we have more 2 adjacent chars left before or after the \n\n #Formally we can merge them in following consditons\n\n # if arr[i-1] == arr[i+1] and len(arr[i])==1 and count(arr[i-1]) > len(arr[i-1])+len(arr[i]) \n\n #examining edges cases , exploration\n #aaabaaacaazhfjdaa\n #another edge case\n #aaaafjofrja #ans we will have to check this case as well\n\n for i in range(0, len(run_len_coded)-2):\n #first check the case for last or first append\n \n \n #check the merge condition\n if run_len_coded[i][0] == run_len_coded[i+2][0] and run_len_coded[i+1][1]== 1:\n if run_len_coded[i][1] + run_len_coded[i+2][1] == count[run_len_coded[i][0]]:\n \n ans = max(ans , run_len_coded[i][1] +run_len_coded[i+2][1])\n elif run_len_coded[i][1] + run_len_coded[i+2][1] < count[run_len_coded[i][0]]:\n ans = max(ans , run_len_coded[i][1] +run_len_coded[i+2][1]+1)\n \n \n \n\n\n return(ans)\n \n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Python 3| O(N) | swap-for-longest-repeated-character-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n\n def solve(text):\n total = {}\n for i in text:\n if i not in total:\n total[i] = 0\n total[i]+=1\n \n # print(total)\n\n i = 0\n start = 0\n curr = None\n val = 0\n maxx = 0\n swap = 1\n while i < len(text):\n if curr == None:\n curr = text[i]\n val+=1\n i+=1\n elif curr!=text[i]:\n #swap\n if total[curr] > val and swap > 0:\n val+=1\n start = i\n i+=1\n swap-=1\n elif swap == 0:\n i = start\n curr = None\n val = 0\n swap = 1\n else:\n curr = None\n val = 0\n swap = 1\n elif curr == text[i]:\n if total[curr] > val:\n val+=1\n i+=1\n else:\n val = 0\n i = start\n curr = None\n maxx = max(val,maxx)\n if total[text[-1]] > val and swap > 0:\n maxx = max(val+1,maxx)\n return maxx\n\n return solve(text)\n # return 2\n \n \n``` | 0 | You are given a string `text`. You can swap two of the characters in the `text`.
Return _the length of the longest substring with repeated characters_.
**Example 1:**
**Input:** text = "ababa "
**Output:** 3
**Explanation:** We can swap the first 'b' with the last 'a', or the last 'b' with the first 'a'. Then, the longest repeated character substring is "aaa " with length 3.
**Example 2:**
**Input:** text = "aaabaaa "
**Output:** 6
**Explanation:** Swap 'b' with the last 'a' (or the first 'a'), and we get longest repeated character substring "aaaaaa " with length 6.
**Example 3:**
**Input:** text = "aaaaa "
**Output:** 5
**Explanation:** No need to swap, longest repeated character substring is "aaaaa " with length is 5.
**Constraints:**
* `1 <= text.length <= 2 * 104`
* `text` consist of lowercase English characters only. | Split the string into words, then look at adjacent triples of words. |
Python 3| O(N) | swap-for-longest-repeated-character-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n\n def solve(text):\n total = {}\n for i in text:\n if i not in total:\n total[i] = 0\n total[i]+=1\n \n # print(total)\n\n i = 0\n start = 0\n curr = None\n val = 0\n maxx = 0\n swap = 1\n while i < len(text):\n if curr == None:\n curr = text[i]\n val+=1\n i+=1\n elif curr!=text[i]:\n #swap\n if total[curr] > val and swap > 0:\n val+=1\n start = i\n i+=1\n swap-=1\n elif swap == 0:\n i = start\n curr = None\n val = 0\n swap = 1\n else:\n curr = None\n val = 0\n swap = 1\n elif curr == text[i]:\n if total[curr] > val:\n val+=1\n i+=1\n else:\n val = 0\n i = start\n curr = None\n maxx = max(val,maxx)\n if total[text[-1]] > val and swap > 0:\n maxx = max(val+1,maxx)\n return maxx\n\n return solve(text)\n # return 2\n \n \n``` | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
easiest python solution, beginner friendly | swap-for-longest-repeated-character-substring | 0 | 1 | \n\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n # Important Question\n \n d=defaultdict(int); out=0; res=0; i=0; c=Counter(text)\n \n for j in range(len(text)):\n d[text[j]]+=1\n while len(d)>2 or (min(d.values())>1 and len(d)>1):\n d[text[i]]-=1\n if not d[text[i]]:del d[text[i]]\n i+=1\n \n \n if len(d)>=2:\n var=max(d.items(),key=lambda x:x[1])[0]\n \n if c[var] > d[var]:\n out=max(out,j-i+1)\n else:\n out=max(out,j-i+1)\n \n \n return out | 0 | You are given a string `text`. You can swap two of the characters in the `text`.
Return _the length of the longest substring with repeated characters_.
**Example 1:**
**Input:** text = "ababa "
**Output:** 3
**Explanation:** We can swap the first 'b' with the last 'a', or the last 'b' with the first 'a'. Then, the longest repeated character substring is "aaa " with length 3.
**Example 2:**
**Input:** text = "aaabaaa "
**Output:** 6
**Explanation:** Swap 'b' with the last 'a' (or the first 'a'), and we get longest repeated character substring "aaaaaa " with length 6.
**Example 3:**
**Input:** text = "aaaaa "
**Output:** 5
**Explanation:** No need to swap, longest repeated character substring is "aaaaa " with length is 5.
**Constraints:**
* `1 <= text.length <= 2 * 104`
* `text` consist of lowercase English characters only. | Split the string into words, then look at adjacent triples of words. |
easiest python solution, beginner friendly | swap-for-longest-repeated-character-substring | 0 | 1 | \n\nclass Solution:\n def maxRepOpt1(self, text: str) -> int:\n # Important Question\n \n d=defaultdict(int); out=0; res=0; i=0; c=Counter(text)\n \n for j in range(len(text)):\n d[text[j]]+=1\n while len(d)>2 or (min(d.values())>1 and len(d)>1):\n d[text[i]]-=1\n if not d[text[i]]:del d[text[i]]\n i+=1\n \n \n if len(d)>=2:\n var=max(d.items(),key=lambda x:x[1])[0]\n \n if c[var] > d[var]:\n out=max(out,j-i+1)\n else:\n out=max(out,j-i+1)\n \n \n return out | 0 | Given a binary tree with the following rules:
1. `root.val == 0`
2. If `treeNode.val == x` and `treeNode.left != null`, then `treeNode.left.val == 2 * x + 1`
3. If `treeNode.val == x` and `treeNode.right != null`, then `treeNode.right.val == 2 * x + 2`
Now the binary tree is contaminated, which means all `treeNode.val` have been changed to `-1`.
Implement the `FindElements` class:
* `FindElements(TreeNode* root)` Initializes the object with a contaminated binary tree and recovers it.
* `bool find(int target)` Returns `true` if the `target` value exists in the recovered binary tree.
**Example 1:**
**Input**
\[ "FindElements ", "find ", "find "\]
\[\[\[-1,null,-1\]\],\[1\],\[2\]\]
**Output**
\[null,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1\]);
findElements.find(1); // return False
findElements.find(2); // return True
**Example 2:**
**Input**
\[ "FindElements ", "find ", "find ", "find "\]
\[\[\[-1,-1,-1,-1,-1\]\],\[1\],\[3\],\[5\]\]
**Output**
\[null,true,true,false\]
**Explanation**
FindElements findElements = new FindElements(\[-1,-1,-1,-1,-1\]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
**Example 3:**
**Input**
\[ "FindElements ", "find ", "find ", "find ", "find "\]
\[\[\[-1,null,-1,-1,null,-1\]\],\[2\],\[3\],\[4\],\[5\]\]
**Output**
\[null,true,false,false,true\]
**Explanation**
FindElements findElements = new FindElements(\[-1,null,-1,-1,null,-1\]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
**Constraints:**
* `TreeNode.val == -1`
* The height of the binary tree is less than or equal to `20`
* The total number of nodes is between `[1, 104]`
* Total calls of `find()` is between `[1, 104]`
* `0 <= target <= 106` | There are two cases: a block of characters, or two blocks of characters between one different character.
By keeping a run-length encoded version of the string, we can easily check these cases. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.