title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅ Python Solution || DP || Aditya Verma Approach||Bottom Up | shortest-common-supersequence | 0 | 1 | PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask.\n# Intuition\nUse Longest Common Subsequence to generated matrix and then matrix to get result string\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(N*M) + O(N+M)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N*M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestCommonSupersequence(self, str1: str, str2: str) -> str:\n #Normal longest common subsequence\n n,m=len(str1),len(str2)\n #initialization\n dp=[[0 for i in range(m+1)]for j in range(n+1)]\n #filing the complete matrix\n for i in range(1,n+1):\n for j in range(1,m+1):\n if str1[i-1]==str2[j-1]:\n dp[i][j]=dp[i-1][j-1]+1\n else:\n dp[i][j]=max(dp[i][j-1],dp[i-1][j])\n #now making supersequence from matrix\n i,j=n,m\n res=""\n #including common element once and rest too\n while i>0 and j>0:\n if str1[i-1]==str2[j-1]:\n res+=str1[i-1]\n i-=1\n j-=1\n else:\n if dp[i-1][j]>dp[i][j-1]:\n res+=str1[i-1]\n i-=1\n else:\n res+=str2[j-1]\n j-=1\n while i>0:\n res+=str1[i-1]\n i-=1\n while j>0:\n res+=str2[j-1]\n j-=1\n #reversing string\n return res[::-1]\n \n```\n\n | 8 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
✅ Python Solution || DP || Aditya Verma Approach||Bottom Up | shortest-common-supersequence | 0 | 1 | PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask.\n# Intuition\nUse Longest Common Subsequence to generated matrix and then matrix to get result string\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(N*M) + O(N+M)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N*M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestCommonSupersequence(self, str1: str, str2: str) -> str:\n #Normal longest common subsequence\n n,m=len(str1),len(str2)\n #initialization\n dp=[[0 for i in range(m+1)]for j in range(n+1)]\n #filing the complete matrix\n for i in range(1,n+1):\n for j in range(1,m+1):\n if str1[i-1]==str2[j-1]:\n dp[i][j]=dp[i-1][j-1]+1\n else:\n dp[i][j]=max(dp[i][j-1],dp[i-1][j])\n #now making supersequence from matrix\n i,j=n,m\n res=""\n #including common element once and rest too\n while i>0 and j>0:\n if str1[i-1]==str2[j-1]:\n res+=str1[i-1]\n i-=1\n j-=1\n else:\n if dp[i-1][j]>dp[i][j-1]:\n res+=str1[i-1]\n i-=1\n else:\n res+=str2[j-1]\n j-=1\n while i>0:\n res+=str1[i-1]\n i-=1\n while j>0:\n res+=str2[j-1]\n j-=1\n #reversing string\n return res[::-1]\n \n```\n\n | 8 | Let the function `f(s)` be the **frequency of the lexicographically smallest character** in a non-empty string `s`. For example, if `s = "dcce "` then `f(s) = 2` because the lexicographically smallest character is `'c'`, which has a frequency of 2.
You are given an array of strings `words` and another array of query strings `queries`. For each query `queries[i]`, count the **number of words** in `words` such that `f(queries[i])` < `f(W)` for each `W` in `words`.
Return _an integer array_ `answer`_, where each_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** queries = \[ "cbd "\], words = \[ "zaaaz "\]
**Output:** \[1\]
**Explanation:** On the first query we have f( "cbd ") = 1, f( "zaaaz ") = 3 so f( "cbd ") < f( "zaaaz ").
**Example 2:**
**Input:** queries = \[ "bbb ", "cc "\], words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** \[1,2\]
**Explanation:** On the first query only f( "bbb ") < f( "aaaa "). On the second query both f( "aaa ") and f( "aaaa ") are both > f( "cc ").
**Constraints:**
* `1 <= queries.length <= 2000`
* `1 <= words.length <= 2000`
* `1 <= queries[i].length, words[i].length <= 10`
* `queries[i][j]`, `words[i][j]` consist of lowercase English letters. | We can find the length of the longest common subsequence between str1[i:] and str2[j:] (for all (i, j)) by using dynamic programming. We can use this information to recover the longest common supersequence. |
Hard made Easy Python solution LCS Easy to Understand | shortest-common-supersequence | 0 | 1 | ```\nclass Solution:\n def LCS(self,s,t):\n m=len(s)\n n=len(t)\n dp=[[0 for i in range(n+1)]for j in range(m+1)]\n for i in range(m+1):\n dp[i][0]=0\n for j in range(n+1):\n dp[0][j]=0\n for i in range(1,m+1):\n for j in range(1,n+1):\n if s[i-1]==t[j-1]:\n dp[i][j]=1+dp[i-1][j-1]\n else:\n dp[i][j]=max(dp[i-1][j],dp[i][j-1])\n return dp\n \n def shortestCommonSupersequence(self, s: str, t: str) -> str:\n dp=self.LCS(s,t)\n m=len(dp)-1\n n=len(dp[0])-1\n ans=""\n i=m\n j=n\n while(i>0 and j>0):\n if s[i-1]==t[j-1]:\n ans+=s[i-1]\n i-=1\n j-=1\n elif dp[i-1][j]>dp[i][j-1]:\n ans+=s[i-1]\n i-=1\n else:\n ans+=t[j-1]\n j-=1\n while(i>0):\n ans+=s[i-1]\n i-=1\n while(j>0):\n ans+=t[j-1]\n j-=1\n return ans[::-1]\n```\n\nIf anyone not got Kindly comment i will explain | 2 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Hard made Easy Python solution LCS Easy to Understand | shortest-common-supersequence | 0 | 1 | ```\nclass Solution:\n def LCS(self,s,t):\n m=len(s)\n n=len(t)\n dp=[[0 for i in range(n+1)]for j in range(m+1)]\n for i in range(m+1):\n dp[i][0]=0\n for j in range(n+1):\n dp[0][j]=0\n for i in range(1,m+1):\n for j in range(1,n+1):\n if s[i-1]==t[j-1]:\n dp[i][j]=1+dp[i-1][j-1]\n else:\n dp[i][j]=max(dp[i-1][j],dp[i][j-1])\n return dp\n \n def shortestCommonSupersequence(self, s: str, t: str) -> str:\n dp=self.LCS(s,t)\n m=len(dp)-1\n n=len(dp[0])-1\n ans=""\n i=m\n j=n\n while(i>0 and j>0):\n if s[i-1]==t[j-1]:\n ans+=s[i-1]\n i-=1\n j-=1\n elif dp[i-1][j]>dp[i][j-1]:\n ans+=s[i-1]\n i-=1\n else:\n ans+=t[j-1]\n j-=1\n while(i>0):\n ans+=s[i-1]\n i-=1\n while(j>0):\n ans+=t[j-1]\n j-=1\n return ans[::-1]\n```\n\nIf anyone not got Kindly comment i will explain | 2 | Let the function `f(s)` be the **frequency of the lexicographically smallest character** in a non-empty string `s`. For example, if `s = "dcce "` then `f(s) = 2` because the lexicographically smallest character is `'c'`, which has a frequency of 2.
You are given an array of strings `words` and another array of query strings `queries`. For each query `queries[i]`, count the **number of words** in `words` such that `f(queries[i])` < `f(W)` for each `W` in `words`.
Return _an integer array_ `answer`_, where each_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** queries = \[ "cbd "\], words = \[ "zaaaz "\]
**Output:** \[1\]
**Explanation:** On the first query we have f( "cbd ") = 1, f( "zaaaz ") = 3 so f( "cbd ") < f( "zaaaz ").
**Example 2:**
**Input:** queries = \[ "bbb ", "cc "\], words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** \[1,2\]
**Explanation:** On the first query only f( "bbb ") < f( "aaaa "). On the second query both f( "aaa ") and f( "aaaa ") are both > f( "cc ").
**Constraints:**
* `1 <= queries.length <= 2000`
* `1 <= words.length <= 2000`
* `1 <= queries[i].length, words[i].length <= 10`
* `queries[i][j]`, `words[i][j]` consist of lowercase English letters. | We can find the length of the longest common subsequence between str1[i:] and str2[j:] (for all (i, j)) by using dynamic programming. We can use this information to recover the longest common supersequence. |
Python3 || Concise || Recursion + Memoization | shortest-common-supersequence | 0 | 1 | ```\n\nfrom functools import lru_cache\n\nclass Solution:\n def shortestCommonSupersequence(self, str1: str, str2: str) -> str:\n \n @lru_cache(maxsize= 8000)\n def helper(first: str, second: str):\n \n if not first and not second:\n return ""\n \n if not first:\n return second\n \n if not second:\n return first\n \n if first[0] == second[0]:\n return first[0] + helper(first[1:], second[1:])\n \n right = second[0] + helper(first, second[1:])\n left = first[0] + helper(first[1:], second)\n \n if len(right) > len(left):\n return left\n return right\n \n return helper(str1, str2)\n\t\t\n``` | 2 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Python3 || Concise || Recursion + Memoization | shortest-common-supersequence | 0 | 1 | ```\n\nfrom functools import lru_cache\n\nclass Solution:\n def shortestCommonSupersequence(self, str1: str, str2: str) -> str:\n \n @lru_cache(maxsize= 8000)\n def helper(first: str, second: str):\n \n if not first and not second:\n return ""\n \n if not first:\n return second\n \n if not second:\n return first\n \n if first[0] == second[0]:\n return first[0] + helper(first[1:], second[1:])\n \n right = second[0] + helper(first, second[1:])\n left = first[0] + helper(first[1:], second)\n \n if len(right) > len(left):\n return left\n return right\n \n return helper(str1, str2)\n\t\t\n``` | 2 | Let the function `f(s)` be the **frequency of the lexicographically smallest character** in a non-empty string `s`. For example, if `s = "dcce "` then `f(s) = 2` because the lexicographically smallest character is `'c'`, which has a frequency of 2.
You are given an array of strings `words` and another array of query strings `queries`. For each query `queries[i]`, count the **number of words** in `words` such that `f(queries[i])` < `f(W)` for each `W` in `words`.
Return _an integer array_ `answer`_, where each_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** queries = \[ "cbd "\], words = \[ "zaaaz "\]
**Output:** \[1\]
**Explanation:** On the first query we have f( "cbd ") = 1, f( "zaaaz ") = 3 so f( "cbd ") < f( "zaaaz ").
**Example 2:**
**Input:** queries = \[ "bbb ", "cc "\], words = \[ "a ", "aa ", "aaa ", "aaaa "\]
**Output:** \[1,2\]
**Explanation:** On the first query only f( "bbb ") < f( "aaaa "). On the second query both f( "aaa ") and f( "aaaa ") are both > f( "cc ").
**Constraints:**
* `1 <= queries.length <= 2000`
* `1 <= words.length <= 2000`
* `1 <= queries[i].length, words[i].length <= 10`
* `queries[i][j]`, `words[i][j]` consist of lowercase English letters. | We can find the length of the longest common subsequence between str1[i:] and str2[j:] (for all (i, j)) by using dynamic programming. We can use this information to recover the longest common supersequence. |
Python simple solution O(n) linear time | statistics-from-a-large-sample | 0 | 1 | # Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n def get_minimum():\n for i in range(len(count)):\n if count[i] > 0:\n return i\n\n def get_maximum():\n for i in reversed(range(len(count))):\n if count[i] > 0:\n return i\n \n def get_mean():\n return sum([e*i for i,e in enumerate(count)])/sum(count)\n \n def get_median():\n return (get_left_median(count) + get_right_median(count))/2\n \n def get_left_median(count):\n total = sum(count)\n cumulative = 0\n for i in range(len(count)):\n cumulative += count[i]\n if cumulative*2 == total:\n return i + 0.5\n if cumulative*2 > total:\n return i\n \n def get_right_median(count):\n return 255 - get_left_median(count[::-1])\n \n def get_mode():\n mode = 0\n for i in range(len(count)):\n if count[i] > count[mode]:\n mode = i\n return mode\n\n return [get_minimum(), get_maximum(), get_mean(), get_median(), get_mode()]\n``` | 1 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Python simple solution O(n) linear time | statistics-from-a-large-sample | 0 | 1 | # Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n def get_minimum():\n for i in range(len(count)):\n if count[i] > 0:\n return i\n\n def get_maximum():\n for i in reversed(range(len(count))):\n if count[i] > 0:\n return i\n \n def get_mean():\n return sum([e*i for i,e in enumerate(count)])/sum(count)\n \n def get_median():\n return (get_left_median(count) + get_right_median(count))/2\n \n def get_left_median(count):\n total = sum(count)\n cumulative = 0\n for i in range(len(count)):\n cumulative += count[i]\n if cumulative*2 == total:\n return i + 0.5\n if cumulative*2 > total:\n return i\n \n def get_right_median(count):\n return 255 - get_left_median(count[::-1])\n \n def get_mode():\n mode = 0\n for i in range(len(count)):\n if count[i] > count[mode]:\n mode = i\n return mode\n\n return [get_minimum(), get_maximum(), get_mean(), get_median(), get_mode()]\n``` | 1 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
Easy to reason about, uses std library to good effect | statistics-from-a-large-sample | 0 | 1 | # Code\n```\nclass Solution:\n def sampleStats(self, count: list[int]) -> list[float]:\n counts = +Counter(dict(enumerate(count)))\n n = counts.total()\n\n _min = next(iter(counts.keys()))\n _max = next(reversed(counts.keys()))\n _mean = sum(map(lambda t: operator.mul(*t), counts.items())) / n\n [_mode, _], *_ = counts.most_common(1)\n\n def _compute_median() -> float:\n floor, odd_sample = divmod(n, 2)\n last_x = _min\n current_pos = 0\n for x, nx in counts.items():\n next_pos = current_pos + nx\n if current_pos == floor:\n return x if odd_sample else (x + last_x) / 2\n elif current_pos < floor < next_pos:\n return x\n current_pos = next_pos\n last_x = x\n\n _median = _compute_median()\n\n return [\n float(_min),\n float(_max),\n float(_mean),\n float(_median),\n float(_mode)\n ]\n\n \n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Easy to reason about, uses std library to good effect | statistics-from-a-large-sample | 0 | 1 | # Code\n```\nclass Solution:\n def sampleStats(self, count: list[int]) -> list[float]:\n counts = +Counter(dict(enumerate(count)))\n n = counts.total()\n\n _min = next(iter(counts.keys()))\n _max = next(reversed(counts.keys()))\n _mean = sum(map(lambda t: operator.mul(*t), counts.items())) / n\n [_mode, _], *_ = counts.most_common(1)\n\n def _compute_median() -> float:\n floor, odd_sample = divmod(n, 2)\n last_x = _min\n current_pos = 0\n for x, nx in counts.items():\n next_pos = current_pos + nx\n if current_pos == floor:\n return x if odd_sample else (x + last_x) / 2\n elif current_pos < floor < next_pos:\n return x\n current_pos = next_pos\n last_x = x\n\n _median = _compute_median()\n\n return [\n float(_min),\n float(_max),\n float(_mean),\n float(_median),\n float(_mode)\n ]\n\n \n``` | 0 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
✅ Python Solution | Little slow but understandable | statistics-from-a-large-sample | 0 | 1 | \n\n# Code\n```\nimport collections\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n totalNumbers = 0\n totalSum = 0\n maxFreq = -1\n maxFreqElem = -1\n minElem = -1\n maxElem = -1\n hashMap = collections.defaultdict(int)\n\n for i, val in enumerate(count):\n if val > 0:\n if minElem == -1:\n minElem = i\n hashMap[i] = val\n totalNumbers += val\n totalSum += (val * i)\n if val > maxFreq:\n maxFreqElem = i\n maxFreq = val\n maxElem = i\n\n minimum = minElem\n maximum = maxElem\n mean = totalSum / totalNumbers\n mode = maxFreqElem\n\n hashMap = sorted(hashMap.items(), key = lambda x:x[0])\n\n oddLength = True\n\n if totalNumbers % 2 == 1:\n medianIndex = (totalNumbers // 2) + 1\n else:\n oddLength = False\n medianIndex1 = (totalNumbers // 2)\n medianIndex2 = (totalNumbers // 2) + 1\n\n index = 0\n median = 0\n firstMedianFound = False\n i = 0\n\n while i < len(hashMap):\n if oddLength:\n if index + hashMap[i][1] < medianIndex:\n index += hashMap[i][1]\n else:\n median = hashMap[i][0]\n break\n i += 1\n else:\n if index + hashMap[i][1] < medianIndex1:\n index += hashMap[i][1]\n i += 1\n continue\n elif not firstMedianFound:\n median += hashMap[i][0]\n firstMedianFound = True\n continue\n if index + hashMap[i][1] < medianIndex2:\n index += hashMap[i][1]\n i += 1\n continue\n else:\n median += hashMap[i][0]\n median /= 2\n break\n\n return [minimum, maximum, mean, median, mode]\n\n\n\n \n\n \n\n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
✅ Python Solution | Little slow but understandable | statistics-from-a-large-sample | 0 | 1 | \n\n# Code\n```\nimport collections\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n totalNumbers = 0\n totalSum = 0\n maxFreq = -1\n maxFreqElem = -1\n minElem = -1\n maxElem = -1\n hashMap = collections.defaultdict(int)\n\n for i, val in enumerate(count):\n if val > 0:\n if minElem == -1:\n minElem = i\n hashMap[i] = val\n totalNumbers += val\n totalSum += (val * i)\n if val > maxFreq:\n maxFreqElem = i\n maxFreq = val\n maxElem = i\n\n minimum = minElem\n maximum = maxElem\n mean = totalSum / totalNumbers\n mode = maxFreqElem\n\n hashMap = sorted(hashMap.items(), key = lambda x:x[0])\n\n oddLength = True\n\n if totalNumbers % 2 == 1:\n medianIndex = (totalNumbers // 2) + 1\n else:\n oddLength = False\n medianIndex1 = (totalNumbers // 2)\n medianIndex2 = (totalNumbers // 2) + 1\n\n index = 0\n median = 0\n firstMedianFound = False\n i = 0\n\n while i < len(hashMap):\n if oddLength:\n if index + hashMap[i][1] < medianIndex:\n index += hashMap[i][1]\n else:\n median = hashMap[i][0]\n break\n i += 1\n else:\n if index + hashMap[i][1] < medianIndex1:\n index += hashMap[i][1]\n i += 1\n continue\n elif not firstMedianFound:\n median += hashMap[i][0]\n firstMedianFound = True\n continue\n if index + hashMap[i][1] < medianIndex2:\n index += hashMap[i][1]\n i += 1\n continue\n else:\n median += hashMap[i][0]\n median /= 2\n break\n\n return [minimum, maximum, mean, median, mode]\n\n\n\n \n\n \n\n``` | 0 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
Python solution with mean calculation using left and right pointers | statistics-from-a-large-sample | 0 | 1 | The max, min, and mean calculations are fairly straightforward. \n\nMedian is a little more complicated. I\'m sure there\'s a more elegant way to approach this, but I\'m using left and right pointers for the beginning and end of *count*. I decrement the number at both ends of the array, until one or both of the numbers is zero, then I move the corresponding pointer one step inwards. \n\nInitially I was decrementing by 1, but I received a timeout exception. It\'s lot more efficient to decrease by the smaller of the two numbers at the left and right pointer indices, ensuring that at least one of those numbers is set to 0. \n\nWorking your way inwards like this, you\'ll reach the median when there\'s only one remaining value in the array, or there are two values sitting next to each other. If that happens, the median is the larger of the two indices, or if they\'re equal, then the median is the average of the two indices.\n\n\n# Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n \n length = len(count)\n minimum = 0\n maximum = 10E9\n\n for i in range(length):\n if count[i] > 0:\n minimum = float(i)\n break\n \n for i in range(length - 1, -1, -1):\n if count[i] > 0:\n maximum = float(i)\n break\n\n count = count[0:int(maximum)+1]\n length = len(count)\n view = []\n\n for i in count:\n view.append(i)\n\n sum = 0\n items = 0\n\n for i in range(length):\n sum += i * view[i]\n items += view[i]\n\n mean = float(1.0 * sum / items)\n\n leftPointer = 0\n rightPointer = length - 1\n index = 0\n median = 0\n\n while True:\n if leftPointer == rightPointer - 1:\n print(view, leftPointer, rightPointer)\n\n if view[leftPointer] == 0:\n leftPointer += 1\n \n if view[rightPointer] == 0:\n rightPointer -= 1\n\n mini = min(view[leftPointer], view[rightPointer])\n view[leftPointer] -= mini\n view[rightPointer] -= mini\n\n if leftPointer == rightPointer - 1:\n print("eval", view, leftPointer, rightPointer)\n\n if leftPointer == rightPointer:\n median = leftPointer\n break\n\n if leftPointer == rightPointer - 1:\n if view[leftPointer] == view[rightPointer]:\n median = (leftPointer + rightPointer) / 2.0\n elif view[leftPointer] > view[rightPointer]:\n median = leftPointer\n else:\n median = rightPointer\n \n break\n\n maxMode = 0\n mode = 0\n\n for i, num in enumerate(count):\n \n if num > maxMode:\n maxMode = num\n mode = i\n\n output = [float(minimum), float(maximum), float(mean), float(median), float(mode)]\n\n return output\n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Python solution with mean calculation using left and right pointers | statistics-from-a-large-sample | 0 | 1 | The max, min, and mean calculations are fairly straightforward. \n\nMedian is a little more complicated. I\'m sure there\'s a more elegant way to approach this, but I\'m using left and right pointers for the beginning and end of *count*. I decrement the number at both ends of the array, until one or both of the numbers is zero, then I move the corresponding pointer one step inwards. \n\nInitially I was decrementing by 1, but I received a timeout exception. It\'s lot more efficient to decrease by the smaller of the two numbers at the left and right pointer indices, ensuring that at least one of those numbers is set to 0. \n\nWorking your way inwards like this, you\'ll reach the median when there\'s only one remaining value in the array, or there are two values sitting next to each other. If that happens, the median is the larger of the two indices, or if they\'re equal, then the median is the average of the two indices.\n\n\n# Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n \n length = len(count)\n minimum = 0\n maximum = 10E9\n\n for i in range(length):\n if count[i] > 0:\n minimum = float(i)\n break\n \n for i in range(length - 1, -1, -1):\n if count[i] > 0:\n maximum = float(i)\n break\n\n count = count[0:int(maximum)+1]\n length = len(count)\n view = []\n\n for i in count:\n view.append(i)\n\n sum = 0\n items = 0\n\n for i in range(length):\n sum += i * view[i]\n items += view[i]\n\n mean = float(1.0 * sum / items)\n\n leftPointer = 0\n rightPointer = length - 1\n index = 0\n median = 0\n\n while True:\n if leftPointer == rightPointer - 1:\n print(view, leftPointer, rightPointer)\n\n if view[leftPointer] == 0:\n leftPointer += 1\n \n if view[rightPointer] == 0:\n rightPointer -= 1\n\n mini = min(view[leftPointer], view[rightPointer])\n view[leftPointer] -= mini\n view[rightPointer] -= mini\n\n if leftPointer == rightPointer - 1:\n print("eval", view, leftPointer, rightPointer)\n\n if leftPointer == rightPointer:\n median = leftPointer\n break\n\n if leftPointer == rightPointer - 1:\n if view[leftPointer] == view[rightPointer]:\n median = (leftPointer + rightPointer) / 2.0\n elif view[leftPointer] > view[rightPointer]:\n median = leftPointer\n else:\n median = rightPointer\n \n break\n\n maxMode = 0\n mode = 0\n\n for i, num in enumerate(count):\n \n if num > maxMode:\n maxMode = num\n mode = i\n\n output = [float(minimum), float(maximum), float(mean), float(median), float(mode)]\n\n return output\n``` | 0 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
Simple easy for beginners using hasmap beats 85 % !!!! | statistics-from-a-large-sample | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n lm=0\n rm=0\n l=0\n sum=0\n sum1=0\n d={}\n res=[]\n for i in range(len(count)):\n if count[i]!=0:\n d[i]=count[i]\n print(d)\n x=d.keys()\n res.append(float(min(x)))\n res.append(float(max(x)))\n for i in d:\n sum=sum+d[i]*i\n sum1=sum1+d[i]\n res.append(sum/sum1)\n if sum1%2==0:\n for i in d:\n if l+d[i]<sum1//2:\n l+=d[i]\n else:\n break\n lm=i\n l=0\n for i in d:\n if l+d[i]<sum1//2+1:\n l+=d[i]\n else:\n break\n rm=i\n res.append((rm+lm)/2)\n if sum1%2==1:\n for i in d:\n if l+d[i]<sum1//2+1:\n l+=d[i]\n else:\n break\n res.append(i)\n y=list(d.values())\n a=max(y)\n for i in d:\n if d[i]==a:\n res.append(float(i))\n break\n return(res)\n\n\n \n\n\n \n \n \n \n \n \n \n \n\n \n\n \n\n \n \n \n \n \n \n \n \n \n\n \n \n \n \n\n \n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Simple easy for beginners using hasmap beats 85 % !!!! | statistics-from-a-large-sample | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n lm=0\n rm=0\n l=0\n sum=0\n sum1=0\n d={}\n res=[]\n for i in range(len(count)):\n if count[i]!=0:\n d[i]=count[i]\n print(d)\n x=d.keys()\n res.append(float(min(x)))\n res.append(float(max(x)))\n for i in d:\n sum=sum+d[i]*i\n sum1=sum1+d[i]\n res.append(sum/sum1)\n if sum1%2==0:\n for i in d:\n if l+d[i]<sum1//2:\n l+=d[i]\n else:\n break\n lm=i\n l=0\n for i in d:\n if l+d[i]<sum1//2+1:\n l+=d[i]\n else:\n break\n rm=i\n res.append((rm+lm)/2)\n if sum1%2==1:\n for i in d:\n if l+d[i]<sum1//2+1:\n l+=d[i]\n else:\n break\n res.append(i)\n y=list(d.values())\n a=max(y)\n for i in d:\n if d[i]==a:\n res.append(float(i))\n break\n return(res)\n\n\n \n\n\n \n \n \n \n \n \n \n \n\n \n\n \n\n \n \n \n \n \n \n \n \n \n\n \n \n \n \n\n \n``` | 0 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
Python 3 solution | statistics-from-a-large-sample | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n minimum = next((i for i, num in enumerate(count) if num), None)\n maximum = next((i for i, num in reversed(\n list(enumerate(count))) if num), None)\n n = sum(count)\n mean = sum(i * c / n for i, c in enumerate(count))\n mode = count.index(max(count))\n\n numCount = 0\n leftMedian = 0\n for i, c in enumerate(count):\n numCount += c\n if numCount >= n / 2:\n leftMedian = i\n break\n\n numCount = 0\n rightMedian = 0\n for i, c in reversed(list(enumerate(count))):\n numCount += c\n if numCount >= n / 2:\n rightMedian = i\n break\n\n return [minimum, maximum, mean, (leftMedian + rightMedian) / 2, mode]\n\n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Python 3 solution | statistics-from-a-large-sample | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sampleStats(self, count: List[int]) -> List[float]:\n minimum = next((i for i, num in enumerate(count) if num), None)\n maximum = next((i for i, num in reversed(\n list(enumerate(count))) if num), None)\n n = sum(count)\n mean = sum(i * c / n for i, c in enumerate(count))\n mode = count.index(max(count))\n\n numCount = 0\n leftMedian = 0\n for i, c in enumerate(count):\n numCount += c\n if numCount >= n / 2:\n leftMedian = i\n break\n\n numCount = 0\n rightMedian = 0\n for i, c in reversed(list(enumerate(count))):\n numCount += c\n if numCount >= n / 2:\n rightMedian = i\n break\n\n return [minimum, maximum, mean, (leftMedian + rightMedian) / 2, mode]\n\n``` | 0 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | statistics-from-a-large-sample | 0 | 1 | \n# Code\n```\nclass Solution:\n def sampleStats(self, count):\n n = sum(count)\n mi = next(i for i in range(256) if count[i]) * 1.0\n ma = next(i for i in range(255, -1, -1) if count[i]) * 1.0\n mean = sum(i * v for i, v in enumerate(count)) * 1.0 / n\n mode = count.index(max(count)) * 1.0\n for i in range(255):\n count[i + 1] += count[i]\n median1 = bisect.bisect(count, (n - 1) / 2)\n median2 = bisect.bisect(count, n / 2)\n median = (median1 + median2) / 2.0\n return [mi, ma, mean, median, mode]\n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9% | statistics-from-a-large-sample | 0 | 1 | \n# Code\n```\nclass Solution:\n def sampleStats(self, count):\n n = sum(count)\n mi = next(i for i in range(256) if count[i]) * 1.0\n ma = next(i for i in range(255, -1, -1) if count[i]) * 1.0\n mean = sum(i * v for i, v in enumerate(count)) * 1.0 / n\n mode = count.index(max(count)) * 1.0\n for i in range(255):\n count[i + 1] += count[i]\n median1 = bisect.bisect(count, (n - 1) / 2)\n median2 = bisect.bisect(count, n / 2)\n median = (median1 + median2) / 2.0\n return [mi, ma, mean, median, mode]\n``` | 0 | Consider a matrix `M` with dimensions `width * height`, such that every cell has value `0` or `1`, and any **square** sub-matrix of `M` of size `sideLength * sideLength` has at most `maxOnes` ones.
Return the maximum possible number of ones that the matrix `M` can have.
**Example 1:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 1
**Output:** 4
**Explanation:**
In a 3\*3 matrix, no 2\*2 sub-matrix can have more than 1 one.
The best solution that has 4 ones is:
\[1,0,1\]
\[0,0,0\]
\[1,0,1\]
**Example 2:**
**Input:** width = 3, height = 3, sideLength = 2, maxOnes = 2
**Output:** 6
**Explanation:**
\[1,0,1\]
\[1,0,1\]
\[1,0,1\]
**Constraints:**
* `1 <= width, height <= 100`
* `1 <= sideLength <= width, height`
* `0 <= maxOnes <= sideLength * sideLength` | The hard part is the median. Write a helper function which finds the k-th element from the sample. |
O(n) solution with code explanation | car-pooling | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this question First thing that comes to my mind is that we just have to answer how many passengers currently we have. So, at every station some passengers are picked up and some may dropped off. To record this number we can use an array, at *from* station passengers count will be increased and at *to* station, count will decresed.\n\nWhen we will have this number we can calculate from the beginning how many passengers are on-boarded. If it is more than the capacity, we will return false.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n passengersAtstations = [0] * 1001 # 1000 stations\n totalPassengers = 0\n\n # record how many passengers at a given station\n for trip in trips:\n passengersAtstations[trip[1]] += trip[0] # on-board\n passengersAtstations[trip[2]] -= trip[0] # drop-off\n\n for passengers in passengersAtstations:\n # calculate total passengers so far\n totalPassengers += passengers\n if totalPassengers > capacity:\n return False\n\n return True\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
O(n) solution with code explanation | car-pooling | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this question First thing that comes to my mind is that we just have to answer how many passengers currently we have. So, at every station some passengers are picked up and some may dropped off. To record this number we can use an array, at *from* station passengers count will be increased and at *to* station, count will decresed.\n\nWhen we will have this number we can calculate from the beginning how many passengers are on-boarded. If it is more than the capacity, we will return false.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n passengersAtstations = [0] * 1001 # 1000 stations\n totalPassengers = 0\n\n # record how many passengers at a given station\n for trip in trips:\n passengersAtstations[trip[1]] += trip[0] # on-board\n passengersAtstations[trip[2]] -= trip[0] # drop-off\n\n for passengers in passengersAtstations:\n # calculate total passengers so far\n totalPassengers += passengers\n if totalPassengers > capacity:\n return False\n\n return True\n``` | 1 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
[Python] Solution with prefix sum - very easy to understand. | car-pooling | 0 | 1 | # Code\n```\nclass Solution:\n def carPooling(self, trips, capacity: int) -> bool: \n n = len(trips)\n prefix = [0]*(1001)\n left = 1e9\n right = 0\n for tpl in trips:\n prefix[tpl[1]] += tpl[0]\n prefix[tpl[2]] -= tpl[0]\n left = min(left, tpl[1])\n right = max(right, tpl[2])\n \n totalPass = 0\n for i in range(left, right+1):\n totalPass += prefix[i]\n if totalPass > capacity: return False\n return True\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
[Python] Solution with prefix sum - very easy to understand. | car-pooling | 0 | 1 | # Code\n```\nclass Solution:\n def carPooling(self, trips, capacity: int) -> bool: \n n = len(trips)\n prefix = [0]*(1001)\n left = 1e9\n right = 0\n for tpl in trips:\n prefix[tpl[1]] += tpl[0]\n prefix[tpl[2]] -= tpl[0]\n left = min(left, tpl[1])\n right = max(right, tpl[2])\n \n totalPass = 0\n for i in range(left, right+1):\n totalPass += prefix[i]\n if totalPass > capacity: return False\n return True\n``` | 1 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
[Python] The algorithm that was not mentioned in the tags (with comments and complexity analysis) | car-pooling | 0 | 1 | # Intuition\nAfter I had read the problem it reminded me about Scanline Algorithm. \nThat usually is used in geometry problems. For example, "How many segments belongs to the point", "The number of intersecting segments" and many more.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1) Create a list of our trip events.\n2) Fill in the list with two types of events boarding (type 1) and leaving (type 0) the car.\nWe use 0 for dropping passengers because, firstly, we finish the prevous trip and after that take new passengers.\n3) Sort the list by time and event type.\n4) Go through the sorted list of events and calculate (add or extract) the current number of the passengers in the car.\n5) If we counted more passengers at some point in time we return $$False$$.\n6) After the for loop we return $$True$$ because in any period of time the number of passengers did not exceed the car capacity.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N*logN)$$, where N is length of $$trips$$\nBecause we sort our data in $$O(N*logN)$$ and have two for loops \n$$O(2*N)$$ ~ $$O(N)$$. All in all, $$O(N*logN)$$ + $$O(N)$$ = $$O(N*logN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$ \nBecause we create new array with length $$2*N$$. We can ignore the constant and get the final space complexity $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n # list/array of our trip events\n a = []\n\n for i in trips:\n # (start_or_end_time, status, number_of_passengers)\n # status can be 0 or 1 :\n # end or start of a trip\n\n a.append((i[2], 0, i[0])) # drop off passengers\n a.append((i[1], 1, i[0])) # boarding passengers\n \n a.sort()\n cur = 0\n\n for i in a: # (time, status, number_of_passengers)\n if (i[1]): # first type of event - new passengers\n cur += i[2]\n\n # if we have more passengers \n # than the capacity we return False\n if (cur > capacity):\n return False\n else: # second type of event - end of a trip\n cur -= i[2]\n\n return True\n```\nAn example of how the algorithm works.\n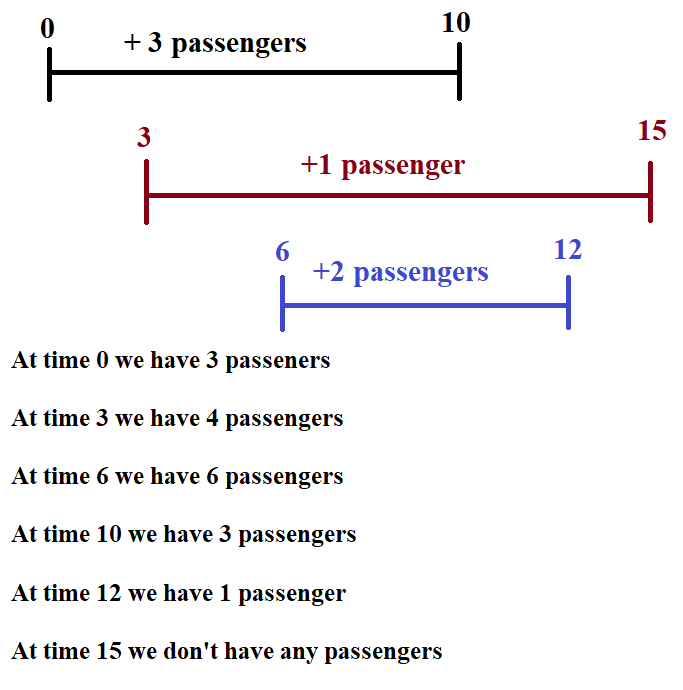\n | 6 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
[Python] The algorithm that was not mentioned in the tags (with comments and complexity analysis) | car-pooling | 0 | 1 | # Intuition\nAfter I had read the problem it reminded me about Scanline Algorithm. \nThat usually is used in geometry problems. For example, "How many segments belongs to the point", "The number of intersecting segments" and many more.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1) Create a list of our trip events.\n2) Fill in the list with two types of events boarding (type 1) and leaving (type 0) the car.\nWe use 0 for dropping passengers because, firstly, we finish the prevous trip and after that take new passengers.\n3) Sort the list by time and event type.\n4) Go through the sorted list of events and calculate (add or extract) the current number of the passengers in the car.\n5) If we counted more passengers at some point in time we return $$False$$.\n6) After the for loop we return $$True$$ because in any period of time the number of passengers did not exceed the car capacity.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N*logN)$$, where N is length of $$trips$$\nBecause we sort our data in $$O(N*logN)$$ and have two for loops \n$$O(2*N)$$ ~ $$O(N)$$. All in all, $$O(N*logN)$$ + $$O(N)$$ = $$O(N*logN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$ \nBecause we create new array with length $$2*N$$. We can ignore the constant and get the final space complexity $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n # list/array of our trip events\n a = []\n\n for i in trips:\n # (start_or_end_time, status, number_of_passengers)\n # status can be 0 or 1 :\n # end or start of a trip\n\n a.append((i[2], 0, i[0])) # drop off passengers\n a.append((i[1], 1, i[0])) # boarding passengers\n \n a.sort()\n cur = 0\n\n for i in a: # (time, status, number_of_passengers)\n if (i[1]): # first type of event - new passengers\n cur += i[2]\n\n # if we have more passengers \n # than the capacity we return False\n if (cur > capacity):\n return False\n else: # second type of event - end of a trip\n cur -= i[2]\n\n return True\n```\nAn example of how the algorithm works.\n\n | 6 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
🔥 [Python3] Beginner friendly, short, using Heap, with comments. | car-pooling | 0 | 1 | ```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n minHeap = []\n for trip in trips:\n # using for \'to\' negative value will help us fristly drop of all passangers in current point\n # and only than pick up others passanger at this point (to save capacity >=0)\n # because for example (1, -1) < (1, 1) and first tuple will be processed first from the heap\n minHeap.extend([(trip[1], trip[0]), (trip[2], -trip[0])])\n heapify(minHeap)\n # stop processing when capacity will be < 0 (not possible transport all passanger) or after process all trips\n while capacity >= 0 and minHeap:\n capacity -= heappop(minHeap)[1]\n # if minHeap not empty it\'s indicator that we haven\'t processed all trips and via versa\n return len(minHeap) == 0\n``` | 8 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
🔥 [Python3] Beginner friendly, short, using Heap, with comments. | car-pooling | 0 | 1 | ```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n minHeap = []\n for trip in trips:\n # using for \'to\' negative value will help us fristly drop of all passangers in current point\n # and only than pick up others passanger at this point (to save capacity >=0)\n # because for example (1, -1) < (1, 1) and first tuple will be processed first from the heap\n minHeap.extend([(trip[1], trip[0]), (trip[2], -trip[0])])\n heapify(minHeap)\n # stop processing when capacity will be < 0 (not possible transport all passanger) or after process all trips\n while capacity >= 0 and minHeap:\n capacity -= heappop(minHeap)[1]\n # if minHeap not empty it\'s indicator that we haven\'t processed all trips and via versa\n return len(minHeap) == 0\n``` | 8 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
linear time most efficeint | car-pooling | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n # O(N) accoriding to input restrictions\n passChange = [0]*1001\n for t in trips:\n numPass,start,end = t\n passChange[start] += numPass\n passChange[end] -= numPass\n\n curPass = 0\n for i in range(1001):\n curPass += passChange[i]\n if curPass > capacity:\n return False\n return True\n\n\n\n``` | 2 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
linear time most efficeint | car-pooling | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n # O(N) accoriding to input restrictions\n passChange = [0]*1001\n for t in trips:\n numPass,start,end = t\n passChange[start] += numPass\n passChange[end] -= numPass\n\n curPass = 0\n for i in range(1001):\n curPass += passChange[i]\n if curPass > capacity:\n return False\n return True\n\n\n\n``` | 2 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
❤ [Python3] STRAIGHTFORWARD (✿◠‿◠), Explained | car-pooling | 0 | 1 | The idea is to create a list `path` with the length of 1000 (from the constraints) and fill it with the number of passengers that will be in the car at the location represented by the index of the list. For example: `path[4] = 30` means that at the 4th kilometer of the path there will be 30 passengers in the car. If at any point of the path the number of passengers exceeds the given capacity, we return `False`.\n\nTime: **O(n^2)** - in worst case, we iterate over whole path for every trip\nSpace: **O(n)** - for the list of locations\n\nRuntime: 451 ms, faster than **5.19%** of Python3 online submissions for Car Pooling.\nMemory Usage: 14.5 MB, less than **98.45%** of Python3 online submissions for Car Pooling.\n\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n path = [0]*1000\n \n for num, a, b in trips:\n for loc in range (a, b):\n path[loc] += num\n if path[loc] > capacity: return False\n \n return True\n``` | 12 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
❤ [Python3] STRAIGHTFORWARD (✿◠‿◠), Explained | car-pooling | 0 | 1 | The idea is to create a list `path` with the length of 1000 (from the constraints) and fill it with the number of passengers that will be in the car at the location represented by the index of the list. For example: `path[4] = 30` means that at the 4th kilometer of the path there will be 30 passengers in the car. If at any point of the path the number of passengers exceeds the given capacity, we return `False`.\n\nTime: **O(n^2)** - in worst case, we iterate over whole path for every trip\nSpace: **O(n)** - for the list of locations\n\nRuntime: 451 ms, faster than **5.19%** of Python3 online submissions for Car Pooling.\nMemory Usage: 14.5 MB, less than **98.45%** of Python3 online submissions for Car Pooling.\n\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n path = [0]*1000\n \n for num, a, b in trips:\n for loc in range (a, b):\n path[loc] += num\n if path[loc] > capacity: return False\n \n return True\n``` | 12 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
Two python solutions with and without min heap. Time: O(nlogn) Space: O(n) | car-pooling | 0 | 1 | # Option 1: without heap\n\n## Intuition\n\nEach interval has two events: first when interval starts then pople hop on the car and the second when interval ends and people hop off the car.\n\n## Approach\n\nThe intervals list of length N can be transformed to an hopOnOff list where each interval will involve a hopOn event when people change are added to the car and an hopOff event when people are removed from the car.\n\nAfter sorting the new list of capacity 2xN by event time and people hopping off before people hopping on the car (people change with negative values before positive values)\n\nTo get the capacity used in the car at any time, just an interation through the list and counting the people change at any event will be enough.\n\n## Complexity\n- Time complexity: $$O(nlogn)$$ (sorting list)\n\n- Space complexity: $$O(n)$$ (new event list)\n\n## Code\n\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n hopOnOff = []\n for count, start, end in trips:\n hopOnOff.append((start, count))\n hopOnOff.append((end, -count))\n\n hopOnOff.sort()\n\n inCar = 0\n for destination, passangers in hopOnOff:\n inCar += passangers\n if inCar > capacity:\n return False\n return True\n```\n\n# Option 2: with minheap\n## Intuition\n\nWhile looking at a trip, count only the people that are in an interval that overlaps with the current trip.\n\n## Approach\n\nIterate over all sorted intervals and find all previous intervals that happened outside the current interval using a min heap to remove the people from the car. Now that all people got off the car, the people from the current interval can find their seats if the capacity allows it. As the current interval has just started, it must be added to the min heap to keep track of it related to the next intervals.\n\n## Complexity\n- Time complexity: $$O(nlogn)$$ (sorting of trips list)\n\n- Space complexity: $$O(n)$$ (size of the min heap in worst case scenario)\n\n## Code\n\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n trips.sort(key = lambda t: t[1])\n\n destinations = []\n inCar = 0\n\n for count, start, end in trips:\n while destinations and destinations[0][0] <= start:\n inCar -= destinations[0][1]\n heapq.heappop(destinations)\n\n inCar += count\n heapq.heappush(destinations, (end, count))\n\n if inCar > capacity:\n return False\n\n return True\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Two python solutions with and without min heap. Time: O(nlogn) Space: O(n) | car-pooling | 0 | 1 | # Option 1: without heap\n\n## Intuition\n\nEach interval has two events: first when interval starts then pople hop on the car and the second when interval ends and people hop off the car.\n\n## Approach\n\nThe intervals list of length N can be transformed to an hopOnOff list where each interval will involve a hopOn event when people change are added to the car and an hopOff event when people are removed from the car.\n\nAfter sorting the new list of capacity 2xN by event time and people hopping off before people hopping on the car (people change with negative values before positive values)\n\nTo get the capacity used in the car at any time, just an interation through the list and counting the people change at any event will be enough.\n\n## Complexity\n- Time complexity: $$O(nlogn)$$ (sorting list)\n\n- Space complexity: $$O(n)$$ (new event list)\n\n## Code\n\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n hopOnOff = []\n for count, start, end in trips:\n hopOnOff.append((start, count))\n hopOnOff.append((end, -count))\n\n hopOnOff.sort()\n\n inCar = 0\n for destination, passangers in hopOnOff:\n inCar += passangers\n if inCar > capacity:\n return False\n return True\n```\n\n# Option 2: with minheap\n## Intuition\n\nWhile looking at a trip, count only the people that are in an interval that overlaps with the current trip.\n\n## Approach\n\nIterate over all sorted intervals and find all previous intervals that happened outside the current interval using a min heap to remove the people from the car. Now that all people got off the car, the people from the current interval can find their seats if the capacity allows it. As the current interval has just started, it must be added to the min heap to keep track of it related to the next intervals.\n\n## Complexity\n- Time complexity: $$O(nlogn)$$ (sorting of trips list)\n\n- Space complexity: $$O(n)$$ (size of the min heap in worst case scenario)\n\n## Code\n\n```\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n trips.sort(key = lambda t: t[1])\n\n destinations = []\n inCar = 0\n\n for count, start, end in trips:\n while destinations and destinations[0][0] <= start:\n inCar -= destinations[0][1]\n heapq.heappop(destinations)\n\n inCar += count\n heapq.heappush(destinations, (end, count))\n\n if inCar > capacity:\n return False\n\n return True\n``` | 1 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
⬆️✅🔥 100% | 0ms | easy | explained | faster | proof 🔥⬆️✅ | car-pooling | 1 | 1 | # Upvote pls\n<!-- Describe your first thoughts on how to solve this problem. -->\nadd passenget at start and remove at the end of the stop.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean carPooling(int[][] T, int C) {\n int A[]= new int[1001];\n for(int[] v:T){\n A[v[1]]+=v[0];\n A[v[2]]-=v[0];\n }\n for(int i=0; i<1001;i++) {\n C-=A[i];\n if(C<0)return false;\n }\n return true;\n }\n}\n``` | 2 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
⬆️✅🔥 100% | 0ms | easy | explained | faster | proof 🔥⬆️✅ | car-pooling | 1 | 1 | # Upvote pls\n<!-- Describe your first thoughts on how to solve this problem. -->\nadd passenget at start and remove at the end of the stop.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean carPooling(int[][] T, int C) {\n int A[]= new int[1001];\n for(int[] v:T){\n A[v[1]]+=v[0];\n A[v[2]]-=v[0];\n }\n for(int i=0; i<1001;i++) {\n C-=A[i];\n if(C<0)return false;\n }\n return true;\n }\n}\n``` | 2 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
Python O(N) Very simple to understand | car-pooling | 0 | 1 | We do lazy propagation. We mark the passanger changes first. We calculate exact passanger counts at the end once.\nWe do a optimization #1. If at any point count is larger than capacity, we return immediately False. \n```py\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n passangers = [0]*1001\n # lazy propagation\n for count, fr, to in trips:\n if count > capacity: return False # optimization 1\n passangers[fr] += count\n passangers[to] -= count\n # calculate now the exact passanger counts and see if we exceed capacity\n for i in range(1, len(passangers)):\n passangers[i] += passangers[i-1]\n if passangers[i] > capacity:\n return False\n return True\n \n``` | 2 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Python O(N) Very simple to understand | car-pooling | 0 | 1 | We do lazy propagation. We mark the passanger changes first. We calculate exact passanger counts at the end once.\nWe do a optimization #1. If at any point count is larger than capacity, we return immediately False. \n```py\nclass Solution:\n def carPooling(self, trips: List[List[int]], capacity: int) -> bool:\n passangers = [0]*1001\n # lazy propagation\n for count, fr, to in trips:\n if count > capacity: return False # optimization 1\n passangers[fr] += count\n passangers[to] -= count\n # calculate now the exact passanger counts and see if we exceed capacity\n for i in range(1, len(passangers)):\n passangers[i] += passangers[i-1]\n if passangers[i] > capacity:\n return False\n return True\n \n``` | 2 | A bus has `n` stops numbered from `0` to `n - 1` that form a circle. We know the distance between all pairs of neighboring stops where `distance[i]` is the distance between the stops number `i` and `(i + 1) % n`.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given `start` and `destination` stops.
**Example 1:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 1
**Output:** 1
**Explanation:** Distance between 0 and 1 is 1 or 9, minimum is 1.
**Example 2:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 2
**Output:** 3
**Explanation:** Distance between 0 and 2 is 3 or 7, minimum is 3.
**Example 3:**
**Input:** distance = \[1,2,3,4\], start = 0, destination = 3
**Output:** 4
**Explanation:** Distance between 0 and 3 is 6 or 4, minimum is 4.
**Constraints:**
* `1 <= n <= 10^4`
* `distance.length == n`
* `0 <= start, destination < n`
* `0 <= distance[i] <= 10^4` | Sort the pickup and dropoff events by location, then process them in order. |
Sidha-Saadha Solution ! | find-in-mountain-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBinary Search\n# Approach\nFind the peak element using binasry search.\nApply binary search on left half of peak element.\nIf item found then return index.\nApply binary search on right half of peak element.\nIf item found then return index.\nReturn -1\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n\n- Time complexity:O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n def find_max_element(arr, low, high):\n if low == high:\n return low # When there\'s only one element left, it\'s the maximum\n\n mid = (low + high) // 2 # Calculate the middle index\n if arr.get(mid) > arr.get(mid + 1):\n return find_max_element(arr, low, mid) # The peak is in the left half\n else:\n return find_max_element(arr, mid + 1, high) \n\n def binary(arr, l, t, r):\n while l <= r:\n mid = (l + r) // 2\n mid_value = arr.get(mid)\n if mid_value == t:\n return mid\n elif mid_value > t:\n r = mid - 1\n else:\n l = mid + 1\n return -1\n def binary2(arr, l, t, r):\n while l <= r:\n mid = (l + r) // 2\n mid_value = arr.get(mid)\n if mid_value == t:\n return mid\n elif mid_value > t:\n l = mid + 1\n else:\n r = mid - 1\n return -1\n\n l = 0\n r = mountain_arr.length() - 1\n ctr = find_max_element(mountain_arr, l, r)\n t = target \n print(ctr)\n r = ctr \n first = binary(mountain_arr, l, t, r)\n print(first)\n if first != -1:\n return first\n r= mountain_arr.length() - 1\n l = ctr+1 \n\n second = binary2(mountain_arr, l, t, r)\n print(second)\n return second\n \n return second\n\n``` | 4 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
Sidha-Saadha Solution ! | find-in-mountain-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBinary Search\n# Approach\nFind the peak element using binasry search.\nApply binary search on left half of peak element.\nIf item found then return index.\nApply binary search on right half of peak element.\nIf item found then return index.\nReturn -1\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n\n- Time complexity:O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n def find_max_element(arr, low, high):\n if low == high:\n return low # When there\'s only one element left, it\'s the maximum\n\n mid = (low + high) // 2 # Calculate the middle index\n if arr.get(mid) > arr.get(mid + 1):\n return find_max_element(arr, low, mid) # The peak is in the left half\n else:\n return find_max_element(arr, mid + 1, high) \n\n def binary(arr, l, t, r):\n while l <= r:\n mid = (l + r) // 2\n mid_value = arr.get(mid)\n if mid_value == t:\n return mid\n elif mid_value > t:\n r = mid - 1\n else:\n l = mid + 1\n return -1\n def binary2(arr, l, t, r):\n while l <= r:\n mid = (l + r) // 2\n mid_value = arr.get(mid)\n if mid_value == t:\n return mid\n elif mid_value > t:\n l = mid + 1\n else:\n r = mid - 1\n return -1\n\n l = 0\n r = mountain_arr.length() - 1\n ctr = find_max_element(mountain_arr, l, r)\n t = target \n print(ctr)\n r = ctr \n first = binary(mountain_arr, l, t, r)\n print(first)\n if first != -1:\n return first\n r= mountain_arr.length() - 1\n l = ctr+1 \n\n second = binary2(mountain_arr, l, t, r)\n print(second)\n return second\n \n return second\n\n``` | 4 | Given a date, return the corresponding day of the week for that date.
The input is given as three integers representing the `day`, `month` and `year` respectively.
Return the answer as one of the following values `{ "Sunday ", "Monday ", "Tuesday ", "Wednesday ", "Thursday ", "Friday ", "Saturday "}`.
**Example 1:**
**Input:** day = 31, month = 8, year = 2019
**Output:** "Saturday "
**Example 2:**
**Input:** day = 18, month = 7, year = 1999
**Output:** "Sunday "
**Example 3:**
**Input:** day = 15, month = 8, year = 1993
**Output:** "Sunday "
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | Based on whether A[i-1] < A[i] < A[i+1], A[i-1] < A[i] > A[i+1], or A[i-1] > A[i] > A[i+1], we are either at the left side, peak, or right side of the mountain. We can binary search to find the peak.
After finding the peak, we can binary search two more times to find whether the value occurs on either side of the peak. |
Python3 Solution | find-in-mountain-array | 0 | 1 | \n```\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n#class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n n=mountain_arr.length()\n low=0\n high=n-1\n max_index=0\n while low<high:\n mid=low+(high-low)//2\n if mountain_arr.get(mid)>mountain_arr.get(mid+1):\n high=mid\n else:\n low=mid+1\n max_index=low\n low=0\n high=max_index\n\n while low<=high:\n mid=low+(high-low)//2\n midarr=mountain_arr.get(mid)\n if midarr<target:\n low=mid+1\n elif midarr>target:\n high=mid-1\n else:\n return mid\n\n low=max_index\n high=n-1\n while low<=high:\n mid=low+(high-low)//2\n midarr=mountain_arr.get(mid)\n if midarr>target:\n low=mid+1\n elif midarr<target:\n high=mid-1\n\n else:\n return mid\n return -1 \n``` | 2 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
Python3 Solution | find-in-mountain-array | 0 | 1 | \n```\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n#class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n n=mountain_arr.length()\n low=0\n high=n-1\n max_index=0\n while low<high:\n mid=low+(high-low)//2\n if mountain_arr.get(mid)>mountain_arr.get(mid+1):\n high=mid\n else:\n low=mid+1\n max_index=low\n low=0\n high=max_index\n\n while low<=high:\n mid=low+(high-low)//2\n midarr=mountain_arr.get(mid)\n if midarr<target:\n low=mid+1\n elif midarr>target:\n high=mid-1\n else:\n return mid\n\n low=max_index\n high=n-1\n while low<=high:\n mid=low+(high-low)//2\n midarr=mountain_arr.get(mid)\n if midarr>target:\n low=mid+1\n elif midarr<target:\n high=mid-1\n\n else:\n return mid\n return -1 \n``` | 2 | Given a date, return the corresponding day of the week for that date.
The input is given as three integers representing the `day`, `month` and `year` respectively.
Return the answer as one of the following values `{ "Sunday ", "Monday ", "Tuesday ", "Wednesday ", "Thursday ", "Friday ", "Saturday "}`.
**Example 1:**
**Input:** day = 31, month = 8, year = 2019
**Output:** "Saturday "
**Example 2:**
**Input:** day = 18, month = 7, year = 1999
**Output:** "Sunday "
**Example 3:**
**Input:** day = 15, month = 8, year = 1993
**Output:** "Sunday "
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | Based on whether A[i-1] < A[i] < A[i+1], A[i-1] < A[i] > A[i+1], or A[i-1] > A[i] > A[i+1], we are either at the left side, peak, or right side of the mountain. We can binary search to find the peak.
After finding the peak, we can binary search two more times to find whether the value occurs on either side of the peak. |
🚀 100% || Binary Search || Explained Intuition 🚀 | find-in-mountain-array | 1 | 1 | # Porblem Description\nThe problem requires **finding** the **minimum** index in a `mountain array` where a given `target` is located. \n\n- A mountain array is defined as an array that satisfies the conditions:\n - The array has a length **greater** than or **equal** to `3`.\n - There exists an index `i` `(0 < i < arr.length - 1)` such that elements from index `0` up to `i` are in strictly **increasing** order, and elements from index `i` onwards are in strictly **decreasing** order.\n\n\n\nThe **task** is to return the **index** of the **target** element in the mountain array using the given `MountainArray` interface. If the target is not present, return `-1`. \nThe solution should not make more than `100` calls to `MountainArray`.get.\n\n- **Constraints:**\n - `3 <= mountain_arr.length() <= 10e4`\n - `0 <= target <= 10e9`\n - `0 <= mountain_arr.get(index) <= 10e9`\n - `Maximum No of calls to MountainArray <= 100`\n\n---\n\n\n\n# Intuition\n\nHi there, Friends. \uD83D\uDE03\n\nLet\'s take a look at today\'s problem.\uD83D\uDC40\nWe have a mountain array and we must find the minimum index of element `target` in it or return `-1` or it doesn\'t exist.\uD83E\uDD14\nAs we know, that mountain array consists of two **parts**: **Increasing** part and **decreasing** part and the **shared** element between them is called the `peak`.\n\nThe **first** thing that can pop into mind \uD83C\uDF7F is why not to use **linear search**?\uD83E\uDD14\nThat\'s the first thing popped into my mind \uD83D\uDE05 since it was the easiest solution.\nbut **Unfotunately**, we are **limited** by number of calls we can make to the `MountainArray` API which is maximum `100` calls and the size of the array can reach $10^4$.\nSo, **linear search** is invalid solution.\uD83D\uDE14\uD83D\uDE14\n\nSadly, We are left only with **logarithmic operations**.\uD83E\uDD28\nHow can we use logarithmic operation to solve our problem?\nI will pretend that I didn\'t say the solution in the title.\uD83D\uDE02\n\nLet\'s look at some **features** of the mountain array:\n```\nEX1: [1, 4, 5, 10, 9, 7, 2]\n```\n```\nEX2: [1, 4, 3, 2, 1]\n```\n```\nEX3: [1, 2, 8, 10, 12, 14, 9]\n```\n\nWhat can we see?\nWe can see that the mountain array consists of two **smaller** array and each of them is **sorted** array.\uD83E\uDD2F\n```\n[1, 4, 5, 10, 9, 7, 2] = [1, 4, 5, 10] + [9, 7, 2]\n```\n```\n[1, 2, 8, 10, 12, 14, 9] = [1, 2, 8, 10, 12, 14] + [9]\n```\nThe **sorting** property is very **important**, how can we make use of it?\uD83E\uDD14\nof course **Binary Search**, the hero of our day.\uD83E\uDDB8\u200D\u2642\uFE0F\n\n**Binary Search** is a logarithmic algorithm in O(log(N)) operations.\nHow can we use **Binary Search**?\nFirst, We need to know the boundaries of our two **sorted** array. By finding the peak element by using **Binary Search**. So we are sure that the elements before it are **sorted** and the elements after it are **sorted**.\uD83E\uDD2F\n\nWhat next\u2753\nSince, we are required to find the **minimum** index if the element exists so we will search the first part of the array using **Binary Search** then the second part also using **Binary Search**.\nBut the **Binary Search** for the second part is reversed **Binary Search** which means that we will move opposite of our regular directions.\n\nBut what if we didn\'t find our element after all?\uD83E\uDD14\nThen simply, it doesn\'t exist in our array and we will return `-1`.\n\nBut we are limited with `100` calls to the API, can this work?\n- Let\'s compute the **number** of calls:\n - **Finding** the `peak` in `log(N)`: $log(10^4)$ = `14`.\n - **Searching** the **first** part in `log(N)`: $log(10^4)$ = `14`.\n - **Searching** the **second** part in `log(N)`: $log(10^4)$ = `14`.\n\nOur total calls to the API if we have an array of size $10^4$ are `14 * 3 = 42` calls which are far less than `100` calls. so we are sure that our approach is a valid one.\u270C\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n\n# Approach\n1. Using a **binary search** `findPeakIndex` to locate the peak index of the mountain array. \n2. Perform a **binary search** for the target in the increasing part of the mountain array `from index 0 to the peak index`. \n - Use the `binarySearch` method with the `reversed` parameter set to `false`.\n - If the target is **found** in the **increasing** part, return the `index`.\n3. If the target is **not found** in the **increasing** part, perform a **binary search** for the target in the **decreasing** part of the mountain array `from the peak index to the end`.\n - Use the `binarySearch` method with the `reversed` parameter set to `true`.\n - If the target is **found** in the **decreasing** part, return the **index**.\n4. If the target is **not found** in **either** part of the array, return `-1` to indicate the **absence** of the target.\n\n\n# Complexity\n- **Time complexity:** $O(log(N))$\nSince we are performing binary search three times: one time to find the peak, another time to find the target in increasing part and last time to find it in decreasing part.\nThis cost us `(3 * log(N))` which is `O(log(N))`.\nwhere `N` is the size of Mountain Array. \n- **Space complexity:** $O(1)$\nSince we are using only constant variables and not using anyother data structures.\n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int findInMountainArray(int target, MountainArray &mountainArr) {\n int length = mountainArr.length();\n\n // Find the index of the peak element in the mountain array.\n int peakIndex = findPeakIndex(1, length - 2, mountainArr);\n\n // Binary search for the target in the increasing part of the mountain array.\n int increasingIndex = binarySearch(0, peakIndex, target, mountainArr, false);\n if (mountainArr.get(increasingIndex) == target) \n return increasingIndex; // Target found in the increasing part.\n\n // Binary search for the target in the decreasing part of the mountain array.\n int decreasingIndex = binarySearch(peakIndex + 1, length - 1, target, mountainArr, true);\n if (mountainArr.get(decreasingIndex) == target) \n return decreasingIndex; // Target found in the decreasing part.\n\n return -1; // Target not found in the mountain array.\n }\n\n int findPeakIndex(int low, int high, MountainArray &mountainArr) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {\n low = mid + 1; // Move to the right side (increasing slope).\n } else {\n high = mid; // Move to the left side (decreasing slope).\n }\n }\n return low; // Return the index of the peak element.\n }\n\n int binarySearch(int low, int high, int target, MountainArray &mountainArr, bool reversed) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (reversed) {\n if (mountainArr.get(mid) > target)\n low = mid + 1; // Move to the right side for a decreasing slope.\n else\n high = mid; // Move to the left side for an increasing slope.\n } else {\n if (mountainArr.get(mid) < target)\n low = mid + 1; // Move to the right side for an increasing slope.\n else\n high = mid; // Move to the left side for a decreasing slope.\n }\n }\n return low; // Return the index where the target should be or would be inserted.\n }\n};\n```\n```Java []\nclass Solution {\n public int findInMountainArray(int target, MountainArray mountainArr) {\n int length = mountainArr.length();\n\n // Find the index of the peak element in the mountain array.\n int peakIndex = findPeakIndex(1, length - 2, mountainArr);\n\n // Binary search for the target in the increasing part of the mountain array.\n int increasingIndex = binarySearch(0, peakIndex, target, mountainArr, false);\n if (mountainArr.get(increasingIndex) == target) \n return increasingIndex; // Target found in the increasing part.\n\n // Binary search for the target in the decreasing part of the mountain array.\n int decreasingIndex = binarySearch(peakIndex + 1, length - 1, target, mountainArr, true);\n if (mountainArr.get(decreasingIndex) == target) \n return decreasingIndex; // Target found in the decreasing part.\n\n return -1; // Target not found in the mountain array.\n }\n\n private int findPeakIndex(int low, int high, MountainArray mountainArr) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {\n low = mid + 1; // Move to the right side (increasing slope).\n } else {\n high = mid; // Move to the left side (decreasing slope).\n }\n }\n return low; // Return the index of the peak element.\n }\n\n private int binarySearch(int low, int high, int target, MountainArray mountainArr, boolean reversed) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (reversed) {\n if (mountainArr.get(mid) > target)\n low = mid + 1; // Move to the right side for a decreasing slope.\n else\n high = mid; // Move to the left side for an increasing slope.\n } else {\n if (mountainArr.get(mid) < target)\n low = mid + 1; // Move to the right side for an increasing slope.\n else\n high = mid; // Move to the left side for a decreasing slope.\n }\n }\n return low; // Return the index where the target should be or would be inserted.\n }\n}\n```\n```Python []\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n length = mountain_arr.length()\n\n # Find the index of the peak element in the mountain array.\n peak_index = self.find_peak_index(1, length - 2, mountain_arr)\n\n # Binary search for the target in the increasing part of the mountain array.\n increasing_index = self.binary_search(0, peak_index, target, mountain_arr, False)\n if mountain_arr.get(increasing_index) == target:\n return increasing_index # Target found in the increasing part.\n\n # Binary search for the target in the decreasing part of the mountain array.\n decreasing_index = self.binary_search(peak_index + 1, length - 1, target, mountain_arr, True)\n if mountain_arr.get(decreasing_index) == target:\n return decreasing_index # Target found in the decreasing part.\n\n return -1 # Target not found in the mountain array.\n\n def find_peak_index(self, low, high, mountainArr):\n while low != high:\n mid = low + (high - low) // 2\n if mountainArr.get(mid) < mountainArr.get(mid + 1):\n low = mid + 1 # Move to the right side (increasing slope).\n else:\n high = mid # Move to the left side (decreasing slope).\n return low # Return the index of the peak element.\n\n def binary_search(self, low, high, target, mountainArr, reversed):\n while low != high:\n mid = low + (high - low) // 2\n if reversed:\n if mountainArr.get(mid) > target:\n low = mid + 1 # Move to the right side for a decreasing slope.\n else:\n high = mid # Move to the left side for an increasing slope.\n else:\n if mountainArr.get(mid) < target:\n low = mid + 1 # Move to the right side for an increasing slope.\n else:\n high = mid # Move to the left side for a decreasing slope.\n return low # Return the index where the target should be or would be inserted.\n```\n\n\n\n\n\n | 120 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
🚀 100% || Binary Search || Explained Intuition 🚀 | find-in-mountain-array | 1 | 1 | # Porblem Description\nThe problem requires **finding** the **minimum** index in a `mountain array` where a given `target` is located. \n\n- A mountain array is defined as an array that satisfies the conditions:\n - The array has a length **greater** than or **equal** to `3`.\n - There exists an index `i` `(0 < i < arr.length - 1)` such that elements from index `0` up to `i` are in strictly **increasing** order, and elements from index `i` onwards are in strictly **decreasing** order.\n\n\n\nThe **task** is to return the **index** of the **target** element in the mountain array using the given `MountainArray` interface. If the target is not present, return `-1`. \nThe solution should not make more than `100` calls to `MountainArray`.get.\n\n- **Constraints:**\n - `3 <= mountain_arr.length() <= 10e4`\n - `0 <= target <= 10e9`\n - `0 <= mountain_arr.get(index) <= 10e9`\n - `Maximum No of calls to MountainArray <= 100`\n\n---\n\n\n\n# Intuition\n\nHi there, Friends. \uD83D\uDE03\n\nLet\'s take a look at today\'s problem.\uD83D\uDC40\nWe have a mountain array and we must find the minimum index of element `target` in it or return `-1` or it doesn\'t exist.\uD83E\uDD14\nAs we know, that mountain array consists of two **parts**: **Increasing** part and **decreasing** part and the **shared** element between them is called the `peak`.\n\nThe **first** thing that can pop into mind \uD83C\uDF7F is why not to use **linear search**?\uD83E\uDD14\nThat\'s the first thing popped into my mind \uD83D\uDE05 since it was the easiest solution.\nbut **Unfotunately**, we are **limited** by number of calls we can make to the `MountainArray` API which is maximum `100` calls and the size of the array can reach $10^4$.\nSo, **linear search** is invalid solution.\uD83D\uDE14\uD83D\uDE14\n\nSadly, We are left only with **logarithmic operations**.\uD83E\uDD28\nHow can we use logarithmic operation to solve our problem?\nI will pretend that I didn\'t say the solution in the title.\uD83D\uDE02\n\nLet\'s look at some **features** of the mountain array:\n```\nEX1: [1, 4, 5, 10, 9, 7, 2]\n```\n```\nEX2: [1, 4, 3, 2, 1]\n```\n```\nEX3: [1, 2, 8, 10, 12, 14, 9]\n```\n\nWhat can we see?\nWe can see that the mountain array consists of two **smaller** array and each of them is **sorted** array.\uD83E\uDD2F\n```\n[1, 4, 5, 10, 9, 7, 2] = [1, 4, 5, 10] + [9, 7, 2]\n```\n```\n[1, 2, 8, 10, 12, 14, 9] = [1, 2, 8, 10, 12, 14] + [9]\n```\nThe **sorting** property is very **important**, how can we make use of it?\uD83E\uDD14\nof course **Binary Search**, the hero of our day.\uD83E\uDDB8\u200D\u2642\uFE0F\n\n**Binary Search** is a logarithmic algorithm in O(log(N)) operations.\nHow can we use **Binary Search**?\nFirst, We need to know the boundaries of our two **sorted** array. By finding the peak element by using **Binary Search**. So we are sure that the elements before it are **sorted** and the elements after it are **sorted**.\uD83E\uDD2F\n\nWhat next\u2753\nSince, we are required to find the **minimum** index if the element exists so we will search the first part of the array using **Binary Search** then the second part also using **Binary Search**.\nBut the **Binary Search** for the second part is reversed **Binary Search** which means that we will move opposite of our regular directions.\n\nBut what if we didn\'t find our element after all?\uD83E\uDD14\nThen simply, it doesn\'t exist in our array and we will return `-1`.\n\nBut we are limited with `100` calls to the API, can this work?\n- Let\'s compute the **number** of calls:\n - **Finding** the `peak` in `log(N)`: $log(10^4)$ = `14`.\n - **Searching** the **first** part in `log(N)`: $log(10^4)$ = `14`.\n - **Searching** the **second** part in `log(N)`: $log(10^4)$ = `14`.\n\nOur total calls to the API if we have an array of size $10^4$ are `14 * 3 = 42` calls which are far less than `100` calls. so we are sure that our approach is a valid one.\u270C\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n\n# Approach\n1. Using a **binary search** `findPeakIndex` to locate the peak index of the mountain array. \n2. Perform a **binary search** for the target in the increasing part of the mountain array `from index 0 to the peak index`. \n - Use the `binarySearch` method with the `reversed` parameter set to `false`.\n - If the target is **found** in the **increasing** part, return the `index`.\n3. If the target is **not found** in the **increasing** part, perform a **binary search** for the target in the **decreasing** part of the mountain array `from the peak index to the end`.\n - Use the `binarySearch` method with the `reversed` parameter set to `true`.\n - If the target is **found** in the **decreasing** part, return the **index**.\n4. If the target is **not found** in **either** part of the array, return `-1` to indicate the **absence** of the target.\n\n\n# Complexity\n- **Time complexity:** $O(log(N))$\nSince we are performing binary search three times: one time to find the peak, another time to find the target in increasing part and last time to find it in decreasing part.\nThis cost us `(3 * log(N))` which is `O(log(N))`.\nwhere `N` is the size of Mountain Array. \n- **Space complexity:** $O(1)$\nSince we are using only constant variables and not using anyother data structures.\n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int findInMountainArray(int target, MountainArray &mountainArr) {\n int length = mountainArr.length();\n\n // Find the index of the peak element in the mountain array.\n int peakIndex = findPeakIndex(1, length - 2, mountainArr);\n\n // Binary search for the target in the increasing part of the mountain array.\n int increasingIndex = binarySearch(0, peakIndex, target, mountainArr, false);\n if (mountainArr.get(increasingIndex) == target) \n return increasingIndex; // Target found in the increasing part.\n\n // Binary search for the target in the decreasing part of the mountain array.\n int decreasingIndex = binarySearch(peakIndex + 1, length - 1, target, mountainArr, true);\n if (mountainArr.get(decreasingIndex) == target) \n return decreasingIndex; // Target found in the decreasing part.\n\n return -1; // Target not found in the mountain array.\n }\n\n int findPeakIndex(int low, int high, MountainArray &mountainArr) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {\n low = mid + 1; // Move to the right side (increasing slope).\n } else {\n high = mid; // Move to the left side (decreasing slope).\n }\n }\n return low; // Return the index of the peak element.\n }\n\n int binarySearch(int low, int high, int target, MountainArray &mountainArr, bool reversed) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (reversed) {\n if (mountainArr.get(mid) > target)\n low = mid + 1; // Move to the right side for a decreasing slope.\n else\n high = mid; // Move to the left side for an increasing slope.\n } else {\n if (mountainArr.get(mid) < target)\n low = mid + 1; // Move to the right side for an increasing slope.\n else\n high = mid; // Move to the left side for a decreasing slope.\n }\n }\n return low; // Return the index where the target should be or would be inserted.\n }\n};\n```\n```Java []\nclass Solution {\n public int findInMountainArray(int target, MountainArray mountainArr) {\n int length = mountainArr.length();\n\n // Find the index of the peak element in the mountain array.\n int peakIndex = findPeakIndex(1, length - 2, mountainArr);\n\n // Binary search for the target in the increasing part of the mountain array.\n int increasingIndex = binarySearch(0, peakIndex, target, mountainArr, false);\n if (mountainArr.get(increasingIndex) == target) \n return increasingIndex; // Target found in the increasing part.\n\n // Binary search for the target in the decreasing part of the mountain array.\n int decreasingIndex = binarySearch(peakIndex + 1, length - 1, target, mountainArr, true);\n if (mountainArr.get(decreasingIndex) == target) \n return decreasingIndex; // Target found in the decreasing part.\n\n return -1; // Target not found in the mountain array.\n }\n\n private int findPeakIndex(int low, int high, MountainArray mountainArr) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {\n low = mid + 1; // Move to the right side (increasing slope).\n } else {\n high = mid; // Move to the left side (decreasing slope).\n }\n }\n return low; // Return the index of the peak element.\n }\n\n private int binarySearch(int low, int high, int target, MountainArray mountainArr, boolean reversed) {\n while (low != high) {\n int mid = low + (high - low) / 2;\n if (reversed) {\n if (mountainArr.get(mid) > target)\n low = mid + 1; // Move to the right side for a decreasing slope.\n else\n high = mid; // Move to the left side for an increasing slope.\n } else {\n if (mountainArr.get(mid) < target)\n low = mid + 1; // Move to the right side for an increasing slope.\n else\n high = mid; // Move to the left side for a decreasing slope.\n }\n }\n return low; // Return the index where the target should be or would be inserted.\n }\n}\n```\n```Python []\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n length = mountain_arr.length()\n\n # Find the index of the peak element in the mountain array.\n peak_index = self.find_peak_index(1, length - 2, mountain_arr)\n\n # Binary search for the target in the increasing part of the mountain array.\n increasing_index = self.binary_search(0, peak_index, target, mountain_arr, False)\n if mountain_arr.get(increasing_index) == target:\n return increasing_index # Target found in the increasing part.\n\n # Binary search for the target in the decreasing part of the mountain array.\n decreasing_index = self.binary_search(peak_index + 1, length - 1, target, mountain_arr, True)\n if mountain_arr.get(decreasing_index) == target:\n return decreasing_index # Target found in the decreasing part.\n\n return -1 # Target not found in the mountain array.\n\n def find_peak_index(self, low, high, mountainArr):\n while low != high:\n mid = low + (high - low) // 2\n if mountainArr.get(mid) < mountainArr.get(mid + 1):\n low = mid + 1 # Move to the right side (increasing slope).\n else:\n high = mid # Move to the left side (decreasing slope).\n return low # Return the index of the peak element.\n\n def binary_search(self, low, high, target, mountainArr, reversed):\n while low != high:\n mid = low + (high - low) // 2\n if reversed:\n if mountainArr.get(mid) > target:\n low = mid + 1 # Move to the right side for a decreasing slope.\n else:\n high = mid # Move to the left side for an increasing slope.\n else:\n if mountainArr.get(mid) < target:\n low = mid + 1 # Move to the right side for an increasing slope.\n else:\n high = mid # Move to the left side for a decreasing slope.\n return low # Return the index where the target should be or would be inserted.\n```\n\n\n\n\n\n | 120 | Given a date, return the corresponding day of the week for that date.
The input is given as three integers representing the `day`, `month` and `year` respectively.
Return the answer as one of the following values `{ "Sunday ", "Monday ", "Tuesday ", "Wednesday ", "Thursday ", "Friday ", "Saturday "}`.
**Example 1:**
**Input:** day = 31, month = 8, year = 2019
**Output:** "Saturday "
**Example 2:**
**Input:** day = 18, month = 7, year = 1999
**Output:** "Sunday "
**Example 3:**
**Input:** day = 15, month = 8, year = 1993
**Output:** "Sunday "
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | Based on whether A[i-1] < A[i] < A[i+1], A[i-1] < A[i] > A[i+1], or A[i-1] > A[i] > A[i+1], we are either at the left side, peak, or right side of the mountain. We can binary search to find the peak.
After finding the peak, we can binary search two more times to find whether the value occurs on either side of the peak. |
Easy Solution || Beginner Friendly || Beats 90% || Line by Line Explanation || | find-in-mountain-array | 0 | 1 | # Intuition\n\nThe problem involves finding a target value within a MountainArray. The MountainArray is a special type of array that increases up to a certain point and then decreases. The task is to determine the index at which the target value is located within the MountainArray.\n\n**Let\'s try to solve this problem together.**\n\n**First, we need to find the peak of the MountainArray. The peak is the point at which the MountainArray transitions from increasing to decreasing.**\n\nTo find the peak, we can use the following algorithm:\n\n```python\ndef find_peak_index(mountain_arr):\n low = 1\n high = mountain_arr.length() - 2\n\n while low != high:\n mid = low + (high - low) // 2\n\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n low = mid + 1\n else:\n high = mid\n\n return low\n```\n\n**Now that we know how to find the peak, we can use it to divide the MountainArray into two parts: the increasing part and the decreasing part.**\n\n**Once we have divided the MountainArray into two parts, we can use binary search to find the target value in each part.**\n\nTo perform binary search, we can use the following algorithm:\n\n```python\ndef binary_search(mountain_arr, low, high, target):\n while low != high:\n mid = low + (high - low) // 2\n\n if mountain_arr.get(mid) == target:\n return mid\n elif mountain_arr.get(mid) < target:\n low = mid + 1\n else:\n high = mid\n\n return -1\n```\n\n# Now, let\'s put all of this together to solve the problem.\n\n\n```python\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n# class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n length = mountain_arr.length()\n peak = self.find_peak_index(1, length - 2, mountain_arr)\n\n increasing_index = self.binary_search(0, peak, target, mountain_arr, is_reversed=False)\n if mountain_arr.get(increasing_index) == target:\n return increasing_index\n decreasing_index = self.binary_search(peak + 1, length - 1, target, mountain_arr, is_reversed=True)\n if mountain_arr.get(decreasing_index) == target:\n return decreasing_index\n return -1\n \n def find_peak_index(self, low, high, mountain_arr):\n while low != high:\n mid = low + (high - low) // 2\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n low = mid + 1\n else:\n high = mid\n return low\n \n def binary_search(self, low, high, target, mountain_arr, is_reversed):\n while low != high:\n mid = low + (high - low) // 2\n if is_reversed:\n if mountain_arr.get(mid) > target:\n low = mid + 1\n else:\n high = mid\n else:\n if mountain_arr.get(mid) < target:\n low = mid + 1\n else:\n high = mid\n return low\n\n | 21 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
Easy Solution || Beginner Friendly || Beats 90% || Line by Line Explanation || | find-in-mountain-array | 0 | 1 | # Intuition\n\nThe problem involves finding a target value within a MountainArray. The MountainArray is a special type of array that increases up to a certain point and then decreases. The task is to determine the index at which the target value is located within the MountainArray.\n\n**Let\'s try to solve this problem together.**\n\n**First, we need to find the peak of the MountainArray. The peak is the point at which the MountainArray transitions from increasing to decreasing.**\n\nTo find the peak, we can use the following algorithm:\n\n```python\ndef find_peak_index(mountain_arr):\n low = 1\n high = mountain_arr.length() - 2\n\n while low != high:\n mid = low + (high - low) // 2\n\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n low = mid + 1\n else:\n high = mid\n\n return low\n```\n\n**Now that we know how to find the peak, we can use it to divide the MountainArray into two parts: the increasing part and the decreasing part.**\n\n**Once we have divided the MountainArray into two parts, we can use binary search to find the target value in each part.**\n\nTo perform binary search, we can use the following algorithm:\n\n```python\ndef binary_search(mountain_arr, low, high, target):\n while low != high:\n mid = low + (high - low) // 2\n\n if mountain_arr.get(mid) == target:\n return mid\n elif mountain_arr.get(mid) < target:\n low = mid + 1\n else:\n high = mid\n\n return -1\n```\n\n# Now, let\'s put all of this together to solve the problem.\n\n\n```python\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n# class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n length = mountain_arr.length()\n peak = self.find_peak_index(1, length - 2, mountain_arr)\n\n increasing_index = self.binary_search(0, peak, target, mountain_arr, is_reversed=False)\n if mountain_arr.get(increasing_index) == target:\n return increasing_index\n decreasing_index = self.binary_search(peak + 1, length - 1, target, mountain_arr, is_reversed=True)\n if mountain_arr.get(decreasing_index) == target:\n return decreasing_index\n return -1\n \n def find_peak_index(self, low, high, mountain_arr):\n while low != high:\n mid = low + (high - low) // 2\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n low = mid + 1\n else:\n high = mid\n return low\n \n def binary_search(self, low, high, target, mountain_arr, is_reversed):\n while low != high:\n mid = low + (high - low) // 2\n if is_reversed:\n if mountain_arr.get(mid) > target:\n low = mid + 1\n else:\n high = mid\n else:\n if mountain_arr.get(mid) < target:\n low = mid + 1\n else:\n high = mid\n return low\n\n | 21 | Given a date, return the corresponding day of the week for that date.
The input is given as three integers representing the `day`, `month` and `year` respectively.
Return the answer as one of the following values `{ "Sunday ", "Monday ", "Tuesday ", "Wednesday ", "Thursday ", "Friday ", "Saturday "}`.
**Example 1:**
**Input:** day = 31, month = 8, year = 2019
**Output:** "Saturday "
**Example 2:**
**Input:** day = 18, month = 7, year = 1999
**Output:** "Sunday "
**Example 3:**
**Input:** day = 15, month = 8, year = 1993
**Output:** "Sunday "
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | Based on whether A[i-1] < A[i] < A[i+1], A[i-1] < A[i] > A[i+1], or A[i-1] > A[i] > A[i+1], we are either at the left side, peak, or right side of the mountain. We can binary search to find the peak.
After finding the peak, we can binary search two more times to find whether the value occurs on either side of the peak. |
first find the peak then do binary search on both sides | find-in-mountain-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(logN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n#class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n l, r = 0, mountain_arr.length() - 1\n peak = -1\n while l < r:\n m = (r + l) // 2\n left, middle, right = mountain_arr.get(m - 1), mountain_arr.get(m), mountain_arr.get(m + 1)\n if left < middle and middle > right:\n peak = m\n break\n if left > middle > right:\n r = m\n if left < middle < right:\n l = m\n\n \n def bisect(l, r, rev):\n res = math.inf\n while l <= r:\n m = (r + l) //2\n middle = mountain_arr.get(m)\n if middle == target:\n res = m\n break\n if not rev:\n if middle > target:\n r = m - 1\n else:\n l = m + 1\n else:\n if middle > target:\n l = m + 1\n else:\n r = m - 1\n return res\n \n left_ans = bisect(0, peak, False)\n right_ans = bisect(peak, mountain_arr.length() - 1, True)\n ans = min(left_ans, right_ans)\n return ans if ans < math.inf else -1\n \n\n``` | 1 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
first find the peak then do binary search on both sides | find-in-mountain-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(logN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n#class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n l, r = 0, mountain_arr.length() - 1\n peak = -1\n while l < r:\n m = (r + l) // 2\n left, middle, right = mountain_arr.get(m - 1), mountain_arr.get(m), mountain_arr.get(m + 1)\n if left < middle and middle > right:\n peak = m\n break\n if left > middle > right:\n r = m\n if left < middle < right:\n l = m\n\n \n def bisect(l, r, rev):\n res = math.inf\n while l <= r:\n m = (r + l) //2\n middle = mountain_arr.get(m)\n if middle == target:\n res = m\n break\n if not rev:\n if middle > target:\n r = m - 1\n else:\n l = m + 1\n else:\n if middle > target:\n l = m + 1\n else:\n r = m - 1\n return res\n \n left_ans = bisect(0, peak, False)\n right_ans = bisect(peak, mountain_arr.length() - 1, True)\n ans = min(left_ans, right_ans)\n return ans if ans < math.inf else -1\n \n\n``` | 1 | Given a date, return the corresponding day of the week for that date.
The input is given as three integers representing the `day`, `month` and `year` respectively.
Return the answer as one of the following values `{ "Sunday ", "Monday ", "Tuesday ", "Wednesday ", "Thursday ", "Friday ", "Saturday "}`.
**Example 1:**
**Input:** day = 31, month = 8, year = 2019
**Output:** "Saturday "
**Example 2:**
**Input:** day = 18, month = 7, year = 1999
**Output:** "Sunday "
**Example 3:**
**Input:** day = 15, month = 8, year = 1993
**Output:** "Sunday "
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | Based on whether A[i-1] < A[i] < A[i+1], A[i-1] < A[i] > A[i+1], or A[i-1] > A[i] > A[i+1], we are either at the left side, peak, or right side of the mountain. We can binary search to find the peak.
After finding the peak, we can binary search two more times to find whether the value occurs on either side of the peak. |
Easy Python3 Solution with explanation | find-in-mountain-array | 0 | 1 | # Intuition\nThe array is sorted in ascending order upto an index which I call as a peak index and from the peak index the array is sorted in descending order.\n\nBinary search not just once, but thrice with different intents:\n\n1. Find the peak element in the mountain array\n2. Find the target in the left half of the mountain array from [0 - peak-index]\n3. If step 2 returns -1 find the target in the right half of the mountain array[peak-index + 1, mountain_arr.length() - 1]\n\n# Approach\n**Step 1**:\nIf you plot a line graph and put the array elements in it there is one element that is tall and that is the peak element. This can be easily found by a modified vannila binary search algorithm in which we find the element index such that the mid element is less than mid + 1 element until the left & right pointers meet:\n```\n def find_peak(n):\n left = 0\n right = n - 1\n\n while left <= right:\n mid = left + (right - left) // 2\n\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n left = mid + 1\n else:\n right = mid - 1\n return left\n```\n**Step 2**:\nNow we have the peak_index from step 1 and it\'s just a plain vannila binary search to find the target in the mountain array from [0 - peak_index]:\n```\ndef binary_search_ascending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n if val == target:\n return mid\n elif target > val:\n left = mid + 1\n else:\n right = mid - 1\n return -1\n```\nIf the binary search in this step returns a valid index we simply return the index as the result because the index is for sure lesser (minimum index) than the peak_index.\n\n**Step 3**:\nIF step 2 returns -1 we need to search the descending sorted mountain array from [peak_index + 1 - mountain_arr.length() - 1]:\n```\ndef binary_search_descending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n\n if val == target:\n return mid\n elif target > val:\n right = mid - 1\n else:\n left = mid + 1\n return -1\n```\n\nThe final piece of the puzzle is just to determine if target is in the range[0 - peak_index], if yes do binary search ascending, if not do binary search descending. This step may not be required, but may well be an optimization.\n```\n peak_index = find_peak(n)\n res = -1\n if target >= mountain_arr.get(0) and target <= mountain_arr.get(peak_index):\n res = binary_search_ascending(0, peak_index)\n \n if res == -1:\n res = binary_search_descending(peak_index + 1, n - 1)\n```\n\n# Complexity\n- Time complexity:\nfind_peak - O(logn)\nbinary_search_ascending - O(logn)\nbinary_search_descending - O(logn)\n\nOverall time complexity is O(logn).\n\n- Space complexity:\nThe algorithm code presented uses constant space O(1).\n\nThank you for reading my solution. If you liked it kindly upvote my solution.\n\n# Code\n```\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n#class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n n = mountain_arr.length()\n def find_peak(n):\n left = 0\n right = n - 1\n\n while left <= right:\n mid = left + (right - left) // 2\n\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n left = mid + 1\n else:\n right = mid - 1\n return left\n\n\n def binary_search_ascending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n if val == target:\n return mid\n elif target > val:\n left = mid + 1\n else:\n right = mid - 1\n return -1\n \n def binary_search_descending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n\n if val == target:\n return mid\n elif target > val:\n right = mid - 1\n else:\n left = mid + 1\n return -1\n\n peak_index = find_peak(n)\n res = -1\n if target >= mountain_arr.get(0) and target <= mountain_arr.get(peak_index):\n res = binary_search_ascending(0, peak_index)\n \n if res == -1:\n res = binary_search_descending(peak_index + 1, n - 1)\n\n return res\n\n``` | 1 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
Easy Python3 Solution with explanation | find-in-mountain-array | 0 | 1 | # Intuition\nThe array is sorted in ascending order upto an index which I call as a peak index and from the peak index the array is sorted in descending order.\n\nBinary search not just once, but thrice with different intents:\n\n1. Find the peak element in the mountain array\n2. Find the target in the left half of the mountain array from [0 - peak-index]\n3. If step 2 returns -1 find the target in the right half of the mountain array[peak-index + 1, mountain_arr.length() - 1]\n\n# Approach\n**Step 1**:\nIf you plot a line graph and put the array elements in it there is one element that is tall and that is the peak element. This can be easily found by a modified vannila binary search algorithm in which we find the element index such that the mid element is less than mid + 1 element until the left & right pointers meet:\n```\n def find_peak(n):\n left = 0\n right = n - 1\n\n while left <= right:\n mid = left + (right - left) // 2\n\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n left = mid + 1\n else:\n right = mid - 1\n return left\n```\n**Step 2**:\nNow we have the peak_index from step 1 and it\'s just a plain vannila binary search to find the target in the mountain array from [0 - peak_index]:\n```\ndef binary_search_ascending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n if val == target:\n return mid\n elif target > val:\n left = mid + 1\n else:\n right = mid - 1\n return -1\n```\nIf the binary search in this step returns a valid index we simply return the index as the result because the index is for sure lesser (minimum index) than the peak_index.\n\n**Step 3**:\nIF step 2 returns -1 we need to search the descending sorted mountain array from [peak_index + 1 - mountain_arr.length() - 1]:\n```\ndef binary_search_descending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n\n if val == target:\n return mid\n elif target > val:\n right = mid - 1\n else:\n left = mid + 1\n return -1\n```\n\nThe final piece of the puzzle is just to determine if target is in the range[0 - peak_index], if yes do binary search ascending, if not do binary search descending. This step may not be required, but may well be an optimization.\n```\n peak_index = find_peak(n)\n res = -1\n if target >= mountain_arr.get(0) and target <= mountain_arr.get(peak_index):\n res = binary_search_ascending(0, peak_index)\n \n if res == -1:\n res = binary_search_descending(peak_index + 1, n - 1)\n```\n\n# Complexity\n- Time complexity:\nfind_peak - O(logn)\nbinary_search_ascending - O(logn)\nbinary_search_descending - O(logn)\n\nOverall time complexity is O(logn).\n\n- Space complexity:\nThe algorithm code presented uses constant space O(1).\n\nThank you for reading my solution. If you liked it kindly upvote my solution.\n\n# Code\n```\n# """\n# This is MountainArray\'s API interface.\n# You should not implement it, or speculate about its implementation\n# """\n#class MountainArray:\n# def get(self, index: int) -> int:\n# def length(self) -> int:\n\nclass Solution:\n def findInMountainArray(self, target: int, mountain_arr: \'MountainArray\') -> int:\n n = mountain_arr.length()\n def find_peak(n):\n left = 0\n right = n - 1\n\n while left <= right:\n mid = left + (right - left) // 2\n\n if mountain_arr.get(mid) < mountain_arr.get(mid + 1):\n left = mid + 1\n else:\n right = mid - 1\n return left\n\n\n def binary_search_ascending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n if val == target:\n return mid\n elif target > val:\n left = mid + 1\n else:\n right = mid - 1\n return -1\n \n def binary_search_descending(left, right):\n while left <= right:\n mid = left + (right - left) // 2\n val = mountain_arr.get(mid)\n\n if val == target:\n return mid\n elif target > val:\n right = mid - 1\n else:\n left = mid + 1\n return -1\n\n peak_index = find_peak(n)\n res = -1\n if target >= mountain_arr.get(0) and target <= mountain_arr.get(peak_index):\n res = binary_search_ascending(0, peak_index)\n \n if res == -1:\n res = binary_search_descending(peak_index + 1, n - 1)\n\n return res\n\n``` | 1 | Given a date, return the corresponding day of the week for that date.
The input is given as three integers representing the `day`, `month` and `year` respectively.
Return the answer as one of the following values `{ "Sunday ", "Monday ", "Tuesday ", "Wednesday ", "Thursday ", "Friday ", "Saturday "}`.
**Example 1:**
**Input:** day = 31, month = 8, year = 2019
**Output:** "Saturday "
**Example 2:**
**Input:** day = 18, month = 7, year = 1999
**Output:** "Sunday "
**Example 3:**
**Input:** day = 15, month = 8, year = 1993
**Output:** "Sunday "
**Constraints:**
* The given dates are valid dates between the years `1971` and `2100`. | Based on whether A[i-1] < A[i] < A[i+1], A[i-1] < A[i] > A[i+1], or A[i-1] > A[i] > A[i+1], we are either at the left side, peak, or right side of the mountain. We can binary search to find the peak.
After finding the peak, we can binary search two more times to find whether the value occurs on either side of the peak. |
[Python3] Concise iterative solution using stack | brace-expansion-ii | 0 | 1 | Use stack for "{" and "}" just like in calculator.\nMaintain two lists:\n1. the previous list before ","\n2. the current list that is still growing\n\nWhen seeing an "alphabet", grow the second list by corss multiplying. So that [a]\\*b will become "ab", [a,c]\\*b will become ["ab", "cb"]\nWhen seeing "," it means the second list can\'t grow anymore. Combine it with the first list and clear the second list.\nWhen seeing "{", push the two lists into stack, \nWhen seeing "}", pop the previous two lists, cross multiplying the result inside "{ }" into the second list.\n\nIf not considering the final sorting before return, the time complexity should be O(n)\n\n```\nclass Solution:\n def braceExpansionII(self, expression: str) -> List[str]:\n stack,res,cur=[],[],[]\n for i in range(len(expression)):\n v=expression[i]\n if v.isalpha():\n cur=[c+v for c in cur or [\'\']]\n elif v==\'{\':\n stack.append(res)\n stack.append(cur)\n res,cur=[],[]\n elif v==\'}\':\n pre=stack.pop()\n preRes=stack.pop()\n cur=[p+c for c in res+cur for p in pre or [\'\']]\n res=preRes\n elif v==\',\':\n res+=cur\n cur=[]\n return sorted(set(res+cur))\n``` | 104 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python3 Stack Solution | brace-expansion-ii | 0 | 1 | ```\nclass Solution:\n def braceExpansionII(self, expression: str) -> List[str]:\n stack, union, product = [],[],[\'\']\n for c in expression:\n if c.isalpha():\n product = [r + c for r in product]\n elif c == \'{\':\n stack.append(union)\n stack.append(product)\n union, product = [], [\'\']\n elif c == \'}\':\n pre_product, pre_union = stack.pop(), stack.pop()\n product = [p + r for r in product + union for p in pre_product]\n union = pre_union\n else:\n union += product\n product = [\'\']\n return sorted(set(union + product))\n``` | 21 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python3: Recursive Parser Pattern | brace-expansion-ii | 0 | 1 | # Intuition\n\nI have a hard time understanding and following the various stack-of-lists solutions, and I suspect your interviewers will have a hard time following them too.\n\nInstead, I prefer the parser pattern:\n* we break the input into the kinds of things we need to parse\n* each `parseThing` method takes the index to start parsing from, and returns the next index to parse from later\n\n# Approach\n\nThe top level expression is something like this:\n```\n<term1><term2>..<termK>\n```\na product of `K` terms. I call it a "product" because the way we combine e.g. `{a,b}{c,d}` is with the direct product of concatenations.\n\nEach individual `term_i` is either\n* a "literal," a sequence of characters\n* or a `{product[,product]*}` expression\n\nA single `{..}` or literal is also a product: a product of 1 term.\n\nSo as we parse, we\'ll find the following:\n* products: `<term1>..<termK>`\n* individual terms: either `{..}` or `letters`\n* literals: `letters`\n* expressions: `{..}`\n\nSo we have 4 parse methods to write.\n\nThe input is a product of 1 or more terms, so we run `parseProduct(0)` to get the output strings.\n\nPersonally I find this WAY more clear than nested stacks and such, but opinions vary.\n\n# Complexity\n- Time complexity: exponential in the length because we can have `{a,b}{c,d}{a,b}{c,d}..` and `2**pairs` runtime\n\n- Space complexity: also exponential, oof\n\nI don\'t think there\'s any way around this, if there are an expoential number of strings then that\'s just how things are.\n\n# Code\n```\nclass Solution:\n def braceExpansionII(self, e: str) -> List[str]:\n # to parse e.g. {..}abc{...}{...}def we have to handle a product of terms: `parseProduct`\n # a term is either {..} or letters: parseTerm\n # expr literal\n # a {..} is an expr, it has { then product[,product]* then }: `parseExpr`\n # s sequence of letters is a literal: `parseLiteral`\n\n E = len(e)\n\n def parseProduct(i: int) -> tuple[set[str], int]:\n """Parses a product of 1 or more {...} and literals"""\n\n ans, j = parseTerm(i)\n while j < E and e[j] != \'}\' and e[j] != \',\':\n term, j = parseTerm(j)\n ans = {a+t for a in ans for t in term} # direct product, concatenations\n \n return ans, j # j is } or , or E\n\n def parseTerm(i: int) -> tuple[set[str], int]:\n if e[i] == \'{\': return parseExpr(i)\n else: return parseLiteral(i)\n\n def parseExpr(i: int) -> tuple[set[str], int]:\n """Parses a {...}, i.e. a ,-delimited sequence of products, wrapped in {..}"""\n\n j = i+1\n ans, j = parseProduct(j)\n while j < E and e[j] == \',\':\n # there\'s a next product\n j += 1\n prod, j = parseProduct(j)\n ans |= prod\n\n assert e[j] == \'}\'\n return ans, j+1 # skip past \'}\', which is part of this {..} expr\n\n def parseLiteral(i: int) -> tuple[set[str], int]:\n j = i+1\n while j < E and e[j].isalpha(): j += 1\n return set([e[i:j]]), j # FIXED: 1-element set, instead of set of unique chars\n\n # input is either {...} by itself, or a literal, or a product\n # the former two are products, just single-term products. so we\'ll parse a product\n ans, _ = parseProduct(0)\n ans = list(ans)\n ans.sort()\n return ans\n``` | 0 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python Clear and Concise, Faster than 73% | Explained | brace-expansion-ii | 0 | 1 | # Intuition\nInitially this may sound as a very overwhelming problem. It has so much unplesant stuff like string expression parsing and full powerset generation. Even the definition sounds vague. But if you spend some time trying to understand the input - it is pretty straighforward.\n\nHere are some of the key takeaways:\n- When the text is joined via comman - it is simply a **union**\n- When a text is concatenated - we **concatenate** the result \n\nMaintaining the uniqueness also gives another hint. This sounds like a perfect spot for a set, isn\'t it?\n\n# Approach\nWhat is `{c,{d,e}}`? Isn\'t it the same as `{c,d,e}`? It is indeed. So key takeaway here is that nested, comma-separated sets are just united. If we make all of our expression to the form: `{a,b,c}{ba,ca,dc,f}` (having single nested level), then we can just do:\n```\nres = {}\nfor expr1 in sub_expr1:\n for expr2 in sub_expr2:\n res.add(expr1 + expr2)\n```\nThis is our Cartesian product part for concatenation. So how do we reach this shallowness? \nWell, recursion is the key. If we solve the problem for some nested `{...{...{1}}}` expression 1, we would then just solve it for the upper level, and so on.\n\nSo:\n\n- To find the solution for the outer level of the expression, find all of the solutions for the nested levels\n- If the nested and outer and joined via comma - do a union of them\n- If they are joined via concatenation - do the Cartesian product as discussed above\n\nAlgorithm in more detail:\n- To maintain such idea scan the expression from left to right and maintain a set of current expressions (those that are not nested and joined via comma)\n- When encounter `{` find the next matching `}` and parse this expression recursively applying all the same logic\n- Join the outer expression with the nested one using the process discussed above (union or Cartesian product)\n\n# Complexity\n- Time complexity:\n_Roughly *_\n```\nl - string length\na - number of elements in answer\n```\n$$O(l*a))$$\n\n- Space complexity:\n\n$$O(a))$$\n\n# Code\n```\nclass Solution:\n def findNext(self, expression: str, start: int):\n balance = 0\n for i, c in enumerate(expression[start:]):\n if c == \'{\':\n balance += 1\n elif c == \'}\':\n balance -= 1\n if balance == 0:\n return start + i\n\n return -1\n\n def backtrack(self, expression: str) -> Set[str]:\n res = set()\n\n pos = 0\n curr_expr = {\'\'}\n while pos < len(expression):\n c = expression[pos]\n\n if c not in \'{},\':\n curr_expr = {expr + c for expr in curr_expr}\n elif c == \',\':\n res = res | curr_expr\n curr_expr = {\'\'}\n elif c == \'{\':\n old_pos = pos + 1\n pos = self.findNext(expression, pos)\n\n # pos - 1 because we find next "}", so we don\'t need to include it\n sub_expr = self.backtrack(expression[old_pos:pos])\n\n tmp_expr = set()\n for expr1 in curr_expr:\n for expr2 in sub_expr:\n tmp_expr.add(expr1 + expr2)\n\n curr_expr = tmp_expr\n pos += 1\n\n res = res | curr_expr\n return res\n\n def braceExpansionII(self, expression: str) -> List[str]:\n return sorted(self.backtrack(expression))\n``` | 0 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python | Beats 96% | Recursion | brace-expansion-ii | 0 | 1 | # Code\n```\nclass Parser:\n def __init__(self, input):\n self.input = input\n self.i = 0\n\n def parse_expr(self):\n if self.input[self.i] == \'{\':\n ret = set()\n self.i += 1\n\n while self.i < len(self.input) and self.input[self.i] != \'}\':\n for i in self.parse_expr():\n ret.add(i)\n if self.input[self.i] == \'}\':\n break\n self.i += 1 # skips \',\'\n\n if self.i+1 < len(self.input):\n nextchar = self.input[self.i+1]\n if nextchar == \'{\' or nextchar.isalpha():\n self.i += 1\n adj = self.parse_expr()\n return [i+j for i in ret for j in adj]\n\n self.i += 1\n return list(ret)\n\n else: # Letter\n bef = self.i\n while self.i < len(self.input) and self.input[self.i].isalpha():\n self.i += 1\n\n word = self.input[bef:self.i]\n if self.i < len(self.input) and self.input[self.i] == \'{\':\n return [word+i for i in self.parse_expr()]\n return [word]\n\n \nclass Solution:\n def braceExpansionII(self, expression: str) -> List[str]:\n """\n Expr :: \'{\' Expr, .. \'}\' | (Expr)(Expr) | a..z\n """\n\n ans = Parser(expression).parse_expr()\n return sorted(ans)\n\n\n``` | 0 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python3 beats 90% short solution | brace-expansion-ii | 0 | 1 | # Code\n```\nclass Solution:\n def braceExpansionII(self, expression: str) -> List[str]:\n groups = [[]]\n level = 0\n for i, c in enumerate(expression):\n if c == \'{\':\n if level == 0:\n start = i+1\n level += 1\n elif c == \'}\':\n level -= 1\n if level == 0:\n groups[-1].append(self.braceExpansionII(expression[start:i]))\n elif c == \',\' and level == 0:\n groups.append([])\n elif level == 0:\n groups[-1].append([c])\n word_set = set()\n for group in groups:\n word_set |= set(map(\'\'.join, itertools.product(*group)))\n return sorted(word_set)\n``` | 0 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python Easy Solution | distribute-candies-to-people | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distributeCandies(self, candies: int, num_people: int) -> List[int]:\n arr = [0 for i in range(num_people)]\n i = 0\n j = 1\n while candies > 0:\n if i == len(arr):\n i = 0\n if candies >= j:\n arr[i] += j\n candies -= j\n j += 1\n else:\n arr[i] += candies\n break\n i += 1\n return arr\n\n\n\n``` | 1 | We distribute some number of `candies`, to a row of **`n = num_people`** people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give `n` candies to the last person.
Then, we go back to the start of the row, giving `n + 1` candies to the first person, `n + 2` candies to the second person, and so on until we give `2 * n` candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length `num_people` and sum `candies`) that represents the final distribution of candies.
**Example 1:**
**Input:** candies = 7, num\_people = 4
**Output:** \[1,2,3,1\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3,0\].
On the fourth turn, ans\[3\] += 1 (because there is only one candy left), and the final array is \[1,2,3,1\].
**Example 2:**
**Input:** candies = 10, num\_people = 3
**Output:** \[5,2,3\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3\].
On the fourth turn, ans\[0\] += 4, and the final array is \[5,2,3\].
**Constraints:**
* 1 <= candies <= 10^9
* 1 <= num\_people <= 1000 | For the minimum: We can always do it in at most 2 moves, by moving one stone next to another, then the third stone next to the other two. When can we do it in 1 move? 0 moves?
For the maximum: Every move, the maximum position minus the minimum position must decrease by at least 1. |
Easy Approach | distribute-candies-to-people | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distributeCandies(self, candies: int, num_people: int) -> List[int]:\n lis=[0]*num_people\n i=1\n j=0\n while(candies):\n if(candies<i):\n lis[j%num_people]+=candies\n break\n if(candies>=i):\n lis[j%num_people]+=i\n candies-=i\n j+=1\n i+=1\n \n return(lis)\n\n \n``` | 3 | We distribute some number of `candies`, to a row of **`n = num_people`** people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give `n` candies to the last person.
Then, we go back to the start of the row, giving `n + 1` candies to the first person, `n + 2` candies to the second person, and so on until we give `2 * n` candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length `num_people` and sum `candies`) that represents the final distribution of candies.
**Example 1:**
**Input:** candies = 7, num\_people = 4
**Output:** \[1,2,3,1\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3,0\].
On the fourth turn, ans\[3\] += 1 (because there is only one candy left), and the final array is \[1,2,3,1\].
**Example 2:**
**Input:** candies = 10, num\_people = 3
**Output:** \[5,2,3\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3\].
On the fourth turn, ans\[0\] += 4, and the final array is \[5,2,3\].
**Constraints:**
* 1 <= candies <= 10^9
* 1 <= num\_people <= 1000 | For the minimum: We can always do it in at most 2 moves, by moving one stone next to another, then the third stone next to the other two. When can we do it in 1 move? 0 moves?
For the maximum: Every move, the maximum position minus the minimum position must decrease by at least 1. |
py3 sol | distribute-candies-to-people | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distributeCandies(self, candies: int, num_people: int) -> List[int]:\n arr = [0 for i in range(num_people)]\n i = 0\n j = 1\n while candies > 0:\n if i == len(arr):\n i = 0\n if candies >= j:\n arr[i] += j\n candies -= j\n j += 1\n else:\n arr[i] += candies\n break\n i += 1\n return arr\n\n\n``` | 1 | We distribute some number of `candies`, to a row of **`n = num_people`** people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give `n` candies to the last person.
Then, we go back to the start of the row, giving `n + 1` candies to the first person, `n + 2` candies to the second person, and so on until we give `2 * n` candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length `num_people` and sum `candies`) that represents the final distribution of candies.
**Example 1:**
**Input:** candies = 7, num\_people = 4
**Output:** \[1,2,3,1\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3,0\].
On the fourth turn, ans\[3\] += 1 (because there is only one candy left), and the final array is \[1,2,3,1\].
**Example 2:**
**Input:** candies = 10, num\_people = 3
**Output:** \[5,2,3\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3\].
On the fourth turn, ans\[0\] += 4, and the final array is \[5,2,3\].
**Constraints:**
* 1 <= candies <= 10^9
* 1 <= num\_people <= 1000 | For the minimum: We can always do it in at most 2 moves, by moving one stone next to another, then the third stone next to the other two. When can we do it in 1 move? 0 moves?
For the maximum: Every move, the maximum position minus the minimum position must decrease by at least 1. |
Solution | Python | distribute-candies-to-people | 0 | 1 | ```\nclass Solution:\n def distributeCandies(self, candies: int, num_people: int) -> List[int]:\n # create an array of size num_people and initialize it with 0\n list_people = [0] * num_people\n \n # starting value\n index = 1\n \n # iterate until the number of candies are more than 0\n while candies > 0:\n \n # if candies are more than index value, add the index value to the location \n if candies > index:\n # we are using mod operation by the num_people to locate the index of the array\n # we are subtracting by 1 because the array index starts at 0\n list_people[(index - 1) % num_people] += index\n else:\n # if candies are less than index value, add all remaining candies to location\n list_people[(index - 1) % num_people] += candies\n \n # subtract the candies with index values\n candies -= index\n \n # increment the index values\n index += 1\n \n # return the resultant array\n return(list_people)\n``` | 12 | We distribute some number of `candies`, to a row of **`n = num_people`** people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give `n` candies to the last person.
Then, we go back to the start of the row, giving `n + 1` candies to the first person, `n + 2` candies to the second person, and so on until we give `2 * n` candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length `num_people` and sum `candies`) that represents the final distribution of candies.
**Example 1:**
**Input:** candies = 7, num\_people = 4
**Output:** \[1,2,3,1\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3,0\].
On the fourth turn, ans\[3\] += 1 (because there is only one candy left), and the final array is \[1,2,3,1\].
**Example 2:**
**Input:** candies = 10, num\_people = 3
**Output:** \[5,2,3\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3\].
On the fourth turn, ans\[0\] += 4, and the final array is \[5,2,3\].
**Constraints:**
* 1 <= candies <= 10^9
* 1 <= num\_people <= 1000 | For the minimum: We can always do it in at most 2 moves, by moving one stone next to another, then the third stone next to the other two. When can we do it in 1 move? 0 moves?
For the maximum: Every move, the maximum position minus the minimum position must decrease by at least 1. |
Optimal Python Solution with clear Explanation of Idea | distribute-candies-to-people | 0 | 1 | Please read with patience for clear understanding - Before proceeding, remember that sum of first n natural numbers is n*(n+1)//2\n```\nclass Solution:\n def distributeCandies(self, candies, num_people):\n \'\'\'\n Idea: Round number k (starting from 1)\n -> give away\n (k-1)*n+1 + (k-1)*n+2 + ... + (k-1)*n + n = \n (k-1)*n^2 + n*(n+1)/2 candies\n \n Assume we have completed K full rounds, then K is the largest integer >= 0 with\n \n K*n*(n+1)/2 + K * (K-1)/2 * n^2 <= candies \n \n Find K by binary search and then simulate the last round.\n \n The person at index i gets\n \n 0*n+i+1 + ... + (K-1)*n+i+1 = K*(i+1) + n*K*(K-1)/2 \n \n candies from rounds 1 to K, plus everything they get on their\n last round.\n \n Important: Allow for the fact that we may not complete a single round.\n\n REVIEW\n\t\t\'\'\'\n\t\t\n lo, hi = 0, candies\n K = 0\n while lo <= hi:\n k = (lo + hi)//2\n if k*(num_people*(num_people+1))//2 + (k*(k-1))//2 * num_people**2 <= candies:\n K = k\n lo = k + 1\n else:\n hi = k - 1\n result = [(i+1)*K+num_people*(K*(K-1))//2 for i in range(num_people)]\n candies -= sum(result)\n for i in range(num_people):\n add = min(candies, K * num_people + i + 1)\n result[i] += add\n candies -= add\n if candies == 0:\n break\n return result \n\t\t```\nIf you came till here - Please Upvote my effort | 10 | We distribute some number of `candies`, to a row of **`n = num_people`** people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give `n` candies to the last person.
Then, we go back to the start of the row, giving `n + 1` candies to the first person, `n + 2` candies to the second person, and so on until we give `2 * n` candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length `num_people` and sum `candies`) that represents the final distribution of candies.
**Example 1:**
**Input:** candies = 7, num\_people = 4
**Output:** \[1,2,3,1\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3,0\].
On the fourth turn, ans\[3\] += 1 (because there is only one candy left), and the final array is \[1,2,3,1\].
**Example 2:**
**Input:** candies = 10, num\_people = 3
**Output:** \[5,2,3\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3\].
On the fourth turn, ans\[0\] += 4, and the final array is \[5,2,3\].
**Constraints:**
* 1 <= candies <= 10^9
* 1 <= num\_people <= 1000 | For the minimum: We can always do it in at most 2 moves, by moving one stone next to another, then the third stone next to the other two. When can we do it in 1 move? 0 moves?
For the maximum: Every move, the maximum position minus the minimum position must decrease by at least 1. |
57 % effective code. | distribute-candies-to-people | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* distributeCandies(int candies, int num_people, int* returnSize){\n *returnSize = num_people;\n int x[num_people];\n int y = 1;\n int *res=(int*)calloc(num_people,sizeof(int));\n while(candies != 0){\n for(int i = 0; i < num_people; i++){\n if(candies < y){\n y = candies;\n }\n res[i] = res[i] + y;\n candies = candies - y;\n y++;\n }\n }\n return res;\n}\n``` | 0 | We distribute some number of `candies`, to a row of **`n = num_people`** people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give `n` candies to the last person.
Then, we go back to the start of the row, giving `n + 1` candies to the first person, `n + 2` candies to the second person, and so on until we give `2 * n` candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length `num_people` and sum `candies`) that represents the final distribution of candies.
**Example 1:**
**Input:** candies = 7, num\_people = 4
**Output:** \[1,2,3,1\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3,0\].
On the fourth turn, ans\[3\] += 1 (because there is only one candy left), and the final array is \[1,2,3,1\].
**Example 2:**
**Input:** candies = 10, num\_people = 3
**Output:** \[5,2,3\]
**Explanation:**
On the first turn, ans\[0\] += 1, and the array is \[1,0,0\].
On the second turn, ans\[1\] += 2, and the array is \[1,2,0\].
On the third turn, ans\[2\] += 3, and the array is \[1,2,3\].
On the fourth turn, ans\[0\] += 4, and the final array is \[5,2,3\].
**Constraints:**
* 1 <= candies <= 10^9
* 1 <= num\_people <= 1000 | For the minimum: We can always do it in at most 2 moves, by moving one stone next to another, then the third stone next to the other two. When can we do it in 1 move? 0 moves?
For the maximum: Every move, the maximum position minus the minimum position must decrease by at least 1. |
Literal Math in Python 3, bottom-up | path-in-zigzag-labelled-binary-tree | 0 | 1 | ```python3\nclass Solution:\n def pathInZigZagTree(self, label: int) -> List[int]:\n def gen():\n nonlocal label\n lv, q = 0, label\n yield label\n while q:\n q, r = divmod(q, 2)\n lv += (q > 0)\n real_parent = label\n for i in range(lv - 1, -1, -1):\n original_parernt = label // 2\n offset = abs(original_parernt - 2 ** (i + 1)) - 1\n real_parent = 2 ** i + offset\n yield real_parent\n label = real_parent\n\n return list(gen())[::-1]\n\n``` | 1 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Complete Binary Tree | Python | path-in-zigzag-labelled-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves finding the path from the root of a zigzag binary tree to a specified node labeled label. In a regular binary tree, finding the parent of any node is straightforward, as it\'s simply the integer division of the node\'s value by 2. However, the zigzag nature of this tree, where each level of the tree alternates between normal and reverse order, adds a layer of complexity. The key insight is to leverage the properties of the complete binary tree and the pattern of the zigzag arrangement to backtrack from the target node to the root.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Determine the Level of the Target Node:** First, find the level of the tree where the target node is located. This is done by increasing the level until the maximum value at that level is at least as large as the label.\n1. **Backtracking to the Root:** Starting from the target node, find its parent in the zigzag tree. Since the tree alternates direction at each level, the parent\'s value is calculated differently for odd and even levels. For a level in normal order, the parent is simply label // 2. For a reversed level, compute the mirror position of the label using the formula mirror = level_min + level_max - label, and then find the parent of this mirrored label.\n1. **Constructing the Path:** Add each visited node to the path. Since the traversal starts from the target node and moves up to the root, the path needs to be reversed at the end to present it from root to target.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(logn)$$. The time complexity is logarithmic in terms of the label\'s value. This is because the depth of the tree (and hence the number of levels) is proportional to the logarithm of the label. The algorithm iterates over each level once.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(logn)$$. The space complexity is also logarithmic, as the longest path in a binary tree is equal to the height of the tree, which is proportional to the logarithm of the highest label in the tree. The path array that is being constructed to store the route will have a size equal to the tree\'s height.\n\n# Code\n```\nclass Solution:\n def pathInZigZagTree(self, label: int) -> List[int]:\n # 1 << level\n # (level)2 -> (level 0)2\n # power(2,level)\n\n # find level first\n level = 0\n while ((1 << (level+1))-1 )< label:\n level += 1\n \n path = []\n while label >= 1:\n path.append(label)\n level_max = (1 << (level+1)) - 1\n level_min = (1 << (level))\n\n label = (level_max + level_min - label) // 2\n level -= 1\n\n return path[::-1]\n\n\n # 1\n # 2 3\n # 4 5 6 7\n # 8 9 10 11 12 13 14 15\n # \uFF5C\n # original position\n\n # \u5728\u4E00\u4E2A\u5B8C\u5168\u4E8C\u53C9\u6811\u4E2D\uFF0C\u5BF9\u4E8E\u4EFB\u4F55\u4E00\u4E2A\u8282\u70B9\u800C\u8A00\uFF0C\u5B83\u7684\u5B50\u8282\u70B9\u53EF\u4EE5\u901A\u8FC7\u4EE5\u4E0B\u65B9\u5F0F\u627E\u5230\uFF1A\n # \u5DE6\u5B50\u8282\u70B9 = \u7236\u8282\u70B9 * 2\n # \u53F3\u5B50\u8282\u70B9 = \u7236\u8282\u70B9 * 2 + 1\n # \u53CD\u8FC7\u6765\uFF0C\u5982\u679C\u4F60\u6709\u4E00\u4E2A\u5B50\u8282\u70B9\uFF0C\u4F60\u53EF\u4EE5\u901A\u8FC7\u6574\u9664 2 \u7684\u64CD\u4F5C\u627E\u5230\u7236\u8282\u70B9\u7684\u6807\u7B7E\uFF1A\n # \u7236\u8282\u70B9 = \u5B50\u8282\u70B9 // 2\n\n # \u5BF9\u4E8E\u5F53\u5C42\u53CD\u5E8F\uFF0C\u6211\u4EEC\u9700\u8981\u627E\u5230\u4ED6\u7684\u955C\u50CF\u4F4D\u7F6E\uFF1A\n # 4 5 6 7\n # -> 15 14 13 12 11 10 9 8\n# \uFF5C\n # mirror position\n # (original position + mirror position) = (level_min + level_max)\n # mirror position = level_min + level_max - original postion\n # parent(mirror position) = (level_min + level_max - original postion) // 2\n\n # \u5BF9\u4E8E\u5F53\u5C42\u987A\u5E8F(\u4E0A\u4E00\u5C42\u53CD\u5E8F)\uFF1A\n # \uFF5C \uFF5C\n # 3 2 2 3\n # -> 4 5 6 7 4 5 6 7\n # \uFF5C \uFF5C\n # \u6211\u4EEC\u4E5F\u53EF\u4EE5\u5148\u627E\u5F53\u524D\u5C42\u7684\u955C\u50CF\u4F4D\u7F6E\uFF0C\u5728\u53BB\u4E0A\u4E00\u5C42\u5BFB\u627Eparent node\n\n\n``` | 1 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Python Solution || With Explanation || Easy to Understand | path-in-zigzag-labelled-binary-tree | 0 | 1 | * How many levels will be there if n=14? The ans is 3 (level 0,level 1, level 2 and level3)\n* How many levels will be there if n=16? The ans is 4.\n* The number of levels in this binary tree will be [log2(n)] where [x] represents floor value. [3.99] = 3\n* The levels in this tree are odd levels and even levels all odd,even levels follows same patterns respectively.\n* for all odd level the parent can be calculated as `label = 2**(level-1)+(2**(level-1)-pos-1)`. i.e. decreasing respective positions.\n* for all even level parent can be calculated as `2**(level) - 1 - pos`. Increasing respective positions\n* for odd level example suppose we have` label = 13 and level = 3` its parent label will be `2**(3-1)+(2**(3-1)-((13-(2**3))//2-1)` that is `4+4-2-1` that is 5.\n* for even level example suppose we have `label = 5 and level = 2` its parent label will be `2**(2) - 1 - (5-2**2)//2` that is 3.\n\n```\nfrom math import log2,floor\nclass Solution:\n def pathInZigZagTree(self, label: int) -> List[int]:\n level = floor(log2(label))\n ans = [label]\n while label!=1:\n c = label - 2**level\n pos = c//2\n if level&1:\n label = 2**(level-1)+(2**(level-1)-pos-1)\n else:\n label = 2**(level) - 1 - pos\n level -= 1\n ans.append(label)\n return ans[::-1]\n``` | 1 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Simple Python Solution | path-in-zigzag-labelled-binary-tree | 0 | 1 | # Intuition\nFirst Calculate at which level the target value will appear and then \ncalculate the path backword. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pathInZigZagTree(self, label: int) -> List[int]:\n def check_level(label, p):\n while True:\n if label <= 2 **(p+1) -1:\n return p\n else:\n p += 1\n level = check_level(label,0)\n \n def find_path(level, label):\n ans = [label]\n while level > 0:\n parent = (2**(level+1) - 1) + (2**(level)) - label\n ans.append(parent//2)\n label = parent//2\n level -= 1\n return ans[::-1]\n return find_path(level,label) \n\n\n \n\n\n\n\n``` | 1 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
68% TC and 72% SC easy python solution | path-in-zigzag-labelled-binary-tree | 0 | 1 | ```\ndef pathInZigZagTree(self, label: int) -> List[int]:\n\tans = [label]\n\twhile(label != 1):\n\t\tpar1 = label//2\n\t\tx = int(log(par1, 2))\n\t\tdiff = par1 - 2**x\n\t\tlabel = 2**(x+1)-1 - diff\n\t\tans.append(label)\n\treturn ans[::-1]\n``` | 1 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Bit masking | path-in-zigzag-labelled-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe parents of zig-zag tree and the original version are mutually exclusive to a factor.\n\nEx: The parent of 23 in the non zig-zag fashion is 23//2 - > 11\nin the zigzag version, it is 15 - 11 + 8 = 12 (15 -> higher bound in powers of 2 and 8 -> lower bound.. pow(2, x) <= parent < pow(2, y); y-x = 1)\n\n# Complexity\n- Time complexity:\nO(logN)\n\n- Space complexity:\n O(1)\n\n# Code\n```\nclass Solution:\n def pathInZigZagTree(self, label: int) -> List[int]:\n \n def getParent(num):\n real_parent = num // 2\n num_bits = len(bin(real_parent)) - 2\n mask = (1 << num_bits - 1) - 1\n foster_parent = real_parent ^ mask\n return foster_parent\n\n output = []\n\n while label:\n output.append(label)\n if label == 1: break\n label = getParent(label)\n\n return output[::-1]\n``` | 0 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Simple Python Solution | path-in-zigzag-labelled-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pathInZigZagTree(self, label: int) -> List[int]:\n def getMaxiMini(level):\n return [2**level-1,2**(level-1)]\n def Solve(label):\n res=[label]\n level=int(math.log(label,2))+1\n while(level!=0):\n if(level%2==0):\n maxi,mini=getMaxiMini(level)\n actual=maxi+mini-label\n parent=actual//2\n label=parent\n else:\n maxi,mini=getMaxiMini(level-1)\n parent=label//2\n actualParent=maxi+mini-parent\n label=actualParent\n res.append(label)\n level-=1\n return res[::-1][1:]\n return Solve(label)\n``` | 0 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Python3 with explanation | path-in-zigzag-labelled-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find a path in a zigzag binary tree, we need to understand the alternating pattern of levels. This involves converting the given label to a regular binary tree label, then tracing back to the root.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nget_level: Determines the tree level of the label.\nget_modified_label: Adjusts labels for zigzag order.\npathInZigZagTree: Finds the path from the label to the root, considering the zigzag pattern.\n\n# Complexity\n- Time complexity: O(log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(log(n))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def get_level(self, label: int):\n level = -1\n while label:\n label = label // 2\n level += 1\n return level\n\n def get_modified_label(self, label: int, level: int) -> int:\n if level % 2 == 1:\n return pow(2, level + 1) - 1 - (label - pow(2, level))\n else:\n return label\n\n def pathInZigZagTree(self, label: int) -> List[int]:\n orig_path = []\n\n temp_label = self.get_modified_label(label, self.get_level(label))\n\n while temp_label:\n orig_path.append(temp_label)\n temp_label = temp_label // 2\n orig_path.reverse()\n\n new_path = []\n for i, val in enumerate(orig_path):\n new_path.append(self.get_modified_label(val, i))\n return new_path\n``` | 0 | In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
Given the `label` of a node in this tree, return the labels in the path from the root of the tree to the node with that `label`.
**Example 1:**
**Input:** label = 14
**Output:** \[1,3,4,14\]
**Example 2:**
**Input:** label = 26
**Output:** \[1,2,6,10,26\]
**Constraints:**
* `1 <= label <= 10^6` | Use a DFS to find every square in the component. Then for each square, color it if it has a neighbor that is outside the grid or a different color. |
Python 3 | DP | Explanation | filling-bookcase-shelves | 0 | 1 | ### Explanation\n- `dp[i]`: Minimum height sum for the first `i` books\n- Given the `i`th book, we just need to decide whether \n\t- It\'s gonna be on its own row, or\n\t- Append to some previous row\n- We can find out above with a nested loop `O(N*N)`\n- Time: `O(N*N)`\n- Space: `O(N)`\n### Implementation\n```\nclass Solution:\n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n n = len(books)\n dp = [sys.maxsize] * n\n dp[0] = books[0][1] # first book will always on it\'s own row\n for i in range(1, n): # for each book\n cur_w, height_max = books[i][0], books[i][1]\n dp[i] = dp[i-1] + height_max # initialize result for current book `dp[i]`\n for j in range(i-1, -1, -1): # for each previou `book[j]`, verify if it can be placed in the same row as `book[i]`\n if cur_w + books[j][0] > shelfWidth: break\n cur_w += books[j][0]\n height_max = max(height_max, books[j][1]) # update current max height\n dp[i] = min(dp[i], (dp[j-1] + height_max) if j-1 >= 0 else height_max) # always take the maximum heigh on current row\n return dp[n-1]\n``` | 12 | You are given an array `books` where `books[i] = [thicknessi, heighti]` indicates the thickness and height of the `ith` book. You are also given an integer `shelfWidth`.
We want to place these books in order onto bookcase shelves that have a total width `shelfWidth`.
We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to `shelfWidth`, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.
Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.
* For example, if we have an ordered list of `5` books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.
Return _the minimum possible height that the total bookshelf can be after placing shelves in this manner_.
**Example 1:**
**Input:** books = \[\[1,1\],\[2,3\],\[2,3\],\[1,1\],\[1,1\],\[1,1\],\[1,2\]\], shelfWidth = 4
**Output:** 6
**Explanation:**
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.
**Example 2:**
**Input:** books = \[\[1,3\],\[2,4\],\[3,2\]\], shelfWidth = 6
**Output:** 4
**Constraints:**
* `1 <= books.length <= 1000`
* `1 <= thicknessi <= shelfWidth <= 1000`
* `1 <= heighti <= 1000` | Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], ... and B[j], B[j+1], ...] are uncrossed, can we write this as a recursion? |
Python 3 | DP | Explanation | filling-bookcase-shelves | 0 | 1 | ### Explanation\n- `dp[i]`: Minimum height sum for the first `i` books\n- Given the `i`th book, we just need to decide whether \n\t- It\'s gonna be on its own row, or\n\t- Append to some previous row\n- We can find out above with a nested loop `O(N*N)`\n- Time: `O(N*N)`\n- Space: `O(N)`\n### Implementation\n```\nclass Solution:\n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n n = len(books)\n dp = [sys.maxsize] * n\n dp[0] = books[0][1] # first book will always on it\'s own row\n for i in range(1, n): # for each book\n cur_w, height_max = books[i][0], books[i][1]\n dp[i] = dp[i-1] + height_max # initialize result for current book `dp[i]`\n for j in range(i-1, -1, -1): # for each previou `book[j]`, verify if it can be placed in the same row as `book[i]`\n if cur_w + books[j][0] > shelfWidth: break\n cur_w += books[j][0]\n height_max = max(height_max, books[j][1]) # update current max height\n dp[i] = min(dp[i], (dp[j-1] + height_max) if j-1 >= 0 else height_max) # always take the maximum heigh on current row\n return dp[n-1]\n``` | 12 | You have some apples and a basket that can carry up to `5000` units of weight.
Given an integer array `weight` where `weight[i]` is the weight of the `ith` apple, return _the maximum number of apples you can put in the basket_.
**Example 1:**
**Input:** weight = \[100,200,150,1000\]
**Output:** 4
**Explanation:** All 4 apples can be carried by the basket since their sum of weights is 1450.
**Example 2:**
**Input:** weight = \[900,950,800,1000,700,800\]
**Output:** 5
**Explanation:** The sum of weights of the 6 apples exceeds 5000 so we choose any 5 of them.
**Constraints:**
* `1 <= weight.length <= 103`
* `1 <= weight[i] <= 103` | Use dynamic programming: dp(i) will be the answer to the problem for books[i:]. |
PYTHON SOL | EXPLAINED WITH PICTURE | RECURSION + MEMO | | filling-bookcase-shelves | 0 | 1 | # EXPLANATION\n```\nWe have 2 choices for each book\n1. Try to put the book on the same row \n2. Make a new row for the book\n\nWe select the choice that leads to minimum height\n\nSo our recursion cases are clear , now the termination will be when no books are left\n\nRemember in memoization we always memoize the variable which are changing in each recursion \n```\n\n\n\n\n\n\n\n# CODE\n```\nclass Solution:\n def recursion(self, idx , n , height , width):\n if idx == n:return height\n \n if (idx,height,width) in self.dp: return self.dp[(idx,height,width)]\n \n choice1 = self.recursion(idx+1,n,max(self.books[idx][1],height), width - self.books[idx][0])\\\n if width >= self.books[idx][0] else float(\'inf\')\n \n choice2 = self.recursion(idx+1,n,self.books[idx][1], self.shelfWidth - self.books[idx][0]) + height\n \n ans = min(choice1,choice2)\n self.dp[(idx,height,width)] = ans\n return ans\n \n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n self.books = books\n self.shelfWidth = shelfWidth\n self.dp = {}\n return self.recursion(0,len(books),0,shelfWidth)\n``` | 6 | You are given an array `books` where `books[i] = [thicknessi, heighti]` indicates the thickness and height of the `ith` book. You are also given an integer `shelfWidth`.
We want to place these books in order onto bookcase shelves that have a total width `shelfWidth`.
We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to `shelfWidth`, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.
Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.
* For example, if we have an ordered list of `5` books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.
Return _the minimum possible height that the total bookshelf can be after placing shelves in this manner_.
**Example 1:**
**Input:** books = \[\[1,1\],\[2,3\],\[2,3\],\[1,1\],\[1,1\],\[1,1\],\[1,2\]\], shelfWidth = 4
**Output:** 6
**Explanation:**
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.
**Example 2:**
**Input:** books = \[\[1,3\],\[2,4\],\[3,2\]\], shelfWidth = 6
**Output:** 4
**Constraints:**
* `1 <= books.length <= 1000`
* `1 <= thicknessi <= shelfWidth <= 1000`
* `1 <= heighti <= 1000` | Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], ... and B[j], B[j+1], ...] are uncrossed, can we write this as a recursion? |
PYTHON SOL | EXPLAINED WITH PICTURE | RECURSION + MEMO | | filling-bookcase-shelves | 0 | 1 | # EXPLANATION\n```\nWe have 2 choices for each book\n1. Try to put the book on the same row \n2. Make a new row for the book\n\nWe select the choice that leads to minimum height\n\nSo our recursion cases are clear , now the termination will be when no books are left\n\nRemember in memoization we always memoize the variable which are changing in each recursion \n```\n\n\n\n\n\n\n\n# CODE\n```\nclass Solution:\n def recursion(self, idx , n , height , width):\n if idx == n:return height\n \n if (idx,height,width) in self.dp: return self.dp[(idx,height,width)]\n \n choice1 = self.recursion(idx+1,n,max(self.books[idx][1],height), width - self.books[idx][0])\\\n if width >= self.books[idx][0] else float(\'inf\')\n \n choice2 = self.recursion(idx+1,n,self.books[idx][1], self.shelfWidth - self.books[idx][0]) + height\n \n ans = min(choice1,choice2)\n self.dp[(idx,height,width)] = ans\n return ans\n \n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n self.books = books\n self.shelfWidth = shelfWidth\n self.dp = {}\n return self.recursion(0,len(books),0,shelfWidth)\n``` | 6 | You have some apples and a basket that can carry up to `5000` units of weight.
Given an integer array `weight` where `weight[i]` is the weight of the `ith` apple, return _the maximum number of apples you can put in the basket_.
**Example 1:**
**Input:** weight = \[100,200,150,1000\]
**Output:** 4
**Explanation:** All 4 apples can be carried by the basket since their sum of weights is 1450.
**Example 2:**
**Input:** weight = \[900,950,800,1000,700,800\]
**Output:** 5
**Explanation:** The sum of weights of the 6 apples exceeds 5000 so we choose any 5 of them.
**Constraints:**
* `1 <= weight.length <= 103`
* `1 <= weight[i] <= 103` | Use dynamic programming: dp(i) will be the answer to the problem for books[i:]. |
1d DP easy solution python3 C++ | filling-bookcase-shelves | 0 | 1 | **Update**\n\n**Ask yourself, how many ways are there to place the i_th book? If you can answer it, then you can solve this problem easily.**\n\nI think this problem is really fantastic! Initially I used DFS which ETL very quickly due to time complexity of O(2**n). Here is my intuition. First of all, it is using DP method, when it comes to DP, the very first question we need to ask ourselives is what the subproblem is. So here the subproblem is to find the minimum total shelf height for i_th book. So a DP array is used to store the minimum total shelf height for each books. dp[i] represents the the minimum total shelf height for first i books, dp[i] actually depends on books in front of i_th book that can be placed on a same shelf with i_th book, ````here you can assume that i_th book is the last book on a shelf````, which is implemented with following code: We are looking backwards to find the minimum total height for i_th book.\n\nPython \n````\nclass Solution:\n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n books = [[0,0]] + books\n dp = [float("inf")] * len(books)\n dp[0] = 0 \n for i in range(1,len(books)):\n width, height = books[i]\n j = i\n while width <= shelfWidth and j>0:\n dp[i] = min(dp[i], dp[j-1]+height)\n j -= 1 \n width += books[j][0]\n height = max(height, books[j][1])\n #print(dp)\n return dp[-1] \n \n````\n\nC++ \n````\nclass Solution {\npublic:\n int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {\n books.insert(books.begin(),{0,0});\n vector<int> dp(books.size(),INT_MAX); // dp[i] represents the minimum total height of shelf for first ith books\n dp[0] = 0;\n int width, height, j;\n for(int i=1;i<books.size();i++){\n width = books[i][0];\n height = books[i][1];\n j = i-1;\n while (0<= j && width<=shelfWidth){\n dp[i] = min(dp[i], dp[j]+height);\n width += books[j][0];\n height = max(height, books[j][1]);\n j--;\n }\n }\n return dp.back();\n \n }\n};\n```` | 4 | You are given an array `books` where `books[i] = [thicknessi, heighti]` indicates the thickness and height of the `ith` book. You are also given an integer `shelfWidth`.
We want to place these books in order onto bookcase shelves that have a total width `shelfWidth`.
We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to `shelfWidth`, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.
Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.
* For example, if we have an ordered list of `5` books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.
Return _the minimum possible height that the total bookshelf can be after placing shelves in this manner_.
**Example 1:**
**Input:** books = \[\[1,1\],\[2,3\],\[2,3\],\[1,1\],\[1,1\],\[1,1\],\[1,2\]\], shelfWidth = 4
**Output:** 6
**Explanation:**
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.
**Example 2:**
**Input:** books = \[\[1,3\],\[2,4\],\[3,2\]\], shelfWidth = 6
**Output:** 4
**Constraints:**
* `1 <= books.length <= 1000`
* `1 <= thicknessi <= shelfWidth <= 1000`
* `1 <= heighti <= 1000` | Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], ... and B[j], B[j+1], ...] are uncrossed, can we write this as a recursion? |
1d DP easy solution python3 C++ | filling-bookcase-shelves | 0 | 1 | **Update**\n\n**Ask yourself, how many ways are there to place the i_th book? If you can answer it, then you can solve this problem easily.**\n\nI think this problem is really fantastic! Initially I used DFS which ETL very quickly due to time complexity of O(2**n). Here is my intuition. First of all, it is using DP method, when it comes to DP, the very first question we need to ask ourselives is what the subproblem is. So here the subproblem is to find the minimum total shelf height for i_th book. So a DP array is used to store the minimum total shelf height for each books. dp[i] represents the the minimum total shelf height for first i books, dp[i] actually depends on books in front of i_th book that can be placed on a same shelf with i_th book, ````here you can assume that i_th book is the last book on a shelf````, which is implemented with following code: We are looking backwards to find the minimum total height for i_th book.\n\nPython \n````\nclass Solution:\n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n books = [[0,0]] + books\n dp = [float("inf")] * len(books)\n dp[0] = 0 \n for i in range(1,len(books)):\n width, height = books[i]\n j = i\n while width <= shelfWidth and j>0:\n dp[i] = min(dp[i], dp[j-1]+height)\n j -= 1 \n width += books[j][0]\n height = max(height, books[j][1])\n #print(dp)\n return dp[-1] \n \n````\n\nC++ \n````\nclass Solution {\npublic:\n int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {\n books.insert(books.begin(),{0,0});\n vector<int> dp(books.size(),INT_MAX); // dp[i] represents the minimum total height of shelf for first ith books\n dp[0] = 0;\n int width, height, j;\n for(int i=1;i<books.size();i++){\n width = books[i][0];\n height = books[i][1];\n j = i-1;\n while (0<= j && width<=shelfWidth){\n dp[i] = min(dp[i], dp[j]+height);\n width += books[j][0];\n height = max(height, books[j][1]);\n j--;\n }\n }\n return dp.back();\n \n }\n};\n```` | 4 | You have some apples and a basket that can carry up to `5000` units of weight.
Given an integer array `weight` where `weight[i]` is the weight of the `ith` apple, return _the maximum number of apples you can put in the basket_.
**Example 1:**
**Input:** weight = \[100,200,150,1000\]
**Output:** 4
**Explanation:** All 4 apples can be carried by the basket since their sum of weights is 1450.
**Example 2:**
**Input:** weight = \[900,950,800,1000,700,800\]
**Output:** 5
**Explanation:** The sum of weights of the 6 apples exceeds 5000 so we choose any 5 of them.
**Constraints:**
* `1 <= weight.length <= 103`
* `1 <= weight[i] <= 103` | Use dynamic programming: dp(i) will be the answer to the problem for books[i:]. |
Python Solution (beats 99%) | filling-bookcase-shelves | 0 | 1 | \n\n# Approach\nThe idea is to use a dp array where `dp[i]` represents the minimum height required to place the first `i` books. We update the `dp` array iteratively, considering the case where the `i-th` book is placed on a new shelf and the case where it is placed with some previous books on the same shelf. The `j` loop checks for the previous books that can be placed on the same shelf as the `i-th` book, while the height is updated to the maximum height of the books placed on the same shelf. The minimum value of these two cases is stored in `dp[i]`.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(n^2), where n is the number of books. This is because the j loop runs in O(n) time and it runs n times, so the overall time complexity is O(n^2).\n\n- Space complexity:\nThe space complexity of this solution is O(n), where n is the number of books. This is because we use a dp array of size n+1 to store the minimum height required to place the first i books.\n\n# More\nMore LeetCode solutions of mine at https://github.com/aurimas13/Solutions-To-Problems.\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n n = len(books)\n dp = [0] * (n + 1)\n for i in range(1, n + 1):\n width, height = books[i - 1]\n dp[i] = dp[i - 1] + height\n j = i - 1\n while j > 0 and width + books[j - 1][0] <= shelfWidth:\n width += books[j - 1][0]\n height = max(height, books[j - 1][1])\n dp[i] = min(dp[i], dp[j - 1] + height)\n j -= 1\n return dp[n]\n\n \n``` | 3 | You are given an array `books` where `books[i] = [thicknessi, heighti]` indicates the thickness and height of the `ith` book. You are also given an integer `shelfWidth`.
We want to place these books in order onto bookcase shelves that have a total width `shelfWidth`.
We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to `shelfWidth`, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.
Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.
* For example, if we have an ordered list of `5` books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.
Return _the minimum possible height that the total bookshelf can be after placing shelves in this manner_.
**Example 1:**
**Input:** books = \[\[1,1\],\[2,3\],\[2,3\],\[1,1\],\[1,1\],\[1,1\],\[1,2\]\], shelfWidth = 4
**Output:** 6
**Explanation:**
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.
**Example 2:**
**Input:** books = \[\[1,3\],\[2,4\],\[3,2\]\], shelfWidth = 6
**Output:** 4
**Constraints:**
* `1 <= books.length <= 1000`
* `1 <= thicknessi <= shelfWidth <= 1000`
* `1 <= heighti <= 1000` | Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], ... and B[j], B[j+1], ...] are uncrossed, can we write this as a recursion? |
Python Solution (beats 99%) | filling-bookcase-shelves | 0 | 1 | \n\n# Approach\nThe idea is to use a dp array where `dp[i]` represents the minimum height required to place the first `i` books. We update the `dp` array iteratively, considering the case where the `i-th` book is placed on a new shelf and the case where it is placed with some previous books on the same shelf. The `j` loop checks for the previous books that can be placed on the same shelf as the `i-th` book, while the height is updated to the maximum height of the books placed on the same shelf. The minimum value of these two cases is stored in `dp[i]`.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(n^2), where n is the number of books. This is because the j loop runs in O(n) time and it runs n times, so the overall time complexity is O(n^2).\n\n- Space complexity:\nThe space complexity of this solution is O(n), where n is the number of books. This is because we use a dp array of size n+1 to store the minimum height required to place the first i books.\n\n# More\nMore LeetCode solutions of mine at https://github.com/aurimas13/Solutions-To-Problems.\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:\n n = len(books)\n dp = [0] * (n + 1)\n for i in range(1, n + 1):\n width, height = books[i - 1]\n dp[i] = dp[i - 1] + height\n j = i - 1\n while j > 0 and width + books[j - 1][0] <= shelfWidth:\n width += books[j - 1][0]\n height = max(height, books[j - 1][1])\n dp[i] = min(dp[i], dp[j - 1] + height)\n j -= 1\n return dp[n]\n\n \n``` | 3 | You have some apples and a basket that can carry up to `5000` units of weight.
Given an integer array `weight` where `weight[i]` is the weight of the `ith` apple, return _the maximum number of apples you can put in the basket_.
**Example 1:**
**Input:** weight = \[100,200,150,1000\]
**Output:** 4
**Explanation:** All 4 apples can be carried by the basket since their sum of weights is 1450.
**Example 2:**
**Input:** weight = \[900,950,800,1000,700,800\]
**Output:** 5
**Explanation:** The sum of weights of the 6 apples exceeds 5000 so we choose any 5 of them.
**Constraints:**
* `1 <= weight.length <= 103`
* `1 <= weight[i] <= 103` | Use dynamic programming: dp(i) will be the answer to the problem for books[i:]. |
⬆️✅🔥 100% | 0MS | DP +1D | 5 LINER | EXPLAINED | PROOF 🔥⬆️✅ | filling-bookcase-shelves | 1 | 1 | # UPVOTE pls\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# Tack the thickness & revist the dp array having min height.\n\n\n\n# Complexity\n- Time complexity:O(M*width)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic int minHeightShelves(int[][] B, int S) {\n int L = B.length, dp[] = new int[L + 1];\n for (int i = 1; i <= L; i++) {\n int ht = B[i - 1][1];\n dp[i] = dp[i - 1] + ht;\n int j = i - 1, wt = B[i - 1][0];\n while (j > 0 && wt + B[j - 1][0] <= S) {\n ht = Math.max(ht, B[j - 1][1]);\n wt += B[j - 1][0];\n dp[i] = Math.min(dp[i], dp[j-- - 1] + ht);\n }\n } return dp[L];\n }\n``` | 2 | You are given an array `books` where `books[i] = [thicknessi, heighti]` indicates the thickness and height of the `ith` book. You are also given an integer `shelfWidth`.
We want to place these books in order onto bookcase shelves that have a total width `shelfWidth`.
We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to `shelfWidth`, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.
Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.
* For example, if we have an ordered list of `5` books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.
Return _the minimum possible height that the total bookshelf can be after placing shelves in this manner_.
**Example 1:**
**Input:** books = \[\[1,1\],\[2,3\],\[2,3\],\[1,1\],\[1,1\],\[1,1\],\[1,2\]\], shelfWidth = 4
**Output:** 6
**Explanation:**
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.
**Example 2:**
**Input:** books = \[\[1,3\],\[2,4\],\[3,2\]\], shelfWidth = 6
**Output:** 4
**Constraints:**
* `1 <= books.length <= 1000`
* `1 <= thicknessi <= shelfWidth <= 1000`
* `1 <= heighti <= 1000` | Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], ... and B[j], B[j+1], ...] are uncrossed, can we write this as a recursion? |
⬆️✅🔥 100% | 0MS | DP +1D | 5 LINER | EXPLAINED | PROOF 🔥⬆️✅ | filling-bookcase-shelves | 1 | 1 | # UPVOTE pls\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# Tack the thickness & revist the dp array having min height.\n\n\n\n# Complexity\n- Time complexity:O(M*width)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic int minHeightShelves(int[][] B, int S) {\n int L = B.length, dp[] = new int[L + 1];\n for (int i = 1; i <= L; i++) {\n int ht = B[i - 1][1];\n dp[i] = dp[i - 1] + ht;\n int j = i - 1, wt = B[i - 1][0];\n while (j > 0 && wt + B[j - 1][0] <= S) {\n ht = Math.max(ht, B[j - 1][1]);\n wt += B[j - 1][0];\n dp[i] = Math.min(dp[i], dp[j-- - 1] + ht);\n }\n } return dp[L];\n }\n``` | 2 | You have some apples and a basket that can carry up to `5000` units of weight.
Given an integer array `weight` where `weight[i]` is the weight of the `ith` apple, return _the maximum number of apples you can put in the basket_.
**Example 1:**
**Input:** weight = \[100,200,150,1000\]
**Output:** 4
**Explanation:** All 4 apples can be carried by the basket since their sum of weights is 1450.
**Example 2:**
**Input:** weight = \[900,950,800,1000,700,800\]
**Output:** 5
**Explanation:** The sum of weights of the 6 apples exceeds 5000 so we choose any 5 of them.
**Constraints:**
* `1 <= weight.length <= 103`
* `1 <= weight[i] <= 103` | Use dynamic programming: dp(i) will be the answer to the problem for books[i:]. |
[Python] Iterative O(n) Solution | parsing-a-boolean-expression | 0 | 1 | ```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n logics = []\n stack = []\n \n def cal(tmp, top, op):\n if op == \'!\':\n tmp = \'t\' if tmp == \'f\' else \'f\'\n elif op == \'&\':\n tmp = \'t\' if (tmp == \'t\' and top == \'t\') else \'f\'\n elif op == \'|\':\n tmp = \'t\' if (tmp == \'t\' or top == \'t\') else \'f\'\n return tmp\n\n for i in expression:\n if i in (\'!\', \'&\', \'|\'):\n logics.append(i)\n elif i == \')\':\n op = logics.pop()\n tmp = stack.pop()\n while stack:\n top = stack.pop()\n # print(tmp, top, op)\n if op == \'!\' and top == \'(\': tmp = cal(tmp, tmp, op)\n if top == \'(\': break\n tmp = cal(tmp, top, op)\n stack.append(tmp)\n elif i == \',\': continue\n else:\n stack.append(i)\n # print(stack, logics, i)\n \n if logics:\n op = logics.pop()\n tmp = stack.pop()\n while stack:\n top = stack.pop()\n tmp = cal(tmp, top, op)\n stack.append(tmp)\n \n return True if stack[0] == \'t\' else False\n \n \n# Time: O(N)\n# Space: O(N)\n``` | 1 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
[Python] Iterative O(n) Solution | parsing-a-boolean-expression | 0 | 1 | ```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n logics = []\n stack = []\n \n def cal(tmp, top, op):\n if op == \'!\':\n tmp = \'t\' if tmp == \'f\' else \'f\'\n elif op == \'&\':\n tmp = \'t\' if (tmp == \'t\' and top == \'t\') else \'f\'\n elif op == \'|\':\n tmp = \'t\' if (tmp == \'t\' or top == \'t\') else \'f\'\n return tmp\n\n for i in expression:\n if i in (\'!\', \'&\', \'|\'):\n logics.append(i)\n elif i == \')\':\n op = logics.pop()\n tmp = stack.pop()\n while stack:\n top = stack.pop()\n # print(tmp, top, op)\n if op == \'!\' and top == \'(\': tmp = cal(tmp, tmp, op)\n if top == \'(\': break\n tmp = cal(tmp, top, op)\n stack.append(tmp)\n elif i == \',\': continue\n else:\n stack.append(i)\n # print(stack, logics, i)\n \n if logics:\n op = logics.pop()\n tmp = stack.pop()\n while stack:\n top = stack.pop()\n tmp = cal(tmp, top, op)\n stack.append(tmp)\n \n return True if stack[0] == \'t\' else False\n \n \n# Time: O(N)\n# Space: O(N)\n``` | 1 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
[Python][Stack]Easy to understand using stack Python (beats 88.89% runtime in python3) | parsing-a-boolean-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* After operator is always (expr1, expr2, ...).\n* You can solve every operator(\'f\', \'t\', ....).\n* Therefore you must solve expr => \'t\' or \'f\'.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* Using stack:\n - for each character in str:\n - if it is not \'(\' push it in stack\n - else if it is \')\': => you have subExpr = operator(\'f\', \'t\', .....) and you can solve it. Remove subExpr out stack and push result in stack.\n - else if it not \',\' push it in stack\n - Continue do the loop\n The answer is the last element in stack\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n stack1 = []\n stack2 = []\n top = \'\'\n for i in expression:\n if i == \',\':\n continue\n \n elif i == \')\':\n top = stack1.pop()\n\n while top != \'(\':\n stack2.append(top)\n top = stack1.pop()\n\n top = stack1.pop()\n\n if top == \'|\':\n stack1.append(\'t\' if \'t\' in stack2 else \'f\')\n \n elif top == \'&\':\n stack1.append(\'f\' if \'f\' in stack2 else \'t\')\n \n elif top == \'!\':\n stack1.append(\'f\' if \'t\' in stack2 else \'t\')\n stack2.clear()\n else:\n stack1.append(i)\n\n return \'t\' in stack1\n\n\n``` | 1 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
[Python][Stack]Easy to understand using stack Python (beats 88.89% runtime in python3) | parsing-a-boolean-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* After operator is always (expr1, expr2, ...).\n* You can solve every operator(\'f\', \'t\', ....).\n* Therefore you must solve expr => \'t\' or \'f\'.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* Using stack:\n - for each character in str:\n - if it is not \'(\' push it in stack\n - else if it is \')\': => you have subExpr = operator(\'f\', \'t\', .....) and you can solve it. Remove subExpr out stack and push result in stack.\n - else if it not \',\' push it in stack\n - Continue do the loop\n The answer is the last element in stack\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n stack1 = []\n stack2 = []\n top = \'\'\n for i in expression:\n if i == \',\':\n continue\n \n elif i == \')\':\n top = stack1.pop()\n\n while top != \'(\':\n stack2.append(top)\n top = stack1.pop()\n\n top = stack1.pop()\n\n if top == \'|\':\n stack1.append(\'t\' if \'t\' in stack2 else \'f\')\n \n elif top == \'&\':\n stack1.append(\'f\' if \'f\' in stack2 else \'t\')\n \n elif top == \'!\':\n stack1.append(\'f\' if \'t\' in stack2 else \'t\')\n stack2.clear()\n else:\n stack1.append(i)\n\n return \'t\' in stack1\n\n\n``` | 1 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
Python super easy solution || Easy to Understand || Override the property || Very Easy | parsing-a-boolean-expression | 0 | 1 | ```\nclass Solution:\n \n def oro(self,*args):\n ans = False\n for elm in args:\n ans|=elm\n return ans\n \n def ando(self,*args):\n ans = True\n for elm in args:\n ans&=elm\n return ans\n \n def noto(self,args):\n return not args\n \n def parseBoolExpr(self, e: str) -> bool:\n e=e.replace(\'f\',\'False\').replace(\'t\',\'True\')\n e=e.replace(\'!\',\'self.noto\').replace(\'|\',\'self.oro\').replace(\'&\',\'self.ando\')\n return eval(e)\n``` | 2 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
Python super easy solution || Easy to Understand || Override the property || Very Easy | parsing-a-boolean-expression | 0 | 1 | ```\nclass Solution:\n \n def oro(self,*args):\n ans = False\n for elm in args:\n ans|=elm\n return ans\n \n def ando(self,*args):\n ans = True\n for elm in args:\n ans&=elm\n return ans\n \n def noto(self,args):\n return not args\n \n def parseBoolExpr(self, e: str) -> bool:\n e=e.replace(\'f\',\'False\').replace(\'t\',\'True\')\n e=e.replace(\'!\',\'self.noto\').replace(\'|\',\'self.oro\').replace(\'&\',\'self.ando\')\n return eval(e)\n``` | 2 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
One pass with stack, 97% speed | parsing-a-boolean-expression | 0 | 1 | \n```\nclass Solution:\n operands = {"!", "&", "|", "t", "f"}\n values = {"t", "f"}\n\n def parseBoolExpr(self, expression: str) -> bool:\n stack = []\n for c in expression:\n if c == ")":\n val = stack.pop()\n args = set()\n while val in Solution.values:\n args.add(val)\n val = stack.pop()\n if val == "!":\n stack.append("f" if "t" in args else "t")\n elif val == "&":\n stack.append("f" if "f" in args else "t")\n elif val == "|":\n stack.append("t" if "t" in args else "f")\n elif c in Solution.operands:\n stack.append(c)\n return stack[0] == "t"\n``` | 5 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
One pass with stack, 97% speed | parsing-a-boolean-expression | 0 | 1 | \n```\nclass Solution:\n operands = {"!", "&", "|", "t", "f"}\n values = {"t", "f"}\n\n def parseBoolExpr(self, expression: str) -> bool:\n stack = []\n for c in expression:\n if c == ")":\n val = stack.pop()\n args = set()\n while val in Solution.values:\n args.add(val)\n val = stack.pop()\n if val == "!":\n stack.append("f" if "t" in args else "t")\n elif val == "&":\n stack.append("f" if "f" in args else "t")\n elif val == "|":\n stack.append("t" if "t" in args else "f")\n elif c in Solution.operands:\n stack.append(c)\n return stack[0] == "t"\n``` | 5 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
Python3: Relatively Simple Stack-Based Parser | parsing-a-boolean-expression | 0 | 1 | # Intuition\n\nUsually I use a recursive parsing pattern, but often I see different solutions involving a stack. So I thought I\'d give one a shot.\n\nAnd, as it turns out, it turns out to be pretty straightforward.\n\nFirst I thought about what we\'d do recursively:\n* if we see a literal \'t\' of \'f\', take it as-is\n* if we see an open parens:\n * recurse to parse all the expressions separated by commas\n * then combine the results with the operator\n * for \'!\' there should only be one operator\n\nWhen we recurse, we create a stack frame: in assembly this is literally function information in a stack.\n\nIn this case, we append to an explicit stack `s`.\n\nSo we do this:\n* if the character is a literal or operator, append it to the current level\n* when we see an \'(\', append an empty list to the stack\n* when we see a \')\', everything in the top level should be either \'t\' or \'f\'. So we can look at the character just before the \'(\', i.e. the last character on the *prior* level, and combine the results. The operator is then replaced with the result\n\n# Example\n\nIf the expression is `|(&(t,f,t),!(t))` then we follow the rules for\n`|(&(t,f,t`. This makes a stack that looks like this\n```\n|(&(t,f,t # input\n\n| # stack |\n & + \')\' ==> f\n t f t\n```\nWhen we see the \')\', the last element of the stack are the arguments, t, f, t. The last character of the prior level is the operator: &. So we combine and merge them.\n\nThen we see `,!t` and get this:\n```\n| |\n f ! + \')\' ==> f f\n t\n```\nso we do the same thing as before when we find the second \')\':\n* the top level are the args: just t\n* the operator is the last character at the prior level: \'!\'\n* the result of !t is f\n\nFinally we get this:\n```\n|\n f f\n```\nThe last ) gives us |(f,f) == f.\n\nSo the result is false.\n\nThus the trickiest part is handling the \')\'. Everything else is appending to the last element of the stack, or adding a new level to the stack.\n\nAnd again, the way I got this structure was to think about recursion and stack frames, and adding a new level to the stack any time we\'d recurse in a recursive/DFS solution.\n\n# Complexity\n- Time complexity: linear in the input length\n\n- Space complexity: linear in the input length\n\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n # usually I just use the parser pattern, but here\'s a chance to try stack parsing instead\n\n # NO SPACES\n\n # we can have\n # a literal\n # or !(e) or &(e[,e]*) or !(e[,e]*)\n # every ( has a ) and a preceding operator\n \n # &(|(f),t)\n\n #\n # &\n # |\n # ( f )\n # at ): look back to prior line to get preceding operator: |, evaluate the op (...) and put result there\n s = [[]]\n for c in expression:\n if c in r\'tf!&|\':\n s[-1].append(c)\n elif c == \'(\':\n s.append([])\n elif c == \')\':\n # \')\' closes current expr\n # operator before current expr is at s[-2][-1]; just before we started this (..)\n op = s[-2][-1]\n # print(f"{op=}, args={s[-1]}")\n if op == \'!\':\n assert len(s[-1]) == 1\n s[-2][-1] = \'t\' if s[-1][0] == \'f\' else \'f\'\n elif op == \'|\':\n s[-2][-1] = \'t\' if any(b == \'t\' for b in s[-1]) else \'f\'\n elif op == \'&\':\n s[-2][-1] = \'t\' if all(b == \'t\' for b in s[-1]) else \'f\'\n else:\n raise RuntimeError(f"Unexpected operator: {c}")\n\n # print(f" res={s[-2][-1]}")\n s.pop()\n elif c == \',\':\n # no nothing\n pass\n else:\n raise RuntimeError(f"Unexpected character: {c}")\n \n assert len(s)==1, "Unclosed expression"\n s = s[0]\n assert len(s)==1, "Multiple terms at top level"\n return True if s[0]==\'t\' else False\n\n # |(&(t,f,t),!(t))\n\n # | | f\n # f ! ==> f f ==> \n # t f t \')\' \')\'\n``` | 0 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
Python3: Relatively Simple Stack-Based Parser | parsing-a-boolean-expression | 0 | 1 | # Intuition\n\nUsually I use a recursive parsing pattern, but often I see different solutions involving a stack. So I thought I\'d give one a shot.\n\nAnd, as it turns out, it turns out to be pretty straightforward.\n\nFirst I thought about what we\'d do recursively:\n* if we see a literal \'t\' of \'f\', take it as-is\n* if we see an open parens:\n * recurse to parse all the expressions separated by commas\n * then combine the results with the operator\n * for \'!\' there should only be one operator\n\nWhen we recurse, we create a stack frame: in assembly this is literally function information in a stack.\n\nIn this case, we append to an explicit stack `s`.\n\nSo we do this:\n* if the character is a literal or operator, append it to the current level\n* when we see an \'(\', append an empty list to the stack\n* when we see a \')\', everything in the top level should be either \'t\' or \'f\'. So we can look at the character just before the \'(\', i.e. the last character on the *prior* level, and combine the results. The operator is then replaced with the result\n\n# Example\n\nIf the expression is `|(&(t,f,t),!(t))` then we follow the rules for\n`|(&(t,f,t`. This makes a stack that looks like this\n```\n|(&(t,f,t # input\n\n| # stack |\n & + \')\' ==> f\n t f t\n```\nWhen we see the \')\', the last element of the stack are the arguments, t, f, t. The last character of the prior level is the operator: &. So we combine and merge them.\n\nThen we see `,!t` and get this:\n```\n| |\n f ! + \')\' ==> f f\n t\n```\nso we do the same thing as before when we find the second \')\':\n* the top level are the args: just t\n* the operator is the last character at the prior level: \'!\'\n* the result of !t is f\n\nFinally we get this:\n```\n|\n f f\n```\nThe last ) gives us |(f,f) == f.\n\nSo the result is false.\n\nThus the trickiest part is handling the \')\'. Everything else is appending to the last element of the stack, or adding a new level to the stack.\n\nAnd again, the way I got this structure was to think about recursion and stack frames, and adding a new level to the stack any time we\'d recurse in a recursive/DFS solution.\n\n# Complexity\n- Time complexity: linear in the input length\n\n- Space complexity: linear in the input length\n\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n # usually I just use the parser pattern, but here\'s a chance to try stack parsing instead\n\n # NO SPACES\n\n # we can have\n # a literal\n # or !(e) or &(e[,e]*) or !(e[,e]*)\n # every ( has a ) and a preceding operator\n \n # &(|(f),t)\n\n #\n # &\n # |\n # ( f )\n # at ): look back to prior line to get preceding operator: |, evaluate the op (...) and put result there\n s = [[]]\n for c in expression:\n if c in r\'tf!&|\':\n s[-1].append(c)\n elif c == \'(\':\n s.append([])\n elif c == \')\':\n # \')\' closes current expr\n # operator before current expr is at s[-2][-1]; just before we started this (..)\n op = s[-2][-1]\n # print(f"{op=}, args={s[-1]}")\n if op == \'!\':\n assert len(s[-1]) == 1\n s[-2][-1] = \'t\' if s[-1][0] == \'f\' else \'f\'\n elif op == \'|\':\n s[-2][-1] = \'t\' if any(b == \'t\' for b in s[-1]) else \'f\'\n elif op == \'&\':\n s[-2][-1] = \'t\' if all(b == \'t\' for b in s[-1]) else \'f\'\n else:\n raise RuntimeError(f"Unexpected operator: {c}")\n\n # print(f" res={s[-2][-1]}")\n s.pop()\n elif c == \',\':\n # no nothing\n pass\n else:\n raise RuntimeError(f"Unexpected character: {c}")\n \n assert len(s)==1, "Unclosed expression"\n s = s[0]\n assert len(s)==1, "Multiple terms at top level"\n return True if s[0]==\'t\' else False\n\n # |(&(t,f,t),!(t))\n\n # | | f\n # f ! ==> f f ==> \n # t f t \')\' \')\'\n``` | 0 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
python super easy too understand recursion + stack counter | parsing-a-boolean-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n \n def parse(s):\n count = 0\n left = 0\n arr = []\n for i in range(len(s)):\n if s[i] == "(":\n count +=1\n if count == 1:\n if i -1 >=0:\n left = i-1\n else:\n left = i\n elif s[i] == ")":\n count -=1\n if count == 0:\n arr.append(s[left:i+1])\n elif s[i] == "t" or s[i] == "f":\n if count == 0:\n arr.append(s[i])\n return arr\n\n def dfs(s):\n if len(s) == 1:\n if s == "t":\n return True\n return False\n\n if s[0] == "!":\n return not dfs(s[2:-1])\n elif s[0] == "&":\n n = parse(s[2:-1])\n return functools.reduce(operator.iand, list(map( lambda x:dfs(x), n)))\n elif s[0] == "|":\n n = parse(s[2:-1])\n return functools.reduce(operator.ior, list(map( lambda x:dfs(x), n)))\n \n return dfs(expression)\n\n \n\n\n``` | 0 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
python super easy too understand recursion + stack counter | parsing-a-boolean-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n \n def parse(s):\n count = 0\n left = 0\n arr = []\n for i in range(len(s)):\n if s[i] == "(":\n count +=1\n if count == 1:\n if i -1 >=0:\n left = i-1\n else:\n left = i\n elif s[i] == ")":\n count -=1\n if count == 0:\n arr.append(s[left:i+1])\n elif s[i] == "t" or s[i] == "f":\n if count == 0:\n arr.append(s[i])\n return arr\n\n def dfs(s):\n if len(s) == 1:\n if s == "t":\n return True\n return False\n\n if s[0] == "!":\n return not dfs(s[2:-1])\n elif s[0] == "&":\n n = parse(s[2:-1])\n return functools.reduce(operator.iand, list(map( lambda x:dfs(x), n)))\n elif s[0] == "|":\n n = parse(s[2:-1])\n return functools.reduce(operator.ior, list(map( lambda x:dfs(x), n)))\n \n return dfs(expression)\n\n \n\n\n``` | 0 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
✅Beginner Solution✅(Python) (Using Two Stacks) | parsing-a-boolean-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Using two stacks. One for storing the last sign encountered and another for storing the values.\n- If value then push into \'stack\'\n- If opening bracket, then push into \'stack\'\n- If closing bracket, pop the values(from \'stack\') and the last sign encountered(from \'sign_stack\') and do the operation. Then pop the opening bracket and push the result in \'stack\'\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n stack = []\n sign_stack = []\n\n op = {\n \'&\': lambda x, y: x and y,\n \'|\': lambda x, y: x or y,\n \'!\': lambda x: not x\n }\n\n for ch in expression:\n # print(stack)\n # print(sign_stack)\n # print()\n if ch in set([\'&\', \'|\', \'!\']):\n sign_stack.append(ch)\n\n elif ch == \'(\':\n stack.append(ch)\n\n elif ch == \')\':\n sign = sign_stack.pop()\n result = stack[-1]\n while stack[-1] != \'(\':\n if sign in set([\'&\', \'|\']):\n result = op[sign](result, stack[-1])\n else:\n result = op[sign](stack[-1])\n stack.pop()\n \n stack.pop()\n stack.append(result)\n\n elif ch in set([\'t\', \'f\']):\n stack.append(True if ch == \'t\' else False)\n\n # print(stack)\n return stack[0]\n\n\n``` | 0 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
✅Beginner Solution✅(Python) (Using Two Stacks) | parsing-a-boolean-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Using two stacks. One for storing the last sign encountered and another for storing the values.\n- If value then push into \'stack\'\n- If opening bracket, then push into \'stack\'\n- If closing bracket, pop the values(from \'stack\') and the last sign encountered(from \'sign_stack\') and do the operation. Then pop the opening bracket and push the result in \'stack\'\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n stack = []\n sign_stack = []\n\n op = {\n \'&\': lambda x, y: x and y,\n \'|\': lambda x, y: x or y,\n \'!\': lambda x: not x\n }\n\n for ch in expression:\n # print(stack)\n # print(sign_stack)\n # print()\n if ch in set([\'&\', \'|\', \'!\']):\n sign_stack.append(ch)\n\n elif ch == \'(\':\n stack.append(ch)\n\n elif ch == \')\':\n sign = sign_stack.pop()\n result = stack[-1]\n while stack[-1] != \'(\':\n if sign in set([\'&\', \'|\']):\n result = op[sign](result, stack[-1])\n else:\n result = op[sign](stack[-1])\n stack.pop()\n \n stack.pop()\n stack.append(result)\n\n elif ch in set([\'t\', \'f\']):\n stack.append(True if ch == \'t\' else False)\n\n # print(stack)\n return stack[0]\n\n\n``` | 0 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
Python solution with two stacks - easy to understand | parsing-a-boolean-expression | 0 | 1 | # Intuition\nWe use two stacks - one for data (`data`) and one for operations (`op`).\n\nWe scan the input from left to right.\n\nThe `t` and `f` in the input appends `True` and `False` to the `data` stack.\n\nThe `!`, `&` , `|` in the inputs appends to the `op` stack.\n\nThe `)` character in the input pops a single operation from the `op` stack and appropriate number of bools from the `data`. To determine what is the "appropriate number", in the `data` in addition to boolean values we also store `(` that plays the role of `end of attributes` marker for a single operation. \nThe result of the operation goes back to `data` stack (in place of `(` that is on the top).\n\nThe `(` in the input appends `(` to the `data` stack as explained above.\n\nThe `,` are skipped.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n op, data = [], []\n for c in expression:\n if c == \'t\': data.append(True)\n if c == \'f\': data.append(False)\n if c in \'!&|\': op.append(c)\n if c == \'(\': data.append(\'(\')\n if c == \')\': \n cop = op.pop()\n if cop == \'!\':\n data[-1] = not data.pop()\n if cop == \'&\':\n res = True\n while data[-1] != \'(\':\n res &= data.pop()\n data[-1] = res\n if cop == \'|\':\n res = False\n while data[-1] != \'(\':\n res |= data.pop()\n data[-1] =res\n return data[0] \n\n \n``` | 0 | A **boolean expression** is an expression that evaluates to either `true` or `false`. It can be in one of the following shapes:
* `'t'` that evaluates to `true`.
* `'f'` that evaluates to `false`.
* `'!(subExpr)'` that evaluates to **the logical NOT** of the inner expression `subExpr`.
* `'&(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical AND** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
* `'|(subExpr1, subExpr2, ..., subExprn)'` that evaluates to **the logical OR** of the inner expressions `subExpr1, subExpr2, ..., subExprn` where `n >= 1`.
Given a string `expression` that represents a **boolean expression**, return _the evaluation of that expression_.
It is **guaranteed** that the given expression is valid and follows the given rules.
**Example 1:**
**Input:** expression = "&(|(f)) "
**Output:** false
**Explanation:**
First, evaluate |(f) --> f. The expression is now "&(f) ".
Then, evaluate &(f) --> f. The expression is now "f ".
Finally, return false.
**Example 2:**
**Input:** expression = "|(f,f,f,t) "
**Output:** true
**Explanation:** The evaluation of (false OR false OR false OR true) is true.
**Example 3:**
**Input:** expression = "!(&(f,t)) "
**Output:** true
**Explanation:**
First, evaluate &(f,t) --> (false AND true) --> false --> f. The expression is now "!(f) ".
Then, evaluate !(f) --> NOT false --> true. We return true.
**Constraints:**
* `1 <= expression.length <= 2 * 104`
* expression\[i\] is one following characters: `'('`, `')'`, `'&'`, `'|'`, `'!'`, `'t'`, `'f'`, and `','`. | If we become stuck, there's either a loop around the source or around the target. If there is a loop around say, the source, what is the maximum number of squares it can have? |
Python solution with two stacks - easy to understand | parsing-a-boolean-expression | 0 | 1 | # Intuition\nWe use two stacks - one for data (`data`) and one for operations (`op`).\n\nWe scan the input from left to right.\n\nThe `t` and `f` in the input appends `True` and `False` to the `data` stack.\n\nThe `!`, `&` , `|` in the inputs appends to the `op` stack.\n\nThe `)` character in the input pops a single operation from the `op` stack and appropriate number of bools from the `data`. To determine what is the "appropriate number", in the `data` in addition to boolean values we also store `(` that plays the role of `end of attributes` marker for a single operation. \nThe result of the operation goes back to `data` stack (in place of `(` that is on the top).\n\nThe `(` in the input appends `(` to the `data` stack as explained above.\n\nThe `,` are skipped.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def parseBoolExpr(self, expression: str) -> bool:\n op, data = [], []\n for c in expression:\n if c == \'t\': data.append(True)\n if c == \'f\': data.append(False)\n if c in \'!&|\': op.append(c)\n if c == \'(\': data.append(\'(\')\n if c == \')\': \n cop = op.pop()\n if cop == \'!\':\n data[-1] = not data.pop()\n if cop == \'&\':\n res = True\n while data[-1] != \'(\':\n res &= data.pop()\n data[-1] = res\n if cop == \'|\':\n res = False\n while data[-1] != \'(\':\n res |= data.pop()\n data[-1] =res\n return data[0] \n\n \n``` | 0 | In an **infinite** chess board with coordinates from `-infinity` to `+infinity`, you have a **knight** at square `[0, 0]`.
A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.
Return _the minimum number of steps needed to move the knight to the square_ `[x, y]`. It is guaranteed the answer exists.
**Example 1:**
**Input:** x = 2, y = 1
**Output:** 1
**Explanation:** \[0, 0\] -> \[2, 1\]
**Example 2:**
**Input:** x = 5, y = 5
**Output:** 4
**Explanation:** \[0, 0\] -> \[2, 1\] -> \[4, 2\] -> \[3, 4\] -> \[5, 5\]
**Constraints:**
* `-300 <= x, y <= 300`
* `0 <= |x| + |y| <= 300`
"t", evaluating to True; "f", evaluating to False; "!(expression)", evaluating to the logical NOT of the expression inside the parentheses; "&(expression1,expression2,...)", evaluating to the logical AND of 2 or more expressions; "|(expression1,expression2,...)", evaluating to the logical OR of 2 or more expressions. | Write a function "parse" which calls helper functions "parse_or", "parse_and", "parse_not". |
Beginner-friendly || Simple solution with TypeScript / Python3 | defanging-an-ip-address | 0 | 1 | # Approach\n1. split `address` into dots, and join to string back again with `[.]` delimeter\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(1)**\n\n# Code in Python3\n```\nclass Solution:\n def defangIPaddr(self, address: str) -> str:\n return \'[.]\'.join(address.split(\'.\'))\n```\n\n# Code in TypeScript\n```\nfunction defangIPaddr(address: string): string {\n return address.split(\'.\').join(\'[.]\')\n};\n``` | 1 | Given a valid (IPv4) IP `address`, return a defanged version of that IP address.
A _defanged IP address_ replaces every period `". "` with `"[.] "`.
**Example 1:**
**Input:** address = "1.1.1.1"
**Output:** "1\[.\]1\[.\]1\[.\]1"
**Example 2:**
**Input:** address = "255.100.50.0"
**Output:** "255\[.\]100\[.\]50\[.\]0"
**Constraints:**
* The given `address` is a valid IPv4 address. | Let's find for every user separately the websites he visited. Consider all possible 3-sequences, find the number of distinct users who visited each of them. How to check if some user visited some 3-sequence ? Store for every user all the 3-sequence he visited. |
EASY PYTHON SOLUTION || DEFANGING IP ADDRESS || O(n) SOLUTION | defanging-an-ip-address | 0 | 1 | Let\'s break it down:\n\nImagine you\'re reading a book (the input string), and you want to make a new version of the book where every time you see a period (\'.\'), you replace it with \'[.]\'. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nThe **time complexity** is like the time it takes for you to read through the book once. You\'re going through each character in the string one by one, so it\'s proportional to the number of characters in the string, or **O(n)**.\n\nThe **space complexity** is like the amount of extra paper you would need to write down the new version of the book. In the worst case, every character is a period, so for each period, you\'re writing down three characters (\'[.]\') instead of one. So, you might need up to three times more paper than the original book. That\'s why we say it\'s **O(n)**. But in reality, not all characters are periods, and Python tries to save paper by reusing parts of the original book when possible. So, the actual amount of extra paper might be less than three times.\n\n# Code\n```\nclass Solution:\n def defangIPaddr(self, address: str) -> str:\n return address.replace(\'.\',\'[.]\')\n \n \n``` | 1 | Given a valid (IPv4) IP `address`, return a defanged version of that IP address.
A _defanged IP address_ replaces every period `". "` with `"[.] "`.
**Example 1:**
**Input:** address = "1.1.1.1"
**Output:** "1\[.\]1\[.\]1\[.\]1"
**Example 2:**
**Input:** address = "255.100.50.0"
**Output:** "255\[.\]100\[.\]50\[.\]0"
**Constraints:**
* The given `address` is a valid IPv4 address. | Let's find for every user separately the websites he visited. Consider all possible 3-sequences, find the number of distinct users who visited each of them. How to check if some user visited some 3-sequence ? Store for every user all the 3-sequence he visited. |
Easy Python Solution to Defang IP Address | defanging-an-ip-address | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe should replace every period (`.`) in a given IPv4 address with `[.]`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can return a copy of the given address with all occurrences of substring **old** (`.`) replaced by **new** (`[.]`) using the following method available for strings in Python:\n\n> `str.replace(old, new)`\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`n` is the length of the input IP address string. In the worst case, we may need to traverse the whole string.\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`n` is the length of the input IP address string. The space required for the output string is proportional to the length of the input IP address.\n\n# Code\n```\nclass Solution:\n def defangIPaddr(self, address: str) -> str:\n return address.replace(".", "[.]")\n \n``` | 2 | Given a valid (IPv4) IP `address`, return a defanged version of that IP address.
A _defanged IP address_ replaces every period `". "` with `"[.] "`.
**Example 1:**
**Input:** address = "1.1.1.1"
**Output:** "1\[.\]1\[.\]1\[.\]1"
**Example 2:**
**Input:** address = "255.100.50.0"
**Output:** "255\[.\]100\[.\]50\[.\]0"
**Constraints:**
* The given `address` is a valid IPv4 address. | Let's find for every user separately the websites he visited. Consider all possible 3-sequences, find the number of distinct users who visited each of them. How to check if some user visited some 3-sequence ? Store for every user all the 3-sequence he visited. |
Simple PYTHON code using if-else statement | defanging-an-ip-address | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def defangIPaddr(self, address: str) -> str:\n st=""\n for i in address:\n if i == ".":\n st+=\'[\'+\'.\'+\']\'\n else:\n st+=i \n return st \n``` | 1 | Given a valid (IPv4) IP `address`, return a defanged version of that IP address.
A _defanged IP address_ replaces every period `". "` with `"[.] "`.
**Example 1:**
**Input:** address = "1.1.1.1"
**Output:** "1\[.\]1\[.\]1\[.\]1"
**Example 2:**
**Input:** address = "255.100.50.0"
**Output:** "255\[.\]100\[.\]50\[.\]0"
**Constraints:**
* The given `address` is a valid IPv4 address. | Let's find for every user separately the websites he visited. Consider all possible 3-sequences, find the number of distinct users who visited each of them. How to check if some user visited some 3-sequence ? Store for every user all the 3-sequence he visited. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.