title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
easy solution using backtracking | splitting-a-string-into-descending-consecutive-values | 0 | 1 | \n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n\n def backtrack(index,prev):\n if index == len(s):\n return True\n\n for j in range(index,len(s)):\n val = int(s[index:j+1])\n if val + 1 == prev and backtrack(j+1,val):\n return True\n return False\n\n for i in range(len(s)-1):\n val = int(s[:i+1])\n if backtrack(i+1,val) : return True\n\n return False\n \n``` | 1 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
easy solution using backtracking | splitting-a-string-into-descending-consecutive-values | 0 | 1 | \n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n\n def backtrack(index,prev):\n if index == len(s):\n return True\n\n for j in range(index,len(s)):\n val = int(s[index:j+1])\n if val + 1 == prev and backtrack(j+1,val):\n return True\n return False\n\n for i in range(len(s)-1):\n val = int(s[:i+1])\n if backtrack(i+1,val) : return True\n\n return False\n \n``` | 1 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
This also works too | splitting-a-string-into-descending-consecutive-values | 0 | 1 | I am sure all you smart pants can figure out the basic algorithm behind this, but the part I had a lot of trouble figuring out was the edge case. However, as long as I made sure that the previous number I had was not int(s) itself, it all worked out itself.\n\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n self.res = False\n self.fake = int(s)\n\n def backtrack(start, prev):\n if start >= len(s) and prev != self.fake:\n self.res = True\n return\n for i in range(start, len(s)):\n num = int(s[start: i+1])\n if num + 1 == prev or prev == -1:\n backtrack(i+1, num)\n \n backtrack(0,-1)\n return self.res\n\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
This also works too | splitting-a-string-into-descending-consecutive-values | 0 | 1 | I am sure all you smart pants can figure out the basic algorithm behind this, but the part I had a lot of trouble figuring out was the edge case. However, as long as I made sure that the previous number I had was not int(s) itself, it all worked out itself.\n\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n self.res = False\n self.fake = int(s)\n\n def backtrack(start, prev):\n if start >= len(s) and prev != self.fake:\n self.res = True\n return\n for i in range(start, len(s)):\n num = int(s[start: i+1])\n if num + 1 == prev or prev == -1:\n backtrack(i+1, num)\n \n backtrack(0,-1)\n return self.res\n\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
💡💡 Neatly coded backtracking solution using python3 | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuitive Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use backtracking (DFS approach) to solve this as we have to go brute anyway to find the different splits possible. \n\nOutside the function:\nWe first loop from 0 to len(s)-2 (we leave the last character for the second part), then we call the backtracking function for the second part (and further splits)\n\nInside the bt function:\nOur backtracking function handles everything after we get the first value. We do it like this as want something to compare our split with i.e. to validate it so that we can perform recursion further. \nSince we have our prev value, we generate string by iterating through the right part of the remaining string. If value + 1 is greater than the prev val, we recurse. Recursion stops as soon as we reach the end of the string. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) + stack space\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n\n def bt(i, prev):\n if i == len(s):\n return True\n for j in range(i, len(s)):\n val = int(s[i:j+1])\n if prev == val+1 and bt(j+1, val):\n return True\n return False\n\n for i in range(len(s)-1):\n val = int(s[:i+1])\n if bt(i+1,val): \n return True\n\n return False\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
💡💡 Neatly coded backtracking solution using python3 | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuitive Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use backtracking (DFS approach) to solve this as we have to go brute anyway to find the different splits possible. \n\nOutside the function:\nWe first loop from 0 to len(s)-2 (we leave the last character for the second part), then we call the backtracking function for the second part (and further splits)\n\nInside the bt function:\nOur backtracking function handles everything after we get the first value. We do it like this as want something to compare our split with i.e. to validate it so that we can perform recursion further. \nSince we have our prev value, we generate string by iterating through the right part of the remaining string. If value + 1 is greater than the prev val, we recurse. Recursion stops as soon as we reach the end of the string. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) + stack space\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n\n def bt(i, prev):\n if i == len(s):\n return True\n for j in range(i, len(s)):\n val = int(s[i:j+1])\n if prev == val+1 and bt(j+1, val):\n return True\n return False\n\n for i in range(len(s)-1):\n val = int(s[:i+1])\n if bt(i+1,val): \n return True\n\n return False\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
Python: 95% | Simple and Detailed Code | DFS | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\nThe main idea of solving this problem is this idea of "chunking" your input string into every possible substring all the while keeping track of the remaining part of the string. These chunks of possible solution and remaining will be passed into futher recursive calls.\n\nI.E. take the string "05004" which should return true.\nWe want to split this into every possible substring\nChunk | Remaining\n0 | 5004\n05 | 004\n050 | 04\n0500 | 4\n05004 | _\n\nWe then "bound/bind" when we make futher recursive calls. In this case, we want each valid substring chunk to have a difference of 1.\n\nThus the current "chunk" we have becomes the previous value we pass into the recursive call. *This makes more sense when reading the code*\n# Approach\n*In-depth comments in the code*\n\n# Complexity\n- Time complexity:\n The time complexity is O(2^N), where N is the length of the input string s.\n\n Explanation:\n\n The recursive function dfs(prev, remaining) explores all possible splits of the input string.\nIn the worst case, each character can be a part of a split or not, leading to 2 possibilities per character.\nSince you\'re exploring all possible combinations of splits, the number of recursive calls grows exponentially with the length of the input string.\n\n- Space complexity:\nThe space complexity of your code is O(N), where N is the length of the input string s.\n\n Explanation:\n\n The space used by the recursion stack is directly proportional to the depth of recursion.\nSince the maximum depth of recursion is determined by the length of the input string, the space complexity is O(N).\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n # This is the dfs code\n # We pass in the previous value, and the remaining s\n # *Note*: It\'s worth scrolling to the bottom where the DFS function\n # is called to see what the initial values are to have a better understanding\n def dfs(prev, remaining):\n\n # if the length of the remaining string is zero we return false\n # this makes sure there is at least 2 seperate values as stated by the\n # problem: "two or more non-empty substrings"\n if len(remaining) == 0:\n return False\n\n # Next we directly check if the remaining s once converted to a int is \n # 1 less then prev. If so we return true.\n # We know this to be valid because we only call recursive calls when\n # all previous values are descending and a difference of 1\n if int(remaining) == prev - 1:\n return True\n\n # If we reach this spot then it is time to iterate acorss the remaining\n # search space\n # We iterate from across the length of the remaining string\n for i in range(len(remaining)):\n\n # Create every single "chunk" of size i to check\n # Convert into an int\n chunk = int(remaining[:i+1])\n\n # Grab the remaining part of the string and MAKE SURE TO NAME IT \n # DIFFERENTLY. This and chunk will be passed into the recursive call\n remaining2 = remaining[i+1:]\n\n # We want to make sure that the "chunk" we have satisfies the difference\n # condition of 1, otherwise there is no point in making futher recursive\n # calls. Also, since we initialize the recursive call below with Infinity\n # we make sure to still make calls when there is no "previous" value\n if chunk == prev - 1 or prev == float("inf"):\n\n # Make the recursive call using the chunk as the previous value, and \n # passing in the new formed remaining2\n # If the recursive call returns True, we make sure to return from this\n # current recursive call as True\n if dfs(chunk,remaining2):\n return True\n\n # If we reach the end of the function without returning True, then there must\n # be no valid splitting, thus return False\n return False\n \n # Make the initial call to the DFS function using Infinity as the prev value, and \n # the whole s as the "remaining"\n return dfs(float("inf"),s)\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
Python: 95% | Simple and Detailed Code | DFS | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\nThe main idea of solving this problem is this idea of "chunking" your input string into every possible substring all the while keeping track of the remaining part of the string. These chunks of possible solution and remaining will be passed into futher recursive calls.\n\nI.E. take the string "05004" which should return true.\nWe want to split this into every possible substring\nChunk | Remaining\n0 | 5004\n05 | 004\n050 | 04\n0500 | 4\n05004 | _\n\nWe then "bound/bind" when we make futher recursive calls. In this case, we want each valid substring chunk to have a difference of 1.\n\nThus the current "chunk" we have becomes the previous value we pass into the recursive call. *This makes more sense when reading the code*\n# Approach\n*In-depth comments in the code*\n\n# Complexity\n- Time complexity:\n The time complexity is O(2^N), where N is the length of the input string s.\n\n Explanation:\n\n The recursive function dfs(prev, remaining) explores all possible splits of the input string.\nIn the worst case, each character can be a part of a split or not, leading to 2 possibilities per character.\nSince you\'re exploring all possible combinations of splits, the number of recursive calls grows exponentially with the length of the input string.\n\n- Space complexity:\nThe space complexity of your code is O(N), where N is the length of the input string s.\n\n Explanation:\n\n The space used by the recursion stack is directly proportional to the depth of recursion.\nSince the maximum depth of recursion is determined by the length of the input string, the space complexity is O(N).\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n # This is the dfs code\n # We pass in the previous value, and the remaining s\n # *Note*: It\'s worth scrolling to the bottom where the DFS function\n # is called to see what the initial values are to have a better understanding\n def dfs(prev, remaining):\n\n # if the length of the remaining string is zero we return false\n # this makes sure there is at least 2 seperate values as stated by the\n # problem: "two or more non-empty substrings"\n if len(remaining) == 0:\n return False\n\n # Next we directly check if the remaining s once converted to a int is \n # 1 less then prev. If so we return true.\n # We know this to be valid because we only call recursive calls when\n # all previous values are descending and a difference of 1\n if int(remaining) == prev - 1:\n return True\n\n # If we reach this spot then it is time to iterate acorss the remaining\n # search space\n # We iterate from across the length of the remaining string\n for i in range(len(remaining)):\n\n # Create every single "chunk" of size i to check\n # Convert into an int\n chunk = int(remaining[:i+1])\n\n # Grab the remaining part of the string and MAKE SURE TO NAME IT \n # DIFFERENTLY. This and chunk will be passed into the recursive call\n remaining2 = remaining[i+1:]\n\n # We want to make sure that the "chunk" we have satisfies the difference\n # condition of 1, otherwise there is no point in making futher recursive\n # calls. Also, since we initialize the recursive call below with Infinity\n # we make sure to still make calls when there is no "previous" value\n if chunk == prev - 1 or prev == float("inf"):\n\n # Make the recursive call using the chunk as the previous value, and \n # passing in the new formed remaining2\n # If the recursive call returns True, we make sure to return from this\n # current recursive call as True\n if dfs(chunk,remaining2):\n return True\n\n # If we reach the end of the function without returning True, then there must\n # be no valid splitting, thus return False\n return False\n \n # Make the initial call to the DFS function using Infinity as the prev value, and \n # the whole s as the "remaining"\n return dfs(float("inf"),s)\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
O(n^n) time | O(n) space | solution explained | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are given a string of digits and need to split it into substrings such that the substrings are in descending order with a difference of 1 between the values that the adjacent substrings represent.\n\nUse backtracking to explore all possible splits and check if it is valid. A split is valid if the resulting substring values are in descending order and the difference is 1 i.e substring2 is 1 less than substring1.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- define a helper function for backtracking\nbacktrack(current index, current partitions, previous substring value)\n - if the current index is the last, we have considered all digits, and check if we were able to split the string i.e current partitions >= 2\n - for each next digit including the current index digit\n - get the current substring value\n - if the previous substring value is greater or the difference between the previous and current is 1, backtrack to explore whether we can make another split. Return true if we can\n - if the loop completes without returning true, we can\'t make any split, return false\n- start backtracking from the first digit at index 0 and return the result\n\n# Complexity\n- Time complexity: O(recursion breadth) \u2192 O(calls at each levele ^ total levels) \u2192 O(n$^n$) but the program runs much faster due to pruning \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(recursion stack) \u2192 O(recursion depth/levels) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n \n def backtrack(i: int, k: int, prev: int) -> bool:\n if i == len(s):\n return k >= 2\n for j in range(i, len(s)):\n cur = int(s[i:j + 1])\n if prev == math.inf or cur == prev - 1:\n if backtrack(j + 1, k + 1, cur):\n return True\n return False\n \n return backtrack(0, 0, math.inf)\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
O(n^n) time | O(n) space | solution explained | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are given a string of digits and need to split it into substrings such that the substrings are in descending order with a difference of 1 between the values that the adjacent substrings represent.\n\nUse backtracking to explore all possible splits and check if it is valid. A split is valid if the resulting substring values are in descending order and the difference is 1 i.e substring2 is 1 less than substring1.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- define a helper function for backtracking\nbacktrack(current index, current partitions, previous substring value)\n - if the current index is the last, we have considered all digits, and check if we were able to split the string i.e current partitions >= 2\n - for each next digit including the current index digit\n - get the current substring value\n - if the previous substring value is greater or the difference between the previous and current is 1, backtrack to explore whether we can make another split. Return true if we can\n - if the loop completes without returning true, we can\'t make any split, return false\n- start backtracking from the first digit at index 0 and return the result\n\n# Complexity\n- Time complexity: O(recursion breadth) \u2192 O(calls at each levele ^ total levels) \u2192 O(n$^n$) but the program runs much faster due to pruning \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(recursion stack) \u2192 O(recursion depth/levels) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n \n def backtrack(i: int, k: int, prev: int) -> bool:\n if i == len(s):\n return k >= 2\n for j in range(i, len(s)):\n cur = int(s[i:j + 1])\n if prev == math.inf or cur == prev - 1:\n if backtrack(j + 1, k + 1, cur):\n return True\n return False\n \n return backtrack(0, 0, math.inf)\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
Python3 Backtracking | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n def backtrack(currIdx, currVal):\n if currIdx == len(s) and currVal != int(s):\n return True\n for i in range(currIdx, len(s)):\n nextVal = int(s[currIdx:i + 1])\n if currVal == float(\'inf\') or (currVal - nextVal == 1):\n if backtrack(i + 1, nextVal):\n return True\n return False\n\n return backtrack(0, float(\'inf\'))\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
Python3 Backtracking | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n def backtrack(currIdx, currVal):\n if currIdx == len(s) and currVal != int(s):\n return True\n for i in range(currIdx, len(s)):\n nextVal = int(s[currIdx:i + 1])\n if currVal == float(\'inf\') or (currVal - nextVal == 1):\n if backtrack(i + 1, nextVal):\n return True\n return False\n\n return backtrack(0, float(\'inf\'))\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
Python (Simple Backtracking) | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s):\n\n def backtrack(s,path):\n if not s and len(path) >= 2:\n res.append(path)\n\n for i in range(1,len(s)+1):\n if path and (int(s[:i]) > int(path[-1]) or (int(s[:i]) - int(path[-1]) != -1)):\n continue\n backtrack(s[i:],path+[s[:i]])\n\n res = []\n backtrack(s,[])\n return len(res) > 0\n \n\n\n\n\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
Python (Simple Backtracking) | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s):\n\n def backtrack(s,path):\n if not s and len(path) >= 2:\n res.append(path)\n\n for i in range(1,len(s)+1):\n if path and (int(s[:i]) > int(path[-1]) or (int(s[:i]) - int(path[-1]) != -1)):\n continue\n backtrack(s[i:],path+[s[:i]])\n\n res = []\n backtrack(s,[])\n return len(res) > 0\n \n\n\n\n\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
Python Solution | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->Check if every digit segments are in decreasing order and differ by one\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBacktracking\n# Complexity\n- Time complexity: O(n^2)/n! (?)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n def backtrack(prevSum,i,segmentCount):\n if i==len(s) and segmentCount > 1:\n return True\n \n currSum=0\n for j in range(i,len(s)):\n currSum=currSum*10+ord(s[j])-ord(\'0\')\n if (prevSum==-1 or currSum==prevSum-1) and \\\n backtrack(currSum,j+1,segmentCount+1):\n return True\n return False\n return backtrack(-1,0,0)\n\n\n\n\n``` | 0 | You are given a string `s` that consists of only digits.
Check if we can split `s` into **two or more non-empty substrings** such that the **numerical values** of the substrings are in **descending order** and the **difference** between numerical values of every two **adjacent** **substrings** is equal to `1`.
* For example, the string `s = "0090089 "` can be split into `[ "0090 ", "089 "]` with numerical values `[90,89]`. The values are in descending order and adjacent values differ by `1`, so this way is valid.
* Another example, the string `s = "001 "` can be split into `[ "0 ", "01 "]`, `[ "00 ", "1 "]`, or `[ "0 ", "0 ", "1 "]`. However all the ways are invalid because they have numerical values `[0,1]`, `[0,1]`, and `[0,0,1]` respectively, all of which are not in descending order.
Return `true` _if it is possible to split_ `s` _as described above__, or_ `false` _otherwise._
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "1234 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Example 2:**
**Input:** s = "050043 "
**Output:** true
**Explanation:** s can be split into \[ "05 ", "004 ", "3 "\] with numerical values \[5,4,3\].
The values are in descending order with adjacent values differing by 1.
**Example 3:**
**Input:** s = "9080701 "
**Output:** false
**Explanation:** There is no valid way to split s.
**Constraints:**
* `1 <= s.length <= 20`
* `s` only consists of digits. | What if we asked for maximum sum, not absolute sum? It's a standard problem that can be solved by Kadane's algorithm. The key idea is the max absolute sum will be either the max sum or the min sum. So just run kadane twice, once calculating the max sum and once calculating the min sum. |
Python Solution | splitting-a-string-into-descending-consecutive-values | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->Check if every digit segments are in decreasing order and differ by one\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBacktracking\n# Complexity\n- Time complexity: O(n^2)/n! (?)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitString(self, s: str) -> bool:\n def backtrack(prevSum,i,segmentCount):\n if i==len(s) and segmentCount > 1:\n return True\n \n currSum=0\n for j in range(i,len(s)):\n currSum=currSum*10+ord(s[j])-ord(\'0\')\n if (prevSum==-1 or currSum==prevSum-1) and \\\n backtrack(currSum,j+1,segmentCount+1):\n return True\n return False\n return backtrack(-1,0,0)\n\n\n\n\n``` | 0 | You are in a city that consists of `n` intersections numbered from `0` to `n - 1` with **bi-directional** roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer `n` and a 2D integer array `roads` where `roads[i] = [ui, vi, timei]` means that there is a road between intersections `ui` and `vi` that takes `timei` minutes to travel. You want to know in how many ways you can travel from intersection `0` to intersection `n - 1` in the **shortest amount of time**.
Return _the **number of ways** you can arrive at your destination in the **shortest amount of time**_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 7, roads = \[\[0,6,7\],\[0,1,2\],\[1,2,3\],\[1,3,3\],\[6,3,3\],\[3,5,1\],\[6,5,1\],\[2,5,1\],\[0,4,5\],\[4,6,2\]\]
**Output:** 4
**Explanation:** The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
**Example 2:**
**Input:** n = 2, roads = \[\[1,0,10\]\]
**Output:** 1
**Explanation:** There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
**Constraints:**
* `1 <= n <= 200`
* `n - 1 <= roads.length <= n * (n - 1) / 2`
* `roads[i].length == 3`
* `0 <= ui, vi <= n - 1`
* `1 <= timei <= 109`
* `ui != vi`
* There is at most one road connecting any two intersections.
* You can reach any intersection from any other intersection. | One solution is to try all possible splits using backtrack Look out for trailing zeros in string |
[Python3] brute-force | minimum-adjacent-swaps-to-reach-the-kth-smallest-number | 0 | 1 | \n```\nclass Solution:\n def getMinSwaps(self, num: str, k: int) -> int:\n num = list(num)\n orig = num.copy()\n \n for _ in range(k): \n for i in reversed(range(len(num)-1)): \n if num[i] < num[i+1]: \n ii = i+1 \n while ii < len(num) and num[i] < num[ii]: ii += 1\n num[i], num[ii-1] = num[ii-1], num[i]\n lo, hi = i+1, len(num)-1\n while lo < hi: \n num[lo], num[hi] = num[hi], num[lo]\n lo += 1\n hi -= 1\n break \n \n ans = 0\n for i in range(len(num)): \n ii = i\n while orig[i] != num[i]: \n ans += 1\n ii += 1\n num[i], num[ii] = num[ii], num[i]\n return ans \n``` | 7 | You are given a string `num`, representing a large integer, and an integer `k`.
We call some integer **wonderful** if it is a **permutation** of the digits in `num` and is **greater in value** than `num`. There can be many wonderful integers. However, we only care about the **smallest-valued** ones.
* For example, when `num = "5489355142 "`:
* The 1st smallest wonderful integer is `"5489355214 "`.
* The 2nd smallest wonderful integer is `"5489355241 "`.
* The 3rd smallest wonderful integer is `"5489355412 "`.
* The 4th smallest wonderful integer is `"5489355421 "`.
Return _the **minimum number of adjacent digit swaps** that needs to be applied to_ `num` _to reach the_ `kth` _**smallest wonderful** integer_.
The tests are generated in such a way that `kth` smallest wonderful integer exists.
**Example 1:**
**Input:** num = "5489355142 ", k = 4
**Output:** 2
**Explanation:** The 4th smallest wonderful number is "5489355421 ". To get this number:
- Swap index 7 with index 8: "5489355142 " -> "5489355412 "
- Swap index 8 with index 9: "5489355412 " -> "5489355421 "
**Example 2:**
**Input:** num = "11112 ", k = 4
**Output:** 4
**Explanation:** The 4th smallest wonderful number is "21111 ". To get this number:
- Swap index 3 with index 4: "11112 " -> "11121 "
- Swap index 2 with index 3: "11121 " -> "11211 "
- Swap index 1 with index 2: "11211 " -> "12111 "
- Swap index 0 with index 1: "12111 " -> "21111 "
**Example 3:**
**Input:** num = "00123 ", k = 1
**Output:** 1
**Explanation:** The 1st smallest wonderful number is "00132 ". To get this number:
- Swap index 3 with index 4: "00123 " -> "00132 "
**Constraints:**
* `2 <= num.length <= 1000`
* `1 <= k <= 1000`
* `num` only consists of digits. | If both ends have distinct characters, no more operations can be made. Otherwise, the only operation is to remove all of the same characters from both ends. We will do this as many times as we can. Note that if the length is equal 1 the answer is 1 |
Python Next Permutation + Minimum Adjacent Swaps | minimum-adjacent-swaps-to-reach-the-kth-smallest-number | 0 | 1 | \n# Complexity\n- Time complexity:O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nextPermutation(self,nums):\n i=len(nums)-2\n while i>=0:\n if nums[i]<nums[i+1]:\n j=len(nums)-1\n while nums[i]>=nums[j]:\n j-=1\n temp=nums[i]\n nums[i]=nums[j]\n nums[j]=temp\n break\n i-=1\n\n t=nums[i+1:]\n t.sort()\n \n return nums[:i+1]+t\n \n def getMinSwaps(self, num: str, k: int) -> int:\n nums=[]\n ar=[]\n for i in range(len(num)):\n nums.append(int(num[i]))\n ar.append(int(num[i]))\n\n for i in range(k):\n t=self.nextPermutation(nums)\n nums=t\n res=0\n for i in range(0,len(nums)):\n j=i\n if ar[i]!=nums[j]:\n while j<len(nums) and i<len(ar) and ar[i]!=nums[j]:\n j+=1\n while i<j:\n temp=nums[j]\n nums[j]=nums[j-1]\n nums[j-1]=temp\n j-=1\n res+=1\n\n return res\n \n\n \n``` | 0 | You are given a string `num`, representing a large integer, and an integer `k`.
We call some integer **wonderful** if it is a **permutation** of the digits in `num` and is **greater in value** than `num`. There can be many wonderful integers. However, we only care about the **smallest-valued** ones.
* For example, when `num = "5489355142 "`:
* The 1st smallest wonderful integer is `"5489355214 "`.
* The 2nd smallest wonderful integer is `"5489355241 "`.
* The 3rd smallest wonderful integer is `"5489355412 "`.
* The 4th smallest wonderful integer is `"5489355421 "`.
Return _the **minimum number of adjacent digit swaps** that needs to be applied to_ `num` _to reach the_ `kth` _**smallest wonderful** integer_.
The tests are generated in such a way that `kth` smallest wonderful integer exists.
**Example 1:**
**Input:** num = "5489355142 ", k = 4
**Output:** 2
**Explanation:** The 4th smallest wonderful number is "5489355421 ". To get this number:
- Swap index 7 with index 8: "5489355142 " -> "5489355412 "
- Swap index 8 with index 9: "5489355412 " -> "5489355421 "
**Example 2:**
**Input:** num = "11112 ", k = 4
**Output:** 4
**Explanation:** The 4th smallest wonderful number is "21111 ". To get this number:
- Swap index 3 with index 4: "11112 " -> "11121 "
- Swap index 2 with index 3: "11121 " -> "11211 "
- Swap index 1 with index 2: "11211 " -> "12111 "
- Swap index 0 with index 1: "12111 " -> "21111 "
**Example 3:**
**Input:** num = "00123 ", k = 1
**Output:** 1
**Explanation:** The 1st smallest wonderful number is "00132 ". To get this number:
- Swap index 3 with index 4: "00123 " -> "00132 "
**Constraints:**
* `2 <= num.length <= 1000`
* `1 <= k <= 1000`
* `num` only consists of digits. | If both ends have distinct characters, no more operations can be made. Otherwise, the only operation is to remove all of the same characters from both ends. We will do this as many times as we can. Note that if the length is equal 1 the answer is 1 |
Python 44ms :) | minimum-adjacent-swaps-to-reach-the-kth-smallest-number | 0 | 1 | \n# Code\n```\n# this function modifies l to a new list, which is\n# strictly after l and before or equal to the k-th successor of l\n# in the lex order.\n# "find the minimum i such that l[i:] is reverse-sorted.\n# find the maximum j >= i with l[j] > l[i - 1].\n# swap l[j] and l[i - 1] and then sort l[i:]."\n# note that after the swap, l[i:] will still be reverse-sorted.\n# so equivalently, just reverse l[i:].\n# shortcut:\n# given a sorted terminal segment, we can do a bit of combinatorics\n# to determine the number of rearrangements of that segment, and\n# often skip quite a number of permutations.\n# it also accepts and returns an upper bound for i, `skip`,\n# since after doing the shortcut, we don\'t need to check\n# the whole reversed suffix.\ndef lex_succ(l, k, skip):\n for i in reversed(range(skip)):\n if l[i] > l[i - 1]:\n break\n # now l[i:] is reverse-sorted.\n # if it\'s also sorted, then switch to the shortcut:\n if k > 1 and l[i] == l[-1]:\n # l[j:] is sorted. How many permutations of l[j:] are there?\n # answer: N! / (N_1! N_2! ... N_t!)\n # where N = len(l[j:]) and N = N_1 + ... + N_t\n # and the N_i are the number of times the distinct elements\n # appear in the list.\n N = 0\n perms = 1\n prev = 10\n for x, g in groupby(reversed(l)):\n if x > prev:\n break\n for Ni in accumulate(1 for _ in g):\n N += 1\n if perms * N // Ni > k + 1:\n N -= 1\n l[-N:] = reversed(l[-N:])\n return perms - 1, len(l) - N + 1\n perms = perms * N // Ni\n prev = x\n l[-N:] = reversed(l[-N:])\n return perms - 1, len(l) - N + 1\n # else produce the successor as normal.\n else:\n # we could use binary search here.\n # but it doesn\'t seem to provide a practical improvement.\n for j in reversed(range(len(l))):\n if l[j] > l[i - 1]:\n break\n l[j], l[i - 1] = l[i - 1], l[j]\n l[i:] = reversed(l[i:])\n return 1, len(l)\n\n# distance between a and b in the "bubble metric".\n# essentially the problem is "how many swaps would bubblesort need to make\n# in order to sort L?"\n# this is basically the problem of counting inversions. There are O(n log n)\n# algorithms: https://stackoverflow.com/questions/337664/counting-inversions-in-an-array/6424847#6424847\n# but they\'re not worth it in this case.\ndef dist(a, b):\n res = 0\n for i, x in enumerate(a):\n if b[i] != x:\n j = b.index(x, i + 1)\n res += j - i\n b.insert(i, b.pop(j))\n return res\n\nclass Solution:\n def getMinSwaps(self, num: str, k: int) -> int:\n kth_wond = list(map(int, num))\n skip = len(kth_wond)\n while k:\n d, skip = lex_succ(kth_wond, k, skip)\n k -= d\n # the first argument to dist may be any iterable.\n return dist(map(int, num), kth_wond)\n``` | 0 | You are given a string `num`, representing a large integer, and an integer `k`.
We call some integer **wonderful** if it is a **permutation** of the digits in `num` and is **greater in value** than `num`. There can be many wonderful integers. However, we only care about the **smallest-valued** ones.
* For example, when `num = "5489355142 "`:
* The 1st smallest wonderful integer is `"5489355214 "`.
* The 2nd smallest wonderful integer is `"5489355241 "`.
* The 3rd smallest wonderful integer is `"5489355412 "`.
* The 4th smallest wonderful integer is `"5489355421 "`.
Return _the **minimum number of adjacent digit swaps** that needs to be applied to_ `num` _to reach the_ `kth` _**smallest wonderful** integer_.
The tests are generated in such a way that `kth` smallest wonderful integer exists.
**Example 1:**
**Input:** num = "5489355142 ", k = 4
**Output:** 2
**Explanation:** The 4th smallest wonderful number is "5489355421 ". To get this number:
- Swap index 7 with index 8: "5489355142 " -> "5489355412 "
- Swap index 8 with index 9: "5489355412 " -> "5489355421 "
**Example 2:**
**Input:** num = "11112 ", k = 4
**Output:** 4
**Explanation:** The 4th smallest wonderful number is "21111 ". To get this number:
- Swap index 3 with index 4: "11112 " -> "11121 "
- Swap index 2 with index 3: "11121 " -> "11211 "
- Swap index 1 with index 2: "11211 " -> "12111 "
- Swap index 0 with index 1: "12111 " -> "21111 "
**Example 3:**
**Input:** num = "00123 ", k = 1
**Output:** 1
**Explanation:** The 1st smallest wonderful number is "00132 ". To get this number:
- Swap index 3 with index 4: "00123 " -> "00132 "
**Constraints:**
* `2 <= num.length <= 1000`
* `1 <= k <= 1000`
* `num` only consists of digits. | If both ends have distinct characters, no more operations can be made. Otherwise, the only operation is to remove all of the same characters from both ends. We will do this as many times as we can. Note that if the length is equal 1 the answer is 1 |
Greedy Python solution | minimum-adjacent-swaps-to-reach-the-kth-smallest-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom bisect import bisect\n\nclass Solution:\n def getMinSwaps(self, num: str, k: int) -> int:\n\n #Generate Kth smallest number\n arr = [*num]\n for _ in range(k):\n brr = [arr.pop()]\n while arr[-1] >= brr[-1]:\n brr.append(arr.pop())\n i = bisect(brr, arr[-1])\n arr[-1], brr[i] = brr[i], arr[-1]\n arr += brr\n \n #Calculate adjacent swaps\n count = 0\n for item in num:\n i = arr.index(item)\n count += i\n arr.pop(i)\n\n return count\n\n``` | 0 | You are given a string `num`, representing a large integer, and an integer `k`.
We call some integer **wonderful** if it is a **permutation** of the digits in `num` and is **greater in value** than `num`. There can be many wonderful integers. However, we only care about the **smallest-valued** ones.
* For example, when `num = "5489355142 "`:
* The 1st smallest wonderful integer is `"5489355214 "`.
* The 2nd smallest wonderful integer is `"5489355241 "`.
* The 3rd smallest wonderful integer is `"5489355412 "`.
* The 4th smallest wonderful integer is `"5489355421 "`.
Return _the **minimum number of adjacent digit swaps** that needs to be applied to_ `num` _to reach the_ `kth` _**smallest wonderful** integer_.
The tests are generated in such a way that `kth` smallest wonderful integer exists.
**Example 1:**
**Input:** num = "5489355142 ", k = 4
**Output:** 2
**Explanation:** The 4th smallest wonderful number is "5489355421 ". To get this number:
- Swap index 7 with index 8: "5489355142 " -> "5489355412 "
- Swap index 8 with index 9: "5489355412 " -> "5489355421 "
**Example 2:**
**Input:** num = "11112 ", k = 4
**Output:** 4
**Explanation:** The 4th smallest wonderful number is "21111 ". To get this number:
- Swap index 3 with index 4: "11112 " -> "11121 "
- Swap index 2 with index 3: "11121 " -> "11211 "
- Swap index 1 with index 2: "11211 " -> "12111 "
- Swap index 0 with index 1: "12111 " -> "21111 "
**Example 3:**
**Input:** num = "00123 ", k = 1
**Output:** 1
**Explanation:** The 1st smallest wonderful number is "00132 ". To get this number:
- Swap index 3 with index 4: "00123 " -> "00132 "
**Constraints:**
* `2 <= num.length <= 1000`
* `1 <= k <= 1000`
* `num` only consists of digits. | If both ends have distinct characters, no more operations can be made. Otherwise, the only operation is to remove all of the same characters from both ends. We will do this as many times as we can. Note that if the length is equal 1 the answer is 1 |
next greater value | minimum-adjacent-swaps-to-reach-the-kth-smallest-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMinSwaps(self, num: str, k: int) -> int:\n def findGreatest(nums):\n nums = list(nums)\n # 1 find pivot\n pivot = None\n for i in range(len(nums) - 1, 0, -1):\n if nums[i] > nums[i - 1]:\n pivot = i - 1\n break\n # 2 swap with pivot if larger than pivot\n for i in range(len(nums) - 1, pivot, -1):\n if nums[i] > nums[pivot]:\n nums[i], nums[pivot] = nums[pivot], nums[i]\n break\n # 3 reverse nums after pivot\n nums[pivot +1: ] = nums[pivot +1: ][::-1]\n return \'\'.join(nums)\n \n origin = list(num[::])\n for i in range(k):\n num = findGreatest(num)\n # swap adjacent greedy\n ans, n = 0, len(num)\n for i in range(n):\n j = origin.index(num[i], i)\n ans += j - i\n origin[i:j+1] = [origin[j]] + origin[i:j]\n return ans\n``` | 0 | You are given a string `num`, representing a large integer, and an integer `k`.
We call some integer **wonderful** if it is a **permutation** of the digits in `num` and is **greater in value** than `num`. There can be many wonderful integers. However, we only care about the **smallest-valued** ones.
* For example, when `num = "5489355142 "`:
* The 1st smallest wonderful integer is `"5489355214 "`.
* The 2nd smallest wonderful integer is `"5489355241 "`.
* The 3rd smallest wonderful integer is `"5489355412 "`.
* The 4th smallest wonderful integer is `"5489355421 "`.
Return _the **minimum number of adjacent digit swaps** that needs to be applied to_ `num` _to reach the_ `kth` _**smallest wonderful** integer_.
The tests are generated in such a way that `kth` smallest wonderful integer exists.
**Example 1:**
**Input:** num = "5489355142 ", k = 4
**Output:** 2
**Explanation:** The 4th smallest wonderful number is "5489355421 ". To get this number:
- Swap index 7 with index 8: "5489355142 " -> "5489355412 "
- Swap index 8 with index 9: "5489355412 " -> "5489355421 "
**Example 2:**
**Input:** num = "11112 ", k = 4
**Output:** 4
**Explanation:** The 4th smallest wonderful number is "21111 ". To get this number:
- Swap index 3 with index 4: "11112 " -> "11121 "
- Swap index 2 with index 3: "11121 " -> "11211 "
- Swap index 1 with index 2: "11211 " -> "12111 "
- Swap index 0 with index 1: "12111 " -> "21111 "
**Example 3:**
**Input:** num = "00123 ", k = 1
**Output:** 1
**Explanation:** The 1st smallest wonderful number is "00132 ". To get this number:
- Swap index 3 with index 4: "00123 " -> "00132 "
**Constraints:**
* `2 <= num.length <= 1000`
* `1 <= k <= 1000`
* `num` only consists of digits. | If both ends have distinct characters, no more operations can be made. Otherwise, the only operation is to remove all of the same characters from both ends. We will do this as many times as we can. Note that if the length is equal 1 the answer is 1 |
Clean Python3 | Sorting & Heap | minimum-interval-to-include-each-query | 0 | 1 | Please upvote if it helps!\n```\nclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n\t\n queries_asc = sorted((q, i) for i, q in enumerate(queries))\n intervals.sort()\n \n i, num_intervals = 0, len(intervals)\n size_heap = [] # (size, left)\n \n for pos, qnum in queries_asc:\n \n while i < num_intervals:\n left, right = intervals[i]\n if left > pos:\n break\n heapq.heappush(size_heap, (right - left + 1, left))\n i += 1\n \n while size_heap:\n size, left = size_heap[0]\n right = left + size - 1\n if right >= pos:\n break\n heapq.heappop(size_heap)\n \n queries[qnum] = size_heap[0][0] if size_heap else -1\n \n return queries | 2 | You are given a 2D integer array `intervals`, where `intervals[i] = [lefti, righti]` describes the `ith` interval starting at `lefti` and ending at `righti` **(inclusive)**. The **size** of an interval is defined as the number of integers it contains, or more formally `righti - lefti + 1`.
You are also given an integer array `queries`. The answer to the `jth` query is the **size of the smallest interval** `i` such that `lefti <= queries[j] <= righti`. If no such interval exists, the answer is `-1`.
Return _an array containing the answers to the queries_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[2,4\],\[3,6\],\[4,4\]\], queries = \[2,3,4,5\]
**Output:** \[3,3,1,4\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,4\] is the smallest interval containing 2. The answer is 4 - 2 + 1 = 3.
- Query = 3: The interval \[2,4\] is the smallest interval containing 3. The answer is 4 - 2 + 1 = 3.
- Query = 4: The interval \[4,4\] is the smallest interval containing 4. The answer is 4 - 4 + 1 = 1.
- Query = 5: The interval \[3,6\] is the smallest interval containing 5. The answer is 6 - 3 + 1 = 4.
**Example 2:**
**Input:** intervals = \[\[2,3\],\[2,5\],\[1,8\],\[20,25\]\], queries = \[2,19,5,22\]
**Output:** \[2,-1,4,6\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,3\] is the smallest interval containing 2. The answer is 3 - 2 + 1 = 2.
- Query = 19: None of the intervals contain 19. The answer is -1.
- Query = 5: The interval \[2,5\] is the smallest interval containing 5. The answer is 5 - 2 + 1 = 4.
- Query = 22: The interval \[20,25\] is the smallest interval containing 22. The answer is 25 - 20 + 1 = 6.
**Constraints:**
* `1 <= intervals.length <= 105`
* `1 <= queries.length <= 105`
* `intervals[i].length == 2`
* `1 <= lefti <= righti <= 107`
* `1 <= queries[j] <= 107` | Sort the events by its startTime. For every event, you can either choose it and consider the next event available, or you can ignore it. You can efficiently find the next event that is available using binary search. |
Clean Python3 | Sorting & Heap | minimum-interval-to-include-each-query | 0 | 1 | Please upvote if it helps!\n```\nclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n\t\n queries_asc = sorted((q, i) for i, q in enumerate(queries))\n intervals.sort()\n \n i, num_intervals = 0, len(intervals)\n size_heap = [] # (size, left)\n \n for pos, qnum in queries_asc:\n \n while i < num_intervals:\n left, right = intervals[i]\n if left > pos:\n break\n heapq.heappush(size_heap, (right - left + 1, left))\n i += 1\n \n while size_heap:\n size, left = size_heap[0]\n right = left + size - 1\n if right >= pos:\n break\n heapq.heappop(size_heap)\n \n queries[qnum] = size_heap[0][0] if size_heap else -1\n \n return queries | 2 | You wrote down many **positive** integers in a string called `num`. However, you realized that you forgot to add commas to seperate the different numbers. You remember that the list of integers was **non-decreasing** and that **no** integer had leading zeros.
Return _the **number of possible lists of integers** that you could have written down to get the string_ `num`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** num = "327 "
**Output:** 2
**Explanation:** You could have written down the numbers:
3, 27
327
**Example 2:**
**Input:** num = "094 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Example 3:**
**Input:** num = "0 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Constraints:**
* `1 <= num.length <= 3500`
* `num` consists of digits `'0'` through `'9'`. | Is there a way to order the intervals and queries such that it takes less time to query? Is there a way to add and remove intervals by going from the smallest query to the largest query to find the minimum size? |
Python 3 || hashMap, priority queue, min-heap | minimum-interval-to-include-each-query | 0 | 1 | \tclass Solution:\n\t\tdef minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n\t\t\thashMap = {}\n\t\t\tintervals.sort()\n\n\t\t\tminHeap = []\n\n\t\t\ti_l = len(intervals)\n\t\t\ti = 0\n\t\t\tfor q in sorted(queries):\n\t\t\t\twhile i < i_l and intervals[i][0] <= q:\n\t\t\t\t\tstart, end = intervals[i]\n\t\t\t\t\theapq.heappush(minHeap, [(end-start+1), end])\n\t\t\t\t\ti += 1\n\n\t\t\t\twhile minHeap and minHeap[0][1] < q:\n\t\t\t\t\theapq.heappop(minHeap)\n\n\t\t\t\thashMap[q] = minHeap[0][0] if minHeap else -1\n\n\t\t\treturn [hashMap[q] for q in queries] | 1 | You are given a 2D integer array `intervals`, where `intervals[i] = [lefti, righti]` describes the `ith` interval starting at `lefti` and ending at `righti` **(inclusive)**. The **size** of an interval is defined as the number of integers it contains, or more formally `righti - lefti + 1`.
You are also given an integer array `queries`. The answer to the `jth` query is the **size of the smallest interval** `i` such that `lefti <= queries[j] <= righti`. If no such interval exists, the answer is `-1`.
Return _an array containing the answers to the queries_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[2,4\],\[3,6\],\[4,4\]\], queries = \[2,3,4,5\]
**Output:** \[3,3,1,4\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,4\] is the smallest interval containing 2. The answer is 4 - 2 + 1 = 3.
- Query = 3: The interval \[2,4\] is the smallest interval containing 3. The answer is 4 - 2 + 1 = 3.
- Query = 4: The interval \[4,4\] is the smallest interval containing 4. The answer is 4 - 4 + 1 = 1.
- Query = 5: The interval \[3,6\] is the smallest interval containing 5. The answer is 6 - 3 + 1 = 4.
**Example 2:**
**Input:** intervals = \[\[2,3\],\[2,5\],\[1,8\],\[20,25\]\], queries = \[2,19,5,22\]
**Output:** \[2,-1,4,6\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,3\] is the smallest interval containing 2. The answer is 3 - 2 + 1 = 2.
- Query = 19: None of the intervals contain 19. The answer is -1.
- Query = 5: The interval \[2,5\] is the smallest interval containing 5. The answer is 5 - 2 + 1 = 4.
- Query = 22: The interval \[20,25\] is the smallest interval containing 22. The answer is 25 - 20 + 1 = 6.
**Constraints:**
* `1 <= intervals.length <= 105`
* `1 <= queries.length <= 105`
* `intervals[i].length == 2`
* `1 <= lefti <= righti <= 107`
* `1 <= queries[j] <= 107` | Sort the events by its startTime. For every event, you can either choose it and consider the next event available, or you can ignore it. You can efficiently find the next event that is available using binary search. |
Python 3 || hashMap, priority queue, min-heap | minimum-interval-to-include-each-query | 0 | 1 | \tclass Solution:\n\t\tdef minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n\t\t\thashMap = {}\n\t\t\tintervals.sort()\n\n\t\t\tminHeap = []\n\n\t\t\ti_l = len(intervals)\n\t\t\ti = 0\n\t\t\tfor q in sorted(queries):\n\t\t\t\twhile i < i_l and intervals[i][0] <= q:\n\t\t\t\t\tstart, end = intervals[i]\n\t\t\t\t\theapq.heappush(minHeap, [(end-start+1), end])\n\t\t\t\t\ti += 1\n\n\t\t\t\twhile minHeap and minHeap[0][1] < q:\n\t\t\t\t\theapq.heappop(minHeap)\n\n\t\t\t\thashMap[q] = minHeap[0][0] if minHeap else -1\n\n\t\t\treturn [hashMap[q] for q in queries] | 1 | You wrote down many **positive** integers in a string called `num`. However, you realized that you forgot to add commas to seperate the different numbers. You remember that the list of integers was **non-decreasing** and that **no** integer had leading zeros.
Return _the **number of possible lists of integers** that you could have written down to get the string_ `num`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** num = "327 "
**Output:** 2
**Explanation:** You could have written down the numbers:
3, 27
327
**Example 2:**
**Input:** num = "094 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Example 3:**
**Input:** num = "0 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Constraints:**
* `1 <= num.length <= 3500`
* `num` consists of digits `'0'` through `'9'`. | Is there a way to order the intervals and queries such that it takes less time to query? Is there a way to add and remove intervals by going from the smallest query to the largest query to find the minimum size? |
📌📌 For Beginners || Easy-Approach || Well-Explained || Clean & Concise 🐍 | minimum-interval-to-include-each-query | 0 | 1 | ## IDEA:\n\uD83D\uDC49 *Sort the intervals by size and the queries in increasing order, then iterate over the intervals.\n\uD83D\uDC49 For each interval (left, right) binary search for the queries (q) that are contained in the interval (left <= q <= right), pop them from the array queries and insert them in the array answers (with size = right - left +1).\n\uD83D\uDC49 Since you\'re looking at the interval from the smallest to the largest, the first answer found is correct.*\n\'\'\'\n\n\tclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n \n intervals.sort(key = lambda x:x[1]-x[0])\n q = sorted([qu,i] for i,qu in enumerate(queries))\n res=[-1]*len(queries)\n\t\t\n for left,right in intervals:\n ind = bisect.bisect(q,[left])\n while ind<len(q) and q[ind][0]<=right:\n res[q.pop(ind)[1]]=right-left+1\n return res\n\t\t\nFeel free to ask if you have any doubt. \uD83E\uDD17\n**Thanku** and do **Upvote** if you got any help !!\uD83E\uDD1E | 5 | You are given a 2D integer array `intervals`, where `intervals[i] = [lefti, righti]` describes the `ith` interval starting at `lefti` and ending at `righti` **(inclusive)**. The **size** of an interval is defined as the number of integers it contains, or more formally `righti - lefti + 1`.
You are also given an integer array `queries`. The answer to the `jth` query is the **size of the smallest interval** `i` such that `lefti <= queries[j] <= righti`. If no such interval exists, the answer is `-1`.
Return _an array containing the answers to the queries_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[2,4\],\[3,6\],\[4,4\]\], queries = \[2,3,4,5\]
**Output:** \[3,3,1,4\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,4\] is the smallest interval containing 2. The answer is 4 - 2 + 1 = 3.
- Query = 3: The interval \[2,4\] is the smallest interval containing 3. The answer is 4 - 2 + 1 = 3.
- Query = 4: The interval \[4,4\] is the smallest interval containing 4. The answer is 4 - 4 + 1 = 1.
- Query = 5: The interval \[3,6\] is the smallest interval containing 5. The answer is 6 - 3 + 1 = 4.
**Example 2:**
**Input:** intervals = \[\[2,3\],\[2,5\],\[1,8\],\[20,25\]\], queries = \[2,19,5,22\]
**Output:** \[2,-1,4,6\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,3\] is the smallest interval containing 2. The answer is 3 - 2 + 1 = 2.
- Query = 19: None of the intervals contain 19. The answer is -1.
- Query = 5: The interval \[2,5\] is the smallest interval containing 5. The answer is 5 - 2 + 1 = 4.
- Query = 22: The interval \[20,25\] is the smallest interval containing 22. The answer is 25 - 20 + 1 = 6.
**Constraints:**
* `1 <= intervals.length <= 105`
* `1 <= queries.length <= 105`
* `intervals[i].length == 2`
* `1 <= lefti <= righti <= 107`
* `1 <= queries[j] <= 107` | Sort the events by its startTime. For every event, you can either choose it and consider the next event available, or you can ignore it. You can efficiently find the next event that is available using binary search. |
📌📌 For Beginners || Easy-Approach || Well-Explained || Clean & Concise 🐍 | minimum-interval-to-include-each-query | 0 | 1 | ## IDEA:\n\uD83D\uDC49 *Sort the intervals by size and the queries in increasing order, then iterate over the intervals.\n\uD83D\uDC49 For each interval (left, right) binary search for the queries (q) that are contained in the interval (left <= q <= right), pop them from the array queries and insert them in the array answers (with size = right - left +1).\n\uD83D\uDC49 Since you\'re looking at the interval from the smallest to the largest, the first answer found is correct.*\n\'\'\'\n\n\tclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n \n intervals.sort(key = lambda x:x[1]-x[0])\n q = sorted([qu,i] for i,qu in enumerate(queries))\n res=[-1]*len(queries)\n\t\t\n for left,right in intervals:\n ind = bisect.bisect(q,[left])\n while ind<len(q) and q[ind][0]<=right:\n res[q.pop(ind)[1]]=right-left+1\n return res\n\t\t\nFeel free to ask if you have any doubt. \uD83E\uDD17\n**Thanku** and do **Upvote** if you got any help !!\uD83E\uDD1E | 5 | You wrote down many **positive** integers in a string called `num`. However, you realized that you forgot to add commas to seperate the different numbers. You remember that the list of integers was **non-decreasing** and that **no** integer had leading zeros.
Return _the **number of possible lists of integers** that you could have written down to get the string_ `num`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** num = "327 "
**Output:** 2
**Explanation:** You could have written down the numbers:
3, 27
327
**Example 2:**
**Input:** num = "094 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Example 3:**
**Input:** num = "0 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Constraints:**
* `1 <= num.length <= 3500`
* `num` consists of digits `'0'` through `'9'`. | Is there a way to order the intervals and queries such that it takes less time to query? Is there a way to add and remove intervals by going from the smallest query to the largest query to find the minimum size? |
SIMPLE HEAP PYTHON (BEATS 100%) | minimum-interval-to-include-each-query | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n intervals.sort(reverse=True)\n heap = []\n ans = {}\n\n for q in sorted(queries):\n while intervals and intervals[-1][0] <= q:\n interval = intervals.pop()\n if interval[1] >= q:\n heappush(heap, [interval[1] - interval[0] + 1, interval[1]])\n \n while heap and heap[0][1] < q:\n heappop(heap)\n \n ans[q] = heap[0][0] if heap else -1\n\n return [ans[q] for q in queries]\n\n\n``` | 0 | You are given a 2D integer array `intervals`, where `intervals[i] = [lefti, righti]` describes the `ith` interval starting at `lefti` and ending at `righti` **(inclusive)**. The **size** of an interval is defined as the number of integers it contains, or more formally `righti - lefti + 1`.
You are also given an integer array `queries`. The answer to the `jth` query is the **size of the smallest interval** `i` such that `lefti <= queries[j] <= righti`. If no such interval exists, the answer is `-1`.
Return _an array containing the answers to the queries_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[2,4\],\[3,6\],\[4,4\]\], queries = \[2,3,4,5\]
**Output:** \[3,3,1,4\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,4\] is the smallest interval containing 2. The answer is 4 - 2 + 1 = 3.
- Query = 3: The interval \[2,4\] is the smallest interval containing 3. The answer is 4 - 2 + 1 = 3.
- Query = 4: The interval \[4,4\] is the smallest interval containing 4. The answer is 4 - 4 + 1 = 1.
- Query = 5: The interval \[3,6\] is the smallest interval containing 5. The answer is 6 - 3 + 1 = 4.
**Example 2:**
**Input:** intervals = \[\[2,3\],\[2,5\],\[1,8\],\[20,25\]\], queries = \[2,19,5,22\]
**Output:** \[2,-1,4,6\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,3\] is the smallest interval containing 2. The answer is 3 - 2 + 1 = 2.
- Query = 19: None of the intervals contain 19. The answer is -1.
- Query = 5: The interval \[2,5\] is the smallest interval containing 5. The answer is 5 - 2 + 1 = 4.
- Query = 22: The interval \[20,25\] is the smallest interval containing 22. The answer is 25 - 20 + 1 = 6.
**Constraints:**
* `1 <= intervals.length <= 105`
* `1 <= queries.length <= 105`
* `intervals[i].length == 2`
* `1 <= lefti <= righti <= 107`
* `1 <= queries[j] <= 107` | Sort the events by its startTime. For every event, you can either choose it and consider the next event available, or you can ignore it. You can efficiently find the next event that is available using binary search. |
SIMPLE HEAP PYTHON (BEATS 100%) | minimum-interval-to-include-each-query | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n intervals.sort(reverse=True)\n heap = []\n ans = {}\n\n for q in sorted(queries):\n while intervals and intervals[-1][0] <= q:\n interval = intervals.pop()\n if interval[1] >= q:\n heappush(heap, [interval[1] - interval[0] + 1, interval[1]])\n \n while heap and heap[0][1] < q:\n heappop(heap)\n \n ans[q] = heap[0][0] if heap else -1\n\n return [ans[q] for q in queries]\n\n\n``` | 0 | You wrote down many **positive** integers in a string called `num`. However, you realized that you forgot to add commas to seperate the different numbers. You remember that the list of integers was **non-decreasing** and that **no** integer had leading zeros.
Return _the **number of possible lists of integers** that you could have written down to get the string_ `num`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** num = "327 "
**Output:** 2
**Explanation:** You could have written down the numbers:
3, 27
327
**Example 2:**
**Input:** num = "094 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Example 3:**
**Input:** num = "0 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Constraints:**
* `1 <= num.length <= 3500`
* `num` consists of digits `'0'` through `'9'`. | Is there a way to order the intervals and queries such that it takes less time to query? Is there a way to add and remove intervals by going from the smallest query to the largest query to find the minimum size? |
💡💡 Neatly coded minheap solution in python3 | minimum-interval-to-include-each-query | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse minheap to store the possible intervals for the current query and pop the minimum interval.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe start with creating a minheap. Now, we sort the queries dynamically as we want to have the order of these queries intact. \nInside the for loop, we haev 2 while loops:\n1. Check the start time of the interval, if q is greater than the start, add it to minheap in the format - (interval, end time) - (l-r+1, r)\n2. Check the end time or r and compare with q. If q > interval, pop it from the minheap. \nNow, append the interval of the minheap element without popping it. \n> We use the second while loop because when we entered the intervals into minheap for earlier queries, we might\'ve pushed intervals that current q might not belong to, so we check and pop.\n\n# Example \n```\nq = [2, 3, 4, 5]\nintervals = [[1, 4], [2, 4], [3, 6], [4, 4]]\nminheap = []\n\nfor q = 2:\ni = 0\nminheap = [(3, 4), (4, 4)]\ni stopped it 2\nres = 3\n\nfor q = 3:\ni = 2\nminheap = [(3, 4), (4, 4), (4, 6)]\ni stopped at 3\nres = 3\n\nfor q = 4:\ni = 2\nminheap = [(1, 4), (3, 4), (4, 4), (4, 6)]\ni exhausted\nres = 1\n\nfor q = 5:\nminheap was [(1, 4), (3, 4), (4, 4), (4, 6)]\nAfter second while loop:\nminheap = [(4, 6)]\nres = 4\n\nres = [3, 3, 1, 4]\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nimport heapq\nclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n intervals = sorted(intervals, key=lambda x: (x[0], x[1]))\n\n i = 0\n minheap = []\n res = {}\n for q in sorted(queries):\n while(i < len(intervals) and q >= intervals[i][0]):\n l = intervals[i][0]\n r = intervals[i][1]\n heapq.heappush(minheap, (r-l+1, r))\n i += 1\n while(minheap and q > minheap[0][1]):\n heapq.heappop(minheap)\n if minheap:\n res[q] = minheap[0][0]\n else:\n res[q] = -1\n\n small = []\n for q in queries:\n small.append(res[q])\n return small\n``` | 0 | You are given a 2D integer array `intervals`, where `intervals[i] = [lefti, righti]` describes the `ith` interval starting at `lefti` and ending at `righti` **(inclusive)**. The **size** of an interval is defined as the number of integers it contains, or more formally `righti - lefti + 1`.
You are also given an integer array `queries`. The answer to the `jth` query is the **size of the smallest interval** `i` such that `lefti <= queries[j] <= righti`. If no such interval exists, the answer is `-1`.
Return _an array containing the answers to the queries_.
**Example 1:**
**Input:** intervals = \[\[1,4\],\[2,4\],\[3,6\],\[4,4\]\], queries = \[2,3,4,5\]
**Output:** \[3,3,1,4\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,4\] is the smallest interval containing 2. The answer is 4 - 2 + 1 = 3.
- Query = 3: The interval \[2,4\] is the smallest interval containing 3. The answer is 4 - 2 + 1 = 3.
- Query = 4: The interval \[4,4\] is the smallest interval containing 4. The answer is 4 - 4 + 1 = 1.
- Query = 5: The interval \[3,6\] is the smallest interval containing 5. The answer is 6 - 3 + 1 = 4.
**Example 2:**
**Input:** intervals = \[\[2,3\],\[2,5\],\[1,8\],\[20,25\]\], queries = \[2,19,5,22\]
**Output:** \[2,-1,4,6\]
**Explanation:** The queries are processed as follows:
- Query = 2: The interval \[2,3\] is the smallest interval containing 2. The answer is 3 - 2 + 1 = 2.
- Query = 19: None of the intervals contain 19. The answer is -1.
- Query = 5: The interval \[2,5\] is the smallest interval containing 5. The answer is 5 - 2 + 1 = 4.
- Query = 22: The interval \[20,25\] is the smallest interval containing 22. The answer is 25 - 20 + 1 = 6.
**Constraints:**
* `1 <= intervals.length <= 105`
* `1 <= queries.length <= 105`
* `intervals[i].length == 2`
* `1 <= lefti <= righti <= 107`
* `1 <= queries[j] <= 107` | Sort the events by its startTime. For every event, you can either choose it and consider the next event available, or you can ignore it. You can efficiently find the next event that is available using binary search. |
💡💡 Neatly coded minheap solution in python3 | minimum-interval-to-include-each-query | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse minheap to store the possible intervals for the current query and pop the minimum interval.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe start with creating a minheap. Now, we sort the queries dynamically as we want to have the order of these queries intact. \nInside the for loop, we haev 2 while loops:\n1. Check the start time of the interval, if q is greater than the start, add it to minheap in the format - (interval, end time) - (l-r+1, r)\n2. Check the end time or r and compare with q. If q > interval, pop it from the minheap. \nNow, append the interval of the minheap element without popping it. \n> We use the second while loop because when we entered the intervals into minheap for earlier queries, we might\'ve pushed intervals that current q might not belong to, so we check and pop.\n\n# Example \n```\nq = [2, 3, 4, 5]\nintervals = [[1, 4], [2, 4], [3, 6], [4, 4]]\nminheap = []\n\nfor q = 2:\ni = 0\nminheap = [(3, 4), (4, 4)]\ni stopped it 2\nres = 3\n\nfor q = 3:\ni = 2\nminheap = [(3, 4), (4, 4), (4, 6)]\ni stopped at 3\nres = 3\n\nfor q = 4:\ni = 2\nminheap = [(1, 4), (3, 4), (4, 4), (4, 6)]\ni exhausted\nres = 1\n\nfor q = 5:\nminheap was [(1, 4), (3, 4), (4, 4), (4, 6)]\nAfter second while loop:\nminheap = [(4, 6)]\nres = 4\n\nres = [3, 3, 1, 4]\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nimport heapq\nclass Solution:\n def minInterval(self, intervals: List[List[int]], queries: List[int]) -> List[int]:\n intervals = sorted(intervals, key=lambda x: (x[0], x[1]))\n\n i = 0\n minheap = []\n res = {}\n for q in sorted(queries):\n while(i < len(intervals) and q >= intervals[i][0]):\n l = intervals[i][0]\n r = intervals[i][1]\n heapq.heappush(minheap, (r-l+1, r))\n i += 1\n while(minheap and q > minheap[0][1]):\n heapq.heappop(minheap)\n if minheap:\n res[q] = minheap[0][0]\n else:\n res[q] = -1\n\n small = []\n for q in queries:\n small.append(res[q])\n return small\n``` | 0 | You wrote down many **positive** integers in a string called `num`. However, you realized that you forgot to add commas to seperate the different numbers. You remember that the list of integers was **non-decreasing** and that **no** integer had leading zeros.
Return _the **number of possible lists of integers** that you could have written down to get the string_ `num`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** num = "327 "
**Output:** 2
**Explanation:** You could have written down the numbers:
3, 27
327
**Example 2:**
**Input:** num = "094 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Example 3:**
**Input:** num = "0 "
**Output:** 0
**Explanation:** No numbers can have leading zeros and all numbers must be positive.
**Constraints:**
* `1 <= num.length <= 3500`
* `num` consists of digits `'0'` through `'9'`. | Is there a way to order the intervals and queries such that it takes less time to query? Is there a way to add and remove intervals by going from the smallest query to the largest query to find the minimum size? |
Python3 O(N) | maximum-population-year | 0 | 1 | ### Steps\n1. For each log, update an array which stores the population changes in each year. The first index corresponds to the year 1950, and the last to the year 2050. \n1. Then, iterate through the years while updating the running sum, max population and year of that max population.\n1. Return that year.\n\n```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n # the timespan 1950-2050 covers 101 years\n\t\tdelta = [0] * 101\n\n\t\t# to make explicit the conversion from the year (1950 + i) to the ith index\n conversionDiff = 1950 \n\t\t\n for l in logs:\n\t\t\t# the log\'s first entry, birth, increases the population by 1\n delta[l[0] - conversionDiff] += 1 \n\t\t\t\n\t\t\t# the log\'s second entry, death, decreases the population by 1\n delta[l[1] - conversionDiff] -= 1\n \n runningSum = 0\n maxPop = 0\n year = 1950\n\t\t\n\t\t# find the year with the greatest population\n for i, d in enumerate(delta):\n runningSum += d\n\t\t\t\n\t\t\t# since we want the first year this population was reached, only update if strictly greater than the previous maximum population\n if runningSum > maxPop:\n maxPop = runningSum\n year = conversionDiff + i\n\t\t\t\t\n return year\n```\n\nThis idea works because we have a limited number of years (101) to track. If this number were higher, we could instead sort then iterate, for an O(nlogn) complexity with O(n) memory solution. | 35 | You are given a 2D integer array `logs` where each `logs[i] = [birthi, deathi]` indicates the birth and death years of the `ith` person.
The **population** of some year `x` is the number of people alive during that year. The `ith` person is counted in year `x`'s population if `x` is in the **inclusive** range `[birthi, deathi - 1]`. Note that the person is **not** counted in the year that they die.
Return _the **earliest** year with the **maximum population**_.
**Example 1:**
**Input:** logs = \[\[1993,1999\],\[2000,2010\]\]
**Output:** 1993
**Explanation:** The maximum population is 1, and 1993 is the earliest year with this population.
**Example 2:**
**Input:** logs = \[\[1950,1961\],\[1960,1971\],\[1970,1981\]\]
**Output:** 1960
**Explanation:**
The maximum population is 2, and it had happened in years 1960 and 1970.
The earlier year between them is 1960.
**Constraints:**
* `1 <= logs.length <= 100`
* `1950 <= birthi < deathi <= 2050` | null |
Simple Python solution with explanation | maximum-population-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n return self.sol1(logs)\n\n def sol1(self, logs):\n\n # First we build an array of length 101, corresponding to the years 1950 to 2050\n\n years = [0] * 101\n\n # next we process each log\n\n # for each record, we increment the value in the array for each year they were alive\n\n for log in logs:\n birth_idx = log[0] - 1950\n death_idx = log[1] - 1950\n\n for i in range(birth_idx, death_idx):\n years[i] += 1\n \n print(years)\n # At this point the years array has a value at each position the number of people that were alive that year\n\n # we simply need to find the idx of the first position with the max population \n\n max_pop = 0\n max_idx = 0\n\n for idx,year in enumerate(years):\n if year > max_pop:\n max_pop = year\n max_idx = idx\n \n\n return max_idx + 1950\n\n\n\n\n``` | 1 | You are given a 2D integer array `logs` where each `logs[i] = [birthi, deathi]` indicates the birth and death years of the `ith` person.
The **population** of some year `x` is the number of people alive during that year. The `ith` person is counted in year `x`'s population if `x` is in the **inclusive** range `[birthi, deathi - 1]`. Note that the person is **not** counted in the year that they die.
Return _the **earliest** year with the **maximum population**_.
**Example 1:**
**Input:** logs = \[\[1993,1999\],\[2000,2010\]\]
**Output:** 1993
**Explanation:** The maximum population is 1, and 1993 is the earliest year with this population.
**Example 2:**
**Input:** logs = \[\[1950,1961\],\[1960,1971\],\[1970,1981\]\]
**Output:** 1960
**Explanation:**
The maximum population is 2, and it had happened in years 1960 and 1970.
The earlier year between them is 1960.
**Constraints:**
* `1 <= logs.length <= 100`
* `1950 <= birthi < deathi <= 2050` | null |
Easy Python Solution for beginners | maximum-population-year | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- This solution iterates through each year in the range of birth years to death years and counts the population by checking if the year falls within the inclusive range for each individual. \n- It then keeps track of the maximum population and the corresponding year. \n- While this solution is less efficient for larger input data, it\'s easy to understand.\n\n# Code\n```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n min_year = float(\'inf\') # To find the minimum birth year\n max_year = float(\'-inf\') # To find the maximum death year\n \n # Find the minimum birth year and maximum death year\n for birth, death in logs:\n min_year = min(min_year, birth)\n max_year = max(max_year, death - 1)\n \n max_population = 0\n max_population_year = None\n \n # Iterate through each year and count the population\n for year in range(min_year, max_year + 1):\n population = 0\n for birth, death in logs:\n if birth <= year <= death - 1:\n population += 1\n if population > max_population:\n max_population = population\n max_population_year = year\n \n return max_population_year\n```\n\n | 2 | You are given a 2D integer array `logs` where each `logs[i] = [birthi, deathi]` indicates the birth and death years of the `ith` person.
The **population** of some year `x` is the number of people alive during that year. The `ith` person is counted in year `x`'s population if `x` is in the **inclusive** range `[birthi, deathi - 1]`. Note that the person is **not** counted in the year that they die.
Return _the **earliest** year with the **maximum population**_.
**Example 1:**
**Input:** logs = \[\[1993,1999\],\[2000,2010\]\]
**Output:** 1993
**Explanation:** The maximum population is 1, and 1993 is the earliest year with this population.
**Example 2:**
**Input:** logs = \[\[1950,1961\],\[1960,1971\],\[1970,1981\]\]
**Output:** 1960
**Explanation:**
The maximum population is 2, and it had happened in years 1960 and 1970.
The earlier year between them is 1960.
**Constraints:**
* `1 <= logs.length <= 100`
* `1950 <= birthi < deathi <= 2050` | null |
Python || 97.44% Faster || O(N) Solution || Hashmap | maximum-population-year | 0 | 1 | ```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n a,n=[0]*101,len(logs)\n for birth,death in logs:\n a[birth-1950]+=1\n a[death-1950]-=1\n c=m=year=0\n for i in range(101):\n c+=a[i]\n if c>m:\n m=c\n year=i+1950\n return year\n```\n\n**An upvote will be encouraging** | 5 | You are given a 2D integer array `logs` where each `logs[i] = [birthi, deathi]` indicates the birth and death years of the `ith` person.
The **population** of some year `x` is the number of people alive during that year. The `ith` person is counted in year `x`'s population if `x` is in the **inclusive** range `[birthi, deathi - 1]`. Note that the person is **not** counted in the year that they die.
Return _the **earliest** year with the **maximum population**_.
**Example 1:**
**Input:** logs = \[\[1993,1999\],\[2000,2010\]\]
**Output:** 1993
**Explanation:** The maximum population is 1, and 1993 is the earliest year with this population.
**Example 2:**
**Input:** logs = \[\[1950,1961\],\[1960,1971\],\[1970,1981\]\]
**Output:** 1960
**Explanation:**
The maximum population is 2, and it had happened in years 1960 and 1970.
The earlier year between them is 1960.
**Constraints:**
* `1 <= logs.length <= 100`
* `1950 <= birthi < deathi <= 2050` | null |
[Python3] greedy | maximum-population-year | 0 | 1 | \n```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n vals = []\n for x, y in logs: \n vals.append((x, 1))\n vals.append((y, -1))\n ans = prefix = most = 0\n for x, k in sorted(vals): \n prefix += k\n if prefix > most: \n ans = x\n most = prefix \n return ans \n``` | 9 | You are given a 2D integer array `logs` where each `logs[i] = [birthi, deathi]` indicates the birth and death years of the `ith` person.
The **population** of some year `x` is the number of people alive during that year. The `ith` person is counted in year `x`'s population if `x` is in the **inclusive** range `[birthi, deathi - 1]`. Note that the person is **not** counted in the year that they die.
Return _the **earliest** year with the **maximum population**_.
**Example 1:**
**Input:** logs = \[\[1993,1999\],\[2000,2010\]\]
**Output:** 1993
**Explanation:** The maximum population is 1, and 1993 is the earliest year with this population.
**Example 2:**
**Input:** logs = \[\[1950,1961\],\[1960,1971\],\[1970,1981\]\]
**Output:** 1960
**Explanation:**
The maximum population is 2, and it had happened in years 1960 and 1970.
The earlier year between them is 1960.
**Constraints:**
* `1 <= logs.length <= 100`
* `1950 <= birthi < deathi <= 2050` | null |
4 liner, hash map solution | maximum-population-year | 0 | 1 | ```\ncount = {}\nfor i in logs:\n for v in range(i[0],i[1]):\n count[v] = count.get(v,0) + 1\n m = max(count.values())\n return min([i for i in count if count[i] == m])\n``` | 2 | You are given a 2D integer array `logs` where each `logs[i] = [birthi, deathi]` indicates the birth and death years of the `ith` person.
The **population** of some year `x` is the number of people alive during that year. The `ith` person is counted in year `x`'s population if `x` is in the **inclusive** range `[birthi, deathi - 1]`. Note that the person is **not** counted in the year that they die.
Return _the **earliest** year with the **maximum population**_.
**Example 1:**
**Input:** logs = \[\[1993,1999\],\[2000,2010\]\]
**Output:** 1993
**Explanation:** The maximum population is 1, and 1993 is the earliest year with this population.
**Example 2:**
**Input:** logs = \[\[1950,1961\],\[1960,1971\],\[1970,1981\]\]
**Output:** 1960
**Explanation:**
The maximum population is 2, and it had happened in years 1960 and 1970.
The earlier year between them is 1960.
**Constraints:**
* `1 <= logs.length <= 100`
* `1950 <= birthi < deathi <= 2050` | null |
Binary Search Python Explained | maximum-distance-between-a-pair-of-values | 0 | 1 | # Intuition\nThrough the given problem we have few conditions\n`1. j >= i`\n`2. nums2[j] > nums1[i]`\n\nNow to satisfy these conditions for every element in of nums1 we have to iterate over nums2(i, len(nums2))\n\nso we will use **binary search** having the above range always\nnow if we find *nums[mid] < nums1[i] => we can\'t consider* this thus shift ur right\n\nif *nums[mid] >= nums1[i] => we know the array is in descending order so store this mid index values as farthestSeen* now and shift left pointer.\n\n`why not return here?` Because to get the farthest position we have to find element > nums1[i] as far as possible from i\n\nCalculate the diff(j-i) and return the maxDiff as your ans :)\n\n# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n def binary(left, right, num):\n farthestPos = 0\n while left < right:\n mid = (left + right) // 2\n if nums2[mid] < num:\n right = mid\n else:\n farthestPos = max(farthestPos, mid)\n left = mid + 1\n if nums2[left] >= num:\n farthestPos = max(farthestPos, left)\n return farthestPos\n maxDiff = 0\n for i in range(min(len(nums1), len(nums2))):\n if nums1[i] > nums2[i]:\n continue\n else:\n j = binary(i, len(nums2)-1, nums1[i])\n maxDiff = max(maxDiff, (j-i))\n return maxDiff\n``` | 2 | You are given two **non-increasing 0-indexed** integer arrays `nums1` and `nums2`.
A pair of indices `(i, j)`, where `0 <= i < nums1.length` and `0 <= j < nums2.length`, is **valid** if both `i <= j` and `nums1[i] <= nums2[j]`. The **distance** of the pair is `j - i`.
Return _the **maximum distance** of any **valid** pair_ `(i, j)`_. If there are no valid pairs, return_ `0`.
An array `arr` is **non-increasing** if `arr[i-1] >= arr[i]` for every `1 <= i < arr.length`.
**Example 1:**
**Input:** nums1 = \[55,30,5,4,2\], nums2 = \[100,20,10,10,5\]
**Output:** 2
**Explanation:** The valid pairs are (0,0), (2,2), (2,3), (2,4), (3,3), (3,4), and (4,4).
The maximum distance is 2 with pair (2,4).
**Example 2:**
**Input:** nums1 = \[2,2,2\], nums2 = \[10,10,1\]
**Output:** 1
**Explanation:** The valid pairs are (0,0), (0,1), and (1,1).
The maximum distance is 1 with pair (0,1).
**Example 3:**
**Input:** nums1 = \[30,29,19,5\], nums2 = \[25,25,25,25,25\]
**Output:** 2
**Explanation:** The valid pairs are (2,2), (2,3), (2,4), (3,3), and (3,4).
The maximum distance is 2 with pair (2,4).
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 105`
* Both `nums1` and `nums2` are **non-increasing**. | null |
Binary Search Python Explained | maximum-distance-between-a-pair-of-values | 0 | 1 | # Intuition\nThrough the given problem we have few conditions\n`1. j >= i`\n`2. nums2[j] > nums1[i]`\n\nNow to satisfy these conditions for every element in of nums1 we have to iterate over nums2(i, len(nums2))\n\nso we will use **binary search** having the above range always\nnow if we find *nums[mid] < nums1[i] => we can\'t consider* this thus shift ur right\n\nif *nums[mid] >= nums1[i] => we know the array is in descending order so store this mid index values as farthestSeen* now and shift left pointer.\n\n`why not return here?` Because to get the farthest position we have to find element > nums1[i] as far as possible from i\n\nCalculate the diff(j-i) and return the maxDiff as your ans :)\n\n# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n def binary(left, right, num):\n farthestPos = 0\n while left < right:\n mid = (left + right) // 2\n if nums2[mid] < num:\n right = mid\n else:\n farthestPos = max(farthestPos, mid)\n left = mid + 1\n if nums2[left] >= num:\n farthestPos = max(farthestPos, left)\n return farthestPos\n maxDiff = 0\n for i in range(min(len(nums1), len(nums2))):\n if nums1[i] > nums2[i]:\n continue\n else:\n j = binary(i, len(nums2)-1, nums1[i])\n maxDiff = max(maxDiff, (j-i))\n return maxDiff\n``` | 2 | You are given a **0-indexed** integer array `nums`, where `nums[i]` represents the score of the `ith` student. You are also given an integer `k`.
Pick the scores of any `k` students from the array so that the **difference** between the **highest** and the **lowest** of the `k` scores is **minimized**.
Return _the **minimum** possible difference_.
**Example 1:**
**Input:** nums = \[90\], k = 1
**Output:** 0
**Explanation:** There is one way to pick score(s) of one student:
- \[**90**\]. The difference between the highest and lowest score is 90 - 90 = 0.
The minimum possible difference is 0.
**Example 2:**
**Input:** nums = \[9,4,1,7\], k = 2
**Output:** 2
**Explanation:** There are six ways to pick score(s) of two students:
- \[**9**,**4**,1,7\]. The difference between the highest and lowest score is 9 - 4 = 5.
- \[**9**,4,**1**,7\]. The difference between the highest and lowest score is 9 - 1 = 8.
- \[**9**,4,1,**7**\]. The difference between the highest and lowest score is 9 - 7 = 2.
- \[9,**4**,**1**,7\]. The difference between the highest and lowest score is 4 - 1 = 3.
- \[9,**4**,1,**7**\]. The difference between the highest and lowest score is 7 - 4 = 3.
- \[9,4,**1**,**7**\]. The difference between the highest and lowest score is 7 - 1 = 6.
The minimum possible difference is 2.
**Constraints:**
* `1 <= k <= nums.length <= 1000`
* `0 <= nums[i] <= 105` | Since both arrays are sorted in a non-increasing way this means that for each value in the first array. We can find the farthest value smaller than it using binary search. There is another solution using a two pointers approach since the first array is non-increasing the farthest j such that nums2[j] ≥ nums1[i] is at least as far as the farthest j such that nums2[j] ≥ nums1[i-1] |
📌 Python3 simple solution using two pointers | maximum-distance-between-a-pair-of-values | 0 | 1 | ```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n length1, length2 = len(nums1), len(nums2)\n i,j = 0,0\n \n result = 0\n while i < length1 and j < length2:\n if nums1[i] > nums2[j]:\n i+=1\n else:\n result = max(result,j-i)\n j+=1\n \n return result\n``` | 6 | You are given two **non-increasing 0-indexed** integer arrays `nums1` and `nums2`.
A pair of indices `(i, j)`, where `0 <= i < nums1.length` and `0 <= j < nums2.length`, is **valid** if both `i <= j` and `nums1[i] <= nums2[j]`. The **distance** of the pair is `j - i`.
Return _the **maximum distance** of any **valid** pair_ `(i, j)`_. If there are no valid pairs, return_ `0`.
An array `arr` is **non-increasing** if `arr[i-1] >= arr[i]` for every `1 <= i < arr.length`.
**Example 1:**
**Input:** nums1 = \[55,30,5,4,2\], nums2 = \[100,20,10,10,5\]
**Output:** 2
**Explanation:** The valid pairs are (0,0), (2,2), (2,3), (2,4), (3,3), (3,4), and (4,4).
The maximum distance is 2 with pair (2,4).
**Example 2:**
**Input:** nums1 = \[2,2,2\], nums2 = \[10,10,1\]
**Output:** 1
**Explanation:** The valid pairs are (0,0), (0,1), and (1,1).
The maximum distance is 1 with pair (0,1).
**Example 3:**
**Input:** nums1 = \[30,29,19,5\], nums2 = \[25,25,25,25,25\]
**Output:** 2
**Explanation:** The valid pairs are (2,2), (2,3), (2,4), (3,3), and (3,4).
The maximum distance is 2 with pair (2,4).
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 105`
* Both `nums1` and `nums2` are **non-increasing**. | null |
📌 Python3 simple solution using two pointers | maximum-distance-between-a-pair-of-values | 0 | 1 | ```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n length1, length2 = len(nums1), len(nums2)\n i,j = 0,0\n \n result = 0\n while i < length1 and j < length2:\n if nums1[i] > nums2[j]:\n i+=1\n else:\n result = max(result,j-i)\n j+=1\n \n return result\n``` | 6 | You are given a **0-indexed** integer array `nums`, where `nums[i]` represents the score of the `ith` student. You are also given an integer `k`.
Pick the scores of any `k` students from the array so that the **difference** between the **highest** and the **lowest** of the `k` scores is **minimized**.
Return _the **minimum** possible difference_.
**Example 1:**
**Input:** nums = \[90\], k = 1
**Output:** 0
**Explanation:** There is one way to pick score(s) of one student:
- \[**90**\]. The difference between the highest and lowest score is 90 - 90 = 0.
The minimum possible difference is 0.
**Example 2:**
**Input:** nums = \[9,4,1,7\], k = 2
**Output:** 2
**Explanation:** There are six ways to pick score(s) of two students:
- \[**9**,**4**,1,7\]. The difference between the highest and lowest score is 9 - 4 = 5.
- \[**9**,4,**1**,7\]. The difference between the highest and lowest score is 9 - 1 = 8.
- \[**9**,4,1,**7**\]. The difference between the highest and lowest score is 9 - 7 = 2.
- \[9,**4**,**1**,7\]. The difference between the highest and lowest score is 4 - 1 = 3.
- \[9,**4**,1,**7**\]. The difference between the highest and lowest score is 7 - 4 = 3.
- \[9,4,**1**,**7**\]. The difference between the highest and lowest score is 7 - 1 = 6.
The minimum possible difference is 2.
**Constraints:**
* `1 <= k <= nums.length <= 1000`
* `0 <= nums[i] <= 105` | Since both arrays are sorted in a non-increasing way this means that for each value in the first array. We can find the farthest value smaller than it using binary search. There is another solution using a two pointers approach since the first array is non-increasing the farthest j such that nums2[j] ≥ nums1[i] is at least as far as the farthest j such that nums2[j] ≥ nums1[i-1] |
Binary Search | maximum-distance-between-a-pair-of-values | 0 | 1 | # Intuition\nWe just have to iterate over the first list and find the index of largest number in the second list using binary search.\n\n# Complexity\nm = len(nums1)\nn = len(nums2)\n- Time complexity:\nO(m*log(n))\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n max_d = 0\n l1, l2 = len(nums1), len(nums2)\n for i in range(l1):\n left, right = i, l2 - 1\n while left <= right:\n index = (left + right) // 2\n if nums2[index] >= nums1[i]:\n left = index + 1\n else:\n right = index - 1\n max_d = max(max_d, right - i)\n return max_d\n``` | 2 | You are given two **non-increasing 0-indexed** integer arrays `nums1` and `nums2`.
A pair of indices `(i, j)`, where `0 <= i < nums1.length` and `0 <= j < nums2.length`, is **valid** if both `i <= j` and `nums1[i] <= nums2[j]`. The **distance** of the pair is `j - i`.
Return _the **maximum distance** of any **valid** pair_ `(i, j)`_. If there are no valid pairs, return_ `0`.
An array `arr` is **non-increasing** if `arr[i-1] >= arr[i]` for every `1 <= i < arr.length`.
**Example 1:**
**Input:** nums1 = \[55,30,5,4,2\], nums2 = \[100,20,10,10,5\]
**Output:** 2
**Explanation:** The valid pairs are (0,0), (2,2), (2,3), (2,4), (3,3), (3,4), and (4,4).
The maximum distance is 2 with pair (2,4).
**Example 2:**
**Input:** nums1 = \[2,2,2\], nums2 = \[10,10,1\]
**Output:** 1
**Explanation:** The valid pairs are (0,0), (0,1), and (1,1).
The maximum distance is 1 with pair (0,1).
**Example 3:**
**Input:** nums1 = \[30,29,19,5\], nums2 = \[25,25,25,25,25\]
**Output:** 2
**Explanation:** The valid pairs are (2,2), (2,3), (2,4), (3,3), and (3,4).
The maximum distance is 2 with pair (2,4).
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 105`
* Both `nums1` and `nums2` are **non-increasing**. | null |
Binary Search | maximum-distance-between-a-pair-of-values | 0 | 1 | # Intuition\nWe just have to iterate over the first list and find the index of largest number in the second list using binary search.\n\n# Complexity\nm = len(nums1)\nn = len(nums2)\n- Time complexity:\nO(m*log(n))\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n max_d = 0\n l1, l2 = len(nums1), len(nums2)\n for i in range(l1):\n left, right = i, l2 - 1\n while left <= right:\n index = (left + right) // 2\n if nums2[index] >= nums1[i]:\n left = index + 1\n else:\n right = index - 1\n max_d = max(max_d, right - i)\n return max_d\n``` | 2 | You are given a **0-indexed** integer array `nums`, where `nums[i]` represents the score of the `ith` student. You are also given an integer `k`.
Pick the scores of any `k` students from the array so that the **difference** between the **highest** and the **lowest** of the `k` scores is **minimized**.
Return _the **minimum** possible difference_.
**Example 1:**
**Input:** nums = \[90\], k = 1
**Output:** 0
**Explanation:** There is one way to pick score(s) of one student:
- \[**90**\]. The difference between the highest and lowest score is 90 - 90 = 0.
The minimum possible difference is 0.
**Example 2:**
**Input:** nums = \[9,4,1,7\], k = 2
**Output:** 2
**Explanation:** There are six ways to pick score(s) of two students:
- \[**9**,**4**,1,7\]. The difference between the highest and lowest score is 9 - 4 = 5.
- \[**9**,4,**1**,7\]. The difference between the highest and lowest score is 9 - 1 = 8.
- \[**9**,4,1,**7**\]. The difference between the highest and lowest score is 9 - 7 = 2.
- \[9,**4**,**1**,7\]. The difference between the highest and lowest score is 4 - 1 = 3.
- \[9,**4**,1,**7**\]. The difference between the highest and lowest score is 7 - 4 = 3.
- \[9,4,**1**,**7**\]. The difference between the highest and lowest score is 7 - 1 = 6.
The minimum possible difference is 2.
**Constraints:**
* `1 <= k <= nums.length <= 1000`
* `0 <= nums[i] <= 105` | Since both arrays are sorted in a non-increasing way this means that for each value in the first array. We can find the farthest value smaller than it using binary search. There is another solution using a two pointers approach since the first array is non-increasing the farthest j such that nums2[j] ≥ nums1[i] is at least as far as the farthest j such that nums2[j] ≥ nums1[i-1] |
[Python 3] Monotomic Stack + Prefix Sum - Simple | maximum-subarray-min-product | 0 | 1 | # Intuition\nsimilar to this problem: https://leetcode.com/problems/largest-rectangle-in-histogram/\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n mod = 10 ** 9 + 7\n ps = [0]\n stack = [-1]\n nums.append(0)\n res = 0\n \n for i in range(len(nums)):\n while nums[stack[-1]] > nums[i]:\n min_val = nums[stack.pop()]\n range_sum = ps[i] - ps[stack[-1] + 1]\n res = max(res, range_sum * min_val)\n stack.append(i)\n ps.append(ps[-1] + nums[i])\n return res % mod\n``` | 4 | The **min-product** of an array is equal to the **minimum value** in the array **multiplied by** the array's **sum**.
* For example, the array `[3,2,5]` (minimum value is `2`) has a min-product of `2 * (3+2+5) = 2 * 10 = 20`.
Given an array of integers `nums`, return _the **maximum min-product** of any **non-empty subarray** of_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`.
Note that the min-product should be maximized **before** performing the modulo operation. Testcases are generated such that the maximum min-product **without** modulo will fit in a **64-bit signed integer**.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,3,2\]
**Output:** 14
**Explanation:** The maximum min-product is achieved with the subarray \[2,3,2\] (minimum value is 2).
2 \* (2+3+2) = 2 \* 7 = 14.
**Example 2:**
**Input:** nums = \[2,3,3,1,2\]
**Output:** 18
**Explanation:** The maximum min-product is achieved with the subarray \[3,3\] (minimum value is 3).
3 \* (3+3) = 3 \* 6 = 18.
**Example 3:**
**Input:** nums = \[3,1,5,6,4,2\]
**Output:** 60
**Explanation:** The maximum min-product is achieved with the subarray \[5,6,4\] (minimum value is 4).
4 \* (5+6+4) = 4 \* 15 = 60.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
[Python 3] Monotomic Stack + Prefix Sum - Simple | maximum-subarray-min-product | 0 | 1 | # Intuition\nsimilar to this problem: https://leetcode.com/problems/largest-rectangle-in-histogram/\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n mod = 10 ** 9 + 7\n ps = [0]\n stack = [-1]\n nums.append(0)\n res = 0\n \n for i in range(len(nums)):\n while nums[stack[-1]] > nums[i]:\n min_val = nums[stack.pop()]\n range_sum = ps[i] - ps[stack[-1] + 1]\n res = max(res, range_sum * min_val)\n stack.append(i)\n ps.append(ps[-1] + nums[i])\n return res % mod\n``` | 4 | You are given an array of strings `nums` and an integer `k`. Each string in `nums` represents an integer without leading zeros.
Return _the string that represents the_ `kth` _**largest integer** in_ `nums`.
**Note**: Duplicate numbers should be counted distinctly. For example, if `nums` is `[ "1 ", "2 ", "2 "]`, `"2 "` is the first largest integer, `"2 "` is the second-largest integer, and `"1 "` is the third-largest integer.
**Example 1:**
**Input:** nums = \[ "3 ", "6 ", "7 ", "10 "\], k = 4
**Output:** "3 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "3 ", "6 ", "7 ", "10 "\].
The 4th largest integer in nums is "3 ".
**Example 2:**
**Input:** nums = \[ "2 ", "21 ", "12 ", "1 "\], k = 3
**Output:** "2 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "1 ", "2 ", "12 ", "21 "\].
The 3rd largest integer in nums is "2 ".
**Example 3:**
**Input:** nums = \[ "0 ", "0 "\], k = 2
**Output:** "0 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "0 ", "0 "\].
The 2nd largest integer in nums is "0 ".
**Constraints:**
* `1 <= k <= nums.length <= 104`
* `1 <= nums[i].length <= 100`
* `nums[i]` consists of only digits.
* `nums[i]` will not have any leading zeros. | Is there a way we can sort the elements to simplify the problem? Can we find the maximum min-product for every value in the array? |
[Python] Disjoint Set Union, iterate from largest to smallest | maximum-subarray-min-product | 0 | 1 | This is a intuition of the process\n- We iterate from the largest number to the smallest number.\n- At every iteration, if the adjacent number(s) is larger than the current number, merge it with the adjacent group(s).\n- After every merge, we update the sum of the group and the minimum value of the group. We update the result if applicable.\n\nWe use a disjoint set union to track the group membership. You can get the disjoint set union template from elsewhere.\n\nWe use another dictionary to track the current sum of each group.\n\n```python\nclass DisjointSet:\n # github.com/not522/ac-library-python/blob/master/atcoder/dsu.py\n\n def __init__(self, n: int = 0) -> None:\n self._n = n\n self.parent_or_size = [-1]*n\n\n def union(self, a: int, b: int) -> int:\n x = self.find(a)\n y = self.find(b)\n\n if x == y:\n return x\n\n if -self.parent_or_size[x] < -self.parent_or_size[y]:\n x, y = y, x\n\n self.parent_or_size[x] += self.parent_or_size[y]\n self.parent_or_size[y] = x\n\n return x\n\n def find(self, a: int) -> int:\n parent = self.parent_or_size[a]\n while parent >= 0:\n if self.parent_or_size[parent] < 0:\n return parent\n self.parent_or_size[a], a, parent = (\n self.parent_or_size[parent],\n self.parent_or_size[parent],\n self.parent_or_size[self.parent_or_size[parent]]\n )\n\n return a\n\n def size(self, a: int) -> int:\n return -self.parent_or_size[self.leader(a)]\n\n\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n \n # we begin from the largest number to the smallest number\n nums = [0] + nums + [0]\n pos = [(x,i) for i,x in enumerate(nums)]\n pos.sort()\n pos.reverse()\n \n # we track the result with this variable\n maxres = 0\n \n # we track the membership of each element\n # d.find(x) == d.find(y) if x and y are in the same group\n d = DisjointSet(len(nums))\n\n # we track the current sum of each group with a dictionary\n # map group_id (which may change over time) to the sum\n segsums = {}\n \n # iterate from the largest to the smallest number and index\n # excluding the two zeros padded at the ends\n for x,i in pos[:-2]:\n minval = x # current value is minimum since we iterate from large to small\n segsum = x\n \n # if the left element is larger\n if nums[i-1] > nums[i]: \n idx = d.find(i-1) # get group index\n segsum += segsums[idx] # include sum of adjacent group\n d.union(i, i-1) # combine groups\n \n # equality because we iterate with decreasing index as well\n if nums[i+1] >= nums[i]:\n idx = d.find(i+1)\n segsum += segsums[idx]\n d.union(i, i+1)\n \n # update sum of group\n segsums[d.find(i)] = segsum \n \n # update the result\n maxres = max(maxres, minval*segsum)\n \n # remember to take modulo\n return maxres%(10**9+7)\n```\n\nThe algorithm runs in O(n log n) due to the sorting. | 8 | The **min-product** of an array is equal to the **minimum value** in the array **multiplied by** the array's **sum**.
* For example, the array `[3,2,5]` (minimum value is `2`) has a min-product of `2 * (3+2+5) = 2 * 10 = 20`.
Given an array of integers `nums`, return _the **maximum min-product** of any **non-empty subarray** of_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`.
Note that the min-product should be maximized **before** performing the modulo operation. Testcases are generated such that the maximum min-product **without** modulo will fit in a **64-bit signed integer**.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,3,2\]
**Output:** 14
**Explanation:** The maximum min-product is achieved with the subarray \[2,3,2\] (minimum value is 2).
2 \* (2+3+2) = 2 \* 7 = 14.
**Example 2:**
**Input:** nums = \[2,3,3,1,2\]
**Output:** 18
**Explanation:** The maximum min-product is achieved with the subarray \[3,3\] (minimum value is 3).
3 \* (3+3) = 3 \* 6 = 18.
**Example 3:**
**Input:** nums = \[3,1,5,6,4,2\]
**Output:** 60
**Explanation:** The maximum min-product is achieved with the subarray \[5,6,4\] (minimum value is 4).
4 \* (5+6+4) = 4 \* 15 = 60.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
[Python] Disjoint Set Union, iterate from largest to smallest | maximum-subarray-min-product | 0 | 1 | This is a intuition of the process\n- We iterate from the largest number to the smallest number.\n- At every iteration, if the adjacent number(s) is larger than the current number, merge it with the adjacent group(s).\n- After every merge, we update the sum of the group and the minimum value of the group. We update the result if applicable.\n\nWe use a disjoint set union to track the group membership. You can get the disjoint set union template from elsewhere.\n\nWe use another dictionary to track the current sum of each group.\n\n```python\nclass DisjointSet:\n # github.com/not522/ac-library-python/blob/master/atcoder/dsu.py\n\n def __init__(self, n: int = 0) -> None:\n self._n = n\n self.parent_or_size = [-1]*n\n\n def union(self, a: int, b: int) -> int:\n x = self.find(a)\n y = self.find(b)\n\n if x == y:\n return x\n\n if -self.parent_or_size[x] < -self.parent_or_size[y]:\n x, y = y, x\n\n self.parent_or_size[x] += self.parent_or_size[y]\n self.parent_or_size[y] = x\n\n return x\n\n def find(self, a: int) -> int:\n parent = self.parent_or_size[a]\n while parent >= 0:\n if self.parent_or_size[parent] < 0:\n return parent\n self.parent_or_size[a], a, parent = (\n self.parent_or_size[parent],\n self.parent_or_size[parent],\n self.parent_or_size[self.parent_or_size[parent]]\n )\n\n return a\n\n def size(self, a: int) -> int:\n return -self.parent_or_size[self.leader(a)]\n\n\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n \n # we begin from the largest number to the smallest number\n nums = [0] + nums + [0]\n pos = [(x,i) for i,x in enumerate(nums)]\n pos.sort()\n pos.reverse()\n \n # we track the result with this variable\n maxres = 0\n \n # we track the membership of each element\n # d.find(x) == d.find(y) if x and y are in the same group\n d = DisjointSet(len(nums))\n\n # we track the current sum of each group with a dictionary\n # map group_id (which may change over time) to the sum\n segsums = {}\n \n # iterate from the largest to the smallest number and index\n # excluding the two zeros padded at the ends\n for x,i in pos[:-2]:\n minval = x # current value is minimum since we iterate from large to small\n segsum = x\n \n # if the left element is larger\n if nums[i-1] > nums[i]: \n idx = d.find(i-1) # get group index\n segsum += segsums[idx] # include sum of adjacent group\n d.union(i, i-1) # combine groups\n \n # equality because we iterate with decreasing index as well\n if nums[i+1] >= nums[i]:\n idx = d.find(i+1)\n segsum += segsums[idx]\n d.union(i, i+1)\n \n # update sum of group\n segsums[d.find(i)] = segsum \n \n # update the result\n maxres = max(maxres, minval*segsum)\n \n # remember to take modulo\n return maxres%(10**9+7)\n```\n\nThe algorithm runs in O(n log n) due to the sorting. | 8 | You are given an array of strings `nums` and an integer `k`. Each string in `nums` represents an integer without leading zeros.
Return _the string that represents the_ `kth` _**largest integer** in_ `nums`.
**Note**: Duplicate numbers should be counted distinctly. For example, if `nums` is `[ "1 ", "2 ", "2 "]`, `"2 "` is the first largest integer, `"2 "` is the second-largest integer, and `"1 "` is the third-largest integer.
**Example 1:**
**Input:** nums = \[ "3 ", "6 ", "7 ", "10 "\], k = 4
**Output:** "3 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "3 ", "6 ", "7 ", "10 "\].
The 4th largest integer in nums is "3 ".
**Example 2:**
**Input:** nums = \[ "2 ", "21 ", "12 ", "1 "\], k = 3
**Output:** "2 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "1 ", "2 ", "12 ", "21 "\].
The 3rd largest integer in nums is "2 ".
**Example 3:**
**Input:** nums = \[ "0 ", "0 "\], k = 2
**Output:** "0 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "0 ", "0 "\].
The 2nd largest integer in nums is "0 ".
**Constraints:**
* `1 <= k <= nums.length <= 104`
* `1 <= nums[i].length <= 100`
* `nums[i]` consists of only digits.
* `nums[i]` will not have any leading zeros. | Is there a way we can sort the elements to simplify the problem? Can we find the maximum min-product for every value in the array? |
[Python3] mono-stack | maximum-subarray-min-product | 0 | 1 | \n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n prefix = [0]\n for x in nums: prefix.append(prefix[-1] + x)\n \n ans = 0 \n stack = []\n for i, x in enumerate(nums + [-inf]): # append "-inf" to force flush all elements\n while stack and stack[-1][1] >= x: \n _, xx = stack.pop()\n ii = stack[-1][0] if stack else -1 \n ans = max(ans, xx*(prefix[i] - prefix[ii+1]))\n stack.append((i, x))\n return ans % 1_000_000_007\n``` | 12 | The **min-product** of an array is equal to the **minimum value** in the array **multiplied by** the array's **sum**.
* For example, the array `[3,2,5]` (minimum value is `2`) has a min-product of `2 * (3+2+5) = 2 * 10 = 20`.
Given an array of integers `nums`, return _the **maximum min-product** of any **non-empty subarray** of_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`.
Note that the min-product should be maximized **before** performing the modulo operation. Testcases are generated such that the maximum min-product **without** modulo will fit in a **64-bit signed integer**.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,3,2\]
**Output:** 14
**Explanation:** The maximum min-product is achieved with the subarray \[2,3,2\] (minimum value is 2).
2 \* (2+3+2) = 2 \* 7 = 14.
**Example 2:**
**Input:** nums = \[2,3,3,1,2\]
**Output:** 18
**Explanation:** The maximum min-product is achieved with the subarray \[3,3\] (minimum value is 3).
3 \* (3+3) = 3 \* 6 = 18.
**Example 3:**
**Input:** nums = \[3,1,5,6,4,2\]
**Output:** 60
**Explanation:** The maximum min-product is achieved with the subarray \[5,6,4\] (minimum value is 4).
4 \* (5+6+4) = 4 \* 15 = 60.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
[Python3] mono-stack | maximum-subarray-min-product | 0 | 1 | \n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n prefix = [0]\n for x in nums: prefix.append(prefix[-1] + x)\n \n ans = 0 \n stack = []\n for i, x in enumerate(nums + [-inf]): # append "-inf" to force flush all elements\n while stack and stack[-1][1] >= x: \n _, xx = stack.pop()\n ii = stack[-1][0] if stack else -1 \n ans = max(ans, xx*(prefix[i] - prefix[ii+1]))\n stack.append((i, x))\n return ans % 1_000_000_007\n``` | 12 | You are given an array of strings `nums` and an integer `k`. Each string in `nums` represents an integer without leading zeros.
Return _the string that represents the_ `kth` _**largest integer** in_ `nums`.
**Note**: Duplicate numbers should be counted distinctly. For example, if `nums` is `[ "1 ", "2 ", "2 "]`, `"2 "` is the first largest integer, `"2 "` is the second-largest integer, and `"1 "` is the third-largest integer.
**Example 1:**
**Input:** nums = \[ "3 ", "6 ", "7 ", "10 "\], k = 4
**Output:** "3 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "3 ", "6 ", "7 ", "10 "\].
The 4th largest integer in nums is "3 ".
**Example 2:**
**Input:** nums = \[ "2 ", "21 ", "12 ", "1 "\], k = 3
**Output:** "2 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "1 ", "2 ", "12 ", "21 "\].
The 3rd largest integer in nums is "2 ".
**Example 3:**
**Input:** nums = \[ "0 ", "0 "\], k = 2
**Output:** "0 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "0 ", "0 "\].
The 2nd largest integer in nums is "0 ".
**Constraints:**
* `1 <= k <= nums.length <= 104`
* `1 <= nums[i].length <= 100`
* `nums[i]` consists of only digits.
* `nums[i]` will not have any leading zeros. | Is there a way we can sort the elements to simplify the problem? Can we find the maximum min-product for every value in the array? |
Python monotonic stack beats 100% | maximum-subarray-min-product | 0 | 1 | a monotonic stack with index and prefix sum\n\n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n mod=int(1e9+7)\n stack=[] # (index, prefix sum at index)\n rsum=0\n res=0\n \n nums.append(0)\n \n for i, v in enumerate(nums):\n while stack and nums[stack[-1][0]] >= v:\n index, _ = stack.pop()\n\t\t\t\t\n\t\t\t\t# if the stack is empty, the subarray sum is the current prefixsum\n arrSum=rsum\n \n if stack:\n arrSum=rsum-stack[-1][1]\n \n\t\t\t\t# update res with subarray sum\n res=max(res, nums[index]*arrSum)\n \n rsum+=v\n stack.append((i, rsum))\n \n return res%mod | 5 | The **min-product** of an array is equal to the **minimum value** in the array **multiplied by** the array's **sum**.
* For example, the array `[3,2,5]` (minimum value is `2`) has a min-product of `2 * (3+2+5) = 2 * 10 = 20`.
Given an array of integers `nums`, return _the **maximum min-product** of any **non-empty subarray** of_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`.
Note that the min-product should be maximized **before** performing the modulo operation. Testcases are generated such that the maximum min-product **without** modulo will fit in a **64-bit signed integer**.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,3,2\]
**Output:** 14
**Explanation:** The maximum min-product is achieved with the subarray \[2,3,2\] (minimum value is 2).
2 \* (2+3+2) = 2 \* 7 = 14.
**Example 2:**
**Input:** nums = \[2,3,3,1,2\]
**Output:** 18
**Explanation:** The maximum min-product is achieved with the subarray \[3,3\] (minimum value is 3).
3 \* (3+3) = 3 \* 6 = 18.
**Example 3:**
**Input:** nums = \[3,1,5,6,4,2\]
**Output:** 60
**Explanation:** The maximum min-product is achieved with the subarray \[5,6,4\] (minimum value is 4).
4 \* (5+6+4) = 4 \* 15 = 60.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
Python monotonic stack beats 100% | maximum-subarray-min-product | 0 | 1 | a monotonic stack with index and prefix sum\n\n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n mod=int(1e9+7)\n stack=[] # (index, prefix sum at index)\n rsum=0\n res=0\n \n nums.append(0)\n \n for i, v in enumerate(nums):\n while stack and nums[stack[-1][0]] >= v:\n index, _ = stack.pop()\n\t\t\t\t\n\t\t\t\t# if the stack is empty, the subarray sum is the current prefixsum\n arrSum=rsum\n \n if stack:\n arrSum=rsum-stack[-1][1]\n \n\t\t\t\t# update res with subarray sum\n res=max(res, nums[index]*arrSum)\n \n rsum+=v\n stack.append((i, rsum))\n \n return res%mod | 5 | You are given an array of strings `nums` and an integer `k`. Each string in `nums` represents an integer without leading zeros.
Return _the string that represents the_ `kth` _**largest integer** in_ `nums`.
**Note**: Duplicate numbers should be counted distinctly. For example, if `nums` is `[ "1 ", "2 ", "2 "]`, `"2 "` is the first largest integer, `"2 "` is the second-largest integer, and `"1 "` is the third-largest integer.
**Example 1:**
**Input:** nums = \[ "3 ", "6 ", "7 ", "10 "\], k = 4
**Output:** "3 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "3 ", "6 ", "7 ", "10 "\].
The 4th largest integer in nums is "3 ".
**Example 2:**
**Input:** nums = \[ "2 ", "21 ", "12 ", "1 "\], k = 3
**Output:** "2 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "1 ", "2 ", "12 ", "21 "\].
The 3rd largest integer in nums is "2 ".
**Example 3:**
**Input:** nums = \[ "0 ", "0 "\], k = 2
**Output:** "0 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "0 ", "0 "\].
The 2nd largest integer in nums is "0 ".
**Constraints:**
* `1 <= k <= nums.length <= 104`
* `1 <= nums[i].length <= 100`
* `nums[i]` consists of only digits.
* `nums[i]` will not have any leading zeros. | Is there a way we can sort the elements to simplify the problem? Can we find the maximum min-product for every value in the array? |
Step by step Intuition for DP Solution | maximum-subarray-min-product | 0 | 1 | # Intuition\nTo find the maximum min-product, we want to check all min products. This means for each element in nums, we want to find the min product it is associated with assuming that element is the minimum.\n\nNow finding and summing up the longest subarray in which each element is the minimum is very costly. **Prefix sums** seem like a good idea, since if we could track a running sum, we wouldn\'t have to recompute subarray sums multiple times. But how can we find the right prefix sum on both sides of the minimum?\n\nOne intuitive idea is that if the elements were sorted, it would be much easier to reason about the subarrays. However, since order must be preserved, this means we can\'t sort the array. Instead, we can maintain an increasing **monotonic stack**. This way, we have structure we can work with. More specifically, if we maintain a monotonic stack, we know that for any element x, any element to the left x must be less than it.\n\n# Approach\nWe will use the strategy outlined above, tracking a stack containing (value, prefix sum) pairs and the current maximum min product.\n\nWe then for loop over nums. At each item, we pop the stack while the top of the stack is greater than the current it, adding the top stack\'s value and its prefix sum to a running total that is initialized at 0. During each pop, we update our answer if (new total * the item we just popped) is the new largest min product. All the while, we track the new prefix sum by adding each stack element greater than or equal to our current item to a running total **psum**.\n\nAfter all elements greater than the current item have been removed, we append the new item with an additional field **psum**.\n\nThen at the end we pop everything from the stack using the same process in order to clean up the remaining elements.\n\n# Complexity\n- Time complexity:\nO(n), since everything can only be added to and removed from the stack once each.\n\n- Space complexity:\nO(n), since the stack only holds one pair of data for every entry in nums.\n\n# Code\n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n modulo = 10**9+7\n stack = []\n ans = 0 \n\n for i in nums:\n psum = 0\n if stack and stack[len(stack)-1][0] > i:\n total = 0\n while stack and stack[len(stack)-1][0] >= i:\n c, csum = stack.pop()\n if c >= i:\n psum += c + csum\n total += c + csum\n ans = max(ans, (total)*c) \n stack.append((i, psum))\n\n # clean up the remaining stack\n total = 0\n while stack:\n c, csum = stack.pop()\n total += c + csum\n ans = max(ans, (total)*c)\n return ans % modulo\n``` | 1 | The **min-product** of an array is equal to the **minimum value** in the array **multiplied by** the array's **sum**.
* For example, the array `[3,2,5]` (minimum value is `2`) has a min-product of `2 * (3+2+5) = 2 * 10 = 20`.
Given an array of integers `nums`, return _the **maximum min-product** of any **non-empty subarray** of_ `nums`. Since the answer may be large, return it **modulo** `109 + 7`.
Note that the min-product should be maximized **before** performing the modulo operation. Testcases are generated such that the maximum min-product **without** modulo will fit in a **64-bit signed integer**.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,3,2\]
**Output:** 14
**Explanation:** The maximum min-product is achieved with the subarray \[2,3,2\] (minimum value is 2).
2 \* (2+3+2) = 2 \* 7 = 14.
**Example 2:**
**Input:** nums = \[2,3,3,1,2\]
**Output:** 18
**Explanation:** The maximum min-product is achieved with the subarray \[3,3\] (minimum value is 3).
3 \* (3+3) = 3 \* 6 = 18.
**Example 3:**
**Input:** nums = \[3,1,5,6,4,2\]
**Output:** 60
**Explanation:** The maximum min-product is achieved with the subarray \[5,6,4\] (minimum value is 4).
4 \* (5+6+4) = 4 \* 15 = 60.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
Step by step Intuition for DP Solution | maximum-subarray-min-product | 0 | 1 | # Intuition\nTo find the maximum min-product, we want to check all min products. This means for each element in nums, we want to find the min product it is associated with assuming that element is the minimum.\n\nNow finding and summing up the longest subarray in which each element is the minimum is very costly. **Prefix sums** seem like a good idea, since if we could track a running sum, we wouldn\'t have to recompute subarray sums multiple times. But how can we find the right prefix sum on both sides of the minimum?\n\nOne intuitive idea is that if the elements were sorted, it would be much easier to reason about the subarrays. However, since order must be preserved, this means we can\'t sort the array. Instead, we can maintain an increasing **monotonic stack**. This way, we have structure we can work with. More specifically, if we maintain a monotonic stack, we know that for any element x, any element to the left x must be less than it.\n\n# Approach\nWe will use the strategy outlined above, tracking a stack containing (value, prefix sum) pairs and the current maximum min product.\n\nWe then for loop over nums. At each item, we pop the stack while the top of the stack is greater than the current it, adding the top stack\'s value and its prefix sum to a running total that is initialized at 0. During each pop, we update our answer if (new total * the item we just popped) is the new largest min product. All the while, we track the new prefix sum by adding each stack element greater than or equal to our current item to a running total **psum**.\n\nAfter all elements greater than the current item have been removed, we append the new item with an additional field **psum**.\n\nThen at the end we pop everything from the stack using the same process in order to clean up the remaining elements.\n\n# Complexity\n- Time complexity:\nO(n), since everything can only be added to and removed from the stack once each.\n\n- Space complexity:\nO(n), since the stack only holds one pair of data for every entry in nums.\n\n# Code\n```\nclass Solution:\n def maxSumMinProduct(self, nums: List[int]) -> int:\n modulo = 10**9+7\n stack = []\n ans = 0 \n\n for i in nums:\n psum = 0\n if stack and stack[len(stack)-1][0] > i:\n total = 0\n while stack and stack[len(stack)-1][0] >= i:\n c, csum = stack.pop()\n if c >= i:\n psum += c + csum\n total += c + csum\n ans = max(ans, (total)*c) \n stack.append((i, psum))\n\n # clean up the remaining stack\n total = 0\n while stack:\n c, csum = stack.pop()\n total += c + csum\n ans = max(ans, (total)*c)\n return ans % modulo\n``` | 1 | You are given an array of strings `nums` and an integer `k`. Each string in `nums` represents an integer without leading zeros.
Return _the string that represents the_ `kth` _**largest integer** in_ `nums`.
**Note**: Duplicate numbers should be counted distinctly. For example, if `nums` is `[ "1 ", "2 ", "2 "]`, `"2 "` is the first largest integer, `"2 "` is the second-largest integer, and `"1 "` is the third-largest integer.
**Example 1:**
**Input:** nums = \[ "3 ", "6 ", "7 ", "10 "\], k = 4
**Output:** "3 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "3 ", "6 ", "7 ", "10 "\].
The 4th largest integer in nums is "3 ".
**Example 2:**
**Input:** nums = \[ "2 ", "21 ", "12 ", "1 "\], k = 3
**Output:** "2 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "1 ", "2 ", "12 ", "21 "\].
The 3rd largest integer in nums is "2 ".
**Example 3:**
**Input:** nums = \[ "0 ", "0 "\], k = 2
**Output:** "0 "
**Explanation:**
The numbers in nums sorted in non-decreasing order are \[ "0 ", "0 "\].
The 2nd largest integer in nums is "0 ".
**Constraints:**
* `1 <= k <= nums.length <= 104`
* `1 <= nums[i].length <= 100`
* `nums[i]` consists of only digits.
* `nums[i]` will not have any leading zeros. | Is there a way we can sort the elements to simplify the problem? Can we find the maximum min-product for every value in the array? |
python3 Solution | largest-color-value-in-a-directed-graph | 0 | 1 | \n```\nclass Solution:\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\n n = len(colors)\n graph = collections.defaultdict(list)\n indegree = [0] * len(colors)\n for u, v in edges:\n graph[v].append(u)\n indegree[u] += 1\n \n count = [collections.defaultdict(int) for _ in range(n)]\n q = collections.deque(filter(lambda i: not indegree[i], range(n)))\n seen = 0\n ans = 0\n while q:\n curr = q.popleft()\n count[curr][colors[curr]] += 1\n ans = max(ans, count[curr][colors[curr]])\n seen += 1\n\n for v in graph[curr]:\n for c in count[curr]:\n count[v][c] = max(count[v][c], count[curr][c])\n indegree[v] -= 1\n if indegree[v] == 0:\n q.append(v)\n \n if seen < n:\n return -1\n return ans\n``` | 2 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
python3 Solution | largest-color-value-in-a-directed-graph | 0 | 1 | \n```\nclass Solution:\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\n n = len(colors)\n graph = collections.defaultdict(list)\n indegree = [0] * len(colors)\n for u, v in edges:\n graph[v].append(u)\n indegree[u] += 1\n \n count = [collections.defaultdict(int) for _ in range(n)]\n q = collections.deque(filter(lambda i: not indegree[i], range(n)))\n seen = 0\n ans = 0\n while q:\n curr = q.popleft()\n count[curr][colors[curr]] += 1\n ans = max(ans, count[curr][colors[curr]])\n seen += 1\n\n for v in graph[curr]:\n for c in count[curr]:\n count[v][c] = max(count[v][c], count[curr][c])\n indegree[v] -= 1\n if indegree[v] == 0:\n q.append(v)\n \n if seen < n:\n return -1\n return ans\n``` | 2 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Simple DFS approach with comments | largest-color-value-in-a-directed-graph | 0 | 1 | Run dfs for each node.\r\nKeep `state` of each node as a dictionary: `letter` to longest count of `letter` starting in this node\r\n\r\nDetect cycles by "algorithm biting on its own tail": `visit[node] == -1`\r\n# Code\r\n```\r\ndef largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n out = [[] for _ in range(n)] # outgoing edges init\r\n for u, v in edges: out[u].append(v) # outgoing edges building of\r\n visit = [0] * n # 0-unvisited, -1 in current stack, 1 visited\r\n state = [defaultdict(int) for _ in range(n)] # [node][letter] -> longest count of letters starting from this node\r\n def dfs(node):\r\n visit[node] = -1 # tmp on current path\r\n for u in out[node]:\r\n if visit[u] == -1: return -1 # cycle detedted\r\n if not visit[u]: # call dfs on unvisited nodes\r\n if dfs(u) == -1: # if there was a cycle\r\n return -1 # then return -1\r\n for k, val in state[u].items(): # update the state for each letter in the child\r\n state[node][k] = max(state[node][k], val)\r\n state[node][colors[node]] += 1 # add the color of the node to the state\r\n visit[node] = 1 # mark visited\r\n return max(state[node].values()) # longest color value for this node\r\n \r\n ret = 0\r\n for u in range(n): # the main loop over all nodes\r\n if not visit[u]:\r\n r = dfs(u)\r\n if r == -1: return -1 # cycle detected\r\n ret = max(ret, r)\r\n return ret\r\n``` | 1 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
Simple DFS approach with comments | largest-color-value-in-a-directed-graph | 0 | 1 | Run dfs for each node.\r\nKeep `state` of each node as a dictionary: `letter` to longest count of `letter` starting in this node\r\n\r\nDetect cycles by "algorithm biting on its own tail": `visit[node] == -1`\r\n# Code\r\n```\r\ndef largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n out = [[] for _ in range(n)] # outgoing edges init\r\n for u, v in edges: out[u].append(v) # outgoing edges building of\r\n visit = [0] * n # 0-unvisited, -1 in current stack, 1 visited\r\n state = [defaultdict(int) for _ in range(n)] # [node][letter] -> longest count of letters starting from this node\r\n def dfs(node):\r\n visit[node] = -1 # tmp on current path\r\n for u in out[node]:\r\n if visit[u] == -1: return -1 # cycle detedted\r\n if not visit[u]: # call dfs on unvisited nodes\r\n if dfs(u) == -1: # if there was a cycle\r\n return -1 # then return -1\r\n for k, val in state[u].items(): # update the state for each letter in the child\r\n state[node][k] = max(state[node][k], val)\r\n state[node][colors[node]] += 1 # add the color of the node to the state\r\n visit[node] = 1 # mark visited\r\n return max(state[node].values()) # longest color value for this node\r\n \r\n ret = 0\r\n for u in range(n): # the main loop over all nodes\r\n if not visit[u]:\r\n r = dfs(u)\r\n if r == -1: return -1 # cycle detected\r\n ret = max(ret, r)\r\n return ret\r\n``` | 1 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
python 3 - DP | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\r\n(This is a fun question!)\r\n\r\nAfter looking at the constraints, you know you need to use DP because input size is large.\r\n\r\nState variables: index of colors\r\nbase case: when reaching leaf node\r\nrecursion: read and return a count dict\r\n\r\nThe hardest part can be: "how to cache".\r\n\r\n# Approach\r\nDP\r\n\r\n# Complexity\r\n- Time complexity:\r\nO(E+V) -> for each index, we loop through all adjacent edges. Since intermediate result is cached, no repeat calculation is made.\r\n\r\n- Space complexity:\r\nO(E+V) -> n2nxt connection graph\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n import collections\r\n\r\n n2nxt = collections.defaultdict(list)\r\n\r\n for a, b in edges:\r\n n2nxt[a].append(b)\r\n\r\n @lru_cache(None)\r\n def cycle_check(n): # return bool, cycle?\r\n nonlocal cycle\r\n if cycle: # checked cycle found\r\n return cycle\r\n if n in visited: # new cycle\r\n cycle = True\r\n return cycle\r\n visited.add(n)\r\n for nxt in n2nxt[n]:\r\n cycle_check(nxt)\r\n if cycle:\r\n return cycle\r\n visited.remove(n)\r\n return False\r\n\r\n visited = set()\r\n cycle = False\r\n for i in range(len(colors)):\r\n cycle_check(i)\r\n if cycle:\r\n return -1\r\n\r\n # no cycle\r\n\r\n @lru_cache(None)\r\n def dfs(n): # return longest color count\r\n if not n2nxt[n]: # no nxt\r\n res = collections.defaultdict(int)\r\n res[colors[n]] += 1\r\n return res\r\n \r\n res = collections.defaultdict(int)\r\n\r\n for nxt in n2nxt[n]:\r\n nxtd = dfs(nxt)\r\n for col, freq in nxtd.items():\r\n res[col] = max(res[col], freq)\r\n\r\n res[colors[n]] += 1\r\n \r\n return res\r\n\r\n ans = 0\r\n for i in range(len(colors)):\r\n dd = dfs(i)\r\n ans = max(ans, dd[colors[i]])\r\n return ans\r\n``` | 1 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
python 3 - DP | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\r\n(This is a fun question!)\r\n\r\nAfter looking at the constraints, you know you need to use DP because input size is large.\r\n\r\nState variables: index of colors\r\nbase case: when reaching leaf node\r\nrecursion: read and return a count dict\r\n\r\nThe hardest part can be: "how to cache".\r\n\r\n# Approach\r\nDP\r\n\r\n# Complexity\r\n- Time complexity:\r\nO(E+V) -> for each index, we loop through all adjacent edges. Since intermediate result is cached, no repeat calculation is made.\r\n\r\n- Space complexity:\r\nO(E+V) -> n2nxt connection graph\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n import collections\r\n\r\n n2nxt = collections.defaultdict(list)\r\n\r\n for a, b in edges:\r\n n2nxt[a].append(b)\r\n\r\n @lru_cache(None)\r\n def cycle_check(n): # return bool, cycle?\r\n nonlocal cycle\r\n if cycle: # checked cycle found\r\n return cycle\r\n if n in visited: # new cycle\r\n cycle = True\r\n return cycle\r\n visited.add(n)\r\n for nxt in n2nxt[n]:\r\n cycle_check(nxt)\r\n if cycle:\r\n return cycle\r\n visited.remove(n)\r\n return False\r\n\r\n visited = set()\r\n cycle = False\r\n for i in range(len(colors)):\r\n cycle_check(i)\r\n if cycle:\r\n return -1\r\n\r\n # no cycle\r\n\r\n @lru_cache(None)\r\n def dfs(n): # return longest color count\r\n if not n2nxt[n]: # no nxt\r\n res = collections.defaultdict(int)\r\n res[colors[n]] += 1\r\n return res\r\n \r\n res = collections.defaultdict(int)\r\n\r\n for nxt in n2nxt[n]:\r\n nxtd = dfs(nxt)\r\n for col, freq in nxtd.items():\r\n res[col] = max(res[col], freq)\r\n\r\n res[colors[n]] += 1\r\n \r\n return res\r\n\r\n ans = 0\r\n for i in range(len(colors)):\r\n dd = dfs(i)\r\n ans = max(ans, dd[colors[i]])\r\n return ans\r\n``` | 1 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Python || 95% TC || Topological Sort (with explanation) | largest-color-value-in-a-directed-graph | 0 | 1 | # Complexity\r\n- Time complexity: $$O(n)$$\r\n\r\n- Space complexity : $$O(n)$$\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n if not edges: return 1 # Edge Case -> no edge -> 1\r\n n = len(colors) # number of nodes\r\n roots = {i for i in range(n)} # to check who are root nodes\r\n graph = defaultdict(set) \r\n indegree = defaultdict(int) \r\n for a, b in edges:\r\n graph[a].add(b) # generate graph\r\n indegree[b] += 1 # save all nodes\'s indegree\r\n roots -= {b} # delete nodes who have parent\r\n \r\n Max = -1\r\n # if we use list[] to do dp, we\'ll use n*26 extra space, and exacly 26 times to update color for all nodes\r\n # so I decide use double hash to optimize TC & MC\r\n # dp define as -> max each color count when reach every node\r\n dp = defaultdict(dict) \r\n for root in roots: # search from every root\r\n indegree[root] = 0 # set root\'s indegree as 0 (cause indegree hash didn\'t data for every root)\r\n dp[root][colors[root]] = 1 # set dp[root]\'s color to 1\r\n q = [root]\r\n while q: # BFS\r\n cur = q.pop(0)\r\n for nxt in graph[cur]:\r\n indegree[nxt] -= 1 # update indegree\r\n # if we meet a node that indegree == -1, means we found a loop, just return -1\r\n # (this situation won\'t happen when using Topological Sort on a graph without loop)\r\n if indegree[nxt] == -1: return -1\r\n # update next node\'s color count\r\n for c in dp[cur]:\r\n dp[nxt].setdefault(c, dp[cur][c])\r\n dp[nxt][c] = max(dp[nxt][c], dp[cur][c])\r\n # if we can finally visited next node\r\n if indegree[nxt] == 0:\r\n q.append(nxt)\r\n cc = colors[nxt] # next node\'s color\r\n # add 1 to next node\'s color count with it\'s own color\r\n dp[nxt].setdefault(cc, 0)\r\n dp[nxt][cc] += 1\r\n Max = max(Max, dp[nxt][cc]) # update Max\r\n return Max\r\n``` | 1 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
Python || 95% TC || Topological Sort (with explanation) | largest-color-value-in-a-directed-graph | 0 | 1 | # Complexity\r\n- Time complexity: $$O(n)$$\r\n\r\n- Space complexity : $$O(n)$$\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n if not edges: return 1 # Edge Case -> no edge -> 1\r\n n = len(colors) # number of nodes\r\n roots = {i for i in range(n)} # to check who are root nodes\r\n graph = defaultdict(set) \r\n indegree = defaultdict(int) \r\n for a, b in edges:\r\n graph[a].add(b) # generate graph\r\n indegree[b] += 1 # save all nodes\'s indegree\r\n roots -= {b} # delete nodes who have parent\r\n \r\n Max = -1\r\n # if we use list[] to do dp, we\'ll use n*26 extra space, and exacly 26 times to update color for all nodes\r\n # so I decide use double hash to optimize TC & MC\r\n # dp define as -> max each color count when reach every node\r\n dp = defaultdict(dict) \r\n for root in roots: # search from every root\r\n indegree[root] = 0 # set root\'s indegree as 0 (cause indegree hash didn\'t data for every root)\r\n dp[root][colors[root]] = 1 # set dp[root]\'s color to 1\r\n q = [root]\r\n while q: # BFS\r\n cur = q.pop(0)\r\n for nxt in graph[cur]:\r\n indegree[nxt] -= 1 # update indegree\r\n # if we meet a node that indegree == -1, means we found a loop, just return -1\r\n # (this situation won\'t happen when using Topological Sort on a graph without loop)\r\n if indegree[nxt] == -1: return -1\r\n # update next node\'s color count\r\n for c in dp[cur]:\r\n dp[nxt].setdefault(c, dp[cur][c])\r\n dp[nxt][c] = max(dp[nxt][c], dp[cur][c])\r\n # if we can finally visited next node\r\n if indegree[nxt] == 0:\r\n q.append(nxt)\r\n cc = colors[nxt] # next node\'s color\r\n # add 1 to next node\'s color count with it\'s own color\r\n dp[nxt].setdefault(cc, 0)\r\n dp[nxt][cc] += 1\r\n Max = max(Max, dp[nxt][cc]) # update Max\r\n return Max\r\n``` | 1 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Beats 99% | O(n) solution | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nfrom string import ascii_lowercase\r\n\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n num_parents = [0]*n\r\n graph = [[] for i in range(n)]\r\n on_stack = [False] * n\r\n freq = [0] * n\r\n\r\n for n1, n2 in edges:\r\n graph[n1].append(n2)\r\n num_parents[n2] += 1\r\n \r\n\r\n def has_cycle(at):\r\n if freq[at] == 1:\r\n return False\r\n if on_stack[at]:\r\n return True\r\n on_stack[at] = True\r\n for to in graph[at]:\r\n if has_cycle(to):\r\n return True\r\n freq[at] = 1\r\n on_stack[at] = False\r\n return False\r\n\r\n\r\n def calc_freq(at, c):\r\n if freq[at] is not None:\r\n return freq[at]\r\n \r\n f = 0\r\n for to in graph[at]:\r\n f = max(f, calc_freq(to, c))\r\n \r\n if colors[at] == c:\r\n f += 1\r\n freq[at] = f\r\n return f\r\n \r\n for i in range(n):\r\n if has_cycle(i):\r\n return -1\r\n\r\n max_freq = -1\r\n for c in set(colors):\r\n for i in range(n):\r\n if num_parents[i] == 0:\r\n freq = [None] * n\r\n max_freq = max(max_freq, calc_freq(i, c))\r\n \r\n return max_freq\r\n\r\n\r\n``` | 1 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
Beats 99% | O(n) solution | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nfrom string import ascii_lowercase\r\n\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n num_parents = [0]*n\r\n graph = [[] for i in range(n)]\r\n on_stack = [False] * n\r\n freq = [0] * n\r\n\r\n for n1, n2 in edges:\r\n graph[n1].append(n2)\r\n num_parents[n2] += 1\r\n \r\n\r\n def has_cycle(at):\r\n if freq[at] == 1:\r\n return False\r\n if on_stack[at]:\r\n return True\r\n on_stack[at] = True\r\n for to in graph[at]:\r\n if has_cycle(to):\r\n return True\r\n freq[at] = 1\r\n on_stack[at] = False\r\n return False\r\n\r\n\r\n def calc_freq(at, c):\r\n if freq[at] is not None:\r\n return freq[at]\r\n \r\n f = 0\r\n for to in graph[at]:\r\n f = max(f, calc_freq(to, c))\r\n \r\n if colors[at] == c:\r\n f += 1\r\n freq[at] = f\r\n return f\r\n \r\n for i in range(n):\r\n if has_cycle(i):\r\n return -1\r\n\r\n max_freq = -1\r\n for c in set(colors):\r\n for i in range(n):\r\n if num_parents[i] == 0:\r\n freq = [None] * n\r\n max_freq = max(max_freq, calc_freq(i, c))\r\n \r\n return max_freq\r\n\r\n\r\n``` | 1 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
[Python] Topological Sort | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n # bfs, topological sort\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n graph = collections.defaultdict(list)\r\n indegree = collections.Counter()\r\n for u, v in edges:\r\n graph[v].append(u)\r\n indegree[u] += 1\r\n\r\n # counter[node][color]\r\n counter = collections.defaultdict(lambda:collections.defaultdict(int))\r\n q = collections.deque(filter(lambda i: indegree[i] == 0, range(n)))\r\n seen = 0\r\n ans = 0\r\n while q:\r\n node = q.popleft()\r\n counter[node][colors[node]] += 1\r\n ans = max(ans, counter[node][colors[node]])\r\n seen += 1\r\n for adj in graph[node]:\r\n for c in counter[node]:\r\n counter[adj][c] = max(counter[adj][c], counter[node][c])\r\n indegree[adj] -= 1\r\n if indegree[adj] == 0: q.append(adj)\r\n \r\n return -1 if seen < n else ans\r\n``` | 1 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
[Python] Topological Sort | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n # bfs, topological sort\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n graph = collections.defaultdict(list)\r\n indegree = collections.Counter()\r\n for u, v in edges:\r\n graph[v].append(u)\r\n indegree[u] += 1\r\n\r\n # counter[node][color]\r\n counter = collections.defaultdict(lambda:collections.defaultdict(int))\r\n q = collections.deque(filter(lambda i: indegree[i] == 0, range(n)))\r\n seen = 0\r\n ans = 0\r\n while q:\r\n node = q.popleft()\r\n counter[node][colors[node]] += 1\r\n ans = max(ans, counter[node][colors[node]])\r\n seen += 1\r\n for adj in graph[node]:\r\n for c in counter[node]:\r\n counter[adj][c] = max(counter[adj][c], counter[node][c])\r\n indegree[adj] -= 1\r\n if indegree[adj] == 0: q.append(adj)\r\n \r\n return -1 if seen < n else ans\r\n``` | 1 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Image Explanation🏆- [Simple BFS - "COMPLETE" Intuition] - C++/Java/Python | largest-color-value-in-a-directed-graph | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\r\n`Largest Color Value in a Directed Graph` by `Aryan Mittal`\r\n\r\n\r\n\r\n\r\n# Approach & Intution\r\n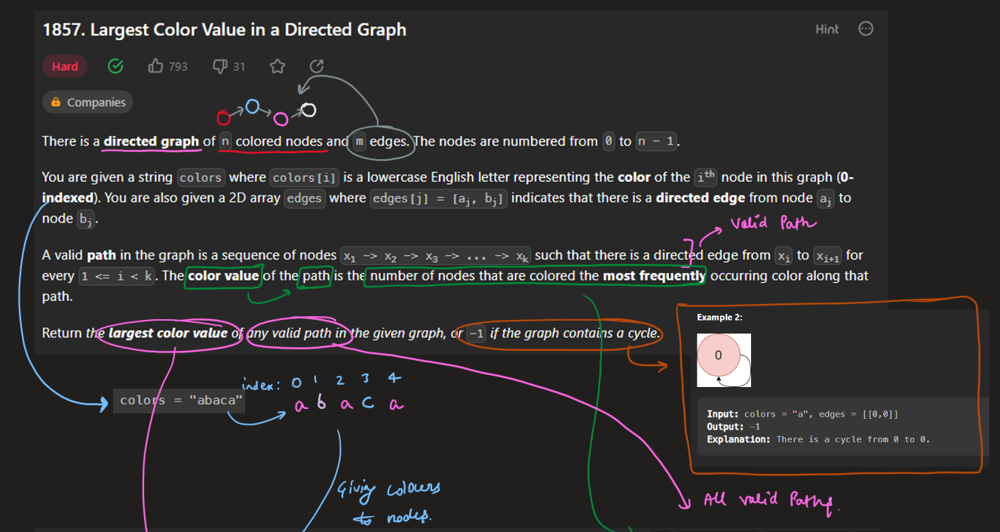\r\n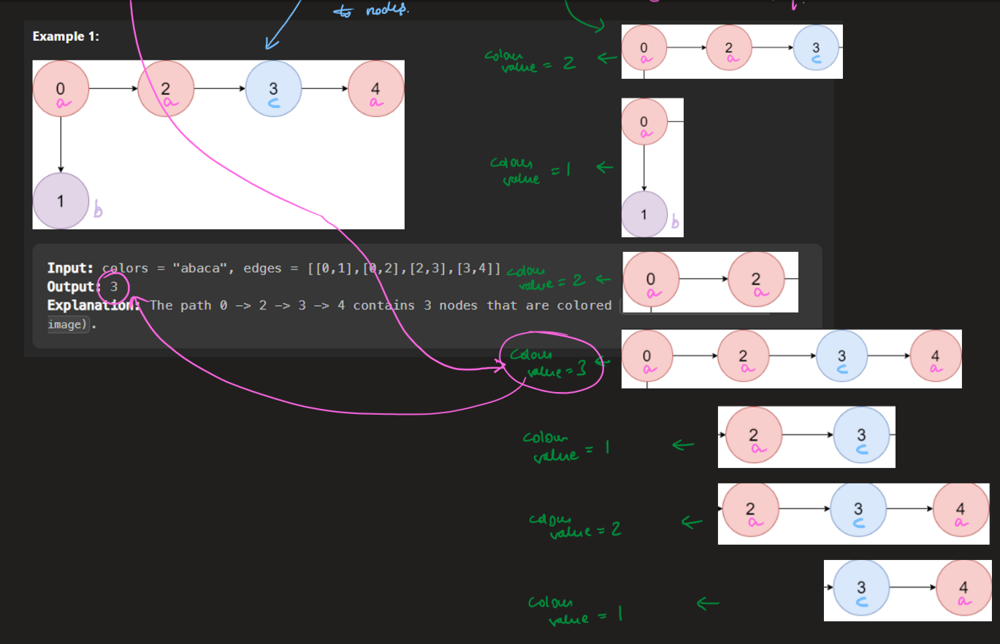\r\n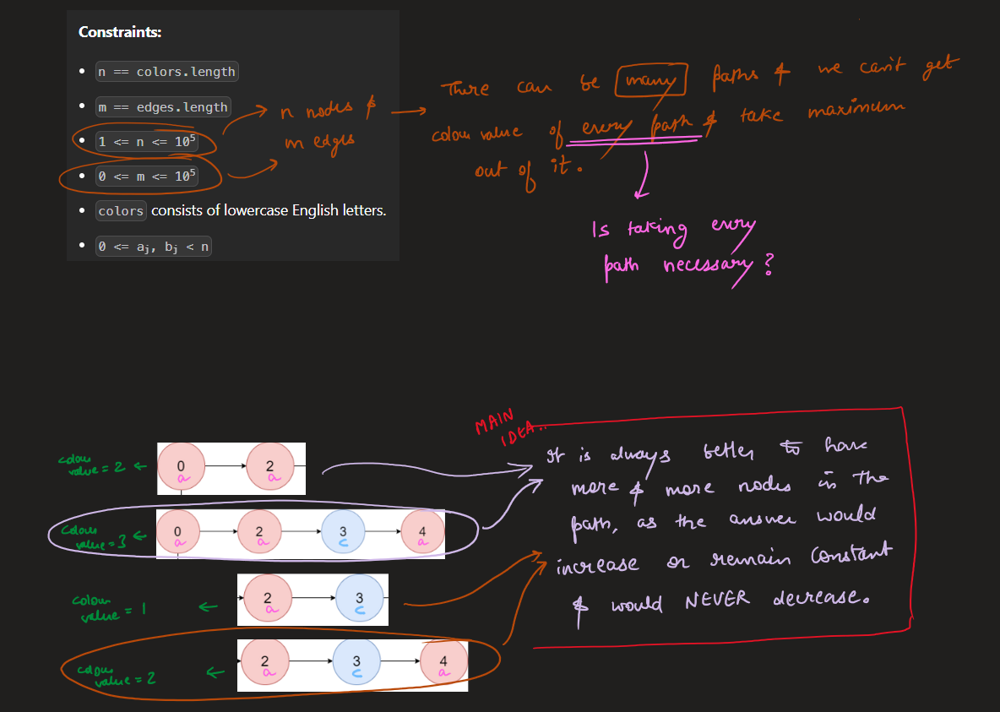\r\n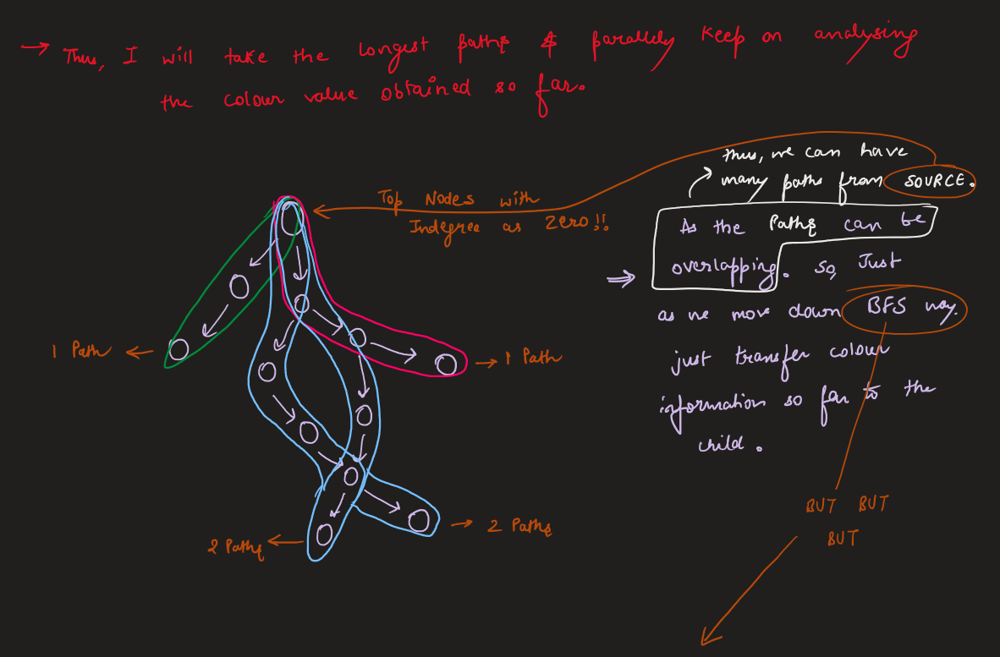\r\n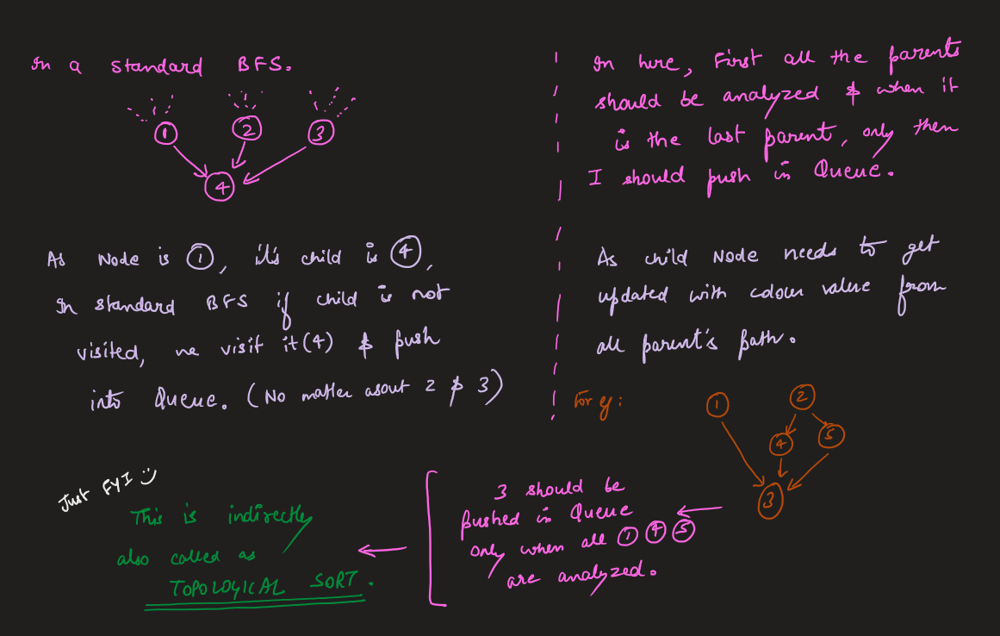\r\n\r\n\r\n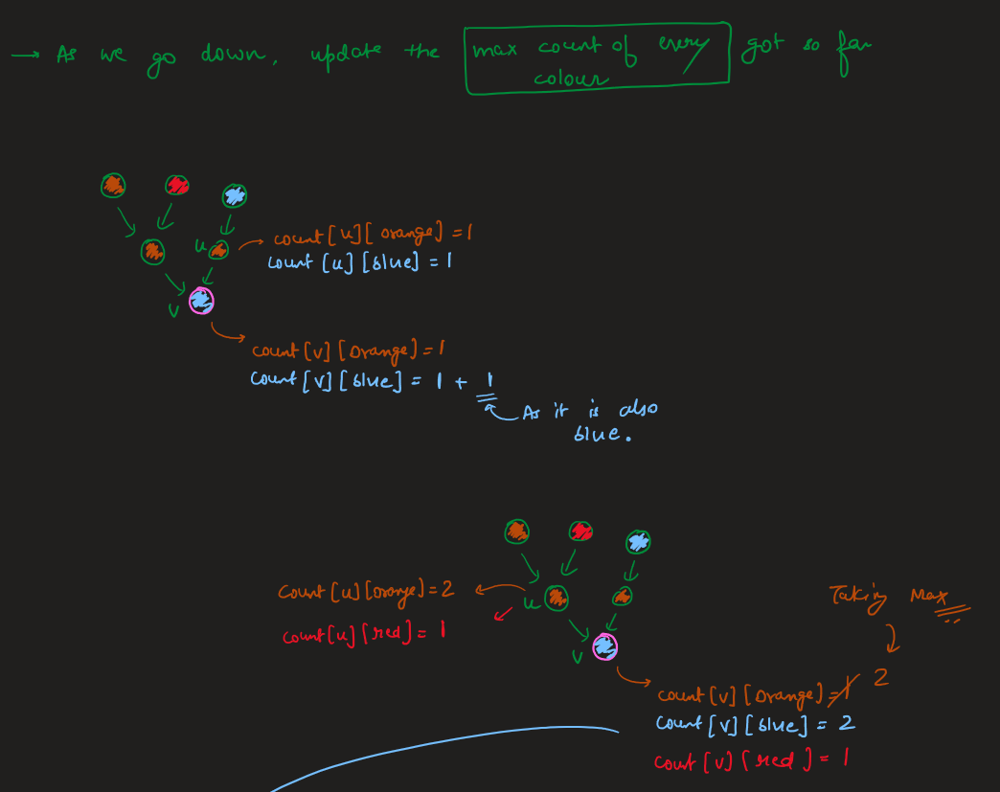\r\n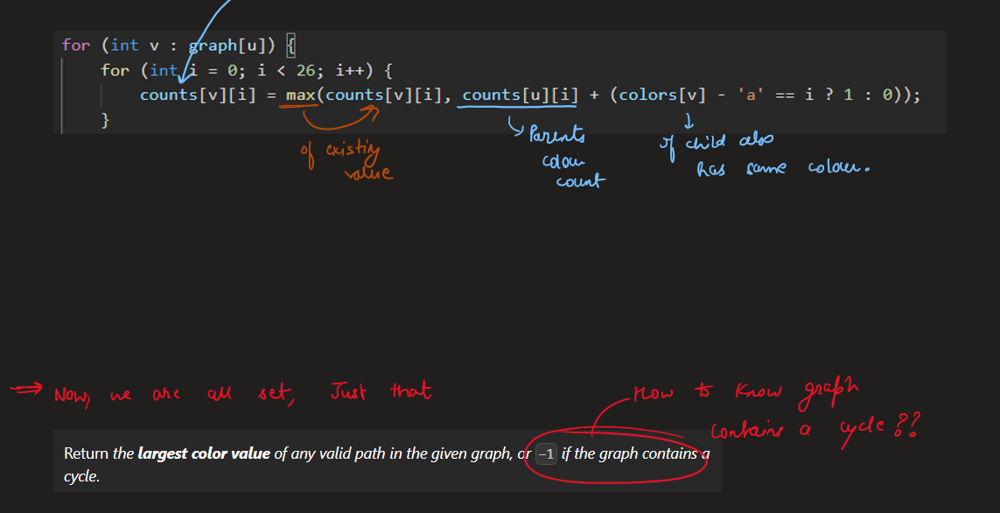\r\n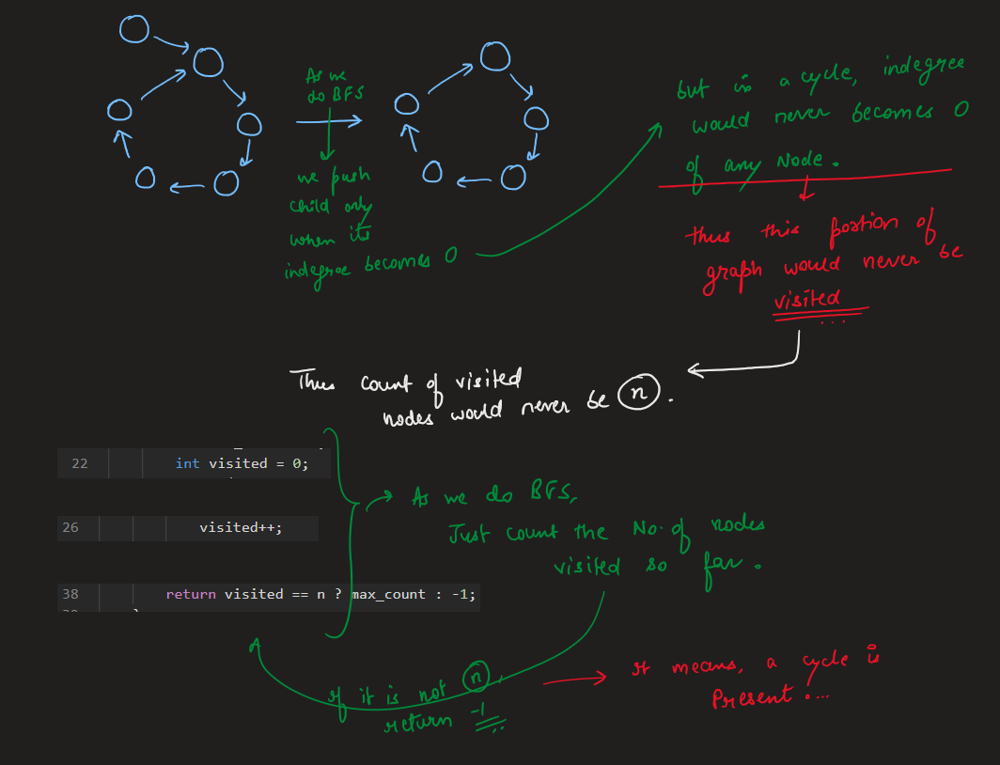\r\n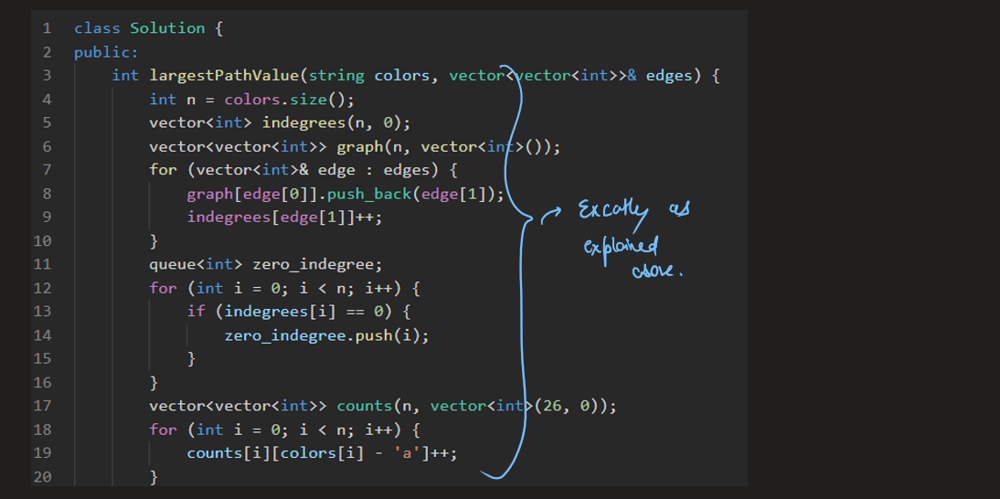\r\n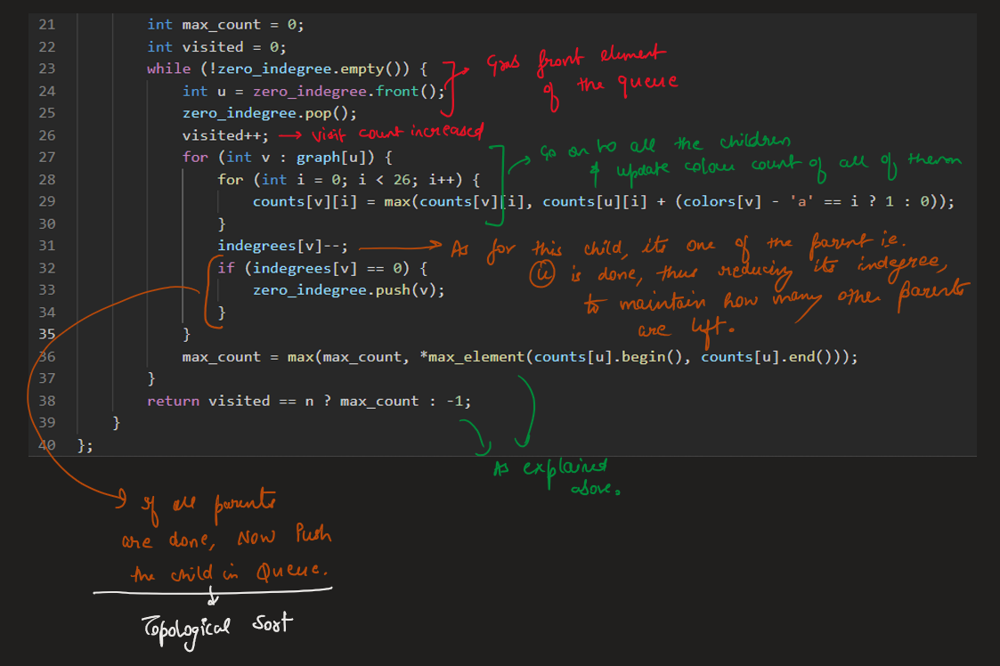\r\n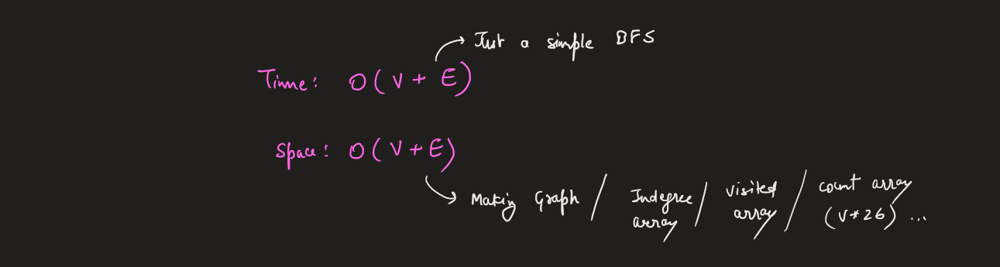\r\n\r\n\r\n# Code\r\n```C++ []\r\nclass Solution {\r\npublic:\r\n int largestPathValue(string colors, vector<vector<int>>& edges) {\r\n int n = colors.size();\r\n vector<int> indegrees(n, 0);\r\n vector<vector<int>> graph(n, vector<int>());\r\n for (vector<int>& edge : edges) {\r\n graph[edge[0]].push_back(edge[1]);\r\n indegrees[edge[1]]++;\r\n }\r\n queue<int> zero_indegree;\r\n for (int i = 0; i < n; i++) {\r\n if (indegrees[i] == 0) {\r\n zero_indegree.push(i);\r\n }\r\n }\r\n vector<vector<int>> counts(n, vector<int>(26, 0));\r\n for (int i = 0; i < n; i++) {\r\n counts[i][colors[i] - \'a\']++;\r\n }\r\n int max_count = 0;\r\n int visited = 0;\r\n while (!zero_indegree.empty()) {\r\n int u = zero_indegree.front();\r\n zero_indegree.pop();\r\n visited++;\r\n for (int v : graph[u]) {\r\n for (int i = 0; i < 26; i++) {\r\n counts[v][i] = max(counts[v][i], counts[u][i] + (colors[v] - \'a\' == i ? 1 : 0));\r\n }\r\n indegrees[v]--;\r\n if (indegrees[v] == 0) {\r\n zero_indegree.push(v);\r\n }\r\n }\r\n max_count = max(max_count, *max_element(counts[u].begin(), counts[u].end()));\r\n }\r\n return visited == n ? max_count : -1;\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n public int largestPathValue(String colors, int[][] edges) {\r\n int n = colors.length();\r\n int[] indegrees = new int[n];\r\n List<List<Integer>> graph = new ArrayList<>();\r\n for (int i = 0; i < n; i++) {\r\n graph.add(new ArrayList<Integer>());\r\n }\r\n for (int[] edge : edges) {\r\n graph.get(edge[0]).add(edge[1]);\r\n indegrees[edge[1]]++;\r\n }\r\n Queue<Integer> zeroIndegree = new LinkedList<>();\r\n for (int i = 0; i < n; i++) {\r\n if (indegrees[i] == 0) {\r\n zeroIndegree.offer(i);\r\n }\r\n }\r\n int[][] counts = new int[n][26];\r\n for (int i = 0; i < n; i++) {\r\n counts[i][colors.charAt(i) - \'a\']++;\r\n }\r\n int maxCount = 0;\r\n int visited = 0;\r\n while (!zeroIndegree.isEmpty()) {\r\n int u = zeroIndegree.poll();\r\n visited++;\r\n for (int v : graph.get(u)) {\r\n for (int i = 0; i < 26; i++) {\r\n counts[v][i] = Math.max(counts[v][i], counts[u][i] + (colors.charAt(v) - \'a\' == i ? 1 : 0));\r\n }\r\n indegrees[v]--;\r\n if (indegrees[v] == 0) {\r\n zeroIndegree.offer(v);\r\n }\r\n }\r\n maxCount = Math.max(maxCount, Arrays.stream(counts[u]).max().getAsInt());\r\n }\r\n return visited == n ? maxCount : -1;\r\n }\r\n}\r\n```\r\n```Python []\r\nfrom typing import List\r\nfrom collections import deque\r\n\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n indegrees = [0] * n\r\n graph = [[] for _ in range(n)]\r\n for edge in edges:\r\n graph[edge[0]].append(edge[1])\r\n indegrees[edge[1]] += 1\r\n zero_indegree = deque()\r\n for i in range(n):\r\n if indegrees[i] == 0:\r\n zero_indegree.append(i)\r\n counts = [[0]*26 for _ in range(n)]\r\n for i in range(n):\r\n counts[i][ord(colors[i]) - ord(\'a\')] += 1\r\n max_count = 0\r\n visited = 0\r\n while zero_indegree:\r\n u = zero_indegree.popleft()\r\n visited += 1\r\n for v in graph[u]:\r\n for i in range(26):\r\n counts[v][i] = max(counts[v][i], counts[u][i] + (ord(colors[v]) - ord(\'a\') == i))\r\n indegrees[v] -= 1\r\n if indegrees[v] == 0:\r\n zero_indegree.append(v)\r\n max_count = max(max_count, max(counts[u]))\r\n return max_count if visited == n else -1\r\n```\r\n | 120 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
Image Explanation🏆- [Simple BFS - "COMPLETE" Intuition] - C++/Java/Python | largest-color-value-in-a-directed-graph | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\r\n`Largest Color Value in a Directed Graph` by `Aryan Mittal`\r\n\r\n\r\n\r\n\r\n# Approach & Intution\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n\r\n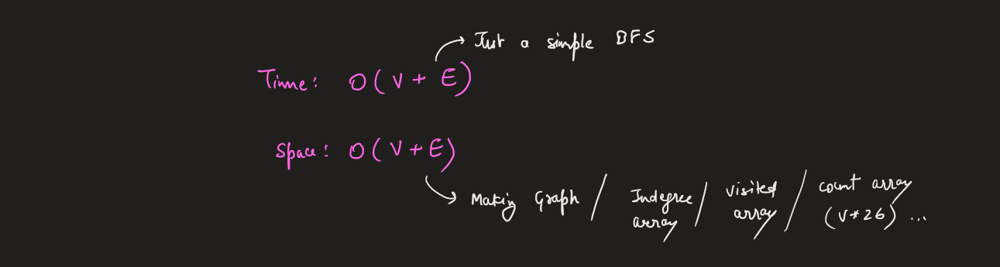\r\n\r\n\r\n# Code\r\n```C++ []\r\nclass Solution {\r\npublic:\r\n int largestPathValue(string colors, vector<vector<int>>& edges) {\r\n int n = colors.size();\r\n vector<int> indegrees(n, 0);\r\n vector<vector<int>> graph(n, vector<int>());\r\n for (vector<int>& edge : edges) {\r\n graph[edge[0]].push_back(edge[1]);\r\n indegrees[edge[1]]++;\r\n }\r\n queue<int> zero_indegree;\r\n for (int i = 0; i < n; i++) {\r\n if (indegrees[i] == 0) {\r\n zero_indegree.push(i);\r\n }\r\n }\r\n vector<vector<int>> counts(n, vector<int>(26, 0));\r\n for (int i = 0; i < n; i++) {\r\n counts[i][colors[i] - \'a\']++;\r\n }\r\n int max_count = 0;\r\n int visited = 0;\r\n while (!zero_indegree.empty()) {\r\n int u = zero_indegree.front();\r\n zero_indegree.pop();\r\n visited++;\r\n for (int v : graph[u]) {\r\n for (int i = 0; i < 26; i++) {\r\n counts[v][i] = max(counts[v][i], counts[u][i] + (colors[v] - \'a\' == i ? 1 : 0));\r\n }\r\n indegrees[v]--;\r\n if (indegrees[v] == 0) {\r\n zero_indegree.push(v);\r\n }\r\n }\r\n max_count = max(max_count, *max_element(counts[u].begin(), counts[u].end()));\r\n }\r\n return visited == n ? max_count : -1;\r\n }\r\n};\r\n```\r\n```Java []\r\nclass Solution {\r\n public int largestPathValue(String colors, int[][] edges) {\r\n int n = colors.length();\r\n int[] indegrees = new int[n];\r\n List<List<Integer>> graph = new ArrayList<>();\r\n for (int i = 0; i < n; i++) {\r\n graph.add(new ArrayList<Integer>());\r\n }\r\n for (int[] edge : edges) {\r\n graph.get(edge[0]).add(edge[1]);\r\n indegrees[edge[1]]++;\r\n }\r\n Queue<Integer> zeroIndegree = new LinkedList<>();\r\n for (int i = 0; i < n; i++) {\r\n if (indegrees[i] == 0) {\r\n zeroIndegree.offer(i);\r\n }\r\n }\r\n int[][] counts = new int[n][26];\r\n for (int i = 0; i < n; i++) {\r\n counts[i][colors.charAt(i) - \'a\']++;\r\n }\r\n int maxCount = 0;\r\n int visited = 0;\r\n while (!zeroIndegree.isEmpty()) {\r\n int u = zeroIndegree.poll();\r\n visited++;\r\n for (int v : graph.get(u)) {\r\n for (int i = 0; i < 26; i++) {\r\n counts[v][i] = Math.max(counts[v][i], counts[u][i] + (colors.charAt(v) - \'a\' == i ? 1 : 0));\r\n }\r\n indegrees[v]--;\r\n if (indegrees[v] == 0) {\r\n zeroIndegree.offer(v);\r\n }\r\n }\r\n maxCount = Math.max(maxCount, Arrays.stream(counts[u]).max().getAsInt());\r\n }\r\n return visited == n ? maxCount : -1;\r\n }\r\n}\r\n```\r\n```Python []\r\nfrom typing import List\r\nfrom collections import deque\r\n\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n n = len(colors)\r\n indegrees = [0] * n\r\n graph = [[] for _ in range(n)]\r\n for edge in edges:\r\n graph[edge[0]].append(edge[1])\r\n indegrees[edge[1]] += 1\r\n zero_indegree = deque()\r\n for i in range(n):\r\n if indegrees[i] == 0:\r\n zero_indegree.append(i)\r\n counts = [[0]*26 for _ in range(n)]\r\n for i in range(n):\r\n counts[i][ord(colors[i]) - ord(\'a\')] += 1\r\n max_count = 0\r\n visited = 0\r\n while zero_indegree:\r\n u = zero_indegree.popleft()\r\n visited += 1\r\n for v in graph[u]:\r\n for i in range(26):\r\n counts[v][i] = max(counts[v][i], counts[u][i] + (ord(colors[v]) - ord(\'a\') == i))\r\n indegrees[v] -= 1\r\n if indegrees[v] == 0:\r\n zero_indegree.append(v)\r\n max_count = max(max_count, max(counts[u]))\r\n return max_count if visited == n else -1\r\n```\r\n | 120 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Beating 67% in speed and my original way - I did not know how to ID circles in directed graphs | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe path starts with a node without ancestor. If we count the max number of nodes with a certain color in paths starting from a certain node and we traverse with all scenarios, the max count is the results, if no circle. And since colors are at most 26, the problem can be done within O(n) with storing the results. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor checking the circle, I came up with an original way (I did not know if this one is used commonly). To save a placeholder of the argument combo in the hashtable and if we see it again in the downstream recursions (which means a circle occurs), we jump out and return a special value to indicate a circle. If this combo is never seen again in its own downstream recursions, we assign the correct value of the combo in the hashtable. \nAlso, since I start only with those nodes without ancestor (starting nodes), I need to keep a record of the nodes I have seen when I go along every path. If I cannot traverse all nodes possibly, it means there are some clusters of nodes forming circles without any starting node. In this case, -1 should be returned as well. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\n\n n = len(colors)\n from collections import defaultdict\n dic = defaultdict(list)\n st = set(range(n))\n for x, y in edges:\n if x == y: \n return -1\n if y in st: \n st.remove(y)\n dic[x].append(y)\n if not st: // No starting nodes\n return -1\n \n dic_res = {} // hash table to save the combo\n self.res = 0\n seen = set() // Keep a record of the nodes I have seen during walking along all possible paths\n \n def calc2(node, color): \n seen.add(node)\n if (node, color) in dic_res:\n if dic_res[(node, color)] is not None: \n res = dic_res[(node, color)]\n self.res = max(self.res, res)\n return res\n else: // Means the combo has been seen before and a circle is there. Jump out the recursion and return None as an indicator\n return None\n else: \n dic_res[(node, color)] = None // Set a placeholder for later recursions to check\n color_node = colors[node]\n res = 0\n for newnode in dic[node]: \n tmp = calc2(newnode, color)\n if tmp == None: // Same as above, jump out the recursions and return None\n return None\n res = max(res, tmp)\n res += color == color_node\n self.res = max(res, self.res)\n // Only when we reach the very end of the recursions and have not seen any node seen before, we assign the values. Color will not change in the recursions. \n dic_res[(node, color)] = res\n return res\n \n for color in set(colors): \n for node in st: \n res = calc2(node, color)\n if res is None: // res is not very useful to us but if it is the indicator - None, there is a circle and we need to return 1\n return -1\n if len(seen) < n: // If I have not traversed all nodes, return -1\n return -1\n return self.res\n \n \n \n \n \n \n \n\n \n``` | 1 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
Beating 67% in speed and my original way - I did not know how to ID circles in directed graphs | largest-color-value-in-a-directed-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe path starts with a node without ancestor. If we count the max number of nodes with a certain color in paths starting from a certain node and we traverse with all scenarios, the max count is the results, if no circle. And since colors are at most 26, the problem can be done within O(n) with storing the results. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor checking the circle, I came up with an original way (I did not know if this one is used commonly). To save a placeholder of the argument combo in the hashtable and if we see it again in the downstream recursions (which means a circle occurs), we jump out and return a special value to indicate a circle. If this combo is never seen again in its own downstream recursions, we assign the correct value of the combo in the hashtable. \nAlso, since I start only with those nodes without ancestor (starting nodes), I need to keep a record of the nodes I have seen when I go along every path. If I cannot traverse all nodes possibly, it means there are some clusters of nodes forming circles without any starting node. In this case, -1 should be returned as well. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\n\n n = len(colors)\n from collections import defaultdict\n dic = defaultdict(list)\n st = set(range(n))\n for x, y in edges:\n if x == y: \n return -1\n if y in st: \n st.remove(y)\n dic[x].append(y)\n if not st: // No starting nodes\n return -1\n \n dic_res = {} // hash table to save the combo\n self.res = 0\n seen = set() // Keep a record of the nodes I have seen during walking along all possible paths\n \n def calc2(node, color): \n seen.add(node)\n if (node, color) in dic_res:\n if dic_res[(node, color)] is not None: \n res = dic_res[(node, color)]\n self.res = max(self.res, res)\n return res\n else: // Means the combo has been seen before and a circle is there. Jump out the recursion and return None as an indicator\n return None\n else: \n dic_res[(node, color)] = None // Set a placeholder for later recursions to check\n color_node = colors[node]\n res = 0\n for newnode in dic[node]: \n tmp = calc2(newnode, color)\n if tmp == None: // Same as above, jump out the recursions and return None\n return None\n res = max(res, tmp)\n res += color == color_node\n self.res = max(res, self.res)\n // Only when we reach the very end of the recursions and have not seen any node seen before, we assign the values. Color will not change in the recursions. \n dic_res[(node, color)] = res\n return res\n \n for color in set(colors): \n for node in st: \n res = calc2(node, color)\n if res is None: // res is not very useful to us but if it is the indicator - None, there is a circle and we need to return 1\n return -1\n if len(seen) < n: // If I have not traversed all nodes, return -1\n return -1\n return self.res\n \n \n \n \n \n \n \n\n \n``` | 1 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Python DFS + DP | largest-color-value-in-a-directed-graph | 0 | 1 | # Approach\r\n\r\nDFS with cycle detection. Similar to Course Schedules.\r\n\r\nImagine each node as having it\'s own dictionary. Each node\'s color values is the max of its children node\'s color values.\r\n\r\nThis approach prevents us from having to do a DFS starting at every node, which would be quadratic time. Since each node has its own dictionary, or in other words, we store the best paths for each node, we don\'t need to go through paths we\'ve already visited.\r\n\r\n# Complexity\r\n- Time complexity: O(v + e)\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity: O(v)\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n\r\n if not edges: return 1\r\n\r\n adj_list = defaultdict(list)\r\n for a, b in edges:\r\n adj_list[a].append(b)\r\n \r\n\r\n def dfs(cur):\r\n \r\n if cur in cycle: return True\r\n if cur in visited: return False\r\n \r\n visited.add(cur)\r\n cycle.add(cur)\r\n\r\n for neigh in adj_list[cur]:\r\n \r\n if dfs(neigh):\r\n return True\r\n \r\n for color in range(26):\r\n dp[cur][color] = max(dp[cur][color], dp[neigh][color])\r\n \r\n\r\n cur_color = ord(colors[cur]) - ord("a")\r\n dp[cur][cur_color] += 1\r\n self.ans = max(self.ans, dp[cur][cur_color])\r\n\r\n cycle.remove(cur)\r\n return False\r\n\r\n\r\n visited = set()\r\n cycle = set()\r\n dp = [[0] * 26 for _ in range(len(colors))]\r\n self.ans = -1\r\n\r\n for node in range(len(colors)):\r\n if node not in visited:\r\n if dfs(node):\r\n return -1\r\n \r\n return self.ans\r\n``` | 3 | There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.
You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the `ith` node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.
A valid **path** in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the **most frequently** occurring color along that path.
Return _the **largest color value** of any valid path in the given graph, or_ `-1` _if the graph contains a cycle_.
**Example 1:**
**Input:** colors = "abaca ", edges = \[\[0,1\],\[0,2\],\[2,3\],\[3,4\]\]
**Output:** 3
**Explanation:** The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored ` "a " (red in the above image)`.
**Example 2:**
**Input:** colors = "a ", edges = \[\[0,0\]\]
**Output:** -1
**Explanation:** There is a cycle from 0 to 0.
**Constraints:**
* `n == colors.length`
* `m == edges.length`
* `1 <= n <= 105`
* `0 <= m <= 105`
* `colors` consists of lowercase English letters.
* `0 <= aj, bj < n` | null |
Python DFS + DP | largest-color-value-in-a-directed-graph | 0 | 1 | # Approach\r\n\r\nDFS with cycle detection. Similar to Course Schedules.\r\n\r\nImagine each node as having it\'s own dictionary. Each node\'s color values is the max of its children node\'s color values.\r\n\r\nThis approach prevents us from having to do a DFS starting at every node, which would be quadratic time. Since each node has its own dictionary, or in other words, we store the best paths for each node, we don\'t need to go through paths we\'ve already visited.\r\n\r\n# Complexity\r\n- Time complexity: O(v + e)\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity: O(v)\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:\r\n\r\n if not edges: return 1\r\n\r\n adj_list = defaultdict(list)\r\n for a, b in edges:\r\n adj_list[a].append(b)\r\n \r\n\r\n def dfs(cur):\r\n \r\n if cur in cycle: return True\r\n if cur in visited: return False\r\n \r\n visited.add(cur)\r\n cycle.add(cur)\r\n\r\n for neigh in adj_list[cur]:\r\n \r\n if dfs(neigh):\r\n return True\r\n \r\n for color in range(26):\r\n dp[cur][color] = max(dp[cur][color], dp[neigh][color])\r\n \r\n\r\n cur_color = ord(colors[cur]) - ord("a")\r\n dp[cur][cur_color] += 1\r\n self.ans = max(self.ans, dp[cur][cur_color])\r\n\r\n cycle.remove(cur)\r\n return False\r\n\r\n\r\n visited = set()\r\n cycle = set()\r\n dp = [[0] * 26 for _ in range(len(colors))]\r\n self.ans = -1\r\n\r\n for node in range(len(colors)):\r\n if node not in visited:\r\n if dfs(node):\r\n return -1\r\n \r\n return self.ans\r\n``` | 3 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Python solution using for loop and list comprehension | sorting-the-sentence | 0 | 1 | # Intuition\nLooking at the test cases I knew I could use the numbers to sort it\n\n# Approach\nI started by converting the string into a list by using .spilt(). I followed that by going into a for loop and getting the last char which is the number. The next step was to put the number at the beginning and to remove the number at the end of the string. Once that was done I put the new string back into the list. Once outside the loop I used .sort() to sort the list. And at the end I used list comprehension to remove the number from all the strings within my list. Finally I made the list into a string again by using .join() and returning the string.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def sortSentence(self, s: str) -> str:\n list_of_words = s.split()\n\n for index in range(len(list_of_words)):\n order_char = list_of_words[index][-1]\n in_process_str = order_char + list_of_words[index]\n in_process_str = in_process_str[:-1]\n list_of_words[index] = in_process_str \n\n list_of_words.sort()\n without_nums = [sub[1:] for sub in list_of_words]\n return " ".join(without_nums)\n \n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Python solution using for loop and list comprehension | sorting-the-sentence | 0 | 1 | # Intuition\nLooking at the test cases I knew I could use the numbers to sort it\n\n# Approach\nI started by converting the string into a list by using .spilt(). I followed that by going into a for loop and getting the last char which is the number. The next step was to put the number at the beginning and to remove the number at the end of the string. Once that was done I put the new string back into the list. Once outside the loop I used .sort() to sort the list. And at the end I used list comprehension to remove the number from all the strings within my list. Finally I made the list into a string again by using .join() and returning the string.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def sortSentence(self, s: str) -> str:\n list_of_words = s.split()\n\n for index in range(len(list_of_words)):\n order_char = list_of_words[index][-1]\n in_process_str = order_char + list_of_words[index]\n in_process_str = in_process_str[:-1]\n list_of_words[index] = in_process_str \n\n list_of_words.sort()\n without_nums = [sub[1:] for sub in list_of_words]\n return " ".join(without_nums)\n \n``` | 0 | There is a **1-based** binary matrix where `0` represents land and `1` represents water. You are given integers `row` and `col` representing the number of rows and columns in the matrix, respectively.
Initially on day `0`, the **entire** matrix is **land**. However, each day a new cell becomes flooded with **water**. You are given a **1-based** 2D array `cells`, where `cells[i] = [ri, ci]` represents that on the `ith` day, the cell on the `rith` row and `cith` column (**1-based** coordinates) will be covered with **water** (i.e., changed to `1`).
You want to find the **last** day that it is possible to walk from the **top** to the **bottom** by only walking on land cells. You can start from **any** cell in the top row and end at **any** cell in the bottom row. You can only travel in the **four** cardinal directions (left, right, up, and down).
Return _the **last** day where it is possible to walk from the **top** to the **bottom** by only walking on land cells_.
**Example 1:**
**Input:** row = 2, col = 2, cells = \[\[1,1\],\[2,1\],\[1,2\],\[2,2\]\]
**Output:** 2
**Explanation:** The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 2.
**Example 2:**
**Input:** row = 2, col = 2, cells = \[\[1,1\],\[1,2\],\[2,1\],\[2,2\]\]
**Output:** 1
**Explanation:** The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 1.
**Example 3:**
**Input:** row = 3, col = 3, cells = \[\[1,2\],\[2,1\],\[3,3\],\[2,2\],\[1,1\],\[1,3\],\[2,3\],\[3,2\],\[3,1\]\]
**Output:** 3
**Explanation:** The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 3.
**Constraints:**
* `2 <= row, col <= 2 * 104`
* `4 <= row * col <= 2 * 104`
* `cells.length == row * col`
* `1 <= ri <= row`
* `1 <= ci <= col`
* All the values of `cells` are **unique**. | Divide the string into the words as an array of strings Sort the words by removing the last character from each word and sorting according to it |
Easiest Python3 Approach | sorting-the-sentence | 0 | 1 | \n# Code\n```\nclass Solution:\n def sortSentence(self, s: str) -> str:\n a = s.split()\n b = [0] * len(a)\n for i in a:\n b[int(i[-1]) - 1] = i[0:-1]\n return " ".join(b)\n``` | 4 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Easiest Python3 Approach | sorting-the-sentence | 0 | 1 | \n# Code\n```\nclass Solution:\n def sortSentence(self, s: str) -> str:\n a = s.split()\n b = [0] * len(a)\n for i in a:\n b[int(i[-1]) - 1] = i[0:-1]\n return " ".join(b)\n``` | 4 | There is a **1-based** binary matrix where `0` represents land and `1` represents water. You are given integers `row` and `col` representing the number of rows and columns in the matrix, respectively.
Initially on day `0`, the **entire** matrix is **land**. However, each day a new cell becomes flooded with **water**. You are given a **1-based** 2D array `cells`, where `cells[i] = [ri, ci]` represents that on the `ith` day, the cell on the `rith` row and `cith` column (**1-based** coordinates) will be covered with **water** (i.e., changed to `1`).
You want to find the **last** day that it is possible to walk from the **top** to the **bottom** by only walking on land cells. You can start from **any** cell in the top row and end at **any** cell in the bottom row. You can only travel in the **four** cardinal directions (left, right, up, and down).
Return _the **last** day where it is possible to walk from the **top** to the **bottom** by only walking on land cells_.
**Example 1:**
**Input:** row = 2, col = 2, cells = \[\[1,1\],\[2,1\],\[1,2\],\[2,2\]\]
**Output:** 2
**Explanation:** The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 2.
**Example 2:**
**Input:** row = 2, col = 2, cells = \[\[1,1\],\[1,2\],\[2,1\],\[2,2\]\]
**Output:** 1
**Explanation:** The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 1.
**Example 3:**
**Input:** row = 3, col = 3, cells = \[\[1,2\],\[2,1\],\[3,3\],\[2,2\],\[1,1\],\[1,3\],\[2,3\],\[3,2\],\[3,1\]\]
**Output:** 3
**Explanation:** The above image depicts how the matrix changes each day starting from day 0.
The last day where it is possible to cross from top to bottom is on day 3.
**Constraints:**
* `2 <= row, col <= 2 * 104`
* `4 <= row * col <= 2 * 104`
* `cells.length == row * col`
* `1 <= ri <= row`
* `1 <= ci <= col`
* All the values of `cells` are **unique**. | Divide the string into the words as an array of strings Sort the words by removing the last character from each word and sorting according to it |
[Java/C++/Python] Solution | incremental-memory-leak | 1 | 1 | **Java**\n\n```\nclass Solution {\n public int[] memLeak(int memory1, int memory2) {\n int i = 1;\n while(Math.max(memory1, memory2) >= i){\n if(memory1 >= memory2)\n memory1 -= i;\n else\n memory2 -= i;\n i++;\n }\n return new int[]{i, memory1, memory2};\n }\n}\n```\n\n**C++**\n```\nclass Solution {\npublic:\n vector<int> memLeak(int memory1, int memory2) {\n int i = 1;\n while(max(memory1, memory2) >= i){\n if(memory1 >= memory2)\n memory1 -= i;\n else\n memory2 -= i;\n i++;\n }\n return {i, memory1, memory2};\n }\n};\n```\n\n**Python**\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n i = 1\n while max(memory1, memory2) >= i:\n if memory1 >= memory2:\n memory1 -= i\n else:\n memory2 -= i\n i += 1\n return [i, memory1, memory2]\n```\n\n```\nclass Solution:\n def memLeak(self, m1: int, m2: int) -> List[int]:\n res = [1,m1,m2]\n while 1:\n if res[2] > res[1]:\n mx = 2\n else:\n mx = 1\n if res[0] > res[mx]:\n return res\n else:\n res[mx] -= res[0]\n res[0]+=1\n``` | 29 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Java/C++/Python] Solution | incremental-memory-leak | 1 | 1 | **Java**\n\n```\nclass Solution {\n public int[] memLeak(int memory1, int memory2) {\n int i = 1;\n while(Math.max(memory1, memory2) >= i){\n if(memory1 >= memory2)\n memory1 -= i;\n else\n memory2 -= i;\n i++;\n }\n return new int[]{i, memory1, memory2};\n }\n}\n```\n\n**C++**\n```\nclass Solution {\npublic:\n vector<int> memLeak(int memory1, int memory2) {\n int i = 1;\n while(max(memory1, memory2) >= i){\n if(memory1 >= memory2)\n memory1 -= i;\n else\n memory2 -= i;\n i++;\n }\n return {i, memory1, memory2};\n }\n};\n```\n\n**Python**\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n i = 1\n while max(memory1, memory2) >= i:\n if memory1 >= memory2:\n memory1 -= i\n else:\n memory2 -= i\n i += 1\n return [i, memory1, memory2]\n```\n\n```\nclass Solution:\n def memLeak(self, m1: int, m2: int) -> List[int]:\n res = [1,m1,m2]\n while 1:\n if res[2] > res[1]:\n mx = 2\n else:\n mx = 1\n if res[0] > res[mx]:\n return res\n else:\n res[mx] -= res[0]\n res[0]+=1\n``` | 29 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
[Python3] simulation | incremental-memory-leak | 0 | 1 | \n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n k = 1\n while k <= memory1 or k <= memory2: \n if memory1 < memory2: memory2 -= k \n else: memory1 -= k \n k += 1\n return [k, memory1, memory2]\n``` | 4 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Python3] simulation | incremental-memory-leak | 0 | 1 | \n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n k = 1\n while k <= memory1 or k <= memory2: \n if memory1 < memory2: memory2 -= k \n else: memory1 -= k \n k += 1\n return [k, memory1, memory2]\n``` | 4 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
[Python3] Solution with using simulation | incremental-memory-leak | 0 | 1 | # Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n memory_in_use, cur_sec = 0,0\n\n while True:\n memory_in_use += 1\n cur_sec += 1\n\n if memory1 < memory_in_use and memory2 < memory_in_use: break\n\n if memory1 >= memory2: memory1 -= memory_in_use\n else: memory2 -= memory_in_use\n \n return [cur_sec, memory1, memory2]\n \n \n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Python3] Solution with using simulation | incremental-memory-leak | 0 | 1 | # Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n memory_in_use, cur_sec = 0,0\n\n while True:\n memory_in_use += 1\n cur_sec += 1\n\n if memory1 < memory_in_use and memory2 < memory_in_use: break\n\n if memory1 >= memory2: memory1 -= memory_in_use\n else: memory2 -= memory_in_use\n \n return [cur_sec, memory1, memory2]\n \n \n``` | 0 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
Simple While Loop Implementation using Python | incremental-memory-leak | 0 | 1 | # Approach\nSimple While Loop Implementation using Python\n\n# Complexity\n- Time complexity:\nO(N) where N is the \n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n crashTime = 1\n memoryAllocation = 1\n while max(memory1, memory2) >= memoryAllocation:\n if memory1 >= memory2:\n memory1-=memoryAllocation\n else:\n memory2-=memoryAllocation\n crashTime+=1\n memoryAllocation+=1\n return [crashTime, memory1, memory2]\n\n \n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
Simple While Loop Implementation using Python | incremental-memory-leak | 0 | 1 | # Approach\nSimple While Loop Implementation using Python\n\n# Complexity\n- Time complexity:\nO(N) where N is the \n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n crashTime = 1\n memoryAllocation = 1\n while max(memory1, memory2) >= memoryAllocation:\n if memory1 >= memory2:\n memory1-=memoryAllocation\n else:\n memory2-=memoryAllocation\n crashTime+=1\n memoryAllocation+=1\n return [crashTime, memory1, memory2]\n\n \n``` | 0 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
[ Python | C++ ] one-liner | incremental-memory-leak | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe could use recursion while simulating memory leak. \n\n# Python\n```\nclass Solution:\n def memLeak(self, a, b, t=1):\n return [t,a,b] if max(a,b)<t else self.memLeak(a-t*(a>=b),b-t*(b>a),t+1)\n```\n\n# C++\n```\nclass Solution {\npublic:\n vector<int> memLeak(int a, int b, int t=1) {\n return max(a,b)<t ? vector({t,a,b}) : memLeak(a-t*(a>=b),b-t*(b>a),t+1);\n }\n};\n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[ Python | C++ ] one-liner | incremental-memory-leak | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe could use recursion while simulating memory leak. \n\n# Python\n```\nclass Solution:\n def memLeak(self, a, b, t=1):\n return [t,a,b] if max(a,b)<t else self.memLeak(a-t*(a>=b),b-t*(b>a),t+1)\n```\n\n# C++\n```\nclass Solution {\npublic:\n vector<int> memLeak(int a, int b, int t=1) {\n return max(a,b)<t ? vector({t,a,b}) : memLeak(a-t*(a>=b),b-t*(b>a),t+1);\n }\n};\n``` | 0 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
Solution Using While Loop Only 8 Lines | incremental-memory-leak | 0 | 1 | # Intuition\nWe need to subtract i from the stick which has more memory left and continue this process until there is no memory left in either of the sticks.\n\n# Approach\ninitialise i=1 which denotes the seconds and create a while loop that checks if either memory1 or memory2 has space and if it does subtract that from the memory.\n\n# Complexity\n- Time complexity:O(n)\n\n- Space complexity:O(1)\n\n# Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n i=1\n while max(memory1,memory2)>=i:\n if memory1>=memory2:\n memory1-=i\n else:\n memory2-=i\n i+=1\n return [i,memory1,memory2]\n\n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
Solution Using While Loop Only 8 Lines | incremental-memory-leak | 0 | 1 | # Intuition\nWe need to subtract i from the stick which has more memory left and continue this process until there is no memory left in either of the sticks.\n\n# Approach\ninitialise i=1 which denotes the seconds and create a while loop that checks if either memory1 or memory2 has space and if it does subtract that from the memory.\n\n# Complexity\n- Time complexity:O(n)\n\n- Space complexity:O(1)\n\n# Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n i=1\n while max(memory1,memory2)>=i:\n if memory1>=memory2:\n memory1-=i\n else:\n memory2-=i\n i+=1\n return [i,memory1,memory2]\n\n``` | 0 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
[Python3] Good enough | incremental-memory-leak | 0 | 1 | ``` Python3 []\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n\n time = 0\n while True:\n time += 1\n if memory1 >= memory2:\n if memory1 - time < 0:\n return [time,memory1,memory2]\n else:\n memory1 -= time\n else:\n if memory2 - time < 0:\n return [time,memory1,memory2]\n else:\n memory2 -= time\n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Python3] Good enough | incremental-memory-leak | 0 | 1 | ``` Python3 []\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n\n time = 0\n while True:\n time += 1\n if memory1 >= memory2:\n if memory1 - time < 0:\n return [time,memory1,memory2]\n else:\n memory1 -= time\n else:\n if memory2 - time < 0:\n return [time,memory1,memory2]\n else:\n memory2 -= time\n``` | 0 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
Brute-Force | incremental-memory-leak | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n time=1\n while True:\n if memory2>memory1:\n if memory2-time>=0:memory2-=time\n else:return [time,memory1,memory2]\n else:\n if memory1-time>=0:memory1-=time\n else:return [time,memory1,memory2]\n time+=1\n \n \n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
Brute-Force | incremental-memory-leak | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def memLeak(self, memory1: int, memory2: int) -> List[int]:\n time=1\n while True:\n if memory2>memory1:\n if memory2-time>=0:memory2-=time\n else:return [time,memory1,memory2]\n else:\n if memory1-time>=0:memory1-=time\n else:return [time,memory1,memory2]\n time+=1\n \n \n``` | 0 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself.
You want to determine if there is a **valid path** that exists from vertex `source` to vertex `destination`.
Given `edges` and the integers `n`, `source`, and `destination`, return `true` _if there is a **valid path** from_ `source` _to_ `destination`_, or_ `false` _otherwise__._
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[2,0\]\], source = 0, destination = 2
**Output:** true
**Explanation:** There are two paths from vertex 0 to vertex 2:
- 0 -> 1 -> 2
- 0 -> 2
**Example 2:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[3,5\],\[5,4\],\[4,3\]\], source = 0, destination = 5
**Output:** false
**Explanation:** There is no path from vertex 0 to vertex 5.
**Constraints:**
* `1 <= n <= 2 * 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ui, vi <= n - 1`
* `ui != vi`
* `0 <= source, destination <= n - 1`
* There are no duplicate edges.
* There are no self edges. | What is the upper bound for the number of seconds? Simulate the process of allocating memory. |
1861. Rotating the Box | rotating-the-box | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe solution first performs a clockwise rotation of the \'box\' by assigning the values from the original matrix box to the new matrix \'res\' in the rotated positions.\n\nNext, the solution iterates through each column of the \'res\' matrix from bottom to top. By keeping track of the start index, the solution simulates gravity by moving stones downwards until they encounter an obstacle or another stone. This is done by swapping the positions of stones and empty spaces in each column.\n\nThe resulting \'res\' matrix represents the \'box\' after the rotation and gravity simulation.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create a new matrix res with dimensions n x m to store the rotated box.\n\n2. Iterate through each cell of the original box matrix. For each cell at index (i, j), assign its value to the corresponding cell in the res matrix at index (i, m-1-j). This step performs the clockwise rotation of the box.\n\n3. Iterate through each column of the res matrix and simulate the effect of gravity on the stones. Start from the bottom of each column and move upwards. Keep track of the index start, which represents the position where the next stone should fall.\n\n4. If the current cell contains an obstacle \'*\', update the start index to j-1 to prevent stones from falling further.\n\n5. If the current cell contains a stone \'#\', update the current cell to \'.\', indicating that the stone has fallen, and assign the value \'#\' to the cell at index (start--, i). Decrementing start ensures that the next stone will fall on top of the previous one.\n\n6. Return the resulting res matrix, which represents the box after the rotation and gravity simulation.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(m * n), where m is the number of rows in the box matrix and n is the number of columns.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n The space complexity is O(m * n) as well, as we use an auxiliary space for keeping the result.\n\n---\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<char>> rotateTheBox(vector<vector<char>>& box) {\n int m = box.size();\n int n = box[0].size();\n\n vector<vector<char>> res(n, vector<char>(m));\n // Trasposing the matrix\n for (int i = 0; i < n; i++) {\n for (int j = m - 1; j >= 0; j--) {\n res[i][m - 1 - j] = box[j][i];\n }\n }\n // Applying the gravity\n for (int i = 0; i < m; i++) {\n int start = n - 1;\n for (int j = start; j >= 0; j--) {\n if (res[j][i] == \'*\') {\n start = j - 1;\n } else if (res[j][i] == \'#\') {\n res[j][i] = \'.\';\n res[start][i] = \'#\';\n start--;\n }\n }\n }\n return res;\n }\n};\n\n```\n```python3 []\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n m, n = len(box), len(box[0])\n\n res = [[\'\'] * m for _ in range(n)]\n # Transposing\n for i in range(n):\n for j in range(m - 1, -1, -1):\n res[i][m - 1 - j] = box[j][i]\n # Applying Gravity\n for i in range(m):\n start = n - 1\n for j in range(start, -1, -1):\n if res[j][i] == \'*\':\n start = j - 1\n elif res[j][i] == \'#\':\n res[j][i] = \'.\'\n res[start][i] = \'#\'\n start -= 1\n\n return res\n\n```\n | 6 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
[Python] Easy explanation | rotating-the-box | 0 | 1 | **First**, move every stone to the right, (or you can rotate the box first and then drop stones. Both as fine).\nThe current location of stone does not matter. \nWe only need to remember how many stones each interval (seperated by obstacles) has, \nand place the stones before the first seeing obstacle.\n\n**Second**, rotate the box. Same as **Leetcode problem # 48 Rotate Image**. \n```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n # move stones to right, row by row\n for i in range(len(box)):\n stone = 0\n for j in range(len(box[0])):\n if box[i][j] == \'#\': # if a stone\n stone += 1\n box[i][j] = \'.\'\n elif box[i][j] == \'*\': # if a obstacle\n for m in range(stone):\n box[i][j-m-1] = \'#\'\n stone = 0\n # if reaches the end of j, but still have stone\n if stone != 0:\n for m in range(stone):\n box[i][j-m] = \'#\'\n \n # rotate box, same as leetcode #48\n box[:] = zip(*box[::-1])\n \n return box\n``` | 13 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python | Two Pointers | rotating-the-box | 0 | 1 | # Algorithm\n1. Create a skeleton matrix with the number of rows and columns interchanged.\n2. Rotate the box -> matrix\n3. Iterate through each column and use two pointers in bottom-up fashion to seach for stone and blanks.\n4. Throughout the entire iteration the points to be kept in mind are:\n\t* \tThe index for stone must be lesser than the index of the blank\n\t* \tSearch for stone and blanks independently\n\t* \tIf while searching for the stone, an obstacle is found make the search for blanks from that index\n\n**NOTE**: The variables **\'stone\'** and **\'blank\'** are keeping track of the **indices** for stone and blank respectively.\n\n# Code\n```\n matrix = []\n rows, cols = len(box), len(box[0])\n \n\t\t# Creation of the new matrix skeleton\n for col in range(cols):\n temp = []\n for row in range(rows):\n temp.append(" ")\n matrix.append(temp)\n \n\t\t# Rotating the box\n for row in range(cols):\n for col in range(rows):\n matrix[row][col] = box[rows - col - 1][row]\n \n rows, cols = cols, rows\n \n\t\t# Main logic\n for col in range(cols):\n blank, stone = rows - 1, rows - 1\n\t\t\t# Iterating till all the rows are iterated over\n while stone >= 0:\n\t\t\t\t# Iterating the column bottom-up till a stone is found\n while stone >= 0 and matrix[stone][col] != \'#\':\n\t\t\t\t\t# If an obstacle is found make its previous index the starting point for the search for blanks\n if matrix[stone][col] == \'*\':\n blank = stone - 1\n stone -= 1\n\t\t\t\t# Iterating the column bottom-up till a blank is found\n while blank >= 0 and matrix[blank][col] != \'.\':\n blank -= 1\n\t\t\t\t# Check for the index values for out of bounds and mainly if the index for stone is lesser than the index for blank\n if blank >= 0 and stone >= 0 and stone < blank:\n matrix[blank][col], matrix[stone][col] = matrix[stone][col], matrix[blank][col]\n stone -= 1\n return matrix\n``` | 3 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
two pointers | Beats 86% | rotating-the-box | 0 | 1 | ```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n m, n = len(box), len(box[0])\n for row in box:\n i, j = len(row) - 2, len(row) - 1\n while i >= 0:\n if row[j] == \'.\':\n if row[i] == \'#\':\n # swap\n row[j] = \'#\'\n row[i] = \'.\'\n j-=1\n i-=1\n elif row[i] == \'.\':\n i-=1\n elif row[i] == \'*\':\n j = i-1\n i = j-1\n else:\n j-=1\n i=j-1\n # take the transpose of the matrix\n new_box = [[0 for _ in range(m)] for _ in range(n)]\n for i in range(m-1, -1, -1):\n for j in range(n):\n new_box[j][m-1-i] = box[i][j]\n return new_box\n``` | 1 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Simple Python Solution | rotating-the-box | 0 | 1 | The idea is to look for the rocks closest to the bottom first. Move them to the the last empty cell (the one left of nearest obstacle).\n\n```\ndef rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n # Constants\n ROWS, COLS = len(box), len(box[0])\n \n # Falling logic\n for r in range(ROWS):\n # Start column scan from "bottom" (R->L)\n for c in range(COLS - 1, -1 , -1):\n # If a rock is found\n if box[r][c] == "#":\n # Scan L->R for next obstacle\n obs = c + 1\n while obs < COLS and box[r][obs] == ".":\n obs += 1\n \n # Mark current cell as empty and cell left of obstacle as rock\n # If the rock doesn\'t move, nothing changes\n box[r][c] = "."\n box[r][obs - 1] = "#"\n \n # Rotation\n rotBox = [[None for _ in range(ROWS)] for _ in range(COLS)]\n curCol = ROWS - 1\n for r in range(ROWS):\n for c in range(COLS):\n rotBox[c][curCol] = box[r][c]\n curCol -= 1\n \n return rotBox\n``` | 1 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
easy solution using sorting || beats 78.95% RT , Memory 61.60 | rotating-the-box | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n lst=[]\n for i in box:\n v=[]\n val=""\n st=""\n for j in i:\n if j!="*":\n st+=j\n else:\n st=sorted(st)\n val+="".join(st[::-1])\n val+="*"\n st=""\n if st:\n st=sorted(st)\n val+="".join(st[::-1])\n for k in val:\n v.append(k)\n lst.append(v)\n lst=lst[::-1]\n ans=[]\n for i in zip(*lst):\n ans.append(i)\n return ans\n \n\n \n``` | 3 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Simple Solution With Lists | rotating-the-box | 0 | 1 | ```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n new_box = []\n for row in box:\n adjusted_row = []\n curr_section = []\n for idx, elem in enumerate(row):\n if elem == ".":\n curr_section.insert(0, elem)\n elif elem == "#":\n curr_section.append(elem)\n elif elem == "*":\n curr_section.append(elem)\n adjusted_row.extend(curr_section)\n curr_section = []\n adjusted_row.extend(curr_section)\n new_box.append(adjusted_row)\n \n return zip(*new_box[::-1])\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python, runtime O(mn), memory O(1) | rotating-the-box | 0 | 1 | ```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n M = len(box)\n N = len(box[0])\n ans = [[\'.\']*M for _ in range(N)]\n for i in range(M):\n q = deque([])\n for j in range(N-1, -1, -1):\n if box[i][j] == \'*\':\n q = deque([])\n ans[j][M-i-1] = \'*\'\n elif box[i][j] == \'.\':\n q.append(j)\n elif box[i][j] == \'#\' and q:\n ans[q.popleft()][M-i-1] = \'#\'\n q.append(j)\n else:\n ans[j][M-i-1] = \'#\'\n\n return ans\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Simple python solution with Sort | 2 mins enough to understand | rotating-the-box | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Iterate over the `box` line by line. For each line:\n + split at each `*` (You can regard each segment as a seperate problem, because all the falling happens independently in the current segment.)\n + Let the little squares "fall to the right". To achieve this, we simply sort the segment.\n + Assemble back the segments into a new line.\n2. Finally, do not forget to transpose the matrix (rotate the matrix).\n\n# Code\n```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n res = []\n for line in box:\n line_seg = \'\'.join(line).split(\'*\')\n line_seg = [\'\'.join(sorted(i, reverse=True)) for i in line_seg]\n new_line = \'*\'.join(line_seg)\n res.append(new_line)\n\n return list(zip(*res[::-1]))\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.