title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python, Java] Elegant & Short | One Pass | sign-of-the-product-of-an-array | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n\n```python []\nclass Solution:\n def arraySign(self, nums: List[int]) -> int:\n sign = 1\n\n for num in nums:\n if num < 0:\n sign *= -1\n if num == 0:\n return 0\n\n return sign\n```\n\n```java []\nclass Solution {\n public int arraySign(int[] nums) {\n int sign = 1;\n\n for (int num : nums) {\n if (num < 0)\n sign *= -1;\n else if (num == 0)\n return 0;\n }\n\n return sign;\n }\n}\n```\n | 1 | You are given an integer array `nums` of size `n`. You are asked to solve `n` queries for each integer `i` in the range `0 <= i < n`.
To solve the `ith` query:
1. Find the **minimum value** in each possible subarray of size `i + 1` of the array `nums`.
2. Find the **maximum** of those minimum values. This maximum is the **answer** to the query.
Return _a **0-indexed** integer array_ `ans` _of size_ `n` _such that_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[0,1,2,4\]
**Output:** \[4,2,1,0\]
**Explanation:**
i=0:
- The subarrays of size 1 are \[0\], \[1\], \[2\], \[4\]. The minimum values are 0, 1, 2, 4.
- The maximum of the minimum values is 4.
i=1:
- The subarrays of size 2 are \[0,1\], \[1,2\], \[2,4\]. The minimum values are 0, 1, 2.
- The maximum of the minimum values is 2.
i=2:
- The subarrays of size 3 are \[0,1,2\], \[1,2,4\]. The minimum values are 0, 1.
- The maximum of the minimum values is 1.
i=3:
- There is one subarray of size 4, which is \[0,1,2,4\]. The minimum value is 0.
- There is only one value, so the maximum is 0.
**Example 2:**
**Input:** nums = \[10,20,50,10\]
**Output:** \[50,20,10,10\]
**Explanation:**
i=0:
- The subarrays of size 1 are \[10\], \[20\], \[50\], \[10\]. The minimum values are 10, 20, 50, 10.
- The maximum of the minimum values is 50.
i=1:
- The subarrays of size 2 are \[10,20\], \[20,50\], \[50,10\]. The minimum values are 10, 20, 10.
- The maximum of the minimum values is 20.
i=2:
- The subarrays of size 3 are \[10,20,50\], \[20,50,10\]. The minimum values are 10, 10.
- The maximum of the minimum values is 10.
i=3:
- There is one subarray of size 4, which is \[10,20,50,10\]. The minimum value is 10.
- There is only one value, so the maximum is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 109` | If there is a 0 in the array the answer is 0 To avoid overflow make all the negative numbers -1 and all positive numbers 1 and calculate the prod |
Simple Python3 & Java Solution|| Upto 100% Faster || O(n) | sign-of-the-product-of-an-array | 0 | 1 | # Intuition\nFor either python or Java we check if Zero or number of negative numbers and return respectively.\nIn Java we donot need to use a Double or Long to get the prod equivalent just check if the number is positive or negative.\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n\n```java []\nclass Solution {\n public int arraySign(int[] nums) {\n int prod = 1;\n for (int i: nums){\n \n prod *= i;\n if (prod ==0){\n return 0;\n } else if (prod < 0){\n prod = -1;\n } else{\n prod = 1;\n }\n //Return Condition\n }\n if (prod ==0){\n return 0;\n } else if (prod < 0){\n return -1;\n } else{\n return 1;\n }\n }\n}\n```\n```python []\nclass Solution:\n def arraySign(self, nums: List[int]) -> int:\n neg = 1\n for i in nums:\n if i==0:\n return 0\n elif i<0:\n neg *= -1\n \n return neg\n``` | 1 | There is a function `signFunc(x)` that returns:
* `1` if `x` is positive.
* `-1` if `x` is negative.
* `0` if `x` is equal to `0`.
You are given an integer array `nums`. Let `product` be the product of all values in the array `nums`.
Return `signFunc(product)`.
**Example 1:**
**Input:** nums = \[-1,-2,-3,-4,3,2,1\]
**Output:** 1
**Explanation:** The product of all values in the array is 144, and signFunc(144) = 1
**Example 2:**
**Input:** nums = \[1,5,0,2,-3\]
**Output:** 0
**Explanation:** The product of all values in the array is 0, and signFunc(0) = 0
**Example 3:**
**Input:** nums = \[-1,1,-1,1,-1\]
**Output:** -1
**Explanation:** The product of all values in the array is -1, and signFunc(-1) = -1
**Constraints:**
* `1 <= nums.length <= 1000`
* `-100 <= nums[i] <= 100` | As with any good dp problem that uses palindromes, try building the palindrome from the edges The prime point is to check that no two adjacent characters are equal, so save the past character while building the palindrome. |
Simple Python3 & Java Solution|| Upto 100% Faster || O(n) | sign-of-the-product-of-an-array | 0 | 1 | # Intuition\nFor either python or Java we check if Zero or number of negative numbers and return respectively.\nIn Java we donot need to use a Double or Long to get the prod equivalent just check if the number is positive or negative.\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n\n```java []\nclass Solution {\n public int arraySign(int[] nums) {\n int prod = 1;\n for (int i: nums){\n \n prod *= i;\n if (prod ==0){\n return 0;\n } else if (prod < 0){\n prod = -1;\n } else{\n prod = 1;\n }\n //Return Condition\n }\n if (prod ==0){\n return 0;\n } else if (prod < 0){\n return -1;\n } else{\n return 1;\n }\n }\n}\n```\n```python []\nclass Solution:\n def arraySign(self, nums: List[int]) -> int:\n neg = 1\n for i in nums:\n if i==0:\n return 0\n elif i<0:\n neg *= -1\n \n return neg\n``` | 1 | You are given an integer array `nums` of size `n`. You are asked to solve `n` queries for each integer `i` in the range `0 <= i < n`.
To solve the `ith` query:
1. Find the **minimum value** in each possible subarray of size `i + 1` of the array `nums`.
2. Find the **maximum** of those minimum values. This maximum is the **answer** to the query.
Return _a **0-indexed** integer array_ `ans` _of size_ `n` _such that_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[0,1,2,4\]
**Output:** \[4,2,1,0\]
**Explanation:**
i=0:
- The subarrays of size 1 are \[0\], \[1\], \[2\], \[4\]. The minimum values are 0, 1, 2, 4.
- The maximum of the minimum values is 4.
i=1:
- The subarrays of size 2 are \[0,1\], \[1,2\], \[2,4\]. The minimum values are 0, 1, 2.
- The maximum of the minimum values is 2.
i=2:
- The subarrays of size 3 are \[0,1,2\], \[1,2,4\]. The minimum values are 0, 1.
- The maximum of the minimum values is 1.
i=3:
- There is one subarray of size 4, which is \[0,1,2,4\]. The minimum value is 0.
- There is only one value, so the maximum is 0.
**Example 2:**
**Input:** nums = \[10,20,50,10\]
**Output:** \[50,20,10,10\]
**Explanation:**
i=0:
- The subarrays of size 1 are \[10\], \[20\], \[50\], \[10\]. The minimum values are 10, 20, 50, 10.
- The maximum of the minimum values is 50.
i=1:
- The subarrays of size 2 are \[10,20\], \[20,50\], \[50,10\]. The minimum values are 10, 20, 10.
- The maximum of the minimum values is 20.
i=2:
- The subarrays of size 3 are \[10,20,50\], \[20,50,10\]. The minimum values are 10, 10.
- The maximum of the minimum values is 10.
i=3:
- There is one subarray of size 4, which is \[10,20,50,10\]. The minimum value is 10.
- There is only one value, so the maximum is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 109` | If there is a 0 in the array the answer is 0 To avoid overflow make all the negative numbers -1 and all positive numbers 1 and calculate the prod |
Easy Python Solution | sign-of-the-product-of-an-array | 0 | 1 | \n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```Python []\nclass Solution:\n def arraySign(self, nums: List[int]) -> int:\n re = 1\n for i in nums:\n re = re*i\n if re<0:\n return -1\n elif re>1:\n return 1\n else:\n return 0\n \n\n``` | 1 | There is a function `signFunc(x)` that returns:
* `1` if `x` is positive.
* `-1` if `x` is negative.
* `0` if `x` is equal to `0`.
You are given an integer array `nums`. Let `product` be the product of all values in the array `nums`.
Return `signFunc(product)`.
**Example 1:**
**Input:** nums = \[-1,-2,-3,-4,3,2,1\]
**Output:** 1
**Explanation:** The product of all values in the array is 144, and signFunc(144) = 1
**Example 2:**
**Input:** nums = \[1,5,0,2,-3\]
**Output:** 0
**Explanation:** The product of all values in the array is 0, and signFunc(0) = 0
**Example 3:**
**Input:** nums = \[-1,1,-1,1,-1\]
**Output:** -1
**Explanation:** The product of all values in the array is -1, and signFunc(-1) = -1
**Constraints:**
* `1 <= nums.length <= 1000`
* `-100 <= nums[i] <= 100` | As with any good dp problem that uses palindromes, try building the palindrome from the edges The prime point is to check that no two adjacent characters are equal, so save the past character while building the palindrome. |
Easy Python Solution | sign-of-the-product-of-an-array | 0 | 1 | \n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```Python []\nclass Solution:\n def arraySign(self, nums: List[int]) -> int:\n re = 1\n for i in nums:\n re = re*i\n if re<0:\n return -1\n elif re>1:\n return 1\n else:\n return 0\n \n\n``` | 1 | You are given an integer array `nums` of size `n`. You are asked to solve `n` queries for each integer `i` in the range `0 <= i < n`.
To solve the `ith` query:
1. Find the **minimum value** in each possible subarray of size `i + 1` of the array `nums`.
2. Find the **maximum** of those minimum values. This maximum is the **answer** to the query.
Return _a **0-indexed** integer array_ `ans` _of size_ `n` _such that_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[0,1,2,4\]
**Output:** \[4,2,1,0\]
**Explanation:**
i=0:
- The subarrays of size 1 are \[0\], \[1\], \[2\], \[4\]. The minimum values are 0, 1, 2, 4.
- The maximum of the minimum values is 4.
i=1:
- The subarrays of size 2 are \[0,1\], \[1,2\], \[2,4\]. The minimum values are 0, 1, 2.
- The maximum of the minimum values is 2.
i=2:
- The subarrays of size 3 are \[0,1,2\], \[1,2,4\]. The minimum values are 0, 1.
- The maximum of the minimum values is 1.
i=3:
- There is one subarray of size 4, which is \[0,1,2,4\]. The minimum value is 0.
- There is only one value, so the maximum is 0.
**Example 2:**
**Input:** nums = \[10,20,50,10\]
**Output:** \[50,20,10,10\]
**Explanation:**
i=0:
- The subarrays of size 1 are \[10\], \[20\], \[50\], \[10\]. The minimum values are 10, 20, 50, 10.
- The maximum of the minimum values is 50.
i=1:
- The subarrays of size 2 are \[10,20\], \[20,50\], \[50,10\]. The minimum values are 10, 20, 10.
- The maximum of the minimum values is 20.
i=2:
- The subarrays of size 3 are \[10,20,50\], \[20,50,10\]. The minimum values are 10, 10.
- The maximum of the minimum values is 10.
i=3:
- There is one subarray of size 4, which is \[10,20,50,10\]. The minimum value is 10.
- There is only one value, so the maximum is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] <= 109` | If there is a 0 in the array the answer is 0 To avoid overflow make all the negative numbers -1 and all positive numbers 1 and calculate the prod |
Beginner-friendly || Simple solution with using Queue DS on Python3 | find-the-winner-of-the-circular-game | 0 | 1 | # Intuition\nLet\'s briefly explain the task and provide some `pseudocode`:\n```\n# There\'re n-friends, playing a game\nfriends = [1,2,3,4,5]\n\n# at each step there\'s an option to SKIP some players in order\nn = 2\ni = 0\n\n# to EXCLUDE the player, that the pointer has stopped at\n# [1, (2), 3, 4, 5]\n# i=1 i=2==k\n\nfriends = [1, 3, 4, 5]\n\n# the process continues UNTIL there will only ONE player\nfriends = [3]\n```\nThis example leads us to create a `queue`, that\'ll represent a source of players, that will leave the `queue`, when `i` **points** at a particular player.\n\n# Approach\n1. initialize a `q` and map `x+1` to the current player\n2. create a loop, that\'ll stop, when there\'ll only **one player** inside of a `q`\n3. at each `c = k-1` step exclude the participant, and continue to iterate\n4. once there\'is only one player, return it\'s index from `q`\n\n# Complexity\n- Time complexity: **O(n^2)**\n\n- Space complexity: **O(n)**\n\n# Code\n```\nclass Solution:\n def findTheWinner(self, n: int, k: int) -> int:\n q = deque([x + 1 for x in range(n)])\n\n while len(q) > 1:\n c = k - 1\n\n while c:\n q.append(q.popleft())\n c -= 1\n \n q.popleft()\n\n return q[0]\n``` | 4 | There are `n` friends that are playing a game. The friends are sitting in a circle and are numbered from `1` to `n` in **clockwise order**. More formally, moving clockwise from the `ith` friend brings you to the `(i+1)th` friend for `1 <= i < n`, and moving clockwise from the `nth` friend brings you to the `1st` friend.
The rules of the game are as follows:
1. **Start** at the `1st` friend.
2. Count the next `k` friends in the clockwise direction **including** the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step `2` **starting** from the friend **immediately clockwise** of the friend who just lost and repeat.
5. Else, the last friend in the circle wins the game.
Given the number of friends, `n`, and an integer `k`, return _the winner of the game_.
**Example 1:**
**Input:** n = 5, k = 2
**Output:** 3
**Explanation:** Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
**Example 2:**
**Input:** n = 6, k = 5
**Output:** 1
**Explanation:** The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
**Constraints:**
* `1 <= k <= n <= 500`
**Follow up:**
Could you solve this problem in linear time with constant space? | Create a function that checks if a character is a vowel, either uppercase or lowercase. |
O(n)->O(klg(n)) with table explanation | find-the-winner-of-the-circular-game | 0 | 1 | This is the josephus problem, [wikipedia](https://en.wikipedia.org/wiki/Josephus_problem)\nThe classic algorithm to this problem is very weird, let me talk with the example1 in "leetcode problem description". \nAt first [aaa,bbb,cac,ddd,eee] is playing this game.\n\n| #alive | aaa | bbb | cac | ddd | eee |\n|-------------|-----|-----|-----|-----|-----|\n| 5 | 1 | 2 | 3 | 4 | 5 |\n| 4 | 4 | (\u2191eliminated) | 1 | 2 | 3 |\n| 3 | 2 | | 3 | (0) | 1 |\n| 2 | | | 1 | | 2 |\n| 1 | | | 1 | | |\n\nEvery different round, we name these people using different number sequences.\nEvery time someone died, the number sequence start again from 1.\nThe table describes how we name these people.\n\nThe winner have a number `1` in the last round. \nYou have to induce his(cac) \'s number in the first round.\nSuppose when there are `i` people alive, cac\'s number is `f(i,\'cac\')`. And when there are `i+1` people alive, cac\'s number is `f(i+1,\'cac\')`.\nThen `f(i+1,\'cac\') == (k + f(i,\'cac\') - 1 )%(i+1) + 1`.\n\n<details><summary> prove </summary><p>\n\n**When there are `i+1` people alive**, person with number *`k % (i+1)`* will be eliminated \n\n**When `i` people alive**, He(\u2191) has a dummy number 0 . So count the next `f(i,\'cac\')` people , ( turn back to round when `i+1` people alive ) number *`(k+f(i,\'cac\')) % (i+1)`* is the value of *`f(i+1, \'cac\')`* . \n\nA good example from this table is when `i==3`. `f(i,\'cac\')` is `3`, \'ddd\' will be eliminated, `f(i+1, \'cac\')` is *`(2+f(i,\'cac\'))%4`*.\n\nNotice, `f(i+1,\'cac\')` can\'t be zero, you need change it to *`(k+f(i,\'cac\')-1)%(i+1)+1`*. ( for example, when `i==2`, the value of *`(k+f(i,\'cac\'))%(i+1)`* maybe `0,1,2`, but indeed, we need `3,1,2`, so additionally map `0` into `3` while remeining other values unchanged. ). \n\nTo avoid this problem, you can make all indices in this problem start from 0, i.e. map all indices from `i` to `i-1`. \n\n---\n</p></details>\n\nThen you can build a relation between each round and finally get the correct answer.\n\nThere is also a `O(klg(n))` hybrid algorithm, I will introduce later.\nThere is also a time `O(lgn)` space `O(1)` formula/algorithm when `k` is `2`, refer to wikipedia.\n## code\n-----\n\ntop-down recursion: time \u0398(n) space \u0398(n)\n```python\nclass Solution:\n def findTheWinner(self, n: int, k: int) -> int:\n if n==1: return 1\n return (k + self.findTheWinner(n-1, k) -1) % n + 1\n```\n\nbottom-up time \u0398(n) space \u0398(1)\n\n```python\ndef findTheWinner(self, n: int, k: int) -> int:\n p = 1\n for i in range(1,n):\n # here i represent number of alive people\n\t\t# p is f(i,\'cac\')\n p=(k+p-1)%(i+1)+1\n\t\t# p is f(i+1, \'cac\')\n return p\n```\n\n## advanced code1\nhttps://stackoverflow.com/a/69891445/7721525\n## advanced code2\n-----\n\nlet\'s use `g(n,k)` to represent answer of this problem.\nIn the previous section, we know for any positive n,k, `g(n,k) = (k + g(n-1, k) -1)%n + 1`.\n\nWhen `n >= k and k!=1`, we can eliminate `floor(n/k)` people in a round, and then use new indices.\nFor example, `n=11, k=3`\n\nhere for convenience, index start from 0\n\n|||||||||||foo||\n|---|---|---|---|---|---|---|---|---|---|---|----|\n| y | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |\n| z | 2 | 3 | / | 4 | 5 | / | 6 | 7 | / | 0 | 1 |\n| x | 0 | 1 | / | 2 | 3 | / | 4 | 5 | / | 6 | 7 |\n|y-x| 0 | 0 | | 1 | 1 | | 2 | 2 | | 3 | 3 |\n\nAs table, on the same column, `x,y,z` are different indices on the same person. From row1 to row2, eliminate `floor(n/k)` people, the indices start again on foo.\n \n+ `nextn = n - floor(n/k)`\n+ `x = (z-n%k) mod nextn ` (`x>=0`)\n+ `y = x + floor(x/(k-1))`\n+ so let `z = g(nextn,k)` we can get `g(n,k)` from `y`\n\n```python\ndef findTheWinner(self, n: int, k: int) -> int:\n if n==1: \n return 1\n elif k==1:\n return n\n elif n>=k:\n next_n = n - n//k\n z = self.findTheWinner(next_n, k) - 1\n x = (z-n%k + next_n) % next_n\n return x + x//(k-1) + 1\n else:\n return (k + self.findTheWinner(n-1, k) -1) % n + 1\n```\n\nthe time complexity `O(klg(n))`, space `O(klg(n))`\n\nSolve `T(n) = T(n*k/(k+1)) + O(1) if n>k else T(n)=T(n-1)+1`, \n`(k/(k+1))^(T(n)-k) = k/n` \n> `T(n) = (log(n/k))/(log(k+1)-log(k)) + k`\n>> `1/(log(k+1)-log(k)) \u2248 k + 0.5` ( logarithm base `math.e`)\n>> \n> `T(n) \u2248 klog(n/k) + k`\n\nSo `klg(n)` is an upper bound, also refer to wikipedia.\n\n## similar problems\n-----\n\n+ leetcode #390 (hard on log(n) solution)\n+ leetcode #1900 (super hard on log(n) solution )\n\n## where I learn from \n\n+ https://maskray.me/blog/2013-08-27-josephus-problem-two-log-n-solutions, but there are some mistakes. | 71 | There are `n` friends that are playing a game. The friends are sitting in a circle and are numbered from `1` to `n` in **clockwise order**. More formally, moving clockwise from the `ith` friend brings you to the `(i+1)th` friend for `1 <= i < n`, and moving clockwise from the `nth` friend brings you to the `1st` friend.
The rules of the game are as follows:
1. **Start** at the `1st` friend.
2. Count the next `k` friends in the clockwise direction **including** the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step `2` **starting** from the friend **immediately clockwise** of the friend who just lost and repeat.
5. Else, the last friend in the circle wins the game.
Given the number of friends, `n`, and an integer `k`, return _the winner of the game_.
**Example 1:**
**Input:** n = 5, k = 2
**Output:** 3
**Explanation:** Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
**Example 2:**
**Input:** n = 6, k = 5
**Output:** 1
**Explanation:** The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
**Constraints:**
* `1 <= k <= n <= 500`
**Follow up:**
Could you solve this problem in linear time with constant space? | Create a function that checks if a character is a vowel, either uppercase or lowercase. |
Python code with Intuition | O(n) | find-the-winner-of-the-circular-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe solution code is of few lines. You just need to understand the pattern here.\n\n## 1) Iterating over queue (If you know how to can skip this)\nBefore that understand how to iterate over the circular queue.\nSuppose no of students in circular queue are 6 starting from 0 index till 5th index.\nLet\'s say we are at 4th index \n\n\n\nincrementing to the next element is no brainer add just to the index\nNow we are at 5th.\nincrementing from here will reach to 6th index which is out of bound.\nUse modulus for incrementing\n## next_index = (current_index+1) % total_students\n next_index = (5+1) % 6 = 0\nThis will work for index less than 6 \n next_index = (4+1) % 6 = 5\n\n## 2) Understanding the pattern\n\nSuppose there are 7 friends are seating in linear way.\n### n = 7 and k = 4\n\n\n\nstarting from 0th index counting till 4 friend at index 3 will loose.\n\n\n\n> Keep in mind that we are counting in circular way even if they are seating in linear. \n\nThe number of students remain are\nn - 1 = 7 - 1 = 6\n\nStarting from 4 the next friend to loose will be at index 0\n\n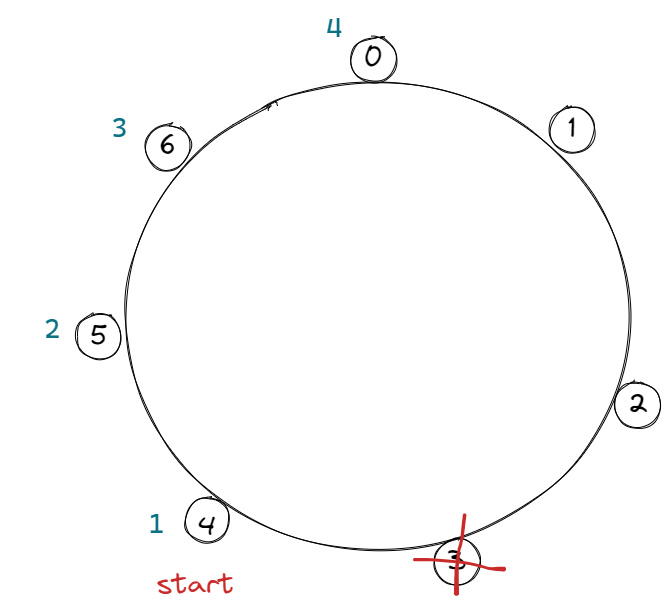\n\n### In linear way\n\n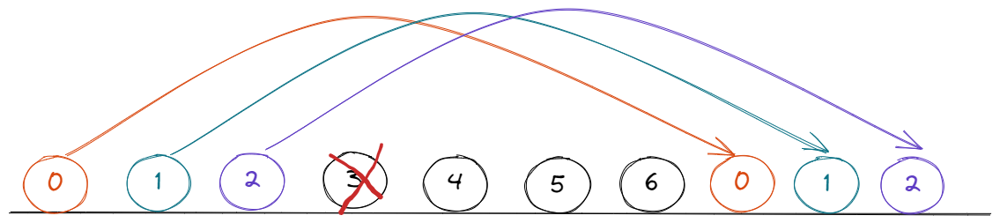\n\nThere are 6 friends now seating in circular fashion and their indices are\n4 5 6 0 1 2\nSo we need to find out which friend will leave the queue if there are 6 friends and k is 4. (k has not changed.)\n\n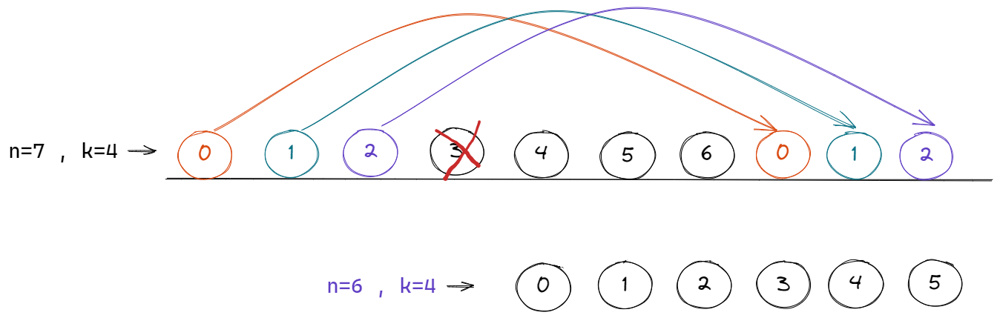\n\nKeep faith in recursion that it will return correct result for n=6 and k=4\n\nbut after the results will be returned we need to find out the relation between our current indices and index returned from the recursion.\n\nObserving first 3 element we can observe that after adding 4 to the indices are n=6 we can get indices of level n=7\n\n\n\nNow to iterate over start index again we will use modulus as it is circular queue.\n\nwe are at level n=7 , k = 4\nthe formula for conversion will be \n#### (findTheWinner(n-1) + k) % n\n\n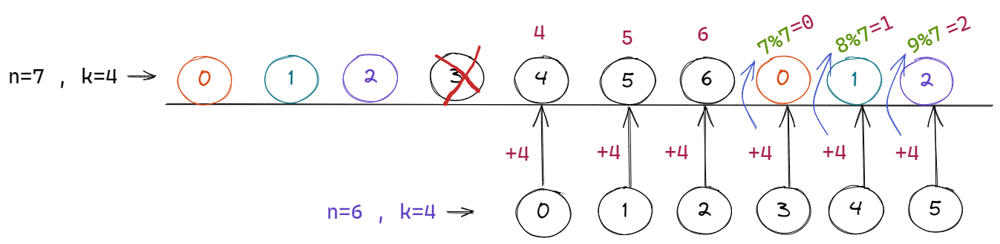\n\n\nThus we can retrieve the indices from the n-1 levels.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n\n# Code\n```\nclass Solution:\n def findTheWinner(self, n: int, k: int) -> int:\n return self.helper(n,k)+1\n\n def helper(self, n:int, k:int)-> int:\n if(n==1):\n return 0\n prevWinner = self.helper(n-1, k)\n return (prevWinner + k) % n\n``` | 15 | There are `n` friends that are playing a game. The friends are sitting in a circle and are numbered from `1` to `n` in **clockwise order**. More formally, moving clockwise from the `ith` friend brings you to the `(i+1)th` friend for `1 <= i < n`, and moving clockwise from the `nth` friend brings you to the `1st` friend.
The rules of the game are as follows:
1. **Start** at the `1st` friend.
2. Count the next `k` friends in the clockwise direction **including** the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step `2` **starting** from the friend **immediately clockwise** of the friend who just lost and repeat.
5. Else, the last friend in the circle wins the game.
Given the number of friends, `n`, and an integer `k`, return _the winner of the game_.
**Example 1:**
**Input:** n = 5, k = 2
**Output:** 3
**Explanation:** Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
**Example 2:**
**Input:** n = 6, k = 5
**Output:** 1
**Explanation:** The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
**Constraints:**
* `1 <= k <= n <= 500`
**Follow up:**
Could you solve this problem in linear time with constant space? | Create a function that checks if a character is a vowel, either uppercase or lowercase. |
Python3 Solutions | find-the-winner-of-the-circular-game | 0 | 1 | # Approach 1: Straight Forward\n```\nclass Solution:\n def findTheWinner(self, n: int, k: int) -> int:\n players = [playerNum+1 for playerNum in range(n)] #setup player numbers\n idx = 0 #starting player index\n while len(players)>1:\n idx = (idx+k-1) % len(players) #get last counter player, mod len(remaining_players) to avoid out of bounds\n players.pop(idx) #pop because it\'s faster than remove\n return players[0] #return last remaining player numbber\n```\n# Approach 2: Recurrsion\n```\nclass Solution:\n def sol(self, n, k, arr, i=0):\n if len(arr) == 1:\n return arr[0]\n else:\n index = (i + k - 1) % len(arr)\n arr.pop(index)\n i = index\n return self.sol(n, k, arr, i)\n\n def findTheWinner(self, n: int, k: int) -> int:\n arr = list(range(1, n + 1))\n return self.sol(n, k, arr)\n``` | 2 | There are `n` friends that are playing a game. The friends are sitting in a circle and are numbered from `1` to `n` in **clockwise order**. More formally, moving clockwise from the `ith` friend brings you to the `(i+1)th` friend for `1 <= i < n`, and moving clockwise from the `nth` friend brings you to the `1st` friend.
The rules of the game are as follows:
1. **Start** at the `1st` friend.
2. Count the next `k` friends in the clockwise direction **including** the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step `2` **starting** from the friend **immediately clockwise** of the friend who just lost and repeat.
5. Else, the last friend in the circle wins the game.
Given the number of friends, `n`, and an integer `k`, return _the winner of the game_.
**Example 1:**
**Input:** n = 5, k = 2
**Output:** 3
**Explanation:** Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
**Example 2:**
**Input:** n = 6, k = 5
**Output:** 1
**Explanation:** The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
**Constraints:**
* `1 <= k <= n <= 500`
**Follow up:**
Could you solve this problem in linear time with constant space? | Create a function that checks if a character is a vowel, either uppercase or lowercase. |
A solution using Python | minimum-sideway-jumps | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSideJumps(self, obstacles: List[int]) -> int:\n dp = [[float("inf")] * len(obstacles) for _ in range(4)]\n dp[2][0] = 0\n\n for i in range(len(obstacles) - 1):\n for j in range(1, 4):\n if obstacles[i + 1] == j:\n for k in range(1, 4):\n if k != j and k != obstacles[i]:\n dp[k][i + 1] = min(dp[k][i + 1], dp[j][i] + 1)\n else:\n dp[j][i + 1] = min(dp[j][i + 1], dp[j][i])\n \n\n ans = float(\'inf\')\n for i in range(1, 4):\n ans = min(ans, dp[i][len(obstacles) - 1])\n\n return ans\n\n``` | 0 | There is a **3 lane road** of length `n` that consists of `n + 1` **points** labeled from `0` to `n`. A frog **starts** at point `0` in the **second** lane and wants to jump to point `n`. However, there could be obstacles along the way.
You are given an array `obstacles` of length `n + 1` where each `obstacles[i]` (**ranging from 0 to 3**) describes an obstacle on the lane `obstacles[i]` at point `i`. If `obstacles[i] == 0`, there are no obstacles at point `i`. There will be **at most one** obstacle in the 3 lanes at each point.
* For example, if `obstacles[2] == 1`, then there is an obstacle on lane 1 at point 2.
The frog can only travel from point `i` to point `i + 1` on the same lane if there is not an obstacle on the lane at point `i + 1`. To avoid obstacles, the frog can also perform a **side jump** to jump to **another** lane (even if they are not adjacent) at the **same** point if there is no obstacle on the new lane.
* For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.
Return _the **minimum number of side jumps** the frog needs to reach **any lane** at point n starting from lane `2` at point 0._
**Note:** There will be no obstacles on points `0` and `n`.
**Example 1:**
**Input:** obstacles = \[0,1,2,3,0\]
**Output:** 2
**Explanation:** The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).
**Example 2:**
**Input:** obstacles = \[0,1,1,3,3,0\]
**Output:** 0
**Explanation:** There are no obstacles on lane 2. No side jumps are required.
**Example 3:**
**Input:** obstacles = \[0,2,1,0,3,0\]
**Output:** 2
**Explanation:** The optimal solution is shown by the arrows above. There are 2 side jumps.
**Constraints:**
* `obstacles.length == n + 1`
* `1 <= n <= 5 * 105`
* `0 <= obstacles[i] <= 3`
* `obstacles[0] == obstacles[n] == 0` | It's optimal to finish the apples that will rot first before those that will rot last You need a structure to keep the apples sorted by their finish time |
A solution using Python | minimum-sideway-jumps | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSideJumps(self, obstacles: List[int]) -> int:\n dp = [[float("inf")] * len(obstacles) for _ in range(4)]\n dp[2][0] = 0\n\n for i in range(len(obstacles) - 1):\n for j in range(1, 4):\n if obstacles[i + 1] == j:\n for k in range(1, 4):\n if k != j and k != obstacles[i]:\n dp[k][i + 1] = min(dp[k][i + 1], dp[j][i] + 1)\n else:\n dp[j][i + 1] = min(dp[j][i + 1], dp[j][i])\n \n\n ans = float(\'inf\')\n for i in range(1, 4):\n ans = min(ans, dp[i][len(obstacles) - 1])\n\n return ans\n\n``` | 0 | Given an integer `n`, return `true` _if_ `n` _has **exactly three positive divisors**. Otherwise, return_ `false`.
An integer `m` is a **divisor** of `n` if there exists an integer `k` such that `n = k * m`.
**Example 1:**
**Input:** n = 2
**Output:** false
**Explantion:** 2 has only two divisors: 1 and 2.
**Example 2:**
**Input:** n = 4
**Output:** true
**Explantion:** 4 has three divisors: 1, 2, and 4.
**Constraints:**
* `1 <= n <= 104` | At a given point, there are only 3 possible states for where the frog can be. Check all the ways to move from one point to the next and update the minimum side jumps for each lane. |
[Python3] Fenwick tree | finding-mk-average | 0 | 1 | \n```\nclass Fenwick: \n\n def __init__(self, n: int):\n self.nums = [0]*(n+1)\n\n def sum(self, k: int) -> int: \n k += 1\n ans = 0\n while k:\n ans += self.nums[k]\n k &= k-1 # unset last set bit \n return ans\n\n def add(self, k: int, x: int) -> None: \n k += 1\n while k < len(self.nums): \n self.nums[k] += x\n k += k & -k \n\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k \n self.data = deque()\n self.value = Fenwick(10**5+1)\n self.index = Fenwick(10**5+1)\n\n def addElement(self, num: int) -> None:\n self.data.append(num)\n self.value.add(num, num)\n self.index.add(num, 1)\n if len(self.data) > self.m: \n num = self.data.popleft()\n self.value.add(num, -num)\n self.index.add(num, -1)\n\n def _getindex(self, k): \n lo, hi = 0, 10**5 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if self.index.sum(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n \n def calculateMKAverage(self) -> int:\n if len(self.data) < self.m: return -1 \n lo = self._getindex(self.k)\n hi = self._getindex(self.m-self.k)\n ans = self.value.sum(hi) - self.value.sum(lo)\n ans += (self.index.sum(lo) - self.k) * lo\n ans -= (self.index.sum(hi) - (self.m-self.k)) * hi\n return ans // (self.m - 2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 46 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
[Python3] Fenwick tree | finding-mk-average | 0 | 1 | \n```\nclass Fenwick: \n\n def __init__(self, n: int):\n self.nums = [0]*(n+1)\n\n def sum(self, k: int) -> int: \n k += 1\n ans = 0\n while k:\n ans += self.nums[k]\n k &= k-1 # unset last set bit \n return ans\n\n def add(self, k: int, x: int) -> None: \n k += 1\n while k < len(self.nums): \n self.nums[k] += x\n k += k & -k \n\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k \n self.data = deque()\n self.value = Fenwick(10**5+1)\n self.index = Fenwick(10**5+1)\n\n def addElement(self, num: int) -> None:\n self.data.append(num)\n self.value.add(num, num)\n self.index.add(num, 1)\n if len(self.data) > self.m: \n num = self.data.popleft()\n self.value.add(num, -num)\n self.index.add(num, -1)\n\n def _getindex(self, k): \n lo, hi = 0, 10**5 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if self.index.sum(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n \n def calculateMKAverage(self) -> int:\n if len(self.data) < self.m: return -1 \n lo = self._getindex(self.k)\n hi = self._getindex(self.m-self.k)\n ans = self.value.sum(hi) - self.value.sum(lo)\n ans += (self.index.sum(lo) - self.k) * lo\n ans -= (self.index.sum(hi) - (self.m-self.k)) * hi\n return ans // (self.m - 2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 46 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python3 solution w/ SortedList, O(logM) add, O(1) calculate | finding-mk-average | 0 | 1 | python3 doesn\'t have a built-in [order statistic tree](https://en.wikipedia.org/wiki/Order_statistic_tree) or even a basic BST and that may be why `sortedcontainers` is one of the few third-party libraries allowed.\n\nAnyway, with a [SortedList](http://www.grantjenks.com/docs/sortedcontainers/sortedlist.html) this solution is conceptually simple. I use both a deque and a SortedList to keep track of the last m numbers, FIFO. It\'s trivial to maintain the total sum of them. To maintain the sum of the smallest/largest k numbers, we examine the index at which the new number will be inserted into the SortedList and the index at which the oldest number will be removed from the SortedList. If the new number to be inserted will become one of the smallest/largest k numbers, we add it to self.first_k/self.last_k and subtract out the current kth smallest/largest number. The operation for removing the oldest number is similar but the reverse. The only gotcha is the off-by-1 error.\n\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.deque = collections.deque()\n self.sl = SortedList()\n self.total = self.first_k = self.last_k = 0\n\n def addElement(self, num: int) -> None:\n self.total += num\n self.deque.append(num)\n index = self.sl.bisect_left(num)\n if index < self.k:\n self.first_k += num\n if len(self.sl) >= self.k:\n self.first_k -= self.sl[self.k - 1]\n if index >= len(self.sl) + 1 - self.k:\n self.last_k += num\n if len(self.sl) >= self.k:\n self.last_k -= self.sl[-self.k]\n self.sl.add(num)\n if len(self.deque) > self.m:\n num = self.deque.popleft()\n self.total -= num\n index = self.sl.index(num)\n if index < self.k:\n self.first_k -= num\n self.first_k += self.sl[self.k]\n elif index >= len(self.sl) - self.k:\n self.last_k -= num\n self.last_k += self.sl[-self.k - 1]\n self.sl.remove(num)\n\n def calculateMKAverage(self) -> int:\n if len(self.sl) < self.m:\n return -1\n return (self.total - self.first_k - self.last_k) // (self.m - 2 * self.k)\n```\n\nTime complexity: O(logM) add due to operations on the SortedList (essentially an [order statistic tree](https://en.wikipedia.org/wiki/Order_statistic_tree)). O(1) calculate is trivial.\nSpace complexity: O(M) due to the deque and SortedList. | 39 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python3 solution w/ SortedList, O(logM) add, O(1) calculate | finding-mk-average | 0 | 1 | python3 doesn\'t have a built-in [order statistic tree](https://en.wikipedia.org/wiki/Order_statistic_tree) or even a basic BST and that may be why `sortedcontainers` is one of the few third-party libraries allowed.\n\nAnyway, with a [SortedList](http://www.grantjenks.com/docs/sortedcontainers/sortedlist.html) this solution is conceptually simple. I use both a deque and a SortedList to keep track of the last m numbers, FIFO. It\'s trivial to maintain the total sum of them. To maintain the sum of the smallest/largest k numbers, we examine the index at which the new number will be inserted into the SortedList and the index at which the oldest number will be removed from the SortedList. If the new number to be inserted will become one of the smallest/largest k numbers, we add it to self.first_k/self.last_k and subtract out the current kth smallest/largest number. The operation for removing the oldest number is similar but the reverse. The only gotcha is the off-by-1 error.\n\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.deque = collections.deque()\n self.sl = SortedList()\n self.total = self.first_k = self.last_k = 0\n\n def addElement(self, num: int) -> None:\n self.total += num\n self.deque.append(num)\n index = self.sl.bisect_left(num)\n if index < self.k:\n self.first_k += num\n if len(self.sl) >= self.k:\n self.first_k -= self.sl[self.k - 1]\n if index >= len(self.sl) + 1 - self.k:\n self.last_k += num\n if len(self.sl) >= self.k:\n self.last_k -= self.sl[-self.k]\n self.sl.add(num)\n if len(self.deque) > self.m:\n num = self.deque.popleft()\n self.total -= num\n index = self.sl.index(num)\n if index < self.k:\n self.first_k -= num\n self.first_k += self.sl[self.k]\n elif index >= len(self.sl) - self.k:\n self.last_k -= num\n self.last_k += self.sl[-self.k - 1]\n self.sl.remove(num)\n\n def calculateMKAverage(self) -> int:\n if len(self.sl) < self.m:\n return -1\n return (self.total - self.first_k - self.last_k) // (self.m - 2 * self.k)\n```\n\nTime complexity: O(logM) add due to operations on the SortedList (essentially an [order statistic tree](https://en.wikipedia.org/wiki/Order_statistic_tree)). O(1) calculate is trivial.\nSpace complexity: O(M) due to the deque and SortedList. | 39 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python3 Keeping Three Containers For Small/Middle/Large Values (Runtime 98%, Memory 94%) | finding-mk-average | 0 | 1 | # Intuition\nSince this data structure deals only with the last m elements from a data stream, it\'s natural to use a deque that only stores the latest m elements (*self.container*). The first solution I came up was precisely that, as can be seen from the commented data block. \n\nIn that straight-forward approach, whenever a valid "calculateMKAverage" query is sent, we will sort *self.container* ad hoc in order to preserve the order of the data stream from sorting. It\'s pretty obvious why that approach is unfeasible with larger m, as each sort operation is an $$O(m log m)$$ operation. I tried implementing a basic cache that only gets refreshed when the data is changed, and the newly added value does not equal to the removed value. This however is inadequate for this question. It was this tinkering with cache that led me to the solution that I finally came up with\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe use *self.container* to keep track of the data stream order, and use three separate sorted containers (*self.smallest, self.middle, self.largest*) to keep track of the minimum/maximum-k elements, and the m-2k elements in the middle. \nUsing SortedList provides many crucial advantages for our purpose:\n1. The sorted nature of the elements means that add, delete and membership operations benefit from binary search algorithm (which is natively provided by the SortedList). As can be seen on https://grantjenks.com/docs/sortedcontainers/sortedlist.html, add, remove and pop operations only have $$O(log(k))$$ time complexity on SortedList\n2. Because the three containers are separately sorted, moving between smallest/middle and largest/middle becomes very easy: we know that it must happen at their respective ends (for example, when a new added value is smaller than existing values in the smallest container, it will naturally be sorted to take the index of middle[0], and the element that no longer is the smallest would sit at the index of smallest[-1] after we move the new value into the smallest container)\n3. Sorting operations have the average time complexity of $$O(n log n)$$. This means that doing a lump-sum sorting of the entire container will certainly be less efficient than doing three sortings of smaller containers($$max(O(klogk), O((m-2k)log(m-2k))$$). What\'s more, by using SortedList we aren\'t even doing a complete sorting each time! A full sorting only happens when we initialize the three containers, and all subsequent operations involve the adding and deleting of single elements, which are $$O(log(k))$$ operations.\n\nThe other optimization is keeping a running sum instead of calculating the sum of *self.middle* every time when average is queried. With any addition and deletion of element it will only impact the running_sum in 2 ways:\n1. When an element is put in the *self.middle* (either as a new element, or moving from the extremes), we add it to the running sum\n2. When an element is removed from *self.middle* (either directly removed, or moving to the extremes), we subtract it from the running sum.\n\n\nLet\'s break down what happens when a new element(*num*) gets added:\n\n1. When the container has not reached m, we simply appended *num* at the end of *self.container*. If after appending it we have reached the target size of m, we initialize the partition of values into *self.smallest, self.middle, self.largest*, and calculate the initial running sum *self.mid_sum*\n\n2. For any subsequent data stream, it will be pushed onto *self.container*, and the oldest one gets popped. After keeping track of stream order with this deque, we move our attention to how this will impact the three containers (Tip: *smallest[-1] == max(smallest), largest[0] == min(largest)*):\n- If both the popped element and the added element belong to the middle container, we don\'t have to worry about anything else: we delete the old value and add the new value to our running sum\n- If the popped element is from the middle, and the added element goes to the extremes, we will check where it will actually go to (*num_small = num<= self.smallest[-1]*). Remember, since only the k number of extreme values get discarded, after adding a new element it will now contain k+1 elements, with the one at their respective end (*max(smallest) and min(largest)*) disqualified and moved back to the middle. We then adjust the running sum based on which one moved into and which one moved out of the midle\n- If the popped element is from the extremes, we will first put the new element in the middle, and move min(middle) or max(middle) to the side the of extreme that has its element just popped. **And here\'s a pitfall: the new value can potentially update the other extreme.** Here\'s the debugging log when you didn\'t check for that: As you can see, we didn\'t check if 64938 can update the largest, resulting in 64938 incorrectly placed in the middle.\n\n```\nSortedList([8272]) SortedList([15456]) SortedList([33433])\nContainer before adding: deque([8272, 33433, 15456])\nPopped: 8272 Num: 64938\nSortedList([15456]) SortedList([64938]) SortedList([33433])\n\n```\n\n- Solving the above mentioned bug is easy: it doesn\'t hurt if we simply try to update the other extreme by moving the potential update candidate there, and pulling back the disqualified one! If the new value doesn\'t update it, nothing happens since they\'ll be pulled back, but if it does, then it will correctly update it.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(log k)$$ for *addElement* since each time it only involves a handful of operations involving adding and removing values from three SortedList.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m)$$, since we store a m-sized deque and a partition of that deque, with total size of 2m\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# from collections import deque\n\n\n# class MKAverage:\n# container = None\n# m = None\n# k = None\n# cached = None\n# def __init__(self, m: int, k: int):\n# self.container = deque()\n# self.m = m\n# self.k = k\n# self.cached = None\n\n# def addElement(self, num: int) -> None:\n# popped = None\n# if len(self.container) < self.m:\n# self.container.append(num)\n# else:\n# popped = self.container.popleft()\n# self.container.append(num)\n# if popped != num:\n# self.cached = None\n\n# def calculateMKAverage(self) -> int:\n# if len(self.container) < self.m:\n# return -1\n# if self.cached is not None:\n# return self.cached\n# m = self.m\n# k = self.k\n# self.cached = int(sum(sorted(self.container)[k:m-k])/(m-2*k))\n# return self.cached\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n\n\nfrom collections import deque\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n\n def __init__(self, m: int, k: int):\n self.smallest = SortedList()\n self.middle = SortedList()\n self.largest = SortedList()\n self.container = deque()\n self.mid_sum = None\n self.m = m\n self.k = k\n \n \n\n def addElement(self, num: int) -> None:\n if len(self.container) < self.m:\n self.container.append(num)\n if len(self.container) == self.m:\n #initializing partition when first filled\n sorted_result = sorted(self.container)\n self.smallest = SortedList(sorted_result[:self.k])\n self.middle = SortedList(sorted_result[self.k:self.m-self.k])\n self.largest = SortedList(sorted_result[-self.k:])\n self.mid_sum = sum(self.middle)\n else:\n #print ("Container before adding:", self.container)\n popped = self.container.popleft()\n self.container.append(num)\n #print ("Popped:", popped, "Num:", num)\n # if popped from middle and added to middle, don\'t worry about anything\n if self.smallest[-1]<popped<self.largest[0] and self.smallest[-1]<num<self.largest[0]:\n self.mid_sum+=num-popped\n self.middle.add(num)\n self.middle.remove(popped)\n\n \n # if popped from the middle and added to the extremes, update corresponding container\n elif self.smallest[-1]<popped<self.largest[0]:\n self.middle.remove(popped)\n # where should num go\n num_small = num<= self.smallest[-1]\n if num_small:\n self.smallest.add(num)\n # element that moved to the middle\n moved = self.smallest.pop()\n else:\n self.largest.add(num)\n # element that moved to the middle\n moved = self.largest.pop(0)\n self.middle.add(moved)\n self.mid_sum += moved-popped\n \n # if popped from the extremes, first putting the new number in the middle, then move\n # popped from smallest\n elif popped<= self.smallest[-1]:\n self.smallest.remove(popped)\n self.middle.add(num)\n # smallest in the middle moved to smallest container\n moved = self.middle.pop(0)\n self.smallest.add(moved)\n # First adding num to middle, then moving moved from middle\n self.mid_sum += num-moved\n # Updating the largest container\n # moving max(middle) to largest\n moved = self.middle.pop()\n self.mid_sum -= moved\n self.largest.add(moved)\n # moving min(largest) to middle\n moved = self.largest.pop(0)\n self.mid_sum += moved\n self.middle.add(moved)\n \n elif popped>= self.largest[0]:\n self.largest.remove(popped)\n self.middle.add(num)\n # largest in the middle moved to largest container\n moved = self.middle.pop()\n self.largest.add(moved)\n # First adding num to middle, then moving moved from middle\n self.mid_sum += num-moved\n # Updating the smallest container\n # moving min(middle) to smallest\n moved = self.middle.pop(0)\n self.mid_sum -= moved\n self.smallest.add(moved)\n # moving max(smallest) to middle\n moved = self.smallest.pop()\n self.mid_sum += moved\n self.middle.add(moved)\n\n \n #print (self.smallest, self.middle, self.largest)\n\n def calculateMKAverage(self) -> int:\n if len(self.container) < self.m:\n return -1\n return self.mid_sum // (self.m - 2* self.k)\n``` | 2 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python3 Keeping Three Containers For Small/Middle/Large Values (Runtime 98%, Memory 94%) | finding-mk-average | 0 | 1 | # Intuition\nSince this data structure deals only with the last m elements from a data stream, it\'s natural to use a deque that only stores the latest m elements (*self.container*). The first solution I came up was precisely that, as can be seen from the commented data block. \n\nIn that straight-forward approach, whenever a valid "calculateMKAverage" query is sent, we will sort *self.container* ad hoc in order to preserve the order of the data stream from sorting. It\'s pretty obvious why that approach is unfeasible with larger m, as each sort operation is an $$O(m log m)$$ operation. I tried implementing a basic cache that only gets refreshed when the data is changed, and the newly added value does not equal to the removed value. This however is inadequate for this question. It was this tinkering with cache that led me to the solution that I finally came up with\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe use *self.container* to keep track of the data stream order, and use three separate sorted containers (*self.smallest, self.middle, self.largest*) to keep track of the minimum/maximum-k elements, and the m-2k elements in the middle. \nUsing SortedList provides many crucial advantages for our purpose:\n1. The sorted nature of the elements means that add, delete and membership operations benefit from binary search algorithm (which is natively provided by the SortedList). As can be seen on https://grantjenks.com/docs/sortedcontainers/sortedlist.html, add, remove and pop operations only have $$O(log(k))$$ time complexity on SortedList\n2. Because the three containers are separately sorted, moving between smallest/middle and largest/middle becomes very easy: we know that it must happen at their respective ends (for example, when a new added value is smaller than existing values in the smallest container, it will naturally be sorted to take the index of middle[0], and the element that no longer is the smallest would sit at the index of smallest[-1] after we move the new value into the smallest container)\n3. Sorting operations have the average time complexity of $$O(n log n)$$. This means that doing a lump-sum sorting of the entire container will certainly be less efficient than doing three sortings of smaller containers($$max(O(klogk), O((m-2k)log(m-2k))$$). What\'s more, by using SortedList we aren\'t even doing a complete sorting each time! A full sorting only happens when we initialize the three containers, and all subsequent operations involve the adding and deleting of single elements, which are $$O(log(k))$$ operations.\n\nThe other optimization is keeping a running sum instead of calculating the sum of *self.middle* every time when average is queried. With any addition and deletion of element it will only impact the running_sum in 2 ways:\n1. When an element is put in the *self.middle* (either as a new element, or moving from the extremes), we add it to the running sum\n2. When an element is removed from *self.middle* (either directly removed, or moving to the extremes), we subtract it from the running sum.\n\n\nLet\'s break down what happens when a new element(*num*) gets added:\n\n1. When the container has not reached m, we simply appended *num* at the end of *self.container*. If after appending it we have reached the target size of m, we initialize the partition of values into *self.smallest, self.middle, self.largest*, and calculate the initial running sum *self.mid_sum*\n\n2. For any subsequent data stream, it will be pushed onto *self.container*, and the oldest one gets popped. After keeping track of stream order with this deque, we move our attention to how this will impact the three containers (Tip: *smallest[-1] == max(smallest), largest[0] == min(largest)*):\n- If both the popped element and the added element belong to the middle container, we don\'t have to worry about anything else: we delete the old value and add the new value to our running sum\n- If the popped element is from the middle, and the added element goes to the extremes, we will check where it will actually go to (*num_small = num<= self.smallest[-1]*). Remember, since only the k number of extreme values get discarded, after adding a new element it will now contain k+1 elements, with the one at their respective end (*max(smallest) and min(largest)*) disqualified and moved back to the middle. We then adjust the running sum based on which one moved into and which one moved out of the midle\n- If the popped element is from the extremes, we will first put the new element in the middle, and move min(middle) or max(middle) to the side the of extreme that has its element just popped. **And here\'s a pitfall: the new value can potentially update the other extreme.** Here\'s the debugging log when you didn\'t check for that: As you can see, we didn\'t check if 64938 can update the largest, resulting in 64938 incorrectly placed in the middle.\n\n```\nSortedList([8272]) SortedList([15456]) SortedList([33433])\nContainer before adding: deque([8272, 33433, 15456])\nPopped: 8272 Num: 64938\nSortedList([15456]) SortedList([64938]) SortedList([33433])\n\n```\n\n- Solving the above mentioned bug is easy: it doesn\'t hurt if we simply try to update the other extreme by moving the potential update candidate there, and pulling back the disqualified one! If the new value doesn\'t update it, nothing happens since they\'ll be pulled back, but if it does, then it will correctly update it.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(log k)$$ for *addElement* since each time it only involves a handful of operations involving adding and removing values from three SortedList.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m)$$, since we store a m-sized deque and a partition of that deque, with total size of 2m\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# from collections import deque\n\n\n# class MKAverage:\n# container = None\n# m = None\n# k = None\n# cached = None\n# def __init__(self, m: int, k: int):\n# self.container = deque()\n# self.m = m\n# self.k = k\n# self.cached = None\n\n# def addElement(self, num: int) -> None:\n# popped = None\n# if len(self.container) < self.m:\n# self.container.append(num)\n# else:\n# popped = self.container.popleft()\n# self.container.append(num)\n# if popped != num:\n# self.cached = None\n\n# def calculateMKAverage(self) -> int:\n# if len(self.container) < self.m:\n# return -1\n# if self.cached is not None:\n# return self.cached\n# m = self.m\n# k = self.k\n# self.cached = int(sum(sorted(self.container)[k:m-k])/(m-2*k))\n# return self.cached\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n\n\nfrom collections import deque\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n\n def __init__(self, m: int, k: int):\n self.smallest = SortedList()\n self.middle = SortedList()\n self.largest = SortedList()\n self.container = deque()\n self.mid_sum = None\n self.m = m\n self.k = k\n \n \n\n def addElement(self, num: int) -> None:\n if len(self.container) < self.m:\n self.container.append(num)\n if len(self.container) == self.m:\n #initializing partition when first filled\n sorted_result = sorted(self.container)\n self.smallest = SortedList(sorted_result[:self.k])\n self.middle = SortedList(sorted_result[self.k:self.m-self.k])\n self.largest = SortedList(sorted_result[-self.k:])\n self.mid_sum = sum(self.middle)\n else:\n #print ("Container before adding:", self.container)\n popped = self.container.popleft()\n self.container.append(num)\n #print ("Popped:", popped, "Num:", num)\n # if popped from middle and added to middle, don\'t worry about anything\n if self.smallest[-1]<popped<self.largest[0] and self.smallest[-1]<num<self.largest[0]:\n self.mid_sum+=num-popped\n self.middle.add(num)\n self.middle.remove(popped)\n\n \n # if popped from the middle and added to the extremes, update corresponding container\n elif self.smallest[-1]<popped<self.largest[0]:\n self.middle.remove(popped)\n # where should num go\n num_small = num<= self.smallest[-1]\n if num_small:\n self.smallest.add(num)\n # element that moved to the middle\n moved = self.smallest.pop()\n else:\n self.largest.add(num)\n # element that moved to the middle\n moved = self.largest.pop(0)\n self.middle.add(moved)\n self.mid_sum += moved-popped\n \n # if popped from the extremes, first putting the new number in the middle, then move\n # popped from smallest\n elif popped<= self.smallest[-1]:\n self.smallest.remove(popped)\n self.middle.add(num)\n # smallest in the middle moved to smallest container\n moved = self.middle.pop(0)\n self.smallest.add(moved)\n # First adding num to middle, then moving moved from middle\n self.mid_sum += num-moved\n # Updating the largest container\n # moving max(middle) to largest\n moved = self.middle.pop()\n self.mid_sum -= moved\n self.largest.add(moved)\n # moving min(largest) to middle\n moved = self.largest.pop(0)\n self.mid_sum += moved\n self.middle.add(moved)\n \n elif popped>= self.largest[0]:\n self.largest.remove(popped)\n self.middle.add(num)\n # largest in the middle moved to largest container\n moved = self.middle.pop()\n self.largest.add(moved)\n # First adding num to middle, then moving moved from middle\n self.mid_sum += num-moved\n # Updating the smallest container\n # moving min(middle) to smallest\n moved = self.middle.pop(0)\n self.mid_sum -= moved\n self.smallest.add(moved)\n # moving max(smallest) to middle\n moved = self.smallest.pop()\n self.mid_sum += moved\n self.middle.add(moved)\n\n \n #print (self.smallest, self.middle, self.largest)\n\n def calculateMKAverage(self) -> int:\n if len(self.container) < self.m:\n return -1\n return self.mid_sum // (self.m - 2* self.k)\n``` | 2 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python Solution SortedList | finding-mk-average | 0 | 1 | ```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.arr = SortedList()\n self.m = m\n self.k = k\n self.q = deque()\n self.total = None\n\n def addElement(self, num: int) -> None:\n self.q.append(num)\n m = self.m\n k = self.k\n if len(self.q) > m:\n val = self.q.popleft() \n ind1 = self.arr.bisect_left(val)\n ind2 = self.arr.bisect_right(val)\n left, right, mid = False, False, False\n kth, mth = self.arr[k], self.arr[m - k - 1]\n if k <= ind1 < m - k or k <= ind2 - 1 < m - k or (ind1 <= k and m - k <= ind2 - 1 < m):\n mid = True\n elif ind1 < k:\n left = True\n elif ind2 - 1 >= m - k:\n right = True \n \n self.arr.remove(val)\n ind1 = self.arr.bisect_left(num)\n ind2 = self.arr.bisect_right(num) \n self.arr.add(num) \n \n if k <= ind1 < m - k or k <= ind2 < m - k or (ind1 <= k and m - k <= ind2 < m):\n if mid:\n self.total += num - val\n if left:\n self.total += num - kth\n if right:\n self.total += num - mth\n elif ind1 < k:\n if mid:\n self.total += self.arr[k] - val\n if left:\n pass\n if right:\n self.total += self.arr[k] - mth\n elif ind2 >= m - k:\n if mid:\n self.total += self.arr[m - k - 1] - val\n if left:\n self.total += self.arr[m - k - 1] - kth\n if right:\n pass\n else:\n self.arr.add(num)\n if self.total is None and len(self.arr) == self.m:\n self.total = sum(self.arr[k:m-k])\n \n\n def calculateMKAverage(self) -> int:\n if len(self.arr) < self.m:\n return -1\n \n return int(self.total / (self.m - 2 * self.k))\n``` | 1 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python Solution SortedList | finding-mk-average | 0 | 1 | ```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.arr = SortedList()\n self.m = m\n self.k = k\n self.q = deque()\n self.total = None\n\n def addElement(self, num: int) -> None:\n self.q.append(num)\n m = self.m\n k = self.k\n if len(self.q) > m:\n val = self.q.popleft() \n ind1 = self.arr.bisect_left(val)\n ind2 = self.arr.bisect_right(val)\n left, right, mid = False, False, False\n kth, mth = self.arr[k], self.arr[m - k - 1]\n if k <= ind1 < m - k or k <= ind2 - 1 < m - k or (ind1 <= k and m - k <= ind2 - 1 < m):\n mid = True\n elif ind1 < k:\n left = True\n elif ind2 - 1 >= m - k:\n right = True \n \n self.arr.remove(val)\n ind1 = self.arr.bisect_left(num)\n ind2 = self.arr.bisect_right(num) \n self.arr.add(num) \n \n if k <= ind1 < m - k or k <= ind2 < m - k or (ind1 <= k and m - k <= ind2 < m):\n if mid:\n self.total += num - val\n if left:\n self.total += num - kth\n if right:\n self.total += num - mth\n elif ind1 < k:\n if mid:\n self.total += self.arr[k] - val\n if left:\n pass\n if right:\n self.total += self.arr[k] - mth\n elif ind2 >= m - k:\n if mid:\n self.total += self.arr[m - k - 1] - val\n if left:\n self.total += self.arr[m - k - 1] - kth\n if right:\n pass\n else:\n self.arr.add(num)\n if self.total is None and len(self.arr) == self.m:\n self.total = sum(self.arr[k:m-k])\n \n\n def calculateMKAverage(self) -> int:\n if len(self.arr) < self.m:\n return -1\n \n return int(self.total / (self.m - 2 * self.k))\n``` | 1 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Solution using BST. Easy to understand | finding-mk-average | 0 | 1 | # Intuition\nUse BST as we are keeping track of sorted items. \n\n# Approach\nThere can be multiple approaches to solve this problem. Let me describe three approaches (note that first two approaches lead to TLE here):\n\n1. Brute force: We can do exactly as the problem says. Maintain a list of all elements. When an add operation comes, append to the list. When a get avg operation comes, slice out last "m" elements, sort the m elements, slice out m-2k elements from middle and return the average of this m-2k elements.\n\nTime complexity of this approach:\nFor One Add: O(1)\nFor One Get: O( m + m log m + (m-2k) ) = O( mlog m)\n\n2. Use two hashmaps: Instead of sorting m elements and slicing out m-2k elements we can maintain sliding window of last m elements using a queue. When adding a new element if the queue size becomes greater than m remove the leftmost element from queue. When calculating the average, construct a min-heap and max-heap of size k and keep track of cumulative sum of these m elements. Then sum of m-2k elements = cumulative_sum-(sum of elements from min heap) - (sum of elements from max heap)\n\nTime complexity:\nOne Get: O( m log k)\n\n3. Use BST: Since we need a sorted list of m elements, we can use a BST for it. For Add operation, add the new element to BST and remove the first element that went out of sliding window of size m. \n\nFor Get operation, get the middle m-2k elements and return the average. However if you do this naively you will get TLE. Instead keep a track of cumulative sum and subtract the sum of k elements from this cumulative sum and then get the average\n\nTC : \nOne Add: (log m)\nOne Get: O(k)\n\n```\nimport sortedcontainers\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.all_elements = []\n self.bst = sortedcontainers.SortedList()\n self.m = m\n self.k = k\n self.m_sum = 0\n\n def addElement(self, num: int) -> None:\n self.all_elements.append(num)\n self.m_sum += num\n self.bst.add(num)\n if len(self.bst) == self.m+1:\n self.bst.remove(self.all_elements[-(self.m+1)])\n self.m_sum -= self.all_elements[-(self.m+1)]\n \n \n\n def calculateMKAverage(self) -> int:\n if len(self.all_elements) < self.m:\n return -1\n min_sum = sum(self.bst[:self.k])\n max_sum = sum(self.bst[-self.k:])\n return (self.m_sum-min_sum-max_sum) // (self.m-2*self.k)\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Solution using BST. Easy to understand | finding-mk-average | 0 | 1 | # Intuition\nUse BST as we are keeping track of sorted items. \n\n# Approach\nThere can be multiple approaches to solve this problem. Let me describe three approaches (note that first two approaches lead to TLE here):\n\n1. Brute force: We can do exactly as the problem says. Maintain a list of all elements. When an add operation comes, append to the list. When a get avg operation comes, slice out last "m" elements, sort the m elements, slice out m-2k elements from middle and return the average of this m-2k elements.\n\nTime complexity of this approach:\nFor One Add: O(1)\nFor One Get: O( m + m log m + (m-2k) ) = O( mlog m)\n\n2. Use two hashmaps: Instead of sorting m elements and slicing out m-2k elements we can maintain sliding window of last m elements using a queue. When adding a new element if the queue size becomes greater than m remove the leftmost element from queue. When calculating the average, construct a min-heap and max-heap of size k and keep track of cumulative sum of these m elements. Then sum of m-2k elements = cumulative_sum-(sum of elements from min heap) - (sum of elements from max heap)\n\nTime complexity:\nOne Get: O( m log k)\n\n3. Use BST: Since we need a sorted list of m elements, we can use a BST for it. For Add operation, add the new element to BST and remove the first element that went out of sliding window of size m. \n\nFor Get operation, get the middle m-2k elements and return the average. However if you do this naively you will get TLE. Instead keep a track of cumulative sum and subtract the sum of k elements from this cumulative sum and then get the average\n\nTC : \nOne Add: (log m)\nOne Get: O(k)\n\n```\nimport sortedcontainers\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.all_elements = []\n self.bst = sortedcontainers.SortedList()\n self.m = m\n self.k = k\n self.m_sum = 0\n\n def addElement(self, num: int) -> None:\n self.all_elements.append(num)\n self.m_sum += num\n self.bst.add(num)\n if len(self.bst) == self.m+1:\n self.bst.remove(self.all_elements[-(self.m+1)])\n self.m_sum -= self.all_elements[-(self.m+1)]\n \n \n\n def calculateMKAverage(self) -> int:\n if len(self.all_elements) < self.m:\n return -1\n min_sum = sum(self.bst[:self.k])\n max_sum = sum(self.bst[-self.k:])\n return (self.m_sum-min_sum-max_sum) // (self.m-2*self.k)\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python, Binary search and double-ended queue. Showing clear thread of thoughts | finding-mk-average | 0 | 1 | # Intuition\n\nThought 1: We start from the naive solution\n* Idea: Keep a container of m elements (data structure: double-ended queue, probably a doubly-linked list in exact implementation)\n* AddElement -> cost O(1)\n* calculateMKAverage -> sort (O(m log m)))\n\nThought 2: Can we do better for calculate MKAverage?\n* Idea: Keep an additional structure, which is sorted\n* AddElement -> find the element to remove O(log m), add the element O(log m).\n(Note: Actually I noticed that cPython list is not a implementation that allows us to insert/remove an element in constant time. An exact data structure suitable would be a binary search tree.)\n* calculateMKAverage -> O(m)\n\nThought 3: MKAverage is still slower than adding element. Can we do even better for calulating MKAverage?\n* Idea: Keep a value of the sum of the elements qualified. Update the sum everytime we add an element.\n\n# Approach\n\nHow do we do even better for calculating MKAverage?\n1. when we remove an element A, if A\n - if among smallest (largest) k, we reduce sum by k+1 smallest (largest) value.\n - if not, we reduce sum by A.\n2. when we add an element B, if B\n - if among smallest (largest) k, we add to sum the k+1 smallest (largest) value.\n - if not, we add B to sum.\n* AddElement -> Still O(log m), as the additional overhead is constant.\n* calculateMKAverage -> O(1).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n* AddElement -> Still O(log m), as the additional overhead is constant.\n* calculateMKAverage -> O(1).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n* O(m) for the deque and sorted list that we keep.\n\n# Code\n```\nimport bisect\nfrom collections import deque\n\nclass MKAverage:\n\n # Naive\n # Keep a container of m elements (data structure: doubl-ended queue)\n # AddElement -> cost O(1)\n # calculateMKAverage -> sort (O(m log m)))\n\n # Can we do better for calculate MKAverage?\n # Keep an additional structure, which is sorted\n # AddElement -> find the element to remove O(log m), add the element O(log m)\n # calculateMKAverage -> O(m)\n\n # Can we do even better for calulating MKAverage?\n # Keep a value of the sum of the elements qualified.\n # Update the average everytime we add an element.\n # How to?\n # 1. when we remove an element A, if A\n # - if among smallest (largest) k, we reduce sum by k+1 smallest (largest) value.\n # - if not, we reduce sum by A\n # 2. when we add an element B, if B\n # - if among smallest (largest) k, we add to sum the k+1 smallest (largest) value.\n # - if not, we add B to sum.\n # calculateMKAverage -> O(1)\n\n def __init__(self, m: int, k: int):\n\n self.m = m\n self.k = k\n\n self.deque = deque()\n self.sorted = list()\n self.total = 0\n \n\n def addElement(self, num: int) -> None:\n\n if len(self.deque) < self.m:\n self.deque.append(num)\n bisect.insort(self.sorted, num)\n if len(self.deque) == self.m:\n self.total = sum(self.sorted[self.k:-self.k]) \n else:\n # remove element\n v = self.deque.popleft()\n index = bisect.bisect_left(self.sorted, v)\n if index < self.k:\n self.total -= self.sorted[self.k]\n elif index >= self.m - self.k:\n self.total -= self.sorted[-self.k-1]\n else:\n self.total -= v\n self.sorted.pop(index)\n\n # add element\n self.deque.append(num)\n index = bisect.bisect_left(self.sorted, num)\n self.sorted.insert(index, num)\n if index < self.k:\n self.total += self.sorted[self.k]\n elif index >= self.m - self.k:\n self.total += self.sorted[-self.k - 1]\n else:\n self.total += num\n\n\n def calculateMKAverage(self) -> int:\n\n if len(self.deque) < self.m:\n return - 1\n\n return int(self.total / (self.m - 2 * self.k) )\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python, Binary search and double-ended queue. Showing clear thread of thoughts | finding-mk-average | 0 | 1 | # Intuition\n\nThought 1: We start from the naive solution\n* Idea: Keep a container of m elements (data structure: double-ended queue, probably a doubly-linked list in exact implementation)\n* AddElement -> cost O(1)\n* calculateMKAverage -> sort (O(m log m)))\n\nThought 2: Can we do better for calculate MKAverage?\n* Idea: Keep an additional structure, which is sorted\n* AddElement -> find the element to remove O(log m), add the element O(log m).\n(Note: Actually I noticed that cPython list is not a implementation that allows us to insert/remove an element in constant time. An exact data structure suitable would be a binary search tree.)\n* calculateMKAverage -> O(m)\n\nThought 3: MKAverage is still slower than adding element. Can we do even better for calulating MKAverage?\n* Idea: Keep a value of the sum of the elements qualified. Update the sum everytime we add an element.\n\n# Approach\n\nHow do we do even better for calculating MKAverage?\n1. when we remove an element A, if A\n - if among smallest (largest) k, we reduce sum by k+1 smallest (largest) value.\n - if not, we reduce sum by A.\n2. when we add an element B, if B\n - if among smallest (largest) k, we add to sum the k+1 smallest (largest) value.\n - if not, we add B to sum.\n* AddElement -> Still O(log m), as the additional overhead is constant.\n* calculateMKAverage -> O(1).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n* AddElement -> Still O(log m), as the additional overhead is constant.\n* calculateMKAverage -> O(1).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n* O(m) for the deque and sorted list that we keep.\n\n# Code\n```\nimport bisect\nfrom collections import deque\n\nclass MKAverage:\n\n # Naive\n # Keep a container of m elements (data structure: doubl-ended queue)\n # AddElement -> cost O(1)\n # calculateMKAverage -> sort (O(m log m)))\n\n # Can we do better for calculate MKAverage?\n # Keep an additional structure, which is sorted\n # AddElement -> find the element to remove O(log m), add the element O(log m)\n # calculateMKAverage -> O(m)\n\n # Can we do even better for calulating MKAverage?\n # Keep a value of the sum of the elements qualified.\n # Update the average everytime we add an element.\n # How to?\n # 1. when we remove an element A, if A\n # - if among smallest (largest) k, we reduce sum by k+1 smallest (largest) value.\n # - if not, we reduce sum by A\n # 2. when we add an element B, if B\n # - if among smallest (largest) k, we add to sum the k+1 smallest (largest) value.\n # - if not, we add B to sum.\n # calculateMKAverage -> O(1)\n\n def __init__(self, m: int, k: int):\n\n self.m = m\n self.k = k\n\n self.deque = deque()\n self.sorted = list()\n self.total = 0\n \n\n def addElement(self, num: int) -> None:\n\n if len(self.deque) < self.m:\n self.deque.append(num)\n bisect.insort(self.sorted, num)\n if len(self.deque) == self.m:\n self.total = sum(self.sorted[self.k:-self.k]) \n else:\n # remove element\n v = self.deque.popleft()\n index = bisect.bisect_left(self.sorted, v)\n if index < self.k:\n self.total -= self.sorted[self.k]\n elif index >= self.m - self.k:\n self.total -= self.sorted[-self.k-1]\n else:\n self.total -= v\n self.sorted.pop(index)\n\n # add element\n self.deque.append(num)\n index = bisect.bisect_left(self.sorted, num)\n self.sorted.insert(index, num)\n if index < self.k:\n self.total += self.sorted[self.k]\n elif index >= self.m - self.k:\n self.total += self.sorted[-self.k - 1]\n else:\n self.total += num\n\n\n def calculateMKAverage(self) -> int:\n\n if len(self.deque) < self.m:\n return - 1\n\n return int(self.total / (self.m - 2 * self.k) )\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python3 sortedlist, barely passes | finding-mk-average | 0 | 1 | # Code\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.l = SortedList([])\n self.k = k\n self.m = m\n self.queue = []\n \n \n\n def addElement(self, num: int) -> None:\n self.l.add(num)\n self.queue.append(num)\n if len(self.queue) > self.m:\n self.l.remove(self.queue.pop(0))\n\n\n \n\n def calculateMKAverage(self) -> int:\n if len(self.l) < self.m: return -1\n s = sum(self.l[self.k:-self.k])\n return s // (self.m - 2*self.k)\n\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python3 sortedlist, barely passes | finding-mk-average | 0 | 1 | # Code\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.l = SortedList([])\n self.k = k\n self.m = m\n self.queue = []\n \n \n\n def addElement(self, num: int) -> None:\n self.l.add(num)\n self.queue.append(num)\n if len(self.queue) > self.m:\n self.l.remove(self.queue.pop(0))\n\n\n \n\n def calculateMKAverage(self) -> int:\n if len(self.l) < self.m: return -1\n s = sum(self.l[self.k:-self.k])\n return s // (self.m - 2*self.k)\n\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Straight forward solution | finding-mk-average | 0 | 1 | # Intuition\nTo compute the MKAverage, we need a rolling window of the last m numbers and an efficient way to exclude the smallest and largest k numbers. A deque is suitable for the rolling window, and a Counter can efficiently track number frequencies.\n\n# Approach\n1. Initialization: Use a deque to maintain the last m numbers and a Counter for their frequencies. Track the sum of middle numbers with middle_sum.\n2. addElement: On new number addition, if deque is full, remove the oldest number. Update deque and Counter. If deque has m numbers, compute the middle_sum by deducting the smallest and largest k values.\n3. calculateMKAverage: If deque size is less than m, return -1. Otherwise, return middle_sum divided by (m - 2 * k).\n\n# Complexity\n- Time complexity:\naddElement is O(m log m) due to sorting. calculateMKAverage is O(1).\n\n- Space complexity:\nThe deque will hold at most m elements and the counter will hold, in the worst case, m unique elements. This gives a space complexity of O(m).\n\n# Code\n```\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.queue = deque()\n self.counter = Counter()\n self.middle_sum = 0\n self.qlen = 0\n\n def addElement(self, num: int) -> None:\n # If m numbers already in queue, remove the leftmost number\n if len(self.queue) == self.m:\n old = self.queue.popleft()\n self.counter[old] -= 1\n if self.counter[old] == 0:\n del self.counter[old]\n else:\n self.qlen += 1\n\n self.queue.append(num)\n self.counter[num] += 1\n\n # If m numbers in the queue, recompute the middle_sum\n if len(self.queue) == self.m:\n self.middle_sum = sum(num * count for num, count in self.counter.items())\n sorted_items = sorted(self.counter.items())\n \n # Deduct smallest k\n c = 0\n remain = self.k\n while remain:\n if sorted_items[c][1] >= remain:\n self.middle_sum -= (sorted_items[c][0] * remain)\n break\n else:\n self.middle_sum -= (sorted_items[c][0] * sorted_items[c][1])\n remain -= sorted_items[c][1]\n c += 1\n\n # Deduct largest k\n c = -1\n remain = self.k\n while remain:\n if sorted_items[c][1] >= remain:\n self.middle_sum -= (sorted_items[c][0] * remain)\n break\n else:\n self.middle_sum -= (sorted_items[c][0] * sorted_items[c][1])\n remain -= sorted_items[c][1]\n c -= 1\n\n def calculateMKAverage(self) -> int:\n if self.qlen < self.m:\n return -1\n return self.middle_sum // (self.m - 2 * self.k)\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Straight forward solution | finding-mk-average | 0 | 1 | # Intuition\nTo compute the MKAverage, we need a rolling window of the last m numbers and an efficient way to exclude the smallest and largest k numbers. A deque is suitable for the rolling window, and a Counter can efficiently track number frequencies.\n\n# Approach\n1. Initialization: Use a deque to maintain the last m numbers and a Counter for their frequencies. Track the sum of middle numbers with middle_sum.\n2. addElement: On new number addition, if deque is full, remove the oldest number. Update deque and Counter. If deque has m numbers, compute the middle_sum by deducting the smallest and largest k values.\n3. calculateMKAverage: If deque size is less than m, return -1. Otherwise, return middle_sum divided by (m - 2 * k).\n\n# Complexity\n- Time complexity:\naddElement is O(m log m) due to sorting. calculateMKAverage is O(1).\n\n- Space complexity:\nThe deque will hold at most m elements and the counter will hold, in the worst case, m unique elements. This gives a space complexity of O(m).\n\n# Code\n```\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.queue = deque()\n self.counter = Counter()\n self.middle_sum = 0\n self.qlen = 0\n\n def addElement(self, num: int) -> None:\n # If m numbers already in queue, remove the leftmost number\n if len(self.queue) == self.m:\n old = self.queue.popleft()\n self.counter[old] -= 1\n if self.counter[old] == 0:\n del self.counter[old]\n else:\n self.qlen += 1\n\n self.queue.append(num)\n self.counter[num] += 1\n\n # If m numbers in the queue, recompute the middle_sum\n if len(self.queue) == self.m:\n self.middle_sum = sum(num * count for num, count in self.counter.items())\n sorted_items = sorted(self.counter.items())\n \n # Deduct smallest k\n c = 0\n remain = self.k\n while remain:\n if sorted_items[c][1] >= remain:\n self.middle_sum -= (sorted_items[c][0] * remain)\n break\n else:\n self.middle_sum -= (sorted_items[c][0] * sorted_items[c][1])\n remain -= sorted_items[c][1]\n c += 1\n\n # Deduct largest k\n c = -1\n remain = self.k\n while remain:\n if sorted_items[c][1] >= remain:\n self.middle_sum -= (sorted_items[c][0] * remain)\n break\n else:\n self.middle_sum -= (sorted_items[c][0] * sorted_items[c][1])\n remain -= sorted_items[c][1]\n c -= 1\n\n def calculateMKAverage(self) -> int:\n if self.qlen < self.m:\n return -1\n return self.middle_sum // (self.m - 2 * self.k)\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Simple and clean Python code to balance 3 sorted lists | finding-mk-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m,self.k,self.total=m,k,0\n self.maxset,self.midset,self.minset,self.temp=SortedList([]),SortedList([]),SortedList([]),[]\n\n def addElement(self, num: int) -> None:\n self.temp.append(num)\n if len(self.temp)==self.m:\n tempsorted=sorted(self.temp)\n for i in range(self.k):\n self.maxset.add(tempsorted[i])\n for i in range(self.k, self.m-self.k):\n self.midset.add(tempsorted[i])\n self.total+=tempsorted[i]\n for i in range(self.m-self.k, self.m):\n self.minset.add(tempsorted[i])\n\n if len(self.temp)>self.m:\n stale=self.temp[-self.m-1]\n if stale>=self.minset[0]:\n self.minset.remove(stale)\n elif stale>=self.midset[0]:\n self.midset.remove(stale)\n self.total-=stale\n else:\n self.maxset.remove(stale)\n if self.minset and num>=self.minset[0]:\n self.minset.add(num)\n elif self.midset and num>=self.midset[0]:\n self.midset.add(num)\n self.total+=num\n else:\n self.maxset.add(num)\n while len(self.minset)>self.k:\n self.total+=self.minset[0]\n self.midset.add(self.minset.pop(0))\n while len(self.midset)>self.m-2*self.k:\n self.total-=self.midset[0]\n self.maxset.add(self.midset.pop(0))\n while len(self.maxset)>self.k:\n self.total+=self.maxset[-1]\n self.midset.add(self.maxset.pop())\n while len(self.midset)>self.m-2*self.k:\n self.total-=self.midset[-1]\n self.minset.add(self.midset.pop())\n\n def calculateMKAverage(self) -> int:\n if len(self.temp)<self.m:\n return -1\n return self.total//(self.m-2*self.k)\n \n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Simple and clean Python code to balance 3 sorted lists | finding-mk-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m,self.k,self.total=m,k,0\n self.maxset,self.midset,self.minset,self.temp=SortedList([]),SortedList([]),SortedList([]),[]\n\n def addElement(self, num: int) -> None:\n self.temp.append(num)\n if len(self.temp)==self.m:\n tempsorted=sorted(self.temp)\n for i in range(self.k):\n self.maxset.add(tempsorted[i])\n for i in range(self.k, self.m-self.k):\n self.midset.add(tempsorted[i])\n self.total+=tempsorted[i]\n for i in range(self.m-self.k, self.m):\n self.minset.add(tempsorted[i])\n\n if len(self.temp)>self.m:\n stale=self.temp[-self.m-1]\n if stale>=self.minset[0]:\n self.minset.remove(stale)\n elif stale>=self.midset[0]:\n self.midset.remove(stale)\n self.total-=stale\n else:\n self.maxset.remove(stale)\n if self.minset and num>=self.minset[0]:\n self.minset.add(num)\n elif self.midset and num>=self.midset[0]:\n self.midset.add(num)\n self.total+=num\n else:\n self.maxset.add(num)\n while len(self.minset)>self.k:\n self.total+=self.minset[0]\n self.midset.add(self.minset.pop(0))\n while len(self.midset)>self.m-2*self.k:\n self.total-=self.midset[0]\n self.maxset.add(self.midset.pop(0))\n while len(self.maxset)>self.k:\n self.total+=self.maxset[-1]\n self.midset.add(self.maxset.pop())\n while len(self.midset)>self.m-2*self.k:\n self.total-=self.midset[-1]\n self.minset.add(self.midset.pop())\n\n def calculateMKAverage(self) -> int:\n if len(self.temp)<self.m:\n return -1\n return self.total//(self.m-2*self.k)\n \n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Easiest Python Solution | finding-mk-average | 0 | 1 | ```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.left = SortedList()\n self.mid = SortedList()\n self.right = SortedList()\n self.total = deque()\n self.m = m\n self.k = k\n self.sum = 0\n\n def addElement(self, num: int) -> None:\n self.total.append(num)\n k = self.k\n m = self.m\n\n self.left.add(num)\n if len(self.left) > k:\n el = self.left.pop()\n self.mid.add(el)\n self.sum += el\n if len(self.mid) > m - 2*k:\n el = self.mid.pop()\n self.right.add(el)\n self.sum -= el\n \n \n if len(self.total) > m:\n last = self.total.popleft()\n\n if self.left[-1] >= last:\n self.left.remove(last)\n elif self.mid[-1] >= last:\n self.mid.remove(last)\n self.sum -= last\n else:\n self.right.remove(last)\n \n\n if len(self.left) < k:\n self.sum -= self.mid[0]\n self.left.add(self.mid[0])\n self.mid.remove(self.mid[0])\n if len(self.mid) < m - 2*k:\n self.sum += self.right[0]\n self.mid.add(self.right[0])\n self.right.remove(self.right[0])\n \n \n def calculateMKAverage(self) -> int:\n if len(self.total) < self.m:\n return -1\n return self.sum // len(self.mid)\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Easiest Python Solution | finding-mk-average | 0 | 1 | ```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.left = SortedList()\n self.mid = SortedList()\n self.right = SortedList()\n self.total = deque()\n self.m = m\n self.k = k\n self.sum = 0\n\n def addElement(self, num: int) -> None:\n self.total.append(num)\n k = self.k\n m = self.m\n\n self.left.add(num)\n if len(self.left) > k:\n el = self.left.pop()\n self.mid.add(el)\n self.sum += el\n if len(self.mid) > m - 2*k:\n el = self.mid.pop()\n self.right.add(el)\n self.sum -= el\n \n \n if len(self.total) > m:\n last = self.total.popleft()\n\n if self.left[-1] >= last:\n self.left.remove(last)\n elif self.mid[-1] >= last:\n self.mid.remove(last)\n self.sum -= last\n else:\n self.right.remove(last)\n \n\n if len(self.left) < k:\n self.sum -= self.mid[0]\n self.left.add(self.mid[0])\n self.mid.remove(self.mid[0])\n if len(self.mid) < m - 2*k:\n self.sum += self.right[0]\n self.mid.add(self.right[0])\n self.right.remove(self.right[0])\n \n \n def calculateMKAverage(self) -> int:\n if len(self.total) < self.m:\n return -1\n return self.sum // len(self.mid)\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python SortedList - intuitive logic and explanation | finding-mk-average | 0 | 1 | Algorithm:\n1. Maintaina queue for keeping items in stream order and 3 sorted lists - lesser, mid and greater for keeping track of the k lesser items, k greater items and m-2k selected items that need to be averaged\n2. When the stream size exceeds m, we need to remove the oldest entry from the stream i.e. the first entry\n\ta. This entry could be in the lesser, mid or greater lists. We simply try each of them. This is ok because we will be balancing their size while adding the new item\n3. Just add the item to the queue and also to the greater list. \n\ta. Then, trickle down the first entry in the greater list to the mid list and similarly from the mid list to the lesser list. \n\tb, Then, if the lesser list size is greater than k, bubble up the last entry to the mid list and similarly from the mid list to the greater list\n\tc. The trickling down ensures that a global sorting order is maintained across the 3 lists and the bubbling up ensures that their sizes remain balanced\n4. For each change in the mid list, keep `self.sum` updated\n5. Return `self.sum` divided by m - 2k as the average\n\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.stream = []\n self.lesser = SortedList()\n self.mid = SortedList()\n self.greater = SortedList()\n self.m = m\n self.k = k\n self.sum = 0 \n\n def addElement(self, num: int) -> None:\n self.stream.append(num)\n \n if len(self.stream) > self.m:\n # remove oldest entry from stream\n old = self.stream.pop(0)\n \n # the oldest entry could be anywhere in the 3 sorted lists\n if old in self.lesser:\n self.lesser.remove(old)\n elif old in self.mid:\n self.mid.remove(old)\n self.sum -= old\n else:\n self.greater.remove(old)\n \n # always add new entry to the greatest list\n # and let it trickle down to mid and lowest lists\n self.greater.add(num)\n extra = self.greater.pop(0)\n self.mid.add(extra)\n self.sum += extra\n extra = self.mid.pop(0)\n self.sum -= extra\n self.lesser.add(extra)\n \n # if lesser list has more than k entries,\n # bubble up last entry to mid\n if len(self.lesser) > self.k:\n extra = self.lesser.pop()\n self.mid.add(extra)\n self.sum += extra\n \n # if mid list has more than m - 2k entries,\n # bubble up last entry to greatest\n if len(self.mid) > self.m - 2 * self.k:\n extra = self.mid.pop()\n self.sum -= extra\n self.greater.add(extra)\n \n\n def calculateMKAverage(self) -> int:\n if len(self.stream) < self.m:\n return -1\n return self.sum // (self.m - 2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python SortedList - intuitive logic and explanation | finding-mk-average | 0 | 1 | Algorithm:\n1. Maintaina queue for keeping items in stream order and 3 sorted lists - lesser, mid and greater for keeping track of the k lesser items, k greater items and m-2k selected items that need to be averaged\n2. When the stream size exceeds m, we need to remove the oldest entry from the stream i.e. the first entry\n\ta. This entry could be in the lesser, mid or greater lists. We simply try each of them. This is ok because we will be balancing their size while adding the new item\n3. Just add the item to the queue and also to the greater list. \n\ta. Then, trickle down the first entry in the greater list to the mid list and similarly from the mid list to the lesser list. \n\tb, Then, if the lesser list size is greater than k, bubble up the last entry to the mid list and similarly from the mid list to the greater list\n\tc. The trickling down ensures that a global sorting order is maintained across the 3 lists and the bubbling up ensures that their sizes remain balanced\n4. For each change in the mid list, keep `self.sum` updated\n5. Return `self.sum` divided by m - 2k as the average\n\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.stream = []\n self.lesser = SortedList()\n self.mid = SortedList()\n self.greater = SortedList()\n self.m = m\n self.k = k\n self.sum = 0 \n\n def addElement(self, num: int) -> None:\n self.stream.append(num)\n \n if len(self.stream) > self.m:\n # remove oldest entry from stream\n old = self.stream.pop(0)\n \n # the oldest entry could be anywhere in the 3 sorted lists\n if old in self.lesser:\n self.lesser.remove(old)\n elif old in self.mid:\n self.mid.remove(old)\n self.sum -= old\n else:\n self.greater.remove(old)\n \n # always add new entry to the greatest list\n # and let it trickle down to mid and lowest lists\n self.greater.add(num)\n extra = self.greater.pop(0)\n self.mid.add(extra)\n self.sum += extra\n extra = self.mid.pop(0)\n self.sum -= extra\n self.lesser.add(extra)\n \n # if lesser list has more than k entries,\n # bubble up last entry to mid\n if len(self.lesser) > self.k:\n extra = self.lesser.pop()\n self.mid.add(extra)\n self.sum += extra\n \n # if mid list has more than m - 2k entries,\n # bubble up last entry to greatest\n if len(self.mid) > self.m - 2 * self.k:\n extra = self.mid.pop()\n self.sum -= extra\n self.greater.add(extra)\n \n\n def calculateMKAverage(self) -> int:\n if len(self.stream) < self.m:\n return -1\n return self.sum // (self.m - 2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
[Python3] SortedList + Deque - O(1) and O(log(N)) | finding-mk-average | 0 | 1 | # Intuition\nUse a queue to store the incoming elements, so we always know which one is the oldest\nKeep 3 sorted lists, one for the leftmost $$k$$ elements, one for the central part (which is used to calculate the average) and one for the rightmost $$k$$ elements.\n\nIf you don\'t have enough elements ($$length < m$$), then just keep the elements in the queue and when we first reach $$m$$ elements, initialize the sorted lists.\n\n# Approach\n\nMaintain the order invariance at every operation. The left array must have $$k$$ elements, the central array must have $$m-2*k$$ elements, the right array must have $$k$$ elements.\n\n# Complexity\n- Time complexity:\n**calculateMKAverage**: $$O(1)$$\n**addElement**: $$O(log(M))$$, but because of the initialization it is $$O(M*log(M))$$ overall in the worst case. The initialization can easily be removed masking it $$O(log(M))$$, but the `_insert_element` method needs to be adjusted.\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.center_len = m - 2 * k\n self.q = deque([])\n self.left = SortedList()\n self.right = SortedList()\n self.center = SortedList()\n self.center_sum = 0\n\n def _initialize_sorted_lists(self):\n sorted_elements = sorted(self.q)\n index = 0\n for num in sorted_elements:\n if index < self.k:\n self.left.add(num)\n elif index >= self.k and index < len(sorted_elements) - self.k:\n self.center.add(num)\n self.center_sum += num\n else:\n self.right.add(num)\n index += 1\n\n def _remove_element(self, num: int) -> None:\n # Remove the element from the first box you can find it in, startig from left\n if num in self.left:\n self.left.remove(num)\n elif num in self.center:\n self.center.remove(num)\n self.center_sum -= num\n elif num in self.right:\n self.right.remove(num)\n else:\n raise Exception(f\'{num} not found in any of the sorted lists\')\n\n def _insert_element(self, num: int) -> None:\n # Insert the element in the right "box" (left, center, right) while maintaining the order\n if (len(self.center) > 0 and num <= self.center[0]) or (len(self.left) > 0 and num <= self.left[-1]):\n self.left.add(num)\n elif (len(self.right) > 0 and num <= self.right[0]) or (len(self.center) > 0 and num <= self.center[-1]):\n self.center.add(num)\n self.center_sum += num\n else:\n self.right.add(num)\n \n # Case 1: the center is too big, move one element to either left or right\n if len(self.center) > self.center_len:\n assert len(self.left) < self.k or len(self.right) < self.k\n if len(self.left) < self.k:\n to_move = self.center.pop(0)\n self.center_sum -= to_move\n self.left.add(to_move)\n elif len(self.right) < self.k:\n to_move = self.center.pop(-1)\n self.center_sum -= to_move\n self.right.add(to_move)\n # Case 2: the center is too small, move one element from left or right to center\n elif len(self.center) < self.center_len:\n assert len(self.left) > self.k or len(self.right) > self.k\n if len(self.left) > self.k:\n to_move = self.left.pop(-1)\n self.center.add(to_move)\n self.center_sum += to_move\n elif len(self.right) > self.k:\n to_move = self.right.pop(0)\n self.center.add(to_move)\n self.center_sum += to_move\n # Case 3: the center is OK, but left is too small and right is too big\n elif len(self.left) < self.k:\n assert len(self.center) == self.center_len and len(self.right) > self.k\n # Move from right to center and from center to left\n to_move1 = self.right.pop(0)\n self.center.add(to_move1)\n self.center_sum += to_move1\n to_move2 = self.center.pop(0)\n self.center_sum -= to_move2\n self.left.add(to_move2)\n # Case 4: the center is OK, but right is too small, and left is too big\n elif len(self.right) < self.k:\n assert len(self.center) == self.center_len and len(self.left) > self.k\n # Move from left to center and from center to right\n to_move1 = self.left.pop(-1)\n self.center.add(to_move1)\n self.center_sum += to_move1\n to_move2 = self.center.pop(-1)\n self.center_sum -= to_move2\n self.right.add(to_move2)\n \n assert len(self.left) == self.k and len(self.right) == self.k and len(self.center) == self.center_len\n\n \n\n def addElement(self, num: int) -> None:\n self.q.append(num)\n if len(self.q) == self.m:\n # This will be called only once, when we first reach "m" elements\n self._initialize_sorted_lists()\n if len(self.q) > self.m:\n to_remove = self.q.popleft()\n self._remove_element(to_remove)\n self._insert_element(num)\n\n\n def calculateMKAverage(self) -> int:\n if len(self.q) < self.m:\n return -1\n return self.center_sum // self.center_len\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
[Python3] SortedList + Deque - O(1) and O(log(N)) | finding-mk-average | 0 | 1 | # Intuition\nUse a queue to store the incoming elements, so we always know which one is the oldest\nKeep 3 sorted lists, one for the leftmost $$k$$ elements, one for the central part (which is used to calculate the average) and one for the rightmost $$k$$ elements.\n\nIf you don\'t have enough elements ($$length < m$$), then just keep the elements in the queue and when we first reach $$m$$ elements, initialize the sorted lists.\n\n# Approach\n\nMaintain the order invariance at every operation. The left array must have $$k$$ elements, the central array must have $$m-2*k$$ elements, the right array must have $$k$$ elements.\n\n# Complexity\n- Time complexity:\n**calculateMKAverage**: $$O(1)$$\n**addElement**: $$O(log(M))$$, but because of the initialization it is $$O(M*log(M))$$ overall in the worst case. The initialization can easily be removed masking it $$O(log(M))$$, but the `_insert_element` method needs to be adjusted.\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.center_len = m - 2 * k\n self.q = deque([])\n self.left = SortedList()\n self.right = SortedList()\n self.center = SortedList()\n self.center_sum = 0\n\n def _initialize_sorted_lists(self):\n sorted_elements = sorted(self.q)\n index = 0\n for num in sorted_elements:\n if index < self.k:\n self.left.add(num)\n elif index >= self.k and index < len(sorted_elements) - self.k:\n self.center.add(num)\n self.center_sum += num\n else:\n self.right.add(num)\n index += 1\n\n def _remove_element(self, num: int) -> None:\n # Remove the element from the first box you can find it in, startig from left\n if num in self.left:\n self.left.remove(num)\n elif num in self.center:\n self.center.remove(num)\n self.center_sum -= num\n elif num in self.right:\n self.right.remove(num)\n else:\n raise Exception(f\'{num} not found in any of the sorted lists\')\n\n def _insert_element(self, num: int) -> None:\n # Insert the element in the right "box" (left, center, right) while maintaining the order\n if (len(self.center) > 0 and num <= self.center[0]) or (len(self.left) > 0 and num <= self.left[-1]):\n self.left.add(num)\n elif (len(self.right) > 0 and num <= self.right[0]) or (len(self.center) > 0 and num <= self.center[-1]):\n self.center.add(num)\n self.center_sum += num\n else:\n self.right.add(num)\n \n # Case 1: the center is too big, move one element to either left or right\n if len(self.center) > self.center_len:\n assert len(self.left) < self.k or len(self.right) < self.k\n if len(self.left) < self.k:\n to_move = self.center.pop(0)\n self.center_sum -= to_move\n self.left.add(to_move)\n elif len(self.right) < self.k:\n to_move = self.center.pop(-1)\n self.center_sum -= to_move\n self.right.add(to_move)\n # Case 2: the center is too small, move one element from left or right to center\n elif len(self.center) < self.center_len:\n assert len(self.left) > self.k or len(self.right) > self.k\n if len(self.left) > self.k:\n to_move = self.left.pop(-1)\n self.center.add(to_move)\n self.center_sum += to_move\n elif len(self.right) > self.k:\n to_move = self.right.pop(0)\n self.center.add(to_move)\n self.center_sum += to_move\n # Case 3: the center is OK, but left is too small and right is too big\n elif len(self.left) < self.k:\n assert len(self.center) == self.center_len and len(self.right) > self.k\n # Move from right to center and from center to left\n to_move1 = self.right.pop(0)\n self.center.add(to_move1)\n self.center_sum += to_move1\n to_move2 = self.center.pop(0)\n self.center_sum -= to_move2\n self.left.add(to_move2)\n # Case 4: the center is OK, but right is too small, and left is too big\n elif len(self.right) < self.k:\n assert len(self.center) == self.center_len and len(self.left) > self.k\n # Move from left to center and from center to right\n to_move1 = self.left.pop(-1)\n self.center.add(to_move1)\n self.center_sum += to_move1\n to_move2 = self.center.pop(-1)\n self.center_sum -= to_move2\n self.right.add(to_move2)\n \n assert len(self.left) == self.k and len(self.right) == self.k and len(self.center) == self.center_len\n\n \n\n def addElement(self, num: int) -> None:\n self.q.append(num)\n if len(self.q) == self.m:\n # This will be called only once, when we first reach "m" elements\n self._initialize_sorted_lists()\n if len(self.q) > self.m:\n to_remove = self.q.popleft()\n self._remove_element(to_remove)\n self._insert_element(num)\n\n\n def calculateMKAverage(self) -> int:\n if len(self.q) < self.m:\n return -1\n return self.center_sum // self.center_len\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
O(logN) addElement, O(1) calculateMKAverage Python SortedList | finding-mk-average | 0 | 1 | The idea is to keep a sorted list of the most recent m elements. the first k elements and last k elements are the k smallest and k largest elements, respectively. Another twist is instead of calculating the sum every time we got an update, we keep a running sum on the two ends of the list (k largest and k smallest) and the sum of the list itself. To keep track of which element to be popped next when we have more than m elements in the list, we keep a separate queue to track the order.\n# Time Complexity:\n- `addElement`: $$O(log(n))$$\n- `calculateMKAverage`: $$O(1)$$\n# Code\n```\nfrom collections import deque\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m,k\n self.ss = SortedList()\n self.running_smallest, self.running_largest = 0, 0\n self.deck = deque()\n self.sum = 0\n\n def addElement(self, num: int) -> None:\n if len(self.ss) == 2*self.k: \n self.running_smallest, self.running_largest = sum(self.ss[:self.k]), sum(self.ss[-self.k:])\n if len(self.ss) >= self.m:\n rm = self.deck.popleft()\n i = self.ss.bisect_left(rm)\n if i < self.k: \n self.running_smallest -= rm\n self.running_smallest += self.ss[self.k]\n elif i>=len(self.ss)-self.k: \n self.running_largest -= rm\n self.running_largest += self.ss[-self.k-1]\n self.ss.pop(self.ss.index(rm))\n self.sum -= rm\n if len(self.ss) >= 2*self.k:\n max_of_smallest = self.ss[self.k-1]\n min_of_largest = self.ss[-self.k]\n if max_of_smallest <= num <= min_of_largest:\n pass\n elif num < max_of_smallest:\n self.running_smallest -= max_of_smallest - num\n elif num > min_of_largest:\n self.running_largest -= min_of_largest - num\n self.deck.append(num)\n self.ss.add(num)\n self.sum += num\n def calculateMKAverage(self) -> int:\n if len(self.ss) < self.m: return -1\n return (self.sum - self.running_smallest - self.running_largest)//(self.m-2*self.k)\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
O(logN) addElement, O(1) calculateMKAverage Python SortedList | finding-mk-average | 0 | 1 | The idea is to keep a sorted list of the most recent m elements. the first k elements and last k elements are the k smallest and k largest elements, respectively. Another twist is instead of calculating the sum every time we got an update, we keep a running sum on the two ends of the list (k largest and k smallest) and the sum of the list itself. To keep track of which element to be popped next when we have more than m elements in the list, we keep a separate queue to track the order.\n# Time Complexity:\n- `addElement`: $$O(log(n))$$\n- `calculateMKAverage`: $$O(1)$$\n# Code\n```\nfrom collections import deque\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m,k\n self.ss = SortedList()\n self.running_smallest, self.running_largest = 0, 0\n self.deck = deque()\n self.sum = 0\n\n def addElement(self, num: int) -> None:\n if len(self.ss) == 2*self.k: \n self.running_smallest, self.running_largest = sum(self.ss[:self.k]), sum(self.ss[-self.k:])\n if len(self.ss) >= self.m:\n rm = self.deck.popleft()\n i = self.ss.bisect_left(rm)\n if i < self.k: \n self.running_smallest -= rm\n self.running_smallest += self.ss[self.k]\n elif i>=len(self.ss)-self.k: \n self.running_largest -= rm\n self.running_largest += self.ss[-self.k-1]\n self.ss.pop(self.ss.index(rm))\n self.sum -= rm\n if len(self.ss) >= 2*self.k:\n max_of_smallest = self.ss[self.k-1]\n min_of_largest = self.ss[-self.k]\n if max_of_smallest <= num <= min_of_largest:\n pass\n elif num < max_of_smallest:\n self.running_smallest -= max_of_smallest - num\n elif num > min_of_largest:\n self.running_largest -= min_of_largest - num\n self.deck.append(num)\n self.ss.add(num)\n self.sum += num\n def calculateMKAverage(self) -> int:\n if len(self.ss) < self.m: return -1\n return (self.sum - self.running_smallest - self.running_largest)//(self.m-2*self.k)\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python (Simple Deque + SortedList) | finding-mk-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage:\n\n def __init__(self, m, k):\n from sortedcontainers import SortedList\n self.m = m\n self.k = k\n self.ans = deque()\n self.res = SortedList()\n self.total = 0\n\n def addElement(self, num):\n self.ans.append(num)\n self.res.add(num)\n self.total += num\n\n if len(self.ans) > self.m:\n x = self.ans.popleft()\n self.res.remove(x)\n self.total -= x\n\n def calculateMKAverage(self):\n if len(self.ans) < self.m:\n return -1\n else:\n remove = sum(self.res[:self.k]) + sum(self.res[-self.k:])\n\n return int((self.total-remove)/(self.m-2*self.k))\n\n \n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Python (Simple Deque + SortedList) | finding-mk-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage:\n\n def __init__(self, m, k):\n from sortedcontainers import SortedList\n self.m = m\n self.k = k\n self.ans = deque()\n self.res = SortedList()\n self.total = 0\n\n def addElement(self, num):\n self.ans.append(num)\n self.res.add(num)\n self.total += num\n\n if len(self.ans) > self.m:\n x = self.ans.popleft()\n self.res.remove(x)\n self.total -= x\n\n def calculateMKAverage(self):\n if len(self.ans) < self.m:\n return -1\n else:\n remove = sum(self.res[:self.k]) + sum(self.res[-self.k:])\n\n return int((self.total-remove)/(self.m-2*self.k))\n\n \n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Use Sorted Containers to help solving this problem | finding-mk-average | 0 | 1 | # Intuition & Approach\nDivide array into 3 sorted arrays: `s1`, `s2` and `s3`; `s1` contains smallest k number, and `s3` contains largest k elements. Use `nums` to remember last m numbers.\n\n# Code\n```\nimport sortedcontainers\nfrom sortedcontainers import SortedList\nfrom collections import deque\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.s1 = SortedList()\n self.s2 = SortedList()\n self.s3 = SortedList()\n self.nums = deque()\n self.sum = 0 # update sum of s2\n self.den = m - 2*k\n\n def addElement(self, n: int) -> None:\n if len(self.nums) < self.m:\n self.s2.add(n)\n self.sum += n\n if len(self.s2) == self.m: # only enter this branch once, first time when length of nums up to m\n for i in range(self.k):\n head = self.s2.pop(0)\n tail = self.s2.pop()\n self.s1.add(head)\n self.s3.add(tail)\n self.sum -= (head + tail)\n else: # move extra number to s2, keep s1 and s3 length == k\n if n <= self.s1[-1]:\n p = self.s1.pop()\n self.s2.add(p)\n self.sum += p\n self.s1.add(n)\n elif n >= self.s3[0]:\n p = self.s3.pop(0)\n self.s2.add(p)\n self.sum += p\n self.s3.add(n)\n else:\n self.s2.add(n)\n self.sum += n\n # delete the oldest number in self.nums\n d = self.nums.popleft()\n if d <= self.s1[-1]:\n self.s1.discard(d)\n p = self.s2.pop(0)\n self.sum -= p\n self.s1.add(p)\n elif d >= self.s3[0]:\n self.s3.discard(d)\n p = self.s2.pop()\n self.sum -= p\n self.s3.add(p)\n else:\n self.s2.discard(d)\n self.sum -= d\n\n # add new number to self.nums\n self.nums.append(n)\n\n def calculateMKAverage(self) -> int:\n if len(self.nums) < self.m:\n return -1\n return self.sum // self.den\n``` | 0 | You are given two integers, `m` and `k`, and a stream of integers. You are tasked to implement a data structure that calculates the **MKAverage** for the stream.
The **MKAverage** can be calculated using these steps:
1. If the number of the elements in the stream is less than `m` you should consider the **MKAverage** to be `-1`. Otherwise, copy the last `m` elements of the stream to a separate container.
2. Remove the smallest `k` elements and the largest `k` elements from the container.
3. Calculate the average value for the rest of the elements **rounded down to the nearest integer**.
Implement the `MKAverage` class:
* `MKAverage(int m, int k)` Initializes the **MKAverage** object with an empty stream and the two integers `m` and `k`.
* `void addElement(int num)` Inserts a new element `num` into the stream.
* `int calculateMKAverage()` Calculates and returns the **MKAverage** for the current stream **rounded down to the nearest integer**.
**Example 1:**
**Input**
\[ "MKAverage ", "addElement ", "addElement ", "calculateMKAverage ", "addElement ", "calculateMKAverage ", "addElement ", "addElement ", "addElement ", "calculateMKAverage "\]
\[\[3, 1\], \[3\], \[1\], \[\], \[10\], \[\], \[5\], \[5\], \[5\], \[\]\]
**Output**
\[null, null, null, -1, null, 3, null, null, null, 5\]
**Explanation**
`MKAverage obj = new MKAverage(3, 1); obj.addElement(3); // current elements are [3] obj.addElement(1); // current elements are [3,1] obj.calculateMKAverage(); // return -1, because m = 3 and only 2 elements exist. obj.addElement(10); // current elements are [3,1,10] obj.calculateMKAverage(); // The last 3 elements are [3,1,10]. // After removing smallest and largest 1 element the container will be [3]. // The average of [3] equals 3/1 = 3, return 3 obj.addElement(5); // current elements are [3,1,10,5] obj.addElement(5); // current elements are [3,1,10,5,5] obj.addElement(5); // current elements are [3,1,10,5,5,5] obj.calculateMKAverage(); // The last 3 elements are [5,5,5]. // After removing smallest and largest 1 element the container will be [5]. // The average of [5] equals 5/1 = 5, return 5`
**Constraints:**
* `3 <= m <= 105`
* `1 <= k*2 < m`
* `1 <= num <= 105`
* At most `105` calls will be made to `addElement` and `calculateMKAverage`. | We can select a subset of tasks and assign it to a worker then solve the subproblem on the remaining tasks |
Use Sorted Containers to help solving this problem | finding-mk-average | 0 | 1 | # Intuition & Approach\nDivide array into 3 sorted arrays: `s1`, `s2` and `s3`; `s1` contains smallest k number, and `s3` contains largest k elements. Use `nums` to remember last m numbers.\n\n# Code\n```\nimport sortedcontainers\nfrom sortedcontainers import SortedList\nfrom collections import deque\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.s1 = SortedList()\n self.s2 = SortedList()\n self.s3 = SortedList()\n self.nums = deque()\n self.sum = 0 # update sum of s2\n self.den = m - 2*k\n\n def addElement(self, n: int) -> None:\n if len(self.nums) < self.m:\n self.s2.add(n)\n self.sum += n\n if len(self.s2) == self.m: # only enter this branch once, first time when length of nums up to m\n for i in range(self.k):\n head = self.s2.pop(0)\n tail = self.s2.pop()\n self.s1.add(head)\n self.s3.add(tail)\n self.sum -= (head + tail)\n else: # move extra number to s2, keep s1 and s3 length == k\n if n <= self.s1[-1]:\n p = self.s1.pop()\n self.s2.add(p)\n self.sum += p\n self.s1.add(n)\n elif n >= self.s3[0]:\n p = self.s3.pop(0)\n self.s2.add(p)\n self.sum += p\n self.s3.add(n)\n else:\n self.s2.add(n)\n self.sum += n\n # delete the oldest number in self.nums\n d = self.nums.popleft()\n if d <= self.s1[-1]:\n self.s1.discard(d)\n p = self.s2.pop(0)\n self.sum -= p\n self.s1.add(p)\n elif d >= self.s3[0]:\n self.s3.discard(d)\n p = self.s2.pop()\n self.sum -= p\n self.s3.add(p)\n else:\n self.s2.discard(d)\n self.sum -= d\n\n # add new number to self.nums\n self.nums.append(n)\n\n def calculateMKAverage(self) -> int:\n if len(self.nums) < self.m:\n return -1\n return self.sum // self.den\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python Easy and Efficient Solution . | minimum-operations-to-make-the-array-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have to Return the minimum number of operations needed to make nums strictly increasing.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTaking the previous value and comparing with the current value and increasing the count with the previous value to meet the rule of \n* nums[i] < nums[i+1] for all 0 <= i < nums.length - 1\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code uses a single loop that iterates through the nums list, and for each element, it performs some constant time operations. Within the loop, there are a few simple conditional checks and arithmetic operations. The time complexity of these operations is linear in the length of the nums list, so the overall time complexity of this code is O(n), where \'n\' is the length of the nums list.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this code is primarily determined by the variables used. There are a few integer variables (count and prev) that are used to store intermediate results, and their memory usage does not depend on the size of the nums list. Therefore, the space complexity is O(1), which means it is constant and does not depend on the input size.\n\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n if len(nums)==1:\n return 0\n count = prev= 0\n for i in nums:\n if i <= prev :\n prev += 1\n count += prev-i\n else:\n prev = i\n return count\n``` | 3 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
Python Easy and Efficient Solution . | minimum-operations-to-make-the-array-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have to Return the minimum number of operations needed to make nums strictly increasing.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTaking the previous value and comparing with the current value and increasing the count with the previous value to meet the rule of \n* nums[i] < nums[i+1] for all 0 <= i < nums.length - 1\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code uses a single loop that iterates through the nums list, and for each element, it performs some constant time operations. Within the loop, there are a few simple conditional checks and arithmetic operations. The time complexity of these operations is linear in the length of the nums list, so the overall time complexity of this code is O(n), where \'n\' is the length of the nums list.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this code is primarily determined by the variables used. There are a few integer variables (count and prev) that are used to store intermediate results, and their memory usage does not depend on the size of the nums list. Therefore, the space complexity is O(1), which means it is constant and does not depend on the input size.\n\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n if len(nums)==1:\n return 0\n count = prev= 0\n for i in nums:\n if i <= prev :\n prev += 1\n count += prev-i\n else:\n prev = i\n return count\n``` | 3 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
python 3 solution beats 99.8% TIME , O(1) SPACE used | minimum-operations-to-make-the-array-increasing | 0 | 1 | # stats\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe can have a temporary variable s and a counting variable c\ns initialized with first element of array\nif s is greater than or equal to current elemnet then we take difference between s and current lement and add 1 to make it number 1 greater than s\n` 5 2` , `s=5`,`c added to 5-2+1`,`s=6` the next element\nelse s is updated to new element \nreturning cdoes the job\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**________O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**________O(1)**\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n c=0\n s=nums[0]\n for i in range(1,len(nums)):\n if s>=nums[i]:\n c+=s-nums[i]+1\n s+=1\n else:\n s=nums[i]\n return c\n``` | 3 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
python 3 solution beats 99.8% TIME , O(1) SPACE used | minimum-operations-to-make-the-array-increasing | 0 | 1 | # stats\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe can have a temporary variable s and a counting variable c\ns initialized with first element of array\nif s is greater than or equal to current elemnet then we take difference between s and current lement and add 1 to make it number 1 greater than s\n` 5 2` , `s=5`,`c added to 5-2+1`,`s=6` the next element\nelse s is updated to new element \nreturning cdoes the job\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**________O(N)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**________O(1)**\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n c=0\n s=nums[0]\n for i in range(1,len(nums)):\n if s>=nums[i]:\n c+=s-nums[i]+1\n s+=1\n else:\n s=nums[i]\n return c\n``` | 3 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
Beginner-friendly || Simple solution in Python3/TypeScript | minimum-operations-to-make-the-array-increasing | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a list of `nums`\n- our goal is to make `nums` **strongly increasing**\n\nThere\'s no need in sorting. The approach is straightforward and requires to calculate difference between adjacent integers.\n\n# Approach\n1. initialize `ans` to store the answer\n2. iterate over `nums`, check if `nums[i] <= nums[i - 1]`, then calculate `diff` and increment `ans`\n3. return `ans`\n\n# Complexity\n- Time complexity: **O(n)**, to iterate over `nums`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space.\n\n# Code in TypeScript\n```\nfunction minOperations(nums: number[]): number {\n let ans = 0\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] <= nums[i - 1]) {\n const diff = Math.abs(nums[i] - nums[i - 1]) + 1\n nums[i] += diff \n ans += diff\n }\n }\n\n return ans\n};\n```\n\n# Code in Python3\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n ans = 0\n\n for i in range(1, len(nums)):\n if nums[i] <= nums[i - 1]:\n diff = abs(nums[i] - nums[i - 1]) + 1\n nums[i] += diff\n ans += diff\n\n return ans\n``` | 2 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
Beginner-friendly || Simple solution in Python3/TypeScript | minimum-operations-to-make-the-array-increasing | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a list of `nums`\n- our goal is to make `nums` **strongly increasing**\n\nThere\'s no need in sorting. The approach is straightforward and requires to calculate difference between adjacent integers.\n\n# Approach\n1. initialize `ans` to store the answer\n2. iterate over `nums`, check if `nums[i] <= nums[i - 1]`, then calculate `diff` and increment `ans`\n3. return `ans`\n\n# Complexity\n- Time complexity: **O(n)**, to iterate over `nums`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space.\n\n# Code in TypeScript\n```\nfunction minOperations(nums: number[]): number {\n let ans = 0\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] <= nums[i - 1]) {\n const diff = Math.abs(nums[i] - nums[i - 1]) + 1\n nums[i] += diff \n ans += diff\n }\n }\n\n return ans\n};\n```\n\n# Code in Python3\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n ans = 0\n\n for i in range(1, len(nums)):\n if nums[i] <= nums[i - 1]:\n diff = abs(nums[i] - nums[i - 1]) + 1\n nums[i] += diff\n ans += diff\n\n return ans\n``` | 2 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
8 lines solution using python3 simplest of all | minimum-operations-to-make-the-array-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n ans=0\n for i in range(len(nums)-1):\n if nums[i]>=nums[i+1]:\n ans=ans+nums[i]-nums[i+1]+1\n nums[i+1]=nums[i]+1\n else:\n ans+=0\n return ans\n\n\n``` | 3 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
8 lines solution using python3 simplest of all | minimum-operations-to-make-the-array-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n ans=0\n for i in range(len(nums)-1):\n if nums[i]>=nums[i+1]:\n ans=ans+nums[i]-nums[i+1]+1\n nums[i+1]=nums[i]+1\n else:\n ans+=0\n return ans\n\n\n``` | 3 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
Python3 simple solution beats 90% users | minimum-operations-to-make-the-array-increasing | 0 | 1 | ```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n count = 0\n for i in range(1,len(nums)):\n if nums[i] <= nums[i-1]:\n x = nums[i]\n nums[i] += (nums[i-1] - nums[i]) + 1\n count += nums[i] - x\n return count\n```\n**If you like this solution, please upvote for this** | 12 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
Python3 simple solution beats 90% users | minimum-operations-to-make-the-array-increasing | 0 | 1 | ```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n count = 0\n for i in range(1,len(nums)):\n if nums[i] <= nums[i-1]:\n x = nums[i]\n nums[i] += (nums[i-1] - nums[i]) + 1\n count += nums[i] - x\n return count\n```\n**If you like this solution, please upvote for this** | 12 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
Python O(n) simple and short solution | minimum-operations-to-make-the-array-increasing | 0 | 1 | **Python :**\n\n```\ndef minOperations(self, nums: List[int]) -> int:\n\tans = 0\n\n\tfor i in range(1, len(nums)):\n\t\tif nums[i] <= nums[i - 1]:\n\t\t\tans += (nums[i - 1] - nums[i] + 1)\n\t\t\tnums[i] = (nums[i - 1] + 1)\n\n\treturn ans\n```\n\n**Like it ? please upvote !** | 9 | You are given an integer array `nums` (**0-indexed**). In one operation, you can choose an element of the array and increment it by `1`.
* For example, if `nums = [1,2,3]`, you can choose to increment `nums[1]` to make `nums = [1,**3**,3]`.
Return _the **minimum** number of operations needed to make_ `nums` _**strictly** **increasing**._
An array `nums` is **strictly increasing** if `nums[i] < nums[i+1]` for all `0 <= i < nums.length - 1`. An array of length `1` is trivially strictly increasing.
**Example 1:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can do the following operations:
1) Increment nums\[2\], so nums becomes \[1,1,**2**\].
2) Increment nums\[1\], so nums becomes \[1,**2**,2\].
3) Increment nums\[2\], so nums becomes \[1,2,**3**\].
**Example 2:**
**Input:** nums = \[1,5,2,4,1\]
**Output:** 14
**Example 3:**
**Input:** nums = \[8\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 5000`
* `1 <= nums[i] <= 104` | null |
Python O(n) simple and short solution | minimum-operations-to-make-the-array-increasing | 0 | 1 | **Python :**\n\n```\ndef minOperations(self, nums: List[int]) -> int:\n\tans = 0\n\n\tfor i in range(1, len(nums)):\n\t\tif nums[i] <= nums[i - 1]:\n\t\t\tans += (nums[i - 1] - nums[i] + 1)\n\t\t\tnums[i] = (nums[i - 1] + 1)\n\n\treturn ans\n```\n\n**Like it ? please upvote !** | 9 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
Python Easy || Simple Geometry | queries-on-number-of-points-inside-a-circle | 0 | 1 | # Code\n```\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n lis=[]\n for circle in queries:\n cnt=0\n for pt in points:\n if ((((circle[0]-pt[0])**2)+((circle[1]-pt[1])**2))**0.5)<=circle[2]:\n cnt+=1\n lis.append(cnt)\n return lis\n\n``` | 1 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Python very easy solution | queries-on-number-of-points-inside-a-circle | 0 | 1 | # Very Easy Soln\n\n# Code\n```\nclass Solution(object):\n def countPoints(self, points, q):\n for i in range(len(q)):\n x,y,r=q[i]\n c=0\n for j,k in points:\n if ((j-x)**2+(k-y)**2)**0.5<=r: c+=1\n q[i]=c\n return q\n``` | 1 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Hashtable + Binary Search, O(RlogN), explained! [Python3] | queries-on-number-of-points-inside-a-circle | 0 | 1 | # Intuition\n\nMost simple solution would be for each circle, check if every point is inside circle using math, then time for each query would be O(N).\n\nAnother idea would be sort points then binary search for points that are within the "square" range that the circle would form from x - r to x + r and y - r to y + r. Worst case you would have to check O(R^2) points if there are that many points per each query, but if R is small and N is big, it could be much faster than O(N).\n\nLast idea is for each circle, for each dx, find the valid range of dy for each circle. Then for each x coordinate within the circle, binary search for points with that x that have a y within the range of the current circle. This would take O(RlogN) for each query.\n\nObjectively, looking at it, it seems that O(RlogN) looks best, but looking at the preconditions for the problem, we see that R >= M > N. So technically the first idea, which is just brute force is the fastest since its O(N). But... if N were big and there were also many circles with varying R, then O(RlogN) would be better. \n\nSo instead of implementing the brute force boring one I did the O(RlogN) solution.\n\n# Complexity\n- Time complexity:\nO(RlogN) for each query\n\n- Space complexity:\nO(N)\n\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n # Preconditions: R >= M > N \n # 1. check every point if inside curr circle, O(NM), each query is O(N)\n # 2. check points that could be within circle range using binary search, O(M * (Rlog(n) + R^2)), each query is O(Rlog(n) + R^2)\n # 3. for each x, find valid range of y for each circle, binary search for valid range O(nlogn + M(RlogN)), O(MRlogN), each query is RlogN\n # based on preconditions, nm is lowkey the move, but ill implement number 3\n point_map = defaultdict(list)\n for x, y in points:\n point_map[x].append(y)\n for key in point_map.keys():\n point_map[key].sort()\n \n ans = []\n for cx, cy, r in queries:\n inside = 0\n for dx in range(-r, r + 1):\n dy = math.sqrt(r ** 2 - dx ** 2)\n x = cx + dx\n lower_y = cy - dy # binary search for leftmost insertion index of lower_y\n upper_y = cy + dy # binary search for rightmost insertion index of upper_y\n lower_ind = bisect.bisect_left(point_map[x], lower_y)\n upper_ind = bisect.bisect_right(point_map[x], upper_y)\n inside += upper_ind - lower_ind\n ans.append(inside)\n return ans\n``` | 2 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Python One-liner | queries-on-number-of-points-inside-a-circle | 0 | 1 | ```\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n return [sum(math.sqrt((x0-x1)**2 + (y0-y1)**2) <= r for x1, y1 in points) for x0, y0, r in queries]\n``` | 28 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Solution of queries on number of points inside a circle problem | queries-on-number-of-points-inside-a-circle | 0 | 1 | # Approach\n- If you select a point on the coordinate plane, you can see that the projections of its coordinates on the x and y axes are the legs of a right triangle. And the hypotenuse of this right triangle just shows the distance from the origin to the point.\n- So, if the length of the hypotenuse is no greater than the radius of the circle, then the point will belong to the circle; otherwise she will be outside it.\n- The length of the hypotenuse is calculated using the Pythagorean theorem: c = \u221Aa^2 + b^2\n# Complexity\n- Time complexity:\n$$O(n * m)$$ - as we are checking all the points for each circle.\n\n# Code\n```\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n answer = []\n for circle in queries:\n count = 0 \n for point in points:\n x = point[0] - circle[0]\n y = point[1] - circle[1]\n c = (x ** 2 + y ** 2) ** 0.5\n if c <= circle[2]:\n count += 1\n answer.append(count)\n return answer\n \n``` | 3 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Simple python code with explanation | queries-on-number-of-points-inside-a-circle | 0 | 1 | # **MOST UNDERSTANDABLE CODE**\n```\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n #create a empty list k \n k = []\n #create a variable and initialise it to 0 \n count = 0 \n #iterate over the elements in the queries\n for i in queries:\n #in each sublist 1st element is x co-ordinate\n x1 = i[0]\n #in each sublist 2nd element is y co-ordinate\n y1 = i[1]\n #in each sublist 3rd element is radius\n r = i[2]\n #iterate ovet the lists in points\n for j in points:\n #in each sublist 1st element is x co-ordinate\n x2 = j[0]\n #in each sublist 2nd element is y co-ordinate\n y2 = j[1]\n #if the distance between those two co-ordinates is less than or equal to radius \n if (((x2 - x1)**2 + (y2 - y1)**2)**0.5) <= r :\n #then the point lies inside the cirle or on the circle\n #then count how many points are inside the circle or on the circle by incrementing count variable\n count = count + 1\n \n #after finishing one co-ordinate in points then add the count value in list k \n k.append(count)\n #then rearrange the value of count to 0 before starting next circle \n count = 0 \n #after finishing all circles return the list k \n return k\n``` | 11 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
[Python 3] 512 ms, faster than 100% using complex numbers | queries-on-number-of-points-inside-a-circle | 0 | 1 | ```\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n points = list(map(complex, *zip(*points)))\n\t\tqueries = ((complex(x, y), r) for x, y, r in queries)\n return [sum(abs(p - q) <= r for p in points) for q, r in queries]\n``` | 17 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Python Easy solution | queries-on-number-of-points-inside-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n answer = []\n for query in queries:\n xj, yj, rj = query\n count = 0\n for xi, yi in points:\n distance = math.sqrt((xi - xj) ** 2 + (yi - yj) ** 2)\n if distance <= rj:\n count += 1\n answer.append(count)\n return answer\n \n``` | 1 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Python My Soln Easy to Follow | queries-on-number-of-points-inside-a-circle | 0 | 1 | def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:\n\n res = []\n for circle in queries:\n count = 0\n for point in points:\n if (circle[0]-point[0]) ** 2 + (circle[1]-point[1]) ** 2 <= circle[2] ** 2:\n count += 1\n res.append(count)\n return res | 1 | You are given an array `points` where `points[i] = [xi, yi]` is the coordinates of the `ith` point on a 2D plane. Multiple points can have the **same** coordinates.
You are also given an array `queries` where `queries[j] = [xj, yj, rj]` describes a circle centered at `(xj, yj)` with a radius of `rj`.
For each query `queries[j]`, compute the number of points **inside** the `jth` circle. Points **on the border** of the circle are considered **inside**.
Return _an array_ `answer`_, where_ `answer[j]` _is the answer to the_ `jth` _query_.
**Example 1:**
**Input:** points = \[\[1,3\],\[3,3\],\[5,3\],\[2,2\]\], queries = \[\[2,3,1\],\[4,3,1\],\[1,1,2\]\]
**Output:** \[3,2,2\]
**Explanation:** The points and circles are shown above.
queries\[0\] is the green circle, queries\[1\] is the red circle, and queries\[2\] is the blue circle.
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\], queries = \[\[1,2,2\],\[2,2,2\],\[4,3,2\],\[4,3,3\]\]
**Output:** \[2,3,2,4\]
**Explanation:** The points and circles are shown above.
queries\[0\] is green, queries\[1\] is red, queries\[2\] is blue, and queries\[3\] is purple.
**Constraints:**
* `1 <= points.length <= 500`
* `points[i].length == 2`
* `0 <= xi, yi <= 500`
* `1 <= queries.length <= 500`
* `queries[j].length == 3`
* `0 <= xj, yj <= 500`
* `1 <= rj <= 500`
* All coordinates are integers.
**Follow up:** Could you find the answer for each query in better complexity than `O(n)`? | Try to define a recursive approach. For the ith candies, there will be one of the two following cases: If the i - 1 previous candies are already distributed into k bags for the ith candy, you can have k * dp[n - 1][k] ways to distribute the ith candy. We need then to solve the state of (n - 1, k). If the i - 1 previous candies are already distributed into k - 1 bags for the ith candy, you can have dp[n - 1][k - 1] ways to distribute the ith candy. We need then to solve the state of (n - 1, k - 1). This approach will be too slow and will traverse some states more than once. We should use memoization to make the algorithm efficient. |
Beginner-friendly || Simple solution with PrefixSum in Python3 / TypeScript | maximum-xor-for-each-query | 0 | 1 | # Intuition\nLet\'s briefly explain, what the problem is:\n- there\'s a list of `nums` and an integer `maximumBit`\n- our goal is to find at each step an integer, that represent **maximum XOR**\n\nThis could be implemented with **Prefix Sum**.\n\nFollowing to the problem\'s description, at each step we should **remove the last** integer from `nums`.\n\nThe way to find this integer is to calculate **prefix** as accumulated **XOR** `nums[i-1] ^ nums[i]`.\n\n# Approach\n1. define `k` as it declared in the problem\'s description and use it as **maximum XOR**\n2. define `prefix` to store accumulated XOR and calculate it\n3. define `ans`\n4. iterate over `nums` in reversed order, remove at each step particular num by `i` index, find **maximum XOR** as `prefix[i] ^ k` and push result into `ans`\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N)**, twice iterating over `nums`\n\n- Space complexity: **O(N)**, the same for filling `ans`\n\n# Code in Python3\n```\nclass Solution:\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n k = 2 ** maximumBit - 1\n prefix = [nums[0]]\n n = len(nums)\n\n for i in range(1, n): prefix.append(prefix[i - 1] ^ nums[i])\n\n ans = []\n \n for i in range(n - 1, -1, -1):\n ans.append(prefix[i] ^ k)\n\n return ans\n\n```\n# Code in TypeScript\n```\nfunction getMaximumXor(nums: number[], maximumBit: number): number[] {\n const k = 2 ** maximumBit - 1\n const prefix = [nums[0]]\n const n = (nums.length)\n\n for (let i = 1; i < n; i++) prefix.push(prefix[i - 1] ^ nums[i])\n\n const ans = []\n\n for (let i = n - 1; i >= 0; i--) ans.push(prefix[i] ^ k)\n\n return ans\n};\n``` | 1 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
reduce() | maximum-xor-for-each-query | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport functools\nclass Solution:\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n max_num = 2**maximumBit-1\n res = []\n # approach 1, time limit exceed\n # while nums:\n # all_xor_now = functools.reduce(lambda a, b: a^b, nums)\n # res.append(all_xor_now^max_num)\n # nums.pop()\n # return res\n all_xor = functools.reduce(lambda a, b: a^b, nums)\n res.append(all_xor^max_num)\n for idx in range(1,len(nums)):\n all_xor = all_xor^nums[-idx]\n res.append(all_xor^max_num)\n return res\n\n``` | 1 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
Simple solution beats 99% | maximum-xor-for-each-query | 0 | 1 | # Code\n```\nclass Solution:\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n ans = [0] * len(nums)\n x = (2**maximumBit-1)\n for i, n in enumerate(nums):\n x = x ^ n\n ans[-1-i] = x\n return ans \n``` | 2 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
Python3 | Prefix Sum With Bit Manip. Fact Max XOR = 2^maximumBit - 1 | maximum-xor-for-each-query | 0 | 1 | ```\nclass Solution:\n #Let n = len(nums)!\n #Time-Complexity: O(n + n) -> O(N)\n #Space-Complexity: O(N)\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n #Approach:\n \n #1. First, initialize prefix sum array of exclusive or results up to each index position!\n \n prefix_sum = [nums[0]]\n for a in range(1, len(nums)):\n prefix_sum.append(prefix_sum[len(prefix_sum)-1] ^ nums[a])\n #2.For each query, take the prefix sum of current index starting from the end and moving left, and\n #utilize binary search on search space of possible values for non-negative integer k, that is \n #maximal and satisfies the inequality!\n comparison = 2 ** maximumBit\n ans = []\n #for each query\n for i in range(len(prefix_sum)-1, -1, -1):\n #get the res so far!\n current_res = prefix_sum[i]\n #largest XOR is going to be 2^maximumBit - (1)!\n #Thus, knowing current_res prefix result and largest possible XOR,\n #if we exclusive or btw the two, we will be able to find \n #non-negative k that maximizes XOR for current query!\n res = current_res ^ (comparison - 1)\n ans.append(res)\n return ans | 1 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
Simple fast solution TIME COMPLEXITY O(n) | maximum-xor-for-each-query | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```python []\nclass Solution:\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n ans = [(1 << maximumBit) - 1]\n for n in nums:\n ans.append(ans[-1] ^ n)\n\n return ans[len(ans)-1:0:-1]\n``` | 2 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
One line solution | maximum-xor-for-each-query | 0 | 1 | ```\nclass Solution:\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n return list(map(xor, accumulate(nums, xor), repeat((1 << maximumBit) - 1)))[::-1] \n``` | 0 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
Python Solution | Easy To Understand | O(N) Runtime & O(1) Space Complexity | maximum-xor-for-each-query | 0 | 1 | \n# Code\n```\nclass Solution:\n def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:\n \n n = len(nums)\n result = [0] * n\n val = 2 ** maximumBit - 1\n\n for i in range(n):\n result[n - i - 1] = val ^ nums[i]\n val = val ^ nums[i]\n\n return result \n``` | 0 | You are given a **sorted** array `nums` of `n` non-negative integers and an integer `maximumBit`. You want to perform the following query `n` **times**:
1. Find a non-negative integer `k < 2maximumBit` such that `nums[0] XOR nums[1] XOR ... XOR nums[nums.length-1] XOR k` is **maximized**. `k` is the answer to the `ith` query.
2. Remove the **last** element from the current array `nums`.
Return _an array_ `answer`_, where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** nums = \[0,1,1,3\], maximumBit = 2
**Output:** \[0,3,2,3\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[0,1,1,3\], k = 0 since 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3.
2nd query: nums = \[0,1,1\], k = 3 since 0 XOR 1 XOR 1 XOR 3 = 3.
3rd query: nums = \[0,1\], k = 2 since 0 XOR 1 XOR 2 = 3.
4th query: nums = \[0\], k = 3 since 0 XOR 3 = 3.
**Example 2:**
**Input:** nums = \[2,3,4,7\], maximumBit = 3
**Output:** \[5,2,6,5\]
**Explanation**: The queries are answered as follows:
1st query: nums = \[2,3,4,7\], k = 5 since 2 XOR 3 XOR 4 XOR 7 XOR 5 = 7.
2nd query: nums = \[2,3,4\], k = 2 since 2 XOR 3 XOR 4 XOR 2 = 7.
3rd query: nums = \[2,3\], k = 6 since 2 XOR 3 XOR 6 = 7.
4th query: nums = \[2\], k = 5 since 2 XOR 5 = 7.
**Example 3:**
**Input:** nums = \[0,1,2,2,5,7\], maximumBit = 3
**Output:** \[4,3,6,4,6,7\]
**Constraints:**
* `nums.length == n`
* `1 <= n <= 105`
* `1 <= maximumBit <= 20`
* `0 <= nums[i] < 2maximumBit`
* `nums` is sorted in **ascending** order. | If we have space for at least one box, it's always optimal to put the box with the most units. Sort the box types with the number of units per box non-increasingly. Iterate on the box types and take from each type as many as you can. |
[Python3] O(n) use combination count and gcd | minimum-number-of-operations-to-make-string-sorted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEvery operation equals to find previous permutation of the tail of s. \nWe process the suffix step by step, to find the correct insert position to insert the current string.\ncnt is used to count all chars after i.\nt is used to store current factorial.\nd is used to store current repeat times. \ng = gcd(d, t) is used to decrease t and d.\nsum(cnt[i] for i in range(c)) // d is to find the insert position.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nfrom math import gcd\n\nclass Solution:\n def makeStringSorted(self, s: str) -> int:\n s = [ord(c) - ord(\'a\') for c in s]\n ans, MOD = 0, 10 ** 9 + 7\n cnt, t, d, step = [0] * 26, 1, 1, 1\n cnt[s[-1]] = 1\n for c in reversed(s[:-1]):\n d *= (cnt[c] + 1)\n t *= step\n g = gcd(d, t)\n d //= g\n t //= g\n ans = (ans + t * sum(cnt[i] for i in range(c)) // d) % MOD\n cnt[c] += 1\n step += 1\n return ans\n``` | 1 | You are given a string `s` (**0-indexed**). You are asked to perform the following operation on `s` until you get a sorted string:
1. Find **the largest index** `i` such that `1 <= i < s.length` and `s[i] < s[i - 1]`.
2. Find **the largest index** `j` such that `i <= j < s.length` and `s[k] < s[i - 1]` for all the possible values of `k` in the range `[i, j]` inclusive.
3. Swap the two characters at indices `i - 1` and `j`.
4. Reverse the suffix starting at index `i`.
Return _the number of operations needed to make the string sorted._ Since the answer can be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "cba "
**Output:** 5
**Explanation:** The simulation goes as follows:
Operation 1: i=2, j=2. Swap s\[1\] and s\[2\] to get s= "cab ", then reverse the suffix starting at 2. Now, s= "cab ".
Operation 2: i=1, j=2. Swap s\[0\] and s\[2\] to get s= "bac ", then reverse the suffix starting at 1. Now, s= "bca ".
Operation 3: i=2, j=2. Swap s\[1\] and s\[2\] to get s= "bac ", then reverse the suffix starting at 2. Now, s= "bac ".
Operation 4: i=1, j=1. Swap s\[0\] and s\[1\] to get s= "abc ", then reverse the suffix starting at 1. Now, s= "acb ".
Operation 5: i=2, j=2. Swap s\[1\] and s\[2\] to get s= "abc ", then reverse the suffix starting at 2. Now, s= "abc ".
**Example 2:**
**Input:** s = "aabaa "
**Output:** 2
**Explanation:** The simulation goes as follows:
Operation 1: i=3, j=4. Swap s\[2\] and s\[4\] to get s= "aaaab ", then reverse the substring starting at 3. Now, s= "aaaba ".
Operation 2: i=4, j=4. Swap s\[3\] and s\[4\] to get s= "aaaab ", then reverse the substring starting at 4. Now, s= "aaaab ".
**Constraints:**
* `1 <= s.length <= 3000`
* `s` consists only of lowercase English letters. | Note that the number of powers of 2 is at most 21 so this turns the problem to a classic find the number of pairs that sum to a certain value but for 21 values You need to use something fasters than the NlogN approach since there is already the log of iterating over the powers so one idea is two pointers |
[Python3] O(n) use combination count and gcd | minimum-number-of-operations-to-make-string-sorted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEvery operation equals to find previous permutation of the tail of s. \nWe process the suffix step by step, to find the correct insert position to insert the current string.\ncnt is used to count all chars after i.\nt is used to store current factorial.\nd is used to store current repeat times. \ng = gcd(d, t) is used to decrease t and d.\nsum(cnt[i] for i in range(c)) // d is to find the insert position.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nfrom math import gcd\n\nclass Solution:\n def makeStringSorted(self, s: str) -> int:\n s = [ord(c) - ord(\'a\') for c in s]\n ans, MOD = 0, 10 ** 9 + 7\n cnt, t, d, step = [0] * 26, 1, 1, 1\n cnt[s[-1]] = 1\n for c in reversed(s[:-1]):\n d *= (cnt[c] + 1)\n t *= step\n g = gcd(d, t)\n d //= g\n t //= g\n ans = (ans + t * sum(cnt[i] for i in range(c)) // d) % MOD\n cnt[c] += 1\n step += 1\n return ans\n``` | 1 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
[Python3] math solution | minimum-number-of-operations-to-make-string-sorted | 0 | 1 | \n```\nclass Solution:\n def makeStringSorted(self, s: str) -> int:\n freq = [0]*26\n for c in s: freq[ord(c) - 97] += 1\n \n MOD = 1_000_000_007\n fac = cache(lambda x: x*fac(x-1)%MOD if x else 1)\n ifac = cache(lambda x: pow(fac(x), MOD-2, MOD)) # Fermat\'s little theorem (a**(p-1) = 1 (mod p))\n \n ans, n = 0, len(s)\n for c in s: \n val = ord(c) - 97\n mult = fac(n-1)\n for k in range(26): mult *= ifac(freq[k])\n for k in range(val): ans += freq[k] * mult\n n -= 1\n freq[val] -= 1\n return ans % MOD\n``` | 2 | You are given a string `s` (**0-indexed**). You are asked to perform the following operation on `s` until you get a sorted string:
1. Find **the largest index** `i` such that `1 <= i < s.length` and `s[i] < s[i - 1]`.
2. Find **the largest index** `j` such that `i <= j < s.length` and `s[k] < s[i - 1]` for all the possible values of `k` in the range `[i, j]` inclusive.
3. Swap the two characters at indices `i - 1` and `j`.
4. Reverse the suffix starting at index `i`.
Return _the number of operations needed to make the string sorted._ Since the answer can be too large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "cba "
**Output:** 5
**Explanation:** The simulation goes as follows:
Operation 1: i=2, j=2. Swap s\[1\] and s\[2\] to get s= "cab ", then reverse the suffix starting at 2. Now, s= "cab ".
Operation 2: i=1, j=2. Swap s\[0\] and s\[2\] to get s= "bac ", then reverse the suffix starting at 1. Now, s= "bca ".
Operation 3: i=2, j=2. Swap s\[1\] and s\[2\] to get s= "bac ", then reverse the suffix starting at 2. Now, s= "bac ".
Operation 4: i=1, j=1. Swap s\[0\] and s\[1\] to get s= "abc ", then reverse the suffix starting at 1. Now, s= "acb ".
Operation 5: i=2, j=2. Swap s\[1\] and s\[2\] to get s= "abc ", then reverse the suffix starting at 2. Now, s= "abc ".
**Example 2:**
**Input:** s = "aabaa "
**Output:** 2
**Explanation:** The simulation goes as follows:
Operation 1: i=3, j=4. Swap s\[2\] and s\[4\] to get s= "aaaab ", then reverse the substring starting at 3. Now, s= "aaaba ".
Operation 2: i=4, j=4. Swap s\[3\] and s\[4\] to get s= "aaaab ", then reverse the substring starting at 4. Now, s= "aaaab ".
**Constraints:**
* `1 <= s.length <= 3000`
* `s` consists only of lowercase English letters. | Note that the number of powers of 2 is at most 21 so this turns the problem to a classic find the number of pairs that sum to a certain value but for 21 values You need to use something fasters than the NlogN approach since there is already the log of iterating over the powers so one idea is two pointers |
[Python3] math solution | minimum-number-of-operations-to-make-string-sorted | 0 | 1 | \n```\nclass Solution:\n def makeStringSorted(self, s: str) -> int:\n freq = [0]*26\n for c in s: freq[ord(c) - 97] += 1\n \n MOD = 1_000_000_007\n fac = cache(lambda x: x*fac(x-1)%MOD if x else 1)\n ifac = cache(lambda x: pow(fac(x), MOD-2, MOD)) # Fermat\'s little theorem (a**(p-1) = 1 (mod p))\n \n ans, n = 0, len(s)\n for c in s: \n val = ord(c) - 97\n mult = fac(n-1)\n for k in range(26): mult *= ifac(freq[k])\n for k in range(val): ans += freq[k] * mult\n n -= 1\n freq[val] -= 1\n return ans % MOD\n``` | 2 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
Python Intuitive solution with dictionary | check-if-the-sentence-is-pangram | 0 | 1 | ```\ndef checkIfPangram(self, sentence: str) -> bool:\n ref = {v:False for i,v in enumerate(\'abcdefghijklmnopqrstuvwxyz\')}\n for i in sentence: \n ref[i] = True\n for i in ref: \n if not ref[i]: \n return False\n return True | 2 | A **pangram** is a sentence where every letter of the English alphabet appears at least once.
Given a string `sentence` containing only lowercase English letters, return `true` _if_ `sentence` _is a **pangram**, or_ `false` _otherwise._
**Example 1:**
**Input:** sentence = "thequickbrownfoxjumpsoverthelazydog "
**Output:** true
**Explanation:** sentence contains at least one of every letter of the English alphabet.
**Example 2:**
**Input:** sentence = "leetcode "
**Output:** false
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` consists of lowercase English letters. | The problem can be reduced to computing Longest Common Subsequence between both arrays. Since one of the arrays has distinct elements, we can consider that these elements describe an arrangement of numbers, and we can replace each element in the other array with the index it appeared at in the first array. Then the problem is converted to finding Longest Increasing Subsequence in the second array, which can be done in O(n log n). |
Python Intuitive solution with dictionary | check-if-the-sentence-is-pangram | 0 | 1 | ```\ndef checkIfPangram(self, sentence: str) -> bool:\n ref = {v:False for i,v in enumerate(\'abcdefghijklmnopqrstuvwxyz\')}\n for i in sentence: \n ref[i] = True\n for i in ref: \n if not ref[i]: \n return False\n return True | 2 | You are given a **0-indexed** string `s` and are tasked with finding two **non-intersecting palindromic** substrings of **odd** length such that the product of their lengths is maximized.
More formally, you want to choose four integers `i`, `j`, `k`, `l` such that `0 <= i <= j < k <= l < s.length` and both the substrings `s[i...j]` and `s[k...l]` are palindromes and have odd lengths. `s[i...j]` denotes a substring from index `i` to index `j` **inclusive**.
Return _the **maximum** possible product of the lengths of the two non-intersecting palindromic substrings._
A **palindrome** is a string that is the same forward and backward. A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "ababbb "
**Output:** 9
**Explanation:** Substrings "aba " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Example 2:**
**Input:** s = "zaaaxbbby "
**Output:** 9
**Explanation:** Substrings "aaa " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Constraints:**
* `2 <= s.length <= 105`
* `s` consists of lowercase English letters. | Iterate over the string and mark each character as found (using a boolean array, bitmask, or any other similar way). Check if the number of found characters equals the alphabet length. |
One if statement python | check-if-the-sentence-is-pangram | 0 | 1 | \n# Code\n```\nclass Solution:\n def checkIfPangram(self, sentence: str) -> bool:\n if \'a\' in sentence and \'s\' in sentence and \'d\' in sentence and \'f\' in sentence and \'g\' in sentence and \'h\' in sentence and \'j\' in sentence and \'k\' in sentence and \'l\' in sentence and \'q\' in sentence and \'w\' in sentence and \'e\' in sentence and \'r\' in sentence and \'t\' in sentence and \'y\' in sentence and \'u\' in sentence and \'i\' in sentence and \'o\' in sentence and \'p\' in sentence and \'z\' in sentence and \'x\' in sentence and \'c\' in sentence and \'v\' in sentence and \'b\' in sentence and \'n\' in sentence and \'m\' in sentence :\n return True\n else:\n return False\n\n``` | 1 | A **pangram** is a sentence where every letter of the English alphabet appears at least once.
Given a string `sentence` containing only lowercase English letters, return `true` _if_ `sentence` _is a **pangram**, or_ `false` _otherwise._
**Example 1:**
**Input:** sentence = "thequickbrownfoxjumpsoverthelazydog "
**Output:** true
**Explanation:** sentence contains at least one of every letter of the English alphabet.
**Example 2:**
**Input:** sentence = "leetcode "
**Output:** false
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` consists of lowercase English letters. | The problem can be reduced to computing Longest Common Subsequence between both arrays. Since one of the arrays has distinct elements, we can consider that these elements describe an arrangement of numbers, and we can replace each element in the other array with the index it appeared at in the first array. Then the problem is converted to finding Longest Increasing Subsequence in the second array, which can be done in O(n log n). |
One if statement python | check-if-the-sentence-is-pangram | 0 | 1 | \n# Code\n```\nclass Solution:\n def checkIfPangram(self, sentence: str) -> bool:\n if \'a\' in sentence and \'s\' in sentence and \'d\' in sentence and \'f\' in sentence and \'g\' in sentence and \'h\' in sentence and \'j\' in sentence and \'k\' in sentence and \'l\' in sentence and \'q\' in sentence and \'w\' in sentence and \'e\' in sentence and \'r\' in sentence and \'t\' in sentence and \'y\' in sentence and \'u\' in sentence and \'i\' in sentence and \'o\' in sentence and \'p\' in sentence and \'z\' in sentence and \'x\' in sentence and \'c\' in sentence and \'v\' in sentence and \'b\' in sentence and \'n\' in sentence and \'m\' in sentence :\n return True\n else:\n return False\n\n``` | 1 | You are given a **0-indexed** string `s` and are tasked with finding two **non-intersecting palindromic** substrings of **odd** length such that the product of their lengths is maximized.
More formally, you want to choose four integers `i`, `j`, `k`, `l` such that `0 <= i <= j < k <= l < s.length` and both the substrings `s[i...j]` and `s[k...l]` are palindromes and have odd lengths. `s[i...j]` denotes a substring from index `i` to index `j` **inclusive**.
Return _the **maximum** possible product of the lengths of the two non-intersecting palindromic substrings._
A **palindrome** is a string that is the same forward and backward. A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "ababbb "
**Output:** 9
**Explanation:** Substrings "aba " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Example 2:**
**Input:** s = "zaaaxbbby "
**Output:** 9
**Explanation:** Substrings "aaa " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Constraints:**
* `2 <= s.length <= 105`
* `s` consists of lowercase English letters. | Iterate over the string and mark each character as found (using a boolean array, bitmask, or any other similar way). Check if the number of found characters equals the alphabet length. |
Python || O(n) || Easy Understanding | check-if-the-sentence-is-pangram | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThinking array of Alphabet Character.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIterating each character in given string mark 1 in charater array.\nThen checking sum of character array if the sum is 26 then it is pangram otherwise not.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(26)\n\n# Code\n```\nclass Solution:\n def checkIfPangram(self, s: str) -> bool:\n l = [0]*26\n for i in range(len(s)):\n l[ord(s[i])-ord(\'a\')] = 1\n return sum(l)==26\n``` | 1 | A **pangram** is a sentence where every letter of the English alphabet appears at least once.
Given a string `sentence` containing only lowercase English letters, return `true` _if_ `sentence` _is a **pangram**, or_ `false` _otherwise._
**Example 1:**
**Input:** sentence = "thequickbrownfoxjumpsoverthelazydog "
**Output:** true
**Explanation:** sentence contains at least one of every letter of the English alphabet.
**Example 2:**
**Input:** sentence = "leetcode "
**Output:** false
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` consists of lowercase English letters. | The problem can be reduced to computing Longest Common Subsequence between both arrays. Since one of the arrays has distinct elements, we can consider that these elements describe an arrangement of numbers, and we can replace each element in the other array with the index it appeared at in the first array. Then the problem is converted to finding Longest Increasing Subsequence in the second array, which can be done in O(n log n). |
Python || O(n) || Easy Understanding | check-if-the-sentence-is-pangram | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThinking array of Alphabet Character.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIterating each character in given string mark 1 in charater array.\nThen checking sum of character array if the sum is 26 then it is pangram otherwise not.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(26)\n\n# Code\n```\nclass Solution:\n def checkIfPangram(self, s: str) -> bool:\n l = [0]*26\n for i in range(len(s)):\n l[ord(s[i])-ord(\'a\')] = 1\n return sum(l)==26\n``` | 1 | You are given a **0-indexed** string `s` and are tasked with finding two **non-intersecting palindromic** substrings of **odd** length such that the product of their lengths is maximized.
More formally, you want to choose four integers `i`, `j`, `k`, `l` such that `0 <= i <= j < k <= l < s.length` and both the substrings `s[i...j]` and `s[k...l]` are palindromes and have odd lengths. `s[i...j]` denotes a substring from index `i` to index `j` **inclusive**.
Return _the **maximum** possible product of the lengths of the two non-intersecting palindromic substrings._
A **palindrome** is a string that is the same forward and backward. A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "ababbb "
**Output:** 9
**Explanation:** Substrings "aba " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Example 2:**
**Input:** s = "zaaaxbbby "
**Output:** 9
**Explanation:** Substrings "aaa " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Constraints:**
* `2 <= s.length <= 105`
* `s` consists of lowercase English letters. | Iterate over the string and mark each character as found (using a boolean array, bitmask, or any other similar way). Check if the number of found characters equals the alphabet length. |
Easy Python solution | check-if-the-sentence-is-pangram | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkIfPangram(self, sentence: str) -> bool:\n return len(set(sentence)) == 26\n``` | 1 | A **pangram** is a sentence where every letter of the English alphabet appears at least once.
Given a string `sentence` containing only lowercase English letters, return `true` _if_ `sentence` _is a **pangram**, or_ `false` _otherwise._
**Example 1:**
**Input:** sentence = "thequickbrownfoxjumpsoverthelazydog "
**Output:** true
**Explanation:** sentence contains at least one of every letter of the English alphabet.
**Example 2:**
**Input:** sentence = "leetcode "
**Output:** false
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` consists of lowercase English letters. | The problem can be reduced to computing Longest Common Subsequence between both arrays. Since one of the arrays has distinct elements, we can consider that these elements describe an arrangement of numbers, and we can replace each element in the other array with the index it appeared at in the first array. Then the problem is converted to finding Longest Increasing Subsequence in the second array, which can be done in O(n log n). |
Easy Python solution | check-if-the-sentence-is-pangram | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkIfPangram(self, sentence: str) -> bool:\n return len(set(sentence)) == 26\n``` | 1 | You are given a **0-indexed** string `s` and are tasked with finding two **non-intersecting palindromic** substrings of **odd** length such that the product of their lengths is maximized.
More formally, you want to choose four integers `i`, `j`, `k`, `l` such that `0 <= i <= j < k <= l < s.length` and both the substrings `s[i...j]` and `s[k...l]` are palindromes and have odd lengths. `s[i...j]` denotes a substring from index `i` to index `j` **inclusive**.
Return _the **maximum** possible product of the lengths of the two non-intersecting palindromic substrings._
A **palindrome** is a string that is the same forward and backward. A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "ababbb "
**Output:** 9
**Explanation:** Substrings "aba " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Example 2:**
**Input:** s = "zaaaxbbby "
**Output:** 9
**Explanation:** Substrings "aaa " and "bbb " are palindromes with odd length. product = 3 \* 3 = 9.
**Constraints:**
* `2 <= s.length <= 105`
* `s` consists of lowercase English letters. | Iterate over the string and mark each character as found (using a boolean array, bitmask, or any other similar way). Check if the number of found characters equals the alphabet length. |
One_liner.py | maximum-ice-cream-bars | 0 | 1 | # Code\n```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n return sum(1 for icecream in sorted(costs) if (coins:= coins-icecream) >= 0)\n```\n | 7 | It is a sweltering summer day, and a boy wants to buy some ice cream bars.
At the store, there are `n` ice cream bars. You are given an array `costs` of length `n`, where `costs[i]` is the price of the `ith` ice cream bar in coins. The boy initially has `coins` coins to spend, and he wants to buy as many ice cream bars as possible.
**Note:** The boy can buy the ice cream bars in any order.
Return _the **maximum** number of ice cream bars the boy can buy with_ `coins` _coins._
You must solve the problem by counting sort.
**Example 1:**
**Input:** costs = \[1,3,2,4,1\], coins = 7
**Output:** 4
**Explanation:** The boy can buy ice cream bars at indices 0,1,2,4 for a total price of 1 + 3 + 2 + 1 = 7.
**Example 2:**
**Input:** costs = \[10,6,8,7,7,8\], coins = 5
**Output:** 0
**Explanation:** The boy cannot afford any of the ice cream bars.
**Example 3:**
**Input:** costs = \[1,6,3,1,2,5\], coins = 20
**Output:** 6
**Explanation:** The boy can buy all the ice cream bars for a total price of 1 + 6 + 3 + 1 + 2 + 5 = 18.
**Constraints:**
* `costs.length == n`
* `1 <= n <= 105`
* `1 <= costs[i] <= 105`
* `1 <= coins <= 108` | Let's note that the altitude of an element is the sum of gains of all the elements behind it Getting the altitudes can be done by getting the prefix sum array of the given array |
One_liner.py | maximum-ice-cream-bars | 0 | 1 | # Code\n```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n return sum(1 for icecream in sorted(costs) if (coins:= coins-icecream) >= 0)\n```\n | 7 | Given a string `s` and an array of strings `words`, determine whether `s` is a **prefix string** of `words`.
A string `s` is a **prefix string** of `words` if `s` can be made by concatenating the first `k` strings in `words` for some **positive** `k` no larger than `words.length`.
Return `true` _if_ `s` _is a **prefix string** of_ `words`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "iloveleetcode ", words = \[ "i ", "love ", "leetcode ", "apples "\]
**Output:** true
**Explanation:**
s can be made by concatenating "i ", "love ", and "leetcode " together.
**Example 2:**
**Input:** s = "iloveleetcode ", words = \[ "apples ", "i ", "love ", "leetcode "\]
**Output:** false
**Explanation:**
It is impossible to make s using a prefix of arr.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 20`
* `1 <= s.length <= 1000`
* `words[i]` and `s` consist of only lowercase English letters. | It is always optimal to buy the least expensive ice cream bar first. Sort the prices so that the cheapest ice cream bar comes first. |
Python 1 Line | maximum-ice-cream-bars | 0 | 1 | ```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n return bisect_right(list(accumulate(sorted(costs))), coins)\n\n``` | 4 | It is a sweltering summer day, and a boy wants to buy some ice cream bars.
At the store, there are `n` ice cream bars. You are given an array `costs` of length `n`, where `costs[i]` is the price of the `ith` ice cream bar in coins. The boy initially has `coins` coins to spend, and he wants to buy as many ice cream bars as possible.
**Note:** The boy can buy the ice cream bars in any order.
Return _the **maximum** number of ice cream bars the boy can buy with_ `coins` _coins._
You must solve the problem by counting sort.
**Example 1:**
**Input:** costs = \[1,3,2,4,1\], coins = 7
**Output:** 4
**Explanation:** The boy can buy ice cream bars at indices 0,1,2,4 for a total price of 1 + 3 + 2 + 1 = 7.
**Example 2:**
**Input:** costs = \[10,6,8,7,7,8\], coins = 5
**Output:** 0
**Explanation:** The boy cannot afford any of the ice cream bars.
**Example 3:**
**Input:** costs = \[1,6,3,1,2,5\], coins = 20
**Output:** 6
**Explanation:** The boy can buy all the ice cream bars for a total price of 1 + 6 + 3 + 1 + 2 + 5 = 18.
**Constraints:**
* `costs.length == n`
* `1 <= n <= 105`
* `1 <= costs[i] <= 105`
* `1 <= coins <= 108` | Let's note that the altitude of an element is the sum of gains of all the elements behind it Getting the altitudes can be done by getting the prefix sum array of the given array |
Python 1 Line | maximum-ice-cream-bars | 0 | 1 | ```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n return bisect_right(list(accumulate(sorted(costs))), coins)\n\n``` | 4 | Given a string `s` and an array of strings `words`, determine whether `s` is a **prefix string** of `words`.
A string `s` is a **prefix string** of `words` if `s` can be made by concatenating the first `k` strings in `words` for some **positive** `k` no larger than `words.length`.
Return `true` _if_ `s` _is a **prefix string** of_ `words`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "iloveleetcode ", words = \[ "i ", "love ", "leetcode ", "apples "\]
**Output:** true
**Explanation:**
s can be made by concatenating "i ", "love ", and "leetcode " together.
**Example 2:**
**Input:** s = "iloveleetcode ", words = \[ "apples ", "i ", "love ", "leetcode "\]
**Output:** false
**Explanation:**
It is impossible to make s using a prefix of arr.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 20`
* `1 <= s.length <= 1000`
* `words[i]` and `s` consist of only lowercase English letters. | It is always optimal to buy the least expensive ice cream bar first. Sort the prices so that the cheapest ice cream bar comes first. |
📌📌Python3 || 838 ms, faster than 92.67% of Python3 || Clean and Easy to Understand | maximum-ice-cream-bars | 0 | 1 | **Logic**\n*1. Sort the Cost array so that we can buy maximum low cost Ice Cream Bars*\n*2. Buy the low cost Ice Cream Bars and reduce the coins as you buy*\n```\ndef maxIceCream(self, costs: List[int], coins: int) -> int:\n result=0\n costs.sort()\n for x,y in enumerate(costs):\n if coins<y:\n break\n result = result + 1\n coins = coins - y\n return result\n```\n\n\n\n | 3 | It is a sweltering summer day, and a boy wants to buy some ice cream bars.
At the store, there are `n` ice cream bars. You are given an array `costs` of length `n`, where `costs[i]` is the price of the `ith` ice cream bar in coins. The boy initially has `coins` coins to spend, and he wants to buy as many ice cream bars as possible.
**Note:** The boy can buy the ice cream bars in any order.
Return _the **maximum** number of ice cream bars the boy can buy with_ `coins` _coins._
You must solve the problem by counting sort.
**Example 1:**
**Input:** costs = \[1,3,2,4,1\], coins = 7
**Output:** 4
**Explanation:** The boy can buy ice cream bars at indices 0,1,2,4 for a total price of 1 + 3 + 2 + 1 = 7.
**Example 2:**
**Input:** costs = \[10,6,8,7,7,8\], coins = 5
**Output:** 0
**Explanation:** The boy cannot afford any of the ice cream bars.
**Example 3:**
**Input:** costs = \[1,6,3,1,2,5\], coins = 20
**Output:** 6
**Explanation:** The boy can buy all the ice cream bars for a total price of 1 + 6 + 3 + 1 + 2 + 5 = 18.
**Constraints:**
* `costs.length == n`
* `1 <= n <= 105`
* `1 <= costs[i] <= 105`
* `1 <= coins <= 108` | Let's note that the altitude of an element is the sum of gains of all the elements behind it Getting the altitudes can be done by getting the prefix sum array of the given array |
📌📌Python3 || 838 ms, faster than 92.67% of Python3 || Clean and Easy to Understand | maximum-ice-cream-bars | 0 | 1 | **Logic**\n*1. Sort the Cost array so that we can buy maximum low cost Ice Cream Bars*\n*2. Buy the low cost Ice Cream Bars and reduce the coins as you buy*\n```\ndef maxIceCream(self, costs: List[int], coins: int) -> int:\n result=0\n costs.sort()\n for x,y in enumerate(costs):\n if coins<y:\n break\n result = result + 1\n coins = coins - y\n return result\n```\n\n\n\n | 3 | Given a string `s` and an array of strings `words`, determine whether `s` is a **prefix string** of `words`.
A string `s` is a **prefix string** of `words` if `s` can be made by concatenating the first `k` strings in `words` for some **positive** `k` no larger than `words.length`.
Return `true` _if_ `s` _is a **prefix string** of_ `words`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "iloveleetcode ", words = \[ "i ", "love ", "leetcode ", "apples "\]
**Output:** true
**Explanation:**
s can be made by concatenating "i ", "love ", and "leetcode " together.
**Example 2:**
**Input:** s = "iloveleetcode ", words = \[ "apples ", "i ", "love ", "leetcode "\]
**Output:** false
**Explanation:**
It is impossible to make s using a prefix of arr.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 20`
* `1 <= s.length <= 1000`
* `words[i]` and `s` consist of only lowercase English letters. | It is always optimal to buy the least expensive ice cream bar first. Sort the prices so that the cheapest ice cream bar comes first. |
Daily LeetCode Challenge (Python 3) | maximum-ice-cream-bars | 0 | 1 | # Intuition\nTo get the maximum amount of icecream in given coins the basic idea is to choose as cheap as icecreams possible.\nFor this we will make the array sorted in increasing order first.\nFor early return of function where it hits the base case of having less coins than req to purchase atleast one icecream compare it to first array element and if smaller return 0 as the child wont be able to buy any icecream. (though this is an optional condition)\nNow for the main cases keep increasing the count of icecream untill and unless the sum==coins available to him.\nThat is our required answer.\n\n\n# Code\n```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n costs.sort() \n if coins < costs[0]:\n return 0\n iceCream = 0\n summ = 0\n for c in costs:\n summ += c\n if summ <= coins:\n iceCream += 1\n return iceCream\n\n``` | 2 | It is a sweltering summer day, and a boy wants to buy some ice cream bars.
At the store, there are `n` ice cream bars. You are given an array `costs` of length `n`, where `costs[i]` is the price of the `ith` ice cream bar in coins. The boy initially has `coins` coins to spend, and he wants to buy as many ice cream bars as possible.
**Note:** The boy can buy the ice cream bars in any order.
Return _the **maximum** number of ice cream bars the boy can buy with_ `coins` _coins._
You must solve the problem by counting sort.
**Example 1:**
**Input:** costs = \[1,3,2,4,1\], coins = 7
**Output:** 4
**Explanation:** The boy can buy ice cream bars at indices 0,1,2,4 for a total price of 1 + 3 + 2 + 1 = 7.
**Example 2:**
**Input:** costs = \[10,6,8,7,7,8\], coins = 5
**Output:** 0
**Explanation:** The boy cannot afford any of the ice cream bars.
**Example 3:**
**Input:** costs = \[1,6,3,1,2,5\], coins = 20
**Output:** 6
**Explanation:** The boy can buy all the ice cream bars for a total price of 1 + 6 + 3 + 1 + 2 + 5 = 18.
**Constraints:**
* `costs.length == n`
* `1 <= n <= 105`
* `1 <= costs[i] <= 105`
* `1 <= coins <= 108` | Let's note that the altitude of an element is the sum of gains of all the elements behind it Getting the altitudes can be done by getting the prefix sum array of the given array |
Daily LeetCode Challenge (Python 3) | maximum-ice-cream-bars | 0 | 1 | # Intuition\nTo get the maximum amount of icecream in given coins the basic idea is to choose as cheap as icecreams possible.\nFor this we will make the array sorted in increasing order first.\nFor early return of function where it hits the base case of having less coins than req to purchase atleast one icecream compare it to first array element and if smaller return 0 as the child wont be able to buy any icecream. (though this is an optional condition)\nNow for the main cases keep increasing the count of icecream untill and unless the sum==coins available to him.\nThat is our required answer.\n\n\n# Code\n```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n costs.sort() \n if coins < costs[0]:\n return 0\n iceCream = 0\n summ = 0\n for c in costs:\n summ += c\n if summ <= coins:\n iceCream += 1\n return iceCream\n\n``` | 2 | Given a string `s` and an array of strings `words`, determine whether `s` is a **prefix string** of `words`.
A string `s` is a **prefix string** of `words` if `s` can be made by concatenating the first `k` strings in `words` for some **positive** `k` no larger than `words.length`.
Return `true` _if_ `s` _is a **prefix string** of_ `words`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "iloveleetcode ", words = \[ "i ", "love ", "leetcode ", "apples "\]
**Output:** true
**Explanation:**
s can be made by concatenating "i ", "love ", and "leetcode " together.
**Example 2:**
**Input:** s = "iloveleetcode ", words = \[ "apples ", "i ", "love ", "leetcode "\]
**Output:** false
**Explanation:**
It is impossible to make s using a prefix of arr.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 20`
* `1 <= s.length <= 1000`
* `words[i]` and `s` consist of only lowercase English letters. | It is always optimal to buy the least expensive ice cream bar first. Sort the prices so that the cheapest ice cream bar comes first. |
Simple Solution using Greedy Algorithm! | maximum-ice-cream-bars | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we will sort the given list `costs` in ascending order, then check if the value of `coins` is strictly less than the 1st element of the sorted `costs` list, If yes then the boy can not buy any ice cream.\n\nIf No, then we will iterate through the list and consider an element by subtracting subsequent costs from the coins and increment the count variable every time we consider an element from the sorted array. We will stop iterating if we reach the end of the list or value of `coins` becomes 0, or else we stop iterating if at any point value of `coins` becomes less than `costs[i]`.\n\nAfter iteration is over we simply return the count.\nThis is Greedy approach beacuse we try to get the correct answer in only one iteration by selecting the lowest costing icecream first.\n# Code\n```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n costs.sort()\n count = 0\n if costs[0] > coins:\n return 0\n i = 0\n while coins > 0 and i < len(costs):\n if coins < costs[i]:\n break\n coins -= costs[i]\n count+=1\n i+=1\n return count\n``` | 2 | It is a sweltering summer day, and a boy wants to buy some ice cream bars.
At the store, there are `n` ice cream bars. You are given an array `costs` of length `n`, where `costs[i]` is the price of the `ith` ice cream bar in coins. The boy initially has `coins` coins to spend, and he wants to buy as many ice cream bars as possible.
**Note:** The boy can buy the ice cream bars in any order.
Return _the **maximum** number of ice cream bars the boy can buy with_ `coins` _coins._
You must solve the problem by counting sort.
**Example 1:**
**Input:** costs = \[1,3,2,4,1\], coins = 7
**Output:** 4
**Explanation:** The boy can buy ice cream bars at indices 0,1,2,4 for a total price of 1 + 3 + 2 + 1 = 7.
**Example 2:**
**Input:** costs = \[10,6,8,7,7,8\], coins = 5
**Output:** 0
**Explanation:** The boy cannot afford any of the ice cream bars.
**Example 3:**
**Input:** costs = \[1,6,3,1,2,5\], coins = 20
**Output:** 6
**Explanation:** The boy can buy all the ice cream bars for a total price of 1 + 6 + 3 + 1 + 2 + 5 = 18.
**Constraints:**
* `costs.length == n`
* `1 <= n <= 105`
* `1 <= costs[i] <= 105`
* `1 <= coins <= 108` | Let's note that the altitude of an element is the sum of gains of all the elements behind it Getting the altitudes can be done by getting the prefix sum array of the given array |
Simple Solution using Greedy Algorithm! | maximum-ice-cream-bars | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we will sort the given list `costs` in ascending order, then check if the value of `coins` is strictly less than the 1st element of the sorted `costs` list, If yes then the boy can not buy any ice cream.\n\nIf No, then we will iterate through the list and consider an element by subtracting subsequent costs from the coins and increment the count variable every time we consider an element from the sorted array. We will stop iterating if we reach the end of the list or value of `coins` becomes 0, or else we stop iterating if at any point value of `coins` becomes less than `costs[i]`.\n\nAfter iteration is over we simply return the count.\nThis is Greedy approach beacuse we try to get the correct answer in only one iteration by selecting the lowest costing icecream first.\n# Code\n```\nclass Solution:\n def maxIceCream(self, costs: List[int], coins: int) -> int:\n costs.sort()\n count = 0\n if costs[0] > coins:\n return 0\n i = 0\n while coins > 0 and i < len(costs):\n if coins < costs[i]:\n break\n coins -= costs[i]\n count+=1\n i+=1\n return count\n``` | 2 | Given a string `s` and an array of strings `words`, determine whether `s` is a **prefix string** of `words`.
A string `s` is a **prefix string** of `words` if `s` can be made by concatenating the first `k` strings in `words` for some **positive** `k` no larger than `words.length`.
Return `true` _if_ `s` _is a **prefix string** of_ `words`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "iloveleetcode ", words = \[ "i ", "love ", "leetcode ", "apples "\]
**Output:** true
**Explanation:**
s can be made by concatenating "i ", "love ", and "leetcode " together.
**Example 2:**
**Input:** s = "iloveleetcode ", words = \[ "apples ", "i ", "love ", "leetcode "\]
**Output:** false
**Explanation:**
It is impossible to make s using a prefix of arr.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 20`
* `1 <= s.length <= 1000`
* `words[i]` and `s` consist of only lowercase English letters. | It is always optimal to buy the least expensive ice cream bar first. Sort the prices so that the cheapest ice cream bar comes first. |
Python minHeap solution. | single-threaded-cpu | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(nlogn)\n- Space complexity:\nO(n)\n# Code\n```\nimport heapq\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n n = len(tasks)\n ind = 0\n for i in tasks:\n i.append(ind)\n ind+=1\n tasks.sort()\n print(tasks)\n\n\n heap = []\n i = 0\n arrivalTime = tasks[0][0]\n while(i < n):\n if tasks[i][0] == arrivalTime:\n heapq.heappush(heap, [tasks[i][1], tasks[i][2]])\n else:\n break \n i+=1\n\n order = []\n while(heap):\n process = heapq.heappop(heap)\n order.append(process[1])\n arrivalTime += (process[0])\n\n while(i < n and tasks[i][0] <= arrivalTime):\n heapq.heappush(heap, [tasks[i][1], tasks[i][2]])\n i+=1\n\n if not heap and i < n:\n arrivalTime = tasks[i][0]\n while(i < n):\n if tasks[i][0] == arrivalTime:\n heapq.heappush(heap, [tasks[i][1], tasks[i][2]])\n else:\n break \n i+=1\n\n return order\n\n``` | 1 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Python minHeap solution. | single-threaded-cpu | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(nlogn)\n- Space complexity:\nO(n)\n# Code\n```\nimport heapq\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n n = len(tasks)\n ind = 0\n for i in tasks:\n i.append(ind)\n ind+=1\n tasks.sort()\n print(tasks)\n\n\n heap = []\n i = 0\n arrivalTime = tasks[0][0]\n while(i < n):\n if tasks[i][0] == arrivalTime:\n heapq.heappush(heap, [tasks[i][1], tasks[i][2]])\n else:\n break \n i+=1\n\n order = []\n while(heap):\n process = heapq.heappop(heap)\n order.append(process[1])\n arrivalTime += (process[0])\n\n while(i < n and tasks[i][0] <= arrivalTime):\n heapq.heappush(heap, [tasks[i][1], tasks[i][2]])\n i+=1\n\n if not heap and i < n:\n arrivalTime = tasks[i][0]\n while(i < n):\n if tasks[i][0] == arrivalTime:\n heapq.heappush(heap, [tasks[i][1], tasks[i][2]])\n else:\n break \n i+=1\n\n return order\n\n``` | 1 | You are given a **0-indexed** integer array `piles`, where `piles[i]` represents the number of stones in the `ith` pile, and an integer `k`. You should apply the following operation **exactly** `k` times:
* Choose any `piles[i]` and **remove** `floor(piles[i] / 2)` stones from it.
**Notice** that you can apply the operation on the **same** pile more than once.
Return _the **minimum** possible total number of stones remaining after applying the_ `k` _operations_.
`floor(x)` is the **greatest** integer that is **smaller** than or **equal** to `x` (i.e., rounds `x` down).
**Example 1:**
**Input:** piles = \[5,4,9\], k = 2
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[5,4,5\].
- Apply the operation on pile 0. The resulting piles are \[3,4,5\].
The total number of stones in \[3,4,5\] is 12.
**Example 2:**
**Input:** piles = \[4,3,6,7\], k = 3
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[4,3,3,7\].
- Apply the operation on pile 3. The resulting piles are \[4,3,3,4\].
- Apply the operation on pile 0. The resulting piles are \[2,3,3,4\].
The total number of stones in \[2,3,3,4\] is 12.
**Constraints:**
* `1 <= piles.length <= 105`
* `1 <= piles[i] <= 104`
* `1 <= k <= 105` | To simulate the problem we first need to note that if at any point in time there are no enqueued tasks we need to wait to the smallest enqueue time of a non-processed element We need a data structure like a min-heap to support choosing the task with the smallest processing time from all the enqueued tasks |
Python | Sort and Heap | Simplified | 100% | Tough Question | single-threaded-cpu | 0 | 1 | # Simplified Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n tasks = sorted([(s,p,i) for i,(s,p) in enumerate(tasks)])\n tasks = tasks+[(float(\'inf\'),0,0)]\n n = len(tasks)\n res, h = [], []\n j = far = 0\n for s, p, i in tasks:\n if s > far:\n if h:\n while h and s > far:\n tmp_p, tmp_i = heappop(h)\n res.append(tmp_i)\n far += tmp_p\n far = max(far, s)\n heappush(h, (p,i))\n return res \n```\n# Previous Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n tasks = [(s,p,i) for i,(s,p) in enumerate(tasks)]\n tasks.sort()\n tasks.append((float(\'inf\'),0,0))\n res = []\n h = []\n far = 0\n j = 0\n n = len(tasks)\n while j < n:\n s, p, i = tasks[j]\n if s > far:\n if h:\n while h and far < s:\n tmp_p, tmp_i = heappop(h)\n res.append(tmp_i)\n far += tmp_p\n else:\n if j == n - 1: break\n while j < n and tasks[j][0] == s:\n s, p, i = tasks[j]\n heappush(h, (p, i))\n j += 1\n tmp_p, tmp_i = heappop(h)\n res.append(tmp_i)\n far = s + tmp_p\n continue\n heappush(h, (p,i))\n j += 1\n return res\n``` | 2 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Python | Sort and Heap | Simplified | 100% | Tough Question | single-threaded-cpu | 0 | 1 | # Simplified Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n tasks = sorted([(s,p,i) for i,(s,p) in enumerate(tasks)])\n tasks = tasks+[(float(\'inf\'),0,0)]\n n = len(tasks)\n res, h = [], []\n j = far = 0\n for s, p, i in tasks:\n if s > far:\n if h:\n while h and s > far:\n tmp_p, tmp_i = heappop(h)\n res.append(tmp_i)\n far += tmp_p\n far = max(far, s)\n heappush(h, (p,i))\n return res \n```\n# Previous Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n tasks = [(s,p,i) for i,(s,p) in enumerate(tasks)]\n tasks.sort()\n tasks.append((float(\'inf\'),0,0))\n res = []\n h = []\n far = 0\n j = 0\n n = len(tasks)\n while j < n:\n s, p, i = tasks[j]\n if s > far:\n if h:\n while h and far < s:\n tmp_p, tmp_i = heappop(h)\n res.append(tmp_i)\n far += tmp_p\n else:\n if j == n - 1: break\n while j < n and tasks[j][0] == s:\n s, p, i = tasks[j]\n heappush(h, (p, i))\n j += 1\n tmp_p, tmp_i = heappop(h)\n res.append(tmp_i)\n far = s + tmp_p\n continue\n heappush(h, (p,i))\n j += 1\n return res\n``` | 2 | You are given a **0-indexed** integer array `piles`, where `piles[i]` represents the number of stones in the `ith` pile, and an integer `k`. You should apply the following operation **exactly** `k` times:
* Choose any `piles[i]` and **remove** `floor(piles[i] / 2)` stones from it.
**Notice** that you can apply the operation on the **same** pile more than once.
Return _the **minimum** possible total number of stones remaining after applying the_ `k` _operations_.
`floor(x)` is the **greatest** integer that is **smaller** than or **equal** to `x` (i.e., rounds `x` down).
**Example 1:**
**Input:** piles = \[5,4,9\], k = 2
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[5,4,5\].
- Apply the operation on pile 0. The resulting piles are \[3,4,5\].
The total number of stones in \[3,4,5\] is 12.
**Example 2:**
**Input:** piles = \[4,3,6,7\], k = 3
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[4,3,3,7\].
- Apply the operation on pile 3. The resulting piles are \[4,3,3,4\].
- Apply the operation on pile 0. The resulting piles are \[2,3,3,4\].
The total number of stones in \[2,3,3,4\] is 12.
**Constraints:**
* `1 <= piles.length <= 105`
* `1 <= piles[i] <= 104`
* `1 <= k <= 105` | To simulate the problem we first need to note that if at any point in time there are no enqueued tasks we need to wait to the smallest enqueue time of a non-processed element We need a data structure like a min-heap to support choosing the task with the smallest processing time from all the enqueued tasks |
Two Heaps | single-threaded-cpu | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe always want to find some minimum (enqueueTime and processingTime) in a list, so using heaps might be a good choice. Therefore we choose to use the Standard library, **heapq**, in Python.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use 2 heaps to keep track:\n* q1: Every task in the list. Everytime we pop a task from p1, we get the min enqueueTime.\n* q2: The task that is executable at the current time. Everytime we pop a task from q2, we get the min processingTime\n\n# Complexity\n- Time complexity: $$O(N~log~N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n clock = 1 # start from t = 1\n result = []\n\n # first queue: tasks sorted by enqueueTime\n q1 = []\n for i, (et, pt) in enumerate(tasks):\n heapq.heappush(q1, (et, pt, i))\n \n # second queue: available tasks sorted by processingTime\n q2 = []\n\n while len(result) < len(tasks):\n # put every available task from first queue into second queue\n while len(q1) > 0 and q1[0][0] <= clock:\n task = heapq.heappop(q1)\n # reorder the info. in task\n # s.t. we get the shorted pt and i when popping\n task = (task[1], task[2], task[0]) # (pt, i, et)\n heapq.heappush(q2, task)\n \n # if no task to execute (q2 is empty)\n # directly jump to the first task in q1\n if len(q2) == 0 and len(q1) > 0 :\n clock = q1[0][0]\n \n # execute task in q2 (pop the task and put it into result)\n else:\n task = heapq.heappop(q2)\n clock += task[0] # processtime\n result.append(task[1])\n return result\n``` | 1 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Two Heaps | single-threaded-cpu | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe always want to find some minimum (enqueueTime and processingTime) in a list, so using heaps might be a good choice. Therefore we choose to use the Standard library, **heapq**, in Python.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use 2 heaps to keep track:\n* q1: Every task in the list. Everytime we pop a task from p1, we get the min enqueueTime.\n* q2: The task that is executable at the current time. Everytime we pop a task from q2, we get the min processingTime\n\n# Complexity\n- Time complexity: $$O(N~log~N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n clock = 1 # start from t = 1\n result = []\n\n # first queue: tasks sorted by enqueueTime\n q1 = []\n for i, (et, pt) in enumerate(tasks):\n heapq.heappush(q1, (et, pt, i))\n \n # second queue: available tasks sorted by processingTime\n q2 = []\n\n while len(result) < len(tasks):\n # put every available task from first queue into second queue\n while len(q1) > 0 and q1[0][0] <= clock:\n task = heapq.heappop(q1)\n # reorder the info. in task\n # s.t. we get the shorted pt and i when popping\n task = (task[1], task[2], task[0]) # (pt, i, et)\n heapq.heappush(q2, task)\n \n # if no task to execute (q2 is empty)\n # directly jump to the first task in q1\n if len(q2) == 0 and len(q1) > 0 :\n clock = q1[0][0]\n \n # execute task in q2 (pop the task and put it into result)\n else:\n task = heapq.heappop(q2)\n clock += task[0] # processtime\n result.append(task[1])\n return result\n``` | 1 | You are given a **0-indexed** integer array `piles`, where `piles[i]` represents the number of stones in the `ith` pile, and an integer `k`. You should apply the following operation **exactly** `k` times:
* Choose any `piles[i]` and **remove** `floor(piles[i] / 2)` stones from it.
**Notice** that you can apply the operation on the **same** pile more than once.
Return _the **minimum** possible total number of stones remaining after applying the_ `k` _operations_.
`floor(x)` is the **greatest** integer that is **smaller** than or **equal** to `x` (i.e., rounds `x` down).
**Example 1:**
**Input:** piles = \[5,4,9\], k = 2
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[5,4,5\].
- Apply the operation on pile 0. The resulting piles are \[3,4,5\].
The total number of stones in \[3,4,5\] is 12.
**Example 2:**
**Input:** piles = \[4,3,6,7\], k = 3
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[4,3,3,7\].
- Apply the operation on pile 3. The resulting piles are \[4,3,3,4\].
- Apply the operation on pile 0. The resulting piles are \[2,3,3,4\].
The total number of stones in \[2,3,3,4\] is 12.
**Constraints:**
* `1 <= piles.length <= 105`
* `1 <= piles[i] <= 104`
* `1 <= k <= 105` | To simulate the problem we first need to note that if at any point in time there are no enqueued tasks we need to wait to the smallest enqueue time of a non-processed element We need a data structure like a min-heap to support choosing the task with the smallest processing time from all the enqueued tasks |
Python Two Heaps - Intuitive | single-threaded-cpu | 0 | 1 | # Complexity\n- Time complexity: O(N lg N), for pushing and popping all tasks to both heaps (each individual operation is a lg N operation)\n\n- Space complexity: O(N), for both heaps\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n not_yet_ready = []\n\n for i, (enqueue_time, _) in enumerate(tasks):\n # add to not_yet_ready queue, prioritize by enqueue time\n heapq.heappush(not_yet_ready, (enqueue_time, i))\n\n result = []\n ready_to_process = []\n next_available_processor_time = 1\n while not_yet_ready or ready_to_process:\n # if nothing is ready to process, fast-forward to enqueue time of next-ready task\n if not ready_to_process:\n time = not_yet_ready[0][0]\n # otherwise, fast-forward to next_available_processor_time\n else:\n time = next_available_processor_time\n\n # add all ready tasks to ready queue, prioritize by processing time then i\n while not_yet_ready and not_yet_ready[0][0] <= time:\n _, i = heapq.heappop(not_yet_ready)\n heapq.heappush(ready_to_process, (tasks[i][1], i))\n\n # if processor is available and a task is ready, begin top-priority task and update result\n if ready_to_process and next_available_processor_time <= time:\n processing_time, i = heapq.heappop(ready_to_process)\n next_available_processor_time = time + processing_time\n result.append(i)\n\n return result\n \n``` | 1 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Python Two Heaps - Intuitive | single-threaded-cpu | 0 | 1 | # Complexity\n- Time complexity: O(N lg N), for pushing and popping all tasks to both heaps (each individual operation is a lg N operation)\n\n- Space complexity: O(N), for both heaps\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def getOrder(self, tasks: List[List[int]]) -> List[int]:\n not_yet_ready = []\n\n for i, (enqueue_time, _) in enumerate(tasks):\n # add to not_yet_ready queue, prioritize by enqueue time\n heapq.heappush(not_yet_ready, (enqueue_time, i))\n\n result = []\n ready_to_process = []\n next_available_processor_time = 1\n while not_yet_ready or ready_to_process:\n # if nothing is ready to process, fast-forward to enqueue time of next-ready task\n if not ready_to_process:\n time = not_yet_ready[0][0]\n # otherwise, fast-forward to next_available_processor_time\n else:\n time = next_available_processor_time\n\n # add all ready tasks to ready queue, prioritize by processing time then i\n while not_yet_ready and not_yet_ready[0][0] <= time:\n _, i = heapq.heappop(not_yet_ready)\n heapq.heappush(ready_to_process, (tasks[i][1], i))\n\n # if processor is available and a task is ready, begin top-priority task and update result\n if ready_to_process and next_available_processor_time <= time:\n processing_time, i = heapq.heappop(ready_to_process)\n next_available_processor_time = time + processing_time\n result.append(i)\n\n return result\n \n``` | 1 | You are given a **0-indexed** integer array `piles`, where `piles[i]` represents the number of stones in the `ith` pile, and an integer `k`. You should apply the following operation **exactly** `k` times:
* Choose any `piles[i]` and **remove** `floor(piles[i] / 2)` stones from it.
**Notice** that you can apply the operation on the **same** pile more than once.
Return _the **minimum** possible total number of stones remaining after applying the_ `k` _operations_.
`floor(x)` is the **greatest** integer that is **smaller** than or **equal** to `x` (i.e., rounds `x` down).
**Example 1:**
**Input:** piles = \[5,4,9\], k = 2
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[5,4,5\].
- Apply the operation on pile 0. The resulting piles are \[3,4,5\].
The total number of stones in \[3,4,5\] is 12.
**Example 2:**
**Input:** piles = \[4,3,6,7\], k = 3
**Output:** 12
**Explanation:** Steps of a possible scenario are:
- Apply the operation on pile 2. The resulting piles are \[4,3,3,7\].
- Apply the operation on pile 3. The resulting piles are \[4,3,3,4\].
- Apply the operation on pile 0. The resulting piles are \[2,3,3,4\].
The total number of stones in \[2,3,3,4\] is 12.
**Constraints:**
* `1 <= piles.length <= 105`
* `1 <= piles[i] <= 104`
* `1 <= k <= 105` | To simulate the problem we first need to note that if at any point in time there are no enqueued tasks we need to wait to the smallest enqueue time of a non-processed element We need a data structure like a min-heap to support choosing the task with the smallest processing time from all the enqueued tasks |
📌📌Python3 || 2007 ms, faster than 90.49% of Python3 || Clean and Easy to Understand | single-threaded-cpu | 0 | 1 | ```\ndef getOrder(self, tasks: List[List[int]]) -> List[int]:\n arr = []\n prev = 0\n output = [] \n tasks= sorted((tasks,i) for i,tasks in enumerate(tasks))\n for (m,n), i in tasks:\n while arr and prev < m:\n p,j,k = heappop(arr)\n prev = max(k,prev)+p\n output.append(j)\n heappush(arr,(n,i,m))\n return output+[i for _, i, _ in sorted(arr)]\n``` | 8 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.