title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 3 || 9 lines, w/ explanation || T/M: 89% / 49% | number-of-orders-in-the-backlog | 0 | 1 | Here\'s the plan:\n1. Establish maxheap `buy` for buy orders and minheap `sell` for sell orders.\n2. Iterate through `orders`. Push each element onto the appropriate heap.\n3. During each iteration, peak at the heads of each list and determine whether they allow a transaction. If so, pop both heads, and if one has a positive amount after the transaction, push it back on its heap, and check the new heads (lather, rinse, repeat... `while`)\n4. After the iteration,`return`the sum of`amt`in the heaps.\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n\n buy,sell = [], [] # <-- 1\n\n for price,amt,order in orders: # <-- 2\n if order: heappush(sell, ( price, amt)) #\n else : heappush(buy , (-price, amt)) #\n \n while buy and sell and -buy[0][0] >= sell[0][0]: # <-- 3\n #\n (buyPrice,buyAmt), (sellPrice,sellAmt) = heappop(buy), heappop(sell) #\n #\n if buyAmt > sellAmt: heappush(buy , (buyPrice , buyAmt -sellAmt)) #\n elif buyAmt < sellAmt: heappush(sell, (sellPrice, sellAmt- buyAmt)) #\n\n return sum(amt for _,amt in buy+sell)% (1000000007) # <-- 4\n```\n[https://leetcode.com/problems/number-of-orders-in-the-backlog/submissions/870707453/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 3 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Python3] priority queue | number-of-orders-in-the-backlog | 0 | 1 | \n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n ans = 0\n buy, sell = [], [] # max-heap & min-heap \n \n for p, q, t in orders: \n ans += q\n if t: # sell order\n while q and buy and -buy[0][0] >= p: # match \n pb, qb = heappop(buy)\n ans -= 2*min(q, qb)\n if q < qb: \n heappush(buy, (pb, qb-q))\n q = 0 \n else: q -= qb \n if q: heappush(sell, (p, q))\n else: # buy order \n while q and sell and sell[0][0] <= p: # match \n ps, qs = heappop(sell)\n ans -= 2*min(q, qs)\n if q < qs: \n heappush(sell, (ps, qs-q))\n q = 0 \n else: q -= qs \n if q: heappush(buy, (-p, q))\n \n return ans % 1_000_000_007\n```\n\nA conciser implementation by @lee215\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], [] # max-heap & min-heap \n for p, q, t in orders: \n if t: heappush(sell, [p, q])\n else: heappush(buy, [-p, q])\n \n while buy and sell and -buy[0][0] >= sell[0][0]: \n qty = min(buy[0][1], sell[0][1])\n buy[0][1] -= qty\n sell[0][1] -= qty\n if not buy[0][1]: heappop(buy)\n if not sell[0][1]: heappop(sell)\n return (sum(q for _, q in sell) + sum(q for _, q in buy)) % 1_000_000_007\n``` | 6 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Python3] priority queue | number-of-orders-in-the-backlog | 0 | 1 | \n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n ans = 0\n buy, sell = [], [] # max-heap & min-heap \n \n for p, q, t in orders: \n ans += q\n if t: # sell order\n while q and buy and -buy[0][0] >= p: # match \n pb, qb = heappop(buy)\n ans -= 2*min(q, qb)\n if q < qb: \n heappush(buy, (pb, qb-q))\n q = 0 \n else: q -= qb \n if q: heappush(sell, (p, q))\n else: # buy order \n while q and sell and sell[0][0] <= p: # match \n ps, qs = heappop(sell)\n ans -= 2*min(q, qs)\n if q < qs: \n heappush(sell, (ps, qs-q))\n q = 0 \n else: q -= qs \n if q: heappush(buy, (-p, q))\n \n return ans % 1_000_000_007\n```\n\nA conciser implementation by @lee215\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], [] # max-heap & min-heap \n for p, q, t in orders: \n if t: heappush(sell, [p, q])\n else: heappush(buy, [-p, q])\n \n while buy and sell and -buy[0][0] >= sell[0][0]: \n qty = min(buy[0][1], sell[0][1])\n buy[0][1] -= qty\n sell[0][1] -= qty\n if not buy[0][1]: heappop(buy)\n if not sell[0][1]: heappop(sell)\n return (sum(q for _, q in sell) + sum(q for _, q in buy)) % 1_000_000_007\n``` | 6 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Heap/PQ solution with logic [Python] | number-of-orders-in-the-backlog | 0 | 1 | Logic is:\n* Since we need to do a lot of **find min/max** operations: use 2 heaps:\n\t* max-heap `b` for buy, min-heap `s` for sell\n\t* So, max buy offer is on top of heap `b`\n\t* Min sell offer is on top of heap `s`\n* Each element of heap is an array: `[price, amount]`\n* *For* each buy/sell order:\n\t* Check for the **good** condition\n\t\t* Good condition is when:\n\t\t\t* Both `b` and `s` are non-empty\n\t\t\t* Top elements satisfy: `s[0][0] <= -b[0][0]` - means `sell price <= buy price`\n\t\t\t* If **good** condition is true: a *sale* will definitely happen\n\t* *While* condition stays **good**, keep performing *sales*\n\t\t* A *sale* means:\n\t\t\t* Pick the top element of both heaps\n\t\t\t* Call their amounts `a1` and `a2`\n\t\t\t* Reduce `a1` and `a2` until one of them becomes `0`\n\t\t\t* If either `a1` or `a2` becomes `0`, pop the heap to which it belongs\n\t\t* Check if the new top of the heap satisfies **good** condition\n* Count the sum of amounts in each heap\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders):\n b, s = [], []\n heapq.heapify(b)\n heapq.heapify(s)\n \n for p,a,o in orders:\n if o == 0:\n heapq.heappush(b, [-p, a])\n \n elif o == 1:\n heapq.heappush(s, [p, a])\n \n # Check "good" condition\n while s and b and s[0][0] <= -b[0][0]:\n a1, a2 = b[0][1], s[0][1]\n \n if a1 > a2:\n b[0][1] -= a2\n heapq.heappop(s)\n elif a1 < a2:\n s[0][1] -= a1\n heapq.heappop(b)\n else:\n heapq.heappop(b)\n heapq.heappop(s)\n \n count = sum([a for p,a in b]) + sum([a for p,a in s])\n return count % (10**9 + 7)\n ``` \n | 9 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Heap/PQ solution with logic [Python] | number-of-orders-in-the-backlog | 0 | 1 | Logic is:\n* Since we need to do a lot of **find min/max** operations: use 2 heaps:\n\t* max-heap `b` for buy, min-heap `s` for sell\n\t* So, max buy offer is on top of heap `b`\n\t* Min sell offer is on top of heap `s`\n* Each element of heap is an array: `[price, amount]`\n* *For* each buy/sell order:\n\t* Check for the **good** condition\n\t\t* Good condition is when:\n\t\t\t* Both `b` and `s` are non-empty\n\t\t\t* Top elements satisfy: `s[0][0] <= -b[0][0]` - means `sell price <= buy price`\n\t\t\t* If **good** condition is true: a *sale* will definitely happen\n\t* *While* condition stays **good**, keep performing *sales*\n\t\t* A *sale* means:\n\t\t\t* Pick the top element of both heaps\n\t\t\t* Call their amounts `a1` and `a2`\n\t\t\t* Reduce `a1` and `a2` until one of them becomes `0`\n\t\t\t* If either `a1` or `a2` becomes `0`, pop the heap to which it belongs\n\t\t* Check if the new top of the heap satisfies **good** condition\n* Count the sum of amounts in each heap\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders):\n b, s = [], []\n heapq.heapify(b)\n heapq.heapify(s)\n \n for p,a,o in orders:\n if o == 0:\n heapq.heappush(b, [-p, a])\n \n elif o == 1:\n heapq.heappush(s, [p, a])\n \n # Check "good" condition\n while s and b and s[0][0] <= -b[0][0]:\n a1, a2 = b[0][1], s[0][1]\n \n if a1 > a2:\n b[0][1] -= a2\n heapq.heappop(s)\n elif a1 < a2:\n s[0][1] -= a1\n heapq.heappop(b)\n else:\n heapq.heappop(b)\n heapq.heappop(s)\n \n count = sum([a for p,a in b]) + sum([a for p,a in s])\n return count % (10**9 + 7)\n ``` \n | 9 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Python] Concise Heap Implementation | number-of-orders-in-the-backlog | 0 | 1 | ### Introduction\n\nWe need to find the total amount of orders that remain un-executed in the backlog of orders after a series of buy and sell orders have passed. A buy order is executed if there exists a sell order in the backlog that has a selling price lower than or equal to the buying price, and a sell order is executed if there exists a buy order in the backlog that has a buying price greater than or equal to the selling price. Each time a buy/sell order comes, we need to compare its price with the sell/buy order with the smallest/greatest price, respectively.\n\nSince we need to obtain the smallest/greatest prices per order, a heap (priority queue) data structure is ideal for this task. For the buy order log, we require a max heap to obtain the greatest buying price; for the sell order log, we require a min heap to obtain the smallest buying price. Note that Python\'s `heapq` library implements a min heap, hence, to maintain a max heap, we need to **negate the buying prices**.\n\nTherefore, each time a buy/sell order with a given buying/selling price and the amount of orders is processed, we retrieve the sell/buy order with the smallest/largest price and execute the orders if the criteria (as mentioned above) is met. We continue to retrieve the sell/buy orders until;\n\n1. The criteria for executing the orders is no longer met.\n2. There are no more orders in the backlog to execute.\n3. There are no more orders in the current order to execute.\n\nAfter which, any remaining un-executed orders gets appended to its corresponding backlog.\n\n---\n\n### Base Implementation\n\nThis implementation features heavily on readability, and is meant to provide readers with a good understanding of how the code should work. If anything here is unclear or could be written better, please let me know in the comments.\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n # note that: buy_log - max heap; sell_log - min heap\n buy_log, sell_log = [], []\n for price, amount, order_type in orders:\n target_log = buy_log if order_type else sell_log\n while amount and target_log:\n # check that the appropriate buy/sell order fits the criteria\n # if order type is sell, ensure buy order price >= current price\n # else if order type is buy, ensure sell order price <= current price\n if (order_type and abs(target_log[0][0]) < price) or \\\n (not order_type and target_log[0][0] > price):\n break\n current_price, current_amount = heappop(target_log)\n # cancel buy and sell orders\n min_amount = min(amount, current_amount)\n amount -= min_amount\n current_amount -= min_amount\n # check if there are remaining target orders\n if current_amount:\n heappush(target_log, (current_price, current_amount))\n # check if there are remaining current orders\n if amount:\n heappush(sell_log if order_type else buy_log,\n # negate price if order type is buy\n # so as to maintain a max heap for buy orders\n (price if order_type else -price, amount))\n return (sum(log_amount for _, log_amount in buy_log) + \\\n sum(log_amount for _, log_amount in sell_log))%int(1e9+7)\n```\n\n---\n\n### Concise Implementation\n\nInstead of having two separate heaps to manage the buy and sell logs, we can combine them into one tuple and use the order type to access the proper logs. If implemented correctly, taking the different comparison operators / min/max heap into account, we can save a lot of lines because none of the code is repeated.\n\nThe following code has been revised for readability, as suggested by [@daBozz](https://leetcode.com/daBozz/).\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n backlog = ([], []) # (buy (max-heap), sell (min-heap))\n for price, amount, order_type in orders:\n # check that the appropriate buy/sell order fits the criteria in the while loop\n # note that le, ge come from the Python operator library\n # equivalent to: le - lambda a, b: a <= b\n # ge - lambda a, b: a >= b\n while amount > 0 and \\\n (target_log := backlog[1-order_type]) and \\\n (le, ge)[order_type](abs(target_log[0][0]), price):\n curr_price, curr_amount = heappop(target_log)\n if (amount := amount-curr_amount) < 0: # there are remaining target orders\n heappush(target_log, (curr_price, -amount))\n if amount > 0: # there are remaining current orders\n heappush(backlog[order_type], (price if order_type else -price, amount))\n # note that itemgetter comes from the Python operator library\n # equivalent to: lambda t: t[1]\n return sum(sum(map(itemgetter(1), log)) for log in backlog)%int(1e9+7)\n```\n\n**TC: O(nlogk)**, where `n` is the number of orders and `k` is the maximum length of either the buy or sell backlogs.\n**SC: O(n)**, taking both backlogs into account.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 4 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Python] Concise Heap Implementation | number-of-orders-in-the-backlog | 0 | 1 | ### Introduction\n\nWe need to find the total amount of orders that remain un-executed in the backlog of orders after a series of buy and sell orders have passed. A buy order is executed if there exists a sell order in the backlog that has a selling price lower than or equal to the buying price, and a sell order is executed if there exists a buy order in the backlog that has a buying price greater than or equal to the selling price. Each time a buy/sell order comes, we need to compare its price with the sell/buy order with the smallest/greatest price, respectively.\n\nSince we need to obtain the smallest/greatest prices per order, a heap (priority queue) data structure is ideal for this task. For the buy order log, we require a max heap to obtain the greatest buying price; for the sell order log, we require a min heap to obtain the smallest buying price. Note that Python\'s `heapq` library implements a min heap, hence, to maintain a max heap, we need to **negate the buying prices**.\n\nTherefore, each time a buy/sell order with a given buying/selling price and the amount of orders is processed, we retrieve the sell/buy order with the smallest/largest price and execute the orders if the criteria (as mentioned above) is met. We continue to retrieve the sell/buy orders until;\n\n1. The criteria for executing the orders is no longer met.\n2. There are no more orders in the backlog to execute.\n3. There are no more orders in the current order to execute.\n\nAfter which, any remaining un-executed orders gets appended to its corresponding backlog.\n\n---\n\n### Base Implementation\n\nThis implementation features heavily on readability, and is meant to provide readers with a good understanding of how the code should work. If anything here is unclear or could be written better, please let me know in the comments.\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n # note that: buy_log - max heap; sell_log - min heap\n buy_log, sell_log = [], []\n for price, amount, order_type in orders:\n target_log = buy_log if order_type else sell_log\n while amount and target_log:\n # check that the appropriate buy/sell order fits the criteria\n # if order type is sell, ensure buy order price >= current price\n # else if order type is buy, ensure sell order price <= current price\n if (order_type and abs(target_log[0][0]) < price) or \\\n (not order_type and target_log[0][0] > price):\n break\n current_price, current_amount = heappop(target_log)\n # cancel buy and sell orders\n min_amount = min(amount, current_amount)\n amount -= min_amount\n current_amount -= min_amount\n # check if there are remaining target orders\n if current_amount:\n heappush(target_log, (current_price, current_amount))\n # check if there are remaining current orders\n if amount:\n heappush(sell_log if order_type else buy_log,\n # negate price if order type is buy\n # so as to maintain a max heap for buy orders\n (price if order_type else -price, amount))\n return (sum(log_amount for _, log_amount in buy_log) + \\\n sum(log_amount for _, log_amount in sell_log))%int(1e9+7)\n```\n\n---\n\n### Concise Implementation\n\nInstead of having two separate heaps to manage the buy and sell logs, we can combine them into one tuple and use the order type to access the proper logs. If implemented correctly, taking the different comparison operators / min/max heap into account, we can save a lot of lines because none of the code is repeated.\n\nThe following code has been revised for readability, as suggested by [@daBozz](https://leetcode.com/daBozz/).\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n backlog = ([], []) # (buy (max-heap), sell (min-heap))\n for price, amount, order_type in orders:\n # check that the appropriate buy/sell order fits the criteria in the while loop\n # note that le, ge come from the Python operator library\n # equivalent to: le - lambda a, b: a <= b\n # ge - lambda a, b: a >= b\n while amount > 0 and \\\n (target_log := backlog[1-order_type]) and \\\n (le, ge)[order_type](abs(target_log[0][0]), price):\n curr_price, curr_amount = heappop(target_log)\n if (amount := amount-curr_amount) < 0: # there are remaining target orders\n heappush(target_log, (curr_price, -amount))\n if amount > 0: # there are remaining current orders\n heappush(backlog[order_type], (price if order_type else -price, amount))\n # note that itemgetter comes from the Python operator library\n # equivalent to: lambda t: t[1]\n return sum(sum(map(itemgetter(1), log)) for log in backlog)%int(1e9+7)\n```\n\n**TC: O(nlogk)**, where `n` is the number of orders and `k` is the maximum length of either the buy or sell backlogs.\n**SC: O(n)**, taking both backlogs into account.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 4 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Python3] OOD | Interview Friendly Solution | number-of-orders-in-the-backlog | 0 | 1 | # Complexity\nTime: $$O(nlogn)$$\nSpace: $$O(n)$$\n\n\n# Code\n```\nimport abc\nimport heapq\nfrom enum import Enum\nfrom abc import ABC, abstractmethod\nfrom typing import Optional, List\n\nMOD = int(1e9+7)\nclass OrderType(Enum):\n BUY = 0\n SELL = 1\n\n @classmethod\n def get(cls, order_type_id: int):\n order_type_map = {k.value: k for k in cls}\n return order_type_map[order_type_id]\n\nclass Backlog(ABC):\n def __init__(self):\n self.__heap = []\n self.__price_amount_map = dict()\n self.__total_amount = 0\n\n def get_total_amount(self) -> int:\n return self.__total_amount%MOD\n\n def add_to_total_amount(self, amount: int):\n self.__total_amount += amount\n\n def remove_from_total_amount(self, amount: int):\n self.__total_amount -= amount\n\n def peek(self) -> Optional[int]:\n if len(self.__heap) == 0:\n return None\n return self.__heap[0]\n\n def push(self, price: int):\n heapq.heappush(self.__heap, price)\n\n def pop(self) -> Optional[int]:\n if self.peek() is None:\n return\n return heapq.heappop(self.__heap)\n\n def get_orders_for_price(self, price: int) -> int:\n return self.__price_amount_map.get(price, 0)\n\n def update_orders_for_price(self, price: int, amount: int):\n self.__price_amount_map[price] = amount\n\n @abstractmethod\n def add(self, price: int, amount: int): ...\n\n @abstractmethod\n def remove(self, amount: int): ...\n\nclass BuyBacklog(Backlog):\n def peek(self) -> Optional[int]:\n top = super().peek()\n if top is None:\n return\n return -top\n\n def push(self, price: int):\n price *= -1\n super().push(price=price)\n\n def pop(self) -> Optional[int]:\n val = super().pop()\n if val is None:\n return\n return -val\n\n def add(self, price: int, amount: int):\n existing_orders_for_price = self.get_orders_for_price(price=price)\n if existing_orders_for_price == 0:\n self.push(price=price)\n new_orders_for_price = existing_orders_for_price + amount\n self.add_to_total_amount(amount=amount)\n self.update_orders_for_price(price=price, amount=new_orders_for_price)\n\n def remove(self, amount: int) -> Optional[int]:\n max_buy_price = self.peek()\n if max_buy_price is None:\n return\n max_price_amount = self.get_orders_for_price(price=max_buy_price)\n amount = min(amount, max_price_amount)\n self.remove_from_total_amount(amount=amount)\n max_price_amount -= amount\n\n self.update_orders_for_price(price=max_buy_price, amount=max_price_amount)\n if max_price_amount == 0:\n self.pop()\n return max_buy_price\n\nclass SellBacklog(Backlog):\n def add(self, price: int, amount: int):\n existing_orders_for_price = self.get_orders_for_price(price=price)\n if existing_orders_for_price == 0:\n self.push(price=price)\n new_orders_for_price = existing_orders_for_price + amount\n self.add_to_total_amount(amount=amount)\n self.update_orders_for_price(price=price, amount=new_orders_for_price)\n\n def remove(self, amount: int) -> Optional[int]:\n min_buy_price = self.peek()\n if min_buy_price is None:\n return\n min_price_amount = self.get_orders_for_price(price=min_buy_price)\n amount = min(amount, min_price_amount)\n self.remove_from_total_amount(amount=amount)\n min_price_amount -= amount\n self.update_orders_for_price(price=min_buy_price, amount=min_price_amount)\n if min_price_amount == 0:\n self.pop()\n return min_buy_price\n\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy_backlog = BuyBacklog()\n sell_backlog = SellBacklog()\n\n for price, amount, order_type_id in orders:\n order_type = OrderType.get(order_type_id=order_type_id)\n if order_type == OrderType.BUY:\n min_sell_price = sell_backlog.peek()\n while amount > 0 and min_sell_price is not None and min_sell_price <= price:\n sell_amount = sell_backlog.get_orders_for_price(price=min_sell_price)\n sell_backlog.remove(amount=amount)\n amount -= sell_amount\n min_sell_price = sell_backlog.peek()\n if amount > 0:\n buy_backlog.add(price=price, amount=amount)\n elif order_type == OrderType.SELL:\n max_buy_price = buy_backlog.peek()\n while amount > 0 and max_buy_price is not None and max_buy_price >= price:\n buy_amount = buy_backlog.get_orders_for_price(price=max_buy_price)\n buy_backlog.remove(amount=amount)\n amount -= buy_amount\n max_buy_price = buy_backlog.peek()\n if amount > 0:\n sell_backlog.add(price=price, amount=amount)\n else:\n raise KeyError(f\'invalid order type\')\n\n total_remaining_amount = (sell_backlog.get_total_amount() + buy_backlog.get_total_amount())%MOD\n return total_remaining_amount\n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Python3] OOD | Interview Friendly Solution | number-of-orders-in-the-backlog | 0 | 1 | # Complexity\nTime: $$O(nlogn)$$\nSpace: $$O(n)$$\n\n\n# Code\n```\nimport abc\nimport heapq\nfrom enum import Enum\nfrom abc import ABC, abstractmethod\nfrom typing import Optional, List\n\nMOD = int(1e9+7)\nclass OrderType(Enum):\n BUY = 0\n SELL = 1\n\n @classmethod\n def get(cls, order_type_id: int):\n order_type_map = {k.value: k for k in cls}\n return order_type_map[order_type_id]\n\nclass Backlog(ABC):\n def __init__(self):\n self.__heap = []\n self.__price_amount_map = dict()\n self.__total_amount = 0\n\n def get_total_amount(self) -> int:\n return self.__total_amount%MOD\n\n def add_to_total_amount(self, amount: int):\n self.__total_amount += amount\n\n def remove_from_total_amount(self, amount: int):\n self.__total_amount -= amount\n\n def peek(self) -> Optional[int]:\n if len(self.__heap) == 0:\n return None\n return self.__heap[0]\n\n def push(self, price: int):\n heapq.heappush(self.__heap, price)\n\n def pop(self) -> Optional[int]:\n if self.peek() is None:\n return\n return heapq.heappop(self.__heap)\n\n def get_orders_for_price(self, price: int) -> int:\n return self.__price_amount_map.get(price, 0)\n\n def update_orders_for_price(self, price: int, amount: int):\n self.__price_amount_map[price] = amount\n\n @abstractmethod\n def add(self, price: int, amount: int): ...\n\n @abstractmethod\n def remove(self, amount: int): ...\n\nclass BuyBacklog(Backlog):\n def peek(self) -> Optional[int]:\n top = super().peek()\n if top is None:\n return\n return -top\n\n def push(self, price: int):\n price *= -1\n super().push(price=price)\n\n def pop(self) -> Optional[int]:\n val = super().pop()\n if val is None:\n return\n return -val\n\n def add(self, price: int, amount: int):\n existing_orders_for_price = self.get_orders_for_price(price=price)\n if existing_orders_for_price == 0:\n self.push(price=price)\n new_orders_for_price = existing_orders_for_price + amount\n self.add_to_total_amount(amount=amount)\n self.update_orders_for_price(price=price, amount=new_orders_for_price)\n\n def remove(self, amount: int) -> Optional[int]:\n max_buy_price = self.peek()\n if max_buy_price is None:\n return\n max_price_amount = self.get_orders_for_price(price=max_buy_price)\n amount = min(amount, max_price_amount)\n self.remove_from_total_amount(amount=amount)\n max_price_amount -= amount\n\n self.update_orders_for_price(price=max_buy_price, amount=max_price_amount)\n if max_price_amount == 0:\n self.pop()\n return max_buy_price\n\nclass SellBacklog(Backlog):\n def add(self, price: int, amount: int):\n existing_orders_for_price = self.get_orders_for_price(price=price)\n if existing_orders_for_price == 0:\n self.push(price=price)\n new_orders_for_price = existing_orders_for_price + amount\n self.add_to_total_amount(amount=amount)\n self.update_orders_for_price(price=price, amount=new_orders_for_price)\n\n def remove(self, amount: int) -> Optional[int]:\n min_buy_price = self.peek()\n if min_buy_price is None:\n return\n min_price_amount = self.get_orders_for_price(price=min_buy_price)\n amount = min(amount, min_price_amount)\n self.remove_from_total_amount(amount=amount)\n min_price_amount -= amount\n self.update_orders_for_price(price=min_buy_price, amount=min_price_amount)\n if min_price_amount == 0:\n self.pop()\n return min_buy_price\n\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy_backlog = BuyBacklog()\n sell_backlog = SellBacklog()\n\n for price, amount, order_type_id in orders:\n order_type = OrderType.get(order_type_id=order_type_id)\n if order_type == OrderType.BUY:\n min_sell_price = sell_backlog.peek()\n while amount > 0 and min_sell_price is not None and min_sell_price <= price:\n sell_amount = sell_backlog.get_orders_for_price(price=min_sell_price)\n sell_backlog.remove(amount=amount)\n amount -= sell_amount\n min_sell_price = sell_backlog.peek()\n if amount > 0:\n buy_backlog.add(price=price, amount=amount)\n elif order_type == OrderType.SELL:\n max_buy_price = buy_backlog.peek()\n while amount > 0 and max_buy_price is not None and max_buy_price >= price:\n buy_amount = buy_backlog.get_orders_for_price(price=max_buy_price)\n buy_backlog.remove(amount=amount)\n amount -= buy_amount\n max_buy_price = buy_backlog.peek()\n if amount > 0:\n sell_backlog.add(price=price, amount=amount)\n else:\n raise KeyError(f\'invalid order type\')\n\n total_remaining_amount = (sell_backlog.get_total_amount() + buy_backlog.get_total_amount())%MOD\n return total_remaining_amount\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python - MaxHeap for Buy Backlog & MinHeap for Sell Backlog ✅ | number-of-orders-in-the-backlog | 0 | 1 | As the problem statement says, if there is a Buy order, we want to quickly get the sell order with the smallest price currently in the backlog, if it exists. If the price of that sell order is <= the price of buy order, we can execute the order. Again, it is not necessary that all the buy orders get executed with the smallest sell order in the backlog. It is possible that only some orders get executed and in that case, we then have to quickly get the next smallest sell order and do the same thing until we can no longer execute further or if all orders are executed.\n\nSimilarly, in case of a sell order, we want to quickly get the buy order with the smallest price currently in the backlog, if it exists. If the price of that buy order is >= the price of sell order, we can execute the order. Again, it is not necessary that all the sell orders get executed with the largest buy order in the backlog. It is possible that only some orders get executed and in that case, we then have to quickly get the next largest buy order and do the same thing until we can no longer execute further or if all orders are executed.\n\nTo quickly get the Smallest Sell Order at any time, we can use a minHeap for the Sell Backlog.\n\nSimilarly, to get the largest buy order at any time, we use a maxHeap for the Buy Backlog.\n\nThe rest is pretty straightforward.\n\n\n```\ndef getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n \n # Mod\n mod = 10**9 + 7\n \n # We want a maxHeap for the buy backlog and a minHeap for the sell backlog\n buyBacklog = []\n sellBacklog = []\n \n # Go over the orders\n for price,amount,orderType in orders:\n \n # If the order is a buy order\n if orderType == 0:\n \n # The order on top of sellBacklog will have the smallest price\n # So, if the price of that sell order is <= price of the current buy order\n while sellBacklog and sellBacklog[0][0] <= price:\n top = heappop(sellBacklog)\n \n # Execute the order accordingly\n if amount > top[1]:\n amount -= top[1]\n else:\n top[1] -= amount\n amount = 0\n heappush(sellBacklog, top)\n break\n \n # If we couldn\'t execute all the Buy orders, put the remaining orders in the buyBacklog\n if amount > 0: heappush(buyBacklog, [-price,amount,orderType])\n\n # If the order is a sell order\n else:\n \n # The order on top of buyBacklog will have the largest price\n # So, if the price of that buy order is >= price of the current sell order\n while buyBacklog and -buyBacklog[0][0] >= price:\n top = heappop(buyBacklog)\n \n # Execute the order accordingly\n if amount > top[1]:\n amount -= top[1]\n else:\n top[1] -= amount\n amount = 0\n heappush(buyBacklog, top)\n break\n \n # If we couldn\'t execute all the Sell orders, put the remaining orders in the sellBacklog\n if amount > 0: heappush(sellBacklog, [price,amount,orderType])\n \n # How many orders are left in backlog\n ordersLeft = 0\n \n while buyBacklog: ordersLeft += heappop(buyBacklog)[1]\n while sellBacklog: ordersLeft += heappop(sellBacklog)[1]\n \n # Finally, return the Number of orders left in the backlog\n return ordersLeft % mod\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Python - MaxHeap for Buy Backlog & MinHeap for Sell Backlog ✅ | number-of-orders-in-the-backlog | 0 | 1 | As the problem statement says, if there is a Buy order, we want to quickly get the sell order with the smallest price currently in the backlog, if it exists. If the price of that sell order is <= the price of buy order, we can execute the order. Again, it is not necessary that all the buy orders get executed with the smallest sell order in the backlog. It is possible that only some orders get executed and in that case, we then have to quickly get the next smallest sell order and do the same thing until we can no longer execute further or if all orders are executed.\n\nSimilarly, in case of a sell order, we want to quickly get the buy order with the smallest price currently in the backlog, if it exists. If the price of that buy order is >= the price of sell order, we can execute the order. Again, it is not necessary that all the sell orders get executed with the largest buy order in the backlog. It is possible that only some orders get executed and in that case, we then have to quickly get the next largest buy order and do the same thing until we can no longer execute further or if all orders are executed.\n\nTo quickly get the Smallest Sell Order at any time, we can use a minHeap for the Sell Backlog.\n\nSimilarly, to get the largest buy order at any time, we use a maxHeap for the Buy Backlog.\n\nThe rest is pretty straightforward.\n\n\n```\ndef getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n \n # Mod\n mod = 10**9 + 7\n \n # We want a maxHeap for the buy backlog and a minHeap for the sell backlog\n buyBacklog = []\n sellBacklog = []\n \n # Go over the orders\n for price,amount,orderType in orders:\n \n # If the order is a buy order\n if orderType == 0:\n \n # The order on top of sellBacklog will have the smallest price\n # So, if the price of that sell order is <= price of the current buy order\n while sellBacklog and sellBacklog[0][0] <= price:\n top = heappop(sellBacklog)\n \n # Execute the order accordingly\n if amount > top[1]:\n amount -= top[1]\n else:\n top[1] -= amount\n amount = 0\n heappush(sellBacklog, top)\n break\n \n # If we couldn\'t execute all the Buy orders, put the remaining orders in the buyBacklog\n if amount > 0: heappush(buyBacklog, [-price,amount,orderType])\n\n # If the order is a sell order\n else:\n \n # The order on top of buyBacklog will have the largest price\n # So, if the price of that buy order is >= price of the current sell order\n while buyBacklog and -buyBacklog[0][0] >= price:\n top = heappop(buyBacklog)\n \n # Execute the order accordingly\n if amount > top[1]:\n amount -= top[1]\n else:\n top[1] -= amount\n amount = 0\n heappush(buyBacklog, top)\n break\n \n # If we couldn\'t execute all the Sell orders, put the remaining orders in the sellBacklog\n if amount > 0: heappush(sellBacklog, [price,amount,orderType])\n \n # How many orders are left in backlog\n ordersLeft = 0\n \n while buyBacklog: ordersLeft += heappop(buyBacklog)[1]\n while sellBacklog: ordersLeft += heappop(sellBacklog)[1]\n \n # Finally, return the Number of orders left in the backlog\n return ordersLeft % mod\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Priority Queue] with Intuition and Approach Explained | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\nWe want to find a way to match the best sell orders with the best buy orders, and vice versa. Since this matching requires us to think about the "minimum" price of the sell orders, and the "maximum" price of the buy orders in the backlog, we know we should use some form of heap or priority queue in order to **think** about accessing the maximum/minimum sells/buy orders.\n\n# Approach\nSo from reading this problem, I started by thinking about how I would count the amount of orders in the backlog, and how I would track these orders. So I started by keeping track of an `ans` variable, which allowed me to track the backlog amount. Each time I added something to the backlog, I would increment this variable, and each time I removed something I would decrement it.\n\nMoving on to actually handling the backlog, from reading the problem I determined how I should be programming the "buy" and "sell" order matching. Basically go through all the orders in the backlog, and try to match them with the current order. Once all of the possible orders have been matched, I would append the rest of the current order into it\'s respective backlog.\n\nI think figured out the best storage system for the backlog to be a heap, since I needed to easily be able to pull minimums and maximums, while also adding data.\n\n# Complexity\n- Time complexity: `O(n)` to loop through all the queries, and `O(log(n))` to access the minimum and maximum orders in the heap, means that our total time complexity is `O(nlogn)`.\n\n- Space complexity: `O(n)` This is because we need to store all the orders in the heap that we\'re saving into the backlog.\n\n# Code\n```\nimport heapq\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buyBacklog = []\n sellBacklog = []\n ans = 0\n for price, amount, orderType in orders:\n if orderType == 0: # Buy order\n while sellBacklog and amount > 0:\n sellPrice, sellAmount = heapq.heappop(sellBacklog)\n if sellPrice <= price:\n if sellAmount > amount:\n sellAmount -= amount\n ans -= amount\n amount = 0\n heapq.heappush(sellBacklog, (sellPrice, sellAmount))\n else:\n amount -= sellAmount\n ans -= sellAmount\n else:\n heapq.heappush(sellBacklog, (sellPrice, sellAmount))\n break\n if amount != 0:\n ans += amount\n heapq.heappush(buyBacklog, (-price, amount))\n\n else:\n while buyBacklog and amount > 0:\n buyPrice, buyAmount = heapq.heappop(buyBacklog)\n buyPrice *= -1\n if buyPrice >= price:\n if buyAmount > amount:\n buyAmount -= amount\n ans -= amount\n amount = 0\n heapq.heappush(buyBacklog, (-buyPrice, buyAmount))\n else:\n amount -= buyAmount\n ans -= buyAmount\n else:\n heapq.heappush(buyBacklog, (-buyPrice, buyAmount))\n break\n \n if amount != 0:\n ans += amount\n heapq.heappush(sellBacklog, (price, amount))\n\n return ans % (10**9 + 7)\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Priority Queue] with Intuition and Approach Explained | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\nWe want to find a way to match the best sell orders with the best buy orders, and vice versa. Since this matching requires us to think about the "minimum" price of the sell orders, and the "maximum" price of the buy orders in the backlog, we know we should use some form of heap or priority queue in order to **think** about accessing the maximum/minimum sells/buy orders.\n\n# Approach\nSo from reading this problem, I started by thinking about how I would count the amount of orders in the backlog, and how I would track these orders. So I started by keeping track of an `ans` variable, which allowed me to track the backlog amount. Each time I added something to the backlog, I would increment this variable, and each time I removed something I would decrement it.\n\nMoving on to actually handling the backlog, from reading the problem I determined how I should be programming the "buy" and "sell" order matching. Basically go through all the orders in the backlog, and try to match them with the current order. Once all of the possible orders have been matched, I would append the rest of the current order into it\'s respective backlog.\n\nI think figured out the best storage system for the backlog to be a heap, since I needed to easily be able to pull minimums and maximums, while also adding data.\n\n# Complexity\n- Time complexity: `O(n)` to loop through all the queries, and `O(log(n))` to access the minimum and maximum orders in the heap, means that our total time complexity is `O(nlogn)`.\n\n- Space complexity: `O(n)` This is because we need to store all the orders in the heap that we\'re saving into the backlog.\n\n# Code\n```\nimport heapq\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buyBacklog = []\n sellBacklog = []\n ans = 0\n for price, amount, orderType in orders:\n if orderType == 0: # Buy order\n while sellBacklog and amount > 0:\n sellPrice, sellAmount = heapq.heappop(sellBacklog)\n if sellPrice <= price:\n if sellAmount > amount:\n sellAmount -= amount\n ans -= amount\n amount = 0\n heapq.heappush(sellBacklog, (sellPrice, sellAmount))\n else:\n amount -= sellAmount\n ans -= sellAmount\n else:\n heapq.heappush(sellBacklog, (sellPrice, sellAmount))\n break\n if amount != 0:\n ans += amount\n heapq.heappush(buyBacklog, (-price, amount))\n\n else:\n while buyBacklog and amount > 0:\n buyPrice, buyAmount = heapq.heappop(buyBacklog)\n buyPrice *= -1\n if buyPrice >= price:\n if buyAmount > amount:\n buyAmount -= amount\n ans -= amount\n amount = 0\n heapq.heappush(buyBacklog, (-buyPrice, buyAmount))\n else:\n amount -= buyAmount\n ans -= buyAmount\n else:\n heapq.heappush(buyBacklog, (-buyPrice, buyAmount))\n break\n \n if amount != 0:\n ans += amount\n heapq.heappush(sellBacklog, (price, amount))\n\n return ans % (10**9 + 7)\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Python3] Two Heap | number-of-orders-in-the-backlog | 0 | 1 | # Code\n```\nimport heapq\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int: \n buyQ = []\n sellQ = []\n\n for o in orders:\n price = o[0]\n amount = o[1]\n if o[2]==0:\n # buy\n while amount > 0 and len(sellQ) > 0:\n if sellQ[0][0] > price:\n break\n sellElement = heapq.heappop(sellQ)\n tradeQauntity = min(sellElement[1], amount)\n amount -= tradeQauntity\n sellElement[1] -= tradeQauntity\n\n if sellElement[1]>0:\n heapq.heappush(sellQ, sellElement)\n\n if amount > 0:\n heapq.heappush(buyQ, [-price, amount])\n\n else:\n # sell\n while amount > 0 and len(buyQ) > 0:\n if -buyQ[0][0] < price:\n break\n buyElement = heapq.heappop(buyQ)\n tradeQauntity = min(buyElement[1], amount)\n amount -= tradeQauntity\n buyElement[1] -= tradeQauntity\n\n if buyElement[1]>0:\n heapq.heappush(buyQ, buyElement)\n\n if amount > 0:\n heapq.heappush(sellQ, [price, amount])\n\n MOD = int(1e9)+7\n ans = 0\n while len(buyQ)>0:\n cur = heapq.heappop(buyQ)\n ans = (ans + cur[1]) % MOD\n while len(sellQ)>0:\n cur = heapq.heappop(sellQ)\n ans = (ans + cur[1]) % MOD\n\n return ans\n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Python3] Two Heap | number-of-orders-in-the-backlog | 0 | 1 | # Code\n```\nimport heapq\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int: \n buyQ = []\n sellQ = []\n\n for o in orders:\n price = o[0]\n amount = o[1]\n if o[2]==0:\n # buy\n while amount > 0 and len(sellQ) > 0:\n if sellQ[0][0] > price:\n break\n sellElement = heapq.heappop(sellQ)\n tradeQauntity = min(sellElement[1], amount)\n amount -= tradeQauntity\n sellElement[1] -= tradeQauntity\n\n if sellElement[1]>0:\n heapq.heappush(sellQ, sellElement)\n\n if amount > 0:\n heapq.heappush(buyQ, [-price, amount])\n\n else:\n # sell\n while amount > 0 and len(buyQ) > 0:\n if -buyQ[0][0] < price:\n break\n buyElement = heapq.heappop(buyQ)\n tradeQauntity = min(buyElement[1], amount)\n amount -= tradeQauntity\n buyElement[1] -= tradeQauntity\n\n if buyElement[1]>0:\n heapq.heappush(buyQ, buyElement)\n\n if amount > 0:\n heapq.heappush(sellQ, [price, amount])\n\n MOD = int(1e9)+7\n ans = 0\n while len(buyQ)>0:\n cur = heapq.heappop(buyQ)\n ans = (ans + cur[1]) % MOD\n while len(sellQ)>0:\n cur = heapq.heappop(sellQ)\n ans = (ans + cur[1]) % MOD\n\n return ans\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Just clean and readable code. | number-of-orders-in-the-backlog | 0 | 1 | # Approach\nWe represent the backlog as tuple of two heaps (or alternatively sorted arrays or priority queues) - one for buy orders (reversed) and one for sell orders. This way if any orders can match they will be at the top. This way we get all $$m$$ matches in the backlog in $$O(m)$$ steps.\n\n# Complexity\n$$n = len(orders)$$\n- Time complexity: $$O(nlogn)$$ - amortized analysis of match_and_execute()\n\n- Space complexity: $$O(n)$$ - space for backlog\n\n# Code\n```\nfrom queue import PriorityQueue\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n M = 10**9+7\n\n def match_and_execute(backlog):\n buy, sell = backlog\n\n while sell and buy:\n p1, a1 = sell[0]\n p2, a2 = buy[0]\n if not(p1 <= -p2):\n break # no more matches left in backlog\n \n if a1 == a2: \n heappop(sell) \n heappop(buy) \n elif a1 < a2: \n heappop(sell) \n buy[0] = (p2, a2-a1)\n else: \n sell[0] = (p1, a1-a2)\n heappop(buy)\n\n return backlog\n \n def simulate_stock(orders, backlog):\n sell, buy = backlog\n for p, a, t in orders:\n if t == 1: \n heappush(sell, (p, a))\n else: \n heappush(buy, (-p, a))\n match_and_execute(backlog)\n return backlog\n\n\n backlog = simulate_stock(orders, ([], []))\n res = 0\n for log in backlog:\n for _, a in log:\n res = (res + a) % M\n return res\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Just clean and readable code. | number-of-orders-in-the-backlog | 0 | 1 | # Approach\nWe represent the backlog as tuple of two heaps (or alternatively sorted arrays or priority queues) - one for buy orders (reversed) and one for sell orders. This way if any orders can match they will be at the top. This way we get all $$m$$ matches in the backlog in $$O(m)$$ steps.\n\n# Complexity\n$$n = len(orders)$$\n- Time complexity: $$O(nlogn)$$ - amortized analysis of match_and_execute()\n\n- Space complexity: $$O(n)$$ - space for backlog\n\n# Code\n```\nfrom queue import PriorityQueue\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n M = 10**9+7\n\n def match_and_execute(backlog):\n buy, sell = backlog\n\n while sell and buy:\n p1, a1 = sell[0]\n p2, a2 = buy[0]\n if not(p1 <= -p2):\n break # no more matches left in backlog\n \n if a1 == a2: \n heappop(sell) \n heappop(buy) \n elif a1 < a2: \n heappop(sell) \n buy[0] = (p2, a2-a1)\n else: \n sell[0] = (p1, a1-a2)\n heappop(buy)\n\n return backlog\n \n def simulate_stock(orders, backlog):\n sell, buy = backlog\n for p, a, t in orders:\n if t == 1: \n heappush(sell, (p, a))\n else: \n heappush(buy, (-p, a))\n match_and_execute(backlog)\n return backlog\n\n\n backlog = simulate_stock(orders, ([], []))\n res = 0\n for log in backlog:\n for _, a in log:\n res = (res + a) % M\n return res\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Heap Python3 Solution | number-of-orders-in-the-backlog | 0 | 1 | ```\nclass Solution:\n \n # O(nlogn) time,\n # O(n) space,\n # Approach: heap, \n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n MOD = 10**9 + 7\n sell_log = []\n buy_log = []\n in_log = 0\n \n for order in orders:\n price, amount, order_type = order\n amount %= MOD\n if order_type == 0:\n while amount > 0 and sell_log and sell_log[0][0] <= price:\n sell_price, sell_amount = heapq.heappop(sell_log)\n left_sell = max(0, sell_amount-amount)\n if left_sell > 0:\n heapq.heappush(sell_log, (sell_price, left_sell))\n in_log -= min(amount, sell_amount)\n amount = max(0, amount-sell_amount)\n if amount > 0:\n heapq.heappush(buy_log, (-price, amount))\n in_log += amount\n else:\n while amount > 0 and buy_log and -buy_log[0][0] >= price:\n buy_price, buy_amount = heapq.heappop(buy_log)\n left_buy = max(0, buy_amount-amount)\n if left_buy > 0:\n heapq.heappush(buy_log, (buy_price, left_buy))\n in_log -= min(amount, buy_amount)\n amount = max(0, amount-buy_amount)\n if amount > 0:\n heapq.heappush(sell_log, (price, amount))\n in_log += amount\n\n return in_log % MOD\n \n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Heap Python3 Solution | number-of-orders-in-the-backlog | 0 | 1 | ```\nclass Solution:\n \n # O(nlogn) time,\n # O(n) space,\n # Approach: heap, \n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n MOD = 10**9 + 7\n sell_log = []\n buy_log = []\n in_log = 0\n \n for order in orders:\n price, amount, order_type = order\n amount %= MOD\n if order_type == 0:\n while amount > 0 and sell_log and sell_log[0][0] <= price:\n sell_price, sell_amount = heapq.heappop(sell_log)\n left_sell = max(0, sell_amount-amount)\n if left_sell > 0:\n heapq.heappush(sell_log, (sell_price, left_sell))\n in_log -= min(amount, sell_amount)\n amount = max(0, amount-sell_amount)\n if amount > 0:\n heapq.heappush(buy_log, (-price, amount))\n in_log += amount\n else:\n while amount > 0 and buy_log and -buy_log[0][0] >= price:\n buy_price, buy_amount = heapq.heappop(buy_log)\n left_buy = max(0, buy_amount-amount)\n if left_buy > 0:\n heapq.heappush(buy_log, (buy_price, left_buy))\n in_log -= min(amount, buy_amount)\n amount = max(0, amount-buy_amount)\n if amount > 0:\n heapq.heappush(sell_log, (price, amount))\n in_log += amount\n\n return in_log % MOD\n \n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python sortedcontainers | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Order:\n def __init__(self, price, amount, order_type):\n self.price = price\n self.amount = amount\n self.order_type = order_type \n \n def __lt__(self, other):\n if self.price < other.price:\n return self.order_type == 1 \n if self.price > other.price:\n return self.order_type == 0 \n return self.amount < other.amount\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n order_list = [SortedList(), SortedList()] \n tot_amount = 0\n for price, amount, order_type in orders:\n order_list[order_type].add(Order(price, amount, order_type))\n tot_amount += amount\n buy_list, sell_list = order_list\n while buy_list and sell_list and buy_list[0].price >= sell_list[0].price:\n top_buy, top_sell = buy_list[0], sell_list[0] \n amount = min(top_buy.amount, top_sell.amount)\n top_buy.amount -= amount\n top_sell.amount -= amount\n tot_amount -= amount + amount\n if not top_buy.amount:\n buy_list.pop(0)\n if not top_sell.amount:\n sell_list.pop(0)\n return tot_amount % 1000000007\n```\n\n\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n total_amount = 0\n buys, sells = [], []\n for price, amount, order_type in orders:\n if order_type == 0:\n while sells:\n sell_price, sell_amount = sells[0]\n if sell_price > price:\n break\n if amount >= sell_amount:\n amount -= sell_amount\n total_amount = (total_amount - sell_amount) % 1000000007\n heappop(sells)\n continue\n sells[0][1] -= amount\n total_amount = (total_amount - amount) % 1000000007\n amount = 0\n break\n if amount:\n total_amount = (total_amount + amount) % 1000000007\n heappush(buys, [-price, amount])\n elif order_type == 1:\n while buys:\n buy_price, buy_amount = buys[0]\n buy_price = -buy_price\n if buy_price < price:\n break\n if amount >= buy_amount:\n amount -= buy_amount\n total_amount = (total_amount - buy_amount) % 1000000007\n heappop(buys)\n continue\n buys[0][1] -= amount\n total_amount = (total_amount - amount) % 1000000007\n amount = 0\n break \n if amount:\n total_amount = (total_amount + amount) % 1000000007\n heappush(sells, [price, amount])\n return total_amount\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Python sortedcontainers | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Order:\n def __init__(self, price, amount, order_type):\n self.price = price\n self.amount = amount\n self.order_type = order_type \n \n def __lt__(self, other):\n if self.price < other.price:\n return self.order_type == 1 \n if self.price > other.price:\n return self.order_type == 0 \n return self.amount < other.amount\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n order_list = [SortedList(), SortedList()] \n tot_amount = 0\n for price, amount, order_type in orders:\n order_list[order_type].add(Order(price, amount, order_type))\n tot_amount += amount\n buy_list, sell_list = order_list\n while buy_list and sell_list and buy_list[0].price >= sell_list[0].price:\n top_buy, top_sell = buy_list[0], sell_list[0] \n amount = min(top_buy.amount, top_sell.amount)\n top_buy.amount -= amount\n top_sell.amount -= amount\n tot_amount -= amount + amount\n if not top_buy.amount:\n buy_list.pop(0)\n if not top_sell.amount:\n sell_list.pop(0)\n return tot_amount % 1000000007\n```\n\n\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n total_amount = 0\n buys, sells = [], []\n for price, amount, order_type in orders:\n if order_type == 0:\n while sells:\n sell_price, sell_amount = sells[0]\n if sell_price > price:\n break\n if amount >= sell_amount:\n amount -= sell_amount\n total_amount = (total_amount - sell_amount) % 1000000007\n heappop(sells)\n continue\n sells[0][1] -= amount\n total_amount = (total_amount - amount) % 1000000007\n amount = 0\n break\n if amount:\n total_amount = (total_amount + amount) % 1000000007\n heappush(buys, [-price, amount])\n elif order_type == 1:\n while buys:\n buy_price, buy_amount = buys[0]\n buy_price = -buy_price\n if buy_price < price:\n break\n if amount >= buy_amount:\n amount -= buy_amount\n total_amount = (total_amount - buy_amount) % 1000000007\n heappop(buys)\n continue\n buys[0][1] -= amount\n total_amount = (total_amount - amount) % 1000000007\n amount = 0\n break \n if amount:\n total_amount = (total_amount + amount) % 1000000007\n heappush(sells, [price, amount])\n return total_amount\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Python] - Using heap T: O(nlogn) S: O(n) | number-of-orders-in-the-backlog | 0 | 1 | \n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n \n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n MOD = 10**9 + 7\n buy_orders = []\n sell_orders = []\n \n for price, amount, order_type in orders:\n if order_type == 0: # buy order\n while sell_orders and sell_orders[0][0] <= price and amount > 0:\n sell_price, sell_amount = heapq.heappop(sell_orders)\n matched_amount = min(amount, sell_amount)\n amount -= matched_amount\n sell_amount -= matched_amount\n if sell_amount > 0:\n heapq.heappush(sell_orders, (sell_price, sell_amount))\n if amount > 0:\n heapq.heappush(buy_orders, (-price, amount))\n else: # sell order\n while buy_orders and -buy_orders[0][0] >= price and amount > 0:\n buy_price, buy_amount = heapq.heappop(buy_orders)\n matched_amount = min(amount, buy_amount)\n amount -= matched_amount\n buy_amount -= matched_amount\n if buy_amount > 0:\n heapq.heappush(buy_orders, (buy_price, buy_amount))\n if amount > 0:\n heapq.heappush(sell_orders, (price, amount))\n \n total_backlog = sum(amount for _, amount in buy_orders) + sum(amount for _, amount in sell_orders)\n return total_backlog % MOD\n\n\n\n\n \n\'\'\'\nImagine you are at a toy store and want to buy a toy. The toy store has a bunch of toys with different prices, and you have some money to spend.\n\nOther people also want to buy toys at the same store, and some of them want to sell toys they already have. The store keeps track of all these orders in a notebook.\n\nWhen you want to buy a toy, the store checks if anyone is selling a toy for a price you can afford. If they find someone selling a toy at that price, you can buy the toy from them. If no one is selling a toy at that price, the store writes down your order in their notebook and waits for someone to sell a toy at that price.\n\nThe same thing happens if someone wants to sell a toy - the store checks if anyone wants to buy a toy at that price, and if so, they match the buyer and seller and the sale is made. If no one wants to buy a toy at that price, the store writes down the order in their notebook and waits for someone to buy a toy at that price.\n\nAt the end of the day, the store counts how many orders they have left in their notebook that they haven\'t been able to match yet. This is called the backlog.\n\nThe problem you are given is to write a computer program that does this toy store order matching automatically, and tells you how many orders are left in the notebook at the end.\n\'\'\'\n \n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Python] - Using heap T: O(nlogn) S: O(n) | number-of-orders-in-the-backlog | 0 | 1 | \n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n \n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n MOD = 10**9 + 7\n buy_orders = []\n sell_orders = []\n \n for price, amount, order_type in orders:\n if order_type == 0: # buy order\n while sell_orders and sell_orders[0][0] <= price and amount > 0:\n sell_price, sell_amount = heapq.heappop(sell_orders)\n matched_amount = min(amount, sell_amount)\n amount -= matched_amount\n sell_amount -= matched_amount\n if sell_amount > 0:\n heapq.heappush(sell_orders, (sell_price, sell_amount))\n if amount > 0:\n heapq.heappush(buy_orders, (-price, amount))\n else: # sell order\n while buy_orders and -buy_orders[0][0] >= price and amount > 0:\n buy_price, buy_amount = heapq.heappop(buy_orders)\n matched_amount = min(amount, buy_amount)\n amount -= matched_amount\n buy_amount -= matched_amount\n if buy_amount > 0:\n heapq.heappush(buy_orders, (buy_price, buy_amount))\n if amount > 0:\n heapq.heappush(sell_orders, (price, amount))\n \n total_backlog = sum(amount for _, amount in buy_orders) + sum(amount for _, amount in sell_orders)\n return total_backlog % MOD\n\n\n\n\n \n\'\'\'\nImagine you are at a toy store and want to buy a toy. The toy store has a bunch of toys with different prices, and you have some money to spend.\n\nOther people also want to buy toys at the same store, and some of them want to sell toys they already have. The store keeps track of all these orders in a notebook.\n\nWhen you want to buy a toy, the store checks if anyone is selling a toy for a price you can afford. If they find someone selling a toy at that price, you can buy the toy from them. If no one is selling a toy at that price, the store writes down your order in their notebook and waits for someone to sell a toy at that price.\n\nThe same thing happens if someone wants to sell a toy - the store checks if anyone wants to buy a toy at that price, and if so, they match the buyer and seller and the sale is made. If no one wants to buy a toy at that price, the store writes down the order in their notebook and waits for someone to buy a toy at that price.\n\nAt the end of the day, the store counts how many orders they have left in their notebook that they haven\'t been able to match yet. This is called the backlog.\n\nThe problem you are given is to write a computer program that does this toy store order matching automatically, and tells you how many orders are left in the notebook at the end.\n\'\'\'\n \n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python (Simple Heap) | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders):\n sell, buy, mod = [], [], 10**9+7\n\n for i,j,l in orders:\n if l == 0:\n heapq.heappush(buy,[-i,j])\n else:\n heapq.heappush(sell,[i,j])\n \n while buy and sell and sell[0][0] <= -buy[0][0]:\n k = min(sell[0][1],buy[0][1])\n sell[0][1] -= k\n buy[0][1] -= k\n if buy[0][1] == 0: heapq.heappop(buy)\n if sell[0][1] == 0: heapq.heappop(sell)\n\n return sum([j for i,j in buy + sell])%mod\n\n\n \n\n\n \n \n \n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Python (Simple Heap) | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders):\n sell, buy, mod = [], [], 10**9+7\n\n for i,j,l in orders:\n if l == 0:\n heapq.heappush(buy,[-i,j])\n else:\n heapq.heappush(sell,[i,j])\n \n while buy and sell and sell[0][0] <= -buy[0][0]:\n k = min(sell[0][1],buy[0][1])\n sell[0][1] -= k\n buy[0][1] -= k\n if buy[0][1] == 0: heapq.heappop(buy)\n if sell[0][1] == 0: heapq.heappop(sell)\n\n return sum([j for i,j in buy + sell])%mod\n\n\n \n\n\n \n \n \n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
PYTHON FASTER SOLUTION - Easy To Understand | number-of-orders-in-the-backlog | 0 | 1 | # Please Upvote If It\'s Helpful :)\n\n# Intuition\nWe keep min heap for selling because we look for the smallest price when there is buying input. And, we also keep max heap for buying because we look for the biggest price when there is selling input. If it is buying, while length of min heap bigger than 0 and amount of bought item bigger than 0, we pop the first element of min heap and decrease it\'s amount if the price condition is fullfilled. If amount of buying has not been reached, we add the buying input to the max heap after we multiply the price with -1 because it\'s a max heap. We are doing the same thing for selling. \n\nAt the end, we pop each element from both max and min heap and take the sum of amounts.\n\n# Complexity\n- Time complexity: O(n**2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n # (price, amount)\n max_heap_for_buy = []\n heapify(max_heap_for_buy)\n min_heap_for_sell = []\n heapify(min_heap_for_sell)\n\n for i in orders:\n if i[2] == 0:\n if len(min_heap_for_sell) > 0:\n amount_wanted_bought = i[1]\n while len(min_heap_for_sell)>0 and amount_wanted_bought>0:\n if min_heap_for_sell[0][0] <= i[0]:\n current_amount = min_heap_for_sell[0][1]\n if current_amount <= amount_wanted_bought:\n amount_wanted_bought -= min_heap_for_sell[0][1]\n heappop(min_heap_for_sell)\n else:\n popped = heappop(min_heap_for_sell)\n price, amount = popped[0], popped[1]\n amount -= amount_wanted_bought\n popped = (price, amount)\n heappush(min_heap_for_sell, popped)\n amount_wanted_bought = 0\n break\n else:\n break\n if amount_wanted_bought != 0:\n heappush(max_heap_for_buy, (i[0]*-1, amount_wanted_bought))\n\n else:\n heappush(max_heap_for_buy, (i[0]*-1, i[1]))\n \n else:\n if len(max_heap_for_buy) > 0:\n amount_wanted_selled = i[1]\n while len(max_heap_for_buy) > 0 and amount_wanted_selled > 0:\n if i[0] <= (max_heap_for_buy[0][0]*-1):\n current_amount = max_heap_for_buy[0][1]\n if current_amount <= amount_wanted_selled:\n amount_wanted_selled -= max_heap_for_buy[0][1]\n heappop(max_heap_for_buy)\n else:\n popped = heappop(max_heap_for_buy)\n price, amount = popped[0], popped[1]\n popped = (price, amount-amount_wanted_selled)\n heappush(max_heap_for_buy, popped)\n amount_wanted_selled = 0\n break\n else:\n break\n if amount_wanted_selled != 0:\n heappush(min_heap_for_sell, (i[0], amount_wanted_selled))\n\n else:\n heappush(min_heap_for_sell, (i[0], i[1]))\n \n ans = 0\n while min_heap_for_sell:\n popped = heappop(min_heap_for_sell)\n ans += (popped[1])\n\n while max_heap_for_buy:\n popped = heappop(max_heap_for_buy)\n ans += popped[1]\n \n return (ans% (pow(10, 9) + 7))\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
PYTHON FASTER SOLUTION - Easy To Understand | number-of-orders-in-the-backlog | 0 | 1 | # Please Upvote If It\'s Helpful :)\n\n# Intuition\nWe keep min heap for selling because we look for the smallest price when there is buying input. And, we also keep max heap for buying because we look for the biggest price when there is selling input. If it is buying, while length of min heap bigger than 0 and amount of bought item bigger than 0, we pop the first element of min heap and decrease it\'s amount if the price condition is fullfilled. If amount of buying has not been reached, we add the buying input to the max heap after we multiply the price with -1 because it\'s a max heap. We are doing the same thing for selling. \n\nAt the end, we pop each element from both max and min heap and take the sum of amounts.\n\n# Complexity\n- Time complexity: O(n**2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n # (price, amount)\n max_heap_for_buy = []\n heapify(max_heap_for_buy)\n min_heap_for_sell = []\n heapify(min_heap_for_sell)\n\n for i in orders:\n if i[2] == 0:\n if len(min_heap_for_sell) > 0:\n amount_wanted_bought = i[1]\n while len(min_heap_for_sell)>0 and amount_wanted_bought>0:\n if min_heap_for_sell[0][0] <= i[0]:\n current_amount = min_heap_for_sell[0][1]\n if current_amount <= amount_wanted_bought:\n amount_wanted_bought -= min_heap_for_sell[0][1]\n heappop(min_heap_for_sell)\n else:\n popped = heappop(min_heap_for_sell)\n price, amount = popped[0], popped[1]\n amount -= amount_wanted_bought\n popped = (price, amount)\n heappush(min_heap_for_sell, popped)\n amount_wanted_bought = 0\n break\n else:\n break\n if amount_wanted_bought != 0:\n heappush(max_heap_for_buy, (i[0]*-1, amount_wanted_bought))\n\n else:\n heappush(max_heap_for_buy, (i[0]*-1, i[1]))\n \n else:\n if len(max_heap_for_buy) > 0:\n amount_wanted_selled = i[1]\n while len(max_heap_for_buy) > 0 and amount_wanted_selled > 0:\n if i[0] <= (max_heap_for_buy[0][0]*-1):\n current_amount = max_heap_for_buy[0][1]\n if current_amount <= amount_wanted_selled:\n amount_wanted_selled -= max_heap_for_buy[0][1]\n heappop(max_heap_for_buy)\n else:\n popped = heappop(max_heap_for_buy)\n price, amount = popped[0], popped[1]\n popped = (price, amount-amount_wanted_selled)\n heappush(max_heap_for_buy, popped)\n amount_wanted_selled = 0\n break\n else:\n break\n if amount_wanted_selled != 0:\n heappush(min_heap_for_sell, (i[0], amount_wanted_selled))\n\n else:\n heappush(min_heap_for_sell, (i[0], i[1]))\n \n ans = 0\n while min_heap_for_sell:\n popped = heappop(min_heap_for_sell)\n ans += (popped[1])\n\n while max_heap_for_buy:\n popped = heappop(max_heap_for_buy)\n ans += popped[1]\n \n return (ans% (pow(10, 9) + 7))\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python3 solution beats 97%. exPlained | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\nMy first thought was to use a greedy approach. For each order, we can check if the order can be fulfilled by a previous order. If not, we can add it to a heap to track the backlog orders.\n\n# Approach\nWe can use two heaps to track all the buy and sell orders. We iterate through the orders and check if the order can be fulfilled by a previous order. If so, we reduce the amount from the previous order, otherwise, we add it to the heap.\n\n# Complexity\n- Time complexity: $$O(n \\log n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy = []\n sell = []\n for o in orders:\n if o[2] == 0:\n while sell and sell[0][0] <= o[0] and o[1] > 0:\n if sell[0][1] <= o[1]:\n o[1] -= sell[0][1]\n heapq.heappop(sell)\n else:\n sell[0][1] -= o[1]\n o[1] = 0\n if o[1] > 0:\n heapq.heappush(buy, [-o[0], o[1]])\n else:\n while buy and -buy[0][0] >= o[0] and o[1] > 0:\n if buy[0][1] <= o[1]:\n o[1] -= buy[0][1]\n heapq.heappop(buy)\n else:\n buy[0][1] -= o[1]\n o[1] = 0\n if o[1] > 0:\n heapq.heappush(sell, [o[0], o[1]])\n return (sum([o[1] for o in buy]) + sum([o[1] for o in sell])) % (10 ** 9 + 7)\n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Python3 solution beats 97%. exPlained | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\nMy first thought was to use a greedy approach. For each order, we can check if the order can be fulfilled by a previous order. If not, we can add it to a heap to track the backlog orders.\n\n# Approach\nWe can use two heaps to track all the buy and sell orders. We iterate through the orders and check if the order can be fulfilled by a previous order. If so, we reduce the amount from the previous order, otherwise, we add it to the heap.\n\n# Complexity\n- Time complexity: $$O(n \\log n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy = []\n sell = []\n for o in orders:\n if o[2] == 0:\n while sell and sell[0][0] <= o[0] and o[1] > 0:\n if sell[0][1] <= o[1]:\n o[1] -= sell[0][1]\n heapq.heappop(sell)\n else:\n sell[0][1] -= o[1]\n o[1] = 0\n if o[1] > 0:\n heapq.heappush(buy, [-o[0], o[1]])\n else:\n while buy and -buy[0][0] >= o[0] and o[1] > 0:\n if buy[0][1] <= o[1]:\n o[1] -= buy[0][1]\n heapq.heappop(buy)\n else:\n buy[0][1] -= o[1]\n o[1] = 0\n if o[1] > 0:\n heapq.heappush(sell, [o[0], o[1]])\n return (sum([o[1] for o in buy]) + sum([o[1] for o in sell])) % (10 ** 9 + 7)\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python easy understand | number-of-orders-in-the-backlog | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n\n# Code\n```\nimport heapq\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], []\n for p, a, t in orders:\n if t == 0:\n while a and sell and sell[0][0] <= p:\n x, y = heappop(sell)\n if a >= y:\n a -= y\n else:\n heappush(sell, (x, y - a))\n a = 0\n if a:\n heappush(buy, (-p, a))\n else:\n while a and buy and -buy[0][0] >= p:\n x, y = heappop(buy)\n if a >= y:\n a -= y\n else:\n heappush(buy, (x, y - a))\n a = 0\n if a:\n heappush(sell, (p, a))\n mod = 10**9 + 7\n return sum(v[1] for v in buy + sell) % mod\n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Python easy understand | number-of-orders-in-the-backlog | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n\n# Code\n```\nimport heapq\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], []\n for p, a, t in orders:\n if t == 0:\n while a and sell and sell[0][0] <= p:\n x, y = heappop(sell)\n if a >= y:\n a -= y\n else:\n heappush(sell, (x, y - a))\n a = 0\n if a:\n heappush(buy, (-p, a))\n else:\n while a and buy and -buy[0][0] >= p:\n x, y = heappop(buy)\n if a >= y:\n a -= y\n else:\n heappush(buy, (x, y - a))\n a = 0\n if a:\n heappush(sell, (p, a))\n mod = 10**9 + 7\n return sum(v[1] for v in buy + sell) % mod\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
[Python3] - Commented SortedList - Better Space efficiency? | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe definetely need some kind of data structure where we can quickly access the minimum/maximum sales price of the orders.\n\nTherefore we could use Min/Maxheaps or a SortedList.\nMy first intuition is to to use a SortedList as we then can also update buy/sell orders of the same price if multiple leftover orders have the same price.\n\nWe can access the smalles element instantly and update prices in logN time.\n\nAlso we keep orders of equal price and type together in the queue by keeping and amount of orders with a certain price.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use the SortedList of the sortedcontainers library, as it provides convenience implementations for several methods we want to use (binary search, inserting and popping)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*logN) as we might need to insert all orders (worst case only buy orders)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) as in the worst case all orders are buy/sell orders and have different prices.\n\nBut using the SortedList instead of the heap allows us to also find orders with an equal price and update the amount of those. Therefore in cases where there are a lot of orders with the same price, we use less space compared to the heap solutions.\n\n**I stand to be corrected on that one. Would love for hints, in case I\'m wrong.**\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n\n # we use sorted lists for the buy and sell backlog\n #\n # when receiving a BUY ORDER we look at the minimum price\n # of the sell queue and subtract everything below that.\n # If something is left we try to find an equal price in the buy queue\n # and add to it or we insert into the buy queue\n #\n # when receiving a SELL ORDER we look at the maximum buy price\n # and subtract everything below that\n # If something is left we try to find an equal sell price in the sell\n # back log and add to it or we insert into the buy queue\n \n # make the sorted lists\n sell = SortedList(key=lambda x: x[0])\n buy = SortedList(key=lambda x: x[0])\n\n # go through each of the orders and process them\n for price, amount, order_type in orders:\n\n # check which type of order we have to process\n if order_type == 0: # buy order\n\n # check the lowest sell orders we have in the backlog\n while sell and price >= sell[0][0] and amount >= sell[0][1]:\n \n # pop the lowest sell orders\n _, sell_amount = sell.pop(0)\n\n # decrease the amount of buy orders\n amount -= sell_amount\n \n # check whether we have more buy orders for a price than sell orders\n if (not sell or price < sell[0][0]) and amount:\n\n # find the right place in the buy queue\n idx = buy.bisect((price, amount))\n\n # check whether we have similar prices\n if idx > 0 and buy[idx-1] == price:\n buy[idx] += amount\n else:\n buy.add([price, amount])\n \n # we have more sell orders for this price\n else:\n sell[0][1] -= amount\n\n elif order_type == 1: # sell order\n\n # check the lowest sell orders we have in the backlog\n while buy and price <= buy[-1][0] and amount >= buy[-1][1]:\n \n # pop the lowest sell orders\n _, buy_amount = buy.pop()\n\n # decrease the amount of buy orders\n amount -= buy_amount\n \n # check whether we have more sell orders for a price than buy orders\n if (not buy or price > buy[-1][0]) and amount:\n\n # find the right place in the sell queue\n idx = sell.bisect((price, amount))\n\n # check whether we have similar prices\n if idx > 0 and sell[idx-1] == price:\n sell[idx] += amount\n else:\n sell.add([price, amount])\n \n # we have more buy orders for this price\n else:\n buy[-1][1] -= amount\n else:\n raise NotImplementedError\n\n # compute the result with the modulo\n MOD = 1_000_000_007\n result = 0\n for _, amount in sell:\n result = (result + amount) % MOD\n for _, amount in buy:\n result = (result + amount) % MOD\n return result \n\n\n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
[Python3] - Commented SortedList - Better Space efficiency? | number-of-orders-in-the-backlog | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe definetely need some kind of data structure where we can quickly access the minimum/maximum sales price of the orders.\n\nTherefore we could use Min/Maxheaps or a SortedList.\nMy first intuition is to to use a SortedList as we then can also update buy/sell orders of the same price if multiple leftover orders have the same price.\n\nWe can access the smalles element instantly and update prices in logN time.\n\nAlso we keep orders of equal price and type together in the queue by keeping and amount of orders with a certain price.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use the SortedList of the sortedcontainers library, as it provides convenience implementations for several methods we want to use (binary search, inserting and popping)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*logN) as we might need to insert all orders (worst case only buy orders)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) as in the worst case all orders are buy/sell orders and have different prices.\n\nBut using the SortedList instead of the heap allows us to also find orders with an equal price and update the amount of those. Therefore in cases where there are a lot of orders with the same price, we use less space compared to the heap solutions.\n\n**I stand to be corrected on that one. Would love for hints, in case I\'m wrong.**\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n\n # we use sorted lists for the buy and sell backlog\n #\n # when receiving a BUY ORDER we look at the minimum price\n # of the sell queue and subtract everything below that.\n # If something is left we try to find an equal price in the buy queue\n # and add to it or we insert into the buy queue\n #\n # when receiving a SELL ORDER we look at the maximum buy price\n # and subtract everything below that\n # If something is left we try to find an equal sell price in the sell\n # back log and add to it or we insert into the buy queue\n \n # make the sorted lists\n sell = SortedList(key=lambda x: x[0])\n buy = SortedList(key=lambda x: x[0])\n\n # go through each of the orders and process them\n for price, amount, order_type in orders:\n\n # check which type of order we have to process\n if order_type == 0: # buy order\n\n # check the lowest sell orders we have in the backlog\n while sell and price >= sell[0][0] and amount >= sell[0][1]:\n \n # pop the lowest sell orders\n _, sell_amount = sell.pop(0)\n\n # decrease the amount of buy orders\n amount -= sell_amount\n \n # check whether we have more buy orders for a price than sell orders\n if (not sell or price < sell[0][0]) and amount:\n\n # find the right place in the buy queue\n idx = buy.bisect((price, amount))\n\n # check whether we have similar prices\n if idx > 0 and buy[idx-1] == price:\n buy[idx] += amount\n else:\n buy.add([price, amount])\n \n # we have more sell orders for this price\n else:\n sell[0][1] -= amount\n\n elif order_type == 1: # sell order\n\n # check the lowest sell orders we have in the backlog\n while buy and price <= buy[-1][0] and amount >= buy[-1][1]:\n \n # pop the lowest sell orders\n _, buy_amount = buy.pop()\n\n # decrease the amount of buy orders\n amount -= buy_amount\n \n # check whether we have more sell orders for a price than buy orders\n if (not buy or price > buy[-1][0]) and amount:\n\n # find the right place in the sell queue\n idx = sell.bisect((price, amount))\n\n # check whether we have similar prices\n if idx > 0 and sell[idx-1] == price:\n sell[idx] += amount\n else:\n sell.add([price, amount])\n \n # we have more buy orders for this price\n else:\n buy[-1][1] -= amount\n else:\n raise NotImplementedError\n\n # compute the result with the modulo\n MOD = 1_000_000_007\n result = 0\n for _, amount in sell:\n result = (result + amount) % MOD\n for _, amount in buy:\n result = (result + amount) % MOD\n return result \n\n\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python | Heap | O(nlogn) | number-of-orders-in-the-backlog | 0 | 1 | # Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buyBacklog = []\n sellBacklog = []\n for p, amount, t in orders:\n if t:\n while amount and buyBacklog and -buyBacklog[0][0] >= p:\n bp, ba = heappop(buyBacklog)\n base = min(amount, ba)\n amount -= base\n ba -= base\n if ba:\n heappush(buyBacklog, (bp, ba))\n if amount:\n heappush(sellBacklog, (p,amount))\n else:\n while amount and sellBacklog and sellBacklog[0][0] <= p:\n sp, sa = heappop(sellBacklog)\n base = min(amount, sa)\n amount -= base\n sa -= base\n if sa:\n heappush(sellBacklog, (sp, sa)) \n if amount:\n heappush(buyBacklog, (-p, amount))\n return (sum([ba for bp, ba in buyBacklog]) + sum([sa for sp, sa in sellBacklog]))%(10**9 + 7)\n\n\n``` | 0 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Python | Heap | O(nlogn) | number-of-orders-in-the-backlog | 0 | 1 | # Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buyBacklog = []\n sellBacklog = []\n for p, amount, t in orders:\n if t:\n while amount and buyBacklog and -buyBacklog[0][0] >= p:\n bp, ba = heappop(buyBacklog)\n base = min(amount, ba)\n amount -= base\n ba -= base\n if ba:\n heappush(buyBacklog, (bp, ba))\n if amount:\n heappush(sellBacklog, (p,amount))\n else:\n while amount and sellBacklog and sellBacklog[0][0] <= p:\n sp, sa = heappop(sellBacklog)\n base = min(amount, sa)\n amount -= base\n sa -= base\n if sa:\n heappush(sellBacklog, (sp, sa)) \n if amount:\n heappush(buyBacklog, (-p, amount))\n return (sum([ba for bp, ba in buyBacklog]) + sum([sa for sp, sa in sellBacklog]))%(10**9 + 7)\n\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | maximum-value-at-a-given-index-in-a-bounded-array | 1 | 1 | # !! BIG ANNOUNCEMENT !!\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for the first 10,000 Subscribers. **DON\'T FORGET** to Subscribe.\n\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution\n\n# Search \uD83D\uDC49 `Maximum Value at a Given Index in a Bounded Array By Tech Wired` \n\n# or\n\n\n# Click the Link in my Profile\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n\n```Python []\nclass Solution:\n def check(self, a):\n left_offset = max(a - self.index, 0)\n result = (a + left_offset) * (a - left_offset + 1) // 2\n right_offset = max(a - ((self.n - 1) - self.index), 0)\n result += (a + right_offset) * (a - right_offset + 1) // 2\n return result - a\n\n def maxValue(self, n, index, maxSum):\n self.n = n\n self.index = index\n\n maxSum -= n\n left, right = 0, maxSum\n while left < right:\n mid = (left + right + 1) // 2\n if self.check(mid) <= maxSum:\n left = mid\n else:\n right = mid - 1\n result = left + 1\n return result\n```\n```Java []\nclass Solution {\n private long check(long a, int index, int n) {\n long leftOffset = Math.max(a - index, 0);\n long result = (a + leftOffset) * (a - leftOffset + 1) / 2;\n long rightOffset = Math.max(a - ((n - 1) - index), 0);\n result += (a + rightOffset) * (a - rightOffset + 1) / 2;\n return result - a;\n }\n\n public int maxValue(int n, int index, int maxSum) {\n maxSum -= n;\n int left = 0, right = maxSum;\n while (left < right) {\n int mid = (left + right + 1) / 2;\n if (check(mid, index, n) <= maxSum) {\n left = mid;\n } else {\n right = mid - 1;\n }\n }\n return left + 1;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n long long check(long long a, int index, int n) {\n long long leftOffset = std::max(a - static_cast<long long>(index), 0LL);\n long long result = (a + leftOffset) * (a - leftOffset + 1) / 2;\n long long rightOffset = std::max(a - static_cast<long long>((n - 1) - index), 0LL);\n result += (a + rightOffset) * (a - rightOffset + 1) / 2;\n return result - a;\n }\n\n int maxValue(int n, int index, int maxSum) {\n maxSum -= n;\n int left = 0, right = maxSum;\n while (left < right) {\n int mid = (left + right + 1) / 2;\n if (check(mid, index, n) <= maxSum) {\n left = mid;\n } else {\n right = mid - 1;\n }\n }\n return left + 1;\n }\n};\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D\n | 11 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | maximum-value-at-a-given-index-in-a-bounded-array | 1 | 1 | # !! BIG ANNOUNCEMENT !!\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for the first 10,000 Subscribers. **DON\'T FORGET** to Subscribe.\n\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution\n\n# Search \uD83D\uDC49 `Maximum Value at a Given Index in a Bounded Array By Tech Wired` \n\n# or\n\n\n# Click the Link in my Profile\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n\n```Python []\nclass Solution:\n def check(self, a):\n left_offset = max(a - self.index, 0)\n result = (a + left_offset) * (a - left_offset + 1) // 2\n right_offset = max(a - ((self.n - 1) - self.index), 0)\n result += (a + right_offset) * (a - right_offset + 1) // 2\n return result - a\n\n def maxValue(self, n, index, maxSum):\n self.n = n\n self.index = index\n\n maxSum -= n\n left, right = 0, maxSum\n while left < right:\n mid = (left + right + 1) // 2\n if self.check(mid) <= maxSum:\n left = mid\n else:\n right = mid - 1\n result = left + 1\n return result\n```\n```Java []\nclass Solution {\n private long check(long a, int index, int n) {\n long leftOffset = Math.max(a - index, 0);\n long result = (a + leftOffset) * (a - leftOffset + 1) / 2;\n long rightOffset = Math.max(a - ((n - 1) - index), 0);\n result += (a + rightOffset) * (a - rightOffset + 1) / 2;\n return result - a;\n }\n\n public int maxValue(int n, int index, int maxSum) {\n maxSum -= n;\n int left = 0, right = maxSum;\n while (left < right) {\n int mid = (left + right + 1) / 2;\n if (check(mid, index, n) <= maxSum) {\n left = mid;\n } else {\n right = mid - 1;\n }\n }\n return left + 1;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n long long check(long long a, int index, int n) {\n long long leftOffset = std::max(a - static_cast<long long>(index), 0LL);\n long long result = (a + leftOffset) * (a - leftOffset + 1) / 2;\n long long rightOffset = std::max(a - static_cast<long long>((n - 1) - index), 0LL);\n result += (a + rightOffset) * (a - rightOffset + 1) / 2;\n return result - a;\n }\n\n int maxValue(int n, int index, int maxSum) {\n maxSum -= n;\n int left = 0, right = maxSum;\n while (left < right) {\n int mid = (left + right + 1) / 2;\n if (check(mid, index, n) <= maxSum) {\n left = mid;\n } else {\n right = mid - 1;\n }\n }\n return left + 1;\n }\n};\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D\n | 11 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
Simple Python solution using Binary Search | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n maxSum -= n\n def check(x):\n y = max(0, x - index)\n ans = (x+y) * (x-y+1) // 2\n y = max(0, x - ((n-1) - index))\n ans += (x+y) * (x-y+1) // 2\n return (ans - x)\n\n l, r = 0, maxSum\n while l < r:\n mid = (l + r + 1) >> 1\n if check(mid) <= maxSum:\n l = mid\n else:\n r = mid - 1\n return l + 1\n \n``` | 3 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Simple Python solution using Binary Search | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n maxSum -= n\n def check(x):\n y = max(0, x - index)\n ans = (x+y) * (x-y+1) // 2\n y = max(0, x - ((n-1) - index))\n ans += (x+y) * (x-y+1) // 2\n return (ans - x)\n\n l, r = 0, maxSum\n while l < r:\n mid = (l + r + 1) >> 1\n if check(mid) <= maxSum:\n l = mid\n else:\n r = mid - 1\n return l + 1\n \n``` | 3 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
Growing the mountain | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn my mind, I visualized `nums` as an array of heights. Maximizing `nums[index]` while adhering to the rules would create a mountain shape. This would be a direct calculation, except that the boundaries of the index could truncate either or both sides. \n\nI decided to start with an approach iterating over a mountain growing within the bounds of the array, from minimum allowed by rules eventually a maximum that went 1 step to far, expecting it to be too expensive... but it worked.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of maintaining an actual `nums` array, I decided to iterate over how the parameters would change growing from a minimum state.\n\nThe answer requires the value before the iteration that exceeds conditions. Detecting the transition from valid to invalid, then backtracking to the last valid answer seemed far easier than attempting to test whether the next iteration would be invalid. Since we plan to overshoot, it\'s ok for the starting state to be after the first iteration, where all `nums[i]` are 1 except `nums[index]` would be one higher at 2. If that exceeds the `maxSum`, no iteration is needed, and backtraking will happen for a quick answer. The only parameters of `nums` we care about are it\'s sum and the value of `nums[index]`. The sum of an index with all values 1, except a singular exception is it\'s length plus the exceptions difference (2 - 1), hence `n+1`\n\n```\n max_num = 2\n\n nums_sum = n + 1\n```\n\nEach iteration, we are checking that our running sum hasn\'t exceeded the allowed max. If it has, we are done, and need to backtrack 1 for the answer. The meat of the iteration is describing how to the parameters we care about change as the mountain bounded within the array grows 1 higher. If we imagined how the array would change, in order to make the peak grow by 1 we\'d need to add a layer of +1 over a range that grew each iteration, until it reached the boundaries of the array. Again, the only parameters we care about are the height of the peak, and the running sum. Each iteration, we update these values by the amount they would change. The peak of the mountain is easy, +1 each time. \n\n while nums_sum <= maxSum:\n max_num += 1\n # TODO increase = ???\n nums_sum += increase\n max_num -= 1\n return max_num\n\nThe increase sum is a bit harder. Because the boundaries could be anywhere relative to the peak, I decided to break it into sub problems, Left side, peak (already solved) and right side. If we did not hit boundaries, each side would be increased by an amount proportional to the height. If we simplified the base height of the mountain to 0, and the height grew from x-1 to x, a range of x-1 numbers to the left of the peak woul all increase by 1 to have it maintain it\'s slope. The same would be be true on the right. because the base on this problem is 1 and not 0, the range is further reduced by 1. So if we don\'t hit an array boundary, every iteration, as the height of the peak grew, each side would grow by height-2.\n\n```\n left_count = max_num - 2\n right_count = max_num - 2\n increase = left_count + 1 + right_count\n```\n\nBut we can and will hit boundaries, and we can handle that. If the range of numbers that needed to grow to support the peak of the mountain hit a boundary, it would be truncated and maintain a fixed increase instead of a growing rate. If we think about how much the left side of the mountain grows as the height grows if the `index` is 1, there is only one spot to the left of that, so every layer only adds 1 to the left side. If the `index` was 2, once it got high enough, a maximum of 2 per layer would be added to the left, it couldn\'t be more and maintain the slope. for the left side, this cap on how much can change is the length from start to index, `index - 0`. the cap on the right side is from the end of the array to the start of the right side, `n - (index + 1)`. So each of the left and right sides will increase by whichever is less, a number based on the height, or the distance from the peak to the boundary.\n\n```\n left_count = min(max_num - 2, index)\n right_count = min(max_num - 2, n - (index + 1))\n```\n\nI ran into failure with this method alone. It could handle wide arrays pretty well, as `maxSum` grew, less and less iterations were needed. Narrow arrays caused excessive calculation, causing time limit exceeded for a particularly narrow array with a very high `maxSum`. It occurred to me that this use case has an optimization availible. The reason this wasn\'t a mathmatical calculation is because the rate of increase changes with growth. If both boundaries of the array are reached, as it quickly would with small values of n, then the rate of change becomes fixed. Once the increase is fixed, it becomes a multiplication problem. So, added a tracking variable, and a condition to detect if the rate of increase stopped growing... and then did that multiplication problem to accelerate past whatever iterations remained. There was a bit of mess when that acceleration turned into rewind, and that was fixed by preventing negative values (instead of testing for additional conditions).\n\n```\n last_increase = 0\n while nums_sum <= maxSum:\n ...\n if increase == last_increase:\n cycles_to_max = max(0, (maxSum - nums_sum) // increase)\n max_num += cycles_to_max\n nums_sum += cycles_to_max * increase\n last_increase = increase\n```\n\nThis was enough to pass all test cases. While this solution is slower than many others, it does act as a proof that sometimes the job can still get done with simpler tools. No arithmetic sequence formula, no using binary search to narrow in on the answer. Just simple iteration keeping running totals with an optimization when the problem simplifies itself.\n\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nmin(O(n), O(log(maxSum))\npretty sure the log(maxSum) is signifigantly slower than the BST solution, but as maxSum grows, a decreasing amount of additional time would be needed.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\nNo collections used, only a few variables to keep track of totals and state.\n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n max_num = 2\n\n nums_sum = n + 1\n last_increase = 0\n while nums_sum <= maxSum:\n # print(f"valid: max:{max_num} sum:{nums_sum}")\n max_num += 1\n left_count = min(max_num - 2, index)\n right_count = min(max_num - 2, n - (index + 1) )\n increase = left_count + 1 + right_count\n nums_sum += increase\n # print(f"increase by {left_count} + 1 + {right_count} = new sum: {nums_sum}")\n if increase == last_increase:\n cycles_to_max = max(0, (maxSum - nums_sum) // increase)\n max_num += cycles_to_max\n nums_sum += cycles_to_max * increase\n print(f"accelerated {cycles_to_max} * {increase}, max:{max_num} sum:{nums_sum}")\n last_increase = increase\n \n max_num -= 1\n \n print(f"answer is:{max_num}, 1 higher gets sum:{nums_sum}")\n return max_num\n``` | 2 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Growing the mountain | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn my mind, I visualized `nums` as an array of heights. Maximizing `nums[index]` while adhering to the rules would create a mountain shape. This would be a direct calculation, except that the boundaries of the index could truncate either or both sides. \n\nI decided to start with an approach iterating over a mountain growing within the bounds of the array, from minimum allowed by rules eventually a maximum that went 1 step to far, expecting it to be too expensive... but it worked.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInstead of maintaining an actual `nums` array, I decided to iterate over how the parameters would change growing from a minimum state.\n\nThe answer requires the value before the iteration that exceeds conditions. Detecting the transition from valid to invalid, then backtracking to the last valid answer seemed far easier than attempting to test whether the next iteration would be invalid. Since we plan to overshoot, it\'s ok for the starting state to be after the first iteration, where all `nums[i]` are 1 except `nums[index]` would be one higher at 2. If that exceeds the `maxSum`, no iteration is needed, and backtraking will happen for a quick answer. The only parameters of `nums` we care about are it\'s sum and the value of `nums[index]`. The sum of an index with all values 1, except a singular exception is it\'s length plus the exceptions difference (2 - 1), hence `n+1`\n\n```\n max_num = 2\n\n nums_sum = n + 1\n```\n\nEach iteration, we are checking that our running sum hasn\'t exceeded the allowed max. If it has, we are done, and need to backtrack 1 for the answer. The meat of the iteration is describing how to the parameters we care about change as the mountain bounded within the array grows 1 higher. If we imagined how the array would change, in order to make the peak grow by 1 we\'d need to add a layer of +1 over a range that grew each iteration, until it reached the boundaries of the array. Again, the only parameters we care about are the height of the peak, and the running sum. Each iteration, we update these values by the amount they would change. The peak of the mountain is easy, +1 each time. \n\n while nums_sum <= maxSum:\n max_num += 1\n # TODO increase = ???\n nums_sum += increase\n max_num -= 1\n return max_num\n\nThe increase sum is a bit harder. Because the boundaries could be anywhere relative to the peak, I decided to break it into sub problems, Left side, peak (already solved) and right side. If we did not hit boundaries, each side would be increased by an amount proportional to the height. If we simplified the base height of the mountain to 0, and the height grew from x-1 to x, a range of x-1 numbers to the left of the peak woul all increase by 1 to have it maintain it\'s slope. The same would be be true on the right. because the base on this problem is 1 and not 0, the range is further reduced by 1. So if we don\'t hit an array boundary, every iteration, as the height of the peak grew, each side would grow by height-2.\n\n```\n left_count = max_num - 2\n right_count = max_num - 2\n increase = left_count + 1 + right_count\n```\n\nBut we can and will hit boundaries, and we can handle that. If the range of numbers that needed to grow to support the peak of the mountain hit a boundary, it would be truncated and maintain a fixed increase instead of a growing rate. If we think about how much the left side of the mountain grows as the height grows if the `index` is 1, there is only one spot to the left of that, so every layer only adds 1 to the left side. If the `index` was 2, once it got high enough, a maximum of 2 per layer would be added to the left, it couldn\'t be more and maintain the slope. for the left side, this cap on how much can change is the length from start to index, `index - 0`. the cap on the right side is from the end of the array to the start of the right side, `n - (index + 1)`. So each of the left and right sides will increase by whichever is less, a number based on the height, or the distance from the peak to the boundary.\n\n```\n left_count = min(max_num - 2, index)\n right_count = min(max_num - 2, n - (index + 1))\n```\n\nI ran into failure with this method alone. It could handle wide arrays pretty well, as `maxSum` grew, less and less iterations were needed. Narrow arrays caused excessive calculation, causing time limit exceeded for a particularly narrow array with a very high `maxSum`. It occurred to me that this use case has an optimization availible. The reason this wasn\'t a mathmatical calculation is because the rate of increase changes with growth. If both boundaries of the array are reached, as it quickly would with small values of n, then the rate of change becomes fixed. Once the increase is fixed, it becomes a multiplication problem. So, added a tracking variable, and a condition to detect if the rate of increase stopped growing... and then did that multiplication problem to accelerate past whatever iterations remained. There was a bit of mess when that acceleration turned into rewind, and that was fixed by preventing negative values (instead of testing for additional conditions).\n\n```\n last_increase = 0\n while nums_sum <= maxSum:\n ...\n if increase == last_increase:\n cycles_to_max = max(0, (maxSum - nums_sum) // increase)\n max_num += cycles_to_max\n nums_sum += cycles_to_max * increase\n last_increase = increase\n```\n\nThis was enough to pass all test cases. While this solution is slower than many others, it does act as a proof that sometimes the job can still get done with simpler tools. No arithmetic sequence formula, no using binary search to narrow in on the answer. Just simple iteration keeping running totals with an optimization when the problem simplifies itself.\n\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nmin(O(n), O(log(maxSum))\npretty sure the log(maxSum) is signifigantly slower than the BST solution, but as maxSum grows, a decreasing amount of additional time would be needed.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\nNo collections used, only a few variables to keep track of totals and state.\n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n max_num = 2\n\n nums_sum = n + 1\n last_increase = 0\n while nums_sum <= maxSum:\n # print(f"valid: max:{max_num} sum:{nums_sum}")\n max_num += 1\n left_count = min(max_num - 2, index)\n right_count = min(max_num - 2, n - (index + 1) )\n increase = left_count + 1 + right_count\n nums_sum += increase\n # print(f"increase by {left_count} + 1 + {right_count} = new sum: {nums_sum}")\n if increase == last_increase:\n cycles_to_max = max(0, (maxSum - nums_sum) // increase)\n max_num += cycles_to_max\n nums_sum += cycles_to_max * increase\n print(f"accelerated {cycles_to_max} * {increase}, max:{max_num} sum:{nums_sum}")\n last_increase = increase\n \n max_num -= 1\n \n print(f"answer is:{max_num}, 1 higher gets sum:{nums_sum}")\n return max_num\n``` | 2 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
Easy, Binary Search Python3 || Beats 63% 🔥 | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | Easy, Intuitive and a bit mathematical solution with commented code.\nSince, we are using binary search, and constant extra space:\n**Time complexity =** $$O(logn)$$\n**Space complexity =** $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n r = n - index - 1 # how many indices are to be filled before the given index\n l = index # how many indices are to be filled after the given index\n start, end = 0, maxSum\n ans = 1 # if in case the given index is zero, we can maximize the index value by 1\n while start <= end:\n mid = (start + end)//2\n sm = mid\n lsum, rsum = 0, 0\n m = mid - 1\n #calculation the sum before the mid index\n if r<=m: rsum = m*(m+1)//2 - (m-r)*(m-r+1)//2\n else: rsum = m*(m+1)//2 + r-m\n #calculating the sum after the mid index\n if l<=m: lsum = m*(m+1)//2 - (m-l)*(m-l+1)//2\n else: lsum = m*(m+1)//2 + l-m\n\n sm += lsum + rsum \n #if the value of the total sum is less than maxSum, update the boundaries we\'re working with \n if sm <= maxSum:\n ans = mid\n start = mid+1\n else: end = mid - 1\n return ans\n``` | 2 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Easy, Binary Search Python3 || Beats 63% 🔥 | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | Easy, Intuitive and a bit mathematical solution with commented code.\nSince, we are using binary search, and constant extra space:\n**Time complexity =** $$O(logn)$$\n**Space complexity =** $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n r = n - index - 1 # how many indices are to be filled before the given index\n l = index # how many indices are to be filled after the given index\n start, end = 0, maxSum\n ans = 1 # if in case the given index is zero, we can maximize the index value by 1\n while start <= end:\n mid = (start + end)//2\n sm = mid\n lsum, rsum = 0, 0\n m = mid - 1\n #calculation the sum before the mid index\n if r<=m: rsum = m*(m+1)//2 - (m-r)*(m-r+1)//2\n else: rsum = m*(m+1)//2 + r-m\n #calculating the sum after the mid index\n if l<=m: lsum = m*(m+1)//2 - (m-l)*(m-l+1)//2\n else: lsum = m*(m+1)//2 + l-m\n\n sm += lsum + rsum \n #if the value of the total sum is less than maxSum, update the boundaries we\'re working with \n if sm <= maxSum:\n ans = mid\n start = mid+1\n else: end = mid - 1\n return ans\n``` | 2 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
python 3 - binary search + greedy + triangle number | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | (This one is quite hard)\n\n# Intuition\nEvery array element has to be 1 in the beginning. At most you case raise nums[i] for (ms - 1), which is the upper boundary. Lower boundary = 0 for sure. -> This is a binary search pattern.\n\nYou will definitely try to raise nums[i] for value x. Value will not be randomly distributed -> Greedy is needed.\n\nIf you choose to raise nums[i] by x, nums[i+1] has to be raised by x - 1, nums[i+2] has to be raised by x - 2 and so on. Same case for the nums[i-1] (opposite side) case.\n\nEdge case: left boundary or right boundary exceed the array. You need to subtract the exceeded part -> You need triangle number formula to do this.\n\n# Approach\nBS + greedy\n\n# Complexity\n- Time complexity:\nO(log(ms)) -> Number of binary search is log(ms). helper function takes O(1) time for checking\n\n- Space complexity:\nO(1) -> just set variables\n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, ms: int) -> int:\n\n def helper(m): # return bool, possible to raise nums[index] by m?\n need = m\n\n # left\n leftb = index - (m - 1)\n need += ((m - 1) * m) // 2\n if leftb < 0:\n tmp = abs(leftb)\n offset = (tmp * (tmp + 1)) // 2\n need -= offset\n\n # right\n rightb = index + (m - 1)\n need += ((m - 1) * m) // 2\n if rightb >= n:\n tmp = rightb - (n - 1)\n offset = (tmp * (tmp + 1)) // 2\n need -= offset\n\n return need <= remain\n\n remain = ms - n\n l, r = 0, remain\n ans = 0\n\n if helper(r): # can take max value initially\n return r + 1\n\n while l < r:\n m = (l + r) // 2\n\n if helper(m): # possible to take\n ans = max(ans, m)\n l = m + 1\n else:\n r = m\n return ans + 1\n``` | 1 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
python 3 - binary search + greedy + triangle number | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | (This one is quite hard)\n\n# Intuition\nEvery array element has to be 1 in the beginning. At most you case raise nums[i] for (ms - 1), which is the upper boundary. Lower boundary = 0 for sure. -> This is a binary search pattern.\n\nYou will definitely try to raise nums[i] for value x. Value will not be randomly distributed -> Greedy is needed.\n\nIf you choose to raise nums[i] by x, nums[i+1] has to be raised by x - 1, nums[i+2] has to be raised by x - 2 and so on. Same case for the nums[i-1] (opposite side) case.\n\nEdge case: left boundary or right boundary exceed the array. You need to subtract the exceeded part -> You need triangle number formula to do this.\n\n# Approach\nBS + greedy\n\n# Complexity\n- Time complexity:\nO(log(ms)) -> Number of binary search is log(ms). helper function takes O(1) time for checking\n\n- Space complexity:\nO(1) -> just set variables\n\n# Code\n```\nclass Solution:\n def maxValue(self, n: int, index: int, ms: int) -> int:\n\n def helper(m): # return bool, possible to raise nums[index] by m?\n need = m\n\n # left\n leftb = index - (m - 1)\n need += ((m - 1) * m) // 2\n if leftb < 0:\n tmp = abs(leftb)\n offset = (tmp * (tmp + 1)) // 2\n need -= offset\n\n # right\n rightb = index + (m - 1)\n need += ((m - 1) * m) // 2\n if rightb >= n:\n tmp = rightb - (n - 1)\n offset = (tmp * (tmp + 1)) // 2\n need -= offset\n\n return need <= remain\n\n remain = ms - n\n l, r = 0, remain\n ans = 0\n\n if helper(r): # can take max value initially\n return r + 1\n\n while l < r:\n m = (l + r) // 2\n\n if helper(m): # possible to take\n ans = max(ans, m)\n l = m + 1\n else:\n r = m\n return ans + 1\n``` | 1 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
Python3 || Tc: O(logn), SC: O(1) || Binary Search || Commented code | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | ```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n low, high = 1, maxSum\n while low <= high: \n mid = (low + high) // 2\n if self.helper(mid, index, maxSum, n):\n ans = mid \n low = mid + 1\n else:\n high = mid - 1\n return ans\n \n def helper(self, val, idx, maxSum, n):\n #no of elements of the given index\n right_total = n-1-idx\n no_of_elements_right_series = min(val-1, right_total)\n remaining_right = max(0, right_total - no_of_elements_right_series)\n \n left_total = idx\n no_of_elements_left_series = min(val-1, left_total)\n remaining_left = max(0, left_total - no_of_elements_left_series)\n \n totalSum = val + self.getAPSum(no_of_elements_right_series, val-1) + self.getAPSum(no_of_elements_left_series, val-1) + remaining_right + remaining_left\n \n if totalSum > maxSum:\n return False\n return True\n \n def getAPSum(self, n, a):\n #ap sum formula = (((n-1)*d + 2a) * n) // 2, a -> start, n->num of elements in the series, \n\t\t#here d = -1 \n return ((2*a + (1-n)) * n) // 2\n \n``` | 1 | You are given three positive integers: `n`, `index`, and `maxSum`. You want to construct an array `nums` (**0-indexed**) that satisfies the following conditions:
* `nums.length == n`
* `nums[i]` is a **positive** integer where `0 <= i < n`.
* `abs(nums[i] - nums[i+1]) <= 1` where `0 <= i < n-1`.
* The sum of all the elements of `nums` does not exceed `maxSum`.
* `nums[index]` is **maximized**.
Return `nums[index]` _of the constructed array_.
Note that `abs(x)` equals `x` if `x >= 0`, and `-x` otherwise.
**Example 1:**
**Input:** n = 4, index = 2, maxSum = 6
**Output:** 2
**Explanation:** nums = \[1,2,**2**,1\] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums\[2\] == 3, so 2 is the maximum nums\[2\].
**Example 2:**
**Input:** n = 6, index = 1, maxSum = 10
**Output:** 3
**Constraints:**
* `1 <= n <= maxSum <= 109`
* `0 <= index < n` | Simulate the given in the statement Calculate those who will eat instead of those who will not. |
Python3 || Tc: O(logn), SC: O(1) || Binary Search || Commented code | maximum-value-at-a-given-index-in-a-bounded-array | 0 | 1 | ```\nclass Solution:\n def maxValue(self, n: int, index: int, maxSum: int) -> int:\n low, high = 1, maxSum\n while low <= high: \n mid = (low + high) // 2\n if self.helper(mid, index, maxSum, n):\n ans = mid \n low = mid + 1\n else:\n high = mid - 1\n return ans\n \n def helper(self, val, idx, maxSum, n):\n #no of elements of the given index\n right_total = n-1-idx\n no_of_elements_right_series = min(val-1, right_total)\n remaining_right = max(0, right_total - no_of_elements_right_series)\n \n left_total = idx\n no_of_elements_left_series = min(val-1, left_total)\n remaining_left = max(0, left_total - no_of_elements_left_series)\n \n totalSum = val + self.getAPSum(no_of_elements_right_series, val-1) + self.getAPSum(no_of_elements_left_series, val-1) + remaining_right + remaining_left\n \n if totalSum > maxSum:\n return False\n return True\n \n def getAPSum(self, n, a):\n #ap sum formula = (((n-1)*d + 2a) * n) // 2, a -> start, n->num of elements in the series, \n\t\t#here d = -1 \n return ((2*a + (1-n)) * n) // 2\n \n``` | 1 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
[Python3] trie | count-pairs-with-xor-in-a-range | 0 | 1 | \n```\nclass Trie: \n def __init__(self): \n self.root = {}\n \n def insert(self, val): \n node = self.root \n for i in reversed(range(15)):\n bit = (val >> i) & 1\n if bit not in node: node[bit] = {"cnt": 0}\n node = node[bit]\n node["cnt"] += 1\n \n def count(self, val, high): \n ans = 0 \n node = self.root\n for i in reversed(range(15)):\n if not node: break \n bit = (val >> i) & 1 \n cmp = (high >> i) & 1\n if cmp: \n if node.get(bit, {}): ans += node[bit]["cnt"]\n node = node.get(1^bit, {})\n else: node = node.get(bit, {})\n return ans \n \n \nclass Solution:\n def countPairs(self, nums: List[int], low: int, high: int) -> int:\n trie = Trie()\n ans = 0\n for x in nums: \n ans += trie.count(x, high+1) - trie.count(x, low)\n trie.insert(x)\n return ans \n``` | 45 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
[Python] O(N log N) using math (Fourier transform) | count-pairs-with-xor-in-a-range | 0 | 1 | We can use some number theory to calculate all possible XOR values of two numbers in the range (0, max(nums)). Obviously this knowledge isn\'t expected in a normal interview, but it can come in handy.\n\nThe trick, which is used in cryptography/signal processing, is to convert our array into a frequency array, then use an [n-dimensional Discrete Fourier Transform](https://en.wikipedia.org/wiki/Fast_Walsh%E2%80%93Hadamard_transform) called the Walsh-Hadamard transform on those frequencies. The algorithm is short, and even has the full Python code on the Wikipedia page. Here, n = log(N) is the bit-length of N, the max value of nums. The transform can be done in N log N steps with divide and conquer (which you can do iteratively with log N loops of length N each). \n\nThen the transformed frequency of pairs with each XOR value becomes the square of each element in our transformed array (using properties of Fourier transforms). Inverting the transform (which is equivalent to the normal transform with an extra division at the end) gives us our desired pair-frequency array.\n\n\n\n```python\ndef countPairs(self, nums, low, high):\n\tdef walsh_hadamard(my_freqs):\n\t\tmy_max = len(my_freqs)\n\n\t\t# If our array\'s length is not a power of 2, \n\t\t# increase its length by padding zeros to the right\n\t\tif my_max & (my_max - 1):\n\t\t\tmy_max = 2 ** (my_max.bit_length())\n\n\t\tif my_max > len(my_freqs):\n\t\t\tmy_freqs.extend([0] * (my_max - len(my_freqs)))\n\n\t\th = 2\n\t\twhile h <= my_max:\n\t\t\thf = h // 2\n\t\t\tfor i in range(0, my_max, h):\n\t\t\t\tfor j in range(hf):\n\t\t\t\t\tu, v = my_freqs[i + j], my_freqs[i + j + hf]\n\t\t\t\t\tmy_freqs[i + j], my_freqs[i + j + hf] = u + v, u - v\n\t\t\th *= 2\n\t\treturn my_freqs\n\n\thigh += 1\n\tmax_num = max(nums) + 1\n\t# If high is larger than any possible XOR,\n\t# we can use a results array of the size of max(nums)\n\tif high.bit_length() > max_num.bit_length():\n\t\tmy_max1 = max_num\n\telse:\n\t\tmy_max1 = max(high, max_num)\n\n\tmy_freq = [0] * my_max1\n\tfor x in nums:\n\t\tmy_freq[x] += 1\n\n\t# Get the WHT transform of our frequencies, square it,\n\t# and take a second transform (which we invert after summing)\n\tmy_freq = walsh_hadamard([x * x for x in walsh_hadamard(my_freq)])\n\n\t# Find the sum of freq in our range,\n\t# divide by 2 to count only (i,j) with i<j,\n\t# and divide by length to invert\n\treturn sum(my_freq[low:high]) // (2 * len(my_freq))\n```\nRun time is O(N log N) here with a slight catch: the N here means the maximum of nums, not the length of our initial array, which means that sparse arrays will have worse runtime than the other solutions, especially the O(n) trie solutions. This can probably be fixed by using a defaultdict to hold our frequencies and modifying the transform code, although that implementation might be a bit tricky. Also, this easily generalizes when we want XOR pairs from 2 different arrays, although the Trie solution can handle that case as well. | 16 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
[C++ || Python || Java] Brief code without explicit Trie | count-pairs-with-xor-in-a-range | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n---\n# Intuition\n1. For the counting pairs problem, the first intuition is to enumerate one of the pair, and count another. Such as [327. Count of Range Sum](https://leetcode.com/problems/count-of-range-sum/). They have the same core with a little difference surfaces. The simplest solution in 327 is Prefix Sum + Binary Indexed Tree, can it be used for this question?\n2. But notice that addition has a property that adding the same number to both sides of an inequality, the inequality remains true. This property makes addition and subtraction can map a continuous interval to another, which $\\oplus$ operation hasn\'t.\n\n TBD\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\nTo solve this kind of problem, unify the problem is a good idea. Similar to the idea of prefix sum: convert the $$\\sum_{i=low}^{high}a[i]$$ to $\\sum_{i=0}^{high}a[i] - \\sum_{i=0}^{low-1}a[i]$.\n\nStudy the process of recursion, take $bound=5$ as an example, draw the recursive diagram:\n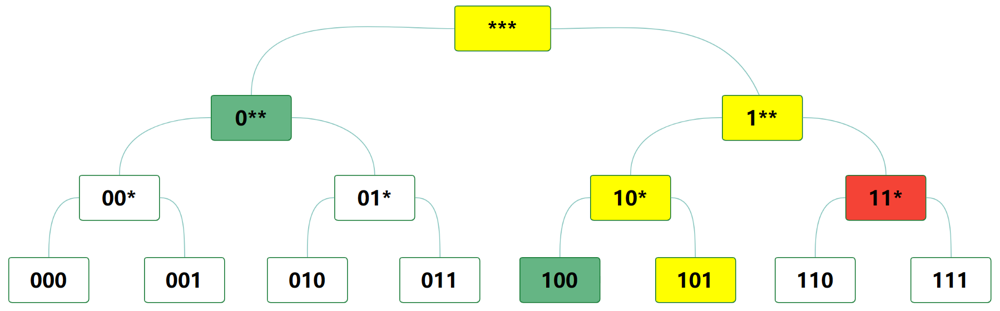\nIn the figure, red means returning 0, green means returning the count of the vertex value $\\oplus x$ , and yellow is the point where recursion continues.\n\nEasy to find that we only need to **accumulate the count of "visited right son\'s brother\'s value$\\oplus x$"** to get the result.\n\nFinally, use these optimizations:\n1. Use loop instead of recursion to improve runtime efficiency.\n2. Use the array instead of explicit 0/1 trie. Suppose the prefix is $p$, the length of prefix is $i$, and the index of this prefix is $2^{i} + p$.\n\n\n# Complexity\n- Time complexity: $O(n \\log (max))$\n- Space complexity: $O(max)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n int countPairs(vector<int>& nums, int low, int high) {\n int maxx = max(*max_element(nums.begin(), nums.end()), high) + 1;\n int bits = 32 - __builtin_clz(maxx);\n vector<int> cnt(1 << bits + 1, 0);\n int res = 0;\n auto less = [&](int x, int bound) -> int {\n int ans = 0;\n for (int i = bits; i >= 0; --i) {\n // find prefix\n int p = bound >> i;\n // if p is a right child, add the left child\n if (p & 1) ans += cnt[(1<<bits-i) + (p^1^x>>i)];\n }\n return ans;\n };\n for (auto x : nums) {\n res += less(x, high + 1) - less(x, low);\n for (int i = 0; i <= bits; ++i) {\n // update each prefix for x\n cnt[(x >> i) + (1 << bits - i)]++;\n }\n }\n return res;\n }\n};\n``` \n``` Java []\nclass Solution {\n public int countPairs(int[] nums, int low, int high) {\n int bits = 15;\n int []cnt = new int[1 << bits + 1];\n int res = 0;\n high += 1\n for (int x : nums) {\n for (int i = bits; i >= 0; --i) {\n // find prefixes of low and high\n int up = high >> i, lp = low >> i;\n // if high is right child, add the left child\n if (up % 2 == 1) res += cnt[(1<<bits-i) + (up^1^x>>i)]; \n // if low is right child, minus the left child\n if (lp % 2 == 1) res -= cnt[(1<<bits-i) + (lp^1^x>>i)];\n }\n for (int i = bits; i >= 0; --i) {\n // update each prefix for x\n cnt[(x >> i) + (1 << bits - i)]++;\n }\n }\n return res;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def countPairs(self, nums: List[int], low: int, high: int) -> int:\n maxx = max(max(nums), high)\n bits = 15\n cnt = [0] * (1 << bits + 1)\n res = 0\n high += 1\n for x in nums:\n for i in range(bits + 1): \n # find prefixes of low and high\n up = high >> i\n lp = low >> i\n # if high is right child, add the left child\n if up & 1: res += cnt[(1<<bits-i) + (up^1^x>>i)]\n # if low is right child, minus the left child\n if lp & 1: res -= cnt[(1<<bits-i) + (lp^1^x>>i)]\n \n for i in range(bits + 1): \n # update each prefix for x\n cnt[(x >> i) + (1 << bits - i)] += 1\n return res\n \n``` | 1 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
[Python3] Trie with diagram and explanations | count-pairs-with-xor-in-a-range | 0 | 1 | ## Idea\n1. We scan the numbers one by one and use a trie to store the counts of existing nums.\n2. Whenever we have a new number `v`, we first find a path in the trie that ensures the XOR between the new number and numbers in the trie to be less than `high`, then we add this number `v` into the trie and update the counts.\n3. The path can be constructed bit-by-bit from the left-most bit. It can be broken down into two scenarios.\n4. Scenario A: If the first bit in `high` is `1`, all numbers that result in `0xx` must be counted. In other words, we can directly add all numbers starting with the same bit because XOR of the same bit results in `0`. However, we are unsure about numbers starting with a different bit because it depends on the remaining bits, which we will move on to check down the trie.\n5. Scenario B: if the first bit in `high` is `0`, the only possible solution is to ensure that the bit in `nums` is the same with the current number `v`, which we check down the trie in the remaining steps.\n6. Because the question is requesting `low <= (nums[i] XOR nums[j]) <= high`, but we are counting `(nums[i] XOR nums[j]) < high` in our function `count(high)`, we need to calculate `final_count += count(high+1) - count(low)`.\n## Figure\nThe figure below shows a trie constructed on the first three numbers `[1,4,2]` (in green) and the current value `v=7` (in yellow). For the first bit, we add the count of `R--1(1)` because it results in `0<1`, and move to the left branch `R--0(2)` which we are unsure about. For the second bit, because the high bit is once again `1`, we add the count of `R--0(2)--1(1)` and move to the left branch `R--0(2)--0(1)`. For the last bit, because the bit is `0` in high, we move to branch `R--0(2)--0(1)--1(1)`. The loop ends here and we do not add this node to the counter.\n\n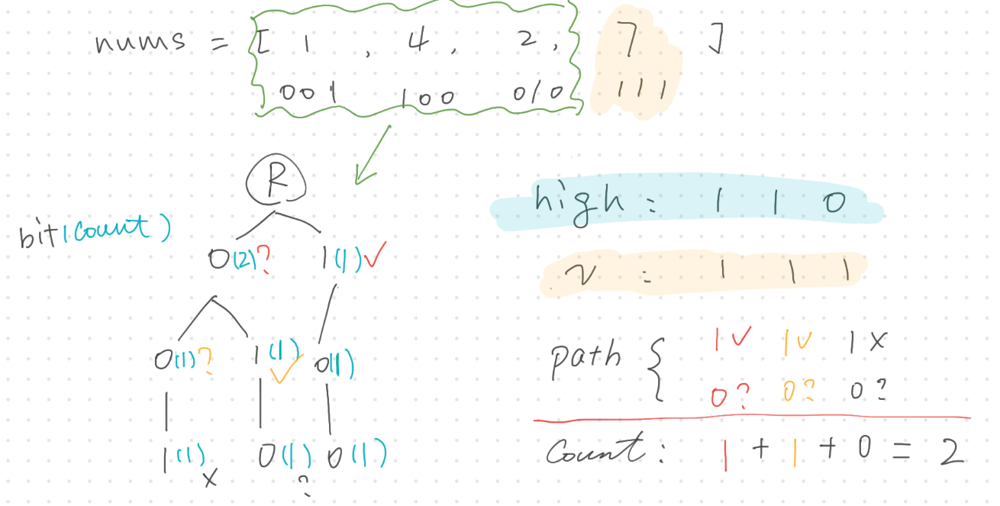\n\n## Code\n```\nclass TrieNode:\n def __init__(self):\n self.children = defaultdict(TrieNode)\n self.count = 0\n \n \nclass Trie:\n def __init__(self, maxbits=None):\n self.root = TrieNode()\n self.maxbits = maxbits\n \n def add(self, v):\n n = self.root\n # build the trie from the left-most bit\n for i in reversed(range(self.maxbits)):\n node_value = (v >> i) & 1\n n.children[node_value].count += 1\n n = n.children[node_value]\n \n def count(self, v, high):\n cnt = 0\n n = self.root\n for i in reversed(range(self.maxbits)):\n if not n: break\n \n high_at_bit_i = (high >> i) & 1\n v_at_bit_i = (v >> i) & 1\n if high_at_bit_i: # x could be v_at_bit_i, and possibly 1-v_at_bit_i\n if v_at_bit_i in n.children:\n cnt += n.children[v_at_bit_i].count\n n = n.children.get(1 - v_at_bit_i, None)\n else: # x must be v_at_bit_i\n n = n.children.get(v_at_bit_i, None)\n \n return cnt\n \n\nclass Solution:\n def countPairs(self, nums: List[int], low: int, high: int) -> int:\n # determine the max number of bits needed in our trie,\n # the # of bits for the largest number in nums and high+1, whichever is the greatest\n max_bits = len(bin(max(nums + [high+1]))) - 2\n \n ans = 0\n trie = Trie(max_bits)\n for num in nums:\n ans += trie.count(num, high+1) - trie.count(num, low) # due to `low <= (nums[i] XOR nums[j]) <= high`\n trie.add(num)\n \n return ans\n``` | 1 | Given a **(0-indexed)** integer array `nums` and two integers `low` and `high`, return _the number of **nice pairs**_.
A **nice pair** is a pair `(i, j)` where `0 <= i < j < nums.length` and `low <= (nums[i] XOR nums[j]) <= high`.
**Example 1:**
**Input:** nums = \[1,4,2,7\], low = 2, high = 6
**Output:** 6
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 1): nums\[0\] XOR nums\[1\] = 5
- (0, 2): nums\[0\] XOR nums\[2\] = 3
- (0, 3): nums\[0\] XOR nums\[3\] = 6
- (1, 2): nums\[1\] XOR nums\[2\] = 6
- (1, 3): nums\[1\] XOR nums\[3\] = 3
- (2, 3): nums\[2\] XOR nums\[3\] = 5
**Example 2:**
**Input:** nums = \[9,8,4,2,1\], low = 5, high = 14
**Output:** 8
**Explanation:** All nice pairs (i, j) are as follows:
- (0, 2): nums\[0\] XOR nums\[2\] = 13
- (0, 3): nums\[0\] XOR nums\[3\] = 11
- (0, 4): nums\[0\] XOR nums\[4\] = 8
- (1, 2): nums\[1\] XOR nums\[2\] = 12
- (1, 3): nums\[1\] XOR nums\[3\] = 10
- (1, 4): nums\[1\] XOR nums\[4\] = 9
- (2, 3): nums\[2\] XOR nums\[3\] = 6
- (2, 4): nums\[2\] XOR nums\[4\] = 5
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i] <= 2 * 104`
* `1 <= low <= high <= 2 * 104` | Iterate on the customers, maintaining the time the chef will finish the previous orders. If that time is before the current arrival time, the chef starts immediately. Else, the current customer waits till the chef finishes, and then the chef starts. Update the running time by the time when the chef starts preparing + preparation time. |
Efficient Python Program Using Map and Regular Expression. | number-of-different-integers-in-a-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(set(map(int,re.findall(r\'\\d+\',word))))\n``` | 1 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Efficient Python Program Using Map and Regular Expression. | number-of-different-integers-in-a-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(set(map(int,re.findall(r\'\\d+\',word))))\n``` | 1 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Efficient Python3 Program Using Regular Expression Method | number-of-different-integers-in-a-string | 0 | 1 | # Intuition:\n\nThe goal is to find and count different integers within the given string, where non-digit characters are replaced with spaces.\n\n# Approach:\n\nImport the re module for regular expressions.\nUse re.findall to extract all the integers from the word string.\nConvert the extracted integers to a set to remove duplicates.\nReturn the count of unique integers in the set.\nComplexity:\n\n# Time complexity:\n The regular expression processing has a time complexity of O(n), where n is the length of the input string. The subsequent set operations have a time complexity of O(m), where m is the number of unique integers in the extracted list. Overall, the time complexity is O(n + m).\nSpace complexity: The space complexity is O(m) for storing the unique integers in the set.\n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n import re \n integers = [ int(i) for i in re.findall(r\'\\d+\',word)]\n integers = set( integers)\n return len(integers)\n``` | 1 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Efficient Python3 Program Using Regular Expression Method | number-of-different-integers-in-a-string | 0 | 1 | # Intuition:\n\nThe goal is to find and count different integers within the given string, where non-digit characters are replaced with spaces.\n\n# Approach:\n\nImport the re module for regular expressions.\nUse re.findall to extract all the integers from the word string.\nConvert the extracted integers to a set to remove duplicates.\nReturn the count of unique integers in the set.\nComplexity:\n\n# Time complexity:\n The regular expression processing has a time complexity of O(n), where n is the length of the input string. The subsequent set operations have a time complexity of O(m), where m is the number of unique integers in the extracted list. Overall, the time complexity is O(n + m).\nSpace complexity: The space complexity is O(m) for storing the unique integers in the set.\n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n import re \n integers = [ int(i) for i in re.findall(r\'\\d+\',word)]\n integers = set( integers)\n return len(integers)\n``` | 1 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Easy method | 3 line code | 80% beats | number-of-different-integers-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n\n\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n result = [int(match) for match in re.findall(r\'\\d+\', word)]\n\n res=set(result)\n\n return len(res)\n\n \n``` | 0 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Easy method | 3 line code | 80% beats | number-of-different-integers-in-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n\n\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n result = [int(match) for match in re.findall(r\'\\d+\', word)]\n\n res=set(result)\n\n return len(res)\n\n \n``` | 0 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Simplest solution for beginners in python beat 80% | number-of-different-integers-in-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n nums=\'0123456789\'\n\n for i in range(len(word)):\n if word[i] not in nums:\n word= word.replace(word[i],\' \')\n num_list=word.split()\n\n res=[]\n for i in range(len(num_list)):\n res.append(int(num_list[i]))\n\n return len(set(res)) \n \n \n``` | 3 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Simplest solution for beginners in python beat 80% | number-of-different-integers-in-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n nums=\'0123456789\'\n\n for i in range(len(word)):\n if word[i] not in nums:\n word= word.replace(word[i],\' \')\n num_list=word.split()\n\n res=[]\n for i in range(len(num_list)):\n res.append(int(num_list[i]))\n\n return len(set(res)) \n \n \n``` | 3 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Python One Line Efficient Solution. | number-of-different-integers-in-a-string | 0 | 1 | # Intuition\n The goal is to find and count different integers within the given string, where non-digit characters are replaced with spaces.\n\n# Approach\n 1. Use regular expressions to extract all the integers from the \'word\' string.\n 2. Convert the extracted integers to a set to remove duplicates.\n 3. Return the count of unique integers in the set.\n\n# Complexity\n - Time complexity: O(n + m), where n is the length of the input string, and m is the number of unique integers in the extracted list.\n - Space complexity: O(m) for storing the unique integers in the set.\n\n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(set([ int(i) for i in re.findall(r\'\\d+\',word)]))\n``` | 1 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Python One Line Efficient Solution. | number-of-different-integers-in-a-string | 0 | 1 | # Intuition\n The goal is to find and count different integers within the given string, where non-digit characters are replaced with spaces.\n\n# Approach\n 1. Use regular expressions to extract all the integers from the \'word\' string.\n 2. Convert the extracted integers to a set to remove duplicates.\n 3. Return the count of unique integers in the set.\n\n# Complexity\n - Time complexity: O(n + m), where n is the length of the input string, and m is the number of unique integers in the extracted list.\n - Space complexity: O(m) for storing the unique integers in the set.\n\n# Code\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(set([ int(i) for i in re.findall(r\'\\d+\',word)]))\n``` | 1 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Python | Easy Solution✅ | number-of-different-integers-in-a-string | 0 | 1 | # Code \u2705\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int: # // word = "a123bc34d8ef34"\n digit_index = 0\n digit_found = False\n number_list = []\n for i in range(len(word)):\n if word[i].isdigit() and not digit_found: # // condition will be true when i = 1,6,9,12\n digit_index = i \n digit_found = True\n if not word[i].isdigit() and digit_found: # // condition will be true when i = 4,8,10\n number_list.append(int(word[digit_index:i]))\n digit_found = False\n if i == len(word) -1 and digit_found: # // condition will be true when i = 13\n number_list.append(int(word[digit_index:i+1])) # // number_list = [123, 34, 8, 34]\n return len(set(number_list)) # // 3\n``` | 5 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Python | Easy Solution✅ | number-of-different-integers-in-a-string | 0 | 1 | # Code \u2705\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int: # // word = "a123bc34d8ef34"\n digit_index = 0\n digit_found = False\n number_list = []\n for i in range(len(word)):\n if word[i].isdigit() and not digit_found: # // condition will be true when i = 1,6,9,12\n digit_index = i \n digit_found = True\n if not word[i].isdigit() and digit_found: # // condition will be true when i = 4,8,10\n number_list.append(int(word[digit_index:i]))\n digit_found = False\n if i == len(word) -1 and digit_found: # // condition will be true when i = 13\n number_list.append(int(word[digit_index:i+1])) # // number_list = [123, 34, 8, 34]\n return len(set(number_list)) # // 3\n``` | 5 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
[Python3] Short and easy to understand | number-of-different-integers-in-a-string | 0 | 1 | We want to return only the part that matches the condition **(\'\\d+)\'** (matches one or more digits), then convert every element to **int** and the length of the **set(nums)** will be the answer.\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n word = re.findall(\'(\\d+)\', word)\n nums = [int(i) for i in word]\n \n return len(set(nums))\n``` | 9 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
[Python3] Short and easy to understand | number-of-different-integers-in-a-string | 0 | 1 | We want to return only the part that matches the condition **(\'\\d+)\'** (matches one or more digits), then convert every element to **int** and the length of the **set(nums)** will be the answer.\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n word = re.findall(\'(\\d+)\', word)\n nums = [int(i) for i in word]\n \n return len(set(nums))\n``` | 9 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Python set comprehension with itertools.groupby | number-of-different-integers-in-a-string | 0 | 1 | ```python []\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(\n set(\n int("".join(grp))\n for k, grp in groupby(word, key=lambda x: x.isdigit())\n if k\n )\n )\n\n``` | 3 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Python set comprehension with itertools.groupby | number-of-different-integers-in-a-string | 0 | 1 | ```python []\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(\n set(\n int("".join(grp))\n for k, grp in groupby(word, key=lambda x: x.isdigit())\n if k\n )\n )\n\n``` | 3 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
Very easy and straightfoward O(n) solution | number-of-different-integers-in-a-string | 0 | 1 | Runtime: 28 ms, faster than 91.62% of Python3 online submissions for Number of Different Integers in a String.\nMemory Usage: 14.1 MB, less than 95.04% of Python3 online submissions for Number of Different Integers in a String.\n\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n out = \'\'\n\t\t\n #Replace every non digits by spaces\n for char in word: \n if char.isdigit():\n out = out + char\n \n else:\n out = out + \' \'\n \n\t\t#Cleaning up None characters (double spaces) and converting digits from str to int\n out = out.split(\' \')\n out_ = []\n \n for number in out: \n if number != \'\':\n out_.append(int(number))\n \n\t\t#Using set() for filtering out repeat numbers\n return len(set(out_))\n``` | 4 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
Very easy and straightfoward O(n) solution | number-of-different-integers-in-a-string | 0 | 1 | Runtime: 28 ms, faster than 91.62% of Python3 online submissions for Number of Different Integers in a String.\nMemory Usage: 14.1 MB, less than 95.04% of Python3 online submissions for Number of Different Integers in a String.\n\n```\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n out = \'\'\n\t\t\n #Replace every non digits by spaces\n for char in word: \n if char.isdigit():\n out = out + char\n \n else:\n out = out + \' \'\n \n\t\t#Cleaning up None characters (double spaces) and converting digits from str to int\n out = out.split(\' \')\n out_ = []\n \n for number in out: \n if number != \'\':\n out_.append(int(number))\n \n\t\t#Using set() for filtering out repeat numbers\n return len(set(out_))\n``` | 4 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
One-line simple solution with regex | number-of-different-integers-in-a-string | 0 | 1 | # Code\n```python\nimport re\n\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(set(map(int, re.sub(r\'[a-z]\', \' \', word).split())))\n\n``` | 0 | You are given a string `word` that consists of digits and lowercase English letters.
You will replace every non-digit character with a space. For example, `"a123bc34d8ef34 "` will become `" 123 34 8 34 "`. Notice that you are left with some integers that are separated by at least one space: `"123 "`, `"34 "`, `"8 "`, and `"34 "`.
Return _the number of **different** integers after performing the replacement operations on_ `word`.
Two integers are considered different if their decimal representations **without any leading zeros** are different.
**Example 1:**
**Input:** word = "a123bc34d8ef34 "
**Output:** 3
**Explanation:** The three different integers are "123 ", "34 ", and "8 ". Notice that "34 " is only counted once.
**Example 2:**
**Input:** word = "leet1234code234 "
**Output:** 2
**Example 3:**
**Input:** word = "a1b01c001 "
**Output:** 1
**Explanation:** The three integers "1 ", "01 ", and "001 " all represent the same integer because
the leading zeros are ignored when comparing their decimal values.
**Constraints:**
* `1 <= word.length <= 1000`
* `word` consists of digits and lowercase English letters. | Choose k 1s and determine how many steps are required to move them into 1 group. Maintain a sliding window of k 1s, and maintain the steps required to group them. When you slide the window across, should you move the group to the right? Once you move the group to the right, it will never need to slide to the left again. |
One-line simple solution with regex | number-of-different-integers-in-a-string | 0 | 1 | # Code\n```python\nimport re\n\nclass Solution:\n def numDifferentIntegers(self, word: str) -> int:\n return len(set(map(int, re.sub(r\'[a-z]\', \' \', word).split())))\n\n``` | 0 | A **value-equal** string is a string where **all** characters are the same.
* For example, `"1111 "` and `"33 "` are value-equal strings.
* In contrast, `"123 "` is not a value-equal string.
Given a digit string `s`, decompose the string into some number of **consecutive value-equal** substrings where **exactly one** substring has a **length of** `2` and the remaining substrings have a **length of** `3`.
Return `true` _if you can decompose_ `s` _according to the above rules. Otherwise, return_ `false`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "000111000 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because \[ "000 ", "111 ", "000 "\] does not have a substring of length 2.
**Example 2:**
**Input:** s = "00011111222 "
**Output:** true
**Explanation:** s can be decomposed into \[ "000 ", "111 ", "11 ", "222 "\].
**Example 3:**
**Input:** s = "011100022233 "
**Output:** false
**Explanation:** s cannot be decomposed according to the rules because of the first '0'.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of only digits `'0'` through `'9'`. | Try to split the string so that each integer is in a different string. Try to remove each integer's leading zeroes and compare the strings to find how many of them are unique. |
[Python3] simulation | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | \n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n ans = 0\n perm = list(range(n))\n while True: \n ans += 1\n perm = [perm[n//2+(i-1)//2] if i&1 else perm[i//2] for i in range(n)]\n if all(perm[i] == i for i in range(n)): return ans\n``` | 4 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
[Python3] simulation | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | \n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n ans = 0\n perm = list(range(n))\n while True: \n ans += 1\n perm = [perm[n//2+(i-1)//2] if i&1 else perm[i//2] for i in range(n)]\n if all(perm[i] == i for i in range(n)): return ans\n``` | 4 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Very Easy Solution | Python3 | Simple To Understand | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Approach\n**Just Following what the problem description is saying thats it.**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n perm = []\n for i in range(0, n):\n perm.append(i)\n\n newPerm = perm\n operation = 0\n while(True):\n a = []\n for i in range(len(newPerm)):\n if i % 2 == 0:\n a.append(newPerm[i // 2])\n \n elif i % 2 == 1:\n a.append(newPerm[n // 2 + (i - 1) // 2])\n\n operation = operation + 1\n\n newPerm = a\n\n if newPerm == perm:\n return operation\n```\n**Please Upvote if you like the Solution :)** | 0 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
Very Easy Solution | Python3 | Simple To Understand | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Approach\n**Just Following what the problem description is saying thats it.**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n perm = []\n for i in range(0, n):\n perm.append(i)\n\n newPerm = perm\n operation = 0\n while(True):\n a = []\n for i in range(len(newPerm)):\n if i % 2 == 0:\n a.append(newPerm[i // 2])\n \n elif i % 2 == 1:\n a.append(newPerm[n // 2 + (i - 1) // 2])\n\n operation = operation + 1\n\n newPerm = a\n\n if newPerm == perm:\n return operation\n```\n**Please Upvote if you like the Solution :)** | 0 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Easy to understand Python3 solution | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n perm = []\n\n for i in range(n):\n perm.append(i)\n\n sample = perm[:]\n\n count = 0\n \n while True:\n test = [0] * len(perm)\n for i in range(len(test)):\n if i % 2 == 0:\n test[i] = perm[i // 2]\n else:\n test[i] = perm[n // 2 + (i-1) // 2]\n count += 1\n if test == sample:\n break\n perm = test\n \n return count\n \n``` | 0 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
Easy to understand Python3 solution | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n perm = []\n\n for i in range(n):\n perm.append(i)\n\n sample = perm[:]\n\n count = 0\n \n while True:\n test = [0] * len(perm)\n for i in range(len(test)):\n if i % 2 == 0:\n test[i] = perm[i // 2]\n else:\n test[i] = perm[n // 2 + (i-1) // 2]\n count += 1\n if test == sample:\n break\n perm = test\n \n return count\n \n``` | 0 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
[Python3] Brutal Force | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n orig = [i for i in range(n)]\n perm = [i for i in range(n)]\n arr = [0]*n\n \n cnt = 1\n for i in range(len(arr)):\n if i%2==0:\n arr[i] = perm[i//2]\n else:\n arr[i] = perm[n//2 + (i-1)//2]\n\n perm = arr\n\n while tuple(orig) != tuple(perm):\n arr = [0]*n\n for i in range(len(arr)):\n if i%2==0:\n arr[i] = perm[i//2]\n else:\n arr[i] = perm[n//2 + (i-1)//2]\n perm = arr\n cnt += 1\n\n return cnt\n``` | 0 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
[Python3] Brutal Force | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n orig = [i for i in range(n)]\n perm = [i for i in range(n)]\n arr = [0]*n\n \n cnt = 1\n for i in range(len(arr)):\n if i%2==0:\n arr[i] = perm[i//2]\n else:\n arr[i] = perm[n//2 + (i-1)//2]\n\n perm = arr\n\n while tuple(orig) != tuple(perm):\n arr = [0]*n\n for i in range(len(arr)):\n if i%2==0:\n arr[i] = perm[i//2]\n else:\n arr[i] = perm[n//2 + (i-1)//2]\n perm = arr\n cnt += 1\n\n return cnt\n``` | 0 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Python 3 - 4 liner Beats 99% | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Intuition\nFind the minimum $m$ such that $2^m - 1 \\text{ mod } n-1 = 0.$\n\n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n if n == 2: return 1\n m = 1\n while (2 ** m) % (n - 1) != 1: m += 1\n return m\n``` | 0 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
Python 3 - 4 liner Beats 99% | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Intuition\nFind the minimum $m$ such that $2^m - 1 \\text{ mod } n-1 = 0.$\n\n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n if n == 2: return 1\n m = 1\n while (2 ** m) % (n - 1) != 1: m += 1\n return m\n``` | 0 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
take care of perm = arr.copy(), you can try change it to perm = arr :P | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | \n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n goal = list(range(n))\n perm = list(range(n))\n arr = list(range(n))\n \n step = 0\n while True:\n for i in range(len(perm)):\n if i % 2==0:\n arr[i] = perm[i//2]\n else:\n arr[i] = perm[n//2 + (i-1)//2]\n step+=1\n perm = arr.copy()\n if arr == goal:\n break\n\n return step\n\n``` | 0 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
take care of perm = arr.copy(), you can try change it to perm = arr :P | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | \n# Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n goal = list(range(n))\n perm = list(range(n))\n arr = list(range(n))\n \n step = 0\n while True:\n for i in range(len(perm)):\n if i % 2==0:\n arr[i] = perm[i//2]\n else:\n arr[i] = perm[n//2 + (i-1)//2]\n step+=1\n perm = arr.copy()\n if arr == goal:\n break\n\n return step\n\n``` | 0 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
minimum-number-of-operations-to-reinitialize-a-permutation | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n b = 0\n l = []\n p = []\n for i in range(n):\n p.append(i)\n l.append(i)\n while True:\n for i in range(len(p)):\n if p[i]%2==0:\n a = (p[i]//2)\n p[i] = a\n elif p[i]%2!=0:\n a = (n//2 + (p[i]-1)//2)\n p[i] = a\n b+=1\n if p==l:\n return b\n break\n``` | 0 | You are given an **even** integer `n`. You initially have a permutation `perm` of size `n` where `perm[i] == i` **(0-indexed)**.
In one operation, you will create a new array `arr`, and for each `i`:
* If `i % 2 == 0`, then `arr[i] = perm[i / 2]`.
* If `i % 2 == 1`, then `arr[i] = perm[n / 2 + (i - 1) / 2]`.
You will then assign `arr` to `perm`.
Return _the minimum **non-zero** number of operations you need to perform on_ `perm` _to return the permutation to its initial value._
**Example 1:**
**Input:** n = 2
**Output:** 1
**Explanation:** perm = \[0,1\] initially.
After the 1st operation, perm = \[0,1\]
So it takes only 1 operation.
**Example 2:**
**Input:** n = 4
**Output:** 2
**Explanation:** perm = \[0,1,2,3\] initially.
After the 1st operation, perm = \[0,2,1,3\]
After the 2nd operation, perm = \[0,1,2,3\]
So it takes only 2 operations.
**Example 3:**
**Input:** n = 6
**Output:** 4
**Constraints:**
* `2 <= n <= 1000`
* `n` is even. | Simulate the tournament as given in the statement. Be careful when handling odd integers. |
minimum-number-of-operations-to-reinitialize-a-permutation | minimum-number-of-operations-to-reinitialize-a-permutation | 0 | 1 | # Code\n```\nclass Solution:\n def reinitializePermutation(self, n: int) -> int:\n b = 0\n l = []\n p = []\n for i in range(n):\n p.append(i)\n l.append(i)\n while True:\n for i in range(len(p)):\n if p[i]%2==0:\n a = (p[i]//2)\n p[i] = a\n elif p[i]%2!=0:\n a = (n//2 + (p[i]-1)//2)\n p[i] = a\n b+=1\n if p==l:\n return b\n break\n``` | 0 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Python Easy to Understand | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def evaluate(self, s: str, knowledge: List[List[str]]) -> str:\n d={}\n for i in knowledge:\n d[i[0]]=i[1]\n temp=\'\'\n res=\'\'\n flag=0\n for i in s:\n if i==\'(\':\n flag=1\n elif i!=\')\' and flag==1:\n temp=temp+i\n elif i==\')\':\n if temp in d.keys():\n res=res+d[temp]\n else:\n res=res+\'?\'\n temp=\'\'\n flag=0\n else:\n res=res+i\n return res\n\n``` | 1 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python: Regular Expression Solution | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | Runtime: 2292 ms, beats 56.60%\nMemory: 52.4 MB, beats 94.04%\n\n```python\nimport re\n\nclass Solution:\n def evaluate(self, s: str, knowledge: list[list[str]]) -> str:\n\t # Transform the list into a dictonary for quick lookups.\n knowledge = {k[0]: k[1] for k in knowledge}\n\t\t\n\t\t# Lookup function taking a Match object returning either the\n\t\t# value associated with a matched key or \'?\' if no such key exists.\n def lookup(match: re.Match) -> str:\n return knowledge.get(match.group(0)[1:-1], \'?\')\n\t\t\n\t\t# Regular expression substitition - pattern lazily looks for zero\n\t\t# or more characters between parentheses.\n return re.sub(r"\\(.*?\\)", lookup, s)\n``` | 1 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
✅ Python Simple Logic ✅ | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def evaluate(self, s: str, knowledge: List[List[str]]) -> str:\n d = {key:sol for key, sol in knowledge}\n ans = add = \'\'\n\n for char in s:\n if char == \'(\':\n ans += add\n add = \'\'\n elif char == \')\':\n ans += d[add] if add in d else \'?\'\n add = \'\'\n else:\n add += char\n\n return ans + add\n\n \n``` | 1 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Concise Two Pointers with HashMap | Beats 100% | Rust & Python | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)\\ extra\\ memory$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Rust Code\n```rust\nuse std::collections::HashMap;\nimpl Solution {\n pub fn evaluate(s: String, k: Vec<Vec<String>>) -> String {\n let map: HashMap<_, _> = k.iter().map(|p| (p[0].as_str(), p[1].as_str())).collect();\n let mut ans = String::with_capacity(s.len());\n let mut l = usize::MAX;\n\n for (r, ch) in s.chars().enumerate() {\n match ch {\n \'(\' => l = r + 1,\n \')\' => {\n ans.push_str(map.get(&s[l..r]).unwrap_or(&"?"));\n l = usize::MAX;\n }\n ch if l == usize::MAX => ans.push(ch),\n _ => (),\n }\n }\n\n ans\n }\n}\n```\n\n# Python3 Code\n```python\nclass Solution:\n def evaluate(self, s: str, knowledge: List[List[str]]) -> str:\n map = { k:v for [k, v] in knowledge }\n res, l = "", 0\n\n for (r, ch) in enumerate(s):\n if ch == \'(\':\n l = r + 1\n elif ch == \')\':\n res += map.get(s[l:r], \'?\')\n l = 0\n elif l == 0:\n res += ch\n \n return res\n``` | 0 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Straight Forward T:O(N)|S:O(N) Approach in Python | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | # Intuition\nSince each opening "(" must be closed by a ")", we can solve in one pass.\n\n# Approach\nConvert 2D list of key value pairs into a hashmap for every lookup. Go through the string and check for opening "(". If found continue untill you see a ")". Note here we are not technically doing an expensive double while loop b/c as per constraints, the length of a key is negligable compared to the size of the string.\n\n# Complexity\n- Time complexity:\nO(n): one time for creating the hashmap of key value pairs for faster lookup and once for iterating through the original string.\n\nO(n) + O(n) --> O(n) \n\n- Space complexity:\nO(n): space needed for hashmap of key value pairs and res list that stores all characters and their changes. \n\nO(n) + O(n) --> O(n) \n\n# Code\n```\nclass Solution:\n def evaluate(self, s: str, knowledge: List[List[str]]) -> str:\n\n # T: O(n) | S: O(n)\n def initial(s, knowledge):\n\n hmap = {}\n for info in knowledge:\n key, value = info\n hmap[key] = value\n\n res = []\n i = 0\n while i <= len(s) - 1:\n\n if s[i] == "(":\n currentWord = []\n i += 1\n while s[i] != ")":\n currentWord.append(s[i])\n i += 1\n \n myKey = "".join(currentWord)\n if myKey in hmap:\n res.append(hmap[myKey])\n else:\n res.append("?")\n\n else:\n res.append(s[i])\n\n i += 1\n\n return "".join(res)\n\n return initial(s, knowledge)\n\n \n``` | 0 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Python simple-solution | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | # Intuition\nUsing the flag to check whether the subsentence should be substituded or not. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def evaluate(self, s: str, knowledge: List[List[str]]) -> str:\n\n key_map = {\n key: value \n for key, value in knowledge\n }\n\n result = ""\n temp_key = ""\n flag = False \n\n for item in s:\n if item == \'(\':\n flag = True \n continue \n \n if item == \')\':\n flag = False \n if temp_key:\n result += key_map.get(temp_key, "?")\n temp_key = ""\n continue \n if not flag:\n result += item \n else:\n temp_key += item \n \n return result \n \n\n \n``` | 0 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
python3 parsing | evaluate-the-bracket-pairs-of-a-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def evaluate(self, s: str, knowledge: List[List[str]]) -> str:\n d = defaultdict(lambda : \'?\')\n res = \'\'\n for x,y in knowledge:\n d[x] = y\n i = 0\n while i < len(s):\n if s[i] != \'(\':\n res += s[i]\n i+=1\n continue\n else:\n i+=1\n temp = \'\'\n while s[i] != \')\':\n temp += s[i]\n i+=1\n res += d[temp]\n i+=1\n return res\n``` | 0 | You are given a string `s` that contains some bracket pairs, with each pair containing a **non-empty** key.
* For example, in the string `"(name)is(age)yearsold "`, there are **two** bracket pairs that contain the keys `"name "` and `"age "`.
You know the values of a wide range of keys. This is represented by a 2D string array `knowledge` where each `knowledge[i] = [keyi, valuei]` indicates that key `keyi` has a value of `valuei`.
You are tasked to evaluate **all** of the bracket pairs. When you evaluate a bracket pair that contains some key `keyi`, you will:
* Replace `keyi` and the bracket pair with the key's corresponding `valuei`.
* If you do not know the value of the key, you will replace `keyi` and the bracket pair with a question mark `"? "` (without the quotation marks).
Each key will appear at most once in your `knowledge`. There will not be any nested brackets in `s`.
Return _the resulting string after evaluating **all** of the bracket pairs._
**Example 1:**
**Input:** s = "(name)is(age)yearsold ", knowledge = \[\[ "name ", "bob "\],\[ "age ", "two "\]\]
**Output:** "bobistwoyearsold "
**Explanation:**
The key "name " has a value of "bob ", so replace "(name) " with "bob ".
The key "age " has a value of "two ", so replace "(age) " with "two ".
**Example 2:**
**Input:** s = "hi(name) ", knowledge = \[\[ "a ", "b "\]\]
**Output:** "hi? "
**Explanation:** As you do not know the value of the key "name ", replace "(name) " with "? ".
**Example 3:**
**Input:** s = "(a)(a)(a)aaa ", knowledge = \[\[ "a ", "yes "\]\]
**Output:** "yesyesyesaaa "
**Explanation:** The same key can appear multiple times.
The key "a " has a value of "yes ", so replace all occurrences of "(a) " with "yes ".
Notice that the "a "s not in a bracket pair are not evaluated.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= knowledge.length <= 105`
* `knowledge[i].length == 2`
* `1 <= keyi.length, valuei.length <= 10`
* `s` consists of lowercase English letters and round brackets `'('` and `')'`.
* Every open bracket `'('` in `s` will have a corresponding close bracket `')'`.
* The key in each bracket pair of `s` will be non-empty.
* There will not be any nested bracket pairs in `s`.
* `keyi` and `valuei` consist of lowercase English letters.
* Each `keyi` in `knowledge` is unique. | Think about if the input was only one digit. Then you need to add up as many ones as the value of this digit. If the input has multiple digits, then you can solve for each digit independently, and merge the answers to form numbers that add up to that input. Thus the answer is equal to the max digit. |
Solution | maximize-number-of-nice-divisors | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors <= 3:\n return primeFactors\n \n MOD = int(1e9 + 7)\n if primeFactors % 3 == 0:\n power = primeFactors // 3\n return self.calculateNiceDivisors(3, power, MOD)\n elif primeFactors % 3 == 1:\n power = (primeFactors // 3) - 1\n return (self.calculateNiceDivisors(3, power, MOD) * 4) % MOD\n else:\n power = primeFactors // 3\n return (self.calculateNiceDivisors(3, power, MOD) * 2) % MOD\n \n def calculateNiceDivisors(self, base: int, power: int, MOD: int) -> int:\n if power == 0:\n return 1\n\n result = self.calculateNiceDivisors(base, power // 2, MOD)\n result = (result * result) % MOD\n\n if power % 2 == 1:\n result = (result * base) % MOD\n\n return result\n\n``` | 0 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Solution | maximize-number-of-nice-divisors | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors <= 3:\n return primeFactors\n \n MOD = int(1e9 + 7)\n if primeFactors % 3 == 0:\n power = primeFactors // 3\n return self.calculateNiceDivisors(3, power, MOD)\n elif primeFactors % 3 == 1:\n power = (primeFactors // 3) - 1\n return (self.calculateNiceDivisors(3, power, MOD) * 4) % MOD\n else:\n power = primeFactors // 3\n return (self.calculateNiceDivisors(3, power, MOD) * 2) % MOD\n \n def calculateNiceDivisors(self, base: int, power: int, MOD: int) -> int:\n if power == 0:\n return 1\n\n result = self.calculateNiceDivisors(base, power // 2, MOD)\n result = (result * result) % MOD\n\n if power % 2 == 1:\n result = (result * base) % MOD\n\n return result\n\n``` | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Python3 solution exPlained | maximize-number-of-nice-divisors | 0 | 1 | # Intuition\nThe goal of this problem is to find the maximum number of nice divisors of a given number, where a nice divisor is a number that is a product of only prime numbers. My first thought is to use a combination of prime factorization and dynamic programming to find the maximum number of nice divisors for a given number.\n\n# Approach\nThe solution to this problem can be found using a combination of prime factorization and dynamic programming. First, the given number must be factorized into its prime factors. Then, we can use dynamic programming to find the maximum number of nice divisors for a given prime factorization. \n\nTo solve this problem using dynamic programming, we can start by considering the base cases of a prime factorization with 1, 2, and 3 prime factors. For a prime factorization with 1 prime factor, the maximum number of nice divisors is 1. For a prime factorization with 2 prime factors, the maximum number of nice divisors is 2. And for a prime factorization with 3 prime factors, the maximum number of nice divisors is 3. \n\nNow, we can use these base cases to find the maximum number of nice divisors for a prime factorization with more than 3 prime factors. To do this, we can consider the prime factorization as a sequence of prime factors, and we can consider each prime factor as a step in the sequence. Then, we can use dynamic programming to find the maximum number of nice divisors for a given sequence of prime factors. \n\nFor example, for a prime factorization with 4 prime factors, the maximum number of nice divisors is 4. This can be seen by considering the prime factorization as a sequence of prime factors, and considering each prime factor as a step in the sequence. Then, we can use dynamic programming to find the maximum number of nice divisors for a given sequence of prime factors. \n\nFor a sequence of 4 prime factors, the maximum number of nice divisors is 4. This can be seen by considering the sequence as a set of 4 prime factors. Then, we can use dynamic programming to find the maximum number of nice divisors for a given set of prime factors. \n\nFor a set of 4 prime factors, the maximum number of nice divisors is 4. This can be seen by considering the set as a product of 4 prime factors. Then, we can use dynamic programming to find the maximum number of nice divisors for a given product of prime factors. \n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors <= 3:\n return primeFactors\n if primeFactors % 3 == 0:\n return pow(3, primeFactors // 3, 1000000007)\n if primeFactors % 3 == 1:\n return pow(3, primeFactors // 3 - 1, 1000000007) * 4 % 1000000007\n return pow(3, primeFactors // 3, 1000000007) * 2 % 1000000007\n``` | 0 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Python3 solution exPlained | maximize-number-of-nice-divisors | 0 | 1 | # Intuition\nThe goal of this problem is to find the maximum number of nice divisors of a given number, where a nice divisor is a number that is a product of only prime numbers. My first thought is to use a combination of prime factorization and dynamic programming to find the maximum number of nice divisors for a given number.\n\n# Approach\nThe solution to this problem can be found using a combination of prime factorization and dynamic programming. First, the given number must be factorized into its prime factors. Then, we can use dynamic programming to find the maximum number of nice divisors for a given prime factorization. \n\nTo solve this problem using dynamic programming, we can start by considering the base cases of a prime factorization with 1, 2, and 3 prime factors. For a prime factorization with 1 prime factor, the maximum number of nice divisors is 1. For a prime factorization with 2 prime factors, the maximum number of nice divisors is 2. And for a prime factorization with 3 prime factors, the maximum number of nice divisors is 3. \n\nNow, we can use these base cases to find the maximum number of nice divisors for a prime factorization with more than 3 prime factors. To do this, we can consider the prime factorization as a sequence of prime factors, and we can consider each prime factor as a step in the sequence. Then, we can use dynamic programming to find the maximum number of nice divisors for a given sequence of prime factors. \n\nFor example, for a prime factorization with 4 prime factors, the maximum number of nice divisors is 4. This can be seen by considering the prime factorization as a sequence of prime factors, and considering each prime factor as a step in the sequence. Then, we can use dynamic programming to find the maximum number of nice divisors for a given sequence of prime factors. \n\nFor a sequence of 4 prime factors, the maximum number of nice divisors is 4. This can be seen by considering the sequence as a set of 4 prime factors. Then, we can use dynamic programming to find the maximum number of nice divisors for a given set of prime factors. \n\nFor a set of 4 prime factors, the maximum number of nice divisors is 4. This can be seen by considering the set as a product of 4 prime factors. Then, we can use dynamic programming to find the maximum number of nice divisors for a given product of prime factors. \n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors <= 3:\n return primeFactors\n if primeFactors % 3 == 0:\n return pow(3, primeFactors // 3, 1000000007)\n if primeFactors % 3 == 1:\n return pow(3, primeFactors // 3 - 1, 1000000007) * 4 % 1000000007\n return pow(3, primeFactors // 3, 1000000007) * 2 % 1000000007\n``` | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Python 3 Solution | Better than 100% at runtime | Better than 91.43% at memory | maximize-number-of-nice-divisors | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors == 1:\n return 1\n Mod = 1_000_000_007\n num2 = -primeFactors%3\n num3 = (primeFactors - primeFactors%3*(-primeFactors%3))//3\n return (pow(2,num2))*(pow(3,num3,Mod))%Mod\n```\n\n# The one-liner\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n return (pow(2,-primeFactors%3))*(pow(3,(primeFactors - primeFactors%3*(-primeFactors%3))//3,1_000_000_007))%1_000_000_007 if primeFactors != 1 else 1\n``` | 0 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Python 3 Solution | Better than 100% at runtime | Better than 91.43% at memory | maximize-number-of-nice-divisors | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors == 1:\n return 1\n Mod = 1_000_000_007\n num2 = -primeFactors%3\n num3 = (primeFactors - primeFactors%3*(-primeFactors%3))//3\n return (pow(2,num2))*(pow(3,num3,Mod))%Mod\n```\n\n# The one-liner\n```\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n return (pow(2,-primeFactors%3))*(pow(3,(primeFactors - primeFactors%3*(-primeFactors%3))//3,1_000_000_007))%1_000_000_007 if primeFactors != 1 else 1\n``` | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Solution | maximize-number-of-nice-divisors | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int maxNiceDivisors(int primeFactors) {\n if (primeFactors <= 3)\n return primeFactors;\n if (primeFactors % 3 == 0)\n return myPow(3, primeFactors / 3) % kMod;\n if (primeFactors % 3 == 1)\n return (4 * myPow(3, (primeFactors - 4) / 3)) % kMod;\n return (2 * myPow(3, (primeFactors - 2) / 3)) % kMod;\n }\n\n private:\n constexpr static int kMod = 1\'000\'000\'007;\n\n long myPow(long x, long n) {\n if (n == 0)\n return 1;\n if (n & 1)\n return x * myPow(x % kMod, (n - 1) % kMod) % kMod;\n return myPow(x * x % kMod, (n / 2) % kMod) % kMod;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors == 1:\n return 1\n Mod = 1_000_000_007\n num2 = -primeFactors%3\n num3 = (primeFactors - primeFactors%3*(-primeFactors%3))//3\n return (pow(2,num2))*(pow(3,num3,Mod))%Mod\n```\n\n```Java []\nclass Solution {\n\nlong mod = 1000000007;\n\npublic int maxNiceDivisors(int n) {\n long ans = 0;\n if(n == 1)\n return 1;\n \n if(n%3 == 0) ans = power(3, n/3);\n if(n%3 == 1) ans = (4*power(3,n/3-1))%mod;\n if(n%3 == 2) ans = (2*power(3,n/3))%mod;\n \n return (int)ans;\n \n}\n\nlong power(int b, int x){\n if(x == 0)\n return 1;\n \n long ans = power(b, x/2);\n \n \n if(x % 2 != 0)\n return (ans*ans*b)%mod;\n \n return (ans*ans)%mod;\n}\n}\n```\n | 0 | You are given a positive integer `primeFactors`. You are asked to construct a positive integer `n` that satisfies the following conditions:
* The number of prime factors of `n` (not necessarily distinct) is **at most** `primeFactors`.
* The number of nice divisors of `n` is maximized. Note that a divisor of `n` is **nice** if it is divisible by every prime factor of `n`. For example, if `n = 12`, then its prime factors are `[2,2,3]`, then `6` and `12` are nice divisors, while `3` and `4` are not.
Return _the number of nice divisors of_ `n`. Since that number can be too large, return it **modulo** `109 + 7`.
Note that a prime number is a natural number greater than `1` that is not a product of two smaller natural numbers. The prime factors of a number `n` is a list of prime numbers such that their product equals `n`.
**Example 1:**
**Input:** primeFactors = 5
**Output:** 6
**Explanation:** 200 is a valid value of n.
It has 5 prime factors: \[2,2,2,5,5\], and it has 6 nice divisors: \[10,20,40,50,100,200\].
There is not other value of n that has at most 5 prime factors and more nice divisors.
**Example 2:**
**Input:** primeFactors = 8
**Output:** 18
**Constraints:**
* `1 <= primeFactors <= 109` | The constraints are small enough for an N^2 solution. Try using dynamic programming. |
Solution | maximize-number-of-nice-divisors | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int maxNiceDivisors(int primeFactors) {\n if (primeFactors <= 3)\n return primeFactors;\n if (primeFactors % 3 == 0)\n return myPow(3, primeFactors / 3) % kMod;\n if (primeFactors % 3 == 1)\n return (4 * myPow(3, (primeFactors - 4) / 3)) % kMod;\n return (2 * myPow(3, (primeFactors - 2) / 3)) % kMod;\n }\n\n private:\n constexpr static int kMod = 1\'000\'000\'007;\n\n long myPow(long x, long n) {\n if (n == 0)\n return 1;\n if (n & 1)\n return x * myPow(x % kMod, (n - 1) % kMod) % kMod;\n return myPow(x * x % kMod, (n / 2) % kMod) % kMod;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxNiceDivisors(self, primeFactors: int) -> int:\n if primeFactors == 1:\n return 1\n Mod = 1_000_000_007\n num2 = -primeFactors%3\n num3 = (primeFactors - primeFactors%3*(-primeFactors%3))//3\n return (pow(2,num2))*(pow(3,num3,Mod))%Mod\n```\n\n```Java []\nclass Solution {\n\nlong mod = 1000000007;\n\npublic int maxNiceDivisors(int n) {\n long ans = 0;\n if(n == 1)\n return 1;\n \n if(n%3 == 0) ans = power(3, n/3);\n if(n%3 == 1) ans = (4*power(3,n/3-1))%mod;\n if(n%3 == 2) ans = (2*power(3,n/3))%mod;\n \n return (int)ans;\n \n}\n\nlong power(int b, int x){\n if(x == 0)\n return 1;\n \n long ans = power(b, x/2);\n \n \n if(x % 2 != 0)\n return (ans*ans*b)%mod;\n \n return (ans*ans)%mod;\n}\n}\n```\n | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.