title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Heap using max difference | maximum-average-pass-ratio | 0 | 1 | use a heap sorted by: currentPassRate - nextPassRate\nthe first element will be the best one since it will have greatest impact\nthe second element is the index which we use to update where we put student\n# Code\n```\ndef maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n classPass = [(a/b - (a+1)/(b+1), i) for i, (a,b) in enumerate(classes)]\n heapq.heapify(classPass)\n toAdd = extraStudents\n # improve lowest\n while toAdd > 0:\n _, i = heapq.heappop(classPass)\n p,t = classes[i]\n classes[i] = [p+1, t+1]\n heapq.heappush(classPass, ((p+1)/(t+1)- (p+2)/(t+2), i))\n toAdd -= 1\n return sum([a/b for a,b in classes]) / len(classes)\n``` | 0 | There is a school that has classes of students and each class will be having a final exam. You are given a 2D integer array `classes`, where `classes[i] = [passi, totali]`. You know beforehand that in the `ith` class, there are `totali` total students, but only `passi` number of students will pass the exam.
You are also given an integer `extraStudents`. There are another `extraStudents` brilliant students that are **guaranteed** to pass the exam of any class they are assigned to. You want to assign each of the `extraStudents` students to a class in a way that **maximizes** the **average** pass ratio across **all** the classes.
The **pass ratio** of a class is equal to the number of students of the class that will pass the exam divided by the total number of students of the class. The **average pass ratio** is the sum of pass ratios of all the classes divided by the number of the classes.
Return _the **maximum** possible average pass ratio after assigning the_ `extraStudents` _students._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** classes = \[\[1,2\],\[3,5\],\[2,2\]\], `extraStudents` = 2
**Output:** 0.78333
**Explanation:** You can assign the two extra students to the first class. The average pass ratio will be equal to (3/4 + 3/5 + 2/2) / 3 = 0.78333.
**Example 2:**
**Input:** classes = \[\[2,4\],\[3,9\],\[4,5\],\[2,10\]\], `extraStudents` = 4
**Output:** 0.53485
**Constraints:**
* `1 <= classes.length <= 105`
* `classes[i].length == 2`
* `1 <= passi <= totali <= 105`
* `1 <= extraStudents <= 105` | In lexicographical order, the elements to the left have higher priority than those that come after. Can you think of a strategy that incrementally builds the answer from left to right? |
Heap || Python3 | maximum-average-pass-ratio | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Check what is the fraction that is adding up most at every stage and add each extra student in that class\n\n# Approach\n- With heap\n\n# Complexity\n- Time complexity:\n- O(NlogN)\n\n- Space complexity:\n- O(N)\n\n# Code\n```\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n heap = []\n for i in range(len(classes)):\n ratio_curr = classes[i][0]/(1.0*classes[i][1])\n ratio = (classes[i][0]+1)/(1.0*(classes[i][1]+1))\n heapq.heappush(heap,(ratio_curr - ratio,i))\n while extraStudents != 0:\n ele = heapq.heappop(heap)\n index = ele[1]\n classes[index][0]+=1\n classes[index][1]+=1\n ratio_curr = classes[index][0]/(1.0*classes[index][1])\n ratio = (classes[index][0]+1)/(1.0*(classes[index][1]+1))\n heapq.heappush(heap,(ratio_curr-ratio,index))\n extraStudents-=1\n total = 0\n for i in range(len(classes)):\n total+=(classes[i][0]/classes[i][1])\n return total/len(classes)\n # return 2\n \n\n\n``` | 0 | There is a school that has classes of students and each class will be having a final exam. You are given a 2D integer array `classes`, where `classes[i] = [passi, totali]`. You know beforehand that in the `ith` class, there are `totali` total students, but only `passi` number of students will pass the exam.
You are also given an integer `extraStudents`. There are another `extraStudents` brilliant students that are **guaranteed** to pass the exam of any class they are assigned to. You want to assign each of the `extraStudents` students to a class in a way that **maximizes** the **average** pass ratio across **all** the classes.
The **pass ratio** of a class is equal to the number of students of the class that will pass the exam divided by the total number of students of the class. The **average pass ratio** is the sum of pass ratios of all the classes divided by the number of the classes.
Return _the **maximum** possible average pass ratio after assigning the_ `extraStudents` _students._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** classes = \[\[1,2\],\[3,5\],\[2,2\]\], `extraStudents` = 2
**Output:** 0.78333
**Explanation:** You can assign the two extra students to the first class. The average pass ratio will be equal to (3/4 + 3/5 + 2/2) / 3 = 0.78333.
**Example 2:**
**Input:** classes = \[\[2,4\],\[3,9\],\[4,5\],\[2,10\]\], `extraStudents` = 4
**Output:** 0.53485
**Constraints:**
* `1 <= classes.length <= 105`
* `classes[i].length == 2`
* `1 <= passi <= totali <= 105`
* `1 <= extraStudents <= 105` | In lexicographical order, the elements to the left have higher priority than those that come after. Can you think of a strategy that incrementally builds the answer from left to right? |
python | maximum-average-pass-ratio | 0 | 1 | Things become a lot easier after looking at hints\n# Code\n```\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], s: int) -> float:\n n = len(classes)\n h = []\n heapq.heapify(h)\n\n for i in range(n):\n change = ((classes[i][0]+1)/(classes[i][1]+1)) - (classes[i][0]/classes[i][1])\n heapq.heappush(h, (-change, i))\n \n while s> 0:\n a, idx = heapq.heappop(h)\n classes[idx][0] += 1\n classes[idx][1] += 1\n s -= 1\n change = ((classes[idx][0]+1)/(classes[idx][1]+1)) - (classes[idx][0]/classes[idx][1])\n heapq.heappush(h, (-change, idx))\n \n res = 0\n for i in range(n):\n res += classes[i][0]/classes[i][1]\n \n return res/n\n\n``` | 0 | There is a school that has classes of students and each class will be having a final exam. You are given a 2D integer array `classes`, where `classes[i] = [passi, totali]`. You know beforehand that in the `ith` class, there are `totali` total students, but only `passi` number of students will pass the exam.
You are also given an integer `extraStudents`. There are another `extraStudents` brilliant students that are **guaranteed** to pass the exam of any class they are assigned to. You want to assign each of the `extraStudents` students to a class in a way that **maximizes** the **average** pass ratio across **all** the classes.
The **pass ratio** of a class is equal to the number of students of the class that will pass the exam divided by the total number of students of the class. The **average pass ratio** is the sum of pass ratios of all the classes divided by the number of the classes.
Return _the **maximum** possible average pass ratio after assigning the_ `extraStudents` _students._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** classes = \[\[1,2\],\[3,5\],\[2,2\]\], `extraStudents` = 2
**Output:** 0.78333
**Explanation:** You can assign the two extra students to the first class. The average pass ratio will be equal to (3/4 + 3/5 + 2/2) / 3 = 0.78333.
**Example 2:**
**Input:** classes = \[\[2,4\],\[3,9\],\[4,5\],\[2,10\]\], `extraStudents` = 4
**Output:** 0.53485
**Constraints:**
* `1 <= classes.length <= 105`
* `classes[i].length == 2`
* `1 <= passi <= totali <= 105`
* `1 <= extraStudents <= 105` | In lexicographical order, the elements to the left have higher priority than those that come after. Can you think of a strategy that incrementally builds the answer from left to right? |
🚀 Monotonic Stack || Explained Intuition 🚀 | maximum-score-of-a-good-subarray | 1 | 1 | # Problem Description\n\nGiven an array of integers `nums` and an integer `k`, find the **maximum** score of a **good** subarray. \nA **good** subarray is one that contains the element at index `k` and is defined by the **product** of the **minimum** value within the subarray and its **length**. Where `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)` and `i <= k <= j`.\n\n- Constraints:\n - `1 <= nums.length <= 10e5`\n - `1 <= nums[i] <= 2 * 10e4`\n - `0 <= k < nums.length`\n\n---\n\n\n\n# Intuition\n\nHi there friends,\uD83D\uDE03\n\nLet\'s take a look\uD83D\uDC40 into our today\'s problem.\nIn our today\'s problem we have some **formula** for calculating the score for a subarray and a number `k` that we must include in our subarray.\uD83E\uDD28\nThe formula indicates that the **minimum** element in the subarray should be **multiplied** by its **length**.\n\nThe **first solution** that can pop\uD83C\uDF7F into mind is to calculate the score for all **possible subarrays** and take the maximum score for subarrays that includes `k` in it.\nUnfortunately, It will give **TLE** since it is $O(N^2)$.\uD83D\uDE22\n\nCan we do better?\uD83E\uDD14\nActually, we can !\uD83E\uDD2F\nI will pretend like every time that I didn\'t say the solution in the title.\uD83D\uDE02\n\n- Let\'s revise what we need in our problem:\n - **good** subarray with element `K` in it.\n - **maximum** score for this subarray.\n\nSome people -I was one of them- can think of **fixing** the `K\'th` element and search **around** it for the best subarray but why don\'t we change our **prespective** a little ?\uD83E\uDD14\nInstead of fixing `K\'th` element why don\'t we iterate over the array and **fix** the `i\'th` element as the **minimum** element in its subarray and search if `k` is within this subarray -that the lower element of it is `i\'th` element-.\n\nLet\'s see for the array: (5, 8, 14, 20, 3, 1, 7), k = 2\n\n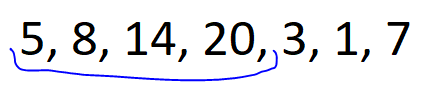\nFor element 5 -> `k` is within the subarray.\nscore = 5 * 4 =20\n\n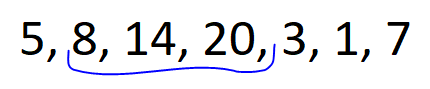\nFor element 8 -> `k` is within the subarray.\nscore = 8 * 3 = 24\n\n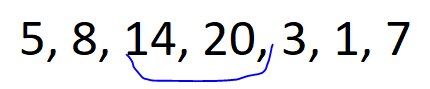\nFor element 14 -> `k` is within the subarray.\nscore = 14 * 2 = 28\n\n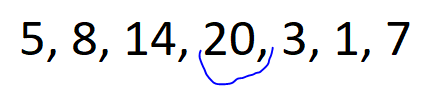\nFor element 20 -> `k` is **not** within the subarray.\n\n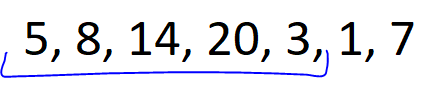\nFor element 3 -> `k` is within the subarray.\nscore = 3 * 5 = 15\n\n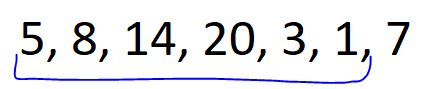\nFor element 1 -> `k` is within the subarray.\nscore = 1 * 6 = 6\n\n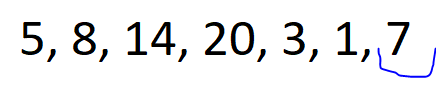\nFor element 20 -> `k` is **not** within the subarray.\n\nThe **best** score = `28` for subarray `(2, 3)` inclusive.\n\nI think, this approach will succesed but how can we implement it?\nThis is a job for our today\'s hero **Monotonic Stack**.\uD83E\uDDB8\u200D\u2642\uFE0F\n\n**Monotonic Stack** is a great data structure that preserve elements in it **sorted** -increasily or decreasily- so we can use it for each element to know the exact element **lower** than them in certain **range**.\nthen after computing the lower element from **left** and **right** we can iterate over each element and see what is the score for the subarray that this element is the **minimum** element in it.\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n\n# Approach\n1. **Initialize** two vectors `leftBoundary` and `rightBoundary`, which will store the next **lower** element to the **left** and **right** of each element, respectively.\n2. Create two **stacks**, `leftStack` and `rightStack`, both functioning as **monotonic** stacks.\n3. Begin by calculating the next **lower** element from the **left** side of the array.\n4. iterate through `nums` in **reverse** order:\n - check if `leftStack` is not empty and if the **current** element is **smaller** than the top element in `leftStack`. \n - If true, set the **left** boundary for the elements in `leftStack` to the current element\'s index and remove them from `leftStack` which indicates that the current element is the next lower for the top of the stack. \n - Push the current element onto `leftStack`.\n5. Continue by calculating the next **lower** element from the **right** side of the array. Iterate through `nums` from the **start** to the end and the same conditions.\n6. **Iterate** through `nums` once more. For each element `i`:\n - check if `k` is **within** the subarray that element `i` is the **minimum** element in it.\n - If true, calculate the **score** for this subarray.\n - Update `maxScore`.\n7. Finally, return `maxScore`.\n\n# Complexity\n- **Time complexity:** $O(N)$\nSince we are iterating over the array **three** times each whith cost `N` then total cost is `3 * N` so the total complexity is `O(N)`.\n- **Space complexity:** $O(N)$\nSince we are for each element, we store the next lower element from right and left and we have two stacks each can store at most `N` elements then total cost is `4 * N` so the total complexity is `O(N)`.\n\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n \n vector<int> leftBoundary(n, -1); // Store the next lower element from the left.\n vector<int> rightBoundary(n, n); // Store the next lower element from the right.\n \n stack<int> leftStack; // Monotonic Stack to help calculate left array.\n stack<int> rightStack; // Monotonic Stack to help calculate right array.\n \n // Calculate next lower element from the left.\n for (int i = n - 1; i >= 0; i--) {\n while (!leftStack.empty() && nums[leftStack.top()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the left boundary for those elements to the current element\'s index.\n leftBoundary[leftStack.top()] = i;\n leftStack.pop();\n }\n leftStack.push(i);\n }\n \n // Calculate next lower element from the right\n for (int i = 0; i < n; i++) {\n while (!rightStack.empty() && nums[rightStack.top()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the right boundary for those elements to the current element\'s index.\n rightBoundary[rightStack.top()] = i; \n rightStack.pop();\n }\n rightStack.push(i);\n }\n \n int maxScore = 0; // Initialize the maximum score to 0.\n \n // Calculate the maximum score for good subarrays\n for (int i = 0; i < n; i++) {\n if (leftBoundary[i] < k && rightBoundary[i] > k) {\n // Calculate the score for the subarray that contains element \'k\'.\n int subarrayScore = nums[i] * (rightBoundary[i] - leftBoundary[i] - 1);\n maxScore = max(maxScore, subarrayScore); // Update the maximum score.\n }\n }\n \n return maxScore; // Return the maximum score for a good subarray.\n }\n};\n\n```\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int n = nums.length;\n\n int[] leftBoundary = new int[n]; // Store the next lower element from the left.\n int[] rightBoundary = new int[n]; // Store the next lower element from the right.\n for(int i = 0 ;i < n ; i ++){\n leftBoundary[i] = -1;\n rightBoundary[i] = n ;\n }\n\n Stack<Integer> leftStack = new Stack<>(); // Monotonic Stack to help calculate left array.\n Stack<Integer> rightStack = new Stack<>(); // Monotonic Stack to help calculate right array.\n\n // Calculate next lower element from the left.\n for (int i = n - 1; i >= 0; i--) {\n while (!leftStack.empty() && nums[leftStack.peek()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the left boundary for those elements to the current element\'s index.\n leftBoundary[leftStack.pop()] = i;\n }\n leftStack.push(i);\n }\n\n // Calculate next lower element from the right\n for (int i = 0; i < n; i++) {\n while (!rightStack.empty() && nums[rightStack.peek()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the right boundary for those elements to the current element\'s index.\n rightBoundary[rightStack.pop()] = i;\n }\n rightStack.push(i);\n }\n\n int maxScore = 0; // Initialize the maximum score to 0.\n\n // Calculate the maximum score for good subarrays\n for (int i = 0; i < n; i++) {\n if (leftBoundary[i] < k && rightBoundary[i] > k) {\n // Calculate the score for the subarray that contains element \'k\'.\n int subarrayScore = nums[i] * (rightBoundary[i] - leftBoundary[i] - 1);\n maxScore = Math.max(maxScore, subarrayScore); // Update the maximum score.\n }\n }\n\n return maxScore; // Return the maximum score for a good subarray.\n }\n}\n```\n```Python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n n = len(nums)\n\n leftBoundary = [-1] * n # Store the next lower element from the left.\n rightBoundary = [n] * n # Store the next lower element from the right.\n\n leftStack = [] # Monotonic Stack to help calculate left array.\n rightStack = [] # Monotonic Stack to help calculate right array.\n\n # Calculate next lower element from the left.\n for i in range(n - 1, -1, -1):\n while leftStack and nums[leftStack[-1]] > nums[i]:\n # If the current element is smaller than elements in the stack,\n # set the left boundary for those elements to the current element\'s index.\n leftBoundary[leftStack[-1]] = i\n leftStack.pop()\n leftStack.append(i)\n\n # Calculate next lower element from the right.\n for i in range(n):\n while rightStack and nums[rightStack[-1]] > nums[i]:\n # If the current element is smaller than elements in the stack,\n # set the right boundary for those elements to the current element\'s index.\n rightBoundary[rightStack[-1]] = i\n rightStack.pop()\n rightStack.append(i)\n\n maxScore = 0 # Initialize the maximum score to 0.\n\n # Calculate the maximum score for good subarrays.\n for i in range(n):\n if leftBoundary[i] < k and rightBoundary[i] > k:\n # Calculate the score for the subarray that contains element \'k\'.\n subarrayScore = nums[i] * (rightBoundary[i] - leftBoundary[i] - 1)\n maxScore = max(maxScore, subarrayScore) # Update the maximum score.\n\n return maxScore # Return the maximum score for a good subarray.\n```\n\n\n\n\n | 29 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
🚀 Monotonic Stack || Explained Intuition 🚀 | maximum-score-of-a-good-subarray | 1 | 1 | # Problem Description\n\nGiven an array of integers `nums` and an integer `k`, find the **maximum** score of a **good** subarray. \nA **good** subarray is one that contains the element at index `k` and is defined by the **product** of the **minimum** value within the subarray and its **length**. Where `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)` and `i <= k <= j`.\n\n- Constraints:\n - `1 <= nums.length <= 10e5`\n - `1 <= nums[i] <= 2 * 10e4`\n - `0 <= k < nums.length`\n\n---\n\n\n\n# Intuition\n\nHi there friends,\uD83D\uDE03\n\nLet\'s take a look\uD83D\uDC40 into our today\'s problem.\nIn our today\'s problem we have some **formula** for calculating the score for a subarray and a number `k` that we must include in our subarray.\uD83E\uDD28\nThe formula indicates that the **minimum** element in the subarray should be **multiplied** by its **length**.\n\nThe **first solution** that can pop\uD83C\uDF7F into mind is to calculate the score for all **possible subarrays** and take the maximum score for subarrays that includes `k` in it.\nUnfortunately, It will give **TLE** since it is $O(N^2)$.\uD83D\uDE22\n\nCan we do better?\uD83E\uDD14\nActually, we can !\uD83E\uDD2F\nI will pretend like every time that I didn\'t say the solution in the title.\uD83D\uDE02\n\n- Let\'s revise what we need in our problem:\n - **good** subarray with element `K` in it.\n - **maximum** score for this subarray.\n\nSome people -I was one of them- can think of **fixing** the `K\'th` element and search **around** it for the best subarray but why don\'t we change our **prespective** a little ?\uD83E\uDD14\nInstead of fixing `K\'th` element why don\'t we iterate over the array and **fix** the `i\'th` element as the **minimum** element in its subarray and search if `k` is within this subarray -that the lower element of it is `i\'th` element-.\n\nLet\'s see for the array: (5, 8, 14, 20, 3, 1, 7), k = 2\n\n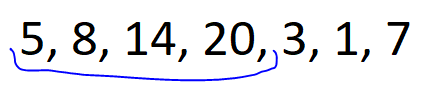\nFor element 5 -> `k` is within the subarray.\nscore = 5 * 4 =20\n\n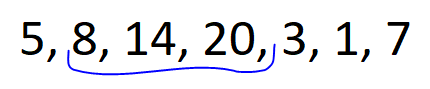\nFor element 8 -> `k` is within the subarray.\nscore = 8 * 3 = 24\n\n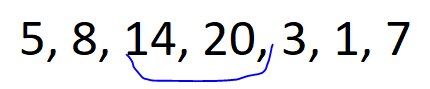\nFor element 14 -> `k` is within the subarray.\nscore = 14 * 2 = 28\n\n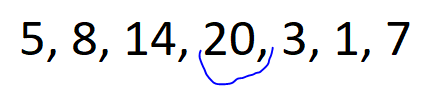\nFor element 20 -> `k` is **not** within the subarray.\n\n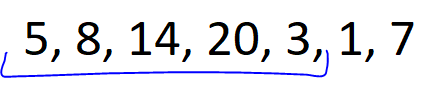\nFor element 3 -> `k` is within the subarray.\nscore = 3 * 5 = 15\n\n\nFor element 1 -> `k` is within the subarray.\nscore = 1 * 6 = 6\n\n\nFor element 20 -> `k` is **not** within the subarray.\n\nThe **best** score = `28` for subarray `(2, 3)` inclusive.\n\nI think, this approach will succesed but how can we implement it?\nThis is a job for our today\'s hero **Monotonic Stack**.\uD83E\uDDB8\u200D\u2642\uFE0F\n\n**Monotonic Stack** is a great data structure that preserve elements in it **sorted** -increasily or decreasily- so we can use it for each element to know the exact element **lower** than them in certain **range**.\nthen after computing the lower element from **left** and **right** we can iterate over each element and see what is the score for the subarray that this element is the **minimum** element in it.\n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n\n\n# Approach\n1. **Initialize** two vectors `leftBoundary` and `rightBoundary`, which will store the next **lower** element to the **left** and **right** of each element, respectively.\n2. Create two **stacks**, `leftStack` and `rightStack`, both functioning as **monotonic** stacks.\n3. Begin by calculating the next **lower** element from the **left** side of the array.\n4. iterate through `nums` in **reverse** order:\n - check if `leftStack` is not empty and if the **current** element is **smaller** than the top element in `leftStack`. \n - If true, set the **left** boundary for the elements in `leftStack` to the current element\'s index and remove them from `leftStack` which indicates that the current element is the next lower for the top of the stack. \n - Push the current element onto `leftStack`.\n5. Continue by calculating the next **lower** element from the **right** side of the array. Iterate through `nums` from the **start** to the end and the same conditions.\n6. **Iterate** through `nums` once more. For each element `i`:\n - check if `k` is **within** the subarray that element `i` is the **minimum** element in it.\n - If true, calculate the **score** for this subarray.\n - Update `maxScore`.\n7. Finally, return `maxScore`.\n\n# Complexity\n- **Time complexity:** $O(N)$\nSince we are iterating over the array **three** times each whith cost `N` then total cost is `3 * N` so the total complexity is `O(N)`.\n- **Space complexity:** $O(N)$\nSince we are for each element, we store the next lower element from right and left and we have two stacks each can store at most `N` elements then total cost is `4 * N` so the total complexity is `O(N)`.\n\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n \n vector<int> leftBoundary(n, -1); // Store the next lower element from the left.\n vector<int> rightBoundary(n, n); // Store the next lower element from the right.\n \n stack<int> leftStack; // Monotonic Stack to help calculate left array.\n stack<int> rightStack; // Monotonic Stack to help calculate right array.\n \n // Calculate next lower element from the left.\n for (int i = n - 1; i >= 0; i--) {\n while (!leftStack.empty() && nums[leftStack.top()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the left boundary for those elements to the current element\'s index.\n leftBoundary[leftStack.top()] = i;\n leftStack.pop();\n }\n leftStack.push(i);\n }\n \n // Calculate next lower element from the right\n for (int i = 0; i < n; i++) {\n while (!rightStack.empty() && nums[rightStack.top()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the right boundary for those elements to the current element\'s index.\n rightBoundary[rightStack.top()] = i; \n rightStack.pop();\n }\n rightStack.push(i);\n }\n \n int maxScore = 0; // Initialize the maximum score to 0.\n \n // Calculate the maximum score for good subarrays\n for (int i = 0; i < n; i++) {\n if (leftBoundary[i] < k && rightBoundary[i] > k) {\n // Calculate the score for the subarray that contains element \'k\'.\n int subarrayScore = nums[i] * (rightBoundary[i] - leftBoundary[i] - 1);\n maxScore = max(maxScore, subarrayScore); // Update the maximum score.\n }\n }\n \n return maxScore; // Return the maximum score for a good subarray.\n }\n};\n\n```\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int n = nums.length;\n\n int[] leftBoundary = new int[n]; // Store the next lower element from the left.\n int[] rightBoundary = new int[n]; // Store the next lower element from the right.\n for(int i = 0 ;i < n ; i ++){\n leftBoundary[i] = -1;\n rightBoundary[i] = n ;\n }\n\n Stack<Integer> leftStack = new Stack<>(); // Monotonic Stack to help calculate left array.\n Stack<Integer> rightStack = new Stack<>(); // Monotonic Stack to help calculate right array.\n\n // Calculate next lower element from the left.\n for (int i = n - 1; i >= 0; i--) {\n while (!leftStack.empty() && nums[leftStack.peek()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the left boundary for those elements to the current element\'s index.\n leftBoundary[leftStack.pop()] = i;\n }\n leftStack.push(i);\n }\n\n // Calculate next lower element from the right\n for (int i = 0; i < n; i++) {\n while (!rightStack.empty() && nums[rightStack.peek()] > nums[i]) {\n // If the current element is smaller than elements in the stack,\n // set the right boundary for those elements to the current element\'s index.\n rightBoundary[rightStack.pop()] = i;\n }\n rightStack.push(i);\n }\n\n int maxScore = 0; // Initialize the maximum score to 0.\n\n // Calculate the maximum score for good subarrays\n for (int i = 0; i < n; i++) {\n if (leftBoundary[i] < k && rightBoundary[i] > k) {\n // Calculate the score for the subarray that contains element \'k\'.\n int subarrayScore = nums[i] * (rightBoundary[i] - leftBoundary[i] - 1);\n maxScore = Math.max(maxScore, subarrayScore); // Update the maximum score.\n }\n }\n\n return maxScore; // Return the maximum score for a good subarray.\n }\n}\n```\n```Python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n n = len(nums)\n\n leftBoundary = [-1] * n # Store the next lower element from the left.\n rightBoundary = [n] * n # Store the next lower element from the right.\n\n leftStack = [] # Monotonic Stack to help calculate left array.\n rightStack = [] # Monotonic Stack to help calculate right array.\n\n # Calculate next lower element from the left.\n for i in range(n - 1, -1, -1):\n while leftStack and nums[leftStack[-1]] > nums[i]:\n # If the current element is smaller than elements in the stack,\n # set the left boundary for those elements to the current element\'s index.\n leftBoundary[leftStack[-1]] = i\n leftStack.pop()\n leftStack.append(i)\n\n # Calculate next lower element from the right.\n for i in range(n):\n while rightStack and nums[rightStack[-1]] > nums[i]:\n # If the current element is smaller than elements in the stack,\n # set the right boundary for those elements to the current element\'s index.\n rightBoundary[rightStack[-1]] = i\n rightStack.pop()\n rightStack.append(i)\n\n maxScore = 0 # Initialize the maximum score to 0.\n\n # Calculate the maximum score for good subarrays.\n for i in range(n):\n if leftBoundary[i] < k and rightBoundary[i] > k:\n # Calculate the score for the subarray that contains element \'k\'.\n subarrayScore = nums[i] * (rightBoundary[i] - leftBoundary[i] - 1)\n maxScore = max(maxScore, subarrayScore) # Update the maximum score.\n\n return maxScore # Return the maximum score for a good subarray.\n```\n\n\n\n\n | 29 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | maximum-score-of-a-good-subarray | 1 | 1 | # Intuition\nThe description accidentally say an answer. lol\n\n---\n\n# Solution Video\n\nhttps://youtu.be/ZiO47ctvu6w\n\n\u25A0 Timeline of the video\n`0:05` Easy way to solve a constraint\n`2:04` How we can move i and j pointers\n`3:59` candidates for minimum number and max score\n`4:29` Demonstrate how it works\n`8:25` Coding\n`11:04` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,778\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nFirst of all, we have two constraints.\n\n---\n\n- min( from nums[i] to nums[j]) * (j - i + 1)\n- i <= k <= j\n\n---\n\nLet\'s focuns on `i <= k <= j`. The problem is it\'s hard to manage 3 indices at the same time.\n\nSo we should change our idea. Simply, since we know that `k` index number,\nI think it\'s good idea to start from `k index`.\n\n`i` index is less than or equal to `k`, so move towards `index 0`. On the other hand, `j` is greater than or equal to `k`, so move towards the last index.\n\n\n---\n\n\u2B50\uFE0F Points\n\nWe should start iterating from `k` index, so that we don\'t have to care about `i <= k <= j` constraint.\n\n---\n\n- How we can move `i` and `j` pointers?\n\nThe next point is "how we can move `i` and `j` pointers". The description says "Return the maximum possible score of a good subarray."\n\nSo, I think we have 3 cases.\n\n\n---\n\n\u2B50\uFE0F Points\n\n1. **not reach end of array at both sides**\n\n In this case, `if nums[i] >= nums[j]`, move `i` with `-1`, if not, move `j` with `+1`, that\'s because we want to get maximum score, so take larger number.\n\n - Why `i` with `-1`, `j` with `+1`?\n\n That\'s because we start from `k` index. Let\'s say k = `2`. As I told you, i move towards `index 0`, so we need to subtract `-1` from `2` to move to `index 1`. `j` is the same reason. we need to add `+1` to move to the last index from `k` index.\n\n2. **reach index `0` first**\n\n In this case, simply move `j` with `+1`\n\n3. **reach the last index first**\n\n In this case, simply move `i` with `-1`\n\n---\n\nVery simple right?\n\n- It\'s time to calculate minimum number and max score\n\nLet\'s calculate minimum number and max score.\n\nRegarding minimum number, we need to compare 3 numbers\n\n---\n\n\u2B50\uFE0F Points\n\ncandidates of minimum number should be\n\n- `current minimum number` (this is initialized with `nums[k]` at first)\n- `nums[i]`\n- `nums[j]`\n\n---\n\nAfter we take current minimum number, it\'s time to calculate max score with the formula.\n\n---\n\n\u2B50\uFE0F Points\n\ncandidates of max score should be\n\n- `current max score`\n- `minimum number * (j - i + 1)`\n\n---\n\nwe compare the two numbers and take a larger number.\n\nwe repeat the same process until `i` reach index `0` and `j` reach the last index.\n\n\n### How it works\n\nLet\'s see how it works with a simple example.\n\n```\nInput: [1,4,3,7], k = 2\n```\n\nWe start from index `k`\n\n```\ni = 2\nj = 2\nminimum = 3 (= nums[k])\nmax score = 3 (= nums[k])\n```\n\n```\nnums[i - 1] = 4\nnums[j + 1] = 7\n\ntake 7, so move j with +1\n\ni = 2\nj = 3\nminimum = 3 (= min(minimum(3), nums[i](3), nums[j](7)))\nmax score = 6 (= max(max_score(3), minimum(3) * (j(3) - i(2) + 1)))\n``` \n\n```\nWe already reached the last index, so move i with -1\n\ni = 1\nj = 3\nminimum = 3 (= min(minimum(3), nums[i](4), nums[j](7)))\nmax score = 9 (= max(max_score(6), minimum(3) * (j(3) - i(1) + 1)))\n``` \n\n```\nWe already reached the last index, so move i with -1\n\ni = 0\nj = 3\nminimum = 1 (= min(minimum(3), nums[i](1), nums[j](7)))\nmax score = 9 (= max(max_score(9), minimum(1) * (j(3) - i(0) + 1)))\n``` \n\n```\nOutput: 9\n```\n\nEasy! Let\'s see a real algorithm!\n\n### Algorithm Overview:\n\nThe algorithm aims to find the maximum score of a good subarray within a given list of numbers, represented by `nums`, with a starting index `k`.\n\n### Detailed Explanation:\n\n1. Initialize necessary variables:\n - Set `minimum` and `max_score` to the value of the element at index `k`. These variables keep track of the minimum element within the subarray and the maximum score found.\n - Initialize `i` and `j` to `k`. These pointers represent the left and right bounds of the subarray under consideration.\n - Determine the length of the input list `n`.\n\n2. Begin a while loop that continues as long as either `i` is greater than 0 or `j` is less than `n - 1`. This loop iteratively expands the subarray and calculates the score.\n\n3. Inside the loop:\n - Check if it\'s possible to expand the subarray towards the left (i > 0) and right (j < n - 1). This is done to ensure we consider the entire list while trying to maximize the score.\n - If both expansions are possible, compare the neighbors at indices `i - 1` and `j + 1`. Expand the subarray towards the side with the larger neighbor. Update `i` or `j` accordingly.\n - If expanding to the left is not possible (i == 0), or expanding to the right is not possible (j == n - 1), expand the subarray in the direction that is feasible.\n\n4. After expanding the subarray, update the `minimum` value by finding the minimum of the following values: `minimum`, `nums[i]`, and `nums[j]`. This keeps track of the minimum element within the current subarray.\n\n5. Calculate the score for the current subarray and update `max_score`. The score is determined by multiplying `minimum` by the width of the subarray, which is `(j - i + 1)`.\n\n6. The loop continues until `i` is not greater than 0 and `j` is not less than `n - 1`. This ensures that the algorithm explores the entire array for maximizing the score.\n\n7. Once the loop ends, return `max_score` as the maximum score of a good subarray.\n\nThe algorithm iterates through the list, expanding the subarray towards the side with the larger neighbor and continuously updating the minimum element and the maximum score. This process is repeated until the subarray cannot be expanded further, ensuring that the maximum score is found.\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n minimum = max_score = nums[k]\n i = j = k\n n = len(nums)\n\n while i > 0 or j < n - 1:\n # Check if we can expand the subarray\n if i > 0 and j < n - 1:\n # Expand the subarray towards the side with the larger neighbor\n if nums[i - 1] >= nums[j + 1]:\n i -= 1\n else:\n j += 1\n elif i == 0 and j < n - 1:\n j += 1\n elif j == n - 1 and i > 0:\n i -= 1\n\n # Update the minimum and the maximum score\n minimum = min(minimum, nums[i], nums[j])\n max_score = max(max_score, minimum * (j - i + 1))\n\n return max_score\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar maximumScore = function(nums, k) {\n let minimum = nums[k];\n let max_score = nums[k];\n let i = k;\n let j = k;\n let n = nums.length;\n\n while (i > 0 || j < n - 1) {\n // Check if we can expand the subarray\n if (i > 0 && j < n - 1) {\n // Expand the subarray towards the side with the larger neighbor\n if (nums[i - 1] >= nums[j + 1]) {\n i--;\n } else {\n j++;\n }\n } else if (i === 0 && j < n - 1) {\n j++;\n } else if (j === n - 1 && i > 0) {\n i--;\n }\n\n // Update the minimum and the maximum score\n minimum = Math.min(minimum, nums[i], nums[j]);\n max_score = Math.max(max_score, minimum * (j - i + 1));\n }\n\n return max_score;\n}\n```\n```java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int minimum = nums[k];\n int max_score = nums[k];\n int i = k;\n int j = k;\n int n = nums.length;\n\n while (i > 0 || j < n - 1) {\n // Check if we can expand the subarray\n if (i > 0 && j < n - 1) {\n // Expand the subarray towards the side with the larger neighbor\n if (nums[i - 1] >= nums[j + 1]) {\n i--;\n } else {\n j++;\n }\n } else if (i == 0 && j < n - 1) {\n j++;\n } else if (j == n - 1 && i > 0) {\n i--;\n }\n\n // Update the minimum and the maximum score\n minimum = Math.min(minimum, Math.min(nums[i], nums[j]));\n max_score = Math.max(max_score, minimum * (j - i + 1));\n }\n\n return max_score; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int minimum = nums[k];\n int max_score = nums[k];\n int i = k;\n int j = k;\n int n = nums.size();\n\n while (i > 0 || j < n - 1) {\n // Check if we can expand the subarray\n if (i > 0 && j < n - 1) {\n // Expand the subarray towards the side with the larger neighbor\n if (nums[i - 1] >= nums[j + 1]) {\n i--;\n } else {\n j++;\n }\n } else if (i == 0 && j < n - 1) {\n j++;\n } else if (j == n - 1 && i > 0) {\n i--;\n }\n\n // Update the minimum and the maximum score\n minimum = min(minimum, min(nums[i], nums[j]));\n max_score = max(max_score, minimum * (j - i + 1));\n }\n\n return max_score; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/power-of-four/solutions/4197554/video-give-me-3-minutes-without-bitwise-operations-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/dy_GA7sG22g\n\n\u25A0 Timeline of the video\n`0:05` Easy way to solve a constraint\n`0:03` Example code with Bitwise Operations\n`0:19` Solution with Build-in function\n`1:23` Coding with Build-in function\n`1:50` Time Complexity and Space Complexity with Build-in function\n`2:15` Coding without Build-in function\n`3:08` Time Complexity and Space Complexity without Build-in function\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/constrained-subsequence-sum/solutions/4191844/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/KuMkwvvesgo\n\n\u25A0 Timeline of the video\n`0:04` Explain a few basic idea\n`3:21` What data we should put in deque?\n`5:10` Demonstrate how it works\n`13:27` Coding\n`16:03` Time Complexity and Space Complexity\n | 23 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | maximum-score-of-a-good-subarray | 1 | 1 | # Intuition\nThe description accidentally say an answer. lol\n\n---\n\n# Solution Video\n\nhttps://youtu.be/ZiO47ctvu6w\n\n\u25A0 Timeline of the video\n`0:05` Easy way to solve a constraint\n`2:04` How we can move i and j pointers\n`3:59` candidates for minimum number and max score\n`4:29` Demonstrate how it works\n`8:25` Coding\n`11:04` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,778\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nFirst of all, we have two constraints.\n\n---\n\n- min( from nums[i] to nums[j]) * (j - i + 1)\n- i <= k <= j\n\n---\n\nLet\'s focuns on `i <= k <= j`. The problem is it\'s hard to manage 3 indices at the same time.\n\nSo we should change our idea. Simply, since we know that `k` index number,\nI think it\'s good idea to start from `k index`.\n\n`i` index is less than or equal to `k`, so move towards `index 0`. On the other hand, `j` is greater than or equal to `k`, so move towards the last index.\n\n\n---\n\n\u2B50\uFE0F Points\n\nWe should start iterating from `k` index, so that we don\'t have to care about `i <= k <= j` constraint.\n\n---\n\n- How we can move `i` and `j` pointers?\n\nThe next point is "how we can move `i` and `j` pointers". The description says "Return the maximum possible score of a good subarray."\n\nSo, I think we have 3 cases.\n\n\n---\n\n\u2B50\uFE0F Points\n\n1. **not reach end of array at both sides**\n\n In this case, `if nums[i] >= nums[j]`, move `i` with `-1`, if not, move `j` with `+1`, that\'s because we want to get maximum score, so take larger number.\n\n - Why `i` with `-1`, `j` with `+1`?\n\n That\'s because we start from `k` index. Let\'s say k = `2`. As I told you, i move towards `index 0`, so we need to subtract `-1` from `2` to move to `index 1`. `j` is the same reason. we need to add `+1` to move to the last index from `k` index.\n\n2. **reach index `0` first**\n\n In this case, simply move `j` with `+1`\n\n3. **reach the last index first**\n\n In this case, simply move `i` with `-1`\n\n---\n\nVery simple right?\n\n- It\'s time to calculate minimum number and max score\n\nLet\'s calculate minimum number and max score.\n\nRegarding minimum number, we need to compare 3 numbers\n\n---\n\n\u2B50\uFE0F Points\n\ncandidates of minimum number should be\n\n- `current minimum number` (this is initialized with `nums[k]` at first)\n- `nums[i]`\n- `nums[j]`\n\n---\n\nAfter we take current minimum number, it\'s time to calculate max score with the formula.\n\n---\n\n\u2B50\uFE0F Points\n\ncandidates of max score should be\n\n- `current max score`\n- `minimum number * (j - i + 1)`\n\n---\n\nwe compare the two numbers and take a larger number.\n\nwe repeat the same process until `i` reach index `0` and `j` reach the last index.\n\n\n### How it works\n\nLet\'s see how it works with a simple example.\n\n```\nInput: [1,4,3,7], k = 2\n```\n\nWe start from index `k`\n\n```\ni = 2\nj = 2\nminimum = 3 (= nums[k])\nmax score = 3 (= nums[k])\n```\n\n```\nnums[i - 1] = 4\nnums[j + 1] = 7\n\ntake 7, so move j with +1\n\ni = 2\nj = 3\nminimum = 3 (= min(minimum(3), nums[i](3), nums[j](7)))\nmax score = 6 (= max(max_score(3), minimum(3) * (j(3) - i(2) + 1)))\n``` \n\n```\nWe already reached the last index, so move i with -1\n\ni = 1\nj = 3\nminimum = 3 (= min(minimum(3), nums[i](4), nums[j](7)))\nmax score = 9 (= max(max_score(6), minimum(3) * (j(3) - i(1) + 1)))\n``` \n\n```\nWe already reached the last index, so move i with -1\n\ni = 0\nj = 3\nminimum = 1 (= min(minimum(3), nums[i](1), nums[j](7)))\nmax score = 9 (= max(max_score(9), minimum(1) * (j(3) - i(0) + 1)))\n``` \n\n```\nOutput: 9\n```\n\nEasy! Let\'s see a real algorithm!\n\n### Algorithm Overview:\n\nThe algorithm aims to find the maximum score of a good subarray within a given list of numbers, represented by `nums`, with a starting index `k`.\n\n### Detailed Explanation:\n\n1. Initialize necessary variables:\n - Set `minimum` and `max_score` to the value of the element at index `k`. These variables keep track of the minimum element within the subarray and the maximum score found.\n - Initialize `i` and `j` to `k`. These pointers represent the left and right bounds of the subarray under consideration.\n - Determine the length of the input list `n`.\n\n2. Begin a while loop that continues as long as either `i` is greater than 0 or `j` is less than `n - 1`. This loop iteratively expands the subarray and calculates the score.\n\n3. Inside the loop:\n - Check if it\'s possible to expand the subarray towards the left (i > 0) and right (j < n - 1). This is done to ensure we consider the entire list while trying to maximize the score.\n - If both expansions are possible, compare the neighbors at indices `i - 1` and `j + 1`. Expand the subarray towards the side with the larger neighbor. Update `i` or `j` accordingly.\n - If expanding to the left is not possible (i == 0), or expanding to the right is not possible (j == n - 1), expand the subarray in the direction that is feasible.\n\n4. After expanding the subarray, update the `minimum` value by finding the minimum of the following values: `minimum`, `nums[i]`, and `nums[j]`. This keeps track of the minimum element within the current subarray.\n\n5. Calculate the score for the current subarray and update `max_score`. The score is determined by multiplying `minimum` by the width of the subarray, which is `(j - i + 1)`.\n\n6. The loop continues until `i` is not greater than 0 and `j` is not less than `n - 1`. This ensures that the algorithm explores the entire array for maximizing the score.\n\n7. Once the loop ends, return `max_score` as the maximum score of a good subarray.\n\nThe algorithm iterates through the list, expanding the subarray towards the side with the larger neighbor and continuously updating the minimum element and the maximum score. This process is repeated until the subarray cannot be expanded further, ensuring that the maximum score is found.\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n minimum = max_score = nums[k]\n i = j = k\n n = len(nums)\n\n while i > 0 or j < n - 1:\n # Check if we can expand the subarray\n if i > 0 and j < n - 1:\n # Expand the subarray towards the side with the larger neighbor\n if nums[i - 1] >= nums[j + 1]:\n i -= 1\n else:\n j += 1\n elif i == 0 and j < n - 1:\n j += 1\n elif j == n - 1 and i > 0:\n i -= 1\n\n # Update the minimum and the maximum score\n minimum = min(minimum, nums[i], nums[j])\n max_score = max(max_score, minimum * (j - i + 1))\n\n return max_score\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar maximumScore = function(nums, k) {\n let minimum = nums[k];\n let max_score = nums[k];\n let i = k;\n let j = k;\n let n = nums.length;\n\n while (i > 0 || j < n - 1) {\n // Check if we can expand the subarray\n if (i > 0 && j < n - 1) {\n // Expand the subarray towards the side with the larger neighbor\n if (nums[i - 1] >= nums[j + 1]) {\n i--;\n } else {\n j++;\n }\n } else if (i === 0 && j < n - 1) {\n j++;\n } else if (j === n - 1 && i > 0) {\n i--;\n }\n\n // Update the minimum and the maximum score\n minimum = Math.min(minimum, nums[i], nums[j]);\n max_score = Math.max(max_score, minimum * (j - i + 1));\n }\n\n return max_score;\n}\n```\n```java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int minimum = nums[k];\n int max_score = nums[k];\n int i = k;\n int j = k;\n int n = nums.length;\n\n while (i > 0 || j < n - 1) {\n // Check if we can expand the subarray\n if (i > 0 && j < n - 1) {\n // Expand the subarray towards the side with the larger neighbor\n if (nums[i - 1] >= nums[j + 1]) {\n i--;\n } else {\n j++;\n }\n } else if (i == 0 && j < n - 1) {\n j++;\n } else if (j == n - 1 && i > 0) {\n i--;\n }\n\n // Update the minimum and the maximum score\n minimum = Math.min(minimum, Math.min(nums[i], nums[j]));\n max_score = Math.max(max_score, minimum * (j - i + 1));\n }\n\n return max_score; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int minimum = nums[k];\n int max_score = nums[k];\n int i = k;\n int j = k;\n int n = nums.size();\n\n while (i > 0 || j < n - 1) {\n // Check if we can expand the subarray\n if (i > 0 && j < n - 1) {\n // Expand the subarray towards the side with the larger neighbor\n if (nums[i - 1] >= nums[j + 1]) {\n i--;\n } else {\n j++;\n }\n } else if (i == 0 && j < n - 1) {\n j++;\n } else if (j == n - 1 && i > 0) {\n i--;\n }\n\n // Update the minimum and the maximum score\n minimum = min(minimum, min(nums[i], nums[j]));\n max_score = max(max_score, minimum * (j - i + 1));\n }\n\n return max_score; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/power-of-four/solutions/4197554/video-give-me-3-minutes-without-bitwise-operations-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/dy_GA7sG22g\n\n\u25A0 Timeline of the video\n`0:05` Easy way to solve a constraint\n`0:03` Example code with Bitwise Operations\n`0:19` Solution with Build-in function\n`1:23` Coding with Build-in function\n`1:50` Time Complexity and Space Complexity with Build-in function\n`2:15` Coding without Build-in function\n`3:08` Time Complexity and Space Complexity without Build-in function\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/constrained-subsequence-sum/solutions/4191844/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/KuMkwvvesgo\n\n\u25A0 Timeline of the video\n`0:04` Explain a few basic idea\n`3:21` What data we should put in deque?\n`5:10` Demonstrate how it works\n`13:27` Coding\n`16:03` Time Complexity and Space Complexity\n | 23 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
✅☑[C++/Java/Python/JavaScript] || 3 Approaches || EXPLAINED🔥 | maximum-score-of-a-good-subarray | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Binary Search)***\n1. The `maximumScore` function is the main function that calculates the maximum score. It takes a vector of integers `nums` and an integer `k` as input.\n\n1. Inside the `maximumScore` function, it first calculates the maximum score using the `solve` function and stores it in the variable `ans`.\n\n1. Then, it reverses the `nums` vector using the `reverse` function. This is done to calculate the maximum score from the other side of the array.\n\n1. Finally, it returns the maximum of the two scores calculated in step 2 and step 3, which effectively returns the overall maximum score.\n\n1. The `solve` function takes two parameters: the `nums` vector and an integer `k`, which represents a pivot point in the vector.\n\n1. It calculates the maximum score starting from the pivot point `k` and moving both left and right in the `nums` vector.\n\n1. The `left` vector is used to store the minimum values found when moving from left to right, starting from the pivot point `k`.\n\n1. The `currMin` variable is initialized with `INT_MAX` to track the minimum value. It is updated while iterating through the vector to find the minimum values.\n\n1. The `for` loop moves from the pivot point `k` towards the beginning of the vector (i.e., from right to left), and it updates the `left` vector with the minimum values encountered.\n\n1. Similarly, the `right` vector is used to store the minimum values found when moving from right to left, starting from the pivot point `k`.\n\n1. Again, the `currMin` variable is initialized with `INT_MAX` to track the minimum value and is updated while iterating through the vector.\n\n1. The second `for` loop moves from the pivot point `k` towards the end of the vector, and it updates the `right` vector with the minimum values encountered.\n\n1. The `ans` variable is used to store the maximum score. It is calculated using a nested for loop that iterates through the `right` vector.\n\n1. For each element in the `right` vector, it calculates the index at which the corresponding minimum value is found in the `left` vector. This is done using the `lower_bound` function.\n\n1. It calculates the size of the subarray by subtracting the index from step 14 from the sum of k and the current iteration variable `j`.\n\n1. The maximum score for the current element is calculated as the product of the minimum value from the `right` vector and the size of the subarray.\n\n1. The maximum score is updated if the calculated score is greater than the current maximum.\n\n1. Finally, the function returns the maximum score calculated.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int ans = solve(nums, k);\n reverse(nums.begin(), nums.end());\n return max(ans, solve(nums, nums.size() - k - 1));\n }\n \n int solve(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> left(k, 0);\n int currMin = INT_MAX;\n for (int i = k - 1; i >= 0; i--) {\n currMin = min(currMin, nums[i]);\n left[i] = currMin;\n }\n \n vector<int> right;\n currMin = INT_MAX;\n for (int i = k; i < n; i++) {\n currMin = min(currMin, nums[i]);\n right.push_back(currMin);\n }\n \n int ans = 0;\n for (int j = 0; j < right.size(); j++) {\n currMin = right[j];\n int i = lower_bound(left.begin(), left.end(), currMin) - left.begin();\n int size = (k + j) - i + 1;\n ans = max(ans, currMin * size);\n }\n \n return ans;\n }\n};\n\n```\n```C []\n\n#include <stdio.h>\n#include <limits.h>\n\nint min(int a, int b) {\n return a < b ? a : b;\n}\n\nint max(int a, int b) {\n return a > b ? a : b;\n}\n\nint lower_bound(int arr[], int size, int value) {\n int left = 0, right = size;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] < value) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n return left;\n}\n\nint solve(int nums[], int size, int k) {\n int *left = (int *)malloc(k * sizeof(int));\n int currMin = INT_MAX;\n for (int i = k - 1; i >= 0; i--) {\n currMin = min(currMin, nums[i]);\n left[i] = currMin;\n }\n\n int *right = (int *)malloc((size - k) * sizeof(int));\n currMin = INT_MAX;\n int rightSize = 0;\n for (int i = k; i < size; i++) {\n currMin = min(currMin, nums[i]);\n right[rightSize] = currMin;\n rightSize++;\n }\n\n int ans = 0;\n for (int j = 0; j < rightSize; j++) {\n currMin = right[j];\n int i = lower_bound(left, k, currMin);\n int size = (k + j) - i + 1;\n ans = max(ans, currMin * size);\n }\n\n free(left);\n free(right);\n return ans;\n}\n\nint maximumScore(int nums[], int size, int k) {\n int ans = solve(nums, size, k);\n int *reversedNums = (int *)malloc(size * sizeof(int));\n for (int i = 0; i < size; i++) {\n reversedNums[i] = nums[size - 1 - i];\n }\n int reversedAns = solve(reversedNums, size, size - k - 1);\n free(reversedNums);\n return max(ans, reversedAns);\n}\n\nint main() {\n int nums[] = {1, 4, 3, 7, 4, 5};\n int size = sizeof(nums) / sizeof(nums[0]);\n int k = 3;\n int result = maximumScore(nums, size, k);\n printf("Maximum Score: %d\\n", result);\n return 0;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int ans = solve(nums, k);\n for (int i = 0; i < nums.length / 2; i++) {\n int temp = nums[i];\n nums[i] = nums[nums.length - i - 1];\n nums[nums.length - i - 1] = temp;\n }\n \n return Math.max(ans, solve(nums, nums.length - k - 1));\n }\n \n public int solve(int[] nums, int k) {\n int n = nums.length;\n int left[] = new int[k];\n int currMin = Integer.MAX_VALUE;\n for (int i = k - 1; i >= 0; i--) {\n currMin = Math.min(currMin, nums[i]);\n left[i] = currMin;\n }\n \n List<Integer> right = new ArrayList();\n currMin = Integer.MAX_VALUE;\n for (int i = k; i < n; i++) {\n currMin = Math.min(currMin, nums[i]);\n right.add(currMin);\n }\n \n int ans = 0;\n for (int j = 0; j < right.size(); j++) {\n currMin = right.get(j);\n int i = binarySearch(left, currMin);\n int size = (k + j) - i + 1;\n ans = Math.max(ans, currMin * size);\n }\n\n return ans;\n }\n \n public int binarySearch(int[] nums, int num) {\n int left = 0;\n int right = nums.length;\n \n while (left < right) {\n int mid = (left + right) / 2;\n if (nums[mid] < num) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n \n return left;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n def solve(nums, k):\n n = len(nums)\n left = [0] * k\n curr_min = inf\n for i in range(k - 1, -1, -1):\n curr_min = min(curr_min, nums[i])\n left[i] = curr_min\n\n right = []\n curr_min = inf\n for i in range(k, n):\n curr_min = min(curr_min, nums[i])\n right.append(curr_min)\n\n ans = 0\n for j in range(len(right)):\n curr_min = right[j]\n i = bisect_left(left, curr_min)\n size = (k + j) - i + 1\n ans = max(ans, curr_min * size)\n \n return ans\n \n return max(solve(nums, k), solve(nums[::-1], len(nums) - k - 1))\n\n```\n\n```javascript []\nfunction maximumScore(nums, k) {\n const ans = solve(nums, k);\n const reversedNums = [...nums].reverse();\n return Math.max(ans, solve(reversedNums, nums.length - k - 1));\n}\n\nfunction solve(nums, k) {\n const n = nums.length;\n const left = new Array(k).fill(0);\n let currMin = Infinity;\n\n for (let i = k - 1; i >= 0; i--) {\n currMin = Math.min(currMin, nums[i]);\n left[i] = currMin;\n }\n\n const right = [];\n currMin = Infinity;\n\n for (let i = k; i < n; i++) {\n currMin = Math.min(currMin, nums[i]);\n right.push(currMin);\n }\n\n let ans = 0;\n\n for (let j = 0; j < right.length; j++) {\n currMin = right[j];\n const i = lowerBound(left, currMin);\n const size = (k + j) - i + 1;\n ans = Math.max(ans, currMin * size);\n }\n\n return ans;\n}\n\nfunction lowerBound(arr, value) {\n let left = 0;\n let right = arr.length;\n\n while (left < right) {\n const mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] < value) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return left;\n}\n\nconst nums = [1, 4, 3, 7, 4, 5];\nconst k = 3;\nconst result = maximumScore(nums, k);\nconsole.log("Maximum Score: " + result);\n\n```\n\n---\n\n#### ***Approach 2 (Monotonic Stack)***\n- This code aims to find the maximum score for a specific element `nums[k]` in an array `nums` by considering elements to its left and right.\n\n- The variable `n` stores the length of the `nums` array.\n\n- The code initializes two arrays, `left` and `right`, with default values of -1 and `n`, respectively. These arrays will be used to store the left and right boundaries for each element in the `nums` array.\n\n- A stack named `stack` is used to help calculate the boundaries of elements as we traverse the array.\n\n- The first loop, moving backward from the end of the array to the beginning, calculates the left boundaries for each element and updates the `left` array. It does this by comparing the current element with the elements in the stack. If the current element is smaller than the element at the top of the stack, the stack element\'s left boundary is set to the current index. This continues until the current element is greater than the element at the top of the stack.\n\n- The second loop, moving forward from the beginning of the array to the end, calculates the right boundaries for each element and updates the `right` array in a similar way to the first loop.\n\n- After calculating the left and right boundaries for each element, the code proceeds to calculate the maximum score. It initializes `ans` to 0 to store the maximum score found so far.\n\n- It then iterates through the `nums` array. For each element at index `i`, it checks if the left boundary (`left[i]`) is less than `k` and the right boundary (`right[i]`) is greater than `k`. This indicates that the element `nums[i]` can be included in the calculation of the maximum score. If these conditions are met, the code calculates the score as `nums[i] * (right[i] - left[i] - 1)`. The `-1` is used to exclude the element `nums[i]` from the scoring calculation.\n\n- For each element, if the calculated score is greater than the current maximum score (ans), it updates `ans` with the newly calculated score.\n\n- Finally, the code returns `ans` as the maximum score for the element at index `k`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> left(n, -1);\n vector<int> stack;\n \n for (int i = n - 1; i >= 0; i--) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n left[stack.back()] = i;\n stack.pop_back();\n }\n \n stack.push_back(i);\n }\n \n vector<int> right(n, n);\n stack.clear();\n for (int i = 0; i < n; i++) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n right[stack.back()] = i;\n stack.pop_back();\n }\n \n stack.push_back(i);\n }\n \n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n \n return ans;\n }\n};\n\n\n```\n```C []\n\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> left(n, -1);\n vector<int> stack;\n\n // Calculate left boundaries for each element.\n for (int i = n - 1; i >= 0; i--) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n left[stack.back()] = i;\n stack.pop_back();\n }\n\n stack.push_back(i);\n }\n\n vector<int> right(n, n);\n stack.clear();\n\n // Calculate right boundaries for each element.\n for (int i = 0; i < n; i++) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n right[stack.back()] = i;\n stack.pop_back();\n }\n\n stack.push_back(i);\n }\n\n int ans = 0;\n\n // Calculate the maximum score for each element.\n for (int i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n\n return ans;\n }\n};\n\n\n```\n\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int n = nums.length;\n int left[] = new int[n];\n Arrays.fill(left, -1);\n Stack<Integer> stack = new Stack<>();\n \n for (int i = n - 1; i >= 0; i--) {\n while (!stack.isEmpty() && nums[stack.peek()] > nums[i]) {\n left[stack.pop()] = i;\n }\n \n stack.push(i);\n }\n \n int right[] = new int[n];\n Arrays.fill(right, n);\n stack = new Stack<>();\n \n for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] > nums[i]) {\n right[stack.pop()] = i;\n }\n \n stack.push(i);\n }\n \n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = Math.max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n \n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n n = len(nums)\n left = [-1] * n\n stack = []\n \n for i in range(n - 1, -1, -1):\n while stack and nums[stack[-1]] > nums[i]:\n left[stack.pop()] = i\n \n stack.append(i)\n \n right = [n] * n\n stack = []\n for i in range(n):\n while stack and nums[stack[-1]] > nums[i]:\n right[stack.pop()] = i\n \n stack.append(i)\n\n ans = 0\n for i in range(n):\n if left[i] < k and right[i] > k:\n ans = max(ans, nums[i] * (right[i] - left[i] - 1))\n \n return ans\n\n```\n\n```javascript []\nclass Solution {\n maximumScore(nums, k) {\n const n = nums.length;\n const left = new Array(n).fill(-1);\n const stack = [];\n\n // Calculate left boundaries for each element.\n for (let i = n - 1; i >= 0; i--) {\n while (stack.length > 0 && nums[stack[stack.length - 1]] > nums[i]) {\n left[stack[stack.length - 1]] = i;\n stack.pop();\n }\n\n stack.push(i);\n }\n\n const right = new Array(n).fill(n);\n stack.length = 0;\n\n // Calculate right boundaries for each element.\n for (let i = 0; i < n; i++) {\n while (stack.length > 0 && nums[stack[stack.length - 1]] > nums[i]) {\n right[stack[stack.length - 1]] = i;\n stack.pop();\n }\n\n stack.push(i);\n }\n\n let ans = 0;\n\n // Calculate the maximum score for each element.\n for (let i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = Math.max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n\n return ans;\n }\n}\n\n```\n\n---\n#### ***Approach 3 (Greedy)***\n- This code aims to find the maximum score for a specific element `nums[k]` in an array `nums` by considering elements to its left and right.\n\n- The variable `n` stores the length of the `nums` array.\n\n- The variables `left` and `right` are initialized with the value of `k`. These variables will be used to keep track of the current left and right boundaries, respectively. `ans` is initialized with the value of `nums[k]`, which represents the initial maximum score.\n\n- The variable `currMin` is also initialized with the value of `nums[k]`. This variable will keep track of the minimum value of the elements within the current range.\n\n- The code enters a `while` loop, and the loop continues as long as either the left or right boundary can be expanded.\n\n- Inside the loop, the code checks which direction to expand. It compares the elements at the left and right boundaries. If the element to the left (`nums[left - 1]`) is smaller or doesn\'t exist (when `left` reaches the beginning of the array), it means it\'s preferable to expand to the right. Otherwise, if the right element (`nums[right + 1]`) is smaller or doesn\'t exist (when `right` reaches the end of the array), the code expands to the left.\n\n- When the code expands the boundaries, it updates `left` or `right` accordingly and also updates `currMin` to the minimum value within the current range.\n\n- In each iteration, the code calculates the score for the current range by multiplying `currMin` by the width of the range (`right - left + 1`). This represents the score of including `nums[k]` along with the elements within the range.\n\n- The calculated score is compared to the current maximum score (`ans`), and if it is greater, the maximum score is updated with the newly calculated score.\n\n- The loop continues to expand the boundaries and calculate the score as long as it\'s possible to do so. It effectively finds the maximum score for `nums[k]` by considering different combinations of left and right boundaries.\n\n- Finally, the code returns `ans` as the maximum score for the element at index `k`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n int left = k;\n int right = k;\n int ans = nums[k];\n int currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1]: 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = min(currMin, nums[right]);\n } else {\n left--;\n currMin = min(currMin, nums[left]);\n }\n \n ans = max(ans, currMin * (right - left + 1));\n }\n \n return ans;\n }\n};\n\n```\n```C []\n#include <stdio.h>\n\nint maximumScore(int nums[], int n, int k) {\n int left = k;\n int right = k;\n int ans = nums[k];\n int currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1] : 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = (currMin < nums[right]) ? currMin : nums[right];\n } else {\n left--;\n currMin = (currMin < nums[left]) ? currMin : nums[left];\n }\n \n int score = currMin * (right - left + 1);\n ans = (ans > score) ? ans : score;\n }\n \n return ans;\n}\n\nint main() {\n int nums[] = {1, 4, 3, 7, 4, 5};\n int n = sizeof(nums) / sizeof(nums[0]);\n int k = 3;\n int result = maximumScore(nums, n, k);\n printf("Maximum Score: %d\\n", result);\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int n = nums.length;\n int left = k;\n int right = k;\n int ans = nums[k];\n int currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1]: 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = Math.min(currMin, nums[right]);\n } else {\n left--;\n currMin = Math.min(currMin, nums[left]);\n }\n \n ans = Math.max(ans, currMin * (right - left + 1));\n }\n \n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n n = len(nums)\n left = k\n right = k\n ans = nums[k]\n curr_min = nums[k]\n \n while left > 0 or right < n - 1:\n if (nums[left - 1] if left else 0) < (nums[right + 1] if right < n - 1 else 0):\n right += 1\n curr_min = min(curr_min, nums[right])\n else:\n left -= 1\n curr_min = min(curr_min, nums[left])\n\n ans = max(ans, curr_min * (right - left + 1))\n \n return ans\n\n```\n\n```javascript []\nfunction maximumScore(nums, k) {\n const n = nums.length;\n let left = k;\n let right = k;\n let ans = nums[k];\n let currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1] : 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = Math.min(currMin, nums[right]);\n } else {\n left--;\n currMin = Math.min(currMin, nums[left]);\n }\n \n const score = currMin * (right - left + 1);\n ans = Math.max(ans, score);\n }\n \n return ans;\n}\n\nconst nums = [1, 4, 3, 7, 4, 5];\nconst k = 3;\nconst result = maximumScore(nums, k);\nconsole.log("Maximum Score:", result);\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
✅☑[C++/Java/Python/JavaScript] || 3 Approaches || EXPLAINED🔥 | maximum-score-of-a-good-subarray | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Binary Search)***\n1. The `maximumScore` function is the main function that calculates the maximum score. It takes a vector of integers `nums` and an integer `k` as input.\n\n1. Inside the `maximumScore` function, it first calculates the maximum score using the `solve` function and stores it in the variable `ans`.\n\n1. Then, it reverses the `nums` vector using the `reverse` function. This is done to calculate the maximum score from the other side of the array.\n\n1. Finally, it returns the maximum of the two scores calculated in step 2 and step 3, which effectively returns the overall maximum score.\n\n1. The `solve` function takes two parameters: the `nums` vector and an integer `k`, which represents a pivot point in the vector.\n\n1. It calculates the maximum score starting from the pivot point `k` and moving both left and right in the `nums` vector.\n\n1. The `left` vector is used to store the minimum values found when moving from left to right, starting from the pivot point `k`.\n\n1. The `currMin` variable is initialized with `INT_MAX` to track the minimum value. It is updated while iterating through the vector to find the minimum values.\n\n1. The `for` loop moves from the pivot point `k` towards the beginning of the vector (i.e., from right to left), and it updates the `left` vector with the minimum values encountered.\n\n1. Similarly, the `right` vector is used to store the minimum values found when moving from right to left, starting from the pivot point `k`.\n\n1. Again, the `currMin` variable is initialized with `INT_MAX` to track the minimum value and is updated while iterating through the vector.\n\n1. The second `for` loop moves from the pivot point `k` towards the end of the vector, and it updates the `right` vector with the minimum values encountered.\n\n1. The `ans` variable is used to store the maximum score. It is calculated using a nested for loop that iterates through the `right` vector.\n\n1. For each element in the `right` vector, it calculates the index at which the corresponding minimum value is found in the `left` vector. This is done using the `lower_bound` function.\n\n1. It calculates the size of the subarray by subtracting the index from step 14 from the sum of k and the current iteration variable `j`.\n\n1. The maximum score for the current element is calculated as the product of the minimum value from the `right` vector and the size of the subarray.\n\n1. The maximum score is updated if the calculated score is greater than the current maximum.\n\n1. Finally, the function returns the maximum score calculated.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int ans = solve(nums, k);\n reverse(nums.begin(), nums.end());\n return max(ans, solve(nums, nums.size() - k - 1));\n }\n \n int solve(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> left(k, 0);\n int currMin = INT_MAX;\n for (int i = k - 1; i >= 0; i--) {\n currMin = min(currMin, nums[i]);\n left[i] = currMin;\n }\n \n vector<int> right;\n currMin = INT_MAX;\n for (int i = k; i < n; i++) {\n currMin = min(currMin, nums[i]);\n right.push_back(currMin);\n }\n \n int ans = 0;\n for (int j = 0; j < right.size(); j++) {\n currMin = right[j];\n int i = lower_bound(left.begin(), left.end(), currMin) - left.begin();\n int size = (k + j) - i + 1;\n ans = max(ans, currMin * size);\n }\n \n return ans;\n }\n};\n\n```\n```C []\n\n#include <stdio.h>\n#include <limits.h>\n\nint min(int a, int b) {\n return a < b ? a : b;\n}\n\nint max(int a, int b) {\n return a > b ? a : b;\n}\n\nint lower_bound(int arr[], int size, int value) {\n int left = 0, right = size;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] < value) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n return left;\n}\n\nint solve(int nums[], int size, int k) {\n int *left = (int *)malloc(k * sizeof(int));\n int currMin = INT_MAX;\n for (int i = k - 1; i >= 0; i--) {\n currMin = min(currMin, nums[i]);\n left[i] = currMin;\n }\n\n int *right = (int *)malloc((size - k) * sizeof(int));\n currMin = INT_MAX;\n int rightSize = 0;\n for (int i = k; i < size; i++) {\n currMin = min(currMin, nums[i]);\n right[rightSize] = currMin;\n rightSize++;\n }\n\n int ans = 0;\n for (int j = 0; j < rightSize; j++) {\n currMin = right[j];\n int i = lower_bound(left, k, currMin);\n int size = (k + j) - i + 1;\n ans = max(ans, currMin * size);\n }\n\n free(left);\n free(right);\n return ans;\n}\n\nint maximumScore(int nums[], int size, int k) {\n int ans = solve(nums, size, k);\n int *reversedNums = (int *)malloc(size * sizeof(int));\n for (int i = 0; i < size; i++) {\n reversedNums[i] = nums[size - 1 - i];\n }\n int reversedAns = solve(reversedNums, size, size - k - 1);\n free(reversedNums);\n return max(ans, reversedAns);\n}\n\nint main() {\n int nums[] = {1, 4, 3, 7, 4, 5};\n int size = sizeof(nums) / sizeof(nums[0]);\n int k = 3;\n int result = maximumScore(nums, size, k);\n printf("Maximum Score: %d\\n", result);\n return 0;\n}\n\n\n```\n\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int ans = solve(nums, k);\n for (int i = 0; i < nums.length / 2; i++) {\n int temp = nums[i];\n nums[i] = nums[nums.length - i - 1];\n nums[nums.length - i - 1] = temp;\n }\n \n return Math.max(ans, solve(nums, nums.length - k - 1));\n }\n \n public int solve(int[] nums, int k) {\n int n = nums.length;\n int left[] = new int[k];\n int currMin = Integer.MAX_VALUE;\n for (int i = k - 1; i >= 0; i--) {\n currMin = Math.min(currMin, nums[i]);\n left[i] = currMin;\n }\n \n List<Integer> right = new ArrayList();\n currMin = Integer.MAX_VALUE;\n for (int i = k; i < n; i++) {\n currMin = Math.min(currMin, nums[i]);\n right.add(currMin);\n }\n \n int ans = 0;\n for (int j = 0; j < right.size(); j++) {\n currMin = right.get(j);\n int i = binarySearch(left, currMin);\n int size = (k + j) - i + 1;\n ans = Math.max(ans, currMin * size);\n }\n\n return ans;\n }\n \n public int binarySearch(int[] nums, int num) {\n int left = 0;\n int right = nums.length;\n \n while (left < right) {\n int mid = (left + right) / 2;\n if (nums[mid] < num) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n \n return left;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n def solve(nums, k):\n n = len(nums)\n left = [0] * k\n curr_min = inf\n for i in range(k - 1, -1, -1):\n curr_min = min(curr_min, nums[i])\n left[i] = curr_min\n\n right = []\n curr_min = inf\n for i in range(k, n):\n curr_min = min(curr_min, nums[i])\n right.append(curr_min)\n\n ans = 0\n for j in range(len(right)):\n curr_min = right[j]\n i = bisect_left(left, curr_min)\n size = (k + j) - i + 1\n ans = max(ans, curr_min * size)\n \n return ans\n \n return max(solve(nums, k), solve(nums[::-1], len(nums) - k - 1))\n\n```\n\n```javascript []\nfunction maximumScore(nums, k) {\n const ans = solve(nums, k);\n const reversedNums = [...nums].reverse();\n return Math.max(ans, solve(reversedNums, nums.length - k - 1));\n}\n\nfunction solve(nums, k) {\n const n = nums.length;\n const left = new Array(k).fill(0);\n let currMin = Infinity;\n\n for (let i = k - 1; i >= 0; i--) {\n currMin = Math.min(currMin, nums[i]);\n left[i] = currMin;\n }\n\n const right = [];\n currMin = Infinity;\n\n for (let i = k; i < n; i++) {\n currMin = Math.min(currMin, nums[i]);\n right.push(currMin);\n }\n\n let ans = 0;\n\n for (let j = 0; j < right.length; j++) {\n currMin = right[j];\n const i = lowerBound(left, currMin);\n const size = (k + j) - i + 1;\n ans = Math.max(ans, currMin * size);\n }\n\n return ans;\n}\n\nfunction lowerBound(arr, value) {\n let left = 0;\n let right = arr.length;\n\n while (left < right) {\n const mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] < value) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return left;\n}\n\nconst nums = [1, 4, 3, 7, 4, 5];\nconst k = 3;\nconst result = maximumScore(nums, k);\nconsole.log("Maximum Score: " + result);\n\n```\n\n---\n\n#### ***Approach 2 (Monotonic Stack)***\n- This code aims to find the maximum score for a specific element `nums[k]` in an array `nums` by considering elements to its left and right.\n\n- The variable `n` stores the length of the `nums` array.\n\n- The code initializes two arrays, `left` and `right`, with default values of -1 and `n`, respectively. These arrays will be used to store the left and right boundaries for each element in the `nums` array.\n\n- A stack named `stack` is used to help calculate the boundaries of elements as we traverse the array.\n\n- The first loop, moving backward from the end of the array to the beginning, calculates the left boundaries for each element and updates the `left` array. It does this by comparing the current element with the elements in the stack. If the current element is smaller than the element at the top of the stack, the stack element\'s left boundary is set to the current index. This continues until the current element is greater than the element at the top of the stack.\n\n- The second loop, moving forward from the beginning of the array to the end, calculates the right boundaries for each element and updates the `right` array in a similar way to the first loop.\n\n- After calculating the left and right boundaries for each element, the code proceeds to calculate the maximum score. It initializes `ans` to 0 to store the maximum score found so far.\n\n- It then iterates through the `nums` array. For each element at index `i`, it checks if the left boundary (`left[i]`) is less than `k` and the right boundary (`right[i]`) is greater than `k`. This indicates that the element `nums[i]` can be included in the calculation of the maximum score. If these conditions are met, the code calculates the score as `nums[i] * (right[i] - left[i] - 1)`. The `-1` is used to exclude the element `nums[i]` from the scoring calculation.\n\n- For each element, if the calculated score is greater than the current maximum score (ans), it updates `ans` with the newly calculated score.\n\n- Finally, the code returns `ans` as the maximum score for the element at index `k`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> left(n, -1);\n vector<int> stack;\n \n for (int i = n - 1; i >= 0; i--) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n left[stack.back()] = i;\n stack.pop_back();\n }\n \n stack.push_back(i);\n }\n \n vector<int> right(n, n);\n stack.clear();\n for (int i = 0; i < n; i++) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n right[stack.back()] = i;\n stack.pop_back();\n }\n \n stack.push_back(i);\n }\n \n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n \n return ans;\n }\n};\n\n\n```\n```C []\n\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> left(n, -1);\n vector<int> stack;\n\n // Calculate left boundaries for each element.\n for (int i = n - 1; i >= 0; i--) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n left[stack.back()] = i;\n stack.pop_back();\n }\n\n stack.push_back(i);\n }\n\n vector<int> right(n, n);\n stack.clear();\n\n // Calculate right boundaries for each element.\n for (int i = 0; i < n; i++) {\n while (!stack.empty() && nums[stack.back()] > nums[i]) {\n right[stack.back()] = i;\n stack.pop_back();\n }\n\n stack.push_back(i);\n }\n\n int ans = 0;\n\n // Calculate the maximum score for each element.\n for (int i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n\n return ans;\n }\n};\n\n\n```\n\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int n = nums.length;\n int left[] = new int[n];\n Arrays.fill(left, -1);\n Stack<Integer> stack = new Stack<>();\n \n for (int i = n - 1; i >= 0; i--) {\n while (!stack.isEmpty() && nums[stack.peek()] > nums[i]) {\n left[stack.pop()] = i;\n }\n \n stack.push(i);\n }\n \n int right[] = new int[n];\n Arrays.fill(right, n);\n stack = new Stack<>();\n \n for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] > nums[i]) {\n right[stack.pop()] = i;\n }\n \n stack.push(i);\n }\n \n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = Math.max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n \n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n n = len(nums)\n left = [-1] * n\n stack = []\n \n for i in range(n - 1, -1, -1):\n while stack and nums[stack[-1]] > nums[i]:\n left[stack.pop()] = i\n \n stack.append(i)\n \n right = [n] * n\n stack = []\n for i in range(n):\n while stack and nums[stack[-1]] > nums[i]:\n right[stack.pop()] = i\n \n stack.append(i)\n\n ans = 0\n for i in range(n):\n if left[i] < k and right[i] > k:\n ans = max(ans, nums[i] * (right[i] - left[i] - 1))\n \n return ans\n\n```\n\n```javascript []\nclass Solution {\n maximumScore(nums, k) {\n const n = nums.length;\n const left = new Array(n).fill(-1);\n const stack = [];\n\n // Calculate left boundaries for each element.\n for (let i = n - 1; i >= 0; i--) {\n while (stack.length > 0 && nums[stack[stack.length - 1]] > nums[i]) {\n left[stack[stack.length - 1]] = i;\n stack.pop();\n }\n\n stack.push(i);\n }\n\n const right = new Array(n).fill(n);\n stack.length = 0;\n\n // Calculate right boundaries for each element.\n for (let i = 0; i < n; i++) {\n while (stack.length > 0 && nums[stack[stack.length - 1]] > nums[i]) {\n right[stack[stack.length - 1]] = i;\n stack.pop();\n }\n\n stack.push(i);\n }\n\n let ans = 0;\n\n // Calculate the maximum score for each element.\n for (let i = 0; i < n; i++) {\n if (left[i] < k && right[i] > k) {\n ans = Math.max(ans, nums[i] * (right[i] - left[i] - 1));\n }\n }\n\n return ans;\n }\n}\n\n```\n\n---\n#### ***Approach 3 (Greedy)***\n- This code aims to find the maximum score for a specific element `nums[k]` in an array `nums` by considering elements to its left and right.\n\n- The variable `n` stores the length of the `nums` array.\n\n- The variables `left` and `right` are initialized with the value of `k`. These variables will be used to keep track of the current left and right boundaries, respectively. `ans` is initialized with the value of `nums[k]`, which represents the initial maximum score.\n\n- The variable `currMin` is also initialized with the value of `nums[k]`. This variable will keep track of the minimum value of the elements within the current range.\n\n- The code enters a `while` loop, and the loop continues as long as either the left or right boundary can be expanded.\n\n- Inside the loop, the code checks which direction to expand. It compares the elements at the left and right boundaries. If the element to the left (`nums[left - 1]`) is smaller or doesn\'t exist (when `left` reaches the beginning of the array), it means it\'s preferable to expand to the right. Otherwise, if the right element (`nums[right + 1]`) is smaller or doesn\'t exist (when `right` reaches the end of the array), the code expands to the left.\n\n- When the code expands the boundaries, it updates `left` or `right` accordingly and also updates `currMin` to the minimum value within the current range.\n\n- In each iteration, the code calculates the score for the current range by multiplying `currMin` by the width of the range (`right - left + 1`). This represents the score of including `nums[k]` along with the elements within the range.\n\n- The calculated score is compared to the current maximum score (`ans`), and if it is greater, the maximum score is updated with the newly calculated score.\n\n- The loop continues to expand the boundaries and calculate the score as long as it\'s possible to do so. It effectively finds the maximum score for `nums[k]` by considering different combinations of left and right boundaries.\n\n- Finally, the code returns `ans` as the maximum score for the element at index `k`.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n = nums.size();\n int left = k;\n int right = k;\n int ans = nums[k];\n int currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1]: 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = min(currMin, nums[right]);\n } else {\n left--;\n currMin = min(currMin, nums[left]);\n }\n \n ans = max(ans, currMin * (right - left + 1));\n }\n \n return ans;\n }\n};\n\n```\n```C []\n#include <stdio.h>\n\nint maximumScore(int nums[], int n, int k) {\n int left = k;\n int right = k;\n int ans = nums[k];\n int currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1] : 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = (currMin < nums[right]) ? currMin : nums[right];\n } else {\n left--;\n currMin = (currMin < nums[left]) ? currMin : nums[left];\n }\n \n int score = currMin * (right - left + 1);\n ans = (ans > score) ? ans : score;\n }\n \n return ans;\n}\n\nint main() {\n int nums[] = {1, 4, 3, 7, 4, 5};\n int n = sizeof(nums) / sizeof(nums[0]);\n int k = 3;\n int result = maximumScore(nums, n, k);\n printf("Maximum Score: %d\\n", result);\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int n = nums.length;\n int left = k;\n int right = k;\n int ans = nums[k];\n int currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1]: 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = Math.min(currMin, nums[right]);\n } else {\n left--;\n currMin = Math.min(currMin, nums[left]);\n }\n \n ans = Math.max(ans, currMin * (right - left + 1));\n }\n \n return ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n n = len(nums)\n left = k\n right = k\n ans = nums[k]\n curr_min = nums[k]\n \n while left > 0 or right < n - 1:\n if (nums[left - 1] if left else 0) < (nums[right + 1] if right < n - 1 else 0):\n right += 1\n curr_min = min(curr_min, nums[right])\n else:\n left -= 1\n curr_min = min(curr_min, nums[left])\n\n ans = max(ans, curr_min * (right - left + 1))\n \n return ans\n\n```\n\n```javascript []\nfunction maximumScore(nums, k) {\n const n = nums.length;\n let left = k;\n let right = k;\n let ans = nums[k];\n let currMin = nums[k];\n \n while (left > 0 || right < n - 1) {\n if ((left > 0 ? nums[left - 1] : 0) < (right < n - 1 ? nums[right + 1] : 0)) {\n right++;\n currMin = Math.min(currMin, nums[right]);\n } else {\n left--;\n currMin = Math.min(currMin, nums[left]);\n }\n \n const score = currMin * (right - left + 1);\n ans = Math.max(ans, score);\n }\n \n return ans;\n}\n\nconst nums = [1, 4, 3, 7, 4, 5];\nconst k = 3;\nconst result = maximumScore(nums, k);\nconsole.log("Maximum Score:", result);\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
Python3 Solution | maximum-score-of-a-good-subarray | 0 | 1 | \n```\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n ans=nums[k]\n MIN=nums[k]\n low=k\n high=k\n n=len(nums)\n while 0<=low-1 or high+1<n:\n\n if low==0 or high+1<n and nums[low-1]<nums[high+1]:\n high+=1\n MIN=min(MIN,nums[high])\n else:\n low-=1\n MIN=min(MIN ,nums[low]) \n ans=max(ans,MIN*(high-low+1))\n return ans \n``` | 3 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
Python3 Solution | maximum-score-of-a-good-subarray | 0 | 1 | \n```\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n ans=nums[k]\n MIN=nums[k]\n low=k\n high=k\n n=len(nums)\n while 0<=low-1 or high+1<n:\n\n if low==0 or high+1<n and nums[low-1]<nums[high+1]:\n high+=1\n MIN=min(MIN,nums[high])\n else:\n low-=1\n MIN=min(MIN ,nums[low]) \n ans=max(ans,MIN*(high-low+1))\n return ans \n``` | 3 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
✅ 92.13% Two Pointers | maximum-score-of-a-good-subarray | 1 | 1 | # Intuition\nThe core of the problem revolves around identifying a subarray where the outcome of multiplying its length by its minimum element is the largest. A vital insight here is recognizing that the subarray yielding the utmost score will invariably encompass the element at index `k`. This observation drives the solution\'s strategy: initiate from the element at index `k` and consistently widen our window in both left and right directions. Throughout this expansion, we meticulously maintain the minimum element within this evolving window. This enables us to determine the score for every possible window and subsequently amplify it to the maximum.\n\n## Live Coding with Comments\nhttps://youtu.be/VZ3q3TMhuXQ?si=HBYf8Oefh8uBrUoM\n\n# Approach\n1. **Initialization**: \n - We kick off by positioning the `left` and `right` pointers at index `k`. \n - The variable `min_val` is promptly initialized with the element present at index `k`.\n - Simultaneously, `max_score` is set to the value of `min_val`. This essentially represents the score of the subarray `[k, k]`, a window with only one element, the `k`-th element.\n\n2. **Expansion**:\n - During every loop iteration, we\'re faced with a decision: Should we shift the `left` pointer to the left, or should we move the `right` pointer to the right?\n - This decision hinges on two factors: \n 1. Ensuring we haven\'t reached the boundaries of the array.\n 2. Comparing the values adjacent to the current `left` and `right` pointers to decide the more promising direction for expansion.\n\n3. **Score Calculation**:\n - Post each expansion step, we refresh the value of `min_val`. This ensures it always mirrors the smallest element within our current window.\n - Subsequent to this update, we compute the score affiliated with the current window. This is straightforward and is the product of `min_val` and the current window\'s length. If this newly calculated score surpasses our existing `max_score`, we update `max_score`.\n\n4. **Termination**:\n - The expansion loop is designed to persevere until it\'s impossible to further extend the window. This state is reached when the `left` pointer touches the start of the array or the `right` pointer hits the array\'s end.\n\n# Complexity\n- **Time complexity**: $$ O(n) $$ - Each element of the array is visited at most twice: once when expanding to the left and once when expanding to the right.\n- **Space complexity**: $$ O(1) $$ - We only use a constant amount of extra space, irrespective of the input size.\n\n# Code\n``` Python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n left, right = k, k\n min_val = nums[k]\n max_score = min_val\n \n while left > 0 or right < len(nums) - 1:\n if left == 0 or (right < len(nums) - 1 and nums[right + 1] > nums[left - 1]):\n right += 1\n else:\n left -= 1\n min_val = min(min_val, nums[left], nums[right])\n max_score = max(max_score, min_val * (right - left + 1))\n \n return max_score\n```\n``` Rust []\nimpl Solution {\n pub fn maximum_score(nums: Vec<i32>, k: i32) -> i32 {\n let mut left = k as usize;\n let mut right = k as usize;\n let mut min_val = nums[k as usize];\n let mut max_score = min_val;\n\n while left > 0 || right < nums.len() - 1 {\n if left == 0 || (right < nums.len() - 1 && nums[right + 1] > nums[left - 1]) {\n right += 1;\n } else {\n left -= 1;\n }\n min_val = min_val.min(nums[left].min(nums[right]));\n max_score = max_score.max(min_val * (right as i32 - left as i32 + 1));\n }\n \n max_score\n }\n}\n```\n``` Go []\nfunc maximumScore(nums []int, k int) int {\n left, right := k, k\n min_val := nums[k]\n max_score := min_val\n\n for left > 0 || right < len(nums) - 1 {\n if left == 0 || (right < len(nums) - 1 && nums[right+1] > nums[left-1]) {\n right++\n } else {\n left--\n }\n min_val = min(min_val, min(nums[left], nums[right]))\n max_score = max(max_score, min_val * (right - left + 1))\n }\n \n return max_score\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int maximumScore(std::vector<int>& nums, int k) {\n int left = k, right = k;\n int min_val = nums[k];\n int max_score = min_val;\n\n while (left > 0 || right < nums.size() - 1) {\n if (left == 0 || (right < nums.size() - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = std::min(min_val, std::min(nums[left], nums[right]));\n max_score = std::max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int maximumScore(int[] nums, int k) {\n int left = k, right = k;\n int min_val = nums[k];\n int max_score = min_val;\n\n while (left > 0 || right < nums.length - 1) {\n if (left == 0 || (right < nums.length - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = Math.min(min_val, Math.min(nums[left], nums[right]));\n max_score = Math.max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int MaximumScore(int[] nums, int k) {\n int left = k, right = k;\n int min_val = nums[k];\n int max_score = min_val;\n\n while (left > 0 || right < nums.Length - 1) {\n if (left == 0 || (right < nums.Length - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = Math.Min(min_val, Math.Min(nums[left], nums[right]));\n max_score = Math.Max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar maximumScore = function(nums, k) {\n let left = k, right = k;\n let min_val = nums[k];\n let max_score = min_val;\n\n while (left > 0 || right < nums.length - 1) {\n if (left == 0 || (right < nums.length - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = Math.min(min_val, Math.min(nums[left], nums[right]));\n max_score = Math.max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n```\n``` PHP []\nclass Solution {\n function maximumScore($nums, $k) {\n $left = $k;\n $right = $k;\n $min_val = $nums[$k];\n $max_score = $min_val;\n\n while ($left > 0 || $right < count($nums) - 1) {\n if ($left == 0 || ($right < count($nums) - 1 && $nums[$right + 1] > $nums[$left - 1])) {\n $right++;\n } else {\n $left--;\n }\n $min_val = min($min_val, min($nums[$left], $nums[$right]));\n $max_score = max($max_score, $min_val * ($right - $left + 1));\n }\n \n return $max_score;\n }\n}\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|------------|---------------------|-------------------|\n| Java | 8 | 59 |\n| Rust | 16 | 3 |\n| JavaScript | 75 | 53.7 |\n| C++ | 127 | 90.1 |\n| Go | 140 | 8.6 |\n| C# | 238 | 55.3 |\n| PHP | 360 | 30.1 |\n| Python3 | 1011 | 26.6 |\n\n\n\n\n# Why It Works\nThis strategy thrives due to the inherent constraint that the optimal subarray must include the element at index `k`. By commencing our search from this element and methodically expanding outwards, we ensure every possible subarray containing the element at `k` is evaluated. By perpetually updating `min_val` and recalculating the score after each expansion, we guarantee that the maximum score is captured by the time the algorithm concludes.\n\n# What We Learned\n- The importance of identifying and leveraging the constraints of a problem. In this case, knowing that the subarray must contain the element at index $$ k $$ is crucial for devising the optimal strategy.\n- The two-pointer approach is a versatile technique, especially for problems involving arrays and strings. By moving the pointers based on certain conditions, we can explore the solution space efficiently.\n | 76 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
✅ 92.13% Two Pointers | maximum-score-of-a-good-subarray | 1 | 1 | # Intuition\nThe core of the problem revolves around identifying a subarray where the outcome of multiplying its length by its minimum element is the largest. A vital insight here is recognizing that the subarray yielding the utmost score will invariably encompass the element at index `k`. This observation drives the solution\'s strategy: initiate from the element at index `k` and consistently widen our window in both left and right directions. Throughout this expansion, we meticulously maintain the minimum element within this evolving window. This enables us to determine the score for every possible window and subsequently amplify it to the maximum.\n\n## Live Coding with Comments\nhttps://youtu.be/VZ3q3TMhuXQ?si=HBYf8Oefh8uBrUoM\n\n# Approach\n1. **Initialization**: \n - We kick off by positioning the `left` and `right` pointers at index `k`. \n - The variable `min_val` is promptly initialized with the element present at index `k`.\n - Simultaneously, `max_score` is set to the value of `min_val`. This essentially represents the score of the subarray `[k, k]`, a window with only one element, the `k`-th element.\n\n2. **Expansion**:\n - During every loop iteration, we\'re faced with a decision: Should we shift the `left` pointer to the left, or should we move the `right` pointer to the right?\n - This decision hinges on two factors: \n 1. Ensuring we haven\'t reached the boundaries of the array.\n 2. Comparing the values adjacent to the current `left` and `right` pointers to decide the more promising direction for expansion.\n\n3. **Score Calculation**:\n - Post each expansion step, we refresh the value of `min_val`. This ensures it always mirrors the smallest element within our current window.\n - Subsequent to this update, we compute the score affiliated with the current window. This is straightforward and is the product of `min_val` and the current window\'s length. If this newly calculated score surpasses our existing `max_score`, we update `max_score`.\n\n4. **Termination**:\n - The expansion loop is designed to persevere until it\'s impossible to further extend the window. This state is reached when the `left` pointer touches the start of the array or the `right` pointer hits the array\'s end.\n\n# Complexity\n- **Time complexity**: $$ O(n) $$ - Each element of the array is visited at most twice: once when expanding to the left and once when expanding to the right.\n- **Space complexity**: $$ O(1) $$ - We only use a constant amount of extra space, irrespective of the input size.\n\n# Code\n``` Python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n left, right = k, k\n min_val = nums[k]\n max_score = min_val\n \n while left > 0 or right < len(nums) - 1:\n if left == 0 or (right < len(nums) - 1 and nums[right + 1] > nums[left - 1]):\n right += 1\n else:\n left -= 1\n min_val = min(min_val, nums[left], nums[right])\n max_score = max(max_score, min_val * (right - left + 1))\n \n return max_score\n```\n``` Rust []\nimpl Solution {\n pub fn maximum_score(nums: Vec<i32>, k: i32) -> i32 {\n let mut left = k as usize;\n let mut right = k as usize;\n let mut min_val = nums[k as usize];\n let mut max_score = min_val;\n\n while left > 0 || right < nums.len() - 1 {\n if left == 0 || (right < nums.len() - 1 && nums[right + 1] > nums[left - 1]) {\n right += 1;\n } else {\n left -= 1;\n }\n min_val = min_val.min(nums[left].min(nums[right]));\n max_score = max_score.max(min_val * (right as i32 - left as i32 + 1));\n }\n \n max_score\n }\n}\n```\n``` Go []\nfunc maximumScore(nums []int, k int) int {\n left, right := k, k\n min_val := nums[k]\n max_score := min_val\n\n for left > 0 || right < len(nums) - 1 {\n if left == 0 || (right < len(nums) - 1 && nums[right+1] > nums[left-1]) {\n right++\n } else {\n left--\n }\n min_val = min(min_val, min(nums[left], nums[right]))\n max_score = max(max_score, min_val * (right - left + 1))\n }\n \n return max_score\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int maximumScore(std::vector<int>& nums, int k) {\n int left = k, right = k;\n int min_val = nums[k];\n int max_score = min_val;\n\n while (left > 0 || right < nums.size() - 1) {\n if (left == 0 || (right < nums.size() - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = std::min(min_val, std::min(nums[left], nums[right]));\n max_score = std::max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int maximumScore(int[] nums, int k) {\n int left = k, right = k;\n int min_val = nums[k];\n int max_score = min_val;\n\n while (left > 0 || right < nums.length - 1) {\n if (left == 0 || (right < nums.length - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = Math.min(min_val, Math.min(nums[left], nums[right]));\n max_score = Math.max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int MaximumScore(int[] nums, int k) {\n int left = k, right = k;\n int min_val = nums[k];\n int max_score = min_val;\n\n while (left > 0 || right < nums.Length - 1) {\n if (left == 0 || (right < nums.Length - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = Math.Min(min_val, Math.Min(nums[left], nums[right]));\n max_score = Math.Max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar maximumScore = function(nums, k) {\n let left = k, right = k;\n let min_val = nums[k];\n let max_score = min_val;\n\n while (left > 0 || right < nums.length - 1) {\n if (left == 0 || (right < nums.length - 1 && nums[right + 1] > nums[left - 1])) {\n right++;\n } else {\n left--;\n }\n min_val = Math.min(min_val, Math.min(nums[left], nums[right]));\n max_score = Math.max(max_score, min_val * (right - left + 1));\n }\n \n return max_score;\n }\n```\n``` PHP []\nclass Solution {\n function maximumScore($nums, $k) {\n $left = $k;\n $right = $k;\n $min_val = $nums[$k];\n $max_score = $min_val;\n\n while ($left > 0 || $right < count($nums) - 1) {\n if ($left == 0 || ($right < count($nums) - 1 && $nums[$right + 1] > $nums[$left - 1])) {\n $right++;\n } else {\n $left--;\n }\n $min_val = min($min_val, min($nums[$left], $nums[$right]));\n $max_score = max($max_score, $min_val * ($right - $left + 1));\n }\n \n return $max_score;\n }\n}\n```\n\n# Performance\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|------------|---------------------|-------------------|\n| Java | 8 | 59 |\n| Rust | 16 | 3 |\n| JavaScript | 75 | 53.7 |\n| C++ | 127 | 90.1 |\n| Go | 140 | 8.6 |\n| C# | 238 | 55.3 |\n| PHP | 360 | 30.1 |\n| Python3 | 1011 | 26.6 |\n\n\n\n\n# Why It Works\nThis strategy thrives due to the inherent constraint that the optimal subarray must include the element at index `k`. By commencing our search from this element and methodically expanding outwards, we ensure every possible subarray containing the element at `k` is evaluated. By perpetually updating `min_val` and recalculating the score after each expansion, we guarantee that the maximum score is captured by the time the algorithm concludes.\n\n# What We Learned\n- The importance of identifying and leveraging the constraints of a problem. In this case, knowing that the subarray must contain the element at index $$ k $$ is crucial for devising the optimal strategy.\n- The two-pointer approach is a versatile technique, especially for problems involving arrays and strings. By moving the pointers based on certain conditions, we can explore the solution space efficiently.\n | 76 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
[python3] Traverse from either sides to find min | maximum-score-of-a-good-subarray | 0 | 1 | There is more scope for optimization but here is a solution that keeps track of minimum from left and right side and then calculate maximum by using formula in the problem. ( right - left +1 ) * nums[i]\n\n```\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n N = len(nums)\n left = [0]*N\n ans = 0\n s = []\n \n for i in range(N):\n while s and nums[i] <= nums[s[-1]]:\n s.pop()\n \n left[i] = (s[-1]+1) if s else 0\n \n s.append(i)\n \n s = []\n \n for i in range(N-1,-1,-1):\n while s and nums[i] <= nums[s[-1]]:\n s.pop()\n \n value = N-1 if not s else (s[-1]-1)\n\n if left[i] <= k and value >= k:\n ans = max(ans, (value - left[i] + 1)*nums[i])\n \n s.append(i) \n \n return ans | 1 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
[python3] Traverse from either sides to find min | maximum-score-of-a-good-subarray | 0 | 1 | There is more scope for optimization but here is a solution that keeps track of minimum from left and right side and then calculate maximum by using formula in the problem. ( right - left +1 ) * nums[i]\n\n```\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n N = len(nums)\n left = [0]*N\n ans = 0\n s = []\n \n for i in range(N):\n while s and nums[i] <= nums[s[-1]]:\n s.pop()\n \n left[i] = (s[-1]+1) if s else 0\n \n s.append(i)\n \n s = []\n \n for i in range(N-1,-1,-1):\n while s and nums[i] <= nums[s[-1]]:\n s.pop()\n \n value = N-1 if not s else (s[-1]-1)\n\n if left[i] <= k and value >= k:\n ans = max(ans, (value - left[i] + 1)*nums[i])\n \n s.append(i) \n \n return ans | 1 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
✅ Beats 100% 🔥 in 4 Languages || Beginner Friendly Eplanation || | maximum-score-of-a-good-subarray | 1 | 1 | ## TypeScript :\n\n\n## PHP :\n\n\n\n## JavaScript :\n\n\n## Ruby :\n\n\n\n# Intuition : \n##### For each index k, find the maximum length of a subarray with minimum value nums[k]. The answer is the maximum of those values.\n<!-- Describe your first thoughts on how to solve this problem. -->\n# Explanation :\n**For each index k, let us find left and right, the boundaries of this subarray. The minimum of nums[left], nums[left + 1], ..., nums[right] will be the answer for this subarray. We can use two pointers to find left and right. The condition for moving our pointers is as follows: we want to move right whenever min(nums[left], nums[left + 1], ..., nums[right]) < min(nums[left], nums[left + 1], ..., nums[right], nums[right + 1]) and left > 0, and we want to move left whenever min(nums[left - 1], nums[left - 2], ..., nums[right]) >= min(nums[left], nums[left + 1], ..., nums[right]). The first condition means that we want to include more elements in our subarray, and the second condition means that we do not want to exclude any elements from our subarray. The subarray we have found is then [left, left + 1, ..., right]. The length is right - left + 1, and the minimum of the subarray is min(nums[left], nums[left + 1], ..., nums[right]). We multiply these together to get the score of this subarray, which is (right - left + 1) * min(nums[left], nums[left + 1], ..., nums[right]). We take the maximum of all these values to get the answer.**\n\n# Approach : Two Pointers\n1. Initialize left = k and right = k.\n2. While left > 0 or right < nums.length - 1:\n 1. If left == 0, then right += 1.\n 2. Else if right == nums.length - 1, then left -= 1.\n 3. Else if nums[left - 1] > nums[right + 1], then left -= 1.\n 4. Else right += 1.\n3. Update the answer as max(answer, (right - left + 1) * min(nums[left], nums[left + 1], ..., nums[right])).\n4. Return answer.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : ***O(n)***, *where n is the length of nums.*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : ***O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n### Please UpVote if this helps you :)\uD83D\uDE03\n\n# Code\n``` Python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n res=nums[k]\n i=k\n j=k\n min_val=nums[k]\n\n while i>0 or j<len(nums)-1:\n if i==0:\n j+=1\n min_val=min(min_val,nums[j])\n elif j==len(nums)-1:\n i-=1\n min_val=min(min_val,nums[i])\n elif nums[i-1]>nums[j+1]:\n i-=1\n min_val=min(min_val,nums[i])\n else:\n j+=1\n min_val=min(min_val,nums[j])\n res=max(res,min_val*(j-i+1))\n return res\n```\n``` C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int res = nums[k];\n int i = k;\n int j = k;\n int min_val = nums[k];\n\n while (i > 0 || j < nums.size() - 1) {\n if (i == 0) {\n j += 1;\n min_val = min(min_val, nums[j]);\n } else if (j == nums.size() - 1) {\n i -= 1;\n min_val = min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = min(min_val, nums[j]);\n }\n\n res = max(res, min_val * (j - i + 1));\n }\n\n return res;\n }\n};\n\n```\n``` Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int res = nums[k];\n int i = k;\n int j = k;\n int min_val = nums[k];\n\n while (i > 0 || j < nums.length - 1) {\n if (i == 0) {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n } else if (j == nums.length - 1) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n }\n\n res = Math.max(res, min_val * (j - i + 1));\n }\n\n return res;\n }\n}\n\n```\n``` C# []\npublic class Solution {\n public int MaximumScore(int[] nums, int k) {\n int res = nums[k];\n int i = k;\n int j = k;\n int min_val = nums[k];\n\n while (i > 0 || j < nums.Length - 1) {\n if (i == 0) {\n j += 1;\n min_val = Math.Min(min_val, nums[j]);\n } else if (j == nums.Length - 1) {\n i -= 1;\n min_val = Math.Min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.Min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.Min(min_val, nums[j]);\n }\n\n res = Math.Max(res, min_val * (j - i + 1));\n }\n\n return res;\n }\n}\n\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar maximumScore = function(nums, k) {\n let res = nums[k];\n let i = k;\n let j = k;\n let min_val = nums[k];\n\n while (i > 0 || j < nums.length - 1) {\n if (i === 0) {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n } else if (j === nums.length - 1) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n }\n\n res = Math.max(res, min_val * (j - i + 1));\n }\n\n return res;\n};\n```\n``` TypeScript []\nfunction maximumScore(nums: number[], k: number): number {\nlet res = nums[k];\n let i = k;\n let j = k;\n let min_val = nums[k];\n\n while (i > 0 || j < nums.length - 1) {\n if (i === 0) {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n } else if (j === nums.length - 1) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n }\n\n res = Math.max(res, min_val * (j - i + 1));\n }\n\n return res;\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @param Integer $k\n * @return Integer\n */\n function maximumScore($nums, $k) {\n $es = $nums[$k];\n $i = $k;\n $j = $k;\n $min_val = $nums[$k];\n $len = count($nums);\n $res = $min_val * ($j - $i + 1);\n\n while ($i > 0 || $j < $len - 1) {\n if ($i == 0) {\n $j += 1;\n $min_val = min($min_val, $nums[$j]);\n } elseif ($j == $len - 1) {\n $i -= 1;\n $min_val = min($min_val, $nums[$i]);\n } elseif ($nums[$i - 1] > $nums[$j + 1]) {\n $i -= 1;\n $min_val = min($min_val, $nums[$i]);\n } else {\n $j += 1;\n $min_val = min($min_val, $nums[$j]);\n }\n\n $res = max($res, $min_val * ($j - $i + 1));\n }\n\n return $res;\n }\n}\n```\n``` Ruby []\n# @param {Integer[]} nums\n# @param {Integer} k\n# @return {Integer}\ndef maximum_score(nums, k)\n res = nums[k]\n i = k\n j = k\n min_val = nums[k]\n\n while i > 0 || j < nums.length - 1\n if i == 0\n j += 1\n min_val = [min_val, nums[j]].min\n elsif j == nums.length - 1\n i -= 1\n min_val = [min_val, nums[i]].min\n elsif nums[i - 1] > nums[j + 1]\n i -= 1\n min_val = [min_val, nums[i]].min\n else\n j += 1\n min_val = [min_val, nums[j]].min\n end\n\n res = [res, min_val * (j - i + 1)].max\n end\n\n res\nend\n``` | 2 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
✅ Beats 100% 🔥 in 4 Languages || Beginner Friendly Eplanation || | maximum-score-of-a-good-subarray | 1 | 1 | ## TypeScript :\n\n\n## PHP :\n\n\n\n## JavaScript :\n\n\n## Ruby :\n\n\n\n# Intuition : \n##### For each index k, find the maximum length of a subarray with minimum value nums[k]. The answer is the maximum of those values.\n<!-- Describe your first thoughts on how to solve this problem. -->\n# Explanation :\n**For each index k, let us find left and right, the boundaries of this subarray. The minimum of nums[left], nums[left + 1], ..., nums[right] will be the answer for this subarray. We can use two pointers to find left and right. The condition for moving our pointers is as follows: we want to move right whenever min(nums[left], nums[left + 1], ..., nums[right]) < min(nums[left], nums[left + 1], ..., nums[right], nums[right + 1]) and left > 0, and we want to move left whenever min(nums[left - 1], nums[left - 2], ..., nums[right]) >= min(nums[left], nums[left + 1], ..., nums[right]). The first condition means that we want to include more elements in our subarray, and the second condition means that we do not want to exclude any elements from our subarray. The subarray we have found is then [left, left + 1, ..., right]. The length is right - left + 1, and the minimum of the subarray is min(nums[left], nums[left + 1], ..., nums[right]). We multiply these together to get the score of this subarray, which is (right - left + 1) * min(nums[left], nums[left + 1], ..., nums[right]). We take the maximum of all these values to get the answer.**\n\n# Approach : Two Pointers\n1. Initialize left = k and right = k.\n2. While left > 0 or right < nums.length - 1:\n 1. If left == 0, then right += 1.\n 2. Else if right == nums.length - 1, then left -= 1.\n 3. Else if nums[left - 1] > nums[right + 1], then left -= 1.\n 4. Else right += 1.\n3. Update the answer as max(answer, (right - left + 1) * min(nums[left], nums[left + 1], ..., nums[right])).\n4. Return answer.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : ***O(n)***, *where n is the length of nums.*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : ***O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n### Please UpVote if this helps you :)\uD83D\uDE03\n\n# Code\n``` Python []\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n res=nums[k]\n i=k\n j=k\n min_val=nums[k]\n\n while i>0 or j<len(nums)-1:\n if i==0:\n j+=1\n min_val=min(min_val,nums[j])\n elif j==len(nums)-1:\n i-=1\n min_val=min(min_val,nums[i])\n elif nums[i-1]>nums[j+1]:\n i-=1\n min_val=min(min_val,nums[i])\n else:\n j+=1\n min_val=min(min_val,nums[j])\n res=max(res,min_val*(j-i+1))\n return res\n```\n``` C++ []\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int res = nums[k];\n int i = k;\n int j = k;\n int min_val = nums[k];\n\n while (i > 0 || j < nums.size() - 1) {\n if (i == 0) {\n j += 1;\n min_val = min(min_val, nums[j]);\n } else if (j == nums.size() - 1) {\n i -= 1;\n min_val = min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = min(min_val, nums[j]);\n }\n\n res = max(res, min_val * (j - i + 1));\n }\n\n return res;\n }\n};\n\n```\n``` Java []\nclass Solution {\n public int maximumScore(int[] nums, int k) {\n int res = nums[k];\n int i = k;\n int j = k;\n int min_val = nums[k];\n\n while (i > 0 || j < nums.length - 1) {\n if (i == 0) {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n } else if (j == nums.length - 1) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n }\n\n res = Math.max(res, min_val * (j - i + 1));\n }\n\n return res;\n }\n}\n\n```\n``` C# []\npublic class Solution {\n public int MaximumScore(int[] nums, int k) {\n int res = nums[k];\n int i = k;\n int j = k;\n int min_val = nums[k];\n\n while (i > 0 || j < nums.Length - 1) {\n if (i == 0) {\n j += 1;\n min_val = Math.Min(min_val, nums[j]);\n } else if (j == nums.Length - 1) {\n i -= 1;\n min_val = Math.Min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.Min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.Min(min_val, nums[j]);\n }\n\n res = Math.Max(res, min_val * (j - i + 1));\n }\n\n return res;\n }\n}\n\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar maximumScore = function(nums, k) {\n let res = nums[k];\n let i = k;\n let j = k;\n let min_val = nums[k];\n\n while (i > 0 || j < nums.length - 1) {\n if (i === 0) {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n } else if (j === nums.length - 1) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n }\n\n res = Math.max(res, min_val * (j - i + 1));\n }\n\n return res;\n};\n```\n``` TypeScript []\nfunction maximumScore(nums: number[], k: number): number {\nlet res = nums[k];\n let i = k;\n let j = k;\n let min_val = nums[k];\n\n while (i > 0 || j < nums.length - 1) {\n if (i === 0) {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n } else if (j === nums.length - 1) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else if (nums[i - 1] > nums[j + 1]) {\n i -= 1;\n min_val = Math.min(min_val, nums[i]);\n } else {\n j += 1;\n min_val = Math.min(min_val, nums[j]);\n }\n\n res = Math.max(res, min_val * (j - i + 1));\n }\n\n return res;\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @param Integer $k\n * @return Integer\n */\n function maximumScore($nums, $k) {\n $es = $nums[$k];\n $i = $k;\n $j = $k;\n $min_val = $nums[$k];\n $len = count($nums);\n $res = $min_val * ($j - $i + 1);\n\n while ($i > 0 || $j < $len - 1) {\n if ($i == 0) {\n $j += 1;\n $min_val = min($min_val, $nums[$j]);\n } elseif ($j == $len - 1) {\n $i -= 1;\n $min_val = min($min_val, $nums[$i]);\n } elseif ($nums[$i - 1] > $nums[$j + 1]) {\n $i -= 1;\n $min_val = min($min_val, $nums[$i]);\n } else {\n $j += 1;\n $min_val = min($min_val, $nums[$j]);\n }\n\n $res = max($res, $min_val * ($j - $i + 1));\n }\n\n return $res;\n }\n}\n```\n``` Ruby []\n# @param {Integer[]} nums\n# @param {Integer} k\n# @return {Integer}\ndef maximum_score(nums, k)\n res = nums[k]\n i = k\n j = k\n min_val = nums[k]\n\n while i > 0 || j < nums.length - 1\n if i == 0\n j += 1\n min_val = [min_val, nums[j]].min\n elsif j == nums.length - 1\n i -= 1\n min_val = [min_val, nums[i]].min\n elsif nums[i - 1] > nums[j + 1]\n i -= 1\n min_val = [min_val, nums[i]].min\n else\n j += 1\n min_val = [min_val, nums[j]].min\n end\n\n res = [res, min_val * (j - i + 1)].max\n end\n\n res\nend\n``` | 2 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
[python3] Intuitive two-pointer method (time beats 98.47%) | maximum-score-of-a-good-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem becomes much easier with this "k condition": the subarray must contains nums[k]. We don\'t need to consider every subarray but only those that grows from index k.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIt is not hard to then think of the following approach: from this nums[k], we expand the subarray to the left and to the right as long as nums[k] is still the min element. When we meet a smaller element in one direction we stop expanding in that direction, we update the answer first, since this is the best we can do with the current smallest, then we take the new smallest as the current smallest, and start expanding again. We do this until we meet both ends of the array.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n l, r = k, k\n cur_min = nums[k]\n ans = float(\'-inf\')\n while l >= 0 or r < len(nums):\n while l >= 0 and nums[l] >= cur_min:\n l -= 1\n while r < len(nums) and nums[r] >= cur_min:\n r += 1\n ans = max(ans, (r - l - 1) * cur_min)\n if l >= 0 and r < len(nums):\n cur_min = max(nums[l], nums[r])\n elif l >= 0:\n cur_min = nums[l]\n elif r < len(nums):\n cur_min = nums[r]\n else:\n break \n return ans\n \n``` | 0 | You are given an array of integers `nums` **(0-indexed)** and an integer `k`.
The **score** of a subarray `(i, j)` is defined as `min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1)`. A **good** subarray is a subarray where `i <= k <= j`.
Return _the maximum possible **score** of a **good** subarray._
**Example 1:**
**Input:** nums = \[1,4,3,7,4,5\], k = 3
**Output:** 15
**Explanation:** The optimal subarray is (1, 5) with a score of min(4,3,7,4,5) \* (5-1+1) = 3 \* 5 = 15.
**Example 2:**
**Input:** nums = \[5,5,4,5,4,1,1,1\], k = 0
**Output:** 20
**Explanation:** The optimal subarray is (0, 4) with a score of min(5,5,4,5,4) \* (4-0+1) = 4 \* 5 = 20.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 2 * 104`
* `0 <= k < nums.length` | Given a target sum x, each pair of nums[i] and nums[n-1-i] would either need 0, 1, or 2 modifications. Can you find the optimal target sum x value such that the sum of modifications is minimized? Create a difference array to efficiently sum all the modifications. |
[python3] Intuitive two-pointer method (time beats 98.47%) | maximum-score-of-a-good-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem becomes much easier with this "k condition": the subarray must contains nums[k]. We don\'t need to consider every subarray but only those that grows from index k.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIt is not hard to then think of the following approach: from this nums[k], we expand the subarray to the left and to the right as long as nums[k] is still the min element. When we meet a smaller element in one direction we stop expanding in that direction, we update the answer first, since this is the best we can do with the current smallest, then we take the new smallest as the current smallest, and start expanding again. We do this until we meet both ends of the array.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maximumScore(self, nums: List[int], k: int) -> int:\n l, r = k, k\n cur_min = nums[k]\n ans = float(\'-inf\')\n while l >= 0 or r < len(nums):\n while l >= 0 and nums[l] >= cur_min:\n l -= 1\n while r < len(nums) and nums[r] >= cur_min:\n r += 1\n ans = max(ans, (r - l - 1) * cur_min)\n if l >= 0 and r < len(nums):\n cur_min = max(nums[l], nums[r])\n elif l >= 0:\n cur_min = nums[l]\n elif r < len(nums):\n cur_min = nums[r]\n else:\n break \n return ans\n \n``` | 0 | Given an integer array `nums` of length `n` and an integer `k`, return _the_ `kth` _**smallest subarray sum**._
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array. A **subarray sum** is the sum of all elements in the subarray.
**Example 1:**
**Input:** nums = \[2,1,3\], k = 4
**Output:** 3
**Explanation:** The subarrays of \[2,1,3\] are:
- \[2\] with sum 2
- \[1\] with sum 1
- \[3\] with sum 3
- \[2,1\] with sum 3
- \[1,3\] with sum 4
- \[2,1,3\] with sum 6
Ordering the sums from smallest to largest gives 1, 2, 3, 3, 4, 6. The 4th smallest is 3.
**Example 2:**
**Input:** nums = \[3,3,5,5\], k = 7
**Output:** 10
**Explanation:** The subarrays of \[3,3,5,5\] are:
- \[3\] with sum 3
- \[3\] with sum 3
- \[5\] with sum 5
- \[5\] with sum 5
- \[3,3\] with sum 6
- \[3,5\] with sum 8
- \[5,5\] with sum 10
- \[3,3,5\], with sum 11
- \[3,5,5\] with sum 13
- \[3,3,5,5\] with sum 16
Ordering the sums from smallest to largest gives 3, 3, 5, 5, 6, 8, 10, 11, 13, 16. The 7th smallest is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 104`
* `1 <= nums[i] <= 5 * 104`
* `1 <= k <= n * (n + 1) / 2` | Try thinking about the prefix before index k and the suffix after index k as two separate arrays. Using two pointers or binary search, we can find the maximum prefix of each array where the numbers are less than or equal to a certain value |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | rearrange-products-table | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python []\ndef rearrange_products_table(products: pd.DataFrame) -> pd.DataFrame:\n return pd.melt(\n products, id_vars=\'product_id\', var_name=\'store\', value_name=\'price\'\n ).dropna()\n```\n```SQL []\nSELECT product_id,\n \'store1\' AS store,\n store1 AS price\n FROM Products\n WHERE store1 IS NOT NULL\n\n UNION\n\n SELECT product_id,\n \'store2\' AS store,\n store2 AS price\n FROM Products\n WHERE store2 IS NOT NULL\n\n UNION\n\n SELECT product_id,\n \'store3\' AS store,\n store3 AS price\n FROM Products\n WHERE store3 IS NOT NULL\n\n ORDER BY product_id, store;\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n | 61 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
the solution of the problem using a command that in pandas library | rearrange-products-table | 0 | 1 | \n# Code\n```\nimport pandas as pd\n\ndef rearrange_products_table(products: pd.DataFrame) -> pd.DataFrame:\n # 1. Saves output in new DataFrame\n df = (\n # 2. .melt() lets you unpivot the table\n products.melt(\n # 3. Columns you want to leave unchanged\n id_vars = [\'product_id\'],\n # 4. Columns you want to unpivot\n value_vars = [\'store1\', \'store2\', \'store3\'], \n # 5. This names the store column\n var_name = \'store\',\n # 6. This names the price column\n value_name = \'price\'\n )\n # 7. .dropna() lets you drop the null values\n .dropna() \n )\n return df\n``` | 1 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
Simplest Python solution | second-largest-digit-in-a-string | 0 | 1 | \n\n# Code\n```\nfrom sortedcontainers import SortedSet\nclass Solution:\n def secondHighest(self, s: str) -> int:\n a = [int(x) for x in s if x.isnumeric()]\n return SortedSet(a)[-2] if len(set(a)) >= 2 else -1\n``` | 3 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
Simplest Python solution | second-largest-digit-in-a-string | 0 | 1 | \n\n# Code\n```\nfrom sortedcontainers import SortedSet\nclass Solution:\n def secondHighest(self, s: str) -> int:\n a = [int(x) for x in s if x.isnumeric()]\n return SortedSet(a)[-2] if len(set(a)) >= 2 else -1\n``` | 3 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
Python | 99% Faster | Easy Solution✅ | second-largest-digit-in-a-string | 0 | 1 | ```\ndef secondHighest(self, s: str) -> int:\n digits = set()\n s = list(set(s))\n for letter in s:\n if letter.isdigit():\n digits.add(letter)\n digits = sorted(list(digits))\n return -1 if len(digits) < 2 else digits[-2]\n```\n\n | 5 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
Python | 99% Faster | Easy Solution✅ | second-largest-digit-in-a-string | 0 | 1 | ```\ndef secondHighest(self, s: str) -> int:\n digits = set()\n s = list(set(s))\n for letter in s:\n if letter.isdigit():\n digits.add(letter)\n digits = sorted(list(digits))\n return -1 if len(digits) < 2 else digits[-2]\n```\n\n | 5 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
✔ Python3 | Faster Solution | Easiest | brute force | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n s=set(s)\n a=[]\n for i in s:\n if i.isnumeric() :\n a.append(int(i))\n a.sort()\n if len(a)<2:\n return -1\n return a[len(a)-2]\n```\n**optimized code**\n```\ndef secondHighest(self, s: str) -> int:\n st = (set(s))\n f1,s2=-1,-1\n for i in st:\n if i.isnumeric():\n i=int(i)\n if i>f1:\n s2=f1\n f1=i\n elif i>s2 and i!=f1:\n s2=i\n return s2\n``` | 5 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
✔ Python3 | Faster Solution | Easiest | brute force | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n s=set(s)\n a=[]\n for i in s:\n if i.isnumeric() :\n a.append(int(i))\n a.sort()\n if len(a)<2:\n return -1\n return a[len(a)-2]\n```\n**optimized code**\n```\ndef secondHighest(self, s: str) -> int:\n st = (set(s))\n f1,s2=-1,-1\n for i in st:\n if i.isnumeric():\n i=int(i)\n if i>f1:\n s2=f1\n f1=i\n elif i>s2 and i!=f1:\n s2=i\n return s2\n``` | 5 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
Clean python with comments | second-largest-digit-in-a-string | 0 | 1 | ```\ndef secondHighest(self, s):\n t = set() # create set to store unique digits\n for i in s:\n if \'0\'<=i<=\'9\':\n t.add(int(i)) # add digit to the set\n if len(t)>1:\n return sorted(list(t))[-2] # sort and return second largest one if number of elements are more than 1 \n return -1 # otherwise return -1\n``` | 16 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
Clean python with comments | second-largest-digit-in-a-string | 0 | 1 | ```\ndef secondHighest(self, s):\n t = set() # create set to store unique digits\n for i in s:\n if \'0\'<=i<=\'9\':\n t.add(int(i)) # add digit to the set\n if len(t)>1:\n return sorted(list(t))[-2] # sort and return second largest one if number of elements are more than 1 \n return -1 # otherwise return -1\n``` | 16 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
PYTHON || EASY TO UNDERSTAND | second-largest-digit-in-a-string | 0 | 1 | \n# Approach\nIndexing and Brute Force\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n lst = []\n for i in range(len(s)):\n if s[i].isdigit():\n lst.append(s[i])\n lst = list(set(lst))\n if len(lst) <= 1:\n return -1\n else:\n lst.sort()\n index = len(lst)-2\n res = lst[index]\n return res\n \n``` | 1 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
PYTHON || EASY TO UNDERSTAND | second-largest-digit-in-a-string | 0 | 1 | \n# Approach\nIndexing and Brute Force\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n lst = []\n for i in range(len(s)):\n if s[i].isdigit():\n lst.append(s[i])\n lst = list(set(lst))\n if len(lst) <= 1:\n return -1\n else:\n lst.sort()\n index = len(lst)-2\n res = lst[index]\n return res\n \n``` | 1 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
Python 3 (30ms) | Fastest Set Solution | Easy to Understand | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n st = (set(s))\n f1,s2=-1,-1\n for i in st:\n if i.isnumeric():\n i=int(i)\n if i>f1:\n s2=f1\n f1=i\n elif i>s2 and i!=f1:\n s2=i\n return s2\n``` | 3 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
Python 3 (30ms) | Fastest Set Solution | Easy to Understand | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n st = (set(s))\n f1,s2=-1,-1\n for i in st:\n if i.isnumeric():\n i=int(i)\n if i>f1:\n s2=f1\n f1=i\n elif i>s2 and i!=f1:\n s2=i\n return s2\n``` | 3 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
✔ Python3 | Without array or sorting | Faster Solution | Easiest | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n st = (set(s))\n f1,s2=-1,-1\n for i in st:\n if i.isnumeric():\n i=int(i)\n if i>f1:\n s2=f1\n f1=i\n elif i>s2 and i!=f1:\n s2=i\n return s2\n``` | 2 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
✔ Python3 | Without array or sorting | Faster Solution | Easiest | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n st = (set(s))\n f1,s2=-1,-1\n for i in st:\n if i.isnumeric():\n i=int(i)\n if i>f1:\n s2=f1\n f1=i\n elif i>s2 and i!=f1:\n s2=i\n return s2\n``` | 2 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
Python3 simple solution using list | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n l = []\n for i in s:\n if i.isdigit() and i not in l:\n l.append(i)\n if len(l) >= 2:\n return int(sorted(l)[-2])\n else:\n return -1\n```\n**If you like this solution, please upvote for this** | 4 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
Python3 simple solution using list | second-largest-digit-in-a-string | 0 | 1 | ```\nclass Solution:\n def secondHighest(self, s: str) -> int:\n l = []\n for i in s:\n if i.isdigit() and i not in l:\n l.append(i)\n if len(l) >= 2:\n return int(sorted(l)[-2])\n else:\n return -1\n```\n**If you like this solution, please upvote for this** | 4 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
Python easy solution without sort and hash | 38ms | second-largest-digit-in-a-string | 0 | 1 | # Intuition\nWhat we need is 2nd largest number, so we just keep track of first and second largest number\n\n# Approach\n1. Initiate first and second to -1, -1\n2. Loop over a string\n3. If item is a number and it\'s greater than `first` then assign that number as `first` and original `first` number to `second`\n4. If number is not greater than `first` but greater than `second` then assign that number as `second`\n\nWhat we are doing is, if number is greater than `first` then shift current largest number to `second`\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\no(1)\n\n# Code\n```python3\nclass Solution:\n def secondHighest(self, s: str) -> int:\n first, second = -1, -1\n for i in s:\n if i.isdigit():\n if int(i) > first:\n first, second = int(i), first\n elif int(i) < first and int(i) > second:\n second = int(i)\n \n return second\n \n``` | 0 | Given an alphanumeric string `s`, return _the **second largest** numerical digit that appears in_ `s`_, or_ `-1` _if it does not exist_.
An **alphanumeric** string is a string consisting of lowercase English letters and digits.
**Example 1:**
**Input:** s = "dfa12321afd "
**Output:** 2
**Explanation:** The digits that appear in s are \[1, 2, 3\]. The second largest digit is 2.
**Example 2:**
**Input:** s = "abc1111 "
**Output:** -1
**Explanation:** The digits that appear in s are \[1\]. There is no second largest digit.
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of only lowercase English letters and/or digits. | If you traverse the tree from right to left, the invalid node will point to a node that has already been visited. |
Python easy solution without sort and hash | 38ms | second-largest-digit-in-a-string | 0 | 1 | # Intuition\nWhat we need is 2nd largest number, so we just keep track of first and second largest number\n\n# Approach\n1. Initiate first and second to -1, -1\n2. Loop over a string\n3. If item is a number and it\'s greater than `first` then assign that number as `first` and original `first` number to `second`\n4. If number is not greater than `first` but greater than `second` then assign that number as `second`\n\nWhat we are doing is, if number is greater than `first` then shift current largest number to `second`\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\no(1)\n\n# Code\n```python3\nclass Solution:\n def secondHighest(self, s: str) -> int:\n first, second = -1, -1\n for i in s:\n if i.isdigit():\n if int(i) > first:\n first, second = int(i), first\n elif int(i) < first and int(i) > second:\n second = int(i)\n \n return second\n \n``` | 0 | You are participating in an online chess tournament. There is a chess round that starts every `15` minutes. The first round of the day starts at `00:00`, and after every `15` minutes, a new round starts.
* For example, the second round starts at `00:15`, the fourth round starts at `00:45`, and the seventh round starts at `01:30`.
You are given two strings `loginTime` and `logoutTime` where:
* `loginTime` is the time you will login to the game, and
* `logoutTime` is the time you will logout from the game.
If `logoutTime` is **earlier** than `loginTime`, this means you have played from `loginTime` to midnight and from midnight to `logoutTime`.
Return _the number of full chess rounds you have played in the tournament_.
**Note:** All the given times follow the 24-hour clock. That means the first round of the day starts at `00:00` and the last round of the day starts at `23:45`.
**Example 1:**
**Input:** loginTime = "09:31 ", logoutTime = "10:14 "
**Output:** 1
**Explanation:** You played one full round from 09:45 to 10:00.
You did not play the full round from 09:30 to 09:45 because you logged in at 09:31 after it began.
You did not play the full round from 10:00 to 10:15 because you logged out at 10:14 before it ended.
**Example 2:**
**Input:** loginTime = "21:30 ", logoutTime = "03:00 "
**Output:** 22
**Explanation:** You played 10 full rounds from 21:30 to 00:00 and 12 full rounds from 00:00 to 03:00.
10 + 12 = 22.
**Constraints:**
* `loginTime` and `logoutTime` are in the format `hh:mm`.
* `00 <= hh <= 23`
* `00 <= mm <= 59`
* `loginTime` and `logoutTime` are not equal. | First of all, get the distinct characters since we are only interested in those Let's note that there might not be any digits. |
Python3: Dictionary + Deque = beat 98% runtime | design-authentication-manager | 0 | 1 | # Intuition\n* The problem has an inherent FIFO nature - tokens are added with strictly increasing timestamps, and the tokens which are added first will also expire first since TTL is the same for all tokens. This should inspire using a queue. \n* I used a hashmap with the queue just to keep track of the tokenids, but it turned out to be redundant.\n* When you get a call to renew or count unexpired tokens, look at the queue and start popping tokens one by one until the head of the queue is an unexpired token. This is amortized O(1) - you do a constant amount of work (queue.popleft()) per expired token. \n\n\n# Complexity\n- Time complexity:\n- Generate: O(1)\n- Renew: O(n)\n- Processing expiry: Amortized O(1)\n- CountUnexpiredTokens: O(1) (once expiry is processed, just get the length of the queue)\n\n- Space complexity: O(n) for queue. \n\n# Code\n```\nfrom collections import deque\n\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.tokens = {} # Dictionary from tokenId to expiry time.\n self.token_queue = deque() # helps keep track of which tokens to expire next. \n self.ttl = timeToLive\n\n def generate(self, tokenId: str, currentTime: int) -> None:\n expiry = currentTime + self.ttl\n self.tokens[tokenId] = expiry\n self.token_queue.append((expiry, tokenId))\n\n\n def process_expiry(self, currentTime: int) -> int:\n count = 0\n while self.token_queue and self.token_queue[0][0] <= currentTime:\n exp, tok = self.token_queue.popleft()\n del self.tokens[tok]\n count += 1\n return count\n\n def renew(self, tokenId: str, currentTime: int) -> None:\n if tokenId not in self.tokens:\n return\n if currentTime >= self.tokens[tokenId]:\n # token is already expired. \n # process expiry\n num_expired = self.process_expiry(currentTime)\n return\n # token not expired, process renewal\n idx = 0\n while self.token_queue[idx][1] != tokenId:\n idx += 1\n del self.token_queue[idx]\n del self.tokens[tokenId]\n self.generate(tokenId, currentTime)\n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.process_expiry(currentTime)\n return len(self.token_queue)\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 1 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Python3: Dictionary + Deque = beat 98% runtime | design-authentication-manager | 0 | 1 | # Intuition\n* The problem has an inherent FIFO nature - tokens are added with strictly increasing timestamps, and the tokens which are added first will also expire first since TTL is the same for all tokens. This should inspire using a queue. \n* I used a hashmap with the queue just to keep track of the tokenids, but it turned out to be redundant.\n* When you get a call to renew or count unexpired tokens, look at the queue and start popping tokens one by one until the head of the queue is an unexpired token. This is amortized O(1) - you do a constant amount of work (queue.popleft()) per expired token. \n\n\n# Complexity\n- Time complexity:\n- Generate: O(1)\n- Renew: O(n)\n- Processing expiry: Amortized O(1)\n- CountUnexpiredTokens: O(1) (once expiry is processed, just get the length of the queue)\n\n- Space complexity: O(n) for queue. \n\n# Code\n```\nfrom collections import deque\n\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.tokens = {} # Dictionary from tokenId to expiry time.\n self.token_queue = deque() # helps keep track of which tokens to expire next. \n self.ttl = timeToLive\n\n def generate(self, tokenId: str, currentTime: int) -> None:\n expiry = currentTime + self.ttl\n self.tokens[tokenId] = expiry\n self.token_queue.append((expiry, tokenId))\n\n\n def process_expiry(self, currentTime: int) -> int:\n count = 0\n while self.token_queue and self.token_queue[0][0] <= currentTime:\n exp, tok = self.token_queue.popleft()\n del self.tokens[tok]\n count += 1\n return count\n\n def renew(self, tokenId: str, currentTime: int) -> None:\n if tokenId not in self.tokens:\n return\n if currentTime >= self.tokens[tokenId]:\n # token is already expired. \n # process expiry\n num_expired = self.process_expiry(currentTime)\n return\n # token not expired, process renewal\n idx = 0\n while self.token_queue[idx][1] != tokenId:\n idx += 1\n del self.token_queue[idx]\n del self.tokens[tokenId]\n self.generate(tokenId, currentTime)\n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.process_expiry(currentTime)\n return len(self.token_queue)\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 1 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
Clean Python with explanation | design-authentication-manager | 0 | 1 | ```\nclass AuthenticationManager(object):\n\n def __init__(self, timeToLive):\n self.token = dict()\n self.time = timeToLive # store timeToLive and create dictionary\n\n def generate(self, tokenId, currentTime):\n self.token[tokenId] = currentTime # store tokenId with currentTime\n\n def renew(self, tokenId, currentTime):\n limit = currentTime-self.time # calculate limit time to filter unexpired tokens\n if tokenId in self.token and self.token[tokenId]>limit: # filter tokens and renew its time\n self.token[tokenId] = currentTime\n\n def countUnexpiredTokens(self, currentTime):\n limit = currentTime-self.time # calculate limit time to filter unexpired tokens\n c = 0\n for i in self.token:\n if self.token[i]>limit: # count unexpired tokens\n c+=1\n return c\n``` | 10 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Clean Python with explanation | design-authentication-manager | 0 | 1 | ```\nclass AuthenticationManager(object):\n\n def __init__(self, timeToLive):\n self.token = dict()\n self.time = timeToLive # store timeToLive and create dictionary\n\n def generate(self, tokenId, currentTime):\n self.token[tokenId] = currentTime # store tokenId with currentTime\n\n def renew(self, tokenId, currentTime):\n limit = currentTime-self.time # calculate limit time to filter unexpired tokens\n if tokenId in self.token and self.token[tokenId]>limit: # filter tokens and renew its time\n self.token[tokenId] = currentTime\n\n def countUnexpiredTokens(self, currentTime):\n limit = currentTime-self.time # calculate limit time to filter unexpired tokens\n c = 0\n for i in self.token:\n if self.token[i]>limit: # count unexpired tokens\n c+=1\n return c\n``` | 10 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
Python3 Easy | design-authentication-manager | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport collections\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.auth = collections.defaultdict()\n self.ttl = timeToLive\n\n def generate(self, tokenId: str, currentTime: int) -> None:\n \n expireTime = currentTime+ self.ttl\n self.auth[tokenId] =expireTime\n\n\n def renew(self, tokenId: str, currentTime: int) -> None:\n if tokenId in self.auth:\n timeToExpire = self.auth[tokenId]\n\n #check if this token has already expired or not (renew unexpired tokens only)\n if timeToExpire > currentTime:\n self.auth[tokenId] = (currentTime+self.ttl)\n \n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n #here we do lazy removal and deletion\n deletion_que = collections.deque()\n liveCount = 0\n for k, v in self.auth.items():\n if v <= currentTime:\n #already expired put for deletion qur\n deletion_que.append(k)\n else:\n liveCount+=1\n\n for k in deletion_que:\n self.auth.pop(k)\n\n return liveCount\n\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n\n``` | 0 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Python3 Easy | design-authentication-manager | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport collections\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.auth = collections.defaultdict()\n self.ttl = timeToLive\n\n def generate(self, tokenId: str, currentTime: int) -> None:\n \n expireTime = currentTime+ self.ttl\n self.auth[tokenId] =expireTime\n\n\n def renew(self, tokenId: str, currentTime: int) -> None:\n if tokenId in self.auth:\n timeToExpire = self.auth[tokenId]\n\n #check if this token has already expired or not (renew unexpired tokens only)\n if timeToExpire > currentTime:\n self.auth[tokenId] = (currentTime+self.ttl)\n \n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n #here we do lazy removal and deletion\n deletion_que = collections.deque()\n liveCount = 0\n for k, v in self.auth.items():\n if v <= currentTime:\n #already expired put for deletion qur\n deletion_que.append(k)\n else:\n liveCount+=1\n\n for k in deletion_que:\n self.auth.pop(k)\n\n return liveCount\n\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n\n``` | 0 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
Simple Python Dictionary Implementation | design-authentication-manager | 0 | 1 | ```\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.mp = {}\n self.life = timeToLive\n \n def generate(self, tokenId: str, currentTime: int) -> None:\n self.mp[tokenId] = (currentTime, currentTime+self.life)\n \n def renew(self, tokenId: str, currentTime: int) -> None:\n self.mp = {key:val for key, val in self.mp.items() if currentTime<val[1]}\n \n if(tokenId in self.mp):\n self.mp[tokenId] = (currentTime, currentTime+self.life)\n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.mp = {key:val for key, val in self.mp.items() if currentTime<val[1]}\n return len(self.mp)\n \n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Simple Python Dictionary Implementation | design-authentication-manager | 0 | 1 | ```\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.mp = {}\n self.life = timeToLive\n \n def generate(self, tokenId: str, currentTime: int) -> None:\n self.mp[tokenId] = (currentTime, currentTime+self.life)\n \n def renew(self, tokenId: str, currentTime: int) -> None:\n self.mp = {key:val for key, val in self.mp.items() if currentTime<val[1]}\n \n if(tokenId in self.mp):\n self.mp[tokenId] = (currentTime, currentTime+self.life)\n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.mp = {key:val for key, val in self.mp.items() if currentTime<val[1]}\n return len(self.mp)\n \n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
Amortized O(1) | design-authentication-manager | 0 | 1 | # Code\n```\nfrom collections import deque\n# Amortized O(1)\nclass AuthenticationManager:\n def __init__(self, timeToLive: int):\n self.ttl = timeToLive \n self.q = deque() # history [(expiry. id)]\n self.tokens = {} # {id : expiry}\n\n def cleanup(self, currentTime): \n for _ in range(len(self.q)):\n if self.q[0][0] <= currentTime:\n _, id = self.q.popleft()\n if id in self.tokens and self.tokens[id] <= currentTime:\n del self.tokens[id]\n\n def generate(self, tokenId: str, currentTime: int) -> None: \n expiry = currentTime + self.ttl\n self.tokens[tokenId] = expiry\n self.q.append((expiry, tokenId))\n \n def renew(self, tokenId: str, currentTime: int) -> None:\n self.cleanup(currentTime)\n if tokenId not in self.tokens:\n return\n self.generate(tokenId, currentTime) \n \n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.cleanup(currentTime)\n return len(self.tokens)\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Amortized O(1) | design-authentication-manager | 0 | 1 | # Code\n```\nfrom collections import deque\n# Amortized O(1)\nclass AuthenticationManager:\n def __init__(self, timeToLive: int):\n self.ttl = timeToLive \n self.q = deque() # history [(expiry. id)]\n self.tokens = {} # {id : expiry}\n\n def cleanup(self, currentTime): \n for _ in range(len(self.q)):\n if self.q[0][0] <= currentTime:\n _, id = self.q.popleft()\n if id in self.tokens and self.tokens[id] <= currentTime:\n del self.tokens[id]\n\n def generate(self, tokenId: str, currentTime: int) -> None: \n expiry = currentTime + self.ttl\n self.tokens[tokenId] = expiry\n self.q.append((expiry, tokenId))\n \n def renew(self, tokenId: str, currentTime: int) -> None:\n self.cleanup(currentTime)\n if tokenId not in self.tokens:\n return\n self.generate(tokenId, currentTime) \n \n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.cleanup(currentTime)\n return len(self.tokens)\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
[Python] Easy to understand: Hash Table | design-authentication-manager | 0 | 1 | # Intuition\nClean old tokens before renewing and counting unexpired tokens\n\n# Code\n```\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.ttl = timeToLive\n self.time = defaultdict(set)\n self.token = {}\n\n def delete_old_tokens(self, currentTime):\n delete = []\n for expiry, tokens in self.time.items():\n if expiry > currentTime:\n break\n delete.append(expiry)\n \n for expiry in delete:\n for tokenId in self.time[expiry]:\n del self.token[tokenId]\n del self.time[expiry]\n\n def generate(self, tokenId: str, currentTime: int) -> None:\n new_expiry = currentTime + self.ttl\n self.token[tokenId] = new_expiry\n self.time[new_expiry].add(tokenId)\n\n def renew(self, tokenId: str, currentTime: int) -> None:\n self.delete_old_tokens(currentTime)\n if tokenId not in self.token: return\n\n expiry = self.token[tokenId]\n self.time[expiry].remove(tokenId)\n new_expiry = currentTime + self.ttl\n self.token[tokenId] = new_expiry\n self.time[new_expiry].add(tokenId)\n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.delete_old_tokens(currentTime)\n return len(self.token)\n \n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
[Python] Easy to understand: Hash Table | design-authentication-manager | 0 | 1 | # Intuition\nClean old tokens before renewing and counting unexpired tokens\n\n# Code\n```\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.ttl = timeToLive\n self.time = defaultdict(set)\n self.token = {}\n\n def delete_old_tokens(self, currentTime):\n delete = []\n for expiry, tokens in self.time.items():\n if expiry > currentTime:\n break\n delete.append(expiry)\n \n for expiry in delete:\n for tokenId in self.time[expiry]:\n del self.token[tokenId]\n del self.time[expiry]\n\n def generate(self, tokenId: str, currentTime: int) -> None:\n new_expiry = currentTime + self.ttl\n self.token[tokenId] = new_expiry\n self.time[new_expiry].add(tokenId)\n\n def renew(self, tokenId: str, currentTime: int) -> None:\n self.delete_old_tokens(currentTime)\n if tokenId not in self.token: return\n\n expiry = self.token[tokenId]\n self.time[expiry].remove(tokenId)\n new_expiry = currentTime + self.ttl\n self.token[tokenId] = new_expiry\n self.time[new_expiry].add(tokenId)\n\n def countUnexpiredTokens(self, currentTime: int) -> int:\n self.delete_old_tokens(currentTime)\n return len(self.token)\n \n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
Simple Python Clean 🔥 | design-authentication-manager | 0 | 1 | \n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n# Code\n```\n\'\'\'\nsess , auth token , TTL secons after curr time\n\nif renewed exp. time = curr time + ttl\n\n\nIn terms of System design we can trade of countUnexpiredTokens\n\'\'\'\n\n\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int): # O(1)\n self.ttl = timeToLive\n self.tokens = {}\n\n def generate(self, tokenId: str, currentTime: int) -> None: # O(1)\n self.tokens[tokenId] = currentTime\n\n def renew(self, tokenId: str, currentTime: int) -> None: # O(1)\n if tokenId in self.tokens and self.tokens[tokenId] + self.ttl > currentTime:\n self.tokens[tokenId] = currentTime\n elif tokenId in self.tokens:\n del self.tokens[tokenId]\n\n def countUnexpiredTokens(self, currentTime: int) -> int: # O(N)\n count = 0\n for t in self.tokens:\n if self.tokens[t] + self.ttl > currentTime:\n count += 1\n return count\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Simple Python Clean 🔥 | design-authentication-manager | 0 | 1 | \n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n# Code\n```\n\'\'\'\nsess , auth token , TTL secons after curr time\n\nif renewed exp. time = curr time + ttl\n\n\nIn terms of System design we can trade of countUnexpiredTokens\n\'\'\'\n\n\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int): # O(1)\n self.ttl = timeToLive\n self.tokens = {}\n\n def generate(self, tokenId: str, currentTime: int) -> None: # O(1)\n self.tokens[tokenId] = currentTime\n\n def renew(self, tokenId: str, currentTime: int) -> None: # O(1)\n if tokenId in self.tokens and self.tokens[tokenId] + self.ttl > currentTime:\n self.tokens[tokenId] = currentTime\n elif tokenId in self.tokens:\n del self.tokens[tokenId]\n\n def countUnexpiredTokens(self, currentTime: int) -> int: # O(N)\n count = 0\n for t in self.tokens:\n if self.tokens[t] + self.ttl > currentTime:\n count += 1\n return count\n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
Heap solution (beats 99%) - O(1) generate, O(1) renew , O(nlogn) count | design-authentication-manager | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst thoughts:\n- Can generate and renew using hashmaps\n- I have to calculate the number of expired tokens for count\n- Brute way is to check and remove each token, is there any faster approach?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHow to solve faster?\n- If i can have the token that\'s gonna expire first with me at all times , i can keep removing tokens until i find the token which has an expiry time> current time.\n- First thoughts whenever you have to keep getting minimum elements should be a heap. heappop will return the token with min expiry time.\nWell so how do i do it actually?\n## Generate\n- push (timeToLive+currentTime,tokenId) to heap\n- make hashmap[tokenid]=timeToLive+currentTime\n- Add 1 to total\n## Renew\nif hashmap[tokenid] exists,\n\n\n*if hashmap[tokenid] value is greater than currentTime*\n- make hashmap[tokenid] = timeToLive+currentTime\n- push (timeToLive+currentTime,tokenId) to heap ( i will explain why you don\'t have to change the pre existing value later on)\n\n*if its value is less than currentTime it has expired*\n- so delete hashmap[tokenid] from hashmap\n- subtract total by 1\n\nNote: we can say that the hashmap stores the **most recently updated value of expiration** for each tokens.\n\n## Count\n\n**while the heap is not empty and the top element has an expiry time less or equal to currentTime :**\n- Remove the top element from heap, lets call it removed.\n- if removed[1] (*ie , the tokenId*) exists in the hashmap\n - if it\'s value is same as removed[0]:\n - subtract 1 from total, because the hashmap stores the recent value of expiration\n - now delete hashmap[removed[1]] from hashmap as it is expired\n - if it\'s value is not same as removed[0]\n - it means that the tokenId(removed[1]) is updated and there exists one more element in heap like: (renewed_exp_time,tokenid)\n - so don\'t do anything.\n- if removed[1] doesnt exist in hashmap, then it has expired and it had been taken into account while renewing.\n\n**return total** \n\n \n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1) generate, O(1) renew , O(nlogn) count\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) - for storing heap\n\n# Code\n```\nfrom heapq import heapify,heappop,heappush\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.heap=[]\n heapify(self.heap)\n self.d={}\n self.total=0\n self.c=[]\n self.time_to_live=timeToLive\n def generate(self, tokenId: str, currentTime: int) -> None:\n self.total+=1\n time=currentTime+self.time_to_live\n self.d[tokenId]=time\n heappush(self.heap,(time,tokenId)) \n def renew(self, tokenId: str, currentTime: int) -> None:\n time=currentTime+self.time_to_live\n if(tokenId in self.d):\n if(self.d[tokenId]>currentTime):\n self.d[tokenId]=time\n heappush(self.heap,(time,tokenId))\n else:\n del(self.d[tokenId])\n self.total-=1 \n def countUnexpiredTokens(self, currentTime: int) -> int:\n time=currentTime\n while(len(self.heap)>0 and self.heap[0][0]<=time):\n t,token=heappop(self.heap)\n if(token in self.d and self.d[token]==t):\n self.total-=1\n del(self.d[token]) \n return self.total\n \n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | There is an authentication system that works with authentication tokens. For each session, the user will receive a new authentication token that will expire `timeToLive` seconds after the `currentTime`. If the token is renewed, the expiry time will be **extended** to expire `timeToLive` seconds after the (potentially different) `currentTime`.
Implement the `AuthenticationManager` class:
* `AuthenticationManager(int timeToLive)` constructs the `AuthenticationManager` and sets the `timeToLive`.
* `generate(string tokenId, int currentTime)` generates a new token with the given `tokenId` at the given `currentTime` in seconds.
* `renew(string tokenId, int currentTime)` renews the **unexpired** token with the given `tokenId` at the given `currentTime` in seconds. If there are no unexpired tokens with the given `tokenId`, the request is ignored, and nothing happens.
* `countUnexpiredTokens(int currentTime)` returns the number of **unexpired** tokens at the given currentTime.
Note that if a token expires at time `t`, and another action happens on time `t` (`renew` or `countUnexpiredTokens`), the expiration takes place **before** the other actions.
**Example 1:**
**Input**
\[ "AuthenticationManager ", "`renew` ", "generate ", "`countUnexpiredTokens` ", "generate ", "`renew` ", "`renew` ", "`countUnexpiredTokens` "\]
\[\[5\], \[ "aaa ", 1\], \[ "aaa ", 2\], \[6\], \[ "bbb ", 7\], \[ "aaa ", 8\], \[ "bbb ", 10\], \[15\]\]
**Output**
\[null, null, null, 1, null, null, null, 0\]
**Explanation**
AuthenticationManager authenticationManager = new AuthenticationManager(5); // Constructs the AuthenticationManager with `timeToLive` = 5 seconds.
authenticationManager.`renew`( "aaa ", 1); // No token exists with tokenId "aaa " at time 1, so nothing happens.
authenticationManager.generate( "aaa ", 2); // Generates a new token with tokenId "aaa " at time 2.
authenticationManager.`countUnexpiredTokens`(6); // The token with tokenId "aaa " is the only unexpired one at time 6, so return 1.
authenticationManager.generate( "bbb ", 7); // Generates a new token with tokenId "bbb " at time 7.
authenticationManager.`renew`( "aaa ", 8); // The token with tokenId "aaa " expired at time 7, and 8 >= 7, so at time 8 the `renew` request is ignored, and nothing happens.
authenticationManager.`renew`( "bbb ", 10); // The token with tokenId "bbb " is unexpired at time 10, so the `renew` request is fulfilled and now the token will expire at time 15.
authenticationManager.`countUnexpiredTokens`(15); // The token with tokenId "bbb " expires at time 15, and the token with tokenId "aaa " expired at time 7, so currently no token is unexpired, so return 0.
**Constraints:**
* `1 <= timeToLive <= 108`
* `1 <= currentTime <= 108`
* `1 <= tokenId.length <= 5`
* `tokenId` consists only of lowercase letters.
* All calls to `generate` will contain unique values of `tokenId`.
* The values of `currentTime` across all the function calls will be **strictly increasing**.
* At most `2000` calls will be made to all functions combined. | You need to check at most 2 characters to determine which character comes next. |
Heap solution (beats 99%) - O(1) generate, O(1) renew , O(nlogn) count | design-authentication-manager | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst thoughts:\n- Can generate and renew using hashmaps\n- I have to calculate the number of expired tokens for count\n- Brute way is to check and remove each token, is there any faster approach?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHow to solve faster?\n- If i can have the token that\'s gonna expire first with me at all times , i can keep removing tokens until i find the token which has an expiry time> current time.\n- First thoughts whenever you have to keep getting minimum elements should be a heap. heappop will return the token with min expiry time.\nWell so how do i do it actually?\n## Generate\n- push (timeToLive+currentTime,tokenId) to heap\n- make hashmap[tokenid]=timeToLive+currentTime\n- Add 1 to total\n## Renew\nif hashmap[tokenid] exists,\n\n\n*if hashmap[tokenid] value is greater than currentTime*\n- make hashmap[tokenid] = timeToLive+currentTime\n- push (timeToLive+currentTime,tokenId) to heap ( i will explain why you don\'t have to change the pre existing value later on)\n\n*if its value is less than currentTime it has expired*\n- so delete hashmap[tokenid] from hashmap\n- subtract total by 1\n\nNote: we can say that the hashmap stores the **most recently updated value of expiration** for each tokens.\n\n## Count\n\n**while the heap is not empty and the top element has an expiry time less or equal to currentTime :**\n- Remove the top element from heap, lets call it removed.\n- if removed[1] (*ie , the tokenId*) exists in the hashmap\n - if it\'s value is same as removed[0]:\n - subtract 1 from total, because the hashmap stores the recent value of expiration\n - now delete hashmap[removed[1]] from hashmap as it is expired\n - if it\'s value is not same as removed[0]\n - it means that the tokenId(removed[1]) is updated and there exists one more element in heap like: (renewed_exp_time,tokenid)\n - so don\'t do anything.\n- if removed[1] doesnt exist in hashmap, then it has expired and it had been taken into account while renewing.\n\n**return total** \n\n \n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1) generate, O(1) renew , O(nlogn) count\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) - for storing heap\n\n# Code\n```\nfrom heapq import heapify,heappop,heappush\nclass AuthenticationManager:\n\n def __init__(self, timeToLive: int):\n self.heap=[]\n heapify(self.heap)\n self.d={}\n self.total=0\n self.c=[]\n self.time_to_live=timeToLive\n def generate(self, tokenId: str, currentTime: int) -> None:\n self.total+=1\n time=currentTime+self.time_to_live\n self.d[tokenId]=time\n heappush(self.heap,(time,tokenId)) \n def renew(self, tokenId: str, currentTime: int) -> None:\n time=currentTime+self.time_to_live\n if(tokenId in self.d):\n if(self.d[tokenId]>currentTime):\n self.d[tokenId]=time\n heappush(self.heap,(time,tokenId))\n else:\n del(self.d[tokenId])\n self.total-=1 \n def countUnexpiredTokens(self, currentTime: int) -> int:\n time=currentTime\n while(len(self.heap)>0 and self.heap[0][0]<=time):\n t,token=heappop(self.heap)\n if(token in self.d and self.d[token]==t):\n self.total-=1\n del(self.d[token]) \n return self.total\n \n\n\n# Your AuthenticationManager object will be instantiated and called as such:\n# obj = AuthenticationManager(timeToLive)\n# obj.generate(tokenId,currentTime)\n# obj.renew(tokenId,currentTime)\n# param_3 = obj.countUnexpiredTokens(currentTime)\n``` | 0 | You are given two `m x n` binary matrices `grid1` and `grid2` containing only `0`'s (representing water) and `1`'s (representing land). An **island** is a group of `1`'s connected **4-directionally** (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in `grid2` is considered a **sub-island** if there is an island in `grid1` that contains **all** the cells that make up **this** island in `grid2`.
Return the _**number** of islands in_ `grid2` _that are considered **sub-islands**_.
**Example 1:**
**Input:** grid1 = \[\[1,1,1,0,0\],\[0,1,1,1,1\],\[0,0,0,0,0\],\[1,0,0,0,0\],\[1,1,0,1,1\]\], grid2 = \[\[1,1,1,0,0\],\[0,0,1,1,1\],\[0,1,0,0,0\],\[1,0,1,1,0\],\[0,1,0,1,0\]\]
**Output:** 3
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
**Example 2:**
**Input:** grid1 = \[\[1,0,1,0,1\],\[1,1,1,1,1\],\[0,0,0,0,0\],\[1,1,1,1,1\],\[1,0,1,0,1\]\], grid2 = \[\[0,0,0,0,0\],\[1,1,1,1,1\],\[0,1,0,1,0\],\[0,1,0,1,0\],\[1,0,0,0,1\]\]
**Output:** 2
**Explanation:** In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
**Constraints:**
* `m == grid1.length == grid2.length`
* `n == grid1[i].length == grid2[i].length`
* `1 <= m, n <= 500`
* `grid1[i][j]` and `grid2[i][j]` are either `0` or `1`. | Using a map, track the expiry times of the tokens. When generating a new token, add it to the map with its expiry time. When renewing a token, check if it's on the map and has not expired yet. If so, update its expiry time. To count unexpired tokens, iterate on the map and check for each token if it's not expired yet. |
merge sort | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nmerge sort\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n prev = 0\n for c in coins:\n if c > prev + 1:\n return prev + 1\n prev += c\n return prev + 1\n \n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
merge sort | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nmerge sort\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n prev = 0\n for c in coins:\n if c > prev + 1:\n return prev + 1\n prev += c\n return prev + 1\n \n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Python greedy with sorting with explanation (330 and 2952 variant) | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Initialize res = 1 since we count from 0;\n2. Sort coins;\n3. For each coin in coins:\n - if coin > res, then the consecutive values cannot expand to the right;\n - if coin == res, then the consecutive values can be just perfectly expanded, res = coin + res;\n - if coin < res, then the consecutive values can be expanded, but not as "efficient" as above, res = coin + res.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy with sorting.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * log(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) due to sorting in Python\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n res = 1\n coins.sort()\n for coin in coins:\n if coin > res:\n break\n else:\n res += coin\n \n return res\n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Python greedy with sorting with explanation (330 and 2952 variant) | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Initialize res = 1 since we count from 0;\n2. Sort coins;\n3. For each coin in coins:\n - if coin > res, then the consecutive values cannot expand to the right;\n - if coin == res, then the consecutive values can be just perfectly expanded, res = coin + res;\n - if coin < res, then the consecutive values can be expanded, but not as "efficient" as above, res = coin + res.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy with sorting.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * log(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) due to sorting in Python\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n res = 1\n coins.sort()\n for coin in coins:\n if coin > res:\n break\n else:\n res += coin\n \n return res\n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Maximum Number of Consecutive Values You Can Make solve with python | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n ans = 1 # next value we want to make\n\n for coin in sorted(coins):\n if coin > ans:\n return ans\n ans += coin\n\n return ans\n\n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Maximum Number of Consecutive Values You Can Make solve with python | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n ans = 1 # next value we want to make\n\n for coin in sorted(coins):\n if coin > ans:\n return ans\n ans += coin\n\n return ans\n\n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Hashmap | O(N + u log u) T | O(u) S | Commented and Explained | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat we care about are the coins we can greedily reach from the coin combinations we can so far generate. As such, we want to track the largest coin combinations we can make as we go over our unique coin types and frequencies in our coins. We want to avoid sorting coins, as it may be very large. Similarly, our range of unique coins can be as uniquely large, but may never be larger by our problem statement. As such, we want to sort the unique coin frequencies, not the coins themselves. \n\nFrom here, we need to build a hashmap and then greedily solve. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGet the frequencies of each unique coin we have in our coins -> Takes time O(N) to go over coins, and space O(U) where U is the unique coin denominations in our coins. U is strictly <= N by problem definition. \n\nSet a largest value of 0 which is our largest combination that can so far be made. We will be looking for largest contiguous value we can make, and as such, we can do this greedily as follows. \n\nFor coin in sorted(coin_frequencies.keys()) \n- If largest + 1 is strictly less than coin, we cannot make it here, break\n- Otherwise, we can make it to this coin, so now largest becomes this coin * this coins frequency \n\nAt end, we need to return largest + 1 to account for the null set \n\n# Complexity\n- Time complexity: O( max (N, U log U))\n - Takes O(N) time to iterate over coins \n - Takes U log U to sort the keys of the coins frequencies \n - As U is strictly less than or equal to N, we can actually use max here to take the maximal time complexity. \n\n- Space complexity: O(U)\n - We store at most U unique coin denominations and their frequencies \n - As U is strictly less than or equal to N, we will represent this as O(U) for clarity \n\n \n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n # get frequencies of unique denominations in coins \n coin_frequencies = collections.Counter(coins)\n # get sorted list of the unique denominations in coin_frequencies\n # for greedy approach, it must be sorted \n coin_keys = sorted(list(coin_frequencies.keys()))\n # largest coin combination so far that we have found \n largest = 0\n # for coin in sorted coin keys \n for coin in coin_keys : \n # if we run into a point where a coin is out of reach of contiguous advancement, \n if coin > largest+1 : \n # break because we will not make it to there \n break\n else : \n # otherwise, increment largest by coin_frequencies[coin] * coin\n largest += (coin_frequencies[coin] * coin)\n # account for the case of zero coins based on problem examples \n return largest + 1\n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Hashmap | O(N + u log u) T | O(u) S | Commented and Explained | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat we care about are the coins we can greedily reach from the coin combinations we can so far generate. As such, we want to track the largest coin combinations we can make as we go over our unique coin types and frequencies in our coins. We want to avoid sorting coins, as it may be very large. Similarly, our range of unique coins can be as uniquely large, but may never be larger by our problem statement. As such, we want to sort the unique coin frequencies, not the coins themselves. \n\nFrom here, we need to build a hashmap and then greedily solve. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGet the frequencies of each unique coin we have in our coins -> Takes time O(N) to go over coins, and space O(U) where U is the unique coin denominations in our coins. U is strictly <= N by problem definition. \n\nSet a largest value of 0 which is our largest combination that can so far be made. We will be looking for largest contiguous value we can make, and as such, we can do this greedily as follows. \n\nFor coin in sorted(coin_frequencies.keys()) \n- If largest + 1 is strictly less than coin, we cannot make it here, break\n- Otherwise, we can make it to this coin, so now largest becomes this coin * this coins frequency \n\nAt end, we need to return largest + 1 to account for the null set \n\n# Complexity\n- Time complexity: O( max (N, U log U))\n - Takes O(N) time to iterate over coins \n - Takes U log U to sort the keys of the coins frequencies \n - As U is strictly less than or equal to N, we can actually use max here to take the maximal time complexity. \n\n- Space complexity: O(U)\n - We store at most U unique coin denominations and their frequencies \n - As U is strictly less than or equal to N, we will represent this as O(U) for clarity \n\n \n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n # get frequencies of unique denominations in coins \n coin_frequencies = collections.Counter(coins)\n # get sorted list of the unique denominations in coin_frequencies\n # for greedy approach, it must be sorted \n coin_keys = sorted(list(coin_frequencies.keys()))\n # largest coin combination so far that we have found \n largest = 0\n # for coin in sorted coin keys \n for coin in coin_keys : \n # if we run into a point where a coin is out of reach of contiguous advancement, \n if coin > largest+1 : \n # break because we will not make it to there \n break\n else : \n # otherwise, increment largest by coin_frequencies[coin] * coin\n largest += (coin_frequencies[coin] * coin)\n # account for the case of zero coins based on problem examples \n return largest + 1\n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Go/Python O(n*log(n)) time | O(1) space | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc getMaximumConsecutive(coins []int) int {\n sort.Ints(coins)\n covered := 0\n for _,value :=range(coins){\n if value <= covered+1{\n covered+=value\n }\n }\n return covered+1\n}\n```\n```python []\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n covered = 0\n for value in coins:\n if value <= covered+1:\n covered+=value\n return covered+1\n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Go/Python O(n*log(n)) time | O(1) space | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc getMaximumConsecutive(coins []int) int {\n sort.Ints(coins)\n covered := 0\n for _,value :=range(coins){\n if value <= covered+1{\n covered+=value\n }\n }\n return covered+1\n}\n```\n```python []\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n covered = 0\n for value in coins:\n if value <= covered+1:\n covered+=value\n return covered+1\n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
[Java/Python] | Greedy | maximum-number-of-consecutive-values-you-can-make | 1 | 1 | Logic is if we have made consecutive sequence [0,K], then next coin coins[i] should be less than equal to K + 1 and next range we will be able to cover is coins[i] + K.\n***Java***\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int curr = 0 ; int n = coins.length;\n for(int i = 0 ; i < n ; i++){\n if (coins[i] <= curr + 1){\n curr = curr + coins[i];\n }\n else{\n break;\n }\n }\n return curr + 1;\n }\n}\n```\n***Python***\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n curr = 0\n n = len(coins)\n for i in range(n):\n if coins[i] <= curr + 1:\n curr = curr + coins[i]\n else:\n break\n return curr + 1\n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
[Java/Python] | Greedy | maximum-number-of-consecutive-values-you-can-make | 1 | 1 | Logic is if we have made consecutive sequence [0,K], then next coin coins[i] should be less than equal to K + 1 and next range we will be able to cover is coins[i] + K.\n***Java***\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int curr = 0 ; int n = coins.length;\n for(int i = 0 ; i < n ; i++){\n if (coins[i] <= curr + 1){\n curr = curr + coins[i];\n }\n else{\n break;\n }\n }\n return curr + 1;\n }\n}\n```\n***Python***\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n curr = 0\n n = len(coins)\n for i in range(n):\n if coins[i] <= curr + 1:\n curr = curr + coins[i]\n else:\n break\n return curr + 1\n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Python | Greedy | O(n) | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n i = 0\n for coin in coins:\n if coin > i+1:\n return i + 1\n else:\n i += coin\n return i + 1\n``` | 0 | You are given an integer array `coins` of length `n` which represents the `n` coins that you own. The value of the `ith` coin is `coins[i]`. You can **make** some value `x` if you can choose some of your `n` coins such that their values sum up to `x`.
Return the _maximum number of consecutive integer values that you **can** **make** with your coins **starting** from and **including**_ `0`.
Note that you may have multiple coins of the same value.
**Example 1:**
**Input:** coins = \[1,3\]
**Output:** 2
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
You can make 2 consecutive integer values starting from 0.
**Example 2:**
**Input:** coins = \[1,1,1,4\]
**Output:** 8
**Explanation:** You can make the following values:
- 0: take \[\]
- 1: take \[1\]
- 2: take \[1,1\]
- 3: take \[1,1,1\]
- 4: take \[4\]
- 5: take \[4,1\]
- 6: take \[4,1,1\]
- 7: take \[4,1,1,1\]
You can make 8 consecutive integer values starting from 0.
**Example 3:**
**Input:** nums = \[1,4,10,3,1\]
**Output:** 20
**Constraints:**
* `coins.length == n`
* `1 <= n <= 4 * 104`
* `1 <= coins[i] <= 4 * 104` | The abstract problem asks to count the number of disjoint pairs with a given sum k. For each possible value x, it can be paired up with k - x. The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2). |
Python | Greedy | O(n) | maximum-number-of-consecutive-values-you-can-make | 0 | 1 | # Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n i = 0\n for coin in coins:\n if coin > i+1:\n return i + 1\n else:\n i += coin\n return i + 1\n``` | 0 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Weak Test Cases: Subexponential Solution Passes All Current Test Cases | maximize-score-after-n-operations | 0 | 1 | This is a greedy solution that tries all first pairs, then greedily chooses the max gcd pair for the remaining pairs.\n\nThis will pass a test case with one layer of "gotchas" like [9088, 9344, 71, 73]. That is, one non-greedy choice is sufficient to greedily make the rest of the choices.\n\nBut, this solution should fail on a test case with more than one "gotcha" like [9088, 9344, 71, 73, 12928, 13184, 101, 103]. This test case requires two non-greedy choices to produce the maximum score.\n\n# Code\n```python3\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort()\n\n # compute gcd of all pairs\n pairs = []\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n pairs.append([gcd(nums[i], nums[j]), i, j])\n\n pairs = sorted(pairs, reverse=True)\n\n max_score = 0\n for fixed_pair in pairs:\n used = [fixed_pair[1], fixed_pair[2]]\n gcds = [fixed_pair[0]]\n\n # first pair fixed, there are n-1 pairs left to find\n for _ in range(len(nums)//2-1):\n for pair in pairs:\n # first pair found has max gcd because sorted in reverse order\n if pair[1] not in used and pair[2] not in used:\n used.append(pair[1])\n used.append(pair[2])\n gcds.append(pair[0])\n \n # compute score of current fixed pair\n gcds.sort()\n cur_score = 0\n for j in range(len(gcds)):\n cur_score += (j+1)*gcds[j]\n max_score = cur_score if cur_score > max_score else max_score\n return max_score\n``` | 4 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
Weak Test Cases: Subexponential Solution Passes All Current Test Cases | maximize-score-after-n-operations | 0 | 1 | This is a greedy solution that tries all first pairs, then greedily chooses the max gcd pair for the remaining pairs.\n\nThis will pass a test case with one layer of "gotchas" like [9088, 9344, 71, 73]. That is, one non-greedy choice is sufficient to greedily make the rest of the choices.\n\nBut, this solution should fail on a test case with more than one "gotcha" like [9088, 9344, 71, 73, 12928, 13184, 101, 103]. This test case requires two non-greedy choices to produce the maximum score.\n\n# Code\n```python3\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort()\n\n # compute gcd of all pairs\n pairs = []\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n pairs.append([gcd(nums[i], nums[j]), i, j])\n\n pairs = sorted(pairs, reverse=True)\n\n max_score = 0\n for fixed_pair in pairs:\n used = [fixed_pair[1], fixed_pair[2]]\n gcds = [fixed_pair[0]]\n\n # first pair fixed, there are n-1 pairs left to find\n for _ in range(len(nums)//2-1):\n for pair in pairs:\n # first pair found has max gcd because sorted in reverse order\n if pair[1] not in used and pair[2] not in used:\n used.append(pair[1])\n used.append(pair[2])\n gcds.append(pair[0])\n \n # compute score of current fixed pair\n gcds.sort()\n cur_score = 0\n for j in range(len(gcds)):\n cur_score += (j+1)*gcds[j]\n max_score = cur_score if cur_score > max_score else max_score\n return max_score\n``` | 4 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
The World Needs Another Python Solution | maximize-score-after-n-operations | 0 | 1 | ```\nfrom math import gcd\nfrom functools import cache\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n n = len(nums)\n @cache\n def rec(nums):\n multiplier = (n-len(nums))//2 + 1\n best = 0\n for i in range(len(nums)-1):\n for j in range(i+1, len(nums)):\n leftover = nums[:i] + nums[i+1:j] + nums[j+1:]\n best = max(best, multiplier*gcd(nums[i], nums[j]) + rec(leftover))\n\n return best\n\n return rec(tuple(nums))\n```\n\nHere it is rewritten to use a bitmask for a marginal memory usage improvement:\n```\nfrom math import gcd\nfrom functools import cache\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n @cache\n def rec(mask, i):\n best = 0\n for x in range(len(nums)-1):\n if mask & (1 << x):\n for y in range(x+1, len(nums)):\n if mask & (1 << y):\n new_mask = mask ^ (1 << x) ^ (1 << y)\n best = max(best, i*gcd(nums[x], nums[y]) + rec(new_mask, i+1))\n\n return best\n \n return rec((1 << (len(nums)+1)) - 1, 1)\n``` | 1 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
The World Needs Another Python Solution | maximize-score-after-n-operations | 0 | 1 | ```\nfrom math import gcd\nfrom functools import cache\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n n = len(nums)\n @cache\n def rec(nums):\n multiplier = (n-len(nums))//2 + 1\n best = 0\n for i in range(len(nums)-1):\n for j in range(i+1, len(nums)):\n leftover = nums[:i] + nums[i+1:j] + nums[j+1:]\n best = max(best, multiplier*gcd(nums[i], nums[j]) + rec(leftover))\n\n return best\n\n return rec(tuple(nums))\n```\n\nHere it is rewritten to use a bitmask for a marginal memory usage improvement:\n```\nfrom math import gcd\nfrom functools import cache\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n @cache\n def rec(mask, i):\n best = 0\n for x in range(len(nums)-1):\n if mask & (1 << x):\n for y in range(x+1, len(nums)):\n if mask & (1 << y):\n new_mask = mask ^ (1 << x) ^ (1 << y)\n best = max(best, i*gcd(nums[x], nums[y]) + rec(new_mask, i+1))\n\n return best\n \n return rec((1 << (len(nums)+1)) - 1, 1)\n``` | 1 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
SOLUTION IN PYTHON3 | maximize-score-after-n-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n def gcd(a,b):\n while b:\n a,b = b,a % b\n return a\n @lru_cache(None)\n def dp(step,mask):\n if mask == (1<<n - 1):\n return 0\n ans = 0\n for i in range(n):\n if mask & (1<<i) == 0:\n for j in range(i+1,n):\n if mask & (1 << j) == 0:\n ans = max(ans,step*gcd(nums[i],nums[j])+dp(step+1,mask |(1<<i)|(1<<j)))\n return ans\n n = len(nums)\n return dp(1,0)\n``` | 1 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
SOLUTION IN PYTHON3 | maximize-score-after-n-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n def gcd(a,b):\n while b:\n a,b = b,a % b\n return a\n @lru_cache(None)\n def dp(step,mask):\n if mask == (1<<n - 1):\n return 0\n ans = 0\n for i in range(n):\n if mask & (1<<i) == 0:\n for j in range(i+1,n):\n if mask & (1 << j) == 0:\n ans = max(ans,step*gcd(nums[i],nums[j])+dp(step+1,mask |(1<<i)|(1<<j)))\n return ans\n n = len(nums)\n return dp(1,0)\n``` | 1 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
[Python3] Greedy-ish, No Bitmask, No Memoization | maximize-score-after-n-operations | 0 | 1 | ```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n """LeetCode 1799\n\n The basic idea is greedy-ish. We want the largest operation to almost always\n conincide with the largest gcd. However, to iterate through all possible\n scenarios, we have to do backtracking where at each gcd index, we can\n choose to take it or not take it.\n\n This will blow up run time, because it will be 2^N. However, there is an\n early termination. Since we go through gcd from large to small, once we\n hit gcd=1, there is no need to keep backtracking, because all the rest\n of the gcds will all be 1. So we can simply add up the rest of the score\n in one go.\n \n O(2^N). Worst case is none of the pairs are co-prime.\n 399 ms, faster than 98.10%\n """\n gcds = []\n for i in range(len(nums)):\n for j in range(i + 1, len(nums)):\n gcds.append((math.gcd(nums[i], nums[j]), i, j))\n gcds.sort()\n self.res = 0\n used = [0] * (len(nums))\n\n def backtrack(op: int, idx: int, cur_score: int) -> None:\n if op == 0:\n self.res = max(self.res, cur_score)\n elif idx >= 0:\n g, i, j = gcds[idx]\n if g == 1:\n # early termination, if the gcd is already 1, the rest of\n # the gcd must all be one. Thus, no need to keep\n # backtracking\n self.res = max(self.res, (op + 1) * op // 2 + cur_score)\n return\n if not used[i] and not used[j]: # take the current i, j\n used[i] = used[j] = 1\n backtrack(op - 1, idx - 1, cur_score + op * g)\n used[i] = used[j] = 0\n # or skip\n backtrack(op, idx - 1, cur_score)\n\n backtrack(len(nums) // 2, len(gcds) - 1, 0)\n return self.res\n``` | 1 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
[Python3] Greedy-ish, No Bitmask, No Memoization | maximize-score-after-n-operations | 0 | 1 | ```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n """LeetCode 1799\n\n The basic idea is greedy-ish. We want the largest operation to almost always\n conincide with the largest gcd. However, to iterate through all possible\n scenarios, we have to do backtracking where at each gcd index, we can\n choose to take it or not take it.\n\n This will blow up run time, because it will be 2^N. However, there is an\n early termination. Since we go through gcd from large to small, once we\n hit gcd=1, there is no need to keep backtracking, because all the rest\n of the gcds will all be 1. So we can simply add up the rest of the score\n in one go.\n \n O(2^N). Worst case is none of the pairs are co-prime.\n 399 ms, faster than 98.10%\n """\n gcds = []\n for i in range(len(nums)):\n for j in range(i + 1, len(nums)):\n gcds.append((math.gcd(nums[i], nums[j]), i, j))\n gcds.sort()\n self.res = 0\n used = [0] * (len(nums))\n\n def backtrack(op: int, idx: int, cur_score: int) -> None:\n if op == 0:\n self.res = max(self.res, cur_score)\n elif idx >= 0:\n g, i, j = gcds[idx]\n if g == 1:\n # early termination, if the gcd is already 1, the rest of\n # the gcd must all be one. Thus, no need to keep\n # backtracking\n self.res = max(self.res, (op + 1) * op // 2 + cur_score)\n return\n if not used[i] and not used[j]: # take the current i, j\n used[i] = used[j] = 1\n backtrack(op - 1, idx - 1, cur_score + op * g)\n used[i] = used[j] = 0\n # or skip\n backtrack(op, idx - 1, cur_score)\n\n backtrack(len(nums) // 2, len(gcds) - 1, 0)\n return self.res\n``` | 1 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
python 3 - dp + bitmask (easy intuition) | maximize-score-after-n-operations | 0 | 1 | # Intuition\nPlease do it by reading the constraint.\n\nSimple backtracking is way tooooo slow which will definitely lead you to TLE. You need a faster solution.\n\nYou see there are similar sub-problems after choosing some numbers. So you need DP. The next question is how to cache.\n\nAs the input isn\'t large, bitmask is a good option to save states, leading to DP with bitmask solution.\n\n# Approach\nbitmask & dp\n\n# Complexity\n- Time complexity:\nO(n^2 * 2^n * log(M)) -> n^2 for double loops. 2^n for possible number of bitmask. log(M) for gcd\'s time, M = average size of number in nums\n\n- Space complexity:\nO(n^2 * 2^n) -> for cache size\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n\n import math\n\n @lru_cache(None)\n def dfs(times, state): # return max score from this state\n nonlocal n\n if times > n:\n return 0\n \n res = 0\n\n for i in range(len(nums)):\n if 1 << i & state: continue # used\n \n state ^= 1 << i\n\n for nxt in range(i+1, len(nums)):\n if 1 << nxt & state: continue\n\n state ^= 1 << nxt\n\n add = math.gcd(nums[i], nums[nxt]) * times\n\n res = max(res, add + dfs(times + 1, state))\n\n state -= 1 << nxt\n\n state -= 1 << i\n return res\n n = len(nums) // 2\n return dfs(1, 0)\n``` | 1 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
python 3 - dp + bitmask (easy intuition) | maximize-score-after-n-operations | 0 | 1 | # Intuition\nPlease do it by reading the constraint.\n\nSimple backtracking is way tooooo slow which will definitely lead you to TLE. You need a faster solution.\n\nYou see there are similar sub-problems after choosing some numbers. So you need DP. The next question is how to cache.\n\nAs the input isn\'t large, bitmask is a good option to save states, leading to DP with bitmask solution.\n\n# Approach\nbitmask & dp\n\n# Complexity\n- Time complexity:\nO(n^2 * 2^n * log(M)) -> n^2 for double loops. 2^n for possible number of bitmask. log(M) for gcd\'s time, M = average size of number in nums\n\n- Space complexity:\nO(n^2 * 2^n) -> for cache size\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n\n import math\n\n @lru_cache(None)\n def dfs(times, state): # return max score from this state\n nonlocal n\n if times > n:\n return 0\n \n res = 0\n\n for i in range(len(nums)):\n if 1 << i & state: continue # used\n \n state ^= 1 << i\n\n for nxt in range(i+1, len(nums)):\n if 1 << nxt & state: continue\n\n state ^= 1 << nxt\n\n add = math.gcd(nums[i], nums[nxt]) * times\n\n res = max(res, add + dfs(times + 1, state))\n\n state -= 1 << nxt\n\n state -= 1 << i\n return res\n n = len(nums) // 2\n return dfs(1, 0)\n``` | 1 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
Python short and clean. 2 solutions. Functional programming. | maximize-score-after-n-operations | 0 | 1 | # Approach 1:\nRecursion with list slicing **(TLE)**\n\n<!-- # Complexity\n- Time complexity: $$O(n ^ 3)$$\n\n- Space complexity: $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def maxScore(self, nums: list[int]) -> int:\n \n def score(xs: list[int]) -> int:\n n = len(xs)\n return max((\n n // 2 * gcd(xs[i], xs[j]) +\n score(xs[:i] + xs[i + 1 : j] + xs[j + 1:])\n for i in range(n)\n for j in range(i + 1, n)),\n default=0,\n )\n \n return score(nums)\n\n\n```\n\n---\n# Approach 2:\nRecursion with bit masking, memoization **(Accepted - 52.53%)**\n\n<!-- # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n n = len(nums)\n \n @cache\n def dfs_score(mask: int) -> int:\n k = (n - mask.bit_count()) // 2\n return max((\n k * math.gcd(nums[i], nums[j]) + \n dfs_score(mask | 1 << i | 1 << j) \n for i in range(n) \n for j in range(i + 1, n)\n if not mask & (1 << i | 1 << j)),\n default=0\n )\n \n return dfs_score(0)\n\n```\n\n---\n# Approach 3:\nRecursion with bit masking, memoization, and pruning **(Accepted - 99.37%)**\n\n<!-- # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$ -->\n\n# Code\n```python\n\nclass Solution:\n def maxScore(self, nums: list[int]) -> int:\n n = len(nums)\n gcds = sorted((\n (gcd(nums[i], nums[j]), 1 << i | 1 << j)\n for i in range(n)\n for j in range(i + 1, n)),\n reverse=True,\n )\n\n \n def score(xs: list[int], mask: int=0) -> int:\n n = len(xs)\n k = (n - mask.bit_count()) // 2\n\n max_score = 0\n for gcd_, ij_mask in gcds:\n if (not (mask & ij_mask) # Prune if the gcd pair is already used.\n and max_score < gcd_ * (k * (k + 1) // 2) # Prune if max possible score on exploring the branch is not greater than current max_score\n ): max_score = max(max_score, k * gcd_ + score(xs, mask | ij_mask))\n \n return max_score\n \n return score(nums)\n\n\n``` | 2 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
Python short and clean. 2 solutions. Functional programming. | maximize-score-after-n-operations | 0 | 1 | # Approach 1:\nRecursion with list slicing **(TLE)**\n\n<!-- # Complexity\n- Time complexity: $$O(n ^ 3)$$\n\n- Space complexity: $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def maxScore(self, nums: list[int]) -> int:\n \n def score(xs: list[int]) -> int:\n n = len(xs)\n return max((\n n // 2 * gcd(xs[i], xs[j]) +\n score(xs[:i] + xs[i + 1 : j] + xs[j + 1:])\n for i in range(n)\n for j in range(i + 1, n)),\n default=0,\n )\n \n return score(nums)\n\n\n```\n\n---\n# Approach 2:\nRecursion with bit masking, memoization **(Accepted - 52.53%)**\n\n<!-- # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n n = len(nums)\n \n @cache\n def dfs_score(mask: int) -> int:\n k = (n - mask.bit_count()) // 2\n return max((\n k * math.gcd(nums[i], nums[j]) + \n dfs_score(mask | 1 << i | 1 << j) \n for i in range(n) \n for j in range(i + 1, n)\n if not mask & (1 << i | 1 << j)),\n default=0\n )\n \n return dfs_score(0)\n\n```\n\n---\n# Approach 3:\nRecursion with bit masking, memoization, and pruning **(Accepted - 99.37%)**\n\n<!-- # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$ -->\n\n# Code\n```python\n\nclass Solution:\n def maxScore(self, nums: list[int]) -> int:\n n = len(nums)\n gcds = sorted((\n (gcd(nums[i], nums[j]), 1 << i | 1 << j)\n for i in range(n)\n for j in range(i + 1, n)),\n reverse=True,\n )\n\n \n def score(xs: list[int], mask: int=0) -> int:\n n = len(xs)\n k = (n - mask.bit_count()) // 2\n\n max_score = 0\n for gcd_, ij_mask in gcds:\n if (not (mask & ij_mask) # Prune if the gcd pair is already used.\n and max_score < gcd_ * (k * (k + 1) // 2) # Prune if max possible score on exploring the branch is not greater than current max_score\n ): max_score = max(max_score, k * gcd_ + score(xs, mask | ij_mask))\n \n return max_score\n \n return score(nums)\n\n\n``` | 2 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
🐍✅Python3 most 🔥optimised🔥 solution | maximize-score-after-n-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using Dynamic programming**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Construct a matrix of greatest common divisors for all pairs of elements in the input array using nested loops and the built-in `gcd()` function.\n- Use dynamic programming to find the maximum score for all possible subsets of the input array using bitwise operations and an array to store the maximum score for each subset.\n- Iterate over all subsets of the input array with an even number of selected elements using bitwise operations and nested loops.\n- Compute the score for the current subset by adding the maximum score for the previous subset and the product of the number of selected elements in the current subset divided by 2 and the greatest common divisor of the two selected elements.\n- Update the maximum score for the current subset in the array storing the maximum score for each subset.\n- Return the maximum score for the subset containing all elements in the input array.\n\n# Complexity\n- Time complexity: O(2^n * n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n # Determine number of elements\n num_elems = len(nums)\n \n # Construct matrix of greatest common divisors for all pairs of elements\n gcd_pairs = [[gcd(nums[i], nums[j]) for j in range(num_elems)] for i in range(num_elems)]\n \n # Use dynamic programming to find maximum score\n max_scores = [0] * (1 << num_elems)\n for state in range(1, 1 << num_elems):\n num_selected = bin(state).count(\'1\')\n \n # Skip states with odd number of selected elements\n if num_selected % 2 == 1:\n continue\n \n # Iterate over all pairs of selected elements\n for i in range(num_elems):\n if not (state & (1 << i)):\n continue\n for j in range(i+1, num_elems):\n if not (state & (1 << j)):\n continue\n \n # Compute score for current state based on previous state and current pair of elements\n prev_state = state ^ (1 << i) ^ (1 << j)\n current_score = max_scores[prev_state] + num_selected // 2 * gcd_pairs[i][j]\n \n # Update maximum score for current state\n max_scores[state] = max(max_scores[state], current_score)\n \n # Return maximum score for state with all elements selected\n return max_scores[(1 << num_elems) - 1]\n\n```\n# Please like and comment below ( \u0361\u2688\u202F\u035C\u0296 \u0361\u2688)\uD83D\uDC49 | 4 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
🐍✅Python3 most 🔥optimised🔥 solution | maximize-score-after-n-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using Dynamic programming**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Construct a matrix of greatest common divisors for all pairs of elements in the input array using nested loops and the built-in `gcd()` function.\n- Use dynamic programming to find the maximum score for all possible subsets of the input array using bitwise operations and an array to store the maximum score for each subset.\n- Iterate over all subsets of the input array with an even number of selected elements using bitwise operations and nested loops.\n- Compute the score for the current subset by adding the maximum score for the previous subset and the product of the number of selected elements in the current subset divided by 2 and the greatest common divisor of the two selected elements.\n- Update the maximum score for the current subset in the array storing the maximum score for each subset.\n- Return the maximum score for the subset containing all elements in the input array.\n\n# Complexity\n- Time complexity: O(2^n * n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n # Determine number of elements\n num_elems = len(nums)\n \n # Construct matrix of greatest common divisors for all pairs of elements\n gcd_pairs = [[gcd(nums[i], nums[j]) for j in range(num_elems)] for i in range(num_elems)]\n \n # Use dynamic programming to find maximum score\n max_scores = [0] * (1 << num_elems)\n for state in range(1, 1 << num_elems):\n num_selected = bin(state).count(\'1\')\n \n # Skip states with odd number of selected elements\n if num_selected % 2 == 1:\n continue\n \n # Iterate over all pairs of selected elements\n for i in range(num_elems):\n if not (state & (1 << i)):\n continue\n for j in range(i+1, num_elems):\n if not (state & (1 << j)):\n continue\n \n # Compute score for current state based on previous state and current pair of elements\n prev_state = state ^ (1 << i) ^ (1 << j)\n current_score = max_scores[prev_state] + num_selected // 2 * gcd_pairs[i][j]\n \n # Update maximum score for current state\n max_scores[state] = max(max_scores[state], current_score)\n \n # Return maximum score for state with all elements selected\n return max_scores[(1 << num_elems) - 1]\n\n```\n# Please like and comment below ( \u0361\u2688\u202F\u035C\u0296 \u0361\u2688)\uD83D\uDC49 | 4 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | maximize-score-after-n-operations | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. Next assignment will be shared tomorrow. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\n\nThe given problem can be solved using dynamic programming. The basic idea is to consider all possible pairs of numbers in the given array and calculate their gcd. Then, we can use a bitmask to represent all possible subsets of indices and use dynamic programming to calculate the maximum score for each subset.\n\nTo calculate the maximum score for a given subset of indices, we can iterate over all possible pairs of indices in the subset and calculate their gcd. We can then add the product of this gcd and half the number of indices in the subset to the maximum score for the subset obtained by removing these indices from the original subset.\n\nThe maximum score for the original subset can then be obtained by considering all possible subsets of indices and choosing the one with the maximum score.\n\n# Intuition:\n\nThe problem requires us to maximize a score that is calculated based on the gcd of pairs of numbers in the given array. We can observe that if we fix a pair of indices, the gcd of the corresponding pair of numbers will be the same for all subsets that contain these indices. Therefore, we can precompute the gcd of all pairs of numbers in the array and use it to calculate the score for each subset.\n\nWe can also observe that if we remove a pair of indices from a subset, the resulting subset will have an even number of indices. This is because the total number of indices in the original subset is even, and removing a pair of indices will reduce this number by 2. Therefore, we can iterate over all possible even-sized subsets of indices and use dynamic programming to calculate the maximum score for each subset.\n\n\n\n\n\n\n```Python []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n n = len(nums)\n \n \n gcd_matrix = [[0] * n for _ in range(n)]\n for i in range(n):\n for j in range(i+1, n):\n gcd_matrix[i][j] = gcd_matrix[j][i] = gcd(nums[i], nums[j])\n \n \n dp = [0] * (1 << n)\n \n \n for state in range(1, 1 << n):\n \n cnt = bin(state).count(\'1\')\n \n \n if cnt % 2 == 1:\n continue\n \n \n for i in range(n):\n if not (state & (1 << i)):\n continue\n for j in range(i+1, n):\n if not (state & (1 << j)):\n continue\n nextState = state ^ (1 << i) ^ (1 << j)\n dp[state] = max(dp[state], dp[nextState] + cnt // 2 * gcd_matrix[i][j])\n \n return dp[(1 << n) - 1]\n\n```\n```Java []\nclass Solution {\n public int maxScore(int[] nums) {\n int n = nums.length;\n \n \n int[][] gcdMatrix = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n gcdMatrix[i][j] = gcdMatrix[j][i] = gcd(nums[i], nums[j]);\n }\n }\n \n \n int[] dp = new int[1 << n];\n \n \n for (int state = 1; state < (1 << n); state++) {\n \n int cnt = Integer.bitCount(state);\n \n \n if (cnt % 2 == 1) {\n continue;\n }\n \n \n for (int i = 0; i < n; i++) {\n if ((state & (1 << i)) == 0) {\n continue;\n }\n for (int j = i + 1; j < n; j++) {\n if ((state & (1 << j)) == 0) {\n continue;\n }\n int nextState = state ^ (1 << i) ^ (1 << j);\n dp[state] = Math.max(dp[state], dp[nextState] + cnt / 2 * gcdMatrix[i][j]);\n }\n }\n }\n \n return dp[(1 << n) - 1];\n }\n \n private int gcd(int a, int b) {\n return b == 0 ? a : gcd(b, a % b);\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int maxScore(vector<int>& nums) {\n int n = nums.size();\n \n \n vector<vector<int>> gcdMatrix(n, vector<int>(n));\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n gcdMatrix[i][j] = gcdMatrix[j][i] = gcd(nums[i], nums[j]);\n }\n }\n \n \n vector<int> dp(1 << n);\n \n \n for (int state = 1; state < (1 << n); state++) {\n \n int cnt = __builtin_popcount(state);\n \n \n if (cnt % 2 == 1) {\n continue;\n }\n \n \n for (int i = 0; i < n; i++) {\n if ((state & (1 << i)) == 0) {\n continue;\n }\n for (int j = i + 1; j < n; j++) {\n if ((state & (1 << j)) == 0) {\n continue;\n }\n int nextState = state ^ (1 << i) ^ (1 << j);\n dp[state] = max(dp[state], dp[nextState] + cnt / 2 * gcdMatrix[i][j]);\n }\n }\n }\n \n return dp[(1 << n) - 1];\n }\n \n int gcd(int a, int b) {\n return b == 0 ? a : gcd(b, a % b);\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 27 | You are given `nums`, an array of positive integers of size `2 * n`. You must perform `n` operations on this array.
In the `ith` operation **(1-indexed)**, you will:
* Choose two elements, `x` and `y`.
* Receive a score of `i * gcd(x, y)`.
* Remove `x` and `y` from `nums`.
Return _the maximum score you can receive after performing_ `n` _operations._
The function `gcd(x, y)` is the greatest common divisor of `x` and `y`.
**Example 1:**
**Input:** nums = \[1,2\]
**Output:** 1
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 2)) = 1
**Example 2:**
**Input:** nums = \[3,4,6,8\]
**Output:** 11
**Explanation:** The optimal choice of operations is:
(1 \* gcd(3, 6)) + (2 \* gcd(4, 8)) = 3 + 8 = 11
**Example 3:**
**Input:** nums = \[1,2,3,4,5,6\]
**Output:** 14
**Explanation:** The optimal choice of operations is:
(1 \* gcd(1, 5)) + (2 \* gcd(2, 4)) + (3 \* gcd(3, 6)) = 1 + 4 + 9 = 14
**Constraints:**
* `1 <= n <= 7`
* `nums.length == 2 * n`
* `1 <= nums[i] <= 106` | The constraints are small enough for a backtrack solution but not any backtrack solution If we use a naive n^k don't you think it can be optimized |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | maximize-score-after-n-operations | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. Next assignment will be shared tomorrow. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\n\nThe given problem can be solved using dynamic programming. The basic idea is to consider all possible pairs of numbers in the given array and calculate their gcd. Then, we can use a bitmask to represent all possible subsets of indices and use dynamic programming to calculate the maximum score for each subset.\n\nTo calculate the maximum score for a given subset of indices, we can iterate over all possible pairs of indices in the subset and calculate their gcd. We can then add the product of this gcd and half the number of indices in the subset to the maximum score for the subset obtained by removing these indices from the original subset.\n\nThe maximum score for the original subset can then be obtained by considering all possible subsets of indices and choosing the one with the maximum score.\n\n# Intuition:\n\nThe problem requires us to maximize a score that is calculated based on the gcd of pairs of numbers in the given array. We can observe that if we fix a pair of indices, the gcd of the corresponding pair of numbers will be the same for all subsets that contain these indices. Therefore, we can precompute the gcd of all pairs of numbers in the array and use it to calculate the score for each subset.\n\nWe can also observe that if we remove a pair of indices from a subset, the resulting subset will have an even number of indices. This is because the total number of indices in the original subset is even, and removing a pair of indices will reduce this number by 2. Therefore, we can iterate over all possible even-sized subsets of indices and use dynamic programming to calculate the maximum score for each subset.\n\n\n\n\n\n\n```Python []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n n = len(nums)\n \n \n gcd_matrix = [[0] * n for _ in range(n)]\n for i in range(n):\n for j in range(i+1, n):\n gcd_matrix[i][j] = gcd_matrix[j][i] = gcd(nums[i], nums[j])\n \n \n dp = [0] * (1 << n)\n \n \n for state in range(1, 1 << n):\n \n cnt = bin(state).count(\'1\')\n \n \n if cnt % 2 == 1:\n continue\n \n \n for i in range(n):\n if not (state & (1 << i)):\n continue\n for j in range(i+1, n):\n if not (state & (1 << j)):\n continue\n nextState = state ^ (1 << i) ^ (1 << j)\n dp[state] = max(dp[state], dp[nextState] + cnt // 2 * gcd_matrix[i][j])\n \n return dp[(1 << n) - 1]\n\n```\n```Java []\nclass Solution {\n public int maxScore(int[] nums) {\n int n = nums.length;\n \n \n int[][] gcdMatrix = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n gcdMatrix[i][j] = gcdMatrix[j][i] = gcd(nums[i], nums[j]);\n }\n }\n \n \n int[] dp = new int[1 << n];\n \n \n for (int state = 1; state < (1 << n); state++) {\n \n int cnt = Integer.bitCount(state);\n \n \n if (cnt % 2 == 1) {\n continue;\n }\n \n \n for (int i = 0; i < n; i++) {\n if ((state & (1 << i)) == 0) {\n continue;\n }\n for (int j = i + 1; j < n; j++) {\n if ((state & (1 << j)) == 0) {\n continue;\n }\n int nextState = state ^ (1 << i) ^ (1 << j);\n dp[state] = Math.max(dp[state], dp[nextState] + cnt / 2 * gcdMatrix[i][j]);\n }\n }\n }\n \n return dp[(1 << n) - 1];\n }\n \n private int gcd(int a, int b) {\n return b == 0 ? a : gcd(b, a % b);\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int maxScore(vector<int>& nums) {\n int n = nums.size();\n \n \n vector<vector<int>> gcdMatrix(n, vector<int>(n));\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n gcdMatrix[i][j] = gcdMatrix[j][i] = gcd(nums[i], nums[j]);\n }\n }\n \n \n vector<int> dp(1 << n);\n \n \n for (int state = 1; state < (1 << n); state++) {\n \n int cnt = __builtin_popcount(state);\n \n \n if (cnt % 2 == 1) {\n continue;\n }\n \n \n for (int i = 0; i < n; i++) {\n if ((state & (1 << i)) == 0) {\n continue;\n }\n for (int j = i + 1; j < n; j++) {\n if ((state & (1 << j)) == 0) {\n continue;\n }\n int nextState = state ^ (1 << i) ^ (1 << j);\n dp[state] = max(dp[state], dp[nextState] + cnt / 2 * gcdMatrix[i][j]);\n }\n }\n }\n \n return dp[(1 << n) - 1];\n }\n \n int gcd(int a, int b) {\n return b == 0 ? a : gcd(b, a % b);\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 27 | The **minimum absolute difference** of an array `a` is defined as the **minimum value** of `|a[i] - a[j]|`, where `0 <= i < j < a.length` and `a[i] != a[j]`. If all elements of `a` are the **same**, the minimum absolute difference is `-1`.
* For example, the minimum absolute difference of the array `[5,2,3,7,2]` is `|2 - 3| = 1`. Note that it is not `0` because `a[i]` and `a[j]` must be different.
You are given an integer array `nums` and the array `queries` where `queries[i] = [li, ri]`. For each query `i`, compute the **minimum absolute difference** of the **subarray** `nums[li...ri]` containing the elements of `nums` between the **0-based** indices `li` and `ri` (**inclusive**).
Return _an **array**_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
A **subarray** is a contiguous sequence of elements in an array.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[2,3\],\[0,3\]\]
**Output:** \[2,1,4,1\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[0,1\]: The subarray is \[1,3\] and the minimum absolute difference is |1-3| = 2.
- queries\[1\] = \[1,2\]: The subarray is \[3,4\] and the minimum absolute difference is |3-4| = 1.
- queries\[2\] = \[2,3\]: The subarray is \[4,8\] and the minimum absolute difference is |4-8| = 4.
- queries\[3\] = \[0,3\]: The subarray is \[1,3,4,8\] and the minimum absolute difference is |3-4| = 1.
**Example 2:**
**Input:** nums = \[4,5,2,2,7,10\], queries = \[\[2,3\],\[0,2\],\[0,5\],\[3,5\]\]
**Output:** \[-1,1,1,3\]
**Explanation:** The queries are processed as follows:
- queries\[0\] = \[2,3\]: The subarray is \[2,2\] and the minimum absolute difference is -1 because all the
elements are the same.
- queries\[1\] = \[0,2\]: The subarray is \[4,5,2\] and the minimum absolute difference is |4-5| = 1.
- queries\[2\] = \[0,5\]: The subarray is \[4,5,2,2,7,10\] and the minimum absolute difference is |4-5| = 1.
- queries\[3\] = \[3,5\]: The subarray is \[2,7,10\] and the minimum absolute difference is |7-10| = 3.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 100`
* `1 <= queries.length <= 2 * 104`
* `0 <= li < ri < nums.length` | Find every way to split the array until n groups of 2. Brute force recursion is acceptable. Calculate the gcd of every pair and greedily multiply the largest gcds. |
Python 32 ms | maximum-ascending-subarray-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n sumx = -1\n for i in range(len(nums)):\n subarr=[nums[i]]\n for j in range(i+1, len(nums)):\n if nums[j]>subarr[-1]:subarr.append(nums[j])\n else:break\n s=sum(subarr)\n if s>sumx:sumx=s\n return sumx\n``` | 1 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Python 32 ms | maximum-ascending-subarray-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n sumx = -1\n for i in range(len(nums)):\n subarr=[nums[i]]\n for j in range(i+1, len(nums)):\n if nums[j]>subarr[-1]:subarr.append(nums[j])\n else:break\n s=sum(subarr)\n if s>sumx:sumx=s\n return sumx\n``` | 1 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
Simple Python3 Solution | Faster than 95.89% | maximum-ascending-subarray-sum | 0 | 1 | ```\n def maxAscendingSum(self, nums: List[int]) -> int:\n res = 0\n \n curr = nums[0]\n for i, n in enumerate(nums[1:]):\n if n <= nums[i]:\n res = max(res, curr)\n curr = n\n else:\n curr += n\n \n return max(res, curr) | 1 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Simple Python3 Solution | Faster than 95.89% | maximum-ascending-subarray-sum | 0 | 1 | ```\n def maxAscendingSum(self, nums: List[int]) -> int:\n res = 0\n \n curr = nums[0]\n for i, n in enumerate(nums[1:]):\n if n <= nums[i]:\n res = max(res, curr)\n curr = n\n else:\n curr += n\n \n return max(res, curr) | 1 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
Straightforward Python Solution | maximum-ascending-subarray-sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n res = 0\n temp = nums[0]\n for i in range(1, len(nums)):\n if nums[i] > nums[i-1]:\n temp += nums[i]\n else:\n res = max(res, temp)\n temp = nums[i]\n return max(res, temp)\n``` | 1 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Straightforward Python Solution | maximum-ascending-subarray-sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n res = 0\n temp = nums[0]\n for i in range(1, len(nums)):\n if nums[i] > nums[i-1]:\n temp += nums[i]\n else:\n res = max(res, temp)\n temp = nums[i]\n return max(res, temp)\n``` | 1 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
[Python3] line sweep | maximum-ascending-subarray-sum | 0 | 1 | \n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n ans = 0\n for i, x in enumerate(nums): \n if not i or nums[i-1] >= nums[i]: val = 0 # reset val \n val += nums[i]\n ans = max(ans, val)\n return ans \n```\n\nEdited on 3/22/2021\nAdding C++ implementation\n```\nclass Solution {\npublic:\n int maxAscendingSum(vector<int>& nums) {\n int ans = 0, val = 0; \n for (int i = 0; i < nums.size(); ++i) {\n if (i == 0 || nums[i-1] >= nums[i]) val = 0; \n val += nums[i]; \n ans = max(ans, val); \n }\n return ans; \n }\n};\n``` | 7 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
[Python3] line sweep | maximum-ascending-subarray-sum | 0 | 1 | \n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n ans = 0\n for i, x in enumerate(nums): \n if not i or nums[i-1] >= nums[i]: val = 0 # reset val \n val += nums[i]\n ans = max(ans, val)\n return ans \n```\n\nEdited on 3/22/2021\nAdding C++ implementation\n```\nclass Solution {\npublic:\n int maxAscendingSum(vector<int>& nums) {\n int ans = 0, val = 0; \n for (int i = 0; i < nums.size(); ++i) {\n if (i == 0 || nums[i-1] >= nums[i]) val = 0; \n val += nums[i]; \n ans = max(ans, val); \n }\n return ans; \n }\n};\n``` | 7 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
PYTHON | Simple python solution | maximum-ascending-subarray-sum | 0 | 1 | ```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n maxSum = 0\n subSum = 0\n \n for i in range(len(nums)):\n \n if i == 0 or nums[i-1] < nums[i]:\n subSum += nums[i]\n maxSum = max(maxSum, subSum)\n else:\n subSum = nums[i]\n \n return maxSum\n``` | 1 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
PYTHON | Simple python solution | maximum-ascending-subarray-sum | 0 | 1 | ```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n maxSum = 0\n subSum = 0\n \n for i in range(len(nums)):\n \n if i == 0 or nums[i-1] < nums[i]:\n subSum += nums[i]\n maxSum = max(maxSum, subSum)\n else:\n subSum = nums[i]\n \n return maxSum\n``` | 1 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
Python3 Solution - Two Pointers | maximum-ascending-subarray-sum | 0 | 1 | # Code :)\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n # Initialize the result to -1 to store the maximum sum\n result = 0\n # Initialize the outer loop index\n i = 0\n \n # Iterate through the list until the end\n while i < len(nums): \n # Initialize a new ascending subarray starting with the current element\n _sum = [nums[i]]\n # Initialize the inner loop index to the next position\n l = i + 1\n \n # Continue adding elements to the ascending subarray while the condition is met\n while l < len(nums) and nums[l] > max(_sum):\n _sum.append(nums[l])\n l += 1\n \n # Update the outer loop index to the next starting position after the inner loop completes\n i = l\n # Update the result with the maximum of the current result and the sum of the current subarray\n result = max(result, sum(_sum))\n \n # Return the final result\n return result\n\n``` | 0 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Python3 Solution - Two Pointers | maximum-ascending-subarray-sum | 0 | 1 | # Code :)\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n # Initialize the result to -1 to store the maximum sum\n result = 0\n # Initialize the outer loop index\n i = 0\n \n # Iterate through the list until the end\n while i < len(nums): \n # Initialize a new ascending subarray starting with the current element\n _sum = [nums[i]]\n # Initialize the inner loop index to the next position\n l = i + 1\n \n # Continue adding elements to the ascending subarray while the condition is met\n while l < len(nums) and nums[l] > max(_sum):\n _sum.append(nums[l])\n l += 1\n \n # Update the outer loop index to the next starting position after the inner loop completes\n i = l\n # Update the result with the maximum of the current result and the sum of the current subarray\n result = max(result, sum(_sum))\n \n # Return the final result\n return result\n\n``` | 0 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
Maximum Ascending Subarray Sum | maximum-ascending-subarray-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n total = 0\n temp = 0\n maxs = 0\n\n for i in range(len(nums)):\n for j in range(i,len(nums)):\n temp = 0\n total = 0\n for k in range(i,j+1):\n if nums[k] > temp:\n temp = nums[k]\n total = total + temp\n else:\n break\n maxs = max(total,maxs)\n return maxs\n\n\n \n``` | 0 | Given an array of positive integers `nums`, return the _maximum possible sum of an **ascending** subarray in_ `nums`.
A subarray is defined as a contiguous sequence of numbers in an array.
A subarray `[numsl, numsl+1, ..., numsr-1, numsr]` is **ascending** if for all `i` where `l <= i < r`, `numsi < numsi+1`. Note that a subarray of size `1` is **ascending**.
**Example 1:**
**Input:** nums = \[10,20,30,5,10,50\]
**Output:** 65
**Explanation:** \[5,10,50\] is the ascending subarray with the maximum sum of 65.
**Example 2:**
**Input:** nums = \[10,20,30,40,50\]
**Output:** 150
**Explanation:** \[10,20,30,40,50\] is the ascending subarray with the maximum sum of 150.
**Example 3:**
**Input:** nums = \[12,17,15,13,10,11,12\]
**Output:** 33
**Explanation:** \[10,11,12\] is the ascending subarray with the maximum sum of 33.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Express the nth number value in a recursion formula and think about how we can do a fast evaluation. |
Maximum Ascending Subarray Sum | maximum-ascending-subarray-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxAscendingSum(self, nums: List[int]) -> int:\n total = 0\n temp = 0\n maxs = 0\n\n for i in range(len(nums)):\n for j in range(i,len(nums)):\n temp = 0\n total = 0\n for k in range(i,j+1):\n if nums[k] > temp:\n temp = nums[k]\n total = total + temp\n else:\n break\n maxs = max(total,maxs)\n return maxs\n\n\n \n``` | 0 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
Python 3 || 9 lines, w/ explanation || T/M: 89% / 49% | number-of-orders-in-the-backlog | 0 | 1 | Here\'s the plan:\n1. Establish maxheap `buy` for buy orders and minheap `sell` for sell orders.\n2. Iterate through `orders`. Push each element onto the appropriate heap.\n3. During each iteration, peak at the heads of each list and determine whether they allow a transaction. If so, pop both heads, and if one has a positive amount after the transaction, push it back on its heap, and check the new heads (lather, rinse, repeat... `while`)\n4. After the iteration,`return`the sum of`amt`in the heaps.\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n\n buy,sell = [], [] # <-- 1\n\n for price,amt,order in orders: # <-- 2\n if order: heappush(sell, ( price, amt)) #\n else : heappush(buy , (-price, amt)) #\n \n while buy and sell and -buy[0][0] >= sell[0][0]: # <-- 3\n #\n (buyPrice,buyAmt), (sellPrice,sellAmt) = heappop(buy), heappop(sell) #\n #\n if buyAmt > sellAmt: heappush(buy , (buyPrice , buyAmt -sellAmt)) #\n elif buyAmt < sellAmt: heappush(sell, (sellPrice, sellAmt- buyAmt)) #\n\n return sum(amt for _,amt in buy+sell)% (1000000007) # <-- 4\n```\n[https://leetcode.com/problems/number-of-orders-in-the-backlog/submissions/870707453/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 3 | You are given a 2D integer array `orders`, where each `orders[i] = [pricei, amounti, orderTypei]` denotes that `amounti` orders have been placed of type `orderTypei` at the price `pricei`. The `orderTypei` is:
* `0` if it is a batch of `buy` orders, or
* `1` if it is a batch of `sell` orders.
Note that `orders[i]` represents a batch of `amounti` independent orders with the same price and order type. All orders represented by `orders[i]` will be placed before all orders represented by `orders[i+1]` for all valid `i`.
There is a **backlog** that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
* If the order is a `buy` order, you look at the `sell` order with the **smallest** price in the backlog. If that `sell` order's price is **smaller than or equal to** the current `buy` order's price, they will match and be executed, and that `sell` order will be removed from the backlog. Else, the `buy` order is added to the backlog.
* Vice versa, if the order is a `sell` order, you look at the `buy` order with the **largest** price in the backlog. If that `buy` order's price is **larger than or equal to** the current `sell` order's price, they will match and be executed, and that `buy` order will be removed from the backlog. Else, the `sell` order is added to the backlog.
Return _the total **amount** of orders in the backlog after placing all the orders from the input_. Since this number can be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** orders = \[\[10,5,0\],\[15,2,1\],\[25,1,1\],\[30,4,0\]\]
**Output:** 6
**Explanation:** Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
**Example 2:**
**Input:** orders = \[\[7,1000000000,1\],\[15,3,0\],\[5,999999995,0\],\[5,1,1\]\]
**Output:** 999999984
**Explanation:** Here is what happens with the orders:
- 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
**Constraints:**
* `1 <= orders.length <= 105`
* `orders[i].length == 3`
* `1 <= pricei, amounti <= 109`
* `orderTypei` is either `0` or `1`. | null |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.