title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python3🐍] [DP] [Drawing✍️] [Easy to understand ✌️] Dynamic Programming solution.✨🍻 | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nConsider we have these three arrarys:\n- groups, provided by input.\n- nums, also provided by input.\n- dp, we create it, the meaning is: **in the current position `i`, how many groups are already matched.**\n For example: `dp[3]=2` means before position `3`, there already has `2` matched groups. And if the `2` is the total number of groups, that\'s done, just return `True`.\n\nSo, let\'s run the dp program:\n\n- for the first step, we\'re trying to match `1st` of groups and nums.\n\n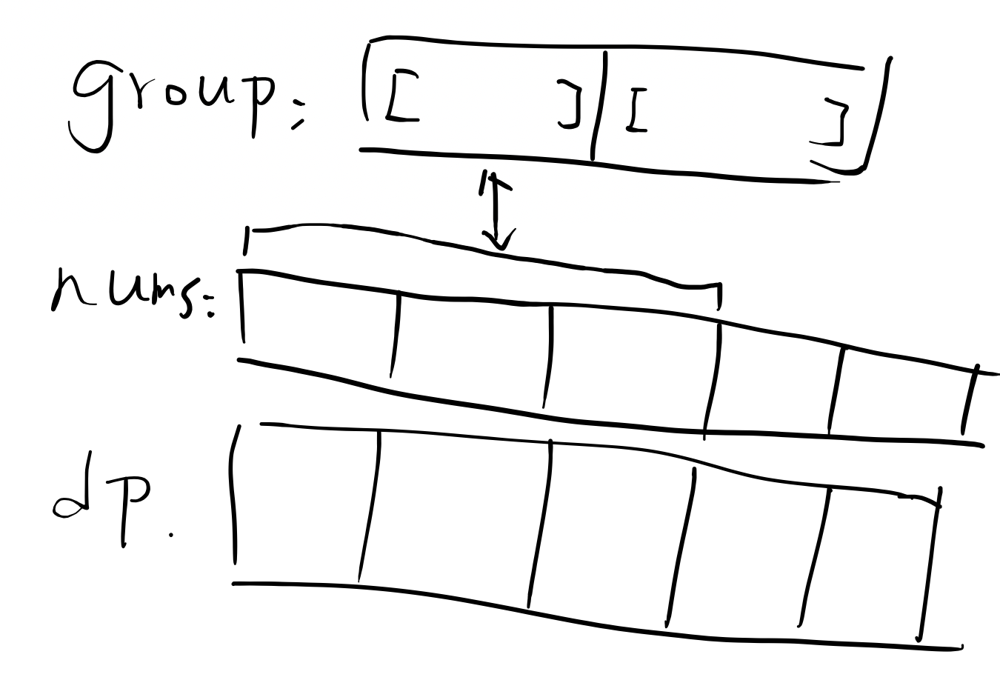\n\n- for the second step, if the first step matched successfully, we\'re trying the match `2nd` of groups and nums.\n\n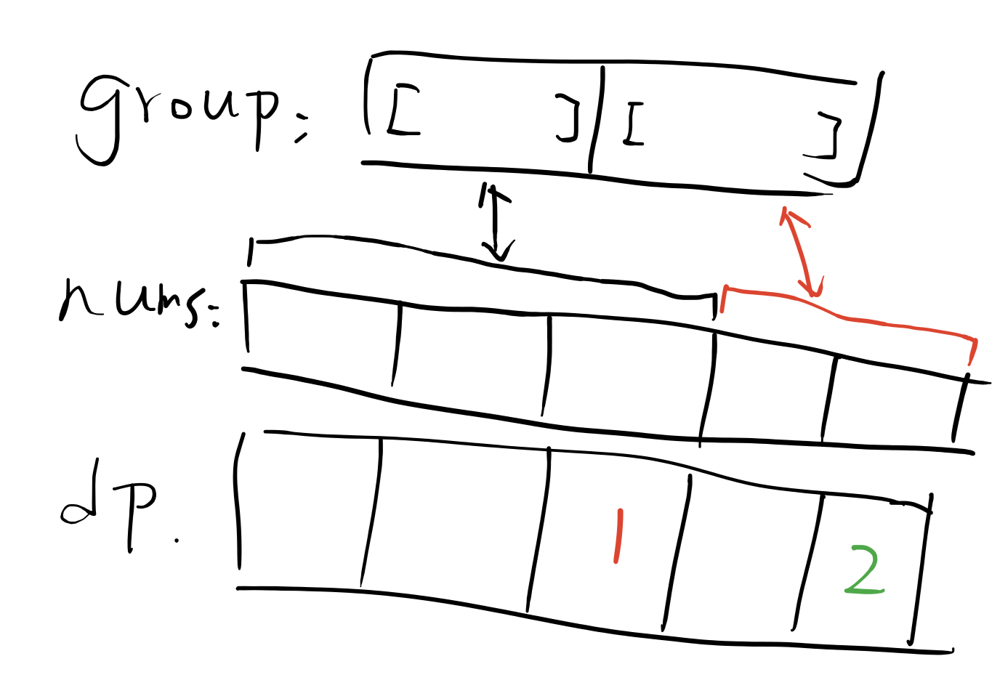\n\n- break condition:\n The number of matched group `>=` total group.\n\n# Complexity\n- Time complexity: O(len(groups) * len(nums))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(len(nums))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n lc = len(nums)\n target = len(groups)\n dp = [0 for j in range(lc)]\n for c in range(lc):\n curGroupIndex = dp[c - 1]\n l = len(groups[curGroupIndex])\n nextIndex = c+l-1\n if nums[c: c+l] == groups[curGroupIndex] and nextIndex < lc:\n dp[nextIndex] = max(dp[nextIndex], curGroupIndex + 1)\n if dp[nextIndex] >= target:\n return True\n dp[c] = max(dp[c-1], dp[c])\n return False\n \n\n``` | 1 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
[Python3] check group one-by-one | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | \n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n i = 0\n for grp in groups: \n for ii in range(i, len(nums)):\n if nums[ii:ii+len(grp)] == grp: \n i = ii + len(grp)\n break \n else: return False\n return True\n``` | 33 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
[Python3] check group one-by-one | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | \n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n i = 0\n for grp in groups: \n for ii in range(i, len(nums)):\n if nums[ii:ii+len(grp)] == grp: \n i = ii + len(grp)\n break \n else: return False\n return True\n``` | 33 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
Easy python solution | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n ln=len(groups)\n idx=0\n for i in groups:\n for j in range(idx,len(nums)):\n if nums[j:j+len(i)]==i:\n idx=j+len(i)\n ln-=1\n break\n return ln==0\n \n``` | 4 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Easy python solution | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n ln=len(groups)\n idx=0\n for i in groups:\n for j in range(idx,len(nums)):\n if nums[j:j+len(i)]==i:\n idx=j+len(i)\n ln-=1\n break\n return ln==0\n \n``` | 4 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
||faster than 99 percent of python solutions||greedy||sliding window|| | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | **# Intuition**\nImagine laying out the groups like train cars on a track, and trying to find matching segments within the nums train to connect them in order. To ensure disjointness, each connected segment cannot overlap with any other.\n\nStart at the front: We begin searching at the beginning of the nums train.\nMatch group by group: For each group car, we try to find a matching "subtrain" within the remaining nums track.\nSlide and compare: We slide a window of size equal to the current group along the remaining nums track, comparing it to the group at each position.\nFind and connect: If a match is found, we "attach" the matched subtrain to the corresponding group and move the starting point of the search to the end of the matched subtrain.\nRepeat and succeed: We repeat this process for all groups. If we successfully find and connect all groups without any overlap, it means we can choose the required subarrays, and we return True. If we fail to find a match for any group, it signifies an overlap or missing segment, and we return False.\n**Approach:**\n\n1. **Iterate through groups:** For each group in the `groups` array:\n - **Slide a window:** Iterate through `nums` using a sliding window of the same size as the current group.\n - **Check for match:** If the window matches the group, mark it as found and move to the next group.\n - **Handle disjointness:** Ensure subsequent windows start after the end of the previously found group to maintain disjointness.\n2. **Return result:** If all groups are found, return `True`, otherwise return `False`.\n\n\n\n**# Complexity**\n\n- **Time complexity:** O(n * m), where n is the number of elements in `nums` and m is the total number of elements in all groups. This is due to the nested loops and potential window sliding.\n- **Space complexity:** O(1), as we only use a constant amount of extra space for variables.\n\n**# Code**\n\n```python\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n index = 0 # Track the current position in nums\n\n for group in groups:\n start = index # Start searching from the current position\n end = index + len(group) - 1 # Calculate the potential end of the group\n\n while end < len(nums):\n if nums[start:end + 1] == group: # Match found\n index = end + 1 # Move to the next possible starting point\n break\n start += 1 # Shift the window if no match\n end += 1\n\n else: # No match found for the current group\n return False\n\n return True # All groups found successfully\n```\n | 0 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
||faster than 99 percent of python solutions||greedy||sliding window|| | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | **# Intuition**\nImagine laying out the groups like train cars on a track, and trying to find matching segments within the nums train to connect them in order. To ensure disjointness, each connected segment cannot overlap with any other.\n\nStart at the front: We begin searching at the beginning of the nums train.\nMatch group by group: For each group car, we try to find a matching "subtrain" within the remaining nums track.\nSlide and compare: We slide a window of size equal to the current group along the remaining nums track, comparing it to the group at each position.\nFind and connect: If a match is found, we "attach" the matched subtrain to the corresponding group and move the starting point of the search to the end of the matched subtrain.\nRepeat and succeed: We repeat this process for all groups. If we successfully find and connect all groups without any overlap, it means we can choose the required subarrays, and we return True. If we fail to find a match for any group, it signifies an overlap or missing segment, and we return False.\n**Approach:**\n\n1. **Iterate through groups:** For each group in the `groups` array:\n - **Slide a window:** Iterate through `nums` using a sliding window of the same size as the current group.\n - **Check for match:** If the window matches the group, mark it as found and move to the next group.\n - **Handle disjointness:** Ensure subsequent windows start after the end of the previously found group to maintain disjointness.\n2. **Return result:** If all groups are found, return `True`, otherwise return `False`.\n\n\n\n**# Complexity**\n\n- **Time complexity:** O(n * m), where n is the number of elements in `nums` and m is the total number of elements in all groups. This is due to the nested loops and potential window sliding.\n- **Space complexity:** O(1), as we only use a constant amount of extra space for variables.\n\n**# Code**\n\n```python\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n index = 0 # Track the current position in nums\n\n for group in groups:\n start = index # Start searching from the current position\n end = index + len(group) - 1 # Calculate the potential end of the group\n\n while end < len(nums):\n if nums[start:end + 1] == group: # Match found\n index = end + 1 # Move to the next possible starting point\n break\n start += 1 # Shift the window if no match\n end += 1\n\n else: # No match found for the current group\n return False\n\n return True # All groups found successfully\n```\n | 0 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
KPM - DP - O(n) - [60%, 55%] | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Complexity\n```\nLet n = sum(len(G) forall g in G) and m = len(A).\nTime complexity: O(n + m)\nSpace complexity: O(n)\n```\n\n# Code\n```python\nclass Solution:\n def canChoose(self, G: List[List[int]], A: List[int]) -> bool:\n # Construct Longest-Proper-Suffix array for each group.\n L = []\n for g in G:\n lps = [0]\n j = 0\n for i in range(1, len(g)):\n while j > 0 and g[j] != g[i]:\n j = lps[j - 1]\n if g[j] == g[i]:\n j += 1\n lps.append(j)\n L.append(lps)\n g, j = 0, 0\n\n for i in range(len(A)):\n if g >= len(G): break\n\n # KPM\n while j > 0 and G[g][j] != A[i]:\n j = L[g][j - 1]\n if G[g][j] == A[i]:\n j += 1\n\n if j >= len(G[g]):\n g += 1\n j = 0\n \n return g == len(G)\n\n\n \n``` | 0 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
KPM - DP - O(n) - [60%, 55%] | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Complexity\n```\nLet n = sum(len(G) forall g in G) and m = len(A).\nTime complexity: O(n + m)\nSpace complexity: O(n)\n```\n\n# Code\n```python\nclass Solution:\n def canChoose(self, G: List[List[int]], A: List[int]) -> bool:\n # Construct Longest-Proper-Suffix array for each group.\n L = []\n for g in G:\n lps = [0]\n j = 0\n for i in range(1, len(g)):\n while j > 0 and g[j] != g[i]:\n j = lps[j - 1]\n if g[j] == g[i]:\n j += 1\n lps.append(j)\n L.append(lps)\n g, j = 0, 0\n\n for i in range(len(A)):\n if g >= len(G): break\n\n # KPM\n while j > 0 and G[g][j] != A[i]:\n j = L[g][j - 1]\n if G[g][j] == A[i]:\n j += 1\n\n if j >= len(G[g]):\n g += 1\n j = 0\n \n return g == len(G)\n\n\n \n``` | 0 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
Intuitive Sliding Window | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUpon reading the question, it can be seen that a sliding window solution might work as we are dealing with subarrays \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart by creating a while loop to go through each group in groups while trying to find a match in nums. Note there are a few edge cases we should take note of in the inner while loops (such as checking the left and right pointers do not exceed len(nums) -1)\n\nafter checking those, we just need to check if the whole group can be found in the current subarray denoted by our left and right pointers. if no, simply shift left and right and try again, if found, move left to right + 1 (next index after the end of current group) and increment curr to signify searching for next group.\n\nAt end, we can use curr to check if we have found all groups (terminating while loop by breaking the curr < len(groups) condition)\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * m) n = len(nums) m = length of longest string in groups \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n \n\n curr = 0\n\n left = 0\n right = 0\n while right < len(nums) and curr < len(groups):\n group = groups[curr]\n right = left + len(group) - 1\n if right >= len(nums):\n break\n while right < len(nums) and nums[left] != group[0]:\n \n left += 1\n right += 1\n if left >= len(nums) or (right == len(nums) and nums[left] != group[0]):\n break\n p = 0\n correct = True\n for i in range(left, right + 1):\n if group[p] == nums[i]:\n p += 1\n continue\n else:\n correct = False\n break\n if not correct:\n left += 1 \n right += 1\n else:\n curr += 1\n left = right + 1\n if curr == len(groups):\n return True\n return False\n\n \n \n\n \n \n\n``` | 0 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Intuitive Sliding Window | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUpon reading the question, it can be seen that a sliding window solution might work as we are dealing with subarrays \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart by creating a while loop to go through each group in groups while trying to find a match in nums. Note there are a few edge cases we should take note of in the inner while loops (such as checking the left and right pointers do not exceed len(nums) -1)\n\nafter checking those, we just need to check if the whole group can be found in the current subarray denoted by our left and right pointers. if no, simply shift left and right and try again, if found, move left to right + 1 (next index after the end of current group) and increment curr to signify searching for next group.\n\nAt end, we can use curr to check if we have found all groups (terminating while loop by breaking the curr < len(groups) condition)\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * m) n = len(nums) m = length of longest string in groups \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n \n\n curr = 0\n\n left = 0\n right = 0\n while right < len(nums) and curr < len(groups):\n group = groups[curr]\n right = left + len(group) - 1\n if right >= len(nums):\n break\n while right < len(nums) and nums[left] != group[0]:\n \n left += 1\n right += 1\n if left >= len(nums) or (right == len(nums) and nums[left] != group[0]):\n break\n p = 0\n correct = True\n for i in range(left, right + 1):\n if group[p] == nums[i]:\n p += 1\n continue\n else:\n correct = False\n break\n if not correct:\n left += 1 \n right += 1\n else:\n curr += 1\n left = right + 1\n if curr == len(groups):\n return True\n return False\n\n \n \n\n \n \n\n``` | 0 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
[Python3] Good enough | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | ``` Python3 []\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n group = 0\n i = len(nums)-len(groups[-1-group])\n while i>=0:\n if nums[i:i+len(groups[-1-group])] == groups[-1-group]:\n if group==len(groups)-1:\n return True\n group += 1\n i -= len(groups[-1-group])\n else:\n i -= 1\n \n return False\n``` | 0 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
[Python3] Good enough | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | ``` Python3 []\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n group = 0\n i = len(nums)-len(groups[-1-group])\n while i>=0:\n if nums[i:i+len(groups[-1-group])] == groups[-1-group]:\n if group==len(groups)-1:\n return True\n group += 1\n i -= len(groups[-1-group])\n else:\n i -= 1\n \n return False\n``` | 0 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
Easy for Beginners | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n lg=len(groups)\n ind=0\n for i in groups:\n for j in range(ind,len(nums)):\n if nums[j:j+len(i)]==i:\n ind=j+len(i)\n lg-=1\n break\n return lg==0\n \n\n \n \n\n``` | 0 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Easy for Beginners | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n lg=len(groups)\n ind=0\n for i in groups:\n for j in range(ind,len(nums)):\n if nums[j:j+len(i)]==i:\n ind=j+len(i)\n lg-=1\n break\n return lg==0\n \n\n \n \n\n``` | 0 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
Simple backtracking | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\nI thought it could be linear time until I realized you have to backtrack and can\'t greedily consume the sub-arrays from groups every time. This makes it $$O(n^2)$$.\n\n# Approach\nIterate over nums and compare and consume items from groups. If a non-match is encountered, backtrack to the beginning of the group and increment by one.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n cur_group = 0\n cur_element_in_group = 0\n backtrack_to = 0\n nums_idx = 0\n while nums_idx < len(nums):\n if nums[nums_idx] == groups[cur_group][cur_element_in_group]:\n cur_element_in_group += 1\n if cur_element_in_group >= len(groups[cur_group]):\n cur_element_in_group = 0\n cur_group += 1\n if cur_group >= len(groups):\n return True\n backtrack_to = nums_idx + 1\n else:\n #print("{} != {}".format(nums[nums_idx], groups[cur_group][cur_element_in_group]))\n cur_element_in_group = 0\n nums_idx = backtrack_to\n backtrack_to = nums_idx + 1\n nums_idx += 1\n return False\n\n``` | 0 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Simple backtracking | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\nI thought it could be linear time until I realized you have to backtrack and can\'t greedily consume the sub-arrays from groups every time. This makes it $$O(n^2)$$.\n\n# Approach\nIterate over nums and compare and consume items from groups. If a non-match is encountered, backtrack to the beginning of the group and increment by one.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n cur_group = 0\n cur_element_in_group = 0\n backtrack_to = 0\n nums_idx = 0\n while nums_idx < len(nums):\n if nums[nums_idx] == groups[cur_group][cur_element_in_group]:\n cur_element_in_group += 1\n if cur_element_in_group >= len(groups[cur_group]):\n cur_element_in_group = 0\n cur_group += 1\n if cur_group >= len(groups):\n return True\n backtrack_to = nums_idx + 1\n else:\n #print("{} != {}".format(nums[nums_idx], groups[cur_group][cur_element_in_group]))\n cur_element_in_group = 0\n nums_idx = backtrack_to\n backtrack_to = nums_idx + 1\n nums_idx += 1\n return False\n\n``` | 0 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
Python 3 | Greedy, Multi-source BFS | Explanation | map-of-highest-peak | 0 | 1 | ### Explanation\n- Start from *water* nodes and BFS until all heights are found\n- NOTE: You don\'t need to worry about getting a skewed peak (by *skewed*, I mean a height with difference greater than 1 on some neighbors), because it will never be possible\n\t- For example: following situation will never be possible\n\t\t```\n\t\t1 2\n\t\t1 0\n\t\t```\n\t- This is because we are using BFS and increment at 1 for each step, in this case, for any node at `(i, j)`, whenever the value is assigned, it will be the highest possible value\n\t- If the same node is re-visited in later step, it can only be the same or larger (larger will be wrong, since you will get a skewed peak), thus, no need to revisited any assigned node `(i, j)`\n### Implementation\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n arr = collections.deque()\n m, n = len(isWater), len(isWater[0])\n for i in range(m):\n for j in range(n):\n if isWater[i][j] == 1:\n arr.append((0, i, j))\n \n ans = [[-1] * n for _ in range(m)]\n while arr:\n val, x, y = arr.popleft() \n if ans[x][y] != -1: continue\n ans[x][y] = val\n for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:\n xx, yy = x+dx, y+dy\n if 0 <= xx < m and 0 <= yy < n and ans[xx][yy] == -1:\n arr.append((val+1, xx, yy))\n return ans\n``` | 6 | You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
* If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
* If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
You must assign each cell a height in a way that follows these rules:
* The height of each cell must be non-negative.
* If the cell is a **water** cell, its height must be `0`.
* Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is **maximized**.
Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
**Example 1:**
**Input:** isWater = \[\[0,1\],\[0,0\]\]
**Output:** \[\[1,0\],\[2,1\]\]
**Explanation:** The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
**Example 2:**
**Input:** isWater = \[\[0,0,1\],\[1,0,0\],\[0,0,0\]\]
**Output:** \[\[1,1,0\],\[0,1,1\],\[1,2,2\]\]
**Explanation:** A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
**Constraints:**
* `m == isWater.length`
* `n == isWater[i].length`
* `1 <= m, n <= 1000`
* `isWater[i][j]` is `0` or `1`.
* There is at least **one** water cell. | Check which edges need to be changed. Let the next node of the (a-1)th node of list1 be the 0-th node in list 2. Let the next node of the last node of list2 be the (b+1)-th node in list 1. |
Python 3 | Greedy, Multi-source BFS | Explanation | map-of-highest-peak | 0 | 1 | ### Explanation\n- Start from *water* nodes and BFS until all heights are found\n- NOTE: You don\'t need to worry about getting a skewed peak (by *skewed*, I mean a height with difference greater than 1 on some neighbors), because it will never be possible\n\t- For example: following situation will never be possible\n\t\t```\n\t\t1 2\n\t\t1 0\n\t\t```\n\t- This is because we are using BFS and increment at 1 for each step, in this case, for any node at `(i, j)`, whenever the value is assigned, it will be the highest possible value\n\t- If the same node is re-visited in later step, it can only be the same or larger (larger will be wrong, since you will get a skewed peak), thus, no need to revisited any assigned node `(i, j)`\n### Implementation\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n arr = collections.deque()\n m, n = len(isWater), len(isWater[0])\n for i in range(m):\n for j in range(n):\n if isWater[i][j] == 1:\n arr.append((0, i, j))\n \n ans = [[-1] * n for _ in range(m)]\n while arr:\n val, x, y = arr.popleft() \n if ans[x][y] != -1: continue\n ans[x][y] = val\n for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:\n xx, yy = x+dx, y+dy\n if 0 <= xx < m and 0 <= yy < n and ans[xx][yy] == -1:\n arr.append((val+1, xx, yy))\n return ans\n``` | 6 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
[Python3] bfs | map-of-highest-peak | 0 | 1 | \n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n m, n = len(isWater), len(isWater[0]) # dimensions \n queue = [(i, j) for i in range(m) for j in range(n) if isWater[i][j]]\n \n ht = 0\n ans = [[0]*n for _ in range(m)]\n seen = set(queue)\n \n while queue: \n newq = []\n for i, j in queue: \n ans[i][j] = ht\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and (ii, jj) not in seen: \n newq.append((ii, jj))\n seen.add((ii, jj))\n queue = newq\n ht += 1\n return ans \n```\n\nAlternative implementation\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n m, n = len(isWater), len(isWater[0]) # dimensions \n \n ans = [[-1]*n for _ in range(m)]\n queue = deque()\n for i in range(m): \n for j in range(n):\n if isWater[i][j]:\n queue.append((i, j))\n ans[i][j] = 0\n\n while queue: \n i, j = queue.popleft()\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and ans[ii][jj] == -1: \n ans[ii][jj] = 1 + ans[i][j]\n queue.append((ii, jj))\n return ans \n``` | 7 | You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
* If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
* If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
You must assign each cell a height in a way that follows these rules:
* The height of each cell must be non-negative.
* If the cell is a **water** cell, its height must be `0`.
* Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is **maximized**.
Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
**Example 1:**
**Input:** isWater = \[\[0,1\],\[0,0\]\]
**Output:** \[\[1,0\],\[2,1\]\]
**Explanation:** The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
**Example 2:**
**Input:** isWater = \[\[0,0,1\],\[1,0,0\],\[0,0,0\]\]
**Output:** \[\[1,1,0\],\[0,1,1\],\[1,2,2\]\]
**Explanation:** A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
**Constraints:**
* `m == isWater.length`
* `n == isWater[i].length`
* `1 <= m, n <= 1000`
* `isWater[i][j]` is `0` or `1`.
* There is at least **one** water cell. | Check which edges need to be changed. Let the next node of the (a-1)th node of list1 be the 0-th node in list 2. Let the next node of the last node of list2 be the (b+1)-th node in list 1. |
[Python3] bfs | map-of-highest-peak | 0 | 1 | \n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n m, n = len(isWater), len(isWater[0]) # dimensions \n queue = [(i, j) for i in range(m) for j in range(n) if isWater[i][j]]\n \n ht = 0\n ans = [[0]*n for _ in range(m)]\n seen = set(queue)\n \n while queue: \n newq = []\n for i, j in queue: \n ans[i][j] = ht\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and (ii, jj) not in seen: \n newq.append((ii, jj))\n seen.add((ii, jj))\n queue = newq\n ht += 1\n return ans \n```\n\nAlternative implementation\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n m, n = len(isWater), len(isWater[0]) # dimensions \n \n ans = [[-1]*n for _ in range(m)]\n queue = deque()\n for i in range(m): \n for j in range(n):\n if isWater[i][j]:\n queue.append((i, j))\n ans[i][j] = 0\n\n while queue: \n i, j = queue.popleft()\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and ans[ii][jj] == -1: \n ans[ii][jj] = 1 + ans[i][j]\n queue.append((ii, jj))\n return ans \n``` | 7 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
📌📌 Greedy || BFS || Well-Explained 🐍 | map-of-highest-peak | 0 | 1 | ## IDEA:\n*Start from water nodes and BFS until all heights are found*\nNOTE: **You don\'t need to worry about height with difference greater than 1 on some neighbors because it will never be possible**\n* For example: following situation will never be possible\n1 1 0\n1 1 2\n2 0 1\n* This is because we are using BFS and increment at 1 for each step, in this case, for any node at (i, j), whenever the value is assigned, it will be the highest possible value\n* If the same node is re-visited in later step, it can only be the same or larger (larger will be wrong, since you will get a skewed peak), thus, no need to revisited any assigned node (i, j).\n\n\'\'\'\n\n\tclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n \n m,n = len(isWater),len(isWater[0])\n q = collections.deque()\n dp = [[float(\'inf\') for _ in range(n)] for _ in range(m)]\n for i in range(m):\n for j in range(n):\n if isWater[i][j]==1:\n dp[i][j] = 0\n q.append([i,j,0])\n \n while q:\n x,y,c = q.popleft()\n for i,j in [(-1,0),(1,0),(0,1),(0,-1)]:\n if 0<=x+i<m and 0<=y+j<n and dp[x+i][y+j]==float(\'inf\'):\n dp[x+i][y+j] = c+1\n q.append([x+i,y+j,c+1])\n \n return dp\n\n### Thanks & Upvote if you got the idea!!\uD83E\uDD1E | 4 | You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
* If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
* If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
You must assign each cell a height in a way that follows these rules:
* The height of each cell must be non-negative.
* If the cell is a **water** cell, its height must be `0`.
* Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is **maximized**.
Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
**Example 1:**
**Input:** isWater = \[\[0,1\],\[0,0\]\]
**Output:** \[\[1,0\],\[2,1\]\]
**Explanation:** The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
**Example 2:**
**Input:** isWater = \[\[0,0,1\],\[1,0,0\],\[0,0,0\]\]
**Output:** \[\[1,1,0\],\[0,1,1\],\[1,2,2\]\]
**Explanation:** A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
**Constraints:**
* `m == isWater.length`
* `n == isWater[i].length`
* `1 <= m, n <= 1000`
* `isWater[i][j]` is `0` or `1`.
* There is at least **one** water cell. | Check which edges need to be changed. Let the next node of the (a-1)th node of list1 be the 0-th node in list 2. Let the next node of the last node of list2 be the (b+1)-th node in list 1. |
📌📌 Greedy || BFS || Well-Explained 🐍 | map-of-highest-peak | 0 | 1 | ## IDEA:\n*Start from water nodes and BFS until all heights are found*\nNOTE: **You don\'t need to worry about height with difference greater than 1 on some neighbors because it will never be possible**\n* For example: following situation will never be possible\n1 1 0\n1 1 2\n2 0 1\n* This is because we are using BFS and increment at 1 for each step, in this case, for any node at (i, j), whenever the value is assigned, it will be the highest possible value\n* If the same node is re-visited in later step, it can only be the same or larger (larger will be wrong, since you will get a skewed peak), thus, no need to revisited any assigned node (i, j).\n\n\'\'\'\n\n\tclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n \n m,n = len(isWater),len(isWater[0])\n q = collections.deque()\n dp = [[float(\'inf\') for _ in range(n)] for _ in range(m)]\n for i in range(m):\n for j in range(n):\n if isWater[i][j]==1:\n dp[i][j] = 0\n q.append([i,j,0])\n \n while q:\n x,y,c = q.popleft()\n for i,j in [(-1,0),(1,0),(0,1),(0,-1)]:\n if 0<=x+i<m and 0<=y+j<n and dp[x+i][y+j]==float(\'inf\'):\n dp[x+i][y+j] = c+1\n q.append([x+i,y+j,c+1])\n \n return dp\n\n### Thanks & Upvote if you got the idea!!\uD83E\uDD1E | 4 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
Easy Python Solution | map-of-highest-peak | 0 | 1 | # Code\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n arr = [[-1 for _ in range(len(isWater[0]))] for _ in range(len(isWater))]\n\n coords = []\n\n for i in range(len(isWater)):\n for j in range(len(isWater[i])):\n if isWater[i][j] == 1:\n arr[i][j] = 0\n coords.append((i, j))\n\n directions = ((-1, 0), (0, -1), (1, 0), (0, 1))\n\n while coords:\n x, y = coords.pop(0)\n for dx, dy in directions:\n fx, fy = x + dx, y + dy\n if (0 <= fx < len(arr) and 0 <= fy < len(arr[0]) and arr[fx][fy] == -1):\n arr[fx][fy] = arr[x][y] + 1\n coords.append((fx, fy))\n\n return arr\n\n``` | 0 | You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
* If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
* If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
You must assign each cell a height in a way that follows these rules:
* The height of each cell must be non-negative.
* If the cell is a **water** cell, its height must be `0`.
* Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is **maximized**.
Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
**Example 1:**
**Input:** isWater = \[\[0,1\],\[0,0\]\]
**Output:** \[\[1,0\],\[2,1\]\]
**Explanation:** The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
**Example 2:**
**Input:** isWater = \[\[0,0,1\],\[1,0,0\],\[0,0,0\]\]
**Output:** \[\[1,1,0\],\[0,1,1\],\[1,2,2\]\]
**Explanation:** A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
**Constraints:**
* `m == isWater.length`
* `n == isWater[i].length`
* `1 <= m, n <= 1000`
* `isWater[i][j]` is `0` or `1`.
* There is at least **one** water cell. | Check which edges need to be changed. Let the next node of the (a-1)th node of list1 be the 0-th node in list 2. Let the next node of the last node of list2 be the (b+1)-th node in list 1. |
Easy Python Solution | map-of-highest-peak | 0 | 1 | # Code\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n arr = [[-1 for _ in range(len(isWater[0]))] for _ in range(len(isWater))]\n\n coords = []\n\n for i in range(len(isWater)):\n for j in range(len(isWater[i])):\n if isWater[i][j] == 1:\n arr[i][j] = 0\n coords.append((i, j))\n\n directions = ((-1, 0), (0, -1), (1, 0), (0, 1))\n\n while coords:\n x, y = coords.pop(0)\n for dx, dy in directions:\n fx, fy = x + dx, y + dy\n if (0 <= fx < len(arr) and 0 <= fy < len(arr[0]) and arr[fx][fy] == -1):\n arr[fx][fy] = arr[x][y] + 1\n coords.append((fx, fy))\n\n return arr\n\n``` | 0 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
python solution | map-of-highest-peak | 0 | 1 | \n# Code\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n q = deque()\n dir=[-1,0,1,0,-1]\n rowsize=len(isWater)\n colsize=len(isWater[0])\n visited=set()\n for i in range(rowsize):\n for j in range(colsize):\n if isWater[i][j]==1:\n q.append([i,j])\n visited.add(tuple([i,j]))\n isWater[i][j]=0\n idx=1\n while q:\n size=len(q)\n for i in range(size):\n [r,c]=q.popleft()\n for i in range(1,len(dir)):\n row,col=r+dir[i-1],c+dir[i]\n if row<0 or row>=rowsize or col<0 or col>=colsize:continue\n if (row,col) in visited:continue\n isWater[row][col]=idx\n visited.add(tuple([row,col]))\n q.append([row,col])\n idx+=1\n return isWater\n\n``` | 0 | You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
* If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
* If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
You must assign each cell a height in a way that follows these rules:
* The height of each cell must be non-negative.
* If the cell is a **water** cell, its height must be `0`.
* Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is **maximized**.
Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
**Example 1:**
**Input:** isWater = \[\[0,1\],\[0,0\]\]
**Output:** \[\[1,0\],\[2,1\]\]
**Explanation:** The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
**Example 2:**
**Input:** isWater = \[\[0,0,1\],\[1,0,0\],\[0,0,0\]\]
**Output:** \[\[1,1,0\],\[0,1,1\],\[1,2,2\]\]
**Explanation:** A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
**Constraints:**
* `m == isWater.length`
* `n == isWater[i].length`
* `1 <= m, n <= 1000`
* `isWater[i][j]` is `0` or `1`.
* There is at least **one** water cell. | Check which edges need to be changed. Let the next node of the (a-1)th node of list1 be the 0-th node in list 2. Let the next node of the last node of list2 be the (b+1)-th node in list 1. |
python solution | map-of-highest-peak | 0 | 1 | \n# Code\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n q = deque()\n dir=[-1,0,1,0,-1]\n rowsize=len(isWater)\n colsize=len(isWater[0])\n visited=set()\n for i in range(rowsize):\n for j in range(colsize):\n if isWater[i][j]==1:\n q.append([i,j])\n visited.add(tuple([i,j]))\n isWater[i][j]=0\n idx=1\n while q:\n size=len(q)\n for i in range(size):\n [r,c]=q.popleft()\n for i in range(1,len(dir)):\n row,col=r+dir[i-1],c+dir[i]\n if row<0 or row>=rowsize or col<0 or col>=colsize:continue\n if (row,col) in visited:continue\n isWater[row][col]=idx\n visited.add(tuple([row,col]))\n q.append([row,col])\n idx+=1\n return isWater\n\n``` | 0 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
Just clean code. | map-of-highest-peak | 0 | 1 | The code speaks for itself. The only trick is in initializing the matrix with -= 1 -> turns water into 0 and land into -1 -> we reuse negative number during bfs as "not visited flag".\n\n\n# Code\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n n, m = len(isWater[0]), len(isWater)\n\n def init():\n nonlocal n, m, isWater\n\n queue = deque()\n for x in range(n):\n for y in range(m):\n isWater[y][x] -= 1\n if isWater[y][x] == 0:\n queue.append((x, y))\n return queue\n \n def bfs(queue):\n nonlocal n, m, isWater\n\n while queue:\n x, y = queue.popleft()\n for a, b in (x+1, y), (x-1, y), (x, y+1), (x, y-1):\n if not(0 <= a < n and 0 <= b < m): continue\n if isWater[b][a] != -1: continue\n isWater[b][a] = isWater[y][x] + 1\n queue.append((a, b))\n\n queue = init()\n bfs(queue)\n return isWater\n\n``` | 0 | You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
* If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
* If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
You must assign each cell a height in a way that follows these rules:
* The height of each cell must be non-negative.
* If the cell is a **water** cell, its height must be `0`.
* Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is **maximized**.
Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
**Example 1:**
**Input:** isWater = \[\[0,1\],\[0,0\]\]
**Output:** \[\[1,0\],\[2,1\]\]
**Explanation:** The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
**Example 2:**
**Input:** isWater = \[\[0,0,1\],\[1,0,0\],\[0,0,0\]\]
**Output:** \[\[1,1,0\],\[0,1,1\],\[1,2,2\]\]
**Explanation:** A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
**Constraints:**
* `m == isWater.length`
* `n == isWater[i].length`
* `1 <= m, n <= 1000`
* `isWater[i][j]` is `0` or `1`.
* There is at least **one** water cell. | Check which edges need to be changed. Let the next node of the (a-1)th node of list1 be the 0-th node in list 2. Let the next node of the last node of list2 be the (b+1)-th node in list 1. |
Just clean code. | map-of-highest-peak | 0 | 1 | The code speaks for itself. The only trick is in initializing the matrix with -= 1 -> turns water into 0 and land into -1 -> we reuse negative number during bfs as "not visited flag".\n\n\n# Code\n```\nclass Solution:\n def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:\n n, m = len(isWater[0]), len(isWater)\n\n def init():\n nonlocal n, m, isWater\n\n queue = deque()\n for x in range(n):\n for y in range(m):\n isWater[y][x] -= 1\n if isWater[y][x] == 0:\n queue.append((x, y))\n return queue\n \n def bfs(queue):\n nonlocal n, m, isWater\n\n while queue:\n x, y = queue.popleft()\n for a, b in (x+1, y), (x-1, y), (x, y+1), (x, y-1):\n if not(0 <= a < n and 0 <= b < m): continue\n if isWater[b][a] != -1: continue\n isWater[b][a] = isWater[y][x] + 1\n queue.append((a, b))\n\n queue = init()\n bfs(queue)\n return isWater\n\n``` | 0 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
[Python3] dfs | tree-of-coprimes | 0 | 1 | **Algo**\nThis is a typical DFS problem. However, the amont of nodes can be huge `10^5` but the values only vary from `0` to `50`. Due to this reason, we can organize what have been seen in a value to location mapping to reduce the amount of nodes to check. \n\n**Implementation**\n```\nclass Solution:\n def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:\n tree = {} # tree as adjacency list \n for u, v in edges: \n tree.setdefault(u, []).append(v)\n tree.setdefault(v, []).append(u)\n \n ans = [-1]*len(nums)\n path = {} # val -> list of position & depth \n seen = {0}\n \n def fn(k, i): \n """Populate ans via dfs."""\n ii = -1 \n for x in path:\n if gcd(nums[k], x) == 1: # coprime \n if path[x] and path[x][-1][1] > ii: \n ans[k] = path[x][-1][0]\n ii = path[x][-1][1]\n \n path.setdefault(nums[k], []).append((k, i))\n for kk in tree.get(k, []): \n if kk not in seen: \n seen.add(kk)\n fn(kk, i+1)\n path[nums[k]].pop()\n \n \n fn(0, 0)\n return ans \n```\n\n**Analysis**\nTime complexity `O(N)` (`O(50N)` to be more specific)\nSpace complexity `O(N)` | 10 | There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`.
To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the `ith` node's value, and each `edges[j] = [uj, vj]` represents an edge between nodes `uj` and `vj` in the tree.
Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`.
An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself.
Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime**, or `-1` _if there is no such ancestor_.
**Example 1:**
**Input:** nums = \[2,3,3,2\], edges = \[\[0,1\],\[1,2\],\[1,3\]\]
**Output:** \[-1,0,0,1\]
**Explanation:** In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
closest valid ancestor.
**Example 2:**
**Input:** nums = \[5,6,10,2,3,6,15\], edges = \[\[0,1\],\[0,2\],\[1,3\],\[1,4\],\[2,5\],\[2,6\]\]
**Output:** \[-1,0,-1,0,0,0,-1\]
**Constraints:**
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[j].length == 2`
* `0 <= uj, vj < n`
* `uj != vj` | Think the opposite direction instead of minimum elements to remove the maximum mountain subsequence Think of LIS it's kind of close |
BFS of GCD adjacency list | Commented and Explained | 100% memory, upper 80-90 T | tree-of-coprimes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a rather hard problem if you are unfamiliar with BFS and GCD. In this intuition and then in approach, I\'ll lay out a standardized solving approach I used and explain the findings from it as we go. To start any problem, I like to layout the limits limits for the problem as stated in the description. We are told that \n- nums are between 1 and 50 \n- we have up to 10^5 values, so a frequency space or related is not a bad idea \n- We have no back edges (no node goes to itself) \n- nums[i] -> ith nodes value \n- edges[j] -> u_j, v_j and is undirected. A key here is found in the examples, where you can note that the value of 0 is used for u_j despite node values being between 1 and 50. This tells you that u_j and v_j are actually the node indices, thus referencing the nodes in question. \n- coprime is the state of acceptance, and is linked to gcd == 1 \n- ancestor of a node is any node other than considered on the shortest path to root \n- asked to return an array of size length of nums, where answer at i is the closest ancestor to node i such that the two are coprime, or -1 if no such ancestor exists \n- As we are asked to find ancestral paths, and asked to do so on the shortest route, BFS is an advisable directionality \n- As we only have values between 1 and 50, computing the gcd graph of the values in that range is not an expensive cost and could be done to start the process. This can be handled in initialization. \n\nIt should be noted from this that we have learned several things, namely that the problem space is well suited for a certain graphical search approach (BFS) and that a related graph (gcd pairings) may be of use and easily constructed. This helps to inform us on our approach which follows. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince we know the set size of the numbers in our gcd pairings, we can actually initialize this during initialization of a Solution object. This allows us to save on some compute time by having initialization handle these components. In this case, we know our solution object should store what it\'s current set size is, and we know we\'ll want to be able to build a gcd set of a certain size. In order to allow for reusability, we should provide an unused functionality to alter the set size, which we leave in a non-optimized form for others to do as part of their own improvements. \n\nTo set up the gcd graph, we need an array of size equal to our range of values, and it needs to store set wise the neighbor values in range. To build this, we doubly loop over the range of values, and if gcd of i and j in this double loop is 1, we add j to i and i to j respectively (see code for explanation of this, but try to set up from here on your own) \n\nTo solve our problem, we then do the following \n- set up nL as a length of nums (we use the variable more than once, so it is advisable to store it) \n- set up a graph as an array of arrays of size nL \n- for src, dst in edges \n - graph[src] -> dst \n - graph[dst] -> src \n- set answer as an array of -1 of size nL \n\nThe following now relates to BFS set up. There are great walkthroughs of BFS elsewhere, so I will omit most of the details. \n\n- Set up for BFS with a current frontier, a next frontier, a seen set, and a depth. Start from root at node id 0. \n- Conduct BFS where we are interested in each entries node id and ancestors dictionary \n - for each ancestor in the ancestors dictionary \n - if ancestor value and our nodes value in our gcd set \n - get ancestor index and depth index from ancestors dictionary\n - if d_i is an improvement over current index depth (gt) \n - update index and depth for this node to a_i, d_i \n - set answer at node to index depth at 0 \n - make a copy of ancestors and add to it this node and depth \n - for neighbor in graph at node \n - if neighbor not visited \n - mark it as visited and push to new frontier \n- At end of current frontier, set frontier to new frontier and set new frontier to empty list. Update depth \n\nWhen done, answer has stored the best valuations. return it. \n\n# Complexity\n- Time complexity : O(N + C) \n - gcd set size takes building of O(50 * 50 * gcd cost)\n - gcd cost time of gcd(a, b) is log a + log b\n - this is small enough to be considered a constant cost C \n - so at worst for set building we incur cost of 2500C \n - call this simply C \n - graph building takes O(E) \n - based on problem space, this is O(N) technically \n - BFS takes O(N) (to convince yourself of why, consider seen) \n - Total then is O(2N + C) \n - This is then N + C \n\n- Space complexity : O(N + c\')\n - Let c be the subset of the factor size of C \n - gcd set has size of c * c -> call this c\' \n - graph stores O(N) \n - BFS never has a frontier or next frontier that contains more than a subset of N \n - As such, treat as N \n - O(2N + c\') \n - This is then O(N + c\')\n\n# Code\n```\nclass Solution:\n # set up with the initial size related to the problem \n def __init__(self, set_size=50) : \n self.gcd_set_size = set_size\n self.build_gcd_set()\n\n # get the gcd set built in a functional manner \n def build_gcd_set(self) : \n # build enough sets in range of size + 1 to account for including the final set size limit \n self.gcd_set = [set() for _ in range(self.gcd_set_size+1)]\n # loop over set size space -> takes O(set size * set size) -> may be expensive for VERY large sets \n for i in range(1, self.gcd_set_size + 1) : \n for j in range(1, self.gcd_set_size+1) : \n # use gcd, may be expensive for very large numbers -> consider lookup memoize version? \n if math.gcd(i, j) == 1 : \n # if coprime, mark as needed \n self.gcd_set[i].add(j)\n self.gcd_set[j].add(i)\n \n # not used for problem but good to include functionality \n def alter_set_size(self, new_size) : \n self.gcd_set_size = new_size \n self.build_gcd_set()\n\n def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:\n # get length of nums \n nL = len(nums)\n # set up graph as a list of lists of length nL \n graph = [[] for _ in range(nL)]\n # for src, dst in edges \n for src, dst in edges : \n # graph at src gets dst, and graph at dst gets src \n graph[src].append(dst)\n graph[dst].append(src)\n\n # answer is set to -1 for length nL \n answer = [-1] * nL\n # frontier is set as list of node id and neighbor graphical dictionary \n frontier = [[0, {}]]\n # next frontier is set as needed \n next_frontier = [] \n # seen contains root to start \n seen = set([0])\n # start at depth 0 \n depth = 0 \n # conduct BFS \n while frontier : \n # empty the frontier \n for node, ancestors in frontier : \n # at each step of doing so, set an index_depth paired tuple \n # this stores the ancestor and the depth of the ancestor related\n index_depth = (-1, -1) \n # for each ancestor in list cast of ancestors keys \n for ancestor in list(ancestors.keys()) : \n # if ancestor in gcd set of nums at node \n if ancestor in self.gcd_set[nums[node]] : \n # get the ancestors index and depth from ancestors \n a_i, d_i = ancestors[ancestor]\n # if the ancestors depth is greater than our current \n if d_i > index_depth[1] : \n # then they are a more recent thus closer to root, set in for this \n index_depth = (a_i, d_i)\n # answer at node is the ancestor\'s indexing that is closest to root \n answer[node] = index_depth[0]\n # make a copy \n copy = ancestors.copy()\n # set into the copy at the value of nums at node the values of this node and this depth \n copy[nums[node]] = (node, depth)\n # this stores this for next loop of bfs progression \n for neighbor in graph[node] : \n # if neighbor of graph at node is not yet visited \n if neighbor not in seen : \n # visit it on the next loop and prevent adding it twice \n seen.add(neighbor)\n next_frontier.append([neighbor, copy])\n # at the end of emptying the current frontier, set up the next \n frontier = next_frontier\n # increase depth and reset next frontier appropriately \n depth += 1 \n next_frontier = [] \n \n # return when done \n return answer \n``` | 0 | There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`.
To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the `ith` node's value, and each `edges[j] = [uj, vj]` represents an edge between nodes `uj` and `vj` in the tree.
Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`.
An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself.
Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime**, or `-1` _if there is no such ancestor_.
**Example 1:**
**Input:** nums = \[2,3,3,2\], edges = \[\[0,1\],\[1,2\],\[1,3\]\]
**Output:** \[-1,0,0,1\]
**Explanation:** In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
closest valid ancestor.
**Example 2:**
**Input:** nums = \[5,6,10,2,3,6,15\], edges = \[\[0,1\],\[0,2\],\[1,3\],\[1,4\],\[2,5\],\[2,6\]\]
**Output:** \[-1,0,-1,0,0,0,-1\]
**Constraints:**
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[j].length == 2`
* `0 <= uj, vj < n`
* `uj != vj` | Think the opposite direction instead of minimum elements to remove the maximum mountain subsequence Think of LIS it's kind of close |
BFS + NumPy; RT 94% | M 94% | tree-of-coprimes | 0 | 1 | \n# Complexity\n- Time complexity: $O(kn)$, where $k=50$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(k+n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```PYTHON\nimport numpy as np\n\nPRIMES = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]\n\nclass Solution:\n def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:\n # find prime factors of each unique number in `nums`\n nums_set = set(nums)\n fact = {\n n: set([p for p in PRIMES if n % p == 0]) \n for n in iter(nums_set)\n }\n\n # coprime[m, n] = True if `gcd(m, n) = 1`, otherwise False.\n coprime = np.zeros((51, 51), dtype=bool)\n for m in iter(nums_set):\n for n in iter(nums_set):\n coprime[m, n] = coprime[n, m] = \\\n bool(fact[m].intersection(fact[n]) == set())\n\n # store edges in a more convenient adjacency list format\n adj_list = {u: [] for u in range(len(nums))}\n for u, v in edges:\n adj_list[u] += [v]\n adj_list[v] += [u]\n\n # nearest[u][m] = nearest node `v` to `u` along the path \n # from `0` s.t. \n # `gcd(m, nums[v]) = 1` for all m = 1,...,50\n nearest = {0: np.full(51, -1, dtype=int)}\n\n # ans[u] = nearest node `v` to `u` along the path from `0` s.t. \n # `gcd(nums[u], nums[v]) = 1`\n ans = np.full(len(nums), -1, dtype=int)\n\n q = deque([0])\n while len(q) > 0:\n u = q.popleft()\n nearest_new = nearest[u].copy()\n\n # mask that indicates which numbers are coprime to `nums[u]`\n coprime_mask = coprime[nums[u]]\n\n # vectorized update\n nearest_new[coprime_mask] = u\n\n # iterate through children of `u`\n for v in adj_list[u]:\n if v not in adj_list:\n continue\n nearest[v] = nearest_new\n ans[v] = nearest_new[nums[v]]\n q += [v]\n \n # mark visited\n adj_list.pop(u) \n\n # `nearest[u]` is no longer needed; release from memory\n nearest.pop(u)\n\n return ans.tolist()\n \n\n``` | 0 | There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`.
To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the `ith` node's value, and each `edges[j] = [uj, vj]` represents an edge between nodes `uj` and `vj` in the tree.
Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`.
An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself.
Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime**, or `-1` _if there is no such ancestor_.
**Example 1:**
**Input:** nums = \[2,3,3,2\], edges = \[\[0,1\],\[1,2\],\[1,3\]\]
**Output:** \[-1,0,0,1\]
**Explanation:** In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
closest valid ancestor.
**Example 2:**
**Input:** nums = \[5,6,10,2,3,6,15\], edges = \[\[0,1\],\[0,2\],\[1,3\],\[1,4\],\[2,5\],\[2,6\]\]
**Output:** \[-1,0,-1,0,0,0,-1\]
**Constraints:**
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[j].length == 2`
* `0 <= uj, vj < n`
* `uj != vj` | Think the opposite direction instead of minimum elements to remove the maximum mountain subsequence Think of LIS it's kind of close |
Simple DFS | tree-of-coprimes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getCoprimes(self, nums, edges):\n @lru_cache(None)\n def func_(node,node_value):\n if node == -1:\n return -1\n\n parent = parent_graph[node]\n\n if math.gcd(node_value,nums[parent]) == 1:\n return parent\n\n return func_(parent,node_value)\n\n dict1 = defaultdict(set)\n\n for i,j in edges:\n dict1[i].add(j)\n dict1[j].add(i)\n\n parent_graph = defaultdict(int)\n\n stack = [(0,-1)]\n\n while stack:\n next_level = []\n\n for node, parent in stack:\n parent_graph[node] = parent\n for neighbor in dict1[node]:\n if neighbor != parent:\n next_level.append((neighbor,node))\n \n stack = next_level\n\n return [func_(i,nums[i]) for i in range(len(nums))]\n\n\n\n\n\n\n``` | 0 | There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`.
To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the `ith` node's value, and each `edges[j] = [uj, vj]` represents an edge between nodes `uj` and `vj` in the tree.
Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`.
An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself.
Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime**, or `-1` _if there is no such ancestor_.
**Example 1:**
**Input:** nums = \[2,3,3,2\], edges = \[\[0,1\],\[1,2\],\[1,3\]\]
**Output:** \[-1,0,0,1\]
**Explanation:** In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
closest valid ancestor.
**Example 2:**
**Input:** nums = \[5,6,10,2,3,6,15\], edges = \[\[0,1\],\[0,2\],\[1,3\],\[1,4\],\[2,5\],\[2,6\]\]
**Output:** \[-1,0,-1,0,0,0,-1\]
**Constraints:**
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[j].length == 2`
* `0 <= uj, vj < n`
* `uj != vj` | Think the opposite direction instead of minimum elements to remove the maximum mountain subsequence Think of LIS it's kind of close |
Least Runtime-Beats 100% Users! Easy to understand code, with step by step explanation. | merge-strings-alternately | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> The goal is to merge two strings, word1 and word2, in an alternating fashion, starting with word1. If one of the strings is longer than the other, append the remaining characters to the end of the merged string. The key intuition is to iterate through both strings simultaneously and concatenate characters in an alternating order.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Determine Minimum Length:** Find the minimum length of the two input strings, minLength = min(len(word1), len(word2)). This is important for ensuring that the loop doesn\'t go out of bounds.\n2. **Alternate Merge:** Use a loop to iterate from 0 to minLength - 1 and concatenate characters from both strings alternately. Append the results to a list.\n3. **Append Remaining Characters:** Append any remaining characters from both strings (if one is longer than the other) to the end of the result list.\n4. **Join Result:** Use \'\'.join(result) to convert the list of characters into a single string.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```JAVA []\nclass Solution {\n public String mergeAlternately(String word1, String word2) {\n\n StringBuilder result = new StringBuilder(word1.length() + word2.length());\n\n int minLength = Math.min(word1.length(), word2.length());\n\n for (int i = 0; i < minLength; i++) {\n result.append(word1.charAt(i)).append(word2.charAt(i));\n }\n\n result.append(word1.substring(minLength)).append(word2.substring(minLength));\n\n return result.toString();\n }\n}\n```\n```C++ []\nusing namespace std;\nclass Solution {\npublic:\n string mergeAlternately(string word1, string word2) {\n string result;\n result.reserve(word1.length() + word2.length());\n\n int minLength = min(word1.length(), word2.length());\n\n for (int i = 0; i < minLength; i++) {\n result.push_back(word1[i]);\n result.push_back(word2[i]);\n }\n\n result.append(word1.substr(minLength)).append(word2.substr(minLength));\n\n return result;\n }\n};\n```\n```Python3 []\n\nclass Solution:\n def mergeAlternately(self, word1: str, word2: str) -> str:\n result = []\n minLength = min(len(word1), len(word2))\n\n for i in range(minLength):\n result.append(word1[i])\n result.append(word2[i])\n\n result.extend([word1[minLength:], word2[minLength:]])\n\n return \'\'.join(result)\n```\n | 5 | You are given two strings `word1` and `word2`. Merge the strings by adding letters in alternating order, starting with `word1`. If a string is longer than the other, append the additional letters onto the end of the merged string.
Return _the merged string._
**Example 1:**
**Input:** word1 = "abc ", word2 = "pqr "
**Output:** "apbqcr "
**Explanation:** The merged string will be merged as so:
word1: a b c
word2: p q r
merged: a p b q c r
**Example 2:**
**Input:** word1 = "ab ", word2 = "pqrs "
**Output:** "apbqrs "
**Explanation:** Notice that as word2 is longer, "rs " is appended to the end.
word1: a b
word2: p q r s
merged: a p b q r s
**Example 3:**
**Input:** word1 = "abcd ", word2 = "pq "
**Output:** "apbqcd "
**Explanation:** Notice that as word1 is longer, "cd " is appended to the end.
word1: a b c d
word2: p q
merged: a p b q c d
**Constraints:**
* `1 <= word1.length, word2.length <= 100`
* `word1` and `word2` consist of lowercase English letters. | Apply the concept of Polymorphism to get a good design Implement the Node class using NumericNode and OperatorNode classes. NumericNode only maintains the value and evaluate returns this value. OperatorNode Maintains the left and right nodes representing the left and right operands, and the evaluate function applies the operator to them. |
Least Runtime-Beats 100% Users! Easy to understand code, with step by step explanation. | merge-strings-alternately | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> The goal is to merge two strings, word1 and word2, in an alternating fashion, starting with word1. If one of the strings is longer than the other, append the remaining characters to the end of the merged string. The key intuition is to iterate through both strings simultaneously and concatenate characters in an alternating order.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Determine Minimum Length:** Find the minimum length of the two input strings, minLength = min(len(word1), len(word2)). This is important for ensuring that the loop doesn\'t go out of bounds.\n2. **Alternate Merge:** Use a loop to iterate from 0 to minLength - 1 and concatenate characters from both strings alternately. Append the results to a list.\n3. **Append Remaining Characters:** Append any remaining characters from both strings (if one is longer than the other) to the end of the result list.\n4. **Join Result:** Use \'\'.join(result) to convert the list of characters into a single string.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```JAVA []\nclass Solution {\n public String mergeAlternately(String word1, String word2) {\n\n StringBuilder result = new StringBuilder(word1.length() + word2.length());\n\n int minLength = Math.min(word1.length(), word2.length());\n\n for (int i = 0; i < minLength; i++) {\n result.append(word1.charAt(i)).append(word2.charAt(i));\n }\n\n result.append(word1.substring(minLength)).append(word2.substring(minLength));\n\n return result.toString();\n }\n}\n```\n```C++ []\nusing namespace std;\nclass Solution {\npublic:\n string mergeAlternately(string word1, string word2) {\n string result;\n result.reserve(word1.length() + word2.length());\n\n int minLength = min(word1.length(), word2.length());\n\n for (int i = 0; i < minLength; i++) {\n result.push_back(word1[i]);\n result.push_back(word2[i]);\n }\n\n result.append(word1.substr(minLength)).append(word2.substr(minLength));\n\n return result;\n }\n};\n```\n```Python3 []\n\nclass Solution:\n def mergeAlternately(self, word1: str, word2: str) -> str:\n result = []\n minLength = min(len(word1), len(word2))\n\n for i in range(minLength):\n result.append(word1[i])\n result.append(word2[i])\n\n result.extend([word1[minLength:], word2[minLength:]])\n\n return \'\'.join(result)\n```\n | 5 | There are `n` students in a class numbered from `0` to `n - 1`. The teacher will give each student a problem starting with the student number `0`, then the student number `1`, and so on until the teacher reaches the student number `n - 1`. After that, the teacher will restart the process, starting with the student number `0` again.
You are given a **0-indexed** integer array `chalk` and an integer `k`. There are initially `k` pieces of chalk. When the student number `i` is given a problem to solve, they will use `chalk[i]` pieces of chalk to solve that problem. However, if the current number of chalk pieces is **strictly less** than `chalk[i]`, then the student number `i` will be asked to **replace** the chalk.
Return _the **index** of the student that will **replace** the chalk pieces_.
**Example 1:**
**Input:** chalk = \[5,1,5\], k = 22
**Output:** 0
**Explanation:** The students go in turns as follows:
- Student number 0 uses 5 chalk, so k = 17.
- Student number 1 uses 1 chalk, so k = 16.
- Student number 2 uses 5 chalk, so k = 11.
- Student number 0 uses 5 chalk, so k = 6.
- Student number 1 uses 1 chalk, so k = 5.
- Student number 2 uses 5 chalk, so k = 0.
Student number 0 does not have enough chalk, so they will have to replace it.
**Example 2:**
**Input:** chalk = \[3,4,1,2\], k = 25
**Output:** 1
**Explanation:** The students go in turns as follows:
- Student number 0 uses 3 chalk so k = 22.
- Student number 1 uses 4 chalk so k = 18.
- Student number 2 uses 1 chalk so k = 17.
- Student number 3 uses 2 chalk so k = 15.
- Student number 0 uses 3 chalk so k = 12.
- Student number 1 uses 4 chalk so k = 8.
- Student number 2 uses 1 chalk so k = 7.
- Student number 3 uses 2 chalk so k = 5.
- Student number 0 uses 3 chalk so k = 2.
Student number 1 does not have enough chalk, so they will have to replace it.
**Constraints:**
* `chalk.length == n`
* `1 <= n <= 105`
* `1 <= chalk[i] <= 105`
* `1 <= k <= 109` | Use two pointers, one pointer for each string. Alternately choose the character from each pointer, and move the pointer upwards. |
Easy Python beats 100% time and space | minimum-number-of-operations-to-move-all-balls-to-each-box | 0 | 1 | Similar to **238. Product of Array Except Self** and **42. Trapping Rain Water**.\nFor each index, the cost to move all boxes to it is sum of the cost ```leftCost``` to move all left boxes to it, and the cost ```rightCost``` to move all right boxes to it.\n- ```leftCost``` for all indexes can be calculted using a single pass from left to right.\n- ```rightCost``` for all indexes can be calculted using a single pass from right to left.\n```\nExample:\nboxes 11010\nleftCount 01223\nleftCost 01358\nrightCount 21100\nrightCost 42100\nans 43458\n```\n\n```\nclass Solution:\n def minOperations(self, boxes: str) -> List[int]:\n ans = [0]*len(boxes)\n leftCount, leftCost, rightCount, rightCost, n = 0, 0, 0, 0, len(boxes)\n for i in range(1, n):\n if boxes[i-1] == \'1\': leftCount += 1\n leftCost += leftCount # each step move to right, the cost increases by # of 1s on the left\n ans[i] = leftCost\n for i in range(n-2, -1, -1):\n if boxes[i+1] == \'1\': rightCount += 1\n rightCost += rightCount\n ans[i] += rightCost\n return ans\n```\n\n | 157 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Easy Python beats 100% time and space | minimum-number-of-operations-to-move-all-balls-to-each-box | 0 | 1 | Similar to **238. Product of Array Except Self** and **42. Trapping Rain Water**.\nFor each index, the cost to move all boxes to it is sum of the cost ```leftCost``` to move all left boxes to it, and the cost ```rightCost``` to move all right boxes to it.\n- ```leftCost``` for all indexes can be calculted using a single pass from left to right.\n- ```rightCost``` for all indexes can be calculted using a single pass from right to left.\n```\nExample:\nboxes 11010\nleftCount 01223\nleftCost 01358\nrightCount 21100\nrightCost 42100\nans 43458\n```\n\n```\nclass Solution:\n def minOperations(self, boxes: str) -> List[int]:\n ans = [0]*len(boxes)\n leftCount, leftCost, rightCount, rightCost, n = 0, 0, 0, 0, len(boxes)\n for i in range(1, n):\n if boxes[i-1] == \'1\': leftCount += 1\n leftCost += leftCount # each step move to right, the cost increases by # of 1s on the left\n ans[i] = leftCost\n for i in range(n-2, -1, -1):\n if boxes[i+1] == \'1\': rightCount += 1\n rightCost += rightCount\n ans[i] += rightCost\n return ans\n```\n\n | 157 | A `k x k` **magic square** is a `k x k` grid filled with integers such that every row sum, every column sum, and both diagonal sums are **all equal**. The integers in the magic square **do not have to be distinct**. Every `1 x 1` grid is trivially a **magic square**.
Given an `m x n` integer `grid`, return _the **size** (i.e., the side length_ `k`_) of the **largest magic square** that can be found within this grid_.
**Example 1:**
**Input:** grid = \[\[7,1,4,5,6\],\[2,5,1,6,4\],\[1,5,4,3,2\],\[1,2,7,3,4\]\]
**Output:** 3
**Explanation:** The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12
**Example 2:**
**Input:** grid = \[\[5,1,3,1\],\[9,3,3,1\],\[1,3,3,8\]\]
**Output:** 2
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 106` | If you want to move a ball from box i to box j, you'll need abs(i-j) moves. To move all balls to some box, you can move them one by one. For each box i, iterate on each ball in a box j, and add abs(i-j) to answers[i]. |
Simple Python3 Solution | minimum-number-of-operations-to-move-all-balls-to-each-box | 0 | 1 | ```\nclass Solution:\n def minOperations(self, boxes: str) -> List[int]:\n arr = []\n \n for i, balls in enumerate(boxes):\n if balls == \'1\':\n arr.append(i)\n \n res = []\n for i in range(len(boxes)):\n tmp = 0\n for index in arr:\n tmp += abs(i - index)\n res.append(tmp)\n \n return res\n``` | 2 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
Simple Python3 Solution | minimum-number-of-operations-to-move-all-balls-to-each-box | 0 | 1 | ```\nclass Solution:\n def minOperations(self, boxes: str) -> List[int]:\n arr = []\n \n for i, balls in enumerate(boxes):\n if balls == \'1\':\n arr.append(i)\n \n res = []\n for i in range(len(boxes)):\n tmp = 0\n for index in arr:\n tmp += abs(i - index)\n res.append(tmp)\n \n return res\n``` | 2 | A `k x k` **magic square** is a `k x k` grid filled with integers such that every row sum, every column sum, and both diagonal sums are **all equal**. The integers in the magic square **do not have to be distinct**. Every `1 x 1` grid is trivially a **magic square**.
Given an `m x n` integer `grid`, return _the **size** (i.e., the side length_ `k`_) of the **largest magic square** that can be found within this grid_.
**Example 1:**
**Input:** grid = \[\[7,1,4,5,6\],\[2,5,1,6,4\],\[1,5,4,3,2\],\[1,2,7,3,4\]\]
**Output:** 3
**Explanation:** The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12
**Example 2:**
**Input:** grid = \[\[5,1,3,1\],\[9,3,3,1\],\[1,3,3,8\]\]
**Output:** 2
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 106` | If you want to move a ball from box i to box j, you'll need abs(i-j) moves. To move all balls to some box, you can move them one by one. For each box i, iterate on each ball in a box j, and add abs(i-j) to answers[i]. |
📌📌 96% faster || Greedy Approach || Well-Explained || For-Beginners 🐍 | minimum-number-of-operations-to-move-all-balls-to-each-box | 0 | 1 | ## IDEA :\nHere, we can create prefix and postfix array of size n\\*2 to store the number of ones before (or after) the index and also information of the number of costs required to collect all the ones at previous index.\n**For Example :** \n\'\'\'\n\n\tstring given = " 0 0 1 0 1 1 "\n\tpostfix array = [[3,11], [3,8], [2,5], [2,3], [1,1], [0,0]] # (starting the array from right for computation).\n\tprefix array = [[0,0], [0,0], [0,0], [1,1], [1,2], [2,4]] # (starting the array from left for computation).\n\t\n\tTake prefix array for explaination:\n\t[0,0] -> 0 number of \'1\' is present left to that position and 0 number of cost required to collect all 1\'s left to it.\n\t[0,0] -> 0 number of \'1\' is present left to that position and 0 number of cost required to collect all 1\'s left to it.\n\t[0,0] -> 0 number of \'1\' is present left to that position and 0 number of cost required to collect all 1\'s left to it.\n\t[1,1] -> 1 number of \'1\' is present left to that position and 1 number of cost required to collect all 1\'s left to it.\n\t[1,2] -> 1 number of \'1\' is present left to that position and 2 number of cost required to collect all 1\'s left to it.\n\t[2,4] -> 2 number of \'1\' is present left to that position and 4 number of cost required to collect all 1\'s left to it.\n\t\n\tFormula used to calculate:\n\tpre[i][0] = boxes[i-1] + pre[i-1][0]\n pre[i][1] = boxes[i-1] + pre[i-1][0] + pre[i-1][1]\n\n### CODE :\n\'\'\'\n\n\tclass Solution:\n def minOperations(self, boxes: str) -> List[int]:\n \n n = len(boxes)\n boxes = [int(i) for i in boxes]\n pre = [[0,0] for i in range(n)]\n post= [[0,0] for i in range(n)]\n \n for i in range(1,n):\n pre[i][0] = boxes[i-1] + pre[i-1][0]\n pre[i][1] = boxes[i-1] + pre[i-1][0] + pre[i-1][1]\n \n for i in range(n-2,-1,-1):\n post[i][0] = boxes[i+1] + post[i+1][0]\n post[i][1] = boxes[i+1] + post[i+1][0] + post[i+1][1]\n \n for i in range(n):\n boxes[i] = pre[i][1]+post[i][1]\n \n return boxes\n\n### Thanks & upvote if you like the idea!!\uD83E\uDD1E | 7 | You have `n` boxes. You are given a binary string `boxes` of length `n`, where `boxes[i]` is `'0'` if the `ith` box is **empty**, and `'1'` if it contains **one** ball.
In one operation, you can move **one** ball from a box to an adjacent box. Box `i` is adjacent to box `j` if `abs(i - j) == 1`. Note that after doing so, there may be more than one ball in some boxes.
Return an array `answer` of size `n`, where `answer[i]` is the **minimum** number of operations needed to move all the balls to the `ith` box.
Each `answer[i]` is calculated considering the **initial** state of the boxes.
**Example 1:**
**Input:** boxes = "110 "
**Output:** \[1,1,3\]
**Explanation:** The answer for each box is as follows:
1) First box: you will have to move one ball from the second box to the first box in one operation.
2) Second box: you will have to move one ball from the first box to the second box in one operation.
3) Third box: you will have to move one ball from the first box to the third box in two operations, and move one ball from the second box to the third box in one operation.
**Example 2:**
**Input:** boxes = "001011 "
**Output:** \[11,8,5,4,3,4\]
**Constraints:**
* `n == boxes.length`
* `1 <= n <= 2000`
* `boxes[i]` is either `'0'` or `'1'`. | Try generating the array. Make sure not to fall in the base case of 0. |
📌📌 96% faster || Greedy Approach || Well-Explained || For-Beginners 🐍 | minimum-number-of-operations-to-move-all-balls-to-each-box | 0 | 1 | ## IDEA :\nHere, we can create prefix and postfix array of size n\\*2 to store the number of ones before (or after) the index and also information of the number of costs required to collect all the ones at previous index.\n**For Example :** \n\'\'\'\n\n\tstring given = " 0 0 1 0 1 1 "\n\tpostfix array = [[3,11], [3,8], [2,5], [2,3], [1,1], [0,0]] # (starting the array from right for computation).\n\tprefix array = [[0,0], [0,0], [0,0], [1,1], [1,2], [2,4]] # (starting the array from left for computation).\n\t\n\tTake prefix array for explaination:\n\t[0,0] -> 0 number of \'1\' is present left to that position and 0 number of cost required to collect all 1\'s left to it.\n\t[0,0] -> 0 number of \'1\' is present left to that position and 0 number of cost required to collect all 1\'s left to it.\n\t[0,0] -> 0 number of \'1\' is present left to that position and 0 number of cost required to collect all 1\'s left to it.\n\t[1,1] -> 1 number of \'1\' is present left to that position and 1 number of cost required to collect all 1\'s left to it.\n\t[1,2] -> 1 number of \'1\' is present left to that position and 2 number of cost required to collect all 1\'s left to it.\n\t[2,4] -> 2 number of \'1\' is present left to that position and 4 number of cost required to collect all 1\'s left to it.\n\t\n\tFormula used to calculate:\n\tpre[i][0] = boxes[i-1] + pre[i-1][0]\n pre[i][1] = boxes[i-1] + pre[i-1][0] + pre[i-1][1]\n\n### CODE :\n\'\'\'\n\n\tclass Solution:\n def minOperations(self, boxes: str) -> List[int]:\n \n n = len(boxes)\n boxes = [int(i) for i in boxes]\n pre = [[0,0] for i in range(n)]\n post= [[0,0] for i in range(n)]\n \n for i in range(1,n):\n pre[i][0] = boxes[i-1] + pre[i-1][0]\n pre[i][1] = boxes[i-1] + pre[i-1][0] + pre[i-1][1]\n \n for i in range(n-2,-1,-1):\n post[i][0] = boxes[i+1] + post[i+1][0]\n post[i][1] = boxes[i+1] + post[i+1][0] + post[i+1][1]\n \n for i in range(n):\n boxes[i] = pre[i][1]+post[i][1]\n \n return boxes\n\n### Thanks & upvote if you like the idea!!\uD83E\uDD1E | 7 | A `k x k` **magic square** is a `k x k` grid filled with integers such that every row sum, every column sum, and both diagonal sums are **all equal**. The integers in the magic square **do not have to be distinct**. Every `1 x 1` grid is trivially a **magic square**.
Given an `m x n` integer `grid`, return _the **size** (i.e., the side length_ `k`_) of the **largest magic square** that can be found within this grid_.
**Example 1:**
**Input:** grid = \[\[7,1,4,5,6\],\[2,5,1,6,4\],\[1,5,4,3,2\],\[1,2,7,3,4\]\]
**Output:** 3
**Explanation:** The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12
**Example 2:**
**Input:** grid = \[\[5,1,3,1\],\[9,3,3,1\],\[1,3,3,8\]\]
**Output:** 2
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 106` | If you want to move a ball from box i to box j, you'll need abs(i-j) moves. To move all balls to some box, you can move them one by one. For each box i, iterate on each ball in a box j, and add abs(i-j) to answers[i]. |
𝗪𝗵𝘆 Greedy Failed? From Level Zero | Beginner-Friendly | Fully Explained | Python | C | maximum-score-from-performing-multiplication-operations | 0 | 1 | # \uD83D\uDE0B Greedy!\n\n**Let\'s go Greedy!**\n\nWe have to pick integer `x` from **either end** of array `nums`. And, multiply that with `multipliers[i]`. Thus, let\'s pick larger `x` from either end. \n\n**`5` vs `3`, we will pick 5. Is it correct?** \nNo! On checking constraints `-1000 \u2264 nums[i], multipliers[i] \u2264 1000`, both arrays can have negative integers. Thus, if `multipliers[i]` is `-10`, we would prefer adding `-30` instead of `-50`. Thus, we should choose, `x` which when multiplied with `multipliers[i]` gives the larger product.\n\n<details><summary><b>\uD83E\uDD73 Let\'s Dry Run! (Click on Left Triangle to see)</b></summary> \n<pre>\n<b>Input :</b> nums = [1,2,3], multipliers = [3,2,1]\n<b>Taking Decision :</b>\n- From multipliers <b>3</b>, nums is [1, 2, 3], from <b>3</b>x1 vs <b>3</b>x3, choose 3, add <u>9</u>.\n- From multipliers <b>2</b>, nums is [1, 2], from <b>2</b>x1 and <b>2</b>x2, choose 2, add <u>4</u>.\n- From multipliers <b>1</b>, nums is [1], add <u>1</u>.\n\n<br/>\n\nTotal Score is <u>9+4+1</u>=<b>14</b>, which is Correct \u2714\uFE0F</pre></details>\n\n<details><summary><b>\uD83D\uDE0E Another Example! (MUST CLICK on Left Triangle to See)</b></summary><pre>\n<b>Input :</b> nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]\n<b>Taking Decision :</b> \n- From multipliers <b>10</b>, nums [-5,-3,-3,-2,7,1], from (<b>-10</b>) (-5) and (<b>-10</b>)(1), choose -5, add <u>50</u>\n- From multipliers <b>-5</b>, nums [-3,-3,-2,7,1], from (<b>-5</b>) (-3) and (<b>-5</b>)(1), choose -3, add <u>15</u>\n- From multipliers <b>3</b>, nums [-3,-2,7,1], from (<b>3</b>) (-3) and (<b>3</b>)(1), choose 1, add <u>3</u>\n- From multipliers <b>4</b>, nums [-3,-2,7], from (<b>4</b>) (-3) and (<b>4</b>)(7), choose 7, add <u>28</u>\n- From multipliers <b>6</b>, nums [-3,-2], from (<b>6</b>) (-3) and (<b>6</b>)(-2), choose -2, add <u>-12</u>\n\n<br/>\n\nTotal Score is <u>50+15+3+28+(-12)</u>=<b>84</b>, which...... \nisn\'t Correct \uD83D\uDE15. 102 is another <u>Optimal Solution</u> \nas given in Problem Example.</pre> </details>\n\nWell, this version of greedy failed! \n\n\n> **How to Prove it?**\n> [\u26A0: Spoiler Alert! Go to these links after reading the complete answer]\n> This was asked on [Computer Science Stack Exchange](https://cs.stackexchange.com/q/151534/143377), and the [answer](https://cs.stackexchange.com/a/151551/143377) and [comments](https://cs.stackexchange.com/questions/151534/formal-proof-on-why-greedy-isnt-working-on-one-particular-problem#comment318613_151534) there suggests that \n>> - "To show that the greedy approach fails, all you have to do is come up with a counterexample. " \n>> - "To prove that the greedy algorithm is not optimal, it suffices to give one counterexample"\n\n> We have given one example, where our version of greedy isn\'t giving <u>Optimal Solution</u>.\n\n*(Another problem where we encounter similar situation is [120. Triangle](https://leetcode.com/problems/triangle/). After reading this answer, you can check the problem and one of the [counter example](https://leetcode.com/problems/triangle/discuss/2146127/why-greedy-fails-intuition-counter-example-dynamic-programming) for the same)* \n\n> **Still, what\'s the logical intuition behind the failure of greedy?**\n> Greedy is `short-sighted`. In hope of global optimum, we take local optimum. But taking this Local Optimum perhaps <ins>may Restrict Potential Larger Positive Product in Future!</ins> \n> \n> Check this example,\n> <pre> <b>Input :</b> nums = [2,1,1,1,1000,1,1,1,1,42], multipliers = [1,1,1,1,1] </pre>\n> If very myopically, we choose 42 over 2, we would never be able to reach our treasure 1000. Since there are only 5 elements in multipliers, the only way to reach 1000 is by taking the Left route only. But one myopic step, and we lost optimal!\n> \n> Another [Example](https://cs.stackexchange.com/a/151551/143377) \n> <pre> <b>Input :</b> nums = [5,4], multipliers = [1,2] </pre>\n> Greedy would choose to multiply the 1 by a 5 rather than 4, giving an output of 1\u22C55+2\u22C54=13. But the second multiplier 2 is larger than the first multiplier and so should have been multiplied with the larger number 5 to get the maximum output (which is 1\u22C54+2\u22C55=14).\n\n\n---\n\n\n**What to do now?**\nLook for every possible combination! Try all scenarios \uD83D\uDE29 \n> - Choose one element from either side from `given nums` and then delete the chosen element (multiply and add to the score) to create `remaining nums` \n> - Choose another element from either side from `remaining nums` and then delete the chosen element (multiply and add to the score) to create `another remaining nums` \n> - Choose again ..... \n\n\u2666 Looking for every possible combination, is, in general not very Efficient. \n\u2666 But, this problem has certain properties.\n\n1. **Optimal Substructure:** To get the maximum score for entire `multipliers`, we should ensure we have the maximum score for every subarray from the first index! For `multipliers[0:1]`, for `multipliers[0:2]`, and so on.... <br>\n\n2. **Overlapping Subproblem:** We may need to compute for a particular (`nums`, `multipliers`) pair multiple times. By computing, we mean solving further from this state. **Rough Example:** `nums = [a,b,c,d,e]` and `multipliers = [u,v,w,x,y,z]`\n - **Pattern-1: Two-Left, One Right**\n - From `multipliers`, we have `u`, from nums `a vs e`, choose `a`\n - From `multipliers`, we have `v`, from nums `b vs e`, choose `b` \n - From `multipliers`, we have `w`, from nums `c vs e`, choose `e`\n - From `multipliers`, we have <u>`x`</u>, from nums `c vs d`, choose <u>`c`</u>\n - **Pattern-2: One-Right, Three Left**\n - From `multipliers`, we have `u`, from nums `a vs e`, choose `e`\n - From `multipliers`, we have `v`, from nums `a vs d`, choose `a` \n - From `multipliers`, we have `w`, from nums `b vs d`, choose `b`\n - From `multipliers`, we have <u>`x`</u>, from nums `c vs d`, choose <u>`c`</u> \n<br>Thus, although beginning with different rules, we have reached a situation where we have to proceed with the same sub-problem/state(<u>`x`</u>-<u>`c`</u>). Thus, we can solve this once, and use its result again and again!\n\n\nHence, **Dynamic Programming**. Choose the best from all possible states. And, instead of computing again and again, save what you have already computed. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity.\n\n\n\n----\n\n\n# \uD83D\uDCD1 Dynamic Programming\nAs evident from the above two examples [Posted as Pattern], to determine a **state**, we essentially need 3 things\n- `L`: left pointer in `nums`. Indicates we have used `L` numbers from left in `nums`.\n- `R`: right pointer in `nums`. Indicates we have used `R` numbers from right in `nums`.\n- `W`: number of operations done. Will be one more than the current index of `multipliers`\n\nHence, there are 3 state variables, `L`, `R`, and `W`. Hence, it\'s a 3D Dynamic Programming Problem. And to memoize it, we may need 3D Array.\n> If there are `n` state variables, then we need an array of <u>atmost</u> `n` dimensions.\n\nBut, without much brain-storming, we CAN reduce 3 state variables to 2. \nThe `R` can be calculated as `(n - 1) - (W - L) `. \n> **How?**\n> Well, there are `n` elements in `nums`. If we have done `W` operations, and left is *ahead* by `L`, means there are `W - L` operations from right. Thus, right should be *behind* `n-1` by `W-L`. Thus, the formula.\n\nThus, in our formulation, the state will be defined by two variables `i` and `j`. Let\'s used `X` to denote state, and thus, `X` represents the array where data will be memoized.\n\n> `X[i][j]` stores the **maximum possible score** after we have done `i` total operations and used `j` numbers from the left/start side.\n\nThus, from this state, we have two options\n- **Choose Left:** Then, the number of operations will increase by one. And, so does the left pointer. Thus, we will multiply `mulitpliers[i]` and `nums[j]` (since we have chosen from left), and add this product to the (optimal) result of state `X[i+1][j+1]`.\n- **Choose Right:** Then also the number of operations will increase by one. Thus, we will multiply `mulitpliers[i]` with `nums[n-1-(i-j)]` (since we have chosen from right), and add this product to the (optimal) result of state `X[i+1][j]` (Now, `j` will not increment since the number has not been chosen from left).\n\nChoose **maximum** of results obtained from choosing from left, or right. \n\nIf `i==m`, means we have performed `m` operations, add 0. The base condition of Recursion.\n\nThus, we can formulate\n\n> [](https://postimg.cc/kRWkLKV6)\n\nAnd, the Code!\n\n----\n\n\n# \uD83D\uDDA5 Code\n\n**Python**\n- Recursive using [@lru_cache(None)](https://docs.python.org/3/library/functools.html#functools.lru_cache) \n\n```python\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n = len(nums)\n m = len(multipliers)\n \n @lru_cache(None)\n #To Save Computed Result\n \n def X(i, left):\n \n if i==m:\n return 0\n \n return max ( (multipliers[i] * nums[left]) + X(i + 1, left + 1), \n (multipliers[i] * nums[n-1-(i-left)]) + X(i + 1, left) ) \n \n #Start from Zero operations\n return X(0,0)\n```\n\n- Iterative.\n\n```python\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [[0] * (m + 1) for _ in range(m + 1)]\n \n for i in range(m - 1, -1, -1):\n for left in range(i, -1, -1):\n \n dp[i][left] = max ( multipliers[i] * nums[left] + dp[i + 1][left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + dp[i + 1][left] ) \n \n return dp[0][0]\n```\n\n**Time Complexity :** O(m<sup>2</sup>) as evident from loops\n**Space Complexity :** O(m<sup>2</sup>) as evident from `dp`\n\n\n----\n\n\n# \u23F3 Optimizing\nWe can optimize this in space dimension. On carefully observing the formula in the image and iterative code, we can conclude that for computing present row `i`, we need next row `i+1` only. Moreover, we can fill the column backward, since present column `left` depends on `left+1` and `left` only. Thus, we are not losing any essential information while filling 1D array this way. \n\n```python\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [0] * (m + 1)\n \n for i in range(m - 1, -1, -1):\n nextRow = dp.copy()\n #Present Row is now nextRow, since iterating upwards\n \n for left in range(i,-1,-1):\n \n dp[left] = max ( multipliers[i] * nums[left] + nextRow[left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + nextRow[left] ) \n \n return dp[0]\n```\n\n**Time Complexity :** O(m<sup>2</sup>) as evident from loops\n**Space Complexity :** O(m) as evident from `dp`\n> [](https://postimg.cc/Y4R2s4GC)\n\n\n---\n\n\n# \uD83D\uDCA1 Conclusion\n\nHence, starting from very intuitive greedy, we realized we were wrong and ultimately we have to check for all possible combinations which isn\'t efficient. Problem has two key properties, thus Dynamic Programming! Here is one of the Final [but not claiming to be most optimized] Code, with O(m<sup>2</sup>) Time Complexity and O(m) Space Complexity.\n\n```c []\nint max(int a, int b) {return a>b ? a : b ;}\n\nint maximumScore(int* nums, int numsSize, int* multipliers, int multipliersSize)\n{\n int n = numsSize, m=multipliersSize;\n register int i, left, k;\n\n int dp[m+1];\n for (k=0; k<=m ; k++) dp[k]=0;\n \n for(i=m-1; i>=0; i--)\n {\n int nextRow[m+1];\n for (register int k=0; k<=m ; k++) nextRow[k]=dp[k];\n \n for (left=i; left>=0; left--)\n {\n dp[left] = max ( multipliers[i] * nums[left] + nextRow[left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + nextRow[left] ); \n }\n }\n \n return dp[0];\n}\n```\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [0] * (m + 1)\n \n for i in range(m - 1, -1, -1):\n nextRow = dp.copy()\n #Present Row is now nextRow, since iterating upwards\n \n for left in range(i,-1,-1):\n \n dp[left] = max ( multipliers[i] * nums[left] + nextRow[left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + nextRow[left] ) \n \n return dp[0]\n```\n\n\n\n<br>\n\n- \u2B06\uFE0F If you have gained some insights, feel free to upvote. Button Below \n- \u2B50 Feel free to add to your Favorite Solutions by clicking on Star.\n- \uD83D\uDE15 If you are confused, or have some doubts, post comments.\n- \uD83D\uDCA1 Any mistake or Have another idea? Share in Comments. \n\n\n----\n\n\n# \uD83E\uDD16 \uD835\uDDD8\uD835\uDDF1\uD835\uDDF6\uD835\uDE01\uD835\uDE00/\uD835\uDDE5\uD835\uDDF2\uD835\uDDFD\uD835\uDDF9\uD835\uDE06\uD835\uDDF6\uD835\uDDFB\uD835\uDDF4 \uD835\uDE01\uD835\uDDFC \uD835\uDDE4\uD835\uDE02\uD835\uDDF2\uD835\uDDFF\uD835\uDDF6\uD835\uDDF2\uD835\uDE00\n\nSpace for your feedback. This Section will take care of Edits and Reply to Comments/Doubts.\n\n**Edit :** Thanks for all the motivating comments. This article was written on Old UI, hence few sections are less readable. Although, I believe content quality isn\'t compromised. \u2764\n\n---------- \n <br>\n | 151 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
𝗪𝗵𝘆 Greedy Failed? From Level Zero | Beginner-Friendly | Fully Explained | Python | C | maximum-score-from-performing-multiplication-operations | 0 | 1 | # \uD83D\uDE0B Greedy!\n\n**Let\'s go Greedy!**\n\nWe have to pick integer `x` from **either end** of array `nums`. And, multiply that with `multipliers[i]`. Thus, let\'s pick larger `x` from either end. \n\n**`5` vs `3`, we will pick 5. Is it correct?** \nNo! On checking constraints `-1000 \u2264 nums[i], multipliers[i] \u2264 1000`, both arrays can have negative integers. Thus, if `multipliers[i]` is `-10`, we would prefer adding `-30` instead of `-50`. Thus, we should choose, `x` which when multiplied with `multipliers[i]` gives the larger product.\n\n<details><summary><b>\uD83E\uDD73 Let\'s Dry Run! (Click on Left Triangle to see)</b></summary> \n<pre>\n<b>Input :</b> nums = [1,2,3], multipliers = [3,2,1]\n<b>Taking Decision :</b>\n- From multipliers <b>3</b>, nums is [1, 2, 3], from <b>3</b>x1 vs <b>3</b>x3, choose 3, add <u>9</u>.\n- From multipliers <b>2</b>, nums is [1, 2], from <b>2</b>x1 and <b>2</b>x2, choose 2, add <u>4</u>.\n- From multipliers <b>1</b>, nums is [1], add <u>1</u>.\n\n<br/>\n\nTotal Score is <u>9+4+1</u>=<b>14</b>, which is Correct \u2714\uFE0F</pre></details>\n\n<details><summary><b>\uD83D\uDE0E Another Example! (MUST CLICK on Left Triangle to See)</b></summary><pre>\n<b>Input :</b> nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]\n<b>Taking Decision :</b> \n- From multipliers <b>10</b>, nums [-5,-3,-3,-2,7,1], from (<b>-10</b>) (-5) and (<b>-10</b>)(1), choose -5, add <u>50</u>\n- From multipliers <b>-5</b>, nums [-3,-3,-2,7,1], from (<b>-5</b>) (-3) and (<b>-5</b>)(1), choose -3, add <u>15</u>\n- From multipliers <b>3</b>, nums [-3,-2,7,1], from (<b>3</b>) (-3) and (<b>3</b>)(1), choose 1, add <u>3</u>\n- From multipliers <b>4</b>, nums [-3,-2,7], from (<b>4</b>) (-3) and (<b>4</b>)(7), choose 7, add <u>28</u>\n- From multipliers <b>6</b>, nums [-3,-2], from (<b>6</b>) (-3) and (<b>6</b>)(-2), choose -2, add <u>-12</u>\n\n<br/>\n\nTotal Score is <u>50+15+3+28+(-12)</u>=<b>84</b>, which...... \nisn\'t Correct \uD83D\uDE15. 102 is another <u>Optimal Solution</u> \nas given in Problem Example.</pre> </details>\n\nWell, this version of greedy failed! \n\n\n> **How to Prove it?**\n> [\u26A0: Spoiler Alert! Go to these links after reading the complete answer]\n> This was asked on [Computer Science Stack Exchange](https://cs.stackexchange.com/q/151534/143377), and the [answer](https://cs.stackexchange.com/a/151551/143377) and [comments](https://cs.stackexchange.com/questions/151534/formal-proof-on-why-greedy-isnt-working-on-one-particular-problem#comment318613_151534) there suggests that \n>> - "To show that the greedy approach fails, all you have to do is come up with a counterexample. " \n>> - "To prove that the greedy algorithm is not optimal, it suffices to give one counterexample"\n\n> We have given one example, where our version of greedy isn\'t giving <u>Optimal Solution</u>.\n\n*(Another problem where we encounter similar situation is [120. Triangle](https://leetcode.com/problems/triangle/). After reading this answer, you can check the problem and one of the [counter example](https://leetcode.com/problems/triangle/discuss/2146127/why-greedy-fails-intuition-counter-example-dynamic-programming) for the same)* \n\n> **Still, what\'s the logical intuition behind the failure of greedy?**\n> Greedy is `short-sighted`. In hope of global optimum, we take local optimum. But taking this Local Optimum perhaps <ins>may Restrict Potential Larger Positive Product in Future!</ins> \n> \n> Check this example,\n> <pre> <b>Input :</b> nums = [2,1,1,1,1000,1,1,1,1,42], multipliers = [1,1,1,1,1] </pre>\n> If very myopically, we choose 42 over 2, we would never be able to reach our treasure 1000. Since there are only 5 elements in multipliers, the only way to reach 1000 is by taking the Left route only. But one myopic step, and we lost optimal!\n> \n> Another [Example](https://cs.stackexchange.com/a/151551/143377) \n> <pre> <b>Input :</b> nums = [5,4], multipliers = [1,2] </pre>\n> Greedy would choose to multiply the 1 by a 5 rather than 4, giving an output of 1\u22C55+2\u22C54=13. But the second multiplier 2 is larger than the first multiplier and so should have been multiplied with the larger number 5 to get the maximum output (which is 1\u22C54+2\u22C55=14).\n\n\n---\n\n\n**What to do now?**\nLook for every possible combination! Try all scenarios \uD83D\uDE29 \n> - Choose one element from either side from `given nums` and then delete the chosen element (multiply and add to the score) to create `remaining nums` \n> - Choose another element from either side from `remaining nums` and then delete the chosen element (multiply and add to the score) to create `another remaining nums` \n> - Choose again ..... \n\n\u2666 Looking for every possible combination, is, in general not very Efficient. \n\u2666 But, this problem has certain properties.\n\n1. **Optimal Substructure:** To get the maximum score for entire `multipliers`, we should ensure we have the maximum score for every subarray from the first index! For `multipliers[0:1]`, for `multipliers[0:2]`, and so on.... <br>\n\n2. **Overlapping Subproblem:** We may need to compute for a particular (`nums`, `multipliers`) pair multiple times. By computing, we mean solving further from this state. **Rough Example:** `nums = [a,b,c,d,e]` and `multipliers = [u,v,w,x,y,z]`\n - **Pattern-1: Two-Left, One Right**\n - From `multipliers`, we have `u`, from nums `a vs e`, choose `a`\n - From `multipliers`, we have `v`, from nums `b vs e`, choose `b` \n - From `multipliers`, we have `w`, from nums `c vs e`, choose `e`\n - From `multipliers`, we have <u>`x`</u>, from nums `c vs d`, choose <u>`c`</u>\n - **Pattern-2: One-Right, Three Left**\n - From `multipliers`, we have `u`, from nums `a vs e`, choose `e`\n - From `multipliers`, we have `v`, from nums `a vs d`, choose `a` \n - From `multipliers`, we have `w`, from nums `b vs d`, choose `b`\n - From `multipliers`, we have <u>`x`</u>, from nums `c vs d`, choose <u>`c`</u> \n<br>Thus, although beginning with different rules, we have reached a situation where we have to proceed with the same sub-problem/state(<u>`x`</u>-<u>`c`</u>). Thus, we can solve this once, and use its result again and again!\n\n\nHence, **Dynamic Programming**. Choose the best from all possible states. And, instead of computing again and again, save what you have already computed. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity.\n\n\n\n----\n\n\n# \uD83D\uDCD1 Dynamic Programming\nAs evident from the above two examples [Posted as Pattern], to determine a **state**, we essentially need 3 things\n- `L`: left pointer in `nums`. Indicates we have used `L` numbers from left in `nums`.\n- `R`: right pointer in `nums`. Indicates we have used `R` numbers from right in `nums`.\n- `W`: number of operations done. Will be one more than the current index of `multipliers`\n\nHence, there are 3 state variables, `L`, `R`, and `W`. Hence, it\'s a 3D Dynamic Programming Problem. And to memoize it, we may need 3D Array.\n> If there are `n` state variables, then we need an array of <u>atmost</u> `n` dimensions.\n\nBut, without much brain-storming, we CAN reduce 3 state variables to 2. \nThe `R` can be calculated as `(n - 1) - (W - L) `. \n> **How?**\n> Well, there are `n` elements in `nums`. If we have done `W` operations, and left is *ahead* by `L`, means there are `W - L` operations from right. Thus, right should be *behind* `n-1` by `W-L`. Thus, the formula.\n\nThus, in our formulation, the state will be defined by two variables `i` and `j`. Let\'s used `X` to denote state, and thus, `X` represents the array where data will be memoized.\n\n> `X[i][j]` stores the **maximum possible score** after we have done `i` total operations and used `j` numbers from the left/start side.\n\nThus, from this state, we have two options\n- **Choose Left:** Then, the number of operations will increase by one. And, so does the left pointer. Thus, we will multiply `mulitpliers[i]` and `nums[j]` (since we have chosen from left), and add this product to the (optimal) result of state `X[i+1][j+1]`.\n- **Choose Right:** Then also the number of operations will increase by one. Thus, we will multiply `mulitpliers[i]` with `nums[n-1-(i-j)]` (since we have chosen from right), and add this product to the (optimal) result of state `X[i+1][j]` (Now, `j` will not increment since the number has not been chosen from left).\n\nChoose **maximum** of results obtained from choosing from left, or right. \n\nIf `i==m`, means we have performed `m` operations, add 0. The base condition of Recursion.\n\nThus, we can formulate\n\n> [](https://postimg.cc/kRWkLKV6)\n\nAnd, the Code!\n\n----\n\n\n# \uD83D\uDDA5 Code\n\n**Python**\n- Recursive using [@lru_cache(None)](https://docs.python.org/3/library/functools.html#functools.lru_cache) \n\n```python\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n = len(nums)\n m = len(multipliers)\n \n @lru_cache(None)\n #To Save Computed Result\n \n def X(i, left):\n \n if i==m:\n return 0\n \n return max ( (multipliers[i] * nums[left]) + X(i + 1, left + 1), \n (multipliers[i] * nums[n-1-(i-left)]) + X(i + 1, left) ) \n \n #Start from Zero operations\n return X(0,0)\n```\n\n- Iterative.\n\n```python\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [[0] * (m + 1) for _ in range(m + 1)]\n \n for i in range(m - 1, -1, -1):\n for left in range(i, -1, -1):\n \n dp[i][left] = max ( multipliers[i] * nums[left] + dp[i + 1][left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + dp[i + 1][left] ) \n \n return dp[0][0]\n```\n\n**Time Complexity :** O(m<sup>2</sup>) as evident from loops\n**Space Complexity :** O(m<sup>2</sup>) as evident from `dp`\n\n\n----\n\n\n# \u23F3 Optimizing\nWe can optimize this in space dimension. On carefully observing the formula in the image and iterative code, we can conclude that for computing present row `i`, we need next row `i+1` only. Moreover, we can fill the column backward, since present column `left` depends on `left+1` and `left` only. Thus, we are not losing any essential information while filling 1D array this way. \n\n```python\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [0] * (m + 1)\n \n for i in range(m - 1, -1, -1):\n nextRow = dp.copy()\n #Present Row is now nextRow, since iterating upwards\n \n for left in range(i,-1,-1):\n \n dp[left] = max ( multipliers[i] * nums[left] + nextRow[left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + nextRow[left] ) \n \n return dp[0]\n```\n\n**Time Complexity :** O(m<sup>2</sup>) as evident from loops\n**Space Complexity :** O(m) as evident from `dp`\n> [](https://postimg.cc/Y4R2s4GC)\n\n\n---\n\n\n# \uD83D\uDCA1 Conclusion\n\nHence, starting from very intuitive greedy, we realized we were wrong and ultimately we have to check for all possible combinations which isn\'t efficient. Problem has two key properties, thus Dynamic Programming! Here is one of the Final [but not claiming to be most optimized] Code, with O(m<sup>2</sup>) Time Complexity and O(m) Space Complexity.\n\n```c []\nint max(int a, int b) {return a>b ? a : b ;}\n\nint maximumScore(int* nums, int numsSize, int* multipliers, int multipliersSize)\n{\n int n = numsSize, m=multipliersSize;\n register int i, left, k;\n\n int dp[m+1];\n for (k=0; k<=m ; k++) dp[k]=0;\n \n for(i=m-1; i>=0; i--)\n {\n int nextRow[m+1];\n for (register int k=0; k<=m ; k++) nextRow[k]=dp[k];\n \n for (left=i; left>=0; left--)\n {\n dp[left] = max ( multipliers[i] * nums[left] + nextRow[left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + nextRow[left] ); \n }\n }\n \n return dp[0];\n}\n```\n```python3 []\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [0] * (m + 1)\n \n for i in range(m - 1, -1, -1):\n nextRow = dp.copy()\n #Present Row is now nextRow, since iterating upwards\n \n for left in range(i,-1,-1):\n \n dp[left] = max ( multipliers[i] * nums[left] + nextRow[left + 1], \n multipliers[i] * nums[n - 1 - (i - left)] + nextRow[left] ) \n \n return dp[0]\n```\n\n\n\n<br>\n\n- \u2B06\uFE0F If you have gained some insights, feel free to upvote. Button Below \n- \u2B50 Feel free to add to your Favorite Solutions by clicking on Star.\n- \uD83D\uDE15 If you are confused, or have some doubts, post comments.\n- \uD83D\uDCA1 Any mistake or Have another idea? Share in Comments. \n\n\n----\n\n\n# \uD83E\uDD16 \uD835\uDDD8\uD835\uDDF1\uD835\uDDF6\uD835\uDE01\uD835\uDE00/\uD835\uDDE5\uD835\uDDF2\uD835\uDDFD\uD835\uDDF9\uD835\uDE06\uD835\uDDF6\uD835\uDDFB\uD835\uDDF4 \uD835\uDE01\uD835\uDDFC \uD835\uDDE4\uD835\uDE02\uD835\uDDF2\uD835\uDDFF\uD835\uDDF6\uD835\uDDF2\uD835\uDE00\n\nSpace for your feedback. This Section will take care of Edits and Reply to Comments/Doubts.\n\n**Edit :** Thanks for all the motivating comments. This article was written on Old UI, hence few sections are less readable. Although, I believe content quality isn\'t compromised. \u2764\n\n---------- \n <br>\n | 151 | You are given a **valid** boolean expression as a string `expression` consisting of the characters `'1'`,`'0'`,`'&'` (bitwise **AND** operator),`'|'` (bitwise **OR** operator),`'('`, and `')'`.
* For example, `"()1|1 "` and `"(1)&() "` are **not valid** while `"1 "`, `"(((1))|(0)) "`, and `"1|(0&(1)) "` are **valid** expressions.
Return _the **minimum cost** to change the final value of the expression_.
* For example, if `expression = "1|1|(0&0)&1 "`, its **value** is `1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1`. We want to apply operations so that the **new** expression evaluates to `0`.
The **cost** of changing the final value of an expression is the **number of operations** performed on the expression. The types of **operations** are described as follows:
* Turn a `'1'` into a `'0'`.
* Turn a `'0'` into a `'1'`.
* Turn a `'&'` into a `'|'`.
* Turn a `'|'` into a `'&'`.
**Note:** `'&'` does **not** take precedence over `'|'` in the **order of calculation**. Evaluate parentheses **first**, then in **left-to-right** order.
**Example 1:**
**Input:** expression = "1&(0|1) "
**Output:** 1
**Explanation:** We can turn "1&(0**|**1) " into "1&(0**&**1) " by changing the '|' to a '&' using 1 operation.
The new expression evaluates to 0.
**Example 2:**
**Input:** expression = "(0&0)&(0&0&0) "
**Output:** 3
**Explanation:** We can turn "(0**&0**)**&**(0&0&0) " into "(0**|1**)**|**(0&0&0) " using 3 operations.
The new expression evaluates to 1.
**Example 3:**
**Input:** expression = "(0|(1|0&1)) "
**Output:** 1
**Explanation:** We can turn "(0|(**1**|0&1)) " into "(0|(**0**|0&1)) " using 1 operation.
The new expression evaluates to 0.
**Constraints:**
* `1 <= expression.length <= 105`
* `expression` only contains `'1'`,`'0'`,`'&'`,`'|'`,`'('`, and `')'`
* All parentheses are properly matched.
* There will be no empty parentheses (i.e: `"() "` is not a substring of `expression`). | At first glance, the solution seems to be greedy, but if you try to greedily take the largest value from the beginning or the end, this will not be optimal. You should try all scenarios but this will be costy. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity, and hence dp is a perfect choice here. |
Solution from Recursion to Space optimization in Python and C++ | maximum-score-from-performing-multiplication-operations | 0 | 1 | **Recursion (TLE)**\n```\nn = len(multipliers)\nm = len(nums)\ndp = [[-1 for i in range(m)] for k in range(n)]\ndef f(ind,i):\n\tif ind==n:\n\t\treturn 0\n\tl = (nums[i]*multipliers[ind])+f(ind+1,i+1)\n\tr = (nums[m-1-(ind-i)]*multipliers[ind])+f(ind+1,i)\n\n\treturn max(l,r)\nreturn f(0,0)\n```\n**Time Complexity: Exponential**\n\n**Memoization (TLE)**\n```\ndef f(ind,i):\n\tif ind==n:\n\t\treturn 0\n\tif dp[ind][i]!=-1: return dp[ind][i]\n\tl = (nums[i]*multipliers[ind])+f(ind+1,i+1)\n\tr = (nums[m-1-(ind-i)]*multipliers[ind])+f(ind+1,i)\n\tdp[ind][i] = max(l,r)\n\treturn dp[ind][i]\nreturn f(0,0)\n```\n**Time Complexity: O(len(multipliers)xlen(multipliers))**\n\n**Tabulation (Accepted)**\n**97% Faster**\n```\ndp = [[0 for i in range(n+1)] for k in range(n+1)]\nfor ind in range(n-1,-1,-1):\n\tfor i in range(ind,-1,-1):\n\t\tl = (nums[i]*multipliers[ind])+dp[ind+1][i+1]\n\t\tr = (nums[m-1-(ind-i)]*multipliers[ind])+dp[ind+1][i]\n\t\tdp[ind][i] = max(l,r)\nreturn dp[0][0]\n```\n**Time Complexity: O(len(multipliers)xlen(multipliers))**\n\n**Space Optimized Code**\n**97% less memory usage**\n```\nahead = [0 for i in range(n+1)]\ncur = [0 for i in range(n+1)]\nfor ind in range(n-1,-1,-1):\n\tfor i in range(ind,-1,-1):\n\t\tl = (nums[i]*multipliers[ind])+ahead[i+1]\n\t\tr = (nums[m-1-(ind-i)]*multipliers[ind])+ahead[i]\n\t\tcur[i] = max(l,r)\n\tahead = cur.copy()\nreturn ahead[0]\n```\n\n**Space Optimized Code in C++**\n```\nint m = multipliers.size();\nint n = nums.size();\nvector<int> ahead(m+1),cur(m+1);\nfor(int ind=m-1;ind>=0;ind--){\n\tfor(int i=ind;i>=0;i--){\n\t\tlong long l=(nums[i]*multipliers[ind])+ahead[i+1];\n\t\tlong long r =(nums[(n-1)-(ind-i)]*multipliers[ind])+ahead[i];\n\t\tcur[i]=max(l,r);\n\t}\n\tahead = cur;\n}\nreturn ahead[0];\n```\n**Please Upvote if you like this solution.** | 4 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
Solution from Recursion to Space optimization in Python and C++ | maximum-score-from-performing-multiplication-operations | 0 | 1 | **Recursion (TLE)**\n```\nn = len(multipliers)\nm = len(nums)\ndp = [[-1 for i in range(m)] for k in range(n)]\ndef f(ind,i):\n\tif ind==n:\n\t\treturn 0\n\tl = (nums[i]*multipliers[ind])+f(ind+1,i+1)\n\tr = (nums[m-1-(ind-i)]*multipliers[ind])+f(ind+1,i)\n\n\treturn max(l,r)\nreturn f(0,0)\n```\n**Time Complexity: Exponential**\n\n**Memoization (TLE)**\n```\ndef f(ind,i):\n\tif ind==n:\n\t\treturn 0\n\tif dp[ind][i]!=-1: return dp[ind][i]\n\tl = (nums[i]*multipliers[ind])+f(ind+1,i+1)\n\tr = (nums[m-1-(ind-i)]*multipliers[ind])+f(ind+1,i)\n\tdp[ind][i] = max(l,r)\n\treturn dp[ind][i]\nreturn f(0,0)\n```\n**Time Complexity: O(len(multipliers)xlen(multipliers))**\n\n**Tabulation (Accepted)**\n**97% Faster**\n```\ndp = [[0 for i in range(n+1)] for k in range(n+1)]\nfor ind in range(n-1,-1,-1):\n\tfor i in range(ind,-1,-1):\n\t\tl = (nums[i]*multipliers[ind])+dp[ind+1][i+1]\n\t\tr = (nums[m-1-(ind-i)]*multipliers[ind])+dp[ind+1][i]\n\t\tdp[ind][i] = max(l,r)\nreturn dp[0][0]\n```\n**Time Complexity: O(len(multipliers)xlen(multipliers))**\n\n**Space Optimized Code**\n**97% less memory usage**\n```\nahead = [0 for i in range(n+1)]\ncur = [0 for i in range(n+1)]\nfor ind in range(n-1,-1,-1):\n\tfor i in range(ind,-1,-1):\n\t\tl = (nums[i]*multipliers[ind])+ahead[i+1]\n\t\tr = (nums[m-1-(ind-i)]*multipliers[ind])+ahead[i]\n\t\tcur[i] = max(l,r)\n\tahead = cur.copy()\nreturn ahead[0]\n```\n\n**Space Optimized Code in C++**\n```\nint m = multipliers.size();\nint n = nums.size();\nvector<int> ahead(m+1),cur(m+1);\nfor(int ind=m-1;ind>=0;ind--){\n\tfor(int i=ind;i>=0;i--){\n\t\tlong long l=(nums[i]*multipliers[ind])+ahead[i+1];\n\t\tlong long r =(nums[(n-1)-(ind-i)]*multipliers[ind])+ahead[i];\n\t\tcur[i]=max(l,r);\n\t}\n\tahead = cur;\n}\nreturn ahead[0];\n```\n**Please Upvote if you like this solution.** | 4 | You are given a **valid** boolean expression as a string `expression` consisting of the characters `'1'`,`'0'`,`'&'` (bitwise **AND** operator),`'|'` (bitwise **OR** operator),`'('`, and `')'`.
* For example, `"()1|1 "` and `"(1)&() "` are **not valid** while `"1 "`, `"(((1))|(0)) "`, and `"1|(0&(1)) "` are **valid** expressions.
Return _the **minimum cost** to change the final value of the expression_.
* For example, if `expression = "1|1|(0&0)&1 "`, its **value** is `1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1`. We want to apply operations so that the **new** expression evaluates to `0`.
The **cost** of changing the final value of an expression is the **number of operations** performed on the expression. The types of **operations** are described as follows:
* Turn a `'1'` into a `'0'`.
* Turn a `'0'` into a `'1'`.
* Turn a `'&'` into a `'|'`.
* Turn a `'|'` into a `'&'`.
**Note:** `'&'` does **not** take precedence over `'|'` in the **order of calculation**. Evaluate parentheses **first**, then in **left-to-right** order.
**Example 1:**
**Input:** expression = "1&(0|1) "
**Output:** 1
**Explanation:** We can turn "1&(0**|**1) " into "1&(0**&**1) " by changing the '|' to a '&' using 1 operation.
The new expression evaluates to 0.
**Example 2:**
**Input:** expression = "(0&0)&(0&0&0) "
**Output:** 3
**Explanation:** We can turn "(0**&0**)**&**(0&0&0) " into "(0**|1**)**|**(0&0&0) " using 3 operations.
The new expression evaluates to 1.
**Example 3:**
**Input:** expression = "(0|(1|0&1)) "
**Output:** 1
**Explanation:** We can turn "(0|(**1**|0&1)) " into "(0|(**0**|0&1)) " using 1 operation.
The new expression evaluates to 0.
**Constraints:**
* `1 <= expression.length <= 105`
* `expression` only contains `'1'`,`'0'`,`'&'`,`'|'`,`'('`, and `')'`
* All parentheses are properly matched.
* There will be no empty parentheses (i.e: `"() "` is not a substring of `expression`). | At first glance, the solution seems to be greedy, but if you try to greedily take the largest value from the beginning or the end, this will not be optimal. You should try all scenarios but this will be costy. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity, and hence dp is a perfect choice here. |
Python Solution | Memoization | Tabulation | maximum-score-from-performing-multiplication-operations | 0 | 1 | ```\ndef maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n s=0\n n=len(nums)\n m=len(multipliers)\n \n # Recursion + Memoization : TLE\n # dp=[[-1]*m for i in range(n)]\n# def helper(low, high, j):\n# if j==m:\n# return 0\n# if dp[low][j]!=None:\n# return dp[low][j]\n# first=nums[low]*multipliers[j]+helper(low+1, high, j+1)\n# last=nums[high]*multipliers[j]+helper(low, high-1, j+1)\n \n# dp[low][j]=max(first, last)\n# return dp[low][j]\n# return helper(0, n-1, 0)\n\n # Tablulation : Accepted\n dp=[[0]*(m+1) for i in range(m+1)]\n for j in range(m-1, -1, -1):\n for low in range(j, -1, -1):\n first=nums[low]*multipliers[j]+dp[j+1][low+1]\n last=nums[n-1-(j-low)]*multipliers[j]+dp[j+1][low]\n dp[j][low]=max(first, last)\n return dp[0][0]\n``` | 4 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
Python Solution | Memoization | Tabulation | maximum-score-from-performing-multiplication-operations | 0 | 1 | ```\ndef maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n s=0\n n=len(nums)\n m=len(multipliers)\n \n # Recursion + Memoization : TLE\n # dp=[[-1]*m for i in range(n)]\n# def helper(low, high, j):\n# if j==m:\n# return 0\n# if dp[low][j]!=None:\n# return dp[low][j]\n# first=nums[low]*multipliers[j]+helper(low+1, high, j+1)\n# last=nums[high]*multipliers[j]+helper(low, high-1, j+1)\n \n# dp[low][j]=max(first, last)\n# return dp[low][j]\n# return helper(0, n-1, 0)\n\n # Tablulation : Accepted\n dp=[[0]*(m+1) for i in range(m+1)]\n for j in range(m-1, -1, -1):\n for low in range(j, -1, -1):\n first=nums[low]*multipliers[j]+dp[j+1][low+1]\n last=nums[n-1-(j-low)]*multipliers[j]+dp[j+1][low]\n dp[j][low]=max(first, last)\n return dp[0][0]\n``` | 4 | You are given a **valid** boolean expression as a string `expression` consisting of the characters `'1'`,`'0'`,`'&'` (bitwise **AND** operator),`'|'` (bitwise **OR** operator),`'('`, and `')'`.
* For example, `"()1|1 "` and `"(1)&() "` are **not valid** while `"1 "`, `"(((1))|(0)) "`, and `"1|(0&(1)) "` are **valid** expressions.
Return _the **minimum cost** to change the final value of the expression_.
* For example, if `expression = "1|1|(0&0)&1 "`, its **value** is `1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1`. We want to apply operations so that the **new** expression evaluates to `0`.
The **cost** of changing the final value of an expression is the **number of operations** performed on the expression. The types of **operations** are described as follows:
* Turn a `'1'` into a `'0'`.
* Turn a `'0'` into a `'1'`.
* Turn a `'&'` into a `'|'`.
* Turn a `'|'` into a `'&'`.
**Note:** `'&'` does **not** take precedence over `'|'` in the **order of calculation**. Evaluate parentheses **first**, then in **left-to-right** order.
**Example 1:**
**Input:** expression = "1&(0|1) "
**Output:** 1
**Explanation:** We can turn "1&(0**|**1) " into "1&(0**&**1) " by changing the '|' to a '&' using 1 operation.
The new expression evaluates to 0.
**Example 2:**
**Input:** expression = "(0&0)&(0&0&0) "
**Output:** 3
**Explanation:** We can turn "(0**&0**)**&**(0&0&0) " into "(0**|1**)**|**(0&0&0) " using 3 operations.
The new expression evaluates to 1.
**Example 3:**
**Input:** expression = "(0|(1|0&1)) "
**Output:** 1
**Explanation:** We can turn "(0|(**1**|0&1)) " into "(0|(**0**|0&1)) " using 1 operation.
The new expression evaluates to 0.
**Constraints:**
* `1 <= expression.length <= 105`
* `expression` only contains `'1'`,`'0'`,`'&'`,`'|'`,`'('`, and `')'`
* All parentheses are properly matched.
* There will be no empty parentheses (i.e: `"() "` is not a substring of `expression`). | At first glance, the solution seems to be greedy, but if you try to greedily take the largest value from the beginning or the end, this will not be optimal. You should try all scenarios but this will be costy. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity, and hence dp is a perfect choice here. |
Python Solution From Recursion To Space Optimisation | maximum-score-from-performing-multiplication-operations | 0 | 1 | ***Recursion(TLE):***\n```\nn = len(nums) \nm = len(multipliers)\n```\n```\ndef f(ind,i,j):\n\tif ind == m:\n\t\treturn 0\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1,j)\n\tr = nums[j]*multipliers[ind]+f(ind+1,i,j-1)\nreturn f(0,0,n-1)\n```\n**Time Complexity:** Exponential\n**Space Complexity:** O(m)\n\n***Memoization(TLE):***\n```\ndef f(ind,i,j):\n\tif ind == m:\n\t\treturn 0\n\tif dp[ind][i][j] != -1:\n\t\treturn dp[ind][i][j]\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1,j)\n\tr = nums[j]*multipliers[ind]+f(ind+1,i,j-1)\n\tdp[ind][i][j] = max(l,r)\n\treturn dp[ind][i][j]\ndp = [[[-1 for i in range(n)]for i in range(n)]for i in range(m)]\nreturn f(0,0,n-1)\n```\n**Time Complexity:** O(n * n * m)\n**Space Complexity:** O(n * n * m) + O(m)\n\n***Tabulation(TLE):***\n```\ndp = [[[0 for i in range(n)]for j in range(n)]for k in range(m+1)]\nfor ind in range(m-1,-1,-1):\n\tfor i in range(n-2,-1,-1):\n\t\tfor j in range(i,n):\n\t\t\tl = nums[i]*multipliers[ind]+dp[ind+1][i+1][j]\n\t\t\tr = nums[j]*multipliers[ind]+dp[ind+1][i][j-1]\n\t\t\tdp[ind][i][j] = max(l,r)\nreturn dp[0][0][n-1]\n```\n**Time Complexity:** O(n * n * m)\n**Space Complexity:** O(n * n * m) \n\n**Optimised Approach:** Instead of using separate pointer for right use n-1-(ind-left) for pointing on right index of nums.\n\n***Recursion(TLE):***\n```\ndef f(ind,i):\n\tif ind == m:\n\t\treturn 0\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1)\n\tr = nums[n-1-(ind-i)]*multipliers[ind]+f(ind+1,i)\n\treturn max(l,r)\nreturn f(0,0)\n```\n**Time Complexity:** Exponential\n**Space Complexity:** O(m)\n\n***Memoization(TLE):***\n```\ndef f(ind,i):\n\tif ind == m:\n\t\treturn 0\n\tif dp[ind][i] != -1:\n\t\treturn dp[ind][i]\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1)\n\tr = nums[n-1-(ind-i)]*multipliers[ind]+f(ind+1,i)\n\tdp[ind][i] = max(l,r)\n\treturn dp[ind][i]\ndp = [[-1 for i in range(n)]for i in range(m)]\nreturn f(0,0)\n```\n**Time Complexity:** O(n * m)\n**Space Complexity:** O(n * m)+ O(m)\n\n***Tabulation(Might Gives TLE in some cases):***\n```\ndp = [[0 for i in range(m+1)]for i in range(m+1)]\nfor ind in range(m-1,-1,-1):\n\tfor left in range(ind,-1,-1):\n\t\tl = nums[left]*multipliers[ind]+dp[ind+1][left+1]\n\t\tr = nums[n-1-(ind-left)]*multipliers[ind]+dp[ind+1][left]\n\t\tdp[ind][left] = max(l,r)\nreturn dp[0][0]\n```\n**Time Complexity:** O(m * m)\n**Space Complexity:** O(m * m)\n\n***Space Optimisation(Accepted):***\n```\nahead = [0 for i in range(m+1)]\ncurr = [0 for i in range(m+1)]\nfor ind in range(m-1,-1,-1):\n\tfor left in range(ind,-1,-1):\n\t\tl = nums[left]*multipliers[ind] + ahead[left+1]\n\t\tr = nums[n-1-(ind-left)]*multipliers[ind] + ahead[left]\n\t\tcurr[left] = max(l,r)\n\tahead = curr.copy()\nreturn ahead[0]\n```\n**Time Complexity:** O(m * m)\n**Space Complexity:** O(m) + O(m)\n\n***Please Upvote if you like this.*** | 3 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
Python Solution From Recursion To Space Optimisation | maximum-score-from-performing-multiplication-operations | 0 | 1 | ***Recursion(TLE):***\n```\nn = len(nums) \nm = len(multipliers)\n```\n```\ndef f(ind,i,j):\n\tif ind == m:\n\t\treturn 0\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1,j)\n\tr = nums[j]*multipliers[ind]+f(ind+1,i,j-1)\nreturn f(0,0,n-1)\n```\n**Time Complexity:** Exponential\n**Space Complexity:** O(m)\n\n***Memoization(TLE):***\n```\ndef f(ind,i,j):\n\tif ind == m:\n\t\treturn 0\n\tif dp[ind][i][j] != -1:\n\t\treturn dp[ind][i][j]\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1,j)\n\tr = nums[j]*multipliers[ind]+f(ind+1,i,j-1)\n\tdp[ind][i][j] = max(l,r)\n\treturn dp[ind][i][j]\ndp = [[[-1 for i in range(n)]for i in range(n)]for i in range(m)]\nreturn f(0,0,n-1)\n```\n**Time Complexity:** O(n * n * m)\n**Space Complexity:** O(n * n * m) + O(m)\n\n***Tabulation(TLE):***\n```\ndp = [[[0 for i in range(n)]for j in range(n)]for k in range(m+1)]\nfor ind in range(m-1,-1,-1):\n\tfor i in range(n-2,-1,-1):\n\t\tfor j in range(i,n):\n\t\t\tl = nums[i]*multipliers[ind]+dp[ind+1][i+1][j]\n\t\t\tr = nums[j]*multipliers[ind]+dp[ind+1][i][j-1]\n\t\t\tdp[ind][i][j] = max(l,r)\nreturn dp[0][0][n-1]\n```\n**Time Complexity:** O(n * n * m)\n**Space Complexity:** O(n * n * m) \n\n**Optimised Approach:** Instead of using separate pointer for right use n-1-(ind-left) for pointing on right index of nums.\n\n***Recursion(TLE):***\n```\ndef f(ind,i):\n\tif ind == m:\n\t\treturn 0\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1)\n\tr = nums[n-1-(ind-i)]*multipliers[ind]+f(ind+1,i)\n\treturn max(l,r)\nreturn f(0,0)\n```\n**Time Complexity:** Exponential\n**Space Complexity:** O(m)\n\n***Memoization(TLE):***\n```\ndef f(ind,i):\n\tif ind == m:\n\t\treturn 0\n\tif dp[ind][i] != -1:\n\t\treturn dp[ind][i]\n\tl = nums[i]*multipliers[ind]+f(ind+1,i+1)\n\tr = nums[n-1-(ind-i)]*multipliers[ind]+f(ind+1,i)\n\tdp[ind][i] = max(l,r)\n\treturn dp[ind][i]\ndp = [[-1 for i in range(n)]for i in range(m)]\nreturn f(0,0)\n```\n**Time Complexity:** O(n * m)\n**Space Complexity:** O(n * m)+ O(m)\n\n***Tabulation(Might Gives TLE in some cases):***\n```\ndp = [[0 for i in range(m+1)]for i in range(m+1)]\nfor ind in range(m-1,-1,-1):\n\tfor left in range(ind,-1,-1):\n\t\tl = nums[left]*multipliers[ind]+dp[ind+1][left+1]\n\t\tr = nums[n-1-(ind-left)]*multipliers[ind]+dp[ind+1][left]\n\t\tdp[ind][left] = max(l,r)\nreturn dp[0][0]\n```\n**Time Complexity:** O(m * m)\n**Space Complexity:** O(m * m)\n\n***Space Optimisation(Accepted):***\n```\nahead = [0 for i in range(m+1)]\ncurr = [0 for i in range(m+1)]\nfor ind in range(m-1,-1,-1):\n\tfor left in range(ind,-1,-1):\n\t\tl = nums[left]*multipliers[ind] + ahead[left+1]\n\t\tr = nums[n-1-(ind-left)]*multipliers[ind] + ahead[left]\n\t\tcurr[left] = max(l,r)\n\tahead = curr.copy()\nreturn ahead[0]\n```\n**Time Complexity:** O(m * m)\n**Space Complexity:** O(m) + O(m)\n\n***Please Upvote if you like this.*** | 3 | You are given a **valid** boolean expression as a string `expression` consisting of the characters `'1'`,`'0'`,`'&'` (bitwise **AND** operator),`'|'` (bitwise **OR** operator),`'('`, and `')'`.
* For example, `"()1|1 "` and `"(1)&() "` are **not valid** while `"1 "`, `"(((1))|(0)) "`, and `"1|(0&(1)) "` are **valid** expressions.
Return _the **minimum cost** to change the final value of the expression_.
* For example, if `expression = "1|1|(0&0)&1 "`, its **value** is `1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1`. We want to apply operations so that the **new** expression evaluates to `0`.
The **cost** of changing the final value of an expression is the **number of operations** performed on the expression. The types of **operations** are described as follows:
* Turn a `'1'` into a `'0'`.
* Turn a `'0'` into a `'1'`.
* Turn a `'&'` into a `'|'`.
* Turn a `'|'` into a `'&'`.
**Note:** `'&'` does **not** take precedence over `'|'` in the **order of calculation**. Evaluate parentheses **first**, then in **left-to-right** order.
**Example 1:**
**Input:** expression = "1&(0|1) "
**Output:** 1
**Explanation:** We can turn "1&(0**|**1) " into "1&(0**&**1) " by changing the '|' to a '&' using 1 operation.
The new expression evaluates to 0.
**Example 2:**
**Input:** expression = "(0&0)&(0&0&0) "
**Output:** 3
**Explanation:** We can turn "(0**&0**)**&**(0&0&0) " into "(0**|1**)**|**(0&0&0) " using 3 operations.
The new expression evaluates to 1.
**Example 3:**
**Input:** expression = "(0|(1|0&1)) "
**Output:** 1
**Explanation:** We can turn "(0|(**1**|0&1)) " into "(0|(**0**|0&1)) " using 1 operation.
The new expression evaluates to 0.
**Constraints:**
* `1 <= expression.length <= 105`
* `expression` only contains `'1'`,`'0'`,`'&'`,`'|'`,`'('`, and `')'`
* All parentheses are properly matched.
* There will be no empty parentheses (i.e: `"() "` is not a substring of `expression`). | At first glance, the solution seems to be greedy, but if you try to greedily take the largest value from the beginning or the end, this will not be optimal. You should try all scenarios but this will be costy. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity, and hence dp is a perfect choice here. |
✅✔ SIMPLE PYTHON3 SOLUTION ✅✔98% less memory and faster | maximum-score-from-performing-multiplication-operations | 0 | 1 | ***UPVOTE*** if it is helpful\n``` \nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n dp = [0] * (len(multipliers) + 1)\n for m in range(len(multipliers) - 1, -1, -1):\n pd = [0] * (m + 1)\n for l in range(m, -1, -1):\n pd[l] = max(dp[l + 1] + multipliers[m] * nums[l], \n dp[l] + multipliers[m] * nums[~(m - l)])\n dp = pd\n return dp[0]\n``` | 2 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
✅✔ SIMPLE PYTHON3 SOLUTION ✅✔98% less memory and faster | maximum-score-from-performing-multiplication-operations | 0 | 1 | ***UPVOTE*** if it is helpful\n``` \nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n dp = [0] * (len(multipliers) + 1)\n for m in range(len(multipliers) - 1, -1, -1):\n pd = [0] * (m + 1)\n for l in range(m, -1, -1):\n pd[l] = max(dp[l + 1] + multipliers[m] * nums[l], \n dp[l] + multipliers[m] * nums[~(m - l)])\n dp = pd\n return dp[0]\n``` | 2 | You are given a **valid** boolean expression as a string `expression` consisting of the characters `'1'`,`'0'`,`'&'` (bitwise **AND** operator),`'|'` (bitwise **OR** operator),`'('`, and `')'`.
* For example, `"()1|1 "` and `"(1)&() "` are **not valid** while `"1 "`, `"(((1))|(0)) "`, and `"1|(0&(1)) "` are **valid** expressions.
Return _the **minimum cost** to change the final value of the expression_.
* For example, if `expression = "1|1|(0&0)&1 "`, its **value** is `1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1`. We want to apply operations so that the **new** expression evaluates to `0`.
The **cost** of changing the final value of an expression is the **number of operations** performed on the expression. The types of **operations** are described as follows:
* Turn a `'1'` into a `'0'`.
* Turn a `'0'` into a `'1'`.
* Turn a `'&'` into a `'|'`.
* Turn a `'|'` into a `'&'`.
**Note:** `'&'` does **not** take precedence over `'|'` in the **order of calculation**. Evaluate parentheses **first**, then in **left-to-right** order.
**Example 1:**
**Input:** expression = "1&(0|1) "
**Output:** 1
**Explanation:** We can turn "1&(0**|**1) " into "1&(0**&**1) " by changing the '|' to a '&' using 1 operation.
The new expression evaluates to 0.
**Example 2:**
**Input:** expression = "(0&0)&(0&0&0) "
**Output:** 3
**Explanation:** We can turn "(0**&0**)**&**(0&0&0) " into "(0**|1**)**|**(0&0&0) " using 3 operations.
The new expression evaluates to 1.
**Example 3:**
**Input:** expression = "(0|(1|0&1)) "
**Output:** 1
**Explanation:** We can turn "(0|(**1**|0&1)) " into "(0|(**0**|0&1)) " using 1 operation.
The new expression evaluates to 0.
**Constraints:**
* `1 <= expression.length <= 105`
* `expression` only contains `'1'`,`'0'`,`'&'`,`'|'`,`'('`, and `')'`
* All parentheses are properly matched.
* There will be no empty parentheses (i.e: `"() "` is not a substring of `expression`). | At first glance, the solution seems to be greedy, but if you try to greedily take the largest value from the beginning or the end, this will not be optimal. You should try all scenarios but this will be costy. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity, and hence dp is a perfect choice here. |
[Python3] bottom-up dp | maximum-score-from-performing-multiplication-operations | 0 | 1 | \n```\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [[0]*m for _ in range(m+1)]\n \n for i in reversed(range(m)):\n for j in range(i, m): \n k = i + m - j - 1\n dp[i][j] = max(nums[i] * multipliers[k] + dp[i+1][j], nums[j-m+n] * multipliers[k] + dp[i][j-1])\n \n return dp[0][-1]\n```\n\nThis is the kind of problems that I really hate as it cannot pass for the plain top-down dp without tricks. Problems like this can be really misleading during contest as it causes people to suspect if it is really a dp. \n\n```\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n \n @lru_cache(2000)\n def fn(lo, hi, k):\n """Return max score from nums[lo:hi+1]."""\n if k == len(multipliers): return 0\n return max(nums[lo] * multipliers[k] + fn(lo+1, hi, k+1), nums[hi] * multipliers[k] + fn(lo, hi-1, k+1))\n \n return fn(0, len(nums)-1, 0)\n``` | 65 | You are given two **0-indexed** integer arrays `nums` and `multipliers` of size `n` and `m` respectively, where `n >= m`.
You begin with a score of `0`. You want to perform **exactly** `m` operations. On the `ith` operation (**0-indexed**) you will:
* Choose one integer `x` from **either the start or the end** of the array `nums`.
* Add `multipliers[i] * x` to your score.
* Note that `multipliers[0]` corresponds to the first operation, `multipliers[1]` to the second operation, and so on.
* Remove `x` from `nums`.
Return _the **maximum** score after performing_ `m` _operations._
**Example 1:**
**Input:** nums = \[1,2,3\], multipliers = \[3,2,1\]
**Output:** 14
**Explanation:** An optimal solution is as follows:
- Choose from the end, \[1,2,**3**\], adding 3 \* 3 = 9 to the score.
- Choose from the end, \[1,**2**\], adding 2 \* 2 = 4 to the score.
- Choose from the end, \[**1**\], adding 1 \* 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.
**Example 2:**
**Input:** nums = \[-5,-3,-3,-2,7,1\], multipliers = \[-10,-5,3,4,6\]
**Output:** 102
**Explanation:** An optimal solution is as follows:
- Choose from the start, \[**\-5**,-3,-3,-2,7,1\], adding -5 \* -10 = 50 to the score.
- Choose from the start, \[**\-3**,-3,-2,7,1\], adding -3 \* -5 = 15 to the score.
- Choose from the start, \[**\-3**,-2,7,1\], adding -3 \* 3 = -9 to the score.
- Choose from the end, \[-2,7,**1**\], adding 1 \* 4 = 4 to the score.
- Choose from the end, \[-2,**7**\], adding 7 \* 6 = 42 to the score.
The total score is 50 + 15 - 9 + 4 + 42 = 102.
**Constraints:**
* `n == nums.length`
* `m == multipliers.length`
* `1 <= m <= 300`
* `m <= n <= 105`
* `-1000 <= nums[i], multipliers[i] <= 1000` | As we can only delete characters, if we have multiple characters having the same frequency, we must decrease all the frequencies of them, except one. Sort the alphabet characters by their frequencies non-increasingly. Iterate on the alphabet characters, keep decreasing the frequency of the current character until it reaches a value that has not appeared before. |
[Python3] bottom-up dp | maximum-score-from-performing-multiplication-operations | 0 | 1 | \n```\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n n, m = len(nums), len(multipliers)\n dp = [[0]*m for _ in range(m+1)]\n \n for i in reversed(range(m)):\n for j in range(i, m): \n k = i + m - j - 1\n dp[i][j] = max(nums[i] * multipliers[k] + dp[i+1][j], nums[j-m+n] * multipliers[k] + dp[i][j-1])\n \n return dp[0][-1]\n```\n\nThis is the kind of problems that I really hate as it cannot pass for the plain top-down dp without tricks. Problems like this can be really misleading during contest as it causes people to suspect if it is really a dp. \n\n```\nclass Solution:\n def maximumScore(self, nums: List[int], multipliers: List[int]) -> int:\n \n @lru_cache(2000)\n def fn(lo, hi, k):\n """Return max score from nums[lo:hi+1]."""\n if k == len(multipliers): return 0\n return max(nums[lo] * multipliers[k] + fn(lo+1, hi, k+1), nums[hi] * multipliers[k] + fn(lo, hi-1, k+1))\n \n return fn(0, len(nums)-1, 0)\n``` | 65 | You are given a **valid** boolean expression as a string `expression` consisting of the characters `'1'`,`'0'`,`'&'` (bitwise **AND** operator),`'|'` (bitwise **OR** operator),`'('`, and `')'`.
* For example, `"()1|1 "` and `"(1)&() "` are **not valid** while `"1 "`, `"(((1))|(0)) "`, and `"1|(0&(1)) "` are **valid** expressions.
Return _the **minimum cost** to change the final value of the expression_.
* For example, if `expression = "1|1|(0&0)&1 "`, its **value** is `1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1`. We want to apply operations so that the **new** expression evaluates to `0`.
The **cost** of changing the final value of an expression is the **number of operations** performed on the expression. The types of **operations** are described as follows:
* Turn a `'1'` into a `'0'`.
* Turn a `'0'` into a `'1'`.
* Turn a `'&'` into a `'|'`.
* Turn a `'|'` into a `'&'`.
**Note:** `'&'` does **not** take precedence over `'|'` in the **order of calculation**. Evaluate parentheses **first**, then in **left-to-right** order.
**Example 1:**
**Input:** expression = "1&(0|1) "
**Output:** 1
**Explanation:** We can turn "1&(0**|**1) " into "1&(0**&**1) " by changing the '|' to a '&' using 1 operation.
The new expression evaluates to 0.
**Example 2:**
**Input:** expression = "(0&0)&(0&0&0) "
**Output:** 3
**Explanation:** We can turn "(0**&0**)**&**(0&0&0) " into "(0**|1**)**|**(0&0&0) " using 3 operations.
The new expression evaluates to 1.
**Example 3:**
**Input:** expression = "(0|(1|0&1)) "
**Output:** 1
**Explanation:** We can turn "(0|(**1**|0&1)) " into "(0|(**0**|0&1)) " using 1 operation.
The new expression evaluates to 0.
**Constraints:**
* `1 <= expression.length <= 105`
* `expression` only contains `'1'`,`'0'`,`'&'`,`'|'`,`'('`, and `')'`
* All parentheses are properly matched.
* There will be no empty parentheses (i.e: `"() "` is not a substring of `expression`). | At first glance, the solution seems to be greedy, but if you try to greedily take the largest value from the beginning or the end, this will not be optimal. You should try all scenarios but this will be costy. Memoizing the pre-visited states while trying all the possible scenarios will reduce the complexity, and hence dp is a perfect choice here. |
[Python 3] simple DP | maximize-palindrome-length-from-subsequences | 0 | 1 | \tclass Solution:\n\t\tdef longestPalindrome(self, word1: str, word2: str) -> int:\n\t\t\tres=0\n\t\t\tnew_word=word1+word2\n\t\t\tn,mid=len(word1)+len(word2),len(word1)\n\t\t\tdp=[[0]*n for _ in range(n)]\n\t\t\tfor i in range(n):\n\t\t\t\tdp[i][i]=1\n\t\t\tfor l in range(n-2,-1,-1):\n\t\t\t\tfor r in range(l+1,n,1):\n\t\t\t\t\tif new_word[l]==new_word[r]:\n\t\t\t\t\t\tdp[l][r]=(dp[l+1][r-1] if r-1>=l+1 else 0)+2\n\t\t\t\t\t\tif l<mid and r>=mid:\n\t\t\t\t\t\t\tres=max(res,dp[l][r])\n\t\t\t\t\telse:\n\t\t\t\t\t\tdp[l][r]=max(dp[l+1][r],dp[l][r-1])\n\t\t\treturn res | 1 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
[Python 3] simple DP | maximize-palindrome-length-from-subsequences | 0 | 1 | \tclass Solution:\n\t\tdef longestPalindrome(self, word1: str, word2: str) -> int:\n\t\t\tres=0\n\t\t\tnew_word=word1+word2\n\t\t\tn,mid=len(word1)+len(word2),len(word1)\n\t\t\tdp=[[0]*n for _ in range(n)]\n\t\t\tfor i in range(n):\n\t\t\t\tdp[i][i]=1\n\t\t\tfor l in range(n-2,-1,-1):\n\t\t\t\tfor r in range(l+1,n,1):\n\t\t\t\t\tif new_word[l]==new_word[r]:\n\t\t\t\t\t\tdp[l][r]=(dp[l+1][r-1] if r-1>=l+1 else 0)+2\n\t\t\t\t\t\tif l<mid and r>=mid:\n\t\t\t\t\t\t\tres=max(res,dp[l][r])\n\t\t\t\t\telse:\n\t\t\t\t\t\tdp[l][r]=max(dp[l+1][r],dp[l][r-1])\n\t\t\treturn res | 1 | You are given an array of strings `words` (**0-indexed**).
In one operation, pick two **distinct** indices `i` and `j`, where `words[i]` is a non-empty string, and move **any** character from `words[i]` to **any** position in `words[j]`.
Return `true` _if you can make **every** string in_ `words` _**equal** using **any** number of operations_, _and_ `false` _otherwise_.
**Example 1:**
**Input:** words = \[ "abc ", "aabc ", "bc "\]
**Output:** true
**Explanation:** Move the first 'a' in `words[1] to the front of words[2], to make` `words[1]` = "abc " and words\[2\] = "abc ".
All the strings are now equal to "abc ", so return `true`.
**Example 2:**
**Input:** words = \[ "ab ", "a "\]
**Output:** false
**Explanation:** It is impossible to make all the strings equal using the operation.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | Let's ignore the non-empty subsequence constraint. We can concatenate the two strings and find the largest palindromic subsequence with dynamic programming. Iterate through every pair of characters word1[i] and word2[j], and see if some palindrome begins with word1[i] and ends with word2[j]. This ensures that the subsequences are non-empty. |
[Python3] top-down dp | maximize-palindrome-length-from-subsequences | 0 | 1 | **Algo**\nFind common characters in `word1` and `word2` and use the anchor to find longest palindromic subsequence. \n\n**Implementation**\n```\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n \n @cache\n def fn(lo, hi):\n """Return length of longest palindromic subsequence."""\n if lo >= hi: return int(lo == hi)\n if word[lo] == word[hi]: return 2 + fn(lo+1, hi-1)\n return max(fn(lo+1, hi), fn(lo, hi-1))\n \n ans = 0\n word = word1 + word2\n for x in ascii_lowercase: \n i = word1.find(x) \n j = word2.rfind(x)\n if i != -1 and j != -1: ans = max(ans, fn(i, j + len(word1)))\n return ans \n```\n\n**Analysis**\nTime complexity `O((M+N)^2)`\nSpace complexity `O((M+N)^2)` | 15 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
[Python3] top-down dp | maximize-palindrome-length-from-subsequences | 0 | 1 | **Algo**\nFind common characters in `word1` and `word2` and use the anchor to find longest palindromic subsequence. \n\n**Implementation**\n```\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n \n @cache\n def fn(lo, hi):\n """Return length of longest palindromic subsequence."""\n if lo >= hi: return int(lo == hi)\n if word[lo] == word[hi]: return 2 + fn(lo+1, hi-1)\n return max(fn(lo+1, hi), fn(lo, hi-1))\n \n ans = 0\n word = word1 + word2\n for x in ascii_lowercase: \n i = word1.find(x) \n j = word2.rfind(x)\n if i != -1 and j != -1: ans = max(ans, fn(i, j + len(word1)))\n return ans \n```\n\n**Analysis**\nTime complexity `O((M+N)^2)`\nSpace complexity `O((M+N)^2)` | 15 | You are given an array of strings `words` (**0-indexed**).
In one operation, pick two **distinct** indices `i` and `j`, where `words[i]` is a non-empty string, and move **any** character from `words[i]` to **any** position in `words[j]`.
Return `true` _if you can make **every** string in_ `words` _**equal** using **any** number of operations_, _and_ `false` _otherwise_.
**Example 1:**
**Input:** words = \[ "abc ", "aabc ", "bc "\]
**Output:** true
**Explanation:** Move the first 'a' in `words[1] to the front of words[2], to make` `words[1]` = "abc " and words\[2\] = "abc ".
All the strings are now equal to "abc ", so return `true`.
**Example 2:**
**Input:** words = \[ "ab ", "a "\]
**Output:** false
**Explanation:** It is impossible to make all the strings equal using the operation.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | Let's ignore the non-empty subsequence constraint. We can concatenate the two strings and find the largest palindromic subsequence with dynamic programming. Iterate through every pair of characters word1[i] and word2[j], and see if some palindrome begins with word1[i] and ends with word2[j]. This ensures that the subsequences are non-empty. |
[Python] Dynamic Programming O((m+n)^2) | maximize-palindrome-length-from-subsequences | 0 | 1 | ```\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n s1 = word1 + word2\n n = len(s1)\n dp = [[0] * n for i in range(n)]\n ans = 0\n for i in range(n-1,-1,-1):\n\t\t# mark every character as a 1 length palindrome\n dp[i][i] = 1\n for j in range(i+1,n):\n\t\t\t# new palindrome is found\n if s1[i] == s1[j]:\n dp[i][j] = dp[i+1][j-1] + 2\n\t\t\t\t\t# if the palindrome includes both string consider it as a valid\n if i < len(word1) and j >= len(word1):\n ans = max(ans,dp[i][j])\n else:\n dp[i][j] = max(dp[i][j-1],dp[i+1][j])\n \n return ans\n``` | 5 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
[Python] Dynamic Programming O((m+n)^2) | maximize-palindrome-length-from-subsequences | 0 | 1 | ```\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n s1 = word1 + word2\n n = len(s1)\n dp = [[0] * n for i in range(n)]\n ans = 0\n for i in range(n-1,-1,-1):\n\t\t# mark every character as a 1 length palindrome\n dp[i][i] = 1\n for j in range(i+1,n):\n\t\t\t# new palindrome is found\n if s1[i] == s1[j]:\n dp[i][j] = dp[i+1][j-1] + 2\n\t\t\t\t\t# if the palindrome includes both string consider it as a valid\n if i < len(word1) and j >= len(word1):\n ans = max(ans,dp[i][j])\n else:\n dp[i][j] = max(dp[i][j-1],dp[i+1][j])\n \n return ans\n``` | 5 | You are given an array of strings `words` (**0-indexed**).
In one operation, pick two **distinct** indices `i` and `j`, where `words[i]` is a non-empty string, and move **any** character from `words[i]` to **any** position in `words[j]`.
Return `true` _if you can make **every** string in_ `words` _**equal** using **any** number of operations_, _and_ `false` _otherwise_.
**Example 1:**
**Input:** words = \[ "abc ", "aabc ", "bc "\]
**Output:** true
**Explanation:** Move the first 'a' in `words[1] to the front of words[2], to make` `words[1]` = "abc " and words\[2\] = "abc ".
All the strings are now equal to "abc ", so return `true`.
**Example 2:**
**Input:** words = \[ "ab ", "a "\]
**Output:** false
**Explanation:** It is impossible to make all the strings equal using the operation.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | Let's ignore the non-empty subsequence constraint. We can concatenate the two strings and find the largest palindromic subsequence with dynamic programming. Iterate through every pair of characters word1[i] and word2[j], and see if some palindrome begins with word1[i] and ends with word2[j]. This ensures that the subsequences are non-empty. |
DP | maximize-palindrome-length-from-subsequences | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can use dynamic programming to find the longest palindrome that can be constructed using subsequences from word1 and word2. We\'ll create a 2D table, dp, where dp[i][j] represents the length of the longest palindrome that can be formed using the subsequences of word1[i:] and word2[j:].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the solution is $$O(n^2)$$, where n is the total length of the combined strings word1 and word2. This is because we are using a nested loop to iterate through the characters of the combined string, and for each character, we perform constant time operations. The nested loop runs for a maximum of $$n^2$$ iterations.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the solution is $$O(n^2)$$ as well. We use a 2D dp table with dimensions n x n to store the intermediate results of the dynamic programming approach. Therefore, the space required is proportional to the square of the length of the combined string.\n# Code\n```\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n combined_word = word1 + word2\n n1, n2, n = len(word1), len(word2), len(combined_word)\n dp = [[0] * n for _ in range(n)]\n\n for i in range(n - 1, -1, -1):\n dp[i][i] = 1\n for j in range(i + 1, n):\n if combined_word[i] == combined_word[j]:\n dp[i][j] = dp[i + 1][j - 1] + 2\n else:\n dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])\n\n max_palindrome = 0\n for i in range(n1):\n for j in range(n2):\n if word1[i] == word2[j]:\n palindrome_len = dp[i][n1 + j]\n max_palindrome = max(max_palindrome, palindrome_len)\n\n return max_palindrome\n\n``` | 0 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
DP | maximize-palindrome-length-from-subsequences | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can use dynamic programming to find the longest palindrome that can be constructed using subsequences from word1 and word2. We\'ll create a 2D table, dp, where dp[i][j] represents the length of the longest palindrome that can be formed using the subsequences of word1[i:] and word2[j:].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the solution is $$O(n^2)$$, where n is the total length of the combined strings word1 and word2. This is because we are using a nested loop to iterate through the characters of the combined string, and for each character, we perform constant time operations. The nested loop runs for a maximum of $$n^2$$ iterations.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the solution is $$O(n^2)$$ as well. We use a 2D dp table with dimensions n x n to store the intermediate results of the dynamic programming approach. Therefore, the space required is proportional to the square of the length of the combined string.\n# Code\n```\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n combined_word = word1 + word2\n n1, n2, n = len(word1), len(word2), len(combined_word)\n dp = [[0] * n for _ in range(n)]\n\n for i in range(n - 1, -1, -1):\n dp[i][i] = 1\n for j in range(i + 1, n):\n if combined_word[i] == combined_word[j]:\n dp[i][j] = dp[i + 1][j - 1] + 2\n else:\n dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])\n\n max_palindrome = 0\n for i in range(n1):\n for j in range(n2):\n if word1[i] == word2[j]:\n palindrome_len = dp[i][n1 + j]\n max_palindrome = max(max_palindrome, palindrome_len)\n\n return max_palindrome\n\n``` | 0 | You are given an array of strings `words` (**0-indexed**).
In one operation, pick two **distinct** indices `i` and `j`, where `words[i]` is a non-empty string, and move **any** character from `words[i]` to **any** position in `words[j]`.
Return `true` _if you can make **every** string in_ `words` _**equal** using **any** number of operations_, _and_ `false` _otherwise_.
**Example 1:**
**Input:** words = \[ "abc ", "aabc ", "bc "\]
**Output:** true
**Explanation:** Move the first 'a' in `words[1] to the front of words[2], to make` `words[1]` = "abc " and words\[2\] = "abc ".
All the strings are now equal to "abc ", so return `true`.
**Example 2:**
**Input:** words = \[ "ab ", "a "\]
**Output:** false
**Explanation:** It is impossible to make all the strings equal using the operation.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | Let's ignore the non-empty subsequence constraint. We can concatenate the two strings and find the largest palindromic subsequence with dynamic programming. Iterate through every pair of characters word1[i] and word2[j], and see if some palindrome begins with word1[i] and ends with word2[j]. This ensures that the subsequences are non-empty. |
Python | O((m+n)**2) | Recursion + Memoization question | maximize-palindrome-length-from-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O((m+n)**2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nfrom bisect import bisect_left,bisect_right\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n dct1 = defaultdict(lambda:-1)\n dct2 = defaultdict(lambda:-1)\n def doItt(s,i,j,isFirst):\n if j<i:return 0\n if i==j:return 1\n if isFirst:\n if dct1[(i,j)]+1:return dct1[(i,j)]\n dct1[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct1[(i,j)] = max(dct1[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct1[(i,j)]\n else:\n if dct2[(i,j)]+1:return dct2[(i,j)]\n dct2[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct2[(i,j)] = max(dct2[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct2[(i,j)]\n doItt(word1,0,len(word1)-1,True)\n doItt(word2,0,len(word2)-1,False)\n dct = defaultdict(lambda:-1)\n arr = word1+word2\n ans = 0\n def doIt(i=0,j=len(arr)-1):\n nonlocal ans\n if j<=i:return max(j-i+1,0)\n if i>=len(word1):return dct2[(i-len(word1),j-len(word1))]\n if j<len(word1):return dct1[(i,j)]\n if dct[(i,j)]+1:return dct[(i,j)]\n if arr[i]==arr[j]:\n dct[i,j] = doIt(i+1,j-1)+2\n if i<len(word1) and j>=len(word1):\n ans = max(ans,dct[i,j])\n else:\n dct[(i,j)] = max(doIt(i,j-1),doIt(i+1,j))\n return dct[(i,j)]\n doIt()\n return ans\n\n\n \n``` | 0 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
Python | O((m+n)**2) | Recursion + Memoization question | maximize-palindrome-length-from-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O((m+n)**2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nfrom bisect import bisect_left,bisect_right\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n dct1 = defaultdict(lambda:-1)\n dct2 = defaultdict(lambda:-1)\n def doItt(s,i,j,isFirst):\n if j<i:return 0\n if i==j:return 1\n if isFirst:\n if dct1[(i,j)]+1:return dct1[(i,j)]\n dct1[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct1[(i,j)] = max(dct1[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct1[(i,j)]\n else:\n if dct2[(i,j)]+1:return dct2[(i,j)]\n dct2[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct2[(i,j)] = max(dct2[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct2[(i,j)]\n doItt(word1,0,len(word1)-1,True)\n doItt(word2,0,len(word2)-1,False)\n dct = defaultdict(lambda:-1)\n arr = word1+word2\n ans = 0\n def doIt(i=0,j=len(arr)-1):\n nonlocal ans\n if j<=i:return max(j-i+1,0)\n if i>=len(word1):return dct2[(i-len(word1),j-len(word1))]\n if j<len(word1):return dct1[(i,j)]\n if dct[(i,j)]+1:return dct[(i,j)]\n if arr[i]==arr[j]:\n dct[i,j] = doIt(i+1,j-1)+2\n if i<len(word1) and j>=len(word1):\n ans = max(ans,dct[i,j])\n else:\n dct[(i,j)] = max(doIt(i,j-1),doIt(i+1,j))\n return dct[(i,j)]\n doIt()\n return ans\n\n\n \n``` | 0 | You are given an array of strings `words` (**0-indexed**).
In one operation, pick two **distinct** indices `i` and `j`, where `words[i]` is a non-empty string, and move **any** character from `words[i]` to **any** position in `words[j]`.
Return `true` _if you can make **every** string in_ `words` _**equal** using **any** number of operations_, _and_ `false` _otherwise_.
**Example 1:**
**Input:** words = \[ "abc ", "aabc ", "bc "\]
**Output:** true
**Explanation:** Move the first 'a' in `words[1] to the front of words[2], to make` `words[1]` = "abc " and words\[2\] = "abc ".
All the strings are now equal to "abc ", so return `true`.
**Example 2:**
**Input:** words = \[ "ab ", "a "\]
**Output:** false
**Explanation:** It is impossible to make all the strings equal using the operation.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | Let's ignore the non-empty subsequence constraint. We can concatenate the two strings and find the largest palindromic subsequence with dynamic programming. Iterate through every pair of characters word1[i] and word2[j], and see if some palindrome begins with word1[i] and ends with word2[j]. This ensures that the subsequences are non-empty. |
Python | O(max(m,n)**2) solution | Recursion + Memoization question | maximize-palindrome-length-from-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(3*(max(m,n)**2))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nfrom bisect import bisect_left,bisect_right\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n dct1 = defaultdict(lambda:-1)\n dct2 = defaultdict(lambda:-1)\n def doItt(s,i,j,isFirst):\n if j<i:return 0\n if i==j:return 1\n if isFirst:\n if dct1[(i,j)]+1:return dct1[(i,j)]\n dct1[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct1[(i,j)] = max(dct1[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct1[(i,j)]\n else:\n if dct2[(i,j)]+1:return dct2[(i,j)]\n dct2[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct2[(i,j)] = max(dct2[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct2[(i,j)]\n doItt(word1,0,len(word1)-1,True)\n doItt(word2,0,len(word2)-1,False)\n dct = defaultdict(lambda:-1)\n arr = word1+word2\n ans = 0\n def doIt(i=0,j=len(arr)-1):\n nonlocal ans\n if j<=i:return max(j-i+1,0)\n if i>=len(word1):return dct2[(i-len(word1),j-len(word1))]\n if j<len(word1):return dct1[(i,j)]\n if dct[(i,j)]+1:return dct[(i,j)]\n if arr[i]==arr[j]:\n dct[i,j] = doIt(i+1,j-1)+2\n if i<len(word1) and j>=len(word1):\n ans = max(ans,dct[i,j])\n else:\n dct[(i,j)] = max(doIt(i,j-1),doIt(i+1,j))\n return dct[(i,j)]\n doIt()\n return ans\n\n\n \n``` | 0 | You are given two strings, `word1` and `word2`. You want to construct a string in the following manner:
* Choose some **non-empty** subsequence `subsequence1` from `word1`.
* Choose some **non-empty** subsequence `subsequence2` from `word2`.
* Concatenate the subsequences: `subsequence1 + subsequence2`, to make the string.
Return _the **length** of the longest **palindrome** that can be constructed in the described manner._ If no palindromes can be constructed, return `0`.
A **subsequence** of a string `s` is a string that can be made by deleting some (possibly none) characters from `s` without changing the order of the remaining characters.
A **palindrome** is a string that reads the same forward as well as backward.
**Example 1:**
**Input:** word1 = "cacb ", word2 = "cbba "
**Output:** 5
**Explanation:** Choose "ab " from word1 and "cba " from word2 to make "abcba ", which is a palindrome.
**Example 2:**
**Input:** word1 = "ab ", word2 = "ab "
**Output:** 3
**Explanation:** Choose "ab " from word1 and "a " from word2 to make "aba ", which is a palindrome.
**Example 3:**
**Input:** word1 = "aa ", word2 = "bb "
**Output:** 0
**Explanation:** You cannot construct a palindrome from the described method, so return 0.
**Constraints:**
* `1 <= word1.length, word2.length <= 1000`
* `word1` and `word2` consist of lowercase English letters. | Greedily sell the most expensive ball. There is some value k where all balls of value > k are sold, and some, (maybe 0) of balls of value k are sold. Use binary search to find this value k, and use maths to find the total sum. |
Python | O(max(m,n)**2) solution | Recursion + Memoization question | maximize-palindrome-length-from-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(3*(max(m,n)**2))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nfrom bisect import bisect_left,bisect_right\nclass Solution:\n def longestPalindrome(self, word1: str, word2: str) -> int:\n dct1 = defaultdict(lambda:-1)\n dct2 = defaultdict(lambda:-1)\n def doItt(s,i,j,isFirst):\n if j<i:return 0\n if i==j:return 1\n if isFirst:\n if dct1[(i,j)]+1:return dct1[(i,j)]\n dct1[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct1[(i,j)] = max(dct1[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct1[(i,j)]\n else:\n if dct2[(i,j)]+1:return dct2[(i,j)]\n dct2[(i,j)] = max(doItt(s,i,j-1,isFirst),doItt(s,i+1,j,isFirst))\n if s[i]==s[j]:\n dct2[(i,j)] = max(dct2[(i,j)],doItt(s,i+1,j-1,isFirst)+2)\n return dct2[(i,j)]\n doItt(word1,0,len(word1)-1,True)\n doItt(word2,0,len(word2)-1,False)\n dct = defaultdict(lambda:-1)\n arr = word1+word2\n ans = 0\n def doIt(i=0,j=len(arr)-1):\n nonlocal ans\n if j<=i:return max(j-i+1,0)\n if i>=len(word1):return dct2[(i-len(word1),j-len(word1))]\n if j<len(word1):return dct1[(i,j)]\n if dct[(i,j)]+1:return dct[(i,j)]\n if arr[i]==arr[j]:\n dct[i,j] = doIt(i+1,j-1)+2\n if i<len(word1) and j>=len(word1):\n ans = max(ans,dct[i,j])\n else:\n dct[(i,j)] = max(doIt(i,j-1),doIt(i+1,j))\n return dct[(i,j)]\n doIt()\n return ans\n\n\n \n``` | 0 | You are given an array of strings `words` (**0-indexed**).
In one operation, pick two **distinct** indices `i` and `j`, where `words[i]` is a non-empty string, and move **any** character from `words[i]` to **any** position in `words[j]`.
Return `true` _if you can make **every** string in_ `words` _**equal** using **any** number of operations_, _and_ `false` _otherwise_.
**Example 1:**
**Input:** words = \[ "abc ", "aabc ", "bc "\]
**Output:** true
**Explanation:** Move the first 'a' in `words[1] to the front of words[2], to make` `words[1]` = "abc " and words\[2\] = "abc ".
All the strings are now equal to "abc ", so return `true`.
**Example 2:**
**Input:** words = \[ "ab ", "a "\]
**Output:** false
**Explanation:** It is impossible to make all the strings equal using the operation.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | Let's ignore the non-empty subsequence constraint. We can concatenate the two strings and find the largest palindromic subsequence with dynamic programming. Iterate through every pair of characters word1[i] and word2[j], and see if some palindrome begins with word1[i] and ends with word2[j]. This ensures that the subsequences are non-empty. |
Solution of count items matching a rule problem | count-items-matching-a-rule | 0 | 1 | # Approach\n- Step one: create table with an index of Each Category\n- Step two: find index of category\n- Step three: count every matches in items list\n\n# Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n\n- Space complexity:\n$$O(n)$$ - as we use extra space for rules table\n\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n rules = {"type": 0, "color": 1, "name": 2}\n idx = rules[ruleKey]\n count = 0\n for i in range(len(items)):\n if items[i][idx] == ruleValue:\n count += 1\n return count\n``` | 1 | You are given an array `items`, where each `items[i] = [typei, colori, namei]` describes the type, color, and name of the `ith` item. You are also given a rule represented by two strings, `ruleKey` and `ruleValue`.
The `ith` item is said to match the rule if **one** of the following is true:
* `ruleKey == "type "` and `ruleValue == typei`.
* `ruleKey == "color "` and `ruleValue == colori`.
* `ruleKey == "name "` and `ruleValue == namei`.
Return _the number of items that match the given rule_.
**Example 1:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "lenovo "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "color ", ruleValue = "silver "
**Output:** 1
**Explanation:** There is only one item matching the given rule, which is \[ "computer ", "silver ", "lenovo "\].
**Example 2:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "phone "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "type ", ruleValue = "phone "
**Output:** 2
**Explanation:** There are only two items matching the given rule, which are \[ "phone ", "blue ", "pixel "\] and \[ "phone ", "gold ", "iphone "\]. Note that the item \[ "computer ", "silver ", "phone "\] does not match.
**Constraints:**
* `1 <= items.length <= 104`
* `1 <= typei.length, colori.length, namei.length, ruleValue.length <= 10`
* `ruleKey` is equal to either `"type "`, `"color "`, or `"name "`.
* All strings consist only of lowercase letters. | null |
Solution of count items matching a rule problem | count-items-matching-a-rule | 0 | 1 | # Approach\n- Step one: create table with an index of Each Category\n- Step two: find index of category\n- Step three: count every matches in items list\n\n# Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n\n- Space complexity:\n$$O(n)$$ - as we use extra space for rules table\n\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n rules = {"type": 0, "color": 1, "name": 2}\n idx = rules[ruleKey]\n count = 0\n for i in range(len(items)):\n if items[i][idx] == ruleValue:\n count += 1\n return count\n``` | 1 | A **triplet** is an array of three integers. You are given a 2D integer array `triplets`, where `triplets[i] = [ai, bi, ci]` describes the `ith` **triplet**. You are also given an integer array `target = [x, y, z]` that describes the **triplet** you want to obtain.
To obtain `target`, you may apply the following operation on `triplets` **any number** of times (possibly **zero**):
* Choose two indices (**0-indexed**) `i` and `j` (`i != j`) and **update** `triplets[j]` to become `[max(ai, aj), max(bi, bj), max(ci, cj)]`.
* For example, if `triplets[i] = [2, 5, 3]` and `triplets[j] = [1, 7, 5]`, `triplets[j]` will be updated to `[max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5]`.
Return `true` _if it is possible to obtain the_ `target` _**triplet**_ `[x, y, z]` _as an **element** of_ `triplets`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** triplets = \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\], target = \[2,7,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and last triplets \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\]. Update the last triplet to be \[max(2,1), max(5,7), max(3,5)\] = \[2,7,5\]. triplets = \[\[2,5,3\],\[1,8,4\],\[2,7,5\]\]
The target triplet \[2,7,5\] is now an element of triplets.
**Example 2:**
**Input:** triplets = \[\[3,4,5\],\[4,5,6\]\], target = \[3,2,5\]
**Output:** false
**Explanation:** It is impossible to have \[3,2,5\] as an element because there is no 2 in any of the triplets.
**Example 3:**
**Input:** triplets = \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\], target = \[5,5,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and third triplets \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\]. Update the third triplet to be \[max(2,1), max(5,2), max(3,5)\] = \[2,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\].
- Choose the third and fourth triplets \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\]. Update the fourth triplet to be \[max(2,5), max(5,2), max(5,3)\] = \[5,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,5,5\]\].
The target triplet \[5,5,5\] is now an element of triplets.
**Constraints:**
* `1 <= triplets.length <= 105`
* `triplets[i].length == target.length == 3`
* `1 <= ai, bi, ci, x, y, z <= 1000` | Iterate on each item, and check if each one matches the rule according to the statement. |
python code in easy | count-items-matching-a-rule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n if(ruleKey=="type"):\n k=0\n elif(ruleKey=="color"):\n k=1\n else:\n k=2\n c=0\n for i in items:\n if(i[k]==ruleValue):\n c=c+1\n return c\n``` | 1 | You are given an array `items`, where each `items[i] = [typei, colori, namei]` describes the type, color, and name of the `ith` item. You are also given a rule represented by two strings, `ruleKey` and `ruleValue`.
The `ith` item is said to match the rule if **one** of the following is true:
* `ruleKey == "type "` and `ruleValue == typei`.
* `ruleKey == "color "` and `ruleValue == colori`.
* `ruleKey == "name "` and `ruleValue == namei`.
Return _the number of items that match the given rule_.
**Example 1:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "lenovo "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "color ", ruleValue = "silver "
**Output:** 1
**Explanation:** There is only one item matching the given rule, which is \[ "computer ", "silver ", "lenovo "\].
**Example 2:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "phone "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "type ", ruleValue = "phone "
**Output:** 2
**Explanation:** There are only two items matching the given rule, which are \[ "phone ", "blue ", "pixel "\] and \[ "phone ", "gold ", "iphone "\]. Note that the item \[ "computer ", "silver ", "phone "\] does not match.
**Constraints:**
* `1 <= items.length <= 104`
* `1 <= typei.length, colori.length, namei.length, ruleValue.length <= 10`
* `ruleKey` is equal to either `"type "`, `"color "`, or `"name "`.
* All strings consist only of lowercase letters. | null |
python code in easy | count-items-matching-a-rule | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n if(ruleKey=="type"):\n k=0\n elif(ruleKey=="color"):\n k=1\n else:\n k=2\n c=0\n for i in items:\n if(i[k]==ruleValue):\n c=c+1\n return c\n``` | 1 | A **triplet** is an array of three integers. You are given a 2D integer array `triplets`, where `triplets[i] = [ai, bi, ci]` describes the `ith` **triplet**. You are also given an integer array `target = [x, y, z]` that describes the **triplet** you want to obtain.
To obtain `target`, you may apply the following operation on `triplets` **any number** of times (possibly **zero**):
* Choose two indices (**0-indexed**) `i` and `j` (`i != j`) and **update** `triplets[j]` to become `[max(ai, aj), max(bi, bj), max(ci, cj)]`.
* For example, if `triplets[i] = [2, 5, 3]` and `triplets[j] = [1, 7, 5]`, `triplets[j]` will be updated to `[max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5]`.
Return `true` _if it is possible to obtain the_ `target` _**triplet**_ `[x, y, z]` _as an **element** of_ `triplets`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** triplets = \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\], target = \[2,7,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and last triplets \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\]. Update the last triplet to be \[max(2,1), max(5,7), max(3,5)\] = \[2,7,5\]. triplets = \[\[2,5,3\],\[1,8,4\],\[2,7,5\]\]
The target triplet \[2,7,5\] is now an element of triplets.
**Example 2:**
**Input:** triplets = \[\[3,4,5\],\[4,5,6\]\], target = \[3,2,5\]
**Output:** false
**Explanation:** It is impossible to have \[3,2,5\] as an element because there is no 2 in any of the triplets.
**Example 3:**
**Input:** triplets = \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\], target = \[5,5,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and third triplets \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\]. Update the third triplet to be \[max(2,1), max(5,2), max(3,5)\] = \[2,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\].
- Choose the third and fourth triplets \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\]. Update the fourth triplet to be \[max(2,5), max(5,2), max(5,3)\] = \[5,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,5,5\]\].
The target triplet \[5,5,5\] is now an element of triplets.
**Constraints:**
* `1 <= triplets.length <= 105`
* `triplets[i].length == target.length == 3`
* `1 <= ai, bi, ci, x, y, z <= 1000` | Iterate on each item, and check if each one matches the rule according to the statement. |
Python 3 | 2-liner | Explanation | count-items-matching-a-rule | 0 | 1 | ### Explanation\n- Create a dict `{ruleKey: index_of_rulekey}`\n- Filter out items that satisfy the condition\n\n### Implementation\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n d = {\'type\': 0, \'color\': 1, \'name\': 2}\n return sum(1 for item in items if item[d[ruleKey]] == ruleValue)\n``` | 64 | You are given an array `items`, where each `items[i] = [typei, colori, namei]` describes the type, color, and name of the `ith` item. You are also given a rule represented by two strings, `ruleKey` and `ruleValue`.
The `ith` item is said to match the rule if **one** of the following is true:
* `ruleKey == "type "` and `ruleValue == typei`.
* `ruleKey == "color "` and `ruleValue == colori`.
* `ruleKey == "name "` and `ruleValue == namei`.
Return _the number of items that match the given rule_.
**Example 1:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "lenovo "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "color ", ruleValue = "silver "
**Output:** 1
**Explanation:** There is only one item matching the given rule, which is \[ "computer ", "silver ", "lenovo "\].
**Example 2:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "phone "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "type ", ruleValue = "phone "
**Output:** 2
**Explanation:** There are only two items matching the given rule, which are \[ "phone ", "blue ", "pixel "\] and \[ "phone ", "gold ", "iphone "\]. Note that the item \[ "computer ", "silver ", "phone "\] does not match.
**Constraints:**
* `1 <= items.length <= 104`
* `1 <= typei.length, colori.length, namei.length, ruleValue.length <= 10`
* `ruleKey` is equal to either `"type "`, `"color "`, or `"name "`.
* All strings consist only of lowercase letters. | null |
Python 3 | 2-liner | Explanation | count-items-matching-a-rule | 0 | 1 | ### Explanation\n- Create a dict `{ruleKey: index_of_rulekey}`\n- Filter out items that satisfy the condition\n\n### Implementation\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n d = {\'type\': 0, \'color\': 1, \'name\': 2}\n return sum(1 for item in items if item[d[ruleKey]] == ruleValue)\n``` | 64 | A **triplet** is an array of three integers. You are given a 2D integer array `triplets`, where `triplets[i] = [ai, bi, ci]` describes the `ith` **triplet**. You are also given an integer array `target = [x, y, z]` that describes the **triplet** you want to obtain.
To obtain `target`, you may apply the following operation on `triplets` **any number** of times (possibly **zero**):
* Choose two indices (**0-indexed**) `i` and `j` (`i != j`) and **update** `triplets[j]` to become `[max(ai, aj), max(bi, bj), max(ci, cj)]`.
* For example, if `triplets[i] = [2, 5, 3]` and `triplets[j] = [1, 7, 5]`, `triplets[j]` will be updated to `[max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5]`.
Return `true` _if it is possible to obtain the_ `target` _**triplet**_ `[x, y, z]` _as an **element** of_ `triplets`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** triplets = \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\], target = \[2,7,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and last triplets \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\]. Update the last triplet to be \[max(2,1), max(5,7), max(3,5)\] = \[2,7,5\]. triplets = \[\[2,5,3\],\[1,8,4\],\[2,7,5\]\]
The target triplet \[2,7,5\] is now an element of triplets.
**Example 2:**
**Input:** triplets = \[\[3,4,5\],\[4,5,6\]\], target = \[3,2,5\]
**Output:** false
**Explanation:** It is impossible to have \[3,2,5\] as an element because there is no 2 in any of the triplets.
**Example 3:**
**Input:** triplets = \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\], target = \[5,5,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and third triplets \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\]. Update the third triplet to be \[max(2,1), max(5,2), max(3,5)\] = \[2,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\].
- Choose the third and fourth triplets \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\]. Update the fourth triplet to be \[max(2,5), max(5,2), max(5,3)\] = \[5,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,5,5\]\].
The target triplet \[5,5,5\] is now an element of triplets.
**Constraints:**
* `1 <= triplets.length <= 105`
* `triplets[i].length == target.length == 3`
* `1 <= ai, bi, ci, x, y, z <= 1000` | Iterate on each item, and check if each one matches the rule according to the statement. |
✅ Explained - Simple and Clear Python3 Code✅ | count-items-matching-a-rule | 0 | 1 | # Intuition\nThe problem requires counting the number of items that match a given rule. We are given an array of items, where each item is represented by its type, color, and name. The rule is defined by a ruleKey and a ruleValue. We need to determine if the ruleKey matches the corresponding attribute of each item, and if so, check if the ruleValue matches the value of that attribute. By counting the items that satisfy the rule, we can determine the final result.\n\n\n# Approach\nWe can solve the problem by iterating over each item in the items array. For each item, we check if the ruleKey matches the corresponding attribute and if the ruleValue matches the value of that attribute. If both conditions are true, we increment a counter variable by 1. Finally, we return the value of the counter variable, which represents the number of items that match the given rule.\n\n\n# Complexity\n- Time complexity:\nThe time complexity of this approach is O(n), where n is the number of items in the input array. We iterate over each item once to check if it matches the given rule.\n\n\n- Space complexity:\nThe space complexity is O(1) because we only use a constant amount of additional space to store the counter variable and the loop variables. The input array is not modified during the process, so we don\'t need any extra space to store intermediate results.\n\n\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n res=0\n for i in items:\n if ruleKey=="type":\n if i[0]==ruleValue:\n res+=1\n elif ruleKey=="color":\n if i[1]==ruleValue:\n res+=1\n elif ruleKey=="name":\n if i[2]==ruleValue:\n res+=1\n return res\n\n``` | 8 | You are given an array `items`, where each `items[i] = [typei, colori, namei]` describes the type, color, and name of the `ith` item. You are also given a rule represented by two strings, `ruleKey` and `ruleValue`.
The `ith` item is said to match the rule if **one** of the following is true:
* `ruleKey == "type "` and `ruleValue == typei`.
* `ruleKey == "color "` and `ruleValue == colori`.
* `ruleKey == "name "` and `ruleValue == namei`.
Return _the number of items that match the given rule_.
**Example 1:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "lenovo "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "color ", ruleValue = "silver "
**Output:** 1
**Explanation:** There is only one item matching the given rule, which is \[ "computer ", "silver ", "lenovo "\].
**Example 2:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "phone "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "type ", ruleValue = "phone "
**Output:** 2
**Explanation:** There are only two items matching the given rule, which are \[ "phone ", "blue ", "pixel "\] and \[ "phone ", "gold ", "iphone "\]. Note that the item \[ "computer ", "silver ", "phone "\] does not match.
**Constraints:**
* `1 <= items.length <= 104`
* `1 <= typei.length, colori.length, namei.length, ruleValue.length <= 10`
* `ruleKey` is equal to either `"type "`, `"color "`, or `"name "`.
* All strings consist only of lowercase letters. | null |
✅ Explained - Simple and Clear Python3 Code✅ | count-items-matching-a-rule | 0 | 1 | # Intuition\nThe problem requires counting the number of items that match a given rule. We are given an array of items, where each item is represented by its type, color, and name. The rule is defined by a ruleKey and a ruleValue. We need to determine if the ruleKey matches the corresponding attribute of each item, and if so, check if the ruleValue matches the value of that attribute. By counting the items that satisfy the rule, we can determine the final result.\n\n\n# Approach\nWe can solve the problem by iterating over each item in the items array. For each item, we check if the ruleKey matches the corresponding attribute and if the ruleValue matches the value of that attribute. If both conditions are true, we increment a counter variable by 1. Finally, we return the value of the counter variable, which represents the number of items that match the given rule.\n\n\n# Complexity\n- Time complexity:\nThe time complexity of this approach is O(n), where n is the number of items in the input array. We iterate over each item once to check if it matches the given rule.\n\n\n- Space complexity:\nThe space complexity is O(1) because we only use a constant amount of additional space to store the counter variable and the loop variables. The input array is not modified during the process, so we don\'t need any extra space to store intermediate results.\n\n\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n res=0\n for i in items:\n if ruleKey=="type":\n if i[0]==ruleValue:\n res+=1\n elif ruleKey=="color":\n if i[1]==ruleValue:\n res+=1\n elif ruleKey=="name":\n if i[2]==ruleValue:\n res+=1\n return res\n\n``` | 8 | A **triplet** is an array of three integers. You are given a 2D integer array `triplets`, where `triplets[i] = [ai, bi, ci]` describes the `ith` **triplet**. You are also given an integer array `target = [x, y, z]` that describes the **triplet** you want to obtain.
To obtain `target`, you may apply the following operation on `triplets` **any number** of times (possibly **zero**):
* Choose two indices (**0-indexed**) `i` and `j` (`i != j`) and **update** `triplets[j]` to become `[max(ai, aj), max(bi, bj), max(ci, cj)]`.
* For example, if `triplets[i] = [2, 5, 3]` and `triplets[j] = [1, 7, 5]`, `triplets[j]` will be updated to `[max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5]`.
Return `true` _if it is possible to obtain the_ `target` _**triplet**_ `[x, y, z]` _as an **element** of_ `triplets`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** triplets = \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\], target = \[2,7,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and last triplets \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\]. Update the last triplet to be \[max(2,1), max(5,7), max(3,5)\] = \[2,7,5\]. triplets = \[\[2,5,3\],\[1,8,4\],\[2,7,5\]\]
The target triplet \[2,7,5\] is now an element of triplets.
**Example 2:**
**Input:** triplets = \[\[3,4,5\],\[4,5,6\]\], target = \[3,2,5\]
**Output:** false
**Explanation:** It is impossible to have \[3,2,5\] as an element because there is no 2 in any of the triplets.
**Example 3:**
**Input:** triplets = \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\], target = \[5,5,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and third triplets \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\]. Update the third triplet to be \[max(2,1), max(5,2), max(3,5)\] = \[2,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\].
- Choose the third and fourth triplets \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\]. Update the fourth triplet to be \[max(2,5), max(5,2), max(5,3)\] = \[5,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,5,5\]\].
The target triplet \[5,5,5\] is now an element of triplets.
**Constraints:**
* `1 <= triplets.length <= 105`
* `triplets[i].length == target.length == 3`
* `1 <= ai, bi, ci, x, y, z <= 1000` | Iterate on each item, and check if each one matches the rule according to the statement. |
Python solution using one for loop | count-items-matching-a-rule | 0 | 1 | # Intuition\nI figured I could match the ruleKey to a number which would make it easier to look at a certain index of the inner list. \n\n# Approach\nFirst I created a total variable to return later. Next I tied a number value to the type of value passed in as ruleKey. Then I used a for loop to loop through the list. I made an if statement to check if ruleValue is the same for each object. And used items[i][ruleKey] i for the outer list and ruleKey is to look at specfic value in the inner list, add 1 to total if the if statement was true. Finally returned the total value.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n total = 0\n\n if ruleKey == "type":\n ruleKey = 0\n elif ruleKey == "color":\n ruleKey = 1\n else:\n ruleKey = 2 \n\n for index in range(len(items)):\n if ruleValue == items[index][ruleKey]:\n total += 1\n \n return total\n``` | 0 | You are given an array `items`, where each `items[i] = [typei, colori, namei]` describes the type, color, and name of the `ith` item. You are also given a rule represented by two strings, `ruleKey` and `ruleValue`.
The `ith` item is said to match the rule if **one** of the following is true:
* `ruleKey == "type "` and `ruleValue == typei`.
* `ruleKey == "color "` and `ruleValue == colori`.
* `ruleKey == "name "` and `ruleValue == namei`.
Return _the number of items that match the given rule_.
**Example 1:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "lenovo "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "color ", ruleValue = "silver "
**Output:** 1
**Explanation:** There is only one item matching the given rule, which is \[ "computer ", "silver ", "lenovo "\].
**Example 2:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "phone "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "type ", ruleValue = "phone "
**Output:** 2
**Explanation:** There are only two items matching the given rule, which are \[ "phone ", "blue ", "pixel "\] and \[ "phone ", "gold ", "iphone "\]. Note that the item \[ "computer ", "silver ", "phone "\] does not match.
**Constraints:**
* `1 <= items.length <= 104`
* `1 <= typei.length, colori.length, namei.length, ruleValue.length <= 10`
* `ruleKey` is equal to either `"type "`, `"color "`, or `"name "`.
* All strings consist only of lowercase letters. | null |
Python solution using one for loop | count-items-matching-a-rule | 0 | 1 | # Intuition\nI figured I could match the ruleKey to a number which would make it easier to look at a certain index of the inner list. \n\n# Approach\nFirst I created a total variable to return later. Next I tied a number value to the type of value passed in as ruleKey. Then I used a for loop to loop through the list. I made an if statement to check if ruleValue is the same for each object. And used items[i][ruleKey] i for the outer list and ruleKey is to look at specfic value in the inner list, add 1 to total if the if statement was true. Finally returned the total value.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n total = 0\n\n if ruleKey == "type":\n ruleKey = 0\n elif ruleKey == "color":\n ruleKey = 1\n else:\n ruleKey = 2 \n\n for index in range(len(items)):\n if ruleValue == items[index][ruleKey]:\n total += 1\n \n return total\n``` | 0 | A **triplet** is an array of three integers. You are given a 2D integer array `triplets`, where `triplets[i] = [ai, bi, ci]` describes the `ith` **triplet**. You are also given an integer array `target = [x, y, z]` that describes the **triplet** you want to obtain.
To obtain `target`, you may apply the following operation on `triplets` **any number** of times (possibly **zero**):
* Choose two indices (**0-indexed**) `i` and `j` (`i != j`) and **update** `triplets[j]` to become `[max(ai, aj), max(bi, bj), max(ci, cj)]`.
* For example, if `triplets[i] = [2, 5, 3]` and `triplets[j] = [1, 7, 5]`, `triplets[j]` will be updated to `[max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5]`.
Return `true` _if it is possible to obtain the_ `target` _**triplet**_ `[x, y, z]` _as an **element** of_ `triplets`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** triplets = \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\], target = \[2,7,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and last triplets \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\]. Update the last triplet to be \[max(2,1), max(5,7), max(3,5)\] = \[2,7,5\]. triplets = \[\[2,5,3\],\[1,8,4\],\[2,7,5\]\]
The target triplet \[2,7,5\] is now an element of triplets.
**Example 2:**
**Input:** triplets = \[\[3,4,5\],\[4,5,6\]\], target = \[3,2,5\]
**Output:** false
**Explanation:** It is impossible to have \[3,2,5\] as an element because there is no 2 in any of the triplets.
**Example 3:**
**Input:** triplets = \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\], target = \[5,5,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and third triplets \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\]. Update the third triplet to be \[max(2,1), max(5,2), max(3,5)\] = \[2,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\].
- Choose the third and fourth triplets \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\]. Update the fourth triplet to be \[max(2,5), max(5,2), max(5,3)\] = \[5,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,5,5\]\].
The target triplet \[5,5,5\] is now an element of triplets.
**Constraints:**
* `1 <= triplets.length <= 105`
* `triplets[i].length == target.length == 3`
* `1 <= ai, bi, ci, x, y, z <= 1000` | Iterate on each item, and check if each one matches the rule according to the statement. |
[PYTHON 3] ONE LINER | count-items-matching-a-rule | 0 | 1 | Runtime: 305 ms, faster than 70.89% of Python3 online submissions for Count Items Matching a Rule.\nMemory Usage: 20.3 MB, less than 34.60% of Python3 online submissions for Count Items Matching a Rule.\n\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n return sum(item_list[{"type": 0, "color": 1, "name": 2}[ruleKey]] == ruleValue for item_list in items) | 5 | You are given an array `items`, where each `items[i] = [typei, colori, namei]` describes the type, color, and name of the `ith` item. You are also given a rule represented by two strings, `ruleKey` and `ruleValue`.
The `ith` item is said to match the rule if **one** of the following is true:
* `ruleKey == "type "` and `ruleValue == typei`.
* `ruleKey == "color "` and `ruleValue == colori`.
* `ruleKey == "name "` and `ruleValue == namei`.
Return _the number of items that match the given rule_.
**Example 1:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "lenovo "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "color ", ruleValue = "silver "
**Output:** 1
**Explanation:** There is only one item matching the given rule, which is \[ "computer ", "silver ", "lenovo "\].
**Example 2:**
**Input:** items = \[\[ "phone ", "blue ", "pixel "\],\[ "computer ", "silver ", "phone "\],\[ "phone ", "gold ", "iphone "\]\], ruleKey = "type ", ruleValue = "phone "
**Output:** 2
**Explanation:** There are only two items matching the given rule, which are \[ "phone ", "blue ", "pixel "\] and \[ "phone ", "gold ", "iphone "\]. Note that the item \[ "computer ", "silver ", "phone "\] does not match.
**Constraints:**
* `1 <= items.length <= 104`
* `1 <= typei.length, colori.length, namei.length, ruleValue.length <= 10`
* `ruleKey` is equal to either `"type "`, `"color "`, or `"name "`.
* All strings consist only of lowercase letters. | null |
[PYTHON 3] ONE LINER | count-items-matching-a-rule | 0 | 1 | Runtime: 305 ms, faster than 70.89% of Python3 online submissions for Count Items Matching a Rule.\nMemory Usage: 20.3 MB, less than 34.60% of Python3 online submissions for Count Items Matching a Rule.\n\n```\nclass Solution:\n def countMatches(self, items: List[List[str]], ruleKey: str, ruleValue: str) -> int:\n return sum(item_list[{"type": 0, "color": 1, "name": 2}[ruleKey]] == ruleValue for item_list in items) | 5 | A **triplet** is an array of three integers. You are given a 2D integer array `triplets`, where `triplets[i] = [ai, bi, ci]` describes the `ith` **triplet**. You are also given an integer array `target = [x, y, z]` that describes the **triplet** you want to obtain.
To obtain `target`, you may apply the following operation on `triplets` **any number** of times (possibly **zero**):
* Choose two indices (**0-indexed**) `i` and `j` (`i != j`) and **update** `triplets[j]` to become `[max(ai, aj), max(bi, bj), max(ci, cj)]`.
* For example, if `triplets[i] = [2, 5, 3]` and `triplets[j] = [1, 7, 5]`, `triplets[j]` will be updated to `[max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5]`.
Return `true` _if it is possible to obtain the_ `target` _**triplet**_ `[x, y, z]` _as an **element** of_ `triplets`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** triplets = \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\], target = \[2,7,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and last triplets \[\[2,5,3\],\[1,8,4\],\[1,7,5\]\]. Update the last triplet to be \[max(2,1), max(5,7), max(3,5)\] = \[2,7,5\]. triplets = \[\[2,5,3\],\[1,8,4\],\[2,7,5\]\]
The target triplet \[2,7,5\] is now an element of triplets.
**Example 2:**
**Input:** triplets = \[\[3,4,5\],\[4,5,6\]\], target = \[3,2,5\]
**Output:** false
**Explanation:** It is impossible to have \[3,2,5\] as an element because there is no 2 in any of the triplets.
**Example 3:**
**Input:** triplets = \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\], target = \[5,5,5\]
**Output:** true
**Explanation:** Perform the following operations:
- Choose the first and third triplets \[\[2,5,3\],\[2,3,4\],\[1,2,5\],\[5,2,3\]\]. Update the third triplet to be \[max(2,1), max(5,2), max(3,5)\] = \[2,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\].
- Choose the third and fourth triplets \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,2,3\]\]. Update the fourth triplet to be \[max(2,5), max(5,2), max(5,3)\] = \[5,5,5\]. triplets = \[\[2,5,3\],\[2,3,4\],\[2,5,5\],\[5,5,5\]\].
The target triplet \[5,5,5\] is now an element of triplets.
**Constraints:**
* `1 <= triplets.length <= 105`
* `triplets[i].length == target.length == 3`
* `1 <= ai, bi, ci, x, y, z <= 1000` | Iterate on each item, and check if each one matches the rule according to the statement. |
[Python3] top-down dp | closest-dessert-cost | 0 | 1 | \n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n toppingCosts *= 2\n \n @cache\n def fn(i, x):\n """Return sum of subsequence of toppingCosts[i:] closest to x."""\n if x < 0 or i == len(toppingCosts): return 0\n return min(fn(i+1, x), toppingCosts[i] + fn(i+1, x-toppingCosts[i]), key=lambda y: (abs(y-x), y))\n \n ans = inf\n for bc in baseCosts: \n ans = min(ans, bc + fn(0, target - bc), key=lambda x: (abs(x-target), x))\n return ans \n```\nTime complexity `O(MNV)`\n\nEdited on 2/28/2021\n\nAdding the version by @lenchen1112\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n \n @cache\n def fn(i, cost):\n """Return sum of subsequence closest to target."""\n if cost >= target or i == len(toppingCosts): return cost\n return min(fn(i+1, cost), fn(i+1, cost+toppingCosts[i]), key=lambda x: (abs(x-target), x))\n \n ans = inf\n toppingCosts *= 2\n for cost in baseCosts: \n ans = min(ans, fn(0, cost), key=lambda x: (abs(x-target), x))\n return ans \n```\n\nAdding binary search implementation\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n top = {0}\n for x in toppingCosts*2: \n top |= {x + xx for xx in top}\n top = sorted(top)\n \n ans = inf \n for bc in baseCosts: \n k = bisect_left(top, target - bc)\n if k < len(top): ans = min(ans, bc + top[k], key=lambda x: (abs(x-target), x))\n if k: ans = min(ans, bc + top[k-1], key=lambda x: (abs(x-target), x))\n return ans \n```\nTime complexity `O(N*2^(2N) + MN)` | 24 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
[Python3] top-down dp | closest-dessert-cost | 0 | 1 | \n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n toppingCosts *= 2\n \n @cache\n def fn(i, x):\n """Return sum of subsequence of toppingCosts[i:] closest to x."""\n if x < 0 or i == len(toppingCosts): return 0\n return min(fn(i+1, x), toppingCosts[i] + fn(i+1, x-toppingCosts[i]), key=lambda y: (abs(y-x), y))\n \n ans = inf\n for bc in baseCosts: \n ans = min(ans, bc + fn(0, target - bc), key=lambda x: (abs(x-target), x))\n return ans \n```\nTime complexity `O(MNV)`\n\nEdited on 2/28/2021\n\nAdding the version by @lenchen1112\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n \n @cache\n def fn(i, cost):\n """Return sum of subsequence closest to target."""\n if cost >= target or i == len(toppingCosts): return cost\n return min(fn(i+1, cost), fn(i+1, cost+toppingCosts[i]), key=lambda x: (abs(x-target), x))\n \n ans = inf\n toppingCosts *= 2\n for cost in baseCosts: \n ans = min(ans, fn(0, cost), key=lambda x: (abs(x-target), x))\n return ans \n```\n\nAdding binary search implementation\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n top = {0}\n for x in toppingCosts*2: \n top |= {x + xx for xx in top}\n top = sorted(top)\n \n ans = inf \n for bc in baseCosts: \n k = bisect_left(top, target - bc)\n if k < len(top): ans = min(ans, bc + top[k], key=lambda x: (abs(x-target), x))\n if k: ans = min(ans, bc + top[k-1], key=lambda x: (abs(x-target), x))\n return ans \n```\nTime complexity `O(N*2^(2N) + MN)` | 24 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Backtracking - Extremely simple, elegant, and beats 98.58%. You will love this! | closest-dessert-cost | 0 | 1 | # Intuition\nFind the minimum over all bases by running DFS over all toppings to find the choices which minimize the absolute difference to the total. We stop when adding more toppings will just take us further from the target as an optimiztion.\n\n\n# Code\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n \n @cache\n def solve(value, j=0):\n\n if j == len(toppingCosts):\n return value\n\n # Pruning makes this really fast!\n if value > target:\n return value\n\n return min( \n solve(value + 2 * toppingCosts[j], j + 1),\n solve(value + toppingCosts[j], j + 1),\n solve(value, j + 1),\n key = lambda x: (abs(target - x), x)\n )\n\n return min([solve(base) for base in baseCosts], key = lambda x: (abs(target - x), x))\n \n\n``` | 1 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Backtracking - Extremely simple, elegant, and beats 98.58%. You will love this! | closest-dessert-cost | 0 | 1 | # Intuition\nFind the minimum over all bases by running DFS over all toppings to find the choices which minimize the absolute difference to the total. We stop when adding more toppings will just take us further from the target as an optimiztion.\n\n\n# Code\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n \n @cache\n def solve(value, j=0):\n\n if j == len(toppingCosts):\n return value\n\n # Pruning makes this really fast!\n if value > target:\n return value\n\n return min( \n solve(value + 2 * toppingCosts[j], j + 1),\n solve(value + toppingCosts[j], j + 1),\n solve(value, j + 1),\n key = lambda x: (abs(target - x), x)\n )\n\n return min([solve(base) for base in baseCosts], key = lambda x: (abs(target - x), x))\n \n\n``` | 1 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Python | BFS | 207ms | 4-line | fast and simple solution | closest-dessert-cost | 0 | 1 | ```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n q = [target - basecost for basecost in baseCosts]\n\n for toppingcost in toppingCosts:\n q += [val - cost for val in q if val > 0 for cost in (toppingcost, toppingcost * 2)]\n\n return target - min(q, key=lambda x: abs(x) * 2 - (x > 0))\n``` | 7 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Python | BFS | 207ms | 4-line | fast and simple solution | closest-dessert-cost | 0 | 1 | ```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n q = [target - basecost for basecost in baseCosts]\n\n for toppingcost in toppingCosts:\n q += [val - cost for val in q if val > 0 for cost in (toppingcost, toppingcost * 2)]\n\n return target - min(q, key=lambda x: abs(x) * 2 - (x > 0))\n``` | 7 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Python 3 solution: Minimizing the error using backtracking | closest-dessert-cost | 0 | 1 | ```python\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n toppingCosts *= 2\n \n best_error = float("inf") # best error can be greater than `target`\n \n @cache\n def findError(index, target):\n if index == len(toppingCosts):\n return target\n elif target < 0:\n return target\n return min(findError(index + 1, target - toppingCosts[index]), \n findError(index + 1, target), key = lambda x : (abs(x), -x))\n\n for base in baseCosts:\n err = findError(0, target - base)\n best_error = min(best_error, err, key = lambda x: (abs(x), -x))\n\n return target - best_error\n``` | 1 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Python 3 solution: Minimizing the error using backtracking | closest-dessert-cost | 0 | 1 | ```python\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n toppingCosts *= 2\n \n best_error = float("inf") # best error can be greater than `target`\n \n @cache\n def findError(index, target):\n if index == len(toppingCosts):\n return target\n elif target < 0:\n return target\n return min(findError(index + 1, target - toppingCosts[index]), \n findError(index + 1, target), key = lambda x : (abs(x), -x))\n\n for base in baseCosts:\n err = findError(0, target - base)\n best_error = min(best_error, err, key = lambda x: (abs(x), -x))\n\n return target - best_error\n``` | 1 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Python easy to read and understand | backtracking | closest-dessert-cost | 0 | 1 | ```\nclass Solution:\n def solve(self, sums, topping, target, index):\n res = abs(sums-target)\n if res < self.diff:\n #print(sums, res)\n self.diff = res\n self.ans = sums\n elif res == self.diff:\n self.ans = min(self.ans, sums)\n if index == len(topping):\n return\n for i in range(3):\n sums += topping[index]*i\n self.solve(sums, topping, target, index+1)\n sums -= topping[index]*i\n \n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n self.ans, self.diff = float("inf"), float("inf")\n for base in baseCosts:\n self.solve(base, toppingCosts, target, 0)\n return self.ans | 1 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Python easy to read and understand | backtracking | closest-dessert-cost | 0 | 1 | ```\nclass Solution:\n def solve(self, sums, topping, target, index):\n res = abs(sums-target)\n if res < self.diff:\n #print(sums, res)\n self.diff = res\n self.ans = sums\n elif res == self.diff:\n self.ans = min(self.ans, sums)\n if index == len(topping):\n return\n for i in range(3):\n sums += topping[index]*i\n self.solve(sums, topping, target, index+1)\n sums -= topping[index]*i\n \n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n self.ans, self.diff = float("inf"), float("inf")\n for base in baseCosts:\n self.solve(base, toppingCosts, target, 0)\n return self.ans | 1 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Python simple DP O(NV) beat 99% | closest-dessert-cost | 0 | 1 | # Intuition\nSimple DP similar to Coin Change II, Time O(M+NV), V is target, N is number of toppings, M is number bases\n\n# Code\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n price=set()\n minb=min(baseCosts)\n if minb>target:\n return minb\n\n currMin=target-minb\n for cost in baseCosts:\n if cost-target>currMin:\n continue\n price.add(cost)\n \n for topcost in toppingCosts:\n for j in range(2):\n nextp=price.copy()\n for p in price:\n v=p+topcost\n if v<target+currMin:\n if abs(v-target)<currMin: currMin=abs(v-target)\n nextp.add(v)\n price=nextp\n \n for i in range(target,0,-1):\n if i in price: return i\n if 2*target-i in price: return 2*target-i\n \n \n \n\n \n``` | 0 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Python simple DP O(NV) beat 99% | closest-dessert-cost | 0 | 1 | # Intuition\nSimple DP similar to Coin Change II, Time O(M+NV), V is target, N is number of toppings, M is number bases\n\n# Code\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n price=set()\n minb=min(baseCosts)\n if minb>target:\n return minb\n\n currMin=target-minb\n for cost in baseCosts:\n if cost-target>currMin:\n continue\n price.add(cost)\n \n for topcost in toppingCosts:\n for j in range(2):\n nextp=price.copy()\n for p in price:\n v=p+topcost\n if v<target+currMin:\n if abs(v-target)<currMin: currMin=abs(v-target)\n nextp.add(v)\n price=nextp\n \n for i in range(target,0,-1):\n if i in price: return i\n if 2*target-i in price: return 2*target-i\n \n \n \n\n \n``` | 0 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Simple python solutions | base solution + 2 heuristics | closest-dessert-cost | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot 3^m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(3^m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\n# base solution\n\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n delta = float(\'inf\')\n results = set()\n\n for base in baseCosts:\n data = {base}\n for topping in toppingCosts:\n for prev_cost in list(data):\n data.add(prev_cost + topping)\n data.add(prev_cost + 2 * topping)\n\n for cost in data:\n current_delta = abs(cost - target)\n if current_delta == delta:\n results.add(cost)\n elif current_delta < delta:\n results = {cost}\n delta = current_delta\n \n return min(results)\n\n```\n``` python3 []\n# solution with 2 heuristics\n\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n delta = float(\'inf\')\n results = set()\n\n for base in baseCosts:\n data = {base}\n for topping in toppingCosts:\n for prev_cost in list(data):\n # first heuristics\n a = prev_cost + topping\n if a <= target + delta:\n data.add(a)\n \n b = prev_cost + 2 * topping\n if b <= target + delta:\n data.add(b)\n\n for cost in data:\n current_delta = abs(cost - target)\n if current_delta == delta:\n results.add(cost)\n elif current_delta < delta:\n results = {cost}\n delta = current_delta\n \n if delta == 0: # second heuristic\n break\n \n return min(results)\n``` | 0 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Simple python solutions | base solution + 2 heuristics | closest-dessert-cost | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot 3^m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(3^m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\n# base solution\n\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n delta = float(\'inf\')\n results = set()\n\n for base in baseCosts:\n data = {base}\n for topping in toppingCosts:\n for prev_cost in list(data):\n data.add(prev_cost + topping)\n data.add(prev_cost + 2 * topping)\n\n for cost in data:\n current_delta = abs(cost - target)\n if current_delta == delta:\n results.add(cost)\n elif current_delta < delta:\n results = {cost}\n delta = current_delta\n \n return min(results)\n\n```\n``` python3 []\n# solution with 2 heuristics\n\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n delta = float(\'inf\')\n results = set()\n\n for base in baseCosts:\n data = {base}\n for topping in toppingCosts:\n for prev_cost in list(data):\n # first heuristics\n a = prev_cost + topping\n if a <= target + delta:\n data.add(a)\n \n b = prev_cost + 2 * topping\n if b <= target + delta:\n data.add(b)\n\n for cost in data:\n current_delta = abs(cost - target)\n if current_delta == delta:\n results.add(cost)\n elif current_delta < delta:\n results = {cost}\n delta = current_delta\n \n if delta == 0: # second heuristic\n break\n \n return min(results)\n``` | 0 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
Python, runtime O(n*3^m), memory O(m) | closest-dessert-cost | 0 | 1 | Backtracking - `n` = len(baseCosts), `m` = len(toppingCosts)\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n\n def recur(cost, index, ans):\n if index == len(toppingCosts):\n if abs(cost-target) < abs(ans-target) or (abs(cost-target) == abs(ans-target) and cost < ans):\n ans = cost\n return ans\n for n in range(3):\n ans = recur(cost+n*toppingCosts[index], index+1, ans)\n return ans\n\n ans = float(\'inf\') # the optimal cost\n for e in baseCosts:\n ans = recur(e, 0, ans)\n return ans\n``` | 0 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
Python, runtime O(n*3^m), memory O(m) | closest-dessert-cost | 0 | 1 | Backtracking - `n` = len(baseCosts), `m` = len(toppingCosts)\n```\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n\n def recur(cost, index, ans):\n if index == len(toppingCosts):\n if abs(cost-target) < abs(ans-target) or (abs(cost-target) == abs(ans-target) and cost < ans):\n ans = cost\n return ans\n for n in range(3):\n ans = recur(cost+n*toppingCosts[index], index+1, ans)\n return ans\n\n ans = float(\'inf\') # the optimal cost\n for e in baseCosts:\n ans = recur(e, 0, ans)\n return ans\n``` | 0 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
[Python3] Using memo without the recursion | closest-dessert-cost | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt looked like a typical knapsack prob to at first.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI suck at recursions for such probs so I used a simple memo to record "reachable points". Think it as the distance you can go given the start gas and top-up gas.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m * 3^n + 10_000)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(20_001)\n\n# Code\n```\nfrom typing import List\n\n\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n n = len(toppingCosts)\n s = set() # starting points\n limit = 20_001\n m = [0] * limit # memo for reachable points\n for b in baseCosts:\n m[b] = 1\n s.add(b)\n for t in toppingCosts:\n nex = [] # given that set can\'t be altered during iteration\n for start in s:\n for reach in [start + t, start + 2 * t]:\n if reach < limit:\n m[reach] = 1\n nex.append(reach)\n for x in nex:\n s.add(x)\n l = r = target\n while l >= 0 or r <= limit: # finding the closest 1 to target\n if l >= 0 and m[l] == 1:\n return l\n if r < limit and m[r] == 1:\n return r\n l -= 1\n r += 1\n return -1\n``` | 0 | You would like to make dessert and are preparing to buy the ingredients. You have `n` ice cream base flavors and `m` types of toppings to choose from. You must follow these rules when making your dessert:
* There must be **exactly one** ice cream base.
* You can add **one or more** types of topping or have no toppings at all.
* There are **at most two** of **each type** of topping.
You are given three inputs:
* `baseCosts`, an integer array of length `n`, where each `baseCosts[i]` represents the price of the `ith` ice cream base flavor.
* `toppingCosts`, an integer array of length `m`, where each `toppingCosts[i]` is the price of **one** of the `ith` topping.
* `target`, an integer representing your target price for dessert.
You want to make a dessert with a total cost as close to `target` as possible.
Return _the closest possible cost of the dessert to_ `target`. If there are multiple, return _the **lower** one._
**Example 1:**
**Input:** baseCosts = \[1,7\], toppingCosts = \[3,4\], target = 10
**Output:** 10
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 7
- Take 1 of topping 0: cost 1 x 3 = 3
- Take 0 of topping 1: cost 0 x 4 = 0
Total: 7 + 3 + 0 = 10.
**Example 2:**
**Input:** baseCosts = \[2,3\], toppingCosts = \[4,5,100\], target = 18
**Output:** 17
**Explanation:** Consider the following combination (all 0-indexed):
- Choose base 1: cost 3
- Take 1 of topping 0: cost 1 x 4 = 4
- Take 2 of topping 1: cost 2 x 5 = 10
- Take 0 of topping 2: cost 0 x 100 = 0
Total: 3 + 4 + 10 + 0 = 17. You cannot make a dessert with a total cost of 18.
**Example 3:**
**Input:** baseCosts = \[3,10\], toppingCosts = \[2,5\], target = 9
**Output:** 8
**Explanation:** It is possible to make desserts with cost 8 and 10. Return 8 as it is the lower cost.
**Constraints:**
* `n == baseCosts.length`
* `m == toppingCosts.length`
* `1 <= n, m <= 10`
* `1 <= baseCosts[i], toppingCosts[i] <= 104`
* `1 <= target <= 104` | Process both linked lists at the same time If the current power of the two heads is equal, add this power with the sum of the coefficients to the answer list. If one head has a larger power, add this power to the answer list and move only this head. |
[Python3] Using memo without the recursion | closest-dessert-cost | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt looked like a typical knapsack prob to at first.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI suck at recursions for such probs so I used a simple memo to record "reachable points". Think it as the distance you can go given the start gas and top-up gas.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m * 3^n + 10_000)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(20_001)\n\n# Code\n```\nfrom typing import List\n\n\nclass Solution:\n def closestCost(self, baseCosts: List[int], toppingCosts: List[int], target: int) -> int:\n n = len(toppingCosts)\n s = set() # starting points\n limit = 20_001\n m = [0] * limit # memo for reachable points\n for b in baseCosts:\n m[b] = 1\n s.add(b)\n for t in toppingCosts:\n nex = [] # given that set can\'t be altered during iteration\n for start in s:\n for reach in [start + t, start + 2 * t]:\n if reach < limit:\n m[reach] = 1\n nex.append(reach)\n for x in nex:\n s.add(x)\n l = r = target\n while l >= 0 or r <= limit: # finding the closest 1 to target\n if l >= 0 and m[l] == 1:\n return l\n if r < limit and m[r] == 1:\n return r\n l -= 1\n r += 1\n return -1\n``` | 0 | There is a tournament where `n` players are participating. The players are standing in a single row and are numbered from `1` to `n` based on their **initial** standing position (player `1` is the first player in the row, player `2` is the second player in the row, etc.).
The tournament consists of multiple rounds (starting from round number `1`). In each round, the `ith` player from the front of the row competes against the `ith` player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.
* For example, if the row consists of players `1, 2, 4, 6, 7`
* Player `1` competes against player `7`.
* Player `2` competes against player `6`.
* Player `4` automatically advances to the next round.
After each round is over, the winners are lined back up in the row based on the **original ordering** assigned to them initially (ascending order).
The players numbered `firstPlayer` and `secondPlayer` are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may **choose** the outcome of this round.
Given the integers `n`, `firstPlayer`, and `secondPlayer`, return _an integer array containing two values, the **earliest** possible round number and the **latest** possible round number in which these two players will compete against each other, respectively_.
**Example 1:**
**Input:** n = 11, firstPlayer = 2, secondPlayer = 4
**Output:** \[3,4\]
**Explanation:**
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4
**Example 2:**
**Input:** n = 5, firstPlayer = 1, secondPlayer = 5
**Output:** \[1,1\]
**Explanation:** The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.
**Constraints:**
* `2 <= n <= 28`
* `1 <= firstPlayer < secondPlayer <= n` | As the constraints are not large, you can brute force and enumerate all the possibilities. |
[Python3] two heaps | equal-sum-arrays-with-minimum-number-of-operations | 0 | 1 | \n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n if 6*len(nums1) < len(nums2) or 6*len(nums2) < len(nums1): return -1 # impossible \n \n if sum(nums1) < sum(nums2): nums1, nums2 = nums2, nums1\n s1, s2 = sum(nums1), sum(nums2)\n \n nums1 = [-x for x in nums1] # max-heap \n heapify(nums1)\n heapify(nums2)\n \n ans = 0\n while s1 > s2: \n x1, x2 = nums1[0], nums2[0]\n if -1-x1 > 6-x2: # change x1 to 1\n s1 += x1 + 1\n heapreplace(nums1, -1)\n else: \n s2 += 6 - x2\n heapreplace(nums2, 6)\n ans += 1\n return ans \n```\n\nEdited on 2/28/2021\nAdding 2-pointer approach \n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n if 6*len(nums1) < len(nums2) or 6*len(nums2) < len(nums1): return -1 # impossible \n \n if sum(nums1) < sum(nums2): nums1, nums2 = nums2, nums1\n s1, s2 = sum(nums1), sum(nums2) # s1 >= s2\n \n nums1.sort()\n nums2.sort()\n \n ans = j = 0\n i = len(nums1)-1\n \n while s1 > s2: \n if j >= len(nums2) or 0 <= i and nums1[i] - 1 > 6 - nums2[j]: \n s1 += 1 - nums1[i]\n i -= 1\n else: \n s2 += 6 - nums2[j]\n j += 1\n ans += 1\n return ans \n``` | 19 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
[Python3] two heaps | equal-sum-arrays-with-minimum-number-of-operations | 0 | 1 | \n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n if 6*len(nums1) < len(nums2) or 6*len(nums2) < len(nums1): return -1 # impossible \n \n if sum(nums1) < sum(nums2): nums1, nums2 = nums2, nums1\n s1, s2 = sum(nums1), sum(nums2)\n \n nums1 = [-x for x in nums1] # max-heap \n heapify(nums1)\n heapify(nums2)\n \n ans = 0\n while s1 > s2: \n x1, x2 = nums1[0], nums2[0]\n if -1-x1 > 6-x2: # change x1 to 1\n s1 += x1 + 1\n heapreplace(nums1, -1)\n else: \n s2 += 6 - x2\n heapreplace(nums2, 6)\n ans += 1\n return ans \n```\n\nEdited on 2/28/2021\nAdding 2-pointer approach \n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n if 6*len(nums1) < len(nums2) or 6*len(nums2) < len(nums1): return -1 # impossible \n \n if sum(nums1) < sum(nums2): nums1, nums2 = nums2, nums1\n s1, s2 = sum(nums1), sum(nums2) # s1 >= s2\n \n nums1.sort()\n nums2.sort()\n \n ans = j = 0\n i = len(nums1)-1\n \n while s1 > s2: \n if j >= len(nums2) or 0 <= i and nums1[i] - 1 > 6 - nums2[j]: \n s1 += 1 - nums1[i]\n i -= 1\n else: \n s2 += 6 - nums2[j]\n j += 1\n ans += 1\n return ans \n``` | 19 | A **peak** element in a 2D grid is an element that is **strictly greater** than all of its **adjacent** neighbors to the left, right, top, and bottom.
Given a **0-indexed** `m x n` matrix `mat` where **no two adjacent cells are equal**, find **any** peak element `mat[i][j]` and return _the length 2 array_ `[i,j]`.
You may assume that the entire matrix is surrounded by an **outer perimeter** with the value `-1` in each cell.
You must write an algorithm that runs in `O(m log(n))` or `O(n log(m))` time.
**Example 1:**
**Input:** mat = \[\[1,4\],\[3,2\]\]
**Output:** \[0,1\]
**Explanation:** Both 3 and 4 are peak elements so \[1,0\] and \[0,1\] are both acceptable answers.
**Example 2:**
**Input:** mat = \[\[10,20,15\],\[21,30,14\],\[7,16,32\]\]
**Output:** \[1,1\]
**Explanation:** Both 30 and 32 are peak elements so \[1,1\] and \[2,2\] are both acceptable answers.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 500`
* `1 <= mat[i][j] <= 105`
* No two adjacent cells are equal. | Let's note that we want to either decrease the sum of the array with a larger sum or increase the array's sum with the smaller sum. You can maintain the largest increase or decrease you can make in a binary search tree and each time get the maximum one. |
Python 3 | Heap, Greedy | Explanations | equal-sum-arrays-with-minimum-number-of-operations | 0 | 1 | ### Explanation\n- There will be a difference (`diff`) between `the sum of nums1` and `the sum of nums2`\n- To make the `diff` converges to 0 the fastest way, we want to make \n\t- The list with larger sum, become smaller\n\t- The list with smaller sum, become larger\n\t- We define `effort` as the absolute difference between the new value & the original value\n\t- In each turn, whoever makes the greater `effort` will get picked (use `heap` for the help)\n- Above is the idea for the first `while` loop\n- If there are `nums1` or `nums2` left over, use them up until the difference is less than or equal to 0\n\t- Second & third `while` loop\n- Return `ans` only if `diff` is less than or equal to 0, otherwise return -1 as there is no way to make `diff` to 0\n### Implementation\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n s1, s2 = sum(nums1), sum(nums2)\n if s1 > s2:\n s1, s2 = s2, s1\n nums1, nums2 = nums2, nums1\n # to make s1 < s2 \n heapq.heapify(nums1) \n nums2 = [-num for num in nums2]\n heapq.heapify(nums2) \n ans = 0\n diff = s2 - s1\n while diff > 0 and nums1 and nums2:\n a = 6 - nums1[0]\n b = - (1 + nums2[0])\n if a > b:\n heapq.heappop(nums1) \n diff -= a\n else:\n heapq.heappop(nums2) \n diff -= b\n ans += 1 \n while diff > 0 and nums1: \n a = 6 - heapq.heappop(nums1) \n diff -= a\n ans += 1 \n while diff > 0 and nums2: \n b = - (1 + heapq.heappop(nums2))\n diff -= b\n ans += 1 \n return ans if diff <= 0 else -1\n``` | 13 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Python 3 | Heap, Greedy | Explanations | equal-sum-arrays-with-minimum-number-of-operations | 0 | 1 | ### Explanation\n- There will be a difference (`diff`) between `the sum of nums1` and `the sum of nums2`\n- To make the `diff` converges to 0 the fastest way, we want to make \n\t- The list with larger sum, become smaller\n\t- The list with smaller sum, become larger\n\t- We define `effort` as the absolute difference between the new value & the original value\n\t- In each turn, whoever makes the greater `effort` will get picked (use `heap` for the help)\n- Above is the idea for the first `while` loop\n- If there are `nums1` or `nums2` left over, use them up until the difference is less than or equal to 0\n\t- Second & third `while` loop\n- Return `ans` only if `diff` is less than or equal to 0, otherwise return -1 as there is no way to make `diff` to 0\n### Implementation\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n s1, s2 = sum(nums1), sum(nums2)\n if s1 > s2:\n s1, s2 = s2, s1\n nums1, nums2 = nums2, nums1\n # to make s1 < s2 \n heapq.heapify(nums1) \n nums2 = [-num for num in nums2]\n heapq.heapify(nums2) \n ans = 0\n diff = s2 - s1\n while diff > 0 and nums1 and nums2:\n a = 6 - nums1[0]\n b = - (1 + nums2[0])\n if a > b:\n heapq.heappop(nums1) \n diff -= a\n else:\n heapq.heappop(nums2) \n diff -= b\n ans += 1 \n while diff > 0 and nums1: \n a = 6 - heapq.heappop(nums1) \n diff -= a\n ans += 1 \n while diff > 0 and nums2: \n b = - (1 + heapq.heappop(nums2))\n diff -= b\n ans += 1 \n return ans if diff <= 0 else -1\n``` | 13 | A **peak** element in a 2D grid is an element that is **strictly greater** than all of its **adjacent** neighbors to the left, right, top, and bottom.
Given a **0-indexed** `m x n` matrix `mat` where **no two adjacent cells are equal**, find **any** peak element `mat[i][j]` and return _the length 2 array_ `[i,j]`.
You may assume that the entire matrix is surrounded by an **outer perimeter** with the value `-1` in each cell.
You must write an algorithm that runs in `O(m log(n))` or `O(n log(m))` time.
**Example 1:**
**Input:** mat = \[\[1,4\],\[3,2\]\]
**Output:** \[0,1\]
**Explanation:** Both 3 and 4 are peak elements so \[1,0\] and \[0,1\] are both acceptable answers.
**Example 2:**
**Input:** mat = \[\[10,20,15\],\[21,30,14\],\[7,16,32\]\]
**Output:** \[1,1\]
**Explanation:** Both 30 and 32 are peak elements so \[1,1\] and \[2,2\] are both acceptable answers.
**Constraints:**
* `m == mat.length`
* `n == mat[i].length`
* `1 <= m, n <= 500`
* `1 <= mat[i][j] <= 105`
* No two adjacent cells are equal. | Let's note that we want to either decrease the sum of the array with a larger sum or increase the array's sum with the smaller sum. You can maintain the largest increase or decrease you can make in a binary search tree and each time get the maximum one. |
Python Short Clean | equal-sum-arrays-with-minimum-number-of-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCalculate the difference in sum between the two lists. Then put them in the same heap. Pull the biggest difference maker each time from the heap until you compensate for the difference or run the heap out of items.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nmax heap is used so everything needs to be negative in python. When calculating how big of a difference a number can make in your calculation need to see how close it is to either 6 or 1. Also need to determine which direction it should go to get you closer to zeroing out the difference.\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) where n is the total length of list1 + list2\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int]) -> int:\n diff, cnt = sum(nums2) - sum(nums1), 0\n \n if diff == 0:\n return 0\n if diff < 0:\n combo = [num - 6 for num in nums2] + [1 - num for num in nums1]\n diff = -diff\n else:\n combo = [num - 6 for num in nums1] + [1 - num for num in nums2]\n heapq.heapify(combo)\n while diff > 0 and combo:\n diff += heapq.heappop(combo)\n cnt += 1\n\n return cnt if cnt and diff <= 0 else -1\n``` | 1 | You are given two arrays of integers `nums1` and `nums2`, possibly of different lengths. The values in the arrays are between `1` and `6`, inclusive.
In one operation, you can change any integer's value in **any** of the arrays to **any** value between `1` and `6`, inclusive.
Return _the minimum number of operations required to make the sum of values in_ `nums1` _equal to the sum of values in_ `nums2`_._ Return `-1` if it is not possible to make the sum of the two arrays equal.
**Example 1:**
**Input:** nums1 = \[1,2,3,4,5,6\], nums2 = \[1,1,2,2,2,2\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2\[0\] to 6. nums1 = \[1,2,3,4,5,6\], nums2 = \[**6**,1,2,2,2,2\].
- Change nums1\[5\] to 1. nums1 = \[1,2,3,4,5,**1**\], nums2 = \[6,1,2,2,2,2\].
- Change nums1\[2\] to 2. nums1 = \[1,2,**2**,4,5,1\], nums2 = \[6,1,2,2,2,2\].
**Example 2:**
**Input:** nums1 = \[1,1,1,1,1,1,1\], nums2 = \[6\]
**Output:** -1
**Explanation:** There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.
**Example 3:**
**Input:** nums1 = \[6,6\], nums2 = \[1\]
**Output:** 3
**Explanation:** You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums1\[0\] to 2. nums1 = \[**2**,6\], nums2 = \[1\].
- Change nums1\[1\] to 2. nums1 = \[2,**2**\], nums2 = \[1\].
- Change nums2\[0\] to 4. nums1 = \[2,2\], nums2 = \[**4**\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[i] <= 6` | Maintain the next id that should be outputted. Maintain the ids that were inserted in the stream. Per each insert, make a loop where you check if the id that has the turn has been inserted, and if so increment the id that has the turn and continue the loop, else break. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.