title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Is Array Sorted and Rotated, Python code made easy | check-if-array-is-sorted-and-rotated | 0 | 1 | ```\nclass Solution:\n def check(self, nums: List[int]) -> bool:\n count = 0\n for i in range(len(nums) - 1):\n if nums[i] > nums[i+1]:\n count += 1\n \n if nums[0] < nums[len(nums)-1]:\n count += 1\n \n return count <= 1\n``` | 4 | You are given an `m x n` integer matrix `grid`.
A **rhombus sum** is the sum of the elements that form **the** **border** of a regular rhombus shape in `grid`. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each **rhombus sum**:
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.
Return _the biggest three **distinct rhombus sums** in the_ `grid` _in **descending order**__. If there are less than three distinct values, return all of them_.
**Example 1:**
**Input:** grid = \[\[3,4,5,1,3\],\[3,3,4,2,3\],\[20,30,200,40,10\],\[1,5,5,4,1\],\[4,3,2,2,5\]\]
**Output:** \[228,216,211\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[20,9,8\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)
**Example 3:**
**Input:** grid = \[\[7,7,7\]\]
**Output:** \[7\]
**Explanation:** All three possible rhombus sums are the same, so return \[7\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 105` | Brute force and check if it is possible for a sorted array to start from each position. |
😎 Find no. of break Points || O(n) FAANG 🥳 Optimized Code💥 | check-if-array-is-sorted-and-rotated | 1 | 1 | # \uD83D\uDDEF\uFE0FIntuition :-\n<!-- Describe your first thoughts on how to solve this problem. -->\nif array is sorted and rotated then, there is only 1 break point where (nums[x] > nums[x+1]),\nif array is only sorted then, there is 0 break point.\n\n# ***Please do Upvote \u270C\uFE0F***\n\n# \uD83D\uDDEF\uFE0FComplexity :-\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \uD83D\uDDEF\uFE0FCode :-\n```\nclass Solution {\npublic:\n bool check(vector<int>& nums) {\n int count=0;\n for(int i=0;i<nums.size();i++){\n if(nums[i]>nums[(i+1)%nums.size()])\n count++;\n }\n return (count<=1);\n }\n};\n```\n\n# **-->why am I doing %size??**\n\nConcider this case: nums = [2,1,3,4]\n\nThis case will give you result true without %size but it is not sorted and rotated. So we have to check last and first element also. | 34 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
😎 Find no. of break Points || O(n) FAANG 🥳 Optimized Code💥 | check-if-array-is-sorted-and-rotated | 1 | 1 | # \uD83D\uDDEF\uFE0FIntuition :-\n<!-- Describe your first thoughts on how to solve this problem. -->\nif array is sorted and rotated then, there is only 1 break point where (nums[x] > nums[x+1]),\nif array is only sorted then, there is 0 break point.\n\n# ***Please do Upvote \u270C\uFE0F***\n\n# \uD83D\uDDEF\uFE0FComplexity :-\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \uD83D\uDDEF\uFE0FCode :-\n```\nclass Solution {\npublic:\n bool check(vector<int>& nums) {\n int count=0;\n for(int i=0;i<nums.size();i++){\n if(nums[i]>nums[(i+1)%nums.size()])\n count++;\n }\n return (count<=1);\n }\n};\n```\n\n# **-->why am I doing %size??**\n\nConcider this case: nums = [2,1,3,4]\n\nThis case will give you result true without %size but it is not sorted and rotated. So we have to check last and first element also. | 34 | You are given an `m x n` integer matrix `grid`.
A **rhombus sum** is the sum of the elements that form **the** **border** of a regular rhombus shape in `grid`. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each **rhombus sum**:
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.
Return _the biggest three **distinct rhombus sums** in the_ `grid` _in **descending order**__. If there are less than three distinct values, return all of them_.
**Example 1:**
**Input:** grid = \[\[3,4,5,1,3\],\[3,3,4,2,3\],\[20,30,200,40,10\],\[1,5,5,4,1\],\[4,3,2,2,5\]\]
**Output:** \[228,216,211\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[20,9,8\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)
**Example 3:**
**Input:** grid = \[\[7,7,7\]\]
**Output:** \[7\]
**Explanation:** All three possible rhombus sums are the same, so return \[7\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 105` | Brute force and check if it is possible for a sorted array to start from each position. |
Easy deque solution- Beats 98% others | check-if-array-is-sorted-and-rotated | 0 | 1 | \n# Code\n```\nclass Solution:\n def check(self, nums: List[int]) -> bool:\n queue =deque(nums)\n for i in range(len(nums)):\n queue.rotate(1)\n if list(queue)==sorted(nums):\n return True\n``` | 1 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Easy deque solution- Beats 98% others | check-if-array-is-sorted-and-rotated | 0 | 1 | \n# Code\n```\nclass Solution:\n def check(self, nums: List[int]) -> bool:\n queue =deque(nums)\n for i in range(len(nums)):\n queue.rotate(1)\n if list(queue)==sorted(nums):\n return True\n``` | 1 | You are given an `m x n` integer matrix `grid`.
A **rhombus sum** is the sum of the elements that form **the** **border** of a regular rhombus shape in `grid`. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each **rhombus sum**:
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.
Return _the biggest three **distinct rhombus sums** in the_ `grid` _in **descending order**__. If there are less than three distinct values, return all of them_.
**Example 1:**
**Input:** grid = \[\[3,4,5,1,3\],\[3,3,4,2,3\],\[20,30,200,40,10\],\[1,5,5,4,1\],\[4,3,2,2,5\]\]
**Output:** \[228,216,211\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[20,9,8\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)
**Example 3:**
**Input:** grid = \[\[7,7,7\]\]
**Output:** \[7\]
**Explanation:** All three possible rhombus sums are the same, so return \[7\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 105` | Brute force and check if it is possible for a sorted array to start from each position. |
Basic Implementation with clear approach | Detailed | check-if-array-is-sorted-and-rotated | 0 | 1 | Time Complexity: O(N)\nSpace Complexity: O(1)\n\n# Approach and Implementation\nTo implement a solution for this problem, you should be aware of what happens when you rotate a sorted array.\n\nLook at the image below. We have a sorted and rotated array:\n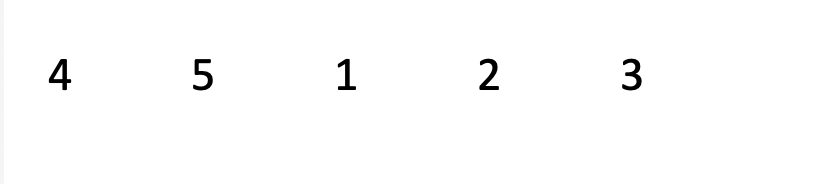\nThe array is rotated 2 times.\n\n\n\nNotice how you only have `one break point`, i.e., `arr[i-1] > arr[i]` happens only once between the elements **5** and **1**.\n\nThis ensures that the arrays is rotated properly and we do not have a random array. \n\nSo now, we have `one breaks`:\n1. Between elements 5 and 1\n\n\n`We can generalize this as nums[i-1] > nums[i]`\n\n# Code\n``` Python []\nclass Solution:\n def check(self, nums: List[int]) -> bool:\n # Initialize the break variable to 0\n breaks = 0\n\n # Iterate over the len(nums)\n for i in range(len(nums)):\n # If you find any break case, increment the break variable\n if nums[i] < nums[i-1]:\n breaks += 1\n \n # If there is atmost 1 breaks, return True\n # Else, return False\n return True if breaks <= 1 else False\n\n```\n``` C++ []\nclass Solution {\npublic:\n bool check(vector<int>& nums) {\n // Initialize the break variable to 1\n int breaks = 0;\n\n // Iterate over the len(nums)\n for(int i = 0; i < nums.size(); i++){\n // If you find any break case, increment the break variable\n if(nums[(i+1) % nums.size()] < nums[i])\n breaks++;\n }\n\n // If there is atmost 1 breaks, return True\n // Else, return False\n return breaks <= 1;\n\n }\n};\n\n```\n\n | 10 | Given an array `nums`, return `true` _if the array was originally sorted in non-decreasing order, then rotated **some** number of positions (including zero)_. Otherwise, return `false`.
There may be **duplicates** in the original array.
**Note:** An array `A` rotated by `x` positions results in an array `B` of the same length such that `A[i] == B[(i+x) % A.length]`, where `%` is the modulo operation.
**Example 1:**
**Input:** nums = \[3,4,5,1,2\]
**Output:** true
**Explanation:** \[1,2,3,4,5\] is the original sorted array.
You can rotate the array by x = 3 positions to begin on the the element of value 3: \[3,4,5,1,2\].
**Example 2:**
**Input:** nums = \[2,1,3,4\]
**Output:** false
**Explanation:** There is no sorted array once rotated that can make nums.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Explanation:** \[1,2,3\] is the original sorted array.
You can rotate the array by x = 0 positions (i.e. no rotation) to make nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | To check if a given sequence is arithmetic, just check that the difference between every two consecutive elements is the same. If and only if a set of numbers can make an arithmetic sequence, then its sorted version makes an arithmetic sequence. So to check a set of numbers, sort it, and check if that sequence is arithmetic. For each query, get the corresponding set of numbers which will be the sub-array represented by the query, sort it, and check if the result sequence is arithmetic. |
Basic Implementation with clear approach | Detailed | check-if-array-is-sorted-and-rotated | 0 | 1 | Time Complexity: O(N)\nSpace Complexity: O(1)\n\n# Approach and Implementation\nTo implement a solution for this problem, you should be aware of what happens when you rotate a sorted array.\n\nLook at the image below. We have a sorted and rotated array:\n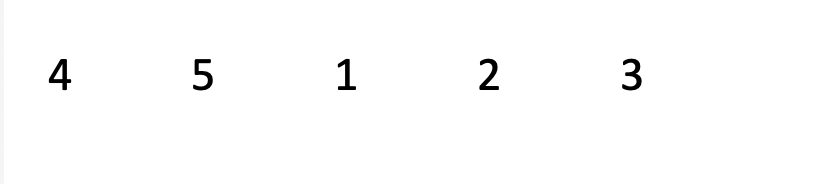\nThe array is rotated 2 times.\n\n\n\nNotice how you only have `one break point`, i.e., `arr[i-1] > arr[i]` happens only once between the elements **5** and **1**.\n\nThis ensures that the arrays is rotated properly and we do not have a random array. \n\nSo now, we have `one breaks`:\n1. Between elements 5 and 1\n\n\n`We can generalize this as nums[i-1] > nums[i]`\n\n# Code\n``` Python []\nclass Solution:\n def check(self, nums: List[int]) -> bool:\n # Initialize the break variable to 0\n breaks = 0\n\n # Iterate over the len(nums)\n for i in range(len(nums)):\n # If you find any break case, increment the break variable\n if nums[i] < nums[i-1]:\n breaks += 1\n \n # If there is atmost 1 breaks, return True\n # Else, return False\n return True if breaks <= 1 else False\n\n```\n``` C++ []\nclass Solution {\npublic:\n bool check(vector<int>& nums) {\n // Initialize the break variable to 1\n int breaks = 0;\n\n // Iterate over the len(nums)\n for(int i = 0; i < nums.size(); i++){\n // If you find any break case, increment the break variable\n if(nums[(i+1) % nums.size()] < nums[i])\n breaks++;\n }\n\n // If there is atmost 1 breaks, return True\n // Else, return False\n return breaks <= 1;\n\n }\n};\n\n```\n\n | 10 | You are given an `m x n` integer matrix `grid`.
A **rhombus sum** is the sum of the elements that form **the** **border** of a regular rhombus shape in `grid`. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each **rhombus sum**:
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.
Return _the biggest three **distinct rhombus sums** in the_ `grid` _in **descending order**__. If there are less than three distinct values, return all of them_.
**Example 1:**
**Input:** grid = \[\[3,4,5,1,3\],\[3,3,4,2,3\],\[20,30,200,40,10\],\[1,5,5,4,1\],\[4,3,2,2,5\]\]
**Output:** \[228,216,211\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211
**Example 2:**
**Input:** grid = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[20,9,8\]
**Explanation:** The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)
**Example 3:**
**Input:** grid = \[\[7,7,7\]\]
**Output:** \[7\]
**Explanation:** All three possible rhombus sums are the same, so return \[7\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j] <= 105` | Brute force and check if it is possible for a sorted array to start from each position. |
Simple solution with Heap/Priority Queue in Python3 | maximum-score-from-removing-stones | 0 | 1 | # Intuition\nHere we have:\n- three integers `a, b, c` respectively\n- our goal is to achieve **maximum score** from decrementing these integers\n\nThere\'re some rules to decrement them:\n- at each step you should take 2 integers and decrement **both**\n- the process repeats until you have **two values == 0**\n\nPresumably we could take **the largest** and **the lowest** integers and decrement them instead of **two largest**.\n\nFor this problem we\'re going to use Heap/Priority Queue to manage integers, since it stores for the first value **maximum/minimum** (depends on implementation).\n\n# Approach\n1. declare `heap` and store **negative** integers to represent a **Maximum Priority Queue (MPQ)** \n2. loop thru `heap`, until it have **more than 1 integer**\n3. decrement two largest integers from `heap`\n4. return them back, if their values **more than** `0`\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N log N)** to manage a MPQ\n\n- Space complexity: **O(1)**\n\n# Code\n```\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n heap = [-a, -b, -c]\n heapify(heap)\n ans = 0\n\n while len(heap) > 1:\n first, sec = heappop(heap) + 1, heappop(heap) + 1\n ans += 1\n\n if first < 0: heappush(heap, first)\n if sec < 0: heappush(heap, sec)\n\n return ans\n``` | 1 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Simple solution with Heap/Priority Queue in Python3 | maximum-score-from-removing-stones | 0 | 1 | # Intuition\nHere we have:\n- three integers `a, b, c` respectively\n- our goal is to achieve **maximum score** from decrementing these integers\n\nThere\'re some rules to decrement them:\n- at each step you should take 2 integers and decrement **both**\n- the process repeats until you have **two values == 0**\n\nPresumably we could take **the largest** and **the lowest** integers and decrement them instead of **two largest**.\n\nFor this problem we\'re going to use Heap/Priority Queue to manage integers, since it stores for the first value **maximum/minimum** (depends on implementation).\n\n# Approach\n1. declare `heap` and store **negative** integers to represent a **Maximum Priority Queue (MPQ)** \n2. loop thru `heap`, until it have **more than 1 integer**\n3. decrement two largest integers from `heap`\n4. return them back, if their values **more than** `0`\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N log N)** to manage a MPQ\n\n- Space complexity: **O(1)**\n\n# Code\n```\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n heap = [-a, -b, -c]\n heapify(heap)\n ans = 0\n\n while len(heap) > 1:\n first, sec = heappop(heap) + 1, heappop(heap) + 1\n ans += 1\n\n if first < 0: heappush(heap, first)\n if sec < 0: heappush(heap, sec)\n\n return ans\n``` | 1 | You are given two integer arrays `nums1` and `nums2` of length `n`.
The **XOR sum** of the two integer arrays is `(nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1])` (**0-indexed**).
* For example, the **XOR sum** of `[1,2,3]` and `[3,2,1]` is equal to `(1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4`.
Rearrange the elements of `nums2` such that the resulting **XOR sum** is **minimized**.
Return _the **XOR sum** after the rearrangement_.
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[2,3\]
**Output:** 2
**Explanation:** Rearrange `nums2` so that it becomes `[3,2]`.
The XOR sum is (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2.
**Example 2:**
**Input:** nums1 = \[1,0,3\], nums2 = \[5,3,4\]
**Output:** 8
**Explanation:** Rearrange `nums2` so that it becomes `[5,4,3]`.
The XOR sum is (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8.
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `1 <= n <= 14`
* `0 <= nums1[i], nums2[i] <= 107` | It's optimal to always remove one stone from the biggest 2 piles Note that the limits are small enough for simulation |
Easy Approach using Max Heap !! | maximum-score-from-removing-stones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom heapq import *\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n count=0\n res=[]\n heappush(res,-a)\n heappush(res,-b)\n heappush(res,-c)\n while len(res)>1:\n a1=heappop(res)\n a2=res.pop()\n a1+=1\n a2+=1\n if a1!=0:\n heappush(res,a1)\n if a2!=0:\n heappush(res,a2)\n count+=1\n return count\n\n\n\n\n\n``` | 2 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Easy Approach using Max Heap !! | maximum-score-from-removing-stones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom heapq import *\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n count=0\n res=[]\n heappush(res,-a)\n heappush(res,-b)\n heappush(res,-c)\n while len(res)>1:\n a1=heappop(res)\n a2=res.pop()\n a1+=1\n a2+=1\n if a1!=0:\n heappush(res,a1)\n if a2!=0:\n heappush(res,a2)\n count+=1\n return count\n\n\n\n\n\n``` | 2 | You are given two integer arrays `nums1` and `nums2` of length `n`.
The **XOR sum** of the two integer arrays is `(nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1])` (**0-indexed**).
* For example, the **XOR sum** of `[1,2,3]` and `[3,2,1]` is equal to `(1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4`.
Rearrange the elements of `nums2` such that the resulting **XOR sum** is **minimized**.
Return _the **XOR sum** after the rearrangement_.
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[2,3\]
**Output:** 2
**Explanation:** Rearrange `nums2` so that it becomes `[3,2]`.
The XOR sum is (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2.
**Example 2:**
**Input:** nums1 = \[1,0,3\], nums2 = \[5,3,4\]
**Output:** 8
**Explanation:** Rearrange `nums2` so that it becomes `[5,4,3]`.
The XOR sum is (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8.
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `1 <= n <= 14`
* `0 <= nums1[i], nums2[i] <= 107` | It's optimal to always remove one stone from the biggest 2 piles Note that the limits are small enough for simulation |
one liner . in O(1) time ans space | maximum-score-from-removing-stones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:1\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:1\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n return min((a+b+c)//2,a+b+c-max(a,b,c))\n``` | 9 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
one liner . in O(1) time ans space | maximum-score-from-removing-stones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:1\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:1\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n return min((a+b+c)//2,a+b+c-max(a,b,c))\n``` | 9 | You are given two integer arrays `nums1` and `nums2` of length `n`.
The **XOR sum** of the two integer arrays is `(nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1])` (**0-indexed**).
* For example, the **XOR sum** of `[1,2,3]` and `[3,2,1]` is equal to `(1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4`.
Rearrange the elements of `nums2` such that the resulting **XOR sum** is **minimized**.
Return _the **XOR sum** after the rearrangement_.
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[2,3\]
**Output:** 2
**Explanation:** Rearrange `nums2` so that it becomes `[3,2]`.
The XOR sum is (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2.
**Example 2:**
**Input:** nums1 = \[1,0,3\], nums2 = \[5,3,4\]
**Output:** 8
**Explanation:** Rearrange `nums2` so that it becomes `[5,4,3]`.
The XOR sum is (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8.
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `1 <= n <= 14`
* `0 <= nums1[i], nums2[i] <= 107` | It's optimal to always remove one stone from the biggest 2 piles Note that the limits are small enough for simulation |
Rutime - 100% beats 💥 || Memory ~ 100% beats 💥 || Fully Explained ✅ || Python ✅ || Java ✅ | maximum-score-from-removing-stones | 1 | 1 | # Approach\n\nThe given approach calculates the maximum score that can be obtained in a solitaire game with three piles of stones, represented by `a`, `b`, and `c`.\n\n1. Calculate the total sum of `a`, `b`, and `c` as `n = a + b + c`. This step determines the total number of stones in the game.\n\n2. Find the maximum value among `a`, `b`, and `c` using the `Math.max(a, b)` function. Assign this maximum value to the variable `max`. \n\n3. Update the value of `max` by comparing it with `c` using the `Math.max(max, c)` function. This ensures that `max` holds the maximum value among `a`, `b`, and `c`.\n\n4. Calculate the maximum score by finding the minimum between two values: `(a + b + c) / 2` and `a + b + c - max`. \n\n - `(a + b + c) / 2` represents half of the total sum of stones. This value represents the maximum score that can be achieved if each turn results in taking one stone from each pile.\n\n - `a + b + c - max` represents the total sum of stones minus the maximum value among `a`, `b`, and `c`. This value represents the maximum score that can be achieved if each turn involves taking stones from different piles, with one of the piles being the pile with the maximum number of stones.\n\n5. Finally, return the minimum value calculated in step 4, which represents the maximum score that can be obtained in the game.\n\nIn summary, the logic of the approach is based on comparing two scenarios: one where each turn involves taking one stone from each pile and another where one of the piles is the pile with the maximum number of stones. The approach then selects the scenario that yields the smaller score, ensuring that the returned value represents the maximum score achievable in the game.\n\n# Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```java []\nclass Solution {\n public int maximumScore(int a, int b, int c) {\n int n = a + b + c;\n int max = Math.max(a, b);\n max = Math.max(max, c);\n return Math.min(n / 2, n - max);\n }\n}\n```\n```python []\nclass Solution(object):\n def maximumScore(self, a, b, c):\n return min((a + b + c) / 2, a + b + c - max(a, b, c))\n\n``` | 3 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
Rutime - 100% beats 💥 || Memory ~ 100% beats 💥 || Fully Explained ✅ || Python ✅ || Java ✅ | maximum-score-from-removing-stones | 1 | 1 | # Approach\n\nThe given approach calculates the maximum score that can be obtained in a solitaire game with three piles of stones, represented by `a`, `b`, and `c`.\n\n1. Calculate the total sum of `a`, `b`, and `c` as `n = a + b + c`. This step determines the total number of stones in the game.\n\n2. Find the maximum value among `a`, `b`, and `c` using the `Math.max(a, b)` function. Assign this maximum value to the variable `max`. \n\n3. Update the value of `max` by comparing it with `c` using the `Math.max(max, c)` function. This ensures that `max` holds the maximum value among `a`, `b`, and `c`.\n\n4. Calculate the maximum score by finding the minimum between two values: `(a + b + c) / 2` and `a + b + c - max`. \n\n - `(a + b + c) / 2` represents half of the total sum of stones. This value represents the maximum score that can be achieved if each turn results in taking one stone from each pile.\n\n - `a + b + c - max` represents the total sum of stones minus the maximum value among `a`, `b`, and `c`. This value represents the maximum score that can be achieved if each turn involves taking stones from different piles, with one of the piles being the pile with the maximum number of stones.\n\n5. Finally, return the minimum value calculated in step 4, which represents the maximum score that can be obtained in the game.\n\nIn summary, the logic of the approach is based on comparing two scenarios: one where each turn involves taking one stone from each pile and another where one of the piles is the pile with the maximum number of stones. The approach then selects the scenario that yields the smaller score, ensuring that the returned value represents the maximum score achievable in the game.\n\n# Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```java []\nclass Solution {\n public int maximumScore(int a, int b, int c) {\n int n = a + b + c;\n int max = Math.max(a, b);\n max = Math.max(max, c);\n return Math.min(n / 2, n - max);\n }\n}\n```\n```python []\nclass Solution(object):\n def maximumScore(self, a, b, c):\n return min((a + b + c) / 2, a + b + c - max(a, b, c))\n\n``` | 3 | You are given two integer arrays `nums1` and `nums2` of length `n`.
The **XOR sum** of the two integer arrays is `(nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1])` (**0-indexed**).
* For example, the **XOR sum** of `[1,2,3]` and `[3,2,1]` is equal to `(1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4`.
Rearrange the elements of `nums2` such that the resulting **XOR sum** is **minimized**.
Return _the **XOR sum** after the rearrangement_.
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[2,3\]
**Output:** 2
**Explanation:** Rearrange `nums2` so that it becomes `[3,2]`.
The XOR sum is (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2.
**Example 2:**
**Input:** nums1 = \[1,0,3\], nums2 = \[5,3,4\]
**Output:** 8
**Explanation:** Rearrange `nums2` so that it becomes `[5,4,3]`.
The XOR sum is (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8.
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `1 <= n <= 14`
* `0 <= nums1[i], nums2[i] <= 107` | It's optimal to always remove one stone from the biggest 2 piles Note that the limits are small enough for simulation |
[Python3] math | maximum-score-from-removing-stones | 0 | 1 | \n```\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n a, b, c = sorted((a, b, c))\n if a + b < c: return a + b\n return (a + b + c)//2\n``` | 18 | You are playing a solitaire game with **three piles** of stones of sizes `a`, `b`, and `c` respectively. Each turn you choose two **different non-empty** piles, take one stone from each, and add `1` point to your score. The game stops when there are **fewer than two non-empty** piles (meaning there are no more available moves).
Given three integers `a`, `b`, and `c`, return _the_ **_maximum_** _**score** you can get._
**Example 1:**
**Input:** a = 2, b = 4, c = 6
**Output:** 6
**Explanation:** The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.
**Example 2:**
**Input:** a = 4, b = 4, c = 6
**Output:** 7
**Explanation:** The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.
**Example 3:**
**Input:** a = 1, b = 8, c = 8
**Output:** 8
**Explanation:** One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.
**Constraints:**
* `1 <= a, b, c <= 105` | Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells. If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost. Binary search the k value. |
[Python3] math | maximum-score-from-removing-stones | 0 | 1 | \n```\nclass Solution:\n def maximumScore(self, a: int, b: int, c: int) -> int:\n a, b, c = sorted((a, b, c))\n if a + b < c: return a + b\n return (a + b + c)//2\n``` | 18 | You are given two integer arrays `nums1` and `nums2` of length `n`.
The **XOR sum** of the two integer arrays is `(nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1])` (**0-indexed**).
* For example, the **XOR sum** of `[1,2,3]` and `[3,2,1]` is equal to `(1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4`.
Rearrange the elements of `nums2` such that the resulting **XOR sum** is **minimized**.
Return _the **XOR sum** after the rearrangement_.
**Example 1:**
**Input:** nums1 = \[1,2\], nums2 = \[2,3\]
**Output:** 2
**Explanation:** Rearrange `nums2` so that it becomes `[3,2]`.
The XOR sum is (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2.
**Example 2:**
**Input:** nums1 = \[1,0,3\], nums2 = \[5,3,4\]
**Output:** 8
**Explanation:** Rearrange `nums2` so that it becomes `[5,4,3]`.
The XOR sum is (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8.
**Constraints:**
* `n == nums1.length`
* `n == nums2.length`
* `1 <= n <= 14`
* `0 <= nums1[i], nums2[i] <= 107` | It's optimal to always remove one stone from the biggest 2 piles Note that the limits are small enough for simulation |
[Python3] greedy | largest-merge-of-two-strings | 0 | 1 | **Algo**\nDefine two pointers `i1` and `i2` for `word1` and `word2` respectively. Pick word from `word1` iff `word1[i1:] > word2[i2]`.\n\n**Implementation**\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n ans = []\n i1 = i2 = 0\n while i1 < len(word1) and i2 < len(word2): \n if word1[i1:] > word2[i2:]: \n ans.append(word1[i1])\n i1 += 1\n else: \n ans.append(word2[i2])\n i2 += 1\n return "".join(ans) + word1[i1:] + word2[i2:]\n```\n\n**Analysis**\nTime complexity `O(N^2)`\nSpace complexity `O(N)` | 6 | You are given two strings `word1` and `word2`. You want to construct a string `merge` in the following way: while either `word1` or `word2` are non-empty, choose **one** of the following options:
* If `word1` is non-empty, append the **first** character in `word1` to `merge` and delete it from `word1`.
* For example, if `word1 = "abc "` and `merge = "dv "`, then after choosing this operation, `word1 = "bc "` and `merge = "dva "`.
* If `word2` is non-empty, append the **first** character in `word2` to `merge` and delete it from `word2`.
* For example, if `word2 = "abc "` and `merge = " "`, then after choosing this operation, `word2 = "bc "` and `merge = "a "`.
Return _the lexicographically **largest**_ `merge` _you can construct_.
A string `a` is lexicographically larger than a string `b` (of the same length) if in the first position where `a` and `b` differ, `a` has a character strictly larger than the corresponding character in `b`. For example, `"abcd "` is lexicographically larger than `"abcc "` because the first position they differ is at the fourth character, and `d` is greater than `c`.
**Example 1:**
**Input:** word1 = "cabaa ", word2 = "bcaaa "
**Output:** "cbcabaaaaa "
**Explanation:** One way to get the lexicographically largest merge is:
- Take from word1: merge = "c ", word1 = "abaa ", word2 = "bcaaa "
- Take from word2: merge = "cb ", word1 = "abaa ", word2 = "caaa "
- Take from word2: merge = "cbc ", word1 = "abaa ", word2 = "aaa "
- Take from word1: merge = "cbca ", word1 = "baa ", word2 = "aaa "
- Take from word1: merge = "cbcab ", word1 = "aa ", word2 = "aaa "
- Append the remaining 5 a's from word1 and word2 at the end of merge.
**Example 2:**
**Input:** word1 = "abcabc ", word2 = "abdcaba "
**Output:** "abdcabcabcaba "
**Constraints:**
* `1 <= word1.length, word2.length <= 3000`
* `word1` and `word2` consist only of lowercase English letters. | null |
[Python3] greedy | largest-merge-of-two-strings | 0 | 1 | **Algo**\nDefine two pointers `i1` and `i2` for `word1` and `word2` respectively. Pick word from `word1` iff `word1[i1:] > word2[i2]`.\n\n**Implementation**\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n ans = []\n i1 = i2 = 0\n while i1 < len(word1) and i2 < len(word2): \n if word1[i1:] > word2[i2:]: \n ans.append(word1[i1])\n i1 += 1\n else: \n ans.append(word2[i2])\n i2 += 1\n return "".join(ans) + word1[i1:] + word2[i2:]\n```\n\n**Analysis**\nTime complexity `O(N^2)`\nSpace complexity `O(N)` | 6 | The **letter value** of a letter is its position in the alphabet **starting from 0** (i.e. `'a' -> 0`, `'b' -> 1`, `'c' -> 2`, etc.).
The **numerical value** of some string of lowercase English letters `s` is the **concatenation** of the **letter values** of each letter in `s`, which is then **converted** into an integer.
* For example, if `s = "acb "`, we concatenate each letter's letter value, resulting in `"021 "`. After converting it, we get `21`.
You are given three strings `firstWord`, `secondWord`, and `targetWord`, each consisting of lowercase English letters `'a'` through `'j'` **inclusive**.
Return `true` _if the **summation** of the **numerical values** of_ `firstWord` _and_ `secondWord` _equals the **numerical value** of_ `targetWord`_, or_ `false` _otherwise._
**Example 1:**
**Input:** firstWord = "acb ", secondWord = "cba ", targetWord = "cdb "
**Output:** true
**Explanation:**
The numerical value of firstWord is "acb " -> "021 " -> 21.
The numerical value of secondWord is "cba " -> "210 " -> 210.
The numerical value of targetWord is "cdb " -> "231 " -> 231.
We return true because 21 + 210 == 231.
**Example 2:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aab "
**Output:** false
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aab " -> "001 " -> 1.
We return false because 0 + 0 != 1.
**Example 3:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aaaa "
**Output:** true
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aaaa " -> "0000 " -> 0.
We return true because 0 + 0 == 0.
**Constraints:**
* `1 <= firstWord.length,` `secondWord.length,` `targetWord.length <= 8`
* `firstWord`, `secondWord`, and `targetWord` consist of lowercase English letters from `'a'` to `'j'` **inclusive**. | Build the result character by character. At each step, you choose a character from one of the two strings. If the next character of the first string is larger than that of the second string, or vice versa, it's optimal to use the larger one. If both are equal, think of a criteria that lets you decide which string to consume the next character from. You should choose the next character from the larger string. |
using two pointers easy-ethiopian nerd | largest-merge-of-two-strings | 0 | 1 | # Intuition\nusnig two pointers\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:o(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:i didnt calculate it\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n for1,for2=0,0\n answer=[]\n while for1<len(word1) and for2<len(word2):\n ele1,ele2=word1[for1],word2[for2]\n if ele1>ele2:\n answer.append(ele1)\n for1+=1\n elif ele1<ele2:\n answer.append(ele2)\n for2+=1\n else:\n temp1=word1[for1:]\n temp2=word2[for2:]\n if temp1>temp2:\n answer.append(ele1)\n for1+=1\n else:\n answer.append(ele2)\n for2+=1\n while for1<len(word1):\n answer.append(word1[for1])\n for1+=1\n while for2<len(word2):\n answer.append(word2[for2])\n for2+=1\n return "".join(answer)\n\n\n``` | 0 | You are given two strings `word1` and `word2`. You want to construct a string `merge` in the following way: while either `word1` or `word2` are non-empty, choose **one** of the following options:
* If `word1` is non-empty, append the **first** character in `word1` to `merge` and delete it from `word1`.
* For example, if `word1 = "abc "` and `merge = "dv "`, then after choosing this operation, `word1 = "bc "` and `merge = "dva "`.
* If `word2` is non-empty, append the **first** character in `word2` to `merge` and delete it from `word2`.
* For example, if `word2 = "abc "` and `merge = " "`, then after choosing this operation, `word2 = "bc "` and `merge = "a "`.
Return _the lexicographically **largest**_ `merge` _you can construct_.
A string `a` is lexicographically larger than a string `b` (of the same length) if in the first position where `a` and `b` differ, `a` has a character strictly larger than the corresponding character in `b`. For example, `"abcd "` is lexicographically larger than `"abcc "` because the first position they differ is at the fourth character, and `d` is greater than `c`.
**Example 1:**
**Input:** word1 = "cabaa ", word2 = "bcaaa "
**Output:** "cbcabaaaaa "
**Explanation:** One way to get the lexicographically largest merge is:
- Take from word1: merge = "c ", word1 = "abaa ", word2 = "bcaaa "
- Take from word2: merge = "cb ", word1 = "abaa ", word2 = "caaa "
- Take from word2: merge = "cbc ", word1 = "abaa ", word2 = "aaa "
- Take from word1: merge = "cbca ", word1 = "baa ", word2 = "aaa "
- Take from word1: merge = "cbcab ", word1 = "aa ", word2 = "aaa "
- Append the remaining 5 a's from word1 and word2 at the end of merge.
**Example 2:**
**Input:** word1 = "abcabc ", word2 = "abdcaba "
**Output:** "abdcabcabcaba "
**Constraints:**
* `1 <= word1.length, word2.length <= 3000`
* `word1` and `word2` consist only of lowercase English letters. | null |
using two pointers easy-ethiopian nerd | largest-merge-of-two-strings | 0 | 1 | # Intuition\nusnig two pointers\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:o(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:i didnt calculate it\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n for1,for2=0,0\n answer=[]\n while for1<len(word1) and for2<len(word2):\n ele1,ele2=word1[for1],word2[for2]\n if ele1>ele2:\n answer.append(ele1)\n for1+=1\n elif ele1<ele2:\n answer.append(ele2)\n for2+=1\n else:\n temp1=word1[for1:]\n temp2=word2[for2:]\n if temp1>temp2:\n answer.append(ele1)\n for1+=1\n else:\n answer.append(ele2)\n for2+=1\n while for1<len(word1):\n answer.append(word1[for1])\n for1+=1\n while for2<len(word2):\n answer.append(word2[for2])\n for2+=1\n return "".join(answer)\n\n\n``` | 0 | The **letter value** of a letter is its position in the alphabet **starting from 0** (i.e. `'a' -> 0`, `'b' -> 1`, `'c' -> 2`, etc.).
The **numerical value** of some string of lowercase English letters `s` is the **concatenation** of the **letter values** of each letter in `s`, which is then **converted** into an integer.
* For example, if `s = "acb "`, we concatenate each letter's letter value, resulting in `"021 "`. After converting it, we get `21`.
You are given three strings `firstWord`, `secondWord`, and `targetWord`, each consisting of lowercase English letters `'a'` through `'j'` **inclusive**.
Return `true` _if the **summation** of the **numerical values** of_ `firstWord` _and_ `secondWord` _equals the **numerical value** of_ `targetWord`_, or_ `false` _otherwise._
**Example 1:**
**Input:** firstWord = "acb ", secondWord = "cba ", targetWord = "cdb "
**Output:** true
**Explanation:**
The numerical value of firstWord is "acb " -> "021 " -> 21.
The numerical value of secondWord is "cba " -> "210 " -> 210.
The numerical value of targetWord is "cdb " -> "231 " -> 231.
We return true because 21 + 210 == 231.
**Example 2:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aab "
**Output:** false
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aab " -> "001 " -> 1.
We return false because 0 + 0 != 1.
**Example 3:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aaaa "
**Output:** true
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aaaa " -> "0000 " -> 0.
We return true because 0 + 0 == 0.
**Constraints:**
* `1 <= firstWord.length,` `secondWord.length,` `targetWord.length <= 8`
* `firstWord`, `secondWord`, and `targetWord` consist of lowercase English letters from `'a'` to `'j'` **inclusive**. | Build the result character by character. At each step, you choose a character from one of the two strings. If the next character of the first string is larger than that of the second string, or vice versa, it's optimal to use the larger one. If both are equal, think of a criteria that lets you decide which string to consume the next character from. You should choose the next character from the larger string. |
simple greedy solution | largest-merge-of-two-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->o(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->o(1)\n\n# Code\n```\nclass Solution:\n def largestMerge(self, w1: str, w2: str) -> str:\n #return w2[:-1]\n #w1=w1[::-1]\n #w2=w2[::-1]\n \n def greedy(w1,w2,res):\n while w1 and w2:\n if w1>w2:\n res+=w1[0]\n w1=w1[1:]\n else:\n res+=w2[0]\n w2=w2[1:]\n #res+=cur\n #print(res)\n res+=w1\n res+=w2\n return res\n res1=greedy(w1,w2,\'\')\n return res1\n \n\n``` | 0 | You are given two strings `word1` and `word2`. You want to construct a string `merge` in the following way: while either `word1` or `word2` are non-empty, choose **one** of the following options:
* If `word1` is non-empty, append the **first** character in `word1` to `merge` and delete it from `word1`.
* For example, if `word1 = "abc "` and `merge = "dv "`, then after choosing this operation, `word1 = "bc "` and `merge = "dva "`.
* If `word2` is non-empty, append the **first** character in `word2` to `merge` and delete it from `word2`.
* For example, if `word2 = "abc "` and `merge = " "`, then after choosing this operation, `word2 = "bc "` and `merge = "a "`.
Return _the lexicographically **largest**_ `merge` _you can construct_.
A string `a` is lexicographically larger than a string `b` (of the same length) if in the first position where `a` and `b` differ, `a` has a character strictly larger than the corresponding character in `b`. For example, `"abcd "` is lexicographically larger than `"abcc "` because the first position they differ is at the fourth character, and `d` is greater than `c`.
**Example 1:**
**Input:** word1 = "cabaa ", word2 = "bcaaa "
**Output:** "cbcabaaaaa "
**Explanation:** One way to get the lexicographically largest merge is:
- Take from word1: merge = "c ", word1 = "abaa ", word2 = "bcaaa "
- Take from word2: merge = "cb ", word1 = "abaa ", word2 = "caaa "
- Take from word2: merge = "cbc ", word1 = "abaa ", word2 = "aaa "
- Take from word1: merge = "cbca ", word1 = "baa ", word2 = "aaa "
- Take from word1: merge = "cbcab ", word1 = "aa ", word2 = "aaa "
- Append the remaining 5 a's from word1 and word2 at the end of merge.
**Example 2:**
**Input:** word1 = "abcabc ", word2 = "abdcaba "
**Output:** "abdcabcabcaba "
**Constraints:**
* `1 <= word1.length, word2.length <= 3000`
* `word1` and `word2` consist only of lowercase English letters. | null |
simple greedy solution | largest-merge-of-two-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->o(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->o(1)\n\n# Code\n```\nclass Solution:\n def largestMerge(self, w1: str, w2: str) -> str:\n #return w2[:-1]\n #w1=w1[::-1]\n #w2=w2[::-1]\n \n def greedy(w1,w2,res):\n while w1 and w2:\n if w1>w2:\n res+=w1[0]\n w1=w1[1:]\n else:\n res+=w2[0]\n w2=w2[1:]\n #res+=cur\n #print(res)\n res+=w1\n res+=w2\n return res\n res1=greedy(w1,w2,\'\')\n return res1\n \n\n``` | 0 | The **letter value** of a letter is its position in the alphabet **starting from 0** (i.e. `'a' -> 0`, `'b' -> 1`, `'c' -> 2`, etc.).
The **numerical value** of some string of lowercase English letters `s` is the **concatenation** of the **letter values** of each letter in `s`, which is then **converted** into an integer.
* For example, if `s = "acb "`, we concatenate each letter's letter value, resulting in `"021 "`. After converting it, we get `21`.
You are given three strings `firstWord`, `secondWord`, and `targetWord`, each consisting of lowercase English letters `'a'` through `'j'` **inclusive**.
Return `true` _if the **summation** of the **numerical values** of_ `firstWord` _and_ `secondWord` _equals the **numerical value** of_ `targetWord`_, or_ `false` _otherwise._
**Example 1:**
**Input:** firstWord = "acb ", secondWord = "cba ", targetWord = "cdb "
**Output:** true
**Explanation:**
The numerical value of firstWord is "acb " -> "021 " -> 21.
The numerical value of secondWord is "cba " -> "210 " -> 210.
The numerical value of targetWord is "cdb " -> "231 " -> 231.
We return true because 21 + 210 == 231.
**Example 2:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aab "
**Output:** false
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aab " -> "001 " -> 1.
We return false because 0 + 0 != 1.
**Example 3:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aaaa "
**Output:** true
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aaaa " -> "0000 " -> 0.
We return true because 0 + 0 == 0.
**Constraints:**
* `1 <= firstWord.length,` `secondWord.length,` `targetWord.length <= 8`
* `firstWord`, `secondWord`, and `targetWord` consist of lowercase English letters from `'a'` to `'j'` **inclusive**. | Build the result character by character. At each step, you choose a character from one of the two strings. If the next character of the first string is larger than that of the second string, or vice versa, it's optimal to use the larger one. If both are equal, think of a criteria that lets you decide which string to consume the next character from. You should choose the next character from the larger string. |
Python3 | Two Pointers | Fast | largest-merge-of-two-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Using two pointers, we can compare the characters.\n\n# Approach\n<!-- Describe your approach to solving the problem. --> Compare each character and append accordingly. When two characters are the same, we need to slice and compare the whole substring and append accordingly.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n merge = \'\'\n i1, i2 = 0,0\n while i1<len(word1) and i2<len(word2):\n if word1[i1]>word2[i2]:\n merge += word1[i1]\n i1+=1\n elif word1[i1] < word2[i2]:\n merge += word2[i2]\n i2 += 1\n else:\n if word1[i1:] > word2[i2:]:\n merge+= word1[i1]\n i1 += 1\n else:\n merge += word2[i2]\n i2 += 1\n if i1<len(word1):\n merge += word1[i1:]\n if i2<len(word2):\n merge+= word2[i2:]\n return merge\n\n``` | 0 | You are given two strings `word1` and `word2`. You want to construct a string `merge` in the following way: while either `word1` or `word2` are non-empty, choose **one** of the following options:
* If `word1` is non-empty, append the **first** character in `word1` to `merge` and delete it from `word1`.
* For example, if `word1 = "abc "` and `merge = "dv "`, then after choosing this operation, `word1 = "bc "` and `merge = "dva "`.
* If `word2` is non-empty, append the **first** character in `word2` to `merge` and delete it from `word2`.
* For example, if `word2 = "abc "` and `merge = " "`, then after choosing this operation, `word2 = "bc "` and `merge = "a "`.
Return _the lexicographically **largest**_ `merge` _you can construct_.
A string `a` is lexicographically larger than a string `b` (of the same length) if in the first position where `a` and `b` differ, `a` has a character strictly larger than the corresponding character in `b`. For example, `"abcd "` is lexicographically larger than `"abcc "` because the first position they differ is at the fourth character, and `d` is greater than `c`.
**Example 1:**
**Input:** word1 = "cabaa ", word2 = "bcaaa "
**Output:** "cbcabaaaaa "
**Explanation:** One way to get the lexicographically largest merge is:
- Take from word1: merge = "c ", word1 = "abaa ", word2 = "bcaaa "
- Take from word2: merge = "cb ", word1 = "abaa ", word2 = "caaa "
- Take from word2: merge = "cbc ", word1 = "abaa ", word2 = "aaa "
- Take from word1: merge = "cbca ", word1 = "baa ", word2 = "aaa "
- Take from word1: merge = "cbcab ", word1 = "aa ", word2 = "aaa "
- Append the remaining 5 a's from word1 and word2 at the end of merge.
**Example 2:**
**Input:** word1 = "abcabc ", word2 = "abdcaba "
**Output:** "abdcabcabcaba "
**Constraints:**
* `1 <= word1.length, word2.length <= 3000`
* `word1` and `word2` consist only of lowercase English letters. | null |
Python3 | Two Pointers | Fast | largest-merge-of-two-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Using two pointers, we can compare the characters.\n\n# Approach\n<!-- Describe your approach to solving the problem. --> Compare each character and append accordingly. When two characters are the same, we need to slice and compare the whole substring and append accordingly.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n merge = \'\'\n i1, i2 = 0,0\n while i1<len(word1) and i2<len(word2):\n if word1[i1]>word2[i2]:\n merge += word1[i1]\n i1+=1\n elif word1[i1] < word2[i2]:\n merge += word2[i2]\n i2 += 1\n else:\n if word1[i1:] > word2[i2:]:\n merge+= word1[i1]\n i1 += 1\n else:\n merge += word2[i2]\n i2 += 1\n if i1<len(word1):\n merge += word1[i1:]\n if i2<len(word2):\n merge+= word2[i2:]\n return merge\n\n``` | 0 | The **letter value** of a letter is its position in the alphabet **starting from 0** (i.e. `'a' -> 0`, `'b' -> 1`, `'c' -> 2`, etc.).
The **numerical value** of some string of lowercase English letters `s` is the **concatenation** of the **letter values** of each letter in `s`, which is then **converted** into an integer.
* For example, if `s = "acb "`, we concatenate each letter's letter value, resulting in `"021 "`. After converting it, we get `21`.
You are given three strings `firstWord`, `secondWord`, and `targetWord`, each consisting of lowercase English letters `'a'` through `'j'` **inclusive**.
Return `true` _if the **summation** of the **numerical values** of_ `firstWord` _and_ `secondWord` _equals the **numerical value** of_ `targetWord`_, or_ `false` _otherwise._
**Example 1:**
**Input:** firstWord = "acb ", secondWord = "cba ", targetWord = "cdb "
**Output:** true
**Explanation:**
The numerical value of firstWord is "acb " -> "021 " -> 21.
The numerical value of secondWord is "cba " -> "210 " -> 210.
The numerical value of targetWord is "cdb " -> "231 " -> 231.
We return true because 21 + 210 == 231.
**Example 2:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aab "
**Output:** false
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aab " -> "001 " -> 1.
We return false because 0 + 0 != 1.
**Example 3:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aaaa "
**Output:** true
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aaaa " -> "0000 " -> 0.
We return true because 0 + 0 == 0.
**Constraints:**
* `1 <= firstWord.length,` `secondWord.length,` `targetWord.length <= 8`
* `firstWord`, `secondWord`, and `targetWord` consist of lowercase English letters from `'a'` to `'j'` **inclusive**. | Build the result character by character. At each step, you choose a character from one of the two strings. If the next character of the first string is larger than that of the second string, or vice versa, it's optimal to use the larger one. If both are equal, think of a criteria that lets you decide which string to consume the next character from. You should choose the next character from the larger string. |
Python3 easy solution | largest-merge-of-two-strings | 0 | 1 | # Code\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n res = []\n while word1 or word2:\n if word1 >= word2:\n res.append(word1[0])\n word1 = word1[1:]\n else:\n res.append(word2[0])\n word2 = word2[1:]\n return "".join(res)\n``` | 0 | You are given two strings `word1` and `word2`. You want to construct a string `merge` in the following way: while either `word1` or `word2` are non-empty, choose **one** of the following options:
* If `word1` is non-empty, append the **first** character in `word1` to `merge` and delete it from `word1`.
* For example, if `word1 = "abc "` and `merge = "dv "`, then after choosing this operation, `word1 = "bc "` and `merge = "dva "`.
* If `word2` is non-empty, append the **first** character in `word2` to `merge` and delete it from `word2`.
* For example, if `word2 = "abc "` and `merge = " "`, then after choosing this operation, `word2 = "bc "` and `merge = "a "`.
Return _the lexicographically **largest**_ `merge` _you can construct_.
A string `a` is lexicographically larger than a string `b` (of the same length) if in the first position where `a` and `b` differ, `a` has a character strictly larger than the corresponding character in `b`. For example, `"abcd "` is lexicographically larger than `"abcc "` because the first position they differ is at the fourth character, and `d` is greater than `c`.
**Example 1:**
**Input:** word1 = "cabaa ", word2 = "bcaaa "
**Output:** "cbcabaaaaa "
**Explanation:** One way to get the lexicographically largest merge is:
- Take from word1: merge = "c ", word1 = "abaa ", word2 = "bcaaa "
- Take from word2: merge = "cb ", word1 = "abaa ", word2 = "caaa "
- Take from word2: merge = "cbc ", word1 = "abaa ", word2 = "aaa "
- Take from word1: merge = "cbca ", word1 = "baa ", word2 = "aaa "
- Take from word1: merge = "cbcab ", word1 = "aa ", word2 = "aaa "
- Append the remaining 5 a's from word1 and word2 at the end of merge.
**Example 2:**
**Input:** word1 = "abcabc ", word2 = "abdcaba "
**Output:** "abdcabcabcaba "
**Constraints:**
* `1 <= word1.length, word2.length <= 3000`
* `word1` and `word2` consist only of lowercase English letters. | null |
Python3 easy solution | largest-merge-of-two-strings | 0 | 1 | # Code\n```\nclass Solution:\n def largestMerge(self, word1: str, word2: str) -> str:\n res = []\n while word1 or word2:\n if word1 >= word2:\n res.append(word1[0])\n word1 = word1[1:]\n else:\n res.append(word2[0])\n word2 = word2[1:]\n return "".join(res)\n``` | 0 | The **letter value** of a letter is its position in the alphabet **starting from 0** (i.e. `'a' -> 0`, `'b' -> 1`, `'c' -> 2`, etc.).
The **numerical value** of some string of lowercase English letters `s` is the **concatenation** of the **letter values** of each letter in `s`, which is then **converted** into an integer.
* For example, if `s = "acb "`, we concatenate each letter's letter value, resulting in `"021 "`. After converting it, we get `21`.
You are given three strings `firstWord`, `secondWord`, and `targetWord`, each consisting of lowercase English letters `'a'` through `'j'` **inclusive**.
Return `true` _if the **summation** of the **numerical values** of_ `firstWord` _and_ `secondWord` _equals the **numerical value** of_ `targetWord`_, or_ `false` _otherwise._
**Example 1:**
**Input:** firstWord = "acb ", secondWord = "cba ", targetWord = "cdb "
**Output:** true
**Explanation:**
The numerical value of firstWord is "acb " -> "021 " -> 21.
The numerical value of secondWord is "cba " -> "210 " -> 210.
The numerical value of targetWord is "cdb " -> "231 " -> 231.
We return true because 21 + 210 == 231.
**Example 2:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aab "
**Output:** false
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aab " -> "001 " -> 1.
We return false because 0 + 0 != 1.
**Example 3:**
**Input:** firstWord = "aaa ", secondWord = "a ", targetWord = "aaaa "
**Output:** true
**Explanation:**
The numerical value of firstWord is "aaa " -> "000 " -> 0.
The numerical value of secondWord is "a " -> "0 " -> 0.
The numerical value of targetWord is "aaaa " -> "0000 " -> 0.
We return true because 0 + 0 == 0.
**Constraints:**
* `1 <= firstWord.length,` `secondWord.length,` `targetWord.length <= 8`
* `firstWord`, `secondWord`, and `targetWord` consist of lowercase English letters from `'a'` to `'j'` **inclusive**. | Build the result character by character. At each step, you choose a character from one of the two strings. If the next character of the first string is larger than that of the second string, or vice versa, it's optimal to use the larger one. If both are equal, think of a criteria that lets you decide which string to consume the next character from. You should choose the next character from the larger string. |
[Python3] divide in half | closest-subsequence-sum | 0 | 1 | **Algo**\nDivide `nums` in half. Collect subsequence subs of the two halves respectively and search for a combined sum that is closest to given `target`. \n\n**Implementation**\n```\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n \n def fn(nums):\n ans = {0}\n for x in nums: \n ans |= {x + y for y in ans}\n return ans \n \n nums0 = sorted(fn(nums[:len(nums)//2]))\n \n ans = inf\n for x in fn(nums[len(nums)//2:]): \n k = bisect_left(nums0, goal - x)\n if k < len(nums0): ans = min(ans, nums0[k] + x - goal)\n if 0 < k: ans = min(ans, goal - x - nums0[k-1])\n return ans \n```\n\n**Analysis**\nTime complexity `O(2^(N/2))`\nSpace complexity `O(2^(N/2))` | 31 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
[Python3] divide in half | closest-subsequence-sum | 0 | 1 | **Algo**\nDivide `nums` in half. Collect subsequence subs of the two halves respectively and search for a combined sum that is closest to given `target`. \n\n**Implementation**\n```\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n \n def fn(nums):\n ans = {0}\n for x in nums: \n ans |= {x + y for y in ans}\n return ans \n \n nums0 = sorted(fn(nums[:len(nums)//2]))\n \n ans = inf\n for x in fn(nums[len(nums)//2:]): \n k = bisect_left(nums0, goal - x)\n if k < len(nums0): ans = min(ans, nums0[k] + x - goal)\n if 0 < k: ans = min(ans, goal - x - nums0[k-1])\n return ans \n```\n\n**Analysis**\nTime complexity `O(2^(N/2))`\nSpace complexity `O(2^(N/2))` | 31 | You are given a very large integer `n`, represented as a string, and an integer digit `x`. The digits in `n` and the digit `x` are in the **inclusive** range `[1, 9]`, and `n` may represent a **negative** number.
You want to **maximize** `n`**'s numerical value** by inserting `x` anywhere in the decimal representation of `n`. You **cannot** insert `x` to the left of the negative sign.
* For example, if `n = 73` and `x = 6`, it would be best to insert it between `7` and `3`, making `n = 763`.
* If `n = -55` and `x = 2`, it would be best to insert it before the first `5`, making `n = -255`.
Return _a string representing the **maximum** value of_ `n`_ after the insertion_.
**Example 1:**
**Input:** n = "99 ", x = 9
**Output:** "999 "
**Explanation:** The result is the same regardless of where you insert 9.
**Example 2:**
**Input:** n = "-13 ", x = 2
**Output:** "-123 "
**Explanation:** You can make n one of {-213, -123, -132}, and the largest of those three is -123.
**Constraints:**
* `1 <= n.length <= 105`
* `1 <= x <= 9`
* The digits in `n` are in the range `[1, 9]`.
* `n` is a valid representation of an integer.
* In the case of a negative `n`, it will begin with `'-'`. | The naive solution is to check all possible subsequences. This works in O(2^n). Divide the array into two parts of nearly is equal size. Consider all subsets of one part and make a list of all possible subset sums and sort this list. Consider all subsets of the other part, and for each one, let its sum = x, do binary search to get the nearest possible value to goal - x in the first part. |
Python | Meet In Middle | Simple Solution | closest-subsequence-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n mid = len(nums) // 2\n subSum1 = self.__getSubsequences(nums[:mid], 0, 0)\n subSum2 = self.__getSubsequences(nums[mid:], 0, 0)\n subSum2.sort()\n ans = sys.maxsize\n for ss in subSum1:\n counterPart = goal - ss\n idx = self.__binarySearchLeft(subSum2, counterPart)\n if idx < len(subSum2):\n ans = min(ans, abs(counterPart-subSum2[idx]))\n if idx > 0:\n ans = min(ans, abs(counterPart-subSum2[idx-1]))\n return ans\n\n \n def __getSubsequences(self, nums, i, subSum):\n if i == len(nums):\n return [subSum]\n current = nums[i]\n taken = self.__getSubsequences(nums, i+1, subSum+current)\n ignored = self.__getSubsequences(nums, i+1, subSum)\n return taken + ignored\n\n def __binarySearchLeft(self, nums, target):\n s, e = 0, len(nums)-1\n ans = -1\n while s <= e:\n m = s + ((e-s)//2)\n if nums[m] >= target:\n ans = m\n e = m-1\n else:\n s = m+1\n return ans\n```\n\n**If you liked the above solution then please upvote!** | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Python | Meet In Middle | Simple Solution | closest-subsequence-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n mid = len(nums) // 2\n subSum1 = self.__getSubsequences(nums[:mid], 0, 0)\n subSum2 = self.__getSubsequences(nums[mid:], 0, 0)\n subSum2.sort()\n ans = sys.maxsize\n for ss in subSum1:\n counterPart = goal - ss\n idx = self.__binarySearchLeft(subSum2, counterPart)\n if idx < len(subSum2):\n ans = min(ans, abs(counterPart-subSum2[idx]))\n if idx > 0:\n ans = min(ans, abs(counterPart-subSum2[idx-1]))\n return ans\n\n \n def __getSubsequences(self, nums, i, subSum):\n if i == len(nums):\n return [subSum]\n current = nums[i]\n taken = self.__getSubsequences(nums, i+1, subSum+current)\n ignored = self.__getSubsequences(nums, i+1, subSum)\n return taken + ignored\n\n def __binarySearchLeft(self, nums, target):\n s, e = 0, len(nums)-1\n ans = -1\n while s <= e:\n m = s + ((e-s)//2)\n if nums[m] >= target:\n ans = m\n e = m-1\n else:\n s = m+1\n return ans\n```\n\n**If you liked the above solution then please upvote!** | 0 | You are given a very large integer `n`, represented as a string, and an integer digit `x`. The digits in `n` and the digit `x` are in the **inclusive** range `[1, 9]`, and `n` may represent a **negative** number.
You want to **maximize** `n`**'s numerical value** by inserting `x` anywhere in the decimal representation of `n`. You **cannot** insert `x` to the left of the negative sign.
* For example, if `n = 73` and `x = 6`, it would be best to insert it between `7` and `3`, making `n = 763`.
* If `n = -55` and `x = 2`, it would be best to insert it before the first `5`, making `n = -255`.
Return _a string representing the **maximum** value of_ `n`_ after the insertion_.
**Example 1:**
**Input:** n = "99 ", x = 9
**Output:** "999 "
**Explanation:** The result is the same regardless of where you insert 9.
**Example 2:**
**Input:** n = "-13 ", x = 2
**Output:** "-123 "
**Explanation:** You can make n one of {-213, -123, -132}, and the largest of those three is -123.
**Constraints:**
* `1 <= n.length <= 105`
* `1 <= x <= 9`
* The digits in `n` are in the range `[1, 9]`.
* `n` is a valid representation of an integer.
* In the case of a negative `n`, it will begin with `'-'`. | The naive solution is to check all possible subsequences. This works in O(2^n). Divide the array into two parts of nearly is equal size. Consider all subsets of one part and make a list of all possible subset sums and sort this list. Consider all subsets of the other part, and for each one, let its sum = x, do binary search to get the nearest possible value to goal - x in the first part. |
python binary search o(2**(n/2) +2**(n/2) ) | closest-subsequence-sum | 0 | 1 | \n\n# Code\n```\nimport bisect\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n a,b = [],[]\n for i in range(len(nums)//2):\n a.append(nums[i])\n for i in range(len(nums)//2,len(nums)):\n b.append(nums[i])\n\n s1,s2 = [0],[0]\n for m in a:\n temp = []\n for n in s1:\n temp.append(n+m)\n s1 = s1+temp\n for m in b:\n temp = []\n for n in s2:\n temp.append(n+m)\n s2 = s2+temp\n \n ans = inf\n s2.sort()\n for e in s1:\n n = goal-e\n idx = bisect.bisect_left(s2,n)\n if idx!=len(s2):\n ans = min(ans,abs(n-s2[idx]))\n if idx!=0:\n ans = min(ans,abs(n-s2[idx-1]))\n\n return ans\n \n\n``` | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
python binary search o(2**(n/2) +2**(n/2) ) | closest-subsequence-sum | 0 | 1 | \n\n# Code\n```\nimport bisect\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n a,b = [],[]\n for i in range(len(nums)//2):\n a.append(nums[i])\n for i in range(len(nums)//2,len(nums)):\n b.append(nums[i])\n\n s1,s2 = [0],[0]\n for m in a:\n temp = []\n for n in s1:\n temp.append(n+m)\n s1 = s1+temp\n for m in b:\n temp = []\n for n in s2:\n temp.append(n+m)\n s2 = s2+temp\n \n ans = inf\n s2.sort()\n for e in s1:\n n = goal-e\n idx = bisect.bisect_left(s2,n)\n if idx!=len(s2):\n ans = min(ans,abs(n-s2[idx]))\n if idx!=0:\n ans = min(ans,abs(n-s2[idx-1]))\n\n return ans\n \n\n``` | 0 | You are given a very large integer `n`, represented as a string, and an integer digit `x`. The digits in `n` and the digit `x` are in the **inclusive** range `[1, 9]`, and `n` may represent a **negative** number.
You want to **maximize** `n`**'s numerical value** by inserting `x` anywhere in the decimal representation of `n`. You **cannot** insert `x` to the left of the negative sign.
* For example, if `n = 73` and `x = 6`, it would be best to insert it between `7` and `3`, making `n = 763`.
* If `n = -55` and `x = 2`, it would be best to insert it before the first `5`, making `n = -255`.
Return _a string representing the **maximum** value of_ `n`_ after the insertion_.
**Example 1:**
**Input:** n = "99 ", x = 9
**Output:** "999 "
**Explanation:** The result is the same regardless of where you insert 9.
**Example 2:**
**Input:** n = "-13 ", x = 2
**Output:** "-123 "
**Explanation:** You can make n one of {-213, -123, -132}, and the largest of those three is -123.
**Constraints:**
* `1 <= n.length <= 105`
* `1 <= x <= 9`
* The digits in `n` are in the range `[1, 9]`.
* `n` is a valid representation of an integer.
* In the case of a negative `n`, it will begin with `'-'`. | The naive solution is to check all possible subsequences. This works in O(2^n). Divide the array into two parts of nearly is equal size. Consider all subsets of one part and make a list of all possible subset sums and sort this list. Consider all subsets of the other part, and for each one, let its sum = x, do binary search to get the nearest possible value to goal - x in the first part. |
Python Soln (Meet in the Middle | combinations) + comments ! | closest-subsequence-sum | 0 | 1 | #### Intuition\nAs all combinations will take too much space so divide the problem in halves & solve inorder to reduce space usage at a time\n\n#### Code\n```\ndef findAllSums(nums):\n res = {0, sum(nums)}\n\n for i in range(1, len(nums)):\n res.update({sum(sub) for sub in combinations(nums, i)})\n \n return res \n\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n \'\'\'Meet in the Middle\'\'\'\n n = len(nums)\n m = n // 2\n sum1 = list(findAllSums(nums[:m]))\n sum2 = sorted(findAllSums(nums[m:]))\n\n ans = abs(goal) \n\n n2 = len(sum2)\n for s1 in sum1:\n t = goal-s1 \n if t == 0: return 0\n\n i = bisect.bisect(sum2, t) # Find pos for {t}\n\n # check two nearest value ie after & before\n if i < n2: # After\n diff = abs(sum2[i] - t)\n if diff == 0: return 0\n ans = min(ans, diff)\n \n if i > 0: # before\n diff = abs(t - sum2[i-1])\n if diff == 0: return 0\n ans = min(ans, diff)\n\n return ans\n``` | 0 | You are given an integer array `nums` and an integer `goal`.
You want to choose a subsequence of `nums` such that the sum of its elements is the closest possible to `goal`. That is, if the sum of the subsequence's elements is `sum`, then you want to **minimize the absolute difference** `abs(sum - goal)`.
Return _the **minimum** possible value of_ `abs(sum - goal)`.
Note that a subsequence of an array is an array formed by removing some elements **(possibly all or none)** of the original array.
**Example 1:**
**Input:** nums = \[5,-7,3,5\], goal = 6
**Output:** 0
**Explanation:** Choose the whole array as a subsequence, with a sum of 6.
This is equal to the goal, so the absolute difference is 0.
**Example 2:**
**Input:** nums = \[7,-9,15,-2\], goal = -5
**Output:** 1
**Explanation:** Choose the subsequence \[7,-9,-2\], with a sum of -4.
The absolute difference is abs(-4 - (-5)) = abs(1) = 1, which is the minimum.
**Example 3:**
**Input:** nums = \[1,2,3\], goal = -7
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 40`
* `-107 <= nums[i] <= 107`
* `-109 <= goal <= 109` | As the array is circular, use modulo to find the correct index. The constraints are low enough for a brute-force solution. |
Python Soln (Meet in the Middle | combinations) + comments ! | closest-subsequence-sum | 0 | 1 | #### Intuition\nAs all combinations will take too much space so divide the problem in halves & solve inorder to reduce space usage at a time\n\n#### Code\n```\ndef findAllSums(nums):\n res = {0, sum(nums)}\n\n for i in range(1, len(nums)):\n res.update({sum(sub) for sub in combinations(nums, i)})\n \n return res \n\nclass Solution:\n def minAbsDifference(self, nums: List[int], goal: int) -> int:\n \'\'\'Meet in the Middle\'\'\'\n n = len(nums)\n m = n // 2\n sum1 = list(findAllSums(nums[:m]))\n sum2 = sorted(findAllSums(nums[m:]))\n\n ans = abs(goal) \n\n n2 = len(sum2)\n for s1 in sum1:\n t = goal-s1 \n if t == 0: return 0\n\n i = bisect.bisect(sum2, t) # Find pos for {t}\n\n # check two nearest value ie after & before\n if i < n2: # After\n diff = abs(sum2[i] - t)\n if diff == 0: return 0\n ans = min(ans, diff)\n \n if i > 0: # before\n diff = abs(t - sum2[i-1])\n if diff == 0: return 0\n ans = min(ans, diff)\n\n return ans\n``` | 0 | You are given a very large integer `n`, represented as a string, and an integer digit `x`. The digits in `n` and the digit `x` are in the **inclusive** range `[1, 9]`, and `n` may represent a **negative** number.
You want to **maximize** `n`**'s numerical value** by inserting `x` anywhere in the decimal representation of `n`. You **cannot** insert `x` to the left of the negative sign.
* For example, if `n = 73` and `x = 6`, it would be best to insert it between `7` and `3`, making `n = 763`.
* If `n = -55` and `x = 2`, it would be best to insert it before the first `5`, making `n = -255`.
Return _a string representing the **maximum** value of_ `n`_ after the insertion_.
**Example 1:**
**Input:** n = "99 ", x = 9
**Output:** "999 "
**Explanation:** The result is the same regardless of where you insert 9.
**Example 2:**
**Input:** n = "-13 ", x = 2
**Output:** "-123 "
**Explanation:** You can make n one of {-213, -123, -132}, and the largest of those three is -123.
**Constraints:**
* `1 <= n.length <= 105`
* `1 <= x <= 9`
* The digits in `n` are in the range `[1, 9]`.
* `n` is a valid representation of an integer.
* In the case of a negative `n`, it will begin with `'-'`. | The naive solution is to check all possible subsequences. This works in O(2^n). Divide the array into two parts of nearly is equal size. Consider all subsets of one part and make a list of all possible subset sums and sort this list. Consider all subsets of the other part, and for each one, let its sum = x, do binary search to get the nearest possible value to goal - x in the first part. |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | recyclable-and-low-fat-products | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```python []\ndef find_products(products: pd.DataFrame) -> pd.DataFrame:\n return products[\n (products[\'low_fats\'] == \'Y\') & \\\n (products[\'recyclable\'] == \'Y\')\n ][[\'product_id\']]\n\n```\n```SQL []\nSELECT product_id\n FROM Products\n WHERE low_fats = \'Y\'\n AND recyclable = \'Y\';\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n | 8 | Alice and Bob take turns playing a game with **Alice starting first**.
In this game, there are `n` piles of stones. On each player's turn, the player should remove any **positive** number of stones from a non-empty pile **of his or her choice**. The first player who cannot make a move loses, and the other player wins.
Given an integer array `piles`, where `piles[i]` is the number of stones in the `ith` pile, return `true` _if Alice wins, or_ `false` _if Bob wins_.
Both Alice and Bob play **optimally**.
**Example 1:**
**Input:** piles = \[1\]
**Output:** true
**Explanation:** There is only one possible scenario:
- On the first turn, Alice removes one stone from the first pile. piles = \[0\].
- On the second turn, there are no stones left for Bob to remove. Alice wins.
**Example 2:**
**Input:** piles = \[1,1\]
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible scenario is:
- On the first turn, Alice removes one stone from the first pile. piles = \[0,1\].
- On the second turn, Bob removes one stone from the second pile. piles = \[0,0\].
- On the third turn, there are no stones left for Alice to remove. Bob wins.
**Example 3:**
**Input:** piles = \[1,2,3\]
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible scenario is:
- On the first turn, Alice removes three stones from the third pile. piles = \[1,2,0\].
- On the second turn, Bob removes one stone from the second pile. piles = \[1,1,0\].
- On the third turn, Alice removes one stone from the first pile. piles = \[0,1,0\].
- On the fourth turn, Bob removes one stone from the second pile. piles = \[0,0,0\].
- On the fifth turn, there are no stones left for Alice to remove. Bob wins.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 7`
* `1 <= piles[i] <= 7`
**Follow-up:** Could you find a linear time solution? Although the linear time solution may be beyond the scope of an interview, it could be interesting to know. | null |
Eazy to understand beat 93% 🚀 | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n count0, count1 = 0, 0\n\n # Iterate through the characters of the string\n for i in range(len(s)):\n # Check if the index is even\n if i % 2 == 0:\n # If the character at this index is not \'0\', increment count0\n if s[i] != \'0\':\n count0 += 1\n # If the character at this index is not \'1\', increment count1\n else:\n count1 += 1\n else:\n # If the index is odd, follow similar logic with count0 and count1\n if s[i] != \'1\':\n count0 += 1\n else:\n count1 += 1\n\n # Return the minimum count of operations required\n return min(count0, count1)\n``` | 1 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Eazy to understand beat 93% 🚀 | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n count0, count1 = 0, 0\n\n # Iterate through the characters of the string\n for i in range(len(s)):\n # Check if the index is even\n if i % 2 == 0:\n # If the character at this index is not \'0\', increment count0\n if s[i] != \'0\':\n count0 += 1\n # If the character at this index is not \'1\', increment count1\n else:\n count1 += 1\n else:\n # If the index is odd, follow similar logic with count0 and count1\n if s[i] != \'1\':\n count0 += 1\n else:\n count1 += 1\n\n # Return the minimum count of operations required\n return min(count0, count1)\n``` | 1 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Python | 51ms Faster than 92% | Soln without '%' or 'sum' | minimum-changes-to-make-alternating-binary-string | 0 | 1 | From an observation we can find that ```s = "0100"``` can have only two solutions which are ``` 0101``` and ```1010```.\n\nIf we find the number of operations to change ```s``` to first solution ```0101```, we can find the number of operations required to change ```s``` to second solution ```1010``` with simple maths.\n```0100 -> 0101``` takes ```1``` operation\n```0100 -> 1010``` takes ```3``` operations, which is nothing but ```len(s) - number of operations for previous solution``` that is ```4 - 1 = 3```\n\nAnother example,\n```s = "100101"``` can have only two solutions which are ```101010``` and ```010101```\n```100101 -> 101010``` takes ```4``` operations\n```100101 -> 010101``` takes ```2``` operations, which is nothing but ```len(s) - number of operations for previous solution``` that is ```6 - 4 = 2```\n\nTime: ```O(n)```\nSpace: ```O(1)```\n```\ndef minOperations(self, s: str) -> int:\n\tstartsWith0 = 0\n\tflag = 0 # here we are first calculating the soln starting with 0, so flag = 0\n\n\tfor c in s:\n\t\tif int(c) != flag:\n\t\t\tstartsWith0 += 1\n\n\t\tflag = not flag # alternates b/w 0 & 1\n\n\tstartsWith1 = len(s) - startsWith0\n\n\treturn min(startsWith0, startsWith1)\n```\n\n\n\n | 15 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python | 51ms Faster than 92% | Soln without '%' or 'sum' | minimum-changes-to-make-alternating-binary-string | 0 | 1 | From an observation we can find that ```s = "0100"``` can have only two solutions which are ``` 0101``` and ```1010```.\n\nIf we find the number of operations to change ```s``` to first solution ```0101```, we can find the number of operations required to change ```s``` to second solution ```1010``` with simple maths.\n```0100 -> 0101``` takes ```1``` operation\n```0100 -> 1010``` takes ```3``` operations, which is nothing but ```len(s) - number of operations for previous solution``` that is ```4 - 1 = 3```\n\nAnother example,\n```s = "100101"``` can have only two solutions which are ```101010``` and ```010101```\n```100101 -> 101010``` takes ```4``` operations\n```100101 -> 010101``` takes ```2``` operations, which is nothing but ```len(s) - number of operations for previous solution``` that is ```6 - 4 = 2```\n\nTime: ```O(n)```\nSpace: ```O(1)```\n```\ndef minOperations(self, s: str) -> int:\n\tstartsWith0 = 0\n\tflag = 0 # here we are first calculating the soln starting with 0, so flag = 0\n\n\tfor c in s:\n\t\tif int(c) != flag:\n\t\t\tstartsWith0 += 1\n\n\t\tflag = not flag # alternates b/w 0 & 1\n\n\tstartsWith1 = len(s) - startsWith0\n\n\treturn min(startsWith0, startsWith1)\n```\n\n\n\n | 15 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Python3 solution | O(n) | Explained | minimum-changes-to-make-alternating-binary-string | 0 | 1 | \'\'\'\nSimple idea:\nIn this problem there are 2 possible valid binary strings. Let\'s take an example:\ns = "010011" the answer is : either "010101" or "101010", but you wanna pick the one that is easier to transform.\nIn order to that you have to iterate through the string and count 2 times how many changes you have to make: one for the first form and one for the latter.\nThen pick the smallest that is the easiest to get to a valid form.\nIf you like it, please upvote! ^^\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n count = 0\n count1 = 0\n for i in range(len(s)):\n if i % 2 == 0:\n if s[i] == \'1\':\n count += 1\n if s[i] == \'0\':\n count1 += 1\n else:\n if s[i] == \'0\':\n count += 1\n if s[i] == \'1\':\n count1 += 1\n return min(count, count1)\n```\n\'\'\' | 14 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python3 solution | O(n) | Explained | minimum-changes-to-make-alternating-binary-string | 0 | 1 | \'\'\'\nSimple idea:\nIn this problem there are 2 possible valid binary strings. Let\'s take an example:\ns = "010011" the answer is : either "010101" or "101010", but you wanna pick the one that is easier to transform.\nIn order to that you have to iterate through the string and count 2 times how many changes you have to make: one for the first form and one for the latter.\nThen pick the smallest that is the easiest to get to a valid form.\nIf you like it, please upvote! ^^\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n count = 0\n count1 = 0\n for i in range(len(s)):\n if i % 2 == 0:\n if s[i] == \'1\':\n count += 1\n if s[i] == \'0\':\n count1 += 1\n else:\n if s[i] == \'0\':\n count += 1\n if s[i] == \'1\':\n count1 += 1\n return min(count, count1)\n```\n\'\'\' | 14 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Python Elegant & Short | Minimum of two | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n return min(\n sum(int(bit) == i & 1 for i, bit in enumerate(s)),\n sum(int(bit) != i & 1 for i, bit in enumerate(s)),\n )\n```\n | 2 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python Elegant & Short | Minimum of two | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n return min(\n sum(int(bit) == i & 1 for i, bit in enumerate(s)),\n sum(int(bit) != i & 1 for i, bit in enumerate(s)),\n )\n```\n | 2 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Python easy solution | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n2 cases by index:\n- \'01010101...\': (0 - even index, 1 - odd index)\n- \'10101010...\': (1 - even index, 0 - odd index)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Case1: Count number of (0 - even index, 1 - odd index) case.\n- Case2: Count number of (1 - even index, 0 - odd index) case.\n\n- If Case1 == len(s) or Case2 == len(s): Alternating Binary String, no change\n- else: number of operations = min(case1, case2)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n numsMap = {\n "1": {\n "even": 0,\n "odd": 0 \n },\n \'0\': {\n "even": 0,\n "odd": 0\n }\n }\n\n # count for numsMap\n n = len(s)\n for i in range(n):\n if i % 2: numsMap[s[i]]["odd"]+=1\n else: numsMap[s[i]]["even"] += 1\n \n case1 = numsMap[\'0\'][\'even\'] + numsMap[\'1\'][\'odd\'] #010101\n case2 = numsMap[\'0\'][\'odd\'] + numsMap[\'1\'][\'even\'] #101010\n \n if case1 == n or case2 == n: return 0 # no change\n if case1 > case2: return case2\n return case1\n\n``` | 1 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python easy solution | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n2 cases by index:\n- \'01010101...\': (0 - even index, 1 - odd index)\n- \'10101010...\': (1 - even index, 0 - odd index)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Case1: Count number of (0 - even index, 1 - odd index) case.\n- Case2: Count number of (1 - even index, 0 - odd index) case.\n\n- If Case1 == len(s) or Case2 == len(s): Alternating Binary String, no change\n- else: number of operations = min(case1, case2)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n numsMap = {\n "1": {\n "even": 0,\n "odd": 0 \n },\n \'0\': {\n "even": 0,\n "odd": 0\n }\n }\n\n # count for numsMap\n n = len(s)\n for i in range(n):\n if i % 2: numsMap[s[i]]["odd"]+=1\n else: numsMap[s[i]]["even"] += 1\n \n case1 = numsMap[\'0\'][\'even\'] + numsMap[\'1\'][\'odd\'] #010101\n case2 = numsMap[\'0\'][\'odd\'] + numsMap[\'1\'][\'even\'] #101010\n \n if case1 == n or case2 == n: return 0 # no change\n if case1 > case2: return case2\n return case1\n\n``` | 1 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Python with explanation | minimum-changes-to-make-alternating-binary-string | 0 | 1 | ```\n# The final string should be either 010101.. or 101010... (depending on the length of string s)\n# Check the number of differences between given string s and the two final strings. \n# Return the one with minimum differences \n\n\tdef minOperations(self, s: str) -> int:\n\t\tstarting_with_01 = \'01\'\n\t\tstarting_with_10 = \'10\'\n\t\tdiff_with_01 = 0\n\t\tdiff_with_10 = 0\n\t\tfor i in range(len(s)):\n\t\t\tif starting_with_01[i%2] != s[i]:\n\t\t\t\tdiff_with_01 += 1\n\t\t\tif starting_with_10[i%2] != s[i]:\n\t\t\t\tdiff_with_10 += 1\n\t\treturn min(diff_with_01, diff_with_10)\n\n``` | 5 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Python with explanation | minimum-changes-to-make-alternating-binary-string | 0 | 1 | ```\n# The final string should be either 010101.. or 101010... (depending on the length of string s)\n# Check the number of differences between given string s and the two final strings. \n# Return the one with minimum differences \n\n\tdef minOperations(self, s: str) -> int:\n\t\tstarting_with_01 = \'01\'\n\t\tstarting_with_10 = \'10\'\n\t\tdiff_with_01 = 0\n\t\tdiff_with_10 = 0\n\t\tfor i in range(len(s)):\n\t\t\tif starting_with_01[i%2] != s[i]:\n\t\t\t\tdiff_with_01 += 1\n\t\t\tif starting_with_10[i%2] != s[i]:\n\t\t\t\tdiff_with_10 += 1\n\t\treturn min(diff_with_01, diff_with_10)\n\n``` | 5 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
5-Lines Python Solution || Faster than 90% || Memory Less than 70% | minimum-changes-to-make-alternating-binary-string | 0 | 1 | ```\n\tdef minOperations(self, s: str) -> int:\n ref0 = \'01\'*(len(s)//2) + \'0\'*(len(s)%2)\n ref1 = \'10\'*(len(s)//2) + \'1\'*(len(s)%2)\n diff0 = sum([1 for i in range(len(s)) if s[i]!=ref0[i]])\n diff1 = sum([1 for i in range(len(s)) if s[i]!=ref1[i]])\n return min(diff0, diff1)\n``` | 2 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
5-Lines Python Solution || Faster than 90% || Memory Less than 70% | minimum-changes-to-make-alternating-binary-string | 0 | 1 | ```\n\tdef minOperations(self, s: str) -> int:\n ref0 = \'01\'*(len(s)//2) + \'0\'*(len(s)%2)\n ref1 = \'10\'*(len(s)//2) + \'1\'*(len(s)%2)\n diff0 = sum([1 for i in range(len(s)) if s[i]!=ref0[i]])\n diff1 = sum([1 for i in range(len(s)) if s[i]!=ref1[i]])\n return min(diff0, diff1)\n``` | 2 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
One line solution with using itertools.cycle and zip | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n return min(sm:= sum(s1==s2 for s1, s2 in zip(s, itertools.cycle("01"))), len(s) - sm)\n\n\n \n \n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
One line solution with using itertools.cycle and zip | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n return min(sm:= sum(s1==s2 for s1, s2 in zip(s, itertools.cycle("01"))), len(s) - sm)\n\n\n \n \n``` | 0 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Beats 88.01% of users with Python3 | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Code\n```\nclass Solution:\n\n def minOperations(self, s: str) -> int:\n # 44ms\n # Beats 88.01% of users with Python3\n ptr = True\n op = {True: "1", False: "0"}\n cnta = cntb = 0\n for i in range(len(s)):\n if s[i] != op[ptr]:\n cnta += 1\n \n if s[i] != op[not ptr]:\n cntb += 1\n\n ptr = not ptr\n \n return min(cnta, cntb)\n\n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Beats 88.01% of users with Python3 | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Code\n```\nclass Solution:\n\n def minOperations(self, s: str) -> int:\n # 44ms\n # Beats 88.01% of users with Python3\n ptr = True\n op = {True: "1", False: "0"}\n cnta = cntb = 0\n for i in range(len(s)):\n if s[i] != op[ptr]:\n cnta += 1\n \n if s[i] != op[not ptr]:\n cntb += 1\n\n ptr = not ptr\n \n return min(cnta, cntb)\n\n``` | 0 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Easy to understand - Python | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n l = len(s)\n a, b = \'01\'*math.ceil(l/2), \'10\'*math.ceil(l/2)\n c, d = 0, 0\n \n if l%2:\n a, b = a[:l], b[:l]\n \n for x, y in zip(s, a):\n if x != y:\n c +=1\n \n for i, j in zip(s, b):\n if i != j:\n d += 1\n \n return min(c, d) \n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Easy to understand - Python | minimum-changes-to-make-alternating-binary-string | 0 | 1 | # Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n l = len(s)\n a, b = \'01\'*math.ceil(l/2), \'10\'*math.ceil(l/2)\n c, d = 0, 0\n \n if l%2:\n a, b = a[:l], b[:l]\n \n for x, y in zip(s, a):\n if x != y:\n c +=1\n \n for i, j in zip(s, b):\n if i != j:\n d += 1\n \n return min(c, d) \n``` | 0 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
Simplest solution ever | minimum-changes-to-make-alternating-binary-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n count1=0\n count2=0\n for i in range(len(s)):\n if i%2==0:\n if s[i]==\'1\':\n count1 += 1\n if s[i]==\'0\':\n count2 += 1\n \n else:\n if s[i]==\'0\':\n count1 += 1\n if s[i]==\'1\':\n count2 += 1\n\n return min(count1,count2)\n\n \n\n\n\n\n \n``` | 0 | You are given a string `s` consisting only of the characters `'0'` and `'1'`. In one operation, you can change any `'0'` to `'1'` or vice versa.
The string is called alternating if no two adjacent characters are equal. For example, the string `"010 "` is alternating, while the string `"0100 "` is not.
Return _the **minimum** number of operations needed to make_ `s` _alternating_.
**Example 1:**
**Input:** s = "0100 "
**Output:** 1
**Explanation:** If you change the last character to '1', s will be "0101 ", which is alternating.
**Example 2:**
**Input:** s = "10 "
**Output:** 0
**Explanation:** s is already alternating.
**Example 3:**
**Input:** s = "1111 "
**Output:** 2
**Explanation:** You need two operations to reach "0101 " or "1010 ".
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`. | Count the frequencies of each number. For example, if nums = [4,4,5,5,5], frequencies = [2,3]. Each customer wants all of their numbers to be the same. This means that each customer will be assigned to one number. Use dynamic programming. Iterate through the numbers' frequencies, and choose some subset of customers to be assigned to this number. |
Simplest solution ever | minimum-changes-to-make-alternating-binary-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minOperations(self, s: str) -> int:\n count1=0\n count2=0\n for i in range(len(s)):\n if i%2==0:\n if s[i]==\'1\':\n count1 += 1\n if s[i]==\'0\':\n count2 += 1\n \n else:\n if s[i]==\'0\':\n count1 += 1\n if s[i]==\'1\':\n count2 += 1\n\n return min(count1,count2)\n\n \n\n\n\n\n \n``` | 0 | You are given **two identical** eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
In each move, you may take an **unbroken** egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** n = 2
**Output:** 2
**Explanation:** We can drop the first egg from floor 1 and the second egg from floor 2.
If the first egg breaks, we know that f = 0.
If the second egg breaks but the first egg didn't, we know that f = 1.
Otherwise, if both eggs survive, we know that f = 2.
**Example 2:**
**Input:** n = 100
**Output:** 14
**Explanation:** One optimal strategy is:
- Drop the 1st egg at floor 9. If it breaks, we know f is between 0 and 8. Drop the 2nd egg starting from floor 1 and going up one at a time to find f within 8 more drops. Total drops is 1 + 8 = 9.
- If the 1st egg does not break, drop the 1st egg again at floor 22. If it breaks, we know f is between 9 and 21. Drop the 2nd egg starting from floor 10 and going up one at a time to find f within 12 more drops. Total drops is 2 + 12 = 14.
- If the 1st egg does not break again, follow a similar process dropping the 1st egg from floors 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100.
Regardless of the outcome, it takes at most 14 drops to determine f.
**Constraints:**
* `1 <= n <= 1000` | Think about how the final string will look like. It will either start with a '0' and be like '010101010..' or with a '1' and be like '10101010..' Try both ways, and check for each way, the number of changes needed to reach it from the given string. The answer is the minimum of both ways. |
【Video】Give me 5 minutes- O(n) time, O(1) space - How we think about a solution | count-number-of-homogenous-substrings | 1 | 1 | # Intuition\nUse two pointers to get length of substring\n\n---\n\n# Solution Video\n\nhttps://youtu.be/VcZrmO045Bo\n\n\u25A0 Timeline of the video\n\n`0:04` Let\'s find a solution pattern\n`1:38` A key point to solve Count Number of Homogenous Substrings\n`2:20` Demonstrate how it works with all the same characters\n`4:55` What if we find different characters\n`7:13` Coding\n`8:21` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,984\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n\u3010Updated\u3011\n\nA few minutes ago, I opened youtube studio and my channel reached 3,000 subscribers. Thank you so much for your support!!\n\n\n\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSeems like we have a lot of patterns, so when I feel that, I usually think about output with small input.\n\n```\nInput = "a"\n```\n```\nPattern\n"a": 1\n\nOutput = 1\n```\n\n```\nInput = "aa"\n```\n```\nPattern\n"a": 2\n"aa": 1\n\nOutput = 3\n```\n\n```\nInput = "aaa"\n```\n```\nPattern\n"a": 3\n"aa": 2\n"aaa": 1\n\nOutput = 6\n```\n```\nInput = "aaaa"\n```\n```\nPattern\n"a": 4\n"aa": 3\n"aaa": 2\n"aaaa": 1\n\nOutput = 10\n```\n```\nInput = "aaaaa"\n```\n```\nPattern\n"a": 5\n"aa": 4\n"aaa": 3\n"aaaa": 2\n"aaaaa": 1\n\nOutput = 15\n```\n\nSeems like we have a solution pattern.\n\n---\n\n\u2B50\uFE0F Points\n\nEvery time we find the same character, we can accumulate `current length of substring` to `ouput`. We will add the numbers from bottom to top (1 + 2 + 3 + 4 + 5) because when we iterate through the input string, length of substring start from minimum to maximum. We use two pointers for length of subtring. Let\'s say `left` and `right`\n\n```\n"a": 5\n"aa": 4\n"aaa": 3\n"aaaa": 2\n"aaaaa": 1 \n\n5 + 4 + 3 + 2 + 1 = 1 + 2 + 3 + 4 + 5\n\n5 + 4 + 3 + 2 + 1 is coming from pyramid above\n1 + 2 + 3 + 4 + 5 is actual calculation in solution code\n```\nThey are the same output.\n\n- How can you calculate length of substring?\n\nSimply\n```\nright - left + 1\n```\nWhy + 1?\n\nThat\'s because `left` and `right` are index number, when both indices are `0`, they are pointing `a`.\n\n```\n0 - 0 = 0?\n```\nThat\'s wrong. We find single `a`. That\'s why we need to add `+1`.\n\n##### How it works\n\n```\nInput: "aaaaa"\n```\n\n```\nleft = 0\nright = 0\n\nFind "a"\noutput: 1\n\n```\n```\nleft = 0\nright = 1\n\noutput: 3 (1 + 2)\n\n1 is current output\n2 is length of substring (= "aa")\n```\n```\nleft = 0\nright = 2\n\noutput: 6 (3 + 3)\n\n(first)3 is current output\n(second)3 is length of substring (= "aaa")\n```\n```\nleft = 0\nright = 3\n\noutput: 10 (6 + 4)\n\n6 is current output\n4 is length of substring (= "aaaa")\n```\n```\nleft = 0\nright = 4\n\noutput: 15 (10 + 5)\n\n10 is current output\n5 is length of substring (= "aaaaa")\n```\n\n```\noutput: 15\n```\n\n### What if we find a different character?\n\nWhen we find the different character, we know that the differnt character is the first new character.\n\nIn that case, \n\n---\n\n\u2B50\uFE0F Points\n\n- We cannot accumulate previous length of subtring anymore, so update `left` with `right`, then we can make a new start from current place\n\n- Add `+1` to current output before we go to the next iteration, because the character is the first character, we know that when we have only one character, output should be `1`. \n\n---\n\n##### How it works\n\n```\nInput: "aabbb"\n```\n```\nleft = 0\nright = 0\n\noutput = 1\n```\n```\nleft = 0\nright = 1\n\noutput = 3 (1 + 2)\n1 is current output\n2 is length of substring(= "aa")\n```\nThen we find a different character. `a` vs `b`\n```\nleft = 0\nright = 2\n\noutput = 4 (3 + 1)\n3 is current output\n1 is length of substring(= "b")\n```\nWe will make a new start from index `2`, so update `left` with `right`.\n\n```\nleft = 2\nright = 3\n\noutput = 6 (4 + 2)\n4 is current output\n2 is length of substring(= "bb")\n```\n\n```\nleft = 2\nright = 4\n\noutput = 9 (6 + 3)\n6 is current output\n3 is length of substring(= "bbb")\n```\n\n```\noutput: 9\n```\n\nEasy! \uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n---\n\n### Algorithm Overview:\n\nUse two pointers to get length of substring, then we will accumulate the length if we find the same characters. If not, we can make a new start.\n\nLet\'s break it down into more detailed steps:\n\n### Detailed Explanation:\n\n1. Initialize `left` and `res` to 0.\n\n2. Start a loop that iterates through each character in the input string `s`.\n\n3. Check if the character at index `left` is equal to the character at index `right`.\n\n4. If the characters are the same:\n - Increment the result `res` by the length of the current substring, which is `right - left + 1`. This accounts for substrings where all characters are the same.\n\n5. If the characters are different:\n - Increment the result `res` by 1 to account for the single character substring.\n - Update the `left` index to the `right` index to start a new substring.\n\n6. Repeat steps 3 to 5 for all characters in the input string.\n\n7. After the loop is completed, return the result `res` modulo `(10^9 + 7)`.\n\nThis algorithm essentially counts the length of consecutive substrings with the same characters within the input string and returns the result modulo `(10^9 + 7)`.\n\n---\n\n# Complexity\n- Time complexity: $$O(n)$$\nWe iterate through all characters one by one.\n\n- Space complexity: $$O(1)$$\nWe don\'t use extra data structure.\n\n```python []\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n\n left = 0\n res = 0\n\n for right in range(len(s)):\n if s[left] == s[right]:\n res += right - left + 1\n else:\n res += 1\n left = right\n \n return res % (10**9 + 7)\n```\n```javascript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar countHomogenous = function(s) {\n let left = 0;\n let res = 0;\n\n for (let right = 0; right < s.length; right++) {\n if (s[left] === s[right]) {\n res += right - left + 1;\n } else {\n res += 1;\n left = right;\n }\n }\n\n return res % (Math.pow(10, 9) + 7); \n};\n```\n```java []\nclass Solution {\n public int countHomogenous(String s) {\n int left = 0;\n long res = 0;\n \n for (int right = 0; right < s.length(); right++) {\n if (s.charAt(left) == s.charAt(right)) {\n res += right - left + 1;\n } else {\n res += 1;\n left = right;\n }\n }\n\n return (int) (res % (1000000007)); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int countHomogenous(string s) {\n int left = 0;\n long long res = 0;\n \n for (int right = 0; right < s.length(); right++) {\n if (s[left] == s[right]) {\n res += right - left + 1;\n } else {\n res += 1;\n left = right;\n }\n }\n\n return (int) (res % (1000000007)); \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/restore-the-array-from-adjacent-pairs/solutions/4271506/video-give-me-5-minutes-on-time-and-space-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/P14SbuALeJ8\n\n\u25A0 Timeline of the video\n\n`0:04` A key point to solve this question\n`1:09` How do you know adjacent number of each number?\n`2:33` Demonstrate how it works\n`6:07` Coding\n`9:07` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/eliminate-maximum-number-of-monsters/solutions/4259212/video-give-me-10-minutes-on-solution-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/7nxGK97CmIw\n\n\u25A0 Timeline of the video\n\n`0:04` How we can calculate x and y distances\n`0:55` We need to consider 2 cases and explain what if start and finish cell are the same position\n`2:20` Explain case 2, what if start and finish cell are different positions\n`4:53` Coding\n`6:18` Time Complexity and Space Complexity | 118 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
Python one line | count-number-of-homogenous-substrings | 0 | 1 | ```python []\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n return sum(\n x * (x + 1) >> 1\n for _, grp in groupby(s)\n for x in [len(list(grp))]\n ) % (10**9 + 7)\n\n``` | 3 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
✅ One Line Solution | count-number-of-homogenous-substrings | 0 | 1 | # Approach 1\nUsing groupby.\n```sum(1 for _ in grp)``` - more time consuming, less memory usage.\n```len(list(grp))``` - less time but more memory.\n\n# Code 1.1\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n return sum((l:=sum(1 for _ in grp))*(l + 1)//2 for _, grp in groupby(s))%(10**9 + 7)\n```\n\n# Code 1.2\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n return sum((l:=len(list(grp)))*(l + 1)//2 for _, grp in groupby(s))%(10**9 + 7)\n```\n\n# Approach 2\nUsing regular expression.\n\n# Code 2\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n return sum((l:=len(m.group()))*(l + 1)//2 for m in re.finditer(r\'(.)\\1*\', s))%(10**9 + 7)\n``` | 3 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
Python 95% beating || Easy solution with explanations || Beginner-friendly | count-number-of-homogenous-substrings | 0 | 1 | # Intuition\nThe problem asks to count the number of substrings in a string such that all the characters in them are the same - and it is important to note that such substrings can and will intersect in the input string.\n# Approach\nMy implementation is quite simple - I go through the string and add to the result the number of substrings with each "group" of characters encountered. The main thing in the problem is to understand one thing - suppose you have the string "####", then how to count the number of substrings in which all the characters are equal for such a string? Let\'s look in more detail, to take a substring of length 4 there is only **one** option - the string itself, to take a substring of length 3 there are only **2** options - we can start counting a substring from index 0 or index 1, a substring of length 2 - **3** options, we can start from 0, 1 and 2, and a substring of length 1 is obviously **4**, since we can take any index - a total of `4 + 3 + 2 + 1 = 10`. In fact, you can write a loop and count like that, but you can use a mathematical solution, since in fact, we get that the number of substrings of the string "#" * N is an arithmetic progression from 1 to N, and the formula for the sum of the arithmetic progression is `N * (N + 1) / 2`. Taking this fact into account, let\'s move on to writing the code.\n\n# Code explanations\nWe declare variables to keep track of the result, the previous letter, and the number of identical letters in the current group (take the first character and start iterating from the second). We will also introduce the \u201Cmod\u201D variable to return the result of this module. Now we go through each character, starting from the second - if it is equal to the previous one, then we simply add it to the group and move on - otherwise, we write the result using the arithmetic progression formula, add it to the result, and also reset the number of characters in a row (group) and the last symbol on the current one - since in fact we are starting a new group. After the end of the cycle, it turns out that we did not count the last group - so we add it manually and return the result.\n\n# Complexity\n- Time complexity:\nO(n), cuz we go through every element in input list once\n\n- Space complexity:\nO(1), cuz we don\'t use any arrays, but only two integer variables and one constant-length string variable.\n\n\n#### Feel free to ask whatever you want if you didn\'t understand something, I would be glad to answer you.\n# Code\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n mod = 10 ** 9 + 7\n res = 0\n last_let = s[0]\n in_row = 1\n\n for char in s[1:]:\n if char == last_let:\n in_row += 1\n else:\n res += in_row * (in_row + 1) / 2\n in_row = 1\n last_let = char\n res += in_row * (in_row + 1) / 2\n \n return int(res) % mod\n```\n\nIf you like my effort you can award me with upvote, it will be a good motivation for me to write such posts in future, thanks and good luck, happy coding! <3\n | 2 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
[Python3] 2 solutions: Two pointer and math using groupby() | count-number-of-homogenous-substrings | 0 | 1 | ```python3 []\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n res, l = 0, 0\n\n for r, c in enumerate(s):\n if c == s[l]:\n res += r - l + 1\n else:\n l = r\n res += 1\n\n return res % (pow(10, 9) + 7)\n```\n###### For those who are confused why are we adding `r - l + 1`, it adds all the subarrays that ends at r (right) starting at l (left) or later. \n###### Example for list with numbers, not string like in the current problem, but the main idea is the same: `s = [1,1,1,1,1,0,0,1], res = 0`\n- `l = 0, r = 0 => [[1],1,1,1,1,0,0,1] => res = 0 + 1 = 1`\n- `l = 0, r = 1 => [[1,1],1,1,1,0,0,1] => res = 1 + 2 = 3`\n- `l = 0, r = 2 => [[1,1,1],1,1,0,0,1] => res = 3 + 3 = 6`\n- `l = 0, r = 3 => [[1,1,1,1],1,0,0,1] => res = 6 + 4 = 10`\n- `l = 0, r = 4 => [[1,1,1,1,1],0,0,1] => res = 10 + 5 = 15`\n- `l = 5, r = 5 => [1,1,1,1,1,[0],0,1] => res = 15 + 1 = 16`\n- `l = 5, r = 6 => [1,1,1,1,1,[0,0],1] => res = 16 + 2 = 18`\n- `l = 7, r = 7 => [1,1,1,1,1,0,0,[1]] => res = 18 + 1 = 19`\n\n###### If you\'re given an array of length\xA0n, it will produce\xA0`(n*(n+1))//2`\xA0total contiguous subarrays (same as doing the sum step by step above).\n```python3 []\n# [k for k, g in groupby(\'AAAABBBCCDAABBB\')] --> A B C D A B\n# [list(g) for k, g in groupby(\'AAAABBBCCD\')] --> AAAA BBB CC D\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n res = 0\n for _, g in groupby(s):\n n = len(list(g))\n res += n * (n + 1) // 2\n \n return res % (pow(10, 9) + 7)\n```\n\n###### Similar Sliding Window problems:\n- [713. Subarray Product Less Than K](https://leetcode.com/problems/subarray-product-less-than-k/)\n- [2302. Count Subarrays With Score Less Than K](https://leetcode.com/problems/count-subarrays-with-score-less-than-k/description/)\n- [1248. Count Number of Nice Subarrays](https://leetcode.com/problems/count-number-of-nice-subarrays/)\n\n\n\n | 14 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
✅☑[C++/Java/Python/JavaScript] || Easy Solution || EXPLAINED🔥 | count-number-of-homogenous-substrings | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n1. if size of `s` is 0 .so,returning 0.\n2. making a vector `len` of same length as `s` and 0 as initial input for all.\n3. let value of `len[0]` be 1 , and hence sum will be 1 too.\n4. run a for loop in `s` string .\n5. make the current len[i] as 1,then check if len[i] is equal to `len[i-1]` ,if yes then add value og `len[i-1]`.\n6. update the `sum` each time.\n7. return the `sum`.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int countHomogenous(string s) {\n int m = 1e9+7;\n if(s.size()==0)return 0;\n\n vector<int>len(s.size(),0);\n len[0]=1;\n int sum =1;\n for(int i =1;i<s.size();i++){\n len[i]=1;\n if(s[i]==s[i-1]){\n len[i] = (len[i] + len[i-1]) %m; //adding the previous possible combinations of the continues sub string \n }\n sum = (sum + len[i]) % m;\n }\n return sum;\n }\n}; \n\n```\n```C []\nint countHomogenous(char *s) {\n int m = 1e9 + 7;\n if(strlen(s)==0)return 0;\n\n int len[100000];\n memset(len, 0, sizeof(len));\n len[0]=1;\n int sum =1;\n for(int i =1;i<strlen(s);i++){\n len[i]=1;\n if(s[i]==s[i-1]){\n len[i] = (len[i] + len[i-1]) %m; //adding the previous possible combinations of the continues sub string \n }\n sum = (sum + len[i]) % m;\n }\n return sum;\n}\n```\n```java []\n\n\nclass Solution {\n public int countHomogenous(String s) {\n int m = 1000000007;\n if(s.length()==0)return 0;\n\n int[] len = new int[s.length()];\n len[0]=1;\n int sum =1;\n for(int i =1;i<s.length();i++){\n len[i]=1;\n if(s.charAt(i)==s.charAt(i-1)){\n len[i] = (len[i] + len[i-1]) %m;\n }\n sum = (sum + len[i]) % m;\n }\n return sum;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n m = 10**9 + 7\n if not s:\n return 0\n\n len_arr = [0] * len(s)\n len_arr[0] = 1\n sum_ = 1\n for i in range(1, len(s)):\n len_arr[i] = 1\n if s[i] == s[i-1]:\n len_arr[i] = (len_arr[i] + len_arr[i-1]) % m\n sum_ = (sum_ + len_arr[i]) % m\n return sum\n```\n```javascript []\nclass Solution {\n countHomogenous(s) {\n let m = 10**9 + 7;\n if(s.length==0)return 0;\n\n let len = new Array(s.length).fill(0);\n len[0]=1;\n let sum =1;\n for(let i =1;i<s.length;i++){\n len[i]=1;\n if(s[i]==s[i-1]){\n len[i] = (len[i] + len[i-1]) %m; //adding the previous possible combinations of the continues sub string \n }\n sum = (sum + len[i]) % m;\n }\n return sum;\n }\n};\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
✅ Python3 | One Line Solution | 90ms | Beats 94% ✅ | count-number-of-homogenous-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nFor a single section of contiguous matching characters, the number of homogenous substrings we can make is equal to $$\\sum_{i=1}^n i$$, where $$n$$ is the length of the section we are looking at. Simplified, that summation is equal to $$n*(n+1) /2$$. So we just need to find the lengths of every section of contiguous matching letters, and apply that formula to each of them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\ngroup the string by contiguous sections of matching letters, then take the sum of $$n*(n+1)//2$$ for each group, where $$n$$ is the length of the group.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n return sum((l:=len(list(g))) * (l+1) // 2 for _, g in itertools.groupby(s)) % (10 ** 9 + 7)\n``` | 1 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
Exaplained code | Java | Python | C++ | JS | Two Pointer Approach | Simple Solution | count-number-of-homogenous-substrings | 1 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```java []\nclass Solution {\n public int countHomogenous(String s) {\n final int MOD = 1000000007;\n int res = 0, i = 0, n = s.length();\n \n while(i < n) {\n int j = i+1;\n char c = s.charAt(i);\n\n // Finding Substring having same characters.\n while(j < n && s.charAt(j) == c) {\n j++;\n }\n\n // Count of Substring having same characters\n long x = j-i;\n\n // Using the simple formula (n*(n+1))/2, we can form all the\n // valid homogenous substring because it will be having same charaters.\n long temp = ((x * (x+1)) / 2l) % MOD; \n\n // Adding the count of valid homogenous substring to the result by MOD \n // to avoid overflow issue. (Given in question description)\n res = (((res % MOD) + (int)temp) % MOD);\n\n // Continue to next iteration for next valid homogenous substring\n i = j;\n }\n \n return res; \n }\n}\n```\n```python []\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n i, res, n, MOD = 0, 0, len(s), 10**9+7\n while i < n:\n j = i+1\n\n # Finding Substring having same characters.\n while j < n and s[i] == s[j]:\n j += 1\n \n # Count of Substring having same characters\n x = j-i\n\n # Using the simple formula (n*(n+1))/2, we can form all the\n # valid homogenous substring because it will be having same charaters.\n res = ((res % MOD) + (x * (x + 1) // 2) % MOD) % MOD\n\n # Continue to next iteration for next valid homogenous substring\n i = j\n \n return res\n```\n```C++ []\nclass Solution {\npublic:\n int countHomogenous(string s) {\n int MOD = 1000000007;\n int res = 0, i = 0, n = s.length();\n \n while(i < n) {\n int j = i+1;\n char c = s[i];\n\n // Finding Substring having same characters.\n while(j < n && s[j] == c) {\n j++;\n }\n\n // Count of Substring having same characters\n long x = j-i;\n\n // Using the simple formula (n*(n+1))/2, we can form all the\n // valid homogenous substring because it will be having same charaters.\n long temp = ((x * (x+1)) / 2l) % MOD; \n\n // Adding the count of valid homogenous substring to the result by MOD \n // to avoid overflow issue. (Given in question description)\n res = (((res % MOD) + (int)temp) % MOD);\n\n // Continue to next iteration for next valid homogenous substring\n i = j;\n }\n \n return res;\n }\n};\n```\n```C# []\npublic class Solution {\n public int CountHomogenous(string s) {\n int MOD = 1000000007;\n int res = 0, i = 0, n = s.Length;\n \n while(i < n) {\n int j = i+1;\n char c = s[i];\n\n // Finding Substring having same characters.\n while(j < n && s[j] == c) {\n j++;\n }\n\n // Count of Substring having same characters\n long x = j-i;\n\n // Using the simple formula (n*(n+1))/2, we can form all the\n // valid homogenous substring because it will be having same charaters.\n long temp = ((x * (x+1)) / 2l) % MOD; \n\n // Adding the count of valid homogenous substring to the result by MOD \n // to avoid overflow issue. (Given in question description)\n res = (((res % MOD) + (int)temp) % MOD);\n\n // Continue to next iteration for next valid homogenous substring\n i = j;\n }\n \n return res;\n }\n}\n```\n```javascript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar countHomogenous = function(s) {\n const MOD = 1000000007;\n let res = 0, i = 0, n = s.length;\n \n while(i < n) {\n let j = i+1;\n let c = s[i];\n\n // Finding Substring having same characters.\n while(j < n && s[j] == c) {\n j++;\n }\n\n // Count of Substring having same characters\n let x = j-i;\n\n // Using the simple formula (n*(n+1))/2, we can form all the\n // valid homogenous substring because it will be having same charaters.\n let temp = ((x * (x+1)) / 2) % MOD; \n\n // Adding the count of valid homogenous substring to the result by MOD \n // to avoid overflow issue. (Given in question description)\n res = (((res % MOD) + temp) % MOD);\n\n // Continue to next iteration for next valid homogenous substring\n i = j;\n }\n \n return res;\n};\n```\n\n | 1 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
Python 4 lines using regex | count-number-of-homogenous-substrings | 0 | 1 | ```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n\n # create list of s segments of consecutive letters\n # ex: splitS = [\'a\', \'bb\', \'ccc\', \'aa\'] for s = \'abbcccaa\'\n pattern = r\'((\\w)\\2*)\'\n splitS = [match.group(1) for match in re.finditer(pattern, s)]\n\n # create list of the length of each segment in splitS\n # ex: charCounts = [1, 2, 3, 2] for splitS above\n charCounts = map(len, splitS)\n\n # sum using Gauss\'s summation\n return sum((cnt * (cnt + 1)) >> 1 for cnt in charCounts) % (10**9 + 7)\n```\n\njust code\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n pattern = r\'((\\w)\\2*)\'\n splitS = [match.group(1) for match in re.finditer(pattern, s)]\n charCounts = map(len, splitS)\n return sum((cnt * (cnt + 1)) >> 1 for cnt in charCounts) % (10**9 + 7) | 1 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
C++ Python sum of n(n+1)/2 ||0 ms Beats 100% | count-number-of-homogenous-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOne pass to find out all longest homogenous substrings in `s` , and store the lengths in a container `len_homo`.\n\nC code is rare & implemented & runs in 0 ms & beats 100%\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nA longest homogenous substring in `s` is the substring with all the same alphabets which is not extendible.\n\nLet `h` be a longest homogenous substring in `s` with length `sz`.\nThere are `sz(sz+1)/2` homogeous substrings in `h`.\nsz homogenous substrings of length 1\nsz-1 homogenous substrings of length 2\nsz-2 homogenous substrings of length 3\n....\n1 homogenous substrings of length sz\n\nSumming them up\n$$\nans=\\sum_{h:s, len(h)=sz}\\frac{sz(sz+1)}{2}\\pmod{ 10^9+7}\n$$\n2nd approach does not use the container `len_homo`, and is fast in 12 ms , SC : O(1).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n+m)$$ where n=len(s) m=len(len_homo)\n$O(n)$ for optimized code\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(m)\\to O(1)$$\n# Code\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n const long long mod=1e9+7;\n int countHomogenous(string s) {\n vector<int> len_homo;\n char prev=\'X\';\n int count=0;\n\n #pragma unroll\n for(char c: s){\n if (c!=prev){\n len_homo.push_back(count);\n count=1;\n }\n else count++;\n prev=c;// update prev\n }\n len_homo.push_back(count);// last one\n\n long long ans=0;\n\n #pragma unroll\n for(int sz: len_homo)\n ans=(ans+(long long)sz*(sz+1)/2)%mod;\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# optimized Code runs in 12 ms\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n const long long mod=1e9+7;\n int countHomogenous(string s) {\n char prev=\'X\';\n int count=0;\n long long ans=0;\n for(char c: s){\n if (c!=prev){\n ans=(ans+(long long)count*(count+1)/2%mod);\n count=1;\n }\n else count++;\n prev=c;// update prev\n }\n ans=(ans+(long long)count*(count+1)/2%mod);// last one\n return ans;\n }\n};\n```\n# Python code \n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n mod=10**9+7\n prev=\'X\'\n count=0\n ans=0\n for c in s:\n if c!=prev:\n ans=(ans+count*(count+1)//2)% mod\n count=1\n else:\n count+=1\n prev=c\n ans=(ans+count*(count+1)//2)% mod\n return ans\n \n```\n\n\n# C code runs in 0 ms beats 100%\n```\n#pragma GCC optimize("O3")\nconst long long mod=1e9+7;\n\nint countHomogenous(char * s){\n int n=strlen(s);\n char prev=\'X\';\n int count=0;\n long long ans=0;\n for(register i=0; i<n; i++){\n if (s[i]!=prev){\n ans=(ans+(long long)count*(count+1)/2%mod);\n count=1;\n }\n else count++;\n prev=s[i];\n }\n ans=(ans+(long long)count*(count+1)/2%mod);// last one\n return ans;\n}\n```\n | 11 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
Simple pattern based intuitive approach!😸 | count-number-of-homogenous-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n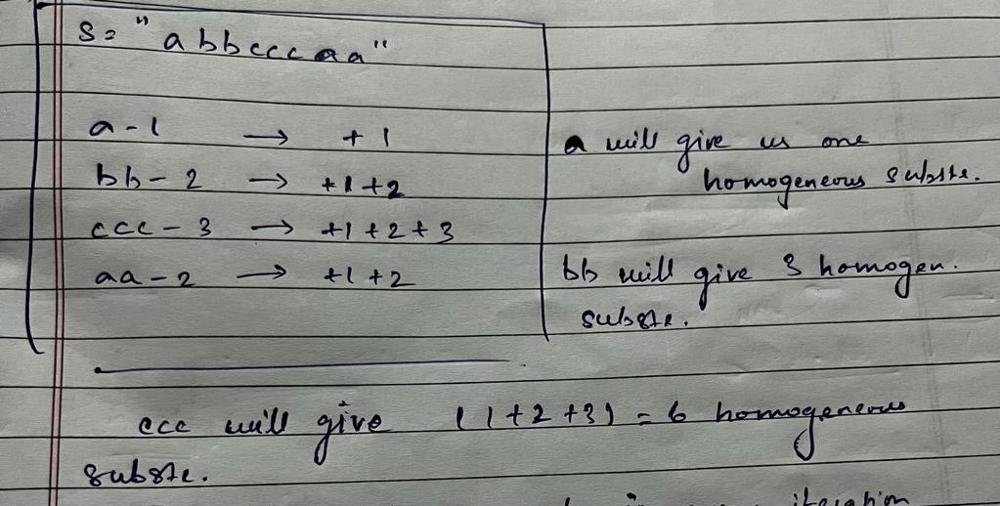\n \nIf there is just one character, the outcome will be one homogenous substr.\n\nWhen two successive characters are the same, it will give (1 + 2 = 3) homogenous substr as result.\n\nWhen three successive characters are the same, the outcome is a homogeneous substr (1 + 2 + 3 = 6).\nSubstrings of ccc - **ccc -> substrings of ccc --> c(1st c) , c(2nd c) , c(3rd c) , cc (first two chars) , cc (last two chars) , ccc (all three chars)**\n\nLikewise, it continues.\n\nTherefore, we will be adding all the answers in our loop.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(1)\n\n\n# Code\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n count , ans = 1 , 1 #since constraints mentioned min length of s as 1\n for i in range(1 , len(s)):\n if s[i] == s[i-1]: \n count += 1\n else:\n count = 1\n ans += count\n return ans % (10**9 + 7)\n``` | 1 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
Solution with Sliding Window in Python3 / TypeScript | count-number-of-homogenous-substrings | 0 | 1 | # Intuition\n\nHere we have:\n\n- a string `s`\n- our goal is to count number of **homogenous** substrings\n\nA string is **homogenous** if all the characters of the string are **the same**.\n\n```\n# Example\ns = \'aab\'\n\n# How much a-s and b-s could construct a homogenous substring?\n# Only four - \'a\', \'a\', \'aa\' and \'b\'\n```\n\nAt each step we want to know, if a string is a **homogenous**.\nWe can track **size of a Sliding Window** and if condition is **broken**, then we **shrink the window**.\n\nIn order to calculate count of **homogenous** substrings at a particular `[left, right]`, we can use an **arithmetic progression formula** as:\n\n```\ncount = n * (n + 1) / 1\n```\n\n# Approach\n\n1. declare `ans` to store count of homogenous substrings\n2. declare **Sliding Window** as with pointers `left` and `right`\n3. use `count` method to find in **O(1)** count of these substrings\n4. iterate over `s`\n5. check, if neighbors in `s` are **equal** and **expand** a window\n6. otherwise **count** valid amount of substrings with `count` function\n7. return `ans`\n\n# Complexity\n\n- Time complexity: **O(N)**, since we iterate over `s`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space.\n\n# Code in Python3\n\n```\nclass Solution:\n def countHomogenous(self, s: str) -> int:\n ans = 0\n left = 0\n right = 1\n\n def count(n):\n return n * (n + 1) / 2\n\n while right < len(s):\n if s[right - 1] != s[right]:\n ans += count(right - left)\n left = right\n\n right += 1\n \n return floor((ans + count(right - left)) % (1e9 + 7))\n```\n# Code in TypeScript\n\n```\nfunction countHomogenous(s: string): number {\n let ans = 0\n let left = 0\n let right = 1\n\n const count = (n: number) => n * (n + 1) / 2\n\n while (right < s.length) {\n if (s[right - 1] != s[right]) {\n ans += count(right - left)\n left = right\n }\n\n right += 1\n\n }\n\n return (ans + count(right - left)) % (1e9 + 7)\n};\n```\n | 1 | Given a string `s`, return _the number of **homogenous** substrings of_ `s`_._ Since the answer may be too large, return it **modulo** `109 + 7`.
A string is **homogenous** if all the characters of the string are the same.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbcccaa "
**Output:** 13
**Explanation:** The homogenous substrings are listed as below:
"a " appears 3 times.
"aa " appears 1 time.
"b " appears 2 times.
"bb " appears 1 time.
"c " appears 3 times.
"cc " appears 2 times.
"ccc " appears 1 time.
3 + 1 + 2 + 1 + 3 + 2 + 1 = 13.
**Example 2:**
**Input:** s = "xy "
**Output:** 2
**Explanation:** The homogenous substrings are "x " and "y ".
**Example 3:**
**Input:** s = "zzzzz "
**Output:** 15
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase letters. | null |
[Python3] brute-force | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | Algo\nCheck all trios and find minimum degrees. \n\nImplementation\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n graph = [[False]*n for _ in range(n)]\n degree = [0]*n\n \n for u, v in edges: \n graph[u-1][v-1] = graph[v-1][u-1] = True\n degree[u-1] += 1\n degree[v-1] += 1\n \n ans = inf\n for i in range(n): \n for j in range(i+1, n):\n if graph[i][j]: \n for k in range(j+1, n):\n if graph[j][k] and graph[k][i]: \n ans = min(ans, degree[i] + degree[j] + degree[k] - 6)\n return ans if ans < inf else -1\n```\n\nAnalysis\nTime complexity `O(V^3)`\nSpace complexity `O(V^2)` | 7 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
[Python3] brute-force | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | Algo\nCheck all trios and find minimum degrees. \n\nImplementation\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n graph = [[False]*n for _ in range(n)]\n degree = [0]*n\n \n for u, v in edges: \n graph[u-1][v-1] = graph[v-1][u-1] = True\n degree[u-1] += 1\n degree[v-1] += 1\n \n ans = inf\n for i in range(n): \n for j in range(i+1, n):\n if graph[i][j]: \n for k in range(j+1, n):\n if graph[j][k] and graph[k][i]: \n ans = min(ans, degree[i] + degree[j] + degree[k] - 6)\n return ans if ans < inf else -1\n```\n\nAnalysis\nTime complexity `O(V^3)`\nSpace complexity `O(V^2)` | 7 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
Python || Beats 100% || O(N^2) | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Code\n``` python3 []\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n E = defaultdict(set)\n for a,b in edges:\n E[a].add(b)\n E[b].add(a)\n ret = len(edges)+1\n L = {k:len(E[k])-2 for k in E.keys()}\n K = sorted(L.keys(), key = lambda k:L[k])\n\n for a in K:\n sa, la = E[a], L[a]\n if la >= ret / 3: break\n while sa:\n b = sa.pop()\n sb, lb = E[b], L[b]\n sb.remove(a)\n for c in sa:\n if c in sb:\n ret = min(la+lb+L[c],ret)\n\n return -1 if ret == len(edges)+1 else ret\n```\nhttps://imgur.com/a/2I7WvZb | 0 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Python || Beats 100% || O(N^2) | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Code\n``` python3 []\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n E = defaultdict(set)\n for a,b in edges:\n E[a].add(b)\n E[b].add(a)\n ret = len(edges)+1\n L = {k:len(E[k])-2 for k in E.keys()}\n K = sorted(L.keys(), key = lambda k:L[k])\n\n for a in K:\n sa, la = E[a], L[a]\n if la >= ret / 3: break\n while sa:\n b = sa.pop()\n sb, lb = E[b], L[b]\n sb.remove(a)\n for c in sa:\n if c in sb:\n ret = min(la+lb+L[c],ret)\n\n return -1 if ret == len(edges)+1 else ret\n```\nhttps://imgur.com/a/2I7WvZb | 0 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
O(m^1.5) algorithm to generate triangles (which is better than O(n^3) or O(n * m)) | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Lemma\n###### For any node there are *O(sqrt(m))* adjacent nodes with bigger degree.\n##### Proof\n1) If degree <= *sqrt(m)*, it\'s obvious.\n2) If degree > *sqrt(m)* there are *O(m / sqrt(m))* = *O(sqrt(m))* nodes with degree > *sqrt(m)*. So there are *O(sqrt(m))* potential nodes with bigger degree.\n\n# Approach\n1) Iterate over edges *O(m)*.\n2) Iterate over one of endpoint of this edge *O(1)*.\n3) For this endpoint iterate over adjacent nodes with bigger degree *O(sqrt(m))*.\n4) This 3 nodes forms triangle in graph.\n\nP.S. This algorithms doesn\'t skip any triangle.\n\n# Complexity\n- Time complexity:\n*O(m) * O(1) * O(sqrt(m)) = O(m^1.5)*\n\n As n^2 >= m we can see that for sparse graphs it\'s better than:\n 1. O(n^3): O(n^3) >= O(sqrt(m)^3) = O(m^1.5)\n 2. O(n * m): O(n * m) >= O(sqrt(m) * m) = O(m^1.5)\n\n- Space complexity:\n*O(m)*\n\n# Code\n```\nINF = 10**9\n\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n g, deg = [set() for _ in range(n)], [0 for _ in range(n)]\n for x, y in edges:\n x, y = x - 1, y - 1\n deg[x] += 1\n deg[y] += 1\n g[x].add(y)\n g[y].add(x)\n\n heavy_g = [[] for _ in range(n)]\n for x, y in edges:\n x, y = x - 1, y - 1\n if deg[x] > deg[y]:\n x, y = y, x\n heavy_g[x].append(y)\n \n res = INF\n for x, y in edges:\n x, y = x - 1, y - 1\n val = deg[x] + deg[y] - 6\n for _ in range(2):\n g_x = g[x]\n for z in heavy_g[y]:\n if z in g_x:\n res = min(res, val + deg[z])\n x, y = y, x\n\n return -1 if res == INF else res\n``` | 0 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
O(m^1.5) algorithm to generate triangles (which is better than O(n^3) or O(n * m)) | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Lemma\n###### For any node there are *O(sqrt(m))* adjacent nodes with bigger degree.\n##### Proof\n1) If degree <= *sqrt(m)*, it\'s obvious.\n2) If degree > *sqrt(m)* there are *O(m / sqrt(m))* = *O(sqrt(m))* nodes with degree > *sqrt(m)*. So there are *O(sqrt(m))* potential nodes with bigger degree.\n\n# Approach\n1) Iterate over edges *O(m)*.\n2) Iterate over one of endpoint of this edge *O(1)*.\n3) For this endpoint iterate over adjacent nodes with bigger degree *O(sqrt(m))*.\n4) This 3 nodes forms triangle in graph.\n\nP.S. This algorithms doesn\'t skip any triangle.\n\n# Complexity\n- Time complexity:\n*O(m) * O(1) * O(sqrt(m)) = O(m^1.5)*\n\n As n^2 >= m we can see that for sparse graphs it\'s better than:\n 1. O(n^3): O(n^3) >= O(sqrt(m)^3) = O(m^1.5)\n 2. O(n * m): O(n * m) >= O(sqrt(m) * m) = O(m^1.5)\n\n- Space complexity:\n*O(m)*\n\n# Code\n```\nINF = 10**9\n\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n g, deg = [set() for _ in range(n)], [0 for _ in range(n)]\n for x, y in edges:\n x, y = x - 1, y - 1\n deg[x] += 1\n deg[y] += 1\n g[x].add(y)\n g[y].add(x)\n\n heavy_g = [[] for _ in range(n)]\n for x, y in edges:\n x, y = x - 1, y - 1\n if deg[x] > deg[y]:\n x, y = y, x\n heavy_g[x].append(y)\n \n res = INF\n for x, y in edges:\n x, y = x - 1, y - 1\n val = deg[x] + deg[y] - 6\n for _ in range(2):\n g_x = g[x]\n for z in heavy_g[y]:\n if z in g_x:\n res = min(res, val + deg[z])\n x, y = y, x\n\n return -1 if res == INF else res\n``` | 0 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
[Python] Don't repeat same trios | Optimization | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | \n# Code\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n adj = [set() for i in range(n)]\n deg = [0]*n\n for u,v in edges:\n u -=1\n v-=1\n adj[u].add(v)\n adj[v].add(u)\n deg[u]+=1\n deg[v] +=1\n res = float(\'inf\')\n for u,v in edges:\n u-=1\n v-=1\n com = adj[u]&adj[v]\n for c in com:\n res = min(res,deg[u] + deg[v] + deg[c] - 6 )\n if u in adj[c]: adj[c].remove(u)\n if v in adj[c]: adj[c].remove(v)\n return -1 if res==float(\'inf\') else res\n``` | 0 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
[Python] Don't repeat same trios | Optimization | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | \n# Code\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n adj = [set() for i in range(n)]\n deg = [0]*n\n for u,v in edges:\n u -=1\n v-=1\n adj[u].add(v)\n adj[v].add(u)\n deg[u]+=1\n deg[v] +=1\n res = float(\'inf\')\n for u,v in edges:\n u-=1\n v-=1\n com = adj[u]&adj[v]\n for c in com:\n res = min(res,deg[u] + deg[v] + deg[c] - 6 )\n if u in adj[c]: adj[c].remove(u)\n if v in adj[c]: adj[c].remove(v)\n return -1 if res==float(\'inf\') else res\n``` | 0 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
Simple Adjacency Matrix iteration with Explanation | Python | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLooking at this problem, the first thing that we should be able to infer is that we need to build out an adjacency list since we want to first find 3 connected nodes.\nWe need to understand the concept of "degree" which means the number of edges for that node. So question is basically asking us to do a search in the graph to find three connected nodes(trio) and then output their collective degree. If there are more than one trio, return the smallest total edges\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Understand that this is an adjacency matrix problem. Build it out so that we know what are the edges for each node\n2. Once we have the edges, we want to iterate through all nodes, and then two of its neighbours(since it is a trio) and check if all these 2 nodes belong to a trio. \n3. If they belong to a trio, store their collective degree in a variable and keep comparing it to the next trio found.\n\nA gotcha here is that when calculating the trio, you should avoid including the edges between the trio nodes itself:\neg: if nodes are A,B,C\nedges to avoid: A-B, B-A, B-C, C-B, A-C, C-A\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n^3)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n # Step 1: Create a defaultdict(set) to represent the graph\n graph = defaultdict(set)\n for u, v in edges:\n graph[u].add(v)\n graph[v].add(u)\n\n min_degree = float(\'inf\')\n\n # Step 2: Iterate through all the nodes\n for i in range(1, n + 1):\n # Iterate through the neighbour\n for j in range(i + 1, n + 1):\n # Nodes i and j are not connected, so skip this pair\n if j not in graph[i]:\n continue\n # Iterate through third node\n for k in range(j + 1, n + 1):\n if k in graph[i] and k in graph[j]: # Nodes i, j, and k are connected (form a trio)\n # for the three nodes i,j,k we want edges that dont include i,j,k \n # ie: i-j, j-i, j-k, k-j, k-i, i-k\n degree = len(graph[i]) + len(graph[j]) + len(graph[k]) - 6\n min_degree = min(min_degree, degree)\n\n return min_degree if min_degree != float(\'inf\') else -1\n\n\n``` | 0 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Simple Adjacency Matrix iteration with Explanation | Python | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLooking at this problem, the first thing that we should be able to infer is that we need to build out an adjacency list since we want to first find 3 connected nodes.\nWe need to understand the concept of "degree" which means the number of edges for that node. So question is basically asking us to do a search in the graph to find three connected nodes(trio) and then output their collective degree. If there are more than one trio, return the smallest total edges\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Understand that this is an adjacency matrix problem. Build it out so that we know what are the edges for each node\n2. Once we have the edges, we want to iterate through all nodes, and then two of its neighbours(since it is a trio) and check if all these 2 nodes belong to a trio. \n3. If they belong to a trio, store their collective degree in a variable and keep comparing it to the next trio found.\n\nA gotcha here is that when calculating the trio, you should avoid including the edges between the trio nodes itself:\neg: if nodes are A,B,C\nedges to avoid: A-B, B-A, B-C, C-B, A-C, C-A\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n^3)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n # Step 1: Create a defaultdict(set) to represent the graph\n graph = defaultdict(set)\n for u, v in edges:\n graph[u].add(v)\n graph[v].add(u)\n\n min_degree = float(\'inf\')\n\n # Step 2: Iterate through all the nodes\n for i in range(1, n + 1):\n # Iterate through the neighbour\n for j in range(i + 1, n + 1):\n # Nodes i and j are not connected, so skip this pair\n if j not in graph[i]:\n continue\n # Iterate through third node\n for k in range(j + 1, n + 1):\n if k in graph[i] and k in graph[j]: # Nodes i, j, and k are connected (form a trio)\n # for the three nodes i,j,k we want edges that dont include i,j,k \n # ie: i-j, j-i, j-k, k-j, k-i, i-k\n degree = len(graph[i]) + len(graph[j]) + len(graph[k]) - 6\n min_degree = min(min_degree, degree)\n\n return min_degree if min_degree != float(\'inf\') else -1\n\n\n``` | 0 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
Python | easy Solution | faster than 100% | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n h = defaultdict(set)\n freq = defaultdict(int)\n for i,j in edges:\n h[i].add(j)\n h[j].add(i)\n freq[i] += 1\n freq[j] += 1\n ans = float(\'inf\')\n for i in range(1, n+1):\n temp = h[i]\n visited = set()\n for j in range(i+1, n+1):\n if j not in visited:\n visited.add(j)\n st = h[j]\n if i in st:\n cnt = st.intersection(temp)\n for x in cnt:\n visited.add(x)\n curr = freq[x]-2 + freq[i]-2+freq[j]-2\n ans = min(ans, curr)\n return ans if ans != float(\'inf\') else -1\n\n\n \n``` | 0 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Python | easy Solution | faster than 100% | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n h = defaultdict(set)\n freq = defaultdict(int)\n for i,j in edges:\n h[i].add(j)\n h[j].add(i)\n freq[i] += 1\n freq[j] += 1\n ans = float(\'inf\')\n for i in range(1, n+1):\n temp = h[i]\n visited = set()\n for j in range(i+1, n+1):\n if j not in visited:\n visited.add(j)\n st = h[j]\n if i in st:\n cnt = st.intersection(temp)\n for x in cnt:\n visited.add(x)\n curr = freq[x]-2 + freq[i]-2+freq[j]-2\n ans = min(ans, curr)\n return ans if ans != float(\'inf\') else -1\n\n\n \n``` | 0 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
Python common sense approach | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Intuition\nA trio is present when the two nodes that are connected by an edge share a neighbor. Count the neighbors of each of these three nodes individually and subtract 6 to account for each member of the trio also having the other two as neighbors.\n\nI was astounded that this worked as it probably has exponential time and space big-O.\n\n# Code\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n nodes = defaultdict(set)\n for e in edges:\n nodes[e[0]].add(e[1])\n nodes[e[1]].add(e[0])\n mindeg = inf\n for node1, node2 in edges:\n neigh1, neigh2 = nodes[node1], nodes[node2]\n if len(neigh1) > 1 and len(neigh2) > 1:\n com_neighs = neigh1 & neigh2\n if len(com_neighs) > 0:\n tmp = len(neigh1) + len(neigh2) - 6\n for c in com_neighs:\n mindeg = min(mindeg, tmp + len(nodes[c]))\n if mindeg == inf:\n mindeg = -1\n return mindeg\n\n``` | 0 | You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`.
A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them.
The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not.
Return _the **minimum** degree of a connected trio in the graph, or_ `-1` _if the graph has no connected trios._
**Example 1:**
**Input:** n = 6, edges = \[\[1,2\],\[1,3\],\[3,2\],\[4,1\],\[5,2\],\[3,6\]\]
**Output:** 3
**Explanation:** There is exactly one trio, which is \[1,2,3\]. The edges that form its degree are bolded in the figure above.
**Example 2:**
**Input:** n = 7, edges = \[\[1,3\],\[4,1\],\[4,3\],\[2,5\],\[5,6\],\[6,7\],\[7,5\],\[2,6\]\]
**Output:** 0
**Explanation:** There are exactly three trios:
1) \[1,4,3\] with degree 0.
2) \[2,5,6\] with degree 2.
3) \[5,6,7\] with degree 2.
**Constraints:**
* `2 <= n <= 400`
* `edges[i].length == 2`
* `1 <= edges.length <= n * (n-1) / 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no repeated edges. | For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it. Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character. In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c). |
Python common sense approach | minimum-degree-of-a-connected-trio-in-a-graph | 0 | 1 | # Intuition\nA trio is present when the two nodes that are connected by an edge share a neighbor. Count the neighbors of each of these three nodes individually and subtract 6 to account for each member of the trio also having the other two as neighbors.\n\nI was astounded that this worked as it probably has exponential time and space big-O.\n\n# Code\n```\nclass Solution:\n def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:\n nodes = defaultdict(set)\n for e in edges:\n nodes[e[0]].add(e[1])\n nodes[e[1]].add(e[0])\n mindeg = inf\n for node1, node2 in edges:\n neigh1, neigh2 = nodes[node1], nodes[node2]\n if len(neigh1) > 1 and len(neigh2) > 1:\n com_neighs = neigh1 & neigh2\n if len(com_neighs) > 0:\n tmp = len(neigh1) + len(neigh2) - 6\n for c in com_neighs:\n mindeg = min(mindeg, tmp + len(nodes[c]))\n if mindeg == inf:\n mindeg = -1\n return mindeg\n\n``` | 0 | Given an integer array `nums`, your goal is to make all elements in `nums` equal. To complete one operation, follow these steps:
1. Find the **largest** value in `nums`. Let its index be `i` (**0-indexed**) and its value be `largest`. If there are multiple elements with the largest value, pick the smallest `i`.
2. Find the **next largest** value in `nums` **strictly smaller** than `largest`. Let its value be `nextLargest`.
3. Reduce `nums[i]` to `nextLargest`.
Return _the number of operations to make all elements in_ `nums` _equal_.
**Example 1:**
**Input:** nums = \[5,1,3\]
**Output:** 3
**Explanation:** It takes 3 operations to make all elements in nums equal:
1. largest = 5 at index 0. nextLargest = 3. Reduce nums\[0\] to 3. nums = \[3,1,3\].
2. largest = 3 at index 0. nextLargest = 1. Reduce nums\[0\] to 1. nums = \[1,1,3\].
3. largest = 3 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1\].
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 0
**Explanation:** All elements in nums are already equal.
**Example 3:**
**Input:** nums = \[1,1,2,2,3\]
**Output:** 4
**Explanation:** It takes 4 operations to make all elements in nums equal:
1. largest = 3 at index 4. nextLargest = 2. Reduce nums\[4\] to 2. nums = \[1,1,2,2,2\].
2. largest = 2 at index 2. nextLargest = 1. Reduce nums\[2\] to 1. nums = \[1,1,1,2,2\].
3. largest = 2 at index 3. nextLargest = 1. Reduce nums\[3\] to 1. nums = \[1,1,1,1,2\].
4. largest = 2 at index 4. nextLargest = 1. Reduce nums\[4\] to 1. nums = \[1,1,1,1,1\].
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `1 <= nums[i] <= 5 * 104` | Consider a trio with nodes u, v, and w. The degree of the trio is just degree(u) + degree(v) + degree(w) - 6. The -6 comes from subtracting the edges u-v, u-w, and v-w, which are counted twice each in the vertex degree calculation. To get the trios (u,v,w), you can iterate on u, then iterate on each w,v such that w and v are neighbors of u and are neighbors of each other. |
Solution with Recursion Beats 93.85% in Runtime | longest-nice-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n\n if len(s)<2:\n return ""\n valid=True\n for i in range(len(s)):\n if ord(s[i])>95 and s[i].upper() in s:\n continue\n elif ord(s[i])<95 and s[i].lower() in s:\n continue\n else:\n valid=False\n break\n if valid:\n return s\n else:\n right=self.longestNiceSubstring(s[:i])\n left=self.longestNiceSubstring(s[i+1:])\n \n if len(left)<=len(right):\n return right\n else:\n return left \n\n``` | 11 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
[Python3] brute-force & divide and conquer | longest-nice-substring | 0 | 1 | \n```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n ans = ""\n for i in range(len(s)):\n for ii in range(i+1, len(s)+1):\n if all(s[k].swapcase() in s[i:ii] for k in range(i, ii)): \n ans = max(ans, s[i:ii], key=len)\n return ans \n```\n\nEdited on 2/23/2021\nApparently, the small size doesn\'t give me enough motivation to seek more efficient algo. Below is the implementation of divide and conquer in Python3 of this [post](https://leetcode.com/problems/longest-nice-substring/discuss/1074589/JavaStraightforward-Divide-and-Conquer). This is indeed a lot faster than the naive solution above. Credit goes to original author. \n```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n if not s: return "" # boundary condition \n ss = set(s)\n for i, c in enumerate(s):\n if c.swapcase() not in ss: \n s0 = self.longestNiceSubstring(s[:i])\n s1 = self.longestNiceSubstring(s[i+1:])\n return max(s0, s1, key=len)\n return s\n``` | 79 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
Python3 - From O(N^2) to O(N) | longest-nice-substring | 0 | 1 | This post is inspired by \nhttps://leetcode.com/problems/longest-nice-substring/discuss/1074677/This-is-a-good-problem-but-it\'s-bad-to-use-small-constraint-and-mark-it-as-an-easy-problem\n\nI want to explain to myself how one can optimize step by step from O(N^2) brute force solution to the optimal solution O(N). \n\n## Approach 1: Brute Force\nThe intuition is simple. We basically check every possible substring to see if it\'s a nice string. We also keep record of the current longest nice substring by remembering the start index of the substring as well as the length of it.\n\n```python\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n N = len(s)\n maxlen = 0\n start = 0\n for i in range(N):\n seen = set()\n missing = 0\n for j in range(i, N):\n\t\t\t# if we haven\'t seen this "type", add it into the seen set\n if s[j] not in seen: \n seen.add(s[j])\n\t\t\t\t\t# since this is the first time we see this "type" of character\n\t\t\t\t\t# we check if the other half has already been seen before\n if (s[j].lower() not in seen) or (s[j].upper() not in seen):\n missing += 1 # we haven\'t seen the other half yet, so adding 1 to the missing type\n else: # otherwise we know this character will compensate the other half which we pushed earlier into the set, so we subtract missing "type" by 1\n missing -= 1\n if missing == 0 and (j - i + 1) > maxlen:\n maxlen = j - i + 1\n start = i\n return s[start:(start + maxlen)]\n```\n**Complexity Analysis**\n\nTime Complexity: O(N^2)\nSpace Complexity: O(26) There are only 26 lowercase English characters\n\n## Approach 2: Divide and Conquer\nThe key observation here is that if a character doesn\'t have its other half (different case but same character) in the given string, it can\'t be included into any of the nice substring.\nFor instance, let\'s look at string **"abcBCEAamM"**. We notice that every alphabet has both cases present in the string except character **E**. So any nice string can\'t have **E** in it. In other words, the longest nice substring must be either in **E**\'s left side or its right side, namely **"abcBC"** or **"AamM"**. We notice that we just create 2 subproblems to find the longest nice substring in **"abcBC"** and **"AamM"**. \n\nWhen we get result from solving left subproblem and right subproblem, we simply compare the length of two strings and return the one with longer length. Note that if both strings have the same length, we need to return the left one since the problem statement explicitly mentions: **If there are multiple, return the substring of the earliest occurrence.**\n\nNow what if we don\'t see any un-paired character after we go through the string? That\'s good because that means the original string is a nice string, so we simply return it since it must be the longest one.\n\nWhat\'s the base case? Well, if the length of string is less than 2, it can\'t be a nice string, so we return empty string in that case.\n\n``` python\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n def helper(i: int, j: int):\n\t\t # string length is less than 2 return empty string\n\t\t # we return a tuple to indicate the start and end index of the string to avoid unncessary string copy operation\n if j - i + 1 < 2: return (0, -1)\n hashset = set()\n\t\t\t# scan the string once and save all char into a set\n for k in range(i, j + 1):\n hashset.add(s[k])\n \n for k in range(i, j + 1):\n\t\t\t # if this char pairs with its other half, we are good\n if s[k].upper() in hashset and s[k].lower() in hashset:\n continue\n\t\t\t # we found `E` !\n slt = helper(i, k - 1)\n srt = helper(k + 1, j)\n return slt if (slt[1] - slt[0] + 1) >= (srt[1] - srt[0] + 1) else srt\n return (i, j)\n lt, rt = helper(0, len(s) - 1)\n return s[lt:(rt + 1)]\n```\n\n**Complexity Analysis**\n\nTime Complexity: O(N x Log(N)) Doesn\'t this look similar to quick sort? In each recursion call, we use O(N) to build the hash set and find the position of un-paired character. Then we create two subproblems whose size was reduced. Ideally if we could reduce size of each subproblem to N/2 every time, then O(N x Log(N) will be the answer for all possible input. However, just like quick sort, dividing each subproblem to N/2 every time is not guaranteed. Consider the following input: **"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"**\n\nEvery time we divide our subproblem to **""** and **"aaaaaaaaaaaaaaaaaaaaaaaaaaaaa"**. It only reduces the subproblem size by 1. So time complexity for this input will be **O(N^2)**\n\nSpace Complexity: **O(N)** There are only 26 lowercase English characters, so the space used by hash set is constant. However, we need to take recursion into consideration. In the worst case we mentioned above, the recursion depth can reach **N**. \n\n## Approach 3: Improved Divide and Conquer\nIf we look at string "AbMab**E**cBC**E**Aam**E**MmdDaA", we notice the un-paired character E appears at multiple location in the original string. That means we can divide our original string into subproblems using E as delimeter:\n**"AbMab"\n"cBC"\n"Aam"\n"MmdDaA"**\n\nWe know one of the factors that determine the time complexity of divide and conqure algorithm is the depth of the recursion tree. Why does dividing subproblems in this way help improve the time complexity? Because every time we are removing one alphabet completely from the data set. There are only 26 lowercase English characters, so at most we only need to remove **26** times, which means the depth of recursion tree is bound to **26**\n\n``` python\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n def helper(i: int, j: int):\n if (j - i + 1) < 2: return (0,-1)\n\n hashset = set()\n for k in range(i, j + 1):\n hashset.add(s[k])\n # use parts array to store position (index) of delimeter in sorted order\n parts = [i - 1]\n for k in range(i, j + 1):\n up = s[k].upper()\n lower = s[k].lower()\n if (up not in hashset) or (lower not in hashset): # un-paired character\n parts.append(k)\n parts.append(j+1) \n\t\t\t# why do we have i - 1 and j + 1 in the array?\n\t\t\t# go through this example aAbbcCEdDEfF\n\t\t\t# the subproblems are:\n\t\t\t# [0, 5], [7, 8], [10, 11]\n max_len_pair = (0, -1)\n\t\t\t# if we don\'t find any delimeter, then the original string is a nice string\n if len(parts) == 2:\n return (i, j)\n\t\t\t# call recursively to solve each subproblem\n for i in range(len(parts) - 1):\n ni, nj = helper(parts[i] + 1, parts[i+1] - 1)\n if (nj - ni + 1) > (max_len_pair[1] - max_len_pair[0] + 1):\n max_len_pair = (ni, nj)\n \n return max_len_pair\n \n lt, rt = helper(0, len(s) - 1)\n return s[lt:(rt+1)]\n```\n**Complexity Analysis**\n\nTime Complexity: O(N x 26) = O(N). Recall the recursion depth is bound to 26\nLet\'s look at the worst case in approach 2 this time **"aaaaaaaa"**\nThe first time we call recursion function, we find **a** is un-paired so we created 9 subprolems of size 0. So it takes O(9) = O(N) to solve it\n\nSpace Complexity: O(26) = O(1). The hashset can contain at most 26 unique characters. The recursion depth is bound to 26\n\n\n | 41 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
Python 🐍 | Simple Solution | Divide and Conquer ✅ | longest-nice-substring | 0 | 1 | \n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def longestNiceSubstring(self, s: str) -> str:\n if len(s) < 2:\n return \'\'\n\n seen = set(s)\n\n for i in range(len(s)):\n if s[i].lower() in seen and s[i].upper() in seen: \n continue\n\n left = self.longestNiceSubstring(s[:i])\n right = self.longestNiceSubstring(s[i + 1:])\n\n return max(left, right, key=len)\n \n return s\n\n \n``` | 1 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
Nice | longest-nice-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n def pper(s):\n for i in s:\n if i.lower() in s and i.upper() in s:\n pass\n else:\n return False\n return True \n m=""\n for i in range(len(s)):\n for j in range(i+1,len(s)):\n if pper(s[i:j+1]) and len(m)<len(s[i:j+1]):\n m=s[i:j+1]\n return m\n``` | 7 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
python3 brute force solution | longest-nice-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestNiceSubstring(self, a: str) -> str:\n # a="wWOExoVhvXebB"\n l=0\n h=len(a)-1\n g=0\n h=[]\n y=0\n k=[]\n for i in range(len(a)):\n for j in range(len(a)):\n b=a[i:len(a)-j]\n for i in range(len(b)):\n if b[i].upper()in b and b[i].lower()in b:\n g=g+1\n if g==len(b) and b!="":\n k.append(b)\n g=0\n u=0\n j=[]\n for i in range(len(k)-1):\n if len(k[i])==len(k[i+1]):\n u=u+1\n if u==len(k)-1 and len(k)>1:\n for i in range(len(k)):\n c=a.find(k[i])\n j.append([c,k[i]])\n g=[100,"a"]\n for i in range(len(j)):\n if j[i][0]<g[0]:\n g=j[i]\n return(g[1])\n else:\n p=""\n max_=-inf\n for i in range(len(k)):\n if len(k[i])>max_:\n max_=len(k[i])\n p=k[i]\n return(p)\n\n``` | 1 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
✅ Elegant Divide and Conquer Approach | longest-nice-substring | 0 | 1 | # Intuition\nWe are using recursion here\n\n# Approach\nWe find the first letter in the string which doesn\'t have complementary and divide string into two substrings - and so on until we find the string without single letters\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n sSet = set(s)\n for i in range(len(s)):\n if s[i].lower() not in sSet or s[i].upper() not in sSet:\n lns1 = self.longestNiceSubstring(s[:i])\n lns2 = self.longestNiceSubstring(s[i+1:])\n\n return max(lns1, lns2, key=len)\n\n return s\n\n``` | 7 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
[Python 3] Using a decreasing sliding window. | longest-nice-substring | 0 | 1 | The intuition behind my approach is to check validity for substings starting with the longest one and decreasing our window size.\n\nThe difficult part was determining how to write a function that would determine "niceness." The intuition behind the function I wrote is that if we compare the number of unique characters in a substring and the number of unique characters in the same substring but lowercased, a "nice" substring would have the property that `len(set(substring.lower())) == len(set(substring))`, since each lowercase letter must have a corresponding uppercase letter.\n\n```\nclass Solution:\n def get_nice(self, s: str) -> bool:\n return len(set(s.lower())) == (len(set(s)) // 2)\n \n def longestNiceSubstring(self, s: str) -> str:\n window_size = len(s)\n \n while window_size:\n for i in range(len(s) - window_size + 1):\n substring = s[i:i + window_size]\n \n if self.get_nice(substring):\n return substring\n \n window_size -= 1\n \n return \'\'\n``` | 12 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
[Python3] Recursive Divide and Conquer Solution (O(n)) | longest-nice-substring | 0 | 1 | ```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n def divcon(s):\n\t\t # string with length 1 or less arent considered nice\n if len(s) < 2:\n return ""\n \n pivot = []\n # get every character that is not nice\n for i, ch in enumerate(s):\n if ch.isupper() and ch.lower() not in s:\n pivot.append(i)\n if ch.islower() and ch.upper() not in s:\n pivot.append(i)\n\t\t\t# if no such character return the string\n if not pivot:\n return s\n\t\t\t# divide the string in half excluding the char that makes the string not nice\n else:\n mid = (len(pivot)) // 2\n return max(divcon(s[:pivot[mid]]),divcon(s[pivot[mid]+1:]),key=len)\n \n return divcon(s)\n``` | 13 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
Python - Simple and Elegant! Multiple Solutions! | longest-nice-substring | 0 | 1 | **Brute Force**:\n```\nclass Solution:\n def longestNiceSubstring(self, s):\n subs = [s[i:j] for i in range(len(s)) for j in range(i+1, len(s)+1)]\n nice = [sub for sub in subs if set(sub)==set(sub.swapcase())]\n return max(nice, key=len, default="")\n```\n\n**Divide and Conquer ([Credit](https://leetcode.com/problems/longest-nice-substring/discuss/1074546/Python3-brute-force-and-divide-and-conquer))**:\n```\nclass Solution:\n def longestNiceSubstring(self, s):\n chars = set(s)\n for i, c in enumerate(s):\n if c.swapcase() not in chars:\n return max(map(self.longestNiceSubstring, [s[:i], s[i+1:]]), key=len)\n return s\n``` | 11 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
Python Stack divide an conquer | longest-nice-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestNiceSubstring(self, s: str) -> str:\n res = ""\n stack = [s]\n while stack:\n word = stack.pop()\n if not word:\n continue\n sset = set(list(word))\n for i,j in enumerate(word):\n if j.swapcase() not in sset:\n stack.append(word[i+1:])\n stack.append(word[:i])\n break\n else:\n res = max(res, word, key=len)\n return res\n``` | 2 | A string `s` is **nice** if, for every letter of the alphabet that `s` contains, it appears **both** in uppercase and lowercase. For example, `"abABB "` is nice because `'A'` and `'a'` appear, and `'B'` and `'b'` appear. However, `"abA "` is not because `'b'` appears, but `'B'` does not.
Given a string `s`, return _the longest **substring** of `s` that is **nice**. If there are multiple, return the substring of the **earliest** occurrence. If there are none, return an empty string_.
**Example 1:**
**Input:** s = "YazaAay "
**Output:** "aAa "
**Explanation: ** "aAa " is a nice string because 'A/a' is the only letter of the alphabet in s, and both 'A' and 'a' appear.
"aAa " is the longest nice substring.
**Example 2:**
**Input:** s = "Bb "
**Output:** "Bb "
**Explanation:** "Bb " is a nice string because both 'B' and 'b' appear. The whole string is a substring.
**Example 3:**
**Input:** s = "c "
**Output:** " "
**Explanation:** There are no nice substrings.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of uppercase and lowercase English letters. | null |
Super Simple Python Solution (check one by one) | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n pointer = 0\n \n groups.reverse()\n \n while pointer <= len(nums):\n if len(groups) == 0:\n return True\n currentGroup = groups[-1]\n if nums[pointer:pointer+len(currentGroup)] == currentGroup:\n pointer += len(currentGroup)\n groups.pop()\n else:\n pointer += 1\n \n return False\n \n``` | 1 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Super Simple Python Solution (check one by one) | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n pointer = 0\n \n groups.reverse()\n \n while pointer <= len(nums):\n if len(groups) == 0:\n return True\n currentGroup = groups[-1]\n if nums[pointer:pointer+len(currentGroup)] == currentGroup:\n pointer += len(currentGroup)\n groups.pop()\n else:\n pointer += 1\n \n return False\n \n``` | 1 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
Hideous Python one liner | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, g: List[List[int]], nums: List[int]) -> bool:\n return (it:=iter(nums)) and all(item in it for item in chain.from_iterable(g)) and (all(any(g[i] == nums[idx[i]:idx[i]+len(g[i])] for *idx, in combinations(range(len(nums)), len(g))) for i in range(len(g))) if len(nums) < 50 else True)\n``` | 1 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Hideous Python one liner | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, g: List[List[int]], nums: List[int]) -> bool:\n return (it:=iter(nums)) and all(item in it for item in chain.from_iterable(g)) and (all(any(g[i] == nums[idx[i]:idx[i]+len(g[i])] for *idx, in combinations(range(len(nums)), len(g))) for i in range(len(g))) if len(nums) < 50 else True)\n``` | 1 | The **product sum** of two equal-length arrays `a` and `b` is equal to the sum of `a[i] * b[i]` for all `0 <= i < a.length` (**0-indexed**).
* For example, if `a = [1,2,3,4]` and `b = [5,2,3,1]`, the **product sum** would be `1*5 + 2*2 + 3*3 + 4*1 = 22`.
Given two arrays `nums1` and `nums2` of length `n`, return _the **minimum product sum** if you are allowed to **rearrange** the **order** of the elements in_ `nums1`.
**Example 1:**
**Input:** nums1 = \[5,3,4,2\], nums2 = \[4,2,2,5\]
**Output:** 40
**Explanation:** We can rearrange nums1 to become \[3,5,4,2\]. The product sum of \[3,5,4,2\] and \[4,2,2,5\] is 3\*4 + 5\*2 + 4\*2 + 2\*5 = 40.
**Example 2:**
**Input:** nums1 = \[2,1,4,5,7\], nums2 = \[3,2,4,8,6\]
**Output:** 65
**Explanation:** We can rearrange nums1 to become \[5,7,4,1,2\]. The product sum of \[5,7,4,1,2\] and \[3,2,4,8,6\] is 5\*3 + 7\*2 + 4\*4 + 1\*8 + 2\*6 = 65.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 100` | When we use a subarray, the room for the next subarrays will be the suffix after the used subarray. If we can match a group with multiple subarrays, we should choose the first one, as this will just leave the largest room for the next subarrays. |
[Python3🐍] [DP] [Drawing✍️] [Easy to understand ✌️] Dynamic Programming solution.✨🍻 | form-array-by-concatenating-subarrays-of-another-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nConsider we have these three arrarys:\n- groups, provided by input.\n- nums, also provided by input.\n- dp, we create it, the meaning is: **in the current position `i`, how many groups are already matched.**\n For example: `dp[3]=2` means before position `3`, there already has `2` matched groups. And if the `2` is the total number of groups, that\'s done, just return `True`.\n\nSo, let\'s run the dp program:\n\n- for the first step, we\'re trying to match `1st` of groups and nums.\n\n\n\n- for the second step, if the first step matched successfully, we\'re trying the match `2nd` of groups and nums.\n\n\n\n- break condition:\n The number of matched group `>=` total group.\n\n# Complexity\n- Time complexity: O(len(groups) * len(nums))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(len(nums))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canChoose(self, groups: List[List[int]], nums: List[int]) -> bool:\n lc = len(nums)\n target = len(groups)\n dp = [0 for j in range(lc)]\n for c in range(lc):\n curGroupIndex = dp[c - 1]\n l = len(groups[curGroupIndex])\n nextIndex = c+l-1\n if nums[c: c+l] == groups[curGroupIndex] and nextIndex < lc:\n dp[nextIndex] = max(dp[nextIndex], curGroupIndex + 1)\n if dp[nextIndex] >= target:\n return True\n dp[c] = max(dp[c-1], dp[c])\n return False\n \n\n``` | 1 | You are given a 2D integer array `groups` of length `n`. You are also given an integer array `nums`.
You are asked if you can choose `n` **disjoint** subarrays from the array `nums` such that the `ith` subarray is equal to `groups[i]` (**0-indexed**), and if `i > 0`, the `(i-1)th` subarray appears **before** the `ith` subarray in `nums` (i.e. the subarrays must be in the same order as `groups`).
Return `true` _if you can do this task, and_ `false` _otherwise_.
Note that the subarrays are **disjoint** if and only if there is no index `k` such that `nums[k]` belongs to more than one subarray. A subarray is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** groups = \[\[1,-1,-1\],\[3,-2,0\]\], nums = \[1,-1,0,1,-1,-1,3,-2,0\]
**Output:** true
**Explanation:** You can choose the 0th subarray as \[1,-1,0,**1,-1,-1**,3,-2,0\] and the 1st one as \[1,-1,0,1,-1,-1,**3,-2,0**\].
These subarrays are disjoint as they share no common nums\[k\] element.
**Example 2:**
**Input:** groups = \[\[10,-2\],\[1,2,3,4\]\], nums = \[1,2,3,4,10,-2\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[**1,2,3,4**,10,-2\] and \[1,2,3,4,**10,-2**\] is incorrect because they are not in the same order as in groups.
\[10,-2\] must come before \[1,2,3,4\].
**Example 3:**
**Input:** groups = \[\[1,2,3\],\[3,4\]\], nums = \[7,7,1,2,3,4,7,7\]
**Output:** false
**Explanation:** Note that choosing the subarrays \[7,7,**1,2,3**,4,7,7\] and \[7,7,1,2,**3,4**,7,7\] is invalid because they are not disjoint.
They share a common elements nums\[4\] (0-indexed).
**Constraints:**
* `groups.length == n`
* `1 <= n <= 103`
* `1 <= groups[i].length, sum(groups[i].length) <= 103`
* `1 <= nums.length <= 103`
* `-107 <= groups[i][j], nums[k] <= 107` | The constraints are low enough for a brute force approach. Try every k value from 0 upwards until word is no longer k-repeating. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.