title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
clean commented code | minimum-number-of-people-to-teach | 0 | 1 | the question is tricky to understand but easy to implement when you overcome that intial hurdle. \n\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n # modify languages to be a set for quick intersection \n languages = {person+1: set(language) for person, language in enumerate(languages)} \n\n # create a set of people with a language barrier between a friend\n barrier = set() \n for u, v in friendships:\n if not languages[u] & languages[v]:\n barrier.add(u)\n barrier.add(v)\n\n # count the spoken languages between people with barriers \n spoken = Counter()\n for person in barrier:\n spoken += Counter(languages[person])\n\n # teach the most common language to those who don\'t know it\n return len(barrier) - max(spoken.values(), default=0)\n\n``` | 0 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Solution | minimum-number-of-people-to-teach | 1 | 1 | ```C++ []\nclass Solution {\nprivate:\n bool intersects(vector<int>& a, vector<int>& b, vector<bool>& vis){\n for(int elem: a){\n vis[elem] = true;\n }\n\n bool intersectionFound = false;\n for(int elem: b){\n if(vis[elem]){\n intersectionFound = true;\n break;\n }\n }\n\n for(int elem: a){\n vis[elem] = false;\n }\n\n return intersectionFound;\n }\n\npublic:\n int minimumTeachings(int L, vector<vector<int>>& languages, vector<vector<int>>& friendships) {\n const int U = languages.size();\n const int F = friendships.size();\n\n vector<bool> isGood(U + 1, true);\n vector<bool> tempVis(L + 1, false);\n for(const vector<int>& V: friendships){\n int a = V[0];\n int b = V[1];\n if(!intersects(languages[a - 1], languages[b - 1], tempVis)){\n isGood[a] = false;\n isGood[b] = false;\n }\n }\n\n int badUsers = 0;\n int maxCount = 0;\n unordered_map<int, int> count;\n for(int user = 1; user <= U; ++user){\n if(!isGood[user]){\n badUsers += 1;\n for(int language: languages[user - 1]){\n count[language] += 1;\n maxCount = max(maxCount, count[language]);\n }\n }\n }\n\n return badUsers - maxCount;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int: \n languages: List[Set[int]] = [set(language) for language in languages] # O(m*n)\n without_contact: Set[int] = set()\n\n FIRST_FRIEND: int = 0\n SECOND_FRIEND: int = 1\n\n friendship: List[int]\n for friendship in friendships: # O(n)\n friend1: int = friendship[FIRST_FRIEND]\n friend2: int = friendship[SECOND_FRIEND]\n\n if not languages[friend1-1].intersection(languages[friend2-1]): # O(m)\n without_contact.add(friend1-1)\n without_contact.add(friend2-1)\n\n languages_spoken: List[int] = []\n\n person: int\n for person in without_contact: # O(m)\n languages_spoken.extend(languages[person])\n\n most_common: int = max(Counter(languages_spoken).values(), default=0) # O(n)\n\n return len(without_contact) - most_common\n```\n\n```Java []\nimport java.util.ArrayList;\nimport java.util.HashSet;\nimport java.util.List;\nimport java.util.Set;\n\npublic class Solution {\n public int minimumTeachings(int n, int[][] languages, int[][] friendships) {\n int m = languages.length;\n boolean[][] speak = new boolean[m + 1][n + 1];\n boolean[][] teach = new boolean[m + 1][n + 1];\n for (int user = 0; user < m; user++) {\n int[] userLanguages = languages[user];\n for (int userLanguage : userLanguages) {\n speak[user + 1][userLanguage] = true;\n }\n }\n List<int[]> listToTeach = new ArrayList<>();\n for (int[] friend : friendships) {\n int userA = friend[0];\n int userB = friend[1];\n boolean hasCommonLanguage = false;\n for (int language = 1; language <= n; language++) {\n if (speak[userA][language] && speak[userB][language]) {\n hasCommonLanguage = true;\n break;\n }\n }\n if (!hasCommonLanguage) {\n for (int language = 1; language <= n; language++) {\n if (!speak[userA][language]) {\n teach[userA][language] = true;\n }\n if (!speak[userB][language]) {\n teach[userB][language] = true;\n }\n }\n listToTeach.add(friend);\n }\n }\n int minLanguage = Integer.MAX_VALUE;\n int languageToTeach = 0;\n for (int language = 1; language <= n; language++) {\n int count = 0;\n for (int user = 1; user <= m; user++) {\n if (teach[user][language]) {\n count++;\n }\n }\n if (count < minLanguage) {\n minLanguage = count;\n languageToTeach = language;\n }\n }\n Set<Integer> setToTeach = new HashSet<>();\n for (int[] friend : listToTeach) {\n int userA = friend[0];\n int userB = friend[1];\n if (!speak[userA][languageToTeach]) {\n setToTeach.add(userA);\n }\n if (!speak[userB][languageToTeach]) {\n setToTeach.add(userB);\n }\n }\n return setToTeach.size();\n }\n}\n```\n | 0 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
Solution | minimum-number-of-people-to-teach | 1 | 1 | ```C++ []\nclass Solution {\nprivate:\n bool intersects(vector<int>& a, vector<int>& b, vector<bool>& vis){\n for(int elem: a){\n vis[elem] = true;\n }\n\n bool intersectionFound = false;\n for(int elem: b){\n if(vis[elem]){\n intersectionFound = true;\n break;\n }\n }\n\n for(int elem: a){\n vis[elem] = false;\n }\n\n return intersectionFound;\n }\n\npublic:\n int minimumTeachings(int L, vector<vector<int>>& languages, vector<vector<int>>& friendships) {\n const int U = languages.size();\n const int F = friendships.size();\n\n vector<bool> isGood(U + 1, true);\n vector<bool> tempVis(L + 1, false);\n for(const vector<int>& V: friendships){\n int a = V[0];\n int b = V[1];\n if(!intersects(languages[a - 1], languages[b - 1], tempVis)){\n isGood[a] = false;\n isGood[b] = false;\n }\n }\n\n int badUsers = 0;\n int maxCount = 0;\n unordered_map<int, int> count;\n for(int user = 1; user <= U; ++user){\n if(!isGood[user]){\n badUsers += 1;\n for(int language: languages[user - 1]){\n count[language] += 1;\n maxCount = max(maxCount, count[language]);\n }\n }\n }\n\n return badUsers - maxCount;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int: \n languages: List[Set[int]] = [set(language) for language in languages] # O(m*n)\n without_contact: Set[int] = set()\n\n FIRST_FRIEND: int = 0\n SECOND_FRIEND: int = 1\n\n friendship: List[int]\n for friendship in friendships: # O(n)\n friend1: int = friendship[FIRST_FRIEND]\n friend2: int = friendship[SECOND_FRIEND]\n\n if not languages[friend1-1].intersection(languages[friend2-1]): # O(m)\n without_contact.add(friend1-1)\n without_contact.add(friend2-1)\n\n languages_spoken: List[int] = []\n\n person: int\n for person in without_contact: # O(m)\n languages_spoken.extend(languages[person])\n\n most_common: int = max(Counter(languages_spoken).values(), default=0) # O(n)\n\n return len(without_contact) - most_common\n```\n\n```Java []\nimport java.util.ArrayList;\nimport java.util.HashSet;\nimport java.util.List;\nimport java.util.Set;\n\npublic class Solution {\n public int minimumTeachings(int n, int[][] languages, int[][] friendships) {\n int m = languages.length;\n boolean[][] speak = new boolean[m + 1][n + 1];\n boolean[][] teach = new boolean[m + 1][n + 1];\n for (int user = 0; user < m; user++) {\n int[] userLanguages = languages[user];\n for (int userLanguage : userLanguages) {\n speak[user + 1][userLanguage] = true;\n }\n }\n List<int[]> listToTeach = new ArrayList<>();\n for (int[] friend : friendships) {\n int userA = friend[0];\n int userB = friend[1];\n boolean hasCommonLanguage = false;\n for (int language = 1; language <= n; language++) {\n if (speak[userA][language] && speak[userB][language]) {\n hasCommonLanguage = true;\n break;\n }\n }\n if (!hasCommonLanguage) {\n for (int language = 1; language <= n; language++) {\n if (!speak[userA][language]) {\n teach[userA][language] = true;\n }\n if (!speak[userB][language]) {\n teach[userB][language] = true;\n }\n }\n listToTeach.add(friend);\n }\n }\n int minLanguage = Integer.MAX_VALUE;\n int languageToTeach = 0;\n for (int language = 1; language <= n; language++) {\n int count = 0;\n for (int user = 1; user <= m; user++) {\n if (teach[user][language]) {\n count++;\n }\n }\n if (count < minLanguage) {\n minLanguage = count;\n languageToTeach = language;\n }\n }\n Set<Integer> setToTeach = new HashSet<>();\n for (int[] friend : listToTeach) {\n int userA = friend[0];\n int userB = friend[1];\n if (!speak[userA][languageToTeach]) {\n setToTeach.add(userA);\n }\n if (!speak[userB][languageToTeach]) {\n setToTeach.add(userB);\n }\n }\n return setToTeach.size();\n }\n}\n```\n | 0 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Python(Simple Maths) | minimum-number-of-people-to-teach | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTeachings(self, n, languages, friendships):\n languages = [set(i) for i in languages]\n\n ans, dict1 = set(), defaultdict(int)\n\n for i,j in friendships:\n i = i-1\n j = j-1\n if languages[i]&languages[j]: continue\n ans.add(i)\n ans.add(j)\n\n for i in ans:\n for j in languages[i]:\n dict1[j] += 1\n\n return 0 if not ans else len(ans) - max(dict1.values())\n\n``` | 0 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
Python(Simple Maths) | minimum-number-of-people-to-teach | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTeachings(self, n, languages, friendships):\n languages = [set(i) for i in languages]\n\n ans, dict1 = set(), defaultdict(int)\n\n for i,j in friendships:\n i = i-1\n j = j-1\n if languages[i]&languages[j]: continue\n ans.add(i)\n ans.add(j)\n\n for i in ans:\n for j in languages[i]:\n dict1[j] += 1\n\n return 0 if not ans else len(ans) - max(dict1.values())\n\n``` | 0 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
[Python] - Commented and Simple Python Solution | minimum-number-of-people-to-teach | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI think this problem is in the harder range of medium problems.\n\nThere are some things you need to consider:\n1) We only deal with users that are disconnected from other users\n2) We need to keep track of the most common known language for each disconnected user\n3) While keeping track of the most common spoken language for each disconnected user, we should be careful to not count users multiple times if they appear in several disconnected friendships (both friends don\'t have a common language)\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe do all of these things in one loop over the friendships, but first we convert all lists of languages to sets of languages to have a quicker way to compute intersections (i.e. finding whether two friends have a common language).\n\nAfter that we iterate over all friendships and immediately continue if two users have a common language and therefore are connected. We do this quickly using a set intersection.\n\nIf users are disconnected, we add their languages to a language counter, but in order to prevent us from counting the languages of a user multiple times (if he has multiple disconnected friendships), we keep track of these disconnected users in a set.\n\nFor the result we then take the most common language from all users and subtract its frequency from the amount of disconnected users. This gives ous the amount of users we would have to teach.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(K*N), where K is the amount of friendships and N is the amount of languages. The K comes from the loop and the N from the set intersection. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) for the counter of languages and the set of visited disconnected users (also N at most).\n\n# Code\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n\n # make languages to a set for quick lookup\n languages = [set(langi) for langi in languages]\n\n # go through the friendships and check whether they can not communicate\n # count the languages these users already know as well as keeping\n # track which user we might have to teach in a visited set.\n visited = set()\n language_cn = collections.Counter()\n for user1, user2 in friendships:\n\n # check whether they already can communicate\n if languages[user1-1].intersection(languages[user2-1]):\n continue\n\n # if we have not added the languages of a disconnected user\n # we use them to keep track of languages disconnected users\n # speek\n if user1 not in visited:\n language_cn.update(languages[user1-1])\n visited.add(user1)\n if user2 not in visited:\n language_cn.update(languages[user2-1])\n visited.add(user2)\n \n # teach the language most of the disconnected users already know, which\n # is the most common language. The number of people we have to teach then\n # are disconnected users minus the ones who already speak the most common\n # language\n return len(visited) - language_cn.most_common(1)[0][1] if visited else 0\n\n``` | 0 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
[Python] - Commented and Simple Python Solution | minimum-number-of-people-to-teach | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI think this problem is in the harder range of medium problems.\n\nThere are some things you need to consider:\n1) We only deal with users that are disconnected from other users\n2) We need to keep track of the most common known language for each disconnected user\n3) While keeping track of the most common spoken language for each disconnected user, we should be careful to not count users multiple times if they appear in several disconnected friendships (both friends don\'t have a common language)\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe do all of these things in one loop over the friendships, but first we convert all lists of languages to sets of languages to have a quicker way to compute intersections (i.e. finding whether two friends have a common language).\n\nAfter that we iterate over all friendships and immediately continue if two users have a common language and therefore are connected. We do this quickly using a set intersection.\n\nIf users are disconnected, we add their languages to a language counter, but in order to prevent us from counting the languages of a user multiple times (if he has multiple disconnected friendships), we keep track of these disconnected users in a set.\n\nFor the result we then take the most common language from all users and subtract its frequency from the amount of disconnected users. This gives ous the amount of users we would have to teach.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(K*N), where K is the amount of friendships and N is the amount of languages. The K comes from the loop and the N from the set intersection. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) for the counter of languages and the set of visited disconnected users (also N at most).\n\n# Code\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n\n # make languages to a set for quick lookup\n languages = [set(langi) for langi in languages]\n\n # go through the friendships and check whether they can not communicate\n # count the languages these users already know as well as keeping\n # track which user we might have to teach in a visited set.\n visited = set()\n language_cn = collections.Counter()\n for user1, user2 in friendships:\n\n # check whether they already can communicate\n if languages[user1-1].intersection(languages[user2-1]):\n continue\n\n # if we have not added the languages of a disconnected user\n # we use them to keep track of languages disconnected users\n # speek\n if user1 not in visited:\n language_cn.update(languages[user1-1])\n visited.add(user1)\n if user2 not in visited:\n language_cn.update(languages[user2-1])\n visited.add(user2)\n \n # teach the language most of the disconnected users already know, which\n # is the most common language. The number of people we have to teach then\n # are disconnected users minus the ones who already speak the most common\n # language\n return len(visited) - language_cn.most_common(1)[0][1] if visited else 0\n\n``` | 0 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
[Python3] Faster than 100% submissions in time and memory, detailed explanation step by step, | minimum-number-of-people-to-teach | 0 | 1 | ```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n """\n 1. Find out users who need to be taught\n 2. If no user needs to be taught, return 0\n 3. For all users who need to be taught a language, find the most popular language among them\n 4. Teach that language to rest of the users who need to be taught. \n """\n need_to_be_taught = set()\n languages = [set(language) for language in languages]\n \n # 1. Find out users who needs to be taught\n for user1, user2 in friendships:\n # Adjust the 1 based indexing to 0 based indexing\n user1 = user1 - 1\n user2 = user2 - 1\n if not (languages[user1] & languages[user2]):\n need_to_be_taught.update([user1, user2])\n \n # 2. If no user needs to be taught, return 0\n if not need_to_be_taught:\n return 0\n \n # 3. For all users who needs to be taught a language, find the most popular language among them\n language_spoken_by = collections.defaultdict(int)\n for user in need_to_be_taught:\n # for each user increment the count of languages he can speak\n for language in languages[user]:\n language_spoken_by[language] += 1\n \n # find occurrence of language spoken by maximum users who can\'t communicate with each other\n popular_language_count = max(language_spoken_by.values())\n \n # 4. Teach that language to rest of the users who need to be taught. \n return len(need_to_be_taught)- popular_language_count\n \n \n \n \n``` | 4 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
[Python3] Faster than 100% submissions in time and memory, detailed explanation step by step, | minimum-number-of-people-to-teach | 0 | 1 | ```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n """\n 1. Find out users who need to be taught\n 2. If no user needs to be taught, return 0\n 3. For all users who need to be taught a language, find the most popular language among them\n 4. Teach that language to rest of the users who need to be taught. \n """\n need_to_be_taught = set()\n languages = [set(language) for language in languages]\n \n # 1. Find out users who needs to be taught\n for user1, user2 in friendships:\n # Adjust the 1 based indexing to 0 based indexing\n user1 = user1 - 1\n user2 = user2 - 1\n if not (languages[user1] & languages[user2]):\n need_to_be_taught.update([user1, user2])\n \n # 2. If no user needs to be taught, return 0\n if not need_to_be_taught:\n return 0\n \n # 3. For all users who needs to be taught a language, find the most popular language among them\n language_spoken_by = collections.defaultdict(int)\n for user in need_to_be_taught:\n # for each user increment the count of languages he can speak\n for language in languages[user]:\n language_spoken_by[language] += 1\n \n # find occurrence of language spoken by maximum users who can\'t communicate with each other\n popular_language_count = max(language_spoken_by.values())\n \n # 4. Teach that language to rest of the users who need to be taught. \n return len(need_to_be_taught)- popular_language_count\n \n \n \n \n``` | 4 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Brute force, 94% speed | minimum-number-of-people-to-teach | 0 | 1 | Runtime: 1352 ms, faster than 93.94%\nMemory Usage: 27.2 MB, less than 59.60%\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n languages = [set(lst) for lst in languages]\n incommunicado_friends = set()\n for friend_1, friend_2 in friendships:\n if not languages[friend_1 - 1] & languages[friend_2 - 1]:\n incommunicado_friends.add(friend_1 - 1)\n incommunicado_friends.add(friend_2 - 1)\n if not incommunicado_friends:\n return 0\n return min(sum(language not in languages[friend]\n for friend in incommunicado_friends)\n for language in range(1, n + 1))\n``` | 1 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
Brute force, 94% speed | minimum-number-of-people-to-teach | 0 | 1 | Runtime: 1352 ms, faster than 93.94%\nMemory Usage: 27.2 MB, less than 59.60%\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n languages = [set(lst) for lst in languages]\n incommunicado_friends = set()\n for friend_1, friend_2 in friendships:\n if not languages[friend_1 - 1] & languages[friend_2 - 1]:\n incommunicado_friends.add(friend_1 - 1)\n incommunicado_friends.add(friend_2 - 1)\n if not incommunicado_friends:\n return 0\n return min(sum(language not in languages[friend]\n for friend in incommunicado_friends)\n for language in range(1, n + 1))\n``` | 1 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
[Python3] count properly | minimum-number-of-people-to-teach | 0 | 1 | **Algo**\nWe collect those who cannot communicate and find the most languages among them. Teach the language to those who haven\'t spoken it yet. \n\n**Implementation**\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n m = len(languages)\n languages = [set(x) for x in languages]\n \n mp = {}\n for u, v in friendships: \n if not languages[u-1] & languages[v-1]: \n for i in range(n):\n if i+1 not in languages[u-1]: mp.setdefault(u-1, set()).add(i)\n if i+1 not in languages[v-1]: mp.setdefault(v-1, set()).add(i)\n \n ans = inf\n for i in range(n): \n val = 0\n for k in range(m): \n if i in mp.get(k, set()): val += 1\n ans = min(ans, val)\n return ans \n```\n\n**Analysis**\nTime complexity `O(MN)`\nSpace complexity `O(M+N)`\n\nEdited on 2/10/2021\nA clearner implementation is given below \n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n languages = [set(x) for x in languages]\n \n users = set()\n for u, v in friendships: \n if not languages[u-1] & languages[v-1]: \n users.add(u-1)\n users.add(v-1)\n \n freq = {}\n for i in users: \n for k in languages[i]:\n freq[k] = 1 + freq.get(k, 0)\n return len(users) - max(freq.values(), default=0)\n``` | 1 | On a social network consisting of `m` users and some friendships between users, two users can communicate with each other if they know a common language.
You are given an integer `n`, an array `languages`, and an array `friendships` where:
* There are `n` languages numbered `1` through `n`,
* `languages[i]` is the set of languages the `ith` user knows, and
* `friendships[i] = [ui, vi]` denotes a friendship between the users `ui` and `vi`.
You can choose **one** language and teach it to some users so that all friends can communicate with each other. Return _the_ _**minimum**_ _number of users you need to teach._
Note that friendships are not transitive, meaning if `x` is a friend of `y` and `y` is a friend of `z`, this doesn't guarantee that `x` is a friend of `z`.
**Example 1:**
**Input:** n = 2, languages = \[\[1\],\[2\],\[1,2\]\], friendships = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** 1
**Explanation:** You can either teach user 1 the second language or user 2 the first language.
**Example 2:**
**Input:** n = 3, languages = \[\[2\],\[1,3\],\[1,2\],\[3\]\], friendships = \[\[1,4\],\[1,2\],\[3,4\],\[2,3\]\]
**Output:** 2
**Explanation:** Teach the third language to users 1 and 3, yielding two users to teach.
**Constraints:**
* `2 <= n <= 500`
* `languages.length == m`
* `1 <= m <= 500`
* `1 <= languages[i].length <= n`
* `1 <= languages[i][j] <= n`
* `1 <= ui < vi <= languages.length`
* `1 <= friendships.length <= 500`
* All tuples `(ui, vi)` are unique
* `languages[i]` contains only unique values | Sort the points by polar angle with the original position. Now only a consecutive collection of points would be visible from any coordinate. We can use two pointers to keep track of visible points for each start point For handling the cyclic condition, it’d be helpful to append the point list to itself after sorting. |
[Python3] count properly | minimum-number-of-people-to-teach | 0 | 1 | **Algo**\nWe collect those who cannot communicate and find the most languages among them. Teach the language to those who haven\'t spoken it yet. \n\n**Implementation**\n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n m = len(languages)\n languages = [set(x) for x in languages]\n \n mp = {}\n for u, v in friendships: \n if not languages[u-1] & languages[v-1]: \n for i in range(n):\n if i+1 not in languages[u-1]: mp.setdefault(u-1, set()).add(i)\n if i+1 not in languages[v-1]: mp.setdefault(v-1, set()).add(i)\n \n ans = inf\n for i in range(n): \n val = 0\n for k in range(m): \n if i in mp.get(k, set()): val += 1\n ans = min(ans, val)\n return ans \n```\n\n**Analysis**\nTime complexity `O(MN)`\nSpace complexity `O(M+N)`\n\nEdited on 2/10/2021\nA clearner implementation is given below \n```\nclass Solution:\n def minimumTeachings(self, n: int, languages: List[List[int]], friendships: List[List[int]]) -> int:\n languages = [set(x) for x in languages]\n \n users = set()\n for u, v in friendships: \n if not languages[u-1] & languages[v-1]: \n users.add(u-1)\n users.add(v-1)\n \n freq = {}\n for i in users: \n for k in languages[i]:\n freq[k] = 1 + freq.get(k, 0)\n return len(users) - max(freq.values(), default=0)\n``` | 1 | You are given `n` tasks labeled from `0` to `n - 1` represented by a 2D integer array `tasks`, where `tasks[i] = [enqueueTimei, processingTimei]` means that the `ith` task will be available to process at `enqueueTimei` and will take `processingTimei` to finish processing.
You have a single-threaded CPU that can process **at most one** task at a time and will act in the following way:
* If the CPU is idle and there are no available tasks to process, the CPU remains idle.
* If the CPU is idle and there are available tasks, the CPU will choose the one with the **shortest processing time**. If multiple tasks have the same shortest processing time, it will choose the task with the smallest index.
* Once a task is started, the CPU will **process the entire task** without stopping.
* The CPU can finish a task then start a new one instantly.
Return _the order in which the CPU will process the tasks._
**Example 1:**
**Input:** tasks = \[\[1,2\],\[2,4\],\[3,2\],\[4,1\]\]
**Output:** \[0,2,3,1\]
**Explanation:** The events go as follows:
- At time = 1, task 0 is available to process. Available tasks = {0}.
- Also at time = 1, the idle CPU starts processing task 0. Available tasks = {}.
- At time = 2, task 1 is available to process. Available tasks = {1}.
- At time = 3, task 2 is available to process. Available tasks = {1, 2}.
- Also at time = 3, the CPU finishes task 0 and starts processing task 2 as it is the shortest. Available tasks = {1}.
- At time = 4, task 3 is available to process. Available tasks = {1, 3}.
- At time = 5, the CPU finishes task 2 and starts processing task 3 as it is the shortest. Available tasks = {1}.
- At time = 6, the CPU finishes task 3 and starts processing task 1. Available tasks = {}.
- At time = 10, the CPU finishes task 1 and becomes idle.
**Example 2:**
**Input:** tasks = \[\[7,10\],\[7,12\],\[7,5\],\[7,4\],\[7,2\]\]
**Output:** \[4,3,2,0,1\]
**Explanation****:** The events go as follows:
- At time = 7, all the tasks become available. Available tasks = {0,1,2,3,4}.
- Also at time = 7, the idle CPU starts processing task 4. Available tasks = {0,1,2,3}.
- At time = 9, the CPU finishes task 4 and starts processing task 3. Available tasks = {0,1,2}.
- At time = 13, the CPU finishes task 3 and starts processing task 2. Available tasks = {0,1}.
- At time = 18, the CPU finishes task 2 and starts processing task 0. Available tasks = {1}.
- At time = 28, the CPU finishes task 0 and starts processing task 1. Available tasks = {}.
- At time = 40, the CPU finishes task 1 and becomes idle.
**Constraints:**
* `tasks.length == n`
* `1 <= n <= 105`
* `1 <= enqueueTimei, processingTimei <= 109` | You can just use brute force and find out for each language the number of users you need to teach Note that a user can appear in multiple friendships but you need to teach that user only once |
Explanations XOR and 1st element [Java, Kotlin, Python] | decode-xored-permutation | 1 | 1 | I was stuck in this seemingly easy question in [contest 44](https://leetcode.com/contest/biweekly-contest-44). How could the answer be unique?\n\n**XOR properties and tips**\n\nLet\'s note `xor` as xor instead of ^\n**1) For `a xor b = c` , you can write \n`b = c xor a` \nor `a = c xor b`** . \nYou can use 2) and 3) to demonstrate 1) .\n2) XOR is commutative, `a xor b = b xor a`\n3) XOR to the same number is always zero `a xor a = 0`\n\n\n# **Intuition**\nIf the first element is determined, the whole array can be decoded.\n> `encoded[i] = perm[i] XOR perm[i + 1]` implies\n\n `perm[i+1] = perm[i] XOR encoded[i]` thanks to 1)\n So you can loop to find the next perm element\nSee [1720. Decode XORed Array](https://leetcode.com/problems/decode-xored-array/discuss/1009844)\n\nBut you still need `perm[0]` , the first element in output array.\n\n\n\n# **Find the first element**\nThat\'s where I was stuck in the contest 44. How could the answer be unique?\nIt took a while to understand after reading other solutions.\n\nI missed an important part in the problem descrition\n> integer array `perm` that is a permutation of the **first `n` positive integers**, where `n` is always odd.\n\nYes, perm is an array with values ranging from [1,2,3 .. n]. The order in the array is permuted.\n\nLet\'s XOR all elements in array `perm`. And perms is an array with **first `n` positive integers**\n`perm[0] XOR perm[1] XOR ... perm[n] = 1 XOR 2 XOR 3 .. XOR n` Order doesn\'t matter, XOR is commutative.\nLet\'s call `totalXor`\n`totalXor = 1 XOR 2 XOR 3 .. XOR n` .\n\nXOR all except the first `perm[0]`\n`perm[0] = totalXor XOR perm[1] XOR perm[2] XOR perm[3] XOR perm[4] XOR ... perm[n]`\n\nLet\'s subsitute (replace) by encoded\n> encoded[i] = perm[i] XOR perm[i + 1]\n\nencoded[1] = perm[1] XOR perm[2]\nencoded[3] = perm[3] XOR perm[4]\n...\nencoded[n-2] = perm[n-2] XOR perm[n-1], remember `n` is the size of perm and is always **odd**\n\n**`perm[0] = totalXor XOR encoded[1] XOR encoded[3] ... encoded[n-2] `**\nOnly the odd indexes of `encoded` are taken.\n\n\n\n\n## Solutions big O\nTime complexity: O(n)\nSpace complexity: O(n)\n\n## Java\n```\n public int[] decode(int[] encoded) {\n int first = 0;\n int n = encoded.length+1;\n for(int i=1;i<=n;i++){\n first ^= i; \n }\n for(int i=1;i<n-1;i+=2) first ^= encoded[i];\n \n int[] perm = new int[n];\n perm[0] = first;\n for(int i=0;i<n-1;i++){\n perm[i+1] = perm[i] ^ encoded[i];\n }\n return perm;\n }\n```\n\n## Kotlin\n```\n fun decode(encoded: IntArray): IntArray {\n var first = 0\n val n = encoded.size + 1\n for(i in 1 .. n){\n first = first xor i\n }\n \n for(i in 1 until n step 2){\n first = first xor encoded[i]\n }\n \n val perm = IntArray(n)\n perm[0] = first\n for (i in 0 until n-1) {\n perm[i + 1] = perm[i] xor encoded[i]\n }\n\n return perm\n }\n```\n\n## Python\n```\n def decode(self, encoded: List[int]) -> List[int]:\n first = 0\n n = len(encoded) + 1\n for i in range(1,n+1):\n first = first ^ i\n\n for i in range(1,n,2):\n first = first ^ encoded[i]\n \n \n perm = [0] * n\n perm[0] = first\n for i in range(n-1):\n perm[i+1] = perm[i] ^ encoded[i]\n return perm\n```\nNot a python pro, the code could be much shorter. | 63 | There is an integer array `perm` that is a permutation of the first `n` positive integers, where `n` is always **odd**.
It was encoded into another integer array `encoded` of length `n - 1`, such that `encoded[i] = perm[i] XOR perm[i + 1]`. For example, if `perm = [1,3,2]`, then `encoded = [2,1]`.
Given the `encoded` array, return _the original array_ `perm`. It is guaranteed that the answer exists and is unique.
**Example 1:**
**Input:** encoded = \[3,1\]
**Output:** \[1,2,3\]
**Explanation:** If perm = \[1,2,3\], then encoded = \[1 XOR 2,2 XOR 3\] = \[3,1\]
**Example 2:**
**Input:** encoded = \[6,5,4,6\]
**Output:** \[2,4,1,5,3\]
**Constraints:**
* `3 <= n < 105`
* `n` is odd.
* `encoded.length == n - 1` | null |
Explanations XOR and 1st element [Java, Kotlin, Python] | decode-xored-permutation | 1 | 1 | I was stuck in this seemingly easy question in [contest 44](https://leetcode.com/contest/biweekly-contest-44). How could the answer be unique?\n\n**XOR properties and tips**\n\nLet\'s note `xor` as xor instead of ^\n**1) For `a xor b = c` , you can write \n`b = c xor a` \nor `a = c xor b`** . \nYou can use 2) and 3) to demonstrate 1) .\n2) XOR is commutative, `a xor b = b xor a`\n3) XOR to the same number is always zero `a xor a = 0`\n\n\n# **Intuition**\nIf the first element is determined, the whole array can be decoded.\n> `encoded[i] = perm[i] XOR perm[i + 1]` implies\n\n `perm[i+1] = perm[i] XOR encoded[i]` thanks to 1)\n So you can loop to find the next perm element\nSee [1720. Decode XORed Array](https://leetcode.com/problems/decode-xored-array/discuss/1009844)\n\nBut you still need `perm[0]` , the first element in output array.\n\n\n\n# **Find the first element**\nThat\'s where I was stuck in the contest 44. How could the answer be unique?\nIt took a while to understand after reading other solutions.\n\nI missed an important part in the problem descrition\n> integer array `perm` that is a permutation of the **first `n` positive integers**, where `n` is always odd.\n\nYes, perm is an array with values ranging from [1,2,3 .. n]. The order in the array is permuted.\n\nLet\'s XOR all elements in array `perm`. And perms is an array with **first `n` positive integers**\n`perm[0] XOR perm[1] XOR ... perm[n] = 1 XOR 2 XOR 3 .. XOR n` Order doesn\'t matter, XOR is commutative.\nLet\'s call `totalXor`\n`totalXor = 1 XOR 2 XOR 3 .. XOR n` .\n\nXOR all except the first `perm[0]`\n`perm[0] = totalXor XOR perm[1] XOR perm[2] XOR perm[3] XOR perm[4] XOR ... perm[n]`\n\nLet\'s subsitute (replace) by encoded\n> encoded[i] = perm[i] XOR perm[i + 1]\n\nencoded[1] = perm[1] XOR perm[2]\nencoded[3] = perm[3] XOR perm[4]\n...\nencoded[n-2] = perm[n-2] XOR perm[n-1], remember `n` is the size of perm and is always **odd**\n\n**`perm[0] = totalXor XOR encoded[1] XOR encoded[3] ... encoded[n-2] `**\nOnly the odd indexes of `encoded` are taken.\n\n\n\n\n## Solutions big O\nTime complexity: O(n)\nSpace complexity: O(n)\n\n## Java\n```\n public int[] decode(int[] encoded) {\n int first = 0;\n int n = encoded.length+1;\n for(int i=1;i<=n;i++){\n first ^= i; \n }\n for(int i=1;i<n-1;i+=2) first ^= encoded[i];\n \n int[] perm = new int[n];\n perm[0] = first;\n for(int i=0;i<n-1;i++){\n perm[i+1] = perm[i] ^ encoded[i];\n }\n return perm;\n }\n```\n\n## Kotlin\n```\n fun decode(encoded: IntArray): IntArray {\n var first = 0\n val n = encoded.size + 1\n for(i in 1 .. n){\n first = first xor i\n }\n \n for(i in 1 until n step 2){\n first = first xor encoded[i]\n }\n \n val perm = IntArray(n)\n perm[0] = first\n for (i in 0 until n-1) {\n perm[i + 1] = perm[i] xor encoded[i]\n }\n\n return perm\n }\n```\n\n## Python\n```\n def decode(self, encoded: List[int]) -> List[int]:\n first = 0\n n = len(encoded) + 1\n for i in range(1,n+1):\n first = first ^ i\n\n for i in range(1,n,2):\n first = first ^ encoded[i]\n \n \n perm = [0] * n\n perm[0] = first\n for i in range(n-1):\n perm[i+1] = perm[i] ^ encoded[i]\n return perm\n```\nNot a python pro, the code could be much shorter. | 63 | The **XOR sum** of a list is the bitwise `XOR` of all its elements. If the list only contains one element, then its **XOR sum** will be equal to this element.
* For example, the **XOR sum** of `[1,2,3,4]` is equal to `1 XOR 2 XOR 3 XOR 4 = 4`, and the **XOR sum** of `[3]` is equal to `3`.
You are given two **0-indexed** arrays `arr1` and `arr2` that consist only of non-negative integers.
Consider the list containing the result of `arr1[i] AND arr2[j]` (bitwise `AND`) for every `(i, j)` pair where `0 <= i < arr1.length` and `0 <= j < arr2.length`.
Return _the **XOR sum** of the aforementioned list_.
**Example 1:**
**Input:** arr1 = \[1,2,3\], arr2 = \[6,5\]
**Output:** 0
**Explanation:** The list = \[1 AND 6, 1 AND 5, 2 AND 6, 2 AND 5, 3 AND 6, 3 AND 5\] = \[0,1,2,0,2,1\].
The XOR sum = 0 XOR 1 XOR 2 XOR 0 XOR 2 XOR 1 = 0.
**Example 2:**
**Input:** arr1 = \[12\], arr2 = \[4\]
**Output:** 4
**Explanation:** The list = \[12 AND 4\] = \[4\]. The XOR sum = 4.
**Constraints:**
* `1 <= arr1.length, arr2.length <= 105`
* `0 <= arr1[i], arr2[j] <= 109` | Compute the XOR of the numbers between 1 and n, and think about how it can be used. Let it be x. Think why n is odd. perm[0] = x XOR encoded[1] XOR encoded[3] XOR encoded[5] ... perm[i] = perm[i-1] XOR encoded[i-1] |
Easy Code in Python | decode-xored-permutation | 0 | 1 | # Code\n```\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n \n # The main goal is to just find the first element in perm\n # After that we can just apply, \n # A XOR B = C ==> B = C XOR A\n\n # So for finding that,\n # We are told that perm has 1 to len(encoded)+1\n # Say, n = len(encoded) + 1\n # Say, encoded = [6,5,4,6] = [a^b,b^c,c^d,d^e]\n # Say, perm = [a,b,c,d,e]\n # Now to find a,\n # (XOR of all elements from 1 to n) ^ (b^c^d^e)\n # i.e, (a^b^c^d^e) ^ (b^c^d^e)\n # For (b^c^d^e), find XOR of alternative elements in encoded\n # encoded = [a^b,b^c,c^d,d^e]\n # XOR(encoded[1]^encoded[3]...)\n\n first = 0\n perm = []\n\n for i in range(1,len(encoded)+2):\n first ^= i\n\n for i in range(1,len(encoded),2):\n first ^= encoded[i]\n \n perm.append(first)\n\n for i in range(len(encoded)):\n perm.append(perm[i] ^ encoded[i])\n\n return perm\n``` | 0 | There is an integer array `perm` that is a permutation of the first `n` positive integers, where `n` is always **odd**.
It was encoded into another integer array `encoded` of length `n - 1`, such that `encoded[i] = perm[i] XOR perm[i + 1]`. For example, if `perm = [1,3,2]`, then `encoded = [2,1]`.
Given the `encoded` array, return _the original array_ `perm`. It is guaranteed that the answer exists and is unique.
**Example 1:**
**Input:** encoded = \[3,1\]
**Output:** \[1,2,3\]
**Explanation:** If perm = \[1,2,3\], then encoded = \[1 XOR 2,2 XOR 3\] = \[3,1\]
**Example 2:**
**Input:** encoded = \[6,5,4,6\]
**Output:** \[2,4,1,5,3\]
**Constraints:**
* `3 <= n < 105`
* `n` is odd.
* `encoded.length == n - 1` | null |
Easy Code in Python | decode-xored-permutation | 0 | 1 | # Code\n```\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n \n # The main goal is to just find the first element in perm\n # After that we can just apply, \n # A XOR B = C ==> B = C XOR A\n\n # So for finding that,\n # We are told that perm has 1 to len(encoded)+1\n # Say, n = len(encoded) + 1\n # Say, encoded = [6,5,4,6] = [a^b,b^c,c^d,d^e]\n # Say, perm = [a,b,c,d,e]\n # Now to find a,\n # (XOR of all elements from 1 to n) ^ (b^c^d^e)\n # i.e, (a^b^c^d^e) ^ (b^c^d^e)\n # For (b^c^d^e), find XOR of alternative elements in encoded\n # encoded = [a^b,b^c,c^d,d^e]\n # XOR(encoded[1]^encoded[3]...)\n\n first = 0\n perm = []\n\n for i in range(1,len(encoded)+2):\n first ^= i\n\n for i in range(1,len(encoded),2):\n first ^= encoded[i]\n \n perm.append(first)\n\n for i in range(len(encoded)):\n perm.append(perm[i] ^ encoded[i])\n\n return perm\n``` | 0 | The **XOR sum** of a list is the bitwise `XOR` of all its elements. If the list only contains one element, then its **XOR sum** will be equal to this element.
* For example, the **XOR sum** of `[1,2,3,4]` is equal to `1 XOR 2 XOR 3 XOR 4 = 4`, and the **XOR sum** of `[3]` is equal to `3`.
You are given two **0-indexed** arrays `arr1` and `arr2` that consist only of non-negative integers.
Consider the list containing the result of `arr1[i] AND arr2[j]` (bitwise `AND`) for every `(i, j)` pair where `0 <= i < arr1.length` and `0 <= j < arr2.length`.
Return _the **XOR sum** of the aforementioned list_.
**Example 1:**
**Input:** arr1 = \[1,2,3\], arr2 = \[6,5\]
**Output:** 0
**Explanation:** The list = \[1 AND 6, 1 AND 5, 2 AND 6, 2 AND 5, 3 AND 6, 3 AND 5\] = \[0,1,2,0,2,1\].
The XOR sum = 0 XOR 1 XOR 2 XOR 0 XOR 2 XOR 1 = 0.
**Example 2:**
**Input:** arr1 = \[12\], arr2 = \[4\]
**Output:** 4
**Explanation:** The list = \[12 AND 4\] = \[4\]. The XOR sum = 4.
**Constraints:**
* `1 <= arr1.length, arr2.length <= 105`
* `0 <= arr1[i], arr2[j] <= 109` | Compute the XOR of the numbers between 1 and n, and think about how it can be used. Let it be x. Think why n is odd. perm[0] = x XOR encoded[1] XOR encoded[3] XOR encoded[5] ... perm[i] = perm[i-1] XOR encoded[i-1] |
Thorough Explanation of Both Usual and Optimized Solution That Gets First Number in O(1) | decode-xored-permutation | 0 | 1 | # Disclaimer!\n\nThis is Part of a series on solving LeetCode problems and understanding rounded solutions with ChatGPT to master DS&A as a self-taught programmer. Check other solutions in here for something more sophisticated and short. Here I do explain the solutions including the optimal one but rather go in depths on my experience confronting the question as an intermediate level self-taught programmer.\n\n# On Bit Manipulation\n\nEncountering this problem, I hadn\'t worked with the XOR operation in depth this way before. I think I\'ve seen a few bit manipulation problems (which is one of the tags), but this problem leaned more toward understanding the XOR operator\'s properties than just manipulating bits.\n\n## Initial Thoughts\n\nMy read-through of the problem wasn\'t great. It was late, and my energy levels might have affected comprehension.\n\nI remember the frustration from the first time 6 months ago when I came across this problem and realized how crucial it is to understand the solution past the attempt, even when you can\'t solve it yourself.\n\nThe first attempt, in retrospect, felt like a wasted effort as it didn\'t add much to my understanding of this second encounter, which felt equally challenging.\n\nThe encoding part was particularly intimidating due to some past unpleasant experiences with similar problems. I ended up thinking that, without prior knowledge of the XOR operation\'s properties, solving this seemed like a long shot, but playing around with bits did teach me a few notions.\n\n## The Solution\n\nThe breakthrough came when I grasped the XOR property, where `A XOR B XOR A` leaves you with `B`. Essentially, any value XORed twice within a chain of XOR operations cancels out, leaving the unaffected values.\n\nThe key to the problem\'s solution is recognizing how the first number in the original list `perm` was the only one not used twice in generating the encoded array.\n\nThen follows that having the first number and the encoded list, one can deduce the rest of the numbers in the original list `perm` by XORing the first number in there with the first in the encoded to get the second in the original, and so on.\n\n```python\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n ans = [0]\n for i in encoded[::-2]:\n ans[0] ^= i\n\n for e in range(len(encoded) + 2):\n ans[0] ^= e\n \n for j in range(1, len(encoded) + 1):\n ans.append(ans[j-1] ^ encoded[j-1])\n \n return ans\n```\n\nThe implemented solution reflected this understanding. I initiated an answer list with zero (`ans = [0]`), exploiting the property that `A XOR 0` equals `A`. I then XORed every other number from the encoded array into a single value, representing the first half of the XOR operations we are going to need to do, giving us as a result a XOR of all the numbers from the original list missing only the first number from the original `perm` array.\n\nI ran another loop, this time through numbers from 1 to `n`, XORing them into the previously obtained value.\n\nThis effectively canceled out all elements except the first one in the original list (because I don\'t have it in half the XORs but do in the other, and every other XORed value is XORed twice, so they cancel out).\n\nIn the final loop, I generated the rest of the numbers in the original list using the first element and the encoded array, following the logic elucidated earlier: taking `perm[0] XOR encoded[0]` to produce `perm[1]` and so on\u200A-\u200A`perm[i] = perm[i-1] xor encoded[i-1]`.\n\nOn Assumptions and ChatGPT\n--------------------------\n\nThis problem was a primer on XOR operations and their properties. Without prior knowledge, solving it would be near impossible.\n\nThe constraints and nomenclature were manageable, though the nuances around XOR required some attention.\n\nThe hints provided didn\'t do much for me initially since the crucial XOR property wasn\'t evident at first.\n\nInteraction with ChatGPT, although a bit misleading because basically listed all properties of XOR at once, eventually led me to the XOR property that broke the problem wide open.\n\nThe problem also brushed on the broader concept of array manipulation and value conversion, albeit in a language-specific manner. It\'s more of a brain teaser grasping the XOR property.\n\nOptimization\n------------\n\nExploring other solutions further on LeetCode, I stumbled upon the `reduce` and `accumulate` Python functions, which mirrored the problem\'s requirements.\n\n\n```Python\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n XOR_all = 1 if (len(encoded)+1) % 4 == 1 else 0\n XOR_tail = reduce(XOR, encoded[::-2])\n return accumulate(encoded, XOR, initial=XOR_tail ^ XOR_all)\n```\n\n### Python Specialized Functions\n\n`reduce` functionally XORs one value with the next sequentially, leaving a single value at the end that is like the cumulative XORed value of everything.\n\nAt the same time `accumulate` does something similar but with an initial value, against a second list, and returns a list where each element is the result of one XOR operation at each step\u200A-\u200AWhich results in the rest of the `perm` array.\n\n### Optimizing Half the Xor Operations\n\nInterestingly, from peaking at rankings for most optimized solutions a pattern emerges while XORing numbers from 1 to `n`, where `n` is always odd in this problem.\n\n```\n Number (n) | XOR from 1 to n\n------------|----------------\n 1 | 1\n 3 | 0\n 5 | 1\n 7 | 0\n 9 | 1\n ... | ...\n```\n\nThe XOR of all numbers 1 to `n` alternates between 1 and 0 for odd values of `n`, reflecting a fascinating optimization opportunity for a constant XOR of all items from 1 to `n`.\n\nThis problem was a blend of bit manipulation, understanding XOR operations, and recognizing patterns, like a brain teaser more like working on DS&A, as I said.\n\nThank you for reading! | 0 | There is an integer array `perm` that is a permutation of the first `n` positive integers, where `n` is always **odd**.
It was encoded into another integer array `encoded` of length `n - 1`, such that `encoded[i] = perm[i] XOR perm[i + 1]`. For example, if `perm = [1,3,2]`, then `encoded = [2,1]`.
Given the `encoded` array, return _the original array_ `perm`. It is guaranteed that the answer exists and is unique.
**Example 1:**
**Input:** encoded = \[3,1\]
**Output:** \[1,2,3\]
**Explanation:** If perm = \[1,2,3\], then encoded = \[1 XOR 2,2 XOR 3\] = \[3,1\]
**Example 2:**
**Input:** encoded = \[6,5,4,6\]
**Output:** \[2,4,1,5,3\]
**Constraints:**
* `3 <= n < 105`
* `n` is odd.
* `encoded.length == n - 1` | null |
Thorough Explanation of Both Usual and Optimized Solution That Gets First Number in O(1) | decode-xored-permutation | 0 | 1 | # Disclaimer!\n\nThis is Part of a series on solving LeetCode problems and understanding rounded solutions with ChatGPT to master DS&A as a self-taught programmer. Check other solutions in here for something more sophisticated and short. Here I do explain the solutions including the optimal one but rather go in depths on my experience confronting the question as an intermediate level self-taught programmer.\n\n# On Bit Manipulation\n\nEncountering this problem, I hadn\'t worked with the XOR operation in depth this way before. I think I\'ve seen a few bit manipulation problems (which is one of the tags), but this problem leaned more toward understanding the XOR operator\'s properties than just manipulating bits.\n\n## Initial Thoughts\n\nMy read-through of the problem wasn\'t great. It was late, and my energy levels might have affected comprehension.\n\nI remember the frustration from the first time 6 months ago when I came across this problem and realized how crucial it is to understand the solution past the attempt, even when you can\'t solve it yourself.\n\nThe first attempt, in retrospect, felt like a wasted effort as it didn\'t add much to my understanding of this second encounter, which felt equally challenging.\n\nThe encoding part was particularly intimidating due to some past unpleasant experiences with similar problems. I ended up thinking that, without prior knowledge of the XOR operation\'s properties, solving this seemed like a long shot, but playing around with bits did teach me a few notions.\n\n## The Solution\n\nThe breakthrough came when I grasped the XOR property, where `A XOR B XOR A` leaves you with `B`. Essentially, any value XORed twice within a chain of XOR operations cancels out, leaving the unaffected values.\n\nThe key to the problem\'s solution is recognizing how the first number in the original list `perm` was the only one not used twice in generating the encoded array.\n\nThen follows that having the first number and the encoded list, one can deduce the rest of the numbers in the original list `perm` by XORing the first number in there with the first in the encoded to get the second in the original, and so on.\n\n```python\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n ans = [0]\n for i in encoded[::-2]:\n ans[0] ^= i\n\n for e in range(len(encoded) + 2):\n ans[0] ^= e\n \n for j in range(1, len(encoded) + 1):\n ans.append(ans[j-1] ^ encoded[j-1])\n \n return ans\n```\n\nThe implemented solution reflected this understanding. I initiated an answer list with zero (`ans = [0]`), exploiting the property that `A XOR 0` equals `A`. I then XORed every other number from the encoded array into a single value, representing the first half of the XOR operations we are going to need to do, giving us as a result a XOR of all the numbers from the original list missing only the first number from the original `perm` array.\n\nI ran another loop, this time through numbers from 1 to `n`, XORing them into the previously obtained value.\n\nThis effectively canceled out all elements except the first one in the original list (because I don\'t have it in half the XORs but do in the other, and every other XORed value is XORed twice, so they cancel out).\n\nIn the final loop, I generated the rest of the numbers in the original list using the first element and the encoded array, following the logic elucidated earlier: taking `perm[0] XOR encoded[0]` to produce `perm[1]` and so on\u200A-\u200A`perm[i] = perm[i-1] xor encoded[i-1]`.\n\nOn Assumptions and ChatGPT\n--------------------------\n\nThis problem was a primer on XOR operations and their properties. Without prior knowledge, solving it would be near impossible.\n\nThe constraints and nomenclature were manageable, though the nuances around XOR required some attention.\n\nThe hints provided didn\'t do much for me initially since the crucial XOR property wasn\'t evident at first.\n\nInteraction with ChatGPT, although a bit misleading because basically listed all properties of XOR at once, eventually led me to the XOR property that broke the problem wide open.\n\nThe problem also brushed on the broader concept of array manipulation and value conversion, albeit in a language-specific manner. It\'s more of a brain teaser grasping the XOR property.\n\nOptimization\n------------\n\nExploring other solutions further on LeetCode, I stumbled upon the `reduce` and `accumulate` Python functions, which mirrored the problem\'s requirements.\n\n\n```Python\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n XOR_all = 1 if (len(encoded)+1) % 4 == 1 else 0\n XOR_tail = reduce(XOR, encoded[::-2])\n return accumulate(encoded, XOR, initial=XOR_tail ^ XOR_all)\n```\n\n### Python Specialized Functions\n\n`reduce` functionally XORs one value with the next sequentially, leaving a single value at the end that is like the cumulative XORed value of everything.\n\nAt the same time `accumulate` does something similar but with an initial value, against a second list, and returns a list where each element is the result of one XOR operation at each step\u200A-\u200AWhich results in the rest of the `perm` array.\n\n### Optimizing Half the Xor Operations\n\nInterestingly, from peaking at rankings for most optimized solutions a pattern emerges while XORing numbers from 1 to `n`, where `n` is always odd in this problem.\n\n```\n Number (n) | XOR from 1 to n\n------------|----------------\n 1 | 1\n 3 | 0\n 5 | 1\n 7 | 0\n 9 | 1\n ... | ...\n```\n\nThe XOR of all numbers 1 to `n` alternates between 1 and 0 for odd values of `n`, reflecting a fascinating optimization opportunity for a constant XOR of all items from 1 to `n`.\n\nThis problem was a blend of bit manipulation, understanding XOR operations, and recognizing patterns, like a brain teaser more like working on DS&A, as I said.\n\nThank you for reading! | 0 | The **XOR sum** of a list is the bitwise `XOR` of all its elements. If the list only contains one element, then its **XOR sum** will be equal to this element.
* For example, the **XOR sum** of `[1,2,3,4]` is equal to `1 XOR 2 XOR 3 XOR 4 = 4`, and the **XOR sum** of `[3]` is equal to `3`.
You are given two **0-indexed** arrays `arr1` and `arr2` that consist only of non-negative integers.
Consider the list containing the result of `arr1[i] AND arr2[j]` (bitwise `AND`) for every `(i, j)` pair where `0 <= i < arr1.length` and `0 <= j < arr2.length`.
Return _the **XOR sum** of the aforementioned list_.
**Example 1:**
**Input:** arr1 = \[1,2,3\], arr2 = \[6,5\]
**Output:** 0
**Explanation:** The list = \[1 AND 6, 1 AND 5, 2 AND 6, 2 AND 5, 3 AND 6, 3 AND 5\] = \[0,1,2,0,2,1\].
The XOR sum = 0 XOR 1 XOR 2 XOR 0 XOR 2 XOR 1 = 0.
**Example 2:**
**Input:** arr1 = \[12\], arr2 = \[4\]
**Output:** 4
**Explanation:** The list = \[12 AND 4\] = \[4\]. The XOR sum = 4.
**Constraints:**
* `1 <= arr1.length, arr2.length <= 105`
* `0 <= arr1[i], arr2[j] <= 109` | Compute the XOR of the numbers between 1 and n, and think about how it can be used. Let it be x. Think why n is odd. perm[0] = x XOR encoded[1] XOR encoded[3] XOR encoded[5] ... perm[i] = perm[i-1] XOR encoded[i-1] |
Python solution | decode-xored-permutation | 0 | 1 | # Intuition\nUsing xor, we can calculate the numbers we are missing.\n\n# Approach\nLet\'s say that `[a, b, c, d, e]` are a permutation of `[1..n+1]`.\nAlso, let\'s call `perm = [a, b, c, d, e].`\n\nThe encoded value is `[a^b, b^c, c^d, d^e]`\n\nWe need to calculate a number x, so that:\n`x = a ^ b ^ c ^ d ^ e`\n\nWith the previous information we know:\n`x = a ^ encoded[1] ^ encoded[3]`, therefore:\n`a = x ^ encoded[1] ^ encoded[3]`\n\nNow, we know `a^b (encoded[0])` and `a`. We also know that `a^a = 0` and `0 ^ b = b`, so: `a^(a^b) = b.`\n\nWe can use this formula to find every number.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n x, n = 0, len(encoded) \n # a, b, c, d, e are a permutation of [1..n+1]\n # let\'s call perm = [a, b, c, d, e]\n # encoded = [a^b, b^c, c^d, d^e]\n # x = a ^ b ^ c ^ d ^ e\n # x = a ^ encoded[1] ^ encoded[3]\n # a = x ^ encoded[1] ^ encoded[3]\n\n # x = 1 ^ 2 ^ 3 ^ ... ^ n + 1\n for i in range(1, n + 2):\n x ^= i\n # find the first number (a) using xor of odd positioned numbers:\n for i in range(1, n, 2):\n x ^= encoded[i]\n perm = [x] # x is now a.\n # We know a^b (encoded[0]) and a. \n # We also know that a^a = 0 and 0 ^ b = b, so: a^(a^b) = b.\n # We use this formula to find every number\n for i in range(len(encoded)):\n x ^= encoded[i]\n perm.append(x)\n return perm\n\n\n\n``` | 0 | There is an integer array `perm` that is a permutation of the first `n` positive integers, where `n` is always **odd**.
It was encoded into another integer array `encoded` of length `n - 1`, such that `encoded[i] = perm[i] XOR perm[i + 1]`. For example, if `perm = [1,3,2]`, then `encoded = [2,1]`.
Given the `encoded` array, return _the original array_ `perm`. It is guaranteed that the answer exists and is unique.
**Example 1:**
**Input:** encoded = \[3,1\]
**Output:** \[1,2,3\]
**Explanation:** If perm = \[1,2,3\], then encoded = \[1 XOR 2,2 XOR 3\] = \[3,1\]
**Example 2:**
**Input:** encoded = \[6,5,4,6\]
**Output:** \[2,4,1,5,3\]
**Constraints:**
* `3 <= n < 105`
* `n` is odd.
* `encoded.length == n - 1` | null |
Python solution | decode-xored-permutation | 0 | 1 | # Intuition\nUsing xor, we can calculate the numbers we are missing.\n\n# Approach\nLet\'s say that `[a, b, c, d, e]` are a permutation of `[1..n+1]`.\nAlso, let\'s call `perm = [a, b, c, d, e].`\n\nThe encoded value is `[a^b, b^c, c^d, d^e]`\n\nWe need to calculate a number x, so that:\n`x = a ^ b ^ c ^ d ^ e`\n\nWith the previous information we know:\n`x = a ^ encoded[1] ^ encoded[3]`, therefore:\n`a = x ^ encoded[1] ^ encoded[3]`\n\nNow, we know `a^b (encoded[0])` and `a`. We also know that `a^a = 0` and `0 ^ b = b`, so: `a^(a^b) = b.`\n\nWe can use this formula to find every number.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n x, n = 0, len(encoded) \n # a, b, c, d, e are a permutation of [1..n+1]\n # let\'s call perm = [a, b, c, d, e]\n # encoded = [a^b, b^c, c^d, d^e]\n # x = a ^ b ^ c ^ d ^ e\n # x = a ^ encoded[1] ^ encoded[3]\n # a = x ^ encoded[1] ^ encoded[3]\n\n # x = 1 ^ 2 ^ 3 ^ ... ^ n + 1\n for i in range(1, n + 2):\n x ^= i\n # find the first number (a) using xor of odd positioned numbers:\n for i in range(1, n, 2):\n x ^= encoded[i]\n perm = [x] # x is now a.\n # We know a^b (encoded[0]) and a. \n # We also know that a^a = 0 and 0 ^ b = b, so: a^(a^b) = b.\n # We use this formula to find every number\n for i in range(len(encoded)):\n x ^= encoded[i]\n perm.append(x)\n return perm\n\n\n\n``` | 0 | The **XOR sum** of a list is the bitwise `XOR` of all its elements. If the list only contains one element, then its **XOR sum** will be equal to this element.
* For example, the **XOR sum** of `[1,2,3,4]` is equal to `1 XOR 2 XOR 3 XOR 4 = 4`, and the **XOR sum** of `[3]` is equal to `3`.
You are given two **0-indexed** arrays `arr1` and `arr2` that consist only of non-negative integers.
Consider the list containing the result of `arr1[i] AND arr2[j]` (bitwise `AND`) for every `(i, j)` pair where `0 <= i < arr1.length` and `0 <= j < arr2.length`.
Return _the **XOR sum** of the aforementioned list_.
**Example 1:**
**Input:** arr1 = \[1,2,3\], arr2 = \[6,5\]
**Output:** 0
**Explanation:** The list = \[1 AND 6, 1 AND 5, 2 AND 6, 2 AND 5, 3 AND 6, 3 AND 5\] = \[0,1,2,0,2,1\].
The XOR sum = 0 XOR 1 XOR 2 XOR 0 XOR 2 XOR 1 = 0.
**Example 2:**
**Input:** arr1 = \[12\], arr2 = \[4\]
**Output:** 4
**Explanation:** The list = \[12 AND 4\] = \[4\]. The XOR sum = 4.
**Constraints:**
* `1 <= arr1.length, arr2.length <= 105`
* `0 <= arr1[i], arr2[j] <= 109` | Compute the XOR of the numbers between 1 and n, and think about how it can be used. Let it be x. Think why n is odd. perm[0] = x XOR encoded[1] XOR encoded[3] XOR encoded[5] ... perm[i] = perm[i-1] XOR encoded[i-1] |
[Python3] Mathematical approach | decode-xored-permutation | 0 | 1 | # Intuition\nWe know the numbers ``1``, ``2``,... ``n`` were use to form ``perm``. \nAlso we know that ``n`` is odd. \n\n``encoded[i]`` = ``perm[i]`` xor ``perm[i+1]``\n\nThus:\n\n``xor_even`` = ``encoded[0]`` xor ``encoded[2]`` xor ... xor ``encoded[n-3]`` = ``perm[0]`` xor ``perm[1]`` xor ... xor ``perm[n-2]``\n\nWe can get ``perm[n-1]`` = ``xor_even`` xor (``1`` xor ``2`` xor ... xor ``n``)\n\nHaving ``perm[n-1]`` and ``encoded`` we can restore original permutation.\n\n# Approach\n1. Get ``n`` as length of ``encoded`` plus 1\n2. Initialize ``result`` of length ``n``\n3. Calculate ``xor_all`` as ``1`` xor ``2`` xor ... xor ``n``\n4. Calculate ``xor_even`` as ``perm[0]`` xor ``perm[1]`` xor ... xor ``perm[n-2]``\n5. Calculate ``perm[n-1]`` as ``xor_even`` xor ``xor_all``\n6. Restore the permutation backwards and return the result\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$ - apart from storage for the output\n\n# Code\n```\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n n = len(encoded) + 1\n result = [0] * n\n xor_all = reduce(lambda r, s: r ^ s, range(1, n+1))\n xor_even = reduce(lambda r, s: r ^ s, encoded[::2])\n result[-1] = xor_even ^ xor_all\n for i in range(n-2, -1, -1):\n result[i] = result[i+1] ^ encoded[i]\n return result\n```\n\nIf you have any questions please ask, and UPVOTE if you like the approach! | 0 | There is an integer array `perm` that is a permutation of the first `n` positive integers, where `n` is always **odd**.
It was encoded into another integer array `encoded` of length `n - 1`, such that `encoded[i] = perm[i] XOR perm[i + 1]`. For example, if `perm = [1,3,2]`, then `encoded = [2,1]`.
Given the `encoded` array, return _the original array_ `perm`. It is guaranteed that the answer exists and is unique.
**Example 1:**
**Input:** encoded = \[3,1\]
**Output:** \[1,2,3\]
**Explanation:** If perm = \[1,2,3\], then encoded = \[1 XOR 2,2 XOR 3\] = \[3,1\]
**Example 2:**
**Input:** encoded = \[6,5,4,6\]
**Output:** \[2,4,1,5,3\]
**Constraints:**
* `3 <= n < 105`
* `n` is odd.
* `encoded.length == n - 1` | null |
[Python3] Mathematical approach | decode-xored-permutation | 0 | 1 | # Intuition\nWe know the numbers ``1``, ``2``,... ``n`` were use to form ``perm``. \nAlso we know that ``n`` is odd. \n\n``encoded[i]`` = ``perm[i]`` xor ``perm[i+1]``\n\nThus:\n\n``xor_even`` = ``encoded[0]`` xor ``encoded[2]`` xor ... xor ``encoded[n-3]`` = ``perm[0]`` xor ``perm[1]`` xor ... xor ``perm[n-2]``\n\nWe can get ``perm[n-1]`` = ``xor_even`` xor (``1`` xor ``2`` xor ... xor ``n``)\n\nHaving ``perm[n-1]`` and ``encoded`` we can restore original permutation.\n\n# Approach\n1. Get ``n`` as length of ``encoded`` plus 1\n2. Initialize ``result`` of length ``n``\n3. Calculate ``xor_all`` as ``1`` xor ``2`` xor ... xor ``n``\n4. Calculate ``xor_even`` as ``perm[0]`` xor ``perm[1]`` xor ... xor ``perm[n-2]``\n5. Calculate ``perm[n-1]`` as ``xor_even`` xor ``xor_all``\n6. Restore the permutation backwards and return the result\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$ - apart from storage for the output\n\n# Code\n```\nclass Solution:\n def decode(self, encoded: List[int]) -> List[int]:\n n = len(encoded) + 1\n result = [0] * n\n xor_all = reduce(lambda r, s: r ^ s, range(1, n+1))\n xor_even = reduce(lambda r, s: r ^ s, encoded[::2])\n result[-1] = xor_even ^ xor_all\n for i in range(n-2, -1, -1):\n result[i] = result[i+1] ^ encoded[i]\n return result\n```\n\nIf you have any questions please ask, and UPVOTE if you like the approach! | 0 | The **XOR sum** of a list is the bitwise `XOR` of all its elements. If the list only contains one element, then its **XOR sum** will be equal to this element.
* For example, the **XOR sum** of `[1,2,3,4]` is equal to `1 XOR 2 XOR 3 XOR 4 = 4`, and the **XOR sum** of `[3]` is equal to `3`.
You are given two **0-indexed** arrays `arr1` and `arr2` that consist only of non-negative integers.
Consider the list containing the result of `arr1[i] AND arr2[j]` (bitwise `AND`) for every `(i, j)` pair where `0 <= i < arr1.length` and `0 <= j < arr2.length`.
Return _the **XOR sum** of the aforementioned list_.
**Example 1:**
**Input:** arr1 = \[1,2,3\], arr2 = \[6,5\]
**Output:** 0
**Explanation:** The list = \[1 AND 6, 1 AND 5, 2 AND 6, 2 AND 5, 3 AND 6, 3 AND 5\] = \[0,1,2,0,2,1\].
The XOR sum = 0 XOR 1 XOR 2 XOR 0 XOR 2 XOR 1 = 0.
**Example 2:**
**Input:** arr1 = \[12\], arr2 = \[4\]
**Output:** 4
**Explanation:** The list = \[12 AND 4\] = \[4\]. The XOR sum = 4.
**Constraints:**
* `1 <= arr1.length, arr2.length <= 105`
* `0 <= arr1[i], arr2[j] <= 109` | Compute the XOR of the numbers between 1 and n, and think about how it can be used. Let it be x. Think why n is odd. perm[0] = x XOR encoded[1] XOR encoded[3] XOR encoded[5] ... perm[i] = perm[i-1] XOR encoded[i-1] |
Solution | decode-xored-permutation | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> decode(vector<int>& encoded) {\n int n = encoded.size()+1;\n \n vector<int> ans(n) ;\n int first = 0;\n\n for(int i = 1 ; i<= n ; i++)\n first ^= i;\n\n for(int i = 0 ; i<n-1 ; i+=2)\n first ^= encoded[i+1]; \n\n ans[0] = first;\n\n for(int i = 1 ; i<n ; i++)\n ans[i] = ans[i-1]^encoded[i-1];\n\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def decode(self, A: List[int]) -> List[int]:\n first = reduce(ixor, A[::-2] + list(range(len(A) + 2)))\n return list(accumulate([first] + A, ixor))\n```\n\n```Java []\nclass Solution {\n public int[] decode(int[] encoded) {\n \n int n = encoded.length + 1;\n int[] result = new int[n];\n int xor_of_all = 0;\n\n if(n%4 == 0){\n xor_of_all = n; \n }\n\n else if(n%4 == 1) {\n xor_of_all = 1; \n }\n\n else if(n%4 == 2) {\n xor_of_all = n+1; \n }\n\n else {\n xor_of_all = 0; \n }\n\n for(int i=0; i<encoded.length; i=i+2) {\n xor_of_all ^= encoded[i];\n }\n\n result[n-1] = xor_of_all;\n for(int i=n-2; i>=0; i--) {\n result[i] = result[i+1] ^ encoded[i];\n }\n\n return result;\n }\n}\n\n```\n | 0 | There is an integer array `perm` that is a permutation of the first `n` positive integers, where `n` is always **odd**.
It was encoded into another integer array `encoded` of length `n - 1`, such that `encoded[i] = perm[i] XOR perm[i + 1]`. For example, if `perm = [1,3,2]`, then `encoded = [2,1]`.
Given the `encoded` array, return _the original array_ `perm`. It is guaranteed that the answer exists and is unique.
**Example 1:**
**Input:** encoded = \[3,1\]
**Output:** \[1,2,3\]
**Explanation:** If perm = \[1,2,3\], then encoded = \[1 XOR 2,2 XOR 3\] = \[3,1\]
**Example 2:**
**Input:** encoded = \[6,5,4,6\]
**Output:** \[2,4,1,5,3\]
**Constraints:**
* `3 <= n < 105`
* `n` is odd.
* `encoded.length == n - 1` | null |
Solution | decode-xored-permutation | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> decode(vector<int>& encoded) {\n int n = encoded.size()+1;\n \n vector<int> ans(n) ;\n int first = 0;\n\n for(int i = 1 ; i<= n ; i++)\n first ^= i;\n\n for(int i = 0 ; i<n-1 ; i+=2)\n first ^= encoded[i+1]; \n\n ans[0] = first;\n\n for(int i = 1 ; i<n ; i++)\n ans[i] = ans[i-1]^encoded[i-1];\n\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def decode(self, A: List[int]) -> List[int]:\n first = reduce(ixor, A[::-2] + list(range(len(A) + 2)))\n return list(accumulate([first] + A, ixor))\n```\n\n```Java []\nclass Solution {\n public int[] decode(int[] encoded) {\n \n int n = encoded.length + 1;\n int[] result = new int[n];\n int xor_of_all = 0;\n\n if(n%4 == 0){\n xor_of_all = n; \n }\n\n else if(n%4 == 1) {\n xor_of_all = 1; \n }\n\n else if(n%4 == 2) {\n xor_of_all = n+1; \n }\n\n else {\n xor_of_all = 0; \n }\n\n for(int i=0; i<encoded.length; i=i+2) {\n xor_of_all ^= encoded[i];\n }\n\n result[n-1] = xor_of_all;\n for(int i=n-2; i>=0; i--) {\n result[i] = result[i+1] ^ encoded[i];\n }\n\n return result;\n }\n}\n\n```\n | 0 | The **XOR sum** of a list is the bitwise `XOR` of all its elements. If the list only contains one element, then its **XOR sum** will be equal to this element.
* For example, the **XOR sum** of `[1,2,3,4]` is equal to `1 XOR 2 XOR 3 XOR 4 = 4`, and the **XOR sum** of `[3]` is equal to `3`.
You are given two **0-indexed** arrays `arr1` and `arr2` that consist only of non-negative integers.
Consider the list containing the result of `arr1[i] AND arr2[j]` (bitwise `AND`) for every `(i, j)` pair where `0 <= i < arr1.length` and `0 <= j < arr2.length`.
Return _the **XOR sum** of the aforementioned list_.
**Example 1:**
**Input:** arr1 = \[1,2,3\], arr2 = \[6,5\]
**Output:** 0
**Explanation:** The list = \[1 AND 6, 1 AND 5, 2 AND 6, 2 AND 5, 3 AND 6, 3 AND 5\] = \[0,1,2,0,2,1\].
The XOR sum = 0 XOR 1 XOR 2 XOR 0 XOR 2 XOR 1 = 0.
**Example 2:**
**Input:** arr1 = \[12\], arr2 = \[4\]
**Output:** 4
**Explanation:** The list = \[12 AND 4\] = \[4\]. The XOR sum = 4.
**Constraints:**
* `1 <= arr1.length, arr2.length <= 105`
* `0 <= arr1[i], arr2[j] <= 109` | Compute the XOR of the numbers between 1 and n, and think about how it can be used. Let it be x. Think why n is odd. perm[0] = x XOR encoded[1] XOR encoded[3] XOR encoded[5] ... perm[i] = perm[i-1] XOR encoded[i-1] |
Prime Factors With Memo | Commented and Explained | Better Version Might Store Factor Results | count-ways-to-make-array-with-product | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe primarily are dealing with prime factors in this case alongside numerical combinations. As such, the math.comb functionality and a list of prime factors in range is most usable. Since we\'re limited to 10^4, we need only factors up to 97 (find the next prime factor to convince yourself of this) \n\nWith that in hand, we should do some prime factorization work. We could also store some prime factorization findings if we so felt like it, and that might help speed things along as well, but I leave that for my students to work on. \n\nTime and Space Complexity left to analyze for student purposes. I can explain in dm if asked. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up your answer array \n- Enumerate queries, catching n_i, k_i with index of occurrence \n - if state of (n_i, k_i) in memo, place at index memoized value \n - otherwise\n - set up k_i_o and n_i_o as original k_i and n_i \n - set a result of 1 \n - decrement n_i by 1 \n - for each p in primes from least to greatest \n - if k_i is a factor of p \n - count c set to 1 \n - k_i is evenly factored by p \n - while k_i is still a factor of p \n - c += 1 \n - k is evenly factored by p \n - result is (result * math.comb(n_i + c, c))%self.mod\n - if doing this as an assignment, you must write out the general form of math.comb procession \n - if k_i is gt 1 \n - result is result * n_i_o % mod \n - answer at index is result \n - memo at n_i_o, k_i_o = result \nreturn answer when done \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # set up mod, primes, and a memo for expensive calculation repeat prevention \n def __init__(self) : \n self.mod = 10**9 + 7 \n self.primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,\n 61, 67, 71, 73, 79, 83, 89, 97]\n self.memo = {}\n\n # solution progression \n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n # set up answer \n answer = [0] * len(queries)\n # enumerate queries \n for index, (n_i, k_i) in enumerate(queries) : \n # if state is stored, mark it again \n if (n_i, k_i) in self.memo : \n answer[index] = self.memo[(n_i, k_i)]\n else : \n # otherwise, preserve initial for proper marking \n k_i_o = k_i \n n_i_o = n_i\n # set up result and decrement n_i \n result = 1 \n n_i -= 1 \n # loop over primes \n for p in self.primes : \n # if k_i is a prime factor \n if k_i % p == 0 : \n # get count of prime factors \n c = 1 \n k_i //= p \n while k_i % p == 0 : \n c += 1 \n k_i //= p \n # and increment result accordingly by combinatorial logic \n result = (result * math.comb(n_i + c, c))% self.mod \n # when done if k_i is gt 1 update result \n if k_i > 1 : \n result = (result * (n_i_o)) % self.mod \n else : \n result *= 1\n # then store result \n answer[index] = result \n self.memo[(n_i_o, k_i_o)] = result \n # return when done \n return answer \n\n``` | 0 | You are given a 2D integer array, `queries`. For each `queries[i]`, where `queries[i] = [ni, ki]`, find the number of different ways you can place positive integers into an array of size `ni` such that the product of the integers is `ki`. As the number of ways may be too large, the answer to the `ith` query is the number of ways **modulo** `109 + 7`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length`_, and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** queries = \[\[2,6\],\[5,1\],\[73,660\]\]
**Output:** \[4,1,50734910\]
**Explanation:** Each query is independent.
\[2,6\]: There are 4 ways to fill an array of size 2 that multiply to 6: \[1,6\], \[2,3\], \[3,2\], \[6,1\].
\[5,1\]: There is 1 way to fill an array of size 5 that multiply to 1: \[1,1,1,1,1\].
\[73,660\]: There are 1050734917 ways to fill an array of size 73 that multiply to 660. 1050734917 modulo 109 + 7 = 50734910.
**Example 2:**
**Input:** queries = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\]
**Output:** \[1,2,3,10,5\]
**Constraints:**
* `1 <= queries.length <= 104`
* `1 <= ni, ki <= 104` | null |
Prime Factors With Memo | Commented and Explained | Better Version Might Store Factor Results | count-ways-to-make-array-with-product | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe primarily are dealing with prime factors in this case alongside numerical combinations. As such, the math.comb functionality and a list of prime factors in range is most usable. Since we\'re limited to 10^4, we need only factors up to 97 (find the next prime factor to convince yourself of this) \n\nWith that in hand, we should do some prime factorization work. We could also store some prime factorization findings if we so felt like it, and that might help speed things along as well, but I leave that for my students to work on. \n\nTime and Space Complexity left to analyze for student purposes. I can explain in dm if asked. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up your answer array \n- Enumerate queries, catching n_i, k_i with index of occurrence \n - if state of (n_i, k_i) in memo, place at index memoized value \n - otherwise\n - set up k_i_o and n_i_o as original k_i and n_i \n - set a result of 1 \n - decrement n_i by 1 \n - for each p in primes from least to greatest \n - if k_i is a factor of p \n - count c set to 1 \n - k_i is evenly factored by p \n - while k_i is still a factor of p \n - c += 1 \n - k is evenly factored by p \n - result is (result * math.comb(n_i + c, c))%self.mod\n - if doing this as an assignment, you must write out the general form of math.comb procession \n - if k_i is gt 1 \n - result is result * n_i_o % mod \n - answer at index is result \n - memo at n_i_o, k_i_o = result \nreturn answer when done \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # set up mod, primes, and a memo for expensive calculation repeat prevention \n def __init__(self) : \n self.mod = 10**9 + 7 \n self.primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,\n 61, 67, 71, 73, 79, 83, 89, 97]\n self.memo = {}\n\n # solution progression \n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n # set up answer \n answer = [0] * len(queries)\n # enumerate queries \n for index, (n_i, k_i) in enumerate(queries) : \n # if state is stored, mark it again \n if (n_i, k_i) in self.memo : \n answer[index] = self.memo[(n_i, k_i)]\n else : \n # otherwise, preserve initial for proper marking \n k_i_o = k_i \n n_i_o = n_i\n # set up result and decrement n_i \n result = 1 \n n_i -= 1 \n # loop over primes \n for p in self.primes : \n # if k_i is a prime factor \n if k_i % p == 0 : \n # get count of prime factors \n c = 1 \n k_i //= p \n while k_i % p == 0 : \n c += 1 \n k_i //= p \n # and increment result accordingly by combinatorial logic \n result = (result * math.comb(n_i + c, c))% self.mod \n # when done if k_i is gt 1 update result \n if k_i > 1 : \n result = (result * (n_i_o)) % self.mod \n else : \n result *= 1\n # then store result \n answer[index] = result \n self.memo[(n_i_o, k_i_o)] = result \n # return when done \n return answer \n\n``` | 0 | Given the `head` of a linked list, find all the values that appear **more than once** in the list and delete the nodes that have any of those values.
Return _the linked list after the deletions._
**Example 1:**
**Input:** head = \[1,2,3,2\]
**Output:** \[1,3\]
**Explanation:** 2 appears twice in the linked list, so all 2's should be deleted. After deleting all 2's, we are left with \[1,3\].
**Example 2:**
**Input:** head = \[2,1,1,2\]
**Output:** \[\]
**Explanation:** 2 and 1 both appear twice. All the elements should be deleted.
**Example 3:**
**Input:** head = \[3,2,2,1,3,2,4\]
**Output:** \[1,4\]
**Explanation:** 3 appears twice and 2 appears three times. After deleting all 3's and 2's, we are left with \[1,4\].
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`
* `1 <= Node.val <= 105` | Prime-factorize ki and count how many ways you can distribute the primes among the ni positions. After prime factorizing ki, suppose there are x amount of prime factor. There are (x + n - 1) choose (n - 1) ways to distribute the x prime factors into k positions, allowing repetitions. |
Using comb in python for combinations with explanation | count-ways-to-make-array-with-product | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nusing permutations and combinations using prime factorization for example 90 = [[2,1],[3,2],[5,1]] which means that 90 = 2^1 * 3^2 * 5^1. Now for each of these 2,3,3,5 we need to assign one value 0,1,...n-1 (n is length of array and initially all values in array are 1). Now here giving 0 to first 3 and 1 to second 3 is same as giving 1 to first 3 and 0 to second 3. Therefore we need to solve differently for each number i,e let n==3\nfor prime factor 2 we have 3 combinations 0,1 or 2\nbut for 3 we only have 6 {(0,0),(0,1),(0,2),(1,1),(1,2),(2,2)}. Therefor for 3 we wil be using formula c(n+r-1,r) where r is 2 as we have 3**2 in 90\ntherefore ans is c(n+r2-1,r2) * c(n+r3-1,r3) * c(n+r5-1,r5) where ri is how many time primefactor i occurs in given main number.\nTherefore ans is c(3+1-1,1) * c(3+2-1,2) * c(3+1-1,1) = 3 * 6 * 3 = 54 total combinations are possilbe\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nimport math\nmod = 10**9+7\ndef primeFactors(n):\n ans = []\n while n % 2 == 0:\n if not ans:ans.append([2,1])\n else:ans[-1][1]+=1\n n = n // 2\n \n # n must be odd at this point\n # so a skip of 2 ( i = i + 2) can be used\n for i in range(3,int(math.sqrt(n))+1,2):\n \n # while i divides n , print i and divide n\n while n % i== 0:\n if not ans or ans[-1][0]!=i:\n ans.append([i,1])\n else:ans[-1][1]+=1\n n = n / i\n \n # Condition if n is a prime\n # number greater than 2\n if n > 2:\n ans.append([n,1])\n return ans\n\ndef given(n,k):\n prime = primeFactors(k)\n ans = 1\n for i,j in prime:\n c = math.comb(n+j-1,j)%mod\n ans *= c\n ans %= mod\n return ans\n\n\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n return [given(n,k) for n,k in queries]\n``` | 0 | You are given a 2D integer array, `queries`. For each `queries[i]`, where `queries[i] = [ni, ki]`, find the number of different ways you can place positive integers into an array of size `ni` such that the product of the integers is `ki`. As the number of ways may be too large, the answer to the `ith` query is the number of ways **modulo** `109 + 7`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length`_, and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** queries = \[\[2,6\],\[5,1\],\[73,660\]\]
**Output:** \[4,1,50734910\]
**Explanation:** Each query is independent.
\[2,6\]: There are 4 ways to fill an array of size 2 that multiply to 6: \[1,6\], \[2,3\], \[3,2\], \[6,1\].
\[5,1\]: There is 1 way to fill an array of size 5 that multiply to 1: \[1,1,1,1,1\].
\[73,660\]: There are 1050734917 ways to fill an array of size 73 that multiply to 660. 1050734917 modulo 109 + 7 = 50734910.
**Example 2:**
**Input:** queries = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\]
**Output:** \[1,2,3,10,5\]
**Constraints:**
* `1 <= queries.length <= 104`
* `1 <= ni, ki <= 104` | null |
Using comb in python for combinations with explanation | count-ways-to-make-array-with-product | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nusing permutations and combinations using prime factorization for example 90 = [[2,1],[3,2],[5,1]] which means that 90 = 2^1 * 3^2 * 5^1. Now for each of these 2,3,3,5 we need to assign one value 0,1,...n-1 (n is length of array and initially all values in array are 1). Now here giving 0 to first 3 and 1 to second 3 is same as giving 1 to first 3 and 0 to second 3. Therefore we need to solve differently for each number i,e let n==3\nfor prime factor 2 we have 3 combinations 0,1 or 2\nbut for 3 we only have 6 {(0,0),(0,1),(0,2),(1,1),(1,2),(2,2)}. Therefor for 3 we wil be using formula c(n+r-1,r) where r is 2 as we have 3**2 in 90\ntherefore ans is c(n+r2-1,r2) * c(n+r3-1,r3) * c(n+r5-1,r5) where ri is how many time primefactor i occurs in given main number.\nTherefore ans is c(3+1-1,1) * c(3+2-1,2) * c(3+1-1,1) = 3 * 6 * 3 = 54 total combinations are possilbe\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nimport math\nmod = 10**9+7\ndef primeFactors(n):\n ans = []\n while n % 2 == 0:\n if not ans:ans.append([2,1])\n else:ans[-1][1]+=1\n n = n // 2\n \n # n must be odd at this point\n # so a skip of 2 ( i = i + 2) can be used\n for i in range(3,int(math.sqrt(n))+1,2):\n \n # while i divides n , print i and divide n\n while n % i== 0:\n if not ans or ans[-1][0]!=i:\n ans.append([i,1])\n else:ans[-1][1]+=1\n n = n / i\n \n # Condition if n is a prime\n # number greater than 2\n if n > 2:\n ans.append([n,1])\n return ans\n\ndef given(n,k):\n prime = primeFactors(k)\n ans = 1\n for i,j in prime:\n c = math.comb(n+j-1,j)%mod\n ans *= c\n ans %= mod\n return ans\n\n\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n return [given(n,k) for n,k in queries]\n``` | 0 | Given the `head` of a linked list, find all the values that appear **more than once** in the list and delete the nodes that have any of those values.
Return _the linked list after the deletions._
**Example 1:**
**Input:** head = \[1,2,3,2\]
**Output:** \[1,3\]
**Explanation:** 2 appears twice in the linked list, so all 2's should be deleted. After deleting all 2's, we are left with \[1,3\].
**Example 2:**
**Input:** head = \[2,1,1,2\]
**Output:** \[\]
**Explanation:** 2 and 1 both appear twice. All the elements should be deleted.
**Example 3:**
**Input:** head = \[3,2,2,1,3,2,4\]
**Output:** \[1,4\]
**Explanation:** 3 appears twice and 2 appears three times. After deleting all 3's and 2's, we are left with \[1,4\].
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`
* `1 <= Node.val <= 105` | Prime-factorize ki and count how many ways you can distribute the primes among the ni positions. After prime factorizing ki, suppose there are x amount of prime factor. There are (x + n - 1) choose (n - 1) ways to distribute the x prime factors into k positions, allowing repetitions. |
Solution | count-ways-to-make-array-with-product | 1 | 1 | ```C++ []\n\n int comb[10013][14] = { 1 }, mod = 1000000007;\nint primes[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, \n 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};\nclass Solution {\npublic:\nvector<int> waysToFillArray(vector<vector<int>>& qs) {\n if (comb[1][1] == 0)\n for (int n = 1; n < 10013; ++n)\n for (int r = 0; r < 14; ++r)\n comb[n][r] = r == 0 ? 1 : (comb[n - 1][r - 1] + comb[n - 1][r]) % mod;\n vector<int> res(qs.size(), 1);\n for (auto i = 0; i < qs.size(); ++i) {\n int n = qs[i][0], k = qs[i][1];\n for (auto p : primes) {\n int r = 0;\n while (k % p == 0) {\n ++r;\n k /= p;\n }\n res[i] = (long)res[i] * comb[n - 1 + r][r] % mod;\n }\n if (k != 1)\n res[i] = (long)res[i] * n % mod;\n }\n return res;\n}\n};\n```\n\n```Python3 []\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n ans = [0] * len(queries)\n MOD = 10 ** 9 + 7\n primes = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]\n \n for i, (n, k) in enumerate(queries):\n ret = 1\n n -= 1\n\n for p in primes:\n if k % p == 0:\n c = 1\n k //= p\n while k % p == 0:\n c += 1\n k //= p\n \n ret = (ret * comb(n + c, c)) % MOD\n \n if k > 1:\n ans[i] = (ret * (n + 1)) % MOD\n else:\n ans[i] = ret\n \n return ans\n```\n\n```Java []\nclass Solution {\n static final long MOD = 1000000007;\n static final int MAX = 10000;\n static final int[] divs = new int[MAX + 1];\n static final int[] counts = new int[MAX + 1];\n\n public int[] waysToFillArray(int[][] queries) {\n int[] res = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n res[i] = waysToFillArray(queries[i][0], queries[i][1]);\n }\n return res;\n }\n\n static int waysToFillArray(int n, int k) {\n long[] c = getCounts(n);\n long r = 1;\n int primeIdx = 0;\n while (k > 1) {\n if (divs[k] == 0) primeIdx = find(primeIdx, k);\n r = (r * c[counts[k]]) % MOD;\n k /= divs[k];\n }\n return (int) r;\n }\n\n static int find(final int primeIdx, final int k) {\n for (int i = primeIdx; i < primes.length; i++) {\n final int p = primes[i];\n if (k % p == 0) {\n int d = p * p;\n int c = 1;\n while (k % d == 0) {\n c++;\n d *= p;\n }\n counts[k] = c;\n divs[k] = d / p;\n return primeIdx + 1;\n }\n }\n divs[k] = k;\n counts[k] = 1;\n return primes.length;\n }\n\n static long[][] cache = new long[MAX + 1][];\n\n private static long[] getCounts(int n) {\n if (cache[n] != null) return cache[n];\n final long[] c = new long[14];\n c[0] = 1;\n c[1] = n;\n c[2] = n * (n + 1) / 2;\n for (int i = 3; i < c.length; i++) {\n c[i] = (((c[i - 1] * (i + n - 1)) % MOD) * inverses[i - 1]) % MOD;\n }\n return cache[n] = c;\n }\n\n static long[] inverses = new long[] {1, 500000004, 333333336, 250000002, 400000003, 166666668, 142857144, 125000001, 111111112, 700000005, 818181824, 83333334, 153846155, 71428572};\n static int[] primes = new int[] { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,\n 79, 83, 89, 97};\n\n}\n```\n | 0 | You are given a 2D integer array, `queries`. For each `queries[i]`, where `queries[i] = [ni, ki]`, find the number of different ways you can place positive integers into an array of size `ni` such that the product of the integers is `ki`. As the number of ways may be too large, the answer to the `ith` query is the number of ways **modulo** `109 + 7`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length`_, and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** queries = \[\[2,6\],\[5,1\],\[73,660\]\]
**Output:** \[4,1,50734910\]
**Explanation:** Each query is independent.
\[2,6\]: There are 4 ways to fill an array of size 2 that multiply to 6: \[1,6\], \[2,3\], \[3,2\], \[6,1\].
\[5,1\]: There is 1 way to fill an array of size 5 that multiply to 1: \[1,1,1,1,1\].
\[73,660\]: There are 1050734917 ways to fill an array of size 73 that multiply to 660. 1050734917 modulo 109 + 7 = 50734910.
**Example 2:**
**Input:** queries = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\]
**Output:** \[1,2,3,10,5\]
**Constraints:**
* `1 <= queries.length <= 104`
* `1 <= ni, ki <= 104` | null |
Solution | count-ways-to-make-array-with-product | 1 | 1 | ```C++ []\n\n int comb[10013][14] = { 1 }, mod = 1000000007;\nint primes[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, \n 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};\nclass Solution {\npublic:\nvector<int> waysToFillArray(vector<vector<int>>& qs) {\n if (comb[1][1] == 0)\n for (int n = 1; n < 10013; ++n)\n for (int r = 0; r < 14; ++r)\n comb[n][r] = r == 0 ? 1 : (comb[n - 1][r - 1] + comb[n - 1][r]) % mod;\n vector<int> res(qs.size(), 1);\n for (auto i = 0; i < qs.size(); ++i) {\n int n = qs[i][0], k = qs[i][1];\n for (auto p : primes) {\n int r = 0;\n while (k % p == 0) {\n ++r;\n k /= p;\n }\n res[i] = (long)res[i] * comb[n - 1 + r][r] % mod;\n }\n if (k != 1)\n res[i] = (long)res[i] * n % mod;\n }\n return res;\n}\n};\n```\n\n```Python3 []\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n ans = [0] * len(queries)\n MOD = 10 ** 9 + 7\n primes = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]\n \n for i, (n, k) in enumerate(queries):\n ret = 1\n n -= 1\n\n for p in primes:\n if k % p == 0:\n c = 1\n k //= p\n while k % p == 0:\n c += 1\n k //= p\n \n ret = (ret * comb(n + c, c)) % MOD\n \n if k > 1:\n ans[i] = (ret * (n + 1)) % MOD\n else:\n ans[i] = ret\n \n return ans\n```\n\n```Java []\nclass Solution {\n static final long MOD = 1000000007;\n static final int MAX = 10000;\n static final int[] divs = new int[MAX + 1];\n static final int[] counts = new int[MAX + 1];\n\n public int[] waysToFillArray(int[][] queries) {\n int[] res = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n res[i] = waysToFillArray(queries[i][0], queries[i][1]);\n }\n return res;\n }\n\n static int waysToFillArray(int n, int k) {\n long[] c = getCounts(n);\n long r = 1;\n int primeIdx = 0;\n while (k > 1) {\n if (divs[k] == 0) primeIdx = find(primeIdx, k);\n r = (r * c[counts[k]]) % MOD;\n k /= divs[k];\n }\n return (int) r;\n }\n\n static int find(final int primeIdx, final int k) {\n for (int i = primeIdx; i < primes.length; i++) {\n final int p = primes[i];\n if (k % p == 0) {\n int d = p * p;\n int c = 1;\n while (k % d == 0) {\n c++;\n d *= p;\n }\n counts[k] = c;\n divs[k] = d / p;\n return primeIdx + 1;\n }\n }\n divs[k] = k;\n counts[k] = 1;\n return primes.length;\n }\n\n static long[][] cache = new long[MAX + 1][];\n\n private static long[] getCounts(int n) {\n if (cache[n] != null) return cache[n];\n final long[] c = new long[14];\n c[0] = 1;\n c[1] = n;\n c[2] = n * (n + 1) / 2;\n for (int i = 3; i < c.length; i++) {\n c[i] = (((c[i - 1] * (i + n - 1)) % MOD) * inverses[i - 1]) % MOD;\n }\n return cache[n] = c;\n }\n\n static long[] inverses = new long[] {1, 500000004, 333333336, 250000002, 400000003, 166666668, 142857144, 125000001, 111111112, 700000005, 818181824, 83333334, 153846155, 71428572};\n static int[] primes = new int[] { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,\n 79, 83, 89, 97};\n\n}\n```\n | 0 | Given the `head` of a linked list, find all the values that appear **more than once** in the list and delete the nodes that have any of those values.
Return _the linked list after the deletions._
**Example 1:**
**Input:** head = \[1,2,3,2\]
**Output:** \[1,3\]
**Explanation:** 2 appears twice in the linked list, so all 2's should be deleted. After deleting all 2's, we are left with \[1,3\].
**Example 2:**
**Input:** head = \[2,1,1,2\]
**Output:** \[\]
**Explanation:** 2 and 1 both appear twice. All the elements should be deleted.
**Example 3:**
**Input:** head = \[3,2,2,1,3,2,4\]
**Output:** \[1,4\]
**Explanation:** 3 appears twice and 2 appears three times. After deleting all 3's and 2's, we are left with \[1,4\].
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`
* `1 <= Node.val <= 105` | Prime-factorize ki and count how many ways you can distribute the primes among the ni positions. After prime factorizing ki, suppose there are x amount of prime factor. There are (x + n - 1) choose (n - 1) ways to distribute the x prime factors into k positions, allowing repetitions. |
No Maths Just Recursion DP we can come up with in interviews -> WA | count-ways-to-make-array-with-product | 0 | 1 | Unable to figure the bug\nGetting Wrong Answer for (73,660)\n\nSolution is just a DP where we take one element\n\ne.g. 6\nwe find a factor e.g. 2\n\nThen subproblem == array of n-1 elements and 6/2 (remaining product)\n\n\n```\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n # brute DP O(NK) where N is max(q[0]) and K is max(q[1])\n @cache\n def dp(n,k):\n \n if k == 1 or n == 1: return 1\n ways = 0\n for factor in range(1, k+1):\n if k % factor == 0:\n ways += dp(n-1, k//factor) # or take the \'3\' part\n ways %= (10**9+7)\n return ways % (10**9+7)\n \n res = [0] * len(queries)\n for i,(n, k) in enumerate(queries):\n res[i] = dp(n,k)\n \n return res\n \n # better solution -> find out how many prime factors a number has.\n # how many ways to group P numbers into N groups (since array has N values only)\n # but you can group in lesser groups and keep 1 1 1 1 as padding in array :(\n```\nBut the optimal solution is:\n```\nclass Solution:\n def waysToFillArray(self, queries, mod = 10**9+7) -> List[int]:\n def getPrimeFactorFreq(n):\n i = 2\n while i*i <= n:\n fre = 0\n while n % i == 0:\n fre += 1\n n //= i\n if fre > 0: yield fre\n i += 1\n if n > 1:\n yield 1\n \n @functools.cache\n def combinations(n, r):\n if n < r: return 0\n elif r == 0 or n == r: return 1\n return (combinations(n-1,r-1) + combinations(n-1,r)) % mod\n \n def getWays(n, k):\n ways = 1\n for fre in getPrimeFactorFreq(k):\n print(\'--\', fre)\n # how many ways to place this factor\n # among N boxes, he has `fre` occurance\n # https://cp-algorithms.com/combinatorics/stars_and_bars.html\n ways_cur_factor = combinations(n+fre-1, fre)\n ways = (ways * ways_cur_factor) % mod\n return ways\n \n \n return [getWays(n,k) for n,k in queries]\n``` | 1 | You are given a 2D integer array, `queries`. For each `queries[i]`, where `queries[i] = [ni, ki]`, find the number of different ways you can place positive integers into an array of size `ni` such that the product of the integers is `ki`. As the number of ways may be too large, the answer to the `ith` query is the number of ways **modulo** `109 + 7`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length`_, and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** queries = \[\[2,6\],\[5,1\],\[73,660\]\]
**Output:** \[4,1,50734910\]
**Explanation:** Each query is independent.
\[2,6\]: There are 4 ways to fill an array of size 2 that multiply to 6: \[1,6\], \[2,3\], \[3,2\], \[6,1\].
\[5,1\]: There is 1 way to fill an array of size 5 that multiply to 1: \[1,1,1,1,1\].
\[73,660\]: There are 1050734917 ways to fill an array of size 73 that multiply to 660. 1050734917 modulo 109 + 7 = 50734910.
**Example 2:**
**Input:** queries = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\]
**Output:** \[1,2,3,10,5\]
**Constraints:**
* `1 <= queries.length <= 104`
* `1 <= ni, ki <= 104` | null |
No Maths Just Recursion DP we can come up with in interviews -> WA | count-ways-to-make-array-with-product | 0 | 1 | Unable to figure the bug\nGetting Wrong Answer for (73,660)\n\nSolution is just a DP where we take one element\n\ne.g. 6\nwe find a factor e.g. 2\n\nThen subproblem == array of n-1 elements and 6/2 (remaining product)\n\n\n```\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n # brute DP O(NK) where N is max(q[0]) and K is max(q[1])\n @cache\n def dp(n,k):\n \n if k == 1 or n == 1: return 1\n ways = 0\n for factor in range(1, k+1):\n if k % factor == 0:\n ways += dp(n-1, k//factor) # or take the \'3\' part\n ways %= (10**9+7)\n return ways % (10**9+7)\n \n res = [0] * len(queries)\n for i,(n, k) in enumerate(queries):\n res[i] = dp(n,k)\n \n return res\n \n # better solution -> find out how many prime factors a number has.\n # how many ways to group P numbers into N groups (since array has N values only)\n # but you can group in lesser groups and keep 1 1 1 1 as padding in array :(\n```\nBut the optimal solution is:\n```\nclass Solution:\n def waysToFillArray(self, queries, mod = 10**9+7) -> List[int]:\n def getPrimeFactorFreq(n):\n i = 2\n while i*i <= n:\n fre = 0\n while n % i == 0:\n fre += 1\n n //= i\n if fre > 0: yield fre\n i += 1\n if n > 1:\n yield 1\n \n @functools.cache\n def combinations(n, r):\n if n < r: return 0\n elif r == 0 or n == r: return 1\n return (combinations(n-1,r-1) + combinations(n-1,r)) % mod\n \n def getWays(n, k):\n ways = 1\n for fre in getPrimeFactorFreq(k):\n print(\'--\', fre)\n # how many ways to place this factor\n # among N boxes, he has `fre` occurance\n # https://cp-algorithms.com/combinatorics/stars_and_bars.html\n ways_cur_factor = combinations(n+fre-1, fre)\n ways = (ways * ways_cur_factor) % mod\n return ways\n \n \n return [getWays(n,k) for n,k in queries]\n``` | 1 | Given the `head` of a linked list, find all the values that appear **more than once** in the list and delete the nodes that have any of those values.
Return _the linked list after the deletions._
**Example 1:**
**Input:** head = \[1,2,3,2\]
**Output:** \[1,3\]
**Explanation:** 2 appears twice in the linked list, so all 2's should be deleted. After deleting all 2's, we are left with \[1,3\].
**Example 2:**
**Input:** head = \[2,1,1,2\]
**Output:** \[\]
**Explanation:** 2 and 1 both appear twice. All the elements should be deleted.
**Example 3:**
**Input:** head = \[3,2,2,1,3,2,4\]
**Output:** \[1,4\]
**Explanation:** 3 appears twice and 2 appears three times. After deleting all 3's and 2's, we are left with \[1,4\].
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`
* `1 <= Node.val <= 105` | Prime-factorize ki and count how many ways you can distribute the primes among the ni positions. After prime factorizing ki, suppose there are x amount of prime factor. There are (x + n - 1) choose (n - 1) ways to distribute the x prime factors into k positions, allowing repetitions. |
[Python3] via sieve & comb | count-ways-to-make-array-with-product | 0 | 1 | **Algo**\nFor any given query, compute prime factorization. For each factor with multiplicity, distribute them into `n` buckets via multiset. \n\n**Implementation**\n```\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n spf = list(range(10001)) # spf = smallest prime factor \n for i in range(4, 10001, 2): spf[i] = 2\n for i in range(3, int(sqrt(10001))+1): \n if spf[i] == i: \n for ii in range(i*i, 10001, i): \n spf[ii] = min(spf[ii], i)\n \n ans = []\n for n, k in queries: \n freq = {} # prime factorization via sieve\n while k != 1: \n freq[spf[k]] = 1 + freq.get(spf[k], 0)\n k //= spf[k]\n val = 1\n for x in freq.values(): \n val *= comb(n+x-1, x)\n ans.append(val % 1_000_000_007)\n return ans \n```\n\n**Analysis**\nTime complexity `O(N+MlogN)`\nSpace complexity `O(N + M)`\n\n```\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n spf = list(range(10001)) # spf = smallest prime factor \n prime = []\n for i in range(2, 10001): \n if spf[i] == i: prime.append(i)\n for x in prime: \n if x <= spf[i] and i*x < 10001: spf[i * x] = x\n else: break \n \n ans = []\n for n, k in queries: \n freq = {} # prime factorization via sieve\n while k != 1: \n freq[spf[k]] = 1 + freq.get(spf[k], 0)\n k //= spf[k]\n val = 1\n for x in freq.values(): \n val *= comb(n+x-1, x)\n ans.append(val % 1_000_000_007)\n return ans \n``` | 0 | You are given a 2D integer array, `queries`. For each `queries[i]`, where `queries[i] = [ni, ki]`, find the number of different ways you can place positive integers into an array of size `ni` such that the product of the integers is `ki`. As the number of ways may be too large, the answer to the `ith` query is the number of ways **modulo** `109 + 7`.
Return _an integer array_ `answer` _where_ `answer.length == queries.length`_, and_ `answer[i]` _is the answer to the_ `ith` _query._
**Example 1:**
**Input:** queries = \[\[2,6\],\[5,1\],\[73,660\]\]
**Output:** \[4,1,50734910\]
**Explanation:** Each query is independent.
\[2,6\]: There are 4 ways to fill an array of size 2 that multiply to 6: \[1,6\], \[2,3\], \[3,2\], \[6,1\].
\[5,1\]: There is 1 way to fill an array of size 5 that multiply to 1: \[1,1,1,1,1\].
\[73,660\]: There are 1050734917 ways to fill an array of size 73 that multiply to 660. 1050734917 modulo 109 + 7 = 50734910.
**Example 2:**
**Input:** queries = \[\[1,1\],\[2,2\],\[3,3\],\[4,4\],\[5,5\]\]
**Output:** \[1,2,3,10,5\]
**Constraints:**
* `1 <= queries.length <= 104`
* `1 <= ni, ki <= 104` | null |
[Python3] via sieve & comb | count-ways-to-make-array-with-product | 0 | 1 | **Algo**\nFor any given query, compute prime factorization. For each factor with multiplicity, distribute them into `n` buckets via multiset. \n\n**Implementation**\n```\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n spf = list(range(10001)) # spf = smallest prime factor \n for i in range(4, 10001, 2): spf[i] = 2\n for i in range(3, int(sqrt(10001))+1): \n if spf[i] == i: \n for ii in range(i*i, 10001, i): \n spf[ii] = min(spf[ii], i)\n \n ans = []\n for n, k in queries: \n freq = {} # prime factorization via sieve\n while k != 1: \n freq[spf[k]] = 1 + freq.get(spf[k], 0)\n k //= spf[k]\n val = 1\n for x in freq.values(): \n val *= comb(n+x-1, x)\n ans.append(val % 1_000_000_007)\n return ans \n```\n\n**Analysis**\nTime complexity `O(N+MlogN)`\nSpace complexity `O(N + M)`\n\n```\nclass Solution:\n def waysToFillArray(self, queries: List[List[int]]) -> List[int]:\n spf = list(range(10001)) # spf = smallest prime factor \n prime = []\n for i in range(2, 10001): \n if spf[i] == i: prime.append(i)\n for x in prime: \n if x <= spf[i] and i*x < 10001: spf[i * x] = x\n else: break \n \n ans = []\n for n, k in queries: \n freq = {} # prime factorization via sieve\n while k != 1: \n freq[spf[k]] = 1 + freq.get(spf[k], 0)\n k //= spf[k]\n val = 1\n for x in freq.values(): \n val *= comb(n+x-1, x)\n ans.append(val % 1_000_000_007)\n return ans \n``` | 0 | Given the `head` of a linked list, find all the values that appear **more than once** in the list and delete the nodes that have any of those values.
Return _the linked list after the deletions._
**Example 1:**
**Input:** head = \[1,2,3,2\]
**Output:** \[1,3\]
**Explanation:** 2 appears twice in the linked list, so all 2's should be deleted. After deleting all 2's, we are left with \[1,3\].
**Example 2:**
**Input:** head = \[2,1,1,2\]
**Output:** \[\]
**Explanation:** 2 and 1 both appear twice. All the elements should be deleted.
**Example 3:**
**Input:** head = \[3,2,2,1,3,2,4\]
**Output:** \[1,4\]
**Explanation:** 3 appears twice and 2 appears three times. After deleting all 3's and 2's, we are left with \[1,4\].
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`
* `1 <= Node.val <= 105` | Prime-factorize ki and count how many ways you can distribute the primes among the ni positions. After prime factorizing ki, suppose there are x amount of prime factor. There are (x + n - 1) choose (n - 1) ways to distribute the x prime factors into k positions, allowing repetitions. |
[Python3] if-elif | latest-time-by-replacing-hidden-digits | 0 | 1 | **Algo**\nReplace `?` based on its location and value. \n\n**Implementation**\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n time = list(time)\n for i in range(len(time)): \n if time[i] == "?": \n if i == 0: time[i] = "2" if time[i+1] in "?0123" else "1"\n elif i == 1: time[i] = "3" if time[0] == "2" else "9"\n elif i == 3: time[i] = "5"\n else: time[i] = "9"\n return "".join(time)\n```\n\n**Analysis**\n`O(1)` for fixed size problem | 28 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
[Python3] if-elif | latest-time-by-replacing-hidden-digits | 0 | 1 | **Algo**\nReplace `?` based on its location and value. \n\n**Implementation**\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n time = list(time)\n for i in range(len(time)): \n if time[i] == "?": \n if i == 0: time[i] = "2" if time[i+1] in "?0123" else "1"\n elif i == 1: time[i] = "3" if time[0] == "2" else "9"\n elif i == 3: time[i] = "5"\n else: time[i] = "9"\n return "".join(time)\n```\n\n**Analysis**\n`O(1)` for fixed size problem | 28 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Very fast (90.58% 🚀) and easy solution!!! | latest-time-by-replacing-hidden-digits | 0 | 1 | class Solution:\n def maximumTime(self, time: str) -> str:\n time_l = list(time)\n new_str = \'\'\n\n if time[0] == \'?\' and time[1] == \'?\':\n time_l[0] = time[0].replace(time[0], \'2\')\n time_l[1] = time[1].replace(time[1], \'3\')\n if time[3] == \'?\' and time[4] == \'?\':\n time_l[3] = time[3].replace(time[3], \'5\')\n time_l[4] = time[4].replace(time[4], \'9\')\n if time[0] == \'?\' and time[1] != \'?\':\n if int(time[1]) < 4:\n time_l[0] = time[0].replace(time[0], \'2\')\n elif int(time[1]) > 3:\n time_l[0] = time[0].replace(time[0], \'1\')\n if time[1] == \'?\' and time[0] != \'?\':\n if int(time[0]) < 2:\n time_l[1] = time[1].replace(time[1], \'9\')\n elif int(time[0]) == 2:\n time_l[1] = time[1].replace(time[1], \'3\')\n if time[3] == \'?\' and time[4] != \'?\':\n time_l[3] = time[3].replace(time[3], \'5\')\n if time[4] == \'?\' and time[3] != \'?\':\n time_l[4] = time[4].replace(time[4], \'9\')\n\n for i in time_l:\n new_str += i\n return new_str\n``` | 2 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
Very fast (90.58% 🚀) and easy solution!!! | latest-time-by-replacing-hidden-digits | 0 | 1 | class Solution:\n def maximumTime(self, time: str) -> str:\n time_l = list(time)\n new_str = \'\'\n\n if time[0] == \'?\' and time[1] == \'?\':\n time_l[0] = time[0].replace(time[0], \'2\')\n time_l[1] = time[1].replace(time[1], \'3\')\n if time[3] == \'?\' and time[4] == \'?\':\n time_l[3] = time[3].replace(time[3], \'5\')\n time_l[4] = time[4].replace(time[4], \'9\')\n if time[0] == \'?\' and time[1] != \'?\':\n if int(time[1]) < 4:\n time_l[0] = time[0].replace(time[0], \'2\')\n elif int(time[1]) > 3:\n time_l[0] = time[0].replace(time[0], \'1\')\n if time[1] == \'?\' and time[0] != \'?\':\n if int(time[0]) < 2:\n time_l[1] = time[1].replace(time[1], \'9\')\n elif int(time[0]) == 2:\n time_l[1] = time[1].replace(time[1], \'3\')\n if time[3] == \'?\' and time[4] != \'?\':\n time_l[3] = time[3].replace(time[3], \'5\')\n if time[4] == \'?\' and time[3] != \'?\':\n time_l[4] = time[4].replace(time[4], \'9\')\n\n for i in time_l:\n new_str += i\n return new_str\n``` | 2 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Easiest & Simplest Python3 Solution with if conditions | 100% Faster | Easy to Understand | latest-time-by-replacing-hidden-digits | 0 | 1 | ```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n s=list(time)\n for i in range(len(s)):\n if s[i]==\'?\':\n if i==0:\n if s[i+1] in [\'0\',\'1\',\'2\',\'3\',\'?\']:\n s[i]=\'2\'\n else:\n s[i]=\'1\'\n elif i==1:\n if s[i-1]==\'1\' or s[i-1]==\'0\':\n s[i]=\'9\'\n else:\n s[i]=\'3\'\n elif i==3:\n s[i]=\'5\'\n elif i==4:\n s[i]=\'9\'\n return \'\'.join(s)\n```\n***Please Upvote, if you found my solution helpful*** | 5 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
Easiest & Simplest Python3 Solution with if conditions | 100% Faster | Easy to Understand | latest-time-by-replacing-hidden-digits | 0 | 1 | ```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n s=list(time)\n for i in range(len(s)):\n if s[i]==\'?\':\n if i==0:\n if s[i+1] in [\'0\',\'1\',\'2\',\'3\',\'?\']:\n s[i]=\'2\'\n else:\n s[i]=\'1\'\n elif i==1:\n if s[i-1]==\'1\' or s[i-1]==\'0\':\n s[i]=\'9\'\n else:\n s[i]=\'3\'\n elif i==3:\n s[i]=\'5\'\n elif i==4:\n s[i]=\'9\'\n return \'\'.join(s)\n```\n***Please Upvote, if you found my solution helpful*** | 5 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Beats 97.98%of users with Python3 | latest-time-by-replacing-hidden-digits | 0 | 1 | # Code\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n m1, m2 = time[3:]\n h1, h2 = time[:2]\n \n match (h1, h2):\n case ("?", "?"):\n h1, h2 = "2", "3"\n case ("?", _):\n if h2 < "4":\n h1 = "2"\n else:\n h1 = "1"\n case (_, "?"):\n if h1 in ["0", "1"]:\n h2 = "9"\n else:\n h2 = "3"\n\n m1 = "5" if m1 == "?" else m1\n m2 = "9" if m2 == "?" else m2\n return "{}{}:{}{}".format(h1, h2, m1, m2)\n``` | 0 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
Beats 97.98%of users with Python3 | latest-time-by-replacing-hidden-digits | 0 | 1 | # Code\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n m1, m2 = time[3:]\n h1, h2 = time[:2]\n \n match (h1, h2):\n case ("?", "?"):\n h1, h2 = "2", "3"\n case ("?", _):\n if h2 < "4":\n h1 = "2"\n else:\n h1 = "1"\n case (_, "?"):\n if h1 in ["0", "1"]:\n h2 = "9"\n else:\n h2 = "3"\n\n m1 = "5" if m1 == "?" else m1\n m2 = "9" if m2 == "?" else m2\n return "{}{}:{}{}".format(h1, h2, m1, m2)\n``` | 0 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Python solution | latest-time-by-replacing-hidden-digits | 0 | 1 | ```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n A, B = time[:2]\n C, D = time[3:]\n\n if A == "?" and B == "?":\n A, B = "2", "3"\n elif A != "?" and A in ["0", "1"] and B == "?":\n B = "9"\n elif A != "?" and B == "?":\n B = "3"\n elif B in ["0", "1", "2", "3"] and A == "?": A = "2"\n elif A == "?": A = "1" \n\n if C == "?": C = "5"\n if D == "?": D = "9"\n\n return f"{A}{B}:{C}{D}" \n``` | 0 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
Python solution | latest-time-by-replacing-hidden-digits | 0 | 1 | ```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n A, B = time[:2]\n C, D = time[3:]\n\n if A == "?" and B == "?":\n A, B = "2", "3"\n elif A != "?" and A in ["0", "1"] and B == "?":\n B = "9"\n elif A != "?" and B == "?":\n B = "3"\n elif B in ["0", "1", "2", "3"] and A == "?": A = "2"\n elif A == "?": A = "1" \n\n if C == "?": C = "5"\n if D == "?": D = "9"\n\n return f"{A}{B}:{C}{D}" \n``` | 0 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Python Solution - Easy To Read!! If Statements!! | latest-time-by-replacing-hidden-digits | 0 | 1 | \n# Code\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n\n if not "?" in time:\n return time\n\n hours, minutes = time.split(":")\n \n if "?" in hours:\n \n if hours == "??": \n hours = "23"\n else:\n hours: list = list(hours)\n if hours[0] == "?":\n if int(hours[1]) > 3: \n hours[0] = "1"\n else: \n hours[0] = "2"\n else:\n if hours[0] == "2": \n hours[1] = "3"\n else: \n hours[1] = "9"\n hours = "".join(hours)\n \n minutes: list = list(minutes)\n \n if "?" in minutes[0]: minutes[0] = "5"\n if "?" in minutes[1]: minutes[1] = "9"\n minutes: str = "".join(minutes)\n\n return f"{hours}:{minutes}"\n \n``` | 0 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
Python Solution - Easy To Read!! If Statements!! | latest-time-by-replacing-hidden-digits | 0 | 1 | \n# Code\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n\n if not "?" in time:\n return time\n\n hours, minutes = time.split(":")\n \n if "?" in hours:\n \n if hours == "??": \n hours = "23"\n else:\n hours: list = list(hours)\n if hours[0] == "?":\n if int(hours[1]) > 3: \n hours[0] = "1"\n else: \n hours[0] = "2"\n else:\n if hours[0] == "2": \n hours[1] = "3"\n else: \n hours[1] = "9"\n hours = "".join(hours)\n \n minutes: list = list(minutes)\n \n if "?" in minutes[0]: minutes[0] = "5"\n if "?" in minutes[1]: minutes[1] = "9"\n minutes: str = "".join(minutes)\n\n return f"{hours}:{minutes}"\n \n``` | 0 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Solve with fewer if statements | 24ms (99%) | latest-time-by-replacing-hidden-digits | 0 | 1 | \n\n\n# Intuition\nTo make the code less cumbersome\n\n# Approach\nTake advantage of the bool value in math formula, where *True* equals 1 and *False* equals 0.\n\n# Complexity\n- Time complexity:\n\n- Space complexity:\n\n# Code\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n time = list(time)\n for i in range(5):\n if time[i] == \'?\':\n if not i:\n time[i] = str(1 + (time[1] == \'?\' or time[1] < \'4\'))\n else:\n time[i] = str(3 + 6*(time[0] < \'2\') if i == 1 else i*2 + (-1)**i)\n\n return \'\'.join(time)\n``` | 0 | You are given a string `time` in the form of `hh:mm`, where some of the digits in the string are hidden (represented by `?`).
The valid times are those inclusively between `00:00` and `23:59`.
Return _the latest valid time you can get from_ `time` _by replacing the hidden_ _digits_.
**Example 1:**
**Input:** time = "2?:?0 "
**Output:** "23:50 "
**Explanation:** The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.
**Example 2:**
**Input:** time = "0?:3? "
**Output:** "09:39 "
**Example 3:**
**Input:** time = "1?:22 "
**Output:** "19:22 "
**Constraints:**
* `time` is in the format `hh:mm`.
* It is guaranteed that you can produce a valid time from the given string. | Convert infix expression to postfix expression. Build an expression tree from the postfix expression. |
Solve with fewer if statements | 24ms (99%) | latest-time-by-replacing-hidden-digits | 0 | 1 | \n\n\n# Intuition\nTo make the code less cumbersome\n\n# Approach\nTake advantage of the bool value in math formula, where *True* equals 1 and *False* equals 0.\n\n# Complexity\n- Time complexity:\n\n- Space complexity:\n\n# Code\n```\nclass Solution:\n def maximumTime(self, time: str) -> str:\n time = list(time)\n for i in range(5):\n if time[i] == \'?\':\n if not i:\n time[i] = str(1 + (time[1] == \'?\' or time[1] < \'4\'))\n else:\n time[i] = str(3 + 6*(time[0] < \'2\') if i == 1 else i*2 + (-1)**i)\n\n return \'\'.join(time)\n``` | 0 | Given an array of strings `words`, find the **longest** string in `words` such that **every prefix** of it is also in `words`.
* For example, let `words = [ "a ", "app ", "ap "]`. The string `"app "` has prefixes `"ap "` and `"a "`, all of which are in `words`.
Return _the string described above. If there is more than one string with the same length, return the **lexicographically smallest** one, and if no string exists, return_ `" "`.
**Example 1:**
**Input:** words = \[ "k ", "ki ", "kir ", "kira ", "kiran "\]
**Output:** "kiran "
**Explanation:** "kiran " has prefixes "kira ", "kir ", "ki ", and "k ", and all of them appear in words.
**Example 2:**
**Input:** words = \[ "a ", "banana ", "app ", "appl ", "ap ", "apply ", "apple "\]
**Output:** "apple "
**Explanation:** Both "apple " and "apply " have all their prefixes in words.
However, "apple " is lexicographically smaller, so we return that.
**Example 3:**
**Input:** words = \[ "abc ", "bc ", "ab ", "qwe "\]
**Output:** " "
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 105`
* `1 <= sum(words[i].length) <= 105` | Trying out all possible solutions from biggest to smallest would fit in the time limit. To check if the solution is okay, you need to find out if it's valid and matches every character |
Frequency Transform | Commented and Explained | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis question is again really asking about how well you can do frequency transformations. In this case, we are asked to find the minimum cost to satisfy one of three conditions. However, all of the conditions come down to a comparison cost of the lengths of the strings as a single space and the combined frequency of the spaces. As such, we can utilize the frequency transform of the problem, once we work out how to do so in the problem space. \n\nThe first clue is that we care about the frequency of the things in a string, so getting the frequency of each char is a good place to start. \n\nThen, we know also that are our lengths define the problem space. In this case, one more than the sum of the lengths is strictly too large no matter what. So, we can now set our upper bound on changes. \n\nSpeaking of upper bounds on changes, we currently have two lexicographic bounds, a and z. Let\'s get rid of one by not considering it in our alphabet. This will necessarily allow us to complete the problem. To do so in an easy manner, let\'s drop off the z \n\nAlright, now we need to figure the cost to alter frequencies from the standpoint of one frequency in regards to another. To do so, we need an upper bound on cost (already established), and a current bound on cost. The current bound on cost is the frequency sum of the first of the frequencies. We also want a secondary bound on cost for the other frequency, which we\'ll start at 0. \n\nNow, we loop through our 1 truncated alphabet \n- update our current bound on cost by decrementing by the frequency of the given char in the first frequency \n- update our secondary bound on cost by incrementing by the frequency of the given char in the second frequency \n\nIn doing so, we are finding the total cost to remove a char from the second frequency if that is a char we are interested in considering in the first frequency. We do this for all the possible components, and so arrive at the best cost in the eyes of the order of the frequencies \n\nWe then do this for frequency of a followed by frequency of b, and vice versa \n\nFinally, we have to consider the alternate cost, which is the cost to get all of them to the same character. This is simply the length of our two strings less the maximum frequencies of each, or our max cost less 1 less the max of each of the frequencies. \n\nNow we have the costs all set up, we simply take the min of each and there\'s the answer \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDictionaries and lists make up the backbone of the data structures\nA simple function and the object fields denote the rest \nIf you follow the intuition you\'ll arrive at the code \n\n# Complexity\n- Time complexity : O(max(a, b, 2 * alphabet)) \n - O(a) + O(b) to build frequencies \n - O(2 * alphabet) to loop over alphabet \n - all others O(1) \n - total then is O(max(a, b, 2 * alphabet)) since all are linear \n - keep the 2* so you know that only in cases of a and b longer than alphabet will you end up with a higher cost \n\n- Space complexity : O(max(a, b)) \n - time complexity is on order of alphabet, and technically a and b are as well. However, a and b also have components, and as such, they may end up being more than alphabet in terms of storage even if less than alphabet in size. As such, report max of a and b as the size requirements. \n\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n # get your frequencies \n frequencies = [dict(collections.Counter(a)), dict(collections.Counter(b))] \n # get your lengths \n aL, bL = len(a), len(b) \n # set your max cost as out of reasonable boundaries \n self.max_cost = (aL + bL) + 1\n # build your alphabet. Notice we leave off z, this is so that we have a definite interval without open ended boundaries \n self.alphabet = \'abcdefghijklmnopqrstuvwxy\'\n # define a function to calculate the cost to alter the frequency of a character in regards to one frequency first \n # this lets us find out the cost / benefit of swapping a certain character from the perspective of a certain string \n def cost_to_alter_frequencies(frequency_1, frequency_2) : \n # calculate initial sum 1 and set initial sum 2 to zero \n initial_sum_1 = sum(frequency_1.values())\n initial_sum_2 = 0 \n # set result to out of bounds value \n result = self.max_cost \n # for each char in alphabet not including the terminal char \n for char in self.alphabet : \n # see if you have it in each case. \n # Update initial sum 1 by decrementing if you already had it, don\'t pay twice! \n initial_sum_1 -= frequency_1.get(char, 0)\n # Update initial sum 2 by incrementing since you never paid for it yet! \n initial_sum_2 += frequency_2.get(char, 0)\n # then, minimize the resulting cost to change frequency by comparing the cost of current versus \n # the cost of removing from initial sum 1 the frequency of char and adding to initial sum 2 the frequency of char \n # this maneuvers the possibilities so that we see the benefit of using a given char\n # versus the benefit of not using a given a char \n result = min(result, initial_sum_1 + initial_sum_2) \n # return the minimzed result \n return result \n \n # get the cost from a\'s viewpoint and the cost from b\'s viewpoint \n cost_to_alter_a = cost_to_alter_frequencies(frequencies[0], frequencies[1]) \n cost_to_alter_b = cost_to_alter_frequencies(frequencies[1], frequencies[0])\n # alternate option depends on length and greatest frequency of items in each relative list (cost to change in place)\n alternate = aL - max(frequencies[0].values()) + bL - max(frequencies[1].values())\n options = [cost_to_alter_a, cost_to_alter_b, alternate]\n # print(options)\n return min(options)\n\n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Frequency Transform | Commented and Explained | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis question is again really asking about how well you can do frequency transformations. In this case, we are asked to find the minimum cost to satisfy one of three conditions. However, all of the conditions come down to a comparison cost of the lengths of the strings as a single space and the combined frequency of the spaces. As such, we can utilize the frequency transform of the problem, once we work out how to do so in the problem space. \n\nThe first clue is that we care about the frequency of the things in a string, so getting the frequency of each char is a good place to start. \n\nThen, we know also that are our lengths define the problem space. In this case, one more than the sum of the lengths is strictly too large no matter what. So, we can now set our upper bound on changes. \n\nSpeaking of upper bounds on changes, we currently have two lexicographic bounds, a and z. Let\'s get rid of one by not considering it in our alphabet. This will necessarily allow us to complete the problem. To do so in an easy manner, let\'s drop off the z \n\nAlright, now we need to figure the cost to alter frequencies from the standpoint of one frequency in regards to another. To do so, we need an upper bound on cost (already established), and a current bound on cost. The current bound on cost is the frequency sum of the first of the frequencies. We also want a secondary bound on cost for the other frequency, which we\'ll start at 0. \n\nNow, we loop through our 1 truncated alphabet \n- update our current bound on cost by decrementing by the frequency of the given char in the first frequency \n- update our secondary bound on cost by incrementing by the frequency of the given char in the second frequency \n\nIn doing so, we are finding the total cost to remove a char from the second frequency if that is a char we are interested in considering in the first frequency. We do this for all the possible components, and so arrive at the best cost in the eyes of the order of the frequencies \n\nWe then do this for frequency of a followed by frequency of b, and vice versa \n\nFinally, we have to consider the alternate cost, which is the cost to get all of them to the same character. This is simply the length of our two strings less the maximum frequencies of each, or our max cost less 1 less the max of each of the frequencies. \n\nNow we have the costs all set up, we simply take the min of each and there\'s the answer \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDictionaries and lists make up the backbone of the data structures\nA simple function and the object fields denote the rest \nIf you follow the intuition you\'ll arrive at the code \n\n# Complexity\n- Time complexity : O(max(a, b, 2 * alphabet)) \n - O(a) + O(b) to build frequencies \n - O(2 * alphabet) to loop over alphabet \n - all others O(1) \n - total then is O(max(a, b, 2 * alphabet)) since all are linear \n - keep the 2* so you know that only in cases of a and b longer than alphabet will you end up with a higher cost \n\n- Space complexity : O(max(a, b)) \n - time complexity is on order of alphabet, and technically a and b are as well. However, a and b also have components, and as such, they may end up being more than alphabet in terms of storage even if less than alphabet in size. As such, report max of a and b as the size requirements. \n\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n # get your frequencies \n frequencies = [dict(collections.Counter(a)), dict(collections.Counter(b))] \n # get your lengths \n aL, bL = len(a), len(b) \n # set your max cost as out of reasonable boundaries \n self.max_cost = (aL + bL) + 1\n # build your alphabet. Notice we leave off z, this is so that we have a definite interval without open ended boundaries \n self.alphabet = \'abcdefghijklmnopqrstuvwxy\'\n # define a function to calculate the cost to alter the frequency of a character in regards to one frequency first \n # this lets us find out the cost / benefit of swapping a certain character from the perspective of a certain string \n def cost_to_alter_frequencies(frequency_1, frequency_2) : \n # calculate initial sum 1 and set initial sum 2 to zero \n initial_sum_1 = sum(frequency_1.values())\n initial_sum_2 = 0 \n # set result to out of bounds value \n result = self.max_cost \n # for each char in alphabet not including the terminal char \n for char in self.alphabet : \n # see if you have it in each case. \n # Update initial sum 1 by decrementing if you already had it, don\'t pay twice! \n initial_sum_1 -= frequency_1.get(char, 0)\n # Update initial sum 2 by incrementing since you never paid for it yet! \n initial_sum_2 += frequency_2.get(char, 0)\n # then, minimize the resulting cost to change frequency by comparing the cost of current versus \n # the cost of removing from initial sum 1 the frequency of char and adding to initial sum 2 the frequency of char \n # this maneuvers the possibilities so that we see the benefit of using a given char\n # versus the benefit of not using a given a char \n result = min(result, initial_sum_1 + initial_sum_2) \n # return the minimzed result \n return result \n \n # get the cost from a\'s viewpoint and the cost from b\'s viewpoint \n cost_to_alter_a = cost_to_alter_frequencies(frequencies[0], frequencies[1]) \n cost_to_alter_b = cost_to_alter_frequencies(frequencies[1], frequencies[0])\n # alternate option depends on length and greatest frequency of items in each relative list (cost to change in place)\n alternate = aL - max(frequencies[0].values()) + bL - max(frequencies[1].values())\n options = [cost_to_alter_a, cost_to_alter_b, alternate]\n # print(options)\n return min(options)\n\n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
✅O(N) || counting | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n a1=[0 for i in range(26)]\n a2=[0 for i in range(26)]\n for i in a:a1[ord(i)-ord(\'a\')]+=1\n for i in b:a2[ord(i)-ord(\'a\')]+=1\n ans=len(a)+len(b)\n maxa=0\n maxb=0\n n=len(a)\n m=len(b)\n for i in range(26):\n ans=min(ans,n+m-a1[i]-a2[i])\n if(i):\n ans=min(ans,maxa+m-maxb)\n ans=min(ans,n+maxb-maxa)\n maxa+=a1[i]\n maxb+=a2[i]\n return ans\n\n \n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
✅O(N) || counting | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n a1=[0 for i in range(26)]\n a2=[0 for i in range(26)]\n for i in a:a1[ord(i)-ord(\'a\')]+=1\n for i in b:a2[ord(i)-ord(\'a\')]+=1\n ans=len(a)+len(b)\n maxa=0\n maxb=0\n n=len(a)\n m=len(b)\n for i in range(26):\n ans=min(ans,n+m-a1[i]-a2[i])\n if(i):\n ans=min(ans,maxa+m-maxb)\n ans=min(ans,n+maxb-maxa)\n maxa+=a1[i]\n maxb+=a2[i]\n return ans\n\n \n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Python solution beats 78.41% | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n la=[0]*26 \n lb=[0]*26\n i0=ord(\'a\') \n for c in a:\n la[ord(c)-i0]+=1\n for c in b:\n lb[ord(c)-i0]+=1\n\n da=sum(la)\n db=sum(lb)\n res=da+db-max(la)-max(lb)\n for i in range(25):\n da+=lb[i]-la[i]\n db+=la[i]-lb[i]\n res=min(res,da,db)\n return res\n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Python solution beats 78.41% | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n la=[0]*26 \n lb=[0]*26\n i0=ord(\'a\') \n for c in a:\n la[ord(c)-i0]+=1\n for c in b:\n lb[ord(c)-i0]+=1\n\n da=sum(la)\n db=sum(lb)\n res=da+db-max(la)-max(lb)\n for i in range(25):\n da+=lb[i]-la[i]\n db+=la[i]-lb[i]\n res=min(res,da,db)\n return res\n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Python3 O(N) Solution use two counter of chars | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#from collections import Counter\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n ct1, ct2 = [0] * 26, [0] * 26\n def countChars(s, arr):\n for c in s:\n arr[ord(c) - ord(\'a\')] += 1\n \n countChars(a, ct1)\n countChars(b, ct2)\n ans = len(a) + len(b)\n def makeStrictLess(arr1, arr2):\n ans = float(\'inf\')\n for i in range(26):\n # set all char less or equal to i-th char\n cnt1 = 0\n for k in range(26):\n if k > i:\n cnt1 += arr1[k]\n \n for j in range(i + 1, 26):\n # # set all char greater or equal to j-th char\n cnt2 = 0\n for k in range(26):\n if k < j:\n cnt2 += arr2[k]\n ans = min(ans, cnt1 + cnt2)\n return ans\n ans = min(ans, makeStrictLess(ct1, ct2), makeStrictLess(ct2, ct1), len(a) + len(b) - max(ct1) - max(ct2))\n return ans\n\n\n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Python3 O(N) Solution use two counter of chars | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#from collections import Counter\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n ct1, ct2 = [0] * 26, [0] * 26\n def countChars(s, arr):\n for c in s:\n arr[ord(c) - ord(\'a\')] += 1\n \n countChars(a, ct1)\n countChars(b, ct2)\n ans = len(a) + len(b)\n def makeStrictLess(arr1, arr2):\n ans = float(\'inf\')\n for i in range(26):\n # set all char less or equal to i-th char\n cnt1 = 0\n for k in range(26):\n if k > i:\n cnt1 += arr1[k]\n \n for j in range(i + 1, 26):\n # # set all char greater or equal to j-th char\n cnt2 = 0\n for k in range(26):\n if k < j:\n cnt2 += arr2[k]\n ans = min(ans, cnt1 + cnt2)\n return ans\n ans = min(ans, makeStrictLess(ct1, ct2), makeStrictLess(ct2, ct1), len(a) + len(b) - max(ct1) - max(ct2))\n return ans\n\n\n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Simple Solution with HashMap | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n counter_a = Counter(ord(ch) - ord(\'a\') for ch in a)\n counter_b = Counter(ord(ch) - ord(\'a\') for ch in b) \n unique = len(a) - max(counter_a.values()) + len(b) - max(counter_b.values())\n #print(counter_a,counter_b, unique)\n min_a = min_b = len(a) + len(b)\n for i in range(25):\n counter_a[i] += counter_a[i-1]\n counter_b[i] += counter_b[i-1]\n min_a = min(min_a , len(a) - counter_a[i] + counter_b[i])\n min_b = min(min_b , len(b) - counter_b[i] + counter_a[i])\n\n return min(min_a,min_b,unique) \n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Simple Solution with HashMap | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n counter_a = Counter(ord(ch) - ord(\'a\') for ch in a)\n counter_b = Counter(ord(ch) - ord(\'a\') for ch in b) \n unique = len(a) - max(counter_a.values()) + len(b) - max(counter_b.values())\n #print(counter_a,counter_b, unique)\n min_a = min_b = len(a) + len(b)\n for i in range(25):\n counter_a[i] += counter_a[i-1]\n counter_b[i] += counter_b[i-1]\n min_a = min(min_a , len(a) - counter_a[i] + counter_b[i])\n min_b = min(min_b , len(b) - counter_b[i] + counter_a[i])\n\n return min(min_a,min_b,unique) \n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Alternative Binary Search approach | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n ca, cb = Counter(a), Counter(b)\n\n o3 = (len(a) - ca.most_common()[0][1]) + (len(b) - cb.most_common()[0][1])\n a = list(sorted(a))\n b = list(sorted(b))\n a_rev = list(reversed(a))\n b_rev = list(reversed(b))\n\n def find(A, B, order=1, skip=\'z\'):\n res = inf\n for i in range(len(A)- 1,-1,-1):\n if A[i] == skip:\n continue\n\n idx = bisect.bisect_right(B, A[i], key=lambda x: order * x)\n res = min(res, (len(A) - i - 1) + idx)\n return res\n\n return min(\n find(a, b),\n find(b, a),\n find(a_rev, b_rev, -1, \'a\'),\n find(b_rev, a_rev, -1, \'a\'),\n o3)\n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Alternative Binary Search approach | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n ca, cb = Counter(a), Counter(b)\n\n o3 = (len(a) - ca.most_common()[0][1]) + (len(b) - cb.most_common()[0][1])\n a = list(sorted(a))\n b = list(sorted(b))\n a_rev = list(reversed(a))\n b_rev = list(reversed(b))\n\n def find(A, B, order=1, skip=\'z\'):\n res = inf\n for i in range(len(A)- 1,-1,-1):\n if A[i] == skip:\n continue\n\n idx = bisect.bisect_right(B, A[i], key=lambda x: order * x)\n res = min(res, (len(A) - i - 1) + idx)\n return res\n\n return min(\n find(a, b),\n find(b, a),\n find(a_rev, b_rev, -1, \'a\'),\n find(b_rev, a_rev, -1, \'a\'),\n o3)\n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Python | PrefixSum | O(n) | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Code\n```\nfrom collections import Counter\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n m, n = len(a), len(b)\n countera = Counter(a)\n counterb = Counter(b)\n prefixa = [0]\n prefixb = [0]\n for c in \'abcdefghijklmnopqrstuvwxyz\':\n prefixa.append(prefixa[-1]+countera[c])\n prefixb.append(prefixb[-1]+counterb[c])\n def solveX(prefixa, prefixb):\n res = float(\'inf\')\n for i in range(2,27):\n res = min(res, prefixa[-1]-prefixa[i-1]+prefixb[i-1])\n return res\n def solveZ(a, b):\n counter = Counter(a) + Counter(b)\n return m+n - max(counter.values())\n return min(solveX(prefixa,prefixb), solveX(prefixb,prefixa), solveZ(a,b))\n\n``` | 0 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
Python | PrefixSum | O(n) | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | # Code\n```\nfrom collections import Counter\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n m, n = len(a), len(b)\n countera = Counter(a)\n counterb = Counter(b)\n prefixa = [0]\n prefixb = [0]\n for c in \'abcdefghijklmnopqrstuvwxyz\':\n prefixa.append(prefixa[-1]+countera[c])\n prefixb.append(prefixb[-1]+counterb[c])\n def solveX(prefixa, prefixb):\n res = float(\'inf\')\n for i in range(2,27):\n res = min(res, prefixa[-1]-prefixa[i-1]+prefixb[i-1])\n return res\n def solveZ(a, b):\n counter = Counter(a) + Counter(b)\n return m+n - max(counter.values())\n return min(solveX(prefixa,prefixb), solveX(prefixb,prefixa), solveZ(a,b))\n\n``` | 0 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
[Python] with explanation | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | Key idea here for satisfying condition 1 and 2 is to try out all the lowercase letters.\nFor example, let\'s choose "b" as the boundary letter. Then cost of converting1st word to consists of letters less than and equal to "b" would be\n`cost_a = len(a) - counter_a["b"]`\nNote counter here is acting like a prefix sum of frequencies. and cost of converting word b to consists of characters only gt than b would be to convert all characters less than equal to "b"\n`cost_b = counter_b["b"]`\nso total cost for using b as the boundary letter and making a less than b would be:\n` a_less_than_b = len(a) - counter_a["b"] + counter_b["b"]`\nsimilar argument applies for `b_less_than_a`\n`b_less_than_a = len(b) - counter_b["b"] + counter_a["b"]`\n\n\nUnique is relatively easier.\n`unique_a = len(a) - max(counter_a.values())`\n`unique_b = len(b) - max(counter_b.values())`\n\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n counter_a = Counter(ord(ch) - ord(\'a\') for ch in a)\n counter_b = Counter(ord(ch) - ord(\'a\') for ch in b)\n # keys will go from 0 to 25\n \n # condition 3\n # min cost to turn a consisting of single character only is len(a) - max_freq_of_character\n unique = len(a) - max(counter_a.values()) + len(b) - max(counter_b.values())\n \n a_less_than_b = b_less_than_a = len(a) + len(b)\n \n # counter maintains a prefix sum and it adds up the frequency of all previous letters upto the letter being tried as boundary letter.\n for i in range(1,26):\n counter_a[i] += counter_a[i-1]\n counter_b[i] += counter_b[i-1]\n # cost to turn a less than b\n a_less_than_b = min(a_less_than_b, len(a) - counter_a[i] + counter_b[i])\n b_less_than_a = min(b_less_than_a, len(b) - counter_b[i] + counter_a[i])\n \n \n\n return min(a_less_than_b, b_less_than_a, unique)\n \n ``` | 3 | You are given two strings `a` and `b` that consist of lowercase letters. In one operation, you can change any character in `a` or `b` to **any lowercase letter**.
Your goal is to satisfy **one** of the following three conditions:
* **Every** letter in `a` is **strictly less** than **every** letter in `b` in the alphabet.
* **Every** letter in `b` is **strictly less** than **every** letter in `a` in the alphabet.
* **Both** `a` and `b` consist of **only one** distinct letter.
Return _the **minimum** number of operations needed to achieve your goal._
**Example 1:**
**Input:** a = "aba ", b = "caa "
**Output:** 2
**Explanation:** Consider the best way to make each condition true:
1) Change b to "ccc " in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb " and b to "aaa " in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa " and b to "aaa " in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).
**Example 2:**
**Input:** a = "dabadd ", b = "cda "
**Output:** 3
**Explanation:** The best way is to make condition 1 true by changing b to "eee ".
**Constraints:**
* `1 <= a.length, b.length <= 105`
* `a` and `b` consist only of lowercase letters. | The depth of any character in the VPS is the ( number of left brackets before it ) - ( number of right brackets before it ) |
[Python] with explanation | change-minimum-characters-to-satisfy-one-of-three-conditions | 0 | 1 | Key idea here for satisfying condition 1 and 2 is to try out all the lowercase letters.\nFor example, let\'s choose "b" as the boundary letter. Then cost of converting1st word to consists of letters less than and equal to "b" would be\n`cost_a = len(a) - counter_a["b"]`\nNote counter here is acting like a prefix sum of frequencies. and cost of converting word b to consists of characters only gt than b would be to convert all characters less than equal to "b"\n`cost_b = counter_b["b"]`\nso total cost for using b as the boundary letter and making a less than b would be:\n` a_less_than_b = len(a) - counter_a["b"] + counter_b["b"]`\nsimilar argument applies for `b_less_than_a`\n`b_less_than_a = len(b) - counter_b["b"] + counter_a["b"]`\n\n\nUnique is relatively easier.\n`unique_a = len(a) - max(counter_a.values())`\n`unique_b = len(b) - max(counter_b.values())`\n\n```\nclass Solution:\n def minCharacters(self, a: str, b: str) -> int:\n counter_a = Counter(ord(ch) - ord(\'a\') for ch in a)\n counter_b = Counter(ord(ch) - ord(\'a\') for ch in b)\n # keys will go from 0 to 25\n \n # condition 3\n # min cost to turn a consisting of single character only is len(a) - max_freq_of_character\n unique = len(a) - max(counter_a.values()) + len(b) - max(counter_b.values())\n \n a_less_than_b = b_less_than_a = len(a) + len(b)\n \n # counter maintains a prefix sum and it adds up the frequency of all previous letters upto the letter being tried as boundary letter.\n for i in range(1,26):\n counter_a[i] += counter_a[i-1]\n counter_b[i] += counter_b[i-1]\n # cost to turn a less than b\n a_less_than_b = min(a_less_than_b, len(a) - counter_a[i] + counter_b[i])\n b_less_than_a = min(b_less_than_a, len(b) - counter_b[i] + counter_a[i])\n \n \n\n return min(a_less_than_b, b_less_than_a, unique)\n \n ``` | 3 | A **sentence** is a list of words that are separated by a single space with no leading or trailing spaces. Each word consists of lowercase and uppercase English letters.
A sentence can be **shuffled** by appending the **1-indexed word position** to each word then rearranging the words in the sentence.
* For example, the sentence `"This is a sentence "` can be shuffled as `"sentence4 a3 is2 This1 "` or `"is2 sentence4 This1 a3 "`.
Given a **shuffled sentence** `s` containing no more than `9` words, reconstruct and return _the original sentence_.
**Example 1:**
**Input:** s = "is2 sentence4 This1 a3 "
**Output:** "This is a sentence "
**Explanation:** Sort the words in s to their original positions "This1 is2 a3 sentence4 ", then remove the numbers.
**Example 2:**
**Input:** s = "Myself2 Me1 I4 and3 "
**Output:** "Me Myself and I "
**Explanation:** Sort the words in s to their original positions "Me1 Myself2 and3 I4 ", then remove the numbers.
**Constraints:**
* `2 <= s.length <= 200`
* `s` consists of lowercase and uppercase English letters, spaces, and digits from `1` to `9`.
* The number of words in `s` is between `1` and `9`.
* The words in `s` are separated by a single space.
* `s` contains no leading or trailing spaces.
1\. All characters in a are strictly less than those in b (i.e., a\[i\] < b\[i\] for all i). 2. All characters in b are strictly less than those in a (i.e., a\[i\] > b\[i\] for all i). 3. All characters in a and b are the same (i.e., a\[i\] = b\[i\] for all i). | Iterate on each letter in the alphabet, and check the smallest number of operations needed to make it one of the following: the largest letter in a and smaller than the smallest one in b, vice versa, or let a and b consist only of this letter. For the first 2 conditions, take care that you can only change characters to lowercase letters, so you can't make 'z' the smallest letter in one of the strings or 'a' the largest letter in one of them. |
Python3 | DP + QuickSelect | Easy to understand | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet\'s construct all possible xors list and use quick select to find the Kth largest value.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirstly I tried brute-forcing the matrix to calculate the i, j xor - solution did not pass. Then I tried using DP and the solution passed.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m*n): DP is always m*n and quick select\'s worst case is m*n.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m*n): quick select\'s additional lists.\n# Code\n```\nfrom random import choice\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n xors = self.construct_xors(matrix)\n return self.quick_select(xors, k)\n\n def construct_xors(self, xors):\n m = len(xors)\n n = len(xors[0])\n\n def valid_coord(i, j):\n return 0 <= i < m and 0 <= j < n\n\n for i in range(m):\n for j in range(n):\n for di, dj in ((-1, 0), (0, -1), (-1, -1)):\n ci, cj = i + di, j + dj\n xors[i][j] ^= xors[ci][cj] * valid_coord(ci, cj)\n \n xors = [xor for row in xors for xor in row]\n return xors\n\n def quick_select(self, container, k):\n pivot = choice(container)\n\n g = [xor for xor in container if xor > pivot]\n e = [xor for xor in container if xor == pivot]\n l = [xor for xor in container if xor < pivot]\n\n if len(g) > k:\n return self.quick_select(g, k)\n if len(g) == k:\n return min(g)\n if len(g) + len(e) >= k:\n return e[0]\n if len(g) + len(e) + len(l) > k:\n return self.quick_select(l, k - len(g) - len(e))\n if len(g) + len(e) + len(l) == k:\n return min(l)\n\n``` | 4 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Python3 | DP + QuickSelect | Easy to understand | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet\'s construct all possible xors list and use quick select to find the Kth largest value.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirstly I tried brute-forcing the matrix to calculate the i, j xor - solution did not pass. Then I tried using DP and the solution passed.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m*n): DP is always m*n and quick select\'s worst case is m*n.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m*n): quick select\'s additional lists.\n# Code\n```\nfrom random import choice\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n xors = self.construct_xors(matrix)\n return self.quick_select(xors, k)\n\n def construct_xors(self, xors):\n m = len(xors)\n n = len(xors[0])\n\n def valid_coord(i, j):\n return 0 <= i < m and 0 <= j < n\n\n for i in range(m):\n for j in range(n):\n for di, dj in ((-1, 0), (0, -1), (-1, -1)):\n ci, cj = i + di, j + dj\n xors[i][j] ^= xors[ci][cj] * valid_coord(ci, cj)\n \n xors = [xor for row in xors for xor in row]\n return xors\n\n def quick_select(self, container, k):\n pivot = choice(container)\n\n g = [xor for xor in container if xor > pivot]\n e = [xor for xor in container if xor == pivot]\n l = [xor for xor in container if xor < pivot]\n\n if len(g) > k:\n return self.quick_select(g, k)\n if len(g) == k:\n return min(g)\n if len(g) + len(e) >= k:\n return e[0]\n if len(g) + len(e) + len(l) > k:\n return self.quick_select(l, k - len(g) - len(e))\n if len(g) + len(e) + len(l) == k:\n return min(l)\n\n``` | 4 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Python3] compute xor O(MNlog(MN)) | O(MNlogK) | O(MN) | find-kth-largest-xor-coordinate-value | 0 | 1 | **Algo**\nCompute `xor` of at `(i, j)` as `xor[i][j] = xor[i-1][j] ^ xor[i][j-1] ^ xor[i-1][j-1] ^ matrix[i][j]`. The return the `k`th largest among observed. \n\n**Implementation**\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0]) # dimensions \n \n ans = []\n for i in range(m): \n for j in range(n): \n if i: matrix[i][j] ^= matrix[i-1][j]\n if j: matrix[i][j] ^= matrix[i][j-1]\n if i and j: matrix[i][j] ^= matrix[i-1][j-1]\n ans.append(matrix[i][j])\n return sorted(ans)[-k] \n```\n\n**Analysis**\nTime complexity `O(MNlog(MN))` (`O(MN)` is possible via quick select)\nSpace complexity `O(MN)`\n\nEdited on 1/24/2021\nAdding two more implementation for improved time complexity \n`O(MNlogK)` time & `logK` space \n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0]) # dimensions \n \n pq = []\n for i in range(m): \n for j in range(n): \n if i: matrix[i][j] ^= matrix[i-1][j]\n if j: matrix[i][j] ^= matrix[i][j-1]\n if i and j: matrix[i][j] ^= matrix[i-1][j-1]\n heappush(pq, matrix[i][j])\n if len(pq) > k: heappop(pq)\n return pq[0]\n```\n\n\n`O(MN)` time & `O(MN)` space \n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0]) # dimensions \n \n vals = []\n for i in range(m): \n for j in range(n): \n if i: matrix[i][j] ^= matrix[i-1][j]\n if j: matrix[i][j] ^= matrix[i][j-1]\n if i and j: matrix[i][j] ^= matrix[i-1][j-1]\n vals.append(matrix[i][j])\n \n def part(lo, hi): \n """Partition vals from lo (inclusive) to hi (exclusive)."""\n i, j = lo+1, hi-1\n while i <= j: \n if vals[i] < vals[lo]: i += 1\n elif vals[lo] < vals[j]: j -= 1\n else: \n vals[i], vals[j] = vals[j], vals[i]\n i += 1\n j -= 1\n vals[lo], vals[j] = vals[j], vals[lo]\n return j \n \n lo, hi = 0, len(vals)\n while lo < hi: \n mid = part(lo, hi)\n if mid + k < len(vals): lo = mid + 1\n else: hi = mid\n return vals[lo]\n``` | 16 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
[Python3] compute xor O(MNlog(MN)) | O(MNlogK) | O(MN) | find-kth-largest-xor-coordinate-value | 0 | 1 | **Algo**\nCompute `xor` of at `(i, j)` as `xor[i][j] = xor[i-1][j] ^ xor[i][j-1] ^ xor[i-1][j-1] ^ matrix[i][j]`. The return the `k`th largest among observed. \n\n**Implementation**\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0]) # dimensions \n \n ans = []\n for i in range(m): \n for j in range(n): \n if i: matrix[i][j] ^= matrix[i-1][j]\n if j: matrix[i][j] ^= matrix[i][j-1]\n if i and j: matrix[i][j] ^= matrix[i-1][j-1]\n ans.append(matrix[i][j])\n return sorted(ans)[-k] \n```\n\n**Analysis**\nTime complexity `O(MNlog(MN))` (`O(MN)` is possible via quick select)\nSpace complexity `O(MN)`\n\nEdited on 1/24/2021\nAdding two more implementation for improved time complexity \n`O(MNlogK)` time & `logK` space \n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0]) # dimensions \n \n pq = []\n for i in range(m): \n for j in range(n): \n if i: matrix[i][j] ^= matrix[i-1][j]\n if j: matrix[i][j] ^= matrix[i][j-1]\n if i and j: matrix[i][j] ^= matrix[i-1][j-1]\n heappush(pq, matrix[i][j])\n if len(pq) > k: heappop(pq)\n return pq[0]\n```\n\n\n`O(MN)` time & `O(MN)` space \n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0]) # dimensions \n \n vals = []\n for i in range(m): \n for j in range(n): \n if i: matrix[i][j] ^= matrix[i-1][j]\n if j: matrix[i][j] ^= matrix[i][j-1]\n if i and j: matrix[i][j] ^= matrix[i-1][j-1]\n vals.append(matrix[i][j])\n \n def part(lo, hi): \n """Partition vals from lo (inclusive) to hi (exclusive)."""\n i, j = lo+1, hi-1\n while i <= j: \n if vals[i] < vals[lo]: i += 1\n elif vals[lo] < vals[j]: j -= 1\n else: \n vals[i], vals[j] = vals[j], vals[i]\n i += 1\n j -= 1\n vals[lo], vals[j] = vals[j], vals[lo]\n return j \n \n lo, hi = 0, len(vals)\n while lo < hi: \n mid = part(lo, hi)\n if mid + k < len(vals): lo = mid + 1\n else: hi = mid\n return vals[lo]\n``` | 16 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
XOR Properties | Commented and Explained | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is really about seeing if a candidate understands xor \nXOR is commutative, associative, self-inverting, and has an identity element of 0. \nBy commutative it really means that a xor b = b xor a (order locally does not matter) \nBy associative it really means that a xor (b xor c) = (a xor b) xor c (order does not matter at all!) \nBy self inverting it really means that a xor a = 0 \nAnd its identity element is 0 which means that a xor 0 = a = 0 xor a \nThe last two together are the key to the problem, as it means that \n- a xor 0 = a = 0 xor a = a xor a xor a \n\nFrom there, the rest takes some trial and error math \nStart with the idea that matrix at 0, 0 is m00 and that xor matrix at 0, 0 is also m00 but we\'ll write x00 \n\nOkay, then what is x01? \n- x01 = m00 xor m01 \n\nWhat about x02? \n- x02 = m00 xor m01 xor m02 \n- x02 = x01 xor m02 \n\nFrom this we can see that our xor matrix at 0, C is \n- xor_matrix[0][C] = xor_matrix[0][C-1] xor matrix[0][C] \n\nWe can also do the same for the rows, so we now have xor_matrix for 0, c and for r, 0 where c and r are the range of columns and rows of matrix \n\nNow we need to consider a more complex element, like x22. From the problem, we know the long form of x22 \n- x22 = m00 xor m01 xor m02 xor m10 xor m20 xor m11 xor m12 xor m21 xor m22\n\nWe also know some other combinations already \n- x02 = m00 xor m01 xor m02 \n- x20 = m00 xor m10 xor m20 \n- x11 = m00 xor m01 xor m10 xor m11 \n\nWhat about x12 and x21 though? \n- x12 = m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n- x21 = m00 xor m01 xor m10 xor m11 xor m20 xor m21 \n\nNow we need to start putting some things together \n- Notice that x22 can be rewritten using some of our combinations \n- x22 = (m00 xor m01 xor m10 xor m11 xor m20 xor m21) xor (m02 xor m12 xor m22) \n- x22 = x21 xor (m02 xor m12 xor m22) \n\nMuch better! What about the rest though? \n- Notice that we already have them all in one row (that\'s important) \n- Remember that xor is self inverting \n- From there, \n - x12 = m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n - x12 xor m00 xor m01 xor m10 xor m11 = xor m00 xor m01 xor m10 xor m11 xor m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n - WHAT A MESS! It\'s not so bad though once you cancel on the right... \n - x12 xor m00 xor m01 xor m10 xor m11 = m02 xor m12 \n - Still a mess on the right, let\'s fix that \n - x12 xor x11 = m02 xor m12 \n - Now we\'ve gotten somewhere! Let\'s go plug it in... \n - x22 = x21 xor (m02 xor m12 xor m22) \n - x22 = x21 xor x12 xor x11 xor m22 \n\nThat last one is the key to the problem in fact. Notice \n- x22 = x21 xor x12 xor x11 xor m22 \n- x12 = m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n- x12 = x02 xor m10 xor m11 xor m12 \n- x12 = x02 xor (m10 xor m11 xor m12) \n - x11 = m00 xor m01 xor m10 xor m11 \n - x11 xor m00 xor m01 = m00 xor m01 xor m00 xor m01 xor m10 xor m11 \n - x11 xor m00 xor m01 = m10 xor m11 \n - x11 xor x01 = m10 xor m11 \n- x12 = x02 xor x11 xor x01 xor m12 \n\nThis shows that we already solved via induction a more difficult case using an assumed case, namely that \n- for i, j in range 1 <= i < rows and 1 <= j < cols \n - xor_matrix[i][j] = xor_matrix[i-1][j] xor xor_matrix[i][j-1] xor xor_matrix[i-1][j-1] xor matrix[i][j] \n\nFrom here, since we know the way to find all the xor matrix values we can use a mapping and frequency to get towards the answer most readily as the approach lays out \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfind your length of rows and cols and set up an xor matrix frequency map and an xor matrix of size similar to the one provided \n\nSet initial as matrix at 0, 0 \nSet xor matrix frequency at initial to 1 \nfill xor matrix at 0, 0 with initial \n\nLoop r in range 1 to rows \n- set xor matrix at r at 0 to xor_matrix at r - 1 at 0 xor matrix at r at 0\n- increment the xor matrix frequency at this value by 1 \n\nDo the same for c in range 1 to cols \n\nFor r in range 1 to rows \n- for c in range 1 to cols \n - if you already filled this, skip it (happens on r = 0 or c = 0, but can do with one check this way if you prefill with negatives in this case) \n - otherwise \n - xor_matrix[r][c] is the value of xor_matrix at r-1, c xor with xor_matrix at r, c-1 xor with xor_matrix at r-1 c-1 xor with matrix at r, c\n - update the frequency of this value in your frequency mapping \n\nSet count = 0 \nGet the unique value keys from your xor matrix frequency mapping sorted \nIf k is 1, return the item in the xor matrix frequency keys at the back \nOtherwise \n- set current index to back of the xor matrix frequency keys \n - while count is lte k \n - get the amount here in the xor matrix frequency using the currently indexed xor matrix frequency keys. \n - If the amount here + count is gte k -> this is the right key \n - return the item at xor matrix frequency keys at current index \n - otherwise, increment count by the amount here and decrement the current index \n - if your current index is now negative, we didn\'t have that many items!!! return -1 \n - otherwise, keep going until you find it \n\n# Complexity\n- Time complexity : O(r * c) \n - O(r * c) to build and fill the xor matrix frequency \n - O(u log u) to sort the unique value keys of our xor matrix frequency keys \n - O(u) to loop over the unique value keys of our xor matrix frequency \n - The number of unique numbers might seem to be as large as r or c or even r*c. However, even if all the numbers were unique, there are some interesting caveats here. Note that the unique numbers when xored with other unique numbers may not have a unique product. This means that the space of xor unique numbers is less than the unique numbers in the matrix. This implies that u is less than r * c, and may in fact imply that u is less than either r or c entirely! The key takeaway is that r * c is gauranteed to be larger than u, and in so doing larger than u log u even. The reason we can say the second is that the subdomain of xored values is at least logarithmicaly smaller than r * c, as we have not only the identity but the self-inversion to deal with. This means that the space of values is cut in half or better (0 xor a = a and a xor a = 0). Thus, u is at least a logarithmic reduction of r * c, so we compare r * c with log (r * c) * log ( log (r * c)). The log of r * c is strictly less than r * c, so it is that u log u is strictly subdomain to r * c \n\n- Space complexity: O(r * c) \n - As it holds for time complexity, so it holds for space complexity \n\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n # 2D matrix of max size one million (1000 * 1000) \n # all values are non-negative (0 or greater) \n # given integer k in range 1 to matrix size \n # value of coordinate a, b of the matrix is the xor of all matrix[i][j] where \n rows = len(matrix) \n cols = len(matrix[0])\n xor_matrix_frequency = collections.defaultdict(int)\n xor_matrix = [[-1]*cols for _ in range(rows)]\n initial = matrix[0][0]\n xor_matrix[0][0] = initial\n xor_matrix_frequency[initial] = 1 \n for r in range(1, rows) : \n xor_matrix[r][0] = (value := xor_matrix[r-1][0] ^ matrix[r][0])\n xor_matrix_frequency[value]+=1 \n\n for c in range(1, cols) : \n xor_matrix[0][c] = (value := xor_matrix[0][c-1] ^ matrix[0][c])\n xor_matrix_frequency[value] += 1 \n\n for r in range(1, rows) : \n for c in range(1, cols) : \n if xor_matrix[r][c] >= 0 : \n continue \n else : \n xor_matrix[r][c] = (value := xor_matrix[r][c-1] ^ xor_matrix[r-1][c] ^ xor_matrix[r-1][c-1] ^ matrix[r][c])\n xor_matrix_frequency[value] += 1 \n\n # uncomment to see matrices and maps \n # for row in matrix : \n # print(row)\n # print()\n # for row in xor_matrix : \n # print(row)\n # print()\n # for key in xor_matrix_frequency : \n # print(f\'The key {key} appears {xor_matrix_frequency[key]} times in the xor matrix\')\n\n count = 0 \n xor_matrix_frequency_keys = sorted(list(xor_matrix_frequency.keys()))\n if k == 1 : \n return xor_matrix_frequency_keys[-1] \n else : \n current_index = len(xor_matrix_frequency_keys) - 1 \n while count <= k : \n if (amount_here := xor_matrix_frequency[xor_matrix_frequency_keys[current_index]]) + count >= k : \n return xor_matrix_frequency_keys[current_index]\n else : \n count += amount_here \n current_index -= 1 \n if current_index < 0 : \n break \n else : \n continue \n return -1 \n``` | 0 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
XOR Properties | Commented and Explained | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is really about seeing if a candidate understands xor \nXOR is commutative, associative, self-inverting, and has an identity element of 0. \nBy commutative it really means that a xor b = b xor a (order locally does not matter) \nBy associative it really means that a xor (b xor c) = (a xor b) xor c (order does not matter at all!) \nBy self inverting it really means that a xor a = 0 \nAnd its identity element is 0 which means that a xor 0 = a = 0 xor a \nThe last two together are the key to the problem, as it means that \n- a xor 0 = a = 0 xor a = a xor a xor a \n\nFrom there, the rest takes some trial and error math \nStart with the idea that matrix at 0, 0 is m00 and that xor matrix at 0, 0 is also m00 but we\'ll write x00 \n\nOkay, then what is x01? \n- x01 = m00 xor m01 \n\nWhat about x02? \n- x02 = m00 xor m01 xor m02 \n- x02 = x01 xor m02 \n\nFrom this we can see that our xor matrix at 0, C is \n- xor_matrix[0][C] = xor_matrix[0][C-1] xor matrix[0][C] \n\nWe can also do the same for the rows, so we now have xor_matrix for 0, c and for r, 0 where c and r are the range of columns and rows of matrix \n\nNow we need to consider a more complex element, like x22. From the problem, we know the long form of x22 \n- x22 = m00 xor m01 xor m02 xor m10 xor m20 xor m11 xor m12 xor m21 xor m22\n\nWe also know some other combinations already \n- x02 = m00 xor m01 xor m02 \n- x20 = m00 xor m10 xor m20 \n- x11 = m00 xor m01 xor m10 xor m11 \n\nWhat about x12 and x21 though? \n- x12 = m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n- x21 = m00 xor m01 xor m10 xor m11 xor m20 xor m21 \n\nNow we need to start putting some things together \n- Notice that x22 can be rewritten using some of our combinations \n- x22 = (m00 xor m01 xor m10 xor m11 xor m20 xor m21) xor (m02 xor m12 xor m22) \n- x22 = x21 xor (m02 xor m12 xor m22) \n\nMuch better! What about the rest though? \n- Notice that we already have them all in one row (that\'s important) \n- Remember that xor is self inverting \n- From there, \n - x12 = m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n - x12 xor m00 xor m01 xor m10 xor m11 = xor m00 xor m01 xor m10 xor m11 xor m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n - WHAT A MESS! It\'s not so bad though once you cancel on the right... \n - x12 xor m00 xor m01 xor m10 xor m11 = m02 xor m12 \n - Still a mess on the right, let\'s fix that \n - x12 xor x11 = m02 xor m12 \n - Now we\'ve gotten somewhere! Let\'s go plug it in... \n - x22 = x21 xor (m02 xor m12 xor m22) \n - x22 = x21 xor x12 xor x11 xor m22 \n\nThat last one is the key to the problem in fact. Notice \n- x22 = x21 xor x12 xor x11 xor m22 \n- x12 = m00 xor m01 xor m02 xor m10 xor m11 xor m12 \n- x12 = x02 xor m10 xor m11 xor m12 \n- x12 = x02 xor (m10 xor m11 xor m12) \n - x11 = m00 xor m01 xor m10 xor m11 \n - x11 xor m00 xor m01 = m00 xor m01 xor m00 xor m01 xor m10 xor m11 \n - x11 xor m00 xor m01 = m10 xor m11 \n - x11 xor x01 = m10 xor m11 \n- x12 = x02 xor x11 xor x01 xor m12 \n\nThis shows that we already solved via induction a more difficult case using an assumed case, namely that \n- for i, j in range 1 <= i < rows and 1 <= j < cols \n - xor_matrix[i][j] = xor_matrix[i-1][j] xor xor_matrix[i][j-1] xor xor_matrix[i-1][j-1] xor matrix[i][j] \n\nFrom here, since we know the way to find all the xor matrix values we can use a mapping and frequency to get towards the answer most readily as the approach lays out \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfind your length of rows and cols and set up an xor matrix frequency map and an xor matrix of size similar to the one provided \n\nSet initial as matrix at 0, 0 \nSet xor matrix frequency at initial to 1 \nfill xor matrix at 0, 0 with initial \n\nLoop r in range 1 to rows \n- set xor matrix at r at 0 to xor_matrix at r - 1 at 0 xor matrix at r at 0\n- increment the xor matrix frequency at this value by 1 \n\nDo the same for c in range 1 to cols \n\nFor r in range 1 to rows \n- for c in range 1 to cols \n - if you already filled this, skip it (happens on r = 0 or c = 0, but can do with one check this way if you prefill with negatives in this case) \n - otherwise \n - xor_matrix[r][c] is the value of xor_matrix at r-1, c xor with xor_matrix at r, c-1 xor with xor_matrix at r-1 c-1 xor with matrix at r, c\n - update the frequency of this value in your frequency mapping \n\nSet count = 0 \nGet the unique value keys from your xor matrix frequency mapping sorted \nIf k is 1, return the item in the xor matrix frequency keys at the back \nOtherwise \n- set current index to back of the xor matrix frequency keys \n - while count is lte k \n - get the amount here in the xor matrix frequency using the currently indexed xor matrix frequency keys. \n - If the amount here + count is gte k -> this is the right key \n - return the item at xor matrix frequency keys at current index \n - otherwise, increment count by the amount here and decrement the current index \n - if your current index is now negative, we didn\'t have that many items!!! return -1 \n - otherwise, keep going until you find it \n\n# Complexity\n- Time complexity : O(r * c) \n - O(r * c) to build and fill the xor matrix frequency \n - O(u log u) to sort the unique value keys of our xor matrix frequency keys \n - O(u) to loop over the unique value keys of our xor matrix frequency \n - The number of unique numbers might seem to be as large as r or c or even r*c. However, even if all the numbers were unique, there are some interesting caveats here. Note that the unique numbers when xored with other unique numbers may not have a unique product. This means that the space of xor unique numbers is less than the unique numbers in the matrix. This implies that u is less than r * c, and may in fact imply that u is less than either r or c entirely! The key takeaway is that r * c is gauranteed to be larger than u, and in so doing larger than u log u even. The reason we can say the second is that the subdomain of xored values is at least logarithmicaly smaller than r * c, as we have not only the identity but the self-inversion to deal with. This means that the space of values is cut in half or better (0 xor a = a and a xor a = 0). Thus, u is at least a logarithmic reduction of r * c, so we compare r * c with log (r * c) * log ( log (r * c)). The log of r * c is strictly less than r * c, so it is that u log u is strictly subdomain to r * c \n\n- Space complexity: O(r * c) \n - As it holds for time complexity, so it holds for space complexity \n\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n # 2D matrix of max size one million (1000 * 1000) \n # all values are non-negative (0 or greater) \n # given integer k in range 1 to matrix size \n # value of coordinate a, b of the matrix is the xor of all matrix[i][j] where \n rows = len(matrix) \n cols = len(matrix[0])\n xor_matrix_frequency = collections.defaultdict(int)\n xor_matrix = [[-1]*cols for _ in range(rows)]\n initial = matrix[0][0]\n xor_matrix[0][0] = initial\n xor_matrix_frequency[initial] = 1 \n for r in range(1, rows) : \n xor_matrix[r][0] = (value := xor_matrix[r-1][0] ^ matrix[r][0])\n xor_matrix_frequency[value]+=1 \n\n for c in range(1, cols) : \n xor_matrix[0][c] = (value := xor_matrix[0][c-1] ^ matrix[0][c])\n xor_matrix_frequency[value] += 1 \n\n for r in range(1, rows) : \n for c in range(1, cols) : \n if xor_matrix[r][c] >= 0 : \n continue \n else : \n xor_matrix[r][c] = (value := xor_matrix[r][c-1] ^ xor_matrix[r-1][c] ^ xor_matrix[r-1][c-1] ^ matrix[r][c])\n xor_matrix_frequency[value] += 1 \n\n # uncomment to see matrices and maps \n # for row in matrix : \n # print(row)\n # print()\n # for row in xor_matrix : \n # print(row)\n # print()\n # for key in xor_matrix_frequency : \n # print(f\'The key {key} appears {xor_matrix_frequency[key]} times in the xor matrix\')\n\n count = 0 \n xor_matrix_frequency_keys = sorted(list(xor_matrix_frequency.keys()))\n if k == 1 : \n return xor_matrix_frequency_keys[-1] \n else : \n current_index = len(xor_matrix_frequency_keys) - 1 \n while count <= k : \n if (amount_here := xor_matrix_frequency[xor_matrix_frequency_keys[current_index]]) + count >= k : \n return xor_matrix_frequency_keys[current_index]\n else : \n count += amount_here \n current_index -= 1 \n if current_index < 0 : \n break \n else : \n continue \n return -1 \n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
Python Easy solution beats 100%. | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\nUse Prefix Sums\n\n# Complexity\n- Time complexity:\nO(mn)\n\n- Space complexity:\nO(mn)\n\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0])\n col_xor = [0] * n\n ans = []\n for i in range(m):\n row_xor = 0\n for j in range(n):\n col_xor[j] ^= matrix[i][j]\n row_xor ^= col_xor[j]\n ans.append(row_xor)\n return sorted(ans, reverse = True)[k - 1]\n``` | 0 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Python Easy solution beats 100%. | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\nUse Prefix Sums\n\n# Complexity\n- Time complexity:\nO(mn)\n\n- Space complexity:\nO(mn)\n\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n m, n = len(matrix), len(matrix[0])\n col_xor = [0] * n\n ans = []\n for i in range(m):\n row_xor = 0\n for j in range(n):\n col_xor[j] ^= matrix[i][j]\n row_xor ^= col_xor[j]\n ans.append(row_xor)\n return sorted(ans, reverse = True)[k - 1]\n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Python3] Prefix sum & heap | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\nWe have two subtasks here:\n1. Calculate coordinate values\n2. Find K-th maximum\n\nFor the first subtask we can use precalculated partial sums for XORs:\n\n```\nps[i][j] = ps[i-1][j-1] ^ ps[i][j-1] ^ ps[i-1][j] ^ matrix[i][j] for i > 0, j > 0\nps[0][0] = matrix[0][0]\nps[i][0] = ps[i-1][0] for i > 0\nps[0][j] = ps[0][j-1] for j > 0\n```\n\nFor the second subtask we can use min-heap - traversing ``ps`` matrix and keeping min-heap of ``k`` maximum values. \n\nThe result will be the root of the heap after traversing ``ps`` matrix.\n\n# Approach\n1. Calculate partial sums\n2. Traverse partial sums matrix ``ps``, keeping track of ``k`` max values in a min-heap\n\n# Complexity\n- Time complexity:\n$$O(n*m*log(k))$$\n\n- Space complexity:\n$$O(n*m+k)$$\n\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n n, m = len(matrix), len(matrix[0])\n ps = [[0] * m for _ in range(n)]\n ps[0][0] = matrix[0][0]\n for i in range(1, n):\n ps[i][0] = ps[i-1][0] ^ matrix[i][0]\n for j in range(1, m):\n ps[0][j] = ps[0][j-1] ^ matrix[0][j]\n for i in range(1, n):\n for j in range(1, m):\n ps[i][j] = ps[i-1][j-1] ^ ps[i-1][j] ^ ps[i][j-1] ^ matrix[i][j]\n h = []\n for i in range(n):\n for j in range(m):\n if len(h) < k:\n heapq.heappush(h, ps[i][j])\n elif h[0] < ps[i][j]:\n heapq.heappop(h)\n heapq.heappush(h, ps[i][j])\n\n return h[0]\n```\n\nShall you have any questions or concerns - please comment! \nPlease UPVOTE if you like it! | 0 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
[Python3] Prefix sum & heap | find-kth-largest-xor-coordinate-value | 0 | 1 | # Intuition\nWe have two subtasks here:\n1. Calculate coordinate values\n2. Find K-th maximum\n\nFor the first subtask we can use precalculated partial sums for XORs:\n\n```\nps[i][j] = ps[i-1][j-1] ^ ps[i][j-1] ^ ps[i-1][j] ^ matrix[i][j] for i > 0, j > 0\nps[0][0] = matrix[0][0]\nps[i][0] = ps[i-1][0] for i > 0\nps[0][j] = ps[0][j-1] for j > 0\n```\n\nFor the second subtask we can use min-heap - traversing ``ps`` matrix and keeping min-heap of ``k`` maximum values. \n\nThe result will be the root of the heap after traversing ``ps`` matrix.\n\n# Approach\n1. Calculate partial sums\n2. Traverse partial sums matrix ``ps``, keeping track of ``k`` max values in a min-heap\n\n# Complexity\n- Time complexity:\n$$O(n*m*log(k))$$\n\n- Space complexity:\n$$O(n*m+k)$$\n\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n n, m = len(matrix), len(matrix[0])\n ps = [[0] * m for _ in range(n)]\n ps[0][0] = matrix[0][0]\n for i in range(1, n):\n ps[i][0] = ps[i-1][0] ^ matrix[i][0]\n for j in range(1, m):\n ps[0][j] = ps[0][j-1] ^ matrix[0][j]\n for i in range(1, n):\n for j in range(1, m):\n ps[i][j] = ps[i-1][j-1] ^ ps[i-1][j] ^ ps[i][j-1] ^ matrix[i][j]\n h = []\n for i in range(n):\n for j in range(m):\n if len(h) < k:\n heapq.heappush(h, ps[i][j])\n elif h[0] < ps[i][j]:\n heapq.heappop(h)\n heapq.heappush(h, ps[i][j])\n\n return h[0]\n```\n\nShall you have any questions or concerns - please comment! \nPlease UPVOTE if you like it! | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
Python Solution | find-kth-largest-xor-coordinate-value | 0 | 1 | 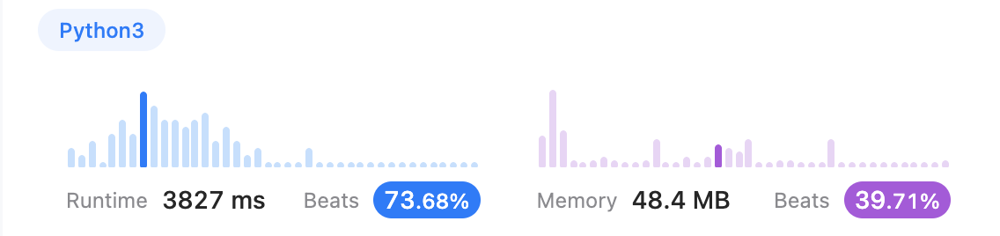\n\n# Approach\n1. The Solution class has a method kthLargestValue that takes in a 2D matrix matrix and an integer k.\n2. We create an empty list xor_vals to store all the XOR values of the matrix.\n3. We loop through each element of the matrix using nested for-loops.\n4. For each element, we calculate its XOR value using the XOR values of the elements to its top, left, and top-left. We use the XOR operator (^) to calculate the XOR value.\n5. We append the XOR value to the xor_vals list.\n6. After all the XOR values have been calculated and added to the xor_vals list, we sort the list in reverse order (highest to lowest) using the sorted function and return the kth element (which is the kth largest XOR value). Note that we subtract 1 from k because the problem is 1-indexed.\n\n# Complexity\n- Time complexity:\n1. Looping through each element in the matrix takes O(mn) time, where m is the number of rows and n is the number of columns.\n2. Calculating the XOR value of each element takes constant time (O(1)).\nAppending the XOR value to the list takes O(1) time.\n3. Sorting the list takes O(nlogn) time, where n is the total number of elements in the matrix (i.e., m x n).\n4. Finally, returning the kth largest XOR value takes O(1) time.\n5. Therefore, the overall time complexity of the function is O(mn + nlogn) or O(n^2 + n log n)\n\n- Space complexity:\n1. We create a list to store all the XOR values, which takes O(mn) space.\n2. We also create some variables to store the loop indices and the XOR values of each element, which take O(1) space.\n3. Therefore, the overall space complexity of the function is O(mn) or O(n^2).\n\n# More \nMore LeetCode problems of mine at https://github.com/aurimas13/Solutions-To-Problems.\nbrute\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n # create an empty list to store all the XOR values\n xor_vals = []\n # loop through each element of the matrix\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n # calculate the XOR value of the current element using the XOR values of the elements to its top, left, and top-left\n if i > 0:\n matrix[i][j] ^= matrix[i-1][j]\n if j > 0:\n matrix[i][j] ^= matrix[i][j-1]\n if i > 0 and j > 0:\n matrix[i][j] ^= matrix[i-1][j-1]\n # append the XOR value to the list of XOR values\n xor_vals.append(matrix[i][j])\n # sort the list of XOR values in reverse order (highest to lowest) and return the kth element (which is the kth largest XOR value)\n return sorted(xor_vals, reverse=True)[k-1]\n\n\n``` | 0 | You are given a 2D `matrix` of size `m x n`, consisting of non-negative integers. You are also given an integer `k`.
The **value** of coordinate `(a, b)` of the matrix is the XOR of all `matrix[i][j]` where `0 <= i <= a < m` and `0 <= j <= b < n` **(0-indexed)**.
Find the `kth` largest value **(1-indexed)** of all the coordinates of `matrix`.
**Example 1:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 1
**Output:** 7
**Explanation:** The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.
**Example 2:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 2
**Output:** 5
**Explanation:** The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.
**Example 3:**
**Input:** matrix = \[\[5,2\],\[1,6\]\], k = 3
**Output:** 4
**Explanation:** The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `0 <= matrix[i][j] <= 106`
* `1 <= k <= m * n` | Try every pair of different cities and calculate its network rank. The network rank of two vertices is almost the sum of their degrees. How can you efficiently check if there is a road connecting two different cities? |
Python Solution | find-kth-largest-xor-coordinate-value | 0 | 1 | \n\n# Approach\n1. The Solution class has a method kthLargestValue that takes in a 2D matrix matrix and an integer k.\n2. We create an empty list xor_vals to store all the XOR values of the matrix.\n3. We loop through each element of the matrix using nested for-loops.\n4. For each element, we calculate its XOR value using the XOR values of the elements to its top, left, and top-left. We use the XOR operator (^) to calculate the XOR value.\n5. We append the XOR value to the xor_vals list.\n6. After all the XOR values have been calculated and added to the xor_vals list, we sort the list in reverse order (highest to lowest) using the sorted function and return the kth element (which is the kth largest XOR value). Note that we subtract 1 from k because the problem is 1-indexed.\n\n# Complexity\n- Time complexity:\n1. Looping through each element in the matrix takes O(mn) time, where m is the number of rows and n is the number of columns.\n2. Calculating the XOR value of each element takes constant time (O(1)).\nAppending the XOR value to the list takes O(1) time.\n3. Sorting the list takes O(nlogn) time, where n is the total number of elements in the matrix (i.e., m x n).\n4. Finally, returning the kth largest XOR value takes O(1) time.\n5. Therefore, the overall time complexity of the function is O(mn + nlogn) or O(n^2 + n log n)\n\n- Space complexity:\n1. We create a list to store all the XOR values, which takes O(mn) space.\n2. We also create some variables to store the loop indices and the XOR values of each element, which take O(1) space.\n3. Therefore, the overall space complexity of the function is O(mn) or O(n^2).\n\n# More \nMore LeetCode problems of mine at https://github.com/aurimas13/Solutions-To-Problems.\nbrute\n# Code\n```\nclass Solution:\n def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:\n # create an empty list to store all the XOR values\n xor_vals = []\n # loop through each element of the matrix\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n # calculate the XOR value of the current element using the XOR values of the elements to its top, left, and top-left\n if i > 0:\n matrix[i][j] ^= matrix[i-1][j]\n if j > 0:\n matrix[i][j] ^= matrix[i][j-1]\n if i > 0 and j > 0:\n matrix[i][j] ^= matrix[i-1][j-1]\n # append the XOR value to the list of XOR values\n xor_vals.append(matrix[i][j])\n # sort the list of XOR values in reverse order (highest to lowest) and return the kth element (which is the kth largest XOR value)\n return sorted(xor_vals, reverse=True)[k-1]\n\n\n``` | 0 | You are given two integers `memory1` and `memory2` representing the available memory in bits on two memory sticks. There is currently a faulty program running that consumes an increasing amount of memory every second.
At the `ith` second (starting from 1), `i` bits of memory are allocated to the stick with **more available memory** (or from the first memory stick if both have the same available memory). If neither stick has at least `i` bits of available memory, the program **crashes**.
Return _an array containing_ `[crashTime, memory1crash, memory2crash]`_, where_ `crashTime` _is the time (in seconds) when the program crashed and_ `memory1crash` _and_ `memory2crash` _are the available bits of memory in the first and second sticks respectively_.
**Example 1:**
**Input:** memory1 = 2, memory2 = 2
**Output:** \[3,1,0\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 1. The first stick now has 1 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 0 bits of available memory.
- At the 3rd second, the program crashes. The sticks have 1 and 0 bits available respectively.
**Example 2:**
**Input:** memory1 = 8, memory2 = 11
**Output:** \[6,0,4\]
**Explanation:** The memory is allocated as follows:
- At the 1st second, 1 bit of memory is allocated to stick 2. The second stick now has 10 bit of available memory.
- At the 2nd second, 2 bits of memory are allocated to stick 2. The second stick now has 8 bits of available memory.
- At the 3rd second, 3 bits of memory are allocated to stick 1. The first stick now has 5 bits of available memory.
- At the 4th second, 4 bits of memory are allocated to stick 2. The second stick now has 4 bits of available memory.
- At the 5th second, 5 bits of memory are allocated to stick 1. The first stick now has 0 bits of available memory.
- At the 6th second, the program crashes. The sticks have 0 and 4 bits available respectively.
**Constraints:**
* `0 <= memory1, memory2 <= 231 - 1` | Use a 2D prefix sum to precalculate the xor-sum of the upper left submatrix. |
[Python3] math | building-boxes | 0 | 1 | **Algo**\nThe **1st observation** is that the base increases as 1, 1+2, 1+2+3, 1+2+3+4, ... When the bases is of the form 1+2+3+...+x, there can be at most `1*x + 2*(x-1) + 3*(x-2) + ... + x*1 = x*(x+1)*(x+2)//6` blocks. So we find the the largest `x` such that `x*(x+1)*(x+2)//6 <= n` as the starting point for which there will be `x*(x+1)//2` blocks at the bottom. \n\nThe **2nd observation** is that once we add blocks to a well-developed piramid \nnext block add 1 bottom block\nnext 2 blocks add 1 bottom block\nnext 3 blocks add 1 bottom block\nThen we can just count how many bottom blocks to add to obsorb all `n` blocks. \n\n**Implementation**\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n x = int((6*n)**(1/3))\n if x*(x+1)*(x+2) > 6*n: x -= 1\n \n ans = x*(x+1)//2\n n -= x*(x+1)*(x+2)//6\n k = 1\n while n > 0: \n ans += 1\n n -= k\n k += 1\n return ans \n```\n\n**Analysis**\nTime complexity `O(sqrt(N))`\nSpace complexity `O(1)`\n\n**Edited on 1/24/2021**\nAdding a `O(1)` solution\nThis implementation is to elaborate on the aforementioned algo. Here, we solve two equations. First, we find largest integer `x` such that `x*(x+1)*(x+2) <= 6*n`. This represents a fully-developed piramid with `x*(x+1)*(x+2)//6` blocks and `x*(x+1)//2` bottom blocks. \nThen, we remove `x*(x+1)*(x+2)//6` from `n`. For the remaining blocks (`rem = n - x*(x+1)*(x+2)//6`), suppose we need another `y` bottom blocks. Then, `1 + 2 + ... + y = y*(y+1) >= rem`, where `y` can be calculated by solving the quadratic equation. \n\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n x = int((6*n)**(1/3))\n if x*(x+1)*(x+2) > 6*n: x -= 1\n n -= x*(x+1)*(x+2)//6\n return x*(x+1)//2 + ceil((sqrt(1+8*n)-1)/2)\n``` | 12 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
[Python3] math | building-boxes | 0 | 1 | **Algo**\nThe **1st observation** is that the base increases as 1, 1+2, 1+2+3, 1+2+3+4, ... When the bases is of the form 1+2+3+...+x, there can be at most `1*x + 2*(x-1) + 3*(x-2) + ... + x*1 = x*(x+1)*(x+2)//6` blocks. So we find the the largest `x` such that `x*(x+1)*(x+2)//6 <= n` as the starting point for which there will be `x*(x+1)//2` blocks at the bottom. \n\nThe **2nd observation** is that once we add blocks to a well-developed piramid \nnext block add 1 bottom block\nnext 2 blocks add 1 bottom block\nnext 3 blocks add 1 bottom block\nThen we can just count how many bottom blocks to add to obsorb all `n` blocks. \n\n**Implementation**\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n x = int((6*n)**(1/3))\n if x*(x+1)*(x+2) > 6*n: x -= 1\n \n ans = x*(x+1)//2\n n -= x*(x+1)*(x+2)//6\n k = 1\n while n > 0: \n ans += 1\n n -= k\n k += 1\n return ans \n```\n\n**Analysis**\nTime complexity `O(sqrt(N))`\nSpace complexity `O(1)`\n\n**Edited on 1/24/2021**\nAdding a `O(1)` solution\nThis implementation is to elaborate on the aforementioned algo. Here, we solve two equations. First, we find largest integer `x` such that `x*(x+1)*(x+2) <= 6*n`. This represents a fully-developed piramid with `x*(x+1)*(x+2)//6` blocks and `x*(x+1)//2` bottom blocks. \nThen, we remove `x*(x+1)*(x+2)//6` from `n`. For the remaining blocks (`rem = n - x*(x+1)*(x+2)//6`), suppose we need another `y` bottom blocks. Then, `1 + 2 + ... + y = y*(y+1) >= rem`, where `y` can be calculated by solving the quadratic equation. \n\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n x = int((6*n)**(1/3))\n if x*(x+1)*(x+2) > 6*n: x -= 1\n n -= x*(x+1)*(x+2)//6\n return x*(x+1)//2 + ceil((sqrt(1+8*n)-1)/2)\n``` | 12 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Math with breakdown and comments | Based on work by other poster | building-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck the comments for the breakdown and go check the original posters work. Was very well done, reposting only to get the math notated and keep for personal use. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# great math breakdown here : https://leetcode.com/problems/building-boxes/solutions/2792603/python-tetrahedral-and-triangular-numbers-o-m-1-3/\n# note some nomenclature mistakes corrected in the comments herein. Hopefully a clearer read. \n# wiki has useful breakdown of triangular numbers here : https://en.wikipedia.org/wiki/Triangular_number\n# wiki has useful breakdown of tetrahedral numbers here : https://en.wikipedia.org/wiki/Tetrahedral_number\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n # set up lambda function for use in problem \n cubic = lambda x : x**(1.0/3.0)\n\n # find the first tetrahedral number gte n \n # spot the wiki equation where a multiplication of 27n occurs here to make math nicer\n first_tetrahedral = cubic(math.sqrt(3)*math.sqrt(243*(n**2) - 1) + 27 * n)\n # find the nth tetrahedral number accordingly again, notice impact of factoring on this part \n nth_tetrahedral = math.ceil(first_tetrahedral/cubic(9) + 1.0/(cubic(3)*first_tetrahedral) - 1)\n\n # if n is the nth triangular number, return the gaussian sum evaluation of the nth tetrahedral\n nth_triangular = nth_tetrahedral*(nth_tetrahedral + 1) * (nth_tetrahedral + 2) // 6\n # gaussian sum of numbers between i and j is n * n + 1 // 2 \n gaussian_sum = nth_tetrahedral * (nth_tetrahedral + 1) // 2 \n # if our n is a triangular number, the answer is a gaussium sum of the nth tetrahedral value \n if n == nth_triangular : \n return gaussian_sum \n else : \n # otherwise, we must start at our limited result and move backwards \n answer = gaussian_sum\n # where our upper limit must be the nth_triangular, which we now know is too much \n limit = nth_triangular + 1 \n while n < limit : \n # where our limit will move by the tetrahedralth valuation \n limit -= nth_tetrahedral\n # our answer will reduce by 1 as we reduce our summation accordingly \n answer -= 1 \n # and our tetrahedral then moves back by one after adjustment elsewhere \n nth_tetrahedral -= 1 \n # we then will be off by 1 due to our limits nature and adjust by 1 \n return answer + 1 \n\n\n``` | 0 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
Math with breakdown and comments | Based on work by other poster | building-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck the comments for the breakdown and go check the original posters work. Was very well done, reposting only to get the math notated and keep for personal use. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# great math breakdown here : https://leetcode.com/problems/building-boxes/solutions/2792603/python-tetrahedral-and-triangular-numbers-o-m-1-3/\n# note some nomenclature mistakes corrected in the comments herein. Hopefully a clearer read. \n# wiki has useful breakdown of triangular numbers here : https://en.wikipedia.org/wiki/Triangular_number\n# wiki has useful breakdown of tetrahedral numbers here : https://en.wikipedia.org/wiki/Tetrahedral_number\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n # set up lambda function for use in problem \n cubic = lambda x : x**(1.0/3.0)\n\n # find the first tetrahedral number gte n \n # spot the wiki equation where a multiplication of 27n occurs here to make math nicer\n first_tetrahedral = cubic(math.sqrt(3)*math.sqrt(243*(n**2) - 1) + 27 * n)\n # find the nth tetrahedral number accordingly again, notice impact of factoring on this part \n nth_tetrahedral = math.ceil(first_tetrahedral/cubic(9) + 1.0/(cubic(3)*first_tetrahedral) - 1)\n\n # if n is the nth triangular number, return the gaussian sum evaluation of the nth tetrahedral\n nth_triangular = nth_tetrahedral*(nth_tetrahedral + 1) * (nth_tetrahedral + 2) // 6\n # gaussian sum of numbers between i and j is n * n + 1 // 2 \n gaussian_sum = nth_tetrahedral * (nth_tetrahedral + 1) // 2 \n # if our n is a triangular number, the answer is a gaussium sum of the nth tetrahedral value \n if n == nth_triangular : \n return gaussian_sum \n else : \n # otherwise, we must start at our limited result and move backwards \n answer = gaussian_sum\n # where our upper limit must be the nth_triangular, which we now know is too much \n limit = nth_triangular + 1 \n while n < limit : \n # where our limit will move by the tetrahedralth valuation \n limit -= nth_tetrahedral\n # our answer will reduce by 1 as we reduce our summation accordingly \n answer -= 1 \n # and our tetrahedral then moves back by one after adjustment elsewhere \n nth_tetrahedral -= 1 \n # we then will be off by 1 due to our limits nature and adjust by 1 \n return answer + 1 \n\n\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python (Simple Maths) | building-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumBoxes(self, n):\n floor,inc,cur = 0,1,0\n\n while cur + floor + inc <= n:\n floor += inc\n inc += 1\n cur += floor\n\n remain, j = n-cur, 1\n\n while remain > 0:\n floor += 1\n remain -= j\n j += 1\n\n return floor\n\n\n\n\n\n\n\n\n\n\n\n \n\n \n\n\n\n \n \n``` | 0 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
Python (Simple Maths) | building-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumBoxes(self, n):\n floor,inc,cur = 0,1,0\n\n while cur + floor + inc <= n:\n floor += inc\n inc += 1\n cur += floor\n\n remain, j = n-cur, 1\n\n while remain > 0:\n floor += 1\n remain -= j\n j += 1\n\n return floor\n\n\n\n\n\n\n\n\n\n\n\n \n\n \n\n\n\n \n \n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Solution | building-boxes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minimumBoxes(int n) {\n int sum = 1, base = 1, row = 1;\n while (sum < n) {\n base += (++row);\n sum += base;\n }\n while (sum > n) {\n --base;\n sum -= (row--);\n }\n return base + (sum < n);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n \n p = -1\n q = 3*n\n r = 2/3\n L = floor((q + (q**2 + (r - p**2)**3)**(1/2))**(1/3) + (q - (q**2 + (r - p**2)**3)**(1/2))**(1/3) + p + 0.0001)\n \n diff = n - (L)*(L+1)*(L+2)//6\n return ceil(((1 + 8*diff)**0.5 - 1)/2) + (L*(L+1))\n```\n\n```Java []\nclass Solution {\n public int minimumBoxes(int n) {\n if (n<=3) {return n;}\n long i = (long)(Math.cbrt(n*6L))-1;\n if ((long)(i+3)*(i+2)*(i+1)<6L*n) {i++;}\n long floor = i*(i+1)/2L, sum = (i+2)*(i+1)*i/6L;\n long diff = n-sum;\n double f = (-1 + Math.sqrt(1.0+4*2*diff))/2.0;\n return (int) floor + (int) Math.ceil(f);\n }\n}\n```\n | 0 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
Solution | building-boxes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minimumBoxes(int n) {\n int sum = 1, base = 1, row = 1;\n while (sum < n) {\n base += (++row);\n sum += base;\n }\n while (sum > n) {\n --base;\n sum -= (row--);\n }\n return base + (sum < n);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n \n p = -1\n q = 3*n\n r = 2/3\n L = floor((q + (q**2 + (r - p**2)**3)**(1/2))**(1/3) + (q - (q**2 + (r - p**2)**3)**(1/2))**(1/3) + p + 0.0001)\n \n diff = n - (L)*(L+1)*(L+2)//6\n return ceil(((1 + 8*diff)**0.5 - 1)/2) + (L*(L+1))\n```\n\n```Java []\nclass Solution {\n public int minimumBoxes(int n) {\n if (n<=3) {return n;}\n long i = (long)(Math.cbrt(n*6L))-1;\n if ((long)(i+3)*(i+2)*(i+1)<6L*n) {i++;}\n long floor = i*(i+1)/2L, sum = (i+2)*(i+1)*i/6L;\n long diff = n-sum;\n double f = (-1 + Math.sqrt(1.0+4*2*diff))/2.0;\n return (int) floor + (int) Math.ceil(f);\n }\n}\n```\n | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Loop based O(n) solution | building-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nanswer for n=1--> 1\nn=2 (1+1)-->2\nn=3 (1+1+1)->3\nn=4 (1+1+2)->3\nn=5 (1+1+2+1)-->4\nn=6 (1+1+2+1+1)->5\nn=7 (1+1+2+1+2)->5\nn=8(1+1+2+1+2+1)->6\nn=9 (1+1+2+1+2+2)->6\nn=10 (1+1+2+1+2+3) ->6\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe need to iterate the loop with jump of corresponding to the pattern described above. We have to keep track of count of numbers in the sequence which is our answer. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) \n# Code\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n answer=curr=i=j=0\n \n while curr<n: \n if j<i:\n j+=1\n else:\n j=1\n i+=1 \n curr+=j\n answer+=1\n\n return answer\n\n \n\n\n \n``` | 0 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
Loop based O(n) solution | building-boxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nanswer for n=1--> 1\nn=2 (1+1)-->2\nn=3 (1+1+1)->3\nn=4 (1+1+2)->3\nn=5 (1+1+2+1)-->4\nn=6 (1+1+2+1+1)->5\nn=7 (1+1+2+1+2)->5\nn=8(1+1+2+1+2+1)->6\nn=9 (1+1+2+1+2+2)->6\nn=10 (1+1+2+1+2+3) ->6\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe need to iterate the loop with jump of corresponding to the pattern described above. We have to keep track of count of numbers in the sequence which is our answer. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) \n# Code\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n answer=curr=i=j=0\n \n while curr<n: \n if j<i:\n j+=1\n else:\n j=1\n i+=1 \n curr+=j\n answer+=1\n\n return answer\n\n \n\n\n \n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
✅Python 3 - Math - fast (80%+) - detailed explanation - with example 😃 | building-boxes | 0 | 1 | 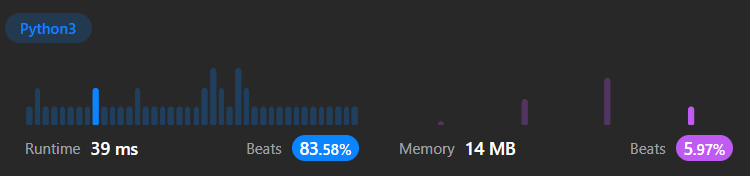\n\n# Approach\n1. find parameters of the perfect corner piramide \nfor `n = 38`: `side = 5`, `square = 15`, `volume = 35`\n\n- we can **decompose** corner piramid **into layouts**\n\n\n```\n5 4 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\n4 3 2 1 = 1 1 1 1 + 1 1 1 + 1 1 + 1 +\n3 2 1 1 1 1 1 1 1\n2 1 1 1 1\n1 1 \n\n35 = 15 + 10 + 6 + 3 + 1 \n```\n- each layout is [triangular number](https://en.wikipedia.org/wiki/Triangular_number), we can compute sum for each layout:\n$$T_n = \\sum_{k=1}^{n} k = 1 + 2 + 3 + .. + n = \\frac{n * (n + 1)}{2} $$\n\n\n```\nside 1: 1 * (1 + 1) / 2 = 1\nside 2: 2 * (2 + 1) / 2 = 3\nside 3: 3 * (3 + 1) / 2 = 6\nside 4: 4 * (4 + 1) / 2 = 10\nside 5: 5 * (5 + 1) / 2 = 15\n\npiramid with side = 5 is already occupied 15 cells\n\n```\n\n- moreover, we can compute volume for perfect piramid by using formula\n**the sum of the first n triangular numbers**:\n$$\\sum_{k=1}^{n}T_k = \\sum_{k=1}^{n} \\frac{k * (k + 1)}{2} = \\frac{n * (n + 1) * (n + 2)}{6} $$\n```\nside 5: 5 * (5 + 1) * (5 + 2) / 6 = 35\n\npiramid with side = 5 contains 35 boxes\n\n```\n#\n\n2. We knew that our piramid with `side = 5` is **already occupied** `15` cells\nGreat! We have `3` extra boxes `n = 38` - ` volume = 35`\n\n- we can **imitate** process for remained boxes\n\n\n```\npiramid add box 1 add box 2 add box 3\n\n5 4 3 2 1 5 4 3 2 1 5 4 3 2 1 5 4 3 2 1\n4 3 2 1 --> 4 3 2 1 --> 4 3 2 1 --> 4 3 2 1 \n3 2 1 3 2 1 3 2 1 3 2 1 \n2 1 2 1 2 1 2 1 \n1 1 1 2<- ->2 2 \n 1<- 1 1\n \n + 1 cell + 1 cell + 0 cell\n\nplus 2 occupied cells \n```\n- we increase counter by one for every 1, 2, 3, 4 .. boxes\n - 1-st occupied cell let us place 1 more box\n - 2-nd occupied cell let us place 2 more boxes\n - 3-rd occupied cell let us place 3 more boxes \nand so on..\n\n# Code\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n\n # compute parameters of piramid: side, square, volume \n side, vol = 0, 0\n while n >= vol: \n side += 1\n vol = side * (side + 1) * (side + 2) // 6\n # we exceeded n, so decrease side by 1\n # compute parameters\n side -= 1\n vol = side * (side + 1) * (side + 2) // 6\n sqr = side * (side + 1) // 2\n \n cnt = sqr \n n -= vol # find number of boxes remained\n \n # imitate process for remained boxes\n i = 1\n while n > 0:\n n -= i\n i += 1\n cnt += 1\n \n return cnt\n``` | 0 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
✅Python 3 - Math - fast (80%+) - detailed explanation - with example 😃 | building-boxes | 0 | 1 | \n\n# Approach\n1. find parameters of the perfect corner piramide \nfor `n = 38`: `side = 5`, `square = 15`, `volume = 35`\n\n- we can **decompose** corner piramid **into layouts**\n\n\n```\n5 4 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\n4 3 2 1 = 1 1 1 1 + 1 1 1 + 1 1 + 1 +\n3 2 1 1 1 1 1 1 1\n2 1 1 1 1\n1 1 \n\n35 = 15 + 10 + 6 + 3 + 1 \n```\n- each layout is [triangular number](https://en.wikipedia.org/wiki/Triangular_number), we can compute sum for each layout:\n$$T_n = \\sum_{k=1}^{n} k = 1 + 2 + 3 + .. + n = \\frac{n * (n + 1)}{2} $$\n\n\n```\nside 1: 1 * (1 + 1) / 2 = 1\nside 2: 2 * (2 + 1) / 2 = 3\nside 3: 3 * (3 + 1) / 2 = 6\nside 4: 4 * (4 + 1) / 2 = 10\nside 5: 5 * (5 + 1) / 2 = 15\n\npiramid with side = 5 is already occupied 15 cells\n\n```\n\n- moreover, we can compute volume for perfect piramid by using formula\n**the sum of the first n triangular numbers**:\n$$\\sum_{k=1}^{n}T_k = \\sum_{k=1}^{n} \\frac{k * (k + 1)}{2} = \\frac{n * (n + 1) * (n + 2)}{6} $$\n```\nside 5: 5 * (5 + 1) * (5 + 2) / 6 = 35\n\npiramid with side = 5 contains 35 boxes\n\n```\n#\n\n2. We knew that our piramid with `side = 5` is **already occupied** `15` cells\nGreat! We have `3` extra boxes `n = 38` - ` volume = 35`\n\n- we can **imitate** process for remained boxes\n\n\n```\npiramid add box 1 add box 2 add box 3\n\n5 4 3 2 1 5 4 3 2 1 5 4 3 2 1 5 4 3 2 1\n4 3 2 1 --> 4 3 2 1 --> 4 3 2 1 --> 4 3 2 1 \n3 2 1 3 2 1 3 2 1 3 2 1 \n2 1 2 1 2 1 2 1 \n1 1 1 2<- ->2 2 \n 1<- 1 1\n \n + 1 cell + 1 cell + 0 cell\n\nplus 2 occupied cells \n```\n- we increase counter by one for every 1, 2, 3, 4 .. boxes\n - 1-st occupied cell let us place 1 more box\n - 2-nd occupied cell let us place 2 more boxes\n - 3-rd occupied cell let us place 3 more boxes \nand so on..\n\n# Code\n```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n\n # compute parameters of piramid: side, square, volume \n side, vol = 0, 0\n while n >= vol: \n side += 1\n vol = side * (side + 1) * (side + 2) // 6\n # we exceeded n, so decrease side by 1\n # compute parameters\n side -= 1\n vol = side * (side + 1) * (side + 2) // 6\n sqr = side * (side + 1) // 2\n \n cnt = sqr \n n -= vol # find number of boxes remained\n \n # imitate process for remained boxes\n i = 1\n while n > 0:\n n -= i\n i += 1\n cnt += 1\n \n return cnt\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python | Tetrahedral and Triangular Numbers | O(m^1/3) | building-boxes | 0 | 1 | # Complexity\n- Time complexity:\nLet $$m$$ be the number number of boxes. The complexity is $$O(m^{1/3})$$ in the worst case, but only $$O(\\log m)$$ if $$m$$ is a tetrahedral number. This follows because the ```while``` loop runs at most $$n$$ times (where $$n$$ refers to the $$n$$th tetrahedral number), and $$m$$ is on the order of $$n^3$$. (The $$n$$th tetrahedral number is given by $$n(n+1)(n+2)/6$$.)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minimumBoxes(self, m: int) -> int:\n def cbrt(x):\n return x**(1. / 3)\n\n # Find the first tetrahedral number greater than\n # or equal to m.\n x = cbrt(sqrt(3)*sqrt(243*(m**2) - 1) + 27*m)\n n = ceil(x/cbrt(9) + 1/(cbrt(3)*x) - 1)\n \n # If m is the nth tetrahedral number, return the\n # nth triangular number (the base).\n t_n =n*(n+1)*(n+2) // 6 \n if m == t_n:\n return n*(n+1)//2\n\n # Otherwise, we must adjust the answer.\n ans = n*(n+1)//2\n j = t_n + 1\n while m < j:\n j -= n\n ans -= 1\n n -= 1\n\n return ans + 1\n\n``` | 0 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
Python | Tetrahedral and Triangular Numbers | O(m^1/3) | building-boxes | 0 | 1 | # Complexity\n- Time complexity:\nLet $$m$$ be the number number of boxes. The complexity is $$O(m^{1/3})$$ in the worst case, but only $$O(\\log m)$$ if $$m$$ is a tetrahedral number. This follows because the ```while``` loop runs at most $$n$$ times (where $$n$$ refers to the $$n$$th tetrahedral number), and $$m$$ is on the order of $$n^3$$. (The $$n$$th tetrahedral number is given by $$n(n+1)(n+2)/6$$.)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minimumBoxes(self, m: int) -> int:\n def cbrt(x):\n return x**(1. / 3)\n\n # Find the first tetrahedral number greater than\n # or equal to m.\n x = cbrt(sqrt(3)*sqrt(243*(m**2) - 1) + 27*m)\n n = ceil(x/cbrt(9) + 1/(cbrt(3)*x) - 1)\n \n # If m is the nth tetrahedral number, return the\n # nth triangular number (the base).\n t_n =n*(n+1)*(n+2) // 6 \n if m == t_n:\n return n*(n+1)//2\n\n # Otherwise, we must adjust the answer.\n ans = n*(n+1)//2\n j = t_n + 1\n while m < j:\n j -= n\n ans -= 1\n n -= 1\n\n return ans + 1\n\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python | Detailed Explanation | building-boxes | 0 | 1 | # Theory\nThe solution I arrived at is based upon a couple of patterns that the problem presents.\n1. The overall shape of the boxes tends toward a quarter-pyramid shape, appearing as a triangle when viewed top-down.\n```\n00000\n0000\n000\n00\n0\n```\n2. Given a full quarter-pyramid taking up `r` rows, the pyramid will have a maximum height of `r` at the top-left corner. Each row down begins at a height 1 less than the previous row, and each column right has a value one less than the previous column in its row. This produces a fairly distinctive pattern.\n```\n54321\n4321\n321\n21\n1\n```\n3. When a full quarter-pyramid is formed, a new box may be placed in a new row, and each additional box placed on the floor (moving up each row) will increase the total number of boxes the quarter-pyramid can hold by one more than the last floor box.\n```text\nbase +1 +2 +3 +4 +5 +6\n54321 54321 54321 54321 54321 54321 654321\n4321 4321 4321 4321 4321 54321 54321\n321 321 321 321 4321 4321 4321\n21 21 21 321 321 321 321\n1 1 21 21 21 21 21\n 1 1 1 1 1 1\n```\nFrom point #1, we know that a complete quarter-pyramid of `r` rows can hold at most `m` floor boxes such that:\n\n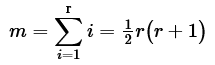\n\nFrom point #2, we know that a complete quarter-pyramid of `r` rows can hold at most `n_upper` total boxes such that:\n\n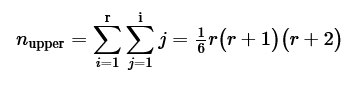\n\nFrom point #3, we know that if we can find the smallest possible `r` such that `n_upper >= n`, then we can begin removing floor boxes by first removing `r` boxes from `n_upper`, then `r-1` boxes, `r-2` boxes, and so on, decrementing `m` each time, until a point is reached where `n_upper` would become less than `n`. At this point, the procedure is aborted and `m` is returned representing the minimum number of floor boxes capable of holding `n` boxes.\n\n---\n\n# Code\n\n```python\nclass Solution:\n\tdef minimumBoxes(self, n: int) -> int:\n\t\tr = 0\n\t\twhile (n_upper := r*(r+1)*(r+2)//6) < n:\n\t\t\tr += 1\n\t\tm = r*(r+1)//2\n\t\tfor i in range(r, 0, -1):\n\t\t\tif (n_upper - i) < n:\n\t\t\t\tbreak\n\t\t\tn_upper -= i\n\t\t\tm -= 1\n\t\treturn m\n``` | 1 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
Python | Detailed Explanation | building-boxes | 0 | 1 | # Theory\nThe solution I arrived at is based upon a couple of patterns that the problem presents.\n1. The overall shape of the boxes tends toward a quarter-pyramid shape, appearing as a triangle when viewed top-down.\n```\n00000\n0000\n000\n00\n0\n```\n2. Given a full quarter-pyramid taking up `r` rows, the pyramid will have a maximum height of `r` at the top-left corner. Each row down begins at a height 1 less than the previous row, and each column right has a value one less than the previous column in its row. This produces a fairly distinctive pattern.\n```\n54321\n4321\n321\n21\n1\n```\n3. When a full quarter-pyramid is formed, a new box may be placed in a new row, and each additional box placed on the floor (moving up each row) will increase the total number of boxes the quarter-pyramid can hold by one more than the last floor box.\n```text\nbase +1 +2 +3 +4 +5 +6\n54321 54321 54321 54321 54321 54321 654321\n4321 4321 4321 4321 4321 54321 54321\n321 321 321 321 4321 4321 4321\n21 21 21 321 321 321 321\n1 1 21 21 21 21 21\n 1 1 1 1 1 1\n```\nFrom point #1, we know that a complete quarter-pyramid of `r` rows can hold at most `m` floor boxes such that:\n\n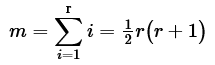\n\nFrom point #2, we know that a complete quarter-pyramid of `r` rows can hold at most `n_upper` total boxes such that:\n\n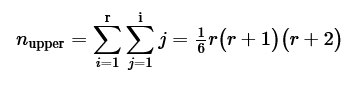\n\nFrom point #3, we know that if we can find the smallest possible `r` such that `n_upper >= n`, then we can begin removing floor boxes by first removing `r` boxes from `n_upper`, then `r-1` boxes, `r-2` boxes, and so on, decrementing `m` each time, until a point is reached where `n_upper` would become less than `n`. At this point, the procedure is aborted and `m` is returned representing the minimum number of floor boxes capable of holding `n` boxes.\n\n---\n\n# Code\n\n```python\nclass Solution:\n\tdef minimumBoxes(self, n: int) -> int:\n\t\tr = 0\n\t\twhile (n_upper := r*(r+1)*(r+2)//6) < n:\n\t\t\tr += 1\n\t\tm = r*(r+1)//2\n\t\tfor i in range(r, 0, -1):\n\t\t\tif (n_upper - i) < n:\n\t\t\t\tbreak\n\t\t\tn_upper -= i\n\t\t\tm -= 1\n\t\treturn m\n``` | 1 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
[python3] Fastest & Most Elegant Script | building-boxes | 0 | 1 | ```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n a = 0\n b = 0\n s = 0\n while n > s:\n a += 1\n b += a\n s += b\n while n <= s:\n s -= a\n a -= 1\n b -= 1\n return b + 1\n``` | 1 | You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
* You can place the boxes anywhere on the floor.
* If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
**Example 1:**
**Input:** n = 3
**Output:** 3
**Explanation:** The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 2:**
**Input:** n = 4
**Output:** 3
**Explanation:** The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.
**Example 3:**
**Input:** n = 10
**Output:** 6
**Explanation:** The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.
**Constraints:**
* `1 <= n <= 109` | Try finding the largest prefix form a that matches a suffix in b Try string matching |
[python3] Fastest & Most Elegant Script | building-boxes | 0 | 1 | ```\nclass Solution:\n def minimumBoxes(self, n: int) -> int:\n a = 0\n b = 0\n s = 0\n while n > s:\n a += 1\n b += a\n s += b\n while n <= s:\n s -= a\n a -= 1\n b -= 1\n return b + 1\n``` | 1 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python3 Solution | Well commented | Better than 94% in Runtime and 90% in Memory distribution | maximum-number-of-balls-in-a-box | 0 | 1 | ```\n\nclass Solution:\n def countBalls(self, lowLimit: int, highLimit: int) -> int:\n \n # Function which will take integer number as an input and return it\'s sum\n # if input is 123 then it\'ll return 6 (1+2+3)\n \n def numberSum(number:int)->int:\n sum1 = 0\n while number:\n sum1 += number%10\n number = number //10\n return sum1\n \n # create a hashmap having key as box number and value as box count\n hashMap = defaultdict(int)\n \n for i in range(lowLimit, highLimit+1):\n # pass i to numberSum function inorder to find it\'s sum1\n # Once sum1 is found, we\'ll use this sum1 as our hash_val\n # If box has alreary one ball avaiable then increment it by one\n hash_val = numberSum(i)\n hashMap[hash_val] += 1\n \n # Check balls in every box\n # hashMap.values() will create an array of balls count in each box.\n values = hashMap.values()\n \n # return maximum balls in boxes\n return max(values)\n\n```\n\nUpvote this post if you like it.\nShare your solution below, let\'s discuss it and learn \u270C | 11 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Python3 Solution | Well commented | Better than 94% in Runtime and 90% in Memory distribution | maximum-number-of-balls-in-a-box | 0 | 1 | ```\n\nclass Solution:\n def countBalls(self, lowLimit: int, highLimit: int) -> int:\n \n # Function which will take integer number as an input and return it\'s sum\n # if input is 123 then it\'ll return 6 (1+2+3)\n \n def numberSum(number:int)->int:\n sum1 = 0\n while number:\n sum1 += number%10\n number = number //10\n return sum1\n \n # create a hashmap having key as box number and value as box count\n hashMap = defaultdict(int)\n \n for i in range(lowLimit, highLimit+1):\n # pass i to numberSum function inorder to find it\'s sum1\n # Once sum1 is found, we\'ll use this sum1 as our hash_val\n # If box has alreary one ball avaiable then increment it by one\n hash_val = numberSum(i)\n hashMap[hash_val] += 1\n \n # Check balls in every box\n # hashMap.values() will create an array of balls count in each box.\n values = hashMap.values()\n \n # return maximum balls in boxes\n return max(values)\n\n```\n\nUpvote this post if you like it.\nShare your solution below, let\'s discuss it and learn \u270C | 11 | You are given a **0-indexed** string `s` that has lowercase English letters in its **even** indices and digits in its **odd** indices.
There is a function `shift(c, x)`, where `c` is a character and `x` is a digit, that returns the `xth` character after `c`.
* For example, `shift('a', 5) = 'f'` and `shift('x', 0) = 'x'`.
For every **odd** index `i`, you want to replace the digit `s[i]` with `shift(s[i-1], s[i])`.
Return `s` _after replacing all digits. It is **guaranteed** that_ `shift(s[i-1], s[i])` _will never exceed_ `'z'`.
**Example 1:**
**Input:** s = "a1c1e1 "
**Output:** "abcdef "
**Explanation:** The digits are replaced as follows:
- s\[1\] -> shift('a',1) = 'b'
- s\[3\] -> shift('c',1) = 'd'
- s\[5\] -> shift('e',1) = 'f'
**Example 2:**
**Input:** s = "a1b2c3d4e "
**Output:** "abbdcfdhe "
**Explanation:** The digits are replaced as follows:
- s\[1\] -> shift('a',1) = 'b'
- s\[3\] -> shift('b',2) = 'd'
- s\[5\] -> shift('c',3) = 'f'
- s\[7\] -> shift('d',4) = 'h'
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists only of lowercase English letters and digits.
* `shift(s[i-1], s[i]) <= 'z'` for all **odd** indices `i`. | Note that both lowLimit and highLimit are of small constraints so you can iterate on all nubmer between them You can simulate the boxes by counting for each box the number of balls with digit sum equal to that box number |
[Python3] freq table | maximum-number-of-balls-in-a-box | 0 | 1 | **Algo**\nScan through all numbers from `lowLimit` to `highLimit` and calculate their sum of digits. Maintain a frequency table to keep track of their frequency. \n\n**Implementation**\n```\nclass Solution:\n def countBalls(self, lowLimit: int, highLimit: int) -> int:\n freq = defaultdict(int)\n for x in range(lowLimit, highLimit+1):\n freq[sum(int(xx) for xx in str(x))] += 1\n return max(freq.values())\n```\n\n**Analysis**\nTime complexity `O(NlogM)`\nSpace complexity `O(logN)` | 13 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
[Python3] freq table | maximum-number-of-balls-in-a-box | 0 | 1 | **Algo**\nScan through all numbers from `lowLimit` to `highLimit` and calculate their sum of digits. Maintain a frequency table to keep track of their frequency. \n\n**Implementation**\n```\nclass Solution:\n def countBalls(self, lowLimit: int, highLimit: int) -> int:\n freq = defaultdict(int)\n for x in range(lowLimit, highLimit+1):\n freq[sum(int(xx) for xx in str(x))] += 1\n return max(freq.values())\n```\n\n**Analysis**\nTime complexity `O(NlogM)`\nSpace complexity `O(logN)` | 13 | You are given a **0-indexed** string `s` that has lowercase English letters in its **even** indices and digits in its **odd** indices.
There is a function `shift(c, x)`, where `c` is a character and `x` is a digit, that returns the `xth` character after `c`.
* For example, `shift('a', 5) = 'f'` and `shift('x', 0) = 'x'`.
For every **odd** index `i`, you want to replace the digit `s[i]` with `shift(s[i-1], s[i])`.
Return `s` _after replacing all digits. It is **guaranteed** that_ `shift(s[i-1], s[i])` _will never exceed_ `'z'`.
**Example 1:**
**Input:** s = "a1c1e1 "
**Output:** "abcdef "
**Explanation:** The digits are replaced as follows:
- s\[1\] -> shift('a',1) = 'b'
- s\[3\] -> shift('c',1) = 'd'
- s\[5\] -> shift('e',1) = 'f'
**Example 2:**
**Input:** s = "a1b2c3d4e "
**Output:** "abbdcfdhe "
**Explanation:** The digits are replaced as follows:
- s\[1\] -> shift('a',1) = 'b'
- s\[3\] -> shift('b',2) = 'd'
- s\[5\] -> shift('c',3) = 'f'
- s\[7\] -> shift('d',4) = 'h'
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists only of lowercase English letters and digits.
* `shift(s[i-1], s[i]) <= 'z'` for all **odd** indices `i`. | Note that both lowLimit and highLimit are of small constraints so you can iterate on all nubmer between them You can simulate the boxes by counting for each box the number of balls with digit sum equal to that box number |
[Python 3] - Easy to understand COMMENTED solution. | maximum-number-of-balls-in-a-box | 0 | 1 | Approach:\n\nIterate through the ```lowLimit``` and ```highLimit```. While doing so, compute the sum of all the elements of the current number and update it\'s count in the frequency table. \nBasically, ```boxes[sum(element)] += 1```, (boxes is my frequency table). Finally, return ```max(boxes)```.\n```\nclass Solution:\n def countBalls(self, lowLimit: int, highLimit: int) -> int:\n boxes = [0] * 100\n \n for i in range(lowLimit, highLimit + 1):\n\t\t\t\n\t\t\t# For the current number "i", convert it into a list of its digits.\n\t\t\t# Compute its sum and increment the count in the frequency table.\n\t\t\t\n boxes[sum([int(j) for j in str(i)])] += 1\n \n return max(boxes)\n``` | 7 | You are working in a ball factory where you have `n` balls numbered from `lowLimit` up to `highLimit` **inclusive** (i.e., `n == highLimit - lowLimit + 1`), and an infinite number of boxes numbered from `1` to `infinity`.
Your job at this factory is to put each ball in the box with a number equal to the sum of digits of the ball's number. For example, the ball number `321` will be put in the box number `3 + 2 + 1 = 6` and the ball number `10` will be put in the box number `1 + 0 = 1`.
Given two integers `lowLimit` and `highLimit`, return _the number of balls in the box with the most balls._
**Example 1:**
**Input:** lowLimit = 1, highLimit = 10
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 2 1 1 1 1 1 1 1 1 0 0 ...
Box 1 has the most number of balls with 2 balls.
**Example 2:**
**Input:** lowLimit = 5, highLimit = 15
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 ...
Ball Count: 1 1 1 1 2 2 1 1 1 0 0 ...
Boxes 5 and 6 have the most number of balls with 2 balls in each.
**Example 3:**
**Input:** lowLimit = 19, highLimit = 28
**Output:** 2
**Explanation:**
Box Number: 1 2 3 4 5 6 7 8 9 10 11 12 ...
Ball Count: 0 1 1 1 1 1 1 1 1 2 0 0 ...
Box 10 has the most number of balls with 2 balls.
**Constraints:**
* `1 <= lowLimit <= highLimit <= 105` | Try sorting the points Think is the y-axis of a point relevant |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.