title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Simple solution. O(n) | rotating-the-box | 0 | 1 | ```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n n = len(box[0])\n ans = [[] for _ in range(n)]\n for row in reversed(box):\n i = 0\n for j, ch in enumerate(row):\n if ch == \'*\':\n for k in range(i, j):\n ans[k].append(\'#\')\n ans[j].append(\'*\')\n i = j+1\n elif ch == \'.\':\n ans[i].append(\'.\')\n i += 1\n for k in range(i, n):\n ans[k].append(\'#\')\n return ans\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python3 solution | rotating-the-box | 0 | 1 | # Intuition\nRotate first, then "apply the gravity". \n\nApplying gravity means starting from the bottom and figuring out how far objects can fall, then making them fall.\n\n# Approach\nFirst, we\'ll rotate the box by copying over the contents to a new box. If the box originally had n rows and m cols, the new box will have m rows and n cols.\n\nBe careful when rotating the box that you aren\'t simply transposing the old box. That is, you can\'t simply take newBox[c][r] = box[r][c].\n\nAs an example, if we originally have a 2 row by 3 col box that looks like this:\n```\n+---+---+---+\n| . | . | . |\n+---+---+---+\n| # | # | # |\n+---+---+---+\n```\nThen the rotated version is this (notice how the contents of row 1 are in column 0, not column 1):\n```\n+---+---+\n| # | . |\n+---+---+\n| # | . |\n+---+---+\n| # | . |\n+---+---+\n```\nOnce we have a rotated box, then we need to drop the leaves if appropriate. We can go column-by-column because objects fall directly downward, not side-to-side at all.\n\nStart from the bottom row and work your way to the top row. We\'ll also keep track of a variable called "drop", that will tell us how far a leaf that we find is currently capable of falling. There are 3 cases:\n\n- You encounter an empty space (newBox[r][c] == "."). In this case, any leaf above this space (that isn\'t blocked by an obstacle) would fall right through this space, so the "drop" will go up by 1.\n- You encounter an obstacle (newBox[r][c] == "*"). In this case, leaves cannot fall through obstacles, so the drop will reset to 0. You can think of this as treating the obstacle as a new bottom to the box.\n- You encounter a leaf (newBox[r][c] == "#"). Leaves will drop by however much they are allowed to (we\'ve save this in the "drop" variable), so drop the leaf by replacing it in newBox[row + drop][c] (remember the larger rows are at the bottom of the box, that\'s why we add to the row). Replace the old leaf\'s position with an empty space.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(n * m)**, where n = rows and m = columns of the input box. The 2 phases are:\n1. Rotation of the box: We iterate through every cell in the box (there are n * m cells in a rectangular matrix) and copy the data (constant time operation), so this phase has a run time of O(n*m)\n2. Dropping of the leaves: For each column, we can drop the leaves by using a single linear scan over the column. The actual dropping of the leaf (switching the leaf and empty space) is a constant time operation that we perform for each cell (n * m cells in the matrix), so the run time of this phase is O(n * m)\n\nAll together, we get O(n * m) + O(n * m) --> 2*O(n * m); but constant multipliers will go away in the algorithmic analysis, so we are left with O(n * m).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is also **O(n * m)**. We copy over the data to a new grid, the new grid having the same total number of cells as the old grid, just with a different orientation. Since we are representing the size of the input grid as the number of cells (n * m), we use additional n * m cells for our new grid, so the total space complexity is O(n * m).\n\nNote that the drop variable we use is just constant space complexity; i.e. no matter how large the input grid is, we only ever use 1 drop variable. In the space complexity analysis, the O(n * m) of the additional grid will dominate the O(1) from the drop variable, so we do not consider it when evaluating the space complexity of this algorithm.\n\n# Code\n```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n oldRows, newCols = len(box), len(box)\n oldCols, newRows = len(box[0]), len(box[0])\n\n # rotate the box (careful, the new box is not directly the transpose)\n newBox = [[0 for c in range(newCols)] for r in range(newRows)]\n for r in range(oldRows):\n for c in range(oldCols):\n newBox[c][oldRows - 1 - r] = box[r][c]\n \n # for each column, start from the bottom of the box and pull contents down, if applicable\n for c in range(newCols):\n # find the first leaf\n drop = 0\n for r in range(newRows - 1, -1, -1):\n if newBox[r][c] == ".":\n drop += 1\n elif newBox[r][c] == "*":\n drop = 0\n elif newBox[r][c] == "#":\n newBox[r][c] = "."\n newBox[r + drop][c] = "#"\n \n return newBox\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
Python: Rotate and drop | rotating-the-box | 0 | 1 | # Complexity\n- Time complexity:\n$$O(m*n)$$\n\n- Space complexity:\n$$O(m*n)$$\n\n# Code\n```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n m = len(box)\n n = len(box[0])\n # rotate matrix\n box_r = [[box[r][c] for r in range(m-1,-1,-1)] for c in range(n)]\n # drop to the bottom\n for c in range(m):\n bottom = n - 1\n for r in range(n-1, -1, -1):\n if box_r[r][c] == \'#\':\n if r != bottom:\n box_r[r][c], box_r[bottom][c] = box_r[bottom][c], box_r[r][c]\n bottom -= 1\n elif box_r[r][c] == \'*\': # our bottom changes\n bottom = r - 1\n return box_r\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
[Python3] Readable, Intuitive Solution with Comments || Faster than 84% of Python submissions | rotating-the-box | 0 | 1 | ```\nclass Solution:\n def rotateTheBox(self, box: List[List[str]]) -> List[List[str]]:\n def convert_rows_to_processed_cols(rows):\n def convert_row_to_processed_col(row):\n insert_stone_ptr = len(row) - 1\n i = len(row) - 1\n \n while i >= 0:\n if row[i] == ".": # open space, no need to overwrite or move the insert_stone_ptr\n pass \n elif row[i] == "*":\n insert_stone_ptr = i - 1 # an obstacle, so move our insert_stone_ptr to before this obstacle\n else: \n row[insert_stone_ptr] = "#"\n if i != insert_stone_ptr: # if i == insert_stone_ptr and the space was a "#", we don\'t want to overwrite with a period.\n # But if we just moved a stone, then we want this space to be empty now.\n row[i] = "."\n \n insert_stone_ptr -= 1\n \n i -= 1\n \n return row\n \n processed_cols = []\n \n for row in rows[::-1]: # the last rows end up being the left-most columns, so we should create columns that are in "reverse"\n processed_cols.append(convert_row_to_processed_col(row))\n \n return processed_cols\n \n def convert_processed_cols_to_rows(processed_cols):\n rows = []\n \n for i in range(len(processed_cols[0])): # go through every stone index in a column\n curr_row = []\n for j in range(len(processed_cols)): # go through this stone index in every column\n curr_row.append(processed_cols[j][i])\n rows.append(curr_row) \n \n return rows\n\n\t\t# simulate falling by converting rows to "processed" columns\n processed_cols = convert_rows_to_processed_cols(box)\n\t\t\n\t\t# convert these columns back into row form\n return convert_processed_cols_to_rows(processed_cols)\n\n``` | 0 | You are given an `m x n` matrix of characters `box` representing a side-view of a box. Each cell of the box is one of the following:
* A stone `'#'`
* A stationary obstacle `'*'`
* Empty `'.'`
The box is rotated **90 degrees clockwise**, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity **does not** affect the obstacles' positions, and the inertia from the box's rotation **does not** affect the stones' horizontal positions.
It is **guaranteed** that each stone in `box` rests on an obstacle, another stone, or the bottom of the box.
Return _an_ `n x m` _matrix representing the box after the rotation described above_.
**Example 1:**
**Input:** box = \[\[ "# ", ". ", "# "\]\]
**Output:** \[\[ ". "\],
\[ "# "\],
\[ "# "\]\]
**Example 2:**
**Input:** box = \[\[ "# ", ". ", "\* ", ". "\],
\[ "# ", "# ", "\* ", ". "\]\]
**Output:** \[\[ "# ", ". "\],
\[ "# ", "# "\],
\[ "\* ", "\* "\],
\[ ". ", ". "\]\]
**Example 3:**
**Input:** box = \[\[ "# ", "# ", "\* ", ". ", "\* ", ". "\],
\[ "# ", "# ", "# ", "\* ", ". ", ". "\],
\[ "# ", "# ", "# ", ". ", "# ", ". "\]\]
**Output:** \[\[ ". ", "# ", "# "\],
\[ ". ", "# ", "# "\],
\[ "# ", "# ", "\* "\],
\[ "# ", "\* ", ". "\],
\[ "# ", ". ", "\* "\],
\[ "# ", ". ", ". "\]\]
**Constraints:**
* `m == box.length`
* `n == box[i].length`
* `1 <= m, n <= 500`
* `box[i][j]` is either `'#'`, `'*'`, or `'.'`. | Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in? The first box should always start in the corner |
[PYTHON] | ALGORITHM | sum-of-floored-pairs | 0 | 1 | \nRuntime: **3561 ms, faster than 73.68%** of Python3 online submissions for Sum of Floored Pairs.\nMemory Usage: **32.6 MB, less than 56.84%** of Python3 online submissions for Sum of Floored Pairs.\n```\n\nclass Solution:\n def sumOfFlooredPairs(self, n: List[int]) -> int:\n f, m, c = Counter(n), max(n), [0]*(max(n)+1)\n for k in f:\n d, r = f[k], 1\n while r*k <= m: c[r*k] += d; r += 1\n r, j = 0, 0\n for i in range(m+1):\n r += c[i]\n if i in f: j += f[i]*r\n return j%(10**9+7)\n\t\t\n```\n**BTW: THIS IS NOT MY COMPLETE IDEA, I MADE `@satendrapandey`\'s VERSION A BIT FASTER** | 1 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
[PYTHON] | ALGORITHM | sum-of-floored-pairs | 0 | 1 | \nRuntime: **3561 ms, faster than 73.68%** of Python3 online submissions for Sum of Floored Pairs.\nMemory Usage: **32.6 MB, less than 56.84%** of Python3 online submissions for Sum of Floored Pairs.\n```\n\nclass Solution:\n def sumOfFlooredPairs(self, n: List[int]) -> int:\n f, m, c = Counter(n), max(n), [0]*(max(n)+1)\n for k in f:\n d, r = f[k], 1\n while r*k <= m: c[r*k] += d; r += 1\n r, j = 0, 0\n for i in range(m+1):\n r += c[i]\n if i in f: j += f[i]*r\n return j%(10**9+7)\n\t\t\n```\n**BTW: THIS IS NOT MY COMPLETE IDEA, I MADE `@satendrapandey`\'s VERSION A BIT FASTER** | 1 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python/Python3 solution BruteForce & Optimized solution using Dictionary | sum-of-floored-pairs | 0 | 1 | **Brute Foce Solution(Time Limit Exceeded)**\n\nThis solution will work if the length of the elements in the testcase is <50000(5 * 10^4).\nIf it exceeds 50000 it will throw TLE error.\n**Code:**\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n sumP = 0 #To store the value of Sum of floor values\n for i in nums: #Traverse every element in nums\n for j in nums: #Traverse every element in nums\n sumP += (j//i) #Simply do floor division and add the number to sumP\n return sumP % (10**9 +7)#return the sumof the pairs\n```\n\n**Optimized Solution**\n\nThe solution is built by using frequency of the prefix elements(freqency prefix sum).\n1. Take the frequency of the elements given in the nums and store ir in dictionary.\n2. After storing calculate the prefix frequency of the nums according to the frequency present in the dictionary.\n3. After computing prefix Frequency just calculate the sum of the floor division.\n* If you need to futher understanding the code kindly watch Part by Part Implementation. \n\n**Code:**\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxi = max(nums) + 1\n dic = {}\n prefix=[0]*maxi\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n #print(prefix,dic)\n sumP = 0\n for i in set(nums):\n for j in range(i,maxi,i):\n sumP += dic[i]*(prefix[-1]-prefix[j-1])\n\t\t\t\t#print(sumP,end = " ")\n return sumP % (10**9 +7)\n```\n**Part by Part Implementation**\n```\n#Part - 1 : Calculating the frequency of the elements in nums to dictionary.\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n dic = {}\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n print(dic)\n```\n**Output:\n{2: 1, 5: 1, 9: 1}**\n\n```\n#Part - 2 : Calculation of Prefix frequency according to the frequency of the nums in dictionary.\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n dic = {}\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n maxi = max(nums) + 1\n prefix=[0]*maxi\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n print(prefix)\n```\n**Output:\n[0, 0, 1, 1, 1, 2, 2, 2, 2, 3]**\n\n```\n#Part - 3 : Calculation of sum of floor division \nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxi = max(nums) + 1\n dic = {}\n prefix=[0]*maxi\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n #print(prefix,dic)\n sumP = 0\n for i in set(nums):\n for j in range(i,maxi,i):\n sumP += dic[i]*(prefix[-1]-prefix[j-1])\n print(sumP,end = " ")\n```\n**Output:\n1 4 6 7 8 10**\n\n***We rise by lifting others*** | 10 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Python/Python3 solution BruteForce & Optimized solution using Dictionary | sum-of-floored-pairs | 0 | 1 | **Brute Foce Solution(Time Limit Exceeded)**\n\nThis solution will work if the length of the elements in the testcase is <50000(5 * 10^4).\nIf it exceeds 50000 it will throw TLE error.\n**Code:**\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n sumP = 0 #To store the value of Sum of floor values\n for i in nums: #Traverse every element in nums\n for j in nums: #Traverse every element in nums\n sumP += (j//i) #Simply do floor division and add the number to sumP\n return sumP % (10**9 +7)#return the sumof the pairs\n```\n\n**Optimized Solution**\n\nThe solution is built by using frequency of the prefix elements(freqency prefix sum).\n1. Take the frequency of the elements given in the nums and store ir in dictionary.\n2. After storing calculate the prefix frequency of the nums according to the frequency present in the dictionary.\n3. After computing prefix Frequency just calculate the sum of the floor division.\n* If you need to futher understanding the code kindly watch Part by Part Implementation. \n\n**Code:**\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxi = max(nums) + 1\n dic = {}\n prefix=[0]*maxi\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n #print(prefix,dic)\n sumP = 0\n for i in set(nums):\n for j in range(i,maxi,i):\n sumP += dic[i]*(prefix[-1]-prefix[j-1])\n\t\t\t\t#print(sumP,end = " ")\n return sumP % (10**9 +7)\n```\n**Part by Part Implementation**\n```\n#Part - 1 : Calculating the frequency of the elements in nums to dictionary.\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n dic = {}\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n print(dic)\n```\n**Output:\n{2: 1, 5: 1, 9: 1}**\n\n```\n#Part - 2 : Calculation of Prefix frequency according to the frequency of the nums in dictionary.\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n dic = {}\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n maxi = max(nums) + 1\n prefix=[0]*maxi\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n print(prefix)\n```\n**Output:\n[0, 0, 1, 1, 1, 2, 2, 2, 2, 3]**\n\n```\n#Part - 3 : Calculation of sum of floor division \nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxi = max(nums) + 1\n dic = {}\n prefix=[0]*maxi\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n #print(prefix,dic)\n sumP = 0\n for i in set(nums):\n for j in range(i,maxi,i):\n sumP += dic[i]*(prefix[-1]-prefix[j-1])\n print(sumP,end = " ")\n```\n**Output:\n1 4 6 7 8 10**\n\n***We rise by lifting others*** | 10 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python most optimized solution | sum-of-floored-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n[[2//2, 2//5, 2//9],\n [5//2, 5//5, 5//9],\n [9//2, 9//5, 9//9]]\n\n let\'s take 9//2 what it represents, it represents that there are total\n of 4 number (2,4,6,8) before 9 that are multiple of 2. so its value \n would be 4. same goes for others like 9//5 its just 1 (5).[next would be\n 10 but its greater than 9 so we cant take that into consideration.]\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwith that knowledege we just have to know for each number how lets say 5 \n how many numbers have its multiple of less than equal to 5 for all number\n smaller than equal to 5[which is in original array nums].\n\n for 5 its just 5\n for 2 its 2, 4 \n\n so there are in total 3 number which gives sum of quotient for all fraction \n that has numerator 5. similarly we can find for all element in array. and \n return its sum.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n \n ls, counter=[0]*(max(nums)+1), Counter(nums)\n for num in counter:\n for j in range(num, len(ls), num):\n ls[j] += counter[num]\n prefix = [ls[0]]\n for i, n in enumerate(ls):\n if i > 0:\n prefix.append(prefix[-1] + n)\n return sum([prefix[num] for num in nums]) % (10**9 + 7)\n``` | 0 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Python most optimized solution | sum-of-floored-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n[[2//2, 2//5, 2//9],\n [5//2, 5//5, 5//9],\n [9//2, 9//5, 9//9]]\n\n let\'s take 9//2 what it represents, it represents that there are total\n of 4 number (2,4,6,8) before 9 that are multiple of 2. so its value \n would be 4. same goes for others like 9//5 its just 1 (5).[next would be\n 10 but its greater than 9 so we cant take that into consideration.]\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwith that knowledege we just have to know for each number how lets say 5 \n how many numbers have its multiple of less than equal to 5 for all number\n smaller than equal to 5[which is in original array nums].\n\n for 5 its just 5\n for 2 its 2, 4 \n\n so there are in total 3 number which gives sum of quotient for all fraction \n that has numerator 5. similarly we can find for all element in array. and \n return its sum.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n \n ls, counter=[0]*(max(nums)+1), Counter(nums)\n for num in counter:\n for j in range(num, len(ls), num):\n ls[j] += counter[num]\n prefix = [ls[0]]\n for i, n in enumerate(ls):\n if i > 0:\n prefix.append(prefix[-1] + n)\n return sum([prefix[num] for num in nums]) % (10**9 + 7)\n``` | 0 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
nlogn solution using maths | sum-of-floored-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n n,ans = 2*max(nums) + 11,0\n p,arr = [0 for _ in range(n)],[]\n for i in nums:\n p[i] += 1 \n if p[i] == 1 : arr.append(i)\n arr.sort()\n for i in range(1,n): p[i] += p[i-1] \n for x in arr : \n i, j, curr = x, x, 0 \n for i in range(x,n,x):\n ans += (p[x] - p[x-1]) * (i//x -1) * (p[i-1]-p[j-1]) \n ans, j = ans%1000000007, i\n \n return ans\n \n``` | 0 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
nlogn solution using maths | sum-of-floored-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n n,ans = 2*max(nums) + 11,0\n p,arr = [0 for _ in range(n)],[]\n for i in nums:\n p[i] += 1 \n if p[i] == 1 : arr.append(i)\n arr.sort()\n for i in range(1,n): p[i] += p[i-1] \n for x in arr : \n i, j, curr = x, x, 0 \n for i in range(x,n,x):\n ans += (p[x] - p[x-1]) * (i//x -1) * (p[i-1]-p[j-1]) \n ans, j = ans%1000000007, i\n \n return ans\n \n``` | 0 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Counting I guesssss | sum-of-floored-pairs | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n + max_num * log(max_num))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(maxnum)$$\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n MOD = 10**9 + 7\n max_num = max(nums)\n freq = [0] * (max_num + 1)\n\n # Count the occurrences of each number\n for num in nums:\n freq[num] += 1\n\n # Calculate prefix sum of frequencies\n prefix_sum = [0] * (max_num + 1)\n for i in range(1, max_num + 1):\n prefix_sum[i] = prefix_sum[i-1] + freq[i]\n\n result = 0\n\n # Calculate the sum of floor divisions\n for i in range(1, max_num + 1):\n if freq[i] == 0:\n continue\n\n # Iterate over all multiples of i\n for j in range(i, max_num + 1, i):\n result += (prefix_sum[min(j + i - 1, max_num)] - prefix_sum[j-1]) * (j // i) * freq[i]\n result %= MOD\n\n return result\n\n``` | 0 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Counting I guesssss | sum-of-floored-pairs | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n + max_num * log(max_num))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(maxnum)$$\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n MOD = 10**9 + 7\n max_num = max(nums)\n freq = [0] * (max_num + 1)\n\n # Count the occurrences of each number\n for num in nums:\n freq[num] += 1\n\n # Calculate prefix sum of frequencies\n prefix_sum = [0] * (max_num + 1)\n for i in range(1, max_num + 1):\n prefix_sum[i] = prefix_sum[i-1] + freq[i]\n\n result = 0\n\n # Calculate the sum of floor divisions\n for i in range(1, max_num + 1):\n if freq[i] == 0:\n continue\n\n # Iterate over all multiples of i\n for j in range(i, max_num + 1, i):\n result += (prefix_sum[min(j + i - 1, max_num)] - prefix_sum[j-1]) * (j // i) * freq[i]\n result %= MOD\n\n return result\n\n``` | 0 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Factor Frequency Prefix Sum w/Num Frequency Product | Commented and Explained | O(N) T/S | sum-of-floored-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem description is deceptively simple and at first a brute force even seems a likely and doable option, for which I got 19/51 and then 25/51 with first Time and then Memory limit expired. From this, it becomes more obvious that we need a more clever solution. \n\nThe first part in any good brute force to get that far was the reduction in time afforded by considering only unique values in nums and using the frequency of those values. \n\nThe second trick was when I considered the contribution of a specific value to a specific total sum. Take 9 and 2. 9 / 2 in floor form gives 4. This can be seen as the statement that there are 4 factors of 2 in 9 (2, 4, 6, 8). This is the key to the second speed up. \n\nIf we keep a number range from 0 to the maximum of nums, then we can account for this contribution exactly. \n\n- For each unique factor in nums \n - for each next factor of this unique factor up to max nums \n - store the frequency of this factor at a point next factor in our number range \n\n- Then, get the prefix sum of the factor frequencies as a list \n- Then, for each actual num in our num frequencies, multiply the prefix sum of the factor frequencies by the frequency of that num. This then gets the other half of the question. \n\nTo simplify, first find out how much and how many items utilize each factor in nums. Then, find out for each of those utilizations what their summed contribution is. Then, sum only the given unique factor contributions present by the frequency of that factor. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIntuitition describes much of the approach, but for completeness, steps outlined here. \n\nGet the frequency of nums \nSet up modulo value as needed \nGet the maximum key in frequency of nums \nSet up a factor frequencies of 0 in range of max key inclusive \n\nFor num and frequency in frequency of nums \n- for factor in range num, max key + 1, num \n - factor frequencies at factor += frequency \n\nGet the prefix sum of factor frequencies \n\nreturn the sum of the product of the prefix sum of factor frequencies for each factor in num frequency with the frequency of that factor \n\n# Complexity\n- Time complexity : O(N) \n - O(N) to get num frequency \n - O(n) to get unique max value \n - O(n * floor(max value / avg other nums)) \n - O(max value) to get prefix sums \n - O(n) to get final value \n - At worst one might think O(N) == O(n) == O(max value) \n - However, when that occurs avg of other nums ~ N \n - Due to this, we can see that the floor mechanism limits \n - Worst would be when n ~ N/2 and n is composed of all values up to N/2 - 1 and N \n - This would give a run time of N/2 * 2 for the loop and shows the value of the floor limit on the run time for the inner loop \n - Thus we can say at worst O(N) \n\n- Space complexity : O(N) \n - As above, at worst is O(N) \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int :\n # uncomment print statements to see in test cases \n # floor nums[i] / nums[j]\n # if nums[i] occurrs multiple times, doing multiple work \n # frequency is first reduction \n num_frequency = collections.Counter(nums)\n mod = 10**9 + 7 \n # second reduction involves consideration of factorization processes \n # for each value in nums, that number will have a number of contributions based on its frequency for its value \n # in relation to all other values. For example, 9 / 2 causes 2 to contribute 4 due to the presence of 9\n # this can be seen as the number of factors of 2 that fit within the value of 9. Due to this, we want to find \n # first the largest value of our num frequency (don\'t search nums! Already did that once to set up num frequency) \n # then we want to find the frequencies related to the factors of a value that fit within range up to that max value \n # this will give us our second reduction, since we can now do loops limited to only unique nums in num frequency \n # as the outer loop and do inner loops over only the factor range for each value, which processes in logarithmic\n # time rather than linear time due to size of steps utilized in advancing towards a set max value \n max_key = max(num_frequency.keys())\n # then, for each factor in range of a num to the max key plus 1 so that the max value is included \n # we will record the frequency that a given factor for any num of nums is found in range and increment \n # by the frequency of the associated base num, as that will denote the contribution frequency times it makes \n # towards the total summation value \n factor_frequencies = [0] * (max_key + 1) \n # loop over num frequency items \n for num, frequency in num_frequency.items() : \n # print(f\'Considering number {num} with frequency {frequency}\')\n # factor values in range of num to max key + 1 in steps of num \n # represents reduction in time by use of multiples of num that are found in floor pairings \n for factor in range(num, max_key + 1, num) : \n # print(f\'Considering factor value {factor} and updating factor frequencies current : {factor_frequencies}\')\n # for which you will have at least frequency occurrences of this value for that partner \n factor_frequencies[factor] += frequency\n # print(f\'New factor_frequencies is {factor_frequencies}\\n\')\n # print(f\'Total factor_frequencies are {factor_frequencies}\')\n # this is the prefix sum of the factors of num frequencies in range of max, accounting for \n # the possible multiple divisions of certain nums by certain other values (i.e. 9 / 2 -> 4)\n prefix_sum_of_factor_frequencies = list(accumulate(factor_frequencies))\n # print(f\'Prefix sum of factor frequencies are {prefix_sum_of_factor_frequencies}\')\n # return the sum of the prefix sum of factor frequencies for each num actually in num frequency multiplied \n # by the frequency of that num. This is because the prefix sum accounts for the number of times it is utilized by others, and now we count by self \n return sum(prefix_sum_of_factor_frequencies[num] * frequency for num, frequency in num_frequency.items()) % mod \n``` | 0 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Factor Frequency Prefix Sum w/Num Frequency Product | Commented and Explained | O(N) T/S | sum-of-floored-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem description is deceptively simple and at first a brute force even seems a likely and doable option, for which I got 19/51 and then 25/51 with first Time and then Memory limit expired. From this, it becomes more obvious that we need a more clever solution. \n\nThe first part in any good brute force to get that far was the reduction in time afforded by considering only unique values in nums and using the frequency of those values. \n\nThe second trick was when I considered the contribution of a specific value to a specific total sum. Take 9 and 2. 9 / 2 in floor form gives 4. This can be seen as the statement that there are 4 factors of 2 in 9 (2, 4, 6, 8). This is the key to the second speed up. \n\nIf we keep a number range from 0 to the maximum of nums, then we can account for this contribution exactly. \n\n- For each unique factor in nums \n - for each next factor of this unique factor up to max nums \n - store the frequency of this factor at a point next factor in our number range \n\n- Then, get the prefix sum of the factor frequencies as a list \n- Then, for each actual num in our num frequencies, multiply the prefix sum of the factor frequencies by the frequency of that num. This then gets the other half of the question. \n\nTo simplify, first find out how much and how many items utilize each factor in nums. Then, find out for each of those utilizations what their summed contribution is. Then, sum only the given unique factor contributions present by the frequency of that factor. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIntuitition describes much of the approach, but for completeness, steps outlined here. \n\nGet the frequency of nums \nSet up modulo value as needed \nGet the maximum key in frequency of nums \nSet up a factor frequencies of 0 in range of max key inclusive \n\nFor num and frequency in frequency of nums \n- for factor in range num, max key + 1, num \n - factor frequencies at factor += frequency \n\nGet the prefix sum of factor frequencies \n\nreturn the sum of the product of the prefix sum of factor frequencies for each factor in num frequency with the frequency of that factor \n\n# Complexity\n- Time complexity : O(N) \n - O(N) to get num frequency \n - O(n) to get unique max value \n - O(n * floor(max value / avg other nums)) \n - O(max value) to get prefix sums \n - O(n) to get final value \n - At worst one might think O(N) == O(n) == O(max value) \n - However, when that occurs avg of other nums ~ N \n - Due to this, we can see that the floor mechanism limits \n - Worst would be when n ~ N/2 and n is composed of all values up to N/2 - 1 and N \n - This would give a run time of N/2 * 2 for the loop and shows the value of the floor limit on the run time for the inner loop \n - Thus we can say at worst O(N) \n\n- Space complexity : O(N) \n - As above, at worst is O(N) \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int :\n # uncomment print statements to see in test cases \n # floor nums[i] / nums[j]\n # if nums[i] occurrs multiple times, doing multiple work \n # frequency is first reduction \n num_frequency = collections.Counter(nums)\n mod = 10**9 + 7 \n # second reduction involves consideration of factorization processes \n # for each value in nums, that number will have a number of contributions based on its frequency for its value \n # in relation to all other values. For example, 9 / 2 causes 2 to contribute 4 due to the presence of 9\n # this can be seen as the number of factors of 2 that fit within the value of 9. Due to this, we want to find \n # first the largest value of our num frequency (don\'t search nums! Already did that once to set up num frequency) \n # then we want to find the frequencies related to the factors of a value that fit within range up to that max value \n # this will give us our second reduction, since we can now do loops limited to only unique nums in num frequency \n # as the outer loop and do inner loops over only the factor range for each value, which processes in logarithmic\n # time rather than linear time due to size of steps utilized in advancing towards a set max value \n max_key = max(num_frequency.keys())\n # then, for each factor in range of a num to the max key plus 1 so that the max value is included \n # we will record the frequency that a given factor for any num of nums is found in range and increment \n # by the frequency of the associated base num, as that will denote the contribution frequency times it makes \n # towards the total summation value \n factor_frequencies = [0] * (max_key + 1) \n # loop over num frequency items \n for num, frequency in num_frequency.items() : \n # print(f\'Considering number {num} with frequency {frequency}\')\n # factor values in range of num to max key + 1 in steps of num \n # represents reduction in time by use of multiples of num that are found in floor pairings \n for factor in range(num, max_key + 1, num) : \n # print(f\'Considering factor value {factor} and updating factor frequencies current : {factor_frequencies}\')\n # for which you will have at least frequency occurrences of this value for that partner \n factor_frequencies[factor] += frequency\n # print(f\'New factor_frequencies is {factor_frequencies}\\n\')\n # print(f\'Total factor_frequencies are {factor_frequencies}\')\n # this is the prefix sum of the factors of num frequencies in range of max, accounting for \n # the possible multiple divisions of certain nums by certain other values (i.e. 9 / 2 -> 4)\n prefix_sum_of_factor_frequencies = list(accumulate(factor_frequencies))\n # print(f\'Prefix sum of factor frequencies are {prefix_sum_of_factor_frequencies}\')\n # return the sum of the prefix sum of factor frequencies for each num actually in num frequency multiplied \n # by the frequency of that num. This is because the prefix sum accounts for the number of times it is utilized by others, and now we count by self \n return sum(prefix_sum_of_factor_frequencies[num] * frequency for num, frequency in num_frequency.items()) % mod \n``` | 0 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python (Simple Hashmap + Prefix Sum) | sum-of-floored-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums):\n ans, dict1, mod = [0]*(max(nums)+1), collections.Counter(nums), 10**9 + 7\n\n for num in dict1:\n for j in range(num,len(ans),num):\n ans[j] += dict1[num]\n\n res = [ans[0]]\n\n for i in ans[1:]:\n res.append(res[-1] + i)\n\n return sum([res[i] for i in nums])%mod\n\n\n\n\n\n \n\n \n``` | 0 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Python (Simple Hashmap + Prefix Sum) | sum-of-floored-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums):\n ans, dict1, mod = [0]*(max(nums)+1), collections.Counter(nums), 10**9 + 7\n\n for num in dict1:\n for j in range(num,len(ans),num):\n ans[j] += dict1[num]\n\n res = [ans[0]]\n\n for i in ans[1:]:\n res.append(res[-1] + i)\n\n return sum([res[i] for i in nums])%mod\n\n\n\n\n\n \n\n \n``` | 0 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python Easy to Understand Solution | Sorting | Binary Search | sum-of-floored-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n res, mod, cache = 0, 1000000007, {}\n for idx, num in enumerate(nums):\n if num in cache:\n res += cache[num]\n else:\n currentRes, j = 0, idx\n while j < len(nums):\n multiplier = nums[j] // num\n lastPosition = bisect_left(nums, num * (multiplier + 1), j)\n currentRes += (lastPosition - j) * multiplier\n j = lastPosition\n cache[num] = currentRes\n res += currentRes\n res %= mod\n return res\n``` | 0 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Python Easy to Understand Solution | Sorting | Binary Search | sum-of-floored-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n res, mod, cache = 0, 1000000007, {}\n for idx, num in enumerate(nums):\n if num in cache:\n res += cache[num]\n else:\n currentRes, j = 0, idx\n while j < len(nums):\n multiplier = nums[j] // num\n lastPosition = bisect_left(nums, num * (multiplier + 1), j)\n currentRes += (lastPosition - j) * multiplier\n j = lastPosition\n cache[num] = currentRes\n res += currentRes\n res %= mod\n return res\n``` | 0 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Python - 8 lines frequency prefix sum | sum-of-floored-pairs | 0 | 1 | ```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n ans, hi, n, c = 0, max(nums)+1, len(nums), Counter(nums)\n pre = [0] * hi\n for i in range(1, hi):\n pre[i] = pre[i-1] + c[i]\n for num in set(nums):\n for i in range(num, hi, num):\n ans += c[num] * (pre[-1] - pre[i-1])\n return ans % (10**9 + 7)\n``` | 4 | Given an integer array `nums`, return the sum of `floor(nums[i] / nums[j])` for all pairs of indices `0 <= i, j < nums.length` in the array. Since the answer may be too large, return it **modulo** `109 + 7`.
The `floor()` function returns the integer part of the division.
**Example 1:**
**Input:** nums = \[2,5,9\]
**Output:** 10
**Explanation:**
floor(2 / 5) = floor(2 / 9) = floor(5 / 9) = 0
floor(2 / 2) = floor(5 / 5) = floor(9 / 9) = 1
floor(5 / 2) = 2
floor(9 / 2) = 4
floor(9 / 5) = 1
We calculate the floor of the division for every pair of indices in the array then sum them up.
**Example 2:**
**Input:** nums = \[7,7,7,7,7,7,7\]
**Output:** 49
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Python - 8 lines frequency prefix sum | sum-of-floored-pairs | 0 | 1 | ```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n ans, hi, n, c = 0, max(nums)+1, len(nums), Counter(nums)\n pre = [0] * hi\n for i in range(1, hi):\n pre[i] = pre[i-1] + c[i]\n for num in set(nums):\n for i in range(num, hi, num):\n ans += c[num] * (pre[-1] - pre[i-1])\n return ans % (10**9 + 7)\n``` | 4 | There is a one-dimensional garden on the x-axis. The garden starts at the point `0` and ends at the point `n`. (i.e The length of the garden is `n`).
There are `n + 1` taps located at points `[0, 1, ..., n]` in the garden.
Given an integer `n` and an integer array `ranges` of length `n + 1` where `ranges[i]` (0-indexed) means the `i-th` tap can water the area `[i - ranges[i], i + ranges[i]]` if it was open.
Return _the minimum number of taps_ that should be open to water the whole garden, If the garden cannot be watered return **\-1**.
**Example 1:**
**Input:** n = 5, ranges = \[3,4,1,1,0,0\]
**Output:** 1
**Explanation:** The tap at point 0 can cover the interval \[-3,3\]
The tap at point 1 can cover the interval \[-3,5\]
The tap at point 2 can cover the interval \[1,3\]
The tap at point 3 can cover the interval \[2,4\]
The tap at point 4 can cover the interval \[4,4\]
The tap at point 5 can cover the interval \[5,5\]
Opening Only the second tap will water the whole garden \[0,5\]
**Example 2:**
**Input:** n = 3, ranges = \[0,0,0,0\]
**Output:** -1
**Explanation:** Even if you activate all the four taps you cannot water the whole garden.
**Constraints:**
* `1 <= n <= 104`
* `ranges.length == n + 1`
* `0 <= ranges[i] <= 100` | Find the frequency (number of occurrences) of all elements in the array. For each element, iterate through its multiples and multiply frequencies to find the answer. |
Solution with Backtracking in Python3 / TypeScript | sum-of-all-subset-xor-totals | 0 | 1 | \n# Intuition\nLet\'s briefly explain what the problem is:\n- there\'s a list of `nums`\n- our goal is to **extract sum** of all **subsets**, that were reduced by **XOR** bit operation between each operands/neighbours.\n\n**Subset** is a part of list, whose indexes could be **shuffled** (**order doesn\'t matter**).\n\n**XOR operation** is achievable between **two operands**, and perform binary comparison between bits. To see some examples of **XOR**, [follow the link](https://en.wikipedia.org/wiki/Exclusive_or).\n\n\n```\n# Example\nnums = [1,3]\nsubsets = [[], [1], [1,3], [3]]\n\n# After XOR\nsubsets = [0, 1, 2, 3] # the sum of all reduced subsets is 6\n\n```\n\nTo find all of the possible subsets of `nums` we\'re going to use [Backtracking approach](https://en.wikipedia.org/wiki/Backtracking).\n\n# Approach\n1. declare an empty `subsets` to store all of the subsets of `nums`\n2. define `bt` function, that accepts `node, path`\n3. at each step put the subset into `subsets`, if `node <== n`\n4. iterate over range `[node, n)`, and fill a current subset\n5. return sum of all subsets, that were reduced by **XOR** between each operands\n\n# Complexity\n- Time complexity: **O(2^n)**, since we\'re building all of the **subsets** from `nums`\n\n- Space complexity: **O(2^n)**, the same for storing these subsets\n\n# Code in Python3\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n subsets = []\n n = len(nums)\n\n def bt(node, path):\n if node <= n:\n subsets.append([*path])\n\n for i in range(node, n):\n path.append(nums[i])\n bt(i + 1, path)\n path.pop()\n\n bt(0, [])\n\n return sum([reduce(lambda a, c: a ^ c, x, 0) for x in subsets])\n```\n# Code in TypeScript\n```\nfunction subsetXORSum(nums: number[]): number {\n const subsets = []\n const n = nums.length;\n\n const bt = (node: number, path: number[]) => {\n if (node <= n) {\n subsets.push([...path])\n\n for (let i = node; i < n; i++) {\n path.push(nums[i])\n bt(i + 1, path)\n path.pop()\n }\n }\n }\n\n bt(0, [])\n\n return subsets.map((s => s.reduce((a, c) => a ^ c, 0))).reduce((a, c) => a + c, 0)\n};\n``` | 1 | The **XOR total** of an array is defined as the bitwise `XOR` of **all its elements**, or `0` if the array is **empty**.
* For example, the **XOR total** of the array `[2,5,6]` is `2 XOR 5 XOR 6 = 1`.
Given an array `nums`, return _the **sum** of all **XOR totals** for every **subset** of_ `nums`.
**Note:** Subsets with the **same** elements should be counted **multiple** times.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`.
**Example 1:**
**Input:** nums = \[1,3\]
**Output:** 6
**Explanation:** The 4 subsets of \[1,3\] are:
- The empty subset has an XOR total of 0.
- \[1\] has an XOR total of 1.
- \[3\] has an XOR total of 3.
- \[1,3\] has an XOR total of 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
**Example 2:**
**Input:** nums = \[5,1,6\]
**Output:** 28
**Explanation:** The 8 subsets of \[5,1,6\] are:
- The empty subset has an XOR total of 0.
- \[5\] has an XOR total of 5.
- \[1\] has an XOR total of 1.
- \[6\] has an XOR total of 6.
- \[5,1\] has an XOR total of 5 XOR 1 = 4.
- \[5,6\] has an XOR total of 5 XOR 6 = 3.
- \[1,6\] has an XOR total of 1 XOR 6 = 7.
- \[5,1,6\] has an XOR total of 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
**Example 3:**
**Input:** nums = \[3,4,5,6,7,8\]
**Output:** 480
**Explanation:** The sum of all XOR totals for every subset is 480.
**Constraints:**
* `1 <= nums.length <= 12`
* `1 <= nums[i] <= 20` | null |
Solution with Backtracking in Python3 / TypeScript | sum-of-all-subset-xor-totals | 0 | 1 | \n# Intuition\nLet\'s briefly explain what the problem is:\n- there\'s a list of `nums`\n- our goal is to **extract sum** of all **subsets**, that were reduced by **XOR** bit operation between each operands/neighbours.\n\n**Subset** is a part of list, whose indexes could be **shuffled** (**order doesn\'t matter**).\n\n**XOR operation** is achievable between **two operands**, and perform binary comparison between bits. To see some examples of **XOR**, [follow the link](https://en.wikipedia.org/wiki/Exclusive_or).\n\n\n```\n# Example\nnums = [1,3]\nsubsets = [[], [1], [1,3], [3]]\n\n# After XOR\nsubsets = [0, 1, 2, 3] # the sum of all reduced subsets is 6\n\n```\n\nTo find all of the possible subsets of `nums` we\'re going to use [Backtracking approach](https://en.wikipedia.org/wiki/Backtracking).\n\n# Approach\n1. declare an empty `subsets` to store all of the subsets of `nums`\n2. define `bt` function, that accepts `node, path`\n3. at each step put the subset into `subsets`, if `node <== n`\n4. iterate over range `[node, n)`, and fill a current subset\n5. return sum of all subsets, that were reduced by **XOR** between each operands\n\n# Complexity\n- Time complexity: **O(2^n)**, since we\'re building all of the **subsets** from `nums`\n\n- Space complexity: **O(2^n)**, the same for storing these subsets\n\n# Code in Python3\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n subsets = []\n n = len(nums)\n\n def bt(node, path):\n if node <= n:\n subsets.append([*path])\n\n for i in range(node, n):\n path.append(nums[i])\n bt(i + 1, path)\n path.pop()\n\n bt(0, [])\n\n return sum([reduce(lambda a, c: a ^ c, x, 0) for x in subsets])\n```\n# Code in TypeScript\n```\nfunction subsetXORSum(nums: number[]): number {\n const subsets = []\n const n = nums.length;\n\n const bt = (node: number, path: number[]) => {\n if (node <= n) {\n subsets.push([...path])\n\n for (let i = node; i < n; i++) {\n path.push(nums[i])\n bt(i + 1, path)\n path.pop()\n }\n }\n }\n\n bt(0, [])\n\n return subsets.map((s => s.reduce((a, c) => a ^ c, 0))).reduce((a, c) => a + c, 0)\n};\n``` | 1 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of the `ith` node. The root of the tree is node `0`, so `parent[0] = -1` since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.
The data structure should support the following functions:
* **Lock:** **Locks** the given node for the given user and prevents other users from locking the same node. You may only lock a node using this function if the node is unlocked.
* **Unlock: Unlocks** the given node for the given user. You may only unlock a node using this function if it is currently locked by the same user.
* **Upgrade****: Locks** the given node for the given user and **unlocks** all of its descendants **regardless** of who locked it. You may only upgrade a node if **all** 3 conditions are true:
* The node is unlocked,
* It has at least one locked descendant (by **any** user), and
* It does not have any locked ancestors.
Implement the `LockingTree` class:
* `LockingTree(int[] parent)` initializes the data structure with the parent array.
* `lock(int num, int user)` returns `true` if it is possible for the user with id `user` to lock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **locked** by the user with id `user`.
* `unlock(int num, int user)` returns `true` if it is possible for the user with id `user` to unlock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **unlocked**.
* `upgrade(int num, int user)` returns `true` if it is possible for the user with id `user` to upgrade the node `num`, or `false` otherwise. If it is possible, the node `num` will be **upgraded**.
**Example 1:**
**Input**
\[ "LockingTree ", "lock ", "unlock ", "unlock ", "lock ", "upgrade ", "lock "\]
\[\[\[-1, 0, 0, 1, 1, 2, 2\]\], \[2, 2\], \[2, 3\], \[2, 2\], \[4, 5\], \[0, 1\], \[0, 1\]\]
**Output**
\[null, true, false, true, true, true, false\]
**Explanation**
LockingTree lockingTree = new LockingTree(\[-1, 0, 0, 1, 1, 2, 2\]);
lockingTree.lock(2, 2); // return true because node 2 is unlocked.
// Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3); // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2); // return true because node 2 was previously locked by user 2.
// Node 2 will now be unlocked.
lockingTree.lock(4, 5); // return true because node 4 is unlocked.
// Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
// Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1); // return false because node 0 is already locked.
**Constraints:**
* `n == parent.length`
* `2 <= n <= 2000`
* `0 <= parent[i] <= n - 1` for `i != 0`
* `parent[0] == -1`
* `0 <= num <= n - 1`
* `1 <= user <= 104`
* `parent` represents a valid tree.
* At most `2000` calls **in total** will be made to `lock`, `unlock`, and `upgrade`. | Is there a way to iterate through all the subsets of the array? Can we use recursion to efficiently iterate through all the subsets? |
Python3 || Beats 99.91 % || Bitmask(or) | sum-of-all-subset-xor-totals | 0 | 1 | The code calculates the bitwise OR of all numbers in the input list using the bitwise OR operator | and stores it in the variable all_or. It then calculates the total number of possible subsets of nums, which is 2^n where n is the length of the list, using the left bit shift operator << and subtracts 1 from it to get the number of subsets excluding the empty set. Finally, it multiplies all_or with the number of subsets to get the sum of XOR of all subsets.\n\nNote that this code does not actually generate all the subsets and calculate their XORs, which would be a brute force approach with O(2^n) time complexity. Instead, it uses a mathematical property of XOR operation that the XOR of two equal numbers is 0 and XOR of a number with 0 is the number itself, and calculates the answer using a formula. This approach has a time complexity of O(n) and is more efficient for larger inputs.\n\n\n# Please Upvote \uD83D\uDE07\n\n## Python3\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n n=len(nums)\n all_or=0\n for i in range(n):\n all_or|=nums[i]\n return all_or*(1<<(n-1))\n```\n | 67 | The **XOR total** of an array is defined as the bitwise `XOR` of **all its elements**, or `0` if the array is **empty**.
* For example, the **XOR total** of the array `[2,5,6]` is `2 XOR 5 XOR 6 = 1`.
Given an array `nums`, return _the **sum** of all **XOR totals** for every **subset** of_ `nums`.
**Note:** Subsets with the **same** elements should be counted **multiple** times.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`.
**Example 1:**
**Input:** nums = \[1,3\]
**Output:** 6
**Explanation:** The 4 subsets of \[1,3\] are:
- The empty subset has an XOR total of 0.
- \[1\] has an XOR total of 1.
- \[3\] has an XOR total of 3.
- \[1,3\] has an XOR total of 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
**Example 2:**
**Input:** nums = \[5,1,6\]
**Output:** 28
**Explanation:** The 8 subsets of \[5,1,6\] are:
- The empty subset has an XOR total of 0.
- \[5\] has an XOR total of 5.
- \[1\] has an XOR total of 1.
- \[6\] has an XOR total of 6.
- \[5,1\] has an XOR total of 5 XOR 1 = 4.
- \[5,6\] has an XOR total of 5 XOR 6 = 3.
- \[1,6\] has an XOR total of 1 XOR 6 = 7.
- \[5,1,6\] has an XOR total of 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
**Example 3:**
**Input:** nums = \[3,4,5,6,7,8\]
**Output:** 480
**Explanation:** The sum of all XOR totals for every subset is 480.
**Constraints:**
* `1 <= nums.length <= 12`
* `1 <= nums[i] <= 20` | null |
Python3 || Beats 99.91 % || Bitmask(or) | sum-of-all-subset-xor-totals | 0 | 1 | The code calculates the bitwise OR of all numbers in the input list using the bitwise OR operator | and stores it in the variable all_or. It then calculates the total number of possible subsets of nums, which is 2^n where n is the length of the list, using the left bit shift operator << and subtracts 1 from it to get the number of subsets excluding the empty set. Finally, it multiplies all_or with the number of subsets to get the sum of XOR of all subsets.\n\nNote that this code does not actually generate all the subsets and calculate their XORs, which would be a brute force approach with O(2^n) time complexity. Instead, it uses a mathematical property of XOR operation that the XOR of two equal numbers is 0 and XOR of a number with 0 is the number itself, and calculates the answer using a formula. This approach has a time complexity of O(n) and is more efficient for larger inputs.\n\n\n# Please Upvote \uD83D\uDE07\n\n## Python3\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n n=len(nums)\n all_or=0\n for i in range(n):\n all_or|=nums[i]\n return all_or*(1<<(n-1))\n```\n | 67 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of the `ith` node. The root of the tree is node `0`, so `parent[0] = -1` since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.
The data structure should support the following functions:
* **Lock:** **Locks** the given node for the given user and prevents other users from locking the same node. You may only lock a node using this function if the node is unlocked.
* **Unlock: Unlocks** the given node for the given user. You may only unlock a node using this function if it is currently locked by the same user.
* **Upgrade****: Locks** the given node for the given user and **unlocks** all of its descendants **regardless** of who locked it. You may only upgrade a node if **all** 3 conditions are true:
* The node is unlocked,
* It has at least one locked descendant (by **any** user), and
* It does not have any locked ancestors.
Implement the `LockingTree` class:
* `LockingTree(int[] parent)` initializes the data structure with the parent array.
* `lock(int num, int user)` returns `true` if it is possible for the user with id `user` to lock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **locked** by the user with id `user`.
* `unlock(int num, int user)` returns `true` if it is possible for the user with id `user` to unlock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **unlocked**.
* `upgrade(int num, int user)` returns `true` if it is possible for the user with id `user` to upgrade the node `num`, or `false` otherwise. If it is possible, the node `num` will be **upgraded**.
**Example 1:**
**Input**
\[ "LockingTree ", "lock ", "unlock ", "unlock ", "lock ", "upgrade ", "lock "\]
\[\[\[-1, 0, 0, 1, 1, 2, 2\]\], \[2, 2\], \[2, 3\], \[2, 2\], \[4, 5\], \[0, 1\], \[0, 1\]\]
**Output**
\[null, true, false, true, true, true, false\]
**Explanation**
LockingTree lockingTree = new LockingTree(\[-1, 0, 0, 1, 1, 2, 2\]);
lockingTree.lock(2, 2); // return true because node 2 is unlocked.
// Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3); // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2); // return true because node 2 was previously locked by user 2.
// Node 2 will now be unlocked.
lockingTree.lock(4, 5); // return true because node 4 is unlocked.
// Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
// Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1); // return false because node 0 is already locked.
**Constraints:**
* `n == parent.length`
* `2 <= n <= 2000`
* `0 <= parent[i] <= n - 1` for `i != 0`
* `parent[0] == -1`
* `0 <= num <= n - 1`
* `1 <= user <= 104`
* `parent` represents a valid tree.
* At most `2000` calls **in total** will be made to `lock`, `unlock`, and `upgrade`. | Is there a way to iterate through all the subsets of the array? Can we use recursion to efficiently iterate through all the subsets? |
Python oneliner | sum-of-all-subset-xor-totals | 0 | 1 | ```py\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n \n return sum(reduce(operator.xor, comb) for i in range(1, len(nums)+1) for comb in combinations(nums, i))\n \n``` | 2 | The **XOR total** of an array is defined as the bitwise `XOR` of **all its elements**, or `0` if the array is **empty**.
* For example, the **XOR total** of the array `[2,5,6]` is `2 XOR 5 XOR 6 = 1`.
Given an array `nums`, return _the **sum** of all **XOR totals** for every **subset** of_ `nums`.
**Note:** Subsets with the **same** elements should be counted **multiple** times.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`.
**Example 1:**
**Input:** nums = \[1,3\]
**Output:** 6
**Explanation:** The 4 subsets of \[1,3\] are:
- The empty subset has an XOR total of 0.
- \[1\] has an XOR total of 1.
- \[3\] has an XOR total of 3.
- \[1,3\] has an XOR total of 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
**Example 2:**
**Input:** nums = \[5,1,6\]
**Output:** 28
**Explanation:** The 8 subsets of \[5,1,6\] are:
- The empty subset has an XOR total of 0.
- \[5\] has an XOR total of 5.
- \[1\] has an XOR total of 1.
- \[6\] has an XOR total of 6.
- \[5,1\] has an XOR total of 5 XOR 1 = 4.
- \[5,6\] has an XOR total of 5 XOR 6 = 3.
- \[1,6\] has an XOR total of 1 XOR 6 = 7.
- \[5,1,6\] has an XOR total of 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
**Example 3:**
**Input:** nums = \[3,4,5,6,7,8\]
**Output:** 480
**Explanation:** The sum of all XOR totals for every subset is 480.
**Constraints:**
* `1 <= nums.length <= 12`
* `1 <= nums[i] <= 20` | null |
Python oneliner | sum-of-all-subset-xor-totals | 0 | 1 | ```py\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n \n return sum(reduce(operator.xor, comb) for i in range(1, len(nums)+1) for comb in combinations(nums, i))\n \n``` | 2 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of the `ith` node. The root of the tree is node `0`, so `parent[0] = -1` since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.
The data structure should support the following functions:
* **Lock:** **Locks** the given node for the given user and prevents other users from locking the same node. You may only lock a node using this function if the node is unlocked.
* **Unlock: Unlocks** the given node for the given user. You may only unlock a node using this function if it is currently locked by the same user.
* **Upgrade****: Locks** the given node for the given user and **unlocks** all of its descendants **regardless** of who locked it. You may only upgrade a node if **all** 3 conditions are true:
* The node is unlocked,
* It has at least one locked descendant (by **any** user), and
* It does not have any locked ancestors.
Implement the `LockingTree` class:
* `LockingTree(int[] parent)` initializes the data structure with the parent array.
* `lock(int num, int user)` returns `true` if it is possible for the user with id `user` to lock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **locked** by the user with id `user`.
* `unlock(int num, int user)` returns `true` if it is possible for the user with id `user` to unlock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **unlocked**.
* `upgrade(int num, int user)` returns `true` if it is possible for the user with id `user` to upgrade the node `num`, or `false` otherwise. If it is possible, the node `num` will be **upgraded**.
**Example 1:**
**Input**
\[ "LockingTree ", "lock ", "unlock ", "unlock ", "lock ", "upgrade ", "lock "\]
\[\[\[-1, 0, 0, 1, 1, 2, 2\]\], \[2, 2\], \[2, 3\], \[2, 2\], \[4, 5\], \[0, 1\], \[0, 1\]\]
**Output**
\[null, true, false, true, true, true, false\]
**Explanation**
LockingTree lockingTree = new LockingTree(\[-1, 0, 0, 1, 1, 2, 2\]);
lockingTree.lock(2, 2); // return true because node 2 is unlocked.
// Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3); // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2); // return true because node 2 was previously locked by user 2.
// Node 2 will now be unlocked.
lockingTree.lock(4, 5); // return true because node 4 is unlocked.
// Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
// Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1); // return false because node 0 is already locked.
**Constraints:**
* `n == parent.length`
* `2 <= n <= 2000`
* `0 <= parent[i] <= n - 1` for `i != 0`
* `parent[0] == -1`
* `0 <= num <= n - 1`
* `1 <= user <= 104`
* `parent` represents a valid tree.
* At most `2000` calls **in total** will be made to `lock`, `unlock`, and `upgrade`. | Is there a way to iterate through all the subsets of the array? Can we use recursion to efficiently iterate through all the subsets? |
Detailed explanation of the topic | sum-of-all-subset-xor-totals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code calculates the XOR sum of all possible subsets of the input list nums and returns the result\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Perform bitwise OR operation: ans |= x performs a bitwise OR operation between the current ans value and the current number x. The bitwise OR operation (|) combines the bits of ans and x, setting a bit to 1 if either of the corresponding bits in ans or x is 1. This step accumulates the XOR values of all the numbers in nums into ans.\n\n2. Calculate the final result: return ans * 2 ** (len(nums)-1) calculates the XOR sum of all subsets. The XOR sum of all subsets can be derived by multiplying the accumulated XOR value ans with 2 ** (len(nums)-1), where 2 ** (len(nums)-1) represents the total number of subsets of nums.\n\nThe expression 2 ** (len(nums)-1) calculates the total number of subsets by taking 2 to the power of len(nums)-1. Since each element in nums can either be included or excluded in a subset, there are 2 choices for each element, resulting in a total of 2 ** len(nums) subsets. By subtracting 1 (len(nums)-1), we exclude the empty set from the count, giving us the total number of non-empty subsets.\nMultiplying ans by 2 ** (len(nums)-1) gives us the XOR sum of all subsets.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\nThe loop for x in nums: iterates through each number in the nums list. Hence, the time complexity of the loop is **O(N)**, where N is the length of the nums list.\nThe bitwise OR operation ans |= x is a constant time operation.\nCalculating 2 ** (len(nums)-1) is also a constant time operation.\nOverall, the time complexity of the code snippet is O(N), where N is the length of the nums list.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nThe space complexity is determined by the usage of additional memory, excluding the input and the output space.\nThe only additional space used in this code snippet is for the variable ans.\nSince ans is a single integer variable, the space complexity is **O(1)**, constant space.\n\n# Code\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n res =0\n for x in nums:\n res |= x\n return res*(2**(len(nums)-1))\n \n``` | 3 | The **XOR total** of an array is defined as the bitwise `XOR` of **all its elements**, or `0` if the array is **empty**.
* For example, the **XOR total** of the array `[2,5,6]` is `2 XOR 5 XOR 6 = 1`.
Given an array `nums`, return _the **sum** of all **XOR totals** for every **subset** of_ `nums`.
**Note:** Subsets with the **same** elements should be counted **multiple** times.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`.
**Example 1:**
**Input:** nums = \[1,3\]
**Output:** 6
**Explanation:** The 4 subsets of \[1,3\] are:
- The empty subset has an XOR total of 0.
- \[1\] has an XOR total of 1.
- \[3\] has an XOR total of 3.
- \[1,3\] has an XOR total of 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
**Example 2:**
**Input:** nums = \[5,1,6\]
**Output:** 28
**Explanation:** The 8 subsets of \[5,1,6\] are:
- The empty subset has an XOR total of 0.
- \[5\] has an XOR total of 5.
- \[1\] has an XOR total of 1.
- \[6\] has an XOR total of 6.
- \[5,1\] has an XOR total of 5 XOR 1 = 4.
- \[5,6\] has an XOR total of 5 XOR 6 = 3.
- \[1,6\] has an XOR total of 1 XOR 6 = 7.
- \[5,1,6\] has an XOR total of 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
**Example 3:**
**Input:** nums = \[3,4,5,6,7,8\]
**Output:** 480
**Explanation:** The sum of all XOR totals for every subset is 480.
**Constraints:**
* `1 <= nums.length <= 12`
* `1 <= nums[i] <= 20` | null |
Detailed explanation of the topic | sum-of-all-subset-xor-totals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code calculates the XOR sum of all possible subsets of the input list nums and returns the result\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Perform bitwise OR operation: ans |= x performs a bitwise OR operation between the current ans value and the current number x. The bitwise OR operation (|) combines the bits of ans and x, setting a bit to 1 if either of the corresponding bits in ans or x is 1. This step accumulates the XOR values of all the numbers in nums into ans.\n\n2. Calculate the final result: return ans * 2 ** (len(nums)-1) calculates the XOR sum of all subsets. The XOR sum of all subsets can be derived by multiplying the accumulated XOR value ans with 2 ** (len(nums)-1), where 2 ** (len(nums)-1) represents the total number of subsets of nums.\n\nThe expression 2 ** (len(nums)-1) calculates the total number of subsets by taking 2 to the power of len(nums)-1. Since each element in nums can either be included or excluded in a subset, there are 2 choices for each element, resulting in a total of 2 ** len(nums) subsets. By subtracting 1 (len(nums)-1), we exclude the empty set from the count, giving us the total number of non-empty subsets.\nMultiplying ans by 2 ** (len(nums)-1) gives us the XOR sum of all subsets.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\nThe loop for x in nums: iterates through each number in the nums list. Hence, the time complexity of the loop is **O(N)**, where N is the length of the nums list.\nThe bitwise OR operation ans |= x is a constant time operation.\nCalculating 2 ** (len(nums)-1) is also a constant time operation.\nOverall, the time complexity of the code snippet is O(N), where N is the length of the nums list.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nThe space complexity is determined by the usage of additional memory, excluding the input and the output space.\nThe only additional space used in this code snippet is for the variable ans.\nSince ans is a single integer variable, the space complexity is **O(1)**, constant space.\n\n# Code\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n res =0\n for x in nums:\n res |= x\n return res*(2**(len(nums)-1))\n \n``` | 3 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of the `ith` node. The root of the tree is node `0`, so `parent[0] = -1` since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.
The data structure should support the following functions:
* **Lock:** **Locks** the given node for the given user and prevents other users from locking the same node. You may only lock a node using this function if the node is unlocked.
* **Unlock: Unlocks** the given node for the given user. You may only unlock a node using this function if it is currently locked by the same user.
* **Upgrade****: Locks** the given node for the given user and **unlocks** all of its descendants **regardless** of who locked it. You may only upgrade a node if **all** 3 conditions are true:
* The node is unlocked,
* It has at least one locked descendant (by **any** user), and
* It does not have any locked ancestors.
Implement the `LockingTree` class:
* `LockingTree(int[] parent)` initializes the data structure with the parent array.
* `lock(int num, int user)` returns `true` if it is possible for the user with id `user` to lock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **locked** by the user with id `user`.
* `unlock(int num, int user)` returns `true` if it is possible for the user with id `user` to unlock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **unlocked**.
* `upgrade(int num, int user)` returns `true` if it is possible for the user with id `user` to upgrade the node `num`, or `false` otherwise. If it is possible, the node `num` will be **upgraded**.
**Example 1:**
**Input**
\[ "LockingTree ", "lock ", "unlock ", "unlock ", "lock ", "upgrade ", "lock "\]
\[\[\[-1, 0, 0, 1, 1, 2, 2\]\], \[2, 2\], \[2, 3\], \[2, 2\], \[4, 5\], \[0, 1\], \[0, 1\]\]
**Output**
\[null, true, false, true, true, true, false\]
**Explanation**
LockingTree lockingTree = new LockingTree(\[-1, 0, 0, 1, 1, 2, 2\]);
lockingTree.lock(2, 2); // return true because node 2 is unlocked.
// Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3); // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2); // return true because node 2 was previously locked by user 2.
// Node 2 will now be unlocked.
lockingTree.lock(4, 5); // return true because node 4 is unlocked.
// Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
// Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1); // return false because node 0 is already locked.
**Constraints:**
* `n == parent.length`
* `2 <= n <= 2000`
* `0 <= parent[i] <= n - 1` for `i != 0`
* `parent[0] == -1`
* `0 <= num <= n - 1`
* `1 <= user <= 104`
* `parent` represents a valid tree.
* At most `2000` calls **in total** will be made to `lock`, `unlock`, and `upgrade`. | Is there a way to iterate through all the subsets of the array? Can we use recursion to efficiently iterate through all the subsets? |
Best Optimal Solution | sum-of-all-subset-xor-totals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n sum = 0\n for i in nums:\n sum |= i\n result = sum*(2**(len(nums)-1))\n return result\n``` | 1 | The **XOR total** of an array is defined as the bitwise `XOR` of **all its elements**, or `0` if the array is **empty**.
* For example, the **XOR total** of the array `[2,5,6]` is `2 XOR 5 XOR 6 = 1`.
Given an array `nums`, return _the **sum** of all **XOR totals** for every **subset** of_ `nums`.
**Note:** Subsets with the **same** elements should be counted **multiple** times.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`.
**Example 1:**
**Input:** nums = \[1,3\]
**Output:** 6
**Explanation:** The 4 subsets of \[1,3\] are:
- The empty subset has an XOR total of 0.
- \[1\] has an XOR total of 1.
- \[3\] has an XOR total of 3.
- \[1,3\] has an XOR total of 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
**Example 2:**
**Input:** nums = \[5,1,6\]
**Output:** 28
**Explanation:** The 8 subsets of \[5,1,6\] are:
- The empty subset has an XOR total of 0.
- \[5\] has an XOR total of 5.
- \[1\] has an XOR total of 1.
- \[6\] has an XOR total of 6.
- \[5,1\] has an XOR total of 5 XOR 1 = 4.
- \[5,6\] has an XOR total of 5 XOR 6 = 3.
- \[1,6\] has an XOR total of 1 XOR 6 = 7.
- \[5,1,6\] has an XOR total of 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
**Example 3:**
**Input:** nums = \[3,4,5,6,7,8\]
**Output:** 480
**Explanation:** The sum of all XOR totals for every subset is 480.
**Constraints:**
* `1 <= nums.length <= 12`
* `1 <= nums[i] <= 20` | null |
Best Optimal Solution | sum-of-all-subset-xor-totals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subsetXORSum(self, nums: List[int]) -> int:\n sum = 0\n for i in nums:\n sum |= i\n result = sum*(2**(len(nums)-1))\n return result\n``` | 1 | You are given a tree with `n` nodes numbered from `0` to `n - 1` in the form of a parent array `parent` where `parent[i]` is the parent of the `ith` node. The root of the tree is node `0`, so `parent[0] = -1` since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.
The data structure should support the following functions:
* **Lock:** **Locks** the given node for the given user and prevents other users from locking the same node. You may only lock a node using this function if the node is unlocked.
* **Unlock: Unlocks** the given node for the given user. You may only unlock a node using this function if it is currently locked by the same user.
* **Upgrade****: Locks** the given node for the given user and **unlocks** all of its descendants **regardless** of who locked it. You may only upgrade a node if **all** 3 conditions are true:
* The node is unlocked,
* It has at least one locked descendant (by **any** user), and
* It does not have any locked ancestors.
Implement the `LockingTree` class:
* `LockingTree(int[] parent)` initializes the data structure with the parent array.
* `lock(int num, int user)` returns `true` if it is possible for the user with id `user` to lock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **locked** by the user with id `user`.
* `unlock(int num, int user)` returns `true` if it is possible for the user with id `user` to unlock the node `num`, or `false` otherwise. If it is possible, the node `num` will become **unlocked**.
* `upgrade(int num, int user)` returns `true` if it is possible for the user with id `user` to upgrade the node `num`, or `false` otherwise. If it is possible, the node `num` will be **upgraded**.
**Example 1:**
**Input**
\[ "LockingTree ", "lock ", "unlock ", "unlock ", "lock ", "upgrade ", "lock "\]
\[\[\[-1, 0, 0, 1, 1, 2, 2\]\], \[2, 2\], \[2, 3\], \[2, 2\], \[4, 5\], \[0, 1\], \[0, 1\]\]
**Output**
\[null, true, false, true, true, true, false\]
**Explanation**
LockingTree lockingTree = new LockingTree(\[-1, 0, 0, 1, 1, 2, 2\]);
lockingTree.lock(2, 2); // return true because node 2 is unlocked.
// Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3); // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2); // return true because node 2 was previously locked by user 2.
// Node 2 will now be unlocked.
lockingTree.lock(4, 5); // return true because node 4 is unlocked.
// Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
// Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1); // return false because node 0 is already locked.
**Constraints:**
* `n == parent.length`
* `2 <= n <= 2000`
* `0 <= parent[i] <= n - 1` for `i != 0`
* `parent[0] == -1`
* `0 <= num <= n - 1`
* `1 <= user <= 104`
* `parent` represents a valid tree.
* At most `2000` calls **in total** will be made to `lock`, `unlock`, and `upgrade`. | Is there a way to iterate through all the subsets of the array? Can we use recursion to efficiently iterate through all the subsets? |
[Python3] greedy | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | \n```\nclass Solution:\n def minSwaps(self, s: str) -> int:\n ones = s.count("1")\n zeros = len(s) - ones \n if abs(ones - zeros) > 1: return -1 # impossible\n \n def fn(x): \n """Return number of swaps if string starts with x."""\n ans = 0 \n for c in s: \n if c != x: ans += 1\n x = "1" if x == "0" else "0"\n return ans//2\n \n if ones > zeros: return fn("1")\n elif ones < zeros: return fn("0")\n else: return min(fn("0"), fn("1")) \n``` | 26 | Given a binary string `s`, return _the **minimum** number of character swaps to make it **alternating**, or_ `-1` _if it is impossible._
The string is called **alternating** if no two adjacent characters are equal. For example, the strings `"010 "` and `"1010 "` are alternating, while the string `"0100 "` is not.
Any two characters may be swapped, even if they are **not adjacent**.
**Example 1:**
**Input:** s = "111000 "
**Output:** 1
**Explanation:** Swap positions 1 and 4: "111000 " -> "101010 "
The string is now alternating.
**Example 2:**
**Input:** s = "010 "
**Output:** 0
**Explanation:** The string is already alternating, no swaps are needed.
**Example 3:**
**Input:** s = "1110 "
**Output:** -1
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`. | null |
[Python3] greedy | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | \n```\nclass Solution:\n def minSwaps(self, s: str) -> int:\n ones = s.count("1")\n zeros = len(s) - ones \n if abs(ones - zeros) > 1: return -1 # impossible\n \n def fn(x): \n """Return number of swaps if string starts with x."""\n ans = 0 \n for c in s: \n if c != x: ans += 1\n x = "1" if x == "0" else "0"\n return ans//2\n \n if ones > zeros: return fn("1")\n elif ones < zeros: return fn("0")\n else: return min(fn("0"), fn("1")) \n``` | 26 | You are given an integer array `nums`. We call a subset of `nums` **good** if its product can be represented as a product of one or more **distinct prime** numbers.
* For example, if `nums = [1, 2, 3, 4]`:
* `[2, 3]`, `[1, 2, 3]`, and `[1, 3]` are **good** subsets with products `6 = 2*3`, `6 = 2*3`, and `3 = 3` respectively.
* `[1, 4]` and `[4]` are not **good** subsets with products `4 = 2*2` and `4 = 2*2` respectively.
Return _the number of different **good** subsets in_ `nums` _**modulo**_ `109 + 7`.
A **subset** of `nums` is any array that can be obtained by deleting some (possibly none or all) elements from `nums`. Two subsets are different if and only if the chosen indices to delete are different.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 6
**Explanation:** The good subsets are:
- \[1,2\]: product is 2, which is the product of distinct prime 2.
- \[1,2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[1,3\]: product is 3, which is the product of distinct prime 3.
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[3\]: product is 3, which is the product of distinct prime 3.
**Example 2:**
**Input:** nums = \[4,2,3,15\]
**Output:** 5
**Explanation:** The good subsets are:
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[2,15\]: product is 30, which is the product of distinct primes 2, 3, and 5.
- \[3\]: product is 3, which is the product of distinct prime 3.
- \[15\]: product is 15, which is the product of distinct primes 3 and 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 30` | Think about all valid strings of length n. Try to count the mismatched positions with each valid string of length n. |
Python 3 | Greedy | Explanation | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | ### Explanation\n- When talking about _**swap**_, it\'s almost always a greedy operation, no easy way around\n- There are only two scenarios, either `010101....` or `101010....`, depends on the length of `s`, you might want to append an extra `0` or `1`\n- Simply count the mismatches and pick the less one, see more explanation in the code comment below\n### Implementation\n```\nclass Solution:\n def minSwaps(self, s: str) -> int:\n ans = n = len(s)\n zero, one = 0, 0\n for c in s: # count number of 0 & 1s\n if c == \'0\':\n zero += 1\n else:\n one += 1\n if abs(zero - one) > 1: return -1 # not possible when cnt differ over 1 \n if zero >= one: # \'010101....\' \n s1 = \'01\' * (n // 2) # when zero == one\n s1 += \'0\' if n % 2 else \'\' # when zero > one \n cnt = sum(c1 != c for c1, c in zip(s1, s))\n ans = cnt // 2\n if zero <= one: # \'101010....\'\n s2 = \'10\' * (n // 2) # when zero == one\n s2 += \'1\' if n % 2 else \'\' # when one > zero \n cnt = sum(c2 != c for c2, c in zip(s2, s))\n ans = min(ans, cnt // 2)\n return ans\n``` | 10 | Given a binary string `s`, return _the **minimum** number of character swaps to make it **alternating**, or_ `-1` _if it is impossible._
The string is called **alternating** if no two adjacent characters are equal. For example, the strings `"010 "` and `"1010 "` are alternating, while the string `"0100 "` is not.
Any two characters may be swapped, even if they are **not adjacent**.
**Example 1:**
**Input:** s = "111000 "
**Output:** 1
**Explanation:** Swap positions 1 and 4: "111000 " -> "101010 "
The string is now alternating.
**Example 2:**
**Input:** s = "010 "
**Output:** 0
**Explanation:** The string is already alternating, no swaps are needed.
**Example 3:**
**Input:** s = "1110 "
**Output:** -1
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`. | null |
Python 3 | Greedy | Explanation | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | ### Explanation\n- When talking about _**swap**_, it\'s almost always a greedy operation, no easy way around\n- There are only two scenarios, either `010101....` or `101010....`, depends on the length of `s`, you might want to append an extra `0` or `1`\n- Simply count the mismatches and pick the less one, see more explanation in the code comment below\n### Implementation\n```\nclass Solution:\n def minSwaps(self, s: str) -> int:\n ans = n = len(s)\n zero, one = 0, 0\n for c in s: # count number of 0 & 1s\n if c == \'0\':\n zero += 1\n else:\n one += 1\n if abs(zero - one) > 1: return -1 # not possible when cnt differ over 1 \n if zero >= one: # \'010101....\' \n s1 = \'01\' * (n // 2) # when zero == one\n s1 += \'0\' if n % 2 else \'\' # when zero > one \n cnt = sum(c1 != c for c1, c in zip(s1, s))\n ans = cnt // 2\n if zero <= one: # \'101010....\'\n s2 = \'10\' * (n // 2) # when zero == one\n s2 += \'1\' if n % 2 else \'\' # when one > zero \n cnt = sum(c2 != c for c2, c in zip(s2, s))\n ans = min(ans, cnt // 2)\n return ans\n``` | 10 | You are given an integer array `nums`. We call a subset of `nums` **good** if its product can be represented as a product of one or more **distinct prime** numbers.
* For example, if `nums = [1, 2, 3, 4]`:
* `[2, 3]`, `[1, 2, 3]`, and `[1, 3]` are **good** subsets with products `6 = 2*3`, `6 = 2*3`, and `3 = 3` respectively.
* `[1, 4]` and `[4]` are not **good** subsets with products `4 = 2*2` and `4 = 2*2` respectively.
Return _the number of different **good** subsets in_ `nums` _**modulo**_ `109 + 7`.
A **subset** of `nums` is any array that can be obtained by deleting some (possibly none or all) elements from `nums`. Two subsets are different if and only if the chosen indices to delete are different.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 6
**Explanation:** The good subsets are:
- \[1,2\]: product is 2, which is the product of distinct prime 2.
- \[1,2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[1,3\]: product is 3, which is the product of distinct prime 3.
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[3\]: product is 3, which is the product of distinct prime 3.
**Example 2:**
**Input:** nums = \[4,2,3,15\]
**Output:** 5
**Explanation:** The good subsets are:
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[2,15\]: product is 30, which is the product of distinct primes 2, 3, and 5.
- \[3\]: product is 3, which is the product of distinct prime 3.
- \[15\]: product is 15, which is the product of distinct primes 3 and 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 30` | Think about all valid strings of length n. Try to count the mismatched positions with each valid string of length n. |
Python, one and only loop | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSwaps(self, s):\n ones_counts = [0, 0] # number of ones in odd indecies and even indecies\n for i in range(len(s)):\n if s[i] == \'1\':\n ones_counts[i%2] += 1\n num_ones = ones_counts[0] + ones_counts[1]\n num_zeros = len(s) - num_ones\n \n if num_zeros - num_ones > 1 or num_zeros - num_ones < -1:\n return -1\n elif num_zeros - num_ones == 1: # num zeroes are num ones + 1\n #return num_ones - ones_counts[1]\n return ones_counts[0]\n elif num_ones - num_zeros == 1:\n return ones_counts[1]\n else:\n return min(ones_counts[0], ones_counts[1])\n``` | 1 | Given a binary string `s`, return _the **minimum** number of character swaps to make it **alternating**, or_ `-1` _if it is impossible._
The string is called **alternating** if no two adjacent characters are equal. For example, the strings `"010 "` and `"1010 "` are alternating, while the string `"0100 "` is not.
Any two characters may be swapped, even if they are **not adjacent**.
**Example 1:**
**Input:** s = "111000 "
**Output:** 1
**Explanation:** Swap positions 1 and 4: "111000 " -> "101010 "
The string is now alternating.
**Example 2:**
**Input:** s = "010 "
**Output:** 0
**Explanation:** The string is already alternating, no swaps are needed.
**Example 3:**
**Input:** s = "1110 "
**Output:** -1
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`. | null |
Python, one and only loop | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSwaps(self, s):\n ones_counts = [0, 0] # number of ones in odd indecies and even indecies\n for i in range(len(s)):\n if s[i] == \'1\':\n ones_counts[i%2] += 1\n num_ones = ones_counts[0] + ones_counts[1]\n num_zeros = len(s) - num_ones\n \n if num_zeros - num_ones > 1 or num_zeros - num_ones < -1:\n return -1\n elif num_zeros - num_ones == 1: # num zeroes are num ones + 1\n #return num_ones - ones_counts[1]\n return ones_counts[0]\n elif num_ones - num_zeros == 1:\n return ones_counts[1]\n else:\n return min(ones_counts[0], ones_counts[1])\n``` | 1 | You are given an integer array `nums`. We call a subset of `nums` **good** if its product can be represented as a product of one or more **distinct prime** numbers.
* For example, if `nums = [1, 2, 3, 4]`:
* `[2, 3]`, `[1, 2, 3]`, and `[1, 3]` are **good** subsets with products `6 = 2*3`, `6 = 2*3`, and `3 = 3` respectively.
* `[1, 4]` and `[4]` are not **good** subsets with products `4 = 2*2` and `4 = 2*2` respectively.
Return _the number of different **good** subsets in_ `nums` _**modulo**_ `109 + 7`.
A **subset** of `nums` is any array that can be obtained by deleting some (possibly none or all) elements from `nums`. Two subsets are different if and only if the chosen indices to delete are different.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 6
**Explanation:** The good subsets are:
- \[1,2\]: product is 2, which is the product of distinct prime 2.
- \[1,2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[1,3\]: product is 3, which is the product of distinct prime 3.
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[3\]: product is 3, which is the product of distinct prime 3.
**Example 2:**
**Input:** nums = \[4,2,3,15\]
**Output:** 5
**Explanation:** The good subsets are:
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[2,15\]: product is 30, which is the product of distinct primes 2, 3, and 5.
- \[3\]: product is 3, which is the product of distinct prime 3.
- \[15\]: product is 15, which is the product of distinct primes 3 and 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 30` | Think about all valid strings of length n. Try to count the mismatched positions with each valid string of length n. |
DIFFERENT SOLUTION IN PYTHON | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSwaps(self, s: str) -> int:\n if abs((s.count("1")-s.count("0")))>1:\n return -1\n c1=s.count("1")\n c0=s.count("0")\n r=len(s)\n str1=""\n str2=""\n i=0\n while(i<r):\n str1+="1"\n i+=1\n if(i<r):\n str1+="0"\n i+=1\n else:\n break\n i=0\n while(i<r):\n str2+="0"\n i+=1\n if(i<r):\n str2+="1"\n i+=1\n else:\n break\n print(str1)\n print(str2) \n ct1=0\n ct2=0\n\n for i in range(len(s)):\n if(s[i]!=str1[i]):\n ct1+=1\n for i in range(len(s)):\n if(s[i]!=str2[i]):\n ct2+=1\n if c1-c0==1:\n return ct1//2\n if c0-c1==1:\n return ct2//2\n else:\n mini=min(ct1,ct2)\n return mini//2\n\n\n \n\n \n``` | 0 | Given a binary string `s`, return _the **minimum** number of character swaps to make it **alternating**, or_ `-1` _if it is impossible._
The string is called **alternating** if no two adjacent characters are equal. For example, the strings `"010 "` and `"1010 "` are alternating, while the string `"0100 "` is not.
Any two characters may be swapped, even if they are **not adjacent**.
**Example 1:**
**Input:** s = "111000 "
**Output:** 1
**Explanation:** Swap positions 1 and 4: "111000 " -> "101010 "
The string is now alternating.
**Example 2:**
**Input:** s = "010 "
**Output:** 0
**Explanation:** The string is already alternating, no swaps are needed.
**Example 3:**
**Input:** s = "1110 "
**Output:** -1
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`. | null |
DIFFERENT SOLUTION IN PYTHON | minimum-number-of-swaps-to-make-the-binary-string-alternating | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSwaps(self, s: str) -> int:\n if abs((s.count("1")-s.count("0")))>1:\n return -1\n c1=s.count("1")\n c0=s.count("0")\n r=len(s)\n str1=""\n str2=""\n i=0\n while(i<r):\n str1+="1"\n i+=1\n if(i<r):\n str1+="0"\n i+=1\n else:\n break\n i=0\n while(i<r):\n str2+="0"\n i+=1\n if(i<r):\n str2+="1"\n i+=1\n else:\n break\n print(str1)\n print(str2) \n ct1=0\n ct2=0\n\n for i in range(len(s)):\n if(s[i]!=str1[i]):\n ct1+=1\n for i in range(len(s)):\n if(s[i]!=str2[i]):\n ct2+=1\n if c1-c0==1:\n return ct1//2\n if c0-c1==1:\n return ct2//2\n else:\n mini=min(ct1,ct2)\n return mini//2\n\n\n \n\n \n``` | 0 | You are given an integer array `nums`. We call a subset of `nums` **good** if its product can be represented as a product of one or more **distinct prime** numbers.
* For example, if `nums = [1, 2, 3, 4]`:
* `[2, 3]`, `[1, 2, 3]`, and `[1, 3]` are **good** subsets with products `6 = 2*3`, `6 = 2*3`, and `3 = 3` respectively.
* `[1, 4]` and `[4]` are not **good** subsets with products `4 = 2*2` and `4 = 2*2` respectively.
Return _the number of different **good** subsets in_ `nums` _**modulo**_ `109 + 7`.
A **subset** of `nums` is any array that can be obtained by deleting some (possibly none or all) elements from `nums`. Two subsets are different if and only if the chosen indices to delete are different.
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** 6
**Explanation:** The good subsets are:
- \[1,2\]: product is 2, which is the product of distinct prime 2.
- \[1,2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[1,3\]: product is 3, which is the product of distinct prime 3.
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[3\]: product is 3, which is the product of distinct prime 3.
**Example 2:**
**Input:** nums = \[4,2,3,15\]
**Output:** 5
**Explanation:** The good subsets are:
- \[2\]: product is 2, which is the product of distinct prime 2.
- \[2,3\]: product is 6, which is the product of distinct primes 2 and 3.
- \[2,15\]: product is 30, which is the product of distinct primes 2, 3, and 5.
- \[3\]: product is 3, which is the product of distinct prime 3.
- \[15\]: product is 15, which is the product of distinct primes 3 and 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 30` | Think about all valid strings of length n. Try to count the mismatched positions with each valid string of length n. |
Python3 Hashmap | Explained | finding-pairs-with-a-certain-sum | 0 | 1 | # Intuition\nHashmap.\n\n# Approach\nUse 2 hashmaps to store the frequency of every number from each array.\nWhen adding we just decrease the number of frequency from that second hashmap of the previous number (before adding) and update it with the current value (increasing the freq). We modify the value in the second array too.\nWhen counting we just iterate through the first hashmap and check if we have a match in the second hashmap and get the final number (we will have 1000 elements to pass at most).\n\n# Complexity\n- Time complexity:\nO(n*m) -> n = number of calls and m = number of elements in the first hashmap\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass FindSumPairs:\n\n def __init__(self, nums1: List[int], nums2: List[int]):\n self.nums2 = nums2\n self.d1, self.d2 = defaultdict(lambda: 0), defaultdict(lambda: 0)\n\n for i in range(len(nums1)):\n self.d1[nums1[i]] += 1\n for i in range(len(nums2)):\n self.d2[nums2[i]] += 1\n\n def add(self, index: int, val: int) -> None:\n number = self.nums2[index]\n self.nums2[index] = number+val\n self.d2[number] -= 1\n self.d2[number+val] += 1\n\n def count(self, tot: int) -> int:\n ans = 0\n for i, element in enumerate(self.d1):\n if tot-element in self.d2:\n ans += self.d1[element]*self.d2[tot-element]\n return ans\n\n\n# Your FindSumPairs object will be instantiated and called as such:\n# obj = FindSumPairs(nums1, nums2)\n# obj.add(index,val)\n# param_2 = obj.count(tot)\n```\nUpvote if you like it!^^ | 0 | You are given two integer arrays `nums1` and `nums2`. You are tasked to implement a data structure that supports queries of two types:
1. **Add** a positive integer to an element of a given index in the array `nums2`.
2. **Count** the number of pairs `(i, j)` such that `nums1[i] + nums2[j]` equals a given value (`0 <= i < nums1.length` and `0 <= j < nums2.length`).
Implement the `FindSumPairs` class:
* `FindSumPairs(int[] nums1, int[] nums2)` Initializes the `FindSumPairs` object with two integer arrays `nums1` and `nums2`.
* `void add(int index, int val)` Adds `val` to `nums2[index]`, i.e., apply `nums2[index] += val`.
* `int count(int tot)` Returns the number of pairs `(i, j)` such that `nums1[i] + nums2[j] == tot`.
**Example 1:**
**Input**
\[ "FindSumPairs ", "count ", "add ", "count ", "count ", "add ", "add ", "count "\]
\[\[\[1, 1, 2, 2, 2, 3\], \[1, 4, 5, 2, 5, 4\]\], \[7\], \[3, 2\], \[8\], \[4\], \[0, 1\], \[1, 1\], \[7\]\]
**Output**
\[null, 8, null, 2, 1, null, null, 11\]
**Explanation**
FindSumPairs findSumPairs = new FindSumPairs(\[1, 1, 2, 2, 2, 3\], \[1, 4, 5, 2, 5, 4\]);
findSumPairs.count(7); // return 8; pairs (2,2), (3,2), (4,2), (2,4), (3,4), (4,4) make 2 + 5 and pairs (5,1), (5,5) make 3 + 4
findSumPairs.add(3, 2); // now nums2 = \[1,4,5,**4**`,5,4`\]
findSumPairs.count(8); // return 2; pairs (5,2), (5,4) make 3 + 5
findSumPairs.count(4); // return 1; pair (5,0) makes 3 + 1
findSumPairs.add(0, 1); // now nums2 = \[**`2`**,4,5,4`,5,4`\]
findSumPairs.add(1, 1); // now nums2 = \[`2`,**5**,5,4`,5,4`\]
findSumPairs.count(7); // return 11; pairs (2,1), (2,2), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,4) make 2 + 5 and pairs (5,3), (5,5) make 3 + 4
**Constraints:**
* `1 <= nums1.length <= 1000`
* `1 <= nums2.length <= 105`
* `1 <= nums1[i] <= 109`
* `1 <= nums2[i] <= 105`
* `0 <= index < nums2.length`
* `1 <= val <= 105`
* `1 <= tot <= 109`
* At most `1000` calls are made to `add` and `count` **each**. | Find the minimum spanning tree of the given graph. Root the tree in an arbitrary node and calculate the maximum weight of the edge from each node to the chosen root. To answer a query, find the lca between the two nodes, and find the maximum weight from each of the query nodes to their lca and compare it to the given limit. |
Python3 Sol using dict. | finding-pairs-with-a-certain-sum | 0 | 1 | \n```\nclass FindSumPairs:\n\n def __init__(self, nums1: List[int], nums2: List[int]):\n self.num2=nums2\n self.dict_num1 = collections.Counter(nums1)\n self.dict_num2 = collections.Counter(nums2)\n def add(self, index: int, val: int) -> None:\n old_val = self.num2[index]\n new_val = self.num2[index] + val\n self.num2[index] = new_val\n self.dict_num2[old_val] -= 1\n self.dict_num2[new_val] += 1\n def count(self, tot: int) -> int:\n count=0\n for key in self.dict_num1:\n reminder = tot - key\n if reminder in self.dict_num2:\n count += (self.dict_num1[key] * self.dict_num2[reminder])\n return count\n \n \n\n\n# Your FindSumPairs object will be instantiated and called as such:\n# obj = FindSumPairs(nums1, nums2)\n# obj.add(index,val)\n# param_2 = obj.count(tot)\n``` | 0 | You are given two integer arrays `nums1` and `nums2`. You are tasked to implement a data structure that supports queries of two types:
1. **Add** a positive integer to an element of a given index in the array `nums2`.
2. **Count** the number of pairs `(i, j)` such that `nums1[i] + nums2[j]` equals a given value (`0 <= i < nums1.length` and `0 <= j < nums2.length`).
Implement the `FindSumPairs` class:
* `FindSumPairs(int[] nums1, int[] nums2)` Initializes the `FindSumPairs` object with two integer arrays `nums1` and `nums2`.
* `void add(int index, int val)` Adds `val` to `nums2[index]`, i.e., apply `nums2[index] += val`.
* `int count(int tot)` Returns the number of pairs `(i, j)` such that `nums1[i] + nums2[j] == tot`.
**Example 1:**
**Input**
\[ "FindSumPairs ", "count ", "add ", "count ", "count ", "add ", "add ", "count "\]
\[\[\[1, 1, 2, 2, 2, 3\], \[1, 4, 5, 2, 5, 4\]\], \[7\], \[3, 2\], \[8\], \[4\], \[0, 1\], \[1, 1\], \[7\]\]
**Output**
\[null, 8, null, 2, 1, null, null, 11\]
**Explanation**
FindSumPairs findSumPairs = new FindSumPairs(\[1, 1, 2, 2, 2, 3\], \[1, 4, 5, 2, 5, 4\]);
findSumPairs.count(7); // return 8; pairs (2,2), (3,2), (4,2), (2,4), (3,4), (4,4) make 2 + 5 and pairs (5,1), (5,5) make 3 + 4
findSumPairs.add(3, 2); // now nums2 = \[1,4,5,**4**`,5,4`\]
findSumPairs.count(8); // return 2; pairs (5,2), (5,4) make 3 + 5
findSumPairs.count(4); // return 1; pair (5,0) makes 3 + 1
findSumPairs.add(0, 1); // now nums2 = \[**`2`**,4,5,4`,5,4`\]
findSumPairs.add(1, 1); // now nums2 = \[`2`,**5**,5,4`,5,4`\]
findSumPairs.count(7); // return 11; pairs (2,1), (2,2), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,4) make 2 + 5 and pairs (5,3), (5,5) make 3 + 4
**Constraints:**
* `1 <= nums1.length <= 1000`
* `1 <= nums2.length <= 105`
* `1 <= nums1[i] <= 109`
* `1 <= nums2[i] <= 105`
* `0 <= index < nums2.length`
* `1 <= val <= 105`
* `1 <= tot <= 109`
* At most `1000` calls are made to `add` and `count` **each**. | Find the minimum spanning tree of the given graph. Root the tree in an arbitrary node and calculate the maximum weight of the edge from each node to the chosen root. To answer a query, find the lca between the two nodes, and find the maximum weight from each of the query nodes to their lca and compare it to the given limit. |
Python Solution using dictionary | finding-pairs-with-a-certain-sum | 0 | 1 | #\n# Code\n```\nclass FindSumPairs:\n\n def __init__(self, nums1: List[int], nums2: List[int]):\n # Keep a copy of nums2 for referencing\n self.num2 = nums2\n\n # Since we only need count of each number occurrences\n # Store nums1 and nums2 as dict counts\n self.dict_num1 = collections.Counter(nums1)\n self.dict_num2 = collections.Counter(nums2)\n\n def add(self, index: int, val: int) -> None:\n # Remove the old value by using the array \n # and then updating the dictionary\n old_val = self.num2[index]\n new_val = self.num2[index] + val\n self.num2[index] = new_val\n self.dict_num2[old_val] -= 1\n self.dict_num2[new_val] += 1\n\n def count(self, tot: int) -> int:\n count = 0\n # Each time we find a pair that their total is equal to tot\n # we increase the count by multiplying the occurrence\n for key in self.dict_num1:\n reminder = tot - key\n if reminder in self.dict_num2:\n count += (self.dict_num1[key] * self.dict_num2[reminder])\n return count\n\n\n# Your FindSumPairs object will be instantiated and called as such:\n# obj = FindSumPairs(nums1, nums2)\n# obj.add(index,val)\n# param_2 = obj.count(tot)\n``` | 0 | You are given two integer arrays `nums1` and `nums2`. You are tasked to implement a data structure that supports queries of two types:
1. **Add** a positive integer to an element of a given index in the array `nums2`.
2. **Count** the number of pairs `(i, j)` such that `nums1[i] + nums2[j]` equals a given value (`0 <= i < nums1.length` and `0 <= j < nums2.length`).
Implement the `FindSumPairs` class:
* `FindSumPairs(int[] nums1, int[] nums2)` Initializes the `FindSumPairs` object with two integer arrays `nums1` and `nums2`.
* `void add(int index, int val)` Adds `val` to `nums2[index]`, i.e., apply `nums2[index] += val`.
* `int count(int tot)` Returns the number of pairs `(i, j)` such that `nums1[i] + nums2[j] == tot`.
**Example 1:**
**Input**
\[ "FindSumPairs ", "count ", "add ", "count ", "count ", "add ", "add ", "count "\]
\[\[\[1, 1, 2, 2, 2, 3\], \[1, 4, 5, 2, 5, 4\]\], \[7\], \[3, 2\], \[8\], \[4\], \[0, 1\], \[1, 1\], \[7\]\]
**Output**
\[null, 8, null, 2, 1, null, null, 11\]
**Explanation**
FindSumPairs findSumPairs = new FindSumPairs(\[1, 1, 2, 2, 2, 3\], \[1, 4, 5, 2, 5, 4\]);
findSumPairs.count(7); // return 8; pairs (2,2), (3,2), (4,2), (2,4), (3,4), (4,4) make 2 + 5 and pairs (5,1), (5,5) make 3 + 4
findSumPairs.add(3, 2); // now nums2 = \[1,4,5,**4**`,5,4`\]
findSumPairs.count(8); // return 2; pairs (5,2), (5,4) make 3 + 5
findSumPairs.count(4); // return 1; pair (5,0) makes 3 + 1
findSumPairs.add(0, 1); // now nums2 = \[**`2`**,4,5,4`,5,4`\]
findSumPairs.add(1, 1); // now nums2 = \[`2`,**5**,5,4`,5,4`\]
findSumPairs.count(7); // return 11; pairs (2,1), (2,2), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,4) make 2 + 5 and pairs (5,3), (5,5) make 3 + 4
**Constraints:**
* `1 <= nums1.length <= 1000`
* `1 <= nums2.length <= 105`
* `1 <= nums1[i] <= 109`
* `1 <= nums2[i] <= 105`
* `0 <= index < nums2.length`
* `1 <= val <= 105`
* `1 <= tot <= 109`
* At most `1000` calls are made to `add` and `count` **each**. | Find the minimum spanning tree of the given graph. Root the tree in an arbitrary node and calculate the maximum weight of the edge from each node to the chosen root. To answer a query, find the lca between the two nodes, and find the maximum weight from each of the query nodes to their lca and compare it to the given limit. |
[Python3] top-down dp | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | \n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n \n @cache \n def fn(n, k): \n """Return number of ways to rearrange n sticks to that k are visible."""\n if n == k: return 1\n if k == 0: return 0\n return ((n-1)*fn(n-1, k) + fn(n-1, k-1)) % 1_000_000_007\n \n return fn(n, k) \n``` | 4 | There are `n` uniquely-sized sticks whose lengths are integers from `1` to `n`. You want to arrange the sticks such that **exactly** `k` sticks are **visible** from the left. A stick is **visible** from the left if there are no **longer** sticks to the **left** of it.
* For example, if the sticks are arranged `[1,3,2,5,4]`, then the sticks with lengths `1`, `3`, and `5` are visible from the left.
Given `n` and `k`, return _the **number** of such arrangements_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 2
**Output:** 3
**Explanation:** \[1,3,2\], \[2,3,1\], and \[2,1,3\] are the only arrangements such that exactly 2 sticks are visible.
The visible sticks are underlined.
**Example 2:**
**Input:** n = 5, k = 5
**Output:** 1
**Explanation:** \[1,2,3,4,5\] is the only arrangement such that all 5 sticks are visible.
The visible sticks are underlined.
**Example 3:**
**Input:** n = 20, k = 11
**Output:** 647427950
**Explanation:** There are 647427950 (mod 109 \+ 7) ways to rearrange the sticks such that exactly 11 sticks are visible.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= k <= n` | Find the first element of nums - it will only appear once in adjacentPairs. The adjacent pairs are like edges of a graph. Perform a depth-first search from the first element. |
[Python3] top-down dp | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | \n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n \n @cache \n def fn(n, k): \n """Return number of ways to rearrange n sticks to that k are visible."""\n if n == k: return 1\n if k == 0: return 0\n return ((n-1)*fn(n-1, k) + fn(n-1, k-1)) % 1_000_000_007\n \n return fn(n, k) \n``` | 4 | You are playing a game that contains multiple characters, and each of the characters has **two** main properties: **attack** and **defense**. You are given a 2D integer array `properties` where `properties[i] = [attacki, defensei]` represents the properties of the `ith` character in the game.
A character is said to be **weak** if any other character has **both** attack and defense levels **strictly greater** than this character's attack and defense levels. More formally, a character `i` is said to be **weak** if there exists another character `j` where `attackj > attacki` and `defensej > defensei`.
Return _the number of **weak** characters_.
**Example 1:**
**Input:** properties = \[\[5,5\],\[6,3\],\[3,6\]\]
**Output:** 0
**Explanation:** No character has strictly greater attack and defense than the other.
**Example 2:**
**Input:** properties = \[\[2,2\],\[3,3\]\]
**Output:** 1
**Explanation:** The first character is weak because the second character has a strictly greater attack and defense.
**Example 3:**
**Input:** properties = \[\[1,5\],\[10,4\],\[4,3\]\]
**Output:** 1
**Explanation:** The third character is weak because the second character has a strictly greater attack and defense.
**Constraints:**
* `2 <= properties.length <= 105`
* `properties[i].length == 2`
* `1 <= attacki, defensei <= 105` | Is there a way to build the solution from a base case? How many ways are there if we fix the position of one stick? |
[Python 3] - Math explanation for deriving top-down DP beats 90% | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | # Explanation\n\nFirstly, when $n=k$, there is a single way to order the sticks. \n\nNow, notice that the largest stick $$n$$ must be the last visible. \n\n\nThen we ask how many sticks are covered by stick $n$? Since we need at least $k-1$ sticks before $n$ to form the $k-1$ visible sequence, the possible choices are $1\\leq i \\leq n-k+1$. Fix an arbitrary $i$. Then there are $\\binom{n}{i}$ ways to choose the covered sticks, and $i!$ ways to order them. Finally, we need to multiply this by the number of ways can we order the sticks which $n$ doesn\'t cover. Since they must form a visible sequence of length $(k-1)$, the answer is $$ \\operatorname{rearrangeSticks\n(n-i,k-1})$$.\n\n Therefore, for a fixed $i$, there are \n\n$$\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\binom{n}{i}\\cdot i!$$\n\nways to order the sticks when the final stick covers exactly $i$ sticks. To find the total number of sticks, we sum over all possible choices of $i$. \n\nTherefore, we arrive at the expression\n\n\n$$\\operatorname{rearrangeSticks\n(n,k})=\\sum_{i=1}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\binom{n}{i}\\cdot i!$$\n\nHowever, if we implement this up as is, we will get a TLE. Therefore, we need to do a small calculation to simplify this expression.\n\n\n$$\\operatorname{rearrangeSticks\n(n,k})\\\\=\\sum_{i=1}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\binom{n}{i}\\cdot i!\\\\\n=\\sum_{i=1}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\frac{(n-1)!}{(n-i)!}\\\\\n=\\operatorname{rearrangeSticks\n(n-1,k-1}) + \\sum_{i=2}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\frac{(n-1)!}{(n-i)!}\\\\\n=\\operatorname{rearrangeSticks\n(n-1,k-1}) + (n-1)\\operatorname{rearrangeSticks\n(n-1,k}).$$\n\nNow, using top down DP, we can implement this expression and achieve an $O(n\\cdot k)$ solution. \n\n\n# Code\n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n\n @cache\n def inner(n,k):\n\n if n == k:\n return 1\n\n if k == 1:\n return math.factorial(n-1)\n\n return (inner(n-1,k-1) + (n-1)*inner(n-1,k)) % (10**9 + 7)\n\n return inner(n,k) % (10**9 + 7)\n``` | 0 | There are `n` uniquely-sized sticks whose lengths are integers from `1` to `n`. You want to arrange the sticks such that **exactly** `k` sticks are **visible** from the left. A stick is **visible** from the left if there are no **longer** sticks to the **left** of it.
* For example, if the sticks are arranged `[1,3,2,5,4]`, then the sticks with lengths `1`, `3`, and `5` are visible from the left.
Given `n` and `k`, return _the **number** of such arrangements_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 2
**Output:** 3
**Explanation:** \[1,3,2\], \[2,3,1\], and \[2,1,3\] are the only arrangements such that exactly 2 sticks are visible.
The visible sticks are underlined.
**Example 2:**
**Input:** n = 5, k = 5
**Output:** 1
**Explanation:** \[1,2,3,4,5\] is the only arrangement such that all 5 sticks are visible.
The visible sticks are underlined.
**Example 3:**
**Input:** n = 20, k = 11
**Output:** 647427950
**Explanation:** There are 647427950 (mod 109 \+ 7) ways to rearrange the sticks such that exactly 11 sticks are visible.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= k <= n` | Find the first element of nums - it will only appear once in adjacentPairs. The adjacent pairs are like edges of a graph. Perform a depth-first search from the first element. |
[Python 3] - Math explanation for deriving top-down DP beats 90% | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | # Explanation\n\nFirstly, when $n=k$, there is a single way to order the sticks. \n\nNow, notice that the largest stick $$n$$ must be the last visible. \n\n\nThen we ask how many sticks are covered by stick $n$? Since we need at least $k-1$ sticks before $n$ to form the $k-1$ visible sequence, the possible choices are $1\\leq i \\leq n-k+1$. Fix an arbitrary $i$. Then there are $\\binom{n}{i}$ ways to choose the covered sticks, and $i!$ ways to order them. Finally, we need to multiply this by the number of ways can we order the sticks which $n$ doesn\'t cover. Since they must form a visible sequence of length $(k-1)$, the answer is $$ \\operatorname{rearrangeSticks\n(n-i,k-1})$$.\n\n Therefore, for a fixed $i$, there are \n\n$$\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\binom{n}{i}\\cdot i!$$\n\nways to order the sticks when the final stick covers exactly $i$ sticks. To find the total number of sticks, we sum over all possible choices of $i$. \n\nTherefore, we arrive at the expression\n\n\n$$\\operatorname{rearrangeSticks\n(n,k})=\\sum_{i=1}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\binom{n}{i}\\cdot i!$$\n\nHowever, if we implement this up as is, we will get a TLE. Therefore, we need to do a small calculation to simplify this expression.\n\n\n$$\\operatorname{rearrangeSticks\n(n,k})\\\\=\\sum_{i=1}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\binom{n}{i}\\cdot i!\\\\\n=\\sum_{i=1}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\frac{(n-1)!}{(n-i)!}\\\\\n=\\operatorname{rearrangeSticks\n(n-1,k-1}) + \\sum_{i=2}^{n-k+1}\\operatorname{rearrangeSticks\n(n-i,k-1})\\cdot \\frac{(n-1)!}{(n-i)!}\\\\\n=\\operatorname{rearrangeSticks\n(n-1,k-1}) + (n-1)\\operatorname{rearrangeSticks\n(n-1,k}).$$\n\nNow, using top down DP, we can implement this expression and achieve an $O(n\\cdot k)$ solution. \n\n\n# Code\n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n\n @cache\n def inner(n,k):\n\n if n == k:\n return 1\n\n if k == 1:\n return math.factorial(n-1)\n\n return (inner(n-1,k-1) + (n-1)*inner(n-1,k)) % (10**9 + 7)\n\n return inner(n,k) % (10**9 + 7)\n``` | 0 | You are playing a game that contains multiple characters, and each of the characters has **two** main properties: **attack** and **defense**. You are given a 2D integer array `properties` where `properties[i] = [attacki, defensei]` represents the properties of the `ith` character in the game.
A character is said to be **weak** if any other character has **both** attack and defense levels **strictly greater** than this character's attack and defense levels. More formally, a character `i` is said to be **weak** if there exists another character `j` where `attackj > attacki` and `defensej > defensei`.
Return _the number of **weak** characters_.
**Example 1:**
**Input:** properties = \[\[5,5\],\[6,3\],\[3,6\]\]
**Output:** 0
**Explanation:** No character has strictly greater attack and defense than the other.
**Example 2:**
**Input:** properties = \[\[2,2\],\[3,3\]\]
**Output:** 1
**Explanation:** The first character is weak because the second character has a strictly greater attack and defense.
**Example 3:**
**Input:** properties = \[\[1,5\],\[10,4\],\[4,3\]\]
**Output:** 1
**Explanation:** The third character is weak because the second character has a strictly greater attack and defense.
**Constraints:**
* `2 <= properties.length <= 105`
* `properties[i].length == 2`
* `1 <= attacki, defensei <= 105` | Is there a way to build the solution from a base case? How many ways are there if we fix the position of one stick? |
Optimized Python O(N*K) Time O(N) Space; Simple Explanation | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | ##### Overview:\n**Paradigm**: Dynamic Programming\n**Input Data Structure(s)**: Integer(s)\n**Auxiliary Data Structure(s)**: Arrays/ArrayLists\n**Core Algorithm(s)**: 2D Bottom-Up Dynamic Programming\n\n\n##### Complexity:\nTime: $$O(N \\times K)$$, to compute `N * K` dp states.\nSpace: $$O(N)$$, to store `2 * N` dp states.\n\n##### Intuition:\nThe nature of this problem requires you to consider various combinations and states to arrive at the solution, making dynamic programming a natural and efficient choice. Starting from some base case, we can probably build up our answer by solving subproblems. Since there are 2 variables, `n` and `k` we likely need to represent subproblems in 2D.\n\n##### Definitions:\n`i` represents how many sticks are available. \n`j` represents the number of sticks that are left visible. \n\n##### Edge cases:\n\n* If we iterate through the subproblems, the edge case `i == j` can only be solved by one ordering, when the values are sorted in ascending order. Hence, `1` way.\n* if `j == 0` we are saying that we want to show 0 sticks which is not possible unless there are 0 sticks total. Hence, `0` ways.\n* if `i == 0` we are saying there are 0 sticks available which is outside the domain of the problem constraints. Hence, `0` ways.\n\n##### Recurrence Relation: \n\n* This means we only need to deal with the situation where `i > 0` and `j > 0` and `i != j`. \n* In this case, let\'s imagine that we are adding in the next smallest stick at each iteration beginning with the largest stick. This seems counterintuitive and wrong at first because the `dp[i][j]` states seem like they represents the smallest $$1 -> i$$ sticks, but this is the wrong way to think about it. Instead imagine that each `dp[i][j]` state represents the `i` biggest sticks. This framing for dp is better because it allows us to solve the problem since placing the newest smallest stick (i-th biggest stick) does not undo or disqualify past state values/work. *On the other hand, placing the next largest stick will disqualify previous past states since the largest stick has potential to obscure the sticks which come after it making it impossible to build off the work in past dp states.*\n* To summarize, this means `dp[i][j]` represents the number of ways to left show `j` sticks when only looking at the `i` biggest sticks. Now the recurrence relation becomes straightforward. At each state `dp[i][j]` there will be `i` places where we can place the next smallest stick.\n* **dp[i-1][j-1] explained:** If we place it at the front of the arrangement, then the number of ways this yields is `dp[i-1][j-1]`. I.e., if there was 1 less stick and we wanted to show 1 less of them. Placing the smallest at the front of these arrangements will not obscure any of the following sticks in any of the arrangements and `j` sticks will become visible (`j-1` from before + 1 for the smallest at the front), so this count propagates. Hence, `dp[i-1][j-1]`. \n* **dp[i-1][j] * (i-1) explained:** Since we want to show `j` sticks, we can also place the smallest stick in any of the `i - 1` positions after the first position. Because we are introducing the smallest stick, placing it after any of these sticks will not obscure any of the sticks in these arrangements. We can find all states where `j` sticks are visible and there was 1 fewer stick and place the newest stick after any of these sticks in any of the arrangements. Hence, `dp[i-1][j] * (i-1)`. \n\nWhen we account for our modulus value, and edge cases, this yields the recurrence relation:\n\n\n$$dp[i][j] =$$\n**{**\n$$\\;\\;\\;\\;0 : if \\; i=0 \\; or \\; j=0,$$\n$$\\;\\;\\;\\;1 : if \\; i = j,$$\n$$\\;\\;\\;\\;dp[i-1][j-1] + dp[i-1][j] \\times (i-1)) % (10^9 + 7)$$ $$: otherwise $$\n**}**\n\n##### Optimization:\n\n**Rolling Array / Sliding Array Technique**: Since each state $$(i, j)$$ only depends on the values from states composed of $$i-1, \\; j-1, \\; and \\; j$$ we do not need to use a 2D DP array to hold all states in memory. We will only need to know all `i` states in the current `j` state set and the previous `j` (`j - 1`) state set. We can reduce space complexity from $$O(N \\times K)$$ to $$O(N)$$ by storing these 2 state sets in 2 dp arrays, `curr_k` which corresponds to `dp[*][j]` and `prev_k` which corresponds to `dp[*][j-1]`.\n\n##### Implementation:\n```python\nclass Solution:\n def rearrangeSticks(self, n, k, mod=10**9 + 7):\n \n prev_k = [0] * (n + 1) # initialize j = 0 state set\n \n for j in range(1, k + 1):\n curr_k = [0] * (n + 1) # initialize j state set\n \n for i in range(1, n + 1):\n \n if i == j: # handle edge case i = j\n curr_k[i] = 1\n continue\n \n # recurrence relation:\n curr_k[i] = (prev_k[i-1] + curr_k[i-1] * (i - 1)) % mod\n\n prev_k = curr_k # roll the arrays, updating j - 1 state set \n\n return curr_k[n]\n\n```\n\n | 0 | There are `n` uniquely-sized sticks whose lengths are integers from `1` to `n`. You want to arrange the sticks such that **exactly** `k` sticks are **visible** from the left. A stick is **visible** from the left if there are no **longer** sticks to the **left** of it.
* For example, if the sticks are arranged `[1,3,2,5,4]`, then the sticks with lengths `1`, `3`, and `5` are visible from the left.
Given `n` and `k`, return _the **number** of such arrangements_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 2
**Output:** 3
**Explanation:** \[1,3,2\], \[2,3,1\], and \[2,1,3\] are the only arrangements such that exactly 2 sticks are visible.
The visible sticks are underlined.
**Example 2:**
**Input:** n = 5, k = 5
**Output:** 1
**Explanation:** \[1,2,3,4,5\] is the only arrangement such that all 5 sticks are visible.
The visible sticks are underlined.
**Example 3:**
**Input:** n = 20, k = 11
**Output:** 647427950
**Explanation:** There are 647427950 (mod 109 \+ 7) ways to rearrange the sticks such that exactly 11 sticks are visible.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= k <= n` | Find the first element of nums - it will only appear once in adjacentPairs. The adjacent pairs are like edges of a graph. Perform a depth-first search from the first element. |
Optimized Python O(N*K) Time O(N) Space; Simple Explanation | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | ##### Overview:\n**Paradigm**: Dynamic Programming\n**Input Data Structure(s)**: Integer(s)\n**Auxiliary Data Structure(s)**: Arrays/ArrayLists\n**Core Algorithm(s)**: 2D Bottom-Up Dynamic Programming\n\n\n##### Complexity:\nTime: $$O(N \\times K)$$, to compute `N * K` dp states.\nSpace: $$O(N)$$, to store `2 * N` dp states.\n\n##### Intuition:\nThe nature of this problem requires you to consider various combinations and states to arrive at the solution, making dynamic programming a natural and efficient choice. Starting from some base case, we can probably build up our answer by solving subproblems. Since there are 2 variables, `n` and `k` we likely need to represent subproblems in 2D.\n\n##### Definitions:\n`i` represents how many sticks are available. \n`j` represents the number of sticks that are left visible. \n\n##### Edge cases:\n\n* If we iterate through the subproblems, the edge case `i == j` can only be solved by one ordering, when the values are sorted in ascending order. Hence, `1` way.\n* if `j == 0` we are saying that we want to show 0 sticks which is not possible unless there are 0 sticks total. Hence, `0` ways.\n* if `i == 0` we are saying there are 0 sticks available which is outside the domain of the problem constraints. Hence, `0` ways.\n\n##### Recurrence Relation: \n\n* This means we only need to deal with the situation where `i > 0` and `j > 0` and `i != j`. \n* In this case, let\'s imagine that we are adding in the next smallest stick at each iteration beginning with the largest stick. This seems counterintuitive and wrong at first because the `dp[i][j]` states seem like they represents the smallest $$1 -> i$$ sticks, but this is the wrong way to think about it. Instead imagine that each `dp[i][j]` state represents the `i` biggest sticks. This framing for dp is better because it allows us to solve the problem since placing the newest smallest stick (i-th biggest stick) does not undo or disqualify past state values/work. *On the other hand, placing the next largest stick will disqualify previous past states since the largest stick has potential to obscure the sticks which come after it making it impossible to build off the work in past dp states.*\n* To summarize, this means `dp[i][j]` represents the number of ways to left show `j` sticks when only looking at the `i` biggest sticks. Now the recurrence relation becomes straightforward. At each state `dp[i][j]` there will be `i` places where we can place the next smallest stick.\n* **dp[i-1][j-1] explained:** If we place it at the front of the arrangement, then the number of ways this yields is `dp[i-1][j-1]`. I.e., if there was 1 less stick and we wanted to show 1 less of them. Placing the smallest at the front of these arrangements will not obscure any of the following sticks in any of the arrangements and `j` sticks will become visible (`j-1` from before + 1 for the smallest at the front), so this count propagates. Hence, `dp[i-1][j-1]`. \n* **dp[i-1][j] * (i-1) explained:** Since we want to show `j` sticks, we can also place the smallest stick in any of the `i - 1` positions after the first position. Because we are introducing the smallest stick, placing it after any of these sticks will not obscure any of the sticks in these arrangements. We can find all states where `j` sticks are visible and there was 1 fewer stick and place the newest stick after any of these sticks in any of the arrangements. Hence, `dp[i-1][j] * (i-1)`. \n\nWhen we account for our modulus value, and edge cases, this yields the recurrence relation:\n\n\n$$dp[i][j] =$$\n**{**\n$$\\;\\;\\;\\;0 : if \\; i=0 \\; or \\; j=0,$$\n$$\\;\\;\\;\\;1 : if \\; i = j,$$\n$$\\;\\;\\;\\;dp[i-1][j-1] + dp[i-1][j] \\times (i-1)) % (10^9 + 7)$$ $$: otherwise $$\n**}**\n\n##### Optimization:\n\n**Rolling Array / Sliding Array Technique**: Since each state $$(i, j)$$ only depends on the values from states composed of $$i-1, \\; j-1, \\; and \\; j$$ we do not need to use a 2D DP array to hold all states in memory. We will only need to know all `i` states in the current `j` state set and the previous `j` (`j - 1`) state set. We can reduce space complexity from $$O(N \\times K)$$ to $$O(N)$$ by storing these 2 state sets in 2 dp arrays, `curr_k` which corresponds to `dp[*][j]` and `prev_k` which corresponds to `dp[*][j-1]`.\n\n##### Implementation:\n```python\nclass Solution:\n def rearrangeSticks(self, n, k, mod=10**9 + 7):\n \n prev_k = [0] * (n + 1) # initialize j = 0 state set\n \n for j in range(1, k + 1):\n curr_k = [0] * (n + 1) # initialize j state set\n \n for i in range(1, n + 1):\n \n if i == j: # handle edge case i = j\n curr_k[i] = 1\n continue\n \n # recurrence relation:\n curr_k[i] = (prev_k[i-1] + curr_k[i-1] * (i - 1)) % mod\n\n prev_k = curr_k # roll the arrays, updating j - 1 state set \n\n return curr_k[n]\n\n```\n\n | 0 | You are playing a game that contains multiple characters, and each of the characters has **two** main properties: **attack** and **defense**. You are given a 2D integer array `properties` where `properties[i] = [attacki, defensei]` represents the properties of the `ith` character in the game.
A character is said to be **weak** if any other character has **both** attack and defense levels **strictly greater** than this character's attack and defense levels. More formally, a character `i` is said to be **weak** if there exists another character `j` where `attackj > attacki` and `defensej > defensei`.
Return _the number of **weak** characters_.
**Example 1:**
**Input:** properties = \[\[5,5\],\[6,3\],\[3,6\]\]
**Output:** 0
**Explanation:** No character has strictly greater attack and defense than the other.
**Example 2:**
**Input:** properties = \[\[2,2\],\[3,3\]\]
**Output:** 1
**Explanation:** The first character is weak because the second character has a strictly greater attack and defense.
**Example 3:**
**Input:** properties = \[\[1,5\],\[10,4\],\[4,3\]\]
**Output:** 1
**Explanation:** The third character is weak because the second character has a strictly greater attack and defense.
**Constraints:**
* `2 <= properties.length <= 105`
* `properties[i].length == 2`
* `1 <= attacki, defensei <= 105` | Is there a way to build the solution from a base case? How many ways are there if we fix the position of one stick? |
[Python] Place from the back | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | \n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n MOD = 10**9+7\n dp = [[-1 for j in range(k+1)] for i in range(n+1)]\n def dfs(n, k):\n if n==k:\n return 1\n if n==0 or k==0:\n return 0\n if dp[n][k] > -1:\n return dp[n][k]\n placeLargest = dfs(n-1, k-1)\n placeRest = (n-1) * dfs(n-1, k)\n dp[n][k] = placeLargest + placeRest\n return dp[n][k]\n return dfs(n, k) % MOD\n \n``` | 0 | There are `n` uniquely-sized sticks whose lengths are integers from `1` to `n`. You want to arrange the sticks such that **exactly** `k` sticks are **visible** from the left. A stick is **visible** from the left if there are no **longer** sticks to the **left** of it.
* For example, if the sticks are arranged `[1,3,2,5,4]`, then the sticks with lengths `1`, `3`, and `5` are visible from the left.
Given `n` and `k`, return _the **number** of such arrangements_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 2
**Output:** 3
**Explanation:** \[1,3,2\], \[2,3,1\], and \[2,1,3\] are the only arrangements such that exactly 2 sticks are visible.
The visible sticks are underlined.
**Example 2:**
**Input:** n = 5, k = 5
**Output:** 1
**Explanation:** \[1,2,3,4,5\] is the only arrangement such that all 5 sticks are visible.
The visible sticks are underlined.
**Example 3:**
**Input:** n = 20, k = 11
**Output:** 647427950
**Explanation:** There are 647427950 (mod 109 \+ 7) ways to rearrange the sticks such that exactly 11 sticks are visible.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= k <= n` | Find the first element of nums - it will only appear once in adjacentPairs. The adjacent pairs are like edges of a graph. Perform a depth-first search from the first element. |
[Python] Place from the back | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | \n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n MOD = 10**9+7\n dp = [[-1 for j in range(k+1)] for i in range(n+1)]\n def dfs(n, k):\n if n==k:\n return 1\n if n==0 or k==0:\n return 0\n if dp[n][k] > -1:\n return dp[n][k]\n placeLargest = dfs(n-1, k-1)\n placeRest = (n-1) * dfs(n-1, k)\n dp[n][k] = placeLargest + placeRest\n return dp[n][k]\n return dfs(n, k) % MOD\n \n``` | 0 | You are playing a game that contains multiple characters, and each of the characters has **two** main properties: **attack** and **defense**. You are given a 2D integer array `properties` where `properties[i] = [attacki, defensei]` represents the properties of the `ith` character in the game.
A character is said to be **weak** if any other character has **both** attack and defense levels **strictly greater** than this character's attack and defense levels. More formally, a character `i` is said to be **weak** if there exists another character `j` where `attackj > attacki` and `defensej > defensei`.
Return _the number of **weak** characters_.
**Example 1:**
**Input:** properties = \[\[5,5\],\[6,3\],\[3,6\]\]
**Output:** 0
**Explanation:** No character has strictly greater attack and defense than the other.
**Example 2:**
**Input:** properties = \[\[2,2\],\[3,3\]\]
**Output:** 1
**Explanation:** The first character is weak because the second character has a strictly greater attack and defense.
**Example 3:**
**Input:** properties = \[\[1,5\],\[10,4\],\[4,3\]\]
**Output:** 1
**Explanation:** The third character is weak because the second character has a strictly greater attack and defense.
**Constraints:**
* `2 <= properties.length <= 105`
* `properties[i].length == 2`
* `1 <= attacki, defensei <= 105` | Is there a way to build the solution from a base case? How many ways are there if we fix the position of one stick? |
DP solution with recursion explained | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | # Intuition\nIt\'s enough to consider two cases of position of 1 in the list. \nThe first one is when 1 takes the first place: then the number f(n,k) (denoting the desired number) when the rray starts with 1 is equal to f(n-1, k-1) as 1 will be visible and among n-1 numbers from 2 to n there should be k-1 visible ones.\nThe second case is when 1 is not on the first place. Then we can surely say that 1 is not visible. This means that we can take numbers from 2 to n with k visible (there are f(n-1, k) of them) and then insert 1 on any position but the first one.\n\n# Approach\nThe rest is just to iteratively calculate that recursion with the help of dynamic programming. We start from n = 1 and each time we calculate f(n, k) from the previous values for n-1\n# Complexity\n- Time complexity: O(n*k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n dp = [[0 for j in range(i+1)] for i in range(n+1)]\n dp[1] = [1, 0]\n for i in range(2,n+1):\n for j in range(i): # j replaces k here for each i\n dp[i][j] = (i - 1) * dp[i-1][j] + dp[i-1][j-1]\n\n return dp[-1][k-1] % 1000000007\n\n``` | 0 | There are `n` uniquely-sized sticks whose lengths are integers from `1` to `n`. You want to arrange the sticks such that **exactly** `k` sticks are **visible** from the left. A stick is **visible** from the left if there are no **longer** sticks to the **left** of it.
* For example, if the sticks are arranged `[1,3,2,5,4]`, then the sticks with lengths `1`, `3`, and `5` are visible from the left.
Given `n` and `k`, return _the **number** of such arrangements_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 2
**Output:** 3
**Explanation:** \[1,3,2\], \[2,3,1\], and \[2,1,3\] are the only arrangements such that exactly 2 sticks are visible.
The visible sticks are underlined.
**Example 2:**
**Input:** n = 5, k = 5
**Output:** 1
**Explanation:** \[1,2,3,4,5\] is the only arrangement such that all 5 sticks are visible.
The visible sticks are underlined.
**Example 3:**
**Input:** n = 20, k = 11
**Output:** 647427950
**Explanation:** There are 647427950 (mod 109 \+ 7) ways to rearrange the sticks such that exactly 11 sticks are visible.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= k <= n` | Find the first element of nums - it will only appear once in adjacentPairs. The adjacent pairs are like edges of a graph. Perform a depth-first search from the first element. |
DP solution with recursion explained | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | # Intuition\nIt\'s enough to consider two cases of position of 1 in the list. \nThe first one is when 1 takes the first place: then the number f(n,k) (denoting the desired number) when the rray starts with 1 is equal to f(n-1, k-1) as 1 will be visible and among n-1 numbers from 2 to n there should be k-1 visible ones.\nThe second case is when 1 is not on the first place. Then we can surely say that 1 is not visible. This means that we can take numbers from 2 to n with k visible (there are f(n-1, k) of them) and then insert 1 on any position but the first one.\n\n# Approach\nThe rest is just to iteratively calculate that recursion with the help of dynamic programming. We start from n = 1 and each time we calculate f(n, k) from the previous values for n-1\n# Complexity\n- Time complexity: O(n*k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n dp = [[0 for j in range(i+1)] for i in range(n+1)]\n dp[1] = [1, 0]\n for i in range(2,n+1):\n for j in range(i): # j replaces k here for each i\n dp[i][j] = (i - 1) * dp[i-1][j] + dp[i-1][j-1]\n\n return dp[-1][k-1] % 1000000007\n\n``` | 0 | You are playing a game that contains multiple characters, and each of the characters has **two** main properties: **attack** and **defense**. You are given a 2D integer array `properties` where `properties[i] = [attacki, defensei]` represents the properties of the `ith` character in the game.
A character is said to be **weak** if any other character has **both** attack and defense levels **strictly greater** than this character's attack and defense levels. More formally, a character `i` is said to be **weak** if there exists another character `j` where `attackj > attacki` and `defensej > defensei`.
Return _the number of **weak** characters_.
**Example 1:**
**Input:** properties = \[\[5,5\],\[6,3\],\[3,6\]\]
**Output:** 0
**Explanation:** No character has strictly greater attack and defense than the other.
**Example 2:**
**Input:** properties = \[\[2,2\],\[3,3\]\]
**Output:** 1
**Explanation:** The first character is weak because the second character has a strictly greater attack and defense.
**Example 3:**
**Input:** properties = \[\[1,5\],\[10,4\],\[4,3\]\]
**Output:** 1
**Explanation:** The third character is weak because the second character has a strictly greater attack and defense.
**Constraints:**
* `2 <= properties.length <= 105`
* `properties[i].length == 2`
* `1 <= attacki, defensei <= 105` | Is there a way to build the solution from a base case? How many ways are there if we fix the position of one stick? |
Python3 classic DP solution | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n\n\n # dp\n dp = [[0] * (k + 1) for _ in range(n + 1)]\n\n # base case\n # if n < k -> 0\n # if n == k -> 1\n \n for i in range(n):\n for j in range(k):\n if i < j:\n dp[i][j] = 0\n elif i == j:\n dp[i][j] = 1\n \n # dp\n for i in range(1, n + 1):\n for j in range(1, k + 1):\n dp[i][j] = dp[i - 1][j - 1] + (i - 1) * dp[i - 1][j]\n\n return dp[n][k] % (10 ** 9 + 7)\n\n\n # instead of 1, 2, 3 in the first position\n # assume they are at the last position \n # n = 3, k = 2\n # 2,3 / 1 -> n = 2, k = 2\n # 1,3 / 2 -> n = 2, k = 2\n # 1,2 / 3 -> n = 2, k = 1\n\n # iterate over the 1, 2, 3 -> survive -> n - i / dies -> i - 1\n # survive / dies k\n # 3 - 1 / 1 - 1 -> 2 / 0 -> 2, 1 * 2! / 2!\n # 3 - 2 / 2 - 1 -> 1 / 1 -> 1, 1 * 2! / 1! 1! \n # n - i / i - 1 -> n - i / k - 1 * (n - 1)! / (i - 1)!\n\n # neetcode\n dp = {(1, 1): 1}\n\n for N in range(2, n + 1):\n for K in range(1, k + 1):\n dp[(N, K)] = (dp.get((N - 1, K - 1), 0) + (N - 1) * dp.get((N - 1, K), 0))\n return dp[(n, k)] % (10 ** 9 + 7)\n\n\n``` | 0 | There are `n` uniquely-sized sticks whose lengths are integers from `1` to `n`. You want to arrange the sticks such that **exactly** `k` sticks are **visible** from the left. A stick is **visible** from the left if there are no **longer** sticks to the **left** of it.
* For example, if the sticks are arranged `[1,3,2,5,4]`, then the sticks with lengths `1`, `3`, and `5` are visible from the left.
Given `n` and `k`, return _the **number** of such arrangements_. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, k = 2
**Output:** 3
**Explanation:** \[1,3,2\], \[2,3,1\], and \[2,1,3\] are the only arrangements such that exactly 2 sticks are visible.
The visible sticks are underlined.
**Example 2:**
**Input:** n = 5, k = 5
**Output:** 1
**Explanation:** \[1,2,3,4,5\] is the only arrangement such that all 5 sticks are visible.
The visible sticks are underlined.
**Example 3:**
**Input:** n = 20, k = 11
**Output:** 647427950
**Explanation:** There are 647427950 (mod 109 \+ 7) ways to rearrange the sticks such that exactly 11 sticks are visible.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= k <= n` | Find the first element of nums - it will only appear once in adjacentPairs. The adjacent pairs are like edges of a graph. Perform a depth-first search from the first element. |
Python3 classic DP solution | number-of-ways-to-rearrange-sticks-with-k-sticks-visible | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rearrangeSticks(self, n: int, k: int) -> int:\n\n\n # dp\n dp = [[0] * (k + 1) for _ in range(n + 1)]\n\n # base case\n # if n < k -> 0\n # if n == k -> 1\n \n for i in range(n):\n for j in range(k):\n if i < j:\n dp[i][j] = 0\n elif i == j:\n dp[i][j] = 1\n \n # dp\n for i in range(1, n + 1):\n for j in range(1, k + 1):\n dp[i][j] = dp[i - 1][j - 1] + (i - 1) * dp[i - 1][j]\n\n return dp[n][k] % (10 ** 9 + 7)\n\n\n # instead of 1, 2, 3 in the first position\n # assume they are at the last position \n # n = 3, k = 2\n # 2,3 / 1 -> n = 2, k = 2\n # 1,3 / 2 -> n = 2, k = 2\n # 1,2 / 3 -> n = 2, k = 1\n\n # iterate over the 1, 2, 3 -> survive -> n - i / dies -> i - 1\n # survive / dies k\n # 3 - 1 / 1 - 1 -> 2 / 0 -> 2, 1 * 2! / 2!\n # 3 - 2 / 2 - 1 -> 1 / 1 -> 1, 1 * 2! / 1! 1! \n # n - i / i - 1 -> n - i / k - 1 * (n - 1)! / (i - 1)!\n\n # neetcode\n dp = {(1, 1): 1}\n\n for N in range(2, n + 1):\n for K in range(1, k + 1):\n dp[(N, K)] = (dp.get((N - 1, K - 1), 0) + (N - 1) * dp.get((N - 1, K), 0))\n return dp[(n, k)] % (10 ** 9 + 7)\n\n\n``` | 0 | You are playing a game that contains multiple characters, and each of the characters has **two** main properties: **attack** and **defense**. You are given a 2D integer array `properties` where `properties[i] = [attacki, defensei]` represents the properties of the `ith` character in the game.
A character is said to be **weak** if any other character has **both** attack and defense levels **strictly greater** than this character's attack and defense levels. More formally, a character `i` is said to be **weak** if there exists another character `j` where `attackj > attacki` and `defensej > defensei`.
Return _the number of **weak** characters_.
**Example 1:**
**Input:** properties = \[\[5,5\],\[6,3\],\[3,6\]\]
**Output:** 0
**Explanation:** No character has strictly greater attack and defense than the other.
**Example 2:**
**Input:** properties = \[\[2,2\],\[3,3\]\]
**Output:** 1
**Explanation:** The first character is weak because the second character has a strictly greater attack and defense.
**Example 3:**
**Input:** properties = \[\[1,5\],\[10,4\],\[4,3\]\]
**Output:** 1
**Explanation:** The third character is weak because the second character has a strictly greater attack and defense.
**Constraints:**
* `2 <= properties.length <= 105`
* `properties[i].length == 2`
* `1 <= attacki, defensei <= 105` | Is there a way to build the solution from a base case? How many ways are there if we fix the position of one stick? |
python3 solution | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | \n```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n best=collections.defaultdict(int)\n for x,t in groupby(s):\n best[x]=max(best[x],len(list(t)))\n \n return best["1"]>best["0"] \n``` | 1 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
✅ 96% || Python3 || 🚀Slicing || ⭐️ Thoroughly Explanation ⭐️ | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | # Intuition\n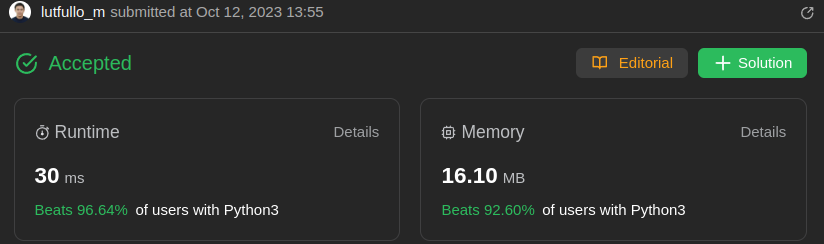\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n one, zero = 0, 0\n front = 0\n max_str = ""\n for x in range(len(s) - 1):\n if s[x] != s[x + 1]:\n max_str = s[front:x + 1]\n front = x + 1\n if "1" in max_str:\n one = max(one, len(max_str))\n else:\n zero = max(zero, len(max_str))\n max_str = s[front:]\n if "1" in max_str:\n one = max(one, len(max_str))\n else:\n zero = max(zero, len(max_str))\n return one > zero\n\n\nobj = Solution()\nprint(obj.checkZeroOnes(s="110100010"))\n\n``` | 1 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Python3 | Time: O(n) | Space: O(1) | Beats 100% solutions in time | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | ```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n best_one, best_zero, current_one, current_zero = 0, 0, 0, 0\n \n for i in s:\n if i == "1":\n current_zero = 0\n current_one += 1\n else:\n current_zero += 1\n current_one = 0\n \n best_one = max(best_one, current_one)\n best_zero = max(best_zero, current_zero)\n \n return best_one > best_zero\n``` | 61 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Python | Easy Solution✅ | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | ```\ndef checkZeroOnes(self, s: str) -> bool:\n one_list = s.split("0")\n zero_list = s.split("1")\n \n one_max = max(one_list, key=len)\n zero_max = max(zero_list, key=len)\n \n if len(one_max) > len(zero_max):\n return True\n else:\n return False\n``` | 12 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Python oneliner | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | ```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n return len(max(s.split(\'0\'),key=len)) > len(max(s.split(\'1\'),key=len))\n``` | 3 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Python beginner friendly solution using split() | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | ```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n one_seg = sorted(s.split("0"), key=len)\n zero_seg = sorted(s.split("1"), key=len)\n return len(one_seg[-1]) > len(zero_seg[-1]) | 2 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Python ✅😎✅ || Faster than 99.27% || Memory beats 97.32% | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | # Code\n```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n zero, one = \'\', \'\'\n mZ, mO = 0, 0\n last = str(int(not int(s[-1])))\n\n for c in s + last:\n if c == \'1\':\n mZ = max(len(zero), mZ)\n zero = \'\'\n one += c\n\n if c == \'0\':\n mO = max(len(one), mO)\n one = \'\'\n zero += c\n return mO > mZ\n```\n\n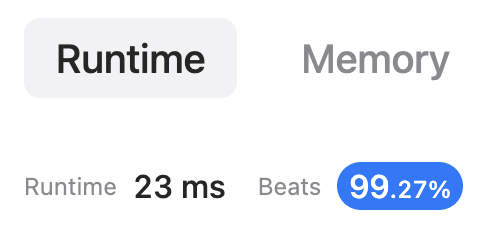\n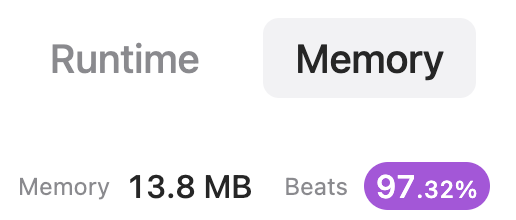\n | 2 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Easy solution in Python using Regular Expressions | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | ```\nfrom re import findall\nclass Solution(object):\n def checkZeroOnes(self, s):\n """\n :type s: str\n :rtype: bool\n """\n o = 0\n z = 0\n try:\n o = len(max(findall("11*",s)))\n z = len(max(findall("00*",s)))\n except:\n None\n return True if o>z else False\n\t``` | 3 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Python || Easy to understand||Beginner solution | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n countOne=0\n countZero=0\n countOneMax=0\n countZeroMax=0\n for i in range(len(s)):\n if s[i]==\'1\':\n countOne+=1\n countOneMax= max(countOneMax,countOne)\n else:\n countOne=0\n if s[i]==\'0\':\n countZero += 1\n countZeroMax = max(countZeroMax, countZero)\n else:\n countZero=0\n return countOneMax > countZeroMax\n \n``` | 0 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
Longer Contiguous Segments of Ones than Zeros | longer-contiguous-segments-of-ones-than-zeros | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkZeroOnes(self, s: str) -> bool:\n return len(max(s.split(\'0\'))) > len(max(s.split(\'1\')))\n\n``` | 0 | Given a binary string `s`, return `true` _if the **longest** contiguous segment of_ `1`'_s is **strictly longer** than the **longest** contiguous segment of_ `0`'_s in_ `s`, or return `false` _otherwise_.
* For example, in `s = "110100010 "` the longest continuous segment of `1`s has length `2`, and the longest continuous segment of `0`s has length `3`.
Note that if there are no `0`'s, then the longest continuous segment of `0`'s is considered to have a length `0`. The same applies if there is no `1`'s.
**Example 1:**
**Input:** s = "1101 "
**Output:** true
**Explanation:**
The longest contiguous segment of 1s has length 2: "1101 "
The longest contiguous segment of 0s has length 1: "1101 "
The segment of 1s is longer, so return true.
**Example 2:**
**Input:** s = "111000 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 3: "111000 "
The longest contiguous segment of 0s has length 3: "111000 "
The segment of 1s is not longer, so return false.
**Example 3:**
**Input:** s = "110100010 "
**Output:** false
**Explanation:**
The longest contiguous segment of 1s has length 2: "110100010 "
The longest contiguous segment of 0s has length 3: "110100010 "
The segment of 1s is not longer, so return false.
**Constraints:**
* `1 <= s.length <= 100`
* `s[i]` is either `'0'` or `'1'`. | null |
C++/Python Koko-like solutions with small searching region | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLike solving the binary search problem\n[875. Koko Eating Bananas\n](https://leetcode.com/problems/koko-eating-bananas/solutions/3685871/w-explanation-easy-binary-search-c-solution/)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n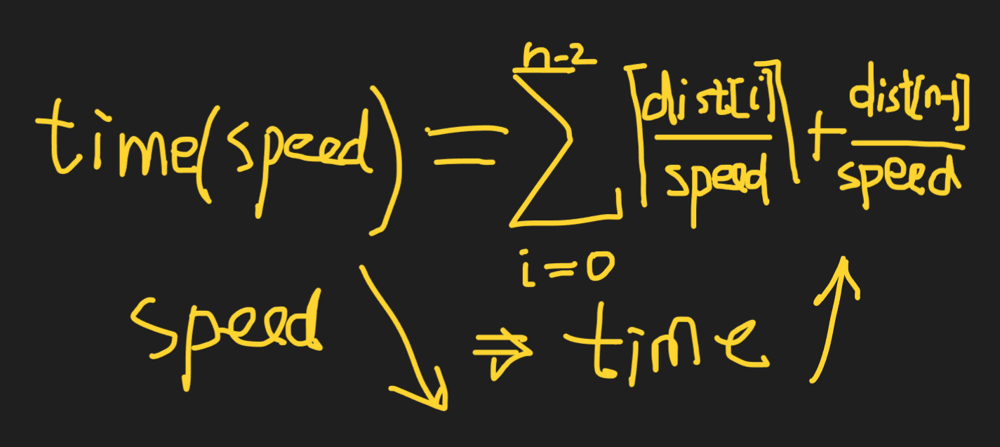\n\nIt is important to know that the function time(speed) is a monotonic (decreasing) function. That is the reason why the binary search can be applied.\n\nTo make the binary search efficient, it is suggested to choose the possible smallest searching range. It can derived as follows\n$$\nhour\\geq time(speed) \\\\\n=\\sum_{i=0}^{n-2}ceil(\\frac{dist[i]}{speed})+\\frac{d[n-1]}{speed}\\\\\n\\geq (n-1)+\\frac{d[n-1]}{speed} , if\\ speed \\geq max_{i=0,\\cdots,n-2} (dist[i])\n$$\nIt implies that\n$$\nspeed\\geq \\frac{dist[n-1]}{hour-n-1}\n$$\nSo we can choose the initial value for right\n```\nright=1+max(*max_element(dist.begin(), dist.end()), int(dist[n-1]/(hour-n+1)))\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n \\log (m))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(1)$\n# Code\n```\nclass Solution {\npublic:\n int n;\n double time(vector<int>& dist, int speed){\n double sum=0;\n for(int i=0; i<n-1; i++)\n sum+=(dist[i]+speed-1)/speed;//ceiling function\n sum+=(double)dist[n-1]/speed;// last one just normal division\n cout<<"speed="<<speed<<",time="<<sum<<endl;\n return sum;\n }\n int minSpeedOnTime(vector<int>& dist, double hour) {\n n=dist.size();\n \n if (hour<=n-1) return -1;\n long long left=1;\n int right=1+max(*max_element(dist.begin(), dist.end()), int(dist[n-1]/(hour-n+1)));\n // cout<<right<<endl;\n int speed;\n while(left<=right)\n {\n int mid=left+(right-left)/2;\n if (time(dist, mid)<=hour){\n speed=mid;\n right=mid-1;\n } \n else left=mid+1;\n }\n return speed;\n }\n};\n```\n# Python code Beats 97.15%\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n n=len(dist)\n if hour<=n-1: return -1\n\n def time(speed):\n sum=0\n for x in dist[:n-1]:\n sum+=(x+speed-1)//speed #ceiling function\n sum+=dist[n-1]/speed\n return sum\n \n left=1\n right=1+max(max(dist), int(dist[-1]//(hour-n+1)))\n speed=0\n while left<=right:\n mid=(left+right)//2\n if time(mid)<= hour:\n speed=mid\n right=mid-1\n else:\n left=mid+1\n return speed\n``` | 7 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
C++/Python Koko-like solutions with small searching region | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLike solving the binary search problem\n[875. Koko Eating Bananas\n](https://leetcode.com/problems/koko-eating-bananas/solutions/3685871/w-explanation-easy-binary-search-c-solution/)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n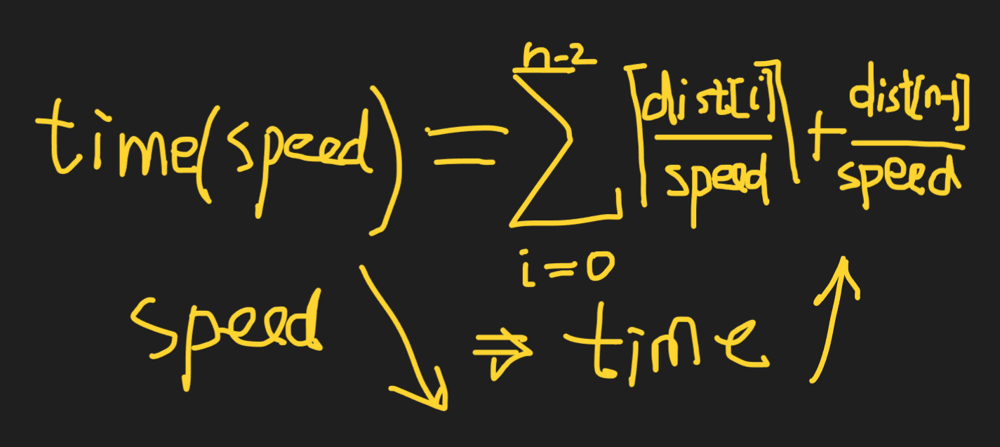\n\nIt is important to know that the function time(speed) is a monotonic (decreasing) function. That is the reason why the binary search can be applied.\n\nTo make the binary search efficient, it is suggested to choose the possible smallest searching range. It can derived as follows\n$$\nhour\\geq time(speed) \\\\\n=\\sum_{i=0}^{n-2}ceil(\\frac{dist[i]}{speed})+\\frac{d[n-1]}{speed}\\\\\n\\geq (n-1)+\\frac{d[n-1]}{speed} , if\\ speed \\geq max_{i=0,\\cdots,n-2} (dist[i])\n$$\nIt implies that\n$$\nspeed\\geq \\frac{dist[n-1]}{hour-n-1}\n$$\nSo we can choose the initial value for right\n```\nright=1+max(*max_element(dist.begin(), dist.end()), int(dist[n-1]/(hour-n+1)))\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n \\log (m))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(1)$\n# Code\n```\nclass Solution {\npublic:\n int n;\n double time(vector<int>& dist, int speed){\n double sum=0;\n for(int i=0; i<n-1; i++)\n sum+=(dist[i]+speed-1)/speed;//ceiling function\n sum+=(double)dist[n-1]/speed;// last one just normal division\n cout<<"speed="<<speed<<",time="<<sum<<endl;\n return sum;\n }\n int minSpeedOnTime(vector<int>& dist, double hour) {\n n=dist.size();\n \n if (hour<=n-1) return -1;\n long long left=1;\n int right=1+max(*max_element(dist.begin(), dist.end()), int(dist[n-1]/(hour-n+1)));\n // cout<<right<<endl;\n int speed;\n while(left<=right)\n {\n int mid=left+(right-left)/2;\n if (time(dist, mid)<=hour){\n speed=mid;\n right=mid-1;\n } \n else left=mid+1;\n }\n return speed;\n }\n};\n```\n# Python code Beats 97.15%\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n n=len(dist)\n if hour<=n-1: return -1\n\n def time(speed):\n sum=0\n for x in dist[:n-1]:\n sum+=(x+speed-1)//speed #ceiling function\n sum+=dist[n-1]/speed\n return sum\n \n left=1\n right=1+max(max(dist), int(dist[-1]//(hour-n+1)))\n speed=0\n while left<=right:\n mid=(left+right)//2\n if time(mid)<= hour:\n speed=mid\n right=mid-1\n else:\n left=mid+1\n return speed\n``` | 7 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Python3 👍||⚡99/99 faster beats, 11 lines🔥|| clean solution || | minimum-speed-to-arrive-on-time | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(m*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n if len(dist) >= hour + 1 : return -1\n left,right = 1, ceil(max(max(dist),dist[-1]/(1 if hour.is_integer() else hour-int(hour))))\n while left<right:\n mid=(left+right)//2\n if sum([ceil(i/mid) for i in dist[:-1]])+(dist[-1]/mid) <= hour :\n right=mid\n else:\n left=mid+1\n return left\n``` | 4 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Python3 👍||⚡99/99 faster beats, 11 lines🔥|| clean solution || | minimum-speed-to-arrive-on-time | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(m*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n if len(dist) >= hour + 1 : return -1\n left,right = 1, ceil(max(max(dist),dist[-1]/(1 if hour.is_integer() else hour-int(hour))))\n while left<right:\n mid=(left+right)//2\n if sum([ceil(i/mid) for i in dist[:-1]])+(dist[-1]/mid) <= hour :\n right=mid\n else:\n left=mid+1\n return left\n``` | 4 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
🚂 [VIDEO] Beats 95% 🚀 All Aboard the Coding Express: Finding the Minimum Speed with Binary Search | minimum-speed-to-arrive-on-time | 1 | 1 | # Intuition\nUpon reading this problem, it quickly becomes clear that there\'s a time constraint on the total journey to the office. This hints towards optimizing the speed of travel. Since we need to find the minimum speed, it seems like a good fit for a binary search algorithm, where we iteratively refine our search for the optimal speed.\n\nhttps://youtu.be/a3VgSDzD-B0\n\n# Approach\nOur approach to solving this problem is to use a binary search algorithm to find the minimum speed. We start by checking whether it\'s possible to reach the office in the given time. If it\'s not possible, we return -1 immediately.\n\nNext, we perform a binary search from 1 to the maximum of the maximum distance and the last distance divided by the remaining time after each train ride takes 1 hour. We define a helper function, `canArriveOnTime`, that checks if we can arrive at the office on time with a given speed. This function calculates the total time taken by adding up the time each train takes to reach the destination. If we can arrive on time with the mid speed, we update the right bound to mid, otherwise, we update the left bound to mid + 1. We repeat this process until we find the minimum speed.\n\n# Complexity\n- Time complexity: The time complexity of this solution is \\(O(n \\log m)\\), where \\(n\\) is the number of train rides and \\(m\\) is the maximum distance. This is because for each possible speed, we check if we can arrive on time, which requires iterating over all the train rides.\n\n- Space complexity: The space complexity is \\(O(1)\\), as we only use a constant amount of space to store the speed, distances, and time.\n\nThis code effectively solves the problem using the power of binary search and some mathematical calculations, demonstrating the flexibility and usefulness of these techniques in solving complex problems.\n\n# Code\n```Python []\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n def canArriveOnTime(speed): \n return sum(math.ceil(d / speed) for d in dist[:-1]) + dist[-1] / speed <= hour \n\n n = len(dist) \n if n - 1 > hour or hour - n + 1 <= 0: \n return -1 \n\n left, right = 1, max(max(dist), math.ceil(dist[-1] / (hour - n + 1))) \n while left < right: \n mid = (left + right) // 2 \n if canArriveOnTime(mid): \n right = mid \n else: \n left = mid + 1 \n\n return left \n```\n``` C++ []\nclass Solution {\npublic:\n int minSpeedOnTime(vector<int>& dist, double hour) {\n int n = dist.size();\n if(n - 1 > hour || hour - n + 1 <= 0) return -1;\n int left = 1, right = max(*max_element(dist.begin(), dist.end()), (int)ceil(dist[n - 1] / (hour - n + 1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n double total_time = 0;\n for(int i = 0; i < n - 1; i++) total_time += ceil((double)dist[i] / mid);\n total_time += (double)dist[n - 1] / mid;\n if(total_time <= hour) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n};\n```\n``` C# []\npublic class Solution {\n public int MinSpeedOnTime(int[] dist, double hour) {\n int n = dist.Length;\n if(n - 1 > hour || hour - n + 1 <= 0) return -1;\n int left = 1, right = Math.Max(dist.Max(), (int)Math.Ceiling(dist[n - 1] / (hour - n + 1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n double total_time = 0;\n for(int i = 0; i < n - 1; i++) total_time += Math.Ceiling((double)dist[i] / mid);\n total_time += (double)dist[n - 1] / mid;\n if(total_time <= hour) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n}\n```\n``` Java []\nclass Solution {\n public int minSpeedOnTime(int[] dist, double hour) {\n int n = dist.length;\n if(n - 1 > hour || hour - n + 1 <= 0) return -1;\n int left = 1, right = Math.max(Arrays.stream(dist).max().getAsInt(), (int)Math.ceil(dist[n - 1] / (hour - n + 1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n double total_time = 0;\n for(int i = 0; i < n - 1; i++) total_time += Math.ceil((double)dist[i] / mid);\n total_time += (double)dist[n - 1] / mid;\n if(total_time <= hour) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} dist\n * @param {number} hour\n * @return {number}\n */\nvar minSpeedOnTime = function(dist, hour) {\n const canArriveOnTime = (speed) => {\n return dist.slice(0, -1).reduce((total, d) => total + Math.ceil(d / speed), 0) + dist[dist.length - 1] / speed <= hour;\n };\n\n let n = dist.length;\n if (n - 1 > hour || hour - n + 1 <= 0) {\n return -1;\n }\n\n let left = 1, right = Math.max(...dist, Math.ceil(dist[dist.length - 1] / (hour - n + 1)));\n while (left < right) {\n let mid = Math.floor((left + right) / 2);\n if (canArriveOnTime(mid)) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return left;\n};\n``` | 3 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
🚂 [VIDEO] Beats 95% 🚀 All Aboard the Coding Express: Finding the Minimum Speed with Binary Search | minimum-speed-to-arrive-on-time | 1 | 1 | # Intuition\nUpon reading this problem, it quickly becomes clear that there\'s a time constraint on the total journey to the office. This hints towards optimizing the speed of travel. Since we need to find the minimum speed, it seems like a good fit for a binary search algorithm, where we iteratively refine our search for the optimal speed.\n\nhttps://youtu.be/a3VgSDzD-B0\n\n# Approach\nOur approach to solving this problem is to use a binary search algorithm to find the minimum speed. We start by checking whether it\'s possible to reach the office in the given time. If it\'s not possible, we return -1 immediately.\n\nNext, we perform a binary search from 1 to the maximum of the maximum distance and the last distance divided by the remaining time after each train ride takes 1 hour. We define a helper function, `canArriveOnTime`, that checks if we can arrive at the office on time with a given speed. This function calculates the total time taken by adding up the time each train takes to reach the destination. If we can arrive on time with the mid speed, we update the right bound to mid, otherwise, we update the left bound to mid + 1. We repeat this process until we find the minimum speed.\n\n# Complexity\n- Time complexity: The time complexity of this solution is \\(O(n \\log m)\\), where \\(n\\) is the number of train rides and \\(m\\) is the maximum distance. This is because for each possible speed, we check if we can arrive on time, which requires iterating over all the train rides.\n\n- Space complexity: The space complexity is \\(O(1)\\), as we only use a constant amount of space to store the speed, distances, and time.\n\nThis code effectively solves the problem using the power of binary search and some mathematical calculations, demonstrating the flexibility and usefulness of these techniques in solving complex problems.\n\n# Code\n```Python []\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n def canArriveOnTime(speed): \n return sum(math.ceil(d / speed) for d in dist[:-1]) + dist[-1] / speed <= hour \n\n n = len(dist) \n if n - 1 > hour or hour - n + 1 <= 0: \n return -1 \n\n left, right = 1, max(max(dist), math.ceil(dist[-1] / (hour - n + 1))) \n while left < right: \n mid = (left + right) // 2 \n if canArriveOnTime(mid): \n right = mid \n else: \n left = mid + 1 \n\n return left \n```\n``` C++ []\nclass Solution {\npublic:\n int minSpeedOnTime(vector<int>& dist, double hour) {\n int n = dist.size();\n if(n - 1 > hour || hour - n + 1 <= 0) return -1;\n int left = 1, right = max(*max_element(dist.begin(), dist.end()), (int)ceil(dist[n - 1] / (hour - n + 1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n double total_time = 0;\n for(int i = 0; i < n - 1; i++) total_time += ceil((double)dist[i] / mid);\n total_time += (double)dist[n - 1] / mid;\n if(total_time <= hour) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n};\n```\n``` C# []\npublic class Solution {\n public int MinSpeedOnTime(int[] dist, double hour) {\n int n = dist.Length;\n if(n - 1 > hour || hour - n + 1 <= 0) return -1;\n int left = 1, right = Math.Max(dist.Max(), (int)Math.Ceiling(dist[n - 1] / (hour - n + 1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n double total_time = 0;\n for(int i = 0; i < n - 1; i++) total_time += Math.Ceiling((double)dist[i] / mid);\n total_time += (double)dist[n - 1] / mid;\n if(total_time <= hour) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n}\n```\n``` Java []\nclass Solution {\n public int minSpeedOnTime(int[] dist, double hour) {\n int n = dist.length;\n if(n - 1 > hour || hour - n + 1 <= 0) return -1;\n int left = 1, right = Math.max(Arrays.stream(dist).max().getAsInt(), (int)Math.ceil(dist[n - 1] / (hour - n + 1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n double total_time = 0;\n for(int i = 0; i < n - 1; i++) total_time += Math.ceil((double)dist[i] / mid);\n total_time += (double)dist[n - 1] / mid;\n if(total_time <= hour) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} dist\n * @param {number} hour\n * @return {number}\n */\nvar minSpeedOnTime = function(dist, hour) {\n const canArriveOnTime = (speed) => {\n return dist.slice(0, -1).reduce((total, d) => total + Math.ceil(d / speed), 0) + dist[dist.length - 1] / speed <= hour;\n };\n\n let n = dist.length;\n if (n - 1 > hour || hour - n + 1 <= 0) {\n return -1;\n }\n\n let left = 1, right = Math.max(...dist, Math.ceil(dist[dist.length - 1] / (hour - n + 1)));\n while (left < right) {\n let mid = Math.floor((left + right) / 2);\n if (canArriveOnTime(mid)) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return left;\n};\n``` | 3 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Easy intuitive two function solution. Beats 90% | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\nThis problem seemed very clearly to be a two pointer / binary search problem. We need to find the lowest value which satisfy certain constraints.\n# Approach\nIntially was to check if it is possible to arrive on time.\nIf there are more trains than hours+1, it is impossible to arrive on time. \n# Complexity\n- Time complexity:\nThe speedcheck function is n and the binary search is log(n) giving us.\n$$O(n*log(n))$$\n\n\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n #Check if it is possible to find a solution.\n if len(dist)-1>=hour:\n return -1\n #A function to check if a certain speed is feasible.\n def speedcheck(speed):\n time=0\n #Adding time for each train rounded up.\n for i in dist[:-1]:\n time+=ceil(i/speed)\n #Not rounding up the last train.\n time+= dist[-1]/speed\n #If the final time is less than required time, return True\n if time<=hour:\n return True\n def search(slow, fastest):\n #Classic binary search starting with 1 as slow and 10^7 as fastest\n l=slow\n r= fastest\n\n while l < r:\n #Find the value in the middle of l and r\n mid = floor((l+r)/2)\n #If the middle value is feasible, move right pointer there.\n if speedcheck(mid):\n r=mid\n continue\n #Otherwise move left pointer to one point right of mid. \n else:\n l=mid+1\n return l\n return search(1,10**7)\n``` | 2 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Easy intuitive two function solution. Beats 90% | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\nThis problem seemed very clearly to be a two pointer / binary search problem. We need to find the lowest value which satisfy certain constraints.\n# Approach\nIntially was to check if it is possible to arrive on time.\nIf there are more trains than hours+1, it is impossible to arrive on time. \n# Complexity\n- Time complexity:\nThe speedcheck function is n and the binary search is log(n) giving us.\n$$O(n*log(n))$$\n\n\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n #Check if it is possible to find a solution.\n if len(dist)-1>=hour:\n return -1\n #A function to check if a certain speed is feasible.\n def speedcheck(speed):\n time=0\n #Adding time for each train rounded up.\n for i in dist[:-1]:\n time+=ceil(i/speed)\n #Not rounding up the last train.\n time+= dist[-1]/speed\n #If the final time is less than required time, return True\n if time<=hour:\n return True\n def search(slow, fastest):\n #Classic binary search starting with 1 as slow and 10^7 as fastest\n l=slow\n r= fastest\n\n while l < r:\n #Find the value in the middle of l and r\n mid = floor((l+r)/2)\n #If the middle value is feasible, move right pointer there.\n if speedcheck(mid):\n r=mid\n continue\n #Otherwise move left pointer to one point right of mid. \n else:\n l=mid+1\n return l\n return search(1,10**7)\n``` | 2 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
99% Faster Python Solution | Clean code | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is quite a classic problem at least on leetcode. We do binary search on the possible solutions in this case is the speed. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem has no solutions if the length of dist - 1 >= hour as that would mean there is\'nt sufficient time for the last trip to be completed as all other trips takes time >= 1.\nThe minimum speed is 1 but the maximum speed requires some calculations. \nThe maximum speed is = max(max(dist), ceil(dist[-1]/tmp)); i.e. the maximum of the max of the dist and the maximum time required for the last trip.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(dist * log(max(max(dist), ceil(dist[-1]/tmp))))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n if len(dist) - 1 >= hour:\n return -1\n mini, maxi = 1, max(dist)\n tmp = hour - len(dist) + 1\n if tmp < 1:\n maxi = max(maxi, ceil(dist[-1]/tmp))\n d1, d2 = dist[:-1], dist[-1]\n res = -1\n while mini <= maxi:\n if mini == maxi:\n return mini\n speed = (mini+maxi)//2\n time = 0\n for d in d1:\n time += ceil(d/speed)\n time += (d2/speed)\n if time <= hour:\n res = speed\n maxi = speed\n else:\n mini = speed + 1\n return res\n``` | 2 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
99% Faster Python Solution | Clean code | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is quite a classic problem at least on leetcode. We do binary search on the possible solutions in this case is the speed. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem has no solutions if the length of dist - 1 >= hour as that would mean there is\'nt sufficient time for the last trip to be completed as all other trips takes time >= 1.\nThe minimum speed is 1 but the maximum speed requires some calculations. \nThe maximum speed is = max(max(dist), ceil(dist[-1]/tmp)); i.e. the maximum of the max of the dist and the maximum time required for the last trip.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(dist * log(max(max(dist), ceil(dist[-1]/tmp))))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n if len(dist) - 1 >= hour:\n return -1\n mini, maxi = 1, max(dist)\n tmp = hour - len(dist) + 1\n if tmp < 1:\n maxi = max(maxi, ceil(dist[-1]/tmp))\n d1, d2 = dist[:-1], dist[-1]\n res = -1\n while mini <= maxi:\n if mini == maxi:\n return mini\n speed = (mini+maxi)//2\n time = 0\n for d in d1:\n time += ceil(d/speed)\n time += (d2/speed)\n if time <= hour:\n res = speed\n maxi = speed\n else:\n mini = speed + 1\n return res\n``` | 2 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Beats 96.92% in time 🔥🔥🔥 | minimum-speed-to-arrive-on-time | 0 | 1 | \n# Code\n```\nimport math\n\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n len_path = len(dist)\n max_dist = max(dist)\n # Paths that will have to the next full hour takes 1 hour each\n if len_path - 1 >= hour:\n return -1\n # If # of paths is equal to hours, they must last at most 1 hour\n if len_path == hour:\n return max_dist\n # If # of paths is equal to # of full hours, the time will be given by the last path\n if len_path - 1 == int(hour):\n return max(max_dist,round(dist[-1]/(hour-int(hour))))\n # Computing the least vel that would work if dist.length = 1\n vel = sum(dist)/hour\n # If this vel is lower than 1, means that the minimum valid vel works\n if vel <= 1:\n return 1\n # Computing a velocity that we are sure doesn\'t work, to the binary search\n vel = math.floor(vel) - 1\n left = vel #Granting left will be the highest that doesn\'t work until now\n right = max_dist #Granting right will be the lowest that worked until now\n aux = (left+right)//2\n while True:\n dur = 0\n # Testing the velocity\n for dis in dist:\n dur += dis/aux\n if dur > hour:\n dur = -1\n break\n else:\n dur = math.ceil(dur)\n if dur == -1:\n left = aux\n else:\n right = aux\n # Ends when left is adjacent to right\n if left == right - 1:\n break\n aux = (left + right)//2\n \n return right\n \n``` | 1 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Beats 96.92% in time 🔥🔥🔥 | minimum-speed-to-arrive-on-time | 0 | 1 | \n# Code\n```\nimport math\n\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n len_path = len(dist)\n max_dist = max(dist)\n # Paths that will have to the next full hour takes 1 hour each\n if len_path - 1 >= hour:\n return -1\n # If # of paths is equal to hours, they must last at most 1 hour\n if len_path == hour:\n return max_dist\n # If # of paths is equal to # of full hours, the time will be given by the last path\n if len_path - 1 == int(hour):\n return max(max_dist,round(dist[-1]/(hour-int(hour))))\n # Computing the least vel that would work if dist.length = 1\n vel = sum(dist)/hour\n # If this vel is lower than 1, means that the minimum valid vel works\n if vel <= 1:\n return 1\n # Computing a velocity that we are sure doesn\'t work, to the binary search\n vel = math.floor(vel) - 1\n left = vel #Granting left will be the highest that doesn\'t work until now\n right = max_dist #Granting right will be the lowest that worked until now\n aux = (left+right)//2\n while True:\n dur = 0\n # Testing the velocity\n for dis in dist:\n dur += dis/aux\n if dur > hour:\n dur = -1\n break\n else:\n dur = math.ceil(dur)\n if dur == -1:\n left = aux\n else:\n right = aux\n # Ends when left is adjacent to right\n if left == right - 1:\n break\n aux = (left + right)//2\n \n return right\n \n``` | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Python short and clean. BinarySearch. Functional programming. | minimum-speed-to-arrive-on-time | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot log(k))$$\n\n- Space complexity: $$O(1)$$\n\nwhere,\n`n is length of dist array`,\n`k is maximum speed possible, i.e 1e7`\n\n# Code\n```python\nclass Solution:\n def minSpeedOnTime(self, dist: list[int], hour: float) -> int:\n n = len(dist)\n if hour <= n - 1: return -1\n\n l = int(max(sum(dist) // hour, 1))\n r = int(max(max(dist), dist[-1] / (hour - (n - 1)))) + 1\n\n while l < r:\n m = (l + r) // 2\n ds = reversed(dist)\n t = sum((ceil(d / m) for d in ds), next(ds) / m)\n l, r = (l, m) if t < hour or isclose(t, hour, rel_tol=1e-12) else (m + 1, r)\n \n return l\n\n\n``` | 1 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Python short and clean. BinarySearch. Functional programming. | minimum-speed-to-arrive-on-time | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot log(k))$$\n\n- Space complexity: $$O(1)$$\n\nwhere,\n`n is length of dist array`,\n`k is maximum speed possible, i.e 1e7`\n\n# Code\n```python\nclass Solution:\n def minSpeedOnTime(self, dist: list[int], hour: float) -> int:\n n = len(dist)\n if hour <= n - 1: return -1\n\n l = int(max(sum(dist) // hour, 1))\n r = int(max(max(dist), dist[-1] / (hour - (n - 1)))) + 1\n\n while l < r:\n m = (l + r) // 2\n ds = reversed(dist)\n t = sum((ceil(d / m) for d in ds), next(ds) / m)\n l, r = (l, m) if t < hour or isclose(t, hour, rel_tol=1e-12) else (m + 1, r)\n \n return l\n\n\n``` | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Binary search in C++/python beats 100% using tighter limits | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\nThe approach I used is a simple binary search, as everybody did. But to get a slight performance improvement, I calculate boundaries for the speed instead of using hard-coded 1 to `1e7` boundary.\n\nWe are given a sequence of distances `dist` denoted as $a_n$, and maximum time `hour` denoted as $c$.\nThen the problem can be restated in the following way:\nFind minimum speed $x \\in \\mathbb{N}$, such that the following holds:\n$$\n\\begin{align}\n\\sum_{i=1}^{n-1}\\left\\lceil\\frac{a_i}{x}\\right\\rceil + \\frac{a_n}{x} \\le c\n\\end{align}\n$$\n\nGiven that all distances and speed are natural numbers, that is, greater or equal to 1, we find that $\\frac{a_i}{x}>0$, therefore $\\left\\lceil\\frac{a_i}{x}\\right\\rceil \\ge 1$.\n\nThen the sum $\\sum_{i=1}^{n-1}\\left\\lceil\\frac{a_i}{x}\\right\\rceil \\ge n-1$ and $\\frac{a_n}{x}>0$. Therefore, if $c<=n-1$, then there is no such $x$ that sutisfy the constraint.\n\nWe know that ceiling function $\\lceil x \\rceil$ always returns result $[x, x+1)$. Therefore, $\\left\\lceil\\frac{a_i}{x}\\right\\rceil$ will be in range $[\\frac{a_i}{x},\\frac{a_i}{x}+1)$. Then the two boundaries of $c$ are:\n\n$$\n\\begin{align}\n\\sum_{i=1}^{n-1}\\frac{a_i}{x} + \\frac{a_n}{x} = c_1 \\\\\n\\sum_{i=1}^{n-1}\\left(\\frac{a_i}{x} + 1 \\right) + \\frac{a_n}{x} = c_2 \\\\\nc_1 \\le c < c_2\n\\end{align}\n$$\n\nAfter some simplifications we get the boundaries of $x$:\n\n$$\n\\begin{align}\n\\frac{\\sum_{i=1}^{n-1}a_i + a_n}{c} = x_1 \\\\\n\\frac{\\sum_{i=1}^{n-1}a_i + a_n}{c-n+1} = x_2 \\\\\nx_1 \\le x < x_2 \\\\\n\\end{align}\n$$\n\nThe code runs faster than 100% in C++:\n\n\n\n# Code\n<iframe src="https://leetcode.com/playground/Qc6KU4dF/shared" frameBorder="0" width="1000" height="500"></iframe> | 1 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Binary search in C++/python beats 100% using tighter limits | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\nThe approach I used is a simple binary search, as everybody did. But to get a slight performance improvement, I calculate boundaries for the speed instead of using hard-coded 1 to `1e7` boundary.\n\nWe are given a sequence of distances `dist` denoted as $a_n$, and maximum time `hour` denoted as $c$.\nThen the problem can be restated in the following way:\nFind minimum speed $x \\in \\mathbb{N}$, such that the following holds:\n$$\n\\begin{align}\n\\sum_{i=1}^{n-1}\\left\\lceil\\frac{a_i}{x}\\right\\rceil + \\frac{a_n}{x} \\le c\n\\end{align}\n$$\n\nGiven that all distances and speed are natural numbers, that is, greater or equal to 1, we find that $\\frac{a_i}{x}>0$, therefore $\\left\\lceil\\frac{a_i}{x}\\right\\rceil \\ge 1$.\n\nThen the sum $\\sum_{i=1}^{n-1}\\left\\lceil\\frac{a_i}{x}\\right\\rceil \\ge n-1$ and $\\frac{a_n}{x}>0$. Therefore, if $c<=n-1$, then there is no such $x$ that sutisfy the constraint.\n\nWe know that ceiling function $\\lceil x \\rceil$ always returns result $[x, x+1)$. Therefore, $\\left\\lceil\\frac{a_i}{x}\\right\\rceil$ will be in range $[\\frac{a_i}{x},\\frac{a_i}{x}+1)$. Then the two boundaries of $c$ are:\n\n$$\n\\begin{align}\n\\sum_{i=1}^{n-1}\\frac{a_i}{x} + \\frac{a_n}{x} = c_1 \\\\\n\\sum_{i=1}^{n-1}\\left(\\frac{a_i}{x} + 1 \\right) + \\frac{a_n}{x} = c_2 \\\\\nc_1 \\le c < c_2\n\\end{align}\n$$\n\nAfter some simplifications we get the boundaries of $x$:\n\n$$\n\\begin{align}\n\\frac{\\sum_{i=1}^{n-1}a_i + a_n}{c} = x_1 \\\\\n\\frac{\\sum_{i=1}^{n-1}a_i + a_n}{c-n+1} = x_2 \\\\\nx_1 \\le x < x_2 \\\\\n\\end{align}\n$$\n\nThe code runs faster than 100% in C++:\n\n\n\n# Code\n<iframe src="https://leetcode.com/playground/Qc6KU4dF/shared" frameBorder="0" width="1000" height="500"></iframe> | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Binary_search.py | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n n = len(dist)\n # if n-1>hour:\n # return -1\n def calc_time(speed):\n time_taken = 0\n ## main logic is here the last time can be in decimal because there is no distance after it..........\n for i in dist[:-1]:\n time_taken+=ceil(i/speed)\n time_taken+=dist[-1]/speed\n return time_taken\n left = 1\n right = 10**7 +1\n\n while left<right:\n mid = (left+right)//2\n if calc_time(mid)<=hour:\n right = mid\n else:\n left = mid+1\n return left if left != 10**7 + 1 else -1\n\n``` | 1 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Binary_search.py | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n n = len(dist)\n # if n-1>hour:\n # return -1\n def calc_time(speed):\n time_taken = 0\n ## main logic is here the last time can be in decimal because there is no distance after it..........\n for i in dist[:-1]:\n time_taken+=ceil(i/speed)\n time_taken+=dist[-1]/speed\n return time_taken\n left = 1\n right = 10**7 +1\n\n while left<right:\n mid = (left+right)//2\n if calc_time(mid)<=hour:\n right = mid\n else:\n left = mid+1\n return left if left != 10**7 + 1 else -1\n\n``` | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
Python 3 | Binary Search | Runtime beats 89% | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAccording to the task\'s description:\n- Speed ranges between $$1$$ and $$10^7$$ km/h.\n- We don\'t need to wait additional time after the last train.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse binary search for the speed, ceil the time taken for each train but the last.\n\n# Complexity \n- Time complexity: $$O(N*LOG(C))$$, where $$C$$ is the range $$[1..10^7]$$, or just $$O(N)$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(1)$$, the algorithm uses constant additional space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```python3\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n def canReach(s):\n return sum([ceil(d / s) for d in dist[:-1]], 0) + dist[-1] / s <= hour\n \n lo, hi = 1, 10 ** 7\n min_speed = -1\n while lo <= hi:\n speed = (hi - lo) // 2 + lo\n if canReach(speed):\n min_speed = speed\n hi = speed - 1\n else:\n lo = speed + 1\n return min_speed\n``` | 1 | You are given a floating-point number `hour`, representing the amount of time you have to reach the office. To commute to the office, you must take `n` trains in sequential order. You are also given an integer array `dist` of length `n`, where `dist[i]` describes the distance (in kilometers) of the `ith` train ride.
Each train can only depart at an integer hour, so you may need to wait in between each train ride.
* For example, if the `1st` train ride takes `1.5` hours, you must wait for an additional `0.5` hours before you can depart on the `2nd` train ride at the 2 hour mark.
Return _the **minimum positive integer** speed **(in kilometers per hour)** that all the trains must travel at for you to reach the office on time, or_ `-1` _if it is impossible to be on time_.
Tests are generated such that the answer will not exceed `107` and `hour` will have **at most two digits after the decimal point**.
**Example 1:**
**Input:** dist = \[1,3,2\], hour = 6
**Output:** 1
**Explanation:** At speed 1:
- The first train ride takes 1/1 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 1 hour mark. The second train takes 3/1 = 3 hours.
- Since we are already at an integer hour, we depart immediately at the 4 hour mark. The third train takes 2/1 = 2 hours.
- You will arrive at exactly the 6 hour mark.
**Example 2:**
**Input:** dist = \[1,3,2\], hour = 2.7
**Output:** 3
**Explanation:** At speed 3:
- The first train ride takes 1/3 = 0.33333 hours.
- Since we are not at an integer hour, we wait until the 1 hour mark to depart. The second train ride takes 3/3 = 1 hour.
- Since we are already at an integer hour, we depart immediately at the 2 hour mark. The third train takes 2/3 = 0.66667 hours.
- You will arrive at the 2.66667 hour mark.
**Example 3:**
**Input:** dist = \[1,3,2\], hour = 1.9
**Output:** -1
**Explanation:** It is impossible because the earliest the third train can depart is at the 2 hour mark.
**Constraints:**
* `n == dist.length`
* `1 <= n <= 105`
* `1 <= dist[i] <= 105`
* `1 <= hour <= 109`
* There will be at most two digits after the decimal point in `hour`. | null |
Python 3 | Binary Search | Runtime beats 89% | minimum-speed-to-arrive-on-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAccording to the task\'s description:\n- Speed ranges between $$1$$ and $$10^7$$ km/h.\n- We don\'t need to wait additional time after the last train.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse binary search for the speed, ceil the time taken for each train but the last.\n\n# Complexity \n- Time complexity: $$O(N*LOG(C))$$, where $$C$$ is the range $$[1..10^7]$$, or just $$O(N)$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(1)$$, the algorithm uses constant additional space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```python3\nclass Solution:\n def minSpeedOnTime(self, dist: List[int], hour: float) -> int:\n def canReach(s):\n return sum([ceil(d / s) for d in dist[:-1]], 0) + dist[-1] / s <= hour\n \n lo, hi = 1, 10 ** 7\n min_speed = -1\n while lo <= hi:\n speed = (hi - lo) // 2 + lo\n if canReach(speed):\n min_speed = speed\n hi = speed - 1\n else:\n lo = speed + 1\n return min_speed\n``` | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
[Simple & Elegant] [O(n) time] [O(maxJump) space] Linear scan using sliding window | jump-game-vii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor computing if any index i is reachable from index 0 or not, we only need the reachability information of indices in the range (i-maxJump, i-1). This is because if index i is reachable and has a path from index 0, then it has to have a predecessor node / index in the range (i-maxJump, i-1).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We linearly scan each index / element of s.\n\n2. For each index i (if s[i] = 0) we check if it\'s reachable from index 0 or not.\n\n3. For this check, we manitain a sliding window that contains all the reachable-from-index-0 indices in the range (i-maxJump, i-1). This window contains all indices in increasing order.\n\n4. So for each i we check if the first element f (smallest and farthest from i) in the window doesn\'t skip i with the smallest possible jump. That is, i >= f + minJump. This is because if i < f + minJump, then no other index j in the window can jump to i (all of them will jump ahead of i).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) for linear scanning of s\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(maxJump) for the sliding window\n\n# Code\n```\nclass Solution:\n def canReach(self, s: str, minJump: int, maxJump: int) -> bool:\n \n window = deque()\n # to keep the list of past maxJump reachable indices\n \n window.append(0)\n for i in range(1, len(s)):\n \n # clear the window beyond maxJump\n if window and window[0] + maxJump < i:\n window.popleft()\n\n # check reachability of i\n if s[i] == \'0\' and window and window[0] + minJump <= i:\n window.append(i)\n\n return window and window[-1] == len(s) - 1\n``` | 3 | You are given a **0-indexed** binary string `s` and two integers `minJump` and `maxJump`. In the beginning, you are standing at index `0`, which is equal to `'0'`. You can move from index `i` to index `j` if the following conditions are fulfilled:
* `i + minJump <= j <= min(i + maxJump, s.length - 1)`, and
* `s[j] == '0'`.
Return `true` _if you can reach index_ `s.length - 1` _in_ `s`_, or_ `false` _otherwise._
**Example 1:**
**Input:** s = "011010 ", minJump = 2, maxJump = 3
**Output:** true
**Explanation:**
In the first step, move from index 0 to index 3.
In the second step, move from index 3 to index 5.
**Example 2:**
**Input:** s = "01101110 ", minJump = 2, maxJump = 3
**Output:** false
**Constraints:**
* `2 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`.
* `s[0] == '0'`
* `1 <= minJump <= maxJump < s.length` | Preprocess checking palindromes in O(1) Note that one string is a prefix and another one is a suffix you can try brute forcing the rest |
python | 100% faster, 5 methods with explanations | jump-game-vii | 0 | 1 | Before I get into the specifics of each method there are 3 cases I checked which make solving the puzzle easier. First, if the target itself can\'t be landed on then there can\'t be a solution. Second, if minJump and maxJump are the same, then there\'s only 1 possible path through the string, does it work? And finally, if minJump is 1, then we can ignore all repeated 0\'s. In practice though, it\'s been faster for me to remove all leading/trailing 0\'s (except for the source/target). Doing this allows the rest of the code to run faster and with less memory usage in some cases. Since I use this code at the start of all of my solutions, I decided to put it here as its own section to save space later.\n\nEdit: I came up with something better for the case when minJump == 1, where instead of removing 0\'s, we can check if a string of 1\'s with length maxJump exists in the puzzle input, since such a string would be impossible to jump over. I\'ve edited the code here to reflect that change, and included the old version of the code at the end of the post for reference. It might be more efficient to find the length of the longest string of 1\'s in the puzzle input, but I didn\'t feel like the extra complexity in the code was worth it. Technically, checking if a run of maxJump \'1\'s exists in the puzzle will disprove the existance of a path for any puzzle, but it\'s only really worth doing this work when minJump is 1.\n\nTime Complexity: O(1) <= O <= O(n)\nSpace Complexity: O(1) <= O <= O(maxJump)\n\n\'\'\'\n\n def canReach(self, s: str, minJump: int, maxJump: int) -> bool:\n #Check for Easy Cases\n I = len(s) - 1 # there are several places having the last index was convenient, so I compute/store it here\n if s[I] == \'1\':\n #It\'s Impossible to Land on the Target\n return False\n elif minJump == maxJump:\n #There\'s Only 1 Possible Path\n return I%minJump == 0 and all(c == \'0\' for c in s[minJump:I:minJump])\n elif minJump == 1:\n #Check if There\'s an Un-Jumpable String of 1\'s\n return \'1\'*maxJump not in s\n else:\n\t\t\t#Solve the Puzzle Using the Method of Your Choice\n\t\t\t...\n\'\'\'\n\n## Method 1: Best-First Search (Simplified A*)\nThis is the first method I tried, and while it is fairly fast, it\'s memory usage is pretty poor. I prioritized indices in a min heap based on their linear distance to the target (which is equivalent to the negated index). The only interesting thing I really did here was that I cast the string to a character array, allowing me to mark nodes as visited in a way that plays nicely in python. I also computed bounds on indecies which can jump directly to the finish, allowing me to end the search a little faster.\n\nTime Complexity: O(nlogn)\nSpace Complexity: O(n)\nBest Performance: 72 ms/19.6 MB : 100%/22%\n\n\'\'\'\n\n\t\t\t...\n\t\t\t\n\t\t\t#Compute the Bounds for Finishing\n X = I - maxJump\n Y = I - minJump\n \n #Update the Minimum Jump for Convenience\n minJump -= 1\n \n #Do a BFS\n s = list(s)\n queue = [0]\n while queue:\n #Get the Next Index\n i = -heappop(queue)\n \n #Check if a Solution was Found\n if i < X:\n #Add Child Nodes to the Queue\n for j in range(i + maxJump, i + minJump, -1):\n #Check if the Index Can be Jumped to\n if s[j] == \'0\':\n #Add the Index to the Queue\n heappush(queue, -j)\n\n #Mark the Index as Visited\n s[j] = \'2\'\n\t\t\t\telif i <= Y:\n\t\t\t\t\treturn True\n \n #No Solution was Found\n return False\n\'\'\'\n\n## Method 2: Depth-First Search\nThis idea here is basically the same as for my bfs, except that I realized that the heuristic I was using basically just gave me a depth-first search anyway, except that the bfs required more work since heap operations run in O(logn) while stack operations run in O(1). The ordering indices are visited isn\'t identical between this dfs and the bfs in method 1, but it\'s close enough that for this puzzle the faster stack operations outweigh the less optimal index ordering, leading to a small performance gain.\n\nTime Complexity: O(n)\nSpace Complexity: O(n)\nBest Performance: 60 ms/18.9 ms : 100%/31%\n\n\'\'\'\n\n\t\t\t...\n\t\t\t\n\t\t\t#Compute the Bounds for Finishing\n X = I - maxJump\n Y = I - minJump\n \n #Update the Maximum Jump for Convenience\n maxJump += 1\n \n #Do a DFS\n s = list(s)\n stack = [0]\n while stack:\n #Get the Next Index\n i = stack.pop()\n \n #Check if a Solution was Found\n if i < X:\n #Add Child Nodes to the Stack\n for j in range(i + minJump, i + maxJump):\n #Check if the Index Can be Jumped to\n if s[j] == \'0\':\n #Add the Index to the Stack\n stack.append(j)\n\n #Mark the Index as Visited\n s[j] = \'2\'\n\t\t\t\telif i <= Y:\n\t\t\t\t\treturn True\n\t\t\t\n #No Solution was Found\n return False\n\'\'\'\n\n## Method 2.5 : DFS with Backtracking\nThis is a much more recent addition to this post, and it was inspired by https://leetcode.com/problems/jump-game-vii/discuss/1400399/python-dfs-%2B-backtracking-44ms-15mb\n\nDoing the DFS with backtracking helps keep the stack smaller, and avoids some unnecessary computation when the path is nice! It still explores nodes in the same order as the DFS in method 2 though, making it a very efficient solution! I\'ve also posted a recursive version of this in the comments which I find a little easier to follow, but performs worse due to the recursive overhead.\n\nTime Complexity: O(n)\nSpace Complexity: O(n)\nBest Performance: 40 ms/15.2 ms : 100%/98%\n\n\'\'\'\n\n ...\n\t\t\t\n\t\t\t#Compute the Bounds for Stopping \n X = I - maxJump\n Y = I - minJump\n \n #Update the Min Jump for Convenience\n minJump -= 1\n \n #Do a DFS With Backtracking\n s = list(s[:Y + 1])\n stack = [(maxJump, minJump)]\n while stack:\n #Get the Next Range Off the Stack\n i, j = stack.pop()\n \n #Find the Next Largest Jump\n for i in range(min(i, Y), j, -1):\n #Check if the Square Can be Jumped to\n if s[i] == \'0\':\n #Mark the Square as Visited/Reachable\n s[i] = \'2\'\n\n #Check the Case (if neither condition is true then the finish isn\'t reachable from the current position)\n if i < X:\n #Add the Current Range Back to the Stack (for backtracking)\n\t\t\t\t\t\t\tstack.append((i, j))\n\t\t\t\t\t\t\t\n #Add the Next Range to the Stack\n stack.append((i + maxJump, i + minJump))\n \n #Move on to the Next Range on the Stack\n break\n else:\n #A Solution was Found\n return True\n \n #No Solution is Possible\n return False\n\'\'\'\n\n## Method 3: 2 Pointer\nIn this method I also cast the string to a character array so that I could mark which nodes were reachable. The basic idea is that we want to know if the position at the right pointer (\'i\') is reachable. The right pointer will be reachable if it\'s open (s[i] == \'0\') and if there\'s a different reachable index in the appropriate range. So, assuming it\'s open, we increment a left pointer searching for indices we could jump to position i from (these indices were previously marked as reachable when the right pointer landed on them). Also, if the left pointer ever catches up to the right pointer then we return False since there was a chain of unreachable points too long for any future points to be reached. (I think the memory usage for this method is still O(n) becasue I casted the string to a character array, but it\'s a much smaller O(n) than either my bfs or dfs).\n\nTime Complexity: O(n)\nSpace Complexity: O(n)\nBest Performance: 108 ms/15.6 MB : 100%/95%\n\n\'\'\'\n\t\t\t\n\t\t\t...\n\t\t\t\n\t\t\t#Cast the String to a Character Array\n s = list(s)\n s[0] = \'2\'\n \n #2 Pointer Solution\n j = 0\n for i in range(minJump, len(s)):\n #Check if the Right Pointer is Open\n if s[i] == \'0\':\n #Increment the Left Pointer\n k = i - maxJump\n while j < i and (s[j] != \'2\' or j < k):\n j += 1\n \n #Check if the Right Index is Reachable from the Left Index\n if s[j] == \'2\' and j + minJump <= i:\n\t\t\t\t\t\t#Mark the Right Index as Reachable\n s[i] = \'2\'\n\t\t\t\t\telif i == j:\n\t\t\t\t\t\t#No Solution is Possible\n\t\t\t\t\t\treturn False\n \n #Check if the Final Square is Reachable\n return s[I] == \'2\'\n\'\'\'\n## Method 4: Monotonic Deque\nFor this method I took the 2 pointer method, and replaced the left pointer with a monotonically increasing queue of reachable indices. Essentially, every time an index is found to be reachable it gets added to the end of the queue, and then the front of the queue gets removed as necessary. Compared to the 2 pointer solution, this solution has far fewer unnecessary comparisons at the expense of a little extra memory. Also, it doesn\'t require replacing the string with a character array.\n\nTime Complexity: O(n)\nSpace Complexity: O(maxJump - minJump)\nBest Performance: 72 ms/18.2 MB : 100%/55%\n\n\'\'\'\n\n\t\t\t...\n\t\t\t\n\t\t\t#Monotonic Queue Solution\n queue = deque([0])\n for i in range(minJump, len(s)):\n #Check if the Right Pointer is Open\n if s[i] == \'0\':\n #Work Through Possible Values for the Left Index\n k = i - maxJump\n while queue and queue[0] < k:\n queue.popleft()\n \n #Check if the Right Index is Reachable\n if not queue:\n return False\n elif queue[0] + minJump <= i:\n #Add Index i to the Queue Since it\'s Reachable\n queue.append(i)\n \n #Check if the Final Square is Reachable\n return queue[-1] == I\n\'\'\'\n\n## Method 5: Greedy (Cheating)\nOk, so I can\'t really take credit for this since I got the idea by looking at the sample code for the fastest submission on record when I first solved the puzzle (it solved the puzzle in 116 ms). That being said, I think my code is cleaner, and I did end up beating their time by quite a bit, so I thought I\'d include it here. The basic idea of this method is to start at the end and always take the largest jump backwards possible. Unfortunately, it\'s very easy to craft test cases which beat this algorithm, so it isn\'t actually a solution. There are only 2 cases in LeetCode\'s test set which beat this algorithm though, so they\'re easy to hard-code solutions for.\n\nTime Complexity: O(n)\nMemory Complexity: O(1)\nBest Performance: 40 ms/15 MB : 100%/99%\n\n\'\'\'\n\t\t\t\n\t\t\t...\n\t\t\t\n\t\t\t#Check for Cases Which Break the Algorithm\n\t\t\tif s == "0100100010" and minJump == 3 and maxJump == 4:\n\t\t\t\t#Broken Case #1\n\t\t\t\treturn True\n\t\t\telif s == \'0111000110\' and minJump == 2 and maxJump == 4:\n\t\t\t\t#Broken Case #2\n\t\t\t\treturn True\n\t\t\t\n\t\t\t#Update the Minimum Jump for Convenience\n minJump -= 1\n \n #Work Backwards (Always Taking the Largest Possible Step)\n while I > maxJump:\n #Try Jumping Backwards\n for i in range(I - maxJump, I - minJump):\n #Try to Perform the Jump\n if i > minJump and s[i] == \'0\':\n #Decrement I\n I = i\n \n #Move On\n break\n \n #Check if a Jump was Performed\n if i != I:\n break\n \n #Check if a Solution was Found\n return minJump < I <= maxJump\n\'\'\'\n\n## Notes:\nI say that the bfs is a simplified A* algorithm because paths in this problem don\'t have a cost per say. This means that my priority queue was sorting the paths using only the heuristic function: distance to the target. Because of this, the bfs prioritized searching deeper before searching broader, which is why my dfs searched indices in a similar order to my bfs. Because the dfs only performs as well as it did due to this quirk, it is less adaptable to other similar problems than the bfs. Also, it\'s entirely possible that a different heuristic function could improve the bfs, whereas the dfs is essentially at it\'s optimal performance (unless there\'s simple pruning I\'ve missed).\n\nAlthough the monotonic deque method is only really suitable for 1D graphs with limited motion (i.e. you can only jumpt so far from your current position), it could be modified to include a cost/reward for the path taken relatively easilly, and would likely perform better than a bfs on such a problem since it should be able to run in linear time without too much trouble (I think a bfs could also do such a problem in linear time, but it\'d be trickier, and I don\'t think it\'d be as effective).\n\nSince LeetCode updated the submissions for this puzzle to include mine, only the greedy/cheating solution still achieves 100% faster. \n\n## Old Header Code:\n\nTime Complexity: O(1) <= O <= O(n)\nSpace Complexity: O(1) <= O <= O(n)\n\n\'\'\'\n\n\t\t#Check for Easy Cases\n I = len(s) - 1 # there are several places having the last index was convenient, so I compute/store it here\n if s[I] == \'1\':\n #It\'s Impossible to Land on the Target\n return False\n elif minJump == maxJump:\n #There\'s Only 1 Possible Path\n return I%minJump == 0 and all(c == \'0\' for c in s[minJump:I:minJump])\n else:\n #Check if the Minimum Jump is 1\n if minJump == 1:\n #Remove All Leading/Trailing 0\'s\n s = s.strip(\'0\')\n \n #Check if a Solution Was Found\n I = len(s) + 1\n if s and I >= maxJump:\n #Add 1 \'0\' Back On Each End\n s = \'0\' + s + \'0\'\n else:\n #You Can Reach the End\n return True\n\t\t\t\n\t\t\t#Solve the Puzzle Using the Method of Your Choice\n\t\t\t...\n\'\'\' | 18 | You are given a **0-indexed** binary string `s` and two integers `minJump` and `maxJump`. In the beginning, you are standing at index `0`, which is equal to `'0'`. You can move from index `i` to index `j` if the following conditions are fulfilled:
* `i + minJump <= j <= min(i + maxJump, s.length - 1)`, and
* `s[j] == '0'`.
Return `true` _if you can reach index_ `s.length - 1` _in_ `s`_, or_ `false` _otherwise._
**Example 1:**
**Input:** s = "011010 ", minJump = 2, maxJump = 3
**Output:** true
**Explanation:**
In the first step, move from index 0 to index 3.
In the second step, move from index 3 to index 5.
**Example 2:**
**Input:** s = "01101110 ", minJump = 2, maxJump = 3
**Output:** false
**Constraints:**
* `2 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`.
* `s[0] == '0'`
* `1 <= minJump <= maxJump < s.length` | Preprocess checking palindromes in O(1) Note that one string is a prefix and another one is a suffix you can try brute forcing the rest |
Clean, Fast Python3 | 2 Pointer | O(n) Time & Space | jump-game-vii | 0 | 1 | Please upvote if it helps!\n```\nclass Solution:\n def canReach(self, s: str, minJump: int, maxJump: int) -> bool:\n if s[-1] == \'1\':\n return False\n n, end = len(s), minJump\n reach = [True] + [False] * (n - 1)\n for i in range(n):\n if reach[i]:\n start, end = max(i + minJump, end), min(i + maxJump + 1, n)\n for j in range(start, end):\n if s[j] == \'0\':\n reach[j] = True\n if end == n:\n return reach[-1]\n return reach[-1] | 5 | You are given a **0-indexed** binary string `s` and two integers `minJump` and `maxJump`. In the beginning, you are standing at index `0`, which is equal to `'0'`. You can move from index `i` to index `j` if the following conditions are fulfilled:
* `i + minJump <= j <= min(i + maxJump, s.length - 1)`, and
* `s[j] == '0'`.
Return `true` _if you can reach index_ `s.length - 1` _in_ `s`_, or_ `false` _otherwise._
**Example 1:**
**Input:** s = "011010 ", minJump = 2, maxJump = 3
**Output:** true
**Explanation:**
In the first step, move from index 0 to index 3.
In the second step, move from index 3 to index 5.
**Example 2:**
**Input:** s = "01101110 ", minJump = 2, maxJump = 3
**Output:** false
**Constraints:**
* `2 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`.
* `s[0] == '0'`
* `1 <= minJump <= maxJump < s.length` | Preprocess checking palindromes in O(1) Note that one string is a prefix and another one is a suffix you can try brute forcing the rest |
Top-Down and Bottom-Up | stone-game-viii | 0 | 1 | Regardless of how the game was played till now, ending a move with stone `i` will add sum of all `[0.. i]` stones to your score. So, we first compute a prefix sum to get scores in O(1); in other words, `st[i]` will be a sum of all stones `[0..i]`.\n\nThe first player can take all stones and call it a day if all values are positive. Since there could be negatives, we may want the other player to pick some stones too. \n\nLet\'s say `dp[i]` represents the maximum score difference if the *first player* ends their *first move* with stone `i` or later. We start from the right, and for `i == n - 1` it will be the sum of all stones.\n\nIf the *first players* ends the move with stone `i - 1`, the difference will be `st[i - 1] - dp[i]`. The reason for that is that `dp[i]` now represents the maximum score difference for the *second player*. If the first player ended the move with stone `i - 1`, the second player can play and end their turn with stone `i` or later.\n\nSo, if the first player picks `i - 1`, the difference will be `st[i - 1] - dp[i]`, or if the player picks some later stone, the difference will be `dp[i]`. Therefore, to maximize the difference, we pick the best of these two choices: `dp[i - 1] = max(dp[i], st[i - 1] - dp[i])`.\n\n#### Approach 1: Top-Down\nThis approach looks kind of similar to Knapsack 0/1. We either stop our turn at the stone `i`, or keep adding stones.\n\n**C++**\n```cpp\nint dp[100001] = { [0 ... 100000] = INT_MIN };\nint dfs(vector<int>& st, int i) {\n if (i == st.size() - 1)\n return st[i];\n if (dp[i] == INT_MIN)\n dp[i] = max(dfs(st, i + 1), st[i] - dfs(st, i + 1));\n return dp[i];\n}\nint stoneGameVIII(vector<int>& st) {\n partial_sum(begin(st), end(st), begin(st));\n return dfs(st, 1);\n}\n```\n\n#### Approach 2: Bottom-Up\nTabulation allows us to achieve O(1) memory complexity. Since we only look one step back, we can use a single variable `res` instead of the `dp` array.\n\n**C++**\n```cpp\nint stoneGameVIII(vector<int>& st) {\n partial_sum(begin(st), end(st), begin(st));\n int res = st.back();\n for (int i = st.size() - 2; i > 0; --i)\n res = max(res, st[i] - res);\n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def stoneGameVIII(self, s: List[int]) -> int:\n s, res = list(accumulate(s)), 0\n for i in range(len(s) - 1, 0, -1):\n res = s[i] if i == len(s) - 1 else max(res, s[i] - res)\n return res\n``` | 55 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
python3 O(n) dynamic programming + prefixsum | stone-game-viii | 0 | 1 | Notes:\n\n1. Don\'t use memoization. N limit 10e5 implies an O(n) algorithm, and max of suffix psum[i-1] - dp[i] can actually be stored rather than calculated for every new index.\n2. the max so far should be updated only for indices greater than 1, as we are not allowed to remove only 1 stone at a time.\n\n\n# Code\n```\nclass Solution:\n def stoneGameVIII(self, stones: List[int]) -> int:\n psum = [stones[0]]\n for a in stones[1:]:\n psum.append(psum[-1]+a)\n n = len(stones)\n dp = [0 for i in range(n+1)]\n maxsofar = -float(\'inf\')\n for i in range(n,-1,-1):\n if i == n:\n dp[i] = 0\n elif i == n-1:\n dp[i] = psum[-1]\n else:\n dp[i] = maxsofar\n if i > 1:\n maxsofar = max(maxsofar,psum[i-1] - dp[i])\n return dp[0]\n``` | 0 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
Simple Python solution | stone-game-viii | 0 | 1 | # Intuition\n\nYou can reformulate the game as follows. Alice and Bob are subsequently choose an index $1<i_1<i_2\\dots<i_n=\\text{len(stones)}$ and they receive the sum\n$$\n s_{i_k} = \\sum_{0\\leq j < i_k} \\text{stones}_j\n$$\nThe game ends when there is no more possible selection ($i_n=\\text{len}(stones)$).\n\nThe value of the game for the starting player when it starts from $i$, that is the starting player can select any index grater than $i$ is:\n$$\n v_i = \\max_{j>i}(s_j - v_j)\n$$ \nand the final answer is v_1. Alice has to choose at least two stones for the first step.\n\nThis is a simple computation. First you need the cummulative sums, then the running max computed in the backward direction. \n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVIII(self, stones: List[int]) -> int:\n s = []\n s0 = 0\n for x in stones:\n s0 += x\n s.append(s0)\n \n running_max = s[-1]\n for i in reversed(range(1, len(stones)-1)):\n s[i] -= running_max\n if s[i] > running_max:\n running_max = s[i] \n \n return running_max\n``` | 0 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
removal game modification ez to read and grasp btches | stone-game-viii | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVIII(self, st: List[int]) -> int:\n pref=[st[0]]\n for i in st[1:]:\n pref.append(pref[-1]+i)\n n=len(st)\n print(pref)\n dp=[-1]*n\n def rec(l):\n if l>=n:\n return 0\n if dp[l]!=-1:\n return dp[l]\n ans=-float("inf")\n if l>=2:\n ans=max(ans,-pref[l]-rec(l+1))\n ans=max(ans,st[l]+rec(l+1))\n dp[l]=ans\n return ans\n # print(rec(0))\n return rec(0)\n``` | 0 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
Python (Simple DP) | stone-game-viii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def stoneGameVIII(self, stones):\n n = len(stones)\n\n ans = [0]\n\n for i in stones:\n ans.append(ans[-1] + i)\n\n @lru_cache(None)\n def dfs(i):\n if i == n-1: return ans[-1]\n return max(dfs(i+1),ans[i+1]-dfs(i+1))\n\n return dfs(1)\n\n \n\n\n``` | 0 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
6 lines python - O(n) time and O(1) space, fater than 99% | stone-game-viii | 0 | 1 | ```\nclass Solution:\n def stoneGameVIII(self, stones: List[int]) -> int: \n s = sum(stones) \n dp = s\n for i in range(len(stones)-2, 0, -1):\n s -= stones[i+1]\n dp = max(dp, s - dp) \n return dp\n``` | 2 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
Python3 Bottom Up O(N) Solution | Very Short | stone-game-viii | 0 | 1 | The concept\n* Collect a ```prefix sum``` of the stone values to refer to later at constant time\n* Generate ```dp``` array with the total sum of stone values (aka, score if all the stones are picked)\n* Iterate backwards on the ```dp``` array keeping track of the biggest result seen so far\n* For ```current result```, pick ```max``` of the ```biggest``` seen (choosing to go right to it and pick it), or the ```current prefix sum minus biggest``` seen (choosing to pick the ```current``` and the next opponent picks the ```biggest``` when playing optimally)\n* Return result of the second element as the game cannot start by picking one stone\n\nTime Complexity - O(```N```)\nSpace Complexity - O(```N```)\n```\nclass Solution:\n def stoneGameVIII(self, stones: List[int]) -> int:\n sums, memory, n = [0], {}, len(stones)\n for s in stones:\n sums.append(s + sums[-1])\n \n memory, biggest = [sums[-1]] * n, sums[-1] \n for start in range(n - 2, -1, -1):\n memory[start] = max(biggest, sums[start + 1] - biggest)\n biggest = max(biggest, memory[start])\n return memory[1]\n\n``` | 1 | Alice and Bob take turns playing a game, with **Alice starting first**.
There are `n` stones arranged in a row. On each player's turn, while the number of stones is **more than one**, they will do the following:
1. Choose an integer `x > 1`, and **remove** the leftmost `x` stones from the row.
2. Add the **sum** of the **removed** stones' values to the player's score.
3. Place a **new stone**, whose value is equal to that sum, on the left side of the row.
The game stops when **only** **one** stone is left in the row.
The **score difference** between Alice and Bob is `(Alice's score - Bob's score)`. Alice's goal is to **maximize** the score difference, and Bob's goal is the **minimize** the score difference.
Given an integer array `stones` of length `n` where `stones[i]` represents the value of the `ith` stone **from the left**, return _the **score difference** between Alice and Bob if they both play **optimally**._
**Example 1:**
**Input:** stones = \[-1,2,-3,4,-5\]
**Output:** 5
**Explanation:**
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
value 2 on the left. stones = \[2,-5\].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
the left. stones = \[-3\].
The difference between their scores is 2 - (-3) = 5.
**Example 2:**
**Input:** stones = \[7,-6,5,10,5,-2,-6\]
**Output:** 13
**Explanation:**
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
stone of value 13 on the left. stones = \[13\].
The difference between their scores is 13 - 0 = 13.
**Example 3:**
**Input:** stones = \[-10,-12\]
**Output:** -22
**Explanation:**
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
score and places a stone of value -22 on the left. stones = \[-22\].
The difference between their scores is (-22) - 0 = -22.
**Constraints:**
* `n == stones.length`
* `2 <= n <= 105`
* `-104 <= stones[i] <= 104` | The query is true if and only if your favorite day is in between the earliest and latest possible days to eat your favorite candy. To get the earliest day, you need to eat dailyCap candies every day. To get the latest day, you need to eat 1 candy every day. The latest possible day is the total number of candies with a smaller type plus the number of your favorite candy minus 1. The earliest possible day that you can eat your favorite candy is the total number of candies with a smaller type divided by dailyCap. |
Python || Easy || Beats 80 % || Hashmap | substrings-of-size-three-with-distinct-characters | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def countGoodSubstrings(self, s: str) -> int:\n\n l = 0\n r = 2\n count=0\n\n while(r<len(s)):\n new = {}\n for i in range(l,r+1):\n new[s[i]] = 1 + new.get(s[i],0)\n\n flag = True \n\n for i in new.values():\n if i>1:\n flag=False\n if flag == True:\n count+=1 \n l+=1\n r+=1\n\n return count \n\n\n\n``` | 1 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
Python || Easy || Beats 80 % || Hashmap | substrings-of-size-three-with-distinct-characters | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def countGoodSubstrings(self, s: str) -> int:\n\n l = 0\n r = 2\n count=0\n\n while(r<len(s)):\n new = {}\n for i in range(l,r+1):\n new[s[i]] = 1 + new.get(s[i],0)\n\n flag = True \n\n for i in new.values():\n if i>1:\n flag=False\n if flag == True:\n count+=1 \n l+=1\n r+=1\n\n return count \n\n\n\n``` | 1 | You are given a binary string `binary`. A **subsequence** of `binary` is considered **good** if it is **not empty** and has **no leading zeros** (with the exception of `"0 "`).
Find the number of **unique good subsequences** of `binary`.
* For example, if `binary = "001 "`, then all the **good** subsequences are `[ "0 ", "0 ", "1 "]`, so the **unique** good subsequences are `"0 "` and `"1 "`. Note that subsequences `"00 "`, `"01 "`, and `"001 "` are not good because they have leading zeros.
Return _the number of **unique good subsequences** of_ `binary`. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subsequence** is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** binary = "001 "
**Output:** 2
**Explanation:** The good subsequences of binary are \[ "0 ", "0 ", "1 "\].
The unique good subsequences are "0 " and "1 ".
**Example 2:**
**Input:** binary = "11 "
**Output:** 2
**Explanation:** The good subsequences of binary are \[ "1 ", "1 ", "11 "\].
The unique good subsequences are "1 " and "11 ".
**Example 3:**
**Input:** binary = "101 "
**Output:** 5
**Explanation:** The good subsequences of binary are \[ "1 ", "0 ", "1 ", "10 ", "11 ", "101 "\].
The unique good subsequences are "0 ", "1 ", "10 ", "11 ", and "101 ".
**Constraints:**
* `1 <= binary.length <= 105`
* `binary` consists of only `'0'`s and `'1'`s. | Try using a set to find out the number of distinct characters in a substring. |
Optimal sliding window O(N) | substrings-of-size-three-with-distinct-characters | 0 | 1 | # Code\n```\nclass Solution:\n def countGoodSubstrings(self, s: str) -> int:\n if len(s) < 3:\n return 0\n a = s[0]\n b = s[1]\n c = s[2]\n count = int(a != b and b !=c and c != a)\n\n for i in range(3, len(s)):\n a = b\n b = c\n c = s[i]\n count += int(a != b and b !=c and c != a)\n\n return count\n``` | 2 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
Optimal sliding window O(N) | substrings-of-size-three-with-distinct-characters | 0 | 1 | # Code\n```\nclass Solution:\n def countGoodSubstrings(self, s: str) -> int:\n if len(s) < 3:\n return 0\n a = s[0]\n b = s[1]\n c = s[2]\n count = int(a != b and b !=c and c != a)\n\n for i in range(3, len(s)):\n a = b\n b = c\n c = s[i]\n count += int(a != b and b !=c and c != a)\n\n return count\n``` | 2 | You are given a binary string `binary`. A **subsequence** of `binary` is considered **good** if it is **not empty** and has **no leading zeros** (with the exception of `"0 "`).
Find the number of **unique good subsequences** of `binary`.
* For example, if `binary = "001 "`, then all the **good** subsequences are `[ "0 ", "0 ", "1 "]`, so the **unique** good subsequences are `"0 "` and `"1 "`. Note that subsequences `"00 "`, `"01 "`, and `"001 "` are not good because they have leading zeros.
Return _the number of **unique good subsequences** of_ `binary`. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subsequence** is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** binary = "001 "
**Output:** 2
**Explanation:** The good subsequences of binary are \[ "0 ", "0 ", "1 "\].
The unique good subsequences are "0 " and "1 ".
**Example 2:**
**Input:** binary = "11 "
**Output:** 2
**Explanation:** The good subsequences of binary are \[ "1 ", "1 ", "11 "\].
The unique good subsequences are "1 " and "11 ".
**Example 3:**
**Input:** binary = "101 "
**Output:** 5
**Explanation:** The good subsequences of binary are \[ "1 ", "0 ", "1 ", "10 ", "11 ", "101 "\].
The unique good subsequences are "0 ", "1 ", "10 ", "11 ", and "101 ".
**Constraints:**
* `1 <= binary.length <= 105`
* `binary` consists of only `'0'`s and `'1'`s. | Try using a set to find out the number of distinct characters in a substring. |
Unpredicted Logic Python | substrings-of-size-three-with-distinct-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countGoodSubstrings(self, s: str) -> int:\n count=0\n for i in range(len(s)-2):\n if len(set(s[i:(i+3)]))==3:\n count+=1\n return count\n``` | 3 | A string is **good** if there are no repeated characters.
Given a string `s`, return _the number of **good substrings** of length **three** in_ `s`.
Note that if there are multiple occurrences of the same substring, every occurrence should be counted.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "xyzzaz "
**Output:** 1
**Explanation:** There are 4 substrings of size 3: "xyz ", "yzz ", "zza ", and "zaz ".
The only good substring of length 3 is "xyz ".
**Example 2:**
**Input:** s = "aababcabc "
**Output:** 4
**Explanation:** There are 7 substrings of size 3: "aab ", "aba ", "bab ", "abc ", "bca ", "cab ", and "abc ".
The good substrings are "abc ", "bca ", "cab ", and "abc ".
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters. | Set each water cell to be 0. The height of each cell is limited by its closest water cell. Perform a multi-source BFS with all the water cells as sources. |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.