title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution in Python 3 (With Detailed Proof) | divisor-game | 0 | 1 | The proof of why this works can be done formally using Mathematical Induction, specifically using <a href="https://en.wikipedia.org/wiki/Mathematical_induction#Complete_(strong)_induction">Strong Mathematical Induction</a>. However an informal proof will also suffice. Note that it is not enough to show that a player who starts on even always wins. One must also show that a player that starts on odd always loses. Otherwise there are more possible ways to guarantee winning aside from starting on even.\n\n**Given:** The Divisor Game as outlined in the problem\n\n**Prove:** Alice will win if and only if N % 2 == 0\n\n_Part 1)_ If Alice starts with an even number she will always win.\n\nIf Alice has an even number, she can always subtract 1, giving Bob an odd number. Odd numbers are not divisible by 2. They are only divisible by odd numbers. Hence Bob must subtract an odd number. Since odd minus odd is even, Bob will always return an even number to Alice. Alice will thus get a smaller even number after each round of play and Bob will get a smaller odd number after each round of play. Eventually Bob will have to play the number 1 and will lose the game since he will have no options.\n\n_Part 2)_ If Alice starts with an odd number she will always lose.\n\nIf Alice has an odd number, she has no choice but to subtract an odd number as odd numbers have no even divisors. Thus Bob will get an even number. Now using the argument from _Part 1_ above, Bob can take this even number and keep giving an odd number back to Alice by subtracting 1. Thus Bob will always get to play even and Alice will always be stuck with an odd number smaller than her previous odd number after each round. Eventually Alice will have to play the number 1 and will lose the game since she will have no options.\n\nThus, assuming both players play optimally, Alice will win the game if and only if she starts on an even number (i.e. N % 2 == 0).\n```\nclass Solution:\n def divisorGame(self, N: int) -> bool:\n return N % 2 == 0\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com | 177 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
Python Easy 1-liner | Faster than 80% | divisor-game | 0 | 1 | Simple. Alice wins on even numbers. Bob wins otherwise\n\n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return not n % 2\n``` | 2 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number `n` on the chalkboard. On each player's turn, that player makes a move consisting of:
* Choosing any `x` with `0 < x < n` and `n % x == 0`.
* Replacing the number `n` on the chalkboard with `n - x`.
Also, if a player cannot make a move, they lose the game.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** n = 2
**Output:** true
**Explanation:** Alice chooses 1, and Bob has no more moves.
**Example 2:**
**Input:** n = 3
**Output:** false
**Explanation:** Alice chooses 1, Bob chooses 1, and Alice has no more moves.
**Constraints:**
* `1 <= n <= 1000` | null |
Python Easy 1-liner | Faster than 80% | divisor-game | 0 | 1 | Simple. Alice wins on even numbers. Bob wins otherwise\n\n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return not n % 2\n``` | 2 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
1 liner python solution | divisor-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return n%2==0\n``` | 5 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number `n` on the chalkboard. On each player's turn, that player makes a move consisting of:
* Choosing any `x` with `0 < x < n` and `n % x == 0`.
* Replacing the number `n` on the chalkboard with `n - x`.
Also, if a player cannot make a move, they lose the game.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** n = 2
**Output:** true
**Explanation:** Alice chooses 1, and Bob has no more moves.
**Example 2:**
**Input:** n = 3
**Output:** false
**Explanation:** Alice chooses 1, Bob chooses 1, and Alice has no more moves.
**Constraints:**
* `1 <= n <= 1000` | null |
1 liner python solution | divisor-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return n%2==0\n``` | 5 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
Python One Liner | divisor-game | 0 | 1 | Yea...\n\n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return True if n%2 == 0 else False\n``` | 1 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number `n` on the chalkboard. On each player's turn, that player makes a move consisting of:
* Choosing any `x` with `0 < x < n` and `n % x == 0`.
* Replacing the number `n` on the chalkboard with `n - x`.
Also, if a player cannot make a move, they lose the game.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** n = 2
**Output:** true
**Explanation:** Alice chooses 1, and Bob has no more moves.
**Example 2:**
**Input:** n = 3
**Output:** false
**Explanation:** Alice chooses 1, Bob chooses 1, and Alice has no more moves.
**Constraints:**
* `1 <= n <= 1000` | null |
Python One Liner | divisor-game | 0 | 1 | Yea...\n\n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return True if n%2 == 0 else False\n``` | 1 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
📚Divisor game || 🫱🏻🫲🏼Beginners friendly || 🐍Python... | divisor-game | 0 | 1 | # KARRAR\n>Divisor game...\n>>Brainteaser...\n>>>Game theory...\n>>>>Optimized code...\n>>>>>Beginners friendly...\n- PLEASE UPVOTE...\uD83D\uDC4D\uD83C\uDFFB\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach:\n Notice that if we subtract 1 from n...\n Answer will be true if result is odd...\n And false if it\'s even...\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Beats 85% (37 ms)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Beats 24% (16 MB)\n\n\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return True if (n-1)%2==1 else False\n``` | 1 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number `n` on the chalkboard. On each player's turn, that player makes a move consisting of:
* Choosing any `x` with `0 < x < n` and `n % x == 0`.
* Replacing the number `n` on the chalkboard with `n - x`.
Also, if a player cannot make a move, they lose the game.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** n = 2
**Output:** true
**Explanation:** Alice chooses 1, and Bob has no more moves.
**Example 2:**
**Input:** n = 3
**Output:** false
**Explanation:** Alice chooses 1, Bob chooses 1, and Alice has no more moves.
**Constraints:**
* `1 <= n <= 1000` | null |
📚Divisor game || 🫱🏻🫲🏼Beginners friendly || 🐍Python... | divisor-game | 0 | 1 | # KARRAR\n>Divisor game...\n>>Brainteaser...\n>>>Game theory...\n>>>>Optimized code...\n>>>>>Beginners friendly...\n- PLEASE UPVOTE...\uD83D\uDC4D\uD83C\uDFFB\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach:\n Notice that if we subtract 1 from n...\n Answer will be true if result is odd...\n And false if it\'s even...\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Beats 85% (37 ms)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Beats 24% (16 MB)\n\n\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def divisorGame(self, n: int) -> bool:\n return True if (n-1)%2==1 else False\n``` | 1 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
[Python] DP | divisor-game | 0 | 1 | ```python\nclass Solution:\n def divisorGame(self, N: int) -> bool:\n dp = [False for i in range(N+1)]\n for i in range(N+1):\n for j in range(1, i//2 + 1):\n if i % j == 0 and (not dp[i - j]):\n dp[i] = True\n break\n return dp[N]\n``` | 55 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number `n` on the chalkboard. On each player's turn, that player makes a move consisting of:
* Choosing any `x` with `0 < x < n` and `n % x == 0`.
* Replacing the number `n` on the chalkboard with `n - x`.
Also, if a player cannot make a move, they lose the game.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** n = 2
**Output:** true
**Explanation:** Alice chooses 1, and Bob has no more moves.
**Example 2:**
**Input:** n = 3
**Output:** false
**Explanation:** Alice chooses 1, Bob chooses 1, and Alice has no more moves.
**Constraints:**
* `1 <= n <= 1000` | null |
[Python] DP | divisor-game | 0 | 1 | ```python\nclass Solution:\n def divisorGame(self, N: int) -> bool:\n dp = [False for i in range(N+1)]\n for i in range(N+1):\n for j in range(1, i//2 + 1):\n if i % j == 0 and (not dp[i - j]):\n dp[i] = True\n break\n return dp[N]\n``` | 55 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
Python3 - One liner, explained maths | divisor-game | 0 | 1 | This is a very nice math problem.\n\nA move is defined as choosing ```x```, a divisor of ```N``` which is lesser than ```N```, and replacing the number with ```N - x```. Since ```x``` is a divisor of ```N```, there exists some positive integer ```d``` such that```N = x*d```.\nNow, the new number will be of the form ```N - x = x*d - x = x * (d-1)```.\n\nNote that if ```N``` is odd, then all of its divisors are odd, therefore ```x``` is odd. So ```N - x``` (the new number) will be even.\nIf ```N``` is even (of the form ```2 * k```), we can choose ```1``` and the new number will be ```N - 1``` (odd nubmer) or we can choose ```2``` (if ```N > 2```) and the new nubmer will be ```2 * k - 2``` (even nubmer).\n\nA player loses when he or she cannot make a move anymore.\nWhen ```N > 1```, the player can always choose ```1``` (which satisfies the requirement), so the player cannot lose. \nWhen ```N = 1```, the player cannot choose any ```x``` strictly between ```0``` and ```1```, so the player will lose.\nIt is easy to see that ```N``` cannot be less than or equal to ```0```.\n\nFrom this, we deduce that the winning strategy will be to **make sure your opponent has ```1``` written on the chalkboard**. In other words, the winning strategy is to **always keep your number even**. This way, you can always write an odd number on the chalkboard so your opponent will have two situations:\n-> the new number is ```1``` and he or she will lose the game;\n-> write a new even number.\n\nIf both players play optimally, Alice will win iff ```N``` is even.\n\n```\nclass Solution:\n def divisorGame(self, N: int) -> bool:\n return N % 2 == 0\n``` | 24 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number `n` on the chalkboard. On each player's turn, that player makes a move consisting of:
* Choosing any `x` with `0 < x < n` and `n % x == 0`.
* Replacing the number `n` on the chalkboard with `n - x`.
Also, if a player cannot make a move, they lose the game.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** n = 2
**Output:** true
**Explanation:** Alice chooses 1, and Bob has no more moves.
**Example 2:**
**Input:** n = 3
**Output:** false
**Explanation:** Alice chooses 1, Bob chooses 1, and Alice has no more moves.
**Constraints:**
* `1 <= n <= 1000` | null |
Python3 - One liner, explained maths | divisor-game | 0 | 1 | This is a very nice math problem.\n\nA move is defined as choosing ```x```, a divisor of ```N``` which is lesser than ```N```, and replacing the number with ```N - x```. Since ```x``` is a divisor of ```N```, there exists some positive integer ```d``` such that```N = x*d```.\nNow, the new number will be of the form ```N - x = x*d - x = x * (d-1)```.\n\nNote that if ```N``` is odd, then all of its divisors are odd, therefore ```x``` is odd. So ```N - x``` (the new number) will be even.\nIf ```N``` is even (of the form ```2 * k```), we can choose ```1``` and the new number will be ```N - 1``` (odd nubmer) or we can choose ```2``` (if ```N > 2```) and the new nubmer will be ```2 * k - 2``` (even nubmer).\n\nA player loses when he or she cannot make a move anymore.\nWhen ```N > 1```, the player can always choose ```1``` (which satisfies the requirement), so the player cannot lose. \nWhen ```N = 1```, the player cannot choose any ```x``` strictly between ```0``` and ```1```, so the player will lose.\nIt is easy to see that ```N``` cannot be less than or equal to ```0```.\n\nFrom this, we deduce that the winning strategy will be to **make sure your opponent has ```1``` written on the chalkboard**. In other words, the winning strategy is to **always keep your number even**. This way, you can always write an odd number on the chalkboard so your opponent will have two situations:\n-> the new number is ```1``` and he or she will lose the game;\n-> write a new even number.\n\nIf both players play optimally, Alice will win iff ```N``` is even.\n\n```\nclass Solution:\n def divisorGame(self, N: int) -> bool:\n return N % 2 == 0\n``` | 24 | Given a list of the scores of different students, `items`, where `items[i] = [IDi, scorei]` represents one score from a student with `IDi`, calculate each student's **top five average**.
Return _the answer as an array of pairs_ `result`_, where_ `result[j] = [IDj, topFiveAveragej]` _represents the student with_ `IDj` _and their **top five average**. Sort_ `result` _by_ `IDj` _in **increasing order**._
A student's **top five average** is calculated by taking the sum of their top five scores and dividing it by `5` using **integer division**.
**Example 1:**
**Input:** items = \[\[1,91\],\[1,92\],\[2,93\],\[2,97\],\[1,60\],\[2,77\],\[1,65\],\[1,87\],\[1,100\],\[2,100\],\[2,76\]\]
**Output:** \[\[1,87\],\[2,88\]\]
**Explanation:**
The student with ID = 1 got scores 91, 92, 60, 65, 87, and 100. Their top five average is (100 + 92 + 91 + 87 + 65) / 5 = 87.
The student with ID = 2 got scores 93, 97, 77, 100, and 76. Their top five average is (100 + 97 + 93 + 77 + 76) / 5 = 88.6, but with integer division their average converts to 88.
**Example 2:**
**Input:** items = \[\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\],\[1,100\],\[7,100\]\]
**Output:** \[\[1,100\],\[7,100\]\]
**Constraints:**
* `1 <= items.length <= 1000`
* `items[i].length == 2`
* `1 <= IDi <= 1000`
* `0 <= scorei <= 100`
* For each `IDi`, there will be **at least** five scores. | If the current number is even, we can always subtract a 1 to make it odd. If the current number is odd, we must subtract an odd number to make it even. |
recursive approach | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\ndef fun(root,mx,mn,ans):\n if(root==None):\n return\n d1=abs(root.val-mx)\n d2=abs(root.val-mn)\n ans[0]=max(d1,d2,ans[0])\n mx=max(mx,root.val)\n mn=min(mn,root.val)\n fun(root.left,mx,mn,ans)\n fun(root.right,mx,mn,ans)\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n ans=[0]\n if(root==None):\n return 0\n fun(root,root.val,root.val,ans)\n return ans[0]\n``` | 3 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
recursive approach | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\ndef fun(root,mx,mn,ans):\n if(root==None):\n return\n d1=abs(root.val-mx)\n d2=abs(root.val-mn)\n ans[0]=max(d1,d2,ans[0])\n mx=max(mx,root.val)\n mn=min(mn,root.val)\n fun(root.left,mx,mn,ans)\n fun(root.right,mx,mn,ans)\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n ans=[0]\n if(root==None):\n return 0\n fun(root,root.val,root.val,ans)\n return ans[0]\n``` | 3 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Python DFS Iterative Solution | maximum-difference-between-node-and-ancestor | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n mini, maxi = root.val, root.val\n ans = 0\n st = [(root, mini, maxi)]\n while st:\n node, a, b = st.pop()\n if node.right:\n mini = min(node.right.val, node.val, a)\n maxi = max(node.right.val, node.val, b)\n ans = max(ans, maxi-mini)\n st.append((node.right,mini , maxi))\n if node.left:\n mini = min(node.left.val, node.val, a)\n maxi = max(node.left.val, node.val, b)\n ans = max(ans, maxi-mini)\n st.append((node.left,mini , maxi))\n return ans\n\n\n``` | 2 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
Python DFS Iterative Solution | maximum-difference-between-node-and-ancestor | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n mini, maxi = root.val, root.val\n ans = 0\n st = [(root, mini, maxi)]\n while st:\n node, a, b = st.pop()\n if node.right:\n mini = min(node.right.val, node.val, a)\n maxi = max(node.right.val, node.val, b)\n ans = max(ans, maxi-mini)\n st.append((node.right,mini , maxi))\n if node.left:\n mini = min(node.left.val, node.val, a)\n maxi = max(node.left.val, node.val, b)\n ans = max(ans, maxi-mini)\n st.append((node.left,mini , maxi))\n return ans\n\n\n``` | 2 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Python | DFS | O(N) | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition\nDFS walk through the binary tree. Save the max value and min value on the path. \n\n# Approach\nImplement a DFS helper function, with ancestor holds the max and min value so far. Recursive terminated at the leaves.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n # ancestor holds [max_val_in_path, min_val_in_path]\n def helper(root, ancestor):\n if not root.left and not root.right:\n # a leaf\n max_ = max(ancestor[0], root.val)\n min_ = min(ancestor[1], root.val)\n return abs(max_ - min_)\n \n left_val, right_val = 0, 0\n prev_max, prev_min = ancestor \n if root.left:\n ancestor[0] = max(ancestor[0], root.val)\n ancestor[1] = min(ancestor[1], root.val)\n left_val = helper(root.left, ancestor)\n ancestor[0], ancestor[1] = prev_max, prev_min\n \n if root.right:\n ancestor[0] = max(ancestor[0], root.val)\n ancestor[1] = min(ancestor[1], root.val)\n right_val = helper(root.right, ancestor)\n ancestor[0], ancestor[1] = prev_max, prev_min\n \n return max(left_val, right_val)\n \n return helper(root, [float("-inf"), float("inf")])\n \n\n\n``` | 1 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
Python | DFS | O(N) | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition\nDFS walk through the binary tree. Save the max value and min value on the path. \n\n# Approach\nImplement a DFS helper function, with ancestor holds the max and min value so far. Recursive terminated at the leaves.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n # ancestor holds [max_val_in_path, min_val_in_path]\n def helper(root, ancestor):\n if not root.left and not root.right:\n # a leaf\n max_ = max(ancestor[0], root.val)\n min_ = min(ancestor[1], root.val)\n return abs(max_ - min_)\n \n left_val, right_val = 0, 0\n prev_max, prev_min = ancestor \n if root.left:\n ancestor[0] = max(ancestor[0], root.val)\n ancestor[1] = min(ancestor[1], root.val)\n left_val = helper(root.left, ancestor)\n ancestor[0], ancestor[1] = prev_max, prev_min\n \n if root.right:\n ancestor[0] = max(ancestor[0], root.val)\n ancestor[1] = min(ancestor[1], root.val)\n right_val = helper(root.right, ancestor)\n ancestor[0], ancestor[1] = prev_max, prev_min\n \n return max(left_val, right_val)\n \n return helper(root, [float("-inf"), float("inf")])\n \n\n\n``` | 1 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Short and easy to understand solution with explanation. TC - O(N) and SC - O(1) | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThis problem can be solved with 2 approaches and with different Time Complexity.\n\n**1st Approach (Naive Solution):-**\nWe can iterate over every node one by one and we will create another function which will traverse its subtree (children nodes).\n\nUsing that, at every point, we can find the absolute value and store the maximum value at every node. \nSimilarly, we can do this for each and every node.\n\nTime Complexity - O(N * N), where N is the no. of nodes in the tree\nSpace Complexity - O(1)\n\n**2nd Approach (Optimal Solution):-**\nWe can iterate over every node and simultaneously we can keep three variables:-\n1. ans - maximum difference ie ans\n2. maxVal - maximum value till now in the current tree wrt its children and ancestor\n3. minVal - minimum value till now in the current tree wrt its children and ancestor\n\nThen we can traverse the tree, and for that, we can create a DFS helper function and in that, we can pass our root and 3 variables as parameters. \n\nIn the DFS function, we can always keep a check of max absolute difference achieved till now, max value in that subtree and min value in that subtree.\n\nThen we can keep on updating those values at every call and in the end just return.\n\nIn the main function, after the completion of the helper function we have got the maximum difference, just return it. \n\n\n# Complexity\n- Time complexity: O(N), where N is the no. of nodes in the tree\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n\n ans = [float("-inf")]\n self.FindMax(root, ans, root.val, root.val)\n return ans[0]\n\n def FindMax(self, root, ans, maxVal, minVal):\n\n if(root is None):\n return \n \n maxVal = max(maxVal, root.val)\n minVal = min(minVal, root.val) \n ans[0] = max(ans[0], abs(maxVal - minVal))\n\n self.FindMax(root.left, ans, maxVal, minVal)\n self.FindMax(root.right, ans, maxVal, minVal)\n return\n``` | 1 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
Short and easy to understand solution with explanation. TC - O(N) and SC - O(1) | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThis problem can be solved with 2 approaches and with different Time Complexity.\n\n**1st Approach (Naive Solution):-**\nWe can iterate over every node one by one and we will create another function which will traverse its subtree (children nodes).\n\nUsing that, at every point, we can find the absolute value and store the maximum value at every node. \nSimilarly, we can do this for each and every node.\n\nTime Complexity - O(N * N), where N is the no. of nodes in the tree\nSpace Complexity - O(1)\n\n**2nd Approach (Optimal Solution):-**\nWe can iterate over every node and simultaneously we can keep three variables:-\n1. ans - maximum difference ie ans\n2. maxVal - maximum value till now in the current tree wrt its children and ancestor\n3. minVal - minimum value till now in the current tree wrt its children and ancestor\n\nThen we can traverse the tree, and for that, we can create a DFS helper function and in that, we can pass our root and 3 variables as parameters. \n\nIn the DFS function, we can always keep a check of max absolute difference achieved till now, max value in that subtree and min value in that subtree.\n\nThen we can keep on updating those values at every call and in the end just return.\n\nIn the main function, after the completion of the helper function we have got the maximum difference, just return it. \n\n\n# Complexity\n- Time complexity: O(N), where N is the no. of nodes in the tree\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n\n ans = [float("-inf")]\n self.FindMax(root, ans, root.val, root.val)\n return ans[0]\n\n def FindMax(self, root, ans, maxVal, minVal):\n\n if(root is None):\n return \n \n maxVal = max(maxVal, root.val)\n minVal = min(minVal, root.val) \n ans[0] = max(ans[0], abs(maxVal - minVal))\n\n self.FindMax(root.left, ans, maxVal, minVal)\n self.FindMax(root.right, ans, maxVal, minVal)\n return\n``` | 1 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Python DFS Simple Solution | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition\nUsing DFS, we find the min and max values and their absolute difference in all the paths from root to leaf nodes.\n\n# Approach\nSolved using DFS Traversal of the Binary Tree.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n self.ans = 0\n\n def dfs(node, mn, mx):\n mx = max(mx, node.val)\n mn = min(mn, node.val)\n self.ans = max( self.ans , abs( mx - mn ) )\n if node.left:\n dfs(node.left, mn, mx)\n if node.right:\n dfs(node.right, mn, mx)\n \n dfs(root, root.val, root.val)\n\n return self.ans\n``` | 1 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
Python DFS Simple Solution | maximum-difference-between-node-and-ancestor | 0 | 1 | # Intuition\nUsing DFS, we find the min and max values and their absolute difference in all the paths from root to leaf nodes.\n\n# Approach\nSolved using DFS Traversal of the Binary Tree.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n self.ans = 0\n\n def dfs(node, mn, mx):\n mx = max(mx, node.val)\n mn = min(mn, node.val)\n self.ans = max( self.ans , abs( mx - mn ) )\n if node.left:\n dfs(node.left, mn, mx)\n if node.right:\n dfs(node.right, mn, mx)\n \n dfs(root, root.val, root.val)\n\n return self.ans\n``` | 1 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Python DFS approach | maximum-difference-between-node-and-ancestor | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n def dfs(root,mini,maxi,res):\n if not root:\n return\n res[0]=max(res[0],abs(mini-root.val),abs(maxi-root.val))\n mini = min(root.val, mini)\n maxi = max(root.val, maxi)\n dfs(root.left,mini,maxi,res)\n dfs(root.right,mini,maxi,res)\n res=[0]\n dfs(root, root.val, root.val, res)\n return res[0]\n``` | 1 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
Python DFS approach | maximum-difference-between-node-and-ancestor | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n def dfs(root,mini,maxi,res):\n if not root:\n return\n res[0]=max(res[0],abs(mini-root.val),abs(maxi-root.val))\n mini = min(root.val, mini)\n maxi = max(root.val, maxi)\n dfs(root.left,mini,maxi,res)\n dfs(root.right,mini,maxi,res)\n res=[0]\n dfs(root, root.val, root.val, res)\n return res[0]\n``` | 1 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Java/Python easy solution using max and min | Backtracking | maximum-difference-between-node-and-ancestor | 1 | 1 | # Please upvote if you find this helpful.\n```java []\nclass Solution {\n public int maxAncestorDiff(TreeNode root) {\n return dfs(root, root.val, root.val);\n }\n\n public int dfs(TreeNode node, int currmax, int currmin) {\n if (node == null) {\n return currmax - currmin;\n }\n currmax = Math.max(currmax, node.val);\n currmin = Math.min(currmin, node.val);\n int left = dfs(node.left, currmax, currmin);\n int right = dfs(node.right, currmax, currmin);\n return Math.max(left, right);\n }\n}\n```\n```python3 []\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n def dfs(node, currmax, currmin):\n if not node:\n return currmax - currmin\n\n currmax = max(currmax, node.val)\n currmin = min(currmin, node.val)\n left = dfs(node.left, currmax, currmin)\n right = dfs(node.right, currmax, currmin)\n return max(left, right)\n\n return dfs(root, root.val, root.val)\n``` | 1 | Given the `root` of a binary tree, find the maximum value `v` for which there exist **different** nodes `a` and `b` where `v = |a.val - b.val|` and `a` is an ancestor of `b`.
A node `a` is an ancestor of `b` if either: any child of `a` is equal to `b` or any child of `a` is an ancestor of `b`.
**Example 1:**
**Input:** root = \[8,3,10,1,6,null,14,null,null,4,7,13\]
**Output:** 7
**Explanation:** We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
**Example 2:**
**Input:** root = \[1,null,2,null,0,3\]
**Output:** 3
**Constraints:**
* The number of nodes in the tree is in the range `[2, 5000]`.
* `0 <= Node.val <= 105` | null |
Java/Python easy solution using max and min | Backtracking | maximum-difference-between-node-and-ancestor | 1 | 1 | # Please upvote if you find this helpful.\n```java []\nclass Solution {\n public int maxAncestorDiff(TreeNode root) {\n return dfs(root, root.val, root.val);\n }\n\n public int dfs(TreeNode node, int currmax, int currmin) {\n if (node == null) {\n return currmax - currmin;\n }\n currmax = Math.max(currmax, node.val);\n currmin = Math.min(currmin, node.val);\n int left = dfs(node.left, currmax, currmin);\n int right = dfs(node.right, currmax, currmin);\n return Math.max(left, right);\n }\n}\n```\n```python3 []\nclass Solution:\n def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:\n def dfs(node, currmax, currmin):\n if not node:\n return currmax - currmin\n\n currmax = max(currmax, node.val)\n currmin = min(currmin, node.val)\n left = dfs(node.left, currmax, currmin)\n right = dfs(node.right, currmax, currmin)\n return max(left, right)\n\n return dfs(root, root.val, root.val)\n``` | 1 | Given two strings `str1` and `str2`, return _the shortest string that has both_ `str1` _and_ `str2` _as **subsequences**_. If there are multiple valid strings, return **any** of them.
A string `s` is a **subsequence** of string `t` if deleting some number of characters from `t` (possibly `0`) results in the string `s`.
**Example 1:**
**Input:** str1 = "abac ", str2 = "cab "
**Output:** "cabac "
**Explanation:**
str1 = "abac " is a subsequence of "cabac " because we can delete the first "c ".
str2 = "cab " is a subsequence of "cabac " because we can delete the last "ac ".
The answer provided is the shortest such string that satisfies these properties.
**Example 2:**
**Input:** str1 = "aaaaaaaa ", str2 = "aaaaaaaa "
**Output:** "aaaaaaaa "
**Constraints:**
* `1 <= str1.length, str2.length <= 1000`
* `str1` and `str2` consist of lowercase English letters. | For each subtree, find the minimum value and maximum value of its descendants. |
Simple DP in Python. | longest-arithmetic-subsequence | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n dp = defaultdict(dict)\n n = len(nums)\n ans = 1\n\n for i in range(n):\n for j in range(i):\n diff = nums[i] - nums[j]\n if diff not in dp[j]:\n dp[j][diff] = 1\n if diff not in dp[i]:\n dp[i][diff] = 0\n dp[i][diff] = dp[j][diff] + 1\n \n ans = max(ans, dp[i][diff])\n \n return ans\n``` | 3 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
Simple DP in Python. | longest-arithmetic-subsequence | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n dp = defaultdict(dict)\n n = len(nums)\n ans = 1\n\n for i in range(n):\n for j in range(i):\n diff = nums[i] - nums[j]\n if diff not in dp[j]:\n dp[j][diff] = 1\n if diff not in dp[i]:\n dp[i][diff] = 0\n dp[i][diff] = dp[j][diff] + 1\n \n ans = max(ans, dp[i][diff])\n \n return ans\n``` | 3 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
Python3 Solution | longest-arithmetic-subsequence | 0 | 1 | \n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n n=len(nums)\n dp=[{} for _ in range(n)]\n ans=0\n for i in range(n):\n dp[i][0]=1\n for j in range(i):\n diff=nums[i]-nums[j]\n\n if diff not in dp[j]:\n dp[i][diff]=2\n\n else:\n dp[i][diff]=dp[j][diff]+1\n\n ans=max(ans,max(dp[i].values()))\n\n return ans \n``` | 2 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
Python3 Solution | longest-arithmetic-subsequence | 0 | 1 | \n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n n=len(nums)\n dp=[{} for _ in range(n)]\n ans=0\n for i in range(n):\n dp[i][0]=1\n for j in range(i):\n diff=nums[i]-nums[j]\n\n if diff not in dp[j]:\n dp[i][diff]=2\n\n else:\n dp[i][diff]=dp[j][diff]+1\n\n ans=max(ans,max(dp[i].values()))\n\n return ans \n``` | 2 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
✅Beats 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | longest-arithmetic-subsequence | 1 | 1 | # Intuition\nThe intuition behind this solution is to use dynamic programming to find the length of the longest arithmetic subsequence in the given array. We iterate through each pair of indices (i, j), where i > j, and check if we can extend the arithmetic subsequence ending at index i by including the element at index j. We update the dynamic programming values based on the common difference between the elements at indices i and j. By keeping track of the maximum length encountered, we can find the length of the longest arithmetic subsequence in the array.\n\n# Approach:\n- If `n` is less than or equal to 2, we can immediately return `n` as the answer since any two elements form a valid arithmetic subsequence.\n- We initialize the variable `longest` to 2, as explained earlier, the minimum length of an arithmetic subsequence is 2.\n- We create a 2D vector `dp` of size `n`, where each element is an unordered map. The purpose of `dp` is to store the dynamic programming values for the lengths of the arithmetic subsequences ending at each index with different common differences.\n- We iterate through each index `i` in the range `[0, n-1]`. This represents the current ending index of the arithmetic subsequences we are considering.\n- For each `i`, we iterate through all previous indices `j` in the range `[0, i-1]`. This allows us to check all the potential elements that can form an arithmetic subsequence with the element at index `i`.\n- We calculate the difference between the elements at indices `i` and `j` and store it in the variable `diff`. This difference represents the common difference of the potential arithmetic subsequence.\n- Next, we update `dp[i][diff]` based on whether we have seen a previous arithmetic subsequence ending at index `j` with a common difference of `diff`.\n - If `dp[j].count(diff)` returns true, it means we have encountered an arithmetic subsequence ending at index `j` with the common difference `diff`. In this case, we update `dp[i][diff]` to be `dp[j][diff] + 1`, which extends the subsequence and increments its length by 1.\n - If `dp[j].count(diff)` returns false, it means we haven\'t seen an arithmetic subsequence ending at index `j` with the common difference `diff`. In this case, we initialize `dp[i][diff]` to 2 because we have found a new arithmetic subsequence of length 2 (nums[j], nums[i]).\n- After updating `dp[i][diff]`, we check if the current length `dp[i][diff]` is greater than the current longest arithmetic subsequence length `longest`. If so, we update `longest` to the new maximum length.\n- Once we finish iterating through all pairs of indices, we have computed the lengths of all possible arithmetic subsequences ending at each index. The maximum length among these subsequences is stored in `longest`, so we return it as the result.\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int longestArithSeqLength(vector<int>& nums) {\n int n = nums.size();\n if (n <= 2)\n return n;\n\n int longest = 2;\n vector<unordered_map<int, int>> dp(n);\n\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < i; j++) {\n int diff = nums[i] - nums[j];\n dp[i][diff] = dp[j].count(diff) ? dp[j][diff] + 1 : 2;\n longest = max(longest, dp[i][diff]);\n }\n }\n\n return longest;\n }\n};\n```\n```Java []\nclass Solution {\n public int longestArithSeqLength(int[] nums) {\n int n = nums.length;\n if (n <= 2)\n return n;\n\n int longest = 2;\n Map<Integer, Integer>[] dp = new HashMap[n];\n\n for (int i = 0; i < n; i++) {\n dp[i] = new HashMap<>();\n for (int j = 0; j < i; j++) {\n int diff = nums[i] - nums[j];\n dp[i].put(diff, dp[j].getOrDefault(diff, 1) + 1);\n longest = Math.max(longest, dp[i].get(diff));\n }\n }\n\n return longest;\n }\n}\n```\n```Python3 []\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n n = len(nums)\n if n <= 2:\n return n\n\n longest = 2\n dp = [{} for _ in range(n)]\n\n for i in range(n):\n for j in range(i):\n diff = nums[i] - nums[j]\n dp[i][diff] = dp[j].get(diff, 1) + 1\n longest = max(longest, dp[i][diff])\n\n return longest\n```\n\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 238 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
✅Beats 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | longest-arithmetic-subsequence | 1 | 1 | # Intuition\nThe intuition behind this solution is to use dynamic programming to find the length of the longest arithmetic subsequence in the given array. We iterate through each pair of indices (i, j), where i > j, and check if we can extend the arithmetic subsequence ending at index i by including the element at index j. We update the dynamic programming values based on the common difference between the elements at indices i and j. By keeping track of the maximum length encountered, we can find the length of the longest arithmetic subsequence in the array.\n\n# Approach:\n- If `n` is less than or equal to 2, we can immediately return `n` as the answer since any two elements form a valid arithmetic subsequence.\n- We initialize the variable `longest` to 2, as explained earlier, the minimum length of an arithmetic subsequence is 2.\n- We create a 2D vector `dp` of size `n`, where each element is an unordered map. The purpose of `dp` is to store the dynamic programming values for the lengths of the arithmetic subsequences ending at each index with different common differences.\n- We iterate through each index `i` in the range `[0, n-1]`. This represents the current ending index of the arithmetic subsequences we are considering.\n- For each `i`, we iterate through all previous indices `j` in the range `[0, i-1]`. This allows us to check all the potential elements that can form an arithmetic subsequence with the element at index `i`.\n- We calculate the difference between the elements at indices `i` and `j` and store it in the variable `diff`. This difference represents the common difference of the potential arithmetic subsequence.\n- Next, we update `dp[i][diff]` based on whether we have seen a previous arithmetic subsequence ending at index `j` with a common difference of `diff`.\n - If `dp[j].count(diff)` returns true, it means we have encountered an arithmetic subsequence ending at index `j` with the common difference `diff`. In this case, we update `dp[i][diff]` to be `dp[j][diff] + 1`, which extends the subsequence and increments its length by 1.\n - If `dp[j].count(diff)` returns false, it means we haven\'t seen an arithmetic subsequence ending at index `j` with the common difference `diff`. In this case, we initialize `dp[i][diff]` to 2 because we have found a new arithmetic subsequence of length 2 (nums[j], nums[i]).\n- After updating `dp[i][diff]`, we check if the current length `dp[i][diff]` is greater than the current longest arithmetic subsequence length `longest`. If so, we update `longest` to the new maximum length.\n- Once we finish iterating through all pairs of indices, we have computed the lengths of all possible arithmetic subsequences ending at each index. The maximum length among these subsequences is stored in `longest`, so we return it as the result.\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int longestArithSeqLength(vector<int>& nums) {\n int n = nums.size();\n if (n <= 2)\n return n;\n\n int longest = 2;\n vector<unordered_map<int, int>> dp(n);\n\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < i; j++) {\n int diff = nums[i] - nums[j];\n dp[i][diff] = dp[j].count(diff) ? dp[j][diff] + 1 : 2;\n longest = max(longest, dp[i][diff]);\n }\n }\n\n return longest;\n }\n};\n```\n```Java []\nclass Solution {\n public int longestArithSeqLength(int[] nums) {\n int n = nums.length;\n if (n <= 2)\n return n;\n\n int longest = 2;\n Map<Integer, Integer>[] dp = new HashMap[n];\n\n for (int i = 0; i < n; i++) {\n dp[i] = new HashMap<>();\n for (int j = 0; j < i; j++) {\n int diff = nums[i] - nums[j];\n dp[i].put(diff, dp[j].getOrDefault(diff, 1) + 1);\n longest = Math.max(longest, dp[i].get(diff));\n }\n }\n\n return longest;\n }\n}\n```\n```Python3 []\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n n = len(nums)\n if n <= 2:\n return n\n\n longest = 2\n dp = [{} for _ in range(n)]\n\n for i in range(n):\n for j in range(i):\n diff = nums[i] - nums[j]\n dp[i][diff] = dp[j].get(diff, 1) + 1\n longest = max(longest, dp[i][diff])\n\n return longest\n```\n\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 238 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
(Python) Longest Arithmetic Subsequence | longest-arithmetic-subsequence | 0 | 1 | # Intuition\nTo find the length of the longest arithmetic subsequence, we can use dynamic programming. We\'ll define a dynamic programming table, dp, where dp[i][diff] represents the length of the longest arithmetic subsequence ending at index i with a common difference of diff.\n# Approach\n1. Initialize the dynamic programming table, dp, as an empty dictionary.\n2. Initialize the maximum length, max_length, to 2 since any two elements form an arithmetic subsequence.\n3. Iterate over each element in the input nums.\n4. For the current element at index i, initialize dp[i] as an empty dictionary.\n5. Iterate over the previous elements from 0 to i-1.\n6. Calculate the difference between the current element nums[i] and the previous element nums[j].\n7. Check if the difference exists in the dp table for the previous element dp[j].\n8. If the difference exists, update dp[i][diff] as dp[j][diff] + 1 since we can extend the arithmetic subsequence.\n9. If the difference doesn\'t exist, initialize dp[i][diff] as 2 since the current element and the previous element form an arithmetic subsequence of length 2.\n10. Update the maximum length, max_length, if dp[i][diff] is greater than max_length.\n11. Return max_length as the result, which represents the length of the longest arithmetic subsequence.\n\n\n\n\n# Complexity\n- Time complexity:\nThe nested loop iterates over all pairs of elements, resulting in a time complexity of O(n^2), where n is the length of the input list nums.\n- Space complexity:\nThe space complexity is also O(n^2) since we use a dynamic programming table of size n^2 to store the lengths of arithmetic subsequences.\n# Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n # Initialize the dynamic programming table\n dp = {}\n n = len(nums)\n max_length = 2\n \n # Iterate over each element in nums\n for i in range(n):\n # Initialize the dp table for the current element\n dp[i] = {}\n \n # Iterate over previous elements\n for j in range(i):\n # Calculate the difference between the current element and previous element\n diff = nums[i] - nums[j]\n \n # Check if the difference exists in the dp table for the previous element\n if diff in dp[j]:\n # If the difference exists, update the dp table for the current element\n dp[i][diff] = dp[j][diff] + 1\n else:\n # If the difference doesn\'t exist, initialize the dp table for the current element with a length of 2\n dp[i][diff] = 2\n \n # Update the maximum length\n max_length = max(max_length, dp[i][diff])\n \n return max_length\n\n``` | 1 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
(Python) Longest Arithmetic Subsequence | longest-arithmetic-subsequence | 0 | 1 | # Intuition\nTo find the length of the longest arithmetic subsequence, we can use dynamic programming. We\'ll define a dynamic programming table, dp, where dp[i][diff] represents the length of the longest arithmetic subsequence ending at index i with a common difference of diff.\n# Approach\n1. Initialize the dynamic programming table, dp, as an empty dictionary.\n2. Initialize the maximum length, max_length, to 2 since any two elements form an arithmetic subsequence.\n3. Iterate over each element in the input nums.\n4. For the current element at index i, initialize dp[i] as an empty dictionary.\n5. Iterate over the previous elements from 0 to i-1.\n6. Calculate the difference between the current element nums[i] and the previous element nums[j].\n7. Check if the difference exists in the dp table for the previous element dp[j].\n8. If the difference exists, update dp[i][diff] as dp[j][diff] + 1 since we can extend the arithmetic subsequence.\n9. If the difference doesn\'t exist, initialize dp[i][diff] as 2 since the current element and the previous element form an arithmetic subsequence of length 2.\n10. Update the maximum length, max_length, if dp[i][diff] is greater than max_length.\n11. Return max_length as the result, which represents the length of the longest arithmetic subsequence.\n\n\n\n\n# Complexity\n- Time complexity:\nThe nested loop iterates over all pairs of elements, resulting in a time complexity of O(n^2), where n is the length of the input list nums.\n- Space complexity:\nThe space complexity is also O(n^2) since we use a dynamic programming table of size n^2 to store the lengths of arithmetic subsequences.\n# Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n # Initialize the dynamic programming table\n dp = {}\n n = len(nums)\n max_length = 2\n \n # Iterate over each element in nums\n for i in range(n):\n # Initialize the dp table for the current element\n dp[i] = {}\n \n # Iterate over previous elements\n for j in range(i):\n # Calculate the difference between the current element and previous element\n diff = nums[i] - nums[j]\n \n # Check if the difference exists in the dp table for the previous element\n if diff in dp[j]:\n # If the difference exists, update the dp table for the current element\n dp[i][diff] = dp[j][diff] + 1\n else:\n # If the difference doesn\'t exist, initialize the dp table for the current element with a length of 2\n dp[i][diff] = 2\n \n # Update the maximum length\n max_length = max(max_length, dp[i][diff])\n \n return max_length\n\n``` | 1 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
Short and Simple 🐍🐍 | longest-arithmetic-subsequence | 0 | 1 | # Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n dp = {}; res = 2\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n diff = nums[j] - nums[i]\n dp[j, diff] = dp.get((i, diff), 1) + 1\n res = max(res, dp[(j, diff)])\n return res\n``` | 1 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
Short and Simple 🐍🐍 | longest-arithmetic-subsequence | 0 | 1 | # Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n dp = {}; res = 2\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n diff = nums[j] - nums[i]\n dp[j, diff] = dp.get((i, diff), 1) + 1\n res = max(res, dp[(j, diff)])\n return res\n``` | 1 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
[Python] DP solution with Japanese explanation | longest-arithmetic-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- \u72B6\u614B\u3092\u914D\u5217\u3067\u306F\u306A\u304Fdict\u578B\u3067\u4FDD\u6301\u3059\u308B\u3068\u76F4\u611F\u7684\u306B\u89E3\u304D\u3084\u3059\u3044\u3002\n- \u5DEE\u5206\u3092\u56FA\u5B9A\u3057\u3066\u8003\u3048\u308B\u3068\u554F\u984C\u304C\u4E00\u6B21\u5143\u306B\u306A\u3063\u3066\u30B7\u30F3\u30D7\u30EB\u306B\u306A\u308B\u3002\n\n# Complexity\n$$N$$: ```nums``` \u306E\u9577\u3055\n$$M$$: ```nums``` \u306E\u8981\u7D20\u306E\u6700\u5927\u5024\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(NM)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(NM)$$: ```calc```\u95A2\u6570\u306E```dp```\u306Edict\u3067O(N)\u4F7F\u7528\u3002O(M)\u56DE```calc```\u95A2\u6570\u304C\u5B9F\u884C\u3055\u308C\u308B\u306E\u3067\u5168\u4F53\u3067\u306FO(NM)\u3002\n\n$$O(N)$$: \u3067\u3082\u6B63\u89E3\u3002\u6B63\u78BA\u306B\u3044\u3046\u3068\u3053\u3061\u3089\u306E\u65B9\u304C\u6B63\u3057\u3044\u3002\u4EE5\u4E0BO(N)\u3068\u7B54\u3048\u308B\u5834\u5408\u306B\u5FC5\u8981\u306A\u88DC\u8DB3\u8AAC\u660E\u3002\n\nPython3 \u3067\u306FGC\u306B\u53C2\u7167\u30AB\u30A6\u30F3\u30C8\u3092\u4F7F\u7528\u3057\u3066\u3044\u307E\u3059\u3002\u305D\u306E\u305F\u3081\u53C2\u7167\u304C\u3055\u308C\u306A\u304F\u306A\u3063\u305F\u30AA\u30D6\u30B8\u30A7\u30AF\u30C8\u306F\u306E\u30E1\u30E2\u30EA\u306F\u89E3\u653E\u3055\u308C\u307E\u3059\u3002\u3053\u306E\u554F\u984C\u3067\u3044\u3046\u3068```calc```\u95A2\u6570\u306E(1)\u3067\u5272\u308A\u5F53\u3066\u3089\u308C\u305F```dp```\u30AA\u30D6\u30B8\u30A7\u30AF\u30C8\u306E\u30E1\u30E2\u30EA\u306F\u95A2\u6570\u306E\u7D42\u4E86\u3068\u3068\u3082\u306B\u89E3\u653E\u3055\u308C\u307E\u3059\u3002\u3053\u308C\u306F\u305D\u3082\u305D\u3082\u95A2\u6570\u306E\u30B9\u30B3\u30FC\u30D7\u5185\u306E\u30AA\u30D6\u30B8\u30A7\u30AF\u30C8\u306A\u306E\u3067\u5F53\u7136\u3068\u3082\u8A00\u3048\u307E\u3059\u3002\u307E\u305F(2)\u3067\u306F```for```\u6587\u306B\u3088\u308B\u9010\u6B21\u5B9F\u884C\u3092\u884C\u306A\u3063\u3066\u3044\u308B\u305F\u3081\u3001\u6BCE\u56DE(1)\u306E```dp```\u306B\u4F7F\u7528\u3057\u3066\u3044\u308B\u30E1\u30E2\u30EA\u306F\u89E3\u653E\u3055\u308C\u3066\u3044\u308B\u3068\u307F\u306A\u305B\u307E\u3059\u3002\u305D\u306E\u305F\u3081\u5168\u4F53\u3068\u3057\u3066\u4F7F\u7528\u3057\u3066\u3044\u308B\u30E1\u30E2\u30EA\u306F\u7D50\u5C40O(N)\u3068\u307F\u306A\u3059\u3053\u3068\u3082\u3067\u304D\u308B\u3068\u8003\u3048\u307E\u3059\u3002\n\n# Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n def calc(diff):\n dp = {} # - (1) \n for num in nums:\n target = num - diff\n if target in dp:\n dp[num] = dp[target] + 1\n else:\n dp[num] = 1\n\n return max(dp.values())\n\n ans = 0\n for diff in range(-max(nums), max(nums)+1): \n ans = max(ans, calc(diff)) # - (2)\n\n return ans \n\n\n\n\n``` | 1 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
[Python] DP solution with Japanese explanation | longest-arithmetic-subsequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- \u72B6\u614B\u3092\u914D\u5217\u3067\u306F\u306A\u304Fdict\u578B\u3067\u4FDD\u6301\u3059\u308B\u3068\u76F4\u611F\u7684\u306B\u89E3\u304D\u3084\u3059\u3044\u3002\n- \u5DEE\u5206\u3092\u56FA\u5B9A\u3057\u3066\u8003\u3048\u308B\u3068\u554F\u984C\u304C\u4E00\u6B21\u5143\u306B\u306A\u3063\u3066\u30B7\u30F3\u30D7\u30EB\u306B\u306A\u308B\u3002\n\n# Complexity\n$$N$$: ```nums``` \u306E\u9577\u3055\n$$M$$: ```nums``` \u306E\u8981\u7D20\u306E\u6700\u5927\u5024\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(NM)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(NM)$$: ```calc```\u95A2\u6570\u306E```dp```\u306Edict\u3067O(N)\u4F7F\u7528\u3002O(M)\u56DE```calc```\u95A2\u6570\u304C\u5B9F\u884C\u3055\u308C\u308B\u306E\u3067\u5168\u4F53\u3067\u306FO(NM)\u3002\n\n$$O(N)$$: \u3067\u3082\u6B63\u89E3\u3002\u6B63\u78BA\u306B\u3044\u3046\u3068\u3053\u3061\u3089\u306E\u65B9\u304C\u6B63\u3057\u3044\u3002\u4EE5\u4E0BO(N)\u3068\u7B54\u3048\u308B\u5834\u5408\u306B\u5FC5\u8981\u306A\u88DC\u8DB3\u8AAC\u660E\u3002\n\nPython3 \u3067\u306FGC\u306B\u53C2\u7167\u30AB\u30A6\u30F3\u30C8\u3092\u4F7F\u7528\u3057\u3066\u3044\u307E\u3059\u3002\u305D\u306E\u305F\u3081\u53C2\u7167\u304C\u3055\u308C\u306A\u304F\u306A\u3063\u305F\u30AA\u30D6\u30B8\u30A7\u30AF\u30C8\u306F\u306E\u30E1\u30E2\u30EA\u306F\u89E3\u653E\u3055\u308C\u307E\u3059\u3002\u3053\u306E\u554F\u984C\u3067\u3044\u3046\u3068```calc```\u95A2\u6570\u306E(1)\u3067\u5272\u308A\u5F53\u3066\u3089\u308C\u305F```dp```\u30AA\u30D6\u30B8\u30A7\u30AF\u30C8\u306E\u30E1\u30E2\u30EA\u306F\u95A2\u6570\u306E\u7D42\u4E86\u3068\u3068\u3082\u306B\u89E3\u653E\u3055\u308C\u307E\u3059\u3002\u3053\u308C\u306F\u305D\u3082\u305D\u3082\u95A2\u6570\u306E\u30B9\u30B3\u30FC\u30D7\u5185\u306E\u30AA\u30D6\u30B8\u30A7\u30AF\u30C8\u306A\u306E\u3067\u5F53\u7136\u3068\u3082\u8A00\u3048\u307E\u3059\u3002\u307E\u305F(2)\u3067\u306F```for```\u6587\u306B\u3088\u308B\u9010\u6B21\u5B9F\u884C\u3092\u884C\u306A\u3063\u3066\u3044\u308B\u305F\u3081\u3001\u6BCE\u56DE(1)\u306E```dp```\u306B\u4F7F\u7528\u3057\u3066\u3044\u308B\u30E1\u30E2\u30EA\u306F\u89E3\u653E\u3055\u308C\u3066\u3044\u308B\u3068\u307F\u306A\u305B\u307E\u3059\u3002\u305D\u306E\u305F\u3081\u5168\u4F53\u3068\u3057\u3066\u4F7F\u7528\u3057\u3066\u3044\u308B\u30E1\u30E2\u30EA\u306F\u7D50\u5C40O(N)\u3068\u307F\u306A\u3059\u3053\u3068\u3082\u3067\u304D\u308B\u3068\u8003\u3048\u307E\u3059\u3002\n\n# Code\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n def calc(diff):\n dp = {} # - (1) \n for num in nums:\n target = num - diff\n if target in dp:\n dp[num] = dp[target] + 1\n else:\n dp[num] = 1\n\n return max(dp.values())\n\n ans = 0\n for diff in range(-max(nums), max(nums)+1): \n ans = max(ans, calc(diff)) # - (2)\n\n return ans \n\n\n\n\n``` | 1 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
python 3 - top down DP with greedy | longest-arithmetic-subsequence | 0 | 1 | # Intuition\nThis question is easy in terms of TC. But getting accepted is kind of "hard".\n\nObviously you need DP. But bottom up can get accepted way easier than top down. For top down DP, you need further optimization.\n\nSince for each diff value, you will ALWAYS get the closest one. So you don\'t need to check the remaining elements once you find (num + diff). If you can\'t find any matching number, just return 0.\n-> So you need greedy too.\n\nIndeed top down dp with greedy has the same tc compare with only bottom up dp. LC checking system is quite harsh in this part.\n\n# Approach\ntop down DP with greedy\n\n# Complexity\n- Time complexity:\nO(n^2) -> state variables of dp + Double loops operations\n\n- Space complexity:\nO(n^2) -> cache size + dict size\n\n# Code\n```\nimport collections\n\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n\n i2diff2list = dict()\n ln = len(nums)\n\n for i in range(ln):\n for nxt in range(ln-1, i, -1):\n if i not in i2diff2list:\n i2diff2list[i] = dict()\n diff = nums[nxt] - nums[i]\n i2diff2list[i][diff] = nxt\n\n @lru_cache(None)\n def dp(i, diff): # return int, longest sequence with this diff\n res = 0\n if i in i2diff2list and diff in i2diff2list[i]:\n nxt = i2diff2list[i][diff]\n res = max(res, dp(nxt, diff))\n return res + 1\n \n ans = 0\n for i in range(ln):\n for nxt in range(i + 1, ln):\n diff = nums[nxt] - nums[i]\n ans = max(ans, dp(nxt, diff) + 1)\n return ans\n``` | 1 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
python 3 - top down DP with greedy | longest-arithmetic-subsequence | 0 | 1 | # Intuition\nThis question is easy in terms of TC. But getting accepted is kind of "hard".\n\nObviously you need DP. But bottom up can get accepted way easier than top down. For top down DP, you need further optimization.\n\nSince for each diff value, you will ALWAYS get the closest one. So you don\'t need to check the remaining elements once you find (num + diff). If you can\'t find any matching number, just return 0.\n-> So you need greedy too.\n\nIndeed top down dp with greedy has the same tc compare with only bottom up dp. LC checking system is quite harsh in this part.\n\n# Approach\ntop down DP with greedy\n\n# Complexity\n- Time complexity:\nO(n^2) -> state variables of dp + Double loops operations\n\n- Space complexity:\nO(n^2) -> cache size + dict size\n\n# Code\n```\nimport collections\n\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n\n i2diff2list = dict()\n ln = len(nums)\n\n for i in range(ln):\n for nxt in range(ln-1, i, -1):\n if i not in i2diff2list:\n i2diff2list[i] = dict()\n diff = nums[nxt] - nums[i]\n i2diff2list[i][diff] = nxt\n\n @lru_cache(None)\n def dp(i, diff): # return int, longest sequence with this diff\n res = 0\n if i in i2diff2list and diff in i2diff2list[i]:\n nxt = i2diff2list[i][diff]\n res = max(res, dp(nxt, diff))\n return res + 1\n \n ans = 0\n for i in range(ln):\n for nxt in range(i + 1, ln):\n diff = nums[nxt] - nums[i]\n ans = max(ans, dp(nxt, diff) + 1)\n return ans\n``` | 1 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
DP Solution Explained by a Novice | longest-arithmetic-subsequence | 0 | 1 | # Intuition\nHi everyone! Today\'s question was challenging maybe just because I\'m a novice at dp. I\'m preparing this section to those who are having hard time to solve dp questions. Hope it would be helpful.\n\nNow if the nums was sorted and we were trying to search arithmetic sequence in subsequent manner then the code like this would be enough:\n\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n if len(nums) == 2: return 2\n # nums.sort()\n max_count = 2\n for i in range(len(nums)-1):\n count = 2\n dif = nums[i+1] - nums[i]\n for j in range(i+2, len(nums)):\n if nums[j] - nums[j-1] == dif:\n count += 1\n else:\n break\n max_count = max(max_count, count)\n\n return max_count\n``` \nAt least first I coded in that way. The real solution is a bit complex than this. We have to store the relative differences for each element in nums. To do that we need a dictionary for each element. In the code below it is called `dp`. Then we start a nested loop. i iterates through each number in nums and j is used for computing relative differences. If the calculated difference in our dict, we increase its count by one. and if not we assign the count as 2 (The smallest sequence) and add a new key having count of 2 to our dictionary. Finally we update the maximum length by comparing maximum length we\'ve tracked so far with the count. The time complexity is O(n^2) {nested loop} and space complexity is also O(n^2) {store ~n variables for n elements.} \n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n n = len(nums)\n dp = [{} for _ in range(n)] \n max_len = 2 \n \n for i in range(n):\n for j in range(i+1, n):\n diff = nums[j] - nums[i] \n if diff in dp[i]:\n count = dp[i][diff] + 1\n else:\n count = 2\n dp[j][diff] = count\n \n \n max_len = max(max_len, count)\n \n return max_len\n``` | 1 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
DP Solution Explained by a Novice | longest-arithmetic-subsequence | 0 | 1 | # Intuition\nHi everyone! Today\'s question was challenging maybe just because I\'m a novice at dp. I\'m preparing this section to those who are having hard time to solve dp questions. Hope it would be helpful.\n\nNow if the nums was sorted and we were trying to search arithmetic sequence in subsequent manner then the code like this would be enough:\n\n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n if len(nums) == 2: return 2\n # nums.sort()\n max_count = 2\n for i in range(len(nums)-1):\n count = 2\n dif = nums[i+1] - nums[i]\n for j in range(i+2, len(nums)):\n if nums[j] - nums[j-1] == dif:\n count += 1\n else:\n break\n max_count = max(max_count, count)\n\n return max_count\n``` \nAt least first I coded in that way. The real solution is a bit complex than this. We have to store the relative differences for each element in nums. To do that we need a dictionary for each element. In the code below it is called `dp`. Then we start a nested loop. i iterates through each number in nums and j is used for computing relative differences. If the calculated difference in our dict, we increase its count by one. and if not we assign the count as 2 (The smallest sequence) and add a new key having count of 2 to our dictionary. Finally we update the maximum length by comparing maximum length we\'ve tracked so far with the count. The time complexity is O(n^2) {nested loop} and space complexity is also O(n^2) {store ~n variables for n elements.} \n```\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n n = len(nums)\n dp = [{} for _ in range(n)] \n max_len = 2 \n \n for i in range(n):\n for j in range(i+1, n):\n diff = nums[j] - nums[i] \n if diff in dp[i]:\n count = dp[i][diff] + 1\n else:\n count = 2\n dp[j][diff] = count\n \n \n max_len = max(max_len, count)\n \n return max_len\n``` | 1 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
Solution | longest-arithmetic-subsequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestArithSeqLength(vector<int>& n)\n { \n int out{1};\n for(int i{}; i<501/out; ++i)\n for(int d[1001]{}, D[1001]{}; const auto & n: n)\n out=max({out, d[n+500]=d[n-i+500]+1, D[n]=D[n+i]+1});\n return out;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n diffToHeadMap = {}\n diff = nums[1] - nums[0]\n diffToHeadMap[diff] = {nums[1]: 2}\n prevSet = set()\n prevSet.add(nums[0])\n prevSet.add(nums[1])\n maxVal = 2\n for i in range(2, len(nums)):\n for prevNum in prevSet:\n diff = nums[i] - prevNum\n if diff not in diffToHeadMap:\n diffToHeadMap[diff] = {nums[i]: 2}\n else:\n mapEntry = diffToHeadMap[diff]\n if prevNum in mapEntry:\n temp = mapEntry[prevNum]\n mapEntry[nums[i]] = temp + 1\n if temp + 1 > maxVal:\n maxVal = temp + 1\n else:\n mapEntry[nums[i]] = 2\n prevSet.add(nums[i])\n return maxVal\n```\n\n```Java []\nclass Solution {\n public int longestArithSeqLength(int[] nums) {\n \n int limit = 500;\n\n int max = Integer.MIN_VALUE;\n int min = Integer.MAX_VALUE;\n\n for (int num : nums) {\n max = Math.max(max, num);\n min = Math.min(min, num);\n }\n int numsLength = 0;\n\n for (int k = 0; k <= max - min; k++) {\n\n if (k * numsLength > max - min) {\n break;\n }\n int[] first = new int[limit + 1];\n int[] second = new int[limit + 1];\n\n for (int num : nums) {\n first[num] = (num + k <= limit) ? (first[num + k] + 1) : 1;\n second[num] = (num - k >= 0) ? (second[num - k] + 1) : 1;\n numsLength = Math.max(numsLength, Math.max(first[num], second[num]));\n }\n }\n return numsLength;\n }\n}\n``` | 1 | Given an array `nums` of integers, return _the length of the longest arithmetic subsequence in_ `nums`.
**Note** that:
* A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
* A sequence `seq` is arithmetic if `seq[i + 1] - seq[i]` are all the same value (for `0 <= i < seq.length - 1`).
**Example 1:**
**Input:** nums = \[3,6,9,12\]
**Output:** 4
**Explanation: ** The whole array is an arithmetic sequence with steps of length = 3.
**Example 2:**
**Input:** nums = \[9,4,7,2,10\]
**Output:** 3
**Explanation: ** The longest arithmetic subsequence is \[4,7,10\].
**Example 3:**
**Input:** nums = \[20,1,15,3,10,5,8\]
**Output:** 4
**Explanation: ** The longest arithmetic subsequence is \[20,15,10,5\].
**Constraints:**
* `2 <= nums.length <= 1000`
* `0 <= nums[i] <= 500` | null |
Solution | longest-arithmetic-subsequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestArithSeqLength(vector<int>& n)\n { \n int out{1};\n for(int i{}; i<501/out; ++i)\n for(int d[1001]{}, D[1001]{}; const auto & n: n)\n out=max({out, d[n+500]=d[n-i+500]+1, D[n]=D[n+i]+1});\n return out;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestArithSeqLength(self, nums: List[int]) -> int:\n diffToHeadMap = {}\n diff = nums[1] - nums[0]\n diffToHeadMap[diff] = {nums[1]: 2}\n prevSet = set()\n prevSet.add(nums[0])\n prevSet.add(nums[1])\n maxVal = 2\n for i in range(2, len(nums)):\n for prevNum in prevSet:\n diff = nums[i] - prevNum\n if diff not in diffToHeadMap:\n diffToHeadMap[diff] = {nums[i]: 2}\n else:\n mapEntry = diffToHeadMap[diff]\n if prevNum in mapEntry:\n temp = mapEntry[prevNum]\n mapEntry[nums[i]] = temp + 1\n if temp + 1 > maxVal:\n maxVal = temp + 1\n else:\n mapEntry[nums[i]] = 2\n prevSet.add(nums[i])\n return maxVal\n```\n\n```Java []\nclass Solution {\n public int longestArithSeqLength(int[] nums) {\n \n int limit = 500;\n\n int max = Integer.MIN_VALUE;\n int min = Integer.MAX_VALUE;\n\n for (int num : nums) {\n max = Math.max(max, num);\n min = Math.min(min, num);\n }\n int numsLength = 0;\n\n for (int k = 0; k <= max - min; k++) {\n\n if (k * numsLength > max - min) {\n break;\n }\n int[] first = new int[limit + 1];\n int[] second = new int[limit + 1];\n\n for (int num : nums) {\n first[num] = (num + k <= limit) ? (first[num + k] + 1) : 1;\n second[num] = (num - k >= 0) ? (second[num - k] + 1) : 1;\n numsLength = Math.max(numsLength, Math.max(first[num], second[num]));\n }\n }\n return numsLength;\n }\n}\n``` | 1 | You are given a string `s` representing a list of words. Each letter in the word has one or more options.
* If there is one option, the letter is represented as is.
* If there is more than one option, then curly braces delimit the options. For example, `"{a,b,c} "` represents options `[ "a ", "b ", "c "]`.
For example, if `s = "a{b,c} "`, the first character is always `'a'`, but the second character can be `'b'` or `'c'`. The original list is `[ "ab ", "ac "]`.
Return all words that can be formed in this manner, **sorted** in lexicographical order.
**Example 1:**
**Input:** s = "{a,b}c{d,e}f"
**Output:** \["acdf","acef","bcdf","bcef"\]
**Example 2:**
**Input:** s = "abcd"
**Output:** \["abcd"\]
**Constraints:**
* `1 <= s.length <= 50`
* `s` consists of curly brackets `'{}'`, commas `','`, and lowercase English letters.
* `s` is guaranteed to be a valid input.
* There are no nested curly brackets.
* All characters inside a pair of consecutive opening and ending curly brackets are different. | null |
Solution with Stack in Python3 | recover-a-tree-from-preorder-traversal | 0 | 1 | # Intuition\nHere we have:\n- a string `traversal`, that denotes to **Preorder Traversal** of a Binary Tree\n- it has nodes as integers and **dashes**, that represent a **depth** of a node\n- our goal is to **recreate** a Binary Tree\n\nAn algorithm implies to **parse** a `traversal` string.\nAt each step we define a **depth** of a particular node, and push it into `stack` to manage relationship between root of a subtree and its leaves.\n\n# Complexity\n- Time complexity: **O(N)**, to restore a Binary Tree from `traversal`\n\n- Space complexity: **O(N)**, since we store all of the nodes (except **dashes**)\n\n# Code\n```\nclass Solution:\n def recoverFromPreorder(self, traversal):\n i, n = 0, len(traversal)\n # define a stack\n stack = []\n num = \'\'\n\n # iterate over traversal and parse tokens\n while i < n:\n # define a depth\n level = 0\n\n # to calculate it for a particular (next) node\n while i < n and traversal[i] == \'-\': \n i += 1\n level += 1\n \n # but if a level is different one, pop redundant\n # elements from stack\n while stack and len(stack) > level: stack.pop()\n\n # then we should parse an integer, since it could have\n # more than 1 digit\n while i < n and traversal[i] != \'-\':\n num += traversal[i]\n i += 1\n\n # create a Binary Tree node\n node = TreeNode(int(num))\n\n # and fill it with children (for left)\n if stack and stack[-1].left is None:\n stack[-1].left = node\n # for right node\n elif stack:\n stack[-1].right = node\n \n # don\'t forget to push a current node into stack\n stack.append(node)\n # and reset a previous integer\n num = \'\'\n \n # the first element of a stack is a root of a recovered tree\n return stack[0]\n``` | 2 | We run a preorder depth-first search (DFS) on the `root` of a binary tree.
At each node in this traversal, we output `D` dashes (where `D` is the depth of this node), then we output the value of this node. If the depth of a node is `D`, the depth of its immediate child is `D + 1`. The depth of the `root` node is `0`.
If a node has only one child, that child is guaranteed to be **the left child**.
Given the output `traversal` of this traversal, recover the tree and return _its_ `root`.
**Example 1:**
**Input:** traversal = "1-2--3--4-5--6--7 "
**Output:** \[1,2,5,3,4,6,7\]
**Example 2:**
**Input:** traversal = "1-2--3---4-5--6---7 "
**Output:** \[1,2,5,3,null,6,null,4,null,7\]
**Example 3:**
**Input:** traversal = "1-401--349---90--88 "
**Output:** \[1,401,null,349,88,90\]
**Constraints:**
* The number of nodes in the original tree is in the range `[1, 1000]`.
* `1 <= Node.val <= 109` | null |
Solution with Stack in Python3 | recover-a-tree-from-preorder-traversal | 0 | 1 | # Intuition\nHere we have:\n- a string `traversal`, that denotes to **Preorder Traversal** of a Binary Tree\n- it has nodes as integers and **dashes**, that represent a **depth** of a node\n- our goal is to **recreate** a Binary Tree\n\nAn algorithm implies to **parse** a `traversal` string.\nAt each step we define a **depth** of a particular node, and push it into `stack` to manage relationship between root of a subtree and its leaves.\n\n# Complexity\n- Time complexity: **O(N)**, to restore a Binary Tree from `traversal`\n\n- Space complexity: **O(N)**, since we store all of the nodes (except **dashes**)\n\n# Code\n```\nclass Solution:\n def recoverFromPreorder(self, traversal):\n i, n = 0, len(traversal)\n # define a stack\n stack = []\n num = \'\'\n\n # iterate over traversal and parse tokens\n while i < n:\n # define a depth\n level = 0\n\n # to calculate it for a particular (next) node\n while i < n and traversal[i] == \'-\': \n i += 1\n level += 1\n \n # but if a level is different one, pop redundant\n # elements from stack\n while stack and len(stack) > level: stack.pop()\n\n # then we should parse an integer, since it could have\n # more than 1 digit\n while i < n and traversal[i] != \'-\':\n num += traversal[i]\n i += 1\n\n # create a Binary Tree node\n node = TreeNode(int(num))\n\n # and fill it with children (for left)\n if stack and stack[-1].left is None:\n stack[-1].left = node\n # for right node\n elif stack:\n stack[-1].right = node\n \n # don\'t forget to push a current node into stack\n stack.append(node)\n # and reset a previous integer\n num = \'\'\n \n # the first element of a stack is a root of a recovered tree\n return stack[0]\n``` | 2 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
[Python] Minimal Code without Stack or Recursion, The Best | recover-a-tree-from-preorder-traversal | 0 | 1 | # Approach\nNote that the empty tree is supported as well.\n\nThe Best!\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def recoverFromPreorder(self, traversal: str) -> Optional[TreeNode]:\n root = None\n for val in traversal.split(\'-\'):\n if not root or val == \'\':\n parent = (parent.right if parent.right else parent.left) if root else (root := TreeNode(int(val)))\n else:\n parent, _ = root, setattr(parent, \'right\' if parent.left else \'left\', TreeNode(int(val)))\n return root\n``` | 1 | We run a preorder depth-first search (DFS) on the `root` of a binary tree.
At each node in this traversal, we output `D` dashes (where `D` is the depth of this node), then we output the value of this node. If the depth of a node is `D`, the depth of its immediate child is `D + 1`. The depth of the `root` node is `0`.
If a node has only one child, that child is guaranteed to be **the left child**.
Given the output `traversal` of this traversal, recover the tree and return _its_ `root`.
**Example 1:**
**Input:** traversal = "1-2--3--4-5--6--7 "
**Output:** \[1,2,5,3,4,6,7\]
**Example 2:**
**Input:** traversal = "1-2--3---4-5--6---7 "
**Output:** \[1,2,5,3,null,6,null,4,null,7\]
**Example 3:**
**Input:** traversal = "1-401--349---90--88 "
**Output:** \[1,401,null,349,88,90\]
**Constraints:**
* The number of nodes in the original tree is in the range `[1, 1000]`.
* `1 <= Node.val <= 109` | null |
[Python] Minimal Code without Stack or Recursion, The Best | recover-a-tree-from-preorder-traversal | 0 | 1 | # Approach\nNote that the empty tree is supported as well.\n\nThe Best!\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def recoverFromPreorder(self, traversal: str) -> Optional[TreeNode]:\n root = None\n for val in traversal.split(\'-\'):\n if not root or val == \'\':\n parent = (parent.right if parent.right else parent.left) if root else (root := TreeNode(int(val)))\n else:\n parent, _ = root, setattr(parent, \'right\' if parent.left else \'left\', TreeNode(int(val)))\n return root\n``` | 1 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
Python Hard | recover-a-tree-from-preorder-traversal | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def recoverFromPreorder(self, traversal: str) -> Optional[TreeNode]:\n mostRecent = {}\n hashCount = 0\n N = len(traversal)\n r = 0\n\n while r < N:\n if traversal[r] == "-":\n hashCount += 1\n r += 1\n\n else:\n num = ""\n while r < N and traversal[r].isnumeric():\n num += traversal[r]\n r += 1\n \n num = int(num)\n\n\n mostRecent[hashCount] = TreeNode(num)\n\n if hashCount - 1 in mostRecent:\n if not mostRecent[hashCount - 1].left:\n mostRecent[hashCount - 1].left = mostRecent[hashCount]\n\n else:\n mostRecent[hashCount - 1].right = mostRecent[hashCount]\n\n \n hashCount = 0\n\n\n\n return mostRecent[0]\n\n \n\n\n \n \n``` | 0 | We run a preorder depth-first search (DFS) on the `root` of a binary tree.
At each node in this traversal, we output `D` dashes (where `D` is the depth of this node), then we output the value of this node. If the depth of a node is `D`, the depth of its immediate child is `D + 1`. The depth of the `root` node is `0`.
If a node has only one child, that child is guaranteed to be **the left child**.
Given the output `traversal` of this traversal, recover the tree and return _its_ `root`.
**Example 1:**
**Input:** traversal = "1-2--3--4-5--6--7 "
**Output:** \[1,2,5,3,4,6,7\]
**Example 2:**
**Input:** traversal = "1-2--3---4-5--6---7 "
**Output:** \[1,2,5,3,null,6,null,4,null,7\]
**Example 3:**
**Input:** traversal = "1-401--349---90--88 "
**Output:** \[1,401,null,349,88,90\]
**Constraints:**
* The number of nodes in the original tree is in the range `[1, 1000]`.
* `1 <= Node.val <= 109` | null |
Python Hard | recover-a-tree-from-preorder-traversal | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def recoverFromPreorder(self, traversal: str) -> Optional[TreeNode]:\n mostRecent = {}\n hashCount = 0\n N = len(traversal)\n r = 0\n\n while r < N:\n if traversal[r] == "-":\n hashCount += 1\n r += 1\n\n else:\n num = ""\n while r < N and traversal[r].isnumeric():\n num += traversal[r]\n r += 1\n \n num = int(num)\n\n\n mostRecent[hashCount] = TreeNode(num)\n\n if hashCount - 1 in mostRecent:\n if not mostRecent[hashCount - 1].left:\n mostRecent[hashCount - 1].left = mostRecent[hashCount]\n\n else:\n mostRecent[hashCount - 1].right = mostRecent[hashCount]\n\n \n hashCount = 0\n\n\n\n return mostRecent[0]\n\n \n\n\n \n \n``` | 0 | You are given a large sample of integers in the range `[0, 255]`. Since the sample is so large, it is represented by an array `count` where `count[k]` is the **number of times** that `k` appears in the sample.
Calculate the following statistics:
* `minimum`: The minimum element in the sample.
* `maximum`: The maximum element in the sample.
* `mean`: The average of the sample, calculated as the total sum of all elements divided by the total number of elements.
* `median`:
* If the sample has an odd number of elements, then the `median` is the middle element once the sample is sorted.
* If the sample has an even number of elements, then the `median` is the average of the two middle elements once the sample is sorted.
* `mode`: The number that appears the most in the sample. It is guaranteed to be **unique**.
Return _the statistics of the sample as an array of floating-point numbers_ `[minimum, maximum, mean, median, mode]`_. Answers within_ `10-5` _of the actual answer will be accepted._
**Example 1:**
**Input:** count = \[0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,3.00000,2.37500,2.50000,3.00000\]
**Explanation:** The sample represented by count is \[1,2,2,2,3,3,3,3\].
The minimum and maximum are 1 and 3 respectively.
The mean is (1+2+2+2+3+3+3+3) / 8 = 19 / 8 = 2.375.
Since the size of the sample is even, the median is the average of the two middle elements 2 and 3, which is 2.5.
The mode is 3 as it appears the most in the sample.
**Example 2:**
**Input:** count = \[0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0\]
**Output:** \[1.00000,4.00000,2.18182,2.00000,1.00000\]
**Explanation:** The sample represented by count is \[1,1,1,1,2,2,2,3,3,4,4\].
The minimum and maximum are 1 and 4 respectively.
The mean is (1+1+1+1+2+2+2+3+3+4+4) / 11 = 24 / 11 = 2.18181818... (for display purposes, the output shows the rounded number 2.18182).
Since the size of the sample is odd, the median is the middle element 2.
The mode is 1 as it appears the most in the sample.
**Constraints:**
* `count.length == 256`
* `0 <= count[i] <= 109`
* `1 <= sum(count) <= 109`
* The mode of the sample that `count` represents is **unique**. | Do an iterative depth first search, parsing dashes from the string to inform you how to link the nodes together. |
✔️ [Python3] 2-LINERS (*´▽`*), Explained | two-city-scheduling | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe idea is simple: sort the input list by cost difference and then choose the first half of the persons in the sorted array to go to the city `a` and the rest of the persons to the city `b`.\n\nTime: **O(nlogn)** - sorting\nSpace: **O(n)** - sorting\n\n```\ndef twoCitySchedCost(self, costs: List[List[int]]) -> int:\n\tcosts, L = sorted(costs, key = lambda a: a[0] - a[1]), len(costs)//2\n\treturn sum(c[0] for c in costs[:L]) + sum(c[1] for c in costs[L:])\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 13 | A company is planning to interview `2n` people. Given the array `costs` where `costs[i] = [aCosti, bCosti]`, the cost of flying the `ith` person to city `a` is `aCosti`, and the cost of flying the `ith` person to city `b` is `bCosti`.
Return _the minimum cost to fly every person to a city_ such that exactly `n` people arrive in each city.
**Example 1:**
**Input:** costs = \[\[10,20\],\[30,200\],\[400,50\],\[30,20\]\]
**Output:** 110
**Explanation:**
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.
The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
**Example 2:**
**Input:** costs = \[\[259,770\],\[448,54\],\[926,667\],\[184,139\],\[840,118\],\[577,469\]\]
**Output:** 1859
**Example 3:**
**Input:** costs = \[\[515,563\],\[451,713\],\[537,709\],\[343,819\],\[855,779\],\[457,60\],\[650,359\],\[631,42\]\]
**Output:** 3086
**Constraints:**
* `2 * n == costs.length`
* `2 <= costs.length <= 100`
* `costs.length` is even.
* `1 <= aCosti, bCosti <= 1000` | null |
✔️ [Python3] 2-LINERS (*´▽`*), Explained | two-city-scheduling | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe idea is simple: sort the input list by cost difference and then choose the first half of the persons in the sorted array to go to the city `a` and the rest of the persons to the city `b`.\n\nTime: **O(nlogn)** - sorting\nSpace: **O(n)** - sorting\n\n```\ndef twoCitySchedCost(self, costs: List[List[int]]) -> int:\n\tcosts, L = sorted(costs, key = lambda a: a[0] - a[1]), len(costs)//2\n\treturn sum(c[0] for c in costs[:L]) + sum(c[1] for c in costs[L:])\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 13 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
O(nlogn) time | O(n) space | solution explained | two-city-scheduling | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to send half people to city A and half to B with minimum cost.\n\nUse the greedy approach. Sort the costs based on the cost difference between the cities. The lower the cost difference, the higher the priority to be sent to city A. Send the first half of the sorted array to city A and the second half to city b.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- sort the costs based on cost difference to get people with low costs for city A at the start (left half) and with high costs at the end (right half)\n- set result res = 0 to track the minimum cost\n- set n = mid of array\n- traverse the left half array\n - add city A cost of left element (i) and city b cost of right element (i + n)\n- return res\n\n# Complexity\n- Time complexity: O(sort + iteration) \u2192 O(nlogn + n/2) \u2192 O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(sort) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoCitySchedCost(self, costs: List[List[int]]) -> int:\n costs.sort(key=lambda x: x[0] - x[1])\n res = 0\n n = len(costs) // 2\n for i in range(n):\n res += costs[i][0] + costs[i + n][1]\n return res \n``` | 2 | A company is planning to interview `2n` people. Given the array `costs` where `costs[i] = [aCosti, bCosti]`, the cost of flying the `ith` person to city `a` is `aCosti`, and the cost of flying the `ith` person to city `b` is `bCosti`.
Return _the minimum cost to fly every person to a city_ such that exactly `n` people arrive in each city.
**Example 1:**
**Input:** costs = \[\[10,20\],\[30,200\],\[400,50\],\[30,20\]\]
**Output:** 110
**Explanation:**
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.
The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
**Example 2:**
**Input:** costs = \[\[259,770\],\[448,54\],\[926,667\],\[184,139\],\[840,118\],\[577,469\]\]
**Output:** 1859
**Example 3:**
**Input:** costs = \[\[515,563\],\[451,713\],\[537,709\],\[343,819\],\[855,779\],\[457,60\],\[650,359\],\[631,42\]\]
**Output:** 3086
**Constraints:**
* `2 * n == costs.length`
* `2 <= costs.length <= 100`
* `costs.length` is even.
* `1 <= aCosti, bCosti <= 1000` | null |
O(nlogn) time | O(n) space | solution explained | two-city-scheduling | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to send half people to city A and half to B with minimum cost.\n\nUse the greedy approach. Sort the costs based on the cost difference between the cities. The lower the cost difference, the higher the priority to be sent to city A. Send the first half of the sorted array to city A and the second half to city b.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- sort the costs based on cost difference to get people with low costs for city A at the start (left half) and with high costs at the end (right half)\n- set result res = 0 to track the minimum cost\n- set n = mid of array\n- traverse the left half array\n - add city A cost of left element (i) and city b cost of right element (i + n)\n- return res\n\n# Complexity\n- Time complexity: O(sort + iteration) \u2192 O(nlogn + n/2) \u2192 O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(sort) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoCitySchedCost(self, costs: List[List[int]]) -> int:\n costs.sort(key=lambda x: x[0] - x[1])\n res = 0\n n = len(costs) // 2\n for i in range(n):\n res += costs[i][0] + costs[i + n][1]\n return res \n``` | 2 | _(This problem is an **interactive problem**.)_
You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some `i` with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given a mountain array `mountainArr`, return the **minimum** `index` such that `mountainArr.get(index) == target`. If such an `index` does not exist, return `-1`.
**You cannot access the mountain array directly.** You may only access the array using a `MountainArray` interface:
* `MountainArray.get(k)` returns the element of the array at index `k` (0-indexed).
* `MountainArray.length()` returns the length of the array.
Submissions making more than `100` calls to `MountainArray.get` will be judged _Wrong Answer_. Also, any solutions that attempt to circumvent the judge will result in disqualification.
**Example 1:**
**Input:** array = \[1,2,3,4,5,3,1\], target = 3
**Output:** 2
**Explanation:** 3 exists in the array, at index=2 and index=5. Return the minimum index, which is 2.
**Example 2:**
**Input:** array = \[0,1,2,4,2,1\], target = 3
**Output:** -1
**Explanation:** 3 does not exist in `the array,` so we return -1.
**Constraints:**
* `3 <= mountain_arr.length() <= 104`
* `0 <= target <= 109`
* `0 <= mountain_arr.get(index) <= 109` | null |
Python 1-line sorting based solution | matrix-cells-in-distance-order | 0 | 1 | ```\ndef allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n return sorted([(i, j) for i in range(R) for j in range(C)], key=lambda p: abs(p[0] - r0) + abs(p[1] - c0))\n```\n\nThe same code, more readable:\n```\ndef allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n def dist(point):\n pi, pj = point\n return abs(pi - r0) + abs(pj - c0)\n\n points = [(i, j) for i in range(R) for j in range(C)]\n return sorted(points, key=dist)\n``` | 88 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Python 1-line sorting based solution | matrix-cells-in-distance-order | 0 | 1 | ```\ndef allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n return sorted([(i, j) for i in range(R) for j in range(C)], key=lambda p: abs(p[0] - r0) + abs(p[1] - c0))\n```\n\nThe same code, more readable:\n```\ndef allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n def dist(point):\n pi, pj = point\n return abs(pi - r0) + abs(pj - c0)\n\n points = [(i, j) for i in range(R) for j in range(C)]\n return sorted(points, key=dist)\n``` | 88 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
python3 Solution | matrix-cells-in-distance-order | 0 | 1 | \n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n res=[]\n for r in range(rows):\n for c in range(cols):\n res.append([r,c])\n \n res.sort(key=lambda x:abs(x[0]-rCenter)+ abs(x[1]-cCenter))\n return res\n``` | 1 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
python3 Solution | matrix-cells-in-distance-order | 0 | 1 | \n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n res=[]\n for r in range(rows):\n for c in range(cols):\n res.append([r,c])\n \n res.sort(key=lambda x:abs(x[0]-rCenter)+ abs(x[1]-cCenter))\n return res\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Using helper function & sort | matrix-cells-in-distance-order | 0 | 1 | ```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n # create a r, c matrix given the rows & cols\n # each element represents a list [r, c] where r is the row & c the col\n # find find the distances of all cells from the center (append to res)\n # sort the result by distance function\n # Time O(M + N) Space O(M + N)\n \n \n def distance(p1, p2):\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n \n matrix = [[i, j] for i in range(rows) for j in range(cols)]\n center = [rCenter, cCenter]\n matrix.sort(key=lambda c: distance(c, center))\n \n return matrix\n``` | 1 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Using helper function & sort | matrix-cells-in-distance-order | 0 | 1 | ```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n # create a r, c matrix given the rows & cols\n # each element represents a list [r, c] where r is the row & c the col\n # find find the distances of all cells from the center (append to res)\n # sort the result by distance function\n # Time O(M + N) Space O(M + N)\n \n \n def distance(p1, p2):\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n \n matrix = [[i, j] for i in range(rows) for j in range(cols)]\n center = [rCenter, cCenter]\n matrix.sort(key=lambda c: distance(c, center))\n \n return matrix\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Python3 || One-liner based on list comprehesion &sorted() || beats 95.3% runtime & 85.6% mem usage | matrix-cells-in-distance-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[r, c] for r in range(rows) for c in range(cols)], key=lambda x: abs(x[0] - rCenter) + abs(x[1] - cCenter))\n``` | 1 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Python3 || One-liner based on list comprehesion &sorted() || beats 95.3% runtime & 85.6% mem usage | matrix-cells-in-distance-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[r, c] for r in range(rows) for c in range(cols)], key=lambda x: abs(x[0] - rCenter) + abs(x[1] - cCenter))\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Simple & Easy Solution by Python 3 | matrix-cells-in-distance-order | 0 | 1 | ```\nclass Solution:\n def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n cells = [[i, j] for i in range(R) for j in range(C)]\n return sorted(cells, key=lambda p: abs(p[0] - r0) + abs(p[1] - c0))\n``` | 6 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Simple & Easy Solution by Python 3 | matrix-cells-in-distance-order | 0 | 1 | ```\nclass Solution:\n def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n cells = [[i, j] for i in range(R) for j in range(C)]\n return sorted(cells, key=lambda p: abs(p[0] - r0) + abs(p[1] - c0))\n``` | 6 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Python3 - Nasty 1 liner | matrix-cells-in-distance-order | 0 | 1 | \n# Complexity\n- Time complexity:\nO(nlogn) \n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n\n return sorted(\n [[r, c] for r in range(0, rows, 1) for c in range(0, cols, 1)],\n key=lambda coord: abs(coord[0] - rCenter) + abs(coord[1] - cCenter),\n )\n\n``` | 1 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Python3 - Nasty 1 liner | matrix-cells-in-distance-order | 0 | 1 | \n# Complexity\n- Time complexity:\nO(nlogn) \n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n\n return sorted(\n [[r, c] for r in range(0, rows, 1) for c in range(0, cols, 1)],\n key=lambda coord: abs(coord[0] - rCenter) + abs(coord[1] - cCenter),\n )\n\n``` | 1 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Easy solution ||python3 | matrix-cells-in-distance-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n a = []\n b = {}\n\n for i in range(rows):\n for j in range(cols):\n a.append((i, j))\n\n for i in a:\n s = abs(i[0] - rCenter) + abs(i[1] - cCenter)\n b[i] = s\n x=[]\n n= sorted(b.items(), key=lambda x: x[1])\n k= [key for key, value in n]\n for i in k:\n x.append(list(i))\n return x\n \n``` | 0 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Easy solution ||python3 | matrix-cells-in-distance-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n a = []\n b = {}\n\n for i in range(rows):\n for j in range(cols):\n a.append((i, j))\n\n for i in a:\n s = abs(i[0] - rCenter) + abs(i[1] - cCenter)\n b[i] = s\n x=[]\n n= sorted(b.items(), key=lambda x: x[1])\n k= [key for key, value in n]\n for i in k:\n x.append(list(i))\n return x\n \n``` | 0 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Logic Build with the question - python | matrix-cells-in-distance-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n res=[]\n for i in range(rows):\n for j in range(cols):\n res.append([i,j])\n res.sort(key = lambda x: abs(x[0]-rCenter)+abs(x[1]-cCenter))\n return res\n``` | 0 | You are given four integers `row`, `cols`, `rCenter`, and `cCenter`. There is a `rows x cols` matrix and you are on the cell with the coordinates `(rCenter, cCenter)`.
Return _the coordinates of all cells in the matrix, sorted by their **distance** from_ `(rCenter, cCenter)` _from the smallest distance to the largest distance_. You may return the answer in **any order** that satisfies this condition.
The **distance** between two cells `(r1, c1)` and `(r2, c2)` is `|r1 - r2| + |c1 - c2|`.
**Example 1:**
**Input:** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**Output:** \[\[0,0\],\[0,1\]\]
**Explanation:** The distances from (0, 0) to other cells are: \[0,1\]
**Example 2:**
**Input:** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**Output:** \[\[0,1\],\[0,0\],\[1,1\],\[1,0\]\]
**Explanation:** The distances from (0, 1) to other cells are: \[0,1,1,2\]
The answer \[\[0,1\],\[1,1\],\[0,0\],\[1,0\]\] would also be accepted as correct.
**Example 3:**
**Input:** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**Output:** \[\[1,2\],\[0,2\],\[1,1\],\[0,1\],\[1,0\],\[0,0\]\]
**Explanation:** The distances from (1, 2) to other cells are: \[0,1,1,2,2,3\]
There are other answers that would also be accepted as correct, such as \[\[1,2\],\[1,1\],\[0,2\],\[1,0\],\[0,1\],\[0,0\]\].
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rCenter < rows`
* `0 <= cCenter < cols` | null |
Logic Build with the question - python | matrix-cells-in-distance-order | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n res=[]\n for i in range(rows):\n for j in range(cols):\n res.append([i,j])\n res.sort(key = lambda x: abs(x[0]-rCenter)+abs(x[1]-cCenter))\n return res\n``` | 0 | There is a car with `capacity` empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer `capacity` and an array `trips` where `trips[i] = [numPassengersi, fromi, toi]` indicates that the `ith` trip has `numPassengersi` passengers and the locations to pick them up and drop them off are `fromi` and `toi` respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return `true` _if it is possible to pick up and drop off all passengers for all the given trips, or_ `false` _otherwise_.
**Example 1:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 4
**Output:** false
**Example 2:**
**Input:** trips = \[\[2,1,5\],\[3,3,7\]\], capacity = 5
**Output:** true
**Constraints:**
* `1 <= trips.length <= 1000`
* `trips[i].length == 3`
* `1 <= numPassengersi <= 100`
* `0 <= fromi < toi <= 1000`
* `1 <= capacity <= 105` | null |
Python 3 || 7 lines, sliding ptrs || T/M: 83% / 56% | maximum-sum-of-two-non-overlapping-subarrays | 0 | 1 | ```\nclass Solution:\n def maxSumTwoNoOverlap(self, nums: List[int], firstLen: int, secondLen: int) -> int:\n\n nums = list(accumulate(nums, initial = 0))\n mx1 = mx2 = mx3 = 0\n \n for sm0,sm1,sm2,sm3 in zip(nums, \n nums[firstLen:],\n nums[secondLen:],\n nums[firstLen+secondLen:]):\n\n mx1 = max(mx1, sm1 - sm0)\n mx2 = max(mx2, sm2 - sm0)\n mx3 = max(mx3, max(mx1 + sm3-sm1, mx2 + sm3-sm2))\n \n return mx3\n```\n[https://leetcode.com/problems/maximum-sum-of-two-non-overlapping-subarrays/submissions/973518314/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~`len(nums)`. | 6 | Given an integer array `nums` and two integers `firstLen` and `secondLen`, return _the maximum sum of elements in two non-overlapping **subarrays** with lengths_ `firstLen` _and_ `secondLen`.
The array with length `firstLen` could occur before or after the array with length `secondLen`, but they have to be non-overlapping.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,6,5,2,2,5,1,9,4\], firstLen = 1, secondLen = 2
**Output:** 20
**Explanation:** One choice of subarrays is \[9\] with length 1, and \[6,5\] with length 2.
**Example 2:**
**Input:** nums = \[3,8,1,3,2,1,8,9,0\], firstLen = 3, secondLen = 2
**Output:** 29
**Explanation:** One choice of subarrays is \[3,8,1\] with length 3, and \[8,9\] with length 2.
**Example 3:**
**Input:** nums = \[2,1,5,6,0,9,5,0,3,8\], firstLen = 4, secondLen = 3
**Output:** 31
**Explanation:** One choice of subarrays is \[5,6,0,9\] with length 4, and \[0,3,8\] with length 3.
**Constraints:**
* `1 <= firstLen, secondLen <= 1000`
* `2 <= firstLen + secondLen <= 1000`
* `firstLen + secondLen <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
Python 3 || 7 lines, sliding ptrs || T/M: 83% / 56% | maximum-sum-of-two-non-overlapping-subarrays | 0 | 1 | ```\nclass Solution:\n def maxSumTwoNoOverlap(self, nums: List[int], firstLen: int, secondLen: int) -> int:\n\n nums = list(accumulate(nums, initial = 0))\n mx1 = mx2 = mx3 = 0\n \n for sm0,sm1,sm2,sm3 in zip(nums, \n nums[firstLen:],\n nums[secondLen:],\n nums[firstLen+secondLen:]):\n\n mx1 = max(mx1, sm1 - sm0)\n mx2 = max(mx2, sm2 - sm0)\n mx3 = max(mx3, max(mx1 + sm3-sm1, mx2 + sm3-sm2))\n \n return mx3\n```\n[https://leetcode.com/problems/maximum-sum-of-two-non-overlapping-subarrays/submissions/973518314/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~`len(nums)`. | 6 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
[Python3] Linear Solution | maximum-sum-of-two-non-overlapping-subarrays | 0 | 1 | # Approach\n1D Dynamic Programming\n- `dp_first[i]` represents the maximum sum of `firstLen` subarray using the first `i` elements in `nums`.\n- `dp_second[i]` represents the maximum sum of `secondLen` subarray using the first `i` elements in `nums`.\n- `dp[i]` represents the maximum sum of elements in two non-overlapping subarrays with lengths firstLen and secondLen ending at `(i-1)th` th element (must including `(i-1)th` element). \n\n# Complexity\n- Time complexity:$$O(n)$$\n- Space complexity: $$O(n)$$\n\n\n# Code\n```python3\nclass Solution:\n def maxSumTwoNoOverlap(self, nums: List[int], firstLen: int, secondLen: int) -> int:\n prefix_sums = [0 for _ in range(len(nums) + 1)]\n for idx in range(1, len(prefix_sums)):\n prefix_sums[idx] = prefix_sums[idx-1] + nums[idx-1]\n \n dp_first = [-2**31 + 1 for _ in range(len(nums)+1)]\n dp_second = [-2**31 + 1 for _ in range(len(nums)+1)]\n dp = [-2**31 + 1 for _ in range(len(nums)+1)]\n\n max_sum = -2**31 + 1\n for i in range(1, len(nums)+1):\n if i >= firstLen:\n dp_first[i] = prefix_sums[i] - prefix_sums[i-firstLen]\n dp[i] = max(dp[i], dp_first[i] + dp_second[i-firstLen])\n if i >= secondLen:\n dp_second[i] = prefix_sums[i] - prefix_sums[i-secondLen]\n dp[i] = max(dp[i], dp_second[i] + dp_first[i-secondLen])\n dp_first[i] = max(dp_first[i], dp_first[i-1])\n dp_second[i] = max(dp_second[i], dp_second[i-1])\n max_sum = max(max_sum, dp[i])\n return max_sum\n``` | 1 | Given an integer array `nums` and two integers `firstLen` and `secondLen`, return _the maximum sum of elements in two non-overlapping **subarrays** with lengths_ `firstLen` _and_ `secondLen`.
The array with length `firstLen` could occur before or after the array with length `secondLen`, but they have to be non-overlapping.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,6,5,2,2,5,1,9,4\], firstLen = 1, secondLen = 2
**Output:** 20
**Explanation:** One choice of subarrays is \[9\] with length 1, and \[6,5\] with length 2.
**Example 2:**
**Input:** nums = \[3,8,1,3,2,1,8,9,0\], firstLen = 3, secondLen = 2
**Output:** 29
**Explanation:** One choice of subarrays is \[3,8,1\] with length 3, and \[8,9\] with length 2.
**Example 3:**
**Input:** nums = \[2,1,5,6,0,9,5,0,3,8\], firstLen = 4, secondLen = 3
**Output:** 31
**Explanation:** One choice of subarrays is \[5,6,0,9\] with length 4, and \[0,3,8\] with length 3.
**Constraints:**
* `1 <= firstLen, secondLen <= 1000`
* `2 <= firstLen + secondLen <= 1000`
* `firstLen + secondLen <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
[Python3] Linear Solution | maximum-sum-of-two-non-overlapping-subarrays | 0 | 1 | # Approach\n1D Dynamic Programming\n- `dp_first[i]` represents the maximum sum of `firstLen` subarray using the first `i` elements in `nums`.\n- `dp_second[i]` represents the maximum sum of `secondLen` subarray using the first `i` elements in `nums`.\n- `dp[i]` represents the maximum sum of elements in two non-overlapping subarrays with lengths firstLen and secondLen ending at `(i-1)th` th element (must including `(i-1)th` element). \n\n# Complexity\n- Time complexity:$$O(n)$$\n- Space complexity: $$O(n)$$\n\n\n# Code\n```python3\nclass Solution:\n def maxSumTwoNoOverlap(self, nums: List[int], firstLen: int, secondLen: int) -> int:\n prefix_sums = [0 for _ in range(len(nums) + 1)]\n for idx in range(1, len(prefix_sums)):\n prefix_sums[idx] = prefix_sums[idx-1] + nums[idx-1]\n \n dp_first = [-2**31 + 1 for _ in range(len(nums)+1)]\n dp_second = [-2**31 + 1 for _ in range(len(nums)+1)]\n dp = [-2**31 + 1 for _ in range(len(nums)+1)]\n\n max_sum = -2**31 + 1\n for i in range(1, len(nums)+1):\n if i >= firstLen:\n dp_first[i] = prefix_sums[i] - prefix_sums[i-firstLen]\n dp[i] = max(dp[i], dp_first[i] + dp_second[i-firstLen])\n if i >= secondLen:\n dp_second[i] = prefix_sums[i] - prefix_sums[i-secondLen]\n dp[i] = max(dp[i], dp_second[i] + dp_first[i-secondLen])\n dp_first[i] = max(dp_first[i], dp_first[i-1])\n dp_second[i] = max(dp_second[i], dp_second[i-1])\n max_sum = max(max_sum, dp[i])\n return max_sum\n``` | 1 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
PYTHON SOL || VERY SIMPLE || EXPLAINED || SLIDING WINDOW || | maximum-sum-of-two-non-overlapping-subarrays | 0 | 1 | \n# EXPLANATION\n```\nFor every firstLen subarray find the maximum sum secondLen size subarray\n\nSay we have arr = [1,2,3,4,5,6,7,8,9,10] firstLen = 3 , secondLen = 4\n\nWe took the subarray with firstLen : [5,6,7]\nNow the secondLen subarray with max sum can be in\n1. [1,2,3,4]\n2. [8,9,10]\n\n\n\n```\n\n# CODE\n```\nclass Solution:\n def getMaxSubarraySum(self,arr,size):\n n = len(arr)\n if n < size: return 0\n best = tmp = sum(arr[:size])\n for i in range(1,n-size+1):\n tmp = tmp + arr[i+size-1] - arr[i-1]\n if tmp > best:best = tmp\n return best\n def maxSumTwoNoOverlap(self, nums: List[int], firstLen: int, secondLen: int) -> int:\n n = len(nums)\n summ = sum(nums[:firstLen])\n ans = summ + self.getMaxSubarraySum(nums[firstLen:],secondLen) \n for i in range(1,n-firstLen+1):\n summ = summ + nums[i+firstLen-1] - nums[i-1]\n a = self.getMaxSubarraySum(nums[:i],secondLen)\n b = self.getMaxSubarraySum(nums[i+firstLen:],secondLen)\n m = a if a > b else b\n if summ + m > ans: ans = summ + m\n return ans\n``` | 5 | Given an integer array `nums` and two integers `firstLen` and `secondLen`, return _the maximum sum of elements in two non-overlapping **subarrays** with lengths_ `firstLen` _and_ `secondLen`.
The array with length `firstLen` could occur before or after the array with length `secondLen`, but they have to be non-overlapping.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,6,5,2,2,5,1,9,4\], firstLen = 1, secondLen = 2
**Output:** 20
**Explanation:** One choice of subarrays is \[9\] with length 1, and \[6,5\] with length 2.
**Example 2:**
**Input:** nums = \[3,8,1,3,2,1,8,9,0\], firstLen = 3, secondLen = 2
**Output:** 29
**Explanation:** One choice of subarrays is \[3,8,1\] with length 3, and \[8,9\] with length 2.
**Example 3:**
**Input:** nums = \[2,1,5,6,0,9,5,0,3,8\], firstLen = 4, secondLen = 3
**Output:** 31
**Explanation:** One choice of subarrays is \[5,6,0,9\] with length 4, and \[0,3,8\] with length 3.
**Constraints:**
* `1 <= firstLen, secondLen <= 1000`
* `2 <= firstLen + secondLen <= 1000`
* `firstLen + secondLen <= nums.length <= 1000`
* `0 <= nums[i] <= 1000` | null |
PYTHON SOL || VERY SIMPLE || EXPLAINED || SLIDING WINDOW || | maximum-sum-of-two-non-overlapping-subarrays | 0 | 1 | \n# EXPLANATION\n```\nFor every firstLen subarray find the maximum sum secondLen size subarray\n\nSay we have arr = [1,2,3,4,5,6,7,8,9,10] firstLen = 3 , secondLen = 4\n\nWe took the subarray with firstLen : [5,6,7]\nNow the secondLen subarray with max sum can be in\n1. [1,2,3,4]\n2. [8,9,10]\n\n\n\n```\n\n# CODE\n```\nclass Solution:\n def getMaxSubarraySum(self,arr,size):\n n = len(arr)\n if n < size: return 0\n best = tmp = sum(arr[:size])\n for i in range(1,n-size+1):\n tmp = tmp + arr[i+size-1] - arr[i-1]\n if tmp > best:best = tmp\n return best\n def maxSumTwoNoOverlap(self, nums: List[int], firstLen: int, secondLen: int) -> int:\n n = len(nums)\n summ = sum(nums[:firstLen])\n ans = summ + self.getMaxSubarraySum(nums[firstLen:],secondLen) \n for i in range(1,n-firstLen+1):\n summ = summ + nums[i+firstLen-1] - nums[i-1]\n a = self.getMaxSubarraySum(nums[:i],secondLen)\n b = self.getMaxSubarraySum(nums[i+firstLen:],secondLen)\n m = a if a > b else b\n if summ + m > ans: ans = summ + m\n return ans\n``` | 5 | Under the grammar given below, strings can represent a set of lowercase words. Let `R(expr)` denote the set of words the expression represents.
The grammar can best be understood through simple examples:
* Single letters represent a singleton set containing that word.
* `R( "a ") = { "a "}`
* `R( "w ") = { "w "}`
* When we take a comma-delimited list of two or more expressions, we take the union of possibilities.
* `R( "{a,b,c} ") = { "a ", "b ", "c "}`
* `R( "{{a,b},{b,c}} ") = { "a ", "b ", "c "}` (notice the final set only contains each word at most once)
* When we concatenate two expressions, we take the set of possible concatenations between two words where the first word comes from the first expression and the second word comes from the second expression.
* `R( "{a,b}{c,d} ") = { "ac ", "ad ", "bc ", "bd "}`
* `R( "a{b,c}{d,e}f{g,h} ") = { "abdfg ", "abdfh ", "abefg ", "abefh ", "acdfg ", "acdfh ", "acefg ", "acefh "}`
Formally, the three rules for our grammar:
* For every lowercase letter `x`, we have `R(x) = {x}`.
* For expressions `e1, e2, ... , ek` with `k >= 2`, we have `R({e1, e2, ...}) = R(e1) ∪ R(e2) ∪ ...`
* For expressions `e1` and `e2`, we have `R(e1 + e2) = {a + b for (a, b) in R(e1) * R(e2)}`, where `+` denotes concatenation, and `*` denotes the cartesian product.
Given an expression representing a set of words under the given grammar, return _the sorted list of words that the expression represents_.
**Example 1:**
**Input:** expression = "{a,b}{c,{d,e}} "
**Output:** \[ "ac ", "ad ", "ae ", "bc ", "bd ", "be "\]
**Example 2:**
**Input:** expression = "{{a,z},a{b,c},{ab,z}} "
**Output:** \[ "a ", "ab ", "ac ", "z "\]
**Explanation:** Each distinct word is written only once in the final answer.
**Constraints:**
* `1 <= expression.length <= 60`
* `expression[i]` consists of `'{'`, `'}'`, `','`or lowercase English letters.
* The given `expression` represents a set of words based on the grammar given in the description. | We can use prefix sums to calculate any subarray sum quickly.
For each L length subarray, find the best possible M length subarray that occurs before and after it. |
Python by search in Trie [w/ Visualization] | stream-of-characters | 0 | 1 | Python by search in Trie\n\n---\n\n**Hint**:\n\nBecause [description](https://leetcode.com/problems/stream-of-characters/) asks us to search from tail, the **last k characters** queried, where k >= 1,\nwe build a trie and search word in **reversed order** to satisfy the requirement.\n\n---\n\n**Visualization**\n\n\n\n\n\n\n\n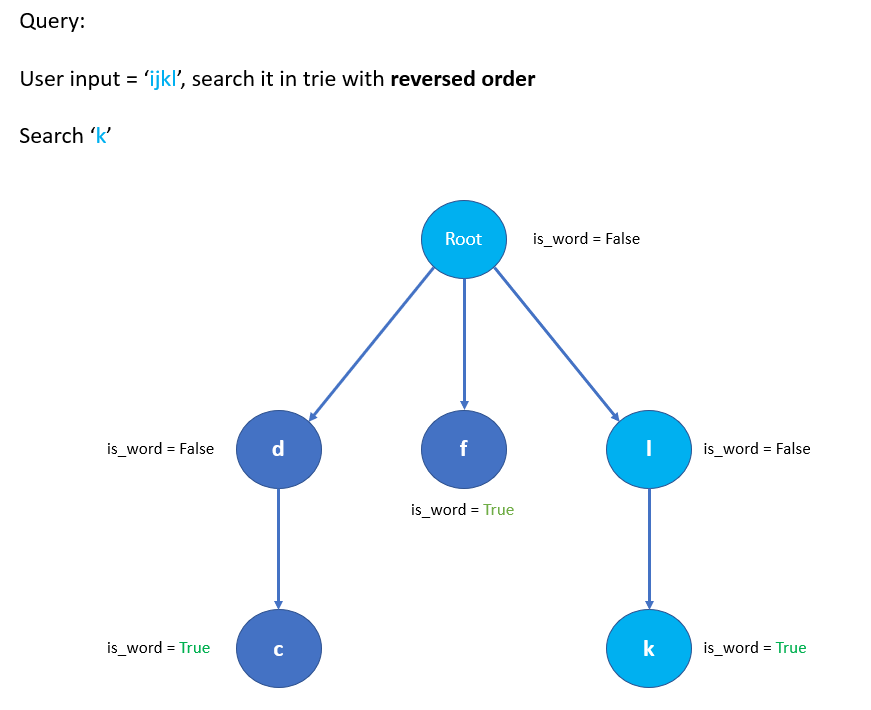\n\n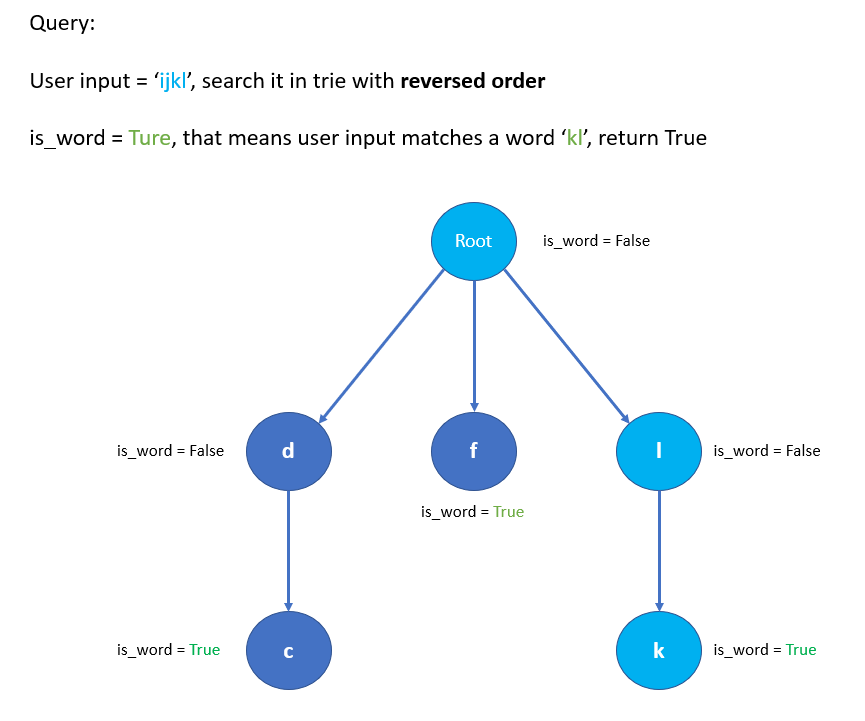\n\n---\n\n**Implementation**:\n\n```\nfrom collections import defaultdict\n\nclass TrieNode:\n \n def __init__(self):\n \n self.dict = defaultdict(TrieNode)\n self.is_word = False\n\n\nclass StreamChecker:\n\n def __init__(self, words: List[str]):\n \'\'\'\n Build a trie for each word in reversed order\n \'\'\'\n\t\t\n # for user query record, init as empty string\n self.prefix = \'\'\n \n # for root node of trie, init as empty Trie\n self.trie = TrieNode()\n \n for word in words:\n \n cur_node = self.trie\n \n\t\t\t# make word in reverse order\n word = word[::-1]\n \n for char in word: \n cur_node = cur_node.dict[ char ]\n \n\t\t\t# mark this trie path as a valid word\n cur_node.is_word = True\n \n \n \n def query(self, letter: str) -> bool:\n \'\'\'\n Search user input in trie with reversed order\n \'\'\'\n\t\t\n self.prefix += letter\n \n cur_node = self.trie\n for char in reversed(self.prefix):\n \n if char not in cur_node.dict:\n # current char not in Trie, impossible to match words\n break\n \n cur_node = cur_node.dict[char]\n \n if cur_node.is_word:\n # user input match a word in Trie\n return True\n \n # No match\n return False\n```\n\n---\n\nReference:\n\n[1] [Wiki: Trie](https://en.wikipedia.org/wiki/Trie) | 34 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
🤌 A very different Trie solution that is O(len(words)), beats 93.1%. With explanation. 🤏 | stream-of-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUnlike the editorial solurion, I don\'t reverse the strings.\nInstead, for the query step, I store the list of non-leaf nodes in the trie that can continue search to find a match. Since the stream comes char by char, I only need to iterate over my chached candidates to see if the new char ends up with a matched word. Each search in a candidate is O(1) since there are only 26 English characters, the number of candidates is O(len(words)). My candidates are refreshed at each char.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUnlike the editorial solurion, I don\'t reverse the strings.\nInstead, for the query step, I store the list of non-leaf nodes in the trie that can continue search to find a match. Since the stream comes char by char, I only need to iterate over my chached candidates to see if the new char ends up with a matched word. Each search in a candidate is O(1) since there are only 26 English characters, the number of candidates is O(len(words)). My candidates are refreshed at each char.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nFor query: O(L) where L is the size of corpus, aka, len(words)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nFor query: O(L) where L is the size of corpus, aka, len(words)\n\n# Code\n```\nclass StreamChecker:\n def __init__(self, words: List[str]):\n # build a trie for the words\n self.trie_root = {}\n # a list of valid nodes that can continue from the previous search\n self.candidates = [] \n\n # build the trie\n for w in words:\n cur = self.trie_root\n for c in w:\n if c in cur:\n cur = cur[c]\n else:\n cur[c] = {}\n cur = cur[c]\n # mark end of word\n cur["#"] = {} \n\n def query(self, letter: str) -> bool:\n new_candidates = []\n found_match = False\n # a new candidate\n if letter in self.trie_root:\n node = self.trie_root[letter]\n if "#" in node:\n found_match = True\n # it\'s possible that the matched word is a prefix \n # of another word\n if len(node) > 1:\n new_candidates.append(node)\n else:\n new_candidates.append(node)\n\n # iterate over candidates to check if the candidates are still valid\n # or if it matches a word (can be both)\n for node in self.candidates:\n if letter in node:\n next_node = node[letter]\n if "#" in next_node:\n found_match = True\n if len(next_node) > 1:\n new_candidates.append(next_node)\n else:\n new_candidates.append(next_node)\n self.candidates = new_candidates\n\n return found_match\n\n\n# Your StreamChecker object will be instantiated and called as such:\n# obj = StreamChecker(words)\n# param_1 = obj.query(letter)\n``` | 2 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
Python no trie | stream-of-characters | 0 | 1 | ```\nclass StreamChecker:\n\n def __init__(self, words: List[str]):\n self.dic = {}\n for word in words:\n if word[-1] not in self.dic:\n self.dic[word[-1]] = [word[:-1]]\n else:\n self.dic[word[-1]].append(word[:-1])\n \n self.string = ""\n\n def query(self, letter: str) -> bool:\n self.string += letter\n if letter in self.dic:\n for word in self.dic[letter]:\n length = len(word) + 1\n complete_word = word + letter\n if len(self.string) >= length and complete_word == self.string[- length:]:\n return True\n return False\n else:\n return False\n```\n\nThe idea is set up a dictionary for the last char for all words in words\nthen add up string and if we see a letter in the dic and the length of string is greater than the word, reverse query the string and see if it matches the words | 7 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
Simple TRIE solution (query in reverse idea) - beats 86% of the submitted solutions in terms of time | stream-of-characters | 0 | 1 | \n\n# Code\n```\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.isWord = False\n \nclass StreamChecker:\n\n def __init__(self, words: List[str]):\n self.trie = TrieNode()\n self.stream = []\n\n for word in words:\n node = self.trie\n for char in reversed(word):\n if char not in node.children:\n node.children[char] = TrieNode()\n node = node.children[char]\n node.isWord = True\n\n def query(self, letter: str) -> bool:\n self.stream.append(letter)\n node = self.trie\n\n for char in reversed(self.stream):\n if char in node.children:\n node = node.children[char]\n if node.isWord:\n return True\n else:\n break\n return False\n\n\n# Your StreamChecker object will be instantiated and called as such:\n# obj = StreamChecker(words)\n# param_1 = obj.query(letter)\n``` | 0 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
Pythonic space-friendly solution | stream-of-characters | 0 | 1 | low memory impact by dint of python\'s "copy by reference" for dicts - hence our list of dicts does not require cloning\n```\nclass StreamChecker:\n\n def __init__(self, words: List[str]):\n self.bank = {}\n for word in words:\n d = self.bank\n for c in word:\n d.setdefault(c, {})\n d = d[c]\n d[None] = None # sentinel for "word end"\n self.candidates = []\n\n def query(self, letter: str) -> bool:\n self.candidates = [\n c for c in (\n candidate.get(letter)\n for candidate in (self.bank, *self.candidates)\n ) if c\n ]\n return any(None in candidate for candidate in self.candidates)\n``` | 0 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
Python3 Trie: Quick to understand solution / excellent readability & code quality | stream-of-characters | 0 | 1 | ```\n# W = # of words\n# L = avg. # of characters in a word\n# Time Complexity:\n# - Initialization: \n# - O(W\xD7L)\n# - Query: \n# - O(N) per call\n# Space Complexity:\n# - Trie: \n# - O(W\xD7L)\n# - Query: \n# - O(N) per call\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.isWord = False\n\nclass StreamChecker:\n def __init__(self, words: List[str]):\n self.trie = TrieNode()\n self.current_nodes = [self.trie]\n for word in words:\n cur = self.trie\n for char in word:\n if not char in cur.children:\n cur.children[char] = TrieNode()\n cur = cur.children[char]\n cur.isWord = True\n\n def query(self, letter: str) -> bool:\n new_nodes = [self.trie]\n is_word = False\n\n for node in self.current_nodes:\n if letter in node.children:\n new_nodes.append(node.children[letter])\n if node.children[letter].isWord:\n is_word = True\n self.current_nodes = new_nodes\n return is_word\n```\n | 0 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
Short Python3 solution; beats 98.92% RT, 70.04% M | stream-of-characters | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nI used the standard trie approach, which stores the words in reverse.\n\n# Complexity\n- Time complexity: $O(\\sum_{w\\in{\\tt words}} {\\rm len}(w))$ to build the trie and $O(\\max_{w\\in{\\tt words}} {\\rm len}(w))$ to query a letter\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(\\sum_{w\\in{\\tt words}} {\\rm len}(w))$ to store the trie and $O(\\#{\\rm queries})$ to store the letters as they arrive\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Python\nclass StreamChecker:\n\n def __init__(self, words: List[str]):\n # store trie as a nested dict\n self.d = {} \n for word in words:\n d = self.d\n for l in reversed(word):\n if l not in d:\n d[l] = {}\n d = d[l]\n # add a leaf node at the end of each word\n d[None] = None \n\n # record the letters as they arrive\n self.letters = []\n \n\n def query(self, letter: str) -> bool:\n self.letters += [letter]\n\n d = self.d\n for l in reversed(self.letters):\n if None in d:\n return True\n if l not in d:\n return False\n d = d[l]\n return None in d\n\n``` | 0 | Design an algorithm that accepts a stream of characters and checks if a suffix of these characters is a string of a given array of strings `words`.
For example, if `words = [ "abc ", "xyz "]` and the stream added the four characters (one by one) `'a'`, `'x'`, `'y'`, and `'z'`, your algorithm should detect that the suffix `"xyz "` of the characters `"axyz "` matches `"xyz "` from `words`.
Implement the `StreamChecker` class:
* `StreamChecker(String[] words)` Initializes the object with the strings array `words`.
* `boolean query(char letter)` Accepts a new character from the stream and returns `true` if any non-empty suffix from the stream forms a word that is in `words`.
**Example 1:**
**Input**
\[ "StreamChecker ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query ", "query "\]
\[\[\[ "cd ", "f ", "kl "\]\], \[ "a "\], \[ "b "\], \[ "c "\], \[ "d "\], \[ "e "\], \[ "f "\], \[ "g "\], \[ "h "\], \[ "i "\], \[ "j "\], \[ "k "\], \[ "l "\]\]
**Output**
\[null, false, false, false, true, false, true, false, false, false, false, false, true\]
**Explanation**
StreamChecker streamChecker = new StreamChecker(\[ "cd ", "f ", "kl "\]);
streamChecker.query( "a "); // return False
streamChecker.query( "b "); // return False
streamChecker.query( "c "); // return False
streamChecker.query( "d "); // return True, because 'cd' is in the wordlist
streamChecker.query( "e "); // return False
streamChecker.query( "f "); // return True, because 'f' is in the wordlist
streamChecker.query( "g "); // return False
streamChecker.query( "h "); // return False
streamChecker.query( "i "); // return False
streamChecker.query( "j "); // return False
streamChecker.query( "k "); // return False
streamChecker.query( "l "); // return True, because 'kl' is in the wordlist
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 200`
* `words[i]` consists of lowercase English letters.
* `letter` is a lowercase English letter.
* At most `4 * 104` calls will be made to query. | null |
Clean Python, beats 100% | moving-stones-until-consecutive | 0 | 1 | Good code should focus on readability instead of being as short as possible.\n\n```\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n x, y, z = sorted([a, b, c])\n if x + 1 == y == z - 1:\n min_steps = 0\n elif y - x > 2 and z - y > 2:\n min_steps = 2\n else:\n min_steps = 1\n max_steps = z - x - 2\n return [min_steps, max_steps]\n``` | 30 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Just IF/Else Only | moving-stones-until-consecutive | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n l = [a, b, c]\n l.sort()\n max_moves = (l[1] - l[0] - 1) + (l[2] - l[1] - 1)\n\n if l[1]-l[0]==l[2]-l[1]==1:\n return [0,max_moves]\n elif l[1]-l[0]==2 or l[2]-l[1]==2 or l[1]-l[0]==1 or l[2]-l[1]==1:\n return [1,max_moves]\n else:\n return [2,max_moves]\n\n\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Python3 | DP approach | moving-stones-until-consecutive | 0 | 1 | # Intuition\nThis problem can be broken down into distinct subtasks whose solutions always remain the same. That is, for some unique configuration of states $(i,j,k)$, the answer for the least and most number of moves to reach the desired configuration of $(v,v+1,v+2)$ will be the aggregated minimum and aggregated maximum of $1 + \\mathrm{dp}(x,y,z)$, respectively, for values of $(x,y,z)$ that were achieved by performing an allowed operation on $(i,j,k)$.\n\n### min number of moves\nFor least number of moves, we would like to move the stones as close to each other as possible in a single move. There are four such ways we can do this, conditionally, for $i < j < k$:\n\n1. If $i < j-1$, then we can consider\n 1. Moving stone at position $i$ to position $j-1$\n 2. Moving stone at position $k$ to position $j-1$\n2. If $k > j+1$, then we can consider\n 1. Moving stone at position $k$ to position $j+1$\n 2. Moving stone at position $i$ to position $j+1$\n\nAnd the answer is the aggregated minimum of all such choices.\n\n### max number of moves\nFor most number of moves, we would like to move the endpoint stones to positions strictly inside the interval (not inclusive) while keeping them as far away from other stones as possible, which can be done in two ways, for $i < j < k$:\n 1. If $i < j -1$, moving stone at position $i$ to position $i+1$\n 2. If $k > j + 1$, moving stone at position $k$ to position $k-1$\n\nAnd the answer is the aggregated maximum of all such choices.\n\n# Approach\nThe states are the positions of the three stones: $a,b$ and $c$. Since $1 \\le a,b,c \\le 100 \\implies abc \\le 10^6$, our cache will be reasonably sized, and we can expect that the solution will *not* exceed the memory limit. We set up the DP as it was outlined in the intuition section of this post.\n\n\n# Code\n```python3 []\nfrom functools import cache\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n a, b, c = sorted([a, b, c])\n\n @cache\n def max_moves(i, j, k):\n if i == j - 1 and j == k - 1: return 0\n moves = 0\n if i < j - 1: moves = 1 + max_moves(i + 1, j, k)\n if k > j + 1: moves = max(moves, 1 + max_moves(i, j, k - 1))\n return moves\n\n @cache\n def min_moves(i, j, k):\n if i == j - 1 and j == k - 1: return 0\n moves = float(\'inf\')\n if i < j - 1:\n moves = 1 + min_moves(j - 1, j, k)\n moves = min(moves, 1 + min_moves(i,j-1,j))\n if k > j + 1:\n moves = min(moves, 1 + min_moves(i, j, j + 1))\n moves = min(moves, 1 + min_moves(j,j+1,k))\n return moves\n\n return [min_moves(a, b, c), max_moves(a, b, c)]\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Simple python3 solution | 3 cases | moving-stones-until-consecutive | 0 | 1 | # Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n a, b, c = sorted((a, b, c))\n\n delta_1 = b - a\n delta_2 = c - b\n\n if delta_1 == delta_2 == 1:\n return [0, 0]\n if min(delta_1, delta_2) <= 2:\n return [1, delta_1 + delta_2 - 2]\n return [2, delta_1 + delta_2 - 2]\n\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Basic Approach Beats 88% | moving-stones-until-consecutive | 0 | 1 | # Approach\nYou need to just study the different types of cases that are mentioned in the below code :).\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n a,b,c=sorted([a,b,c])\n d,e=abs(b-a),abs(c-b)\n if d==e==1:\n return [0,0]\n if d==1 or e==1 or d==2 or e==2:\n return [1,e+d-2]\n return [2,e+d-2]\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Python easy to understand beats 91.77% | moving-stones-until-consecutive | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nminimum move:\n1.if no any gap between stones, return 0\n \u25CF\u25CF\u25CF\n2.if there have only a gap between 2 stones, return 1 \n \u25CF\u25C9\u25CF--\u25CB\n3.in the other case, you gotta move 2 stone anyway, return 2 \n \u25CF\u25C9\u25C9-\u25CB-\u25CB\n\nmaximum move:\njust count all the gap between first stone and last stone\n\u25CF--\u25CF-\u25CF\n\u25CF--\u25CF\u25C9\u25CB\n\u25CF-\u25C9\u25CF\u25CB-\n\u25CF\u25C9\u25CF\u25CB--\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n stone=sorted([a,b,c])\n return [ 0 if stone[0]+1==stone[1] and stone[1]+1==stone[2] else 1 if stone[1]-stone[0]<=2 or stone[2]-stone[1]<=2 else 2 ,(stone[2]-stone[0])-2]\n\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Solution | moving-stones-until-consecutive | 1 | 1 | ```C++ []\nclass Solution {\n public:\n vector<int> numMovesStones(int a, int b, int c) {\n vector<int> nums = {a, b, c};\n\n sort(begin(nums), end(nums));\n\n if (nums[2] - nums[0] == 2)\n return {0, 0};\n return {min(nums[1] - nums[0], nums[2] - nums[1]) <= 2 ? 1 : 2,\n nums[2] - nums[0] - 2};\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n pos = sorted([a, b, c])\n\n if (pos[1] - pos[0] == 1 and pos[2] - pos[1] == 1):\n minVal = 0\n elif (pos[1] - pos[0] <= 2 or pos[2] - pos[1] <= 2):\n minVal = 1\n else:\n minVal = 2\n\n maxVal = pos[2] - pos[0] - 2\n\n return [minVal, maxVal]\n```\n\n```Java []\nclass Solution {\n public int[] numMovesStones(int a, int b, int c) {\n int low=Math.min(Math.min(a,b),c);\n int high=Math.max(Math.max(a,b),c);\n int mid=0;\n int min=0;\n if(a>low && a<high) mid=a;\n if(b>low && b<high) mid=b;\n if(c>low && c<high) mid=c;\n int max=mid-low-1+high-mid-1;\n if(mid-low-1<1 && high-mid-1<1) min=0;\n else\n if( mid-low-1<=1 || high-mid-1<=1) min=1;\n else min=2;\n return new int[]{min,max};\n }\n}\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
| Python3 - 4 Lines | ✔ | moving-stones-until-consecutive | 0 | 1 | Python3 Solution\n\n# Code\n```\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n a,b,c=sorted([a,b,c])\n if b-a==1 and c-b==1: return [0,b-(a+1)+c-(b+1)]\n elif b-a==1 or c-b==1 or c-a==1 or b-a==2 or c-b==2 or c-a==2: return [1,b-(a+1)+c-(b+1)]\n else: return [2,b-(a+1)+c-(b+1)]\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Python - easy space reduction with 3 rules | moving-stones-until-consecutive | 0 | 1 | # Intuition\nProblem is about reduction of spaces within range.\nTake spaces in between middle item and edge items, those spaces are area you can move within. Max steps is just sum of those.\nMin steps is reduced to 3 cases:\n1. If both zero then number of moves is 0.\n2. if just one is zero or one then there is one step needed. Other can be fixed with just one step.\n3. Otherwise you need minimum 2 steps, why: move one edge element in between middle element and other edge element just next to middle element and then move other edge element next to it, that needs exactly 2 steps.\n\n\n# Approach\nSort input to simply life, calculate spaces between edge elements and middle element. Take sum of those as max. To get min value apply those 3 rules above.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def min_steps(self, a, b):\n if max(a, b) == 0: return 0\n if min(a, b) in [0, 1]: return 1\n return 2\n \n def get_spaces(self, A):\n a, b, c = sorted(A)\n return b - a - 1, c - b - 1\n\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n space1, space2 = self.get_spaces([a, b, c])\n return [self.min_steps(space1, space2), space1 + space2]\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Clean Python | 6 lines | High Speed | O(n) time, O(1) space | Beats 96.9% | moving-stones-until-consecutive | 0 | 1 | \n# Code\n```\nclass Solution:\n def numMovesStones(self, a: int, b: int, c: int) -> List[int]:\n x, y, z = sorted([a, b, c])\n if x + 1 == y == z - 1: min_steps = 0\n elif y - x > 2 and z - y > 2: min_steps = 2\n else: min_steps = 1\n max_steps = z - x - 2\n return [min_steps, max_steps]\n``` | 0 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
BFS | Beats 99% | Easy to Understand | coloring-a-border | 0 | 1 | Question is poorly articulated so I\'ll try to explain a bit.\nAdjacency - Two squares are adjacent id they are in one of the four (up, down, left, right) directions of each other.\nConnected Component - A connected component is a set of squares which are adjacent to at least one of the squares in the connected component and carry the same color\nBoundary - A square is said to be a boundary square of a connected component if it\'s either adjacent to a square of different color or is a boundary square of our grid i.e a square of first or last row or column.\n\nNow the question asks us to paint the boundary of the said connected component with a particular given color.\n\n**Solution-**\nNow the solution to it is pretty easy, you traverse the whole conncted component and change the color of each square whose all 4 adjacent sides does not contain the original color.\n\n**Simple readable code with the said logic-**\n\n\n\n```\nclass Solution:\n def colorBorder(self, grid: List[List[int]], row: int, col: int, color: int) -> List[List[int]]:\n m = len(grid)\n n = len(grid[0])\n\n change = []\n \n queue = [[row, col]]\n q = 1 \n \n ori = grid[row][col]\n \n vis = [[0]*n for i in range(m)]\n vis[row][col] = 1 \n \n while q > 0:\n r, c = queue.pop(0)\n q -= 1\n \n sides = 0\n \n if r-1 >= 0:\n if grid[r-1][c] == ori:\n sides += 1\n if not vis[r-1][c]:\n vis[r-1][c] = 1 \n if grid[r-1][c] == ori:\n queue.append([r-1, c])\n q += 1 \n \n if c-1 >= 0:\n if grid[r][c-1] == ori:\n sides += 1\n if not vis[r][c-1]:\n vis[r][c-1] = 1 \n if grid[r][c-1] == ori:\n queue.append([r, c-1])\n q += 1 \n \n if r+1 < m:\n if grid[r+1][c] == ori:\n sides += 1\n if not vis[r+1][c]:\n vis[r+1][c] = 1 \n if grid[r+1][c] == ori:\n queue.append([r+1, c])\n q += 1 \n \n if c+1 < n:\n if grid[r][c+1] == ori:\n sides += 1\n if not vis[r][c+1]:\n vis[r][c+1] = 1 \n if grid[r][c+1] == ori:\n queue.append([r, c+1])\n q += 1 \n \n if sides != 4:\n change.append([r, c])\n \n for r, c in change:\n grid[r][c] = color \n \n return grid | 2 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Detailed Explanation With Pictures | coloring-a-border | 0 | 1 | ` Suppose given `\n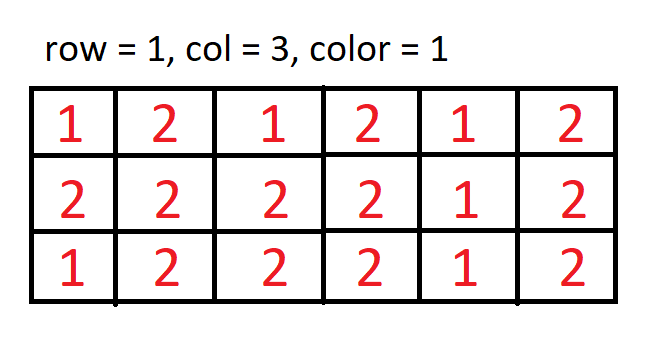\n\n``` \nAll the neighbour(4 directions) of grid[1][3] including neighbours of the neighbours of \ngrid[1][3]\n```\n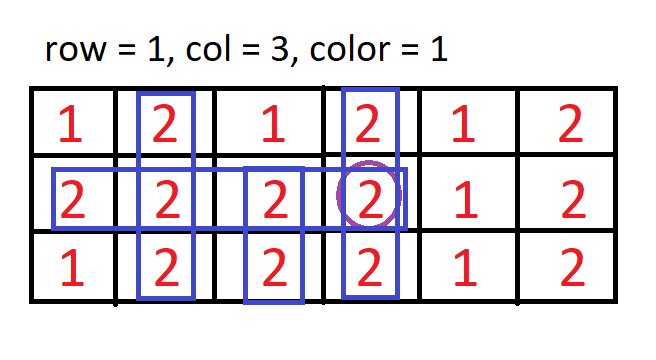\n\n```\nNow you have to go through the all of those grid[1][3]\'s neighbours and change the color of \nthose cells which are on the border(cell whose 4 direction cells values are not equal to\n that cell value)\n```\n```\nLet\'s look at the cell grid[1][2].\n```\n\n\n```\nHere only the upper neighbour(green marked) is not same as grid[1][2] (purple marked).\nSo grid[1][2] is on the border and thus we color it to 1.\n```\n```\nFor grid[1][1] : \n```\n\n\n```\nFor grid[1][1](purple marked) all it\'s neighbour has the same value as grid[1][1] has, means\nthis cell is not on the border and that\'s why we won\'t color it to 1.\n```\n```\nFinal Output : (red = previous color, blue = new color)\n```\n\n\n\n### My Solution Explanation :\n```\nIf you want to run the dfs and change the border cell to new color in the dfs it would\nbe huge messy : \n```\n\n\n```\nIf I change the color of grid[1][3] and grid[1][2] at the same time in dfs function, then \nfor grid[1][1] (purple marked) it\'s right neighbour(grid[1][2]) is 1 and grid[1][1] will be \ncolored to 1 as it\'s all neighbours value are not same as grid[1][1] BUT grid[1][1] can\'t be\ncolored to 1 as in the Q it\'s all neighbour has the same value as its.\n```\n```\nInstead I made a boolean array of the same size as grid and marked all the neighbours of \ngrid[row][col] as 1 in dfs(). Now I can easily traverse the \'visited\' array and change the \nborder cells of \'grid\' to \'color\'.\n```\n\n\n```\nTo check if the current cell (grid[r][c]) is on the border or not :\n\n1. If the cell is on the first or the last row as \'CELLS ON THE FIRST ROW MISSING UPPER \n NEIGHBOUR\' AND \'LAST ROW BOTTOM NEIGHBOUR\'.\n2. If the cell is on the first colomn(missing left neighbour) or the last colomn(missing right \n neighbour)\n3. If the cell in the middle, then check if all the neighbour has 1 in the \'visited\' array, \n because if one of them is 0 means it\'s a border cell. \n\n NO NEED TO CHECK IF THE CELL (WHOSE NEIGHBOURS HAS 1 OR NOT) HAS ALSO 1 BECAUSE UNLESS THAT \n CELL HAD NOT 1 WE WOULDN\'T BE CHECKING IF ALL ITS NEIGHBOURS AS 1 OR NOT. \n```\n\n```CPP []\nclass Solution \n{\npublic:\n vector<vector<int>> diff = {{0, -1}, {-1, 0}, {0, 1}, {1, 0}}; // left up right down\n \n bool on_border_or_neighbours_not_equal(vector<vector<bool>>& visited, int r, int c){\n if(r == 0 || r == visited.size()-1 || c == 0 || c == visited[0].size()-1) // on border conditions\n return true;\n int left = visited[r][c-1], up = visited[r-1][c], right = visited[r][c+1], down = visited[r+1][c];\n return left != 1 || up != 1 || right != 1 || down != 1; // at least one neighbour is different conditions\n }\n \n void create_border(vector<vector<int>>& grid, vector<vector<bool>> &visited, int newcolor)\n {\n for(int r=0; r<visited.size(); r++)\n {\n for(int c=0; c<visited[0].size(); c++)\n if(visited[r][c] == 1 && on_border_or_neighbours_not_equal(visited, r, c))\n grid[r][c] = newcolor;\n }\n }\n\n void dfs(vector<vector<int>>& grid, int r, int c, int oldcolor, vector<vector<bool>> &visited)\n {\n if(r<0 || r>=grid.size() || c<0 || c>=grid[0].size() || visited[r][c] == 1 || grid[r][c] != oldcolor)\n return;\n visited[r][c] = 1;\n for(const auto &d : diff)\n dfs(grid, r+d[0], c+d[1], oldcolor, visited);\n }\n\n vector<vector<int>> colorBorder(vector<vector<int>>& grid, int row, int col, int color)\n {\n vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size()));\n dfs(grid, row, col, grid[row][col], visited);\n create_border(grid, visited, color);\n return grid;\n }\n};\n```\n```Python []\nclass Solution:\n def colorBorder(self, grid: List[List[int]], row: int, col: int, color: int) -> List[List[int]]:\n ROW, COL, oldcolor = len(grid), len(grid[0]), grid[row][col]\n visited = [ [0 for _ in range(COL)] for _ in range(ROW) ]\n\n def dfs(r:int, c:int):\n if r<0 or r>=ROW or c<0 or c>=COL or visited[r][c] == 1 or grid[r][c] != oldcolor :\n return\n visited[r][c] = 1\n [ dfs(r+x, c+y) for (x,y) in ((0, -1), (-1, 0), (0, 1), (1, 0)) ]\n \n def on_border_or_neighbours_not_equal(r:int, c:int) -> bool:\n if r == 0 or r == ROW-1 or c == 0 or c == COL-1 : # on border\n return True\n left, up, right, down = visited[r][c-1], visited[r-1][c], visited[r][c+1], visited[r+1][c]\n return left != 1 or up != 1 or right != 1 or down != 1 # min 1 neighbour is different or not\n \n def create_border():\n for r in range(ROW):\n for c in range(COL):\n if visited[r][c] == 1 and on_border_or_neighbours_not_equal(r, c):\n grid[r][c] = color\n\n dfs(row, col)\n create_border()\n return grid\n```\n```\nTime complexity : O(m*n)\nSpace complexity : O(m*n)\n```\n### It took me plenty time to explain everything. If the post was useful to you, an upvote will really make me happy. Thank you for reading it till the end. | 6 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
DFS, intuitive with is_valid_pixel and is_border helpers | coloring-a-border | 0 | 1 | # Intuition\nAt first glance, the problem requires us to change the color of the border of a region in an image. Since the region is defined as all pixels with the same color that are 4-directionally connected (meaning they are connected either vertically or horizontally), the natural inclination is to solve this problem using depth-first search (DFS), a well-known algorithm used for traversing or searching tree or graph data structures. We use DFS to visit all pixels in the region. While doing this, we also check if the current pixel is on the border of the region, and if so, we color it with the new color.\n\n# Approach\nThe approach to solve this problem involves three helper functions: `is_valid_pixel`, `is_border`, and `dfs`. `is_valid_pixel` checks if a pixel is inside the image and if it has the original color. `is_border` checks if a pixel is on the border of the image or is adjacent to a pixel that is not part of the region and has not yet been visited. If a pixel satisfies these conditions, it\'s a border pixel.\n\nThe `dfs` function is where we perform the depth-first search. It checks if the current pixel is valid and unvisited. If it is a border pixel, we change its color to the new color. We then visit all four directions from the current pixel.\n\nFinally, the condition `original_color != newColor` prevents infinite loops when the new color is the same as the original color.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(n), where n is the number of pixels in the image. In the worst-case scenario, every pixel in the image is visited once.\n \n- Space complexity: The space complexity is also O(n), where n is the number of pixels in the image. The space complexity comes from the memory used to store the visited set and the memory used for the stack in the recursive DFS function. In the worst-case scenario, the depth of recursion could go up to n. This worst-case scenario would occur if all pixels have the same color and the starting pixel is at one corner of the image.\n\n# Code\n```\nclass Solution:\n def colorBorder(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:\n DIRECTIONS = [(0, 1), (0, -1), (-1, 0), (1, 0)]\n R = len(image); C = len(image[0])\n original_color = image[sr][sc]\n visited = set()\n\n # return true if the pixel is in the image\n def is_valid_pixel(row, col):\n return 0 <= row < R and 0 <= col < C and image[row][col] == original_color\n\n # return True if the pixel is at the border\n def is_border(row, col):\n return row == 0 or row == R-1 or col == 0 or col == C-1 or any(\n 0 <= row + dr < R and 0 <= col + dc < C and image[row + dr][col + dc] != original_color and (row+dr, col+dc) not in visited\n for dr, dc in DIRECTIONS\n )\n\n def dfs(row, col):\n if not is_valid_pixel(row, col) or (row, col) in visited:\n return\n if is_border(row, col):\n image[row][col] = newColor\n visited.add((row, col))\n for dr, dc in DIRECTIONS:\n dfs(row + dr, col + dc)\n\n if original_color != newColor:\n dfs(sr, sc)\n return image\n\n```\n\n# is_border\n`is_border` determines whether a given pixel, specified by its row and column indices, is on the border of a region with the same color in the image.\n\nHere is a detailed explanation of the logic:\n\n- `row == 0 or row == R-1 or col == 0 or col == C-1`: This condition checks if the pixel is on the edge of the image. If it is, it\'s part of the border by definition.\n\n- `any(0 <= row + dr < R and 0 <= col + dc < C and image[row + dr][col + dc] != original_color and (row+dr, col+dc) not in visited for dr, dc in DIRECTIONS)`: This condition uses the `any` function, which returns `True` if any element in the iterable it\'s given is `True`. It\'s iterating over the four possible directions from the current pixel (up, down, left, right) represented by `DIRECTIONS`.\n\n - `0 <= row + dr < R and 0 <= col + dc < C`: These conditions check that the pixel in the direction `(dr, dc)` is still within the image bounds.\n\n - `image[row + dr][col + dc] != original_color`: This condition checks that the color of the pixel in the direction `(dr, dc)` is different from the original color. This would mean that the current pixel is next to a pixel of a different color, and is therefore on the border of its region.\n\n - `(row+dr, col+dc) not in visited`: This condition checks that the pixel in the direction `(dr, dc)` has not been visited. This is to ensure that we don\'t count pixels that have already been recolored as being different, as they might have been the same color originally. \nIf any of these conditions is `True`, the function will return `True`, indicating that the pixel is indeed a border pixel.\n\n | 2 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
80% TC and 76% Sc easy python solution | coloring-a-border | 0 | 1 | ```\ndef colorBorder(self, grid: List[List[int]], row: int, col: int, color: int) -> List[List[int]]:\n\tm, n = len(grid), len(grid[0])\n\tdir = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\tdef calc(i, j, c):\n\t\tif not(0<=i<m and 0<=j<n): return 1\n\t\treturn grid[i][j] != c and grid[i][j] != -1\n\t\t\n\tdef dfs(i, j):\n\t\tif not(0<=i<m and 0<=j<n):\n\t\t\treturn\n\t\tvis.add((i, j))\n\t\tc = grid[i][j]\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<m and 0<=j+y<n and grid[i+x][j+y] == c and (i+x, j+y) not in vis):\n\t\t\t\tdfs(i+x, j+y) \n\t\tif(calc(i-1, j, c) or calc(i+1, j, c) or calc(i, j+1, c) or calc(i, j-1, c)):\n\t\t\tgrid[i][j] = -1\n\t\t\n\tvis = set()\n\tdfs(row, col)\n\tfor i in range(m):\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j] == -1):\n\t\t\t\tgrid[i][j] = color\n\treturn(grid)\n``` | 1 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Simple python3 solution | DFS | coloring-a-border | 0 | 1 | # Complexity\n- Time complexity: $$O(m \\cdot n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m \\cdot n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def colorBorder(self, grid: List[List[int]], row: int, col: int, color: int) -> List[List[int]]:\n if grid[row][col] == color:\n return grid\n \n m = len(grid)\n n = len(grid[0])\n\n prev_color = grid[row][col]\n\n q = [(row, col)]\n in_progress = {(row, col)}\n to_color = set()\n\n while q:\n i, j = q.pop()\n\n for x, y in ((i - 1, j), (i + 1, j),\n (i, j - 1), (i, j + 1)):\n if (\n 0 <= x < m \n and 0 <= y < n\n and grid[x][y] == prev_color\n ):\n if (x, y) not in in_progress:\n in_progress.add((x, y))\n q.append((x, y))\n else:\n to_color.add((i, j))\n \n for i, j in to_color:\n grid[i][j] = color\n\n return grid\n\n``` | 0 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Python3: Simple DFS with a Stack, and a List of Border Cells | coloring-a-border | 0 | 1 | # Intuition\n\nTo find the border we can start with `(r, c)` and use DFS or BFS to find all cells on the border. We can record them in a `list`.\n\nThen for each cell in the border list we switch the color to `color`.\n\n# Approach\n\nSee the code docs for details. Briefly:\n* I used DFS without recursion (stack, not queue)\n* a cell is on the border per the problem statement if it\'s adjacent to an OOB cell or something with another color\n* I used a `set` to keep track of cells already visited. I was tempted to use the visited array in place, but doing so means you have to change each cell so some other value, then change non-border cells back. It looked complicated so I didn\'t do it.\n\nHaving seen some other solutions, the "change grid cells to visited already" is indeed kind of complicated. I wouldn\'t do it for an interview.\n\n# Complexity\n- Time complexity: $O(M N)$ worst case to visit all the cells\n\n- Space complexity: $O(M N)$ worst case for the visited array\n\nChanging grid cells in place to some "I visited this" value probably reduces the memory complexity. But also makes it way more likely for there to be errors in your code. So tough call.\n\n# Code\n```\nclass Solution:\n def colorBorder(self, grid: List[List[int]], r: int, c: int, color: int) -> List[List[int]]:\n # border cells: every cell in (r, c)\'s CC that is on the border of the grid or adj to another color\n\n # brute force: run DFS/BFS on grid to find all border cells\n # then turn the border cells back to `color`\n \n if grid[r][c] == color: return grid # border is already the right color\n\n M = len(grid)\n N = len(grid[0])\n\n seen = {(r, c)}\n stack = [(r, c)]\n border = []\n while stack:\n i, j = stack.pop()\n\n # if i,j is a border cell, record in border: if adj cell is OOB or different color\n # as we go, enqueue same-color neighbors not already seen\n isBorder = False\n for di, dj in [(-1, 0), (+1, 0), (0, -1), (0, +1)]:\n ii, jj = i+di, j+dj\n\n if 0 <= ii < M and 0 <= jj < N:\n # in bounds\n if grid[ii][jj] != grid[r][c]:\n isBorder = True # i,j adj to diff color -> on border; don\'t enqueue ii,jj b/c it\'s not the same color\n elif (ii, jj) not in seen:\n # not necessarily on the border, but ii,jj is same color so keep exploring\n seen.add((ii, jj))\n stack.append((ii, jj))\n else:\n # OOB, on border\n isBorder = True\n\n if isBorder:\n border.append((i, j))\n\n for i,j in border:\n grid[i][j] = color\n\n return grid\n``` | 0 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.